2.1. Colliding vortex rings

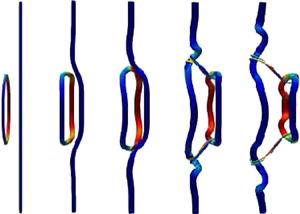
We first consider the interaction of two circular vortex rings, which are symmetrically placed with the initial inclination angle $\theta ={\rm \pi} /4$ (figure 2a). The initial radius of the ring is selected as $R_0=1$. In addition, the initial minimum distance between these two vortex rings is chosen as $\delta _0=0.2$ so that the interaction between the vortices can be considered as localized ($\sigma _0\ll \delta _0\ll R_0$). Note that this vortex set-up represents the typical antiparallel configuration. The evolution of the flow structure for $Re_\Gamma =2000$ is shown in the insets of figure 2 and also in supplementary movies 1 and 2. The structures for $Re_\Gamma = 4000$, which are quite similar, are not shown due to high computational cost for rendering. Several features that distinctly differ from quantum reconnection deserve to be noted. First, as the rings approach each other under self-induction, they also undergo significant core deformation and form two thin vortex sheets. Second, the reconnection process is not discrete as for quantized vortices, and circulation transfer rate and the reconnection time strongly depend on viscosity $\nu$, and hence on $Re_\Gamma$ (Hussain & Duraisamy Reference Hussain and Duraisamy2011; Yao & Hussain Reference Yao and Hussain2020b). Finally, reconnection is never complete; as a consequence, the circulation in the reconnected bridges is relatively smaller than the initial circulation $\Gamma _0$ of the vortices.

Figure 2. Reconnection of colliding vortex rings: (a) initial configuration, and evolution of $\delta ^2(t)$ at $Re_\Gamma =2000$ () and $4000$ (, red) for (b) pre- and (c) post-reconnection phases. The blue dashed lines indicate the linear scaling. The insets are flow structures represented by vorticity isosurface at 5 % of maximum initial vorticity $|\boldsymbol {\omega }| = 0.05\omega _0$ for $Re_\Gamma =2000$; and $\delta$ as a function of $|t-t_0|$ for $Re_\Gamma =4000$ with the dashed line referring the $t^{1/2}$ scaling.

The appropriate determination of $\delta (t)$ relies heavily on the accurate tracking of the location of the vortex axis (Fonda et al. Reference Fonda, Meichle, Ouellette, Hormoz and Lathrop2014; Villois et al. Reference Villois, Krstulovic, Proment and Salman2016), which is rather challenging in classical fluids. First, unlike vortex filaments or quantized vortices, where the axis location is almost precise, the vorticity field in classical fluids is continuously distributed. Second, vortex cores are typically distributed in irregular shapes without any clear centre: before reconnection, the vortices undergo significant core deformation, and, after reconnection, the reconnected vortex lines take some time to collect together to form the bridge.

Due to the twofold symmetry of the initial condition considered, the minimum distance $\delta$ between these two interacting rings before and after reconnection should occur in the symmetry $S_s$ and collision $S_c$ planes, respectively – which makes the determination of $\delta (t)$ relatively easy. Following Hussain & Duraisamy (Reference Hussain and Duraisamy2011) and Yao & Hussain (Reference Yao and Hussain2020a), we take the vorticity centroid (computed as the centroid of above 75 % of its maximum) to be the centre for vortices in these two planes. Figure 2(b) displays the evolution of $\delta ^2(t)$ for the pre-reconnection event, with the top inset showing $\delta$ as a function of $t_0-t$ on a log–log scale for $Re_\Gamma =4000$. The clear following of linear scaling for $\delta ^2(t)$ at the early time suggests that $\delta (t)\sim a^{-} (t^-_0-t)^{1/2}$, with $a^{-}$ the constant prefactors for pre-reconnection corresponding to $A^-\Gamma ^{1/2}$ in (1.1), and $t^-_0$ the critical time when $\delta \to 0$. For both $Re_\Gamma$ cases, $\delta ^2(t)$ collapses initially and then slowly deviates from linear scaling when $\delta \sim {O}(\sigma )$. The deviation happens earlier for the $Re_\Gamma =2000$ case, which is due to the more rapid increase of the core size caused by stronger viscous diffusion. A linear fit on $\delta ^2(t)$ between $0<t<0.15$ for $Re_\Gamma =4000$ gives $t^-_0=0.26$ and $a^{-}=0.38$ (table 1). As the circulation remains constant at $\Gamma =1$ during this time, the dimensionless prefactor $A^{-}=a^{-}=0.38$, which is quite close to $A=0.4$ reported in de Waele & Aarts (Reference de Waele and Aarts1994).

Table 1. Fitted values of the prefactors $a^{\pm }$ and $t^{\pm }_0$ for the minimum distance scaling $\delta (t)\sim a^{\pm }|t-t^\pm _0|^{1/2}$. The superscript $\pm$ stands for before ($-$) and after ($+$) the reconnection, respectively.

When two bridges move sufficiently apart from the interacting region, a clear linear scaling for $\delta ^2(t)$ can be observed for both $Re_\Gamma$ cases (figure 2c). Hence, $\delta \sim a^{+}(t-t^{+}_0)^{1/2}$ scaling also holds in the post-reconnection dynamics when the two bridges’ vortices are mainly governed by the mutual interaction. The early evolution of $\delta ^2(t)$ deviates from the linear scaling, presumably for two main reasons. First, when the bridges are too close, they are under the influence of other unreconnected structures, such as threads, and other parameters besides $\Gamma$ may be relevant in determining $\delta$. Second, the reconnected vortex lines, initially in a thin vortex sheet shape, take time to accumulate to form a circular shape, and the circulation $\Gamma$ continuously increases during this phase. A fit in the linear region gives $t^+_0\approx 0.30$ for both $Re_\Gamma$ cases, and $a^+=2.19$ and $2.27$ for $Re_\Gamma =2000$ and $4000$, respectively (table 1). Different from quantized vortices, where reconnection is discrete and $t_0$ is almost the same for pre- and post-reconnection, here reconnection is a continuous process, and hence $t^+_0$ is slightly larger than $t^-_0$. Consistent with previous studies, $a^+$ is always larger than $a^-$, indicating that the vortices separate much faster than their approach. Compared to the pre-reconnection process, the effect of $Re_\Gamma$ on $\delta (t)$ is more apparent for the post-reconnection. It is because, in classical fluids, the dynamics of reconnection, such as the reconnection time and the circulation transfer rate, strongly depends on the viscosity $\nu$. In general, reconnection is faster at higher $Re_\Gamma$, which explains why $\delta ^2(t)$ follows linear scaling earlier at $Re_\Gamma =4000$. In addition, as $Re_\Gamma$ increases, reconnection is more complete (Yao & Hussain Reference Yao and Hussain2020a). The variation of $a^+$ with respect to $Re_\Gamma$ is mainly attributed to different circulations $\Gamma$ in the reconnected bridges – which is difficult to be precisely determined.

2.2. Orthogonal vortex tubes

As one of the simplest configurations, the reconnection of orthogonal vortex tubes has been extensively studied for both classical (Boratav et al. Reference Boratav, Pelz and Zabusky1992; Beardsell, Dufresne & Dumas Reference Beardsell, Dufresne and Dumas2016; Jaque & Fuentes Reference Jaque and Fuentes2017) and quantum (Zuccher et al. Reference Zuccher, Caliari, Baggaley and Barenghi2012; Galantucci etal. Reference Galantucci, Baggaley, Parker and Barenghi2019) fluids. Similar to Case I, here the initial distance between these two rectilinear vortices is chosen as $\delta _0=0.2$. The insets in figures 3(a) and 3(b) and also supplementary movie 3 show the evolution of the flow structures for $Re_\Gamma =2000$. The evolution is quite similar to that in Boratav et al. (Reference Boratav, Pelz and Zabusky1992) for the thick vortex core case: the vortex tubes first develop into locally antiparallel configuration under mutual induction, then collide with each other due to self-induction; after reconnection, they recede away. Different from quantum cases (Villois et al. Reference Villois, Proment and Krstulovic2017; Galantucci et al. Reference Galantucci, Baggaley, Parker and Barenghi2019), the unreconnected threads, which wrap around the bridges, are distinct after reconnection. In addition, a Kelvin wave is observed after reconnection. In quantum fluids, nonlinear interaction of Kelvin waves creates waves of shorter and shorter wavelength, which is considered as the main mechanism for energy cascade (Baggaley & Barenghi Reference Baggaley and Barenghi2011); in classical fluids, however, the Kelvin wave would rapidly decay due to viscous effect. It would be interesting to compare the difference in the Kelvin wave evolution as well as its role on energy cascade between the quantum and classical reconnections.

Figure 3. Reconnection of orthogonal vortex tubes: time evolution of $\delta ^2(t)$ at $Re_\Gamma =2000$ () and $4000$ (, red) for $(a)$ the pre- and $(b)$ post-reconnection phases, with the dashed lines indicating linear scaling. The insets are flow structures represented by vorticity isosurface $|\boldsymbol {\omega }| = 0.05\omega _0$; the bottom inset in $(b)$ is $\delta$ as a function of $|t-t_0|$ for $Re_\Gamma =4000$ with the dashed line indicating the $t^{1/2}$ scaling.

To determine the minimum distance $\delta (t)$ between these two vortex tubes, the axis of the vortex tubes needs to be tracked. Here, we propose a vortex tracking method based on the vortex lines that go through the vortex centre at the boundary. First, the centriod of the vortex tubes at the planes $x=-{\rm \pi}$ and $y=-{\rm \pi}$ is determined using the same procedure as discussed above. Then, vortex lines that seed from these two centres are integrated using the ‘stream3’ function in Matlab. Figure 4 (and supplementary movie 4) show the time evolution of the vortex axis for $Re_\Gamma =2000$, and the evolution at $Re_\Gamma =4000$ is quantitatively the same. It is clear that the axis of vortex tubes is unambiguously identified. Finally, $\delta$ is taken as the shortest distance between these two vortex lines.

Figure 4. Evolution of the vortex axes for the orthogonal vortex tubes case at $Re_\Gamma =2000$: $(a)$$t=0$, $(b)$$t=0.45$, $(c)$$t=0.8$ and $(d)$$t=1.2$.

For the pre-reconnection, $\delta ^2(t)$ initially varies slowly during the phase of the formation of antiparallel configuration (figure 3a). Then, the perturbed vortex tubes approach each other rapidly with $\delta ^2(t)$ following a clear linear scaling. A slight difference in the evolution of $\delta ^2(t)$ can be observed between $Re_\Gamma =2000$ and $4000$ cases, indicating a weak Reynolds number effect on the pre-reconnection evolution. For both $Re_\Gamma$ cases, the linear fit shows that $a^-\approx 0.29$, which is slightly smaller than the case of the colliding rings. Figure 3$(b)$ shows that $\delta ^2(t)$ also follows linear scaling after reconnection, and the $\delta \sim t^{1/2}$ scaling extends far beyond the initial separation distance $\delta _0$. Consistent with Case I, the prefactor increases with $Re_\Gamma$, with $a^+=0.93$ and $0.99$ for $Re_\Gamma =2000$ and $4000$, respectively. Again, the vortices move faster after the reconnection than before it. Similar to the finding in Villois et al. (Reference Villois, Proment and Krstulovic2017), the prefactors $a^+$ are smaller than those in Case I, which might be due to a smaller curvature of the cusps generated after reconnection in this case.

2.3. Vortex ring and tube interaction

The third case we considered is a vortex ring interacting with an isolated rectilinear vortex tube. The radius of the ring is the same as the colliding vortex rings case, namely, $R_0=1$. To reveal the cross-over from driven ($\delta \sim t$) to interaction ($\delta \sim t^{1/2}$) region observed in Galantucci et al. (Reference Galantucci, Baggaley, Parker and Barenghi2019), the initial distance is chosen as twice the previous cases, namely, $\delta _0=0.4$. The vortex set-up and the subsequent evolution for $Re_\Gamma =2000$ represented by vortex surfaces and tracked vortex axis are shown in the top insets in figures 5(a) and 5(b), respectively (see also supplementary movies 5 and 6). Due to the self-induction, the vortex ring approaches the vortex tube; during this phase, both the vortex ring and tube are perturbed; at close approach, the vortex ring and tube are also deformed into locally antiparallel configuration (i.e. $t=1$). It further confirms the argument that reconnection physics of two vortices should be independent of the initial spatial configuration (Siggia & Pumir Reference Siggia and Pumir1985). After reconnection, parts of the vortex ring and tube exchange with each other, and, due to the Kelvin wave, the newly formed vortex ring and tube become further perturbed with the threads connecting them.

Figure 5. Evolution of flow structures for vortex ring and tube interaction for $Re_\Gamma =2000$: $(a)$ represented by vorticity isosurface at 5 % of maximum initial vorticity, i.e. at $|\boldsymbol {\omega }| = 0.05\omega _0$, and $(b)$ by tracked vortex axis.

Figure 6$(a)$ displays the evolution of $\delta (t)$, with figures 6$(b)$ and 6$(c)$ showing $\delta ^2(t)$ before and after reconnection, respectively. Initially, $\delta (t)$ scales almost linearly with $t$ and the approaching velocity can be approximately determined by the initial self-induced velocity of the ring and the mutual-induced velocity between the ring and the tube. Consistent with the previous two cases, when the two vortices are close to each other, a clear $t^{1/2}$ scaling for $\delta$ is observed (inset in figure 6b). The transition between driven ($\delta \sim t$) and interaction ($\delta \sim t^{1/2}$) regions happens at $\delta \sim 0.3$. The prefactor for $Re_\Gamma =4000$ is $a^-=0.40$, which is very close to Case I.

Figure 6. Interaction of vortex ring and tube: $(a)$ time evolution of $\delta (t)$; and $\delta ^2(t)$ for $(b)$ the pre-reconnection and $(c)$ post-reconnection phases. Symbols and , red, refer to $Re_\Gamma =2000$ and $4000$, respectively, and the blue dashed lines indicate linear scaling. The insets in ($b$) and ($c$) show separation distance $\delta$ as a function of $|t-t_0|$ for $Re_\Gamma =4000$ with the dashed line indicating the $t^{1/2}$ scaling.

From figure 6$(c)$, it is clear that $\delta (t)\sim t^{1/2}$ scaling holds after reconnection, with the prefactor $a^+=1.28$ and $1.34$ for $Re_\Gamma =2000$ and $4000$, respectively. The values are between the colliding vortex rings and orthogonal tubes cases. The $1/2$ scaling breaks down when the vortex ring moves sufficiently far away from the tube. Note that the cross-over between the $t^{1/2}$ to $t^1$ scalings for $\delta (t)$ in the post-reconnection is not observed. Instead, for this case $\delta (t)$ remains almost constant after some time. The reason is that the travelling velocity of the perturbed vortex ring is roughly the same as that of the perturbed part of the tube. When the oscillations in the vortex tube and ring die out and the vortex ring regains its circular shape, we should expect $\delta(t) \sim t$ as suggested in Galantucci et al. (Reference Galantucci, Baggaley, Parker and Barenghi2019).