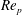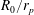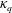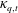1 Introduction
The migration of charged particles in an electrostatic field is ubiquitous in a variety of fields, such as aerosol removal in an electrostatic precipitator (Marshall & Li Reference Marshall and Li2014), fabrication of functional films using electrophoretic deposition (Cordelair & Greil Reference Cordelair and Greil2004) and dust devils in the Martian atmosphere (Matthews, Shotorban & Truell Reference Matthews, Shotorban and Truell2013; Izvekova & Popel Reference Izvekova and Popel2016), where both long-range hydrodynamic and electrostatic interactions among particles result in complex collective dynamics. In most of these processes, particle sizes are around a micrometre and the relevant Reynolds number can be very small; thus the hydrodynamic interaction can be simulated by solving the Stokes/Oseen equations: the disturbance of every particle on the flow field can be linearly summed to obtain the flow field at the positions of other particles (Guazzelli & Morris Reference Guazzelli and Morris2011).
Earlier studies of sedimenting clouds have been carried out in the absence of electrostatic interactions. A common feature therein is that, while settling down, most particles tend to stay as a cohesive blob, resulting in a mean settling velocity that can be several times larger than the Stokes velocity of an isolated particle.
The settling velocity and the shape of a particle cloud during gravity settling are first studied in conditions where inertia is negligible (Nitsche & Batchelor Reference Nitsche and Batchelor1997; Metzger, Nicolas & Guazzelli Reference Metzger, Nicolas and Guazzelli2007). An initially spherical cloud is found to evolve into a torus shape and eventually to break up into two secondary subclouds, each of which will further break again. In conditions with small but finite Reynolds number, the inflow at the rear of the cloud plays a key role in the cloud’s evolution into a torus shape, and the deformation is accelerated as inertia is increased (Pignatel, Nicolas & Guazzelli Reference Pignatel, Nicolas and Guazzelli2011). Subramanian & Koch (Reference Subramanian and Koch2008) were one of the first to consider inertial clouds and organized their behaviour into different regimes (see figure 1). They also presented a theoretical prediction of the long-time dynamics of a sedimenting cloud, wherein a settling cloud is characterized by a number density field
$n$
and a corresponding induced velocity field
$u_{r}$
(only the radial component appears due to symmetry). According to their prediction, for both planar axisymmetric clouds and spherical clouds, the evolution equation admits a self-similar expansion.
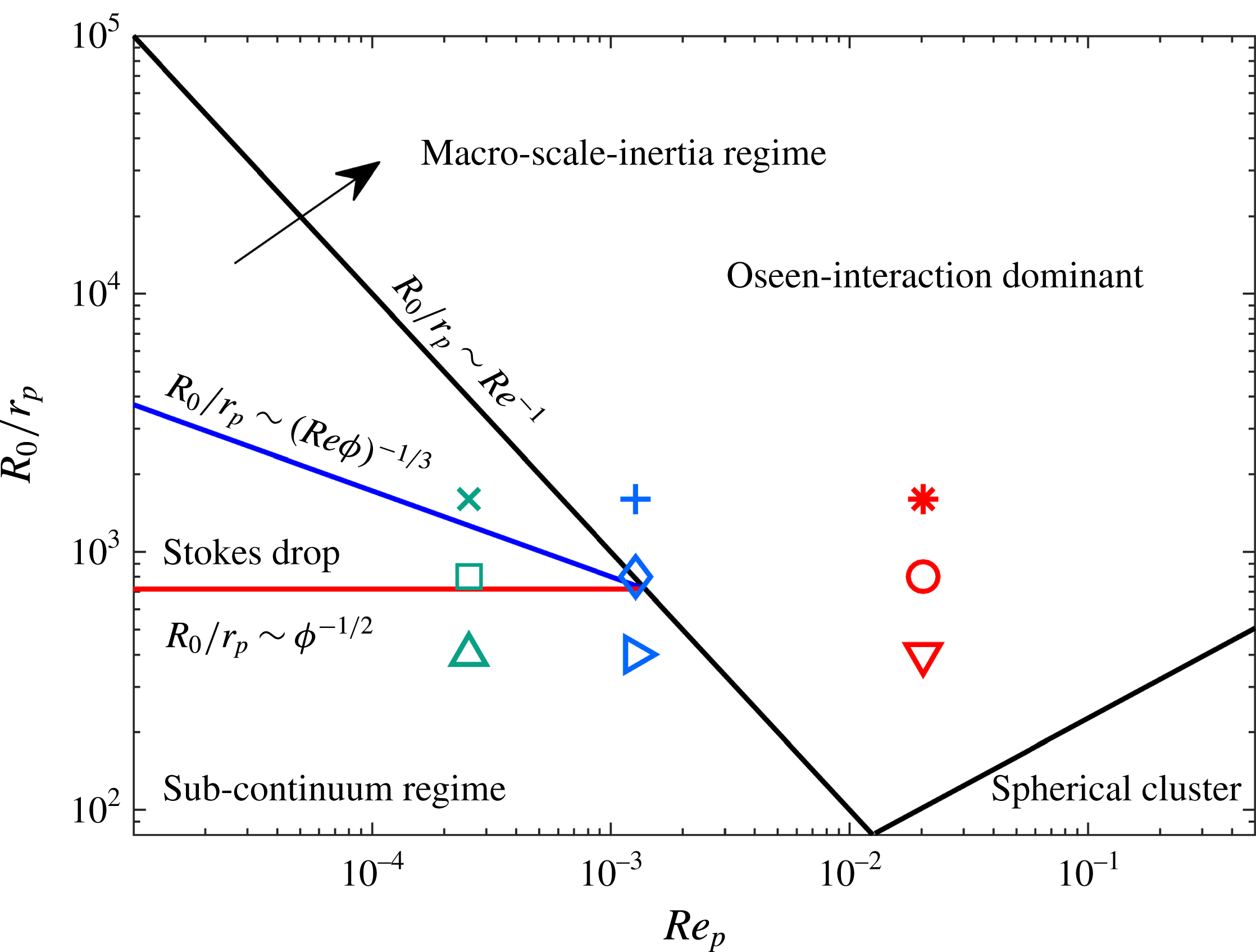
Figure 1. Regimes of evolution for a migrating cloud characterized by particle Reynolds number
$Re_{p}$
and cloud-to-particle size ratio
$R_{0}/r_{p}$
. The points are the specific cases studied in this paper.
Recently, Chraibi & Amarouchene (Reference Chraibi and Amarouchene2013) and Yang, Li & Marshall (Reference Yang, Li and Marshall2015) performed ‘Oseenlet’ simulations of spherical or cylindrical clouds to study the effects of fluid inertia and cloud shape, in which an analytical solution for zero-time cloud settling velocity is proposed. Tao, Guo & Wang (Reference Tao, Guo and Wang2017) studied the effect of surface slip on the sedimentation process and found that slippery particles inside the particle cloud generally increase the fluctuations in vertical velocity and position in the accelerated falling stage.
In the absence of electrostatic interactions, a cloud containing a sufficiently large number of particles is quite unstable. The instability and breakup phenomena are found to be sensitive to the polydispersity (size or density) of the particles: a greater degree of polydispersity tends to cause the cloud to persist as a cohesive entity for a shorter period of time (Faletra et al. Reference Faletra, Marshall, Yang and Li2015; Ho, Phan-Thien & Khoo Reference Ho, Phan-Thien and Khoo2016). High instability poses huge challenges in predicting long-time dynamics of a migrating cloud. Therefore, theoretical predictions of evolution can be made only for isotropic clouds with sufficiently low number density: particles in the cloud are outside the wake of any other particle, and the evolution of the cloud is governed by repulsive source–field interactions (Subramanian & Koch Reference Subramanian and Koch2008).
If particles are unipolarly charged, the Coulomb repulsion will act against the hydrodynamic stress and tend to separate particles. This long-range repulsion has been found to have significant effects on particle packing structure (Chen et al.
Reference Chen, Li, Liu and Makse2016a
; Schella, Herminghaus & Schröter Reference Schella, Herminghaus and Schröter2017), clustering of particles in turbulence (Lu et al.
Reference Lu, Nordsiek, Saw and Shaw2010), shear-induced ordering in suspensions (Nazockdast & Morris Reference Nazockdast and Morris2012) and clogging/non-clogging transition in colloids and aerosols (Agbangla, Bacchin & Climent Reference Agbangla, Bacchin and Climent2014; Chen, Liu & Li Reference Chen, Liu and Li2016b
). However, the migration behaviour of particle clouds with a coupling effect of both hydrodynamic and electrostatic interactions is still less investigated. In this paper, we incorporate electrostatic interactions in a rigorous manner and perform Oseenlet simulations of migrating clouds in a wide range of particle Reynolds number
$Re_{p}$
and cloud-to-particle size ratio
$R_{0}/r_{p}$
to show how the Coulomb repulsion affects the evolution of a migrating cloud.
2 Formulation of the problem
We consider a spherical cloud with initial radius
$R_{0}$
containing
$N$
unipolarly charged non-Brownian particles (with charge number
$q_{0}$
). The particles are randomly seeded in the cloud with an initial volume fraction
$\unicode[STIX]{x1D719}=2\times 10^{-6}$
and are assumed to be neutrally buoyant to avoid a gravity effect. In such dilute condition, particle–particle collisions can be prevented, and higher-order multipoles, e.g. dipoles or quadrupoles, which decay sufficiently fast with distance, can be ignored. The cloud is immersed in unbounded stationary fluid and migrates under the action of a uniform electric field
$E_{0}$
(in the vertical
$x$
direction). The hydrodynamic interactions among particles are modelled by Oseen equations, and we simultaneously consider the long-rang electrostatic forces: a uniform external electrostatic force (
$E_{0}q_{0}$
) and a pairwise Coulomb repulsion
$(q_{0}^{2}/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}r_{ij}^{2})$
, where
$\unicode[STIX]{x1D700}_{f}=8.85\times 10^{-12}~\text{F}~\text{m}^{-1}$
is the permittivity of the fluid and
$r_{ij}=|\boldsymbol{r}_{i}-\boldsymbol{r}_{j}|$
is the distance from the centroid of a source particle to that of a target particle.
A phase diagram, adapted from Subramanian & Koch (Reference Subramanian and Koch2008), is presented in figure 1 to show different regimes of evolution for a settling cloud of particles. In figure 1, all the physical quantities that influence the properties of a migrating cloud, including the particle radius
$r_{p}$
and density
$\unicode[STIX]{x1D70C}_{p}$
, the fluid viscosity
$\unicode[STIX]{x1D707}_{f}$
and density
$\unicode[STIX]{x1D70C}_{f}$
, as well as the cloud radius
$R_{0}$
, can be grouped into two dimensionless parameters: one is particle Reynolds number
$Re_{p}$
, which is related to the driving force by
$Re_{p}=E_{0}q_{0}\unicode[STIX]{x1D70C}_{f}/6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}^{2}$
; the other is cloud-to-particle size ratio
$R_{0}/r_{p}$
. Since we have fixed the volume fraction
$\unicode[STIX]{x1D719}$
, parameters like particle number
$N=\unicode[STIX]{x1D719}(R_{0}/r_{p})^{3}$
and dimensionless inertial length
$l^{\ast }=(r_{p}/R_{0})/Re_{p}$
can be directly derived from
$Re_{p}$
and
$R_{0}/r_{p}$
. It is noted that the Stokes number
$St=(2/9)(\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f})Re_{p}$
, which is kept in the range of
$10^{-4}{-}10^{-2}$
, does not play a key role here. We pick out nine points located in four different regimes in the phase diagram (
$Re_{p}=2.54\times 10^{-4},1.27\times 10^{-3},2.03\times 10^{-2}$
and
$R_{0}/r_{p}=400,800,1600$
) and systematically perform particle dynamic simulations by changing the strength of long-range Coulomb repulsion.
The equation of motion for
$i$
th particle can be written as
$$\begin{eqnarray}\boldsymbol{u}_{i}=\boldsymbol{u}_{f,i}+\boldsymbol{u}_{s,i}=\displaystyle \mathop{\sum }_{j\neq i}\boldsymbol{W}_{ij}\boldsymbol{u}_{s,j}+{\displaystyle \frac{1}{6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}r_{p}}}\left(\boldsymbol{E}_{0}q_{0}+\displaystyle \mathop{\sum }_{j\neq i}{\displaystyle \frac{q_{0}^{2}\boldsymbol{r}_{ij}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}r_{ij}^{3}}}\right).\end{eqnarray}$$
Here,
$\boldsymbol{u}_{f,i}$
is the fluid velocity at the centre of particle
$i$
and
$\boldsymbol{u}_{s,i}$
is the particle slip velocity. Since the Stokes number is sufficiently small, the particle inertia is negligible, and
$\boldsymbol{u}_{s}$
can be directly calculated from the external force acting on the particle through
$\boldsymbol{u}_{s}=\boldsymbol{F}_{ext}/6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}r_{p}$
. Vector
$\boldsymbol{r}_{ij}=\boldsymbol{r}_{i}-\boldsymbol{r}_{j}$
is that from source point
$j$
to target point
$i$
. The interaction kernel
$\boldsymbol{W}_{ij}=\boldsymbol{W}(\boldsymbol{r}_{i},\boldsymbol{r}_{j})$
is a function of the positions of particles and can be obtained based on the Oseen solution for the flow around a particle:
$$\begin{eqnarray}\displaystyle u_{r,Oseen} & = & \displaystyle {\displaystyle \frac{u_{s}r_{p}^{2}}{r^{2}}}\Bigg\{-{\displaystyle \frac{r_{p}\cos \unicode[STIX]{x1D703}}{2r}}-{\displaystyle \frac{3(1-\cos \unicode[STIX]{x1D703})r}{4r_{p}}}\exp \left(-{\displaystyle \frac{Re_{s}r(1+\cos \unicode[STIX]{x1D703})}{2r_{p}}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{3}{2Re_{s}}}\left[1-\exp \left(-{\displaystyle \frac{Re_{s}r(1+\cos \unicode[STIX]{x1D703})}{2r_{p}}}\right)\right]\Bigg\},\end{eqnarray}$$
$$\begin{eqnarray}u_{\unicode[STIX]{x1D703},Oseen}=-{\displaystyle \frac{u_{s}r_{p}}{r}}\sin \unicode[STIX]{x1D703}\left[{\displaystyle \frac{r_{p}^{2}}{4r^{2}}}+{\displaystyle \frac{3}{4}}\exp \left(-{\displaystyle \frac{Re_{s}r(1+\cos \unicode[STIX]{x1D703})}{2r_{p}}}\right)\right],\end{eqnarray}$$
with the polar axis (
$\unicode[STIX]{x1D703}=0$
) coincident with the direction of particle motion. Finally,
$Re_{S}=2r_{p}u_{s}\unicode[STIX]{x1D70C}_{f}/\unicode[STIX]{x1D707}_{f}$
is the instantaneous particle Reynolds number based on its slip velocity
$u_{s}$
.
Normalizing the velocity by the migrating velocity of an isolated particle
$U_{0}=E_{0}q_{0}/6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}r_{p}$
and the length by the initial radius of the cloud
$R_{0}$
, (2.1) becomes
$$\begin{eqnarray}\hat{\boldsymbol{u}}_{p,i}=\displaystyle \mathop{\sum }_{j\neq i}\hat{\boldsymbol{W}}_{ij}\hat{\boldsymbol{u}}_{s,j}+\boldsymbol{e}_{x}+\unicode[STIX]{x1D705}_{q}\unicode[STIX]{x1D731}_{i}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D731}_{i}=(1/N)\sum _{j\neq i}(\hat{\boldsymbol{r}}_{ij}/\hat{r}_{ij}^{3})$
is a function of the position vectors
$(\hat{\boldsymbol{r}}_{1},\hat{\boldsymbol{r}}_{2},\ldots ,\hat{\boldsymbol{r}}_{N})$
of the particles. A dimensionless charge parameter is indicated as
$$\begin{eqnarray}\unicode[STIX]{x1D705}_{q}={\displaystyle \frac{q_{0}N}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}E_{0}R_{0}^{2}}},\end{eqnarray}$$
which is interpreted as the ratio of the velocity caused by particle–particle Coulomb repulsion to the velocity driven by the external field. The
$3N$
coupled equations of motion of the particles (2.4) are solved by the Adams–Bashforth method with sufficiently small time steps. The information of all the particles is simultaneously recorded and thus the temporal evolution of the migrating cloud can be easily captured.
Before presenting the results from particle dynamics simulations, we introduce a continuum description of cloud expansion in terms of number density field
$n(\hat{\boldsymbol{r}},\hat{t})$
and induced velocity field
$\hat{\boldsymbol{u}}(\hat{\boldsymbol{r}},\hat{t})$
. A continuity equation can be built based on the conservation of particle number (Subramanian & Koch Reference Subramanian and Koch2008):
$$\begin{eqnarray}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}n(\hat{\boldsymbol{r}},\hat{t})+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\hat{\boldsymbol{u}}(\hat{\boldsymbol{r}},\hat{t})n(\hat{\boldsymbol{r}},\hat{t}))=0.\end{eqnarray}$$
A similarity solution of (2.6) for a spherical cloud settling under gravity was given in the condition of a sufficiently low number density (
$N/R_{0}\ll U_{0}/\unicode[STIX]{x1D708}_{f},\unicode[STIX]{x1D708}_{f}=\unicode[STIX]{x1D707}_{f}/\unicode[STIX]{x1D70C}_{f}$
). Under such a constraint, most particles in the cloud are outside the wake of any other particle, and the evolution of the cloud is governed by repulsive source–field interactions
$u_{f,r}=3\unicode[STIX]{x1D708}_{f}r_{p}/(2r^{2})$
(Batchelor Reference Batchelor2000). Under such conditions, the expansion rate
$\hat{u} _{r}(\hat{R}_{cl},\hat{t})$
and the relative increase of the migrating velocity
$\unicode[STIX]{x0394}\hat{U} =(U-U_{0})/U_{0}$
(
$U$
is defined as the average velocity of all particles) of the cloud can be estimated as
$\hat{u} _{r}(\hat{R}_{cl},\hat{t})=3r_{p}N\unicode[STIX]{x1D708}_{f}/(2R_{0}^{2}U_{0})\ll 1$
and
$\unicode[STIX]{x0394}\hat{U} =(6/5)N(r_{p}/R_{0})3/(3+Re_{p}R_{0}/r_{p})\approx 18r_{p}N\unicode[STIX]{x1D708}_{f}/(5R_{0}^{2}U_{0})\ll 1$
, respectively (Yang et al.
Reference Yang, Li and Marshall2015). It indicates an extremely weak hydrodynamic interaction between particles and the particles behave like isolated ones.
Figure 2. Typical evolution of clouds in the Stokes regime with
$Re_{p}=2.54\times 10^{-4}$
,
$R_{0}/r_{p}=800$
, and with (a)
$\unicode[STIX]{x1D705}_{q}=0$
and (b)
$\unicode[STIX]{x1D705}_{q}=1.0$
.
3 Results
3.1 Effect of Coulomb repulsion on Stokes clouds
We first consider two migrating clouds in the Stokes regime (
$Re_{p}=2.54\times 10^{-4}$
) with the same
$R_{0}/r_{p}$
and initial cloud configuration
$(\hat{\boldsymbol{r}}_{1},\hat{\boldsymbol{r}}_{2},\ldots ,\hat{\boldsymbol{r}}_{N})$
. In the first case, we set the interparticle Coulomb repulsion to zero, whereas a strong repulsion is employed in the second case. The typical evolution of the two clouds is displayed in figure 2. The cloud with
$\unicode[STIX]{x1D705}_{q}=0$
is seen to flatten and to expand in the horizontal direction. A circulation of the particles inside the cloud is also observed, which can be regarded as a typical feature for Stokes clouds or drops (Yang et al.
Reference Yang, Li and Marshall2015). (The circulation is more clear in figure 5(a).) At the same time, a leakage of particles occurs at the rear of the cloud (figure 2
a). The flat cloud further expands and breaks up into two subclouds, each of which further breaks again. All these features qualitatively resemble the numerical and experimental results of Stokes cloud settling under gravity (Metzger et al.
Reference Metzger, Nicolas and Guazzelli2007; Pignatel et al.
Reference Pignatel, Nicolas and Guazzelli2011), indicating that, with extremely weak Coulomb repulsion (
$\unicode[STIX]{x1D705}_{q}\rightarrow 0$
), the effect of external electrostatic field (
$E_{0}$
) is similar to that of gravity. In the presence of strong Coulomb repulsion (figure 2
b), the cloud undergoes an expansion without breakup during a long-term observation (
$\hat{t}\sim 100$
). After a compression in the vertical direction in the initial stage, the cloud then undergoes a self-similar expansion with size increased and geometrical shape unchanged. Figure 3 clearly shows the distribution of particles in the two clouds. In the case without Coulomb repulsion, two distinct subclouds with high local volume fraction are displayed. Both subclouds have rugged surfaces, which may lead to further destabilization. However, with strong repulsion, the cloud has relatively smooth boundary, with particles uniformly distributed.
Figure 3. Scatter plots of particle dispersion in migrating clouds with
$Re_{p}=2.54\times 10^{-4}$
,
$R_{0}/r_{p}=800$
, and with (a)
$\unicode[STIX]{x1D705}_{q}=0$
and (b)
$\unicode[STIX]{x1D705}_{q}=1.0$
. The particle position relative to the centre of mass of the cloud with their local volume fraction is plotted at
$\hat{t}=60$
. Top and bottom panels correspond to top views and side views of the clouds, respectively.
In figure 4, the evolution of horizontal-to-vertical aspect ratio
$\unicode[STIX]{x1D6FE}=R_{h}/R_{v}$
for clouds with different repulsion is shown. The horizontal radius
$R_{h}$
is defined as the average of the maximum distances from the centre of mass over four quadrants in the horizontal plane. And the vertical radius
$R_{v}$
is defined as the distance from the front leading particle to the centre of mass of the cloud. It can be seen that aspect ratio increases in all cases due to the expansion in the horizontal direction. Obvious fluctuations appear in the case with
$\unicode[STIX]{x1D705}_{q}=0$
, which is a result of the coupling between the toroidal circulation of the cloud and the expansion in the horizontal direction (Metzger et al.
Reference Metzger, Nicolas and Guazzelli2007). When the cloud breaks up, particles in the subclouds that have a relatively higher particle concentration migrate faster than those out of the subclouds. It leads to a stretch of the cloud in the vertical direction, and thus
$\unicode[STIX]{x1D6FE}$
drops remarkably at
$\hat{t}\approx 30$
. In cases with strong Coulomb repulsions, the fluctuation in
$\unicode[STIX]{x1D6FE}$
is significantly inhibited, and the growth rate of
$\unicode[STIX]{x1D6FE}$
decreases as
$\unicode[STIX]{x1D705}_{q}$
increases. When a sufficiently large repulsion is imposed,
$\unicode[STIX]{x1D6FE}$
stays close to unity, indicating that the cloud can keep its spherical shape.
Figure 4. Evolution of the aspect ratio of clouds in the Stokes regime with
$Re_{p}=2.54\times 10^{-4}$
and
$R_{0}/r_{p}=800$
. We show results with four different strengths of Coulomb repulsion:
$\unicode[STIX]{x1D705}_{q}=0$
(circles),
$\unicode[STIX]{x1D705}_{q}=0.11$
(upward-pointing triangles),
$\unicode[STIX]{x1D705}_{q}=1.0$
(squares) and
$\unicode[STIX]{x1D705}_{q}=11$
(right-pointing triangles).
3.2 Effect of fluid inertia
Here, we also simulate clouds with distinct particle Reynolds numbers to elucidate the effect of fluid inertia. According to figure 1, when inertia increases, a cloud first transits from the Stokes drop-like regime into the regime dominated by microscale inertia (
$R_{0}/r_{p}\sim (Re\unicode[STIX]{x1D719})^{-1/3}$
), and then enters into the Oseen interactions-dominant regime (
$R_{0}/r_{p}\sim Re^{-1}$
). In our simulation, Oseen solution is adopted and is valid in all these regimes.
In figure 5, we plot the velocities of particles in clouds with the same configuration but different
$Re_{p}$
and
$\unicode[STIX]{x1D705}_{q}$
. When the Coulomb repulsion is extremely weak (
$\unicode[STIX]{x1D705}_{q}=0.01$
in figure 5
a–c), we found the following characteristics that are qualitatively similar to clouds settling under gravity: (1) a conspicuous circulation in a toroidal vortex is observed in the Stokes drop-like cloud; and (2) as the inertia increases, the inflow at the rear of the cloud becomes stronger and drastically diminishes the particle leakage (Bosse et al.
Reference Bosse, Kleiser, Härtel and Meiburg2005; Pignatel et al.
Reference Pignatel, Nicolas and Guazzelli2011). With a sufficiently strong repulsion (
$\unicode[STIX]{x1D705}_{q}=5.0$
), the velocities of particles become radial. With such a high
$\unicode[STIX]{x1D705}_{q}$
, the direct Coulomb interaction term (
$\unicode[STIX]{x1D705}_{q}\unicode[STIX]{x1D731}_{i}$
) becomes dominant and the evolution of clouds is no longer affected by fluid inertia (see figure 5
g–i). We check all the simulation runs with different
$R_{0}/r_{p}$
and
$Re_{p}$
and find that, when a sufficiently large
$\unicode[STIX]{x1D705}_{q}$
is given, the clouds always remain in a stable shape.
It is worth noting that the velocity vectors in figure 5(f) have a pattern that is closer to an isotropic form than those in figure 5(d). It indicates that the cloud with higher
$Re_{p}$
transits from the hydrodynamically controlled regime to the isotropic expansion regime at relatively lower
$\unicode[STIX]{x1D705}_{q}$
. This effect of fluid inertia can be understood at a first level by considering the hydrodynamic interaction between two identical particles. Figure 6(a) shows a simple case where particle
$i$
has a unit slip velocity and generates induced velocity at the location of particle
$j$
. According to the Oseen solution in (2.2) and (2.3), the induced velocity is a function of the ratio between the distance and the particle radius
$r/r_{p}$
, the angle
$\unicode[STIX]{x1D703}$
between the direction of slip velocity and the vector from particle
$i$
to particle
$j$
, and the particle Reynolds number
$Re_{p}$
. Here
$r/r_{p}$
is fixed as
$10$
and the magnitude of velocities in the radial direction (
$|\hat{u} _{r,Oseen}|$
in figure 6
b) and tangential velocity (
$|\hat{u} _{\unicode[STIX]{x1D703},Oseen}|$
in figure 6
c) at different
$\unicode[STIX]{x1D703}$
are plotted for four distinct
$Re_{p}$
(
$0.001$
,
$0.01$
,
$0.1$
and
$0.5$
). It is evident that
$|\hat{u} _{r,Oseen}|$
(
$|\hat{u} _{\unicode[STIX]{x1D703},Oseen}|$
) reaches its maximum at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
(
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
). The induced velocities in both radial and tangential directions decrease with increasing
$Re_{p}$
(except at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
). Given the same
$\unicode[STIX]{x1D705}_{q}$
, clouds with higher
$Re_{p}$
will have relatively weaker hydrodynamic interaction (i.e. smaller
$\sum _{j\neq i}\hat{\boldsymbol{W}}_{ij}\hat{\boldsymbol{u}}_{s,j}$
in (2.4)). This result confirms the findings in figure 5 that clouds with higher
$Re_{p}$
transit into the isotropic expansion regime at a relatively lower
$\unicode[STIX]{x1D705}_{q}$
.
Figure 5. Velocity vectors of particles in clouds with the same configuration but different Reynolds number (
$Re_{p}$
) and repulsion (
$\unicode[STIX]{x1D705}_{q}$
). Each column has the same
$Re_{p}$
, with
$Re_{p}=2.54\times 10^{-4}$
,
$1.27\times 10^{-3}$
and
$2.03\times 10^{-2}$
from left to right; and each row has the same
$\unicode[STIX]{x1D705}_{q}$
, with
$\unicode[STIX]{x1D705}_{q}=0.01$
,
$1.0$
and
$5.0$
from top to bottom. The cloud-to-particle size ratio is fixed as
$R_{0}/r_{p}=800$
. For clarity, only
$300$
particles near the plane of
$\hat{z}=0$
are drawn for each case.
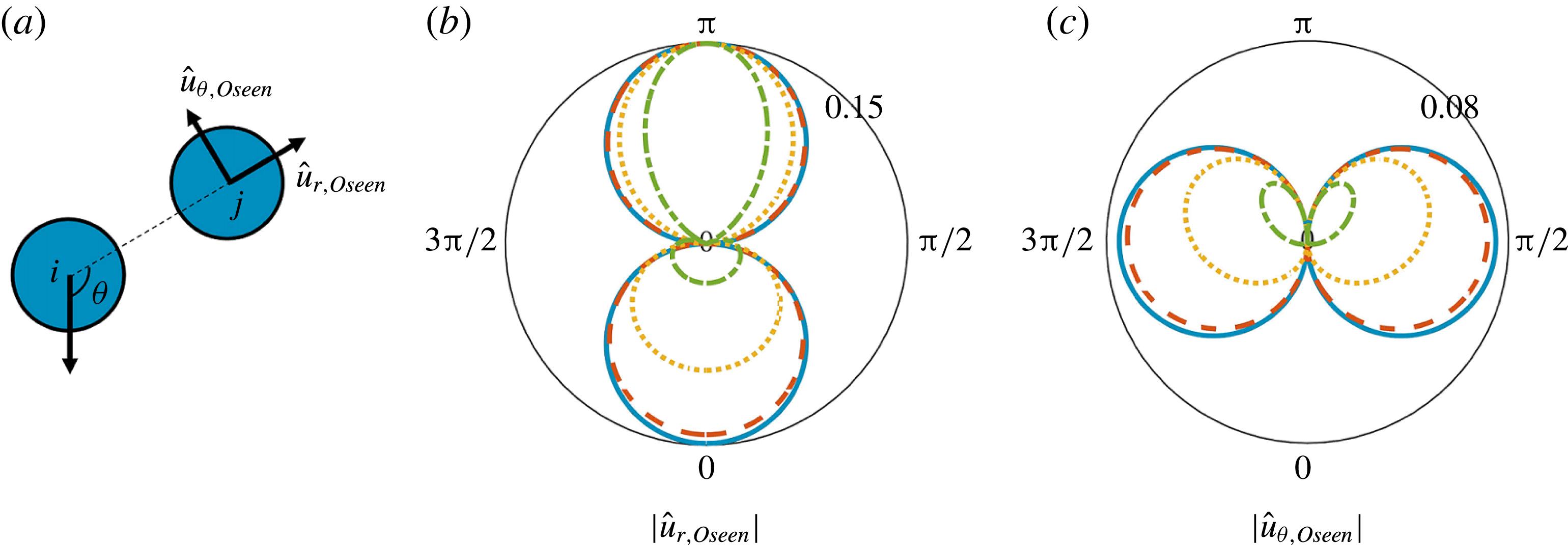
Figure 6. (a) Alignment of two particles and the magnitude of velocities in the radial direction (b) and tangential direction (c) at the location of particle
$j$
induced by the slip velocity of particle
$i$
. In (b) and (c)
$\unicode[STIX]{x1D703}$
stands for the angle between the direction of slip velocity and the vector from particle
$i$
to particle
$j$
. Results for four different particle Reynolds numbers are presented:
$Re_{p}=0.001$
(blue solid lines),
$Re_{p}=0.01$
(red dashed lines),
$Re_{p}=0.1$
(yellow dotted lines) and
$Re_{p}=0.5$
(green dash-dotted lines).
In the following section, we will focus on the effect of Coulomb repulsion and try to answer the questions: how to characterize the transition from unstable migrating cloud to the stable cloud without breakup, and what rules the stable cloud would follow during its evolution.
3.3 Scaling analysis and continuum description
To answer the questions above, the influence of Coulomb repulsion is evaluated by a scaling analysis of the particles’ equation of motion (2.4). The simplest term in (2.4) is the mobility caused by the external field (
$\boldsymbol{e}_{x}$
), which has no effect on the evolution of the cloud shape. Here we compare the contribution from the remaining two terms: the mobility due to Coulomb repulsion from other particles (
$(\unicode[STIX]{x1D705}_{q}/N)\sum _{j\neq i}(\hat{\boldsymbol{r}}_{ij}/\hat{r}_{ij}^{3})$
) and the fluid velocity induced by the slip velocities of other particles (
$\sum _{j\neq i}\hat{\boldsymbol{W}}_{ij}\hat{\boldsymbol{u}}_{s,j}$
). In the second term,
$\hat{\boldsymbol{u}}_{s,j}$
can be calculated from the external force and the repulsive forces on particle
$j$
. It thus can be regarded as an indirect effect of the imposed external field and the interparticle electrostatic repulsions.
The relative magnitudes of these two terms can be estimated as:
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{i}={\displaystyle \frac{\left|\displaystyle \mathop{\sum }_{j\neq i}\hat{\boldsymbol{W}}_{ij}\hat{\boldsymbol{u}}_{s,j}\right|}{\left|{\displaystyle \frac{\unicode[STIX]{x1D705}_{q}}{N}}\displaystyle \mathop{\sum }_{j\neq i}{\displaystyle \frac{\hat{\boldsymbol{r}}_{ij}}{\hat{r}_{ij}^{3}}}\right|}}={\displaystyle \frac{\left|\displaystyle \mathop{\sum }_{j\neq i}\hat{\boldsymbol{W}}_{ij}\left(\boldsymbol{e}_{x}+{\displaystyle \frac{\unicode[STIX]{x1D705}_{q}}{N}}\displaystyle \mathop{\sum }_{k\neq j}{\displaystyle \frac{\hat{\boldsymbol{r}}_{jk}}{\hat{r}_{jk}^{3}}}\right)\right|}{\left|{\displaystyle \frac{\unicode[STIX]{x1D705}_{q}}{N}}\displaystyle \mathop{\sum }_{j\neq i}{\displaystyle \frac{\hat{\boldsymbol{r}}_{ij}}{\hat{r}_{ij}^{3}}}\right|}}=\unicode[STIX]{x1D6F9}_{i,ext}+\unicode[STIX]{x1D6F9}_{i,Coul}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D6F9}_{i,ext}$
is the ratio of the velocity caused by the indirect effect of the imposed external field to the mobility caused by the direct Coulomb repulsion, and
$\unicode[STIX]{x1D6F9}_{i,Coul}$
is the ratio between the velocities from the indirect and direct effects of Coulomb repulsion. Note that the only anisotropic term (
$\boldsymbol{e}_{x}$
) is included in
$\unicode[STIX]{x1D6F9}_{i,ext}$
, and thus the clouds will undergo an isotropic expansion if
$\unicode[STIX]{x1D6F9}_{i,ext}\ll 1$
. If
$\unicode[STIX]{x1D6F9}_{i,Coul}\ll 1$
as well, the isotropic expansion will be determined by the direct repulsive interaction. Scaling analysis shows that
$\unicode[STIX]{x1D6F9}_{i,ext}\sim (1/\unicode[STIX]{x1D705}_{q})N\hat{r}_{p}\hat{R}_{cl}$
and
$\unicode[STIX]{x1D6F9}_{i,Coul}\sim N\hat{r}_{p}\hat{R}_{cl}$
(see appendix A). It is natural to see whether a cloud will undergo an isotropic expansion based on its initial configuration. Substituting
$\hat{R}_{cl}$
with its initial value
$1$
into the direct-repulsion-dominant condition (
$\unicode[STIX]{x1D6F9}_{i,ext}\ll 1$
and
$\unicode[STIX]{x1D6F9}_{i,Coul}\ll 1$
), a new regime of isotropic expansion is identified as
$$\begin{eqnarray}\unicode[STIX]{x1D705}_{q}\gg \left({\displaystyle \frac{R_{0}}{r_{p}}}\right)^{2}\unicode[STIX]{x1D719}\equiv \unicode[STIX]{x1D705}_{q,t}\quad \text{and}\quad \unicode[STIX]{x1D705}_{q,t}\ll 1.\end{eqnarray}$$
A migrating cloud in this regime will undergo an isotropic expansion before its radius reaches a critical value
$\hat{R}_{cl,crit}$
(see appendix A). Equation (2.4) (in a reference frame moving with velocity
$U_{0}$
) is simply reduced to
$\hat{\boldsymbol{u}}_{p,i}\approx \unicode[STIX]{x1D705}_{q}\unicode[STIX]{x1D731}_{i}$
, which can be transformed into a continuous form:
$$\begin{eqnarray}\hat{\boldsymbol{u}}(\hat{\boldsymbol{r}},\hat{t})={\displaystyle \frac{\unicode[STIX]{x1D705}_{q}}{N}}\int _{V_{cl}}{\displaystyle \frac{\hat{\boldsymbol{r}}-\hat{\boldsymbol{r}}^{\prime }}{|\hat{\boldsymbol{r}}-\hat{\boldsymbol{r}}^{\prime }|^{3}}}n(\hat{\boldsymbol{r}}^{\prime },\hat{t})\,\text{d}V^{\prime }(\hat{\boldsymbol{r}}^{\prime }).\end{eqnarray}$$
It gives the induced velocity in (2.6). Then, for a spherical cloud with initial density field independent of angular coordinates, (2.6) and (3.3) take the forms
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}\hat{t}}}+{\displaystyle \frac{1}{\hat{r}^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\hat{r}}}[\hat{u} _{r}(\hat{r},\hat{t})\hat{r}^{2}n]=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{u} _{r}(\hat{r},\hat{t})={\displaystyle \frac{\unicode[STIX]{x1D705}_{q}}{N}}\int _{0}^{\hat{R}_{cl}}\!\int _{0}^{\unicode[STIX]{x03C0}}{\displaystyle \frac{(\hat{r}-\hat{r}^{\prime }\cos \unicode[STIX]{x1D6FD})n(\hat{r}^{\prime },\hat{t})}{(\hat{r}^{2}+\hat{r}^{\prime 2}-2\hat{r}\hat{r}^{\prime }\cos \unicode[STIX]{x1D6FD})^{3/2}}}\sin \unicode[STIX]{x1D6FD}\,\text{d}\unicode[STIX]{x1D6FD}\,\hat{r}^{\prime 2}\,\text{d}\hat{r}^{\prime }, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}$
is the azimuthal angle between
$\hat{\boldsymbol{r}}$
and
$\hat{\boldsymbol{r}}^{\prime }$
.
We then extend the derivation of Subramanian & Koch (Reference Subramanian and Koch2008) to obtain the solution that includes the influence of Coulomb repulsion for the number density field and the cloud radius (see appendix B):
$$\begin{eqnarray}\displaystyle & \displaystyle n(\hat{r},\hat{t})={\displaystyle \frac{N}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}_{q}\hat{t}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{R}_{cl}(\hat{t})=(3\unicode[STIX]{x1D705}_{q}\hat{t})^{1/3}. & \displaystyle\end{eqnarray}$$
Applying (3.6) and (3.7) in (3.5), the induced velocity field reduces to
$$\begin{eqnarray}\hat{u} _{r}(\hat{r},\hat{t})=\left({\displaystyle \frac{\unicode[STIX]{x1D705}_{q}}{9\hat{t}^{2}}}\right)^{1/3}{\displaystyle \frac{\hat{r}}{\hat{R}_{cl}}}.\end{eqnarray}$$
In this sense, the isotropic expansion can be well described by the charge parameter
$\unicode[STIX]{x1D705}_{q}$
.
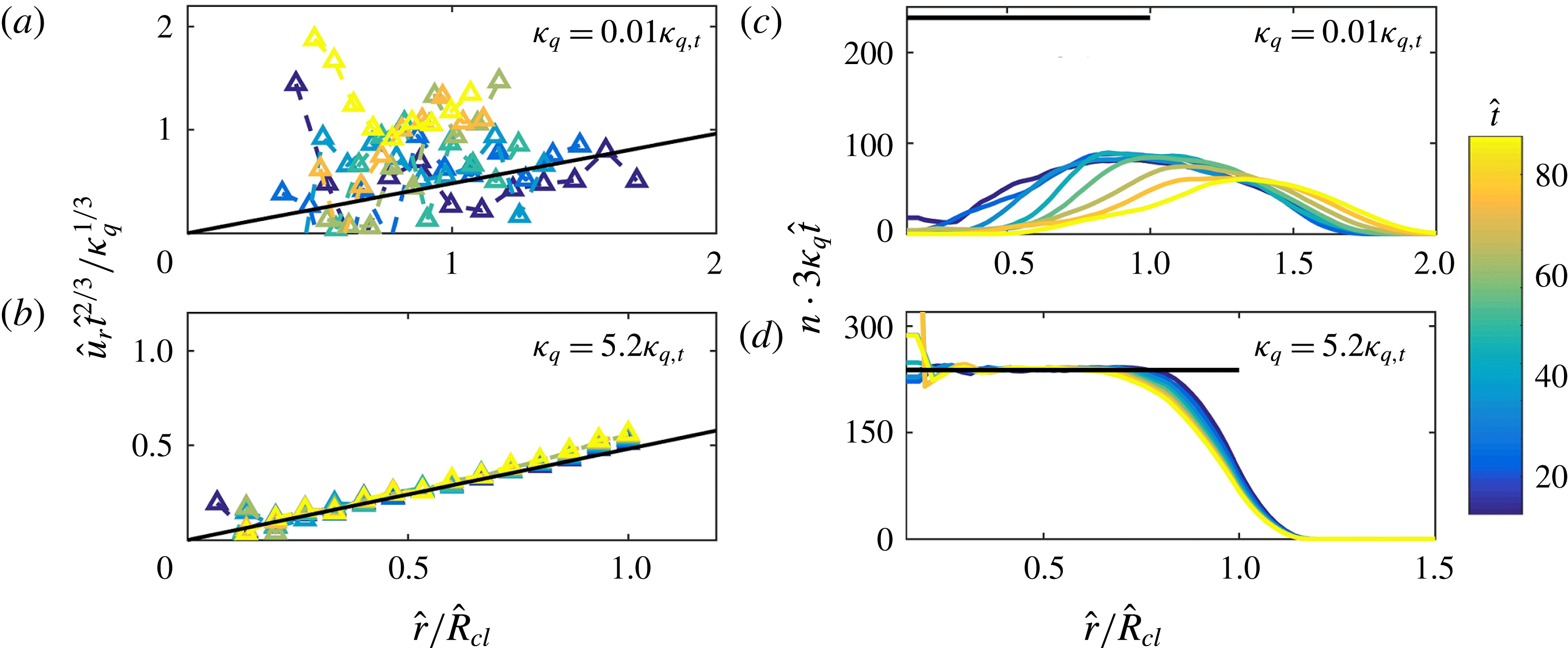
Figure 7. Normalized velocity
$\hat{u} _{r}\hat{t}^{2/3}/\unicode[STIX]{x1D705}_{q}^{1/3}$
as a function of
$\hat{r}/R_{cl}$
for a cloud with (
$a$
)
$\unicode[STIX]{x1D705}_{q}=0.01\unicode[STIX]{x1D705}_{q,t}$
and (
$b$
)
$\unicode[STIX]{x1D705}_{q}=5.2\unicode[STIX]{x1D705}_{q,t}$
; (
$c$
) and (
$d$
) are the corresponding rescaled density field
$3n\unicode[STIX]{x1D705}_{q}\hat{t}$
. Colour code spans from blue to yellow with increasing time (from
$\hat{t}=20$
to
$\hat{t}=90$
) and black solid lines are theoretical predictions given by (3.8) and (3.6).
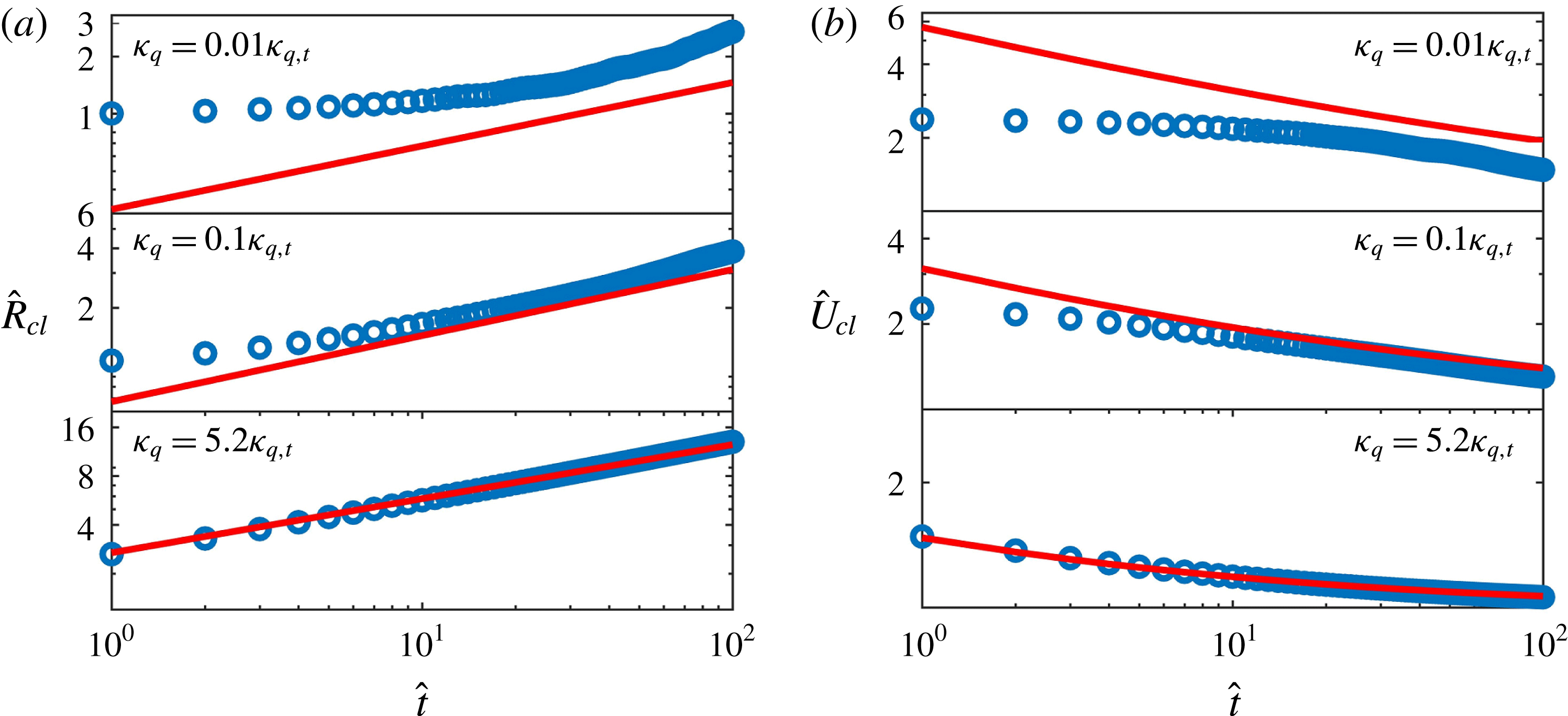
Figure 8. Evolution of (a) cloud radius
$\hat{R}_{cl}$
and (b) migrating velocity
$\hat{U} _{cl}$
with
$\unicode[STIX]{x1D705}_{q}=0.01\unicode[STIX]{x1D705}_{q,t}$
,
$\unicode[STIX]{x1D705}_{q}=0.1\unicode[STIX]{x1D705}_{q,t}$
and
$\unicode[STIX]{x1D705}_{q}=5.2\unicode[STIX]{x1D705}_{q,t}$
. The particle Reynolds number is
$Re_{p}=2.54\times 10^{-4}$
and cloud-to-particle size ratio is
$R_{0}/r_{p}=800$
. Red lines are theoretical predictions of (3.7) and (3.9).
In figure 7, we plot the induced velocity (in radial direction) in clouds with weak (
$\unicode[STIX]{x1D705}_{q}=0.01\unicode[STIX]{x1D705}_{q,t}$
) and strong (
$\unicode[STIX]{x1D705}_{q}=5.2\unicode[STIX]{x1D705}_{q,t}$
) repulsions and the corresponding particle density profiles. The coloured scatterplots and lines are the results from particle dynamic simulations, and the black solid lines are the scaling laws in (3.8) and (3.6). An evident result is that the normalized induced velocities
$\hat{u} _{r}\hat{t}^{2/3}/\hat{\unicode[STIX]{x1D705}}_{q}^{1/3}$
for clouds with strong repulsion all collapse onto a single universal curve (figure 7
b) formulated by (3.8). The corresponding number density profiles, plotted in a rescaled form
$n3\unicode[STIX]{x1D705}_{q}\hat{t}$
, at different times also collapse (figure 7
d). The number density almost remains constant across the entire cloud, and its value can be simply derived from the initial condition of number density
$n_{0}$
through
$n(\hat{t})=n_{0}/\hat{R}_{cl}^{3}(\hat{t})$
. These results indicate that a cloud with strong repulsion undergoes a self-similar expansion, which is well predicted by our scalings.
Figure 9. Scaled cloud radius
$\hat{R}_{cl}/(\hat{t}\unicode[STIX]{x1D705}_{q,t})^{1/3}$
and migrating velocity
$\hat{U} _{cl}^{\ast }=5(\hat{U} _{cl}-1)(\hat{t}\unicode[STIX]{x1D705}_{q,t})^{1/3}/(6Nf(R^{\ast })\hat{r}_{p})$
as functions of
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}$
at
$\hat{t}=10$
. The scatters are results of Oseenlet simulations and the black lines are corresponding theoretical prediction. Legend is the same as in figure 1.
When the repulsion interaction is weak (
$\unicode[STIX]{x1D705}_{q}\ll \unicode[STIX]{x1D705}_{q,t}$
), the scaling may break down. This is because, in such circumstances, the particles’ motion is dominated by hydrodynamic interaction. Particles are circulating in the clouds, which results in a significant scatter of the data points in figure 7(a). The cloud will break into subclouds with a local high particle concentration (as shown in figure 3
a), corresponding to peaks in density profile in figure 7(c).
Figure 8(a) shows how the cloud radius
$\hat{R}_{cl}$
evolves as
$\hat{t}$
increases for different
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}$
. The analytical solution (3.7) can well predict the evolution of the radius for a cloud with
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}=5.2$
, whereas it underestimates the radius for a cloud with
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}=0.01$
, where the separation between subclouds becomes the main cause of the increase of the cloud radius. Besides the cloud radius, the cloud migrating velocity
$\hat{U} _{cl}$
is also of great significance for the design of industrial units. For neutral clouds, one can only predict the velocity at a very early stage before breakup occurs. With strong repulsion, the formation of relatively stable configurations enables us to predict long-term evolution of
$\hat{U} _{cl}$
. Based on the analytical expression for cloud settling velocity under gravity in our earlier study (Yang et al.
Reference Yang, Li and Marshall2015) and the prediction of cloud radius
$\hat{R}_{cl}$
in (3.7), we construct a new formula for the migrating velocity of a cloud of charged particles in repulsion-dominant regime:
$$\begin{eqnarray}\hat{U} _{cl}(\hat{t})={\displaystyle \frac{6}{5}}Nf(R^{\ast }){\displaystyle \frac{\hat{r}_{p}}{(3\unicode[STIX]{x1D705}_{q}\hat{t})^{1/3}}}+1.\end{eqnarray}$$
Here
$R^{\ast }=Re_{p}R_{cl}/r_{p}=1/l^{\ast }$
is the instantaneous system inertia scale and
$f(R^{\ast })=3/(3+R^{\ast })$
is the correction factor for fluid inertia. Figure 8(b) shows that the simulation results nicely collapse onto the theoretical line (3.9) in the condition of strong repulsion.
To generalize these results, we run a large number of simulations for clouds with different particle Reynolds number
$Re_{p}$
and cloud-to-particle size ratio
$R_{0}/r_{p}$
(as shown in figure 1) with
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}$
ranging from
$10^{-3}$
to
$10^{1}$
. We rewrite (3.7) as
$\hat{R}_{cl}/(\hat{t}\unicode[STIX]{x1D705}_{q,t})^{1/3}=(3\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t})^{1/3}$
and (3.9) as
$5(\hat{U} _{cl}-1)(\hat{t}\unicode[STIX]{x1D705}_{q,t})^{1/3}/(6Nf(R^{\ast })\hat{r}_{p})=(3\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t})^{-1/3}$
, and plot all the simulation results at
$\hat{t}=10$
as a function of
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}$
in figure 9. It can be seen that, for
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}\ll 1$
, the scatters in the data are large; whereas, for
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}>1$
, the scaled cloud radius and migrating velocity both fall into a narrow range around the theoretical curves. Figure 9 also displays snapshots of clouds at different
$Re_{p}$
. We observe that, for
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}<1$
, the clouds are compressed into different shapes, while the clouds with
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}>1$
stay spherical. Therefore, combining our results for
$\hat{R}_{cl}(\hat{t})$
and
$\hat{U} _{cl}(\hat{t})$
highlights a Coulomb-repulsion-controlled regime characterized by the dimensionless ratio
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}$
.
4 Discussion
By imposing electrostatic interactions into Oseenlet simulations, we have been able to study the behaviour of a migrating cloud of charged particles. We have shown that strong long-range Coulomb repulsion can prevent the breakup of the clouds covering a wide range of particle Reynolds number
$Re_{p}$
and cloud-to-particle size ratio
$R_{0}/r_{p}$
. The simulated results with strong repulsion can be described with a continuum convection equation, which predicts the evolution of the density field, the radius and the migrating velocity of the cloud. A dimensionless charge parameter
$\unicode[STIX]{x1D705}_{q}$
is proposed to quantify the effect of the repulsion, and the ratio
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}$
successfully captures the transition from hydrodynamically controlled regime
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}<1$
to repulsion-controlled regime
$\unicode[STIX]{x1D705}_{q}/\unicode[STIX]{x1D705}_{q,t}>1$
.
Indeed, Subramanian & Koch (Reference Subramanian and Koch2008) have presented a theoretical analysis of the long-time dynamics of sedimenting neutral clouds, wherein particle interactions were dominated by the source–field interaction. Owing to the high instability of neutral clouds, their analysis may be valid only for clouds with extremely low particle volume fraction. Introducing a strong Coulomb repulsion makes the cloud more stable and extends the continuum description to a wider regime, which is the key difference between our study and the previous works. Our Oseenlet simulation not only, for the first time, provides a direct support for the utility of the continuum description, but also extended it to include long-range Coulomb interaction.
For the dilute clouds considered here, the isotropic expansion condition can also be understood at a first level by the force balance between the hydrodynamic drag
$6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}r_{p}\unicode[STIX]{x0394}u_{r,Oseen}$
and the pairwise Coulomb repulsion
$(1/(6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}r_{p}))(\sum _{j\neq i}q_{0}^{2}\boldsymbol{r}_{ij}/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}r_{ij}^{3}))$
. Substituting
$\unicode[STIX]{x0394}u_{r,Oseen}$
with maximum inward flow velocity at the rear boundary of the cloud
$(E_{0}q/(6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}r_{p}))6Nr_{p}/(5R_{0})$
(Yang et al.
Reference Yang, Li and Marshall2015), we can reproduce (3.2) as
$\unicode[STIX]{x1D705}_{q,t}\sim (R_{0}/r_{p})^{2}\unicode[STIX]{x1D719}$
. A balance length scale can be calculated as
$\hat{l}_{q}^{\ast }\sim q_{0}/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}E_{0}r_{p}N^{1/3})$
, and the isotropic condition will be satisfied if the typical distance between neighbouring particles
$l$
is smaller than
$\hat{l}_{q}^{\ast }$
. It is straightforward to see from (3.7) that
$\hat{l}$
increases with time as
$\hat{l}\sim \hat{t}^{1/3}$
. Therefore, an initially isotropic expanding cloud will evolve into the hydrodynamically controlled regime after a sufficiently long time. We have simulated some cases to observe this transition and find that an expanding cloud will finally resemble the behaviour of a neutral cloud settling under gravity. The subsequent evolution is then determined by the instant cloud radius
$R(t)$
, the cloud-to-particle size ratio
$R(t)/r_{p}$
, the volume fraction
$\unicode[STIX]{x1D719}$
and the particle Reynolds number
$Re_{p}$
. Recall that the condition of a sufficiently low number density (
$N/R_{0}\ll U_{0}/\unicode[STIX]{x1D708}_{f}$
) indicates another length scale
$\hat{l}_{f}^{\ast }\sim N^{2/3}r_{p}/(Re_{p}R_{0})$
. If the transition happens at
$\hat{l}\gg \hat{l}_{f}^{\ast }$
, the wake interactions remain negligible, and the hydrodynamics is continuously controlled by
$O(1/r^{2})$
type interaction. Then the clouds dynamics, such as the temporal evolution of cloud radius
$\hat{R}_{cl}(\hat{t})$
, when presented in a log–log plot, only has a change in the intercept (see appendix C).
It should be noted that, owing to the low particle volume fraction in our simulation, it is reasonable to consider a particle as a point when calculating electrostatic and hydrodynamic interactions. However, for a sufficiently dense cloud, the finite size of the particles substantially affects the interactions between particles: (1) higher-order multipoles in electrostatic interaction, e.g. dipoles or quadrupoles, cannot be neglected; and (2) higher-order moments of the traction taken over the particle surface should be considered. A reasonable estimation of the volume fraction over which the point force condition is valid can be obtained by comparing the relative magnitude of: (1) the interaction between point charged particles (
$F_{Coul}$
) versus that between induced dipoles (
$F_{dipole}$
); and (2) the flow field induced by point force (
$U_{PF}$
) versus that induced by the degenerate quadrupole (
$U_{DQ}$
) (finite size term). These conditions can be written as
$$\begin{eqnarray}\underbrace{{\displaystyle \frac{q_{0}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}l^{2}}}}_{F_{Coul}}\gg \underbrace{{\displaystyle \frac{3p^{2}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}l^{4}}}}_{F_{dipole}}\quad \text{and }\quad \underbrace{{\displaystyle \frac{F_{ext}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}l}}}_{U_{PF}}\gg \underbrace{{\displaystyle \frac{r_{p}^{2}F_{ext}}{12\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{f}l^{3}}}}_{U_{DQ}}.\end{eqnarray}$$
Here,
$p=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}Kr_{p}^{3}E_{0}$
is the dipole moment of a particle induced by the external field (Jones Reference Jones2005), and the Clausius–Mossotti factor
$K=(\unicode[STIX]{x1D700}_{p}-\unicode[STIX]{x1D700}_{f})/(\unicode[STIX]{x1D700}_{p}+2\unicode[STIX]{x1D700}_{f})$
is a function of particle permittivity
$\unicode[STIX]{x1D700}_{p}$
and fluid permittivity
$\unicode[STIX]{x1D700}_{f}$
; and
$l$
is the typical distance between two neighbouring particles, which scales as
$l=\unicode[STIX]{x1D719}^{-1/3}r_{p}$
. Therefore, the point force simplification is valid when the volume fraction satisfies
$$\begin{eqnarray}\unicode[STIX]{x1D719}\ll \left({\displaystyle \frac{q_{0}}{10\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{f}Kr_{p}^{2}E_{0}}}\right)^{3}\quad \text{and}\quad \unicode[STIX]{x1D719}\ll {\displaystyle \frac{1}{3}}.\end{eqnarray}$$
Particularly, it would be of great interest to compare the present study with Wigner glass transition in colloidal suspension. In a Wigner glass, electrostatic repulsion among charged particles becomes the dominant interaction. The long-range electrostatic repulsion effectively holds the particles away from each other. Thus, a stabilized glass phase can be formed at a very low density (Lindsay & Chaikin Reference Lindsay and Chaikin1982; Klix, Royall & Tanaka Reference Klix, Royall and Tanaka2010; Ruzicka & Zaccarelli Reference Ruzicka and Zaccarelli2011). Our system has the following characteristics in common with a Wigner glass: (1) the dynamics is driven by the long-ranged electrostatic repulsion; and (2) a homogeneous and stable configuration can be obtained with strong repulsive interactions. The glassy properties have also been found in clogging transitions: when charged particles accumulate near a microchannel bottleneck, a force network is built up and the electrostatic repulsion keeps the particles apart, prohibiting further collisions or depositions of the particles (Agbangla et al. Reference Agbangla, Bacchin and Climent2014; Chen et al. Reference Chen, Li, Liu and Makse2016a ; Sendekie & Bacchin Reference Sendekie and Bacchin2016). This kind of force network may help the migrating cloud hold its shape and keep a uniform density profile.
Several avenues for future investigation have also been indicated based on our results. First, it still remains a real challenge to extend the continuum theory to predict the behaviour of a sufficiently dense migrating cloud, where the effect of higher-order multipoles should be included. Moreover, the current work focuses on the cloud migrating in infinite space. A hindering effect – migrating velocity decreases with the increase of particle concentration – is found in the sedimentation of uniform suspensions with periodic boundary condition (Brady & Bossis Reference Brady and Bossis1988; Hamid, Molina & Yamamoto Reference Hamid, Molina and Yamamoto2013). Thus, it is of interest to simulate migrating of electrically charged uniform suspensions, where the typical distance between neighbouring particles remains unchanged, to find out how the presence of long-range repulsion influences the distribution of particles and whether a ‘Wigner glass’ can be formed.
Acknowledgements
This work has been jointly funded by the National Key Research and Development Program of China (2016YFB0600602) and the National Fund for Distinguished Young Scholars of China (51725601). We are grateful to Jeff Marshall at Vermont and Corey O’Hern at Yale for fruitful discussions, and Professor Q. Yao and Dr M. Yang at Tsinghua University for their useful suggestions.
Appendix A. Scaling analysis of (3.1)
According to (3.1),
$\unicode[STIX]{x1D6F9}_{i,ext}$
and
$\unicode[STIX]{x1D6F9}_{i,Coul}$
can be written as
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{i,ext}={\displaystyle \frac{1}{\unicode[STIX]{x1D705}_{q}}}{\displaystyle \frac{\left|\displaystyle \mathop{\sum }_{j\neq i}\hat{\boldsymbol{W}}_{ij}\boldsymbol{e}_{x}\right|}{|\unicode[STIX]{x1D731}_{i}|}}\quad \text{and}\quad \unicode[STIX]{x1D6F9}_{i,Coul}={\displaystyle \frac{\left|\displaystyle \mathop{\sum }_{j\neq i}\hat{\boldsymbol{W}}_{ij}\unicode[STIX]{x1D731}_{j}\right|}{|\unicode[STIX]{x1D731}_{i}|}}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D731}_{i}=(1/N)\sum _{j\neq i}(\hat{\boldsymbol{r}}_{ij}/\hat{r}_{ij}^{3})$
is a function only of the particles’ positions. For simplicity, we ignore the effect of fluid inertia here, so that
$\hat{\boldsymbol{W}}_{ij}$
is also determined by the particles’ positions. According to (2.2), (2.3) and figure 6, the maximum induced radial velocity
$\hat{u} _{r,Oseen}$
at the position of particle
$i$
due to particle
$j$
(at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
) scales as
$O(\hat{r}_{p}/\hat{r}_{ij})$
; and the maximum of
$\hat{u} _{\unicode[STIX]{x1D703},Oseen}$
(at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
) also scales as
$O(\hat{r}_{p}/\hat{r}_{ij})$
. Thus
$\sum _{j\neq i}\hat{\boldsymbol{W}}_{ij}$
can be estimated as
$\sum _{j\neq i}(\hat{r}_{p}\hat{\boldsymbol{r}}_{ij})/\hat{r}_{ij}^{2}$
. Here, we assume that the target particle
$i$
is located close to the boundary of the cloud and use integration to approximate the summation. Then
$|\unicode[STIX]{x1D731}_{i}|$
and
$|\!\sum _{j\neq i}\hat{\boldsymbol{W}}_{ij}|$
can be estimated as
$$\begin{eqnarray}\displaystyle & \displaystyle |\unicode[STIX]{x1D731}_{i}|=\left|{\displaystyle \frac{1}{N}}\displaystyle \mathop{\sum }_{j\neq i}{\displaystyle \frac{\hat{\boldsymbol{r}}_{ij}}{\hat{r}_{ij}^{3}}}\right|\sim \left|{\displaystyle \frac{1}{\hat{V}_{cl}}}\int _{\hat{V}_{cl}}{\displaystyle \frac{\hat{\boldsymbol{r}_{i}}-\hat{\boldsymbol{r}}^{\prime }}{|\hat{\boldsymbol{r}_{i}}-\hat{\boldsymbol{r}}^{\prime }|^{3}}}\,\text{d}\hat{V}^{\prime }(\hat{\boldsymbol{r}}^{\prime })\right|\sim O(\hat{R}_{cl}^{-2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left|\displaystyle \mathop{\sum }_{j\neq i}\hat{\boldsymbol{W}}_{ij}\right|\approx \left|\displaystyle \mathop{\sum }_{j\neq i}{\displaystyle \frac{\hat{r}_{p}\hat{\boldsymbol{r}}_{ij}}{\hat{r}_{ij}^{2}}}\right|\sim \left|{\displaystyle \frac{N\hat{r_{p}}}{\hat{V}_{cl}}}\int _{\hat{V}_{cl}}{\displaystyle \frac{\hat{\boldsymbol{r}_{i}}-\hat{\boldsymbol{r}}^{\prime }}{|\hat{\boldsymbol{r}_{i}}-\hat{\boldsymbol{r}}^{\prime }|^{2}}}\,\text{d}\hat{V}^{\prime }(\hat{\boldsymbol{r}}^{\prime })\right|\sim O(N\hat{r}_{p}\hat{R}_{cl}^{-1}). & \displaystyle\end{eqnarray}$$
Here,
$\hat{R}_{cl}=R(t)/R_{0}$
and
$R(t)$
is the cloud radius at time
$t$
. Then (A 1) take the form
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{i,ext}\sim {\displaystyle \frac{1}{\unicode[STIX]{x1D705}_{q}}}N\hat{r}_{p}\hat{R}_{cl}\propto R(t)\quad \text{and }\quad \unicode[STIX]{x1D6F9}_{i,Coul}\sim N\hat{r}_{p}\hat{R}_{cl}\propto R(t).\end{eqnarray}$$
It is straightforward that the condition
$\unicode[STIX]{x1D6F9}_{i,ext}\ll 1$
can always be met through increasing
$\unicode[STIX]{x1D705}_{q}$
. However,
$\unicode[STIX]{x1D6F9}_{i,Coul}$
is independent of
$\unicode[STIX]{x1D705}_{q}$
, so that the relative magnitude of the direct and indirect contributions of the Coulomb repulsion is determined only by the cloud configuration. Both
$\unicode[STIX]{x1D6F9}_{i,ext}$
and
$\unicode[STIX]{x1D6F9}_{i,Coul}$
are proportional to cloud radius
$R(t)$
, indicating that a repulsion-dominant cloud will evolve into the hydrodynamically controlled regime (with either
$\unicode[STIX]{x1D6F9}_{i,ext}\sim 1$
or
$\unicode[STIX]{x1D6F9}_{i,Coul}\sim 1$
) when its radius reaches a critical value
$\hat{R}_{cl,crit}\sim \text{min}\{(N\hat{r}_{p})^{-1},\unicode[STIX]{x1D705}_{q}(N\hat{r}_{p})^{-1}\}$
.
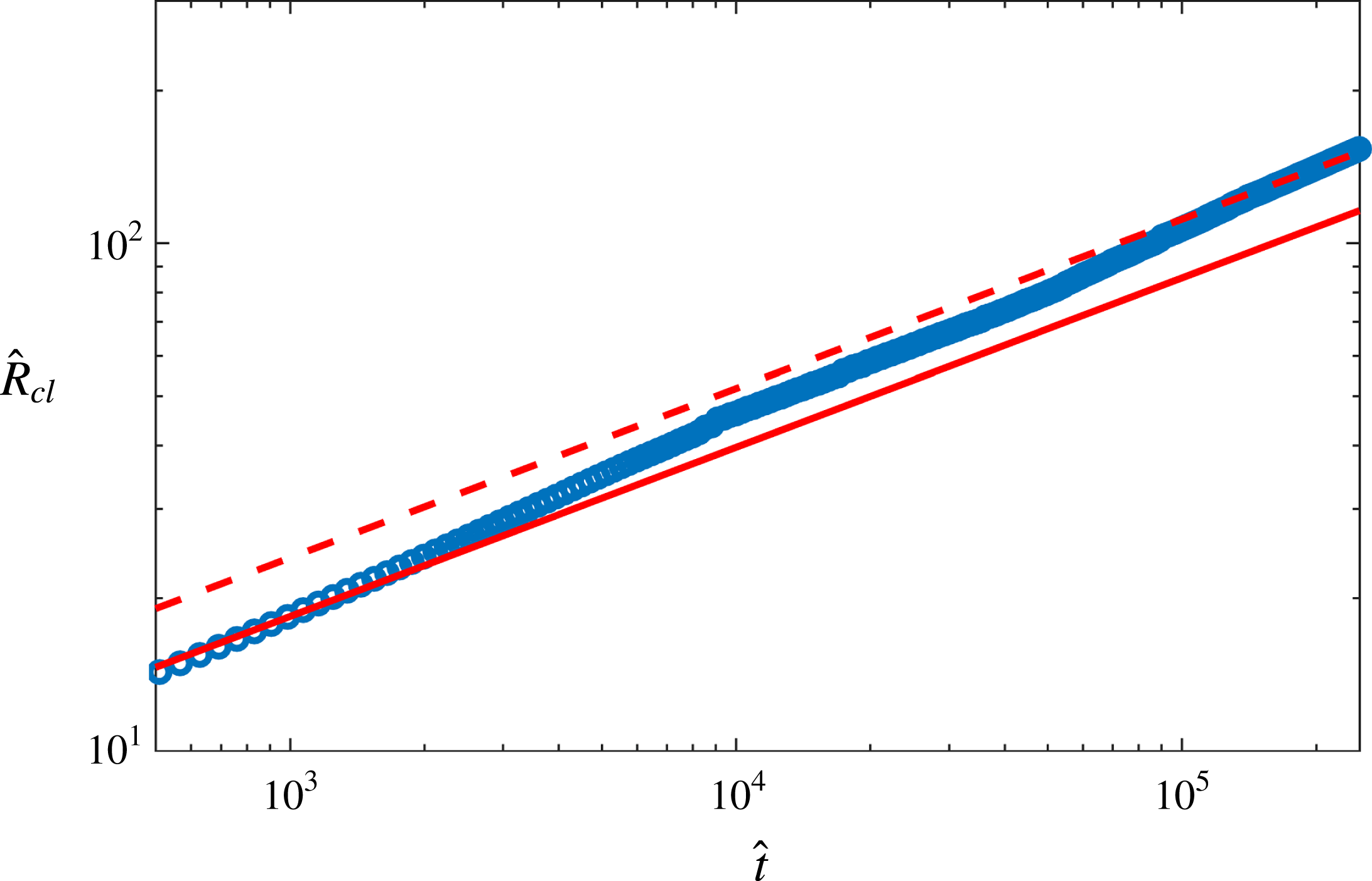
Figure 10. Long-time evolution of cloud radius
$\hat{R}_{cl}$
. The solid line is the theoretical prediction for electrostatic-interaction-dominant expansion (3.7) and the dashed line is the theoretical prediction (C 1) of Subramanian & Koch (Reference Subramanian and Koch2008) for a neutral cloud with
$O(1/r^{2})$
type source interactions.
Appendix B. Similarity solution of (3.4)
Here, we briefly introduce the standard similarity solution of (3.4) including the influence of Coulomb repulsion. A similarity formulation is employed as
$n=f(\hat{t}){\hat{g}}(\bar{\unicode[STIX]{x1D702}})$
with the similarity variable
$\bar{\unicode[STIX]{x1D702}}=\hat{r}/\hat{t}^{\unicode[STIX]{x1D6FE}}$
. Transforming (3.4), we obtain
$$\begin{eqnarray}{\displaystyle \frac{\text{d}\,f(\hat{t})}{\text{d}\hat{t}}}{\hat{g}}-\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D702}}{\displaystyle \frac{\,f(\hat{t})}{\hat{t}}}{\displaystyle \frac{\unicode[STIX]{x2202}{\hat{g}}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D702}}}}=-f^{2}(\hat{t}){\displaystyle \frac{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}_{q}}{\bar{\unicode[STIX]{x1D702}}^{2}N}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D702}}}}\left[{\hat{g}}(\bar{\unicode[STIX]{x1D702}})\int _{0}^{\bar{\unicode[STIX]{x1D702}}}{\hat{g}}(\bar{\unicode[STIX]{x1D702}}^{\prime })\bar{\unicode[STIX]{x1D702}}^{\prime 2}\,\text{d}\bar{\unicode[STIX]{x1D702}}^{\prime }\right].\end{eqnarray}$$
There should be no explicit time dependence in (B 1) to ensure the work of the similarity solution, implying that
$f(\hat{t})\sim 1/\hat{t}$
. The integral constraint of a constant total number of particles in a cloud gives
$\unicode[STIX]{x1D6FE}=1/3$
. Then another non-dimensional similarity variable, defined as
$\unicode[STIX]{x1D702}=\bar{\unicode[STIX]{x1D702}}/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}_{q}/N)^{1/3}=\hat{r}/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}_{q}\hat{t}/N)^{1/3}$
is used to form a dimensionless number density, given by
$g(\unicode[STIX]{x1D702})=4\unicode[STIX]{x03C0}{\hat{g}}\unicode[STIX]{x1D705}_{q}/N$
, and (B 1) takes the form
$$\begin{eqnarray}{\displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D702}}}(g\unicode[STIX]{x1D702}^{3})=3{\displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D702}}}\left[g\int _{0}^{\unicode[STIX]{x1D702}}g(\unicode[STIX]{x1D702}^{\prime }){\unicode[STIX]{x1D702}^{\prime }}^{2}\,\text{d}\unicode[STIX]{x1D702}^{\prime }\right].\end{eqnarray}$$
Integrating (B 2) and taking the limit
$\unicode[STIX]{x1D702}\rightarrow \infty$
to determine an integration constant, we can obtain an integral equation for
$g(\unicode[STIX]{x1D702})$
,
$$\begin{eqnarray}3\int _{0}^{\unicode[STIX]{x1D702}}g{\unicode[STIX]{x1D702}^{\prime }}^{2}\,\text{d}\unicode[STIX]{x1D702}^{\prime }=\unicode[STIX]{x1D702}^{3}\quad (\unicode[STIX]{x1D702}\leqslant \unicode[STIX]{x1D702}_{m}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D702}_{m}$
is the radial dimension of the cloud in similarity coordinates. The solution of (B 3),
$g=1$
, is straightforward. Thus, the number density field (3.6) for an isotropic expanding spherical cloud is
$n(\hat{r},\hat{t})=N/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}_{q}\hat{t})$
and the cloud radius (3.7) can be easily obtained using the condition of constant number of particles.
Appendix C. Transition from the repulsion-controlled to the hydrodynamically controlled regime
In this section, we consider the transition from the repulsion-controlled to the hydrodynamically controlled regime that happens at
$\hat{l}\gg N^{2/3}r_{p}/(Re_{p}R_{0})$
. The further evolution will still be controlled by
$O(1/r^{2})$
type source interaction
$u_{f,r}=3\unicode[STIX]{x1D708}_{f}r_{p}/(2r^{2})$
(Batchelor Reference Batchelor2000). Then evolution of the cloud radius
$\hat{R}_{cl}$
is given as (Subramanian & Koch Reference Subramanian and Koch2008)
$$\begin{eqnarray}\hat{R}_{cl}(\hat{t})=\left({\displaystyle \frac{3NQ}{4\unicode[STIX]{x03C0}U_{0}R_{0}^{2}}}\hat{t}\right)^{1/3},\end{eqnarray}$$
with
$Q=6\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}_{f}r_{p}$
. In figure 10, we present a typical case of a long-time evolution of the cloud radius
$\hat{R}_{cl}$
to show the transition. The evolution only has a change in intercept when presented in log–log coordinates.
