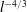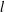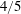1 Introduction
The dynamics of slender rods (or fibres) in turbulence has wide-ranging applications in environmental and industrial processes (for example, see the review by Voth & Soldati (Reference Voth and Soldati2017)). These applications include aerosols in the atmosphere (Newsom & Bruce Reference Newsom and Bruce1994, Reference Newsom and Bruce1998; Spurny Reference Spurny2000), textile and paper manufacture (Marheineke & Wegener Reference Marheineke and Wegener2006; Lundell, Söderberg & Alfredsson Reference Lundell, Söderberg and Alfredsson2011), the microstructure of clouds and precipitation (Pruppacher & Klett Reference Pruppacher and Klett2012), the scattering of electromagnetic radiation (Alyones & Bruce Reference Alyones and Bruce2015) and plankton hydrodynamics (Dusenbery Reference Dusenbery2009; Bordoloi & Variano Reference Bordoloi and Variano2017; Niazi et al. Reference Niazi, Sardina, Brandt, Karp-Boss, Bearon and Variano2017). The focus on rods also follows from the fact that they are analytically and numerically tractable using slender-body theory (e.g. Batchelor Reference Batchelor1970; Cox Reference Cox1970; Khayat & Cox Reference Khayat and Cox1989; Shin & Koch Reference Shin and Koch2005; Subramanian & Kock Reference Subramanian and Kock2005; Guazzelli & Hinch Reference Guazzelli and Hinch2011; Lopez & Guazzelli Reference Lopez and Guazzelli2017).
More generally, the study of rods, discs and triaxial ellipsoids that follow fluid trajectories but rotate in response to local velocity gradients has provided a way to investigate the Lagrangian structure of the smallest scales in turbulence (e.g. Parsa et al. Reference Parsa, Calzavarini, Toschi and Voth2012; Chevillard & Meneveau Reference Chevillard and Meneveau2013; Gustavsson, Einarsson & Mehlig Reference Gustavsson, Einarsson and Mehlig2014; Ni, Ouellette & Voth Reference Ni, Ouellette and Voth2014; Byron et al. Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015; Ni et al. Reference Ni, Kramel, Ouellette and Voth2015; Pujara & Variano Reference Pujara and Variano2017). This approach has shown that small rods (or, equivalently, infinitesimal material lines) strongly align with vorticity (Pumir & Wilkinson Reference Pumir and Wilkinson2011; Parsa et al. Reference Parsa, Calzavarini, Toschi and Voth2012), and both rods and vorticity come to align with the Lagrangian fluid stretching direction (Ni et al. Reference Ni, Ouellette and Voth2014). Herein, we extend this approach to larger scales and rods that are no longer small enough to follow fluid trajectories. Applications for this include predicting the motion of large anisotropic particles (e.g. Chen, Jin & Zhang Reference Chen, Jin and Zhang2015; Bordoloi & Variano Reference Bordoloi and Variano2017; Ravnik, Marchioli & Soldati Reference Ravnik, Marchioli and Soldati2017; Pujara et al. Reference Pujara, Oehmke, Bordoloi and Variano2018) and modelling the subgrid-scale stress tensor in large-eddy simulations (e.g. Sreenivasan & Antonia Reference Sreenivasan and Antonia1997; Meneveau & Katz Reference Meneveau and Katz2000; He, Rubinstein & Wang Reference He, Rubinstein and Wang2002; Yang, He & Wang Reference Yang, He and Wang2008). Studying the dynamics of longer rods also presents an opportunity to further the understanding of inertial-range dynamics of turbulence.
An important feature of the inertial range is internal intermittency (see e.g. Frisch Reference Frisch1995). In the inertial range, there exists a detailed phenomenology of the energy cascade and intermittency, where the majority of intermittency models focus on spatio-temporal variations of a scalar quantity such as the energy dissipation rate or the enstrophy in the spirit of Kolmogorov’s refined similarity hypothesis (e.g. Kolmogorov Reference Kolmogorov1962; Oboukhov Reference Oboukhov1962; Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1991; Chen et al. Reference Chen, Sreenivasan, Nelkin and Cao1997; Nelkin Reference Nelkin1999; Donzis, Yeung & Sreenivasan Reference Donzis, Yeung and Sreenivasan2008). This assumes that the local average of a single scalar captures the relevant fluctuations in the energy cascade at a given scale and that the structure of the associated fluid motions is not important. However, as we summarise below, recent work on the structure of turbulent flow at scales in the inertial range have provided new insights.
Chertkov, Pumir & Shraiman (Reference Chertkov, Pumir and Shraiman1999) introduced the idea of ‘tetrad dynamics’ where the Lagrangian evolution of four points is studied to understand coarse-grained velocity gradients. This approach of multi-particle statistics has been used to understand the effects of small-scale motions on larger-scale motions and how coarse-grained vorticity aligns in the coarse-grained strain-rate eigenframe (Naso & Pumir Reference Naso and Pumir2005; Luthi et al. Reference Luthi, Ott, Berg and Mann2007; Xu, Pumir & Bodenschatz Reference Xu, Pumir and Bodenschatz2011; Pumir, Bodenschatz & Xu Reference Pumir, Bodenschatz and Xu2013). Li & Meneveau (Reference Li and Meneveau2005, Reference Li and Meneveau2006) used a heavily simplified model for the Lagrangian evolution of two-point velocity increments derived from the Navier–Stokes equation (the ‘advected delta-vee system’) to study the origins of intermittency. They found that this system was able to reproduce key features of inertial-range intermittency, such as heavy tails in the probability distribution of transverse velocity increments and negative skewness of the longitudinal velocity increments, starting from initial Gaussian conditions. Hamlington, Schumacher & Dahm (Reference Hamlington, Schumacher and Dahm2008) and Leung, Swaminathan & Davidson (Reference Leung, Swaminathan and Davidson2012) examined vortical structures at different scales and showed that their shape becomes more worm-like with decreasing scale and that they align with the most stretching direction of strain at scales several times larger than the vortical structures. In laboratory experiments, Sinhuber, Bewley & Bodenschatz (Reference Sinhuber, Bewley and Bodenschatz2017) found that oscillations in power-law behaviour for moments of longitudinal velocity increments occur at fixed multiples of the Kolmogorov length scale, independent of Reynolds number, revealing the influence of dissipation-range fluid motions on inertial-range velocity statistics. Danish & Meneveau (Reference Danish and Meneveau2018) used coarse-grained velocity fields in turbulence and investigated the population fractions of different flow topologies as a function of scale and connected them to alignment of coarse-grained vorticity.
We aim to add to this knowledge of inertial-range dynamics by investigating rods that naturally respond to features in the flow and become aligned by fluid motions whose scale is near the rod length. We also build on the previous results from laboratory experiments which investigated the rod tumbling rate (rate of change of rod orientation (Parsa & Voth Reference Parsa and Voth2014)) and the rod stretching rate (longitudinal velocity increment across the rod (Kramel et al. Reference Kramel, Voth, Tympel and Toschi2016)) for rods with lengths in the inertial range. To do so, we use direct numerical simulation (DNS) data of isotropic turbulence in which we compute the motion of long rods (or, equivalently, rigid material lines). Along rod trajectories, we record the fluid velocity gradients filtered at the scale of the particle. We explore how the rods align with these perceived velocity gradients; this alignment is important in explaining the dynamics of rod rotation and rod stretching rates as a function of rod length. Because the moments of rod rotation and rod stretching directly probe the degree of alignment and how it behaves for rare events, we check whether the refined similarity hypothesis is able correctly to predict these moments.
The remainder of this paper is organised as follows. In § 2 we show the equations of rod motion and the methods used to track rods in a turbulent flow. This section also shows our method for computing the perceived velocity gradients around each rod as it travels through the flow. In § 3, we discuss the results, starting with properties of the perceived velocity gradient tensor (§§ 3.1 and 3.2), and how these relate to the power-law behaviour of rod dynamics in the inertial range (§§ 3.3 and 3.4) and scaling exponents of their higher-order moments (§ 3.5). We end with the conclusions in § 4.
2 Methods
2.1 Equations of rod motion
Figure 1(a) shows a planar slice of a turbulent fluid velocity field and a rigid, neutrally buoyant rod of length
![]() $l$
and infinitesimal diameter suspended in it. Shin & Koch (Reference Shin and Koch2005) derived the equations of motion for a rod such as this in a turbulent velocity field from slender-body theory (Batchelor Reference Batchelor1970; Cox Reference Cox1970). Slender-body theory uses matched asymptotic expansions in which the particle is replaced by a line of forces. In the limit
$l$
and infinitesimal diameter suspended in it. Shin & Koch (Reference Shin and Koch2005) derived the equations of motion for a rod such as this in a turbulent velocity field from slender-body theory (Batchelor Reference Batchelor1970; Cox Reference Cox1970). Slender-body theory uses matched asymptotic expansions in which the particle is replaced by a line of forces. In the limit
![]() $\ln (2l/d_{r})\gg 1$
, where
$\ln (2l/d_{r})\gg 1$
, where
![]() $d_{r}$
is the rod diameter and
$d_{r}$
is the rod diameter and
![]() $(l/d_{r})$
is the rod aspect ratio, Shin & Koch (Reference Shin and Koch2005) showed that the solution from slender-body theory could be simplified. To the same order of accuracy, they also showed that rod motion could be computed using one-way forcing, i.e. the reaction of the rod onto the fluid could be ignored. This is equivalent to ignoring the inertia of the rod in comparison to the inertia of the fluid at scale
$(l/d_{r})$
is the rod aspect ratio, Shin & Koch (Reference Shin and Koch2005) showed that the solution from slender-body theory could be simplified. To the same order of accuracy, they also showed that rod motion could be computed using one-way forcing, i.e. the reaction of the rod onto the fluid could be ignored. This is equivalent to ignoring the inertia of the rod in comparison to the inertia of the fluid at scale
![]() $l$
. For our purposes, the rod can be considered to be of very small diameter (or very high aspect ratio) so that this approximation is valid. Under this approximation, we do not account for the influence of rods on the fluid velocity. We also do not account for the interactions between rods since we are interested in the motion of an ensemble of rods rather than how rods affect each other. In this framework, the equations of motion for rod translation and rod orientation are, respectively,
$l$
. For our purposes, the rod can be considered to be of very small diameter (or very high aspect ratio) so that this approximation is valid. Under this approximation, we do not account for the influence of rods on the fluid velocity. We also do not account for the interactions between rods since we are interested in the motion of an ensemble of rods rather than how rods affect each other. In this framework, the equations of motion for rod translation and rod orientation are, respectively,

Figure 1. (a) A rigid, neutrally buoyant rod of length
![]() $l$
with orientation vector
$l$
with orientation vector
![]() $\boldsymbol{p}$
and with velocity of translation
$\boldsymbol{p}$
and with velocity of translation
![]() $\boldsymbol{u}_{\boldsymbol{p}}$
suspended in a fluid velocity field
$\boldsymbol{u}_{\boldsymbol{p}}$
suspended in a fluid velocity field
![]() $\boldsymbol{u}(\boldsymbol{x},t)$
. (b) Locations of velocity samples used to calculate the perceived velocity gradients around the rod. Large dots are on the surface of a sphere of diameter
$\boldsymbol{u}(\boldsymbol{x},t)$
. (b) Locations of velocity samples used to calculate the perceived velocity gradients around the rod. Large dots are on the surface of a sphere of diameter
![]() $l$
and are the 20 vertices of a regular dodecahedron. Small dots within the sphere are the six vertices of a regular octahedron.
$l$
and are the 20 vertices of a regular dodecahedron. Small dots within the sphere are the six vertices of a regular octahedron.
Equation (2.1a
) states that the rod translation velocity is the average of the fluid velocity sampled by the rod along its length. Equation (2.1b
) states that the rod tumbling is given by integrating the moment about the rod centre of the fluid velocity component that is perpendicular to the rod orientation. In the limit
![]() $l\rightarrow 0$
, the rod translational velocity equals the local fluid velocity and the rod acts as a fluid tracer. This simplifies (2.1a
) to
$l\rightarrow 0$
, the rod translational velocity equals the local fluid velocity and the rod acts as a fluid tracer. This simplifies (2.1a
) to
![]() $\boldsymbol{u}_{\boldsymbol{p}}=\boldsymbol{u}$
. In this limit, equation (2.1b
) can also be simplified since velocity variations are linear across the rod length. Also,
$\boldsymbol{u}_{\boldsymbol{p}}=\boldsymbol{u}$
. In this limit, equation (2.1b
) can also be simplified since velocity variations are linear across the rod length. Also,
![]() $\boldsymbol{u}$
in (2.1b
) can be replaced by
$\boldsymbol{u}$
in (2.1b
) can be replaced by
![]() $\boldsymbol{u}-\boldsymbol{u}_{\boldsymbol{p}}$
without changing the equation. Thus, the quantity in square brackets in (2.1b
) can be expressed in terms of the local velocity gradients. The correct expression, which considers the along-rod gradient of the velocity perpendicular to the rod, is given by
$\boldsymbol{u}-\boldsymbol{u}_{\boldsymbol{p}}$
without changing the equation. Thus, the quantity in square brackets in (2.1b
) can be expressed in terms of the local velocity gradients. The correct expression, which considers the along-rod gradient of the velocity perpendicular to the rod, is given by
![]() $[\unicode[STIX]{x1D63C}\,\boldsymbol{p}-(\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p})\boldsymbol{p}]s$
, where
$[\unicode[STIX]{x1D63C}\,\boldsymbol{p}-(\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p})\boldsymbol{p}]s$
, where
![]() $\unicode[STIX]{x1D63C}$
is the velocity gradient tensor and
$\unicode[STIX]{x1D63C}$
is the velocity gradient tensor and
![]() $\unicode[STIX]{x1D64E}$
is its symmetric part. Since the velocity gradients are uniform, they can be taken outside the integral, leaving (2.1b
) to simplify to Jeffery’s (Reference Jeffery1922) equation for tumbling of an infinite-aspect-ratio prolate spheroid:
$\unicode[STIX]{x1D64E}$
is its symmetric part. Since the velocity gradients are uniform, they can be taken outside the integral, leaving (2.1b
) to simplify to Jeffery’s (Reference Jeffery1922) equation for tumbling of an infinite-aspect-ratio prolate spheroid:
The first term in this equation is responsible for rod tumbling whereas the second term serves to keep
![]() $\boldsymbol{p}$
to unit length.
$\boldsymbol{p}$
to unit length.
In the limit
![]() $l\rightarrow 0$
, the rod stretching rate is given by the along-rod gradient of the fluid velocity parallel to the rod, which is given by the expression
$l\rightarrow 0$
, the rod stretching rate is given by the along-rod gradient of the fluid velocity parallel to the rod, which is given by the expression
![]() $\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
. For longer rods, the stretching rate is given by the integral of
$\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
. For longer rods, the stretching rate is given by the integral of
![]() $\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
over the rod length divided by the rod length. The integral of
$\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
over the rod length divided by the rod length. The integral of
![]() $\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
over the rod length simplifies to the longitudinal velocity increment between the rod end points,
$\boldsymbol{p}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
over the rod length simplifies to the longitudinal velocity increment between the rod end points,
where
![]() $\unicode[STIX]{x0394}_{r}u$
denotes the fluid velocity increment across the rod length for the velocity component parallel to the rod.
$\unicode[STIX]{x0394}_{r}u$
denotes the fluid velocity increment across the rod length for the velocity component parallel to the rod.
In this paper, the rod dynamics we focus on are the rod tumbling rate,
![]() $\dot{\boldsymbol{p}}$
, and the rod stretching rate,
$\dot{\boldsymbol{p}}$
, and the rod stretching rate,
![]() $\unicode[STIX]{x0394}_{r}u/l$
.
$\unicode[STIX]{x0394}_{r}u/l$
.
2.2 Numerical computations
We examine the dynamics of rods of different lengths in homogeneous isotropic turbulence. The turbulent fluid velocity field is taken from DNS data in the Johns Hopkins Turbulence Database (Perlman et al.
Reference Perlman, Burns, Li and Meneveau2007; Li et al.
Reference Li, Perlman, Wan, Yang, Meneveau, Burns, Chen, Szalay and Eyink2008; Yu et al.
Reference Yu, Kanov, Perlman, Graham, Frederix, Burns, Szalay, Eyink and Meneveau2012). The forced isotropic turbulence dataset consists of velocity and pressure data on a triply periodic cubic domain where the Taylor-scale Reynolds number is
![]() $Re_{\unicode[STIX]{x1D706}}\approx 430$
. The ratio of the integral length scale,
$Re_{\unicode[STIX]{x1D706}}\approx 430$
. The ratio of the integral length scale,
![]() $L$
, to the Kolmogorov length scale,
$L$
, to the Kolmogorov length scale,
![]() $\unicode[STIX]{x1D702}$
, is
$\unicode[STIX]{x1D702}$
, is
![]() $L\approx 480\unicode[STIX]{x1D702}$
, and the ratio of the integral time scale,
$L\approx 480\unicode[STIX]{x1D702}$
, and the ratio of the integral time scale,
![]() $T_{L}$
, to the Kolmogorov time scale,
$T_{L}$
, to the Kolmogorov time scale,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, is
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, is
![]() $T_{L}\approx 45\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
.
$T_{L}\approx 45\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
.
Rods of length
![]() $l$
spanning the range
$l$
spanning the range
![]() $\unicode[STIX]{x1D702}\leqslant l\leqslant 200\unicode[STIX]{x1D702}$
(
$\unicode[STIX]{x1D702}\leqslant l\leqslant 200\unicode[STIX]{x1D702}$
(
![]() $0.002L\leqslant l\leqslant 0.42L$
) are tracked in the flow. The position and orientation of each rod are tracked by integrating discretised forms of (2.1) in which the rod is represented by a nine-point stencil. In sensitivity tests, it was found that using more than nine points to represent the rod gave only marginally improved accuracy for the variance of rod tumbling (less than 2.5 % even for the longest rods considered). The integrations are carried out using second-order Runge–Kutta algorithms with a time step of
$0.002L\leqslant l\leqslant 0.42L$
) are tracked in the flow. The position and orientation of each rod are tracked by integrating discretised forms of (2.1) in which the rod is represented by a nine-point stencil. In sensitivity tests, it was found that using more than nine points to represent the rod gave only marginally improved accuracy for the variance of rod tumbling (less than 2.5 % even for the longest rods considered). The integrations are carried out using second-order Runge–Kutta algorithms with a time step of
![]() $0.009\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, which is twice the value of the time step used in the DNS integration. Rod data are recorded every five integration steps.
$0.009\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, which is twice the value of the time step used in the DNS integration. Rod data are recorded every five integration steps.
For each rod length, 7500 rods are initialised at random positions and random orientations and tracked from
![]() $t=0$
to
$t=0$
to
![]() $t=2T_{L}$
. Initial-time statistics show the behaviour of randomly oriented rods and are calculated as an ensemble average over all rods at
$t=2T_{L}$
. Initial-time statistics show the behaviour of randomly oriented rods and are calculated as an ensemble average over all rods at
![]() $t=0$
. Long-time statistics show the behaviour of rods in a statistically steady alignment with the turbulent flow and are calculated as an ensemble average over all rods and over time for
$t=0$
. Long-time statistics show the behaviour of rods in a statistically steady alignment with the turbulent flow and are calculated as an ensemble average over all rods and over time for
![]() $40\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}\leqslant t\leqslant 2T_{L}$
. Rods of all lengths have reached a statistically steady alignment with the flow by
$40\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}\leqslant t\leqslant 2T_{L}$
. Rods of all lengths have reached a statistically steady alignment with the flow by
![]() $t=40\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. Rod alignment is discussed in more detail in the following section.
$t=40\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. Rod alignment is discussed in more detail in the following section.
2.3 Perceived velocity gradient tensor
In addition to tracking rod position and orientation, we also compute velocity gradients around each rod as it travels through the flow. For rods in the tracer limit, the relevant velocity gradients are given by the velocity gradient tensor along Lagrangian fluid trajectories, denoted as
![]() $\unicode[STIX]{x1D63C}$
. For longer rods, the relevant velocity gradients are given by the ‘perceived velocity gradient tensor’,
$\unicode[STIX]{x1D63C}$
. For longer rods, the relevant velocity gradients are given by the ‘perceived velocity gradient tensor’,
![]() $\tilde{\unicode[STIX]{x1D63C}}$
, along the rod trajectory. The tensor
$\tilde{\unicode[STIX]{x1D63C}}$
, along the rod trajectory. The tensor
![]() $\tilde{\unicode[STIX]{x1D63C}}$
shows gradients in fluid motion at the rod length scale,
$\tilde{\unicode[STIX]{x1D63C}}$
shows gradients in fluid motion at the rod length scale,
![]() $l$
.
$l$
.
We compute
![]() $\tilde{\unicode[STIX]{x1D63C}}$
by a least-squares fit to velocity data at sample points within a region of interest surrounding the rod following Chertkov et al. (Reference Chertkov, Pumir and Shraiman1999) and Pumir et al. (Reference Pumir, Bodenschatz and Xu2013). To do this, we use velocity data at 26 points distributed around the rod centre (figure 1
b), where 20 points form a regular dodecahedron that can be circumscribed by a sphere of diameter
$\tilde{\unicode[STIX]{x1D63C}}$
by a least-squares fit to velocity data at sample points within a region of interest surrounding the rod following Chertkov et al. (Reference Chertkov, Pumir and Shraiman1999) and Pumir et al. (Reference Pumir, Bodenschatz and Xu2013). To do this, we use velocity data at 26 points distributed around the rod centre (figure 1
b), where 20 points form a regular dodecahedron that can be circumscribed by a sphere of diameter
![]() $l$
. The remaining six points form a regular octahedron whose vertices are at the centres of the six faces of the cube formed by eight vertices of the dodecahedron (orange circles in figure 1
b). The orientation of both polyhedra with respect to the simulation grid is held constant, i.e. it does not depend on rod orientation. The distribution of these 26 points is chosen because it is isotropic and most of the data (20 points) are at a distance
$l$
. The remaining six points form a regular octahedron whose vertices are at the centres of the six faces of the cube formed by eight vertices of the dodecahedron (orange circles in figure 1
b). The orientation of both polyhedra with respect to the simulation grid is held constant, i.e. it does not depend on rod orientation. The distribution of these 26 points is chosen because it is isotropic and most of the data (20 points) are at a distance
![]() $l/2$
from the rod centre. Additionally, tests with fewer points arranged at the vertices of fewer-sided regular polyhedra showed that the rod tumbling variance calculated using the perceived velocity gradients and Jeffery’s equation converged to within 2.5 % after using more points than the 20 vertices of the dodecahedron. To calculate the perceived velocity gradients, the fluid velocity at the rod centre is subtracted from the velocity at the 26 sample points. Then,
$l/2$
from the rod centre. Additionally, tests with fewer points arranged at the vertices of fewer-sided regular polyhedra showed that the rod tumbling variance calculated using the perceived velocity gradients and Jeffery’s equation converged to within 2.5 % after using more points than the 20 vertices of the dodecahedron. To calculate the perceived velocity gradients, the fluid velocity at the rod centre is subtracted from the velocity at the 26 sample points. Then,
![]() $\tilde{\unicode[STIX]{x1D63C}}$
is computed from a least-squares fit (equation (4) in Pumir et al.
Reference Pumir, Bodenschatz and Xu2013). Finally, continuity is imposed by subtracting
$\tilde{\unicode[STIX]{x1D63C}}$
is computed from a least-squares fit (equation (4) in Pumir et al.
Reference Pumir, Bodenschatz and Xu2013). Finally, continuity is imposed by subtracting
![]() $(1/3)\tilde{\unicode[STIX]{x1D608}}_{ii}\unicode[STIX]{x1D6FF}_{ij}$
from the least-squares solution to make the final
$(1/3)\tilde{\unicode[STIX]{x1D608}}_{ii}\unicode[STIX]{x1D6FF}_{ij}$
from the least-squares solution to make the final
![]() $\tilde{\unicode[STIX]{x1D63C}}$
trace-free.
$\tilde{\unicode[STIX]{x1D63C}}$
trace-free.
Like the velocity gradient tensor, the perceived velocity gradient tensor can be decomposed into a vorticity vector and a strain-rate tensor. Thus, there are four key directions associated with
![]() $\tilde{\unicode[STIX]{x1D63C}}$
: the direction of vorticity, represented by the unit vector
$\tilde{\unicode[STIX]{x1D63C}}$
: the direction of vorticity, represented by the unit vector
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
, and the eigenvectors of the strain-rate tensor, represented by the unit vectors
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
, and the eigenvectors of the strain-rate tensor, represented by the unit vectors
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}},\tilde{\boldsymbol{e}}_{\mathbf{2}},\tilde{\boldsymbol{e}}_{\mathbf{3}}$
. The most extensional direction is labelled
$\tilde{\boldsymbol{e}}_{\mathbf{1}},\tilde{\boldsymbol{e}}_{\mathbf{2}},\tilde{\boldsymbol{e}}_{\mathbf{3}}$
. The most extensional direction is labelled
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
and corresponds to the most positive eigenvalue,
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
and corresponds to the most positive eigenvalue,
![]() $\tilde{\unicode[STIX]{x1D706}}_{1}$
. The most compressional direction is labelled
$\tilde{\unicode[STIX]{x1D706}}_{1}$
. The most compressional direction is labelled
![]() $\tilde{\boldsymbol{e}}_{\mathbf{3}}$
and corresponds to the most negative eigenvalue,
$\tilde{\boldsymbol{e}}_{\mathbf{3}}$
and corresponds to the most negative eigenvalue,
![]() $\tilde{\unicode[STIX]{x1D706}}_{3}$
. The intermediate direction is
$\tilde{\unicode[STIX]{x1D706}}_{3}$
. The intermediate direction is
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
and corresponds to
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
and corresponds to
![]() $\tilde{\unicode[STIX]{x1D706}}_{2}$
, which can take either sign. Continuity requires that
$\tilde{\unicode[STIX]{x1D706}}_{2}$
, which can take either sign. Continuity requires that
![]() $\tilde{\unicode[STIX]{x1D706}}_{1}+\tilde{\unicode[STIX]{x1D706}}_{2}+\tilde{\unicode[STIX]{x1D706}}_{3}=0$
. Within the constraints of continuity and the ordering of the eigenvalues, the strain state can be quantified with a single dimensionless number given by (Lund & Rogers Reference Lund and Rogers1994)
$\tilde{\unicode[STIX]{x1D706}}_{1}+\tilde{\unicode[STIX]{x1D706}}_{2}+\tilde{\unicode[STIX]{x1D706}}_{3}=0$
. Within the constraints of continuity and the ordering of the eigenvalues, the strain state can be quantified with a single dimensionless number given by (Lund & Rogers Reference Lund and Rogers1994)
Here
![]() $\tilde{s}^{\ast }$
varies in the range
$\tilde{s}^{\ast }$
varies in the range
![]() $[-1,+1]$
;
$[-1,+1]$
;
![]() $\tilde{s}^{\ast }=+1$
is the limit of axisymmetric extension, where a spherical fluid element evolves into a disc, and
$\tilde{s}^{\ast }=+1$
is the limit of axisymmetric extension, where a spherical fluid element evolves into a disc, and
![]() $\tilde{s}^{\ast }=-1$
is the limit of axisymmetric contraction, where a spherical fluid element evolves into rod. The ratio
$\tilde{s}^{\ast }=-1$
is the limit of axisymmetric contraction, where a spherical fluid element evolves into rod. The ratio
![]() $\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}$
, which varies in the range
$\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}$
, which varies in the range
![]() $[-0.5,+1]$
, is also helpful in picturing the strain state, with
$[-0.5,+1]$
, is also helpful in picturing the strain state, with
![]() $\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}=-0.5$
being the limit of axisymmetric contraction, and
$\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}=-0.5$
being the limit of axisymmetric contraction, and
![]() $\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}=+1$
being the limit of axisymmetric extension. It is worth noting that the probability density function (p.d.f.) of
$\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}=+1$
being the limit of axisymmetric extension. It is worth noting that the probability density function (p.d.f.) of
![]() $\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}$
at the extreme values vanishes due to kinematic reasons rather than a lack of existence of such strain states (see Lund & Rogers Reference Lund and Rogers1994).
$\tilde{\unicode[STIX]{x1D706}}_{2}/\tilde{\unicode[STIX]{x1D706}}_{1}$
at the extreme values vanishes due to kinematic reasons rather than a lack of existence of such strain states (see Lund & Rogers Reference Lund and Rogers1994).
2.4 Lagrangian stretching directions
The time evolution of rod orientation relative to the directions of the velocity gradient tensor is more intuitive in the Lagrangian framework given by the Cauchy–Green strain tensors than with respect to the instantaneous velocity gradients given by
![]() $\tilde{\unicode[STIX]{x1D63C}}$
. For a fluid element undergoing deformation due to velocity gradients given by
$\tilde{\unicode[STIX]{x1D63C}}$
. For a fluid element undergoing deformation due to velocity gradients given by
![]() $\tilde{\unicode[STIX]{x1D63C}}(t)$
, the deformation gradient tensor,
$\tilde{\unicode[STIX]{x1D63C}}(t)$
, the deformation gradient tensor,
![]() $\tilde{\unicode[STIX]{x1D641}}$
, is given by integrating the differential relation
$\tilde{\unicode[STIX]{x1D641}}$
, is given by integrating the differential relation
![]() $\text{d}\tilde{\unicode[STIX]{x1D641}}(t)/\text{d}t=\tilde{\unicode[STIX]{x1D60D}}_{ij}(t)\tilde{\unicode[STIX]{x1D608}}_{jk}(t)$
. We calculate
$\text{d}\tilde{\unicode[STIX]{x1D641}}(t)/\text{d}t=\tilde{\unicode[STIX]{x1D60D}}_{ij}(t)\tilde{\unicode[STIX]{x1D608}}_{jk}(t)$
. We calculate
![]() $\tilde{\unicode[STIX]{x1D641}}$
by carrying out this integration using a fourth-order Runge–Kutta algorithm with the initial condition
$\tilde{\unicode[STIX]{x1D641}}$
by carrying out this integration using a fourth-order Runge–Kutta algorithm with the initial condition
![]() $\tilde{\unicode[STIX]{x1D641}}(t=40\unicode[STIX]{x1D702})=\unicode[STIX]{x1D6FF}_{ij}$
. The integration is carried out for
$\tilde{\unicode[STIX]{x1D641}}(t=40\unicode[STIX]{x1D702})=\unicode[STIX]{x1D6FF}_{ij}$
. The integration is carried out for
![]() $40\unicode[STIX]{x1D702}\leqslant t\leqslant 2T_{L}$
during which rods are in a statistically steady alignment with the flow.
$40\unicode[STIX]{x1D702}\leqslant t\leqslant 2T_{L}$
during which rods are in a statistically steady alignment with the flow.
The deformation gradient tensor can be written as
![]() $\tilde{\unicode[STIX]{x1D641}}=\tilde{\unicode[STIX]{x1D64D}}\tilde{\unicode[STIX]{x1D650}}$
or as
$\tilde{\unicode[STIX]{x1D641}}=\tilde{\unicode[STIX]{x1D64D}}\tilde{\unicode[STIX]{x1D650}}$
or as
![]() $\tilde{\unicode[STIX]{x1D641}}=\tilde{\unicode[STIX]{x1D651}}\tilde{\unicode[STIX]{x1D64D}}$
, depending upon whether the deformation is described as stretching (
$\tilde{\unicode[STIX]{x1D641}}=\tilde{\unicode[STIX]{x1D651}}\tilde{\unicode[STIX]{x1D64D}}$
, depending upon whether the deformation is described as stretching (
![]() $\tilde{\unicode[STIX]{x1D650}}$
) followed by rotation (
$\tilde{\unicode[STIX]{x1D650}}$
) followed by rotation (
![]() $\tilde{\unicode[STIX]{x1D64D}}$
) or rotation (
$\tilde{\unicode[STIX]{x1D64D}}$
) or rotation (
![]() $\tilde{\unicode[STIX]{x1D64D}}$
) followed by stretching (
$\tilde{\unicode[STIX]{x1D64D}}$
) followed by stretching (
![]() $\tilde{\unicode[STIX]{x1D651}}$
) (see e.g. Gonzalez & Stuart Reference Gonzalez and Stuart2009). Thus,
$\tilde{\unicode[STIX]{x1D651}}$
) (see e.g. Gonzalez & Stuart Reference Gonzalez and Stuart2009). Thus,
![]() $\tilde{\unicode[STIX]{x1D650}}$
and
$\tilde{\unicode[STIX]{x1D650}}$
and
![]() $\tilde{\unicode[STIX]{x1D651}}$
are the right and left stretch tensors, respectively. Using the inner product of
$\tilde{\unicode[STIX]{x1D651}}$
are the right and left stretch tensors, respectively. Using the inner product of
![]() $\tilde{\unicode[STIX]{x1D641}}$
with itself, we can isolate the stretching components of the deformation gradient:
$\tilde{\unicode[STIX]{x1D641}}$
with itself, we can isolate the stretching components of the deformation gradient:
![]() $\tilde{\unicode[STIX]{x1D63E}}_{R}=\tilde{\unicode[STIX]{x1D641}}^{\text{T}}\tilde{\unicode[STIX]{x1D641}}=\tilde{\unicode[STIX]{x1D650}}^{2}$
or
$\tilde{\unicode[STIX]{x1D63E}}_{R}=\tilde{\unicode[STIX]{x1D641}}^{\text{T}}\tilde{\unicode[STIX]{x1D641}}=\tilde{\unicode[STIX]{x1D650}}^{2}$
or
![]() $\tilde{\unicode[STIX]{x1D63E}}_{L}=\tilde{\unicode[STIX]{x1D641}}\tilde{\unicode[STIX]{x1D641}}^{\text{T}}=\tilde{\unicode[STIX]{x1D651}}^{2}$
, where
$\tilde{\unicode[STIX]{x1D63E}}_{L}=\tilde{\unicode[STIX]{x1D641}}\tilde{\unicode[STIX]{x1D641}}^{\text{T}}=\tilde{\unicode[STIX]{x1D651}}^{2}$
, where
![]() $\tilde{\unicode[STIX]{x1D63E}}_{R}$
and
$\tilde{\unicode[STIX]{x1D63E}}_{R}$
and
![]() $\tilde{\unicode[STIX]{x1D63E}}_{L}$
are the right Cauchy–Green strain tensor and the left Cauchy–Green strain tensor, respectively. The eigenframes of
$\tilde{\unicode[STIX]{x1D63E}}_{L}$
are the right Cauchy–Green strain tensor and the left Cauchy–Green strain tensor, respectively. The eigenframes of
![]() $\tilde{\unicode[STIX]{x1D63E}}_{R}$
and
$\tilde{\unicode[STIX]{x1D63E}}_{R}$
and
![]() $\tilde{\unicode[STIX]{x1D63E}}_{L}$
provide useful descriptions of fluid strain and we denote the unit vectors in the most extensional directions (associated with the most positive eigenvalues) of these tensors as
$\tilde{\unicode[STIX]{x1D63E}}_{L}$
provide useful descriptions of fluid strain and we denote the unit vectors in the most extensional directions (associated with the most positive eigenvalues) of these tensors as
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
and
$\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
, respectively. Physically,
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
, respectively. Physically,
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
is the direction of greatest fluid stretching at the initial time being considered and
$\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
is the direction of greatest fluid stretching at the initial time being considered and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
is the direction of greatest fluid stretching after taking into account the cumulative effect of velocity gradients over
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
is the direction of greatest fluid stretching after taking into account the cumulative effect of velocity gradients over
![]() $\unicode[STIX]{x0394}t$
.
$\unicode[STIX]{x0394}t$
.
2.5 Scale-local time scales
The characteristic time scale for fluid motions at rod length scale
![]() $l$
is a ‘scale-local’ time scale. Two such time scales are constructed using two-point fluid velocity statistics, otherwise known as structure functions (see e.g. Pope Reference Pope2000). If longitudinal velocity increments in the flow are denoted as
$l$
is a ‘scale-local’ time scale. Two such time scales are constructed using two-point fluid velocity statistics, otherwise known as structure functions (see e.g. Pope Reference Pope2000). If longitudinal velocity increments in the flow are denoted as
![]() $\unicode[STIX]{x0394}_{L}u$
, and transverse velocity increments are denoted as
$\unicode[STIX]{x0394}_{L}u$
, and transverse velocity increments are denoted as
![]() $\unicode[STIX]{x0394}_{N}u$
,
$\unicode[STIX]{x0394}_{N}u$
,
![]() $\langle (\unicode[STIX]{x0394}_{L}u)^{2}\rangle$
and
$\langle (\unicode[STIX]{x0394}_{L}u)^{2}\rangle$
and
![]() $\langle (\unicode[STIX]{x0394}_{N}u)^{2}\rangle$
are the second-order longitudinal and transverse velocity structure functions, respectively. The scale-local time scales are then given by
$\langle (\unicode[STIX]{x0394}_{N}u)^{2}\rangle$
are the second-order longitudinal and transverse velocity structure functions, respectively. The scale-local time scales are then given by
![]() $\unicode[STIX]{x1D70F}_{L}=l/(\sqrt{15\langle (\unicode[STIX]{x0394}_{L}u)^{2}\rangle })$
and
$\unicode[STIX]{x1D70F}_{L}=l/(\sqrt{15\langle (\unicode[STIX]{x0394}_{L}u)^{2}\rangle })$
and
![]() $\unicode[STIX]{x1D70F}_{N}=l/(\sqrt{(15/2)\langle (\unicode[STIX]{x0394}_{N}u)^{2}\rangle })$
, respectively, where
$\unicode[STIX]{x1D70F}_{N}=l/(\sqrt{(15/2)\langle (\unicode[STIX]{x0394}_{N}u)^{2}\rangle })$
, respectively, where
![]() $\unicode[STIX]{x0394}_{L}u$
and
$\unicode[STIX]{x0394}_{L}u$
and
![]() $\unicode[STIX]{x0394}_{N}u$
are evaluated at scale
$\unicode[STIX]{x0394}_{N}u$
are evaluated at scale
![]() $l$
. Defined in this way,
$l$
. Defined in this way,
![]() $\unicode[STIX]{x1D70F}_{L}$
and
$\unicode[STIX]{x1D70F}_{L}$
and
![]() $\unicode[STIX]{x1D70F}_{N}$
transition smoothly from a value of
$\unicode[STIX]{x1D70F}_{N}$
transition smoothly from a value of
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
in the limit of
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
in the limit of
![]() $l\rightarrow 0$
to a Kolmogorov (Reference Kolmogorov1941, henceforth K41) scaling in the inertial range, where
$l\rightarrow 0$
to a Kolmogorov (Reference Kolmogorov1941, henceforth K41) scaling in the inertial range, where
![]() $\unicode[STIX]{x1D70F}_{L}$
and
$\unicode[STIX]{x1D70F}_{L}$
and
![]() $\unicode[STIX]{x1D70F}_{N}$
scale as
$\unicode[STIX]{x1D70F}_{N}$
scale as
![]() $l^{2/3}$
.
$l^{2/3}$
.
We compute
![]() $\unicode[STIX]{x1D70F}_{L}$
and
$\unicode[STIX]{x1D70F}_{L}$
and
![]() $\unicode[STIX]{x1D70F}_{N}$
from
$\unicode[STIX]{x1D70F}_{N}$
from
![]() $\unicode[STIX]{x0394}_{L}u$
and
$\unicode[STIX]{x0394}_{L}u$
and
![]() $\unicode[STIX]{x0394}_{N}u$
taken from velocity data at the 20 vertices of the dodecahedron used to compute
$\unicode[STIX]{x0394}_{N}u$
taken from velocity data at the 20 vertices of the dodecahedron used to compute
![]() $\tilde{\unicode[STIX]{x1D63C}}$
. These form 10 pairs of points, where each pair consists of diametrically opposite points separated by distance
$\tilde{\unicode[STIX]{x1D63C}}$
. These form 10 pairs of points, where each pair consists of diametrically opposite points separated by distance
![]() $l$
.
$l$
.
2.6 Rod dynamics from Jeffery’s equation and rod tumbling from rod end points
We will refer to rod dynamics, i.e. position, orientation, velocity and tumbling, obtained by integrating (2.1) as ‘fully resolved’ rod dynamics. These data will be compared to rod dynamics obtained from two alternative methods, which we now introduce.
The first alternative method is to compute rod orientation and tumbling via integration of Jeffery’s equation using the perceived velocity gradient tensor,
![]() $\tilde{\unicode[STIX]{x1D63C}}(t)$
, along each rod trajectory. This is done by integrating equation (2.2) using a fourth-order Runge–Kutta algorithm with the same initial conditions as the fully resolved rod dynamics. Rod orientation and tumbling obtained using Jeffery’s equation are denoted as
$\tilde{\unicode[STIX]{x1D63C}}(t)$
, along each rod trajectory. This is done by integrating equation (2.2) using a fourth-order Runge–Kutta algorithm with the same initial conditions as the fully resolved rod dynamics. Rod orientation and tumbling obtained using Jeffery’s equation are denoted as
![]() $p_{i,J}$
and
$p_{i,J}$
and
![]() ${\dot{p}}_{i,J}$
, respectively.
${\dot{p}}_{i,J}$
, respectively.
The second alternative method pertains only to the rod tumbling. In this method, the rod trajectories and the rod orientation time histories from fully resolved rod dynamics are used, but an alternative measure of rod tumbling is computed using only the fluid velocity at the rod end points. If only the rod end points are used, (2.1b
) simplifies to
![]() $\unicode[STIX]{x0394}_{r}[\boldsymbol{u}-\boldsymbol{p}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{p})]/l$
, where
$\unicode[STIX]{x0394}_{r}[\boldsymbol{u}-\boldsymbol{p}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{p})]/l$
, where
![]() $\unicode[STIX]{x0394}_{r}[\boldsymbol{u}-\boldsymbol{p}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{p})]$
is the transverse velocity increment across the rod. In other words, the rod tumbling is determined by the increment of the fluid velocity across the rod length using the component perpendicular to the rod. The rod tumbling obtained in this way is denoted as
$\unicode[STIX]{x0394}_{r}[\boldsymbol{u}-\boldsymbol{p}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{p})]$
is the transverse velocity increment across the rod. In other words, the rod tumbling is determined by the increment of the fluid velocity across the rod length using the component perpendicular to the rod. The rod tumbling obtained in this way is denoted as
![]() ${\dot{p}}_{i,E}$
.
${\dot{p}}_{i,E}$
.
3 Results
3.1 Rod alignment
Figure 2 shows the rod alignment for fully resolved rod dynamics and rod dynamics from integrating Jeffery’s equation. Rod alignment is quantified by the inner product between the rod orientation
![]() $\boldsymbol{p}$
and the directions associated with
$\boldsymbol{p}$
and the directions associated with
![]() $\tilde{\unicode[STIX]{x1D63C}}$
. Mean-square values close to
$\tilde{\unicode[STIX]{x1D63C}}$
. Mean-square values close to
![]() $1$
indicate a propensity for the two vectors to be aligned with each other and mean-square values close to
$1$
indicate a propensity for the two vectors to be aligned with each other and mean-square values close to
![]() $0$
indicate a propensity for the two vectors to be orthogonal to each other. Two unit vectors with no correlation in their alignment would produce a mean-square value of
$0$
indicate a propensity for the two vectors to be orthogonal to each other. Two unit vectors with no correlation in their alignment would produce a mean-square value of
![]() $1/3$
. The data show that there is a scale-independent preferred alignment of rods in the tracer limit (
$1/3$
. The data show that there is a scale-independent preferred alignment of rods in the tracer limit (
![]() $l<5\unicode[STIX]{x1D702}$
) that follows the order
$l<5\unicode[STIX]{x1D702}$
) that follows the order
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}>\tilde{\boldsymbol{e}}_{\mathbf{2}}>\tilde{\boldsymbol{e}}_{\mathbf{1}}$
(see also Pumir & Wilkinson Reference Pumir and Wilkinson2011; Chevillard & Meneveau Reference Chevillard and Meneveau2013; Byron et al.
Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015; Ni et al.
Reference Ni, Kramel, Ouellette and Voth2015; Pujara & Variano Reference Pujara and Variano2017). As the rod length transitions to the inertial range, rod alignment with
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}>\tilde{\boldsymbol{e}}_{\mathbf{2}}>\tilde{\boldsymbol{e}}_{\mathbf{1}}$
(see also Pumir & Wilkinson Reference Pumir and Wilkinson2011; Chevillard & Meneveau Reference Chevillard and Meneveau2013; Byron et al.
Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015; Ni et al.
Reference Ni, Kramel, Ouellette and Voth2015; Pujara & Variano Reference Pujara and Variano2017). As the rod length transitions to the inertial range, rod alignment with
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
decreases and rod alignment in the strain-rate eigenframe shifts from being more aligned with
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
decreases and rod alignment in the strain-rate eigenframe shifts from being more aligned with
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
to being more aligned with
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
to being more aligned with
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
. There appears to be an almost scale-independent preferred rod alignment in the inertial range (
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
. There appears to be an almost scale-independent preferred rod alignment in the inertial range (
![]() $l>60\unicode[STIX]{x1D702}$
) that follows the order
$l>60\unicode[STIX]{x1D702}$
) that follows the order
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}>\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}>\tilde{\boldsymbol{e}}_{\mathbf{2}}$
.
$\tilde{\boldsymbol{e}}_{\mathbf{1}}>\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}>\tilde{\boldsymbol{e}}_{\mathbf{2}}$
.

Figure 2. Mean rod alignment with the directions of
![]() $\tilde{\unicode[STIX]{x1D63C}}$
as a function of
$\tilde{\unicode[STIX]{x1D63C}}$
as a function of
![]() $l/\unicode[STIX]{x1D702}$
. Symbols are data from fully resolved rod dynamics and dashed lines are data from integrating Jeffery’s equation. The dotted line is at a value of
$l/\unicode[STIX]{x1D702}$
. Symbols are data from fully resolved rod dynamics and dashed lines are data from integrating Jeffery’s equation. The dotted line is at a value of
![]() $1/3$
, which corresponds to random alignment.
$1/3$
, which corresponds to random alignment.
The agreement in figure 2 between data from fully resolved rod dynamics and data from integrating Jeffery’s equation using
![]() $\tilde{\unicode[STIX]{x1D63C}}$
shows that
$\tilde{\unicode[STIX]{x1D63C}}$
shows that
![]() $\tilde{\unicode[STIX]{x1D63C}}$
captures the flow features that are responsible for rod tumbling. This is not surprising given that velocity increments separated by length
$\tilde{\unicode[STIX]{x1D63C}}$
captures the flow features that are responsible for rod tumbling. This is not surprising given that velocity increments separated by length
![]() $l$
have the greatest weight in determining the rod tumbling rate in (2.1b
) and also in computing
$l$
have the greatest weight in determining the rod tumbling rate in (2.1b
) and also in computing
![]() $\tilde{\unicode[STIX]{x1D63C}}$
. The p.d.f.s of alignment (not plotted) show that alignment in fully resolved rod dynamics tends to be slightly more skewed than in rod data obtained from Jeffery’s equation, but the net effect of this difference on the mean alignment value is small, as seen in figure 2. Having checked that
$\tilde{\unicode[STIX]{x1D63C}}$
. The p.d.f.s of alignment (not plotted) show that alignment in fully resolved rod dynamics tends to be slightly more skewed than in rod data obtained from Jeffery’s equation, but the net effect of this difference on the mean alignment value is small, as seen in figure 2. Having checked that
![]() $\tilde{\unicode[STIX]{x1D63C}}$
is able to reproduce the statistics of rod orientation, we can proceed to understand rod alignment in terms of the properties of
$\tilde{\unicode[STIX]{x1D63C}}$
is able to reproduce the statistics of rod orientation, we can proceed to understand rod alignment in terms of the properties of
![]() $\tilde{\unicode[STIX]{x1D63C}}$
.
$\tilde{\unicode[STIX]{x1D63C}}$
.
Figure 3 shows how the properties of the perceived strain-rate tensor, and in particular the strain state, change with scale. At the smallest scale (
![]() $l=\unicode[STIX]{x1D702}$
), the data are similar to those in Lund & Rogers (Reference Lund and Rogers1994). The most likely strain state for all scales is
$l=\unicode[STIX]{x1D702}$
), the data are similar to those in Lund & Rogers (Reference Lund and Rogers1994). The most likely strain state for all scales is
![]() $\tilde{s}^{\ast }=+1$
(axisymmetric extension), but the likelihood of
$\tilde{s}^{\ast }=+1$
(axisymmetric extension), but the likelihood of
![]() $\tilde{s}^{\ast }=-1$
(axisymmetric contraction) increases with increasing scale. This changing distribution of the strain state provides at least a partial explanation for changing rod alignment with
$\tilde{s}^{\ast }=-1$
(axisymmetric contraction) increases with increasing scale. This changing distribution of the strain state provides at least a partial explanation for changing rod alignment with
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
: with increasing
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
: with increasing
![]() $l/\unicode[STIX]{x1D702}$
, strain states tend towards one dominant direction of stretching, which improves rod alignment with this direction. In other words, there is less competition for rod alignment between
$l/\unicode[STIX]{x1D702}$
, strain states tend towards one dominant direction of stretching, which improves rod alignment with this direction. In other words, there is less competition for rod alignment between
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
and
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
allowing rods to be more aligned with
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
allowing rods to be more aligned with
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
.
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
.

Figure 3. Properties of
![]() $\tilde{\unicode[STIX]{x1D64E}}$
as a function of
$\tilde{\unicode[STIX]{x1D64E}}$
as a function of
![]() $l/\unicode[STIX]{x1D702}$
: (a) p.d.f.s of the strain state,
$l/\unicode[STIX]{x1D702}$
: (a) p.d.f.s of the strain state,
![]() $\tilde{s}^{\ast }$
; (b) p.d.f.s of the ratio of eigenvalues
$\tilde{s}^{\ast }$
; (b) p.d.f.s of the ratio of eigenvalues
![]() $\tilde{\unicode[STIX]{x1D706}_{2}}/\tilde{\unicode[STIX]{x1D706}_{1}}$
; (c) mean value of
$\tilde{\unicode[STIX]{x1D706}_{2}}/\tilde{\unicode[STIX]{x1D706}_{1}}$
; (c) mean value of
![]() $\tilde{s}^{\ast }$
; and (d) mean value of
$\tilde{s}^{\ast }$
; and (d) mean value of
![]() $\tilde{\unicode[STIX]{x1D706}_{2}}/\tilde{\unicode[STIX]{x1D706}_{1}}$
.
$\tilde{\unicode[STIX]{x1D706}_{2}}/\tilde{\unicode[STIX]{x1D706}_{1}}$
.

Figure 4. Alignment of rods with the most stretching direction of the right and left Cauchy–Green strain tensors as a function of the time delay. (a) Mean alignment between rods and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
. (b) Mean alignment between rods and
$\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
. (b) Mean alignment between rods and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. The dotted lines are at a value of
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. The dotted lines are at a value of
![]() $1/3$
, which corresponds to random alignment.
$1/3$
, which corresponds to random alignment.
The effects of a time delay on rod alignment are shown in figure 4. Figure 4(a) shows that rods have a maximum in alignment with
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
for some positive value of
$\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
for some positive value of
![]() $\unicode[STIX]{x0394}t$
. For longer rods, the maximum value is higher and occurs at smaller multiples of the scale-local time scale
$\unicode[STIX]{x0394}t$
. For longer rods, the maximum value is higher and occurs at smaller multiples of the scale-local time scale
![]() $\unicode[STIX]{x1D70F}_{N}$
. The maxima in figure 4(a) indicate that, for a strain-rate tensor
$\unicode[STIX]{x1D70F}_{N}$
. The maxima in figure 4(a) indicate that, for a strain-rate tensor
![]() $\tilde{\unicode[STIX]{x1D64E}}$
at a given time
$\tilde{\unicode[STIX]{x1D64E}}$
at a given time
![]() $t_{0}$
, the strongest alignment of rods with the most stretching direction of
$t_{0}$
, the strongest alignment of rods with the most stretching direction of
![]() $\tilde{\unicode[STIX]{x1D64E}}(t_{0})$
occurs with some optimum time delay at
$\tilde{\unicode[STIX]{x1D64E}}(t_{0})$
occurs with some optimum time delay at
![]() $t_{0}+\unicode[STIX]{x0394}t$
. When rod alignment is computed with respect to
$t_{0}+\unicode[STIX]{x0394}t$
. When rod alignment is computed with respect to
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
, figure 4(b) shows that it reaches a steady-state plateau. For longer rods, the plateaued alignment is weaker, but it is reached in smaller multiples of
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
, figure 4(b) shows that it reaches a steady-state plateau. For longer rods, the plateaued alignment is weaker, but it is reached in smaller multiples of
![]() $\unicode[STIX]{x1D70F}_{N}$
. Rod alignment with
$\unicode[STIX]{x1D70F}_{N}$
. Rod alignment with
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
shows the rod response to the cumulative effects of the strain-rate tensor over a time
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
shows the rod response to the cumulative effects of the strain-rate tensor over a time
![]() $\unicode[STIX]{x0394}t$
. Ni et al. (Reference Ni, Ouellette and Voth2014) showed that tracer rods approach perfect alignment with
$\unicode[STIX]{x0394}t$
. Ni et al. (Reference Ni, Ouellette and Voth2014) showed that tracer rods approach perfect alignment with
![]() $\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
given a large enough
$\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
given a large enough
![]() $\unicode[STIX]{x0394}t$
, consistent with the fact that rod orientation in the tracer limit is driven only by the term
$\unicode[STIX]{x0394}t$
, consistent with the fact that rod orientation in the tracer limit is driven only by the term
![]() $\unicode[STIX]{x1D63C}\,\boldsymbol{p}$
(2.2). In contrast, figure 4(b) shows that rods outside of the tracer limit do not reach perfect alignment with
$\unicode[STIX]{x1D63C}\,\boldsymbol{p}$
(2.2). In contrast, figure 4(b) shows that rods outside of the tracer limit do not reach perfect alignment with
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. With increasing rod length, the decreasing plateau of alignment with
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. With increasing rod length, the decreasing plateau of alignment with
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
indicates that fluid motions at scales smaller than
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
indicates that fluid motions at scales smaller than
![]() $l$
prevent perfect rod alignment with
$l$
prevent perfect rod alignment with
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. This is confirmed by the alignment of
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. This is confirmed by the alignment of
![]() $\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
with
$\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
with
![]() $\boldsymbol{p}_{J}$
, where rod orientations are obtained from integrating Jeffery’s equation and fluid motions at scales smaller than
$\boldsymbol{p}_{J}$
, where rod orientations are obtained from integrating Jeffery’s equation and fluid motions at scales smaller than
![]() $l$
are removed in
$l$
are removed in
![]() $\tilde{\unicode[STIX]{x1D63C}}$
from coarse-graining. In this case, we find that plots of
$\tilde{\unicode[STIX]{x1D63C}}$
from coarse-graining. In this case, we find that plots of
![]() $\langle (\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p}_{J})^{2}\rangle$
against
$\langle (\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p}_{J})^{2}\rangle$
against
![]() $\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}_{N}$
(not shown) collapse for rods of all lengths and show an approach towards perfect alignment.
$\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}_{N}$
(not shown) collapse for rods of all lengths and show an approach towards perfect alignment.
In figures 2 and 4, the statistics of rod alignment are weakly non-monotonic with increasing
![]() $l/\unicode[STIX]{x1D702}$
. In figure 2 the mean rod alignment with
$l/\unicode[STIX]{x1D702}$
. In figure 2 the mean rod alignment with
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
becomes stronger in the inertial range with a ‘bump’ at
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
becomes stronger in the inertial range with a ‘bump’ at
![]() $l\approx 60\unicode[STIX]{x1D702}$
. Figure 4(a) shows a similar variation in the maximum rod alignment with
$l\approx 60\unicode[STIX]{x1D702}$
. Figure 4(a) shows a similar variation in the maximum rod alignment with
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
as a function of
$\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
as a function of
![]() $l/\unicode[STIX]{x1D702}$
. The monotonic variation in the properties of
$l/\unicode[STIX]{x1D702}$
. The monotonic variation in the properties of
![]() $\tilde{\unicode[STIX]{x1D64E}}$
in figure 3 show that this ‘bump’ cannot be explained by the p.d.f. of
$\tilde{\unicode[STIX]{x1D64E}}$
in figure 3 show that this ‘bump’ cannot be explained by the p.d.f. of
![]() $\tilde{s}^{\ast }$
. More likely, it is caused by the changing structure of time correlations for the elements of
$\tilde{s}^{\ast }$
. More likely, it is caused by the changing structure of time correlations for the elements of
![]() $\tilde{\unicode[STIX]{x1D63C}}$
as a function of
$\tilde{\unicode[STIX]{x1D63C}}$
as a function of
![]() $l/\unicode[STIX]{x1D702}$
.
$l/\unicode[STIX]{x1D702}$
.
3.2 Vorticity alignment
The alignment of vorticity in the strain-rate eigenframe of
![]() $\tilde{\unicode[STIX]{x1D64E}}$
is an important property of
$\tilde{\unicode[STIX]{x1D64E}}$
is an important property of
![]() $\tilde{\unicode[STIX]{x1D63C}}$
for turbulent flow. Figure 5 shows how this alignment changes with
$\tilde{\unicode[STIX]{x1D63C}}$
for turbulent flow. Figure 5 shows how this alignment changes with
![]() $l/\unicode[STIX]{x1D702}$
using the same statistical measures as in the previous section. In figure 5(a), we see that the alignment between
$l/\unicode[STIX]{x1D702}$
using the same statistical measures as in the previous section. In figure 5(a), we see that the alignment between
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
increases with increasing scale, whereas the alignment between
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
increases with increasing scale, whereas the alignment between
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
decreases with increasing scale. The orthogonality between
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
decreases with increasing scale. The orthogonality between
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{3}}$
also decreases with increasing scale. These results are consistent with previous data (Luthi et al.
Reference Luthi, Ott, Berg and Mann2007; Pumir et al.
Reference Pumir, Bodenschatz and Xu2013; Danish & Meneveau Reference Danish and Meneveau2018) where
$\tilde{\boldsymbol{e}}_{\mathbf{3}}$
also decreases with increasing scale. These results are consistent with previous data (Luthi et al.
Reference Luthi, Ott, Berg and Mann2007; Pumir et al.
Reference Pumir, Bodenschatz and Xu2013; Danish & Meneveau Reference Danish and Meneveau2018) where
![]() $\tilde{\unicode[STIX]{x1D63C}}$
was computed using different coarse-graining methods. In figure 5(b), we see that vorticity reaches a peak alignment with
$\tilde{\unicode[STIX]{x1D63C}}$
was computed using different coarse-graining methods. In figure 5(b), we see that vorticity reaches a peak alignment with
![]() $\boldsymbol{e}_{\boldsymbol{R}\mathbf{1}}$
after a time delay of
$\boldsymbol{e}_{\boldsymbol{R}\mathbf{1}}$
after a time delay of
![]() $\unicode[STIX]{x0394}t\approx 3\unicode[STIX]{x1D70F}_{N}$
, almost independent of the scale
$\unicode[STIX]{x0394}t\approx 3\unicode[STIX]{x1D70F}_{N}$
, almost independent of the scale
![]() $l/\unicode[STIX]{x1D702}$
(Xu et al.
Reference Xu, Pumir and Bodenschatz2011; Pumir et al.
Reference Pumir, Bodenschatz and Xu2013). The initial growth in alignment of vorticity with
$l/\unicode[STIX]{x1D702}$
(Xu et al.
Reference Xu, Pumir and Bodenschatz2011; Pumir et al.
Reference Pumir, Bodenschatz and Xu2013). The initial growth in alignment of vorticity with
![]() $\boldsymbol{e}_{\boldsymbol{R}\mathbf{1}}$
is consistent with previous arguments for the evolution of vorticity in the tracer limit, i.e. it is caused by the vortex stretching term in the dynamical equation of
$\boldsymbol{e}_{\boldsymbol{R}\mathbf{1}}$
is consistent with previous arguments for the evolution of vorticity in the tracer limit, i.e. it is caused by the vortex stretching term in the dynamical equation of
![]() $\unicode[STIX]{x1D63C}$
(Chevillard & Meneveau Reference Chevillard and Meneveau2011; Ni et al.
Reference Ni, Kramel, Ouellette and Voth2015). Outside the tracer limit, the curves are nearly scale-independent when time is made dimensionless by the scale-local time scale,
$\unicode[STIX]{x1D63C}$
(Chevillard & Meneveau Reference Chevillard and Meneveau2011; Ni et al.
Reference Ni, Kramel, Ouellette and Voth2015). Outside the tracer limit, the curves are nearly scale-independent when time is made dimensionless by the scale-local time scale,
![]() $\unicode[STIX]{x1D70F}_{N}$
. This shows that small-scale motions do not affect the alignment of coarse-grained vorticity with
$\unicode[STIX]{x1D70F}_{N}$
. This shows that small-scale motions do not affect the alignment of coarse-grained vorticity with
![]() $\boldsymbol{e}_{\boldsymbol{R}\mathbf{1}}$
. In figure 5(c), we see that vorticity alignment with
$\boldsymbol{e}_{\boldsymbol{R}\mathbf{1}}$
. In figure 5(c), we see that vorticity alignment with
![]() $\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
increases with time until it reaches a plateau. The plateau’s value decreases with increasing scale, which shows that smaller scales disrupt the alignment of vorticity with the direction of greatest stretching given by the cumulative deformation of the strain-rate tensor.
$\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
increases with time until it reaches a plateau. The plateau’s value decreases with increasing scale, which shows that smaller scales disrupt the alignment of vorticity with the direction of greatest stretching given by the cumulative deformation of the strain-rate tensor.

Figure 5. Alignment of vorticity in the strain-rate and Cauchy–Green eigenframes as a function of scale. (a) Mean alignment of
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
within the perceived strain-rate eigenframe. (b) Mean alignment between the
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
within the perceived strain-rate eigenframe. (b) Mean alignment between the
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
. (c) Mean alignment between the
$\tilde{\boldsymbol{e}}_{\boldsymbol{R}\mathbf{1}}$
. (c) Mean alignment between the
![]() $\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
$\tilde{\boldsymbol{e}}_{\unicode[STIX]{x1D74E}}$
and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. The dotted lines are at a value of
$\tilde{\boldsymbol{e}}_{\boldsymbol{L}\mathbf{1}}$
. The dotted lines are at a value of
![]() $1/3$
, which corresponds to random alignment.
$1/3$
, which corresponds to random alignment.
The above results point towards a partial analogy between infinitesimal rods and vorticity in turbulent flows. As pointed out previously (Pumir & Wilkinson Reference Pumir and Wilkinson2011), the vortex stretching term,
![]() $\unicode[STIX]{x1D64E}\,\unicode[STIX]{x1D74E}$
, in the vorticity evolution equation has an analogous term in Jeffery’s equation for evolution of rod orientation,
$\unicode[STIX]{x1D64E}\,\unicode[STIX]{x1D74E}$
, in the vorticity evolution equation has an analogous term in Jeffery’s equation for evolution of rod orientation,
![]() $\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
. However, unlike rods, vorticity is an active vector that is coupled to the strain rate in its evolution equation and affected by viscosity (e.g. Guala et al.
Reference Guala, Luthi, Liberzon, Tsinober and Kinzelbach2005; Luthi, Tsinober & Kinzelbach Reference Luthi, Tsinober and Kinzelbach2005; Pumir & Wilkinson Reference Pumir and Wilkinson2011). Hence, unlike rods, vorticity does not reach perfect alignment with
$\unicode[STIX]{x1D64E}\,\boldsymbol{p}$
. However, unlike rods, vorticity is an active vector that is coupled to the strain rate in its evolution equation and affected by viscosity (e.g. Guala et al.
Reference Guala, Luthi, Liberzon, Tsinober and Kinzelbach2005; Luthi, Tsinober & Kinzelbach Reference Luthi, Tsinober and Kinzelbach2005; Pumir & Wilkinson Reference Pumir and Wilkinson2011). Hence, unlike rods, vorticity does not reach perfect alignment with
![]() $\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
in the tracer limit. With increasing
$\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
in the tracer limit. With increasing
![]() $l/\unicode[STIX]{x1D702}$
, the action of fluid motions at scales smaller than
$l/\unicode[STIX]{x1D702}$
, the action of fluid motions at scales smaller than
![]() $l$
on dynamics at scale
$l$
on dynamics at scale
![]() $l$
leads to decreasing plateaus of alignment with
$l$
leads to decreasing plateaus of alignment with
![]() $\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
for both rods and coarse-grained vorticity, but the effects of smaller scales on coarse-grained vorticity are more complex since the vorticity also affects the velocity field. This makes the dynamics of rods and vorticity diverge even further with increasing
$\boldsymbol{e}_{\boldsymbol{L}\mathbf{1}}$
for both rods and coarse-grained vorticity, but the effects of smaller scales on coarse-grained vorticity are more complex since the vorticity also affects the velocity field. This makes the dynamics of rods and vorticity diverge even further with increasing
![]() $l/\unicode[STIX]{x1D702}$
, as indicated by the decreased alignment between rods and vorticity in figure 2.
$l/\unicode[STIX]{x1D702}$
, as indicated by the decreased alignment between rods and vorticity in figure 2.
3.3 Lower-order moments of rod tumbling
The rod tumbling rate is best characterised in terms of its variance,
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle$
, since the mean of any single component of the rod tumbling vector is zero due to flow isotropy. For randomly oriented rods, the rod tumbling variance can be derived from (2.1b
) to be (see Olson & Kerekes Reference Olson and Kerekes1998; Shin & Koch Reference Shin and Koch2005):
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle$
, since the mean of any single component of the rod tumbling vector is zero due to flow isotropy. For randomly oriented rods, the rod tumbling variance can be derived from (2.1b
) to be (see Olson & Kerekes Reference Olson and Kerekes1998; Shin & Koch Reference Shin and Koch2005):
where
![]() $R_{NN}$
is the dimensionless transverse velocity correlation function.
$R_{NN}$
is the dimensionless transverse velocity correlation function.
In the tracer limit, equation (3.1) simplifies to
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=4/15$
(Shin & Koch Reference Shin and Koch2005) since the transverse velocity correlation can be written in terms of the velocity gradients, whose variance can in turn be written in terms of the mean dissipation rate in isotropic turbulence (Pope Reference Pope2000). In the inertial range, K41 parametrisations can be used to simplify (3.1). From K41 theory,
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=4/15$
(Shin & Koch Reference Shin and Koch2005) since the transverse velocity correlation can be written in terms of the velocity gradients, whose variance can in turn be written in terms of the mean dissipation rate in isotropic turbulence (Pope Reference Pope2000). In the inertial range, K41 parametrisations can be used to simplify (3.1). From K41 theory,
![]() $R_{NN}=1-(2/3u_{rms}^{2})C_{2}(\langle \unicode[STIX]{x1D716}\rangle l)^{2/3}$
and
$R_{NN}=1-(2/3u_{rms}^{2})C_{2}(\langle \unicode[STIX]{x1D716}\rangle l)^{2/3}$
and
![]() $\unicode[STIX]{x1D70F}_{N}=(l^{2}/\langle \unicode[STIX]{x1D716}\rangle )^{1/3}/\sqrt{10C_{2}}$
, where
$\unicode[STIX]{x1D70F}_{N}=(l^{2}/\langle \unicode[STIX]{x1D716}\rangle )^{1/3}/\sqrt{10C_{2}}$
, where
![]() $C_{2}$
is a universal constant and is set to
$C_{2}$
is a universal constant and is set to
![]() $2.0$
here. From these expressions, equation (3.1) simplifies to
$2.0$
here. From these expressions, equation (3.1) simplifies to
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=108/350$
for rods in the inertial range. The inertial-range result can also be expressed in terms of the Kolmogorov scales as
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=108/350$
for rods in the inertial range. The inertial-range result can also be expressed in terms of the Kolmogorov scales as
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}=(108/35)C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
, revealing that rod tumbling variance for randomly oriented rods in the inertial range should scale as
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}=(108/35)C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
, revealing that rod tumbling variance for randomly oriented rods in the inertial range should scale as
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \sim l^{-4/3}$
. Parsa & Voth (Reference Parsa and Voth2014) derived this expression and also provided a physical argument: rod tumbling in the inertial range is driven primarily by turbulent motions of size
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \sim l^{-4/3}$
. Parsa & Voth (Reference Parsa and Voth2014) derived this expression and also provided a physical argument: rod tumbling in the inertial range is driven primarily by turbulent motions of size
![]() $l$
and thus the rod tumbling variance should scale as the inverse square of the turnover time of these turbulent motions.
$l$
and thus the rod tumbling variance should scale as the inverse square of the turnover time of these turbulent motions.

Figure 6. Variance of rod tumbling calculated from (i) fully resolved rod data,
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle$
(circles), (ii) Jeffery’s equation,
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle$
(circles), (ii) Jeffery’s equation,
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle _{J}$
(dashed line), and (iii) rod end points,
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle _{J}$
(dashed line), and (iii) rod end points,
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle _{E}$
(thick line). Initial-time data are shown in grey and long-time data in black. (a) Variance of rod tumbling made dimensionless by
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle _{E}$
(thick line). Initial-time data are shown in grey and long-time data in black. (a) Variance of rod tumbling made dimensionless by
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
(dotted line is
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
(dotted line is
![]() $(108/35)C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
). (b) Variance of rod tumbling made dimensionless by
$(108/35)C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
). (b) Variance of rod tumbling made dimensionless by
![]() $\unicode[STIX]{x1D70F}_{N}$
.
$\unicode[STIX]{x1D70F}_{N}$
.
Figure 6(a) shows that the initial-time data (randomly oriented rods) agree well with the prediction from K41 theory (
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}=(108/35)C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
) in the inertial range (
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}=(108/35)C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
) in the inertial range (
![]() $l>60\unicode[STIX]{x1D702}$
). These data are examined more closely in figure 6(b), where they are made dimensionless using the scale-local time scale
$l>60\unicode[STIX]{x1D702}$
). These data are examined more closely in figure 6(b), where they are made dimensionless using the scale-local time scale
![]() $\unicode[STIX]{x1D70F}_{N}$
. There is good agreement with the predictions in the tracer limit:
$\unicode[STIX]{x1D70F}_{N}$
. There is good agreement with the predictions in the tracer limit:
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=4/15$
for
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=4/15$
for
![]() $l<5\unicode[STIX]{x1D702}$
. In the transition to the inertial range, there is a non-monotonic variation (or ‘bump’) before the data show agreement with the inertial-range prediction:
$l<5\unicode[STIX]{x1D702}$
. In the transition to the inertial range, there is a non-monotonic variation (or ‘bump’) before the data show agreement with the inertial-range prediction:
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=108/350$
for
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}=108/350$
for
![]() $l>100\unicode[STIX]{x1D702}$
. The non-monotonic variation between the tracer limit value and the inertial-range value shows that transverse velocity increments, which are used to compute
$l>100\unicode[STIX]{x1D702}$
. The non-monotonic variation between the tracer limit value and the inertial-range value shows that transverse velocity increments, which are used to compute
![]() $\unicode[STIX]{x1D70F}_{N}$
, start to show inertial-range scaling at lower values of
$\unicode[STIX]{x1D70F}_{N}$
, start to show inertial-range scaling at lower values of
![]() $l/\unicode[STIX]{x1D702}$
compared to rod tumbling. Physically, this means that considering only the velocity increments across the rod length underpredicts the rod tumbling variance at transition scales for randomly oriented rods.
$l/\unicode[STIX]{x1D702}$
compared to rod tumbling. Physically, this means that considering only the velocity increments across the rod length underpredicts the rod tumbling variance at transition scales for randomly oriented rods.
The long-time values of rod tumbling variance are significantly lower than the initial-time values because rods of all lengths show preferential alignment with the fluid vorticity, which suppresses their tumbling (Parsa et al.
Reference Parsa, Calzavarini, Toschi and Voth2012). The behaviour of rod tumbling variance for rods in statistically steady equilibrium with the turbulent flow, i.e. the long-time data, shows a non-monotonic variation, similar to the initial-time data. Though its size and location are changed, the cause of the ‘bump’ in the long-time data is again the difference between transverse velocity increments and the transverse velocity correlation function, where both quantities are now evaluated in the frame of the rod. This is demonstrated by the fact that data from using only the rod end points (
![]() ${\dot{p}}_{i,E}$
) show a monotonic increase from the dissipation range to the inertial range without a ‘bump’.
${\dot{p}}_{i,E}$
) show a monotonic increase from the dissipation range to the inertial range without a ‘bump’.
The configuration of alignment in figure 2 is responsible for reducing the size of the ‘bump’, meaning that preferential rod alignment causes the value of
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}$
to be flatter in the inertial range and improves the agreement with the
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \unicode[STIX]{x1D70F}_{N}^{2}$
to be flatter in the inertial range and improves the agreement with the
![]() $\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \sim l^{-4/3}$
scaling. Rod alignment is not accounted for in Parsa & Voth’s (Reference Parsa and Voth2014) physical argument that rod tumbling in the inertial range is driven primarily by turbulent motions of size
$\langle {\dot{p}}_{i}{\dot{p}}_{i}\rangle \sim l^{-4/3}$
scaling. Rod alignment is not accounted for in Parsa & Voth’s (Reference Parsa and Voth2014) physical argument that rod tumbling in the inertial range is driven primarily by turbulent motions of size
![]() $l$
, but it appears that preferential rod alignment causes the rod tumbling variance to better agree with predictions made from this argument.
$l$
, but it appears that preferential rod alignment causes the rod tumbling variance to better agree with predictions made from this argument.
3.4 Lower-order moments of rod stretching
The p.d.f.s of rod stretching are shown in figure 7(a) with their moments shown in figure 7(b–e). In most cases, the rod stretching has been made dimensionless with the scale-local time scale
![]() $\unicode[STIX]{x1D70F}_{L}$
. In this dimensionless form, the longitudinal velocity increments across the rod are normalised by longitudinal velocity increments in random orientations, thereby making the effects of rod alignment explicit.
$\unicode[STIX]{x1D70F}_{L}$
. In this dimensionless form, the longitudinal velocity increments across the rod are normalised by longitudinal velocity increments in random orientations, thereby making the effects of rod alignment explicit.

Figure 7. Statistics of rod stretching as a function of
![]() $l/\unicode[STIX]{x1D702}$
: (i) from fully resolved rod data,
$l/\unicode[STIX]{x1D702}$
: (i) from fully resolved rod data,
![]() $(\unicode[STIX]{x0394}_{r}u/l)$
(triangles), and (ii) from Jeffery’s equation,
$(\unicode[STIX]{x0394}_{r}u/l)$
(triangles), and (ii) from Jeffery’s equation,
![]() $(\unicode[STIX]{x0394}_{r}u/l)_{J}$
(dashed lines). Initial-time data are shown in grey and long-time data in purple. (a) P.d.f.s of the long-time values of
$(\unicode[STIX]{x0394}_{r}u/l)_{J}$
(dashed lines). Initial-time data are shown in grey and long-time data in purple. (a) P.d.f.s of the long-time values of
![]() $(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}$
from fully resolved rod data. (b) Mean value,
$(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}$
from fully resolved rod data. (b) Mean value,
![]() $\langle \unicode[STIX]{x0394}_{r}u/l\rangle \unicode[STIX]{x1D70F}_{L}$
. (c) Skewness value,
$\langle \unicode[STIX]{x0394}_{r}u/l\rangle \unicode[STIX]{x1D70F}_{L}$
. (c) Skewness value,
![]() $\text{Skew}(\unicode[STIX]{x0394}_{r}u/l)$
. (d) Variance value normalised by the Kolmogorov time scale,
$\text{Skew}(\unicode[STIX]{x0394}_{r}u/l)$
. (d) Variance value normalised by the Kolmogorov time scale,
![]() $\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}$
with the dotted line showing
$\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}$
with the dotted line showing
![]() $C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
. (e) Variance value normalised by scale-local time scale,
$C_{2}(l/\unicode[STIX]{x1D702})^{-4/3}$
. (e) Variance value normalised by scale-local time scale,
![]() $\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{N}^{2}$
with the dotted line as labelled.
$\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{N}^{2}$
with the dotted line as labelled.
The initial-time mean of rod stretching,
![]() $\langle \unicode[STIX]{x0394}_{r}u/l\rangle$
, vanishes due to fluid incompressibility, but the long-time value of
$\langle \unicode[STIX]{x0394}_{r}u/l\rangle$
, vanishes due to fluid incompressibility, but the long-time value of
![]() $\langle \unicode[STIX]{x0394}_{r}u/l\rangle$
is not zero because rods show preferential alignment in the perceived strain-rate eigenframe. The effects of preferential rod alignment on the mean rod stretching can be observed in figure 7(b). It shows that
$\langle \unicode[STIX]{x0394}_{r}u/l\rangle$
is not zero because rods show preferential alignment in the perceived strain-rate eigenframe. The effects of preferential rod alignment on the mean rod stretching can be observed in figure 7(b). It shows that
![]() $\langle \unicode[STIX]{x0394}_{r}u/l\rangle \unicode[STIX]{x1D70F}_{L}$
increases non-monotonically from a value of approximately
$\langle \unicode[STIX]{x0394}_{r}u/l\rangle \unicode[STIX]{x1D70F}_{L}$
increases non-monotonically from a value of approximately
![]() $0.12$
in the tracer limit to a value of approximately
$0.12$
in the tracer limit to a value of approximately
![]() $0.18$
in the inertial range, with a small ‘bump’ at
$0.18$
in the inertial range, with a small ‘bump’ at
![]() $l\approx 100\unicode[STIX]{x1D702}$
. The tracer limit result is in agreement with previous data (Girimaji & Pope Reference Girimaji and Pope1990). Given that rod stretching is achieved by strain at the scale of the rod length, it is not surprising that the non-monotonic variation in
$l\approx 100\unicode[STIX]{x1D702}$
. The tracer limit result is in agreement with previous data (Girimaji & Pope Reference Girimaji and Pope1990). Given that rod stretching is achieved by strain at the scale of the rod length, it is not surprising that the non-monotonic variation in
![]() $\langle \unicode[STIX]{x0394}_{r}u/l\rangle \unicode[STIX]{x1D70F}_{L}$
reflects the non-monotonic variation in alignment between
$\langle \unicode[STIX]{x0394}_{r}u/l\rangle \unicode[STIX]{x1D70F}_{L}$
reflects the non-monotonic variation in alignment between
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
in figure 2. In particular, the location of the ‘bump’ in the mean rod stretching from Jeffery’s equations,
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
in figure 2. In particular, the location of the ‘bump’ in the mean rod stretching from Jeffery’s equations,
![]() $\langle \unicode[STIX]{x0394}_{r}u/l\rangle _{J}\unicode[STIX]{x1D70F}_{L}$
, almost exactly matches the location of the ‘bump’ in
$\langle \unicode[STIX]{x0394}_{r}u/l\rangle _{J}\unicode[STIX]{x1D70F}_{L}$
, almost exactly matches the location of the ‘bump’ in
![]() $\langle (\tilde{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p})^{2}\rangle$
.
$\langle (\tilde{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p})^{2}\rangle$
.
Figure 7(c) shows the skewness of rod stretching, which is defined as
![]() $\text{Skew}(a)=\langle (a-\langle a\rangle )^{3}\rangle /\langle (a-\langle a\rangle )^{2}\rangle ^{3/2}$
. Since the mean stretching is zero for randomly oriented rods, the initial-time value of skewness is equivalent to the third-order longitudinal velocity structure function in the inertial range and to the third moment of longitudinal velocity gradients in the tracer limit. In this case, the data show agreement with Kolmogorov’s 4/5th law in the inertial range,
$\text{Skew}(a)=\langle (a-\langle a\rangle )^{3}\rangle /\langle (a-\langle a\rangle )^{2}\rangle ^{3/2}$
. Since the mean stretching is zero for randomly oriented rods, the initial-time value of skewness is equivalent to the third-order longitudinal velocity structure function in the inertial range and to the third moment of longitudinal velocity gradients in the tracer limit. In this case, the data show agreement with Kolmogorov’s 4/5th law in the inertial range,
![]() $\langle \unicode[STIX]{x0394}_{r}u^{3}\rangle /\langle \unicode[STIX]{x0394}_{r}u^{2}\rangle ^{3/2}\approx -(4/5)C_{2}^{-3/2}$
, and with previous data in the tracer limit
$\langle \unicode[STIX]{x0394}_{r}u^{3}\rangle /\langle \unicode[STIX]{x0394}_{r}u^{2}\rangle ^{3/2}\approx -(4/5)C_{2}^{-3/2}$
, and with previous data in the tracer limit
![]() $\langle \unicode[STIX]{x0394}_{r}u^{3}\rangle /\langle \unicode[STIX]{x0394}_{r}u^{2}\rangle ^{3/2}\approx -0.4$
(summarised in Sreenivasan & Antonia (Reference Sreenivasan and Antonia1997) and Davidson (Reference Davidson2015)). The long-time rod stretching skewness data reflect the fact that rod alignment alters the rod stretching statistics. Alignment changes the sign of the rod stretching skewness so that the long-time value is positive for
$\langle \unicode[STIX]{x0394}_{r}u^{3}\rangle /\langle \unicode[STIX]{x0394}_{r}u^{2}\rangle ^{3/2}\approx -0.4$
(summarised in Sreenivasan & Antonia (Reference Sreenivasan and Antonia1997) and Davidson (Reference Davidson2015)). The long-time rod stretching skewness data reflect the fact that rod alignment alters the rod stretching statistics. Alignment changes the sign of the rod stretching skewness so that the long-time value is positive for
![]() $l<100\unicode[STIX]{x1D702}$
. As
$l<100\unicode[STIX]{x1D702}$
. As
![]() $l/\unicode[STIX]{x1D702}$
increases, the long-time skewness value decreases from
$l/\unicode[STIX]{x1D702}$
increases, the long-time skewness value decreases from
![]() $\text{Skew}(\unicode[STIX]{x0394}_{r}u/l)\approx 0.25$
for tracer rods (see also Kramel et al.
Reference Kramel, Voth, Tympel and Toschi2016) and becomes negative after crossing zero at
$\text{Skew}(\unicode[STIX]{x0394}_{r}u/l)\approx 0.25$
for tracer rods (see also Kramel et al.
Reference Kramel, Voth, Tympel and Toschi2016) and becomes negative after crossing zero at
![]() $l\approx 100\unicode[STIX]{x1D702}$
. The negative values for rods well into the inertial range suggests that long rods experience stronger extremes of compression than of extension. It is also interesting to note that our data do not appear to show a scale-invariant behaviour for the long-time skewness for rods with lengths in the inertial range.
$l\approx 100\unicode[STIX]{x1D702}$
. The negative values for rods well into the inertial range suggests that long rods experience stronger extremes of compression than of extension. It is also interesting to note that our data do not appear to show a scale-invariant behaviour for the long-time skewness for rods with lengths in the inertial range.
The variance of rod stretching, defined as
![]() $\text{Var}(a)=\langle (a-\langle a\rangle )^{2}\rangle$
, is shown in figure 7(d,e). Figure 7(d) shows that the variance of rod stretching follows a power-law scaling
$\text{Var}(a)=\langle (a-\langle a\rangle )^{2}\rangle$
, is shown in figure 7(d,e). Figure 7(d) shows that the variance of rod stretching follows a power-law scaling
![]() $\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\sim l^{-4/3}$
in the inertial range. The physical argument behind this scaling is the same as that for the rod tumbling variance: rod stretching is driven primarily by fluid motions of size
$\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\sim l^{-4/3}$
in the inertial range. The physical argument behind this scaling is the same as that for the rod tumbling variance: rod stretching is driven primarily by fluid motions of size
![]() $l$
, whose turnover time scales as
$l$
, whose turnover time scales as
![]() ${\sim}l^{2/3}$
in the inertial range from K41 theory.
${\sim}l^{2/3}$
in the inertial range from K41 theory.
In figure 7(e), we plot the rod stretching variance made dimensionless by the scale-local time scale
![]() $\unicode[STIX]{x1D70F}_{L}^{2}$
to further examine the
$\unicode[STIX]{x1D70F}_{L}^{2}$
to further examine the
![]() $l^{-4/3}$
scaling. At the initial time, rod stretching variance and
$l^{-4/3}$
scaling. At the initial time, rod stretching variance and
![]() $\unicode[STIX]{x1D70F}_{L}^{2}$
are essentially the same quantities with different constants and the initial-time variance of rod stretching rate can be written as
$\unicode[STIX]{x1D70F}_{L}^{2}$
are essentially the same quantities with different constants and the initial-time variance of rod stretching rate can be written as
![]() $\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}^{2}=1/15$
. At long time, the value of
$\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}^{2}=1/15$
. At long time, the value of
![]() $\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}^{2}$
is lower than at the initial time because preferential alignment of rods means they sample a smaller variation of stretching and compression compared to randomly oriented rods. As
$\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}^{2}$
is lower than at the initial time because preferential alignment of rods means they sample a smaller variation of stretching and compression compared to randomly oriented rods. As
![]() $l/\unicode[STIX]{x1D702}$
increases, rod alignment with the perceived velocity gradients weakens, causing
$l/\unicode[STIX]{x1D702}$
increases, rod alignment with the perceived velocity gradients weakens, causing
![]() $\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}^{2}$
to increase towards the random orientation limit. Data of rod stretching variance from Jeffery’s equation at long time show a decrease relative to
$\text{Var}(\unicode[STIX]{x0394}_{r}u/l)\unicode[STIX]{x1D70F}_{L}^{2}$
to increase towards the random orientation limit. Data of rod stretching variance from Jeffery’s equation at long time show a decrease relative to
![]() $\unicode[STIX]{x1D70F}_{L}^{2}$
as
$\unicode[STIX]{x1D70F}_{L}^{2}$
as
![]() $l/\unicode[STIX]{x1D702}$
increases; this is due to the fact that velocity gradients in
$l/\unicode[STIX]{x1D702}$
increases; this is due to the fact that velocity gradients in
![]() $\tilde{\unicode[STIX]{x1D63C}}$
are weaker than two-point velocity increments.
$\tilde{\unicode[STIX]{x1D63C}}$
are weaker than two-point velocity increments.
3.5 Higher-order moments of rod tumbling and rod stretching
The power-law behaviour of higher-order moments of rod tumbling and rod stretching can be used to understand how internal intermittency affects rod dynamics. One manifestation of intermittency in the inertial range is that power-law exponents of the moments of velocity increments, i.e. structure functions, show anomalous scaling (Frisch Reference Frisch1995). From figures 6 and 7, we conclude that the variances of rod tumbling and rod stretching in the inertial range are primarily due to velocity increments over a distance
![]() $l$
. This implies that intermittency corrections for higher-order moments of rod dynamics should behave similarly to those for velocity increments in the flow. To test this, we compare the power-law scaling exponents for moments of rod tumbling,
$l$
. This implies that intermittency corrections for higher-order moments of rod dynamics should behave similarly to those for velocity increments in the flow. To test this, we compare the power-law scaling exponents for moments of rod tumbling,
![]() $({\dot{p}}_{i}{\dot{p}}_{i})^{1/2}$
, and rod stretching,
$({\dot{p}}_{i}{\dot{p}}_{i})^{1/2}$
, and rod stretching,
![]() $(\unicode[STIX]{x0394}_{r}u-\langle \unicode[STIX]{x0394}_{r}u\rangle )$
, to those of transverse velocity increments,
$(\unicode[STIX]{x0394}_{r}u-\langle \unicode[STIX]{x0394}_{r}u\rangle )$
, to those of transverse velocity increments,
![]() $\unicode[STIX]{x0394}_{N}u$
, and longitudinal velocity increments,
$\unicode[STIX]{x0394}_{N}u$
, and longitudinal velocity increments,
![]() $\unicode[STIX]{x0394}_{L}u$
. The moments of rod stretching are calculated after removing the mean, but results are unaffected within the statistical uncertainty because the mean is small compared to the standard deviation (figure 7
a). To facilitate comparison to other quantities, rod tumbling is converted into velocity units by multiplying by the rod length,
$\unicode[STIX]{x0394}_{L}u$
. The moments of rod stretching are calculated after removing the mean, but results are unaffected within the statistical uncertainty because the mean is small compared to the standard deviation (figure 7
a). To facilitate comparison to other quantities, rod tumbling is converted into velocity units by multiplying by the rod length,
![]() $({\dot{p}}_{i}{\dot{p}}_{i})^{1/2}l$
. This does not affect the deviation of its power-law exponents from K41 predictions.
$({\dot{p}}_{i}{\dot{p}}_{i})^{1/2}l$
. This does not affect the deviation of its power-law exponents from K41 predictions.
The power-law exponents are measured over
![]() $80\unicode[STIX]{x1D702}\leqslant l\leqslant 200\unicode[STIX]{x1D702}$
. Over this range, logarithmic derivatives calculated using finite differencing are reasonably flat for all quantities, confirming power-law behaviour. It is known that the range of scales for which there is clear power-law behaviour is different for
$80\unicode[STIX]{x1D702}\leqslant l\leqslant 200\unicode[STIX]{x1D702}$
. Over this range, logarithmic derivatives calculated using finite differencing are reasonably flat for all quantities, confirming power-law behaviour. It is known that the range of scales for which there is clear power-law behaviour is different for
![]() $\unicode[STIX]{x0394}_{L}u$
and
$\unicode[STIX]{x0394}_{L}u$
and
![]() $\unicode[STIX]{x0394}_{N}u$
, as well as being a function of moment order and Reynolds number (Ishihara, Gotoh & Kaneda Reference Ishihara, Gotoh and Kaneda2009), but for moments up to
$\unicode[STIX]{x0394}_{N}u$
, as well as being a function of moment order and Reynolds number (Ishihara, Gotoh & Kaneda Reference Ishihara, Gotoh and Kaneda2009), but for moments up to
![]() $n=6$
,
$n=6$
,
![]() $\unicode[STIX]{x0394}_{L}u$
and
$\unicode[STIX]{x0394}_{L}u$
and
![]() $\unicode[STIX]{x0394}_{N}u$
both show power-law behaviour over
$\unicode[STIX]{x0394}_{N}u$
both show power-law behaviour over
![]() $80\unicode[STIX]{x1D702}\leqslant l\leqslant 200\unicode[STIX]{x1D702}$
. In plots of pre-multiplied moments (not shown), we also observe reasonable convergence of moments up to
$80\unicode[STIX]{x1D702}\leqslant l\leqslant 200\unicode[STIX]{x1D702}$
. In plots of pre-multiplied moments (not shown), we also observe reasonable convergence of moments up to
![]() $n=6$
in our data. We compute the power-law scaling exponents by a least-squares fit in log space with error bars to show 95 % confidence intervals from the uncertainty in the fitting. Comparison of these results with scaling exponents calculated using extended self-similarity (not shown), where higher-order moments are plotted as a function of the second-moment instead of as a function of
$n=6$
in our data. We compute the power-law scaling exponents by a least-squares fit in log space with error bars to show 95 % confidence intervals from the uncertainty in the fitting. Comparison of these results with scaling exponents calculated using extended self-similarity (not shown), where higher-order moments are plotted as a function of the second-moment instead of as a function of
![]() $l$
, show that the results are the same within the statistical uncertainty.
$l$
, show that the results are the same within the statistical uncertainty.
The scaling exponents of higher-order moments are compared to predictions from the Kolmogorov hypotheses (K41 theory) and the refined Kolmogorov hypotheses (Kolmogorov Reference Kolmogorov1962; Oboukhov Reference Oboukhov1962; henceforth K62 theory). In K41 theory, moments of velocity increments in the inertial range conditioned on the mean dissipation rate,
![]() $\langle \unicode[STIX]{x1D716}\rangle$
, are assumed to be universal and to scale as
$\langle \unicode[STIX]{x1D716}\rangle$
, are assumed to be universal and to scale as
![]() $\langle (\unicode[STIX]{x0394}_{L}u)^{n}\rangle \sim (\langle \unicode[STIX]{x1D716}\rangle l)^{\unicode[STIX]{x1D701}_{n}}$
, where
$\langle (\unicode[STIX]{x0394}_{L}u)^{n}\rangle \sim (\langle \unicode[STIX]{x1D716}\rangle l)^{\unicode[STIX]{x1D701}_{n}}$
, where
![]() $\unicode[STIX]{x1D701}_{n}$
is a function only of
$\unicode[STIX]{x1D701}_{n}$
is a function only of
![]() $n$
and universal constants. The K41 prediction is
$n$
and universal constants. The K41 prediction is
![]() $\unicode[STIX]{x1D701}_{n,K41}=n/3$
. However, it is well known that internal intermittency causes deviations from the K41 predictions (Frisch Reference Frisch1995; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). Taking the intermittent spatial distribution of dissipation into account, K62 theory predicts that
$\unicode[STIX]{x1D701}_{n,K41}=n/3$
. However, it is well known that internal intermittency causes deviations from the K41 predictions (Frisch Reference Frisch1995; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). Taking the intermittent spatial distribution of dissipation into account, K62 theory predicts that
![]() $\unicode[STIX]{x1D701}_{n,K62}=(n/3)-\unicode[STIX]{x1D707}(n/6)[(n/3)-1]$
. Here,
$\unicode[STIX]{x1D701}_{n,K62}=(n/3)-\unicode[STIX]{x1D707}(n/6)[(n/3)-1]$
. Here,
![]() $\unicode[STIX]{x1D707}$
is the intermittency exponent whose value is set to
$\unicode[STIX]{x1D707}$
is the intermittency exponent whose value is set to
![]() $\unicode[STIX]{x1D707}=0.25$
(Pope Reference Pope2000). This model of intermittency assumes that a locally averaged value of
$\unicode[STIX]{x1D707}=0.25$
(Pope Reference Pope2000). This model of intermittency assumes that a locally averaged value of
![]() $\unicode[STIX]{x1D716}$
is sufficient to predict statistics of velocity increments and that the dissipation follows a log-normal distribution.
$\unicode[STIX]{x1D716}$
is sufficient to predict statistics of velocity increments and that the dissipation follows a log-normal distribution.

Figure 8. The power-law exponents for moments of velocity increments and rod dynamics in the inertial range as a function of moment order. K41 theory,
![]() $\unicode[STIX]{x1D701}_{n}=n/3$
(solid line); K62 theory,
$\unicode[STIX]{x1D701}_{n}=n/3$
(solid line); K62 theory,
![]() $\unicode[STIX]{x1D701}_{n}=(n/3)-\unicode[STIX]{x1D707}(n/6)[(n/3)-1]$
with intermittency exponent
$\unicode[STIX]{x1D701}_{n}=(n/3)-\unicode[STIX]{x1D707}(n/6)[(n/3)-1]$
with intermittency exponent
![]() $\unicode[STIX]{x1D707}=0.25$
(dashed line). Error bars represent 95 % confidence intervals to the power-law fit.
$\unicode[STIX]{x1D707}=0.25$
(dashed line). Error bars represent 95 % confidence intervals to the power-law fit.
The scaling exponent data are shown in figure 8. In figure 8(a), we observe that
![]() $\unicode[STIX]{x0394}_{N}u$
shows a larger departure from K41 theory than
$\unicode[STIX]{x0394}_{N}u$
shows a larger departure from K41 theory than
![]() $\unicode[STIX]{x0394}_{L}u$
, which is in agreement with previous data (e.g. Chen et al.
Reference Chen, Sreenivasan, Nelkin and Cao1997), though data from higher-Reynolds-number simulations suggest that this difference exists only at low Reynolds numbers (Iyer, Sreenivasan & Yeung Reference Iyer, Sreenivasan and Yeung2017). In figure 8(b), we include data of rod dynamics, first examining initial-time data of
$\unicode[STIX]{x0394}_{L}u$
, which is in agreement with previous data (e.g. Chen et al.
Reference Chen, Sreenivasan, Nelkin and Cao1997), though data from higher-Reynolds-number simulations suggest that this difference exists only at low Reynolds numbers (Iyer, Sreenivasan & Yeung Reference Iyer, Sreenivasan and Yeung2017). In figure 8(b), we include data of rod dynamics, first examining initial-time data of
![]() ${\dot{p}}_{i}$
(data where rods are randomly oriented). These scaling exponents match those of the transverse velocity increments quite well. Figure 8(c) shows data for rods in statistically steady alignment with the flow, computed from rod dynamics using velocity increments across the rod end points,
${\dot{p}}_{i}$
(data where rods are randomly oriented). These scaling exponents match those of the transverse velocity increments quite well. Figure 8(c) shows data for rods in statistically steady alignment with the flow, computed from rod dynamics using velocity increments across the rod end points,
![]() ${\dot{p}}_{i,E}$
(rod tumbling computed using only rod end points) and
${\dot{p}}_{i,E}$
(rod tumbling computed using only rod end points) and
![]() $\unicode[STIX]{x0394}_{r}u-\langle \unicode[STIX]{x0394}_{r}u\rangle$
(rod stretching). Since these rod data are computed using two-point velocity increments aligned with the rod, they should explicitly reveal the effects of preferential alignment on scaling exponents. The scaling exponents of rod tumbling match the transverse velocity increments and those of rod stretching match the longitudinal velocity increments. Thus, it appears that rod alignment does not affect the intermittency within the statistical uncertainty in our data.
$\unicode[STIX]{x0394}_{r}u-\langle \unicode[STIX]{x0394}_{r}u\rangle$
(rod stretching). Since these rod data are computed using two-point velocity increments aligned with the rod, they should explicitly reveal the effects of preferential alignment on scaling exponents. The scaling exponents of rod tumbling match the transverse velocity increments and those of rod stretching match the longitudinal velocity increments. Thus, it appears that rod alignment does not affect the intermittency within the statistical uncertainty in our data.
In figure 8(d), the rod tumbling data from using fully resolved rod dynamics for rods in statistically steady alignment with the flow are used to compute the scaling exponents. In this case, we observe that the scaling exponents of higher-order moments of rod tumbling show a further departure from K41 theory than transverse velocity increments. The statistical uncertainty associated with these data is large, but, within this uncertainty, it does seem that rod tumbling is more intermittent than transverse velocity increments in the flow. If this additional intermittency is real, it must be due to the distribution of transverse velocity over the rod length, which evidently increases the likelihood of extreme values of rod tumbling.
Finally, in figure 8(e), we show scaling exponents from rod data computed from Jeffery’s equation. In this case, we observe that rod dynamics shows less intermittency compared to velocity increments in the flow. This shows that our computation of
![]() $\tilde{\unicode[STIX]{x1D63C}}$
not only gives weaker velocity gradients, but also leads to less intermittent rod dynamics, compared to estimates from two-point velocity increments. Less intermittency in rod tumbling computed from Jeffery’s equation compared to rod tumbling from fully resolved rods in the flow further highlights the role of fluid motions at scales smaller than the rod length in generating extreme values of rod tumbling.
$\tilde{\unicode[STIX]{x1D63C}}$
not only gives weaker velocity gradients, but also leads to less intermittent rod dynamics, compared to estimates from two-point velocity increments. Less intermittency in rod tumbling computed from Jeffery’s equation compared to rod tumbling from fully resolved rods in the flow further highlights the role of fluid motions at scales smaller than the rod length in generating extreme values of rod tumbling.
4 Conclusions
By tracking rods of different lengths in an isotropic turbulent flow, we study the effects and structure of turbulent fluid motions at different scales on slender rods. We find that the preferential alignment of rods with the directions of the perceived velocity gradient tensor changes with the rod length. In the dissipation range, there is a well-defined scale-independent preferred alignment where rods are most strongly aligned with the vorticity. In the inertial range, there is a different well-defined preferred alignment that is almost scale-independent where rods are most strongly aligned with the most extensional eigenvector of the strain-rate tensor.
In the inertial range, we find that the variances of both rod tumbling and rod stretching scale as
![]() $l^{-4/3}$
, where
$l^{-4/3}$
, where
![]() $l$
is the rod length. This scaling can be derived from the physical argument that rod tumbling and stretching are driven primarily by fluid motions of the same size as the rod length combined with K41 scaling relationships for the time scale of these turbulent fluid motions (see also Parsa & Voth Reference Parsa and Voth2014). A closer examination of the rod tumbling variance reveals that its value is higher than expected at transitional scales between the dissipation range and the inertial range (specifically, at
$l$
is the rod length. This scaling can be derived from the physical argument that rod tumbling and stretching are driven primarily by fluid motions of the same size as the rod length combined with K41 scaling relationships for the time scale of these turbulent fluid motions (see also Parsa & Voth Reference Parsa and Voth2014). A closer examination of the rod tumbling variance reveals that its value is higher than expected at transitional scales between the dissipation range and the inertial range (specifically, at
![]() $l\approx 60\unicode[STIX]{x1D702}$
). By comparing rod tumbling data from different methods, we conclude that this is because fluid motions at scales smaller than
$l\approx 60\unicode[STIX]{x1D702}$
). By comparing rod tumbling data from different methods, we conclude that this is because fluid motions at scales smaller than
![]() $l$
do not cancel out over the rod, but rather contribute to rod tumbling variance. For rod stretching statistics, we find that there is interesting behaviour at
$l$
do not cancel out over the rod, but rather contribute to rod tumbling variance. For rod stretching statistics, we find that there is interesting behaviour at
![]() $l\approx 100\unicode[STIX]{x1D702}$
. At this scale, the mean rod stretching relative to longitudinal fluid velocity increments shows a maximum and the skewness of rod stretching changes sign from being positive for rods in the tracer limit to becoming negative for rods well into the inertial range. Thus, the skewness of longitudinal velocity increments in the frame of rods in statistically steady alignment with the turbulent flow do not display scale independence in the inertial range; this is a marked contrast relative to longitudinal velocity increments taken in random orientations whose scale independence in the inertial range is predicted from Kolmogorov’s
$l\approx 100\unicode[STIX]{x1D702}$
. At this scale, the mean rod stretching relative to longitudinal fluid velocity increments shows a maximum and the skewness of rod stretching changes sign from being positive for rods in the tracer limit to becoming negative for rods well into the inertial range. Thus, the skewness of longitudinal velocity increments in the frame of rods in statistically steady alignment with the turbulent flow do not display scale independence in the inertial range; this is a marked contrast relative to longitudinal velocity increments taken in random orientations whose scale independence in the inertial range is predicted from Kolmogorov’s
![]() $4/5$
law.
$4/5$
law.
The power-law scaling exponents of higher-order moments of rod tumbling and rod stretching show anomalous scaling as a consequence of turbulent intermittency. The scaling exponents for rod stretching compare well to scaling exponents for longitudinal velocity increments in the flow and predictions from the refined similarity hypothesis (K62 theory). When the rod tumbling is computed from two-point transverse velocity increments across the rod length, the rod tumbling scaling exponents agree with the scaling exponents of transverse velocity increments in the flow. Together, this suggests that evaluating velocity increments in directions associated with fluid deformation does not seem to increase the departure of their scaling exponents from K41 theory predictions, though this departure is within the uncertainty limits of the data. However, if the rod tumbling is computed from fully resolved rod dynamics that take into account the fluid velocity variation along the full length of the rod, the scaling exponents do show a further departure from K41 theory predictions. This means that rod alignment does not necessarily cause rod dynamics to be more intermittent in comparison to structure functions in the inertial range, but that the effects of small-scale fluid motions on rod tumbling in combination with rod alignment does appear to result in additional intermittency.
Acknowledgements
N.P. and E.A.V. acknowledge support from the Army Research Office (grant no. W911NF-16-1-0284). G.A.V. acknowledges support from the National Science Foundation (grant no. DMR-1508575) and the Army Research Office (grant no. W911NF-15-1-0205). The authors also thank C. Lalescu and M. Wilczek for stimulating discussions. This research benefited from the use of the Savio computational cluster resource provided by the Berkeley Research Computing programme supported by the University of California, Berkeley.