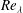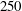1 Introduction
According to the classical theory of turbulence, the turbulent kinetic energy is contained at the large scales, and it is then transferred in an inviscid process to the small scales that dissipate it into heat (Pope Reference Pope2000). This inviscid transfer of energy occurs across the inertial subrange, whose span in the power spectrum depends on the turbulence level of the flow, i.e. the Reynolds number. At sufficiently large Reynolds number, and according to the Kolmogorov’s hypothesis of local isotropy, the small scales are statistically isotropic, whereas the large scales are anisotropic, especially in shear flows (Pope Reference Pope2000). This suggests that in the transfer of energy across scales, the characteristics of the large scales are lost and not perceptible at the small-scale level. For this reason, large and small scales have been considered independent of each other for a long time.
Nonetheless, Batchelor & Townsend (Reference Batchelor and Townsend1949) were the first to postulate that the turbulent kinetic energy can be transferred to the small scales without a direct involvement of the intermediate range of scales contained in the inertial subrange. Later, Yeung, Brasseur & Wang (Reference Yeung, Brasseur and Wang1995) showed that the energy transfer from large to small scales can be a single step process. Recent works reported that in a turbulent boundary layer (TBL) at high Reynolds number, the large scales modulate the small scales both in amplitude (Hutchins & Marusic Reference Hutchins and Marusic2007; Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009a ; Mathis et al. Reference Mathis, Monty, Hutchins and Marusic2009b ; Chung & McKeon Reference Chung and McKeon2010) and in frequency (Ganapathisubramani et al. Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012). In Mathis et al. (Reference Mathis, Hutchins and Marusic2009a ), the large-scale signal (i.e. low pass filtered velocity signal) was correlated with the large-scale filtered envelope of the small-scale signal (i.e. high pass filtered velocity signal), at different positions within the TBL. It was found that in the near-wall region of a TBL, positive fluctuations of the large-scale signal correlate with higher amplitudes of the small-scale signal, whereas in the wake region of the flow, these signals are negatively correlated. Similar observations were made in other wall-bounded flows, such as a channel flow and a pipe flow (Mathis et al. Reference Mathis, Monty, Hutchins and Marusic2009b ). At the centreline of a mixing layer, Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) found a scale interaction analogous to the outer region of a TBL, while, in a jet, the large-scale amplitude modulation of the small scales is similar to the near-wall region of wall-bounded flows (Fiscaletti, Ganapathisubramani & Elsinga Reference Fiscaletti, Ganapathisubramani and Elsinga2015). In their work, Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015) pointed out the different level of amplitude modulation in time signals (from hot-wire anemometry) and in space (from PIV). The strength of the small-scale amplitude modulation in the spatial signal was found to be only 25 % of the value obtained from the time signal. The elevated level of amplitude modulation in the latter was attributed to the fixed spectral band filter used to obtain the large- and the small-scale signals, which does not consider the local convection velocity. All of these findings are consistent with the pioneering study by Bandyopadhyay & Hussain (Reference Bandyopadhyay and Hussain1984), who explored many different turbulent flows in relation to scale interaction. Therefore, the nature of the scale interaction appears to be strongly dependent not only on the type of flow, but also on the location within the same flow. On the other hand, this seems to be at conflict with the classical theories of turbulence, according to which turbulence is a universal phenomenon.
The universality of the interaction between large and small scales was suggested by Elsinga & Marusic (Reference Elsinga and Marusic2010), who evaluated the average flow patterns in the local coordinate system defined by the eigenvectors of the strain-rate tensor. They found that the small-scale vortical structures have the tendency to be located in regions of shear, produced by the interaction of large-scale structures. This statistical tendency has been observed in both numerical and experimental datasets of different flows, including homogeneous isotropic turbulence and wall-bounded turbulence. These observations are in agreement with the theoretical predictions by Hunt et al. (Reference Hunt, Eames, Westerweel, Davidson, Voropayev, Fernando and Braza2010). According to this theory, thin layers of intense shear are found at the interface between large-scale motions, and are characterized by strong dissipation of turbulent kinetic energy. These thin layers play a major role in the small-scale dynamics of turbulence, and their importance increases with the Reynolds number of the flow. The measurements by Worth & Nickels (Reference Worth and Nickels2011) and the direct numerical simulations (DNS) of homogeneous isotropic turbulence by Ishihara, Kaneda & Hunt (Reference Ishihara, Kaneda and Hunt2013) supported these theories. This body of recent literature suggests that the large-scale velocity gradients could be directly related to the small scales of turbulence, and that this relationship between scales is the same in all turbulent flows. The correlation between the large-scale gradient and the small-scale amplitude was explored in a turbulent channel by Jiménez (Reference Jiménez2012). His results showed a nearly constant positive correlation throughout most of the channel. The Smagorinsky model as well as other subgrid scale (SGS) models used in large eddy simulations (LES) also link the activity of the small scales to larger-scale gradients by invoking scale invariance (Meneveau & Katz Reference Meneveau and Katz2000).
In the references mentioned above, the small-scale activity is related to the large-scale velocity fluctuations. If the analysis is performed in this way, the interaction between the large and the small scales depends on both the flow and the position within the flow. In the present paper, we investigate the modulation of the small scales by the large-scale velocity gradients in a DNS of a mixing layer (Attili & Bisetti Reference Attili and Bisetti2012). The modulation by the large-scale gradients is hypothesized to be insensitive to the position within the flow, as discussed above. The DNS is ideally suited for this purpose, as it allows access to all velocity gradients at all relevant scales. Indeed, we will show that the large-scale shear velocity gradients modulate the small scales in the same way throughout the mixing layer, in contrast to the modulation by the large-scale velocity which depends on the position within the layer. In addition, the correlation between large-scale velocity fluctuations and the small scales is shown to reflect the spatial organization of the large-scale structures within the flow rather than an actual interaction between large and small scales. The large scales are flow dependent, which explains why this correlation (between large-scale velocity fluctuations and the small scales) depends on the position within the flow, and varies between different flows. Finally, the small-scale vorticity within vortical structures is shown to be statistically aligned with large-scale vorticity. As a consequence of their directional coupling with larger scales, the small scales of turbulence are found to be anisotropic, as already observed by Yeung et al. (Reference Yeung, Brasseur and Wang1995) and Shen & Warhaft (Reference Shen and Warhaft2000) among others.
2 Methods
The DNS presented in this work is performed by solving the unsteady, incompressible Navier–Stokes equations. The parallel flow solver ‘NGA’ by Desjardins et al. (Reference Desjardins, Blanquart, Balarac and Pitsch2008), developed at Stanford University, is used to solve the transport equations. The solver implements a finite difference method on a spatially and temporally staggered grid with the semi-implicit fractional step method of Kim & Moin (Reference Kim and Moin1985). Velocity and scalar spatial derivatives are discretized with a second-order finite differences centred scheme.
A complete description of the flow parameters and methods used for the simulation are provided in Attili & Bisetti (Reference Attili and Bisetti2012, Reference Attili and Bisetti2013) and Attili, Cristancho & Bisetti (Reference Attili, Cristancho and Bisetti2014), together with a detailed analysis of the spatial evolution of the flow in the transitional and fully developed turbulent regions. Therefore, only a brief summary is presented here. The flow is imposed at the inlet plane (
$x=0$
) and free convective outflow (Ol’Shanskii & Staroverov Reference Ol’Shanskii and Staroverov2000) is specified at
$x=L_{x}$
. The boundary conditions are periodic in the spanwise direction
$z$
and free slip in the cross-wise direction
$y$
. The flow at the inlet (
$x=0$
) is a hyperbolic tangent profile for the streamwise velocity
$U$
with prescribed vorticity thickness
${\it\delta}_{{\it\omega},0}$
:
$U(x=0,y,z)=U_{c}+1/2{\rm\Delta}U\tanh (2y/{\it\delta}_{{\it\omega},0})$
, where
$U_{c}=(U_{1}+U_{2})/2$
is the convective velocity,
$U_{1}$
and
$U_{2}$
are the high- and low-speed stream velocities and
${\rm\Delta}U=U_{1}-U_{2}$
is the velocity difference across the layer. The ratio of the two velocities is
$U_{1}/U_{2}=3$
. Low amplitude white noise is superimposed on the hyperbolic tangent profile, resulting in the onset of the Kelvin–Helmholtz instability at a short distance downstream of the inlet (
$x\approx 50{\it\delta}_{{\it\omega},0}$
). The cross-wise and spanwise velocity components are perturbed in the same manner.
The computational domain extends over
$L_{x}=473{\it\delta}_{{\it\omega},0}$
,
$L_{y}=290{\it\delta}_{{\it\omega},0}$
,
$L_{z}=157.5{\it\delta}_{{\it\omega},0}$
in the streamwise (
$x$
), cross-wise (
$y$
) and spanwise (
$z$
) directions, respectively. The domain is discretized with
$3072\times 940\times 1024\approx 3\times 10^{9}$
grid points (
$N_{x}\times N_{y}\times N_{z}$
). In the region centred around
$y=0$
(
$|y|\leqslant 45{\it\delta}_{{\it\omega},0}$
), the grid is homogeneous in the three directions:
${\rm\Delta}x={\rm\Delta}y={\rm\Delta}z=0.15{\it\delta}_{{\it\omega},0}$
. Outside the core region for
$|y|>45{\it\delta}_{{\it\omega},0}$
, the grid is stretched linearly until
${\rm\Delta}y=0.6{\it\delta}_{{\it\omega},0}$
at
$|y|=55{\it\delta}_{{\it\omega},0}$
and then is constant again up to the boundary. Overall, the spatial resolution is such that
${\rm\Delta}x={\rm\Delta}y={\rm\Delta}z\leqslant 2.5{\it\eta}$
everywhere, where
${\it\eta}={\it\nu}^{3/4}{\it\varepsilon}^{-1/4}$
is the Kolmogorov scale and
${\it\varepsilon}$
the average turbulent kinetic energy dissipation. As shown in Attili & Bisetti (Reference Attili and Bisetti2012), the high-order structure functions display the expected viscous scaling at scales of the order of the Kolmogorov’s length, indicating that the resolution is adequate. The time step size is calculated in order to have a unity Courant–Friedrichs–Lewy (CFL) number.
The simulation was performed on the IBM Blue Gene/P system ‘Shaheen’ available at King Abdullah University of Science and Technology, using up to 65 536 processing cores (16 racks of the Blue Gene/P architecture). The simulation required around 10 million CPU hours and produced around 100 TB of data.
The Reynolds number based on the vorticity (momentum) thickness at the inlet is
$\mathit{Re}_{{\it\omega}}=600$
(resp.
$\mathit{Re}_{{\it\theta}}=150$
), increasing up to
$\mathit{Re}_{{\it\omega}}=25\,000$
(resp.
$\mathit{Re}_{{\it\theta}}=4250$
) as the mixing layer develops. In the fully developed region, the flow achieves a Reynolds number based on the Taylor microscale
$Re_{{\it\lambda}}=250$
.
The present analysis of scale interaction was performed in the far field of the mixing layer, in a region where the velocity statistics are self-similar and turbulence is fully developed. Twenty-one three-dimensional subdomains of size
$16.7{\it\lambda}\times 13.3{\it\lambda}\times 68.3{\it\lambda}$
(
${\it\lambda}\approx 30{\it\eta}$
is the Taylor microscale), collected at different time instants, were considered in the analysis. The centre of these subdomains is located at a streamwise position
$x=375{\it\delta}_{{\it\omega},0}$
and at
$y=0$
. The convective distance between two consecutive subdomains, computed after applying the Taylor’s hypotheses, is 167
${\it\delta}_{{\it\omega},0}$
, corresponding to approximately 68 Taylor microscales and 2000 Kolmogorov scales; therefore, the subdomains are statistically independent. The subdomains span the entire length of the simulation domain in the spanwise direction
$z$
. Since the DNS subdomains have been obtained at different time instants, all the variables obtained from these subdomains throughout the whole paper are also dependent on time, which is indicated with
$t$
. Furthermore, the vorticity root-mean-square (r.m.s.) was calculated to be approximately eight times larger than the mean vorticity everywhere throughout the subdomain.
A coordinate system,
$\tilde{x}{\tilde{y}}\tilde{z}$
, is introduced; it is centred at
$x=375{\it\delta}_{{\it\omega},0}$
,
$y=0$
,
$z=0$
and non-dimensionalized by the Taylor length scale
${\it\lambda}$
. The coordinate system is oriented so that positive values of
${\tilde{y}}$
are on the high velocity side of the mixing layer. A sketch of the coordinate systems and the numerical flow domain is presented in figure 1.
Figure 1. Schematics of the spatially developing mixing layer. The frame of reference of the simulation is indicated by the axes
$x$
,
$y$
and
$z$
, while the
$\tilde{x}$
,
${\tilde{y}}$
and
$\tilde{z}$
axes show the frame of reference centred in the region under analysis, marked by the black box. The background figure represents a two-dimensional cut of a passive scalar field, which shows the streamwise evolution of the mixing layer.
2.1 Large- and small-scale signals in physical space
With the aim of studying the modulation of the small scales by the large scales, large- and small-scale signals were created in physical space. The ‘small scales’ were defined as the range of length scales smaller than the Taylor length scale (
${\it\lambda}$
). At a given cross-wise position
${\tilde{y}}$
, one signal that represents the small-scale activity was constructed (
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
), and a number of different signals representative of the large scales were created, considering both large-scale velocity fluctuations (
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
), and large-scale velocity gradients (
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
${\hat{g}}_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
). To construct the large- and small-scale signals in physical space, each of the twenty-one three-dimensional subdomains described in the previous section was subdivided into cubes with sides of one Taylor length scale (
${\it\lambda}$
), and centred on
${\tilde{y}}$
. The following signals were then constructed.
-
(i) The local vorticity r.m.s.
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
was computed inside each cube. The following relationship was used: (2.1)where
$$\begin{eqnarray}A(\tilde{x},{\tilde{y}},\tilde{z},t)=\sqrt{\frac{1}{N}\mathop{\sum }_{i=1}^{N}[({\it\omega}_{x}|_{i}-\bar{{\it\omega}}_{x})^{2}+({\it\omega}_{y}|_{i}-\bar{{\it\omega}}_{y})^{2}+({\it\omega}_{z}|_{i}-\bar{{\it\omega}}_{z})^{2}]},\end{eqnarray}$$
${\it\omega}_{x}|_{i}$
,
${\it\omega}_{y}|_{i}$
and
${\it\omega}_{z}|_{i}$
are the components of the vorticity vector in the directions
$\tilde{x}$
,
${\tilde{y}}$
and
$\tilde{z}$
, respectively, in the
$i$
th point within the cube centred on
$(\tilde{x},{\tilde{y}},\tilde{z},t)$
;
$\bar{{\it\omega}}_{x}$
,
$\bar{{\it\omega}}_{y}$
, and
$\bar{{\it\omega}}_{z}$
are the corresponding vorticity components averaged over the cube, e.g.
$\bar{{\it\omega}}_{x}=(1/N)\sum _{i=1}^{N}{\it\omega}_{x}|_{i}$
;
$N$
is the number of points inside each cube, equal to
$3375$
.
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
was non-dimensionalized by its overall average,
$\bar{A}({\tilde{y}})$
, at a given
${\tilde{y}}$
, which is denoted
$A^{\ast }(\tilde{x},{\tilde{y}},\tilde{z},t)=A(\tilde{x},{\tilde{y}},\tilde{z},t)/\bar{A}({\tilde{y}})$
. The superscript
$\ast$
denotes non-dimensional quantities throughout the whole paper. The local vorticity r.m.s.,
$A$
, was used to quantify the local strength of the small-scale activity.
-
(ii) The mean streamwise velocity
$U_{av}(\tilde{x},{\tilde{y}},\tilde{z},t)$
was calculated inside each cube. The strength of the local non-dimensional large-scale fluctuation was determined as
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)=U_{av}(\tilde{x},{\tilde{y}},\tilde{z},t)-U_{m}({\tilde{y}})$
, where
$U_{m}({\tilde{y}})$
is the ensemble average streamwise velocity at
${\tilde{y}}$
. The large-scale velocity fluctuations were non-dimensionalized by the velocity difference over the mixing layer
${\rm\Delta}U$
, therefore
$u_{L}^{\ast }(\tilde{x},{\tilde{y}},\tilde{z},t)=u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)/{\rm\Delta}U$
. -
(iii) A moving average filter with a cube side of one Taylor length scale (
${\it\lambda}$
, case 1.) and three Taylor length scales (
$3{\it\lambda}$
, case 2.) was applied to the twenty-one 3-D velocity vector fields. From this procedure, the 3-D filtered velocity fields
$U_{L}$
,
$V_{L}$
,
$W_{L}$
were obtained. The spectral leakage associated to the moving average filtering was assessed by comparison with a Gaussian filter (characterized by the same cube size, and by a standard deviation of
$0.65$
the cube size), and it was found to be negligible for aims of the present analysis. The local large-scale gradient signal
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
, computed in each cube centred on
$(\tilde{x},{\tilde{y}},\tilde{z})$
, at time
$t$
, was calculated using the following relationship, which includes only the derivatives associated with shear: (2.2)The derivatives were computed with a central difference scheme from the discrete dataset in each point of the cube, and averaged over the number of mesh points inside each cube
$$\begin{eqnarray}g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)=\frac{1}{N}\mathop{\sum }_{i=1}^{N}\sqrt{\left(\left.\frac{\text{d}U_{L}}{\text{d}{\tilde{y}}}\right|_{i}^{2}+\left.\frac{\text{d}U_{L}}{\text{d}\tilde{z}}\right|_{i}^{2}+\left.\frac{\text{d}V_{L}}{\text{d}\tilde{x}}\right|_{i}^{2}+\left.\frac{\text{d}V_{L}}{\text{d}\tilde{z}}\right|_{i}^{2}+\left.\frac{\text{d}W_{L}}{\text{d}\tilde{x}}\right|_{i}^{2}+\left.\frac{\text{d}W_{L}}{\text{d}{\tilde{y}}}\right|_{i}^{2}\right)}.\end{eqnarray}$$
$N$
. Only the shear components of the gradients have been included in
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
(2.2), since the acceleration terms were found to be not important in modulating the small scales, in agreement with the conceptual picture of small-scale structures being organized in large-scale shear layers, as discussed in the Introduction. The validity of this assumption is confirmed later in the article.
-
(iv) A signal
${\hat{g}}_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
was also constructed, retaining in this case only the first term of (2.2), which represents the dominant contribution to
$g_{L}$
. Accordingly,
${\hat{g}}_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
was defined as: (2.3)
$$\begin{eqnarray}{\hat{g}}_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)=\frac{1}{N}\left|\mathop{\sum }_{i=1}^{N}\left.\frac{\text{d}U_{L}}{\text{d}{\tilde{y}}}\right|_{i}\right|.\end{eqnarray}$$
In this definition of
${\hat{g}}_{L}$
, we chose to calculate the absolute value of the sum, and not the sum of the absolute value. In consequence of this, an inhomogeneity in the sign of
$\text{d}U_{L}/\text{d}{\tilde{y}}$
over a cube results in a lower
${\hat{g}}_{L}$
compared to that obtained with the absolute value of the sum. Note that this effect is small since
$U_{L}$
is already filtered to the size of the cube, or larger.
In the construction of the large-scale signals, the appropriate length scale for large-scale filtering was considered to be the Taylor microscale (and larger length scales). This is justified by the fact that the dissipation spectrum has a peak at a length scale close to the Taylor length scale, meaning that the length scales larger than the Taylor length scale contribute progressively less to dissipation and can be considered large scales. In §§ 3 and 4, the small-scale signal
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
will be related to the large-scale signals
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
,
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
${\hat{g}}_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
to study possible interactions between large and small scales of turbulence.
3 The interaction between large-scale velocity fluctuations and small scales
We first investigate the interaction between the large-scale velocity fluctuations and the small scales of turbulence in the fully developed region of the mixing layer, analogous to earlier modulation studies. At different cross-wise locations
${\tilde{y}}$
, we consider the signals
$A^{\ast }(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
$u_{L}^{\ast }(\tilde{x},{\tilde{y}},\tilde{z},t)$
described in the previous section. Equally spaced
$u_{L}^{\ast }$
bins with a spacing of
$0.05$
ranging from
$u_{L}^{\ast }=-0.2$
to
$u_{L}^{\ast }=0.2$
are generated. The average vorticity r.m.s. conditioned on the strength of the local large-scale fluctuation
$u_{L}^{\ast }$
is calculated, and denoted by
$A_{u_{L}}^{\ast }$
. The minimum number of samples that contributed to the statistics was
$556$
, which was obtained at
${\tilde{y}}=+3.4$
, for the bin
$-0.2<u_{L}^{\ast }<-0.15$
.
The results of this analysis are presented in figure 2. It is worth noting that the interaction between large and small scales depends on the cross-wise position (
${\tilde{y}}$
) within the flow. On the low velocity side of the mixing layer (negative values of
${\tilde{y}}$
), positive fluctuations of the large-scale signal
$u_{L}^{\ast }$
are associated with a stronger activity of the small scales. Moreover, it can be observed that the extent of this scale modulation decreases as
${\tilde{y}}=0$
is approached. At
${\tilde{y}}=-0.2$
, the slope is inverted, and the activity of the small scales is now stronger for negative large-scale fluctuations, even if the scale interaction is rather weak here. This negative dependence grows stronger towards the top of the mixing layer, i.e. the high velocity side corresponding to positive
${\tilde{y}}$
.
Figure 2. Local vorticity r.m.s.
$A_{u_{L}}^{\ast }$
conditioned on the fluctuations of the large-scale signal
$u_{L}^{\ast }$
, at
${\tilde{y}}=-7.13$
(dot-dashed line),
${\tilde{y}}=-3.93$
(crosses, ‘
$+$
’),
${\tilde{y}}=-1.80$
(circles, ‘○’),
${\tilde{y}}=-0.20$
(triangles, ‘◃’),
${\tilde{y}}=+1.40$
(diamonds, ‘♢’) and
${\tilde{y}}=+3.40$
(asterisks, ‘
$\ast$
’).
It is worth pointing out that the inversion in the trend of the scale modulation does not occur at
${\tilde{y}}=0$
, but on the low velocity side of the mixing layer, which is in agreement with the works by Buxton (Reference Buxton2011) and Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014). This asymmetry is consistent with a slow drift of the mixing layer centre towards the low speed-side. This occurs in spatially evolving flows (Bell & Mehta Reference Bell and Mehta1990; Attili & Bisetti Reference Attili and Bisetti2012), but it is not present in temporally evolving mixing layer often employed in other DNS (e.g. Rogers & Moser Reference Rogers and Moser1994).
In their study, Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015) explained the observed amplitude modulation in terms of a spatially inhomogeneous distribution of the small-scale coherent structures of vorticity and of intense dissipation. According to this explanation, the small-scale structures are characterized by instantaneous convection velocities that are on average higher than the average streamwise velocity of the flow in regions of positive amplitude modulation, and vice versa. By positive/negative amplitude modulation we mean that the strength of the small-scale signal is stronger for positive/negative large-scale fluctuations. Therefore, when positive (negative) fluctuations of the large-scale velocity signal determine locally a stronger amplitude of the small-scale signal, the small-scale structures are more probably located in high velocity (low velocity) regions of the flow, which means that they are characterized by convection velocities higher (lower) than the mean. Then, for
${\tilde{y}}>-1.78$
, we expect the small-scale structures to have a higher probability of being located in regions of the flow characterized by a streamwise velocity lower than the average velocity, whereas an opposite behaviour occurs for
${\tilde{y}}<-1.78$
. From the present DNS dataset, this trend is confirmed, but not shown for the sake of brevity. These inferences on the spatial organization of the small-scale structures are consistent with the measurements by Buxton, de Kat & Ganapathisubramani (Reference Buxton, de Kat and Ganapathisubramani2013), who found that the convection velocities of the small-scale fluctuations are on average higher than the mean velocity on the low velocity side, and lower than the mean velocity on the high velocity side. The nature of the interaction between large-scale fluctuations and the small scales in a mixing layer is similar to the scale interaction in a TBL, where positive and negative amplitude modulation occurs at different positions within the flow (Mathis et al.
Reference Mathis, Hutchins and Marusic2009a
; Ganapathisubramani et al.
Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012). A jet and a wake behave similarly to the low velocity region of the mixing layer, and to the near-wall region of the TBL, and the scale interaction does not depend on the location within the flow (Bandyopadhyay & Hussain Reference Bandyopadhyay and Hussain1984).
Furthermore, we examined the interaction between large-scale fluctuations and small scales from time series. One hundred and twenty-eight uncorrelated time series were recorded at the two cross-wise positions
${\tilde{y}}=\pm 4.13$
and analysed. The length of each time series is
$1.15\times 10^{3}{\it\tau}_{{\it\eta}}$
, where
${\it\tau}_{{\it\eta}}$
is the Kolmogorov time scale. The length of the signals is more than three orders of magnitude larger than the eddy turnover time of one Taylor length scale. The time resolution of the signals is
${\rm\Delta}t=0.025{\it\tau}_{{\it\eta}}$
. A spectral filter is applied to these time series, analogously to Mathis et al. (Reference Mathis, Hutchins and Marusic2009a
), Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) and Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015). Two signals are constructed, representing the large- (large-scale signal), and the small-scale motions (small-scale signal), respectively. The wavelength ranges in the large- and in the small-scale signals are
$[3{\it\lambda},18{\it\lambda}]$
and
$[1.5{\it\eta},5{\it\eta}]$
, respectively, when assuming a constant convection velocity equal to the mean velocity in the application of the Taylor hypothesis. A measure of the level of scale interaction is obtained by the correlation coefficients between the large-scale signal and a signal representative of the local amplitude of the small-scale signal. The latter is obtained by Hilbert transforming and low pass filtering the small-scale signal, analogous to Mathis et al. (Reference Mathis, Hutchins and Marusic2009a
). It can be thought of as the filtered envelope of the small-scale signal. These correlation coefficients were calculated for different time delays between the two signals. The correlation coefficients
$R$
revealed a peak for time delays comparable to one Kolmogorov time scale (
${\it\tau}_{{\it\eta}}$
) at both locations (
$R=0.46$
and
$R=-0.35$
, at
${\tilde{y}}=-4.13$
and
${\tilde{y}}=+4.13$
, respectively). This finding suggests that the scales interact concurrently, and the time delays can be considered negligible. Consistently, Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014) found a concurrent interaction between large and small scales at
${\tilde{y}}=0$
.
It is also of interest to compare amplitude modulation in physical space with modulation in the time series. To determine the strength of the large-scale velocity fluctuations in physical space
$u_{L}^{\ast }$
, a procedure analogous to Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015) was applied, where the local mean of the streamwise velocity
$U$
was calculated within squares of
$2.3{\it\lambda}\times 1.3{\it\lambda}$
in size, on the
$\tilde{x}{-}{\tilde{y}}$
plane. The planes were taken at a distance of
$16{\it\eta}$
in the spanwise direction. The large-scale velocity fluctuations were obtained by subtracting from
$U$
the overall average streamwise velocity at
${\tilde{y}}$
. The large-scale velocity fluctuations were non-dimensionalized by the velocity difference over the mixing layer
${\rm\Delta}U$
. (Note that in the present analysis we define the large-scale signal
$u_{L}^{\ast }$
in a slightly different way than in § 2. This allows us to draw an analogy with Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015).) The strength of the small-scale activity was estimated as the local r.m.s. of the fluctuating streamwise velocity
$U$
within the corresponding square,
$U_{rms}$
. The fluctuations of the streamwise velocity in this case are relative to the mean within the square. The quantity
$U_{rms}$
was non-dimensionalized by
$\overline{U}_{rms}$
, which is the mean of all the values of
$U_{rms}$
at each
${\tilde{y}}$
. A total number of
$26\times 10^{3}$
samples (squares) were considered in this estimate of amplitude modulation in physical space. The use of the local r.m.s. of the streamwise velocity
$U$
instead of the local vorticity r.m.s. (to create
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
as described in § 2) allows us to compare amplitude modulation in time and in space. From the time series, the strength of the small-scale activity conditioned on
$u_{L}^{\ast }$
is represented by the r.m.s. of the conditional small-scale signal
${\it\sigma}_{u_{L}}^{\ast }$
. A detailed description of the procedure is presented in Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) (figure 3 of their paper). The same procedure has been used also by Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015).
Figure 3. Circles (○) represent the amplitude modulation in physical space (the local r.m.s. streamwise velocity
$U_{rms}/\overline{U}_{rms}$
conditioned on the fluctuations of the large-scale signal
$u_{L}^{\ast }$
), triangles (◃) represent amplitude modulation from time series (the r.m.s. of the small-scale signal
${\it\sigma}_{u_{L}}^{\ast }$
, conditioned on the fluctuations of the large-scale signal
$u_{L}^{\ast }$
), at (a)
${\tilde{y}}=-4.13$
, and (b)
${\tilde{y}}=4.13$
.
Statistics of the small-scale activity conditioned on the large-scale velocity fluctuations are shown in figure 3, for both the spatial data and the time series. At
${\tilde{y}}=-4.13$
(low velocity side of the mixing layer), the magnitude of amplitude modulation in space is approximately 50 % lower than that computed from time series. The nonlinearity of amplitude modulation in physical space makes it difficult to quantify the gap between amplitude modulation in physical space and from time series by a single number. At
${\tilde{y}}=+4.13$
(high velocity side of the mixing layer), amplitude modulation from time series largely underestimates the value obtained from spatial data. This analysis confirms the finding by Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015) in a turbulent round jet. They showed that a positive amplitude modulation from time series (observed in a jet) overestimates the value obtained from spatial data. This was attributed to the fixed spectral band filter used to obtain the large and the small scales in the time signals, as this filter does not take into account the local convection velocity. In consequence of this, the parts of the small-scale signal associated with positive large-scale fluctuations are characterized by a higher convection velocity and thereby a locally longer spatial wavelength, which contains a higher amount of turbulent kinetic energy. In the context of amplitude modulation, the low velocity side of a mixing layer is similar to a jet (positive amplitude modulation), while the high velocity side compares well with the wake region of a TBL (negative amplitude modulation). On the low velocity side, the assessment of amplitude modulation from time series largely overestimates the phenomenon when compared to physical space, analogous to the jet examined by Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015). Also, the extent of amplitude modulation in the wake region of a TBL is expected to be stronger when evaluated in physical space, because the intense small scales in the time signal are associated with low convection velocities, hence shorter spatial wavelength and lower energy content. These results should be taken into consideration when interpreting amplitude modulation from time series.
In the available literature on the topic, the correlation coefficient has been largely used to quantify the coupling between large and small scales (Bandyopadhyay & Hussain Reference Bandyopadhyay and Hussain1984; Mathis et al. Reference Mathis, Hutchins and Marusic2009a ; Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010, among others), and its dependency on the skewness has been recently discussed (Schlatter & Örlü Reference Schlatter and Örlü2010; Bernardini & Pirozzoli Reference Bernardini and Pirozzoli2011; Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2011). Till now, only the correlation coefficient between the large- and the small-scale velocity fluctuations has been considered. In the next section, the interaction between large and small scales of turbulence is quantified in space by computing the correlation coefficient between large-scale velocity gradients and the small-scale activity.
4 A quantification based on the correlation coefficient: the role of large-scale gradients
A correlation between the small scales and the local large-scale gradients has been suggested by Elsinga & Marusic (Reference Elsinga and Marusic2010), Hunt et al. (Reference Hunt, Eames, Westerweel, Davidson, Voropayev, Fernando and Braza2010), Jiménez (Reference Jiménez2012), and assumed in the subgrid scale (SGS) models used in LES such as the Smagorinsky model (Smagorinsky Reference Smagorinsky1963; Lilly Reference Lilly1967), and the dynamic model (Germano et al. Reference Germano, Piomelli, Moin and Cabot1991). The coupling between the large-scale gradients and the small scales is expected to be a flow-independent feature, as opposed to the large-scale velocity to small-scale interaction, which is not only dependent on the flow, as evident from the literature, but also dependent on the location within a given flow, as shown in § 3.
Therefore, the interaction between the large-scale gradients and the small-scale activity is investigated, by computing the correlation coefficient at different cross-wise locations within the mixing layer. It is important to stress that the mean of some signals in the analysis, i.e.
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
,
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
${\hat{g}}_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
, is not zero. Therefore, the correlation coefficients obtained from these signals are different to the same correlation coefficients computed after subtracting their mean. Nevertheless, the use of correlation coefficients between signals characterized by non-zero mean is justified by typical LES modelling, in which the mean of the large-scale signal and the small scales are also non-zero. In the following, we show first that the correlation coefficient between
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
can be approximated by the product between the correlation coefficient between
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
and the correlation coefficient between
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
. We start from the correlation coefficient at a given
${\tilde{y}}$
between
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
, denoted as
$R_{uA}({\tilde{y}})$
, and given by:
$$\begin{eqnarray}R_{uA}({\tilde{y}})=\mathop{\sum }_{\tilde{x},\tilde{z},t}\frac{u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)A(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert \Vert A(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }\end{eqnarray}$$
the signals
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
,
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
can be considered as state vectors, with corresponding length norm indicated by
$\Vert \cdot \Vert$
. Then, the following decomposition is applied:
$$\begin{eqnarray}\frac{A(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert A(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }={\it\alpha}({\tilde{y}})\frac{g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }+B(\tilde{x},{\tilde{y}},\tilde{z},t),\end{eqnarray}$$
where the coefficient
${\it\alpha}({\tilde{y}})$
is chosen such that
$B(\tilde{x},{\tilde{y}},\tilde{z},t)$
is orthogonal to
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
. From the scalar product between
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and (4.2), and from trigonometric considerations we obtain the coefficient
${\it\alpha}({\tilde{y}})$
, which can be expressed as:
$$\begin{eqnarray}{\it\alpha}({\tilde{y}})=\mathop{\sum }_{\tilde{x},\tilde{z},t}\frac{A(\tilde{x},{\tilde{y}},\tilde{z},t)g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert A(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert \Vert g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }=R_{gA}({\tilde{y}}),\end{eqnarray}$$
where
$R_{gA}({\tilde{y}})$
is the correlation coefficient between
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
and
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
at a given
${\tilde{y}}$
. It is worth noting that
${\it\alpha}({\tilde{y}})$
is independent of the directions
$\tilde{x}$
and
$\tilde{z}$
. Then, using (4.2) and (4.3), (4.1) is written as:
$$\begin{eqnarray}\displaystyle R_{uA}({\tilde{y}}) & = & \displaystyle \mathop{\sum }_{\tilde{x},\tilde{z},t}\frac{A(\tilde{x},{\tilde{y}},\tilde{z},t)g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert \Vert A(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }\mathop{\sum }_{\tilde{x},\tilde{z},t}\frac{u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert \Vert u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\tilde{x},\tilde{z},t}\frac{u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)B(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }.\end{eqnarray}$$
A large value of
${\it\alpha}({\tilde{y}})$
(close to unity) indicates a strong correlation between the activity of the small scales and the large-scale gradients (essentially an LES-type model in the sense that small scales are correlated with large-scale gradients), and implies a small value of
$B(\tilde{x},{\tilde{y}},\tilde{z},t)$
(4.2). Therefore, for large
${\it\alpha}({\tilde{y}})$
, i.e. large
$R_{gA}({\tilde{y}})$
, (4.4) reduces to:
$$\begin{eqnarray}\displaystyle R_{uA}({\tilde{y}}) & {\approx} & \displaystyle \mathop{\sum }_{\tilde{x},\tilde{z},t}\frac{g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)A(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert \Vert A(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }\mathop{\sum }_{\tilde{x},\tilde{z},t}\frac{u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)}{\Vert u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert \Vert g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)\Vert }\nonumber\\ \displaystyle & {\approx} & \displaystyle R_{gA}({\tilde{y}})R_{ug}({\tilde{y}}),\end{eqnarray}$$
which states that the correlation coefficient between the large-scale velocity fluctuations
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and the small-scale signal
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
is approximately equal to the product of the correlation coefficient between the large-scale gradients
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and the small-scale signal
$A(\tilde{x},{\tilde{y}},\tilde{z},t)$
and the correlation coefficient between the large-scale velocity signal
$u_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
and the large-scale velocity gradients
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
. An identical relation may be derived for the velocity gradient
$\hat{g_{L}}$
(2.3), instead of
$g_{L}$
, assuming the correlation coefficient
$R_{{\hat{g}}A}$
is large.
Figure 4. Correlation coefficients between: (a,b) asterisks (
$\ast$
),
$g_{L}-A$
, triangles (◃)
${\hat{g}}_{L}-A$
, for two different sizes of the large-scale filter, (a) at one Taylor length scale
${\it\lambda}$
(case 1), and (b) at three Taylor length scales
$3{\it\lambda}$
(case 2); (c,d) circles (○)
$u_{L}-A$
, diamonds (♢)
$u_{L}-g_{L}$
, triangles (◃)
$u_{L}-{\hat{g}}_{L}$
, for two different sizes of the large-scale filter (c) at one Taylor length scale
${\it\lambda}$
(case 1), and (d) at three Taylor length scales
$3{\it\lambda}$
(case 2).
The correlation coefficients
$R_{uA}$
,
$R_{gA}$
,
$R_{{\hat{g}}A}$
,
$R_{u{\hat{g}}}$
,
$R_{ug}$
computed at different cross-wise positions
${\tilde{y}}$
within the mixing layer, are presented in figure 4. The correlation coefficients were calculated directly from the signals
$u_{L}$
,
$A$
,
$g_{L}$
and
$\hat{g_{L}}$
, as defined in § 2, and not from the relationships expressed in the equations above. Hence, the results can be used to test the validity of (4.5). According to the assumption leading to (4.5),
$R_{gA}$
is large across
${\tilde{y}}$
, i.e. close to unity. Figure 4(a,b) confirm the validity of this assumption. Moreover,
$R_{gA}$
is approximately constant throughout the flow, in agreement with the initial expectations. It can also be observed that the values of
$R_{gA}$
seem rather independent of the size of the large-scale filter used to obtain the large-scale gradients. The correlation coefficients
$R_{{\hat{g}}A}$
between
${\hat{g}}_{L}$
and
$A$
have a very similar trend to
$R_{gA}$
(figure 4
a,b), thus revealing the dominating weight of the term
$\text{d}U_{L}/\text{d}{\tilde{y}}$
in the large-scale gradients
$g_{L}$
. With a large-scale filter of three Taylor length scales
$3{\it\lambda}$
,
$R_{{\hat{g}}A}$
is closer to unity than with a large-scale filter of one Taylor length scale
${\it\lambda}$
. This shows that at larger scales, the contribution of the main gradient of the flow to the large-scale small-scale coupling is predominant. Additionally, the other large-scale gradients in (2.2) contribute to a stronger modulating activity of the small scales in the range
$[1{\it\lambda},3{\it\lambda}]$
rather than at larger scales. Similarly to
$g_{L}$
, a signal containing all the nine components of the velocity gradient tensor (VGT) was also constructed, analogous to (2.2), and correlated with the local vorticity r.m.s. (
$A$
) at different cross-wise positions
${\tilde{y}}$
. The corresponding correlation coefficients present a remarkable overlap with
$R_{gA}$
, and for sake of clarity they are not reported in figure 4(a,b). This observation indicates that the acceleration terms of the VGT do not contribute significantly to the coupling between large-scale gradients and small scales. This implies that the shear components of the VGT modulate the small scales, which is in agreement with the expectations and consistent with the aforementioned references. Furthermore, different choices for the large-scale gradient signal, i.e. the large-scale vorticity and the Frobenius norm of the large-scale strain-rate tensor, yielded a high correlation with the small-scale signal
$A$
throughout the mixing layer, almost matching with
$R_{gA}$
in figure 4. These results are not shown for brevity.
The correlation coefficients
$R_{uA}$
between
$u_{L}$
and
$A$
range from positive values in the low velocity region of the mixing layer to negative values in the high velocity region, as already found in § 3. It is also of interest to note that the change in the sign of the correlation coefficient does not occur at the centreline, but inside the low velocity region of the mixing layer, consistent with figure 4 presented and discussed in § 3. The trend of the correlation coefficients
$R_{ug}$
between
$u_{L}$
and
$g_{L}$
across the different cross-wise positions
${\tilde{y}}$
is very similar to the trend of
$R_{uA}$
, both for a large-scale filter of one Taylor length scale (figure 4
c), and three Taylor length scales (figure 4
d). The similarity between
$R_{uA}$
and
$R_{ug}$
is again consistent with (4.5) and the observed nearly constant value of
$R_{gA}$
close to unity.
These observations have some important physical implications. According to the decomposition shown in (4.5),
$R_{uA}$
can be approximated as the product of
$R_{ug}$
and
$R_{gA}$
. The correlation
$R_{ug}$
is a term involving only the large scales, and represents the spatial organization of the large-scale structures within the flow. The term
$R_{gA}$
quantifies the local interaction between large-scale gradients and the small scales, and was found to be constant and close to unity throughout the flow. The value close to unity of
$R_{gA}$
and its independence of the
${\tilde{y}}$
position is an evidence that the cascade of turbulent kinetic energy occurs in the presence of large-scale velocity gradients. In other words, the link between large and small scales is represented by the large-scale gradients, and not by the large-scale fluctuations, which provides the physical support for the current SGS models for LES. Also in a channel flow, the correlation coefficient between the local velocity gradient and the small-scale activity is approximately independent of the wall-normal distance apart from a small region very close to the wall, as shown in figure 3(b) of Jiménez (Reference Jiménez2012). The deviations may be attributed to difficulties in defining a large-scale fluctuation so close to the wall. Then, with
$R_{gA}$
constant and positive, the trends in
$R_{uA}$
previously reported in the literature are actually directly driven by
$R_{ug}$
(4.5), hence in our view they should be interpreted as a large-scale behaviour, and not as a measure of the interaction between large and small scales.
After clarifying the role of the large-scale gradients in modulating the small scales, we intend to quantify the extent of this scale interaction depending on the local strength of the large-scale gradients. The procedure we apply is analogous to the procedure described in § 3. The large-scale gradients
$g_{L}(\tilde{x},{\tilde{y}},\tilde{z},t)$
at the cross-wise position
${\tilde{y}}$
are non-dimensionalized by the average of the large-scale gradients at
${\tilde{y}}$
,
$\overline{g}_{L}({\tilde{y}})$
, thus constructing a new signal
$g_{L}^{\ast }=g_{L}/\overline{g}_{L}$
representative of the fluctuations of the large-scale gradients. Statistics of the activity of the small scales conditioned on the large-scale gradients are shown in figure 5. Large-scale gradients above the average (
$g_{L}^{\ast }>1$
) determine statistically an increase of the local vorticity r.m.s. independently of the cross-wise position
${\tilde{y}}$
within the mixing layer, whereas a decrease is obtained for large-scale gradients below the average (
$g_{L}^{\ast }<1$
). This is consistent with expectations, and with the positive correlation coefficients between
$g_{L}$
and
$A$
being close to unity. For a filter size of one Taylor length scale (figure 5
a), the increase of the local vorticity r.m.s.
$A_{g_{L}}^{\ast }$
with the strength of the large-scale gradients is almost linear, and highly independent of the cross-wise location
${\tilde{y}}$
. At cross-wise positions closer to
${\tilde{y}}=0$
, the slope is slightly smaller than 1. For a filter size of three Taylor length scales (figure 5
b), the increase of the local vorticity r.m.s.
$A_{g_{L}}^{\ast }$
with the strength of the large-scale gradients is again confirmed, even if the slope tends to decrease near the centreline. This analysis allows us to conclude that, independently of the large-scale filter used, the local level of enstrophy in a turbulent mixing layer increases statistically with the increase of the local strength of the large-scale gradients.
Figure 5. Local vorticity r.m.s.
$A_{g_{L}}^{\ast }$
conditioned on the fluctuations of the large-scale gradients
$g_{L}^{\ast }$
for two different sizes of the large-scale filter, (a) at one Taylor length scale
${\it\lambda}$
(case 1), and (b) at three Taylor length scales
$3{\it\lambda}$
(case 2), at
${\tilde{y}}=-7.13$
(dot-dashed line),
${\tilde{y}}=-3.93$
(crosses, ‘
$+$
’),
${\tilde{y}}=-1.80$
(circles, ‘○’),
${\tilde{y}}=-0.20$
(triangles, ‘◃’),
${\tilde{y}}=+1.40$
(diamonds, ‘♢’), and
${\tilde{y}}=+3.40$
(asterisks, ‘
$\ast$
’).
5 The local orientation of the small-scale structures
In the previous section, the local interaction between the large-scale gradients and the small scales has been examined statistically in terms of its magnitude. In the present section, the alignment between the vorticity vector
${\bf\omega}$
and the large-scale vorticity vector
${\bf\omega}_{L}$
is examined both within vortical tubes and unconditionally, i.e. considering all points in the flow within the subdomains (§ 2). Results show a preferential alignment, which is an evidence of a direct coupling between eddies of different sizes. The implications on the isotropy of the small scales are also discussed. The analysis is restricted to the local alignment of the vorticity vectors. At present, we do not intend to relate these results to the energy cascade process or to the non-local effects produced by the large-scale straining regions on the small-scale vorticity (their importance has been pointed out in Ferré et al. (Reference Ferré, Mumford, Savill and Giralt1990) and in Vernet et al. (Reference Vernet, Kopp, Ferré and Giralt1999), among others).
To detect the small-scale vortical structures, the
${\it\lambda}_{ci}$
-criterion (Zhou et al.
Reference Zhou, Adrian, Balachandar and Kendall1999) based on the local swirling strength is adopted. The criterion uses the imaginary part of the eigenvalues of the VGT,
${\it\lambda}_{ci}$
, where non-zero values indicate a local swirling motion. A threshold value for
${\it\lambda}_{ci}$
(
${\it\lambda}_{ci,thr}$
) was determined as a multiple of the r.m.s. of
${\it\lambda}_{ci}$
, computed on the set of points where
${\it\lambda}_{ci}$
was non-zero. A point is considered as part of a vortex if the local swirling strength satisfies:
$$\begin{eqnarray}{\it\lambda}_{ci}>K{\it\lambda}_{ci,rms}={\it\lambda}_{ci,thr},\end{eqnarray}$$
where
$K$
is a constant. In each point satisfying this criterion (5.1), the vorticity vector was considered,
${\bf\omega}$
, which was used in place of the small-scale vorticity vector, under the hypothesis that the two quantities are similar. Furthermore, a moving average filter was applied to the 3-D velocity vector fields with a cubic kernel with a linear dimension of one, two and three Taylor length scales (
${\it\lambda}$
). In the same points, the large-scale vorticity vectors
${\bf\omega}_{L}$
were determined from the filtered velocity vector fields for all three cases. The large-scale vorticity,
${\bf\omega}_{L}$
, in this case includes the mean shear. The cosine alignment between the vorticity vectors both from the filtered,
${\bf\omega}_{L}$
, and the unfiltered velocity fields,
${\bf\omega}$
, was calculated in each point satisfying the criterion of (5.1) as:
$$\begin{eqnarray}\cos ({\it\theta})=\frac{{\bf\omega}\boldsymbol{\cdot }{\bf\omega}_{L}}{\Vert {\bf\omega}\Vert \Vert {\bf\omega}_{L}\Vert },\end{eqnarray}$$
where
${\it\theta}$
represents the angle between the small-scale and the large-scale vorticity vectors. The cosine alignment cos(
${\it\theta}$
) was calculated for
$K=3.5$
, and for the three different large-scale filter lengths. More than
$1.4\times 10^{6}$
points contributed to the statistics. In addition, the cosine alignment was also calculated in all the points of the flow, without considering the criterion of (5.1), for the same three large-scale filter lengths. In figure 6, the probability density functions (p.d.f.s) of cos(
${\it\theta}$
) are shown for all the points (figure 6
a), and for
$K=3.5$
in the criterion defined in (5.1) (figure 6
b). The peak in the p.d.f.s at
$\cos ({\it\theta})=1$
indicates a preferential alignment between
${\bf\omega}$
and
${\bf\omega}_{L}$
, in particular inside intense vortices (figure 6
b). The peak in the p.d.f.s drops significantly as the box size of the filter increases, even if a preferential alignment is still found for a box size of three Taylor length scales (
$3{\it\lambda}$
). The findings presented in figure 6 represent evidence for a preferential alignment between vorticity at the small-scale and the large-scale level. The structures of vorticity in the range of scales above the Taylor length scale thus have an influence on the local orientation of the small-scale structures. The choice of approximating the small-scale vorticity vectors with the raw unfiltered vorticity vectors did not affect importantly these results. Similar findings were obtained when the small-scale vorticity vectors (defined as
${\bf\omega}_{S}={\bf\omega}-{\bf\omega}_{L}$
) were considered in (5.2), instead of the raw unfiltered vorticity vectors
${\bf\omega}$
.
Figure 6. P.d.f.s of the cosine of the angle between the vorticity vectors from the filtered velocity vector fields (representative of the large scales), and the vorticity vectors from the unfiltered velocity vector fields (representative of the small scales), in all the points of the flow (a), and in the points satisfying the
${\it\lambda}_{ci}$
-criterion (5.1), with
$K=3.5$
(b). The size of the filter applied to the velocity vector fields is one Taylor length scale (
${\it\lambda}$
, continuous line), two Taylor length scales (
$2{\it\lambda}$
, dashed line) and three Taylor length scales (
$3{\it\lambda}$
, dash-dotted line).
To further elaborate these findings, we examine in the following the alignment between the vorticity vectors from filtered and unfiltered data and the three axes
$\tilde{x}$
,
${\tilde{y}}$
and
$\tilde{z}$
of the coordinate system. Again, we considered only points complying with the criterion of (5.1), with
$K=3.5$
. The result of this analysis is presented in figure 7. The cosine alignment between the vorticity vectors within the vortex tubes and the
$\tilde{x}$
- and
${\tilde{y}}$
-axis reveals a very similar orientation for
$1{\it\lambda}$
-filtered and unfiltered data. In particular, the cosine alignment between the vorticity vectors and the
${\tilde{y}}$
-axis is almost independent of the filtering of the velocity vector fields.
Figure 7. P.d.f.s of the cosine of the angle between the
$\tilde{x}$
-axis (a), the
${\tilde{y}}$
-axis (b) and the
$\tilde{z}$
-axis (c) and the vorticity vectors from the unfiltered velocity vector fields (continuous line), and the vorticity vectors from the filtered velocity vector fields, where the size of the filter is one Taylor length scales (
$1{\it\lambda}$
, dash-dotted line) and two Taylor length scales (
$2{\it\lambda}$
, dashed line). The alignment was calculated in points satisfying the
${\it\lambda}_{ci}$
-criterion (5.1) with
$K=3.5$
.
Moreover, figure 7(c) shows that the vorticity vectors from the filtered data are preferentially aligned with the
$\tilde{z}$
-axis. This result is expected, in that the mean vorticity of the flow, which is oriented parallel to the
$\tilde{z}$
-axis, contributes significantly to the filtered dataset (Brown & Roshko Reference Brown and Roshko1974). The analysis of the vorticity computed from the unfiltered velocity fields (continuous line) shows that the statistical predominance of this
$\tilde{z}$
-axis alignment is lost, although values of the cos(
${\it\theta}$
) lower than
$-0.6$
are still more likely than cos(
${\it\theta}$
)
${>}0.6$
. Examining the alignment between the vorticity vectors and the
$\tilde{x}$
-axis, it appears that the vorticity vectors for a filtering of
$2{\it\lambda}$
have a stronger tendency to be oriented orthogonally to the
$\tilde{x}$
-axis than those computed for the unfiltered and for the
$1{\it\lambda}$
-filtered fields. This is consistent with the increasing probability of the vorticity vectors from the
$2{\it\lambda}$
-filtered data to be aligned with the
$\tilde{z}$
-axis.
In conclusion, the (unfiltered) vorticity within the small-scale vortical structures tends to assume a preferential orientation in the far field of the mixing layer, as the related p.d.f.s (figure 7, continuous lines) do not show a uniform distribution. This preferential orientation appears to be affected by the large-scale vorticity. These findings have some important implications for the small-scale turbulence. In particular, the results provide evidence for the so-called ‘scale invariance’ (Meneveau & Katz Reference Meneveau and Katz2000) and suggest that part of the characteristics of the large scales are not lost at the small scales (i.e. higher frequencies). Instead, the small scales are similarly anisotropic, even in a statistical sense, as shown clearly in figure 7. This implies that in the cascade mechanism the organization of the scales may not be significantly altered across the inertial subrange. On the contrary, the anisotropy seems to be partially preserved and transferred to the smaller scales (figure 7 c). It is worth stressing that these results are based on the analysis of one flow at moderately high Reynolds number. Nonetheless, recent DNS simulations of homogeneous isotropic turbulence at very high Reynolds numbers (Ishihara et al. Reference Ishihara, Kaneda and Hunt2013) show that the small-scale vortical structures cluster in thin layers of intense shear. Their results suggest a preferential orientation of the axes of the vortical tubes belonging to the same thin layer, which supports the local anisotropy of the small scales. Further investigations of flows at higher Reynolds number are required to explore the dependence of these results on the Reynolds number itself.
Finally, the evidence of the anisotropic organization of the small scales presented in this section is consistent with the observations by Yeung et al. (Reference Yeung, Brasseur and Wang1995), Ferchichi & Tavoularis (Reference Ferchichi and Tavoularis2000), Shen & Warhaft (Reference Shen and Warhaft2000), and with the already mentioned work of Ishihara et al. (Reference Ishihara, Kaneda and Hunt2013). In addition, the experimental investigations by Hunt et al. (Reference Hunt, Ishihara, Worth and Kaneda2014) suggest a direct coupling between large-scale shear and small-scale enstrophy.
6 Conclusions
In the present work, the interaction between large and small scales is investigated in a DNS of a turbulent mixing layer at the Reynolds number based on the Taylor microscale (
$Re_{{\it\lambda}}$
) of
$250$
. The analysis is conducted directly in physical space, since important differences have been found in the strength of the scale interaction when quantified from time series, analogous to Fiscaletti et al. (Reference Fiscaletti, Ganapathisubramani and Elsinga2015). The local vorticity r.m.s., taken as a measure of the small-scale activity, is found to be modulated by the large-scale velocity fluctuations. In particular, on the low-speed side of the mixing layer, positive large-scale velocity fluctuations correspond to a higher vorticity r.m.s., whereas on the high-speed side, they correspond to a lower vorticity r.m.s., consistent with Buxton et al. (Reference Buxton, de Kat and Ganapathisubramani2013) and Buxton & Ganapathisubramani (Reference Buxton and Ganapathisubramani2014). Therefore, the interaction between large and small scales depends on the position within the mixing layer, similar to a turbulent boundary layer (Bandyopadhyay & Hussain Reference Bandyopadhyay and Hussain1984; Hutchins & Marusic Reference Hutchins and Marusic2007; Mathis et al.
Reference Mathis, Hutchins and Marusic2009a
). In the literature, this modulation has been quantified by the correlation coefficient between the large-scale and the small-scale velocity fluctuations.
Here, we showed that the correlation coefficient between large-scale velocity fluctuations and small-scale vorticity r.m.s. (
$R_{uA}$
) can be approximated by the product of
$R_{gA}$
and
$R_{ug}$
(
$R_{uA}\approx R_{gA}R_{ug}$
), which respectively are the correlation coefficient between vorticity r.m.s.,
$A$
, and the large-scale shear velocity gradients,
$g_{L}$
, and the correlation coefficient between the large-scale velocity fluctuations,
$u_{L}$
, and the large-scale shear velocity gradients,
$g_{L}$
. The term
$R_{gA}$
was found to be nearly constant throughout the mixing layer and close to unity. This reveals that large and small scales present a strong interaction independent of the position within the flow when the large-scale velocity gradients are considered, instead of the large-scale velocity fluctuations, as used in the existing literature on amplitude modulation (Bandyopadhyay & Hussain Reference Bandyopadhyay and Hussain1984; Mathis et al.
Reference Mathis, Hutchins and Marusic2009a
; Bernardini & Pirozzoli Reference Bernardini and Pirozzoli2011, among others). With
$R_{gA}$
constant and close to unity, it follows that
$R_{uA}\approx R_{ug}$
, meaning that the correlation coefficient between the large-scale velocity fluctuations and the small scales (
$R_{uA}$
) can be viewed as depending exclusively on the spatial organization of the large-scale signals, i.e.
$u_{L}$
and
$g_{L}$
. The present results confirm this approximation. As such,
$R_{uA}$
does not reflect a scale interaction. Because
$R_{uA}$
depends exclusively on the large scales, which are flow dependent,
$R_{uA}$
can vary between flows and with position in the same flow, as was indeed observed in the literature.
The observed strong correlation between large-scale gradients and small scales suggested further investigation of possible evidence of the so-called ‘scale invariance’ (Meneveau & Katz Reference Meneveau and Katz2000). It was found that the vorticity from unfiltered (small scales) and from low pass filtered (large scales) velocity vector fields tend to be aligned. This suggests that the vorticity direction does not vary significantly across the scales. At the Reynolds number of the present investigation, the anisotropy of the large scales is partially preserved at the small-scale level. This seems to be in contrast with the Kolmogorov’s hypothesis of local isotropy (Kolmogorov Reference Kolmogorov1941a ,Reference Kolmogorov b ), even if further investigations of flows at even higher Reynolds numbers are necessary.
