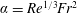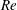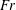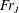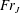1 Introduction
We examine the thin-film flow as a result of a circular jet impinging on a stationary disk. A circular hydraulic jump is expected to arise when a fluid jet falling vertically at high Reynolds number impacts the disk. The fluid spreads radially as a thin film until reaching a critical radius at which the film rises abruptly. Although the impingement of a circular jet has been extensively considered, there remain important issues as to a fully predictive theoretical formulation, particularly concerning the prediction of the jump location and height. Early predictions for the jump radius based on inviscid theory were reported by Rayleigh (Reference Rayleigh1914), which did not yield a good agreement with experiment (Watson Reference Watson1964). Although Tani (Reference Tani1949) considered viscous effects later, the dominant influence of viscosity was addressed much later. In fact, Watson (Reference Watson1964) formulated an appropriate description of the developing boundary layer and the fully viscous layer upstream of the jump. Watson (Reference Watson1964) studied both the radial and planar jet spreads for steady laminar and turbulent flows. Watson’s thin-film approach became the basis for numerous theoretical and experimental studies. The jump location is of major fundamental significance, and its prediction remains somewhat incomplete, as far as a coherent and simple theory is concerned, despite the various existing theoretical and numerical approaches in the literature. It will be a major focus in the present study. In particular, we explore the role of gravity and its influence on the location of the jump. We demonstrate the crucial role of gravity for liquids of relatively large viscosity and low surface tension. The influence of surface tension was the focus of the recent study of Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018).
Numerous existing studies follow essentially the same approach as proposed by Watson (Reference Watson1964), where the flow domain comprises a developing boundary layer followed by a supercritical viscous film layer ahead of the jump and a subcritical layer downstream of the jump. This description appears to mimic well the flow for a type I hydraulic jump, where the jump is relatively abrupt, followed by flow separation and the emergence of a vortex downstream. Upstream of the jump, the location where the boundary layer reaches the free surface separates the developing boundary-layer region from the fully viscous region. The boundary-layer height before this transition point is typically determined using a Kármán–Pohlhausen approach and the similarity profile for the velocity. Downstream of the transition point, the same similarity profile is assumed to (approximately) hold. Based on the balance of forces, a relation between the jump location and the height is also obtained for both laminar and turbulent flows. Watson’s theory was tested in a number of experimental investigations, including those of Watson himself, Craik et al. (Reference Craik, Latham, Fawkes and Gibbon1981), Stevens & Webb (Reference Stevens and Webb1992), Bush & Aristoff (Reference Bush and Aristoff2003) and Baonga, Gualous & Imbert (Reference Baonga, Gualous and Imbert2006). Liu & Lienhard (Reference Liu and Lienhard1993) observed that Watson’s predictions are least satisfactory in the limit of relatively weak jump. Surface tension effect was neglected in Watson’s work, and was later included by Bush and co-workers for a small circular jump radius, which led to a better agreement with experiment. They elucidated the influence of surface tension on the circular hydraulic jump, on both its size (Bush & Aristoff Reference Bush and Aristoff2003) and its stability (Bush, Aristoff & Hosoi Reference Bush, Aristoff and Hosoi2006) through combined theoretical and experimental investigations. The instability and the transition to polygonal hydraulic jump were originally reported by Ellegaard et al. (Reference Ellegaard, Hansen, Haaning, Marcussen, Bohr, Hansen and Watanabe1998, Reference Ellegaard, Hansen, Haaning, Hansen, Marcussen, Bohr, Hansen and Watanabe1999). The transition to type II and polygonal jump will not be considered here.
Watson’s theory is generally considered to be adequate for a circular jump with relatively large radius and height. Some extensions have been considered, such as the spread of an impinging non-Newtonian jet by Zhao & Khayat (Reference Zhao and Khayat2008), the formation of hydraulic jump on an inclined plane by Kate, Das & Chakraborty (Reference Kate, Das and Chakraborty2007) and Benilov (Reference Benilov2015), and the impingement on a rotating disk by Ozar, Cetegen & Faghri (Reference Ozar, Cetegen and Faghri2003) and Wang & Khayat (Reference Wang and Khayat2018). The influence of slip was also examined by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010), Prince, Maynes & Crockett (Reference Prince, Maynes and Crockett2012) and Khayat (Reference Khayat2016). Another extension involves the influence of gravity on the jump radius (Avedisian & Zhao Reference Avedisian and Zhao2000).
The fully theoretical prediction of the simultaneous location and height of the jump remains lacking in typical analyses. We recall that Watson’s approach and similar formulations provide only one relation between the jump radius and height in the form of an averaged momentum equation discretized across the jump. A second relation is therefore required. Moreover, the location of the jump is not always identifiable in reality, especially for high-viscosity liquids and flow at low rate. Avedisian & Zhao (Reference Avedisian and Zhao2000) published photographs of the transition across the jump from submerged views, which illustrate the difficulty in identifying the jump location when the height changes gradually as result of a sudden reduction of gravity. The numerical simulation of Rojas, Argentina & Tirapegui (Reference Rojas, Argentina and Tirapegui2010) also depicts the ambiguity in the jump location. Their numerical film profiles in their figure 2 illustrate how the abrupt jump ceases to exist with increasing viscosity, giving way to a smoother profile.
The full prediction of the jump location has been the focus of several studies. Following the approach of Tani (Reference Tani1949), Bohr, Dimon & Putzkaradze (Reference Bohr, Dimon and Putzkaradze1993) obtained the shallow-water equations for the average radial velocity and fluid depth by averaging the axisymmetric Navier–Stokes equations and in the vertical direction. They eliminated the depth from the averaged mass and momentum equations, and derived an ordinary differential equation for the average velocity. The equation turned out to have a single critical point which is a spiral (see Tani (Reference Tani1949)), and can exhibit an essential singularity at some finite distance. Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) argued that the jump location is close to the critical spiral point of their averaged equation, and deduced that the jump radius scales as
![]() $Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
, where
$Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
, where
![]() $Q$
is the jet flow rate,
$Q$
is the jet flow rate,
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity and g is the acceleration due to gravity. They also identified the location of the disk edge where the singularity occurs. The influence of the flow rate, the viscosity and the nozzle-to-disk distance on the hydraulic jump radius was investigated experimentally by Brechet & Neda (Reference Brechet and Neda1999), who reached a scaling law similar to that proposed by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993). They also observed that the nozzle-to-disk distance has no influence on the jump location. Kasimov (Reference Kasimov2008) modified the formulation of Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) by adding the effect of surface tension and incorporating the shape of a flat plate with a falling edge. He studied the influence of surface tension on the stability of the hydraulic jump, and found that a steady jump may not exist at high surface tension. In a later work, Bohr, Putkaradze & Watanabe (Reference Bohr, Putkaradze and Watanabe1997) and Watanabe, Putkaradze & Bohr (Reference Watanabe, Putkaradze and Bohr2003) adopted a non-self-similar cubic profile for the velocity that allowed them to avoid the critical point and the singularity of the averaged equations. However, two experimental points are needed in their solution to fix the boundary conditions, and some prior knowledge of the location of the jump was required. We shall refer back to the contributions of Bohr and associates later in this study.
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and g is the acceleration due to gravity. They also identified the location of the disk edge where the singularity occurs. The influence of the flow rate, the viscosity and the nozzle-to-disk distance on the hydraulic jump radius was investigated experimentally by Brechet & Neda (Reference Brechet and Neda1999), who reached a scaling law similar to that proposed by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993). They also observed that the nozzle-to-disk distance has no influence on the jump location. Kasimov (Reference Kasimov2008) modified the formulation of Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) by adding the effect of surface tension and incorporating the shape of a flat plate with a falling edge. He studied the influence of surface tension on the stability of the hydraulic jump, and found that a steady jump may not exist at high surface tension. In a later work, Bohr, Putkaradze & Watanabe (Reference Bohr, Putkaradze and Watanabe1997) and Watanabe, Putkaradze & Bohr (Reference Watanabe, Putkaradze and Bohr2003) adopted a non-self-similar cubic profile for the velocity that allowed them to avoid the critical point and the singularity of the averaged equations. However, two experimental points are needed in their solution to fix the boundary conditions, and some prior knowledge of the location of the jump was required. We shall refer back to the contributions of Bohr and associates later in this study.
Additional studies of numerical nature were also done. Passandideh-Fard, Teymourtash & Khavari (Reference Passandideh-Fard, Teymourtash and Khavari2011) proposed a numerical approach to determine the hydraulic jump location. The free surface was tracked by a volume-of-fluid approach. In their calculation domain, the downstream depth was imposed at the disk edge. Rojas et al. (Reference Rojas, Argentina and Tirapegui2010), Rojas, Argentina & Tirapegui (Reference Rojas, Argentina and Tirapegui2013), Rojas & Tirapegui (Reference Rojas and Tirapegui2015) developed and implemented a spectral representation for the velocity profile in the vertical direction. The projected averaged dynamical system is multidimensional in this case. More details on the work of Rojas and associates will be given when we compare our predictions with theirs.
Duchesne, Lebon & Limat (Reference Duchesne, Lebon and Limat2014) showed experimentally that the Froude number based on the jump height and velocity is independent of the flow rate, the viscosity and the surface tension. This critical Froude number, denoted here by
![]() $Fr_{J}$
, is therefore a constant, and should in principle provide the desired additional relation, which when coupled with Watson’s discretized momentum relation, would allow the full prediction of the jump location and height. However, no theoretical justification was provided. More recently, the measurements of Mohajer & Li (Reference Mohajer and Li2015) do indeed support the claim of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), but found that the Froude number is not independent of the surface tension. Recently, Wang & Khayat (Reference Wang and Khayat2018) revisited this issue in their study of the flow on a rotating disk, and provided some theoretical arguments and comparison with experiment in support of the claim of Duchesne et al. (Reference Duchesne, Lebon and Limat2014). The thickness at the edge of the disk was determined as a combination of static and dynamic contributions based on the local minimization of energy. The Froude number was found to remain essentially independent of the flow rate. However, the predictions were limited to low-viscosity liquids and high flow rates.
$Fr_{J}$
, is therefore a constant, and should in principle provide the desired additional relation, which when coupled with Watson’s discretized momentum relation, would allow the full prediction of the jump location and height. However, no theoretical justification was provided. More recently, the measurements of Mohajer & Li (Reference Mohajer and Li2015) do indeed support the claim of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), but found that the Froude number is not independent of the surface tension. Recently, Wang & Khayat (Reference Wang and Khayat2018) revisited this issue in their study of the flow on a rotating disk, and provided some theoretical arguments and comparison with experiment in support of the claim of Duchesne et al. (Reference Duchesne, Lebon and Limat2014). The thickness at the edge of the disk was determined as a combination of static and dynamic contributions based on the local minimization of energy. The Froude number was found to remain essentially independent of the flow rate. However, the predictions were limited to low-viscosity liquids and high flow rates.
This brings us to the main objective of the present study, focused on the theoretical prediction of the jump location and height for liquids of high viscosity. In this case, gravity becomes important for the supercritical flow. We therefore explore the interplay among inertia, viscosity and gravity for a thin film flowing axisymmetrically on a stationary disk as a result of jet impingement. In § 2, we outline the problem by giving the governing equations and boundary conditions in each region of the physical domain. The overall solution strategy is also discussed. In § 3, the Kármán–Pohlhausen (KP) approach is adopted to determine the boundary-layer structure and the film thickness upstream of the jump. The transition point is also located, where the boundary-layer edge and the free surface meet. In § 4, the KP approach is employed again to examine the viscous boundary-layer region, and assess the influence of gravity on the thin-film flow and jump location. Comparison with experiment is also carried out. In § 5, the height of the hydraulic jump is determined using a momentum balance across the jump, and the effect of gravity on the jump is analysed. The drawback of this approach is discussed. Alternatively, we propose an approach based on the knowledge of the edge thickness, which is established following the recent study of Wang & Khayat (Reference Wang and Khayat2018). Finally, concluding remarks and discussion are given in § 6.
2 Physical domain and problem statement
Consider the steady laminar incompressible flow of a circular (axisymmetric) jet of a Newtonian fluid emerging from a nozzle of radius
![]() $a$
, impinging at a volume flow rate
$a$
, impinging at a volume flow rate
![]() $Q$
on a flat disk lying normal to the jet direction. The flow configuration is depicted schematically in figure 1, where dimensionless variables and parameters are used. The problem is formulated in the
$Q$
on a flat disk lying normal to the jet direction. The flow configuration is depicted schematically in figure 1, where dimensionless variables and parameters are used. The problem is formulated in the
![]() $(r,\unicode[STIX]{x1D703},z)$
fixed coordinates, with the origin coinciding with the disk centre. The flow is assumed to be independent of
$(r,\unicode[STIX]{x1D703},z)$
fixed coordinates, with the origin coinciding with the disk centre. The flow is assumed to be independent of
![]() $\unicode[STIX]{x1D703}$
, thus excluding polygonal flow. In this case,
$\unicode[STIX]{x1D703}$
, thus excluding polygonal flow. In this case,
![]() $u(r,z)$
and
$u(r,z)$
and
![]() $w(r,z)$
are the corresponding dimensionless velocity components in the radial and vertical directions, respectively. The
$w(r,z)$
are the corresponding dimensionless velocity components in the radial and vertical directions, respectively. The
![]() $r$
-axis is taken along the disk radius and the
$r$
-axis is taken along the disk radius and the
![]() $z$
-axis is taken parallel to the jet. The length and the velocity scales are conveniently taken to be the radius of the jet,
$z$
-axis is taken parallel to the jet. The length and the velocity scales are conveniently taken to be the radius of the jet,
![]() $a$
, and
$a$
, and
![]() $Q/\unicode[STIX]{x03C0}a^{2}$
both in the radial and vertical directions. Since the pressure is expected to be predominantly hydrostatic for a thin film, it will be scaled by
$Q/\unicode[STIX]{x03C0}a^{2}$
both in the radial and vertical directions. Since the pressure is expected to be predominantly hydrostatic for a thin film, it will be scaled by
![]() $\unicode[STIX]{x1D70C}ga$
. Two main dimensionless groups emerge in this case: the Reynolds number
$\unicode[STIX]{x1D70C}ga$
. Two main dimensionless groups emerge in this case: the Reynolds number
![]() $Re=Q/\unicode[STIX]{x03C0}a\unicode[STIX]{x1D708}$
, where
$Re=Q/\unicode[STIX]{x03C0}a\unicode[STIX]{x1D708}$
, where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity, and the Froude number
$\unicode[STIX]{x1D708}$
is the kinematic viscosity, and the Froude number
![]() $Fr=Q/\unicode[STIX]{x03C0}\sqrt{a^{5}g}$
,
$Fr=Q/\unicode[STIX]{x03C0}\sqrt{a^{5}g}$
,
![]() $g$
being the acceleration due to gravity. We shall see that the problem can be reduced to a one-parameter problem, but the two parameters remain useful when comparing with experiment.
$g$
being the acceleration due to gravity. We shall see that the problem can be reduced to a one-parameter problem, but the two parameters remain useful when comparing with experiment.

Figure 1. Schematic illustration of the axisymmetric jet flow impinging on a flat stationary disk and the hydraulic jump of type I with one vortex downstream. Shown are the stagnation region (i), the developing boundary-layer region (ii), the fully developed viscous region (iii) and the hydraulic jump region (iv). All notations are dimensionless.
2.1 The physical domain
Following the treatment of Watson (Reference Watson1964), we identify four distinct flow regions for the jet over a circular disk, with smooth passage from one region to the next (see figure 1): a stagnation flow region (i), a developing boundary-layer region (ii), where the boundary layer grows until it reaches the film surface at the transition location
![]() $r=r_{0}$
and a fully viscous thin-film region (iii). A hydraulic jump emerges in region (iv), located at a radius
$r=r_{0}$
and a fully viscous thin-film region (iii). A hydraulic jump emerges in region (iv), located at a radius
![]() $r=r_{J}$
. We observe that
$r=r_{J}$
. We observe that
![]() $r=O(1)$
near the stagnation point in region (i). The velocity outside the boundary layer rises rapidly from 0 at the stagnation point to the impingement velocity in the inviscid far region. In region (ii), and as we shall confirm, the boundary layer is not expected to grow like
$r=O(1)$
near the stagnation point in region (i). The velocity outside the boundary layer rises rapidly from 0 at the stagnation point to the impingement velocity in the inviscid far region. In region (ii), and as we shall confirm, the boundary layer is not expected to grow like
![]() $\sqrt{r/Re}$
in the presence of gravity. The speed outside the boundary layer remains almost constant, as the fluid here is unaffected by the viscous stresses. For
$\sqrt{r/Re}$
in the presence of gravity. The speed outside the boundary layer remains almost constant, as the fluid here is unaffected by the viscous stresses. For
![]() $r\gg 1$
, the flow field in region (ii) is not significantly affected by the stagnation flow of region (i). The region
$r\gg 1$
, the flow field in region (ii) is not significantly affected by the stagnation flow of region (i). The region
![]() $1\ll r<r_{0}$
will be referred to as the developing boundary-layer region, with boundary-layer thickness
$1\ll r<r_{0}$
will be referred to as the developing boundary-layer region, with boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}(r)$
, outside which the flow is inviscid and uniform. Here
$\unicode[STIX]{x1D6FF}(r)$
, outside which the flow is inviscid and uniform. Here
![]() $r_{0}$
is the location of the transition point at which the viscous stresses become appreciable right up to the free surface, where the whole flow is of the boundary-layer type. At this point, in the absence of gravity, the velocity profile changes from the Blasius type to the self-similar profile. In contrast, in the presence of gravity, a similarity profile does not exist. The flow in region (iii),
$r_{0}$
is the location of the transition point at which the viscous stresses become appreciable right up to the free surface, where the whole flow is of the boundary-layer type. At this point, in the absence of gravity, the velocity profile changes from the Blasius type to the self-similar profile. In contrast, in the presence of gravity, a similarity profile does not exist. The flow in region (iii),
![]() $r>r_{0}$
, which will be referred to as the fully developed viscous region, is bounded by the disk and the free surface
$r>r_{0}$
, which will be referred to as the fully developed viscous region, is bounded by the disk and the free surface
![]() $z=h(r)$
.
$z=h(r)$
.
Finally, the hydraulic jump in region (iv) occurs at a location
![]() $r=r_{J}$
, which is larger than
$r=r_{J}$
, which is larger than
![]() $r_{0}$
since the jump typically occurs downstream of the transition point. Referring to figure 1, we conveniently introduce the supercritical film thickness (upstream of the jump) as
$r_{0}$
since the jump typically occurs downstream of the transition point. Referring to figure 1, we conveniently introduce the supercritical film thickness (upstream of the jump) as
![]() $h(r)=h(r<r_{J})$
, and the subcritical thickness (downstream of the jump) as
$h(r)=h(r<r_{J})$
, and the subcritical thickness (downstream of the jump) as
![]() $H(r)\equiv h(r>r_{J})$
. The height immediately upstream of the jump is denoted by
$H(r)\equiv h(r>r_{J})$
. The height immediately upstream of the jump is denoted by
![]() $h_{J}\equiv h(r=r_{J})$
, and the height immediately downstream of the jump is denoted by
$h_{J}\equiv h(r=r_{J})$
, and the height immediately downstream of the jump is denoted by
![]() $H_{J}\equiv H(r=r_{J})$
. The subcritical height
$H_{J}\equiv H(r=r_{J})$
. The subcritical height
![]() $H(r)$
is generally not constant and is different from the height
$H(r)$
is generally not constant and is different from the height
![]() $H_{J}$
. In this study, the fluid is assumed to be drained at the edge of the disk, at
$H_{J}$
. In this study, the fluid is assumed to be drained at the edge of the disk, at
![]() $r=r_{\infty }$
, and the flow remains steady, with the film thickness denoted by
$r=r_{\infty }$
, and the flow remains steady, with the film thickness denoted by
![]() $H_{\infty }=H(r=r_{\infty })$
. Although it is common practice to assume the jump height to remain equal to
$H_{\infty }=H(r=r_{\infty })$
. Although it is common practice to assume the jump height to remain equal to
![]() $H_{J}$
, this assumption is valid for fluids of low viscosity. The edge thickness is not expected to depend heavily on the flow rate (Rojas et al.
Reference Rojas, Argentina and Tirapegui2013; Mohajer & Li Reference Mohajer and Li2015).
$H_{J}$
, this assumption is valid for fluids of low viscosity. The edge thickness is not expected to depend heavily on the flow rate (Rojas et al.
Reference Rojas, Argentina and Tirapegui2013; Mohajer & Li Reference Mohajer and Li2015).
2.2 Governing equations and boundary conditions
Unless otherwise specified, the Reynolds number is assumed to be moderately large so that our analysis is confined to the laminar regime. Consequently, for steady axisymmetric thin-film flow, in the presence of gravity, the mass and momentum conservation equations are formulated using a thin-film or Prandtl boundary-layer approach, which amounts to assuming that the radial flow varies much slower than the vertical flow (Schlichtling Reference Schlichtling2000). By letting a subscript with respect to
![]() $r$
or
$r$
or
![]() $z$
denote partial differentiation, the reduced dimensionless conservation equations become
$z$
denote partial differentiation, the reduced dimensionless conservation equations become
These are the thin-film equations commonly used to model the spreading liquid flow (Tani Reference Tani1949; Bohr et al.
Reference Bohr, Dimon and Putzkaradze1993, Reference Bohr, Ellegaard, Hansen and Haaning1996; Kasimov Reference Kasimov2008). We observe that the pressure for a thin film is hydrostatic as a result of its vanishing at the film surface (in the absence of surface tension) and the small thickness of the film. In addition, upstream of the jump, the variation of the film thickness with the radius is expected to be smooth and gradual. In this case, the radial variation of the hydrostatic pressure is also small. Unlike the case of liquids of low viscosity, gravity cannot be neglected in the supercritical range. At the disk, the no-slip and no-penetration conditions are assumed to hold for any
![]() $r$
. In this case:
$r$
. In this case:
At the free surface
![]() $z=h(r<r_{J})$
or
$z=h(r<r_{J})$
or
![]() $z=H(r>r_{J})$
, the kinematic and dynamic conditions for steady flow take the form
$z=H(r>r_{J})$
, the kinematic and dynamic conditions for steady flow take the form
Here a prime denotes total differentiation. The flow field is sought separately in the developing boundary-layer region (ii) for
![]() $0<r<r_{0}$
, the fully developed viscous boundary-layer region (iii) for
$0<r<r_{0}$
, the fully developed viscous boundary-layer region (iii) for
![]() $r_{0}<r<r_{J}$
and the hydraulic jump region (iv) for
$r_{0}<r<r_{J}$
and the hydraulic jump region (iv) for
![]() $r_{J}<r<r_{\infty }$
. We observe that region (i) is neglected and will not be considered here. In this case, the leading edge of the boundary layer in region (ii) is taken to coincide with the disk centre. Consequently, the additional boundary conditions are as follows. In region (ii), the flow is assumed to be sufficiently inertial for inviscid flow to prevail between the boundary-layer outer edge and the free surface (see figure 1). In this case, the following conditions at the outer edge of the boundary layer and beyond must hold:
$r_{J}<r<r_{\infty }$
. We observe that region (i) is neglected and will not be considered here. In this case, the leading edge of the boundary layer in region (ii) is taken to coincide with the disk centre. Consequently, the additional boundary conditions are as follows. In region (ii), the flow is assumed to be sufficiently inertial for inviscid flow to prevail between the boundary-layer outer edge and the free surface (see figure 1). In this case, the following conditions at the outer edge of the boundary layer and beyond must hold:
Integrating (2.1c
) subject to condition (2.3b
), the pressure becomes
![]() $p(r,z)=h(r)-z$
, which is then eliminated so that (2.1b
) reduces to
$p(r,z)=h(r)-z$
, which is then eliminated so that (2.1b
) reduces to
Finally, the conservation of mass at any location upstream and downstream of the jump yields the following relation in dimensionless form:
The presence of gravity causes the flow to be non-self-similar in character. Therefore, in the present study, approximate solutions are sought in each region. An integral approach of the Kármán–Pohlhausen (KP) type (Schlichtling Reference Schlichtling2000) is adopted upstream of the jump, similar to the formulation of Prince et al. (Reference Prince, Maynes and Crockett2012) for a jet impinging on a disk with slip. The cubic profile is used for the velocity, which is considered to be the leading-order solution in a comprehensive spectral approach when inertia is included (Khayat & Kim Reference Khayat and Kim2006; Rojas et al. Reference Rojas, Argentina and Tirapegui2010). The cubic profile seems to be amply adequate as it leads to close agreement with Watson’s (Reference Watson1964) similarity solution for a jet impinging on a stationary disk (Prince et al. Reference Prince, Maynes and Crockett2012). The cubic profile was also assessed by Khayat (Reference Khayat2016) for a planar jet impinging on a surface with slip, and was found to yield a good agreement against his numerical solution. See also Rao & Arakeri (Reference Rao and Arakeri1998) for an integral analysis of a rotating film. Higher-order polynomial velocity profiles were also used. In their study on flow separation and wave breaking, Bohr et al. (Reference Bohr, Ellegaard, Hansen and Haaning1996) used a quartic profile to illustrate the emergence of a singularity at the separation point for a thin film. The coefficients in the polynomial expansion were not obtained explicitly. A cubic velocity profile was later adopted by Bohr et al. (Reference Bohr, Putkaradze and Watanabe1997), accounting for regions of separation. The cubic profile was also adopted in our recent study for a jet impinging on a rotating disk (Wang & Khayat Reference Wang and Khayat2018), and was found to yield close agreement with experiment.
3 The flow in the developing boundary layer and the transition location
Throughout this study, the stagnation region (i) under the impinging jet will not be considered. The velocity outside the boundary layer rises rapidly from 0 at the stagnation point to the impingement velocity in the inviscid far region. The impinging jet is predominantly inviscid close to the stagnation point, and the boundary-layer thickness remains negligibly small. Obviously, this is the case for a jet at relatively large Reynolds number. Ideally, the flow at the boundary-layer edge should correspond to the (almost parabolic) potential flow near the stagnating jet, with the boundary-layer leading edge coinciding with the stagnation point (Liu, Gabour & Lienhard Reference Liu, Gabour and Lienhard1993). However, the assumption of uniform horizontal flow near the wall and outside the boundary layer (as illustrated in figure 1) is reasonable. The distance from the stagnation point for the inviscid flow to reach uniform horizontal velocity is small, of the order of the jet radius (Lienhard Reference Lienhard2006). In the absence of gravity, the flow acquires a similarity character. In this case, the position or effect of the leading edge is irrelevant. This is not the case in the presence of gravity, where, as we shall see, a non-self-similar solution should be sought subject to initial conditions at the leading edge. However, the dominance of inertia near the stagnation point, albeit weakened by gravity, should make plausible the assumption of uniform horizontal flow. This assumption was adopted initially by Watson (Reference Watson1964), and is commonly used in the existing theories (see, for instance, Higuera (Reference Higuera1994), Bush & Aristoff (Reference Bush and Aristoff2003), Prince et al. (Reference Prince, Maynes and Crockett2012)).
We therefore start by examining the flow in region (ii), where the inviscid flow dominates the upper layer
![]() $(\unicode[STIX]{x1D6FF}\leqslant z<h)$
of the film in the radial direction. Consequently, the radial velocity above the boundary layer remains equal to one:
$(\unicode[STIX]{x1D6FF}\leqslant z<h)$
of the film in the radial direction. Consequently, the radial velocity above the boundary layer remains equal to one:
![]() $U(r)=1$
. The boundary-layer height
$U(r)=1$
. The boundary-layer height
![]() $\unicode[STIX]{x1D6FF}$
is determined by considering the mass and momentum balance over the boundary-layer region (ii). Therefore, we consider first the integral form of the convective term in (2.5). The vertical velocity component is eliminated by noting from (2.1a
) that
$\unicode[STIX]{x1D6FF}$
is determined by considering the mass and momentum balance over the boundary-layer region (ii). Therefore, we consider first the integral form of the convective term in (2.5). The vertical velocity component is eliminated by noting from (2.1a
) that
![]() $w(r,z)=-(1/r)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)(r\int _{0}^{z}u(r,z)\,\text{d}z)$
. In this case,
$w(r,z)=-(1/r)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)(r\int _{0}^{z}u(r,z)\,\text{d}z)$
. In this case,
Consequently, upon integrating (3.1) across the boundary-layer thickness, we obtain the integral form of the momentum equation in the boundary-layer region:
The boundary layer grows with radial distance, eventually invading the entire film width, reaching the jet free surface at
![]() $r=r_{0}$
. For
$r=r_{0}$
. For
![]() $r<r_{0}$
and above the boundary-layer outer edge, at some height
$r<r_{0}$
and above the boundary-layer outer edge, at some height
![]() $z=h(r)>\unicode[STIX]{x1D6FF}(r)$
, lies the free surface. The height of the free surface in region (ii) is then determined from mass conservation inside and outside the boundary layer. Therefore, for
$z=h(r)>\unicode[STIX]{x1D6FF}(r)$
, lies the free surface. The height of the free surface in region (ii) is then determined from mass conservation inside and outside the boundary layer. Therefore, for
![]() $r<r_{0}$
,
$r<r_{0}$
,
For simplicity, we choose a cubic profile for the velocity. Thus, we let
where
![]() $\unicode[STIX]{x1D702}=z/\unicode[STIX]{x1D6FF}$
. The cubic profile (3.4) is obviously one of many that can be used. The cubic profile, which will also be modified and implemented in the fully viscous region (iii), does not satisfy the momentum equation at
$\unicode[STIX]{x1D702}=z/\unicode[STIX]{x1D6FF}$
. The cubic profile (3.4) is obviously one of many that can be used. The cubic profile, which will also be modified and implemented in the fully viscous region (iii), does not satisfy the momentum equation at
![]() $z=0$
except in the absence of a pressure gradient. But so do many profiles used in the literature, including the parabolic profile used by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) and Kasimov (Reference Kasimov2008). The inclusion of the pressure gradient yields a non-self-similar profile, making the problem mathematically more cumbersome. For this reason, simple profiles are often adopted in the literature, including the cubic profile used by Prince et al. for a flow on a disk with isotropic (Reference Prince, Maynes and Crockett2012) and anisotropic (2014) slip, Watson’s (axisymmetric) similarity profile used by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) to simulate non-axisymmetric hydraulic jump patterns. None of these profiles satisfy the momentum equation at the disk, yet they all lead to an accurate description. See, for instance, the comparisons of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010), Prince et al. (Reference Prince, Maynes and Crockett2012) and Khayat (Reference Khayat2016). The profile (3.4) fulfils desirable criteria as it is simple and, and as we shall see, yields accurate results.
$z=0$
except in the absence of a pressure gradient. But so do many profiles used in the literature, including the parabolic profile used by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) and Kasimov (Reference Kasimov2008). The inclusion of the pressure gradient yields a non-self-similar profile, making the problem mathematically more cumbersome. For this reason, simple profiles are often adopted in the literature, including the cubic profile used by Prince et al. for a flow on a disk with isotropic (Reference Prince, Maynes and Crockett2012) and anisotropic (2014) slip, Watson’s (axisymmetric) similarity profile used by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) to simulate non-axisymmetric hydraulic jump patterns. None of these profiles satisfy the momentum equation at the disk, yet they all lead to an accurate description. See, for instance, the comparisons of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010), Prince et al. (Reference Prince, Maynes and Crockett2012) and Khayat (Reference Khayat2016). The profile (3.4) fulfils desirable criteria as it is simple and, and as we shall see, yields accurate results.
Upon inserting (3.4) into (3.2) and (3.3), we obtain the following coupled equations for the boundary-layer and free-surface heights:
These equations are solved subject to
![]() $\unicode[STIX]{x1D6FF}(r=0)=0$
. In the absence of gravity
$\unicode[STIX]{x1D6FF}(r=0)=0$
. In the absence of gravity
![]() $(Fr\rightarrow \infty )$
, equations (3.5) are easily solved to yield the following boundary-layer and film thicknesses:
$(Fr\rightarrow \infty )$
, equations (3.5) are easily solved to yield the following boundary-layer and film thicknesses:
which agree with the
![]() $\unicode[STIX]{x1D6FF}\approx \sqrt{r/Re}$
behaviour established from the dimensional argument of (2.5). In this case,
$\unicode[STIX]{x1D6FF}\approx \sqrt{r/Re}$
behaviour established from the dimensional argument of (2.5). In this case,
![]() $h$
decreases rapidly, like
$h$
decreases rapidly, like
![]() $1/r$
, near the disk centre, reaching a minimum, and increases like
$1/r$
, near the disk centre, reaching a minimum, and increases like
![]() $\sqrt{r}$
further downstream. The transition location is determined by equating
$\sqrt{r}$
further downstream. The transition location is determined by equating
![]() $h(r_{0})$
and
$h(r_{0})$
and
![]() $\unicode[STIX]{x1D6FF}(r_{0})$
to obtain
$\unicode[STIX]{x1D6FF}(r_{0})$
to obtain
![]() $r_{0}=((78/875)Re)^{1/3}$
.
$r_{0}=((78/875)Re)^{1/3}$
.
In the presence of gravity, the system (3.5) must be solved numerically. The problem can be reduced to a one-parameter problem by introducing the following transformation:
Eliminating the film height and using (3.7), the equation for the boundary-layer height reduces to, along with the film thickness:
Here, we introduced
which becomes the only parameter in the problem. Equation (3.8a
) is solved numerically subject to
![]() $\bar{\unicode[STIX]{x1D6FF}}(\bar{r}=0)=0$
, yielding in turn the height from (3.8b
).
$\bar{\unicode[STIX]{x1D6FF}}(\bar{r}=0)=0$
, yielding in turn the height from (3.8b
).
Figure 2 illustrates the influence of gravity on the boundary-layer height. In the limit of infinite Froude number, the classical boundary-layer result is recovered (Watson Reference Watson1964; Schlichtling Reference Schlichtling2000). As expected, gravity can have a tangible effect as the profiles in figure 2 show a departure from the classical parabolic character of the boundary layer height. In fact, it is not difficult to show that the asymptotic solution of equation (3.8a
) for small
![]() $r$
that the behaviour of the boundary-layer height near impingement is linear with distance. More precisely,
$r$
that the behaviour of the boundary-layer height near impingement is linear with distance. More precisely,
![]() $\bar{\unicode[STIX]{x1D6FF}}=\sqrt{3\unicode[STIX]{x1D6FC}}\bar{r}+O(\bar{r}^{2})$
, or
$\bar{\unicode[STIX]{x1D6FF}}=\sqrt{3\unicode[STIX]{x1D6FC}}\bar{r}+O(\bar{r}^{2})$
, or
![]() $\unicode[STIX]{x1D6FF}\approx \sqrt{3}(Fr/\sqrt{Re})r$
as opposed to
$\unicode[STIX]{x1D6FF}\approx \sqrt{3}(Fr/\sqrt{Re})r$
as opposed to
![]() $\unicode[STIX]{x1D6FF}=2\sqrt{(70/39)r/Re}$
in the absence of gravity. The linear growth is clearly reflected by the
$\unicode[STIX]{x1D6FF}=2\sqrt{(70/39)r/Re}$
in the absence of gravity. The linear growth is clearly reflected by the
![]() $\unicode[STIX]{x1D6FC}=10$
curve. Thus, the boundary-layer height approaches the linear behaviour with a diminishing slope as the level of gravity (or
$\unicode[STIX]{x1D6FC}=10$
curve. Thus, the boundary-layer height approaches the linear behaviour with a diminishing slope as the level of gravity (or
![]() $\unicode[STIX]{x1D6FC}$
) increases. We observe from (3.8b
) that, since the boundary-layer height is small near the origin, the film height decays like
$\unicode[STIX]{x1D6FC}$
) increases. We observe from (3.8b
) that, since the boundary-layer height is small near the origin, the film height decays like
![]() $\bar{h}\sim 1/2\bar{r}$
regardless of the level of gravity. This behaviour is also reflected by the h curves in figure 2, showing a narrow spread when
$\bar{h}\sim 1/2\bar{r}$
regardless of the level of gravity. This behaviour is also reflected by the h curves in figure 2, showing a narrow spread when
![]() $\unicode[STIX]{x1D6FC}$
is varied compared to
$\unicode[STIX]{x1D6FC}$
is varied compared to
![]() $\unicode[STIX]{x1D6FF}$
. Gravity tends to lower the boundary-layer height.
$\unicode[STIX]{x1D6FF}$
. Gravity tends to lower the boundary-layer height.
The behaviour in figure 2 can also be deduced qualitatively from (2.5), where the effect of gravity tends to enhance the effect of inertia as a result of the decaying film thickness with distance. The level of inertia is reflected by the radial convective term
![]() $Re\,uu_{r}$
. An estimate of the order of magnitude of this term is reached by taking
$Re\,uu_{r}$
. An estimate of the order of magnitude of this term is reached by taking
![]() $u$
to correspond to the free-surface value. In this case, we see that
$u$
to correspond to the free-surface value. In this case, we see that
![]() $Re\,uu_{r}$
decays with distance like
$Re\,uu_{r}$
decays with distance like
![]() $Re\,r^{-1}$
. There is an additional contribution to inertia stemming from gravity, namely through
$Re\,r^{-1}$
. There is an additional contribution to inertia stemming from gravity, namely through
![]() $-(Re/Fr^{2})h^{\prime }\sim (Re/2Fr^{2})r^{-2}$
for small
$-(Re/Fr^{2})h^{\prime }\sim (Re/2Fr^{2})r^{-2}$
for small
![]() $r$
, making the boundary-layer height behaves roughly like
$r$
, making the boundary-layer height behaves roughly like
![]() $\unicode[STIX]{x1D6FF}\sim \sqrt{r/Re}(1+1/2Fr^{2}r)^{-1/2}$
, which clearly shows the diminishing influence of gravity on the boundary-layer height. Thus, for dominant gravity, this relation reduces to
$\unicode[STIX]{x1D6FF}\sim \sqrt{r/Re}(1+1/2Fr^{2}r)^{-1/2}$
, which clearly shows the diminishing influence of gravity on the boundary-layer height. Thus, for dominant gravity, this relation reduces to
![]() $\unicode[STIX]{x1D6FF}\sim (Fr/Re)r$
, which is the linear behaviour based on (3.8).
$\unicode[STIX]{x1D6FF}\sim (Fr/Re)r$
, which is the linear behaviour based on (3.8).
Figure 3 depicts the influence of gravity on the transition location
![]() $r_{0}$
and corresponding film thickness
$r_{0}$
and corresponding film thickness
![]() $h(r_{0})$
, which are determined by setting
$h(r_{0})$
, which are determined by setting
![]() $h(r_{0})=\unicode[STIX]{x1D6FF}(r_{0})$
. The transition location is further from impingement for a thinner film with increasing gravity effect as inertia is enhanced by gravity. This is the same trend predicted for the effect of slip (see figure 8 of Khayat (Reference Khayat2016)). Similar to slip, gravity results in an asymptotic behaviour of the thickness for large
$h(r_{0})=\unicode[STIX]{x1D6FF}(r_{0})$
. The transition location is further from impingement for a thinner film with increasing gravity effect as inertia is enhanced by gravity. This is the same trend predicted for the effect of slip (see figure 8 of Khayat (Reference Khayat2016)). Similar to slip, gravity results in an asymptotic behaviour of the thickness for large
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.

Figure 2. Influence of gravity in the developing boundary-layer region (ii). The rescaled boundary-layer height,
![]() $\unicode[STIX]{x1D6FF}$
, and film thickness,
$\unicode[STIX]{x1D6FF}$
, and film thickness,
![]() $h$
, are plotted against the normalized radial distance. The transition location coincides with the intersection of the two heights (at the cusps in the figure). We only indicate the transition location by a vertical line for
$h$
, are plotted against the normalized radial distance. The transition location coincides with the intersection of the two heights (at the cusps in the figure). We only indicate the transition location by a vertical line for
![]() $\unicode[STIX]{x1D6FC}=10$
.
$\unicode[STIX]{x1D6FC}=10$
.

Figure 3. Dependence of the location and film thickness at the transition point between the developing and viscous boundary-layer regions (ii) and (iii) on gravity.
4 The fully viscous layer and prediction of the jump location
In this section, we formulate the problem for the film thickness in region (iii) and examine the flow field in this region. We then determine the location of the jump based on the supercritical flow without recourse to the subcritical solution. The approach is validated against existing measurements of the jump radius and its dependence on the flow rate.
4.1 The equation for the film thickness
In region (iii), the potential flow in the radial direction ceases to exist, with the velocity
![]() $U(r)=u(r,z=h)$
at the free surface becoming dependent on
$U(r)=u(r,z=h)$
at the free surface becoming dependent on
![]() $r$
. We again assume a cubic velocity profile subject to conditions (2.3a
) and (2.3b
). In this case, the radial velocity profile is given as function of the surface velocity
$r$
. We again assume a cubic velocity profile subject to conditions (2.3a
) and (2.3b
). In this case, the radial velocity profile is given as function of the surface velocity
![]() $U(r)$
as
$U(r)$
as
Here, we observe that
![]() $f(\unicode[STIX]{x1D702})$
is still given by (3.4). Using the mass conservation (2.6) yields the following relation:
$f(\unicode[STIX]{x1D702})$
is still given by (3.4). Using the mass conservation (2.6) yields the following relation:
This equation agrees with equation (15) of Prince et al. (Reference Prince, Maynes and Crockett2012) when setting their slip parameter equal to zero.
Similar to (3.2), the integral form of the momentum equation reads:
Substituting (4.1) into (4.3) and using (4.2) to eliminate
![]() $U$
, we obtain the equation for the film thickness in the fully viscous region:
$U$
, we obtain the equation for the film thickness in the fully viscous region:
which is solved for
![]() $r\geqslant r_{0}$
subject to
$r\geqslant r_{0}$
subject to
![]() $h(r=r_{0})=\unicode[STIX]{x1D6FF}(r_{0})$
. We observe that the flow in the absence of gravity is recovered in the limit
$h(r=r_{0})=\unicode[STIX]{x1D6FF}(r_{0})$
. We observe that the flow in the absence of gravity is recovered in the limit
![]() $Fr\rightarrow \infty$
. In this case, the problem reduces to the following equation and boundary condition:
$Fr\rightarrow \infty$
. In this case, the problem reduces to the following equation and boundary condition:
which admits
as solution, where we recall
![]() $r_{0}=((78/875)Re)^{1/3}$
. For comparison, Watson’s expression is reproduced here in dimensionless form:
$r_{0}=((78/875)Re)^{1/3}$
. For comparison, Watson’s expression is reproduced here in dimensionless form:
Thus, we have
![]() $h\approx 1.21(r^{2}/Re)+0.685(1/r)$
from (4.6) compared to Watson’s
$h\approx 1.21(r^{2}/Re)+0.685(1/r)$
from (4.6) compared to Watson’s
![]() $h\approx 1.28(r^{2}/Re)+0.69(1/r)$
from (4.7), showing a surprisingly close agreement, and validity of the cubic profile.
$h\approx 1.28(r^{2}/Re)+0.69(1/r)$
from (4.7), showing a surprisingly close agreement, and validity of the cubic profile.
4.2 The supercritical flow and the location of the hydraulic jump
Equation (4.4) indicates that a singularity exists, occurring at some distance where the slope of the free surface becomes infinite. An equation similar to (4.4) was obtained by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) by approximating the mean of the derivative of
![]() $u^{2}$
in the averaged momentum equation (4.3) in terms of the derivative of the mean square. They showed that the singularity is not an artefact of the averaging process, but is inherent to the thin-film equations. Of closer relevance is the equation obtained by Kasimov (Reference Kasimov2008) using a parabolic velocity profile, incorporating the shape of a finite disk with a sudden falling edge (see below).
$u^{2}$
in the averaged momentum equation (4.3) in terms of the derivative of the mean square. They showed that the singularity is not an artefact of the averaging process, but is inherent to the thin-film equations. Of closer relevance is the equation obtained by Kasimov (Reference Kasimov2008) using a parabolic velocity profile, incorporating the shape of a finite disk with a sudden falling edge (see below).
We conjecture that the location of the singularity coincides with the radius of the jump. Consequently, we now have a relation between the jump radius
![]() $r_{J}$
and the film height
$r_{J}$
and the film height
![]() $h_{J}$
immediately upstream of the jump:
$h_{J}$
immediately upstream of the jump:
We therefore identify the jump location or radius to occur when the slope of the free surface upstream of the jump becomes infinite, that is
![]() $h^{\prime }(r=r_{J})\rightarrow \infty$
, which coincides with the occurrence of the singularity of equation (4.4). At this location the relation between the jump radius and height is given by (4.8). Obviously, this claim is bold and needs to be validated, which we shall do shortly. The jump location is found by simply integrating (4.4) numerically subject to
$h^{\prime }(r=r_{J})\rightarrow \infty$
, which coincides with the occurrence of the singularity of equation (4.4). At this location the relation between the jump radius and height is given by (4.8). Obviously, this claim is bold and needs to be validated, which we shall do shortly. The jump location is found by simply integrating (4.4) numerically subject to
![]() $h(r_{0})=\unicode[STIX]{x1D6FF}(r_{0})$
from
$h(r_{0})=\unicode[STIX]{x1D6FF}(r_{0})$
from
![]() $r_{0}$
to a distance
$r_{0}$
to a distance
![]() $r_{J}$
until (4.8) is satisfied to within a certain tolerance. More details on the numerical treatment are given below.
$r_{J}$
until (4.8) is satisfied to within a certain tolerance. More details on the numerical treatment are given below.
Before comparing the predicted jump radius with existing measurements, it is helpful to explore the general supercritical flow behaviour (upstream of the jump). Once again, the flow becomes governed by a one-parameter problem when transformation (3.7) is used. In this case, (4.4) reduces to
where we recall
![]() $\unicode[STIX]{x1D6FC}$
from (3.9). In this case, relation (4.8) becomes
$\unicode[STIX]{x1D6FC}$
from (3.9). In this case, relation (4.8) becomes
We observe that the velocity at the free surface remains invariant under transformation (3.7). Equation (4.9) is integrated numerically subject to the condition
![]() $\bar{h}(\bar{r}=\bar{r}_{0})=\bar{\unicode[STIX]{x1D6FF}}(\bar{r}_{0})$
at the transition point, using MATLAB sixth-order Runge–Kutta scheme. The integration is carried out at equal steps in the distance taken equal to
$\bar{h}(\bar{r}=\bar{r}_{0})=\bar{\unicode[STIX]{x1D6FF}}(\bar{r}_{0})$
at the transition point, using MATLAB sixth-order Runge–Kutta scheme. The integration is carried out at equal steps in the distance taken equal to
![]() $10^{-3}$
, until the turning point is reached at the singularity. The program is terminated when the slope
$10^{-3}$
, until the turning point is reached at the singularity. The program is terminated when the slope
![]() $h^{\prime }>10^{2}$
, giving an accuracy in the jump location
$h^{\prime }>10^{2}$
, giving an accuracy in the jump location
![]() $r_{J}$
to the third decimal. The pre-jump height
$r_{J}$
to the third decimal. The pre-jump height
![]() $h_{J}$
is then deduced from (4.10).
$h_{J}$
is then deduced from (4.10).
We observe that equation (4.9), similar to equation (33) of Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) and equation (3.1)) of Kasimov (Reference Kasimov2008) for a flat disk, has only one critical point
![]() $\bar{h}_{c}=(6\unicode[STIX]{x1D6FC}/5)^{1/4},\bar{r}_{c}=\sqrt{272/875}(5/6)^{3/8}\unicode[STIX]{x1D6FC}^{1/8}$
, which is the root of the system
$\bar{h}_{c}=(6\unicode[STIX]{x1D6FC}/5)^{1/4},\bar{r}_{c}=\sqrt{272/875}(5/6)^{3/8}\unicode[STIX]{x1D6FC}^{1/8}$
, which is the root of the system
![]() $1/\unicode[STIX]{x1D6FC}-(272/875)(1/\bar{r}^{2}\bar{h}^{3})=(272/875)(1/\bar{r}^{2})-6/5\bar{h}=0$
, corresponding to a pair of complex conjugate eigenvalues of the Jacobian of the linearized two-dimensional dynamical system (Kasimov Reference Kasimov2008). The real part is positive, indicating that the critical point is an unstable spiral, which in turn indicates that the solution cannot pass through the critical point. Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) estimated that the jump is located close to the critical point. They computed the flow and the free surface by choosing the pre-jump (inner) branch to correspond to a constant average velocity, and chose the post-jump (outer) branch that emanates from the point of singularity. The two branches are then joined by the shock when they reach the same radial position, at a point that is identified as the jump radius (see their figure 3). This method led them to deduce the scaling for the jump radius to be
$1/\unicode[STIX]{x1D6FC}-(272/875)(1/\bar{r}^{2}\bar{h}^{3})=(272/875)(1/\bar{r}^{2})-6/5\bar{h}=0$
, corresponding to a pair of complex conjugate eigenvalues of the Jacobian of the linearized two-dimensional dynamical system (Kasimov Reference Kasimov2008). The real part is positive, indicating that the critical point is an unstable spiral, which in turn indicates that the solution cannot pass through the critical point. Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) estimated that the jump is located close to the critical point. They computed the flow and the free surface by choosing the pre-jump (inner) branch to correspond to a constant average velocity, and chose the post-jump (outer) branch that emanates from the point of singularity. The two branches are then joined by the shock when they reach the same radial position, at a point that is identified as the jump radius (see their figure 3). This method led them to deduce the scaling for the jump radius to be
![]() $R_{J}\approx Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
. In fact, if we assume the jump to occur at or near the critical point and recall (3.9), we obtain
$R_{J}\approx Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
. In fact, if we assume the jump to occur at or near the critical point and recall (3.9), we obtain
![]() $\bar{r}_{J}\approx \bar{r}_{c}=\sqrt{272/875}(5/6)^{3/8}(Re^{3}Fr^{2})^{1/8}$
, which is the dimensionless form of the scaling deduced by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993).
$\bar{r}_{J}\approx \bar{r}_{c}=\sqrt{272/875}(5/6)^{3/8}(Re^{3}Fr^{2})^{1/8}$
, which is the dimensionless form of the scaling deduced by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993).
Later, Kasimov (Reference Kasimov2008) derived an equation of closer similarity to (4.9) but introduced the shape of a flat disk with a cutoff at the edge. See his equation (3.1) and figure 2. The addition of the variable disk shape led to the existence of a critical saddle point near the disk edge, in addition to the spiral critical point. Kasimov determined the flow and the surface height on the two sides of the jump. The upstream branch is sought by solving his equation (3.1) subject to an initial condition corresponding the location where the jet velocity at impact equals the free-surface velocity. The downstream branch is sought by integrating (3.1) inward toward the jump starting at the far critical saddle point through which the solution effectively must pass. The integration is terminated on each side at the turning points, corresponding to an infinite slope in the surface height or the singularity in (3.1). The two heights computed on either side are subsequently used to determine the location of the jump by applying the discretized momentum equation.
Figure 4 gives an overview of the influence of gravity on the film thickness distribution up to the jump location. The film thickness exhibits a minimum typically downstream of the transition location. In general, gravity does not seem to have much of an effect until the jump is reached. In particular, and as expected by inspecting (2.5), near the minimum, gravity has a negligible effect. The jump occurs sooner and closer to transition point for a flow with stronger gravity.

Figure 4. Influence of gravity on the developing boundary-layer height and film thickness for supercritical flow. Also indicated in vertical lines are the locations of the hydraulic jump location
![]() $Re^{-1/3}r_{J}$
for different
$Re^{-1/3}r_{J}$
for different
![]() $\unicode[STIX]{x1D6FC}$
values.
$\unicode[STIX]{x1D6FC}$
values.
The influence of gravity on the corresponding free-surface velocity profiles is depicted in figure 5. Here the velocity in the developing boundary-layer region (ii) outside the boundary layer is equal to 1 (the uniform jet velocity), which then decreases monotonically with distance downstream of the transition location. In the absence of gravity
![]() $(\unicode[STIX]{x1D6FC}\rightarrow \infty )$
, the surface velocity decreases rapidly. This behaviour is easily deduced from (4.2) by substituting (4.6) to obtain
$(\unicode[STIX]{x1D6FC}\rightarrow \infty )$
, the surface velocity decreases rapidly. This behaviour is easily deduced from (4.2) by substituting (4.6) to obtain
In this case,
![]() $U$
decreases like
$U$
decreases like
![]() $r^{-3}$
at large distance. The figure indicates that gravity tends to enhance the radial flow near the transition point similar to the effects of disk rotation (Wang & Khayat Reference Wang and Khayat2018) and slip (Prince et al.
Reference Prince, Maynes and Crockett2012; Khayat Reference Khayat2016). The rate at which the surface velocity decays with radial distance is also enhanced by gravity. However, further downstream, gravity inhibits flow movement as the film thickens ahead of the jump.
$r^{-3}$
at large distance. The figure indicates that gravity tends to enhance the radial flow near the transition point similar to the effects of disk rotation (Wang & Khayat Reference Wang and Khayat2018) and slip (Prince et al.
Reference Prince, Maynes and Crockett2012; Khayat Reference Khayat2016). The rate at which the surface velocity decays with radial distance is also enhanced by gravity. However, further downstream, gravity inhibits flow movement as the film thickens ahead of the jump.

Figure 5. Influence of gravity on the free-surface velocity for supercritical flow.
Figure 6 illustrates the development of the dimensionless wall shear stress at the disk (skin friction) for the same gravity levels as in figures 4 and 5. The figure shows that the wall shear stress is always larger for higher gravity except near the jump. This larger shear stress, which reflects a larger shear rate at the disk, is the result of a thinner film thickness and a greater free-surface velocity caused by a higher gravity effect as already reported in figures 4 and 5. The shear stress decays rapidly with radial distance in the developing boundary-layer region. In the absence of gravity,
For any gravity level, after the rapid drop,
![]() $\unicode[STIX]{x1D70F}_{w}$
exhibits a maximum before decaying monotonically. At large radial distance, the shear stress decays like
$\unicode[STIX]{x1D70F}_{w}$
exhibits a maximum before decaying monotonically. At large radial distance, the shear stress decays like
![]() $r^{-5}$
in the absence of gravity effect. The strength of the maximum is essentially uninfluenced by gravity, but tends to occur further downstream with increasing gravity effect.
$r^{-5}$
in the absence of gravity effect. The strength of the maximum is essentially uninfluenced by gravity, but tends to occur further downstream with increasing gravity effect.
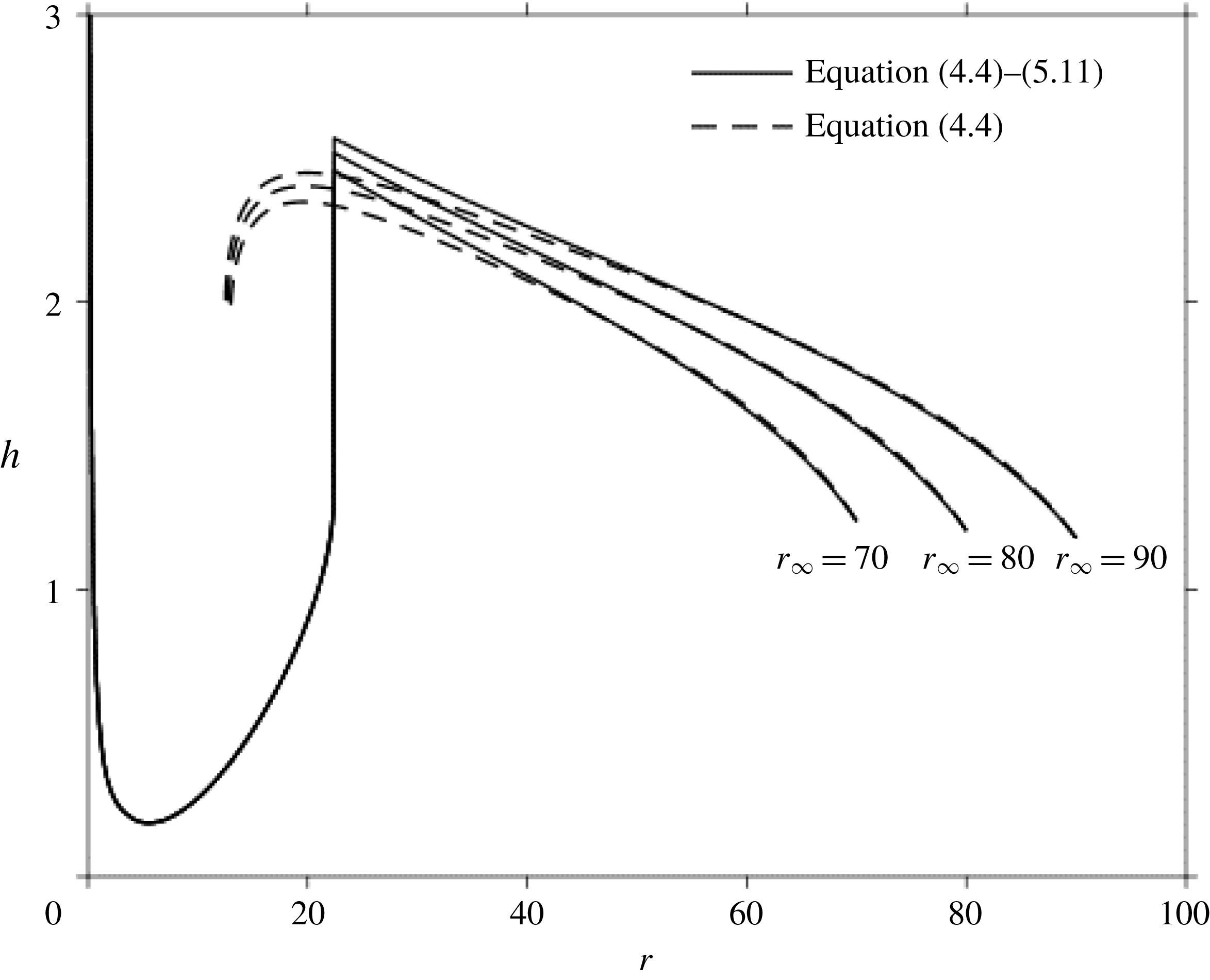
Although both the film height in figure 4 and the free-surface velocity in figure 5 are not significantly influenced by gravity, the location of the jump reflects a significant influence. This is depicted in figure 7 where the jump radius and corresponding film thickness immediately upstream of the jump are plotted against
![]() $\unicode[STIX]{x1D6FC}$
. The growth of the jump radius and the height closely follows the overall behaviour
$\unicode[STIX]{x1D6FC}$
. The growth of the jump radius and the height closely follows the overall behaviour
![]() $\bar{r}_{J}\approx \unicode[STIX]{x1D6FC}^{1/6}$
and
$\bar{r}_{J}\approx \unicode[STIX]{x1D6FC}^{1/6}$
and
![]() $\bar{h}_{J}\approx \unicode[STIX]{x1D6FC}^{2/9}$
, yielding
$\bar{h}_{J}\approx \unicode[STIX]{x1D6FC}^{2/9}$
, yielding
![]() $\bar{r}_{J}^{2}\bar{h}_{J}^{3}\approx \unicode[STIX]{x1D6FC}$
, which agrees with the original expression (4.10). The fractional power growth is also reflected from the position of the vertical lines in figure 4 as well.
$\bar{r}_{J}^{2}\bar{h}_{J}^{3}\approx \unicode[STIX]{x1D6FC}$
, which agrees with the original expression (4.10). The fractional power growth is also reflected from the position of the vertical lines in figure 4 as well.

Figure 6. Influence of gravity on the wall shear stress for supercritical flow.

Figure 7. Dependence on the jump location and height immediately upstream of the jump on
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
4.3 Comparison with experiment
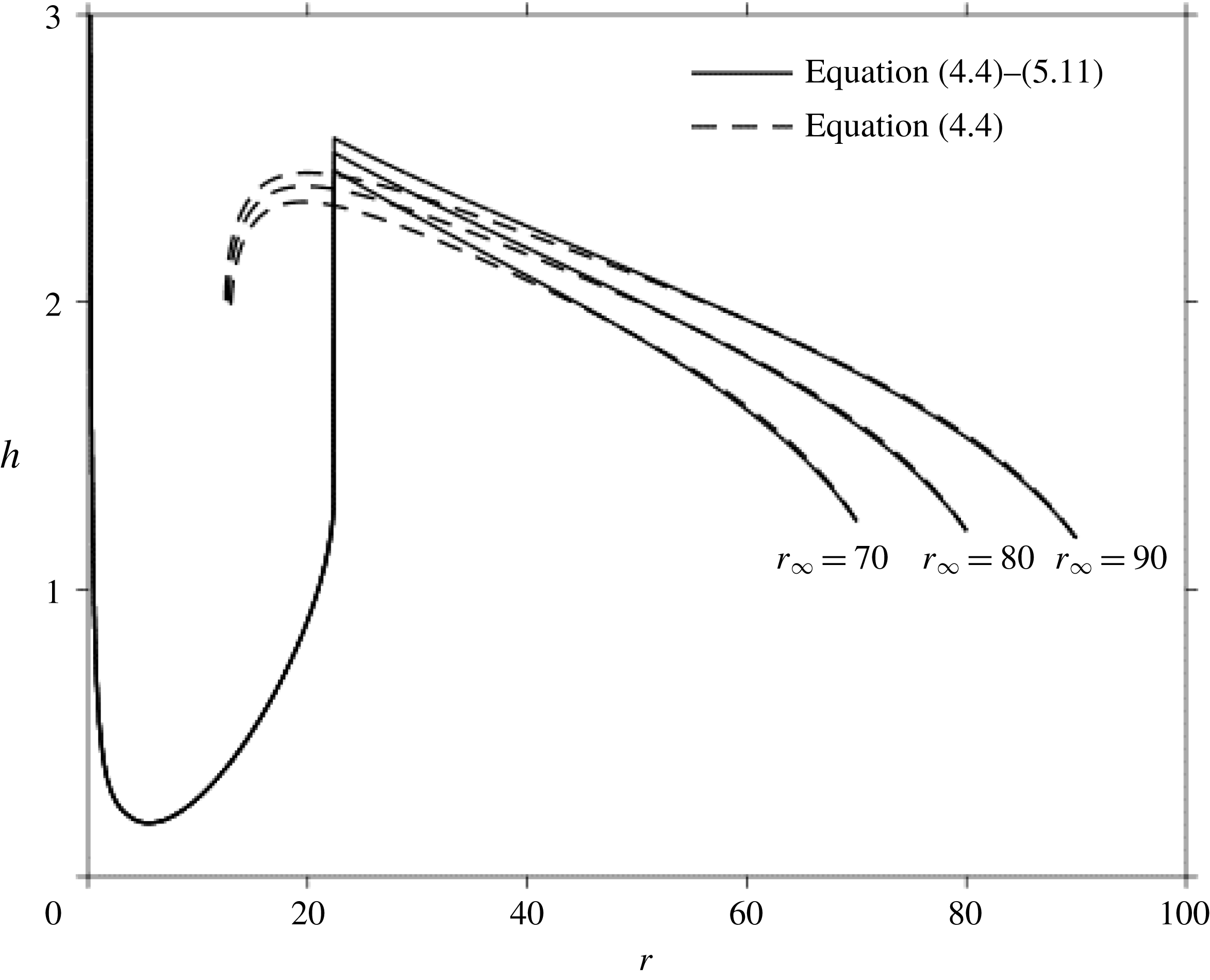
Figure 8 shows the dependence of the dimensional jump location on the flow rate, where comparison is carried out with the measurements of Hansen et al. (Reference Hansen, Horluck, Zauner, Dimon, Ellegaard and Creagh1997) as well as the numerical predictions of Rojas et al. (Reference Rojas, Argentina and Tirapegui2010) for silicon oils of two different viscosities. The same experimental data were also used by Rojas et al. (Reference Rojas, Argentina and Tirapegui2010) when they validated their spectral solution. We have included our results using the same log–log ranges used by Rojas et al. (Reference Rojas, Argentina and Tirapegui2010) in their figure 2. Our predictions are in excellent agreement with their numerical results. The qualitative and quantitative agreement for the highest-viscosity case
![]() $\unicode[STIX]{x1D708}=95~\text{cS}$
is especially encouraging given the simplicity of the present approach compared to their spectral approach. In particular, and in contrast to the numerical approach, the present formulation does not require imposing a boundary condition downstream of the jump. The agreement with experiment appears to suggest that the location of the jump can be determined without knowledge of downstream conditions such as the disk diameter or the thickness at the edge of the disk. This observation corroborates well the experimental findings of Brechet & Neda (Reference Brechet and Neda1999). We recall that Rojas et al. (Reference Rojas, Argentina and Tirapegui2010) had to impose the thickness at the edge of the disk as measured by Hansen et al. (Reference Hansen, Horluck, Zauner, Dimon, Ellegaard and Creagh1997). Both the present theoretical and existing numerical predictions tend to overestimate slightly the jump radius compared to experiment. The discrepancy appears to be higher for low flow rates, for a given liquid. A plausible explanation for the discrepancy is the difficulty to accurately locate the jump radius in reality. Moreover, it is likely that the jump for
$\unicode[STIX]{x1D708}=95~\text{cS}$
is especially encouraging given the simplicity of the present approach compared to their spectral approach. In particular, and in contrast to the numerical approach, the present formulation does not require imposing a boundary condition downstream of the jump. The agreement with experiment appears to suggest that the location of the jump can be determined without knowledge of downstream conditions such as the disk diameter or the thickness at the edge of the disk. This observation corroborates well the experimental findings of Brechet & Neda (Reference Brechet and Neda1999). We recall that Rojas et al. (Reference Rojas, Argentina and Tirapegui2010) had to impose the thickness at the edge of the disk as measured by Hansen et al. (Reference Hansen, Horluck, Zauner, Dimon, Ellegaard and Creagh1997). Both the present theoretical and existing numerical predictions tend to overestimate slightly the jump radius compared to experiment. The discrepancy appears to be higher for low flow rates, for a given liquid. A plausible explanation for the discrepancy is the difficulty to accurately locate the jump radius in reality. Moreover, it is likely that the jump for
![]() $\unicode[STIX]{x1D708}=95~\text{cSt}$
is of type II, with two vortex rolls downstream of the jump.
$\unicode[STIX]{x1D708}=95~\text{cSt}$
is of type II, with two vortex rolls downstream of the jump.

Figure 8. Dependence of the hydraulic jump radius on the flow rate. The figure shows the comparison between the present theoretical predictions and the measurements of Hansen et al. (Reference Hansen, Horluck, Zauner, Dimon, Ellegaard and Creagh1997) for two silicon oils of viscosities
![]() $\unicode[STIX]{x1D708}=15~\text{cSt}$
and 95 cSt. The numerical predictions of Rojas et al. (Reference Rojas, Argentina and Tirapegui2010) are also included.
$\unicode[STIX]{x1D708}=15~\text{cSt}$
and 95 cSt. The numerical predictions of Rojas et al. (Reference Rojas, Argentina and Tirapegui2010) are also included.
We further assess the validity of our approach by comparison against the scaling law proposed by Rojas et al. (Reference Rojas, Argentina and Tirapegui2013), which relates the radius of the jump, in particular, to the height downstream of the jump (see their relation (15)). In the absence of surface tension, the relation, written here as
![]() $R_{J}\approx ((9/70)(Q^{3}/\unicode[STIX]{x03C0}^{3}\unicode[STIX]{x1D708}g\tilde{H}_{\infty }))^{1/4}$
, becomes based on their spectral approach for inertial lubrication flow (Rojas et al.
Reference Rojas, Argentina and Tirapegui2010) and the inviscid Belanger equation (White Reference White2006). Figure 9 shows the comparison between our predictions and the scaling law.
$R_{J}\approx ((9/70)(Q^{3}/\unicode[STIX]{x03C0}^{3}\unicode[STIX]{x1D708}g\tilde{H}_{\infty }))^{1/4}$
, becomes based on their spectral approach for inertial lubrication flow (Rojas et al.
Reference Rojas, Argentina and Tirapegui2010) and the inviscid Belanger equation (White Reference White2006). Figure 9 shows the comparison between our predictions and the scaling law.

Figure 9. Dependence of the hydraulic jump radius on the flow rate. The figure shows the comparison between the present theoretical predictions (solid lines) and the ones based on the scaling law (dashed lines) of Rojas et al. (Reference Rojas, Argentina and Tirapegui2013) for two silicon oils of viscosities
![]() $\unicode[STIX]{x1D708}=15~\text{cSt}$
and 95 cSt.
$\unicode[STIX]{x1D708}=15~\text{cSt}$
and 95 cSt.
Finally, we observe that our earlier approach (Wang & Khayat Reference Wang and Khayat2018), where gravity is neglected in the supercritical regime, could not capture the location of the jump in comparison to experiment for heavily viscous liquids. On the other hand, the case of water is not considered here, not just because of the low viscosity but also due to the high surface tension. We considered the case of water in our recent work dealing with high surface tension liquids along with comparisons with experiment (Wang & Khayat Reference Wang and Khayat2018). In the present work, we neglect surface tension upstream in order to investigate the role of gravity on the hydraulic jump. Our objective is to also confirm or dismiss the claim and observation of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for highly viscous liquids. Further comparison with other existing measurements, including those of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), will be carried out in § 5.
4.4 Further validation
As further general assessment of the validity of equation (4.9), we examine its solution against that of the shallow-water equations for weak gravity. Thus, we set
![]() $\unicode[STIX]{x1D700}\equiv \unicode[STIX]{x1D6FC}^{-1}$
as the small parameter, and expand the thickness as
$\unicode[STIX]{x1D700}\equiv \unicode[STIX]{x1D6FC}^{-1}$
as the small parameter, and expand the thickness as
![]() $\bar{h}(\bar{r})=\sum _{m=0}\unicode[STIX]{x1D700}^{m}\bar{h}_{m}(\bar{r})$
. To leading order, (4.9) yields the following equation for
$\bar{h}(\bar{r})=\sum _{m=0}\unicode[STIX]{x1D700}^{m}\bar{h}_{m}(\bar{r})$
. To leading order, (4.9) yields the following equation for
![]() $\bar{h}_{0}$
:
$\bar{h}_{0}$
:
which corresponds to the thickness in the absence of gravity. The solution of this equation was already given earlier and is equivalent to (4.6). To next order:
We next examine the corresponding solution of the shallow-water equations, which are first rescaled to involve the only parameter
![]() $\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$
by recalling (3.7) and introducing all the barred variables as
$\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$
by recalling (3.7) and introducing all the barred variables as
In this case, equations (2.1a ), (2.5) and (2.6) become
In the presence of gravity, a similarity solution is possible only under some conditions.
Starting with the mapping
![]() $\bar{\unicode[STIX]{x1D709}}(\bar{r},\bar{z})=\bar{r},\bar{\unicode[STIX]{x1D702}}(\bar{r},\bar{z})=\bar{z}/\bar{h}(\bar{r})$
, and taking
$\bar{\unicode[STIX]{x1D709}}(\bar{r},\bar{z})=\bar{r},\bar{\unicode[STIX]{x1D702}}(\bar{r},\bar{z})=\bar{z}/\bar{h}(\bar{r})$
, and taking
![]() $\bar{u}(\bar{r},\bar{z})=\bar{U}(\bar{\unicode[STIX]{x1D709}})g(\bar{\unicode[STIX]{x1D702}})$
, (4.16a
) becomes
$\bar{u}(\bar{r},\bar{z})=\bar{U}(\bar{\unicode[STIX]{x1D709}})g(\bar{\unicode[STIX]{x1D702}})$
, (4.16a
) becomes
Isolating
![]() $\bar{w}_{\bar{\unicode[STIX]{x1D702}}}$
and rearranging terms:
$\bar{w}_{\bar{\unicode[STIX]{x1D702}}}$
and rearranging terms:
Now, from conservation of mass or (4.16c ), we have
 $$\begin{eqnarray}\displaystyle \bar{U}\bar{h}\bar{r}=\frac{1}{2\displaystyle \int _{0}^{1}g\,\text{d}\bar{\unicode[STIX]{x1D702}}}=\text{Const., yielding}\quad (\bar{\unicode[STIX]{x1D709}}\bar{h}\bar{U})^{\prime }=0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{U}\bar{h}\bar{r}=\frac{1}{2\displaystyle \int _{0}^{1}g\,\text{d}\bar{\unicode[STIX]{x1D702}}}=\text{Const., yielding}\quad (\bar{\unicode[STIX]{x1D709}}\bar{h}\bar{U})^{\prime }=0. & & \displaystyle\end{eqnarray}$$
Consequently, (4.18) reduces to
![]() $\bar{w}_{\bar{\unicode[STIX]{x1D702}}}=\bar{h}^{\prime }\bar{U}(\bar{\unicode[STIX]{x1D702}}g)_{\bar{\unicode[STIX]{x1D702}}}$
. Integrating and recalling that
$\bar{w}_{\bar{\unicode[STIX]{x1D702}}}=\bar{h}^{\prime }\bar{U}(\bar{\unicode[STIX]{x1D702}}g)_{\bar{\unicode[STIX]{x1D702}}}$
. Integrating and recalling that
![]() $\bar{w}(\bar{\unicode[STIX]{x1D709}},\bar{\unicode[STIX]{x1D702}}=0)=0$
, we get
$\bar{w}(\bar{\unicode[STIX]{x1D709}},\bar{\unicode[STIX]{x1D702}}=0)=0$
, we get
![]() $\bar{w}=\bar{h}^{\prime }\bar{U}\bar{\unicode[STIX]{x1D702}}g(\bar{\unicode[STIX]{x1D702}})$
.
$\bar{w}=\bar{h}^{\prime }\bar{U}\bar{\unicode[STIX]{x1D702}}g(\bar{\unicode[STIX]{x1D702}})$
.
We thus have so far
where (4.20c
) is deduced from (4.16c
). Substituting the velocity components from (4.20a,b
) into equation (4.16b
), and eliminating
![]() $\bar{U}$
using (4.20c
), yields the following problem for
$\bar{U}$
using (4.20c
), yields the following problem for
![]() $g$
:
$g$
:
We again seek the solution by expanding the thickness as
![]() $\bar{h}(\bar{r})=\sum _{m=0}\unicode[STIX]{x1D700}^{m}\bar{h}_{m}(\bar{r})$
. To leading order, we recover the classical equation of Watson (Reference Watson1964):
$\bar{h}(\bar{r})=\sum _{m=0}\unicode[STIX]{x1D700}^{m}\bar{h}_{m}(\bar{r})$
. To leading order, we recover the classical equation of Watson (Reference Watson1964):
which suggests that
![]() $\bar{r}^{-2}(\bar{r}\bar{h}_{0})^{\prime }$
must be constant. Multiplying (4.22) by
$\bar{r}^{-2}(\bar{r}\bar{h}_{0})^{\prime }$
must be constant. Multiplying (4.22) by
![]() $g_{\bar{\unicode[STIX]{x1D702}}}$
, and integrating using the conditions in (4.21), yields the following equation:
$g_{\bar{\unicode[STIX]{x1D702}}}$
, and integrating using the conditions in (4.21), yields the following equation:
The value of
![]() $C$
is determined by noting that
$C$
is determined by noting that
![]() $c=g_{\bar{\unicode[STIX]{x1D702}}}/\sqrt{1-g^{3}}$
, yielding
$c=g_{\bar{\unicode[STIX]{x1D702}}}/\sqrt{1-g^{3}}$
, yielding
![]() $\int _{0}^{1}g\,\text{d}g=\int _{0}^{1}g\,\text{d}g/\sqrt{1-g^{3}}=0.615$
, so that
$\int _{0}^{1}g\,\text{d}g=\int _{0}^{1}g\,\text{d}g/\sqrt{1-g^{3}}=0.615$
, so that
![]() $C=0.813$
. To the next order in
$C=0.813$
. To the next order in
![]() $\unicode[STIX]{x1D700}$
, (4.21) gives
$\unicode[STIX]{x1D700}$
, (4.21) gives
where
![]() $c\int _{0}^{1}g^{2}\,\text{d}\unicode[STIX]{x1D702}=(1/3)\int _{0}^{1}\text{d}g^{3}/\sqrt{1-g^{3}}=2/3$
was used. Comparison between the numerical coefficients of (4.14) and (4.24) indicates a discrepancy of 6 %. The discrepancy for the first-order contribution is 1 % when (4.15) is compared with (4.24).
$c\int _{0}^{1}g^{2}\,\text{d}\unicode[STIX]{x1D702}=(1/3)\int _{0}^{1}\text{d}g^{3}/\sqrt{1-g^{3}}=2/3$
was used. Comparison between the numerical coefficients of (4.14) and (4.24) indicates a discrepancy of 6 %. The discrepancy for the first-order contribution is 1 % when (4.15) is compared with (4.24).
Finally, it is worth observing that Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) and Rojas et al. (Reference Rojas, Argentina and Tirapegui2013) found that the jump radius scales roughly as
![]() $R_{J}\approx Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
. Using the current scaling, the dimensionless form of the estimate of Bohr et al. can be written as
$R_{J}\approx Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
. Using the current scaling, the dimensionless form of the estimate of Bohr et al. can be written as
![]() $r_{J}\approx Re^{3/8}Fr^{1/4}$
. Avedisian & Zhao (Reference Avedisian and Zhao2000) investigated the circular hydraulic jump experimentally for normal and reduced gravity conditions. They measured the jump diameter and shape at the free liquid surface for an impinging jet on a stationary disk. Based on the reported two values of the flow rate and two gravitational acceleration data provided, we find that the location of the jump behaves close to
$r_{J}\approx Re^{3/8}Fr^{1/4}$
. Avedisian & Zhao (Reference Avedisian and Zhao2000) investigated the circular hydraulic jump experimentally for normal and reduced gravity conditions. They measured the jump diameter and shape at the free liquid surface for an impinging jet on a stationary disk. Based on the reported two values of the flow rate and two gravitational acceleration data provided, we find that the location of the jump behaves close to
![]() $g^{-1/9}$
, roughly confirming the scaling of Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) for low gravity. We can also estimate the behaviour of the jump radius from (4.8) by assuming the thickness from (4.6) or (4.7) for large distance or
$g^{-1/9}$
, roughly confirming the scaling of Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) for low gravity. We can also estimate the behaviour of the jump radius from (4.8) by assuming the thickness from (4.6) or (4.7) for large distance or
![]() $h_{J}\approx r_{J}^{2}/Re$
. When inserted in (4.8), we obtain
$h_{J}\approx r_{J}^{2}/Re$
. When inserted in (4.8), we obtain
![]() $r_{J}\approx Re^{3/8}Fr^{1/4}$
, which is precisely the scaling suggested by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) cast in dimensionless form. Interestingly, this scaling law can also be expressed in terms of only one parameter as
$r_{J}\approx Re^{3/8}Fr^{1/4}$
, which is precisely the scaling suggested by Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) cast in dimensionless form. Interestingly, this scaling law can also be expressed in terms of only one parameter as
![]() $\bar{r}_{J}\approx \unicode[STIX]{x1D6FC}^{1/8}$
.
$\bar{r}_{J}\approx \unicode[STIX]{x1D6FC}^{1/8}$
.
5 The influence of gravity on the hydraulic jump height and the subcritical flow
Now that the jump location has been determined, we are in a position to examine the flow and the film height in the subcritical region downstream of the jump, in particular the height of the jump. Here, we consider two alternatives and assess their validity, the first consisting of applying the conservation of momentum across the jump, and the second involving the use of the film thickness at the edge of the disk and integrating the momentum equation (backwards) to determine the jump height. We conveniently let
![]() $r=r_{J-}$
and
$r=r_{J-}$
and
![]() $r=r_{J+}$
denote the radial position immediately up- and downstream of the jump, respectively, with corresponding film heights
$r=r_{J+}$
denote the radial position immediately up- and downstream of the jump, respectively, with corresponding film heights
![]() $h_{J}\equiv h(r=r_{J-})$
and
$h_{J}\equiv h(r=r_{J-})$
and
![]() $H_{J}\equiv h(r=r_{J+})$
.
$H_{J}\equiv h(r=r_{J+})$
.
5.1 Conservation of momentum across the jump
We first recall the integral form (4.3) of the momentum conservation equation, which holds for any position
![]() $r>r_{0}$
in the super- and subcritical regions. Across the jump, equation (4.3) is applied for a control volume of width
$r>r_{0}$
in the super- and subcritical regions. Across the jump, equation (4.3) is applied for a control volume of width
![]() $\unicode[STIX]{x0394}r$
in the radial direction, taking the following discretized form:
$\unicode[STIX]{x0394}r$
in the radial direction, taking the following discretized form:
Since the width of the jump
![]() $\unicode[STIX]{x0394}r$
is assumed to be small, equation (5.1) reduces to
$\unicode[STIX]{x0394}r$
is assumed to be small, equation (5.1) reduces to
We observe that the supercritical velocity is already available from (4.1) and (4.2), yielding
![]() $u(r_{J-},z)=(4/5r_{J}h_{J})f(\unicode[STIX]{x1D702})$
, where
$u(r_{J-},z)=(4/5r_{J}h_{J})f(\unicode[STIX]{x1D702})$
, where
![]() $\unicode[STIX]{x1D702}=z/h_{J}$
and
$\unicode[STIX]{x1D702}=z/h_{J}$
and
![]() $f(\unicode[STIX]{x1D702})$
is given in (3.4). We also use relation (4.8) to eliminate
$f(\unicode[STIX]{x1D702})$
is given in (3.4). We also use relation (4.8) to eliminate
![]() $h_{J}$
, In this case, (5.2) becomes
$h_{J}$
, In this case, (5.2) becomes
Thus, the jump height is completely determined as a function of the Froude and the Reynolds numbers once the subcritical velocity profile
![]() $u(r_{J+},z)$
is imposed. Various assumptions have been adopted in the literature, ranging from inviscid to fully viscous flows. Both regimes will be explored next.
$u(r_{J+},z)$
is imposed. Various assumptions have been adopted in the literature, ranging from inviscid to fully viscous flows. Both regimes will be explored next.
We first consider the flow to be inviscid downstream of the jump. Although the present work is focused on heavily viscous liquids, the inviscid subcritical flow would correspond to a jump that is relatively high. A boundary layer always exists, but it is relatively thin in this case. Consequently, the velocity right downstream of the jump would be essentially uniform. This is an assumption that has been widely adopted in the literature in various contexts (see, for instance, Watson Reference Watson1964; Bush & Aristoff Reference Bush and Aristoff2003; Dressaire et al. Reference Dressaire, Courbin, Crest and Stone2010; Prince et al. Reference Prince, Maynes and Crockett2012). At the very least, the inclusion of the uniform subcritical flow is helpful as a reference limit. The assumption of uniform flow does not necessarily have to hold over the entire domain downstream of the jump. It is not unreasonable to assume that the velocity is uniform right downstream of the jump, which allows the jump height to be readily determined from (5.3). Further downstream, the flow may be considered fully viscous, and can be determined by taking the jump height and velocity as initial conditions.
Thus, assuming uniform flow downstream of the jump, and using the mass conservation equation (2.6), equation (5.3) reduces to
Equation (5.4) takes an interesting form when cast in terms of the Froude number based on the jump radius and height. In this regard, there is a close connection with the recent experimental findings and claim of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), which we will now explore.
Duchesne et al. (Reference Duchesne, Lebon and Limat2014) introduced the Froude number defined in terms of the jump height and the average velocity immediately after the jump, namely
![]() $Fr_{J}=Fr/2r_{J}H_{J}^{3/2}$
in our notations. Their measurements suggest that
$Fr_{J}=Fr/2r_{J}H_{J}^{3/2}$
in our notations. Their measurements suggest that
![]() $Fr_{J}$
remains sensibly independent of the flow rate (constant with respect to
$Fr_{J}$
remains sensibly independent of the flow rate (constant with respect to
![]() $Fr$
). However, they could not explain or theoretically support this observation, which, in turn, begs the question whether the constancy of
$Fr$
). However, they could not explain or theoretically support this observation, which, in turn, begs the question whether the constancy of
![]() $Fr_{J}$
has any theoretical basis. This turns out to be indeed the case as we shall now demonstrate.
$Fr_{J}$
has any theoretical basis. This turns out to be indeed the case as we shall now demonstrate.
It is easy to see that (5.4) yields the following equation for
![]() $Fr_{J}$
:
$Fr_{J}$
:
This equation indicates that
![]() $Fr_{J}$
is indeed a constant that is independent of the
$Fr_{J}$
is indeed a constant that is independent of the
![]() $Fr$
or, equivalently, of the flow rate, confirming the observation of Duchesne et al. (Reference Duchesne, Lebon and Limat2014). This is a cubic equation in
$Fr$
or, equivalently, of the flow rate, confirming the observation of Duchesne et al. (Reference Duchesne, Lebon and Limat2014). This is a cubic equation in
![]() $Fr_{J}^{2/3}$
, admitting
$Fr_{J}^{2/3}$
, admitting
![]() $Fr_{J}=0.58$
as a solution. Thus, we have established the constancy of
$Fr_{J}=0.58$
as a solution. Thus, we have established the constancy of
![]() $Fr_{J}$
when the subcritical flow to be inviscid.
$Fr_{J}$
when the subcritical flow to be inviscid.
We next address the question whether
![]() $Fr_{J}$
remains actually independent of the flow rate if the subcritical flow is assumed to be viscous, and see whether this yields a closer constant
$Fr_{J}$
remains actually independent of the flow rate if the subcritical flow is assumed to be viscous, and see whether this yields a closer constant
![]() $Fr_{J}$
value to the one measured by Duchesne et al. (Reference Duchesne, Lebon and Limat2014). We follow Duchesne et al. (Reference Duchesne, Lebon and Limat2014), and adopt a lubrication flow approach. In this case, a differential equation for
$Fr_{J}$
value to the one measured by Duchesne et al. (Reference Duchesne, Lebon and Limat2014). We follow Duchesne et al. (Reference Duchesne, Lebon and Limat2014), and adopt a lubrication flow approach. In this case, a differential equation for
![]() $H$
can be obtained by neglecting the inertial terms in equation (2.5), yielding the following profile for the radial velocity:
$H$
can be obtained by neglecting the inertial terms in equation (2.5), yielding the following profile for the radial velocity:
Inserting
![]() $u$
into the mass conservation (2.6) and integrating, the equation governing the film thickness downstream of the jump becomes
$u$
into the mass conservation (2.6) and integrating, the equation governing the film thickness downstream of the jump becomes
which leads to the velocity profile just downstream of the jump as
Finally, inserting (5.8) into (5.3), we obtain the following equation for
![]() $Fr_{J}$
:
$Fr_{J}$
:
Similar to (5.5), equation (5.9) also confirms that
![]() $Fr_{J}$
is independent of
$Fr_{J}$
is independent of
![]() $Fr$
(flow rate), with
$Fr$
(flow rate), with
![]() $Fr_{J}=0.71$
.
$Fr_{J}=0.71$
.
What we have established so far, based on the discretized mass and momentum equations across the jump, is that
![]() $Fr_{J}$
is indeed constant (independent of the flow rate) as Duchesne et al. (Reference Duchesne, Lebon and Limat2014) claim from their measurements. Surprisingly, this is the case whether the subcritical flow is assumed to be inviscid or viscous obeying the lubrication regime, thus covering a wide range of viscosity and flow rate. The value of
$Fr_{J}$
is indeed constant (independent of the flow rate) as Duchesne et al. (Reference Duchesne, Lebon and Limat2014) claim from their measurements. Surprisingly, this is the case whether the subcritical flow is assumed to be inviscid or viscous obeying the lubrication regime, thus covering a wide range of viscosity and flow rate. The value of
![]() $Fr_{J}$
is found to be slightly lower for inviscid compared to viscous subcritical flow. However, both values remain higher than the measured value by Duchesne et al. (Reference Duchesne, Lebon and Limat2014):
$Fr_{J}$
is found to be slightly lower for inviscid compared to viscous subcritical flow. However, both values remain higher than the measured value by Duchesne et al. (Reference Duchesne, Lebon and Limat2014):
![]() $Fr_{J}\approx 0.35{-}0.40$
. It is important to observe that the values of
$Fr_{J}\approx 0.35{-}0.40$
. It is important to observe that the values of
![]() $Fr_{J}$
can be found theoretically without the knowledge of downstream conditions of the jump such as the disk radius or the thickness at the edge of the disk. Such conditions are not needed when the discretized conservation equations are invoked. Another important observation to make is whether the discretized (5.2) itself is valid. It is expected that (5.2) remains reasonably valid for low-viscosity liquids or at high flow rate since the jump is of negligible thickness and its location is well defined. However, for high-viscosity liquids such as the silicon oils used by Duchesne et al. (Reference Duchesne, Lebon and Limat2014), the jump is expected to be wide, and (5.2) cannot be entirely valid. This brings us to the second alternative when seeking the subcritical flow.
$Fr_{J}$
can be found theoretically without the knowledge of downstream conditions of the jump such as the disk radius or the thickness at the edge of the disk. Such conditions are not needed when the discretized conservation equations are invoked. Another important observation to make is whether the discretized (5.2) itself is valid. It is expected that (5.2) remains reasonably valid for low-viscosity liquids or at high flow rate since the jump is of negligible thickness and its location is well defined. However, for high-viscosity liquids such as the silicon oils used by Duchesne et al. (Reference Duchesne, Lebon and Limat2014), the jump is expected to be wide, and (5.2) cannot be entirely valid. This brings us to the second alternative when seeking the subcritical flow.
5.2 The influence of disk radius and edge thickness
We proceed by examining the flow in the subcritical range, downstream of the jump, without invoking (5.3). In this case, an approximate or asymptotic solution of (4.4) can be found by keeping the three dominant terms for large distance, reducing it to a lubrication-like equation for
![]() $H$
:
$H$
:
Subject to
![]() $H(r=r_{\infty })=H_{\infty }$
, (5.10) can be integrated analytically to give
$H(r=r_{\infty })=H_{\infty }$
, (5.10) can be integrated analytically to give
The prediction of the edge thickness was considered in our recent study for the flow on a rotating disk (Wang & Khayat Reference Wang and Khayat2018). The case of a stationary disk was also examined. Both static and dynamic contributions were considered, which yielded an accurate prediction established by comparing against experiment for the edge thickness. Direct measurements by Duchesne et al. (Reference Duchesne, Lebon and Limat2014) of the edge thickness, performed at nearly 5 mm of the disk perimeter in their experiment, give a nearly constant value of 1.5 mm with a weak power-law variation with the flow rate, not exceeding a few per cent. This constant thickness value, for a liquid of surface tension
![]() $\unicode[STIX]{x1D6FE}$
, is very close to the capillary length
$\unicode[STIX]{x1D6FE}$
, is very close to the capillary length
![]() $\sqrt{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g}$
of the fluid, which results from the balance of forces between the hydrostatic pressure and the surface tension at the disk perimeter. This value is also consistent with the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010). Consequently, we assumed that the film thickness at the edge of the disk is essentially equal to the film thickness the liquid exhibits under static conditions. Lubarda & Talke (Reference Lubarda and Talke2011) proposed an expression for this static thickness as
$\sqrt{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g}$
of the fluid, which results from the balance of forces between the hydrostatic pressure and the surface tension at the disk perimeter. This value is also consistent with the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010). Consequently, we assumed that the film thickness at the edge of the disk is essentially equal to the film thickness the liquid exhibits under static conditions. Lubarda & Talke (Reference Lubarda and Talke2011) proposed an expression for this static thickness as
![]() $h_{s}=2\sqrt{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g}\sin (\unicode[STIX]{x1D703}_{Y}/2)$
, based on the minimum free energy principle. Here
$h_{s}=2\sqrt{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g}\sin (\unicode[STIX]{x1D703}_{Y}/2)$
, based on the minimum free energy principle. Here
![]() $\unicode[STIX]{x1D703}_{Y}$
is the contact angle, which depends on both the liquid and the solid, and may then be deduced from experiment. For water, we achieved an excellent agreement with the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) for the jump radius by taking
$\unicode[STIX]{x1D703}_{Y}$
is the contact angle, which depends on both the liquid and the solid, and may then be deduced from experiment. For water, we achieved an excellent agreement with the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) for the jump radius by taking
![]() $\unicode[STIX]{x1D703}_{Y}=90^{\circ }$
. This value is within the range of values measured for water on polydimethylsiloxane (Diversified Enterprises 2009), which is the material used by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) for their disk. For water flowing on glass,
$\unicode[STIX]{x1D703}_{Y}=90^{\circ }$
. This value is within the range of values measured for water on polydimethylsiloxane (Diversified Enterprises 2009), which is the material used by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) for their disk. For water flowing on glass,
![]() $\unicode[STIX]{x1D703}_{Y}=35^{\circ }$
(Vicente, Andre & Ferreira Reference Vicente, Andre and Ferreira2012), a value used recently in our comparison with the measurements of Hansen et al. (Reference Hansen, Horluck, Zauner, Dimon, Ellegaard and Creagh1997) for water (Wang & Khayat Reference Wang and Khayat2018).
$\unicode[STIX]{x1D703}_{Y}=35^{\circ }$
(Vicente, Andre & Ferreira Reference Vicente, Andre and Ferreira2012), a value used recently in our comparison with the measurements of Hansen et al. (Reference Hansen, Horluck, Zauner, Dimon, Ellegaard and Creagh1997) for water (Wang & Khayat Reference Wang and Khayat2018).
In addition to the static contribution, and in order to explore the small variation of edge thickness with flow rate as observed by Duchesne et al. (Reference Duchesne, Lebon and Limat2014), we resorted to a minimum mechanical energy principle (Yang & Chen Reference Yang and Chen1992; Yang, Chen & Hsu Reference Yang, Chen and Hsu1997), which states that a fluid flowing over the edge of a disk under the influence of a hydrostatic pressure gradient will adjust itself so that the mechanical energy within the fluid will be minimum with respect to the film thickness at the disk edge. Consequently, the contribution to the thickness at the edge of the disk is determined by setting the derivative of the mechanical energy with respect to the film thickness equal to zero. In dimensionless form, the total energy is
![]() $E=\int _{0}^{H}(Fr^{2}(u^{2}/2)+z+p)\,\text{d}z$
. Since the pressure is hydrostatic:
$E=\int _{0}^{H}(Fr^{2}(u^{2}/2)+z+p)\,\text{d}z$
. Since the pressure is hydrostatic:
![]() $p=-z+H$
, yielding
$p=-z+H$
, yielding
![]() $E=\int _{0}^{H}(Fr^{2}(u^{2}/2)+H)\,\text{d}z$
. Consequently, we set
$E=\int _{0}^{H}(Fr^{2}(u^{2}/2)+H)\,\text{d}z$
. Consequently, we set
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}H\int _{0}^{H}(Fr^{2}(u^{2}/2)+H)\,\text{d}z=0$
at the edge of the disk. Using (5.8), we obtain the dimensionless film thickness at the edge as
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}H\int _{0}^{H}(Fr^{2}(u^{2}/2)+H)\,\text{d}z=0$
at the edge of the disk. Using (5.8), we obtain the dimensionless film thickness at the edge as
Here the Bond number is given by
![]() $Bo=\unicode[STIX]{x1D70C}ga^{2}/\unicode[STIX]{x1D6FE}$
. Clearly, in the presence of relatively strong gravity or surface tension and large disk radius, the second term tends to be dominated by the static contribution. As we shall see next, even the static contribution will turn out to be uninfluential for the heavily viscous liquids considered in the present work.
$Bo=\unicode[STIX]{x1D70C}ga^{2}/\unicode[STIX]{x1D6FE}$
. Clearly, in the presence of relatively strong gravity or surface tension and large disk radius, the second term tends to be dominated by the static contribution. As we shall see next, even the static contribution will turn out to be uninfluential for the heavily viscous liquids considered in the present work.
Indeed, once the thickness
![]() $H(r=r_{\infty })=H_{\infty }$
at the edge of the disk is determined as per (5.12), we obtain the film thickness distribution downstream of the jump from (5.10). In particular, and given that the jump location has already been determined, the jump height is now obtained through
$H(r=r_{\infty })=H_{\infty }$
at the edge of the disk is determined as per (5.12), we obtain the film thickness distribution downstream of the jump from (5.10). In particular, and given that the jump location has already been determined, the jump height is now obtained through
In this case, it is not difficult to confirm that, for a large disk and relatively small Reynolds number, the logarithmic term dominates on the right-hand side of (5.13). This is obviously the case of very viscous liquids. As a comparison, the Reynolds number for the flow of silicon oils (Duchesne et al.
Reference Duchesne, Lebon and Limat2014) is of the order of
![]() $10^{2}$
, whereas for water (Dressaire et al.
Reference Dressaire, Courbin, Crest and Stone2010) its order is closer to
$10^{2}$
, whereas for water (Dressaire et al.
Reference Dressaire, Courbin, Crest and Stone2010) its order is closer to
![]() $10^{4}$
. It is important to note that the range of Froude number in both sets of measurements is essentially the same. Based on the range of Froude numbers in figure 10 below, it is not difficult to deduce that the static contribution to the edge thickness is also dominated. In fact, experiment (Duchesne et al.
Reference Duchesne, Lebon and Limat2014) indicate that
$10^{4}$
. It is important to note that the range of Froude number in both sets of measurements is essentially the same. Based on the range of Froude numbers in figure 10 below, it is not difficult to deduce that the static contribution to the edge thickness is also dominated. In fact, experiment (Duchesne et al.
Reference Duchesne, Lebon and Limat2014) indicate that
![]() $H_{\infty }=O(1)$
at most, and
$H_{\infty }=O(1)$
at most, and
![]() $H_{\infty }\approx 0$
for a liquid of high viscosity.
$H_{\infty }\approx 0$
for a liquid of high viscosity.
We now turn, once again, to examining conditions where
![]() $Fr_{J}$
may remain independent of the flow rate. This time, (5.13) is used instead of (5.3). In this case, since the pre-jump height
$Fr_{J}$
may remain independent of the flow rate. This time, (5.13) is used instead of (5.3). In this case, since the pre-jump height
![]() $h_{J}$
and the jump radius
$h_{J}$
and the jump radius
![]() $r_{J}$
must be computed numerically, it is not possible to derive a closed form equation similar to (5.5) or (5.9), confirming that
$r_{J}$
must be computed numerically, it is not possible to derive a closed form equation similar to (5.5) or (5.9), confirming that
![]() $Fr_{J}$
is constant. In fact, (5.13) suggests that
$Fr_{J}$
is constant. In fact, (5.13) suggests that
![]() $Fr_{J}$
is not independent of
$Fr_{J}$
is not independent of
![]() $Fr$
. However, the dependence on
$Fr$
. However, the dependence on
![]() $Fr$
turns out to be weak, as figure 10 suggests. The figure shows the variation of
$Fr$
turns out to be weak, as figure 10 suggests. The figure shows the variation of
![]() $Fr_{J}$
against
$Fr_{J}$
against
![]() $Fr$
for the silicon oil of viscosity 20 cSt used by Duchesne et al. (Reference Duchesne, Lebon and Limat2014) in their measurements, which are also shown in the figure. The experimental data are reproduced in dimensionless form. Surprisingly, the figure indicates that
$Fr$
for the silicon oil of viscosity 20 cSt used by Duchesne et al. (Reference Duchesne, Lebon and Limat2014) in their measurements, which are also shown in the figure. The experimental data are reproduced in dimensionless form. Surprisingly, the figure indicates that
![]() $Fr_{J}$
not only is indeed sensibly constant but agrees closely with experiment. Some discrepancy is, however, noted for low flow rates, which is not surprising given the difficulty in measuring accurately the jump radius and height.
$Fr_{J}$
not only is indeed sensibly constant but agrees closely with experiment. Some discrepancy is, however, noted for low flow rates, which is not surprising given the difficulty in measuring accurately the jump radius and height.

Figure 10. Dependence of
![]() $Fr_{J}$
on the flow rate (Froude number). The solid line correspond to predictions based on relations (4.4) and (5.13). The experimental data corresponding to silicon oil are from Duchesne et al. (Reference Duchesne, Lebon and Limat2014). Also added as dashed and dash-dotted lines the result based on (5.5) and (5.9), respectively.
$Fr_{J}$
on the flow rate (Froude number). The solid line correspond to predictions based on relations (4.4) and (5.13). The experimental data corresponding to silicon oil are from Duchesne et al. (Reference Duchesne, Lebon and Limat2014). Also added as dashed and dash-dotted lines the result based on (5.5) and (5.9), respectively.
Now that the solution is available in the supercritical and subcritical regions, we are in a position to validate our model over the entire domain, against existing numerical results and experiment. We also take the opportunity to assess the validity of the parabolic profile. For the supercritical range, an equation similar to (4.4) is obtained when using the parabolic profile:
![]() $f(\unicode[STIX]{x1D702})=2\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}^{2}$
, namely
$f(\unicode[STIX]{x1D702})=2\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}^{2}$
, namely
We observe that the asymptotic form of (5.14) for large
![]() $r$
is precisely the lubrication (5.7), which when integrated yields
$r$
is precisely the lubrication (5.7), which when integrated yields
Figure 11 shows the comparison between the present theory and the numerical results of Rojas & Tirapegui (Reference Rojas and Tirapegui2015) as well as the measurements of Ellegaard et al. (Reference Ellegaard, Hansen, Haaning, Hansen and Bohr1996) for ethylene glycol. Both formulations based on the parabolic and cubic profiles are represented. The results for the free-surface velocity are reported in dimensionless form, with corresponding parameters being
![]() $Re=334$
,
$Re=334$
,
![]() $Fr=14.4$
and
$Fr=14.4$
and
![]() $Bo=1.21$
. The contact angle used to determine the edge thickness is
$Bo=1.21$
. The contact angle used to determine the edge thickness is
![]() $\unicode[STIX]{x1D703}_{Y}=70^{\circ }$
, yielding a total edge thickness of
$\unicode[STIX]{x1D703}_{Y}=70^{\circ }$
, yielding a total edge thickness of
![]() $H_{\infty }=1.7$
, including the height of the vertical edge. While the position of the jump is well reproduced by the present theory based on the cubic profile and the numerical method, figure 11 shows that the theory tends to slightly underestimate the level of the surface velocity in both the super- and subcritical ranges. Figure 11 indicates that the numerical approach of Rojas et al. tends to agree slightly better with experiment than the present theory. The figure also indicates a larger discrepancy when the parabolic profile is used.
$H_{\infty }=1.7$
, including the height of the vertical edge. While the position of the jump is well reproduced by the present theory based on the cubic profile and the numerical method, figure 11 shows that the theory tends to slightly underestimate the level of the surface velocity in both the super- and subcritical ranges. Figure 11 indicates that the numerical approach of Rojas et al. tends to agree slightly better with experiment than the present theory. The figure also indicates a larger discrepancy when the parabolic profile is used.
Figure 11. Free-surface velocity in the supercritical and subcritical domains. Comparison between the present theory (solid line), the numerical results of Rojas & Tirapegui (Reference Rojas and Tirapegui2015), as well as the experimental data of Ellegaard et al. (Reference Ellegaard, Hansen, Haaning, Hansen and Bohr1996). Also added is the velocity distribution based on the parabolic profile.
We next examine the shape of the entire film under general flow conditions. For this, we rescale (5.11) using (3.7) to reduce the problem in terms of the parameter
![]() $\unicode[STIX]{x1D6FC}$
:
$\unicode[STIX]{x1D6FC}$
:
Here
![]() $\bar{H}_{\infty }=2\sqrt{Re^{2/3}/Bo}\sin (\unicode[STIX]{x1D703}_{Y}/2)+((3/40)\unicode[STIX]{x1D6FC}/\bar{r}_{\infty }^{2})^{1/3}$
from (5.12). The overall effect of gravity is illustrated in figure 12, which depicts the film thickness over the entire disk. The jump height decreases with increasing gravity, simultaneously as the jump location is pushed upstream toward the stagnation point and away from the edge of the disk. We can also observe the logarithmic increase in height reported earlier in figure 7.
$\bar{H}_{\infty }=2\sqrt{Re^{2/3}/Bo}\sin (\unicode[STIX]{x1D703}_{Y}/2)+((3/40)\unicode[STIX]{x1D6FC}/\bar{r}_{\infty }^{2})^{1/3}$
from (5.12). The overall effect of gravity is illustrated in figure 12, which depicts the film thickness over the entire disk. The jump height decreases with increasing gravity, simultaneously as the jump location is pushed upstream toward the stagnation point and away from the edge of the disk. We can also observe the logarithmic increase in height reported earlier in figure 7.

Figure 12. Influence of gravity on the film thickness plotted against radial distance in regions (ii), (iii) and (iv).
While the use of (4.4) or (4.9) is imperative in the supercritical range ahead of the jump, allowing us to locate the jump, it is not necessarily so for the subcritical flow, where we have the choice to use different approximations. For instance, as the flow slows down downstream of the shock, we saw that the lubrication assumption holds well between the jump and the edge of the disk, yielding a good agreement with experiment (see figures 10 and 11). Our calculations of the subcritical flow so far are based on the asymptotic form (5.11) of (4.4) or (5.16) of (4.9) for large
![]() $r$
as it is convenient to use, given the analytical distribution of the thickness (and velocity) downstream of the jump and its direct relation to the edge thickness and the disk radius. Alternatively, we now consider using (4.4), and apply it directly to capture the subcritical flow, which should allow us to assess the validity of (5.11). Simultaneously, we examine the effect of the disk radius. The comparison is reported in figure 13 for the film thickness distribution with distance in the super- and subcritical ranges for three different values of the disk radius. We take
$r$
as it is convenient to use, given the analytical distribution of the thickness (and velocity) downstream of the jump and its direct relation to the edge thickness and the disk radius. Alternatively, we now consider using (4.4), and apply it directly to capture the subcritical flow, which should allow us to assess the validity of (5.11). Simultaneously, we examine the effect of the disk radius. The comparison is reported in figure 13 for the film thickness distribution with distance in the super- and subcritical ranges for three different values of the disk radius. We take
![]() $Re=628$
,
$Re=628$
,
![]() $Fr=63$
,
$Fr=63$
,
![]() $Bo=1.1$
and
$Bo=1.1$
and
![]() $\unicode[STIX]{x1D6E9}_{Y}=55^{\circ }$
. In this case, the values of the thickness at the edge of the disk are determined from (5.12) are
$\unicode[STIX]{x1D6E9}_{Y}=55^{\circ }$
. In this case, the values of the thickness at the edge of the disk are determined from (5.12) are
![]() $H_{\infty }=1.24$
, 1.2 and 1.18, corresponding to
$H_{\infty }=1.24$
, 1.2 and 1.18, corresponding to
![]() $r_{\infty }=70$
, 80 and 90, respectively.
$r_{\infty }=70$
, 80 and 90, respectively.
Several observations are worth making here. Figure 13 shows that the subcritical branches exhibit a turning point corresponding to the singularity of (4.4), which occurs slightly upstream of the jump location. As expected, the profile of the asymptotic solution (5.11) collapses onto the profile based on (4.4) at a distance not too far from the jump. This distance, nevertheless, increases with the disk radius. The asymptotic solution yields a jump height
![]() $H_{J}$
that is slightly above the one based on the exact solution of (4.4). Finally, despite the important spread in the values of the disk radius, the location of the singularity reached by the subcritical branches is essentially the same, as reflected in the saturation near the turning point. This seems to suggest that the location of the jump in reality, if it were to fall half-way, say, between the two locations of the singularity, is independent of downstream conditions. We seem to reach this observation regardless of which branch, super- or subcritical, we are referring to.
$H_{J}$
that is slightly above the one based on the exact solution of (4.4). Finally, despite the important spread in the values of the disk radius, the location of the singularity reached by the subcritical branches is essentially the same, as reflected in the saturation near the turning point. This seems to suggest that the location of the jump in reality, if it were to fall half-way, say, between the two locations of the singularity, is independent of downstream conditions. We seem to reach this observation regardless of which branch, super- or subcritical, we are referring to.
Next, we pursue our assessment of the validity of (4.4) and the asymptotic form (5.11) against experiment. The comparison is reported in figure 14 for the film thickness distribution with distance in the super- and subcritical regions against the measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for silicon oil (20 cSt). The data are reproduced here in dimensionless form from their figure 2, corresponding to
![]() $Re=169$
,
$Re=169$
,
![]() $Fr=14.88$
,
$Fr=14.88$
,
![]() $Bo=1.19$
,
$Bo=1.19$
,
![]() $\unicode[STIX]{x1D6E9}_{Y}=55^{\circ }$
and
$\unicode[STIX]{x1D6E9}_{Y}=55^{\circ }$
and
![]() $\bar{r}_{\infty }=94$
. In this case, the value of the thickness at the edge of the disk is determined from (5.12) as
$\bar{r}_{\infty }=94$
. In this case, the value of the thickness at the edge of the disk is determined from (5.12) as
![]() $\bar{H}_{\infty }=0.95$
. Several observations are worth making here. Figure 14 shows that the theoretical predictions, based on the solution of (4.4), are generally in good agreement with the experiment of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), slightly underestimating their measurements. The location of the jump is predicted to be close to the level of the turning point or the singularity of the supercritical branch upstream of the jump. The subcritical branch also exhibits a turning point corresponding to the singularity of (4.4), occurring slightly downstream of the jump location (see figure 13). The behaviour of the two branches is in close (qualitative) agreement with the theoretical predictions of Kasimov (Reference Kasimov2008) who incorporated the shape of the bottom (flat disk with a sharp cut off at the edge). The reader is particularly referred to figure 3(a) from Kasimov (Reference Kasimov2008). The asymptotic solution cannot mimic the downward turning trend observed in the experiment, yielding a jump height HJ that is slightly above the one based on the exact solution of (4.4). Interestingly, there is no need here to integrate from a critical point coinciding with at the edge of the disk to obtain the subcritical branch as Kasimov (Reference Kasimov2008) did. Kasimov estimated the location of the jump to be somewhere between the upstream and downstream singularities, which seems to be case here. However, this may not always be the case. Based on the agreement between theory and experiment in previous figures, we saw that the location of the jump coincides rather with the upstream singularity of the averaged momentum equation.
$\bar{H}_{\infty }=0.95$
. Several observations are worth making here. Figure 14 shows that the theoretical predictions, based on the solution of (4.4), are generally in good agreement with the experiment of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), slightly underestimating their measurements. The location of the jump is predicted to be close to the level of the turning point or the singularity of the supercritical branch upstream of the jump. The subcritical branch also exhibits a turning point corresponding to the singularity of (4.4), occurring slightly downstream of the jump location (see figure 13). The behaviour of the two branches is in close (qualitative) agreement with the theoretical predictions of Kasimov (Reference Kasimov2008) who incorporated the shape of the bottom (flat disk with a sharp cut off at the edge). The reader is particularly referred to figure 3(a) from Kasimov (Reference Kasimov2008). The asymptotic solution cannot mimic the downward turning trend observed in the experiment, yielding a jump height HJ that is slightly above the one based on the exact solution of (4.4). Interestingly, there is no need here to integrate from a critical point coinciding with at the edge of the disk to obtain the subcritical branch as Kasimov (Reference Kasimov2008) did. Kasimov estimated the location of the jump to be somewhere between the upstream and downstream singularities, which seems to be case here. However, this may not always be the case. Based on the agreement between theory and experiment in previous figures, we saw that the location of the jump coincides rather with the upstream singularity of the averaged momentum equation.

Figure 14. Free-surface profile. Comparison between theoretical predictions and the measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for silicon oil (20 cSt). Results plotted in dimensionless form with
![]() $Re=169$
,
$Re=169$
,
![]() $Fr=14.88$
,
$Fr=14.88$
,
![]() $Bo=1.19$
,
$Bo=1.19$
,
![]() $\unicode[STIX]{x1D6E9}_{Y}=55^{\circ }$
and
$\unicode[STIX]{x1D6E9}_{Y}=55^{\circ }$
and
![]() $\bar{r}_{\infty }=94$
. Theoretical profiles based on current theory or (4.4) (solid lines) and asymptotic subcritical (5.11) (dashed line).
$\bar{r}_{\infty }=94$
. Theoretical profiles based on current theory or (4.4) (solid lines) and asymptotic subcritical (5.11) (dashed line).
Finally, an interesting observation can be made regarding the (constant) value of
![]() $Fr_{J}$
and its independence of
$Fr_{J}$
and its independence of
![]() $Fr$
(or the flow rate). The measurements of the film profile for heavily viscous liquids seem to give a rough estimate of the height
$Fr$
(or the flow rate). The measurements of the film profile for heavily viscous liquids seem to give a rough estimate of the height
![]() $H_{J}$
immediately downstream of the relative the height
$H_{J}$
immediately downstream of the relative the height
![]() $h_{J}$
upstream of the jump. More precisely, experiment suggests that
$h_{J}$
upstream of the jump. More precisely, experiment suggests that
![]() $H_{J}\approx 2h_{J}$
(see, for instance, the measurements of Ellegaard et al. (Reference Ellegaard, Hansen, Haaning, Hansen and Bohr1996), and those in figure 2 of Duchesne et al. (Reference Duchesne, Lebon and Limat2014). By substituting
$H_{J}\approx 2h_{J}$
(see, for instance, the measurements of Ellegaard et al. (Reference Ellegaard, Hansen, Haaning, Hansen and Bohr1996), and those in figure 2 of Duchesne et al. (Reference Duchesne, Lebon and Limat2014). By substituting
![]() $h_{J}=H_{J}/2$
in (4.8) and recalling that
$h_{J}=H_{J}/2$
in (4.8) and recalling that
![]() $Fr_{J}=Fr/2r_{J}H_{J}^{3/2}$
, we deduce that
$Fr_{J}=Fr/2r_{J}H_{J}^{3/2}$
, we deduce that
which is very close to 0.33, the value measured by Duchesne et al. (Reference Duchesne, Lebon and Limat2014). Another way of obtaining the same result is to assume that the singularity yielding (4.8) occurs at a height half-way along the jump, where we expect the slope to be largest (infinite). In this case, one would replace
![]() $h_{J}$
in (4.8) by the average height, which, in turn, can be approximated as
$h_{J}$
in (4.8) by the average height, which, in turn, can be approximated as
![]() $(H_{J}+h_{J})/2\approx H_{J}/2$
if one assumes that
$(H_{J}+h_{J})/2\approx H_{J}/2$
if one assumes that
![]() $h_{J}\ll H_{J}$
(Watson Reference Watson1964), and obtain (5.17). The estimated value in (5.17) confirms the important observation in this study that the jump characteristics appear to be dictated only by the supercritical flow and upstream conditions.
$h_{J}\ll H_{J}$
(Watson Reference Watson1964), and obtain (5.17). The estimated value in (5.17) confirms the important observation in this study that the jump characteristics appear to be dictated only by the supercritical flow and upstream conditions.
6 Concluding remarks and discussion
In this study, the flow of a high-viscosity jet impinging on a stationary disk is examined theoretically. The present study focuses on the role of gravity in the prediction of both the location and height of the circular hydraulic jump, and is restricted to laminar circular steady jump of type I, which exhibits a sharp transition and is marked by unidirectional surface flow with boundary-layer separation beyond the jump (Bohr et al. Reference Bohr, Ellegaard, Hansen and Haaning1996; Bush & Aristoff Reference Bush and Aristoff2003). See figure 1. Despite the numerous theoretical and numerical studies in the literature, this prediction remains somewhat difficult to achieve through a simple and practical theoretical model. This issue was recently addressed in our work on a jet impinging on a rotating disk, but was limited to low-viscosity liquids (Wang & Khayat Reference Wang and Khayat2018). Typical theoretical models in the literature seem to rely on some empirical input to generate boundary conditions, or lack the additional relation needed along with the discretized momentum balance across the jump when an approach similar to Watson’s is used. The additional relation is needed in order to determine uniquely the location and height of the jump. In the present study, we show how a closure to the problem can be brought by establishing a simple relation between the jump location and pre-jump height by including the effect of gravity in the developing boundary layer and the supercritical region of the flow domain. In fact, we show that the Froude number based on the pre-jump height and jump radius is constant (see relation (4.8) or (4.10)).
The flow is assumed to remain steady and axisymmetric. A model is developed based on the Kármán–Pohlhausen integral approach to describe the behaviour of the flow in the developing boundary-layer region (ii) and the fully developed viscous region (iii). The integral form of the continuity and momentum equations, governing the flow of a thin film, is treated numerically separately in each region, and the flow is matched at the transition point. Unlike the flow in the absence of gravity, the problem does not admit a similarity solution. However, a self-similar cubic profile is nevertheless assumed for the velocity, which is commonly used and was previously shown to be accurate. Although two dimensionless parameters are involved in the absence of surface tension, namely the Reynolds number
![]() $Re$
and the Froude number
$Re$
and the Froude number
![]() $Fr$
defined in terms of the jet radius and the flow rate, we show that the problem can be cast in terms of only one parameter:
$Fr$
defined in terms of the jet radius and the flow rate, we show that the problem can be cast in terms of only one parameter:
![]() $\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$
.
$\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$
.
We find that gravity tends to enhance inertia, leading to a drop in the boundary-layer height as well as the film thickness in region (ii). Near the stagnation point, the boundary layer departs from the
![]() $\sqrt{r/Re}$
behaviour to grow increasingly linearly with distance like
$\sqrt{r/Re}$
behaviour to grow increasingly linearly with distance like
![]() $\unicode[STIX]{x1D6FF}\approx \sqrt{3}(Fr/\sqrt{Re})r$
under the influence of gravity. The transition point, where the outer edge of the boundary layer intersects the film surface, moves towards the perimeter of the disk with increasing gravity while the film thickness at the transition location diminishes (figures 2 and 3).
$\unicode[STIX]{x1D6FF}\approx \sqrt{3}(Fr/\sqrt{Re})r$
under the influence of gravity. The transition point, where the outer edge of the boundary layer intersects the film surface, moves towards the perimeter of the disk with increasing gravity while the film thickness at the transition location diminishes (figures 2 and 3).
In the fully viscous region (iii), the shallow-water equations are reduced to a first-order equation for the thickness (4.4) or (4.9). We show that this equation exhibits an essential singularity in the presence of gravity at a distance identified as the jump location. As the flow slows down, inertia weakens and friction increases with radial distance. At some distance gravity and viscous effects become equal, causing the singularity and therefore the jump to occur.
The numerical solution indicates that the film thickness decreases rapidly near impingement and exhibits a minimum that strengthens with gravity (figure 4), accompanied by an increase in the surface velocity that decays at a slower rate with radial distance (figure 5). Interestingly, unlike the film thickness, the surface velocity decays monotonically with distance. In contrast, the shear stress along the wall exhibits a weak maximum that shifts downstream as the effect of gravity increases (figure 6).
We show that, for a flat disk, the jump radius can be determined independently of its height or downstream conditions, in agreement with experimental observations. Based on their measurements, Brechet & Neda (Reference Brechet and Neda1999) concluded that ‘the boundary conditions on a perfectly flat plate do not influence the radius of the hydraulic jump’. These findings are validated against existing experimental data and numerical simulation. Comparison between the predicted and measured jump locations in figure 8 confirm that, for a circular jump, the jump radius is independent of the subcritical flow downstream of the jump, nor is it affected by the radius of the disk or the thickness at the edge of a flat disk. Despite the simplicity of the present approach, the predicted jump location shows surprisingly close agreement with existing numerical results based on a spectral methodology.
We consider two alternatives to determine the jump height and assess the empirical claim of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) concerning the constancy of the Froude number
![]() $Fr_{J}$
based on the jump radius and height, and its independence of the flow rate. The first approach, following Watson and many others, consists of applying a momentum balance across the (infinitely thin) hydraulic jump, yielding (5.3). We demonstrate theoretically that for both uniform and lubrication flows downstream of the jump, the Froude number is indeed constant as Duchesne et al. (Reference Duchesne, Lebon and Limat2014) claim. However, the predicted values in both cases are higher than their measured value. This simultaneously suggests that the discretized momentum balance approach is not adequate, which is not surprising given the finite thickness of the jump for high-viscosity liquids. This brings us to the second alternative, which consists of solving the film (4.4), either directly or by deducing an asymptotic form far from impingement, taking the thickness
$Fr_{J}$
based on the jump radius and height, and its independence of the flow rate. The first approach, following Watson and many others, consists of applying a momentum balance across the (infinitely thin) hydraulic jump, yielding (5.3). We demonstrate theoretically that for both uniform and lubrication flows downstream of the jump, the Froude number is indeed constant as Duchesne et al. (Reference Duchesne, Lebon and Limat2014) claim. However, the predicted values in both cases are higher than their measured value. This simultaneously suggests that the discretized momentum balance approach is not adequate, which is not surprising given the finite thickness of the jump for high-viscosity liquids. This brings us to the second alternative, which consists of solving the film (4.4), either directly or by deducing an asymptotic form far from impingement, taking the thickness
![]() $H_{\infty }$
of the film at the edge of the disk as the boundary condition and integrating (upstream) towards the jump location to determine the height. This approach turns out to be the method of choice as it yields close agreement with the measured Froude number for silicon oil (see figure 10). The value of
$H_{\infty }$
of the film at the edge of the disk as the boundary condition and integrating (upstream) towards the jump location to determine the height. This approach turns out to be the method of choice as it yields close agreement with the measured Froude number for silicon oil (see figure 10). The value of
![]() $H_{\infty }$
is determined theoretically as a combined static and dynamic contributions as was done for low-viscosity liquids (Wang & Khayat Reference Wang and Khayat2018) but turns out to be relatively much smaller for high-viscosity liquids. Finally, the influence of gravity on the film shape in the entire flow domain is assessed (figure 13).
$H_{\infty }$
is determined theoretically as a combined static and dynamic contributions as was done for low-viscosity liquids (Wang & Khayat Reference Wang and Khayat2018) but turns out to be relatively much smaller for high-viscosity liquids. Finally, the influence of gravity on the film shape in the entire flow domain is assessed (figure 13).
We observe that the self-similar cubic profiles (3.4) and (4.1) are obviously adopted here for their simplicity, and turned out to be consistently accurate in our comparisons with existing numerical results and experiment. The self-similar cubic profile does not satisfy the momentum equation at the disk, which would break the similarity. The accuracy of the profile used here, despite its simplicity, seems to suggest that, in the KP averaging formulation, the effect of gravity or the pressure gradient in general is not significant at the level of thee solid disk where shearing is dominant. On the other hand, a non-self-similar cubic profile would yield a smooth jump as opposed to the presently predicted shock. Building on the earlier work of Bohr et al. (Reference Bohr, Putkaradze and Watanabe1997), Watanabe et al. (Reference Watanabe, Putkaradze and Bohr2003) used a non-self-similar cubic profile: expression (2.20) in their paper. They obtained the system (2.26) of two ordinary differential equations from their averaged momentum and mass conservation equations. The two unknowns were the film thickness
![]() $h(r)$
and a shape parameter
$h(r)$
and a shape parameter
![]() $\unicode[STIX]{x1D706}(r)$
related to the profile coefficients in (2.20). A singularity occurs when
$\unicode[STIX]{x1D706}(r)$
related to the profile coefficients in (2.20). A singularity occurs when
![]() $h=0$
or
$h=0$
or
![]() $\unicode[STIX]{x1D706}=7/2$
, which is not encountered for the flow they sought. In particular, when
$\unicode[STIX]{x1D706}=7/2$
, which is not encountered for the flow they sought. In particular, when
![]() $\unicode[STIX]{x1D706}=7/2$
, their equation (2.24b) reduces to
$\unicode[STIX]{x1D706}=7/2$
, their equation (2.24b) reduces to
![]() $h^{\prime }=-41/2rh^{3}$
when their relation (2.14) is used. This expression for the slope indicates that, for the singularity to occur, the slope must be necessarily negative, which is practically not the case for the flow they considered. Their solution was sought by imposing the film heights at two locations obtained from experiment. In that case, the slope is positive or at most mildly negative, and the singularity was thus avoided. This is particularly the case in the subcritical region where the film thickness is high. We refer the reader to figures 4 and 5 in Watanabe et al. (Reference Watanabe, Putkaradze and Bohr2003). We also note that
$h^{\prime }=-41/2rh^{3}$
when their relation (2.14) is used. This expression for the slope indicates that, for the singularity to occur, the slope must be necessarily negative, which is practically not the case for the flow they considered. Their solution was sought by imposing the film heights at two locations obtained from experiment. In that case, the slope is positive or at most mildly negative, and the singularity was thus avoided. This is particularly the case in the subcritical region where the film thickness is high. We refer the reader to figures 4 and 5 in Watanabe et al. (Reference Watanabe, Putkaradze and Bohr2003). We also note that
![]() $\unicode[STIX]{x1D706}$
was always negative.
$\unicode[STIX]{x1D706}$
was always negative.
However, the singularity is not always avoidable. In particular, when the disk radius is sufficiently large, the film thickness at the edge of the disk can be small enough for
![]() $h^{\prime }$
to remain negative downstream of the jump, thus causing the singularity to occur in the subcritical region. See, for instance, figures 1 and 2 in Duchesne et al. (Reference Duchesne, Lebon and Limat2014), and our own figures 12–14. Consequently, although a non-self-similar cubic profile may yield a smooth jump zone, one may still have to deal with the singularity further downstream. In fact, Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) did encounter the singularity downstream, and attributed its presence to the edge of the disk.
$h^{\prime }$
to remain negative downstream of the jump, thus causing the singularity to occur in the subcritical region. See, for instance, figures 1 and 2 in Duchesne et al. (Reference Duchesne, Lebon and Limat2014), and our own figures 12–14. Consequently, although a non-self-similar cubic profile may yield a smooth jump zone, one may still have to deal with the singularity further downstream. In fact, Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) did encounter the singularity downstream, and attributed its presence to the edge of the disk.
In closing, we highlight the main points that distinguish our method from the main theoretical literature:
Our approach involves the actual physical domain, ranging from the point of impingement to the edge of the disk, as opposed to the domain located between two arbitrarily chosen points as in Bohr et al. (Reference Bohr, Putkaradze and Watanabe1997) and Watanabe et al. (Reference Watanabe, Putkaradze and Bohr2003).
In this regard, our model does not require any degree of empiricism (other than the flow parameters) such as the imposition of the film heights at the boundary(ies) from experiment (Bohr et al. Reference Bohr, Putkaradze and Watanabe1997; Watanabe et al. Reference Watanabe, Putkaradze and Bohr2003; Rojas et al. Reference Rojas, Argentina and Tirapegui2013).
Given the essential singularity, the domain is clearly separated, at the level of the shock, into a supercritical flow ahead of the jump and a subcritical flow after the jump. Therefore, there is no overlap in the solution domains on the two sides of the shock as in Kasimov (Reference Kasimov2008).
Both the supercritical and subcritical flows are sought separately as initial-value problems, starting at theoretically determined initial conditions that correspond to the transition point upstream of the jump and the thickness at the edge downstream.
The jump location is precisely identified to coincide with the location of the singularity of the averaged momentum thin-film equation. In other words, the singularity is inherent to the momentum and not necessarily to the energy equation as in Bhagat et al. (Reference Bhagat, Jha, Linden and Wilson2018).
We attribute the emergence of the jump as the result of the balance between gravity and viscosity, at a point where inertia has sufficiently weakened by the mounting friction, coinciding with the location of the singularity, and not somewhere between the two singularities of the averaged momentum equation as Kasimov (Reference Kasimov2008) suggested.
The jump location (not height) is determined independently of downstream conditions, such as the disk radius and the edge thickness, in agreement with experiment (Brechet & Neda Reference Brechet and Neda1999).
The jump height as well as the entire subcritical flow can be sought a posteriori, subject to a well-established boundary conditions at the edge of the disk (static and dynamic contributions at the edge).
Finally, we show the conditions where the Froude number based on the jump height and location is independent of the flow rate, in agreement with the measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014).
In conclusion, we demonstrate the crucial role of gravity and its influence on the emergence of the circular hydraulic jump for liquids of relatively large viscosity. We propose a simple and complete theoretical model to predict the location of the jump as well as the flow in the entire domain.
Acknowledgements
The financial support of the Natural Sciences and Engineering Council of Canada is gratefully acknowledged. R.E.K. would like to acknowledge the helpful discussions he had with Professor E. Benilov during his stay at the University of Limerick.