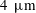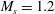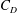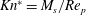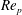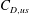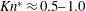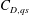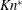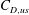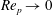1 Introduction
Shocked multiphase flows involve complex transfer of mass, momentum and energy between the dispersed and carrier phases. The passage of a shock wave through a multiphase medium causes the particles to first accelerate behind the shock and eventually relax into mechanical and thermal equilibrium with the post-shock carrier phase (Rudinger Reference Rudinger1964). The two-phase interactions in the relaxation zone often result in evaporation, deformation and breakup of the dispersed particles as well as modulation of the carrier phase turbulence (Gore & Crowe Reference Gore and Crowe1989; Smolders & van Dongen Reference Smolders and van Dongen1992; Strecker & Roth Reference Strecker and Roth1994).
The physics of particles accelerating behind a shock wave requires an understanding of the drag experienced by individual particles during the relaxation phase. Over the past few decades, the experimental work on unsteady drag behind a shock wave has primarily been limited to the bulk motion of a particle cloud (Rudinger Reference Rudinger1970; Murakama & Ishikawa Reference Murakama and Ishikawa1978; Miura & Glass Reference Miura and Glass1983; Boiko et al.
Reference Boiko, Kiselev, Kiselev, Papyrin, Poplavsky and Fomin1997; Geng & Groenig Reference Geng and Groenig2000). Rudinger (Reference Rudinger1970) measured particle drag coefficients (
![]() $C_{D}$
) from the traces of bulk particle trajectories and found the local
$C_{D}$
) from the traces of bulk particle trajectories and found the local
![]() $C_{D}$
to be two orders of magnitude larger than the expected values from standard drag equations. They proposed a qualitative model for the drag of the cloud accounting for the nonlinear phase interactions that cause longitudinal and lateral perturbations to individual particles from their mean trajectory. Sommerfeld (Reference Sommerfeld1985) measured particle velocity using laser Doppler anemometry and proposed an empirical correlation for particle
$C_{D}$
to be two orders of magnitude larger than the expected values from standard drag equations. They proposed a qualitative model for the drag of the cloud accounting for the nonlinear phase interactions that cause longitudinal and lateral perturbations to individual particles from their mean trajectory. Sommerfeld (Reference Sommerfeld1985) measured particle velocity using laser Doppler anemometry and proposed an empirical correlation for particle
![]() $C_{D}$
in the range
$C_{D}$
in the range
![]() $50<Re_{p}<500$
. Igra & Takayama (Reference Igra and Takayama1993) measured
$50<Re_{p}<500$
. Igra & Takayama (Reference Igra and Takayama1993) measured
![]() $C_{D}$
based on double-exposure holography images for spherical particles placed initially on the shock tube floor. These measurements also showed significantly large unsteady drag coefficients. Jourdan et al. (Reference Jourdan, Houas, Igra, Estivalezes, Devals and Meshkov2007) extended the drag measurement of a single particle to the relaxation zone using shadowgraphy and estimated
$C_{D}$
based on double-exposure holography images for spherical particles placed initially on the shock tube floor. These measurements also showed significantly large unsteady drag coefficients. Jourdan et al. (Reference Jourdan, Houas, Igra, Estivalezes, Devals and Meshkov2007) extended the drag measurement of a single particle to the relaxation zone using shadowgraphy and estimated
![]() $C_{D}$
on particles of millimetre size (
$C_{D}$
on particles of millimetre size (
![]() $d_{p}=0.62{-}6.5$
mm) attached to a spider web. Their measurements for a range of particle densities (
$d_{p}=0.62{-}6.5$
mm) attached to a spider web. Their measurements for a range of particle densities (
![]() $\unicode[STIX]{x1D70C}_{p}=25{-}1096~\text{kg}~\text{m}^{-3}$
) yielded
$\unicode[STIX]{x1D70C}_{p}=25{-}1096~\text{kg}~\text{m}^{-3}$
) yielded
![]() $C_{D}$
values over 50 % higher than standard predictions. Sun et al. (Reference Sun, Saito, Takayama and Tanno2005) observed a steep increase in drag for large spheres (
$C_{D}$
values over 50 % higher than standard predictions. Sun et al. (Reference Sun, Saito, Takayama and Tanno2005) observed a steep increase in drag for large spheres (
![]() $d_{p}=80$
mm) suspended on a thin wire during the passage of a shock.
$d_{p}=80$
mm) suspended on a thin wire during the passage of a shock.
The dynamics of dispersed particles in gas have been studied under various unsteady conditions (Kulick, Fessler & Eaton Reference Kulick, Fessler and Eaton1994; Tanaka & Eaton Reference Tanaka and Eaton2010). The total unsteady force (
![]() $F_{p}$
) on a small rigid sphere is modelled using quasi-steady (
$F_{p}$
) on a small rigid sphere is modelled using quasi-steady (
![]() $F_{qs}$
), inviscid unsteady (
$F_{qs}$
), inviscid unsteady (
![]() $F_{iu}$
, pressure gradient and added mass), viscous unsteady (
$F_{iu}$
, pressure gradient and added mass), viscous unsteady (
![]() $F_{vu}$
, Basset history force), gravity (
$F_{vu}$
, Basset history force), gravity (
![]() $F_{g}$
) and lift (
$F_{g}$
) and lift (
![]() $F_{l}$
) forces (Maxey & Riley Reference Maxey and Riley1983; Magnaudet & Eames Reference Magnaudet and Eames2000). Theoretical and empirical models for the forces on shock accelerated particles have been proposed by Miles (Reference Miles1951), Longhorn (Reference Longhorn1952), Henderson (Reference Henderson1976), Saito et al. (Reference Saito, Saba, Sun and Takayama2007), Loth (Reference Loth2008) and Parmar, Haselbacher & Balachandar (Reference Parmar, Haselbacher and Balachandar2008, Reference Parmar, Haselbacher and Balachandar2009, Reference Parmar, Haselbacher and Balachandar2010). Henderson (Reference Henderson1976), Loth (Reference Loth2008) and Parmar et al. (Reference Parmar, Haselbacher and Balachandar2010) proposed empirical correlations for the quasi-steady drag on spherical particles in compressible multiphase flows. Parmar et al. (Reference Parmar, Haselbacher and Balachandar2008) and Parmar et al. (Reference Parmar, Haselbacher and Balachandar2009) proposed a model for the inviscid component of drag based on an unsteady force kernel. They showed that the unsteady drag on a particle reaches a peak that is an order of magnitude higher than the standard drag during the passage of the shock across the particle, and this peak is primarily caused by the inviscid unsteady (
$F_{l}$
) forces (Maxey & Riley Reference Maxey and Riley1983; Magnaudet & Eames Reference Magnaudet and Eames2000). Theoretical and empirical models for the forces on shock accelerated particles have been proposed by Miles (Reference Miles1951), Longhorn (Reference Longhorn1952), Henderson (Reference Henderson1976), Saito et al. (Reference Saito, Saba, Sun and Takayama2007), Loth (Reference Loth2008) and Parmar, Haselbacher & Balachandar (Reference Parmar, Haselbacher and Balachandar2008, Reference Parmar, Haselbacher and Balachandar2009, Reference Parmar, Haselbacher and Balachandar2010). Henderson (Reference Henderson1976), Loth (Reference Loth2008) and Parmar et al. (Reference Parmar, Haselbacher and Balachandar2010) proposed empirical correlations for the quasi-steady drag on spherical particles in compressible multiphase flows. Parmar et al. (Reference Parmar, Haselbacher and Balachandar2008) and Parmar et al. (Reference Parmar, Haselbacher and Balachandar2009) proposed a model for the inviscid component of drag based on an unsteady force kernel. They showed that the unsteady drag on a particle reaches a peak that is an order of magnitude higher than the standard drag during the passage of the shock across the particle, and this peak is primarily caused by the inviscid unsteady (
![]() $F_{iu}$
) force. This model reinforces the observations of Sun et al. (Reference Sun, Saito, Takayama and Tanno2005) but is not extended beyond a very short time period,
$F_{iu}$
) force. This model reinforces the observations of Sun et al. (Reference Sun, Saito, Takayama and Tanno2005) but is not extended beyond a very short time period,
![]() $O(\unicode[STIX]{x1D70F}_{s}=d_{p}/u_{s})$
, compared with the total relaxation time, where
$O(\unicode[STIX]{x1D70F}_{s}=d_{p}/u_{s})$
, compared with the total relaxation time, where
![]() $\unicode[STIX]{x1D70F}_{s}$
,
$\unicode[STIX]{x1D70F}_{s}$
,
![]() $d_{p}$
and
$d_{p}$
and
![]() $u_{s}$
are the acoustic time scale, particle diameter and shock speed.
$u_{s}$
are the acoustic time scale, particle diameter and shock speed.
Some progress has been made in modelling unsteady viscous forces. Mei & Adrian (Reference Mei and Adrian1992) used a linearised asymptotic analysis based on the numerical results by Mei, Lawrencce & Adrian (Reference Mei, Lawrencce and Adrian1991) for small oscillations about a mean flow around a sphere and proposed an approximate model for the Basset history kernel. Parmar, Haselbacher & Balachandar (Reference Parmar, Haselbacher and Balachandar2011) accounted for the compressibility effects and proposed a model for the linearised Basset–Boussinesq–Oseen (BBO) equation in the limit of
![]() $M_{p}\rightarrow 0$
and
$M_{p}\rightarrow 0$
and
![]() $Re_{p}\rightarrow 0$
accounting for the history kernel in
$Re_{p}\rightarrow 0$
accounting for the history kernel in
![]() $F_{vu}$
. The understanding of the viscous unsteady component of drag for shock driven flows is limited to these linearised models, but the unsteady drag on the particle through the relaxation phase is likely to be caused by nonlinear effects.
$F_{vu}$
. The understanding of the viscous unsteady component of drag for shock driven flows is limited to these linearised models, but the unsteady drag on the particle through the relaxation phase is likely to be caused by nonlinear effects.
Many experimental studies observe high drag coefficients for bulk and individual particles, but the physical mechanisms behind the high drag remain unclear. We have designed shock tube experiments to precisely measure particle displacements for shock accelerated microparticles. The effects of compressibility observed by Boiko et al. (Reference Boiko, Kiselev, Kiselev, Papyrin, Poplavsky and Fomin1997) and Wagner et al. (Reference Wagner, Beresh, Kearney, Pruett and Wright2012) are avoided by keeping the particle Mach number in the subsonic range (
![]() $M_{p}<0.6$
). Unlike most of the previous studies, unsteady drag is calculated for individual particles through particle relaxation.
$M_{p}<0.6$
). Unlike most of the previous studies, unsteady drag is calculated for individual particles through particle relaxation.
2 Experimental set-up and methods
Experiments are conducted in a 6.5 m horizontal shock tube (HST) with a
![]() $76.2\times 76.2~\text{mm}^{2}$
cross-section. The shock tube generates repeatable shock waves using a diaphragmless pneumatic driver that keeps the shock tube free of contamination from diaphragm fragments (Martinez, Orlicz & Prestridge Reference Martinez, Orlicz and Prestridge2015; Mejia-Alvarez et al.
Reference Mejia-Alvarez, Wilson, Leftwich, Martinez and Prestridge2015). Six pressure transducers (PT1–PT6, PCB Piezotronics Inc. Model 113B27), with PT4 being exactly at the centre of the measurement section, are incorporated along the length of the tube to measure shock speed and to trigger the imaging diagnostics. A detailed description of the HST can be found in Martinez et al. (Reference Martinez, Orlicz and Prestridge2015). The driver pressure is set between 0.14 and 0.4 MPa to obtain incident shock Mach numbers of
$76.2\times 76.2~\text{mm}^{2}$
cross-section. The shock tube generates repeatable shock waves using a diaphragmless pneumatic driver that keeps the shock tube free of contamination from diaphragm fragments (Martinez, Orlicz & Prestridge Reference Martinez, Orlicz and Prestridge2015; Mejia-Alvarez et al.
Reference Mejia-Alvarez, Wilson, Leftwich, Martinez and Prestridge2015). Six pressure transducers (PT1–PT6, PCB Piezotronics Inc. Model 113B27), with PT4 being exactly at the centre of the measurement section, are incorporated along the length of the tube to measure shock speed and to trigger the imaging diagnostics. A detailed description of the HST can be found in Martinez et al. (Reference Martinez, Orlicz and Prestridge2015). The driver pressure is set between 0.14 and 0.4 MPa to obtain incident shock Mach numbers of
![]() $M_{s}=1.2$
, 1.3 and 1.4. Table 1 summarises the detailed experimental parameters for each Mach number.
$M_{s}=1.2$
, 1.3 and 1.4. Table 1 summarises the detailed experimental parameters for each Mach number.
Table 1. Experimental parameters and values. Here, the pre-shock speed of sound,
![]() $c=344~\text{m}~\text{s}^{-1}$
at 294.8 K. Post-shock properties, including the speed of sound,
$c=344~\text{m}~\text{s}^{-1}$
at 294.8 K. Post-shock properties, including the speed of sound,
![]() $c_{2}$
, are calculated using one-dimensional normal shock relations (Anderson Reference Anderson1990).
$c_{2}$
, are calculated using one-dimensional normal shock relations (Anderson Reference Anderson1990).

Nylon particles (TSI 10084) with mean diameter
![]() $d_{p}=4~\unicode[STIX]{x03BC}\text{m}$
and mass density
$d_{p}=4~\unicode[STIX]{x03BC}\text{m}$
and mass density
![]() $\unicode[STIX]{x1D70C}_{p}=1140~\text{kg}~\text{m}^{-3}$
are used for all experiments. The particles are driven through a pipe, enter the shock tube through an inlet port with area
$\unicode[STIX]{x1D70C}_{p}=1140~\text{kg}~\text{m}^{-3}$
are used for all experiments. The particles are driven through a pipe, enter the shock tube through an inlet port with area
![]() $484~\text{mm}^{2}$
located near the driver and exit through a similar port located near the end of the tube. A fan keeps the average pre-shock speed of a particle to approximately
$484~\text{mm}^{2}$
located near the driver and exit through a similar port located near the end of the tube. A fan keeps the average pre-shock speed of a particle to approximately
![]() $0.6~\text{m}~\text{s}^{-1}$
, which is negligibly small compared with the speed of the shock and the post-shock gas. The post-shock gas velocity (
$0.6~\text{m}~\text{s}^{-1}$
, which is negligibly small compared with the speed of the shock and the post-shock gas. The post-shock gas velocity (
![]() $u_{g}$
) is estimated based on the Rankine–Hugoniot relationship for normal shocks, and the estimate is confirmed experimentally. The particles are dispersed in a dilute concentration (
$u_{g}$
) is estimated based on the Rankine–Hugoniot relationship for normal shocks, and the estimate is confirmed experimentally. The particles are dispersed in a dilute concentration (
![]() $C\approx 10^{-7}$
) such that there is no particle–particle interaction, and the particles do not affect the post-shock properties of the gas (Rudinger Reference Rudinger1964).
$C\approx 10^{-7}$
) such that there is no particle–particle interaction, and the particles do not affect the post-shock properties of the gas (Rudinger Reference Rudinger1964).

Figure 1. Schematic of the test section in the horizontal shock tube. The shock moves from right to left. The inset shows the field of view (FOV) with an example shock position. The camera images the shadowgraph and scattered light from the particles within the laser sheet.
The current measurements are conducted in the test section schematically shown in figure 1. Particles are illuminated by four dual-head Nd : YAG 532 nm lasers (Quantel Twins CFR300, repetition rate 15 Hz), each head being timed independently to produce a single pulse of light sheet with a width of 1 mm. The particles and shock are imaged simultaneously at 5.83 m from the driver using an eight-frame SIMD high-speed framing camera positioned orthogonal to the laser sheet. The output laser pulse timing is measured with a photodiode, and particle images are calibrated using a precision chrome-on-glass cross-hair grid (Edmund Optics FA79E-58509). The depth of field of 0.75 mm was measured using a DOF 5-15 target with the camera aperture set at
![]() $f/22$
(Martinez et al.
Reference Martinez, Orlicz and Prestridge2015). The image resolution is
$f/22$
(Martinez et al.
Reference Martinez, Orlicz and Prestridge2015). The image resolution is
![]() $2.14~\unicode[STIX]{x03BC}\text{m}~\text{pixel}^{-1}$
at a magnification of 3, and the total field of view is
$2.14~\unicode[STIX]{x03BC}\text{m}~\text{pixel}^{-1}$
at a magnification of 3, and the total field of view is
![]() $2.74\times 2.05~\text{mm}^{2}$
. The shock position is measured on either frame two or three with a shadowgraph from a pulsed LED light source (Luminus 18A, CBT-120 Green LED).
$2.74\times 2.05~\text{mm}^{2}$
. The shock position is measured on either frame two or three with a shadowgraph from a pulsed LED light source (Luminus 18A, CBT-120 Green LED).
The absolute shock location and shock speed (
![]() $V_{s}$
) determine when each particle interacts with the shock. We calculate the shock speed using the pressure traces from transducers PT1–PT4 and the position from shadowgraph images. Figure 2(a) shows sample pressure traces obtained from transducers PT3 and PT4 for an experiment with
$V_{s}$
) determine when each particle interacts with the shock. We calculate the shock speed using the pressure traces from transducers PT1–PT4 and the position from shadowgraph images. Figure 2(a) shows sample pressure traces obtained from transducers PT3 and PT4 for an experiment with
![]() $M_{s}=1.3$
. As the shock wave traverses the transducer head, the pressure signal rises from zero to a maximum value. Assuming that the shock reaches the centre of a transducer when the pressure is half that of the maximum, the shock speed (
$M_{s}=1.3$
. As the shock wave traverses the transducer head, the pressure signal rises from zero to a maximum value. Assuming that the shock reaches the centre of a transducer when the pressure is half that of the maximum, the shock speed (
![]() $V_{s}$
) is the interval between the two half-peak times and the centre-to-centre distance between transducers PT3 and PT4. The location (
$V_{s}$
) is the interval between the two half-peak times and the centre-to-centre distance between transducers PT3 and PT4. The location (
![]() $x_{s}$
) of the shock is obtained for each shot from a shadowgraph image containing the shock wave at a known time,
$x_{s}$
) of the shock is obtained for each shot from a shadowgraph image containing the shock wave at a known time,
![]() $t_{s}$
(see figure 2
b). The band in the shadowgraph (typically 50–150 pixels wide) is caused by diffraction of light about the edge of the shock (Settles Reference Settles2006). The shock location in figure 2(b) is measured by taking a mean intensity along the
$t_{s}$
(see figure 2
b). The band in the shadowgraph (typically 50–150 pixels wide) is caused by diffraction of light about the edge of the shock (Settles Reference Settles2006). The shock location in figure 2(b) is measured by taking a mean intensity along the
![]() $y$
-axis after background subtraction and a Gaussian noise filter are applied, giving 0.5 pixel accuracy in the shock location.
$y$
-axis after background subtraction and a Gaussian noise filter are applied, giving 0.5 pixel accuracy in the shock location.

Figure 2. (a) Time traces of pressure signals from transducers PT3 and PT4 with the framing camera timing and (b) sample shadowgraph image superposed with the mean intensity profile (red). The shock location is indicated by a dashed line. Image contrast has been enhanced to better show the shock shadowgraph, and the resulting speckle in the image is background noise, not experimental particles.
3 Results and discussion
The history of particle drag is calculated along the one-dimensional Lagrangian particle trajectories reconstructed from eight independent images. To reconstruct particle trajectories through the entire relaxation zone, we acquire
![]() $O(50)$
measurements at different post-shock times. For any given particle, usually four to seven post-shock trajectory images are captured. A large interframe time step (
$O(50)$
measurements at different post-shock times. For any given particle, usually four to seven post-shock trajectory images are captured. A large interframe time step (
![]() $\unicode[STIX]{x0394}t$
) is optimal for obtaining the particle trajectory through the relaxation time. A small
$\unicode[STIX]{x0394}t$
) is optimal for obtaining the particle trajectory through the relaxation time. A small
![]() $\unicode[STIX]{x0394}t$
, on the other hand, is optimal for capturing particle displacements during the initial stage of unsteady particle acceleration. We address these opposing criteria by repeating the experiments with multiple time steps (
$\unicode[STIX]{x0394}t$
, on the other hand, is optimal for capturing particle displacements during the initial stage of unsteady particle acceleration. We address these opposing criteria by repeating the experiments with multiple time steps (
![]() $\unicode[STIX]{x0394}t=0.5~\unicode[STIX]{x03BC}\text{s}$
,
$\unicode[STIX]{x0394}t=0.5~\unicode[STIX]{x03BC}\text{s}$
,
![]() $1.0~\unicode[STIX]{x03BC}\text{s}$
and
$1.0~\unicode[STIX]{x03BC}\text{s}$
and
![]() $2.0~\unicode[STIX]{x03BC}\text{s}$
). The typical image size of a particle is approximately nine pixels across, with average displacement of approximately 50 pixels. The pre-shock particle location is registered in the first frame based on peak intensity, and the particle is tracked using cross-correlation between frames, with an uncertainty of one pixel.
$2.0~\unicode[STIX]{x03BC}\text{s}$
). The typical image size of a particle is approximately nine pixels across, with average displacement of approximately 50 pixels. The pre-shock particle location is registered in the first frame based on peak intensity, and the particle is tracked using cross-correlation between frames, with an uncertainty of one pixel.
For one-dimensional flows, the relationship between
![]() $C_{D}$
and the physical and kinematic properties of a particle and the post-shock gas reduces to (Igra & Takayama Reference Igra and Takayama1993)
$C_{D}$
and the physical and kinematic properties of a particle and the post-shock gas reduces to (Igra & Takayama Reference Igra and Takayama1993)
 $$\begin{eqnarray}\frac{{\displaystyle \frac{\text{d}^{2}x_{p}}{\text{d}t^{2}}}}{\left(u_{g}-{\displaystyle \frac{\text{d}x_{p}}{\text{d}t}}\right)^{2}}=\frac{3\unicode[STIX]{x1D70C}_{g}C_{D}}{4\unicode[STIX]{x1D70C}_{p}d_{p}}={\mathcal{A}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\displaystyle \frac{\text{d}^{2}x_{p}}{\text{d}t^{2}}}}{\left(u_{g}-{\displaystyle \frac{\text{d}x_{p}}{\text{d}t}}\right)^{2}}=\frac{3\unicode[STIX]{x1D70C}_{g}C_{D}}{4\unicode[STIX]{x1D70C}_{p}d_{p}}={\mathcal{A}}.\end{eqnarray}$$
Here,
![]() $\text{d}x_{p}/\text{d}t$
and
$\text{d}x_{p}/\text{d}t$
and
![]() $\text{d}^{2}x_{p}/\text{d}t^{2}$
are the velocity and acceleration of the particle;
$\text{d}^{2}x_{p}/\text{d}t^{2}$
are the velocity and acceleration of the particle;
![]() $\unicode[STIX]{x1D70C}_{p}$
and
$\unicode[STIX]{x1D70C}_{p}$
and
![]() $\unicode[STIX]{x1D70C}_{g}$
are the densities of the particle and post-shock gas. Estimation of
$\unicode[STIX]{x1D70C}_{g}$
are the densities of the particle and post-shock gas. Estimation of
![]() $C_{D}$
directly from (3.1) requires that the time derivatives of position are calculated from each trajectory. However, when calculating the acceleration using numerical differentiation, even a small error in particle locations can lead to substantially large errors (Christensen & Adrian Reference Christensen and Adrian2002). We avoid differentiation of the experimental data by adopting a method of piecewise fitting of measured particle locations, as described below.
$C_{D}$
directly from (3.1) requires that the time derivatives of position are calculated from each trajectory. However, when calculating the acceleration using numerical differentiation, even a small error in particle locations can lead to substantially large errors (Christensen & Adrian Reference Christensen and Adrian2002). We avoid differentiation of the experimental data by adopting a method of piecewise fitting of measured particle locations, as described below.

Figure 3. (a) Particle location (
![]() $x_{p}$
) for
$x_{p}$
) for
![]() $M_{s}=1.3$
experiments obtained from particle tracking with
$M_{s}=1.3$
experiments obtained from particle tracking with
![]() $\unicode[STIX]{x0394}t=0.5~\unicode[STIX]{x03BC}\text{s}$
,
$\unicode[STIX]{x0394}t=0.5~\unicode[STIX]{x03BC}\text{s}$
,
![]() $1.0~\unicode[STIX]{x03BC}\text{s}$
and
$1.0~\unicode[STIX]{x03BC}\text{s}$
and
![]() $2.0~\unicode[STIX]{x03BC}\text{s}$
, and the corresponding (b) fitting parameter
$2.0~\unicode[STIX]{x03BC}\text{s}$
, and the corresponding (b) fitting parameter
![]() ${\mathcal{A}}$
(see (3.2)), (c) velocity
${\mathcal{A}}$
(see (3.2)), (c) velocity
![]() $u_{p}$
(see (3.3)) with the post-shock gas velocity (
$u_{p}$
(see (3.3)) with the post-shock gas velocity (
![]() $u_{g}$
, – ⋅ – ⋅ –) and (d) acceleration
$u_{g}$
, – ⋅ – ⋅ –) and (d) acceleration
![]() $a_{p}$
(see (3.1)) obtained from piecewise nonlinear fitting (—○—). The dashed lines (– – –) show the values expected from Clift–Gauvin drag (3.4). Four individual particle trajectories,
$a_{p}$
(see (3.1)) obtained from piecewise nonlinear fitting (—○—). The dashed lines (– – –) show the values expected from Clift–Gauvin drag (3.4). Four individual particle trajectories,
![]() $T_{1}{-}T_{4}$
, are highlighted for reference.
$T_{1}{-}T_{4}$
, are highlighted for reference.
Integrating (3.1) twice with initial conditions
![]() $u_{p}=0$
and
$u_{p}=0$
and
![]() $x_{p}=x_{p,0}$
at
$x_{p}=x_{p,0}$
at
![]() $t=t_{0}$
, we obtain
$t=t_{0}$
, we obtain
Since
![]() $C_{D}$
is not known a priori, we derive (3.2) by making a first-order approximation that
$C_{D}$
is not known a priori, we derive (3.2) by making a first-order approximation that
![]() $C_{D}$
is constant about three successive particle locations (
$C_{D}$
is constant about three successive particle locations (
![]() $x_{p,i-1}$
,
$x_{p,i-1}$
,
![]() $x_{p,i}$
,
$x_{p,i}$
,
![]() $x_{p,i+1}$
) in a trajectory. Three successive particle locations are piecewise fitted to the fifth order Taylor series expansion of (3.2) with three fitting parameters,
$x_{p,i+1}$
) in a trajectory. Three successive particle locations are piecewise fitted to the fifth order Taylor series expansion of (3.2) with three fitting parameters,
![]() $x_{p,0}$
,
$x_{p,0}$
,
![]() $t_{0}$
and
$t_{0}$
and
![]() ${\mathcal{A}}$
. Before performing the fit, the time axis is shifted to the reference time,
${\mathcal{A}}$
. Before performing the fit, the time axis is shifted to the reference time,
![]() $t_{0}=t_{s}-(x_{s}-x_{p})/V_{s}$
, the time when the shock location coincides with the particle position
$t_{0}=t_{s}-(x_{s}-x_{p})/V_{s}$
, the time when the shock location coincides with the particle position
![]() $x_{p,0}$
. Here,
$x_{p,0}$
. Here,
![]() $x_{s}$
and
$x_{s}$
and
![]() $x_{p}$
are the shock and particle positions at time
$x_{p}$
are the shock and particle positions at time
![]() $t_{s}$
. The particle drag coefficient
$t_{s}$
. The particle drag coefficient
![]() $C_{D}$
at time
$C_{D}$
at time
![]() $t_{i}$
for each piecewise fit of the trajectory is obtained from the parameter
$t_{i}$
for each piecewise fit of the trajectory is obtained from the parameter
![]() ${\mathcal{A}}$
(see (3.1)). Through the fitting method, we obtain
${\mathcal{A}}$
(see (3.1)). Through the fitting method, we obtain
![]() $n-2$
instantaneous
$n-2$
instantaneous
![]() $C_{D}$
values for every
$C_{D}$
values for every
![]() $n$
available post-shock particle locations.
$n$
available post-shock particle locations.
Figure 3(a) shows particle locations (
![]() $x_{p}$
) for 32 trajectories for
$x_{p}$
) for 32 trajectories for
![]() $M_{s}=1.3$
. Four example trajectories (
$M_{s}=1.3$
. Four example trajectories (
![]() $T_{1}{-}T_{4}$
) are highlighted with their corresponding piecewise fits. The fitting parameter
$T_{1}{-}T_{4}$
) are highlighted with their corresponding piecewise fits. The fitting parameter
![]() ${\mathcal{A}}$
for each trajectory is shown in figure 3(b). The particle velocities (see figure 3
c) are obtained by invoking parameter
${\mathcal{A}}$
for each trajectory is shown in figure 3(b). The particle velocities (see figure 3
c) are obtained by invoking parameter
![]() ${\mathcal{A}}$
in the first integral of (3.1),
${\mathcal{A}}$
in the first integral of (3.1),
and accelerations (see figure 3
d) are obtained from (3.1). The dashed line in each plot shows the values expected based on standard drag. The particle kinematics captured in figure 3 show the characteristics of the post-shock relaxation zone: (i) the particle acceleration reaches a peak immediately after the shock and then decreases (see figure 3
d); (ii) the particle velocity continuously increases and asymptotically approaches the post-shock gas velocity (
![]() $u_{g}$
) as the acceleration monotonically approaches zero (see figure 3
c). The relaxation period is approximately
$u_{g}$
) as the acceleration monotonically approaches zero (see figure 3
c). The relaxation period is approximately
![]() $10~\unicode[STIX]{x03BC}\text{s}$
or
$10~\unicode[STIX]{x03BC}\text{s}$
or
![]() $1000\unicode[STIX]{x1D70F}_{s}$
for these flow conditions.
$1000\unicode[STIX]{x1D70F}_{s}$
for these flow conditions.

Figure 4. The total drag coefficient
![]() $C_{D}$
(solid line), the quasi-steady component
$C_{D}$
(solid line), the quasi-steady component
![]() $C_{D,qs}$
(dashed line) and the unsteady component
$C_{D,qs}$
(dashed line) and the unsteady component
![]() $C_{D,us}$
(dotted line) with respect to time normalised by the acoustic time scale (
$C_{D,us}$
(dotted line) with respect to time normalised by the acoustic time scale (
![]() $\unicode[STIX]{x1D70F}_{s}$
) for trajectories (a)
$\unicode[STIX]{x1D70F}_{s}$
) for trajectories (a)
![]() $T_{1}$
,
$T_{1}$
,
![]() $T_{2}$
and (b)
$T_{2}$
and (b)
![]() $T_{3}$
,
$T_{3}$
,
![]() $T_{4}$
.
$T_{4}$
.
Drag coefficients for the trajectories
![]() $T_{1},T_{2}$
and
$T_{1},T_{2}$
and
![]() $T_{3},T_{4}$
are shown in figure 4(a,b). Here, 95 % confidence intervals for
$T_{3},T_{4}$
are shown in figure 4(a,b). Here, 95 % confidence intervals for
![]() $C_{D}$
are obtained from bootstrapping, with bounds generated via Monte-Carlo simulation. The particle location (
$C_{D}$
are obtained from bootstrapping, with bounds generated via Monte-Carlo simulation. The particle location (
![]() $x_{p}$
), shock speed (
$x_{p}$
), shock speed (
![]() $V_{s}$
) and absolute shock location (
$V_{s}$
) and absolute shock location (
![]() $x_{s}$
) are perturbed over a random Gaussian distribution with standard deviation
$x_{s}$
) are perturbed over a random Gaussian distribution with standard deviation
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x0394}p/\sqrt{12}$
. The
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x0394}p/\sqrt{12}$
. The
![]() $\unicode[STIX]{x0394}p$
values for
$\unicode[STIX]{x0394}p$
values for
![]() $x_{p}$
,
$x_{p}$
,
![]() $V_{s}$
and
$V_{s}$
and
![]() $x_{s}$
are 1 pixel,
$x_{s}$
are 1 pixel,
![]() $0.05~\text{m}~\text{s}^{-1}$
and 0.5 pixel. The
$0.05~\text{m}~\text{s}^{-1}$
and 0.5 pixel. The
![]() $C_{D}$
at the earliest resolved post-shock time (
$C_{D}$
at the earliest resolved post-shock time (
![]() ${\approx}2\unicode[STIX]{x1D70F}_{s}$
) is 6.3 (see figure 4
a). This early-time drag after shock is consistent with the prediction based on the inviscid unsteady model by Parmar et al. (Reference Parmar, Haselbacher and Balachandar2009). This model, validated for stationary particles, predicts that
${\approx}2\unicode[STIX]{x1D70F}_{s}$
) is 6.3 (see figure 4
a). This early-time drag after shock is consistent with the prediction based on the inviscid unsteady model by Parmar et al. (Reference Parmar, Haselbacher and Balachandar2009). This model, validated for stationary particles, predicts that
![]() $C_{D}$
decreases sharply after
$C_{D}$
decreases sharply after
![]() $t=2\unicode[STIX]{x1D70F}_{s}$
and attains a constant value equal to the quasi-steady drag after
$t=2\unicode[STIX]{x1D70F}_{s}$
and attains a constant value equal to the quasi-steady drag after
![]() $t\approx 8\unicode[STIX]{x1D70F}_{s}$
. Although the acoustic-time drag is consistent with this model, figure 4(a,b) shows that the particles experience a continuously increasing drag through the relaxation zone. As the particle relaxes into mechanical equilibrium with the background gas,
$t\approx 8\unicode[STIX]{x1D70F}_{s}$
. Although the acoustic-time drag is consistent with this model, figure 4(a,b) shows that the particles experience a continuously increasing drag through the relaxation zone. As the particle relaxes into mechanical equilibrium with the background gas,
![]() $C_{D}$
increases by an order of magnitude compared with the time just after shock interaction.
$C_{D}$
increases by an order of magnitude compared with the time just after shock interaction.
As mentioned in § 1, there are many possible forces that could contribute to the increased drag observed in figure 4. Under shock acceleration, the particle acceleration due to the shock is much larger than gravity, so we assume that
![]() $F_{g}=0$
. The lift force (
$F_{g}=0$
. The lift force (
![]() $F_{l}$
) is negligible for the smooth spherical particles used in this study, and images show that the particles experience no vertical movement. Elimination of lift and drag effects leaves a combination of quasi-steady (
$F_{l}$
) is negligible for the smooth spherical particles used in this study, and images show that the particles experience no vertical movement. Elimination of lift and drag effects leaves a combination of quasi-steady (
![]() $F_{qs}$
) and unsteady (
$F_{qs}$
) and unsteady (
![]() $F_{us}=F_{iu}+F_{vu}$
) forces acting on the particles.
$F_{us}=F_{iu}+F_{vu}$
) forces acting on the particles.
The models that could be used to estimate quasi-steady and unsteady forces (Parmar et al.
Reference Parmar, Haselbacher and Balachandar2009, Reference Parmar, Haselbacher and Balachandar2011) are assessed in table 2 for applicability to these experiments. The quasi-steady model is applicable to the HST experiments, but the models for the unsteady forces are designed for much shorter time scales than the relaxation times we are studying. For the range of particle Mach numbers (
![]() $M_{p}\leqslant 0.5$
) and Knudsen numbers (
$M_{p}\leqslant 0.5$
) and Knudsen numbers (
![]() $Kn\approx 0.01$
) in this study, the quasi-steady component of the drag coefficient (
$Kn\approx 0.01$
) in this study, the quasi-steady component of the drag coefficient (
![]() $C_{D,qs}$
) can be estimated using an incompressible model given by the Clift–Gauvin equation (Clift & Gauvin Reference Clift and Gauvin1970),
$C_{D,qs}$
) can be estimated using an incompressible model given by the Clift–Gauvin equation (Clift & Gauvin Reference Clift and Gauvin1970),
To understand how much of the drag in our experiment might be coming from unsteady forces, we estimate the quasi-steady component of drag based on (3.4) and calculate the unsteady component as
The quasi-steady (
![]() $C_{D,qs}$
) and unsteady (
$C_{D,qs}$
) and unsteady (
![]() $C_{D,us}$
) components of the drag coefficient for our sample trajectories are shown in figure 4. The quasi-steady force contributes only a small amount to the overall drag at early times, but it increases steadily through the relaxation zone. The combination of decreasing slip between the particle and the surrounding gas, and the large acceleration immediately after the passage of the shock causes some of the high levels of unsteady drag (see (3.1)).
$C_{D,us}$
) components of the drag coefficient for our sample trajectories are shown in figure 4. The quasi-steady force contributes only a small amount to the overall drag at early times, but it increases steadily through the relaxation zone. The combination of decreasing slip between the particle and the surrounding gas, and the large acceleration immediately after the passage of the shock causes some of the high levels of unsteady drag (see (3.1)).
The existing force models for the unsteady components of drag do not predict the large magnitude of
![]() $C_{D,us}$
observed in figure 4. The force kernel for the inviscid unsteady component proposed in Parmar et al. (Reference Parmar, Haselbacher and Balachandar2009) decays to zero near
$C_{D,us}$
observed in figure 4. The force kernel for the inviscid unsteady component proposed in Parmar et al. (Reference Parmar, Haselbacher and Balachandar2009) decays to zero near
![]() $t<\unicode[STIX]{x1D70F}_{s}$
, well before the relaxation period (see table 2). The linearised models for the Basset history kernels proposed in Mei et al. (Reference Mei, Lawrencce and Adrian1991) and Parmar et al. (Reference Parmar, Haselbacher and Balachandar2011) require a convective time scale
$t<\unicode[STIX]{x1D70F}_{s}$
, well before the relaxation period (see table 2). The linearised models for the Basset history kernels proposed in Mei et al. (Reference Mei, Lawrencce and Adrian1991) and Parmar et al. (Reference Parmar, Haselbacher and Balachandar2011) require a convective time scale
![]() $\unicode[STIX]{x1D70F}_{c}\ll 1/(Re_{p}M_{s})$
, where
$\unicode[STIX]{x1D70F}_{c}\ll 1/(Re_{p}M_{s})$
, where
![]() $\unicode[STIX]{x1D70F}_{c}=t(u_{g}-u_{p})/d_{p}$
. During the relaxation phase of these experiments,
$\unicode[STIX]{x1D70F}_{c}=t(u_{g}-u_{p})/d_{p}$
. During the relaxation phase of these experiments,
![]() $\unicode[STIX]{x1D70F}_{c}>1/Re_{p}$
(see table 2). In this regime, defined by Parmar et al. (Reference Parmar, Haselbacher and Balachandar2011) as ‘regime IV: very long time’, nonlinear effects become important and the relationship between drag,
$\unicode[STIX]{x1D70F}_{c}>1/Re_{p}$
(see table 2). In this regime, defined by Parmar et al. (Reference Parmar, Haselbacher and Balachandar2011) as ‘regime IV: very long time’, nonlinear effects become important and the relationship between drag,
![]() $Re_{p}$
and
$Re_{p}$
and
![]() $M_{s}$
becomes complex (Mei & Adrian Reference Mei and Adrian1992; Parmar et al.
Reference Parmar, Haselbacher and Balachandar2011).
$M_{s}$
becomes complex (Mei & Adrian Reference Mei and Adrian1992; Parmar et al.
Reference Parmar, Haselbacher and Balachandar2011).
Table 2. Range of applicability of the models of Parmar et al. (Reference Parmar, Haselbacher and Balachandar2009, Reference Parmar, Haselbacher and Balachandar2011) for quasi-steady and unsteady forces compared to experimental values.

To understand the unsteady particle dynamics in the relaxation zone, we examine the drag as a function of a modified Knudsen number,
![]() $Kn^{\ast }=M_{s}/Re_{p}$
, for all three Mach numbers,
$Kn^{\ast }=M_{s}/Re_{p}$
, for all three Mach numbers,
![]() $M_{s}=1.2$
, 1.3 and 1.4. Figure 5 shows that the variation of
$M_{s}=1.2$
, 1.3 and 1.4. Figure 5 shows that the variation of
![]() $C_{D}$
with respect to
$C_{D}$
with respect to
![]() $Kn^{\ast }$
is weakly sensitive to
$Kn^{\ast }$
is weakly sensitive to
![]() $M_{s}$
within the range of our experiments. With
$M_{s}$
within the range of our experiments. With
![]() $C_{D}\propto a_{p}/Re_{p}^{2}$
and the behaviour of
$C_{D}\propto a_{p}/Re_{p}^{2}$
and the behaviour of
![]() $a_{p}$
shown in figure 3(d), we choose a second-order power-law expression
$a_{p}$
shown in figure 3(d), we choose a second-order power-law expression
![]() $C_{D}=a-b{Kn^{\ast }}^{c}$
for a least-squares fit to the data, with
$C_{D}=a-b{Kn^{\ast }}^{c}$
for a least-squares fit to the data, with
![]() $a=167.5$
,
$a=167.5$
,
![]() $b=92.2$
and
$b=92.2$
and
![]() $c=-0.18$
for the range of
$c=-0.18$
for the range of
![]() $Kn^{\ast }=0.04{-}3.92$
. The bounds of this fit, shown in light grey solid and dashed lines, are predicted using simultaneous functional and observational bounds with 95 % confidence validated with Monte-Carlo simulations.
$Kn^{\ast }=0.04{-}3.92$
. The bounds of this fit, shown in light grey solid and dashed lines, are predicted using simultaneous functional and observational bounds with 95 % confidence validated with Monte-Carlo simulations.

Figure 5. Total drag coefficient
![]() $C_{D}$
, quasi-steady (
$C_{D}$
, quasi-steady (
![]() $C_{D,qs}$
) and unsteady (
$C_{D,qs}$
) and unsteady (
![]() $C_{D,us}$
) components with respect to
$C_{D,us}$
) components with respect to
![]() $M_{s}/Re_{p}$
. The red line is a least-squares fit to the experimental data,
$M_{s}/Re_{p}$
. The red line is a least-squares fit to the experimental data,
![]() $C_{D}=a-b(M_{s}/Re_{p})^{c}$
, with
$C_{D}=a-b(M_{s}/Re_{p})^{c}$
, with
![]() $a=167.5$
,
$a=167.5$
,
![]() $b=92.2$
and
$b=92.2$
and
![]() $c=-0.18$
. The grey solid and dashed lines are simultaneous functional and observational 95 % confidence bounds.
$c=-0.18$
. The grey solid and dashed lines are simultaneous functional and observational 95 % confidence bounds.
For the experimentally measured data with all three incident Mach numbers, we can again calculate the contributions from the quasi-steady model ((3.4), as shown in figure 5), with the remaining unsteady drag contribution shown by the green dotted line in figure 5. Here,
![]() $C_{D,us}$
is the primary contributor to the overall drag until
$C_{D,us}$
is the primary contributor to the overall drag until
![]() $Kn^{\ast }\approx 1$
, with maximum values in the range
$Kn^{\ast }\approx 1$
, with maximum values in the range
![]() $0.5\leqslant Kn^{\ast }\leqslant 1.0$
. For all Mach numbers,
$0.5\leqslant Kn^{\ast }\leqslant 1.0$
. For all Mach numbers,
![]() $C_{D,qs}$
increases almost linearly through the relaxation period. After
$C_{D,qs}$
increases almost linearly through the relaxation period. After
![]() $Kn^{\ast }\approx 1.0$
, the unsteady force contribution declines, and it intersects the increasing quasi-steady force contribution at
$Kn^{\ast }\approx 1.0$
, the unsteady force contribution declines, and it intersects the increasing quasi-steady force contribution at
![]() $Kn^{\ast }\approx 2$
.
$Kn^{\ast }\approx 2$
.
As indicated in table 1, our data are limited to
![]() $Re_{p}>0.3$
. As
$Re_{p}>0.3$
. As
![]() $Re_{p}\rightarrow 0$
, the total drag should approach the Stokes flow regime, when the quasi-steady drag will completely dominate the total drag. This trend is shown with a dashed red line in figure 5, where the red empirical curve is connected to the Mach 1.3 quasi-steady (black dashed) line.
$Re_{p}\rightarrow 0$
, the total drag should approach the Stokes flow regime, when the quasi-steady drag will completely dominate the total drag. This trend is shown with a dashed red line in figure 5, where the red empirical curve is connected to the Mach 1.3 quasi-steady (black dashed) line.
4 Conclusions
The unsteady drag coefficients of shock accelerated microparticles through the relaxation period are higher than the drag coefficients predicted by either standard drag or any current quasi-steady and unsteady drag models. The high drag coefficients measured just after shock passage (near the acoustic time scales) agree with the drag coefficients reported in previous studies, but the measured drag coefficients at later times quickly exceed model predictions. The coefficient of drag is highly sensitive to the time-dependent particle slip velocity. This dependence, represented by a modified time-dependent Knudsen number,
![]() $Kn^{\ast }=M_{s}/Re_{p}$
, results in a power-law behaviour of the unsteady drag coefficient. The increased drag is caused by unsteady forces that are not approximated by current linearised models, and these forces are higher than the quasi-steady drag until
$Kn^{\ast }=M_{s}/Re_{p}$
, results in a power-law behaviour of the unsteady drag coefficient. The increased drag is caused by unsteady forces that are not approximated by current linearised models, and these forces are higher than the quasi-steady drag until
![]() $Kn^{\ast }\approx 2$
. Because the physical mechanisms affecting drag are coupled in a nonlinear way during the relaxation time period, it is difficult to assess how the time-dependent drag will change when there are compressibility effects (
$Kn^{\ast }\approx 2$
. Because the physical mechanisms affecting drag are coupled in a nonlinear way during the relaxation time period, it is difficult to assess how the time-dependent drag will change when there are compressibility effects (
![]() $M_{p}>0.6$
), or whether there are other additional forces such as temperature changes or particle deformation at higher Mach numbers. Simulations may provide some insights into these complex dynamics.
$M_{p}>0.6$
), or whether there are other additional forces such as temperature changes or particle deformation at higher Mach numbers. Simulations may provide some insights into these complex dynamics.