2.1 Theory

We consider a neutrally buoyant, cantilever beam of length $L$ , width $W$ and thickness $D$ , placed perpendicular to a uniform oscillatory flow of velocity $\boldsymbol{U}(t)=A\unicode[STIX]{x1D6FA}\sin (\unicode[STIX]{x1D6FA}t)\boldsymbol{e}_{\boldsymbol{x}}$ in a fluid of density $\unicode[STIX]{x1D70C}$ (see figure 1). The amplitude $A$ corresponds to the maximal horizontal excursion of the fluid particles over one cycle, while $\unicode[STIX]{x1D6FA}$ is the angular frequency of the oscillations.

Figure 1. (a) Side view of the bending structure. (b) Dimensions of the undeformed blade.

We assume the thickness of the plate is small compared to its width ( $D\ll W$ ) so that deflection under the effect of the flow is confined in the $xz$ -plane. We also assume the structure is slender ( $L\gg W$ ) so we can model it as a two-dimensional inextensible Euler–Bernoulli beam of bending stiffness $EI$ and mass per unit length $m$ (see Audoly & Pomeau Reference Audoly and Pomeau2010). The curvilinear coordinate $s$ represents the distance from the clamped edge along the span, and we use the prime symbol $(\cdot )^{\prime }$ to denote differentiation with respect to $s$ . Hereafter, $\unicode[STIX]{x1D703}$ is the local angle of the tangent $\unicode[STIX]{x1D749}=\boldsymbol{r}^{\prime }$ with the vertical axis $\boldsymbol{e}_{\boldsymbol{z}}$ , where $\boldsymbol{r}=x(s,t)\boldsymbol{e}_{\boldsymbol{x}}+z(s,t)\boldsymbol{e}_{\boldsymbol{z}}$ is the position vector. Following Audoly & Pomeau (Reference Audoly and Pomeau2010), the dynamic equilibrium reads

(2.1) $$\begin{eqnarray}m\ddot{\boldsymbol{r}}=\boldsymbol{F}^{\prime }+\boldsymbol{q},\end{eqnarray}$$

where $\boldsymbol{q}$ is the external load per unit length on the structure, $\boldsymbol{F}=T\unicode[STIX]{x1D749}+Q\boldsymbol{n}$ is the internal force vector, with $T$ the tension and $Q$ the shear force and the overdot stands for time derivation. The internal bending moment $M$ is related to the local curvature $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D703}^{\prime }$ by $M=EI\unicode[STIX]{x1D705}$ , and the shear force $Q$ is given by $Q=-M^{\prime }=-EI\unicode[STIX]{x1D705}^{\prime }$ . Clamping implies $x=z=\unicode[STIX]{x1D703}=0$ at $s=0$ , while the free tip condition reads $T=M=Q=0$ at $s=L$ .

Because the structure is neutrally buoyant, its density is also $\unicode[STIX]{x1D70C}$ and gravity and buoyancy forces cancel each other. We assume large Reynolds number so that friction forces are negligible. Following Eloy, Kofman & Schouveiler (Reference Eloy, Kofman and Schouveiler2012), Singh, Michelin & de Langre (Reference Singh, Michelin and de Langre2012), Michelin & Doaré (Reference Michelin and Doaré2013), Piñeirua et al. (Reference Piñeirua, Thiria and Godoy-Diana2017) we model the effect of the relative flow as a combination of two external loads distributed along the span. First, the resistive drag (Taylor Reference Taylor1952)

(2.2) $$\begin{eqnarray}\boldsymbol{q}_{\boldsymbol{d}}=-1/2\unicode[STIX]{x1D70C}C_{D}W|U_{n}|U_{n}\boldsymbol{n}\end{eqnarray}$$

due to the pressure in the wake is purely normal. It is proportional to the square of the normal component $U_{n}$ of the relative velocity $\boldsymbol{U}_{\boldsymbol{r}}=U_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D749}+U_{n}\boldsymbol{n}=\dot{\boldsymbol{r}}-\boldsymbol{U}$ . The drag coefficient $C_{D}$ depends on the geometry of the cross-section and is typically of order $O(1)$ . In pure sinusoidal flow, it slightly varies with the frequency through the Keulegan–Carpenter number $K_{C}=U/Wf=2\unicode[STIX]{x03C0}A/W$ (Keulegan & Carpenter Reference Keulegan and Carpenter1958). But in the case of a deformable body, the relative flow varies along the span and is not purely sinusoidal because of the motion of the structure itself. The exact value of $C_{D}$ is however not critical here so we will simply use the value for steady flows. We will also assume a rectangular cross-section so we will use $C_{D}=2$ . The second force component is the reactive (or added mass) force (Lighthill Reference Lighthill1971; Candelier, Boyer & Leroyer Reference Candelier, Boyer and Leroyer2011)

(2.3) $$\begin{eqnarray}\boldsymbol{q}_{\boldsymbol{a}\boldsymbol{m}}=-m_{a}\left[\unicode[STIX]{x2202}_{t}(U_{n}\boldsymbol{n})-\unicode[STIX]{x2202}_{s}(U_{n}U_{\unicode[STIX]{x1D70F}}\boldsymbol{n})+{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}_{s}(U_{n}^{2}\unicode[STIX]{x1D749})\right],\end{eqnarray}$$

where the added mass is given by $m_{a}=\unicode[STIX]{x1D70C}\unicode[STIX]{x03C0}W^{2}/4$ . This expression involves the normal component but also the tangential component $U_{\unicode[STIX]{x1D70F}}$ of the relative velocity. In the case of an inextensible beam, this force becomes purely normal and its expression may be simplified in

(2.4) $$\begin{eqnarray}\boldsymbol{q}_{\boldsymbol{a}\boldsymbol{m}}=-m_{a}\left[(\ddot{\boldsymbol{r}}-\dot{\boldsymbol{U}})\boldsymbol{\cdot }\boldsymbol{n}-2\dot{\unicode[STIX]{x1D703}}U_{\unicode[STIX]{x1D70F}}+\unicode[STIX]{x1D705}\left(U_{\unicode[STIX]{x1D70F}}^{2}-{\textstyle \frac{1}{2}}U_{n}^{2}\right)\right]\boldsymbol{n}.\end{eqnarray}$$

Finally, because the fluid itself is accelerated, a third force component has to be considered, called the virtual buoyancy force (Blevins Reference Blevins1990)

(2.5) $$\begin{eqnarray}\boldsymbol{q}_{\boldsymbol{v}\boldsymbol{b}}=m_{d}\dot{\boldsymbol{U}}.\end{eqnarray}$$

This term is due to the pressure gradient induced by the acceleration of the fluid. It is equivalent to the Archimedes force, only the acceleration of gravity is replaced by the acceleration of the fluid. It is proportional to the displaced mass per unit length $m_{d}=\unicode[STIX]{x1D70C}WD$ . We have assumed so far that the structure is fixed in an oscillating fluid. If the clamped edge of the structure was set into a forced horizontal motion of velocity $\boldsymbol{U}_{\boldsymbol{f}}=U_{f}\boldsymbol{e}_{\boldsymbol{x}}$ , then the equilibrium equation in the frame of the structure (2.1) would include an additional load due to the inertial pseudo-force $\boldsymbol{q}_{\boldsymbol{i}}=-m\dot{\boldsymbol{U}_{f}}$ . For a neutrally buoyant structure the displaced mass is equal to the structural mass ( $m_{d}=m$ ), so this inertial force has the same expression as the virtual buoyancy term (2.5) if $U_{f}=-U$ . Thus, oscillating a plate in a still fluid is actually equivalent to having a fixed structure in an oscillating flow, providing that the structure has the same density as the fluid. For practical reasons, in the experiments of § 3, we set the structure into motion rather than the fluid.

In the following, we will only consider very thin blades $D\ll W$ (equivalently $m=m_{d}\ll m_{a}$ ) so that we may neglect the structural inertia and the virtual buoyancy. The dynamic equilibrium (2.1) then reads

(2.6) $$\begin{eqnarray}\left[T+{\textstyle \frac{1}{2}}EI\unicode[STIX]{x1D705}^{2}\right]^{\prime }\unicode[STIX]{x1D749}+[\unicode[STIX]{x1D705}T-EI\unicode[STIX]{x1D705}^{\prime \prime }]\boldsymbol{n}+\boldsymbol{q}_{\boldsymbol{ d}}+\boldsymbol{q}_{\boldsymbol{a}\boldsymbol{m}}=0.\end{eqnarray}$$

After projection on the tangential and normal directions and elimination of the unknown tension $T$ , we finally obtain a single differential equation for the kinematic variables $\unicode[STIX]{x1D705}$ , $\unicode[STIX]{x1D703}$ , $\boldsymbol{r}$

(2.7) $$\begin{eqnarray}\displaystyle & & \displaystyle EI\left[\unicode[STIX]{x1D705}^{\prime \prime }+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D705}^{3}\right]+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}C_{D}W|U_{n}|U_{n}\nonumber\\ \displaystyle & & \displaystyle \quad +\,m_{a}\left[\ddot{\boldsymbol{r}}\boldsymbol{\cdot }\boldsymbol{n}+\unicode[STIX]{x1D705}\left(U_{\unicode[STIX]{x1D70F}}^{2}-{\textstyle \frac{1}{2}}U_{n}^{2}\right)-2\dot{\unicode[STIX]{x1D703}}U_{\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D6FA}^{2}A\cos \unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D6FA}t)\right]=0.\end{eqnarray}$$

We non-dimensionalize all the variables using the length of the structure $L$ and the scale of the natural period of the structure in small-amplitude oscillations in the fluid $T_{s}=L^{2}\sqrt{m_{a}/EI}$ . We finally obtain, in non-dimensional form

(2.8) $$\begin{eqnarray}\unicode[STIX]{x1D705}^{\prime \prime }+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D705}^{3}+\unicode[STIX]{x1D706}|U_{n}|U_{n}+\ddot{\boldsymbol{r}}\boldsymbol{\cdot }\boldsymbol{n}+\unicode[STIX]{x1D705}\left(U_{\unicode[STIX]{x1D70F}}^{2}-{\textstyle \frac{1}{2}}U_{n}^{2}\right)-2\dot{\unicode[STIX]{x1D703}}U_{\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D714}t)=0,\end{eqnarray}$$

with boundary conditions $\boldsymbol{r}=0$ and $\unicode[STIX]{x1D703}=0$ at the clamped edge $s=0$ and $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}^{\prime }=0$ at the free tip $s=1$ , and the tangential and normal relative velocities $U_{\unicode[STIX]{x1D70F}}=\dot{\boldsymbol{r}}\boldsymbol{\cdot }\unicode[STIX]{x1D749}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}\sin (\unicode[STIX]{x1D714}t)\sin \unicode[STIX]{x1D703}$ and $U_{n}=\dot{\boldsymbol{r}}\boldsymbol{\cdot }\boldsymbol{n}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}\sin (\unicode[STIX]{x1D714}t)\cos \unicode[STIX]{x1D703}$ . This system is ruled by three non-dimensional parameters that are

(2.9a-c ) $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{A}{L},\quad \unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}T_{s},\quad \unicode[STIX]{x1D706}=\frac{\unicode[STIX]{x1D70C}C_{D}WL}{2m_{a}}=\left(\frac{2}{\unicode[STIX]{x03C0}}C_{D}\right)\frac{L}{W}.\end{eqnarray}$$

The first two parameters $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D714}$ respectively scale the amplitude and frequency of the background flow to the length and natural frequency of the structure, while $\unicode[STIX]{x1D706}=O(L/W)$ is mostly a slenderness parameter specific to the structure alone. Because our model is only valid for slender structures, we are restricted to $\unicode[STIX]{x1D706}\gg 1$ . Note that, when studying the influence of flexibility on the loads endured by a structure, the classical non-dimensional parameter that describes the competition between the fluid loading stemming from the resistive drag and the elastic restoring force is the Cauchy number $C_{Y}$ (Tickner & Sacks Reference Tickner and Sacks1969; Chakrabarti Reference Chakrabarti2002; de Langre Reference de Langre2008). Following the definition of Gosselin et al. (Reference Gosselin, de Langre and Machado-Almeida2010) in the case of the static reconfiguration of cantilever beams, we may here define a Cauchy number based on the maximum velocity of the flow ( $A\unicode[STIX]{x1D6FA}$ ) as $C_{Y}=\unicode[STIX]{x1D70C}C_{D}WL^{3}(A\unicode[STIX]{x1D6FA})^{2}/EI=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D714}^{2}$ . In the governing equation (2.8), given the scaling of the normal relative velocity component $U_{n}=O(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714})$ , the resistive drag term $\unicode[STIX]{x1D706}|U_{n}|U_{n}$ directly scales as $\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D714}^{2}=C_{Y}$ owing to the choice of characteristic length and time chosen for normalization.

2.2 Numerical resolution

We numerically solve (2.8) along with the boundary conditions using a time stepping scheme. The one-dimensional structure is discretized using the Gauss–Lobatto distribution $s_{k}=1/2(1-\cos ((k-1)/(N-1)\unicode[STIX]{x03C0}))$ with $N=100$ points. The curvilinear derivatives and integrals are computed respectively by Chebyshev collocation and the Clenshaw–Curtis quadrature formulae. We evaluate the time derivatives at time $t_{n}$ with implicit second-order accurate finite differences with $10^{3}$ time steps per forcing cycle in most cases. The time step is reduced further to maintain good accuracy when a smaller time scale is involved in §§ 4.2 and 5.4. At each time step, we solve the boundary value problem in $\unicode[STIX]{x1D705}_{n}(s)$ with a pseudo-Newton solver (method of Broyden Reference Broyden1965). The computations are carried on until a limit cycle is found.

4.1 Small amplitude of flow oscillation $\unicode[STIX]{x1D6FC}=A/L\ll 1$

Let us first consider the situation where the amplitude of forcing is small ( $\unicode[STIX]{x1D6FC}\ll 1$ ). The excursion of the fluid particles being small compared to the length of the blade, we may also assume that the deflection remains small as well $|x(s,t)|\ll 1$ . Neglecting all the geometrical nonlinearities in (2.8) thus yields the small-amplitude equation

(4.1) $$\begin{eqnarray}x^{(4)}+\ddot{x}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}^{2}\cos (\unicode[STIX]{x1D714}t)-\unicode[STIX]{x1D706}|{\dot{x}}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}\sin (\unicode[STIX]{x1D714}t)|({\dot{x}}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}\sin (\unicode[STIX]{x1D714}t)),\end{eqnarray}$$

with boundary conditions $x=x^{\prime }=0$ at $s=0$ and $x^{\prime \prime }=x^{\prime \prime \prime }=0$ at $s=1$ . Equation (4.1) is the standard cantilever beam linear oscillator, forced on the right-hand side by the fluid inertia and the resistive drag. Note that only the nonlinearities of geometrical nature have been removed but the quadratic relative velocity term of the resistive drag has been retained at this point. Indeed, the slenderness parameter $\unicode[STIX]{x1D706}$ that scales this term is large and the order of magnitude of the whole resistive drag term depends as much on the scaling of $\unicode[STIX]{x1D706}$ as it depends on that of $\unicode[STIX]{x1D6FC}$ . Besides, no assumption has been made regarding the characteristic time scale for the variations of $x$ , and there is no reason to presume that ${\dot{x}}$ should be small compared to the free-stream velocity based on the sole assumption that $x$ is small.

If the period of the forcing is large compared to the characteristic response time of the structure ( $\unicode[STIX]{x1D714}<1$ ), we may assume that the structure is in static equilibrium with the fluid forcing at all times. Consequently, we may neglect the velocity and acceleration of the structure and (4.1) reduces to the small-amplitude static equation

(4.2) $$\begin{eqnarray}x^{(4)}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}^{2}[\cos (\unicode[STIX]{x1D714}t)+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC})|\text{sin}(\unicode[STIX]{x1D714}t)|\sin (\unicode[STIX]{x1D714}t)].\end{eqnarray}$$

The left-hand side of this equation now involves only the linearized stiffness force, while the fluid forcing on the right-hand side is the same as that a perfectly rigid blade would endure.

On the other hand, if the forcing varies with a period comparable to the characteristic structural response time or faster ( $\unicode[STIX]{x1D714}>1$ ), we may then assume that the amplitude and the frequency of the response will scale as those of the forcing, as is usually the case for linear oscillators (see for instance Blevins Reference Blevins1990). We thus define the rescaled deflection and time $\tilde{x}=x/\unicode[STIX]{x1D6FC}$ , $\tilde{t}=\unicode[STIX]{x1D714}t$ , so that the small-amplitude equation (4.1) can be written

(4.3) $$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D714}^{2}}\tilde{x}^{(4)}+\ddot{\tilde{x}}=\cos (\tilde{t})-K_{C}|\dot{\tilde{x}}-\sin (\tilde{t})|(\dot{\tilde{x}}-\sin (\tilde{t})),\end{eqnarray}$$

which now only depends on two parameters: the frequency parameter $\unicode[STIX]{x1D714}$ and a new amplitude parameter $K_{C}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}=(2C_{D}/\unicode[STIX]{x03C0})A/W$ that compares the fluid particles excursion to the width instead of the length of the blade. This parameter is a problem-specific formulation of the classical Keulegan–Carpenter number that compares the respective magnitudes of the drag and the fluid inertial forces. When $K_{C}$ is small, the fluid inertia dominates over drag and vice versa.

Let us first look at the asymptotic limit of infinitely small amplitude of the forcing $K_{C}\rightarrow 0$ . The nonlinear drag term can be neglected and (4.3) then simply describes a linear oscillator with sinusoidal forcing due to the fluid inertial term. It can be solved analytically and the solution is

(4.4) $$\begin{eqnarray}\tilde{x}(s,\tilde{t})=2\mathop{\sum }_{m=0}^{+\infty }\frac{\unicode[STIX]{x1D70E}_{m}}{k_{m}}\frac{\unicode[STIX]{x1D714}^{2}}{k_{m}^{4}-\unicode[STIX]{x1D714}^{2}}X_{m}(s)\cos \tilde{t},\end{eqnarray}$$

with the wavenumbers $k_{m}$ satisfying $\cos k_{m}\cosh k_{m}+1=0$ , the classical cantilever beam modes $X_{m}(s)=[\cosh (k_{m}s)-\cos (k_{m}s)]-\unicode[STIX]{x1D70E}_{m}[\sinh (k_{m}s)-\sin (k_{m}s)]$ and $\unicode[STIX]{x1D70E}_{m}=(\sinh k_{m}-\sin k_{m})/(\cosh k_{m}+\cos k_{m})$ (see Weaver, Timoshenko & Young Reference Weaver, Timoshenko and Young1990).

Figure 5(a) compares the amplitude of the maximum deflection for different values of $K_{C}$ , and for the asymptotic solution (4.4), as a function of $\unicode[STIX]{x1D714}$ . This analytical solution is in good agreement with the model predictions for any $K_{C}\leqslant 1$ , and it shows that the system behaves as a high-pass filter in this range of the parameter space. As the frequency increases, successive beam modes are excited and resonances occur when the frequency of the forcing matches one of the natural modes of the structure $\unicode[STIX]{x1D714}=k_{m}^{2}$ . For finite but small $K_{C}$ , drag acts as a damping term that saturates the amplitude of the resonances but does not seem to affect significantly the modal shape of the deforming structure. The deformation of the beam close to the first three resonances ( $\unicode[STIX]{x1D714}_{1}=3.5$ , $\unicode[STIX]{x1D714}_{2}=22.0$ , $\unicode[STIX]{x1D714}_{3}=61.7$ ) for $K_{C}=10^{-2}$ in figure 5(b) is indeed similar to the corresponding beam modes $X_{1}$ , $X_{2}$ , $X_{3}$ involved in the asymptotic solution (4.4). Note that when $K_{C}$ is close to 1, the nonlinear drag term is also responsible for a drift of the resonance frequencies that has been studied in Arellano Castro et al. (Reference Arellano Castro, Guillamot, Cros and Eloy2014). This effect is not obvious in figure 5(a) because of the very strong attenuation of the resonance peak for $K_{C}=1$ , but is more visible in the structural stress analysis of figure 9(a).

Figure 5. (a) Amplitude of the maximum scaled deflection obtained with (4.3) against the frequency ratio. $K_{C}=10^{-2}$ (——), $K_{C}=10^{0}$ (– – –), $K_{C}=10^{2}$ (— ⋅ —). Analytical solution for $K_{C}\rightarrow 0$ ( $\cdots \cdots$ ). (b) Snapshots of the beam over one cycle obtained with (4.3) for $K_{C}=10^{-2}$ (modal regime) and for $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{1}$ (resonance of mode 1), $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{2}$ (resonance of mode 2), $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{3}$ (resonance of mode 3). (c) Same as (b) but with $K_{C}=10^{2}$ (convective regime).

On the other hand, if we increase the fluid particles excursion beyond the width of the structure ( $K_{C}\gg 1$ ), a change in physical behaviour occurs. Drag becomes the dominant term in (4.3). The leading-order solution now is $\tilde{x}(s,\tilde{t})=\cos \tilde{t}$ , which amounts to considering that the structure is convected exactly with the fluid particles. Therefore, we may call this regime the convective regime. This solution is however incompatible with the boundary condition at the clamped edge $\tilde{x}(0,\tilde{t})=0$ , so an elastic boundary layer develops close to the clamping point. The relative magnitude of the terms in (4.3) suggests that the thickness of the boundary layer scales as $\unicode[STIX]{x1D6FF}=(K_{C}\,\unicode[STIX]{x1D714}^{2})^{-1/4}$ . Rescaling the curvilinear coordinate ${\hat{s}}=s/\unicode[STIX]{x1D6FF}$ in (4.3) provides the leading-order equation for the inner solution

(4.5) $$\begin{eqnarray}\unicode[STIX]{x2202}_{{\hat{s}}}^{4}\tilde{x}=|\dot{\tilde{x}}-\sin (\tilde{t})|(\dot{\tilde{x}}-\sin (\tilde{t})),\end{eqnarray}$$

with boundary conditions $\tilde{x}=\unicode[STIX]{x2202}_{{\hat{s}}}\tilde{x}=0$ at ${\hat{s}}=0$ and $\unicode[STIX]{x2202}_{{\hat{s}}}^{2}\tilde{x}=\unicode[STIX]{x2202}_{{\hat{s}}}^{3}\tilde{x}=0$ at ${\hat{s}}=1/\unicode[STIX]{x1D6FF}$ .

The dynamic deformation of the structure displayed in figure 5(c) for $K_{C}=10^{2}$ for the same values of frequency ratios as in figure 5(b) clearly shows the concentration of the curvature close to the clamped edge and the passive convection of the main part of the structure. The resonances previously observed in the modal regime in figure 5(a) are now completely damped out when $K_{C}=10^{2}$ . Compared to the case $K_{C}=1$ , this curve is shifted one decade to the left as the proper scaling parameter is now $\sqrt{K_{C}}\,\unicode[STIX]{x1D714}$ instead of $\unicode[STIX]{x1D714}$ , and $\sqrt{K_{C}}=10$ for $K_{C}=10^{2}$ . The scaling of the boundary layer thickness $\unicode[STIX]{x1D6FF}$ is similar to that of the effective length of Luhar & Nepf (Reference Luhar and Nepf2016), as it is based on the equilibrium between the same forces. A similar problem had also been considered in Mullarney & Henderson (Reference Mullarney and Henderson2010). In the case of a wave-like flow, the authors neglected the quadratic nonlinearity in order to get an analytical solution.

4.2 Large amplitude of flow oscillation $\unicode[STIX]{x1D6FC}=A/L\gg 1$

In the convective regime discussed above, the structure is purely convected with the fluid particles on most of its span over the whole cycle. But when the amplitude becomes larger than the length of the structure, geometric saturation of the deflection occurs because the structure cannot extend further than its own length. The deflection is now of order $x=O(1)$ and so we cannot neglect the geometrical nonlinearities of (2.8) anymore. The slenderness $\unicode[STIX]{x1D706}$ becomes the relevant parameter to compare drag to the fluid inertial forces in lieu of the Keulegan–Carpenter number $K_{C}$ . Because we only consider elongated structures $\unicode[STIX]{x1D706}\gg 1$ in this study, drag will always be the dominant term in the large-amplitude regime.

The dynamic deformations obtained with (2.8) in two cases with similar amplitude $\unicode[STIX]{x1D6FC}=10^{2}$ and slenderness $\unicode[STIX]{x1D706}=12.7$ but different frequencies are compared in figure 6 with 100 snapshots per cycle with constant time interval. In the small frequency case (a), the deformation looks quasi-static. Transition from one side to the other is slow (many snapshots distributed from left to right) and the curvature is essentially concentrated near the clamped edge during the whole cycle. On the other hand, in the larger frequency case (b), the structure switches sides very fast (few snapshots visible in the centre while many are superimposed on the sides) and curvature waves propagate very quickly along the span during reversal. Therefore, the cycle may be decomposed into two steps: first, a fast reversal period during which the structure switches from one side to the other immediately after flow reversal, followed by a longer period of quasi-static adaptation to the increasing magnitude of the drag. Because the dominant drag force $\unicode[STIX]{x1D706}|U_{n}|U_{n}\propto \unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D714}^{2}$ is proportional to $\unicode[STIX]{x1D714}^{2}$ , the maximum drag is larger in the large frequency case in figure 6, which explains why the maximum deflection is enhanced.

Figure 6. Snapshots of the deforming structure over one cycle (——) and tip trajectory (– – –) obtained with (2.8) for $\unicode[STIX]{x1D706}=12.7$ , $\unicode[STIX]{x1D6FC}=10^{2}$ . (a) $\unicode[STIX]{x1D714}=10^{-2}$ , (b) $\unicode[STIX]{x1D714}=1$ .

To estimate the time scale of reversal $T_{r}$ , let us assume that shortly before flow reversal, the structure is fully reconfigured on one side $x(s=1,t=0)=-1$ . At flow reversal $t=0$ , drag starts pushing the structure to the other side. Let us assume that the blade is purely convected until it is fully reconfigured on the other side at the end of the reversal time $x(s=1,t=T_{r})=1$ . In that case, we may write

(4.6) $$\begin{eqnarray}2=x_{tip}(T_{r})-x_{tip}(0)=\int _{0}^{T_{r}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}\sin (\unicode[STIX]{x1D714}t)\,\text{d}t\simeq \int _{0}^{T_{r}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}^{2}t\,\text{d}t=\frac{1}{2}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D714}T_{r})^{2},\end{eqnarray}$$

where the linearization holds owing to the fact that reversal occurs on a time scale much smaller than the period of the cycle ( $\unicode[STIX]{x1D714}T_{r}\ll 2\unicode[STIX]{x03C0}$ ). We finally obtain $T_{r}=2/(\unicode[STIX]{x1D714}\sqrt{\unicode[STIX]{x1D6FC}})$ . This expression of the reversal time is normalized by the scale of the natural period of the structure. It is more relevant than $\unicode[STIX]{x1D714}$ to assess the quasi-steady nature of the deformation in the large-amplitude regime because it compares only the time scale on which structural motion is significant (instead of the whole cycle period) to the characteristic structural response time. Indeed, in figure 6(a), the large reversal time $T_{r}=20$ allows the structure to be in quasi-static equilibrium with the fluid loading at all times. Conversely, in figure 6(b) the small reversal time $T_{r}=0.2$ is responsible for the propagation of curvature waves during reversal. Hence, when $T_{r}\gg 1$ , the structure is in static equilibrium with the fluid forces during the whole cycle, while the quasi-static character of the deformation is lost during the fast reversal when $T_{r}\ll 1$ .

A zoom on the trajectory of the tip around flow reversal in the case of figure 6(b) shown in figure 7 (solid line) confirms that reversal occurs approximately between $t/T_{r}=0$ and $t/T_{r}=1$ . When the slenderness parameter is increased (broken lines, $\unicode[STIX]{x1D706}=127$ ), the time scale of the dynamics remains unchanged. The same graphs for the same $T_{r}$ but for a smaller or a larger amplitude ( $\unicode[STIX]{x1D6FC}=10$ and $\unicode[STIX]{x1D6FC}=10^{3}$ respectively), not shown here, are practically indistinguishable from that in figure 7. This result confirms that the amplitude and frequency parameters influence the kinematics of the reversal exclusively through the combined parameter $T_{r}$ . Besides, because the structural mass was neglected, no dynamic excitation possibly resulting from the violent reversal is allowed to persist after $T_{r}$ .

Figure 7. Horizontal displacement of the tip during flow reversal against the rescaled time $t/T_{r}$ , for $\unicode[STIX]{x1D6FC}=10^{2}$ , $T_{r}=0.2$ ( $\unicode[STIX]{x1D714}=1$ ) and $\unicode[STIX]{x1D706}=12.7$ (——), $\unicode[STIX]{x1D706}=127$ (– – –).

Figure 8. Schematic view of the kinematic regimes in the amplitude–frequency space.

4.3 Summary of the kinematic regimes

So far we have found that depending on the amplitude and frequency of the oscillating flow with respect to the dimensions and natural frequencies of the blade, four different kinematic regimes may exist. Their respective locations in the parameter space are summarized in figure 8.

First, if the amplitude is much smaller than the length of the blade ( $\unicode[STIX]{x1D6FC}\ll 1$ or equivalently $A\ll L$ ) and the frequency of the flow smaller than that of the structure ( $\unicode[STIX]{x1D714}<1$ or equivalently $\unicode[STIX]{x1D6FA}<1/T_{s}$ ), the structure is in static equilibrium with the fluid forces at all times. On the other hand, if the frequency is now comparable or larger than the characteristic structural frequency ( $\unicode[STIX]{x1D714}>1$ or equivalently $\unicode[STIX]{x1D6FA}>1/T_{s}$ ), the kinematics further depends on the ratio of the amplitude of the flow to the width of the structure. If the amplitude is much smaller than the width of the blade ( $A\ll W$ , or equivalently $K_{C}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}\ll 1$ ), the structure behaves as a linear oscillator and we are in the modal regime. If the amplitude is large compared to the width, but small compared to the length ( $W\ll A\ll L$ , or equivalently $K_{C}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}\gg 1$ and $\unicode[STIX]{x1D6FC}\ll 1$ ), an elastic boundary layer develops close to the clamped edge in which all the curvature is confined, while the rest of the structure is passively convected with the fluid particles. This convective regime occurs because of the saturation of the drag term in the small-amplitude equation (4.1).

Now, if the amplitude is increased further and becomes larger than the length of the blade ( $A\gg L$ or equivalently $\unicode[STIX]{x1D6FC}\gg 1$ ), the convection of the blade by the fluid is limited to its own length and the blade deformation is subject to geometric saturation. The convection process is therefore limited in time to a short reversal period, right after flow reversal, and during which the blade switches side at the speed of the fluid particles, followed by a longer period of quasi-static adaptation to the increasing magnitude of the drag force. If reversal occurs on a longer time scale than the characteristic structural response time ( $T_{r}\sim 1/(\unicode[STIX]{x1D714}\sqrt{\unicode[STIX]{x1D6FC}})\gg 1$ ), the structure has time to reach the static equilibrium with the fluid forces at all time. Conversely, if reversal is faster than the characteristic time of the structure ( $T_{r}\sim 1/(\unicode[STIX]{x1D714}\sqrt{\unicode[STIX]{x1D6FC}})\ll 1$ ), the quasi-static nature of the large-amplitude structural response is lost during the short time needed for reversal.

5.1 Stress reduction due to flexibility

Depending on the kinematic regime, we expect that the consequences of flexibility in terms of magnitude and repartition of the internal stresses will vary. Our main interest is to assess whether flexibility makes a blade more or less likely to break in a given flow. Structural failure may occur when, at a given time $t$ , the stress due to the loads exceeds a given threshold called the breaking strength, at some location within the structure. For an Euler–Bernoulli beam in two-dimensional bending, the stress tensor may essentially be reduced to two components, the tensile (or compressive) stress $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$ and the shear stress $\unicode[STIX]{x1D70E}_{n}$ . Both quantities vary along the span but also within the cross-section. The maximum tensile stress is reached at the edges of the cross-section and depends linearly on the internal bending moment $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\propto MD/I\propto M/WD^{2}$ . Conversely, the shear stress reaches its maximum on the neutral axis and it is proportional to the internal shear force $\unicode[STIX]{x1D70E}_{n}\propto Q/WD$ . Thus, following the dedicated terminology of Gosselin et al. (Reference Gosselin, de Langre and Machado-Almeida2010), we may define two reconfiguration numbers

(5.1a,b ) $$\begin{eqnarray}{\mathcal{R}}_{\unicode[STIX]{x1D70F}}=\frac{\max |M(s,t)|}{\max |M_{rigid}(s,t)|},\quad {\mathcal{R}}_{n}=\frac{\max |Q(s,t)|}{\max |Q_{rigid}(s,t)|}\end{eqnarray}$$

that compare the maximum stresses endured over a cycle at any point along the structure to the maximum value the same structure would have to endure if it were rigid. The reconfiguration numbers are smaller than one if the flexibility is beneficial in terms of internal stresses, and larger than unity if it is detrimental.

Our shear reconfiguration number ${\mathcal{R}}_{n}$ is equivalent to the reconfiguration number defined in Gosselin et al. (Reference Gosselin, de Langre and Machado-Almeida2010) and Leclercq & de Langre (Reference Leclercq and de Langre2016) in the static case. Their definition is based on the total drag $Q(s=0)$ instead of the maximum of the shear force $\max |Q|$ , but the shear force is in fact maximum at the clamped edge in their case so it is equal to the total drag. Our ${\mathcal{R}}_{n}$ is also quite similar to the effective length defined by Luhar & Nepf (Reference Luhar and Nepf2016), only the latter was based on the root-mean-square value of the total drag $Q(s=0)$ instead of the spatio-temporal maximum of $Q$ . This is so because the goal of Luhar & Nepf (Reference Luhar and Nepf2016) was to provide insight about how flexibility affects energy dissipation in the background flow, while our focus is the ability of the structure to withstand the fluid loads. For the sake of simplicity, in the rest of this article we will only present results about the shear stress $\unicode[STIX]{x1D70E}_{n}$ and shear reconfiguration number ${\mathcal{R}}_{n}$ . The results about the tensile stress are actually quite similar and will be provided in appendix A.

5.2 Rigid case

In the case of a perfectly rigid structure, the combination of the external fluid forces (2.2) and (2.4) results in a span-invariant, purely horizontal load

(5.2) $$\begin{eqnarray}q_{rigid}(t)=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}^{2}[\cos (\unicode[STIX]{x1D714}t)+(\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC})|\text{sin}(\unicode[STIX]{x1D714}t)|\sin (\unicode[STIX]{x1D714}t)]\end{eqnarray}$$

that also reads, in terms of the Cauchy number ( $C_{Y}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D714}^{2}$ ) and Keulegan–Carpenter number ( $K_{C}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}$ )

(5.3) $$\begin{eqnarray}q_{rigid}(t)=\frac{C_{Y}}{K_{C}}[\cos (\unicode[STIX]{x1D714}t)+K_{C}|\text{sin}(\unicode[STIX]{x1D714}t)|\sin (\unicode[STIX]{x1D714}t)].\end{eqnarray}$$

The first term is an inertia term, proportional to the flow acceleration, while the second term is the resistive drag force proportional to the velocity squared. Integration from the free tip provides the internal bending moment and shear force

(5.4a,b ) $$\begin{eqnarray}M_{rigid}(s,t)=-{\textstyle \frac{1}{2}}q_{rigid}(t)(1-s)^{2},\quad Q_{rigid}(s,t)=-q_{rigid}(t)(1-s)\end{eqnarray}$$

that are maximum at the clamped edge and $\max |M_{rigid}(s,t)|=1/2\max |Q_{rigid}(s,t)|=1/2\max |q_{rigid}(t)|$ with

(5.5a,b ) $$\begin{eqnarray}\max |q_{rigid}(t)|=\frac{C_{Y}}{K_{C}}\quad \text{if }K_{C}\leqslant \frac{1}{2};\quad C_{Y}\left(1+\frac{1}{4K_{C}^{2}}\right)\quad \text{if }K_{C}\geqslant \frac{1}{2}.\end{eqnarray}$$

Figure 9. Shear reconfiguration number (a) and location of maximum shear stress along the span (b), in the modal regime, against the frequency ratio, for $K_{C}=10^{-2}$ (——), $K_{C}=10^{-1}$ (— ⋅ —), $K_{C}=10^{0}$ (– – –) and analytical solution for $K_{C}\rightarrow 0$ ( $\cdots \cdots$ ).

5.3 Small amplitude of flow oscillation $\unicode[STIX]{x1D6FC}=A/L\ll 1$

As for the kinematics, let us first consider the case where the amplitude of forcing is small compared to the length of the structure ( $\unicode[STIX]{x1D6FC}\ll 1$ ). Depending on the value of the Keulegan–Carpenter number $K_{C}$ , the system will be in the modal or convective regime.

The variations of the shear reconfiguration number with the frequency ratio are shown in figure 9(a) for different values of $K_{C}$ in the modal regime. Because the system behaves as a high-pass filter, the blade remains rigid in the quasi-static limit $\unicode[STIX]{x1D714}<1$ and so there is no drag reduction in this regime ${\mathcal{R}}_{n}\sim 1$ . For larger frequencies, the reconfiguration number decreases overall but peaks at the successive resonances. The magnitude of the peaks is mitigated when the Keulegan–Carpenter number is increased due to damping by the drag term. The resonance frequencies are decreased as well owing to the nonlinearity of the drag term, as explained in Arellano Castro et al. (Reference Arellano Castro, Guillamot, Cros and Eloy2014). But when $K_{C}$ is small enough, the reconfiguration number may even exceed unity close to the first resonances. In these particular cases, flexibility may therefore be responsible for a magnification of the shear stress. Apart from the resonances, the slope of the overall decay may be estimated by a scaling argument. Far from the resonances, the amplitude of the deflection is of the order of the fluid particles excursion $x=O(\unicode[STIX]{x1D6FC})$ . The non-dimensional shear force $Q=\unicode[STIX]{x1D705}^{\prime }$ , is thus of order $O(\unicode[STIX]{x1D6FC}\times k^{3})$ with the wavenumber of the dominant mode $k\sim \sqrt{\unicode[STIX]{x1D714}}$ , while the rigid shear force is of order $O(C_{Y}/K_{C})=O(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}^{2})$ according to (5.5). Thus, the shear reconfiguration number is ${\mathcal{R}}_{n}\sim k^{-1}\sim \unicode[STIX]{x1D714}^{-1/2}$ , which is consistent with the slope observed in figure 9(a).

As shown in figure 9(b), the location $s_{n}$ along the span of the blade where the maximum shear stress $\max (\unicode[STIX]{x1D70E}_{n})$ is reached varies with the frequency. In the rigid domain $\unicode[STIX]{x1D714}<1$ the maximum stress remains at the clamped edge, until the first resonance is reached. After $\unicode[STIX]{x1D714}_{1}$ , the maximum stress starts moving from the clamped edge towards the free tip as ${\mathcal{R}}_{n}$ decreases, before suddenly going back to the clamping point as ${\mathcal{R}}_{n}$ starts increasing again, until the second resonance is attained. Similarly, after $\unicode[STIX]{x1D714}_{2}$ , the locus moves again as ${\mathcal{R}}_{n}$ decreases and then comes back as ${\mathcal{R}}_{n}$ starts increasing towards the next resonance, and so on. This trajectory of the most solicited spot is independent of $K_{C}$ , except close to the transition towards the convective regime. Indeed, for $K_{C}=1$ , the maximum shear stress remains at the clamping point for any value of the frequency ratio.

In the convective regime $K_{C}>1$ , we have shown that all the curvature concentrates within an elastic boundary layer of typical size $\unicode[STIX]{x1D6FF}=(K_{C}\,\unicode[STIX]{x1D714}^{2})^{-1/4}$ close to the attachment point. Consequently, the location of the maximum stress is always located at the clamping point in the convective regime. Besides, the variations of the shear reconfiguration number ${\mathcal{R}}_{n}$ , displayed as a function of the frequency ratio in figure 10(a), all collapse on the same curve when replotted as a function of $K_{C}\,\unicode[STIX]{x1D714}^{2}$ in figure 10(b). Even the transition case $K_{C}=1$ also follows the same trend on average, but still exhibits some variations and small resonances due to the persistent modal nature of the response. When $K_{C}\,\unicode[STIX]{x1D714}^{2}<1$ , the scale of the boundary layer exceeds the length of the structure so the blade behaves rigidly and ${\mathcal{R}}_{n}\sim 1$ . Conversely when $K_{C}\,\unicode[STIX]{x1D714}^{2}>1$ , the motion allowed by the flexibility is responsible for an alleviation of the internal shear stress. We may estimate the slope of the asymptotic decay by a similar argument as in the modal regime. Assuming that the characteristic bending length scales as the boundary layer thickness $\unicode[STIX]{x1D6FF}$ , we now have $Q\sim O(\unicode[STIX]{x1D6FC}\times \unicode[STIX]{x1D6FF}^{-3})$ and the rigid shear force of order $O(C_{Y})=O(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}^{-4})$ . We thus obtain ${\mathcal{R}}_{n}\sim \unicode[STIX]{x1D6FF}\sim (K_{C}\,\unicode[STIX]{x1D714}^{2})^{-1/4}$ , in agreement with figure 10(b). Note that, as illustrated in figure 10(a), reconfiguration in the elastic boundary layer occurs even in the quasi-static regime $\unicode[STIX]{x1D714}<1$ provided that $K_{C}\,\unicode[STIX]{x1D714}^{2}>1$ . Indeed, in this particular case, the rigid force $q_{rigid}$ that appears on the right-hand side of the small-amplitude static equation (4.2) would actually lead to static deformations exceeding the excursion of the fluid particles. This is not possible in this drag-dominated regime as only strong inertial forces can cause the structure to overshoot the fluid particles. The drag term of (4.3) thus ensures the limitation of the structural excursion to that of the fluid particles, while only the elastic boundary layer that develops close to the clamped edge actually satisfies the quasi-static equilibrium between the elasticity forces and the drag (which amounts to neglecting the $\dot{\tilde{x}}$ terms in the boundary layer equation (4.5)). Consequently, the scaling of the drag associated with reconfiguration in the elastic boundary layer remains valid in this domain as well.

Figure 10. Shear reconfiguration number in the convective regime against (a) the frequency ratio $\unicode[STIX]{x1D714}$ , (b) the rescaled parameter $K_{C}\,\unicode[STIX]{x1D714}^{2}$ , for $K_{C}=10^{0}$ (– – –), $K_{C}=10^{1}$ (— ⋅ —), $K_{C}=10^{2}$ (——).

5.4 Large amplitude of flow oscillation $\unicode[STIX]{x1D6FC}=A/L\gg 1$

In the large-amplitude regime ( $\unicode[STIX]{x1D6FC}>1$ ), we have proven that significant structural motion may only occur during a short period of time $T_{r}$ following flow reversal ( $\unicode[STIX]{x1D714}t=0$ ). During that time, the flow magnitude is close to zero and the drag force is at its minimum. Drag being the dominant term of the equation, we expect the largest stress to be experienced when it is at its maximum around $\unicode[STIX]{x1D714}t=\pm \unicode[STIX]{x03C0}/2$ , at a time where the structure is in quasi-static equilibrium with the flow forces. Besides, the flow acceleration cancels out when the flow magnitude is maximum so that, at the time where the stress peaks, equation (2.8) reduces to the static equation

(5.6) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}^{\prime \prime }+\frac{1}{2}\unicode[STIX]{x1D705}^{3}-C_{Y}\left[|\text{cos}\,\unicode[STIX]{x1D703}|\cos \unicode[STIX]{x1D703}-\frac{1}{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D705}\left(\sin ^{2}\unicode[STIX]{x1D703}-\frac{1}{2}\cos ^{2}\unicode[STIX]{x1D703}\right)\right]=0. & & \displaystyle\end{eqnarray}$$

In the quasi-static part of the cycle, the amplitude and frequency parameter influence the shape of the structure and the internal stress only through the Cauchy number $C_{Y}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D714}^{2}$ . Consequently, the evolution of the shear reconfiguration number shown in figure 11(a) as a function of the frequency ratio $\unicode[STIX]{x1D714}$ (for $\unicode[STIX]{x1D706}=12.7$ ) collapse very well on the static curve obtained with (5.6) when replotted as a function of the Cauchy number in figure 11(b). The curves are perfectly superimposed for $\unicode[STIX]{x1D6FC}=10$ , but even for $\unicode[STIX]{x1D6FC}$ as small as 1, agreement is already very good. When the Cauchy number is less than 1, deflection is negligible so (5.6) actually reduces to the small-amplitude static equation (4.2). In this limit, even though the amplitude of the forcing is large $\unicode[STIX]{x1D6FC}>1$ , we actually recover the small-amplitude static regime in which the structure experiences the same amount of stress as if it were rigid ${\mathcal{R}}_{n}\sim 1$ .

On the other hand, when the Cauchy number is large $C_{Y}>1$ , the stress is much reduced. In the limit where drag dominates over the added mass corrective term (limit of infinite slenderness $\unicode[STIX]{x1D706}\rightarrow \infty$ ), the static equation (5.6) has a self-similar structure. The scaling of the terms of the equation provides the length of the self-similar boundary layer $\ell _{s}=C_{Y}^{-1/3}$ within which all the curvature concentrates. Consequently we may here again estimate the asymptotic behaviour of the shear reconfiguration number by a scaling argument. In this case, the saturated angle $\unicode[STIX]{x1D703}$ is of order $O(1)$ so the shear force $Q=\unicode[STIX]{x1D705}^{\prime }\sim O(1\times \ell _{s}^{-2})$ . The rigid shear force is of order $O(C_{Y})=O(\ell _{s}^{-3})$ so we get ${\mathcal{R}}_{n}\sim \ell _{s}\sim C_{Y}^{-1/3}$ . The slope in figure 11(b) is close but differs slightly from that estimation. The analysis of appendix B shows that this discrepancy is due to the rather small value of $\unicode[STIX]{x1D706}=12.7$ . For any larger slenderness, the asymptotic scaling provided here matches very well the numerical results. Note that this bending length is similar to that previously found by Gosselin et al. (Reference Gosselin, de Langre and Machado-Almeida2010) who neglected the cubic term in curvature in their governing equation, as well as that found by Alben et al. (Reference Alben, Shelley and Zhang2004) for the case of a two-dimensional plate (opposite limit of infinite width). The extended validity of this static bending length to the case of large-amplitude unsteady flows was moreover suggested in Luhar & Nepf (Reference Luhar and Nepf2016).

Note finally that this analysis is independent of the magnitude of the reversal time $T_{r}$ . The key point of this analysis lies in the fact that even if significant dynamics may be involved during reversal when $T_{r}\gg 1$ , the maximum stress is endured at a time when the structure is in static equilibrium with the fluid forces. This remains obviously true when $T_{r}\ll 1$ and static equilibrium is enforced at all times.

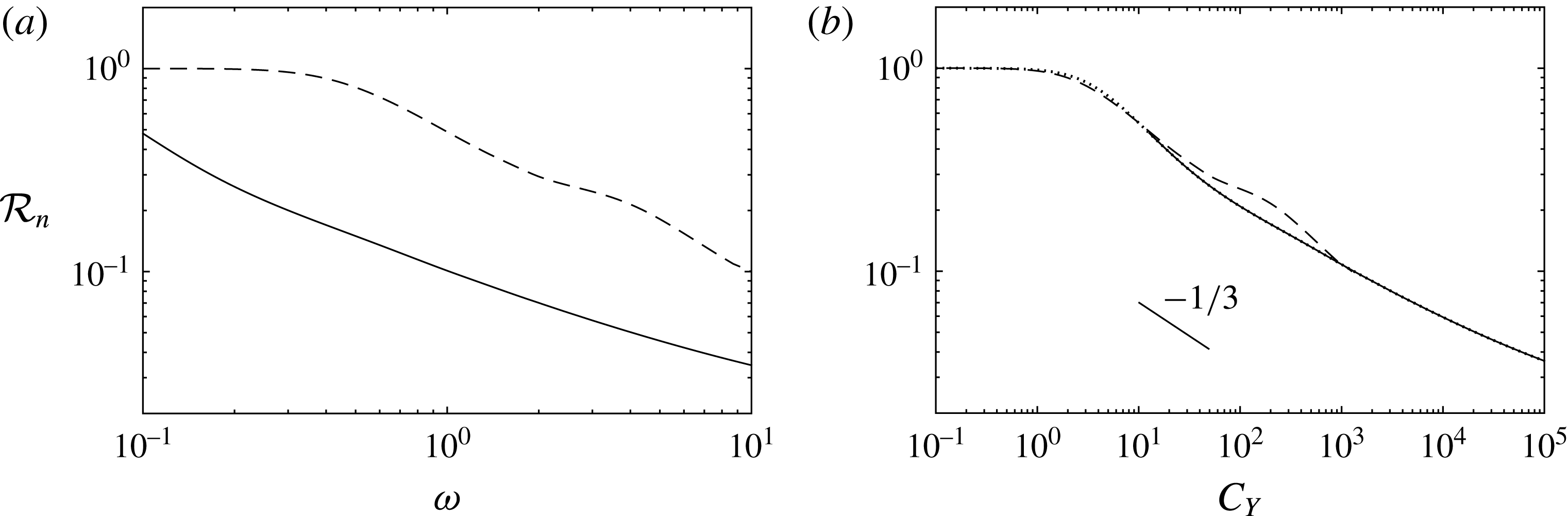
Figure 11. Shear reconfiguration number in the large-amplitude regime for $\unicode[STIX]{x1D706}=12.7$ , against (a) the frequency ratio $\unicode[STIX]{x1D714}$ , (b) the Cauchy number $C_{Y}$ , for $\unicode[STIX]{x1D6FC}=10^{0}$ (– – –), $\unicode[STIX]{x1D6FC}=10^{1}$ (——). Static solution obtained with (5.6) ( $\cdots \cdots$ , on (b) only).