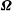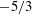1 Introduction
Rotating turbulent flows are ubiquitous and their studies have long become one of the areas of classical fluid mechanics (Greenspan Reference Greenspan1968; Vanyo Reference Vanyo1993; Sagaut & Cambon Reference Sagaut and Cambon2008; Davidson Reference Davidson2013, see also a recent review by Godeferd & Moisy Reference Godeferd and Moisy2015). Rotation is a primary factor affecting circulations of planetary and terrestrial atmospheres and oceans (Pedlosky Reference Pedlosky1998; Vallis Reference Vallis2006; Sánchez-Lavega Reference Sánchez-Lavega2011). Environments with a background rotation are conducive to anisotropization of dynamical and transport properties of a fluid flow and excitation of inertial waves. Practical needs and theoretical interest in understanding and predicting rotating turbulent flows yielded accumulation of extensive and ever expanding volume of experimental, observational, heuristic and computational information.
Different flow regimes emerging in rotating systems can be characterized in terms of spatial and temporal scales and ensuing non-dimensional parameters derived from heuristic, semi-empirical and analytical theories (see e.g. Cambon & Jacquin Reference Cambon and Jacquin1989; Godeferd & Cambon Reference Godeferd and Cambon1994; Bartello Reference Bartello1995; Cambon & Scott Reference Cambon and Scott1999; Cambon Reference Cambon2001; Smith & Waleffe Reference Smith and Waleffe2002; Sagaut & Cambon Reference Sagaut and Cambon2008; Davidson Reference Davidson2013). Despite the ongoing effort, however, we are still far away from full understanding of the intricacies of rotating turbulence. As in the case of stable stratification, progressive anisotropization of transport properties on increasing spatial scales is one of the most challenging aspects of turbulence with rotation. The mathematical description of this phenomenon evokes tensorial apparatus whose complexity is exacerbated by the presence of inertial waves (Cambon & Jacquin Reference Cambon and Jacquin1989; Gaite Reference Gaite2003). Due to the anisotropization, the isotropic spectrum provides only partial representation of the dynamics of rotating flows (appropriate discussions can be found in Zeman Reference Zeman1994; Canuto & Dubovikov Reference Canuto and Dubovikov1997; Yeung & Zhou Reference Yeung and Zhou1998; Thangam & Wang Reference Thangam and Wang1999; Gledzer Reference Gledzer2008). More detailed analysis requires consideration of various one-dimensional (1-D) spectra as was done in e.g. Cambon, Mansour & Godeferd (Reference Cambon, Mansour and Godeferd1997), Yang & Domaradzki (Reference Yang and Domaradzki2004), Thiele & Müller (Reference Thiele and Müller2009), Baerenzung et al. (Reference Baerenzung, Mininni, Pouquet, Politano and Ponty2010) and Mininni & Pouquet (Reference Mininni and Pouquet2010).
Many analytical investigations of rotating turbulence utilize a spectral approach employing some version of the eddy-damped quasi-normal Markovian (EDQNM) theory (Orszag Reference Orszag, Balian and Peabe1977; Cambon et al. Reference Cambon, Mansour and Godeferd1997; Sagaut & Cambon Reference Sagaut and Cambon2008; Baerenzung et al. Reference Baerenzung, Politano, Ponty and Pouquet2008; Sen et al. Reference Sen, Mininni, Rosenberg and Pouquet2012) based upon consideration of wave vector triad interactions. In anisotropic turbulent flows with dispersive waves, in addition to the vector triads, one must consider frequency resonances associated with the interacting vectors which narrow down the number of the interacting triads and preferentially select those that funnel energy into waveless (and thus slow mode) subsets lying in the hypersurfaces orthogonal to or enclosing the directions of zero frequency (e.g. Rhines Reference Rhines1975; Bartello Reference Bartello1995; Huang, Galperin & Sukoriansky Reference Huang, Galperin and Sukoriansky2001; Smith & Waleffe Reference Smith and Waleffe2002; Chen et al. Reference Chen, Chen, Eyink and Holm2005; Bourouiba & Bartello Reference Bourouiba and Bartello2007; Sagaut & Cambon Reference Sagaut and Cambon2008).
The recently developed quasi-normal scale elimination (QNSE) theory (Sukoriansky, Galperin & Staroselsky Reference Sukoriansky, Galperin and Staroselsky2003, Reference Sukoriansky, Galperin and Staroselsky2005; Galperin & Sukoriansky Reference Galperin and Sukoriansky2010; Sukoriansky & Galperin Reference Sukoriansky and Galperin2013; Sukoriansky & Zemach Reference Sukoriansky and Zemach2016) operates at the level of the momentum equation and is thus simpler than EDQNM. It is amenable to closed-form analytical solutions for basic neutrally stratified flows and for flows with extra strains (following the terminology by Bradshaw Reference Bradshaw1973) produced by stable stratification and/or system rotation. The theory is well suited for explicit accounting of the combined effect of anisotropy and waves upon initially isotropic turbulence. QNSE can be used to complement the EDQNM-based theories as it provides a framework for computing the spectra, eddy viscosities and eddy diffusivities necessary for evaluation of the time decorrelation exponents (e.g. Cambon et al. Reference Cambon, Mansour and Godeferd1997; Sen et al. Reference Sen, Mininni, Rosenberg and Pouquet2012).
Physically, QNSE aims at establishing a self-consistent coarse-graining procedure yielding the effective viscosity as a function of the grain size, i.e. the smallest explicit (or resolved) scale. The QNSE formalism utilizes the key fact that for a small shell (denoted
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
) of the velocity modes adjacent to the dissipation cutoff wavenumber, the Reynolds number,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
) of the velocity modes adjacent to the dissipation cutoff wavenumber, the Reynolds number,
![]() $Re$
, is of
$Re$
, is of
![]() $O(1)$
. Using the Langevin equation to represent forcing of a given mode by all other modes due to nonlinear interactions, that shell is mapped onto a randomly forced vector field with quasi-normal statistics. The coarse graining is achieved by ensemble averaging over the modes in the shell
$O(1)$
. Using the Langevin equation to represent forcing of a given mode by all other modes due to nonlinear interactions, that shell is mapped onto a randomly forced vector field with quasi-normal statistics. The coarse graining is achieved by ensemble averaging over the modes in the shell
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
. The averaging generates a small,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
. The averaging generates a small,
![]() $O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
, correction to the viscosity which accounts for the transport processes taking place within that shell. Along with the increase of the effective viscosity, the effective dissipation wavenumber,
$O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
, correction to the viscosity which accounts for the transport processes taking place within that shell. Along with the increase of the effective viscosity, the effective dissipation wavenumber,
![]() $\unicode[STIX]{x1D6EC}$
, decreases. The effective
$\unicode[STIX]{x1D6EC}$
, decreases. The effective
![]() $Re$
built upon the scales pertinent to the new value of
$Re$
built upon the scales pertinent to the new value of
![]() $\unicode[STIX]{x1D6EC}$
remains of
$\unicode[STIX]{x1D6EC}$
remains of
![]() $O(1)$
thus enabling a cyclic repetition of the averaging procedure. Taking a limit
$O(1)$
thus enabling a cyclic repetition of the averaging procedure. Taking a limit
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
, one obtains a differential equation relating the effective viscosity to the current value of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
, one obtains a differential equation relating the effective viscosity to the current value of
![]() $\unicode[STIX]{x1D6EC}$
. The effective,
$\unicode[STIX]{x1D6EC}$
. The effective,
![]() $\unicode[STIX]{x1D6EC}$
-dependent viscosity emerging in this procedure can be used as a subgrid-scale (SGS) viscosity in large eddy simulations (LES) where
$\unicode[STIX]{x1D6EC}$
-dependent viscosity emerging in this procedure can be used as a subgrid-scale (SGS) viscosity in large eddy simulations (LES) where
![]() $\unicode[STIX]{x1D6EC}$
is determined by the grid resolution. The combination of a modal quasi-normal forcing and an eddy damping by the effective viscosity places QNSE in the class of the quasi-normal eddy-damped theories of turbulence (Orszag Reference Orszag, Balian and Peabe1977; Chasnov Reference Chasnov1991; McComb Reference McComb1991). The algorithm of successive small-scale elimination was initially developed within the renormalization group theory of turbulence (RNG) (Forster, Nelson & Stephen Reference Forster, Nelson and Stephen1977; Yakhot & Orszag Reference Yakhot and Orszag1986; Smith & Woodruff Reference Smith and Woodruff1998; Zhou Reference Zhou2010). QNSE methodology significantly differs from the RNG, however, because it employs neither the
$\unicode[STIX]{x1D6EC}$
is determined by the grid resolution. The combination of a modal quasi-normal forcing and an eddy damping by the effective viscosity places QNSE in the class of the quasi-normal eddy-damped theories of turbulence (Orszag Reference Orszag, Balian and Peabe1977; Chasnov Reference Chasnov1991; McComb Reference McComb1991). The algorithm of successive small-scale elimination was initially developed within the renormalization group theory of turbulence (RNG) (Forster, Nelson & Stephen Reference Forster, Nelson and Stephen1977; Yakhot & Orszag Reference Yakhot and Orszag1986; Smith & Woodruff Reference Smith and Woodruff1998; Zhou Reference Zhou2010). QNSE methodology significantly differs from the RNG, however, because it employs neither the
![]() $\unicode[STIX]{x1D716}$
-expansion nor the fixed point arguments (note that
$\unicode[STIX]{x1D716}$
-expansion nor the fixed point arguments (note that
![]() $\unicode[STIX]{x1D716}$
denotes the expansion parameter in the original renormalization group theory by Forster et al. (Reference Forster, Nelson and Stephen1977) in this paragraph only). Instead, QNSE exploits the quasi-normality assumption within the shell
$\unicode[STIX]{x1D716}$
denotes the expansion parameter in the original renormalization group theory by Forster et al. (Reference Forster, Nelson and Stephen1977) in this paragraph only). Instead, QNSE exploits the quasi-normality assumption within the shell
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
(Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003, Reference Sukoriansky, Galperin and Staroselsky2005).
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
(Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003, Reference Sukoriansky, Galperin and Staroselsky2005).
In neutral flows with no extra strains, QNSE replicates all known RNG results. Those include the derivation from nearly first principles of the classical Kolmogorov and Corrsin–Obukhov spectra of the kinetic energy and temperature variance and computing their respective universal constants.
Applied to flows with stable stratification, QNSE yields expressions for the anisotropic effective viscosities and effective diffusivities valid in a broad range of stratification strength (Sukoriansky et al. Reference Sukoriansky, Galperin and Staroselsky2005). In the limit of weak stratification, the theory allows for a fully analytical description of the transition from the isotropic, Kolmogorov to anisotropic buoyancy-dominated turbulence regime (Sukoriansky & Galperin Reference Sukoriansky and Galperin2013). Other important QNSE results include 1-D spectra of the kinetic and potential energies, the dispersion relationships for internal waves in the presence of turbulence and the demonstration of the absence of the critical Richardson number (Galperin, Sukoriansky & Anderson Reference Galperin, Sukoriansky and Anderson2007). Reviews by Galperin & Sukoriansky (Reference Galperin and Sukoriansky2010) and Sukoriansky & Galperin (Reference Sukoriansky and Galperin2013) detail the QNSE results and compare them with observations and other theories.
The present study broadens the range of QNSE applications by focusing it on a neutrally stratified turbulent flow in a coordinate frame rotating with a constant angular velocity
![]() $\unicode[STIX]{x1D734}$
which, without the loss of generality, is assumed to be aligned vertically. The rotation evokes an inertial pseudo-force, the Coriolis force (e.g. Landau & Lifshitz Reference Landau and Lifshitz1993). Despite obvious differences in the large-scale behaviour of rotating and stably stratified flows, they also exhibit some similarities. Those include the spatial anisotropization of the eddy viscosities and eddy diffusivities and emergence of slow modes. In agreement with the Taylor–Proudman theorem, the slow modes in rotating flows are represented by cyclonic and anticyclonic vortices whose axes are aligned with the axis of rotation. Such an alignment has been observed in numerous laboratory experiments (e.g. Hopfinger, Browand & Gagne Reference Hopfinger, Browand and Gagne1982) and computer simulations. Rotating flows also feature componentality (Sagaut & Cambon Reference Sagaut and Cambon2008; Godeferd & Moisy Reference Godeferd and Moisy2015), i.e. different velocity components being affected by the rotation-modified eddy viscosities in different ways.
$\unicode[STIX]{x1D734}$
which, without the loss of generality, is assumed to be aligned vertically. The rotation evokes an inertial pseudo-force, the Coriolis force (e.g. Landau & Lifshitz Reference Landau and Lifshitz1993). Despite obvious differences in the large-scale behaviour of rotating and stably stratified flows, they also exhibit some similarities. Those include the spatial anisotropization of the eddy viscosities and eddy diffusivities and emergence of slow modes. In agreement with the Taylor–Proudman theorem, the slow modes in rotating flows are represented by cyclonic and anticyclonic vortices whose axes are aligned with the axis of rotation. Such an alignment has been observed in numerous laboratory experiments (e.g. Hopfinger, Browand & Gagne Reference Hopfinger, Browand and Gagne1982) and computer simulations. Rotating flows also feature componentality (Sagaut & Cambon Reference Sagaut and Cambon2008; Godeferd & Moisy Reference Godeferd and Moisy2015), i.e. different velocity components being affected by the rotation-modified eddy viscosities in different ways.
Stably stratified flows tend to develop direct energy cascade and a Kolmogorov 1-D spectrum in the direction orthogonal to the gravity vector (Riley & Lindborg Reference Riley and Lindborg2008; Galperin & Sukoriansky Reference Galperin and Sukoriansky2010). Rotating flows, on the other hand, exhibit complicated scale-dependent energy transfer between different directions and different velocity components (e.g. Godeferd & Cambon Reference Godeferd and Cambon1994; Bourouiba & Bartello Reference Bourouiba and Bartello2007; Staplehurst, Davidson & Dalziel Reference Staplehurst, Davidson and Dalziel2008; Bourouiba, Straub & Waite Reference Bourouiba, Straub and Waite2012). Yeung & Xu (Reference Yeung and Xu2004) note two well-known effects of rotation: (i) reduced energy transfer to small scales and, thus, reduced rate of viscous dissipation despite the Coriolis term not entering the turbulence kinetic energy equation explicitly, and (ii) strong anisotropization of the characteristic length scales of turbulence as they become quite different in the directions parallel (
![]() $k_{\Vert }$
) and orthogonal (
$k_{\Vert }$
) and orthogonal (
![]() $k_{\bot }$
) to the axis of rotation. If the forcing is localized on intermediate scales, rotation causes gradually increasing with scale redirection of the energy flux from smaller to larger scales in the plane orthogonal to
$k_{\bot }$
) to the axis of rotation. If the forcing is localized on intermediate scales, rotation causes gradually increasing with scale redirection of the energy flux from smaller to larger scales in the plane orthogonal to
![]() $\unicode[STIX]{x1D734}$
and on scales smaller than the forcing scale. This redirection can be identified with the energy backscatter or the inverse energy cascade (e.g. Chen et al.
Reference Chen, Chen, Eyink and Holm2005). The inverse cascade facilitates the reduction of the viscous dissipation rate mentioned in (i) (also see e.g. Bardina, Ferziger & Rogallo Reference Bardina, Ferziger and Rogallo1985; Dubrulle & Valdettaro Reference Dubrulle and Valdettaro1992) and concurrent decrease of the horizontal eddy viscosity that may become negative, the point beyond which QNSE derivations cannot be continued. The increase of the length scale in the direction
$\unicode[STIX]{x1D734}$
and on scales smaller than the forcing scale. This redirection can be identified with the energy backscatter or the inverse energy cascade (e.g. Chen et al.
Reference Chen, Chen, Eyink and Holm2005). The inverse cascade facilitates the reduction of the viscous dissipation rate mentioned in (i) (also see e.g. Bardina, Ferziger & Rogallo Reference Bardina, Ferziger and Rogallo1985; Dubrulle & Valdettaro Reference Dubrulle and Valdettaro1992) and concurrent decrease of the horizontal eddy viscosity that may become negative, the point beyond which QNSE derivations cannot be continued. The increase of the length scale in the direction
![]() $k_{\Vert }$
mentioned in (ii) above can be related to the conservation of the angular momentum and formation of the Taylor columns (Davidson Reference Davidson2013).
$k_{\Vert }$
mentioned in (ii) above can be related to the conservation of the angular momentum and formation of the Taylor columns (Davidson Reference Davidson2013).
Even though QNSE cannot be extended to large scales in 3-D flows that combine fully 3-D and quasi-2-D dynamics on small and large scales, respectively, the method allows one to analyse the transition from the classical Kolmogorov 3-D to the anisotropic rotation-dominated turbulence regime, just as was done by Sukoriansky & Galperin (Reference Sukoriansky and Galperin2013) for flows with stable stratification and by Sukoriansky & Zemach (Reference Sukoriansky and Zemach2016) for magneto-hydrodynamic flows with low magnetic Reynolds number. In both cases, the derivations are amenable to closed-form analytical treatment. This transition is of great theoretical interest on its own sake and in addition, QNSE allows one to focus on the analogies and differences between the effects of rotation and stable stratification. Along with ever increasing computing power and concurrent proliferation of numerical investigations of rotating turbulence with continually increasing resolution (Godeferd & Moisy Reference Godeferd and Moisy2015), comprehensive theoretical investigations have been scarce and the present study to some degree addresses this void.
The layout of the paper is as follows. Section 2 elaborates the anisotropization of the viscosity and diffusivity under the action of rotation and introduces new variables that will be used in the formal analysis in § 3. That section presents the mathematical formulation of the problem of neutrally stratified turbulence in a rotating frame and outlines the basic assumptions and methods of QNSE. The relation between the Navier–Stokes and the Langevin equations underlying the idea of the quasi-Gaussian mapping is explained. Section 4 clarifies the procedure of successive small-scale elimination, i.e. coarse graining, for the momentum equation while § 5 explains the spectral gap approximation. Section 6 extends this procedure to the diffusion equation. Section 7 details the computation of the effective viscosities and effective diffusivities and considers the limit of weak rotation. Section 8 considers the relationship between the forcing amplitude and an observable parameter, the rate of the viscous dissipation
![]() $\unicode[STIX]{x1D716}$
, which allows one to express the effective turbulent transport coefficients as functions of
$\unicode[STIX]{x1D716}$
, which allows one to express the effective turbulent transport coefficients as functions of
![]() $\unicode[STIX]{x1D716}$
. These expressions are derived and elaborated in § 9. All turbulence transport coefficients are shown to depend on a non-dimensional parameter
$\unicode[STIX]{x1D716}$
. These expressions are derived and elaborated in § 9. All turbulence transport coefficients are shown to depend on a non-dimensional parameter
![]() $k/k_{\unicode[STIX]{x1D6FA}}$
, where
$k/k_{\unicode[STIX]{x1D6FA}}$
, where
![]() $k$
is a running wavenumber,
$k$
is a running wavenumber,
![]() $k_{\unicode[STIX]{x1D6FA}}=(f^{3}/\unicode[STIX]{x1D716})^{1/2}$
,
$k_{\unicode[STIX]{x1D6FA}}=(f^{3}/\unicode[STIX]{x1D716})^{1/2}$
,
![]() $f=2\unicode[STIX]{x1D6FA}$
is the Coriolis parameter and
$f=2\unicode[STIX]{x1D6FA}$
is the Coriolis parameter and
![]() $\unicode[STIX]{x1D6FA}=|\unicode[STIX]{x1D734}|$
. The wavenumber
$\unicode[STIX]{x1D6FA}=|\unicode[STIX]{x1D734}|$
. The wavenumber
![]() $k_{\unicode[STIX]{x1D6FA}}$
is the rotational analogue of the Ozmidov wavenumber,
$k_{\unicode[STIX]{x1D6FA}}$
is the rotational analogue of the Ozmidov wavenumber,
![]() $k_{O}=(N^{3}/\unicode[STIX]{x1D716})^{1/2}$
,
$k_{O}=(N^{3}/\unicode[STIX]{x1D716})^{1/2}$
,
![]() $N$
being the Brunt-Väisälä frequency, which has been used to quantify the effect of stable stratification on turbulent flow field (Dougherty Reference Dougherty1961; Ozmidov Reference Ozmidov1965). The scalings with
$N$
being the Brunt-Väisälä frequency, which has been used to quantify the effect of stable stratification on turbulent flow field (Dougherty Reference Dougherty1961; Ozmidov Reference Ozmidov1965). The scalings with
![]() $k/k_{\unicode[STIX]{x1D6FA}}$
and
$k/k_{\unicode[STIX]{x1D6FA}}$
and
![]() $k/k_{O}$
are explored to clarify the analogies and differences between the effects of rotation and stable stratification. Section 10 analyses the effect of turbulence on the dispersion relationship for inertial waves. Section 11 provides analytical expressions for various 1-D and 3-D spectra of the kinetic energy and passive-scalar variance. Section 12 discusses the anisotropy of spectral energy transfers and demonstrates that it indeed corresponds to columnar self-organization. Section 13 offers the interpretation of the decreasing eddy viscosities as a manifestation of the inverse energy cascade. Finally, § 14 provides discussion and conclusions which include situations when both rotation and stratification are present.
$k/k_{O}$
are explored to clarify the analogies and differences between the effects of rotation and stable stratification. Section 10 analyses the effect of turbulence on the dispersion relationship for inertial waves. Section 11 provides analytical expressions for various 1-D and 3-D spectra of the kinetic energy and passive-scalar variance. Section 12 discusses the anisotropy of spectral energy transfers and demonstrates that it indeed corresponds to columnar self-organization. Section 13 offers the interpretation of the decreasing eddy viscosities as a manifestation of the inverse energy cascade. Finally, § 14 provides discussion and conclusions which include situations when both rotation and stratification are present.
2 Directionality and componentality of turbulent transport anisotropization under the action of rotation; horizontal and vertical eddy viscosities and eddy diffusivities
The anisotropy introduced by the system rotation causes the effective viscosity and diffusivity to transform differently in the directions parallel and orthogonal to the direction of rotation (i.e. along
![]() $k_{\Vert }$
and
$k_{\Vert }$
and
![]() $k_{\bot }$
, respectively) whose unity vector is aligned vertically and given by
$k_{\bot }$
, respectively) whose unity vector is aligned vertically and given by
![]() $\boldsymbol{e}_{3}=\unicode[STIX]{x1D734}/|\unicode[STIX]{x1D734}|$
. In this coordinate system, vectors collinear with
$\boldsymbol{e}_{3}=\unicode[STIX]{x1D734}/|\unicode[STIX]{x1D734}|$
. In this coordinate system, vectors collinear with
![]() $k_{\bot }$
and
$k_{\bot }$
and
![]() $k_{\Vert }$
become
$k_{\Vert }$
become
![]() $k_{h}$
(‘horizontal’) and
$k_{h}$
(‘horizontal’) and
![]() $k_{z}\equiv k_{3}$
(‘vertical’), respectively, such that
$k_{z}\equiv k_{3}$
(‘vertical’), respectively, such that
In the process of small-scale elimination, there will emerge two types of anisotropization – by direction and by component (hence componentality). Utilizing the least restrictive and most general approach, we assume that the renormalized viscosities differ in different directions and for different components. For the horizontal velocity components, the effective viscosities in the horizontal and vertical directions are, respectively,
![]() $\unicode[STIX]{x1D708}_{h}$
and
$\unicode[STIX]{x1D708}_{h}$
and
![]() $\unicode[STIX]{x1D708}_{z}$
,
$\unicode[STIX]{x1D708}_{z}$
,
and for the vertical velocity component
![]() $v_{3}$
they are
$v_{3}$
they are
In (2.2) and (2.3), the terms with
![]() $\unicode[STIX]{x1D6FF}$
mark anisotropic corrections to viscosity. These corrections are small for weak rotation, the limit in the focus of this investigation. This smallness will be utilized later in small parameter expansions.
$\unicode[STIX]{x1D6FF}$
mark anisotropic corrections to viscosity. These corrections are small for weak rotation, the limit in the focus of this investigation. This smallness will be utilized later in small parameter expansions.
The spectral viscosity operator acting on the horizontal velocity components is
while that acting on
![]() $v_{3}$
is
$v_{3}$
is
The renormalized diffusivity is directionally dependent and given by
in the horizontal and vertical directions, respectively, while the spectral diffusivity operator is
3 Governing equations
Consider the dynamics of fully three-dimensional, incompressible turbulent flow in a coordinate system rotating with the angular velocity
![]() $\unicode[STIX]{x1D734}$
. The flow occupies an infinite domain and its dynamics is governed by the momentum (Navier–Stokes) and continuity equations,
$\unicode[STIX]{x1D734}$
. The flow occupies an infinite domain and its dynamics is governed by the momentum (Navier–Stokes) and continuity equations,
In the spectral domain bounded by the viscous dissipation (or Kolmogorov) wavenumber
![]() $k_{d}\propto (\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}_{0}^{3})^{1/4}$
, a space–time Fourier transform of the velocity is given by
$k_{d}\propto (\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}_{0}^{3})^{1/4}$
, a space–time Fourier transform of the velocity is given by
where
![]() $d\,(=3)$
is the dimension of space.
$d\,(=3)$
is the dimension of space.
In the original Navier–Stokes equation all scales are resolved, and the Fourier transform of the viscous term is simply
![]() $\unicode[STIX]{x1D708}_{0}k^{2}$
. In the rotating coordinate frame, however, this term undergoes anisotropization elaborated in § 2. Anticipating this anisotropization, we added new viscous terms in (3.4) with which the Fourier-transformed momentum equation becomes
$\unicode[STIX]{x1D708}_{0}k^{2}$
. In the rotating coordinate frame, however, this term undergoes anisotropization elaborated in § 2. Anticipating this anisotropization, we added new viscous terms in (3.4) with which the Fourier-transformed momentum equation becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\text{i}\unicode[STIX]{x1D714}v_{\unicode[STIX]{x1D6FC}}(\hat{k})+\text{i}k_{\unicode[STIX]{x1D6FD}}\int v_{\unicode[STIX]{x1D6FC}}(\hat{q})v_{\unicode[STIX]{x1D6FD}}(\hat{k}-\hat{q})\,\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}f_{\unicode[STIX]{x1D6FD}}v_{\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{i}k_{\unicode[STIX]{x1D6FC}}P(\hat{k})-(\unicode[STIX]{x1D708}k^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}k_{z}^{2})v_{\unicode[STIX]{x1D6FC}}(\hat{k})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}k^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}k_{z}^{2})v_{3}(\hat{k})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}3}+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}^{0}(\hat{k}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\text{i}\unicode[STIX]{x1D714}v_{\unicode[STIX]{x1D6FC}}(\hat{k})+\text{i}k_{\unicode[STIX]{x1D6FD}}\int v_{\unicode[STIX]{x1D6FC}}(\hat{q})v_{\unicode[STIX]{x1D6FD}}(\hat{k}-\hat{q})\,\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}f_{\unicode[STIX]{x1D6FD}}v_{\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{i}k_{\unicode[STIX]{x1D6FC}}P(\hat{k})-(\unicode[STIX]{x1D708}k^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}k_{z}^{2})v_{\unicode[STIX]{x1D6FC}}(\hat{k})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}k^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}k_{z}^{2})v_{3}(\hat{k})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}3}+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}^{0}(\hat{k}),\end{eqnarray}$$
where
![]() $\hat{k}=(\unicode[STIX]{x1D714},\boldsymbol{k})$
,
$\hat{k}=(\unicode[STIX]{x1D714},\boldsymbol{k})$
,
![]() $\hat{q}=(\unicode[STIX]{x1D71B},\boldsymbol{q})$
,
$\hat{q}=(\unicode[STIX]{x1D71B},\boldsymbol{q})$
,
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{0}(\hat{k})$
is the Fourier transform of the external forcing and
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{0}(\hat{k})$
is the Fourier transform of the external forcing and
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}$
is the permutation tensor. Of course, in the limit
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}$
is the permutation tensor. Of course, in the limit
![]() $\unicode[STIX]{x1D6FA}\rightarrow 0$
, all anisotropic corrections disappear (see (7.26), (7.27), (7.45)–(7.47) below) and the process of small-scale elimination will only produce the isotropic eddy viscosity term,
$\unicode[STIX]{x1D6FA}\rightarrow 0$
, all anisotropic corrections disappear (see (7.26), (7.27), (7.45)–(7.47) below) and the process of small-scale elimination will only produce the isotropic eddy viscosity term,
![]() $\unicode[STIX]{x1D708}k^{2}$
, as in Sukoriansky et al. (Reference Sukoriansky, Galperin and Staroselsky2003).
$\unicode[STIX]{x1D708}k^{2}$
, as in Sukoriansky et al. (Reference Sukoriansky, Galperin and Staroselsky2003).
The Fourier-transformed continuity equation is
The pressure term is evaluated by taking the divergence of (3.4) using the continuity equation (3.5),
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}}{k^{2}}\int v_{\unicode[STIX]{x1D6FC}}(\hat{q})v_{\unicode[STIX]{x1D6FD}}(\hat{k}-\hat{q})\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}+\text{i}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}\frac{k_{\unicode[STIX]{x1D6FC}}}{k^{2}}f_{\unicode[STIX]{x1D6FD}}v_{\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & & \displaystyle \quad +\text{i}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}k^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}k_{3}^{2})\frac{k_{3}}{k^{2}}v_{3}(\hat{k})=P(\hat{k}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}}{k^{2}}\int v_{\unicode[STIX]{x1D6FC}}(\hat{q})v_{\unicode[STIX]{x1D6FD}}(\hat{k}-\hat{q})\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}+\text{i}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}\frac{k_{\unicode[STIX]{x1D6FC}}}{k^{2}}f_{\unicode[STIX]{x1D6FD}}v_{\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & & \displaystyle \quad +\text{i}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}k^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}k_{3}^{2})\frac{k_{3}}{k^{2}}v_{3}(\hat{k})=P(\hat{k}),\end{eqnarray}$$
where the standard nonlinear term on the left-hand side is complemented by contributions due to the Coriolis force and terms expected to emerge from eddy viscosity anisotropization.
Substituting (3.6) in (3.4) and symmetrizing the resulting equation using the tensor
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}(\boldsymbol{k})$
(e.g. Lesieur Reference Lesieur1997), where
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}(\boldsymbol{k})$
(e.g. Lesieur Reference Lesieur1997), where
and
is the operator that projects any vector to a plane normal to
![]() $\boldsymbol{k}$
, one can transform (3.4) into
$\boldsymbol{k}$
, one can transform (3.4) into
Here, the inverse Green function,
is a non-diagonal tensor conditioned by the rotation-imposed anisotropy,
is the inverse auxiliary scalar Green function and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the Kronecker delta.
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the Kronecker delta.
The momentum equation (3.9) can be rearranged in the form of the canonical equation,
used in the procedure of coarse graining. This equation preserves its form in flows with different extra strains while the strains’ effect is absorbed in the tensorial Green function.
The canonical equation appears as the Langevin equation,
where
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
represents nonlinear stirring of a mode
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
represents nonlinear stirring of a mode
![]() $\hat{k}$
by all other modes (Kraichnan Reference Kraichnan1987; McComb Reference McComb1991; Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003) and is associated with the ‘dressed’ force. Generally, replacing the nonlinear term in the Navier–Stokes equations by a random stochastic force has been one of the tools used in theories of turbulence (e.g. Lesieur Reference Lesieur1997).
$\hat{k}$
by all other modes (Kraichnan Reference Kraichnan1987; McComb Reference McComb1991; Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003) and is associated with the ‘dressed’ force. Generally, replacing the nonlinear term in the Navier–Stokes equations by a random stochastic force has been one of the tools used in theories of turbulence (e.g. Lesieur Reference Lesieur1997).
We distinguish between the ‘bare’ and ‘dressed’ forces,
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{0}(\hat{k})$
and
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{0}(\hat{k})$
and
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
(Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005). The ‘bare’ force mimics the effect of large-scale instabilities and provides forcing that maintains turbulence in statistically steady state. In 3-D isotropic flows, this force is isotropic; it generates direct energy cascade characterized by the Kolmogorov kinetic energy spectrum. Due to the anisotropy of the Coriolis force, rotating flows are inherently anisotropic. A bare forcing may introduce additional complications if it is also anisotropic and produces helicity on large scales. A flow of this kind, with Beltrami forcing, was studied in direct numerical simulations (DNS) by Mininni, Rosenberg & Pouquet (Reference Mininni, Rosenberg and Pouquet2012). They found, however, that on scales smaller than the Woods scale,
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
(Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005). The ‘bare’ force mimics the effect of large-scale instabilities and provides forcing that maintains turbulence in statistically steady state. In 3-D isotropic flows, this force is isotropic; it generates direct energy cascade characterized by the Kolmogorov kinetic energy spectrum. Due to the anisotropy of the Coriolis force, rotating flows are inherently anisotropic. A bare forcing may introduce additional complications if it is also anisotropic and produces helicity on large scales. A flow of this kind, with Beltrami forcing, was studied in direct numerical simulations (DNS) by Mininni, Rosenberg & Pouquet (Reference Mininni, Rosenberg and Pouquet2012). They found, however, that on scales smaller than the Woods scale,
![]() $L_{\unicode[STIX]{x1D6FA}}=k_{\unicode[STIX]{x1D6FA}}^{-1}$
(the wavenumber
$L_{\unicode[STIX]{x1D6FA}}=k_{\unicode[STIX]{x1D6FA}}^{-1}$
(the wavenumber
![]() $k_{\unicode[STIX]{x1D6FA}}$
is defined by (7.36); the naming of the scale
$k_{\unicode[STIX]{x1D6FA}}$
is defined by (7.36); the naming of the scale
![]() $L_{\unicode[STIX]{x1D6FA}}$
will be elucidated in § 7.1.3), the helicity cascade breaks down and a flow returns to isotropic Kolmogorov turbulence. This result is consistent with a general study by Biferale & Procaccia (Reference Biferale and Procaccia2005) showing that on small scales, the isotropic solution is always of leading order. Being informed of these results, it is assumed here that the bare and the dressed forces are isotropic and that the forcing scale,
$L_{\unicode[STIX]{x1D6FA}}$
will be elucidated in § 7.1.3), the helicity cascade breaks down and a flow returns to isotropic Kolmogorov turbulence. This result is consistent with a general study by Biferale & Procaccia (Reference Biferale and Procaccia2005) showing that on small scales, the isotropic solution is always of leading order. Being informed of these results, it is assumed here that the bare and the dressed forces are isotropic and that the forcing scale,
![]() $L_{\unicode[STIX]{x1D709}}$
, does not significantly exceed
$L_{\unicode[STIX]{x1D709}}$
, does not significantly exceed
![]() $L_{\unicode[STIX]{x1D6FA}}$
. The ensuing results are correct on scales smaller than
$L_{\unicode[STIX]{x1D6FA}}$
. The ensuing results are correct on scales smaller than
![]() $L_{\unicode[STIX]{x1D709}}$
. It is possible that they will remain correct for
$L_{\unicode[STIX]{x1D709}}$
. It is possible that they will remain correct for
![]() $L_{\unicode[STIX]{x1D709}}/L_{\unicode[STIX]{x1D6FA}}\gg 1$
but we do not know that a priori. In a study that follows up, we shall investigate the limits of validity of the theory and present comparisons with observations.
$L_{\unicode[STIX]{x1D709}}/L_{\unicode[STIX]{x1D6FA}}\gg 1$
but we do not know that a priori. In a study that follows up, we shall investigate the limits of validity of the theory and present comparisons with observations.
The ‘dressed’, or effective, force,
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
, acts upon every mode
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
, acts upon every mode
![]() $k$
and represents nonlinear stirring of that mode by all other modes. The Langevin equation (3.13) is used in the coarse-graining procedure for which
$k$
and represents nonlinear stirring of that mode by all other modes. The Langevin equation (3.13) is used in the coarse-graining procedure for which
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
needs to be determined. Unfortunately, a complete mathematical representation of this force cannot be derived from first principles at the present time (McComb Reference McComb1991; Canuto & Dubovikov Reference Canuto and Dubovikov1996). Since we consider an incompressible, homogeneous in space, stochastically steady-state turbulent flow in an infinite domain, the force
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
needs to be determined. Unfortunately, a complete mathematical representation of this force cannot be derived from first principles at the present time (McComb Reference McComb1991; Canuto & Dubovikov Reference Canuto and Dubovikov1996). Since we consider an incompressible, homogeneous in space, stochastically steady-state turbulent flow in an infinite domain, the force
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
must be solenoidal, zero mean and homogeneous in space and time. The rate of the energy injection into the mode
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\hat{k})$
must be solenoidal, zero mean and homogeneous in space and time. The rate of the energy injection into the mode
![]() $k$
must be proportional to the energy dissipation rate
$k$
must be proportional to the energy dissipation rate
![]() $\unicode[STIX]{x1D716}$
. These requirements yield the correlation function in the form
$\unicode[STIX]{x1D716}$
. These requirements yield the correlation function in the form
where the multiplicative factor
![]() $k^{-3}$
ensures correct dimensionality and numerical coefficients are introduced for convenience. The correlator’s amplitude
$k^{-3}$
ensures correct dimensionality and numerical coefficients are introduced for convenience. The correlator’s amplitude
![]() $D$
is proportional to the mean rate of energy transfer through the mode
$D$
is proportional to the mean rate of energy transfer through the mode
![]() $k$
. The relationship between
$k$
. The relationship between
![]() $D$
and
$D$
and
![]() $\unicode[STIX]{x1D716}$
in neutrally stratified non-rotating flows can be calculated using the energy balance considerations (Yakhot & Orszag Reference Yakhot and Orszag1986) which yield (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005)
$\unicode[STIX]{x1D716}$
in neutrally stratified non-rotating flows can be calculated using the energy balance considerations (Yakhot & Orszag Reference Yakhot and Orszag1986) which yield (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005)
We shall use (3.15) as a zero-order approximation; the next-order correction will be considered in § 13.
Note that the assumption of isotropic
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D714},\boldsymbol{k})$
is well justified only in non-rotating neutral flows (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003). Various extra strains may invalidate this assumption. Indeed, diverse numerical simulations point to a sensitivity of the results to the nature of the forcing. However, similarly to the case of stable stratification (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005), it is assumed here that flow anisotropization due to rotation will chiefly manifest itself through the anisotropization of the Green functions. This assumption is particularly well justified for the case of weak rotation which is the main subject of the present study.
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D714},\boldsymbol{k})$
is well justified only in non-rotating neutral flows (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003). Various extra strains may invalidate this assumption. Indeed, diverse numerical simulations point to a sensitivity of the results to the nature of the forcing. However, similarly to the case of stable stratification (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005), it is assumed here that flow anisotropization due to rotation will chiefly manifest itself through the anisotropization of the Green functions. This assumption is particularly well justified for the case of weak rotation which is the main subject of the present study.
Equation (3.12) is the starting point of the scale elimination procedure. It requires the inversion of the tensorial operator
![]() $[G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})]^{-1}$
given by (3.10)–(3.11). Since
$[G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})]^{-1}$
given by (3.10)–(3.11). Since
![]() $\boldsymbol{f}$
is aligned with the vertical axis in the chosen coordinate system, the second term on the right-hand side of (3.10) is
$\boldsymbol{f}$
is aligned with the vertical axis in the chosen coordinate system, the second term on the right-hand side of (3.10) is
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}}(\boldsymbol{k})\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}f_{\unicode[STIX]{x1D6FE}}=fP_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}e_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}\equiv fS_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
, where
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}}(\boldsymbol{k})\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}f_{\unicode[STIX]{x1D6FE}}=fP_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}e_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}\equiv fS_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
, where
and the matrix representation of the tensor
![]() $e_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is
$e_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is
 $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}ccc@{}}0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0\end{array}\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}ccc@{}}0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0\end{array}\right). & & \displaystyle\end{eqnarray}$$
Retaining only the terms up to
![]() $O(f^{2})$
in the limit of weak rotation, one can invert (3.9) to obtain
$O(f^{2})$
in the limit of weak rotation, one can invert (3.9) to obtain
where
In the derivation of (3.18) we took into account that the Green function
![]() $G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})$
acts upon the solenoidal vector field
$G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})$
acts upon the solenoidal vector field
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D714},\boldsymbol{k})$
and, as will be shown later,
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D714},\boldsymbol{k})$
and, as will be shown later,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}=O(f^{2})$
.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}=O(f^{2})$
.
4 The procedure of successive coarse graining
The scale elimination formalism consists of the following steps (Sukoriansky et al. Reference Sukoriansky, Galperin and Staroselsky2005):
-
(i) Introduction of the dynamic dissipation cutoff wavenumber,
 $\unicode[STIX]{x1D6EC}$
, a small shell
$\unicode[STIX]{x1D6EC}$
, a small shell
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
,
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}\ll 1$
, which is subject to elimination, and ‘slow’ and ‘fast’ modes.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}\ll 1$
, which is subject to elimination, and ‘slow’ and ‘fast’ modes. -
(ii) Computing
 $O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
correction to the inverse Green function resulting from the ensemble averaging of the fast modes over
$O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
correction to the inverse Green function resulting from the ensemble averaging of the fast modes over
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
. This correction generates
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
. This correction generates
 $O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
accruals to all renormalized viscosities defined in § 2 while otherwise preserving the analytical form of the governing equations.
$O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
accruals to all renormalized viscosities defined in § 2 while otherwise preserving the analytical form of the governing equations. -
(iii) All viscosities are updated and the process moves forward towards elimination of the next shell
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
.
These steps are similar to those in flows with stable stratification (Sukoriansky et al. Reference Sukoriansky, Galperin and Staroselsky2005) and so they will only be described briefly.
The wavenumber of the dynamic dissipation cutoff,
![]() $\unicode[STIX]{x1D6EC}$
, defines the current domain of definition of the canonical equation (3.12),
$\unicode[STIX]{x1D6EC}$
, defines the current domain of definition of the canonical equation (3.12),
![]() $D=(0,\unicode[STIX]{x1D6EC}]$
. At the first iteration, when all scales are included,
$D=(0,\unicode[STIX]{x1D6EC}]$
. At the first iteration, when all scales are included,
![]() $\unicode[STIX]{x1D6EC}=k_{d}$
. A small shell
$\unicode[STIX]{x1D6EC}=k_{d}$
. A small shell
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
subdivides the domain onto
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
subdivides the domain onto
![]() $D^{{<}}=(0,\unicode[STIX]{x1D6EC}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}]$
and
$D^{{<}}=(0,\unicode[STIX]{x1D6EC}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}]$
and
![]() $D^{{>}}=(\unicode[STIX]{x1D6EC}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}]$
, such that
$D^{{>}}=(\unicode[STIX]{x1D6EC}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}]$
, such that
![]() $D=D^{{<}}\cup D^{{>}}$
. At every step of the scale elimination procedure, modes within the shell
$D=D^{{<}}\cup D^{{>}}$
. At every step of the scale elimination procedure, modes within the shell
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
undergo ensemble averaging which results in shrinking of the domain of definition from
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
undergo ensemble averaging which results in shrinking of the domain of definition from
![]() $D$
to
$D$
to
![]() $D^{{<}}$
and corresponding modifications of the viscosity and diffusivity which renders them
$D^{{<}}$
and corresponding modifications of the viscosity and diffusivity which renders them
![]() $\unicode[STIX]{x1D6EC}$
dependent or ‘dressed’. The ‘dressed’ Green functions employ these ‘dressed’ viscosities and diffusivities. After every step of this process, the governing equations reproduce their form precisely and ‘forget’ about the molecular values.
$\unicode[STIX]{x1D6EC}$
dependent or ‘dressed’. The ‘dressed’ Green functions employ these ‘dressed’ viscosities and diffusivities. After every step of this process, the governing equations reproduce their form precisely and ‘forget’ about the molecular values.
The ‘slow’ (
![]() $\boldsymbol{v}^{{<}}$
) and ‘fast’ (
$\boldsymbol{v}^{{<}}$
) and ‘fast’ (
![]() $\boldsymbol{v}^{{>}}$
) velocity modes are defined such that
$\boldsymbol{v}^{{>}}$
) velocity modes are defined such that
![]() $k\in D^{{<}}$
for
$k\in D^{{<}}$
for
![]() $\boldsymbol{v}^{{<}}(\hat{k})$
and
$\boldsymbol{v}^{{<}}(\hat{k})$
and
![]() $k\in D^{{>}}$
for
$k\in D^{{>}}$
for
![]() $\boldsymbol{v}^{{>}}(\hat{k})$
. The velocity mode
$\boldsymbol{v}^{{>}}(\hat{k})$
. The velocity mode
![]() $v_{\unicode[STIX]{x1D6FC}}$
is represented as a sum,
$v_{\unicode[STIX]{x1D6FC}}$
is represented as a sum,
![]() $v_{\unicode[STIX]{x1D6FC}}=v_{\unicode[STIX]{x1D6FC}}^{{<}}+v_{\unicode[STIX]{x1D6FC}}^{{>}}$
, substitution of which in the canonical equation (3.12) yields
$v_{\unicode[STIX]{x1D6FC}}=v_{\unicode[STIX]{x1D6FC}}^{{<}}+v_{\unicode[STIX]{x1D6FC}}^{{>}}$
, substitution of which in the canonical equation (3.12) yields
 $$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D6FC}}(\hat{k}) & = & \displaystyle G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{0}-\frac{\text{i}}{2}G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})P_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}(\boldsymbol{k})\int [\!v_{\unicode[STIX]{x1D707}}^{{<}}(\hat{q})v_{\unicode[STIX]{x1D708}}^{{<}}(\hat{k}-\hat{q})\nonumber\\ \displaystyle & & \displaystyle +\,2v_{\unicode[STIX]{x1D707}}^{{>}}(\hat{q})v_{\unicode[STIX]{x1D708}}^{{<}}(\hat{k}-\hat{q})+v_{\unicode[STIX]{x1D707}}^{{>}}(\hat{q})v_{\unicode[STIX]{x1D708}}^{{>}}(\hat{k}-\hat{q})\!]\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D6FC}}(\hat{k}) & = & \displaystyle G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{0}-\frac{\text{i}}{2}G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\hat{k})P_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}(\boldsymbol{k})\int [\!v_{\unicode[STIX]{x1D707}}^{{<}}(\hat{q})v_{\unicode[STIX]{x1D708}}^{{<}}(\hat{k}-\hat{q})\nonumber\\ \displaystyle & & \displaystyle +\,2v_{\unicode[STIX]{x1D707}}^{{>}}(\hat{q})v_{\unicode[STIX]{x1D708}}^{{<}}(\hat{k}-\hat{q})+v_{\unicode[STIX]{x1D707}}^{{>}}(\hat{q})v_{\unicode[STIX]{x1D708}}^{{>}}(\hat{k}-\hat{q})\!]\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}.\end{eqnarray}$$
This equation holds for either
![]() $k\in D^{{<}}$
or
$k\in D^{{<}}$
or
![]() $k\in D^{{>}}$
and so (4.1) applies to both
$k\in D^{{>}}$
and so (4.1) applies to both
![]() $v_{\unicode[STIX]{x1D6FC}}^{{<}}$
and
$v_{\unicode[STIX]{x1D6FC}}^{{<}}$
and
![]() $v_{\unicode[STIX]{x1D6FC}}^{{>}}$
.
$v_{\unicode[STIX]{x1D6FC}}^{{>}}$
.
Schematically, the equation for
![]() $v^{{<}}$
contains
$v^{{<}}$
contains
![]() $v^{{>}}$
in the second and third terms of the integrand. In order to derive a self-contained equation for
$v^{{>}}$
in the second and third terms of the integrand. In order to derive a self-contained equation for
![]() $v^{{<}}$
, we iterate this equation once by substituting (4.1) itself, written for
$v^{{<}}$
, we iterate this equation once by substituting (4.1) itself, written for
![]() $v^{{<}}$
and
$v^{{<}}$
and
![]() $v^{{>}}$
, in the second and third terms, respectively. We then replace
$v^{{>}}$
, in the second and third terms, respectively. We then replace
![]() $v^{{>}}$
by the Langevin equation (3.13) and perform ensemble averaging over the force
$v^{{>}}$
by the Langevin equation (3.13) and perform ensemble averaging over the force
![]() $\unicode[STIX]{x1D743}^{{>}}$
. Details of this procedure are given in Sukoriansky et al. (Reference Sukoriansky, Galperin and Staroselsky2005). The final expression for the correction to the inverse Green function produced by the elimination of the shell
$\unicode[STIX]{x1D743}^{{>}}$
. Details of this procedure are given in Sukoriansky et al. (Reference Sukoriansky, Galperin and Staroselsky2005). The final expression for the correction to the inverse Green function produced by the elimination of the shell
![]() $D^{{>}}$
is
$D^{{>}}$
is
where
Equation (4.2) contains the velocity correlation tensor,
![]() $U_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D71B},\boldsymbol{q})$
, which can be evaluated using the Langevin equation (3.13) and (3.18),
$U_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D71B},\boldsymbol{q})$
, which can be evaluated using the Langevin equation (3.13) and (3.18),
 $$\begin{eqnarray}\displaystyle U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D714},\boldsymbol{k}) & = & \displaystyle \frac{|G(\unicode[STIX]{x1D714},\boldsymbol{k})|^{2}}{|d(\unicode[STIX]{x1D714},\boldsymbol{k})|^{2}}D(k)[\!A(\unicode[STIX]{x1D714},\boldsymbol{k})P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})+B(\unicode[STIX]{x1D714},\boldsymbol{k})Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle +\,C(\unicode[STIX]{x1D714},\boldsymbol{k})P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{k})P_{3\unicode[STIX]{x1D6FD}}(\boldsymbol{k})\!],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D714},\boldsymbol{k}) & = & \displaystyle \frac{|G(\unicode[STIX]{x1D714},\boldsymbol{k})|^{2}}{|d(\unicode[STIX]{x1D714},\boldsymbol{k})|^{2}}D(k)[\!A(\unicode[STIX]{x1D714},\boldsymbol{k})P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})+B(\unicode[STIX]{x1D714},\boldsymbol{k})Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle +\,C(\unicode[STIX]{x1D714},\boldsymbol{k})P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{k})P_{3\unicode[STIX]{x1D6FD}}(\boldsymbol{k})\!],\end{eqnarray}$$
where
The integral in (4.2) is calculated in the long-time limit,
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
, and using the spectral gap approximation which is explained in the next section.
$\unicode[STIX]{x1D714}\rightarrow 0$
, and using the spectral gap approximation which is explained in the next section.
Concluding this section we remark that a requirement imposed upon the ‘dressed’ force
![]() $\unicode[STIX]{x1D743}$
in the Langevin equation (3.13) is that
$\unicode[STIX]{x1D743}$
in the Langevin equation (3.13) is that
![]() $\langle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}(\boldsymbol{p})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\rangle =0$
for all vector triads
$\langle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}(\boldsymbol{p})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\rangle =0$
for all vector triads
![]() $(\boldsymbol{p},\boldsymbol{q},\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\in \unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
,
$(\boldsymbol{p},\boldsymbol{q},\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\in \unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
being a shell subject to elimination (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003, Reference Sukoriansky, Galperin and Staroselsky2005). This requirement is somewhat weaker than the global quasi-Gaussianity implied in classical theories such as the EDQNM. The quasi-Gaussianity in the shell
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
being a shell subject to elimination (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003, Reference Sukoriansky, Galperin and Staroselsky2005). This requirement is somewhat weaker than the global quasi-Gaussianity implied in classical theories such as the EDQNM. The quasi-Gaussianity in the shell
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
alone suffices to develop a rigorous self-contained mathematical procedure of successive coarse graining. There is no need for the force
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
alone suffices to develop a rigorous self-contained mathematical procedure of successive coarse graining. There is no need for the force
![]() $\unicode[STIX]{x1D743}(\hat{k})$
to be quasi-Gaussian in the entire domain although such field would fulfil the above condition. In general terms,
$\unicode[STIX]{x1D743}(\hat{k})$
to be quasi-Gaussian in the entire domain although such field would fulfil the above condition. In general terms,
![]() $\unicode[STIX]{x1D743}(\hat{k})$
could be characterized as quasi-normal. The combination of a quasi-normal forcing and eddy damping represented by the renormalized viscosity places the QNSE theory in the class of quasi-normal eddy-damped theories of turbulence elucidated by e.g. Orszag (Reference Orszag, Balian and Peabe1977), Chasnov (Reference Chasnov1991), McComb (Reference McComb1991), Sagaut & Cambon (Reference Sagaut and Cambon2008).
$\unicode[STIX]{x1D743}(\hat{k})$
could be characterized as quasi-normal. The combination of a quasi-normal forcing and eddy damping represented by the renormalized viscosity places the QNSE theory in the class of quasi-normal eddy-damped theories of turbulence elucidated by e.g. Orszag (Reference Orszag, Balian and Peabe1977), Chasnov (Reference Chasnov1991), McComb (Reference McComb1991), Sagaut & Cambon (Reference Sagaut and Cambon2008).
5 The spectral gap approximation
The concept of viscosity implies the existence of a spectral gap between the resolvable (explicit) and subgrid (implicit) scales which may be either molecular or computational. While in the former case the gap is real, in the latter it does not exist and as a result, the effect of the subgrid scales on the explicit ones in the vicinity of
![]() $\unicode[STIX]{x1D6EC}$
differs from that away from it. Recognizing this physics, Kraichnan (Reference Kraichnan1976) introduced a two-parametric viscosity denoted
$\unicode[STIX]{x1D6EC}$
differs from that away from it. Recognizing this physics, Kraichnan (Reference Kraichnan1976) introduced a two-parametric viscosity denoted
![]() $\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})$
which depends on the local explicit wavenumber
$\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})$
which depends on the local explicit wavenumber
![]() $k$
and the dynamic dissipation cutoff
$k$
and the dynamic dissipation cutoff
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
The idea of a spectral gap is used to simplify the computation of the correction to the inverse Green function given by (4.2). In this computation, only the terms up to
![]() $O[(k/\unicode[STIX]{x1D6EC})^{2}]$
are retained. This is equivalent to introducing a virtual spectral gap and taking all renormalized viscosities constant and equal to their values at
$O[(k/\unicode[STIX]{x1D6EC})^{2}]$
are retained. This is equivalent to introducing a virtual spectral gap and taking all renormalized viscosities constant and equal to their values at
![]() $\unicode[STIX]{x1D6EC}$
. This method will be named a spectral gap approximation, or SGA. Note that in Yakhot & Orszag (Reference Yakhot and Orszag1986), as well as in our earlier publications, this method was referred to as the distant interaction approximation, or DIA. This abbreviation conflicts with DIA introduced by Kraichnan (Reference Kraichnan1959) for the direct interaction approximation. The new name mitigates this conflict.
$\unicode[STIX]{x1D6EC}$
. This method will be named a spectral gap approximation, or SGA. Note that in Yakhot & Orszag (Reference Yakhot and Orszag1986), as well as in our earlier publications, this method was referred to as the distant interaction approximation, or DIA. This abbreviation conflicts with DIA introduced by Kraichnan (Reference Kraichnan1959) for the direct interaction approximation. The new name mitigates this conflict.
To illustrate the effect of the SGA, figure 1 shows the two-parametric viscosity,
![]() $\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})$
, computed following Kraichnan (Reference Kraichnan1976) for 3-D non-rotating flows and normalized with
$\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})$
, computed following Kraichnan (Reference Kraichnan1976) for 3-D non-rotating flows and normalized with
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
evaluated using the QNSE theory and SGA. The two-parametric viscosity displays a cusp-like behaviour at
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
evaluated using the QNSE theory and SGA. The two-parametric viscosity displays a cusp-like behaviour at
![]() $k\rightarrow \unicode[STIX]{x1D6EC}$
the nature of which was elaborated by Kraichnan (Reference Kraichnan1976). Even though the cusp is lost in QNSE, it gives reliable subgrid scale parameterization in 3-D flows featuring direct energy cascade.
$k\rightarrow \unicode[STIX]{x1D6EC}$
the nature of which was elaborated by Kraichnan (Reference Kraichnan1976). Even though the cusp is lost in QNSE, it gives reliable subgrid scale parameterization in 3-D flows featuring direct energy cascade.

Figure 1. Plot of
![]() $\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})/\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
(solid line) in non-rotating 3-D flows. Here
$\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})/\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
(solid line) in non-rotating 3-D flows. Here
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
is evaluated using QNSE with SGA.
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
is evaluated using QNSE with SGA.
In flows with inverse energy cascade, the SGA becomes problematic because
![]() $\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})$
changes sign and grows negative at
$\unicode[STIX]{x1D708}(k|\unicode[STIX]{x1D6EC})$
changes sign and grows negative at
![]() $k\rightarrow 0$
, as shown in figure 2 (also see Chekhlov et al.
Reference Chekhlov, Orszag, Sukoriansky, Galperin and Staroselsky1994). A problem of this kind arises in 3-D flows with a solid body rotation where the energy is gradually channelled into a manifold occupying a conical region orthogonal to the axis of rotation giving rise to the inverse energy cascade (Sagaut & Cambon Reference Sagaut and Cambon2008). In such flows, the QNSE formalism can only be applied on relatively small scales in the assumption that the forcing acts on scales where the eddy viscosity remains positive. In other words, in flows with rotation, the QNSE theory can only be used in the limit of weak rotation or on scales where the effect of rotation is weak. Although this limitation constrains the applicability of the QNSE theory to rotating flows, it does not preclude the possibility of developing an analytical theory of transition from Kolmogorov to rotation-dominated turbulence which is a subject of the forthcoming sections. Note in this respect that the QNSE theory was also used to develop an analytical theory of the transition from Kolmogorov to stable stratification-dominated turbulence where it provided a deep physical insight of flow anisotropization and turbulence–internal wave interaction (Sukoriansky & Galperin Reference Sukoriansky and Galperin2013).
$k\rightarrow 0$
, as shown in figure 2 (also see Chekhlov et al.
Reference Chekhlov, Orszag, Sukoriansky, Galperin and Staroselsky1994). A problem of this kind arises in 3-D flows with a solid body rotation where the energy is gradually channelled into a manifold occupying a conical region orthogonal to the axis of rotation giving rise to the inverse energy cascade (Sagaut & Cambon Reference Sagaut and Cambon2008). In such flows, the QNSE formalism can only be applied on relatively small scales in the assumption that the forcing acts on scales where the eddy viscosity remains positive. In other words, in flows with rotation, the QNSE theory can only be used in the limit of weak rotation or on scales where the effect of rotation is weak. Although this limitation constrains the applicability of the QNSE theory to rotating flows, it does not preclude the possibility of developing an analytical theory of transition from Kolmogorov to rotation-dominated turbulence which is a subject of the forthcoming sections. Note in this respect that the QNSE theory was also used to develop an analytical theory of the transition from Kolmogorov to stable stratification-dominated turbulence where it provided a deep physical insight of flow anisotropization and turbulence–internal wave interaction (Sukoriansky & Galperin Reference Sukoriansky and Galperin2013).

Figure 2. Normalized two-parametric eddy viscosity in isotropic 2-D flows from DNS (dots), the test field model (dashed line) and the renormalization group theory (solid line). (After Sukoriansky & Zemach Reference Sukoriansky and Zemach2016, © The Royal Swedish Academy of Sciences. Reproduced by permission of IOP Publishing. All rights reserved.)
6 Passive-scalar diffusion equation and its successive coarse graining
The procedure of successive quasi-normal coarse graining can be developed for the scalar diffusion equation. The resulting equation and (4.2) will be used later to compute scale-dependent eddy viscosities and eddy diffusivities.
The diffusion of a passive scalar
![]() $c$
is described by a standard diffusion equation
$c$
is described by a standard diffusion equation
where
![]() $\unicode[STIX]{x1D705}_{0}$
is the molecular diffusivity. Space–time Fourier-transformed representation of (6.1) is
$\unicode[STIX]{x1D705}_{0}$
is the molecular diffusivity. Space–time Fourier-transformed representation of (6.1) is
where
![]() $G_{D}(\hat{k})$
is the diffusion Green function,
$G_{D}(\hat{k})$
is the diffusion Green function,
where following § 2 an anisotropic correction is included.
Similar to (3.13), (6.2) can be written in the form of the Langevin equation for a scalar
![]() $c$
,
$c$
,
where
![]() $\unicode[STIX]{x1D709}_{c}(\hat{k})$
represents nonlinear stirring of a mode
$\unicode[STIX]{x1D709}_{c}(\hat{k})$
represents nonlinear stirring of a mode
![]() $\hat{k}$
by all other modes.
$\hat{k}$
by all other modes.
Successive coarse graining of the diffusion equation (6.2) is performed using a two-part procedure similar to that outlined in § 4 for the momentum equation. Namely, ‘slow’,
![]() $c^{{<}}$
, and ‘fast’,
$c^{{<}}$
, and ‘fast’,
![]() $c^{{>}}$
, scalar modes are introduced and the expansion
$c^{{>}}$
, scalar modes are introduced and the expansion
![]() $c=c^{{<}}+c^{{>}}$
is substituted in (6.2) yielding
$c=c^{{<}}+c^{{>}}$
is substituted in (6.2) yielding
 $$\begin{eqnarray}\displaystyle c(\hat{k}) & = & \displaystyle -\text{i}G_{D}^{0}(\hat{k})k_{\unicode[STIX]{x1D6FC}}\int [\!v_{\unicode[STIX]{x1D6FC}}^{{<}}(\hat{q})c^{{<}}(\hat{k}-\hat{q})+v_{\unicode[STIX]{x1D6FC}}^{{<}}(\hat{q})c^{{>}}(\hat{k}-\hat{q})\nonumber\\ \displaystyle & & \displaystyle +\,v_{\unicode[STIX]{x1D6FC}}^{{>}}(\hat{q})c^{{<}}(\hat{k}-\hat{q})+v_{\unicode[STIX]{x1D6FC}}^{{>}}(\hat{q})c^{{>}}(\hat{k}-\hat{q})\!]\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c(\hat{k}) & = & \displaystyle -\text{i}G_{D}^{0}(\hat{k})k_{\unicode[STIX]{x1D6FC}}\int [\!v_{\unicode[STIX]{x1D6FC}}^{{<}}(\hat{q})c^{{<}}(\hat{k}-\hat{q})+v_{\unicode[STIX]{x1D6FC}}^{{<}}(\hat{q})c^{{>}}(\hat{k}-\hat{q})\nonumber\\ \displaystyle & & \displaystyle +\,v_{\unicode[STIX]{x1D6FC}}^{{>}}(\hat{q})c^{{<}}(\hat{k}-\hat{q})+v_{\unicode[STIX]{x1D6FC}}^{{>}}(\hat{q})c^{{>}}(\hat{k}-\hat{q})\!]\frac{\text{d}\hat{q}}{(2\unicode[STIX]{x03C0})^{d+1}}.\end{eqnarray}$$
Similarly to (4.1), this equation is valid for either
![]() $k\in D^{{<}}$
or
$k\in D^{{<}}$
or
![]() $k\in D^{{>}}$
.
$k\in D^{{>}}$
.
Then, an equation for
![]() $c^{{<}}(\hat{k})$
is derived by manipulating (6.5) written for
$c^{{<}}(\hat{k})$
is derived by manipulating (6.5) written for
![]() $c^{{<}}(\hat{k})$
. The second and third terms are iterated by substituting the ‘slow’ mode equations for
$c^{{<}}(\hat{k})$
. The second and third terms are iterated by substituting the ‘slow’ mode equations for
![]() $c^{{<}}$
and
$c^{{<}}$
and
![]() $v^{{<}}$
, respectively, while the term
$v^{{<}}$
, respectively, while the term
![]() $v^{{>}}c^{{>}}$
is iterated by substituting the equation for
$v^{{>}}c^{{>}}$
is iterated by substituting the equation for
![]() $c^{{>}}$
. Then, replacing the ‘fast’ variables
$c^{{>}}$
. Then, replacing the ‘fast’ variables
![]() $v^{{>}}$
and
$v^{{>}}$
and
![]() $c^{{>}}$
by their respective Langevin equations (3.13) and (6.4) and ensemble averaging the result over the fast modes
$c^{{>}}$
by their respective Langevin equations (3.13) and (6.4) and ensemble averaging the result over the fast modes
![]() $\unicode[STIX]{x1D743}^{{>}}$
and
$\unicode[STIX]{x1D743}^{{>}}$
and
![]() $\unicode[STIX]{x1D743}_{c}^{{>}}$
, we compute corrections to the inverse Green function produced by the elimination of the shell
$\unicode[STIX]{x1D743}_{c}^{{>}}$
, we compute corrections to the inverse Green function produced by the elimination of the shell
![]() $D^{{>}}$
,
$D^{{>}}$
,
Similarly to (4.2), the integral in (6.6) is calculated in the long-time limit,
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
, and using the spectral gap approximation.
$\unicode[STIX]{x1D714}\rightarrow 0$
, and using the spectral gap approximation.
Note that (6.6) depends on the velocity correlator
![]() $U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D71B},\boldsymbol{q})$
and so the statistics of the scalar forcing
$U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D71B},\boldsymbol{q})$
and so the statistics of the scalar forcing
![]() $\unicode[STIX]{x1D709}_{c}(\hat{k})$
is immaterial. The closure is achieved by neglecting the odd velocity-scalar moments of the fast modes in the iterated (6.5) (see Sukoriansky et al. (Reference Sukoriansky, Galperin and Staroselsky2005) for details).
$\unicode[STIX]{x1D709}_{c}(\hat{k})$
is immaterial. The closure is achieved by neglecting the odd velocity-scalar moments of the fast modes in the iterated (6.5) (see Sukoriansky et al. (Reference Sukoriansky, Galperin and Staroselsky2005) for details).
7 Computation of the effective viscosities and diffusivities
Evaluation of the integrals in (4.2) and (6.6) is accomplished in the following steps:
-
(i) Contour integration over the frequency
 $\unicode[STIX]{x1D71B}$
.
$\unicode[STIX]{x1D71B}$
. -
(ii) Invoking the spectral gap approximation.
-
(iii) Integration over the spherical shell
 $D^{{>}}$
which is a two-step operation combining multiplication by
$D^{{>}}$
which is a two-step operation combining multiplication by
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
and the angular integration over the surface of a sphere with the radius
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
and the angular integration over the surface of a sphere with the radius
 $\unicode[STIX]{x1D6EC}$
. The inherent anisotropy due to the system rotation complicates the integration. However, by utilizing the isotropy of the integrand in the plane normal to
$\unicode[STIX]{x1D6EC}$
. The inherent anisotropy due to the system rotation complicates the integration. However, by utilizing the isotropy of the integrand in the plane normal to
 $\unicode[STIX]{x1D734}$
one can carry out all calculations analytically.
$\unicode[STIX]{x1D734}$
one can carry out all calculations analytically.
In the next sections it will be shown that the corrections to the inverse velocity and diffusion Green functions caused by the elimination of the fast shell
![]() $D^{{>}}$
result in
$D^{{>}}$
result in
![]() $O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
corrections to eddy viscosities and eddy diffusivities such that both
$O(\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC})$
corrections to eddy viscosities and eddy diffusivities such that both
![]() $G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{-1}(0,k,k_{z})+\unicode[STIX]{x0394}G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{-1}(0,k,k_{z})$
and
$G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{-1}(0,k,k_{z})+\unicode[STIX]{x0394}G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{-1}(0,k,k_{z})$
and
![]() $G_{D}^{-1}(0,k,k_{z})+\unicode[STIX]{x0394}G_{D}^{-1}(0,k,k_{z})$
preserve their forms. The procedure also generates a correction proportional to
$G_{D}^{-1}(0,k,k_{z})+\unicode[STIX]{x0394}G_{D}^{-1}(0,k,k_{z})$
preserve their forms. The procedure also generates a correction proportional to
![]() $fk^{2}S_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(k,k_{z})$
. This correction corresponds to renormalization of
$fk^{2}S_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(k,k_{z})$
. This correction corresponds to renormalization of
![]() $\unicode[STIX]{x1D6FA}$
. It should be discarded as being
$\unicode[STIX]{x1D6FA}$
. It should be discarded as being
![]() $O(k^{2})$
small whereas the original term is
$O(k^{2})$
small whereas the original term is
![]() $O(1)$
. Finally, by dividing
$O(1)$
. Finally, by dividing
![]() $\unicode[STIX]{x0394}G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{-1}(0,k,k_{z})$
and
$\unicode[STIX]{x0394}G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{-1}(0,k,k_{z})$
and
![]() $\unicode[STIX]{x0394}G_{D}^{-1}(0,k,k_{z})$
by
$\unicode[STIX]{x0394}G_{D}^{-1}(0,k,k_{z})$
by
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
and taking the limit
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
and taking the limit
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
, we obtain a system of coupled ordinary differential equations for all eddy viscosities and eddy diffusivities.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
, we obtain a system of coupled ordinary differential equations for all eddy viscosities and eddy diffusivities.
In the process of computation, the integral in (6.6) will be evaluated first. This integral is simpler of the two and its evaluation provides a good illustration for calculation of the other integral. In all the forthcoming derivations, the continuity equation (3.5) will be routinely enforced. This means that if a term, such as the integral (4.2), is factored with
![]() $v_{\unicode[STIX]{x1D6FD}}(\hat{k})$
then any part of this term proportional to
$v_{\unicode[STIX]{x1D6FD}}(\hat{k})$
then any part of this term proportional to
![]() $k_{\unicode[STIX]{x1D6FD}}$
will be set to zero automatically. Other simplifying relationships are related to the symmetry and solenoidality properties of the projection operator, i.e.
$k_{\unicode[STIX]{x1D6FD}}$
will be set to zero automatically. Other simplifying relationships are related to the symmetry and solenoidality properties of the projection operator, i.e.
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})=P_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}(\boldsymbol{k})$
and
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})=P_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}(\boldsymbol{k})$
and
![]() $k_{\unicode[STIX]{x1D6FC}}P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})=0$
, and zeroing out the contractions of symmetric and antisymmetric tensors (e.g.
$k_{\unicode[STIX]{x1D6FC}}P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})=0$
, and zeroing out the contractions of symmetric and antisymmetric tensors (e.g.
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
and
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
and
![]() $Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
or
$Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
or
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
and
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
and
![]() $e_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
). All related simplifications will usually be implemented without specific mentioning.
$e_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
). All related simplifications will usually be implemented without specific mentioning.
7.1 Effective diffusivities
7.1.1 Simplification of the integrand
Turn now to (6.6) in the limit
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
where the integrand is
$\unicode[STIX]{x1D714}\rightarrow 0$
where the integrand is
As explained earlier in § 5, the application of the spectral gap approximation implies that the calculation of the expression in the right-hand side of (6.6) needs to be carried out only up to the order of
![]() $O(k^{2})$
. The presence of the product
$O(k^{2})$
. The presence of the product
![]() $k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}$
in front of the integral makes the calculation of terms smaller than
$k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}$
in front of the integral makes the calculation of terms smaller than
![]() $O(1)$
in the integrand (7.1) unnecessary and so, one can set
$O(1)$
in the integrand (7.1) unnecessary and so, one can set
![]() $k=0$
in
$k=0$
in
![]() $G_{D}$
yielding
$G_{D}$
yielding
Using (4.4), one can represent
![]() $I_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{D}$
as
$I_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{D}$
as
 $$\begin{eqnarray}\displaystyle I_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{D} & = & \displaystyle \frac{|G(\unicode[STIX]{x1D71B},q,q_{3})|^{2}}{|d(\unicode[STIX]{x1D71B},q,q_{3})|^{2}}D(q)[\!A(\unicode[STIX]{x1D71B},q,q_{3})P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})+B(\unicode[STIX]{x1D71B},q,q_{3})Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\nonumber\\ \displaystyle & & \displaystyle +\,C(\unicode[STIX]{x1D71B},q,q_{3})P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{q})P_{3\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\!]G_{D}(-\unicode[STIX]{x1D71B},q,q_{3}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{D} & = & \displaystyle \frac{|G(\unicode[STIX]{x1D71B},q,q_{3})|^{2}}{|d(\unicode[STIX]{x1D71B},q,q_{3})|^{2}}D(q)[\!A(\unicode[STIX]{x1D71B},q,q_{3})P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})+B(\unicode[STIX]{x1D71B},q,q_{3})Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\nonumber\\ \displaystyle & & \displaystyle +\,C(\unicode[STIX]{x1D71B},q,q_{3})P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{q})P_{3\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\!]G_{D}(-\unicode[STIX]{x1D71B},q,q_{3}).\end{eqnarray}$$
We keep in mind that the second term in (7.3) zeroes out upon contraction of the antisymmetric tensor
![]() $Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})$
with the symmetric product
$Q_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})$
with the symmetric product
![]() $k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}$
in front of the integral in (6.6). After this simplification, the integrand (7.1) can be factorized,
$k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}$
in front of the integral in (6.6). After this simplification, the integrand (7.1) can be factorized,
where
7.1.2 Frequency integration
The
![]() $\unicode[STIX]{x1D71B}$
-integration in (6.6) reduces to the integration of
$\unicode[STIX]{x1D71B}$
-integration in (6.6) reduces to the integration of
![]() $R_{1}(\unicode[STIX]{x1D71B},q,q_{3})$
and
$R_{1}(\unicode[STIX]{x1D71B},q,q_{3})$
and
![]() $R_{2}(\unicode[STIX]{x1D71B},q,q_{3})$
which can be performed using the contour methods. Both functions
$R_{2}(\unicode[STIX]{x1D71B},q,q_{3})$
which can be performed using the contour methods. Both functions
![]() $R_{1}(\unicode[STIX]{x1D71B},q,q_{3})$
and
$R_{1}(\unicode[STIX]{x1D71B},q,q_{3})$
and
![]() $R_{2}(\unicode[STIX]{x1D71B},q,q_{3})$
have 5 poles,
$R_{2}(\unicode[STIX]{x1D71B},q,q_{3})$
have 5 poles,
Three of these poles are located in the upper half-plane while the other two belong in the lower half-plane. The frequency integrals are computed over the lower half-plane and yield
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{R}_{1}(q,q_{3})=\int R_{1}(\unicode[STIX]{x1D71B},q,q_{3})\frac{\text{d}\unicode[STIX]{x1D71B}}{2\unicode[STIX]{x03C0}}=\frac{\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D}}{2\unicode[STIX]{x1D714}_{q}[f_{1}+(\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D})^{2}]},\\ \displaystyle \mathscr{R}_{2}(q,q_{3})=\int R_{2}(\unicode[STIX]{x1D71B},q,q_{3})\frac{\text{d}\unicode[STIX]{x1D71B}}{2\unicode[STIX]{x03C0}}=-\frac{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}q^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}q_{3}^{2})(2\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D})}{2(f_{1}+\unicode[STIX]{x1D714}_{q}^{2})[f_{1}+(\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D})^{2}]}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{R}_{1}(q,q_{3})=\int R_{1}(\unicode[STIX]{x1D71B},q,q_{3})\frac{\text{d}\unicode[STIX]{x1D71B}}{2\unicode[STIX]{x03C0}}=\frac{\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D}}{2\unicode[STIX]{x1D714}_{q}[f_{1}+(\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D})^{2}]},\\ \displaystyle \mathscr{R}_{2}(q,q_{3})=\int R_{2}(\unicode[STIX]{x1D71B},q,q_{3})\frac{\text{d}\unicode[STIX]{x1D71B}}{2\unicode[STIX]{x03C0}}=-\frac{(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}q^{2}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}q_{3}^{2})(2\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D})}{2(f_{1}+\unicode[STIX]{x1D714}_{q}^{2})[f_{1}+(\unicode[STIX]{x1D714}_{q}+\unicode[STIX]{x1D714}_{q}^{D})^{2}]}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The integration in (6.6) is now reduced to integration of the product
![]() $D(q)P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\mathscr{R}(q,q_{3})$
over the spherical shell
$D(q)P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\mathscr{R}(q,q_{3})$
over the spherical shell
![]() $D^{{>}}$
.
$D^{{>}}$
.
7.1.3 Integration over spherical shell
 $D^{{>}}$
$D^{{>}}$
The integration over
![]() $D^{{>}}$
consists of the integration in the radial direction (which results in multiplication by
$D^{{>}}$
consists of the integration in the radial direction (which results in multiplication by
![]() $-\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
; the negative sign is due to contraction of the domain when scales are eliminated) and subsequent integration over the surface of a
$-\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}$
; the negative sign is due to contraction of the domain when scales are eliminated) and subsequent integration over the surface of a
![]() $d$
-dimensional sphere,
$d$
-dimensional sphere,
![]() $\unicode[STIX]{x1D6F4}_{d}$
, whose radius is
$\unicode[STIX]{x1D6F4}_{d}$
, whose radius is
![]() $\unicode[STIX]{x1D6EC}$
. Some of the calculations are performed in
$\unicode[STIX]{x1D6EC}$
. Some of the calculations are performed in
![]() $d$
-dimensional space with the understanding that
$d$
-dimensional space with the understanding that
![]() $d=3$
. In the isotropic case, the angular integration yields sums of products of the Kronecker
$d=3$
. In the isotropic case, the angular integration yields sums of products of the Kronecker
![]() $\unicode[STIX]{x1D6FF}$
-symbols (Yakhot & Orszag Reference Yakhot and Orszag1986; Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003). In flows with system rotation the integrand is anisotropic and the procedure of angular integration requires further development. Similarly to the case of stable stratification (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005), the isotropy is preserved in horizontal planes. Utilizing this observation, the angular integration over the surface of a
$\unicode[STIX]{x1D6FF}$
-symbols (Yakhot & Orszag Reference Yakhot and Orszag1986; Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2003). In flows with system rotation the integrand is anisotropic and the procedure of angular integration requires further development. Similarly to the case of stable stratification (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005), the isotropy is preserved in horizontal planes. Utilizing this observation, the angular integration over the surface of a
![]() $d$
-dimensional sphere,
$d$
-dimensional sphere,
![]() $\unicode[STIX]{x1D6F4}_{d}$
, is performed, firstly, by integrating over the surface of a
$\unicode[STIX]{x1D6F4}_{d}$
, is performed, firstly, by integrating over the surface of a
![]() $d-1$
-dimensional sphere
$d-1$
-dimensional sphere
![]() $\unicode[STIX]{x1D6F4}_{d-1}$
(clearly, for
$\unicode[STIX]{x1D6F4}_{d-1}$
(clearly, for
![]() $d-1=2$
, this is merely a circle in the horizontal plane) and, secondly, integrating over the vertical semi-circle:
$d-1=2$
, this is merely a circle in the horizontal plane) and, secondly, integrating over the vertical semi-circle:
In the integration over
![]() $\unicode[STIX]{x1D6F4}_{d-1}$
, the horizontal radius
$\unicode[STIX]{x1D6F4}_{d-1}$
, the horizontal radius
![]() $q_{h}$
is a function of the vertical coordinate,
$q_{h}$
is a function of the vertical coordinate,
where
![]() $\unicode[STIX]{x1D703}$
is the angle between the vector
$\unicode[STIX]{x1D703}$
is the angle between the vector
![]() $\boldsymbol{q}$
and the vertical axis;
$\boldsymbol{q}$
and the vertical axis;
![]() $q$
is replaced by
$q$
is replaced by
![]() $\unicode[STIX]{x1D6EC}$
reflecting the fact that
$\unicode[STIX]{x1D6EC}$
reflecting the fact that
![]() $D^{{>}}$
is a spherical shell of the radius
$D^{{>}}$
is a spherical shell of the radius
![]() $\unicode[STIX]{x1D6EC}$
. Note that by (3.8),
$\unicode[STIX]{x1D6EC}$
. Note that by (3.8),
The horizontal isotropy comes into play by representing the vector
![]() $\boldsymbol{q}$
as a sum of its horizontal and vertical projections,
$\boldsymbol{q}$
as a sum of its horizontal and vertical projections,
![]() $\boldsymbol{q}_{h}=(q_{1},q_{2},0)$
and
$\boldsymbol{q}_{h}=(q_{1},q_{2},0)$
and
![]() $q_{3}$
, respectively,
$q_{3}$
, respectively,
This decomposition enables one to perform the integration over
![]() $\unicode[STIX]{x1D6F4}_{d-1}$
analytically. The integration over a
$\unicode[STIX]{x1D6F4}_{d-1}$
analytically. The integration over a
![]() $d-1$
-dimensional spherical surface of the radius
$d-1$
-dimensional spherical surface of the radius
![]() $\unicode[STIX]{x1D6EC}$
can be accomplished by utilizing the following auxiliary relationships valid for the horizontal components of the vector
$\unicode[STIX]{x1D6EC}$
can be accomplished by utilizing the following auxiliary relationships valid for the horizontal components of the vector
![]() $\boldsymbol{q}$
,
$\boldsymbol{q}$
,
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6F4}_{d-1}}{q_{h}}_{\unicode[STIX]{x1D6FC}}{q_{h}}_{\unicode[STIX]{x1D6FD}}{q_{h}}_{\unicode[STIX]{x1D6FE}}{q_{h}}_{\unicode[STIX]{x1D6FF}}\text{d}^{d-2}q & = & \displaystyle S_{d-1}(\unicode[STIX]{x1D6EC}\sin \unicode[STIX]{x1D703})^{d+2}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}}+\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}}+\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}}{(d-1)(d+1)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6F4}_{d-1}}{q_{h}}_{\unicode[STIX]{x1D6FC}}{q_{h}}_{\unicode[STIX]{x1D6FD}}{q_{h}}_{\unicode[STIX]{x1D6FE}}{q_{h}}_{\unicode[STIX]{x1D6FF}}\text{d}^{d-2}q & = & \displaystyle S_{d-1}(\unicode[STIX]{x1D6EC}\sin \unicode[STIX]{x1D703})^{d+2}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}}+\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}}+\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}}{(d-1)(d+1)},\end{eqnarray}$$
where
![]() $S_{d}=2\unicode[STIX]{x03C0}^{d/2}/\unicode[STIX]{x1D6E4}(d/2)$
is the surface area of a
$S_{d}=2\unicode[STIX]{x03C0}^{d/2}/\unicode[STIX]{x1D6E4}(d/2)$
is the surface area of a
![]() $d$
-dimensional unit sphere and
$d$
-dimensional unit sphere and
![]() $\unicode[STIX]{x1D6FC}$
through
$\unicode[STIX]{x1D6FC}$
through
![]() $\unicode[STIX]{x1D6FF}$
are indexes in the horizontal plane.
$\unicode[STIX]{x1D6FF}$
are indexes in the horizontal plane.
With the use of the auxiliary relationships for the integration in the horizontal plane one finds
 $$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}\int _{\unicode[STIX]{x1D6F4}_{d-1}}P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\text{d}^{d-2}q & = & \displaystyle S_{d-1}(\unicode[STIX]{x1D6EC}\sin \unicode[STIX]{x1D703})^{d-2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[k^{2}\left(1-\frac{\sin ^{2}\unicode[STIX]{x1D703}}{d-1}\right)+k_{3}^{2}\left(\frac{d}{d-1}\sin ^{2}\unicode[STIX]{x1D703}-1\right)\right]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}\int _{\unicode[STIX]{x1D6F4}_{d-1}}P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{q})\text{d}^{d-2}q & = & \displaystyle S_{d-1}(\unicode[STIX]{x1D6EC}\sin \unicode[STIX]{x1D703})^{d-2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[k^{2}\left(1-\frac{\sin ^{2}\unicode[STIX]{x1D703}}{d-1}\right)+k_{3}^{2}\left(\frac{d}{d-1}\sin ^{2}\unicode[STIX]{x1D703}-1\right)\right]\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}\int _{\unicode[STIX]{x1D6F4}_{d-1}}P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{q})P_{3\unicode[STIX]{x1D6FD}}\text{d}^{d-2}q & = & \displaystyle \frac{S_{d-1}}{d-1}(\unicode[STIX]{x1D6EC}\sin \unicode[STIX]{x1D703})^{d-2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[k^{2}\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D703}+k_{3}^{2}\sin ^{2}\unicode[STIX]{x1D703}(d\sin ^{2}\unicode[STIX]{x1D703}-1)\right].\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{\unicode[STIX]{x1D6FC}}k_{\unicode[STIX]{x1D6FD}}\int _{\unicode[STIX]{x1D6F4}_{d-1}}P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{q})P_{3\unicode[STIX]{x1D6FD}}\text{d}^{d-2}q & = & \displaystyle \frac{S_{d-1}}{d-1}(\unicode[STIX]{x1D6EC}\sin \unicode[STIX]{x1D703})^{d-2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[k^{2}\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D703}+k_{3}^{2}\sin ^{2}\unicode[STIX]{x1D703}(d\sin ^{2}\unicode[STIX]{x1D703}-1)\right].\quad\end{eqnarray}$$
Terms proportional to
![]() $k^{2}$
and
$k^{2}$
and
![]() $k_{3}^{2}$
in (7.19) and (7.20) give corrections to
$k_{3}^{2}$
in (7.19) and (7.20) give corrections to
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $\unicode[STIX]{x1D705}_{z}$
, respectively. After collecting all the factors, taking the limit
$\unicode[STIX]{x1D705}_{z}$
, respectively. After collecting all the factors, taking the limit
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
and substituting
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
and substituting
![]() $d=3$
and
$d=3$
and
![]() $x=\cos \unicode[STIX]{x1D703}$
, we obtain differential equations for
$x=\cos \unicode[STIX]{x1D703}$
, we obtain differential equations for
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $\unicode[STIX]{x1D705}_{z}$
,
$\unicode[STIX]{x1D705}_{z}$
,
 $$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D705}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle \frac{D}{8\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}}\int _{-1}^{1}\left\{\frac{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})(1+x^{2})}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}(2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})x^{2}(1-x^{2})}{(f^{2}x^{2}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{2})[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right\}\,\text{d}x,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D705}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle \frac{D}{8\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}}\int _{-1}^{1}\left\{\frac{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})(1+x^{2})}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}(2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})x^{2}(1-x^{2})}{(f^{2}x^{2}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{2})[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right\}\,\text{d}x,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D705}_{z}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle -\frac{D}{4\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}}\int _{-1}^{1}\left\{\frac{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})(1-x^{2})}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}(2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})(1-x^{2})^{2}}{(f^{2}x^{2}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{2})[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right\}\,\text{d}x,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D705}_{z}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle -\frac{D}{4\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}}\int _{-1}^{1}\left\{\frac{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})(1-x^{2})}{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}(2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})(1-x^{2})^{2}}{(f^{2}x^{2}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{2})[f^{2}x^{2}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}^{D})^{2}]}\right\}\,\text{d}x,\end{eqnarray}$$
In the approximation of weak rotation, the integrals simplify significantly and reduce to
 $$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D705}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle -\frac{D}{3\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}^{5}\unicode[STIX]{x1D708}^{2}(1+\unicode[STIX]{x1D6FC})}\left\{1-\frac{1}{1+\unicode[STIX]{x1D6FC}}\left[\frac{2}{5(1+\unicode[STIX]{x1D6FC})}Ro^{-2}+\frac{2}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{z}}{\unicode[STIX]{x1D708}_{n}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\left.\frac{2(2+\unicode[STIX]{x1D6FC})}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}}{\unicode[STIX]{x1D708}_{n}}+\frac{2+\unicode[STIX]{x1D6FC}}{10}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}}{\unicode[STIX]{x1D708}_{n}}+\frac{3(2+\unicode[STIX]{x1D6FC})}{70}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}}{\unicode[STIX]{x1D708}_{n}}\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D705}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle -\frac{D}{3\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}^{5}\unicode[STIX]{x1D708}^{2}(1+\unicode[STIX]{x1D6FC})}\left\{1-\frac{1}{1+\unicode[STIX]{x1D6FC}}\left[\frac{2}{5(1+\unicode[STIX]{x1D6FC})}Ro^{-2}+\frac{2}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{z}}{\unicode[STIX]{x1D708}_{n}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\left.\frac{2(2+\unicode[STIX]{x1D6FC})}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}}{\unicode[STIX]{x1D708}_{n}}+\frac{2+\unicode[STIX]{x1D6FC}}{10}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}}{\unicode[STIX]{x1D708}_{n}}+\frac{3(2+\unicode[STIX]{x1D6FC})}{70}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}}{\unicode[STIX]{x1D708}_{n}}\right]\right\},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{z}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle -\frac{D}{3\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}^{5}\unicode[STIX]{x1D708}_{n}^{2}(1+\unicode[STIX]{x1D6FC})^{2}}\left[\frac{1}{5(1+\unicode[STIX]{x1D6FC})}Ro^{-2}+\frac{1}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{z}}{\unicode[STIX]{x1D708}_{n}}+\frac{2+\unicode[STIX]{x1D6FC}}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}}{\unicode[STIX]{x1D708}_{n}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{7(2+\unicode[STIX]{x1D6FC})}{10}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}}{\unicode[STIX]{x1D708}_{n}}-\frac{2+\unicode[STIX]{x1D6FC}}{14}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}}{\unicode[STIX]{x1D708}_{n}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{z}}{\text{d}\unicode[STIX]{x1D6EC}} & = & \displaystyle -\frac{D}{3\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D6EC}^{5}\unicode[STIX]{x1D708}_{n}^{2}(1+\unicode[STIX]{x1D6FC})^{2}}\left[\frac{1}{5(1+\unicode[STIX]{x1D6FC})}Ro^{-2}+\frac{1}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D705}_{z}}{\unicode[STIX]{x1D708}_{n}}+\frac{2+\unicode[STIX]{x1D6FC}}{5}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}}{\unicode[STIX]{x1D708}_{n}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{7(2+\unicode[STIX]{x1D6FC})}{10}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}}{\unicode[STIX]{x1D708}_{n}}-\frac{2+\unicode[STIX]{x1D6FC}}{14}\frac{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}}{\unicode[STIX]{x1D708}_{n}}\right],\end{eqnarray}$$
where for
![]() $d=3$
,
$d=3$
,
In non-rotating flows, (7.26) reduces to
where for
![]() $d=3$
,
$d=3$
,
and
![]() $\unicode[STIX]{x1D708}_{n}$
is given by (7.28). The solution to (7.30) is
$\unicode[STIX]{x1D708}_{n}$
is given by (7.28). The solution to (7.30) is
from which one finds
Furthermore,
is a spectral Rossby number which is the ratio of the time scale of system rotation and the eddy turnover time at a local scale
![]() $\unicode[STIX]{x1D6EC}$
. In (7.34), the eddy viscosity
$\unicode[STIX]{x1D6EC}$
. In (7.34), the eddy viscosity
![]() $\unicode[STIX]{x1D708}_{n}(\unicode[STIX]{x1D6EC})$
can be used instead of
$\unicode[STIX]{x1D708}_{n}(\unicode[STIX]{x1D6EC})$
can be used instead of
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
. The spectral Rossby number is analogous to the spectral Froude number in stably stratified turbulence (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005) and is an important characteristic of the scalewise effect of rotation on turbulence. Clearly, turbulence is isotropic on scales where
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6EC})$
. The spectral Rossby number is analogous to the spectral Froude number in stably stratified turbulence (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005) and is an important characteristic of the scalewise effect of rotation on turbulence. Clearly, turbulence is isotropic on scales where
![]() $Ro>1$
while the effects of inertial waves and anisotropy become strong on scales where
$Ro>1$
while the effects of inertial waves and anisotropy become strong on scales where
![]() $Ro<1$
. Such classification of flow regimes is consistent with experimental results, see e.g. Jacquin et al. (Reference Jacquin, Leuchter, Cambon and Mathieu1990).
$Ro<1$
. Such classification of flow regimes is consistent with experimental results, see e.g. Jacquin et al. (Reference Jacquin, Leuchter, Cambon and Mathieu1990).
It will be shown later in (8.3) that in zero-order approximation,
![]() $D\simeq 13.1\unicode[STIX]{x1D716}$
. Then,
$D\simeq 13.1\unicode[STIX]{x1D716}$
. Then,
![]() $Ro(k)$
can be presented in an alternative form reminiscent of flows with stable stratification (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005),
$Ro(k)$
can be presented in an alternative form reminiscent of flows with stable stratification (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005),
where
is a wavenumber analogous to the Ozmidov wavenumber,
![]() $k_{O}$
, in stably stratified flows. The wavenumber
$k_{O}$
, in stably stratified flows. The wavenumber
![]() $k_{\unicode[STIX]{x1D6FA}}$
identifies a scale at which turbulence eddy turnover time is commensurate with the time scale of system rotation. Similarly to
$k_{\unicode[STIX]{x1D6FA}}$
identifies a scale at which turbulence eddy turnover time is commensurate with the time scale of system rotation. Similarly to
![]() $Ro$
, the ratio
$Ro$
, the ratio
![]() $k/k_{\unicode[STIX]{x1D6FA}}$
is a non-dimensional parameter characterizing scalewise strength of the effect of rotation. It is weak on scales where
$k/k_{\unicode[STIX]{x1D6FA}}$
is a non-dimensional parameter characterizing scalewise strength of the effect of rotation. It is weak on scales where
![]() $k/k_{\unicode[STIX]{x1D6FA}}>1$
and strong on scales where
$k/k_{\unicode[STIX]{x1D6FA}}>1$
and strong on scales where
![]() $k/k_{\unicode[STIX]{x1D6FA}}\lesssim 1$
. In some studies,
$k/k_{\unicode[STIX]{x1D6FA}}\lesssim 1$
. In some studies,
![]() $k_{\unicode[STIX]{x1D6FA}}$
is defined in terms of the angular velocity of system rotation,
$k_{\unicode[STIX]{x1D6FA}}$
is defined in terms of the angular velocity of system rotation,
![]() $\unicode[STIX]{x1D6FA}$
. Here, we use the definition based upon
$\unicode[STIX]{x1D6FA}$
. Here, we use the definition based upon
![]() $f$
because this is a variable recognized by the governing equation (3.1). Both representations (7.35) and (7.36) will be utilized in studies of explicit modifications of eddy viscosities and eddy diffusivities by rotation.
$f$
because this is a variable recognized by the governing equation (3.1). Both representations (7.35) and (7.36) will be utilized in studies of explicit modifications of eddy viscosities and eddy diffusivities by rotation.
Mininni et al. (Reference Mininni, Rosenberg and Pouquet2012) propose to name the scale
![]() $L_{\unicode[STIX]{x1D6FA}}=k_{\unicode[STIX]{x1D6FA}}^{-1}$
after Zeman following Zeman (Reference Zeman1994). Earlier, however, following Hopfinger & Browand (Reference Hopfinger and Browand1981), Gibson (Reference Gibson1991) referred to
$L_{\unicode[STIX]{x1D6FA}}=k_{\unicode[STIX]{x1D6FA}}^{-1}$
after Zeman following Zeman (Reference Zeman1994). Earlier, however, following Hopfinger & Browand (Reference Hopfinger and Browand1981), Gibson (Reference Gibson1991) referred to
![]() $L_{\unicode[STIX]{x1D6FA}}$
as the Hopfinger scale. A similar scale was introduced in the analysis of the effects of rotation on thermal convection (Fernando, Boyer & Chen Reference Fernando, Boyer and Chen1989; Fernando, Chen & Boyer Reference Fernando, Chen and Boyer1991) but the role of
$L_{\unicode[STIX]{x1D6FA}}$
as the Hopfinger scale. A similar scale was introduced in the analysis of the effects of rotation on thermal convection (Fernando, Boyer & Chen Reference Fernando, Boyer and Chen1989; Fernando, Chen & Boyer Reference Fernando, Chen and Boyer1991) but the role of
![]() $\unicode[STIX]{x1D716}$
there played the kinematic surface heat flux. That scale, referred to by Gibson (Reference Gibson1991) as the Fernando scale, has become one of the main characteristics of convective turbulence. Two decades earlier, the scale
$\unicode[STIX]{x1D716}$
there played the kinematic surface heat flux. That scale, referred to by Gibson (Reference Gibson1991) as the Fernando scale, has become one of the main characteristics of convective turbulence. Two decades earlier, the scale
![]() $L_{\unicode[STIX]{x1D6FA}}$
was introduced in the works by Woods (Reference Woods1973, Reference Woods1974, Reference Woods1980) and following these papers, it was included in the discussions of the variety of scales of oceanic and atmospheric circulations in the books by Monin & Ozmidov (Reference Monin and Ozmidov1985) and Kamenkovich, Koshlyakov & Monin (Reference Kamenkovich, Koshlyakov and Monin1986). To the best of our knowledge, Woods was the first to recognize the importance of
$L_{\unicode[STIX]{x1D6FA}}$
was introduced in the works by Woods (Reference Woods1973, Reference Woods1974, Reference Woods1980) and following these papers, it was included in the discussions of the variety of scales of oceanic and atmospheric circulations in the books by Monin & Ozmidov (Reference Monin and Ozmidov1985) and Kamenkovich, Koshlyakov & Monin (Reference Kamenkovich, Koshlyakov and Monin1986). To the best of our knowledge, Woods was the first to recognize the importance of
![]() $L_{\unicode[STIX]{x1D6FA}}$
as a scale characterizing the effect of rotation on turbulence and for this reason, it would be appropriate to refer to
$L_{\unicode[STIX]{x1D6FA}}$
as a scale characterizing the effect of rotation on turbulence and for this reason, it would be appropriate to refer to
![]() $L_{\unicode[STIX]{x1D6FA}}$
as the Woods scale (Gibson (Reference Gibson1991) also credited Woods with the invention of the term ‘fossil turbulence’ in Woods (Reference Woods1969)).
$L_{\unicode[STIX]{x1D6FA}}$
as the Woods scale (Gibson (Reference Gibson1991) also credited Woods with the invention of the term ‘fossil turbulence’ in Woods (Reference Woods1969)).
7.2 Effective viscosities
Derivation of
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $\unicode[STIX]{x1D708}_{z}$
,
$\unicode[STIX]{x1D708}_{z}$
,
![]() $\unicode[STIX]{x1D708}_{3}$
and
$\unicode[STIX]{x1D708}_{3}$
and
![]() $\unicode[STIX]{x1D708}_{3z}$
follows the pattern employed for the computation of
$\unicode[STIX]{x1D708}_{3z}$
follows the pattern employed for the computation of
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $\unicode[STIX]{x1D705}_{z}$
. Setting
$\unicode[STIX]{x1D705}_{z}$
. Setting
![]() $\unicode[STIX]{x1D714}=0$
and bringing the factor
$\unicode[STIX]{x1D714}=0$
and bringing the factor
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}}(\boldsymbol{k})$
inside the integral in (4.2) yields
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}}(\boldsymbol{k})$
inside the integral in (4.2) yields
Substitution of (3.18) for the Green function and (4.4) for the velocity correlator result in factorization of the integrand,
where the tensorial and scalar terms are given in the appendix A. Note that the scalar terms are frequency dependent only.
7.2.1 Frequency integration
Altogether, functions
![]() $R^{i}$
have 9 poles determined by various products of the expressions (A 19)–(A 21) in the denominators of (A 10)–(A 18) given in the appendix A. Those poles are:
$R^{i}$
have 9 poles determined by various products of the expressions (A 19)–(A 21) in the denominators of (A 10)–(A 18) given in the appendix A. Those poles are:
Six of these poles are in the upper half-plane while the other three are in the lower half-plane. The frequency integration is performed over the lower half-plane yielding
where the expressions for
![]() $\mathscr{R}^{i}(q,q_{3},k,k_{3})$
expanded up to
$\mathscr{R}^{i}(q,q_{3},k,k_{3})$
expanded up to
![]() $O(f^{2})$
are given in the appendix A.
$O(f^{2})$
are given in the appendix A.
After frequency integration, expression (7.38) reduces to
7.2.2 Spectral gap approximation and integration over the shell
 $D^{{>}}$
$D^{{>}}$
Since the integrand (7.38) is calculated up to
![]() $O(k^{2})$
and
$O(k^{2})$
and
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}}(\boldsymbol{k})=O(k)$
, only the terms up to
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}}(\boldsymbol{k})=O(k)$
, only the terms up to
![]() $O(k)$
need to be retained in the product
$O(k)$
need to be retained in the product
![]() $\unicode[STIX]{x1D61B}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FD}}^{i}\mathscr{R}^{i}$
in (7.44). By expanding this product in powers of
$\unicode[STIX]{x1D61B}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FD}}^{i}\mathscr{R}^{i}$
in (7.44). By expanding this product in powers of
![]() $k$
and contracting the result with
$k$
and contracting the result with
![]() $P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}}(\boldsymbol{k})$
using the properties of the Kronecker delta and projection operators, (7.44) can be brought to an expression that can be integrated in the horizontal plane
$P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}}(\boldsymbol{k})$
using the properties of the Kronecker delta and projection operators, (7.44) can be brought to an expression that can be integrated in the horizontal plane
![]() $q_{h}$
and over
$q_{h}$
and over
![]() $q_{3}$
. Upon completing this final step, we collect all the terms into groups proportional to
$q_{3}$
. Upon completing this final step, we collect all the terms into groups proportional to
![]() $k^{2}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
,
$k^{2}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
,
![]() $k_{3}^{2}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
,
$k_{3}^{2}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
,
![]() $k^{2}P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{k})\unicode[STIX]{x1D6FF}_{3\unicode[STIX]{x1D6FD}}$
and
$k^{2}P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{k})\unicode[STIX]{x1D6FF}_{3\unicode[STIX]{x1D6FD}}$
and
![]() $k_{3}^{2}P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{k})\unicode[STIX]{x1D6FF}_{3\unicode[STIX]{x1D6FD}}$
and take the limit
$k_{3}^{2}P_{3\unicode[STIX]{x1D6FC}}(\boldsymbol{k})\unicode[STIX]{x1D6FF}_{3\unicode[STIX]{x1D6FD}}$
and take the limit
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
which yields a coupled system of four ordinary differential equations for
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6EC}\rightarrow 0$
which yields a coupled system of four ordinary differential equations for
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}$
,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{z}$
,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}$
,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}$
,
Equation (7.48) is solved first. By substituting
![]() $\unicode[STIX]{x1D708}_{n}(\unicode[STIX]{x1D6EC})$
from (7.28), we obtain the equation
$\unicode[STIX]{x1D708}_{n}(\unicode[STIX]{x1D6EC})$
from (7.28), we obtain the equation
whose solution is
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=C\unicode[STIX]{x1D6EC}^{-28/27}$
. Since
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=C\unicode[STIX]{x1D6EC}^{-28/27}$
. Since
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=0$
at the start of scale elimination,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=0$
at the start of scale elimination,
![]() $C=0$
and so
$C=0$
and so
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=0$
for any
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=0$
for any
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
For practical applications, the solutions for the eddy viscosities and eddy diffusivities need to be expressed in terms of the observable variables such as the dissipation rate
![]() $\unicode[STIX]{x1D716}$
. This can be done by finding a relationship between
$\unicode[STIX]{x1D716}$
. This can be done by finding a relationship between
![]() $\unicode[STIX]{x1D716}$
and the forcing amplitude
$\unicode[STIX]{x1D716}$
and the forcing amplitude
![]() $D$
which enters equation (7.28). This relationship is elaborated in the next section.
$D$
which enters equation (7.28). This relationship is elaborated in the next section.
8 The forcing amplitude
It is relatively straightforward to determine the forcing amplitude
![]() $D$
in (3.14) in the non-rotating case in which the velocity correlation tensor is
$D$
in (3.14) in the non-rotating case in which the velocity correlation tensor is
![]() $U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(k,\unicode[STIX]{x1D714})=|G_{0}(k,\unicode[STIX]{x1D714})|^{2}D(k)P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
and the 3-D energy spectrum is
$U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(k,\unicode[STIX]{x1D714})=|G_{0}(k,\unicode[STIX]{x1D714})|^{2}D(k)P_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\boldsymbol{k})$
and the 3-D energy spectrum is
(
![]() $E_{0}(k)$
denotes the energy spectrum in a non-rotating flow). Let
$E_{0}(k)$
denotes the energy spectrum in a non-rotating flow). Let
![]() $k_{c}$
be the dynamic dissipation cutoff bounding the range of eliminated (or implicit) modes
$k_{c}$
be the dynamic dissipation cutoff bounding the range of eliminated (or implicit) modes
![]() $p>k_{c}$
. The effective viscosity
$p>k_{c}$
. The effective viscosity
![]() $\unicode[STIX]{x1D708}_{n}(k_{c})$
is a result of this scale elimination. It acts on the resolved (explicit) modes in such a way as to ensure that the energy loss in the range
$\unicode[STIX]{x1D708}_{n}(k_{c})$
is a result of this scale elimination. It acts on the resolved (explicit) modes in such a way as to ensure that the energy loss in the range
![]() $0<p<k_{c}$
is equal precisely to the dissipation rate
$0<p<k_{c}$
is equal precisely to the dissipation rate
![]() $\unicode[STIX]{x1D716}$
,
$\unicode[STIX]{x1D716}$
,
Substituting (7.28) and (8.1) into (8.2), we find
which makes it possible to relate the eddy viscosity and the energy spectrum of non-rotating turbulence to
![]() $\unicode[STIX]{x1D716}$
,
$\unicode[STIX]{x1D716}$
,
9 Eddy viscosities, eddy diffusivities and flow regimes in rotating and stably stratified turbulence
The solution
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=0$
simplifies (7.26), (7.27) and (7.45)–(7.47) which now can be solved analytically in the lowest order of
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{3z}=0$
simplifies (7.26), (7.27) and (7.45)–(7.47) which now can be solved analytically in the lowest order of
![]() $Ro(k)^{-1}$
. Designating the independent variable as
$Ro(k)^{-1}$
. Designating the independent variable as
![]() $k$
(instead of
$k$
(instead of
![]() $\unicode[STIX]{x1D6EC}$
) one obtains the scale-dependent eddy viscosities,
$\unicode[STIX]{x1D6EC}$
) one obtains the scale-dependent eddy viscosities,
With no rotation, i.e. in the limit
![]() $Ro^{-1}\rightarrow 0$
, the flow becomes isotropic,
$Ro^{-1}\rightarrow 0$
, the flow becomes isotropic,
![]() $\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{z}=\unicode[STIX]{x1D708}_{3}=\unicode[STIX]{x1D708}_{3z}$
. For
$\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{z}=\unicode[STIX]{x1D708}_{3}=\unicode[STIX]{x1D708}_{3z}$
. For
![]() $k/k_{\unicode[STIX]{x1D6FA}}\gtrsim 10$
, the deviations of
$k/k_{\unicode[STIX]{x1D6FA}}\gtrsim 10$
, the deviations of
![]() $\unicode[STIX]{x1D708}_{h}$
,
$\unicode[STIX]{x1D708}_{h}$
,
![]() $\unicode[STIX]{x1D708}_{z}$
,
$\unicode[STIX]{x1D708}_{z}$
,
![]() $\unicode[STIX]{x1D708}_{3}$
and
$\unicode[STIX]{x1D708}_{3}$
and
![]() $\unicode[STIX]{x1D708}_{3z}$
from their values in non-rotating flows are within 5 %. On larger scales, rotation causes gradual decrease of the first three ratios,
$\unicode[STIX]{x1D708}_{3z}$
from their values in non-rotating flows are within 5 %. On larger scales, rotation causes gradual decrease of the first three ratios,
![]() $\unicode[STIX]{x1D708}_{h}/\unicode[STIX]{x1D708}_{n}$
,
$\unicode[STIX]{x1D708}_{h}/\unicode[STIX]{x1D708}_{n}$
,
![]() $\unicode[STIX]{x1D708}_{z}/\unicode[STIX]{x1D708}_{n}$
and
$\unicode[STIX]{x1D708}_{z}/\unicode[STIX]{x1D708}_{n}$
and
![]() $\unicode[STIX]{x1D708}_{3}/\unicode[STIX]{x1D708}_{n}$
, and the increase of the fourth one. The decreasing viscosities, especially
$\unicode[STIX]{x1D708}_{3}/\unicode[STIX]{x1D708}_{n}$
, and the increase of the fourth one. The decreasing viscosities, especially
![]() $\unicode[STIX]{x1D708}_{h}\rightarrow 0$
, point to a decreasing energy flux to small scales. The concurrent energy redirection to large scales can be interpreted as energy backscatter or the inverse cascade. From (9.1)–(9.3) one infers that the horizontal viscosity decreases at the fastest rate and may become zero at
$\unicode[STIX]{x1D708}_{h}\rightarrow 0$
, point to a decreasing energy flux to small scales. The concurrent energy redirection to large scales can be interpreted as energy backscatter or the inverse cascade. From (9.1)–(9.3) one infers that the horizontal viscosity decreases at the fastest rate and may become zero at
![]() $k/k_{\unicode[STIX]{x1D6FA}}=O(1)$
. Numerical solution of the system (7.45)–(7.48), which can be carried out for larger values of
$k/k_{\unicode[STIX]{x1D6FA}}=O(1)$
. Numerical solution of the system (7.45)–(7.48), which can be carried out for larger values of
![]() $\unicode[STIX]{x1D6FA}$
than it is feasible in the weak rotation approximation, indicates that
$\unicode[STIX]{x1D6FA}$
than it is feasible in the weak rotation approximation, indicates that
![]() $\unicode[STIX]{x1D708}_{h}\rightarrow 0$
at considerably smaller values of
$\unicode[STIX]{x1D708}_{h}\rightarrow 0$
at considerably smaller values of
![]() $k/k_{\unicode[STIX]{x1D6FA}}$
. This result is consistent with numerical simulations by Smith & Waleffe (Reference Smith and Waleffe1999) and Lindborg (Reference Lindborg2005) who showed that at
$k/k_{\unicode[STIX]{x1D6FA}}$
. This result is consistent with numerical simulations by Smith & Waleffe (Reference Smith and Waleffe1999) and Lindborg (Reference Lindborg2005) who showed that at
![]() $k_{\unicode[STIX]{x1D709}}/k_{\unicode[STIX]{x1D6FA}}\simeq 0.01$
,
$k_{\unicode[STIX]{x1D709}}/k_{\unicode[STIX]{x1D6FA}}\simeq 0.01$
,
![]() $k_{\unicode[STIX]{x1D709}}$
being the wavenumber of the forcing, a 3-D flow develops strong inverse energy cascade and acquires features of a ‘negative viscosity phenomenon’ (Starr Reference Starr1968).
$k_{\unicode[STIX]{x1D709}}$
being the wavenumber of the forcing, a 3-D flow develops strong inverse energy cascade and acquires features of a ‘negative viscosity phenomenon’ (Starr Reference Starr1968).
Have we reached a dead end by arriving at the negative eddy viscosity? The answer is ‘no’ because, as explained in Galperin et al. (Reference Galperin, Sukoriansky, Orszag and Staroselsky1993), Sukoriansky et al. (Reference Sukoriansky, Chekhlov, Orszag, Galperin and Staroselsky1996) and Sukoriansky, Galperin & Chekhlov (Reference Sukoriansky, Galperin and Chekhlov1999), the negative Laplacian viscosity in quasi-2-D flows represents only part of the physics. The other part can be gleaned from figure 2 showing that, on smaller scales, the effect of the negative viscosity is compensated by a biharmonic and, possibly, higher-order dissipative hyperviscosities. Thus emerging SGS parameterization was coined a stabilized negative viscosity, or SNV by Sukoriansky et al. (Reference Sukoriansky, Chekhlov, Orszag, Galperin and Staroselsky1996) and Sukoriansky et al. (Reference Sukoriansky, Galperin and Chekhlov1999). The negative Laplacian viscosity in SNV assumes the role of the unresolved subgrid-scale forcing which otherwise would be unaccounted for in estimating the large-scale eddy kinetic energy and the global energy balance. It is well possible that an SNV representation can be developed within the QNSE formalism for 3-D flows to alleviate the problems posed by the use of the spectral gap approximation as elaborated in § 5.
As was already noted,
![]() $\unicode[STIX]{x1D708}_{h}$
decreases faster than
$\unicode[STIX]{x1D708}_{h}$
decreases faster than
![]() $\unicode[STIX]{x1D708}_{z}$
and
$\unicode[STIX]{x1D708}_{z}$
and
![]() $\unicode[STIX]{x1D708}_{3}$
with the increasing scale. This result is consistent with the experiments by Jacquin et al. (Reference Jacquin, Leuchter, Cambon and Mathieu1990). Numerical simulations by Yeung & Zhou (Reference Yeung and Zhou1998) demonstrated that the spectral energy transfer in the direction of rotation is similar to that in non-rotating flows, but in the normal direction, the transfer weakens significantly. The ratios,
$\unicode[STIX]{x1D708}_{3}$
with the increasing scale. This result is consistent with the experiments by Jacquin et al. (Reference Jacquin, Leuchter, Cambon and Mathieu1990). Numerical simulations by Yeung & Zhou (Reference Yeung and Zhou1998) demonstrated that the spectral energy transfer in the direction of rotation is similar to that in non-rotating flows, but in the normal direction, the transfer weakens significantly. The ratios,
![]() $\unicode[STIX]{x1D708}_{z}/\unicode[STIX]{x1D708}_{h}$
and
$\unicode[STIX]{x1D708}_{z}/\unicode[STIX]{x1D708}_{h}$
and
![]() $\unicode[STIX]{x1D708}_{3}/\unicode[STIX]{x1D708}_{h}$
,
$\unicode[STIX]{x1D708}_{3}/\unicode[STIX]{x1D708}_{h}$
,
Equations (9.1)–(9.3) make it possible to solve (7.26) and (7.27) analytically and derive expressions for the horizontal and vertical eddy diffusivities in the limit of weak rotation,
On the first sight, the increase of the horizontal diffusivity versus the decrease of its vertical counterpart seems to contradict the data. For instance, using analytical and numerical tools, Cambon et al. (Reference Cambon, Godeferd, Nicolleau and Vassilicos2004) and Rodriguez Imazio & Mininni (Reference Rodriguez Imazio and Mininni2013) show that in rotating flows, the vertical diffusivity increases while the horizontal diffusivity decreases; eventually, their ratio attains the value of approximately 2. Their analysis, however, pertains not to scale-dependent eddy diffusivities, such as
![]() $\unicode[STIX]{x1D705}_{h}(k)$
and
$\unicode[STIX]{x1D705}_{h}(k)$
and
![]() $\unicode[STIX]{x1D705}_{z}(k)$
, but the total eddy diffusivities obtained by averaging over all fluctuating scales. Those diffusivities grow with the integral scales in the respective directions. Since the integral length scale is larger in the vertical direction (Yeung & Zhou Reference Yeung and Zhou1998; Müller & Thiele Reference Müller and Thiele2007; Godeferd & Moisy Reference Godeferd and Moisy2015), the total vertical diffusivity may become larger than the horizontal one.
$\unicode[STIX]{x1D705}_{z}(k)$
, but the total eddy diffusivities obtained by averaging over all fluctuating scales. Those diffusivities grow with the integral scales in the respective directions. Since the integral length scale is larger in the vertical direction (Yeung & Zhou Reference Yeung and Zhou1998; Müller & Thiele Reference Müller and Thiele2007; Godeferd & Moisy Reference Godeferd and Moisy2015), the total vertical diffusivity may become larger than the horizontal one.
The increase of the horizontal spectral diffusivity in rotating flows undergoing two-dimensionalization pointed to by (9.7) can be better understood by comparing the values of
![]() $\unicode[STIX]{x1D705}_{h}$
in isotropic turbulence with 2-D versus 3-D geometry. Solving (7.30) for
$\unicode[STIX]{x1D705}_{h}$
in isotropic turbulence with 2-D versus 3-D geometry. Solving (7.30) for
![]() $d=2$
and
$d=2$
and
![]() $d=3$
and taking a note that for
$d=3$
and taking a note that for
![]() $d=2$
,
$d=2$
,
![]() $A_{d}=(16\unicode[STIX]{x03C0})^{-1}$
and
$A_{d}=(16\unicode[STIX]{x03C0})^{-1}$
and
![]() $K_{d}=(4\unicode[STIX]{x03C0})^{-1}$
, one derives
$K_{d}=(4\unicode[STIX]{x03C0})^{-1}$
, one derives
such that
![]() $\unicode[STIX]{x1D705}_{n}^{2D}/\unicode[STIX]{x1D708}_{n}$
is approximately 1.4 times larger than
$\unicode[STIX]{x1D705}_{n}^{2D}/\unicode[STIX]{x1D708}_{n}$
is approximately 1.4 times larger than
![]() $\unicode[STIX]{x1D705}_{n}^{3D}/\unicode[STIX]{x1D708}_{n}=\unicode[STIX]{x1D6FC}\sim 1.4$
. In other words, the ratio
$\unicode[STIX]{x1D705}_{n}^{3D}/\unicode[STIX]{x1D708}_{n}=\unicode[STIX]{x1D6FC}\sim 1.4$
. In other words, the ratio
![]() $\unicode[STIX]{x1D705}_{h}/\unicode[STIX]{x1D708}_{n}$
increases from
$\unicode[STIX]{x1D705}_{h}/\unicode[STIX]{x1D708}_{n}$
increases from
![]() $\unicode[STIX]{x1D6FC}=1.39$
to approximately 2 with increasing scale and expanding two-dimensionalization.
$\unicode[STIX]{x1D6FC}=1.39$
to approximately 2 with increasing scale and expanding two-dimensionalization.

Figure 3. Vertical and horizontal eddy viscosities and eddy diffusivities normalized with
![]() $\unicode[STIX]{x1D708}_{n}$
for turbulence with rotation (a) and stable stratification (b) (after Sukoriansky & Galperin Reference Sukoriansky and Galperin2013). Horizontal and vertical eddy viscosities and vertical eddy diffusivities exhibit opposite tendencies.
$\unicode[STIX]{x1D708}_{n}$
for turbulence with rotation (a) and stable stratification (b) (after Sukoriansky & Galperin Reference Sukoriansky and Galperin2013). Horizontal and vertical eddy viscosities and vertical eddy diffusivities exhibit opposite tendencies.
Figure 3 compares the behaviours of the eddy viscosities and eddy diffusivities in rotating versus stably stratified flows as analysed by Sukoriansky & Galperin (Reference Sukoriansky and Galperin2013). Immediately obvious is the similarity between the scalings with
![]() $k/k_{\unicode[STIX]{x1D6FA}}$
in the former and
$k/k_{\unicode[STIX]{x1D6FA}}$
in the former and
![]() $k/k_{O}$
in the latter which highlights the affinity between the Woods and Ozmidov scales in flows with different extra strains.
$k/k_{O}$
in the latter which highlights the affinity between the Woods and Ozmidov scales in flows with different extra strains.
On relatively small scales, the effect of either extra strain is miniscule and practically not felt by the flow. Rotational effects become sizeable at respective scales of approximately 0.1
![]() $L_{\unicode[STIX]{x1D6FA}}$
and 0.1
$L_{\unicode[STIX]{x1D6FA}}$
and 0.1
![]() $L_{O}$
where one observes increasing with scale anisotropization of both flows. The tendencies to anisotropization expressed by the horizontal and vertical eddy viscosities and eddy diffusivities under the action of rotation and stable stratification are switched around as
$L_{O}$
where one observes increasing with scale anisotropization of both flows. The tendencies to anisotropization expressed by the horizontal and vertical eddy viscosities and eddy diffusivities under the action of rotation and stable stratification are switched around as
![]() $\unicode[STIX]{x1D708}_{h}/\unicode[STIX]{x1D708}_{n}$
decreases with decreasing
$\unicode[STIX]{x1D708}_{h}/\unicode[STIX]{x1D708}_{n}$
decreases with decreasing
![]() $k/k_{\unicode[STIX]{x1D6FA}}$
in the former case and increases with decreasing
$k/k_{\unicode[STIX]{x1D6FA}}$
in the former case and increases with decreasing
![]() $k/k_{O}$
in the latter. On the other hand, while
$k/k_{O}$
in the latter. On the other hand, while
![]() $\unicode[STIX]{x1D705}_{z}/\unicode[STIX]{x1D708}_{n}$
stays nearly constant with
$\unicode[STIX]{x1D705}_{z}/\unicode[STIX]{x1D708}_{n}$
stays nearly constant with
![]() $k/k_{\unicode[STIX]{x1D6FA}}$
, it decreases and tends to zero with
$k/k_{\unicode[STIX]{x1D6FA}}$
, it decreases and tends to zero with
![]() $k/k_{O}$
. These differences are stipulated by the action of different types of extra strains whose directions of zero frequency are orthogonal.
$k/k_{O}$
. These differences are stipulated by the action of different types of extra strains whose directions of zero frequency are orthogonal.
On larger scales, while the horizontal viscosity in rotating flows decreases due to inverse energy cascade, the eddy diffusivities always remain positive definite regardless of the direction of energy transfer (e.g. Kraichnan Reference Kraichnan1976). The increase in
![]() $\unicode[STIX]{x1D705}_{h}/\unicode[STIX]{x1D708}_{n}$
from approximately 1.4 to approximately 2 confirms the tendency towards flow two-dimensionalization under the action of rotation, and is quantitatively consistent with (9.9). On the other hand, the ratio
$\unicode[STIX]{x1D705}_{h}/\unicode[STIX]{x1D708}_{n}$
from approximately 1.4 to approximately 2 confirms the tendency towards flow two-dimensionalization under the action of rotation, and is quantitatively consistent with (9.9). On the other hand, the ratio
![]() $\unicode[STIX]{x1D705}_{z}/\unicode[STIX]{x1D708}_{n}$
is almost
$\unicode[STIX]{x1D705}_{z}/\unicode[STIX]{x1D708}_{n}$
is almost
![]() $\unicode[STIX]{x1D6FA}$
-independent.
$\unicode[STIX]{x1D6FA}$
-independent.
Although QNSE implies the arbitrarily small molecular viscosity, consideration of the viscous effects is necessary for practical purposes. On very small scales, of the order of the Kolmogorov microscale,
![]() $L_{K}=(\unicode[STIX]{x1D708}_{0}^{3}/\unicode[STIX]{x1D716})^{1/4}$
, both rotating and stably stratified flows are strongly impacted by the effect of the molecular viscosity. For the latter class of flows, the range of scales between
$L_{K}=(\unicode[STIX]{x1D708}_{0}^{3}/\unicode[STIX]{x1D716})^{1/4}$
, both rotating and stably stratified flows are strongly impacted by the effect of the molecular viscosity. For the latter class of flows, the range of scales between
![]() $L_{O}$
and
$L_{O}$
and
![]() $L_{K}$
is quantified by the buoyancy Reynolds number
$L_{K}$
is quantified by the buoyancy Reynolds number
![]() $Re_{b}$
(also known as the isotropy index, Thorpe Reference Thorpe2005),
$Re_{b}$
(also known as the isotropy index, Thorpe Reference Thorpe2005),
The value
![]() $Re_{b}\simeq 10^{2}$
is an approximate threshold below which the viscous dissipation becomes increasingly anisotropic (e.g. Galperin & Sukoriansky Reference Galperin and Sukoriansky2010, and references therein).
$Re_{b}\simeq 10^{2}$
is an approximate threshold below which the viscous dissipation becomes increasingly anisotropic (e.g. Galperin & Sukoriansky Reference Galperin and Sukoriansky2010, and references therein).
A similar parameter can be introduced for rotating flows,
where
![]() $Re_{\unicode[STIX]{x1D6FA}}$
can be referred to as the rotational Reynolds number. It is plausible to assume that the threshold of the viscous dissipation anisotropization in rotating flows is about the same as in stratified flows, i.e.
$Re_{\unicode[STIX]{x1D6FA}}$
can be referred to as the rotational Reynolds number. It is plausible to assume that the threshold of the viscous dissipation anisotropization in rotating flows is about the same as in stratified flows, i.e.
![]() $Re_{\unicode[STIX]{x1D6FA}}\simeq 10^{2}$
. Since
$Re_{\unicode[STIX]{x1D6FA}}\simeq 10^{2}$
. Since
![]() $Re_{\unicode[STIX]{x1D6FA}}\gg Re_{b}$
in geophysical flows, this criterion is of little consequence. It may be important in computer simulations of rotating flows, however, where the Reynolds numbers are still relatively low.
$Re_{\unicode[STIX]{x1D6FA}}\gg Re_{b}$
in geophysical flows, this criterion is of little consequence. It may be important in computer simulations of rotating flows, however, where the Reynolds numbers are still relatively low.
10 Dispersion relation for inertial waves in the presence of turbulence
Consider now the effect of turbulence on inertial waves. Sukoriansky et al. (Reference Sukoriansky, Galperin and Staroselsky2005) showed that turbulence modifies the classical dispersion relation for linear internal waves and it is important to know whether or not turbulence has a similar effect on the inertial waves. This can be done using the Langevin equation (3.13) that describes a linear, forced, stochastic oscillator and whose eigenfrequencies are given by the real parts of the roots of the secular equation
These roots are the poles of the Green function
![]() $G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D71B},\boldsymbol{k})$
given by (7.40). Recalling (7.7), one writes the eigenfrequencies as
$G_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D71B},\boldsymbol{k})$
given by (7.40). Recalling (7.7), one writes the eigenfrequencies as
where
![]() $\unicode[STIX]{x1D703}$
being the angle between the wave vector
$\unicode[STIX]{x1D703}$
being the angle between the wave vector
![]() $\boldsymbol{k}$
and the vertical axis, is the classical dispersion relationship for linear inertial waves (Landau & Lifshitz Reference Landau and Lifshitz1993). Thus, turbulence does not change the linear wave frequency. The imaginary part of
$\boldsymbol{k}$
and the vertical axis, is the classical dispersion relationship for linear inertial waves (Landau & Lifshitz Reference Landau and Lifshitz1993). Thus, turbulence does not change the linear wave frequency. The imaginary part of
![]() $\unicode[STIX]{x1D71B}$
is related to turbulent dissipation and, as elaborated by Galperin, Sukoriansky & Dikovskaya (Reference Galperin, Sukoriansky and Dikovskaya2010) in the appendix A, it broadens the spectral peak associated with the wave.
$\unicode[STIX]{x1D71B}$
is related to turbulent dissipation and, as elaborated by Galperin, Sukoriansky & Dikovskaya (Reference Galperin, Sukoriansky and Dikovskaya2010) in the appendix A, it broadens the spectral peak associated with the wave.
The dispersion relationship (10.2) underscores the difference between the inertial and internal waves. Recall that in the case of stable stratification, turbulence does modify the linear wave frequency. Moreover, internal waves are completely eradicated on scales where turbulence contribution renders
![]() $\unicode[STIX]{x1D714}$
imaginary (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005).
$\unicode[STIX]{x1D714}$
imaginary (Sukoriansky et al.
Reference Sukoriansky, Galperin and Staroselsky2005).
We emphasize that even though turbulence does not shift the frequency of the inertial waves in the QNSE theory, turbulence and waves are considered as one entity in exactly the same fashion as it was done in the case of flows with stable stratification (Sukoriansky et al. Reference Sukoriansky, Galperin and Staroselsky2005).
We also notice that though turbulence affects the dispersion relation for internal waves, their range of existence,
![]() $\unicode[STIX]{x1D714}\leqslant N$
, remains the same as in the case of purely linear waves. As shown above, turbulence does not affect the dispersion relation for inertial waves at all. Therefore, the range of existence of the mixed internal–inertial waves,
$\unicode[STIX]{x1D714}\leqslant N$
, remains the same as in the case of purely linear waves. As shown above, turbulence does not affect the dispersion relation for inertial waves at all. Therefore, the range of existence of the mixed internal–inertial waves,
![]() $f\leqslant \unicode[STIX]{x1D714}\leqslant N$
(Phillips Reference Phillips1977), should remain the same as in the case of linear waves even if the waves coexist with turbulence.
$f\leqslant \unicode[STIX]{x1D714}\leqslant N$
(Phillips Reference Phillips1977), should remain the same as in the case of linear waves even if the waves coexist with turbulence.
11 Spectra of kinetic energy and scalar variance
Laboratory experiments, numerical simulations, ocean currents and various layers of the atmosphere exhibit a remarkable and ubiquitous vertical spectrum of the horizontal velocity obeying a spectral law
![]() $E_{1}(k_{z})\propto N^{2}k_{z}^{-3}$
(Smith, Fritts & VanZandt Reference Smith, Fritts and Vanzandt1987; Galperin & Sukoriansky Reference Galperin and Sukoriansky2010; Sukoriansky & Galperin Reference Sukoriansky and Galperin2013). The horizontal layering in such flows can be associated with modes with zero frequency, i.e. slow modes (e.g. Sagaut & Cambon Reference Sagaut and Cambon2008). This spectrum is peculiar because, while being aligned in the direction of zero frequency, it nevertheless depends on
$E_{1}(k_{z})\propto N^{2}k_{z}^{-3}$
(Smith, Fritts & VanZandt Reference Smith, Fritts and Vanzandt1987; Galperin & Sukoriansky Reference Galperin and Sukoriansky2010; Sukoriansky & Galperin Reference Sukoriansky and Galperin2013). The horizontal layering in such flows can be associated with modes with zero frequency, i.e. slow modes (e.g. Sagaut & Cambon Reference Sagaut and Cambon2008). This spectrum is peculiar because, while being aligned in the direction of zero frequency, it nevertheless depends on
![]() $N$
. In fact, this spectrum depends on
$N$
. In fact, this spectrum depends on
![]() $N$
and
$N$
and
![]() $k_{z}$
only and is, thus, independent of the forcing, seasons and altitude, if the atmospheric realization is considered (Smith et al.
Reference Smith, Fritts and Vanzandt1987). In QNSE, this spectrum was derived in the approximation of weakly stratified turbulence which reduces to Kolmogorov turbulence on small scales. Since the large-scale spectrum also depends on
$k_{z}$
only and is, thus, independent of the forcing, seasons and altitude, if the atmospheric realization is considered (Smith et al.
Reference Smith, Fritts and Vanzandt1987). In QNSE, this spectrum was derived in the approximation of weakly stratified turbulence which reduces to Kolmogorov turbulence on small scales. Since the large-scale spectrum also depends on
![]() $N$
and
$N$
and
![]() $k_{z}$
only, the QNSE results appear applicable well beyond their domain of validity. The importance of this result is underscored by the fact that the non-dimensional coefficient in the spectrum expression turned out to be invariant across the scales. In fact, this is the only existing theoretical derivation of this coefficient. Note also that the QNSE theory attributes this spectrum to the interaction between turbulence and internal waves rather than accepting the traditional view that the spectrum is a product of internal wave saturation (see e.g. Dewan Reference Dewan1979; Dewan & Good Reference Dewan and Good1986).
$k_{z}$
only, the QNSE results appear applicable well beyond their domain of validity. The importance of this result is underscored by the fact that the non-dimensional coefficient in the spectrum expression turned out to be invariant across the scales. In fact, this is the only existing theoretical derivation of this coefficient. Note also that the QNSE theory attributes this spectrum to the interaction between turbulence and internal waves rather than accepting the traditional view that the spectrum is a product of internal wave saturation (see e.g. Dewan Reference Dewan1979; Dewan & Good Reference Dewan and Good1986).
In analogy to turbulence with stable stratification, various 1-D and 3-D spectra of turbulence with rotation will be derived in the approximation of weak rotation. Being a product of interaction between turbulence and inertial waves, they are of considerable interest, particularly if they also turn out to be applicable beyond the domain of their derivation.
In computing the spectra, we follow the nomenclature in Monin & Yaglom (Reference Monin and Yaglom1975) and define by
![]() $E_{1}(k_{1})$
a 1-D longitudinal spectrum of the velocity component
$E_{1}(k_{1})$
a 1-D longitudinal spectrum of the velocity component
![]() $v_{1}$
, while
$v_{1}$
, while
![]() $E_{1}(k_{2})$
and
$E_{1}(k_{2})$
and
![]() $E_{1}(k_{3})$
are the transverse spectra of
$E_{1}(k_{3})$
are the transverse spectra of
![]() $v_{1}$
in the horizontal and vertical directions. In the case of weak rotation, all 1-D spectra can be calculated analytically. For instance, for the 1-D longitudinal horizontal spectrum
$v_{1}$
in the horizontal and vertical directions. In the case of weak rotation, all 1-D spectra can be calculated analytically. For instance, for the 1-D longitudinal horizontal spectrum
![]() $E_{1}(k_{1})$
one finds
$E_{1}(k_{1})$
one finds
 $$\begin{eqnarray}\displaystyle E_{1}(k_{1}) & = & \displaystyle \frac{4}{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\frac{\text{d}k_{2}\text{d}k_{3}}{(2\unicode[STIX]{x03C0})^{2}}\int _{-\infty }^{\infty }\frac{\text{d}\unicode[STIX]{x1D714}}{2\unicode[STIX]{x03C0}}U_{11}(\unicode[STIX]{x1D714},\boldsymbol{k})\nonumber\\ \displaystyle & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}+0.0926f^{2}k_{1}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}\left[1+0.197\left(\frac{k_{1}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}(k_{1}) & = & \displaystyle \frac{4}{\unicode[STIX]{x03C0}}\int _{0}^{\infty }\int _{0}^{\infty }\frac{\text{d}k_{2}\text{d}k_{3}}{(2\unicode[STIX]{x03C0})^{2}}\int _{-\infty }^{\infty }\frac{\text{d}\unicode[STIX]{x1D714}}{2\unicode[STIX]{x03C0}}U_{11}(\unicode[STIX]{x1D714},\boldsymbol{k})\nonumber\\ \displaystyle & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}+0.0926f^{2}k_{1}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}\left[1+0.197\left(\frac{k_{1}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right].\end{eqnarray}$$
Generally, any other 1-D spectrum
![]() $E_{i}(k_{j})$
can be computed in a similar way by integrating the spectral tensor
$E_{i}(k_{j})$
can be computed in a similar way by integrating the spectral tensor
![]() $U_{ii}(\unicode[STIX]{x1D714},\boldsymbol{k})$
, no summation over
$U_{ii}(\unicode[STIX]{x1D714},\boldsymbol{k})$
, no summation over
![]() $i$
is implied, over the frequency
$i$
is implied, over the frequency
![]() $\unicode[STIX]{x1D714}$
and the two wavenumbers different from
$\unicode[STIX]{x1D714}$
and the two wavenumbers different from
![]() $k_{j}$
.
$k_{j}$
.
Those other 1-D spectra are
 $$\begin{eqnarray}\displaystyle E_{1}(k_{2}) & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{2}^{-5/3}+0.240f^{2}k_{2}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{2}^{-5/3}\left[1+0.385\left(\frac{k_{2}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}(k_{2}) & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{2}^{-5/3}+0.240f^{2}k_{2}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{2}^{-5/3}\left[1+0.385\left(\frac{k_{2}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle E_{1}(k_{3}) & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}+0.144f^{2}k_{3}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}\left[1+0.230\left(\frac{k_{3}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}(k_{3}) & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}+0.144f^{2}k_{3}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}\left[1+0.230\left(\frac{k_{3}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle E_{3}(k_{1}) & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}+0.059f^{2}k_{1}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}\left[1+0.095\left(\frac{k_{1}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{3}(k_{1}) & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}+0.059f^{2}k_{1}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.626\unicode[STIX]{x1D716}^{2/3}k_{1}^{-5/3}\left[1+0.095\left(\frac{k_{1}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle E_{3}(k_{3}) & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}+0.037f^{2}k_{3}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}\left[1+0.079\left(\frac{k_{3}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{3}(k_{3}) & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}+0.037f^{2}k_{3}^{-3}\nonumber\\ \displaystyle & = & \displaystyle 0.47\unicode[STIX]{x1D716}^{2/3}k_{3}^{-5/3}\left[1+0.079\left(\frac{k_{3}}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right].\end{eqnarray}$$
Note that the effect of rotation on the vertical velocity component is weaker than that on the two horizontal ones.
The 3-D energy spectrum is computed as
 $$\begin{eqnarray}\displaystyle E(k) & = & \displaystyle \frac{1}{2}k^{2}\int _{-\infty }^{\infty }\frac{\text{d}\unicode[STIX]{x1D714}}{2\unicode[STIX]{x03C0}}\int _{\unicode[STIX]{x2202}S}\frac{\text{d}\unicode[STIX]{x1D6F4}}{(2\unicode[STIX]{x03C0})^{3}}U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D714},\boldsymbol{k})\nonumber\\ \displaystyle & = & \displaystyle 1.458\unicode[STIX]{x1D716}^{2/3}k^{-5/3}+0.564f^{2}k^{-3}=E_{0}(k)+\unicode[STIX]{x1D6FF}E(k)\nonumber\\ \displaystyle & = & \displaystyle 1.458\unicode[STIX]{x1D716}^{2/3}k^{-5/3}\left[1+0.387\left(\frac{k}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E(k) & = & \displaystyle \frac{1}{2}k^{2}\int _{-\infty }^{\infty }\frac{\text{d}\unicode[STIX]{x1D714}}{2\unicode[STIX]{x03C0}}\int _{\unicode[STIX]{x2202}S}\frac{\text{d}\unicode[STIX]{x1D6F4}}{(2\unicode[STIX]{x03C0})^{3}}U_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D714},\boldsymbol{k})\nonumber\\ \displaystyle & = & \displaystyle 1.458\unicode[STIX]{x1D716}^{2/3}k^{-5/3}+0.564f^{2}k^{-3}=E_{0}(k)+\unicode[STIX]{x1D6FF}E(k)\nonumber\\ \displaystyle & = & \displaystyle 1.458\unicode[STIX]{x1D716}^{2/3}k^{-5/3}\left[1+0.387\left(\frac{k}{k_{\unicode[STIX]{x1D6FA}}}\right)^{-4/3}\right],\end{eqnarray}$$
where
![]() $E_{0}(k)$
is given by (8.5) and
$E_{0}(k)$
is given by (8.5) and
![]() $\unicode[STIX]{x1D6FF}E(k)$
is the lowest-order correction to
$\unicode[STIX]{x1D6FF}E(k)$
is the lowest-order correction to
![]() $E_{0}(k)$
due to rotation. Here,
$E_{0}(k)$
due to rotation. Here,
![]() $\int _{\unicode[STIX]{x2202}S}\text{d}\unicode[STIX]{x1D6F4}$
denotes integration over the surface of a 3-D unit sphere. These equations demonstrate that within QNSE, rotation provides positive contributions to all Kolmogorov 1-D and 3-D spectra; they are all proportional to the respective factors
$\int _{\unicode[STIX]{x2202}S}\text{d}\unicode[STIX]{x1D6F4}$
denotes integration over the surface of a 3-D unit sphere. These equations demonstrate that within QNSE, rotation provides positive contributions to all Kolmogorov 1-D and 3-D spectra; they are all proportional to the respective factors
![]() $f^{2}k_{i}^{-3}$
,
$f^{2}k_{i}^{-3}$
,
![]() $i=1,2,3$
.
$i=1,2,3$
.
Comparing these results with numerical simulations recall that turbulence isotropization on scales smaller than the Woods scale was observed by Mininni et al. (Reference Mininni, Rosenberg and Pouquet2012) and Sen et al. (Reference Sen, Mininni, Rosenberg and Pouquet2012). The relevance of the Coriolis term-related additions
![]() $\propto f^{2}k_{\bot }^{-3}$
to the isotropic Kolmogorov horizontal spectra can be assessed via comparison with computer simulations. Two factors ought to be kept in mind in making such comparisons. (i) It is well known that physical and spectral space characteristics of rotating turbulence profoundly depend on the way it is being forced (e.g. Smith, Chasnov & Waleffe Reference Smith, Chasnov and Waleffe1996; Bourouiba et al.
Reference Bourouiba, Straub and Waite2012; Sen et al.
Reference Sen, Mininni, Rosenberg and Pouquet2012). The QNSE formalism developed in this paper implies isotropic ‘bare’ forcing which is then projected onto isotropic ‘dressed’ modal forcing specified by (3.14). Thus, numerical results based upon isotropic forcing are most suitable for comparison with QNSE predictions. In principle, QNSE could be extended to anisotropic and other types of forcing by modification of (3.14) but this is a separate effort which is outside the scope of the present study. (ii) The resolution of simulations performed to date was sufficient to attain only relatively small values of the rotational Reynolds number,
$\propto f^{2}k_{\bot }^{-3}$
to the isotropic Kolmogorov horizontal spectra can be assessed via comparison with computer simulations. Two factors ought to be kept in mind in making such comparisons. (i) It is well known that physical and spectral space characteristics of rotating turbulence profoundly depend on the way it is being forced (e.g. Smith, Chasnov & Waleffe Reference Smith, Chasnov and Waleffe1996; Bourouiba et al.
Reference Bourouiba, Straub and Waite2012; Sen et al.
Reference Sen, Mininni, Rosenberg and Pouquet2012). The QNSE formalism developed in this paper implies isotropic ‘bare’ forcing which is then projected onto isotropic ‘dressed’ modal forcing specified by (3.14). Thus, numerical results based upon isotropic forcing are most suitable for comparison with QNSE predictions. In principle, QNSE could be extended to anisotropic and other types of forcing by modification of (3.14) but this is a separate effort which is outside the scope of the present study. (ii) The resolution of simulations performed to date was sufficient to attain only relatively small values of the rotational Reynolds number,
![]() $Re_{\unicode[STIX]{x1D6FA}}\lesssim 70$
, and oftentimes, they were much smaller. QNSE, on the other hand, implies arbitrarily large
$Re_{\unicode[STIX]{x1D6FA}}\lesssim 70$
, and oftentimes, they were much smaller. QNSE, on the other hand, implies arbitrarily large
![]() $Re_{\unicode[STIX]{x1D6FA}}$
such that some differences in flow regimes are unavoidable.
$Re_{\unicode[STIX]{x1D6FA}}$
such that some differences in flow regimes are unavoidable.
Early simulations by Smith & Waleffe (Reference Smith and Waleffe1999) provided evidence of the
![]() $k_{\bot }^{-3}$
spectral scaling but the transition to the small-scale Kolmogorov range was unresolved.
$k_{\bot }^{-3}$
spectral scaling but the transition to the small-scale Kolmogorov range was unresolved.
Mininni et al. (Reference Mininni, Rosenberg and Pouquet2012) performed simulations with the resolution of 3072
![]() $^{3}$
points in which the Woods scale was more than an order of magnitude larger than the dissipation scale thus allowing for the ranges of the large-scale inverse energy cascade, direct cascades of energy and helicity, and the Kolmogorov cascade to small-scale dissipation to be resolved reasonably well. Even though these simulations employed the Beltrami forcing that evokes a helical flow regime, they presented clear evidence of flow three-dimensionalization and establishing the Kolmogorov
$^{3}$
points in which the Woods scale was more than an order of magnitude larger than the dissipation scale thus allowing for the ranges of the large-scale inverse energy cascade, direct cascades of energy and helicity, and the Kolmogorov cascade to small-scale dissipation to be resolved reasonably well. Even though these simulations employed the Beltrami forcing that evokes a helical flow regime, they presented clear evidence of flow three-dimensionalization and establishing the Kolmogorov
![]() $k_{\bot }^{-5/3}$
spectral laws for both energy and helicity on scales smaller than
$k_{\bot }^{-5/3}$
spectral laws for both energy and helicity on scales smaller than
![]() $L_{\unicode[STIX]{x1D6FA}}$
.
$L_{\unicode[STIX]{x1D6FA}}$
.
Sen et al. (Reference Sen, Mininni, Rosenberg and Pouquet2012) investigated rotating flows with inverse cascade at a fixed small Rossby number and a linear resolution of 384 points. They considered a flow in a periodic box with the aspect ratio of unity and employed both helical and non-helical forcing functions. To attain reasonably high Reynolds numbers, they employed LES in which the EDQNM-based SGS parameterization included the effect of helicity. Following Mininni et al. (Reference Mininni, Rosenberg and Pouquet2012), this model assumed that turbulence returns to 3-D isotropy on scales smaller than
![]() $L_{\unicode[STIX]{x1D6FA}}$
. In addition, following Baerenzung et al. (Reference Baerenzung, Politano, Ponty and Pouquet2008), it included energy backscatter. The simulated large-scale energy spectrum attained either the
$L_{\unicode[STIX]{x1D6FA}}$
. In addition, following Baerenzung et al. (Reference Baerenzung, Politano, Ponty and Pouquet2008), it included energy backscatter. The simulated large-scale energy spectrum attained either the
![]() $k_{\bot }^{-5/3}$
power law consistent with the inverse energy cascade of quasi-2-D turbulence or a steeper
$k_{\bot }^{-5/3}$
power law consistent with the inverse energy cascade of quasi-2-D turbulence or a steeper
![]() $k_{\bot }^{-3}$
slope in which 3-D modes release significant amount of energy to 2-D modes. The spectral shape ultimately depended on forcing isotropy: the
$k_{\bot }^{-3}$
slope in which 3-D modes release significant amount of energy to 2-D modes. The spectral shape ultimately depended on forcing isotropy: the
![]() $k_{\bot }^{-5/3}$
law was associated with the forcing that selectively injected energy into 2-D modes while the
$k_{\bot }^{-5/3}$
law was associated with the forcing that selectively injected energy into 2-D modes while the
![]() $k_{\bot }^{-3}$
law was more endemic to isotropic forcing.
$k_{\bot }^{-3}$
law was more endemic to isotropic forcing.
Thiele & Müller (Reference Thiele and Müller2009) found that turbulence, driven by a large-scale forcing, exhibits a 1-D stationary scaling
![]() $\propto k_{\bot }^{-2}$
in the rotation-dominated inertial range. The spectrum was computed in analogy to (11.1) or (11.2) with the integration over
$\propto k_{\bot }^{-2}$
in the rotation-dominated inertial range. The spectrum was computed in analogy to (11.1) or (11.2) with the integration over
![]() $k_{3}$
. The individual spectra, without the integration over
$k_{3}$
. The individual spectra, without the integration over
![]() $k_{3}$
, exhibited the spectral slope
$k_{3}$
, exhibited the spectral slope
![]() $\propto k^{-3}$
.
$\propto k^{-3}$
.
Generally, the horizontal spectra (11.1) and (11.2) are equivalents of the spectrum
![]() $E_{1}(k_{3})$
in the case of stable stratification. Similar to the latter, they demonstrate the transition from the Kolmogorov spectrum to a steeper spectrum
$E_{1}(k_{3})$
in the case of stable stratification. Similar to the latter, they demonstrate the transition from the Kolmogorov spectrum to a steeper spectrum
![]() $\propto f^{2}k_{\bot }^{-3}$
that depends on
$\propto f^{2}k_{\bot }^{-3}$
that depends on
![]() $f$
and
$f$
and
![]() $k\bot$
only. Unfortunately, almost no spectrum obtained in simulations and exhibiting the
$k\bot$
only. Unfortunately, almost no spectrum obtained in simulations and exhibiting the
![]() $k_{\bot }^{-3}$
slope was checked for the
$k_{\bot }^{-3}$
slope was checked for the
![]() $f^{2}$
dependence as well and so the nature of the
$f^{2}$
dependence as well and so the nature of the
![]() $k_{\bot }^{-3}$
scaling is difficult to ascertain even though it may be important for explaining the horizontal spectra of atmospheric winds and ocean currents that often exhibit such slopes.
$k_{\bot }^{-3}$
scaling is difficult to ascertain even though it may be important for explaining the horizontal spectra of atmospheric winds and ocean currents that often exhibit such slopes.
One may also inquire about a possible connection between the present results and studies of turbulence in the limit of fast rotation. For instance, Galtier (Reference Galtier2003) considered rotating turbulence in the limit of small Rossby number using weak turbulence theory which yielded the energy spectrum in the form
![]() $E(k)\propto k_{\bot }^{-5/2}k_{\Vert }^{-1/2}$
. This distribution is quite different from those obtained here. Note, however, that Galtier (Reference Galtier2003) considered a limit of weak turbulence and strong wave interaction while the regime considered here implies strong turbulence and weak wave interaction. The former regime does not converge to Kolmogorov turbulence for
$E(k)\propto k_{\bot }^{-5/2}k_{\Vert }^{-1/2}$
. This distribution is quite different from those obtained here. Note, however, that Galtier (Reference Galtier2003) considered a limit of weak turbulence and strong wave interaction while the regime considered here implies strong turbulence and weak wave interaction. The former regime does not converge to Kolmogorov turbulence for
![]() $\unicode[STIX]{x1D734}\rightarrow 0$
and for this reason, there is no analytical transition between the two limits.
$\unicode[STIX]{x1D734}\rightarrow 0$
and for this reason, there is no analytical transition between the two limits.
Spectra of a passive-scalar variance (labelled with
![]() $\unicode[STIX]{x1D703}$
) can be computed using the passive-scalar Langevin equation (6.4) and scalar variance dissipation equation that, in analogy to (8.2), equates the loss of the scalar variance due to the action of the effective diffusivity
$\unicode[STIX]{x1D703}$
) can be computed using the passive-scalar Langevin equation (6.4) and scalar variance dissipation equation that, in analogy to (8.2), equates the loss of the scalar variance due to the action of the effective diffusivity
![]() $\unicode[STIX]{x1D705}(k_{c})$
in the resolved range
$\unicode[STIX]{x1D705}(k_{c})$
in the resolved range
![]() $0<p<k_{c}$
to the scalar dissipation rate
$0<p<k_{c}$
to the scalar dissipation rate
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
,
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$
,
Unlike the energy spectra, all rotation-related terms in (11.7)–(11.9) are negative such that all three spectra fall below the Kolmogorov law with increasing scale. Rodriguez Imazio & Mininni (Reference Rodriguez Imazio and Mininni2011, Reference Rodriguez Imazio and Mininni2015) advanced a simple phenomenological scaling argument for rotating non-helical flows according to which, if the energy spectrum follows a power law
![]() $E(k)\propto k^{-n}$
, then the spectrum of a passive-scalar variance is
$E(k)\propto k^{-n}$
, then the spectrum of a passive-scalar variance is
![]() $E_{\unicode[STIX]{x1D703}}(k)\propto k^{-m}$
, where
$E_{\unicode[STIX]{x1D703}}(k)\propto k^{-m}$
, where
![]() $m=(5-n)/2$
. Accordingly, since all energy spectra, (11.1)–(11.6), undergo the transition from the Kolmogorov
$m=(5-n)/2$
. Accordingly, since all energy spectra, (11.1)–(11.6), undergo the transition from the Kolmogorov
![]() $k^{-5/3}$
to
$k^{-5/3}$
to
![]() $k^{-3}$
power law with the increasing scale, then the slope of the corresponding scalar variance spectra can be expected to flatten from the
$k^{-3}$
power law with the increasing scale, then the slope of the corresponding scalar variance spectra can be expected to flatten from the
![]() $k^{-5/3}$
to
$k^{-5/3}$
to
![]() $k^{-1}$
which indeed (11.7)–(11.9) may be indicative of since the coefficients
$k^{-1}$
which indeed (11.7)–(11.9) may be indicative of since the coefficients
![]() $C_{1}$
,
$C_{1}$
,
![]() $C_{13}$
and
$C_{13}$
and
![]() $C_{11}$
are all negative. The results do not extend far enough, however, to determine whether or not the
$C_{11}$
are all negative. The results do not extend far enough, however, to determine whether or not the
![]() $k^{-1}$
slope is attained.
$k^{-1}$
slope is attained.
12 The anisotropy of spectral energy transfers
Equations (11.1)–(11.5) make it possible to analyse the energy transfers between different directions and different velocity components in rotating turbulence. One observes that contributions to the horizontal spectra exceed those to their vertical counterparts, which is true for both the transverse, i.e.
![]() $E_{1}(k_{2})>E_{1}(k_{3})$
, and the longitudinal, i.e.
$E_{1}(k_{2})>E_{1}(k_{3})$
, and the longitudinal, i.e.
![]() $E_{1}(k_{1})>E_{3}(k_{3})$
, spectra. These tendencies are produced by turbulence energy redistribution between different directions and concentration in the equatorial plane in the spectral space. This concentration is consistent with the Taylor–Proudman constraint that causes the appearance of columnar vortices or ‘cigars’. The coherence inside these ‘cigars’ increases while vertical gradients diminish leading to decimation of the vortex stretching and development of the inverse cascade on large scales in the horizontal planes. Even though the flow remains three-dimensional, in the sense that it possesses all three velocity components, it virtually depends on two horizontal coordinates and develops properties of 2-D turbulence. This behaviour is opposite to the case of stable stratification in which the energy concentrates inside vertically aligned cone and the slow modes are comprised of horizontal sheets, or ‘pancakes’ with strong gradients between them. These gradients enhance vortex stretching and facilitate vorticity generation on ever smaller scales thus precluding the development of the inverse energy cascade. Extensive studies of the energy redistribution in rotating and stably stratified flows was undertaken over the years by the scientists of the Lyon group (see extensive reviews by Sagaut & Cambon Reference Sagaut and Cambon2008; Godeferd & Moisy Reference Godeferd and Moisy2015); their results are schematically presented in figure 4 adopted from Sagaut & Cambon (Reference Sagaut and Cambon2008).
$E_{1}(k_{1})>E_{3}(k_{3})$
, spectra. These tendencies are produced by turbulence energy redistribution between different directions and concentration in the equatorial plane in the spectral space. This concentration is consistent with the Taylor–Proudman constraint that causes the appearance of columnar vortices or ‘cigars’. The coherence inside these ‘cigars’ increases while vertical gradients diminish leading to decimation of the vortex stretching and development of the inverse cascade on large scales in the horizontal planes. Even though the flow remains three-dimensional, in the sense that it possesses all three velocity components, it virtually depends on two horizontal coordinates and develops properties of 2-D turbulence. This behaviour is opposite to the case of stable stratification in which the energy concentrates inside vertically aligned cone and the slow modes are comprised of horizontal sheets, or ‘pancakes’ with strong gradients between them. These gradients enhance vortex stretching and facilitate vorticity generation on ever smaller scales thus precluding the development of the inverse energy cascade. Extensive studies of the energy redistribution in rotating and stably stratified flows was undertaken over the years by the scientists of the Lyon group (see extensive reviews by Sagaut & Cambon Reference Sagaut and Cambon2008; Godeferd & Moisy Reference Godeferd and Moisy2015); their results are schematically presented in figure 4 adopted from Sagaut & Cambon (Reference Sagaut and Cambon2008).

Figure 4. Angular energy drain for stably stratified (a) and rotating (c) turbulence; spectral transfers (a,c) versus structures in physical space (b,d). (After Sagaut & Cambon (Reference Sagaut and Cambon2008); reprinted with the permission of Cambridge University Press.)
13 Direct and inverse energy transfers
The tendency of the rotating flows to develop the inverse energy cascade on large scales is so prolific that doubts have been raised as to whether or not the large-scale energy of the atmospheric and oceanic circulation can ever be delivered to the scales at which it can become involved in the direct cascade and dissipate (Pouquet & Marino Reference Pouquet and Marino2013). On the other hand, the co-existence of the direct and inverse cascades in rotating flows has been known at least since the early studies by Smith et al. (Reference Smith, Chasnov and Waleffe1996). It was also evident in simulations of oceanic flows by Klein et al. (Reference Klein, Hua, Lapeyre, Capet, Gentil and Sasaki2008). Pouquet & Marino (Reference Pouquet and Marino2013) showed that a dual, direct and inverse, energy cascade at constant rates
![]() $\unicode[STIX]{x1D716}_{D}$
and
$\unicode[STIX]{x1D716}_{D}$
and
![]() $\unicode[STIX]{x1D716}_{I}$
, respectively, can develop in rotating stratified turbulence. Furthering these findings, Marino, Pouquet & Rosenberg (Reference Marino, Pouquet and Rosenberg2015) performed high-resolution DNS of rotating stratified flows and identified a double cascade of the kinetic and potential energies to large and to small scales. All these efforts alleviate the paradox of the small-scale mixing in the presence of the inverse energy cascade. QNSE results provide an additional framework that can be used to analyse this paradox from a different viewpoint.
$\unicode[STIX]{x1D716}_{I}$
, respectively, can develop in rotating stratified turbulence. Furthering these findings, Marino, Pouquet & Rosenberg (Reference Marino, Pouquet and Rosenberg2015) performed high-resolution DNS of rotating stratified flows and identified a double cascade of the kinetic and potential energies to large and to small scales. All these efforts alleviate the paradox of the small-scale mixing in the presence of the inverse energy cascade. QNSE results provide an additional framework that can be used to analyse this paradox from a different viewpoint.
Denote the energy dissipation in the non-rotating case, (8.2), as
In the lowest order in
![]() $Ro(k)^{-1}$
, the total energy flux through a wavenumber
$Ro(k)^{-1}$
, the total energy flux through a wavenumber
![]() $k$
can be computed as a sum of two terms,
$k$
can be computed as a sum of two terms,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716} & = & \displaystyle \unicode[STIX]{x1D716}_{0}+2\int _{k}^{\infty }p^{2}[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}(p)E_{0}(p)+\unicode[STIX]{x1D708}_{n}(p)\unicode[STIX]{x1D6FF}E(p)]\,\text{d}p\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{0}\left[1-0.39\left(\frac{k_{\unicode[STIX]{x1D6FA}}}{k}\right)^{4/3}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716} & = & \displaystyle \unicode[STIX]{x1D716}_{0}+2\int _{k}^{\infty }p^{2}[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}(p)E_{0}(p)+\unicode[STIX]{x1D708}_{n}(p)\unicode[STIX]{x1D6FF}E(p)]\,\text{d}p\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{0}\left[1-0.39\left(\frac{k_{\unicode[STIX]{x1D6FA}}}{k}\right)^{4/3}\right],\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}E(k)=E(k)-E_{0}(k)$
is the correction to the total spectrum as defined in (11.6) and
$\unicode[STIX]{x1D6FF}E(k)=E(k)-E_{0}(k)$
is the correction to the total spectrum as defined in (11.6) and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}(p)=\unicode[STIX]{x1D708}(p)-\unicode[STIX]{x1D708}_{n}(p)$
. While
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}(p)=\unicode[STIX]{x1D708}(p)-\unicode[STIX]{x1D708}_{n}(p)$
. While
![]() $\unicode[STIX]{x1D716}_{0}$
is computed by integration over the interval
$\unicode[STIX]{x1D716}_{0}$
is computed by integration over the interval
![]() $(0,k)$
as it quantifies the energy transfer from the explicit to the implicit, or SGS domain
$(0,k)$
as it quantifies the energy transfer from the explicit to the implicit, or SGS domain
![]() $(k,\infty )$
, the correction
$(k,\infty )$
, the correction
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}$
is computed by integration over the interval
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}$
is computed by integration over the interval
![]() $(k,\infty )$
as it quantifies the energy transfer from the implicit to explicit domain. Since
$(k,\infty )$
as it quantifies the energy transfer from the implicit to explicit domain. Since
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}<0$
, one infers that it effectively quantifies energy backscatter due to rotation which, in fact, is the
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}<0$
, one infers that it effectively quantifies energy backscatter due to rotation which, in fact, is the
![]() $k$
-dependent rate of the inverse energy cascade.
$k$
-dependent rate of the inverse energy cascade.
Based upon the other two corrections to the vertical viscosity, we can compute the angular and component-wise redistributions of the energy flux,
and
Note that both
![]() $\unicode[STIX]{x1D716}_{z}(k)$
and
$\unicode[STIX]{x1D716}_{z}(k)$
and
![]() $\unicode[STIX]{x1D716}_{3}(k)$
are negative meaning that the energy is withdrawn both from the vertical component and the
$\unicode[STIX]{x1D716}_{3}(k)$
are negative meaning that the energy is withdrawn both from the vertical component and the
![]() $z$
(or
$z$
(or
![]() $k_{\Vert }$
) direction of all components. The energy loss of the third component (which is rather minor, (13.4)) is the gain of the two other horizontal components. More significant is the energy transfer from the
$k_{\Vert }$
) direction of all components. The energy loss of the third component (which is rather minor, (13.4)) is the gain of the two other horizontal components. More significant is the energy transfer from the
![]() $k_{\Vert }$
direction to the horizontal plane (for which
$k_{\Vert }$
direction to the horizontal plane (for which
![]() $k_{\Vert }=0$
) given by (13.3). This picture agrees well with the process of energy redistribution as presented schematically on figure 4. This analysis also indicates that while the direct cascade diminishes with the increasing scale, the inverse cascade gradually increases, consistently with the evidence of the dual cascade discussed in Pouquet & Marino (Reference Pouquet and Marino2013) and Marino et al. (Reference Marino, Pouquet and Rosenberg2015). Clearly, this reasoning is qualitative only and valid for
$k_{\Vert }=0$
) given by (13.3). This picture agrees well with the process of energy redistribution as presented schematically on figure 4. This analysis also indicates that while the direct cascade diminishes with the increasing scale, the inverse cascade gradually increases, consistently with the evidence of the dual cascade discussed in Pouquet & Marino (Reference Pouquet and Marino2013) and Marino et al. (Reference Marino, Pouquet and Rosenberg2015). Clearly, this reasoning is qualitative only and valid for
![]() $\unicode[STIX]{x1D708}_{h}>0$
.
$\unicode[STIX]{x1D708}_{h}>0$
.
14 Discussion and conclusions
The QNSE theory has been extended to include the case of forced rotating flows in a steady state. The process of small-scale elimination produces componentality which manifests via eddy viscosities acting in different ways on different velocity components and in different directions. In fact, the eddy viscosity
![]() $\unicode[STIX]{x1D708}_{3}$
acting on the vertical velocity component alone has been obtained here for the first time. All but
$\unicode[STIX]{x1D708}_{3}$
acting on the vertical velocity component alone has been obtained here for the first time. All but
![]() $\unicode[STIX]{x1D708}_{3z}$
eddy viscosities decrease with increasing scales compared to their values in non-rotating flows. In the vicinity of the Woods scale,
$\unicode[STIX]{x1D708}_{3z}$
eddy viscosities decrease with increasing scales compared to their values in non-rotating flows. In the vicinity of the Woods scale,
![]() $L_{\unicode[STIX]{x1D6FA}}$
, the horizontal eddy viscosity,
$L_{\unicode[STIX]{x1D6FA}}$
, the horizontal eddy viscosity,
![]() $\unicode[STIX]{x1D708}_{h}$
, tends to zero and the process of successive scale elimination cannot proceed beyond that point. The decrease in eddy viscosities is associated with gradual reorientation of the energy flux from small to large scales, i.e. increasing energy backscatter or inverse energy transfer inherent to turbulence with rotation. This behaviour of the eddy viscosities sets apart QNSE results for the cases of stably stratified and rotating turbulence. While in the former, the QNSE procedure produced positive viscosities for any stratification and so it could be carried out to any scale, in the latter, the procedure can only be used in the limit of weak rotation for as long as
$\unicode[STIX]{x1D708}_{h}$
, tends to zero and the process of successive scale elimination cannot proceed beyond that point. The decrease in eddy viscosities is associated with gradual reorientation of the energy flux from small to large scales, i.e. increasing energy backscatter or inverse energy transfer inherent to turbulence with rotation. This behaviour of the eddy viscosities sets apart QNSE results for the cases of stably stratified and rotating turbulence. While in the former, the QNSE procedure produced positive viscosities for any stratification and so it could be carried out to any scale, in the latter, the procedure can only be used in the limit of weak rotation for as long as
![]() $\unicode[STIX]{x1D708}_{h}>0$
. The results are nevertheless important because they provide an analytical closed-form description of the transition from the isotropic 3-D Kolmogorov turbulence to anisotropic, rotation-dominated, quasi-2-D, three-component flow field emerging under the action of rotation. With regard to the frequencies of the inertial waves, turbulence appears not to affect them and so they remain unchanged compared to the linear case.
$\unicode[STIX]{x1D708}_{h}>0$
. The results are nevertheless important because they provide an analytical closed-form description of the transition from the isotropic 3-D Kolmogorov turbulence to anisotropic, rotation-dominated, quasi-2-D, three-component flow field emerging under the action of rotation. With regard to the frequencies of the inertial waves, turbulence appears not to affect them and so they remain unchanged compared to the linear case.
The QNSE-generated eddy viscosities and eddy diffusivities can be used as SGS parameterization for rotating flows on scales with positive eddy viscosities. Several LES studies of rotating turbulence used the EDQNM formalism to develop the SGS parameterization. Since the spectra in this approach are unknown, it was assumed that in the SGS range the deviations from the Kolmogorov spectrum are small (e.g Baerenzung et al.
Reference Baerenzung, Politano, Ponty and Pouquet2008; Sen et al.
Reference Sen, Mininni, Rosenberg and Pouquet2012; Pouquet et al.
Reference Pouquet, Sen, Rosenberg, Mininni and Baerenzung2013). QNSE could possibly improve such SGS schemes because it provides simple analytical expressions for the response functions needed by EDQNM. Furthermore, an adequate resolution of the Kolmogorov inertial subrange in simulations of turbulence with rotation requires that the values of the rotational Reynolds number,
![]() $Re_{f}=\unicode[STIX]{x1D716}/(\unicode[STIX]{x1D708}_{0}f^{2})$
, be relatively large, well in excess of
$Re_{f}=\unicode[STIX]{x1D716}/(\unicode[STIX]{x1D708}_{0}f^{2})$
, be relatively large, well in excess of
![]() $10^{2}$
. QNSE perfectly addresses this requirement as it implies an arbitrarily large
$10^{2}$
. QNSE perfectly addresses this requirement as it implies an arbitrarily large
![]() $Re_{f}$
. Clearly, QNSE offers many advantages which are yet to be tested within EDQNM.
$Re_{f}$
. Clearly, QNSE offers many advantages which are yet to be tested within EDQNM.
Planetary rotation and density stratification significantly influence the dynamics of the Earth’s atmosphere and oceans as well as many other planetary circulations (Read Reference Read2011). Their combined effect is scale dependent and can be characterized in terms of the ratio of the Ozmidov and Woods scales,
![]() $L_{O}/L_{\unicode[STIX]{x1D6FA}}=(f/N)^{3/2}$
, where
$L_{O}/L_{\unicode[STIX]{x1D6FA}}=(f/N)^{3/2}$
, where
![]() $f/N$
is sometimes referred to as the Prandtl’s ratio (e.g. Dritschel & McKiver Reference Dritschel and McKiver2015). The paramount role of this ratio in the dynamics of the Earth’s atmosphere was elaborated by Charney (Reference Charney1971). The complicated and often opposing tendencies of the rotation- and stratification-affected eddy viscosities and eddy diffusivities shown in figure 3 can be expected to have different and even opposing effects on flows on different scales. Recent numerical investigation by Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013) showed that the energy transfer from 3-D to 2-D modes is most efficient for
$f/N$
is sometimes referred to as the Prandtl’s ratio (e.g. Dritschel & McKiver Reference Dritschel and McKiver2015). The paramount role of this ratio in the dynamics of the Earth’s atmosphere was elaborated by Charney (Reference Charney1971). The complicated and often opposing tendencies of the rotation- and stratification-affected eddy viscosities and eddy diffusivities shown in figure 3 can be expected to have different and even opposing effects on flows on different scales. Recent numerical investigation by Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013) showed that the energy transfer from 3-D to 2-D modes is most efficient for
![]() $1/2\leqslant f/N\leqslant 2$
, or
$1/2\leqslant f/N\leqslant 2$
, or
![]() $0.35\lesssim L_{O}/L_{\unicode[STIX]{x1D6FA}}\lesssim 2.8$
. Within this interval, the stratification is most effective at creating large-scale structures and facilitating inverse energy cascade. On the other hand, the inverse cascade diminishes when stratification becomes predominant.
$0.35\lesssim L_{O}/L_{\unicode[STIX]{x1D6FA}}\lesssim 2.8$
. Within this interval, the stratification is most effective at creating large-scale structures and facilitating inverse energy cascade. On the other hand, the inverse cascade diminishes when stratification becomes predominant.
One of the most important outcomes of the competition between the effects of rotation and stratification is the behaviour of the energy spectra. As was elaborated in Galperin & Sukoriansky (Reference Galperin and Sukoriansky2010), in the case of stratification with no rotation, a flow tends to develop a universal spectrum
![]() $\propto N^{2}k_{z}^{-3}$
for the horizontal velocity in the vertical direction, i.e. the direction along which the phase speed of the internal waves is zero. It is quite possible that a similar universal spectrum emerges for the horizontal spectrum of the horizontal velocity in rotating flows. Note in this respect that the energy spectral laws and changes in the power laws exponents are often explained in terms of cross-overs between 3-D and 2-D turbulence. For the Earth’s atmosphere and ocean,
$\propto N^{2}k_{z}^{-3}$
for the horizontal velocity in the vertical direction, i.e. the direction along which the phase speed of the internal waves is zero. It is quite possible that a similar universal spectrum emerges for the horizontal spectrum of the horizontal velocity in rotating flows. Note in this respect that the energy spectral laws and changes in the power laws exponents are often explained in terms of cross-overs between 3-D and 2-D turbulence. For the Earth’s atmosphere and ocean,
![]() $f/N\sim 10^{-2}$
, and so, according to Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013), such a transition would be quite inefficient. In addition, the dimensional cross-overs, if such exist, are difficult, if at all possible, to capture within the paradigms of isotropic or geostrophic turbulence. The QNSE formalism is free from this difficulty because it operates with the full set of 3-D Navier–Stokes and continuity equations with extra strains; no approximations regarding the character of a flow are made. In this 3-D framework, the emergence of flow two-dimensionalization and inverse energy cascade originate from anisotropic energy transfers reflected in the anisotropization of the Green function and velocity correlation tensor, the basic processes within the anisotropic turbulence paradigm. This paradigm has also been promoted by Schertzer & Lovejoy (Reference Schertzer and Lovejoy1985) and Lovejoy et al. (Reference Lovejoy, Tuck, Schertzer and Hovde2009) for atmospheric flows.
$f/N\sim 10^{-2}$
, and so, according to Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013), such a transition would be quite inefficient. In addition, the dimensional cross-overs, if such exist, are difficult, if at all possible, to capture within the paradigms of isotropic or geostrophic turbulence. The QNSE formalism is free from this difficulty because it operates with the full set of 3-D Navier–Stokes and continuity equations with extra strains; no approximations regarding the character of a flow are made. In this 3-D framework, the emergence of flow two-dimensionalization and inverse energy cascade originate from anisotropic energy transfers reflected in the anisotropization of the Green function and velocity correlation tensor, the basic processes within the anisotropic turbulence paradigm. This paradigm has also been promoted by Schertzer & Lovejoy (Reference Schertzer and Lovejoy1985) and Lovejoy et al. (Reference Lovejoy, Tuck, Schertzer and Hovde2009) for atmospheric flows.
Acknowledgements
The authors are grateful to Professor Sagaut who contributed figure 4. We are also thankful to the anonymous reviewers for providing insightful comments that helped to improve and clarify the manuscript. S.S. was partially supported by the ISF grant no. 408/15. B.G. and S.S. gratefully acknowledge partial support by ARO grant W911NF-09-1-0018 and ONR grant N00014-07-1-1065.
Appendix A. Tensorial and scalar terms used in derivation of the effective viscosities
In § 7.2 equations for effective viscosities have been derived. These derivations involved lengthy and cumbersome expressions for the tensorial (
![]() $T_{abc}$
) and scalar
$T_{abc}$
) and scalar
![]() $(R)$
terms which are given below.
$(R)$
terms which are given below.
where
The scalar functions
![]() $R^{i}$
are integrated over the frequency
$R^{i}$
are integrated over the frequency
![]() $\unicode[STIX]{x1D71B}$
using standard contour methods. The results of this integration, schematically shown by (7.43) and expanded up to
$\unicode[STIX]{x1D71B}$
using standard contour methods. The results of this integration, schematically shown by (7.43) and expanded up to
![]() $O(f^{2})$
, are as follows:
$O(f^{2})$
, are as follows:
 $$\begin{eqnarray}\displaystyle \mathscr{R}^{3}(q,q_{3},k,k_{3}) & = & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{q}\left\{-\unicode[STIX]{x1D714}_{q}^{2}(\unicode[STIX]{x1D714}_{k-q}+\unicode[STIX]{x1D714}_{q})^{2}(\unicode[STIX]{x1D714}_{k-q}+2\unicode[STIX]{x1D714}_{q})\right.\nonumber\\ \displaystyle & & \displaystyle +\,f^{2}\left\{[1-P_{33}(\boldsymbol{k}-\boldsymbol{q})]\unicode[STIX]{x1D714}_{q}^{2}(\unicode[STIX]{x1D714}_{k-q}+4\unicode[STIX]{x1D714}_{q})\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,[1-P_{33}(\boldsymbol{q})](\unicode[STIX]{x1D714}_{k-q}+2\unicode[STIX]{x1D714}_{q})(\unicode[STIX]{x1D714}_{k-q}^{2}+2\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D714}_{q}+2\unicode[STIX]{x1D714}_{q}^{2})\right\}\!\right\}/(2\unicode[STIX]{x1D714}_{q}^{4}d_{1}^{4}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{R}^{3}(q,q_{3},k,k_{3}) & = & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{q}\left\{-\unicode[STIX]{x1D714}_{q}^{2}(\unicode[STIX]{x1D714}_{k-q}+\unicode[STIX]{x1D714}_{q})^{2}(\unicode[STIX]{x1D714}_{k-q}+2\unicode[STIX]{x1D714}_{q})\right.\nonumber\\ \displaystyle & & \displaystyle +\,f^{2}\left\{[1-P_{33}(\boldsymbol{k}-\boldsymbol{q})]\unicode[STIX]{x1D714}_{q}^{2}(\unicode[STIX]{x1D714}_{k-q}+4\unicode[STIX]{x1D714}_{q})\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,[1-P_{33}(\boldsymbol{q})](\unicode[STIX]{x1D714}_{k-q}+2\unicode[STIX]{x1D714}_{q})(\unicode[STIX]{x1D714}_{k-q}^{2}+2\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D714}_{q}+2\unicode[STIX]{x1D714}_{q}^{2})\right\}\!\right\}/(2\unicode[STIX]{x1D714}_{q}^{4}d_{1}^{4}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{R}^{9}(q,q_{3},k,k_{3}) & = & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{q}\left\{\unicode[STIX]{x1D714}_{q}^{2}(\unicode[STIX]{x1D714}_{k-q}+\unicode[STIX]{x1D714}_{q})^{2}(\unicode[STIX]{x1D714}_{k-q}+3\unicode[STIX]{x1D714}_{q})\right.\nonumber\\ \displaystyle & & \displaystyle +\,P_{33}(\boldsymbol{q})f^{2}(\unicode[STIX]{x1D714}_{k-q}^{3}+5\unicode[STIX]{x1D714}_{k-q}^{2}\unicode[STIX]{x1D714}_{q}+10\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D714}_{q}^{2}+10\unicode[STIX]{x1D714}_{q}^{3})\nonumber\\ \displaystyle & & \displaystyle -\,f^{2}\left\{\unicode[STIX]{x1D714}_{k-q}^{3}+5\unicode[STIX]{x1D714}_{k-q}^{2}\unicode[STIX]{x1D714}_{q}+[11-P_{33}(\boldsymbol{k}-\boldsymbol{q})]\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D714}_{q}^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,5[3-P_{33}(\boldsymbol{k}-\boldsymbol{q})]\unicode[STIX]{x1D714}_{q}^{3}\right\}\!\right\}/(2\unicode[STIX]{x1D714}_{q}^{4}d_{1}^{5}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{R}^{9}(q,q_{3},k,k_{3}) & = & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{q}\left\{\unicode[STIX]{x1D714}_{q}^{2}(\unicode[STIX]{x1D714}_{k-q}+\unicode[STIX]{x1D714}_{q})^{2}(\unicode[STIX]{x1D714}_{k-q}+3\unicode[STIX]{x1D714}_{q})\right.\nonumber\\ \displaystyle & & \displaystyle +\,P_{33}(\boldsymbol{q})f^{2}(\unicode[STIX]{x1D714}_{k-q}^{3}+5\unicode[STIX]{x1D714}_{k-q}^{2}\unicode[STIX]{x1D714}_{q}+10\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D714}_{q}^{2}+10\unicode[STIX]{x1D714}_{q}^{3})\nonumber\\ \displaystyle & & \displaystyle -\,f^{2}\left\{\unicode[STIX]{x1D714}_{k-q}^{3}+5\unicode[STIX]{x1D714}_{k-q}^{2}\unicode[STIX]{x1D714}_{q}+[11-P_{33}(\boldsymbol{k}-\boldsymbol{q})]\unicode[STIX]{x1D714}_{k-q}\unicode[STIX]{x1D714}_{q}^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,5[3-P_{33}(\boldsymbol{k}-\boldsymbol{q})]\unicode[STIX]{x1D714}_{q}^{3}\right\}\!\right\}/(2\unicode[STIX]{x1D714}_{q}^{4}d_{1}^{5}),\end{eqnarray}$$
where
The tensorial terms
![]() $\unicode[STIX]{x1D61B}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FD}}^{i}$
are
$\unicode[STIX]{x1D61B}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FD}}^{i}$
are
![]() $\unicode[STIX]{x1D71B}$
-independent and only affect the angular integration.
$\unicode[STIX]{x1D71B}$
-independent and only affect the angular integration.