1 Introduction
Transition processes and convective mechanisms of complex flows and geometries have gained great visibility in recent decades due to the advances in computational resources and stability methods, and have been investigated to understand the physical mechanisms of flows in idealized biological models. These models include time-dependent flows in confined geometries with separated flow, which are prone to strong instabilities. Considering channel flows, direct numerical simulations and large-eddy simulations were employed to study pulsatile flow in a planar channel with a one-sided semicircular constriction with 50 % occlusion by Mittal, Simmons & Najjar (Reference Mittal, Simmons and Najjar2003). It was observed that the transition to turbulence for pulsatile flow happened for Reynolds numbers higher than 1000. Pitt (Reference Pitt2005) reported biglobal stability analysis and direct numerical simulations for a pulsatile flow in a constricted channel with 60 % occlusion. Critical Reynolds numbers were obtained for different Womersley numbers, and the bifurcation through which the flow went for a certain reduced velocity was found to be supercritical. Khair, Wang & Kuhn (Reference Khair, Wang and Kuhn2016) studied a more realistic physiological pulsatile flow in a constricted channel. Three-dimensional direct numerical simulations were carried out for different degrees of the stenosis and pulsatile conditions in order to investigate the flow transition. On the other hand, in axisymmetric geometries, Sherwin & Blackburn (Reference Sherwin and Blackburn2005) studied three-dimensional instabilities and flow transition in pulsatile flows in an axisymmetric constricted tube with 75 % occlusion. The pulsatile flows became unstable through a subcritical bifurcation and the primary instability was identified as a period-doubling bifurcation: the vortex rings which were ejected from the throat presented alternating tilting with each pulse. However, the tilting vortex rings quickly broke down, producing localized turbulence approximately four diameters downstream from the stenosis. Blackburn & Sherwin (Reference Blackburn and Sherwin2007) demonstrated that, differently from their previous work for long-period pulsatile flows, in lower reduced velocities the primary instability is normally manifested as azimuthal waves of low wavenumber that grow on each vortex ring. Griffith et al. (Reference Griffith, Leweke, Thompson and Hourigan2009) carried out numerical and experimental investigations of a pulsatile flow in stenotic geometries and comparisons were made between Floquet stability analysis results and the instabilities observed experimentally.
Spatial symmetry-breaking bifurcations appear in many channel flows. The earliest experimental and computational studies of the flow-field characterization of symmetric channels with sudden expansion were carried out by Durst, Melling & Whitelaw (Reference Durst, Melling and Whitelaw1974), Cherdron, Durst & Whitelaw (Reference Cherdron, Durst and Whitelaw1978), Fearn, Mullin & Cliffe (Reference Fearn, Mullin and Cliffe1990). In recent investigations, Fani, Camarri & Salvetti (Reference Fani, Camarri and Salvetti2012) performed linear stability and sensitivity analyses for two-dimensional steady flow in a symmetric channel with a sudden expansion in order to design a passive control by introducing a small cylinder in the flow with the aim of stabilizing the unstable symmetric flow (asymmetric steady flow). Lashgari et al. (Reference Lashgari, Tammisola, Citro, Juniper and Brandt2014) explored bifurcations and control in a symmetric channel junction by means of linear stability analysis and direct numerical simulations, such that the observed instability mechanisms were stabilized or destabilized by boundary modifications. Isler, Gioria & Carmo (Reference Isler, Gioria and Carmo2018) reported the physical mechanism of the primary bifurcation of a symmetric steady flow in a constricted channel. During the transition process, energy from the three-dimensional modes was transferred to the two-dimensional mode, leading the system to a two-dimensional asymmetric steady flow, and this bifurcation exhibited a hysteretic behaviour.
The symmetry-breaking bifurcations in steady constricted channel flows are naturally bistable solutions. The equilibrium states have similar energy, since the asymmetric solution observed after the bifurcation can deflect the flow upwards or downwards (Durst et al. Reference Durst, Melling and Whitelaw1974). In non-symmetric systems, the bistability arises with different energy levels. Pralits, Brandt & Giannetti (Reference Pralits, Brandt and Giannetti2010) demonstrated that there are two-dimensional flows that differ slightly in lift force for flow around a rotating circular cylinder. However, in this paper, we explore the bistability in a symmetric geometry in which the equilibrium states differ slightly in energy and both states are symmetric in space.
The intent of this study is to extend the previous work by Isler et al. (Reference Isler, Gioria and Carmo2018), in which symmetric and asymmetric steady flows, the last being a result of the primary instability, were investigated in a constricted channel in order to comprehend the bifurcations and convective instabilities in these two flow regimes. The aim of this paper is to understand the base flow behaviour and the equilibrium states (bistability) observed at subcritical Reynolds number of pulsatile flow in the same geometry.
2 Problem description and dimensionless parameters
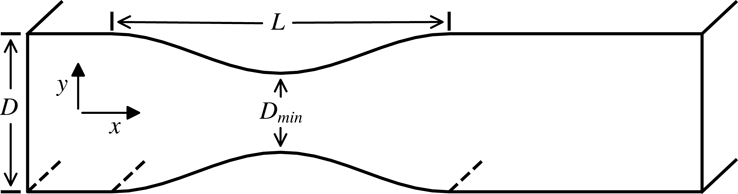
The constricted channel geometry with 50 % occlusion under investigation is similar to that used in Isler et al. (Reference Isler, Gioria and Carmo2018), having the same stenotic shape (figure 1). The channel has width
$D$
, throat spacing
$D_{min}$
and stenosis length
$L=2D$
. In our investigation, the width ratio is
$D_{min}/D=0.5$
, so the relative occlusion is
$s=1-D_{min}/D=0.5$
. The base flow is generated with a time periodic inflow. Note that, although stenotic tubes are the most common geometry studied using periodic inflows, the geometry analysed here is planar.
Figure 1. Constricted channel geometry and parameters (not to scale).
The time-dependent inlet,
$\bar{u}(t)$
, has a uniform cross-sectional velocity, which implies that it does not depend on space coordinates, such that it does not vary in the wall-normal direction. Thus, the time-dependent inlet is
$\bar{\boldsymbol{u}}(\boldsymbol{x},t)=\bar{u}(t)\hat{\boldsymbol{x}}$
and the temporal-averaged flow velocity is
$\bar{u}_{m}=1/T\int _{0}^{T}\bar{u}(t)\,\text{d}t$
, where
$T$
is the pulse period and
$\hat{\boldsymbol{x}}$
is the vector component along the
$x$
-direction. The channel width
$D$
and the average velocity
$\bar{u}_{m}$
are used as length and velocity scales, respectively, so the time scale is
$D/\bar{u}_{m}$
.
We can now define the dimensionless parameters of the flow, which are the time-averaged Reynolds number
$Re=\bar{u}_{m}D/\unicode[STIX]{x1D708}$
and the reduced velocity
$U_{red}=\bar{u}_{m}T/D$
, where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of the fluid. Another dimensionless parameter commonly employed in pulsatile flows is the Womersley number
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x03C0}Re/2U_{red})^{1/2}$
. In our study we fixed the reduced velocity, and varied the Reynolds number by changing the viscosity only.
The pulse oscillates around the temporal-averaged flow velocity with a sinusoidal shape, so that the velocity waveform applied in the pulsatile flow is a single-harmonic pulse given by
$$\begin{eqnarray}\bar{u}(t)=\bar{u}_{m}\{1+0.75\sin (2\unicode[STIX]{x03C0}t/T)\}.\end{eqnarray}$$
Pulsatile flows with a single-harmonic pulse have been used in many experiments (Ahmed & Giddens Reference Ahmed and Giddens1984; Ojha et al. Reference Ojha, Cobbold, Johnston and Hummel1989), and this specific pulsatile fluctuation was chosen based on computational works in constricted channel (Pitt Reference Pitt2005) and stenotic tubes (Sherwin & Blackburn Reference Sherwin and Blackburn2005; Blackburn & Sherwin Reference Blackburn and Sherwin2007; Griffith et al. Reference Griffith, Leweke, Thompson and Hourigan2009).
In the present paper, the reduced velocity employed was
$U_{red}=9$
and we explored a range of
$Re$
up to
$270$
. In addition, it is worth mentioning that the results were mainly analysed at
$t/T=0$
, since at this phase it was possible to extract all the information necessary to discuss the findings, although the flow is time-dependent.
3 Formulation
The fluid is considered to be Newtonian and governed by the Navier–Stokes equations. These equations can be written in non-dimensional form as
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\boldsymbol{u}=-(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}-\unicode[STIX]{x1D735}p+Re^{-1}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u},\quad \text{with }\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0\text{ in }\unicode[STIX]{x1D6FA},\end{eqnarray}$$
where
$\boldsymbol{u}(\boldsymbol{x},t)=(u,v,w)(\boldsymbol{x},t)$
is the velocity vector,
$p(\boldsymbol{x},t)$
is the pressure field and
$\unicode[STIX]{x1D6FA}$
is the domain. The base flows were two-dimensional. The boundary conditions employed on these equations are described as follows. For the velocity, at the inflow boundary we imposed Dirichlet boundary conditions, no-slip conditions were imposed at the solid walls and Neumann conditions were specified at the outflow boundary. The pressure was set to zero at the outflow boundary and high-order pressure boundary conditions were imposed at the inflow and walls, as described in Karniadakis, Israeli & Orszag (Reference Karniadakis, Israeli and Orszag1991). In addition, since we are exploring a two-dimensional geometry, which is invariant in the
$z$
-direction, a homogeneous decomposition in the spanwise direction can be employed to assess the three dimensionality of normal modes (Karniadakis Reference Karniadakis1990). We can define the spanwise wavelength as
$L_{z}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}$
(
$\unicode[STIX]{x1D6FD}$
is the spanwise wavenumber).
The interest of the linear stability analysis is in the evolution of small perturbations of the form
$\boldsymbol{u}^{\prime }(x,y,z,t)$
in a time-dependent base flow
$\boldsymbol{U}(x,y,t)$
(pulsatile flow). The linearized Navier–Stokes equations were applied to evolve infinitesimal perturbations
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\boldsymbol{u}^{\prime }=-(\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}^{\prime }-(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{U}-\unicode[STIX]{x1D735}p^{\prime }+Re^{-1}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}^{\prime },\quad \text{with }\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}^{\prime }=0\text{ in }\unicode[STIX]{x1D6FA},\end{eqnarray}$$
where
$p^{\prime }(x,y,z,t)$
is the perturbation pressure.
An operator
${\mathcal{A}}(\unicode[STIX]{x1D70F})$
can be defined in order to represent the action of the linearized equations (3.2) on an initial perturbation
$\boldsymbol{u}^{\prime }(t=0)$
. So it is possible to evolve an initial perturbation over an time interval
$\unicode[STIX]{x1D70F}$
by calculating
$\boldsymbol{u}^{\prime }(\unicode[STIX]{x1D70F})={\mathcal{A}}(\unicode[STIX]{x1D70F})\boldsymbol{u}^{\prime }(0)$
. The solution of the linear system (3.2) can be decomposed as a sum of eigenmodes
$\boldsymbol{u}^{\prime }(\boldsymbol{x},t)=\sum _{j}\text{exp}(\unicode[STIX]{x1D70E}_{j}t)\tilde{\boldsymbol{u}_{j}}+\text{c.c.}$
, where
$\unicode[STIX]{x1D70E}_{j}$
is the complex growth rate of the eigenfunction
$\tilde{\boldsymbol{u}_{j}}$
and c.c. stands for complex conjugate. The evolution of each eigenmode is given by the dynamics of the system
$$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D70F})\tilde{\boldsymbol{u}}_{j}=\unicode[STIX]{x1D707}_{j}\tilde{\boldsymbol{u}}_{j},\quad \unicode[STIX]{x1D707}_{j}\equiv \text{exp}(\unicode[STIX]{x1D70E}_{j}\unicode[STIX]{x1D70F}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D70E}_{j}$
is the eigenvalue of the system (3.2) and
$\unicode[STIX]{x1D707}_{j}$
is called a Floquet multiplier of the forward operator
${\mathcal{A}}(\unicode[STIX]{x1D70F})$
. Since the base flow
$\boldsymbol{U}$
is
$T$
-periodic, we set
$\unicode[STIX]{x1D70F}=T$
and consider this as a temporal Floquet problem. The eigenmodes of
$A(\unicode[STIX]{x1D70F})$
are
$T$
-periodic Floquet modes
$\boldsymbol{u}_{j}(\boldsymbol{x},t+T)=\boldsymbol{u}_{j}(\boldsymbol{x},t)$
. A mode is linearly unstable if the real part of the growth rate,
$\unicode[STIX]{x1D70E}_{j}$
, is positive, which corresponds to
$|\unicode[STIX]{x1D707}_{j}|>1$
. On the other hand, a mode is linearly stable when the real part of
$\unicode[STIX]{x1D70E}_{j}$
is negative, which corresponds to
$|\unicode[STIX]{x1D707}_{j}|<1$
. To solve this eigenproblem, we imposed
$\boldsymbol{u}^{\prime }=\mathbf{0}$
and
$\unicode[STIX]{x2202}\boldsymbol{u}^{\prime }/\unicode[STIX]{x2202}\boldsymbol{n}=\mathbf{0}$
on boundaries where Dirichlet and Neumann conditions are specified for the base flow, respectively.
The dimensionless flow kinetic energy was employed as a measure of the amplitude of the perturbation in this investigation and is defined as
$$\begin{eqnarray}E_{k}=\frac{1}{2A\bar{u}_{m}^{2}}\int _{A}\hat{\boldsymbol{u}}_{k}\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{k}^{\ast }\,\text{d}A,\end{eqnarray}$$
where
$A$
is the area of two-dimensional cross-section of the domain
$\unicode[STIX]{x1D6FA}$
,
$\hat{\boldsymbol{u}}_{k}$
is the velocity data in the
$k$
th Fourier mode and
$\hat{\boldsymbol{u}}_{k}^{\ast }$
is its complex conjugate. For the discretization in the spanwise direction we mostly used
$8$
Fourier modes (16 planes of data in the spanwise direction), however numerical simulations were also performed with 32 Fourier modes in order to ensure the independence of our results with respect to the number of Fourier modes. Periodic boundary conditions were enforced on the planes at the boundaries parallel to the
$xy$
plane.
4 Computational simulations
The three-dimensional computational simulations were carried out using a three-dimensional version of the Navier–Stokes solver which employs a Spectral/hp element discretization in the
$xy$
plane (Karniadakis & Sherwin Reference Karniadakis and Sherwin2005) and Fourier modes in the spanwise direction. The quadrilateral mesh approach around the throat applied in Isler et al. (Reference Isler, Gioria and Carmo2018) was used here with almost the same level of refinement. The two-dimensional computational mesh was composed by
$2136$
spectral elements,
$1994$
being quadrilateral and
$42$
triangular.
Table 1. Convergence of the three-dimensional leading eigenvalues at
$Re=315$
for
$\unicode[STIX]{x1D6FD}=1$
with respect the variation of the spectral element polynomial order
$N$
.
Floquet stability analysis was chosen as the subject to perform the convergence tests – in addition this method was employed considering the highest Reynolds number in the present study. Polynomials of degree
$4$
(i.e. fifth-order accuracy in space) achieved excellent convergence results (table 1). Just to be rigorous with our calculations, polynomials of degree
$6$
were used in the discretization of the mesh for the two-dimensional base flows and stability calculations. However, the fully three-dimensional simulations were carried out with polynomials of degree
$5$
, due to the high computational cost. The inflow and outflow lengths were chosen as
$30D$
and
$40D$
measured from the throat of the stenosis, such that there was no influence of the mesh length in the stability calculations.
Equation (3.1) was used to solve the two-dimensional pulsatile base flows, employing the stiffly stable splitting scheme presented by Karniadakis et al. (Reference Karniadakis, Israeli and Orszag1991). Time integration was carried out using a second-order velocity-correction scheme with a value of the non-dimensional time step of 0.001 for the two-dimensional base flows and normal stability analyses and 0.002 for the three-dimensional simulations. For Floquet stability calculations, the pulsatile base flows were pre-computed and stored as data:
$192$
time slices were stored (Blackburn, Sherwin & Barkley Reference Blackburn, Sherwin and Barkley2008) and the base flows were reconstructed from these data, using Fourier interpolation.
5 Results
5.1 Floquet stability calculations
Figure 2(a) shows the leading eigenvalues,
$\unicode[STIX]{x1D70E}$
, as functions of spanwise wavenumber
$\unicode[STIX]{x1D6FD}$
for different Reynolds numbers. All leading eigenvalues found were real and correspond to positive Floquet multipliers. Figure 2(b) depicts the neutral stability curve for the primary instability for Reynolds numbers up to
$270$
. The critical Reynolds number and corresponding spanwise wavenumber are
$Re_{c}=247.8\pm 0.1$
and
$\unicode[STIX]{x1D6FD}_{c}=0.78\pm 0.01$
, respectively, for
$U_{red}=9$
(
$\unicode[STIX]{x1D6FC}=6.6$
).
Figure 2. Floquet stability analysis for pulsatile flow in a constricted channel. (a) Plot of the leading eigenvalues,
$\unicode[STIX]{x1D70E}$
, against spanwise wavenumber for different Reynolds numbers. (b) Neutral stability curve for the primary instability. The critical Reynolds number is
$Re_{c}=247.8$
.
5.2 Nonlinear characterization of the pulsatile flow
The next step of our study was the nonlinear characterization of the flow and understanding of the physical mechanisms behind the pulsatile flow and flow-field behaviour.
5.2.1 Equilibrium states: bistable system
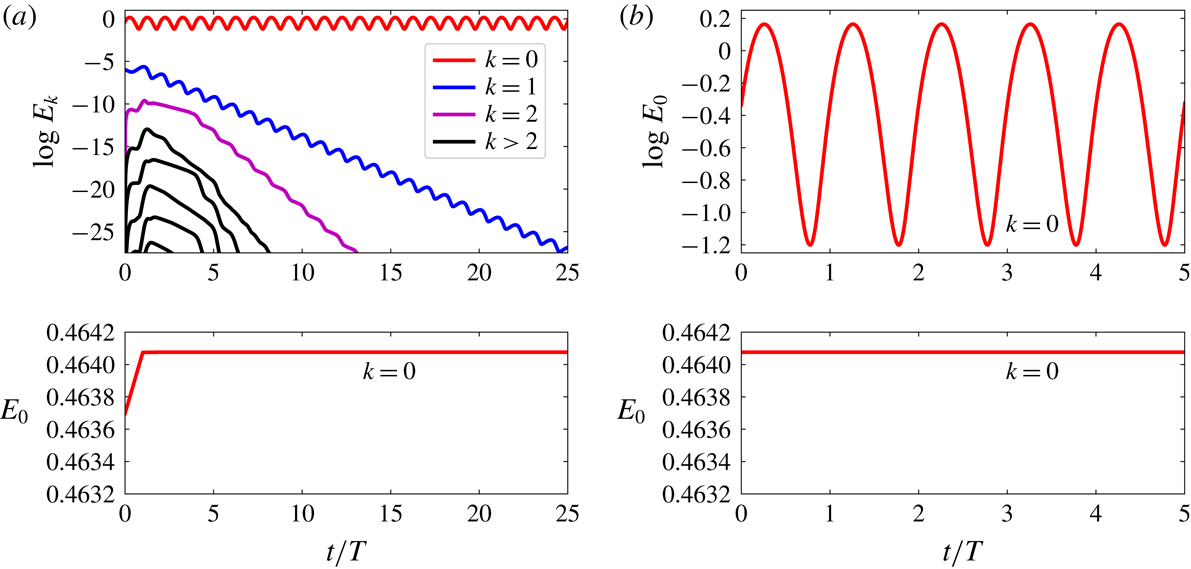
Results from three-dimensional direct numerical simulation of the pulsatile base flow seeded with the least stable mode taken from the Floquet stability analysis at
$Re=225$
and
$\unicode[STIX]{x1D6FD}=0.78$
are shown in figure 3(a). As expected in a linearly stable region, the energy of the three-dimensional Fourier modes went to zero; however, the energy of the two-dimensional mode increased slightly, achieving an upper energy level (nonlinear saturated state), which demonstrates an unexpected behaviour. In addition, when the three-dimensional simulation started, the energy grew abruptly, almost reaching its upper energy level in one period cycle. It is worth mentioning that, although we employed a Floquet mode as initial condition in this numerical simulation, a white noise with very small energy was applied for this set up and it was also able to lead the two-dimensional mode to the upper energy level.
Figure 3. (a) Three-dimensional simulation at
$Re=225$
for
$\unicode[STIX]{x1D6FD}=0.78$
seeded with the least stable mode. (b) Two-dimensional simulation at
$Re=225$
seeded with the two-dimensional Fourier mode at the upper energy level. The time series of energies
$E_{k}$
in spanwise Fourier modes are shown above. The growth and saturation of the energy of the two-dimensional Fourier mode with points in steps of
$T$
are shown below.
The three-dimensional perturbation was able to trigger the two-dimensional flow to another (two-dimensional) equilibrium state. A two-dimensional simulation was initialized with the two-dimensional mode at the upper energy level at
$Re=225$
as illustrated in figure 3(b), in order to verify whether the nonlinear saturated state of the two-dimensional mode could survive in a two-dimensional regime. It can be seen that the energy of the two-dimensional mode stayed at the same energy level during the five period cycles, thus the system was sustained at the upper energy level, showing that it has two equilibrium states. Therefore, we can conclude that this system is bistable in two dimensions. However, when three-dimensional simulations are performed, the energy of the two-dimensional mode always goes to the upper energy level, such that only the upper energy state exists in three dimensions.
An important point to be mentioned is that small differences between bistable flows were also observed in the literature for other geometries. See for instance Pralits et al. (Reference Pralits, Brandt and Giannetti2010) for flow around a rotating circular cylinder. They have found two stable two-dimensional flows that differ slightly in lift force.
5.2.2 Two-dimensional Fourier mode behaviour
To analyse the bistable system further, diagrams were built with the energies of the two-dimensional Fourier modes at the lower and upper energy levels (both equilibrium states) at the beginning of the pulse (
$t/T=0$
), as shown in figure 4. Note that the energy diagrams only deal with energy from two-dimensional simulations and for subcritical Reynolds number. Figure 4(a) depicts the energies of the lower and upper energy levels for a range of Reynolds number. The energies of the two-dimensional Fourier modes are higher for the lower Reynolds numbers, but when the Reynolds number is increased they suffer a sharp fall, such that their energies reach a minimum and afterwards start to increase again. It should be noted that, before the energy minimum the curves have a nonlinear behaviour, but after that they increase almost linearly. The energy minimum occurs at
$Re=154.8$
for the lower energy state and at
$Re=156.3$
for the upper energy state, which corresponds to a Womersley number of
$\unicode[STIX]{x1D6FC}\approx 5.2$
.
Figure 4. Energy diagrams with the two-dimensional component (
$k=0$
) of the Fourier modes. The energies were computed at the beginning of the pulse (
$t/T=0$
) in two-dimensional simulations. (a) Energies at the upper and lower energy states. (b) Difference between the energies of the upper and lower energy levels.
Now let the focus be on the observed difference of the energy curves (energy gaps) in figure 4(a), which is the additional energy in the two-dimensional Fourier modes that led the system to the upper energy level. Surprisingly, the energy gap is higher for lower Reynolds numbers and gets smaller when the Reynolds number increases, having an intriguing behaviour. Besides that, at the end the energy gap decreases linearly, as shown in figure 4(b). Thus, not only the energy of the two-dimensional modes increases linearly with
$Re$
(figure 4
a), but also the energy gap between the upper and lower energy levels starts to decrease linearly with
$Re$
after the energy minimum. It should be noted that, in figure 4(b), the decrease in the energy gap indicates that the bistable system is converging to a unique solution at higher Reynolds number, since the energy gap is tending to zero. In addition, it is noteworthy that this energy diagram (figure 4
b) is the opposite of that found by Isler et al. (Reference Isler, Gioria and Carmo2018) for a symmetric steady flow, where the energy gap of the two-dimensional modes increased with Reynolds number due to the spatial symmetry-breaking nature of the flow bifurcation. However, both phenomena, the primary bifurcation of the symmetric steady flow and changes between the equilibrium states of the pulsatile flow, occur at approximately the same energy level, of approximately
$10^{-4}$
.
5.2.3 Pulse front emission
In order to find a physical explanation for the energy minimum of the two-dimensional modes, contours of vorticity of the two-dimensional base flow at the beginning of the pulse for Reynolds numbers before and after the energy minimum are illustrated in figure 5(a–c). At
$Re=90$
, in figure 5(a), it is easy to verify that there is no pulse front detached from the shear layers. However, at
$Re=270$
, a pulse front is observed travelling downstream of the throat (figure 5
c), which is stronger than that found at
$Re=225$
(figure 5
b), so that the only effect in the flow field is the strengthening of the pulse front at higher Reynolds numbers. In addition, when the pulse front begins to be observed downstream of the throat (after the energy minimum), the energy of the two-dimensional modes increases almost linearly, as shown in figure 4(a).
Figure 5. Contours of vorticity for the two-dimensional base flow
$(-10<\unicode[STIX]{x1D714}_{z}D/\bar{u}_{m}<10)$
at
$t/T=0$
. (a)
$Re=90$
(before the energy minimum); (b)
$Re=225$
and (c)
$Re=270$
(after the energy minimum). (d)
$y$
-velocity (velocity perpendicular to the channel centreline) against time at
$(x,y)/D=(6,0.25)$
during one pulse cycle for Reynolds numbers before and after the energy minimum of the two-dimensional mode.
Exploring the two flow regimes further, figure 5(d) shows the
$y$
-velocity against time at
$(x,y)/D=(6,0.25)$
for Reynolds numbers before and after the energy minimum. After the energy minimum, the
$y$
-velocities present positive and negative values along the cycle period, which means that the pulse front travelled through this point. In addition, since the pulse front at
$Re=225$
is weaker than at
$Re=270$
and we are evaluating the top part of the channel, there is a positive velocity at
$t/T=0$
because the vorticity centre is behind
$x/D=6$
. However, at
$Re=270$
the vorticity centre is downstream from this point, such that the velocity is negative at
$t/T=0$
. On the other hand, before the energy minimum, the velocity peaks are lower than after the energy minimum. At
$Re=90$
there is just a short interval with negative velocity around
$t/T=0.24$
, after which the velocity becomes positive again, and at
$Re=45$
no negative velocity was observed along the cycle period. Thus, these velocity patterns demonstrate that they are not pulse fronts propagating downstream of the throat, but just velocity deviations caused by the separated flow, which quickly die away.
Therefore, it was possible to identify two distinct flow behaviours, one before and another after the energy minimum. After the energy minimum there is one pulse front per cycle detaching from the throat and propagating downstream. Before the energy minimum the separated flow from the throat simply weakens and no pulse front is observed downstream of the throat.
5.2.4 Energy gap effects
Now we are going to explore the effects caused in the flow field when the system achieves the upper energy level. Since the energy gaps between the lower and upper energy levels are very small, as observed in figure 4(b), the change in the flow field is subtle (even so it is remarkable). So, the fundamental question here is: what happens in the flow field when the two-dimensional Fourier mode goes to the upper energy state of the bistable system?
Figure 6. Contours of vorticity of the Fourier mode
$0$
from the upper energy state subtracted from the lower energy state at
$t/T=0$
. (a)
$Re=45$
; (b)
$Re=90$
; (c)
$Re=225$
; (d)
$Re=270$
. Contours of vorticity vary from
$\unicode[STIX]{x1D714}_{z}D/\bar{u}_{m}=-0.005$
(dark contours) to
$\unicode[STIX]{x1D714}_{z}D/\bar{u}_{m}=0.005$
(light countours).
In order to answer this question, contours of vorticity of the Fourier mode 0 from the upper energy state subtracted from the lower energy state (difference between the equilibrium states) at
$t/T=0$
are shown in figure 6. At
$Re=45$
, the vorticity of this resulting flow field is mostly located just downstream of the throat, in the recirculation bubbles of the separated flow. Increasing the Reynolds number, the flow vorticity starts to be distributed downstream of the throat and as a consequence a vortex pair begins to grow soon after the separated flow with opposite vorticity, as can be observed at
$Re=90$
. Moreover, even though the two-dimensional modes have almost the same energy level at
$Re=90$
and
$Re=225$
(figure 4
a), these Reynolds numbers being before and after the energy minimum, respectively, the wake is stronger and extends far away downstream at
$Re=225$
. This happens because for Reynolds numbers higher than that of the energy minimum the flow shows one pulse front per cycle downstream of the throat. Finally, at
$Re=270$
the vortex pair was broken into two parts, which is explained by the pulse front strengthening. The first part lies around
$x/D=4$
and the second part is leaving the picture at
$x/D=10$
, so that the vortex pair travels together with the pulse front.
Once we understood the emergence of the vortex pair and its development process with Reynolds number, we believe that it could be the cause of the energy gap decrease observed in figure 4(b). Since the vortex pair has opposite vorticity compared to the recirculation bubbles of the separated flow at the upper energy state, it produces high energy dissipation in this region, which may slightly reduce the energy of the upper energy state compared to the lower energy state where the vortex pair does not exist. Moreover, the vortex pair becomes larger with Reynolds number, hence explaining why the energy diagram has a monotonic decrease.
6 Conclusion
The pulse front emission through the throat for a pulsatile flow in a constricted channel was found to be related to the energy of the two-dimensional Fourier mode. In the subcritical regime, the energy of the two-dimensional modes went through a minimum for a specific Reynolds number which marked the critical value for which one pulse front started to be emitted per period cycle. Thus, before the energy minimum there was no pulse front propagating downstream of the throat. However, for Reynolds numbers higher than the energy minimum we observed one pulse front per cycle being emitted from the throat, so that the system has two flow regimes at subcritical Reynolds number. In addition, this physical mechanism related to the energy minimum of the two-dimensional mode could be a possible explanation for pulse front emissions in any constricted channel using a single-harmonic pulse in the inflow, although different stenotic shapes and occlusions would change the Reynolds number which triggers the pulse front emission.
The flow investigated presented a bistable behaviour in two dimensions, which was also dictated by the energy of the two-dimensional mode, but this bistability did not appear in three dimensions, being a purely two-dimensional effect. The two-dimensional bistability was characterized by two equilibrium states which have distinct energy levels. Although it was demonstrated that the equilibrium states have similar energy levels, the state with higher energy provoked the emergence of a vortex pair soon after the recirculation bubbles of the separated flow with opposite vorticity, which developed and became wider when the Reynolds number was increased. Finally, the energy difference between the equilibrium states decreased monotonically from the lower to the higher Reynolds numbers, which indicates that the system was tending towards an unique solution at higher Reynolds numbers.
Acknowledgement
J.A.I. gratefully acknowledges CAPES for financial support during his PhD.
