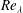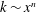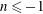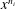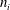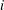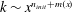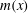1. Introduction
Since the pioneering work of Taylor (Reference Taylor1935), homogeneous isotropic turbulence (HIT) has been extensively studied in grid turbulence, which consists in passing a uniform flow through a grid made of vertical and horizontal bars placed normal to the main flow. Accordingly, over almost 80 years, grid turbulence has been used for testing various theories of HIT including, for example, self-similarity laws, Kolmogorov’s similarities (Kolmogorov (Reference Kolmogorov1941a
,Reference Kolmogorov
b
), hereafter denoted K41) and the decay law of the turbulent kinetic energy. One of the main difficulties with grid turbulence is to generate turbulence at high Reynolds numbers (e.g.
$Re_{{\it\lambda}}$
, the Taylor microscale Reynolds number;
$Re_{{\it\lambda}}=u^{\prime }{\it\lambda}/{\it\nu}$
, where
$u^{\prime }$
is the r.m.s. velocity,
${\it\lambda}$
the Taylor microscale and
${\it\nu}$
the kinematic viscosity of the fluid). Only a few experiments were successful in achieving relatively high
$Re_{{\it\lambda}}$
by using so-called active grids (e.g. Mydlarski & Warhaft Reference Mydlarski and Warhaft1996, Reference Mydlarski and Warhaft1998; Larssen & Davenport Reference Larssen and Davenport2001; Kang, Chester & Meneveau Reference Kang, Chester and Meneveau2003). Recently, in a very interesting experiment, Sinhuber, Bodenschatz & Bewley (Reference Sinhuber, Bodenschatz and Bewley2015) carried out measurements in passive grid turbulence with very high Reynolds number in the range
$5\leqslant x/M\leqslant 40$
by using air and pressurized sulphur hexafluoride (
$x$
is the distance downstream of the grid and
$M$
the grid mesh size). Note though that the results need to be analysed with care because, as shown by Isaza, Salazar & Warhaft (Reference Isaza, Salazar and Warhaft2014) (see also Lavoie Reference Lavoie2006), turbulence in the region
$x/M\leqslant 10{-}15$
has an ‘anomalous’ behaviour similar to that seen in fractal-grid turbulence, i.e. a larger decay power-law exponent and a turbulent kinetic energy dissipation coefficient that varies like
$Re_{{\it\lambda}}^{-1}$
(Valente & Vassilicos Reference Valente and Vassilicos2011) (it should be mentioned that the latter variation is also observed in the 3D periodic turbulence of Goto & Vassilicos (Reference Goto and Vassilocos2015)). In the near-field region downstream of the grid, the streamwise inhomogeneity may not be sufficiently weak to be neglected. Also the variation of
$Re_{{\it\lambda}}$
with
$x$
is strong enough so that it cannot be ignored. The reason for working with turbulence at high Reynolds number is to test HIT theories when there is a large separation between the large and small scales, i.e. when an inertial range exists and is represented by the
$5/3$
law in the Kolmogorov-normalized velocity spectrum or the
$2/3$
law in the second-order velocity structure function (K41). While the experimental implementation of high
$Re_{{\it\lambda}}$
grid turbulence is challenging, the realizability of very low
$Re_{{\it\lambda}}$
grid turbulence (i.e. final stage of decaying turbulence (Batchelor & Townsend Reference Batchelor and Townsend1948)) is equally challenging. In this latter case, the intensity of the background turbulence level is of the order of or greater than the turbulence generated by the grid, thus making the measurements of the decay practically impossible. There is also the practical issue associated with the fact that low
$Re_{{\it\lambda}}$
grid turbulence requires long distances downstream of the grid for the turbulence to become homogeneous in planes perpendicular to the mean flow. Thus, an experimental study of the final period of decaying turbulence is extremely difficult, if not impossible. There have been a few experimental investigations of the final period (e.g. Tan & Ling Reference Tan and Ling1963; Ling & Huang Reference Ling and Huang1970; Tavoularis, Bennett & Corrsin Reference Tavoularis, Bennett and Corrsin1978), but the results are still inconclusive for the reason cited above.
The difficulties encountered in achieving decaying grid turbulence with either very high or very low Reynolds number mean that the issue of the decay of the turbulent kinetic energy,
$k$
, is yet to be resolved. The lack of ideal flow conditions (e.g. very high or very low
$Re_{{\it\lambda}}$
) forces researchers to investigate the decay of turbulence in grid turbulence with low to moderate Reynolds number, e.g.
$Re_{{\it\lambda}}$
ranging from about 30 to 80. It is commonly believed that turbulence decays as a power law of the form
$k\sim x^{n}$
, where
$x$
is the downstream distance behind the grid and
$n$
is a negative constant. So far, the theoretical predictions show that turbulence may decay according to Batchelor (Reference Batchelor1949) or Saffman (Reference Saffman1967). Note though that these predictions are valid only at very high and very low
$Re_{{\it\lambda}}$
. The first measurements in grid turbulence appeared to show that
$n=-1$
(e.g. Batchelor & Townsend Reference Batchelor and Townsend1947). But it is now well accepted that
$n\leqslant -1$
, at least in grid turbulence generated in laboratories where
$Re_{{\it\lambda}}$
is neither very high nor very small. Under these conditions, the decay of turbulence is yet to be resolved, as illustrated by the various values of
$n$
reported in the literature. For example, in recent times, Krogstad & Davidson (Reference Krogstad and Davidson2010), who carried out measurements in grid turbulence with several grid geometries, argued that the turbulence behind a grid decays according to Saffman (
$n=-1.2$
, Saffman Reference Saffman1967). Hearst & Lavoie (Reference Hearst and Lavoie2014) reported values of
$n$
of about
$-1.37$
and
$-1.39$
in turbulence behind a fractal grid (for various values of
$n$
in decaying turbulence behind classical grids see Mohamed & LaRue (Reference Mohamed and LaRue1990) and Lavoie, Djenidi & Antonia (Reference Lavoie, Djenidi and Antonia2007)).
Recent numerical simulations (Meldi & Sagaut Reference Meldi and Sagaut2013) based on the eddy-damped quasi-normal Markovian (EDQNM) model of decaying HIT showed that the turbulence is in a transition period (from the initial to the final stages) when
$Re_{{\it\lambda}}$
ranges from approximately 1 to 100. The EDQNM results imply that, if one assumes that the turbulence decays according to a power law, then the power exponent
$n$
cannot be constant. Interestingly, this transition regime covers the range of
$Re_{{\it\lambda}}$
at which experiments in grid turbulence are carried out. Since it is well accepted that
$|n_{init}|\leqslant |n_{final}|$
, where
$|n_{init}|$
and
$|n_{final}|$
are the decay exponents at the initial and final stages of the decay, respectively, then
$n$
must vary from its initial period value to its final period value (as shown by Meldi & Sagaut Reference Meldi and Sagaut2013). In an earlier numerical study of decaying HIT, Orlandi & Antonia (Reference Orlandi and Antonia2004), who compared results based on EDQNM, pseudospectral DNS and finite differences DNS, also reported a variation of
$n$
for
$4\leqslant Re_{{\it\lambda}}\leqslant 2000$
.
The non-constancy of
$n$
would suggest that one needs to use a family of power laws of the form
$t^{n_{i}}$
, where
$n_{i}$
is a different constant over a portion
$i$
of the decay time during this transition period. If one then accepts that a series of power laws with different decay exponents is required to describe the decay of turbulence in the transition period, one is then forced to conclude that it is not possible to assess whether the turbulence decays according to Saffman (
$n_{init}=-1.2$
,
$n_{final}=-1.5$
; Saffman Reference Saffman1967), Batchelor (
$n_{init}=-10/7$
,
$n_{final}=-2.5$
; Batchelor Reference Batchelor1949) or any other possible type of decay from a single grid turbulence experiment if either the initial or the final stage of the decay is not part of the decay range covered by the measurements. Bekritskaya & Pavel’ev (Reference Bekritskaya and Pavel’ev1983) analysed the data of Batchelor (Reference Batchelor1948) and Gad-el-Hak & Corrsin (Reference Gad-el-Hak and Corrsin1974) and suggested that the decay could be approximated by a power law provided that the exponent increases with decreasing Reynolds number.
The present work focuses on the decay of a grid-generated turbulence when
$Re_{{\it\lambda}}$
varies from about 6 to 100. The aim of the study is to assess the appropriateness of a power-law decay of the form
$k\sim x^{n}$
and the behaviour of the exponent
$n$
.
2. Experimental set-up and measurement technique
The experiment is carried out in an open-circuit wind tunnel that was also used by Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) and Lee et al. (Reference Lee, Benaissa, Djenidi, Lavoie and Antonia2012). The air flow is driven by a centrifugal blower which is controlled by a variable-cycle (0–1500 r.p.m.) power supply. The blower is supported by dampers and connected to the tunnel by a flexible joint to minimize possible vibrations. At the inlet to a plenum chamber, an air filter
$(594~\text{mm}\times 594~\text{mm}\times 96~\text{mm})$
captures particles from the flow and a honeycomb
$(l/d\simeq 4.3)$
removes residual swirl. A wire screen with an open area ratio of 63 % and a smooth 9:1 primary contraction at the outlet of the plenum chamber improve the uniformity of the flow. A secondary (1.36:1) short contraction is mounted at a fixed location downstream of the turbulence generator, which corresponds to
$x/M=6.2$
, 19.2 and 54 for the LSQ43, SSQ43 and WMD36 grids (see below), respectively. This contraction is used to improve global isotropy (Comte-Bellot & Corrsin Reference Comte-Bellot and Corrsin1966) (more information on the secondary contraction can be found in Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007)). Because the velocity of the flow is accelerated when fluid flows through the secondary contraction an ‘equivalent’ time is defined as follows (Comte-Bellot & Corrsin Reference Comte-Bellot and Corrsin1966; Mohamed & LaRue Reference Mohamed and LaRue1990; Lavoie et al.
Reference Lavoie, Djenidi and Antonia2007):
$$\begin{eqnarray}t=\int _{0}^{x}\frac{\text{d}s}{\langle U(s)\rangle }\end{eqnarray}$$
where
$\langle U(s)\rangle$
is measured at the centreline of the working section. The angular brackets denote time averaging.
Figure 1. The geometry of the two different perforated grids (LSQ43 and SSQ43) and the woven mesh grid (WMG36).
Three grids are used to generate turbulence in the wind tunnel (figure 1). The first (LSQ43) is a flat plate perforated with large square holes yielding a mesh of size
$M=43.75$
mm and solidity,
${\it\sigma}$
, of about 43 %. The second, also made from a flat plate perforated with small square holes (SSQ43), has a mesh size
$M=14.15$
mm and the same solidity as the LSQ43 grid. The mesh size ratio between LSQ43 and SSQ43 is 3:1. The third is a woven mesh grid (WMG36) with
${\it\sigma}=36\,\%$
and
$M=5$
mm. The effect of the grid mesh Reynolds number
$Re_{M}=U_{0}M/{\it\nu}$
on the decay of turbulence is investigated at several different speeds. The use of these three grids and different values of
$U_{0}$
, the incoming velocity, yielded values of
$Re_{{\it\lambda}}$
in the range 6–100.
Figure 2. Streamwise variation of
$Re_{{\it\lambda}}$
for the grids used in the study. Red open symbols: ♢, ▫, ○
$\text{LSQ}43$
grid (
$Re_{M}=37\,500,17\,900$
and
$12\,950$
); black open symbols: ▫, ○
$\text{SSQ}43$
grid (
$Re_{M}=5800$
and 4170); blue open symbols: ▫, ○ WMG36 grid (
$Re_{M}=1474$
and 1200).
The streamwise variation of
$Re_{{\it\lambda}}$
for the three grids is presented in figure 2. Notice how the rate of decrease of
$Re_{{\it\lambda}}$
reduces as
$Re_{M}$
decreases. This makes the measurements at small Reynolds numbers quite difficult as a very large distance is required for
$Re_{{\it\lambda}}$
to change significantly.
The measurements of the velocity fluctuations
$u$
and
$v$
in the longitudinal and lateral directions, respectively, were carried out using hot-wire anemometry; both single and X wires were used. The wires (diameter
$d\approx 2.5~{\rm\mu}$
m and length
$l=200d$
) were etched from a coil of Wollaston (platinum) and were operated with in-house constant-temperature anemometers (hereafter, CTA) at overheat ratio of 1.5. The output signals from CTA circuits were amplified, offset and low-pass filtered at a cutoff frequency (
$f_{c}$
) close to the Kolmogorov frequency
$f_{K}=U_{0}/2{\rm\pi}{\it\eta}$
, where
${\it\eta}\,(={\it\nu}^{3/4}\langle {\it\epsilon}\rangle ^{-1/4})$
is the Kolmogorov length scale;
$\langle {\it\epsilon}\rangle$
is the mean dissipation rate of the turbulent kinetic energy. The sampling frequency
$f_{s}$
was at least
$2f_{c}$
. The hot-wire signals were digitized into a PC using a
$\pm 10$
V and 16 bit AD converter. Measurements were conducted at several distances downstream from the grid. The ratio
${\it\eta}/l$
varied from about 0.26 to about 3.6 across all measurement sets.
3. Results
3.1.
$Re_{{\it\lambda}}$
dependence of the power-law decay
The decay of the mean turbulent kinetic energy downstream of a grid is commonly represented by a power law:
$$\begin{eqnarray}\langle q^{2}\rangle =A(x-x_{0})^{n}\end{eqnarray}$$
where
$\langle q^{2}\rangle =\langle u^{2}\rangle +\langle v^{2}\rangle +\langle w^{2}\rangle$
is twice the turbulent kinetic energy,
$x$
(
$=tU_{0}/M$
,
$t$
is the time) is a distance downstream of the grid,
$x_{0}$
is a virtual origin and
$n\leqslant -1$
;
$A$
,
$x_{0}$
and
$n$
are to be determined empirically. Note that, strictly, the distance
$x$
as used in (3.1) is not the actual distance downstream of the grid but an equivalent one as it accounts for the acceleration of the flow through the short contraction (i.e.
$t$
is given by (2.1)). Since
$v^{2}=w^{2}$
in the turbulence generated by each grid, we have
$\langle q^{2}\rangle =\langle u^{2}\rangle +2\langle v^{2}\rangle$
, which eliminates the necessity to measure the third velocity component. For the single-wire measurements, we used
$\langle q^{2}\rangle =\langle u^{2}\rangle (1+2/r_{uv})$
with
$r_{uv}=\langle u^{2}\rangle /\langle v^{2}\rangle$
estimated from the X-wire measurements.
$A$
,
$x_{0}$
and
$n$
are assumed to be constant in (3.1). Yet, one expects that
$|n|$
should increase to reach its final value
$n_{final}$
when
$Re_{{\it\lambda}}$
decreases. In grid turbulence,
$Re_{{\it\lambda}}$
decreases with increasing
$x$
, as shown in figure 2, and thus one can expect that
$|n|$
increases with
$x$
. However, if the rate of change in
$Re_{{\it\lambda}}$
over some distance
$x$
is small enough (see figure 2), one may assume
$n$
to be constant to a first approximation; this is the usual approach reported in the literature. Figure 2 indicates that, while such an approximation seems valid for SSQ43 and WMG36 over a relatively long distance, it is not as evident for LSQ43 because of the relatively short distance. Nevertheless, we follow the common practice of assuming that the variation in
$Re_{{\it\lambda}}$
for the LSQ43 grid is small enough in the region
$U_{0}t/M\geqslant 25$
to ignore. Thus, for each set of measurements with the three grids,
$n$
will be assumed to be independent of
$x$
and (3.1) will hold, as illustrated in figure 3, which shows, in a log–log representation, the variation of both
$\langle q^{2}\rangle$
and
$\langle {\it\epsilon}\rangle$
with the distance
$(x-x_{0})/M$
. The figure shows that
$\langle q^{2}\rangle$
follows a straight line relatively well for each grid, supporting the law (3.1) over the range of
$x$
considered. Since the transport equation for
$\langle q^{2}\rangle$
in grid turbulence is
$$\begin{eqnarray}\langle {\it\epsilon}\rangle =-\frac{U_{0}}{2}\frac{\partial \langle q^{2}\rangle }{\partial x},\end{eqnarray}$$
then using (3.1) leads to
$\langle {\it\epsilon}\rangle \sim (x-x_{0})^{n-1}$
. It is important to stress that, strictly, (3.2) holds when the production of the turbulent and viscous diffusions of
$\langle q^{2}\rangle$
is zero, which is the case in grid turbulence when
$x$
is at least larger than
$20M$
–
$25M$
. Djenidi & Antonia (Reference Djenidi and Antonia2014) showed that
$\langle {\it\epsilon}\rangle =({\it\nu}/2)\langle (\partial u_{i}/\partial x_{j})+(\partial u_{j}/\partial x_{i})\rangle$
, with all terms included, satisfies (3.2) when
$x/M\geqslant 25$
behind a grid made of floating flat square elements and with a solidity of about 25 %. They also found that (3.2) cannot be used to obtain
$\langle {\it\epsilon}\rangle$
when
$x/M\leqslant 25$
(see also Lavoie Reference Lavoie2006). The power-law decay of
$\langle {\it\epsilon}\rangle$
is supported by the data in figure 3. The slope of the straight lines, which gives the value of
$|n|$
, increases as
$Re_{M}$
(or equivalently
$Re_{{\it\lambda}}$
) decreases, confirming that the magnitude of
$n$
increases with a decreasing
$Re_{{\it\lambda}}$
. It is interesting that the value of
$\langle {\it\epsilon}\rangle$
inferred from (3.2) is equal to the isotropic value
$\langle {\it\epsilon}_{iso}\rangle$
, which Djenidi & Antonia (Reference Djenidi and Antonia2014) showed is equal to the actual value of
$\langle {\it\epsilon}\rangle$
for
$x/M\geqslant 10$
.
Figure 3. Decay of
$\langle q^{2}\rangle$
and
$\langle {\it\epsilon}\rangle$
for different grids and
$Re_{M}$
. Open red symbols: LSQ43, ▫:
$Re_{M}=17900$
, ▵:
$Re_{M}=12950$
. Open black symbols: SSQ43, ▫:
$Re_{M}=5800$
, ▵:
$Re_{M}=4170$
. Open blue symbols: WMG36, ▫:
$Re_{M}=2000$
, ▵:
$Re_{M}=1474$
.
Table 1. Decay exponent
$n$
for LSQ43, SSQ43 and WMG36.
The determination of
$n$
is conditioned by
$x_{0}$
. It is then critical that
$x_{0}$
is obtained as accurately and unambiguously as possible. In this study, it was estimated by using a trial-and-error method adopted by Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1966) and later Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007). Assuming the decay laws (3.1) and (3.2), we have
${\it\lambda}^{2}=10{\it\nu}(q^{2}/\langle {\it\epsilon}\rangle )=-(10{\it\nu}/U_{0}n)((tU_{0}/M_{0})-(t_{0}U_{0}/M))$
. Different values of
$tU_{0}/M~(=x_{0})$
were tried until
${\it\lambda}^{2}/MU_{0}(t-x_{0})$
exhibited the longest plateau when plotted against
$U_{0}(t-t_{0})/M$
. This is illustrated in figure 4 for SSQ43 at
$Re_{M}=4710$
. Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) showed that the uncertainty in
$x_{0}$
is about
$\pm 1$
, which results in a
$\pm 0.03$
variation in the estimate of
$n$
.
Figure 4. Examples of plots used for estimating the virtual origin. Ratio
${\it\lambda}^{2}/MU_{0}(t-t_{0})$
for SSQ43 and
$U_{0}=4.6$
m s
$^{-1}$
. The curve exhibiting the longest plateau corresponds to
$U_{0}t_{0}/M$
used in the power law (3.1).
Table 1 contains values of
$U_{0}$
,
$x_{0}$
,
$n$
, the ratio
$r_{uv}$
,
$Re_{{\it\lambda}}$
,
$Re_{M}$
,
${\it\eta}/M$
and
$L/M$
. Interestingly, the values of
$x_{0}$
and
$r_{uv}$
for a given grid appear to be independent of
$Re_{M}$
. Of interest are the values of
${\it\eta}/M$
and
$L/M$
across the various set of measurements. The maximum value of
$L/M$
is about 1.9, which suggests that the lateral dimensions of the tunnel are large enough to neglect any effect they may have on the decay of turbulence. Figure 5(a) shows the variation of
$n$
as function of
$Re_{{\it\lambda}}$
. We also show in figure 5(b) various values of
$n$
extracted from several studies cited in table 2. The trend of the present data (figure 5
a) is consistent with that seen in figure 5(b), i.e. the value of
$-n$
increases when
$Re_{{\it\lambda}}$
decreases. When
$Re_{{\it\lambda}}$
becomes large,
$n$
tends to approach a constant. It is not clear whether the scatter observed for
$n$
at large
$Re_{{\it\lambda}}$
is due to measurement uncertainties or reflects an actual effect of the initial conditions. These measurements were obtained in active decaying grid turbulence (see table 2 for the references).
Figure 5 highlights the need to exercise caution when interpreting the results of decaying grid turbulence in the context of determining whether it follows the Saffman (
$n=-1.2$
; Saffman Reference Saffman1967) or Batchelor (
$n=-10/7$
; Batchelor Reference Batchelor1948) decay laws at low
$Re_{{\it\lambda}}$
. In particular, when the Reynolds number is below about 100, one cannot conclude, solely on the basis of the value of
$n$
, whether the turbulence decays according to Saffman (Reference Saffman1967) or Batchelor (Reference Batchelor1948) because
$n$
has departed from its value at high Reynolds number, and
$Re_{{\it\lambda}}$
is not small enough for
$n$
to have reached its ‘final period’ value. The present results do not agree with the results of Ling & Huang (Reference Ling and Huang1970), who argue that
$n=-2$
when
$Re_{{\it\lambda}}\leqslant 30$
.
Figure 5. Decay exponent
$n$
as function of
$Re_{{\it\lambda}}$
. (a) Present three grids. (b) Selection of data from the literature. See table 2 for the symbols and their references.
Figure 6. Variation of
$n$
as function of
$Re_{{\it\lambda}}$
. Solid circles, same as in figure 5; stars, present data using (3.3) (the thin dash-dotted line through the symbols is used only as a visual guide); solid triangles, EDQNM (Orlandi & Antonia Reference Orlandi and Antonia2004); ▫, pseudospectral (Orlandi & Antonia Reference Orlandi and Antonia2004); lines, EDQNM (Meldi & Sagaut Reference Meldi and Sagaut2013) with
$n_{init}=-10/7$
(dashed) or
$n_{init}=-1.2$
(solid). The transition regime is only tentatively delimited by the vertical lines. This range corresponds to that in which the majority of the data for
$n$
, as inferred from decaying turbulence behind passive grids, has been reported.
Table 2. Reference table for the decay exponent. Symbols are used in figure 5(b). The data were compiled by Lee et al. (Reference Lee, Djenidi, Antonia and Danaila2013).
The present variation of the decay exponent with
$Re_{{\it\lambda}}$
is compared (figure 6) with that from the numerical simulations of Orlandi & Antonia (Reference Orlandi and Antonia2004) and Meldi & Sagaut (Reference Meldi and Sagaut2013). The data of Orlandi & Antonia (Reference Orlandi and Antonia2004) correspond to Batchelor decaying turbulence, while those of Meldi & Sagaut (Reference Meldi and Sagaut2013) correspond to both Batchelor and Saffman decaying turbulence. Meldi & Sagaut (Reference Meldi and Sagaut2013) showed that different curves
$n=f(Re_{{\it\lambda}})$
are obtained with different initial values of
$n_{init}$
. Although the EDQNM curves deviate from the experimental data, both the experiments and simulations indicate unambiguously that
$n$
varies in the transition period, thus revealing that the decay of turbulence cannot strictly follow a unique power law in this transition period. Nevertheless, one may consider using a family of power laws of the form
$x^{n_{i}}$
, where
$n_{i}$
is a different constant over a portion
$i$
of the decay time during this transition period or region. A possible practical alternative that one can infer from figure 6 is to use a power law of the form
$\langle q^{2}\rangle \sim x^{n_{init}+m(x)}$
, where the continuous function
$m(x)$
is such that
$n_{final}-n_{init}\leqslant m(x)\leqslant 0$
. This latter form could be used to describe the entire decay (i.e. initial, transient and final stages). Since most of the grid turbulence measurements are carried out in the transition region, it is not surprising that a rather large range of values of
$n$
has been reported in the literature and mistakenly assigned to the initial period of decay. Interestingly, the experimental values of
$-n$
at the higher
$Re_{{\it\lambda}}$
fall below those of both Saffman and Batchelor. While no definite conclusion can be drawn from figure 6 on the actual type of decay, this result does not support the argument that grid turbulence, at least when generated by the present grids, is likely to follow Saffman (Krogstad & Davidson Reference Krogstad and Davidson2010), although it is closer to Saffman than Batchelor. Further, the data in figure 5(b) suggest that the decay of turbulence behind active grids follows neither Saffman nor Batchelor, as indicated by the values of
$n$
at large
$Re_{{\it\lambda}}$
.
Recently, Djenidi & Antonia (Reference Djenidi and Antonia2015) used a self-preservation (SP) analysis on the scale-by-scale energy budget equation for decaying HIT and developed an expression for
$n$
with an explicit dependence on
$Re_{l}$
:
$$\begin{eqnarray}n=-1+2(t-t_{0})\frac{1}{Re_{l}}\frac{\text{d}Re_{l}}{\text{d}t}.\end{eqnarray}$$
where
$Re_{l}$
is a Reynolds number based on a set of velocity and length scales conforming with SP. Expression (3.3) is valid strictly when SP is satisfied at all scales of motion. If one assumes that SP is approximately satisfied in decaying grid turbulence, i.e.
$Re_{{\it\lambda}}$
varies weakly downstream of the grid, then one can expect (3.3) with
$Re_{{\it\lambda}}$
replacing
$Re_{l}$
to be approximately valid. This appears to be confirmed in figure 6, where the values of
$n$
calculated with (3.3) are reported. There is relatively good agreement between these latter values and those of
$n$
inferred from the power-law decay.
Note that care must be taken when measuring
$n$
when a power-law decay is assumed. One must ensure that
$Re_{{\it\lambda}}$
decreases weakly in the region considered. This is not the case in the near-grid region, as highlighted in figure 2. This is most evident for a fractal-grid turbulence (Valente & Vassilicos Reference Valente and Vassilicos2011; Hearst & Lavoie Reference Hearst and Lavoie2014) where the near-grid region is larger than for conventional grid turbulence. Despite this shortcoming, Valente & Vassilicos (Reference Valente and Vassilicos2011) and Hearst & Lavoie (Reference Hearst and Lavoie2014) measured
$n$
and found values of about
$-$
2.5 and
$-$
2.79, respectively, in the near-grid region. Associated with a rapid decay of turbulence in the near grid, one must also consider the effect of the lateral inhomogeneity of the flow caused by the individual wakes generated by the grid elements. Corrsin (Reference Corrsin1963) proposed at least three criteria that must be satisfied for ensuring homogeneity in grid turbulence (grid made of horizontal and vertical bars): (i) large grid porosity, (ii) large
$L=M$
(
$L$
is the height/diameter of the wind tunnel) and (iii) measurements should be taken at least
$40M$
downstream of the grid (see also Grant & Nisbet Reference Grant and Nisbet1957). As mentioned in the introduction, recently Sinhuber et al. (Reference Sinhuber, Bodenschatz and Bewley2015) carried out measurements in a (conventional) passive grid turbulence with very high Reynolds number (
$10^{4}\leqslant Re_{M}\leqslant 5\times 10^{6}$
; unfortunately no value of
$Re_{{\it\lambda}}$
is provided in their paper). They measured
$n=-1.18$
, and argued that the turbulence decays according to Saffman. However, while the Reynolds number is very high, the range of
$x/M$
over which they measured
$n$
falls within the region where turbulence is not homogeneous. Further, the results of Sinhuber et al. (Reference Sinhuber, Bodenschatz and Bewley2015) contrast with those of Isaza et al. (Reference Isaza, Salazar and Warhaft2014), who showed that the turbulence in the region
$5\leqslant x/M\leqslant 15$
is not homogeneous and
$n=-1.9$
, while
$n=-1.34$
for
$15\leqslant x/M\leqslant 70$
. They also showed that turbulence in the first range (referred to as the near-field) displays an anomalous behaviour similar to that observed in fractal-grid turbulence. Nevertheless, it is noteworthy to point out that Sinhuber et al. (Reference Sinhuber, Bodenschatz and Bewley2015) made a compilation of values of
$n$
as a function of
$Re_{M}$
from previous studies in decaying HIT. The trend shown by the data is in good agreement with the present results. However, the authors did not identify the transitional period and attributed the variation of
$n$
with
$Re_{M}$
to changes in initial and boundary conditions between experiments.
Finally, comments are warranted on the nature of the initial and transition periods of decay in HIT. The initial period is associated with a high
$Re_{{\it\lambda}}$
and an approximately constant
$n$
followed by the transition period where
$n$
varies. In grid turbulence, the hypothesis of HIT can only be valid when the flow becomes homogeneous in a plane perpendicular to the main flow and very weakly inhomogeneous along the main flow, which, according to Corrsin (Reference Corrsin1963), is well observed when
$x/M\geqslant 40$
. It is thus important not to associate the decay of turbulence in the region
$x/M\leqslant 40$
with the initial period, even though
$Re_{{\it\lambda}}$
can be large; or at least one must ensure that turbulence is homogeneous in a plane perpendicular to the main flow in that region. On the other hand, so far, the decay in passive grid turbulence observed in the literature for
$x/M\geqslant 40$
where the values of
$n$
fall within the range obtained here is consistent with the transition period observed in this study.
4. Conclusion
A grid-generated turbulence at moderate to low
$Re_{{\it\lambda}}$
was investigated with the aim of ascertaining whether the commonly used power-law decay of the turbulent kinetic energy,
$k$
, is appropriate. Several grid geometries were used to allow
$Re_{{\it\lambda}}$
to vary from about 6 to 100, a range that covers most of the Reynolds numbers obtained in passive grid turbulence reported in the literature. It is shown that the decay of turbulence does not strictly follow a power law of the form
$k\sim x^{n}$
with
$n$
constant. The results, supported by the numerical data of decaying HIT (Orlandi & Antonia Reference Orlandi and Antonia2004; Meldi & Sagaut Reference Meldi and Sagaut2013) and the experimental results (see Sinhuber et al. (Reference Sinhuber, Bodenschatz and Bewley2015) for a compilation of values of
$n$
in various experiments and simulations of decaying HIT), suggest that, on an empirical ground at least, one may consider using a family of power laws of the form
$x^{n_{i}}$
, where
$n_{i}$
is a different constant over a portion
$i$
of the decay time during this transition period, with
$|n_{i}|$
increasing as
$Re_{{\it\lambda}}$
decreases, and
$n_{final}\leqslant n_{i}\leqslant n_{init}$
. A possible practical alternative for describing the entire decay is
$\langle q^{2}\rangle \sim x^{n_{init}+m(x)}$
, where
$n_{final}-n_{init}\leqslant m(x)\leqslant 0$
.
The present study sheds light on the lack of consensus in the literature on the value of
$n$
for what is presumed to be the initial period of decay for grid turbulence. It also underlines the current impossibility of differentiating between the Batchelor and Saffman predictions for the value of
$n$
in the initial period. The range
$-$
1.4 to
$-$
1.1 for
$n$
reported in the literature indicates that the measurements have almost certainly been carried out in what should more appropriately be designated as the transition period of decay, at least for passive decaying grid turbulence.
To address properly the question of the decay of turbulence behind a grid, one is required to perform measurements in a very long wind tunnel so the variation of
$Re_{{\it\lambda}}$
downstream of the grid is significant enough to lead to a non-negligible variation in
$n$
, if a solution in the form of a power law is sought. The range of
$x/M$
to consider for such a study should correspond to the range where turbulence is homogeneous in the lateral directions and weakly inhomogeneous in the streamwise direction. This range is beyond the near-grid region of classical grid turbulence that Hearst & Lavoie (Reference Hearst and Lavoie2014) and Isaza et al. (Reference Isaza, Salazar and Warhaft2014) identified with the ‘anomalous’ behaviour range.
The present results (e.g. figure 6) suggest that, ideally, the Taylor microscale Reynolds number should vary from about 0.1 to about 300. Sinhuber et al. (Reference Sinhuber, Bodenschatz and Bewley2015) showed that a very high
$Re_{M}$
can be achieved with conventional passive grids in the region
$x/M\leqslant 30$
. However, these high
$Re_{M}$
measurements need to be extended in the region
$x/M\geqslant 40$
and over a long distance so both the initial and the transition periods of the decay can be observed in grid turbulence. The final period of decay can be achieved over a long distance downstream of the grid, but the background turbulence prevents any reliable measurements.
Acknowledgement
The financial support of the Australian Research Council is gratefully acknowledged.
