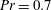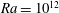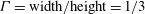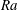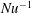1. Introduction
Rayleigh–Bénard (RB) convection (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012) is a system in which a fluid is heated from below and cooled from above and convection arises due to the density differences induced by the different temperatures. This system is used to model natural convection, preserving most of the relevant phenomena while reducing the complexity of the problem. As is commonly done and well justified, we adopt the Boussinesq approximation, i.e. the fluid properties are assumed to be independent of the temperature except in the buoyancy term of the momentum equation.
RB convection features ubiquitous coherent structures, which continue to survive in strong turbulence. The most prevalent structures are thermal plumes and large-scale circulation (LSC). The thermal plumes and LSC are intrinsically coupled (Grossmann & Lohse Reference Grossmann and Lohse2004), as thermal plumes cluster to form a LSC (Parodi et al. Reference Parodi, von Hardenberg, Passoni, Provenzale and Spiegel2004; Xi, Lam & Xia Reference Xi, Lam and Xia2004) and fragment in the bulk (Bosbach, Weiss & Ahlers Reference Bosbach, Weiss and Ahlers2012). In addition, both thermal and shear instabilities can result in the emission of buoyant fluid parcels, as was shown by Hunt et al. (Reference Hunt, Vrieling, Nieuwstadt and Fernando2003), who distinguished between plumes and puffs. Here this distinction is not made, and all buoyant parcels are classified as plumes, irrespective of the mechanism behind their origin. Zhou, Sun & Xia (Reference Zhou, Sun and Xia2007) divided the plumes into ‘sheet’ or ‘line’ plumes of elongated shape and circular ‘mushroom’ plumes. They showed that the plumes are predominantly sheetlike close to the plates and mushroomlike higher in the system. Eventually the numbers of both types of plumes are shown to decrease with height. We will connect this phenomenon to the clustering of plumes by using a plume identification criterion and image segmentation.
The concept of thermal plumes has been used to directly and indirectly derive scaling laws for the heat flux by Castaing et al. (Reference Castaing, Gunaratne, Heslot, Kadanoff, Libchaber, Thomae, Wu, Zaleski and Zanetti1989) and Grossmann & Lohse (Reference Grossmann and Lohse2004), respectively. This is because the contribution of thermal plumes to the total heat flux, relative to that of the LSC, is substantial (Belmonte, Tilgner & Libchaber Reference Belmonte, Tilgner and Libchaber1993). It is generally assumed that thermal plumes have a characteristic width equal to that of the thermal boundary layer, which stems from the understanding that thermal plumes are detached thermal boundary layers. This assumption is used by Castaing et al. (Reference Castaing, Gunaratne, Heslot, Kadanoff, Libchaber, Thomae, Wu, Zaleski and Zanetti1989) and Grossmann & Lohse (Reference Grossmann and Lohse2004) to derive scaling laws for the heat flux through the system. We attempt to extract the plume width and thereby substantiate this assumption.
The dynamics of plumes is complex. Plumes move not only vertically but also horizontally, being advected by the LSC, as was observed by Sano, Wu & Libchaber (Reference Sano, Wu and Libchaber1989). In addition, the dynamics of the LSC is highly non-trivial (Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005; Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009; Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), affecting the collective motion of the thermal plumes through an opposing pressure gradient. This complicates the simple (two-dimensional) picture of a stationary LSC with thermal plumes moving alongside it that was sketched by Kadanoff (Reference Kadanoff2001) (see figure 1), as Ching et al. (Reference Ching, Guo, Shang, Tong and Xia2004) and Emran & Schumacher (Reference Emran and Schumacher2012) have shown that plumes are found in the centre of the cell and even throughout the entire volume. Recently, Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014) found in a Taylor–Couette (TC) flow that the boundary layer transition from laminar to turbulent occurs in plume-ejecting locations at lower driving than in the wind-sheared region. It was shown by Eckhardt, Grossmann & Lohse (Reference Eckhardt, Grossmann and Lohse2007) that RB is analogous to TC, which raises the question of whether this phenomenon can also be observed in RB. Because the driving in RB is less efficient than in TC, turbulent boundary layers, such as those seen in RB by Ahlers et al. (Reference Ahlers, Bodenschatz, Funfschilling, Grossmann, He, Lohse, Stevens and Verzicco2012), are difficult to observe due to the required high
$\mathit{Ra}$
and long averaging time. This prevents a study in RB convection comparable to the TC flow study by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014). However, it is possible to study the connection between wind shear and plume ejection and hence gain insights into how shear is related to thermal plumes and in turn to boundary layer turbulence. The turbulent boundary layer in RB is an important ingredient in expected heat flux scaling arguments by Kraichnan (Reference Kraichnan1962) and Grossmann & Lohse (Reference Grossmann and Lohse2011) for the ultimate regime.
Figure 1. Sketch of a confined Rayleigh–Bénard system with
${\it\Gamma}\approx 1$
. A large-scale circulation and plume paths are indicated, as well as the positions of the three different horizontal boundary regions: impacting, wind-shearing and ejecting. The corner rolls are not shown.
2. Method
Direct numerical simulations (DNS) of the Boussinesq equations were performed using a second-order staggered finite difference scheme by Verzicco & Camussi (Reference Verzicco and Camussi1999, Reference Verzicco and Camussi2003) that is energy conserving. The governing equations in dimensionless form are
$$\begin{eqnarray}\displaystyle & \partial _{t}u_{i}+u_{j}\partial _{j}u_{i}=-\partial _{i}p+\sqrt{\displaystyle \frac{\mathit{ Pr }}{\mathit{Ra }}}\,\partial _{j}^{2}u_{i}+{\it\theta}{\it\delta}_{i3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \partial _{t}{\it\theta}+u_{j}\partial _{j}{\it\theta}=\displaystyle \frac{1}{\sqrt{\mathit{Ra }\,\mathit{Pr}}}\,\partial _{j}^{2}{\it\theta}, & \displaystyle\end{eqnarray}$$
$\hat{\boldsymbol{e}}_{3}$
is the unit vector that is antiparallel to gravity,
$u_{i}$
is the velocity normalized by the free-fall velocity
$\sqrt{g{\it\beta}{\rm\Delta}L}$
,
$t$
is the time normalized by the free-fall time
$\sqrt{L/(g{\it\beta}{\rm\Delta})}$
and
${\it\theta}$
is the temperature normalized by
${\rm\Delta}$
, the temperature difference between the top and bottom plates. The control parameters of the system are the non-dimensional temperature difference, i.e. the Rayleigh number
$\mathit{Ra}=g{\it\beta}{\rm\Delta}L^{3}/({\it\nu}{\it\kappa})$
, the Prandtl number
$\mathit{Pr}={\it\nu}/{\it\kappa}$
of the fluid and the aspect ratio
${\it\Gamma}=D/L$
, where
$L$
is the height of the sample and
$D$
is its width,
$g$
is the gravitational acceleration,
${\it\beta}$
is the thermal expansion coefficient,
${\it\nu}$
is the kinematic viscosity and
${\it\kappa}$
is the thermal diffusivity. The boundary conditions chosen are no-slip conditions on all walls for the velocity, adiabatic conditions on the sidewall and isothermal conditions on the horizontal plates for temperature. The numerical set-up has a Prandtl number of
$\mathit{Pr}=0.7$
and an aspect ratio of
${\it\Gamma}=1/3$
. In addition, for fixed
$\mathit{Ra}$
, a low-aspect-ratio domain is computationally less demanding than a large-aspect-ratio domain due to the smaller volume. The resolutions used are up to
$1536\times 512\times 2048$
for Rayleigh number
$\mathit{Ra}=10^{12}$
with clustering of grid points near the boundaries similar to the previous high-
$\mathit{Ra}$
DNS of Stevens, Lohse & Verzicco (Reference Stevens, Lohse and Verzicco2011). The Nusselt number
$\mathit{Nu}$
, which quantifies the area-averaged heat flux, is calculated as both an area average of the convective term,
$\mathit{Nu}=\sqrt{\mathit{Ra }\,\mathit{Pr}}\,\langle u_{z}{\it\theta}\rangle _{r,{\it\phi},t}+1$
, and a line average on the horizontal plates of the diffusive term,
$\mathit{Nu}=-\langle \partial _{z}{\it\theta}|_{z=0,L}\rangle _{r,{\it\phi},t}$
. We verify these results for
$\mathit{Nu}$
by also calculating
$\mathit{Nu}$
through the kinetic and thermal dissipation rates (Shraiman & Siggia Reference Shraiman and Siggia1990; Siggia Reference Siggia1994). Horizontal cross-sections of
$u_{r,{\it\phi},z}(r,{\it\phi})$
and
${\it\theta}(r,{\it\phi})$
are used that have a time interval of 0.5 free-fall time. This interval is tested for statistical independence and shown to be sufficient. The number of cross-sections required for statistical convergence is approximately 100.
Figure 2 shows the compensated
$\mathit{Nu}$
as a function of
$\mathit{Ra}$
compared with previous results obtained at
${\it\Gamma}=1/2$
. It is apparent that the heat fluxes for
${\it\Gamma}=1/3$
and
${\it\Gamma}=1/2$
are within the error bars of the data. In addition, no transition in the
$\mathit{Nu}$
(
$\mathit{Ra}$
) scaling towards the steeper scaling (the so-called ultimate regime) is observed, and the system can be considered to be in the classical regime, i.e. the boundary layers are not yet turbulent, consistent with the theoretical expectation at
$\mathit{Ra}\leqslant 10^{12}$
(Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2011; Stevens et al.
Reference Stevens, van der Poel, Grossmann and Lohse2013).
Figure 2. Compensated Nusselt number
$\mathit{Nu}/\mathit{Ra}^{1/3}$
as a function of
$\mathit{Ra}$
. The blue squares indicate the DNS data for
${\it\Gamma}=1/2$
of Stevens et al. (Reference Stevens, Lohse and Verzicco2011); the data used in this paper for
${\it\Gamma}=1/3$
is represented by the orange triangles; the solid black curve is the result of the Grossmann–Lohse fit for
$\mathit{Pr}=0.7$
from Stevens et al. (Reference Stevens, van der Poel, Grossmann and Lohse2013).
Various methods for detecting plumes have been used previously, as reviewed by Ching et al. (Reference Ching, Guo, Shang, Tong and Xia2004). We define a thermal plume as the set of coordinates
$P$
where
${\it\theta}(r,{\it\phi})-\langle {\it\theta}\rangle _{r,{\it\phi}}>c{\it\theta}_{RMS}$
and
$\sqrt{\mathit{Ra }\,\mathit{Pr}}\,u_{z}(r,{\it\phi}){\it\theta}(r,{\it\phi})>c\,\mathit{Nu}$
, as Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) did in their study on confined RB convection. This criterion selects coordinates based on a high temperature anomaly and an excess of convective heat flux. Only hot plumes in the lower half of the domain are considered. The empirical constant
$c$
was chosen to be 0.8 in Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013), but here we take
$c=1.2$
to better separate the plumes from the background and emphasize their core structure. In addition, this choice of
$c$
matches the absolute value of the plume with the thermal boundary layer thickness, as will become apparent later on. A similar threshold based only on
$u_{z}{\it\theta}$
was used by Emran & Schumacher (Reference Emran and Schumacher2012), where they found no qualitative differences in their results when the threshold was varied by two orders of magnitude. Along the lines of what was already shown there, quantitatively our results do depend on the value of threshold
$c$
. In figure 3(d–f) the results of applying this criterion to the temperature snapshots shown in figure 3(a–c) are depicted. It should be noted that this method of extracting thermal plume information limits the analysis to treating the plume as a two-dimensional entity, although in reality it is three-dimensional.
Figure 3. Temperature field snapshots for
$\mathit{Ra}=10^{11}$
at (a)
$z/L=0.004$
, (b)
$z/L=0.04$
and (c)
$z/L=0.2$
; hot and cold are indicated by red and blue, respectively, with colour maps displayed above the corresponding snapshots. Detection of thermal plumes
$P$
corresponding to the temperature field snapshots in (a)–(c) are shown in (d)–(f), respectively, where white indicates a plume.
3. Plume size as a function of vertical position
Previous studies have revealed a log–normal distribution for the area of the plume (Zhou et al.
Reference Zhou, Sun and Xia2007), for the length of the plumes (Bosbach et al.
Reference Bosbach, Weiss and Ahlers2012) and for the spacing between the plumes (Puthenveettil & Arakeri Reference Puthenveettil and Arakeri2005). These results suggest that the three quantities are intrinsically related to each other. The log–normal distribution suggests a fragmentation process that can be dealt with by the central limit theorem. The physical mechanism resulting in this distribution is that the fluctuations, acting on all scales, fragment the plumes (Zhou & Xia Reference Zhou and Xia2010). When modelling this process, the fragmentations are iterated, and a new sample is drawn from some distribution at each individual fragmentation. After many of these iterations, in each of which the plume area is always subdivided, a log–normal distribution results. We use the data at
$\mathit{Ra}=10^{11}$
to analyse the resulting plume area distribution as a function of
$z$
, because this gives the optimum available
$\mathit{Ra}$
with respect to minimum sidewall influence and the amount of statistics collected.
In figure 4(a) we plot the probability density functions of the plume areas at three vertical locations for
$\mathit{Ra}=10^{11}$
. Closest to the plate, the distribution is unimodal and log–normal, which is illustrated by the quite accurate Gaussian fit to the data in the semi-log plot. Higher in the cell, the distribution becomes weakly bimodal. We interpret the second mode, indicating a larger plume area, as a reflection of plume clustering, which is a signature of the LSC, as the large-scale roll contains clusters of hot plumes in its upwelling region. The small area peaks indicate the existence of fragmented smaller plumes traversing the bulk. This view is supported by the data displayed in figure 4(b), where the most probable area is plotted as a function of the vertical location
$z$
. For all
$z$
, the most probable area is characterized by the smaller plumes, as in all of these bimodal distributions at
$\mathit{Ra}=10^{11}$
the right peak is considerably smaller than the left one. In figure 4(b) the thermal boundary layer thickness
${\it\lambda}_{{\it\theta}}$
based on the time- and volume-averaged
$\mathit{Nu}$
is shown. It can be seen that for
$\mathit{Ra}=10^{11}$
there is a region, extending much beyond
${\it\lambda}_{{\it\theta}}$
, where the most probable area is nearly constant. Beyond that region, the area of the small plumes decreases with height, a reflection of the fact that thermal plumes dissipate most of their energy near the plates (Kaczorowski & Wagner Reference Kaczorowski and Wagner2009) and are weakened through molecular and turbulent diffusion while moving towards the bulk of the flow higher in the cell (Tilgner, Belmonte & Libchaber Reference Tilgner, Belmonte and Libchaber1993). The small plumes either become smaller or cluster to become part of the LSC, thus driving it.
Figure 4. (a) Probability density functions (PDF) of the plume areas
$A_{P}$
(normalized by the total area) at different vertical locations
$z$
indicated in the legend for
$\mathit{Ra}=10^{11}$
; the solid curve is a log–normal fit to the data at
$z/L=0.002$
, and the grey dashed line indicates the characteristic plume area
$A_{c}$
. (b) The most probable value (Mo) of the PDF at each of the measured
$z$
values; the blue dashed line indicates the mean thermal boundary layer thickness
${\it\lambda}_{{\it\theta}}=1/(2\mathit{Nu})$
.
The clustering is further highlighted by the behaviour of the plume number
$N_{p}$
as a function of height
$z$
, plotted in figure 5(a). It can be seen that
$N_{p}$
decreases strongly with
$z$
in the bulk, indicating the clustering and dissipation of plumes. In addition, there appears to be a region close to the lower boundary where
$N_{p}$
is approximately constant. The vertical extent of this region decreases with
$\mathit{Ra}$
, which signifies the relation of this region to the boundary layer thickness. Close to the upper boundary,
$N_{p}$
displays a steep drop-off, the location of which depends on
$\mathit{Ra}$
: the hot plumes travel further in the vertical direction for higher
$\mathit{Ra}$
. In figure 5(b), the normalized
$N_{p}^{\prime }$
is plotted as function of
$z/{\it\lambda}_{{\it\theta}}$
. Here
$N_{p}^{\prime }$
is the number of plumes normalized by
$N_{p}$
at
$z/{\it\lambda}_{{\it\theta}}=4.5$
. The profiles for
$\mathit{Ra}=10^{11}$
and
$\mathit{Ra}=10^{12}$
look strikingly similar, hinting at a universal profile for high
$\mathit{Ra}$
.
Figure 5. (a) The number
$N_{p}$
of hot plumes plotted as a function of height
$z/L$
for
$\mathit{Ra}=10^{10},10^{11}$
and
$10^{12}$
; the error bars increase with increasing height but are omitted from the last few data points for clarity. (b) The normalized number of plumes,
$N_{p}^{\prime }$
, plotted as a function of
$z/{\it\lambda}_{{\it\theta}}$
, where
$N_{p}^{\prime }$
is the number of plumes normalized by
$N_{p}$
at
$z/{\it\lambda}_{{\it\theta}}=4.5$
.
4. Scaling of the plume width with
$\mathit{Ra}$
One could think of two parameters that determine the area of a plume. Close to the plates and thus for line plumes, the length of the plumes should be determined by the domain width
$D=L{\it\Gamma}$
, while their thickness is determined by the width
${\it\lambda}_{{\it\theta}}$
of the thermal boundary layer, characterized by
${\it\lambda}_{{\it\theta}}=L/(2\mathit{Nu})$
. The resulting characteristic non-dimensional plume area is then
$A_{c}=L{\it\Gamma}/(2\mathit{Nu})$
. Illustratively,
$A_{c}$
is the area of a plume that is as long as the diameter of the cell and as wide as the thermal boundary layer. This characteristic plume area is indicated in figure 4(a). It can be seen that most of the plume areas are smaller than
$A_{c}$
; either the plume length, the plume width or both can differ from the dimensional expectation. Conceptually, the line plumes can be understood as detached thermal boundary layers of similar width; cf. Grossmann & Lohse (Reference Grossmann and Lohse2000). This has also been observed by Shishkina & Wagner (Reference Shishkina and Wagner2008) using a different method. We expect that the observation that
$A_{c}$
approximately separates the two distributions at higher
$z/L$
is coincidental, as the assumptions associated with the definition of
$A_{c}$
are not applicable to plumes at this height.
As the absolute value of a quantity obtained from any thermal plume identification depends on the threshold, we compare the scaling of the width with the scaling of
$\mathit{Nu}$
. To be more precise, we compare the plume width with the thermal boundary layer thickness
${\it\lambda}_{{\it\theta}}$
, which scales approximately as
${\it\lambda}_{{\it\theta}}/L\sim \mathit{Ra}^{-0.31}$
for the data points
$\mathit{Ra}=10^{9},10^{10}$
and
$10^{11}$
. The data for
$\mathit{Ra}=10^{12}$
are not used in this analysis due to lack of statistical convergence.
The data at
$z/L=0.002$
are inside (for
$\mathit{Ra}=10^{9}$
and
$\mathit{Ra}=10^{10}$
) or on the edge (for
$\mathit{Ra}=10^{11}$
) of the thermal boundary layer. It is non-trivial to extract the width of the plumes from the results of the plume detection method used, as displayed in figure 3(d). We obtain the average plume width
$W_{P}$
by defining
$\mathscr{D}$
as a so-called distance transform on
$P$
and
$\mathscr{T}$
as a so-called thinning operation on
$P$
. These are defined as follows. For every plume element, the distance transform
$\mathscr{D}$
gives the Euclidean distance to the closest non-plume element (figure 7
b); the thinning operation
$\mathscr{T}$
reduces
$P$
to minimally connected lines (figure 7
a). These minimally connected lines are set to 1 and the rest of
$\mathscr{T}$
is set to zero. The resulting set characterizes the ‘backbone’ of the plume. The plume width is obtained from
$W_{P}=2\langle (\mathscr{D}:\mathscr{T})/(\mathscr{T}:\mathscr{T})\rangle _{t}$
, where
$\mathscr{D}:\mathscr{T}$
denotes the componentwise inner product of
$\mathscr{D}$
and
$\mathscr{T}$
, namely
$\sum _{i,j}\mathscr{D}_{ij}\mathscr{T}_{ij}$
with the sum
$\sum _{i,j}$
taken over all points of the set
$P$
. An alternative approach that gives identical results involves iterating over all the coordinates in
$\mathscr{T}$
and time-averaging the minimum distance to the edge of a plume in
$P$
, which is more intuitive but much slower computationally.
The data are obtained at absolute vertical positions, constant for each
$\mathit{Ra}$
value. Consequently, the vertical position relative to the boundary layer thickness varies, as the boundary layer thickness decreases with
$\mathit{Ra}$
. In figure 4(b) we see that the most probable plume area can be approximated as constant between
$z/L=10^{-3}$
and
$10^{-2}$
, revealing insensitivity to the vertical position over a substantial range. However, this insensitivity is only for the plume area and not for the plume width. Therefore, performing the analysis at a fixed vertical position introduces an uncertainty that is added to the data. The uncertainty is obtained from the variation of the plume width between
$z/L=0.002$
and
$0.004$
and is included in the error bar on each data point in figure 6(a), where the results of the plume width quantification are shown. The results demonstrate that the scaling of
$W_{P}$
is similar to the scaling of
${\it\lambda}_{{\it\theta}}$
. We emphasize that the close similarity of the absolute values is incidental, as the absolute value of
$W_{P}$
depends on
$c$
. On the other hand, this shows that
$c=1.2$
is a reasonable value for
$c$
. The scaling of
$W_{P}$
agrees approximately with that of
${\it\lambda}_{{\it\theta}}$
, which shows that the method used for plume identification provides the expected results and that it is the length of the plumes that gives rise to the deviations from
$A_{c}$
as a characteristic plume area.
Figure 6. (a) Thermal boundary layer thickness
${\it\lambda}_{{\it\theta}}/L=1/(2\mathit{Nu})$
and plume thickness
$W_{P}$
, as defined in the text, plotted as functions of
$\mathit{Ra}$
; the solid black line represents
$\mathit{Ra}^{-0.31}$
, where the exponent is obtained from a fit to the
${\it\lambda}_{{\it\theta}}$
points. (b) Mean plume area inside the sliding window conditioned on the shear velocity outside the plume,
$\langle A_{P\cap C}\mid u_{C\setminus P}\rangle$
, for two values of
$\mathit{Ra}$
.
Figure 7. (a) Thinning operation
$\mathscr{T}$
, indicated by the thin lines, on an arbitrary subset of the domain at
$z/L=0.004$
; here
$\mathscr{T}$
is drawn on
$P$
for clarity, and we emphasize that
$\mathscr{T}$
equals 1 on the thin lines and 0 elsewhere. (b) Distance function
$\mathscr{D}$
on the same subset as in (a); the dark shading inside the plumes reflects the distance of the location to the edge of the plume in units of
${\it\lambda}_{{\it\theta}}$
.
5. Relation between wind shear and plume emission locations
The boundary layer of RB convection can conceptually be divided into three regions, namely the ejecting, wind-shearing and impacting regions, as Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014) has shown for TC flow, which has similar topology. We refer to figure 1 for an indication of these regions in RB convection. In the ejecting region, the plumes are emitted from the corresponding boundary layer, whereas in the impacting regions, the descending current and thermal plumes originating from the opposite boundary impact the boundary layer under consideration. Between these two regions is the wind-shearing region, where the large-scale wind shear is high and the velocity is predominantly horizontal. In TC flow, Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014) used this classification to rationalize the different boundary layer profiles found in each of these regions. As the ejecting region is defined by the emission of a large number of thermal plumes and the wind-shearing region is defined by high shear, this classification implies that regions of high shear emit fewer plumes than regions with low shear. This is opposite to what is observed in pressure-driven flows, where it is the high shear that results in bursts of momentum, concentration or temperature being emitted from the boundary layer into the bulk. This effect of plume emission being anticorrelated with large shear will now be quantified using our numerical data. A circle
$C$
with diameter
$D_{c}=0.05\,L{\it\Gamma}$
is used as a non-overlapping sliding window in which the mean shear velocity outside a plume,
$u_{C\setminus P}=\langle \surd (u_{{\it\phi}}^{2}+u_{r}^{2})\rangle _{C\setminus P}$
, and the plume area in that circle,
$A_{P\cap C}$
, are calculated. The velocity and area are normalized with the free-fall velocity and total area, respectively. For the shear velocity, only the area in the circle outside of the plume is considered, to avoid the contribution that the plume makes to the shear. We focus on the effect of the large-scale flow on the plumes by considering only the shear outside of a plume in the circle average. One of the contributions is the horizontal inflow near the boundary due to continuity. Conditioning
$A_{P\cap C}$
on
$u_{C\setminus P}$
gives
$\langle A_{P\cap C}\mid u_{C\setminus P}\rangle$
averaged over
$r$
,
${\it\phi}$
and
$t$
, a quantity that can be used to quantify and study the effect of shear on plume emission. We find that only the amplitude of
$\langle A_{P\cap C}\mid u_{C\setminus P}\rangle$
depends on
$D_{c}$
; in contrast, the trend does not, as long as
$1\gg D_{c}/{\it\Gamma}\gg 1/(2\mathit{Nu})$
. The analysis is performed on the data at
$z/L=0.002$
, which is inside or on the edge of the viscous boundary layer for
$\mathit{Ra}=10^{10}$
and
$10^{11}$
. At this height, the horizontal velocity can be interpreted as being proportional to the vertical gradient of horizontal velocity, averaged over
$0\leqslant z/L\leqslant 0.002$
. In figure 6(b), the quantity
$\langle A_{P\cap C}\mid u_{C\setminus P}\rangle$
is plotted for these two values of
$\mathit{Ra}$
. The trend is clear: regions of the boundary layer where the large-scale shear is high emit fewer plumes than regions where the shear is low. We emphasize that this analysis only accounts for the emitted plumes; plumes originating from the opposing plate that impact the boundary layer may display different behaviour, although we expect the behaviour to be similar.
6. Summary
In summary, we have studied three-dimensional thermal plumes using their cross-sections with horizontal planes at different heights in a cylindrical RB system. We have shown that the log–normal distribution of the thermal plume areas becomes weakly bimodal at higher vertical locations. This observation, together with the decline in the number of plumes, shows that there is clustering of plumes not only during a transient, as was studied by Parodi et al. (Reference Parodi, von Hardenberg, Passoni, Provenzale and Spiegel2004), but also in a statistically stationary state. In addition, the weakly bimodal distribution indicates that plumes either cluster or lose energy while traversing the system. Both these mechanisms result in the number of plumes decreasing with increasing vertical position, an observation noted here and previously by Zhou et al. (Reference Zhou, Sun and Xia2007). As was used in scaling law derivations by Castaing et al. (Reference Castaing, Gunaratne, Heslot, Kadanoff, Libchaber, Thomae, Wu, Zaleski and Zanetti1989) and Grossmann & Lohse (Reference Grossmann and Lohse2004), the assumption that the width of the plumes close to the plates is determined by the thermal boundary layer thickness is shown to be reasonable. The length of the plumes is not simply determined by the domain size; it originates from the flow structure and from the instability mechanism (Bosbach et al. Reference Bosbach, Weiss and Ahlers2012). The plumes are more likely to be emitted in regions of low shear, an observation used by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014) in TC flow to study the transition into turbulence of the boundary layers. The turbulent boundary layer is an important ingredient in the asymptotic scaling laws of Kraichnan (Reference Kraichnan1962) and Grossmann & Lohse (Reference Grossmann and Lohse2011), and our finding supports the classification of different horizontal regions of the boundary layer into ejecting, wind-shearing and impacting regions in RB convection as well. It provides an argument for conceptually dividing the RB cell not only vertically into bulk and boundary layer regions, but also horizontally into the aforementioned three regions. The existence of different boundary layer properties in these regions and their relative sizes can play an important role in understanding the transition to the ultimate regime in RB convection.
Acknowledgements
The authors thank R. Ostilla-Mónico, C. Sun, R. C. A. van der Veen and S. G. Huisman for useful discussions. This work was supported by the Foundation for Fundamental Research on Matter (FOM) and PRACE grant no. 2012061135.
