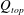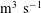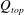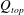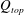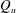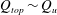1 Introduction
A fountain is formed as dense fluid is ejected vertically upwards from a localised source into a lighter environment. Gravity opposes the rise of the flow, thus, close to some terminal height, the flow collapses back under gravity to shroud the upflow. During this collapse, ambient fluid is entrained into the fountain top, which causes the flow to dilute. Our focus in this paper is to assess the rate of this entrainment, which we refer to as ‘fountain-top entrainment’. Herein, we consider axisymmetric fountains in uniform and quiescent surroundings that are miscible, Boussinesq, fully turbulent and that may be regarded as forced (Turner Reference Turner1966; Kaye & Hunt Reference Kaye and Hunt2006).
Along with jets and plumes, fountains represent a canonical example of environmental flows. These elegant flows occur extensively in nature and in engineering, from the evaporative cycles observed atop cumulus clouds (Turner Reference Turner1966) to the dilution of industrial waste in the ocean (Koh & Brooks Reference Koh and Brooks1975). An account of their wider applications can be found in the review article by Hunt & Burridge (Reference Hunt and Burridge2015).
Several theoretical models describing the time-averaged behaviour of forced fountains have emerged since the seminal study by Turner (Reference Turner1966). These models each define the fountain in terms of an upflow and a counterflow, the latter being characterised either implicitly (Carazzo, Kaminski & Tait Reference Carazzo, Kaminski and Tait2010; Mehaddi et al. Reference Mehaddi, Vaux, Candelier and Vauquelin2015) or explicitly (McDougall Reference McDougall1981; Bloomfield & Kerr Reference Bloomfield and Kerr2000). Strikingly, with the exception of McDougall (Reference McDougall1981), all have omitted to include a region near the top of the fountain where the flow is allowed to reverse under the influence of buoyancy (hereinafter ‘cap’). Significantly, none explicitly model entrainment into the fountain via the fountain top.
This omission comes as somewhat of a surprise. Indeed, the issue of lateral entrainment and of appropriately parameterising this entrainment lies at the heart of the modelling of fountains (see, e.g., the discussion in Carazzo et al. (Reference Carazzo, Kaminski and Tait2010)). There is no obvious reason why entrainment into the cap should receive less rigorous a treatment. Notably, the experimental measurements of Lin & Linden (Reference Lin and Linden2005), the large eddy simulations of Devenish, Rooney & Thomson (Reference Devenish, Rooney and Thomson2010) and the direct numerical simulations of Williamson, Armfield & Lin (Reference Williamson, Armfield and Lin2011) have each indicated that entrainment into the cap is by no means negligible. Devenish et al. (Reference Devenish, Rooney and Thomson2010), for instance, simulated the rise of a plume through a stably stratified environment. Beyond the height of neutral buoyancy, the plume became negatively buoyant and thereby reached a terminal height before reversing as a fountain. The amount of ambient fluid entrained through the reversing plume top (effectively, a fountain top) was then calculated as the difference between the flux of volume supplied to the plume top from the upflow (
![]() $Q_{u}$
) and that leaving the plume top in the counterflow (
$Q_{u}$
) and that leaving the plume top in the counterflow (
![]() $Q_{c}$
), i.e. as
$Q_{c}$
), i.e. as
![]() $Q_{top}=Q_{c}-Q_{u}$
. Over the investigated range, they found that
$Q_{top}=Q_{c}-Q_{u}$
. Over the investigated range, they found that
![]() $Q_{top}/Q_{u}=1$
–3. Though exceeding the values measured by Lin & Linden (Reference Lin and Linden2005), who report
$Q_{top}/Q_{u}=1$
–3. Though exceeding the values measured by Lin & Linden (Reference Lin and Linden2005), who report
![]() $Q_{top}/Q_{u}=0.5$
–0.8, Devenish et al. (Reference Devenish, Rooney and Thomson2010, p. 98) acknowledge that this discrepancy is primarily due to the volume fluxes being measured at different heights. In the absence of a unifying theoretical framework and a systematic empirical means for isolating the cap from the remainder of the fountain, such differences in convention are to be expected. Adjusting their notation to be consistent with the formalism of Lin & Linden (Reference Lin and Linden2005), and indeed with the notation adopted in § 2, one obtains
$Q_{top}/Q_{u}=0.5$
–0.8, Devenish et al. (Reference Devenish, Rooney and Thomson2010, p. 98) acknowledge that this discrepancy is primarily due to the volume fluxes being measured at different heights. In the absence of a unifying theoretical framework and a systematic empirical means for isolating the cap from the remainder of the fountain, such differences in convention are to be expected. Adjusting their notation to be consistent with the formalism of Lin & Linden (Reference Lin and Linden2005), and indeed with the notation adopted in § 2, one obtains
![]() $Q_{top}/Q_{u}\approx 1$
. Despite some uncertainty surrounding the precise value of
$Q_{top}/Q_{u}\approx 1$
. Despite some uncertainty surrounding the precise value of
![]() $Q_{top}$
, this broad agreement suggests that fountain-top entrainment is of a similar magnitude as the incident volume flux
$Q_{top}$
, this broad agreement suggests that fountain-top entrainment is of a similar magnitude as the incident volume flux
![]() $Q_{u}$
.
$Q_{u}$
.
With this scale for
![]() $Q_{top}$
in mind, it becomes clear that neglecting to account for fountain-top entrainment will upset the internal balance of fluxes in an established fountain. Without the additional dilution at the top, the counterflow remains relatively undiluted and, hence, relatively energetic. This results in an enhanced shear rate at the interface between the upflow and the counterflow. Notably, this implies that a greater fraction of the momentum in the upflow is lost in turbulent exchanges. One immediate consequence of this excess loss would be a reduction in predicted rise height. McDougall’s (Reference McDougall1981) model, for instance, which features a non-entraining cap, necessitates the introduction underneath the cap of a cylindrical region of arbitrary height to achieve rise heights that compare favourably with measurements. The importance of including fountain-top entrainment was also upheld by Devenish et al. (Reference Devenish, Rooney and Thomson2010), who showed that the model predictions of Bloomfield & Kerr (Reference Bloomfield and Kerr2000) could be improved by allowing for a finite volume of fluid to be entrained during flow reversal. Here, the authors did not specify how external fluid was entrained. Instead, entrainment was achieved numerically by formulating
$Q_{top}$
in mind, it becomes clear that neglecting to account for fountain-top entrainment will upset the internal balance of fluxes in an established fountain. Without the additional dilution at the top, the counterflow remains relatively undiluted and, hence, relatively energetic. This results in an enhanced shear rate at the interface between the upflow and the counterflow. Notably, this implies that a greater fraction of the momentum in the upflow is lost in turbulent exchanges. One immediate consequence of this excess loss would be a reduction in predicted rise height. McDougall’s (Reference McDougall1981) model, for instance, which features a non-entraining cap, necessitates the introduction underneath the cap of a cylindrical region of arbitrary height to achieve rise heights that compare favourably with measurements. The importance of including fountain-top entrainment was also upheld by Devenish et al. (Reference Devenish, Rooney and Thomson2010), who showed that the model predictions of Bloomfield & Kerr (Reference Bloomfield and Kerr2000) could be improved by allowing for a finite volume of fluid to be entrained during flow reversal. Here, the authors did not specify how external fluid was entrained. Instead, entrainment was achieved numerically by formulating
![]() $Q_{c}$
as a multiple (
$Q_{c}$
as a multiple (
![]() ${>}1$
) of
${>}1$
) of
![]() $Q_{u}$
. (By comparison, Bloomfield & Kerr’s original formulation assumes
$Q_{u}$
. (By comparison, Bloomfield & Kerr’s original formulation assumes
![]() $Q_{c}=Q_{u}$
.) For
$Q_{c}=Q_{u}$
.) For
![]() $Q_{c}=2Q_{u}$
, the predicted volume fluxes accurately matched those in their reversing plume simulations. Again, this hints at
$Q_{c}=2Q_{u}$
, the predicted volume fluxes accurately matched those in their reversing plume simulations. Again, this hints at
![]() $Q_{top}\sim Q_{u}$
.
$Q_{top}\sim Q_{u}$
.
Devenish et al.’s (Reference Devenish, Rooney and Thomson2010) adjustment, albeit ingenious, is purely numerical. As such, it cannot provide an explanation of the physical mechanisms underlying the entrainment process. Without physical substantiation, the associated choice of multiplicative factor appears somewhat arbitrary. Nevertheless, their approach reaffirms the need to account for fountain-top entrainment in theoretical treatments of forced fountains. As exemplified by McDougall (Reference McDougall1981), the inclusion of an entrainment flux
![]() $Q_{top}$
is central to developing a suitable model for the region of flow reversal and, hence, for a forced fountain in general (see, e.g., the models of Bloomfield & Kerr (Reference Bloomfield and Kerr2000) and Carazzo et al. (Reference Carazzo, Kaminski and Tait2010), for whom the absence of a cap is cause for breakdown close to the steady-state rise height). Thus, by evaluating
$Q_{top}$
is central to developing a suitable model for the region of flow reversal and, hence, for a forced fountain in general (see, e.g., the models of Bloomfield & Kerr (Reference Bloomfield and Kerr2000) and Carazzo et al. (Reference Carazzo, Kaminski and Tait2010), for whom the absence of a cap is cause for breakdown close to the steady-state rise height). Thus, by evaluating
![]() $Q_{top}$
we pave the way towards providing a complete model for a forced fountain.
$Q_{top}$
we pave the way towards providing a complete model for a forced fountain.
The aim of this paper is twofold: (i) to identify the physical processes by which ambient fluid is entrained into the fountain top, and (ii) to estimate the ensuing rate of entrainment
![]() $Q_{top}$
. We continue with a detailed inspection of the dynamics of the flow at the fountain top in § 2.1. Two independent estimates of
$Q_{top}$
. We continue with a detailed inspection of the dynamics of the flow at the fountain top in § 2.1. Two independent estimates of
![]() $Q_{top}$
are then derived based on arguments developed by Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956) (§ 2.2) and by Shrinivas & Hunt (Reference Shrinivas and Hunt2014) (§ 2.3). During these derivations, careful attention is paid to what each formulation implies for the bulk flow. Arguing that neither capture the primary entraining mechanism that is observed in practice, in § 2.4 we develop a new phenomenological model that takes into account the role of rise-height fluctuations in the engulfment of external fluid. Drawing from our model, we then show how to implement the entraining fountain top in existing descriptions for forced fountains. Finally, in § 3 we contrast our findings and discuss what should be regarded as a suitable value for
$Q_{top}$
are then derived based on arguments developed by Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956) (§ 2.2) and by Shrinivas & Hunt (Reference Shrinivas and Hunt2014) (§ 2.3). During these derivations, careful attention is paid to what each formulation implies for the bulk flow. Arguing that neither capture the primary entraining mechanism that is observed in practice, in § 2.4 we develop a new phenomenological model that takes into account the role of rise-height fluctuations in the engulfment of external fluid. Drawing from our model, we then show how to implement the entraining fountain top in existing descriptions for forced fountains. Finally, in § 3 we contrast our findings and discuss what should be regarded as a suitable value for
![]() $Q_{top}$
.
$Q_{top}$
.
2 Fountain-top entrainment models
2.1 Description of the fountain top
Before concentrating on the modelling of entrainment into the cap, it is helpful to first consider the general aspects of the fountain top.
In its instantaneous nature, there is no well-defined region of flow reversal (cf. figure 1 a). Instead, the flow atop a fountain appears to be highly irregular. Observations reveal that the pulsating fountain top undergoes large-amplitude fluctuations, shedding blobs or lobes of fluid. These lobes subsequently descend around the upflow to form the counterflow. A comprehensive study of the fountain top undertaken by Burridge & Hunt (Reference Burridge and Hunt2013) clarifies the picture (see also Pantzlaff & Lueptow Reference Pantzlaff and Lueptow1999). Burridge & Hunt (Reference Burridge and Hunt2013) analysed the time series of rise height produced by the motion of the fountain front. They found that there was a discernible rhythm, or periodicity, to the dominant mode of fluctuations occurring at the fountain top. For forced fountains, the dominant period of fluctuation was found to correspond approximately to the timescale of (large) eddies forming on the scale of the upflow radius at (the level of) the fountain top. Thereafter, these eddies collapse onto the counterflow, completing the fluctuation cycle. Thus, Burridge & Hunt (Reference Burridge and Hunt2013) argue that the fluctuations atop forced fountains can be assimilated as quasi-periodic cycles of formation and collapse of large-scale eddies.
To date, no attempt has been made (to the authors’ knowledge) to implement fluctuations into a model for fountains. By the same token, the potential links between these fluctuations and the entrainment of ambient fluid at the fountain top have seemingly been overlooked. In immiscible fountains, the reversing flow absorbs large pockets of surrounding fluid into the body of the fountain (Friedman et al. Reference Friedman, Vadakoot, Meyer and Carey2007). A similar phenomenon takes place in miscible fountains: as large-scale eddies spill off the fountain top, they wrap up external fluid into billow-like structures. Thereby, ambient fluid is entrained into the body of the fountain. It therefore seems essential that a faithful model for fountain-top entrainment incorporates the effects of fluctuations.

Figure 1. Structure of a turbulent forced fountain. (a) Instantaneous snapshot of an aqueous-saline fountain (source diameter 0.6 cm) with steady-state rise height and vertical extent of a characteristic large-scale fluctuation marked (cf. measurements by Burridge & Hunt (Reference Burridge and Hunt2013)). (b) Time-averaged image of the same fountain. The modelled, time-averaged fountain-top morphology is depicted in (c). The dotted lines in (b) and (c) outline the approximate boundaries of upflow, fountain top and counterflow.
Next, the question of the shape of the fountain top must be addressed. To the experimentalist who has observed these flows in controlled laboratory tests, this question is relatively straightforward to answer. This is mirrored by the fact that across the literature, schematics of fountains are depicted similarly: namely with an approximately hemispherical structure at their top (e.g. Turner Reference Turner1966; Mizushina et al.
Reference Mizushina, Ogino, Takeuchi and Ikawa1982; Cresswell & Szczepura Reference Cresswell and Szczepura1993; Burridge & Hunt Reference Burridge and Hunt2012). The broadly hemispherical morphology is also apparent from figure 1(b), which was obtained by averaging over time instantaneous snapshots, such as that shown in figure 1(a). Thus, in line with a long history of observations, we adopt a time-averaged description of the cap as a hemisphere of height
![]() $z_{t}$
, as illustrated in figure 1(c). At its base, the cap is fed by an incoming volume flux of dense fluid from the fountain upflow,
$z_{t}$
, as illustrated in figure 1(c). At its base, the cap is fed by an incoming volume flux of dense fluid from the fountain upflow,
![]() $Q_{u}\propto {\rm\pi}b_{u}^{2}w_{u}$
, characterised by a reduced gravity
$Q_{u}\propto {\rm\pi}b_{u}^{2}w_{u}$
, characterised by a reduced gravity
![]() $g_{u}^{\prime }=g({\it\rho}_{u}-{\it\rho}_{a})/{\it\rho}_{a}$
. Here,
$g_{u}^{\prime }=g({\it\rho}_{u}-{\it\rho}_{a})/{\it\rho}_{a}$
. Here,
![]() $b_{u}$
,
$b_{u}$
,
![]() $w_{u}$
and
$w_{u}$
and
![]() ${\it\rho}_{u}$
denote the radius, velocity and density of the upflow, respectively, at a height corresponding to the onset of flow reversal, and
${\it\rho}_{u}$
denote the radius, velocity and density of the upflow, respectively, at a height corresponding to the onset of flow reversal, and
![]() ${\it\rho}_{a}$
the ambient density (figure 1
c). For convenience, we adopt a top-hat profile for
${\it\rho}_{a}$
the ambient density (figure 1
c). For convenience, we adopt a top-hat profile for
![]() $w_{u}$
, thus
$w_{u}$
, thus
![]() $Q_{u}={\rm\pi}b_{u}^{2}w_{u}$
. A local Froude number, indicative of the relative strengths of inertial and buoyant forces in the cap, can be formed as
$Q_{u}={\rm\pi}b_{u}^{2}w_{u}$
. A local Froude number, indicative of the relative strengths of inertial and buoyant forces in the cap, can be formed as
This balance between the two competing forces determines the dynamics of the (time-averaged) fountain top and needs to be specified. In order to select a sensible value for
![]() $Fr_{u}$
, we may reason as follows. We know that a (large) eddy of nominal width
$Fr_{u}$
, we may reason as follows. We know that a (large) eddy of nominal width
![]() $2b_{u}$
will reverse at the fountain top when the gravitational downward pull exceeds the upward thrust of momentum. The height at which the flow starts to reverse can therefore be defined by the ‘tipping’ point
$2b_{u}$
will reverse at the fountain top when the gravitational downward pull exceeds the upward thrust of momentum. The height at which the flow starts to reverse can therefore be defined by the ‘tipping’ point
![]() $w_{u}=\sqrt{2b_{u}g_{u}^{\prime }}$
, i.e. by
$w_{u}=\sqrt{2b_{u}g_{u}^{\prime }}$
, i.e. by
![]() $Fr_{u}=\sqrt{2}$
. A similar argument is developed by McDougall (Reference McDougall1981), who initiates his cap at the height at which conditions locally in the upflow are characterised by
$Fr_{u}=\sqrt{2}$
. A similar argument is developed by McDougall (Reference McDougall1981), who initiates his cap at the height at which conditions locally in the upflow are characterised by
![]() $Fr_{u}=\sqrt{2}$
.
$Fr_{u}=\sqrt{2}$
.
2.2 Morton–Taylor–Turner entrainment closure
When faced with a flow for which (macroscopic) entrainment is a prominent feature, it is tempting to rely on the closure popularised by Morton et al. (Reference Morton, Taylor and Turner1956) (hereinafter MTT). MTT postulated that the entrainment velocity across the outskirts of a jet or a plume is directly proportional to the time-averaged centreline velocity. The constant of proportionality, the entrainment coefficient
![]() ${\it\alpha}$
, varies across applications, but typically
${\it\alpha}$
, varies across applications, but typically
![]() ${\it\alpha}\approx 0.1$
. Their ‘entrainment assumption’ has since been successfully applied to many different types of flow; see Turner (Reference Turner1986) for a review. Crucially, our interest lies primarily in describing the physical phenomena responsible for entrainment into the cap. In the following, we apply MTT’s closure to the fountain cap and discuss its appropriateness with regard to the dynamics of a forced fountain.
${\it\alpha}\approx 0.1$
. Their ‘entrainment assumption’ has since been successfully applied to many different types of flow; see Turner (Reference Turner1986) for a review. Crucially, our interest lies primarily in describing the physical phenomena responsible for entrainment into the cap. In the following, we apply MTT’s closure to the fountain cap and discuss its appropriateness with regard to the dynamics of a forced fountain.
In order to apply MTT, we seek a characteristic vertical velocity,
![]() ${\hat{w}}$
, in the cap. As relatively dense fluid from the upflow rises through the buoyancy-dominated cap, it experiences a downward acceleration
${\hat{w}}$
, in the cap. As relatively dense fluid from the upflow rises through the buoyancy-dominated cap, it experiences a downward acceleration
![]() $g_{u}^{\prime }$
. Some fluid elements reach the crest of the cap (
$g_{u}^{\prime }$
. Some fluid elements reach the crest of the cap (
![]() $r=0$
,
$r=0$
,
![]() $z=z_{t}$
, figure 1), where the vertical velocity has reduced to zero. Eventually, these fluid elements reverse direction and are accelerated under gravity. Assuming that pressure remains hydrostatic throughout the cap, an estimate of
$z=z_{t}$
, figure 1), where the vertical velocity has reduced to zero. Eventually, these fluid elements reverse direction and are accelerated under gravity. Assuming that pressure remains hydrostatic throughout the cap, an estimate of
![]() ${\hat{w}}$
is obtained on applying the Bernoulli equation along a streamline from the crest to a point at height
${\hat{w}}$
is obtained on applying the Bernoulli equation along a streamline from the crest to a point at height
![]() $z$
. This yields
$z$
. This yields
The characteristic entrainment (or inflow) velocity is therefore
In order to evaluate the entrained volume flux
![]() $Q_{top}$
, we must integrate the inflow velocity (2.3) over the cap. For a hemispherical geometry, the radius of the cap
$Q_{top}$
, we must integrate the inflow velocity (2.3) over the cap. For a hemispherical geometry, the radius of the cap
![]() $b_{t}$
is given by
$b_{t}$
is given by
![]() $b_{t}^{2}(z)+z^{2}=z_{t}^{2}$
. Thus, integrating leads to an entrainment flux of
$b_{t}^{2}(z)+z^{2}=z_{t}^{2}$
. Thus, integrating leads to an entrainment flux of
 $$\begin{eqnarray}Q_{top}=2{\rm\pi}{\it\alpha}\int _{0}^{z_{t}}b_{t}(z){\hat{w}}(z)\,\text{d}z=\underbrace{\frac{4{\it\alpha}\sqrt{2}}{15}(8\sqrt{2}-7)}_{{\it\delta}}\frac{z_{t}^{5/2}}{Fr_{u}b_{u}^{5/2}}Q_{u},\end{eqnarray}$$
$$\begin{eqnarray}Q_{top}=2{\rm\pi}{\it\alpha}\int _{0}^{z_{t}}b_{t}(z){\hat{w}}(z)\,\text{d}z=\underbrace{\frac{4{\it\alpha}\sqrt{2}}{15}(8\sqrt{2}-7)}_{{\it\delta}}\frac{z_{t}^{5/2}}{Fr_{u}b_{u}^{5/2}}Q_{u},\end{eqnarray}$$
where
![]() ${\it\delta}=0.163$
(to three decimal places) with
${\it\delta}=0.163$
(to three decimal places) with
![]() ${\it\alpha}=0.1$
, and
${\it\alpha}=0.1$
, and
![]() $Q_{u}(={\rm\pi}b_{u}^{2}w_{u})$
is the volume flux supplied to the cap by the upflow. In (2.4), the factor multiplying
$Q_{u}(={\rm\pi}b_{u}^{2}w_{u})$
is the volume flux supplied to the cap by the upflow. In (2.4), the factor multiplying
![]() $Q_{u}$
is a constant whose numerical value evidently depends on the geometry of the cap and on the characteristic local balance between inertia and buoyancy.
$Q_{u}$
is a constant whose numerical value evidently depends on the geometry of the cap and on the characteristic local balance between inertia and buoyancy.
In a similar configuration, Shrinivas & Hunt (Reference Shrinivas and Hunt2014) (see § 2.3) obtained an expression for
![]() $z_{t}$
(namely
$z_{t}$
(namely
![]() $z_{t}=0.94b_{u}Fr_{u}^{2}$
) based on the assumption that there was an efficient conversion of kinetic to potential energy in the cap. Although their study pertains to localised interfacial mixing induced by an impinging jet, later we motivate why it is reasonable to apply directly some of their results to a fountain cap, rather than solely to an impingement dome for which their model was developed. Therefore, for
$z_{t}=0.94b_{u}Fr_{u}^{2}$
) based on the assumption that there was an efficient conversion of kinetic to potential energy in the cap. Although their study pertains to localised interfacial mixing induced by an impinging jet, later we motivate why it is reasonable to apply directly some of their results to a fountain cap, rather than solely to an impingement dome for which their model was developed. Therefore, for
![]() $Fr_{u}=\sqrt{2}$
, (2.4) evaluates to
$Fr_{u}=\sqrt{2}$
, (2.4) evaluates to
Equation (2.5) is promising in that it confirms our intuition that
![]() $Q_{top}$
should scale on
$Q_{top}$
should scale on
![]() $Q_{u}$
. That said, one should be mindful of applying MTT to the fountain top. In plumes, a typical entrainment event consists of peripheral eddies engulfing ambient fluid into the plume (Turner Reference Turner1986). The MTT entrainment assumption gives a time-averaged representation of this engulfment process. As outlined in § 2.1, we indeed expect ‘engulfment’ to be the primary driver of fountain-top entrainment. There is a difference, however, between ‘engulfment’ in the context of slender flows such as plumes, and in the context of a fountain top. Slender flows have eddies on their perimeter that entrain patches of external fluid into the bulk flow as they propagate. Significantly, these eddies do not occupy the whole cross-section of the flow (e.g. plate 166 in Van Dyke (Reference Van Dyke1982)). By contrast, observations of the dominant fluctuation mode suggest that the instantaneous fountain top consists of single large-scale eddies shed in succession (e.g. Burridge & Hunt (Reference Burridge and Hunt2013)). It is therefore unclear a priori that the same closure should hold in a flow which, like the fountain top, comprises one such notional eddy. A related concern is the requirement within the MTT closure to define a meaningful time-averaged velocity. In the fluctuating fountain top, where the velocity changes sign over the course of a fluctuation, the existence of such a time-averaged velocity is questionable.
$Q_{u}$
. That said, one should be mindful of applying MTT to the fountain top. In plumes, a typical entrainment event consists of peripheral eddies engulfing ambient fluid into the plume (Turner Reference Turner1986). The MTT entrainment assumption gives a time-averaged representation of this engulfment process. As outlined in § 2.1, we indeed expect ‘engulfment’ to be the primary driver of fountain-top entrainment. There is a difference, however, between ‘engulfment’ in the context of slender flows such as plumes, and in the context of a fountain top. Slender flows have eddies on their perimeter that entrain patches of external fluid into the bulk flow as they propagate. Significantly, these eddies do not occupy the whole cross-section of the flow (e.g. plate 166 in Van Dyke (Reference Van Dyke1982)). By contrast, observations of the dominant fluctuation mode suggest that the instantaneous fountain top consists of single large-scale eddies shed in succession (e.g. Burridge & Hunt (Reference Burridge and Hunt2013)). It is therefore unclear a priori that the same closure should hold in a flow which, like the fountain top, comprises one such notional eddy. A related concern is the requirement within the MTT closure to define a meaningful time-averaged velocity. In the fluctuating fountain top, where the velocity changes sign over the course of a fluctuation, the existence of such a time-averaged velocity is questionable.
2.3 Entrainment by baroclinic vortices
An alternative account of the time-averaged entrainment process in fountain tops may be drawn from the work of Shrinivas & Hunt (Reference Shrinivas and Hunt2014) (hereinafter SH14). In the context of a two-layer stratified system, SH14 present a closure for the entrainment caused by a jet weakly impinging on a density interface. This localised impingement penetrates the interface as a recirculating bulge (or ‘dome’) which, as we shall see, shares notable similarities with a fountain top. In their account, inspired from experiments by Shy (Reference Shy1995) and Cotel et al. (Reference Cotel, Gjestvang, Ramkhelawan and Breidenthal1997), external fluid is entrained into a dome through the action of small baroclinic vortices located on the dome’s periphery (figure 2). Herein, we briefly recount some of the SH14 arguments to motivate why their closure warrants inspection and to illustrate the fundamental differences between their conceptual picture and an MTT-based approach.
Interested in the mixing dynamics of a jet, Shy (Reference Shy1995) performed a series of experiments in which a turbulent jet impinged on an interface across which there was a buoyancy jump
![]() ${\rm\Delta}g^{\prime }$
. When the impingement was weak, the interface distorted locally into a dome-like structure. For sufficiently energetic impingements, the jet penetrated the interface into a region of lower density fluid as a fountain. Using laser-induced fluorescence, Shy was able to distinguish fractions of the fountain which had mixed with the surroundings from fractions which had merely been ‘stirred’. In his flow visualisation, a fluorescent layer, indicative of mixing, persisted around the dark bulk silhouette of the fountain. Around the fountain top specifically, this fluorescent layer was thin, hinting that eddies responsible for the entrainment of ambient fluid were mostly confined to a thin region around its periphery. Later, Cotel et al. (Reference Cotel, Gjestvang, Ramkhelawan and Breidenthal1997) confirmed that for moderately energetic impingements (again forming a dome) this narrow layer was comprised of small, sustained baroclinic vortices. Performing several rotations in place before dislodging, these persistent eddies were responsible for drawing ambient fluid into the dome. A diagram of this conceptual picture is shown in figure 2(a).
${\rm\Delta}g^{\prime }$
. When the impingement was weak, the interface distorted locally into a dome-like structure. For sufficiently energetic impingements, the jet penetrated the interface into a region of lower density fluid as a fountain. Using laser-induced fluorescence, Shy was able to distinguish fractions of the fountain which had mixed with the surroundings from fractions which had merely been ‘stirred’. In his flow visualisation, a fluorescent layer, indicative of mixing, persisted around the dark bulk silhouette of the fountain. Around the fountain top specifically, this fluorescent layer was thin, hinting that eddies responsible for the entrainment of ambient fluid were mostly confined to a thin region around its periphery. Later, Cotel et al. (Reference Cotel, Gjestvang, Ramkhelawan and Breidenthal1997) confirmed that for moderately energetic impingements (again forming a dome) this narrow layer was comprised of small, sustained baroclinic vortices. Performing several rotations in place before dislodging, these persistent eddies were responsible for drawing ambient fluid into the dome. A diagram of this conceptual picture is shown in figure 2(a).

Figure 2. Diagram of the shear-driven entrainment model. Confined to a thin vortical layer (shaded region), baroclinic vortices, shown in (a), drive a volume flux
![]() $Q_{top}$
of external fluid of density
$Q_{top}$
of external fluid of density
![]() ${\it\rho}_{a}$
into the dome. In (b), mean flow streamlines through the vortical layer are illustrated. After Shrinivas & Hunt (Reference Shrinivas and Hunt2014, figure 5).
${\it\rho}_{a}$
into the dome. In (b), mean flow streamlines through the vortical layer are illustrated. After Shrinivas & Hunt (Reference Shrinivas and Hunt2014, figure 5).
Significantly, this picture suggests a physical origin for entrainment that is different from MTT: the primary entraining mechanism observed is a near-steady drawing in of external fluid effectuated by the sustained rotation of small vortices, rather than a quasi-periodical engulfment event averaged over time (as in MTT).
There is, however, more than a passing resemblance between the ‘entrainment dome’ formed when a jet-like flow impinges on a density interface and the time-averaged fountain top in uniform surroundings: both flows are dominated by their buoyancy and are approximately hemispherical in shape. Their close connection is reinforced on considering that, if one increases the forcing at the interface (or decreases the buoyancy jump), the entrainment dome naturally transitions into a fountain top. This is apparent in the experiments of Shy (Reference Shy1995) and, to a lesser extent, in those of Lin & Linden (Reference Lin and Linden2005). Thus, in light of these similarities and seeking a time-averaged entrainment closure, it seems natural to inspect the rate of entrainment which baroclinic eddies drive into the fountain top.
In the arguments that follow we distinguish between
![]() ${\rm\Delta}g^{\prime }$
, the reduced gravity across a density interface and pertinent to the interfacial dome, and
${\rm\Delta}g^{\prime }$
, the reduced gravity across a density interface and pertinent to the interfacial dome, and
![]() $g_{u}^{\prime }$
, the reduced gravity at the onset of flow reversal in a fountain (in an unstratified environment), and characteristic of the buoyancy in the cap. Similarly, we use ‘dome’ to designate the interfacial dome, depicted in figure 2, and ‘cap’ to refer to the top of a fountain rising through a uniform environment.
$g_{u}^{\prime }$
, the reduced gravity at the onset of flow reversal in a fountain (in an unstratified environment), and characteristic of the buoyancy in the cap. Similarly, we use ‘dome’ to designate the interfacial dome, depicted in figure 2, and ‘cap’ to refer to the top of a fountain rising through a uniform environment.
If there were not a sustained flux of vorticity into the dome, the baroclinic torque, a torque resulting from the misalignment of pressure and density isolines, would ‘unwrap’ the dense dome into a horizontal surface. The upflow provides the dome with a sustained influx of vorticity that maintains the persistent rotation of eddies, or vortices, within the vortical layer. The steady vorticity equation for a baroclinic vortex revolving at mean radial and vertical velocity,
![]() $u_{v}(z)$
and
$u_{v}(z)$
and
![]() $w_{v}(z)$
, respectively, is given by
$w_{v}(z)$
, respectively, is given by
where
![]() $P(z)$
designates the pressure in the environment, assumed hydrostatic, and
$P(z)$
designates the pressure in the environment, assumed hydrostatic, and
![]() ${\it\Omega}_{v}(z)$
the vorticity of a baroclinic vortex. In (2.6), the left-hand side represents the rate of rotation induced by the upflow. This is counteracted by the right-hand side, the baroclinic torque acting on the dome. Vortex stretching is absent because the time-averaged morphology of the dome is unchanging. SH14 established that
${\it\Omega}_{v}(z)$
the vorticity of a baroclinic vortex. In (2.6), the left-hand side represents the rate of rotation induced by the upflow. This is counteracted by the right-hand side, the baroclinic torque acting on the dome. Vortex stretching is absent because the time-averaged morphology of the dome is unchanging. SH14 established that
![]() $u_{v}/w_{v}\ll 1$
, such that (2.6) simplifies to
$u_{v}/w_{v}\ll 1$
, such that (2.6) simplifies to
without significantly affecting the analysis: neglecting the contribution of
![]() $u_{v}$
modifies their final estimate of the entrained volume flux by less than 2 % (Shrinivas & Hunt Reference Shrinivas and Hunt2014).
$u_{v}$
modifies their final estimate of the entrained volume flux by less than 2 % (Shrinivas & Hunt Reference Shrinivas and Hunt2014).
The small baroclinic vortices, driving entrainment at a mean velocity
![]() $u_{e}(z)$
, are fuelled by an incident vorticity flux from the upflow over a length scale
$u_{e}(z)$
, are fuelled by an incident vorticity flux from the upflow over a length scale
![]() $b_{u}$
. Thus, their mean circulation scales as
$b_{u}$
. Thus, their mean circulation scales as
![]() ${\it\Gamma}_{v}\propto u_{e}b_{u}$
and their vorticity
${\it\Gamma}_{v}\propto u_{e}b_{u}$
and their vorticity
![]() ${\it\Omega}_{v}$
scales as
${\it\Omega}_{v}$
scales as
The baroclinic vorticity is generated at a mean rate
Substituting for
![]() ${\it\Omega}_{v}$
from (2.8) and for the baroclinic torque from (2.9) into the vorticity equation (2.7) yields
${\it\Omega}_{v}$
from (2.8) and for the baroclinic torque from (2.9) into the vorticity equation (2.7) yields
It remains to determine
![]() $w_{v}$
. To that end, consider the mean flow within the dome, illustrated in figure 2(b). As in § 2.2, the ascent of fluid in the cap is stifled by its negative buoyancy. Due to the combined action of the weak inflow engendered by the entrainment flux and of the internal recirculation, some fluid is steered into the vortical layer and begins rotating at a velocity
$w_{v}$
. To that end, consider the mean flow within the dome, illustrated in figure 2(b). As in § 2.2, the ascent of fluid in the cap is stifled by its negative buoyancy. Due to the combined action of the weak inflow engendered by the entrainment flux and of the internal recirculation, some fluid is steered into the vortical layer and begins rotating at a velocity
![]() $\{u_{v},w_{v}\}$
; cf. streamline
$\{u_{v},w_{v}\}$
; cf. streamline
![]() $R$
on figure 2(b). Therefore, applying the Bernoulli equation along streamline
$R$
on figure 2(b). Therefore, applying the Bernoulli equation along streamline
![]() $R$
, we approximate
$R$
, we approximate
![]() $w_{v}$
as
$w_{v}$
as
since the radial velocity
![]() $u_{v}$
has negligible magnitude. Using (2.11), equation (2.10) becomes
$u_{v}$
has negligible magnitude. Using (2.11), equation (2.10) becomes
where
![]() ${\it\alpha}$
denotes a constant of proportionality.
${\it\alpha}$
denotes a constant of proportionality.
Equation (2.12), which states that the mean entrainment velocity is proportional to the mean vertical velocity of a vortex, is formally identical to the entrainment velocity (2.3) found in § 2.2: remarkably, the MTT entrainment closure is recovered. This assertion comes despite the different entrainment mechanism at the start of the argument. Thus, if one were to assume that the SH14 dome is an appropriate representation of the time-averaged fountain top, with reference to (2.5) we retrieve
![]() $Q_{top}=0.525Q_{u}$
(taking, for consistency,
$Q_{top}=0.525Q_{u}$
(taking, for consistency,
![]() ${\it\alpha}=0.1$
).
${\it\alpha}=0.1$
).
Here too, caution is advisable. Some aspects of the entraining mechanism proposed by SH14 for the dome appear to be incompatible with the flow atop a fountain. Pertinently, the SH14 closure, or at least route to closure, would rely on the presence of sustained baroclinic vortices surrounding the fountain top. This requirement may seem somewhat contrived, even in a time-averaged sense, in a fountain top that is perpetually fluctuating. As a whole, the entrainment process presumed in SH14 (a steady, regular drawing in of external fluid), though successful in describing entrainment in an interfacial dome, does not comply well with the engulfing events that are observed in forced fountains (e.g. Burridge & Hunt Reference Burridge and Hunt2013).
In light of these concerns, it is advisable to search for different methods to quantify entrainment. Ideally in the context of forced fountains, an entrainment closure should replicate the characteristic large-scale fluctuations at the fountain top. This forms the focus of § 2.4.
2.4 Entrainment by vortical engulfment
So far, we have considered two separate approaches to evaluate fountain-top entrainment: MTT and SH14, each based on very distinct conceptualisations of the bulk flow. A noteworthy preliminary result is that they both predict
![]() $Q_{top}=0.525Q_{u}$
.
$Q_{top}=0.525Q_{u}$
.
There remain, however, open questions regarding the pertinence of either approach when applied to the fountain top. These questions centre around how meaningful it is to adopt a time-averaged representation of the fountain top. Indeed we argue that fluctuations play a fundamental role in engulfing external fluid into the fountain body. It then seems difficult to reconcile this fluctuating behaviour with a time-averaged view of the flow.
Seeking a time-averaged entrainment closure has the obvious benefit that entrainment through the cap may be expressed as an entrainment rate,
![]() $Q_{top}$
, rather than an entrained volume,
$Q_{top}$
, rather than an entrained volume,
![]() $V_{top}$
. However, for the purposes of developing the arguments that follow (and indeed to alleviate some of the previous concerns), it is useful to shift our mindset from a time-averaged to a periodical representation of the cap.
$V_{top}$
. However, for the purposes of developing the arguments that follow (and indeed to alleviate some of the previous concerns), it is useful to shift our mindset from a time-averaged to a periodical representation of the cap.
Once we adopt a periodical framework, the fluctuations can readily be implemented into an entrainment model. To achieve this, we represent fluctuations conceptually as periodical cycles of ‘filling’ (first half-cycle) and ‘draining’ (second half-cycle) of the cap, during which the fountain top forms and collapses, respectively. Simultaneously, the cap rises during the first half-cycle and subsequently falls back in the second half-cycle. The two stages are depicted schematically in figures 3 and 4, respectively.

Figure 3. First half-cycle,
![]() $0\leqslant t\leqslant T_{p}/2$
: schematic depicting three stages in the formation of a fountain top by a filling process. (a) Initially, the cap is empty. (b) The cap gradually forms due to the inflow
$0\leqslant t\leqslant T_{p}/2$
: schematic depicting three stages in the formation of a fountain top by a filling process. (a) Initially, the cap is empty. (b) The cap gradually forms due to the inflow
![]() $Q_{u}$
from below. In (c), the cap has reached the peak fluctuation height
$Q_{u}$
from below. In (c), the cap has reached the peak fluctuation height
![]() $z_{m}$
. The dashed line depicts the outline of the cap at maximal volume.
$z_{m}$
. The dashed line depicts the outline of the cap at maximal volume.

Figure 4. Second half-cycle,
![]() $T_{p}/2\leqslant t\leqslant T_{p}$
: schematic depicting three stages in the collapse of a fountain top by a draining process. (a) The cap has reached a maximal volume at the peak height of a fluctuation cycle and starts to drain. (b) As the cap collapses, vortical motion entrains ambient fluid into the counterflow by engulfment. The cap is fully depleted in (c). Dashed outline as in figure 3.
$T_{p}/2\leqslant t\leqslant T_{p}$
: schematic depicting three stages in the collapse of a fountain top by a draining process. (a) The cap has reached a maximal volume at the peak height of a fluctuation cycle and starts to drain. (b) As the cap collapses, vortical motion entrains ambient fluid into the counterflow by engulfment. The cap is fully depleted in (c). Dashed outline as in figure 3.
We now consider, in turn, how external fluid is absorbed into the cap during formation and collapse. Suppose that, in the first instance, the cap gradually ‘fills up’ via the volume flux supplied by the upflow. The kinetic energy provided by this influx is stored as potential energy in the growing cap; simultaneously, it enables the cap to rise to the maximal quasi-steady fluctuation height
![]() $z_{m}=z(T_{p}/2)$
(figure 3
c), where the time
$z_{m}=z(T_{p}/2)$
(figure 3
c), where the time
![]() $t=T_{p}/2$
denotes the end of the first half-cycle. Based on the assumption that this raising of the cap results from a conversion of kinetic to potential energy, we may write
$t=T_{p}/2$
denotes the end of the first half-cycle. Based on the assumption that this raising of the cap results from a conversion of kinetic to potential energy, we may write
The rise to a height
![]() $z_{m}$
concludes the first half of a single oscillation cycle. At this stage, the amount of fluid entrained (i.e. for
$z_{m}$
concludes the first half of a single oscillation cycle. At this stage, the amount of fluid entrained (i.e. for
![]() $0\leqslant t\leqslant T_{p}/2$
) by engulfment is expected to be negligible. In practice, we expect some fluid to spill weakly from the fountain top and to roll up into tiny billows at its rear, although their contribution to entrainment is likely to be small. The actual entrainment is probably occurring at a smaller scale, akin to that in SH14. However, as discussed, the applicability of their model to a periodical framework is questionable. Therefore, it seems reasonable to neglect entrainment altogether during the first half-cycle. We will see later that our conclusions are largely unaffected by this assumption.
$0\leqslant t\leqslant T_{p}/2$
) by engulfment is expected to be negligible. In practice, we expect some fluid to spill weakly from the fountain top and to roll up into tiny billows at its rear, although their contribution to entrainment is likely to be small. The actual entrainment is probably occurring at a smaller scale, akin to that in SH14. However, as discussed, the applicability of their model to a periodical framework is questionable. Therefore, it seems reasonable to neglect entrainment altogether during the first half-cycle. We will see later that our conclusions are largely unaffected by this assumption.

Figure 5. Illustration of the modelling approach whereby the engulfment is driven by a thin vortex ring of circulation
![]() ${\it\Gamma}$
with core at height
${\it\Gamma}$
with core at height
![]() $z_{c}(t)$
(the italicised subscript ‘c’ reading ‘core’) across a cylindrical stem of radius
$z_{c}(t)$
(the italicised subscript ‘c’ reading ‘core’) across a cylindrical stem of radius
![]() $b_{u}$
. To avoid ill-posedness, the vortex-induced velocity
$b_{u}$
. To avoid ill-posedness, the vortex-induced velocity
![]() $U_{v}$
follows the velocity of a Rankine vortex.
$U_{v}$
follows the velocity of a Rankine vortex.
In the second half-cycle, the collapsing cap wraps around and thereby engulfs ambient fluid as it falls. To describe this engulfment mechanism, a new model is needed.
Figure 5 illustrates the modelling approach that we have taken. Whilst its application to the fountain top is novel, a similar approach has been used to describe entrainment in the near-field of fires (Cetegen Reference Cetegen1998) and, qualitatively, in jets (Sreenivas & Prasad Reference Sreenivas and Prasad2000). The swirling motion induced by the inflow of ambient fluid and simultaneous collapse of the fountain top is modelled by a thin vortex ring to which we assign a diameter
![]() $2b_{u}$
and a constant strength
$2b_{u}$
and a constant strength
![]() ${\it\Gamma}$
(
${\it\Gamma}$
(
![]() $\text{m}^{2}~\text{s}^{-1}$
). This vortex ring induces a lateral velocity
$\text{m}^{2}~\text{s}^{-1}$
). This vortex ring induces a lateral velocity
![]() $U_{v}$
which drives a volume flux across an extension of the upflow. For simplicity, this extension is modelled as a cylindrical stem of perimeter
$U_{v}$
which drives a volume flux across an extension of the upflow. For simplicity, this extension is modelled as a cylindrical stem of perimeter
![]() $2{\rm\pi}b_{u}$
and of height
$2{\rm\pi}b_{u}$
and of height
![]() $z_{c}$
. The position of the core of the vortex ring,
$z_{c}$
. The position of the core of the vortex ring,
![]() $z_{c}(t)$
, varies over the course of one half-cycle from
$z_{c}(t)$
, varies over the course of one half-cycle from
![]() $z=z_{m}$
at
$z=z_{m}$
at
![]() $t=T_{p}/2$
to
$t=T_{p}/2$
to
![]() $z=0$
at
$z=0$
at
![]() $t=T_{p}$
.
$t=T_{p}$
.
Since we only consider
![]() $U_{v}$
along the perimeter of a vertical cylinder, we can express
$U_{v}$
along the perimeter of a vertical cylinder, we can express
![]() $U_{v}$
as
$U_{v}$
as
![]() $U_{v}(z)$
, with
$U_{v}(z)$
, with
![]() $0\leqslant z\leqslant z_{c}(t)$
. The profile of
$0\leqslant z\leqslant z_{c}(t)$
. The profile of
![]() $U_{v}(z)$
is shown qualitatively on figure 5. To bypass the difficulty of the velocity tending to infinity on the vortex core, we specify a length scale
$U_{v}(z)$
is shown qualitatively on figure 5. To bypass the difficulty of the velocity tending to infinity on the vortex core, we specify a length scale
![]() $z_{sb}$
over which the flow rotates as a solid body. This is formally known as a Rankine vortex (Saffman Reference Saffman1992, p. 22), where
$z_{sb}$
over which the flow rotates as a solid body. This is formally known as a Rankine vortex (Saffman Reference Saffman1992, p. 22), where
![]() $z_{sb}$
is generally introduced to account for viscous effects. We shall see later that the choice of
$z_{sb}$
is generally introduced to account for viscous effects. We shall see later that the choice of
![]() $z_{sb}$
is immaterial to the final solution, provided that it is small. The velocity induced by a vortex ring with a viscous core of extent
$z_{sb}$
is immaterial to the final solution, provided that it is small. The velocity induced by a vortex ring with a viscous core of extent
![]() $z_{sb}$
follows
$z_{sb}$
follows
 $$\begin{eqnarray}U_{v}(\mathscr{Z})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{{\it\Gamma}}{2{\rm\pi}\mathscr{Z}}\left(\frac{\mathscr{Z}}{z_{sb}}\right)^{2},\quad & 0<\mathscr{Z}<z_{sb},\\ \displaystyle \frac{{\it\Gamma}}{2{\rm\pi}\mathscr{Z}},\quad & \mathscr{Z}\geqslant z_{sb},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}U_{v}(\mathscr{Z})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{{\it\Gamma}}{2{\rm\pi}\mathscr{Z}}\left(\frac{\mathscr{Z}}{z_{sb}}\right)^{2},\quad & 0<\mathscr{Z}<z_{sb},\\ \displaystyle \frac{{\it\Gamma}}{2{\rm\pi}\mathscr{Z}},\quad & \mathscr{Z}\geqslant z_{sb},\end{array}\right.\end{eqnarray}$$
where
![]() $\mathscr{Z}(t)=z_{c}(t)-z$
is a local coordinate pointing radially outward from the vortex core (figure 5). The total volume
$\mathscr{Z}(t)=z_{c}(t)-z$
is a local coordinate pointing radially outward from the vortex core (figure 5). The total volume
![]() $V_{top}$
entrained over a duration
$V_{top}$
entrained over a duration
![]() $t$
is therefore
$t$
is therefore
Substituting for
![]() $U_{v}$
from (2.14), we evaluate the inner integral of (2.15) as
$U_{v}$
from (2.14), we evaluate the inner integral of (2.15) as
where
represent contributions to
![]() $I$
(2.15) over the solid body of rotation (
$I$
(2.15) over the solid body of rotation (
![]() $\mathscr{F}$
) and over the free vortex (
$\mathscr{F}$
) and over the free vortex (
![]() $\mathscr{G}$
), respectively. Denoting the vertical velocity of the core as
$\mathscr{G}$
), respectively. Denoting the vertical velocity of the core as
![]() $w_{c}$
and making the substitution of variables
$w_{c}$
and making the substitution of variables
![]() $\text{d}t^{\prime }=\text{d}z_{c}/w_{c}$
transforms the integral (2.15) into
$\text{d}t^{\prime }=\text{d}z_{c}/w_{c}$
transforms the integral (2.15) into
where
![]() $z_{c,max}$
designates the maximal height attained by the core of the cap over one complete cycle. Given that the collapsing cap experiences a reduced gravity
$z_{c,max}$
designates the maximal height attained by the core of the cap over one complete cycle. Given that the collapsing cap experiences a reduced gravity
![]() $g_{u}^{\prime }$
, we may express its vertical velocity as
$g_{u}^{\prime }$
, we may express its vertical velocity as
Substituting for
![]() $w_{c}$
from (2.19) and for
$w_{c}$
from (2.19) and for
![]() $\mathscr{F}$
and
$\mathscr{F}$
and
![]() $\mathscr{G}$
from (2.17) into (2.18), on integrating we obtain
$\mathscr{G}$
from (2.17) into (2.18), on integrating we obtain
with
and
It remains to estimate the bounds of integration
![]() $z_{sb}$
and
$z_{sb}$
and
![]() $z_{c,max}$
, and to specify the form of the vortex circulation
$z_{c,max}$
, and to specify the form of the vortex circulation
![]() ${\it\Gamma}$
. Over one draining cycle, as depicted on figure 4, we readily recover
${\it\Gamma}$
. Over one draining cycle, as depicted on figure 4, we readily recover
As alluded to previously, the precise form of
![]() $z_{sb}$
is inconsequential. For convenience, we may assume that it scales on the length scale pertinent to the fountain top, i.e.
$z_{sb}$
is inconsequential. For convenience, we may assume that it scales on the length scale pertinent to the fountain top, i.e.
with
![]() $B\ll A$
to ensure that
$B\ll A$
to ensure that
![]() $z_{sb}$
is suitably small (
$z_{sb}$
is suitably small (
![]() $z_{sb}/z_{m}\ll 1$
). Further, in order to determine
$z_{sb}/z_{m}\ll 1$
). Further, in order to determine
![]() ${\it\Gamma}$
, we use the knowledge that the upflow velocity
${\it\Gamma}$
, we use the knowledge that the upflow velocity
![]() $w_{u}$
(at level
$w_{u}$
(at level
![]() $z=0$
) generates circulation over an area
$z=0$
) generates circulation over an area
![]() ${\rm\pi}b_{u}^{2}$
. It follows that
${\rm\pi}b_{u}^{2}$
. It follows that
![]() ${\it\Gamma}\propto {\rm\pi}b_{u}w_{u}$
, i.e.
${\it\Gamma}\propto {\rm\pi}b_{u}w_{u}$
, i.e.
where
![]() $C$
is an order one constant. Crucially, knowing the form of
$C$
is an order one constant. Crucially, knowing the form of
![]() ${\it\Gamma}$
enables us to evaluate the total volume entrained by engulfment into the fountain top over one half of an oscillation cycle of duration
${\it\Gamma}$
enables us to evaluate the total volume entrained by engulfment into the fountain top over one half of an oscillation cycle of duration
![]() $T_{p}/2$
. Substituting (2.25) and the bounds (2.23) and (2.24) into (2.20) yields our estimate
$T_{p}/2$
. Substituting (2.25) and the bounds (2.23) and (2.24) into (2.20) yields our estimate
Two comments need to be made on (2.26) so as to ascertain its validity. First,
![]() ${\it\beta}>0$
for all positive values of
${\it\beta}>0$
for all positive values of
![]() $B<A$
, so that the entrained volume
$B<A$
, so that the entrained volume
![]() $V_{top}$
is always positive. Second, we recall that the length scale
$V_{top}$
is always positive. Second, we recall that the length scale
![]() $z_{sb}$
was introduced as a modelling artefact which, ideally, should approach zero. Whilst the factor
$z_{sb}$
was introduced as a modelling artefact which, ideally, should approach zero. Whilst the factor
![]() ${\it\beta}$
is unbounded in the limit as
${\it\beta}$
is unbounded in the limit as
![]() $B\rightarrow 0$
, for small but finite
$B\rightarrow 0$
, for small but finite
![]() $B$
,
$B$
,
![]() ${\it\beta}$
is well-behaved. Indeed,
${\it\beta}$
is well-behaved. Indeed,
![]() $\text{arctanh}(x)$
asymptotes to infinity slowly as
$\text{arctanh}(x)$
asymptotes to infinity slowly as
![]() $x\rightarrow 1$
. These two points are illustrated in figure 6, where we plot
$x\rightarrow 1$
. These two points are illustrated in figure 6, where we plot
![]() ${\it\beta}$
against
${\it\beta}$
against
![]() $B/A$
. Moreover, for small
$B/A$
. Moreover, for small
![]() $B$
,
$B$
,
![]() $V_{top,\mathscr{F}}\rightarrow 0$
(2.21). Given
$V_{top,\mathscr{F}}\rightarrow 0$
(2.21). Given
![]() $Q_{u}={\rm\pi}b_{u}^{2}w_{u}$
, we may approximate the entrained volume as
$Q_{u}={\rm\pi}b_{u}^{2}w_{u}$
, we may approximate the entrained volume as
In (2.27) the ratio
![]() $w_{u}/g_{u}^{\prime }$
represents a timescale
$w_{u}/g_{u}^{\prime }$
represents a timescale
![]() $T_{u}$
that is indicative of the fluctuation period. In terms of average entrainment rates therefore, we recover that
$T_{u}$
that is indicative of the fluctuation period. In terms of average entrainment rates therefore, we recover that
Equation (2.28) shows that the rate of entrainment through the fountain top is a constant fraction of the volume flux provided by the upflow. Thus, our model for vortical entrainment predicts the same functional dependence as models based on MTT or SH14. In the case of MTT, this functional agreement should perhaps not come as a surprise. The entraining mechanism which forms the basis of (2.27) resembles MTT: large eddies, whose size and velocity scale on the mean flow, engulf ambient fluid. The main novelty and indeed primary outcome of our approach is that, by coupling the engulfing motion with the large-amplitude fluctuations that typify a forced fountain top, equation (2.27) faithfully replicates the phenomenology that is observed in practice. Significantly, one key implication of this agreement is that a time-averaged description of entrainment successfully captures the dynamic processes in the fountain top. This result enables the direct implementation of a mechanistic approach for fountain-top entrainment into a (three-region) model for a forced fountain. First, one replaces McDougall’s (Reference McDougall1981) cap with a hemispherical fountain top (figure 1
c) diluting at a rate
![]() $Q_{top}$
. Then, following McDougall’s lead, but crucially including the additional dilution, one obtains a modified set of outflow conditions for fluid leaving the fountain top. Given that these conditions drive the counterflow, the effects of fountain-top entrainment are incorporated into a complete description for a forced fountain. The details of this implementation, which lie beyond the desired scope of this paper, can be found in Hunt & Debugne (Reference Hunt and Debugne0000).
$Q_{top}$
. Then, following McDougall’s lead, but crucially including the additional dilution, one obtains a modified set of outflow conditions for fluid leaving the fountain top. Given that these conditions drive the counterflow, the effects of fountain-top entrainment are incorporated into a complete description for a forced fountain. The details of this implementation, which lie beyond the desired scope of this paper, can be found in Hunt & Debugne (Reference Hunt and Debugne0000).

Figure 6. Numerical value of the factor
![]() ${\it\beta}$
(thick line) normalised by
${\it\beta}$
(thick line) normalised by
![]() $Fr_{u}\sqrt{b_{u}}\sqrt{A}$
against different ratios
$Fr_{u}\sqrt{b_{u}}\sqrt{A}$
against different ratios
![]() $B/A$
for
$B/A$
for
![]() $A=0.9$
. Also plotted are the contributions to
$A=0.9$
. Also plotted are the contributions to
![]() ${\it\beta}$
of the individual terms in (2.26) (thin lines, annotated).
${\it\beta}$
of the individual terms in (2.26) (thin lines, annotated).
We can gain some insight into the magnitude of
![]() $Q_{top}$
by giving estimates for
$Q_{top}$
by giving estimates for
![]() $A$
and
$A$
and
![]() $T_{u}$
. The relative lack of internal fountain statistics prevents us from deducing these estimates purely from the literature. In appendix A, we show how data from Burridge & Hunt (Reference Burridge and Hunt2013) can be coupled with our model for forced fountains (presented in a complementary paper, Hunt & Debugne (Reference Hunt and Debugne0000)) to yield
$T_{u}$
. The relative lack of internal fountain statistics prevents us from deducing these estimates purely from the literature. In appendix A, we show how data from Burridge & Hunt (Reference Burridge and Hunt2013) can be coupled with our model for forced fountains (presented in a complementary paper, Hunt & Debugne (Reference Hunt and Debugne0000)) to yield
![]() $A\approx 0.9$
and
$A\approx 0.9$
and
![]() $T_{u}\approx 0.1T_{p}$
. From these estimates and taking
$T_{u}\approx 0.1T_{p}$
. From these estimates and taking
![]() ${\it\beta}\approx 10Fr_{u}\sqrt{b_{u}}\sqrt{A}$
(figure 6), we can deduce the approximation
${\it\beta}\approx 10Fr_{u}\sqrt{b_{u}}\sqrt{A}$
(figure 6), we can deduce the approximation
![]() $Q_{top}/Q_{u}\approx 0.81C$
. Given that the magnitudes of
$Q_{top}/Q_{u}\approx 0.81C$
. Given that the magnitudes of
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $C$
are independent in the limit of a vanishingly thin vortex ring (
$C$
are independent in the limit of a vanishingly thin vortex ring (
![]() $B\rightarrow 0$
), it is difficult to assign a precise value to
$B\rightarrow 0$
), it is difficult to assign a precise value to
![]() $C$
, however, by construction we expect
$C$
, however, by construction we expect
![]() $C\sim 1$
(2.25). Therefore, our model for vortical engulfment suggests
$C\sim 1$
(2.25). Therefore, our model for vortical engulfment suggests
![]() $Q_{top}/Q_{u}\sim 1$
.
$Q_{top}/Q_{u}\sim 1$
.
3 Discussion and conclusions
We have presented a novel approach to assess how external fluid is entrained into a fountain cap. By taking into account the role of rise-height fluctuations at the fountain top in the engulfment of external fluid, our model (2.27) closely mimics the dynamic behaviour of a (forced) fountain top. We predict that the entrained volume flux is a constant fraction of the incoming volume flux (as indeed follows from elementary dimensional considerations) and an order-of-magnitude estimate of (2.27) suggests that
![]() $Q_{top}\sim Q_{u}$
. This result is consistent with the large-eddy simulations of Devenish et al. (Reference Devenish, Rooney and Thomson2010) (
$Q_{top}\sim Q_{u}$
. This result is consistent with the large-eddy simulations of Devenish et al. (Reference Devenish, Rooney and Thomson2010) (
![]() $Q_{top}\approx Q_{u}$
) and with the experimental measurements of Lin & Linden (Reference Lin and Linden2005) (
$Q_{top}\approx Q_{u}$
) and with the experimental measurements of Lin & Linden (Reference Lin and Linden2005) (
![]() $Q_{top}/Q_{u}=0.5$
–0.8). Moreover, the oscillatory and engulfing motion encompassed within our model is in accord with observations (Friedman et al.
Reference Friedman, Vadakoot, Meyer and Carey2007; Burridge & Hunt Reference Burridge and Hunt2013).
$Q_{top}/Q_{u}=0.5$
–0.8). Moreover, the oscillatory and engulfing motion encompassed within our model is in accord with observations (Friedman et al.
Reference Friedman, Vadakoot, Meyer and Carey2007; Burridge & Hunt Reference Burridge and Hunt2013).
Relatively few assumptions underpin our model (§ 2.4). Notably, we have assumed that:
-
(i) over the course of a fluctuation, kinetic energy is converted into potential energy (and vice versa);
-
(ii) the rotational motion of a typical engulfment event can be modelled as the inflow produced by a vortex ring of strength
 ${\it\Gamma}\propto b_{u}w_{u}$
.
${\it\Gamma}\propto b_{u}w_{u}$
.
From (i), we deduced the relevant length scale (2.13) and velocity (2.19). Energy losses that occur during the reversal of a lobe of fluid are implicit in the quantity
![]() $A$
(2.13). Then, (ii) constitutes the main modelling approach: it is an approximation based on an idealised representation of entrainment as induced by a single translating vortex ring. Together, (i) and (ii) allow one to reduce the process of engulfment at the fountain top to a tractable form (2.27). Significantly, our closure (2.27) combines a fountain’s fluctuating nature with a mechanistic account of entrainment.
$A$
(2.13). Then, (ii) constitutes the main modelling approach: it is an approximation based on an idealised representation of entrainment as induced by a single translating vortex ring. Together, (i) and (ii) allow one to reduce the process of engulfment at the fountain top to a tractable form (2.27). Significantly, our closure (2.27) combines a fountain’s fluctuating nature with a mechanistic account of entrainment.
Ideally, an estimate of the constants
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
would enable the direct implementation of (2.27), which, from a phenomenological viewpoint, seems to provide a more faithful account of fountain-top entrainment. Whilst the magnitude of
$C$
would enable the direct implementation of (2.27), which, from a phenomenological viewpoint, seems to provide a more faithful account of fountain-top entrainment. Whilst the magnitude of
![]() $A$
can be inferred from the fluctuation height data provided by Burridge & Hunt (Reference Burridge and Hunt2013) (appendix A), the physical interpretation of the constants
$A$
can be inferred from the fluctuation height data provided by Burridge & Hunt (Reference Burridge and Hunt2013) (appendix A), the physical interpretation of the constants
![]() $B$
and
$B$
and
![]() $C$
is less clear. Nor is it straightforward to devise an experiment by which to measure these constants. Nevertheless, there is evidently a strong connection between our theoretical description (2.27) and the entrainment closure of MTT (2.5), both starting from the engulfing motion by large-scale eddies, and both subsequently predicting
$C$
is less clear. Nor is it straightforward to devise an experiment by which to measure these constants. Nevertheless, there is evidently a strong connection between our theoretical description (2.27) and the entrainment closure of MTT (2.5), both starting from the engulfing motion by large-scale eddies, and both subsequently predicting
![]() $Q_{top}\sim Q_{u}$
. We might therefore reasonably anticipate that evaluation of (2.27) should lead to a similar result as (2.5).
$Q_{top}\sim Q_{u}$
. We might therefore reasonably anticipate that evaluation of (2.27) should lead to a similar result as (2.5).
This outcome bolsters the inclusion into full-fledged models of forced fountains (as per § 2.4) of a time-averaged fountain top, modelled as a hemispherical cap and entraining ambient fluid at a rate
![]() $Q_{top}=0.525Q_{u}$
. This rate of entrainment, which emerges from MTT, is not a figure that is set in stone (in reference to fountain tops). Future theoretical refinements or new insights arising from a series of dedicated experiments may well refine its numerical value. In the meantime, and indeed in light of the arguments developed herein, it would seem reasonable to take
$Q_{top}=0.525Q_{u}$
. This rate of entrainment, which emerges from MTT, is not a figure that is set in stone (in reference to fountain tops). Future theoretical refinements or new insights arising from a series of dedicated experiments may well refine its numerical value. In the meantime, and indeed in light of the arguments developed herein, it would seem reasonable to take
![]() $Q_{top}=0.5Q_{u}$
.
$Q_{top}=0.5Q_{u}$
.
As an aside, it is interesting to contemplate that this is the same closure used to quantify interfacial entrainment in SH14. Although both flows differ profoundly, the entrainment mechanisms underlying SH14 and the present model need not be incompatible. In the absence of a density interface, the thickness of the thin vortical layer in SH14 is likely to increase towards
![]() $b_{u}$
, which is akin to the cap consisting of one large eddy entraining fluid during a typical engulfment event. Alternatively, instabilities may prompt the growth of the small baroclinic vortices into larger eddies, whereby we again recover an engulfing mechanism. The actual picture for fountain-top entrainment likely lies somewhere between both descriptions; both the phenomena modelled in SH14 and in the present study are relevant.
$b_{u}$
, which is akin to the cap consisting of one large eddy entraining fluid during a typical engulfment event. Alternatively, instabilities may prompt the growth of the small baroclinic vortices into larger eddies, whereby we again recover an engulfing mechanism. The actual picture for fountain-top entrainment likely lies somewhere between both descriptions; both the phenomena modelled in SH14 and in the present study are relevant.
Acknowledgements
A.L.R.D. and G.R.H. would like to thank Qualcomm European Research Studentships in Technology and the Engineering and Physical Sciences Research Council (EPSRC) for their financial support (EPSRC grant number EP/L504920/1).
Appendix A. Estimates of
 $A$
and
$A$
and
 $T_{u}$
from Burridge & Hunt (Reference Burridge and Hunt2013)
$T_{u}$
from Burridge & Hunt (Reference Burridge and Hunt2013)
In this appendix we seek to assess the approximate magnitudes of
![]() $A$
and
$A$
and
![]() $T_{u}$
. In their experimental study of the fountain top, Burridge & Hunt (Reference Burridge and Hunt2013) relate the average vertical extent of a fluctuation
$T_{u}$
. In their experimental study of the fountain top, Burridge & Hunt (Reference Burridge and Hunt2013) relate the average vertical extent of a fluctuation
![]() ${\it\delta}z$
to the time-averaged width of the cap
${\it\delta}z$
to the time-averaged width of the cap
![]() $\widetilde{b}_{ss}$
by
$\widetilde{b}_{ss}$
by
In order to acquire meaningful statistics, Burridge & Hunt (Reference Burridge and Hunt2013) performed their averages only over intervals during which the instantaneous front of the fountain was above its steady-state height. This precaution means it is not clear how their variables relate to the corresponding variables in this paper. Nevertheless, given that we wish to extract only their magnitude, it is reasonable to equate the variables
![]() ${\it\delta}z\approx z_{m}$
and
${\it\delta}z\approx z_{m}$
and
![]() $\widetilde{b}_{ss}\approx b_{u}$
. Then, for
$\widetilde{b}_{ss}\approx b_{u}$
. Then, for
![]() $Fr_{u}=\sqrt{2}$
, we have
$Fr_{u}=\sqrt{2}$
, we have
Unfortunately we cannot rely solely on data from Burridge & Hunt (Reference Burridge and Hunt2013) to link
![]() $T_{u}$
to the dominant period of fluctuation
$T_{u}$
to the dominant period of fluctuation
![]() $T_{p}$
. Burridge & Hunt (Reference Burridge and Hunt2013) report the latter in terms of source variables as
$T_{p}$
. Burridge & Hunt (Reference Burridge and Hunt2013) report the latter in terms of source variables as
![]() $T_{p}=2w_{0}/g_{0}^{\prime }$
. However, unlike plumes which accept closed-form solutions, in fountains it is not known how local variables (which define
$T_{p}=2w_{0}/g_{0}^{\prime }$
. However, unlike plumes which accept closed-form solutions, in fountains it is not known how local variables (which define
![]() $T_{u}$
) relate to their source values.
$T_{u}$
) relate to their source values.
To gain an estimate of
![]() $T_{u}$
, we must therefore resort to model predictions. We simulate time-averaged forced fountain behaviour by means of the model presented in Hunt & Debugne (Reference Hunt and Debugne0000). This allows one to relate
$T_{u}$
, we must therefore resort to model predictions. We simulate time-averaged forced fountain behaviour by means of the model presented in Hunt & Debugne (Reference Hunt and Debugne0000). This allows one to relate
![]() $T_{u}$
to
$T_{u}$
to
![]() $T_{p}$
as
$T_{p}$
as
Note that estimates of
![]() $A$
from the same model return
$A$
from the same model return
![]() $A\approx 0.7$
, which broadly agrees with (A 1).
$A\approx 0.7$
, which broadly agrees with (A 1).