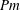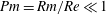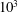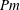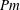1 Introduction
The existence of planetary and stellar magnetic fields is attributed to the dynamo instability, the mechanism by which a background turbulent flow spontaneously generates a magnetic field by the constructive refolding of magnetic field lines (Moffatt Reference Moffatt1978). Many efforts have been made by several experimental groups to reproduce the dynamo instability in the laboratory using liquid metals (Gailitis et al.
Reference Gailitis, Lielausis, Platacis, Dement’ev, Cifersons, Gerbeth, Gundrum, Stefani, Christen and Will2001; Stieglitz & Mueller Reference Stieglitz and Mueller2001; Shew & Lathrop Reference Shew and Lathrop2005; Nornberg et al.
Reference Nornberg, Spence, Kendrick, Jacobson and Forest2006; Monchaux et al.
Reference Monchaux, Berhanu, Bourgoin, Moulin, Odier, Pinton, Volk, Fauve, Mordant and Pétrélis2007; Giesecke et al.
Reference Giesecke, Stefani, Gundrum, Gerbeth, Nore and Lorat2012). However, so far, unconstrained dynamos driven just by turbulent flows have not been achieved in the laboratory. Successful experimental dynamos rely either on constraining the flow or using ferromagnetic materials. One of the major challenges to achieving a liquid metal dynamo is the large energy injection rate required to reach the dynamo onset, which is determined by the magnetic Reynolds number
$Rm=UL/\unicode[STIX]{x1D702}$
(where
$U$
is the r.m.s. velocity,
$L$
is the domain size and
$\unicode[STIX]{x1D702}$
is the magnetic diffusivity), which should be larger than a critical value
$Rm_{c}$
. The low value of the magnetic Prandtl number
$Pm\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D702}\sim 10^{-5}$
of liquid metals (where
$\unicode[STIX]{x1D708}$
is the viscosity) implies that the required Reynolds number
$Re=UL/\unicode[STIX]{x1D708}=Rm/Pm$
must be very large. The energy injection rate
$\unicode[STIX]{x1D716}$
is proportional to the cubic power of
$Re$
, which makes the dynamo onset extremely costly (in energy consumption) to reach in the laboratory. Given that technical constraints limit the size
$L$
of laboratory experiments on liquid metal to be no more than a couple of metres, the magnetic diffusivity of liquid sodium is
$\unicode[STIX]{x1D702}\simeq 10^{-1}~\text{m}^{2}~\text{s}^{-1}$
and its density
$\unicode[STIX]{x1D70C}\simeq 10^{3}~\text{kg}~\text{m}^{-3}$
, we arrive at an energy consumption rate larger than 100 kW assuming
$Rm_{c}\simeq 50$
, which is approximately the critical Reynolds number in the constrained dynamos mentioned above (see Pétrélis, Mordant & Fauve Reference Pétrélis, Mordant and Fauve2007). The VKS dynamo, for example, consumed 300 kW at its peak (Monchaux et al.
Reference Monchaux, Berhanu, Bourgoin, Moulin, Odier, Pinton, Volk, Fauve, Mordant and Pétrélis2007). This large required size and the large energy consumption rate limit dynamo experiments to laboratories of industrial size. Note that a reduction of
$Rm_{c}$
even by a factor of 2, i.e.
$Rm_{c}\simeq 25$
, reduces this consumption rate to
${\sim}$
10 kW, which is attainable in small-scale laboratories.
From the other side, numerical simulations in the last decade have been able to reach high enough Reynolds numbers to study the dependence of
$Rm_{c}$
as the low
$Pm$
limit is approached (Mininni & Montgomery Reference Mininni and Montgomery2005; Ponty et al.
Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005; Iskakov et al.
Reference Iskakov, Schekochihin, Cowley, McWilliams and Proctor2007). It was shown that as
$Re$
was increased the turbulent fluctuations prevented the dynamo instability, resulting in a value of
$Rm_{c}$
much larger than that of organized laminar flows. The value of
$Rm_{c}$
was shown to increase monotonically for values of
$Pm$
around 1, but finally for high enough values of
$Re$
(low enough
$Pm$
) a finite value of
$Rm_{c}$
was reached independent of
$Re$
. This finite value is the turbulent critical magnetic Reynolds number defined as
$Rm_{c}^{turb}\equiv \lim _{Re\rightarrow \infty }Rm_{c}$
. Different values of
$Rm_{c}^{turb}$
were obtained for the different flows under study, implying that this number is not universal and that the flows can be optimized to reduce
$Rm_{c}^{turb}$
. This was performed in Sadek, Alexakis & Fauve (Reference Sadek, Alexakis and Fauve2016) by varying the forcing length scale.
In this work we demonstrate that rotation can be used to reduce the dynamo threshold
$Rm_{c}^{turb}$
. Rotation is recognized as one of the key elements that determines the main characteristics of the resulting flows and magnetic fields of planets and stars (Proctor & Gilbert Reference Proctor and Gilbert1994). This is confirmed by observations over the last decade, which have measured the magnetic activity of stars as a function of their rotation period (Reiners, Basri & Browning Reference Reiners, Basri and Browning2009; Morin et al.
Reference Morin, Donati, Petit, Delfosse, Forveille and Jardine2010). It has also been argued that rotation can reduce the dynamo onset (Christensen & Aubert Reference Christensen and Aubert2006). At fast rotation rates variations along the axis of rotation are suppressed, rendering the flow quasi-2-D in the sense that the flow varies weakly along the direction of rotation while retaining all three velocity components (Alexakis Reference Alexakis2015; Dallas & Tobias Reference Dallas and Tobias2016), a situation referred to in the literature as 2.5-dimensional (2.5-D) flow. These 2.5-D flows have been shown to be effective dynamos (Smith & Tobias Reference Smith and Tobias2004; Seshasayanan & Alexakis Reference Seshasayanan and Alexakis2016a
,Reference Seshasayanan and Alexakis
b
). The fact that turbulent fluctuations inhibit the dynamo instability while more organized flows reduce the dynamo threshold (Tobias & Cattaneo Reference Tobias and Cattaneo2008a
,Reference Tobias and Cattaneo
b
; Tobias, Cattaneo & Boldyrev Reference Tobias, Cattaneo, Boldyrev, Davidson, Kaneda and Sreenivasan2011) indicates that background rotation can provide an efficient way to suppress fluctuations and optimize the flow so that the value of
$Rm_{c}^{turb}$
is reduced. In this work, we demonstrate that this is indeed the case. The effort to achieve the dynamo onset in rotating turbulent flows is modest in comparison to that in non-rotating turbulent flows, with the columnar vortices playing a key role in the spontaneous generation of the magnetic field.
2 Numerical set-up
In this paper we study the kinematic dynamo problem in a rotating frame of reference. Thus, the governing equations involved in this study are
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}\boldsymbol{u}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}=-\frac{1}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}p-2\unicode[STIX]{x1D734}\times \boldsymbol{u}+\unicode[STIX]{x1D708}\unicode[STIX]{x0394}\boldsymbol{u}+\boldsymbol{f}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}\boldsymbol{B}=\unicode[STIX]{x1D735}\times \left(\boldsymbol{u}\times \boldsymbol{B}\right)+\unicode[STIX]{x1D702}\unicode[STIX]{x0394}\boldsymbol{B}, & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{u}$
and
$\boldsymbol{B}$
are the velocity and the magnetic field respectively with
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}=0$
,
$\unicode[STIX]{x1D70C}$
is the mass density and
$p$
is the pressure. The rotation
$\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\hat{\boldsymbol{e}}_{z}$
is applied along the
$z$
-direction. We integrate these equations numerically in a cubic periodic box of length
$2\unicode[STIX]{x03C0}L$
using the pseudo-spectral code ghost (Mininni et al.
Reference Mininni, Rosenberg, Reddy and Pouquet2011) with a fourth-order Runge–Kutta scheme for the time advancement and the
$2/3$
de-aliasing rule. The body force is taken to be a 2.5-D non-helical Roberts flow,
$\boldsymbol{f}=f_{0}(\cos (k_{f}y),\sin (k_{f}x),\cos (k_{f}y)+\sin (k_{f}x))$
. Since we are interested in optimizing the flow to reduce the energy consumption in dynamo experiments, we define the non-dimensional parameters in terms of the energy injection/dissipation rate in the system measured by
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}\langle |\unicode[STIX]{x1D735}\boldsymbol{u}|^{2}\rangle$
, where
$\langle \cdot \rangle$
denotes volume and time average. The non-dimensional parameters in terms of
$\unicode[STIX]{x1D716}$
are the Reynolds number
$Re=(\unicode[STIX]{x1D716}/k_{f})^{1/3}/(k_{f}\unicode[STIX]{x1D708})$
, the magnetic Reynolds number
$Rm=(\unicode[STIX]{x1D716}/k_{f})^{1/3}/(k_{f}\unicode[STIX]{x1D702})$
and the Rossby number
$Ro=(\unicode[STIX]{x1D716}/k_{f})^{1/3}k_{f}/(2\unicode[STIX]{x1D6FA})$
. With this choice of non-dimensionalization
$Rm_{c}^{turb}$
can be related directly to the power
$\unicode[STIX]{x1D716}_{c}$
required to obtain a dynamo by
$\unicode[STIX]{x1D716}_{c}=\unicode[STIX]{x1D70C}(2\unicode[STIX]{x03C0}L)^{3}k_{f}^{4}\unicode[STIX]{x1D702}^{3}(Rm_{c}^{turb})^{3}$
. To recover other definitions based on the r.m.s. velocity
$U=\langle |\boldsymbol{u}^{2}|\rangle ^{1/2}$
of the flow,
$Re_{_{U}}=U/(k_{f}\unicode[STIX]{x1D708})$
and
$Ro_{_{U}}=Uk_{f}/(2\unicode[STIX]{x1D6FA})$
, we provide the dependence of
$\unicode[STIX]{x1D716}$
and
$U$
on the control parameters of the system in figure 1(a,b) and their asymptotic values in table 1.
We are interested in different limits of the parameters in this problem. To model the limit
$Re\gg 1$
(or the limit
$Pm\ll 1$
) we also use hyperviscosity where the Laplacian in the Navier–Stokes equation (2.1) is changed to
$\unicode[STIX]{x0394}^{4}$
. The use of hyperviscosity assumes that the large scales do not depend on the exact mechanism by which energy is dissipated in the small scales, and thus in principle it should always be compared to the results of large
$Re$
simulations.
The other limit we would like to reach is the fast rotating limit
$Ro\ll 1$
, in which the flow becomes 2.5-D (Gallet Reference Gallet2015). In this case the velocity field becomes invariant along the axis of rotation, and its evolution reduces to the 2-D Navier–Stokes equation for the horizontal components
$\boldsymbol{u}_{_{2D}}$
and an advection diffusion equation for the vertical component
$u_{z}$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}\boldsymbol{u}_{_{2D}}+\boldsymbol{u}_{_{2D}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\,\boldsymbol{u}_{_{2D}}=-\unicode[STIX]{x1D735}P+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}_{_{2D}}+\boldsymbol{f}_{_{2D}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}u_{z}+\boldsymbol{u}_{_{2D}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\,u_{z}=+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}u_{z}+f_{z}. & \displaystyle\end{eqnarray}$$
The magnetic field in this case can be expressed in the form
$\boldsymbol{B}=\boldsymbol{b}(x,y,t)\text{e}^{\text{i}k_{z}z}$
due to the invariance of the flow along the
$z$
-direction, where
$\boldsymbol{b}$
is a three-component complex vector field. Each
$k_{z}$
-mode evolves independently and the induction equation in this case reads
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\boldsymbol{b}+\boldsymbol{u}_{_{2D}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}+u_{z}\text{i}k_{z}\boldsymbol{b}=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D702}(\unicode[STIX]{x0394}-k_{z}^{2})\boldsymbol{b}.\end{eqnarray}$$
Then, the divergence-free condition
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}=0$
for each magnetic mode gives
$$\begin{eqnarray}\unicode[STIX]{x2202}_{x}b_{x}(x,y,t)+\unicode[STIX]{x2202}_{x}b_{y}(x,y,t)=-\text{i}k_{z}b_{z}(x,y,t).\end{eqnarray}$$
In this limit we follow only the
$k_{z}=1$
mode, which corresponds to the largest mode in our cubic domain and was found to be the most unstable mode (Smith & Tobias Reference Smith and Tobias2004; Seshasayanan & Alexakis Reference Seshasayanan and Alexakis2016b
). The range of the parameters used can be found in table 1.
Figure 1. The normalized total velocity squared
$U^{2}/(f_{0}/k_{f})$
(a) and the normalized dissipation rate
$\unicode[STIX]{x1D716}/(U^{3}k_{f})$
(b) as functions of the Reynolds number
$Re$
for different values of the rotation rate as mentioned in the legend. The points denoted by
$\star$
at
$Re=2000$
denote hyperviscosity runs.
Table 1. Numerical parameters of the simulations. For all runs
$f_{0}=1$
,
$L=1$
and
$k_{f}=4$
.
$N$
denotes the grid size. The reported values are for the largest values of
$Re$
(regular viscosity);
$Rm_{c}^{turb}$
is based on the hyperviscous runs.
$\unicode[STIX]{x1D6FA}=\infty$
corresponds to the 2.5-D simulations.
3 Results
We first describe the effect of rotation on the flow. Rotation affects the velocity field through the Coriolis term. At low
$Re$
the flow is laminar and
$\unicode[STIX]{x1D6FA}$
does not modify the velocity field because the laminar flow is invariant along the direction of rotation. As we increase
$Re$
beyond a threshold the flow becomes turbulent, varying along all three directions, and hence the effect of
$\unicode[STIX]{x1D6FA}$
becomes more important.
For
$\unicode[STIX]{x1D6FA}\lesssim 1$
, the effect of rotation is not dominant and the underlying flow is not far away from 3-D isotropic turbulence (compared to the cases with
$\unicode[STIX]{x1D6FA}\geqslant 3$
). The total energy
$U^{2}$
normalized by
$f_{0}/k_{f}$
and the normalized dissipation rate
$\unicode[STIX]{x1D716}/(U^{3}k_{f})$
reach asymptotic values for
$Re\rightarrow \infty$
as shown in figure 1. These asymptotic values match those obtained by the hyperviscous simulations, which are denoted by star symbols
$\star$
, and they are connected with the rest of the data set by dashed lines. This is the classical Kolmogorov turbulence where the large-scale quantities become independent of viscosity at large
$Re$
, and all the injected energy cascades via the nonlinearities to the small scales, where it is dissipated at a finite rate (Frisch Reference Frisch1995).
For
$\unicode[STIX]{x1D6FA}=3$
the flow becomes anisotropic with lesser fluctuations along the
$z$
-direction. There is an inverse cascade present in the system, which forms condensates. The growth of the condensate saturates when the counter-rotating vortex locally cancels the effect of global rotation for
$U\sim \unicode[STIX]{x1D6FA}L$
(Bartello, Métais & Lesieur Reference Bartello, Métais and Lesieur1994; Alexakis Reference Alexakis2015). The normalized dissipation rate
$\unicode[STIX]{x1D716}/(U^{3}k_{f})$
approaches an asymptote but at a much smaller value than in the non-rotating case. For larger rotation rates
$\unicode[STIX]{x1D6FA}=50$
and
$\unicode[STIX]{x1D6FA}=\infty$
saturation comes from viscous forces and
$\unicode[STIX]{x1D716}/(U^{3}k_{f})$
decreases with
$Re$
. An
$Re$
-independent scaling of the
$\unicode[STIX]{x1D6FA}=50$
case is also expected at large values of
$Re$
where a condensate of amplitude
$U\sim \unicode[STIX]{x1D6FA}L$
is reached. However, the realization of this behaviour at this large value of
$\unicode[STIX]{x1D6FA}$
is not possible even with hyperviscous runs. Furthermore the 2.5-D runs (
$\unicode[STIX]{x1D6FA}=\infty$
) will saturate due to viscous forces at high amplitudes inversely proportional to viscosity. For these reasons we do not investigate the
$\unicode[STIX]{x1D6FA}=50$
and
$\unicode[STIX]{x1D6FA}=\infty$
runs with hyperviscosity.
Figure 2. Relative helicity
$\unicode[STIX]{x1D70C}_{_{H}}$
as a function of time
$t$
for different values of
$\unicode[STIX]{x1D6FA}$
mentioned in the legend. Darker shades of blue correspond to larger values of
$\unicode[STIX]{x1D6FA}$
.
Another quantity that is important for large-scale dynamo action is the helicity
$H=\left\langle \boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}\right\rangle$
where
$\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
is the vorticity of the flow. Figure 2 shows the normalized helicity
$\unicode[STIX]{x1D70C}_{_{H}}=H/(\Vert \boldsymbol{u}\Vert \Vert \unicode[STIX]{x1D74E}\Vert )$
as a function of time for different values of
$\unicode[STIX]{x1D6FA}$
(here
$\Vert \cdot \Vert$
denotes the
$L_{2}$
norm). As we can see for
$\unicode[STIX]{x1D6FA}=3$
, we observe much larger fluctuations of
$\unicode[STIX]{x1D70C}_{_{H}}$
whose average over time is zero. Note that the time scale of the fluctuations is much longer than the eddy turnover time scale
$L/U\simeq 0.2$
. These fluctuations are due to the formation of the condensate (Dallas & Tobias Reference Dallas and Tobias2016). At small
$\unicode[STIX]{x1D6FA}$
the helicity fluctuations are governed by the small scales, for which the eddy turnover time is very short; for large
$\unicode[STIX]{x1D6FA}$
the helicity fluctuation is governed by the
$k_{z}=0$
mode, which fluctuates over a much longer time scale. We note that when a condensate forms, most of the energy is concentrated in the largest scales and thus there is no scale separation that would allow us to interpret our dynamo results in terms of an
$\unicode[STIX]{x1D6FC}$
dynamo (Moffatt Reference Moffatt1978).
Figure 3. Critical magnetic Reynolds number
$Rm_{c}$
as a function of
$Re$
for different values of
$\unicode[STIX]{x1D6FA}$
shown in the legend. The points denoted by
$\star$
at
$Re=2000$
denote hyperviscosity runs.
A priori we do not know whether the transition from a flow with no inverse cascade to a flow with an inverse cascade will decrease the dynamo threshold. To look at the effect of rotation on a dynamo we need to solve for the evolution of the magnetic field. To calculate
$Rm_{c}$
we run simulations of the same flow (same
$Re$
and
$Ro$
) but with different values of
$Rm$
.
$Rm_{c}$
was determined by linear interpolation of the growth rate between runs with a dynamo (positive growth rate) and runs without (negative growth rate). We then repeat the runs for larger values of
$Re$
, thus approaching the low
$Pm$
limit. Figure 3 shows the critical Reynolds number
$Rm_{c}$
as a function of
$Re$
for different values of
$\unicode[STIX]{x1D6FA}$
. The cases of
$\unicode[STIX]{x1D6FA}=0$
and 1 display similar behaviour to other studies of non-rotating flows (Mininni & Montgomery Reference Mininni and Montgomery2005; Ponty et al.
Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005; Iskakov et al.
Reference Iskakov, Schekochihin, Cowley, McWilliams and Proctor2007) in which
$Rm_{c}$
initially increases with
$Re$
, until it begins to become constant at large
$Re$
. For
$\unicode[STIX]{x1D6FA}=1$
the asymptotic value
$Rm_{c}^{turb}$
is larger than the
$\unicode[STIX]{x1D6FA}=0$
case, expressing an initial hindering effect for the dynamo by rotation. For
$\unicode[STIX]{x1D6FA}\geqslant 3$
, however, we see a much lower threshold for the dynamo instability and no such increase due to turbulence is observed. In fact the threshold for
$\unicode[STIX]{x1D6FA}=3$
appears no different to that for
$\unicode[STIX]{x1D6FA}=\infty$
, implying that the destructive effect of the 3-D turbulent fluctuations on the dynamo has already disappeared. The ratio between
$Rm_{c}^{turb}$
for the case of
$\unicode[STIX]{x1D6FA}=0$
and that for
$\unicode[STIX]{x1D6FA}=3$
for the hyperviscous runs is approximately
${\sim}12$
. The injected power
$\unicode[STIX]{x1D716}$
scales like
$(Rm_{c}^{turb})^{3}$
, implying a reduction in the power required for a dynamo instability by a factor of
$2\times 10^{3}$
between
$\unicode[STIX]{x1D6FA}=0$
and 3 and a factor of
$8\times 10^{3}$
between
$\unicode[STIX]{x1D6FA}=1$
and 3 (see figure 3).
Figure 4. (a) Compensated kinetic energy spectra
$k^{2}E(k)$
and (b) magnetic energy spectra for the two different cases of
$\unicode[STIX]{x1D6FA}=0$
and 3 for the hyperviscous runs (i.e.
$Pm\ll 1$
).
Figure 5. (a) Colour plot of the vertical vorticity
$\unicode[STIX]{x1D714}_{z}$
. (b) Vertical current
$j_{z}$
. Red corresponds to positive (co-rotating) values and blue to negative (counter-rotating) values. Both panels have
$\unicode[STIX]{x1D6FA}=3$
,
$Re\approx 60$
,
$Pm=0.0375$
and are extracted at the same time.
To decipher the reason behind this drop in
$Rm_{c}^{turb}$
at
$\unicode[STIX]{x1D6FA}=3$
we display in figure 4(a) the enstrophy spectra
$k^{2}E(k)$
for
$\unicode[STIX]{x1D6FA}=0$
and
$\unicode[STIX]{x1D6FA}=3$
obtained from the hyperviscous runs. Large enstrophy implies a larger stretching rate of the magnetic field lines (although not necessarily constructive). For
$\unicode[STIX]{x1D6FA}=0$
a behaviour close to Kolmogorov type is observed, with the enstrophy spectrum
$k^{2}E(k)$
increasing with
$k$
after the forcing scale
$k_{f}=4$
. The strongest stretching rate is thus clearly at the small incoherent scales. In contrast, for
$\unicode[STIX]{x1D6FA}=3$
the enstrophy spectrum
$k^{2}E(k)$
is decreasing with
$k$
. Only at the smallest scales does
$k^{2}E(k)$
start to increase again. Thus, the small-scale fluctuations are suppressed and the dominant stretching rate
$u_{\ell }/\ell$
is restricted to the large coherent scales. Figure 5(b) shows the vertical vorticity field
$\unicode[STIX]{x1D714}_{z}$
for
$\unicode[STIX]{x1D6FA}=3$
, displaying a strong coherent co-rotating vortex aligned with the global rotation and a counter-rotating vortex responsible for the energy cascade to small scales. Note that the same structure is observed in a flow driven by a Taylor–Green forcing (Alexakis Reference Alexakis2015) and in rotating convection (Guervilly, Hughes & Jones Reference Guervilly, Hughes and Jones2014). Thus, this structure is not related to the particular choice of forcing used. The dynamo thus behaves as if it is driven just by the organized large scales that act as a laminar flow (i.e. it behaves similarly to a high
$Pm$
dynamo) even though the actual Reynolds number is much higher than the magnetic Reynolds number (i.e. low
$Pm$
).
This suppression of small-scale fluctuations, however, is not due to a dissipative mechanism since the Coriolis term is not dissipative and thus does not lead to an extra cost in energy injection.
The magnetic energy spectra for
$Rm$
close to the onset (i.e. at the kinematic phase of the dynamo) are shown in figure 4(b). For the case of
$\unicode[STIX]{x1D6FA}=0$
the magnetic energy spectrum is almost flat with an exponential decay at high wavenumbers. The unstable eigenmode (not shown here) takes the form of thin filamentary structures. On the other hand, for
$\unicode[STIX]{x1D6FA}=3$
the magnetic energy spectrum decreases fast with
$k$
. The peak of the magnetic energy is at the forcing scale (
$k_{f}=4$
), while the energy of the large-scale component (
$k=1$
) is more than an order of magnitude smaller. Thus despite the presence of helicity this is not a large-scale dynamo (Ponty & Plunian Reference Ponty and Plunian2011; Cameron & Alexakis Reference Cameron and Alexakis2016). The structure of the vertical current field
$j_{z}$
from an unstable eigenmode of the dynamo at
$\unicode[STIX]{x1D6FA}=3$
is shown in figure 5(b). The magnetic field as seen previously in the spectra is present at large scales, with the
$k_{z}=1$
mode being dominant. Most of the magnetic energy is concentrated along the coherent co-rotating vortex in two oppositely directed spiral flux tubes.
4 Conclusions
The present study shows that global rotation can play a positive role in the dynamo instability by (i) suppressing turbulent fluctuations and (ii) organizing the large scales in space and time, making them more effective in performing a constructive refolding of the magnetic field lines. These two effects lead the flow to be more efficient in driving the dynamo (at present we cannot be explicit on which of the two effects is more important). This discovery provides a new paradigm for the design of new dynamo experiments that include global rotation.
Our study was performed in an idealized set-up of a triple periodic box. Thus, the question that arises naturally is to what extent these results can carry over to more realistic domains and boundary conditions. Boundaries can delay the inverse cascade (as has been noted in rotating convection (Kunnen et al.
Reference Kunnen, Ostilla-Mónico, van der Poel, Verzicco and Lohse2016; Plumley et al.
Reference Plumley, Julien, Marti and Stellmach2016)) and can also introduce further dissipation mechanisms in the boundary layers such as Ekman friction. To answer this question, further work needs to be pursued with simulations in more realistic domains. Nevertheless we note that reaching rotation rates in the laboratory that lead to quasi-2-D flows is feasible and has already been achieved in water-tank experiments (Yarom, Vardi & Sharon Reference Yarom, Vardi and Sharon2013; Campagne et al.
Reference Campagne, Gallet, Moisy and Cortet2014). Furthermore, in Campagne et al. (Reference Campagne, Machicoane, Gallet, Cortet and Moisy2016) the dissipated power in rotating turbulence was directly measured and was shown to decrease by a factor of 10 at the highest rotation examined, compared to the dissipated power in non-rotating turbulence, due to a two-dimensionalization of the flow. At the examined rotation rates no enhancement of the viscous dissipation due to Ekman layers was observed. So, suppressing turbulent fluctuations and decreasing energy dissipation by adding global rotation is indeed feasible experimentally. The additional energy cost of maintaining the rotation is probably minimal compared to the large gain of the order of
$10^{3}$
due to the suppression of turbulent fluctuations. Another issue that needs to be considered is the design of the domain and the forcing, which should guarantee that all three velocity components are present, so that the flow becomes 2.5-D and not 2-D. This difficulty can be overcome by the proper design of the forcing mechanism that amplifies all velocity components.
Finally, we note that this result also shows that in fast rotating systems, such as the Earth, the critical magnetic Reynolds number based on the energy injected to sustain a dynamo instability might stay very small,
$Rm\sim O(1)$
, even at large Reynolds numbers.
Acknowledgements
The authors acknowledge enlightening discussions with S. Fauve. V.D. acknowledges support from the Royal Society and the British Academy of Sciences (Newton International Fellowship, NF140631). The computations were performed using the HPC resources from GENCI-TGCC-CURIE (Project no. x2016056421) and ARC1, part of the High Performance Computing facilities at the University of Leeds, UK.
