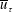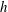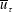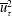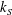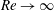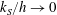1 Introduction
Non-circular ducts are of interest as they generate secondary flows of the second kind according to Prandtl’s definition (Bradshaw Reference Bradshaw1987), which reveal the rich effects of turbulence, and have a definite practical importance particularly in convex corner flows. They expose the weakness of the Boussinesq approximation used in the widespread linear eddy-viscosity models, thus providing a helpful starting point for nonlinear models (Spalart Reference Spalart2000). The straight duct with a square cross-sectional shape has been prevalent (Raiesi, Piomelli & Pollard Reference Raiesi, Piomelli and Pollard2011; Pirozzoli et al.
Reference Pirozzoli, Modesti, Orlandi and Grasso2017). The complexity of the physics naturally leads one to expect non-trivial and shape-dependent quantitative behaviour for the primary measure of this flow, namely the skin friction, which makes the simple prediction discussed in this note somewhat remarkable. While there is much practical interest in developing flows, the work here concerns only fully developed flows, independent of the streamwise coordinate
$x$
, other than the gradual pressure drop of course. Also of interest is the scaling (as the Reynolds number varies) of the secondary flow velocities and the Reynolds stresses, possibly proportional to a single velocity scale
$\overline{u}_{\unicode[STIX]{x1D70F}}$
with the nature of a friction velocity. Such a scaling is somewhat established for the core regions of two-dimensional channels and circular pipes, but controversies remain active in particular over the existence of plateaus on the stress profiles, and the imperfect universality near the wall. See, among others, Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013) for both smooth and rough walls in pipes. Conveniently, in fully developed channel and pipe flows the Reynolds stresses which suffer from controversies do not enter the momentum equation, so that universal behaviour of the velocity profile is possible even with these questions unanswered.
The present note can be considered as the extension to more general ducts of the work of Pullin, Inoue & Saito (Reference Pullin, Inoue and Saito2013) in channels, pipes and boundary layers; we note their term ‘gigantic’ for the Reynolds number and the requirement that
$\log (Re)\gg 1$
. We also note their words ‘the asymptotic state of the wall layer is a slip-flow bounded by a vortex sheet at the wall with weakly nonlinear internal structure’, which are fully consistent with our findings.
As mentioned above, after the presentation of the theory we use solutions with conventional Reynolds-averaged Navier–Stokes (RANS) turbulence models to verify the assumed scaling over a wide Reynolds-number range, and check that it spontaneously appears. We consider that essentially all current models will have the same qualitative behaviour. However, these findings do not constitute independent physical evidence, because the models interact with the mean flow field in precisely the same framework that the theory is built on: the momentum equation, and the control of the turbulence-model equations by production terms based on the mean deformation tensor. In addition, the Spalart–Allmaras model (Spalart & Allmaras Reference Spalart and Allmaras1994) contains an explicit term that depends on the distance to the wall, which is very consistent with the present theory. A rigorous independent validation could come from direct numerical simulation, but of course large Reynolds numbers are out of the question for direct numerical simulation (DNS), and much judgment will be needed to extract indications from DNS (Pirozzoli et al. Reference Pirozzoli, Modesti, Orlandi and Grasso2017). Wall-modelled large-eddy simulation can be used, but it is not at all free of near-wall assumptions which again communicate with the theory. Very high Reynolds numbers have been reached in experiments in circular pipe flow and could be reached in a non-circular duct, at the expense of building a new duct or insert (which could be a simple floor).
The note proceeds with basic definitions in § 2, the approximations in § 3, turbulence-model studies in § 4 and a discussion in § 5.
2 Definitions
Let
$\text{d}p/\text{d}x$
be the mean streamwise pressure gradient and
$h$
the characteristic dimension, for which a helpful specific definition is
$h\equiv 2A/P$
, where
$A$
is the area of the cross-section and
$P$
its perimeter (it gives the half-width for a square, and the radius for a circle). Thus,
$2h$
is the hydraulic diameter. As mentioned in the abstract, a geometry with two disparate characteristic dimensions, say a rectangle with
$h_{1}\ll h_{2}$
, would not qualify as
$h_{1}$
would dominate; an elongated triangle would be an even worse proposition. We define a global average friction velocity,
$\overline{u}_{\unicode[STIX]{x1D70F}}\equiv \sqrt{A|\text{d}p/\text{d}x|/(\unicode[STIX]{x1D70C}P)}$
. Velocities in these wall units will be denoted with a bar also:
$\overline{U}^{+}\equiv U/\overline{u}_{\unicode[STIX]{x1D70F}}$
. Finally,
$Re_{\unicode[STIX]{x1D70F}}\equiv h\overline{u}_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$
is the friction Reynolds number. There are other Reynolds numbers, but they are all functions of each other for a given shape.
We use both the
$(y,z)$
Cartesian coordinate system and a curvilinear
$(s,n)$
system along the wall, in which
$s\in [0,P]$
,
$n=0$
at the wall, and
$n\ll h$
in the region where the overlap argument is made. At corners, the
$(s,n)$
system becomes ambiguous, and the argument fails for physical reasons. These regions shrink as the Reynolds number rises, so that the asymptotic result holds over more and more of the perimeter.
The basic assumption about the fully developed turbulent flow is that for each shape, there exist the following unique functions:
$\overline{U}^{+}(y/h,z/h,Re_{\unicode[STIX]{x1D70F}})$
,
$\overline{V}^{+}(y/h,z/h,Re_{\unicode[STIX]{x1D70F}})$
,
$\overline{W}^{+}(y/h,z/h,Re_{\unicode[STIX]{x1D70F}})$
and the equivalent for the Reynolds stresses and pressure field. These give, for each shape, unique functions for integral quantities, for instance the bulk velocity
$\overline{U}_{b}^{+}$
is a function of
$Re_{\unicode[STIX]{x1D70F}}$
.
3 Approximations and their consequences
Here, approximations based on the Reynolds number being high,
$Re_{\unicode[STIX]{x1D70F}}\rightarrow \infty$
, or the roughness small,
$k_{S}/h\rightarrow 0$
, are introduced.
3.1 Core region
For the core region, we can consider deviations from the bulk velocity
$U_{b}$
or from the centreline (or peak) velocity
$U_{max}$
, but to leading order, the difference between them is proportional to
$\overline{u}_{\unicode[STIX]{x1D70F}}$
, so that the approximations are equivalent. We use the symbol
$f(\cdot )$
to mean ‘is a function of’.
We posit, after Townsend (Reference Townsend1961) and others that, exactly as in channel and pipe flows, outside the viscous or roughness-influenced regions (i.e. for
$n^{+}\gg 1$
or
$n/k_{S}\gg 1$
):
$$\begin{eqnarray}\overline{U}^{+}-\overline{U}_{b}^{+}=f_{uc}\left(\frac{y}{h},\frac{z}{h}\right),\quad \overline{V}^{+}=f_{vc}\left(\frac{y}{h},\frac{z}{h}\right),\quad \overline{W}^{+}=f_{wc}\left(\frac{y}{h},\frac{z}{h}\right),\end{eqnarray}$$
where ‘
$uc$
’ stands for ‘
$U$
in the core’ with similar notations for turbulence quantities
$$\begin{eqnarray}\overline{\langle u_{i}u_{j}\rangle }^{+}=f_{ijc}\left(\frac{y}{h},\frac{z}{h}\right).\end{eqnarray}$$
The same scaling applies to the pressure. As usual, capitals denote averaged quantities, and lower-case letters fluctuating quantities. The terms in the continuity equation are proportional to
$\overline{u}_{\unicode[STIX]{x1D70F}}/h$
. All the terms except the viscous term in the momentum equation are proportional to
$\overline{u}_{\unicode[STIX]{x1D70F}}^{2}/h$
and therefore balance is possible to leading order, with the neglected viscous term being of relative order
$1/Re_{\unicode[STIX]{x1D70F}}$
.
3.2 Wall regions
These satisfy
$n\ll h$
. The local skin friction gives a local-friction velocity
$u_{\unicode[STIX]{x1D70F}}(s/h)$
. To leading order, it can be based either on the wall shear stress in the
$x$
direction or on the magnitude in the
$(x,s)$
plane, since the flow angle tends to 0 as
$Re_{\unicode[STIX]{x1D70F}}$
increases. We expect a unique local-friction function
$u_{\unicode[STIX]{x1D70F}}(s/h)/\overline{u}_{\unicode[STIX]{x1D70F}}=f_{lf}(s/h)$
; this is a further assumption, of the same nature as those made in the core region.
The primary approximation here is that for a smooth wall, with
$n^{+}\equiv nu_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$
$$\begin{eqnarray}\frac{U}{u_{\unicode[STIX]{x1D70F}}}=f_{SW}(n^{+}).\end{eqnarray}$$
This is the ‘law of the wall’. It is based on the local friction velocity.
The approximation for a fully rough wall with a local roughness
$k_{S}(s/h)$
(and therefore
$k_{S}^{+}\gg 1$
) is
$$\begin{eqnarray}\frac{U}{u_{\unicode[STIX]{x1D70F}}}=f_{RW}\left(\frac{n}{k_{S}}\right).\end{eqnarray}$$
It is also based on the local friction velocity. We assume that the local roughness at different
$s$
locations tends to zero at the same rate, that is, we have
$k_{S}(s/h)=f_{lr}(s/h)k_{S0}$
, and
$f_{lr}$
is fixed while
$k_{S0}/h\rightarrow 0$
. In simple cases,
$f_{lr}=1$
.
3.3 Overlap region, smooth wall
The key identity in the band which satisfies both
$n\ll h$
and
$n^{+}\gg 1$
(which is possible only for large Reynolds number) is the overlap between (3.3) on the left-hand side and equation (3.1a
) on the right-hand side, inserting the relationship
$n^{+}=f_{lf}(s/h)[n/h]Re_{\unicode[STIX]{x1D70F}}$
:
$$\begin{eqnarray}f_{lf}\left(\frac{s}{h}\right)f_{SW}\left(f_{lf}\left(\frac{s}{h}\right)\frac{n}{h}Re_{\unicode[STIX]{x1D70F}}\right)=\overline{U}^{+}=\overline{U}_{b}^{+}+f_{uc}\left(\frac{s}{h},\frac{n}{h}\right),\end{eqnarray}$$
where the function
$f_{uc}$
was mapped from
$(y/h,z/h)$
to
$(s/h,n/h)$
.
This overlap argument is most closely associated with Millikan’s (Reference Millikan1938) paper. However we believe, first, that the physical content is equivalent to that of von Kármán in the 1920s and many other treatises and, second, that the mathematical steps can be taken in a number of different orders without altering the conclusion. Our choice is to bring out the consequences of (3.5) by differentiating it or exploiting dependencies with respect to
$Re_{\unicode[STIX]{x1D70F}}$
, then to
$n$
, then to
$s$
.
The derivative of (3.5) with respect to
$Re_{\unicode[STIX]{x1D70F}}$
at fixed
$(s/h,n/h)$
is
$$\begin{eqnarray}f_{lf}^{2}\left(\frac{s}{h}\right)\frac{n}{h}f_{SW}^{\prime }\left(f_{lf}\left(\frac{s}{h}\right)\frac{n}{h}Re_{\unicode[STIX]{x1D70F}}\right)=\frac{\text{d}\overline{U}_{b}^{+}}{\text{d}Re_{\unicode[STIX]{x1D70F}}},\end{eqnarray}$$
where the prime denotes a derivative. We now exploit the dependence on
$n/h$
. The only factors that vary with
$n/h$
are
$n/h$
itself or equivalently
$n^{+}$
and
$f_{SW}^{\prime }(n^{+})$
, therefore
$n^{+}f_{SW}^{\prime }$
must be a constant denoted by
$1/\unicode[STIX]{x1D705}$
, which leads to the log law for velocity, namely,
$U^{+}\equiv U/u_{\unicode[STIX]{x1D70F}}(s/h)=\log (n^{+})/\unicode[STIX]{x1D705}+C$
. Assuming a universal von Kármán constant
$\unicode[STIX]{x1D705}$
and intercept
$C$
as implied by (3.3), (3.6) becomes
$$\begin{eqnarray}f_{lf}\left(\frac{s}{h}\right)\frac{1}{\unicode[STIX]{x1D705}Re_{\unicode[STIX]{x1D70F}}}=\frac{\text{d}\overline{U}_{b}^{+}}{\text{d}Re_{\unicode[STIX]{x1D70F}}}.\end{eqnarray}$$
The right-hand side is independent of
$s$
, which means
$f_{lf}$
is uniform. The average of its square being 1,
$f_{lf}$
can only equal 1. This is our key new prediction: the skin friction is independent of
$s$
.
This equation then gives the skin-friction law
$$\begin{eqnarray}\overline{U}_{b}^{+}=\frac{1}{\unicode[STIX]{x1D705}}\log Re_{\unicode[STIX]{x1D70F}}+C_{SW}^{\prime }.\end{eqnarray}$$
The constant
$C_{SW}^{\prime }$
depends only on the shape of the cross-section. This is very consistent with the findings of Pirozzoli et al. (Reference Pirozzoli, Modesti, Orlandi and Grasso2017), although in other respects they do not agree with the present theory, as discussed in § 5.
3.4 Overlap region, rough wall
The key identity is now the overlap between (3.4) on the left-hand side and equation (3.1a
) on the right-hand side, with
$k_{S}\ll n\ll h$
, in
$$\begin{eqnarray}f_{lf}\left(\frac{s}{h}\right)f_{RW}\left(\frac{n}{f_{lr}(s/h)k_{S0}}\right)=\overline{U}^{+}=\overline{U}_{b}^{+}+f_{uc}\left(\frac{s}{h},\frac{n}{h}\right).\end{eqnarray}$$
Again, we arrive at the consequences of (3.9) by differentiating it or exploiting dependencies with respect to
$k_{S0}/h$
, then to
$n$
, then to
$s$
. The derivative of (3.9) with respect to
$k_{S0}/h$
at fixed
$(s/h,n/h)$
is
$$\begin{eqnarray}-f_{lf}\left(\frac{s}{h}\right)\frac{nh}{f_{lr}(s/h)k_{S0}^{2}}f_{RW}^{\prime }\left(\frac{n}{f_{lr}(s/h)k_{S0}}\right)=\frac{\text{d}\overline{U}_{b}^{+}}{\text{d}(k_{S0}/h)}.\end{eqnarray}$$
We now exploit the dependence on
$n$
. The only factors that vary with
$n/h$
are
$n/h$
itself and
$f_{RW}^{\prime }$
, therefore
$(n/k_{S})f_{RW}^{\prime }$
must be a constant giving a log law, and
$$\begin{eqnarray}-f_{lf}\left(\frac{s}{h}\right)\frac{h}{k_{S0}}\frac{1}{\unicode[STIX]{x1D705}}=\frac{\text{d}\overline{U}_{b}^{+}}{\text{d}(k_{S0}/h)}.\end{eqnarray}$$
The right-hand side is independent of
$s$
, which means
$f_{lf}$
is uniform and equals 1. Again, the skin friction is independent of
$s$
, even if the roughness is not uniform (but scales at the same rate independent of
$s$
).
This equation then gives the skin-friction law
$$\begin{eqnarray}\overline{U}_{b}^{+}=-\frac{1}{\unicode[STIX]{x1D705}}\log \left(\frac{k_{S0}}{h}\right)+C_{RW}^{\prime }.\end{eqnarray}$$
The constant
$C_{RW}^{\prime }$
depends on the shape of the cross-section, and the
$f_{lr}$
function.
4 Turbulence-model studies
The RANS models used are as follows. The Spalart–Allmaras (SA) model, aimed at aerodynamic flows (Spalart & Allmaras Reference Spalart and Allmaras1994) relies on a single empirical equation to produce an eddy viscosity, and was calibrated on a few thin shear flows. It has eight primary adjustable constants. The QCR or quadratic constitutive relation (Spalart Reference Spalart2000) uses the eddy viscosity from any chosen model (i.e. it is not limited to SA), but instead of using the straightforward Boussinesq constitutive relation, the Reynolds stresses also contain terms proportional to the product of the rotation tensor and the strain tensor. This improves the anisotropy of the stresses, and allows eddy-viscosity models to capture turbulent secondary flows of the second kind (the linear SA model would not reproduce the
$y{-}z$
motion in non-circular ducts, as predicted by Speziale Reference Speziale1982). The QCR here depends only on one additional constant.
The grids obeyed standard guidelines for the value of the first
$n^{+}$
spacing and the stretching ratio in
$n$
; in the ellipses the wall-to-centre grid count ranged from 124 at the lowest Reynolds number to 256 at the highest
$Re_{\unicode[STIX]{x1D70F}}$
. The distribution versus
$s$
was tested with different levels of resolution; the 4-to-1 ellipse required rather strong refinement near the tight concave region, leading to 532 nodes for the entire perimeter.
Figure 1. Streamwise and secondary velocities in square and elliptical ducts, as predicted by the Spalart–Allmaras QCR (SAQCR) model.
4.1 Square duct
Figure 1 provides a perspective of the secondary flows, as predicted by a nonlinear RANS model. They are in good qualitative agreement with DNS (Nikitin & Yakhot Reference Nikitin and Yakhot2005; Pirozzoli et al.
Reference Pirozzoli, Modesti, Orlandi and Grasso2017). The different symmetries of the two geometries result in eight vortices in the square and only four in the ellipse; it appears the turbulence ‘maximizes’ the size of the vortices, and consistently directs the secondary flow towards the tighter concave regions, which happens to promote uniformity. The secondary motion is not strong (less than 1 % of the bulk velocity), but it is sufficient to very noticeably alter the skin friction along the wall, as confirmed in figure 2 by results from the linear SA model (which fails to generate secondary flow) and the nonlinear SAQCR model (which does generate secondary flow). As usual, evidence from turbulence models is to be treated with caution, but is not meaningless. It appears likely that all the models in this general class will miss the surge in skin friction revealed by the DNS near the corner; results from two-equation and Reynolds stress transport models, not shown, are very consistent with this prediction. This surge moves closer to the corner as
$Re$
increases (Pirozzoli et al.
Reference Pirozzoli, Modesti, Orlandi and Grasso2017). The existing nonlinear models appear to capture the gross corner effect, but not the subtler, localized one.
Figure 2. Skin friction in square duct, from DNS (Raiesi et al. Reference Raiesi, Piomelli and Pollard2011; Pirozzoli et al. Reference Pirozzoli, Modesti, Orlandi and Grasso2017) and from two models.
Figure 3 strongly supports the idea that the secondary motion at the point in the centre of each quadrant is proportional to the global friction velocity, in agreement with the tentative theory (3.1), rather than the bulk velocity (as is predicted by Pirozzoli et al.
Reference Pirozzoli, Modesti, Orlandi and Grasso2017, but note that the trend we are referring to is not yet established for the Reynolds numbers of their simulations). Finally, figure 4 gives strong support to the prediction of uniform skin friction along the sides of the square duct, excepting the corners. The trend towards uniformity versus
$s$
as the Reynolds number is raised is very convincing. For the corner regions, the condition
$n^{+}\gg 1$
is not satisfied if
$n$
is measured from the other wall which intersects the wall on which skin friction is examined. The skin friction must fall to zero at the corner, but that happens increasingly steeply for higher Reynolds number.
Figure 3. Secondary velocities at
$(y,z)=(h/2,h/2)$
in square duct of side
$2h$
, for different
$Re$
, as predicted by the SAQCR model.
Figure 4. Skin friction in square duct, for different
$Re$
, as predicted by the SAQCR model.
Figure 5. Skin friction around elliptical duct, as predicted by the SAQCR model. (a) The 2-to-1 shape; (b) the 4-to-1 shape. Notice the very different scales.
Figure 6. Skin-friction law for elliptical ducts, as predicted by the SAQCR model.
4.2 Elliptical duct
The results in an ellipse with 2-to-1 ratio of its axes are even more favourable than those in the square. Here,
$h$
is approximately
$0.65a$
where
$a$
is the major axis. Figure 5(a) shows that the
$f_{lf}$
variations are of the order of
$\pm 1\,\%$
at the lowest Reynolds number (whereas the range for laminar flow is from 0.78 to 1.11), and then steadily decrease as the Reynolds number is repeatedly multiplied by 100. Admittedly, the evolution is slow: a factor-of-
$10^{6}$
increase fails to make the variation vanish. This means that, at manageable Reynolds numbers, the residual non-uniformity of the skin friction (of order
$\overline{u}_{\unicode[STIX]{x1D70F}}/U_{b}$
) will provide a test of a turbulence model of some interest, similar to the comparison with DNS in figure 2. The 4-to-1 ellipse in figure 5(b) admits much larger variations, although it is not truly a geometry with ‘
$h_{1}\ll h_{2}$
’, but the trend versus
$Re_{\unicode[STIX]{x1D70F}}$
is similar. Finally, figure 6 verifies the skin-friction law (3.8), confirming the prediction that the maximum velocity differs from the bulk velocity by a constant multiple of
$\overline{u}_{\unicode[STIX]{x1D70F}}$
and also making the point that the bulk velocity in wall units is very close between the two ellipses; this happens because almost all the velocity rise occurs inside the wall layer (Pullin et al.
Reference Pullin, Inoue and Saito2013).
We attempted to exhibit a linear dependency of the maximum skin-friction deviation on
$1/\log (Re_{\unicode[STIX]{x1D70F}})$
(it being amply clear from figure 5 that scaling with
$1/Re_{\unicode[STIX]{x1D70F}}$
is ruled out). The problem with such an exercise is that the function is really
$1/\log (Re_{\unicode[STIX]{x1D70F}}/Re_{\unicode[STIX]{x1D70F}0})$
where
$Re_{\unicode[STIX]{x1D70F}0}$
is arbitrary, so that the curvature of the line can be altered at will (this was not an issue in figure 6 since altering
$Re_{\unicode[STIX]{x1D70F}0}$
simply moves the curves up or down). This greatly weakens any conclusions.
5 Discussion
A simple theory of fully developed turbulence in straight ducts with non-circular cross-section was presented, and found to be consistent with conventional turbulence models. In short, it generalizes the defect law from one-dimensional to two-dimensional fields, containing secondary turbulent flows of the second kind. It is limited to shapes of moderate aspect ratio, well characterized by a single length scale. Its prediction that the skin friction around the duct will be uniform away from corners in the limit of large Reynolds number was a surprise to us, and has the merit of amounting to a simple fact and being testable. If it stands the test of time, it will represent a small but non-trivial addition to turbulence theory.
The DNS results of Pirozzoli et al. in a square duct are unfortunately not supportive of the theory; in particular, an ‘educated guess’ based in their skin-friction figure would probably predict that the high-Reynolds-number asymptote curves down for roughly
$z/h<0.3$
. It is fair to write that the DNS results do not ‘suggest’ a uniform skin-friction distribution. The scaling of the secondary velocity with
$\overline{u}_{\unicode[STIX]{x1D70F}}$
is no more convincing, as they favour a scaling with
$U_{b}$
(their figures 4 and 7 and S. Pirozzoli, personal communication 2017). One should not blame ‘low-Reynolds-number effects’ for every disappointing comparison but we note that in channel flow, with
$Re_{\unicode[STIX]{x1D70F}}$
values five times larger, DNS is still not decisively confirming the logarithmic law. The gap from DNS Reynolds numbers to those that fully enable the theory remains wide.
The results of Nikitin & Yakhot (Reference Nikitin and Yakhot2005) for elliptical ducts were limited to lower Reynolds than those of Pirozzoli et al. in the square duct, but the trend in their figure 8 is qualitatively very favourable in our opinion: namely, the skin friction is far closer to uniform for the turbulent than for the laminar flow. This is also true for results of turbulence modelling, in both the square and elliptical geometries.
Acknowledgements
We are grateful for the comments of P. Bradshaw, O. Gonzalez, S. Pirozzoli, M. Shur and M. Strelets. The addition of rough-wall reasoning was suggested by one of the referees.
