1 Introduction
It is a common experience to observe that when a jet of water falls vertically from a tap on to the base of a domestic sink, the water spreads radially outwards in a thin film until it reaches a radius where the film thickness increases abruptly. This abrupt change in depth is the circular hydraulic jump shown in figure 1(a). Beyond the jump, the thicker downstream liquid film then spreads until it reaches the edge of the sink. Up to this point, the hydraulic jump radius remains approximately at the same location (see supplementary movie 1 available at https://doi.org/10.1017/jfm.2018.558). Once the liquid reaches the edge of the sink, the boundary condition for the liquid film changes, the downstream liquid film thickness increases and the initial steady hydraulic jump radius moves inwards. In the present study, we are interested in the steady hydraulic jump before the liquid reaches the edge of the plate.

Figure 1. Hydraulic jumps caused by a water jet impinging normally on surfaces with different orientations. In these three cases the jets are identical, produced from the same nozzle at the same flow rate,
![]() $Q=1~\text{L}~\text{min}^{-1}$
, and the radius of the jump is observed to be independent of the orientation of the surface. (a) Horizontal surface; jet impinging from above, (b) vertical surface; jet impinging horizontally, (c) horizontal surface; jet impinging from below.
$Q=1~\text{L}~\text{min}^{-1}$
, and the radius of the jump is observed to be independent of the orientation of the surface. (a) Horizontal surface; jet impinging from above, (b) vertical surface; jet impinging horizontally, (c) horizontal surface; jet impinging from below.
The hydraulic jump has been studied for over four hundred years. An early account was presented by Leonardo de Vinci in the 16th century (Hager Reference Hager2013). The Italian mathematician Bidone (Reference Bidone1819) published experimental results on the topic and Rayleigh (1914) subsequently provided the first theoretical explanation for the planar hydraulic jump based on inviscid theory.
Figures 1(b) and 1(c) show that the same abrupt change in film thickness occurs on a vertical plane impacted by a horizontal jet and a horizontal plane impacted from below by an upwards directed jet, respectively. Further, as can be seen in figure 1, for a given jet diameter and flow rate, the radius of the initial jump is the same in all cases, irrespective of the orientation of the surface. Thus we conclude that gravity plays no role in the initial formation of the jump.
To the best of our knowledge all existing explanations for thin-film hydraulic jumps on the scales we are considering in this paper invoke gravity as a significant force in its formation. The purpose of this paper is to show that this view is incorrect and that the appropriate force balance in these jumps critically involves surface tension and that gravity is unimportant. To achieve this aim we review the previous theories and experiments in § 2. We describe our experiments in § 3, and then carry out a scaling analysis in § 4, and show that this collapses our experimental data. We further develop a detailed theory for the flow in § 5 and explain the role of surface tension in the force balance, and compare the theoretical predictions with the experimental data for different surface orientations and fluid properties in § 6. Our conclusions are given in § 7.
2 Previous studies
We are concerned here with the initiation of the jump shown by the schematic in figure 2(a), so we consider the impact of a jet normally on an infinite plane. In practice, all experiments involve a plane of finite dimensions and eventually the liquid drains from the edges of the surface. Consequently, we restrict ourselves to considerations of the flow before it reaches the edge of the surface, and ignore the changes that occur once the downstream boundary condition changes (see supplementary movie 2).
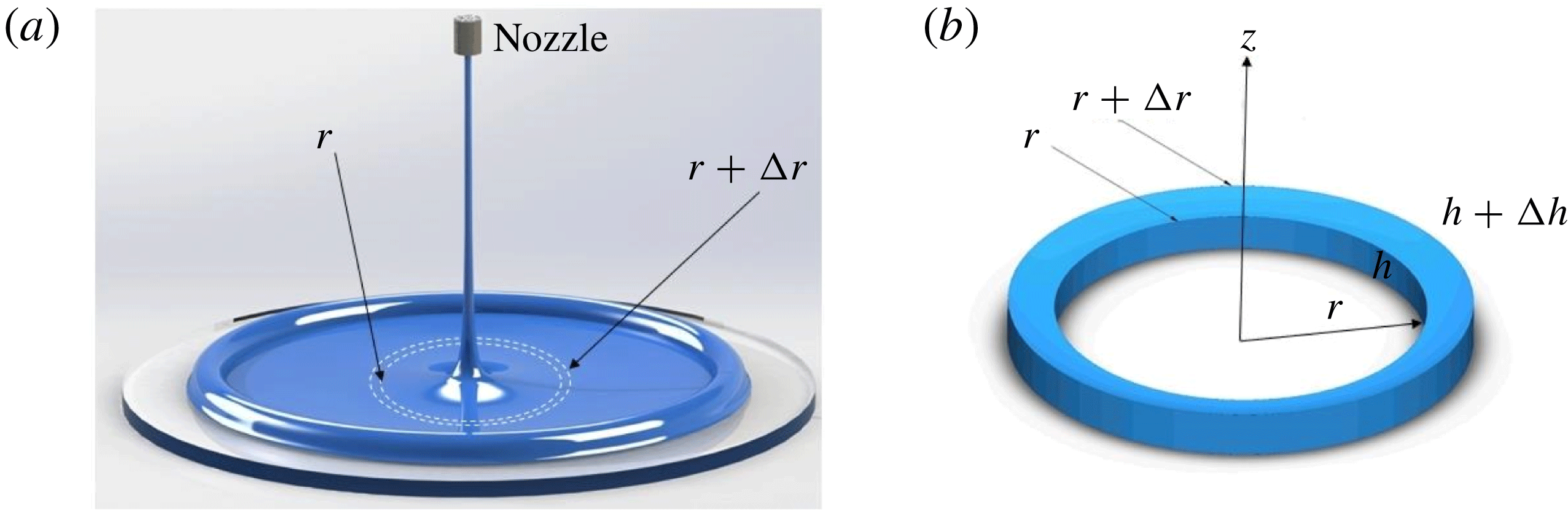
Figure 2. (a) Schematic of the liquid film and hydraulic jump created by an impinging jet. (b) Control volume of the film element on which the energy balance is applied.
Watson (Reference Watson1964) developed a similarity solution for radial flow in a thin liquid film, which we describe further below. He also proposed the first description of a thin-film circular hydraulic jump incorporating viscous friction in the film, ignoring the tangential stress due to surface tension, and balanced the momentum and hydrostatic pressure across the jump. Watson’s solution, which involves gravity, requires experimental measurement of the film thickness at the jump location to predict the jump radius, and overpredicts the radius for smaller jumps by as much as 50 %. Bush & Aristoff (Reference Bush and Aristoff2003) added surface tension to Watson’s theory but stated that its influence was small, as they argued its effect was confined to the hoop stress associated with the increase in circumference of the jump. They recognised that addition of a surfactant substantially (20 %) increased the jump radius but they did not pursue this aspect further, owing to the complications involved with surfactants. Mathur et al. (Reference Mathur, DasGupta, Selvi, John, Kulkarni and Govindarajan2007) presented results for hydraulic jumps in liquid metals where the jump radii are in range of micrometres. They recognised that jumps on this scale are created due to surface tension but are associated with very high curvature and small jump radii. However, they remarked that gravity is the key to all jumps on the scale of the kitchen sink hydraulic jump.
Earlier analysis by Kurihara (Reference Kurihara1946) and Tani (Reference Tani1949) used thin-film boundary layer equations including gravity to model circular hydraulic jumps. This analysis was critiqued by Bohr, Dimon & Putkaradze (Reference Bohr, Dimon and Putkaradze1993), who solved the axisymmetric shallow water equations, which again, naturally, include gravity. Bohr et al. (Reference Bohr, Dimon and Putkaradze1993) found that the outer solution of the equations became singular at a finite radius. Consequently, they solved the equations inwards from the edge of the plate or the boundary from where liquid drains due to gravity, and connected the inner and the outer solutions for radial flow through a shock. This analysis gave a scaling relation for the jump radius
![]() $R\sim Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
, where
$R\sim Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
, where
![]() $Q,\unicode[STIX]{x1D708}$
and
$Q,\unicode[STIX]{x1D708}$
and
![]() $g$
are the jet volume flux, the kinematic viscosity of the fluid and the acceleration due to gravity, respectively. They argued that the jump could be understood qualitatively in terms of the interplay between gravity, viscosity and the momentum of the liquid. A similar axisymmetric shallow water model was also proposed by Kasimov (Reference Kasimov2008). Again this study did not consider the initial formation of the jump, but connected the thin film with a deeper flow established as a result of a downstream boundary condition at the edge of the domain.
$g$
are the jet volume flux, the kinematic viscosity of the fluid and the acceleration due to gravity, respectively. They argued that the jump could be understood qualitatively in terms of the interplay between gravity, viscosity and the momentum of the liquid. A similar axisymmetric shallow water model was also proposed by Kasimov (Reference Kasimov2008). Again this study did not consider the initial formation of the jump, but connected the thin film with a deeper flow established as a result of a downstream boundary condition at the edge of the domain.
Two studies considered the case where gravity is unimportant. Godwin (Reference Godwin1993) assumed the jet diameter was an important parameter and showed that the jump radius, when independent of gravity, scales as
![]() $R\sim Q^{1/3}d^{2/3}\unicode[STIX]{x1D708}^{-1/3}$
, where
$R\sim Q^{1/3}d^{2/3}\unicode[STIX]{x1D708}^{-1/3}$
, where
![]() $d$
is the jet diameter. We argue that, since
$d$
is the jet diameter. We argue that, since
![]() $R\gg d$
, the jet diameter is not a relevant parameter. Avedisian & Zhao (Reference Avedisian and Zhao2000) studied the circular hydraulic jump at low gravity in a drop tower. In these experiments, a horizontal plate was submerged in a pool of liquid to impose a constant downstream liquid thickness condition and was impacted by a liquid jet to create a hydraulic jump. They found that, at normal gravity, the jump radius decreased when the depth of the downstream liquid film increased. However, at low gravity, the downstream liquid film height had no effect, and the jump radius increased compared to its value under normal gravity. Capillary waves were also observed, and they concluded that at low gravity the jumps were dominated by viscosity and surface tension.
$R\gg d$
, the jet diameter is not a relevant parameter. Avedisian & Zhao (Reference Avedisian and Zhao2000) studied the circular hydraulic jump at low gravity in a drop tower. In these experiments, a horizontal plate was submerged in a pool of liquid to impose a constant downstream liquid thickness condition and was impacted by a liquid jet to create a hydraulic jump. They found that, at normal gravity, the jump radius decreased when the depth of the downstream liquid film increased. However, at low gravity, the downstream liquid film height had no effect, and the jump radius increased compared to its value under normal gravity. Capillary waves were also observed, and they concluded that at low gravity the jumps were dominated by viscosity and surface tension.
Hansen et al. (Reference Hansen, Hørlück, Zauner, Dimon, Ellegaard and Creagh1997) studied surface waves in circular hydraulic jumps. They reported that the hydraulic jump radius scales as
![]() $R\propto Q^{0.77}$
for water, and
$R\propto Q^{0.77}$
for water, and
![]() $R\propto Q^{0.72}$
for less viscous oils. They concluded that, on a flat plate without any reflectors, the waves are gravity–capillary waves. Further, in the limit of zero surface tension, Rojas, Argentina & Tirapegui (Reference Rojas, Argentina and Tirapegui2013) reported that
$R\propto Q^{0.72}$
for less viscous oils. They concluded that, on a flat plate without any reflectors, the waves are gravity–capillary waves. Further, in the limit of zero surface tension, Rojas, Argentina & Tirapegui (Reference Rojas, Argentina and Tirapegui2013) reported that
![]() $R\sim Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}H^{-1/2}g^{-1/4}$
, where
$R\sim Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}H^{-1/2}g^{-1/4}$
, where
![]() $H$
is the height of the film downstream of the hydraulic jump.
$H$
is the height of the film downstream of the hydraulic jump.
In the experiments described below we observed that, under the same flow conditions, normal impingement of a liquid jet gives a circular hydraulic jump with the same initial radius irrespective of the orientation of the surface (figure 1). On a vertical plate, where the spreading liquid film and gravity are coplanar, an approximately circular hydraulic jump is still formed (figure 1
b). The thicker liquid film beyond the hydraulic jump then drains downwards due to gravity and above the point of impingement the location of the jump remains constant in time. Our experiments on a surface inclined at
![]() $45^{\circ }$
also produced circular jumps. A similar lack of dependence of the radius on both vertical and inclined surfaces has also been observed by Wilson et al. (Reference Wilson, Le, Dao, Lai, Morison and Davidson2012), Wang, Davidson & Wilson (Reference Wang, Davidson and Wilson2015), Bhagat & Wilson (Reference Bhagat and Wilson2016). Similarly, when a jet impinges onto a horizontal surface from below, an abrupt increase in film thickness is also observed (figure 1
c). Under the influence of gravity, the thicker liquid film falls as droplets or as a continuous film forming a water bell (Jameson et al.
Reference Jameson, Jenkins, Button and Sader2010). In our experiments we changed the surface tension of the liquid by preparing homogeneous water–alcohol solutions and a surfactant. Supplementary movie 3 shows the change in a kitchen-sink-scale hydraulic jump by changing the surface tension
$45^{\circ }$
also produced circular jumps. A similar lack of dependence of the radius on both vertical and inclined surfaces has also been observed by Wilson et al. (Reference Wilson, Le, Dao, Lai, Morison and Davidson2012), Wang, Davidson & Wilson (Reference Wang, Davidson and Wilson2015), Bhagat & Wilson (Reference Bhagat and Wilson2016). Similarly, when a jet impinges onto a horizontal surface from below, an abrupt increase in film thickness is also observed (figure 1
c). Under the influence of gravity, the thicker liquid film falls as droplets or as a continuous film forming a water bell (Jameson et al.
Reference Jameson, Jenkins, Button and Sader2010). In our experiments we changed the surface tension of the liquid by preparing homogeneous water–alcohol solutions and a surfactant. Supplementary movie 3 shows the change in a kitchen-sink-scale hydraulic jump by changing the surface tension
![]() $\unicode[STIX]{x1D6FE}$
when
$\unicode[STIX]{x1D6FE}$
when
![]() $Q$
and
$Q$
and
![]() $\unicode[STIX]{x1D708}$
are kept constant. The existing treatments are unable to explain this behaviour, as they hold that surface tension only becomes significant for much smaller jump radii.
$\unicode[STIX]{x1D708}$
are kept constant. The existing treatments are unable to explain this behaviour, as they hold that surface tension only becomes significant for much smaller jump radii.
3 Experiments
Circular hydraulic jumps were produced by impinging a liquid jet normally onto a planar surface. Both a vertical jet impinging on a horizontal plate from above and below, and normal impingement on a vertical plate and a plate inclined at
![]() $45^{\circ }$
to the horizontal were studied. For most experiments the jet nozzle diameter was 2 mm and the jet flow rate
$45^{\circ }$
to the horizontal were studied. For most experiments the jet nozzle diameter was 2 mm and the jet flow rate
![]() $Q$
varied from
$Q$
varied from
![]() $0.49{-}2~\text{L}~\text{min}^{-1}$
. For low flow rates (
$0.49{-}2~\text{L}~\text{min}^{-1}$
. For low flow rates (
![]() $Q<1.3~\text{L}~\text{min}^{-1}$
), liquid was supplied from a constant-head apparatus to glass Pasteur pipettes. For higher
$Q<1.3~\text{L}~\text{min}^{-1}$
), liquid was supplied from a constant-head apparatus to glass Pasteur pipettes. For higher
![]() $Q$
a centrifugal pump and a brass nozzle were used (Wang et al.
Reference Wang, Davidson and Wilson2015). Target plates were PerspexTM, glass or Teflon® sheets. The horizontal plate was a 0.25 m diameter circular disk; horizontal and inclined planes consisted of a
$Q$
a centrifugal pump and a brass nozzle were used (Wang et al.
Reference Wang, Davidson and Wilson2015). Target plates were PerspexTM, glass or Teflon® sheets. The horizontal plate was a 0.25 m diameter circular disk; horizontal and inclined planes consisted of a
![]() $1\times 0.4~\text{m}^{2}$
rectangular plate. It was found that the jump radius was independent of the plate material and we will not consider this factor further. Nozzle diameters of 1 and 3 mm were also used, and no significant difference in the jump radius was observed when measured from the edge of the resulting jet.
$1\times 0.4~\text{m}^{2}$
rectangular plate. It was found that the jump radius was independent of the plate material and we will not consider this factor further. Nozzle diameters of 1 and 3 mm were also used, and no significant difference in the jump radius was observed when measured from the edge of the resulting jet.
The viscosity and surface tension were varied by using mixtures of water with 1-propanol (5 and 20 w/w %, labelled as
![]() $\text{WP95}/5$
and
$\text{WP95}/5$
and
![]() $\text{WP80}/20$
, respectively) and with glycerol (70 and 90 w/w %, labelled as
$\text{WP80}/20$
, respectively) and with glycerol (70 and 90 w/w %, labelled as
![]() $\text{WG30}/70$
and
$\text{WG30}/70$
and
![]() $\text{WG10}/90$
, respectively). We also used a
$\text{WG10}/90$
, respectively). We also used a
![]() $3~\text{mmol}~\text{L}^{-1}$
solution of sodium dodecyl benzene sulphonate (SDBS). The surface tension was varied by an approximate factor of three and the kinematic viscosity by a factor of nearly 100. The fluid properties are listed in table 1.
$3~\text{mmol}~\text{L}^{-1}$
solution of sodium dodecyl benzene sulphonate (SDBS). The surface tension was varied by an approximate factor of three and the kinematic viscosity by a factor of nearly 100. The fluid properties are listed in table 1.
Table 1. Properties of the liquids used.
A Photron Fastcam SA3 was used to acquire images of the liquid film and the hydraulic jump at up to 2000 f.p.s. These were subsequently processed using MATLAB and ImageJ to obtain the jump radius
![]() $R$
as a function of the jet and fluid properties. In total over 150 experiments were conducted. Error bars were determined by the standard deviation of repeated experiments.
$R$
as a function of the jet and fluid properties. In total over 150 experiments were conducted. Error bars were determined by the standard deviation of repeated experiments.
4 Scaling analysis
We consider the axisymmetric flow shown schematically in figure 2. The jump is characterised by its radius
![]() $R$
and depth
$R$
and depth
![]() $h$
, along with the radial velocity
$h$
, along with the radial velocity
![]() $u$
of the film. Based on our observations we assume that gravity is unimportant and hence the flow depends on the jet flow rate
$u$
of the film. Based on our observations we assume that gravity is unimportant and hence the flow depends on the jet flow rate
![]() $Q$
, the jet diameter
$Q$
, the jet diameter
![]() $d$
, the film thickness
$d$
, the film thickness
![]() $h$
and the fluid properties (i.e. the density
$h$
and the fluid properties (i.e. the density
![]() $\unicode[STIX]{x1D70C}$
, viscosity
$\unicode[STIX]{x1D70C}$
, viscosity
![]() $\unicode[STIX]{x1D708}$
and the surface tension
$\unicode[STIX]{x1D708}$
and the surface tension
![]() $\unicode[STIX]{x1D6FE}$
). Since observations (e.g. figure 1) show that the jump radius
$\unicode[STIX]{x1D6FE}$
). Since observations (e.g. figure 1) show that the jump radius
![]() $R\gg d$
and we observed no dependence on
$R\gg d$
and we observed no dependence on
![]() $d$
, we will ignore the jet diameter. We then have six parameters;
$d$
, we will ignore the jet diameter. We then have six parameters;
![]() $R,h,\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FE}$
and
$R,h,\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FE}$
and
![]() $Q$
(or equivalently
$Q$
(or equivalently
![]() $u$
) and three dimensions, giving three dimensionless parameters: the Reynolds number
$u$
) and three dimensions, giving three dimensionless parameters: the Reynolds number
![]() $Re$
, the dimensionless film thickness,
$Re$
, the dimensionless film thickness,
![]() $\unicode[STIX]{x1D6FC}$
, and the Weber number,
$\unicode[STIX]{x1D6FC}$
, and the Weber number,
![]() $We$
, given by
$We$
, given by
We assume that the radial flow is balanced by viscous drag
![]() $u/R\sim \unicode[STIX]{x1D708}/h^{2}$
which implies
$u/R\sim \unicode[STIX]{x1D708}/h^{2}$
which implies
![]() $\unicode[STIX]{x1D6FC}Re=O(1)$
. Then, if we further assume that surface tension is important and that, at the jump
$\unicode[STIX]{x1D6FC}Re=O(1)$
. Then, if we further assume that surface tension is important and that, at the jump
![]() $We\sim 1$
, and use the fact that continuity implies
$We\sim 1$
, and use the fact that continuity implies
![]() $Q\sim uhR$
, we find
$Q\sim uhR$
, we find
![]() $R/R_{0}=\text{const.}$
, where the characteristic length
$R/R_{0}=\text{const.}$
, where the characteristic length
![]() $R_{0}$
is given by
$R_{0}$
is given by
We plot the measurements of the dimensionless jump radius
![]() $R/R_{0}$
against the jet flow rate
$R/R_{0}$
against the jet flow rate
![]() $Q$
in figure 3. The data from experiments covering the full range of
$Q$
in figure 3. The data from experiments covering the full range of
![]() $Q$
, surface material and orientation and fluid properties (table 1) all collapse on to the line
$Q$
, surface material and orientation and fluid properties (table 1) all collapse on to the line
![]() $R/R_{0}=0.289\pm 0.015$
. This collapse of the data, consistent with (4.2), implies that the dominant balance in the formation of thin-film jumps is associated with surface tension and viscous drag, and that gravity is irrelevant. In § 5, we will develop a more quantitative estimate of the jump radius.
$R/R_{0}=0.289\pm 0.015$
. This collapse of the data, consistent with (4.2), implies that the dominant balance in the formation of thin-film jumps is associated with surface tension and viscous drag, and that gravity is irrelevant. In § 5, we will develop a more quantitative estimate of the jump radius.

Figure 3. Dimensionless jump radius plotted against the flow rate for all our experiments with different liquids and surface orientation.
5 Theory
We consider a cylindrical coordinates
![]() $r$
and
$r$
and
![]() $z$
, the radial and jet-axial coordinates, respectively,
$z$
, the radial and jet-axial coordinates, respectively,
![]() $u$
and
$u$
and
![]() $w$
, the associated velocity components (figure 2), and assume circular symmetry about the jet axis. In order to analyse the jump we use the ansatz developed by Watson (Reference Watson1964) for the velocity within the thin film. We write the radial velocity as
$w$
, the associated velocity components (figure 2), and assume circular symmetry about the jet axis. In order to analyse the jump we use the ansatz developed by Watson (Reference Watson1964) for the velocity within the thin film. We write the radial velocity as
![]() $u=u_{s}\,f(\unicode[STIX]{x1D702})$
,
$u=u_{s}\,f(\unicode[STIX]{x1D702})$
,
![]() $\unicode[STIX]{x1D702}\equiv z/h(r)$
(
$\unicode[STIX]{x1D702}\equiv z/h(r)$
(
![]() $0\leqslant \unicode[STIX]{x1D702}\leqslant 1$
), where
$0\leqslant \unicode[STIX]{x1D702}\leqslant 1$
), where
![]() $\unicode[STIX]{x1D702}$
is the dimensionless thickness of the film and
$\unicode[STIX]{x1D702}$
is the dimensionless thickness of the film and
![]() $u_{s}$
is the velocity at the free surface. Using continuity we define the flux-average velocity
$u_{s}$
is the velocity at the free surface. Using continuity we define the flux-average velocity
![]() $\bar{u}\equiv C_{1}u_{s}$
by
$\bar{u}\equiv C_{1}u_{s}$
by
where
![]() $C_{1}=\int _{0}^{1}f(\unicode[STIX]{x1D702})\,\text{d}\unicode[STIX]{x1D702}=0.6137$
is a shape factor determined from the similarity solution.
$C_{1}=\int _{0}^{1}f(\unicode[STIX]{x1D702})\,\text{d}\unicode[STIX]{x1D702}=0.6137$
is a shape factor determined from the similarity solution.
We now balance the flux of mechanical energy across an annular control volume shown in figure 2(b), from
![]() $r$
to
$r$
to
![]() $r+\unicode[STIX]{x0394}r$
and from 0 to
$r+\unicode[STIX]{x0394}r$
and from 0 to
![]() $h$
(where we have cancelled out the common factor
$h$
(where we have cancelled out the common factor
![]() $2\unicode[STIX]{x03C0}$
),
$2\unicode[STIX]{x03C0}$
),
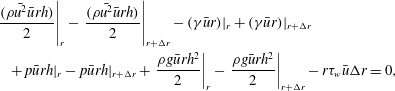 $$\begin{eqnarray}\displaystyle & & \displaystyle \left.\frac{(\unicode[STIX]{x1D70C}\bar{u^{2}}\bar{u}rh)}{2}\right|_{r}-\left.\frac{(\unicode[STIX]{x1D70C}\bar{u^{2}}\bar{u}rh)}{2}\right|_{r+\unicode[STIX]{x0394}r}-(\unicode[STIX]{x1D6FE}\bar{u}r)|_{r}+(\unicode[STIX]{x1D6FE}\bar{u}r)|_{r+\unicode[STIX]{x0394}r}\nonumber\\ \displaystyle & & \displaystyle \quad +\,p\bar{u}rh|_{r}-p\bar{u}rh|_{r+\unicode[STIX]{x0394}r}+\left.\frac{\unicode[STIX]{x1D70C}g\bar{u}rh^{2}}{2}\right|_{r}-\left.\frac{\unicode[STIX]{x1D70C}g\bar{u}rh^{2}}{2}\right|_{r+\unicode[STIX]{x0394}r}-r\unicode[STIX]{x1D70F}_{w}\bar{u}\unicode[STIX]{x0394}r=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left.\frac{(\unicode[STIX]{x1D70C}\bar{u^{2}}\bar{u}rh)}{2}\right|_{r}-\left.\frac{(\unicode[STIX]{x1D70C}\bar{u^{2}}\bar{u}rh)}{2}\right|_{r+\unicode[STIX]{x0394}r}-(\unicode[STIX]{x1D6FE}\bar{u}r)|_{r}+(\unicode[STIX]{x1D6FE}\bar{u}r)|_{r+\unicode[STIX]{x0394}r}\nonumber\\ \displaystyle & & \displaystyle \quad +\,p\bar{u}rh|_{r}-p\bar{u}rh|_{r+\unicode[STIX]{x0394}r}+\left.\frac{\unicode[STIX]{x1D70C}g\bar{u}rh^{2}}{2}\right|_{r}-\left.\frac{\unicode[STIX]{x1D70C}g\bar{u}rh^{2}}{2}\right|_{r+\unicode[STIX]{x0394}r}-r\unicode[STIX]{x1D70F}_{w}\bar{u}\unicode[STIX]{x0394}r=0,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}(u_{s}/h)f^{\prime }(0)$
is the wall shear stress and, from the velocity profile ansatz, we have
$\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}(u_{s}/h)f^{\prime }(0)$
is the wall shear stress and, from the velocity profile ansatz, we have
![]() $f^{\prime }(0)=1.402$
.
$f^{\prime }(0)=1.402$
.
In these jump conditions, the first term is the flux of kinetic energy which is balanced by pressure, gravity and viscous work, given by the third, fourth and fifth terms, respectively. These are standard and the new term is the second term
![]() $\unicode[STIX]{x1D6FE}\bar{u}r$
, which represents the flux of surface energy that has been neglected in previous studies. This term results from the increase of surface area across the control volume as a result of the increase in the circumference from
$\unicode[STIX]{x1D6FE}\bar{u}r$
, which represents the flux of surface energy that has been neglected in previous studies. This term results from the increase of surface area across the control volume as a result of the increase in the circumference from
![]() $r$
to
$r$
to
![]() $r+\unicode[STIX]{x0394}r$
.
$r+\unicode[STIX]{x0394}r$
.
Dividing (5.2) by
![]() $\unicode[STIX]{x0394}r$
, taking the limit
$\unicode[STIX]{x0394}r$
, taking the limit
![]() $\unicode[STIX]{x0394}r\rightarrow 0$
and using the fact that
$\unicode[STIX]{x0394}r\rightarrow 0$
and using the fact that
![]() $\bar{u}rh=\text{const.}$
(see (5.1)) yields
$\bar{u}rh=\text{const.}$
(see (5.1)) yields
From the boundary layer velocity profile ansatz we write
![]() $\bar{u^{2}}=\int _{0}^{1}u^{2}\,\text{d}\unicode[STIX]{x1D702}\equiv C_{2}u_{s}^{2}$
, where
$\bar{u^{2}}=\int _{0}^{1}u^{2}\,\text{d}\unicode[STIX]{x1D702}\equiv C_{2}u_{s}^{2}$
, where
![]() $C_{2}\equiv \int _{0}^{1}f^{2}(\unicode[STIX]{x1D702})\,\text{d}\unicode[STIX]{x1D702}=0.4755$
is a second shape factor. Then (5.3) implies
$C_{2}\equiv \int _{0}^{1}f^{2}(\unicode[STIX]{x1D702})\,\text{d}\unicode[STIX]{x1D702}=0.4755$
is a second shape factor. Then (5.3) implies
Note that the shape factor
![]() $C_{1}$
cancels out in this equation, and so plays no role. Again using (5.1), we write
$C_{1}$
cancels out in this equation, and so plays no role. Again using (5.1), we write
![]() $u_{s}r(\text{d}h/\text{d}r)=-h(\text{d}(u_{s}r)/\text{d}r)$
in (5.4), to obtain
$u_{s}r(\text{d}h/\text{d}r)=-h(\text{d}(u_{s}r)/\text{d}r)$
in (5.4), to obtain
Finally, rearranging (5.5) we find that the gradient of the radial velocity satisfies
 $$\begin{eqnarray}\frac{\text{d}u_{s}}{\text{d}r}=\frac{-u_{s}rh{\displaystyle \frac{\text{d}p}{\text{d}r}}+\unicode[STIX]{x1D6FE}u_{s}+{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D70C}gu_{s}h^{2}-\unicode[STIX]{x1D70F}_{w}ru_{s}}{\left(1-{\displaystyle \frac{1}{We}}-{\displaystyle \frac{1}{Fr^{2}}}\right)(C_{2}\unicode[STIX]{x1D70C}u_{s}^{2}hr)}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}u_{s}}{\text{d}r}=\frac{-u_{s}rh{\displaystyle \frac{\text{d}p}{\text{d}r}}+\unicode[STIX]{x1D6FE}u_{s}+{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D70C}gu_{s}h^{2}-\unicode[STIX]{x1D70F}_{w}ru_{s}}{\left(1-{\displaystyle \frac{1}{We}}-{\displaystyle \frac{1}{Fr^{2}}}\right)(C_{2}\unicode[STIX]{x1D70C}u_{s}^{2}hr)}.\end{eqnarray}$$
Here, we define the Weber number and Froude number as, respectively,
It is clear that (5.6) is singular when
and that the hydraulic jump occurs where this condition is satisfied.
In order to obtain quantitative results, (5.6) was solved for
![]() $u_{s}$
using the similarity velocity profile and the initial condition obtained from Watson (Reference Watson1964). The boundary layer first occupies the full depth of the film at
$u_{s}$
using the similarity velocity profile and the initial condition obtained from Watson (Reference Watson1964). The boundary layer first occupies the full depth of the film at
![]() $r_{b}$
, given by
$r_{b}$
, given by
![]() $r_{b}/d=0.1833Re_{j}^{1/3}$
, where the jet Reynolds number
$r_{b}/d=0.1833Re_{j}^{1/3}$
, where the jet Reynolds number
![]() $Re_{j}=4Q/\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}d$
. At this location, which for the present values of
$Re_{j}=4Q/\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}d$
. At this location, which for the present values of
![]() $Re_{j}\sim 10^{4}$
,
$Re_{j}\sim 10^{4}$
,
![]() $r_{b}\ll R$
,
$r_{b}\ll R$
,
![]() $u_{s}$
is set equal to the mean jet velocity, and (5.6) provides its subsequent radial values. The solution of (5.6) is not sensitive to the initial condition obtained using Watson’s similarity profile, as other boundary layer velocity profiles yield similar values of
$u_{s}$
is set equal to the mean jet velocity, and (5.6) provides its subsequent radial values. The solution of (5.6) is not sensitive to the initial condition obtained using Watson’s similarity profile, as other boundary layer velocity profiles yield similar values of
![]() $r_{b}$
. We then calculate
$r_{b}$
. We then calculate
![]() $R$
as the location where
$R$
as the location where
![]() $We^{-1}+Fr^{-2}=1$
, and (5.6) becomes singular. This condition provides a more precise estimate and a physical basis for the scaling argument (4.2), and also includes the effect of gravity.
$We^{-1}+Fr^{-2}=1$
, and (5.6) becomes singular. This condition provides a more precise estimate and a physical basis for the scaling argument (4.2), and also includes the effect of gravity.
6 Results
6.1 Effect of surface orientations
We showed in figure 1 that for normal jet impingement the orientation of the surface does not affect the radius of the jump. In figure 1(b), for a vertical wall, the jump is very close to circular, which is further evidence that gravity plays no significant role. A direct comparison between the four cases of a horizontal plane impinged from above and below, a vertical plane and a surface inclined at
![]() $45^{\circ }$
is shown in figure 4. The theoretical curve, obtained ignoring gravity by setting
$45^{\circ }$
is shown in figure 4. The theoretical curve, obtained ignoring gravity by setting
![]() $g=0$
in (5.6), agrees closely with the data from the vertical, inclined and horizontal plate from above. The observed radius is slightly larger for the horizontal plate impinged from below. This is presumably because the ultimate transition to dripping flow or a water bell is affected by gravity and occurs after the film initially thickens.
$g=0$
in (5.6), agrees closely with the data from the vertical, inclined and horizontal plate from above. The observed radius is slightly larger for the horizontal plate impinged from below. This is presumably because the ultimate transition to dripping flow or a water bell is affected by gravity and occurs after the film initially thickens.

Figure 4. Jump radius plotted against jet flow rate for the four surface orientations. In each case the liquid was pure water. The theoretical prediction (line) is obtained ignoring gravity by setting
![]() $g=0$
in (5.6).
$g=0$
in (5.6).
6.2 Effect of fluid properties: surface tension and viscosity
Figure 5(a) compares experimental measurements with theoretical predictions of
![]() $R$
for pure water,
$R$
for pure water,
![]() $\text{WP95}/5$
and the aqueous SDBS solution for a jet impinging on a horizontal plate from above. SDBS and pure water have similar viscosities but differ in their surface tensions, while
$\text{WP95}/5$
and the aqueous SDBS solution for a jet impinging on a horizontal plate from above. SDBS and pure water have similar viscosities but differ in their surface tensions, while
![]() $\text{WP95}/5$
and SDBS have different viscosities but similar surface tensions. Lowering the surface tension (SDBS cf. water) increases
$\text{WP95}/5$
and SDBS have different viscosities but similar surface tensions. Lowering the surface tension (SDBS cf. water) increases
![]() $R$
while increasing the viscosity (
$R$
while increasing the viscosity (
![]() $\text{WP95}/5$
cf. SDBS) reduces
$\text{WP95}/5$
cf. SDBS) reduces
![]() $R$
. The corresponding theoretical curves obtained from (5.6), again with
$R$
. The corresponding theoretical curves obtained from (5.6), again with
![]() $g=0$
, shown in figure 5(a), capture these variations with liquid properties and agree with the experimental measurements.
$g=0$
, shown in figure 5(a), capture these variations with liquid properties and agree with the experimental measurements.
Figure 5(b) compares data reported by Jameson et al. (Reference Jameson, Jenkins, Button and Sader2010) for liquid jets of 70 and 90 w/w % glycerol/water solutions,
![]() $\text{WG30}/70$
and
$\text{WG30}/70$
and
![]() $\text{WG10}/90$
, at
$\text{WG10}/90$
, at
![]() $19\,^{\circ }\text{C}$
and
$19\,^{\circ }\text{C}$
and
![]() $28\,^{\circ }\text{C}$
, respectively, impinging on the underside of a horizontal surface consisting of either glass or Teflon®. For a given flow rate, the measured departure radius
$28\,^{\circ }\text{C}$
, respectively, impinging on the underside of a horizontal surface consisting of either glass or Teflon®. For a given flow rate, the measured departure radius
![]() $R_{b}$
is smaller for the more viscous solution: the surface tensions are comparable. Our theoretical curves obtained by setting
$R_{b}$
is smaller for the more viscous solution: the surface tensions are comparable. Our theoretical curves obtained by setting
![]() $g=0$
in (5.6) slightly underpredict the radius, but they capture the effect of the viscosity changes. In their theoretical description of the water bell departure radius, Button et al. (Reference Button, Davidson, Jameson and Sader2010) expected that
$g=0$
in (5.6) slightly underpredict the radius, but they capture the effect of the viscosity changes. In their theoretical description of the water bell departure radius, Button et al. (Reference Button, Davidson, Jameson and Sader2010) expected that
![]() $R_{b}$
would depend on the surface wettability or the contact angle between the surface and the liquid. As can be seen in figure 5(b) there is only a very small difference between the glass (hydrophilic) and Teflon® (hydrophobic) surfaces. Although they observed a change in the local contact angle at the rim of the radial flow, the water bell formation radius was at the same location, as predicted by our theory.
$R_{b}$
would depend on the surface wettability or the contact angle between the surface and the liquid. As can be seen in figure 5(b) there is only a very small difference between the glass (hydrophilic) and Teflon® (hydrophobic) surfaces. Although they observed a change in the local contact angle at the rim of the radial flow, the water bell formation radius was at the same location, as predicted by our theory.
6.3 Return to scaling
We can now use the solution to determine the constant in the scaling relation (4.2). Using (5.1), (5.7) and the expression for the wall stress we find that
which is close to the experimental best fit to the data
![]() $0.289\pm 0.015$
quoted in § 4.2. Thus, as expected, the theory allows us to quantify our scaling relation.
$0.289\pm 0.015$
quoted in § 4.2. Thus, as expected, the theory allows us to quantify our scaling relation.
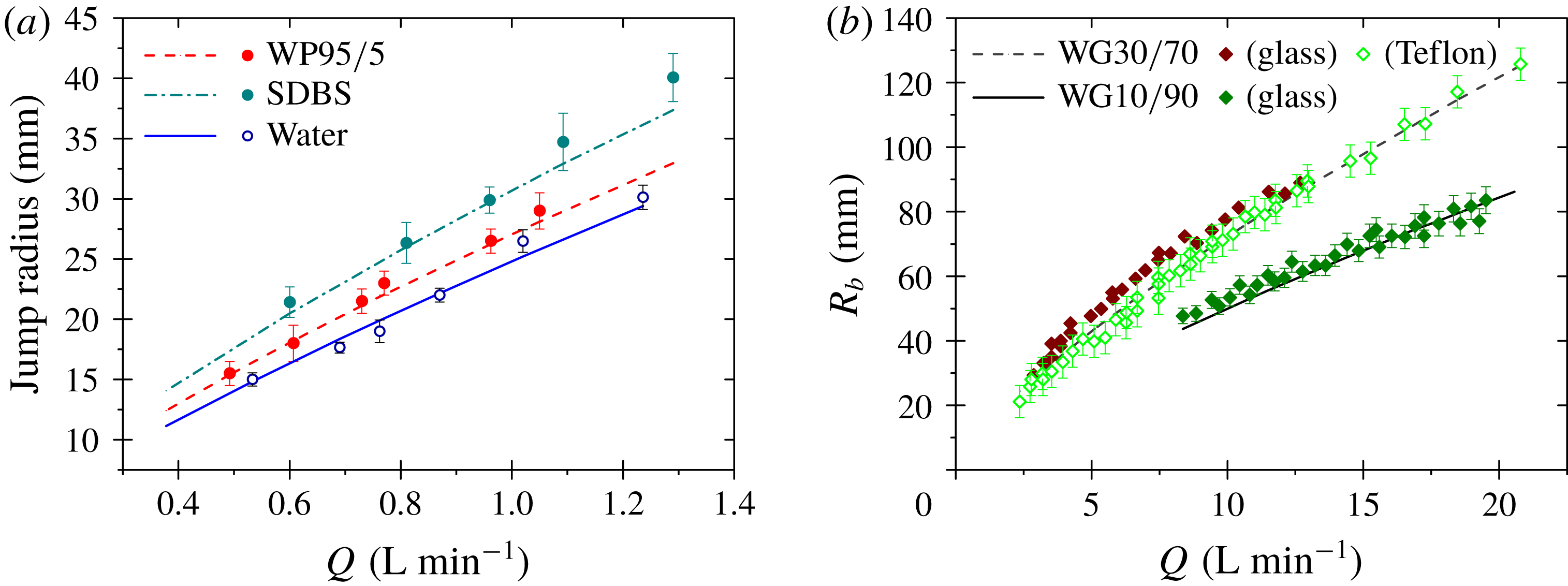
Figure 5. (a) Effect of surface tension. Initial jump radius for normal impingement on a horizontal plate from above, for water, water–propanol (
![]() $\text{WP95}/5$
) and SDBS. Curves are the predictions obtained from solutions of (5.6). The predictions lie within the uncertainty in the experimental measurements. (b) Effect of kinematic viscosity. Measured water bell departure radius, from Jameson et al. (Reference Jameson, Jenkins, Button and Sader2010), alongside predictions (curves), obtained by solving (5.6) with
$\text{WP95}/5$
) and SDBS. Curves are the predictions obtained from solutions of (5.6). The predictions lie within the uncertainty in the experimental measurements. (b) Effect of kinematic viscosity. Measured water bell departure radius, from Jameson et al. (Reference Jameson, Jenkins, Button and Sader2010), alongside predictions (curves), obtained by solving (5.6) with
![]() $g=0$
. The liquids were water–glycerol mixtures
$g=0$
. The liquids were water–glycerol mixtures
![]() $\text{WG30}/70$
and
$\text{WG30}/70$
and
![]() $\text{WG10}/90$
.
$\text{WG10}/90$
.
7 Conclusions
This paper provides a resolution to the question: what determines the radius of a circular hydraulic jump in a thin liquid film on an infinite plane? We derived a scaling relationship (4.2) that collapses our data and shows that the jump location is determined by the viscosity and the surface tension of the liquid. Using a similarity solution due to Watson (Reference Watson1964), with the addition of surface tension, we made quantitative predictions of the jump radius
![]() $R$
that are in excellent agreement with our measurements for different surface orientations and fluid properties.
$R$
that are in excellent agreement with our measurements for different surface orientations and fluid properties.
We found that the hydraulic jump, or the supercritical to subcritical transition, occurs when
![]() $We^{-1}+Fr^{-2}=1$
. From (5.6) we infer that the transport of surface energy becomes dominant for the expanding films at larger radii. The left-hand side of (5.5) indicates that the liquid momentum must overcome the hydrostatic pressure and surface tension. The jump is formed where the hydrostatic pressure term
$We^{-1}+Fr^{-2}=1$
. From (5.6) we infer that the transport of surface energy becomes dominant for the expanding films at larger radii. The left-hand side of (5.5) indicates that the liquid momentum must overcome the hydrostatic pressure and surface tension. The jump is formed where the hydrostatic pressure term
![]() $\unicode[STIX]{x1D70C}gh^{2}r$
and surface force
$\unicode[STIX]{x1D70C}gh^{2}r$
and surface force
![]() $\unicode[STIX]{x1D6FE}r$
are greater than or equal to the momentum. This behaviour was previously attributed to the hydrostatic force alone, which is a special case of the general solution.
$\unicode[STIX]{x1D6FE}r$
are greater than or equal to the momentum. This behaviour was previously attributed to the hydrostatic force alone, which is a special case of the general solution.
Previous analyses have incorporated surface tension, but only through the hoop stress, which, we agree, is small on the scale of these jumps and is effectively incorporated in the pressure term in (5.2). It is the loss of energy associated with the radial transport of surface energy that implies that the flow can no longer provide the kinetic energy to maintain the thin film. At this point the flow decelerates rapidly, the depth of the flow increases and the hydraulic jump occurs. This is equivalent to the surface tension force associated with curvature of a film of thickness
![]() $h$
, and hence this thickness is the relevant length scale in the Weber number used to obtain the scaling relation (4.2). Comparing our scaling relation (4.2),
$h$
, and hence this thickness is the relevant length scale in the Weber number used to obtain the scaling relation (4.2). Comparing our scaling relation (4.2),
![]() $R\sim \unicode[STIX]{x1D70C}^{1/4}Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}\unicode[STIX]{x1D6FE}^{-1/4}$
, with the result obtained by Rojas et al. (Reference Rojas, Argentina and Tirapegui2013) in the limit of zero surface tension,
$R\sim \unicode[STIX]{x1D70C}^{1/4}Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}\unicode[STIX]{x1D6FE}^{-1/4}$
, with the result obtained by Rojas et al. (Reference Rojas, Argentina and Tirapegui2013) in the limit of zero surface tension,
![]() $R\sim Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}H^{-1/2}g^{-1/4}$
, implies that the depth of liquid downstream of the jump scales with the capillary length scale
$R\sim Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}H^{-1/2}g^{-1/4}$
, implies that the depth of liquid downstream of the jump scales with the capillary length scale
![]() $H\sim (\unicode[STIX]{x1D6FE}/g\unicode[STIX]{x1D70C})^{1/2}$
.
$H\sim (\unicode[STIX]{x1D6FE}/g\unicode[STIX]{x1D70C})^{1/2}$
.
It is also worth noting that the dependence of
![]() $R$
on
$R$
on
![]() $Q$
and
$Q$
and
![]() $\unicode[STIX]{x1D708}$
our scaling relation (
$\unicode[STIX]{x1D708}$
our scaling relation (
![]() $Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}$
) is very similar to that obtained by Bohr et al. (Reference Bohr, Dimon and Putkaradze1993) quoted in § 2, namely,
$Q^{3/4}\unicode[STIX]{x1D708}^{-1/4}$
) is very similar to that obtained by Bohr et al. (Reference Bohr, Dimon and Putkaradze1993) quoted in § 2, namely,
![]() $Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}$
. Consequently, these and other authors were able to fit their data to the latter scaling, which involves gravity and not surface tension, since these latter two parameters were not changed between experiments. Similarly, Hansen et al. (Reference Hansen, Hørlück, Zauner, Dimon, Ellegaard and Creagh1997) found empirically that the jump radius for water,
$Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}$
. Consequently, these and other authors were able to fit their data to the latter scaling, which involves gravity and not surface tension, since these latter two parameters were not changed between experiments. Similarly, Hansen et al. (Reference Hansen, Hørlück, Zauner, Dimon, Ellegaard and Creagh1997) found empirically that the jump radius for water,
![]() $R\propto Q^{0.77}$
which is close to our scaling relationship,
$R\propto Q^{0.77}$
which is close to our scaling relationship,
![]() $R\propto Q^{3/4}$
. However, they concluded that it is consistent with the scaling relation obtained by Bohr et al. (Reference Bohr, Dimon and Putkaradze1993), which predicts
$R\propto Q^{3/4}$
. However, they concluded that it is consistent with the scaling relation obtained by Bohr et al. (Reference Bohr, Dimon and Putkaradze1993), which predicts
![]() $R\propto Q^{5/8}$
.
$R\propto Q^{5/8}$
.
The critical Weber number based on the film thickness at the jump implies that the flow speed is
![]() $\sqrt{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}h}$
, which is the speed of capillary waves with wavenumbers comparable to the inverse of the film thickness. Consequently, capillary waves play a similar role in this situation to gravity waves in the traditional hydraulic jump.
$\sqrt{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}h}$
, which is the speed of capillary waves with wavenumbers comparable to the inverse of the film thickness. Consequently, capillary waves play a similar role in this situation to gravity waves in the traditional hydraulic jump.
It should again be emphasised that we are only concerned with the location of the jump on an infinite plane. For vertical jet impingement on a horizontal surface from above, the liquid film eventually reaches and flows off the edge of the surface. At that point there will be another boundary condition resulting from this flow off the edge which will result in information travelling upstream through the subcritical region to the initial jump location. This will effectively flood that control and, in general, the jump will move inwards from its initial location, reducing
![]() $R$
.
$R$
.
Finally, it is worth considering what constitutes a thin film in this context. As shown in § 4.2, balancing the deceleration with the viscous drag implies that the film aspect ratio
![]() $\unicode[STIX]{x1D6FC}\sim Re^{-1}$
. For the values of
$\unicode[STIX]{x1D6FC}\sim Re^{-1}$
. For the values of
![]() $Re\sim 1000$
in our experiments
$Re\sim 1000$
in our experiments
![]() $h\sim R\cdot 10^{-3}\sim 100~\unicode[STIX]{x03BC}\text{m}$
.
$h\sim R\cdot 10^{-3}\sim 100~\unicode[STIX]{x03BC}\text{m}$
.
Acknowledgements
Funding for R.K.B. from the Commonwealth Scholarship Commission is gratefully acknowledged. N.K.J. acknowledges the support of an EPSRC grant EP/K50375/1.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2018.558.









