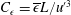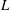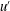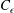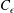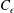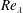1 Introduction
It is commonly believed that the constancy of the non-dimensional dissipation rate parameter
![]() $C_{\unicode[STIX]{x1D716}}=\overline{\unicode[STIX]{x1D716}}L/u^{\prime 3}$
(where
$C_{\unicode[STIX]{x1D716}}=\overline{\unicode[STIX]{x1D716}}L/u^{\prime 3}$
(where
![]() $\overline{\unicode[STIX]{x1D716}}$
is the dissipation rate of the mean turbulent kinetic energy,
$\overline{\unicode[STIX]{x1D716}}$
is the dissipation rate of the mean turbulent kinetic energy,
![]() $C_{\unicode[STIX]{x1D716}}$
is the dissipation coefficient and constant,
$C_{\unicode[STIX]{x1D716}}$
is the dissipation coefficient and constant,
![]() $u^{\prime }$
is the velocity root-mean-square and
$u^{\prime }$
is the velocity root-mean-square and
![]() $L$
an integral length scale; the overbar represents time average) is a cornerstone assumption of turbulence, e.g. Tennekes & Lumley (Reference Tennekes and Lumley1972), McComb et al. (Reference McComb, Berera, Yoffe and Linkmann2015), Vassilicos (Reference Vassilicos2015); see also McComb (Reference McComb2014) for a brief review. It is often interpreted as representing the transfer of energy from larger to smaller scales of motion (Tennekes & Lumley Reference Tennekes and Lumley1972). Interestingly, this interpretation was not made by Taylor (Reference Taylor1935) who first introduced this constant. In fact, it is his attempt to connect
$L$
an integral length scale; the overbar represents time average) is a cornerstone assumption of turbulence, e.g. Tennekes & Lumley (Reference Tennekes and Lumley1972), McComb et al. (Reference McComb, Berera, Yoffe and Linkmann2015), Vassilicos (Reference Vassilicos2015); see also McComb (Reference McComb2014) for a brief review. It is often interpreted as representing the transfer of energy from larger to smaller scales of motion (Tennekes & Lumley Reference Tennekes and Lumley1972). Interestingly, this interpretation was not made by Taylor (Reference Taylor1935) who first introduced this constant. In fact, it is his attempt to connect
![]() $\overline{\unicode[STIX]{x1D716}}$
to the velocity correlation function that led him to this dissipation scaling. Since the focus of this study is on
$\overline{\unicode[STIX]{x1D716}}$
to the velocity correlation function that led him to this dissipation scaling. Since the focus of this study is on
![]() $C_{\unicode[STIX]{x1D716}}$
, it is worthwhile reproducing Taylor’s introduction of
$C_{\unicode[STIX]{x1D716}}$
, it is worthwhile reproducing Taylor’s introduction of
![]() $C_{\unicode[STIX]{x1D716}}$
. He wrote:
$C_{\unicode[STIX]{x1D716}}$
. He wrote:
It has been shown by von Kármán that if the surface stress in a pipe is expressed in the form
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70C}v_{x}^{2}$
then
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70C}v_{x}^{2}$
then
where
![]() $U_{c}$
is the maximum velocity in the middle of the pipe and
$U_{c}$
is the maximum velocity in the middle of the pipe and
![]() $U$
is the velocity at radius
$U$
is the velocity at radius
![]() $r$
. This relationship is associated with the conception that the Reynolds stresses are proportional to the squares of the turbulent component of velocity. It seems that the rate of dissipation of energy in such a system must be proportional, so far as changes in linear dimension, velocity and density are concerned, to
$r$
. This relationship is associated with the conception that the Reynolds stresses are proportional to the squares of the turbulent component of velocity. It seems that the rate of dissipation of energy in such a system must be proportional, so far as changes in linear dimension, velocity and density are concerned, to
![]() $\unicode[STIX]{x1D70C}u^{\prime 3}/l$
, where
$\unicode[STIX]{x1D70C}u^{\prime 3}/l$
, where
![]() $l$
is some linear dimension defining the scale of the system. For turbulence produced by geometrically similar boundaries therefore
$l$
is some linear dimension defining the scale of the system. For turbulence produced by geometrically similar boundaries therefore
For such systems therefore
where
![]() $C$
depends on the positions relative to the solid boundaries of the point at which observations are made and on the element used for defining
$C$
depends on the positions relative to the solid boundaries of the point at which observations are made and on the element used for defining
![]() $l$
.
$l$
.
Here,
![]() $\unicode[STIX]{x1D70C}$
is the fluid density,
$\unicode[STIX]{x1D70C}$
is the fluid density,
![]() $\unicode[STIX]{x1D706}$
is the Taylor microscale,
$\unicode[STIX]{x1D706}$
is the Taylor microscale,
![]() $\unicode[STIX]{x1D70F}$
is the shear stress and
$\unicode[STIX]{x1D70F}$
is the shear stress and
![]() $vx$
is a scaling velocity. For convenience we identify the constant in (1.2) as
$vx$
is a scaling velocity. For convenience we identify the constant in (1.2) as
![]() $C_{T}$
. Note also that there is some ambiguity about
$C_{T}$
. Note also that there is some ambiguity about
![]() $l$
, which is not necessarily the integral length scale
$l$
, which is not necessarily the integral length scale
![]() $L$
, although it should characterize the large-scale motion. A few remarks can be made. First, equation (1.2) leads immediately to
$L$
, although it should characterize the large-scale motion. A few remarks can be made. First, equation (1.2) leads immediately to
![]() $C_{T}=(15/Re_{l})l^{2}/\unicode[STIX]{x1D706}^{2}$
, where
$C_{T}=(15/Re_{l})l^{2}/\unicode[STIX]{x1D706}^{2}$
, where
![]() $Re_{l}=lu^{\prime }/\unicode[STIX]{x1D708}$
is a scaling Reynolds number. Clearly, since
$Re_{l}=lu^{\prime }/\unicode[STIX]{x1D708}$
is a scaling Reynolds number. Clearly, since
![]() $C_{T}$
is constant, then
$C_{T}$
is constant, then
![]() $l/\unicode[STIX]{x1D706}\sim \sqrt{Re_{l}}$
. Second, Taylor uses dimensional arguments for stating that
$l/\unicode[STIX]{x1D706}\sim \sqrt{Re_{l}}$
. Second, Taylor uses dimensional arguments for stating that
![]() $\overline{\unicode[STIX]{x1D716}}\sim \unicode[STIX]{x1D70C}u^{\prime 3}/l$
. Third, he uses the local isotropy assumption as is evident from the last term on the right in (1.2). Fourth, the constant
$\overline{\unicode[STIX]{x1D716}}\sim \unicode[STIX]{x1D70C}u^{\prime 3}/l$
. Third, he uses the local isotropy assumption as is evident from the last term on the right in (1.2). Fourth, the constant
![]() $C=(15/C_{T})$
may depend on the initial and boundary conditions. Fifth, the statement referring to the Reynolds stresses and expression (1.1) indicates that Taylor assumes the turbulent flow to be in self-preservation (hereafter denoted SP). The hypothesis of SP development of a turbulent flow assumes that all aspects of motion have similar forms at all stages, the differences being described by changes of velocity and length scales which are functions of time (in decaying turbulence) or of position in the flow direction (Townsend Reference Townsend1976); in other words, all mean turbulent quantities are expressible non-dimensionally through suitable scales of length and velocity, and the forms of the normalized distributions remain unchanged at all stages of the flow evolution. Thus, Taylor introduced the constant
$C=(15/C_{T})$
may depend on the initial and boundary conditions. Fifth, the statement referring to the Reynolds stresses and expression (1.1) indicates that Taylor assumes the turbulent flow to be in self-preservation (hereafter denoted SP). The hypothesis of SP development of a turbulent flow assumes that all aspects of motion have similar forms at all stages, the differences being described by changes of velocity and length scales which are functions of time (in decaying turbulence) or of position in the flow direction (Townsend Reference Townsend1976); in other words, all mean turbulent quantities are expressible non-dimensionally through suitable scales of length and velocity, and the forms of the normalized distributions remain unchanged at all stages of the flow evolution. Thus, Taylor introduced the constant
![]() $C_{T}$
under the condition that the flow is in SP and isotropy is satisfied. Interestingly, no reference to the Reynolds number is made by Taylor.
$C_{T}$
under the condition that the flow is in SP and isotropy is satisfied. Interestingly, no reference to the Reynolds number is made by Taylor.
Kolmogorov (Reference Kolmogorov1941b
) showed that
![]() $\overline{\unicode[STIX]{x1D716}}=Ck^{3/2}/L$
(
$\overline{\unicode[STIX]{x1D716}}=Ck^{3/2}/L$
(
![]() $k$
is the turbulent kinetic energy) with
$k$
is the turbulent kinetic energy) with
![]() $C=(2g/C_{K})^{2/3}$
, not necessarily the same as in (1.2), where
$C=(2g/C_{K})^{2/3}$
, not necessarily the same as in (1.2), where
![]() $g$
is supposed to be a constant and
$g$
is supposed to be a constant and
![]() $C_{K}$
the Kolmogorov constant (defined in
$C_{K}$
the Kolmogorov constant (defined in
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}=C_{K}(\overline{\unicode[STIX]{x1D716}}r)^{2/3}$
,
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}=C_{K}(\overline{\unicode[STIX]{x1D716}}r)^{2/3}$
,
![]() $\unicode[STIX]{x1D6FF}u$
is the velocity increment and
$\unicode[STIX]{x1D6FF}u$
is the velocity increment and
![]() $r$
is the spatial increment). Here,
$r$
is the spatial increment). Here,
![]() $L$
is related to the Loitsiansky length scale
$L$
is related to the Loitsiansky length scale
![]() $\unicode[STIX]{x1D6EC}$
as
$\unicode[STIX]{x1D6EC}$
as
![]() $L=(\unicode[STIX]{x1D6EC}/k)^{1/5}$
. Kolmogorov developed the expression of
$L=(\unicode[STIX]{x1D6EC}/k)^{1/5}$
. Kolmogorov developed the expression of
![]() $C_{\unicode[STIX]{x1D716}}$
for separations in the range
$C_{\unicode[STIX]{x1D716}}$
for separations in the range
![]() $\unicode[STIX]{x1D706}\ll r\ll L$
and by assuming SP for
$\unicode[STIX]{x1D706}\ll r\ll L$
and by assuming SP for
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
, i.e.
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
, i.e.
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}=k\unicode[STIX]{x1D713}(r/L)$
,
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}=k\unicode[STIX]{x1D713}(r/L)$
,
![]() $\unicode[STIX]{x1D713}$
is a dimensionless function of
$\unicode[STIX]{x1D713}$
is a dimensionless function of
![]() $r/L$
. Clearly, Kolmogorov used
$r/L$
. Clearly, Kolmogorov used
![]() $L$
as a SP scaling variable. It is evident that he assumed the existence of an inertial range, which suggests that he assumed a very, if not infinitely, large Reynolds number.
$L$
as a SP scaling variable. It is evident that he assumed the existence of an inertial range, which suggests that he assumed a very, if not infinitely, large Reynolds number.
It is interesting to note that both Taylor and Kolmogorov required some form of SP in their respective approaches to obtain
![]() $C_{\unicode[STIX]{x1D716}}$
, suggesting that the constancy of
$C_{\unicode[STIX]{x1D716}}$
, suggesting that the constancy of
![]() $C_{\unicode[STIX]{x1D716}}$
too requires some form of SP. Accordingly, testing the constancy of
$C_{\unicode[STIX]{x1D716}}$
too requires some form of SP. Accordingly, testing the constancy of
![]() $C_{\unicode[STIX]{x1D716}}$
, as defined by both Taylor and Kolmogorov, requires that SP should be closely approximated. However, since the work of Taylor and Kolmogorov, the reference to the SP requirement for obtaining
$C_{\unicode[STIX]{x1D716}}$
, as defined by both Taylor and Kolmogorov, requires that SP should be closely approximated. However, since the work of Taylor and Kolmogorov, the reference to the SP requirement for obtaining
![]() $C_{\unicode[STIX]{x1D716}}$
appears to have been largely ignored (with some exceptions, e.g. Antonia, Satyaprakash & Hussain (Reference Antonia, Satyaprakash and Hussain1980)) and the focus has been almost invariably on the dimensional arguments (e.g. Batchelor Reference Batchelor1953; Tennekes & Lumley Reference Tennekes and Lumley1972; Sreenivasan Reference Sreenivasan1984; Monin & Yaglom Reference Monin and Yaglom2007). This has led to testing the constancy of
$C_{\unicode[STIX]{x1D716}}$
appears to have been largely ignored (with some exceptions, e.g. Antonia, Satyaprakash & Hussain (Reference Antonia, Satyaprakash and Hussain1980)) and the focus has been almost invariably on the dimensional arguments (e.g. Batchelor Reference Batchelor1953; Tennekes & Lumley Reference Tennekes and Lumley1972; Sreenivasan Reference Sreenivasan1984; Monin & Yaglom Reference Monin and Yaglom2007). This has led to testing the constancy of
![]() $C_{\unicode[STIX]{x1D716}}$
in many turbulent flows which do not necessarily comply with SP, as originally assumed by Taylor and Kolmogorov, such as grid turbulence (Djenidi, Kamruzzaman & Antonia Reference Djenidi, Kamruzzaman and Antonia2015; Sinhuber, Bodenschatz & Bewley Reference Sinhuber, Bodenschatz and Bewley2015). For example, Batchelor (Reference Batchelor1953) presented values of
$C_{\unicode[STIX]{x1D716}}$
in many turbulent flows which do not necessarily comply with SP, as originally assumed by Taylor and Kolmogorov, such as grid turbulence (Djenidi, Kamruzzaman & Antonia Reference Djenidi, Kamruzzaman and Antonia2015; Sinhuber, Bodenschatz & Bewley Reference Sinhuber, Bodenschatz and Bewley2015). For example, Batchelor (Reference Batchelor1953) presented values of
![]() $C_{\unicode[STIX]{x1D716}}$
for grid turbulence at several Reynolds numbers. Despite the scatter in the data, the trend is clear:
$C_{\unicode[STIX]{x1D716}}$
for grid turbulence at several Reynolds numbers. Despite the scatter in the data, the trend is clear:
![]() $C_{\unicode[STIX]{x1D716}}$
shows a systematic, albeit weak, decrease with increasing downstream distance and increasing Reynolds number. The Reynolds number dependence was further confirmed by Sreenivasan (Reference Sreenivasan1984), who showed that
$C_{\unicode[STIX]{x1D716}}$
shows a systematic, albeit weak, decrease with increasing downstream distance and increasing Reynolds number. The Reynolds number dependence was further confirmed by Sreenivasan (Reference Sreenivasan1984), who showed that
![]() $C_{\unicode[STIX]{x1D716}}$
varies strongly when
$C_{\unicode[STIX]{x1D716}}$
varies strongly when
![]() $0\leqslant Re_{\unicode[STIX]{x1D706}}\leqslant 50$
, but becomes constant with a value of approximately 1 when
$0\leqslant Re_{\unicode[STIX]{x1D706}}\leqslant 50$
, but becomes constant with a value of approximately 1 when
![]() $Re_{\unicode[STIX]{x1D706}}\geqslant 50$
. Recently Vassilicos (Reference Vassilicos2015) presented a review of
$Re_{\unicode[STIX]{x1D706}}\geqslant 50$
. Recently Vassilicos (Reference Vassilicos2015) presented a review of
![]() $C_{\unicode[STIX]{x1D716}}$
over the past 60 years and discussed its non-universality. He further proposed, on empirical grounds, that for decaying turbulence, such as wake and grid turbulence,
$C_{\unicode[STIX]{x1D716}}$
over the past 60 years and discussed its non-universality. He further proposed, on empirical grounds, that for decaying turbulence, such as wake and grid turbulence,
![]() $C_{\unicode[STIX]{x1D716}}\sim Re_{I}^{m}/Re_{L}^{n}$
with
$C_{\unicode[STIX]{x1D716}}\sim Re_{I}^{m}/Re_{L}^{n}$
with
![]() $m\simeq n\simeq 1$
where
$m\simeq n\simeq 1$
where
![]() $Re_{I}=Ul_{b}/\unicode[STIX]{x1D708}$
is a global or inlet Reynolds number characterizing the inlet condition (
$Re_{I}=Ul_{b}/\unicode[STIX]{x1D708}$
is a global or inlet Reynolds number characterizing the inlet condition (
![]() $l_{b}$
is a length scale defined by the grid e.g. the grid mesh size
$l_{b}$
is a length scale defined by the grid e.g. the grid mesh size
![]() $M$
).
$M$
).
While dimensional analysis has proven to be quite useful, it lacks the rigour of an analysis based on the equations of motion. Only a very few analyses of
![]() $C_{\unicode[STIX]{x1D716}}$
were carried out within the framework of the Navier–Stokes equations. Lohse (Reference Lohse1994) was probably first to transcend dimensional analysis. He used a mean field theory closure of the Kármán–Howarth equation and obtained
$C_{\unicode[STIX]{x1D716}}$
were carried out within the framework of the Navier–Stokes equations. Lohse (Reference Lohse1994) was probably first to transcend dimensional analysis. He used a mean field theory closure of the Kármán–Howarth equation and obtained
![]() $C_{\unicode[STIX]{x1D716}}=C_{\unicode[STIX]{x1D716},\infty }\sqrt{1+\unicode[STIX]{x1D6FC}/Re_{\unicode[STIX]{x1D706}}^{2}}$
, where
$C_{\unicode[STIX]{x1D716}}=C_{\unicode[STIX]{x1D716},\infty }\sqrt{1+\unicode[STIX]{x1D6FC}/Re_{\unicode[STIX]{x1D706}}^{2}}$
, where
![]() $C_{\unicode[STIX]{x1D716},\infty }$
is the value of
$C_{\unicode[STIX]{x1D716},\infty }$
is the value of
![]() $C_{\unicode[STIX]{x1D716}}$
as
$C_{\unicode[STIX]{x1D716}}$
as
![]() $Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
and
$Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
and
![]() $\unicode[STIX]{x1D6FC}$
a constant. He ignored the term accounting for the large-scale motions in the Kármán–Howarth equation. Using the Navier–Stokes equations, Doering & Foias (Reference Doering and Foias2002) established the following expression
$\unicode[STIX]{x1D6FC}$
a constant. He ignored the term accounting for the large-scale motions in the Kármán–Howarth equation. Using the Navier–Stokes equations, Doering & Foias (Reference Doering and Foias2002) established the following expression
![]() $C_{\unicode[STIX]{x1D716}}\leqslant (a/Re_{l}+b)$
(
$C_{\unicode[STIX]{x1D716}}\leqslant (a/Re_{l}+b)$
(
![]() $a$
and
$a$
and
![]() $b$
are constants independent of the Reynolds number) or equivalently
$b$
are constants independent of the Reynolds number) or equivalently
![]() $C_{\unicode[STIX]{x1D716}}\leqslant (b/2)(1+\sqrt{1+(4a/b^{2})/Re_{\unicode[STIX]{x1D706}}^{2}})$
for a ‘steadily’ driven turbulence in a periodic domain without boundary. It should be noted that in their expression (28) of
$C_{\unicode[STIX]{x1D716}}\leqslant (b/2)(1+\sqrt{1+(4a/b^{2})/Re_{\unicode[STIX]{x1D706}}^{2}})$
for a ‘steadily’ driven turbulence in a periodic domain without boundary. It should be noted that in their expression (28) of
![]() $\overline{\unicode[STIX]{x1D716}}$
, Doering & Foias (Reference Doering and Foias2002) used the following form for the time-independent forcing,
$\overline{\unicode[STIX]{x1D716}}$
, Doering & Foias (Reference Doering and Foias2002) used the following form for the time-independent forcing,
![]() $f=F\unicode[STIX]{x1D6F7}(x/l)$
with
$f=F\unicode[STIX]{x1D6F7}(x/l)$
with
![]() $l=\unicode[STIX]{x1D6FC}L$
where
$l=\unicode[STIX]{x1D6FC}L$
where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $L$
are an integer and the size of the system, respectively. More recently, McComb et al. (Reference McComb, Berera, Yoffe and Linkmann2015) used the Kármán–Howarth equation with a forcing term to develop a model for
$L$
are an integer and the size of the system, respectively. More recently, McComb et al. (Reference McComb, Berera, Yoffe and Linkmann2015) used the Kármán–Howarth equation with a forcing term to develop a model for
![]() $C_{\unicode[STIX]{x1D716}}$
for forced homogeneous isotropic turbulence (HIT). Using
$C_{\unicode[STIX]{x1D716}}$
for forced homogeneous isotropic turbulence (HIT). Using
![]() $L$
as a scaling length scale and applying asymptotic expansions for the second- and third-order velocity structure functions into the Kármán–Howarth equation, they obtained
$L$
as a scaling length scale and applying asymptotic expansions for the second- and third-order velocity structure functions into the Kármán–Howarth equation, they obtained
![]() $C_{\unicode[STIX]{x1D716}}=C_{\unicode[STIX]{x1D716},\infty }+C/Re_{L}$
, where
$C_{\unicode[STIX]{x1D716}}=C_{\unicode[STIX]{x1D716},\infty }+C/Re_{L}$
, where
![]() $C_{\unicode[STIX]{x1D716},\infty }=0.468\pm 0.006$
and
$C_{\unicode[STIX]{x1D716},\infty }=0.468\pm 0.006$
and
![]() $C=18.9\pm 1.3$
are constant with respect to
$C=18.9\pm 1.3$
are constant with respect to
![]() $Re_{L}$
and the dimensionless variable
$Re_{L}$
and the dimensionless variable
![]() $r/L$
. Further, they used the expression
$r/L$
. Further, they used the expression
![]() $Re_{L}=C_{\unicode[STIX]{x1D716}}Re_{\unicode[STIX]{x1D706}}^{2}/15$
, albeit without justification, to show that
$Re_{L}=C_{\unicode[STIX]{x1D716}}Re_{\unicode[STIX]{x1D706}}^{2}/15$
, albeit without justification, to show that
![]() $C_{\unicode[STIX]{x1D716}}=A(1+\sqrt{1+(B)/Re_{\unicode[STIX]{x1D706}}^{2}})$
, where
$C_{\unicode[STIX]{x1D716}}=A(1+\sqrt{1+(B)/Re_{\unicode[STIX]{x1D706}}^{2}})$
, where
![]() $A$
and
$A$
and
![]() $B$
are constant with respect to
$B$
are constant with respect to
![]() $Re_{\unicode[STIX]{x1D706}}$
, which is similar to the upper bound of
$Re_{\unicode[STIX]{x1D706}}$
, which is similar to the upper bound of
![]() $C_{\unicode[STIX]{x1D716}}$
of Doering & Foias (Reference Doering and Foias2002). In this paper, we present a derivation for an analytical expression of
$C_{\unicode[STIX]{x1D716}}$
of Doering & Foias (Reference Doering and Foias2002). In this paper, we present a derivation for an analytical expression of
![]() $C_{\unicode[STIX]{x1D716}}$
based on the Navier–Stokes equations. The approach follows the work of Lohse (Reference Lohse1994) and McComb et al. (Reference McComb, Berera, Yoffe and Linkmann2015), in that the starting point of the analysis is the transport equation for
$C_{\unicode[STIX]{x1D716}}$
based on the Navier–Stokes equations. The approach follows the work of Lohse (Reference Lohse1994) and McComb et al. (Reference McComb, Berera, Yoffe and Linkmann2015), in that the starting point of the analysis is the transport equation for
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
. However, we avoid using any model closure or asymptotic expansion in the analysis, although we work within the framework of SP, which is aligned with the approach taken by both Taylor (Reference Taylor1935) and Kolmogorov (Reference Kolmogorov1941b
).
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
. However, we avoid using any model closure or asymptotic expansion in the analysis, although we work within the framework of SP, which is aligned with the approach taken by both Taylor (Reference Taylor1935) and Kolmogorov (Reference Kolmogorov1941b
).
The aim of the study is to assess the Reynolds number dependence of
![]() $C_{\unicode[STIX]{x1D716}}$
in decaying turbulence. Two cases of decaying turbulence are considered: HIT such as closely approximated in grid turbulence and locally homogeneous and isotropic turbulence such as on the axis of a turbulent round jet (§ 2). The analytical results are tested against the experimental data in § 3. It should be stressed that the quest for an answer to the issue regarding whether or not
$C_{\unicode[STIX]{x1D716}}$
in decaying turbulence. Two cases of decaying turbulence are considered: HIT such as closely approximated in grid turbulence and locally homogeneous and isotropic turbulence such as on the axis of a turbulent round jet (§ 2). The analytical results are tested against the experimental data in § 3. It should be stressed that the quest for an answer to the issue regarding whether or not
![]() $C_{\unicode[STIX]{x1D716}}$
is Reynolds number dependent or has a universal value (i.e. independent of the Reynolds number and flow configurations) has an important practical implication considering that
$C_{\unicode[STIX]{x1D716}}$
is Reynolds number dependent or has a universal value (i.e. independent of the Reynolds number and flow configurations) has an important practical implication considering that
![]() $\overline{\unicode[STIX]{x1D716}}$
plays a fundamental role in the theory of turbulence and is a critical controlling variable in many processes (e.g. mixing, chemical reactions, interfacial exchanges). For example, considering that
$\overline{\unicode[STIX]{x1D716}}$
plays a fundamental role in the theory of turbulence and is a critical controlling variable in many processes (e.g. mixing, chemical reactions, interfacial exchanges). For example, considering that
![]() $\overline{\unicode[STIX]{x1D716}}$
is practically impossible to measure during field experiments (e.g. atmospheric, oceanic and industrial measurements) the knowledge (i) that
$\overline{\unicode[STIX]{x1D716}}$
is practically impossible to measure during field experiments (e.g. atmospheric, oceanic and industrial measurements) the knowledge (i) that
![]() $C_{\unicode[STIX]{x1D716}}$
is universal and (ii) of its actual value would greatly benefit such experiments. Indeed, if
$C_{\unicode[STIX]{x1D716}}$
is universal and (ii) of its actual value would greatly benefit such experiments. Indeed, if
![]() $C_{\unicode[STIX]{x1D716}}$
is a universal constant, then it allows a relatively simple practical way for estimating
$C_{\unicode[STIX]{x1D716}}$
is a universal constant, then it allows a relatively simple practical way for estimating
![]() $\overline{\unicode[STIX]{x1D716}}$
in any turbulent flow, at least at high Reynolds numbers. One would be required to measure both the turbulence intensity,
$\overline{\unicode[STIX]{x1D716}}$
in any turbulent flow, at least at high Reynolds numbers. One would be required to measure both the turbulence intensity,
![]() $u^{\prime }$
, and the integral length scale,
$u^{\prime }$
, and the integral length scale,
![]() $L$
, which are relatively straightforward to measure.
$L$
, which are relatively straightforward to measure.
2 Theoretical considerations
2.1 Homogeneous and isotropic turbulence
For the sake of convenience, we reproduce here the first stages of the SP analytical development of Djenidi & Antonia (Reference Djenidi and Antonia2015) (hereafter denoted DA15), which we then extend to derive an expression for
![]() $C_{\unicode[STIX]{x1D716}}$
. The starting point of the analysis is the transport equation for the second-order velocity structure function,
$C_{\unicode[STIX]{x1D716}}$
. The starting point of the analysis is the transport equation for the second-order velocity structure function,
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
where the velocity increment is
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
where the velocity increment is
![]() $\unicode[STIX]{x1D6FF}u=(u(x+r,t)-u(x,t))$
, (Danaila et al.
Reference Danaila, Anselmet, Zhou and Antonia1999; Antonia et al.
Reference Antonia, Smalley, Zhou, Anselmet and Danaila2003)
$\unicode[STIX]{x1D6FF}u=(u(x+r,t)-u(x,t))$
, (Danaila et al.
Reference Danaila, Anselmet, Zhou and Antonia1999; Antonia et al.
Reference Antonia, Smalley, Zhou, Anselmet and Danaila2003)
where
![]() $\overline{\unicode[STIX]{x1D716}}=-(2/3)(\unicode[STIX]{x2202}\overline{u^{2}}/\unicode[STIX]{x2202}t)$
is the mean turbulent kinetic energy dissipation rate ((2.1) is also called the scale-by-scale (SBS) energy budget). Following Barenblatt & Gavrilov (Reference Barenblatt and Gavrilov1974), we assume the following SP expressions for
$\overline{\unicode[STIX]{x1D716}}=-(2/3)(\unicode[STIX]{x2202}\overline{u^{2}}/\unicode[STIX]{x2202}t)$
is the mean turbulent kinetic energy dissipation rate ((2.1) is also called the scale-by-scale (SBS) energy budget). Following Barenblatt & Gavrilov (Reference Barenblatt and Gavrilov1974), we assume the following SP expressions for
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
and
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
and
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{3}}$
viz.
$\overline{(\unicode[STIX]{x1D6FF}u)^{3}}$
viz.
where
![]() $r^{\ast }=r/l(t)$
;
$r^{\ast }=r/l(t)$
;
![]() $l(t)$
,
$l(t)$
,
![]() $u_{2}(t)$
and
$u_{2}(t)$
and
![]() $u_{3}(t)$
are the length scale and velocity scaling functions to be determined while
$u_{3}(t)$
are the length scale and velocity scaling functions to be determined while
![]() $f$
and
$f$
and
![]() $g$
are dimensionless functions. For convenience, we hereafter drop the variable
$g$
are dimensionless functions. For convenience, we hereafter drop the variable
![]() $t$
. Their analysis introduces the skewness of the longitudinal velocity increment,
$t$
. Their analysis introduces the skewness of the longitudinal velocity increment,
![]() $S(r)(\equiv \overline{(\unicode[STIX]{x1D6FF}u)^{3}}/\overline{(\unicode[STIX]{x1D6FF}u)^{2}}^{3/2})$
, as a SP controlling parameter. Using (2.2) and (2.3), one can write
$S(r)(\equiv \overline{(\unicode[STIX]{x1D6FF}u)^{3}}/\overline{(\unicode[STIX]{x1D6FF}u)^{2}}^{3/2})$
, as a SP controlling parameter. Using (2.2) and (2.3), one can write
![]() $S=c(t)\unicode[STIX]{x1D719}(r/l)$
where
$S=c(t)\unicode[STIX]{x1D719}(r/l)$
where
![]() $c(t)$
and
$c(t)$
and
![]() $\unicode[STIX]{x1D719}(r/l)$
are dimensionless functions of time and
$\unicode[STIX]{x1D719}(r/l)$
are dimensionless functions of time and
![]() $(r/l)$
, respectively. DA15’s SP framework allowed a critical appraisal of the specific assumptions that have been made in previous SP analyses. Specifically, SP is achieved when
$(r/l)$
, respectively. DA15’s SP framework allowed a critical appraisal of the specific assumptions that have been made in previous SP analyses. Specifically, SP is achieved when
![]() $cRe_{l}=\text{const.}$
, where
$cRe_{l}=\text{const.}$
, where
![]() $Re_{l}=u_{2}l/\unicode[STIX]{x1D708}$
is the ‘scaling’ Reynolds number. DA15 further show that when
$Re_{l}=u_{2}l/\unicode[STIX]{x1D708}$
is the ‘scaling’ Reynolds number. DA15 further show that when
![]() $c(t)$
is constant, then
$c(t)$
is constant, then
![]() $Re_{l}=\text{const.}$
, the length scale
$Re_{l}=\text{const.}$
, the length scale
![]() $l$
can hence be identified not only with the Kolmogorov length scale
$l$
can hence be identified not only with the Kolmogorov length scale
![]() $\unicode[STIX]{x1D702}$
, but with any other characteristic length scale which is proportional to
$\unicode[STIX]{x1D702}$
, but with any other characteristic length scale which is proportional to
![]() $\unicode[STIX]{x1D702}$
. The implication is that SP is complete or exact i.e. the ratio between any two length scales is constant (similarly for any two velocity scales) even when
$\unicode[STIX]{x1D702}$
. The implication is that SP is complete or exact i.e. the ratio between any two length scales is constant (similarly for any two velocity scales) even when
![]() $Re_{l}$
is relatively small. Recent measurements in the far field of a cylinder wake (Tang et al.
Reference Tang, Antonia, Djenidi and Zhou2015b
) show that
$Re_{l}$
is relatively small. Recent measurements in the far field of a cylinder wake (Tang et al.
Reference Tang, Antonia, Djenidi and Zhou2015b
) show that
![]() $S(r)$
collapses onto a single distribution, confirming that
$S(r)$
collapses onto a single distribution, confirming that
![]() $S=c(t)\unicode[STIX]{x1D719}(r/l)$
with
$S=c(t)\unicode[STIX]{x1D719}(r/l)$
with
![]() $c(t)=\text{const.}$
(i.e.
$c(t)=\text{const.}$
(i.e.
![]() $Re_{l}=\text{const.}$
). This is remarkable considering that the turbulence in the far wake is neither homogeneous nor isotropic, and the Taylor microscale Reynolds number is small. This suggests that the DA15 SP analysis can be extended to anisotropic turbulence and in particular that the SP constraint
$Re_{l}=\text{const.}$
). This is remarkable considering that the turbulence in the far wake is neither homogeneous nor isotropic, and the Taylor microscale Reynolds number is small. This suggests that the DA15 SP analysis can be extended to anisotropic turbulence and in particular that the SP constraint
![]() $cRe_{l}=\text{const.}$
appears to be a general requirement that needs to be satisfied in any turbulent flow if SP is to be achieved. This constraint presents two cases of SP, discussed in DA15. One, as observed in Tang et al. (Reference Tang, Antonia, Djenidi and Zhou2015b
) (see their figure 13), in which
$cRe_{l}=\text{const.}$
appears to be a general requirement that needs to be satisfied in any turbulent flow if SP is to be achieved. This constraint presents two cases of SP, discussed in DA15. One, as observed in Tang et al. (Reference Tang, Antonia, Djenidi and Zhou2015b
) (see their figure 13), in which
![]() $c(t)$
is constant and the second which allows
$c(t)$
is constant and the second which allows
![]() $c(t)$
to vary. However, so far, experimental and numerical evidence show that SP is observed when
$c(t)$
to vary. However, so far, experimental and numerical evidence show that SP is observed when
![]() $Re_{l}$
is constant during decay, implying that
$Re_{l}$
is constant during decay, implying that
![]() $c(t)$
is constant too. The case of non-constant
$c(t)$
is constant too. The case of non-constant
![]() $c(t)$
under SP is yet to be observed. Accordingly, the SP analysis presented below concerns mainly SP where
$c(t)$
under SP is yet to be observed. Accordingly, the SP analysis presented below concerns mainly SP where
![]() $c(t)$
is constant during the decay, which we know can be observed experimentally and numerically.
$c(t)$
is constant during the decay, which we know can be observed experimentally and numerically.
Following Djenidi & Antonia (Reference Djenidi and Antonia2015), we substitute (2.2), (2.3) and
![]() $S(r)$
into (2.1). After some trivial manipulations, we obtain
$S(r)$
into (2.1). After some trivial manipulations, we obtain
with
where
![]() $s^{\ast }$
is a dummy variable of integration. Equation (2.4) holds at all scales if
$s^{\ast }$
is a dummy variable of integration. Equation (2.4) holds at all scales if
![]() $\unicode[STIX]{x1D6E4}_{1}\sim r^{\ast 5}$
and
$\unicode[STIX]{x1D6E4}_{1}\sim r^{\ast 5}$
and
![]() $\unicode[STIX]{x1D6E4}_{2}\sim r^{\ast 5}$
when
$\unicode[STIX]{x1D6E4}_{2}\sim r^{\ast 5}$
when
![]() $r^{\ast }\rightarrow \infty$
. Since
$r^{\ast }\rightarrow \infty$
. Since
![]() $f(r^{\ast })\rightarrow \text{const.}$
and
$f(r^{\ast })\rightarrow \text{const.}$
and
![]() $f^{\prime }(r^{\ast })\rightarrow 0$
when
$f^{\prime }(r^{\ast })\rightarrow 0$
when
![]() $r^{\ast }\rightarrow \infty$
, it is easy to show that these conditions are satisfied. Note also that when
$r^{\ast }\rightarrow \infty$
, it is easy to show that these conditions are satisfied. Note also that when
![]() $r^{\ast }\rightarrow 0$
,
$r^{\ast }\rightarrow 0$
,
![]() $f\sim r^{\ast 2}$
. Thus,
$f\sim r^{\ast 2}$
. Thus,
![]() $\unicode[STIX]{x1D6E4}_{1}\sim r^{\ast 7}$
and
$\unicode[STIX]{x1D6E4}_{1}\sim r^{\ast 7}$
and
![]() $\unicode[STIX]{x1D6E4}_{2}\sim r^{\ast 7}$
; they approach zero more rapidly than
$\unicode[STIX]{x1D6E4}_{2}\sim r^{\ast 7}$
; they approach zero more rapidly than
![]() $r^{\ast 4}$
.
$r^{\ast 4}$
.
The SP constraints are:
where
![]() $Re_{l}=u_{2}l/\unicode[STIX]{x1D708}$
is a scaling Reynolds number. Evidently, the above constraints, i.e.
$Re_{l}=u_{2}l/\unicode[STIX]{x1D708}$
is a scaling Reynolds number. Evidently, the above constraints, i.e.
![]() $C_{i}$
must be independent of
$C_{i}$
must be independent of
![]() $t$
(since the coefficient of the first term on the left-hand side of (2.4) is a constant), apply for all separations
$t$
(since the coefficient of the first term on the left-hand side of (2.4) is a constant), apply for all separations
![]() $r^{\ast }$
while the numerical value of the constants
$r^{\ast }$
while the numerical value of the constants
![]() $C_{i}$
depend on the scaling variables. Combining (2.7) and (2.10) and using the definition of
$C_{i}$
depend on the scaling variables. Combining (2.7) and (2.10) and using the definition of
![]() $Re_{l}$
yields
$Re_{l}$
yields
Now, substituting (2.11) into (2.10) leads to
Recognizing that
![]() $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\overline{\unicode[STIX]{x1D716}})^{1/4}$
and
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\overline{\unicode[STIX]{x1D716}})^{1/4}$
and
![]() $v_{K}=(\unicode[STIX]{x1D708}\overline{\unicode[STIX]{x1D716}})^{1/4}$
, the Kolmogorov length and velocity scales, respectively, we can write
$v_{K}=(\unicode[STIX]{x1D708}\overline{\unicode[STIX]{x1D716}})^{1/4}$
, the Kolmogorov length and velocity scales, respectively, we can write
![]() $l=C_{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D702}$
and
$l=C_{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D702}$
and
![]() $u_{2}=C_{v_{K}}v_{K}$
. Clearly,
$u_{2}=C_{v_{K}}v_{K}$
. Clearly,
![]() $C_{\unicode[STIX]{x1D702}}$
and
$C_{\unicode[STIX]{x1D702}}$
and
![]() $C_{v_{K}}$
are constant if
$C_{v_{K}}$
are constant if
![]() $c$
or equivalently
$c$
or equivalently
![]() $Re_{l}$
is constant. So far, experimental and numerical evidence indicate that SP occurs when the scaling Reynolds number is constant. We thus will take
$Re_{l}$
is constant. So far, experimental and numerical evidence indicate that SP occurs when the scaling Reynolds number is constant. We thus will take
![]() $c$
or
$c$
or
![]() $Re_{l}$
to be constant under SP. Note that if
$Re_{l}$
to be constant under SP. Note that if
![]() $c$
is constant, one can, without loss of generality, take
$c$
is constant, one can, without loss of generality, take
![]() $u_{3}=u_{2}$
and (2.7) becomes
$u_{3}=u_{2}$
and (2.7) becomes
![]() $Re_{l}=C_{0}$
. Expressions (2.11) and (2.12) reveal that, under SP,
$Re_{l}=C_{0}$
. Expressions (2.11) and (2.12) reveal that, under SP,
![]() $\overline{\unicode[STIX]{x1D716}}$
and
$\overline{\unicode[STIX]{x1D716}}$
and
![]() $\unicode[STIX]{x1D708}$
are the relevant natural parameters for the velocity increments.
$\unicode[STIX]{x1D708}$
are the relevant natural parameters for the velocity increments.
The above derivation of the SP constraints (2.7)–(2.10) is similar to that of DA15. The rest of the analysis departs from DA15. We can now rewrite (2.4) as
![]() $C_{1}=-2C_{2}$
under SP (DA15), then
$C_{1}=-2C_{2}$
under SP (DA15), then
First we write (2.14) as
If
![]() $l=\unicode[STIX]{x1D706}$
and
$l=\unicode[STIX]{x1D706}$
and
![]() $u_{2}=u^{\prime }$
(i.e.
$u_{2}=u^{\prime }$
(i.e.
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $u^{\prime }$
are scaling variables satisfying SP requirements) and writing
$u^{\prime }$
are scaling variables satisfying SP requirements) and writing
![]() $C_{3,\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D716}\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D708}u^{\prime 2})=C_{\unicode[STIX]{x1D716}}(\unicode[STIX]{x1D706}/L)Re_{\unicode[STIX]{x1D706}}$
, we have the following expression for
$C_{3,\unicode[STIX]{x1D706}}=(\unicode[STIX]{x1D716}\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D708}u^{\prime 2})=C_{\unicode[STIX]{x1D716}}(\unicode[STIX]{x1D706}/L)Re_{\unicode[STIX]{x1D706}}$
, we have the following expression for
![]() $C_{\unicode[STIX]{x1D716}}$
:
$C_{\unicode[STIX]{x1D716}}$
:
where
![]() $r_{L}^{\ast }=L/\unicode[STIX]{x1D706}$
and
$r_{L}^{\ast }=L/\unicode[STIX]{x1D706}$
and
![]() $C_{3,\unicode[STIX]{x1D706}}=15$
;
$C_{3,\unicode[STIX]{x1D706}}=15$
;
![]() $L$
is a length scale characteristic of the large-scale motions. This expression reveals a non-trivial
$L$
is a length scale characteristic of the large-scale motions. This expression reveals a non-trivial
![]() $Re_{\unicode[STIX]{x1D706}}$
dependency of
$Re_{\unicode[STIX]{x1D706}}$
dependency of
![]() $C_{\unicode[STIX]{x1D716}}$
felt at all scales of motion. Also,
$C_{\unicode[STIX]{x1D716}}$
felt at all scales of motion. Also,
![]() $C_{\unicode[STIX]{x1D716}}$
must be independent of
$C_{\unicode[STIX]{x1D716}}$
must be independent of
![]() $r^{\ast }$
, which is easily verified. For example, when
$r^{\ast }$
, which is easily verified. For example, when
![]() $r^{\ast }\rightarrow \infty$
, we obtain these asymptotic values,
$r^{\ast }\rightarrow \infty$
, we obtain these asymptotic values,
![]() $f(r^{\ast })\simeq 2$
,
$f(r^{\ast })\simeq 2$
,
![]() $f^{\prime }(r^{\ast })=0$
,
$f^{\prime }(r^{\ast })=0$
,
![]() $S(r^{\ast })=0$
. Then it follows that
$S(r^{\ast })=0$
. Then it follows that
![]() $\unicode[STIX]{x1D6E4}_{1}\simeq (2/5)r^{\ast 5}$
,
$\unicode[STIX]{x1D6E4}_{1}\simeq (2/5)r^{\ast 5}$
,
![]() $\unicode[STIX]{x1D6E4}_{2}\simeq 0$
and the right-hand side of (2.16) becomes
$\unicode[STIX]{x1D6E4}_{2}\simeq 0$
and the right-hand side of (2.16) becomes
where
![]() $r_{L}^{\ast }=Re_{L}/Re_{\unicode[STIX]{x1D706}}$
and
$r_{L}^{\ast }=Re_{L}/Re_{\unicode[STIX]{x1D706}}$
and
![]() $C_{1}=-10$
(for HIT under SP, i.e. constant
$C_{1}=-10$
(for HIT under SP, i.e. constant
![]() $Re_{\unicode[STIX]{x1D706}}$
; see DA15). We can also recover this expression when
$Re_{\unicode[STIX]{x1D706}}$
; see DA15). We can also recover this expression when
![]() $r^{\ast }\rightarrow 0$
. Indeed, expanding
$r^{\ast }\rightarrow 0$
. Indeed, expanding
![]() $f(r^{\ast })$
around
$f(r^{\ast })$
around
![]() $r^{\ast }=0$
and using Taylor series expansion to order 4 yields
$r^{\ast }=0$
and using Taylor series expansion to order 4 yields
where
![]() $\unicode[STIX]{x1D6FC}=(l^{2}/u_{2}^{2})\overline{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}}$
and
$\unicode[STIX]{x1D6FC}=(l^{2}/u_{2}^{2})\overline{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}}$
and
![]() $\unicode[STIX]{x1D6FD}=(l^{4}/u_{2}^{2})\overline{(\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}x^{2})^{2}}$
are constant under SP and whose values depend on the choice of
$\unicode[STIX]{x1D6FD}=(l^{4}/u_{2}^{2})\overline{(\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}x^{2})^{2}}$
are constant under SP and whose values depend on the choice of
![]() $l$
and
$l$
and
![]() $u_{2}$
. Since we selected
$u_{2}$
. Since we selected
![]() $u_{2}=u^{\prime }$
and
$u_{2}=u^{\prime }$
and
![]() $l=\unicode[STIX]{x1D706}$
then
$l=\unicode[STIX]{x1D706}$
then
![]() $\unicode[STIX]{x1D6FC}=1$
, and
$\unicode[STIX]{x1D6FC}=1$
, and
![]() $\unicode[STIX]{x1D6FD}=G=(u^{\prime 2}\overline{(\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}x^{2})^{2}}/\overline{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}}^{2})$
, often called the enstrophy destruction coefficient of
$\unicode[STIX]{x1D6FD}=G=(u^{\prime 2}\overline{(\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}x^{2})^{2}}/\overline{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}}^{2})$
, often called the enstrophy destruction coefficient of
![]() $\overline{\unicode[STIX]{x1D716}}$
. Substituting (2.18) into (2.16) with
$\overline{\unicode[STIX]{x1D716}}$
. Substituting (2.18) into (2.16) with
![]() $(\unicode[STIX]{x1D6E4}_{1}+1/2\unicode[STIX]{x1D6E4}_{2})=(2/7)r^{\ast 7}$
as
$(\unicode[STIX]{x1D6E4}_{1}+1/2\unicode[STIX]{x1D6E4}_{2})=(2/7)r^{\ast 7}$
as
![]() $r^{\ast }\rightarrow 0$
yields
$r^{\ast }\rightarrow 0$
yields
which leads to
![]() $C_{\unicode[STIX]{x1D716}}\simeq 15(L/\unicode[STIX]{x1D706})/Re_{\unicode[STIX]{x1D706}}$
for very small
$C_{\unicode[STIX]{x1D716}}\simeq 15(L/\unicode[STIX]{x1D706})/Re_{\unicode[STIX]{x1D706}}$
for very small
![]() $r^{\ast }$
. The expression inside the parentheses is of interest. Since
$r^{\ast }$
. The expression inside the parentheses is of interest. Since
![]() $C_{\unicode[STIX]{x1D716}}$
must be independent of
$C_{\unicode[STIX]{x1D716}}$
must be independent of
![]() $r^{\ast }$
$r^{\ast }$
This expression, which is in fact the transport equation for
![]() $\overline{\unicode[STIX]{x1D716}}$
first written and tested by Batchelor & Townsend (Reference Batchelor and Townsend1947) and analysed in detail by Djenidi & Antonia (Reference Djenidi and Antonia2014) using direct numerical simulation based on the lattice Boltzmann method (Succi Reference Succi2001), was recently extensively used to determine the behaviours of
$\overline{\unicode[STIX]{x1D716}}$
first written and tested by Batchelor & Townsend (Reference Batchelor and Townsend1947) and analysed in detail by Djenidi & Antonia (Reference Djenidi and Antonia2014) using direct numerical simulation based on the lattice Boltzmann method (Succi Reference Succi2001), was recently extensively used to determine the behaviours of
![]() $S_{(r^{\ast }\rightarrow 0)}$
and
$S_{(r^{\ast }\rightarrow 0)}$
and
![]() $G$
when
$G$
when
![]() $Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
in several turbulent flows (Lee et al.
Reference Lee, Djenidi, Antonia and Danaila2013; Thiesset, Antonia & Djenidi Reference Thiesset, Antonia and Djenidi2014; Antonia et al.
Reference Antonia, Tang, Djenidi and Danaila2015; Tang et al.
Reference Tang, Antonia, Djenidi, Abe, Zhou., Danaila and Zhou2015a
,Reference Tang, Antonia, Djenidi and Zhou
b
,Reference Tang, Antonia, Djenidi and Zhou
c
) in the context of assessing whether the small-scale statistics are consistent with the original similarity hypothesis (Kolmogorov Reference Kolmogorov1941a
) or the modified one (Kolmogorov Reference Kolmogorov1962), i.e. whether
$Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
in several turbulent flows (Lee et al.
Reference Lee, Djenidi, Antonia and Danaila2013; Thiesset, Antonia & Djenidi Reference Thiesset, Antonia and Djenidi2014; Antonia et al.
Reference Antonia, Tang, Djenidi and Danaila2015; Tang et al.
Reference Tang, Antonia, Djenidi, Abe, Zhou., Danaila and Zhou2015a
,Reference Tang, Antonia, Djenidi and Zhou
b
,Reference Tang, Antonia, Djenidi and Zhou
c
) in the context of assessing whether the small-scale statistics are consistent with the original similarity hypothesis (Kolmogorov Reference Kolmogorov1941a
) or the modified one (Kolmogorov Reference Kolmogorov1962), i.e. whether
![]() $S_{(r^{\ast }\rightarrow 0)}\rightarrow \text{const.}$
or
$S_{(r^{\ast }\rightarrow 0)}\rightarrow \text{const.}$
or
![]() $S_{(r^{\ast }\rightarrow 0)}\sim Re_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FC}}$
;
$S_{(r^{\ast }\rightarrow 0)}\sim Re_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FC}}$
;
![]() $S_{(r^{\ast }\rightarrow 0)}$
is the velocity derivative skewness. If one accepts that
$S_{(r^{\ast }\rightarrow 0)}$
is the velocity derivative skewness. If one accepts that
![]() $C_{\unicode[STIX]{x1D716}}$
approaches a constant as
$C_{\unicode[STIX]{x1D716}}$
approaches a constant as
![]() $Re_{\unicode[STIX]{x1D706}}$
increases, then one must accept that (2.20) holds. Thus, since
$Re_{\unicode[STIX]{x1D706}}$
increases, then one must accept that (2.20) holds. Thus, since
![]() $C_{1}$
is constant (
$C_{1}$
is constant (
![]() $\equiv -10$
), equation (2.20) reduces to
$\equiv -10$
), equation (2.20) reduces to
![]() $S_{(r^{\ast }\rightarrow 0)}+2G/Re_{\unicode[STIX]{x1D706}}\rightarrow 0$
as
$S_{(r^{\ast }\rightarrow 0)}+2G/Re_{\unicode[STIX]{x1D706}}\rightarrow 0$
as
![]() $Re_{\unicode[STIX]{x1D706}}$
increases.
$Re_{\unicode[STIX]{x1D706}}$
increases.
We can write (2.16) in the generic form
where
![]() $A(r^{\ast })$
and
$A(r^{\ast })$
and
![]() $B(r^{\ast })$
are functions of
$B(r^{\ast })$
are functions of
![]() $r^{\ast }$
, possibly of the Reynolds number too, and
$r^{\ast }$
, possibly of the Reynolds number too, and
We can easily relate
![]() $C_{\unicode[STIX]{x1D716}}$
to the SP constants
$C_{\unicode[STIX]{x1D716}}$
to the SP constants
![]() $C_{0}$
and
$C_{0}$
and
![]() $C_{3}$
. If we rewrite (2.7) as
$C_{3}$
. If we rewrite (2.7) as
and substitute it into (2.10), we obtain
If
![]() $l=L$
(i.e.
$l=L$
(i.e.
![]() $L$
is assumed to be a scaling length satisfying the SP requirement) and
$L$
is assumed to be a scaling length satisfying the SP requirement) and
![]() $u_{2}=u^{\prime }$
, then we have
$u_{2}=u^{\prime }$
, then we have
where
![]() $Re_{L}=u^{\prime }L/\unicode[STIX]{x1D708}$
. Note that
$Re_{L}=u^{\prime }L/\unicode[STIX]{x1D708}$
. Note that
![]() $C_{3,L}\neq 15$
. This is readily shown as follows. In the context of SP, if both
$C_{3,L}\neq 15$
. This is readily shown as follows. In the context of SP, if both
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $L$
are scaling lengths then (2.10) holds for both these quantities and we have
$L$
are scaling lengths then (2.10) holds for both these quantities and we have
where we used
![]() $u_{2}=u^{\prime }$
. This leads to
$u_{2}=u^{\prime }$
. This leads to
2.2 Locally homogeneous and isotropic turbulence
The analysis carried out above for HIT can be experimentally tested only approximately in grid turbulence, which remains, as far as we are aware, the closest approximation to HIT in the laboratory. Another flow that is amenable to a SP analysis and where HIT can be locally observed is the far field of a turbulent round jet. Burattini, Lavoie & Antonia (Reference Burattini, Lavoie and Antonia2005b ) showed that the SBS energy budget on the axis of the jet is given the following generic form:
where
![]() $I_{u}$
represents the contribution of the large-scale motions. The term
$I_{u}$
represents the contribution of the large-scale motions. The term
![]() $I_{u}$
is
$I_{u}$
is
and represents the contributions from the advection (first term) and production (second term) mechanisms, respectively. Darisse, Lemay & Benaissa (Reference Darisse, Lemay and Benaissa2015) showed that the energy contribution from the pressure diffusion, turbulent diffusion and molecular diffusion are negligible in the turbulent kinetic energy budget on the axis of the round jet, which allows us to neglect them in
![]() $I_{u}(r)$
. Seeking SP solutions of similar forms as (2.2) and (2.3) and after following the same trivial manipulations as above we obtain
$I_{u}(r)$
. Seeking SP solutions of similar forms as (2.2) and (2.3) and after following the same trivial manipulations as above we obtain
where
![]() $\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{1}$
and
![]() $\unicode[STIX]{x1D6E4}_{2}$
are similar to (2.5) and (2.6), respectively, and
$\unicode[STIX]{x1D6E4}_{2}$
are similar to (2.5) and (2.6), respectively, and
In the Appendix we reproduce, for the sake of convenience, the first stages of the analytical development of Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) for the transport equation of
![]() $\overline{(\unicode[STIX]{x1D6FF}q)^{2}}=\overline{(\unicode[STIX]{x1D6FF}u)^{2}}+\overline{(\unicode[STIX]{x1D6FF}v)^{2}}+\overline{(\unicode[STIX]{x1D6FF}w)^{2}}$
and then develop a similar expression to (2.30), albeit with different numerical coefficients.
$\overline{(\unicode[STIX]{x1D6FF}q)^{2}}=\overline{(\unicode[STIX]{x1D6FF}u)^{2}}+\overline{(\unicode[STIX]{x1D6FF}v)^{2}}+\overline{(\unicode[STIX]{x1D6FF}w)^{2}}$
and then develop a similar expression to (2.30), albeit with different numerical coefficients.
The objective of the next section is to test the analysis against experimental data in grid turbulence and on the axis of a turbulent round jet.

Figure 1. Streamwise variation of
![]() $C_{\unicode[STIX]{x1D716}}$
in grid turbulence and on the axis of a round jet. LSQ43: perforated plate with large square holes with solidity 43 %; SSQ36: perforated plate with small square holes with a solidity 36 %; WMG36: woven mesh grid with a solidity 36 %; FG: fractal grid; for FG,
$C_{\unicode[STIX]{x1D716}}$
in grid turbulence and on the axis of a round jet. LSQ43: perforated plate with large square holes with solidity 43 %; SSQ36: perforated plate with small square holes with a solidity 36 %; WMG36: woven mesh grid with a solidity 36 %; FG: fractal grid; for FG,
![]() $M$
corresponds to the mesh size of the background grid supporting the fractal elements.
$M$
corresponds to the mesh size of the background grid supporting the fractal elements.
3 Discussion and experimental results
The theoretical analysis developed above indicates that the constancy of
![]() $C_{\unicode[STIX]{x1D716}}$
in a decaying turbulence for a given Reynolds number is a consequence of the turbulence decaying under the SP requirement. To assess these theoretical results, we report measurements of
$C_{\unicode[STIX]{x1D716}}$
in a decaying turbulence for a given Reynolds number is a consequence of the turbulence decaying under the SP requirement. To assess these theoretical results, we report measurements of
![]() $C_{\unicode[STIX]{x1D716}}$
in decaying grid turbulence and on the axis of a turbulent round jet in figure 1. Whilst grid turbulence does not satisfy SP (Djenidi et al.
Reference Djenidi, Kamruzzaman and Antonia2015), the far-field flow along the jet axis complies well with SP (Djenidi et al.
Reference Djenidi, Antonia, Lefeuvre and Lemay2016). The measurements in grid turbulence were made using three different grids; two were constructed from perforated plates, but with different (square) hole sizes (denoted LSQ43 and SSQ36, 46 and 36 % solidity), and one is a woven mesh (WMG36, 36 % solidity). Details of the grid turbulence experiments can be found in Djenidi et al. (Reference Djenidi, Kamruzzaman and Antonia2015), while details of the round jet measurements can be found in Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016). Figure 1 reports also the measurements of Hearst & Lavoie (Reference Hearst and Lavoie2014) obtained in fractal grid (FG) turbulence and the results of Burattini, Antonia & Danaila (Reference Burattini, Antonia and Danaila2005a
) in the turbulent round jet. All values of
$C_{\unicode[STIX]{x1D716}}$
in decaying grid turbulence and on the axis of a turbulent round jet in figure 1. Whilst grid turbulence does not satisfy SP (Djenidi et al.
Reference Djenidi, Kamruzzaman and Antonia2015), the far-field flow along the jet axis complies well with SP (Djenidi et al.
Reference Djenidi, Antonia, Lefeuvre and Lemay2016). The measurements in grid turbulence were made using three different grids; two were constructed from perforated plates, but with different (square) hole sizes (denoted LSQ43 and SSQ36, 46 and 36 % solidity), and one is a woven mesh (WMG36, 36 % solidity). Details of the grid turbulence experiments can be found in Djenidi et al. (Reference Djenidi, Kamruzzaman and Antonia2015), while details of the round jet measurements can be found in Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016). Figure 1 reports also the measurements of Hearst & Lavoie (Reference Hearst and Lavoie2014) obtained in fractal grid (FG) turbulence and the results of Burattini, Antonia & Danaila (Reference Burattini, Antonia and Danaila2005a
) in the turbulent round jet. All values of
![]() $C_{\unicode[STIX]{x1D716}}$
are calculated using
$C_{\unicode[STIX]{x1D716}}$
are calculated using
![]() $L$
defined as
$L$
defined as
where
![]() $r_{o}$
is the first zero crossing of the auto-correlation of the longitudinal velocity. The trend in the variation of
$r_{o}$
is the first zero crossing of the auto-correlation of the longitudinal velocity. The trend in the variation of
![]() $C_{\unicode[STIX]{x1D716}}$
along
$C_{\unicode[STIX]{x1D716}}$
along
![]() $x$
in grid turbulence is clear:
$x$
in grid turbulence is clear:
![]() $C_{\unicode[STIX]{x1D716}}$
decreases with increasing
$C_{\unicode[STIX]{x1D716}}$
decreases with increasing
![]() $x$
. This is consistent with the measurements of Krogstad & Davidson (Reference Krogstad and Davidson2011) in decaying turbulence downstream of multiscale grids. For the SSQ and WMG data,
$x$
. This is consistent with the measurements of Krogstad & Davidson (Reference Krogstad and Davidson2011) in decaying turbulence downstream of multiscale grids. For the SSQ and WMG data,
![]() $C_{\unicode[STIX]{x1D716}}$
first increases before decreasing. The increase reflects the non-homogeneity of the turbulence which is still in a development stage immediately downstream of the grid. This region expands as
$C_{\unicode[STIX]{x1D716}}$
first increases before decreasing. The increase reflects the non-homogeneity of the turbulence which is still in a development stage immediately downstream of the grid. This region expands as
![]() $Re_{M}$
decreases, as the comparison between the SSQ and LSQ data illustrates. This region is further extended behind a FG as Hearst & Lavoie (Reference Hearst and Lavoie2014) showed in their comparative study between a classical grid and a FG. After an initial increase behind the FG,
$Re_{M}$
decreases, as the comparison between the SSQ and LSQ data illustrates. This region is further extended behind a FG as Hearst & Lavoie (Reference Hearst and Lavoie2014) showed in their comparative study between a classical grid and a FG. After an initial increase behind the FG,
![]() $C_{\unicode[STIX]{x1D716}}$
appears to decrease. However, a much longer distance is required to assess the definitive trend for this type of grid turbulence. The data for the round jet indicate that
$C_{\unicode[STIX]{x1D716}}$
appears to decrease. However, a much longer distance is required to assess the definitive trend for this type of grid turbulence. The data for the round jet indicate that
![]() $C_{\unicode[STIX]{x1D716}}$
remains practically constant along the axis for a given Reynolds number, after an initial increase. The variation of
$C_{\unicode[STIX]{x1D716}}$
remains practically constant along the axis for a given Reynolds number, after an initial increase. The variation of
![]() $C_{\unicode[STIX]{x1D716}}$
with
$C_{\unicode[STIX]{x1D716}}$
with
![]() $x/M$
in grid turbulence is consistent with a lack of SP at all scales of motion. Djenidi et al. (Reference Djenidi, Kamruzzaman and Antonia2015) showed that decaying grid turbulence obtained in the laboratory is not in SP. Their experimental results confirm the results of the eddy-damped quasi-normal Markovian (EDQNM) simulation of decaying HIT by Meldi & Sagaut (Reference Meldi and Sagaut2013) and the analysis of Djenidi & Antonia (Reference Djenidi and Antonia2015) for decaying HIT. The latter derived an analytical expression relating the power-law decay exponent
$x/M$
in grid turbulence is consistent with a lack of SP at all scales of motion. Djenidi et al. (Reference Djenidi, Kamruzzaman and Antonia2015) showed that decaying grid turbulence obtained in the laboratory is not in SP. Their experimental results confirm the results of the eddy-damped quasi-normal Markovian (EDQNM) simulation of decaying HIT by Meldi & Sagaut (Reference Meldi and Sagaut2013) and the analysis of Djenidi & Antonia (Reference Djenidi and Antonia2015) for decaying HIT. The latter derived an analytical expression relating the power-law decay exponent
![]() $n$
and
$n$
and
![]() $Re_{\unicode[STIX]{x1D706}}$
, which shows that SP at all scales of motion can only be achieved if
$Re_{\unicode[STIX]{x1D706}}$
, which shows that SP at all scales of motion can only be achieved if
![]() $Re_{\unicode[STIX]{x1D706}}\simeq \infty$
or finite
$Re_{\unicode[STIX]{x1D706}}\simeq \infty$
or finite
![]() $Re_{\unicode[STIX]{x1D706}}$
provided
$Re_{\unicode[STIX]{x1D706}}$
provided
![]() $Re_{\unicode[STIX]{x1D706}}$
is constant, which would lead to
$Re_{\unicode[STIX]{x1D706}}$
is constant, which would lead to
![]() $n=-1$
. So far, experimental and numerical evidence point to a decrease in
$n=-1$
. So far, experimental and numerical evidence point to a decrease in
![]() $Re_{\unicode[STIX]{x1D706}}$
in decaying HIT. By contrast, the constancy of
$Re_{\unicode[STIX]{x1D706}}$
in decaying HIT. By contrast, the constancy of
![]() $C_{\unicode[STIX]{x1D716}}$
on the jet axis reflects the validity of SP at all scales of motion (e.g. Burattini et al.
Reference Burattini, Antonia and Danaila2005a
; Djenidi et al.
Reference Djenidi, Antonia, Lefeuvre and Lemay2016). Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) showed analytically that the requirement for SP on the axis of a turbulent round jet is similar to that for decaying HIT (i.e. constancy of
$C_{\unicode[STIX]{x1D716}}$
on the jet axis reflects the validity of SP at all scales of motion (e.g. Burattini et al.
Reference Burattini, Antonia and Danaila2005a
; Djenidi et al.
Reference Djenidi, Antonia, Lefeuvre and Lemay2016). Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) showed analytically that the requirement for SP on the axis of a turbulent round jet is similar to that for decaying HIT (i.e. constancy of
![]() $Re_{\unicode[STIX]{x1D706}}$
). Their measurements along the jet axis showed not only that
$Re_{\unicode[STIX]{x1D706}}$
). Their measurements along the jet axis showed not only that
![]() $Re_{\unicode[STIX]{x1D706}}$
is constant, but both the one-point and two-point turbulence statistics evolve in a manner which complies with SP, in the far field. Accordingly, for a given initial condition, (i.e. a given global Reynolds number such as
$Re_{\unicode[STIX]{x1D706}}$
is constant, but both the one-point and two-point turbulence statistics evolve in a manner which complies with SP, in the far field. Accordingly, for a given initial condition, (i.e. a given global Reynolds number such as
![]() $Re_{M}$
in grid turbulence or
$Re_{M}$
in grid turbulence or
![]() $Re_{D}$
for a jet), one should expect that
$Re_{D}$
for a jet), one should expect that
![]() $C_{\unicode[STIX]{x1D716}}$
varies with
$C_{\unicode[STIX]{x1D716}}$
varies with
![]() $x$
in decaying grid turbulence, and to remain constant along the axis in the far field of a turbulent round jet.
$x$
in decaying grid turbulence, and to remain constant along the axis in the far field of a turbulent round jet.

Figure 2. Streamwise variation of
![]() $L_{u}/\unicode[STIX]{x1D706}$
in grid turbulence and along the axis of a turbulent round jet. The dashed line is used only as a visual guide to make it clearer that the data for
$L_{u}/\unicode[STIX]{x1D706}$
in grid turbulence and along the axis of a turbulent round jet. The dashed line is used only as a visual guide to make it clearer that the data for
![]() $R_{M}=2000$
actually decrease as
$R_{M}=2000$
actually decrease as
![]() $x$
increases.
$x$
increases.
Likewise, SP at all scales of motion also implies that
![]() $r_{L}^{\ast }=L/\unicode[STIX]{x1D706}$
must be a constant as the turbulence decays at any one Reynolds number. We show in figure 2 the variation of
$r_{L}^{\ast }=L/\unicode[STIX]{x1D706}$
must be a constant as the turbulence decays at any one Reynolds number. We show in figure 2 the variation of
![]() $L_{u}/\unicode[STIX]{x1D706}(=r_{L_{u}}^{\ast })$
with
$L_{u}/\unicode[STIX]{x1D706}(=r_{L_{u}}^{\ast })$
with
![]() $x$
for the data reported in figure 1; a log scale is used for the ordinate to highlight more effectively any streamwise variation at small
$x$
for the data reported in figure 1; a log scale is used for the ordinate to highlight more effectively any streamwise variation at small
![]() $r_{L_{u}}^{\ast }$
. In grid turbulence,
$r_{L_{u}}^{\ast }$
. In grid turbulence,
![]() $r_{L_{u}}^{\ast }\simeq 3.3{-}7$
for LSQ43,
$r_{L_{u}}^{\ast }\simeq 3.3{-}7$
for LSQ43,
![]() $r_{L_{u}}^{\ast }\simeq 1.5{-}2.5$
for SSQ43,
$r_{L_{u}}^{\ast }\simeq 1.5{-}2.5$
for SSQ43,
![]() $r_{L_{u}}^{\ast }\simeq 1.1{-}1.25$
for WMG36 (the measurement uncertainties are 6 %, 7.3 % and 9.65 % for LSW, SSQ and WWG, respectively). For the FG data (not shown here),
$r_{L_{u}}^{\ast }\simeq 1.1{-}1.25$
for WMG36 (the measurement uncertainties are 6 %, 7.3 % and 9.65 % for LSW, SSQ and WWG, respectively). For the FG data (not shown here),
![]() $r_{L_{u}}^{\ast }\simeq 6{-}7.3$
and decreases with
$r_{L_{u}}^{\ast }\simeq 6{-}7.3$
and decreases with
![]() $x$
;
$x$
;
![]() $Re_{\unicode[STIX]{x1D706}}$
also decreases (see figure 10 of Hearst & Lavoie (Reference Hearst and Lavoie2014)). The variation of
$Re_{\unicode[STIX]{x1D706}}$
also decreases (see figure 10 of Hearst & Lavoie (Reference Hearst and Lavoie2014)). The variation of
![]() $r_{L_{u}}^{\ast }$
with
$r_{L_{u}}^{\ast }$
with
![]() $x$
is consistent with a lack of SP. On the jet axis, the ratio
$x$
is consistent with a lack of SP. On the jet axis, the ratio
![]() $r_{L_{u}}^{\ast }$
increases initially at a steep rate. It then approaches a plateau, notwithstanding the jitter in the data at high
$r_{L_{u}}^{\ast }$
increases initially at a steep rate. It then approaches a plateau, notwithstanding the jitter in the data at high
![]() $x/D$
, associated with the difficulty in determining the first zero crossing of the velocity auto-correlation function; the distance
$x/D$
, associated with the difficulty in determining the first zero crossing of the velocity auto-correlation function; the distance
![]() $x/D$
for the
$x/D$
for the
![]() $r_{L_{u}}^{\ast }$
distributions to approach a plateau increases with the Reynolds number. This is consistent with the observation that the onset of the SP solutions moves downstream as
$r_{L_{u}}^{\ast }$
distributions to approach a plateau increases with the Reynolds number. This is consistent with the observation that the onset of the SP solutions moves downstream as
![]() $Re_{D}$
increases. For example, Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) showed that SP starts at
$Re_{D}$
increases. For example, Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) showed that SP starts at
![]() $x/D\simeq 15$
and 40 when
$x/D\simeq 15$
and 40 when
![]() $Re_{D}=3.4\times 10^{4}$
and
$Re_{D}=3.4\times 10^{4}$
and
![]() $13\times 10^{4}$
, respectively. It should be noted that these far-field measurements in a turbulent jet are difficult because the turbulence intensity becomes (i) low and (ii) susceptible to the environment (the measurement uncertainty in
$13\times 10^{4}$
, respectively. It should be noted that these far-field measurements in a turbulent jet are difficult because the turbulence intensity becomes (i) low and (ii) susceptible to the environment (the measurement uncertainty in
![]() $L_{u}$
varies from 8 % for
$L_{u}$
varies from 8 % for
![]() $Re_{D}=33\,000$
to 15 % for
$Re_{D}=33\,000$
to 15 % for
![]() $Re_{D}=105\,000$
). This explains in part the jitter in the data and why far-field data are rather scant in a turbulent jet.
$Re_{D}=105\,000$
). This explains in part the jitter in the data and why far-field data are rather scant in a turbulent jet.

Figure 3. Dependence of
![]() $L_{u}/\unicode[STIX]{x1D706}$
on
$L_{u}/\unicode[STIX]{x1D706}$
on
![]() $Re_{\unicode[STIX]{x1D706}}$
in grid turbulence and along the axis of a turbulent round jet and a plane jet. The dashed line is a linear fit used only as reference for the behaviour
$Re_{\unicode[STIX]{x1D706}}$
in grid turbulence and along the axis of a turbulent round jet and a plane jet. The dashed line is a linear fit used only as reference for the behaviour
![]() $L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
. The data for Gomes-Fernandes, Ganapathisubramani & Vassilicos (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012) are for two fractal grids defined as SFG8 and SFG17 with the same solidity. Inset: comparison between the distributions of the main plot (black circles) with the distribution from the forced HIT of Kaneda et al. (Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003).
$L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
. The data for Gomes-Fernandes, Ganapathisubramani & Vassilicos (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012) are for two fractal grids defined as SFG8 and SFG17 with the same solidity. Inset: comparison between the distributions of the main plot (black circles) with the distribution from the forced HIT of Kaneda et al. (Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003).
For a given flow configuration, the streamwise behaviour of
![]() $r_{L_{u}}^{\ast }$
with downstream distance is independent of the ‘inlet’ Reynolds number,
$r_{L_{u}}^{\ast }$
with downstream distance is independent of the ‘inlet’ Reynolds number,
![]() $Re_{D}$
for the jet and
$Re_{D}$
for the jet and
![]() $Re_{M}$
for grid turbulence:
$Re_{M}$
for grid turbulence:
![]() $r_{L_{u}}^{\ast }$
becomes constant after an increase in the former case, while it decreases continuously in the latter. However, for both flows,
$r_{L_{u}}^{\ast }$
becomes constant after an increase in the former case, while it decreases continuously in the latter. However, for both flows,
![]() $r_{L_{u}}^{\ast }$
increases with the ‘inlet’ Reynolds number or equivalently with
$r_{L_{u}}^{\ast }$
increases with the ‘inlet’ Reynolds number or equivalently with
![]() $Re_{\unicode[STIX]{x1D706}}$
. This is well illustrated in figure 3, which shows the variation of
$Re_{\unicode[STIX]{x1D706}}$
. This is well illustrated in figure 3, which shows the variation of
![]() $r_{L_{u}}^{\ast }$
with
$r_{L_{u}}^{\ast }$
with
![]() $Re_{\unicode[STIX]{x1D706}}$
. The value of
$Re_{\unicode[STIX]{x1D706}}$
. The value of
![]() $r_{L_{u}}^{\ast }$
for each grid turbulence is taken at the last
$r_{L_{u}}^{\ast }$
for each grid turbulence is taken at the last
![]() $x/M$
position, while for the round jet we used the value of
$x/M$
position, while for the round jet we used the value of
![]() $r_{L_{u}}^{\ast }$
averaged over the region over which it is practically constant. Sreenivasan (Reference Sreenivasan1984) showed that
$r_{L_{u}}^{\ast }$
averaged over the region over which it is practically constant. Sreenivasan (Reference Sreenivasan1984) showed that
![]() $L_{u}/\unicode[STIX]{x1D706}\simeq (\unicode[STIX]{x03C0}/2)^{1/2}$
for grid turbulence at very low Reynolds numbers where the energy transfer is very weak such as in the final period of decay. The present results suggest that the final period of decay has not yet been reached, even though the smallest
$L_{u}/\unicode[STIX]{x1D706}\simeq (\unicode[STIX]{x03C0}/2)^{1/2}$
for grid turbulence at very low Reynolds numbers where the energy transfer is very weak such as in the final period of decay. The present results suggest that the final period of decay has not yet been reached, even though the smallest
![]() $Re_{\unicode[STIX]{x1D706}}$
is approximately 9 in the woven mesh grid turbulence. Note however that Djenidi et al. (Reference Djenidi, Tardu, Antonia and Danaila2014) showed that the Kolmogorov scaling breaks down when
$Re_{\unicode[STIX]{x1D706}}$
is approximately 9 in the woven mesh grid turbulence. Note however that Djenidi et al. (Reference Djenidi, Tardu, Antonia and Danaila2014) showed that the Kolmogorov scaling breaks down when
![]() $Re_{\unicode[STIX]{x1D706}}$
drops below approximately 20, underlining the persistence of the Reynolds number dependence of
$Re_{\unicode[STIX]{x1D706}}$
drops below approximately 20, underlining the persistence of the Reynolds number dependence of
![]() $L_{u}/\unicode[STIX]{x1D706}$
. We have also added data for a plane jet (Pearson & Antonia Reference Pearson and Antonia2001; Zhou, Pearson & Antonia Reference Zhou, Pearson and Antonia2001) and the fractal grid turbulence of Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) (see also figure 3 in Vassilicos (Reference Vassilicos2015)) and Gomes-Fernandes et al. (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012) (for both fractal grids only the last
$L_{u}/\unicode[STIX]{x1D706}$
. We have also added data for a plane jet (Pearson & Antonia Reference Pearson and Antonia2001; Zhou, Pearson & Antonia Reference Zhou, Pearson and Antonia2001) and the fractal grid turbulence of Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) (see also figure 3 in Vassilicos (Reference Vassilicos2015)) and Gomes-Fernandes et al. (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012) (for both fractal grids only the last
![]() $x$
station was used, but similar results are observed upstream of that position). It is evident that
$x$
station was used, but similar results are observed upstream of that position). It is evident that
![]() $r_{L_{u}}^{\ast }$
increases with increasing
$r_{L_{u}}^{\ast }$
increases with increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
, regardless of the flow configuration. Further, the data seem to collapse remarkably and unexpectedly well onto a single line, as suggested in the inset of figure 3 where the data are redrawn but without differentiating between the sets of data. For comparison, we have reported
$Re_{\unicode[STIX]{x1D706}}$
, regardless of the flow configuration. Further, the data seem to collapse remarkably and unexpectedly well onto a single line, as suggested in the inset of figure 3 where the data are redrawn but without differentiating between the sets of data. For comparison, we have reported
![]() $r_{L_{u}}^{\ast }$
for the high Reynolds number direct numerical simulation (DNS) of a three-dimensional periodic forced turbulence or forced HIT (Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003). It seems that the distribution of
$r_{L_{u}}^{\ast }$
for the high Reynolds number direct numerical simulation (DNS) of a three-dimensional periodic forced turbulence or forced HIT (Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003). It seems that the distribution of
![]() $r_{L_{u}}^{\ast }$
for all decaying turbulence (black circles) tends to become parallel to the
$r_{L_{u}}^{\ast }$
for all decaying turbulence (black circles) tends to become parallel to the
![]() $r_{L_{u}}^{\ast }$
distribution of forced turbulence as
$r_{L_{u}}^{\ast }$
distribution of forced turbulence as
![]() $Re_{\unicode[STIX]{x1D706}}$
increases. Note the latter is relatively well represented by
$Re_{\unicode[STIX]{x1D706}}$
increases. Note the latter is relatively well represented by
![]() $L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
for the whole range of
$L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
for the whole range of
![]() $Re_{\unicode[STIX]{x1D706}}$
used, although there is a deviation from that behaviour for the largest Reynolds number. At this stage, it is unfortunately not possible to determine whether or not the curve formed by the black circles will eventually remain parallel to the data for forced HIT and thus behave like
$Re_{\unicode[STIX]{x1D706}}$
used, although there is a deviation from that behaviour for the largest Reynolds number. At this stage, it is unfortunately not possible to determine whether or not the curve formed by the black circles will eventually remain parallel to the data for forced HIT and thus behave like
![]() $L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
. If, from a purely practical point of view, one considers the flow configurations separately, one may argue that, in a first approximation,
$L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
. If, from a purely practical point of view, one considers the flow configurations separately, one may argue that, in a first approximation,
![]() $L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
with the constant of proportionality changing between the flows (this is represented by the dashed-dotted lines). It is interesting to note that it is perhaps not a coincidence that the value of the constant of proportionality corresponds to different ranges of
$L_{u}/\unicode[STIX]{x1D706}\sim Re_{\unicode[STIX]{x1D706}}$
with the constant of proportionality changing between the flows (this is represented by the dashed-dotted lines). It is interesting to note that it is perhaps not a coincidence that the value of the constant of proportionality corresponds to different ranges of
![]() $Re_{\unicode[STIX]{x1D706}}$
, and that it decreases as
$Re_{\unicode[STIX]{x1D706}}$
, and that it decreases as
![]() $Re_{\unicode[STIX]{x1D706}}$
increases. Applying a simple linear curve fit to each set of data (grid turbulence, round jet and plane jet) of figure 3 we then obtain
$Re_{\unicode[STIX]{x1D706}}$
increases. Applying a simple linear curve fit to each set of data (grid turbulence, round jet and plane jet) of figure 3 we then obtain
where the pair of coefficients
![]() $(a^{\dagger },b^{\dagger })$
is (0.6, 0.0533), (1.23, 0.042), (3, 0.0357) and (6.015, 0.0281) for the grid turbulence, the fractal grid turbulence and the axes of the round and plane jets, respectively (the symbol
$(a^{\dagger },b^{\dagger })$
is (0.6, 0.0533), (1.23, 0.042), (3, 0.0357) and (6.015, 0.0281) for the grid turbulence, the fractal grid turbulence and the axes of the round and plane jets, respectively (the symbol
![]() $\dagger$
in (3.2) and in (3.3), below, is a reminder that the empirical constants, which, by the empirical nature of their derivation, may be Reynolds number dependent and flow dependent). Using (2.17) with (3.2) yields the following empirical relation for
$\dagger$
in (3.2) and in (3.3), below, is a reminder that the empirical constants, which, by the empirical nature of their derivation, may be Reynolds number dependent and flow dependent). Using (2.17) with (3.2) yields the following empirical relation for
![]() $C_{\unicode[STIX]{x1D716}}$
$C_{\unicode[STIX]{x1D716}}$
where
![]() $(c^{\dagger },d^{\dagger })$
is (9, 0.7995), (18.45, 0.623), (45, 0.5355) and (90.4, 0.421) for standard grid turbulence, fractal grid turbulence, the axis of the round jet and the centreline of the plane jet, respectively. It seems that (3.3) would provide the asymptotic value
$(c^{\dagger },d^{\dagger })$
is (9, 0.7995), (18.45, 0.623), (45, 0.5355) and (90.4, 0.421) for standard grid turbulence, fractal grid turbulence, the axis of the round jet and the centreline of the plane jet, respectively. It seems that (3.3) would provide the asymptotic value
![]() $C_{\unicode[STIX]{x1D716},\infty }=d^{\dagger }$
when
$C_{\unicode[STIX]{x1D716},\infty }=d^{\dagger }$
when
![]() $Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
, which would appear to depend on the flow configuration;
$Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
, which would appear to depend on the flow configuration;
![]() $C_{\unicode[STIX]{x1D716},\infty }\simeq 0.8$
, 0.62, 0.54 and 0.42 for standard grid turbulence, fractal grid turbulence, round jet axis and plane jet centreline, respectively. These results suggest that
$C_{\unicode[STIX]{x1D716},\infty }\simeq 0.8$
, 0.62, 0.54 and 0.42 for standard grid turbulence, fractal grid turbulence, round jet axis and plane jet centreline, respectively. These results suggest that
![]() $C_{\unicode[STIX]{x1D716},\infty }$
is controlled by the rate of growth of
$C_{\unicode[STIX]{x1D716},\infty }$
is controlled by the rate of growth of
![]() $r_{L_{u}}^{\ast }$
; the larger the growth, the larger
$r_{L_{u}}^{\ast }$
; the larger the growth, the larger
![]() $C_{\unicode[STIX]{x1D716},\infty }$
. This rate of growth decreases with increasing
$C_{\unicode[STIX]{x1D716},\infty }$
. This rate of growth decreases with increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
. However, it is clear that the empirical constants obtained above are only valid for the corresponding flow configuration considered and the range of
$Re_{\unicode[STIX]{x1D706}}$
. However, it is clear that the empirical constants obtained above are only valid for the corresponding flow configuration considered and the range of
![]() $Re_{\unicode[STIX]{x1D706}}$
over which the curve fit was applied, which leads to an important issue requiring further investigation and which relates to the asymptotic behaviour of
$Re_{\unicode[STIX]{x1D706}}$
over which the curve fit was applied, which leads to an important issue requiring further investigation and which relates to the asymptotic behaviour of
![]() $r_{L_{u}}^{\ast }$
with increasing
$r_{L_{u}}^{\ast }$
with increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
in different turbulent flows. Determining whether this behaviour is universal (i.e. the same for all turbulent flows) or not requires measurements in a various turbulent flows at very high Reynolds numbers. As stated above, if the trend shown in the inset of figure 3 is confirmed, that is
$Re_{\unicode[STIX]{x1D706}}$
in different turbulent flows. Determining whether this behaviour is universal (i.e. the same for all turbulent flows) or not requires measurements in a various turbulent flows at very high Reynolds numbers. As stated above, if the trend shown in the inset of figure 3 is confirmed, that is
![]() $L_{u}/\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FC}Re_{\unicode[STIX]{x1D706}}$
(
$L_{u}/\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FC}Re_{\unicode[STIX]{x1D706}}$
(
![]() $\unicode[STIX]{x1D6FC}$
is a constant and the same for all turbulent flows) at very large Reynolds numbers, then
$\unicode[STIX]{x1D6FC}$
is a constant and the same for all turbulent flows) at very large Reynolds numbers, then
![]() $C_{\unicode[STIX]{x1D716},\infty }$
would reach an asymptotic (universal) limit, yet to be properly determined. When
$C_{\unicode[STIX]{x1D716},\infty }$
would reach an asymptotic (universal) limit, yet to be properly determined. When
![]() $Re_{\unicode[STIX]{x1D706}}$
approaches infinitely large values, the turbulence reaches its isotropic steady state regardless of the turbulent flow configuration (at least away of any solid boundaries). If one accepts that such turbulence is adequately represented by forced HIT at a finite but large Reynolds number, then
$Re_{\unicode[STIX]{x1D706}}$
approaches infinitely large values, the turbulence reaches its isotropic steady state regardless of the turbulent flow configuration (at least away of any solid boundaries). If one accepts that such turbulence is adequately represented by forced HIT at a finite but large Reynolds number, then
![]() $C_{\unicode[STIX]{x1D716}}$
for such turbulence is equal to
$C_{\unicode[STIX]{x1D716}}$
for such turbulence is equal to
![]() $C_{\unicode[STIX]{x1D716},\infty }$
. Thus, the possibility that
$C_{\unicode[STIX]{x1D716},\infty }$
. Thus, the possibility that
![]() $C_{\unicode[STIX]{x1D716},\infty }$
is a universal constant should not be excluded.
$C_{\unicode[STIX]{x1D716},\infty }$
is a universal constant should not be excluded.

Figure 4. Dependence of
![]() $C_{\unicode[STIX]{x1D716}}$
on
$C_{\unicode[STIX]{x1D716}}$
on
![]() $Re_{\unicode[STIX]{x1D706}}$
in several turbulent flows.
$Re_{\unicode[STIX]{x1D706}}$
in several turbulent flows.
The derivation of the empirical expression (3.3) is based on the relation (2.17) valid for isotropic or locally isotropic turbulence. Thus, a convenient and simple way to test isotropy or local isotropy is to compare the measured
![]() $C_{\unicode[STIX]{x1D716}}$
with the calculated one using (2.17). However, this requires the true dissipation
$C_{\unicode[STIX]{x1D716}}$
with the calculated one using (2.17). However, this requires the true dissipation
![]() $\overline{\unicode[STIX]{x1D716}}_{t}$
, which necessitates the measurement of 12 terms. So far, only in grid turbulence can
$\overline{\unicode[STIX]{x1D716}}_{t}$
, which necessitates the measurement of 12 terms. So far, only in grid turbulence can
![]() $\overline{\unicode[STIX]{x1D716}}_{t}$
be estimated reliably from the turbulence kinetic energy budget in HIT (
$\overline{\unicode[STIX]{x1D716}}_{t}$
be estimated reliably from the turbulence kinetic energy budget in HIT (
![]() $\overline{\unicode[STIX]{x1D716}}_{t}=-(U_{o})(\text{d}k/\text{d}x)$
,
$\overline{\unicode[STIX]{x1D716}}_{t}=-(U_{o})(\text{d}k/\text{d}x)$
,
![]() $U_{o}$
is the local velocity). Of course,
$U_{o}$
is the local velocity). Of course,
![]() $\overline{\unicode[STIX]{x1D716}}_{t}$
is easily calculated with DNS data. Often in measurements,
$\overline{\unicode[STIX]{x1D716}}_{t}$
is easily calculated with DNS data. Often in measurements,
![]() $\overline{\unicode[STIX]{x1D716}}_{t}$
is approximated by its (local) isotropic surrogate
$\overline{\unicode[STIX]{x1D716}}_{t}$
is approximated by its (local) isotropic surrogate
![]() $\overline{\unicode[STIX]{x1D716}}_{iso}$
. We reported in figure 4 the measured
$\overline{\unicode[STIX]{x1D716}}_{iso}$
. We reported in figure 4 the measured
![]() $C_{\unicode[STIX]{x1D716}}$
and the calculated one using (2.17) for the same flows as reported in figure 3; we also added the DNS data for forced HIT (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Donzis, Sreenivasan & Yeung Reference Donzis, Sreenivasan and Yeung2005; Yeung, Donzis & Sreenivasan Reference Yeung, Donzis and Sreenivasan2012). For grid turbulence, we used
$C_{\unicode[STIX]{x1D716}}$
and the calculated one using (2.17) for the same flows as reported in figure 3; we also added the DNS data for forced HIT (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Donzis, Sreenivasan & Yeung Reference Donzis, Sreenivasan and Yeung2005; Yeung, Donzis & Sreenivasan Reference Yeung, Donzis and Sreenivasan2012). For grid turbulence, we used
![]() $\overline{\unicode[STIX]{x1D716}}_{t}$
while for the two jets we used
$\overline{\unicode[STIX]{x1D716}}_{t}$
while for the two jets we used
![]() $\overline{\unicode[STIX]{x1D716}}_{iso}$
. For the jet flows, it was found that
$\overline{\unicode[STIX]{x1D716}}_{iso}$
. For the jet flows, it was found that
![]() $\overline{\unicode[STIX]{x1D716}}_{iso}$
is a reasonable surrogate for
$\overline{\unicode[STIX]{x1D716}}_{iso}$
is a reasonable surrogate for
![]() $\overline{\unicode[STIX]{x1D716}}$
(Darisse et al. (Reference Darisse, Lemay and Benaissa2015); Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) for the round jet, and Antonia, Anselmet & Chambers (Reference Antonia, Anselmet and Chambers1986) for the plane jet), justifying the use of
$\overline{\unicode[STIX]{x1D716}}$
(Darisse et al. (Reference Darisse, Lemay and Benaissa2015); Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) for the round jet, and Antonia, Anselmet & Chambers (Reference Antonia, Anselmet and Chambers1986) for the plane jet), justifying the use of
![]() $\overline{\unicode[STIX]{x1D716}}_{iso}$
; in any case, the comparison between
$\overline{\unicode[STIX]{x1D716}}_{iso}$
; in any case, the comparison between
![]() $C_{\overline{\unicode[STIX]{x1D716}}_{iso}}$
and (2.17) constitutes a check for self-consistency. Also reported in the figure, are the values calculated using the second equality of (2.16) for grid turbulence where we evaluated all the terms on the right-hand side at
$C_{\overline{\unicode[STIX]{x1D716}}_{iso}}$
and (2.17) constitutes a check for self-consistency. Also reported in the figure, are the values calculated using the second equality of (2.16) for grid turbulence where we evaluated all the terms on the right-hand side at
![]() $r=L_{u}$
; in the case of the round jet, we used (2.30) in which we ignored the term
$r=L_{u}$
; in the case of the round jet, we used (2.30) in which we ignored the term
![]() $\unicode[STIX]{x1D6E4}_{3}$
because we did not have the data for
$\unicode[STIX]{x1D6E4}_{3}$
because we did not have the data for
![]() $f_{v}(r)$
. Of course, this is strictly not correct, and the values of
$f_{v}(r)$
. Of course, this is strictly not correct, and the values of
![]() $C_{\unicode[STIX]{x1D716}}$
obtained with (2.30) will be only an approximation. Note though that one should expect
$C_{\unicode[STIX]{x1D716}}$
obtained with (2.30) will be only an approximation. Note though that one should expect
![]() $\unicode[STIX]{x1D6E4}_{3}$
to be smaller than
$\unicode[STIX]{x1D6E4}_{3}$
to be smaller than
![]() $\unicode[STIX]{x1D6E4}_{1}$
since
$\unicode[STIX]{x1D6E4}_{1}$
since
![]() $(f_{u}(r)-f_{v}(r))$
is smaller than
$(f_{u}(r)-f_{v}(r))$
is smaller than
![]() $f_{u}(r)$
. There is a general good agreement between the measured
$f_{u}(r)$
. There is a general good agreement between the measured
![]() $C_{\unicode[STIX]{x1D716}}$
and that calculated using either (2.17) or (2.16) and (2.30) for each turbulent flow. The agreement between the measurements and (2.17) for the grid turbulence indicates that local isotropy is well approximated. For forced HIT where all turbulence statistics are time independent, the agreement is perfect. Notice also the good agreement between the forced HIT data obtained in various DNS studies. For the round jet, the measurements too agree well with (2.17). This is not surprising since the constraint (2.10), which leads to
$C_{\unicode[STIX]{x1D716}}$
and that calculated using either (2.17) or (2.16) and (2.30) for each turbulent flow. The agreement between the measurements and (2.17) for the grid turbulence indicates that local isotropy is well approximated. For forced HIT where all turbulence statistics are time independent, the agreement is perfect. Notice also the good agreement between the forced HIT data obtained in various DNS studies. For the round jet, the measurements too agree well with (2.17). This is not surprising since the constraint (2.10), which leads to
![]() $C_{\unicode[STIX]{x1D716}}=15(L/\unicode[STIX]{x1D706})(1/Re_{\unicode[STIX]{x1D706}})$
, applies equally to equation (2.28) and we used
$C_{\unicode[STIX]{x1D716}}=15(L/\unicode[STIX]{x1D706})(1/Re_{\unicode[STIX]{x1D706}})$
, applies equally to equation (2.28) and we used
![]() $\unicode[STIX]{x1D716}_{iso}$
as a surrogate to
$\unicode[STIX]{x1D716}_{iso}$
as a surrogate to
![]() $\unicode[STIX]{x1D716}$
. The agreement with (2.30) is not as good (notice the systematic downward shift), possibly due to the neglect of
$\unicode[STIX]{x1D716}$
. The agreement with (2.30) is not as good (notice the systematic downward shift), possibly due to the neglect of
![]() $\unicode[STIX]{x1D6E4}_{3}$
. Whilst the agreement between (2.30) and the measurements is expected because the turbulence decays in conformity with SP on the jet axis, the agreement observed for grid turbulence between the measurements and (2.16) may be less evident, since SP is strictly not satisfied, as can be seen in figure 1. The most possible explanation for this rather unexpected observation relates to the fact that the large-scale inhomogeneity in grid turbulence is weak, as reflected in the weak decrease of
$\unicode[STIX]{x1D6E4}_{3}$
. Whilst the agreement between (2.30) and the measurements is expected because the turbulence decays in conformity with SP on the jet axis, the agreement observed for grid turbulence between the measurements and (2.16) may be less evident, since SP is strictly not satisfied, as can be seen in figure 1. The most possible explanation for this rather unexpected observation relates to the fact that the large-scale inhomogeneity in grid turbulence is weak, as reflected in the weak decrease of
![]() $Re_{\unicode[STIX]{x1D706}}$
with the distance
$Re_{\unicode[STIX]{x1D706}}$
with the distance
![]() $x/M$
; the lower the initial Reynolds number, the smaller the rate of decrease. If this inhomogeneity is small enough for allowing
$x/M$
; the lower the initial Reynolds number, the smaller the rate of decrease. If this inhomogeneity is small enough for allowing
![]() $Re_{\unicode[STIX]{x1D706}}$
to be considered approximately constant over the distance
$Re_{\unicode[STIX]{x1D706}}$
to be considered approximately constant over the distance
![]() $x/M$
covered by the measurements, then one can expect to observe an approximately constant
$x/M$
covered by the measurements, then one can expect to observe an approximately constant
![]() $C_{\unicode[STIX]{x1D716}}$
over that distance. Interestingly, the observation that the measurements satisfy both equalities of (2.16) suggests that local isotropy and SP are verified by the small scales even though globally both SP and isotropy are not strictly satisfied. While direct comparisons between DNS and experiments of HIT are not possible, one can still compare decaying grid turbulence, a close surrogate for decaying HIT, to DNS data for decaying HIT. To carry out such a comparison, we report in figure 4 the data of Wang et al. (Reference Wang, Chen, Brasseur and Wyngaard1996) for decaying HIT. The DNS data follow the measurement trend adequately, thus lending confidence in the measurements.
$C_{\unicode[STIX]{x1D716}}$
over that distance. Interestingly, the observation that the measurements satisfy both equalities of (2.16) suggests that local isotropy and SP are verified by the small scales even though globally both SP and isotropy are not strictly satisfied. While direct comparisons between DNS and experiments of HIT are not possible, one can still compare decaying grid turbulence, a close surrogate for decaying HIT, to DNS data for decaying HIT. To carry out such a comparison, we report in figure 4 the data of Wang et al. (Reference Wang, Chen, Brasseur and Wyngaard1996) for decaying HIT. The DNS data follow the measurement trend adequately, thus lending confidence in the measurements.
The behaviour of
![]() $C_{\unicode[STIX]{x1D716}}$
depicted in figure 4 is similar to that reported by McComb (Reference McComb2014) (see also Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003; Burattini et al.
Reference Burattini, Lavoie and Antonia2005b
) for DNS data of decaying and forced HIT. It is worthwhile commenting on this similarity considering that none of the turbulent flows investigated here, with the exception of grid turbulence, are considered HIT nor are they in ‘steady state’ (they decay spatially). Although it should be pointed out that while grid turbulence and the jets decay in the direction of the mean flow, there is still some ‘forcing’ associated with the large-scale non-homogeneity, as seen in (2.1) and (A 1). Kaneda et al. (Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003) reported that
$C_{\unicode[STIX]{x1D716}}$
depicted in figure 4 is similar to that reported by McComb (Reference McComb2014) (see also Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003; Burattini et al.
Reference Burattini, Lavoie and Antonia2005b
) for DNS data of decaying and forced HIT. It is worthwhile commenting on this similarity considering that none of the turbulent flows investigated here, with the exception of grid turbulence, are considered HIT nor are they in ‘steady state’ (they decay spatially). Although it should be pointed out that while grid turbulence and the jets decay in the direction of the mean flow, there is still some ‘forcing’ associated with the large-scale non-homogeneity, as seen in (2.1) and (A 1). Kaneda et al. (Reference Kaneda, Ishihara, Yokokawa, Itakura and Uni2003) reported that
![]() $C_{\unicode[STIX]{x1D716}}$
can be grouped in two groups when
$C_{\unicode[STIX]{x1D716}}$
can be grouped in two groups when
![]() $Re_{\unicode[STIX]{x1D706}}\leqslant 250$
, which was also noted by Sreenivasan (Reference Sreenivasan1998): decaying HIT and forced HIT. However, the two groups merge as
$Re_{\unicode[STIX]{x1D706}}\leqslant 250$
, which was also noted by Sreenivasan (Reference Sreenivasan1998): decaying HIT and forced HIT. However, the two groups merge as
![]() $Re_{\unicode[STIX]{x1D706}}$
increases beyond 250 and
$Re_{\unicode[STIX]{x1D706}}$
increases beyond 250 and
![]() $C_{\unicode[STIX]{x1D716}}$
becomes independent of
$C_{\unicode[STIX]{x1D716}}$
becomes independent of
![]() $Re_{\unicode[STIX]{x1D706}}$
. Figure 4 also shows that while the data for forced HIT can be clearly distinguished from those for grid turbulence and jets when
$Re_{\unicode[STIX]{x1D706}}$
. Figure 4 also shows that while the data for forced HIT can be clearly distinguished from those for grid turbulence and jets when
![]() $Re_{\unicode[STIX]{x1D706}}\leqslant 500$
, they tend to merge at higher
$Re_{\unicode[STIX]{x1D706}}\leqslant 500$
, they tend to merge at higher
![]() $Re_{\unicode[STIX]{x1D706}}$
where
$Re_{\unicode[STIX]{x1D706}}$
where
![]() $C_{\unicode[STIX]{x1D716}}$
appears to become independent of
$C_{\unicode[STIX]{x1D716}}$
appears to become independent of
![]() $Re_{\unicode[STIX]{x1D706}}$
. These observations lead naturally to the issue of the universality of
$Re_{\unicode[STIX]{x1D706}}$
. These observations lead naturally to the issue of the universality of
![]() $C_{\unicode[STIX]{x1D716}}$
(i.e. the
$C_{\unicode[STIX]{x1D716}}$
(i.e. the
![]() $Re_{\unicode[STIX]{x1D706}}$
independence of
$Re_{\unicode[STIX]{x1D706}}$
independence of
![]() $C_{\unicode[STIX]{x1D716}}$
for any flow). Unfortunately, it is not possible to address this question at present but, as figure 4 shows, it is essential that any assessment of this universality to be carried out at very large Reynolds numbers.
$C_{\unicode[STIX]{x1D716}}$
for any flow). Unfortunately, it is not possible to address this question at present but, as figure 4 shows, it is essential that any assessment of this universality to be carried out at very large Reynolds numbers.
Finally, it is worth commenting on the following seemingly paradox: the present analysis indicates that, under SP,
![]() $C_{\unicode[STIX]{x1D716}}$
(or any SP constant) remains constant during decay and yet its value can vary with the Reynolds number as seen in figure 1. This paradox may be cleared by considering the two forms of similarity hypothesis introduced by Townsend (Reference Townsend1956). The first similarity hypothesis asserts that at sufficiently high Reynolds numbers non-dimensional mean-value functions are independent of the Reynolds number; this is often called Reynolds number similarity. The second similarity hypothesis is that of self-preservation at any one Reynolds number, where the flow structure at all values of
$C_{\unicode[STIX]{x1D716}}$
(or any SP constant) remains constant during decay and yet its value can vary with the Reynolds number as seen in figure 1. This paradox may be cleared by considering the two forms of similarity hypothesis introduced by Townsend (Reference Townsend1956). The first similarity hypothesis asserts that at sufficiently high Reynolds numbers non-dimensional mean-value functions are independent of the Reynolds number; this is often called Reynolds number similarity. The second similarity hypothesis is that of self-preservation at any one Reynolds number, where the flow structure at all values of
![]() $t$
(or
$t$
(or
![]() $x$
in the case of spatially evolving turbulent flows) is similar. Figure 1 illustrates the second similarity hypothesis for the round jet centreline: SP is satisfied at different Reynolds numbers, as illustrated by the constancy of both
$x$
in the case of spatially evolving turbulent flows) is similar. Figure 1 illustrates the second similarity hypothesis for the round jet centreline: SP is satisfied at different Reynolds numbers, as illustrated by the constancy of both
![]() $Re_{\unicode[STIX]{x1D706}}$
and
$Re_{\unicode[STIX]{x1D706}}$
and
![]() $C_{\unicode[STIX]{x1D716}}$
along
$C_{\unicode[STIX]{x1D716}}$
along
![]() $x$
. On the other hand, figure 4 illustrates the Reynolds number similarity, where
$x$
. On the other hand, figure 4 illustrates the Reynolds number similarity, where
![]() $C_{\unicode[STIX]{x1D716}}$
becomes independent of as
$C_{\unicode[STIX]{x1D716}}$
becomes independent of as
![]() $Re_{\unicode[STIX]{x1D706}}$
becomes large. Townsend stated that ‘if, as must be assumed, Reynolds number similarity of self-preserving flows exits, the form of the self-preserving functions are universal for any one type of flow’. The question that remains to be answered is: are all turbulent flows at an infinitely large Reynolds number of one type only? The fate of the universality of
$Re_{\unicode[STIX]{x1D706}}$
becomes large. Townsend stated that ‘if, as must be assumed, Reynolds number similarity of self-preserving flows exits, the form of the self-preserving functions are universal for any one type of flow’. The question that remains to be answered is: are all turbulent flows at an infinitely large Reynolds number of one type only? The fate of the universality of
![]() $C_{\unicode[STIX]{x1D716}}$
may well rest on the answer to this question.
$C_{\unicode[STIX]{x1D716}}$
may well rest on the answer to this question.
4 Conclusions
It is shown that, for decaying HIT and decaying local HIT,
![]() $C_{\unicode[STIX]{x1D716}}$
can be recovered from the Navier–Stokes equations when self-preservation is assumed, thus avoiding the use of dimensional analysis for its derivation. It is further shown that
$C_{\unicode[STIX]{x1D716}}$
can be recovered from the Navier–Stokes equations when self-preservation is assumed, thus avoiding the use of dimensional analysis for its derivation. It is further shown that
![]() $C_{\unicode[STIX]{x1D716}}$
is intimately related to SP requirements, which fits well with Taylor’s initial introduction of
$C_{\unicode[STIX]{x1D716}}$
is intimately related to SP requirements, which fits well with Taylor’s initial introduction of
![]() $C_{\unicode[STIX]{x1D716}}$
. When the turbulence decays/evolves in accordance with SP requirements,
$C_{\unicode[STIX]{x1D716}}$
. When the turbulence decays/evolves in accordance with SP requirements,
![]() $C_{\unicode[STIX]{x1D716}}$
remains constant for a given flow condition. Measurements in grid turbulence, which do not satisfy SP, and a turbulent round jet, which comply with SP in the far field, confirm these analytical results. The measurements show that after an initial increase associated with the development of turbulence,
$C_{\unicode[STIX]{x1D716}}$
remains constant for a given flow condition. Measurements in grid turbulence, which do not satisfy SP, and a turbulent round jet, which comply with SP in the far field, confirm these analytical results. The measurements show that after an initial increase associated with the development of turbulence,
![]() $C_{\unicode[STIX]{x1D716}}$
decreases with increasing
$C_{\unicode[STIX]{x1D716}}$
decreases with increasing
![]() $x$
in grid turbulence and is constant along the axis in the far field of a round jet. However, the measurements also show that
$x$
in grid turbulence and is constant along the axis in the far field of a round jet. However, the measurements also show that
![]() $C_{\unicode[STIX]{x1D716}}$
decreases when the Reynolds number (e.g.
$C_{\unicode[STIX]{x1D716}}$
decreases when the Reynolds number (e.g.
![]() $Re_{\unicode[STIX]{x1D706}}$
) increases in grid turbulence, a round jet and a plane jet. The rate at which
$Re_{\unicode[STIX]{x1D706}}$
) increases in grid turbulence, a round jet and a plane jet. The rate at which
![]() $C_{\unicode[STIX]{x1D716}}$
decreases continues to diminish as
$C_{\unicode[STIX]{x1D716}}$
decreases continues to diminish as
![]() $Re_{\unicode[STIX]{x1D706}}$
increases. This trend, in agreement with earlier studies (e.g. Sreenivasan Reference Sreenivasan1984; Pearson, Krogstad & van de Water Reference Pearson, Krogstad and van de Water2002), suggests that one cannot exclude the possibility that
$Re_{\unicode[STIX]{x1D706}}$
increases. This trend, in agreement with earlier studies (e.g. Sreenivasan Reference Sreenivasan1984; Pearson, Krogstad & van de Water Reference Pearson, Krogstad and van de Water2002), suggests that one cannot exclude the possibility that
![]() $C_{\unicode[STIX]{x1D716}}$
decreases towards a universal constant, which would be equal to the magnitude of
$C_{\unicode[STIX]{x1D716}}$
decreases towards a universal constant, which would be equal to the magnitude of
![]() $C_{\unicode[STIX]{x1D716}}$
in forced HIT, i.e. approximately 0.5.
$C_{\unicode[STIX]{x1D716}}$
in forced HIT, i.e. approximately 0.5.
A final word may be worthwhile on the SP solutions of the present analysis. Both the theory and experiments show that
![]() $Re_{\unicode[STIX]{x1D706}}$
is constant under SP. However, the theory also shows that SP under which
$Re_{\unicode[STIX]{x1D706}}$
is constant under SP. However, the theory also shows that SP under which
![]() $Re_{\unicode[STIX]{x1D706}}$
varies can exist. Whether or not this form of SP leads to a constant or non-constant
$Re_{\unicode[STIX]{x1D706}}$
varies can exist. Whether or not this form of SP leads to a constant or non-constant
![]() $C_{\unicode[STIX]{x1D716}}$
during decay cannot be answered by the present theory and is yet to be observed experimentally (or numerically), but which may well exist. This situation is reminiscent of the SP solutions of Sedov (see Batchelor Reference Batchelor1948) who showed two possible cases of SP for HIT; one with constant
$C_{\unicode[STIX]{x1D716}}$
during decay cannot be answered by the present theory and is yet to be observed experimentally (or numerically), but which may well exist. This situation is reminiscent of the SP solutions of Sedov (see Batchelor Reference Batchelor1948) who showed two possible cases of SP for HIT; one with constant
![]() $Re_{\unicode[STIX]{x1D706}}$
during decay and the other with
$Re_{\unicode[STIX]{x1D706}}$
during decay and the other with
![]() $Re_{\unicode[STIX]{x1D706}}$
increasing with time toward an asymptotic value.
$Re_{\unicode[STIX]{x1D706}}$
increasing with time toward an asymptotic value.
Acknowledgement
The financial support of the Australian Research Council is acknowledged.
Appendix. SP analysis of locally homogeneous and isotropic turbulence based on
 $\overline{(\unicode[STIX]{x1D6FF}q)^{2}}$
$\overline{(\unicode[STIX]{x1D6FF}q)^{2}}$
In § 2.2 we developed an expression of
![]() $C_{\unicode[STIX]{x1D716}}$
based on the transport equation for
$C_{\unicode[STIX]{x1D716}}$
based on the transport equation for
![]() $\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
. To make the analysis somewhat more general, here, we develop an expression of
$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$
. To make the analysis somewhat more general, here, we develop an expression of
![]() $C_{\unicode[STIX]{x1D716}}$
based on the transport equation for
$C_{\unicode[STIX]{x1D716}}$
based on the transport equation for
![]() $\overline{(\unicode[STIX]{x1D6FF}q)^{2}}=\overline{(\unicode[STIX]{x1D6FF}u)^{2}}+\overline{(\unicode[STIX]{x1D6FF}v)^{2}}+\overline{(\unicode[STIX]{x1D6FF}w)^{2}}$
whose generic form is (Burattini et al.
Reference Burattini, Antonia and Danaila2005a
; Djenidi et al.
Reference Djenidi, Antonia, Lefeuvre and Lemay2016):
$\overline{(\unicode[STIX]{x1D6FF}q)^{2}}=\overline{(\unicode[STIX]{x1D6FF}u)^{2}}+\overline{(\unicode[STIX]{x1D6FF}v)^{2}}+\overline{(\unicode[STIX]{x1D6FF}w)^{2}}$
whose generic form is (Burattini et al.
Reference Burattini, Antonia and Danaila2005a
; Djenidi et al.
Reference Djenidi, Antonia, Lefeuvre and Lemay2016):
where
![]() $I_{q}$
represents the contribution of the large-scale motions which varies from flow to flow. Let us for example focus on the centreline of a turbulent round jet. The term
$I_{q}$
represents the contribution of the large-scale motions which varies from flow to flow. Let us for example focus on the centreline of a turbulent round jet. The term
![]() $I_{q}$
is of the form
$I_{q}$
is of the form
which represents the contributions from the advection and production mechanisms, respectively. We now follow Djenidi et al. (Reference Djenidi, Antonia, Lefeuvre and Lemay2016) and seek SP requirements for (A 1) by assuming the following SP expressions
with
![]() $r^{\ast }=r/l_{q}$
, and
$r^{\ast }=r/l_{q}$
, and
![]() $l_{q}$
,
$l_{q}$
,
![]() $q_{\ast }$
,
$q_{\ast }$
,
![]() $u_{\ast }$
,
$u_{\ast }$
,
![]() $v_{\ast }$
,
$v_{\ast }$
,
![]() $w_{\ast }$
and
$w_{\ast }$
and
![]() $(uq)_{\ast }^{1/3}$
the length and velocity scaling functions to be determined;
$(uq)_{\ast }^{1/3}$
the length and velocity scaling functions to be determined;
![]() $f_{q}$
,
$f_{q}$
,
![]() $g$
,
$g$
,
![]() $h_{u}$
,
$h_{u}$
,
![]() $h_{v}$
and
$h_{v}$
and
![]() $h_{w}$
are dimensionless functions. Note that
$h_{w}$
are dimensionless functions. Note that
![]() $\overline{(\unicode[STIX]{x1D6FF}v)^{2}}=\overline{(\unicode[STIX]{x1D6FF}w)^{2}}$
on the axis of the jet. Let us introduce the mixed skewness increment,
$\overline{(\unicode[STIX]{x1D6FF}v)^{2}}=\overline{(\unicode[STIX]{x1D6FF}w)^{2}}$
on the axis of the jet. Let us introduce the mixed skewness increment,
![]() $S_{q}(r)(\equiv \overline{(\unicode[STIX]{x1D6FF}u)(\unicode[STIX]{x1D6FF}q)^{2}}/[\overline{(\unicode[STIX]{x1D6FF}u)^{2}}^{1/2}\overline{(\unicode[STIX]{x1D6FF}q)^{2}}])$
, as a SP controlling parameter; this helps for expressing
$S_{q}(r)(\equiv \overline{(\unicode[STIX]{x1D6FF}u)(\unicode[STIX]{x1D6FF}q)^{2}}/[\overline{(\unicode[STIX]{x1D6FF}u)^{2}}^{1/2}\overline{(\unicode[STIX]{x1D6FF}q)^{2}}])$
, as a SP controlling parameter; this helps for expressing
![]() $\overline{(\unicode[STIX]{x1D6FF}u)(\unicode[STIX]{x1D6FF}q)^{2}}$
in terms of
$\overline{(\unicode[STIX]{x1D6FF}u)(\unicode[STIX]{x1D6FF}q)^{2}}$
in terms of
![]() $\overline{(\unicode[STIX]{x1D6FF}q)^{2}}$
. If SP is satisfied, then
$\overline{(\unicode[STIX]{x1D6FF}q)^{2}}$
. If SP is satisfied, then
![]() $S_{q}$
has also the SP expression
$S_{q}$
has also the SP expression
![]() $S_{q}(r)=c_{q}\unicode[STIX]{x1D719}_{q}(r^{\ast })$
(where
$S_{q}(r)=c_{q}\unicode[STIX]{x1D719}_{q}(r^{\ast })$
(where
![]() $c_{q}$
is in general a function of
$c_{q}$
is in general a function of
![]() $x$
and
$x$
and
![]() $\unicode[STIX]{x1D719}_{q}(r^{\ast })$
a function of
$\unicode[STIX]{x1D719}_{q}(r^{\ast })$
a function of
![]() $r^{\ast }$
), and we can write
$r^{\ast }$
), and we can write
![]() $(uq)_{\ast }=c_{q}u_{\ast }q_{\ast }^{2}$
. Note also that since we can express
$(uq)_{\ast }=c_{q}u_{\ast }q_{\ast }^{2}$
. Note also that since we can express
![]() $f_{q}$
as
$f_{q}$
as
and it is independent of
![]() $x$
, we must have
$x$
, we must have
![]() $q_{\ast }^{2}\sim u_{\ast }^{2}\sim v_{\ast }^{2}\sim w_{\ast }^{2}$
if SP holds. Thus, we can take
$q_{\ast }^{2}\sim u_{\ast }^{2}\sim v_{\ast }^{2}\sim w_{\ast }^{2}$
if SP holds. Thus, we can take
![]() $u_{\ast }=v_{\ast }=w_{\ast }$
without loss of generality. Substituting (A 3), (A 4) and the definition of
$u_{\ast }=v_{\ast }=w_{\ast }$
without loss of generality. Substituting (A 3), (A 4) and the definition of
![]() $S_{q}(r)$
in (A 1) leads to
$S_{q}(r)$
in (A 1) leads to
with
where
![]() $s^{\ast }$
is a dummy variable of integration. SP implies that all coefficients
$s^{\ast }$
is a dummy variable of integration. SP implies that all coefficients
where
![]() $R_{l_{q}}=u_{\ast }l_{q}/\unicode[STIX]{x1D708}$
is a scaling Reynolds number, are independent of
$R_{l_{q}}=u_{\ast }l_{q}/\unicode[STIX]{x1D708}$
is a scaling Reynolds number, are independent of
![]() $x$
, since the coefficient of the second term in (A 6) is a constant. We can now write
$x$
, since the coefficient of the second term in (A 6) is a constant. We can now write
After trivial manipulations we obtain:
 $$\begin{eqnarray}\displaystyle C_{\unicode[STIX]{x1D716}} & = & \displaystyle -\frac{3}{4}S(r_{L_{q}}^{\ast })f_{q}(r_{L_{q}}^{\ast })h_{u}(r_{L_{q}}^{\ast })^{1/2}\frac{r_{L_{q}}^{\ast }}{r^{\ast }}+\frac{3}{2}\frac{f_{q}^{\prime }(r_{L_{q}}^{\ast })}{Re_{\unicode[STIX]{x1D706}_{q}}}\frac{r_{L_{q}}^{\ast }}{r^{\ast }}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{Re_{\unicode[STIX]{x1D706}_{q}}}\frac{r_{L_{q}}^{\ast }}{r^{\ast }}\left\{\frac{3}{4r_{L_{q}}^{\ast 2}}(C_{2}\unicode[STIX]{x1D6E4}_{1}-C_{3}\unicode[STIX]{x1D6E4}_{2}+2C_{4}\unicode[STIX]{x1D6E4}_{3})\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{\unicode[STIX]{x1D716}} & = & \displaystyle -\frac{3}{4}S(r_{L_{q}}^{\ast })f_{q}(r_{L_{q}}^{\ast })h_{u}(r_{L_{q}}^{\ast })^{1/2}\frac{r_{L_{q}}^{\ast }}{r^{\ast }}+\frac{3}{2}\frac{f_{q}^{\prime }(r_{L_{q}}^{\ast })}{Re_{\unicode[STIX]{x1D706}_{q}}}\frac{r_{L_{q}}^{\ast }}{r^{\ast }}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{Re_{\unicode[STIX]{x1D706}_{q}}}\frac{r_{L_{q}}^{\ast }}{r^{\ast }}\left\{\frac{3}{4r_{L_{q}}^{\ast 2}}(C_{2}\unicode[STIX]{x1D6E4}_{1}-C_{3}\unicode[STIX]{x1D6E4}_{2}+2C_{4}\unicode[STIX]{x1D6E4}_{3})\right\},\end{eqnarray}$$
where we used
![]() $l_{q}=\unicode[STIX]{x1D706}_{q}$
(
$l_{q}=\unicode[STIX]{x1D706}_{q}$
(
![]() $q=2k$
) and
$q=2k$
) and
![]() $u_{\ast }=q^{1/2}$
(
$u_{\ast }=q^{1/2}$
(
![]() $q=2k$
). We can now apply similar arguments as in HIT to find an expression for
$q=2k$
). We can now apply similar arguments as in HIT to find an expression for
![]() $C_{\unicode[STIX]{x1D716}}$
when
$C_{\unicode[STIX]{x1D716}}$
when
![]() $r^{\ast }$
is large enough so that
$r^{\ast }$
is large enough so that
![]() $f_{q}=h_{u}=h_{v}\simeq 2$
and
$f_{q}=h_{u}=h_{v}\simeq 2$
and
![]() $S(r^{\ast })=0$
. This leads to
$S(r^{\ast })=0$
. This leads to
which is equivalent to the isotropic form (2.17).