1. Introduction
The particle-laden turbulent flow is a common scene in nature (Grabowski & Wang Reference Grabowski and Wang2013) and engineering applications (Sahu, Hardalupas & Tayler Reference Sahu, Hardalupas and Tayler2014; Pouransari & Mani Reference Pouransari and Mani2017). In this multi-phase flow system, the particle–turbulence interaction can significantly modulate the turbulence, and impact the kinetic and thermal behaviour of particles. This further results in various important dynamics (Elghobashi Reference Elghobashi1994; Balachandar & Eaton Reference Balachandar and Eaton2010) that are crucial in natural and industrial processes.
Particles of sufficient inertia in turbulence can concentrate in clusters away from vorticity core under the centrifugal effect and sweep-stick mechanism (Squires & Eaton Reference Squires and Eaton1991; Wang & Maxey Reference Wang and Maxey1993); they can also tend to cluster in the region close to the wall due to the turbophoresis in the wall-bounded flow (Reeks Reference Reeks1983; Bragg, Richter & Wang Reference Bragg, Richter and Wang2021). Thus the particles significantly alter the flow structures and the heat transfer of the flow. For instance, it is found that particles transfer their momentum to the small-scale flow, which increases the local velocity gradients (Ahmed & Elghobashi Reference Ahmed and Elghobashi2000) and further increases the viscous dissipation (Druzhinin & Elghobashi Reference Druzhinin and Elghobashi1999). Moreover, Ferrante & Elghobashi (Reference Ferrante and Elghobashi2003) found that the preferential concentration of settling particles significantly stretches the vortical structures in the gravitational direction, thus the turbulent energy redistributes from the horizontal to the vertical direction. Wang & Richter (Reference Wang and Richter2020) further investigated the multiscale interaction of inertial particles with turbulent flow structures in the turbulent channel flow. They highlight that the interaction between inertial particles and large-scale motions is crucial for the interphase energy transport. When the thermal buoyancy is negligible, the temperature is treated as a passive scalar. The modulation of fluid heat transfer and temperature field by particles are well investigated in the turbulent homogeneous shear flow and turbulent channel flow (Shotorban, Mashayek & Pandya Reference Shotorban, Mashayek and Pandya2003; Liu et al. Reference Liu, Tang, Dong and Shen2018). Moreover, the multiscale thermal properties of particles and their contribution to fluid temperature are characterized (Carbone, Bragg & Iovieno Reference Carbone, Bragg and Iovieno2019). In many conditions, the thermal buoyancy is very important and even is the driving force of the flow system. The single-phase buoyancy-driven flow, which is abstracted as the paradigmatic model Rayleigh–Bénard (RB) convection, has been investigated extensively (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Wang, Zhou & Sun Reference Wang, Zhou and Sun2020). However, the study of particle-laden RB convection is a new field that has not been investigated widely. Oresta & Prosperetti (Reference Oresta and Prosperetti2013) found that the alteration of heat transfer is dominated by the thermal coupling for small particles, and the mechanical coupling plays an increasingly important role as the increasing of particle diameter in the cylindrical cell. Park, O'Keefe & Richter (Reference Park, O'Keefe and Richter2018) investigated the RB convection laden with non-isothermal particles in a three-dimensional rectangular cell, where particles are limited in the artificially tiny gravity. They found that the effect of preferential concentration results in the significant enhancement of the Nusselt number (
$Nu$). Our recent work investigates the dynamic coupling between carrier fluid and particles in RB convection laden with particles (Yang et al. Reference Yang, Zhang, Wang, Dong and Zhou2022b). We found that particles with medium Stokes number significantly enhance the Nusselt number due to strong coupling of the two phases, where the particle-induced kinetic energy is dominated.
As one of the strategies to utilize renewable energy efficiently, concentrating solar power (CSP) systems use low-cost materials to capture, store and transfer solar energy in the form of radiant heat through particulate two-phase flow, which can substantially reduce power generation costs and improve green energy supply. The particle solar receiver plays a key role in CSP, which can be regarded as a radiatively heated particle-laden two-phase flow (Tan & Chen Reference Tan and Chen2010; Ho Reference Ho2016). At present, some scholars have carried out some research for engineering applications. Chen et al. (Reference Chen, Chen, Hsieh and Siegel2007) investigated numerically the gas-particle flow in a solid-particle solar receiver. They found that particles with small size are easy to heat up, and higher temperatures can be achieved. Kim et al. (Reference Kim, Siegel, Kolb, Rangaswamy and Moujaes2009) studied the kinetic behaviour of heated particles in the solar particle receiver. They observed that the local concentration of particles results in the higher energy collection efficiency as it is more optically dense. Chinnici et al. (Reference Chinnici, Arjomanidi, Tian, Lu and Nathan2015) investigated the particle residence time in the solar vortex reactor with different geometry. They found that the turbulent vortex structures strongly impact the resident time of particles. Researchers also abstracted the particle-based solar receivers as simpler multi-phase flow system to study the intrinsically physical mechanism. For instance, Pouransari & Mani (Reference Pouransari and Mani2017, Reference Pouransari and Mani2018) found that the preferential concentration of heated particles reduces the heat transfer between particles and gas in a square channel. Rahmani et al. (Reference Rahmani, Geraci, Iaccarino and Mani2018) considered the particle polydispersity in a square channel. They found that the polydisperse heated particles perform better in transferring heat to the gas than the monodisperse particles. Frankel et al. (Reference Frankel, Pouransari, Coletti and Mani2016) analysed the influence of settling of heated particles on the turbulent structures in homogeneous turbulence. They found that the heated particles shed plumes of buoyant gas, which further modifies the turbulent structures. In this way, the turbulent kinetic energy varies non-monotonically as the increasing of radiation intensity due to the competing effects between the downward gravity and the upward buoyancy. Banko et al. (Reference Banko, Villafñe, Kim and Eaton2020) investigated experimentally the temperature statistics in the heated particle-laden turbulent square duct flow. The temperature statistics exhibit qualitatively differently at the duct centreline and the near wall under the effect of preferential concentration of particles and the streamwise elongated streaks in the centre and the near-wall regions, respectively. Zamansky et al. (Reference Zamansky, Coletti, Massot and Mani2014, Reference Zamansky, Coletti, Massot and Mani2016) investigated the turbulent thermal convection driven by heated inertial particles. They found that the fluid temperature properties and dissipation characteristics of energy are the result of the different forcing mechanisms that depend on the distribution of the particles. We note that works exploring the complete physics of particle–turbulence–radiation interaction are scarce, and the mechanisms and efficiency of energy transport in radiatively heated particle-laden flows are not well investigated. For example, little information exists that can address how the density ratio impacts exothermic and endothermic laws between phases. In addition, regarding the application of using solar radiant energy, the captured thermal energy tends to be high radiation intensity and causes considerable temperature differences in which the non-Oberbeck–Boussinesq effects should be considered, but this aspect is missing in previous studies. This has stimulated our enthusiasm to study related issues.
When fluid flow laden with solid particles is subject to radiative heating, it is often accompanied by the thermal buoyancy driving flow. There are temperature differences as well as strong thermal convection in the particle solar receiver; the radiatively heated particle-laden RB flow therefore can be regarded as one of the simplified models of particle solar receiver. To our knowledge, there is a lack of theoretical analysis on the interphase heat exchange of RB convection laden with heated particles, as well as an understanding of the relationship among particle motion, distribution, thermal variation of the flow field, and radiation intensity. Here, we focus on the energy transport characteristics and the heat transfer efficiency. We study numerically and theoretically the plate heat transfer and the interphase energy transport in the RB convection laden with heated particles, and investigate the correlation between particle–fluid density ratio versus Rayleigh number and radiation intensity.
The remainder of this paper is organized as follows. In § 2, we describe briefly the mathematical model and numerical procedure. Results and discussion are presented in § 3, which is divided into five parts. We describe the flow organization in § 3.1, and discuss the flow heat transfer and Reynolds number in § 3.2. In § 3.3, we derive the theoretical relation of the Nusselt number for the interphase heat transfer in a particle-laden RB convection system, and further analyse the specific relation between the interphase heat transfer and the normalized density ratio. Section 3.4 analyses the energy transport characteristics and discusses the kinetic energy and thermal energy. Section 3.5 discusses the scaling law of the critical density ratio versus the radiation intensity and the Rayleigh number. Finally, we give a conclusion for this work in § 4.
2. Mathematical model and numerical procedure
The configuration of the RB convection laden with heated particles is shown in figure 1, with cell width 
${W}$, height 
${H}$ and depth 
${D}$. We consider air as the working fluid; the temperature variation of fluid may be large under the effect of the heated particles, thus the fluid flow is governed by the low-Mach-number Navier–Stokes equations (Paolucci Reference Paolucci1982). Additionally, the air is an optically transparent gas, thus we ignore the effect of thermal radiation on gas temperature. In addition, this work assumes that no portion of the radiation is absorbed or reflected by the cavity walls. That implies that all radiated heat is captured equally by the particles. The volume occupied by the particles is very small; we write the momentum equations and the energy equation, in dimensionless form, as
$$\begin{gather} \frac{{\partial}\rho}{{\partial} t}+\frac{{\partial}\rho u_j}{{\partial} x_j}=0, \end{gather}$$
$$\begin{gather}\frac{{\partial}\rho u_i}{{\partial} t}+\frac{{\partial}\rho u_i u_j}{{\partial} x_j}={-}\frac{{\partial} p}{{\partial} x_j}+\frac{1}{(Ra/Pr)^{1/2}}\,\frac{{\partial}\tau_{i,j}}{{\partial} x_j}+\frac{1}{2\varepsilon}\,(\rho-1)\delta_{3i}+F_i, \end{gather}$$
$$\begin{gather}\rho c_p\left(\frac{{\partial} T}{{\partial} t}+u_j\,\frac{{\partial} T}{{\partial} x_j}\right)=\frac{1}{(Ra\, Pr)^{1/2}}\,\frac{{\partial}}{{\partial} x_j}k\,\frac{{\partial} T}{{\partial} x_j}+\varGamma\,\frac{{\rm d} p_{th}}{{\rm d} t}+Q, \end{gather}$$
$$\begin{gather}p_{th}=\rho T, \end{gather}$$
where 
$\rho$, 
$u$, 
$T$, 
$p$ and 
$p_{th}$ are, respectively, the fluid density, velocity, temperature, hydrodynamic pressure and thermostatic pressure; 
$\tau _{i,j}=\mu ( {\partial } u_i/ {\partial } x_j+ {\partial } u_j/ {\partial } x_i)$ 
$-(2/3)\delta _{ij}\mu ( {\partial } u_k/ {\partial } x_k)$ is the viscosity stress tensor, where 
$\mu$ is the dynamical viscosity, 
$\lambda =-2\mu /3$ is the volume viscosity, and 
$\delta _{ij}$ is the Kronecker delta; 
$c_p$ is the isobaric specific heat and is fixed at unity; 
$\varGamma =(\gamma -1)/\gamma$ represents the resilience of the fluid, with the ratio of specific heats 
$\gamma =1.4$. The dimensionless thermal conductivity 
$k$ and dynamic viscosity 
$\mu$ for air are governed by Sutherland's law
\begin{equation} k=T^{1.5}(1+S_k)/(T+S_k),\quad \mu=T^{1.5}(1+S_{\mu})/(T+S_{\mu}), \end{equation}
where 
$S_k=0.648$ and 
$S_\mu =0.368$ for the reference temperature 
${T}_0=300\,\mathrm {K}$ (Suslov & Paolucci Reference Suslov and Paolucci1999; Suslov Reference Suslov2010). Sutherland's law is developed based on the kinetic theory of ideal gases and an idealized intermolecular force potential (Sutherland Reference Sutherland1893), thus fairly accurate results can be obtained with an error less than a few per cent over a wide range of temperatures. The terms 
$F_i$ and 
$Q$, respectively, represent the momentum and thermal feedback of the dispersed phase, which will be described later. The non-dimensional equations (2.1)–(2.4) are obtained by the cell height 
${H}$, the arithmetic average temperature 
${T}_0$, the averaged density 
${\rho }_0$, the characteristic velocity 
$u^*=(2\varepsilon {{g}{H}})^{1/2}$, and the reference thermodynamic pressure 
${\rho }_0{R}{T}_0$, where 
${g}$ is the acceleration due to gravity, and 
${R}$ is the gas constant. The fluid properties at the reference temperature and the thermodynamic pressure are also the reference quantities, including 
${c}_{p,0}$, 
${\mu }_0$ and 
${k}_0$. The dimensionless temperature differential 
$\varepsilon$, the Rayleigh number and the Prandtl number are defined as
\begin{equation} \varepsilon=\frac{\Delta {T}}{2{T}_0},\quad Ra=\frac{2\varepsilon {c}_{p,0} {\rho}_0^2 {g} {H}^3}{{\mu}_0 {k}_0},\quad Pr=\frac{{c}_{p,0}{\mu}_0}{{k}_0}. \end{equation}
Figure 1. Configuration of turbulent RB convection laden with heated particles.
In this work, the particles in air are highly dilute and optically thin, thus we can neglect particle–particle interaction (Elghobashi Reference Elghobashi1994, Reference Elghobashi2019) and assume that every particle receives the same amount of radiation (Frankel, Iaccarino & Mani Reference Frankel, Iaccarino and Mani2017). In addition, the density of particles is much higher than that of the fluid, and particle diameters are small compared with the Kolmogorov scale of turbulence. All the constant properties of the simulations are shown in table 1. Under the above assumptions, movement of particles is conducted by Stokes drag and gravity (Elghobashi & Truesdell Reference Elghobashi and Truesdell1992; Guha Reference Guha2008; Balachandar & Eaton Reference Balachandar and Eaton2010). Therefore, we write the particle equations, in dimensionless form, as
$$\begin{gather} \frac{\mathrm{d}x_{p,i}}{\mathrm{d} t}=u_{p,i}, \end{gather}$$
$$\begin{gather}\frac{\mathrm{d} u_{p,i}}{\mathrm{d} t}={-}\frac{1}{Fr^2_p}\,\delta_{3i}-\frac{C_D}{St_f}\,(u_{p,i}-u_i), \end{gather}$$
$$\begin{gather}\frac{\mathrm{d} T_p}{\mathrm{d} t}=\frac{Nu_p}{2}\,\frac{T_f-T_p}{St_T}+q, \end{gather}$$
where 
$x_p$, 
$u_p$ and 
$T_p$ are the particle dimensionless position, velocity and temperature, respectively; 
$T_f$ is the fluid temperature at the particle location; 
$Fr_p=(2\varepsilon )^{1/2}$ represents the ratio of inertia force of fluid to gravity of a particle; 
$C_D=1+0.15\,Re_p^{0.678}$ represents the drag correction coefficient that applies when the particle Reynolds number 
$Re_p=({d}_p/{H})(\rho /\mu )\,|\boldsymbol {u}-\boldsymbol {u}_p|\,(Ra/Pr)^{1/2}$ exceeds unity, where 
${d}_p$ is the particle diameter, and the notation 
$|\boldsymbol {u}-\boldsymbol {u}_p|$ refers to the magnitude of the vector difference between the fluid and particle velocities. The particle Nusselt number 
${Nu_p}$ is given by a well-known empirical correlation as 
$Nu_p=2+0.6\,Re_p^{1/2}\,Pr^{1/3}$ (Ranz & Marshall Reference Ranz and Marshall1952). The particle Stokes number and the thermal Stokes number based on the integral time scale are given by 
$St_f=(1/18)({\rho }_p/{\rho }_0)({d}_p/{H})^2({\mu }_0/{\mu })(Ra/Pr)^{1/2}$ and 
$St_T=(1/12)({c}_{p,p}/{c}_{p,0})({\rho }_p/{\rho }_0)({d}_p/{H})^2({k_0}/{k})(Ra\, Pr)^{1/2}$, respectively, where 
${\rho }_p$ denotes the particle density. In this study, the non-Oberbeck–Boussinesq effect is considered, thus the thermal conductivity 
$k$ and dynamic viscosity 
$\mu$ are not constants. That is, both Stokes numbers vary with the location of particles in the cell. They represent respectively the inertia and the thermal inertia of a particle in turbulence. Here, 
$q={\phi }_p/{\phi }_p^*$ is the heat absorption by a particle with the radiation intensity 
${\phi }$, where 
${\phi }_p=({\rm \pi} /4){d}_p^2{\phi }$ and 
${\phi }_p^*={c}_{p,p}{m}_p{T}_0/({H}/(2\varepsilon {g}))^{1/2}$, and 
$m_p$ is the mass of a particle.
Table 1. Summary of the fluid and particle properties used in the simulation. Here, the heights of the convection cell are 0.07, 0.12 and 0.26 m for 
$Ra=2\times 10^6$, 
$10^7$ and 
$10^8$, respectively.
According to previous studies, in the case of particle mass fraction in table 1, the interaction between particles and fluid is significant, thus particles change the turbulent structures (Elghobashi & Truesdell Reference Elghobashi and Truesdell1992). The size of particles is far less than the Kolmogorov scale of the flow field, so the point-particle model applies. In (2.2) and (2.3), 
$F_i$ and 
$Q$ respectively represent the total force and heat exerted on the fluid by the point-particle in each fluid cell (Oresta & Prosperetti Reference Oresta and Prosperetti2013; Liu et al. Reference Liu, Tang, Dong and Shen2018). Thus 
$F_i$ and 
$Q$ are expressed as
$$\begin{gather} F_i={-}\frac{\rm \pi}{6}\,\frac{{\rho}_p}{{\rho}_0}\,\frac{{d}_p^3}{{V}}\sum_{j=1}^{N} \left({\frac{\mathrm{d} u_{p,i}^j}{\mathrm{d} t}-\left(-\frac{1}{Fr_p^2}\,\delta_{3i}\right)}\right), \end{gather}$$
$$\begin{gather}Q={-}\frac{\rm \pi}{6}\,\frac{{c}_{p,p}}{{c}_{p,0}}\,\frac{{\rho}_p}{{\rho}_0}\, \frac{{d}_p^3}{{V}}\sum_{j=1}^{N}\left({\frac{\mathrm{d} T_{p}^j}{\mathrm{d} t}-q}\right), \end{gather}$$
where 
${V}$ is the fluid volume of the cell, and 
$N$ is the number of particles in the cell.
The RB convection models that we consider here are both two-dimensional (2-D) and three-dimensional (3-D). For the 2-D cases, it can be an approximate cross-section of the two-phase flow in a square pipe with 
$H/L=1$. Here, we consider the fluid layer thickness in the 
$y$-direction 
$W$ to be very thin, with 
$W=H/(N_p)^{1/2}$, and 
$N_p$ is the total number of particles. In this way, on average, a specific particle will occupy a 3-D box with sides equal to 
$H/(N_p)^{1/2}$. The coupling between fluid and particle features is 3-D to some extent, while the flow characteristics tend to be generally 2-D. The reasonableness of this approximation includes mainly the following. (i) Many well-cited theories for turbulent RB systems are essentially 2-D, e.g. the popular Grossmann–Lohse theory (Grossmann & Lohse Reference Grossmann and Lohse2000) and the Whitehead–Doering theory for the ultimate regime (Whitehead & Doering Reference Whitehead and Doering2011). (ii) The 2-D turbulence has been a possible application to intermediate-scale meteorological flow (Kraichnan Reference Kraichnan1967), and it can be used to better understand the physical mechanisms of 3-D convection (van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2013). (iii) Many of the important physical processes found in 3-D flows laden with inertial particles are also present in the 2-D model (Patočka, Calzavarini & Tosi Reference Patočka, Calzavarini and Tosi2020; Xu et al. Reference Xu, Tao, Shi and Xi2020). For the 3-D cases, the geometry of the flow system is a cavity with 
$H/L=1$ and 
$H/W=1$. For both the 2-D and 3-D cases, the bottom and top walls are respectively fixed at constant temperatures 
$1+\varepsilon$ and 
$1-\varepsilon$, while the lateral walls are assumed to be thermally adiabatic; in addition, no-penetration and no-slip velocity boundary conditions are applied to all solid walls. Here, we study both the 2-D and 3-D cases to compare the similarities and the differences of heat transfer as well as the energy transport mechanism in different geometries.
The governing equations (2.1)–(2.3) are discretized using the second-order central difference method. The fractional-step method is used to solve the equations (Verzicco & Orlandi Reference Verzicco and Orlandi1996). A multi-grid strategy (Briggs, Henson & McCormick Reference Briggs, Henson and McCormick2000) is adopted to solve the pressure Poisson equation. For time advancement, the wall-normal viscous terms are treated semi-implicitly with the Crank–Nicolson scheme, while all other terms are discretized by the third-order Runge–Kutta scheme. The numerical details and validations of the code have been elaborated in previous works (Xia et al. Reference Xia, Wan, Liu, Wang and Sun2016; Liu et al. Reference Liu, Xia, Yan, Wan and Sun2018; Wang et al. Reference Wang, Xia, Yan, Sun and Wan2019). After the flow field is fully developed, particles are injected into the flow field at a random position, with their velocities and temperatures set to those of the local fluid, then we continue the simulation of the particle-laden flow. In the computation, Lagrangian particle tracking is employed to obtain the position and the velocity of the particles. Equations of particles’ evolution are advanced in time by a second-order Adams–Bashforth method (Dong & Chen Reference Dong and Chen2011). For particles, an elastic reflection is enforced at the upper wall and the lateral walls. When a particle reaches the bottom of the cell, it is removed from the calculation and a new particle is re-injected at a random position on the top plate with velocity zero and temperature 
$1-\varepsilon$, which is the same as the top temperature. This assumption means that the volume fraction of discrete phases in the system remains unchanged, and each particle injected is always at the same temperature as the surrounding fluid. The present particle re-entry model was supported by previous numerical studies (Oresta & Prosperetti Reference Oresta and Prosperetti2013). In fact, newly injected particles here do not represent the subsequent behaviour of removing particles. The thermal modulation at small scales can be due only to the local non-uniformity of the thermal coupling between interphases. The momentum and energy of the carrier phase and discrete phase can be in equilibrium. Generally speaking, this approximation is reasonable when the residence time of the particles in the flow is short, in view of the comparatively smaller volumetric heat capacity of the fluid. To reveal systematically the properties of the heat transfer and energy transport in the heated particle-laden RB convection, we carried out both 2-D and 3-D direct numerical simulations (DNS) cases as shown in table 2, where radiation intensity is 
$1\le \phi /\phi _{solar}\le 100$, spanning the density ratio range 
$854.7\le \rho _p/\rho _0 \le 8547$. All the simulations are performed at fixed Prandtl number 
$Pr=0.71$, Froude number 
$Fr_p=0.447$, mass loading 
$\varPhi _m=0.01$, temperature differential 
$\varepsilon =0.1$, and particle diameter 
$d_p=40\,\mathrm {\mu } {\rm m}$. We adopt the non-uniform grid with more grid points clustered near walls to achieve a full resolution of the boundary layer and the smallest scale of the flow. For 2-D DNS cases, the grid numbers are set to be 
$N_x\times N_z=256\times 256$, 
$384\times 384$ and 
$768\times 768$ for 
$Ra=2\times 10^6$, 
$10^7$ and 
$10^8$, respectively. For 3-D cases, 
$Ra=10^7$ and 
$N_x\times N_y\times N_z=192\times 192\times 192$ were used.
Table 2. Simulation parameters. For all cases, the Prandtl number is 
$Pr=0.71$, the Froude number is 
$Fr_p=0.447$, the mass loading is 
$\varPhi _m=0.01$, the temperature differential is 
$\varepsilon =0.1$, and the particle diameter is 
$d_p=40\,\mathrm {\mu } {\rm m}$.
3. Results
3.1. Flow organization
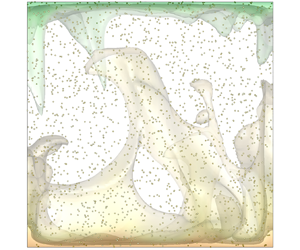
The instantaneous temperature field and flow structures in the 2-D convection cell at 
$Ra=10^7$ and 
$\phi =50\times \phi _{solar}$ for the single-phase case and the particle-laden cases with three density ratios, i.e. 
$\rho _p/\rho _0=2564.1$, 
$4273.5$ and 
$8547.0$, are shown in figures 2(a–d). In the 2-D simulations, a large-scale circulation accompanied by small secondary rolls is observed in the single-phase case in figure 2(a); the thermal plumes self-organize into a large-scale coherent structure, and move along side walls (Xu et al. Reference Xu, Wang, He, Wang, Schumacher, Huang and Tong2021). For the small-density-ratio case 
$\rho _p/\rho _0=2564.1$, there are more secondary rolls as the flow is speeded up by the particle cluster, as shown in figure 2(b). This is in line with the observation of our previous work in the RB convection laden with isothermal particles (Yang et al. Reference Yang, Zhang, Wang, Dong and Zhou2022b). Moreover, the temperature of bulk increases significantly due to the heated particles transferring their heat to the fluid. The flow structures and the temperature field vary a little at the medium-density-ratio case 
$\rho _p/\rho _0=4273.5$. For the large-density-ratio case 
$\rho _p/\rho _0=8547.0$, the flow structures change a small amount. The temperature of the bulk surprisingly drops a little, which implies that the heated particles absorb heat from the fluid. In the 3-D simulations, vigorous sheet-like plumes are ejected from the bottom and top plates, as shown in figure 2(e). For the particle-laden case at the small density ratio 
$\rho _p/\rho _0=2564.1$, the hot plumes stretch into the bulk, which indicates that the bulk is heated significantly.
Figure 2. Typical snapshots of the 2-D instantaneous temperature field (colour) and streamlines (black lines with arrows) for 
$Ra=10^7$ at 
$Pr=0.71$, 
$\varepsilon =0.1$ and 
$\phi =50\times \phi _{solar}$: (a) single-phase, (b) 
$\rho _p/\rho _0=2564.1$, (c) 
$\rho _p/\rho _0=4273.5$, and (d) 
$\rho _p/\rho _0=8547.0$. (e, f) Instantaneous temperature isosurfaces of 3-D cases with the opacity set to be 50 % and the distribution of particles for 
$Ra=10^7$ at 
$Pr=0.71$, 
$\varepsilon =0.1$ and 
$\phi =50\times \phi _{solar}$: (e) single-phase, ( f) 
$\rho _p/\rho _0=2564.1$. Here, 50 % and 1 % of the total number of particles are shown for the 2-D cases and 3-D case, respectively.
Additionally, the distribution of particles is also given in figures 2(b–d) for 2-D cases, and figure 2(e) for 3-D simulation. For small density ratio 
$\rho _p/\rho _0=2564.1$, particles cluster into bands along the edge of the large-scale circulation as the effect of preferential sweeping (Wang & Maxey Reference Wang and Maxey1993) for the 2-D case, as shown in figure 2(b). The clusters that act on the edge of the eddy can change the strength and shape of the eddy, as shown in figure 2(b). This is decided by the transport patterns of particles. Particles with a particular density ratio (or Stokes number) can cluster into bands that correlate to the edges of eddies, which is named as channel transport mode (Yang et al. Reference Yang, Wang, Tang, Zhou and Dong2022a). The preferential concentration of particles is also observed repeatedly for RB convection, mixing layer and jet flow (Lázaro & Lasheras Reference Lázaro and Lasheras1992; Longmire & Eaton Reference Longmire and Eaton1992). But in the 3-D case, the distribution of particles is uniform, as shown in figure 2(e), as the flow strength is rather weaker than in the 2-D case, and the preferential sweeping cannot significantly impact the distribution of particles. For the medium and large density ratios 
$\rho _p/\rho _0=4273.5$ and 
$8547.0$, the particle motion is dominated by its gravity; consequently, the distribution of particles has no significant correlation with the structures of eddies, and particles distribute uniformly in the flow field, as shown in figures 2(c,d).
3.2. Flow heat transfer and Reynolds number
The cold-plate Nusselt number and the hot-plate Nusselt number are shown in figure 3. For the cold-plate Nusselt number 
$Nu_c$ as shown in figures 3(a,b), 
$Nu_c$ is decreased almost monotonically as the increase of the density ratio 
$\rho _p/\rho _0$, and it also noted that 
$Nu_c$ becomes larger for large radiation intensity. The trends between the 2-D cases and the 3-D cases are basically the same. The particles with a small density ratio and large radiation intensity can substantially increase the cold-plate heat transfer of the convection cell; this implies that in this situation, the temperature of particles is significantly larger than that of the cold plate, thus it becomes important that the heat transfers between the hot particles and the top plate. For the hot-plate Nusselt number 
$Nu_h$ as shown in figures 3(c,d), there is little difference between the 2-D cases and 3-D cases. For the 2-D cases, 
$Nu_h$ climbs to a peak then goes down near the heat transfer of the single-phase case with increasing density ratio, when the radiation intensity is lower than 
$50\times \phi _{solar}$. At larger radiation intensity, for example, 
$\phi =100\times \phi _{solar}$ as shown in figure 3(c), 
$Nu_h$ increases monotonically to the heat transfer of the single-phase case with increasing density ratio. Note that slight ‘bump-like’ variations can be observed in the Nusselt numbers at high density ratios in figures 3(a,c). This is related to thermal and mechanical fluid–particle coupling. The acceleration that the particles impart to the colder, descending fluid stream is re-balanced by the retardation that they cause on the warmer fluid. Meanwhile, the larger drag that they impose on the flow in the thermal boundary layers is responsible for the decline of 
$Nu_c$ in the bump-like variation at high density ratio. For the 3-D cases, 
$Nu_h$ becomes monotonically larger for the large density ratio, and reaches a value that is slightly larger than the heat transfer of the single-phase case. Moreover, for both the 2-D cases and 3-D cases, it is noted that 
$Nu_h$ can become negative, with a very large absolute value at small density ratio and large radiation intensity, which means that a large heat flux goes down. This implies that the temperature of the heated particle at a small density ratio and large radiation intensity is significantly larger than the hot-plate temperature; consequently, heat is transported from particles with a higher position than the bottom wall to the hot plate. What is more, as the density ratio becomes very large, the dependence of 
$Nu_c$ (or 
$Nu_h$) on the radiation intensity becomes inconspicuous.
Figure 3. Cold-plate Nusselt number 
$Nu_c$ as a function of density ratio 
$\rho _p/\rho _0$ for (a) 2-D cases and (b) 3-D cases. Hot-plate Nusselt number 
$Nu_h$ as a function of density ratio 
$\rho _p/\rho _0$ for (c) 2-D cases and (d) 3-D cases. For all the cases, 
$Ra=10^7$, 
$Pr=0.71$ and 
$\varepsilon =0.1$. The black dashed lines denote the volume-averaged Nusselt number for 2-D and 3-D single-phase cases.
The heated particles also change significantly the turbulent momentum transport. The Reynolds number (
$Re$) of the thermal convection system can imply the activity of the turbulent momentum, and is calculated as 
$Re=U_{rms}(Ra/Pr)^{1/2}$, where 
$U_{rms}=\langle \boldsymbol {u}\boldsymbol {\cdot } \boldsymbol {u}\rangle ^{1/2}$, in which 
$\langle {\cdot }\rangle$ denotes an ensemble (or space–time) average. We show 
$Re$ for different density ratios and radiation intensities in figures 4(a,b). For the 2-D cases, 
$Re$ is increased significantly, by up to 280 % for small density ratio as the particle clusters acting on the edges of the eddy, called a circling transport pattern, as shown in figure 2(b), vastly accelerate the motion of the fluid and then enhance the turbulent momentum transport of the cell. In addition, a significant decline of 
$Re$ is observed for large-density-ratio cases, where particles settle uniformly due to large inertia, called a downpour transport pattern, as shown in figures 2(c,d). Particles cannot transfer their momentum effectively to fluid, instead increasing the dissipation of fluid kinetic energy, and causing a substantial change in the Reynolds number. Our recent work (Yang et al. Reference Yang, Wang, Tang, Zhou and Dong2022a) found that the flow structure and heat transfer processes can change significantly with different particle motion patterns. This also implies that the buoyancy contribution from heated particles is less for large-density-ratio particle-laden cases. For the 3-D cases, the physical model and the boundary conditions (especially the constraints on the front and back walls) are different from the 2-D cases. Particle clusters and the aforementioned particle transport patterns are not observed within the current parameters; the particles tend to be distributed uniformly in the flow field at all times – see figure 2( f). Thus the Reynolds number shows a continuous variation following the density ratio, and it is less than the single-phase Reynolds number for small density ratio (small inertia particles). This is in line with the observations in a cylindrical RB convection system by Oresta & Prosperetti (Reference Oresta and Prosperetti2013).
Figure 4. 
$Re$ as functions of 
$\rho _p/\rho _0$ for different values of radiation intensity for (a) 2-D cases and (b) 3-D cases, for 
$Ra=10^7$ at 
$Pr=0.71$ and 
$\varepsilon =0.1$.
3.3. Interphase heat transfer efficiency
The interphase heat transfer is one of the key focuses in the RB convection laden with heated inertial particles. It is strongly related to how to exchange and store thermal energy in the particle solar receiver flow system. Here, based on the energy equation and the continuity equation of fluid, we derive the theoretical relation between the cold/hot plate heat transfer and the interphase heat transfer. The fluid continuity equation and the energy equation are given as equations (2.1) and (2.3). Here, for a closed system with no-slip and no-penetration boundary conditions, the time derivative of thermodynamic pressure is
\begin{equation} \frac{\mathrm{d}p_{th}}{\mathrm{d}t}=\frac{1}{(Ra\,Pr)^{1/2}}\, \frac{1}{(1-\varGamma)V}\int_S k\,\frac{{\partial} T}{{\partial} x_j}\,n_j\,{\rm d} S. \end{equation}We combine this with the time-averaged fluid continuity equation (2.3) to get
\begin{equation} c_p\left(\frac{{\partial} (\rho T)}{{\partial} t}+\frac{{\partial} (\rho u_jT)}{{\partial} x_j}\right)= \frac{1}{(Ra\, Pr)^{1/2}}\,\frac{{\partial}}{{\partial} x_j}k\,\frac{{\partial} T}{{\partial} x_j}+\varGamma\, \frac{\mathrm{d}p_{th}}{\mathrm{d}t}+Q. \end{equation}
Applying stationarity (i.e. the first term on the left-hand side equals zero) and the 
$z$-plane average for (3.2), and combining the no-penetration boundary condition at all side walls, 
$\int _{A}({ {\partial } (\rho uT)}/{ {\partial } x}+{ {\partial } (\rho vT)}/{ {\partial } y})\,{\rm d} x\,{\rm d} y$ vanishes; 
$\int _{A}(({ {\partial }}/{ {\partial } x})k({ {\partial } T}/{ {\partial } x})+({ {\partial }}/{ {\partial } y})k({ {\partial } T}/{ {\partial } y}))\,{\rm d} x\,{\rm d} y=0$ as there is no heat flux at all side walls.
Thus
\begin{equation} \left\langle c_p\,\frac{{\partial} (\rho wT)}{{\partial} z}\right\rangle_{A,t}= \frac{1}{(Ra\, Pr)^{1/2}}\left\langle\frac{{\partial}}{{\partial} z}k\,\frac{{\partial} T}{{\partial} z}\right\rangle_{A,t}+ \left\langle\varGamma\,\frac{\mathrm{d}p_{th}}{\mathrm{d}t}\right\rangle_{A,t}+ \left\langle Q\right\rangle_{A,t}, \end{equation}
where 
$\langle {\cdot }\rangle _{A,t}$ denotes the 
$z$-plane time average. We use the given definitions of 
$Nu_c$ and 
$Nu_h$ to write
$$\begin{gather} Nu_c=\left\langle\left.\left({-}k_{d}\,\frac{{\partial} T_d}{{\partial} z_d}\right)\right|_H \Bigg/ \left(k_0\,\frac{\Delta T}{H}\right) \right\rangle_{A,t}={-} \frac{k}{2\varepsilon}\left.\left\langle\frac{{\partial} T}{{\partial} z}\right\rangle_{A,t}\right|_1, \end{gather}$$
$$\begin{gather}Nu_h=\left\langle\left.\left({-}k_{d}\,\frac{{\partial} T_d}{{\partial} z_d}\right)\right|_0 \Bigg/ \left(k_0\,\frac{\Delta T}{H}\right) \right\rangle_{A,t}={-} \frac{k}{2\varepsilon}\left.\left\langle\frac{{\partial} T}{{\partial} z}\right\rangle_{A,t}\right|_0. \end{gather}$$
Then we perform the integration over 
$0\le z\le z_1$ and 
$z_1\le z\le 1$. We can obtain the non-dimensional heat flux of the hot plate and cold plate as
\begin{align} Nu_h &= \left.\frac{(Ra\, Pr)^{1/2}}{2\varepsilon}\left\langle\rho wT\right\rangle_{A,t}\right|_{z_1}- \left.\left\langle\frac{k(z_1)}{2\varepsilon}\,\frac{{\partial} T}{{\partial} z}\right\rangle_{A,t}\right|_{z_1} \nonumber\\ &\quad -\frac{(Ra\, Pr)^{1/2}}{2\varepsilon}\int_{0}^{z_1} \left\langle Q\right\rangle_{A,t}{\rm d} z-(\gamma-1)z_1\left(Nu_c-Nu_h\right), \end{align}
\begin{align} Nu_c &= \left.\frac{(Ra\, Pr)^{1/2}}{2\varepsilon} \left\langle\rho wT\right\rangle_{A,t}\right|_{z_1}-\left.\left\langle \frac{k(z_1)}{2\varepsilon}\,\frac{{\partial} T}{{\partial} z}\right\rangle_{A,t}\right|_{z_1} \nonumber\\ &\quad +\frac{(Ra\, Pr)^{1/2}}{2\varepsilon}\int_{z_1}^{1} \left\langle Q\right\rangle_{A,t}{\rm d} z+(\gamma-1)(1-z_1)\left(Nu_c-Nu_h\right). \end{align}Equation (3.7) minus (3.6) gives
\begin{align} Nu_c-Nu_h &= \frac{(Ra\,Pr)^{1/2}}{2\varepsilon\gamma}\int_{0}^{1} \left\langle Q\right\rangle_{A,t}{\rm d} z \nonumber\\ &={-}\frac{(Ra\, Pr)^{1/2}}{2\varepsilon\gamma}\,\frac{\rm \pi}{6}\, \frac{{c}_{p,p}}{{c}_{p,0}}\,\frac{{\rho}_p}{{\rho}_0}\, \frac{{d}_p^3}{HLW}\left\langle\sum_{i=1}^{N} \left({\frac{\mathrm{d} T_{p,i}}{\mathrm{d} t}-q}\right)\right\rangle_{t}=Nu_q. \end{align}
Here, 
$Nu_q$ denotes the difference between the Nusselt numbers of the cold and hot plates. Equation (3.8) shows that 
$Nu_q$ is the result of the interphase heat transfer in the cell. We can also verify our numerical resolution utilizing (3.8). Figure 5 compares 
$Nu_c$ and 
$Nu_h+Nu_q$ for various density ratios at different radiation intensities and at fixed 
$Ra=10^7$. It is seen from the figure that 
$Nu_c/(Nu_h+Nu_q)$ is quite close to unity for different radiation intensities and density ratios, which indicates that the grid resolutions are fine enough to obtain accurate results that are very close to the theory results, and the small flow structures can be well captured. What is more, it also indicates that both the momentum feedback and the thermal feedback imposed by the heated particles are properly calculated.
Figure 5. 
$Nu_c / (Nu_h+Nu_q)$ as functions of 
$\rho _p/\rho _0$ for different values of radiation intensity at 
$Ra=10^7$ for (a) 2-D cases and (b) 3-D cases.
We further plot the variation of 
$Nu_q$ with density ratio at different radiation intensities and at fixed 
$Ra=10^7$ in figures 6(a,b). Despite the small difference in magnitudes, it is noted that the variation of 
$Nu_q$ with density ratio is similar for 2-D cases and 3-D cases. As the density ratio is increased, 
$Nu_q$ decreases very rapidly at first, and then slowly becomes less than 0. This indicates that the small-density-ratio particles can absorb more radiation heat and then transfer relatively more heat to the fluid, as the settling of small-density-ratio particles is slow. It is also noted that particles with a large density ratio always absorb heat from fluid even at very large radiation intensity 
$\phi =100\times \phi _{solar}$, as the temperature of particles is increased a little under the process of fast settling. Two different regimes can be identified: the exothermal particle regime where 
$Nu_q$ is larger than 0, and the endothermal particle regime where 
$Nu_q$ is less than 0. The division between the two regimes gives a critical density ratio 
$\rho _c/\rho _0$ at which 
$Nu_q$ crosses 0. The regime shifts towards larger 
$\rho _p/\rho _0$ when the radiation intensity is increased, suggesting that the exothermal particle regime occurs more easily at larger radiation intensity. To better compare the 
$Nu_q$ values at different radiation intensities, we adopt 
$\rho _c/\rho _0$ and the single-phase Nusselt number 
$Nu^*$ to normalize the data, and the results are plotted in figures 6(c,d). It is seen that all symbols can collapse on a curve for both 2-D and 3-D cases. The two curves can be well described by 
$Nu_q / Nu^*=C_q[(\rho _p/\rho _c)^{-1}-1]$, where the constant parameter 
$C_q$ equals 0.6 for the 2-D simulations, and 0.4 for the 3-D simulations. This indicates that 
$\rho _c/\rho _0$ is indeed a relevant typical density ratio for the problem. This signals that the interphase heat transfers for all cases studied exhibit universal properties and are governed by the same transfer mechanism. In addition, 
$Nu_q$ values increase linearly with the radiation intensity, and their slopes become large as the density ratio decreases, as shown in figure 7(a). Here, 
$\alpha$ is the growth rate of 
$Nu_q$ with radiation intensity. In figure 7(b), we summarize 
$\alpha$ in the best linear relation fits of 
$Nu_q\sim \alpha (\phi /\phi _{solar})$ as a function of the density ratio and the Rayleigh number. One sees that all data collapse onto a single curve, and the best power-law fits to the data yield 
$\alpha \sim (\rho _p/\rho _0)^{-1.11}\,Ra^{0.65}$.
Figure 6. Plots of 
$Nu_q$ as a function of 
$\rho _p/\rho _0$ obtained at various 
$\phi$ and fixed 
$Ra=10^7$ for (a) 2-D cases and (b) 3-D cases. Ratio 
$Nu_q/Nu^*$ as a function of the normalized density ratio 
$\rho _p/\rho _c$ for (c) all 2-D cases and (d) all 3-D cases; the black solid curves are the best power function fits to the respective data. Here, 
$\phi _1$, 
$\phi _2$, 
$\phi _3$, 
$\phi _4$ and 
$\phi _5$ represent the radiation strengths of 
$\phi _{solar}$, 
$10\phi _{solar}$, 
$20\phi _{solar}$, 
$50\phi _{solar}$ and 
$100\phi _{solar}$, respectively.
Figure 7. (a) Plots of 
$Nu_q$ as functions of 
$\phi /\phi _{solar}$ obtained at various density ratios 
$\rho _p/\rho _0$ and fixed 
$Ra=10^7$ for 2-D cases. The solid and dashed lines are eye guides. (b) Fitted slope in the linear relation 
$Nu_q\sim \alpha (\phi /\phi _{solar})$ as a function of the product 
$(\rho _p/\rho _0)^{-1.11}\,Ra^{0.65}$ for both 2-D and 3-D cases. The black dashed line is the fitted relation for 
$\alpha$ versus 
$(\rho _p/\rho _0)^{-1.11}\,Ra^{0.65}$.
3.4. The energy transport
We plot the schematic of the energy process in the particle-laden RB convection as shown in figure 8. In this flow system, the fluid energy includes kinetic energy and thermal energy. Fluid kinetic energy can be obtained through interaction between thermal buoyancy or particle and fluid, and finally dissipated by fluid viscosity. The injected kinetic energy is from the work done by the driving buoyancy and the momentum feedback of particles 
$\boldsymbol {F}\boldsymbol {\cdot } \boldsymbol {u}$; the injected thermal energy includes the part of the heat flux from the hot/cold plate and the thermal feedback of particles 
$Q T$. The energy finally dissipates due to the fluid viscosity and the thermal diffusivity.
Figure 8. The schematic of the energy process in the RB convection laden with heated particles.
The kinetic energy of the fluid in RB convection can be revealed by the Reynolds number, as shown in figure 4 and discussed in § 3.2. For the 2-D cases, the particle-induced kinetic energy 
$\langle \boldsymbol {F}\boldsymbol {\cdot }\boldsymbol {u}\rangle _{V,t}$ is important for a small-density-ratio particle, as shown in figure 9(a). Our recent work revealed that the mechanism for the increased 
$Re$ as shown in figure 4(a) results from particle-induced kinetic energy, therefore it enhances the strength of turbulence (Yang et al. Reference Yang, Zhang, Wang, Dong and Zhou2022b). For the 3-D cases, the particle-induced kinetic energy decreases with the increasing of 
$\rho _p/\rho _0$, while the fluid kinetic energy increases at larger 
$\rho _p/\rho _0$. This implies that the thermal plumes shed from heated particles accelerate the motion of flow eddies, and its contribution to the fluid is larger than that of particle-induced kinetic energy. That explains why the alteration of fluid kinetic energy is dominated by the particle-induced kinetic energy for the 2-D cases, while it is dominated by the buoyancy-induced kinetic energy by the heated particles for the 3-D cases.
Figure 9. The particle-induced kinetic energy as functions of 
$\rho _p/\rho _0$ obtained at various 
$\phi$ and fixed 
$Ra=10^7$ for (a) 2-D cases and (b) 3-D cases.
The volume-averaged temperature of the fluid can reflect the fluid thermal energy; figure 10 shows the volume-averaged temperature 
$\langle T\rangle _{V,t}$ of the fluid as functions of 
$\rho _p/\rho _0$ at fixed 
$Ra=10^7$. Despite the different magnitudes, both the data sets exhibit a similar trend with 
$Nu_q$, i.e. 
$\langle T\rangle _{V,t}$ decreases with increasing 
$\rho _p/\rho _0$, and reaches a value less than the single-phase temperature, for both the 2-D and 3-D cases. The 
$\langle T\rangle _{V,t}$ value tends to be larger for large radiation intensity. Notably, the 
$\langle T\rangle _{V,t}$ value of the 3-D simulations is significantly larger than that of 2-D simulations at small 
$\rho _p/\rho _0$ for large radiation intensities 
$\phi =50\times \phi _{solar}$ and 
$100\times \phi _{solar}$, even if there is little difference 
$Nu_q$ between the 2-D and 3-D simulations, as shown in figure 6. This implies that 
$Nu_q$ is an important reference quantity for fluid heating, but it is not the only factor. It also involves the dynamics of RB turbulent convection.
Figure 10. The volume-averaged temperature as functions of 
$\rho _p/\rho _0$ obtained at various 
$\phi$ and fixed 
$Ra=10^7$ for (a) 2-D cases and (b) 3-D cases.
The particle-induced thermal energy is described by 
$\langle Q\rangle _{V,t}$, and we plot 
$\langle Q T\rangle _{V,t}$ as functions of 
$\rho _p/\rho _0$ at fixed 
$Ra=10^7$ and at different radiation intensities, as shown in figures 11(a,b). Here, 
$\langle Q T\rangle _{V,t}$ and 
$Nu_q$ have similar trends as functions of 
$\rho _p/\rho _0$ at different radiation intensities. Namely, with increasing 
$\rho _p/\rho _0$, 
$\langle Q T\rangle _{V,t}$ decreases rapidly at first, and then decreases slowly below 0. The particles with small 
$\rho _p/\rho _0$ can transport more thermal energy to the fluid. The exothermal particle regime and endothermal particle regime are also observed, and the critical density ratio 
$\rho _c/\rho _0$ between the two regimes is the same as that of 
$Nu_q$ for specific radiation intensity. This implies that the interphase heat transfer mechanism is consistent with the interphase thermal energy transport mechanism. We further rescale 
$\langle Q T\rangle _{V,t}$ by the thermal dissipation rate of the single-phase case, and 
$\rho _p/\rho _0$ by the critical density ratio 
$\rho _c/\rho _0$, as shown in figures 11(c,d). This rescaling leads to the converging of the data onto a single curve for 2-D and 3-D cases, representing the functions 
$\langle Q T\rangle _{V,t}/\langle \varepsilon ^*_T\rangle _{V,t}=C_{qt}[(\rho _p/\rho _c)^{-1}-1]$ with the constant equal to 4.5 and 3.0 for the 2-D and 3-D cases, respectively, where the thermal dissipation rate of single-phase is expressed as 
$\varepsilon ^*_T=1/(Ra\,Pr)^{1/2}k\sum _{i}( {\partial } T/ {\partial } x_i)^2$. Moreover, 
$\langle Q T\rangle _{V,t}$ increases linearly with increasing radiation intensity at different density ratios 
$\rho _p/\rho _0$. The linear slope increases with the decrease of the density ratio 
$\rho _p/\rho _0$, as shown in figure 12(a). Figure 12(b) plots the growth rate 
$\beta$ of particle-induced thermal energy with radiation intensity in the linear relation 
$1000\langle Q T\rangle _{V,t}\sim \beta (\phi /\phi _{solar})$ at various 
$Ra$ and 
$\rho _p/\rho _0$. One sees that all growth rates converge onto a curve, and the scaling relation of growth rate 
$\beta$ versus Rayleigh number and density ratio can be obtained, i.e. 
$\beta \sim (\rho _p/\rho _0)^{-1.20}\,Ra^{0.18}$.
Figure 11. The particle-to-fluid thermal energy 
$\langle Q T\rangle _{V,t}$ as a function of 
$\rho _p/\rho _0$ obtained at various 
$\phi$ and fixed 
$Ra=10^7$ for (a) 2-D cases and (b) 3-D cases. Ratio 
$\langle Q T\rangle _{V,t}/\langle \varepsilon ^*_T\rangle _{V,t}$ as a function of the normalized density ratio 
$\rho _p/\rho _c$ for (c) all 2-D cases and (d) all 3-D cases; the black solid curves are the best power function fits to the respective data. Here, 
$\phi _1$, 
$\phi _2$, 
$\phi _3$, 
$\phi _4$ and 
$\phi _5$ represent the radiation strengths of 
$\phi _{solar}$, 
$10\phi _{solar}$, 
$20\phi _{solar}$, 
$50\phi _{solar}$ and 
$100\phi _{solar}$, respectively.
Figure 12. (a) Plots of 
$\langle Q T\rangle _{V,t}$ as functions of 
$\phi /\phi _{solar}$ obtained at various density ratios 
$\rho _p/\rho _0$ and fixed 
$Ra=10^7$ for 2-D cases. The solid and dashed lines are eye guides. (b) Fitted slope in the linear relation 
$1000\langle Q T\rangle _{V,t}\sim \beta (\phi /\phi _{solar})$ as a function of the product 
$(\rho _p/\rho _0)^{-1.2}\,Ra^{0.18}$ for both 2-D and 3-D cases. The black dashed line is the fitted relation for 
$\beta$ versus 
$(\rho _p/\rho _0)^{-1.2}\,Ra^{0.18}$.
3.5. The critical density ratio
It is noted that there are two regimes, i.e. the exothermal particle regime and the endothermal particle regime; a critical density ratio divides the two regimes, at which both 
$Nu_q$ and 
$\langle Q T\rangle _{V,t}$ equal 0. The critical density is crucial for the interphase heat transfer and thermal energy transport. The critical density ratios 
$\rho _p/\rho _c$ as functions of radiation intensity and Rayleigh number are illustrated in figures 13(a,b). One sees that the critical density ratio 
$\rho _p/\rho _c$ of 2-D cases collapses onto a single curve that is well described by the power law 
$\rho _p/\rho _c \sim (\phi /\phi _{solar})^{3/4}\,Ra^{0.18}$. For the 3-D cases, the critical density ratio is larger than that of the 2-D cases at the present radiation intensity, as shown in figures 6(a,b). Nevertheless, the 
$\rho _p/\rho _c-(\phi /\phi _{solar})$ data set approaches the scaling of 
$\rho _p/\rho _c\sim (\phi /\phi _{solar})^{0.55}$, which is not as steep as the 2-D cases.
Figure 13. (a) The characteristic density ratio 
$\rho _p/\rho _0$ as a function of the product 
$(\phi /\phi _{solar})^{3/4}\,Ra^{0.18}$ for all the 2-D cases. (b) The characteristic density ratio 
$\rho _p/\rho _0$ as a function of the product 
$(\phi /\phi _{solar})^{0.55}$ for all the 3-D cases. The black dashed lines are the best functions that fit the respective data.
To deeply understand the above dependencies, we first idealize the scene for the critical-density particle-laden cases as the situation where the temperature of particles is consistently equal to the local fluid temperature during the settling of particles; particles settle directly towards the bottom plate and are not advected into the bulk region again. Based on this, the particle thermal equation is
\begin{equation} \frac{\mathrm{d} T_p}{\mathrm{d} t}=\frac{Nu_p}{2}\,\frac{T_f-T_p}{St_T}+q. \end{equation}According to the above approximation, the first term of the right-hand side vanishes, so
\begin{equation} \frac{\mathrm{d} T_p}{\mathrm{d} t}=q. \end{equation}
We integrate both sides of (3.10) from 
$t_1$ to 
$t_2$ for a specific particle, where the particle is released from the top plate at 
$t_1$ and reaches the bottom plate at 
$t_2$. According to the boundary condition of the convection cell, we can get
\begin{equation} \frac{T_p(t_2)-T_p(t_1)}{t_2-t_1}=\frac{2\varepsilon}{1/S_p}=q, \end{equation}
where 
$S_p$ is the averaged settling velocity of particles. Additionally, we give the formulation of 
$q$ as
\begin{equation} q=\frac{({\rm \pi}/4){d}_p^2{\phi}}{{c}_{p,p}{m}_p{T}_0/({H}/(2\varepsilon {g}))^{1/2}}, \end{equation}reforming it to get
\begin{equation} q=\frac{3}{2}\,\frac{\phi}{\phi_{solar}}\left(\frac{{c}_{p,p}}{{c}_{p,0}}\, \frac{{\rho}_c}{{\rho}_0}\,\frac{{d}_p}{H}\right)^{{-}1}\frac{\phi_{solar}}{k_0T_0/H}\,(Ra\, Pr)^{{-}1/2}. \end{equation}
According to Yang et al. (Reference Yang, Zhang, Wang, Dong and Zhou2022b), 
$S_p\simeq \frac {1}{18}({1}/{Fr_p^2})({\rho _c}/{\rho _0}) ({d_p^2}/{H^2})({{Ra}/{Pr}})^{1/2}$ in the RB convection. Consequently, for the cases with critical density, we can get that
\begin{equation} \left(\frac{\rho_c}{\rho_0}\right)^2\sim \frac{Fr_p^2}{2\varepsilon}\, \frac{\phi}{\phi_{solar}}\,\frac{\phi_{solar}}{k_0T_0/H}\left(\frac{d_p}{H}\right)^{{-}3} \left(\frac{{c}_{p,p}}{{c}_{p,0}}\right)^{{-}1}Ra^{{-}1}. \end{equation}
In the present study, the non-dimensional temperature difference 
$\varepsilon$ between the top and bottom plates is constant. Also, the working fluid is air at 300 K, and the physical properties are also constant. Based on these facts, we can get 
$H\sim Ra^{1/3}$, and consequently
\begin{equation} \frac{\rho_c}{\rho_0}\sim \left(\frac{\phi}{\phi_{solar}}\right)^{1/2}Ra^{1/3}. \end{equation}On account of the approximate assumption and the simplification in the derivative procedure, there are three causes that can result in a small adjustment in the scaling exponent for (3.15):
(1) In real turbulent circumstances, the transport modes of particles are complex and diverse due to the interaction between turbulence and particles, and the particles near the bottom plate can be brought into the bulk again by the fluid.
(2) The temperature of particles would not be consistently equal to the local fluid temperature during the settling of particles.
(3) The kinetic and dynamic behaviour of particles in turbulence can result in some small adjustments for the expression of particle settling velocity
$S_p$, according to the discussion of Yang et al. (Reference Yang, Zhang, Wang, Dong and Zhou2022b).
Specifically, for the 2-D cases, the scaling relation 
$\rho _c/\rho _0\sim (\phi /\phi _{solar})^{3/4}\,Ra^{0.18}$ of the computed data has relative large difference with the derived scaling 
$\rho _c/\rho _0\sim (\phi /\phi _{solar})^{1/2}\,Ra^{1/3}$ on account of the transport modes of particles being diverse and not as simple as the simplification. For the 3-D cases, the derived scaling 
$\rho _c/\rho _0\sim (\phi /\phi _{solar})^{1/2}$ is very close to the obtained scaling relation 
$\rho _c/\rho _0\sim (\phi /\phi _{solar})^{0.55}$ from computed data as the transport of particles is similar to the approximation. What is more, we predict the critical density ratio to be 
$\rho _c/\rho _0=2155.48$ for 
$\phi /\phi _{solar}=50$ at 
$Ra=10^6$ and 
$Pr=0.71$ by using the scaling 
$\rho _c/\rho _0\sim (\phi /\phi _{solar})^{0.55}\,Ra^{1/3}$, and the computed result shows 
$Nu_q=0.848$, which is close to 0; this shows that the predicted critical density ratio is very close to the real critical density ratio. This indicates that the theoretically predicted scaling can well describe the relation between the critical density ratio and the control parameters for the 3-D cases.
4. Conclusion
We carried out the DNS combined with the Lagrangian point-particle mode for the RB convection laden with heated inertial particles, where the two-phase flow is relevant to particle-based solar receivers. We consider the particle–turbulence system in the ranges of density ratio 
$854.7\le \rho _p/\rho _0 \le 8547$ and radiation intensity 
$1\le \phi /\phi _{solar}\le 100$ for 2-D and 3-D simulations. Three Rayleigh numbers, 
$Ra=2\times 10^6$, 
$1\times 10^7$ and 
$1\times 10^8$ are considered for 2-D simulations, and 
$Ra=1\times 10^7$ is considered for 3-D simulations at fixed 
$Pr=0.71$. We also theoretically derive and analyse the exact relation for the interphase heat transfer in the heated particle-laden RB convection, which shows that the Nusselt number difference between the cold and hot plates is caused by the interphase heat transfer in the cell.
We found that particles with small density ratio and encountering strong radiation significantly alter the flow momentum transport and fluid heat transfer, especially enhancing the top plate heat transport, so the fluid temperature of the bulk is remarkably heated. This indicates that the small-density-ratio particles absorb more radiant heat in the slow settlement process, which further leads to the increase of heat flux between the top plate and particles. Also, the heat transfer of the bottom plate becomes small at a small density ratio, and the heat flux changes from positive to negative, and increases gradually under the high radiation intensity. The negative value of heat transfer means that the direction of heat flux is from up to down; this is because the temperature of particles is significant higher than that of the bottom plate. Due to the preferential sweeping of particles, particle clusters are relevant to the edges of eddies at small density ratio for the 2-D cases, where particles can effectively do work on these eddies; this significantly enhances the momentum transport of fluid.
What is more, two different regimes are observed: the exothermal particle regime and the endothermal particle regime. By using the critical density ratio, the Nusselt number and the energy dissipation rate of the single-phase flow as characteristic quantities to normalize the data, both the interphase heat transfer and the interphase thermal energy transport exhibit universal properties that are governed by the specific transfer mechanism, respectively. They can be well described by 
$Nu_q / Nu^*=C_q[(\rho _p/\rho _c)^{-1}-1]$ and 
$\langle Q T\rangle _{V,t}/\langle \varepsilon ^*_T\rangle _{V,t}=C_{qt}[(\rho _p/\rho _c)^{-1}-1]$, respectively, where the constant parameter 
$C_q$ equals 0.6 for the 2-D simulations and 0.4 for the 3-D simulations, and with the constant 
$C_{qt}$ equal to 4.5 and 3.0 for the 2-D and 3-D cases, respectively. Additionally, both the interphase heat transfer and the interphase thermal energy transport also increase linearly with the increasing of radiation intensity. The linear growth rates in 
$Nu_q\sim \alpha (\phi /\phi _{solar})$ and 
$1000\langle Q T\rangle _{V,t}\sim \beta (\phi /\phi _{solar})$ exhibit the scaling relations 
$\alpha \sim (\rho _p/\rho _0)^{-1.11}\,Ra^{0.65}$ and 
$\beta \sim (\rho _p/\rho _0)^{-1.20}\,Ra^{0.18}$, respectively.
Finally, the critical density ratios where the two regimes are divided are the same for both the interphase heat transfer and the interphase thermal energy transport at specific radiation intensity. The scaling relations of critical density ratio versus radiation intensity and Rayleigh number are described by the power law 
$\rho _p/\rho _c \sim (\phi /\phi _{solar})^{3/4}\, Ra^{0.18}$ for the 2-D cases, and 
$\rho _p/\rho _c\sim (\phi /\phi _{solar})^{0.55}\,Ra^{\gamma }$ for the 3-D simulations. We further predict theoretically the power-law relation of the critical density ratios versus Rayleigh number and radiation intensity, i.e. 
$\rho _p/\rho _c \sim (\phi /\phi _{solar})^{1/2}Ra^{1/3}$, which is in remarkable agreement with our 3-D simulations.
Funding
This work was supported by the Natural Science Foundation of China (grant nos 12172207, 92052201 and 11825204), and the Shanghai Science and Technology Program under project no. 19JC1412802.
Declaration of interests
The authors report no conflict of interest.
