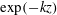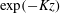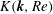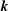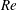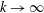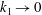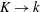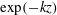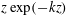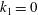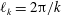1 Introduction
When analysing turbulent flow over rough surfaces, flow statistics are often averaged over wall-parallel planes. The difference between mean flow and horizontally averaged mean flow yields dispersive velocities, and leads to so-called dispersive or coherent stresses in the horizontally averaged mean momentum equations (Raupach & Shaw Reference Raupach and Shaw1982; Finnigan Reference Finnigan2000; Nikora et al. Reference Nikora, McEwan, McLean, Coleman, Pokrajac and Walters2007). The effects of the shape and distribution of surface roughness on turbulent wall-flows is typically assumed to be confined to the roughness sub-layer where the dispersive motions are dominant and complement Reynolds shear stresses (Raupach, Antonia & Rajagopalan Reference Raupach, Antonia and Rajagopalan1991; Manes et al. Reference Manes, Pokrajac, Coceal and McEwan2008). In this region, the mean flow statistics are complex and three-dimensional, governed by the complex shape of the roughness itself.
In flows over homogeneous rough surfaces, the roughness sub-layer is typically found to extend vertically two to five times the representative roughness heights, which can be the equivalent sandgrain roughness or the maximum roughness height or a root-mean-square roughness height, depending on the type of roughness (Raupach et al. Reference Raupach, Antonia and Rajagopalan1991; Nikora et al. Reference Nikora, Goring, McEwan and Griffiths2001; Jiménez Reference Jiménez2004; Flack, Schultz & Connelly Reference Flack, Schultz and Connelly2007). When moving away from the wall, the dispersive stress contribution to the total stress gradually decays, in accordance with the picture of an outer layer that is dominated by Reynolds stresses. Therefore, beyond this roughness sub-layer, the outer layer of the flow is usually independent of local details of surface roughness, resulting in a mean flow that is nearly homogeneous in wall-parallel directions, with flow statistics that mainly depend on the wall-normal direction (Townsend Reference Townsend1956, Reference Townsend1976; Castro Reference Castro2007). However, for rough surfaces with spatial heterogeneities where dominant spanwise length scales of the roughness distribution are of the order of the outer length scale of the flow, large secondary motions are excited by the roughness arrangement, and can penetrate into the outer layer (Nezu & Nakagawa Reference Nezu and Nakagawa1984; Wang & Cheng Reference Wang and Cheng2005; Barros & Christensen Reference Barros and Christensen2014; Anderson et al. Reference Anderson, Barros, Christensen and Awasthi2015; Vanderwel & Ganapathisubramani Reference Vanderwel and Ganapathisubramani2015; Kevin et al. Reference Kevin, Monty, Bai, Pathikonda, Nugroho, Barros, Christensen and Hutchins2017; Hwang & Lee Reference Hwang and Lee2018; Medjnoun, Vanderwel & Ganapathisubramani Reference Medjnoun, Vanderwel and Ganapathisubramani2018). Therefore, dispersive stress can be significant across the entire turbulent layer.
Recent work has shown that the decay of dispersive stresses (or secondary motions) scales with the spanwise roughness wavelength when the roughness is geometrically scaled (proportional increase in both roughness height and wavelength) and when the wavelength increases at fixed roughness height (Chan et al. Reference Chan, MacDonald, Chung, Hutchins and Ooi2018; Yang & Anderson Reference Yang and Anderson2018). Very recently, Morgan & McKeon (Reference Morgan and McKeon2018) analysed the spatial and wave-number structure of dispersive motions in a boundary layer with periodic roughness elements. In the current work, a new analytical framework is proposed that allows one to study this decay of dispersive motions systematically. The paper is organised as follows. First in § 2, the theory is presented, and approximate solutions for dispersive motions in the outer layer of a boundary layer are derived. Next, a comparison with experiments is shown in § 3. Lastly, discussion and conclusions are stated in § 4.
2 Approximate solutions for the dispersive velocity field
2.1 Horizontally averaged Navier–Stokes equations and linearization
Consider an incompressible turbulent boundary layer over a rough wall, with
$x_{1}$
,
$x_{2}$
and
$x_{3}$
oriented in the streamwise, spanwise and wall-normal directions, respectively. Further,
$\overline{\boldsymbol{u}}$
represents the Reynolds-averaged velocity field, with fluctuation
$\boldsymbol{u}^{\prime }$
. The focus is on rough boundary layers with either periodic roughness elements or a roughness distribution that is statistically homogeneous in the horizontal directions, and the horizontally averaged and Reynolds-averaged flow is denoted with
$\langle \overline{\boldsymbol{u}}\rangle \triangleq (U,0,W)$
. Furthermore,
$\overline{\boldsymbol{u}}^{\prime \prime }$
is introduced, so that
$\overline{\boldsymbol{u}}=U\boldsymbol{e}_{1}+W\boldsymbol{e}_{3}+\overline{\boldsymbol{u}}^{\prime \prime }$
.
It is further presumed that the boundary layer is sufficiently developed for the streamwise evolution of mean velocity components to be negligible, so that the time-averaged and horizontally averaged Navier–Stokes equation follows as
$$\begin{eqnarray}W\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}x_{3}}-\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}x_{3}^{2}}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p_{\infty }}{\unicode[STIX]{x2202}x_{1}}=-\frac{\unicode[STIX]{x2202}\langle \overline{u_{1}^{\prime }u_{3}^{\prime }}\rangle }{\unicode[STIX]{x2202}x_{3}}-\frac{\unicode[STIX]{x2202}\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle }{\unicode[STIX]{x2202}x_{3}},\end{eqnarray}$$
with
$\langle \overline{u_{1}^{\prime }u_{3}^{\prime }}\rangle$
and
$\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle$
being the plane-averaged Reynolds stress and dispersive stress, respectively,
$p_{\infty }$
the background pressure,
$\unicode[STIX]{x1D708}$
the kinematic viscosity, and where the density
$\unicode[STIX]{x1D70C}$
is presumed to be constant.
The equations for the dispersive velocity fluctuations
$\overline{\boldsymbol{u}}^{\prime \prime }$
further follow from subtracting (2.1) from the standard Navier–Stokes equations, yielding
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\overline{u}_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{i}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U\frac{\unicode[STIX]{x2202}\overline{u}_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{1}}+\overline{u}_{j}^{\prime \prime }\frac{\unicode[STIX]{x2202}\overline{u}_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{j}}+\overline{u}_{3}^{\prime \prime }\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6FF}_{i1}=-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}\overline{p}^{\prime \prime }}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}\langle \overline{u_{1}^{\prime }u_{3}^{\prime }}\rangle }{\unicode[STIX]{x2202}x_{3}}\unicode[STIX]{x1D6FF}_{i1}+\frac{\unicode[STIX]{x2202}\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle }{\unicode[STIX]{x2202}x_{3}}\unicode[STIX]{x1D6FF}_{i1}-\frac{\unicode[STIX]{x2202}\overline{u_{i}^{\prime }u_{j}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}+\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}u_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{j}x_{j}}, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x1D6FF}_{ij}$
the Kronecker delta. Here, terms with products of
$W$
and
$\overline{u}_{i}^{\prime \prime }$
are considered as being negligible, and the short-hand notation
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}x_{3}$
is used.
For
$\overline{\boldsymbol{u}}^{\prime \prime }$
sufficiently small, the dispersive velocity equations can be linearized around the mean background flow, neglecting all higher-order terms. This leads to
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\overline{u}_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{i}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U\frac{\unicode[STIX]{x2202}\overline{u}_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{1}}+\overline{u}_{3}^{\prime \prime }\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6FF}_{i1}=-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}\overline{p}^{\prime \prime }}{\unicode[STIX]{x2202}x_{i}}-\frac{\unicode[STIX]{x2202}(\overline{u_{i}^{\prime }u_{j}^{\prime }})^{\prime \prime }}{\unicode[STIX]{x2202}x_{j}}+\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}u_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{j}x_{j}}. & \displaystyle\end{eqnarray}$$
In particular, the solution of these equations are investigated in the outer layer, since we expect
$\overline{\boldsymbol{u}}^{\prime \prime }$
to be small for
$x_{3}\rightarrow \unicode[STIX]{x1D6FF}$
, with
$\unicode[STIX]{x1D6FF}$
the boundary layer thickness.
2.2 Turbulence closure
In order to solve (2.5), a closure is required for the Reynolds stresses
$R_{ij}^{\prime \prime }=(\overline{u_{i}^{\prime }u_{j}^{\prime }})^{\prime \prime }$
. To this end, first, a simple closure for the background flow is posed. Providing that conditions for the linearization hold, it is reasonable to assume that the background corresponds to a standard outer layer solution in the absence of any dispersive terms. Pertaining to the Reynolds forces, an exact parametrization then corresponds to
$$\begin{eqnarray}F_{i}\triangleq -\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left(R_{ij}-\frac{1}{3}\unicode[STIX]{x1D6FF}_{ij}R_{kk}\right)=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\unicode[STIX]{x1D708}_{e}\left(\frac{\unicode[STIX]{x2202}\overline{u}_{i}}{\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}\overline{u}_{i}}{\unicode[STIX]{x2202}x_{j}}\right)=\unicode[STIX]{x1D6FF}_{i1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D708}_{e}\unicode[STIX]{x1D6E4}}{\unicode[STIX]{x2202}x_{3}},\end{eqnarray}$$
where as usual, the trace of the Reynolds stress is absorbed in the pressure term, and the eddy viscosity
$\unicode[STIX]{x1D708}_{e}$
is straightforwardly determined from
$\unicode[STIX]{x1D708}_{e}=-\langle \overline{u_{1}^{\prime }u_{3}^{\prime }}\rangle /\unicode[STIX]{x1D6E4}$
, using known experimental, numerical or analytical profiles for
$\unicode[STIX]{x1D6E4}$
and
$\overline{u_{1}^{\prime }u_{3}^{\prime }}$
in the outer layer of a boundary layer. For later use in § 2.3, the total viscous force is introduced as
$G_{i}\triangleq F_{i}+\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{j}[\unicode[STIX]{x1D708}(\unicode[STIX]{x2202}\overline{u}_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}\overline{u}_{i}/\unicode[STIX]{x2202}x_{j})]$
.
The linearization of the Reynolds forces now follows from the chain rule as
$$\begin{eqnarray}F_{i}^{\prime \prime }=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left[\unicode[STIX]{x1D708}_{e}\left(\frac{\unicode[STIX]{x2202}\overline{u}_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}\overline{u}_{i}^{\prime \prime }}{\unicode[STIX]{x2202}x_{j}}\right)+\unicode[STIX]{x1D6FF}_{i1}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D708}_{e}^{\prime \prime }\unicode[STIX]{x1D6E4}\right].\end{eqnarray}$$
Unfortunately, the dispersive turbulent viscosity
$\unicode[STIX]{x1D708}_{e}^{\prime \prime }$
is not known. However, when
$\unicode[STIX]{x1D6E4}\ll 1$
, which is generally true in boundary layers for
$x_{3}\rightarrow \unicode[STIX]{x1D6FF}$
, the term with
$\unicode[STIX]{x1D708}_{e}^{\prime \prime }\unicode[STIX]{x1D6E4}$
disappears. Alternatively, this result is also obtained by linearizing the Navier–Stokes equations around a constant background velocity
$U_{\infty }$
instead of
$U$
. The resulting equations are the same as (2.5), but with
$U_{\infty }$
instead of
$U$
and
$\unicode[STIX]{x1D6E4}=0$
. The linearization in that case is valid, as long as
$|U_{\infty }-U|\ll 1$
, which again holds for
$x_{3}\rightarrow \unicode[STIX]{x1D6FF}$
. Thus, for this particular case, (2.7) with
$\unicode[STIX]{x1D6E4}=0$
yields an exact closure of the linearized Reynolds forces. Finally, it should be noted that the above proposed closure is not exact in terms of the Reynolds stresses themselves. This closure determines the Reynolds stresses up to an addition of a divergence-free tensor (see, for example, Deser Reference Deser1967; Wu, Zhou & Wu Reference Wu, Zhou and Wu1996; Jiménez Reference Jiménez2016). The latter will have no influence on the Reynolds force, but will change the individual stress components. In particular, it is well understood that a classical eddy viscosity model leads to a stress tensor with a zero diagonal (corresponding to
$\overline{u_{1}^{\prime }u_{1}^{\prime }}=\overline{u_{2}^{\prime }u_{2}^{\prime }}=\overline{u_{3}^{\prime }u_{3}^{\prime }}$
), which is generally not the case in boundary layers. Here, this is not an issue, as the Reynolds stresses are not directly needed in the remainder of this work.
2.3 Representation using Fourier modes
Given periodic roughness elements, the linearized Navier–Stokes equations can be solved using periodic boundaries in the
$x_{1}$
and
$x_{2}$
directions. Thus, solutions can be expressed based on a Fourier series. To this end,
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{u}_{i}^{\prime \prime }=\mathop{\sum }_{\boldsymbol{k}}\widetilde{u}_{i}(\boldsymbol{k},z)\exp (\text{i}(k_{1}x_{1}+k_{2}x_{2})), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{p}^{\prime \prime }=\mathop{\sum }_{\boldsymbol{k}}\widetilde{p}(\boldsymbol{k},z)\exp (\text{i}(k_{1}x_{1}+k_{2}x_{2})), & \displaystyle\end{eqnarray}$$
etc., are introduced with
$\boldsymbol{k}=(k_{1},k_{2})$
, and
$z\triangleq x_{3}$
. Furthermore,
$k_{1}=i2\unicode[STIX]{x03C0}/L_{x}$
,
$k_{2}=j2\unicode[STIX]{x03C0}/L_{y}$
, with
$i,j\in \mathbb{Z}$
, and
$L_{x},L_{y}$
the roughness periods in
$x_{1}$
and
$x_{2}$
directions respectively. We note that in the case of a roughness distribution, which is statistically homogeneous in horizontal directions (instead of periodic roughness elements), the above Fourier series can be replaced by Fourier integrals in the horizontal planes, without further affecting results below. In this case, it is assumed that the largest horizontal length scales in the roughness distributions are sufficiently small for the streamwise homogeneity assumption of the dispersive-flow equations (2.2), (2.3) to hold.
Since solving linear equations is the aim, solutions can now be found mode by mode. To this end, the continuity equation is first eliminated by using
$\widetilde{u}_{3}$
and
$\widetilde{\unicode[STIX]{x1D714}}_{3}=-\text{i}k_{2}\widetilde{u}_{1}+\text{i}k_{1}\widetilde{u}_{2}$
as independent variables. Thus for
$(k_{1},k_{2})\neq (0,0)$
,
$$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{u}_{1}=\frac{\text{i}k_{1}}{k^{2}}\frac{\text{d}\widetilde{u}_{3}}{\text{d}z}+\frac{\text{i}k_{2}}{k^{2}}\widetilde{\unicode[STIX]{x1D714}}_{3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{u}_{2}=\frac{\text{i}k_{2}}{k^{2}}\frac{\text{d}\widetilde{u}_{3}}{\text{d}z}-\frac{\text{i}k_{1}}{k^{2}}\widetilde{\unicode[STIX]{x1D714}}_{3}, & \displaystyle\end{eqnarray}$$
with
$k=(k_{1}^{2}+k_{2}^{2})^{1/2}$
.
Inserting (2.10) and (2.11) in the linearized momentum equations (2.5), and further eliminating the pressure, then leads to following set of equations
$$\begin{eqnarray}\displaystyle & \displaystyle -k_{1}U\widetilde{\unicode[STIX]{x1D714}}_{3}+k_{2}\widetilde{u}_{3}\unicode[STIX]{x1D6E4}=k_{2}\tilde{G}_{1}-k_{1}\tilde{G}_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle k_{1}U\frac{\text{d}^{2}\widetilde{u}_{3}}{\text{d}z^{2}}-k_{1}\widetilde{u}_{3}\frac{\text{d}\unicode[STIX]{x1D6E4}}{\text{d}z}-k_{1}Uk^{2}\widetilde{u}_{3}=-k_{1}\frac{\text{d}\tilde{G}_{1}}{\text{d}z}-k_{2}\frac{\text{d}\tilde{G}_{2}}{\text{d}z}+\text{i}k^{2}\tilde{G}_{3}, & \displaystyle\end{eqnarray}$$
which constitutes a set of two coupled ordinary differential equations. Finally, using (2.7) and
$\unicode[STIX]{x1D6E4}=0$
in the above equations, using
$U\approx U_{\infty }$
, and some straightforward but cumbersome algebraic manipulations, leads to
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}z}\unicode[STIX]{x1D708}_{t}\frac{\text{d}\widetilde{\unicode[STIX]{x1D714}}_{3}}{\text{d}z}-(\text{i}U_{\infty }k_{1}+\unicode[STIX]{x1D708}_{t}k^{2})\widetilde{\unicode[STIX]{x1D714}}_{3}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}}{\text{d}z^{2}}\unicode[STIX]{x1D708}_{t}\frac{\text{d}^{2}\widetilde{u}_{3}}{\text{d}z^{2}}-\frac{\text{d}}{\text{d }z}\left[(\text{i}k_{1}U_{\infty }+2k^{2}\unicode[STIX]{x1D708}_{t})\frac{\text{d}\widetilde{u}_{3}}{\text{d}z}\right]+\left(\text{i}k_{1}U_{\infty }+k^{2}\unicode[STIX]{x1D708}_{t}+\frac{\text{d}^{2}\unicode[STIX]{x1D708}_{t}}{\text{d}z^{2}}\right)k^{2}\widetilde{u}_{3}=0,\qquad & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x1D708}_{t}=\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{e}$
the total viscosity. For a classical developing boundary layer, boundary conditions at
$z=\infty$
correspond to
$\widetilde{\unicode[STIX]{x1D714}}_{3}(\infty )=0$
,
$\widetilde{u}_{3}(\infty )=0$
and
$\text{d}\widetilde{u}_{3}/\text{d}z|_{z=\infty }=0$
. Three more boundary conditions are required to uniquely determine solutions. They should be given at a location
$z$
which is sufficiently far from the wall for the linearized equations to hold. These additional conditions are not a priori known, and depend on the shape of the wall roughness and the nonlinear dynamics of the flow close to the wall.
2.4 Analytical solutions
Given an outer layer parametrization of
$\unicode[STIX]{x1D708}_{e}(z)$
, and appropriate boundary conditions, (2.14) and (2.15) can be solved. Here, however, the approach is further simplified by considering a constant eddy viscosity, for which solutions are analytically tractable. Although this is a rather strong assumption, it is not unreasonable. For instance, using DNS data by Schlatter & Örlü (Reference Schlatter and Örlü2010) for
$Re_{\unicode[STIX]{x1D703}}=4060$
, we find that
$0.06<\unicode[STIX]{x1D708}_{e}/(u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF})<0.07$
for
$0.2<z/\unicode[STIX]{x1D6FF}<0.6$
, though
$\unicode[STIX]{x1D708}_{e}/(u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF})$
drops to
$0.03$
at
$z/\unicode[STIX]{x1D6FF}=1$
.
When
$\unicode[STIX]{x1D708}_{t}=\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{e}$
is constant, (2.14), (2.15) simplify to
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}\widetilde{\unicode[STIX]{x1D714}}_{3}}{\text{d}z^{2}}-(\text{i}U_{\infty }k_{1}/\unicode[STIX]{x1D708}_{t}+k^{2})\widetilde{\unicode[STIX]{x1D714}}_{3}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{4}\widetilde{u}_{3}}{\text{d}z^{4}}-(\text{i}k_{1}U_{\infty }/\unicode[STIX]{x1D708}_{t}+2k^{2})\frac{\text{d}^{2}\widetilde{u}_{3}}{\text{d}z^{2}}+(\text{i}k_{1}U_{\infty }/\unicode[STIX]{x1D708}_{t}+k^{2})k^{2}\widetilde{u}_{3}=0. & \displaystyle\end{eqnarray}$$
The first equation has two characteristic roots, i.e.
$\pm K=\pm k(1+\text{i}Uk_{1}/k^{2}/\unicode[STIX]{x1D708}_{t})^{1/2}$
, or elaborated in its real and imaginary parts:
$$\begin{eqnarray}K=k\left[\sqrt{\frac{1}{2}\left(1+\left(\frac{U_{\infty }k_{1}}{\unicode[STIX]{x1D708}_{t}k^{2}}\right)^{2}\right)^{1/2}+\frac{1}{2}}+\text{i}\sqrt{\frac{1}{2}\left(1+\left(\frac{U_{\infty }k_{1}}{\unicode[STIX]{x1D708}_{t}k^{2}}\right)^{2}\right)^{1/2}-\frac{1}{2}}\right].\end{eqnarray}$$
The second equation has four characteristic roots, i.e.
$\pm k$
and
$\pm K$
. The root
$K$
depends on
$U_{\infty }k_{1}/(\unicode[STIX]{x1D708}_{t}k^{2})$
. Introducing
$\ell _{k}\triangleq 2\unicode[STIX]{x03C0}/k$
, it can be elaborated as
$$\begin{eqnarray}\frac{U_{\infty }k_{1}}{\unicode[STIX]{x1D708}_{t}k^{2}}=\frac{U_{\infty }\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D708}_{t}}\frac{\ell _{k}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}}\frac{k_{1}}{k}=\left[\sqrt{\frac{c_{f}}{2}}\frac{\unicode[STIX]{x1D708}_{e}}{u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}}+\frac{1}{Re}\right]^{-1}\frac{\ell _{k}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}}\frac{k_{1}}{k},\end{eqnarray}$$
with the Reynolds number
$Re\triangleq U_{\infty }\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$
and
$c_{f}$
the skin friction coefficient. For
$Re\rightarrow \infty$
, it is expected that
$\unicode[STIX]{x1D708}_{e}/(u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF})=O(1)$
, so that
$U_{\infty }k_{1}/(\unicode[STIX]{x1D708}_{t}k^{2})\sim c_{f}^{-1/2}(\ell _{k}/\unicode[STIX]{x1D6FF})(k_{1}/k)$
. Other interesting limits correspond to
$k_{1}/k\rightarrow 0$
and
$\ell _{k}/\unicode[STIX]{x1D6FF}\rightarrow 0$
. In both cases,
$U_{\infty }k_{1}/(\unicode[STIX]{x1D708}_{t}k^{2})\rightarrow 0$
and
$K\rightarrow k$
(independent of Reynolds number).
Using the boundary conditions at
$z=\infty$
, and presuming
$U_{\infty }k_{1}/k^{2}\neq 0$
, solutions correspond to
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D714}}_{3}=A\exp (-Kz)\quad \text{and}\quad \widetilde{u}_{3}=B\exp (-kz)+C\exp (-Kz),\end{eqnarray}$$
with
$A$
,
$B$
,
$C$
complex numbers that can only be determined if additional boundary conditions are known. For
$U_{\infty }k_{1}/k^{2}=0$
,
$K=k$
, and solutions correspond to
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D714}}_{3}=A\exp (-kz)\quad \text{and}\quad \widetilde{u}_{3}=Bz\exp (-kz)+C\exp (-kz).\end{eqnarray}$$
Moreover, for the limit of
$k_{1}/k\rightarrow 0$
or
$\ell _{k}/\unicode[STIX]{x1D6FF}\rightarrow 0$
, (2.20) converges to (2.21).
Finally, we note that for
$\unicode[STIX]{x1D708}_{t}=0$
, the potential-flow solution is recovered. Inserting
$\unicode[STIX]{x1D708}_{t}=0$
in (2.14), (2.15) leads to
$\tilde{\unicode[STIX]{x1D714}}_{3}=0$
, while
$\tilde{u} _{3}=A\exp (-kz)$
. Interestingly, for the case of spanwise constant roughness (
$k_{2}=0$
) and irrotational flow, Morgan & McKeon (Reference Morgan and McKeon2018) mention an equivalent solution.
3 Experimental verification
In order to evaluate the relations derived above, experiments by Vanderwel & Ganapathisubramani (Reference Vanderwel and Ganapathisubramani2015) are examined. These experiments consist of a series of particle image velocimetry (PIV) measurements in rough-wall boundary layers with Lego-brick roughness elements that are periodically organized with different spanwise spacings. An overview of the experiment and some mean velocity fields is shown in figure 1. The roughness structure is such that
$k_{1}=0$
, while spanwise spacings of the different experiments correspond to
$S/\unicode[STIX]{x1D6FF}=0.3$
,
$S/\unicode[STIX]{x1D6FF}=0.45$
,
$S/\unicode[STIX]{x1D6FF}=0.88$
,
$S/\unicode[STIX]{x1D6FF}=1.2$
,
$S/\unicode[STIX]{x1D6FF}=1.8$
, with
$S$
the wavelength and
$\unicode[STIX]{x1D6FF}$
the boundary layer thickness. Velocity measurements are obtained in a wall-normal–spanwise plane, which allows one to fully characterize the dispersive velocity field (given
$k_{1}=0$
). Full details of the experiment are found in Vanderwel & Ganapathisubramani (Reference Vanderwel and Ganapathisubramani2015).
Figure 1. Overview of the experiments by Vanderwel & Ganapathisubramani (Reference Vanderwel and Ganapathisubramani2015). Left to right: contours of streamwise velocity
$U/U_{\infty }$
shown in a spanwise–wall-normal plane obtained from the different experiments. Roughness elements are aligned in the streamwise direction and have a different spanwise spacing per experiment. The shape of the elements is outlined at the bottom of the pictures.
The PIV measurement planes in the experiments extended approximately 240 mm in the spanwise direction. The extent of these planes does not exactly correspond to an integer multiple of the spanwise roughness spacing (i.e.
$S=$
32 mm, 48 mm, 96 mm, 128 mm and 192 mm) in the experiments. Therefore, the outer portions of the plane are truncated, and the velocity and Reynolds stress measurements are resampled in spanwise direction so that an integer number of spanwise periods and grid points is retained. Linear interpolation is used for the resampling; keeping the resolution as close as possible to the original. For the different cases (
$S/\unicode[STIX]{x1D6FF}=0.3$
,
$0.45$
,
$0.88$
,
$1.2$
,
$1.8$
), this yields periods of 7, 4, 2, 1 and 1, respectively. These results are then averaged in the spanwise direction and used to obtain the dispersive stress fields as a function of wall-normal direction.
First of all, in figure 2 an overview is provided of the total stresses as a function of wall distance for the different experiments, as well as of the
$\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{1}^{\prime \prime }\rangle$
,
$\langle \overline{u}_{3}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle$
, and
$\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle$
dispersive stresses. Moreover, based on the maximum of the total stress, the skin friction coefficients for the various cases are also estimated. Figure 2 shows that the total stress depends non-monotonously on the spanwise roughness spacing, with the lowest skin friction at
$S/\unicode[STIX]{x1D6FF}=0.3$
, which increases to a maximum around
$S/\unicode[STIX]{x1D6FF}=0.88$
, and subsequently decreases again when
$S/\unicode[STIX]{x1D6FF}$
is further increased to
$1.8$
. Similar differences in skin friction as a function of the spanwise spacing were, for example, also observed by Hwang & Lee (Reference Hwang and Lee2018), Medjnoun et al. (Reference Medjnoun, Vanderwel and Ganapathisubramani2018).
Figure 2. (a) Total stress as function of wall distance, normalized by dynamic pressure. (b,c,d)
$\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{1}^{\prime \prime }\rangle$
,
$\langle \overline{u}_{3}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle$
, and
$-\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle$
respectively, as function of wall distance. Linetypes (——, – –, –
$\cdot$
,
$\cdots \,$
, –
$+$
) correspond to different spacings as labelled.
Further in figure 2(c–d), it is observed that the maximum magnitudes of the dispersive stresses (observed around
$z/\unicode[STIX]{x1D6FF}\approx 0.2$
) are reasonably correlated with the total skin friction, in particular for the cases with
$S/\unicode[STIX]{x1D6FF}\leqslant 0.88$
. For wider spacings, trends are less clear. Differences in dispersive stresses result from processes induced by the shape and spacing of the roughness elements as well as the flow in the inner layer of the boundary layer. They essentially serve as a boundary condition for the outer layer decay relations derived in § 2.
Finally, it is seen in figure 2(c,d) that the dispersive stresses roughly decay exponentially with increasing wall-normal distance, as suggested by the analysis in § 2. However, there is no clear single slope to be identified, as the stresses result from a sum over all the modes present in the flow; each decaying at their own rate. To this end, the decay should be analysed mode by mode (cf. below). It is further acknowledged that the decay saturates towards the top of the boundary layer, as measurement noise starts to play an important role in the very small remaining dispersive stress components. Exploring this error in detail is beyond the scope of the current study. However, we obtain a direct estimate of the error by looking at the free-stream level (at
$z/\unicode[STIX]{x1D6FF}\approx 1.1$
) of the dispersive stresses
$\langle \overline{u}^{\prime \prime }\overline{u}^{\prime \prime }\rangle$
and
$\langle \overline{w}^{\prime \prime }\overline{w}^{\prime \prime }\rangle$
, corresponding respectively to
$5\times 10^{-3}u_{\unicode[STIX]{x1D70F}}^{2}$
and
$10^{-3}u_{\unicode[STIX]{x1D70F}}^{2}$
. At this location, dispersive stresses are expected to be zero, so that the observed magnitudes correspond to the respective error levels. It is seen that the error on
$\langle \overline{u}^{\prime \prime }\overline{u}^{\prime \prime }\rangle$
is larger than that on
$\langle \overline{w}^{\prime \prime }\overline{w}^{\prime \prime }\rangle$
. This is consistent with the measurement set-up, where
$w$
is an in-plane component that can be estimated directly while
$u$
is the out-of-plane component that has to be reconstructed by combining the displacements observed by the two cameras in the PIV set-up (Vanderwel & Ganapathisubramani Reference Vanderwel and Ganapathisubramani2015). The ratio of the uncertainty in the out-of-plane component to the uncertainty of the in-plane components is approximately
$1/\tan \unicode[STIX]{x1D703}$
, where
$\unicode[STIX]{x1D703}$
is the included half-angle of the cameras (see Prasad Reference Prasad2000 for details). In the set-up of Vanderwel & Ganapathisubramani (Reference Vanderwel and Ganapathisubramani2015),
$\unicode[STIX]{x1D703}$
is 35 degrees, so that the uncertainty ratio between
$u$
and
$w$
components is 1.43, or approximately 2 when comparing
$\langle \overline{u}^{\prime \prime }\overline{u}^{\prime \prime }\rangle$
and
$\langle \overline{w}^{\prime \prime }\overline{w}^{\prime \prime }\rangle$
.
Now turning to the evaluation of the decay of dispersive stresses per mode, a Fourier transform in the spanwise direction on the dispersive velocity field
$\overline{\boldsymbol{u}}^{\prime \prime }$
is performed. The decay of the spectra of stream and wall-normal dispersive velocity components is the focal point, respectively, defined as
$S_{uu}(k_{2},z)=\overline{u}_{1}(k_{2},z)\overline{u}_{1}^{\ast }(k_{2},z)$
and
$S_{ww}(k_{2},z)=\overline{u}_{3}(k_{2},z)\overline{u}_{3}^{\ast }(k_{2},z)$
, where
$\ast$
is used for the complex conjugate. Given the relations (2.21) and (2.10),
$$\begin{eqnarray}\displaystyle & \displaystyle S_{uu}=D_{1}\exp (-2k_{2}z), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle S_{ww}=\exp (-2k_{2}z)(D_{2}+D_{3}z+D_{4}z^{2}), & \displaystyle\end{eqnarray}$$
is expected, where
$D_{1}$
–
$D_{4}$
are constants that can, for example, be found by matching the linear solution to the near-wall nonlinear solution at a location sufficiently far from the wall.
In figure 3, decay of
$S_{uu}$
and
$S_{ww}$
is shown as function of wall distance for the different cases (panels a–e). Results are shown on a semi-log scale, and up to four modes are shown, corresponding to those modes that contribute most to the
$\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle$
dispersive stress at
$z=0.2\unicode[STIX]{x1D6FF}$
. For
$S_{uu}$
the slopes
$-2k_{2}$
(corresponding to (3.1)) are also plotted for the different modes, while for
$S_{ww}$
least-squares fits of (3.2) over the range
$0.2<z/\unicode[STIX]{x1D6FF}<1.0$
are shown. Note that in figure 3(a–c) only two and three modes are shown, as other contributing modes fall within the noise level of the measurements. Similar to before, a dynamic range of two to three decades in the spectra is observed, but for modes with less energy content, the dynamic range can be significantly lower (see, for example, mode
$k\unicode[STIX]{x1D6FF}/(2\unicode[STIX]{x03C0})=5.1$
in figure 3
e). In order to visually illustrate the noise level of the measurements relative to the magnitude of the different modes, a marker on each mode indicating the level
$10^{-3}u_{\unicode[STIX]{x1D70F}}^{2}$
relative to the scaling used for the modes is included. Note that this represents the estimated error level for
$S_{ww}$
, while the error on
$S_{uu}$
is two to five times higher (cf. discussion above).
Figure 3. Decay of Fourier modes of streamwise
$S_{uu}$
and normal
$S_{ww}$
dispersive components as function of wall distance
$z/\unicode[STIX]{x1D6FF}$
. (a)
$S/\unicode[STIX]{x1D6FF}=0.3$
(b)
$S/\unicode[STIX]{x1D6FF}=0.45$
; (c)
$S/\unicode[STIX]{x1D6FF}=0.88$
; (d)
$S/\unicode[STIX]{x1D6FF}=1.2$
; (e)
$S/\unicode[STIX]{x1D6FF}=1.8$
. (—— ▴, – – ▪, –
$\cdot$
●,
$\cdots \,$
♦): up to four Fourier modes with the highest contribution to the dispersive shear component
$\langle \overline{u}_{1}^{\prime \prime }\overline{u}_{3}^{\prime \prime }\rangle$
; line types are ordered according to the magnitude of the contributing mode. Lines are shifted by half a decade for visibility. Grey line in streamwise plots: slope corresponding to
$\exp (-2k_{2}z)$
. Grey line in normal plots: least-squares fit of
$\exp (-2k_{2}z)(D_{2}+D_{3}z+D_{4}z^{2})$
to the data in the range
$0.2<z<1.0$
. (♦, ▪, ●, ♦): markers on the different Fourier modes are inserted at level
$10^{-3}u_{\unicode[STIX]{x1D70F}}^{2}/S_{uu}(k,0.2)$
and
$10^{-3}u_{\unicode[STIX]{x1D70F}}^{2}/S_{ww}(k,0.2)$
, respectively.
Looking at figure 3, it is observed that the fits of
$S_{ww}$
match the data very well between
$z/\unicode[STIX]{x1D6FF}=0.2$
and
$z/\unicode[STIX]{x1D6FF}=0.6$
for all cases and modes. At higher wall distances, the measurements are saturated with noise, such that no meaningful comparison can be performed. Considering the matching of
$\exp (-2k_{2}z)$
to
$S_{uu}$
in figure 3, the picture is more diverse. For the first two cases (panels a,b), a good agreement is found between
$z/\unicode[STIX]{x1D6FF}=0.2$
and
$z/\unicode[STIX]{x1D6FF}=0.3$
to 0.4. Beyond that, the noise level starts to dominate the measurements. For the other cases (panels c,d), an adequate matching for higher modes is generally found, i.e. in particular for
$k\unicode[STIX]{x1D6FF}/(2\unicode[STIX]{x03C0})=\unicode[STIX]{x1D6FF}/\ell _{k}>2$
. For lower modes, the experimental slopes do not correspond well with the analytical slope, and are typically lower in absolute value.
4 Discussion
Given the strong assumptions made in the development of analytical solutions in § 2.4, the correspondence with experiments is good, in particular when considering
$S_{ww}$
. The results for
$S_{uu}$
are mixed, and differences could be attributed to nonlinear effects, the lack of streamwise mean-flow homogeneity, or using
$\unicode[STIX]{x1D6E4}=0$
in the linearisation, as further discussed below.
First, when considering the quality of fits in § 3, nonlinear effects can play a role, in particular since modes that are poorly predicted tend to occur mainly for
$S/\unicode[STIX]{x1D6FF}=0.88$
,
$1.2$
and
$1.8$
, which have the strongest dispersive shear stresses relative to the friction velocity (see figure 2). Values for these spacings correspond, respectively, to 30 %, 18 % and 11 %, versus 9 % and 1 % for
$S/\unicode[STIX]{x1D6FF}=0.45$
, and
$0.3$
. Nevertheless, since also the former values remain relatively small, and since
$S_{ww}$
fits the data reasonably well, other effects (discussed below) are seemingly more probable. Furthermore, contributions from
$\overline{u}^{\prime \prime }\overline{u}^{\prime \prime }$
, which are much larger relative to the friction velocity (see figure 2
b), do not play a role in the nonlinear equations (2.3) when
$k_{1}=0$
.
A further assumption in the derivation of (2.14), (2.15) is that the streamwise evolution of mean velocity components can be neglected in (2.1) and (2.3). For
$k_{1}\rightarrow 0$
, this assumption does not hold. Consequently, the limit
$k_{1}/k\rightarrow 0$
in (2.18) is not viable, and only
$\ell _{k}/\unicode[STIX]{x1D6FF}\rightarrow 0$
(and thus,
$k\unicode[STIX]{x1D6FF}\rightarrow \infty$
) may be expected to lead to (2.21). The picture in figure 3 above is consistent with that, showing a good match between theory and results for
$\unicode[STIX]{x1D6FF}/\ell _{k}>2$
. This is also in agreement with results from Vanderwel & Ganapathisubramani (Reference Vanderwel and Ganapathisubramani2015) and Hwang & Lee (Reference Hwang and Lee2018) that show that the excitation of secondary motions is most effective around a spanwise roughness spacing of
$S/\unicode[STIX]{x1D6FF}={\mathcal{O}}(1)$
, but decreases drastically when
$S$
is decreased.
Third, also
$\unicode[STIX]{x1D6E4}\approx 0$
and
$U\approx U_{\infty }$
are strong simplifications in the derivation of (2.14), (2.15): for example, around
$z/\unicode[STIX]{x1D6FF}=0.2$
, the velocity deficit is already approximately 30 % of the free-stream velocity. Interestingly, for
$k_{1}/k\rightarrow 0$
, the effect of
$\unicode[STIX]{x1D6E4}$
in (2.13) disappears, so that (2.15) and solutions for
$\tilde{u} _{3}$
remain the same when
$\unicode[STIX]{x1D6E4}\neq 0$
. This is not the case for (2.13), i.e.
$\unicode[STIX]{x1D6E4}\neq 0$
leads to an additional term
$\text{i}k_{2}\tilde{u} _{3}\unicode[STIX]{x1D6E4}$
in (2.14). Thus related solutions for
$\unicode[STIX]{x1D714}_{3}$
and
$u_{1}$
may depend on
$u_{3}$
and
$\unicode[STIX]{x1D6E4}$
. For
$\ell _{k}/\unicode[STIX]{x1D6FF}\rightarrow 0$
(
$k\rightarrow \infty$
), the relative importance of the additional term
$\text{i}k_{2}\tilde{u} _{3}\unicode[STIX]{x1D6E4}$
decreases in (2.14), since other terms scale with
$k^{2}$
. This remains consistent with observations in § 3, that
$S_{uu}$
matches data better when
$\ell _{k}/\unicode[STIX]{x1D6FF}$
is sufficiently small. It should be noted that for
$\unicode[STIX]{x1D6E4}\neq 0$
, the dispersive eddy viscosity
$\unicode[STIX]{x1D708}_{e}^{\prime \prime }$
and the last term on the right-hand side of (2.7) may also become important; finding exact (linear) expressions for this term is however akin to the classical turbulence closure problem, and not further considered here.
The current analytical model may shed some further light on the characterization of roughness length scales in rough boundary layers. Whereas the classical roughness ‘height’ is directly associated with the skin friction drag, the horizontal roughness length
$\ell _{k}$
dictates how fast dispersive flow perturbations decay in the outer layer, supporting the notion of spanwise homogeneous outer flow behavior that is independent of the near-wall flow when
$\ell _{k}$
is sufficiently small. Current findings may also be of interest for the development of rough-wall stress conditions for simulations, in particular in situations with multi-scale roughness (for example, prevalent in the atmospheric boundary layer) in which only part of the roughness is resolved by the mesh (Anderson & Meneveau Reference Anderson and Meneveau2011).
5 Summary
A framework is presented to study the decay of dispersive stresses in the outer layer of a rough-wall boundary layer by using a linearization of the Navier–Stokes equations. By formulating the problem in Fourier space, this leads to two coupled ordinary differential equations per horizontal wavevector. These equations require the unperturbed background velocity
$U(z)$
and eddy viscosity
$\unicode[STIX]{x1D708}(t)$
as input, and are expected to be exact to first order when
$\unicode[STIX]{x1D6E4}\ll 1$
, as is the case near the top of the boundary layer. A further approximation that uses
$\unicode[STIX]{x1D6E4}=0$
, and assumes a constant eddy viscosity, allows for solutions that are analytically tractable. These solutions were compared to the experimental data from Vanderwel & Ganapathisubramani (Reference Vanderwel and Ganapathisubramani2015), showing a reasonable agreement with the measurements, given the assumptions that were made to obtain the analytical model.
In the future, it will be of interest to investigate more involved solutions of (2.14), (2.15) using detailed parametrizations of
$\unicode[STIX]{x1D708}_{e}(z)$
in the outer layer of a boundary layer, or by directly solving the coupled system (2.12), (2.13) using an additional parametrization of
$\unicode[STIX]{x1D6E4}(z)$
and
$U(z)$
. In this case, analytically tractable solutions may no longer exist, but numerical solutions should be obtained without much complication. In this context, more extensive comparison with data, in particular including also roughness elements with
$k_{1}\neq 0$
, is also relevant.
Acknowledgements
J.M. acknowledges support from the Research Foundation – Flanders (FWO grant no. V4.255.17N). B.G. acknowledges financial support from the Engineering and Physical Sciences Research Council of the United Kingdom (EPSRC grant ref. nos EP/R034370/1 and EP/P021476/1).
