1. Introduction
Dielectrophoresis is defined as the motion of matter caused by polarisation effects in a non-uniform electric field (Pohl Reference Pohl1958, Reference Pohl1978). The use of dielectrophoresis forces to stimulate fluid motion is of interest in optics due to potential applications in the development of novel switchable liquid optical devices (Brown et al. Reference Brown, Wells, Newton and McHale2009). In particular, the motivation for the present study relates to tracking the motion of an oil–air interface arising from switching on an electric potential at the base of the oil film, as studied experimentally for a set of interdigitated electrodes at the base of thin film of hexadecane in Brown et al. (Reference Brown, Wells, Newton and McHale2009). This ‘switch on problem’ has been further studied in relation to the dynamics of thin sessile drops by Corson et al. (Reference Corson, Mottram, Duffy, Wilson, Tsakonas and Brown2016), and related steady-state analysis of such drops in both an experimental and theoretical setting is given by Corson et al. (Reference Corson, Tsakonas, Duffy, Mottram, Sage, Brown and Wilson2014) and Tsakonas et al. (Reference Tsakonas, Corson, Sage and Brown2014). We consider a general multiphysics model describing the dynamics of an interface between two viscous fluids in a periodic half-plane, under the influence of dielectrophoresis forces. The time-dependent interface position is given as the solution of a so-called transmission problem for a Stokes flow with a kinematic boundary condition along the interface. We enforce continuity conditions on the stress field at the interface by solving an associated transmission problem for the Laplace equation for the normal and tangential derivatives of the potential on the interface (Chappell Reference Chappell2015).
Related work on the simulation of electrified fluid droplets and liquid bridges has been carried out using a range of techniques including asymptotic approaches (Yeo & Chang Reference Yeo and Chang2006), level set methods (Walker & Shapiro Reference Walker and Shapiro2006), finite element approaches for coupled fluid flow and dynamic interface models (Falk & Walker Reference Falk and Walker2013) and boundary integral methods for coupled potential and dynamic interface problems (Volkov, Papageorgiou & Petropoulos Reference Volkov, Papageorgiou and Petropoulos2005; Sorgentone, Tornberg & Vlahovska Reference Sorgentone, Tornberg and Vlahovska2019). A number of researchers have proposed nonlinear long-wave asymptotic theories for two-fluid systems, where one fluid region is assumed to be slender and the other region has an electric field applied; see, for example Papageorgiou, Maldarelli & Rumschitzki (Reference Papageorgiou, Maldarelli and Rumschitzki1990) and Kalogirou et al. (Reference Kalogirou, Cîmpeanu, Keaveny and Papageorgiou2016). In addition, leaky dielectric two-fluid systems, where there is the possibility of free charge conduction between the fluids, have been studied in the long-wave limit (Pease & Russel Reference Pease and Russel2002; Shankar & Sharma Reference Shankar and Sharma2004) as well as more generally (Papageorgiou & Petropoulos Reference Papageorgiou and Petropoulos2004). The presence of non-zero conductivity has been found to have a significant effect on the interface stability, giving rise to pattern formation (Craster & Matar Reference Craster and Matar2005; Wang & Papageorgiou Reference Wang and Papageorgiou2016). More recent studies have considered the application of electric fields on perfectly conducting liquid films to control travelling wave flows on vertical fibres (Ding & Willis Reference Ding and Willis2019) or to suppress dripping from inverted substrates (Tomlin, Cîmpeanu & Papageorgiou Reference Tomlin, Cîmpeanu and Papageorgiou2020).
A comprehensive summary of the literature on electrified film flows can be found in the recent review article (Papageorgiou Reference Papageorgiou2019). Of particular relevance to the study here is the simplified analysis of Brown, McHale & Mottram (Reference Brown, McHale and Mottram2011) and the dynamic thin-film asymptotic models proposed by Tseluiko & Papageorgiou (Reference Tseluiko and Papageorgiou2006, Reference Tseluiko and Papageorgiou2007) and Tseluiko et al. (Reference Tseluiko, Blyth, Papageorgiou and Vanden-Broeck2008, Reference Tseluiko, Blyth, Papageorgiou and Vanden-Broeck2010). In the former, a theoretical treatment of the static wrinkle formation observed experimentally in Brown et al. (Reference Brown, Wells, Newton and McHale2009) is given, in which both the applied potential at the film base and the surface deformation are assumed to be steady sinusoids, thereby allowing analytical expressions to be obtained in the steady-state case. In the latter, a perfectly conducting viscous film in contact with a solid surface on one side and a semi-infinite passive dielectric medium on the other side is considered. A rigorous study of a thin-film asymptotic model showing the global boundedness of positive periodic smooth solutions for a film on a horizontal plate in the presence of a vertical electric field is given in Tseluiko & Papageorgiou (Reference Tseluiko and Papageorgiou2007). The effect of a normal electric field on the gravity driven flow of a thin viscous film down an inclined plane is considered in Tseluiko & Papageorgiou (Reference Tseluiko and Papageorgiou2006) and parameter ranges that support travelling wave solutions and chaotic interfacial oscillations are identified. This study is then extended to model flow down an inclined plane with periodic indentations in Tseluiko et al. (Reference Tseluiko, Blyth, Papageorgiou and Vanden-Broeck2008) and flow in the presence of finite electrodes in Tseluiko et al. (Reference Tseluiko, Blyth, Papageorgiou and Vanden-Broeck2010). Here, the thin-film asymptotic model for a viscous film flow over a step on an inclined plane is compared to a Stokes flow based boundary element model.
In this work, we consider both asymptotic and boundary integral techniques to study the motion of a thin viscous film under the influence of dielectrophoresis forces arising from a spatially periodic potential applied at its base, and apply these formulations to the experimental results of Brown et al. (Reference Brown, Wells, Newton and McHale2009) wherein the potential arises from an array of interdigitated electrodes. Thereby, we provide both fully numerical and reduced descriptions that allow consideration of the full film surface dynamics for arbitrary (periodic) electrode arrangement, and which are valid across a range of film thicknesses. We note that the dynamic problem considered here has received little attention within the experimental community until relatively recently (see, for example, Saxena Reference Saxena2017) because accurately tracking the dynamics of thin films through time is rather more challenging than measuring the static steady-state profile. The models we provide can be used to study the influence of various experimentally controllable parameters on the growth rates of the film disturbance amplitude as well as the evolution of the interface position itself, from which we envisage useful future contribution to the design of liquid optical devices.
The boundary integral formulation that we employ comprises the coupling, via a temporally discretised kinematic boundary condition, of that for the electrostatic problem (considered in Chappell Reference Chappell2015) and for the Stokes flow (adapted from Pozrikidis Reference Pozrikidis1992). A commonly cited advantage of boundary integral methods is the reduction in dimensionality (by one) to the boundary of the domain being studied. Here, we go one step further and reduce our study to the interfacial part of the boundary only by making use of the Green's functions for the Laplace and Stokes flow problems in a periodic half-space. There are three further major reasons that a boundary integral approach is favourable here. Firstly, the relevant Green's functions are available in a closed form (Newhouse & Pozrikidis Reference Newhouse and Pozrikidis1990; Pozrikidis Reference Pozrikidis1992) making it relatively simple to implement a boundary integral method (compared to, for example, Volkov et al. (Reference Volkov, Papageorgiou and Petropoulos2005), where the periodic Green's function must be approximated via fast summation methods). Secondly, the infinite domains are dealt with intrinsically in the boundary integral formulation, both along and perpendicular to the direction of periodicity. This means that the imposition of artificial boundaries, as would be required for finite element and finite difference approaches, is not necessary. Thirdly, the dynamic interface is dealt with very naturally by the boundary integral method where the updated position of the interface curve becomes the new region of integration after each time step and the re-meshing effort is therefore very simple in comparison to re-meshing both fluid domains at each time step for a finite difference or finite element method.
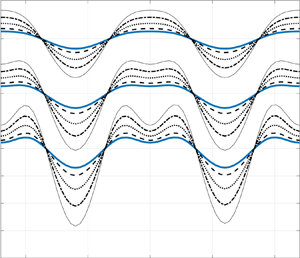
While the boundary integral method is a natural choice for numerically solving the full problem, the complexity of the model at hand means that we are essentially solving three coupled partial differential equations (PDEs) including the kinematic boundary condition for describing the interface motion. In order to simplify the model and permit some analytical progress, we concentrate on an oil–air interface, and derive two asymptotic reductions of the model, which both apply under the assumption of an asymptotically thin viscous film with a fluid of significantly lower viscosity surrounding it. The first model simplifies the fluid flow problem to one described by a single thin-film PDE for the interface motion (see, e.g. Oron, Davis & Bankoff (Reference Oron, Davis and Bankoff1997) for an excellent review of thin-film approaches), coupled to the electrostatic problem via an inhomogeneous forcing term that is obtained via the Laplace equation boundary integral model described above. Subsequently, we go one step further and consider the corresponding asymptotic limit for the potential problem, thereby obtaining a formula for the electrostatic forcing in terms of the (known) applied potential at the electrodes. By comparison with numerical solutions of the full model in suitable parameter regimes, we investigate the validity of these approximations. Finally, we present results for a parameter choice with practical relevance for the experiments of Brown et al. (Reference Brown, Wells, Newton and McHale2009).
The paper is structured as follows: in the next section we outline the governing PDEs describing the motion of a thin viscous film due to dielectrophoresis forces. In § 3 we reformulate our PDE model as a set of boundary integral equations, making use of the periodic half-space Green's functions for the Laplace and Stokes flow models to reduce the formulation to one posed on the interfacial part of the solution domain only. Section 4 provides two asymptotic reductions of the PDE formulation in § 2, which are both derived under the assumption that the height of the periodic viscous film domain is small in comparison to the period. In § 5, the discretisation methods employed for the models presented in §§ 3 and 4 are detailed, before applying them to perform a series of numerical experiments in § 6.
2. Governing partial differential equations
Let ![]() $H=\{(x,y)\in \mathbb {R}^2|y>0\}$ and assume
$H=\{(x,y)\in \mathbb {R}^2|y>0\}$ and assume ![]() $h:\mathbb {R}\times \mathbb {R}_{\geq 0}\rightarrow \mathbb {R}$ defines a dynamic interface at
$h:\mathbb {R}\times \mathbb {R}_{\geq 0}\rightarrow \mathbb {R}$ defines a dynamic interface at ![]() $y=h(x,t)$ dividing
$y=h(x,t)$ dividing ![]() $H$ into
$H$ into ![]() $\varOmega _1=\{(x,y)\in H|y < h(x,t)\}$ and
$\varOmega _1=\{(x,y)\in H|y < h(x,t)\}$ and ![]() $\varOmega _2=\{(x,y)\in H|y>h(x,t)\}$. Here,
$\varOmega _2=\{(x,y)\in H|y>h(x,t)\}$. Here, ![]() $\varOmega _1$ represents a thin film of viscous fluid with boundary
$\varOmega _1$ represents a thin film of viscous fluid with boundary ![]() $\varGamma _1=\varGamma _I\cup \varGamma _0$, where
$\varGamma _1=\varGamma _I\cup \varGamma _0$, where ![]() $\varGamma _I=\{(x,y)\in \mathbb {R}^2|y=h(x,t)\}$ and
$\varGamma _I=\{(x,y)\in \mathbb {R}^2|y=h(x,t)\}$ and ![]() $\varGamma _0=\{(x,y)\in \mathbb {R}^2|y=0\}$. The domain
$\varGamma _0=\{(x,y)\in \mathbb {R}^2|y=0\}$. The domain ![]() $\varOmega _2$ represents the surrounding fluid and has boundary
$\varOmega _2$ represents the surrounding fluid and has boundary ![]() $\varGamma _2=\varGamma _I$. The problem setup is shown in figure 1. We will assume that
$\varGamma _2=\varGamma _I$. The problem setup is shown in figure 1. We will assume that ![]() $h$ is positive and
$h$ is positive and ![]() $C^{k}$ for some
$C^{k}$ for some ![]() $k\geq 2$. We consider a multiphysics model comprising an electrostatic problem for the potential
$k\geq 2$. We consider a multiphysics model comprising an electrostatic problem for the potential ![]() $\phi _{\alpha }$,
$\phi _{\alpha }$, ![]() $\alpha =1,2$ coupled to a fluid flow
$\alpha =1,2$ coupled to a fluid flow ![]() $\boldsymbol {u}_{\alpha }=(u_{\alpha },\ v_{\alpha })^{\textrm {T}}$, which drives the motion of the interface governed by a kinematic boundary condition.
$\boldsymbol {u}_{\alpha }=(u_{\alpha },\ v_{\alpha })^{\textrm {T}}$, which drives the motion of the interface governed by a kinematic boundary condition.

Figure 1. A ![]() $2L$-periodic wrinkle of a viscous film
$2L$-periodic wrinkle of a viscous film ![]() $\varOmega _1$ beneath a semi-infinite fluid layer
$\varOmega _1$ beneath a semi-infinite fluid layer ![]() $\varOmega _2$. The two fluids meet at the interface
$\varOmega _2$. The two fluids meet at the interface ![]() $\varGamma _I$, whose motion is driven by an imposed potential.
$\varGamma _I$, whose motion is driven by an imposed potential.
The problem for the electric potential is given by
 \begin{gather} \left[\epsilon_{\alpha} \frac{\partial\phi_{\alpha}}{\partial \boldsymbol{\nu}}\right]_{\alpha=1}^2=0 \quad \mathrm{on}\ \varGamma_I. \end{gather}
\begin{gather} \left[\epsilon_{\alpha} \frac{\partial\phi_{\alpha}}{\partial \boldsymbol{\nu}}\right]_{\alpha=1}^2=0 \quad \mathrm{on}\ \varGamma_I. \end{gather}
Here, ![]() $\epsilon _{\alpha }$ is the dielectric constant in
$\epsilon _{\alpha }$ is the dielectric constant in ![]() $\varOmega _{\alpha }$,
$\varOmega _{\alpha }$, ![]() $\partial /\partial \boldsymbol {\nu }$ denotes the derivative in the direction of the unit normal vector
$\partial /\partial \boldsymbol {\nu }$ denotes the derivative in the direction of the unit normal vector ![]() $\boldsymbol {\nu }=(\nu _x,\nu _y)^{\textrm {T}}$ pointing out of
$\boldsymbol {\nu }=(\nu _x,\nu _y)^{\textrm {T}}$ pointing out of ![]() $\varOmega _1$ and
$\varOmega _1$ and ![]() $[\cdot ]_{\alpha =1}^2$ denotes the jump between domains
$[\cdot ]_{\alpha =1}^2$ denotes the jump between domains ![]() $\varOmega _1$ and
$\varOmega _1$ and ![]() $\varOmega _2$. In addition we prescribe the boundary conditions
$\varOmega _2$. In addition we prescribe the boundary conditions
Here, ![]() $f(x)$ is a
$f(x)$ is a ![]() $2L$-periodic function representing an input voltage through an array of electrodes applied at
$2L$-periodic function representing an input voltage through an array of electrodes applied at ![]() $y=0$, giving rise to a potential in
$y=0$, giving rise to a potential in ![]() $\varOmega _{\alpha }$ (
$\varOmega _{\alpha }$ (![]() $\alpha =1,2$) and, in particular, along
$\alpha =1,2$) and, in particular, along ![]() $\varGamma _I$, this henceforth being denoted by
$\varGamma _I$, this henceforth being denoted by ![]() $\phi$. We additionally assume that the induced potential decays at infinity as described by (2.5). In general, the input voltage will vary with time (to model switchable liquid optical devices, for example), imparting quasi-time-dependence in the above electrostatic model; however, herein, we consider only time-independent choices for
$\phi$. We additionally assume that the induced potential decays at infinity as described by (2.5). In general, the input voltage will vary with time (to model switchable liquid optical devices, for example), imparting quasi-time-dependence in the above electrostatic model; however, herein, we consider only time-independent choices for ![]() $f$, with time-dependence imparted to the flow problem in the sense of ‘switching on’ the input voltage only driving the evolution of the interface
$f$, with time-dependence imparted to the flow problem in the sense of ‘switching on’ the input voltage only driving the evolution of the interface ![]() $\varGamma _I$ from rest. We further assume that the function
$\varGamma _I$ from rest. We further assume that the function ![]() $h(x,t)$ describing the interface
$h(x,t)$ describing the interface ![]() $\varGamma _I$ is
$\varGamma _I$ is ![]() $2L$-periodic in space, thereby reducing the problem to the study of a single periodic cell of
$2L$-periodic in space, thereby reducing the problem to the study of a single periodic cell of ![]() $H$ with
$H$ with ![]() $-L\leq x < L$. This periodicity is physically reasonable, since in relevant experiments, the potential is typically applied by a regularly spaced array of electrodes – see § 6.2.
$-L\leq x < L$. This periodicity is physically reasonable, since in relevant experiments, the potential is typically applied by a regularly spaced array of electrodes – see § 6.2.
The fluid is assumed to satisfy the following linear creeping-flow model
Here, ![]() $\mu _{\alpha }$ is the fluid viscosity and
$\mu _{\alpha }$ is the fluid viscosity and ![]() $p_{\alpha }$ is the fluid pressure in
$p_{\alpha }$ is the fluid pressure in ![]() $\varOmega _{\alpha }$. In addition, at the interface
$\varOmega _{\alpha }$. In addition, at the interface ![]() $\varGamma _I$ we have denoted the unit tangent vector as
$\varGamma _I$ we have denoted the unit tangent vector as ![]() $\boldsymbol {\tau }$, the curvature as
$\boldsymbol {\tau }$, the curvature as ![]() $\kappa$ and the surface tension as
$\kappa$ and the surface tension as ![]() $\gamma$. These fluid equations are connected to the electric potential problem through the stress tensor
$\gamma$. These fluid equations are connected to the electric potential problem through the stress tensor ![]() $\boldsymbol {\sigma }^{\alpha }=\boldsymbol {\sigma }_{v}^{\alpha }+\boldsymbol {\sigma }_{M}^{\alpha }$, wherein
$\boldsymbol {\sigma }^{\alpha }=\boldsymbol {\sigma }_{v}^{\alpha }+\boldsymbol {\sigma }_{M}^{\alpha }$, wherein ![]() $\boldsymbol {\sigma }_v^{\alpha }$ denotes the standard stress tensor for a viscous flow and
$\boldsymbol {\sigma }_v^{\alpha }$ denotes the standard stress tensor for a viscous flow and ![]() $\boldsymbol {\sigma }_M^{\alpha }$ denotes the Maxwell stress arising due to the applied electric field; namely
$\boldsymbol {\sigma }_M^{\alpha }$ denotes the Maxwell stress arising due to the applied electric field; namely
where ![]() $\boldsymbol{\mathsf{I}}$ is the
$\boldsymbol{\mathsf{I}}$ is the ![]() $2\times 2$ identity matrix and
$2\times 2$ identity matrix and ![]() $\epsilon _0$ is the permittivity of free space.
$\epsilon _0$ is the permittivity of free space.
We also prescribe the following boundary conditions
describing no slip of the viscous fluid at ![]() $y=0$, no flow in the far field and a kinematic condition describing the interfacial evolution, respectively.
$y=0$, no flow in the far field and a kinematic condition describing the interfacial evolution, respectively.
In what follows, we consider the evolution of the interface ![]() $h(x,t)$ under the action of the applied voltage, from initial data comprising
$h(x,t)$ under the action of the applied voltage, from initial data comprising ![]() $h(x,0)=h_0>0$,
$h(x,0)=h_0>0$, ![]() $\boldsymbol {u}_{\alpha }(\boldsymbol {x},0)=\boldsymbol {0}$.
$\boldsymbol {u}_{\alpha }(\boldsymbol {x},0)=\boldsymbol {0}$.
3. Boundary integral formulation
In this section we recast the problem (2.2)–(2.14) described in the previous section as a set of boundary integral equations on a single periodic section of the interface ![]() $\varGamma _I$. We highlight that the boundary integral model for the electrostatic problem is taken from Chappell (Reference Chappell2015) (note that therein, only electrostatics are considered) and that for the Stokes flow is adapted from those summarised in Pozrikidis (Reference Pozrikidis1992); in the present work these two models are coupled together via a (temporally discretised) kinematic boundary condition.
$\varGamma _I$. We highlight that the boundary integral model for the electrostatic problem is taken from Chappell (Reference Chappell2015) (note that therein, only electrostatics are considered) and that for the Stokes flow is adapted from those summarised in Pozrikidis (Reference Pozrikidis1992); in the present work these two models are coupled together via a (temporally discretised) kinematic boundary condition.
3.1. Green's functions and the periodic half-plane potential
A key ingredient in our boundary integral formulation will be the ![]() $2L$-periodic (in
$2L$-periodic (in ![]() $x$) half-plane Green's functions for the Laplace and Stokes equations. For the Laplace equation we have the following expression for the
$x$) half-plane Green's functions for the Laplace and Stokes equations. For the Laplace equation we have the following expression for the ![]() $2L$-periodic Green's function (see, for example, Linton Reference Linton1999)
$2L$-periodic Green's function (see, for example, Linton Reference Linton1999)
where ![]() $\boldsymbol {x}=(x,y)\in H$,
$\boldsymbol {x}=(x,y)\in H$, ![]() $z=x+\textrm {i}y$,
$z=x+\textrm {i}y$, ![]() $\boldsymbol {x}_0=(x_0,y_0)\in \overline{H}$ and
$\boldsymbol {x}_0=(x_0,y_0)\in \overline{H}$ and ![]() $z_0=x_0+\textrm {i}y_0$. The over-bar notation is used to represent the closure of the set, here meaning the union of
$z_0=x_0+\textrm {i}y_0$. The over-bar notation is used to represent the closure of the set, here meaning the union of ![]() $H$ and its boundary
$H$ and its boundary ![]() $y=0$. It follows from the method of images that the periodic Green's function on
$y=0$. It follows from the method of images that the periodic Green's function on ![]() $H$ may be written
$H$ may be written
where ![]() $\boldsymbol {x}_0'=(x_0,-y_0)$ is the mirror image of
$\boldsymbol {x}_0'=(x_0,-y_0)$ is the mirror image of ![]() $\boldsymbol {x}_0$ in
$\boldsymbol {x}_0$ in ![]() $\varGamma _0$.
$\varGamma _0$.
We also consider the problem (2.1)–(2.5) in the absence of an interface, which will be useful for the boundary integral reformulation of the potential problem introduced in the following section. In this case the problem reduces to the Laplace equation on ![]() $\varOmega _1=H$, with boundary conditions comprising
$\varOmega _1=H$, with boundary conditions comprising ![]() $2L$-periodic Dirichlet data
$2L$-periodic Dirichlet data ![]() $f$ along
$f$ along ![]() $\varGamma _0$ (2.4), and (2.5). Using Green's representation formula for
$\varGamma _0$ (2.4), and (2.5). Using Green's representation formula for ![]() $\boldsymbol {x}\in H$, the solution of this half-plane problem
$\boldsymbol {x}\in H$, the solution of this half-plane problem ![]() $\phi ^H$ may be expressed in the form (Chappell Reference Chappell2015)
$\phi ^H$ may be expressed in the form (Chappell Reference Chappell2015)
In the sequel we make use of the following reduced notation ![]() $A:=G(\boldsymbol {x},\boldsymbol {x}_0)$ and
$A:=G(\boldsymbol {x},\boldsymbol {x}_0)$ and ![]() $A':=G(\boldsymbol {x},\boldsymbol {x}'_0)$. For the Stokes equation, the
$A':=G(\boldsymbol {x},\boldsymbol {x}'_0)$. For the Stokes equation, the ![]() $2L$-periodic Green's function is given by the matrix (Pozrikidis Reference Pozrikidis1992)
$2L$-periodic Green's function is given by the matrix (Pozrikidis Reference Pozrikidis1992)
 \begin{equation} \boldsymbol{\mathsf{G}}(\boldsymbol{x},\boldsymbol{x}_0)= \left[\begin{matrix} -A-\lambda(y-y_0)A_y-\dfrac{1}{2{\rm \pi}} & \lambda(y-y_0)A_x\\ \lambda(y-y_0)A_x & -A+\lambda(y-y_0)A_y \end{matrix}\right], \end{equation}
\begin{equation} \boldsymbol{\mathsf{G}}(\boldsymbol{x},\boldsymbol{x}_0)= \left[\begin{matrix} -A-\lambda(y-y_0)A_y-\dfrac{1}{2{\rm \pi}} & \lambda(y-y_0)A_x\\ \lambda(y-y_0)A_x & -A+\lambda(y-y_0)A_y \end{matrix}\right], \end{equation}
where the wavenumber ![]() $\lambda ={\rm \pi} /L$ and the subscripts
$\lambda ={\rm \pi} /L$ and the subscripts ![]() $x$ and
$x$ and ![]() $y$ denote partial derivatives with respect to the variables
$y$ denote partial derivatives with respect to the variables ![]() $\lambda x$ and
$\lambda x$ and ![]() $\lambda y$. In this case, the periodic Green's function on the half-space
$\lambda y$. In this case, the periodic Green's function on the half-space ![]() $H$ is given by (Pozrikidis Reference Pozrikidis1992)
$H$ is given by (Pozrikidis Reference Pozrikidis1992)
where
 \begin{equation} \boldsymbol{\mathsf{G}}^D(\boldsymbol{x},\boldsymbol{x}_0')= \left[\begin{matrix} A'_{yy} & A'_{xy}\\ -A'_{xy} & A'_{yy}\end{matrix}\right] \end{equation}
\begin{equation} \boldsymbol{\mathsf{G}}^D(\boldsymbol{x},\boldsymbol{x}_0')= \left[\begin{matrix} A'_{yy} & A'_{xy}\\ -A'_{xy} & A'_{yy}\end{matrix}\right] \end{equation}and
 \begin{equation} \boldsymbol{\mathsf{G}}^S\left(\boldsymbol{x},\boldsymbol{x}'_0\right)= \left[\begin{matrix} -\lambda(y+y_0)A'_{yy} & -A'_x-\lambda(y+y_0)A'_{xy}\\ -A'_x+\lambda(y+y_0)A'_{xy} & -\lambda(y+y_0)A'_{yy} \end{matrix}\right]. \end{equation}
\begin{equation} \boldsymbol{\mathsf{G}}^S\left(\boldsymbol{x},\boldsymbol{x}'_0\right)= \left[\begin{matrix} -\lambda(y+y_0)A'_{yy} & -A'_x-\lambda(y+y_0)A'_{xy}\\ -A'_x+\lambda(y+y_0)A'_{xy} & -\lambda(y+y_0)A'_{yy} \end{matrix}\right]. \end{equation}
In addition to the Green's functions ![]() $G^H$ and
$G^H$ and ![]() $\boldsymbol{\mathsf{G}}^H$, our boundary integral formulations will also require the 2
$\boldsymbol{\mathsf{G}}^H$, our boundary integral formulations will also require the 2![]() $L$-periodic normal stress term
$L$-periodic normal stress term
 \begin{align}
\boldsymbol{\mathsf{T}}(\boldsymbol{x},\boldsymbol{x}_0)&=2\nu_x\left[\begin{matrix}
-2A_x-\lambda(y-y_0)A_{xy} &
\lambda(y-y_0)A_{xx}-A_y\\
\lambda(y-y_0)A_{xx}-A_y & \lambda(y-y_0)A_{xy}
\end{matrix}\right]\nonumber\\ &\quad
+2\nu_y\left[\begin{array}{ccc} \lambda(y-y_0)A_{xx}-A_y &
\lambda(y-y_0)A_{xy}\\
\lambda(y-y_0)A_{xy} & -\lambda(y-y_0)A_{xx}-A_y
\end{array}\right].
\end{align}
\begin{align}
\boldsymbol{\mathsf{T}}(\boldsymbol{x},\boldsymbol{x}_0)&=2\nu_x\left[\begin{matrix}
-2A_x-\lambda(y-y_0)A_{xy} &
\lambda(y-y_0)A_{xx}-A_y\\
\lambda(y-y_0)A_{xx}-A_y & \lambda(y-y_0)A_{xy}
\end{matrix}\right]\nonumber\\ &\quad
+2\nu_y\left[\begin{array}{ccc} \lambda(y-y_0)A_{xx}-A_y &
\lambda(y-y_0)A_{xy}\\
\lambda(y-y_0)A_{xy} & -\lambda(y-y_0)A_{xx}-A_y
\end{array}\right].
\end{align}
The periodic normal stress on the half-space ![]() $H$ is then given by (Pozrikidis Reference Pozrikidis1992)
$H$ is then given by (Pozrikidis Reference Pozrikidis1992)
where
 \begin{equation} \boldsymbol{\mathsf{T}}^D(\boldsymbol{x},\boldsymbol{x}_0')=\nu_x\left[\begin{matrix} 2A'_{yyx} & 2A'_{xyx} \\ A'_{yyy}-A'_{xyx} & 2A'_{xyy}\end{matrix}\right]+\nu_y\left[\begin{matrix} A'_{yyy}-A'_{xyx} & 2A'_{xyy} \\ -2A'_{xyy} & 2A'_{yyy} \end{matrix}\right] \end{equation}
\begin{equation} \boldsymbol{\mathsf{T}}^D(\boldsymbol{x},\boldsymbol{x}_0')=\nu_x\left[\begin{matrix} 2A'_{yyx} & 2A'_{xyx} \\ A'_{yyy}-A'_{xyx} & 2A'_{xyy}\end{matrix}\right]+\nu_y\left[\begin{matrix} A'_{yyy}-A'_{xyx} & 2A'_{xyy} \\ -2A'_{xyy} & 2A'_{yyy} \end{matrix}\right] \end{equation}and
 \begin{align}
\boldsymbol{\mathsf{T}}^S(\boldsymbol{x},\boldsymbol{x}'_0)&=\nu_x\left[\begin{matrix}
-2A'_{xy}-2\lambda(y+y_0)A'_{yyx} &
4A'_{yy}-2\lambda(y+y_0)A'_{xyx}\\
\lambda(y+y_0)(A'_{xyx}-A'_{yyy}) &
-2A'_{xy}-2\lambda(y+y_0)A'_{xyy}
\end{matrix}\right]\nonumber\\ &\quad
+\nu_y\left[\begin{matrix}
\lambda(y+y_0)(A'_{xyx}-A'_{yyy}) &
-2A'_{xy}-2\lambda(y+y_0)A'_{xyy}\\
-2A'_{xy}+2\lambda(y+y_0)A'_{xyy} &
-2\lambda(y+y_0)A'_{yyy} \end{matrix}\right].
\end{align}
\begin{align}
\boldsymbol{\mathsf{T}}^S(\boldsymbol{x},\boldsymbol{x}'_0)&=\nu_x\left[\begin{matrix}
-2A'_{xy}-2\lambda(y+y_0)A'_{yyx} &
4A'_{yy}-2\lambda(y+y_0)A'_{xyx}\\
\lambda(y+y_0)(A'_{xyx}-A'_{yyy}) &
-2A'_{xy}-2\lambda(y+y_0)A'_{xyy}
\end{matrix}\right]\nonumber\\ &\quad
+\nu_y\left[\begin{matrix}
\lambda(y+y_0)(A'_{xyx}-A'_{yyy}) &
-2A'_{xy}-2\lambda(y+y_0)A'_{xyy}\\
-2A'_{xy}+2\lambda(y+y_0)A'_{xyy} &
-2\lambda(y+y_0)A'_{yyy} \end{matrix}\right].
\end{align}3.2. Boundary integral model
We now detail the interface-only boundary integral formulation of (2.2)–(2.14). The advantages of such a formulation are that it provides a significant increase in computational efficiency though reducing the size of the domain to be discretised, as well as alleviating problems due to near singularities associated with boundary integral methods in long slender domains.
For the fluid problem (2.6)–(2.14), the simplest formulation is an indirect model using a single layer potential solution ansatz (Pozrikidis Reference Pozrikidis1992, chap. 5). In addition to giving a relatively simple interface-only formulation of the problem, this approach also has the advantage that the same equation can be used to determine the fluid velocity on both sides of the interface ![]() $\varGamma _I$. This is a consequence of the continuity of the Green's function (3.5) across the interface. We therefore assume that for
$\varGamma _I$. This is a consequence of the continuity of the Green's function (3.5) across the interface. We therefore assume that for ![]() $\boldsymbol {x}\in \overline{\Omega} _{\alpha }$ (
$\boldsymbol {x}\in \overline{\Omega} _{\alpha }$ (![]() $\alpha =1,2$), the fluid velocity
$\alpha =1,2$), the fluid velocity ![]() $\boldsymbol {u}_{\alpha }$ may be expressed in the form (Pozrikidis Reference Pozrikidis1992)
$\boldsymbol {u}_{\alpha }$ may be expressed in the form (Pozrikidis Reference Pozrikidis1992)
where the second equality follows from the property that ![]() $\boldsymbol{\mathsf{G}}^H(\boldsymbol {x},\boldsymbol {x}_0)$ vanishes for
$\boldsymbol{\mathsf{G}}^H(\boldsymbol {x},\boldsymbol {x}_0)$ vanishes for ![]() $\boldsymbol {x}_0\in \varGamma _0$. The vector
$\boldsymbol {x}_0\in \varGamma _0$. The vector ![]() $\boldsymbol {q}$ is an unknown density term to be computed by solving the second-kind boundary integral equation
$\boldsymbol {q}$ is an unknown density term to be computed by solving the second-kind boundary integral equation
with ![]() $\boldsymbol {x}\in \varGamma _I$. The existence and uniqueness of solutions to (3.13) are discussed in Pozrikidis (Reference Pozrikidis1992, § 5.4), and holds provided both
$\boldsymbol {x}\in \varGamma _I$. The existence and uniqueness of solutions to (3.13) are discussed in Pozrikidis (Reference Pozrikidis1992, § 5.4), and holds provided both ![]() $\mu _1,\ \mu _2>0$. We now make use of the symmetry of
$\mu _1,\ \mu _2>0$. We now make use of the symmetry of ![]() $\boldsymbol {\sigma }_v^{\alpha }$ (
$\boldsymbol {\sigma }_v^{\alpha }$ (![]() $\alpha =1,2$), the definitions ((2.10) and (2.11)) and the interface conditions ((2.8) and (2.9)) to rewrite the right-hand side of (3.13) via
$\alpha =1,2$), the definitions ((2.10) and (2.11)) and the interface conditions ((2.8) and (2.9)) to rewrite the right-hand side of (3.13) via
Here, we have made use of the fact that ![]() $\boldsymbol {\tau }\boldsymbol {\cdot }(\boldsymbol {\sigma }_M^1-\boldsymbol {\sigma }_M^2)\boldsymbol {\cdot }\boldsymbol {\nu }=0$ due to the interface conditions ((2.2) and (2.3)), which provides
$\boldsymbol {\tau }\boldsymbol {\cdot }(\boldsymbol {\sigma }_M^1-\boldsymbol {\sigma }_M^2)\boldsymbol {\cdot }\boldsymbol {\nu }=0$ due to the interface conditions ((2.2) and (2.3)), which provides
 \begin{equation} \boldsymbol{\nu}\boldsymbol{\cdot}\left(\boldsymbol{\sigma}_M^1-\boldsymbol{\sigma}_M^2\right)\boldsymbol{\cdot}\boldsymbol{\nu}=\frac{\epsilon_0}{2\epsilon_2}(\epsilon_2-\epsilon_1)\left(\epsilon_1\left(\frac{\partial\phi_1}{\partial \boldsymbol{\nu}}\right)^2+\epsilon_2\left(\frac{\partial\phi_1}{\partial \boldsymbol{\tau}}\right)^2\right). \end{equation}
\begin{equation} \boldsymbol{\nu}\boldsymbol{\cdot}\left(\boldsymbol{\sigma}_M^1-\boldsymbol{\sigma}_M^2\right)\boldsymbol{\cdot}\boldsymbol{\nu}=\frac{\epsilon_0}{2\epsilon_2}(\epsilon_2-\epsilon_1)\left(\epsilon_1\left(\frac{\partial\phi_1}{\partial \boldsymbol{\nu}}\right)^2+\epsilon_2\left(\frac{\partial\phi_1}{\partial \boldsymbol{\tau}}\right)^2\right). \end{equation}The final expression for the right-hand side of (3.13) is therefore
 \begin{equation} \frac{1}{{4{\rm \pi}}(\mu_1+\mu_2)}\left(\frac{\epsilon_0}{\epsilon_2}(\epsilon_2-\epsilon_1)\left(\epsilon_1\left(\frac{\partial\phi_1}{\partial \boldsymbol{\nu}}\right)^2+\epsilon_2\left(\frac{\partial\phi_1}{\partial \boldsymbol{\tau}}\right)^2\right)-\gamma\kappa\right)\boldsymbol{\nu}. \end{equation}
\begin{equation} \frac{1}{{4{\rm \pi}}(\mu_1+\mu_2)}\left(\frac{\epsilon_0}{\epsilon_2}(\epsilon_2-\epsilon_1)\left(\epsilon_1\left(\frac{\partial\phi_1}{\partial \boldsymbol{\nu}}\right)^2+\epsilon_2\left(\frac{\partial\phi_1}{\partial \boldsymbol{\tau}}\right)^2\right)-\gamma\kappa\right)\boldsymbol{\nu}. \end{equation} For the electrical potential problem (2.1)–(2.5), a single layer potential solution ansatz fails because ![]() $G^H$ vanishes on
$G^H$ vanishes on ![]() $\varGamma _0$ where the boundary condition
$\varGamma _0$ where the boundary condition ![]() $f$ is prescribed. A double layer potential solution ansatz would lead to a more complicated equation for computing the Neumann data on the interface
$f$ is prescribed. A double layer potential solution ansatz would lead to a more complicated equation for computing the Neumann data on the interface ![]() $\varGamma _I$ and so we instead turn to a direct formulation based on Green's representation formula, as derived in Chappell (Reference Chappell2015). This has the additional advantage that the unknowns appearing in the boundary integral equations are the physical quantities (potentials) that we wish to compute. In order to obtain an interface-only formulation in this case we make use of the half-space solution
$\varGamma _I$ and so we instead turn to a direct formulation based on Green's representation formula, as derived in Chappell (Reference Chappell2015). This has the additional advantage that the unknowns appearing in the boundary integral equations are the physical quantities (potentials) that we wish to compute. In order to obtain an interface-only formulation in this case we make use of the half-space solution ![]() $\phi ^H$. We obtain the following second-kind Fredholm integral equation for the potential
$\phi ^H$. We obtain the following second-kind Fredholm integral equation for the potential ![]() $\phi =\phi _1=\phi _2$ at a point
$\phi =\phi _1=\phi _2$ at a point ![]() $\boldsymbol {x}\in \varGamma _I$:
$\boldsymbol {x}\in \varGamma _I$:
The notation ![]() $\boldsymbol {\nu }_0$ is used to specify that the normal derivative in this case is taken at
$\boldsymbol {\nu }_0$ is used to specify that the normal derivative in this case is taken at ![]() $\boldsymbol {x}_0$, rather than at
$\boldsymbol {x}_0$, rather than at ![]() $\boldsymbol {x}$ as before. Clearly the case
$\boldsymbol {x}$ as before. Clearly the case ![]() $\epsilon _1=\epsilon _2$ reduces to
$\epsilon _1=\epsilon _2$ reduces to ![]() $\phi =\phi ^H$ as expected. Note that here we are effectively treating
$\phi =\phi ^H$ as expected. Note that here we are effectively treating ![]() $\phi ^H$ as our boundary data on
$\phi ^H$ as our boundary data on ![]() $\varGamma _I$ and that, since
$\varGamma _I$ and that, since ![]() $\phi ^H$ is harmonic, it is analytic. In the examples considered later, a closed form expression will be available for
$\phi ^H$ is harmonic, it is analytic. In the examples considered later, a closed form expression will be available for ![]() $\phi ^H$; however, in general it may be necessary to approximate
$\phi ^H$; however, in general it may be necessary to approximate ![]() $\phi ^H$ by, for example, a truncated Fourier series (if solving the half-plane problem via separation of variables) or quadrature (if computing
$\phi ^H$ by, for example, a truncated Fourier series (if solving the half-plane problem via separation of variables) or quadrature (if computing ![]() $\phi ^H$ directly from the boundary integral formula (3.3)). It is shown in Chappell (Reference Chappell2015) that the integral equation (3.17) has a unique bounded solution for any
$\phi ^H$ directly from the boundary integral formula (3.3)). It is shown in Chappell (Reference Chappell2015) that the integral equation (3.17) has a unique bounded solution for any ![]() $\epsilon _1,\ \epsilon _2>0$.
$\epsilon _1,\ \epsilon _2>0$.
In order to combine the above-described fluid and electric potential models, we note that the fluid equations depend on the normal and tangential derivatives of ![]() $\phi$ on
$\phi$ on ![]() $\varGamma _I$ (see (3.16)), rather than on
$\varGamma _I$ (see (3.16)), rather than on ![]() $\phi$ itself. The tangential derivative may be computed from
$\phi$ itself. The tangential derivative may be computed from ![]() $\phi$ relatively simply using interpolation of
$\phi$ relatively simply using interpolation of ![]() $\varGamma _I$ by trigonometric polynomials as discussed later. The normal derivative will be computed from the result for
$\varGamma _I$ by trigonometric polynomials as discussed later. The normal derivative will be computed from the result for ![]() $\phi$ by making use of the Dirichlet-to-Neumann operator (Chappell Reference Chappell2015), which results from solving the following first-kind integral equation for
$\phi$ by making use of the Dirichlet-to-Neumann operator (Chappell Reference Chappell2015), which results from solving the following first-kind integral equation for ![]() $\partial \phi _{\alpha }/\partial \boldsymbol {\nu }_0$,
$\partial \phi _{\alpha }/\partial \boldsymbol {\nu }_0$, ![]() $\alpha =1,2$:
$\alpha =1,2$:
In Chappell (Reference Chappell2015) it is shown that (3.18) has a unique bounded solution in the Sobolev space ![]() $H^{-1/2}(\varGamma _I)$ – see for example Kress (Reference Kress1989, § 8.2) for an introduction to Sobolev spaces.
$H^{-1/2}(\varGamma _I)$ – see for example Kress (Reference Kress1989, § 8.2) for an introduction to Sobolev spaces.
The solution procedure is thus to first find the potential ![]() $\phi$ correponding to the initially flat interface
$\phi$ correponding to the initially flat interface ![]() $y=h_0$ by solving (3.17), and to compute the required normal derivative via (3.18). The associated flow
$y=h_0$ by solving (3.17), and to compute the required normal derivative via (3.18). The associated flow ![]() $\boldsymbol {u}_1$ along
$\boldsymbol {u}_1$ along ![]() $\varGamma _I$ is computed via (3.13) and the formula (3.12), and the kinematic boundary condition (2.14) provides the updated interfacial position
$\varGamma _I$ is computed via (3.13) and the formula (3.12), and the kinematic boundary condition (2.14) provides the updated interfacial position ![]() $h$. This process is then repeated to obtain the time evolution of the interface
$h$. This process is then repeated to obtain the time evolution of the interface ![]() $h(x,t)$.
$h(x,t)$.
4. Long-wavelength reduction
In this section we describe a restriction and asymptotic reduction of the general formulation described earlier. In particular, we restrict attention to a model appropriate to the oil–air interface in Brown et al. (Reference Brown, Wells, Newton and McHale2009, Reference Brown, McHale and Mottram2011). Firstly, to permit some analytical progress we adopt the long-wavelength limit that is typically applied in the context of lubrication theory, thereby reducing the flow problem to a PDE describing the motion of the free interface ![]() $\varGamma _I$ coupled to forcing supplied from the electrostatic problem. We then consider a corresponding reduced representation for the electrical potential, consistent with this limit, reducing the entire problem to a single PDE model at leading order.
$\varGamma _I$ coupled to forcing supplied from the electrostatic problem. We then consider a corresponding reduced representation for the electrical potential, consistent with this limit, reducing the entire problem to a single PDE model at leading order.
4.1. Thin-film flow model
We first non-dimensionalise the governing equations by introducing the following scalings:
 \begin{equation} \left. \begin{aligned} (x,y) & =L(\tilde{x},\delta\tilde{h}(x,t)\tilde{y}),\quad t=\mu_1 L\gamma^{-1}\delta^{-3}\tilde{t},\ \phi_1 = \Phi\tilde{\phi_1},\\ (u_1,v_1) & = \delta^3\gamma\mu_1^{-1}(\tilde{u}_1,\delta\tilde{v}_1),\quad p_1=\gamma\delta L^{-1}\tilde{p}_1, \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} (x,y) & =L(\tilde{x},\delta\tilde{h}(x,t)\tilde{y}),\quad t=\mu_1 L\gamma^{-1}\delta^{-3}\tilde{t},\ \phi_1 = \Phi\tilde{\phi_1},\\ (u_1,v_1) & = \delta^3\gamma\mu_1^{-1}(\tilde{u}_1,\delta\tilde{v}_1),\quad p_1=\gamma\delta L^{-1}\tilde{p}_1, \end{aligned} \right\} \end{equation}
where tildes denote dimensionless quantities and ![]() $\Phi$ denotes the amplitude of the applied voltage
$\Phi$ denotes the amplitude of the applied voltage ![]() $f(x)$ appearing in (2.4). We highlight that we have chosen a frame of reference where the interface is fixed (following Secomb Reference Secomb1978; O'Dea & Waters Reference O'Dea and Waters2006); in particular, the free interface
$f(x)$ appearing in (2.4). We highlight that we have chosen a frame of reference where the interface is fixed (following Secomb Reference Secomb1978; O'Dea & Waters Reference O'Dea and Waters2006); in particular, the free interface ![]() $\varGamma _I$ has been mapped to the flat surface at
$\varGamma _I$ has been mapped to the flat surface at ![]() $\tilde {y}=1$. The dimensionless parameter
$\tilde {y}=1$. The dimensionless parameter ![]() $\delta =h_0/L$ denotes the (mean) aspect ratio of the thin viscous film domain
$\delta =h_0/L$ denotes the (mean) aspect ratio of the thin viscous film domain ![]() $\varOmega _1$; to simplify the governing equations, we adopt the long-wavelength limit, setting
$\varOmega _1$; to simplify the governing equations, we adopt the long-wavelength limit, setting ![]() $0<\delta \ll 1$. We assume, consistent with the oil–air interface application of interest, that the viscosity and pressure in the thin film dominate those in the surrounding fluid (
$0<\delta \ll 1$. We assume, consistent with the oil–air interface application of interest, that the viscosity and pressure in the thin film dominate those in the surrounding fluid (![]() $\mu _1\gg \mu _2$,
$\mu _1\gg \mu _2$, ![]() $p_1\gg p_2$), under which scaling the interface motion may be expressed entirely in terms of variables defined in
$p_1\gg p_2$), under which scaling the interface motion may be expressed entirely in terms of variables defined in ![]() $\varOmega _1$ and so we do not consider scalings for the dependent variables associated with
$\varOmega _1$ and so we do not consider scalings for the dependent variables associated with ![]() $\varOmega _2$ here.
$\varOmega _2$ here.
At leading order, the dimensionless versions of (2.6), (2.7) governing the flow in ![]() $\varOmega _1$ are
$\varOmega _1$ are
The leading-order dimensionless boundary conditions (2.8), (2.9), (2.12) and (2.14) read
Here, ![]() $M_1$ is the contribution from the Maxwell stress, given by
$M_1$ is the contribution from the Maxwell stress, given by
 \begin{equation} M_1=\frac{\epsilon_1}{\delta^2\tilde{h}^2}\left(\frac{\partial\tilde{\phi}_1}{\partial \tilde{y}}\right)^2+\epsilon_2\left(\frac{\partial\tilde{\phi}_1}{\partial \tilde{x}}-\frac{\tilde{y}}{\tilde{h}}\frac{\partial \tilde{h}}{\partial \tilde{x}}\frac{\partial\tilde{\phi}_1}{\partial \tilde{y}}\right)^2 \end{equation}
\begin{equation} M_1=\frac{\epsilon_1}{\delta^2\tilde{h}^2}\left(\frac{\partial\tilde{\phi}_1}{\partial \tilde{y}}\right)^2+\epsilon_2\left(\frac{\partial\tilde{\phi}_1}{\partial \tilde{x}}-\frac{\tilde{y}}{\tilde{h}}\frac{\partial \tilde{h}}{\partial \tilde{x}}\frac{\partial\tilde{\phi}_1}{\partial \tilde{y}}\right)^2 \end{equation}
evaluated at ![]() $\tilde {y}=1$, and the corresponding coefficient
$\tilde {y}=1$, and the corresponding coefficient ![]() $K$ is
$K$ is
Note that the apparent ![]() $O(\delta ^{-2})$ term in (4.8) is actually
$O(\delta ^{-2})$ term in (4.8) is actually ![]() $O(1)$ since, as we shall see in the next section,
$O(1)$ since, as we shall see in the next section, ![]() $\partial \tilde {\phi }_1/\partial \tilde {y}=O(\delta )$. We note that in (4.8) we have used the interface conditions ((2.2) and (2.3)) for the electrostatic problem to express
$\partial \tilde {\phi }_1/\partial \tilde {y}=O(\delta )$. We note that in (4.8) we have used the interface conditions ((2.2) and (2.3)) for the electrostatic problem to express ![]() $M_1$ in terms of the potential in
$M_1$ in terms of the potential in ![]() $\varOmega _1$ only; this follows on from the procedure outlined in the previous section for the boundary integral model (see (3.15) and (3.16)).
$\varOmega _1$ only; this follows on from the procedure outlined in the previous section for the boundary integral model (see (3.15) and (3.16)).
The second of (4.3) provides ![]() $\tilde {p}_1 = \tilde {p}_1(\tilde {x},\tilde {t})$, in view of which, we may integrate (4.2) and the first of (4.3), imposing the relevant no-slip and interface conditions, to obtain
$\tilde {p}_1 = \tilde {p}_1(\tilde {x},\tilde {t})$, in view of which, we may integrate (4.2) and the first of (4.3), imposing the relevant no-slip and interface conditions, to obtain
where ![]() $\tilde {\boldsymbol {x}}=(\tilde {x},\tilde {y}).$
$\tilde {\boldsymbol {x}}=(\tilde {x},\tilde {y}).$
The dimensionless kinematic boundary condition (4.7), exploiting (4.10) and (4.11) at ![]() $\tilde {y}=1$, gives
$\tilde {y}=1$, gives
 \begin{equation} \frac{\partial \tilde{h}}{\partial \tilde{t}}=\frac{\partial}{\partial\tilde{x}}\left(\frac{\tilde{h}^3}{3}\frac{\partial\tilde{p}_1}{\partial\tilde{x}}\right). \end{equation}
\begin{equation} \frac{\partial \tilde{h}}{\partial \tilde{t}}=\frac{\partial}{\partial\tilde{x}}\left(\frac{\tilde{h}^3}{3}\frac{\partial\tilde{p}_1}{\partial\tilde{x}}\right). \end{equation}
Applying the normal stress condition (4.4) gives a PDE for the interface position ![]() $\tilde {h}$ in terms of input data from the solution of the electrostatic problem (2.1)–(2.5), that is
$\tilde {h}$ in terms of input data from the solution of the electrostatic problem (2.1)–(2.5), that is
 \begin{equation} \frac{\partial \tilde{h}}{\partial \tilde{t}}=\frac{\partial}{\partial\tilde{x}}\left(\frac{\tilde{h}^3}{3}\left(K\frac{\partial M_1}{\partial\tilde{x}}-\frac{\partial^3 \tilde{h}}{\partial\tilde{x}^3}\right)\right). \end{equation}
\begin{equation} \frac{\partial \tilde{h}}{\partial \tilde{t}}=\frac{\partial}{\partial\tilde{x}}\left(\frac{\tilde{h}^3}{3}\left(K\frac{\partial M_1}{\partial\tilde{x}}-\frac{\partial^3 \tilde{h}}{\partial\tilde{x}^3}\right)\right). \end{equation}The discretisation and numerical solution of (4.13) will be described in the subsequent sections.
4.2. Reduced electrostatic model
We now consider a correspondingly reduced asymptotic model for the electrostatic problem (2.1)–(2.5), in order to obtain an analytical expression for ![]() $\tilde {\phi }_1$ and thereby decouple the numerical solution of (4.13) from the electrostatic problem.
$\tilde {\phi }_1$ and thereby decouple the numerical solution of (4.13) from the electrostatic problem.
Consider first the electrostatic problem in ![]() $\varOmega _1$. Assuming an asymptotic expansion for the potential of the form
$\varOmega _1$. Assuming an asymptotic expansion for the potential of the form ![]() $\tilde {\phi }_1=\tilde {\phi }_{10}+\delta \tilde {\phi }_{11}+\ldots\,$, under the scalings (4.1), (2.1) and (2.5) at leading order and at
$\tilde {\phi }_1=\tilde {\phi }_{10}+\delta \tilde {\phi }_{11}+\ldots\,$, under the scalings (4.1), (2.1) and (2.5) at leading order and at ![]() $O(\delta )$ read
$O(\delta )$ read
for ![]() $0<\tilde {y}<1$,
$0<\tilde {y}<1$, ![]() $i=0,1$;
$i=0,1$;
We hence obtain
wherein ![]() $\tilde {f}=f/\Phi$ is the dimensionless applied potential.
$\tilde {f}=f/\Phi$ is the dimensionless applied potential.
In (4.16) and (4.17), ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are determined from the interface conditions ((2.2) and (2.3)) on specification of
$\beta$ are determined from the interface conditions ((2.2) and (2.3)) on specification of ![]() $\tilde {\phi }_2=\phi _2/\Phi$, which we now consider. Firstly, we note that the thin-film scaling is not appropriate for the potential model in
$\tilde {\phi }_2=\phi _2/\Phi$, which we now consider. Firstly, we note that the thin-film scaling is not appropriate for the potential model in ![]() $\varOmega _2$, apart from in a thin layer near the interface; instead we consider an alternative non-dimensionalisation
$\varOmega _2$, apart from in a thin layer near the interface; instead we consider an alternative non-dimensionalisation ![]() $y=L\tilde {Y}$. Under this scaling, and since the oil film
$y=L\tilde {Y}$. Under this scaling, and since the oil film ![]() $\varOmega _1$ is thin (
$\varOmega _1$ is thin (![]() $\delta \ll 1$), the interfacial conditions are now applied at
$\delta \ll 1$), the interfacial conditions are now applied at ![]() $\tilde {Y}=0$;
$\tilde {Y}=0$; ![]() $\varOmega _1$ and
$\varOmega _1$ and ![]() $\varOmega _2$ are ‘inner’ and ‘outer’ layers, the connection between which occurring at
$\varOmega _2$ are ‘inner’ and ‘outer’ layers, the connection between which occurring at ![]() $\tilde {y}=1$ or
$\tilde {y}=1$ or ![]() $\tilde {Y}=\delta \tilde {h}$. To leading order in
$\tilde {Y}=\delta \tilde {h}$. To leading order in ![]() $\delta$ the electrostatic problem in
$\delta$ the electrostatic problem in ![]() $\varOmega _2$ is therefore
$\varOmega _2$ is therefore
for ![]() $\tilde {Y}>0$,
$\tilde {Y}>0$,
as ![]() $\tilde {Y}\rightarrow \infty$, with interface conditions applied at
$\tilde {Y}\rightarrow \infty$, with interface conditions applied at ![]() $\tilde {Y}=0$.
$\tilde {Y}=0$.
Applying the interface continuity condition yields ![]() $\tilde {\phi }_2(\tilde {x},0)=\tilde {f}(\tilde {x})$ and hence
$\tilde {\phi }_2(\tilde {x},0)=\tilde {f}(\tilde {x})$ and hence ![]() $\tilde {\phi }_2$ is the half-plane solution
$\tilde {\phi }_2$ is the half-plane solution ![]() $\phi ^{H}$ from (3.3) written in
$\phi ^{H}$ from (3.3) written in ![]() $(\tilde {x},\tilde {Y})$ coordinates
$(\tilde {x},\tilde {Y})$ coordinates
 \begin{equation} \tilde{\phi}_2(\tilde{x},\tilde{Y}) = \frac{1}{2}\int_{-1}^1\frac{\sinh({\rm \pi}\tilde{Y})\tilde{f}(\tilde{x}_0)}{\cosh({\rm \pi}\tilde{Y})-\cos({\rm \pi}(\tilde{x}-\tilde{x}_0))}\,\mathrm{d}\tilde{x}_0. \end{equation}
\begin{equation} \tilde{\phi}_2(\tilde{x},\tilde{Y}) = \frac{1}{2}\int_{-1}^1\frac{\sinh({\rm \pi}\tilde{Y})\tilde{f}(\tilde{x}_0)}{\cosh({\rm \pi}\tilde{Y})-\cos({\rm \pi}(\tilde{x}-\tilde{x}_0))}\,\mathrm{d}\tilde{x}_0. \end{equation}Expressed in their respective coordinates for clarity, the normal derivative jump condition reads
 \begin{equation} \frac{\epsilon_1}{\delta \tilde{h}}\left.\frac{\partial\tilde{\phi}_1}{\partial \tilde{y}}\right|_{\tilde{y}=1}=\epsilon_2\left.\frac{\partial\tilde{\phi}_2}{\partial \tilde{Y}}\right|_{\tilde{Y}=0}, \end{equation}
\begin{equation} \frac{\epsilon_1}{\delta \tilde{h}}\left.\frac{\partial\tilde{\phi}_1}{\partial \tilde{y}}\right|_{\tilde{y}=1}=\epsilon_2\left.\frac{\partial\tilde{\phi}_2}{\partial \tilde{Y}}\right|_{\tilde{Y}=0}, \end{equation}
and hence ![]() $\alpha =0$, with
$\alpha =0$, with ![]() $\beta$ determined from
$\beta$ determined from ![]() $\tilde {\phi }_2$ via (4.21) as follows:
$\tilde {\phi }_2$ via (4.21) as follows:
 \begin{equation} \beta = \frac{\epsilon_2\tilde{h}}{\epsilon_1} \left.\frac{\partial\tilde{\phi}_{2}}{\partial \tilde{Y}}\right|_{\tilde{Y}=0}. \end{equation}
\begin{equation} \beta = \frac{\epsilon_2\tilde{h}}{\epsilon_1} \left.\frac{\partial\tilde{\phi}_{2}}{\partial \tilde{Y}}\right|_{\tilde{Y}=0}. \end{equation}We thereby obtain
and substitution into the expression for ![]() $M_1$ (4.8), provides, to leading order in
$M_1$ (4.8), provides, to leading order in ![]() $\delta$,
$\delta$,
 \begin{equation} M_1=\frac{\epsilon_2^2{\rm \pi}^2}{4\epsilon_1} \left( \int_{-1}^1\frac{\tilde{f}(\tilde{x}_0)}{1-\cos({\rm \pi}(\tilde{x}-\tilde{x}_0))}\,\mathrm{d}\tilde{x}_0 \right)^2+\epsilon_2\left(\frac{\mathrm{d}\tilde{f}}{\mathrm{d}\tilde{x}}\right)^2. \end{equation}
\begin{equation} M_1=\frac{\epsilon_2^2{\rm \pi}^2}{4\epsilon_1} \left( \int_{-1}^1\frac{\tilde{f}(\tilde{x}_0)}{1-\cos({\rm \pi}(\tilde{x}-\tilde{x}_0))}\,\mathrm{d}\tilde{x}_0 \right)^2+\epsilon_2\left(\frac{\mathrm{d}\tilde{f}}{\mathrm{d}\tilde{x}}\right)^2. \end{equation}The expression (4.24) may then be applied in the equation for the interface position (4.13) to model the evolution of the interface geometry.
We remark in passing that straightforward analytical progress can be made by taking the additional limit of small amplitude variations in the applied voltage; e.g. ![]() $\tilde {f}(\tilde {x})=1+\varepsilon \mathcal {F}(\tilde {x})$, for some
$\tilde {f}(\tilde {x})=1+\varepsilon \mathcal {F}(\tilde {x})$, for some ![]() $|\varepsilon |\ll 1$. Here, one may solve the potential problem, and the associated linear fourth-order PDE for
$|\varepsilon |\ll 1$. Here, one may solve the potential problem, and the associated linear fourth-order PDE for ![]() $\tilde {h}$ directly; however, this additional linearisation procedure results in simplified interfacial dynamics that does not reflect that observed experimentally (in particular, the amplitude growth rate obtained is independent of the applied potential amplitude) and so we do not pursue this here.
$\tilde {h}$ directly; however, this additional linearisation procedure results in simplified interfacial dynamics that does not reflect that observed experimentally (in particular, the amplitude growth rate obtained is independent of the applied potential amplitude) and so we do not pursue this here.
5. Discretisation procedures
In this section we describe the discretisation of the integral equations (3.13), (3.17) and (3.18) using the Nyström method with suitable quadratures. The evaluation of the formula (3.12) using appropriate numerical integration rules, and suitable finite difference methods for the discretisation of the time evolution equations (2.14) and (4.13) will also be detailed. With this in hand, we have three possible numerical solution approaches to the problem under consideration. These are as follows:
(i) Full boundary integral approach.
Numerically solve (3.17) and (3.18) with a flat interface to provide the right-hand side of (3.13). Here, we make use of expression (3.16) and note that the tangential derivative is computed using interpolation by trigonometric polynomials, as will be discussed later in this section. Equation (3.13) is then solved using the Nyström method, and the result is used to compute the fluid velocity components on the interface via (3.12). The problem is then advanced to the next time step by using a finite difference formula for the time derivative in (2.14) to obtain
 $h(x,{\rm \Delta} t)$, where
$h(x,{\rm \Delta} t)$, where  ${\rm \Delta} t$ is the step size for the time discretisation. This process is repeated until a desired final solution time or termination criterion is reached.
${\rm \Delta} t$ is the step size for the time discretisation. This process is repeated until a desired final solution time or termination criterion is reached.(ii) Boundary integral approach with long-wavelength asymptotics.
Numerically solve (3.17) and (3.18) with a flat interface to provide the Maxwell stress term
 $M_1$, which in dimensional form can be expressed as
(5.1)The problem is then advanced to the next time step by using an appropriate finite difference scheme for the PDE (4.13).
$M_1$, which in dimensional form can be expressed as
(5.1)The problem is then advanced to the next time step by using an appropriate finite difference scheme for the PDE (4.13). \begin{equation} M_1=\epsilon_1\left(\frac{\partial\phi_1}{\partial \boldsymbol{\nu}}\right)^2+\epsilon_2\left(\frac{\partial\phi_1}{\partial \boldsymbol{\tau}}\right)^2. \end{equation}
\begin{equation} M_1=\epsilon_1\left(\frac{\partial\phi_1}{\partial \boldsymbol{\nu}}\right)^2+\epsilon_2\left(\frac{\partial\phi_1}{\partial \boldsymbol{\tau}}\right)^2. \end{equation}(iii) Fully asymptotic approach.
Use the formula (4.24) for provide the Maxwell stress term
 $M_1$ as well as its derivative with respect to
$M_1$ as well as its derivative with respect to  $\tilde {x}$, and then use an appropriate finite difference scheme for the PDE (4.13) and proceed as in approach (ii).
$\tilde {x}$, and then use an appropriate finite difference scheme for the PDE (4.13) and proceed as in approach (ii).
Note that we approximate the tangential derivative ![]() $\partial \phi _1/\partial \boldsymbol {\tau }$ appearing in (5.1), as well as the derivative of
$\partial \phi _1/\partial \boldsymbol {\tau }$ appearing in (5.1), as well as the derivative of ![]() $M_1$ with respect to
$M_1$ with respect to ![]() $\tilde {x}$, by interpolating with trigonometric polynomials and first computing the derivative with respect to
$\tilde {x}$, by interpolating with trigonometric polynomials and first computing the derivative with respect to ![]() $x$. This involves applying a fast Fourier transform (FFT) and then differentiating the Fourier components, which is also the same procedure that we carry out for approximating the derivative
$x$. This involves applying a fast Fourier transform (FFT) and then differentiating the Fourier components, which is also the same procedure that we carry out for approximating the derivative ![]() $\partial h/\partial x$ of the interface position function
$\partial h/\partial x$ of the interface position function ![]() $h$. One then obtains an approximation to the tangential derivative of
$h$. One then obtains an approximation to the tangential derivative of ![]() $\phi _1$ by correcting for arclength via division by a factor of
$\phi _1$ by correcting for arclength via division by a factor of ![]() $\sqrt {1+(\partial h/\partial x)^2}$. A similar procedure is described and rigorously analysed in Preston, Chamberlain & Chandler-Wilde (Reference Preston, Chamberlain and Chandler-Wilde2011), where super-algebraic convergence of the approximation is shown.
$\sqrt {1+(\partial h/\partial x)^2}$. A similar procedure is described and rigorously analysed in Preston, Chamberlain & Chandler-Wilde (Reference Preston, Chamberlain and Chandler-Wilde2011), where super-algebraic convergence of the approximation is shown.
5.1. Discretisation for the full boundary integral approach
The discretisation of the integral equations (3.17) and (3.18) using spectrally convergent Nyström methods is detailed in Chappell (Reference Chappell2015); here we give a brief summary. Let us first consider the second-kind Fredholm equation (3.17).
Under the assumption of an infinitely differentiable interface (in space), we also have an infinitely differentiable kernel in (3.17) and as discussed in § 3.2, the data term ![]() $\phi ^H$ is also infinitely differentiable. In this situation a simple application of the trapezoidal rule yields a super-algebraically convergent method (Preston et al. Reference Preston, Chamberlain and Chandler-Wilde2011; Atkinson Reference Atkinson1997). To implement this scheme we note that
$\phi ^H$ is also infinitely differentiable. In this situation a simple application of the trapezoidal rule yields a super-algebraically convergent method (Preston et al. Reference Preston, Chamberlain and Chandler-Wilde2011; Atkinson Reference Atkinson1997). To implement this scheme we note that ![]() $\boldsymbol {x}=(x,h(x,t))$ on
$\boldsymbol {x}=(x,h(x,t))$ on ![]() $\varGamma _I$, and hence the trapezoidal rule approximation to the integral over
$\varGamma _I$, and hence the trapezoidal rule approximation to the integral over ![]() $\varGamma _I$ of a function
$\varGamma _I$ of a function ![]() $F(\boldsymbol {x})=\hat {F}(x)$ may be written
$F(\boldsymbol {x})=\hat {F}(x)$ may be written
 \begin{equation} \left. \begin{aligned} \int_{\varGamma_I}F(\boldsymbol{x})\,\mathrm{d}\varGamma_I(\boldsymbol{x}) & =\int_{-L}^{L}\hat{F}(x)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x,t)}\right)^2}\,\mathrm{d}x\\ & \approx\frac{2L}{n}\sum_{j=1}^{n}\hat{F}\left(x_j\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}, \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \int_{\varGamma_I}F(\boldsymbol{x})\,\mathrm{d}\varGamma_I(\boldsymbol{x}) & =\int_{-L}^{L}\hat{F}(x)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x,t)}\right)^2}\,\mathrm{d}x\\ & \approx\frac{2L}{n}\sum_{j=1}^{n}\hat{F}\left(x_j\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}, \end{aligned} \right\} \end{equation}
where ![]() $x_j=-L+2L(j-1)/n$ denotes a uniform spatial discretisation of the (dynamic) interface
$x_j=-L+2L(j-1)/n$ denotes a uniform spatial discretisation of the (dynamic) interface ![]() $\varGamma _I$, and we highlight that throughout this work we suppress the time dependence of
$\varGamma _I$, and we highlight that throughout this work we suppress the time dependence of ![]() $\varGamma _I$ for concision. Note that because we have assumed above that
$\varGamma _I$ for concision. Note that because we have assumed above that ![]() $h$ is given by trigonometric interpolation, its derivative
$h$ is given by trigonometric interpolation, its derivative ![]() $\partial h/\partial x$ may be computed simply by differentiating its Fourier components as described in Preston et al. (Reference Preston, Chamberlain and Chandler-Wilde2011). Applying the formula (5.2) to the integral in (3.17) yields the following approximation:
$\partial h/\partial x$ may be computed simply by differentiating its Fourier components as described in Preston et al. (Reference Preston, Chamberlain and Chandler-Wilde2011). Applying the formula (5.2) to the integral in (3.17) yields the following approximation:
 \begin{equation} \int_{\varGamma_I}\frac{\partial G^H}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x},\boldsymbol{x}_0)\phi(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\approx\frac{2L}{n}\sum_{j=1}^{n}k_{i,j}\hat{\phi}(x_j)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}, \end{equation}
\begin{equation} \int_{\varGamma_I}\frac{\partial G^H}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x},\boldsymbol{x}_0)\phi(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\approx\frac{2L}{n}\sum_{j=1}^{n}k_{i,j}\hat{\phi}(x_j)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}, \end{equation}where
 \begin{equation} k_{i,j}=\frac{1}{\sqrt{1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2}}\left.\left(\dfrac{\partial G^H}{\partial y_0}(\boldsymbol{x},\boldsymbol{x}_0)-\dfrac{\partial h}{\partial x}{(x_j,t)}\dfrac{\partial G^H}{\partial x_0}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_i,\ \boldsymbol{x}_0=\boldsymbol{x}_j)} \end{equation}
\begin{equation} k_{i,j}=\frac{1}{\sqrt{1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2}}\left.\left(\dfrac{\partial G^H}{\partial y_0}(\boldsymbol{x},\boldsymbol{x}_0)-\dfrac{\partial h}{\partial x}{(x_j,t)}\dfrac{\partial G^H}{\partial x_0}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_i,\ \boldsymbol{x}_0=\boldsymbol{x}_j)} \end{equation}
for ![]() $i\neq j$ and
$i\neq j$ and ![]() $\hat {\phi }(x_j):=\phi (\boldsymbol {x}_j)$. In addition,
$\hat {\phi }(x_j):=\phi (\boldsymbol {x}_j)$. In addition, ![]() $\boldsymbol {x}_i=(x_i,h(x_i,t))$ (and similarly for
$\boldsymbol {x}_i=(x_i,h(x_i,t))$ (and similarly for ![]() $\boldsymbol {x}_j$) and
$\boldsymbol {x}_j$) and ![]() $k_{i,j}$ corresponds to the directional derivative of
$k_{i,j}$ corresponds to the directional derivative of ![]() $G_H$ (3.2) with respect to
$G_H$ (3.2) with respect to ![]() $\boldsymbol {\nu }$ at the quadrature node
$\boldsymbol {\nu }$ at the quadrature node ![]() $\boldsymbol {x}_j$. When
$\boldsymbol {x}_j$. When ![]() $i=j$, the formula (5.4) contains an apparent singularity at
$i=j$, the formula (5.4) contains an apparent singularity at ![]() $x_i=x_j$ (see (3.1) and (3.2)). However, one may utilise the smoothness of the interface profile
$x_i=x_j$ (see (3.1) and (3.2)). However, one may utilise the smoothness of the interface profile ![]() $h$ to derive the following (non-singular) formula for
$h$ to derive the following (non-singular) formula for ![]() $k_{j,j}$ in terms of
$k_{j,j}$ in terms of ![]() $h$ and its spatial derivatives (for similar derivations see Preston et al. (Reference Preston, Chamberlain and Chandler-Wilde2011) and Atkinson (Reference Atkinson1997, chap. 7)):
$h$ and its spatial derivatives (for similar derivations see Preston et al. (Reference Preston, Chamberlain and Chandler-Wilde2011) and Atkinson (Reference Atkinson1997, chap. 7)):
 \begin{equation} k_{j,j}=\frac{\dfrac{\partial^2 h}{\partial x^2}{(x_j,t)}}{4{\rm \pi}\left(1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2\right)}+\frac{1}{4L\sqrt{1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2}}\coth\left(\frac{{\rm \pi} }{L}h(x_j,t)\right). \end{equation}
\begin{equation} k_{j,j}=\frac{\dfrac{\partial^2 h}{\partial x^2}{(x_j,t)}}{4{\rm \pi}\left(1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2\right)}+\frac{1}{4L\sqrt{1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2}}\coth\left(\frac{{\rm \pi} }{L}h(x_j,t)\right). \end{equation}
As with the first derivative, ![]() $\partial ^2 h/\partial x^2$ may be computed simply by differentiation of the Fourier components for
$\partial ^2 h/\partial x^2$ may be computed simply by differentiation of the Fourier components for ![]() $h$. Applying the approximation (5.3) to the second-kind integral equation (3.17) leads to the following Nyström scheme for the approximate solution
$h$. Applying the approximation (5.3) to the second-kind integral equation (3.17) leads to the following Nyström scheme for the approximate solution ![]() $\phi ^n$:
$\phi ^n$:
 \begin{equation} \phi^{n}(x_i)+\frac{4L(\epsilon_1-\epsilon_2)}{n(\epsilon_1+\epsilon_2)}\sum_{j=1}^{n}k_{i,j}\phi^{n}(x_j)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}=\frac{2\epsilon_1\phi^H(x_i,h(x_i,t))}{(\epsilon_1+\epsilon_2)} \end{equation}
\begin{equation} \phi^{n}(x_i)+\frac{4L(\epsilon_1-\epsilon_2)}{n(\epsilon_1+\epsilon_2)}\sum_{j=1}^{n}k_{i,j}\phi^{n}(x_j)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}=\frac{2\epsilon_1\phi^H(x_i,h(x_i,t))}{(\epsilon_1+\epsilon_2)} \end{equation}
for ![]() $i=1,\ldots ,n$. The super-algebraic convergence of
$i=1,\ldots ,n$. The super-algebraic convergence of ![]() $\phi ^n$ to
$\phi ^n$ to ![]() $\phi$ for increasing
$\phi$ for increasing ![]() $n$ is a consequence of Preston et al. (Reference Preston, Chamberlain and Chandler-Wilde2011, theorem 3.12).
$n$ is a consequence of Preston et al. (Reference Preston, Chamberlain and Chandler-Wilde2011, theorem 3.12).
We now consider a Nyström method for the solution of (3.18), which is a first-kind integral equation for ![]() $\partial \phi _{\alpha }/\partial \nu _0$,
$\partial \phi _{\alpha }/\partial \nu _0$, ![]() $\alpha =1,2$. In particular, we note that the kernel function
$\alpha =1,2$. In particular, we note that the kernel function ![]() $G^H$ contains a logarithmic singularity and (3.18) falls into the class of first-kind equations analysed in Kress & Sloan (Reference Kress and Sloan1993). The approach here is therefore based on the scheme presented in Kress & Sloan (Reference Kress and Sloan1993) (see also Kress (Reference Kress1989) and references therein). Super-algebraic convergence rates will then be attained due to Kress & Sloan (Reference Kress and Sloan1993, theorem 2.3) if the right-hand side of (3.18) is infinitely differentiable. We note that
$G^H$ contains a logarithmic singularity and (3.18) falls into the class of first-kind equations analysed in Kress & Sloan (Reference Kress and Sloan1993). The approach here is therefore based on the scheme presented in Kress & Sloan (Reference Kress and Sloan1993) (see also Kress (Reference Kress1989) and references therein). Super-algebraic convergence rates will then be attained due to Kress & Sloan (Reference Kress and Sloan1993, theorem 2.3) if the right-hand side of (3.18) is infinitely differentiable. We note that ![]() $\phi$ will be replaced by the numerical solution
$\phi$ will be replaced by the numerical solution ![]() $\phi ^n$ in the right-hand side of (3.18) and therefore trigonometric polynomials will be used to obtain an infinitely differentiable interpolant. The right-hand side of (3.18) will then be infinitely differentiable for
$\phi ^n$ in the right-hand side of (3.18) and therefore trigonometric polynomials will be used to obtain an infinitely differentiable interpolant. The right-hand side of (3.18) will then be infinitely differentiable for ![]() $h(\cdot ,t)\in C^{\infty }([-L,L])$ for all
$h(\cdot ,t)\in C^{\infty }([-L,L])$ for all ![]() $t\geq 0$ (Chappell Reference Chappell2015).
$t\geq 0$ (Chappell Reference Chappell2015).
We now outline the quadrature rule we employ to approximate the integral on the left-hand side of (3.18). We first define
and note that on ![]() $\varGamma _I$ where
$\varGamma _I$ where ![]() $y=h(x,t)$ and
$y=h(x,t)$ and ![]() $h(\cdot ,t)\in C^{\infty }([-L,L])$, then
$h(\cdot ,t)\in C^{\infty }([-L,L])$, then ![]() $V$ is infinitely differentiable with respect to both
$V$ is infinitely differentiable with respect to both ![]() $x$ and
$x$ and ![]() $x_0$ (Chappell Reference Chappell2015). We then decompose the integral on the left-hand side of (3.18) as
$x_0$ (Chappell Reference Chappell2015). We then decompose the integral on the left-hand side of (3.18) as
 \begin{align} &\int_{\varGamma_I}G^H(\boldsymbol{x},\boldsymbol{x}_0)\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0) = \int_{\varGamma_I}(V(\boldsymbol{x},\boldsymbol{x}_0)-G(\boldsymbol{x},\boldsymbol{x}'_0))\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0) \nonumber\\ &\qquad -\frac{1}{4{\rm \pi}}\int_{\varGamma_I}\ln\left(4\sin^2\left(\frac{\rm \pi}{2L}(x-x_0)\right)\right)\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0), \end{align}
\begin{align} &\int_{\varGamma_I}G^H(\boldsymbol{x},\boldsymbol{x}_0)\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0) = \int_{\varGamma_I}(V(\boldsymbol{x},\boldsymbol{x}_0)-G(\boldsymbol{x},\boldsymbol{x}'_0))\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0) \nonumber\\ &\qquad -\frac{1}{4{\rm \pi}}\int_{\varGamma_I}\ln\left(4\sin^2\left(\frac{\rm \pi}{2L}(x-x_0)\right)\right)\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0), \end{align}
where the logarithmic singularity of the integral on the left-hand side is only present in the final integral on the right-hand side. In fact, ![]() $V(\boldsymbol {x},\boldsymbol {x}_0)-G(\boldsymbol {x},\boldsymbol {x}'_0)$ is infinitely differentiable with respect to both
$V(\boldsymbol {x},\boldsymbol {x}_0)-G(\boldsymbol {x},\boldsymbol {x}'_0)$ is infinitely differentiable with respect to both ![]() $x$ and
$x$ and ![]() $x_0$ on
$x_0$ on ![]() $\varGamma _I$ and so the first integral on the right of (5.8) may be well approximated using the trapezoidal rule as before. For the term containing the logarithmic singularity we employ a quadrature rule of the form
$\varGamma _I$ and so the first integral on the right of (5.8) may be well approximated using the trapezoidal rule as before. For the term containing the logarithmic singularity we employ a quadrature rule of the form
 \begin{equation} \frac{-1}{4{\rm \pi}}\int_{-L}^{L}\ln\left(4\sin^2\left(\frac{\rm \pi}{2L}(x-x_0)\right)\right)\hat{F}(x_0)\,\mathrm{d}x_0\approx\sum_{j=1}^{2N}R_{j}(x)\hat{F}\left(x_j\right), \end{equation}
\begin{equation} \frac{-1}{4{\rm \pi}}\int_{-L}^{L}\ln\left(4\sin^2\left(\frac{\rm \pi}{2L}(x-x_0)\right)\right)\hat{F}(x_0)\,\mathrm{d}x_0\approx\sum_{j=1}^{2N}R_{j}(x)\hat{F}\left(x_j\right), \end{equation}
for positive integer ![]() $N=n/2$ (assuming
$N=n/2$ (assuming ![]() $n$ is even), with
$n$ is even), with ![]() $x_j=-L+L(j-1)/n$,
$x_j=-L+L(j-1)/n$, ![]() $j=1,\ldots ,n$, as before. The quadrature weight function
$j=1,\ldots ,n$, as before. The quadrature weight function ![]() $R_{j}(x)$ is given by
$R_{j}(x)$ is given by
 \begin{equation} R_{j}(x)=\frac{L}{2{\rm \pi} n}\left\{\sum_{m=1}^{N-1}\frac{1}{m}\cos\left(\frac{m{\rm \pi}}{L}(x-x_j)\right)+\frac{1}{n}\cos\left(\frac{N{\rm \pi}}{L}(x-x_j)\right)\right\}. \end{equation}
\begin{equation} R_{j}(x)=\frac{L}{2{\rm \pi} n}\left\{\sum_{m=1}^{N-1}\frac{1}{m}\cos\left(\frac{m{\rm \pi}}{L}(x-x_j)\right)+\frac{1}{n}\cos\left(\frac{N{\rm \pi}}{L}(x-x_j)\right)\right\}. \end{equation}
This choice of quadrature computes the integral in (5.9) exactly when ![]() $\hat {F}$ has been replaced by its trigonometric interpolation polynomial. To see this replace
$\hat {F}$ has been replaced by its trigonometric interpolation polynomial. To see this replace ![]() $\hat {F}$ in (5.9) by the Lagrange trigonometric polynomial of order
$\hat {F}$ in (5.9) by the Lagrange trigonometric polynomial of order ![]() $j$, then the formula (5.10) may be derived for the integral on the left-hand side; see Kress & Sloan (Reference Kress and Sloan1993) and Kress (Reference Kress1989, p. 208) for details.
$j$, then the formula (5.10) may be derived for the integral on the left-hand side; see Kress & Sloan (Reference Kress and Sloan1993) and Kress (Reference Kress1989, p. 208) for details.
We therefore arrive at the following approximation for the integral on the left-hand side of (3.18) evaluated at the ![]() $i$th quadrature node for any
$i$th quadrature node for any ![]() $i=1,\ldots ,n$:
$i=1,\ldots ,n$:
 \begin{align} & \int_{\varGamma_I} G^H(\boldsymbol{x}_i,\boldsymbol{x}_0)\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\nonumber\\ &\qquad \approx\sum_{j=1}^{n}\frac{\partial\phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_j)\left(R_{j}(x_i)+\frac{2L}{n}s_{i,j}\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2} \end{align}
\begin{align} & \int_{\varGamma_I} G^H(\boldsymbol{x}_i,\boldsymbol{x}_0)\frac{\partial \phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\nonumber\\ &\qquad \approx\sum_{j=1}^{n}\frac{\partial\phi_{\alpha}}{\partial\boldsymbol{\nu}_0}(\boldsymbol{x}_j)\left(R_{j}(x_i)+\frac{2L}{n}s_{i,j}\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2} \end{align}
for ![]() $\alpha =1,2$. Here,
$\alpha =1,2$. Here, ![]() $s_{i,j}=V(\boldsymbol {x}_i,\boldsymbol {x}_j)-G(\boldsymbol {x}_i,\boldsymbol {x}'_j)$ and
$s_{i,j}=V(\boldsymbol {x}_i,\boldsymbol {x}_j)-G(\boldsymbol {x}_i,\boldsymbol {x}'_j)$ and ![]() $\boldsymbol {x}'_j=(x_j,-h(x_j,t))$. For the diagonal case this may be reduced to
$\boldsymbol {x}'_j=(x_j,-h(x_j,t))$. For the diagonal case this may be reduced to
 \begin{equation} s_{j,j}=\frac{-1}{4{\rm \pi}}\left\{\ln\left(1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2\right)-\ln\left(4\sinh^2\left(\frac{\rm \pi}{L}h(x_j,t)\right)\right)\right\}. \end{equation}
\begin{equation} s_{j,j}=\frac{-1}{4{\rm \pi}}\left\{\ln\left(1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2\right)-\ln\left(4\sinh^2\left(\frac{\rm \pi}{L}h(x_j,t)\right)\right)\right\}. \end{equation}
Applying the approximation (5.11) to the first-kind integral equation (3.18) leads to the following Nyström scheme for the approximate solution ![]() $\partial \phi ^n_{\alpha }/\partial \nu _0$:
$\partial \phi ^n_{\alpha }/\partial \nu _0$:
 \begin{align} &\sum_{j=1}^{n}\frac{\partial\phi^n_{\alpha}}{\partial\nu_0}(x_j)\left(R_{j}(x_i)+\frac{2L}{n}s_{i,j}\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}\nonumber\\ &\qquad =\frac{\epsilon_2}{\epsilon_{\alpha}}\left(\frac{-\phi^n(x_i)}{2}+\frac{2L}{n}\sum_{j=1}^{n}k_{i,j}\phi^{n}(x_j)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}\right), \end{align}
\begin{align} &\sum_{j=1}^{n}\frac{\partial\phi^n_{\alpha}}{\partial\nu_0}(x_j)\left(R_{j}(x_i)+\frac{2L}{n}s_{i,j}\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}\nonumber\\ &\qquad =\frac{\epsilon_2}{\epsilon_{\alpha}}\left(\frac{-\phi^n(x_i)}{2}+\frac{2L}{n}\sum_{j=1}^{n}k_{i,j}\phi^{n}(x_j)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}\right), \end{align}
for ![]() $i=1,\ldots ,n$ and
$i=1,\ldots ,n$ and ![]() $\alpha =1,2$.
$\alpha =1,2$.
The vectorial boundary integral equation (3.13) may also be discretised via the Nyström method following approaches analogous to that for (3.17) described above. Instead of the directional derivative of ![]() $G^H=A-A'$ with respect to
$G^H=A-A'$ with respect to ![]() $\boldsymbol {\nu }_0$ found in (3.17), the matrix kernel function
$\boldsymbol {\nu }_0$ found in (3.17), the matrix kernel function ![]() $\boldsymbol{\mathsf{T}}^{H}$ (3.9) contains derivatives of
$\boldsymbol{\mathsf{T}}^{H}$ (3.9) contains derivatives of ![]() $A$ and
$A$ and ![]() $A'$ between first and third order with respect to both
$A'$ between first and third order with respect to both ![]() $\lambda x$ and
$\lambda x$ and ![]() $\lambda y$, as well as mixed derivatives. We note that in most cases there are no singularities to consider in the integrand in (3.13); in the expression (3.9), the latter three terms are all evaluated at
$\lambda y$, as well as mixed derivatives. We note that in most cases there are no singularities to consider in the integrand in (3.13); in the expression (3.9), the latter three terms are all evaluated at ![]() $\boldsymbol {x}'_0$, which is the reflection of the point
$\boldsymbol {x}'_0$, which is the reflection of the point ![]() $\boldsymbol {x}_0$ in
$\boldsymbol {x}_0$ in ![]() $\varGamma _0$ and, as such, can never coincide with the point
$\varGamma _0$ and, as such, can never coincide with the point ![]() $\boldsymbol {x}\in \varGamma _I$. In these cases we base our Nyström method discretisation on the standard trapezoidal rule as outlined above. For the first term in (3.9), however, we must take care of the singularities at
$\boldsymbol {x}\in \varGamma _I$. In these cases we base our Nyström method discretisation on the standard trapezoidal rule as outlined above. For the first term in (3.9), however, we must take care of the singularities at ![]() $\boldsymbol {x}=\boldsymbol {x}_0$ in the quadrature scheme for
$\boldsymbol {x}=\boldsymbol {x}_0$ in the quadrature scheme for ![]() $\int _{\varGamma _I}\boldsymbol{\mathsf{T}}(\boldsymbol {x},\boldsymbol {x}_0)\boldsymbol {q}(\boldsymbol {x}_0)\mathrm {d}\varGamma _I(\boldsymbol {x}_0)$. In particular, we need to evaluate
$\int _{\varGamma _I}\boldsymbol{\mathsf{T}}(\boldsymbol {x},\boldsymbol {x}_0)\boldsymbol {q}(\boldsymbol {x}_0)\mathrm {d}\varGamma _I(\boldsymbol {x}_0)$. In particular, we need to evaluate ![]() $A_x$,
$A_x$, ![]() $A_y$,
$A_y$, ![]() $\lambda (y-y_0)A_{xx}$ and
$\lambda (y-y_0)A_{xx}$ and ![]() $\lambda (y-y_0)A_{xy}$ in the case
$\lambda (y-y_0)A_{xy}$ in the case ![]() $i=j$, where
$i=j$, where ![]() $i$ is the index of the quadrature node at which the solution is sought and
$i$ is the index of the quadrature node at which the solution is sought and ![]() $j$ is the index of the quadrature node for the numerical integration over
$j$ is the index of the quadrature node for the numerical integration over ![]() $\varGamma _I$ as above. To do so, we utilise the following relations:
$\varGamma _I$ as above. To do so, we utilise the following relations:
 \begin{gather} \left.\left( A_x\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left(\frac{\partial G}{\partial x}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0, \end{gather}
\begin{gather} \left.\left( A_x\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left(\frac{\partial G}{\partial x}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0, \end{gather} \begin{gather} \left.\left( A_y\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left(\frac{\partial G}{\partial y}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{\dfrac{\partial^2 h}{\partial x^2}{(x_j,t)}}{4{\rm \pi}\lambda\left(1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2\right)}, \end{gather}
\begin{gather} \left.\left( A_y\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left(\frac{\partial G}{\partial y}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{\dfrac{\partial^2 h}{\partial x^2}{(x_j,t)}}{4{\rm \pi}\lambda\left(1+\left(\dfrac{\partial h}{\partial x}{(x_j,t)}\right)^2\right)}, \end{gather} \begin{gather} \left.\left(\lambda(y-y_0) A_{xx}\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left((y-y_0)\frac{\partial^2 G}{\partial x^2}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0, \end{gather}
\begin{gather} \left.\left(\lambda(y-y_0) A_{xx}\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left((y-y_0)\frac{\partial^2 G}{\partial x^2}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0, \end{gather} \begin{gather} \left.\left(\lambda(y-y_0) A_{xy}\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left((y-y_0)\frac{\partial^2 G}{\partial x\partial y}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0. \end{gather}
\begin{gather} \left.\left(\lambda(y-y_0) A_{xy}\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\frac{1}{\lambda}\left.\left((y-y_0)\frac{\partial^2 G}{\partial x\partial y}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0. \end{gather}
For the case ![]() $i\neq j$, we simply employ a standard trapezoidal rule to evaluate
$i\neq j$, we simply employ a standard trapezoidal rule to evaluate ![]() $\int _{\varGamma _I}\boldsymbol{\mathsf{T}}(\boldsymbol {x},\boldsymbol {x}_0)\boldsymbol {q}(\boldsymbol {x}_0)\mathrm {d}\varGamma _I(\boldsymbol {x}_0)$. For reasons of brevity we omit to write out the numerical scheme for (3.13) in full, but instead note simply that it is analogous to the procedure for the scalar equation (3.17), except using the relations above for the diagonal case.
$\int _{\varGamma _I}\boldsymbol{\mathsf{T}}(\boldsymbol {x},\boldsymbol {x}_0)\boldsymbol {q}(\boldsymbol {x}_0)\mathrm {d}\varGamma _I(\boldsymbol {x}_0)$. For reasons of brevity we omit to write out the numerical scheme for (3.13) in full, but instead note simply that it is analogous to the procedure for the scalar equation (3.17), except using the relations above for the diagonal case.
Once (3.13) has been solved for ![]() $\boldsymbol {q}$, the solution for the fluid velocity
$\boldsymbol {q}$, the solution for the fluid velocity ![]() $\boldsymbol {u}$ on
$\boldsymbol {u}$ on ![]() $\varGamma _I$ may be evaluated using the formula (3.12). We evaluate this formula using a quadrature rule that is consistent with the Nyström method scheme applied to solve (3.13). In particular, the trapezoidal rule is applied, together with a treatment of singularities that is analogous the scheme for (3.18) detailed above. We note that as for
$\varGamma _I$ may be evaluated using the formula (3.12). We evaluate this formula using a quadrature rule that is consistent with the Nyström method scheme applied to solve (3.13). In particular, the trapezoidal rule is applied, together with a treatment of singularities that is analogous the scheme for (3.18) detailed above. We note that as for ![]() $\boldsymbol{\mathsf{T}}^H$, it is only in the first of the four terms (
$\boldsymbol{\mathsf{T}}^H$, it is only in the first of the four terms (![]() $\boldsymbol{\mathsf{G}}$) that are summed to form the matrix
$\boldsymbol{\mathsf{G}}$) that are summed to form the matrix ![]() $\boldsymbol{\mathsf{G}}^H$ (3.5) (the kernel function in (3.12)) that singularities can occur. For the four entries of the matrix
$\boldsymbol{\mathsf{G}}^H$ (3.5) (the kernel function in (3.12)) that singularities can occur. For the four entries of the matrix ![]() $\boldsymbol{\mathsf{G}}$ we need to evaluate
$\boldsymbol{\mathsf{G}}$ we need to evaluate ![]() $A$,
$A$, ![]() $\lambda (y-y_0)A_x$ and
$\lambda (y-y_0)A_x$ and ![]() $\lambda (y-y_0)A_y$ in the case
$\lambda (y-y_0)A_y$ in the case ![]() $i=j$, where
$i=j$, where ![]() $i$ and
$i$ and ![]() $j$ are as above. For the latter two terms, it is clear from the above relations for (3.13) that we have
$j$ are as above. For the latter two terms, it is clear from the above relations for (3.13) that we have
 \begin{gather} \left.\left( \lambda(y-y_0)A_x\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\left.\left((y-y_0)\frac{\partial G}{\partial x}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0, \end{gather}
\begin{gather} \left.\left( \lambda(y-y_0)A_x\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\left.\left((y-y_0)\frac{\partial G}{\partial x}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0, \end{gather} \begin{gather} \left.\left( \lambda(y-y_0)A_y\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\left.\left((y-y_0)\frac{\partial G}{\partial y}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0. \end{gather}
\begin{gather} \left.\left( \lambda(y-y_0)A_y\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=\left.\left((y-y_0)\frac{\partial G}{\partial y}(\boldsymbol{x},\boldsymbol{x}_0)\right)\right|_{(\boldsymbol{x}=\boldsymbol{x}_j,\,\boldsymbol{x}_0=\boldsymbol{x}_j)}=0. \end{gather}
For the terms containing ![]() $A$, we need to evaluate
$A$, we need to evaluate
where the function ![]() $q$ can be either entry from the vector function
$q$ can be either entry from the vector function ![]() $\boldsymbol {q}$. This can be done using an analogous splitting to the one in (5.8) as follows:
$\boldsymbol {q}$. This can be done using an analogous splitting to the one in (5.8) as follows:
 \begin{align} &\int_{\varGamma_I}G(\boldsymbol{x},\boldsymbol{x}_0)q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0) =\int_{\varGamma_I}V(\boldsymbol{x},\boldsymbol{x}_0)q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\nonumber\\ &\qquad -\frac{1}{4{\rm \pi}} \int_{\varGamma_I}\ln\left(4\sin^2\left(\frac{\rm \pi}{2L}(x-x_0)\right)\right)q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0). \end{align}
\begin{align} &\int_{\varGamma_I}G(\boldsymbol{x},\boldsymbol{x}_0)q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0) =\int_{\varGamma_I}V(\boldsymbol{x},\boldsymbol{x}_0)q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\nonumber\\ &\qquad -\frac{1}{4{\rm \pi}} \int_{\varGamma_I}\ln\left(4\sin^2\left(\frac{\rm \pi}{2L}(x-x_0)\right)\right)q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0). \end{align}
Following the same steps as for (3.18) leads to the following approximation for the integral (5.20) evaluated at the ![]() $i$th quadrature node for any
$i$th quadrature node for any ![]() $i=1,\ldots ,n$:
$i=1,\ldots ,n$:
 \begin{align} &\int_{\varGamma_I}G(\boldsymbol{x}_i,\boldsymbol{x}_0) q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\nonumber\\ &\qquad \approx\sum_{j=1}^{n}q(\boldsymbol{x}_j)\left(R_{j}(x_i)+\frac{2L}{n}V(\boldsymbol{x}_i,\boldsymbol{x}_j)\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}. \end{align}
\begin{align} &\int_{\varGamma_I}G(\boldsymbol{x}_i,\boldsymbol{x}_0) q(\boldsymbol{x}_0)\,\mathrm{d}\varGamma_I(\boldsymbol{x}_0)\nonumber\\ &\qquad \approx\sum_{j=1}^{n}q(\boldsymbol{x}_j)\left(R_{j}(x_i)+\frac{2L}{n}V(\boldsymbol{x}_i,\boldsymbol{x}_j)\right)\sqrt{1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2}. \end{align}
For the diagonal case ![]() $i=j$ we note that
$i=j$ we note that
 \begin{equation} V(\boldsymbol{x}_j,\boldsymbol{x}_j)=\frac{-1}{4{\rm \pi}}\ln\left(1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2\right). \end{equation}
\begin{equation} V(\boldsymbol{x}_j,\boldsymbol{x}_j)=\frac{-1}{4{\rm \pi}}\ln\left(1+\left(\frac{\partial h}{\partial x}{(x_j,t)}\right)^2\right). \end{equation} Finally, we describe the time evolution of the interface ![]() $h(x,t)$ via a discretised form of (2.14) with time step
$h(x,t)$ via a discretised form of (2.14) with time step ![]() ${\rm \Delta} t$ and spatial mesh size
${\rm \Delta} t$ and spatial mesh size ![]() ${\rm \Delta} x$. We denote
${\rm \Delta} x$. We denote ![]() $h_i^k=h(x_i,t_k)$ for
$h_i^k=h(x_i,t_k)$ for ![]() $i=1,\ldots ,n$,
$i=1,\ldots ,n$, ![]() $k=1,2,\ldots$ and apply Euler's method to approximate
$k=1,2,\ldots$ and apply Euler's method to approximate ![]() $h_i^{k+1}=h(x_i,t_{k+1})$ as follows:
$h_i^{k+1}=h(x_i,t_{k+1})$ as follows:
 \begin{equation} h_i^{k+1}=h_i^k+{\rm \Delta} t\left.\left(u\frac{\partial h}{\partial x}-v \right)\right|_{(x_i,t_k)}. \end{equation}
\begin{equation} h_i^{k+1}=h_i^k+{\rm \Delta} t\left.\left(u\frac{\partial h}{\partial x}-v \right)\right|_{(x_i,t_k)}. \end{equation}
Note that the flow ![]() $\boldsymbol {u}_1=\boldsymbol {u}=(u,v)^{\textrm {T}}$ corresponding to the interface position at
$\boldsymbol {u}_1=\boldsymbol {u}=(u,v)^{\textrm {T}}$ corresponding to the interface position at ![]() $t=t_k$ is obtained as described above, where the spatial variation of
$t=t_k$ is obtained as described above, where the spatial variation of ![]() $h$ at each time point is given by trigonometric interpolation and hence its spatial derivative may be computed simply by differentiating its Fourier components. We further remark that since the velocity terms on the right-hand side of (5.24) are only known at the current time then we are somewhat restricted in terms of our choice of time discretisation method. In the next section, we will discuss the additional discretisation methods employed for the two asymptotic reductions introduced above.
$h$ at each time point is given by trigonometric interpolation and hence its spatial derivative may be computed simply by differentiating its Fourier components. We further remark that since the velocity terms on the right-hand side of (5.24) are only known at the current time then we are somewhat restricted in terms of our choice of time discretisation method. In the next section, we will discuss the additional discretisation methods employed for the two asymptotic reductions introduced above.
5.2. Discretisation for the asymptotic approaches
In this section we describe two approaches for the discretisation of the interface evolution equation (4.13).
First, we consider an explicit Euler scheme as follows:
 \begin{equation} \tilde{h}_i^{k+1}=\tilde{h}_i^k+{\rm \Delta} t\left.\left(\frac{\partial}{\partial \tilde{x}}\left(\frac{\tilde{h}^3}{3}\left(K\frac{\partial M_1}{\partial \tilde{x}}-\frac{\partial^3 \tilde{h}}{\partial \tilde{x}^3}\right) \right)\right)\right|_{(\tilde{x}_i,\tilde{t}_k)}, \end{equation}
\begin{equation} \tilde{h}_i^{k+1}=\tilde{h}_i^k+{\rm \Delta} t\left.\left(\frac{\partial}{\partial \tilde{x}}\left(\frac{\tilde{h}^3}{3}\left(K\frac{\partial M_1}{\partial \tilde{x}}-\frac{\partial^3 \tilde{h}}{\partial \tilde{x}^3}\right) \right)\right)\right|_{(\tilde{x}_i,\tilde{t}_k)}, \end{equation}
with corresponding notation to that employed in (5.24), but with the tildes denoting the non-dimensional variables in (4.13) as before. Note that the spatial derivatives of ![]() $M_1$ are computed either by Fourier interpolation in the case of scheme 2, or analytically in the case of the (fully asymptotic) scheme 3.
$M_1$ are computed either by Fourier interpolation in the case of scheme 2, or analytically in the case of the (fully asymptotic) scheme 3.
The presence of a ‘stiff’ fourth-order spatial derivative on the right-hand side of (4.13) places restrictive stability constraints on the time-stepping scheme. For example, a standard von Neumann stability analysis reveals that an explicit finite difference discretisation with ![]() $n$ spatial mesh points leads to a requirement of the form
$n$ spatial mesh points leads to a requirement of the form ![]() ${\rm \Delta} t\propto n^{-4}$. We remark that such an analysis is presented in, for example, Momoniat, Harley & Adlem (Reference Momoniat, Harley and Adlem2010), in which the generalised lubrication equation (i.e.
${\rm \Delta} t\propto n^{-4}$. We remark that such an analysis is presented in, for example, Momoniat, Harley & Adlem (Reference Momoniat, Harley and Adlem2010), in which the generalised lubrication equation (i.e. ![]() $K=0$ in (4.13)) is considered; however, the result can be extended to the inhomogeneous case under the assumption of an upper bound on the maximal film height. We also find in practice that the scheme (5.25) requires a time step
$K=0$ in (4.13)) is considered; however, the result can be extended to the inhomogeneous case under the assumption of an upper bound on the maximal film height. We also find in practice that the scheme (5.25) requires a time step ![]() ${\rm \Delta} t\propto n^{-4}$ for stability, even when the spatial derivatives of
${\rm \Delta} t\propto n^{-4}$ for stability, even when the spatial derivatives of ![]() $\tilde {h}$ are computed by Fourier interpolation in place of finite difference formulæ. Nonetheless, the relevant terms may be evaluated relatively quickly, particularly in the case of scheme 3 (fully asymptotic), meaning that it is feasible to compute solutions within the confines of the stability constraint, provided not too fine a spatial grid is required. Generally this should be the case provided that the applied voltage
$\tilde {h}$ are computed by Fourier interpolation in place of finite difference formulæ. Nonetheless, the relevant terms may be evaluated relatively quickly, particularly in the case of scheme 3 (fully asymptotic), meaning that it is feasible to compute solutions within the confines of the stability constraint, provided not too fine a spatial grid is required. Generally this should be the case provided that the applied voltage ![]() $f$ is smooth and periodic, since then the interpolation by trigonometric polynomials should converge spectrally.
$f$ is smooth and periodic, since then the interpolation by trigonometric polynomials should converge spectrally.
In order to circumvent the stability constraint when necessary, we additionally consider the implicit–explicit finite difference scheme presented in Momoniat et al. (Reference Momoniat, Harley and Adlem2010), which treats the ![]() $\partial ^3\tilde {h}/\partial \tilde {x}^3$ term in (4.13) implicitly. Alternative approaches include Crank–Nicolson based schemes for both driven (Ha, Kim & Myers Reference Ha, Kim and Myers2008) and interface relaxation problems (Momoniat et al. Reference Momoniat, Harley and Adlem2010; Li & Kim Reference Li and Kim2013) or finite difference schemes that preserve the positivity of the interface height (Zhornitskaya & Bertozzi Reference Zhornitskaya and Bertozzi1999). In higher-dimensional settings it may be preferable to consider finite element approximations for nonlinear fourth-order degenerate PDEs, see for example Barrett, Blowey & Garcke (Reference Barrett, Blowey and Garcke1998).
$\partial ^3\tilde {h}/\partial \tilde {x}^3$ term in (4.13) implicitly. Alternative approaches include Crank–Nicolson based schemes for both driven (Ha, Kim & Myers Reference Ha, Kim and Myers2008) and interface relaxation problems (Momoniat et al. Reference Momoniat, Harley and Adlem2010; Li & Kim Reference Li and Kim2013) or finite difference schemes that preserve the positivity of the interface height (Zhornitskaya & Bertozzi Reference Zhornitskaya and Bertozzi1999). In higher-dimensional settings it may be preferable to consider finite element approximations for nonlinear fourth-order degenerate PDEs, see for example Barrett, Blowey & Garcke (Reference Barrett, Blowey and Garcke1998).
Our implicit–explicit finite difference scheme may be derived by first approximating the outer spatial derivative using a standard second-order central difference formula with step size ![]() ${\rm \Delta} x$, while evaluating the third-order spatial derivative at the advanced time as follows:
${\rm \Delta} x$, while evaluating the third-order spatial derivative at the advanced time as follows:
 \begin{align} \tilde{h}_i^{k+1}&=\tilde{h}_i^k+\frac{K{\rm \Delta} t}{6{\rm \Delta} x}\left(\left(\tilde{h}_{i+1}^k\right)^3-\left(\tilde{h}_{i-1}^k\right)^3\right)\left.\frac{\partial M_1}{\partial \tilde{x}}\right|_{(\tilde{x}_i,\tilde{t}_k)}\nonumber\\ &\quad -\frac{{\rm \Delta} t}{6{\rm \Delta} x}\left(\left(\tilde{h}_{i+1}^k\right)^3\frac{\partial^3\tilde{h}_{i+1}^{k+1}}{\partial\tilde{x}^3}-\left(\tilde{h}_{i-1}^k\right)^3\frac{\partial^3\tilde{h}_{i-1}^{k+1}}{\partial\tilde{x}^3}\right). \end{align}
\begin{align} \tilde{h}_i^{k+1}&=\tilde{h}_i^k+\frac{K{\rm \Delta} t}{6{\rm \Delta} x}\left(\left(\tilde{h}_{i+1}^k\right)^3-\left(\tilde{h}_{i-1}^k\right)^3\right)\left.\frac{\partial M_1}{\partial \tilde{x}}\right|_{(\tilde{x}_i,\tilde{t}_k)}\nonumber\\ &\quad -\frac{{\rm \Delta} t}{6{\rm \Delta} x}\left(\left(\tilde{h}_{i+1}^k\right)^3\frac{\partial^3\tilde{h}_{i+1}^{k+1}}{\partial\tilde{x}^3}-\left(\tilde{h}_{i-1}^k\right)^3\frac{\partial^3\tilde{h}_{i-1}^{k+1}}{\partial\tilde{x}^3}\right). \end{align}
Recall that the spatial derivatives of ![]() $M_1$ are computed either by Fourier interpolation in the case of scheme 2, or analytically in the case of scheme 3 and thus finite difference approximations of these derivatives are not required. The fully discrete scheme is then obtained on application of the second-order central difference formula
$M_1$ are computed either by Fourier interpolation in the case of scheme 2, or analytically in the case of scheme 3 and thus finite difference approximations of these derivatives are not required. The fully discrete scheme is then obtained on application of the second-order central difference formula
adjusted for the appropriate spatial grid positions. We note that this scheme is shown to be unconditionally stable in the case of the homogeneous switch-off model (![]() $K=0$) for the relaxation of an initially disturbed interface in Momoniat et al. (Reference Momoniat, Harley and Adlem2010), providing a significant improvement over an explicit scheme. However, in our case this comes at the cost of a lower precision approximation of the spatial derivatives (second order instead of spectral convergence). In the next section we consider the three numerical solution approaches outlined above in order to understand the extent of the validity of the asymptotic models and to perform tests with parameters corresponding to those used in typical experimental set-ups (Brown et al. Reference Brown, Wells, Newton and McHale2009, Reference Brown, McHale and Mottram2011).
$K=0$) for the relaxation of an initially disturbed interface in Momoniat et al. (Reference Momoniat, Harley and Adlem2010), providing a significant improvement over an explicit scheme. However, in our case this comes at the cost of a lower precision approximation of the spatial derivatives (second order instead of spectral convergence). In the next section we consider the three numerical solution approaches outlined above in order to understand the extent of the validity of the asymptotic models and to perform tests with parameters corresponding to those used in typical experimental set-ups (Brown et al. Reference Brown, Wells, Newton and McHale2009, Reference Brown, McHale and Mottram2011).
6. Numerical experiments
6.1. Investigation of the asymptotic models
In this section we first perform a series of experiments to investigate the validity of the asymptotic models derived in § 4. We test our models using the same boundary condition for (2.4) as employed in Brown et al. (Reference Brown, McHale and Mottram2011) for a static applied potential; namely: ![]() $f(x)=\Phi \cos ({\rm \pi} x/L)$, where
$f(x)=\Phi \cos ({\rm \pi} x/L)$, where ![]() $\Phi$ is a constant amplitude term. Note that one can then derive the half-space solution
$\Phi$ is a constant amplitude term. Note that one can then derive the half-space solution ![]() $\phi ^H$, either using separation of variables or directly from the boundary integral formula (3.3), to obtain
$\phi ^H$, either using separation of variables or directly from the boundary integral formula (3.3), to obtain
One may also evaluate the asymptotic formula for the Maxwell stress ![]() $M_1$ (4.24) as
$M_1$ (4.24) as
In addition we set the parameter ![]() $\epsilon _1=8$ and
$\epsilon _1=8$ and ![]() $\epsilon _2=1$ to reflect typical values for oil and air in our application of interest (Brown et al. Reference Brown, McHale and Mottram2011).
$\epsilon _2=1$ to reflect typical values for oil and air in our application of interest (Brown et al. Reference Brown, McHale and Mottram2011).
We use the methods described in the previous section to approximate the evolution of the film profile ![]() $h(x,t)$ from an initial constant profile
$h(x,t)$ from an initial constant profile ![]() $h(x,0)=h_0$ until the profile reaches a steady-state wrinkle where the effect of the applied potential is exactly balanced by the forces arising from the surface tension on a curved interface profile. Figure 2 shows the amplitude of the final steady-state wrinkle estimated by all three models: full boundary integral approach for a Stokes’ flow, hybrid long-wavelength asymptotic approach coupled to the boundary integral solution of the electrostatic problem and finally the fully asymptotic approach. The effect of different force terms is assessed by varying the magnitude of the surface tension
$h(x,0)=h_0$ until the profile reaches a steady-state wrinkle where the effect of the applied potential is exactly balanced by the forces arising from the surface tension on a curved interface profile. Figure 2 shows the amplitude of the final steady-state wrinkle estimated by all three models: full boundary integral approach for a Stokes’ flow, hybrid long-wavelength asymptotic approach coupled to the boundary integral solution of the electrostatic problem and finally the fully asymptotic approach. The effect of different force terms is assessed by varying the magnitude of the surface tension ![]() $\gamma$, which enters the loading term in both the Stokes flow model (3.16) and the asymptotic model via the parameter
$\gamma$, which enters the loading term in both the Stokes flow model (3.16) and the asymptotic model via the parameter ![]() $K$ in (4.13). In particular, a larger surface tension will lead to lower steady-state amplitudes by amplifying the curvature driven motion of the interface relative to the dielectrophoretic motion. We fix the parameters
$K$ in (4.13). In particular, a larger surface tension will lead to lower steady-state amplitudes by amplifying the curvature driven motion of the interface relative to the dielectrophoretic motion. We fix the parameters ![]() $L=1$,
$L=1$, ![]() $\Phi =1$,
$\Phi =1$, ![]() $\mu _1=\epsilon _0$ and
$\mu _1=\epsilon _0$ and ![]() $\mu _2=\mu _1\times 10^{-4}$ so that the assumption
$\mu _2=\mu _1\times 10^{-4}$ so that the assumption ![]() $\mu _1\gg \mu _2$ introduced in § 4.1 is valid for these results.
$\mu _1\gg \mu _2$ introduced in § 4.1 is valid for these results.

Figure 2. Comparison of the results from all three models (full boundary integral approach for a Stokes flow, hybrid long-wavelength asymptotic approach coupled to the boundary integral solution of the electrostatic problem and fully asymptotic approach) for the final steady-state wrinkle amplitude with three different force terms: case 1 with ![]() $\gamma =\epsilon _0/50$, case 2 with
$\gamma =\epsilon _0/50$, case 2 with ![]() $\gamma =\epsilon _0/500$ and case 3 with
$\gamma =\epsilon _0/500$ and case 3 with ![]() $\gamma =\epsilon _0/5000$.
$\gamma =\epsilon _0/5000$.
For all three forcing cases tested, one observes convergence of the numerical and hybrid asymptotic approaches to the fully asymptotic (leading order in ![]() $\delta$) result as
$\delta$) result as ![]() $\delta \rightarrow 0$ and the leading-order approximation becomes reasonable in the regime
$\delta \rightarrow 0$ and the leading-order approximation becomes reasonable in the regime ![]() $\delta <0.05$. The fully numerical (Stokes flow) simulation loses accuracy as
$\delta <0.05$. The fully numerical (Stokes flow) simulation loses accuracy as ![]() $\delta$ becomes smaller, and the issue is particularly evident for larger force terms. In these situations, a large number of quadrature nodes may be required in the Nyström discretisation to obtain convergence to a steady state. This imposed a practical limitation on the minimum
$\delta$ becomes smaller, and the issue is particularly evident for larger force terms. In these situations, a large number of quadrature nodes may be required in the Nyström discretisation to obtain convergence to a steady state. This imposed a practical limitation on the minimum ![]() $\delta$ value that could be simulated in the full numerical model for each of the three forcing cases ranging from
$\delta$ value that could be simulated in the full numerical model for each of the three forcing cases ranging from ![]() $\delta =0.025$ for the lightest forcing (case 3 in figure 2) to
$\delta =0.025$ for the lightest forcing (case 3 in figure 2) to ![]() $\delta =0.1$ for the strongest forcing (case 1 in figure 2). A similar limitation is present for the hybrid approach, although the computation of each step is much quicker due to only employing the boundary integral method for the electrostatic part of the simulation. The main computational limitation of this approach is rather the very small time steps necessary for stability of the explicit time-stepping scheme (5.25). In this case, the situation deteriorates further when using the implicit–explicit scheme (5.26) due to a build up of numerical errors and the lower precision of the finite difference approximation for the spatial derivatives; the situation could potentially be improved with the development of a semi-implicit spectral approach in future work. Stable calculations for the fully asymptotic approach can, however, be obtained using the implicit–explicit scheme (5.26) without the strong time-step limitation and this was by far the most computationally efficient approach of the three.
$\delta =0.1$ for the strongest forcing (case 1 in figure 2). A similar limitation is present for the hybrid approach, although the computation of each step is much quicker due to only employing the boundary integral method for the electrostatic part of the simulation. The main computational limitation of this approach is rather the very small time steps necessary for stability of the explicit time-stepping scheme (5.25). In this case, the situation deteriorates further when using the implicit–explicit scheme (5.26) due to a build up of numerical errors and the lower precision of the finite difference approximation for the spatial derivatives; the situation could potentially be improved with the development of a semi-implicit spectral approach in future work. Stable calculations for the fully asymptotic approach can, however, be obtained using the implicit–explicit scheme (5.26) without the strong time-step limitation and this was by far the most computationally efficient approach of the three.
In figure 3 we investigate the thin-film cases more closely in order to examine not only how close the final amplitudes are, but also the growth behaviour over time and the match of the steady-state profile. In addition, we investigate the case of two viscous fluids of comparable viscosity, replacing ![]() $\mu _2=\mu _1\times 10^{-4}$ with
$\mu _2=\mu _1\times 10^{-4}$ with ![]() $\mu _2=\mu _1/2$. Note that the two asymptotic approaches are both independent of
$\mu _2=\mu _1/2$. Note that the two asymptotic approaches are both independent of ![]() $\mu _2$, being derived under the assumption that
$\mu _2$, being derived under the assumption that ![]() $\mu _1\gg \mu _2$, and so only one new curve appears on each panel labelled ‘Stokes viscous’. In all cases we observe a similar final wrinkle profile for all four experiments with the largest discrepancy occurring in the stronger forcing case (case 1) for the numerical boundary integral simulation with a more viscous fluid in
$\mu _1\gg \mu _2$, and so only one new curve appears on each panel labelled ‘Stokes viscous’. In all cases we observe a similar final wrinkle profile for all four experiments with the largest discrepancy occurring in the stronger forcing case (case 1) for the numerical boundary integral simulation with a more viscous fluid in ![]() $\varOmega _2$; here, the greater viscosity leads to a slightly larger final wrinkle amplitude. The differences between the simulations are more evident in the amplitude evolution plots in the left column. However, for the lighter forcing case with
$\varOmega _2$; here, the greater viscosity leads to a slightly larger final wrinkle amplitude. The differences between the simulations are more evident in the amplitude evolution plots in the left column. However, for the lighter forcing case with ![]() $\delta =0.025$, we still see a good agreement between the two asymptotic predictions and the fully numerical results with both
$\delta =0.025$, we still see a good agreement between the two asymptotic predictions and the fully numerical results with both ![]() $\mu _2$ values tested. For the stronger forcing case with
$\mu _2$ values tested. For the stronger forcing case with ![]() $\delta =0.1$ we now observe clear differences in not only the time taken to reach the steady state, but also the steady-state amplitude (due to the finer scale on the vertical axis compared with the final profile plots). These differences can mainly be attributed to the assumptions under which the asymptotic models are derived not being fully satisfied for
$\delta =0.1$ we now observe clear differences in not only the time taken to reach the steady state, but also the steady-state amplitude (due to the finer scale on the vertical axis compared with the final profile plots). These differences can mainly be attributed to the assumptions under which the asymptotic models are derived not being fully satisfied for ![]() $\delta =0.1$, and additionally for
$\delta =0.1$, and additionally for ![]() $\mu _2=\mu _1/2$ in the ‘Stokes Viscous’ case.
$\mu _2=\mu _1/2$ in the ‘Stokes Viscous’ case.

Figure 3. The time evolution of the wrinkle amplitude from flat to steady state ![]() $(a{,}c)$ and the final steady-state wrinkle profile
$(a{,}c)$ and the final steady-state wrinkle profile ![]() $(b{,}d)$. The rows represent the thinnest-film experiment shown in figure 2 for two of the three forcing cases: case 1 with
$(b{,}d)$. The rows represent the thinnest-film experiment shown in figure 2 for two of the three forcing cases: case 1 with ![]() $\gamma =\epsilon _0/50$ (a,b) and case 3 with
$\gamma =\epsilon _0/50$ (a,b) and case 3 with ![]() $\gamma =\epsilon _0/5000$ (c,d). The dash-dot curve (Stokes viscous) shows the effect of reducing the viscosity ratio between
$\gamma =\epsilon _0/5000$ (c,d). The dash-dot curve (Stokes viscous) shows the effect of reducing the viscosity ratio between ![]() $\varOmega _1$ and
$\varOmega _1$ and ![]() $\varOmega _2$ in the Stokes flow boundary integral model from
$\varOmega _2$ in the Stokes flow boundary integral model from ![]() $10^4$ to
$10^4$ to ![]() $2$.
$2$.
A perhaps surprising observation on the results in figure 2 is how closely the wrinkle amplitudes predicted by the numerically simulated Stokes flow model and the hybrid asymptotic approach agree for thick films, suggesting that it is the additional asymptotic reduction of the electrostatic model that is more limiting. We investigate this further in figure 4 where the growth behaviour of a thick film (![]() $\delta =0.5$) over time and the match of the steady-state profile predicted by the numerically simulated Stokes flow model and the hybrid asymptotic approach are compared. The results show that both methods predict essentially the same steady-state result, but the hybrid asymptotic approach is not able to correctly capture the time dynamics and predicts a much faster onset of the steady state than the full model. However, if only the steady state itself were of interest then either method could reasonably be used.
$\delta =0.5$) over time and the match of the steady-state profile predicted by the numerically simulated Stokes flow model and the hybrid asymptotic approach are compared. The results show that both methods predict essentially the same steady-state result, but the hybrid asymptotic approach is not able to correctly capture the time dynamics and predicts a much faster onset of the steady state than the full model. However, if only the steady state itself were of interest then either method could reasonably be used.

Figure 4. The time evolution of the wrinkle amplitude from flat to steady state ![]() $(a)$ and the final steady-state wrinkle profile
$(a)$ and the final steady-state wrinkle profile ![]() $(b)$ for a thick film with
$(b)$ for a thick film with ![]() $\delta =0.5$ and
$\delta =0.5$ and ![]() $\gamma =\epsilon _0/5000$.
$\gamma =\epsilon _0/5000$.
To summarise, between the three approaches tested, at least one can give reasonably accurate results for any possible ![]() $\delta$ value and for
$\delta$ value and for ![]() $\delta <0.05$ one can use the fully asymptotic method for maximal computational efficiency. Note that here we have only presented results where the steady-state amplitude has converged to three significant figures. We have not reported any verification of the discretisation methods or their convergence properties. For the boundary integral model of the electrostatic problem, such an analysis can be found in Chappell (Reference Chappell2015). We have also independently verified that the boundary integral model employed for the fluid dynamical simulations here is in agreement with the solution of Orchard (Reference Orchard1963) for the surface tension driven levelling of an initially perturbed oil–air interface. Finally, the agreement between the three different models presented here for appropriate parameter choices provides verification of their correctness.
$\delta <0.05$ one can use the fully asymptotic method for maximal computational efficiency. Note that here we have only presented results where the steady-state amplitude has converged to three significant figures. We have not reported any verification of the discretisation methods or their convergence properties. For the boundary integral model of the electrostatic problem, such an analysis can be found in Chappell (Reference Chappell2015). We have also independently verified that the boundary integral model employed for the fluid dynamical simulations here is in agreement with the solution of Orchard (Reference Orchard1963) for the surface tension driven levelling of an initially perturbed oil–air interface. Finally, the agreement between the three different models presented here for appropriate parameter choices provides verification of their correctness.
6.2. Application to an experimental set-up
In this section we present results for a more experimentally realistic system where the applied potential originates from an array of interdigitated electrodes. In particular, we base our model set up on the experimental work presented in Brown et al. (Reference Brown, Wells, Newton and McHale2009) for the dynamics of an oil–air interface using a thin film of hexadecane. Therein, an interdigital array of striped coplanar electrodes was shown to spread a droplet of oil into a thin uniform film at low voltage and that increasing the voltage drop between neighbouring electrodes gave rise to a periodic undulation at the surface of the oil. A list of the relevant material parameters for this set-up is provided in table 1; we direct the reader to Brown et al. (Reference Brown, Wells, Newton and McHale2009) for a detailed description of the experimental set-up. We apply a modified form of the potential model for interdigitated electrodes from den Otter (Reference den Otter2002), but with a minor modification in order to better model the electrode configuration in Brown et al. (Reference Brown, Wells, Newton and McHale2009). Explicitly, we take
 \begin{equation} f(x)=\frac{2\Phi}{\rm \pi}\sum_{j=1}^{\infty}\frac{1}{2j-1}J_0\left(\frac{(2j-1){\rm \pi}}{4}\right)\left(1+\sin\left(\frac{(2j-1){\rm \pi} x}{L}\right)\right), \end{equation}
\begin{equation} f(x)=\frac{2\Phi}{\rm \pi}\sum_{j=1}^{\infty}\frac{1}{2j-1}J_0\left(\frac{(2j-1){\rm \pi}}{4}\right)\left(1+\sin\left(\frac{(2j-1){\rm \pi} x}{L}\right)\right), \end{equation}
as shown in figure 5 with ![]() $\Phi =400$ and
$\Phi =400$ and ![]() $L=240\ \mathrm {\mu }\text {m}$. The infinite sum in (6.3) has been truncated at
$L=240\ \mathrm {\mu }\text {m}$. The infinite sum in (6.3) has been truncated at ![]() $N=1,3$ and
$N=1,3$ and ![]() $11$ terms for the different curves in the plot. For
$11$ terms for the different curves in the plot. For ![]() $N=1$ we have a simple (raised) sine curve and would expect similar profiles to those obtained in the previous section and not the more interesting profiles observed experimentally in Brown et al. (Reference Brown, Wells, Newton and McHale2009). We may further obtain that
$N=1$ we have a simple (raised) sine curve and would expect similar profiles to those obtained in the previous section and not the more interesting profiles observed experimentally in Brown et al. (Reference Brown, Wells, Newton and McHale2009). We may further obtain that
 \begin{equation} \phi^H(\boldsymbol{x})=\frac{2\Phi}{\rm \pi}\sum_{j=1}^{\infty}\frac{1}{j_{{o}}}J_0\left(\frac{\rm \pi}{4}\right)\left(1+\sin\left(\frac{j_{{o}}{\rm \pi} x}{L}\right)\exp\left(-\frac{j_{{o}}{\rm \pi} y}{L}\right)\right), \end{equation}
\begin{equation} \phi^H(\boldsymbol{x})=\frac{2\Phi}{\rm \pi}\sum_{j=1}^{\infty}\frac{1}{j_{{o}}}J_0\left(\frac{\rm \pi}{4}\right)\left(1+\sin\left(\frac{j_{{o}}{\rm \pi} x}{L}\right)\exp\left(-\frac{j_{{o}}{\rm \pi} y}{L}\right)\right), \end{equation}
where the notation ![]() $j_{{o}}=2j-1$ has been introduced for brevity and
$j_{{o}}=2j-1$ has been introduced for brevity and ![]() $J_0$ is the zeroth-order Bessel function of the first kind as usual. The corresponding Maxwell stress is then be derived as
$J_0$ is the zeroth-order Bessel function of the first kind as usual. The corresponding Maxwell stress is then be derived as
 \begin{equation} M_1=4\epsilon_2\left(\left(\sum_{j=1}^{\infty} J_0\left(\frac{j_{{o}}{\rm \pi}}{4}\right)\cos(\,j_{{o}}{\rm \pi} \tilde{x})\right)^2+\frac{\epsilon_2}{\epsilon_1}\left(\sum_{j=1}^{\infty} J_0\left(\frac{j_{{o}}{\rm \pi}}{4}\right)\sin(\,j_{{o}}{\rm \pi} \tilde{x})\right)^2\right). \end{equation}
\begin{equation} M_1=4\epsilon_2\left(\left(\sum_{j=1}^{\infty} J_0\left(\frac{j_{{o}}{\rm \pi}}{4}\right)\cos(\,j_{{o}}{\rm \pi} \tilde{x})\right)^2+\frac{\epsilon_2}{\epsilon_1}\left(\sum_{j=1}^{\infty} J_0\left(\frac{j_{{o}}{\rm \pi}}{4}\right)\sin(\,j_{{o}}{\rm \pi} \tilde{x})\right)^2\right). \end{equation}
Figure 5. Modelling the electric potential from an array of interdigitated electrodes using (6.3) with parameters ![]() $\Phi =400\ \textrm {V}$,
$\Phi =400\ \textrm {V}$, ![]() $L=240\ \mathrm {\mu }\textrm {m}$ and truncating the sum after
$L=240\ \mathrm {\mu }\textrm {m}$ and truncating the sum after ![]() $N$ terms as specified in the legend.
$N$ terms as specified in the legend.
Table 1. Parameters used in the hexadecane oil–air interface model.

Figure 6 shows the steady-state wrinkle profiles for the set-up described above with electrode pitch ![]() $L=240\ \mathrm {\mu }\textrm {m}$ and a variety of different applied voltages
$L=240\ \mathrm {\mu }\textrm {m}$ and a variety of different applied voltages ![]() $\Phi$ between 275 V and 550 V using (6.3) with the sums truncated after three terms. The small parameter
$\Phi$ between 275 V and 550 V using (6.3) with the sums truncated after three terms. The small parameter ![]() $\delta$ for the asymptotic models ranges from 0.025 with
$\delta$ for the asymptotic models ranges from 0.025 with ![]() $h_0=6\ \mathrm {\mu }\textrm {m}$ up to 0.125 with
$h_0=6\ \mathrm {\mu }\textrm {m}$ up to 0.125 with ![]() $h_0=30\ \mathrm {\mu }\textrm {m}$ and so the results in the previous section suggest that the fully asymptotic model should at least be appropriate in the former case. The plots are all scaled consistently, but their position on the vertical axis has been shifted for ease of comparison between the plots for different values of
$h_0=30\ \mathrm {\mu }\textrm {m}$ and so the results in the previous section suggest that the fully asymptotic model should at least be appropriate in the former case. The plots are all scaled consistently, but their position on the vertical axis has been shifted for ease of comparison between the plots for different values of ![]() $h_0$. Note that as before, convergence issues arise in the fully numerical Stokes flow code for thin films in combination with relatively large applied voltages leading to prohibitive computational costs in these cases. For this reason, the profiles in this case are only calculated for the thickest film (
$h_0$. Note that as before, convergence issues arise in the fully numerical Stokes flow code for thin films in combination with relatively large applied voltages leading to prohibitive computational costs in these cases. For this reason, the profiles in this case are only calculated for the thickest film (![]() $30\ \mathrm {\mu }\textrm {m}$) and for a limited range of amplitudes for the
$30\ \mathrm {\mu }\textrm {m}$) and for a limited range of amplitudes for the ![]() $16.5\ \mathrm {\mu }\textrm {m}$ film. The fully asymptotic model has only been plotted for the thinnest-film case since this is the only case where the leading order in
$16.5\ \mathrm {\mu }\textrm {m}$ film. The fully asymptotic model has only been plotted for the thinnest-film case since this is the only case where the leading order in ![]() $\delta$ result is approximately valid. The hybrid numerical-asymptotic model can be applied to compute the steady-state wrinkle profile throughout the range of applied voltages and different film thickness values, but we note that as before, we only expect the growth behaviour with respect to time to be well approximated for thinner films.
$\delta$ result is approximately valid. The hybrid numerical-asymptotic model can be applied to compute the steady-state wrinkle profile throughout the range of applied voltages and different film thickness values, but we note that as before, we only expect the growth behaviour with respect to time to be well approximated for thinner films.

Figure 6. The steady-state wrinkle profile of a hexadecane oil–air interface predicted by ![]() $(a)$ the Stokes flow numerical model,
$(a)$ the Stokes flow numerical model, ![]() $(b)$ the hybrid numerical-asymptotic model and
$(b)$ the hybrid numerical-asymptotic model and ![]() $(c)$ the fully asymptotic model. The mean film height
$(c)$ the fully asymptotic model. The mean film height ![]() $h_0$ is chosen as
$h_0$ is chosen as ![]() $h_0= 6\ \mathrm {\mu }\text {m},\ 16.5\ \mathrm {\mu }\text {m},\ 30\ \mathrm {\mu }\text {m}$, corresponding to a small parameter
$h_0= 6\ \mathrm {\mu }\text {m},\ 16.5\ \mathrm {\mu }\text {m},\ 30\ \mathrm {\mu }\text {m}$, corresponding to a small parameter ![]() $\delta$ ranging from
$\delta$ ranging from ![]() $0.025$ to
$0.025$ to ![]() $0.125$, and results for each model are presented in appropriate regimes (see text). A simulated array of interdigitated electrodes is applied to excite the system via (6.3) and truncating the sum after three terms. The applied potential is indicated in the legend of (c), and is consistent throughout all panels. The plots are all scaled consistently, but their position on the vertical axis has been shifted for ease of comparison between different values of
$0.125$, and results for each model are presented in appropriate regimes (see text). A simulated array of interdigitated electrodes is applied to excite the system via (6.3) and truncating the sum after three terms. The applied potential is indicated in the legend of (c), and is consistent throughout all panels. The plots are all scaled consistently, but their position on the vertical axis has been shifted for ease of comparison between different values of ![]() $h_0$.
$h_0$.
The results in figure 6 show that the steady-state profile predicted by the hybrid numerical asymptotic model (figure 6b) agrees reasonably closely with both the numerical Stokes flow model for the thicker films (figure 6a) and the fully asymptotic model for the thinnest film with ![]() $h_0=6\ \mathrm {\mu }\textrm {m}$ at lower applied potentials (figure 6c). Some discrepancies can also be observed, with the hybrid model typically predicting slightly lower wrinkle amplitudes than the other two models; note that this observation is consistent with the results from the previous subsection as shown in figure 2. The fully asymptotic model also predicts larger amplitudes and a stronger influence of the higher-order expansion terms in (6.3), which can be observed through the deeper trough in the wrinkle profiles at
$h_0=6\ \mathrm {\mu }\textrm {m}$ at lower applied potentials (figure 6c). Some discrepancies can also be observed, with the hybrid model typically predicting slightly lower wrinkle amplitudes than the other two models; note that this observation is consistent with the results from the previous subsection as shown in figure 2. The fully asymptotic model also predicts larger amplitudes and a stronger influence of the higher-order expansion terms in (6.3), which can be observed through the deeper trough in the wrinkle profiles at ![]() $x=0$ in panel (c). The reason for this can be found by inspection of the asymptotic formula for the Maxwell stress term
$x=0$ in panel (c). The reason for this can be found by inspection of the asymptotic formula for the Maxwell stress term ![]() $M_1$ in (6.5) and recalling that inhomogeneous part of the thin film (4.13) depends on
$M_1$ in (6.5) and recalling that inhomogeneous part of the thin film (4.13) depends on ![]() $\partial M_1/\partial \tilde {x}$ and
$\partial M_1/\partial \tilde {x}$ and ![]() $\partial ^2 M_1/\partial \tilde {x}^2$. After differentiation with respect to
$\partial ^2 M_1/\partial \tilde {x}^2$. After differentiation with respect to ![]() $\tilde {x}$, the sums in (6.5) become divergent and hence the match between the fully asymptotic model and the other two will deteriorate if we include more terms in the sum (6.3) than the three considered here. The other two models depend instead on the half-space solution (6.4) via (3.17), in which the higher-order terms in (6.3) have increasing exponential decay rates.
$\tilde {x}$, the sums in (6.5) become divergent and hence the match between the fully asymptotic model and the other two will deteriorate if we include more terms in the sum (6.3) than the three considered here. The other two models depend instead on the half-space solution (6.4) via (3.17), in which the higher-order terms in (6.3) have increasing exponential decay rates.
Finally, we note that the results in figure 6 bear a strong similarity to the experimental findings published in figure 5 of Brown et al. (Reference Brown, Wells, Newton and McHale2009), both in terms of the observed profile shapes and amplitudes. In particular, the experimental results also show a simple sinusoidal profile when ![]() $h_0=30\ \mathrm {\mu }\textrm {m}$ and a flattening of the peak at
$h_0=30\ \mathrm {\mu }\textrm {m}$ and a flattening of the peak at ![]() $x=0$, followed by the increasing emergence of a trough as
$x=0$, followed by the increasing emergence of a trough as ![]() $h_0$ is decreased.
$h_0$ is decreased.
7. Conclusions
We have provided appropriate mathematical models to study the fluid motion of a thin viscous film under the influence of dielectrophoresis forces, which are valid across a range of film thicknesses. The first approach is to numerically solve the full Stokes flow–electrostatic problem using a boundary integral method. This model has the widest range of validity but provides a considerable challenge in the case of thin films since direct numerical simulations for the Stokes flow problem become prohibitively costly. To address this, we consider two asymptotic reductions, in the limit of a thin viscous film below a fluid of significantly lower viscosity. The first of these (the ‘hybrid approach’) retains a dependence on the film thickness from the electrostatic part of the model (the solution to which is obtained numerically), while the fully asymptotic approach reduces the problem to a single nonlinear PDE for the film height. For suitably thin films, both approaches provide excellent approximations to the film dynamics and eventual steady state profile. For thicker films, the hybrid approach is able to describe the steady-state profile, but not the correct time dependence of the wrinkle growth. All three approaches can be shown to reproduce experimental measurements of the final steady-state profile within the ranges of validity and practical applicability described above.
Future work from a numerical simulation perspective could consider modifications to the boundary integral scheme to give better convergence for thinner films, or develop a suitable accurate semi-implicit time discretisation for the hybrid method to avoid the strong time-step restrictions. From an asymptotic perspective, our results suggest that reduction of the electrostatic problem is the key factor affecting the accuracy of our fully asymptotic scheme. The consideration of higher order contributions and, for example, explicit treatment of the potential within regions near the film–air interface would be of interest, and may permit the time-dependent dynamics observed in experiment, as well as the decay in the steady-state film amplitude, to be captured. Finally, from an applications perspective, future work (in progress) will consider the growth rate of the film disturbance in the switch on problem considered here in comparison to the decay rate for the corresponding switch off problem, where an initially disturbed film relaxes to a flat profile. Furthermore, the evolution of the interface position to its final steady state will be of interest for further study in order to understand the influence of various parameters (electrode configuration, applied voltage, film thickness and material etc.) and ultimately facilitate the design of profiles with particular optical properties.
Acknowledgements
We acknowledge helpful discussions with Professor C. Brown and Professor J. R. King.
Declaration of interests
The authors report no conflict of interest.