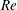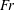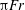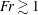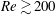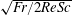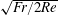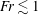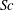1. Introduction
Atmospheric and oceanic flows are under the influence of stratification, and the horizontal velocity component is usually much larger than the vertical component since the horizontal length scale is much larger than the vertical scale which is limited by the total depth of the atmosphere or the ocean. Therefore, most of the studies on stratified flows have been concentrated on horizontal flows, including the flow past a mountain which generates internal gravity waves (e.g. Castro, Snyder & Marsh Reference Castro, Snyder and Marsh1983) or horizontal eddies in a blocked fluid under strong stratification (e.g. Hunt & Snyder Reference Hunt and Snyder1980).
On the other hand, vertical flows have rarely been studied, while they often become important in small-scale processes. For example, development of a Lagrangian float to observe the deep ocean requires an estimation of the vertical drag at speeds less than
![]() $20~\text{cm}~\text{s}^{-1}$
(D’Asaro Reference D’Asaro2003). Small organic matter such as plankton controls the carbon cycle in the ocean, and the prediction of its vertical movement requires the investigation of spherical particles at low Reynolds numbers (Srdić-Mitrović, Mohamed & Fernando Reference Srdić-Mitrović, Mohamed and Fernando1999; Abaid et al.
Reference Abaid, Adalsteinsson, Agyapong and McLaughlin2004; Camassa et al.
Reference Camassa, Falcon, Lin, McLaughlin and Parker2009, Reference Camassa, Falcon, Lin, McLaughlin and Mykins2010; Yick et al.
Reference Yick, Torres, Peacock and Stocker2009).
$20~\text{cm}~\text{s}^{-1}$
(D’Asaro Reference D’Asaro2003). Small organic matter such as plankton controls the carbon cycle in the ocean, and the prediction of its vertical movement requires the investigation of spherical particles at low Reynolds numbers (Srdić-Mitrović, Mohamed & Fernando Reference Srdić-Mitrović, Mohamed and Fernando1999; Abaid et al.
Reference Abaid, Adalsteinsson, Agyapong and McLaughlin2004; Camassa et al.
Reference Camassa, Falcon, Lin, McLaughlin and Parker2009, Reference Camassa, Falcon, Lin, McLaughlin and Mykins2010; Yick et al.
Reference Yick, Torres, Peacock and Stocker2009).
One of the earliest studies on the flow around a vertically moving obstacle in salt-stratified fluids is the paper by Mowbray & Rarity (Reference Mowbray and Rarity1967), in which the internal waves generated by a sphere moving vertically in a quiescent stratified fluid were observed by a schlieren method. Ochoa & Van Woert (Reference Ochoa and Van Woert1977) observed the flow generated by a descending sphere by a shadowgraph method, and identified a vertical plume-like flow above the sphere. A similar flow pattern has also been observed in the flow generated by free buoyant oscillations of a sphere (Levitskii & Chashechkin Reference Levitskii and Chashechkin1999; Chashechkin & Levitskii Reference Chashechkin and Levitskii2003).
It is important to note that the flow pattern becomes inverted if the sphere is moving upward instead of moving downward. Namely, if the sphere is moving upward, a strong downward jet is generated below the sphere. This can be verified from the symmetry of the governing equations under the Boussinesq approximation, and can be observed readily in experiments when the sphere is pulled up to its original height for the next downward movement.
In a numerical study, Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000) found that the plume-like flow is actually a ‘jet’ whose upward velocity is much faster than the downward sphere velocity. The jet appears instead of the standing vortex observed in a neutrally stratified fluid. The vortex observed at
![]() $\mathit{Re}=200$
is completely collapsed even in a weakly stratified fluid of
$\mathit{Re}=200$
is completely collapsed even in a weakly stratified fluid of
![]() $\mathit{Fr}\simeq 19$
. The parameters
$\mathit{Fr}\simeq 19$
. The parameters
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $\mathit{Fr}$
are here defined by
$\mathit{Fr}$
are here defined by
![]() $\mathit{Re}=2Wa/{\it\nu}$
and
$\mathit{Re}=2Wa/{\it\nu}$
and
![]() $\mathit{Fr}=W/Na$
, where
$\mathit{Fr}=W/Na$
, where
![]() $W$
is the sphere velocity,
$W$
is the sphere velocity,
![]() $a$
is the sphere radius,
$a$
is the sphere radius,
![]() ${\it\nu}$
is the dynamic viscosity of fluid and
${\it\nu}$
is the dynamic viscosity of fluid and
![]() $N$
is the Brunt–Väisälä frequency. Along with the appearance of the jet, the drag coefficient
$N$
is the Brunt–Väisälä frequency. Along with the appearance of the jet, the drag coefficient
![]() $C_{D}$
of the sphere increases significantly under strong stratification, corresponding to the large upward velocity or the reduced pressure above the sphere.
$C_{D}$
of the sphere increases significantly under strong stratification, corresponding to the large upward velocity or the reduced pressure above the sphere.
More recently, Hanazaki, Konishi & Okamura (Reference Hanazaki, Konishi and Okamura2009b ) investigated the effects of Schmidt number by a numerical simulation, and found that the jet becomes much broader as the Schmidt/Prandtl number decreases from 700 (salt in water) to 0.7 (heat in the air), and the velocity in the jet decreases significantly. This shows that the formation of the jet is controlled largely by the diffusion process of stratifying agents.
In an experimental study on the flow around a vertically moving sphere at moderate Reynolds numbers, Hanazaki, Kashimoto & Okamura (Reference Hanazaki, Kashimoto and Okamura2009a
) identified seven types of wake or jet structures in the parameter range of
![]() $0.2\lesssim \mathit{Fr}\lesssim 70$
and
$0.2\lesssim \mathit{Fr}\lesssim 70$
and
![]() $30\lesssim \mathit{Re}\lesssim 4000$
. One of the conspicuous phenomena found in that paper is the ‘bell-shaped’ structure which appears under strong stratification, accompanying a thin jet. It appears at approximately three sphere radii above the rear/upper stagnation point of the sphere when
$30\lesssim \mathit{Re}\lesssim 4000$
. One of the conspicuous phenomena found in that paper is the ‘bell-shaped’ structure which appears under strong stratification, accompanying a thin jet. It appears at approximately three sphere radii above the rear/upper stagnation point of the sphere when
![]() $\mathit{Fr}\sim 0.3~(\mathit{Re}=247)$
. Although the relation to internal waves was suggested in that paper using the velocity distribution obtained by particle image velocimetry (PIV), further investigations are necessary to confirm that conjecture.
$\mathit{Fr}\sim 0.3~(\mathit{Re}=247)$
. Although the relation to internal waves was suggested in that paper using the velocity distribution obtained by particle image velocimetry (PIV), further investigations are necessary to confirm that conjecture.
One of the fundamental processes in which we are interested is the unsteady development of the flow leading to the generation of a jet. The final approach to a steady flow is also of interest to understand the whole process of jet formation. We know that, as far as the density is materially conserved, isopycnal surfaces are simply pulled down by the sphere for an indefinitely long distance. This means at the same time that a steady flow is never realised, since the upper light fluid travels down with the sphere, continuously generating a larger density perturbation around the sphere. Here, ‘steady flow’ means that the density perturbation from the quiescent fluid is independent of time, and the velocity also has a constant value. Steady flow is realised by density diffusion since the diffusion can stop the indefinite pulling down of an isopycnal surface by the sphere. It will change the fluid density around the sphere surface and generate a horizontal circular hole along the sphere surface in the isopycnal surface, allowing the fluid of altered density to go up to near its original height.
In this numerical study, we will first investigate the origin of the bell-shaped structure observed in previous experiments (Hanazaki et al. Reference Hanazaki, Kashimoto and Okamura2009a ) and will clarify its relation with the internal gravity waves. Then, we will focus on the unsteady generation process of the jet, especially the flow development near the sphere surface and in the jet, which is important to understanding how the steady patterns are established by the diffusive processes of density.
2. Numerical methods
We consider a sphere moving vertically at a constant speed in a linearly stratified fluid. The governing equations are the momentum equation under the Boussinesq approximation, the density equation, and the mass-conservation equation. In the laboratory (i.e. stationary) frame, they are given in dimensional form by
where
![]() $t$
is the time,
$t$
is the time,
![]() $\boldsymbol{u}$
is the velocity,
$\boldsymbol{u}$
is the velocity,
![]() $p$
is the pressure,
$p$
is the pressure,
![]() ${\it\rho}$
is the density,
${\it\rho}$
is the density,
![]() $g$
is the acceleration due to gravity,
$g$
is the acceleration due to gravity,
![]() ${\it\mu}$
is the viscosity coefficient and
${\it\mu}$
is the viscosity coefficient and
![]() ${\it\kappa}$
is the diffusivity coefficient. We use cylindrical coordinates with the cylindrical axis
${\it\kappa}$
is the diffusivity coefficient. We use cylindrical coordinates with the cylindrical axis
![]() $z$
in the vertical direction (figure 1), so that
$z$
in the vertical direction (figure 1), so that
![]() $\hat{\boldsymbol{z}}$
is the unit vector in the vertical direction.
$\hat{\boldsymbol{z}}$
is the unit vector in the vertical direction.

Figure 1. Schematic figure of the flow considered in this study. A frame moving vertically downward with the sphere is used for the computation, i.e. linearly stratified fluid moves up at a constant speed
![]() $W$
relative to the sphere.
$W$
relative to the sphere.
To examine the fundamental process of jet formation without complications by three-dimensional effects, we consider the cases in which essentially axisymmetric flow has been observed in the experiments. Then, we assume axisymmetric flow in the computation, and the velocity has only two components
![]() $\boldsymbol{u}=(u,w)$
, with
$\boldsymbol{u}=(u,w)$
, with
![]() $u$
and
$u$
and
![]() $w$
being the horizontal (radial) and vertical components,
$w$
being the horizontal (radial) and vertical components,
In the numerical simulation we use a coordinate frame moving downward with the sphere at a constant speed
![]() $W$
(figure 1). The flow observed in the moving frame is equivalent to that generated when the stratified fluid layers move upward at the same speed. The basic fluid density
$W$
(figure 1). The flow observed in the moving frame is equivalent to that generated when the stratified fluid layers move upward at the same speed. The basic fluid density
![]() $\overline{{\it\rho}}$
and the hydrostatic pressure
$\overline{{\it\rho}}$
and the hydrostatic pressure
![]() $\overline{p}$
are functions of time and height
$\overline{p}$
are functions of time and height
![]() $z$
:
$z$
:
and
where
![]() $z$
is the vertical coordinate measured from the centre of the sphere,
$z$
is the vertical coordinate measured from the centre of the sphere,
![]() $\partial \overline{{\it\rho}}/\partial z$
is the vertical gradient of the basic density field which is constant for a linearly stratified fluid, and
$\partial \overline{{\it\rho}}/\partial z$
is the vertical gradient of the basic density field which is constant for a linearly stratified fluid, and
![]() $\overline{{\it\rho}}(0,0)$
is the initial density at the equator level (
$\overline{{\it\rho}}(0,0)$
is the initial density at the equator level (
![]() $z=0$
) of the sphere. The term
$z=0$
) of the sphere. The term
![]() $-Wt$
in (2.4) appears since we have adopted a moving frame.
$-Wt$
in (2.4) appears since we have adopted a moving frame.
We decompose the total density and the total pressure into the basic states and the perturbations from them, i.e.
and
where the primes denote perturbations.
Substituting (2.6) and (2.7) into (2.1), subtracting the basic state and using the Boussinesq approximation, the momentum equation becomes
where
![]() ${\it\rho}_{0}=\overline{{\it\rho}}(0,0)$
and
${\it\rho}_{0}=\overline{{\it\rho}}(0,0)$
and
![]() ${\it\nu}={\it\mu}/{\it\rho}_{0}$
is the kinematic viscosity. Similarly, substitution of (2.6) into (2.2) gives
${\it\nu}={\it\mu}/{\it\rho}_{0}$
is the kinematic viscosity. Similarly, substitution of (2.6) into (2.2) gives
We scale length by the sphere diameter
![]() $2a$
, velocity by the mean flow or the downward velocity of the sphere
$2a$
, velocity by the mean flow or the downward velocity of the sphere
![]() $W$
, pressure perturbation by
$W$
, pressure perturbation by
![]() ${\it\rho}_{0}W^{2}$
, and density perturbation by
${\it\rho}_{0}W^{2}$
, and density perturbation by
![]() $-2a(\partial \overline{{\it\rho}}/\partial z)$
. Then, the non-dimensional equations are
$-2a(\partial \overline{{\it\rho}}/\partial z)$
. Then, the non-dimensional equations are
and
The non-dimensional parameters in these equations are the Reynolds number
![]() $\mathit{Re}=W2a/{\it\nu}$
, Froude number
$\mathit{Re}=W2a/{\it\nu}$
, Froude number
![]() $\mathit{Fr}=W/Na$
and Schmidt number
$\mathit{Fr}=W/Na$
and Schmidt number
![]() $\mathit{Sc}={\it\nu}/{\it\kappa}$
, where
$\mathit{Sc}={\it\nu}/{\it\kappa}$
, where
![]() $N$
is the Brunt–Väisälä frequency defined by
$N$
is the Brunt–Väisälä frequency defined by
We may rewrite (2.4) in non-dimensional form as
Comparison with (2.4) reveals that
![]() $-z$
represents linear stable stratification and
$-z$
represents linear stable stratification and
![]() $t$
represents the density increase due to the downward movement of the sphere or the mean upward movement of the stratified fluid. The non-dimensional total density then becomes
$t$
represents the density increase due to the downward movement of the sphere or the mean upward movement of the stratified fluid. The non-dimensional total density then becomes
When there is no initial density perturbation (
![]() ${\it\rho}^{\prime }(\boldsymbol{x},0)=0$
), substitution of
${\it\rho}^{\prime }(\boldsymbol{x},0)=0$
), substitution of
![]() $t=0$
into (2.14) recovers the initial density distribution as
$t=0$
into (2.14) recovers the initial density distribution as
As an initial condition, we have used an impulsive start, i.e. vertical mean flow is instantly raised to its maximum and constant speed
![]() $W$
at
$W$
at
![]() $t=0$
.
$t=0$
.
Numerical methods for solving the governing equations are essentially the same as those in Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000) or Hanazaki et al. (Reference Hanazaki, Konishi and Okamura2009b ). Namely, the finite difference method combined with the marker and cell (MAC) method (Harlow & Welch Reference Harlow and Welch1965) is used for the simulation of the flow of incompressible stratified fluid (Hanazaki Reference Hanazaki1988).
We mainly consider the flow at the Reynolds number of 200, below which axisymmetric flow has been observed in homogeneous fluids (Taneda Reference Taneda1956), while the Froude number is changed in the range of
![]() $0.3\leqslant \mathit{Fr}\leqslant 10$
. In some cases, we have simulated the case of different
$0.3\leqslant \mathit{Fr}\leqslant 10$
. In some cases, we have simulated the case of different
![]() $\mathit{Re}~(20\leqslant \mathit{Re}\leqslant 1000)$
at fixed
$\mathit{Re}~(20\leqslant \mathit{Re}\leqslant 1000)$
at fixed
![]() $\mathit{Fr}\;(=1)$
to investigate the Reynolds number effects. For comparison with previous experiments, we have also simulated the case of
$\mathit{Fr}\;(=1)$
to investigate the Reynolds number effects. For comparison with previous experiments, we have also simulated the case of
![]() $\mathit{Fr}=0.3$
and
$\mathit{Fr}=0.3$
and
![]() $\mathit{Re}=247$
(as will be seen later in figure 3). Schmidt number is fixed at
$\mathit{Re}=247$
(as will be seen later in figure 3). Schmidt number is fixed at
![]() $\mathit{Sc}=700$
throughout this study to correspond to the salt stratification used in the previous experiments.
$\mathit{Sc}=700$
throughout this study to correspond to the salt stratification used in the previous experiments.
The governing equations originally written in cylindrical coordinates (
![]() $z,r$
) are transformed to body-fitted curvilinear coordinates with variables
$z,r$
) are transformed to body-fitted curvilinear coordinates with variables
![]() ${\it\xi}$
and
${\it\xi}$
and
![]() ${\it\eta}$
(figure 2
a), and the computation is executed on the transformed coordinates. Since the density boundary layer is very thin for a salt-stratified fluid with a high Schmidt number (
${\it\eta}$
(figure 2
a), and the computation is executed on the transformed coordinates. Since the density boundary layer is very thin for a salt-stratified fluid with a high Schmidt number (
![]() $\mathit{Sc}=700$
) even at moderate Reynolds numbers, grid points are highly concentrated near the sphere surface along which
$\mathit{Sc}=700$
) even at moderate Reynolds numbers, grid points are highly concentrated near the sphere surface along which
![]() ${\it\eta}$
is constant, to resolve a large density variation in a narrow region. The mesh number in the density boundary layer is approximately six if we estimate the thickness of the density boundary layer by
${\it\eta}$
is constant, to resolve a large density variation in a narrow region. The mesh number in the density boundary layer is approximately six if we estimate the thickness of the density boundary layer by
![]() $1/\sqrt{\mathit{Re }\mathit{ Sc}}$
, which is
$1/\sqrt{\mathit{Re }\mathit{ Sc}}$
, which is
![]() $2.67\times 10^{-3}$
for
$2.67\times 10^{-3}$
for
![]() $\mathit{Re}=200$
, and
$\mathit{Re}=200$
, and
![]() $1.20\times 10^{-3}$
for
$1.20\times 10^{-3}$
for
![]() $\mathit{Re}=1000$
, although we will show later in figures 21 and 22 that the boundary layer is in many cases much thicker than this passive-scalar limit (
$\mathit{Re}=1000$
, although we will show later in figures 21 and 22 that the boundary layer is in many cases much thicker than this passive-scalar limit (
![]() $\mathit{Fr}\rightarrow \infty$
). An even finer mesh is used near the
$\mathit{Fr}\rightarrow \infty$
). An even finer mesh is used near the
![]() $z$
-axis, on which a thin vertical jet is generated and large horizontal density variation is expected, especially under strong stratification (figure 2
b). The grid lines are parallel to the
$z$
-axis, on which a thin vertical jet is generated and large horizontal density variation is expected, especially under strong stratification (figure 2
b). The grid lines are parallel to the
![]() $z$
axis to obtain a good resolution near the
$z$
axis to obtain a good resolution near the
![]() $z$
axis.
$z$
axis.

Figure 2. Grid used for the computation of the flow with
![]() $\mathit{Re}=200$
and
$\mathit{Re}=200$
and
![]() $\mathit{Sc}=700$
. (a) Grid near the sphere. Only every other grid line is drawn in both the
$\mathit{Sc}=700$
. (a) Grid near the sphere. Only every other grid line is drawn in both the
![]() ${\it\xi}$
and
${\it\xi}$
and
![]() ${\it\eta}$
directions. (b) Close-up view of the grid very near the rear/upper stagnation point of the sphere located at
${\it\eta}$
directions. (b) Close-up view of the grid very near the rear/upper stagnation point of the sphere located at
![]() $(r,z)=(0,0.5)$
. (c) Steady distribution of density perturbation
$(r,z)=(0,0.5)$
. (c) Steady distribution of density perturbation
![]() ${\it\rho}^{\prime }~(\mathit{Fr}=0.3,\mathit{Re}=200)$
on the horizontal and straight grid line of
${\it\rho}^{\prime }~(\mathit{Fr}=0.3,\mathit{Re}=200)$
on the horizontal and straight grid line of
![]() $z=0$
, which originates from the equator (
$z=0$
, which originates from the equator (
![]() ${\it\theta}=90^{\circ }$
) of the sphere (cf. figure 6
a). The abscissa
${\it\theta}=90^{\circ }$
) of the sphere (cf. figure 6
a). The abscissa
![]() $d$
is the distance from the sphere surface, and the black squares (▪) denote the position of grid points.
$d$
is the distance from the sphere surface, and the black squares (▪) denote the position of grid points.

Figure 3. Typical results at a low Froude number (
![]() $\mathit{Fr}=0.3$
,
$\mathit{Fr}=0.3$
,
![]() $\mathit{Re}=247$
, steady state at
$\mathit{Re}=247$
, steady state at
![]() $t=30$
). (a) Velocity vectors in laboratory/stationary frame. The arrow at the centre of the sphere shows the downward velocity of the sphere. (b) Contours of vertical velocity in laboratory/stationary frame, i.e. (
$t=30$
). (a) Velocity vectors in laboratory/stationary frame. The arrow at the centre of the sphere shows the downward velocity of the sphere. (b) Contours of vertical velocity in laboratory/stationary frame, i.e. (
![]() $w-1$
), drawn at intervals of
$w-1$
), drawn at intervals of
![]() ${\rm\Delta}(w-1)=(w_{max}-1)/10$
for
${\rm\Delta}(w-1)=(w_{max}-1)/10$
for
![]() $w-1>0$
(solid lines), and
$w-1>0$
(solid lines), and
![]() $|w_{min}-1|/10$
for
$|w_{min}-1|/10$
for
![]() $w-1<0$
(dashed lines). Thick lines represent
$w-1<0$
(dashed lines). Thick lines represent
![]() $w-1=0$
. (c) Grey-scale image of the distribution of molecular diffusion of density
$w-1=0$
. (c) Grey-scale image of the distribution of molecular diffusion of density
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
.
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
.
The total number of grid points on the transformed plane, i.e.
![]() ${\it\xi}{-}{\it\eta}$
plane, is
${\it\xi}{-}{\it\eta}$
plane, is
![]() $360\times 1000$
. The grid resolution near the
$360\times 1000$
. The grid resolution near the
![]() $z$
-axis is much higher than in Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000) and is comparable to the case of highest resolution (
$z$
-axis is much higher than in Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000) and is comparable to the case of highest resolution (
![]() $360\times 241$
) in Hanazaki et al. (Reference Hanazaki, Konishi and Okamura2009b
) where the smallest grid spacing used along the
$360\times 241$
) in Hanazaki et al. (Reference Hanazaki, Konishi and Okamura2009b
) where the smallest grid spacing used along the
![]() $z$
-axis is
$z$
-axis is
![]() ${\rm\Delta}r=6\times 10^{-4}$
. The outer boundary of the computational domain is a circle whose radius is
${\rm\Delta}r=6\times 10^{-4}$
. The outer boundary of the computational domain is a circle whose radius is
![]() $\sqrt{r^{2}+z^{2}}=100\times 2a$
, where
$\sqrt{r^{2}+z^{2}}=100\times 2a$
, where
![]() $2a$
is the diameter of the sphere. A large area is used, since it takes a long time before a steady state is realised in weakly stratified fluids, in which the light upper fluid is pulled down by the sphere for a long distance. The computed area is much larger than in Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000) and Hanazaki et al. (Reference Hanazaki, Konishi and Okamura2009b
), in which the outer boundary is located at most twenty times the sphere diameter. This is realised by the use of many more grid points in the
$2a$
is the diameter of the sphere. A large area is used, since it takes a long time before a steady state is realised in weakly stratified fluids, in which the light upper fluid is pulled down by the sphere for a long distance. The computed area is much larger than in Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000) and Hanazaki et al. (Reference Hanazaki, Konishi and Okamura2009b
), in which the outer boundary is located at most twenty times the sphere diameter. This is realised by the use of many more grid points in the
![]() ${\it\eta}$
direction (
${\it\eta}$
direction (
![]() $=1000$
) normal to the sphere surface. Isopycnals initially located at the height of the sphere centre, i.e. at
$=1000$
) normal to the sphere surface. Isopycnals initially located at the height of the sphere centre, i.e. at
![]() $z=0$
, move upward relative to the sphere at speed
$z=0$
, move upward relative to the sphere at speed
![]() $W$
, and they reach the upper boundary of the computational domain at time
$W$
, and they reach the upper boundary of the computational domain at time
![]() $Wt/2a=100$
. Computation should be stopped before that time since the large deformation of the isopycnal surface at the upper boundary, if it exists, would reduce the accuracy of the solution. In other words, at large times which satisfy
$Wt/2a=100$
. Computation should be stopped before that time since the large deformation of the isopycnal surface at the upper boundary, if it exists, would reduce the accuracy of the solution. In other words, at large times which satisfy
![]() $Wt/2a>100$
, the isopycnal surface initially deformed and dragged by the sphere can no longer be traced.
$Wt/2a>100$
, the isopycnal surface initially deformed and dragged by the sphere can no longer be traced.
Under weak stratification, the isopycnal surface is pulled down for a very long distance as we will see later in figure 7, for example. The remote outer boundary also helps to reduce the effects of internal wave reflection at the boundary, compared with the laboratory experiments in which the tank dimension is often less than
![]() $2a\times 100$
.
$2a\times 100$
.
The boundary conditions for the numerical simulations are specified as follows (Hanazaki et al. Reference Hanazaki, Konishi and Okamura2009b ). On the sphere surface, velocity satisfies the no-slip boundary condition
and the density satisfies the no-flux or adiabatic condition
where
![]() $\boldsymbol{n}$
is the unit normal to the sphere surface. Substitution of (2.14) into (2.17) gives the boundary condition for the density perturbation
$\boldsymbol{n}$
is the unit normal to the sphere surface. Substitution of (2.14) into (2.17) gives the boundary condition for the density perturbation
while the substitution of (2.16) into the momentum equation (2.8) gives the boundary condition for the perturbation pressure
On the outer boundary where perturbations are small, the density and the pressure are given by
and
where
![]() $\boldsymbol{n}$
is the unit normal to the outer boundary. The velocity is specified as
$\boldsymbol{n}$
is the unit normal to the outer boundary. The velocity is specified as
except near the
![]() $z$
-axis in the upper wake region where it is given by
$z$
-axis in the upper wake region where it is given by
To illustrate the resolution of the density boundary layer on the sphere surface, an example of the density distribution near the equator of the sphere is plotted in figure 2(c). This shows that the density boundary layer is well resolved and the boundary condition (2.17) is satisfied, although it may appear later in figure 5 that the isopycnals are not normal to the sphere surface. This illusory contradiction occurs since the density boundary layer is very thin, even thinner than the width of the contour lines.
3. Results
3.1. Bell-shaped structure and internal waves at a low Froude number
Since the bell-shaped structure is one of the most conspicuous structures observed in the experiments and the results under strong stratification give a good insight into the overall phenomena, we first discuss that structure. In figure 3 the bell-shaped structure observed at the lowest Froude number (
![]() $\mathit{Fr}=0.3$
,
$\mathit{Fr}=0.3$
,
![]() $\mathit{Re}=247$
) is presented in three different physical quantities, i.e. velocity vector (figure 3
a), vertical velocity component in the laboratory frame (figure 3
b) and molecular diffusion of density (figure 3
c). Reynolds number is 247 only in this figure for a direct comparison with previous experiments.
$\mathit{Re}=247$
) is presented in three different physical quantities, i.e. velocity vector (figure 3
a), vertical velocity component in the laboratory frame (figure 3
b) and molecular diffusion of density (figure 3
c). Reynolds number is 247 only in this figure for a direct comparison with previous experiments.
The structure can be most clearly observed in figure 3(c), since the figure corresponds most directly to shadowgraph experiments in which this particular structure was first observed. In experiments it was found that a large downward velocity exists near the bell-shaped structure, the position of the bell relative to the sphere is time invariant, and the bell moves down at the same speed as the sphere. This lead to a conjecture that the internal lee wave is the origin of the bell-shaped structure. In this numerical study, contours of vertical velocity in the laboratory frame, i.e.
![]() $w-1$
, show steady diverging lee waves (figure 3
b) as observed by PIV (figure 13 of Hanazaki et al.
Reference Hanazaki, Kashimoto and Okamura2009a
), and the position of the bell-shaped structure (figure 3
c) agrees with the position of the largest downward velocity. Then, the bell-shaped structure is supported by a ‘steady’ lee wave whose wavelength determines the time-independent distance of the structure from the sphere. This will become clearer in figure 9, where the Froude number dependence is discussed.
$w-1$
, show steady diverging lee waves (figure 3
b) as observed by PIV (figure 13 of Hanazaki et al.
Reference Hanazaki, Kashimoto and Okamura2009a
), and the position of the bell-shaped structure (figure 3
c) agrees with the position of the largest downward velocity. Then, the bell-shaped structure is supported by a ‘steady’ lee wave whose wavelength determines the time-independent distance of the structure from the sphere. This will become clearer in figure 9, where the Froude number dependence is discussed.

Figure 4. Typical deformation process of an isopycnal surface (
![]() $\mathit{Fr}=0.3$
,
$\mathit{Fr}=0.3$
,
![]() $\mathit{Re}=200$
). The surface is initially located at
$\mathit{Re}=200$
). The surface is initially located at
![]() $z=-1$
as a horizontal plane. (a)
$z=-1$
as a horizontal plane. (a)
![]() $t=1$
; (b)
$t=1$
; (b)
![]() $t=2$
; (c)
$t=2$
; (c)
![]() $t=3$
; (d)
$t=3$
; (d)
![]() $t=4$
.
$t=4$
.
Comparison between figure 3(a–c) shows that there is a small but discernible difference between the height of the bell-shaped structure and the height of largest downward velocity. This can be understood through the phase difference between
![]() $w$
and
$w$
and
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }$
. To be more explicit, we assume the form of vertical velocity to be (e.g. Gill Reference Gill1982)
${\rm\nabla}^{2}{\it\rho}^{\prime }$
. To be more explicit, we assume the form of vertical velocity to be (e.g. Gill Reference Gill1982)
in the linearised inviscid and non-diffusive governing equations, where
![]() $\boldsymbol{k}$
is the wavenumber,
$\boldsymbol{k}$
is the wavenumber,
![]() $\boldsymbol{x}$
is the position and
$\boldsymbol{x}$
is the position and
![]() ${\it\omega}$
is the frequency. Then, the Laplacian of the density perturbation becomes
${\it\omega}$
is the frequency. Then, the Laplacian of the density perturbation becomes
showing that
![]() $w$
has a phase advance of
$w$
has a phase advance of
![]() ${\rm\pi}/2$
, or a quarter-wavelength, compared to
${\rm\pi}/2$
, or a quarter-wavelength, compared to
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }$
. The phase difference can be more clearly identified if we compare the contours of
${\rm\nabla}^{2}{\it\rho}^{\prime }$
. The phase difference can be more clearly identified if we compare the contours of
![]() $w-1$
and
$w-1$
and
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }$
, although the contours of
${\rm\nabla}^{2}{\it\rho}^{\prime }$
, although the contours of
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }$
are not presented here.
${\rm\nabla}^{2}{\it\rho}^{\prime }$
are not presented here.
An example of three-dimensional images of the initial deforming process of an isopycnal surface is presented in figure 4, where the movement of an isopycnal surface initially located horizontally at
![]() $z=-1$
is depicted. It moves up to
$z=-1$
is depicted. It moves up to
![]() $z=0$
at
$z=0$
at
![]() $t=1$
(figure 4
a) since the stratified fluid in the moving frame goes up relative to the sphere at a constant speed
$t=1$
(figure 4
a) since the stratified fluid in the moving frame goes up relative to the sphere at a constant speed
![]() $W\;(=1)$
. As long as the density is conserved, the isopycnal surface is trapped by the sphere and simply deforms along the sphere surface without being ruptured, as observed at
$W\;(=1)$
. As long as the density is conserved, the isopycnal surface is trapped by the sphere and simply deforms along the sphere surface without being ruptured, as observed at
![]() $t=1$
and 2 (figure 4
a,b). If the density is conserved for an indefinitely long time, the sphere will pull down the isopycnal surface for an infinitely long distance. In reality, however, molecular diffusion of density given by
$t=1$
and 2 (figure 4
a,b). If the density is conserved for an indefinitely long time, the sphere will pull down the isopycnal surface for an infinitely long distance. In reality, however, molecular diffusion of density given by
![]() ${\rm\nabla}^{2}{\it\rho}$
in the density equation becomes larger as time elapses. It becomes significant in the density boundary layer on the sphere surface. We note that before
${\rm\nabla}^{2}{\it\rho}$
in the density equation becomes larger as time elapses. It becomes significant in the density boundary layer on the sphere surface. We note that before
![]() $t=3$
(figure 4
c), molecular diffusion alters the value of density on the isopycnal surface, generating a circular hole along the sphere surface. The hole is at the height of
$t=3$
(figure 4
c), molecular diffusion alters the value of density on the isopycnal surface, generating a circular hole along the sphere surface. The hole is at the height of
![]() $z\sim 0.1$
in figure 4(c), for example. The appearance of a hole means that a new closed isopycnal line is generated along the circumference of the hole, and the density has been changed. The fluid of non-conserved density is no longer pulled down by the sphere, and it will return, by the buoyancy force, to a position in the neighbourhood of, but possibly different from, its original height since the original density has been changed by the molecular diffusion.
$z\sim 0.1$
in figure 4(c), for example. The appearance of a hole means that a new closed isopycnal line is generated along the circumference of the hole, and the density has been changed. The fluid of non-conserved density is no longer pulled down by the sphere, and it will return, by the buoyancy force, to a position in the neighbourhood of, but possibly different from, its original height since the original density has been changed by the molecular diffusion.
To examine the time development of density distributions more quantitatively, contours of total density
![]() ${\it\rho}$
are presented in figure 5 at a contour interval of
${\it\rho}$
are presented in figure 5 at a contour interval of
![]() ${\rm\Delta}{\it\rho}=0.5$
. Density contours on the sphere surface, which appear as straight horizontal lines due to the axisymmetry of the flow, are also depicted. The contours on the sphere surface represent circular holes in the isopycnal surface. The orange line at
${\rm\Delta}{\it\rho}=0.5$
. Density contours on the sphere surface, which appear as straight horizontal lines due to the axisymmetry of the flow, are also depicted. The contours on the sphere surface represent circular holes in the isopycnal surface. The orange line at
![]() $z=-0.5$
when
$z=-0.5$
when
![]() $t=0.5$
(figure 5
a), which existed initially at
$t=0.5$
(figure 5
a), which existed initially at
![]() $z=-1$
corresponds to the isopycnal surface depicted in figure 4. The contour rises vertically and is simply deformed along the sphere surface at least until
$z=-1$
corresponds to the isopycnal surface depicted in figure 4. The contour rises vertically and is simply deformed along the sphere surface at least until
![]() $t=2$
, as observed in figure 4(b). A circular hole appears in the isopycnal surface before
$t=2$
, as observed in figure 4(b). A circular hole appears in the isopycnal surface before
![]() $t=3$
(figure 4
c), and by the time when the contour has risen to
$t=3$
(figure 4
c), and by the time when the contour has risen to
![]() $z=9$
at
$z=9$
at
![]() $t=10$
(figure 5
c), many new circular holes appear on the sphere surface. The number of isopycnal lines on the sphere increases with time, meaning that more stratified layers are affected by the molecular diffusion and change their densities, generating a hole in each layer. We should note that the time development of velocity shows that the jet develops (cf. figure 3
a) in the vertical range where large vertical displacement of isopycnal surface exists (e.g.
$t=10$
(figure 5
c), many new circular holes appear on the sphere surface. The number of isopycnal lines on the sphere increases with time, meaning that more stratified layers are affected by the molecular diffusion and change their densities, generating a hole in each layer. We should note that the time development of velocity shows that the jet develops (cf. figure 3
a) in the vertical range where large vertical displacement of isopycnal surface exists (e.g.
![]() $0.5\lesssim z\lesssim 1.8$
in figure 5
b), although the figures are not presented here.
$0.5\lesssim z\lesssim 1.8$
in figure 5
b), although the figures are not presented here.

Figure 5. Time development of the isopycnal lines of total density
![]() ${\it\rho}~(\mathit{Fr}=0.3,\mathit{Re}=200)$
. Horizontal lines on the sphere represent the density distribution on the sphere surface. Contour interval
${\it\rho}~(\mathit{Fr}=0.3,\mathit{Re}=200)$
. Horizontal lines on the sphere represent the density distribution on the sphere surface. Contour interval
![]() ${\rm\Delta}{\it\rho}$
is 0.5. (a)
${\rm\Delta}{\it\rho}$
is 0.5. (a)
![]() $t=0.5$
; (b)
$t=0.5$
; (b)
![]() $t=1.0$
; (c)
$t=1.0$
; (c)
![]() $t=10.0$
.
$t=10.0$
.
We mention here that at this low Froude number (
![]() $\mathit{Fr}=0.3$
), velocity and density near the sphere become steady in a short time, and figure 5(c) (
$\mathit{Fr}=0.3$
), velocity and density near the sphere become steady in a short time, and figure 5(c) (
![]() $t=10$
) shows the established steady distribution of
$t=10$
) shows the established steady distribution of
![]() ${\it\rho}^{\prime }$
near the sphere. Throughout this study, the word ‘steady’ means that the perturbation fields such as
${\it\rho}^{\prime }$
near the sphere. Throughout this study, the word ‘steady’ means that the perturbation fields such as
![]() $u^{\prime }$
,
$u^{\prime }$
,
![]() $w^{\prime }$
and
$w^{\prime }$
and
![]() ${\it\rho}^{\prime }$
are independent of time, while the mean density field
${\it\rho}^{\prime }$
are independent of time, while the mean density field
![]() $\overline{{\it\rho}}(z,t)$
and the total density
$\overline{{\it\rho}}(z,t)$
and the total density
![]() ${\it\rho}$
are changing linearly with time. Once the steady state is established, isopycnals in figure 5(c) drawn at the vertical interval of
${\it\rho}$
are changing linearly with time. Once the steady state is established, isopycnals in figure 5(c) drawn at the vertical interval of
![]() ${\rm\Delta}z=0.5$
, would also represent the time development of a single isopycnal surface at the time interval of
${\rm\Delta}z=0.5$
, would also represent the time development of a single isopycnal surface at the time interval of
![]() ${\rm\Delta}t=0.5$
as it rises up across the sphere.
${\rm\Delta}t=0.5$
as it rises up across the sphere.
Since the molecular diffusion on the sphere surface is essential to establish a steady state, the time development of the density perturbation
![]() ${\it\rho}^{\prime }$
and the molecular diffusion
${\it\rho}^{\prime }$
and the molecular diffusion
![]() $(1/\mathit{Re}\mathit{Sc}){\rm\nabla}^{2}{\it\rho}^{\prime }$
at various points on the sphere is presented in figure 6. In figure 6(a) the time development of
$(1/\mathit{Re}\mathit{Sc}){\rm\nabla}^{2}{\it\rho}^{\prime }$
at various points on the sphere is presented in figure 6. In figure 6(a) the time development of
![]() ${\it\rho}^{\prime }$
is initially (
${\it\rho}^{\prime }$
is initially (
![]() $t\lesssim 0.5$
) independent of the position (
$t\lesssim 0.5$
) independent of the position (
![]() ${\it\theta}$
) on the sphere. Since
${\it\theta}$
) on the sphere. Since
![]() ${\it\rho}^{\prime }$
changes according to (2.14), i.e.
${\it\rho}^{\prime }$
changes according to (2.14), i.e.
and the initial density distribution is given by (2.15), invariance of density with time at a fixed position (
![]() ${\it\rho}(\boldsymbol{x},t)={\it\rho}(\boldsymbol{x},0)$
) is equivalent to
${\it\rho}(\boldsymbol{x},t)={\it\rho}(\boldsymbol{x},0)$
) is equivalent to
showing that
![]() ${\it\rho}^{\prime }$
decreases linearly with time.
${\it\rho}^{\prime }$
decreases linearly with time.

Figure 6. (a) Time development of the density perturbation
![]() ${\it\rho}^{\prime }$
at six selected points on the sphere surface. The angle
${\it\rho}^{\prime }$
at six selected points on the sphere surface. The angle
![]() ${\it\theta}$
is measured from the forward/lower stagnation point of the sphere. (b) Time development of the density diffusion
${\it\theta}$
is measured from the forward/lower stagnation point of the sphere. (b) Time development of the density diffusion
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
. (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
. (
![]() $\mathit{Fr}=0.3$
in both figures).
$\mathit{Fr}=0.3$
in both figures).

Figure 7. Isopycnals of total density
![]() ${\it\rho}$
in steady state (
${\it\rho}$
in steady state (
![]() ${\rm\Delta}{\it\rho}=2$
). (a)
${\rm\Delta}{\it\rho}=2$
). (a)
![]() $\mathit{Fr}=0.3~(t=30)$
; (b)
$\mathit{Fr}=0.3~(t=30)$
; (b)
![]() $\mathit{Fr}=1.5~(t=30)$
; (c)
$\mathit{Fr}=1.5~(t=30)$
; (c)
![]() $\mathit{Fr}=10~(t=90)$
. The data used for (a) are almost the same as figure 5(c), since the flow at
$\mathit{Fr}=10~(t=90)$
. The data used for (a) are almost the same as figure 5(c), since the flow at
![]() $\mathit{Fr}=0.3$
is almost steady near the sphere for
$\mathit{Fr}=0.3$
is almost steady near the sphere for
![]() $t\gtrsim 10$
.
$t\gtrsim 10$
.
On the sphere surface where velocity is zero (
![]() $u=w=0$
), the Lagrangian derivative agrees with the partial time derivative (
$u=w=0$
), the Lagrangian derivative agrees with the partial time derivative (
![]() $\text{D}{\it\rho}/\text{D}t=\partial {\it\rho}/\partial t$
). Then
$\text{D}{\it\rho}/\text{D}t=\partial {\it\rho}/\partial t$
). Then
![]() ${\it\rho}(\boldsymbol{x},t)={\it\rho}(\boldsymbol{x},0)$
, i.e.
${\it\rho}(\boldsymbol{x},t)={\it\rho}(\boldsymbol{x},0)$
, i.e.
![]() $\partial {\it\rho}/\partial t=0$
, means that the density is conserved (
$\partial {\it\rho}/\partial t=0$
, means that the density is conserved (
![]() $\text{D}{\it\rho}/\text{D}t=0$
). Therefore, on the sphere surface, (3.4) means density conservation.
$\text{D}{\it\rho}/\text{D}t=0$
). Therefore, on the sphere surface, (3.4) means density conservation.
The violation of conservation of density is obviously due to molecular diffusion. On the sphere surface where velocity is zero, (2.11) reduces to
In the case of no initial perturbation (
![]() ${\it\rho}^{\prime }(\boldsymbol{x},0)=0$
), time integration gives
${\it\rho}^{\prime }(\boldsymbol{x},0)=0$
), time integration gives
which shows that the cumulative molecular diffusion represented by the integral is the origin of deviation from (3.4). We note at the same time that, when a steady state is realised,
![]() $\partial {\it\rho}^{\prime }/\partial t=0$
in (3.5), and the diffusion term approaches unity, i.e.
$\partial {\it\rho}^{\prime }/\partial t=0$
in (3.5), and the diffusion term approaches unity, i.e.
As demonstrated in figure 6(b), molecular diffusion is generally small initially (
![]() $t=0$
) and is nearly zero at the stagnation points (
$t=0$
) and is nearly zero at the stagnation points (
![]() ${\it\theta}=0^{\circ },180^{\circ }$
), while it is already non-zero near the equator (
${\it\theta}=0^{\circ },180^{\circ }$
), while it is already non-zero near the equator (
![]() ${\it\theta}=90^{\circ }$
) of the sphere. In the succeeding period (
${\it\theta}=90^{\circ }$
) of the sphere. In the succeeding period (
![]() $1\lesssim t\lesssim 2$
), however, diffusion increases and approaches unity rapidly on the lower hemisphere, especially near the lower stagnation point (
$1\lesssim t\lesssim 2$
), however, diffusion increases and approaches unity rapidly on the lower hemisphere, especially near the lower stagnation point (
![]() ${\it\theta}=0^{\circ }$
). As can be easily understood from (3.5) or (3.6),
${\it\theta}=0^{\circ }$
). As can be easily understood from (3.5) or (3.6),
![]() $(1/\mathit{Re}\mathit{Sc}){\rm\nabla}^{2}{\it\rho}^{\prime }=1$
corresponds to constant
$(1/\mathit{Re}\mathit{Sc}){\rm\nabla}^{2}{\it\rho}^{\prime }=1$
corresponds to constant
![]() ${\it\rho}^{\prime }$
. Then, the steady state is realised sooner on the lower hemisphere. On the rear/upper stagnation point (
${\it\rho}^{\prime }$
. Then, the steady state is realised sooner on the lower hemisphere. On the rear/upper stagnation point (
![]() ${\it\theta}=180^{\circ }$
), density is conserved for the longest period (
${\it\theta}=180^{\circ }$
), density is conserved for the longest period (
![]() $t\lesssim 2$
), and the steady state is not realised until
$t\lesssim 2$
), and the steady state is not realised until
![]() $t\sim 10$
.
$t\sim 10$
.
Since the diffusion term increases to unity sooner and the decrease of
![]() ${\it\rho}^{\prime }$
stops sooner, the final steady value of
${\it\rho}^{\prime }$
stops sooner, the final steady value of
![]() ${\it\rho}^{\prime }$
is larger at lower heights as demonstrated in figure 6(a). Near the rear stagnation point, it takes the longest time before the density diffusion approaches unity, and the final steady value of
${\it\rho}^{\prime }$
is larger at lower heights as demonstrated in figure 6(a). Near the rear stagnation point, it takes the longest time before the density diffusion approaches unity, and the final steady value of
![]() ${\it\rho}^{\prime }$
is smallest there. Thus, the total density decreases more significantly at higher positions on the sphere surface. This can be identified in figure 5(c), where the steady total-density distribution on the sphere shows that the vertical distance between the contours is smaller at larger heights.
${\it\rho}^{\prime }$
is smallest there. Thus, the total density decreases more significantly at higher positions on the sphere surface. This can be identified in figure 5(c), where the steady total-density distribution on the sphere shows that the vertical distance between the contours is smaller at larger heights.
3.2. Froude number dependence
We next examine the effect of the Froude number. Steady isopycnals are shown in figure 7 including the higher Froude numbers of
![]() $\mathit{Fr}=1.5$
and 10. The figure shows that a larger number of isopycnals are dragged downward under weaker stratification (note that the contour interval
$\mathit{Fr}=1.5$
and 10. The figure shows that a larger number of isopycnals are dragged downward under weaker stratification (note that the contour interval
![]() ${\rm\Delta}{\it\rho}$
in figure 7 is four times that in figure 5). At the same time, a larger number of isopycnals exist on the sphere surface, and the diameter of the bundle of vertical isopycnals concentrated around the
${\rm\Delta}{\it\rho}$
in figure 7 is four times that in figure 5). At the same time, a larger number of isopycnals exist on the sphere surface, and the diameter of the bundle of vertical isopycnals concentrated around the
![]() $z$
axis becomes larger, corresponding to an increased radius of the jet. These results suggest that the density diffusion becomes smaller and the density is better conserved under weaker stratification.
$z$
axis becomes larger, corresponding to an increased radius of the jet. These results suggest that the density diffusion becomes smaller and the density is better conserved under weaker stratification.
This change is not abrupt throughout the range of Froude number investigated in this numerical study (
![]() $0.3\leqslant \mathit{Fr}\leqslant 10$
), suggesting that the transition between type A (thin jet) and C (broad jet) in the shadowgraph experiments would be actually continuous. In experiments, larger
$0.3\leqslant \mathit{Fr}\leqslant 10$
), suggesting that the transition between type A (thin jet) and C (broad jet) in the shadowgraph experiments would be actually continuous. In experiments, larger
![]() $\mathit{Fr}$
for the same
$\mathit{Fr}$
for the same
![]() $\mathit{Re}$
means that
$\mathit{Re}$
means that
![]() $N$
is smaller for the same
$N$
is smaller for the same
![]() $W$
and
$W$
and
![]() $a$
. Then, the black and white contrast of the shadowgraph would be weakened. On the other hand, if
$a$
. Then, the black and white contrast of the shadowgraph would be weakened. On the other hand, if
![]() $N$
is kept constant, sphere size
$N$
is kept constant, sphere size
![]() $2a$
must be smaller and
$2a$
must be smaller and
![]() $W$
must be larger to keep the value of
$W$
must be larger to keep the value of
![]() $W\times 2a\;(\propto \mathit{Re})$
constant. This reduces the resolution of the image per unit length (
$W\times 2a\;(\propto \mathit{Re})$
constant. This reduces the resolution of the image per unit length (
![]() $=2a$
). These two effects would have prohibited the clear observation of transition region between type A and C, as discussed in Hanazaki et al. (Reference Hanazaki, Kashimoto and Okamura2009a
).
$=2a$
). These two effects would have prohibited the clear observation of transition region between type A and C, as discussed in Hanazaki et al. (Reference Hanazaki, Kashimoto and Okamura2009a
).
While we can observe the overall density distributions in figures 5 and 7, the density distribution in the jet, particularly near its centre axis (
![]() $r\sim 0$
), is not discernible in these figures since many isopycnals are concentrated in a thin region. Enlarged figures, although not shown here, reveal that a local maximum of density appears on the
$r\sim 0$
), is not discernible in these figures since many isopycnals are concentrated in a thin region. Enlarged figures, although not shown here, reveal that a local maximum of density appears on the
![]() $z$
axis. Below that point, lighter fluid exists at lower heights, suggesting a strong buoyancy force above the rear/upper stagnation point of the sphere. Indeed, the vertical flow is significantly accelerated there. On the other hand, above the point of local maximum, density decreases in the upward direction, constituting a stable stratification which would decelerate the vertical flow.
$z$
axis. Below that point, lighter fluid exists at lower heights, suggesting a strong buoyancy force above the rear/upper stagnation point of the sphere. Indeed, the vertical flow is significantly accelerated there. On the other hand, above the point of local maximum, density decreases in the upward direction, constituting a stable stratification which would decelerate the vertical flow.
Steady velocity distributions in figure 8 (
![]() $\mathit{Fr}=0.3$
, 0.8, 1.5) show that the flow of larger Froude number supports a jet of larger radius. In addition, the vertical wavelength of the internal wave increases in proportion to
$\mathit{Fr}=0.3$
, 0.8, 1.5) show that the flow of larger Froude number supports a jet of larger radius. In addition, the vertical wavelength of the internal wave increases in proportion to
![]() $\mathit{Fr}$
. This proportionality to the Froude number can be predicted by the linear internal-wave theory (Mowbray & Rarity Reference Mowbray and Rarity1967) and has also been identified in previous numerical simulations (Torres et al.
Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000). On the other hand, in experiments, the height of the bell-shaped structure has been found to be proportional to the Froude number, but its relationship to internal waves has not been so clear. Figure 8 shows an upward movement of the bell-shaped structure with
$\mathit{Fr}$
. This proportionality to the Froude number can be predicted by the linear internal-wave theory (Mowbray & Rarity Reference Mowbray and Rarity1967) and has also been identified in previous numerical simulations (Torres et al.
Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000). On the other hand, in experiments, the height of the bell-shaped structure has been found to be proportional to the Froude number, but its relationship to internal waves has not been so clear. Figure 8 shows an upward movement of the bell-shaped structure with
![]() $\mathit{Fr}$
, as observed in the shadowgraph experiments (cf. figure 8 of Hanazaki et al. (Reference Hanazaki, Kashimoto and Okamura2009a
) where
$\mathit{Fr}$
, as observed in the shadowgraph experiments (cf. figure 8 of Hanazaki et al. (Reference Hanazaki, Kashimoto and Okamura2009a
) where
![]() $\mathit{Fr}=0.32$
, 0.77 and 1.5), as well as the diverging pattern of internal gravity waves.
$\mathit{Fr}=0.32$
, 0.77 and 1.5), as well as the diverging pattern of internal gravity waves.

Figure 8. Velocity vectors in steady state (
![]() $t=30$
) under strong stratification. (a)
$t=30$
) under strong stratification. (a)
![]() $\mathit{Fr}=0.3$
; (b)
$\mathit{Fr}=0.3$
; (b)
![]() $\mathit{Fr}=0.8$
; (c)
$\mathit{Fr}=0.8$
; (c)
![]() $\mathit{Fr}=1.5$
.
$\mathit{Fr}=1.5$
.
Contours of steady vertical velocity in the laboratory frame (
![]() $w-1$
) in figure 9(a–c) show clearly the increase of vertical wavelength with the Froude number. In each plot, positive and negative vertical velocity appear alternately in the vertical direction, while the amplitude of internal waves decreases with height. Then, the bell-shaped structure is observed only at the height where the downward flow is fastest (e.g.
$w-1$
) in figure 9(a–c) show clearly the increase of vertical wavelength with the Froude number. In each plot, positive and negative vertical velocity appear alternately in the vertical direction, while the amplitude of internal waves decreases with height. Then, the bell-shaped structure is observed only at the height where the downward flow is fastest (e.g.
![]() $1.5<z<2.0$
in figures 8
a and 9
a), i.e. where the downward flow is first encountered if we go up from the rear/upper stagnation point of the sphere (excluding the region very near the upper stagnation point of the sphere where the fluid has to move downward with the sphere). Therefore, the vertical position of the bell-shaped structure is determined by the vertical wavelength of internal waves, which is proportional to the Froude number. When
$1.5<z<2.0$
in figures 8
a and 9
a), i.e. where the downward flow is first encountered if we go up from the rear/upper stagnation point of the sphere (excluding the region very near the upper stagnation point of the sphere where the fluid has to move downward with the sphere). Therefore, the vertical position of the bell-shaped structure is determined by the vertical wavelength of internal waves, which is proportional to the Froude number. When
![]() $\mathit{Fr}=0.3$
, the minimum value of
$\mathit{Fr}=0.3$
, the minimum value of
![]() $w-1$
is
$w-1$
is
![]() $-1.44$
, so that
$-1.44$
, so that
![]() $(w-1)_{min}<-1$
and
$(w-1)_{min}<-1$
and
![]() $w_{min}$
is negative. This means that the fluid moves downward faster than the sphere, as a manifestation of large downward velocity in the bell-shaped structure. As the Froude number increases, downward velocity decreases, and
$w_{min}$
is negative. This means that the fluid moves downward faster than the sphere, as a manifestation of large downward velocity in the bell-shaped structure. As the Froude number increases, downward velocity decreases, and
![]() $(w-1)_{min}=-1$
(i.e.
$(w-1)_{min}=-1$
(i.e.
![]() $w_{min}=0$
) for
$w_{min}=0$
) for
![]() $\mathit{Fr}\gtrsim 1.5$
, meaning that the fastest downward flow occurs at the upper stagnation point so that no fluid descends faster than the sphere.
$\mathit{Fr}\gtrsim 1.5$
, meaning that the fastest downward flow occurs at the upper stagnation point so that no fluid descends faster than the sphere.

Figure 9. Contours of steady vertical velocity in the laboratory frame, i.e. (
![]() $w-1$
), at
$w-1$
), at
![]() $t=30$
. Thick lines denote
$t=30$
. Thick lines denote
![]() $w-1=0$
, solid lines denote
$w-1=0$
, solid lines denote
![]() $w-1>0$
with interval of
$w-1>0$
with interval of
![]() $(w_{max}-1)/10$
, and dashed lines denote
$(w_{max}-1)/10$
, and dashed lines denote
![]() $w-1<0$
with interval of
$w-1<0$
with interval of
![]() $|w_{min}-1|/10$
. Values written on the sphere are the maximum and minimum velocity in each case. (a)
$|w_{min}-1|/10$
. Values written on the sphere are the maximum and minimum velocity in each case. (a)
![]() $\mathit{Fr}=0.3$
; (b)
$\mathit{Fr}=0.3$
; (b)
![]() $\mathit{Fr}=0.8$
; (c)
$\mathit{Fr}=0.8$
; (c)
![]() $\mathit{Fr}=1.5$
.
$\mathit{Fr}=1.5$
.
The corresponding distribution of molecular diffusion of density
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in grey-scale image is given in figure 10. These plots compare well with the shadowgraphs at approximately the same Froude numbers (figure 8 of Hanazaki et al.
Reference Hanazaki, Kashimoto and Okamura2009a
), although the unsteady non-axisymmetric behaviour sometimes observed in experiments at large height (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in grey-scale image is given in figure 10. These plots compare well with the shadowgraphs at approximately the same Froude numbers (figure 8 of Hanazaki et al.
Reference Hanazaki, Kashimoto and Okamura2009a
), although the unsteady non-axisymmetric behaviour sometimes observed in experiments at large height (
![]() $z\gtrsim 3$
) cannot be reproduced in this numerical simulation. Vertical positions of the bell in the numerical simulation at
$z\gtrsim 3$
) cannot be reproduced in this numerical simulation. Vertical positions of the bell in the numerical simulation at
![]() $\mathit{Re}=200$
agree with the experiments, in which the Reynolds number was varied in the range of
$\mathit{Re}=200$
agree with the experiments, in which the Reynolds number was varied in the range of
![]() $200\lesssim \mathit{Re}\lesssim 500$
. This shows that the height of the bell is determined only by the Froude number which determines the vertical wavelength of the internal wave, confirming the conjecture in experiments that the origin of the bell-shaped structure is in internal gravity waves.
$200\lesssim \mathit{Re}\lesssim 500$
. This shows that the height of the bell is determined only by the Froude number which determines the vertical wavelength of the internal wave, confirming the conjecture in experiments that the origin of the bell-shaped structure is in internal gravity waves.

Figure 10. Distribution of density diffusion
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in steady state (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in steady state (
![]() $t=30$
) depicted in grey scale. (a)
$t=30$
) depicted in grey scale. (a)
![]() $\mathit{Fr}=0.3$
; (b)
$\mathit{Fr}=0.3$
; (b)
![]() $\mathit{Fr}=0.8$
; (c)
$\mathit{Fr}=0.8$
; (c)
![]() $\mathit{Fr}=1.5$
.
$\mathit{Fr}=1.5$
.
Temporal variations of density perturbation on the rear/upper stagnation point of the sphere are shown in figure 11 for various Froude numbers. We observe that as
![]() $\mathit{Fr}$
increases, density is better conserved and (3.4) is satisfied for a longer period. The duration of density conservation
$\mathit{Fr}$
increases, density is better conserved and (3.4) is satisfied for a longer period. The duration of density conservation
![]() $t_{c}$
can be described in its simplest form by
$t_{c}$
can be described in its simplest form by
where constant
![]() $A$
is
$A$
is
![]() $A\sim 3.5$
for
$A\sim 3.5$
for
![]() $\mathit{Fr}\gtrsim 1$
. The duration of conservation also represents the vertical distance that the upper fluid is dragged downward since
$\mathit{Fr}\gtrsim 1$
. The duration of conservation also represents the vertical distance that the upper fluid is dragged downward since
![]() $t_{c}$
is equal to
$t_{c}$
is equal to
![]() $Wt_{c}^{\ast }/2a$
, i.e. the dragged length
$Wt_{c}^{\ast }/2a$
, i.e. the dragged length
![]() $Wt_{c}^{\ast }$
divided by
$Wt_{c}^{\ast }$
divided by
![]() $2a$
(asterisk denotes the dimensional quantity).
$2a$
(asterisk denotes the dimensional quantity).

Figure 11. Time development of density perturbation
![]() ${\it\rho}^{\prime }$
on the rear/upper stagnation point of the sphere (
${\it\rho}^{\prime }$
on the rear/upper stagnation point of the sphere (
![]() ${\it\theta}=180^{\circ }$
) for various Froude numbers.
${\it\theta}=180^{\circ }$
) for various Froude numbers.
Potential energy
![]() $\mathit{PE}$
due to the vertical movement of fluid from its initial height to the dragged height is given by
$\mathit{PE}$
due to the vertical movement of fluid from its initial height to the dragged height is given by
where
![]() ${\it\rho}^{\prime }$
is the density difference between the dragged fluid and the surrounding fluid before density diffusion becomes significant. It is given by
${\it\rho}^{\prime }$
is the density difference between the dragged fluid and the surrounding fluid before density diffusion becomes significant. It is given by
![]() ${\it\rho}^{\prime }=-t_{c}$
at the rear stagnation point where the density conservation lasts longest. Then, the proportionality
${\it\rho}^{\prime }=-t_{c}$
at the rear stagnation point where the density conservation lasts longest. Then, the proportionality
![]() $t_{c}=A\,\mathit{Fr}$
gives
$t_{c}=A\,\mathit{Fr}$
gives
meaning that the maximum non-dimensional potential energy
![]() $\mathit{PE}_{c}$
attained during the density conservation is independent of
$\mathit{PE}_{c}$
attained during the density conservation is independent of
![]() $\mathit{Fr}$
for weak stratification. This shows that the vertically dragged length of fluid is determined by some critical value
$\mathit{Fr}$
for weak stratification. This shows that the vertically dragged length of fluid is determined by some critical value
![]() $\mathit{PE}_{c}$
of potential energy. Regardless of the ‘number’ of dragged isopycnals depicted in figure 7, the maximum potential energy due to the vertical displacement of fluid is the same.
$\mathit{PE}_{c}$
of potential energy. Regardless of the ‘number’ of dragged isopycnals depicted in figure 7, the maximum potential energy due to the vertical displacement of fluid is the same.
To confirm the approximate proportionality given by (3.8), we plot in figure 12 the value of
![]() $t_{c}$
determined by the time when the total density
$t_{c}$
determined by the time when the total density
![]() ${\it\rho}$
at the rear stagnation point becomes slightly larger than its initial value, i.e.
${\it\rho}$
at the rear stagnation point becomes slightly larger than its initial value, i.e.
![]() ${\it\rho}=-0.5+{\it\alpha}$
(
${\it\rho}=-0.5+{\it\alpha}$
(
![]() ${\it\alpha}=0.001$
and 0.01). Figure 12(a) shows a proportionality between
${\it\alpha}=0.001$
and 0.01). Figure 12(a) shows a proportionality between
![]() $t_{c}$
and
$t_{c}$
and
![]() $\mathit{Fr}$
except for small
$\mathit{Fr}$
except for small
![]() $\mathit{Fr}\;({<}1)$
. Figure 12(b) shows that
$\mathit{Fr}\;({<}1)$
. Figure 12(b) shows that
![]() $t_{c}$
is quite independent of
$t_{c}$
is quite independent of
![]() $\mathit{Re}$
for sufficiently large Reynolds numbers
$\mathit{Re}$
for sufficiently large Reynolds numbers
![]() $(\mathit{Re}\gtrsim 200)$
at a fixed
$(\mathit{Re}\gtrsim 200)$
at a fixed
![]() $\mathit{Fr}$
. Therefore,
$\mathit{Fr}$
. Therefore,
![]() $\mathit{PE}_{c}$
has only a weak dependence on sufficiently large Froude numbers and Reynolds numbers. At low
$\mathit{PE}_{c}$
has only a weak dependence on sufficiently large Froude numbers and Reynolds numbers. At low
![]() $\mathit{Fr}\;({\lesssim}1)$
and low
$\mathit{Fr}\;({\lesssim}1)$
and low
![]() $\mathit{Re}\lesssim 200$
,
$\mathit{Re}\lesssim 200$
,
![]() $t_{c}$
shows faster decrease, indicating that strong stratification and large viscosity prevents the conservation of density.
$t_{c}$
shows faster decrease, indicating that strong stratification and large viscosity prevents the conservation of density.

Figure 12. Duration of density conservation on the rear/upper stagnation point (
![]() $t_{c}$
) determined by the time when the density becomes
$t_{c}$
) determined by the time when the density becomes
![]() ${\it\rho}=-0.5+{\it\alpha}$
(
${\it\rho}=-0.5+{\it\alpha}$
(
![]() ${\it\alpha}=0.001$
and 0.01). (a) Froude number dependence (
${\it\alpha}=0.001$
and 0.01). (a) Froude number dependence (
![]() $\mathit{Re}=200$
); (b) Reynolds number dependence (
$\mathit{Re}=200$
); (b) Reynolds number dependence (
![]() $\mathit{Fr}=1$
).
$\mathit{Fr}=1$
).
We can also consider that the buoyancy time
![]() $t_{N}^{\ast }=2{\rm\pi}/N^{-1}$
determines the time scale for the development of a density boundary layer and hence the vertically dragged length of the isopycnals. Under this assumption, dragged length would be estimated by
$t_{N}^{\ast }=2{\rm\pi}/N^{-1}$
determines the time scale for the development of a density boundary layer and hence the vertically dragged length of the isopycnals. Under this assumption, dragged length would be estimated by
giving the non-dimensional dragged length as
which is proportional to the Froude number, and differs from
![]() $t_{c}\;(=Wt_{c}^{\ast }/2a\sim 3.5\mathit{Fr})$
(cf. (3.8)) only by a small difference in the proportionality constant, which is approximately 3.14 in (3.12) and 3.5 in (3.8). The inclination of the graph between
$t_{c}\;(=Wt_{c}^{\ast }/2a\sim 3.5\mathit{Fr})$
(cf. (3.8)) only by a small difference in the proportionality constant, which is approximately 3.14 in (3.12) and 3.5 in (3.8). The inclination of the graph between
![]() $\mathit{Fr}=2$
and 10 in figure 12(a) is indeed close to 3.1, rather than 3.5. This shows that the buoyancy time controls the initial unsteady process of density diffusion which determines the duration of density conservation.
$\mathit{Fr}=2$
and 10 in figure 12(a) is indeed close to 3.1, rather than 3.5. This shows that the buoyancy time controls the initial unsteady process of density diffusion which determines the duration of density conservation.
To understand the physical meaning of the above results, it is useful to consider the energy conversion from kinetic energy to potential energy as discussed by Higginson, Dalziel & Linden (Reference Higginson, Dalziel and Linden2003). Indeed, the length scale determined by the ratio between the vertical velocity and the buoyancy frequency, such as (3.11), can also be obtained from the energy balance between kinetic energy and potential energy (Pearson, Puttock & Hunt Reference Pearson, Puttock and Hunt1983). Since the dimensional potential energy per unit mass is given by
![]() $\mathit{PE}^{\ast }=\mathit{PE}\,W^{2}$
while the kinetic energy of fluid generated by the sphere per unit mass would be estimated by
$\mathit{PE}^{\ast }=\mathit{PE}\,W^{2}$
while the kinetic energy of fluid generated by the sphere per unit mass would be estimated by
![]() $\mathit{KE}^{\ast }=(1/2)\,W^{2}$
, these two have the relation
$\mathit{KE}^{\ast }=(1/2)\,W^{2}$
, these two have the relation
Therefore, non-dimensional potential energy
![]() $\mathit{PE}$
represents how much of the kinetic energy generated by the sphere is converted into the potential energy. Constant
$\mathit{PE}$
represents how much of the kinetic energy generated by the sphere is converted into the potential energy. Constant
![]() $\mathit{PE}_{c}$
means that the energy conversion ratio from kinetic to potential is independent of
$\mathit{PE}_{c}$
means that the energy conversion ratio from kinetic to potential is independent of
![]() $\mathit{Fr}$
and
$\mathit{Fr}$
and
![]() $\mathit{Re}$
. Conversely, the threshold value of potential energy
$\mathit{Re}$
. Conversely, the threshold value of potential energy
![]() $\mathit{PE}_{c}$
determined by the system (e.g. obstacle shape) will determine the maximum vertical movement
$\mathit{PE}_{c}$
determined by the system (e.g. obstacle shape) will determine the maximum vertical movement
![]() $t_{c}$
of the fluid according to (3.10), which is proportional to
$t_{c}$
of the fluid according to (3.10), which is proportional to
![]() $\mathit{Fr}$
.
$\mathit{Fr}$
.
We note that
![]() $\mathit{PE}_{c}$
is larger than unity here, while it should be of
$\mathit{PE}_{c}$
is larger than unity here, while it should be of
![]() $O(1)$
if we consider the energy conversion. However,
$O(1)$
if we consider the energy conversion. However,
![]() $t_{c}$
or
$t_{c}$
or
![]() ${\it\rho}^{\prime }$
is the value at the single stagnation point, and it is the largest possible value among all the fluid dragged by the sphere. Since the diffusion becomes effective sooner on other points of the sphere surface (figure 6), the mean value of
${\it\rho}^{\prime }$
is the value at the single stagnation point, and it is the largest possible value among all the fluid dragged by the sphere. Since the diffusion becomes effective sooner on other points of the sphere surface (figure 6), the mean value of
![]() $\mathit{PE}_{c}$
of all the dragged fluid would be much smaller. For example, on the equator of the sphere (
$\mathit{PE}_{c}$
of all the dragged fluid would be much smaller. For example, on the equator of the sphere (
![]() ${\it\theta}=90^{\circ }$
) where the length of the latitude line is longest and the contribution to the mean value would be largest, diffusion is effective from the very initial moment (
${\it\theta}=90^{\circ }$
) where the length of the latitude line is longest and the contribution to the mean value would be largest, diffusion is effective from the very initial moment (
![]() $t\ll 1$
, cf. figure 6
b).
$t\ll 1$
, cf. figure 6
b).
We should also mention that Yick et al. (Reference Yick, Torres, Peacock and Stocker2009) found that the dragged length is proportional to
![]() $\mathit{Fr}^{1/2}$
at low Reynolds numbers (
$\mathit{Fr}^{1/2}$
at low Reynolds numbers (
![]() $\mathit{Re}=0.05,0.5$
), suggesting the difference due to strong viscosity.
$\mathit{Re}=0.05,0.5$
), suggesting the difference due to strong viscosity.
Temporal variation of the distribution of
![]() ${\it\rho}^{\prime }$
on the sphere surface for the largest
${\it\rho}^{\prime }$
on the sphere surface for the largest
![]() $\mathit{Fr}\;(=10)$
is shown in figure 13. Near the upper stagnation point at
$\mathit{Fr}\;(=10)$
is shown in figure 13. Near the upper stagnation point at
![]() ${\it\theta}=180^{\circ }$
, density is conserved for a long time, and (3.4) is satisfied until
${\it\theta}=180^{\circ }$
, density is conserved for a long time, and (3.4) is satisfied until
![]() $t\sim 30$
. On the other hand, on the lower hemisphere of the sphere (
$t\sim 30$
. On the other hand, on the lower hemisphere of the sphere (
![]() ${\it\theta}<90^{\circ }$
), density diffusion becomes significant in a short time and
${\it\theta}<90^{\circ }$
), density diffusion becomes significant in a short time and
![]() ${\it\rho}^{\prime }$
attains its final steady value before
${\it\rho}^{\prime }$
attains its final steady value before
![]() $t=10$
. The final distribution of
$t=10$
. The final distribution of
![]() ${\it\rho}^{\prime }$
on the lower hemisphere is relatively independent of the Froude number under weak stratification (
${\it\rho}^{\prime }$
on the lower hemisphere is relatively independent of the Froude number under weak stratification (
![]() $\mathit{Fr}\gtrsim 2$
). For all the Froude numbers investigated, steady state is realised sooner on the lower hemisphere of the sphere where density diffusion is more significant, and it is realised more slowly on the upper hemisphere.
$\mathit{Fr}\gtrsim 2$
). For all the Froude numbers investigated, steady state is realised sooner on the lower hemisphere of the sphere where density diffusion is more significant, and it is realised more slowly on the upper hemisphere.

Figure 13. Temporal variation of the perturbation density distribution on the sphere at the weakest stratification (
![]() $\mathit{Fr}=10$
). The angle
$\mathit{Fr}=10$
). The angle
![]() ${\it\theta}$
is measured from the lower/forward stagnation point of the sphere along the sphere surface, as indicated in figure 6(a).
${\it\theta}$
is measured from the lower/forward stagnation point of the sphere along the sphere surface, as indicated in figure 6(a).
On the rear/upper stagnation point where the density boundary layer does not exist, the longest time is necessary before the steady state for density is realised. Since the steady value of
![]() ${\it\rho}^{\prime }$
is as low as
${\it\rho}^{\prime }$
is as low as
![]() $-50$
for the weakest stratification (
$-50$
for the weakest stratification (
![]() $\mathit{Fr}=10$
), the fluid would have been pulled down for more than 50 sphere diameters. In addition, the density distribution becomes steady only after
$\mathit{Fr}=10$
), the fluid would have been pulled down for more than 50 sphere diameters. In addition, the density distribution becomes steady only after
![]() $t\sim 80$
(figure 11) and we continued computation until
$t\sim 80$
(figure 11) and we continued computation until
![]() $t=90$
.
$t=90$
.
3.3. Flow on the vertical axis of symmetry
We next describe the flow on the vertical symmetry axis. Distributions of
![]() ${\it\rho}$
and
${\it\rho}$
and
![]() ${\it\rho}^{\prime }$
on the
${\it\rho}^{\prime }$
on the
![]() $z$
axis and their temporal variation under strong stratification (
$z$
axis and their temporal variation under strong stratification (
![]() $\mathit{Fr}=0.3$
) are presented in figure 14. We notice that the density perturbation
$\mathit{Fr}=0.3$
) are presented in figure 14. We notice that the density perturbation
![]() ${\it\rho}^{\prime }$
is nearly zero above
${\it\rho}^{\prime }$
is nearly zero above
![]() $z\sim t+0.8$
. Since
$z\sim t+0.8$
. Since
![]() $z=t$
is the initial height of the sphere at each instant (
$z=t$
is the initial height of the sphere at each instant (
![]() $=t$
), this means that the fluid is strongly perturbed only where the sphere has passed through. Fluid in the jet would not rise much beyond its initial height, although some overshoot of the jet and the far-field perturbation of internal gravity waves exists. In the initial time development at
$=t$
), this means that the fluid is strongly perturbed only where the sphere has passed through. Fluid in the jet would not rise much beyond its initial height, although some overshoot of the jet and the far-field perturbation of internal gravity waves exists. In the initial time development at
![]() $t=1.0$
(figure 14
a), the constant value of
$t=1.0$
(figure 14
a), the constant value of
![]() ${\it\rho}$
and the increase of
${\it\rho}$
and the increase of
![]() ${\it\rho}^{\prime }$
proportional to
${\it\rho}^{\prime }$
proportional to
![]() $z$
just above the sphere (
$z$
just above the sphere (
![]() $0.5\leqslant z\lesssim 1.7$
) show density conservation along the almost vertical isopycnal surface observed in figures 4(c) and 5(b). As already observed in figure 6, density is conserved on the rear/upper stagnation point until
$0.5\leqslant z\lesssim 1.7$
) show density conservation along the almost vertical isopycnal surface observed in figures 4(c) and 5(b). As already observed in figure 6, density is conserved on the rear/upper stagnation point until
![]() $t\sim 3$
, and
$t\sim 3$
, and
![]() ${\it\rho}$
agrees with its initial value
${\it\rho}$
agrees with its initial value
![]() $({\it\rho}=-0.5)$
(figure 14
a,b). At
$({\it\rho}=-0.5)$
(figure 14
a,b). At
![]() $t=3$
(figure 14
b), density above the rear stagnation point begins to change due to molecular diffusion within the jet, and the plots of
$t=3$
(figure 14
b), density above the rear stagnation point begins to change due to molecular diffusion within the jet, and the plots of
![]() ${\it\rho}$
and
${\it\rho}$
and
![]() ${\it\rho}^{\prime }$
are slightly curved in the range of
${\it\rho}^{\prime }$
are slightly curved in the range of
![]() $0.5<z\lesssim 3.5$
. As time proceeds (
$0.5<z\lesssim 3.5$
. As time proceeds (
![]() $t>3$
), the change becomes more significant near the sphere, and
$t>3$
), the change becomes more significant near the sphere, and
![]() ${\it\rho}^{\prime }$
approaches its final steady value at
${\it\rho}^{\prime }$
approaches its final steady value at
![]() $t\sim 5$
. After
$t\sim 5$
. After
![]() $t=10$
, the density distribution is steady, i.e. the curve of
$t=10$
, the density distribution is steady, i.e. the curve of
![]() ${\it\rho}^{\prime }$
is independent of time, and the curve of
${\it\rho}^{\prime }$
is independent of time, and the curve of
![]() ${\it\rho}$
moves upward in proportion to time without changing its form.
${\it\rho}$
moves upward in proportion to time without changing its form.

Figure 14. Distribution of density perturbation
![]() ${\it\rho}^{\prime }$
and total density
${\it\rho}^{\prime }$
and total density
![]() ${\it\rho}$
on the
${\it\rho}$
on the
![]() $z$
-axis under strong stratification (
$z$
-axis under strong stratification (
![]() $\mathit{Fr}=0.3$
). (a)
$\mathit{Fr}=0.3$
). (a)
![]() $t=1$
; (b)
$t=1$
; (b)
![]() $t=3$
; (c)
$t=3$
; (c)
![]() $t=5$
; (d)
$t=5$
; (d)
![]() $t=10$
. Steady state is achieved before
$t=10$
. Steady state is achieved before
![]() $t=10$
. Height
$t=10$
. Height
![]() $z=0.5$
is the rear/upper stagnation point of the sphere. In these plots the two curves cross at
$z=0.5$
is the rear/upper stagnation point of the sphere. In these plots the two curves cross at
![]() $z=t$
since
$z=t$
since
![]() $\overline{{\it\rho}}(0,0)=0$
is assumed in (3.3) for convenience in drawing figures.
$\overline{{\it\rho}}(0,0)=0$
is assumed in (3.3) for convenience in drawing figures.
Figure 15 shows a similar plot for a weak stratification (
![]() $\mathit{Fr}=5$
). The overall behaviour has some similarity to the case of strong stratification, but one significant difference is that density is better conserved in the whole region for a long time (until
$\mathit{Fr}=5$
). The overall behaviour has some similarity to the case of strong stratification, but one significant difference is that density is better conserved in the whole region for a long time (until
![]() $t\sim 20$
). This means that much longer time is necessary before the molecular diffusion becomes effective and steady state is realised. Under weak stratification, the flow near
$t\sim 20$
). This means that much longer time is necessary before the molecular diffusion becomes effective and steady state is realised. Under weak stratification, the flow near
![]() $z=t$
is still unsteady even at
$z=t$
is still unsteady even at
![]() $t=90$
(figure 15
b) since the fluid dragged by the sphere for a long distance returns nearly to its original height (
$t=90$
(figure 15
b) since the fluid dragged by the sphere for a long distance returns nearly to its original height (
![]() $z=t$
at time
$z=t$
at time
![]() $t$
) along the jet. Then, the steady state is not yet realised. Under strong stratification, the fluid is dragged only for a short length, and it returns to the original height in a short time, leading to an earlier realisation of the steady flow. We observe small undulations in the plot of
$t$
) along the jet. Then, the steady state is not yet realised. Under strong stratification, the fluid is dragged only for a short length, and it returns to the original height in a short time, leading to an earlier realisation of the steady flow. We observe small undulations in the plot of
![]() ${\it\rho}$
(figure 15
b) due to internal gravity waves. Each undulation corresponds to one wavelength of internal waves.
${\it\rho}$
(figure 15
b) due to internal gravity waves. Each undulation corresponds to one wavelength of internal waves.

Figure 15. Distribution of density perturbation
![]() ${\it\rho}^{\prime }$
and total density
${\it\rho}^{\prime }$
and total density
![]() ${\it\rho}$
on the
${\it\rho}$
on the
![]() $z$
axis under weak stratification (
$z$
axis under weak stratification (
![]() $\mathit{Fr}=5$
). (a)
$\mathit{Fr}=5$
). (a)
![]() $t=20$
; (b)
$t=20$
; (b)
![]() $t=90$
. The two curves cross at
$t=90$
. The two curves cross at
![]() $z=t$
since
$z=t$
since
![]() $\overline{{\it\rho}}(0,0)=0$
is assumed in (3.3) for convenience in drawing figures.
$\overline{{\it\rho}}(0,0)=0$
is assumed in (3.3) for convenience in drawing figures.
To investigate the process of density diffusion, the time evolution of each term of the density equation (2.11) on the
![]() $z$
axis is shown in figure 16 (
$z$
axis is shown in figure 16 (
![]() $\mathit{Fr}=0.3$
). Vertical velocity increases initially with time but the jet (
$\mathit{Fr}=0.3$
). Vertical velocity increases initially with time but the jet (
![]() $w-1$
) is well developed before
$w-1$
) is well developed before
![]() $t=5$
and it is already steady for a short distance above the sphere (
$t=5$
and it is already steady for a short distance above the sphere (
![]() $z\lesssim 4$
), although unsteadiness in velocity is still observed at higher altitude (
$z\lesssim 4$
), although unsteadiness in velocity is still observed at higher altitude (
![]() $z\gtrsim 4$
).
$z\gtrsim 4$
).

Figure 16. Distribution of each term in the density equation (2.11) on the
![]() $z$
axis under strong stratification (
$z$
axis under strong stratification (
![]() $\mathit{Fr}=0.3$
) at selected times: (a)
$\mathit{Fr}=0.3$
) at selected times: (a)
![]() $t=1$
; (b)
$t=1$
; (b)
![]() $t=3$
; (c)
$t=3$
; (c)
![]() $t=5$
; (d)
$t=5$
; (d)
![]() $t=10$
.
$t=10$
.
At time
![]() $t=1$
(figure 16
a), the time derivative has a constant value of
$t=1$
(figure 16
a), the time derivative has a constant value of
![]() $\partial {\it\rho}^{\prime }/\partial t=-1$
just above the sphere (
$\partial {\it\rho}^{\prime }/\partial t=-1$
just above the sphere (
![]() $0.5\leqslant z\lesssim 1.7$
) since the density is conserved and isopycnals are simply pulled down by the sphere (cf. figure 5
b). This can be explained as follows. First, we note that
$0.5\leqslant z\lesssim 1.7$
) since the density is conserved and isopycnals are simply pulled down by the sphere (cf. figure 5
b). This can be explained as follows. First, we note that
![]() $\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\rho}^{\prime }=w\partial {\it\rho}^{\prime }/\partial z$
is satisfied on the
$\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\rho}^{\prime }=w\partial {\it\rho}^{\prime }/\partial z$
is satisfied on the
![]() $z$
axis since
$z$
axis since
![]() $u=0$
on the symmetry axis. If the isopycnals are vertical (
$u=0$
on the symmetry axis. If the isopycnals are vertical (
![]() $\partial {\it\rho}/\partial z=0$
) and also if the mean stratification is uniform (
$\partial {\it\rho}/\partial z=0$
) and also if the mean stratification is uniform (
![]() $\text{d}\overline{{\it\rho}}/\text{d}z=-1$
), density perturbation satisfies
$\text{d}\overline{{\it\rho}}/\text{d}z=-1$
), density perturbation satisfies
![]() $\partial {\it\rho}^{\prime }/\partial z=1$
. Then,
$\partial {\it\rho}^{\prime }/\partial z=1$
. Then,
is satisfied. This simplifies the density equation (2.11) to (3.5), which we have already encountered on the sphere surface. Therefore, if the density is conserved and density diffusion is negligible (
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }=0$
), (3.5) further reduces to
${\rm\nabla}^{2}{\it\rho}^{\prime }=0$
), (3.5) further reduces to
![]() $\partial {\it\rho}^{\prime }/\partial t=-1$
.
$\partial {\it\rho}^{\prime }/\partial t=-1$
.
As time proceeds (
![]() $t=3\sim 10$
), diffusion (
$t=3\sim 10$
), diffusion (
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
) increases in the jet, near the rear stagnation point (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
) increases in the jet, near the rear stagnation point (
![]() $z=0.5$
) in particular. Note that on the sphere surface where the fluid velocity is zero, the final steady value of the diffusion term is unity (cf. (3.7)). On the other hand, on the
$z=0.5$
) in particular. Note that on the sphere surface where the fluid velocity is zero, the final steady value of the diffusion term is unity (cf. (3.7)). On the other hand, on the
![]() $z$
axis away from the sphere, (3.5) is not satisfied unless density is conserved, i.e. (3.7) is not satisfied in steady state in which the molecular diffusion is essential. Therefore,
$z$
axis away from the sphere, (3.5) is not satisfied unless density is conserved, i.e. (3.7) is not satisfied in steady state in which the molecular diffusion is essential. Therefore,
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
can increase beyond unity.
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
can increase beyond unity.
At
![]() $t=10$
, a nearly steady state is achieved on the whole
$t=10$
, a nearly steady state is achieved on the whole
![]() $z$
axis at this low Froude number (
$z$
axis at this low Froude number (
![]() $\mathit{Fr}=0.3$
), and
$\mathit{Fr}=0.3$
), and
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
asymptotes to unity on the rear stagnation point (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
asymptotes to unity on the rear stagnation point (
![]() $z=0.5$
), while its maximum value (
$z=0.5$
), while its maximum value (
![]() ${\sim}8$
) is much larger than unity. We again observe undulations due to internal waves, in the distributions of
${\sim}8$
) is much larger than unity. We again observe undulations due to internal waves, in the distributions of
![]() $\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\rho}^{\prime }$
and
$\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\rho}^{\prime }$
and
![]() $w-1$
in particular. It is of interest to note that the distribution of
$w-1$
in particular. It is of interest to note that the distribution of
![]() $\partial {\it\rho}^{\prime }/\partial t$
is flat at low Froude numbers, and approaches zero at approximately the same time in the whole range of the jet (
$\partial {\it\rho}^{\prime }/\partial t$
is flat at low Froude numbers, and approaches zero at approximately the same time in the whole range of the jet (
![]() $0.5\leqslant z\lesssim t$
), meaning that the flow becomes steady on the
$0.5\leqslant z\lesssim t$
), meaning that the flow becomes steady on the
![]() $z$
axis with a short time lag.
$z$
axis with a short time lag.
3.4. Radius of the round jet
To investigate the Froude number dependence of the radius of a jet, we show in figure 17 the steady distributions of
![]() $w-1$
in the jet as functions of
$w-1$
in the jet as functions of
![]() $r$
, at the heights where the vertical velocity on the
$r$
, at the heights where the vertical velocity on the
![]() $z$
axis becomes maximum. The radius of the jet increases with
$z$
axis becomes maximum. The radius of the jet increases with
![]() $\mathit{Fr}$
as we have observed in figure 8, while the maximum vertical velocity decreases. This means that the jet becomes less concentrated under weak stratification. We note also that the velocity becomes maximum at larger height for larger
$\mathit{Fr}$
as we have observed in figure 8, while the maximum vertical velocity decreases. This means that the jet becomes less concentrated under weak stratification. We note also that the velocity becomes maximum at larger height for larger
![]() $\mathit{Fr}$
, corresponding to the larger pulled-down length by the sphere or the larger vertical wavelength of internal waves.
$\mathit{Fr}$
, corresponding to the larger pulled-down length by the sphere or the larger vertical wavelength of internal waves.

Figure 17. Froude number dependence of the distribution of vertical velocity (
![]() $w-1$
) near the
$w-1$
) near the
![]() $z$
axis. The distribution at the height where
$z$
axis. The distribution at the height where
![]() $w$
becomes maximum is drawn for each
$w$
becomes maximum is drawn for each
![]() $\mathit{Fr}$
.
$\mathit{Fr}$
.
Unsteady development of the molecular diffusion of density in the jet is shown in figure 18, for both strong and weak stratification. The value of
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
is considered here since it directly corresponds to the previous shadowgraph experiments (Hanazaki et al.
Reference Hanazaki, Kashimoto and Okamura2009a
), and more faithfully represents a boundary layer or a jet where the diffusive term is dominant, compared to the isopycnals significantly deformed by the sphere. Under strong stratification (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
is considered here since it directly corresponds to the previous shadowgraph experiments (Hanazaki et al.
Reference Hanazaki, Kashimoto and Okamura2009a
), and more faithfully represents a boundary layer or a jet where the diffusive term is dominant, compared to the isopycnals significantly deformed by the sphere. Under strong stratification (
![]() $\mathit{Fr}=0.3$
), full development of the jet is established much sooner at around
$\mathit{Fr}=0.3$
), full development of the jet is established much sooner at around
![]() $t=10$
, while under weak stratification (
$t=10$
, while under weak stratification (
![]() $\mathit{Fr}=10$
), almost no development of the jet is observed until
$\mathit{Fr}=10$
), almost no development of the jet is observed until
![]() $t=15$
, and it takes a much longer time (
$t=15$
, and it takes a much longer time (
![]() $t\sim 90$
) for the full development.
$t\sim 90$
) for the full development.

Figure 18. Time development of
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
near the
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
near the
![]() $z$
axis at the height where maximum value is observed in steady state. (a)
$z$
axis at the height where maximum value is observed in steady state. (a)
![]() $\mathit{Fr}=0.3~(z=0.56)$
; (b)
$\mathit{Fr}=0.3~(z=0.56)$
; (b)
![]() $\mathit{Fr}=10~(z=0.60)$
.
$\mathit{Fr}=10~(z=0.60)$
.
Comparison of figure 18 with figure 17 shows that the radius observed in the distribution of density diffusion is much smaller than that observed in the vertical velocity. The difference at the same Froude number is approximately sixty times, reflecting mainly the difference between the boundary-layer thickness of velocity and density on the sphere surface at a high Schmidt number (
![]() $\sqrt{Sc}=\sqrt{700}\sim 27$
), although this is partly because the velocity is used instead of its Laplacian (
$\sqrt{Sc}=\sqrt{700}\sim 27$
), although this is partly because the velocity is used instead of its Laplacian (
![]() ${\rm\nabla}^{2}w/\mathit{Re}$
), for which the estimated radius reduces to
${\rm\nabla}^{2}w/\mathit{Re}$
), for which the estimated radius reduces to
![]() $1/3{-}1/4$
times the value presented here. These are the straightforward results since the vertical jet is a continuation of the viscous and diffusive boundary layer on the sphere surface, across the rear stagnation point of the sphere.
$1/3{-}1/4$
times the value presented here. These are the straightforward results since the vertical jet is a continuation of the viscous and diffusive boundary layer on the sphere surface, across the rear stagnation point of the sphere.
The Froude number dependence of the jet radius, defined by the half-width at half-maximum (HWHM) of density diffusion, is shown in figure 19(a). We observe that the radius is proportional to
![]() $\mathit{Fr}^{1/2}$
. Similar Froude number dependence holds also for the velocity (figure 19
b), although saturation appears for
$\mathit{Fr}^{1/2}$
. Similar Froude number dependence holds also for the velocity (figure 19
b), although saturation appears for
![]() $\mathit{Fr}^{1/2}\gtrsim 2~(\mathit{Fr}\gtrsim 4)$
. The reason why the radius of a jet or the thickness of a density boundary layer on the sphere is proportional to
$\mathit{Fr}^{1/2}\gtrsim 2~(\mathit{Fr}\gtrsim 4)$
. The reason why the radius of a jet or the thickness of a density boundary layer on the sphere is proportional to
![]() $\mathit{Fr}^{1/2}$
may be explained as follows. A plausible assumption is that in stratified fluids, the length scale of density is determined by a combination of the buoyancy frequency
$\mathit{Fr}^{1/2}$
may be explained as follows. A plausible assumption is that in stratified fluids, the length scale of density is determined by a combination of the buoyancy frequency
![]() $N$
and the diffusion coefficient of density
$N$
and the diffusion coefficient of density
![]() ${\it\kappa}$
, since the jet defined by the density anomaly is a continuation of the density boundary layer on the sphere surface and the process of jet formation would be controlled by the density boundary layer where the density diffusion is significant.
${\it\kappa}$
, since the jet defined by the density anomaly is a continuation of the density boundary layer on the sphere surface and the process of jet formation would be controlled by the density boundary layer where the density diffusion is significant.

Figure 19. Froude number dependence of the HWHM of (a)
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
and (b)
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
and (b)
![]() $w-1$
at
$w-1$
at
![]() $\mathit{Re}=200$
.
$\mathit{Re}=200$
.
The dimensional analysis gives a fundamental length scale:
which can be rewritten in non-dimensional form as
If we substitute
![]() $\mathit{Re}=200$
,
$\mathit{Re}=200$
,
![]() $\mathit{Sc}=700$
and
$\mathit{Sc}=700$
and
![]() $\mathit{Fr}=1$
into (3.16),
$\mathit{Fr}=1$
into (3.16),
![]() $l_{{\it\kappa}}/2a=1.9\times 10^{-3}$
is obtained, which is close to the simulated value in figure 20(a) (
$l_{{\it\kappa}}/2a=1.9\times 10^{-3}$
is obtained, which is close to the simulated value in figure 20(a) (
![]() ${\sim}1.2\times 10^{-3}$
). This example shows that the above assumptions give a good estimation.
${\sim}1.2\times 10^{-3}$
). This example shows that the above assumptions give a good estimation.

Figure 20. Reynolds number dependence of the HWHM of (a)
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
and (b)
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
and (b)
![]() $w-1$
at
$w-1$
at
![]() $\mathit{Fr}=1$
.
$\mathit{Fr}=1$
.
Similarly, we may consider that the length scale of velocity in stratified fluids is controlled by stratification, and is determined by a combination of the buoyancy frequency
![]() $N$
and the viscosity of fluid
$N$
and the viscosity of fluid
![]() ${\it\nu}$
. The velocity length scale
${\it\nu}$
. The velocity length scale
![]() $\sqrt{{\it\nu}/N}$
thus obtained by dimensional analysis was originally used in the literature on stratified turbulence as the primitive length scale (e.g. Gibson Reference Gibson and Nihoul1980; Barry et al.
Reference Barry, Ivey, Winters and Imberger2001), and was used in the context of a vertically moving sphere in stratified fluids to estimate the thickness of a fluid shell dragged by the sphere (Yick et al.
Reference Yick, Torres, Peacock and Stocker2009). If we assume that the thickness of the velocity shear layer in the jet
$\sqrt{{\it\nu}/N}$
thus obtained by dimensional analysis was originally used in the literature on stratified turbulence as the primitive length scale (e.g. Gibson Reference Gibson and Nihoul1980; Barry et al.
Reference Barry, Ivey, Winters and Imberger2001), and was used in the context of a vertically moving sphere in stratified fluids to estimate the thickness of a fluid shell dragged by the sphere (Yick et al.
Reference Yick, Torres, Peacock and Stocker2009). If we assume that the thickness of the velocity shear layer in the jet
![]() $l_{{\it\nu}}$
is estimated by this length scale, we obtain
$l_{{\it\nu}}$
is estimated by this length scale, we obtain
i.e.
If we substitute
![]() $\mathit{Re}=200$
and
$\mathit{Re}=200$
and
![]() $\mathit{Fr}=1$
into (3.18), we obtain
$\mathit{Fr}=1$
into (3.18), we obtain
![]() $l_{{\it\nu}}/2a=5\times 10^{-2}$
. This value is close to the simulated value in figure 20(b) (
$l_{{\it\nu}}/2a=5\times 10^{-2}$
. This value is close to the simulated value in figure 20(b) (
![]() ${\sim}7\times 10^{-2}$
), and gives good agreement. If we use
${\sim}7\times 10^{-2}$
), and gives good agreement. If we use
![]() ${\rm\nabla}^{2}w$
instead of
${\rm\nabla}^{2}w$
instead of
![]() $w-1$
, the HWHM value would be approximately
$w-1$
, the HWHM value would be approximately
![]() $1/3{-}1/4$
times that of figure 20(b) and reduces to
$1/3{-}1/4$
times that of figure 20(b) and reduces to
![]() ${\sim}2\times 10^{-2}$
for example, but the agreement is still reasonable.
${\sim}2\times 10^{-2}$
for example, but the agreement is still reasonable.
This length scale
![]() $l_{{\it\nu}}$
has the same proportionality (
$l_{{\it\nu}}$
has the same proportionality (
![]() $\propto \!(\mathit{Fr}/\mathit{Re})^{1/2}$
) as
$\propto \!(\mathit{Fr}/\mathit{Re})^{1/2}$
) as
![]() $l_{{\it\kappa}}$
, and if
$l_{{\it\kappa}}$
, and if
![]() $\mathit{Sc}$
is constant, it is equivalent to
$\mathit{Sc}$
is constant, it is equivalent to
![]() $l_{{\it\kappa}}$
except for a proportionality constant (
$l_{{\it\kappa}}$
except for a proportionality constant (
![]() $=\;\mathit{Sc}^{-1/2}$
). Indeed, in numerical results by Yick et al. (Reference Yick, Torres, Peacock and Stocker2009), proportionality to
$=\;\mathit{Sc}^{-1/2}$
). Indeed, in numerical results by Yick et al. (Reference Yick, Torres, Peacock and Stocker2009), proportionality to
![]() $(\mathit{Fr}/\mathit{Re})^{1/2}$
was observed at low Reynolds numbers (
$(\mathit{Fr}/\mathit{Re})^{1/2}$
was observed at low Reynolds numbers (
![]() $\mathit{Re}=0.05,0.5$
) for a single Prandtl/Schmidt number (
$\mathit{Re}=0.05,0.5$
) for a single Prandtl/Schmidt number (
![]() $\mathit{Pr}=700$
).
$\mathit{Pr}=700$
).
To explore the limiting behaviour as
![]() $\mathit{Fr}\rightarrow \infty$
, computation at larger
$\mathit{Fr}\rightarrow \infty$
, computation at larger
![]() $\mathit{Fr}$
is necessary. However, larger
$\mathit{Fr}$
is necessary. However, larger
![]() $\mathit{Fr}$
requires a larger time to establish a steady state, meaning that a larger vertical computational area and a more exhaustive computation are necessary. Since the time necessary to establish a steady state at the rear stagnation point is approximately
$\mathit{Fr}$
requires a larger time to establish a steady state, meaning that a larger vertical computational area and a more exhaustive computation are necessary. Since the time necessary to establish a steady state at the rear stagnation point is approximately
![]() $8\mathit{Fr}$
(cf. figure 11), we can estimate, for example in the case of
$8\mathit{Fr}$
(cf. figure 11), we can estimate, for example in the case of
![]() $\mathit{Fr}=30$
, that a steady state would be realised after
$\mathit{Fr}=30$
, that a steady state would be realised after
![]() $t=240$
. Then, the top boundary of the computational domain should be higher than
$t=240$
. Then, the top boundary of the computational domain should be higher than
![]() $z=240$
, which is an extremely large value.
$z=240$
, which is an extremely large value.
In order to examine the Reynolds number dependence of the radius of a jet, HWHM of
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
and
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
and
![]() $w-1$
are presented in figure 20 for Reynolds numbers in the range of
$w-1$
are presented in figure 20 for Reynolds numbers in the range of
![]() $20\leqslant \mathit{Re}\leqslant 1000$
at a fixed Froude number
$20\leqslant \mathit{Re}\leqslant 1000$
at a fixed Froude number
![]() $(\mathit{Fr}=1)$
. Approximate proportionality to
$(\mathit{Fr}=1)$
. Approximate proportionality to
![]() $\mathit{Re}^{-1/2}$
is observed, supporting the applicability of (3.16) and (3.18).
$\mathit{Re}^{-1/2}$
is observed, supporting the applicability of (3.16) and (3.18).
Since the radius of a jet would have a strong correlation with the boundary layer thickness on the sphere, it would be appropriate to investigate the distribution of density diffusion near the sphere surface. Figure 21 shows that the thickness of the density boundary layer on the equator of the sphere (
![]() ${\it\theta}=90^{\circ }$
) actually increases with
${\it\theta}=90^{\circ }$
) actually increases with
![]() $\mathit{Fr}$
, with similarity to the radius of a jet.
$\mathit{Fr}$
, with similarity to the radius of a jet.

Figure 21. Distribution of
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in the density boundary layer on the equator of the sphere (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in the density boundary layer on the equator of the sphere (
![]() ${\it\theta}=90^{\circ }$
), where
${\it\theta}=90^{\circ }$
), where
![]() $d$
is the distance from the sphere surface (
$d$
is the distance from the sphere surface (
![]() $\mathit{Re}=200$
).
$\mathit{Re}=200$
).
We see in figure 22 that the thickness of the density boundary layer on the sphere surface is four to ten times larger than the radius of a jet (figures 19
a, 20
a) at the same
![]() $\mathit{Fr}$
and
$\mathit{Fr}$
and
![]() $\mathit{Re}$
, although the jet is a continuation of the density boundary layer on the sphere surface so that an approximate equality between the thickness and radius might be expected. For example, the thickness at
$\mathit{Re}$
, although the jet is a continuation of the density boundary layer on the sphere surface so that an approximate equality between the thickness and radius might be expected. For example, the thickness at
![]() $\mathit{Re}=200$
in figure 22(a) is larger than the passive-scalar boundary layer in homogeneous fluids (
$\mathit{Re}=200$
in figure 22(a) is larger than the passive-scalar boundary layer in homogeneous fluids (
![]() $(1/\mathit{Re}\mathit{Sc})^{1/2}=2.67\times 10^{-3}$
) for all the Froude numbers investigated. We should note that (3.16) agrees with the passive-scalar limit (
$(1/\mathit{Re}\mathit{Sc})^{1/2}=2.67\times 10^{-3}$
) for all the Froude numbers investigated. We should note that (3.16) agrees with the passive-scalar limit (
![]() $\mathit{Fr}\rightarrow \infty$
) at
$\mathit{Fr}\rightarrow \infty$
) at
![]() $\mathit{Fr}=2$
(i.e.
$\mathit{Fr}=2$
(i.e.
![]() $\mathit{Fr}^{1/2}=1.4$
) and further increase of
$\mathit{Fr}^{1/2}=1.4$
) and further increase of
![]() $\mathit{Fr}$
in (3.16) would give an underestimation. A density boundary layer thicker than
$\mathit{Fr}$
in (3.16) would give an underestimation. A density boundary layer thicker than
![]() $(1/\mathit{Re}\mathit{Sc})^{1/2}$
has also been observed in the previous numerical simulations (Torres et al.
Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000). Phenomenologically, it would be caused by the accumulated isopycnal surfaces pulled down by the sphere. In figure 22(b), the thickness of the density boundary layer at
$(1/\mathit{Re}\mathit{Sc})^{1/2}$
has also been observed in the previous numerical simulations (Torres et al.
Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000). Phenomenologically, it would be caused by the accumulated isopycnal surfaces pulled down by the sphere. In figure 22(b), the thickness of the density boundary layer at
![]() $\mathit{Fr}=1$
increases
$\mathit{Fr}=1$
increases
![]() $\propto \mathit{Re}^{-1/2}$
in agreement with (3.16), since there would be no restriction on the value of
$\propto \mathit{Re}^{-1/2}$
in agreement with (3.16), since there would be no restriction on the value of
![]() $\mathit{Re}$
, in contrast to the upper limit of
$\mathit{Re}$
, in contrast to the upper limit of
![]() $\mathit{Fr}$
.
$\mathit{Fr}$
.

Figure 22. Thickness of the density boundary layer on the equator of the sphere (
![]() ${\it\theta}=90^{\circ }$
) defined by the position of the negative peak of
${\it\theta}=90^{\circ }$
) defined by the position of the negative peak of
![]() ${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in figure 21. (a) Froude number dependence (
${\rm\nabla}^{2}{\it\rho}^{\prime }/\mathit{Re}\mathit{Sc}$
in figure 21. (a) Froude number dependence (
![]() $\mathit{Re}=200$
); (b) Reynolds number dependence (
$\mathit{Re}=200$
); (b) Reynolds number dependence (
![]() $\mathit{Fr}=1$
).
$\mathit{Fr}=1$
).
The Froude number dependence of the drag coefficient which would be important in applications is shown in figure 23. The value of the drag in homogeneous fluid is 0.81 at
![]() $\mathit{Re}=200$
, and the plot shows that the drag increase due to stratification, i.e.
$\mathit{Re}=200$
, and the plot shows that the drag increase due to stratification, i.e.
![]() $C_{S}\;(=C_{D}-0.81)$
, is proportional to
$C_{S}\;(=C_{D}-0.81)$
, is proportional to
![]() $1/\mathit{Fr}$
. This is in agreement with the numerical simulations by Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000), although this point was not explicitly discussed in that paper. More recently, Higginson et al. (Reference Higginson, Dalziel and Linden2003) measured the drag on a grid of bars, and derived a formula for the buoyancy drag coefficient
$1/\mathit{Fr}$
. This is in agreement with the numerical simulations by Torres et al. (Reference Torres, Hanazaki, Ochoa, Castillo and Van Woert2000), although this point was not explicitly discussed in that paper. More recently, Higginson et al. (Reference Higginson, Dalziel and Linden2003) measured the drag on a grid of bars, and derived a formula for the buoyancy drag coefficient
![]() $C_{S}$
which predicts
$C_{S}$
which predicts
![]() $C_{S}\propto 1/\mathit{Fr}$
(cf. their equation (16)), assuming that
$C_{S}\propto 1/\mathit{Fr}$
(cf. their equation (16)), assuming that
![]() $C_{S}$
is due to the gravitational restoring force working on the vertically dragged fluid. Our results suggest that their formula is also applicable to a sphere.
$C_{S}$
is due to the gravitational restoring force working on the vertically dragged fluid. Our results suggest that their formula is also applicable to a sphere.

Figure 23. Froude number dependence of the drag coefficient of a sphere (
![]() $\mathit{Re}=200$
).
$\mathit{Re}=200$
).
4. Conclusions
We have investigated the generation of a buoyant jet by a sphere moving vertically in a stratified fluid. An unsteady process showed that the density is almost materially conserved initially, but molecular diffusion becomes significant after a certain period, and a horizontal circular hole appears along the sphere surface in the isopycnal surface. Density conservation is violated first near the equator of the sphere and finally at the rear/upper stagnation point of the sphere. The non-conserved light fluid can continuously move upward owing to the buoyancy force, and it generates a vertical jet along the symmetry axis of the flow.
The vertical dragging time of an isopycnal surface is very close to the buoyancy time
![]() $t_{N}^{\ast }\;(=2{\rm\pi}/N)$
, and the corresponding non-dimensional dragged length of the isopycnal surface is proportional to the Froude number and well estimated by
$t_{N}^{\ast }\;(=2{\rm\pi}/N)$
, and the corresponding non-dimensional dragged length of the isopycnal surface is proportional to the Froude number and well estimated by
![]() ${\rm\pi}\mathit{Fr}$
for
${\rm\pi}\mathit{Fr}$
for
![]() $\mathit{Fr}\gtrsim 1$
and
$\mathit{Fr}\gtrsim 1$
and
![]() $\mathit{Re}\gtrsim 200$
at the rear/upper stagnation point. Potential energy due to the vertical displacement of fluid is approximately constant and independent of
$\mathit{Re}\gtrsim 200$
at the rear/upper stagnation point. Potential energy due to the vertical displacement of fluid is approximately constant and independent of
![]() $\mathit{Fr}$
and
$\mathit{Fr}$
and
![]() $\mathit{Re}$
.
$\mathit{Re}$
.
The radius of the jet determined by the density distribution is estimated by
![]() $\sqrt{{\it\kappa}/N}$
, or in non-dimensional form by
$\sqrt{{\it\kappa}/N}$
, or in non-dimensional form by
![]() $\sqrt{\mathit{Fr }/2\mathit{Re }\mathit{ Sc}}$
, which would be the fundamental length scale in stratified diffusive fluids. The radius of the jet determined by the velocity distribution is estimated by
$\sqrt{\mathit{Fr }/2\mathit{Re }\mathit{ Sc}}$
, which would be the fundamental length scale in stratified diffusive fluids. The radius of the jet determined by the velocity distribution is estimated by
![]() $\sqrt{{\it\nu}/N}$
, or in non-dimensional form by
$\sqrt{{\it\nu}/N}$
, or in non-dimensional form by
![]() $\sqrt{\mathit{Fr }/2\mathit{Re}}$
, which has been considered as a ‘primitive’ length scale in stratified turbulence. The thickness of the density boundary layer on the sphere is significantly larger than the radius of the jet determined from the density distribution, while the thickness of the velocity boundary layer on the sphere is comparable to the radius of a jet determined from the velocity distribution. The difference is due to the isopycnal surfaces dragged by the sphere.
$\sqrt{\mathit{Fr }/2\mathit{Re}}$
, which has been considered as a ‘primitive’ length scale in stratified turbulence. The thickness of the density boundary layer on the sphere is significantly larger than the radius of the jet determined from the density distribution, while the thickness of the velocity boundary layer on the sphere is comparable to the radius of a jet determined from the velocity distribution. The difference is due to the isopycnal surfaces dragged by the sphere.
It is found that a large downward velocity related to the internal waves generates a bell-shaped structure under strong stratification, and the vertical distance between the bell and the sphere corresponds to the wavelength of internal waves, which is proportional to the Froude number.
In weakly stratified fluids (
![]() $\mathit{Fr}\gg 1$
), isopycnal surfaces can be dragged vertically for a very long distance. At time
$\mathit{Fr}\gg 1$
), isopycnal surfaces can be dragged vertically for a very long distance. At time
![]() $t$
, the density distribution might be still unsteady near the height of
$t$
, the density distribution might be still unsteady near the height of
![]() $z=t$
, at which the sphere was initially located, although the possibility of whether this actually occurs would depend largely on the Reynolds number and the Schmidt number. When this occurs, however, upper boundary of the computational domain should be higher than
$z=t$
, at which the sphere was initially located, although the possibility of whether this actually occurs would depend largely on the Reynolds number and the Schmidt number. When this occurs, however, upper boundary of the computational domain should be higher than
![]() $z=t$
to capture the large deformation of isopycnal surfaces.
$z=t$
to capture the large deformation of isopycnal surfaces.
Acknowledgements
The authors would like to thank Mr Arai and Mr Shimobata, graduate students of Kyoto University, for their technical support during the course of this study.