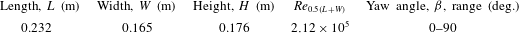1 Introduction
Flows around bluff bodies are important in a wide range of engineering disciplines. Many structures pertinent to industrial applications, including cables, girders and power lines, may be represented as long circular cylinders, while towers and skyscrapers often have rectangular cross-sections. In such cases, the length dimension is typically at least an order of magnitude greater than the other dimensions, and three-dimensional flow effects are often neglected (Zdravkovich Reference Zdravkovich2003a ). However, many applications exist in which short, finite-length bluff bodies are of interest. One example is in the area of tethered loads in aviation and construction. In aviation operations, a wide variety of bluff bodies may be transported underneath a helicopter attached by a system of cables. These configurations result in complex aerodynamic–dynamic interactions of the tethered load, which are also coupled with the dynamics of the tether system and helicopter (Greenwell Reference Greenwell2011; Prosser & Smith Reference Prosser and Smith2015a ). Typical tethered loads include cargo containers such as the CONEX, which is a short rectangular bluff body (or rectangular prism), and oil drums and engine canisters, which may be approximately represented as short finite cylinders. Other applications requiring finite bluff body aerodynamics include towed bodies, air drops, and store separation.
Numerous researchers have studied the aerodynamics of two-dimensional (or infinite) bluff bodies. Zdravkovich (Reference Zdravkovich2003a
,Reference Zdravkovich
b
) has presented a comprehensive review of the aerodynamics of circular cylinders, including finite aspect ratio effects as well as the effects of incidence angle. Both of these effects are important to (for instance) the tethered load applications, in which finite bluff bodies undergo large changes in incidence angle relative to the free-stream flow. However, these two effects (finite aspect ratio and incidence) are considered together in the review of Zdravkovich only in the case of long or infinite cylinders (with aspect ratio,
$L/D$
, greater than 20 or with end plates).
In comparison, there has been very little focus on short, finite-length cylinders with two free ends. One of the earliest experimental studies was undertaken by Wieselsberger (Reference Wieselsberger1922), in which the drag coefficient of cylinders in normal flow (the orientation where the curved surface is normal to the flow) was measured over a broad range of Reynolds numbers. Both infinite (without free ends) and finite circular cylinders with
$L/D=5$
were considered. Wieselsberger observed that, in the subcritical and transitional Reynolds number regimes, the drag of the finite cylinder was significantly less than that of the infinite cylinder. However, this difference vanished at supercritical Reynolds numbers of the order of
$10^{6}$
. Additionally, the changes between subcritical, transitional, and supercritical flow occurred at similar Reynolds numbers for the infinite and short circular cylinders. The magnitude of the change in drag during these transitions was also comparable.
Zdravkovich et al. (Reference Zdravkovich, Brand, Mathew and Weston1989) performed wind-tunnel experiments in the subcritical Reynolds number regime on finite cylinders (
$2\leqslant L/D\leqslant 10$
). Their observations were similar to those of Wieselsberger, in that decreasing the aspect ratio resulted in a decrease in drag. However, below
$L/D=5$
, further decreases in aspect ratio resulted in little if any additional drag decrease. The researchers also found that the Strouhal number for short circular cylinders with
$L/D<5$
was in the range 0.15–0.27, but the shedding behaviour was highly irregular and difficult to assign a single dominant frequency. This irregular shedding was attributed to the turbulent shear layers and three-dimensional flow interactions. Hoerner (Reference Hoerner1958) compiled drag data for circular cylinders and disks in axial flow (with the flat face normal to the flow). In this orientation, the drag was found to decrease abruptly as the aspect ratio increased from zero (circular disk) to two, but it then remained approximately constant as the aspect ratio was increased further. Other than the normal flow and axial flow orientations, very little information is available regarding the aerodynamics of short circular cylinders.
In the case of two-dimensional rectangular bluff bodies, more extensive treatment of incidence angle effects is present. Norberg (Reference Norberg1993) performed experimental investigations of two-dimensional flow around rectangular bluff bodies with the ratio of length to width (
$L/W$
) ranging from one to five at Reynolds numbers in the range 400–30 000. The Strouhal number, drag, lift, and moment coefficients were measured for each of the bluff bodies as functions of the Reynolds number and the angle of incidence, which ranged from 0° to 90°. Abrupt changes in the forces and moments were found to occur when shear layer reattachment occurred, which has also been confirmed by Matsumoto et al. (Reference Matsumoto, Ishizaki, Matsuoka, Daito, Ichikawa and Shimahara1998).
Robertson et al. (Reference Robertson, Wedding, Peterka and Cermak1978) recorded wall pressures of reattachment on square bluff bodies in two-dimensional flow for angles of attack ranging from 0° to 45°. This study identified low-pressure separation bubble, pressure recovery and attached flow regions that occur during shear layer reattachment, and quantified how the extents of these distinct regions change as the angle of attack increases. It was also observed that, for the square bluff body, the portions of the pressure distributions leading up to the attached flow region collapse onto a single curve for the two-dimensional square bluff body when particular normalizations are applied involving the reattachment distance and maximum pressure coefficient.
Motivated by the large changes in forces and moments that are caused by shear layer reattachment, Greenwell (Reference Greenwell2011) developed empirical models describing the reattachment behaviour of two-dimensional rectangular bluff bodies, drawing from available experimental data, including that of Robertson et al. (Reference Robertson, Wedding, Peterka and Cermak1978), Norberg (Reference Norberg1993), Matsumoto et al. (Reference Matsumoto, Ishizaki, Matsuoka, Daito, Ichikawa and Shimahara1998). A major contribution of his work was the development of an empirical equation which indicated that the reattachment distance for these bluff bodies, when normalized by the dimensional perpendicular to the side on which reattachment occurs, depends on the angle of incidence but not the aspect ratio. This empirical model is significant because it predicts the reattachment angle, at which sudden changes in the forces and moments occur, for two-dimensional rectangular bluff bodies. Greenwell also studied three-dimensional rectangular prisms. A comparison of the reattachment behaviours of the two- and three-dimensional bluff bodies was made for a few specific cases, but it was not thoroughly characterized. Greenwell also developed empirical reconstructions of the attached flow portion of the pressure distribution, which can be applied to either reattaching or fully attached shear layers.
The available literature indicates that shear layer behaviour plays a major role in dictating the surface pressure distribution on bluff bodies. However, there remains a marked lack of understanding of this behaviour for finite bluff bodies. Empirical models quantifying some aspects of the shear layer behaviour (including the reattachment angle) have been developed for two-dimensional rectangular bluff bodies, but these have not been characterized for common three-dimensional bluff bodies, including rectangular prisms and circular cylinders. In the current work, the aerodynamics of short rectangular prisms and circular cylinders are examined via high-fidelity numerical experiments. The primary goal of the examination is to begin to characterize the aerodynamics of these geometries over the range of angles and Reynolds numbers required by applications such as tethered loads, air drops, store separation, and towed bodies. The configurations, numerical methods, and validation of the numerical model are first discussed. Subsequently, techniques for ascertaining the mean shear layer behaviour in unsteady flow are explained, and empirical models for important shear layer quantities, including the reattachment distance, stagnation point location, and relevant pressure coefficients, are developed. As part of the characterization process, sensitivities with respect to bluff body geometry, face shape, aspect ratio, Reynolds number and incidence angle are determined.
2 Configurations
Several bluff body configurations have been selected for this investigation. All have small aspect ratio (for cylinders, the ratio of length to diameter, or
$L/D$
; for rectangular prisms, the ratio of length to width, or
$L/W$
) of the order of one to two, so three-dimensional aerodynamics are highly important. The configurations represent canonical configurations, meaning that basic geometries (i.e., rectangular prisms and circular cylinders) are modelled. Secondary geometric features such as surface imperfections and wind-tunnel mounting hardware are not modelled. This approach is important, because it ensures that the results are representative of fundamental aerodynamic behaviours that are also applicable to more complex shapes. The canonical geometries are also common in many engineering applications, so the findings are broadly pertinent.
Figure 1. Bluff body types modelled and the full-scale sling loads they represent (Cicolani et al. Reference Cicolani, Lusardi, Greaves, Robinson, Rosen and Raz2010).
The specific configurations investigated are rectangular prisms and circular cylinders. These have been selected due to prevalence in a wide range of applications, including helicopter and crane tethered loads, as well as air drops. Figure 1 depicts two of the computational models and full-scale tethered loads they represent. Figure 1(b) is a
$6\times 6\times 8$
ft. CONtainer EXpress (CONEX) cargo container. Prior evaluations (Rosen, Cecutta & Yaffe Reference Rosen, Cecutta and Yaffe1999; Raz et al.
Reference Raz, Rosen, Carmeli, Lusardi, Cicolani and Robinson2010) have indicated that the corrugations and skids do not play a major role in the integrated forces and moments for this bluff body. Short finite cylinders with aspect ratios of 1.0 and 2.0 were also evaluated. These cylinders are also representative of common tethered loads; for instance, engine canisters (as depicted in figure 1
d) and oil drums.
Table 1. Rectangular prism dimensions and flow conditions.
Figure 2. Convention for the angles
${\it\alpha}$
and
${\it\beta}$
.
Table 2. Cylinder dimensions and flow conditions.
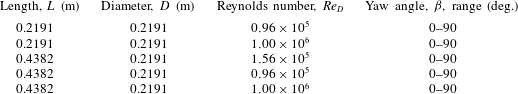
The dimensions and flow conditions examined are listed in tables 1 and 2. The Mach numbers are not listed here but are very low (below 0.1). Only a single Reynolds number was considered for the rectangular prism, which was selected to compare with available wind-tunnel test data. Several investigators (Raz et al. Reference Raz, Rosen, Carmeli, Lusardi, Cicolani and Robinson2010, Reference Raz, Rosen, Cicolani, Lusardi, Gassaway and Thompson2011, Reference Raz, Rosen, Cicolani and Lusardi2014) have noted that the rectangular prism is insensitive to Reynolds number, because separation is fixed at the sharp leading edges of the faces. Conversely, cylinders are known to be sensitive to Reynolds number when separation occurs on the curved face. Therefore, the flow around the cylinders was examined over a broad range of Reynolds numbers ranging from values typical of a low-speed wind tunnel to a full-scale tethered load.
In each case, the yaw angle was varied in the range 0°–90°, but symmetry considerations can be applied to complete the range of yaw angles from
$-180^{\circ }$
to 180°. The angle of attack was held constant at 0°. The convention for the yaw angle is as follows: for the rectangular prism, a yaw angle of 0° corresponds to the broader side (the length) facing into the free-stream flow, which is the highest-drag configuration for this geometry. At a yaw angle of 90°, the shorter side (the width) faces into the flow. For the circular cylinder, a yaw angle of 0° corresponds to the curved surface facing into the free-stream flow (the normal flow configuration), and a yaw angle of 90° corresponds to the flat surface facing into the flow (the axial flow configuration). For both geometries, a positive yaw angle represents a counterclockwise rotation when viewed from above. The conventions used for these angles are presented in figure 2.
3 Numerical model
A methodology that couples the unsteady Reynolds-averaged Navier–Stokes (URANS) equations with a subgrid-scale turbulence closure for large eddy simulations (LES) has been developed and validated using both structured and unstructured solvers. The development of the model, including details on the turbulence closure modelling, validation of the approach on a wide range of canonical problems, and demonstration with experimental correlation on complex configurations can be found in Kim & Menon (Reference Kim and Menon1999), Sánchez-Rocha & Menon (Reference Sánchez-Rocha and Menon2009, Reference Sánchez-Rocha and Menon2011), Lynch & Smith (Reference Lynch and Smith2011), Smith, Liggett & Koukol (Reference Smith, Liggett and Koukol2011), Shenoy, Smith & Park (Reference Shenoy, Smith and Park2014), Hodara & Smith (Reference Hodara and Smith2015), and Hodara et al. (Reference Hodara, Lind, Jones and Smith2016). As the focus of the paper is not on the hybrid methodology development, but rather its application for studying fluid physics, a short review of the methodology is provided here for the reader who may wish to replicate the computational assessment.
3.1 Governing equations and numerical methods
FUN3D, NASA’s URANS flow solver for unstructured grids (Anderson, Rausch & Bonhaus Reference Anderson, Rausch and Bonhaus1996), is employed in this work. FUN3D is capable of solving the URANS equations in fully compressible or incompressible formulations on mixed-element grids. To accurately resolve the turbulent wake in bluff body flows, a hybrid Reynolds-averaged Navier–Stokes – large eddy simulation (HRLES) turbulence closure (Sánchez-Rocha & Menon Reference Sánchez-Rocha and Menon2009, Reference Sánchez-Rocha and Menon2011) has been implemented into and validated in FUN3D (see Lynch & Smith Reference Lynch and Smith2011). Consider the compressible Navier–Stokes equations, defined by
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial {\it\rho}}{\partial t}+\frac{\partial }{\partial x_{j}}({\it\rho}u_{j})=0,\\ \displaystyle \frac{\partial }{\partial t}({\it\rho}u_{i})+\frac{\partial }{\partial x_{j}}({\it\rho}u_{i}u_{j})=\frac{\partial }{\partial x_{j}}(-p{\it\delta}_{ij}+{\it\tau}_{ij}),\\ \displaystyle \frac{\partial }{\partial t}({\it\rho}E)+\frac{\partial }{\partial x_{j}}({\it\rho}u_{j}E)=\frac{\partial }{\partial x_{j}}\left({\it\kappa}\frac{\partial T}{\partial x_{j}}+(-p{\it\delta}_{ij}+{\it\tau}_{ij})u_{i}\right),\end{array}\right\}\end{eqnarray}$$
where
$t$
is time,
$x$
is a spatial coordinate,
${\it\rho}$
is the fluid density,
$u$
is a fluid velocity component,
$p$
is the static pressure,
${\bf\tau}$
is the fluid stress tensor,
$E$
is the total energy,
${\it\kappa}$
is the thermal conductivity,
$T$
is the temperature, and
${\it\delta}$
is the Kronecker delta function, which is equal to one if
$i=j$
and zero otherwise. The fluid is assumed to be an ideal gas; thus,
$p={\it\rho}RT$
, where
$R$
is the gas constant. The total energy is defined as
$E=c_{v}T+(u_{k}u_{k})/2$
, where
$c_{v}$
is the specific heat at constant volume. The stress tensor
${\it\tau}_{ij}$
is defined as
$$\begin{eqnarray}{\it\tau}_{ij}=2{\it\mu}\left(\unicode[STIX]{x1D61A}_{ij}-\frac{1}{3}\unicode[STIX]{x1D61A}_{kk}{\it\delta}_{ij}\right),\quad \text{where}~\unicode[STIX]{x1D61A}_{ij}=\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right),\end{eqnarray}$$
and where
${\it\mu}$
is the dynamic viscosity. In the HRLES formulation, the density, pressure, and thermal conductivity are Reynolds-averaged, while the remaining variables are Favre-averaged. A mathematical description of these two averaging (or filtering) approaches is available in Sánchez-Rocha & Menon (Reference Sánchez-Rocha and Menon2009). The filtering process results in several fluctuating terms which are not present in the original Navier–Stokes equations, including the turbulent viscous stress,
$({\it\tau}_{ij})_{\mathit{turb}}=-\overline{{\it\rho}u_{i}^{\prime \prime }u_{j}^{\prime \prime }}$
, and the turbulent heat flux,
$(q_{i})_{\mathit{turb}}=\overline{{\it\rho}u_{i}^{\prime \prime }H^{\prime \prime }}$
, where
$H$
is the total enthalpy,
$E+p/{\it\rho}$
. Here, the operator
$\overline{(\cdot )}$
is the Reynolds-averaging operator and the notation
$(\cdot )^{\prime \prime }$
signifies the fluctuating component of a Favre-averaged variable. These fluctuating terms arising from the filtering process are not resolved by the grid and must be closed by a turbulence model.
Closure for the turbulent viscous stress is achieved by the Boussinesq approximation,
$$\begin{eqnarray}({\it\tau}_{ij})_{\mathit{turb}}=2\overline{{\it\rho}}\left({\it\nu}_{T}\unicode[STIX]{x1D61A}_{ij}-{\textstyle \frac{1}{3}}k{\it\delta}_{ij}\right)\!,\end{eqnarray}$$
where
${\it\nu}_{T}$
is the known as the eddy viscosity and
$k$
is the turbulent kinetic energy. In the HRLES approach,
$k$
is calculated via a linear blending of the URANS and subgrid-scale (SGS) LES model equations of the turbulent kinetic energy,
$G(k)=FG_{1}(k^{URANS})+(1-F)G_{2}(k^{SGS})$
. In this work, the two-equation
$k$
–
${\it\omega}$
SST model of Menter (Reference Menter1994) is applied as the URANS turbulence model, while the LES turbulent kinetic energy equation of Kim & Menon (Reference Kim and Menon1999) is employed to model
$k^{SGS}$
. The eddy viscosity,
${\it\nu}_{T}$
, is computed by blending the URANS and LES eddy viscosities, which are functions of
$k^{URANS}$
and
$k^{SGS}$
, respectively. The function
$F_{1}$
of the
$k$
–
${\it\omega}$
SST model (Menter Reference Menter1994) is selected as the blending function, which varies smoothly from one in attached boundary layers to zero in separated wakes. More information on blending functions is available in Lynch & Smith (Reference Lynch and Smith2011) and Smith et al. (Reference Smith, Cook, Sánchez-Rocha, Shenoy and Menon2013). It has been demonstrated that an approach which resolves turbulence in the wake, such as HRLES, is necessary for massively separated flows around airfoils undergoing static and dynamic stall (Sánchez-Rocha, Kirtas & Menon Reference Sánchez-Rocha, Kirtas and Menon2006; Liggett & Smith Reference Liggett and Smith2012) and bluff bodies (Theron et al.
Reference Theron, Gordon, Rosen, Cicolani, Duque and Halsey2006; Lynch & Smith Reference Lynch and Smith2011; Shenoy et al.
Reference Shenoy, Holmes, Smith and Komerath2013; Prosser & Smith Reference Prosser and Smith2014).
As the flow conditions of interest in this work correspond to very low Mach number (less than 0.1), the incompressible path is taken to solve the governing flow equations. In FUN3D, incompressible flows are treated using the method of artificial compressibility of Chorin (Reference Chorin1967). In this method,
${\it\rho}$
in the continuity equation is replaced by
${\it\Gamma}p$
, where
${\it\Gamma}$
is the artificial compressibility parameter. Additionally,
${\it\rho}$
is replaced by the free-stream value in the momentum equation, and the energy equation no longer needs to be solved. As a consequence, the pressure is not resolved by the ideal gas law but rather is evolved as part of the flow solution. This formulation is both powerful and convenient because it maintains the same form of the governing equations, permitting algorithms developed for solution of the compressible flow equations to also be applied in incompressible flow.
FUN3D uses a finite-volume spatial discretization; thus, (3.1) is transformed into the integral form using the divergence theorem in the numerical method. The discretization is second-order accurate spatially, which is typical for unstructured finite-volume solvers. Inviscid fluxes are resolved using Roe’s approximate Riemann solver, and flow gradients for viscous fluxes are computed via least squares. As bluff body flows are highly unsteady, time-accurate computations are required. FUN3D applies a backwards differentiation (BDF) scheme to achieve temporal accuracy that is formally second order but has lower truncation error than the standard second-order BDF scheme. The form is given by (3.4) (see Biedron, Vatsa & Atkins Reference Biedron, Vatsa and Atkins2005):
$$\begin{eqnarray}\frac{V}{{\rm\Delta}t}({\it\theta}_{n+1}\boldsymbol{Q}^{n+1}+{\it\theta}_{n}\boldsymbol{Q}^{n}+{\it\theta}_{n-1}\boldsymbol{Q}^{n-1}+{\it\theta}_{n-2}\boldsymbol{Q}^{n-2})=\boldsymbol{R}^{n+1}.\end{eqnarray}$$
Here,
$V$
is the cell volume,
$n$
is the physical time level,
${\rm\Delta}t$
is the physical time-step size,
$\boldsymbol{Q}$
is the vector of conserved variables and
${\it\theta}$
are the backwards differentiation coefficients, given by Biedron et al. (Reference Biedron, Vatsa and Atkins2005).
$\boldsymbol{R}$
is the residual vector, which encompasses all the terms that are not operated on by
$\partial /\partial t$
in (3.1). Since
$\boldsymbol{R}^{n+1}$
is not known, it is typically evaluated using a Taylor-series linearization of the form
$$\begin{eqnarray}\boldsymbol{R}^{n+1}\approx \boldsymbol{R}^{n}+\frac{\partial \boldsymbol{R}^{n}}{\partial \boldsymbol{Q}^{n}}(\boldsymbol{Q}^{n+1}-\boldsymbol{Q}^{n}).\end{eqnarray}$$
This linearization introduces additional error, but this is mitigated by the introduction of pseudo time terms and a pseudo time-stepping process which simultaneously causes these artificial terms to vanish and
$\boldsymbol{R}^{n+1}$
to be recovered during a convergent time step. More information on this approach is available in Biedron et al. (Reference Biedron, Vatsa and Atkins2005) and Prosser (Reference Prosser2015). The time-step size and number of pseudo time steps have been selected so that the residual vector converges by several orders of magnitude for both the momentum and turbulence equations.
Though unstructured grid topologies are already able to handle a wide range of complex geometries, further flexibility is afforded by overset grids. In this approach, multiple grids are placed on top of each other and solved simultaneously. Holes are cut in nodes of the background grids that are enclosed by a solid body in the near-body grids. Outer boundary conditions on the near-body grids are handled by interpolation from the background grid, which implies that the grid resolution must be similar at the interface between the grids and that there must be sufficient overlap. FUN3D supports overset grid simulations through the SUGGAR++ (Noack Reference Noack2005b ) and DiRTlib (Noack Reference Noack2005a ) libraries. SUGGAR++ determines blanked cells, donors and recipients, while DiRTlib interpolates data to and from overset grids. In addition to simplifying the grid generation process for complex geometries, this method is also beneficial for static simulations of internal flows when the body of interest must change orientations multiple times, as it allows the same near-body and background grids to be reused for each orientation.
3.2 Computational grids and grid convergence
Grids have been created for the bluff body geometries using best practices established for similar configurations during validation of the HRLES turbulence closure (Lynch & Smith Reference Lynch and Smith2011; Smith et al.
Reference Smith, Liggett and Koukol2011; Shenoy et al.
Reference Shenoy, Holmes, Smith and Komerath2013). The grids are unstructured and overset, with hexahedral boundary layer cells aligned with the wall-normal direction. At least 35 cells are present in this normal growth layer, with dimensionless wall distance,
$y^{+}=({\it\rho}u^{\ast }y)/{\it\mu}$
, less than 1.0 at the wall. Here,
$u^{\ast }$
is the friction velocity,
$u^{\ast }=\sqrt{{\it\tau}_{w}/{\it\rho}}$
, and
${\it\tau}_{w}$
is the shear stress at the wall. It has been previously demonstrated that a
$y^{+}$
value and number of normal-growth-layer cells similar to those applied here are important to capture separation and reattachment on surfaces at high angles of incidence (Lynch & Smith Reference Lynch and Smith2011; Smith et al.
Reference Smith, Liggett and Koukol2011; Liggett & Smith Reference Liggett and Smith2012). Figure 3 shows representative views of the grid spacing on the surface. The surface spacing is non-uniform, with points clustered near the sharp edges where separation occurs. In all cases, there are at least 300–400 cells around the perimeter in either of the surface tangential directions, and the maximum surface cell width is in all cases less than 2 % of the length or diameter.
Figure 3. Representative surface grid spacing.
Outside the boundary layer region, grid cells are tetrahedral. As the results are compared with wind-tunnel data, the near-body grids are superimposed on a background grid representing the wind-tunnel test section. The tunnel walls extend approximately 10.5 times the cylinder diameter upstream and downstream, and tunnel blockage is 1.85 % at maximum, which occurs for the cylinder with
$L/D=2$
at a yaw angle of 0°. Sensitivity studies have indicated that the effect of this blockage is minimal (see Prosser Reference Prosser2015). The wind-tunnel mounting hardware is not included in the grids to avoid interactions that would not be present for true canonical geometries.
Appropriate grid resolution has been determined by grid convergence studies, validation of integrated quantities with experimental data (see § 4), and established best practices. In the case of the rectangular prism, results accurate to within experimental uncertainty have been verified with 3.5 million total nodes. For the cylinder, experimental data are not available over most of the range of yaw angles investigated, so a grid convergence study has been performed to determine the required number of nodes (see below). The final cylinder grids have 6.5–8 million nodes, with the higher count pertaining to the longer cylinder. The higher grid resolution required for the cylinders is a direct consequence of the separation location on the curved face being sensitive to grid resolution, whereas the rectangular prism has fixed separation points. The number of nodes in the finite cylinder grids is also greater than, but of the same order of magnitude as, previous validated computations for a cylinder between walls at
$Re_{D}=3900$
(Lynch & Smith Reference Lynch and Smith2011).
Figure 4. Side views of bluff body overset grids.
Three side views of the grids are presented in figure 4. Figure 4(a) illustrates the grid for the cylinder with
$L/D=1.0$
from a perspective that includes the top and bottom walls of the wind tunnel. In addition to the fact that the near-body grid has fine resolution, the background grid resolution is also increased in the vicinity of the cylinder and its wake to prevent orphans (nodes lacking an adequate interpolation stencil at overset grid boundaries) and to ensure that wake turbulence is accurately captured. Figure 4(b) depicts the same configuration, but from a closer perspective so that the normal growth region is visible. Figure 4(c) is a side view of the rectangular prism, which is coarser than the cylinder near-body grid. Similar grid resolution and characteristics are present in the top and front views, which are not shown.
While comparisons with wind-tunnel data have confirmed that accurate integrated loads are obtained for the rectangular prism on 3.5-million-node grids, a grid convergence study has been performed for the cylinder. The sensitivity has been evaluated by comparison of the forces and moments on grids with various levels of refinement at low yaw angles, where the sensitivity is expected to be the highest. The Reynolds number based on diameter for the grid sensitivity study is
$3.2\times 10^{5}$
, which is between the low and high range of Reynolds numbers investigated in the rest of this paper. The aspect ratio of the cylinder is 1.0 for the sensitivity study. Two different refinement techniques have been applied:
-
(i) uniform refinement, and
-
(ii) feature-based adaptation to vorticity magnitude.
Figure 5. Side views of cylinder grids refined via feature-based adaptation.
Feature-based adaptation capability has been introduced in FUN3D for overset grids by Shenoy et al. (see Shenoy & Smith Reference Shenoy and Smith2011; Shenoy et al.
Reference Shenoy, Smith and Park2014). In this technique, flow features of interest (such as separated shear layers and shed vortices) can be resolved while reducing the number of grid points in regions of smooth flow. The baseline grid contains 3.7 million nodes, which is only slightly larger than the rectangular prism grids, while the finest grid has 8.5 million nodes. In both the feature-based and uniform refinement approaches, the node count has been increased by clustering points near the surface and in the wake. Illustrations of the uniformly refined grid are included in figure 4(a,b). Figure 5(a,b) presents similar depictions of the cylinder grids after one and two cycles of feature-based refinement, respectively. The feature-based adaptation strategy follows the approach of Shenoy et al. (Reference Shenoy, Smith and Park2014), in which a vorticity-based indicator
$F_{|{\it\omega}|}$
is constructed for each edge over time. The indicator is defined as
$$\begin{eqnarray}F_{|{\it\omega}|}=0.5l(|{\it\omega}_{n1}|+|{\it\omega}_{n2}|),\end{eqnarray}$$
where
$l$
is the edge length,
$n1$
and
$n2$
are the two nodes defining the edge, and
${\it\omega}$
is the instantaneous non-dimensional vorticity. To account for unsteadiness in the flow,
$F_{|{\it\omega}|}$
is tracked throughout the grid over enough steps to resolve several cycles of vortex shedding. Following this period, the maximum value of the indicator over time at each edge is used to establish an adaptation intensity field to define the regions of grid refinement. Coarsening may also occur up to approximately 15 % of the original spacing. More information on the feature-based algorithm is available in Shenoy & Smith (Reference Shenoy and Smith2011) and Shenoy et al. (Reference Shenoy, Smith and Park2014). As is apparent in figure 5, this approach is effective in clustering grid points in the wake region between the two separated shear layers where vorticity magnitude is large. The figure also shows that the algorithm is able to traverse overset grid boundaries effectively.
Figure 6. Grid sensitivity study, cylinder with an aspect ratio of 1.0 at low yaw angle and a Reynolds number of
$3.2\times 10^{5}$
. (a) Drag coefficient, (b) side force coefficient, (c) yaw moment coefficient.
The mean drag, side force, and yaw moment between yaw angles of 0° and 10° are presented in figure 6. The reference area used for non-dimensionalization here is the frontal area,
$LD$
, and the reference length for normalizing the yaw moment is the diameter,
$D$
. While increasing the node count reduces the drag, the 5.5-million-node grid is within 5 % the drag of the finest grid. The side force behaviour is more sensitive to grid refinement than the drag, particularly between the coarsest grid and any of the finer grids. The coarsest grid predicts an incorrect side force trend between yaw angles of 0° and 2.5°; on the coarsest grid, the side force is positive at a yaw angle of 2.5°, while it is negative on the finer grids. The side force at a yaw angle of zero is also further from the expected value of zero (based on geometric symmetry) on the coarsest grid. Wind-tunnel experiments (see Zdravkovich et al.
Reference Zdravkovich, Brand, Mathew and Weston1989) have indicated that the asymmetric behaviour occurs due to the bi-stable nature of vortex shedding for very short cylinders with two free ends at low yaw angles. In terms of the side force, all of the grids with node counts of 5.5 million and above offer comparable results. The yaw moment trends are the same for all grids evaluated, and the variation in yaw moment is less than the variation in drag and side force coefficients across the grids evaluated.
Based on the results of the grid sensitivity analysis, acceptable grid convergence is observed with the finest grids in figure 6, so the final grids were created with node counts in the range 6.5–8 million. Point spacings on the surface and the wake are similar in all cases; the higher node counts correspond to the cylinder with higher aspect ratio. Though feature-based adaptive refinement has been applied in the grid convergence study, uniform refinement has been leveraged here to generate the final grids, as adaptive refinement needs to be performed at each yaw angle to account for the changing shear layer behaviour, and thus would introduce significant additional cost.
Because the numerical solver is unstructured, the simulation is limited to a second-order spatial algorithm. This approach requires a finer grid than is required for a higher-order structured solver to obtain similar results. A study on the effect of dissipation in the wake, separation location, and pressures was previously conducted with an infinite circular cylinder at a Reynolds number of 3900 (Lynch & Smith Reference Lynch and Smith2011). From the results of this canonical test case, used extensively for large eddy simulation assessment, the unstructured grid topology and numerical options necessary to minimize dissipation in simulations with separation and turbulent wakes was determined. This grid topology has been applied here to ensure that numerical dissipation was minimized for the configurations evaluated.
4 Approach validation
Static force and moment coefficients have been compiled for the rectangular prism and circular cylinders for the configurations and flow conditions listed in tables 1 and 2. These are compared with wind-tunnel experiments performed at the Georgia Institute of Technology (Mantri et al.
Reference Mantri, Raghav, Komerath and Smith2011) and other extant data (Wieselsberger Reference Wieselsberger1922; Hoerner Reference Hoerner1958; Rosen et al.
Reference Rosen, Cecutta and Yaffe1999), where available. The reference area used for non-dimensionalizing the forces and moments is, for the rectangular prism,
$0.5H(L+W)$
, the average area of the two vertical faces. Similarly, the reference length for moments is
$0.5(L+W)$
, and the moments are computed about the geometric centre of the prism. The cylinder force and moment coefficients are typically presented with
$LD$
as the reference area and
$D$
as the reference length for moments, which are also taken about the geometric centre. The planform area (
$LD$
) as the reference for the short cylinders, rather than the circular face area
$({\rm\pi}/4)D^{2}$
, has been selected so that force coefficients in the normal flow orientation may be compared directly with two-dimensional results, as in various experimental studies (Wieselsberger Reference Wieselsberger1922; Hoerner Reference Hoerner1958; Zdravkovich et al.
Reference Zdravkovich, Brand, Mathew and Weston1989).
The numerical simulations are time-accurate and the integrated loads are unsteady, so the forces and moments are time-averaged and presented as mean values with fluctuations plotted as dashed lines (they are not uncertainties, but rather an indication of the influence of vortex shedding fluctuations). To ensure that no bias due to vortex shedding is present in the time-averaging process, the time-averaging procedure described in § 5.1 was applied to these variables.
Figure 7. Rectangular prism computed force and moment coefficients and comparison with experimental data (Rosen et al. Reference Rosen, Cecutta and Yaffe1999; Mantri et al. Reference Mantri, Raghav, Komerath and Smith2011). Dashed lines represent min and max values for the unsteady simulations. (a) Drag coefficient, (b) side force coefficient, (c) yaw moment coefficient.
Figure 7 depicts the drag, side force, and yaw moment coefficients for the rectangular prism. The experimental data were measured using a load cell attached to the wind-tunnel model, and in the Georgia Tech experiments the reported uncertainty in these measurements is
$\pm 3.5\,\%$
for forces and
$\pm 5\,\%$
for moments. The agreement between these quantities and both sets of data is satisfactory, as the computed values are typically within 7 % of at least one of the experimental data sets. There is some variation between the two sets of wind-tunnel data, but in general at least one of the two experimental sets lies within the bounds of unsteadiness of the computations, and the computations generally lie between the two experimental data sets. While the data by Rosen et al. (Reference Rosen, Cecutta and Yaffe1999) were taken at a lower Reynolds number (
$Re=1.5\times 10^{5}$
rather than the Reynolds number,
$Re=2.1\times 10^{5}$
, of the other data), these minor variations in Reynolds number are not expected to have a significant effect on the integrated loads for bodies with sharp-edge separation (Raz et al.
Reference Raz, Rosen, Carmeli, Lusardi, Cicolani and Robinson2010, Reference Raz, Rosen, Cicolani, Lusardi, Gassaway and Thompson2011, Reference Raz, Rosen, Cicolani and Lusardi2014). In comparison with other computational evaluations of the CONEX rectangular prism and similar bluff bodies to date, the present computations better predict the forces and moments measured experimentally. This improved correlation is thought to be due in large part to the HRLES turbulence approach that resolves large turbulent wake structures. The prior evaluations with traditional URANS models have proved less successful, particularly in the prediction of side of side force (Theron et al.
Reference Theron, Duque, Cicolani and Halsey2005, Reference Theron, Gordon, Rosen, Cicolani, Duque and Halsey2006; Cicolani et al.
Reference Cicolani, Cone, Theron, Robinson, Lusardi, Tischler, Rosen and Raz2009). Similar findings have been reported across a broad spectrum of configurations (with smooth curves and sharp corners) at moderate and high Reynolds numbers where separation and reattachment is present, including airfoils and wings at high and reverse angles of attack (Smith et al.
Reference Smith, Liggett and Koukol2011; Hodara et al.
Reference Hodara, Lind, Jones and Smith2016) and rotor–fuselage interactions (Shenoy et al.
Reference Shenoy, Smith and Park2014), for example. These latter simulations were performed with both URANS and HRLES using the same grids and otherwise the same numerical parameters, verifying the inability of the URANS turbulence methods to correctly capture the leeward-side physics of all of these configurations.
The present numerical analysis approach has also been previously validated for flows over infinite cylinders via comparisons with experiments in the subcritical Reynolds number regime at
$Re_{D}=3900$
(Lynch & Smith Reference Lynch and Smith2011). The drag coefficient, shedding frequency, and separation location were all well within the error bounds of experimental measurements in that study. Because many of the applications of this work typically involve larger Reynolds numbers, here the focus is on transitional and supercritical flows. The computations are compared with experimental data at yaw angles of 0° and 90°, as other orientations are not available in the literature for short finite cylinders.
Figure 8. Comparison of the current computations in normal and axial flow configurations with experimental data by Wieselsberger (Reference Wieselsberger1922), Hoerner (Reference Hoerner1958), and previous computations by Lynch & Smith (Reference Lynch and Smith2011).
Figure 8 presents the drag coefficients of the present computations in normal flow with the experimental data of Wieselsberger (Reference Wieselsberger1922) and the prior computations by Lynch & Smith (Reference Lynch and Smith2011). Here, the drag coefficient is computed with the frontal area (
$LD$
) as the reference area. It is apparent from this figure that the agreement with experimental data is excellent (within 4 % of experimental measurements) in both the subcritical and supercritical regimes. Furthermore, in both the transitional and supercritical regimes, the difference in drag between aspect ratios of 1.0 and 2.0 is small, as the difference in drag is less than 7 % at both Reynolds numbers when the aspect ratio changes from 1.0 to 2.0. This result is in agreement with experimental observations of Zdravkovich et al. (Reference Zdravkovich, Brand, Mathew and Weston1989), who found that the drag coefficient is insensitive to aspect ratio for
$L/D\leqslant 5$
in the normal flow orientation (the change in drag was also less than 10 % when the aspect ratio is decreased from 5.0 to 1.0).
The finite cylinder drag predictions in the range of Reynolds numbers from
$0.96\times 10^{5}$
to
$1.56\times 10^{5}$
are somewhat lower than the experimental data for the cylinder with an aspect ratio of 5.0, with only minor variation across this range. However, they are comparable to the experimental drag in the transitional regime, which occurs at a somewhat higher Reynolds number, and over a small range of Reynolds numbers, in the experiments. The URANS model active inside the boundary layer in this work is the two-equation Menter
$k$
–
${\it\omega}$
shear stress transport (SST) model (Menter, Kuntz & Langtry Reference Menter, Kuntz and Langtry2003), which assumes a fully turbulent boundary layer. Hodara & Smith (Reference Hodara and Smith2015) have developed a new transition-based HRLES approach (tHRLES), which shows improved prediction of integrated forces in the transitional regime than both URANS and the present original HRLES model. While this model was not available for this study, it holds promise for future applications of the hybrid turbulence closure. Despite this transition modelling shortcoming, Prosser (Reference Prosser2015) demonstrated that the transition prediction primarily affects the drag for yaw angles below 30° but has minimal influence on most other quantities of interest. Furthermore, it will be shown later that many of the shear layer behaviours are insensitive to Reynolds number, so transition does not have a significant impact on the main quantities of interest for this work.
The drag in axial flow is compared with experimental data from Hoerner (Reference Hoerner1958) for circular disks and finite cylinders in figure 8(b). The drag force is again normalized by the frontal area, which in this orientation is
$({\rm\pi}/4)D^{2}$
instead of
$LD$
. Complete details of the flow conditions for the experimental data were not available, but at least some of the tests were performed with Reynolds numbers in the range
$10^{5}$
–
$10^{6}$
. In any case, the computational results in figure 8(b) indicate that in axial flow, there is no sensitivity of the drag to the Reynolds number, at least over the range investigated here. This result is not surprising, as in this orientation separation occurs at the sharp edges of the flat face, whereas in normal flow separation occurs from the curved face and is dependent on the boundary layer and wake turbulence characteristics. The present computations at an aspect ratio of 1.0 result in drag comparable to a circular disk in the experimental data. The data indicate that there is a sharp decrease in drag near this aspect ratio corresponding to a change in the shear layer behaviour. Due to the abruptness of this change, it is not unusual for the drop in drag to occur at a slightly different aspect ratio depending on the flow conditions (in particular, the wind-tunnel turbulence level, which was not recorded in the wind-tunnel data). The computations for the cylinders with an aspect ratio of 2.0 are consistent with the experimental data.
Figure 9. Time-averaged contours of pressure coefficient and streamlines in a top-down view for the axial flow condition of the circular cylinder.
Figure 9 highlights the differences in shear layer behaviour for cylinders with two different aspect ratios (1 and 2) in axial flow. Time-averaged streamlines and pressure coefficient contours are shown in a planform view. Separation occurs at the sharp edges of the front face, promoting the formation of low-pressure, vortical separation bubbles that draw the outer flow back towards the surface. For the cylinder with an aspect ratio of 2.0, the shear layer reattaches on the aft portion of the curved face, but it remains separated for the shorter cylinder, as its length is not sufficient for reattachment to occur. Reattachment is accompanied by a pressure recovery, resulting in significantly lower base pressure and drag for the longer cylinder.
5 Shear layer behaviour
The significant unsteadiness and complex turbulent structures in flows about short three-dimensional bluff bodies present challenges in characterizing the shear layer behaviour. To illustrate these difficulties, figure 10 presents flow-field snapshots for a cylinder with an aspect ratio of 2.0 at a yaw angle of 10° and a rectangular prism at a yaw angle of 25°. Surfaces of constant
$Q$
-criterion in the wake are rendered as smoke, while the surface is coloured by contours of pressure coefficient.
$Q$
is defined as:
$$\begin{eqnarray}Q={\textstyle \frac{1}{2}}(\Vert {\it\bf\Omega}\Vert ^{2}-\Vert \unicode[STIX]{x1D64E}\Vert ^{2}),\end{eqnarray}$$
where
${\it\bf\Omega}$
is the vorticity tensor and
$\unicode[STIX]{x1D64E}$
is the strain rate tensor (Haller Reference Haller2005). In both snapshots, there exist complex, highly three-dimensional turbulent structures that are resolved by the hybrid RANS–LES turbulence methodology. For example, in figure 10(a), ‘roller’ vortices originating from the separation point on the curved face are visible, but these structures break down as they blend with the vortices shed from the flat face. The interactions between these structures emanating from the different faces of short bluff bodies result in multi-modal and variable shedding frequencies that have also been observed in wind-tunnel tests (Ayoub & Karamcheti Reference Ayoub and Karamcheti1982; Zdravkovich et al.
Reference Zdravkovich, Brand, Mathew and Weston1989) as well as computations (Prosser & Smith Reference Prosser and Smith2014, Reference Prosser and Smith2015b
).
Figure 10. Unsteady flow snapshots on various short bluff bodies. Flow direction is from right to left.
Figure 11. Illustration of shear layer behaviour for a rectangular bluff body. (1) Fully separated, (2) reattaching, and (3) fully attached.
In addition to the turbulent structures, multiple different shear layer behaviours are visible in each illustration. There are three possible behaviours, including (1) separated shear layer, (2) reattaching shear layer, and (3) attached shear layer. These three behaviours are illustrated in figure 11, which is representative of the rectangular prism in a top view. At low yaw angles, the shear layers are both fully separated (1). As the yaw angle increases, the shear layer eventually reattaches on the right side, marked by (2), but the flow is fully attached on the front side, identified by (3). Increasing the yaw angle further results in full attachment on the side marked by (3), while a separation bubble and reattaching flow occurs on the side, (2), and eventually fully separated flow on this side, (1).
Each of these three shear layer behaviours is also visible in figure 10. For example, reattachment is evidenced by a rapid increase in pressure over a short distance leading up to the reattachment point. As clearly displayed in figure 10, large, unsteady turbulent eddies are present during reattachment, unlike the diagram in figure 11 suggests. As in figure 10(a), the shear layer often breaks up into discrete vortical structures that travel downstream and either interact with the reattached boundary layer or are drawn into the separation bubble. The large, sudden changes in pressure caused by reattachment also have a significant influence on the mean forces and moments, but the unsteady, turbulent nature of the shear layer and its interaction with the surface create difficulty in assessing these relationships with the mean integrated loads.
Figure 12. Unsteady and time-averaged reattachment behaviour for
$L/D=1$
cylinder,
$Re_{D}=0.96\times 10^{5}$
,
${\it\beta}=2.5^{\circ }$
; top view shown. (The circular flat face is normal to the page in this view.) (a) Unsteady flow field, (b) time-averaged flow field.
5.1 Time averaging
To overcome these difficulties related to unsteady flow, the flow fields themselves have been time-averaged to permit the mean separation and reattachment behaviours to be studied. To illustrate the effect of time averaging, figure 12(a) presents a snapshot of the unsteady non-dimensional vorticity magnitude,
$|{\it\omega}|=\sqrt{(\boldsymbol{{\rm\nabla}}\times \boldsymbol{ u})^{2}}$
, around a circular cylinder with an aspect ratio of 1.0. In this orientation, shear layer reattachment occurs near the aft end of the cylinder, but it is weak and highly unsteady. Time averaging the flow field, as illustrated in figure 12(b), smooths out discrete turbulent structures and permits the mean trajectory of the shear layer and its reattachment point on the side of the circular cylinder to be identified. Similar benefits of time averaging have also been noted in direct numerical simulations of turbulent flows around bluff bodies. For example, Vinuesa et al. (Reference Vinuesa, Schlatter, Malm, Mavriplis and Henningson2015) found that a large horseshoe vortex became visible in turbulent flows around wall-mounted rectangular prisms only after time averaging. In instantaneous flow visualizations, small-scale turbulence was too prevalent to distinguish the horseshoe vortex.
To ensure that no bias due to vortex shedding is present in the time-averaging process, the following procedure was developed and verified. Each numerical experiment was performed over 40–60 vortex shedding cycles based on a Strouhal number of 0.2. As the flow fields were initialized from steady-state solutions, in some cases transients were apparent in the forces and moments for up to the first ten cycles, so this period of time was not included in the averaging. The flow fields (as well as the forces and moments) were, therefore, averaged over a minimum of 30 cycles, which was found to result in converged reattachment locations and wall pressures. This length of time corresponds to approximately 150 convective time units,
$t^{\ast }=tU_{\infty }/L_{ref}$
(where
$U_{\infty }$
is the speed of the incoming flow and
$L_{ref}$
is the reference length), for the circular cylinder with
$D$
taken as the reference length. The averaging time in convective units is also similar for the rectangular prism with
$0.5(L+W)$
taken as the reference length. The window for time averaging was selected so that the endpoints corresponded to peaks in the forces and moments, ensuring that the time-averaging process did not include partial vortex shedding cycles. An example time-averaging window is illustrated in figure 13, which represents the drag coefficient for a circular cylinder with
$L/D=1$
at
$Re_{D}=10^{6}$
.
Figure 13. Example time-averaging window of the drag coefficient (
$C_{D}$
) time history for a circular cylinder with
$L/D=1$
at
$Re_{D}=10^{6}$
.
Figure 14. Typical pressure distributions and definition of empirical modelling parameters. (a) Reattaching flow, (b) attached flow.
Similar to
$|{\it\omega}|$
, the surface pressure distributions also become smooth and steady as a result of the time-averaging process. This behaviour is important because the time-averaged pressure distributions are directly related to the mean forces and moments acting on the bluff body. Figure 14 presents typical pressure distributions along the centreline of faces subject to shear layer reattachment and fully attached flow. There are four important parameters in the reattaching pressure distribution (figure 14
a): the base pressure,
$c_{p_{b}}$
, the separation bubble pressure,
$c_{p_{S}}$
, the maximum pressure at reattachment,
$c_{p_{M}}$
, and the reattachment distance,
$x_{M}$
, defined as the distance from the leading edge to the location of
$c_{p_{M}}$
. In attached flow (figure 14
b), the maximum pressure coefficient remains constant at 1.0 (the incompressible stagnation pressure coefficient), and there is no separation bubble. As a result, the fully attached pressure distribution can be characterized by just the stagnation point location,
$x_{0}$
. In fully separated flow (the behaviour labelled (1) in figure 11), Robertson et al. (Reference Robertson, Wedding, Peterka and Cermak1978) observed that the pressure distribution is nearly constant, with a value close to the base pressure.
In § 5.2, the data in figure 14 are assessed using the time-averaged pressure distribution data from the numerical experiments. The variations are characterized with bluff body type, face shape, orientation angle, aspect ratio, and Reynolds number.
5.2 Empirical modelling
Due to the inherent unsteadiness and nonlinearity resulting from transition, separation, and reattachment in bluff body flows, simplified analytical theories are generally not available. Empirical modelling represents an alternative to analytical modelling, with similar benefits to applications such as real-time or training simulations that require a method with low computational cost. Some development in the area of empirical modelling of shear layer behaviour has been published by Greenwell (Reference Greenwell2011) for two-dimensional rectangular bluff bodies. This work develops similar empirical models for the mean behaviour of short three-dimensional bluff bodies.
Figure 15. Depiction of the incidence angle,
${\it\phi}$
, and the incidence angle at which reattachment first occurs,
${\it\phi}_{R}$
. Arrows indicate the free-stream flow direction.
One key parameter relevant to the shear layer behaviour is the incidence angle,
${\it\phi}$
, which is the angle of the free stream relative to a given face. This angle is related to the yaw angle but also depends on the orientation of the face at a yaw angle of 0°, and, moreover, at a given yaw angle, each individual face of a bluff body has a different incidence angle. This angle is depicted for a single face of a bluff body in a top view in figure 15(a). The most relevant angle in the reattachment process is the angle at which reattachment on a given face first occurs, or
${\it\phi}_{R}$
, which is illustrated in figure 15(b). As shown in the illustration, the separation bubble spans the entire face when
${\it\phi}={\it\phi}_{R}$
. If the incidence angle is further increased, the separation bubble will shrink, or, alternatively, the shear layer will become fully separated if the incidence angle is decreased from
${\it\phi}_{R}$
. The angle
${\it\phi}_{R}$
can be considered constant for a given face of a bluff body at a particular free-stream condition.
Figure 16 quantifies the variation of the normalized reattachment distance with incidence angle. Data from the present numerical experiments are included in this figure as well as wind-tunnel data from Robertson et al. (Reference Robertson, Wedding, Peterka and Cermak1978) for two-dimensional rectangular prisms. For the rectangular prisms, the reattachment distance is normalized by the length of the side adjacent to the face on which reattachment occurs; for the circular cylinders it is normalized by the diameter. These figures clearly indicate that the normalized reattachment distance correlates with the geometry type and face shape, but not the aspect ratio or Reynolds number. Though similar trends occur for all three canonical configurations, the normalized reattachment distance is largest for a given incidence angle on the rectangular prism, followed by the curved face of the circular cylinder. It is smallest on the flat faces of the circular cylinder. The incidence angle at which reattachment first occurs (
${\it\phi}_{R}$
) can be determined from these empirical relationships by determining the reattachment distance equal to the length of the relevant face and identifying the incidence angle from the curve fit in figure 16.
Figure 16. Normalized reattachment distance as a function of incidence angle. Two-dimensional rectangular prism data from Robertson et al. (Reference Robertson, Wedding, Peterka and Cermak1978). (a) Flat cylinder faces, (b) curved cylinder faces, (c) rectangular prism faces.
Empirical models of the four reattachment pressure distribution parameters are presented in figure 17. Most collapse onto a single curve when normalized appropriately. The incidence angle, for instance, can be normalized as
$({\it\phi}-{\it\phi}_{R})/$
$(45^{\circ }-{\it\phi}_{R})$
. Similarly, the pressure coefficients can be normalized as
$(c_{p}-c_{p_{b,{\it\phi}=0}})/$
$(1.0-c_{p_{b,{\it\phi}=0}})$
, where
$c_{p_{b,{\it\phi}=0}}$
is the base pressure coefficient at an incidence angle of 0°. When normalized in this manner, the variation in reattachment distance can be described with a single quadratic curve with coefficient of determination (
$R^{2}$
) of 0.97. The normalized reattachment distance is independent of the surface type, canonical geometry type (cylinders and two- or three-dimensional rectangular bluff bodies), aspect ratio, and Reynolds number. Conversely, if
${\it\phi}_{R}$
is not subtracted, as in figure 16, then the empirical equations vary with geometry and surface type. This result indicates that these geometric differences have a significant effect on the incidence angle at which reattachment begins, but the variation of the reattachment distance with incidence angle after reattachment begins follows a similar trend in all cases. Therefore, the models provided in figure 16 can be used to determine the incidence angle at which reattachment begins, and then the equation in figure 17(a) can be applied.
Figure 17. Reattachment parameter variations with
${\it\phi}$
and empirical curve fits. (a)
$x_{M}$
, (b)
$c_{p_{M}}$
, (c)
$c_{p_{S}}$
, (d)
$c_{p_{b}}$
.
The maximum pressure coefficient during reattachment,
$c_{p_{M}}$
, exhibits similar independence when normalized appropriately. All geometries evaluated collapse onto a single empirical curve with a coefficient of determination of 0.96, and the maximum pressure coefficient increases with incidence angle in a cubic relationship. The separation bubble pressure coefficient,
$c_{p_{S}}$
, collapses similarly, but in this case, there are differences with respect to the type of surface. For reattachment on flat faces (cylinder finite ends or rectangular bluff bodies), the separation bubble pressure can be modelled by an empirical curve fit with a coefficient of determination of 0.98. However, curved faces do not fit this trend; data for curved faces are highlighted in red in figure 17(c). In fact, the separation bubble pressure on curved faces is found to depend not only on the incidence angle but also the aspect ratio and Reynolds number. The base pressure coefficient,
$c_{p_{b}}$
, exhibits significant scatter and is not amenable to fitting by an empirical curve. However, this parameter is difficult to determine, as the pressure coefficient drops off rapidly at the aft end of the face (see figure 14
a). Due to this rapid drop-off, the value of this coefficient is not expected to significantly influence the integrated loads, and a representative value for a given geometry could reasonably be applied at all yaw angles.
Figure 18 presents the variation of the stagnation point with incidence angle. As stagnation on a given face implies that reattachment does not occur on the same face, the incidence angle at which reattachment begins is not subtracted from the incidence angle for normalization. Instead, since the transition from reattaching to fully attached flow occurs at 45°, the incidence angle is normalized as
$({\it\phi}-45^{\circ })/45^{\circ }$
. Figure 18 demonstrates that the stagnation point, when normalized in this manner, also depends on the surface type. As was the case with the separation bubble pressure, the normalized stagnation point collapses onto a single empirical curve for flat faces, including both finite cylinders and rectangular bluff bodies. However, curved-face stagnation (labelled on the figures) does not fit the same trend. On curved faces, the stagnation point is found to depend on the aspect ratio but not the Reynolds number.
Figure 18. Variation of
$x_{0}$
with
${\it\phi}$
and empirical curve fit.
6 Conclusions
The aerodynamics of short three-dimensional bluff bodies have received very little attention in the literature, particularly over a broad range of angles and at high Reynolds number as required by applications including tethered loads, air drops, store separation, and towed bodies. The present work addresses this gap by analysing the flow around canonical three-dimensional bluff bodies, including rectangular prisms and finite circular cylinders, with high-fidelity numerical experiments. Aspect ratios of the bluff bodies for this work are in the range one to two, the Reynolds number ranges from
$0.96\times 10^{5}$
–
$1.0\times 10^{6}$
, and the yaw angle varies from 0° to 90°. The primary findings are as follows:
-
(i) Time averaging of the unsteady flow fields is required to quantify the characteristics of the phenomena responsible for sudden changes in the mean forces and moments at particular yaw angles. The time-averaging procedure permits clear identification of shear layer behaviour through evaluation of surface pressure indicators.
-
(ii) Given the range of geometric characteristics and flow conditions evaluated in this study:
-
(1) The normalized reattachment distance can be correlated with bluff body type and surface type. In the configurations evaluated, this distance is greatest, at a given incidence angle, for the rectangular prism. The next greatest distance corresponds to the curved faces of the circular cylinder, while the shortest distance corresponds to the flat faces of the circular cylinder.
-
(2) The distance to reattachment and the maximum pressure coefficient at reattachment may be modelled empirically as functions of incidence angle only. These quantities have been found to be independent of geometry type, surface shape (flat or curved), Reynolds number, and aspect ratio for the configurations examined, provided the proper normalization is applied to compute the incidence angle when reattachment first occurs.
-
(3) The pressure coefficient in the separation bubble can be modelled empirically as a single-valued function of incidence angle for flat bluff body faces when normalized appropriately. On curved cylinder faces, this parameter also depends on the Reynolds number and aspect ratio.
-
(4) The normalized stagnation point location is also a single-valued function of incidence angle for flat bluff body faces. On curved cylinder faces, this parameter also depends on the aspect ratio but not the Reynolds number.
-
Ongoing and future development related to this work include further validation of the numerical predictions of the numerical method for finite cylinders at yaw angles other than the normal and axial flow orientations, when experimental data become available for comparison. Additionally, the shear layer behaviours will be investigated for other canonical geometries and variations of those evaluated here (i.e., additional aspect ratios). Methods to predict the mean forces and moments from the empirical characterizations of shear layer behaviour are under development, as the shear layer behaviour is largely responsible for the shape of the surface pressure distribution, and, therefore, the mean forces and moments.
Acknowledgements
This research is funded through the US Army/Navy/NASA Vertical Lift Rotorcraft Center of Excellence at Georgia Tech under Task 10 ‘Dynamic-Aerodynamic Interactions of Bluff Bodies: Computational Investigations’ under the direction of M. Bhagwat of AFDD, Agreement No. W911W6-11-2-0010. The authors would like to thank the technical points of contact of this project, M. Moulton and T. Thompson of AMRDEC, and G. Yamauchi of NASA for their insights, as well as noted researchers in the area of bluff body flows: L. Cicolani, D. Greenwell and A. Rosen. The US Government is authorized to reproduce and distribute reprints notwithstanding any copyright notation thereon. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the US Government.
