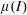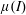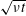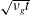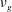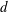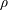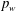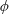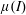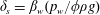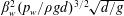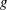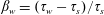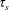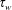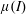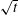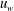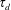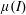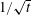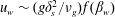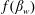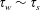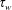1 Introduction
Flowing matter containing a dense collection of grains like sand, gravel, cereals, sugar, etc. is ubiquitous in nature as well as in many industrial processes. Such granular media exist in various states at any given common flow situation depending strongly on the energy supplied by external deformation and/or shear stresses (Jaeger, Nagel & Behringer Reference Jaeger, Nagel and Behringer1996). And so, they show a very rich phenomenology (Liu & Nagel Reference Liu and Nagel1998; Gray, Tai & Noelle Reference Gray, Tai and Noelle2003; Aranson & Tsimring Reference Aranson and Tsimring2006): a gaseous regime wherein the flow is very rapid and dilute, and the particles interact by collision (Jenkins & Savage Reference Jenkins and Savage1983), and a quasi-static regime in which the material deformation is extremely slow wherein frictional contacts between particles dominate the rheology, as is often the case in soil mechanics (Hutter & Rajagopal Reference Hutter and Rajagopal1994). Indeed, there exists an intermediate regime in the presence of both collisions and friction that result in huge dissipation. Here, a dense granular medium behaves like a viscoplastic liquid (Forterre & Pouliquen Reference Forterre and Pouliquen2008; Andreotti, Forterre & Pouliquen Reference Andreotti, Forterre and Pouliquen2011). A decade ago, generalising the scalar rheology of Midi (Reference Midi2004), Jop, Forterre & Pouliquen (Reference Jop, Forterre and Pouliquen2006) proposed the so-called
![]() $\unicode[STIX]{x1D707}(I)$
-rheology to describe such a dense granular liquid state. It has since been well exploited, often via direct numerical simulations, to study and model many common flow configurations (Kamrin Reference Kamrin2010; Cawthorn Reference Cawthorn2011; Lagrée, Staron & Popinet Reference Lagrée, Staron and Popinet2011; Staron, Lagrée & Popinet Reference Staron, Lagrée and Popinet2012; Chauchat & Médale Reference Chauchat and Médale2014; Gray & Edwards Reference Gray and Edwards2014; Baker, Barker & Gray Reference Baker, Barker and Gray2016).
$\unicode[STIX]{x1D707}(I)$
-rheology to describe such a dense granular liquid state. It has since been well exploited, often via direct numerical simulations, to study and model many common flow configurations (Kamrin Reference Kamrin2010; Cawthorn Reference Cawthorn2011; Lagrée, Staron & Popinet Reference Lagrée, Staron and Popinet2011; Staron, Lagrée & Popinet Reference Staron, Lagrée and Popinet2012; Chauchat & Médale Reference Chauchat and Médale2014; Gray & Edwards Reference Gray and Edwards2014; Baker, Barker & Gray Reference Baker, Barker and Gray2016).
However, recent works by Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015), Goddard & Lee (Reference Goddard and Lee2017) and Martin et al. (Reference Martin, Ionescu, Mangeney, Bouchut and Farin2017) illustrate that the governing equations of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology can exhibit ill-posed behaviour in the parameter range corresponding to quasi-gaseous and quasi-static regimes, respectively. Joseph & Saut (Reference Joseph and Saut1990) showed that ill-posed problems suffer from the so-called Hadamard instability and they characterised the ill-posedness through a stability analysis that identifies exponential temporal growth of short-wavelength perturbations. As a consequence, grid-dependent numerical results may not converge as the spatial refinement is enhanced for these cases (see Joseph & Saut Reference Joseph and Saut1990, p. 224). In particular, Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015) demonstrated both theoretically and numerically the governing equations of the
$\unicode[STIX]{x1D707}(I)$
-rheology can exhibit ill-posed behaviour in the parameter range corresponding to quasi-gaseous and quasi-static regimes, respectively. Joseph & Saut (Reference Joseph and Saut1990) showed that ill-posed problems suffer from the so-called Hadamard instability and they characterised the ill-posedness through a stability analysis that identifies exponential temporal growth of short-wavelength perturbations. As a consequence, grid-dependent numerical results may not converge as the spatial refinement is enhanced for these cases (see Joseph & Saut Reference Joseph and Saut1990, p. 224). In particular, Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015) demonstrated both theoretically and numerically the governing equations of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology are Hadamard unstable even for the simple case of Bagnold flow. More recently, Martin et al. (Reference Martin, Ionescu, Mangeney, Bouchut and Farin2017) also observed it in their numerical simulations for the case of granular column collapse on inclined channels. Nonetheless novel attempts to regularise the governing equations via a proper functional form of
$\unicode[STIX]{x1D707}(I)$
-rheology are Hadamard unstable even for the simple case of Bagnold flow. More recently, Martin et al. (Reference Martin, Ionescu, Mangeney, Bouchut and Farin2017) also observed it in their numerical simulations for the case of granular column collapse on inclined channels. Nonetheless novel attempts to regularise the governing equations via a proper functional form of
![]() $\unicode[STIX]{x1D707}(I)$
, at least in the quasi-static regime, have already been proposed by Barker & Gray (Reference Barker and Gray2017) and Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017). They successfully simulated granular roll waves in two dimensions and it now remains to see if their regularisation is valid also in direct computations of other unsteady granular flows.
$\unicode[STIX]{x1D707}(I)$
, at least in the quasi-static regime, have already been proposed by Barker & Gray (Reference Barker and Gray2017) and Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017). They successfully simulated granular roll waves in two dimensions and it now remains to see if their regularisation is valid also in direct computations of other unsteady granular flows.
In this context, this work aims to determine, both numerically and theoretically, the time evolution characteristics of the unsteady, non-uniform velocity and shear-stress fields arising in the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology for a canonical flow situation, namely, the so-called Stokes’ first problem (Stokes Reference Stokes1851) of the fluid motion that is brought about by impulsively starting an infinite wall. Unlike the classical case, the granular medium is placed underneath the plate (see figure 1). It is the simplest unsteady parallel flow in which some important features of fluid flows, such as transverse momentum transfer and the resulting boundary layer development due to direct balance between local fluid acceleration and the friction forces, can be treated. It is also known as the dragged-plate problem in Andreotti et al. (Reference Andreotti, Forterre and Pouliquen2011) and Cawthorn (Reference Cawthorn2011), where only a steady-state analytical solution can so far been found. The objective of the present work is to treat the transient solution and its characteristics.
$\unicode[STIX]{x1D707}(I)$
-rheology for a canonical flow situation, namely, the so-called Stokes’ first problem (Stokes Reference Stokes1851) of the fluid motion that is brought about by impulsively starting an infinite wall. Unlike the classical case, the granular medium is placed underneath the plate (see figure 1). It is the simplest unsteady parallel flow in which some important features of fluid flows, such as transverse momentum transfer and the resulting boundary layer development due to direct balance between local fluid acceleration and the friction forces, can be treated. It is also known as the dragged-plate problem in Andreotti et al. (Reference Andreotti, Forterre and Pouliquen2011) and Cawthorn (Reference Cawthorn2011), where only a steady-state analytical solution can so far been found. The objective of the present work is to treat the transient solution and its characteristics.

Figure 1. Schematic of the problem: an impulsively started, infinitely long flat plate over a semi-infinite dense granular medium consisting of mono-dispersed spherical grains.
Note that there has been a steady interest in Stokes’ first problem for non-Newtonian fluids, in particular, viscoelastic fluids (see Morrison Reference Morrison1956; Tanner Reference Tanner1962; Preziosi & Joseph Reference Preziosi and Joseph1987; Devakar & Iyengar Reference Devakar and Iyengar2008, Reference Devakar and Iyengar2009). Similarly, Stokes’ second problem (Panton Reference Panton1968; Schlichting Reference Schlichting1968), which considers the time evolution of the velocity field due to a horizontally oscillating infinite flat plate, has recently been studied for viscoelastic fluids by Devakar & Iyengar (Reference Devakar and Iyengar2008). Its applications include high-frequency microfluidics (Yakhot & Colosqui Reference Yakhot and Colosqui2007; Ekinci, Karabacak & Yakhot Reference Ekinci, Karabacak and Yakhot2008) for viscoelastic materials and rheometers for viscoplastic (Balmforth, Forterre & Pouliquen Reference Balmforth, Forterre and Pouliquen2009) and power law fluids (Pritchard, McArdle & Wilson Reference Pritchard, McArdle and Wilson2011). Recent literature also considers a third type of Stokes’ problem wherein a transient velocity field is set up by suddenly applying a body force to a fluid that is initially at rest. In fact, for a granular medium, Jop, Forterre & Pouliquen (Reference Jop, Forterre and Pouliquen2007) used this configuration to numerically validate their proposed
![]() $\unicode[STIX]{x1D707}(I)$
-rheology. This was later referred to as Stokes’ third problem by Ancey & Bates (Reference Ancey and Bates2017) for a Herschel–Bulkley material and interestingly, for the numerical resolution, the authors resorted to a Stefan problem, with a moving interface (boundary condition) that separates the sheared and unsheared regions.
$\unicode[STIX]{x1D707}(I)$
-rheology. This was later referred to as Stokes’ third problem by Ancey & Bates (Reference Ancey and Bates2017) for a Herschel–Bulkley material and interestingly, for the numerical resolution, the authors resorted to a Stefan problem, with a moving interface (boundary condition) that separates the sheared and unsheared regions.
The constitutive laws for many non-Newtonian fluids are often nonlinear but they can be simplified in the case of Stokes’ problems. The yield stress of the granular material varies in space since the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology proposes a constitutive law for dense granular flows wherein the medium behaves like a viscoplastic liquid with the local viscosity nonlinearly related to the local strain rate as well as the local pressure. Moreover, care should be taken to express a well-posed initial-value problem using the
$\unicode[STIX]{x1D707}(I)$
-rheology proposes a constitutive law for dense granular flows wherein the medium behaves like a viscoplastic liquid with the local viscosity nonlinearly related to the local strain rate as well as the local pressure. Moreover, care should be taken to express a well-posed initial-value problem using the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology to avoid Hadamard instability. Finally, it is only recently that dense granular flows have been successfully studied using a continuum model, so the governing equations have so far been unexplored even for Stokes’ first problem. In addition, apart from the simple case of steady Bagnold flow over an inclined plane, the constant shear flow case, and the steady-state solution of Stokes’ first problem (Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011; Cawthorn Reference Cawthorn2011), there exist only a few analytical results describing unsteady dense granular flows (see the notable recent exception of Capart, Hung & Stark (Reference Capart, Hung and Stark2015), who gave entrainment rates in the case of transient heap flows from the depth-integrated layer dynamics assuming a local
$\unicode[STIX]{x1D707}(I)$
-rheology to avoid Hadamard instability. Finally, it is only recently that dense granular flows have been successfully studied using a continuum model, so the governing equations have so far been unexplored even for Stokes’ first problem. In addition, apart from the simple case of steady Bagnold flow over an inclined plane, the constant shear flow case, and the steady-state solution of Stokes’ first problem (Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011; Cawthorn Reference Cawthorn2011), there exist only a few analytical results describing unsteady dense granular flows (see the notable recent exception of Capart, Hung & Stark (Reference Capart, Hung and Stark2015), who gave entrainment rates in the case of transient heap flows from the depth-integrated layer dynamics assuming a local
![]() $\unicode[STIX]{x1D707}(I)$
-rheology). Therefore, this brief note is aimed at bringing out the key features of this canonical problem as predicted by the
$\unicode[STIX]{x1D707}(I)$
-rheology). Therefore, this brief note is aimed at bringing out the key features of this canonical problem as predicted by the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology.
$\unicode[STIX]{x1D707}(I)$
-rheology.
The article is structured as follows. Firstly, the governing equations are shown to result in a single nonlinear shear-stress diffusion equation. Its numerical solution is then computed for the case when the wall shear stress is imposed while letting the wall velocity develop with time. Some approximate unsteady solutions are obtained and compared with computations. Finally, a brief note on Stokes’ first problem with imposed wall speed is given.
2 Governing equations
2.1 Constitutive laws:
 $\unicode[STIX]{x1D707}(I)$
-rheology
$\unicode[STIX]{x1D707}(I)$
-rheology
Analogous to Coulomb’s friction law, using dimensional arguments, experiments and numerical simulations, Iordanoff & Khonsari (Reference Iordanoff and Khonsari2004), Midi (Reference Midi2004) and Da Cruz et al. (Reference Da Cruz, Emam, Prochnow, Roux and Chevoir2005) demonstrated that the shear stress
![]() $\unicode[STIX]{x1D70F}$
is proportional to the normal stress
$\unicode[STIX]{x1D70F}$
is proportional to the normal stress
![]() $P$
for two-dimensional (2-D) dense granular flows of rigid particles so that
$P$
for two-dimensional (2-D) dense granular flows of rigid particles so that
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}(I)P$
where the local friction coefficient
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}(I)P$
where the local friction coefficient
![]() $\unicode[STIX]{x1D707}$
is only a function of a dimensionless parameter called the inertial number
$\unicode[STIX]{x1D707}$
is only a function of a dimensionless parameter called the inertial number
![]() $I=\dot{\unicode[STIX]{x1D6FE}}d/\sqrt{P/\unicode[STIX]{x1D70C}}$
. Here,
$I=\dot{\unicode[STIX]{x1D6FE}}d/\sqrt{P/\unicode[STIX]{x1D70C}}$
. Here,
![]() $\dot{\unicode[STIX]{x1D6FE}}$
is the local shear rate which is related to the macroscopic time scale of the granular flow and
$\dot{\unicode[STIX]{x1D6FE}}$
is the local shear rate which is related to the macroscopic time scale of the granular flow and
![]() $d\sqrt{\unicode[STIX]{x1D70C}/P}$
is the microscopic time scale corresponding to any local rearrangement of grains of diameter
$d\sqrt{\unicode[STIX]{x1D70C}/P}$
is the microscopic time scale corresponding to any local rearrangement of grains of diameter
![]() $d$
and density
$d$
and density
![]() $\unicode[STIX]{x1D70C}$
subjected to a local normal stress
$\unicode[STIX]{x1D70C}$
subjected to a local normal stress
![]() $P$
. Note that
$P$
. Note that
![]() $I$
is also the square root of the Savage or the Coulomb number as used in Savage (Reference Savage1984) or Ancey, Coussot & Evesque (Reference Ancey, Coussot and Evesque1999), respectively. In general, the dimensionless local friction coefficient is given by (Midi Reference Midi2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006)
$I$
is also the square root of the Savage or the Coulomb number as used in Savage (Reference Savage1984) or Ancey, Coussot & Evesque (Reference Ancey, Coussot and Evesque1999), respectively. In general, the dimensionless local friction coefficient is given by (Midi Reference Midi2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006)
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D707}(I)=\unicode[STIX]{x1D707}_{s}+{\displaystyle \frac{\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}}{\left(1+{\displaystyle \frac{I_{0}}{I}}\right)}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D707}(I)=\unicode[STIX]{x1D707}_{s}+{\displaystyle \frac{\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}}{\left(1+{\displaystyle \frac{I_{0}}{I}}\right)}}, & \displaystyle\end{eqnarray}$$
whereby
![]() $\unicode[STIX]{x1D707}$
saturates towards two fundamental constants for a dense granular medium
$\unicode[STIX]{x1D707}$
saturates towards two fundamental constants for a dense granular medium
![]() $\unicode[STIX]{x1D707}_{s}$
or
$\unicode[STIX]{x1D707}_{s}$
or
![]() $\unicode[STIX]{x1D707}_{d}$
depending respectively on the inertial number
$\unicode[STIX]{x1D707}_{d}$
depending respectively on the inertial number
![]() $I\ll 1$
(quasi-static regime) or
$I\ll 1$
(quasi-static regime) or
![]() $I\gg 1$
(kinetic or gaseous regime). Jop et al. (Reference Jop, Forterre and Pouliquen2006) proposed a 3-D generalisation of this scalar constitutive relation for a granular material by decomposing the Cauchy stress tensor into an isotropic contribution from the local pressure
$I\gg 1$
(kinetic or gaseous regime). Jop et al. (Reference Jop, Forterre and Pouliquen2006) proposed a 3-D generalisation of this scalar constitutive relation for a granular material by decomposing the Cauchy stress tensor into an isotropic contribution from the local pressure
![]() $p$
and a traceless deviatoric stress tensor
$p$
and a traceless deviatoric stress tensor
![]() $\unicode[STIX]{x1D70F}_{ij}$
while assuming that
$\unicode[STIX]{x1D70F}_{ij}$
while assuming that
![]() $\unicode[STIX]{x1D70F}_{ij}$
is aligned with the strain rate tensor
$\unicode[STIX]{x1D70F}_{ij}$
is aligned with the strain rate tensor
![]() $\dot{\unicode[STIX]{x1D6FE}}_{ij}=1/2(\unicode[STIX]{x2202}_{i}u_{j}+\unicode[STIX]{x2202}_{j}u_{i})$
(where
$\dot{\unicode[STIX]{x1D6FE}}_{ij}=1/2(\unicode[STIX]{x2202}_{i}u_{j}+\unicode[STIX]{x2202}_{j}u_{i})$
(where
![]() $u_{i}$
represent components of the velocity field). So, if
$u_{i}$
represent components of the velocity field). So, if
![]() $\boldsymbol{x}$
is the position vector and
$\boldsymbol{x}$
is the position vector and
![]() $t$
represents time, then the Cauchy stress tensor
$t$
represents time, then the Cauchy stress tensor
where
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta and
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta and
![]() $\unicode[STIX]{x1D70F}_{ij}(\boldsymbol{x},t)=\unicode[STIX]{x1D702}(\boldsymbol{x},t)\dot{\unicode[STIX]{x1D6FE}}_{ij}(\boldsymbol{x},t)$
and the local granular liquid viscosity
$\unicode[STIX]{x1D70F}_{ij}(\boldsymbol{x},t)=\unicode[STIX]{x1D702}(\boldsymbol{x},t)\dot{\unicode[STIX]{x1D6FE}}_{ij}(\boldsymbol{x},t)$
and the local granular liquid viscosity
is, thereby, a nonlinear function of the local pressure
![]() $p$
and the local second invariant of the strain rate tensor
$p$
and the local second invariant of the strain rate tensor
![]() $|\dot{\unicode[STIX]{x1D6FE}}|=\sqrt{1/2\dot{\unicode[STIX]{x1D6FE}}_{ij}\dot{\unicode[STIX]{x1D6FE}}_{ij}}$
via the local friction coefficient given by (2.1) and the inertial number for the
$|\dot{\unicode[STIX]{x1D6FE}}|=\sqrt{1/2\dot{\unicode[STIX]{x1D6FE}}_{ij}\dot{\unicode[STIX]{x1D6FE}}_{ij}}$
via the local friction coefficient given by (2.1) and the inertial number for the
![]() $3$
-D case
$3$
-D case
In addition, the solid volume fraction
![]() $\unicode[STIX]{x1D719}$
is also a linear function of
$\unicode[STIX]{x1D719}$
is also a linear function of
![]() $I$
(see Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011, p. 238) but, in general, it varies very little and so, for the sake of simplicity, it is taken to be a constant in the following.
$I$
(see Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011, p. 238) but, in general, it varies very little and so, for the sake of simplicity, it is taken to be a constant in the following.
2.2 Stokes’ first problem and its steady-state solution
Consider an infinite rigid flat plate placed at rest (
![]() $t=0$
) on top of a semi-infinite dense granular medium. As illustrated in figure 1, the plate is set in motion impulsively at
$t=0$
) on top of a semi-infinite dense granular medium. As illustrated in figure 1, the plate is set in motion impulsively at
![]() $t>0$
by applying a tangential shear stress
$t>0$
by applying a tangential shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
(along the
$\unicode[STIX]{x1D70F}_{w}$
(along the
![]() $x$
-direction) in the presence of a normal stress
$x$
-direction) in the presence of a normal stress
![]() $p_{w}$
(along the
$p_{w}$
(along the
![]() $y$
-direction). It is then natural to restrict the analysis to two dimensions. In fact, the absence of any horizontal length scale implies that the flow properties should depend only on
$y$
-direction). It is then natural to restrict the analysis to two dimensions. In fact, the absence of any horizontal length scale implies that the flow properties should depend only on
![]() $y$
and
$y$
and
![]() $t$
. Incompressibility and the initial condition then imply that the vertical velocity is uniformly zero for all
$t$
. Incompressibility and the initial condition then imply that the vertical velocity is uniformly zero for all
![]() $t\geqslant 0$
. And so the only non-zero components of the strain rate tensor are
$t\geqslant 0$
. And so the only non-zero components of the strain rate tensor are
![]() $\dot{\unicode[STIX]{x1D6FE}}_{xy}=\dot{\unicode[STIX]{x1D6FE}}_{yx}=(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)/2$
, where
$\dot{\unicode[STIX]{x1D6FE}}_{xy}=\dot{\unicode[STIX]{x1D6FE}}_{yx}=(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)/2$
, where
![]() $u$
is the
$u$
is the
![]() $x$
-component of the velocity field. Therefore, the
$x$
-component of the velocity field. Therefore, the
![]() $2$
-D shear-stress tensor is completely determined by a single scalar shear field
$2$
-D shear-stress tensor is completely determined by a single scalar shear field
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
so that the
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
so that the
![]() $x$
and
$x$
and
![]() $y$
momentum equations become, respectively,
$y$
momentum equations become, respectively,
where
![]() $g$
is the acceleration due to gravity. Initially the granular medium is at rest (
$g$
is the acceleration due to gravity. Initially the granular medium is at rest (
![]() $u(y,t=0)=0$
) but a static granular material can support a wide variety of shear-stress and pressure distributions so long as the yield stress is not exceeded so that
$u(y,t=0)=0$
) but a static granular material can support a wide variety of shear-stress and pressure distributions so long as the yield stress is not exceeded so that
![]() $\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D707}_{s}p$
. Within the context of the
$\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D707}_{s}p$
. Within the context of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology, the only possible configuration where the granular liquid is at rest corresponds to the case
$\unicode[STIX]{x1D707}(I)$
-rheology, the only possible configuration where the granular liquid is at rest corresponds to the case
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}_{s}p$
. For all other static states, the constitutive law
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}_{s}p$
. For all other static states, the constitutive law
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
is violated, so the
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
is violated, so the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology is no longer applicable. Therefore, in the following, the initial conditions correspond to a specific static state wherein the shear stress equals the yield stress throughout the granular medium
$\unicode[STIX]{x1D707}(I)$
-rheology is no longer applicable. Therefore, in the following, the initial conditions correspond to a specific static state wherein the shear stress equals the yield stress throughout the granular medium
with
![]() $p$
the hydrostatic pressure. Whereas the boundary conditions for all
$p$
the hydrostatic pressure. Whereas the boundary conditions for all
![]() $t>0$
are
$t>0$
are
along with the condition that the grains sufficiently far from the plate remain static, i.e.
![]() $u(y=\infty ,t)=0$
, and so
$u(y=\infty ,t)=0$
, and so
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
at
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
at
![]() $y=\infty$
. In contrast to the classical Stokes’ problem (Stokes Reference Stokes1851) for a Newtonian fluid, firstly, the frictional force (right-hand side of equation (2.5)) is not only non-uniform due to the hydrostatic pressure
$y=\infty$
. In contrast to the classical Stokes’ problem (Stokes Reference Stokes1851) for a Newtonian fluid, firstly, the frictional force (right-hand side of equation (2.5)) is not only non-uniform due to the hydrostatic pressure
![]() $p(y)=p_{w}+\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}gy$
but also nonlinear since
$p(y)=p_{w}+\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}gy$
but also nonlinear since
![]() $\unicode[STIX]{x1D707}$
depends on both
$\unicode[STIX]{x1D707}$
depends on both
![]() $p(y)$
and
$p(y)$
and
![]() $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$
via (2.1). And secondly, there exists a non-trivial steady-state solution wherein the shear stress is constant throughout the medium such that
$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$
via (2.1). And secondly, there exists a non-trivial steady-state solution wherein the shear stress is constant throughout the medium such that
![]() $\unicode[STIX]{x1D707}p=\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}_{w}p_{w}$
, as already shown in Andreotti et al. (Reference Andreotti, Forterre and Pouliquen2011, pp.
$\unicode[STIX]{x1D707}p=\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}_{w}p_{w}$
, as already shown in Andreotti et al. (Reference Andreotti, Forterre and Pouliquen2011, pp.
![]() $254$
–
$254$
–
![]() $256$
) and Cawthorn (Reference Cawthorn2011, pp.
$256$
) and Cawthorn (Reference Cawthorn2011, pp.
![]() $46$
–
$46$
–
![]() $50$
). Since
$50$
). Since
![]() $\unicode[STIX]{x1D707}\in [\unicode[STIX]{x1D707}_{s},\unicode[STIX]{x1D707}_{d}]$
and
$\unicode[STIX]{x1D707}\in [\unicode[STIX]{x1D707}_{s},\unicode[STIX]{x1D707}_{d}]$
and
![]() $p(y)$
increases linearly with the depth
$p(y)$
increases linearly with the depth
![]() $y$
, it follows that
$y$
, it follows that
for all
![]() $y\leqslant \unicode[STIX]{x1D6FF}_{s}$
and
$y\leqslant \unicode[STIX]{x1D6FF}_{s}$
and
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
otherwise; here, the critical depth
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
otherwise; here, the critical depth
![]() $\unicode[STIX]{x1D6FF}_{s}$
is given by
$\unicode[STIX]{x1D6FF}_{s}$
is given by
with
![]() $\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D707}_{s}-1)$
. This denotes the depth beyond which the granular medium does not flow
$\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D707}_{s}-1)$
. This denotes the depth beyond which the granular medium does not flow
![]() $y\geqslant \unicode[STIX]{x1D6FF}_{s}$
. Note that the term
$y\geqslant \unicode[STIX]{x1D6FF}_{s}$
. Note that the term
![]() $\unicode[STIX]{x1D6FD}_{w}$
represents the surplus in wall shear stress over the yield criterion at the wall. The steady-state solution (2.10) can be used to obtain the corresponding velocity profile. As previously shown by Cawthorn (Reference Cawthorn2011, pp.
$\unicode[STIX]{x1D6FD}_{w}$
represents the surplus in wall shear stress over the yield criterion at the wall. The steady-state solution (2.10) can be used to obtain the corresponding velocity profile. As previously shown by Cawthorn (Reference Cawthorn2011, pp.
![]() $46$
–
$46$
–
![]() $50$
), the resulting relation between the wall velocity (if the no-slip condition is allowed) and the shear layer thickness compares qualitatively well with the molecular dynamic simulations of Thompson & Grest (Reference Thompson and Grest1991).
$50$
), the resulting relation between the wall velocity (if the no-slip condition is allowed) and the shear layer thickness compares qualitatively well with the molecular dynamic simulations of Thompson & Grest (Reference Thompson and Grest1991).
2.3 Stokes’ first problem: shear-stress diffusion equation
Most numerical studies obtain the velocity field by solving the momentum equations that account for the constitutive law (2.2). Note that the latter is coupled with the expressions for the local friction coefficient (2.1) and the inertial number
![]() $I$
. However, it is possible to write a single equation for the shear stress in the case of Stokes’ first problem within the context of the
$I$
. However, it is possible to write a single equation for the shear stress in the case of Stokes’ first problem within the context of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology. Since
$\unicode[STIX]{x1D707}(I)$
-rheology. Since
![]() $I=-(1/2)(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)\sqrt{\unicode[STIX]{x1D70C}d^{2}/p}$
, the local friction coefficient (2.1) can be rewritten as
$I=-(1/2)(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)\sqrt{\unicode[STIX]{x1D70C}d^{2}/p}$
, the local friction coefficient (2.1) can be rewritten as
which when differentiated with respect to time and using
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
yields
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
yields
where
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}>0$
. By allowing
$\unicode[STIX]{x0394}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}>0$
. By allowing
![]() $\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}y\unicode[STIX]{x2202}t=\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}t\unicode[STIX]{x2202}y$
and then introducing (2.5) in the above expression, this leads to a single nonlinear shear-stress diffusion equation
$\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}y\unicode[STIX]{x2202}t=\unicode[STIX]{x2202}^{2}u/\unicode[STIX]{x2202}t\unicode[STIX]{x2202}y$
and then introducing (2.5) in the above expression, this leads to a single nonlinear shear-stress diffusion equation
Finally, by taking
![]() $\unicode[STIX]{x1D708}_{g}=(d/2\unicode[STIX]{x1D719}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}I_{0})\sqrt{p_{w}/\unicode[STIX]{x1D70C}}$
as a proper diffusion coefficient and the steady-state shear-layer thickness
$\unicode[STIX]{x1D708}_{g}=(d/2\unicode[STIX]{x1D719}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}I_{0})\sqrt{p_{w}/\unicode[STIX]{x1D70C}}$
as a proper diffusion coefficient and the steady-state shear-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{s}$
as the characteristic length scale, the non-dimensional time and space coordinates are
$\unicode[STIX]{x1D6FF}_{s}$
as the characteristic length scale, the non-dimensional time and space coordinates are
![]() $\tilde{t}=\unicode[STIX]{x1D708}_{g}t/\unicode[STIX]{x1D6FF}_{s}^{2}$
and
$\tilde{t}=\unicode[STIX]{x1D708}_{g}t/\unicode[STIX]{x1D6FF}_{s}^{2}$
and
![]() ${\tilde{y}}=y/\unicode[STIX]{x1D6FF}_{s}$
, respectively. Thus, in terms of the normalised pressure
${\tilde{y}}=y/\unicode[STIX]{x1D6FF}_{s}$
, respectively. Thus, in terms of the normalised pressure
![]() $\tilde{p}=p(y)/p_{w}$
and shear stress
$\tilde{p}=p(y)/p_{w}$
and shear stress
![]() $\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}(y,t)/\unicode[STIX]{x1D70F}_{w}$
, the above equation becomes
$\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}(y,t)/\unicode[STIX]{x1D70F}_{w}$
, the above equation becomes
with boundary conditions
![]() $\tilde{\unicode[STIX]{x1D70F}}(0,\tilde{t})=\tilde{\unicode[STIX]{x1D70F}}(1,\tilde{t})=1$
and an initial condition
$\tilde{\unicode[STIX]{x1D70F}}(0,\tilde{t})=\tilde{\unicode[STIX]{x1D70F}}(1,\tilde{t})=1$
and an initial condition
![]() $\tilde{\unicode[STIX]{x1D70F}}({\tilde{y}},0)=\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
. The steady-state solution for the non-dimensional shear stress is
$\tilde{\unicode[STIX]{x1D70F}}({\tilde{y}},0)=\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
. The steady-state solution for the non-dimensional shear stress is
![]() $\tilde{\unicode[STIX]{x1D70F}}=1$
. Unlike the steady-state local friction coefficient
$\tilde{\unicode[STIX]{x1D70F}}=1$
. Unlike the steady-state local friction coefficient
![]() $\unicode[STIX]{x1D707}$
, the steady-state shear stress is a continuous and infinitely differentiable function for all
$\unicode[STIX]{x1D707}$
, the steady-state shear stress is a continuous and infinitely differentiable function for all
![]() $y\geqslant 0$
. So, it is expected that
$y\geqslant 0$
. So, it is expected that
![]() $\tilde{\unicode[STIX]{x1D70F}}$
remains smooth also for the unsteady case. In fact, the term
$\tilde{\unicode[STIX]{x1D70F}}$
remains smooth also for the unsteady case. In fact, the term
![]() $(\unicode[STIX]{x1D707}_{d}\tilde{p}-\unicode[STIX]{x1D707}_{w}\tilde{\unicode[STIX]{x1D70F}})$
is positive–definite. Hence, it is quite straightforward to homogenise the boundary conditions and numerically solve the above equation using a second-order centred finite difference scheme for spatial derivatives and a second-order Crank–Nicolson one for temporal integration. The updated
$(\unicode[STIX]{x1D707}_{d}\tilde{p}-\unicode[STIX]{x1D707}_{w}\tilde{\unicode[STIX]{x1D70F}})$
is positive–definite. Hence, it is quite straightforward to homogenise the boundary conditions and numerically solve the above equation using a second-order centred finite difference scheme for spatial derivatives and a second-order Crank–Nicolson one for temporal integration. The updated
![]() $\tilde{\unicode[STIX]{x1D70F}}$
is obtained by an iterative Richardson minimal residual process.
$\tilde{\unicode[STIX]{x1D70F}}$
is obtained by an iterative Richardson minimal residual process.
2.4 Well-posedness of the shear-stress diffusion equation
Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015) demonstrated that the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology is well-posed for intermediate values of inertial number
$\unicode[STIX]{x1D707}(I)$
-rheology is well-posed for intermediate values of inertial number
![]() $I$
, but that it is ill-posed for both high and low inertial numbers. In the present case,
$I$
, but that it is ill-posed for both high and low inertial numbers. In the present case,
![]() $I\gg 1$
in the neighbourhood of the wall when either the applied wall shear
$I\gg 1$
in the neighbourhood of the wall when either the applied wall shear
![]() $\unicode[STIX]{x1D70F}_{w}$
is close to the critical wall shear
$\unicode[STIX]{x1D70F}_{w}$
is close to the critical wall shear
![]() $\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D707}_{d}p_{w}$
or when wall speed
$\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D707}_{d}p_{w}$
or when wall speed
![]() $u_{w}$
is sufficiently large. In addition, there is always a zone where
$u_{w}$
is sufficiently large. In addition, there is always a zone where
![]() $I\ll 1$
(or
$I\ll 1$
(or
![]() $\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{s}$
) since the medium is slowly moving or stationary when
$\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{s}$
) since the medium is slowly moving or stationary when
![]() $y\sim \unicode[STIX]{x1D6FF}_{s}$
. As already shown by Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015) this should provoke Hadamard instability (Joseph & Saut Reference Joseph and Saut1990) whereby infinitesimally small short-wave perturbations are amplified indefinitely. Thus, numerical solutions may not converge as the grid is refined and so, before proceeding any further, it is important to verify that the shear-stress diffusion (2.15) is indeed well-posed for all values of the inertial number
$y\sim \unicode[STIX]{x1D6FF}_{s}$
. As already shown by Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015) this should provoke Hadamard instability (Joseph & Saut Reference Joseph and Saut1990) whereby infinitesimally small short-wave perturbations are amplified indefinitely. Thus, numerical solutions may not converge as the grid is refined and so, before proceeding any further, it is important to verify that the shear-stress diffusion (2.15) is indeed well-posed for all values of the inertial number
![]() $I$
.
$I$
.
In fact, this nonlinear diffusion equation (2.15) is one-dimensional and when it is linearised about an arbitrary base state, as in Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015, see p. 799), the resulting dispersion equation of the normal mode analysis in the high-wavenumber limit should be
where
![]() $\unicode[STIX]{x1D706}$
is the complex frequency,
$\unicode[STIX]{x1D706}$
is the complex frequency,
![]() $\unicode[STIX]{x1D709}_{y}$
is the wavenumber in the
$\unicode[STIX]{x1D709}_{y}$
is the wavenumber in the
![]() ${\tilde{y}}$
-direction and
${\tilde{y}}$
-direction and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}(\tilde{p}^{0},\tilde{\unicode[STIX]{x1D70F}}^{0})$
is some function of the base state pressure
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}(\tilde{p}^{0},\tilde{\unicode[STIX]{x1D70F}}^{0})$
is some function of the base state pressure
![]() $\tilde{p}^{0}$
and shear stress
$\tilde{p}^{0}$
and shear stress
![]() $\tilde{\unicode[STIX]{x1D70F}}^{0}$
. Since the real part of the complex frequency
$\tilde{\unicode[STIX]{x1D70F}}^{0}$
. Since the real part of the complex frequency
![]() $\unicode[STIX]{x1D706}$
provides the perturbation growth rate, it is straightforward to see that (2.15) is stable for short waves along the
$\unicode[STIX]{x1D706}$
provides the perturbation growth rate, it is straightforward to see that (2.15) is stable for short waves along the
![]() $y$
-coordinate.
$y$
-coordinate.
Note that this is a one-dimensional analysis since it takes into account only plane waves along the
![]() ${\tilde{y}}$
-axis in order to analyse the well-posedness of (2.15) for one-dimensional, time-dependent computations. For two-dimensional codes that consider the granular Stokes’ problem as a test case, the situation is more complex. In this case, as previously shown by Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015), the equations are still ill-posed since oblique two-dimensional short waves are unstable in the region
${\tilde{y}}$
-axis in order to analyse the well-posedness of (2.15) for one-dimensional, time-dependent computations. For two-dimensional codes that consider the granular Stokes’ problem as a test case, the situation is more complex. In this case, as previously shown by Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015), the equations are still ill-posed since oblique two-dimensional short waves are unstable in the region
![]() $y\sim \unicode[STIX]{x1D6FF}_{s}$
(or close to the wall for
$y\sim \unicode[STIX]{x1D6FF}_{s}$
(or close to the wall for
![]() $\unicode[STIX]{x1D707}_{w}\sim \unicode[STIX]{x1D707}_{d}$
).
$\unicode[STIX]{x1D707}_{w}\sim \unicode[STIX]{x1D707}_{d}$
).
3 Unsteady solutions and their characteristics
Figure 2 presents the results of such numerical solutions (continuous lines) for three typical values of applied wall shear stress when
![]() $\unicode[STIX]{x1D707}_{s}=\tan 21^{\circ }$
and
$\unicode[STIX]{x1D707}_{s}=\tan 21^{\circ }$
and
![]() $\unicode[STIX]{x1D707}_{d}=\tan 33^{\circ }$
(typical values for spherical mono-dispersed glass beads as in Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011). Each graphic (top) depicts the normalised shear stress
$\unicode[STIX]{x1D707}_{d}=\tan 33^{\circ }$
(typical values for spherical mono-dispersed glass beads as in Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011). Each graphic (top) depicts the normalised shear stress
![]() $\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
variation in the
$\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
variation in the
![]() $y$
-direction at various times
$y$
-direction at various times
![]() $\tilde{t}=10^{-4},10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
for typical values of the normalised wall friction coefficient
$\tilde{t}=10^{-4},10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
for typical values of the normalised wall friction coefficient
![]() $(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
(where,
$(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
(where,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}$
). In all cases, the static initial condition
$\unicode[STIX]{x0394}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}$
). In all cases, the static initial condition
![]() $\tilde{\unicode[STIX]{x1D70F}}(0,{\tilde{y}})=\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
(dashed line), wherein the local shear stress is taken to be the yield criterion
$\tilde{\unicode[STIX]{x1D70F}}(0,{\tilde{y}})=\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
(dashed line), wherein the local shear stress is taken to be the yield criterion
![]() $\unicode[STIX]{x1D707}_{s}p$
, evolves continuously towards the steady-state solution
$\unicode[STIX]{x1D707}_{s}p$
, evolves continuously towards the steady-state solution
![]() $\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}\tilde{p}/\unicode[STIX]{x1D707}_{w}=1$
. The spatial variation of
$\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}\tilde{p}/\unicode[STIX]{x1D707}_{w}=1$
. The spatial variation of
![]() $\tilde{\unicode[STIX]{x1D70F}}$
shows that there exists a layer in which
$\tilde{\unicode[STIX]{x1D70F}}$
shows that there exists a layer in which
![]() $\tilde{\unicode[STIX]{x1D70F}}$
is greater than the yield stress, so the granular medium should flow in this region. If the size of this shear layer, say
$\tilde{\unicode[STIX]{x1D70F}}$
is greater than the yield stress, so the granular medium should flow in this region. If the size of this shear layer, say
![]() $\unicode[STIX]{x1D6FF}(\tilde{t})$
, is defined as the region where
$\unicode[STIX]{x1D6FF}(\tilde{t})$
, is defined as the region where
![]() $\tilde{\unicode[STIX]{x1D70F}}=0.999\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
, figure 2 (bottom) clearly illustrates that
$\tilde{\unicode[STIX]{x1D70F}}=0.999\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
, figure 2 (bottom) clearly illustrates that
![]() $\unicode[STIX]{x1D6FF}(\tilde{t})$
increases with time as
$\unicode[STIX]{x1D6FF}(\tilde{t})$
increases with time as
![]() $\sqrt{\tilde{t}}$
until
$\sqrt{\tilde{t}}$
until
![]() $\tilde{t}\sim O(1)$
, after which it saturates to the steady-state limit. Therefore, it is expected from these results that, for any general
$\tilde{t}\sim O(1)$
, after which it saturates to the steady-state limit. Therefore, it is expected from these results that, for any general
![]() $\unicode[STIX]{x1D707}_{d}$
and
$\unicode[STIX]{x1D707}_{d}$
and
![]() $\unicode[STIX]{x1D707}_{s}$
, approximate solutions to (2.15) can be obtained at both
$\unicode[STIX]{x1D707}_{s}$
, approximate solutions to (2.15) can be obtained at both
![]() $\tilde{t}\ll 1$
and
$\tilde{t}\ll 1$
and
![]() $\tilde{t}\gg 1$
by properly linearising it.
$\tilde{t}\gg 1$
by properly linearising it.

Figure 2. Temporal evolution of the normalised shear stress
![]() $\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
(top) and shear layer thickness
$\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
(top) and shear layer thickness
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
(bottom) for typical values of the normalised wall friction coefficient
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
(bottom) for typical values of the normalised wall friction coefficient
![]() $(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
(a)
$(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
(a)
![]() $0.9$
, (b)
$0.9$
, (b)
![]() $0.5$
and (c)
$0.5$
and (c)
![]() $0.1$
as computed directly using (2.15) with initial condition
$0.1$
as computed directly using (2.15) with initial condition
![]() $\tilde{\unicode[STIX]{x1D70F}}(0,{\tilde{y}})=\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
corresponding to a no-flow regime (shaded region). Note that
$\tilde{\unicode[STIX]{x1D70F}}(0,{\tilde{y}})=\unicode[STIX]{x1D707}_{s}\tilde{p}/\unicode[STIX]{x1D707}_{w}$
corresponding to a no-flow regime (shaded region). Note that
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}$
.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s}$
.
3.1 Self-similarity at
 $\tilde{t}\ll 1$
$\tilde{t}\ll 1$
When
![]() $\tilde{t}\ll 1$
, the non-dimensional shear layer thickness
$\tilde{t}\ll 1$
, the non-dimensional shear layer thickness
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
is small, as observed in figure 2 (bottom). By taking the non-dimensional local pressure
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
is small, as observed in figure 2 (bottom). By taking the non-dimensional local pressure
![]() $\tilde{p}=1+\unicode[STIX]{x1D6FD}_{w}{\tilde{y}}$
and local shear stress
$\tilde{p}=1+\unicode[STIX]{x1D6FD}_{w}{\tilde{y}}$
and local shear stress
![]() $\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}(1+\unicode[STIX]{x1D6FD}_{w}{\tilde{y}})/\unicode[STIX]{x1D707}_{w}$
, the diffusion equation (2.15) becomes
$\tilde{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}(1+\unicode[STIX]{x1D6FD}_{w}{\tilde{y}})/\unicode[STIX]{x1D707}_{w}$
, the diffusion equation (2.15) becomes
with
![]() $\unicode[STIX]{x1D707}({\tilde{y}},0)=\unicode[STIX]{x1D707}_{s}$
,
$\unicode[STIX]{x1D707}({\tilde{y}},0)=\unicode[STIX]{x1D707}_{s}$
,
![]() $\unicode[STIX]{x1D707}(0,\tilde{t})=\unicode[STIX]{x1D707}_{w}$
and
$\unicode[STIX]{x1D707}(0,\tilde{t})=\unicode[STIX]{x1D707}_{w}$
and
![]() $\unicode[STIX]{x1D707}(1,\tilde{t})=\unicode[STIX]{x1D707}_{s}$
. Note that, in general,
$\unicode[STIX]{x1D707}(1,\tilde{t})=\unicode[STIX]{x1D707}_{s}$
. Note that, in general,
![]() $\unicode[STIX]{x1D6FD}_{w}<1$
and hence, for
$\unicode[STIX]{x1D6FD}_{w}<1$
and hence, for
![]() $\tilde{t}\ll 1$
, the highest-order derivative of
$\tilde{t}\ll 1$
, the highest-order derivative of
![]() $\unicode[STIX]{x1D707}$
should dominate if
$\unicode[STIX]{x1D707}$
should dominate if
![]() ${\tilde{y}}\leqslant \unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
so that
${\tilde{y}}\leqslant \unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
so that
![]() $\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{w}-(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s})y/\unicode[STIX]{x1D6FF}$
. And in the outer region,
$\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{w}-(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s})y/\unicode[STIX]{x1D6FF}$
. And in the outer region,
![]() $\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{s}$
. As the spatial variations of the local friction coefficient
$\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{s}$
. As the spatial variations of the local friction coefficient
![]() $\unicode[STIX]{x1D707}$
are stronger inside the shear layer (i.e. when
$\unicode[STIX]{x1D707}$
are stronger inside the shear layer (i.e. when
![]() $\unicode[STIX]{x1D6FD}_{w}{\tilde{y}}\ll 1$
), it is reasonable to simplify (3.1) to
$\unicode[STIX]{x1D6FD}_{w}{\tilde{y}}\ll 1$
), it is reasonable to simplify (3.1) to
at the leading order with the same boundary conditions as before. By taking
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D707}-(\unicode[STIX]{x1D707}_{w}-(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s}){\tilde{y}})$
, the above equation admits a self-similar solution for
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D707}-(\unicode[STIX]{x1D707}_{w}-(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s}){\tilde{y}})$
, the above equation admits a self-similar solution for
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D702})$
with
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D702})$
with
![]() $\unicode[STIX]{x1D702}={\tilde{y}}/(2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}})$
satisfying the initial and the boundary conditions for all
$\unicode[STIX]{x1D702}={\tilde{y}}/(2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}})$
satisfying the initial and the boundary conditions for all
![]() $\tilde{t}\geqslant 0$
. Thereby, the local friction coefficient is deduced to be
$\tilde{t}\geqslant 0$
. Thereby, the local friction coefficient is deduced to be
which implies that the shear layer thickness should grow as
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}\sim 4.66\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
.
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}\sim 4.66\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
.
The expression (3.3) is presented in figure 3 (top) where the time evolution of the local friction coefficient is displayed as function of
![]() ${\tilde{y}}$
at different times
${\tilde{y}}$
at different times
![]() $\tilde{t}=10^{-4},10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
for the same values of
$\tilde{t}=10^{-4},10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
for the same values of
![]() $(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
as in figure 2. When compared with numerical solutions of
$(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
as in figure 2. When compared with numerical solutions of
![]() $\unicode[STIX]{x1D707}$
(and also,
$\unicode[STIX]{x1D707}$
(and also,
![]() $\unicode[STIX]{x1D6FF}$
) as seen in figure 3 (top) (and figure 2, respectively), these approximations are very satisfactory for all
$\unicode[STIX]{x1D6FF}$
) as seen in figure 3 (top) (and figure 2, respectively), these approximations are very satisfactory for all
![]() $\tilde{t}\ll 1$
. Indeed, the expression (3.3) for the local friction coefficient, and especially the estimations of the time evolution of the shear layer thickness
$\tilde{t}\ll 1$
. Indeed, the expression (3.3) for the local friction coefficient, and especially the estimations of the time evolution of the shear layer thickness
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}\sim 4.66\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
, are reasonably good even when
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}\sim 4.66\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
, are reasonably good even when
![]() $\tilde{t}$
is of order
$\tilde{t}$
is of order
![]() $1$
.
$1$
.

Figure 3. Comparison between self-similar approximation (top) and the long-time diffusion approximation (bottom) with the direct numerical solution (continuous lines) for various normalised wall friction coefficients
![]() $(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
(a)
$(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
(a)
![]() $0.9$
, (b)
$0.9$
, (b)
![]() $0.5$
and (c)
$0.5$
and (c)
![]() $0.1$
.
$0.1$
.
3.2 Diffusion at
 $\tilde{t}\gg 1$
$\tilde{t}\gg 1$
As soon as
![]() $\tilde{t}\sim O(1)$
the non-dimensional shear layer thickness is no longer small, and hence a singular perturbation of (3.1) cannot be obtained with the present scaling for the
$\tilde{t}\sim O(1)$
the non-dimensional shear layer thickness is no longer small, and hence a singular perturbation of (3.1) cannot be obtained with the present scaling for the
![]() $y$
-coordinate. However, by using the non-dimensional pressure
$y$
-coordinate. However, by using the non-dimensional pressure
![]() $\tilde{p}$
as an equivalent normalised spatial variable
$\tilde{p}$
as an equivalent normalised spatial variable
![]() ${\hat{y}}=1+\unicode[STIX]{x1D6FD}_{w}{\tilde{y}}$
, it is possible to show that
${\hat{y}}=1+\unicode[STIX]{x1D6FD}_{w}{\tilde{y}}$
, it is possible to show that
which is singular if
![]() $(\unicode[STIX]{x1D6FD}_{w}\unicode[STIX]{x0394}\unicode[STIX]{x1D707})^{2}$
tends to zero. This is often true since
$(\unicode[STIX]{x1D6FD}_{w}\unicode[STIX]{x0394}\unicode[STIX]{x1D707})^{2}$
tends to zero. This is often true since
![]() $(\unicode[STIX]{x1D6FD}_{w}(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}))^{2}$
is of the order of
$(\unicode[STIX]{x1D6FD}_{w}(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}))^{2}$
is of the order of
![]() $(\unicode[STIX]{x1D6FD}_{w}\unicode[STIX]{x0394}\unicode[STIX]{x1D707})^{2}$
and
$(\unicode[STIX]{x1D6FD}_{w}\unicode[STIX]{x0394}\unicode[STIX]{x1D707})^{2}$
and
![]() ${\hat{y}}\sim O(1)$
. Thus, taking
${\hat{y}}\sim O(1)$
. Thus, taking
![]() $\unicode[STIX]{x1D6FD}_{w}(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707})\sim \unicode[STIX]{x1D6FD}_{w}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
at the leading order in (3.4), it becomes linear and admits a WKB approximation in the
$\unicode[STIX]{x1D6FD}_{w}(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707})\sim \unicode[STIX]{x1D6FD}_{w}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
at the leading order in (3.4), it becomes linear and admits a WKB approximation in the
![]() ${\hat{y}}$
-coordinate. Thereby, the local shear stress
${\hat{y}}$
-coordinate. Thereby, the local shear stress
![]() $\tilde{\unicode[STIX]{x1D70F}}$
can be shown to be
$\tilde{\unicode[STIX]{x1D70F}}$
can be shown to be
where
Note that it is possible to solve the linearised version of (3.4) directly by separation of variables as well. In that case, the general solution is an infinite sum of Bessel functions in the
![]() ${\hat{y}}$
-direction. But it is advantageous to work with the approximate solution (3.5) when
${\hat{y}}$
-direction. But it is advantageous to work with the approximate solution (3.5) when
![]() $m$
is large. Nevertheless, the comparison between the WKB approximation (3.5) (dot-dash lines in figure 3) and the numerical solution for the local friction coefficient is good. In particular, the agreement is excellent when the applied friction coefficient
$m$
is large. Nevertheless, the comparison between the WKB approximation (3.5) (dot-dash lines in figure 3) and the numerical solution for the local friction coefficient is good. In particular, the agreement is excellent when the applied friction coefficient
![]() $\unicode[STIX]{x1D707}_{w}$
is close to yield friction coefficient
$\unicode[STIX]{x1D707}_{w}$
is close to yield friction coefficient
![]() $\unicode[STIX]{x1D707}_{s}$
.
$\unicode[STIX]{x1D707}_{s}$
.
3.3 Velocity field development
It is now possible to compute the temporal evolution of the velocity field using local shear stress
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
. By rewriting (2.5) in terms of
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
. By rewriting (2.5) in terms of
![]() $\tilde{t}$
and
$\tilde{t}$
and
![]() ${\tilde{y}}$
, a natural normalisation for the velocity
${\tilde{y}}$
, a natural normalisation for the velocity
![]() $u$
can be shown to be
$u$
can be shown to be
where
![]() $\unicode[STIX]{x1D6FF}_{s}$
is the steady-state shear layer thickness (2.11),
$\unicode[STIX]{x1D6FF}_{s}$
is the steady-state shear layer thickness (2.11),
![]() $\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s})/\unicode[STIX]{x1D707}_{s}$
and
$\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s})/\unicode[STIX]{x1D707}_{s}$
and
![]() $\unicode[STIX]{x1D708}_{g}=(d/\unicode[STIX]{x1D719}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}I_{0})\sqrt{p_{w}/\unicode[STIX]{x1D70C}}$
is the diffusion coefficient which appears in the granular Stokes’ equation (2.14). Using this normalisation and by taking
$\unicode[STIX]{x1D708}_{g}=(d/\unicode[STIX]{x1D719}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}I_{0})\sqrt{p_{w}/\unicode[STIX]{x1D70C}}$
is the diffusion coefficient which appears in the granular Stokes’ equation (2.14). Using this normalisation and by taking
the equation for the shear rate (2.12) becomes
which can then be integrated to study the velocity field. In the following, the no-slip condition is assumed so that the wall speed and the velocity of the granular medium right next to it (
![]() ${\tilde{y}}=0$
) are equal.
${\tilde{y}}=0$
) are equal.

Figure 4. Normalised wall velocity as a function of the non-dimensional time
![]() $\tilde{t}$
for various applied wall shear stresses:
$\tilde{t}$
for various applied wall shear stresses:
![]() $(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
(a)
$(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
(a)
![]() $0.9$
, (b)
$0.9$
, (b)
![]() $0.5$
and (c)
$0.5$
and (c)
![]() $0.1$
. The different symbols denote calculations from the numerical solution using (2.15) (filled circles), the self-similar solution (3.3) (▫) and the long-time approximate solution (3.5) (
$0.1$
. The different symbols denote calculations from the numerical solution using (2.15) (filled circles), the self-similar solution (3.3) (▫) and the long-time approximate solution (3.5) (
![]() $+$
).
$+$
).
Figure 4 compares the normalised wall velocity
![]() $\tilde{u} _{w}=\tilde{u} ({\tilde{y}}=0,\tilde{t})$
when obtained from the numerical solution of (2.15) (filled circles), the self-similar solution (3.3) (▫) and the long-time approximate solution (3.5) (
$\tilde{u} _{w}=\tilde{u} ({\tilde{y}}=0,\tilde{t})$
when obtained from the numerical solution of (2.15) (filled circles), the self-similar solution (3.3) (▫) and the long-time approximate solution (3.5) (
![]() $+$
) for a given boundary condition at the wall. Each panel shows the temporal evolution of
$+$
) for a given boundary condition at the wall. Each panel shows the temporal evolution of
![]() $\tilde{u} _{w}$
when the wall friction coefficient is taken as
$\tilde{u} _{w}$
when the wall friction coefficient is taken as
![]() $(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
(a)
$(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
(a)
![]() $0.9$
, (b)
$0.9$
, (b)
![]() $0.5$
and (c)
$0.5$
and (c)
![]() $0.1$
. In all cases, the wall velocity grows monotonically by following a power law in
$0.1$
. In all cases, the wall velocity grows monotonically by following a power law in
![]() $\tilde{t}$
as long as
$\tilde{t}$
as long as
![]() $\tilde{t}\leqslant 1$
and then it saturates at the steady-state value
$\tilde{t}\leqslant 1$
and then it saturates at the steady-state value
![]() $\tilde{u} _{w}^{\infty }=\tilde{u} ({\tilde{y}}=0,\tilde{t}=\infty )$
. Firstly, the self-similar solution (3.3) gives good qualitative agreement with the numerical results, and also, it matches well with the power law
$\tilde{u} _{w}^{\infty }=\tilde{u} ({\tilde{y}}=0,\tilde{t}=\infty )$
. Firstly, the self-similar solution (3.3) gives good qualitative agreement with the numerical results, and also, it matches well with the power law
![]() $\tilde{u} _{w}(\tilde{t})\sim \sqrt{\tilde{t}}$
. The long-time WKB approximation (3.5) matches very well with the numerical solution at all times
$\tilde{u} _{w}(\tilde{t})\sim \sqrt{\tilde{t}}$
. The long-time WKB approximation (3.5) matches very well with the numerical solution at all times
![]() $\tilde{t}>1$
. Secondly, it is observed that the steady-state wall velocity
$\tilde{t}>1$
. Secondly, it is observed that the steady-state wall velocity
![]() $\tilde{u} _{w}^{\infty }$
depends largely on the imposed wall shear via
$\tilde{u} _{w}^{\infty }$
depends largely on the imposed wall shear via
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
as already shown by previous works (Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011; Cawthorn Reference Cawthorn2011). In fact, for the steady-state solution, Cawthorn (Reference Cawthorn2011, p. 49) had already given an asymptotic solution for the wall speed
$\tilde{\unicode[STIX]{x1D707}}_{w}=(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
as already shown by previous works (Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011; Cawthorn Reference Cawthorn2011). In fact, for the steady-state solution, Cawthorn (Reference Cawthorn2011, p. 49) had already given an asymptotic solution for the wall speed
![]() $\tilde{u} _{w}^{\infty }$
when the applied shear stress is just above the yield shear, i.e. when
$\tilde{u} _{w}^{\infty }$
when the applied shear stress is just above the yield shear, i.e. when
![]() $\unicode[STIX]{x1D707}({\tilde{y}}=0,\tilde{t})$
approaches
$\unicode[STIX]{x1D707}({\tilde{y}}=0,\tilde{t})$
approaches
![]() $\unicode[STIX]{x1D707}_{s}$
from above (or
$\unicode[STIX]{x1D707}_{s}$
from above (or
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}\sim 1$
). However, it is also possible to obtain expressions for
$\tilde{\unicode[STIX]{x1D707}}_{w}\sim 1$
). However, it is also possible to obtain expressions for
![]() $\tilde{u} _{w}^{\infty }$
for a wide range of
$\tilde{u} _{w}^{\infty }$
for a wide range of
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}$
via the self-similar solution (3.3) since, as suggested by figure 4, this gives a good approximation to the steady-state wall speed. In the limit when
$\tilde{\unicode[STIX]{x1D707}}_{w}$
via the self-similar solution (3.3) since, as suggested by figure 4, this gives a good approximation to the steady-state wall speed. In the limit when
![]() $\tilde{t}\gg 1$
, the approximate solution (3.3) becomes a function only of
$\tilde{t}\gg 1$
, the approximate solution (3.3) becomes a function only of
![]() ${\tilde{y}}$
, and so, in terms of the normalised friction coefficient (3.9), it is given by
${\tilde{y}}$
, and so, in terms of the normalised friction coefficient (3.9), it is given by
![]() $\tilde{\unicode[STIX]{x1D707}}\sim \tilde{\unicode[STIX]{x1D707}}_{w}+(1-\tilde{\unicode[STIX]{x1D707}}_{w}){\tilde{y}}$
. Using this expression in (3.10), it reads
$\tilde{\unicode[STIX]{x1D707}}\sim \tilde{\unicode[STIX]{x1D707}}_{w}+(1-\tilde{\unicode[STIX]{x1D707}}_{w}){\tilde{y}}$
. Using this expression in (3.10), it reads
and since
![]() $\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D707}_{s}-1)<1$
, it could be further developed to obtain a simple expression for the steady-state wall velocity
$\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D707}_{s}-1)<1$
, it could be further developed to obtain a simple expression for the steady-state wall velocity
Noting that
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=1-\unicode[STIX]{x1D707}_{s}\unicode[STIX]{x1D6FD}_{w}/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
, it is straightforward to see that the first term in the above expression cancels out when
$\tilde{\unicode[STIX]{x1D707}}_{w}=1-\unicode[STIX]{x1D707}_{s}\unicode[STIX]{x1D6FD}_{w}/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
, it is straightforward to see that the first term in the above expression cancels out when
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}\sim 1$
(or
$\tilde{\unicode[STIX]{x1D707}}_{w}\sim 1$
(or
![]() $\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D707}_{s}-1)\ll 1$
), and thereby, it gives
$\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D707}_{s}-1)\ll 1$
), and thereby, it gives
![]() $\tilde{u} _{w}^{\infty }\sim O(\unicode[STIX]{x1D6FD}_{w})$
. In this case, as already deduced by Cawthorn (Reference Cawthorn2011, p. 49), the above integral leads to
$\tilde{u} _{w}^{\infty }\sim O(\unicode[STIX]{x1D6FD}_{w})$
. In this case, as already deduced by Cawthorn (Reference Cawthorn2011, p. 49), the above integral leads to
For the case when
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}$
tends to zero (or
$\tilde{\unicode[STIX]{x1D707}}_{w}$
tends to zero (or
![]() $\unicode[STIX]{x1D707}\rightarrow \unicode[STIX]{x1D707}_{d}$
), the integral (3.11) will exhibit a logarithmic singularity at
$\unicode[STIX]{x1D707}\rightarrow \unicode[STIX]{x1D707}_{d}$
), the integral (3.11) will exhibit a logarithmic singularity at
![]() ${\tilde{y}}=0$
, and so
${\tilde{y}}=0$
, and so
![]() $\tilde{u} _{w}^{\infty }\sim -\log \tilde{\unicode[STIX]{x1D707}}_{w}/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
. For the sake of completeness, it is pointed out that, even when
$\tilde{u} _{w}^{\infty }\sim -\log \tilde{\unicode[STIX]{x1D707}}_{w}/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
. For the sake of completeness, it is pointed out that, even when
![]() $\unicode[STIX]{x1D6FD}_{w}$
is not smaller than one, an expression similar to (3.12) could be developed at
$\unicode[STIX]{x1D6FD}_{w}$
is not smaller than one, an expression similar to (3.12) could be developed at
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}\ll 1$
by exploiting the logarithmic singularity in the integral (3.11).
$\tilde{\unicode[STIX]{x1D707}}_{w}\ll 1$
by exploiting the logarithmic singularity in the integral (3.11).

Figure 5. Comparison between direct computations and approximate expressions of the steady-state wall speed
![]() $\tilde{u} _{w}^{\infty }=\tilde{u} ({\tilde{y}}=0,\tilde{t}\gg 1)$
as a function for the entire range of normalised wall friction coefficient
$\tilde{u} _{w}^{\infty }=\tilde{u} ({\tilde{y}}=0,\tilde{t}\gg 1)$
as a function for the entire range of normalised wall friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
. Black circles denote the numerical solution using (2.15). The continuous line (blue) and the dashed line (red) are obtained using the expressions (3.12) and (3.13), respectively. The latter gives a good match when the applied shear stress is just above the yield shear stress
$\tilde{\unicode[STIX]{x1D707}}_{w}=(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{w})/(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707}_{s})$
. Black circles denote the numerical solution using (2.15). The continuous line (blue) and the dashed line (red) are obtained using the expressions (3.12) and (3.13), respectively. The latter gives a good match when the applied shear stress is just above the yield shear stress
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}\sim 1$
(or
$\tilde{\unicode[STIX]{x1D707}}_{w}\sim 1$
(or
![]() $\unicode[STIX]{x1D707}_{w}\sim \unicode[STIX]{x1D707}_{s}$
), whereas the former captures the trend for all values of
$\unicode[STIX]{x1D707}_{w}\sim \unicode[STIX]{x1D707}_{s}$
), whereas the former captures the trend for all values of
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}\in [0,1]$
.
$\tilde{\unicode[STIX]{x1D707}}_{w}\in [0,1]$
.

Figure 6. Velocity profile at different times
![]() $\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
in the shear layer for various normalised wall friction coefficients
$\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
in the shear layer for various normalised wall friction coefficients
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=0.9$
(a),
$\tilde{\unicode[STIX]{x1D707}}_{w}=0.9$
(a),
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=0.5$
(b) and
$\tilde{\unicode[STIX]{x1D707}}_{w}=0.5$
(b) and
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=0.1$
(c). The thick dashed line represents the steady-state solution. These data are obtained by directly integrating the numerical solution of the non-dimensional shear-stress equation (2.15). The data collapse features in the second and third rows imply that the
$\tilde{\unicode[STIX]{x1D707}}_{w}=0.1$
(c). The thick dashed line represents the steady-state solution. These data are obtained by directly integrating the numerical solution of the non-dimensional shear-stress equation (2.15). The data collapse features in the second and third rows imply that the
![]() $\tilde{u} ({\tilde{y}},\tilde{t})\sim \tilde{u} _{w}^{\infty }\sqrt{\tilde{t}}f({\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}})$
, where
$\tilde{u} ({\tilde{y}},\tilde{t})\sim \tilde{u} _{w}^{\infty }\sqrt{\tilde{t}}f({\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}})$
, where
![]() $\tilde{u} _{w}^{\infty }$
is given by the expression (3.12).
$\tilde{u} _{w}^{\infty }$
is given by the expression (3.12).
The expressions (3.12) and (3.13) for
![]() $\tilde{u} _{w}^{\infty }$
can now be verified by plotting the steady-state wall speed with respect to the normalised wall friction coefficient
$\tilde{u} _{w}^{\infty }$
can now be verified by plotting the steady-state wall speed with respect to the normalised wall friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}$
as in figure 5. Here, the exact wall speed (open circles) is computed by substituting the steady-state solution (2.10) in (3.10) and integrating it numerically. The asymptotic results (3.12) and (3.13) are displayed as continuous (blue) and dashed (red) lines, respectively. The normalised wall velocity varies slowly with the normalised friction coefficient
$\tilde{\unicode[STIX]{x1D707}}_{w}$
as in figure 5. Here, the exact wall speed (open circles) is computed by substituting the steady-state solution (2.10) in (3.10) and integrating it numerically. The asymptotic results (3.12) and (3.13) are displayed as continuous (blue) and dashed (red) lines, respectively. The normalised wall velocity varies slowly with the normalised friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}$
as long as
$\tilde{\unicode[STIX]{x1D707}}_{w}$
as long as
![]() $1-\tilde{\unicode[STIX]{x1D707}}_{w}$
is small (or
$1-\tilde{\unicode[STIX]{x1D707}}_{w}$
is small (or
![]() $\unicode[STIX]{x1D707}_{w}\sim \unicode[STIX]{x1D707}_{s}$
). Thus, for a given normal stress
$\unicode[STIX]{x1D707}_{w}\sim \unicode[STIX]{x1D707}_{s}$
). Thus, for a given normal stress
![]() $p_{w}$
at the wall,
$p_{w}$
at the wall,
![]() $\tilde{u} _{w}$
varies linearly with the applied shear stress
$\tilde{u} _{w}$
varies linearly with the applied shear stress
![]() $\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}_{w}p_{w}$
if the latter is sufficiently close to the yield shear stress
$\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}_{w}p_{w}$
if the latter is sufficiently close to the yield shear stress
![]() $\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D707}_{s}p_{w}$
. Then the wall velocity increases rapidly with
$\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D707}_{s}p_{w}$
. Then the wall velocity increases rapidly with
![]() $1-\tilde{\unicode[STIX]{x1D707}}_{w}$
and it becomes logarithmically large as
$1-\tilde{\unicode[STIX]{x1D707}}_{w}$
and it becomes logarithmically large as
![]() $\unicode[STIX]{x1D707}_{w}$
approaches
$\unicode[STIX]{x1D707}_{w}$
approaches
![]() $\unicode[STIX]{x1D707}_{d}$
. This is not surprising since when
$\unicode[STIX]{x1D707}_{d}$
. This is not surprising since when
![]() $\unicode[STIX]{x1D70F}_{w}$
approaches
$\unicode[STIX]{x1D70F}_{w}$
approaches
![]() $\unicode[STIX]{x1D707}_{d}p_{w}$
, the inertial number satisfies
$\unicode[STIX]{x1D707}_{d}p_{w}$
, the inertial number satisfies
![]() $I\gg 1$
in such a manner that frictional grain–grain contacts become less dominant compared to grain–grain collisions, as internal grain rearrangements are very frequent compared to the local deformation rate (Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011). Thus, a highly agitated flow can occur near the wall. Indeed, beyond this critical value, there is no longer an equilibrium between the applied shear stress and the internal resistance via frictional contacts as previously pointed out by Cawthorn (Reference Cawthorn2011). A more relevant description is given by models inspired by the kinetic theory of gases (Jenkins & Savage Reference Jenkins and Savage1983; Goldhirsch Reference Goldhirsch2003). Furthermore, figure 5 indicates that the expression (3.13) provides a very good approximation to the steady-state wall speed when the applied shear stress is just above the yield stress
$I\gg 1$
in such a manner that frictional grain–grain contacts become less dominant compared to grain–grain collisions, as internal grain rearrangements are very frequent compared to the local deformation rate (Andreotti et al.
Reference Andreotti, Forterre and Pouliquen2011). Thus, a highly agitated flow can occur near the wall. Indeed, beyond this critical value, there is no longer an equilibrium between the applied shear stress and the internal resistance via frictional contacts as previously pointed out by Cawthorn (Reference Cawthorn2011). A more relevant description is given by models inspired by the kinetic theory of gases (Jenkins & Savage Reference Jenkins and Savage1983; Goldhirsch Reference Goldhirsch2003). Furthermore, figure 5 indicates that the expression (3.13) provides a very good approximation to the steady-state wall speed when the applied shear stress is just above the yield stress
![]() $\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D707}_{s}p_{w}$
and the expression (3.12) remarkably captures the wall speed variation for all applied shear stresses
$\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D707}_{s}p_{w}$
and the expression (3.12) remarkably captures the wall speed variation for all applied shear stresses
![]() $\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}_{w}p_{w}\in [\unicode[STIX]{x1D707}_{s}p_{w},\unicode[STIX]{x1D707}_{d}p_{w}]$
.
$\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D707}_{w}p_{w}\in [\unicode[STIX]{x1D707}_{s}p_{w},\unicode[STIX]{x1D707}_{d}p_{w}]$
.
The above result that the wall speed
![]() $\tilde{u} _{w}(\tilde{t})\propto \sqrt{\tilde{t}}$
along with the fact that
$\tilde{u} _{w}(\tilde{t})\propto \sqrt{\tilde{t}}$
along with the fact that
![]() $\tilde{u} _{w}(\tilde{t}\gg 1)$
follows a universal trend (3.12) suggests that the velocity profile can be approximately deduced from the short-time asymptotic solution (3.3). This hypothesis is explored in figure 6, which shows three different normalisations of the velocity field as a function of time. Each column corresponds to specific wall boundary conditions corresponding to
$\tilde{u} _{w}(\tilde{t}\gg 1)$
follows a universal trend (3.12) suggests that the velocity profile can be approximately deduced from the short-time asymptotic solution (3.3). This hypothesis is explored in figure 6, which shows three different normalisations of the velocity field as a function of time. Each column corresponds to specific wall boundary conditions corresponding to
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=0.9$
(a),
$\tilde{\unicode[STIX]{x1D707}}_{w}=0.9$
(a),
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=0.5$
(b) and
$\tilde{\unicode[STIX]{x1D707}}_{w}=0.5$
(b) and
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=0.1$
(c). The steady-state solution is displayed as a thick dashed line only in the first row but it is left out in the rest of the graphs for the sake of clarity. In this row, all figures present the time development of the velocity
$\tilde{\unicode[STIX]{x1D707}}_{w}=0.1$
(c). The steady-state solution is displayed as a thick dashed line only in the first row but it is left out in the rest of the graphs for the sake of clarity. In this row, all figures present the time development of the velocity
![]() $\tilde{u} ({\tilde{y}},\tilde{t})$
as computed by numerically integrating (3.10) at each
$\tilde{u} ({\tilde{y}},\tilde{t})$
as computed by numerically integrating (3.10) at each
![]() $\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
. As seen before in figure 4, it can be readily observed that the wall velocity
$\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
. As seen before in figure 4, it can be readily observed that the wall velocity
![]() $\tilde{u} ({\tilde{y}}=0,\tilde{t})$
increases in time and attains a steady-state value which in turn depends on the applied wall shear stress. The numerical solution at
$\tilde{u} ({\tilde{y}}=0,\tilde{t})$
increases in time and attains a steady-state value which in turn depends on the applied wall shear stress. The numerical solution at
![]() $\tilde{t}=10^{1}$
is already superimposed on the steady-state solution (dashed line) for all the cases of
$\tilde{t}=10^{1}$
is already superimposed on the steady-state solution (dashed line) for all the cases of
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}$
shown here. The second and the third rows in figure 6 display the same data when the velocity field is normalised with the wall speed
$\tilde{\unicode[STIX]{x1D707}}_{w}$
shown here. The second and the third rows in figure 6 display the same data when the velocity field is normalised with the wall speed
![]() $\tilde{u} _{w}(\tilde{t})=\tilde{u} ({\tilde{y}}=0,\tilde{t})$
and
$\tilde{u} _{w}(\tilde{t})=\tilde{u} ({\tilde{y}}=0,\tilde{t})$
and
![]() $\tilde{u} _{w}^{\infty }\sqrt{\tilde{t}}$
, respectively, as a function of
$\tilde{u} _{w}^{\infty }\sqrt{\tilde{t}}$
, respectively, as a function of
![]() ${\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
. Note that
${\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
. Note that
![]() $\tilde{u} _{w}^{\infty }$
is taken from the expression (3.12). Irrespective of the velocity normalisation, all the velocity profiles collapse onto a unique curve except for the cases when
$\tilde{u} _{w}^{\infty }$
is taken from the expression (3.12). Irrespective of the velocity normalisation, all the velocity profiles collapse onto a unique curve except for the cases when
![]() $\tilde{t}>O(1)$
, as expected from the previous results. However, the collapse is only marginally good when
$\tilde{t}>O(1)$
, as expected from the previous results. However, the collapse is only marginally good when
![]() $\tilde{\unicode[STIX]{x1D707}}_{w}=0.1$
when
$\tilde{\unicode[STIX]{x1D707}}_{w}=0.1$
when
![]() $\tilde{t}\sim O(1)$
or greater. This implies that this observation may apply at shorter and shorter times as
$\tilde{t}\sim O(1)$
or greater. This implies that this observation may apply at shorter and shorter times as
![]() $\unicode[STIX]{x1D707}_{w}$
tends towards
$\unicode[STIX]{x1D707}_{w}$
tends towards
![]() $\unicode[STIX]{x1D707}_{d}$
. Nonetheless, as long as
$\unicode[STIX]{x1D707}_{d}$
. Nonetheless, as long as
![]() $\tilde{t}\leqslant O(1)$
, the velocity field should be given by
$\tilde{t}\leqslant O(1)$
, the velocity field should be given by
![]() $\tilde{u} ({\tilde{y}},\tilde{t})\sim \tilde{u} _{w}^{\infty }\sqrt{\tilde{t}}f({\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}})$
, where
$\tilde{u} ({\tilde{y}},\tilde{t})\sim \tilde{u} _{w}^{\infty }\sqrt{\tilde{t}}f({\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}})$
, where
![]() $\tilde{u} _{w}^{\infty }$
is given by the expression (3.12).
$\tilde{u} _{w}^{\infty }$
is given by the expression (3.12).
3.4 Stokes’ first problem with imposed wall velocity
So far in this article Stokes’ first problem has been considered for the case when the wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
is imposed externally. Therefore, the wall velocity developed with time and, as the internal resistance of the granular medium balances out the applied stresses, it saturated to a constant value
$\unicode[STIX]{x1D70F}_{w}$
is imposed externally. Therefore, the wall velocity developed with time and, as the internal resistance of the granular medium balances out the applied stresses, it saturated to a constant value
![]() $u_{w}$
. In contrast, it should be possible to set the granular medium in motion by imposing the wall speed
$u_{w}$
. In contrast, it should be possible to set the granular medium in motion by imposing the wall speed
![]() $u_{w}$
. Here, the resulting shear stress experienced by the wall should vary temporally as the internal resistance of the granular medium develops with time. However, it should also ultimately saturate to a constant value
$u_{w}$
. Here, the resulting shear stress experienced by the wall should vary temporally as the internal resistance of the granular medium develops with time. However, it should also ultimately saturate to a constant value
![]() $\unicode[STIX]{x1D70F}_{w}$
so that it gives precisely the same steady-state solution as for the imposed shear-stress case. In this subsection, a brief note on this variant of Stokes’ first problem is presented.
$\unicode[STIX]{x1D70F}_{w}$
so that it gives precisely the same steady-state solution as for the imposed shear-stress case. In this subsection, a brief note on this variant of Stokes’ first problem is presented.
As already seen in figure 5, in the steady-state solution, for each wall friction coefficient there exists one and only one wall velocity. Therefore, it is reasonable to leave the normalised variables of the previous sections as such. Now by using the normalised local friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
, (3.1) can be rewritten as
$\tilde{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}_{d}-\unicode[STIX]{x1D707})/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
, (3.1) can be rewritten as
which for the case of Stokes’ first problem with imposed wall velocity should satisfy the initial condition
![]() $\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t}=0)=1$
(or
$\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t}=0)=1$
(or
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
) along with the boundary conditions
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
) along with the boundary conditions
and
![]() $\tilde{\unicode[STIX]{x1D707}}({\tilde{y}}=1,\tilde{t})=1$
. Here, the initial and lower boundary conditions are chosen so as to satisfy
$\tilde{\unicode[STIX]{x1D707}}({\tilde{y}}=1,\tilde{t})=1$
. Here, the initial and lower boundary conditions are chosen so as to satisfy
![]() $\tilde{u} =0$
, which is possible only when
$\tilde{u} =0$
, which is possible only when
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
in the
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}$
in the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology. The integral condition imposes the wall velocity on the choice of the vertical distribution of the normalised local friction coefficient
$\unicode[STIX]{x1D707}(I)$
-rheology. The integral condition imposes the wall velocity on the choice of the vertical distribution of the normalised local friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}$
. In particular, note that the parameter
$\tilde{\unicode[STIX]{x1D707}}$
. In particular, note that the parameter
![]() $\unicode[STIX]{x1D6FD}_{w}=\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D6FF}_{s}/p_{w}$
as in (2.11) since the steady-state solution (2.10) for Stokes’ first problem with applied shear stress should also apply to this case where the wall speed is externally imposed. Thus
$\unicode[STIX]{x1D6FD}_{w}=\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D6FF}_{s}/p_{w}$
as in (2.11) since the steady-state solution (2.10) for Stokes’ first problem with applied shear stress should also apply to this case where the wall speed is externally imposed. Thus
![]() $\unicode[STIX]{x1D6FD}_{w}=\unicode[STIX]{x1D707}_{w}^{\infty }/\unicode[STIX]{x1D707}_{s}-1$
, where
$\unicode[STIX]{x1D6FD}_{w}=\unicode[STIX]{x1D707}_{w}^{\infty }/\unicode[STIX]{x1D707}_{s}-1$
, where
![]() $\unicode[STIX]{x1D707}_{w}^{\infty }$
is the steady-state wall friction coefficient that is needed to sustain the applied wall speed
$\unicode[STIX]{x1D707}_{w}^{\infty }$
is the steady-state wall friction coefficient that is needed to sustain the applied wall speed
![]() $u_{w}$
.
$u_{w}$
.

Figure 7. Numerical results for Stokes’ first problem with imposed wall velocity showing the evolution of the velocity
![]() $\tilde{u} ({\tilde{y}},\tilde{t})$
(top) and the normalised friction coefficient
$\tilde{u} ({\tilde{y}},\tilde{t})$
(top) and the normalised friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t})$
(bottom) at different times
$\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t})$
(bottom) at different times
![]() $\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
for various imposed wall speeds
$\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
for various imposed wall speeds
![]() $\tilde{u} _{w}$
. These data are obtained by directly integrating the numerical solution of the non-dimensional shear-stress equation (3.14) with the wall boundary condition (3.15). The thick dashed line represents the steady-state solution. The imposed wall speed
$\tilde{u} _{w}$
. These data are obtained by directly integrating the numerical solution of the non-dimensional shear-stress equation (3.14) with the wall boundary condition (3.15). The thick dashed line represents the steady-state solution. The imposed wall speed
![]() $\tilde{u} _{w}$
was chosen to match with the steady-state wall speed in figure 6.
$\tilde{u} _{w}$
was chosen to match with the steady-state wall speed in figure 6.

Figure 8. Temporal evolution of the shear layer thickness
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
for the profiles presented in figure 7. Different symbols correspond to various imposed wall velocities (▫,
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{s}$
for the profiles presented in figure 7. Different symbols correspond to various imposed wall velocities (▫,
![]() $\tilde{u} _{w}=0.198$
; ○,
$\tilde{u} _{w}=0.198$
; ○,
![]() $\tilde{u} _{w}=1.334$
; ♢,
$\tilde{u} _{w}=1.334$
; ♢,
![]() $\tilde{u} _{w}=4.629$
). As already seen in figure 2 (bottom) for the case when the wall shear stress is imposed, the shear layer grows as
$\tilde{u} _{w}=4.629$
). As already seen in figure 2 (bottom) for the case when the wall shear stress is imposed, the shear layer grows as
![]() $\sqrt{\tilde{t}}$
until approximately
$\sqrt{\tilde{t}}$
until approximately
![]() $\tilde{t}\sim O(1)$
.
$\tilde{t}\sim O(1)$
.
Figure 7 presents the velocity
![]() $\tilde{u} ({\tilde{y}},\tilde{t})$
(top) and the normalised friction coefficient
$\tilde{u} ({\tilde{y}},\tilde{t})$
(top) and the normalised friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t})$
(bottom) profiles that are obtained by numerically solving (3.14) for
$\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t})$
(bottom) profiles that are obtained by numerically solving (3.14) for
![]() $\tilde{\unicode[STIX]{x1D707}}$
satisfying the imposed wall velocity condition as given by (3.15). Each continuous line represents a different time as indicated in the figure
$\tilde{\unicode[STIX]{x1D707}}$
satisfying the imposed wall velocity condition as given by (3.15). Each continuous line represents a different time as indicated in the figure
![]() $(\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1})$
and the thick dashed line represents the steady-state solution. Note that particular wall speeds ((a)
$(\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1})$
and the thick dashed line represents the steady-state solution. Note that particular wall speeds ((a)
![]() $\tilde{u} _{w}=0.198$
, (b)
$\tilde{u} _{w}=0.198$
, (b)
![]() $\tilde{u} _{w}=1.334$
and (c)
$\tilde{u} _{w}=1.334$
and (c)
![]() $\tilde{u} _{w}=4.629$
) were chosen so that the resulting steady-state velocity and local friction coefficient profiles are the same as that obtained in figure 6 for the case when wall shear stress is imposed. As expected, in all figures, the velocity profile (top) and the related boundary layer develops with time in such a way that the velocity at the wall is equal to the applied wall speed
$\tilde{u} _{w}=4.629$
) were chosen so that the resulting steady-state velocity and local friction coefficient profiles are the same as that obtained in figure 6 for the case when wall shear stress is imposed. As expected, in all figures, the velocity profile (top) and the related boundary layer develops with time in such a way that the velocity at the wall is equal to the applied wall speed
![]() $\tilde{u} _{w}$
at all times, and the size of the mobile layer increases until approximately
$\tilde{u} _{w}$
at all times, and the size of the mobile layer increases until approximately
![]() $\tilde{t}\sim O(1)$
. This is true for the normalised wall friction coefficient (bottom) as well. Also, both
$\tilde{t}\sim O(1)$
. This is true for the normalised wall friction coefficient (bottom) as well. Also, both
![]() $\tilde{u} ({\tilde{y}},\tilde{t})$
and
$\tilde{u} ({\tilde{y}},\tilde{t})$
and
![]() $\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t})$
match with their respective steady-state profiles (thick dashed line) for sufficiently large time
$\tilde{\unicode[STIX]{x1D707}}({\tilde{y}},\tilde{t})$
match with their respective steady-state profiles (thick dashed line) for sufficiently large time
![]() $\tilde{t}>O(1)$
.
$\tilde{t}>O(1)$
.
With these data, it is then possible to calculate the size of the mobile layer, say
![]() $\unicode[STIX]{x1D6FF}(\tilde{t})$
, where the local shear stress is just above the threshold shear
$\unicode[STIX]{x1D6FF}(\tilde{t})$
, where the local shear stress is just above the threshold shear
![]() $\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D707}_{s}p$
. Figure 8 illustrates that
$\unicode[STIX]{x1D70F}_{s}=\unicode[STIX]{x1D707}_{s}p$
. Figure 8 illustrates that
![]() $\unicode[STIX]{x1D6FF}(\tilde{t})$
increases with time as
$\unicode[STIX]{x1D6FF}(\tilde{t})$
increases with time as
![]() $\sqrt{\tilde{t}}$
until
$\sqrt{\tilde{t}}$
until
![]() $\tilde{t}\sim O(1)$
, after which it saturates to the steady-state limit. Even though this is similar to what was observed previously for the case of Stokes’ problem when the wall shear is imposed, as seen in figure 2 (bottom), the evolution of the wall friction coefficient
$\tilde{t}\sim O(1)$
, after which it saturates to the steady-state limit. Even though this is similar to what was observed previously for the case of Stokes’ problem when the wall shear is imposed, as seen in figure 2 (bottom), the evolution of the wall friction coefficient
![]() $\unicode[STIX]{x1D707}_{w}(\tilde{t})$
takes place in two stages (see figure 9). It is observed that
$\unicode[STIX]{x1D707}_{w}(\tilde{t})$
takes place in two stages (see figure 9). It is observed that
![]() $\unicode[STIX]{x1D707}_{w}(\tilde{t})$
is close to
$\unicode[STIX]{x1D707}_{w}(\tilde{t})$
is close to
![]() $\unicode[STIX]{x1D707}_{d}$
for sufficiently small times, say up to when
$\unicode[STIX]{x1D707}_{d}$
for sufficiently small times, say up to when
![]() $\tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}d}$
. Then it decreases as
$\tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}d}$
. Then it decreases as
![]() $1/\sqrt{\tilde{t}}$
until it attains the steady state at
$1/\sqrt{\tilde{t}}$
until it attains the steady state at
![]() $\tilde{t}\sim \tilde{t}_{\unicode[STIX]{x1D707}w}$
. Thus, the corresponding wall shear stress
$\tilde{t}\sim \tilde{t}_{\unicode[STIX]{x1D707}w}$
. Thus, the corresponding wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}(\tilde{t})=\unicode[STIX]{x1D707}_{w}(\tilde{t})p_{w}$
initially remains sufficiently close to the critical shear stress
$\unicode[STIX]{x1D70F}_{w}(\tilde{t})=\unicode[STIX]{x1D707}_{w}(\tilde{t})p_{w}$
initially remains sufficiently close to the critical shear stress
![]() $\unicode[STIX]{x1D707}_{d}p_{w}$
before decreasing monotonically towards the wall shear stress that is needed to sustain the applied wall velocity
$\unicode[STIX]{x1D707}_{d}p_{w}$
before decreasing monotonically towards the wall shear stress that is needed to sustain the applied wall velocity
![]() $\tilde{u} _{w}$
. It suggests that the time at which these two stages occur should depend on
$\tilde{u} _{w}$
. It suggests that the time at which these two stages occur should depend on
![]() $\tilde{u} _{w}$
and these time scales are different from
$\tilde{u} _{w}$
and these time scales are different from
![]() $\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g}$
.
$\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g}$
.

Figure 9. Evolution of the wall friction coefficient
![]() $\unicode[STIX]{x1D707}({\tilde{y}}=0,\tilde{t})=\unicode[STIX]{x1D707}_{w}(\tilde{t})$
for various imposed wall velocities (▫,
$\unicode[STIX]{x1D707}({\tilde{y}}=0,\tilde{t})=\unicode[STIX]{x1D707}_{w}(\tilde{t})$
for various imposed wall velocities (▫,
![]() $\tilde{u} _{w}=0.198$
; ○,
$\tilde{u} _{w}=0.198$
; ○,
![]() $\tilde{u} _{w}=1.334$
; ♢,
$\tilde{u} _{w}=1.334$
; ♢,
![]() $\tilde{u} _{w}=4.629$
). Figures on the right display the same data as a function of two different normalisations of the time variable based on the scaling laws (3.17) and (3.18).
$\tilde{u} _{w}=4.629$
). Figures on the right display the same data as a function of two different normalisations of the time variable based on the scaling laws (3.17) and (3.18).
For
![]() $\tilde{t}_{\unicode[STIX]{x1D707}d}\leqslant \tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}w}$
, an order of magnitude analysis of (2.5) gives
$\tilde{t}_{\unicode[STIX]{x1D707}d}\leqslant \tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}w}$
, an order of magnitude analysis of (2.5) gives
![]() $u_{w}/t\sim (\unicode[STIX]{x1D707}_{w}(t)-\unicode[STIX]{x1D707}_{s})p_{w}/\unicode[STIX]{x1D6FF}(t)$
. In terms of the non-dimensional time
$u_{w}/t\sim (\unicode[STIX]{x1D707}_{w}(t)-\unicode[STIX]{x1D707}_{s})p_{w}/\unicode[STIX]{x1D6FF}(t)$
. In terms of the non-dimensional time
![]() $\tilde{t}$
and wall velocity
$\tilde{t}$
and wall velocity
![]() $\tilde{u} _{w}$
, this can be rewritten as
$\tilde{u} _{w}$
, this can be rewritten as
since
![]() $\unicode[STIX]{x1D6FF}\sim 3.66\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
as shown by figure 8. Since when
$\unicode[STIX]{x1D6FF}\sim 3.66\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
as shown by figure 8. Since when
![]() $\tilde{t}\sim \tilde{t}_{\unicode[STIX]{x1D707}d}$
,
$\tilde{t}\sim \tilde{t}_{\unicode[STIX]{x1D707}d}$
,
![]() $\unicode[STIX]{x1D707}_{w}(\tilde{t})-\unicode[STIX]{x1D707}_{s}\approx \unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
, this implies that the wall friction coefficient should be around
$\unicode[STIX]{x1D707}_{w}(\tilde{t})-\unicode[STIX]{x1D707}_{s}\approx \unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
, this implies that the wall friction coefficient should be around
![]() $\unicode[STIX]{x1D707}_{d}$
until some time
$\unicode[STIX]{x1D707}_{d}$
until some time
Thus, according to
![]() $\unicode[STIX]{x1D707}(I)$
-rheology, in order to sustain an applied wall speed
$\unicode[STIX]{x1D707}(I)$
-rheology, in order to sustain an applied wall speed
![]() $\tilde{u} _{w}$
with the no-slip condition, the granular medium develops a strong shear stress (about
$\tilde{u} _{w}$
with the no-slip condition, the granular medium develops a strong shear stress (about
![]() $\unicode[STIX]{x1D707}_{d}p_{w}$
) near the wall for all times
$\unicode[STIX]{x1D707}_{d}p_{w}$
) near the wall for all times
![]() $\tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}d}$
. From this point onwards, the wall shear stress should decrease monotonically as
$\tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}d}$
. From this point onwards, the wall shear stress should decrease monotonically as
![]() $1/\sqrt{\tilde{t}}$
until the local friction coefficient (or the local shear stress) distribution has reached the steady-state solution to give
$1/\sqrt{\tilde{t}}$
until the local friction coefficient (or the local shear stress) distribution has reached the steady-state solution to give
![]() $\unicode[STIX]{x1D707}_{w}(\tilde{t}\gg 1)=\unicode[STIX]{x1D707}_{w}^{\infty }$
. Here,
$\unicode[STIX]{x1D707}_{w}(\tilde{t}\gg 1)=\unicode[STIX]{x1D707}_{w}^{\infty }$
. Here,
![]() $\unicode[STIX]{x1D707}_{w}^{\infty }$
is a function of the applied wall speed and it can be either estimated directly by integrating the steady-state profile (2.10) or approximately via the expression (3.12). Using (3.16), it is seen that the wall friction coefficient, and hence the wall shear stress, should attain a steady-state value at some time
$\unicode[STIX]{x1D707}_{w}^{\infty }$
is a function of the applied wall speed and it can be either estimated directly by integrating the steady-state profile (2.10) or approximately via the expression (3.12). Using (3.16), it is seen that the wall friction coefficient, and hence the wall shear stress, should attain a steady-state value at some time
These two time scales can be verified by plotting the data from figure 9(a) as a function of properly rescaled time with respect to the relations (3.17) and (3.18). This is done in figure 9 (see plots b,c) where the data collapse indicates a good agreement with the above scaling laws.

Figure 10. The same data as in figure 7 (bottom) for different times
![]() $\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
but plotted here against the self-similar variable
$\tilde{t}=10^{-3},10^{-2},10^{-1},10^{0},10^{1}$
but plotted here against the self-similar variable
![]() $\unicode[STIX]{x1D702}={\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
. A reasonably good collapse is observed.
$\unicode[STIX]{x1D702}={\tilde{y}}/2\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
. A reasonably good collapse is observed.
Finally, an approximate expression can now be elaborated for
![]() $\unicode[STIX]{x1D707}({\tilde{y}},\tilde{t})$
due to the fact that the shear layer
$\unicode[STIX]{x1D707}({\tilde{y}},\tilde{t})$
due to the fact that the shear layer
![]() $\tilde{\unicode[STIX]{x1D6FF}}$
is small up to
$\tilde{\unicode[STIX]{x1D6FF}}$
is small up to
![]() $\tilde{t}\sim O(1)$
. As done before in § 3.1, (3.14) becomes
$\tilde{t}\sim O(1)$
. As done before in § 3.1, (3.14) becomes
at short time
![]() $\tilde{t}$
. This equation is singular near the wall region
$\tilde{t}$
. This equation is singular near the wall region
![]() ${\tilde{y}}\ll 1$
since
${\tilde{y}}\ll 1$
since
![]() $\tilde{\unicode[STIX]{x1D707}}\sim 0$
at least until
$\tilde{\unicode[STIX]{x1D707}}\sim 0$
at least until
![]() $\tilde{t}_{\unicode[STIX]{x1D707}d}$
(see figure 9). Nonetheless, the chosen initial condition
$\tilde{t}_{\unicode[STIX]{x1D707}d}$
(see figure 9). Nonetheless, the chosen initial condition
![]() $\unicode[STIX]{x1D70F}(y,t=0)=\unicode[STIX]{x1D707}_{s}p$
implies that there exists a zone where
$\unicode[STIX]{x1D70F}(y,t=0)=\unicode[STIX]{x1D707}_{s}p$
implies that there exists a zone where
![]() $\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{s}$
(or
$\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{s}$
(or
![]() $\tilde{\unicode[STIX]{x1D707}}\sim 1$
) away from the wall until the shear layer is completely developed, i.e. for all
$\tilde{\unicode[STIX]{x1D707}}\sim 1$
) away from the wall until the shear layer is completely developed, i.e. for all
![]() $\tilde{t}\leqslant O(1)$
. In this outer zone
$\tilde{t}\leqslant O(1)$
. In this outer zone
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\tilde{\unicode[STIX]{x1D707}}\sim \unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
and hence the above equation reduces to a simple diffusion equation wherein the outer solution should be
$\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\tilde{\unicode[STIX]{x1D707}}\sim \unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
and hence the above equation reduces to a simple diffusion equation wherein the outer solution should be
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}+A\,\text{erfc}\,({\tilde{y}}/2\unicode[STIX]{x0394}\sqrt{t})$
. Here
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{s}+A\,\text{erfc}\,({\tilde{y}}/2\unicode[STIX]{x0394}\sqrt{t})$
. Here
![]() $A$
is an arbitrary constant that could be deduced by matching this solution to the inner region where the friction coefficient
$A$
is an arbitrary constant that could be deduced by matching this solution to the inner region where the friction coefficient
![]() $\tilde{\unicode[STIX]{x1D707}}\sim 0$
. Here,
$\tilde{\unicode[STIX]{x1D707}}\sim 0$
. Here,
![]() $\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{w}(\tilde{t})$
and therefore
$\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}_{w}(\tilde{t})$
and therefore
is obtained as an approximate expression for the friction coefficient
![]() $\unicode[STIX]{x1D707}({\tilde{y}},\tilde{t})$
as long as
$\unicode[STIX]{x1D707}({\tilde{y}},\tilde{t})$
as long as
![]() $\tilde{t}$
is sufficiently small. When this expression is compared with the numerical results (see figure 10) a reasonable fit is observed for all
$\tilde{t}$
is sufficiently small. When this expression is compared with the numerical results (see figure 10) a reasonable fit is observed for all
![]() $\tilde{t}\leqslant O(1)$
. As previously shown from computational data in figure 9, it is pointed out here that
$\tilde{t}\leqslant O(1)$
. As previously shown from computational data in figure 9, it is pointed out here that
![]() $\unicode[STIX]{x1D707}_{w}(\tilde{t})-\unicode[STIX]{x1D707}_{s}\sim \unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
for all
$\unicode[STIX]{x1D707}_{w}(\tilde{t})-\unicode[STIX]{x1D707}_{s}\sim \unicode[STIX]{x0394}\unicode[STIX]{x1D707}$
for all
![]() $\tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}d}$
and
$\tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}d}$
and
![]() $\unicode[STIX]{x1D707}_{w}(\tilde{t})-\unicode[STIX]{x1D707}_{s}\sim \tilde{u} _{w}/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
when
$\unicode[STIX]{x1D707}_{w}(\tilde{t})-\unicode[STIX]{x1D707}_{s}\sim \tilde{u} _{w}/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\tilde{t}}$
when
![]() $\tilde{t}_{\unicode[STIX]{x1D707}d}\leqslant \tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}w}$
.
$\tilde{t}_{\unicode[STIX]{x1D707}d}\leqslant \tilde{t}\leqslant \tilde{t}_{\unicode[STIX]{x1D707}w}$
.
4 Conclusion
Using the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology, the so-called Stokes’ first problem on the motion of a granular liquid set up by an impulsively started flat plate is studied both numerically and theoretically. The problem is first well-posed in terms of a nonlinear diffusion equation for the local shear stress with proper initial and boundary conditions in order to avoid the Hadamard instability. Numerical solutions are then obtained for both externally imposed wall stress and speed. Approximate solutions at short and long times are also illustrated to capture the main features of the numerical results.
$\unicode[STIX]{x1D707}(I)$
-rheology, the so-called Stokes’ first problem on the motion of a granular liquid set up by an impulsively started flat plate is studied both numerically and theoretically. The problem is first well-posed in terms of a nonlinear diffusion equation for the local shear stress with proper initial and boundary conditions in order to avoid the Hadamard instability. Numerical solutions are then obtained for both externally imposed wall stress and speed. Approximate solutions at short and long times are also illustrated to capture the main features of the numerical results.
For the case when the dense granular flow is brought about by applying constant shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
at
$\unicode[STIX]{x1D70F}_{w}$
at
![]() $t>0$
, if
$t>0$
, if
![]() $\unicode[STIX]{x1D70F}_{w}$
is greater than the yield stress at the wall
$\unicode[STIX]{x1D70F}_{w}$
is greater than the yield stress at the wall
![]() $\unicode[STIX]{x1D707}_{s}p_{w}$
(where
$\unicode[STIX]{x1D707}_{s}p_{w}$
(where
![]() $p_{w}$
is the applied pressure at the wall) then the
$p_{w}$
is the applied pressure at the wall) then the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology implies that it is diffused into the granular medium until the shear stress is uniform throughout the medium such that, at any time
$\unicode[STIX]{x1D707}(I)$
-rheology implies that it is diffused into the granular medium until the shear stress is uniform throughout the medium such that, at any time
![]() $t$
, the applied shear stress reaches a depth proportional to
$t$
, the applied shear stress reaches a depth proportional to
![]() $\sqrt{\unicode[STIX]{x1D708}_{g}t}$
where
$\sqrt{\unicode[STIX]{x1D708}_{g}t}$
where
![]() $\unicode[STIX]{x1D708}_{g}=(d/2\unicode[STIX]{x1D719}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}I_{0})\sqrt{p_{w}/\unicode[STIX]{x1D70C}}$
denotes the diffusion coefficient for the local shear stress. A steady state, wherein a finite zone of grains (of thickness, say,
$\unicode[STIX]{x1D708}_{g}=(d/2\unicode[STIX]{x1D719}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}I_{0})\sqrt{p_{w}/\unicode[STIX]{x1D70C}}$
denotes the diffusion coefficient for the local shear stress. A steady state, wherein a finite zone of grains (of thickness, say,
![]() $\unicode[STIX]{x1D6FF}_{s}$
) yield, and hence flow, due to the applied shear, is thus shown to occur at a finite time of the approximate order
$\unicode[STIX]{x1D6FF}_{s}$
) yield, and hence flow, due to the applied shear, is thus shown to occur at a finite time of the approximate order
![]() $\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g}$
. Here, if
$\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g}$
. Here, if
![]() $\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s})/\unicode[STIX]{x1D707}_{s}$
, the shear layer depth
$\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D707}_{w}-\unicode[STIX]{x1D707}_{s})/\unicode[STIX]{x1D707}_{s}$
, the shear layer depth
![]() $\unicode[STIX]{x1D6FF}_{s}$
is
$\unicode[STIX]{x1D6FF}_{s}$
is
![]() $\unicode[STIX]{x1D6FD}_{w}p_{w}/\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}g$
as already obtained by Andreotti et al. (Reference Andreotti, Forterre and Pouliquen2011) and Cawthorn (Reference Cawthorn2011). If the no-slip condition is allowed, the wall velocity develops in time as
$\unicode[STIX]{x1D6FD}_{w}p_{w}/\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}g$
as already obtained by Andreotti et al. (Reference Andreotti, Forterre and Pouliquen2011) and Cawthorn (Reference Cawthorn2011). If the no-slip condition is allowed, the wall velocity develops in time as
![]() $u_{w}^{\infty }\sqrt{\unicode[STIX]{x1D708}_{g}t}/\unicode[STIX]{x1D6FF}_{s}$
until approximately a time
$u_{w}^{\infty }\sqrt{\unicode[STIX]{x1D708}_{g}t}/\unicode[STIX]{x1D6FF}_{s}$
until approximately a time
![]() $t\sim O(\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g})$
.
$t\sim O(\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g})$
.
If the dense granular flow is set up by suddenly imparting a constant speed
![]() $u_{w}$
on the wall at
$u_{w}$
on the wall at
![]() $t>0$
, the internal resistance of the medium develops in a small region close to the wall and later it is diffused into the shear layer. As a result, the
$t>0$
, the internal resistance of the medium develops in a small region close to the wall and later it is diffused into the shear layer. As a result, the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology suggests that, initially when the wall is set in motion, the shear stress experienced by the granular medium in the neighbourhood of the velocity-driven wall should be sufficiently close to the critical shear stress
$\unicode[STIX]{x1D707}(I)$
-rheology suggests that, initially when the wall is set in motion, the shear stress experienced by the granular medium in the neighbourhood of the velocity-driven wall should be sufficiently close to the critical shear stress
![]() $\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D707}_{d}p_{w}$
until some time
$\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D707}_{d}p_{w}$
until some time
![]() $t_{\unicode[STIX]{x1D707}d}$
proportional to
$t_{\unicode[STIX]{x1D707}d}$
proportional to
![]() $\unicode[STIX]{x1D708}_{g}(u_{w}/g\unicode[STIX]{x1D6FF}_{s})^{2}$
. Thereafter, the wall shear stress
$\unicode[STIX]{x1D708}_{g}(u_{w}/g\unicode[STIX]{x1D6FF}_{s})^{2}$
. Thereafter, the wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
decreases with time as a power law
$\unicode[STIX]{x1D70F}_{w}$
decreases with time as a power law
![]() $1/\sqrt{t}$
before reaching its steady-state value necessary to support the externally imposed wall speed
$1/\sqrt{t}$
before reaching its steady-state value necessary to support the externally imposed wall speed
![]() $u_{w}$
. At this stage the shear stress becomes uniform in the bulk of the mobile layer.
$u_{w}$
. At this stage the shear stress becomes uniform in the bulk of the mobile layer.
In both variants of Stokes’ problem in granular media, a properly rescaled friction coefficient (or the shear stress) is illustrated to be approximately self-similar with respect to the variable
![]() $y/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\unicode[STIX]{x1D708}_{g}t}$
. Moreover, the steady-state wall speed, wall shear stress and the applied wall pressure are related by a simple approximate expression (3.12) which in terms of dimensional parameters can be given as
$y/\unicode[STIX]{x0394}\unicode[STIX]{x1D707}\sqrt{\unicode[STIX]{x1D708}_{g}t}$
. Moreover, the steady-state wall speed, wall shear stress and the applied wall pressure are related by a simple approximate expression (3.12) which in terms of dimensional parameters can be given as
![]() $u_{w}\sim (g\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g})f(\unicode[STIX]{x1D6FD}_{w})$
, where
$u_{w}\sim (g\unicode[STIX]{x1D6FF}_{s}^{2}/\unicode[STIX]{x1D708}_{g})f(\unicode[STIX]{x1D6FD}_{w})$
, where
![]() $f(\unicode[STIX]{x1D6FD}_{w})$
is a function of the surplus steady-state wall shear stress
$f(\unicode[STIX]{x1D6FD}_{w})$
is a function of the surplus steady-state wall shear stress
![]() $\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D70F}_{w}-\unicode[STIX]{x1D707}_{s}p_{w})/\unicode[STIX]{x1D707}_{s}p_{w}$
such that it is either
$\unicode[STIX]{x1D6FD}_{w}=(\unicode[STIX]{x1D70F}_{w}-\unicode[STIX]{x1D707}_{s}p_{w})/\unicode[STIX]{x1D707}_{s}p_{w}$
such that it is either
![]() $O(1)$
when the wall shear stress is just above the yield stress
$O(1)$
when the wall shear stress is just above the yield stress
![]() $\unicode[STIX]{x1D70F}_{w}\sim \unicode[STIX]{x1D70F}_{s}$
or logarithmically large as
$\unicode[STIX]{x1D70F}_{w}\sim \unicode[STIX]{x1D70F}_{s}$
or logarithmically large as
![]() $\unicode[STIX]{x1D70F}_{w}$
approaches
$\unicode[STIX]{x1D70F}_{w}$
approaches
![]() $\unicode[STIX]{x1D70F}_{d}$
.
$\unicode[STIX]{x1D70F}_{d}$
.
Note that when the local friction coefficient
![]() $\unicode[STIX]{x1D707}$
approaches
$\unicode[STIX]{x1D707}$
approaches
![]() $\unicode[STIX]{x1D707}_{d}$
, the local inertial number, which compares the time scale of grain–grain rearrangements with that arising from the macroscopic deformation of the medium, should be very large (
$\unicode[STIX]{x1D707}_{d}$
, the local inertial number, which compares the time scale of grain–grain rearrangements with that arising from the macroscopic deformation of the medium, should be very large (
![]() $I\gg 1$
). Therefore, the aforementioned result that, for
$I\gg 1$
). Therefore, the aforementioned result that, for
![]() $t\leqslant t_{\unicode[STIX]{x1D707}d}$
, the local shear stress
$t\leqslant t_{\unicode[STIX]{x1D707}d}$
, the local shear stress
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
tends towards
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}p$
tends towards
![]() $\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D707}_{d}p$
in the immediate vicinity of the region where velocity is imposed, suggests that a highly agitated granular flow could occur in this zone. A viscoplastic description of the
$\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D707}_{d}p$
in the immediate vicinity of the region where velocity is imposed, suggests that a highly agitated granular flow could occur in this zone. A viscoplastic description of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology might, in fact, not be suitable in such zones as the local shear stress therein cannot be supported by internal grain–grain frictional resistance alone. Here, a proper model for rapid granular flows (Jenkins & Savage Reference Jenkins and Savage1983; Goldhirsch Reference Goldhirsch2003) should be more pertinent. Furthermore, if the applied wall speed
$\unicode[STIX]{x1D707}(I)$
-rheology might, in fact, not be suitable in such zones as the local shear stress therein cannot be supported by internal grain–grain frictional resistance alone. Here, a proper model for rapid granular flows (Jenkins & Savage Reference Jenkins and Savage1983; Goldhirsch Reference Goldhirsch2003) should be more pertinent. Furthermore, if the applied wall speed
![]() $u_{w}$
is much larger than
$u_{w}$
is much larger than
![]() $\unicode[STIX]{x1D708}_{g}/g\unicode[STIX]{x1D6FF}_{s}^{2}$
so that
$\unicode[STIX]{x1D708}_{g}/g\unicode[STIX]{x1D6FF}_{s}^{2}$
so that
![]() $t_{\unicode[STIX]{x1D707}d}$
becomes sufficiently large, the resulting unsteady granular flow as computed from the
$t_{\unicode[STIX]{x1D707}d}$
becomes sufficiently large, the resulting unsteady granular flow as computed from the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology may even be incorrect.
$\unicode[STIX]{x1D707}(I)$
-rheology may even be incorrect.
It is expected that this study will motivate investigations of the further validity of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology for unsteady dense granular flows using simple experiments. These results should also be helpful to better understand shear layers, effective viscosity, drag force and characteristic diffusion time scales in future studies with the
$\unicode[STIX]{x1D707}(I)$
-rheology for unsteady dense granular flows using simple experiments. These results should also be helpful to better understand shear layers, effective viscosity, drag force and characteristic diffusion time scales in future studies with the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology. Especially in the context of the ill-posedness of the
$\unicode[STIX]{x1D707}(I)$
-rheology. Especially in the context of the ill-posedness of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology as an initial-value problem, it might be essential to identify what features predicted by this rheology are still meaningful. It will be of some interest to include the spatio-temporal variation of the solid fraction
$\unicode[STIX]{x1D707}(I)$
-rheology as an initial-value problem, it might be essential to identify what features predicted by this rheology are still meaningful. It will be of some interest to include the spatio-temporal variation of the solid fraction
![]() $\unicode[STIX]{x1D719}$
as well – via, for example, a linear function of the inertial number
$\unicode[STIX]{x1D719}$
as well – via, for example, a linear function of the inertial number
![]() $I$
as in Jop et al. (Reference Jop, Forterre and Pouliquen2006). Non-local effects by which a granular medium can yield even if the local shear stress is below the yield criterion are omitted in the present short note for the sake of simplicity, but they might play an important role under common experimental conditions. Finally, it is pointed out that Stokes’ second problem with an oscillating wall boundary condition remains a very interesting open problem, as it might shed light on how static and dynamic zones can simultaneously appear and move around in unsteady flow fields predicted by the
$I$
as in Jop et al. (Reference Jop, Forterre and Pouliquen2006). Non-local effects by which a granular medium can yield even if the local shear stress is below the yield criterion are omitted in the present short note for the sake of simplicity, but they might play an important role under common experimental conditions. Finally, it is pointed out that Stokes’ second problem with an oscillating wall boundary condition remains a very interesting open problem, as it might shed light on how static and dynamic zones can simultaneously appear and move around in unsteady flow fields predicted by the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology of dense granular flows. However, the
$\unicode[STIX]{x1D707}(I)$
-rheology of dense granular flows. However, the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology can neither account for the history of the shear stress in the bulk of the medium nor consider other static initial conditions that are different from the yield criterion. It is nonetheless important to study these configurations using the
$\unicode[STIX]{x1D707}(I)$
-rheology can neither account for the history of the shear stress in the bulk of the medium nor consider other static initial conditions that are different from the yield criterion. It is nonetheless important to study these configurations using the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology to further advance knowledge about continuum models for unsteady dense granular flows.
$\unicode[STIX]{x1D707}(I)$
-rheology to further advance knowledge about continuum models for unsteady dense granular flows.
Acknowledgements
The authors acknowledge vital inputs from S. Dagois Bohy and all correspondences with D. Doppler and P. Jop.