2 Formulation

We consider a supersonic flow of an ideal gas with uniform free-stream velocity $U_{\infty }^{\ast }$ , temperature $T_{\infty }^{\ast }$ , dynamic viscosity $\unicode[STIX]{x1D707}_{\infty }^{\ast }$ and density $\unicode[STIX]{x1D70C}_{\infty }^{\ast }$ past an infinitely thin flat plate and suppose that a small amplitude harmonic distortion with angular frequency $\unicode[STIX]{x1D714}^{\ast }$ is superimposed on the flow. We also suppose that the time $t$ is normalized by $\unicode[STIX]{x1D714}^{\ast }$ , the velocities by $U_{\infty }^{\ast }$ , the pressure fluctuation by $\unicode[STIX]{x1D70C}_{\infty }^{\ast }(U_{\infty }^{\ast })^{2}$ , the temperature by $T_{\infty }^{\ast }$ and the dynamic viscosity by $\unicode[STIX]{x1D707}_{\infty }^{\ast }$ . We let $\{x,y,z\}$ denote Cartesian coordinates normalized by $L^{\ast }\equiv U_{\infty }^{\ast }/\unicode[STIX]{x1D714}^{\ast }$ with the coordinate $y$ being perpendicular to the surface of the plate.

As indicated in the introduction, the present paper assumes the Reynolds number $\unicode[STIX]{x1D70C}^{\ast }U_{\infty }^{\ast }L^{\ast }/\unicode[STIX]{x1D707}_{\infty }^{\ast }$ to be large and uses asymptotic theory to explain how the imposed harmonic distortion generates oblique instabilities at large downstream distances in the viscous boundary layer that forms on the surface of the plate. The distortion will therefore be inviscid at lowest approximation and, as is well known (Kovasznay Reference Kovasznay1953), can be decomposed into an acoustic component that carries no vorticity, and vortical and entropic components that produce no pressure fluctuations.

We only consider the first two for simplicity. The vortical velocity $\boldsymbol{u}_{v}$ is given by

where $\hat{\unicode[STIX]{x1D6FF}}\ll 1$ and $u_{\infty },v_{\infty },w_{\infty }$ satisfy the continuity condition

but are otherwise arbitrary constants while the acoustic component is governed by the linear wave equation which has a fundamental plane wave solution

for the velocity and pressure perturbation where

where, as noted in the introduction, $M_{\infty }$ denotes the free-stream Mach number.

The leading edge interaction will produce large scattered fields when the incidence angle $\tan ^{-1}(v_{a}/u_{a})=\tan ^{-1}(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FC})$ of the acoustic wave and $\tan ^{-1}(v_{v}/u_{v})$ of the vortical disturbance are $\mathit{O}(1)$ . In order to avoid this complication, we only consider the case where the incidence angle of the vortical disturbance is small, which requires that

and the case where the incidence angle of the acoustic disturbance is zero, which requires that

where the subscripts $\mp$ refer to the slow/fast acoustic modes. Equation (2.6) shows that the slow mode wavenumber becomes infinite when the obliqueness angle is equal to the critical angle referred to in the introduction.

As indicated above our interest here is in explaining how the incident harmonic distortions generate oblique instabilities at large downstream distances in the viscous boundary layer where the mean temperature, density and streamwise velocity, say $T$ , $\unicode[STIX]{x1D70C}$ , $U$ , respectively, can be expressed as functions of the Dorodnitsyn–Howarth variable

and determined from the similarity equations (Stewartson Reference Stewartson1964)

where $\unicode[STIX]{x1D6FE}_{r}$ is the specific heat ratio and the mean viscosity $\unicode[STIX]{x1D707}$ is assumed to depend on the temperature. The prime is used to denote differentiation with respect to $\unicode[STIX]{x1D702}$ and $\mathit{Pr}$ is used to denote the Prandtl number.

The natural small parameter for the asymptotic expansion turns out to be

where, as indicated in the introduction,

denotes the frequency parameter. We begin by considering the unsteady flow generated by the upstream vorticity.

3 Boundary layer disturbances generated by free-stream vorticity

4 Boundary layer disturbances generated by the Fedorov/Khokhlov mechanism for obliqueness angles close to critical angle

F/K analysed the generation of Mack mode instabilities in flat plate boundary layers by oblique acoustic waves of the form (2.3) where the wavenumbers $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D6FD}$ satisfy the dispersion relation (2.6) when the incidence angle $\unicode[STIX]{x1D6FE}$ is equal to zero, which, for reasons given in § 2, is the case of interest here. The focus of the present paper is on the moderate supersonic regime (the Mach number is less than approximately 4) where the most rapidly growing disturbances are usually highly oblique 1st Mack modes. (As indicated above, the obliqueness angle of the most rapidly growing 1st mode lies between $50^{\circ }$ and $70^{\circ }$ for an insulated wall when the Mach number is between 2 and 6, Mack Reference Mack1984.) F/K showed that diffraction of the slow acoustic wave by the non-parallel mean boundary layer flow can produce a 1st Mack mode instability in the downstream region where $x=\mathit{O}(\unicode[STIX]{x1D716}^{-6})$ when its obliqueness angle $\unicode[STIX]{x1D703}$ is less than the critical angle

and the deviation

is $\mathit{O}(1)$ . Their analysis shows that the diffraction occurs in the downstream region where $x=\mathit{O}(\unicode[STIX]{x1D716}^{-3})$ and the unsteady flow has a three layer structure: a passive Stokes layer near the wall, a main boundary layer region that fills the mean boundary layer and an outer diffraction region of thickness $\mathit{O}(\unicode[STIX]{x1D716}^{-3/2})$ . The instability emerges from the downstream limit of the solution in this region.

As noted above our interest here is in comparing the unstable flow produced by this mechanism with that produced by the vortical disturbances. It is natural to do this comparison at the same scaled spanwise wavenumber and scaled time (and, therefore, the same period for the periodic motion being considered here). But, as noted above, the vortical disturbances must have large spanwise wavenumber $\unicode[STIX]{x1D6FD}$ in order to produce oblique instability waves in the downstream region. The corresponding acoustic disturbances will only have large spanwise wavenumbers when their obliqueness angles $\unicode[STIX]{x1D703}$ are close to the critical angle $\unicode[STIX]{x1D703}_{c}$ , i.e. when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\ll 1$ . And since

when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\ll 1$ , it follows from (2.6) that

and

where

are $\mathit{O}(1)$ constants when this occurs. This shows that $\unicode[STIX]{x1D6FC}$ also becomes large when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\ll 1$ and that $\unicode[STIX]{x1D6FC}$ will expand in powers of $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ as indicated in (4.6), if $\unicode[STIX]{x1D6FD}$ is fixed at (4.5) to all orders in $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ (which we now assume to be the case). But the F/K diffraction region equations do not provide an appropriate asymptotic balance when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\ll 1$ and new equations have to be derived before that analysis can be extended into the small- $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ regime. The relevant equations are derived in this section.

We begin by rescaling the F/K diffraction region equations. F/K showed that the $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(1)$ solution, say $\{u,v,w,\unicode[STIX]{x1D717},p\}$ , for the velocity, temperature and pressure in the outer diffraction region (region 2 in their notation) is of the form

where

and the pressure is determined by

subject to the boundary conditions

where the wall normal velocity $v_{1}(x_{2},\infty )=\lim _{\unicode[STIX]{x1D702}\rightarrow \infty }v_{1}(x_{2},\unicode[STIX]{x1D702})$ is determined by the solution in the boundary layer where $\unicode[STIX]{x1D702}=\mathit{O}(1)$ . This solution shows that $v_{1}(x_{2},\infty )$ is related to the boundary layer pressure $p_{1}$ by

where $k$ is a constant.

Equations (4.10) and (4.12) become

when the obliqueness angle is close to the critical angle. But, as noted above, these equations have to be rescaled in order to obtain an asymptotically balanced result because now $\unicode[STIX]{x1D6FC}\gg 1$ . Appendix A shows that they will remain unchanged, i.e. they can be written as

if we put

where we now allow the rescaled proportionality constant $\tilde{k}(\tilde{\tilde{x}}_{2})$ to depend on $\tilde{\tilde{x}}_{2}$ in order to accommodate the altered boundary layer flow which determines (4.18). The scale factor $\unicode[STIX]{x0394}\unicode[STIX]{x1D711}\ll 1$ is introduced to account for the fact this flow now develops a double layer structure below the outer diffraction region when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\rightarrow 0$ : a main boundary layer where $\unicode[STIX]{x1D702}=\mathit{O}(1)$ and a wall layer where

The solution to (4.16), which is essentially the same as that in F/K, implies that the wall boundary condition (4.17) can be written as

It turns out that the wall layer flow can be balanced if the lowest-order solution $\{u,v,w,p\}$ in the main boundary layer behaves like

with

The wall layer flow will be completely viscous when the convective and viscous terms in the wall layer equations, which are proportional to $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D702}$ and $(2x)^{-1}\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}$ respectively, are of the same order. This occurs when

or

and, since $\tilde{\tilde{x}}_{2}=\mathit{O}(1)$ , it follows from (4.19) that this occurs when

or equivalently when

Inserting (4.26) into (4.19) shows that

The distinguished limit corresponds to the case where the wall layer flow is also time dependent. This occurs when $\unicode[STIX]{x0394}\unicode[STIX]{x1D711}=\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ or, in view of (4.27), when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(\unicode[STIX]{x1D716}^{2/3})$ . The corresponding wall layer solution, which is given in appendix B, shows that the wall normal velocity $v_{1}(\tilde{\tilde{x}}_{2},\infty )=\lim _{\unicode[STIX]{x1D702}\rightarrow \infty }v_{1}(\tilde{\tilde{x}}_{2},\unicode[STIX]{x1D702})$ is given in terms of the integral $\int _{\unicode[STIX]{x1D709}_{0}}^{\infty }\text{Ai}(\unicode[STIX]{x1D709})\,\text{d}\unicode[STIX]{x1D709}$ and the derivative $\text{Ai}^{\prime }(\unicode[STIX]{x1D709}_{0})$ of the Airy function $\text{Ai}(\unicode[STIX]{x1D709}_{0})$ by

which behaves like

as $\tilde{\tilde{x}}_{2}\rightarrow \infty$ since (Abramowitz & Stegun Reference Abramowitz and Stegun1964, pp. 446–447)

Inserting (4.17) and (4.30) into (4.21) shows that

where

which is formally the same as the equation considered by F/K who showed that the solution is given by

This result also applies when

But the wall layer flow will be inviscid when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}>\unicode[STIX]{x1D716}^{2/3}$ and the time dependent term must again balance the convective term in the wall layer equations, which means that the wall layer scale factor $\unicode[STIX]{x0394}\unicode[STIX]{x1D711}$ must also be set equal to $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ in this case. Equation (4.19) then becomes

which is consistent with (4.28) when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D716}^{2/3}$ and shows that the diffraction region moves upstream when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\rightarrow 0$ . The expansion breaks down when the length of the diffraction region $x=(\unicode[STIX]{x0394}\unicode[STIX]{x1D703})^{5/2}\tilde{\tilde{x}}_{2}\unicode[STIX]{x1D716}^{-3}$ is equal to the wavelength $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\unicode[STIX]{x1D716}^{-2}=\mathit{O}(1)$ .

Equation (4.27) shows that $\unicode[STIX]{x0394}\unicode[STIX]{x1D711}(\unicode[STIX]{x0394}\unicode[STIX]{x1D703})^{-1}\gg 1$ when $\unicode[STIX]{x1D716}^{2/3}(\unicode[STIX]{x0394}\unicode[STIX]{x1D703})^{-1}\gg 1$ . This implies that the time dependent terms will drop out of the wall layer equations when $\unicode[STIX]{x1D716}^{2/3}(\unicode[STIX]{x0394}\unicode[STIX]{x1D703})^{-1}\gg 1$ , which occurs when $\unicode[STIX]{x1D709}$ is replaced by $\overline{\unicode[STIX]{x1D709}}$ in the analysis of appendix B. The relevant solution for the wall normal velocity $v_{1}$ can therefore be obtained from (4.29) by taking the limit $\unicode[STIX]{x1D709}_{0}\rightarrow 0$ , with $p_{1},\unicode[STIX]{x1D709}_{0}$ held fixed. And, since (Abramowitz & Stegun Reference Abramowitz and Stegun1964, pp. 448–449)

where $\unicode[STIX]{x1D6E4}(x)$ denotes the gamma function, it follows that

And inserting (4.17) and (4.38) into (4.21) shows that

where

is a constant.

Equation (4.39) possesses a power series solution of the form

where

which is somewhat different from the corresponding solution obtained by F/K. Inserting (4.42) into (4.39), equating coefficients of like powers of $Z$ , summing the resulting recurrence relation and using equations (6.1.8), (6.2.1) and (6.2.2) of Abramowitz & Stegun (Reference Abramowitz and Stegun1964) shows that

It therefore follows from (4.42) and (C 5) that

where $\unicode[STIX]{x1D6FE}_{1}$ is given by (4.40). Equations (4.17) and (4.22) show that the pressure $p(\tilde{\tilde{x}}_{2})$ in the main boundary layer is given by

The acoustically generated boundary layer disturbance considered in this section as well as the vortically generated disturbance considered in § 3 will eventually evolve into propagating eigensolutions in regions that lie further downstream. The resulting flow will have a triple-deck structure of the type considered by Smith (Reference Smith1989), Wu (Reference Wu1999) and Ricco & Wu (Reference Ricco and Wu2007) in the latter (i.e. vortically generated) case. But the acoustically generated disturbance considered in the present section can also potentially have a triple-deck structure when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(\unicode[STIX]{x1D716})$ . We therefore begin by considering the flow in this region and show that the resulting triple-deck solution will match onto the compressible Lam–Rott eigensolutions (3.16) and (3.17). We then further investigate whether an analogous matching occurs for the acoustically generated small- $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ F/K solution.

5 The triple-deck region

As shown by Smith (Reference Smith1989), Wu (Reference Wu1999) and Ricco & Wu (Reference Ricco and Wu2007) the linearized Navier–Stokes equations possess an eigensolution of the form

in the triple-deck region where

and

is a scaled transverse coordinate and, as noted in Goldstein (Reference Goldstein1983), $\unicode[STIX]{x1D705}$ has the expansion

where the lowest-order term in this expansion satisfies the dispersion relation

and

which is easily obtained by rewriting equation (5.2) of Ricco & Wu (Reference Ricco and Wu2007) or equation (3.17) of Wu (Reference Wu1999) in the present notation.

The solution in the main boundary layer where $\unicode[STIX]{x1D702}=\mathit{O}(1)$ is given by

where $\hat{\unicode[STIX]{x1D6FF}}\ll 1$ is the common scale factor used in (3.6).

The solution in the upper deck where

is given by

when the branch of the square root is chosen so that

in order to exclude solutions exhibiting unphysical wall normal exponential growth.

Continuity of pressure and wall normal velocity requires that

which implies that $\overline{P}$ and $\overline{A}$ are related by

The equation for $w$ can be written as

As expected these equations reduce to equations (5.2) and (5.3) of Goldstein (Reference Goldstein1983) with $H$ defined by the right-hand side of (4.52) of that reference when $\overline{\unicode[STIX]{x1D6FD}}$ and $M_{\infty }$ are set to zero.

6 The next stage of evolution

It follows from (4.31), (5.5) and (5.6) that

when $x_{1}\rightarrow \infty$ and, therefore, that

when $\unicode[STIX]{x1D705}_{0}$ is allowed to approach zero when $x_{1}\rightarrow \infty$ , and that

when it is not. Substituting this latter result into (5.5) shows that the constant $c$ is given by

We exclude this latter case because it does not seem to match onto a non-trivial solution downstream.

It is easy to show that the solution to the reduced dispersion relation (5.24) satisfies the rescaled version

of (6.2), which can be considered to be a special case of this result if we allow $r$ to lie in the half-closed interval $0\leqslant r<1$ instead of the open interval (5.22). (The subset $0<r<1/3$ will be of little interest since there are no global solutions in this range.) The expansion (5.4) then generalizes to

where

and $\hat{x}_{1}$ is defined in (5.23).

Equation (6.5) implies that the streamwise wavenumber goes to zero as the disturbance propagates downstream. Its growth rate approaches or is equal to zero but does not become negative. The spanwise length scale remains constant at $\mathit{O}(\unicode[STIX]{x1D716}^{1-r})$ , but the boundary layer thickness continues to increase and the triple-deck scaling breaks down when the boundary layer thickness, which is of $\mathit{O}(\unicode[STIX]{x1D716}^{3}\sqrt{x})$ , becomes of the order of the spanwise length scale. This occurs when

which is upstream of the location where the unsteady flow is governed by the full Rayleigh equation considered in F/K. The instability wave becomes more oblique in this limit and it follows from (5.4) and (5.23) that

where $\overline{\unicode[STIX]{x1D6FC}}(\overline{x}_{1})$ is an $\mathit{O}(1)$ function of $\overline{x}_{1}$ (given by (6.8)) and

which means that the solution should be proportional to $\exp \{\text{i}[\unicode[STIX]{x1D716}^{-(4+2r)}\int _{0}^{\overline{x}_{1}}\overline{\unicode[STIX]{x1D6FC}}(\overline{x}_{1},\unicode[STIX]{x1D716})\,\text{d}\overline{x}_{1}+\overline{\overline{\unicode[STIX]{x1D6FD}}}\overline{\overline{z}}-t]\}$ , where $\overline{\unicode[STIX]{x1D6FC}}(\overline{x}_{1})$ is an $\mathit{O}(1)$ function of $\overline{x}_{1}$ that behaves like

in this next stage and should exhibit a double layer structure consisting of an inviscid region whose thickness is of the order of the boundary layer thickness and a completely passive viscous wall layer (i.e. a Stokes layer). The scaled variable

will be $\mathit{O}(1)$ in the latter region and the scaled variable

will be $\mathit{O}(1)$ in the former region since the boundary layer thickness is now of the order of the spanwise length scale, $\mathit{O}(\unicode[STIX]{x1D716}^{1-r})$ . It therefore follows from (6.8) and (6.13) that the transverse pressure gradients are expected to come into play and the solution in this region should expand like

where ${\mathcal{A}}(\overline{x}_{1})$ is a function of the slow variable $\overline{x}_{1}$ . Substituting this into the linearized Navier–Stokes equations shows that

since the density and temperature fluctuations can be eliminated between the energy equation and continuity equations to obtain a single equation for the pressure and velocity fluctuations at this order of approximation (Goldstein Reference Goldstein1976, Reference Goldstein2003). Eliminating the velocity between (6.15)–(6.18) leads to the incompressible reduced Rayleigh equation

for a variable temperature mean flow. Equation (6.19) is a limiting form of the full (compressible) reduced Rayleigh equation

It is well known that the incompressible Rayleigh equation can also be expressed in terms of the wall normal velocity $v$ . In fact, substituting (6.17) into (6.20) and differentiating with respect to $\overline{y}$ shows that

and therefore that

whose solution must satisfy the following boundary conditions:

Matching with the upstream solution (5.1) and (5.4) requires that $\overline{\unicode[STIX]{x1D6FC}}(\overline{x}_{1})$ satisfy the matching condition (6.11) as $\overline{x}_{1}\rightarrow 0$ .

Inserting (2.7), (2.11) and (6.13) into (6.22) and using (6.24) shows that

which means that

where

clearly approaches zero when

which means $\overline{\unicode[STIX]{x1D6FC}}$ that will be consistent with the matching condition (6.9) if we require that it behave like

where $\unicode[STIX]{x1D6FC}_{0}=\unicode[STIX]{x1D706}/T_{w}^{2}$ and $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\ldots$ are (in general complex) constants such that

and

We therefore need to consider the expansion (6.30) in order to show that the solution matches with the triple-deck solution. Substituting (6.30) into (6.25) shows that

which suggests that $\overline{v}$ should expand like

when $\unicode[STIX]{x1D702}=\mathit{O}(1)$ . Inserting (6.34) into (6.33) and equating coefficients of like powers of $\widehat{\unicode[STIX]{x1D6FD}}$ yields

and (6.24) implies that

But (6.25) also shows that

when

which means that

in this region. And, since expanding (6.40) for small $\hat{\unicode[STIX]{x1D702}}$ shows that

matching the inner solution (6.34), (6.35) and (6.37) to this result implies that

Inserting (6.42) into (6.36) and integrating the result yields

where $c$ and ${\hat{c}}_{1}$ are integration constants. Matching (6.43) with (6.41) and imposing the boundary condition (6.37) shows that

and it therefore follows from (6.30) and (6.32) that

which is consistent with the matching condition (6.11). Notice that (6.42) is consistent with (5.7).

While $\overline{\unicode[STIX]{x1D6FC}}$ is initially real it can eventually become complex and thereby produce exponential growth or decay because $\left(U^{\prime }/T^{2}\right)^{\prime }$ can equal zero at some finite value of $\unicode[STIX]{x1D702}$ and (6.25) can, therefore, have the equivalent of a generalized inflection point there.

7 Numerical procedures

The Newton–Raphson method was used to solve the dispersion relation (5.5). The complex eigenvalue $\unicode[STIX]{x1D705}_{0}$ was first computed at small- $x_{1}$ values, where quick numerical convergence was achieved by using the asymptotic formula (5.15) as an initial guess for the iterative procedure. The numerically computed $\unicode[STIX]{x1D705}_{0}$ values at the two previous $x_{1}$ locations were interpolated to construct the initial guess for the $\unicode[STIX]{x1D705}_{0}$ calculations at larger $x_{1}$ locations. The same procedure was used to solve (5.24). The Airy function was computed with an in-house code based on the method developed by Gil, Segura & Temme (Reference Gil, Segura and Temme2002).

An implicit second-order finite-difference scheme was used to solve the modified Rayleigh boundary value problem (6.23), (6.25) and (6.26). The eigenvalue $\overline{\unicode[STIX]{x1D6FC}}$ was computed by setting $\text{d}\overline{v}/\text{d}\unicode[STIX]{x1D702}|_{\unicode[STIX]{x1D702}=0}$ to an order-one constant and using the Newton–Raphson method to iteratively update the computed value of $\overline{\unicode[STIX]{x1D6FC}}$ until $|\overline{v}(0)|$ was smaller than $10^{-8}$ , and the difference between the absolute values of two successively computed values of $\overline{\unicode[STIX]{x1D6FC}}$ was also smaller than $10^{-8}$ . The computation was first performed at small $\widehat{\unicode[STIX]{x1D6FD}}$ values, where quick numerical convergence was achieved by using the asymptotic formula (6.11) as an initial guess for the iterative procedure. The numerically computed $\overline{\unicode[STIX]{x1D6FC}}$ values at the two smaller $\widehat{\unicode[STIX]{x1D6FD}}$ values were interpolated to construct the initial guess for the $\overline{\unicode[STIX]{x1D6FC}}$ calculations at the larger $\widehat{\unicode[STIX]{x1D6FD}}$ values.

8 Results and discussion

This paper uses asymptotic analysis to compare the generation of oblique 1st Mack mode instabilities by free-stream acoustic disturbances with those generated by elongated vortical disturbances. The focus is on explaining the relevant physics and not on obtaining accurate numerical predictions. The appropriate small expansion parameter turns out to be $\unicode[STIX]{x1D716}={\mathcal{F}}^{1/6}$ , where ${\mathcal{F}}$ denotes the frequency parameter defined in (2.14).

The free-stream vortical disturbances generate unsteady flows in the leading edge region that produce short spanwise wavelength instabilities in a viscous triple-deck region which lies at an $\mathit{O}(\unicode[STIX]{x1D716}^{-2})$ distance downstream. The mechanism is analogous to the one considered by Goldstein (Reference Goldstein1983) in incompressible flows, but the instability onset occurs much further upstream in the present supersonic case and is, therefore, much more robust. The triple-deck instability does not possess an upper branch and evolves into an inviscid 1st Mack mode instability with short spanwise wavelength at an $\mathit{O}(\unicode[STIX]{x1D716}^{-4})$ distance downstream.

Figure 2. $\text{Re}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ as a function of the scaled streamwise coordinate $x_{1}^{\dagger }$ calculated from the dispersion relation (5.5) together with the Lam–Rott initial condition (5.15) for $M_{\infty }=2,3,4$ (double dot-dashed, dot-dashed and solid lines, respectively) and three values of the frequency-scaled transverse wavenumber $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }\geqslant 2$ . In the main graph, the dashed curve is the rescaled large- $x_{1}^{\dagger }$ asymptote (6.5).

Slow free-stream acoustic waves whose obliqueness angles differ from the critical angle $\unicode[STIX]{x1D703}_{c}$ by an $\mathit{O}(1)$ amount generate slow boundary layer disturbances over a relatively long region of length $\mathit{O}(\unicode[STIX]{x1D716}^{-3})$ . And these latter disturbances then produce $\mathit{O}(1)$ spanwise wavelength inviscid 1st Mack mode instabilities at a much larger $\mathit{O}(\unicode[STIX]{x1D716}^{-6})$ distance downstream. But the physical streamwise distance $x^{\ast }=(U_{\infty }^{\ast })^{3}/[(\unicode[STIX]{x1D714}^{\ast })^{2}\unicode[STIX]{x1D708}_{\infty }^{\ast }]$ corresponding to this scaled downstream location is at least equal to approximately 7 m for the typical supersonic flight conditions at $M_{\infty }=3$ ( $U_{\infty }^{\ast }=888~\text{m}~\text{s}^{-1}$ , $\unicode[STIX]{x1D708}_{\infty }^{\ast }=0.000264~\text{m}^{2}~\text{s}^{-1}$ ) at an altitude of 20 km, with an upper bound of 100 kHz for typical ‘low’ characteristic frequency. This means that this instability occurs too far downstream to be any practical interest.

However, the present results show that the slow boundary layer disturbances are generated over shorter streamwise length scales and produce (possibly unstable) eigensolutions in a region that lies at an $\mathit{O}(\unicode[STIX]{x1D716}^{-(4+2r)})$ distance downstream when the deviation $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ of the acoustic wave obliqueness angle from its critical angle $\unicode[STIX]{x1D703}_{c}$ is reduced to $\mathit{O}(\unicode[STIX]{x1D716}^{1-r})$ , with $1/3\leqslant r<1$ . This region lies closer to the leading edge and the latter eigensolutions are therefore more likely to be of practical interest than the $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(1)$ 1st Mack mode instabilities that appear in the F/K analysis. The relevant flow structure is depicted in figure 1.

The dispersion relation (5.5), which determines the complex wavenumber of the triple-deck instabilities, is expected to have at least one root corresponding to each of the infinitely many roots of the Lam–Rott dispersion relation (3.19). But only the lowest-order $n=0$ root of (3.19) can produce the spatially growing modes of (5.5). The wall temperature $T_{w}$ and viscosity $\unicode[STIX]{x1D707}_{w}$ can be scaled out of this equation by introducing the rescaled variables

Figures 2 and 3 are plots of the real and negative imaginary parts, respectively, of the scaled wavenumber $\unicode[STIX]{x1D705}_{0}^{\dagger }$ as a function of the scaled streamwise coordinate $\overline{x}_{1}^{\dagger }$ calculated from (5.5) together with the $n=0$ Lam–Rott initial condition (5.15) for $M_{\infty }=2,3,4$ and three values of the frequency-scaled transverse wavenumber $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }\geqslant 2$ . The dashed curves in the main plot of figure 2 show the re-scaled large- $\overline{x}_{1}^{\dagger }$ asymptote (6.2). The insets are included to more clearly show the changes at small $\overline{x}_{1}^{\dagger }$ . The dashed curves in the insets denote the real and imaginary parts of the small- $\overline{x}_{1}^{\dagger }$ asymptotic formula (5.15). The composite Lam–Rott triple-deck eigensolution can undergo a significant amount of damping before it turns into a spatially growing instability wave at the lower branch with the amount of damping determined by the upstream behaviour of the triple-deck solution (5.1) since this solution actually contains the Lam–Rott solution as an upstream limit. Equation (5.1) shows that the exponential damping factor is proportional to $\text{Im}[\int _{0}^{x_{LB}}\unicode[STIX]{x1D705}(x_{1})\,\text{d}x]=\unicode[STIX]{x1D716}^{-2}$ $\text{Im}[\int _{0}^{(x_{1})_{LB}}\unicode[STIX]{x1D705}(x_{1})\,\text{d}x]$ , where $x_{LB}$ denotes the streamwise location of the lower branch of the neutral stability curve and $(x_{1})_{LB}$ denotes the scaled streamwise location of that curve. In other words it is proportional to the area under the growth rate curve in figure 3 between zero and the lower branch. The inset in figure 3 is particularly relevant because it shows that the length $\unicode[STIX]{x0394}x_{1}^{\dagger }=0.01$ of this upstream region is very short and therefore that the amount of damping is relatively small. The supersonic leading edge receptivity mechanism is therefore expected to be much more relevant than in the incompressible case considered by Goldstein (Reference Goldstein1983).

Figure 3. $-\text{Im}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ as a function of the scaled streamwise coordinate $x_{1}^{\dagger }$ calculated from the dispersion relation (5.5) together with the Lam–Rott initial condition (5.15) for $M_{\infty }=2,3,4$ (double dot-dashed, dot-dashed and solid lines, respectively) and three values of the frequency-scaled transverse wavenumber $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }\geqslant 2$ .

The rapid changes allow small changes in $x_{1}^{\dagger }$ to produce order-one changes in $\unicode[STIX]{x1D705}_{0}^{\dagger }$ which means that the asymptotic expansion will not be accurate in the region where $x_{1}^{\dagger }\in \unicode[STIX]{x0394}x_{1}^{\dagger }$ unless the small expansion parameter $\unicode[STIX]{x1D716}$ is much smaller than $\unicode[STIX]{x0394}x_{1}^{\dagger }$ (although it is still likely to be accurate in the region where $x_{1}^{\dagger }=\mathit{O}(1)$ ). This requirement will probably not be satisfied at realistic values of $\unicode[STIX]{x1D716}$ and the full linearized Navier–Stokes equations will then have to be used to obtain accurate results in this upstream region. This was done by Wanderley & Corke (Reference Wanderley and Corke2001) for the incompressible case considered by Goldstein (Reference Goldstein1983). Analogous calculations were carried out by Ricco & Wu (Reference Ricco and Wu2007) who solved the boundary region equations driven by highly oblique free-stream disturbances and obtained exponentially growing (i.e. unstable) solutions which exactly correspond to the large $\overline{\unicode[STIX]{x1D6FD}}$ limit of the triple-deck dispersion relation (5.5). But the full linearized Navier–Stokes equations would have to be used in the present case in order to account for the streamwise pressure gradients that enter into the $\overline{\unicode[STIX]{x1D6FD}}=\mathit{O}(1)$ triple-deck solutions.

Since these results show that the complex wavenumber $\unicode[STIX]{x1D705}_{0}^{\dagger }$ is nearly independent of the Mach number for the Mach number range being considered here, the remaining discussion of the triple-deck regime is restricted to the $M_{\infty }=3$ case.

Realistic values of the actual unscaled streamwise location of the triple-deck region can be estimated by first selecting the characteristic scaled spanwise wavenumber $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ and taking $x_{1}^{\dagger }$ to be the streamwise coordinate of the downstream location of maximum growth rate. It follows from figure 3 that typical values of $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ and $x_{1}^{\dagger }$ are $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }=2$ and $x_{1}^{\dagger }=0.25$ , which satisfy the requirement, alluded to above, that the scaled streamwise location $x_{1}^{\dagger }$ be significantly larger than the short streamwise region of length $\unicode[STIX]{x0394}x_{1}^{\dagger }=0.01$ where the gradient of the growth rate is too large for the asymptotic balance to be valid. By expressing $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ and $x_{1}^{\dagger }$ in terms of dimensional quantities, $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }=2\unicode[STIX]{x03C0}(U_{\infty }^{\ast })^{2/3}(\unicode[STIX]{x1D708}_{\infty }^{\ast })^{1/6}T_{w}^{2/3}/[\unicode[STIX]{x1D706}_{z}^{\ast }(\unicode[STIX]{x1D714}^{\ast })^{2/3}]$ , and eliminating the frequency $\unicode[STIX]{x1D714}^{\ast }$ , the dimensional (unscaled) downstream location can be estimated as $x^{\ast }=x_{1}^{\dagger }(\overline{\unicode[STIX]{x1D6FD}}^{\dagger }\unicode[STIX]{x1D706}_{z}^{\ast })^{8/5}(U_{\infty }^{\ast })^{3/5}/[(2\unicode[STIX]{x03C0})^{8/5}(\unicode[STIX]{x1D708}_{\infty }^{\ast })^{3/5}T_{w}^{12/5}]$ . The streamwise locations of the points of maximum instability wave growth are given in table 1 for typical supersonic flight conditions and realistic values of the spanwise wavelength $\unicode[STIX]{x1D706}_{z}^{\ast }=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}^{\ast }$ . We therefore conclude that the triple-deck instability can play an important role in the boundary layer transition process on actual supersonic aircraft wings.

Figure 4 is a plot of the real part of $\hat{\unicode[STIX]{x1D705}}_{0}$ as a function of the frequency-scaled transverse wavenumber $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ for various values of the scaled streamwise coordinate $x_{1}^{\dagger }$ calculated from the dispersion relation (5.5) together with the Lam–Rott initial condition (5.15) for $M_{\infty }=3$ . It shows that the results are well approximated by the (appropriately rescaled) large- $x_{1}$ asymptote (6.2) and therefore that this formula is also the lowest-order term in the large- $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ asymptotic expansion of $\hat{\unicode[STIX]{x1D705}}_{0}$ at fixed $x_{1}$ for $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }>2$ .

Figure 4. $\text{Re}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ as a function of the frequency-scaled transverse wavenumber $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ for three values of the scaled streamwise coordinate $x_{1}^{\dagger }$ calculated from the dispersion relation (5.5) together with the Lam–Rott initial condition (5.15) for $M_{\infty }=3$ . The dashed curve is the rescaled large- $x_{1}^{\dagger }$ asymptote (6.5), which shows that this result is also valid when $\overline{\overline{\unicode[STIX]{x1D6FD}}}\rightarrow \infty$ and $x_{1}^{\dagger }=\mathit{O}(1)$ .

Figure 5 is a plot of the complex wavenumber $\unicode[STIX]{x1D705}_{0}^{\dagger }$ for $M_{\infty }=3$ and various values of $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }<5$ . The $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }<0.978$ curves are discontinued at the value of $\overline{x}_{1}^{\dagger }$ where $\text{Im}(\hat{\unicode[STIX]{x1D705}}_{0})=0$ because the upper-deck solution, which is proportional to $\exp \left[-\overline{y}\sqrt{\overline{\unicode[STIX]{x1D6FD}}^{2}-(M_{\infty }^{2}-1)\unicode[STIX]{x1D705}_{0}^{2}}\right]$ , becomes unbounded at large $\overline{y}$ when the curves are continued to larger $x_{1}^{\dagger }$ values. Similar behaviour was found to occur in rotating-disk boundary layers (Healey Reference Healey2006). The inset in figure 5 shows that the bifurcation occurs at $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }=0.978$ and $x_{1}^{\dagger }=0.025$ . Figure 6 shows that this happens because the real part of the exponent $\sqrt{\overline{\unicode[STIX]{x1D6FD}}^{2}-(M_{\infty }^{2}-1)\unicode[STIX]{x1D705}_{0}^{2}}$ becomes negative when $\text{Im}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ becomes negative if $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }<0.978$ but remains positive if $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }>0.978$ , which means that the $n=0$ Lam–Rott solution cannot be continued into the downstream region when $M_{\infty }=3$ and $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }\leqslant 0.978$ and a linear steady state (time periodic) global solution will not exist. But the higher-order $n>0$ modes shown in figure 7 exist for all $x_{1}^{\dagger }$ when $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }>0.978$ , which means that there will be at least one global solution for all values of $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ . The lowest-order $n=0$ modes have a positive growth rates for at least some values of $x_{1}^{\dagger }$ when $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }>0.978$ and have negative or zero growth at all $x_{1}^{\dagger }$ values when $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ is less than this critical value 0.978. The higher-order $n>0$ modes have negative growth rates for all values of $x_{1}^{\dagger }$ .

Figure 5. (a) $\text{Re}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ , (b) scaled growth rate $-\text{Im}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ as a function of the scaled streamwise coordinate $\overline{x}_{1}^{\dagger }$ calculated from the dispersion relation (5.5) together with the initial condition given by (5.15) with $n=0$ for $M_{\infty }=3$ and various values of the frequency-scaled transverse wavenumber $\overline{\unicode[STIX]{x1D6FD}}^{\dagger }<5$ .

Figure 6. Constant $\overline{\unicode[STIX]{x1D6FD}}$ curves in $\sqrt{\overline{\unicode[STIX]{x1D6FD}}^{2}-(M_{\infty }^{2}-1)\unicode[STIX]{x1D705}_{0}^{2}}$ -plane for $M_{\infty }=3$ .

Figure 7. (a) $\text{Re}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ , (b) scaled growth rate $-\text{Im}(\unicode[STIX]{x1D705}_{0}^{\dagger })$ as a function of the scaled streamwise coordinate $x_{1}^{\dagger }$ calculated from the dispersion relation (5.5) with the initial condition given by (5.15) with $n>0$ for $M_{\infty }=3$ and $\overline{\unicode[STIX]{x1D6FD}}_{0}^{\dagger }=0.6$ .

The dashed curves in figure 5 show the small- $\overline{x}_{1}^{\dagger }$ asymptote (5.15) which is the initial condition for the calculation. The dashed curves in figure 7 show the small- $\overline{x}_{1}^{\dagger }$ asymptotes (5.15) for $n>0$ .

While the slow F/K solution constructed in § 4 can be matched onto a viscous triple-deck solution when $\overline{\unicode[STIX]{x1D6FD}}\equiv \unicode[STIX]{x1D716}/\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(1)$ , we have shown (after (5.21)) that this result is unphysical because it does not remain bounded at large wall normal distances from the plate. This means that a global triple-deck solution can only exist at larger $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ , which corresponds to the scaling

with $0<r<1$ . But § 5 shows that the resulting solution can only be matched onto the slow F/K solution when $1/3\leqslant r<1$ , which means that the F/K solution cannot be continued into the downstream region when $0\leqslant r<1/3$ . The minimum $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ , which is determined by $\overline{\overline{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D716}^{2/3}/\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(1)$ in (8.2), corresponds to an upstream diffraction region solution that matches onto an inviscid triple-deck solution in the downstream region where $\hat{x}_{1}=x_{1}\unicode[STIX]{x1D716}^{4/3}=\mathit{O}(1)$ , which is still further downstream than the viscous triple-deck region where $x_{1}=\mathit{O}(1)$ but upstream of the full Rayleigh equation region where the $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(1)$ solution becomes unstable.

Figure 8 is a plot of the scaled wavenumber $\overline{\unicode[STIX]{x1D705}}_{0}/\overline{\overline{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D705}_{0}/\overline{\unicode[STIX]{x1D6FD}}$ as a function of the scaled streamwise coordinate $(\overline{\overline{\unicode[STIX]{x1D6FD}}}T_{w})^{4}\hat{x}_{1}/\unicode[STIX]{x1D706}^{2}=(\overline{\unicode[STIX]{x1D6FD}}T_{w})^{4}x_{1}/\unicode[STIX]{x1D706}^{2}$ for various values of the free-stream Mach number $M_{\infty }$ calculated from the inviscid triple-deck dispersion relation (5.24) together with the F/K asymptotic initial condition (5.25) which is shown by the dashed curves in the figure. The wavenumber is now completely real and the disturbance growth rates are therefore zero. This means that these F/K disturbances are potentially much less significant than the Lam–Rott instabilities which occur upstream and can exhibit significant streamwise growth.

Figure 8. Scaled wavenumber $\overline{\unicode[STIX]{x1D705}}_{0}/\overline{\overline{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D705}_{0}/\overline{\unicode[STIX]{x1D6FD}}$ as a function of the scaled streamwise coordinate $(\overline{\overline{\unicode[STIX]{x1D6FD}}}T_{w})^{4}\hat{x}_{1}/\unicode[STIX]{x1D706}^{2}=(\overline{\unicode[STIX]{x1D6FD}}T_{w})^{4}x_{1}/\unicode[STIX]{x1D706}^{2}$ for various values of the free-stream Mach number $M_{\infty }$ . The solid lines represent the numerical solution while the dashed lines represent the asymptotic solution (5.25).

The non-local Lam–Rott instabilities are low frequency disturbances that occur when the scaled frequency parameter $\overline{\unicode[STIX]{x1D6FD}}^{-1}$ is less than the critical value $1/0.4925$ for $M_{\infty }=3$ and the non-local F/K instabilities are high frequency disturbances that occur when $\overline{\unicode[STIX]{x1D6FD}}^{-1}=\unicode[STIX]{x1D716}^{-r}$ , $1/3\leqslant r<1$ . Since $\unicode[STIX]{x1D716}^{1/3}$ could easily be equal to 0.4925 numerically and since the leading edge shock wave can convert acoustic disturbances into convected disturbances, this may explain the results plotted in figure 13 of Fedorov (Reference Fedorov2003) which show that the F/K solution significantly underpredicts the experimental data of Maslov et al. (Reference Maslov, Shiplyuk, Sidorenko and Arnal2001) in the vicinity of the critical angle.

We have also shown that the solutions in the (viscous or inviscid) triple-deck regions eventually evolve into a Rayleigh equation phase whose eigenvalues $\overline{\unicode[STIX]{x1D6FC}}$ are determined by the boundary value problem (6.23), (6.25) and (6.26) and must therefore occur in complex conjugate pairs since the coefficients in (6.25) are all real. These equations suggest that $\overline{\unicode[STIX]{x1D6FC}}$ will depend on the single parameter $\widehat{\unicode[STIX]{x1D6FD}}$ , but it will, in reality, also be Mach number dependent since (2.8)–(2.11) show that the mean streamwise velocity $U=F^{\prime }(\unicode[STIX]{x1D702})$ and mean temperature distribution $T(\unicode[STIX]{x1D702})$ exhibit this dependence. The eigenvalues that satisfy this non-local problem must also satisfy the initial conditions (6.30)–(6.32). We assume in the following that the Prandtl number $\mathit{Pr}$ is equal to unity and that the viscosity $\unicode[STIX]{x1D707}(T)$ satisfies the simple linear relation $\unicode[STIX]{x1D707}(T)=T(\unicode[STIX]{x1D702})$ .

Figures 9 and 10 are plots of the real and imaginary parts respectively of these eigenvalues as a function of $\widehat{\unicode[STIX]{x1D6FD}}$ . They clearly show that $\text{Im}(\overline{\unicode[STIX]{x1D6FC}})$ undergoes very rapid changes at small values of $\widehat{\unicode[STIX]{x1D6FD}}$ . But, as in the triple-deck case, these changes again allow small changes in $\widehat{\unicode[STIX]{x1D6FD}}$ , say $\unicode[STIX]{x0394}\widehat{\unicode[STIX]{x1D6FD}}=0.05$ , to produce order-one changes in $\overline{\unicode[STIX]{x1D6FC}}$ which means that the asymptotic solution may not be accurate in the region where $\widehat{\unicode[STIX]{x1D6FD}}\in \unicode[STIX]{x0394}\widehat{\unicode[STIX]{x1D6FD}}$ . It may even lead to unphysical results unless the expansion parameter is much smaller than $\unicode[STIX]{x0394}\widehat{\unicode[STIX]{x1D6FD}}$ , although, analogously to the triple-deck solution, it should still be accurate in the region where $\widehat{\unicode[STIX]{x1D6FD}}=\mathit{O}(1)$ and the results should still be qualitatively correct for all $\widehat{\unicode[STIX]{x1D6FD}}$ . It is again unlikely that this restriction on $\unicode[STIX]{x1D716}$ will be satisfied for realistic values of $~epsilon$ and the full linearized Navier–Stokes equations may again have to be used to obtain accurate solutions in this region.

Figure 9. $\text{Re}(\bar{\unicode[STIX]{x1D6FC}})$ versus $\widehat{\unicode[STIX]{x1D6FD}}$ calculated from the modified Rayleigh equation eigenvalue problem. The dashed curves are calculated from the asymptotic formula (6.11).

Figure 10. $|\text{Im}(\bar{\unicode[STIX]{x1D6FC}})|$ versus $\widehat{\unicode[STIX]{x1D6FD}}$ calculated from the modified Rayleigh solution. The dashed lines in the inset are $|\text{Im}(\bar{\unicode[STIX]{x1D6FC}})|=C\widehat{\unicode[STIX]{x1D6FD}}$ , where the following values for the scale factor $C$ were obtained by optimizing the fit to the computations: $C=36$ for $M_{\infty }=2$ , $C=129.4$ for $M_{\infty }=3$ and $C=340.1$ for $M_{\infty }=4$ .

Figures 9 and 10 also show that the numerical solution for $\overline{\unicode[STIX]{x1D6FC}}$ is consistent with the initial conditions (6.11) and (6.32) provided that $\text{Im}(\unicode[STIX]{x1D6FC}_{1})=\text{Im}[\lim _{\hat{x}_{1}\rightarrow \infty }\overline{\unicode[STIX]{x1D705}}_{1}(\hat{x}_{1})]=0$ and $\unicode[STIX]{x1D6FC}_{2}=\lim _{\hat{x}_{1}\rightarrow \infty }\overline{\unicode[STIX]{x1D705}}_{2}(\hat{x}_{1})/\overline{\overline{\unicode[STIX]{x1D6FD}}}\sqrt{2\hat{x}_{1}}=\pm \text{i}C$ , where the values of $C$ are given in the caption of figure 10.

The last of these three conditions would determine the sign of $\text{Im}(\overline{\unicode[STIX]{x1D6FC}})$ and therefore whether the Rayleigh instability will grow or decay, if the solution for the second-order term in the triple-deck expansion (5.4) was known. We do not pursue this further since $\overline{\unicode[STIX]{x1D705}}_{2}(\hat{x}_{1})$ is determined by a very complicated higher-order triple-deck problem. But (6.8) and (6.28) show that actual streamwise length of the region where $|\text{Im}(\overline{\unicode[STIX]{x1D6FC}})|>0$ increases as $r\rightarrow 1$ (i.e. the flow will become more unstable when $\text{Im}(\overline{\unicode[STIX]{x1D6FC}})<0$ ) and setting $\overline{\unicode[STIX]{x1D6FD}}$ equal to $\unicode[STIX]{x1D716}/\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ in (5.23) suggests that present solution will merge into the $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(1)$ solution constructed by Fedorov (Reference Fedorov2003) when $r$ approaches this limit, which tends to support the positive growth option for the F/K result since the Fedorov solution is known to produce spatially growing instabilities. But the Lam–Rott instability may exhibit negative growth at large values of $\overline{\unicode[STIX]{x1D6FD}}$ since the Ricco & Wu (Reference Ricco and Wu2007) boundary region equation solutions suggest that its amplitude exhibits a single peak as it increases from zero and eventually decays back to zero at large streamwise distances (refer to their figure 10). But the present results allow us to compare the F/K and Lam–Rott transition mechanisms even when this issue remains unresolved. The comparison is most meaningful with $\overline{\overline{\unicode[STIX]{x1D6FD}}}$ rather than $\overline{\unicode[STIX]{x1D6FD}}$ held fixed. Equations (5.1) and (5.2) show that the maximum scaled growth rate of the Lam–Rott instability is $\mathit{O}(\unicode[STIX]{x1D716}^{-1})$ and occurs at $x=\mathit{O}(\unicode[STIX]{x1D716}^{-2})$ while (6.8) and (6.14) now show that the maximum scaled growth rate of the F/K instability can only be $\mathit{O}(1)$ and must occur further downstream at $x=\mathit{O}(\unicode[STIX]{x1D716}^{-(4+2r)})$ for $1/3\leqslant r<1$ .

The computations show that the growth rates go to zero when $\widehat{\unicode[STIX]{x1D6FD}}=0.477$ and that no solutions, other than the trivial solution

exist beyond this point, which might suggest that there are no global solutions to the receptivity problem. But (6.25) has a critical layer at the point where $U(\unicode[STIX]{x1D702})=\overline{\unicode[STIX]{x1D6FC}}^{-1}$ when $\overline{\unicode[STIX]{x1D6FC}}$ is real. The Rayleigh equation solution will be regular (i.e. analytic) there since this point coincides with the generalized inflection point where $(U^{\prime }/T^{2})^{\prime }=0$ . But viscous effects must be taken into account within a thin critical layer surrounding this point before continuing the solution into the downstream region because the streamwise and spanwise velocity perturbations still become singular there.

The viscous effects actually come into play in a thin critical layer at the point, say $x_{c}$ , where $\text{Im}(\overline{\unicode[STIX]{x1D6FC}})=\mathit{O}(\unicode[STIX]{x1D716}^{4/3})$ which lies slightly upstream of the neutral stability point $x_{n.s.}$ . The difference between the corresponding scaled streamwise coordinates, say $\overline{x}_{1c}-\overline{x}_{n.s.}$ , will also be $\mathit{O}(\unicode[STIX]{x1D716}^{4/3})$ at this point, but its actual location can otherwise be arbitrarily specified. The critical layer flow can only be balanced by allowing the unsteady flow to evolve on the relatively fast streamwise length scale

which can be done by changing the amplitude function in (6.14) and using (6.16) to show that the streamwise velocity outside of the critical layer should expand like

where $\overline{x}_{1c}$ denotes the scaled streamwise coordinate $\overline{x}_{1}$ at the location of the critical point

and $\overline{v}(\unicode[STIX]{x1D702};\overline{x}_{1})$ denotes the solution to the Rayleigh equation (6.25) described in § 6. The second-order solution can be determined from (6.15)–(6.18) with $\overline{\unicode[STIX]{x1D6FC}}$ replaced by the operator $\overline{\unicode[STIX]{x1D6FC}}_{c}+\unicode[STIX]{x1D716}^{4/3}\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{\overline{x}}_{1}$ but the $\mathit{O}(\unicode[STIX]{x1D716}^{2(1-r)})$ terms have to be included when $1/3\leqslant r\leqslant 1$ , which is the range of $r$ -values associated with the F/K solutions.

Since (6.8) and (8.4) show that $\overline{\overline{x}}_{1}\equiv \unicode[STIX]{x1D716}^{4/3}(\overline{x}_{1}-\overline{x}_{1c})/\unicode[STIX]{x1D716}^{4+2r}$ and since $\overline{x}_{1c}-\overline{x}_{1n.s.}$ must be $\mathit{O}(\unicode[STIX]{x1D716}^{4/3})$ the relatively short streamwise distance $\overline{\overline{x}}_{1}$ can be as large as $\unicode[STIX]{x1D716}^{-(2r+4/3)}$ and still lie in the upstream region where the Rayleigh problem can be solved, which means that the limit $\overline{\overline{x}}_{1}\rightarrow \infty$ will also lie in this region in a strict asymptotic sense. The outer solution (8.5) will therefore still exist and be compatible with the trivial solution (8.3) if the, as yet undetermined, amplitude function ${\mathcal{A}}(\overline{\overline{x}}_{1})$ goes to zero as $\overline{\overline{x}}_{1}\rightarrow \infty$ . But it now has a singularity at the critical point which must be eliminated by accounting for viscous effects.

Balancing the viscous and convective terms shows that the streamwise velocity within the critical layer should expand like

where the lowest-order scaled dependent variable $\overline{\overline{u}}_{0}$ is determined by

where $\unicode[STIX]{x1D702}_{c}$ denotes the transverse location of the critical layer,

$T_{c}$ and $U_{c}^{\prime }$ denote the mean temperature and mean velocity derivative at that level and

The solution to (8.8) is given by

where

Integrating by parts shows that

and, therefore, that (8.11) matches with (8.7).

The slowly varying amplitude ${\mathcal{A}}(\overline{\overline{x}}_{1})$ is determined by requiring that the change in the second-order outer streamwise velocity $\overline{u}_{1}(\unicode[STIX]{x1D702},\overline{\overline{x}}_{1};\overline{\overline{x}}_{1c})$ balance the change in the second-order inner streamwise velocity $\overline{\overline{u}}_{1}(\overline{\overline{y}},\overline{\overline{x}}_{1})$ across the critical layer. We will not go through the details here but the results are expected to show that ${\mathcal{A}}(\overline{\overline{x}}_{1})\rightarrow 0$ as $\overline{\overline{x}}_{1}\rightarrow \infty$ which, as noted above, implies that the instability wave will vanish on the relative fast streamwise length scale $\overline{\overline{x}}_{1}$ and is therefore compatible with the non-existence of a non-trivial Rayleigh equation solution downstream of the neutral point.

The dimensional streamwise location of the neutral stability point (which lies well outside the small region $\unicode[STIX]{x0394}\widehat{\unicode[STIX]{x1D6FD}}$ where the complex wavenumber $\overline{\unicode[STIX]{x1D6FC}}$ undergoes rapid change and the modified Rayleigh equation is therefore expected to accurately predict the unsteady flow at this location) is given by $x^{\ast }=\hat{\unicode[STIX]{x1D6FD}}^{2}U_{\infty }^{\ast }(\unicode[STIX]{x1D706}_{z}^{\ast })^{2}/(8\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D708}_{\infty }^{\ast })$ , where $\unicode[STIX]{x1D706}_{z}^{\ast }=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}^{\ast }$ is the spanwise wavelength. We can estimate the downstream distance to this point under typical supersonic flight conditions for the case where $M_{\infty }=3$ as we did for the $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\mathit{O}(1)$ F/K Rayleigh instability and for the triple-deck instability. The results, which are given in table 2, show that these distances are probably too large to be relevant to the transition process on actual aircraft wings and we therefore do not further pursue the critical layer analysis.

Figure 11 is a plot of the Rayleigh solution wall normal velocity profiles as a function of the transverse Blasius coordinate $\unicode[STIX]{x1D702}$ defined by (2.7) for small and intermediate values of $\widehat{\unicode[STIX]{x1D6FD}}$ . The dashed curves denote the one-term uniformly valid composite solution $\overline{v}=\text{e}^{-\widehat{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D702}}+U-1+\cdots \,$ , constructed from (6.40)–(6.42). The numerical results are in excellent agreement with the asymptotic results when $\widehat{\unicode[STIX]{x1D6FD}}\ll 1$ .

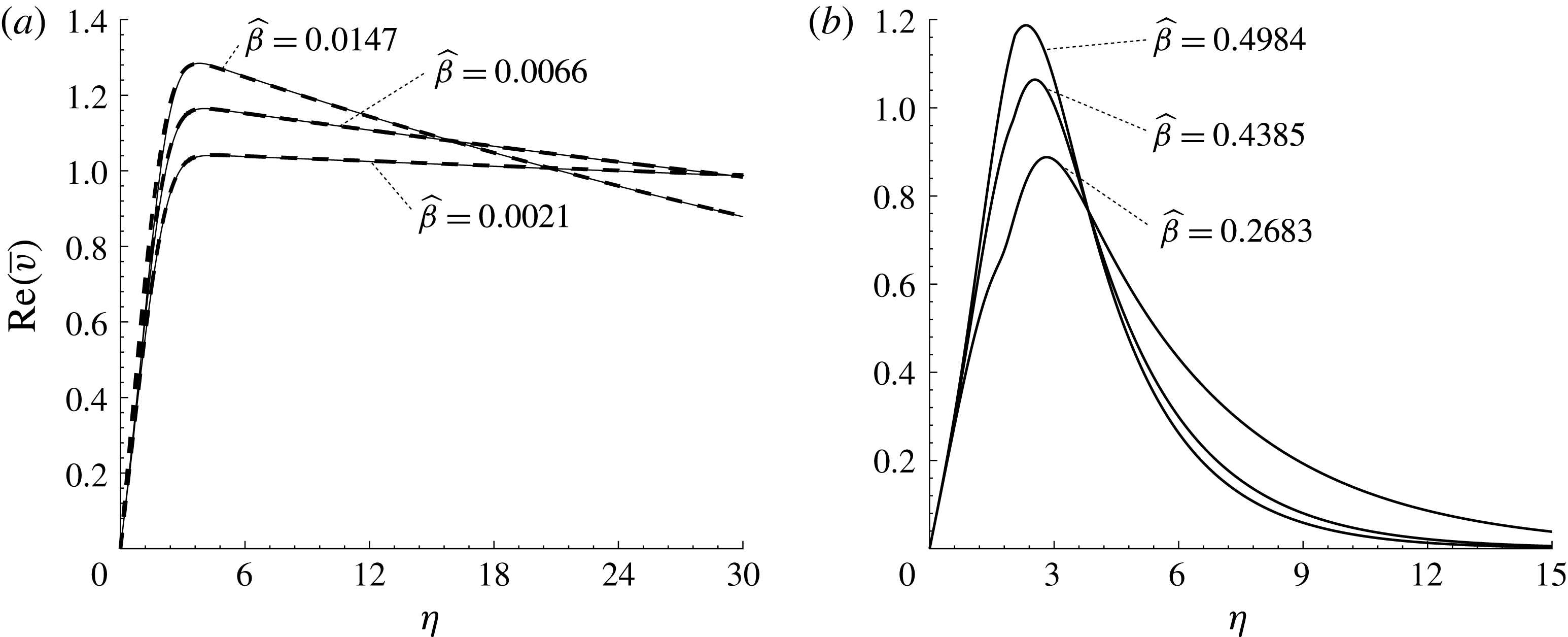
Figure 11. Wall normal velocity profiles of the real parts of the Rayleigh solution as a function of the transverse Blasius coordinate $\unicode[STIX]{x1D702}$ for $M_{\infty }=3$ . (a) For small values of $\widehat{\unicode[STIX]{x1D6FD}}$ (dashed curves denote uniformly valid composite solution constructed from (6.40)–(6.42). (b) For intermediate values of $\widehat{\unicode[STIX]{x1D6FD}}$ .

The Rayleigh equation (6.25) develops a critical layer when $\overline{\unicode[STIX]{x1D6FC}}$ becomes real, which occurs when $\widehat{\unicode[STIX]{x1D6FD}}\rightarrow 0$ . It follows from the expansion (6.30) that the critical layer moves toward the wall and lies at $\unicode[STIX]{x1D702}=\widehat{\unicode[STIX]{x1D6FD}}(T_{w}/\unicode[STIX]{x1D706})^{2}$ when $\widehat{\unicode[STIX]{x1D6FD}}\rightarrow 0$ . It eventually moves into the viscous wall layer when $\overline{x}_{1}=\mathit{O}(\unicode[STIX]{x1D716}^{2+r})$ . This corresponds to $\hat{x}_{1}=\mathit{O}(\unicode[STIX]{x1D716}^{3r})\leqslant \mathit{O}(1)$ which will lie well within the triple-deck region for realistic values of  $\unicode[STIX]{x1D716}$ .

The present study can also be extended to two-dimensional mean flow boundary layers on slightly curved surfaces. And while the analysis is probably not relevant for the boundary layers on highly swept wings such as the ones on current subsonic transports, it is expected to be very relevant to boundary layer transition on the nearly straight wing on aircraft such as the low-sweep Aerion AS2 supersonic Bizjet, shown in figure 12 – especially for wind tunnel testing, where strong acoustic disturbances are generated on the wind tunnel walls.

Figure 12. Low-sweep Aerion AS2 supersonic Bizjet. Posted by Tim Brown on the manufacturer Newsletter.

The analysis is also easily extended to supersonic wedge flows. It would directly apply to the flow behind the leading edge shock if the free-stream disturbance downstream of the shock rather than the disturbance field upstream of the shock were taken as input. But the shock wave will now couple the acoustic and vortical (as well as the entropic) free-stream disturbances and the downstream boundary layer can even produce reflected acoustic disturbance, which, as shown by the theoretical analyses of Duck, Lasseigne & Hussaini (Reference Duck, Lasseigne and Hussaini1997) and Cowley & Hall (Reference Cowley and Hall1990), will not play a significant role in the moderate supersonic Mach number regime being considered in this paper. The simultaneous consideration of the acoustic and vortical free-stream disturbances is however essential in this case. And finally it should be noted that the F/K disturbances are expected to become more significant than the Lam–Rott disturbances at sufficiently high free-stream Mach numbers (say, $M_{\infty }>4$ ) and/or sufficiently cold walls (for which $T_{w}$ is smaller than the adiabatic wall temperature), where the growth rate of the second Mack mode becomes larger than that of the oblique first mode. In fact, the main purpose of the F/K analysis was to deal with such hypersonic cases.

9 Concluding remarks

High Reynolds number asymptotics was used to study the non-local behaviour of boundary layer instabilities generated by small amplitude free-stream disturbances at moderate supersonic Mach numbers. The vortical disturbances produce an unsteady boundary flow that develops into oblique instability waves with a viscous triple-deck structure in the downstream region where the frequency-scaled streamwise coordinate $x$ is $\mathit{O}(\unicode[STIX]{x1D716}^{-2})$ . The analysis is analogous to the leading edge receptivity analysis carried by Goldstein (Reference Goldstein1983) in the incompressible limit, but the present results are expected to be much more robust because the instability waves now undergo very little decay before they begin to grow. F/K analysed the generation of inviscid instabilities in supersonic boundary layers by fast and slow acoustic disturbances in the free stream. They considered the case where the deviation $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\equiv \unicode[STIX]{x1D703}_{c}-\unicode[STIX]{x1D703}$ of the obliqueness angle from its critical value is $\mathit{O}(1)$ and showed that downstream propagating slow acoustic disturbances with $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}>0$ generate unsteady boundary layer disturbances that match onto the inviscid 1st Mack instability mode when the frequency-scaled distance $x$ is $\mathit{O}(\unicode[STIX]{x1D716}^{-6})=\mathit{O}({\mathcal{F}}^{-1})$ which is much further downstream than the region where the viscous triple-deck instability emerges from the vortically generated unsteady boundary layer flow. But, as shown in § 8, this instability emerges too far downstream to be of interest when scaled up to actual flight conditions for the small incidence angle disturbances considered in this paper. However, the inviscid instability, which first appears at an $\mathit{O}(\unicode[STIX]{x1D716}^{-(4+2r)})$ distance downstream when $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$ is reduced to $\mathit{O}(\unicode[STIX]{x1D716}^{1-r})$ with $1/3\leqslant r<1$ , can be of considerable importance when scaled to flight conditions. It is therefore appropriate to compare the vortically generated instabilities with the instabilities generated by oblique acoustic disturbances with obliqueness angles in this range as is done in this paper. These acoustic disturbances generate slow boundary layer disturbances which eventually develop into oblique stable disturbances with inviscid triple-deck structure in a region that lies downstream of the viscous triple-deck region. The acoustically generated oblique F/K disturbances are therefore likely to be insignificant compared to the vortically generated Lam–Rott instabilities. The paper shows that both of these instabilities eventually develop into modified Rayleigh-type instabilities (which can either grow or decay) further downstream.

The global Lam–Rott instabilities are low frequency disturbances that occur when the scaled frequency parameter $1/\overline{\unicode[STIX]{x1D6FD}}^{\dagger }$ is less than the critical value $1/0.978$ and the global F/K instabilities are high frequency disturbances that occur when $1/\overline{\unicode[STIX]{x1D6FD}}=1/\unicode[STIX]{x1D716}^{r}$ , $1/3\leqslant r<1$ . Since $\unicode[STIX]{x1D716}^{1/3}$ could easily be equal to 0.978 numerically and since the leading edge shock wave can convert acoustic disturbance into convected disturbances, this may explain the results given in Fedorov (Reference Fedorov2003) which show that the F/K solution significantly underpredicts the experimental data of Maslov et al. (Reference Maslov, Shiplyuk, Sidorenko and Arnal2001) in the vicinity of the critical angle.