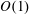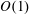1 Introduction
The transition from a laminar to a turbulent state in boundary layers, although studied for over a century, still represents one of the outstanding unsolved problems in fluid mechanics. A thorough understanding of the physics underlying this phenomenon is of great importance from a fundamental as well as from a practical point of view. The wall shear stress and heat transfer characteristics change dramatically depending on the flow regime being laminar, transitional or turbulent. Therefore, quantitative prediction and control of transition play a decisive role in determining the operating conditions and performance of flows around high-speed airfoils in a variety of industrial applications. Relevant examples are commercial and high-speed aircraft, space capsule re-entry into the atmosphere and flows around turbine stator vanes or rotor blades.
Boundary-layer transition is known to be strongly influenced by disturbances present in the oncoming stream, which penetrate into the boundary layer and eventually lead to the breakdown of the laminar flow. Such perturbations consist of acoustic (pressure), kinematic (vortical) and entropy (temperature) fluctuations, and may exist independently of each other when they are of sufficiently small amplitude.
In this paper we are concerned with free-stream vortical perturbations whose intensities are high enough (
![]() $Tu=1\,\%$
or more, where
$Tu=1\,\%$
or more, where
![]() $Tu$
is the root-mean-square value of the velocity fluctuations) for transition to occur rather early, bypassing the so-called orderly route via viscous Tollmien–Schlichting (T–S) waves. In this scenario, referred to as bypass transition (Morkovin Reference Morkovin1984), the laminar boundary-layer breakdown is preceded and caused by unsteady streamwise-elongated regions of high and low streamwise velocity. These structures have been referred to as breathing modes (Taylor Reference Taylor, Den Hartog and Peters1939) because of their resemblance to a thickening and thinning of the layer, Klebanoff modes (Kendall Reference Kendall1985) after the experiments of Klebanoff (Reference Klebanoff1971), or laminar streaks. The focus of our work is on the generation and nonlinear evolution of streaks in the compressible regime because in high-speed flows transition occurs more frequently through the bypass route than via the T–S wave growth described by the classical stability theory.
$Tu$
is the root-mean-square value of the velocity fluctuations) for transition to occur rather early, bypassing the so-called orderly route via viscous Tollmien–Schlichting (T–S) waves. In this scenario, referred to as bypass transition (Morkovin Reference Morkovin1984), the laminar boundary-layer breakdown is preceded and caused by unsteady streamwise-elongated regions of high and low streamwise velocity. These structures have been referred to as breathing modes (Taylor Reference Taylor, Den Hartog and Peters1939) because of their resemblance to a thickening and thinning of the layer, Klebanoff modes (Kendall Reference Kendall1985) after the experiments of Klebanoff (Reference Klebanoff1971), or laminar streaks. The focus of our work is on the generation and nonlinear evolution of streaks in the compressible regime because in high-speed flows transition occurs more frequently through the bypass route than via the T–S wave growth described by the classical stability theory.
1.1 Experiments and direct numerical simulations
Experimental works (Arnal & Juillen Reference Arnal and Juillen1978; Kendall Reference Kendall1985, Reference Kendall1990, Reference Kendall, Reda, Reed and Kobayashi1991; Westin et al. Reference Westin, Boiko, Klingmann, Kozlov and Alfredsson1994, Reference Westin, Bakchinov, Kozlov and Alfredsson1998; Matsubara & Alfredsson Reference Matsubara and Alfredsson2001; Fransson, Matsubara & Alfredsson Reference Fransson, Matsubara and Alfredsson2005) and direct numerical simulations (DNS) using realistic free-stream disturbances (Nagarajan, Lele & Ferziger Reference Nagarajan, Lele and Ferziger2007; Ovchinnikov, Choudhari & Piomelli Reference Ovchinnikov, Choudhari and Piomelli2008; Brinkerhoff & Yaras Reference Brinkerhoff and Yaras2015) have provided an overall picture of bypass transition induced by free-stream turbulence in the incompressible regime. The reader is also referred to DNS studies (e.g. Jacobs & Durbin Reference Jacobs and Durbin2001; Brandt, Schlatter & Henningson Reference Brandt, Schlatter and Henningson2004; Zaki & Durbin Reference Zaki and Durbin2005) using inflow conditions synthesized through the continuous modes of the Orr–Sommerfeld/Squire equations. Despite its importance in high-speed aircraft design and turbomachinery applications, the literature available on bypass transition in compressible flows is more limited than for incompressible flows. Supersonic wind tunnel experiments (Laufer Reference Laufer1961; Kendall Reference Kendall1967; Pate & Schueler Reference Pate and Schueler1969; Schneider Reference Schneider2001) showed that the transition behaviour is dominated by the noise radiated from the turbulent boundary layers on the walls. Transition may occur earlier in laboratory experiments than in flight conditions because of the high levels of tunnel noise (Schneider Reference Schneider2001). This discrepancy prevents the direct use of laboratory data for high-speed vehicle design. Although most of the experimental studies in the last few decades have focussed on acoustic disturbances, it should be recognized that more attention needs to be devoted to vortical disturbances. As speculated by Kendall (Reference Kendall1975), at low speeds the tunnel sound might be less effective than other type of disturbances, such as the vortical fluctuations. In flight conditions vortical disturbances are the main source of perturbation influencing transition, while acoustic modes are weak and only become relevant at locations affected by the noise radiated by the engine.
Mayer, Von Terzi & Fasel (Reference Mayer, Von Terzi and Fasel2011) performed DNS of the downstream development of a pair of oblique instability waves in a supersonic flat-plate boundary layer. They showed that transition in supersonic two-dimensional boundary layers can be initiated by very low disturbance levels (e.g. less than
![]() $0.01\,\%$
), which explains the practical relevance of the oblique breakdown mechanism for quiet environment such as free flight. Joo & Durbin (Reference Joo and Durbin2012) carried out DNS of the transition initiated by discrete instability modes and continuous vortical modes in a Mach 4.5 boundary layer. As in Jacobs & Durbin (Reference Jacobs and Durbin2001) and Zaki & Durbin (Reference Zaki and Durbin2005), their approach consisted of specifying the inflow conditions in terms of a superposition of the continuous spectra of the Orr–Sommerfeld and Squire operators. Such a practice has been questioned by Dong & Wu (Reference Dong and Wu2013) and Wu & Dong (Reference Wu and Dong2016), who showed that continuous spectra exhibit non-physical features (i.e. entanglement of Fourier components and abnormal size of the streamwise free-stream velocity) because non-parallel flow effects in the boundary layer are neglected. Non-parallelism actually plays a leading-order role in the entrainment of free-stream vortical disturbances into the boundary layer.
$0.01\,\%$
), which explains the practical relevance of the oblique breakdown mechanism for quiet environment such as free flight. Joo & Durbin (Reference Joo and Durbin2012) carried out DNS of the transition initiated by discrete instability modes and continuous vortical modes in a Mach 4.5 boundary layer. As in Jacobs & Durbin (Reference Jacobs and Durbin2001) and Zaki & Durbin (Reference Zaki and Durbin2005), their approach consisted of specifying the inflow conditions in terms of a superposition of the continuous spectra of the Orr–Sommerfeld and Squire operators. Such a practice has been questioned by Dong & Wu (Reference Dong and Wu2013) and Wu & Dong (Reference Wu and Dong2016), who showed that continuous spectra exhibit non-physical features (i.e. entanglement of Fourier components and abnormal size of the streamwise free-stream velocity) because non-parallel flow effects in the boundary layer are neglected. Non-parallelism actually plays a leading-order role in the entrainment of free-stream vortical disturbances into the boundary layer.
1.2 Theoretical works
In order to include the interaction between free-stream disturbances and the boundary layer, a rigorous mathematical formulation has been developed by Goldstein and co-workers (Goldstein, Leib & Cowley Reference Goldstein, Leib and Cowley1992; Goldstein & Leib Reference Goldstein and Leib1993; Goldstein Reference Goldstein1997; Wundrow & Goldstein Reference Wundrow and Goldstein2001). Goldstein’s theory is based on the boundary-region equations (Kemp Reference Kemp1951), which are the rigorous asymptotic limit of the Navier–Stokes equations for low-frequency and long-wavelength perturbations. For these disturbances, the streamwise derivatives in the viscous and pressure gradient terms are negligible, while the spanwise viscous diffusion is retained. In the limit of small-amplitude disturbances or short downstream distance, the boundary-region equations can be linearized about the Blasius solution. Leib, Wundrow & Goldstein (Reference Leib, Wundrow and Goldstein1999) used the linearized unsteady boundary-region equations (LUBR) to investigate the response of an incompressible laminar boundary layer to free-stream unsteady vortical fluctuations of the convected-gust type. Wu & Choudhari (Reference Wu and Choudhari2003) and Wu & Luo (Reference Wu and Luo2003) studied the instability of a Blasius boundary layer in the presence of steady and unsteady streaks, and showed that inviscid instability may occur when the distortion of the Klebanoff modes reaches a certain threshold value.
The linear analysis of Leib et al. (Reference Leib, Wundrow and Goldstein1999) was extended by Ricco, Luo & Wu (Reference Ricco, Luo and Wu2011) to include nonlinear effects. Nonlinearity was found to attenuate the amplification of the streaks and to distort the mean-flow profile significantly. A secondary instability analysis was carried out on the nonlinear streaks, proving that the streaky boundary layer may become inviscidly unstable during certain phases of the time modulation.
Ricco & Wu (Reference Ricco and Wu2007) extended the incompressible analysis by Leib et al. (Reference Leib, Wundrow and Goldstein1999) to the compressible case and explained the formation and growth of thermal streaks, which are thought to play a significant role in the secondary instability. Ricco, Tran & Ye (Reference Ricco, Tran and Ye2009) and Ricco, Shah & Hicks (Reference Ricco, Shah and Hicks2013) further studied the influence of wall heat transfer and wall suction, respectively, on the thermal streaks. The boundary-layer signature in the region relatively close to the leading edge corresponds to the inhomogeneous solution forced by the free-stream disturbance. However, Ricco & Wu (Reference Ricco and Wu2007) also observed that sufficiently downstream exponentially growing disturbances are formed. For high subsonic and supersonic Mach numbers, the appearance of the amplifying disturbances was in the streamwise region of practical interest. Ricco & Wu (Reference Ricco and Wu2007) showed that the growing disturbances evolved from the so-called quasi-three-dimensional Lam–Rott eigensolutions, which are excited by the free-stream disturbance and may be identified as highly oblique low-frequency T–S waves in the so-called first-mode family (Mack Reference Mack1975, Reference Mack1984). Ricco et al. (Reference Ricco, Tran and Ye2009) found that wall cooling suppresses the streaks and enhances the growth of the instability waves.
The parabolized-stability equations (PSE) approach has been developed and used to study the evolution of instability modes in compressible boundary layers (see e.g. Chang et al. Reference Chang, Malik, Erlebacher and Hussaini1991). This methodology is based on the assumption that the base flow varies slowly in the streamwise direction and thus a Wentzel–Kramers–Brillouin (WKB) type of analysis is employed to parabolize the Navier–Stokes equations. The method requires, however, an ad hoc iterative procedure to identify a local streamwise wavenumber, and, furthermore, the presence of the streamwise pressure gradient causes some numerical instability due to a residual ellipticity in the equations (Li & Malik Reference Li and Malik1996). Neither of these problems occurs in the boundary-region equation approach because the local streamwise wavenumber tends to zero in the low-frequency asymptotic limit, and the equations are strictly parabolic. It should be pointed out that what we referred to as the boundary-region equation approach consists of appropriate initial (upstream) and boundary conditions, which correctly describe the entrainment of physically realizable free-stream disturbances. This is in contrast to the so-called optimal perturbation theory (Andersson, Berggren & Henningson Reference Andersson, Berggren and Henningson1999; Zuccher, Bottaro & Luchini Reference Zuccher, Bottaro and Luchini2006), which uses the adjoint of the boundary-region equations or of the PSE to find the initial (upstream) disturbances that undergo the maximum gain when evolving to a pre-selected streamwise location. Free-stream disturbances, the very factor causing bypass transition, are not taken into account in the latter formulation.
1.3 Objectives
As in the incompressible case, bypass transition in compressible boundary layers is of relevance for engineering applications, but it is also challenging theoretically because of the difficult mathematics involved and the complex physical mechanisms at play. As an essential step towards understanding and predicting compressible bypass transition, we formulate a rigorous description of the formation and nonlinear development of the unsteady compressible streaks induced by free-stream vortical fluctuations. Such a mathematical theory for compressible disturbances responsible for bypass transition is still absent. A further goal is to explain the nonlinear interactions between the free-stream flow and the viscous boundary-layer flow, which occur through the displacement effect.
In § 2, the mathematical formulation and the scalings adopted are presented. In § 2.1 the free-stream perturbation is described and in § 2.2 the nonlinear unsteady compressible boundary-region equations are derived. In § 2.3 the outer-flow solution is obtained and matched with the inner solution in § 2.4. The numerical procedure to solve the boundary-region problem is outlined in § 3. The outer-flow velocity and pressure fields are shown in § 4 for the subsonic and supersonic regimes. In § 5.1 three different cases are considered, i.e. a turbomachinery flow (§ 5.1.1), a free flight flow (§ 5.1.2) and a supersonic wind tunnel flow (§ 5.1.3). The relevant results for the unsteady compressible streaks are presented in §§ 5.2 and 5.3. A summary and conclusions are given in § 6.
2 Formulation: scalings and governing equations
An air flow with a mean uniform velocity
![]() $U_{\infty }^{\ast }$
and constant temperature
$U_{\infty }^{\ast }$
and constant temperature
![]() $T_{\infty }^{\ast }$
is considered; hereinafter, the symbol
$T_{\infty }^{\ast }$
is considered; hereinafter, the symbol
![]() $^{\ast }$
is used to indicate dimensional quantities. Superimposed on the mean flow are homogeneous, statistically stationary turbulent vortical fluctuations, which are of the convected-gust type, i.e. they are passively advected by
$^{\ast }$
is used to indicate dimensional quantities. Superimposed on the mean flow are homogeneous, statistically stationary turbulent vortical fluctuations, which are of the convected-gust type, i.e. they are passively advected by
![]() $U_{\infty }^{\ast }$
. The oncoming flow is considered isentropic and air is treated as a perfect gas. The speed of sound in the free stream is:
$U_{\infty }^{\ast }$
. The oncoming flow is considered isentropic and air is treated as a perfect gas. The speed of sound in the free stream is:
where
![]() $\unicode[STIX]{x1D6FE}=1.4$
is the ratio of the specific heats and
$\unicode[STIX]{x1D6FE}=1.4$
is the ratio of the specific heats and
![]() ${\mathcal{R}}^{\ast }$
is the universal gas constant (
${\mathcal{R}}^{\ast }$
is the universal gas constant (
![]() ${\mathcal{R}}^{\ast }=287.05~\text{N}~\text{m}~\text{kg}^{-1}~\text{K}^{-1}$
). The Mach number is defined as
${\mathcal{R}}^{\ast }=287.05~\text{N}~\text{m}~\text{kg}^{-1}~\text{K}^{-1}$
). The Mach number is defined as
In the Cartesian coordinate system employed to describe the flow, a point is represented by a position vector
![]() $\boldsymbol{x}^{\ast }=x^{\ast }\boldsymbol{i}+y^{\ast }\boldsymbol{j}+z^{\ast }\boldsymbol{k}$
, where
$\boldsymbol{x}^{\ast }=x^{\ast }\boldsymbol{i}+y^{\ast }\boldsymbol{j}+z^{\ast }\boldsymbol{k}$
, where
![]() $x^{\ast }$
,
$x^{\ast }$
,
![]() $y^{\ast }$
and
$y^{\ast }$
and
![]() $z^{\ast }$
define the streamwise, wall-normal and spanwise directions, respectively. The spatial coordinates are non-dimensionalized by a suitable reference length scale
$z^{\ast }$
define the streamwise, wall-normal and spanwise directions, respectively. The spatial coordinates are non-dimensionalized by a suitable reference length scale
![]() $\unicode[STIX]{x1D706}^{\ast }$
, which we shall specify below. The velocity and temperature reference scales are
$\unicode[STIX]{x1D706}^{\ast }$
, which we shall specify below. The velocity and temperature reference scales are
![]() $U_{\infty }^{\ast }$
and
$U_{\infty }^{\ast }$
and
![]() $T_{\infty }^{\ast }$
. The fluid properties, such as the density
$T_{\infty }^{\ast }$
. The fluid properties, such as the density
![]() $\unicode[STIX]{x1D70C}^{\ast }$
and the dynamic viscosity
$\unicode[STIX]{x1D70C}^{\ast }$
and the dynamic viscosity
![]() $\unicode[STIX]{x1D707}^{\ast }$
, are scaled by their respective constant free-stream values,
$\unicode[STIX]{x1D707}^{\ast }$
, are scaled by their respective constant free-stream values,
![]() $\unicode[STIX]{x1D70C}_{\infty }^{\ast }$
and
$\unicode[STIX]{x1D70C}_{\infty }^{\ast }$
and
![]() $\unicode[STIX]{x1D707}_{\infty }^{\ast }$
. The time
$\unicode[STIX]{x1D707}_{\infty }^{\ast }$
. The time
![]() $t^{\ast }$
and the pressure
$t^{\ast }$
and the pressure
![]() $p^{\ast }$
are non-dimensionalized by
$p^{\ast }$
are non-dimensionalized by
![]() $\unicode[STIX]{x1D706}^{\ast }/U_{\infty }^{\ast }$
and
$\unicode[STIX]{x1D706}^{\ast }/U_{\infty }^{\ast }$
and
![]() $\unicode[STIX]{x1D70C}_{\infty }^{\ast }U_{\infty }^{\ast 2}$
, respectively.
$\unicode[STIX]{x1D70C}_{\infty }^{\ast }U_{\infty }^{\ast 2}$
, respectively.
It should be pointed out that in the supersonic regime shocks appear when the aerodynamic body (including a flat plate) has a finite thickness, and that at sufficiently high Mach numbers shocks can also arise for the idealized case of a flat plate with zero thickness due to the significant displacement produced by the viscous boundary-layer motion near the leading edge. The presence of a shock may change the boundary-layer instability properties if it is sufficiently close to the boundary layer (Chang, Malik & Hussaini Reference Chang, Malik and Hussaini1990; Cowley & Hall Reference Cowley and Hall1990). Moreover, when any of the three types of perturbations, e.g. a vortical fluctuation, interacts with a shock, all three disturbances may appear downstream of the shock (McKenzie & Westphal Reference McKenzie and Westphal1968). The acoustic and entropy perturbations may influence transition via receptivity mechanisms (Fedorov & Khokhlov Reference Fedorov and Khokhlov2003; Zhong & Wang Reference Zhong and Wang2012; Qin & Wu Reference Qin and Wu2016). In the present study, effects of shocks are neglected on the grounds that the plate is sufficiently thin and the Mach number is moderate so that shocks are weak and distant from the boundary. In this case, the interaction of unsteady disturbances with the shock is decoupled from their subsequent interaction with the boundary layer (Qin & Wu Reference Qin and Wu2016). The response of the boundary layer to each type of free-stream disturbance downstream of a shock can be analysed separately.
2.1 Free-stream disturbances and scaling
Free-stream turbulence is in general of broadband nature. For simplicity, we consider the case of vortical perturbation consisting of a pair of vortical modes with the same frequency (and hence streamwise wavenumber), but opposite spanwise wavenumber
![]() $\pm k_{z}^{\ast }$
. In the incompressible analysis of Ricco et al. (Reference Ricco, Luo and Wu2011), this choice of free-stream disturbance has led to good quantitative agreement between the theoretical prediction and wind tunnel experimental data. A similar behaviour is expected in the compressible case. The formulation and computation can be extended to realistic free-stream perturbations, which are of broadband nature as was shown by Zhang et al. (Reference Zhang, Zaki, Sherwin and Wu2011) for incompressible flows.
$\pm k_{z}^{\ast }$
. In the incompressible analysis of Ricco et al. (Reference Ricco, Luo and Wu2011), this choice of free-stream disturbance has led to good quantitative agreement between the theoretical prediction and wind tunnel experimental data. A similar behaviour is expected in the compressible case. The formulation and computation can be extended to realistic free-stream perturbations, which are of broadband nature as was shown by Zhang et al. (Reference Zhang, Zaki, Sherwin and Wu2011) for incompressible flows.
The velocity field of free-stream convected gusts of the assumed form can be expressed as
where
![]() $\hat{\boldsymbol{u}}_{\pm }^{\infty }=\{\hat{u} _{x,\pm }^{\infty },\hat{u} _{y,\pm }^{\infty },\hat{u} _{z,\pm }^{\infty }\}=O(1)$
is a real vector,
$\hat{\boldsymbol{u}}_{\pm }^{\infty }=\{\hat{u} _{x,\pm }^{\infty },\hat{u} _{y,\pm }^{\infty },\hat{u} _{z,\pm }^{\infty }\}=O(1)$
is a real vector,
![]() $\unicode[STIX]{x1D716}\ll 1$
is a measure of the free-stream perturbation level and c.c. indicates the complex conjugate. From the continuity equation, it follows that
$\unicode[STIX]{x1D716}\ll 1$
is a measure of the free-stream perturbation level and c.c. indicates the complex conjugate. From the continuity equation, it follows that
It is appropriate and convenient to take
![]() $\unicode[STIX]{x1D706}^{\ast }=1/k_{z}^{\ast }$
, so that
$\unicode[STIX]{x1D706}^{\ast }=1/k_{z}^{\ast }$
, so that
![]() $k_{z}=1$
. The characteristic Reynolds number is
$k_{z}=1$
. The characteristic Reynolds number is
Only the components of the free-stream disturbance with
![]() $k_{x}\ll 1$
are considered as they have been shown in experiments to be the ones that can penetrate the most into the boundary layer to form streaks.
$k_{x}\ll 1$
are considered as they have been shown in experiments to be the ones that can penetrate the most into the boundary layer to form streaks.
According to the result of Leib et al. (Reference Leib, Wundrow and Goldstein1999), the velocity perturbation is maximum when
![]() $x=O(k_{x}^{-1})$
. The following scaling is thus introduced:
$x=O(k_{x}^{-1})$
. The following scaling is thus introduced:
As a measure of the ratio between the boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
and the spanwise length scale
$\unicode[STIX]{x1D6FF}^{\ast }$
and the spanwise length scale
![]() $\unicode[STIX]{x1D706}^{\ast }$
at
$\unicode[STIX]{x1D706}^{\ast }$
at
![]() $\bar{x}=O(1)$
, a scaled spanwise wavenumber is defined as
$\bar{x}=O(1)$
, a scaled spanwise wavenumber is defined as
The interest is in the downstream viscous region where
![]() $\unicode[STIX]{x1D6FF}^{\ast }=O(\unicode[STIX]{x1D706}^{\ast })$
so that viscous diffusion effects in the spanwise and wall-normal directions are comparable. This occurs at streamwise locations
$\unicode[STIX]{x1D6FF}^{\ast }=O(\unicode[STIX]{x1D706}^{\ast })$
so that viscous diffusion effects in the spanwise and wall-normal directions are comparable. This occurs at streamwise locations
![]() $x^{\ast }=O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, which, together with (2.6), leads to
$x^{\ast }=O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, which, together with (2.6), leads to
![]() $k_{x}=O(R_{\unicode[STIX]{x1D706}}^{-1})$
, or, equivalently,
$k_{x}=O(R_{\unicode[STIX]{x1D706}}^{-1})$
, or, equivalently,
![]() $\unicode[STIX]{x1D705}=O(1)$
. As shown by Leib et al. (Reference Leib, Wundrow and Goldstein1999),
$\unicode[STIX]{x1D705}=O(1)$
. As shown by Leib et al. (Reference Leib, Wundrow and Goldstein1999),
![]() $O(\unicode[STIX]{x1D716})$
free-stream disturbances can produce
$O(\unicode[STIX]{x1D716})$
free-stream disturbances can produce
![]() $O(\unicode[STIX]{x1D716}/k_{x})$
fluctuations of the streamwise velocity component within the boundary layer. Nonlinear effects become of leading order when
$O(\unicode[STIX]{x1D716}/k_{x})$
fluctuations of the streamwise velocity component within the boundary layer. Nonlinear effects become of leading order when
![]() $\unicode[STIX]{x1D716}/k_{x}=O(1)$
, i.e. when the turbulent Reynolds number
$\unicode[STIX]{x1D716}/k_{x}=O(1)$
, i.e. when the turbulent Reynolds number
since
![]() $k_{x}=O(R_{\unicode[STIX]{x1D706}}^{-1})$
. A schematic illustration of the flow domain and its asymptotic structure is shown in figure 1.
$k_{x}=O(R_{\unicode[STIX]{x1D706}}^{-1})$
. A schematic illustration of the flow domain and its asymptotic structure is shown in figure 1.

Figure 1. Sketch of the flow configuration representing the asymptotic regions (adapted from Leib et al. Reference Leib, Wundrow and Goldstein1999).
2.2 The inner region: nonlinear unsteady compressible streaks
In the boundary layer the solution is expressed as the superimposition of the unsteady perturbation on the steady laminar compressible boundary layer. The velocities and temperature of the Blasius flow have the similarity solution (Stewartson Reference Stewartson1964)
where the prime indicates differentiation with respect to the similarity variable
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
and
![]() $\unicode[STIX]{x1D702}_{c}=T^{-1}\int _{0}^{\unicode[STIX]{x1D702}}T(\check{\unicode[STIX]{x1D702}})\,\text{d}\check{\unicode[STIX]{x1D702}}$
. The
$\unicode[STIX]{x1D702}_{c}=T^{-1}\int _{0}^{\unicode[STIX]{x1D702}}T(\check{\unicode[STIX]{x1D702}})\,\text{d}\check{\unicode[STIX]{x1D702}}$
. The
![]() $x$
-momentum and the energy equations are:
$x$
-momentum and the energy equations are:
where
![]() $T_{w}$
is the imposed wall temperature (isothermal condition). For
$T_{w}$
is the imposed wall temperature (isothermal condition). For
![]() $\unicode[STIX]{x1D702}\gg 1$
,
$\unicode[STIX]{x1D702}\gg 1$
,
![]() $F\rightarrow \bar{\unicode[STIX]{x1D702}}\equiv \unicode[STIX]{x1D702}-\unicode[STIX]{x1D6FD}_{c}$
, where
$F\rightarrow \bar{\unicode[STIX]{x1D702}}\equiv \unicode[STIX]{x1D702}-\unicode[STIX]{x1D6FD}_{c}$
, where
![]() $\unicode[STIX]{x1D6FD}_{c}$
depends on
$\unicode[STIX]{x1D6FD}_{c}$
depends on
![]() $M_{\infty }$
. Using the equation of state, the density
$M_{\infty }$
. Using the equation of state, the density
![]() $\unicode[STIX]{x1D70C}$
is given by
$\unicode[STIX]{x1D70C}$
is given by
The viscosity
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(T)$
is assumed to follow a power law,
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}(T)$
is assumed to follow a power law,
This relation has been proved to be more appropriate than the linear Chapman law (
![]() $\unicode[STIX]{x1D714}=1$
) in the Mach number range of interest
$\unicode[STIX]{x1D714}=1$
) in the Mach number range of interest
![]() $M_{\infty }<4$
(Stewartson Reference Stewartson1964).
$M_{\infty }<4$
(Stewartson Reference Stewartson1964).
The total boundary-layer flow is decomposed as the sum of the Blasius flow and the perturbation induced by the free-stream disturbance, namely,
 $$\begin{eqnarray}\displaystyle \left\{u_{tot},v_{tot},w_{tot},p_{tot},\unicode[STIX]{x1D70F}_{tot}\right\} & = & \displaystyle \left\{U,V,0,-\frac{1}{2},T\right\}+r_{t}\left\{\bar{u}(\bar{x},\unicode[STIX]{x1D702},z,t),\sqrt{\frac{2\bar{x}k_{x}}{R_{\unicode[STIX]{x1D706}}}}\bar{v}(\bar{x},\unicode[STIX]{x1D702},z,t),\right.\nonumber\\ \displaystyle & & \displaystyle \left.\frac{k_{x}}{k_{z}}\bar{w}(\bar{x},\unicode[STIX]{x1D702},z,t),\frac{k_{x}}{R_{\unicode[STIX]{x1D706}}}\bar{p}(\bar{x},\unicode[STIX]{x1D702},z,t),\bar{\unicode[STIX]{x1D70F}}(\bar{x},\unicode[STIX]{x1D702},z,t)\vphantom{\sqrt{\frac{2\bar{x}k_{x}}{R_{\unicode[STIX]{x1D706}}}}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{u_{tot},v_{tot},w_{tot},p_{tot},\unicode[STIX]{x1D70F}_{tot}\right\} & = & \displaystyle \left\{U,V,0,-\frac{1}{2},T\right\}+r_{t}\left\{\bar{u}(\bar{x},\unicode[STIX]{x1D702},z,t),\sqrt{\frac{2\bar{x}k_{x}}{R_{\unicode[STIX]{x1D706}}}}\bar{v}(\bar{x},\unicode[STIX]{x1D702},z,t),\right.\nonumber\\ \displaystyle & & \displaystyle \left.\frac{k_{x}}{k_{z}}\bar{w}(\bar{x},\unicode[STIX]{x1D702},z,t),\frac{k_{x}}{R_{\unicode[STIX]{x1D706}}}\bar{p}(\bar{x},\unicode[STIX]{x1D702},z,t),\bar{\unicode[STIX]{x1D70F}}(\bar{x},\unicode[STIX]{x1D702},z,t)\vphantom{\sqrt{\frac{2\bar{x}k_{x}}{R_{\unicode[STIX]{x1D706}}}}}\right\},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70F}_{tot}$
stands for the temperature. The Blasius flow does not correspond to the mean flow; the latter also consists of the time-independent components generated by the nonlinear interactions, which are included in the perturbation. The scaling (2.8) and the decomposition (2.16) indicate that for low-frequency free-stream disturbances with spanwise wavelength comparable with the boundary-layer thickness and streamwise wavelength of
$\unicode[STIX]{x1D70F}_{tot}$
stands for the temperature. The Blasius flow does not correspond to the mean flow; the latter also consists of the time-independent components generated by the nonlinear interactions, which are included in the perturbation. The scaling (2.8) and the decomposition (2.16) indicate that for low-frequency free-stream disturbances with spanwise wavelength comparable with the boundary-layer thickness and streamwise wavelength of
![]() $O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, the streamwise velocity and the temperature of the induced streaks acquire an amplitude of
$O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, the streamwise velocity and the temperature of the induced streaks acquire an amplitude of
![]() $O(\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D706}})$
, which is much larger than
$O(\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D706}})$
, which is much larger than
![]() $O(\unicode[STIX]{x1D716})$
transverse velocity components (and the intensity of free-stream disturbances). The boundary-layer signature therefore bears all hallmarks of streaks observed in experiments. For the assumed simple composition of free-stream disturbance, the seeded oblique-mode pair would be dominant in the earlier stage, and is expected to remain the most significant in the nonlinear stage downstream. However, nonlinear interactions generate harmonics and the mean-flow distortion. The disturbance can be expressed as a Fourier series in time and
$O(\unicode[STIX]{x1D716})$
transverse velocity components (and the intensity of free-stream disturbances). The boundary-layer signature therefore bears all hallmarks of streaks observed in experiments. For the assumed simple composition of free-stream disturbance, the seeded oblique-mode pair would be dominant in the earlier stage, and is expected to remain the most significant in the nonlinear stage downstream. However, nonlinear interactions generate harmonics and the mean-flow distortion. The disturbance can be expressed as a Fourier series in time and
![]() $z$
,
$z$
,
where
![]() $\{\hat{u} _{m,n},\hat{v}_{m,n},{\hat{w}}_{m,n},\hat{p}_{m,n},\hat{\unicode[STIX]{x1D70F}}_{m,n}\}$
are functions of
$\{\hat{u} _{m,n},\hat{v}_{m,n},{\hat{w}}_{m,n},\hat{p}_{m,n},\hat{\unicode[STIX]{x1D70F}}_{m,n}\}$
are functions of
![]() $\bar{x}$
and
$\bar{x}$
and
![]() $\unicode[STIX]{x1D702}$
. Unless otherwise specified, hereinafter the upper and lower limits of the summations are
$\unicode[STIX]{x1D702}$
. Unless otherwise specified, hereinafter the upper and lower limits of the summations are
![]() $\pm \infty$
. As the physical quantities are real, the Fourier coefficients are Hermitian,
$\pm \infty$
. As the physical quantities are real, the Fourier coefficients are Hermitian,
where
![]() $\hat{q}$
indicates any of
$\hat{q}$
indicates any of
![]() $\{\hat{u} ,\hat{v},{\hat{w}},\hat{p},\hat{\unicode[STIX]{x1D70F}}\}$
and the symbol
$\{\hat{u} ,\hat{v},{\hat{w}},\hat{p},\hat{\unicode[STIX]{x1D70F}}\}$
and the symbol
![]() $^{\star }$
denotes the complex conjugate. The total density is decomposed as
$^{\star }$
denotes the complex conjugate. The total density is decomposed as
![]() $\unicode[STIX]{x1D70C}_{tot}=\unicode[STIX]{x1D70C}+r_{t}\bar{\unicode[STIX]{x1D70C}}$
, where
$\unicode[STIX]{x1D70C}_{tot}=\unicode[STIX]{x1D70C}+r_{t}\bar{\unicode[STIX]{x1D70C}}$
, where
![]() $\unicode[STIX]{x1D70C}$
is given by (2.14). Substituting the total flow into the equation of state, one finds
$\unicode[STIX]{x1D70C}$
is given by (2.14). Substituting the total flow into the equation of state, one finds
It follows that the total density is:
The total viscosity is expressed by applying (2.15) to the total flow and by expanding it using the binomial formula as
where
![]() $(\unicode[STIX]{x1D714})_{j}=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D714}-1)(\unicode[STIX]{x1D714}-2)\ldots (\unicode[STIX]{x1D714}-j+1)$
,
$(\unicode[STIX]{x1D714})_{j}=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D714}-1)(\unicode[STIX]{x1D714}-2)\ldots (\unicode[STIX]{x1D714}-j+1)$
,
![]() $\unicode[STIX]{x1D707}^{\prime }=\text{d}\unicode[STIX]{x1D707}/\text{d}T$
and
$\unicode[STIX]{x1D707}^{\prime }=\text{d}\unicode[STIX]{x1D707}/\text{d}T$
and
![]() $\bar{\unicode[STIX]{x1D707}}$
is the nonlinear part of the viscosity perturbation, which is decomposed as
$\bar{\unicode[STIX]{x1D707}}$
is the nonlinear part of the viscosity perturbation, which is decomposed as
The nonlinearity of the viscosity comes from the power law exponent
![]() $\unicode[STIX]{x1D714}\neq 1$
and the turbulent Reynolds number
$\unicode[STIX]{x1D714}\neq 1$
and the turbulent Reynolds number
![]() $r_{t}=O(1)$
. The nonlinear part
$r_{t}=O(1)$
. The nonlinear part
![]() $\bar{\unicode[STIX]{x1D707}}$
is null when either (i)
$\bar{\unicode[STIX]{x1D707}}$
is null when either (i)
![]() $\unicode[STIX]{x1D714}=1\;\forall \,r_{t}$
or (ii)
$\unicode[STIX]{x1D714}=1\;\forall \,r_{t}$
or (ii)
![]() $r_{t}=0\;\forall \unicode[STIX]{x1D714}$
in (2.21). As long as
$r_{t}=0\;\forall \unicode[STIX]{x1D714}$
in (2.21). As long as
![]() $|r_{t}\bar{\unicode[STIX]{x1D70F}}|<1$
, which applies to all the cases considered, the series in (2.21) is absolutely convergent.
$|r_{t}\bar{\unicode[STIX]{x1D70F}}|<1$
, which applies to all the cases considered, the series in (2.21) is absolutely convergent.
By inserting (2.16) and (2.17) into the continuity, momentum and energy equations, using (2.20)–(2.22), and taking the limits
![]() $k_{x}\ll k_{z}$
,
$k_{x}\ll k_{z}$
,
![]() $R_{\unicode[STIX]{x1D706}}\gg 1$
with
$R_{\unicode[STIX]{x1D706}}\gg 1$
with
![]() $k_{x}R_{\unicode[STIX]{x1D706}}=O(1)$
, the nonlinear unsteady compressible boundary-region equations are found as follows.
$k_{x}R_{\unicode[STIX]{x1D706}}=O(1)$
, the nonlinear unsteady compressible boundary-region equations are found as follows.
The continuity equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{T^{\prime }}{T}\hat{u} _{m,n}+\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{T^{\prime }}{T^{2}}\hat{v}_{m,n}+\frac{1}{T}\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\text{i}n{\hat{w}}_{m,n}-\left(\frac{\text{i}m}{T}+\frac{FT^{\prime }}{2\bar{x}T^{2}}\right)\hat{\unicode[STIX]{x1D70F}}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{F^{\prime }}{T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}+\frac{F}{2\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}=r_{t}\hat{{\mathcal{C}}}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{T^{\prime }}{T}\hat{u} _{m,n}+\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{T^{\prime }}{T^{2}}\hat{v}_{m,n}+\frac{1}{T}\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\text{i}n{\hat{w}}_{m,n}-\left(\frac{\text{i}m}{T}+\frac{FT^{\prime }}{2\bar{x}T^{2}}\right)\hat{\unicode[STIX]{x1D70F}}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{F^{\prime }}{T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}+\frac{F}{2\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}=r_{t}\hat{{\mathcal{C}}}_{m,n},\end{eqnarray}$$
the
![]() $x$
-momentum equation
$x$
-momentum equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\text{i}m-\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}F^{\prime \prime }+\unicode[STIX]{x1D705}^{2}n^{2}T\unicode[STIX]{x1D707}\right)\hat{u} _{m,n}+F^{\prime }\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{1}{2\bar{x}}\left(F+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{T}-\frac{\unicode[STIX]{x1D707}T^{\prime }}{T^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D707}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{F^{\prime \prime }}{T}\hat{v}_{m,n}+\left(\frac{FF^{\prime \prime }-\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime \prime }-\unicode[STIX]{x1D707}^{\prime \prime }F^{\prime \prime }T^{\prime }}{2\bar{x}T}+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }F^{\prime \prime }}{2\bar{x}T^{2}}\right)\hat{\unicode[STIX]{x1D70F}}_{m,n}-\frac{\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}=r_{t}\hat{{\mathcal{X}}}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\text{i}m-\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}F^{\prime \prime }+\unicode[STIX]{x1D705}^{2}n^{2}T\unicode[STIX]{x1D707}\right)\hat{u} _{m,n}+F^{\prime }\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{1}{2\bar{x}}\left(F+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{T}-\frac{\unicode[STIX]{x1D707}T^{\prime }}{T^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D707}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{F^{\prime \prime }}{T}\hat{v}_{m,n}+\left(\frac{FF^{\prime \prime }-\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime \prime }-\unicode[STIX]{x1D707}^{\prime \prime }F^{\prime \prime }T^{\prime }}{2\bar{x}T}+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }F^{\prime \prime }}{2\bar{x}T^{2}}\right)\hat{\unicode[STIX]{x1D70F}}_{m,n}-\frac{\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}=r_{t}\hat{{\mathcal{X}}}_{m,n},\end{eqnarray}$$
the
![]() $y$
-momentum equation
$y$
-momentum equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{4\bar{x}^{2}}\left[FT+\unicode[STIX]{x1D702}_{c}(FT^{\prime }-TF^{\prime })-\unicode[STIX]{x1D702}_{c}^{2}F^{\prime \prime }T\right]\hat{u} _{m,n}+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{3\bar{x}}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{\unicode[STIX]{x1D707}}{6\bar{x}}\frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\unicode[STIX]{x2202}\bar{x}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{12\bar{x}^{2}}\left(\unicode[STIX]{x1D707}+\unicode[STIX]{x1D702}_{c}T^{\prime }\unicode[STIX]{x1D707}^{\prime }-\frac{\unicode[STIX]{x1D707}T^{\prime }\unicode[STIX]{x1D702}_{c}}{T}\right)\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}}{12\bar{x}^{2}}\frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\text{i}m+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}F^{\prime \prime }+\frac{F^{\prime }}{2\bar{x}}-\frac{FT^{\prime }}{2\bar{x}T}+\unicode[STIX]{x1D705}^{2}n^{2}\unicode[STIX]{x1D707}T\right)\hat{v}_{m,n}+F^{\prime }\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{\bar{x}}\left(\frac{F}{2}+\frac{2\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{3T}-\frac{2\unicode[STIX]{x1D707}T^{\prime }}{3T^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{2\unicode[STIX]{x1D707}}{3\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}+\text{i}n\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{3\bar{x}}{\hat{w}}_{m,n}-\text{i}n\frac{\unicode[STIX]{x1D707}}{6\bar{x}}\frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{4\bar{x}^{2}}\left[\unicode[STIX]{x1D702}_{c}\left((FF^{\prime })^{\prime }-T\left(\frac{\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{T}\right)^{\prime }\right)-FF^{\prime }-\frac{F^{2}T^{\prime }}{T}-\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }+\frac{4}{3}\left(\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }F}{T}\right)^{\prime }\right]\hat{\unicode[STIX]{x1D70F}}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}+\left(\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }F}{3\bar{x}^{2}T}-\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{4\bar{x}^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{1}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{p}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}=r_{t}\hat{{\mathcal{Y}}}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{4\bar{x}^{2}}\left[FT+\unicode[STIX]{x1D702}_{c}(FT^{\prime }-TF^{\prime })-\unicode[STIX]{x1D702}_{c}^{2}F^{\prime \prime }T\right]\hat{u} _{m,n}+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{3\bar{x}}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{\unicode[STIX]{x1D707}}{6\bar{x}}\frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\unicode[STIX]{x2202}\bar{x}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{12\bar{x}^{2}}\left(\unicode[STIX]{x1D707}+\unicode[STIX]{x1D702}_{c}T^{\prime }\unicode[STIX]{x1D707}^{\prime }-\frac{\unicode[STIX]{x1D707}T^{\prime }\unicode[STIX]{x1D702}_{c}}{T}\right)\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}}{12\bar{x}^{2}}\frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\text{i}m+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}F^{\prime \prime }+\frac{F^{\prime }}{2\bar{x}}-\frac{FT^{\prime }}{2\bar{x}T}+\unicode[STIX]{x1D705}^{2}n^{2}\unicode[STIX]{x1D707}T\right)\hat{v}_{m,n}+F^{\prime }\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{\bar{x}}\left(\frac{F}{2}+\frac{2\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{3T}-\frac{2\unicode[STIX]{x1D707}T^{\prime }}{3T^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{2\unicode[STIX]{x1D707}}{3\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}+\text{i}n\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{3\bar{x}}{\hat{w}}_{m,n}-\text{i}n\frac{\unicode[STIX]{x1D707}}{6\bar{x}}\frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{4\bar{x}^{2}}\left[\unicode[STIX]{x1D702}_{c}\left((FF^{\prime })^{\prime }-T\left(\frac{\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{T}\right)^{\prime }\right)-FF^{\prime }-\frac{F^{2}T^{\prime }}{T}-\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }+\frac{4}{3}\left(\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }F}{T}\right)^{\prime }\right]\hat{\unicode[STIX]{x1D70F}}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}+\left(\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }F}{3\bar{x}^{2}T}-\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{4\bar{x}^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{1}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{p}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}=r_{t}\hat{{\mathcal{Y}}}_{m,n},\end{eqnarray}$$
the
![]() $z$
-momentum equation
$z$
-momentum equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}^{\prime }T^{\prime }T}{2\bar{x}}\hat{u} _{m,n}-\text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D707}T}{3}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}+\text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}T}{6\bar{x}}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }T^{\prime }\hat{v}_{m,m}-\text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D707}}{3}\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\text{i}m+\frac{4n^{2}\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}T}{3}\right){\hat{w}}_{m,n}+F^{\prime }\frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{1}{2\bar{x}}\left(F+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{T}-\frac{\unicode[STIX]{x1D707}T^{\prime }}{T^{2}}\right)\frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\unicode[STIX]{x1D707}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}-\frac{\text{i}n\unicode[STIX]{x1D705}^{2}FT^{\prime }\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}}\hat{\unicode[STIX]{x1D70F}}_{m,n}+\text{i}n\unicode[STIX]{x1D705}^{2}T\hat{p}_{m,n}=r_{t}\hat{{\mathcal{Z}}}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}^{\prime }T^{\prime }T}{2\bar{x}}\hat{u} _{m,n}-\text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D707}T}{3}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\bar{x}}+\text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}T}{6\bar{x}}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }T^{\prime }\hat{v}_{m,m}-\text{i}n\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x1D707}}{3}\frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left(\text{i}m+\frac{4n^{2}\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}T}{3}\right){\hat{w}}_{m,n}+F^{\prime }\frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{1}{2\bar{x}}\left(F+\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{T}-\frac{\unicode[STIX]{x1D707}T^{\prime }}{T^{2}}\right)\frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\unicode[STIX]{x1D707}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}-\frac{\text{i}n\unicode[STIX]{x1D705}^{2}FT^{\prime }\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}}\hat{\unicode[STIX]{x1D70F}}_{m,n}+\text{i}n\unicode[STIX]{x1D705}^{2}T\hat{p}_{m,n}=r_{t}\hat{{\mathcal{Z}}}_{m,n},\end{eqnarray}$$
and the energy equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{2\bar{x}}\hat{u} _{m,n}-\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}F^{\prime \prime }}{\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T}\hat{v}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[\text{i}m+\frac{FT^{\prime }}{2\bar{x}T}-\frac{1}{2Pr\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{T}\right)^{\prime }-\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}^{\prime }(F^{\prime \prime })^{2}}{2\bar{x}T}+\frac{\unicode[STIX]{x1D707}n^{2}\unicode[STIX]{x1D705}^{2}T}{Pr}\right]\hat{\unicode[STIX]{x1D70F}}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,F^{\prime }\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{1}{2\bar{x}}\left(F+\frac{2\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{PrT}-\frac{\unicode[STIX]{x1D707}T^{\prime }}{PrT^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D707}}{2Pr\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}=r_{t}\hat{{\mathcal{E}}}_{m,n},\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{2\bar{x}}\hat{u} _{m,n}-\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}F^{\prime \prime }}{\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T}\hat{v}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[\text{i}m+\frac{FT^{\prime }}{2\bar{x}T}-\frac{1}{2Pr\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{T}\right)^{\prime }-\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}^{\prime }(F^{\prime \prime })^{2}}{2\bar{x}T}+\frac{\unicode[STIX]{x1D707}n^{2}\unicode[STIX]{x1D705}^{2}T}{Pr}\right]\hat{\unicode[STIX]{x1D70F}}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,F^{\prime }\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\bar{x}}-\frac{1}{2\bar{x}}\left(F+\frac{2\unicode[STIX]{x1D707}^{\prime }T^{\prime }}{PrT}-\frac{\unicode[STIX]{x1D707}T^{\prime }}{PrT^{2}}\right)\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D707}}{2Pr\bar{x}T}\frac{\unicode[STIX]{x2202}^{2}\hat{\unicode[STIX]{x1D70F}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}=r_{t}\hat{{\mathcal{E}}}_{m,n},\qquad\end{eqnarray}$$
where the terms
![]() $\hat{{\mathcal{C}}}_{m,n}$
,
$\hat{{\mathcal{C}}}_{m,n}$
,
![]() $\hat{{\mathcal{X}}}_{m,n}$
,
$\hat{{\mathcal{X}}}_{m,n}$
,
![]() $\hat{{\mathcal{Y}}}_{m,n}$
,
$\hat{{\mathcal{Y}}}_{m,n}$
,
![]() $\hat{{\mathcal{Z}}}_{m,n}$
,
$\hat{{\mathcal{Z}}}_{m,n}$
,
![]() $\hat{{\mathcal{E}}}_{m,n}$
arise due to nonlinearity and are given in appendix A. The right-hand sides of (2.23)–(2.27), where the nonlinear terms are collected, vanish as
$\hat{{\mathcal{E}}}_{m,n}$
arise due to nonlinearity and are given in appendix A. The right-hand sides of (2.23)–(2.27), where the nonlinear terms are collected, vanish as
![]() $r_{t}\rightarrow 0$
so that the linearized compressible unsteady boundary-region equations of Ricco & Wu (Reference Ricco and Wu2007) are recovered. Note that the above fully nonlinear equations are to be used to predict the entire development of streaks even though the disturbance evolves through a linear stage near the leading edge.
$r_{t}\rightarrow 0$
so that the linearized compressible unsteady boundary-region equations of Ricco & Wu (Reference Ricco and Wu2007) are recovered. Note that the above fully nonlinear equations are to be used to predict the entire development of streaks even though the disturbance evolves through a linear stage near the leading edge.
2.3 The outer flow
The outer-flow dynamics is influenced by the displacement of the underlying boundary-layer flow. The displacement effect becomes of leading order at downstream distances where
![]() $\bar{x}=O(1)$
and the streamwise velocity fluctuations acquire an
$\bar{x}=O(1)$
and the streamwise velocity fluctuations acquire an
![]() $O(1)$
amplitude. The disturbance in the outer region consists of the three-dimensional vortical perturbation convected from upstream and of the two-dimensional disturbance arising from the boundary-layer displacement effect due to the nonlinear interactions in the boundary layer. The two-dimensional component attenuates over a wall-normal distance
$O(1)$
amplitude. The disturbance in the outer region consists of the three-dimensional vortical perturbation convected from upstream and of the two-dimensional disturbance arising from the boundary-layer displacement effect due to the nonlinear interactions in the boundary layer. The two-dimensional component attenuates over a wall-normal distance
![]() $O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, and thus depends on the relatively slow wall-normal variable
$O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, and thus depends on the relatively slow wall-normal variable
![]() $\bar{y}=k_{x}y=O(1)$
. The three-dimensional component depends on
$\bar{y}=k_{x}y=O(1)$
. The three-dimensional component depends on
![]() $y$
and, a priori, also on
$y$
and, a priori, also on
![]() $\bar{y}$
because its governing equations involve the two-dimensional component as we will discuss later. Following the approach of Wundrow & Goldstein (Reference Wundrow and Goldstein2001) and Ricco et al. (Reference Ricco, Luo and Wu2011), the outer-region solution is expanded as:
$\bar{y}$
because its governing equations involve the two-dimensional component as we will discuss later. Following the approach of Wundrow & Goldstein (Reference Wundrow and Goldstein2001) and Ricco et al. (Reference Ricco, Luo and Wu2011), the outer-region solution is expanded as:
where
![]() $\bar{t}\equiv k_{x}t=O(1)$
,
$\bar{t}\equiv k_{x}t=O(1)$
,
![]() $\boldsymbol{Q}$
is the uniform mean flow, and
$\boldsymbol{Q}$
is the uniform mean flow, and
![]() $\bar{\boldsymbol{q}_{0}}$
and
$\bar{\boldsymbol{q}_{0}}$
and
![]() $\boldsymbol{q}_{i}$
(
$\boldsymbol{q}_{i}$
(
![]() $i=0,1,\ldots$
) indicate the two-dimensional and three-dimensional disturbances, respectively.
$i=0,1,\ldots$
) indicate the two-dimensional and three-dimensional disturbances, respectively.
2.3.1 Linearized inviscid subsonic and supersonic flows
The two-dimensional inviscid part of the perturbation is considered first: the subsonic and supersonic regimes are analysed by extending the approach of Ricco et al. (Reference Ricco, Luo and Wu2011) to take compressibility into account. The transonic case is however beyond the scope of the present analysis. The two-dimensional terms
![]() $\{\bar{u}_{0},\bar{v}_{0},\bar{p}_{0},\bar{\unicode[STIX]{x1D70F}}_{0},\bar{\unicode[STIX]{x1D70C}}_{0}\}$
satisfy the linearized unsteady compressible Euler equations:
$\{\bar{u}_{0},\bar{v}_{0},\bar{p}_{0},\bar{\unicode[STIX]{x1D70F}}_{0},\bar{\unicode[STIX]{x1D70C}}_{0}\}$
satisfy the linearized unsteady compressible Euler equations:
where the density has been eliminated from the continuity equation by using the energy equation and the equation of state,
The displacement effect is associated with the transpiration velocity, i.e. the spanwise-averaged wall-normal velocity component at the boundary-layer outer edge. The continuity equation,
is integrated first with respect to
![]() $z$
over a spanwise period
$z$
over a spanwise period
![]() $\unicode[STIX]{x1D706}_{z}=2\unicode[STIX]{x03C0}/k_{z}$
and with respect to
$\unicode[STIX]{x1D706}_{z}=2\unicode[STIX]{x03C0}/k_{z}$
and with respect to
![]() $y$
from
$y$
from
![]() $0$
to
$0$
to
![]() $\infty$
. For the term
$\infty$
. For the term
![]() $\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}_{tot}w_{tot})/\unicode[STIX]{x2202}z$
a change in the order of integration is performed. At supersonic speeds this step is justified by the assumption that shock waves, if present, are of infinitesimal strength and therefore the flow remains smooth and isentropic. It follows that
$\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}_{tot}w_{tot})/\unicode[STIX]{x2202}z$
a change in the order of integration is performed. At supersonic speeds this step is justified by the assumption that shock waves, if present, are of infinitesimal strength and therefore the flow remains smooth and isentropic. It follows that
The first term on the right-hand side of (2.32) represents the derivative with respect to
![]() $\bar{x}$
of the spanwise-averaged boundary-layer displacement thickness, defined as
$\bar{x}$
of the spanwise-averaged boundary-layer displacement thickness, defined as
The second term on the right-hand side of (2.32) is due to compressibility effects and is not present in Ricco et al. (Reference Ricco, Luo and Wu2011). It can be written as the derivative with respect to
![]() $\bar{t}$
of a spanwise-averaged boundary-layer thickness
$\bar{t}$
of a spanwise-averaged boundary-layer thickness
![]() $\bar{\unicode[STIX]{x1D6FF}}^{c}$
defined as
$\bar{\unicode[STIX]{x1D6FF}}^{c}$
defined as
Matching the left-hand side of (2.32) with the outer flow gives
where the terms
![]() $O(\unicode[STIX]{x1D716}^{2})$
have been neglected. Therefore, equation (2.32) leads to
$O(\unicode[STIX]{x1D716}^{2})$
have been neglected. Therefore, equation (2.32) leads to
where the compressibility effects appear in the definition of the displacement thickness
![]() $\bar{\unicode[STIX]{x1D6FF}}$
and in the additional term
$\bar{\unicode[STIX]{x1D6FF}}$
and in the additional term
![]() $\bar{\unicode[STIX]{x1D6FF}}^{c}$
. Equation (2.36) is used as a boundary condition on the system (2.29).
$\bar{\unicode[STIX]{x1D6FF}}^{c}$
. Equation (2.36) is used as a boundary condition on the system (2.29).
The proof employed by Ricco et al. (Reference Ricco, Luo and Wu2011) to show the irrotationality of the two-dimensional flow holds for the compressible case as long as the flow remains isentropic (i.e. shock waves are absent or, if present, their effect is negligible). Therefore, the potential
![]() $\bar{\unicode[STIX]{x1D719}}_{0}$
is introduced such that
$\bar{\unicode[STIX]{x1D719}}_{0}$
is introduced such that
![]() $\unicode[STIX]{x1D735}_{\bar{x}\bar{y}}\bar{\unicode[STIX]{x1D719}}_{0}=\{\bar{u}_{0},\bar{v}_{0}\}$
, where
$\unicode[STIX]{x1D735}_{\bar{x}\bar{y}}\bar{\unicode[STIX]{x1D719}}_{0}=\{\bar{u}_{0},\bar{v}_{0}\}$
, where
![]() $\unicode[STIX]{x1D735}_{\bar{x}\bar{y}}$
denotes the gradient operator in the
$\unicode[STIX]{x1D735}_{\bar{x}\bar{y}}$
denotes the gradient operator in the
![]() $\bar{x}{-}\bar{y}$
plane. By rewriting (2.29) in terms of
$\bar{x}{-}\bar{y}$
plane. By rewriting (2.29) in terms of
![]() $\bar{\unicode[STIX]{x1D719}}_{0}$
and eliminating the pressure from the continuity equation with the aid of the momentum equations, a single equation for the potential is derived,
$\bar{\unicode[STIX]{x1D719}}_{0}$
and eliminating the pressure from the continuity equation with the aid of the momentum equations, a single equation for the potential is derived,
which is a wave (i.e. hyperbolic) equation, indicating the acoustic nature of the perturbation. It is interesting that streaks emit sound waves spontaneously during their nonlinear evolution. Equation (2.37) is of the same form as the linearized perturbation velocity potential equation governing the flow over a thin airfoil performing small unsteady (periodic) oscillations in the transverse direction (refer to Landahl Reference Landahl1989, equation (1.7)). The small thickness of the airfoil is represented here by the boundary-layer displacement thickness, the equivalent body being semi-infinite rather than finite and closed (i.e. with null thickness at both ends of the body).
The problem of the flow over a thin oscillating airfoil has been widely studied in aeroelasticity because of the loads and vibrations occurring on the wing. Thanks to the linearization, two separated cases are distinguished: the thickness problem (symmetrical) and the lifting problem (anti-symmetrical). Aeroelasticians are usually interested in the latter because of the contribution to the lift experienced by the wing (Dowell Reference Dowell2014). Here it suffices to state that the analogy between the boundary-layer displacement effect and the thin airfoil theory only concerns the thickness problem, as circulatory flow is absent. This analogy was first suggested by Lighthill (Reference Lighthill1958) for incompressible flows and its use in the study of steady flows outside boundary layers has been well established (Van Dyke Reference Van Dyke1975). However, to the best of our knowledge, this analogy has never been considered for unsteady boundary layers.
By employing Fourier decomposition in time,
equation (2.37) is recast into a generalized Helmholtz differential equation (i.e. telegraph equation) for the Fourier coefficients
![]() $\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y})$
:
$\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y})$
:
Performing the change
![]() $\hat{\unicode[STIX]{x1D719}}_{m}\rightarrow \hat{\unicode[STIX]{x1D6F7}}_{m}$
, where
$\hat{\unicode[STIX]{x1D719}}_{m}\rightarrow \hat{\unicode[STIX]{x1D6F7}}_{m}$
, where
the telegraph equation (2.39) is reduced to either the Helmholtz equation if
![]() $M_{\infty }<1$
or the Klein–Gordon equation if
$M_{\infty }<1$
or the Klein–Gordon equation if
![]() $M_{\infty }>1$
:
$M_{\infty }>1$
:
where the
![]() $+$
or
$+$
or
![]() $-$
sign correspond to the subsonic or supersonic case, respectively. The appropriate boundary conditions for (2.41) are:
$-$
sign correspond to the subsonic or supersonic case, respectively. The appropriate boundary conditions for (2.41) are:
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D6F7}}_{m}}{\unicode[STIX]{x2202}\bar{y}}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{k_{x}}{\unicode[STIX]{x1D716}}(\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c})\text{e}^{b\bar{x}/2},\quad & \bar{y}=0,\bar{x}\geqslant 0,\\ 0,\quad & \bar{y}=0,\bar{x}<0;\end{array}\right. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D6F7}}_{m}}{\unicode[STIX]{x2202}\bar{y}}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{k_{x}}{\unicode[STIX]{x1D716}}(\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c})\text{e}^{b\bar{x}/2},\quad & \bar{y}=0,\bar{x}\geqslant 0,\\ 0,\quad & \bar{y}=0,\bar{x}<0;\end{array}\right. & \displaystyle\end{eqnarray}$$
In the supersonic case it is convenient to solve for
![]() $\hat{\unicode[STIX]{x1D719}}_{m}$
directly. The fluid ahead of the body remains undisturbed and so the Laplace transform in the
$\hat{\unicode[STIX]{x1D719}}_{m}$
directly. The fluid ahead of the body remains undisturbed and so the Laplace transform in the
![]() $\bar{x}$
direction can be employed,
$\bar{x}$
direction can be employed,
The telegraph equation (2.39) and the boundary condition (2.42a
) for
![]() $\bar{x}\geqslant 0$
become:
$\bar{x}\geqslant 0$
become:
where
![]() $c^{2}=s^{2}(M_{\infty }^{2}-1)+mM_{\infty }^{2}(2\text{i}s-m)$
and
$c^{2}=s^{2}(M_{\infty }^{2}-1)+mM_{\infty }^{2}(2\text{i}s-m)$
and
![]() $\tilde{v}_{m}(s,0)$
indicates the Laplace transform of
$\tilde{v}_{m}(s,0)$
indicates the Laplace transform of
![]() $\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D719}}_{m}/\unicode[STIX]{x2202}\bar{y}$
at
$\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D719}}_{m}/\unicode[STIX]{x2202}\bar{y}$
at
![]() $\bar{y}=0$
. The solution to (2.44) is
$\bar{y}=0$
. The solution to (2.44) is
Inverting (2.45) and using the convolution theorem, one finds
 $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }>1) & = & \displaystyle -\frac{k_{x}}{\unicode[STIX]{x1D716}\sqrt{M_{\infty }^{2}-1}}\int _{0}^{\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1}}\!\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{-(\text{i}mM_{\infty }^{2}/(M_{\infty }^{2}-1))(\bar{x}-\bar{x}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,J_{0}\left[\frac{mM_{\infty }}{M_{\infty }^{2}-1}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}-\left(M_{\infty }^{2}-1\right)\bar{y}^{2}}\right]\,\text{d}\bar{x}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }>1) & = & \displaystyle -\frac{k_{x}}{\unicode[STIX]{x1D716}\sqrt{M_{\infty }^{2}-1}}\int _{0}^{\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1}}\!\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{-(\text{i}mM_{\infty }^{2}/(M_{\infty }^{2}-1))(\bar{x}-\bar{x}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,J_{0}\left[\frac{mM_{\infty }}{M_{\infty }^{2}-1}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}-\left(M_{\infty }^{2}-1\right)\bar{y}^{2}}\right]\,\text{d}\bar{x}_{0},\end{eqnarray}$$
where
![]() $J_{0}$
is the zeroth-order Bessel function of the first kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The procedure to derive (2.46) closely follows the theory proposed by Stewartson (Reference Stewartson1950) for harmonically oscillating thin airfoils in supersonic flows.
$J_{0}$
is the zeroth-order Bessel function of the first kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The procedure to derive (2.46) closely follows the theory proposed by Stewartson (Reference Stewartson1950) for harmonically oscillating thin airfoils in supersonic flows.
In the subsonic case, the disturbance is felt in all directions and so the use of the Laplace transform in
![]() $\bar{x}$
is not appropriate. The Fourier transform is instead employed and the analytic continuation of the Neumann boundary condition (2.42a
) to the complex plane
$\bar{x}$
is not appropriate. The Fourier transform is instead employed and the analytic continuation of the Neumann boundary condition (2.42a
) to the complex plane
![]() $\bar{\unicode[STIX]{x1D709}}=\bar{x}+\text{i}\bar{y}$
is considered. The solution reads
$\bar{\unicode[STIX]{x1D709}}=\bar{x}+\text{i}\bar{y}$
is considered. The solution reads
 $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }<1) & = & \displaystyle -\frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}\sqrt{1-M_{\infty }^{2}}}\int _{\bar{x}-\text{i}\bar{y}\sqrt{1-M_{\infty }^{2}}}^{\bar{x}+\text{i}\bar{y}\sqrt{1-M_{\infty }^{2}}}\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{\unicode[STIX]{x1D709}})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{\unicode[STIX]{x1D709}})\right]\text{e}^{(\text{i}mM_{\infty }^{2}/(1-M_{\infty }^{2}))(\bar{x}-\bar{\unicode[STIX]{x1D709}})}\nonumber\\ \displaystyle & & \displaystyle \times \,J_{0}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{\left(\bar{x}-\bar{\unicode[STIX]{x1D709}}\right)^{2}+\left(1-M_{\infty }^{2}\right)\bar{y}^{2}}\right]\,\text{d}\bar{\unicode[STIX]{x1D709}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }<1) & = & \displaystyle -\frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}\sqrt{1-M_{\infty }^{2}}}\int _{\bar{x}-\text{i}\bar{y}\sqrt{1-M_{\infty }^{2}}}^{\bar{x}+\text{i}\bar{y}\sqrt{1-M_{\infty }^{2}}}\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{\unicode[STIX]{x1D709}})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{\unicode[STIX]{x1D709}})\right]\text{e}^{(\text{i}mM_{\infty }^{2}/(1-M_{\infty }^{2}))(\bar{x}-\bar{\unicode[STIX]{x1D709}})}\nonumber\\ \displaystyle & & \displaystyle \times \,J_{0}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{\left(\bar{x}-\bar{\unicode[STIX]{x1D709}}\right)^{2}+\left(1-M_{\infty }^{2}\right)\bar{y}^{2}}\right]\,\text{d}\bar{\unicode[STIX]{x1D709}}.\end{eqnarray}$$
The solution can also be expressed in terms of the Green’s function by modelling the boundary-layer thickness as a distribution of pulsating sources as suggested by Lighthill’s theory. The free-space Green’s function associated with the Helmholtz equation (2.41) is given by Dragos (Reference Dragos2004) on p. 33 for a single source located in the origin. Considering a line distribution of these sources at the point
![]() $(\bar{x}_{0},0)$
, where
$(\bar{x}_{0},0)$
, where
![]() $\bar{x}_{0}$
spans the
$\bar{x}_{0}$
spans the
![]() $\bar{x}$
axis, and using the method of images to include the boundary
$\bar{x}$
axis, and using the method of images to include the boundary
![]() $\bar{y}=0$
, we obtain
$\bar{y}=0$
, we obtain
 $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }<1) & = & \displaystyle \frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}\sqrt{1-M_{\infty }^{2}}}\int _{0}^{\infty }\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{(\text{i}mM_{\infty }^{2}/(1-M_{\infty }^{2}))\left(\bar{x}-\bar{x}_{0}\right)}\nonumber\\ \displaystyle & & \displaystyle \times \,H_{0}^{(2)}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}+\left(1-M_{\infty }^{2}\right)\bar{y}^{2}}\right]\,\text{d}\bar{x}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }<1) & = & \displaystyle \frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}\sqrt{1-M_{\infty }^{2}}}\int _{0}^{\infty }\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{(\text{i}mM_{\infty }^{2}/(1-M_{\infty }^{2}))\left(\bar{x}-\bar{x}_{0}\right)}\nonumber\\ \displaystyle & & \displaystyle \times \,H_{0}^{(2)}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}+\left(1-M_{\infty }^{2}\right)\bar{y}^{2}}\right]\,\text{d}\bar{x}_{0},\end{eqnarray}$$
where
![]() $H_{0}^{(2)}$
is the zeroth-order Hankel function of the second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The solution with
$H_{0}^{(2)}$
is the zeroth-order Hankel function of the second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The solution with
![]() $H_{0}^{(2)}$
has been chosen instead of that with
$H_{0}^{(2)}$
has been chosen instead of that with
![]() $H_{0}^{(1)}$
to ensure outgoing waves radiating from the source. As
$H_{0}^{(1)}$
to ensure outgoing waves radiating from the source. As
![]() $M_{\infty }\rightarrow 0$
, equation (2.47) matches the solution obtained in the incompressible case (Ricco et al.
Reference Ricco, Luo and Wu2011):
$M_{\infty }\rightarrow 0$
, equation (2.47) matches the solution obtained in the incompressible case (Ricco et al.
Reference Ricco, Luo and Wu2011):
 $$\begin{eqnarray}\displaystyle \lim _{M_{\infty }\rightarrow 0}\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }<1) & = & \displaystyle -\frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}}\int _{\bar{x}-\text{i}\bar{y}}^{\bar{x}+\text{i}\bar{y}}\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\unicode[STIX]{x1D709})\,\text{d}\unicode[STIX]{x1D709}=-\frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}}[\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{x}+\text{i}\bar{y})-\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{x}-\text{i}\bar{y})]\nonumber\\ \displaystyle & = & \displaystyle \frac{k_{x}}{\unicode[STIX]{x1D716}}\operatorname{Im}[\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{x}+\text{i}\bar{y})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{M_{\infty }\rightarrow 0}\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y};M_{\infty }<1) & = & \displaystyle -\frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}}\int _{\bar{x}-\text{i}\bar{y}}^{\bar{x}+\text{i}\bar{y}}\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\unicode[STIX]{x1D709})\,\text{d}\unicode[STIX]{x1D709}=-\frac{\text{i}k_{x}}{2\unicode[STIX]{x1D716}}[\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{x}+\text{i}\bar{y})-\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{x}-\text{i}\bar{y})]\nonumber\\ \displaystyle & = & \displaystyle \frac{k_{x}}{\unicode[STIX]{x1D716}}\operatorname{Im}[\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{x}+\text{i}\bar{y})],\end{eqnarray}$$
where
![]() $\operatorname{Im}$
indicates the imaginary part and use has been made of the property of holomorphic functions,
$\operatorname{Im}$
indicates the imaginary part and use has been made of the property of holomorphic functions,
![]() $\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{\unicode[STIX]{x1D709}}^{\star })=$
$\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{\unicode[STIX]{x1D709}}^{\star })=$
![]() $\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{\unicode[STIX]{x1D709}})^{\star }$
. The limit
$\hat{\unicode[STIX]{x1D6FF}}_{m}(\bar{\unicode[STIX]{x1D709}})^{\star }$
. The limit
![]() $M_{\infty }\rightarrow \infty$
is not considered because for very large hypersonic Mach numbers the Blasius boundary-layer assumption of negligible wall-normal pressure gradient is invalid (refer to Anderson Reference Anderson2006, p. 275).
$M_{\infty }\rightarrow \infty$
is not considered because for very large hypersonic Mach numbers the Blasius boundary-layer assumption of negligible wall-normal pressure gradient is invalid (refer to Anderson Reference Anderson2006, p. 275).
The pressure is obtained from the
![]() $y$
-momentum equation (2.29) as
$y$
-momentum equation (2.29) as
or, in Fourier space,
From substitution of the supersonic and subsonic expressions for the potential, equations (2.46) and (2.48), into (2.51), it follows that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hat{p}_{m}(\bar{x},\bar{y};M_{\infty }>1)=\frac{k_{x}}{\unicode[STIX]{x1D716}\sqrt{M_{\infty }^{2}-1}}\left\{\int _{0}^{\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1}}f(\bar{x_{0}},\bar{x},\bar{y})\,\text{d}\bar{x}_{0}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \left.\vphantom{\int _{0}^{\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1}}}-\,\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1})\right]\text{e}^{-(\text{i}mM_{\infty }^{2}/\sqrt{M_{\infty }^{2}-1})\bar{y}}\right\}\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hat{p}_{m}(\bar{x},\bar{y};M_{\infty }>1)=\frac{k_{x}}{\unicode[STIX]{x1D716}\sqrt{M_{\infty }^{2}-1}}\left\{\int _{0}^{\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1}}f(\bar{x_{0}},\bar{x},\bar{y})\,\text{d}\bar{x}_{0}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \left.\vphantom{\int _{0}^{\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1}}}-\,\left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}-\bar{y}\sqrt{M_{\infty }^{2}-1})\right]\text{e}^{-(\text{i}mM_{\infty }^{2}/\sqrt{M_{\infty }^{2}-1})\bar{y}}\right\}\qquad\end{eqnarray}$$
in the supersonic case, where
 $$\begin{eqnarray}\displaystyle f & = & \displaystyle \left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{-(\text{i}mM_{\infty }^{2}/(M_{\infty }^{2}-1))\left(\bar{x}-\bar{x}_{0}\right)}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\frac{\text{i}m}{M_{\infty }^{2}-1}J_{0}\left[\frac{mM_{\infty }}{M_{\infty }^{2}-1}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}-\left(M_{\infty }^{2}-1\right)\bar{y}^{2}}\right]\vphantom{\frac{mM_{\infty }}{\sqrt{(\bar{x}-\bar{x}_{0})^{2}-(M_{\infty }^{2}-1)\bar{y}^{2}}}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{mM_{\infty }(\bar{x}-\bar{x}_{0})}{(M_{\infty }^{2}-1)\sqrt{(\bar{x}-\bar{x}_{0})^{2}-(M_{\infty }^{2}-1)\bar{y}^{2}}}J_{1}\left[\frac{mM_{\infty }}{M_{\infty }^{2}-1}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}-\left(M_{\infty }^{2}-1\right)\bar{y}^{2}}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f & = & \displaystyle \left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{-(\text{i}mM_{\infty }^{2}/(M_{\infty }^{2}-1))\left(\bar{x}-\bar{x}_{0}\right)}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\frac{\text{i}m}{M_{\infty }^{2}-1}J_{0}\left[\frac{mM_{\infty }}{M_{\infty }^{2}-1}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}-\left(M_{\infty }^{2}-1\right)\bar{y}^{2}}\right]\vphantom{\frac{mM_{\infty }}{\sqrt{(\bar{x}-\bar{x}_{0})^{2}-(M_{\infty }^{2}-1)\bar{y}^{2}}}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{mM_{\infty }(\bar{x}-\bar{x}_{0})}{(M_{\infty }^{2}-1)\sqrt{(\bar{x}-\bar{x}_{0})^{2}-(M_{\infty }^{2}-1)\bar{y}^{2}}}J_{1}\left[\frac{mM_{\infty }}{M_{\infty }^{2}-1}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}-\left(M_{\infty }^{2}-1\right)\bar{y}^{2}}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and
![]() $J_{1}$
is the first-order Bessel function of the first kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964), and in the subsonic case
$J_{1}$
is the first-order Bessel function of the first kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964), and in the subsonic case
where
 $$\begin{eqnarray}\displaystyle g & = & \displaystyle \left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{(\text{i}mM_{\infty }^{2}/(1-M_{\infty }^{2}))(\bar{x}-\bar{x}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\frac{\text{i}m}{1-M_{\infty }^{2}}H_{0}^{(2)}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}+\left(1-M_{\infty }^{2}\right)\bar{y}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{mM_{\infty }\left(\bar{x}-\bar{x}_{0}\right)}{(1-M_{\infty }^{2})\sqrt{(\bar{x}-\bar{x}_{0})^{2}+(1-M_{\infty }^{2})\bar{y}^{2}}}\nonumber\\ \displaystyle & & \displaystyle \left.\times \,H_{1}^{(2)}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{(\bar{x}-\bar{x}_{0})^{2}+(1-M_{\infty }^{2})\bar{y}^{2}}\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g & = & \displaystyle \left[\hat{\unicode[STIX]{x1D6FF}}_{m}^{\prime }(\bar{x}_{0})+\text{i}m\hat{\unicode[STIX]{x1D6FF}}_{m}^{c}(\bar{x}_{0})\right]\text{e}^{(\text{i}mM_{\infty }^{2}/(1-M_{\infty }^{2}))(\bar{x}-\bar{x}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\frac{\text{i}m}{1-M_{\infty }^{2}}H_{0}^{(2)}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{\left(\bar{x}-\bar{x}_{0}\right)^{2}+\left(1-M_{\infty }^{2}\right)\bar{y}^{2}}\right]\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{mM_{\infty }\left(\bar{x}-\bar{x}_{0}\right)}{(1-M_{\infty }^{2})\sqrt{(\bar{x}-\bar{x}_{0})^{2}+(1-M_{\infty }^{2})\bar{y}^{2}}}\nonumber\\ \displaystyle & & \displaystyle \left.\times \,H_{1}^{(2)}\left[\frac{mM_{\infty }}{1-M_{\infty }^{2}}\sqrt{(\bar{x}-\bar{x}_{0})^{2}+(1-M_{\infty }^{2})\bar{y}^{2}}\right]\right\},\end{eqnarray}$$
and
![]() $H_{1}^{(2)}$
is the first-order Hankel function of the second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The temperature is found from the energy equation (2.30) as
$H_{1}^{(2)}$
is the first-order Hankel function of the second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The temperature is found from the energy equation (2.30) as
2.3.2 Viscous three-dimensional flow
By substituting the expansion (2.28) into the Navier–Stokes equations and subtracting the equations (2.29) and (2.30) for the displacement-induced disturbance, the leading-order three-dimensional part of the perturbation is found to satisfy the equations:
 $$\begin{eqnarray}\left\{\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{t}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D716}}{k_{x}}\left[(\bar{v}_{0}+v_{0})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}+w_{0}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\right]\right\}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ \unicode[STIX]{x1D70F}_{0}\end{array}\right\}=-\frac{\unicode[STIX]{x1D716}}{k_{x}}\left\{\begin{array}{@{}c@{}}0\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}y\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}z\\ 0\end{array}\right\}+\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D6FB}_{yz}^{2}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ Pr^{-1}\unicode[STIX]{x1D70F}_{0}\end{array}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\left\{\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{t}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D716}}{k_{x}}\left[(\bar{v}_{0}+v_{0})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}+w_{0}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\right]\right\}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ \unicode[STIX]{x1D70F}_{0}\end{array}\right\}=-\frac{\unicode[STIX]{x1D716}}{k_{x}}\left\{\begin{array}{@{}c@{}}0\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}y\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}z\\ 0\end{array}\right\}+\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D6FB}_{yz}^{2}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ Pr^{-1}\unicode[STIX]{x1D70F}_{0}\end{array}\right\},\end{eqnarray}$$
where
![]() $p_{0}=0$
without loss of generality and
$p_{0}=0$
without loss of generality and
![]() $\unicode[STIX]{x1D735}_{yz}$
is the gradient operator in the
$\unicode[STIX]{x1D735}_{yz}$
is the gradient operator in the
![]() $y{-}z$
plane.
$y{-}z$
plane.
The three-dimensional part of the perturbation in (2.57) and (2.58) does not directly depend on the slow variable
![]() $\bar{y}$
at the leading order, but the momentum equations (2.58) include the inviscid wall-normal velocity component
$\bar{y}$
at the leading order, but the momentum equations (2.58) include the inviscid wall-normal velocity component
![]() $\bar{v}_{0}$
, which depends on
$\bar{v}_{0}$
, which depends on
![]() $\bar{y}$
. Therefore, the dependence of the leading-order three-dimensional disturbance upon
$\bar{y}$
. Therefore, the dependence of the leading-order three-dimensional disturbance upon
![]() $\bar{y}$
is parametric. The aim of the following analysis is to decouple (2.58) from
$\bar{y}$
is parametric. The aim of the following analysis is to decouple (2.58) from
![]() $\bar{v}_{0}$
to obtain a system of equations in the only unknowns
$\bar{v}_{0}$
to obtain a system of equations in the only unknowns
![]() $\left\{u_{0},v_{0},w_{0},\unicode[STIX]{x1D70F}_{0},p_{1}\right\}$
. This is accomplished by introducing the Prandtl transformation,
$\left\{u_{0},v_{0},w_{0},\unicode[STIX]{x1D70F}_{0},p_{1}\right\}$
. This is accomplished by introducing the Prandtl transformation,
![]() ${\hat{y}}=y-\operatorname{Re}[\unicode[STIX]{x1D6E5}(\bar{\unicode[STIX]{x1D709}},\bar{t})]$
, where
${\hat{y}}=y-\operatorname{Re}[\unicode[STIX]{x1D6E5}(\bar{\unicode[STIX]{x1D709}},\bar{t})]$
, where
![]() $\operatorname{Re}$
denotes the real part and
$\operatorname{Re}$
denotes the real part and
![]() $\unicode[STIX]{x1D6E5}$
is suitably chosen to eliminate the coupling between
$\unicode[STIX]{x1D6E5}$
is suitably chosen to eliminate the coupling between
![]() $\left\{u_{0},v_{0},w_{0},\unicode[STIX]{x1D70F}_{0},p_{1}\right\}$
and
$\left\{u_{0},v_{0},w_{0},\unicode[STIX]{x1D70F}_{0},p_{1}\right\}$
and
![]() $\bar{v}_{0}$
from (2.58). The new variable
$\bar{v}_{0}$
from (2.58). The new variable
![]() ${\hat{y}}$
is written in this form for consistency with the previous analyses of Wundrow & Goldstein (Reference Wundrow and Goldstein2001) and Ricco et al. (Reference Ricco, Luo and Wu2011), although it will turn out that only the dependence of
${\hat{y}}$
is written in this form for consistency with the previous analyses of Wundrow & Goldstein (Reference Wundrow and Goldstein2001) and Ricco et al. (Reference Ricco, Luo and Wu2011), although it will turn out that only the dependence of
![]() $\unicode[STIX]{x1D6E5}$
on the real variables
$\unicode[STIX]{x1D6E5}$
on the real variables
![]() $\bar{x}$
and
$\bar{x}$
and
![]() $\bar{t}$
is relevant since we are interested in the matching at
$\bar{t}$
is relevant since we are interested in the matching at
![]() $\bar{y}=0$
. Written in terms of
$\bar{y}=0$
. Written in terms of
![]() ${\hat{y}}$
, equations (2.57) and (2.58) become
${\hat{y}}$
, equations (2.57) and (2.58) become
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{N}}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ \unicode[STIX]{x1D70F}_{0}\end{array}\right\}=-\frac{\unicode[STIX]{x1D716}}{k_{x}}\left\{\begin{array}{@{}c@{}}0\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}{\hat{y}}\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}z\\ 0\end{array}\right\}+\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D6FB}_{{\hat{y}}z}^{2}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ Pr^{-1}\unicode[STIX]{x1D70F}_{0}\end{array}\right\}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{N}}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ \unicode[STIX]{x1D70F}_{0}\end{array}\right\}=-\frac{\unicode[STIX]{x1D716}}{k_{x}}\left\{\begin{array}{@{}c@{}}0\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}{\hat{y}}\\ \unicode[STIX]{x2202}p_{1}/\unicode[STIX]{x2202}z\\ 0\end{array}\right\}+\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D6FB}_{{\hat{y}}z}^{2}\left\{\begin{array}{@{}c@{}}u_{0}\\ v_{0}\\ w_{0}\\ Pr^{-1}\unicode[STIX]{x1D70F}_{0}\end{array}\right\}, & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D735}_{{\hat{y}}z}$
is the gradient operator in the
$\unicode[STIX]{x1D735}_{{\hat{y}}z}$
is the gradient operator in the
![]() ${\hat{y}}{-}z$
plane and
${\hat{y}}{-}z$
plane and
![]() ${\mathcal{N}}$
is the differential operator:
${\mathcal{N}}$
is the differential operator:
The dependence on
![]() $\bar{v}_{0}$
is removed by choosing
$\bar{v}_{0}$
is removed by choosing
![]() $\unicode[STIX]{x1D6E5}$
to satisfy (Ricco et al.
Reference Ricco, Luo and Wu2011)
$\unicode[STIX]{x1D6E5}$
to satisfy (Ricco et al.
Reference Ricco, Luo and Wu2011)
which, in view of (2.36), becomes
Decomposing
![]() $\unicode[STIX]{x1D6E5}$
into Fourier series as
$\unicode[STIX]{x1D6E5}$
into Fourier series as
and using the time Fourier series of
![]() $\bar{\unicode[STIX]{x1D6FF}}$
and
$\bar{\unicode[STIX]{x1D6FF}}$
and
![]() $\bar{\unicode[STIX]{x1D6FF}}^{c}$
, we obtain the expression for
$\bar{\unicode[STIX]{x1D6FF}}^{c}$
, we obtain the expression for
![]() $\hat{\unicode[STIX]{x1D6E5}}_{m}$
,
$\hat{\unicode[STIX]{x1D6E5}}_{m}$
,
where the condition
![]() $\unicode[STIX]{x1D6E5}(0,\bar{t})=0$
,
$\unicode[STIX]{x1D6E5}(0,\bar{t})=0$
,
![]() $\forall \bar{t}>0$
has been employed.
$\forall \bar{t}>0$
has been employed.
Equation (2.60) shows that the streamwise velocity
![]() $u_{0}$
and the temperature
$u_{0}$
and the temperature
![]() $\unicode[STIX]{x1D70F}_{0}$
are decoupled from the transverse velocities
$\unicode[STIX]{x1D70F}_{0}$
are decoupled from the transverse velocities
![]() $\{v_{0},w_{0}\}$
and from the pressure
$\{v_{0},w_{0}\}$
and from the pressure
![]() $p_{1}$
. At leading order, only
$p_{1}$
. At leading order, only
![]() $\{v_{0},w_{0},p_{1}\}$
enter the matching with the boundary-layer solution, while the matching of
$\{v_{0},w_{0},p_{1}\}$
enter the matching with the boundary-layer solution, while the matching of
![]() $\{u_{0},\unicode[STIX]{x1D70F}_{0}\}$
needs to be considered when a solution with an order of accuracy higher than
$\{u_{0},\unicode[STIX]{x1D70F}_{0}\}$
needs to be considered when a solution with an order of accuracy higher than
![]() $O(R_{\unicode[STIX]{x1D706}}^{-1})$
is sought.
$O(R_{\unicode[STIX]{x1D706}}^{-1})$
is sought.
In view of the continuity equation (2.59), the streamfunction
![]() $\unicode[STIX]{x1D713}_{0}(\bar{x},{\hat{y}},z,\bar{t})$
is introduced such that
$\unicode[STIX]{x1D713}_{0}(\bar{x},{\hat{y}},z,\bar{t})$
is introduced such that
![]() $\unicode[STIX]{x1D735}_{{\hat{y}}z}\unicode[STIX]{x1D713}_{0}=\{-w_{0},v_{0}\}$
. In terms of the streamfunction the transverse momentum equations are recast into a transport equation for the longitudinal vorticity
$\unicode[STIX]{x1D735}_{{\hat{y}}z}\unicode[STIX]{x1D713}_{0}=\{-w_{0},v_{0}\}$
. In terms of the streamfunction the transverse momentum equations are recast into a transport equation for the longitudinal vorticity
![]() $\unicode[STIX]{x1D6FB}_{{\hat{y}}z}^{2}\unicode[STIX]{x1D713}_{0}$
,
$\unicode[STIX]{x1D6FB}_{{\hat{y}}z}^{2}\unicode[STIX]{x1D713}_{0}$
,
along with the Poisson equation for the pressure,
In the general case of a full spectrum of free-stream vortical disturbances, the streamfunction is decomposed as:
By substituting (2.68) into (2.66) and expanding the resulting equation for a pair of oblique forcing modes, the nonlinear terms cancel out and (2.66) reduces to
with
![]() $\{m,j,n\}=\{1,-1,\pm 1\}$
. The solution is:
$\{m,j,n\}=\{1,-1,\pm 1\}$
. The solution is:
where
![]() $c_{\infty }=1/k_{y}$
is chosen to normalize the amplitude of the free-stream spanwise velocity to unity. From (2.68) and (2.70) it follows that
$c_{\infty }=1/k_{y}$
is chosen to normalize the amplitude of the free-stream spanwise velocity to unity. From (2.68) and (2.70) it follows that
The transverse velocities are obtained as
By inserting (2.71) into (2.67), the pressure is found to be
At
![]() $\bar{y}=0$
, the expression
$\bar{y}=0$
, the expression
![]() ${\hat{y}}=y-\unicode[STIX]{x1D6E5}(\bar{x},\bar{t})$
is substituted into (2.71)–(2.73), and the time-dependent terms are expanded into Fourier series,
${\hat{y}}=y-\unicode[STIX]{x1D6E5}(\bar{x},\bar{t})$
is substituted into (2.71)–(2.73), and the time-dependent terms are expanded into Fourier series,
Rewriting (2.72) and (2.73) with the aid of (2.74), the outer-flow solution for
![]() $y=O(1)$
is obtained as
$y=O(1)$
is obtained as
with
2.4 Initial and boundary conditions
As the boundary-region equations (2.23)–(2.27) constitute a parabolic system in the streamwise direction, initial conditions are needed for
![]() $\bar{x}\ll 1$
. Since the velocity and temperature fluctuations are of small amplitude near the leading edge, their governing equations become linear. This was elucidated by Ricco et al. (Reference Ricco, Luo and Wu2011), who showed that the full nonlinear regime develops gradually from the initial linear stage in the upstream region corresponding to
$\bar{x}\ll 1$
. Since the velocity and temperature fluctuations are of small amplitude near the leading edge, their governing equations become linear. This was elucidated by Ricco et al. (Reference Ricco, Luo and Wu2011), who showed that the full nonlinear regime develops gradually from the initial linear stage in the upstream region corresponding to
![]() $R_{\unicode[STIX]{x1D706}}^{-1}\ll \bar{x}\ll 1$
. The initial conditions for the forced modes
$R_{\unicode[STIX]{x1D706}}^{-1}\ll \bar{x}\ll 1$
. The initial conditions for the forced modes
![]() $(m,n)=(1,\pm 1)$
are thus the same as those in Ricco & Wu (Reference Ricco and Wu2007).
$(m,n)=(1,\pm 1)$
are thus the same as those in Ricco & Wu (Reference Ricco and Wu2007).
The upstream conditions are found by first seeking the power series solution for
![]() $\unicode[STIX]{x1D702}=O(1)$
and
$\unicode[STIX]{x1D702}=O(1)$
and
![]() $\bar{x}\ll 1$
,
$\bar{x}\ll 1$
,
and by constructing a composite solution that is valid for
![]() $\bar{x}\ll 1$
and
$\bar{x}\ll 1$
and
![]() $\forall \unicode[STIX]{x1D702}$
:
$\forall \unicode[STIX]{x1D702}$
:
where
![]() $\{U_{in},V_{in},W_{in},T_{in},P_{in}\}$
are equal to the right-hand sides of equations (4.12)–(4.16) in Ricco & Wu (Reference Ricco and Wu2007). The term
$\{U_{in},V_{in},W_{in},T_{in},P_{in}\}$
are equal to the right-hand sides of equations (4.12)–(4.16) in Ricco & Wu (Reference Ricco and Wu2007). The term
![]() $u_{z,w,\pm }$
represents the spanwise slip velocity at the surface of the plate (refer to Leib et al.
Reference Leib, Wundrow and Goldstein1999, equation (3.14)). In the case of a pair of oblique modes, it is given by
$u_{z,w,\pm }$
represents the spanwise slip velocity at the surface of the plate (refer to Leib et al.
Reference Leib, Wundrow and Goldstein1999, equation (3.14)). In the case of a pair of oblique modes, it is given by
For all the other harmonics generated by nonlinear effects, null initial velocity, temperature and pressure profiles are imposed.
The velocity fluctuations are required to vanish at the wall (no-slip condition). Two types of different thermal boundary conditions at the wall may be imposed: the Dirichlet boundary condition,
![]() $\bar{\unicode[STIX]{x1D70F}}(0)=0$
, which was also employed by Ricco & Wu (Reference Ricco and Wu2007), and the Neumann boundary condition,
$\bar{\unicode[STIX]{x1D70F}}(0)=0$
, which was also employed by Ricco & Wu (Reference Ricco and Wu2007), and the Neumann boundary condition,
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{\unicode[STIX]{x1D702}=0}=0$
. The condition
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}|_{\unicode[STIX]{x1D702}=0}=0$
. The condition
![]() $\bar{\unicode[STIX]{x1D70F}}(0)=0$
is used herein as Ricco et al. (Reference Ricco, Tran and Ye2009) showed that there is no substantial difference in the development of the Klebanoff modes.
$\bar{\unicode[STIX]{x1D70F}}(0)=0$
is used herein as Ricco et al. (Reference Ricco, Tran and Ye2009) showed that there is no substantial difference in the development of the Klebanoff modes.
As
![]() $\unicode[STIX]{x1D702}\rightarrow \infty$
, the boundary-region solution must match to the limit
$\unicode[STIX]{x1D702}\rightarrow \infty$
, the boundary-region solution must match to the limit
![]() $\bar{y}\rightarrow 0$
of the outer flow. On taking into account the decomposition (2.16) and (2.17) within the boundary layer, the matching with the outer solution (2.75) requires that
$\bar{y}\rightarrow 0$
of the outer flow. On taking into account the decomposition (2.16) and (2.17) within the boundary layer, the matching with the outer solution (2.75) requires that
for
![]() $\bar{x}=O(1)$
, where the condition on
$\bar{x}=O(1)$
, where the condition on
![]() $\hat{v}_{m,n}$
holds only for
$\hat{v}_{m,n}$
holds only for
![]() $n\neq 0$
. In the spanwise-averaged equations (
$n\neq 0$
. In the spanwise-averaged equations (
![]() $n=0$
) the pressure only appears in the
$n=0$
) the pressure only appears in the
![]() $y$
-momentum equation. The velocities and the temperature are calculated by solving the continuity,
$y$
-momentum equation. The velocities and the temperature are calculated by solving the continuity,
![]() $x$
- and
$x$
- and
![]() $z$
-momentum and the energy equations. The condition on
$z$
-momentum and the energy equations. The condition on
![]() $\hat{v}_{m,0}$
as
$\hat{v}_{m,0}$
as
![]() $\unicode[STIX]{x1D702}\rightarrow \infty$
is not needed because the order of the system has decreased. As an a posteriori check, the free-stream value of
$\unicode[STIX]{x1D702}\rightarrow \infty$
is not needed because the order of the system has decreased. As an a posteriori check, the free-stream value of
![]() $\hat{v}_{m,0}$
is obtained from the large-
$\hat{v}_{m,0}$
is obtained from the large-
![]() $\unicode[STIX]{x1D702}$
limit of the continuity equation,
$\unicode[STIX]{x1D702}$
limit of the continuity equation,
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -\int _{0}^{\infty }\left(\frac{\unicode[STIX]{x2202}\hat{u} _{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\hat{u} _{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}+\int _{0}^{\infty }\frac{F^{\prime }}{T}\left(\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\hat{\unicode[STIX]{x1D70F}}_{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}+\int _{0}^{\infty }\frac{\text{i}m}{T}\hat{\unicode[STIX]{x1D70F}}_{m,0}\text{d}\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}\int _{0}^{\infty }T\left(\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}_{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}_{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}+r_{t}\int _{0}^{\infty }\frac{\text{i}m}{T}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}_{m,0}\,\text{d}\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle +\,r_{t}\int _{0}^{\infty }F^{\prime }\left(\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}_{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}_{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}\quad \text{as}~\unicode[STIX]{x1D702}\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -\int _{0}^{\infty }\left(\frac{\unicode[STIX]{x2202}\hat{u} _{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\hat{u} _{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}+\int _{0}^{\infty }\frac{F^{\prime }}{T}\left(\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70F}}_{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\hat{\unicode[STIX]{x1D70F}}_{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}+\int _{0}^{\infty }\frac{\text{i}m}{T}\hat{\unicode[STIX]{x1D70F}}_{m,0}\text{d}\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}\int _{0}^{\infty }T\left(\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}_{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}_{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}+r_{t}\int _{0}^{\infty }\frac{\text{i}m}{T}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}_{m,0}\,\text{d}\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle +\,r_{t}\int _{0}^{\infty }F^{\prime }\left(\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}_{m,0}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}_{m,0}}{2\bar{x}}\right)\,\text{d}\unicode[STIX]{x1D702}\quad \text{as}~\unicode[STIX]{x1D702}\rightarrow \infty ,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}_{bl}$
is the compressible Blasius displacement thickness,
$\unicode[STIX]{x1D6FF}_{bl}$
is the compressible Blasius displacement thickness,
and
![]() $\unicode[STIX]{x1D6FE}_{c}=\unicode[STIX]{x1D702}_{c}-\unicode[STIX]{x1D702}$
as
$\unicode[STIX]{x1D6FE}_{c}=\unicode[STIX]{x1D702}_{c}-\unicode[STIX]{x1D702}$
as
![]() $\unicode[STIX]{x1D702}\rightarrow \infty$
. In the limit
$\unicode[STIX]{x1D702}\rightarrow \infty$
. In the limit
![]() $M_{\infty }\rightarrow 0$
the result of Ricco et al. (Reference Ricco, Luo and Wu2011) is recovered:
$M_{\infty }\rightarrow 0$
the result of Ricco et al. (Reference Ricco, Luo and Wu2011) is recovered:
where
![]() $\unicode[STIX]{x1D6FF}_{bl}=\int _{0}^{\infty }[1-F^{\prime }(\unicode[STIX]{x1D702})]\,\text{d}y=\unicode[STIX]{x1D6FD}\sqrt{2\bar{x}/k_{x}R_{\unicode[STIX]{x1D706}}}$
is the incompressible Blasius displacement thickness and
$\unicode[STIX]{x1D6FF}_{bl}=\int _{0}^{\infty }[1-F^{\prime }(\unicode[STIX]{x1D702})]\,\text{d}y=\unicode[STIX]{x1D6FD}\sqrt{2\bar{x}/k_{x}R_{\unicode[STIX]{x1D706}}}$
is the incompressible Blasius displacement thickness and
![]() $\unicode[STIX]{x1D6FD}=1.2168$
. In the compressible case the additional term related to
$\unicode[STIX]{x1D6FD}=1.2168$
. In the compressible case the additional term related to
![]() $\bar{\unicode[STIX]{x1D6FF}}^{c}$
in (2.81) is present or absent depending on the motion being unsteady or steady, while in the incompressible case the transpiration velocity is not affected by unsteady effects.
$\bar{\unicode[STIX]{x1D6FF}}^{c}$
in (2.81) is present or absent depending on the motion being unsteady or steady, while in the incompressible case the transpiration velocity is not affected by unsteady effects.
3 Numerical procedures
The Fourier coefficients
![]() $\{\hat{u} _{m,n},\hat{v}_{m,n},{\hat{w}}_{m,n},\hat{\unicode[STIX]{x1D70F}}_{m,n},\hat{p}_{m,n}\}$
are obtained by solving the boundary-region equations (2.23)–(2.27) with the initial conditions (2.78) and the boundary conditions (2.80). The wall-normal domain extends to
$\{\hat{u} _{m,n},\hat{v}_{m,n},{\hat{w}}_{m,n},\hat{\unicode[STIX]{x1D70F}}_{m,n},\hat{p}_{m,n}\}$
are obtained by solving the boundary-region equations (2.23)–(2.27) with the initial conditions (2.78) and the boundary conditions (2.80). The wall-normal domain extends to
![]() $\unicode[STIX]{x1D702}_{max}=60$
and
$\unicode[STIX]{x1D702}_{max}=60$
and
![]() $2000$
grid points are used in this direction. The typical step size in the marching direction is
$2000$
grid points are used in this direction. The typical step size in the marching direction is
![]() $\unicode[STIX]{x0394}\bar{x}=10^{-3}$
. The resulting block tri-diagonal system is solved using a standard block elimination algorithm. In order to avoid the pressure decoupling phenomenon, the pressure is computed on a grid that is staggered in the
$\unicode[STIX]{x0394}\bar{x}=10^{-3}$
. The resulting block tri-diagonal system is solved using a standard block elimination algorithm. In order to avoid the pressure decoupling phenomenon, the pressure is computed on a grid that is staggered in the
![]() $\unicode[STIX]{x1D702}$
direction with respect to the grid for the velocity and temperature. The nonlinear terms are evaluated using the pseudo-spectral method (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988). Dealiasing is performed by following the so-called 3/2-rule, which prevents the spurious cascade from the unresolved higher-frequency modes into the resolved low-frequency modes (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988).
$\unicode[STIX]{x1D702}$
direction with respect to the grid for the velocity and temperature. The nonlinear terms are evaluated using the pseudo-spectral method (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988). Dealiasing is performed by following the so-called 3/2-rule, which prevents the spurious cascade from the unresolved higher-frequency modes into the resolved low-frequency modes (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988).
The density fluctuations are calculated using (2.19), where the first term is neglected with respect to the other two because
![]() $k_{x}/R_{\unicode[STIX]{x1D706}}\ll 1$
. The viscosity fluctuations are evaluated using (2.21) and by excluding the mean flow and the linear part of the disturbance from (2.21). The following steps are performed to obtain
$k_{x}/R_{\unicode[STIX]{x1D706}}\ll 1$
. The viscosity fluctuations are evaluated using (2.21) and by excluding the mean flow and the linear part of the disturbance from (2.21). The following steps are performed to obtain
![]() $\hat{\unicode[STIX]{x1D70C}}_{m,n}$
and
$\hat{\unicode[STIX]{x1D70C}}_{m,n}$
and
![]() $\hat{\unicode[STIX]{x1D707}}_{m,n}$
.
$\hat{\unicode[STIX]{x1D707}}_{m,n}$
.
-
(1) The temperature fluctuation
 $\hat{\unicode[STIX]{x1D70F}}_{m,n}$
is transformed from the spectral to the physical space to calculate
$\hat{\unicode[STIX]{x1D70F}}_{m,n}$
is transformed from the spectral to the physical space to calculate
 $\bar{\unicode[STIX]{x1D70F}}$
.
$\bar{\unicode[STIX]{x1D70F}}$
. -
(2) The fluctuations of density and viscosity are evaluated as follows
(3.1a,b ) $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}=-\frac{\bar{\unicode[STIX]{x1D70F}}}{T(T+r_{t}\bar{\unicode[STIX]{x1D70F}})},\quad \bar{\unicode[STIX]{x1D707}}=\mathop{\sum }_{j=2}^{\infty }\frac{(\unicode[STIX]{x1D714}_{j})}{j!}T^{\unicode[STIX]{x1D714}-j}r_{t}^{\,j-2}\bar{\unicode[STIX]{x1D70F}}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}=-\frac{\bar{\unicode[STIX]{x1D70F}}}{T(T+r_{t}\bar{\unicode[STIX]{x1D70F}})},\quad \bar{\unicode[STIX]{x1D707}}=\mathop{\sum }_{j=2}^{\infty }\frac{(\unicode[STIX]{x1D714}_{j})}{j!}T^{\unicode[STIX]{x1D714}-j}r_{t}^{\,j-2}\bar{\unicode[STIX]{x1D70F}}^{j}.\end{eqnarray}$$
-
(3) The latter are transformed back to the spectral space to obtain
 $\hat{\unicode[STIX]{x1D70C}}_{m,n}$
and
$\hat{\unicode[STIX]{x1D70C}}_{m,n}$
and
 $\hat{\unicode[STIX]{x1D707}}_{m,n}$
.
$\hat{\unicode[STIX]{x1D707}}_{m,n}$
.
A second-order predictor–corrector scheme is used to calculate the nonlinear terms while marching downstream. Extensive resolution checks have been carried out to verify the accuracy of the code. The amplitudes of the truncated Fourier series are six or seven orders of magnitude smaller than that of the forcing modes and so they do not significantly affect the flow dynamics. Use of
![]() $N_{t}=N_{z}=9$
is sufficient to capture the nonlinear effects in the case
$N_{t}=N_{z}=9$
is sufficient to capture the nonlinear effects in the case
![]() $r_{t}=2$
, while for
$r_{t}=2$
, while for
![]() $r_{t}=4$
an accuracy of the same order is obtained with
$r_{t}=4$
an accuracy of the same order is obtained with
![]() $N_{t}=N_{z}=13$
.
$N_{t}=N_{z}=13$
.
To calculate the outer-flow field in the subsonic case, we solve the Helmholtz equation (2.41) numerically with
![]() $M_{\infty }<1$
to obtain
$M_{\infty }<1$
to obtain
![]() $\hat{\unicode[STIX]{x1D6F7}}_{m}(\bar{x},\bar{y})$
, and the Fourier coefficients
$\hat{\unicode[STIX]{x1D6F7}}_{m}(\bar{x},\bar{y})$
, and the Fourier coefficients
![]() $\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y})$
are then retrieved from (2.40). The computational domain for
$\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y})$
are then retrieved from (2.40). The computational domain for
![]() $\bar{x}\geqslant 0$
extends sufficiently downstream for the forcing at
$\bar{x}\geqslant 0$
extends sufficiently downstream for the forcing at
![]() $\bar{y}=0$
to vanish. The symmetry about
$\bar{y}=0$
to vanish. The symmetry about
![]() $\bar{y}=0$
implies that the homogeneous Neumann boundary condition
$\bar{y}=0$
implies that the homogeneous Neumann boundary condition
![]() $\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D6F7}}_{m}/\unicode[STIX]{x2202}\bar{y}=0$
is used at
$\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D6F7}}_{m}/\unicode[STIX]{x2202}\bar{y}=0$
is used at
![]() $\bar{y}=0$
and
$\bar{y}=0$
and
![]() $\bar{x}<0$
. Careful resolution checks have been performed to ensure that the solution is independent of the size of the computational domain. The Helmholtz equation is discretized with a second-order finite difference scheme in
$\bar{x}<0$
. Careful resolution checks have been performed to ensure that the solution is independent of the size of the computational domain. The Helmholtz equation is discretized with a second-order finite difference scheme in
![]() $\bar{x}$
and
$\bar{x}$
and
![]() $\bar{y}$
. The resulting block tri-diagonal matrix is solved at each point using the generalized minimum residual method (Saad & Schultz Reference Saad and Schultz1986) with diagonal preconditioner implemented in the iterative methods library, IML++ (Dongarra et al.
Reference Dongarra, Lumsdaine, Pozo and Remington2006).
$\bar{y}$
. The resulting block tri-diagonal matrix is solved at each point using the generalized minimum residual method (Saad & Schultz Reference Saad and Schultz1986) with diagonal preconditioner implemented in the iterative methods library, IML++ (Dongarra et al.
Reference Dongarra, Lumsdaine, Pozo and Remington2006).
4 Results for the outer flow
The solution for the irrotational part of the outer flow
![]() $\bar{\boldsymbol{q}}_{0}(\bar{x},\bar{y},\bar{t})$
(refer to (2.28)) is studied in this section. The streamwise and wall-normal velocity components,
$\bar{\boldsymbol{q}}_{0}(\bar{x},\bar{y},\bar{t})$
(refer to (2.28)) is studied in this section. The streamwise and wall-normal velocity components,
![]() $\bar{u}_{0}(\bar{x},\bar{y},\bar{t})$
and
$\bar{u}_{0}(\bar{x},\bar{y},\bar{t})$
and
![]() $\bar{v}_{0}(\bar{x},\bar{y},\bar{t})$
, are calculated for two different flow regimes: a subsonic case with
$\bar{v}_{0}(\bar{x},\bar{y},\bar{t})$
, are calculated for two different flow regimes: a subsonic case with
![]() $\{M_{\infty },R_{\unicode[STIX]{x1D706}},r_{t},\unicode[STIX]{x1D705}\}=\{0.69,600,3.6,1.3\}$
and a supersonic case with
$\{M_{\infty },R_{\unicode[STIX]{x1D706}},r_{t},\unicode[STIX]{x1D705}\}=\{0.69,600,3.6,1.3\}$
and a supersonic case with
![]() $\{M_{\infty },R_{\unicode[STIX]{x1D706}},r_{t},\unicode[STIX]{x1D705}\}=\{3,1000,3.6,1.12\}$
.
$\{M_{\infty },R_{\unicode[STIX]{x1D706}},r_{t},\unicode[STIX]{x1D705}\}=\{3,1000,3.6,1.12\}$
.
The displacement-induced transverse velocity
![]() $\hat{v}_{m,0}$
given in (2.82) represents, after multiplication by
$\hat{v}_{m,0}$
given in (2.82) represents, after multiplication by
![]() $\sqrt{2\bar{x}}/\unicode[STIX]{x1D705}$
, the Neumann boundary condition at
$\sqrt{2\bar{x}}/\unicode[STIX]{x1D705}$
, the Neumann boundary condition at
![]() $\bar{y}=0$
for
$\bar{y}=0$
for
![]() $\hat{\unicode[STIX]{x1D719}}_{m}$
and is shown for the subsonic and supersonic cases in figure 2. Only the real part of the modes with
$\hat{\unicode[STIX]{x1D719}}_{m}$
and is shown for the subsonic and supersonic cases in figure 2. Only the real part of the modes with
![]() $|m|=0$
,
$|m|=0$
,
![]() $2$
,
$2$
,
![]() $4$
is considered, as the imaginary part is similar to the real part and higher harmonics are negligible. Physically, the terms
$4$
is considered, as the imaginary part is similar to the real part and higher harmonics are negligible. Physically, the terms
![]() $\hat{v}_{m,0}(\bar{x},\unicode[STIX]{x1D702}\gg 1)$
represent the harmonics of a spanwise-averaged time-periodic modulation which is superimposed onto the slope of the Blasius displacement thickness. In the light of the thin airfoil theory analogy, this modulation is interpreted as the strength of the pulse source distribution.
$\hat{v}_{m,0}(\bar{x},\unicode[STIX]{x1D702}\gg 1)$
represent the harmonics of a spanwise-averaged time-periodic modulation which is superimposed onto the slope of the Blasius displacement thickness. In the light of the thin airfoil theory analogy, this modulation is interpreted as the strength of the pulse source distribution.

Figure 2. Large-
![]() $\unicode[STIX]{x1D702}$
limit of
$\unicode[STIX]{x1D702}$
limit of
![]() $\hat{v}_{m,0}$
for
$\hat{v}_{m,0}$
for
![]() $M_{\infty }=0.69$
(a) and
$M_{\infty }=0.69$
(a) and
![]() $M_{\infty }=3$
(b).
$M_{\infty }=3$
(b).
In the subsonic case, due to the difficulty in calculating the integral in (2.47), the solution is obtained numerically, as explained in § 3. In the supersonic case, the solution (2.46) is employed to calculate the Fourier coefficients
![]() $\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y})$
, from which
$\hat{\unicode[STIX]{x1D719}}_{m}(\bar{x},\bar{y})$
, from which
![]() $\bar{u}_{0}(\bar{x},\bar{y},\bar{t})$
and
$\bar{u}_{0}(\bar{x},\bar{y},\bar{t})$
and
![]() $\bar{v}_{0}(\bar{x},\bar{y},\bar{t})$
are obtained. The pressure
$\bar{v}_{0}(\bar{x},\bar{y},\bar{t})$
are obtained. The pressure
![]() $\bar{p}_{0}(\bar{x},\bar{y},\bar{t})$
is derived from (2.50).
$\bar{p}_{0}(\bar{x},\bar{y},\bar{t})$
is derived from (2.50).
Contours of
![]() $\bar{u}_{0}$
,
$\bar{u}_{0}$
,
![]() $\bar{v}_{0}$
and
$\bar{v}_{0}$
and
![]() $\bar{p}_{0}$
in the
$\bar{p}_{0}$
in the
![]() $\bar{x}{-}\bar{y}$
plane, which represent the acoustic field emitted by streaks, are shown in figures 3 and 4 at two different times
$\bar{x}{-}\bar{y}$
plane, which represent the acoustic field emitted by streaks, are shown in figures 3 and 4 at two different times
![]() $\bar{t}$
for the subsonic and supersonic cases, respectively. According to (2.56) the temperature
$\bar{t}$
for the subsonic and supersonic cases, respectively. According to (2.56) the temperature
![]() $\bar{\unicode[STIX]{x1D70F}}_{0}$
differs from
$\bar{\unicode[STIX]{x1D70F}}_{0}$
differs from
![]() $\bar{p}_{0}$
by a factor
$\bar{p}_{0}$
by a factor
![]() $(\unicode[STIX]{x1D6FE}-1)M_{\infty }^{2}$
, which is equal to
$(\unicode[STIX]{x1D6FE}-1)M_{\infty }^{2}$
, which is equal to
![]() $0.19$
and
$0.19$
and
![]() $3.6$
in the two flow regimes. The scale for the temperature
$3.6$
in the two flow regimes. The scale for the temperature
![]() $\bar{\unicode[STIX]{x1D70F}}_{0}$
is thus reported together with that for the pressure.
$\bar{\unicode[STIX]{x1D70F}}_{0}$
is thus reported together with that for the pressure.

Figure 3. Contours of the streamwise and wall-normal velocity components,
![]() $\bar{u}_{0}$
and
$\bar{u}_{0}$
and
![]() $\bar{v}_{0}$
, the pressure
$\bar{v}_{0}$
, the pressure
![]() $\bar{p}_{0}$
and the temperature
$\bar{p}_{0}$
and the temperature
![]() $\bar{\unicode[STIX]{x1D70F}}_{0}$
in
$\bar{\unicode[STIX]{x1D70F}}_{0}$
in
![]() $\bar{x}{-}\bar{y}$
plane, at different times
$\bar{x}{-}\bar{y}$
plane, at different times
![]() $\bar{t}$
for
$\bar{t}$
for
![]() $M_{\infty }=0.69$
.
$M_{\infty }=0.69$
.

Figure 4. Contours of the streamwise and wall-normal velocity components,
![]() $\bar{u}_{0}$
and
$\bar{u}_{0}$
and
![]() $\bar{v}_{0}$
, the pressure
$\bar{v}_{0}$
, the pressure
![]() $\bar{p}_{0}$
and the temperature
$\bar{p}_{0}$
and the temperature
![]() $\bar{\unicode[STIX]{x1D70F}}_{0}$
in the
$\bar{\unicode[STIX]{x1D70F}}_{0}$
in the
![]() $\bar{x}{-}\bar{y}$
plane, at different times
$\bar{x}{-}\bar{y}$
plane, at different times
![]() $\bar{t}$
for
$\bar{t}$
for
![]() $M_{\infty }=3$
. The dashed lines represent the Mach line
$M_{\infty }=3$
. The dashed lines represent the Mach line
![]() $\bar{y}=\bar{x}/\sqrt{M_{\infty }^{2}-1}$
.
$\bar{y}=\bar{x}/\sqrt{M_{\infty }^{2}-1}$
.
In the subsonic case, the influence of the boundary-layer thickness pulsation propagates in all directions from the plate and gradually diminishes as the distance from the body increases. The streamwise modulation of the solution is caused by the oscillatory forcing at
![]() $\bar{y}=0$
, which corresponds to a sequence of sources with positive and negative strength (refer to figure 2). The apparent ‘wavelength’ of modulation is
$\bar{y}=0$
, which corresponds to a sequence of sources with positive and negative strength (refer to figure 2). The apparent ‘wavelength’ of modulation is
![]() $\unicode[STIX]{x0394}\bar{x}\approx 0.5$
. The outer-flow solution shows the most intense peaks for
$\unicode[STIX]{x0394}\bar{x}\approx 0.5$
. The outer-flow solution shows the most intense peaks for
![]() $0.5<\bar{x}<2$
, i.e. where the forcing is strongest.
$0.5<\bar{x}<2$
, i.e. where the forcing is strongest.
The supersonic solution, shown in figure 4, is non-zero only inside the Mach dihedron delimited by the Mach line
![]() $\bar{y}=\bar{x}/\sqrt{M_{\infty }^{2}-1}$
, as in the thin airfoil theory (Dragos Reference Dragos2004, p. 32). The magnitude of the disturbance is constant along the Mach line and thus the perturbations do not vanish as
$\bar{y}=\bar{x}/\sqrt{M_{\infty }^{2}-1}$
, as in the thin airfoil theory (Dragos Reference Dragos2004, p. 32). The magnitude of the disturbance is constant along the Mach line and thus the perturbations do not vanish as
![]() $\bar{y}\rightarrow \infty$
.
$\bar{y}\rightarrow \infty$
.
5 Results for the boundary-layer streaks
The parameters for the numerical results are selected to be representative of two possible applications: subsonic turbomachinery and supersonic flight conditions. The former is characterized by a relatively low Mach number and an intense turbulence level, while the latter features a higher Mach number and a quieter disturbance environment. An idealized case of a supersonic wind tunnel flow with no acoustic modes is also considered. In all the cases, the scaled amplitudes of the free-stream turbulence velocity components are:
![]() $\hat{u} _{x,\pm }^{\infty }=\hat{u} _{y,\pm }^{\infty }=1$
and
$\hat{u} _{x,\pm }^{\infty }=\hat{u} _{y,\pm }^{\infty }=1$
and
![]() $\hat{u} _{z,\pm }^{\infty }=\mp 1$
. Through continuity (2.4), this leads to the following relation for the wavenumbers:
$\hat{u} _{z,\pm }^{\infty }=\mp 1$
. Through continuity (2.4), this leads to the following relation for the wavenumbers:
![]() $k_{x}+k_{y}-1=0$
.
$k_{x}+k_{y}-1=0$
.
In the following, the parameters employed for the three sets of calculations are presented and the relevant results are shown. The reader may skip § 5.1 without loss of clarity.
5.1 Choice of parameters
5.1.1 Turbomachinery applications
With a reference to typical experimental works on turbomachinery applications (e.g. Camci & Arts Reference Camci and Arts1990) the following parameters are adopted: unit Reynolds number
![]() $R_{1\infty }^{\ast }=$
$R_{1\infty }^{\ast }=$
![]() $U_{\infty }^{\ast }/\unicode[STIX]{x1D708}_{\infty }^{\ast }=8\times 10^{6}~\text{ m}^{-1}$
, chord length
$U_{\infty }^{\ast }/\unicode[STIX]{x1D708}_{\infty }^{\ast }=8\times 10^{6}~\text{ m}^{-1}$
, chord length
![]() $\ell ^{\ast }=8~\text{ cm}$
, free-stream temperature
$\ell ^{\ast }=8~\text{ cm}$
, free-stream temperature
![]() $T_{\infty }^{\ast }=500~\text{ K}$
and kinematic viscosity of air
$T_{\infty }^{\ast }=500~\text{ K}$
and kinematic viscosity of air
![]() $\unicode[STIX]{x1D708}_{\infty }^{\ast }=3.9\times 10^{-5}~\text{ m}^{2}~\text{s}^{-1}$
, free-stream Mach number
$\unicode[STIX]{x1D708}_{\infty }^{\ast }=3.9\times 10^{-5}~\text{ m}^{2}~\text{s}^{-1}$
, free-stream Mach number
![]() $M_{\infty }=0.69$
and turbulence level
$M_{\infty }=0.69$
and turbulence level
![]() $Tu=0.8-5.2\,\%$
. Although we have chosen our flow parameters to be as close as possible to the experimental ones, important extra factors are present in real experimental and technological flow systems, such as acoustic free-stream forcing, surface curvature, pressure gradient and wall cooling. These can be taken into account by suitable extensions of the present framework. For example, the boundary-region equation approach has been extended to study the generation and development of Görtler vortices in the incompressible boundary layer over a concave wall (Wu, Zhao & Luo Reference Wu, Zhao and Luo2011). With further progress, precise quantitative comparisons with experiments and applications to practical situations would be possible. Presently, the results are of qualitative value as far as their relevance to turbomachinery is concerned. The adiabatic wall temperature is calculated using the following relation valid for a perfect gas,
$Tu=0.8-5.2\,\%$
. Although we have chosen our flow parameters to be as close as possible to the experimental ones, important extra factors are present in real experimental and technological flow systems, such as acoustic free-stream forcing, surface curvature, pressure gradient and wall cooling. These can be taken into account by suitable extensions of the present framework. For example, the boundary-region equation approach has been extended to study the generation and development of Görtler vortices in the incompressible boundary layer over a concave wall (Wu, Zhao & Luo Reference Wu, Zhao and Luo2011). With further progress, precise quantitative comparisons with experiments and applications to practical situations would be possible. Presently, the results are of qualitative value as far as their relevance to turbomachinery is concerned. The adiabatic wall temperature is calculated using the following relation valid for a perfect gas,
where
![]() $C_{t}=\sqrt{Pr}$
is the recovery factor for a laminar boundary layer over a flat plate. The resulting adiabatic wall temperature,
$C_{t}=\sqrt{Pr}$
is the recovery factor for a laminar boundary layer over a flat plate. The resulting adiabatic wall temperature,
![]() $T_{ad}^{\ast }=540.5~\text{ K}$
, is in the range of typical turbine rotor applications. The ratio of the wall temperature to the adiabatic wall temperature
$T_{ad}^{\ast }=540.5~\text{ K}$
, is in the range of typical turbine rotor applications. The ratio of the wall temperature to the adiabatic wall temperature
![]() $T_{w}^{\ast }/T_{ad}^{\ast }=0.7$
is chosen to mimic realistic aero-engine conditions (Zhang & He Reference Zhang and He2014), where blade cooling is most often applied to avoid excessive surface temperature. The resulting non-dimensional wall temperature is
$T_{w}^{\ast }/T_{ad}^{\ast }=0.7$
is chosen to mimic realistic aero-engine conditions (Zhang & He Reference Zhang and He2014), where blade cooling is most often applied to avoid excessive surface temperature. The resulting non-dimensional wall temperature is
![]() $T_{w}=0.75$
.
$T_{w}=0.75$
.
As the relevant length scales and spectra of the free-stream turbulence are not documented in the experiments, we choose to assume that the ratio of the streamwise integral scale to the chord is equal to
![]() $1.5$
. It follows that
$1.5$
. It follows that
![]() $\unicode[STIX]{x1D706}_{x}^{\ast }=0.12~\text{ m}$
and the frequency
$\unicode[STIX]{x1D706}_{x}^{\ast }=0.12~\text{ m}$
and the frequency
![]() $f^{\ast }=U_{\infty }^{\ast }/\unicode[STIX]{x1D706}_{x}^{\ast }=2.5~\text{ kHz}$
. At downstream locations where
$f^{\ast }=U_{\infty }^{\ast }/\unicode[STIX]{x1D706}_{x}^{\ast }=2.5~\text{ kHz}$
. At downstream locations where
![]() $x^{\ast }=O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, the boundary-layer thickness is comparable with the spanwise length scale
$x^{\ast }=O(\unicode[STIX]{x1D706}^{\ast }R_{\unicode[STIX]{x1D706}})$
, the boundary-layer thickness is comparable with the spanwise length scale
![]() $\unicode[STIX]{x1D706}^{\ast }$
. The laminar boundary-layer thickness is proportional to
$\unicode[STIX]{x1D706}^{\ast }$
. The laminar boundary-layer thickness is proportional to
![]() $\sqrt{\unicode[STIX]{x1D708}_{\infty }^{\ast }x^{\ast }/U_{\infty }^{\ast }}$
, and it is estimated that transition occurs at
$\sqrt{\unicode[STIX]{x1D708}_{\infty }^{\ast }x^{\ast }/U_{\infty }^{\ast }}$
, and it is estimated that transition occurs at
![]() $x_{T}^{\ast }/\ell ^{\ast }=0.67$
(i.e.
$x_{T}^{\ast }/\ell ^{\ast }=0.67$
(i.e.
![]() $x_{T}^{\ast }=5.36~\text{ cm}$
), which corresponds to a critical Reynolds number of
$x_{T}^{\ast }=5.36~\text{ cm}$
), which corresponds to a critical Reynolds number of
![]() $5\times 10^{5}$
(Schlichting & Gersten Reference Schlichting and Gersten2000). It follows that the boundary-layer thickness
$5\times 10^{5}$
(Schlichting & Gersten Reference Schlichting and Gersten2000). It follows that the boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{99}^{\ast }$
, defined as the wall-normal location where
$\unicode[STIX]{x1D6FF}_{99}^{\ast }$
, defined as the wall-normal location where
![]() $U=0.99$
, is
$U=0.99$
, is
![]() $0.41~\text{ mm}$
, and the displacement thickness is
$0.41~\text{ mm}$
, and the displacement thickness is
![]() $\unicode[STIX]{x1D6FF}^{\ast }=0.14~\text{ mm}$
. The latter value is taken as the reference length scale
$\unicode[STIX]{x1D6FF}^{\ast }=0.14~\text{ mm}$
. The latter value is taken as the reference length scale
![]() $\unicode[STIX]{x1D706}^{\ast }$
. The Reynolds number
$\unicode[STIX]{x1D706}^{\ast }$
. The Reynolds number
![]() $R_{\unicode[STIX]{x1D706}}$
and the scaled streamwise wavenumber
$R_{\unicode[STIX]{x1D706}}$
and the scaled streamwise wavenumber
![]() $\unicode[STIX]{x1D705}$
are worked out by use of (2.5) and (2.7). The free-stream disturbance intensity is defined as
$\unicode[STIX]{x1D705}$
are worked out by use of (2.5) and (2.7). The free-stream disturbance intensity is defined as
![]() $Tu=2\unicode[STIX]{x1D716}\sqrt{(\hat{u} _{x,+}^{\infty })^{2}+(\hat{u} _{x,-}^{\infty })^{2}}$
. For our choice of
$Tu=2\unicode[STIX]{x1D716}\sqrt{(\hat{u} _{x,+}^{\infty })^{2}+(\hat{u} _{x,-}^{\infty })^{2}}$
. For our choice of
![]() $\hat{u} _{x,\pm }^{\infty }=1$
,
$\hat{u} _{x,\pm }^{\infty }=1$
,
![]() $Tu=2\sqrt{2}\unicode[STIX]{x1D716}$
. Given
$Tu=2\sqrt{2}\unicode[STIX]{x1D716}$
. Given
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $R_{\unicode[STIX]{x1D706}}$
, the turbulence Reynolds number
$R_{\unicode[STIX]{x1D706}}$
, the turbulence Reynolds number
![]() $r_{t}$
is calculated from (2.8). The influence of nonlinear effects is investigated by varying the turbulence level (i.e.
$r_{t}$
is calculated from (2.8). The influence of nonlinear effects is investigated by varying the turbulence level (i.e.
![]() $\unicode[STIX]{x1D716}$
) with all the other parameters kept constant, as shown in table 1(a). Two different values of
$\unicode[STIX]{x1D716}$
) with all the other parameters kept constant, as shown in table 1(a). Two different values of
![]() $\unicode[STIX]{x1D706}_{x}^{\ast }/\ell ^{\ast }=0.77$
,
$\unicode[STIX]{x1D706}_{x}^{\ast }/\ell ^{\ast }=0.77$
,
![]() $3.1$
are considered in order to study the effect of the streamwise wavenumber (refer to table 1(b)). The relation between
$3.1$
are considered in order to study the effect of the streamwise wavenumber (refer to table 1(b)). The relation between
![]() $\unicode[STIX]{x1D706}_{z}^{\ast }$
, shown in table 1, and
$\unicode[STIX]{x1D706}_{z}^{\ast }$
, shown in table 1, and
![]() $\unicode[STIX]{x1D706}^{\ast }$
is
$\unicode[STIX]{x1D706}^{\ast }$
is
![]() $\unicode[STIX]{x1D706}_{z}^{\ast }=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}^{\ast }$
.
$\unicode[STIX]{x1D706}_{z}^{\ast }=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}^{\ast }$
.
Table 1. Choice of the parameters for the turbomachinery, flight and wind tunnel cases.

5.1.2 Flight conditions
The data reported in Schneider (Reference Schneider1999) are analysed to infer typical parameters for supersonic flight conditions. The following values are adopted: free-stream Mach number
![]() $M_{\infty }=3$
, unit Reynolds number
$M_{\infty }=3$
, unit Reynolds number
![]() $R_{1\infty }^{\ast }=3.33\times 10^{6}~\text{ m}^{-1}$
and wall temperature ratio
$R_{1\infty }^{\ast }=3.33\times 10^{6}~\text{ m}^{-1}$
and wall temperature ratio
![]() $T_{w}^{\ast }/T_{ad}^{\ast }=0.5$
. The latter value is in the typical range of high supersonic flight speeds, where, in addition to aerodynamic heating, radiative cooling also occurs due to the solid wall of the body radiating energy from the surface (Fedorov & Khokhlov Reference Fedorov and Khokhlov2001). A free-stream temperature
$T_{w}^{\ast }/T_{ad}^{\ast }=0.5$
. The latter value is in the typical range of high supersonic flight speeds, where, in addition to aerodynamic heating, radiative cooling also occurs due to the solid wall of the body radiating energy from the surface (Fedorov & Khokhlov Reference Fedorov and Khokhlov2001). A free-stream temperature
![]() $T_{\infty }^{\ast }=218~\text{ K}$
is assumed at a typical altitude for supersonic flight of
$T_{\infty }^{\ast }=218~\text{ K}$
is assumed at a typical altitude for supersonic flight of
![]() $20~\text{ km}$
(Wilson, Love & Larson Reference Wilson, Love and Larson1971). It follows that the velocity and the kinematic viscosity of air in the free stream are
$20~\text{ km}$
(Wilson, Love & Larson Reference Wilson, Love and Larson1971). It follows that the velocity and the kinematic viscosity of air in the free stream are
![]() $U_{\infty }^{\ast }=888~\text{ ms}^{-1}$
and
$U_{\infty }^{\ast }=888~\text{ ms}^{-1}$
and
![]() $\unicode[STIX]{x1D708}_{\infty }^{\ast }=2.67\times 10^{-4}~\text{ m}^{2}~\text{s}^{-1}$
. From (5.1) the adiabatic wall temperature
$\unicode[STIX]{x1D708}_{\infty }^{\ast }=2.67\times 10^{-4}~\text{ m}^{2}~\text{s}^{-1}$
. From (5.1) the adiabatic wall temperature
![]() $T_{ad}^{\ast }=548~\text{ K}$
is obtained. It follows that
$T_{ad}^{\ast }=548~\text{ K}$
is obtained. It follows that
![]() $T_{w}^{\ast }=274~\text{ K}$
. The boundary-layer thickness
$T_{w}^{\ast }=274~\text{ K}$
. The boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
at high Mach number is assumed to grow as
$\unicode[STIX]{x1D6FF}^{\ast }$
at high Mach number is assumed to grow as
![]() $x^{\ast }M_{\infty }^{2}/\sqrt{R_{x}}$
, where
$x^{\ast }M_{\infty }^{2}/\sqrt{R_{x}}$
, where
![]() $R_{x}$
is the local Reynolds number at the edge of the boundary layer (refer to Anderson Reference Anderson2006, equation (7.9)). At the transition-onset location
$R_{x}$
is the local Reynolds number at the edge of the boundary layer (refer to Anderson Reference Anderson2006, equation (7.9)). At the transition-onset location
![]() $x_{T}^{\ast }=0.1~\text{ m}$
(Schneider Reference Schneider1999) and
$x_{T}^{\ast }=0.1~\text{ m}$
(Schneider Reference Schneider1999) and
![]() $\unicode[STIX]{x1D6FF}^{\ast }=1.5~\text{ mm}$
, which is taken as the reference length scale, i.e.
$\unicode[STIX]{x1D6FF}^{\ast }=1.5~\text{ mm}$
, which is taken as the reference length scale, i.e.
![]() $\unicode[STIX]{x1D706}^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }$
.
$\unicode[STIX]{x1D706}^{\ast }=\unicode[STIX]{x1D6FF}^{\ast }$
.
Considering the data reported in figure 6 of Wilson et al. (Reference Wilson, Love and Larson1971) and figure 1 of Hocking (Reference Hocking1985) on the atmospheric turbulence power spectra and scales, a streamwise wavelength
![]() $\unicode[STIX]{x1D706}_{x}^{\ast }=3.68~\text{ m}$
is chosen. The corresponding frequency is
$\unicode[STIX]{x1D706}_{x}^{\ast }=3.68~\text{ m}$
is chosen. The corresponding frequency is
![]() $f^{\ast }=240.8~\text{ Hz}$
. In-flight measurements by Riedel & Sitzmann (Reference Riedel and Sitzmann1998) and Saric (Reference Saric2008) indicate that the turbulence level in subsonic flight for the quiescent air atmosphere is 0.05 %–0.06 %. For the high-altitude environment of a supersonic aircraft, Coleman & Steiner (Reference Coleman and Steiner1960) and Ehernberger & Love (Reference Ehernberger and Love1975) report even lower turbulence intensities. However, close to inversion layers (i.e. areas where the usual trend of decrease in air temperature with increasing altitude is reversed) or within clouds, large turbulence levels in the range
$f^{\ast }=240.8~\text{ Hz}$
. In-flight measurements by Riedel & Sitzmann (Reference Riedel and Sitzmann1998) and Saric (Reference Saric2008) indicate that the turbulence level in subsonic flight for the quiescent air atmosphere is 0.05 %–0.06 %. For the high-altitude environment of a supersonic aircraft, Coleman & Steiner (Reference Coleman and Steiner1960) and Ehernberger & Love (Reference Ehernberger and Love1975) report even lower turbulence intensities. However, close to inversion layers (i.e. areas where the usual trend of decrease in air temperature with increasing altitude is reversed) or within clouds, large turbulence levels in the range
![]() $0.1\,\%<Tu<1\,\%$
or more may occur (Zanin Reference Zanin1985). The turbulence levels for our simulations are chosen as representative of these atmospheric conditions (
$0.1\,\%<Tu<1\,\%$
or more may occur (Zanin Reference Zanin1985). The turbulence levels for our simulations are chosen as representative of these atmospheric conditions (
![]() $0.1\,\%<Tu<0.3\,\%$
).
$0.1\,\%<Tu<0.3\,\%$
).
The influence of compressibility is investigated by varying
![]() $M_{\infty }$
. It is assumed that the variation of
$M_{\infty }$
. It is assumed that the variation of
![]() $M_{\infty }$
is only due to a variation of the free-stream velocity
$M_{\infty }$
is only due to a variation of the free-stream velocity
![]() $U_{\infty }^{\ast }$
, while the free-stream temperature
$U_{\infty }^{\ast }$
, while the free-stream temperature
![]() $T_{\infty }^{\ast }$
is unchanged. Therefore,
$T_{\infty }^{\ast }$
is unchanged. Therefore,
![]() $a_{\infty }^{\ast }$
and
$a_{\infty }^{\ast }$
and
![]() $\unicode[STIX]{x1D708}_{\infty }^{\ast }$
are also constant. The wall temperature is the same in all the cases, while
$\unicode[STIX]{x1D708}_{\infty }^{\ast }$
are also constant. The wall temperature is the same in all the cases, while
![]() $T_{ad}^{\ast }$
varies according to (5.1) for different Mach numbers. The dimensional amplitude of the gust is kept fixed at
$T_{ad}^{\ast }$
varies according to (5.1) for different Mach numbers. The dimensional amplitude of the gust is kept fixed at
![]() $2.39~\text{ m}~\text{s}^{-1}$
. It follows that the turbulence level decreases as the free-stream velocity increases, but the turbulence Reynolds number, which is defined by (2.8), does not change because
$2.39~\text{ m}~\text{s}^{-1}$
. It follows that the turbulence level decreases as the free-stream velocity increases, but the turbulence Reynolds number, which is defined by (2.8), does not change because
![]() $R_{\unicode[STIX]{x1D706}}$
increases linearly with
$R_{\unicode[STIX]{x1D706}}$
increases linearly with
![]() $U_{\infty }^{\ast }$
. The dimensional frequency is kept constant and it corresponds to different
$U_{\infty }^{\ast }$
. The dimensional frequency is kept constant and it corresponds to different
![]() $\unicode[STIX]{x1D706}_{x}^{\ast }$
depending on
$\unicode[STIX]{x1D706}_{x}^{\ast }$
depending on
![]() $U_{\infty }^{\ast }$
, as presented in table 1(c). In order to analyse the effect of nonlinearity at supersonic speeds, two different turbulence levels,
$U_{\infty }^{\ast }$
, as presented in table 1(c). In order to analyse the effect of nonlinearity at supersonic speeds, two different turbulence levels,
![]() $Tu=0.19\,\%$
and
$Tu=0.19\,\%$
and
![]() $0.35\,\%$
, are considered for
$0.35\,\%$
, are considered for
![]() $M_{\infty }=3$
(refer to table 1(d)).
$M_{\infty }=3$
(refer to table 1(d)).
5.1.3 Wind tunnel conditions
The following parameters are chosen as representative of typical supersonic wind tunnel experiments (Beckwith & Miller Reference Beckwith and Miller1990; Graziosi & Brown Reference Graziosi and Brown2002; Fedorov et al.
Reference Fedorov, Shiplyuk, Maslov, Burov and Malmuth2003):
![]() $M_{\infty }=3$
,
$M_{\infty }=3$
,
![]() $U_{\infty }^{\ast }=646~\text{ m}~\text{s}^{-1}$
,
$U_{\infty }^{\ast }=646~\text{ m}~\text{s}^{-1}$
,
![]() $\unicode[STIX]{x1D708}_{\infty }^{\ast }=3.7\times 10^{-5}~\text{ m}^{2}~\text{s}^{-1}$
,
$\unicode[STIX]{x1D708}_{\infty }^{\ast }=3.7\times 10^{-5}~\text{ m}^{2}~\text{s}^{-1}$
,
![]() $T_{\infty }^{\ast }=115.4~\text{ K}$
,
$T_{\infty }^{\ast }=115.4~\text{ K}$
,
![]() $f^{\ast }=500~\text{ Hz}$
,
$f^{\ast }=500~\text{ Hz}$
,
![]() $k_{x}=1.55\times 10^{-3}$
,
$k_{x}=1.55\times 10^{-3}$
,
![]() $R_{\unicode[STIX]{x1D706}}=5400$
and
$R_{\unicode[STIX]{x1D706}}=5400$
and
![]() $\unicode[STIX]{x1D705}=0.34$
. The calculations are performed for three different turbulence levels,
$\unicode[STIX]{x1D705}=0.34$
. The calculations are performed for three different turbulence levels,
![]() $Tu=0.11\,\%$
,
$Tu=0.11\,\%$
,
![]() $0.23\,\%$
,
$0.23\,\%$
,
![]() $0.31\,\%$
, which correspond to
$0.31\,\%$
, which correspond to
![]() $r_{t}=2.1$
, 4.4, 6 (refer to table 1(e)). The representation is idealized since acoustic disturbances are excluded.
$r_{t}=2.1$
, 4.4, 6 (refer to table 1(e)). The representation is idealized since acoustic disturbances are excluded.
For these cases the ratio between the wall temperature and the adiabatic wall temperature provided by Graziosi & Brown (Reference Graziosi and Brown2002),
![]() $T_{w}^{\ast }/T_{ad}^{\ast }=1.1$
, is employed. The results for this hot-wall condition will be compared with those obtained with the adiabatic condition
$T_{w}^{\ast }/T_{ad}^{\ast }=1.1$
, is employed. The results for this hot-wall condition will be compared with those obtained with the adiabatic condition
![]() $T_{w}^{\ast }=T_{ad}^{\ast }$
and with the cold-wall condition employed by Fedorov et al. (Reference Fedorov, Shiplyuk, Maslov, Burov and Malmuth2003), where
$T_{w}^{\ast }=T_{ad}^{\ast }$
and with the cold-wall condition employed by Fedorov et al. (Reference Fedorov, Shiplyuk, Maslov, Burov and Malmuth2003), where
![]() $T_{w}^{\ast }/T_{ad}^{\ast }=0.8$
.
$T_{w}^{\ast }/T_{ad}^{\ast }=0.8$
.
5.2 Evolution of nonlinear compressible streaks
As anticipated on the basis of the linear analysis by Ricco & Wu (Reference Ricco and Wu2007), free-stream disturbances of the hydrodynamic kind (i.e. convected gusts) generate thermal fluctuations inside the boundary layer due to the velocity–temperature coupling. Just as the temperature profile affects the stability of a two-dimensional flow (Lees Reference Lees1947; Mack Reference Mack1975), thermal streaks are bound to influence the secondary instability of the streaky boundary layer. We will therefore focus on the fluctuations of the streamwise velocity and temperature inside the boundary layer.
The overall intensity of the streak signature, which comprises all the harmonics in the nonlinear regime, is measured by the root-mean-square (r.m.s. hereinafter) of the fluctuating quantity, defined as
 $$\begin{eqnarray}q_{rms}\equiv r_{t}\sqrt{\mathop{\sum }_{m=-\bar{N}_{t}}^{\bar{N}_{t}}\mathop{\sum }_{n=-\bar{N}_{z}}^{\bar{N}_{z}}|\hat{q}_{m,n}|^{2}},\quad m\neq 0,\end{eqnarray}$$
$$\begin{eqnarray}q_{rms}\equiv r_{t}\sqrt{\mathop{\sum }_{m=-\bar{N}_{t}}^{\bar{N}_{t}}\mathop{\sum }_{n=-\bar{N}_{z}}^{\bar{N}_{z}}|\hat{q}_{m,n}|^{2}},\quad m\neq 0,\end{eqnarray}$$
where
![]() $q$
may stand for the streamwise velocity or the temperature and
$q$
may stand for the streamwise velocity or the temperature and
![]() $\bar{N}_{t}=(N_{t}-1)/2$
,
$\bar{N}_{t}=(N_{t}-1)/2$
,
![]() $\bar{N}_{z}=(N_{z}-1)/2$
. The downstream development of the maximum
$\bar{N}_{z}=(N_{z}-1)/2$
. The downstream development of the maximum
![]() $q_{rms}$
along
$q_{rms}$
along
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
is shown in figures 5 (turbomachinery case), 6 (flight case) and 7 (wind tunnel case), where the nonlinear solutions are compared with the corresponding linearized approximations for different values of
![]() $Tu$
. In the linear case, the peak of the r.m.s. is given by
$Tu$
. In the linear case, the peak of the r.m.s. is given by
where
![]() $\bar{q}_{l}$
represents the solution provided by Ricco & Wu (Reference Ricco and Wu2007). Since
$\bar{q}_{l}$
represents the solution provided by Ricco & Wu (Reference Ricco and Wu2007). Since
![]() $|u_{z,w,+}|=|u_{z,w,-}|=|u_{z,w}|$
, (5.4) simplifies to:
$|u_{z,w,+}|=|u_{z,w,-}|=|u_{z,w}|$
, (5.4) simplifies to:
Sufficiently upstream, the linear and nonlinear solutions overlap as the influence of nonlinearity is still weak. Due to the continued amplification of the disturbance, the streak signature becomes stronger and the linear and nonlinear solutions start diverging for moderate
![]() $r_{t}$
. In the case with the lowest
$r_{t}$
. In the case with the lowest
![]() $r_{t}$
for all the three scenarios considered, the linear and nonlinear curves are almost indistinguishable. In the cases with higher
$r_{t}$
for all the three scenarios considered, the linear and nonlinear curves are almost indistinguishable. In the cases with higher
![]() $r_{t}$
, a stabilizing effect of nonlinearity is observed on the streamwise velocity and temperature and, as the turbulence intensity increases, the attenuation of the disturbances is enhanced. The higher the turbulence level, the slower and the weaker the disturbance growth becomes, and the farther upstream the nonlinear effects start asserting their influence. The stabilizing effect of nonlinearity was already observed by Ricco et al. (Reference Ricco, Luo and Wu2011) in the incompressible regime for high turbulence levels. Here, it is shown that nonlinear effects play the same role on thermal (temperature) streaks.
$r_{t}$
, a stabilizing effect of nonlinearity is observed on the streamwise velocity and temperature and, as the turbulence intensity increases, the attenuation of the disturbances is enhanced. The higher the turbulence level, the slower and the weaker the disturbance growth becomes, and the farther upstream the nonlinear effects start asserting their influence. The stabilizing effect of nonlinearity was already observed by Ricco et al. (Reference Ricco, Luo and Wu2011) in the incompressible regime for high turbulence levels. Here, it is shown that nonlinear effects play the same role on thermal (temperature) streaks.

Figure 5. Evolution of the maximum r.m.s. of the streamwise velocity (a) and the temperature (b) for different values of the turbulence Reynolds number:
![]() $r_{t}=2.7$
(solid lines),
$r_{t}=2.7$
(solid lines),
![]() $r_{t}=7.9$
(dashed lines) at
$r_{t}=7.9$
(dashed lines) at
![]() $M_{\infty }=0.69$
(refer to table 1(a)). Thick lines: nonlinear solutions, thin lines: linearized solution.
$M_{\infty }=0.69$
(refer to table 1(a)). Thick lines: nonlinear solutions, thin lines: linearized solution.

Figure 6. Evolution of the maximum r.m.s. of the streamwise velocity (a) and the temperature (b) for different values of the turbulence Reynolds number:
![]() $r_{t}=3.37$
(solid line),
$r_{t}=3.37$
(solid line),
![]() $r_{t}=6.25$
(dashed lines) at
$r_{t}=6.25$
(dashed lines) at
![]() $M_{\infty }=3$
(refer to table 1(d)). Thick lines: nonlinear solutions, thin lines: linearized solutions.
$M_{\infty }=3$
(refer to table 1(d)). Thick lines: nonlinear solutions, thin lines: linearized solutions.

Figure 7. Evolution of the maximum r.m.s. of the streamwise velocity (a) and temperature (b) for different values of the turbulence Reynolds number:
![]() $r_{t}=2.1$
(dashed-dotted lines),
$r_{t}=2.1$
(dashed-dotted lines),
![]() $r_{t}=4.4$
(dashed lines),
$r_{t}=4.4$
(dashed lines),
![]() $r_{t}=6$
(solid lines) at
$r_{t}=6$
(solid lines) at
![]() $M_{\infty }=3$
(refer to table 1(e)). Thick lines: nonlinear solutions, thin lines: linearized solutions.
$M_{\infty }=3$
(refer to table 1(e)). Thick lines: nonlinear solutions, thin lines: linearized solutions.
For the turbomachinery case (figure 5), the attenuation of the streaks is more pronounced than in flight conditions as the turbulence levels are higher, and the deviation of the kinematic and thermal streaks from the linearized solution is of similar magnitude. The kinematic fluctuations are approximately one order of magnitude higher than the thermal streaks relatively to the correspondent free-stream mean velocity and temperature.
In flight conditions (figure 6), because of a higher Mach number, the temperature fluctuation acquires a large intensity, which is comparable with that of the velocity fluctuation. Although the influence of
![]() $Tu$
on the streamwise velocity is quite weak even in the highest turbulence intensity case,
$Tu$
on the streamwise velocity is quite weak even in the highest turbulence intensity case,
![]() $r_{t}=6.25$
, appreciable attenuation of the nonlinear thermal streaks with respect to the linearized ones is observed. The stabilizing effect is more marked on the temperature than on the streamwise velocity. The nonlinear and linear r.m.s. of the temperature streaks diverge farther upstream than the r.m.s. of the streamwise velocity. Even for a low-disturbance environment such as free flight, it seems necessary to describe the formation and amplification of the streaks correctly by taking into account the nonlinear interactions inside the boundary layer.
$r_{t}=6.25$
, appreciable attenuation of the nonlinear thermal streaks with respect to the linearized ones is observed. The stabilizing effect is more marked on the temperature than on the streamwise velocity. The nonlinear and linear r.m.s. of the temperature streaks diverge farther upstream than the r.m.s. of the streamwise velocity. Even for a low-disturbance environment such as free flight, it seems necessary to describe the formation and amplification of the streaks correctly by taking into account the nonlinear interactions inside the boundary layer.
In the wind tunnel case shown in figure 7, a peculiar behaviour of the nonlinear curve for the highest turbulence level case is observed. A sharp deviation of the nonlinear solution from the linear one occurs at
![]() $\bar{x}\approx 0.5$
, which corresponds to a physical downstream position of
$\bar{x}\approx 0.5$
, which corresponds to a physical downstream position of
![]() $x^{\ast }\approx 10~\text{ cm}$
. This phenomenon was not observed in the incompressible cases studied by Ricco et al. (Reference Ricco, Luo and Wu2011). The parameters used in this case are very similar to those of the flight case with highest
$x^{\ast }\approx 10~\text{ cm}$
. This phenomenon was not observed in the incompressible cases studied by Ricco et al. (Reference Ricco, Luo and Wu2011). The parameters used in this case are very similar to those of the flight case with highest
![]() $r_{t}$
(refer to tables 1(d) and 1(e)), except that
$r_{t}$
(refer to tables 1(d) and 1(e)), except that
![]() $k_{x}$
is approximately half of that in the flight case. As a consequence, the effect of nonlinearity is stronger. The streamwise wavenumber of the wind tunnel case is comparable with that of the flight case with
$k_{x}$
is approximately half of that in the flight case. As a consequence, the effect of nonlinearity is stronger. The streamwise wavenumber of the wind tunnel case is comparable with that of the flight case with
![]() $M_{\infty }=6$
(refer to table 1(c)) but
$M_{\infty }=6$
(refer to table 1(c)) but
![]() $r_{t}$
is smaller and
$r_{t}$
is smaller and
![]() $M_{\infty }$
is higher in the latter, thus resulting in weaker nonlinear effects. Additional calculations suggest that this abrupt change occurs when a sufficiently small streamwise wavenumber is employed, i.e.
$M_{\infty }$
is higher in the latter, thus resulting in weaker nonlinear effects. Additional calculations suggest that this abrupt change occurs when a sufficiently small streamwise wavenumber is employed, i.e.
![]() $k_{x}\leqslant 1.5\times 10^{-3}$
, together with a high turbulence Reynolds number,
$k_{x}\leqslant 1.5\times 10^{-3}$
, together with a high turbulence Reynolds number,
![]() $r_{t}\geqslant 6$
, at supersonic speed. In the subsonic regime no such sharp deviation was observed, even at high
$r_{t}\geqslant 6$
, at supersonic speed. In the subsonic regime no such sharp deviation was observed, even at high
![]() $r_{t}$
.
$r_{t}$
.
The effect of the frequency is displayed in figure 8, where the downstream evolutions of
![]() $u_{rms,max}$
and
$u_{rms,max}$
and
![]() $\unicode[STIX]{x1D70F}_{rms,max}$
are plotted for different values of
$\unicode[STIX]{x1D70F}_{rms,max}$
are plotted for different values of
![]() $k_{x}$
in the turbomachinery case (refer to table 1(b)). The fluctuations of the streamwise velocity and temperature are higher for smaller
$k_{x}$
in the turbomachinery case (refer to table 1(b)). The fluctuations of the streamwise velocity and temperature are higher for smaller
![]() $k_{x}$
, but the dependence of the stabilizing effect of nonlinearity on the frequency is very weak and it is the same for the streamwise velocity component and the temperature. For
$k_{x}$
, but the dependence of the stabilizing effect of nonlinearity on the frequency is very weak and it is the same for the streamwise velocity component and the temperature. For
![]() $k_{x}\geqslant 0.01$
the amplitude saturates at an almost constant value before decaying farther downstream.
$k_{x}\geqslant 0.01$
the amplitude saturates at an almost constant value before decaying farther downstream.

Figure 8. Evolution of the maximum r.m.s. of the streamwise velocity (a) and the temperature (b) for different streamwise wavenumber:
![]() $k_{x}=0.0036$
(solid lines) and
$k_{x}=0.0036$
(solid lines) and
![]() $k_{x}=0.0142$
(dashed lines) at
$k_{x}=0.0142$
(dashed lines) at
![]() $M_{\infty }=0.69$
(refer to table 1(b)). Thick lines: nonlinear solutions, thin lines: linearized solutions.
$M_{\infty }=0.69$
(refer to table 1(b)). Thick lines: nonlinear solutions, thin lines: linearized solutions.
Figure 9 displays the signature of the streamwise velocity and temperature for different Mach numbers in the flight case (refer to table 1(c)). The variation of
![]() $M_{\infty }$
is only due to a variation of
$M_{\infty }$
is only due to a variation of
![]() $U_{\infty }^{\ast }$
, while
$U_{\infty }^{\ast }$
, while
![]() $T_{\infty }^{\ast }$
is constant. As the Mach number increases the r.m.s. of the streamwise velocity is attenuated while the temperature fluctuations are intensified. For
$T_{\infty }^{\ast }$
is constant. As the Mach number increases the r.m.s. of the streamwise velocity is attenuated while the temperature fluctuations are intensified. For
![]() $M_{\infty }=6$
, the latter acquire an intensity as large as 26 % of
$M_{\infty }=6$
, the latter acquire an intensity as large as 26 % of
![]() $T_{\infty }^{\ast }$
, whereas the velocity fluctuations merely reach 5 % of
$T_{\infty }^{\ast }$
, whereas the velocity fluctuations merely reach 5 % of
![]() $U_{\infty }^{\ast }$
. The result suggests that thermal streaks are likely to be the primary cause of secondary instability in high speed flows. Figure 9 also shows that the attenuation effect on the velocity is stronger than the enhancement of the temperature. For example, tripling the Mach number from 2 to 6 results in a decrease of more than three times in the r.m.s. of the streamwise velocity and an increase of twice in the temperature signature at
$U_{\infty }^{\ast }$
. The result suggests that thermal streaks are likely to be the primary cause of secondary instability in high speed flows. Figure 9 also shows that the attenuation effect on the velocity is stronger than the enhancement of the temperature. For example, tripling the Mach number from 2 to 6 results in a decrease of more than three times in the r.m.s. of the streamwise velocity and an increase of twice in the temperature signature at
![]() $x=600$
. Despite
$x=600$
. Despite
![]() $r_{t}$
being the same, for higher
$r_{t}$
being the same, for higher
![]() $M_{\infty }$
the stabilizing effect of nonlinearity becomes less pronounced and this is more evident for the streamwise velocity r.m.s., whose nonlinear evolution is indistinguishable from the linearized curve in the highest
$M_{\infty }$
the stabilizing effect of nonlinearity becomes less pronounced and this is more evident for the streamwise velocity r.m.s., whose nonlinear evolution is indistinguishable from the linearized curve in the highest
![]() $M_{\infty }$
case. This behaviour is attributed to the turbulence level being smaller for higher values of the free-stream velocity, although
$M_{\infty }$
case. This behaviour is attributed to the turbulence level being smaller for higher values of the free-stream velocity, although
![]() $r_{t}$
is the same in all the cases.
$r_{t}$
is the same in all the cases.

Figure 9. Evolution of the maximum r.m.s. of the streamwise velocity (a) and the temperature (b) for different free-stream Mach numbers:
![]() $M_{\infty }=2$
(dashed lines),
$M_{\infty }=2$
(dashed lines),
![]() $M_{\infty }=6$
(solid lines). The turbulence Reynolds number is
$M_{\infty }=6$
(solid lines). The turbulence Reynolds number is
![]() $r_{t}=4.8$
(refer to table 1(c)). Thick lines: nonlinear solutions, thin lines: linearized solutions.
$r_{t}=4.8$
(refer to table 1(c)). Thick lines: nonlinear solutions, thin lines: linearized solutions.
In figure 10 the results obtained in the wind tunnel case with
![]() $r_{t}=6$
for the hot-wall condition
$r_{t}=6$
for the hot-wall condition
![]() $T_{w}^{\ast }/T_{ad}^{\ast }=1.1$
are compared with those relative to a cold-wall condition
$T_{w}^{\ast }/T_{ad}^{\ast }=1.1$
are compared with those relative to a cold-wall condition
![]() $T_{w}^{\ast }/T_{ad}^{\ast }=0.8$
and an adiabatic temperature at the wall
$T_{w}^{\ast }/T_{ad}^{\ast }=0.8$
and an adiabatic temperature at the wall
![]() $T_{w}^{\ast }=T_{ad}^{\ast }$
. As the wall heat flux increases from negative (heating), to zero (adiabatic) and to positive (cooling), the signature of the streamwise velocity is enhanced while the temperature disturbance is attenuated. The position where the abrupt deviation occurs moves from
$T_{w}^{\ast }=T_{ad}^{\ast }$
. As the wall heat flux increases from negative (heating), to zero (adiabatic) and to positive (cooling), the signature of the streamwise velocity is enhanced while the temperature disturbance is attenuated. The position where the abrupt deviation occurs moves from
![]() $\bar{x}\approx 0.5$
in the hot-wall case to
$\bar{x}\approx 0.5$
in the hot-wall case to
![]() $\bar{x}\approx 0.7$
in the cold-wall case. Therefore the wall heat flux influences the position where the onset of the stabilizing effect due to nonlinearity occurs. This suggests that the employment of the adiabatic wall condition in wind tunnel experiments may lead to an inaccurate prediction of the transition location for high Mach number supersonic flight conditions, where wall cooling usually needs to be employed for thermal protection.
$\bar{x}\approx 0.7$
in the cold-wall case. Therefore the wall heat flux influences the position where the onset of the stabilizing effect due to nonlinearity occurs. This suggests that the employment of the adiabatic wall condition in wind tunnel experiments may lead to an inaccurate prediction of the transition location for high Mach number supersonic flight conditions, where wall cooling usually needs to be employed for thermal protection.

Figure 10. Evolution of the maximum r.m.s. of the streamwise velocity (a) and the temperature (b) for different wall temperature conditions: hot wall (h.w.), adiabatic wall (a.w.) and cold wall (c.w.) at
![]() $M_{\infty }=3$
.
$M_{\infty }=3$
.
5.3 Wall-normal profiles of the perturbation for flight condition
The wall-normal profiles of the streamwise velocity and the temperature are now examined for flight conditions with
![]() $M_{\infty }=3$
and
$M_{\infty }=3$
and
![]() $r_{t}=4.8$
, as this case features significant effects of nonlinearity and compressibility, whereas in the turbomachinery case compressible effects are weak. The parameters correspond to case (d) in table 1, except that
$r_{t}=4.8$
, as this case features significant effects of nonlinearity and compressibility, whereas in the turbomachinery case compressible effects are weak. The parameters correspond to case (d) in table 1, except that
![]() $Tu=0.27\,\%$
and
$Tu=0.27\,\%$
and
![]() $r_{t}=4.8$
. The flow is symmetric with respect to the
$r_{t}=4.8$
. The flow is symmetric with respect to the
![]() $z$
direction because the Fourier forcing modes have opposite spanwise wavenumbers but equal amplitude. Therefore, results will only be presented for modes with
$z$
direction because the Fourier forcing modes have opposite spanwise wavenumbers but equal amplitude. Therefore, results will only be presented for modes with
![]() $n\geqslant 0$
, since modes
$n\geqslant 0$
, since modes
![]() $(m,n)$
and
$(m,n)$
and
![]() $(m,-n)$
have the same amplitude and shape.
$(m,-n)$
have the same amplitude and shape.
Figure 11 shows the profiles of the spanwise-uniform time-averaged flow distortion
![]() $(0,0)$
, the forcing mode
$(0,0)$
, the forcing mode
![]() $(-1,1)$
, and the second and third harmonics with
$(-1,1)$
, and the second and third harmonics with
![]() $|m|=|n|$
, i.e.
$|m|=|n|$
, i.e.
![]() $(-2,2)$
and
$(-2,2)$
and
![]() $(-3,3)$
, at
$(-3,3)$
, at
![]() $\bar{x}=0.5$
and
$\bar{x}=0.5$
and
![]() $1.2$
. As expected, the forcing mode has a higher amplitude than the other components. The mean-flow distortion makes a significant contribution to the overall flow. The magnitude of the higher harmonics decreases so quickly that the third harmonic becomes almost negligible. The profiles of the temperature perturbation are similar to those of the streamwise velocity and evolve in a similar manner, but the amplitude of the thermal fluctuations is slightly higher than those of the streamwise velocity (relatively to the free-stream values).
$1.2$
. As expected, the forcing mode has a higher amplitude than the other components. The mean-flow distortion makes a significant contribution to the overall flow. The magnitude of the higher harmonics decreases so quickly that the third harmonic becomes almost negligible. The profiles of the temperature perturbation are similar to those of the streamwise velocity and evolve in a similar manner, but the amplitude of the thermal fluctuations is slightly higher than those of the streamwise velocity (relatively to the free-stream values).

Figure 11. Profiles of the streamwise velocity (a,b) and the temperature (c,d) of the mean-flow distortion and harmonics with
![]() $|m|=|n|=1,2,3$
at
$|m|=|n|=1,2,3$
at
![]() $\bar{x}=0.5$
(a,c) and
$\bar{x}=0.5$
(a,c) and
![]() $\bar{x}=1.2$
(b,d). The parameters correspond to the flight case with
$\bar{x}=1.2$
(b,d). The parameters correspond to the flight case with
![]() $M_{\infty }=3$
and
$M_{\infty }=3$
and
![]() $r_{t}=4.8$
.
$r_{t}=4.8$
.
The streamwise velocity and temperature of the seeded modes attain their respective maxima at
![]() $\unicode[STIX]{x1D702}=1.5$
and
$\unicode[STIX]{x1D702}=1.5$
and
![]() $\unicode[STIX]{x1D702}=2$
. The most pronounced peak of the second harmonic occurs at a larger wall-normal distance,
$\unicode[STIX]{x1D702}=2$
. The most pronounced peak of the second harmonic occurs at a larger wall-normal distance,
![]() $\unicode[STIX]{x1D702}=3$
. The mean-flow distortion of the streamwise velocity is positive near the wall and negative for
$\unicode[STIX]{x1D702}=3$
. The mean-flow distortion of the streamwise velocity is positive near the wall and negative for
![]() $\unicode[STIX]{x1D702}>2$
, while the temperature profile
$\unicode[STIX]{x1D702}>2$
, while the temperature profile
![]() $(0,0)$
is negative close to the plate (excluding a small positive region at
$(0,0)$
is negative close to the plate (excluding a small positive region at
![]() $\unicode[STIX]{x1D702}<0.5$
) and positive in the outer layer. The
$\unicode[STIX]{x1D702}<0.5$
) and positive in the outer layer. The
![]() $(0,0)$
components of the streamwise velocity and temperature grow significantly with the downstream distance and their amplitudes become greater than that of the seeded modes in the outer portion of the boundary layer,
$(0,0)$
components of the streamwise velocity and temperature grow significantly with the downstream distance and their amplitudes become greater than that of the seeded modes in the outer portion of the boundary layer,
![]() $\unicode[STIX]{x1D702}>4$
. The difference between the maximum values of the linear and nonlinear profiles is larger for the temperature than for the streamwise velocity. This confirms the stronger effect of nonlinearity on temperature for high-speed flows, which was already observed in figure 6. At
$\unicode[STIX]{x1D702}>4$
. The difference between the maximum values of the linear and nonlinear profiles is larger for the temperature than for the streamwise velocity. This confirms the stronger effect of nonlinearity on temperature for high-speed flows, which was already observed in figure 6. At
![]() $\bar{x}=0.5$
the linear solution of
$\bar{x}=0.5$
the linear solution of
![]() $r_{t}|\hat{u} _{-1,1}|$
and
$r_{t}|\hat{u} _{-1,1}|$
and
![]() $r_{t}|\hat{\unicode[STIX]{x1D70F}}_{-1,1}|$
are almost indistinguishable from their nonlinear counterparts. At
$r_{t}|\hat{\unicode[STIX]{x1D70F}}_{-1,1}|$
are almost indistinguishable from their nonlinear counterparts. At
![]() $\bar{x}=1.2$
the peaks of
$\bar{x}=1.2$
the peaks of
![]() $r_{t}|\hat{u} _{-1,1}|$
and
$r_{t}|\hat{u} _{-1,1}|$
and
![]() $r_{t}|\hat{\unicode[STIX]{x1D70F}}_{-1,1}|$
in the nonlinear case have moved closer to the wall and have decreased in comparison to the linear case. After reaching their maxima, the nonlinear solutions decay more slowly and become larger than the linearized approximations in the outer region of the boundary layer. The mean-flow distortion acquires an amplitude comparable with that of the seeded modes. Therefore, the effect of nonlinearity is to move the location of the disturbance peaks nearer to the wall, to weaken the fluctuations in the core of the boundary layer while enhancing them close to the free stream, and most notably to generate significant mean-flow distortion.
$r_{t}|\hat{\unicode[STIX]{x1D70F}}_{-1,1}|$
in the nonlinear case have moved closer to the wall and have decreased in comparison to the linear case. After reaching their maxima, the nonlinear solutions decay more slowly and become larger than the linearized approximations in the outer region of the boundary layer. The mean-flow distortion acquires an amplitude comparable with that of the seeded modes. Therefore, the effect of nonlinearity is to move the location of the disturbance peaks nearer to the wall, to weaken the fluctuations in the core of the boundary layer while enhancing them close to the free stream, and most notably to generate significant mean-flow distortion.
As was pointed out by Ricco (Reference Ricco2006), the nonlinear interactions generate only Fourier modes with
![]() $m=n$
when the flow is forced by a single free-stream mode, while in the case of a pair of oblique free-stream modes additional components with
$m=n$
when the flow is forced by a single free-stream mode, while in the case of a pair of oblique free-stream modes additional components with
![]() $m\neq n$
are induced. The nonlinearly generated modes are those with
$m\neq n$
are induced. The nonlinearly generated modes are those with
![]() $|m|+|n|$
equal to an even integer, i.e. they are arranged as a checkerboard in spectral space. Those generated at the second and third orders are displayed in figure 12 at the downstream locations
$|m|+|n|$
equal to an even integer, i.e. they are arranged as a checkerboard in spectral space. Those generated at the second and third orders are displayed in figure 12 at the downstream locations
![]() $\bar{x}=0.5$
and
$\bar{x}=0.5$
and
![]() $1.2$
. The amplitudes of the components
$1.2$
. The amplitudes of the components
![]() $(-2,0)$
and
$(-2,0)$
and
![]() $(0,2)$
are comparable with each other but approximately three times smaller than that of the mean-flow distortion
$(0,2)$
are comparable with each other but approximately three times smaller than that of the mean-flow distortion
![]() $(0,0)$
. At
$(0,0)$
. At
![]() $\bar{x}=0.5$
, the peak positions and the magnitudes of the modes
$\bar{x}=0.5$
, the peak positions and the magnitudes of the modes
![]() $(-2,0)$
and
$(-2,0)$
and
![]() $(0,2)$
are very similar (or almost identical for
$(0,2)$
are very similar (or almost identical for
![]() $\unicode[STIX]{x1D702}>2$
), while at
$\unicode[STIX]{x1D702}>2$
), while at
![]() $\bar{x}=1.2$
the first peak of the mode
$\bar{x}=1.2$
the first peak of the mode
![]() $(-2,0)$
becomes much higher than that of the component
$(-2,0)$
becomes much higher than that of the component
![]() $(0,2)$
and the second peak moves further from the wall. The third-order harmonics feature two or three humps, with the first or second peak being coincident with the valley of the second-order components. Profiles with three peaks were not observed in the incompressible case (Ricco et al.
Reference Ricco, Luo and Wu2011) and they are more evident in the temperature streaks.
$(0,2)$
and the second peak moves further from the wall. The third-order harmonics feature two or three humps, with the first or second peak being coincident with the valley of the second-order components. Profiles with three peaks were not observed in the incompressible case (Ricco et al.
Reference Ricco, Luo and Wu2011) and they are more evident in the temperature streaks.

Figure 12. Profiles of the streamwise velocity (a,b) and the temperature (c,d) of harmonics with
![]() $m\neq n$
at
$m\neq n$
at
![]() $\bar{x}=0.5$
(a,c) and
$\bar{x}=0.5$
(a,c) and
![]() $\bar{x}=1.2$
(b,d). The parameters correspond to the flight case with
$\bar{x}=1.2$
(b,d). The parameters correspond to the flight case with
![]() $M_{\infty }=3$
and
$M_{\infty }=3$
and
![]() $r_{t}=4.8$
.
$r_{t}=4.8$
.
The profiles of the cross-flow velocity components and of the pressure are displayed in figure 13. No mean spanwise velocity component is generated because the disturbances are symmetric with respect to the plane
![]() $z=0$
. The profiles of
$z=0$
. The profiles of
![]() $\hat{v}_{m,0}$
asymptotically approach a constant value (with respect to
$\hat{v}_{m,0}$
asymptotically approach a constant value (with respect to
![]() $\unicode[STIX]{x1D702}$
) in the free stream, as the right-hand side of (2.82) is a function of
$\unicode[STIX]{x1D702}$
) in the free stream, as the right-hand side of (2.82) is a function of
![]() $\bar{x}$
only. The amplitudes of the wall-normal and spanwise velocity components are much smaller than that of the streamwise velocity, as
$\bar{x}$
only. The amplitudes of the wall-normal and spanwise velocity components are much smaller than that of the streamwise velocity, as
![]() $\sqrt{k_{x}/R_{\unicode[STIX]{x1D706}}}=O(10^{-4})$
and
$\sqrt{k_{x}/R_{\unicode[STIX]{x1D706}}}=O(10^{-4})$
and
![]() $k_{x}/k_{z}=O(10^{-3})$
.
$k_{x}/k_{z}=O(10^{-3})$
.

Figure 13. Profiles of the wall-normal velocity (a,b), spanwise velocity (c,d) and the pressure (e,f) of the mean-flow distortion and harmonics at
![]() $\bar{x}=1.2$
. The parameters correspond to the flight case with
$\bar{x}=1.2$
. The parameters correspond to the flight case with
![]() $M_{\infty }=3$
and
$M_{\infty }=3$
and
![]() $r_{t}=4.8$
.
$r_{t}=4.8$
.
The pressure fluctuations at the wall are analysed in order to show that these do not represent an aeroelasticity problem. The root-mean-square of the wall pressure is calculated and transformed in dimensional terms by multiplying it by
![]() $\unicode[STIX]{x1D70C}_{\infty }^{\ast }U_{\infty }^{\ast 2}$
, where
$\unicode[STIX]{x1D70C}_{\infty }^{\ast }U_{\infty }^{\ast 2}$
, where
![]() $U_{\infty }^{\ast }=888~\text{ m}~\text{s}^{-1}$
(table 1(d)) and
$U_{\infty }^{\ast }=888~\text{ m}~\text{s}^{-1}$
(table 1(d)) and
![]() $\unicode[STIX]{x1D70C}_{\infty }^{\ast }=0.09~\text{kg}~\text{m}^{-3}$
at
$\unicode[STIX]{x1D70C}_{\infty }^{\ast }=0.09~\text{kg}~\text{m}^{-3}$
at
![]() $20~\text{ km}$
altitude (Champion, Cole & Kantor Reference Champion, Cole and Kantor1985). The value obtained
$20~\text{ km}$
altitude (Champion, Cole & Kantor Reference Champion, Cole and Kantor1985). The value obtained
![]() $p_{rms}^{\ast }=0.055~\text{ Pa}$
is compared to the pressure difference on the wing. The latter is derived from the lift coefficient
$p_{rms}^{\ast }=0.055~\text{ Pa}$
is compared to the pressure difference on the wing. The latter is derived from the lift coefficient
![]() $C_{l}$
, which is evaluated using the supersonic linearized theory (refer to Anderson Reference Anderson2007, equation (12.23)) and assuming an angle of attack equal to
$C_{l}$
, which is evaluated using the supersonic linearized theory (refer to Anderson Reference Anderson2007, equation (12.23)) and assuming an angle of attack equal to
![]() $10^{\circ }$
. The resulting pressure difference
$10^{\circ }$
. The resulting pressure difference
![]() $\unicode[STIX]{x0394}p^{\ast }=4200~\text{ Pa}$
is five orders of magnitude higher than the pressure oscillations obtained in our calculations. A comparison is also performed with the wall pressure oscillations in a turbulent boundary layer for the same set of parameters. The experimental data provided by Tsuji et al. (Reference Tsuji, Fransson, Alfredsson and Johansson2007), who measured the r.m.s. of the wall pressure at different friction Reynolds number
$\unicode[STIX]{x0394}p^{\ast }=4200~\text{ Pa}$
is five orders of magnitude higher than the pressure oscillations obtained in our calculations. A comparison is also performed with the wall pressure oscillations in a turbulent boundary layer for the same set of parameters. The experimental data provided by Tsuji et al. (Reference Tsuji, Fransson, Alfredsson and Johansson2007), who measured the r.m.s. of the wall pressure at different friction Reynolds number
![]() $R_{\unicode[STIX]{x1D70F}}$
, are used to evaluate the
$R_{\unicode[STIX]{x1D70F}}$
, are used to evaluate the
![]() $p_{rms}$
at the wall at the current friction Reynolds number
$p_{rms}$
at the wall at the current friction Reynolds number
![]() $R_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}^{\ast }x^{\ast }/\unicode[STIX]{x1D708}_{\infty }^{\ast }$
, where
$R_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}^{\ast }x^{\ast }/\unicode[STIX]{x1D708}_{\infty }^{\ast }$
, where
![]() $u_{\unicode[STIX]{x1D70F}}^{\ast }$
is the friction velocity and
$u_{\unicode[STIX]{x1D70F}}^{\ast }$
is the friction velocity and
![]() $x^{\ast }$
is the distance from the leading edge. From our calculations we obtain
$x^{\ast }$
is the distance from the leading edge. From our calculations we obtain
![]() $u_{\unicode[STIX]{x1D70F}}^{\ast }=13~\text{ m}~\text{s}^{-1}$
and we choose
$u_{\unicode[STIX]{x1D70F}}^{\ast }=13~\text{ m}~\text{s}^{-1}$
and we choose
![]() $x^{\ast }=0.7~\text{ m}$
corresponding to
$x^{\ast }=0.7~\text{ m}$
corresponding to
![]() $\bar{x}=1.2$
. It follows that
$\bar{x}=1.2$
. It follows that
![]() $R_{\unicode[STIX]{x1D70F}}=3.4\times 10^{4}$
. The relation proposed by Farabee & Casarella (Reference Farabee and Casarella1991)
$R_{\unicode[STIX]{x1D70F}}=3.4\times 10^{4}$
. The relation proposed by Farabee & Casarella (Reference Farabee and Casarella1991)
![]() $(p_{rms}^{+})^{2}=6.5+1.86\ln (R_{\unicode[STIX]{x1D70F}}/333)$
is employed to extrapolate the wall pressure r.m.s.
$(p_{rms}^{+})^{2}=6.5+1.86\ln (R_{\unicode[STIX]{x1D70F}}/333)$
is employed to extrapolate the wall pressure r.m.s.
![]() $p_{rms}^{+}$
scaled with inner viscous units. The experiments of Tsuji et al. (Reference Tsuji, Fransson, Alfredsson and Johansson2007) refer to an incompressible boundary layer and therefore the effect of the Mach number on the wall pressure needs to be included in our calculations. As a first estimate, the effect of compressibility on the skin-friction coefficient
$p_{rms}^{+}$
scaled with inner viscous units. The experiments of Tsuji et al. (Reference Tsuji, Fransson, Alfredsson and Johansson2007) refer to an incompressible boundary layer and therefore the effect of the Mach number on the wall pressure needs to be included in our calculations. As a first estimate, the effect of compressibility on the skin-friction coefficient
![]() $C_{f}$
is evaluated by means of figure 19.1 of Schlichting & Gersten (Reference Schlichting and Gersten2000) and the same ratio
$C_{f}$
is evaluated by means of figure 19.1 of Schlichting & Gersten (Reference Schlichting and Gersten2000) and the same ratio
![]() $C_{f}(M_{\infty }=3)/C_{f}(M_{\infty }=0)=0.6$
is assumed to be valid for the wall pressure. It follows that
$C_{f}(M_{\infty }=3)/C_{f}(M_{\infty }=0)=0.6$
is assumed to be valid for the wall pressure. It follows that
![]() $p_{rms}^{\ast }=35~\text{Pa}$
and therefore the ratio between the wall pressure turbulent and pre-transitional fluctuations is approximately
$p_{rms}^{\ast }=35~\text{Pa}$
and therefore the ratio between the wall pressure turbulent and pre-transitional fluctuations is approximately
![]() $6\times 10^{2}$
.
$6\times 10^{2}$
.
The total time-averaged (
![]() $m=0$
) streaks of the streamwise velocity and temperature, which will be referred to as
$m=0$
) streaks of the streamwise velocity and temperature, which will be referred to as
![]() $u_{str}$
and
$u_{str}$
and
![]() $\unicode[STIX]{x1D70F}_{str}$
, are defined as
$\unicode[STIX]{x1D70F}_{str}$
, are defined as
in which only modes with
![]() $n=0,2,4,\ldots$
provide a non-zero contribution, but the component
$n=0,2,4,\ldots$
provide a non-zero contribution, but the component
![]() $(0,4)$
is almost negligible. They represent a time-averaged spanwise modulation superimposed onto the Blasius boundary layer.
$(0,4)$
is almost negligible. They represent a time-averaged spanwise modulation superimposed onto the Blasius boundary layer.
Figure 14 shows the contours of the time-averaged streamwise velocity and the temperature streaks plotted in the
![]() $\unicode[STIX]{x1D702}{-}z$
plane at different downstream locations. A positive value of the contours means that the mean flow is higher than the local Blasius solution, while a negative value means that it is lower. Therefore, near the wall the flow is accelerated and cooled, while close to the free stream it is decelerated and heated. The mean-flow distortion of the streamwise velocity has been interpreted as an increase of the mean wall shear stress and backward jets at the edge of the boundary layer, both of which have been observed in experiments (Ricco et al.
Reference Ricco, Luo and Wu2011).
$\unicode[STIX]{x1D702}{-}z$
plane at different downstream locations. A positive value of the contours means that the mean flow is higher than the local Blasius solution, while a negative value means that it is lower. Therefore, near the wall the flow is accelerated and cooled, while close to the free stream it is decelerated and heated. The mean-flow distortion of the streamwise velocity has been interpreted as an increase of the mean wall shear stress and backward jets at the edge of the boundary layer, both of which have been observed in experiments (Ricco et al.
Reference Ricco, Luo and Wu2011).

Figure 14. Contours of the time-averaged streamwise velocity streaks
![]() $u_{str}$
(a,b) and the temperature streaks
$u_{str}$
(a,b) and the temperature streaks
![]() $\unicode[STIX]{x1D70F}_{str}$
(c,d) in the
$\unicode[STIX]{x1D70F}_{str}$
(c,d) in the
![]() $\unicode[STIX]{x1D702}{-}z$
plane, at different downstream locations:
$\unicode[STIX]{x1D702}{-}z$
plane, at different downstream locations:
![]() $\bar{x}=0.5$
(a,c),
$\bar{x}=0.5$
(a,c),
![]() $\bar{x}=1.2$
(b,d). The parameters correspond to the flight case with
$\bar{x}=1.2$
(b,d). The parameters correspond to the flight case with
![]() $M_{\infty }=3$
and
$M_{\infty }=3$
and
![]() $r_{t}=4.8$
.
$r_{t}=4.8$
.
6 Summary and conclusions
The present work investigated the nonlinear response of a compressible boundary layer to free-stream unsteady vortical fluctuations of the convected-gust type. Attention is focused on the low-frequency and long streamwise components of the disturbances because these penetrate the most into the core of the boundary layer to form kinematic and thermal streaks (or Klebanoff modes). Thanks to this assumption, the mathematical framework of the compressible boundary-region equations (i.e. the Navier–Stokes equations with the streamwise derivative being neglected in the pressure and viscous terms) can be employed. The free-stream perturbation is assumed to be sufficiently strong that the amplitude of the induced streaks is comparable with the mean flow. Nonlinear effects must therefore be taken into account. The previous works by Ricco & Wu (Reference Ricco and Wu2007) and Ricco et al. (Reference Ricco, Luo and Wu2011) were extended to take into account both compressibility and nonlinear effects.
The boundary-layer displacement effect influences the outer-flow solution at leading order, that is, nonlinear interactions within the boundary layer generate a spanwise-independent flow, which drives an unsteady two-dimensional flow of acoustic nature in the outer inviscid region. The analysis shows that the displacement-induced part of the outer perturbation assumes different forms depending on the regime being subsonic or supersonic. Thanks to the well-known analogy with the flow over a thin oscillating airfoil, analytical linearized solutions in the subsonic and supersonic cases are derived. This analogy is used here for the first time to study unsteady boundary layers. In the subsonic regime the disturbances propagate in all directions from the plate, while at supersonic speeds the fluid ahead of the body remains undisturbed and the perturbations are confined within the Mach dihedron.
An initial boundary-value problem, comprising the nonlinear unsteady compressible boundary-region equations and appropriate upstream and far-field conditions, is presented to study the formation and evolution of the streaks. The initial boundary-value problem is solved for the case where the convected gust consists of a pair of oblique modes with the same frequency but opposite spanwise wavenumbers. It is shown that nonlinear interactions inside the boundary layer generate higher harmonics and a mean-flow distortion. Kinematic and thermal streaks arise, which represent an unsteady spanwise modulation of the velocity and temperature superimposed onto the Blasius boundary layer. Nonlinearity attenuates the fluctuations of the streamwise velocity and a similar stabilizing effect on the temperature is identified. Near the wall the new mean streamwise velocity is higher than the local Blasius value, while the temperature profile exhibits a deficit with respect to the Blasius solution. At the edge of the boundary layer the flow is instead decelerated and heated. The effect of the free-stream Mach number is also investigated: as the Mach number increases, the streamwise velocity fluctuations are inhibited, while the temperature ones are enhanced.
For the first time we have constructed the unsteady and three-dimensional base flow generated by the free-stream forcing and by the nonlinear interactions inside the boundary layer. This is the first step towards the formulation of the secondary instability problem, which, in the compressible case, must account for both the velocity and thermal streaks. Furthermore, by combining the present methodology and solutions, which pertain to very low-frequency disturbances, with the analytical results of Wu & Dong (Reference Wu and Dong2016) for components of
![]() $O(1)$
or higher frequency, it is now possible, for given broadband free-stream disturbances, to specify the appropriate inlet perturbations required by DNS of bypass transition in compressible boundary layers.
$O(1)$
or higher frequency, it is now possible, for given broadband free-stream disturbances, to specify the appropriate inlet perturbations required by DNS of bypass transition in compressible boundary layers.
Acknowledgements
We would like to thank the Department of Mechanical Engineering at the University of Sheffield and the Institute of High Performance Computing in Singapore for funding this work. This research would have not been possible without the use of the high performance computing facilities of the A*Star Computational Resource Centre. P.R. is supported by UKTC EPSRC grant EP/L000261/1. Part of this material is based upon work carried out by P.R. and supported by the Air Force Office of Scientific Research under award number AFOSR Grant FA8655-13-1-3073. The authors are also grateful to Drs V.-T. Nguyen and M. Skote for helpful discussions and to Drs P. Hicks, D. Wise, W. Brevis, E. Klaseboer and Professor G. Vittori for insightful suggestions on a preliminary version of the manuscript. Part of this work was presented by E.M. at the 24th International Congress of Applied Mechanics in Montréal, Canada, in August 2016 and at the IUTAM-ABCM 8th Symposium on Laminar Turbulent Transition, Rio de Janeiro, Brazil, in September 2014.
Appendix A. Nonlinear terms of the boundary-region equations
The nonlinear terms
![]() $\hat{{\mathcal{C}}}_{m,n}$
,
$\hat{{\mathcal{C}}}_{m,n}$
,
![]() $\hat{{\mathcal{X}}}_{m,n}$
,
$\hat{{\mathcal{X}}}_{m,n}$
,
![]() $\hat{{\mathcal{Y}}}_{m,n}$
,
$\hat{{\mathcal{Y}}}_{m,n}$
,
![]() $\hat{{\mathcal{Z}}}_{m,n}$
,
$\hat{{\mathcal{Z}}}_{m,n}$
,
![]() $\hat{{\mathcal{E}}}_{m,n}$
of (2.23)–(2.27) are:
$\hat{{\mathcal{E}}}_{m,n}$
of (2.23)–(2.27) are:
 $$\begin{eqnarray}\displaystyle \hat{{\mathcal{X}}}_{m,n} & = & \displaystyle \left\{\left(-\text{i}mT+\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}F^{\prime \prime }+\frac{FT^{\prime }}{2\bar{x}}\right)\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}-F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{T^{\prime }}{T}\widehat{\bar{u}\,\bar{u}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\,\bar{u}}}{\unicode[STIX]{x2202}\bar{x}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\,\bar{u}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{u}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{u}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-F^{\prime \prime }\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{u}\bar{v}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}n\widehat{\bar{u}\bar{w}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{w}}-\frac{FF^{\prime \prime }}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}+\frac{1}{2\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}n\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}+\frac{1}{2\bar{x}}\left(\frac{F^{\prime \prime }}{T}\right)^{\prime }\hat{\unicode[STIX]{x1D707}}+\frac{F^{\prime \prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{r_{t}T^{\prime }}{2\bar{x}T^{2}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{r_{t}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,r_{t}\text{i}nT\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right\}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{{\mathcal{X}}}_{m,n} & = & \displaystyle \left\{\left(-\text{i}mT+\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}F^{\prime \prime }+\frac{FT^{\prime }}{2\bar{x}}\right)\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}-F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{T^{\prime }}{T}\widehat{\bar{u}\,\bar{u}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\,\bar{u}}}{\unicode[STIX]{x2202}\bar{x}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\,\bar{u}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{u}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{u}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-F^{\prime \prime }\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{u}\bar{v}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}n\widehat{\bar{u}\bar{w}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{w}}-\frac{FF^{\prime \prime }}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}+\frac{1}{2\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}n\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}+\frac{1}{2\bar{x}}\left(\frac{F^{\prime \prime }}{T}\right)^{\prime }\hat{\unicode[STIX]{x1D707}}+\frac{F^{\prime \prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{r_{t}T^{\prime }}{2\bar{x}T^{2}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{r_{t}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,r_{t}\text{i}nT\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right\}_{m,n},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{{\mathcal{Y}}}_{m,n} & = & \displaystyle \left\{-\frac{T}{4\bar{x}^{2}}\left[FT+\unicode[STIX]{x1D702}_{c}(FT^{\prime }-TF^{\prime })-\unicode[STIX]{x1D702}_{c}^{2}F^{\prime \prime }T\right]\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left(\text{i}mT+\frac{\unicode[STIX]{x1D702}_{c}TF^{\prime \prime }+F^{\prime }T}{2\bar{x}}-\frac{FT^{\prime }}{\bar{x}}\right)\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}\nonumber\\ \displaystyle & & \displaystyle -\,F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{1}{2\bar{x}}\left(1+\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{T}\right)\widehat{\bar{u}\bar{v}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D702}}}-r_{t}\frac{T}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{v}\bar{v}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{v}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\widehat{\bar{v}\bar{w}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{w}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{T}{4\bar{x}^{2}}\left[-\unicode[STIX]{x1D702}_{c}(FF^{\prime })^{\prime }+FF^{\prime }+\frac{F^{2}T^{\prime }}{T}\right]\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}-\frac{\unicode[STIX]{x1D707}^{\prime \prime }T^{\prime }}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}-\frac{\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{12\bar{x}^{2}}\left[\unicode[STIX]{x1D707}^{\prime }+\unicode[STIX]{x1D702}_{c}T\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\right]\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)-\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}^{\prime }}{12\bar{x}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2}{3\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{2\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)+\text{i}n\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}+\frac{\text{i}n\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-\frac{\unicode[STIX]{x1D707}^{\prime \prime }T^{\prime }}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\right)+\left[\frac{F(T^{\prime })^{2}}{3\bar{x}^{2}T^{2}}+\frac{F^{\prime \prime }}{4\bar{x}^{2}}-\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }F^{\prime \prime }}{4\bar{x}^{2}T}-\frac{(FT^{\prime })^{\prime }}{3\bar{x}^{2}T}+\frac{\unicode[STIX]{x1D702}_{c}F^{\prime \prime \prime }}{4\bar{x}^{2}}\right]\hat{\unicode[STIX]{x1D707}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{F^{\prime \prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\bar{x}}+\left(\frac{\unicode[STIX]{x1D702}_{c}F^{\prime \prime }}{4\bar{x}^{2}}-\frac{FT^{\prime }}{3\bar{x}^{2}T}\right)\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{r_{t}}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}\right)+\frac{r_{t}}{12\bar{x}^{2}}\left(\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{T}-1\right)\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{r_{t}}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)-\frac{r_{t}\unicode[STIX]{x1D702}_{c}}{12\bar{x}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)-r_{t}\frac{2T^{\prime }}{3\bar{x}T^{2}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{2r_{t}}{3\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,r_{t}\text{i}nT\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}+r_{t}\frac{\text{i}n}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-\frac{r_{t}}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\right)\right\}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{{\mathcal{Y}}}_{m,n} & = & \displaystyle \left\{-\frac{T}{4\bar{x}^{2}}\left[FT+\unicode[STIX]{x1D702}_{c}(FT^{\prime }-TF^{\prime })-\unicode[STIX]{x1D702}_{c}^{2}F^{\prime \prime }T\right]\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left(\text{i}mT+\frac{\unicode[STIX]{x1D702}_{c}TF^{\prime \prime }+F^{\prime }T}{2\bar{x}}-\frac{FT^{\prime }}{\bar{x}}\right)\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}\nonumber\\ \displaystyle & & \displaystyle -\,F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{1}{2\bar{x}}\left(1+\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{T}\right)\widehat{\bar{u}\bar{v}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D702}}}-r_{t}\frac{T}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{v}\bar{v}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{v}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{v}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\widehat{\bar{v}\bar{w}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{w}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{T}{4\bar{x}^{2}}\left[-\unicode[STIX]{x1D702}_{c}(FF^{\prime })^{\prime }+FF^{\prime }+\frac{F^{2}T^{\prime }}{T}\right]\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}-\frac{\unicode[STIX]{x1D707}^{\prime \prime }T^{\prime }}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}-\frac{\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{12\bar{x}^{2}}\left[\unicode[STIX]{x1D707}^{\prime }+\unicode[STIX]{x1D702}_{c}T\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\right]\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)-\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D707}^{\prime }}{12\bar{x}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2}{3\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{2\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)+\text{i}n\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}+\frac{\text{i}n\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-\frac{\unicode[STIX]{x1D707}^{\prime \prime }T^{\prime }}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D707}^{\prime }}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\right)+\left[\frac{F(T^{\prime })^{2}}{3\bar{x}^{2}T^{2}}+\frac{F^{\prime \prime }}{4\bar{x}^{2}}-\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }F^{\prime \prime }}{4\bar{x}^{2}T}-\frac{(FT^{\prime })^{\prime }}{3\bar{x}^{2}T}+\frac{\unicode[STIX]{x1D702}_{c}F^{\prime \prime \prime }}{4\bar{x}^{2}}\right]\hat{\unicode[STIX]{x1D707}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{F^{\prime \prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\bar{x}}+\left(\frac{\unicode[STIX]{x1D702}_{c}F^{\prime \prime }}{4\bar{x}^{2}}-\frac{FT^{\prime }}{3\bar{x}^{2}T}\right)\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{r_{t}}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}\right)+\frac{r_{t}}{12\bar{x}^{2}}\left(\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{T}-1\right)\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{r_{t}}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)-\frac{r_{t}\unicode[STIX]{x1D702}_{c}}{12\bar{x}^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)-r_{t}\frac{2T^{\prime }}{3\bar{x}T^{2}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{2r_{t}}{3\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,r_{t}\text{i}nT\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}+r_{t}\frac{\text{i}n}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-\frac{r_{t}}{3\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\right)\right\}_{m,n},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{{\mathcal{Z}}}_{m,n} & = & \displaystyle \left\{\left(-\text{i}mT+\frac{FT^{\prime }}{2\bar{x}}\right)\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}}-F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{2\bar{x}T}\widehat{\bar{u}\bar{w}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{v}\bar{w}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{v}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\widehat{\bar{w}\bar{w}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}\bar{w}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2\text{i}nT\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }}{3}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}+\frac{\text{i}nT\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D702}_{c}}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime \prime }TT^{\prime }}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}+T\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)-\frac{2\text{i}n\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }}{3}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\unicode[STIX]{x1D707}^{\prime \prime }T^{\prime }\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}+\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)+\frac{4\unicode[STIX]{x1D707}^{\prime }\text{i}nT\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}+\frac{\text{i}n\unicode[STIX]{x1D705}^{2}FT^{\prime }}{3\bar{x}}\hat{\unicode[STIX]{x1D707}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}\frac{2\text{i}nT\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}+r_{t}\frac{\text{i}nT\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D702}_{c}}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+r_{t}T\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)-r_{t}\frac{\unicode[STIX]{x1D702}_{c}T\unicode[STIX]{x1D705}^{2}}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}\frac{2\text{i}n\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+r_{t}\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}\right)-r_{t}\frac{T^{\prime }}{2\bar{x}T^{2}}\widehat{\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{r_{t}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,r_{t}\frac{4\text{i}nT\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\right\}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{{\mathcal{Z}}}_{m,n} & = & \displaystyle \left\{\left(-\text{i}mT+\frac{FT^{\prime }}{2\bar{x}}\right)\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}}-F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{2\bar{x}T}\widehat{\bar{u}\bar{w}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{v}\bar{w}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{v}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{w}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\widehat{\bar{w}\bar{w}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}\bar{w}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2\text{i}nT\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }}{3}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}+\frac{\text{i}nT\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D702}_{c}}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime \prime }TT^{\prime }}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}+T\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D702}_{c}\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)-\frac{2\text{i}n\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D707}^{\prime }}{3}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\unicode[STIX]{x1D707}^{\prime \prime }T^{\prime }\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}+\unicode[STIX]{x1D707}^{\prime }\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\bar{x}}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)+\frac{4\unicode[STIX]{x1D707}^{\prime }\text{i}nT\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}+\frac{\text{i}n\unicode[STIX]{x1D705}^{2}FT^{\prime }}{3\bar{x}}\hat{\unicode[STIX]{x1D707}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}\frac{2\text{i}nT\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\bar{x}}}+r_{t}\frac{\text{i}nT\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D702}_{c}}{3\bar{x}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+r_{t}T\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\bar{x}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)-r_{t}\frac{\unicode[STIX]{x1D702}_{c}T\unicode[STIX]{x1D705}^{2}}{2\bar{x}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,r_{t}\frac{2\text{i}n\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+r_{t}\unicode[STIX]{x1D705}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}\hat{z}}}\right)-r_{t}\frac{T^{\prime }}{2\bar{x}T^{2}}\widehat{\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{r_{t}}{2\bar{x}T}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,r_{t}\frac{4\text{i}nT\unicode[STIX]{x1D705}^{2}}{3}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{w}}{\unicode[STIX]{x2202}\hat{z}}}\right\}_{m,n},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \hat{\{}_{m,n} & = & \displaystyle \left\{\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }T}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}-r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-T^{\prime }\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}\bar{\unicode[STIX]{x1D70F}}}-\text{i}mT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{2\bar{x}T}\widehat{\bar{u}\bar{\unicode[STIX]{x1D70F}}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{v}\bar{\unicode[STIX]{x1D70F}}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{v}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\widehat{\bar{w}\bar{\unicode[STIX]{x1D70F}}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D707}^{\prime }Tn^{2}\unicode[STIX]{x1D705}^{2}}{2Pr}\widehat{\bar{\unicode[STIX]{x1D70F}}^{2}}+\frac{1}{2\bar{x}Pr}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}PrT}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}}{2\bar{x}T}\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)^{2}}+\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{\bar{x}T}\widehat{\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\bar{\unicode[STIX]{x1D70F}}}+r_{t}\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}T}\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)^{2}}\bar{\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & & \displaystyle +\,M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}\right)^{2}}+M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)r_{t}\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}\right)^{2}\bar{\unicode[STIX]{x1D70F}}}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{1}{2\bar{x}Pr}\left(\frac{T^{\prime }}{T}\right)^{\prime }+\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)(F^{\prime \prime })^{2}}{2\bar{x}T}\right]\hat{\unicode[STIX]{x1D707}}+\frac{T^{\prime }}{2\bar{x}PrT}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle +\,r_{t}\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)F^{\prime \prime }}{\bar{x}T}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+r_{t}^{2}\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)}{2\bar{x}T}\widehat{\bar{\unicode[STIX]{x1D707}}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)^{2}}\!+r_{t}^{2}M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)T\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D707}}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}\right)^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\left.r_{t}\frac{T^{\prime }}{2\bar{x}PrT^{2}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{r_{t}}{2\bar{x}PrT}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)+r_{t}\frac{\text{i}nT\unicode[STIX]{x1D705}^{2}}{Pr}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\hat{z}}}\right\}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{\{}_{m,n} & = & \displaystyle \left\{\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }T}{2\bar{x}}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}}-r_{t}T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\bar{x}}+r_{t}\frac{\unicode[STIX]{x1D702}_{c}T}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-T^{\prime }\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}}-r_{t}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{v}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-r_{t}\text{i}nT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{w}\bar{\unicode[STIX]{x1D70F}}}-\text{i}mT\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,F^{\prime }T\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{FT}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{\unicode[STIX]{x1D70C}}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x1D702}_{c}T^{\prime }}{2\bar{x}T}\widehat{\bar{u}\bar{\unicode[STIX]{x1D70F}}}-\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\bar{x}}+\frac{\unicode[STIX]{x1D702}_{c}}{2\bar{x}}\frac{\unicode[STIX]{x2202}\widehat{\bar{u}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{T^{\prime }}{T^{2}}\widehat{\bar{v}\bar{\unicode[STIX]{x1D70F}}}-\frac{1}{T}\frac{\unicode[STIX]{x2202}\widehat{\bar{v}\bar{\unicode[STIX]{x1D70F}}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\text{i}n\widehat{\bar{w}\bar{\unicode[STIX]{x1D70F}}}\left.\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D707}^{\prime }Tn^{2}\unicode[STIX]{x1D705}^{2}}{2Pr}\widehat{\bar{\unicode[STIX]{x1D70F}}^{2}}+\frac{1}{2\bar{x}Pr}\left(\frac{\unicode[STIX]{x1D707}^{\prime }}{T}\right)^{\prime }\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}PrT}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}}{2\bar{x}T}\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)^{2}}+\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}^{\prime }F^{\prime \prime }}{\bar{x}T}\widehat{\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\bar{\unicode[STIX]{x1D70F}}}+r_{t}\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D707}^{\prime }}{2\bar{x}T}\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)^{2}}\bar{\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & & \displaystyle +\,M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}\right)^{2}}+M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)r_{t}\unicode[STIX]{x1D705}^{2}T\unicode[STIX]{x1D707}^{\prime }\widehat{\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}\right)^{2}\bar{\unicode[STIX]{x1D70F}}}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{1}{2\bar{x}Pr}\left(\frac{T^{\prime }}{T}\right)^{\prime }+\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)(F^{\prime \prime })^{2}}{2\bar{x}T}\right]\hat{\unicode[STIX]{x1D707}}+\frac{T^{\prime }}{2\bar{x}PrT}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D707}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle +\,r_{t}\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)F^{\prime \prime }}{\bar{x}T}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+r_{t}^{2}\frac{M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)}{2\bar{x}T}\widehat{\bar{\unicode[STIX]{x1D707}}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)^{2}}\!+r_{t}^{2}M_{\infty }^{2}(\unicode[STIX]{x1D6FE}-1)T\unicode[STIX]{x1D705}^{2}\widehat{\bar{\unicode[STIX]{x1D707}}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}\hat{z}}\right)^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\left.r_{t}\frac{T^{\prime }}{2\bar{x}PrT^{2}}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}+\frac{r_{t}}{2\bar{x}PrT}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\right)+r_{t}\frac{\text{i}nT\unicode[STIX]{x1D705}^{2}}{Pr}\widehat{\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x2202}\hat{z}}}\right\}_{m,n},\end{eqnarray}$$
where
![]() $\hat{z}=k_{z}z$
.
$\hat{z}=k_{z}z$
.