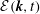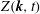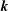1 Introduction
Turbulence and stability in rotating shear flows are essential in many contexts ranging from engineering – as in e.g. turbomachinery or hydroelectric power generation – to geophysics and astrophysics. Among various combinations of mean-flow gradients and system rotation, the case with mean plane shear rotating in the spanwise direction (figure 1) has widespread applications. Stabilization and destabilization of turbulence are found in these flows depending on cyclonic or anticyclonic asymmetries of mean shear vorticity and system vorticity, for instance in the experimental study of rotating plane channel flow by Johnston, Halleent & Lezius (Reference Johnston, Halleent and Lezius1972). Similar effects are also exhibited in rotating Couette flows (Hiwatashi et al. Reference Hiwatashi, Alfredsson, Tillmark and Nagata2007) and rotating wakes (Perret et al. Reference Perret, Stegner, Farge and Pichon2006; Dong, McWilliams & Shchepetkin Reference Dong, McWilliams and Shchepetkin2007) with the interaction of mean shear and the Coriolis force.
Figure 1. Coordinate system for a flow with pure plane mean shear and rotating in the spanwise direction.
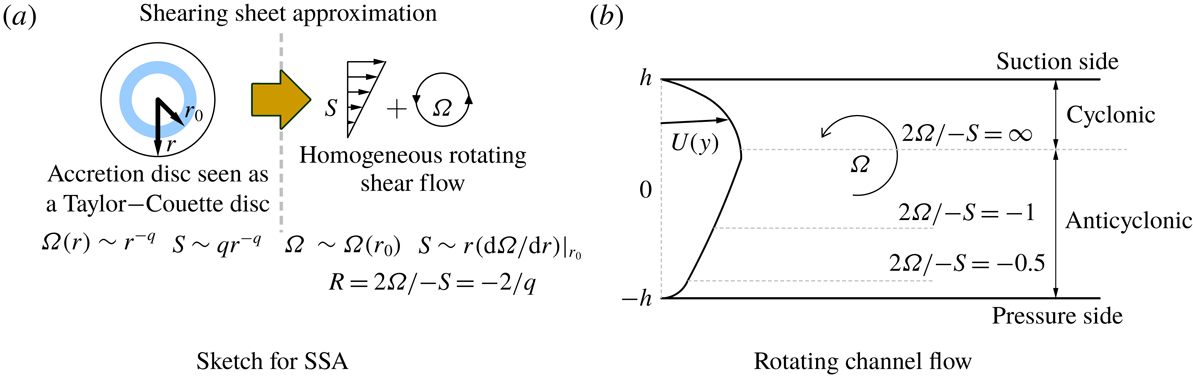
A simple model for spatially uniform turbulent shear flow is used in astrophysics for the study of turbulent accretion discs, which can be seen as Taylor–Couette flow (figure 2
a). According to the shearing sheet approximation (SSA) by Balbus & Hawley (Reference Balbus and Hawley1998) – also called the local shearing box – the rotation rate
$\unicode[STIX]{x1D6FA}$
is approximately uniform and the shear rate
$S$
can be represented by differential rotation at a specific radial position
$r_{0}$
, namely
$\unicode[STIX]{x1D6FA}\sim \unicode[STIX]{x1D6FA}(r_{0})$
and
$S=r(\text{d}\unicode[STIX]{x1D6FA}/\text{d}r)|_{r_{0}}$
. The simple model of homogeneous turbulent rotating shear flow is also useful in engineering for interblade flow in turbomachinery, and in geophysical flows. Figure 2(b) illustrates how the context of homogeneous anisotropic turbulence (HAT) can be locally relevant for rotating channel flow, e.g. in the centre region where constant mean shear rate
$S$
and uniform spanwise rotation
$\unicode[STIX]{x1D6FA}$
apply.
Figure 2. Schematic of the geometrical simplification of complex flows leading to local homogeneous anisotropic turbulence modelling: (a) accretion disc in astrophysics; (b) rotating channel flow.
Although inhomogeneity is discarded, these flows are still difficult to describe with single-point statistics because the dynamics of anisotropic turbulence depends on the relevant length scale. Considering single-point closures, while the basic two-equation
${\mathcal{K}}$
–
$\unicode[STIX]{x1D700}$
model altogether ignores the effect of rotation in the rotating shear case, others take it into account to some extent. This is the case of the Reynolds-stress models (RSM, e.g. Launder, Reece & Rodi Reference Launder, Reece and Rodi1975), or of the more sophisticated structure-based models (Kassinos, Reynolds & Rogers Reference Kassinos, Reynolds and Rogers2001). Alternately, spectral theory with a two-point statistical approach is very popular for the study of HAT, in which the distorting mean flow is represented by uniform mean-velocity and density gradients, and by body forces such as the Coriolis force (Sagaut & Cambon Reference Sagaut and Cambon2018). The two-point spectral description starts with the spectral tensor
$\hat{\unicode[STIX]{x1D64D}}(\boldsymbol{k},t)$
, which is the Fourier transform of the two-point second-order velocity correlation tensor
$\unicode[STIX]{x1D619}_{ij}(\boldsymbol{r},t)=\langle u_{i}(\boldsymbol{x},t)u_{j}(\boldsymbol{x}+\boldsymbol{r},t)\rangle$
in physical space. Closed nonlinear equations for the evolution of
$\hat{\unicode[STIX]{x1D64D}}(\boldsymbol{k},t)$
can be obtained and permit the study of statistical properties of anisotropic flows, such as scale-by-scale anisotropy or turbulent cascade.
In turbulent shear flows, the interplay between linear and nonlinear mechanisms can be very complex and subtle. For linear terms, spectral linear theory (SLT) is very efficient for solving linear operators of homogeneous turbulence. It was originally introduced as ‘rapid distortion theory’ (RDT) for irrotational mean flows by Batchelor & Proudman (Reference Batchelor and Proudman1954), and applied to the shear flow case by Moffatt (Reference Moffatt, Yaglom and Tatarsky1967). SLT was then extended to rotating shear flows by Salhi & Cambon (Reference Salhi and Cambon1997) and to stratified shear flows by Hanazaki & Hunt (Reference Hanazaki and Hunt2004) using a refined analytical approach. Salhi & Cambon (Reference Salhi and Cambon2010) unified this approach for the case of rotating stratified shear flows. All these studies show the global relevance of the Bradshaw number
$B$
(Bradshaw Reference Bradshaw1969) for characterizing the stability of the flow:
$B=R(R+1)$
, in which
$R=2\unicode[STIX]{x1D6FA}/-S$
is the ratio of system vorticity
$2\unicode[STIX]{x1D6FA}$
to shear-induced vorticity
$-S$
. Cases with
$B<0$
or
$-1<R<0$
correspond to exponential growth of turbulent kinetic energy, and
$B>0$
to exponential decay. Neutral cases are found for both
$R=0$
(no background rotation) and
$R=-1$
(zero absolute vorticity). However, SLT is limited in principle to short evolution times, and more specifically to the largest scales of the turbulent flow, since its focus is the linear influence of the mean flow on fluctuations rather than the nonlinear interaction of the fluctuating flow with itself. In addition, from the point of view of linear dynamics, the passage from a two-point spectral description to a single-point one implies a loss of non-locality in the pressure/velocity relationship in physical space. As a consequence, modelling the ‘rapid’ pressure–strain rate tensor in the RSM equations is very difficult, as recently discussed by Mishra & Girimaji (Reference Mishra and Girimaji2017) in line with exact SLT analysis. Surprisingly, the Bradshaw criterion is globally relevant for explaining the stability when considering production terms in the RSM equations (see also Brethouwer Reference Brethouwer2005). This is also supported by a coarse pressureless model (Salhi, Cambon & Speziale Reference Salhi, Cambon and Speziale1997; Leblanc & Cambon Reference Leblanc and Cambon1998) which also brings forward the role of
$R=2\unicode[STIX]{x1D6FA}/-S$
. A criterion similar to that of Bradshaw was also proposed in the SSA, using the epicyclic frequency
$\unicode[STIX]{x1D705}=\sqrt{2\unicode[STIX]{x1D6FA}(2\unicode[STIX]{x1D6FA}+S)}$
. The stability of the flow is thus related to a Rayleigh criterion, ignoring again the effects of fluctuating pressure. Moreover,
$B=\unicode[STIX]{x1D705}^{2}/S^{2}$
in the rotating shear case is sometimes called the ‘rotational Richardson number’; it is analogous to the Richardson number
$Ri=N^{2}/S^{2}$
of the stratified shear case, where
$N$
is the Brunt–Väisälä frequency.
Regarding nonlinear closures of homogeneous isotropic turbulence (HIT), a few models are based on Heisenberg’s transfer model (e.g. Canuto & Dubovikov Reference Canuto and Dubovikov1996a ,Reference Canuto and Dubovikov b ; Canuto et al. Reference Canuto, Dubovikov, Cheng and Dienstfrey1996). Other more sophisticated and successful models employ high-order closures using the eddy damped quasi-normal Markovian (EDQNM) technique (Orszag Reference Orszag1969), which can be extended to shear-driven or buoyancy-driven flows, and accounts for coupled fields, e.g. in magnetohydrodynamics (see review in Cambon et al. Reference Cambon, Mons, Gréa and Rubinstein2017; Sagaut & Cambon Reference Sagaut and Cambon2018). In the case of HAT, different versions of EDQNM closure can be chosen depending on the flow regimes and on the available computational resources. These versions involve physical assumptions which are sometimes justified only for specific flows, but their validity are in practice checked by implementation of the model and the related numerical results. Briefly, the EDQNM closure model can be developed in different versions depending on the retained physical assumptions and on the chosen method of resolution.
First, physical assumptions permit closures of the basic equations written for single-time three-point third-order correlations, and transformed in Fourier space for solving pressure fluctuation via the divergence-free property of velocity. In these equations, linear terms represent the effect of mean gradients, body forces and viscous terms, whereas fourth-order moments account for nonlinearity. These moments are expressed as the sum of a quasi-normal contribution and a contribution from fourth-order cumulants. The closure consists in attributing a damping effect to the contribution from cumulants to express the departure from Gaussianity. This is the eddy-damped (ED) quasi-normal (QN) assumption. In addition, one assumes that the time scale of triple correlations is much larger than that of double correlations embedded in the quasi-normal term. This is the Markovian (M) assumption. On the basis of these assumptions, one can derive a series of models that differ by the degree of refinement chosen for representing linear versus nonlinear mechanisms, and for representing anisotropy. For instance, the EDQNM1 model – from which the MCS (Mons, Cambon, Sagaut) model is derived – neglects explicit anisotropic linear terms in the equations for triple correlations. This restricts the models to turbulent flows where linear effects induced by mean-flow gradients have no essential qualitative effects on the dynamics of triple correlations compared with the induced production effects in the equations for second-order correlations. It is questionable in purely rotating turbulence in which the Coriolis force does not affect the energy balance equation directly, i.e. induces no production. A refinement of the EDQNM1 model can use an anisotropic eddy damping, or keep it similar to its form in HIT. Overall, EDQNM1 compares well with direct numerical simulation (DNS) when linear terms are associated with energy production in double correlations equations (e.g. unstably stratified homogeneous turbulence in Burlot et al. Reference Burlot, Gréa, Godeferd, Cambon and Griffond2015).
Second, various formulations and resolution methods can be chosen. For instance, the EDQNM1 approach results in a closure for two-point transfer terms using a vector of variables
$({\mathcal{E}},Z,{\mathcal{H}})$
that represent the complete spectral tensor of double correlations. Moreover, the helicity spectrum
${\mathcal{H}}$
can be used in general (Bellet et al.
Reference Bellet, Godeferd, Scott and Cambon2006), but it will be neglected in our case of homogeneous shear-driven turbulence, since it cannot emerge spontaneously unless introduced explicitly in the initial conditions. Accordingly, all the information from the closure strategy will be concentrated in two generalized transfers denoted
$T^{({\mathcal{E}})}$
and
$T^{(Z)}$
. At this stage, the complexity and the numerical cost of the model remains high, even in axisymmetric flows, because of the anisotropy which renders all two-point statistics dependent on the three-dimensional (3-D) wave vector
$\boldsymbol{k}$
. In order to derive a numerically tractable model, the description of anisotropy of the second-order spectral tensor is simplified by using low-degree expansions in terms of angular harmonics. The initial model in terms
$\boldsymbol{k}$
-vector thus becomes a model in terms of spherically averaged descriptors that depend only on
$k$
– the modulus of
$\boldsymbol{k}$
, e.g. the MCS model by Mons, Cambon & Sagaut (Reference Mons, Cambon and Sagaut2016) which retains the first two degrees in the spherical harmonics expansion. Although validated for different flows, comparisons of the MCS model to SLT and DNS at long times suggest that this low-degree expansion is much less adapted to the representation of linear terms angular variations than it is for the nonlinear terms. The purpose of the present article is therefore to restore the full angular dependence of linear terms in the equations for
${\mathcal{E}}(\boldsymbol{k},t)$
and
$Z(\boldsymbol{k},t)$
and to restrict to nonlinear transfer terms the use of low-degree expansion inspired from MCS. This appears as the only way to check the validity of the nonlinear closure per se, given the subtle interplay of linear and nonlinear terms. In addition, this also permits validation of other models which use no assumption for modelling the linear terms, with unexpected results. The model by Weinstock (Reference Weinstock1982, Reference Weinstock2013) for the pure plane shear without system rotation is particularly interesting because it relies on purely isotropic EDQNM model for the energy transfer, with a weakly anisotropic part to force the return to isotropy. One of the most surprising results of our work is the fact that a hybrid model combining the nonlinear closure from both MCS and Weinstock is relevant for the pure shear flow without system rotation.
The paper is organized as follows. In § 2 we recall the decomposition of
$\hat{\unicode[STIX]{x1D64D}}(\boldsymbol{k},t)$
in terms of the scalar
${\mathcal{E}}(\boldsymbol{k},t)$
and pseudo-scalar
$Z(\boldsymbol{k},t)$
, their governing equations and the simplified anisotropic closure based on EDQNM, then we propose a hybrid nonlinear model combining simplified anisotropic EDQNM closure and Weinstock’s model. We present the numerical scheme and spectral space discretization in § 3. In § 4, the validation of the model in the linear limit is described and we obtain results of the complete nonlinear models. A dedicated discussion for the non-rotating shear flow case is proposed in § 5. Finally, § 6 is devoted to conclusions and perspectives.
2 Background equations
Following Batchelor (Reference Batchelor1953) and Craya (Reference Craya1957), we consider the general case of statistical homogeneity restricted to fluctuations. An extensional mean flow with velocity components
$U_{i}$
injects energy and anisotropy into the fluctuating flow via a spatially uniform mean-velocity gradient
$A_{ij}$
:
$$\begin{eqnarray}A_{ij}=\frac{\unicode[STIX]{x2202}U_{i}}{\unicode[STIX]{x2202}x_{j}}=\mathit{S}_{ij}+\frac{1}{2}\unicode[STIX]{x1D716}_{imj}W_{m},\end{eqnarray}$$
combining contributions from strain
$\mathit{S}_{ij}$
– the symmetric part – and mean vorticity
$\boldsymbol{W}$
– the antisymmetric part (
$\unicode[STIX]{x1D716}_{imj}$
is the Levi-Civita pseudo-tensor). In addition, the whole flow – mean flow plus fluctuations – is placed in a frame rotating at angular velocity
$\unicode[STIX]{x1D734}$
. This corresponds to various possible applications, such as rotating shear or precessing flows.
We consider the two-point correlation of fluctuating velocity
$\unicode[STIX]{x1D619}_{ij}(\boldsymbol{r},t)$
and its Fourier transform producing a spectrum of Fourier coefficients
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
. In the incompressible homogeneous anisotropic flow with the mean gradients
$A_{ij}$
of (2.1) and in the frame rotating at
$\unicode[STIX]{x1D734}$
,
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
is governed by
$$\begin{eqnarray}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}-A_{ln}k_{l}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k_{n}}+2\unicode[STIX]{x1D708}k^{2}\right)\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)+M_{in}(\boldsymbol{k})\hat{\unicode[STIX]{x1D619}}_{nj}(\boldsymbol{k},t)+M_{jn}(\boldsymbol{k})\hat{\unicode[STIX]{x1D619}}_{ni}(\boldsymbol{k},t)=T_{ij}(\boldsymbol{k},t),\end{eqnarray}$$
with the linear operator induced by mean-velocity gradients:
$$\begin{eqnarray}M_{ij}(\boldsymbol{k})=\left(\unicode[STIX]{x1D6FF}_{in}-2\frac{k_{i}k_{n}}{k^{2}}\right)A_{nj}+2P_{in}(\unicode[STIX]{x1D736})\unicode[STIX]{x1D700}_{lnj}\unicode[STIX]{x1D6FA}_{l},\end{eqnarray}$$
and the nonlinear transfer
$T_{ij}(\boldsymbol{k},t)$
gathers contributions for third-order two-point velocity correlations (see § 2.2), which need to be closed. Equation (2.2) is derived by Fourier transform of the Navier–Stokes equations, in which
$\unicode[STIX]{x1D736}=\boldsymbol{k}/k$
is the unit vector along wave vector
$\boldsymbol{k}$
,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$P_{ij}(\unicode[STIX]{x1D736})=\unicode[STIX]{x1D6FF}_{ij}-(k_{i}k_{j}/k^{2})$
is the projection tensor.
Figure 3. Polar-spherical system of coordinates for
$\boldsymbol{k}$
and related Craya–Herring frame of reference
$(\boldsymbol{e}^{(1)},\boldsymbol{e}^{(2)},\unicode[STIX]{x1D736}=\boldsymbol{e}^{(3)})$
.
2.1 Equations for the state vector (
${\mathcal{E}},Z$
)
The two-point second-order velocity correlation tensor is given by
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k})$
(and also
$\unicode[STIX]{x1D619}_{ij}(\boldsymbol{r})$
), which is a priori 9-component. It contains the complete information pertaining to second-order velocity statistics of the flow. Thanks to incompressibility and Hermitian symmetry, it can be replaced by a basic state vector
$({\mathcal{E}},Z,{\mathcal{H}})$
(see Cambon & Jacquin Reference Cambon and Jacquin1989; Sagaut & Cambon Reference Sagaut and Cambon2018) such that
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)={\mathcal{E}}(\boldsymbol{k},t)P_{ij}(\unicode[STIX]{x1D736})+\text{Re}(Z(\boldsymbol{k},t)N_{i}(\unicode[STIX]{x1D736})N_{j}(\unicode[STIX]{x1D736}))+\text{i}\unicode[STIX]{x1D716}_{ijn}{\mathcal{H}}(\boldsymbol{k},t)\unicode[STIX]{x1D6FC}_{n}.\end{eqnarray}$$
The first term displays the directional anisotropy, that is generated by the departure of the 3-D energy spectrum
${\mathcal{E}}=\hat{\unicode[STIX]{x1D619}}_{nn}/2$
from its spherically averaged counterpart
$E(k,t)/4\unicode[STIX]{x03C0}k^{2}$
, where
$E(k,t)=\int _{S_{k}}{\mathcal{E}}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}$
is the classical spherically integrated energy spectrum. The second term represents the polarization tensor (see also Cambon & Rubinstein Reference Cambon and Rubinstein2006) generated by the complex-valued pseudo-scalar
$Z$
. The last term involves the 3-D helicity spectrum
$k{\mathcal{H}}(\boldsymbol{k},t)$
and is purely imaginary (
$\text{i}^{2}=-1$
) and antisymmetric. It is neglected in this study. This decomposition relies on the use of the three unit vectors (
$\boldsymbol{N},\boldsymbol{N}^{\ast },\unicode[STIX]{x1D736}$
) of an orthonormal frame onto which the fluctuating velocity in Fourier space
$\hat{\boldsymbol{u}}(\boldsymbol{k},t)$
is projected. The helical modes
$\boldsymbol{N}$
and conjugate
$\boldsymbol{N}^{\ast }$
are closely related to the Craya–Herring frame of reference
$(\boldsymbol{e}^{(1)},\boldsymbol{e}^{(2)},\unicode[STIX]{x1D736}=\boldsymbol{e}^{(3)})$
with polar axis
$\boldsymbol{n}$
illustrated in figure 3 (Herring Reference Herring1974; Cambon & Jacquin Reference Cambon and Jacquin1989; Waleffe Reference Waleffe1992; Cambon, Mansour & Godeferd Reference Cambon, Mansour and Godeferd1997)
$$\begin{eqnarray}\boldsymbol{N}(\unicode[STIX]{x1D736})=\boldsymbol{e}^{(2)}(\unicode[STIX]{x1D736})-\text{i}\boldsymbol{e}^{(1)}(\unicode[STIX]{x1D736}),\quad \unicode[STIX]{x1D736}=\frac{\boldsymbol{k}}{|\boldsymbol{k}|},\boldsymbol{e}^{(1)}(\unicode[STIX]{x1D736})=\frac{\unicode[STIX]{x1D736}\times \boldsymbol{n}}{|\unicode[STIX]{x1D736}\times \boldsymbol{n}|},\boldsymbol{e}^{(2)}(\unicode[STIX]{x1D736})=\unicode[STIX]{x1D736}\times \boldsymbol{e}^{(1)}.\end{eqnarray}$$
The governing equations for the state vector
$({\mathcal{E}},Z)$
are obtained from (2.2) as
$$\begin{eqnarray}\displaystyle & \dot{(k{\mathcal{E}})}+2\unicode[STIX]{x1D708}k^{3}{\mathcal{E}}+\text{Re}(kZ(\boldsymbol{k},t)\mathit{S}_{ij}N_{i}(\unicode[STIX]{x1D736})N_{j}(\unicode[STIX]{x1D736}))=kT^{({\mathcal{E}})}(\boldsymbol{k},t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \dot{(kZ)}+2\unicode[STIX]{x1D708}k^{3}Z+k{\mathcal{E}}(\boldsymbol{k},t)\mathit{S}_{ij}N_{i}(-\unicode[STIX]{x1D736})N_{j}(-\unicode[STIX]{x1D736})-\text{i}kZ(\boldsymbol{k},t)((\boldsymbol{W}+4\unicode[STIX]{x1D734})\boldsymbol{\cdot }\unicode[STIX]{x1D736}-2\unicode[STIX]{x1D6FA}_{E}) & \displaystyle \nonumber\\ \displaystyle & \quad =kT^{(Z)}(\boldsymbol{k},t). & \displaystyle\end{eqnarray}$$
The overdot denotes the advection operator due to the presence of the mean flow, namely
$\dot{(...)}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t-A_{mn}k_{m}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}k_{n})$
. The left-hand sides of (2.6) represent the linear effects of the mean flow as in viscous SLT, with geometric coefficients that depend on the orientation of the wave vector
$\unicode[STIX]{x1D736}$
via helical modes
$\boldsymbol{N}(\pm \unicode[STIX]{x1D736})$
.
$\unicode[STIX]{x1D6FA}_{E}$
is the rotation rate induced by the advection operator, and corresponds to the rotation required for transforming the Craya–Herring frame at time
$t=0$
to that at subsequent time
$t$
. We retain it here for the sake of completeness, but it can be removed from consideration in the special applications used in this article. The right-hand sides of (2.6) gather the contributions from two-point third-order correlations mediated by the quadratic nonlinearity of the basic Navier–Stokes equations and are closed in § 2.2. Equation (2.6) is presented in a simplified form using
$k$
as an integrating factor in the products of
$k{\mathcal{E}}$
and
$kZ$
. The left-hand sides of both (2.6a
) and (2.6b
) contain viscous terms, and similar symmetric straining terms, but the antisymmetric part of the mean-velocity gradients only affects the equation for polarization through a combination of mean and system vorticity (the ‘stropholysis’ effect coined by Kassinos et al.
Reference Kassinos, Reynolds and Rogers2001).
2.2 Closure of nonlinear transfer terms with simplified anisotropic EDQNM
Principles of the fully 3-D EDQNM1 model were recalled in the Introduction, and detailed equations are given in Mons et al. (Reference Mons, Cambon and Sagaut2016). However, the numerical resolution cost of EDQNM1 may be large since the transfer terms involve 3-D triadic integrals similar to convolutions. A significant reduction of the complexity and of the numerical cost was obtained by MCS which replaces the model for
$\boldsymbol{k}$
-dependent spectra by a model in terms of spherically averaged descriptors. The method relies on expansions in terms of angular harmonics of the form:
$$\begin{eqnarray}{\mathcal{E}}(\boldsymbol{k},t)={\mathcal{E}}^{(2)}(\boldsymbol{k},t)+{\mathcal{E}}^{+}(\boldsymbol{k},t),\quad Z(\boldsymbol{k},t)=Z^{(2)}(\boldsymbol{k},t)+Z^{+}(\boldsymbol{k},t),\end{eqnarray}$$
in which the terms containing information of degrees no more than two are
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\mathcal{E}}^{(2)}(\boldsymbol{k},t)={\displaystyle \frac{E(k,t)}{4\unicode[STIX]{x03C0}k^{2}}}(1-15\unicode[STIX]{x1D60F}_{mn}^{(dir)}(k,t)\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D6FC}_{n}),\\ Z^{(2)}(\boldsymbol{k},t)={\displaystyle \frac{5}{2}}{\displaystyle \frac{E(k,t)}{4\unicode[STIX]{x03C0}k^{2}}}\unicode[STIX]{x1D60F}_{mn}^{(pol)}(k,t)N_{m}^{\ast }(\unicode[STIX]{x1D736})N_{n}^{\ast }(\unicode[STIX]{x1D736}),\end{array}\right\}\end{eqnarray}$$
and
${\mathcal{E}}^{+}(\boldsymbol{k},t)$
and
$Z^{+}(\boldsymbol{k},t)$
hold for higher-degree contributions. When restricted to degree 2, the expansions use only the non-dimensional deviatoric tensors
$\unicode[STIX]{x1D60F}_{mn}^{(dir)}(k,t)$
and
$\unicode[STIX]{x1D60F}_{mn}^{(pol)}(k,t)$
which are obtained by integrating the isotropic, directional and polarization components of
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
in (2.4) over spherical shells of radius
$k$
, such that
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{ij}(k,t)=\int _{S_{k}}\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)d^{2}\boldsymbol{k}=2E(k,t)\left(\frac{1}{3}\unicode[STIX]{x1D6FF}_{ij}+\unicode[STIX]{x1D60F}_{ij}^{(dir)}(k,t)+\unicode[STIX]{x1D60F}_{ij}^{(pol)}(k,t)\right),\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}2E(k,t)\unicode[STIX]{x1D60F}_{ij}^{(dir)}(k,t)=\displaystyle \int _{S_{k}}\left({\mathcal{E}}(\boldsymbol{k},t)-{\displaystyle \frac{E(k,t)}{4\unicode[STIX]{x03C0}k^{2}}}\right)P_{ij}(\unicode[STIX]{x1D736})\,\text{d}^{2}\boldsymbol{k},\\ 2E(k,t)\unicode[STIX]{x1D60F}_{ij}^{(pol)}(k,t)=\displaystyle \int _{S_{k}}\text{Re}(Z(\boldsymbol{k},t)N_{i}(\unicode[STIX]{x1D736})N_{j}(\unicode[STIX]{x1D736}))\,\text{d}^{2}\boldsymbol{k}.\end{array}\right\}\end{eqnarray}$$
In the recent study by Clark, Kurien & Rubinstein (Reference Clark, Kurien and Rubinstein2018), expansions of angular harmonics to arbitrary degree are analytically derived, to represent inviscid SLT solutions for irrotational strain with dependence on the orientation of
$\boldsymbol{k}$
only, without need for its modulus. This is not suitable in our study since we consider various initial data and
$k$
-spectrum, and we include viscous terms and nonlinear source terms, in which a
$k$
-grid is needed.
Note that it is possible to extract the set of spherically averaged descriptors
$(E,\unicode[STIX]{x1D60F}_{ij}^{(dir)},\unicode[STIX]{x1D60F}_{ij}^{(pol)})$
from an arbitrary anisotropic spectral tensor
$\hat{\unicode[STIX]{x1D619}}_{ij}$
. Conversely, one can reconstruct an approximation of the full spectral tensor based on these descriptors, by using (2.8). Consistently, the generalized transfer terms use the same truncated expansions:
$$\begin{eqnarray}T^{({\mathcal{E}})}(\boldsymbol{k},t)=T^{({\mathcal{E}})2}(\boldsymbol{k},t)+T^{({\mathcal{E}})+}(\boldsymbol{k},t),\quad T^{(Z)}(\boldsymbol{k},t)=T^{(Z)2}(\boldsymbol{k},t)+T^{(Z)+}(\boldsymbol{k},t)\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}T^{({\mathcal{E}})2}(\boldsymbol{k},t)={\displaystyle \frac{T(k,t)}{4\unicode[STIX]{x03C0}k^{2}}}(1-15\tilde{S}_{mn}^{\mathit{NL(dir)}}(k,t)\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D6FC}_{n}),\\ T^{(Z)2}(\boldsymbol{k},t)={\displaystyle \frac{5}{2}}{\displaystyle \frac{T(k,t)}{4\unicode[STIX]{x03C0}k^{2}}}\tilde{S}_{mn}^{\mathit{NL(pol)}}(k,t)N_{m}^{\ast }(\unicode[STIX]{x1D736})N_{n}^{\ast }(\unicode[STIX]{x1D736}).\end{array}\right\}\end{eqnarray}$$
Note also that all anisotropic spectra and thus spectral anisotropic descriptors vanish in isotropic turbulence.
The MCS model describes the evolution of spherical descriptors of the second-order spectral tensor –
$E(k,t)$
,
$\unicode[STIX]{x1D60F}_{mn}^{(dir)}(k,t)$
and
$\unicode[STIX]{x1D60F}_{mn}^{(pol)}(k,t)$
– governed by spherically averaged linear terms along with the nonlinear transfer terms –
$T(k,t)$
,
$\tilde{S}_{ij}^{\mathit{NL(dir)}}(k,t)$
,
$\tilde{S}_{ij}^{\mathit{NL(pol)}}(k,t)$
. The final equations are presented in appendix A and can be obtained by spherically integrating corresponding equations in the EDQNM1 model with the truncated expansions of (2.8) and (2.12). Predictions of the model were computed by Mons et al. (Reference Mons, Cambon and Sagaut2016) for flows submitted to irrotational straining or plane shear, and for assessing the return to isotropy when an anisotropic flow is no more submitted to mean-velocity gradients.
Equations (2.4) and (2.8) imply that the set of (
$E$
,
$\unicode[STIX]{x1D643}^{(dir)}$
,
$\unicode[STIX]{x1D643}^{(pol)}$
) can regenerate the first two-degree spherical harmonics expansion of the tensor
$\hat{\unicode[STIX]{x1D64D}}$
exactly. That means the MCS model only pictures the anisotropy of
$\hat{\unicode[STIX]{x1D64D}}(\boldsymbol{k},t)$
decomposed with spherical harmonics in degrees no higher than two, and neglects higher-degree anisotropy terms in
$\unicode[STIX]{x1D643}^{(dir)}(k,t)$
and
$\unicode[STIX]{x1D643}^{(pol)}(k,t)$
, both due to linear and nonlinear mechanisms. These restrictions prevent the MCS model describing flows in which higher-degree anisotropy is significant. To solve this, the fully angular dependency of
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
(or of
${\mathcal{E}}(\boldsymbol{k},t)$
and
$Z(\boldsymbol{k},t)$
) is restored in our first proposed model, coined ZCG. The linear terms of ZCG are the same as those on the left-hand side of (2.6), and the simplified nonlinear terms in MCS are retained with the form in (2.12) to avoid the large computational cost in EDQNM1.
At this stage, the ZCG model contains the exact linear evolution of
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
, but the anisotropic nonlinear evolution higher than degree two is ignored. That means anisotropy of
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
in higher degrees – either produced by the linear mechanism or introduced explicitly from the initial field – cannot decay when the strain
$A_{ij}$
is removed. We fix this problem of the nonlinear closure by a further modification inspired by the model of Weinstock (Reference Weinstock1982, Reference Weinstock2013) which includes isotropic nonlinear transfer and a return to isotropy (RTI) term (also proposed by Rotta (Reference Rotta1951) for one-point statistics). In terms of equations for
${\mathcal{E}}$
and
$Z$
, Weinstock’s model amounts to
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}T^{({\mathcal{E}})}(\boldsymbol{k},t)={\displaystyle \frac{T(k,t)}{4\unicode[STIX]{x03C0}k^{2}}}-\unicode[STIX]{x1D711}^{\mathit{(RTI)}}(k,t)\left({\mathcal{E}}(\boldsymbol{k},t)-{\displaystyle \frac{E(k,t)}{4\unicode[STIX]{x03C0}k^{2}}}\right),\\ T^{(Z)}(\boldsymbol{k},t)=-\unicode[STIX]{x1D711}^{\mathit{(RTI)}}(k,t)Z(\boldsymbol{k},t).\end{array}\right\}\end{eqnarray}$$
$T(k,t)$
is closed by isotropic EDQNM, in terms of
$E$
, again as in MCS, but the RTI effect is forced via a single relaxation parameter suggested by weakly anisotropic EDQNM:
$$\begin{eqnarray}\unicode[STIX]{x1D711}(k,t)^{\mathit{(RTI)}}=\frac{1}{5\unicode[STIX]{x03C0}}\iint _{\unicode[STIX]{x1D6E5}k}\unicode[STIX]{x1D703}_{kpq}\frac{k^{3}E(p,t)E(q,t)}{pqE(k,t)}(1-y^{2})\,\text{d}p\,\text{d}q,\end{eqnarray}$$
in which
$\unicode[STIX]{x1D703}_{kpq}$
is the EDQNM decorrelation time scale for third-order statistics (details in appendix A). Comparing (2.13) and (2.12), it appears that the anisotropic terms
$T^{({\mathcal{E}})2}$
and
$T^{(Z)2}$
in ZCG are replaced by explicit RTI terms in (2.13). We therefore propose a mixed model in which the growth of angular harmonics of degree larger than two by linear mechanisms is balanced by the damping from the RTI term. We call it the ‘hybrid’ model, which is computed as
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}T^{({\mathcal{E}})}(\boldsymbol{k},t)=T^{({\mathcal{E}})2}-\unicode[STIX]{x1D711}^{\mathit{(RTI)}}(k,t)({\mathcal{E}}(\boldsymbol{k},t)-{\mathcal{E}}^{(2)}(\boldsymbol{k},t)),\\ T^{(Z)}(\boldsymbol{k},t)=T^{(Z)2}-\unicode[STIX]{x1D711}^{\mathit{(RTI)}}(k,t)(Z(\boldsymbol{k},t)-Z^{(2)}(\boldsymbol{k},t)),\end{array}\right\}\end{eqnarray}$$
in which
$T^{({\mathcal{E}})2}$
,
$T^{(Z)2}$
,
${\mathcal{E}}^{(2)}$
and
$Z^{(2)}$
are given by (2.12) and (2.8) respectively.
Briefly speaking, the two proposed models in terms of equations for
${\mathcal{E}}$
and
$Z$
both have the same exact linear operator as the left-hand side of (2.6) (or as those in EDQNM1). Concerning the nonlinear closure, the ZCG model retains the simplified EDQNM technique of MCS with (2.12), whereas the hybrid model brings in further RTI effects as in (2.15).
3 Numerical procedure: method and discretization
The first goal of this study is to numerically solve the system of (2.6) for various mean-flow gradients, with controlled accuracy for the linear terms and generalized transfer terms given by (2.12) or (2.15).
In both ZCG and hybrid models, the nonlinear terms are EDQNM-closed integrals of spherically averaged descriptors
$T(k,t)$
,
$\tilde{S}_{ij}^{\mathit{NL(dir)}}(k,t)$
,
$\tilde{S}_{ij}^{\mathit{NL(pol)}}(k,t)$
(see appendix A) or
$\unicode[STIX]{x1D711}(k,t)^{\mathit{(RTI)}}$
. Thanks to the simplified EDQNM technique, the 3-D triadic integral for each
$\boldsymbol{k}$
point in EDQNM1 is reduced to the plane triadic integral for each one-dimensional
$k$
point. Hence, the computational cost and memory for nonlinear terms are much smaller than those in the paradigmatic DNS algorithm by Rogallo (Reference Rogallo1981) which calculates full 3-D convolution with a pseudo-spectral method.
The main difficulty is to solve the advection operators in (2.6). In the commonly used approach of SLT, as well as in fully nonlinear DNS by Rogallo (Reference Rogallo1981) and Lesur & Longaretti (Reference Lesur and Longaretti2005), the scheme amounts to following the characteristic lines in terms of
$\boldsymbol{k}(t)$
which are related to the mean Lagrangian trajectories in physical space (details in appendix B). Accordingly, the wave vector is time dependent so that the time evolution of a statistical quantity
$\unicode[STIX]{x1D6F7}$
appears as
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D6F7}}(\boldsymbol{k}(t),t)=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}k_{i}}\frac{\text{d}k_{i}}{\text{d}t},\end{eqnarray}$$
with
$\dot{k}_{i}=-A_{ji}k_{j}$
the eikonal equation. This method can perform very well simulations in triple-periodic boxes without too complex numerical consideration. However, the computational domain can be strongly distorted at large times, so that periodic remeshing is required, as illustrated in figure 4. Therefore, the distorted grids are difficult to couple with nonlinear models based on spherically averaged descriptors, and the following remeshing and interpolation have a consequence on accuracy, especially considering spherically averaged statistics.
A different method is chosen here. We use a finite-difference scheme for evaluating the
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}k_{n}$
-derivatives, with a discretization of the wave vector consistent with the polar-spherical coordinates presented in figure 3. With respect to the method of characteristics, there is no need for interpolation or remeshing, but special attention should be paid to the numerical convergence problem induced by the finite-difference method for the advection operator. The orientation of the wave vector is represented with high accuracy by using refined grids on spheres in spectral space, and the number of spherical grid points depends on the anisotropy of flows rather than the Reynolds number. As in EDQNM calculations and shell models (Plunian & Stepanov Reference Plunian and Stepanov2007), a logarithmic distribution of discretized
$k$
is used for an accurate representation at the smallest and largest scales. This permits the present models to simulate flows with really high Reynolds number compared to DNS.
In polar-spherical coordinates, the advection operator is
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k_{n}}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}\unicode[STIX]{x1D6FC}_{n}+\frac{1}{k}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\text{e}_{n}^{(2)}(\unicode[STIX]{x1D736})-\frac{1}{k\sin \unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}\text{e}_{n}^{(1)}(\unicode[STIX]{x1D736}).\end{eqnarray}$$
Accordingly,
$k$
,
$\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D711}$
can be discretized independently and the local frame defined by (2.5) and sketched in figure 3 is used. However, the governing equations for
${\mathcal{E}}(\boldsymbol{k},t)$
and
$Z(\boldsymbol{k},t)$
become singular at the pole (along
$\boldsymbol{n}$
) where the Craya frame is not uniquely defined. We solve this by using a degenerate equation (2.2) at the pole by replacing the Craya frame by the Cartesian frame,
$$\begin{eqnarray}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+2\unicode[STIX]{x1D708}k^{2}\right)\hat{\unicode[STIX]{x1D619}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(k,\boldsymbol{n},t)+(A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}+2\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FC}m\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FA}_{m})\hat{\unicode[STIX]{x1D619}}_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}+(A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}+2\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6FD}m\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FA}_{m})\hat{\unicode[STIX]{x1D619}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}=T_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}},\end{eqnarray}$$
in which the spectral tensor
$\hat{\unicode[STIX]{x1D619}}_{ij}$
reduces to four non-zero components because of incompressibility so that Greek indices are restricted to 1, 2,
$n_{i}=\unicode[STIX]{x1D6FF}_{i3}$
, and the advection operator vanishes since
$A_{mn}n_{m}=0$
. We compute
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
rather than the set (
${\mathcal{E}}(\boldsymbol{k},t)$
,
$Z(\boldsymbol{k},t)$
) in a neighbourhood of the pole, and we exchange values with neighbour grid points to provide the required boundary conditions (see figure 5). Overall, the special treatment of the pole improves the numerical accuracy obviously when the advection along
$\unicode[STIX]{x1D703}$
direction is significant.
Figure 4. Illustration of the resolution grid when using the method of characteristics for uniform mean shear.
Figure 5. Illustration of the interaction between the two numerical regions in the latitude direction. In the polar region, fixed-frame equations are specifically used, and both regions exchange information to recover the complete spectral information.
A large number of tests have been done for the numerical implementation, e.g. various finite-difference schemes (FDSs), integration schemes for time evolution and the convergence study in terms of grids. The FDS we use for discretizing derivatives with respect to
$k_{m}$
in the advection term is a sixth-order explicit centred scheme, and the classical fourth-order Runge–Kutta scheme is employed for time marching. In practice, the strongest accuracy constraint for computing
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}k_{m}$
appeared to be in the small-scale range (large wavenumbers), where mesh elements distribution is relatively sparse. We use a ‘high-order FDS, low resolution grids’ strategy for computational efficiency, which provides excellent accuracy for the sheared turbulence case.
All details on the numerical simulation method can be found in Zhu (Reference Zhu2019).
4 Validation of the proposed models versus SLT and DNS for rotating shear flow
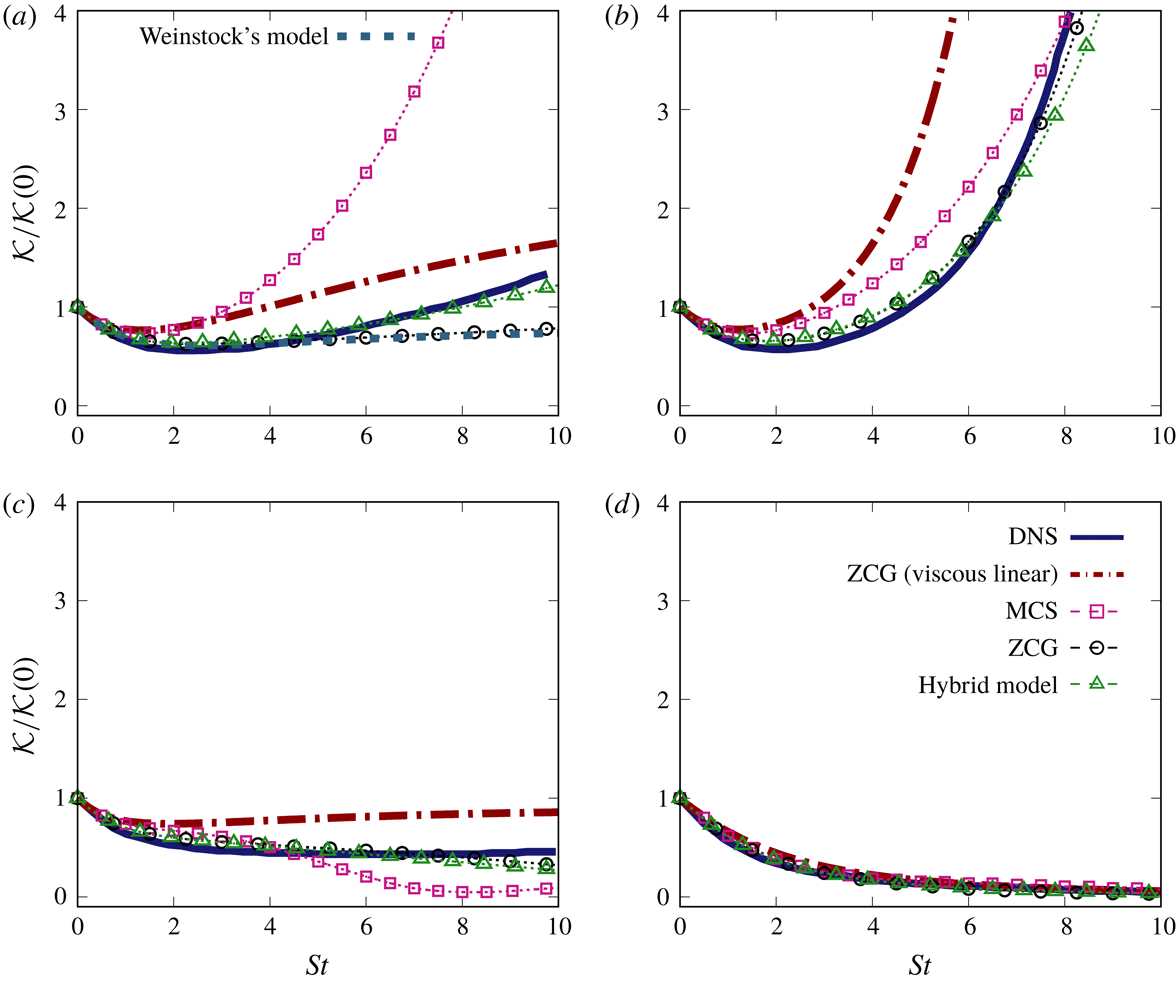
We begin the validation of the ZCG model by considering different flows in both the inviscid and viscous linear limits, and compare with SLT results, and with results of MCS, in § 4.1. In § 4.2 we compare fully nonlinear results provided by: (i) the ZCG model, (ii) the MCS model, (iii) the hybrid model and (iv) direct numerical simulations by Salhi et al. (Reference Salhi, Jacobitz, Schneider and Cambon2014).
4.1 Validation in the linear limit
The linear limit regime is obtained by considering only the left-hand side of (2.6) with zero right-hand side. This limit is very subtle and difficult to capture as introduced in § 3. We consider a flow with mean plane shear
$S$
such that the mean-velocity gradient is
$A_{ij}=S\unicode[STIX]{x1D6FF}_{i1}\unicode[STIX]{x1D6FF}_{j2}$
. The indices 1, 2 and 3 refer to streamwise, cross-gradient and spanwise directions respectively (see figure 1). As in Salhi et al. (Reference Salhi, Jacobitz, Schneider and Cambon2014), we add system vorticity
$2\unicode[STIX]{x1D6FA}$
in the spanwise direction, and choose the same flow parameters and initial spectrum: at initial time, the Taylor-scale-based Reynolds number is
$Re=(2{\mathcal{K}})^{1/2}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}=56$
, and the shear number is
$S{\mathcal{K}}/\unicode[STIX]{x1D716}=2$
, where
${\mathcal{K}}$
is the kinetic energy,
$\unicode[STIX]{x1D716}$
its dissipation and
$\unicode[STIX]{x1D706}$
the Taylor length scale. Rotation is chosen such that the Rossby number
$R=-5$
,
$-1$
,
$-1/2$
and 0.
The numerical linear results from Salhi et al. (Reference Salhi, Jacobitz, Schneider and Cambon2014) are denoted as ‘SLT’ in this section, which are not obtained by merely cancelling nonlinear terms in pseudo-spectral DNS, as sometimes done, but using an accurate resolution of the time-dependent linear equation (B 4) recalled in appendix B. Some predictions concerning the pure shear case without additional system vorticity are also given by spectral linear theory denoted as ‘theo’. These theoretical predictions correspond to the exact resolution of (B 6) for
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$
in which an integral Green’s function (B 11) is computed analytically (details in appendix B). Therefore, in the comparison with models, the SLT is a reliable reference.
Figure 6. Time evolution of turbulent kinetic energy in the inviscid and viscous linear limits, as a function of non-dimensional time
$St$
. ZCG–MCS–SLT comparisons with four typical
$R$
ratios: (a)
$R=0$
, in which the inviscid and viscous analytical exact solutions are also plotted; (b)
$R=-0.5$
; (c)
$R=-1$
; and (d)
$R=-5$
.
4.1.1 Turbulent kinetic energy
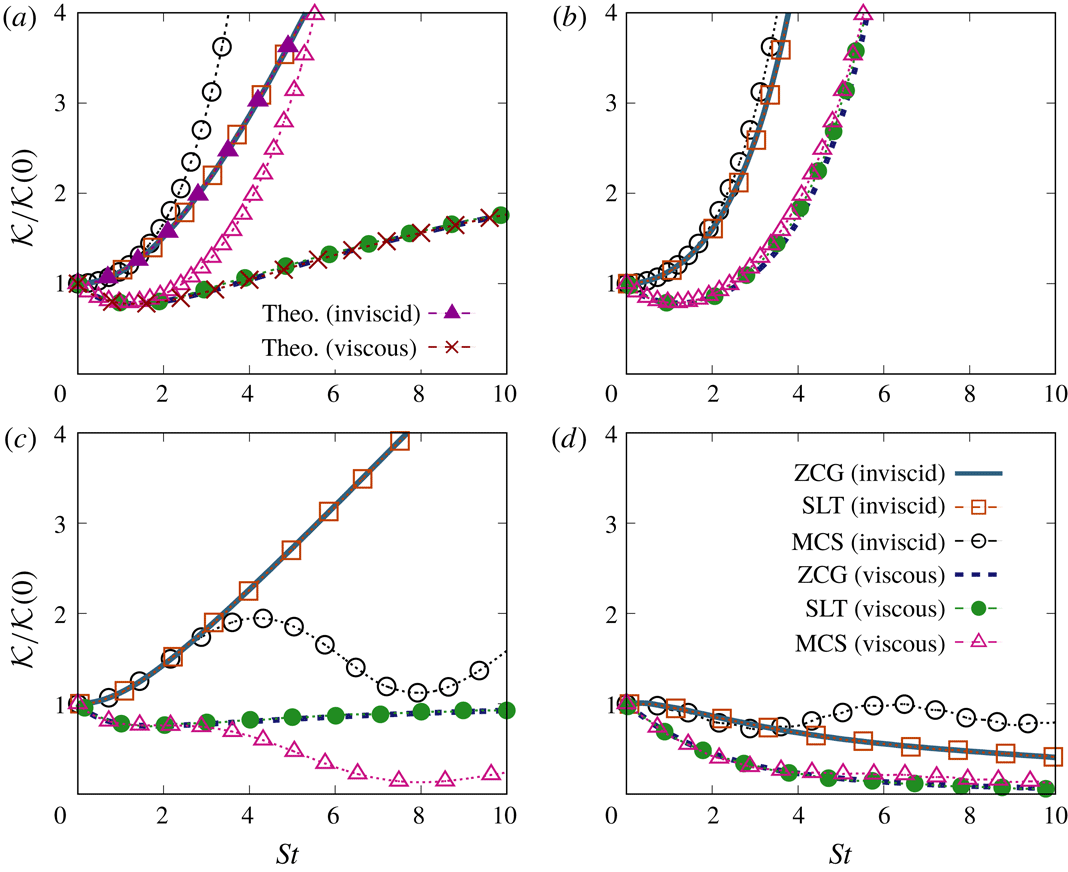
The present model’s numerical predictions of turbulent kinetic energy are shown in figure 6, along with those of MCS and the results of SLT. Typical cases with different combinations of strain and rotation are plotted:
$R=-5$
or
$\unicode[STIX]{x1D6FA}=5S/2$
corresponds to a stabilizing, anticyclonic case;
$R=-1$
or
$\unicode[STIX]{x1D6FA}=S/2$
for a neutral case with zero absolute vorticity, as encountered in the central region of a rotating channel;
$R=-1/2$
or
$\unicode[STIX]{x1D6FA}=S/4$
for a maximum destabilization, anticyclonic case, as in the pressure side of a rotating channel; and
$R=0$
with no rotation.
First of all, figure 6 shows excellent agreement between results of the ZCG model and SLT for all the four cases, and also the agreement with the theoretical results in the case without system rotation in figure 6(a). This is true for the inviscid runs but also, without surprise, for the viscous ones. The figure shows that the time evolution of kinetic energy is accurately reproduced by our present model, thus confirming that our discretization and choice of numerical FDS are adequate in this limit.
In contrast, the MCS model departs rapidly from SLT at
$St\gtrsim 3$
, for both viscous or inviscid cases at
$R=0,-1$
(figure 6
a,c), and for the inviscid case at
$R=-5$
(figure 6
d). In the viscous exponentially stable
$R=-5$
case, which is stabilizing, the damping of energy is strong so that the relative departure of MCS from SLT is not as clear but still noticeable. MCS is close to SLT in the maximum destabilization case
$R=-1/2$
(figure 6
b), exponentially unstable, where the kinetic energy growth is largest. Clearly, for the
$R=0$
case, the algebraic growth of kinetic energy is missed by MCS and exponential growth is predicted instead. On the contrary, our ZCG model predicts the linear growth of kinetic energy rightly.
Note that, in the inviscid case of zero absolute vorticity
$R=-1$
, inviscid MCS gives an evolution not far from periodic, probably close to the evolution of a one-point Reynolds-stress model (RSM), in strong contrast with the expected algebraic growth.
Figure 7. Time evolution of the spherically averaged kinetic energy with
$R=-5$
,
$-1$
,
$-1/2$
,
$-1/4$
, 0 in the linear inviscid limit by the ZCG model.
We have finally gathered in figure 7 the kinetic energy evolution for all the previous inviscid cases, as well as for the intermediate case at
$R=-1/4$
which is not documented in Salhi et al. (Reference Salhi, Jacobitz, Schneider and Cambon2014). The figure shows that kinetic energy decays only for
$R=-5$
, and that kinetic energy grows in all other cases, including the neutral case
$R=-1$
. Moreover, there is very few difference between cases
$R=-1/2$
and
$-1/4$
. This is consistent with the criterion in terms of Rossby number
$R$
, from the stability analysis discussed in the Introduction.
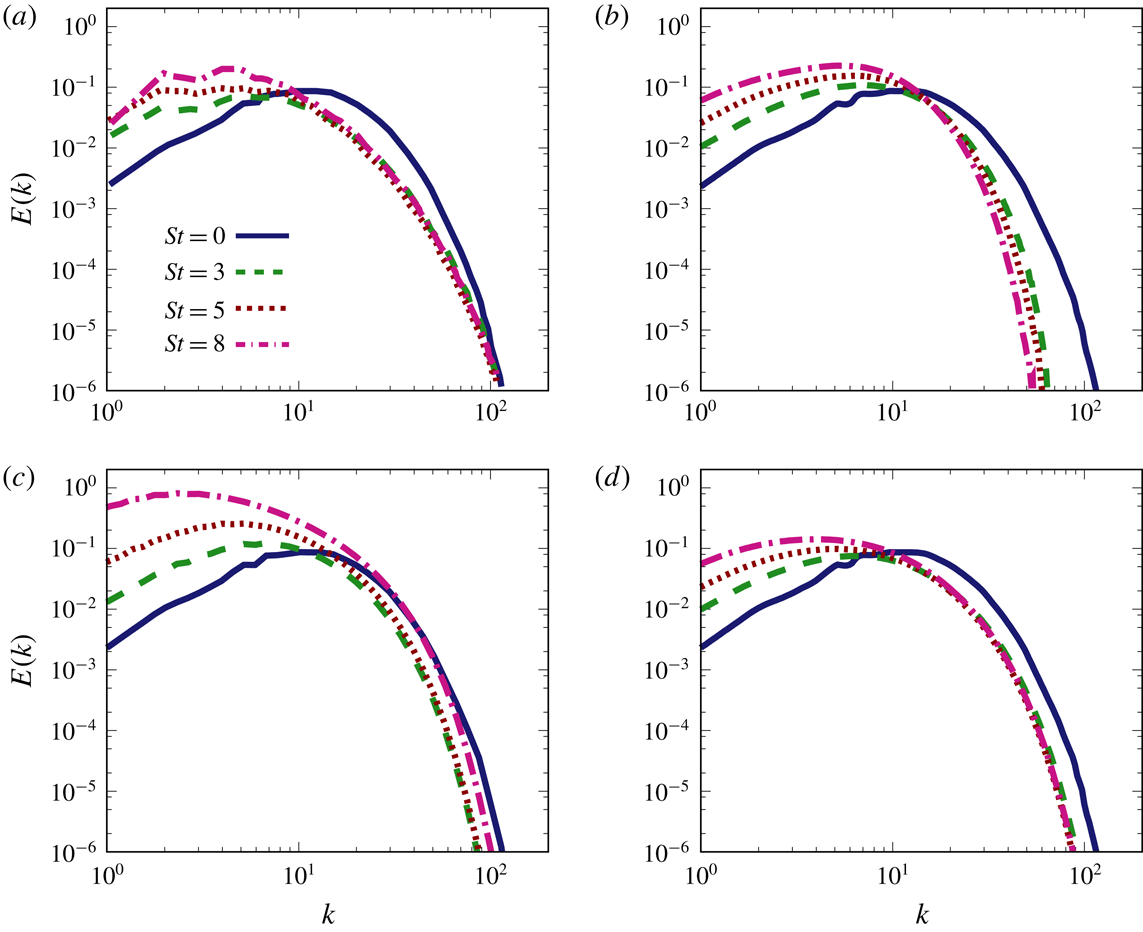
4.1.2 Kinetic energy spectra for pure shear
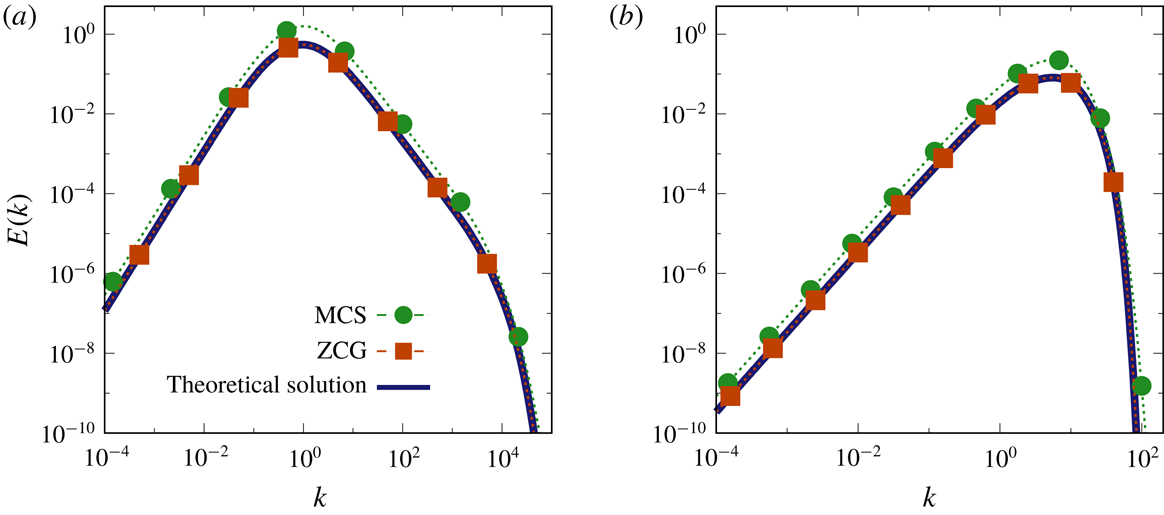
Figure 8. Spherically averaged energy spectra for pure shear case at
$St=5$
. MCS–ZCG–theoretical solution comparisons in both (a) inviscid linear and (b) viscous linear limits.
Figure 9. Time evolution of spherically averaged energy spectra. Comparison of results from the present model with SLT in the viscous linear limit for the pure shear case
$R=0$
.
The time evolution of the spectrum
$E(k,t)$
is governed by
$$\begin{eqnarray}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+2\unicode[STIX]{x1D708}k^{2}\right)E(k,t)+S^{L}(k,t)-P(k,t)=T(k,t),\end{eqnarray}$$
in which the spherically averaged production spectrum is
$$\begin{eqnarray}P(k,t)=-2SE(k,t)\unicode[STIX]{x1D60F}_{12}(k,t)\end{eqnarray}$$
for shear flows, where the anisotropy tensor
$\unicode[STIX]{x1D643}(k,t)$
is
$\unicode[STIX]{x1D60F}_{ij}(k,t)=\unicode[STIX]{x1D60F}_{ij}^{(dir)}(k,t)+\unicode[STIX]{x1D60F}_{ij}^{(pol)}(k,t)$
.
Spherically averaged kinetic energy spectra obtained from ZCG, MCS and the theoretical SLT solutions are plotted in figure 8 for
$R=0$
at
$St=5$
, and in figure 9 from ZCG only at different times.
Figure 8 shows that the ZCG model not only predicts correctly the total kinetic energy evolution but also the scale distribution at all spectral subranges when compared with the theoretical prediction. This is the case for both the inviscid limit (figure 8 a) and the viscous one (figure 8 b), so that the agreement cannot be only due to the effect of viscosity. As expected from the above comparison on the total kinetic energy, the energy spectra of the viscous or inviscid MCS model do not match the theoretical prediction. The departure is observed in the small-scale range and in the inertial spectral range, less so in the viscous subrange where viscous dissipation is dominant and is solved exactly in the models.
The time evolution of the kinetic energy spectra is shown in figure 9, where the ZCG model spectra are compared to SLT spectra up to
$St=8$
. The agreement is excellent, and it is particularly worth noticing that the peaks of the ZCG spectra follow closely those of the SLT solution, indicating that the large scales are well resolved. The correspondence between the models in terms of the peak wavenumber evolution can also be observed in the nonlinear validation in § 4.2.
4.1.3 Production for pure shear
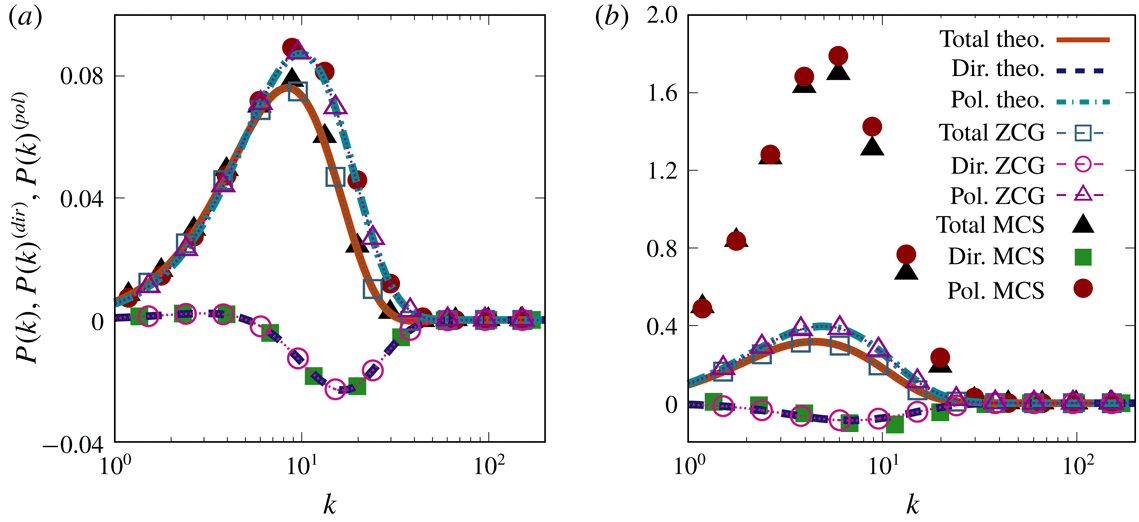
Figure 10. Time evolution of (a) the deviatoric component
$\unicode[STIX]{x1D623}_{12}$
of the Reynolds-stress tensor, which is a production-related term, and its contributions from (b) directional and (c) polarization anisotropies. MCS–ZCG–theoretical solution comparisons for pure shear case
$R=0$
in the viscous linear limit.
The analysis of production in one-point statistics is obtained by spherically averaging the
${\mathcal{E}}$
-equation (2.6a
) or integrating (4.1) over wavenumber
$k$
. Since the mean shear is in the
$(x_{1},x_{2})$
plane, the one-point production term is
$\langle u_{1}u_{2}\rangle$
, but we rather compute the corresponding component
$\unicode[STIX]{x1D623}_{12}$
of the deviator of the Reynolds-stress tensor (RST), namely
$\unicode[STIX]{x1D623}_{ij}=\langle u_{i}u_{j}\rangle /(2{\mathcal{K}})-\unicode[STIX]{x1D6FF}_{ij}/3$
, which is obtained from
$$\begin{eqnarray}\unicode[STIX]{x1D623}_{ij}(t)={\mathcal{K}}(t)^{-1}\int _{0}^{\infty }E(k,t)\unicode[STIX]{x1D60F}_{ij}(k,t)\,\text{d}k.\end{eqnarray}$$
At
$R=0$
, the time development of
$\unicode[STIX]{x1D623}_{12}$
is shown in figure 10 in the viscous linear limit. The present model allows us to correctly capture the total deviatoric part of the Reynolds-stress tensor (figure 10
a), along with its directional (figure 10
b) and polarization contributions (figure 10
c). The figures also show that MCS predicts quite well the development of the directional component
$\unicode[STIX]{x1D623}_{12}^{(dir)}$
, but not that of the polarization component
$\unicode[STIX]{x1D623}_{12}^{(pol)}$
, so that its prediction for
$\unicode[STIX]{x1D623}_{12}$
is not correct after
$St\simeq 1$
. The overestimation of the magnitude of
$\unicode[STIX]{x1D623}_{12}^{(pol)}$
by MCS, with its plateau at large
$St$
, is connected to the erroneous prediction of the exponential growth of total kinetic energy which is given by
$$\begin{eqnarray}\frac{1}{{\mathcal{K}}}\frac{\text{d}{\mathcal{K}}}{\text{d}t}=-2S\unicode[STIX]{x1D623}_{12}-\frac{\unicode[STIX]{x1D700}}{{\mathcal{K}}}.\end{eqnarray}$$
Predictions of the production spectrum (4.2) by the ZCG model with comparison to the results of MCS and the theoretical ones are reported in figure 11. Figure 11(a) at short time
$St=0.5$
shows a good agreement between both models and the theoretical predictions, due to the fact that anisotropy development is still limited at this time. However, figure 11(b) at longer time
$St=5$
shows that the MCS model prediction is not correct, mainly due to the polarization spectrum whose amplitude is not adequately captured, notwithstanding the proper prediction of the directional anisotropy production spectrum. The ZCG model compares very well with the theoretical prediction for both production spectra. This indicates clearly that the representation of anisotropy has to be complete, in terms of directional accumulation of energy (in latitude in spectral space), but importantly also in terms of the more complex polarization anisotropic contents of the flow, which is related to its structure. This was also observed in homogeneous turbulence, for magnetohydrodynamic, rotating or stratified flows (Sagaut & Cambon Reference Sagaut and Cambon2018, and references therein).
These results are confirmed when rotation is added, in figure 12. Polarization anisotropy of the production spectrum is overestimated by MCS, except in the most unstable case (figure 12
b). The directional part is much better reproduced than the polarization part in almost all other cases except the one in figure 12(d). MCS is not good even for the directional part of anisotropy for this case at
$R=-5$
in contrast with figure 12(b) at
$R=-0.5$
.
Note finally from figure 12 that the amplitude of the production spectrum peak is larger for the case
$R=-1/2$
and decreases with absolute value of
$R$
from
$-1$
to
$-5$
, in which case it is only a hundredth of that of
$R=-1/2$
.
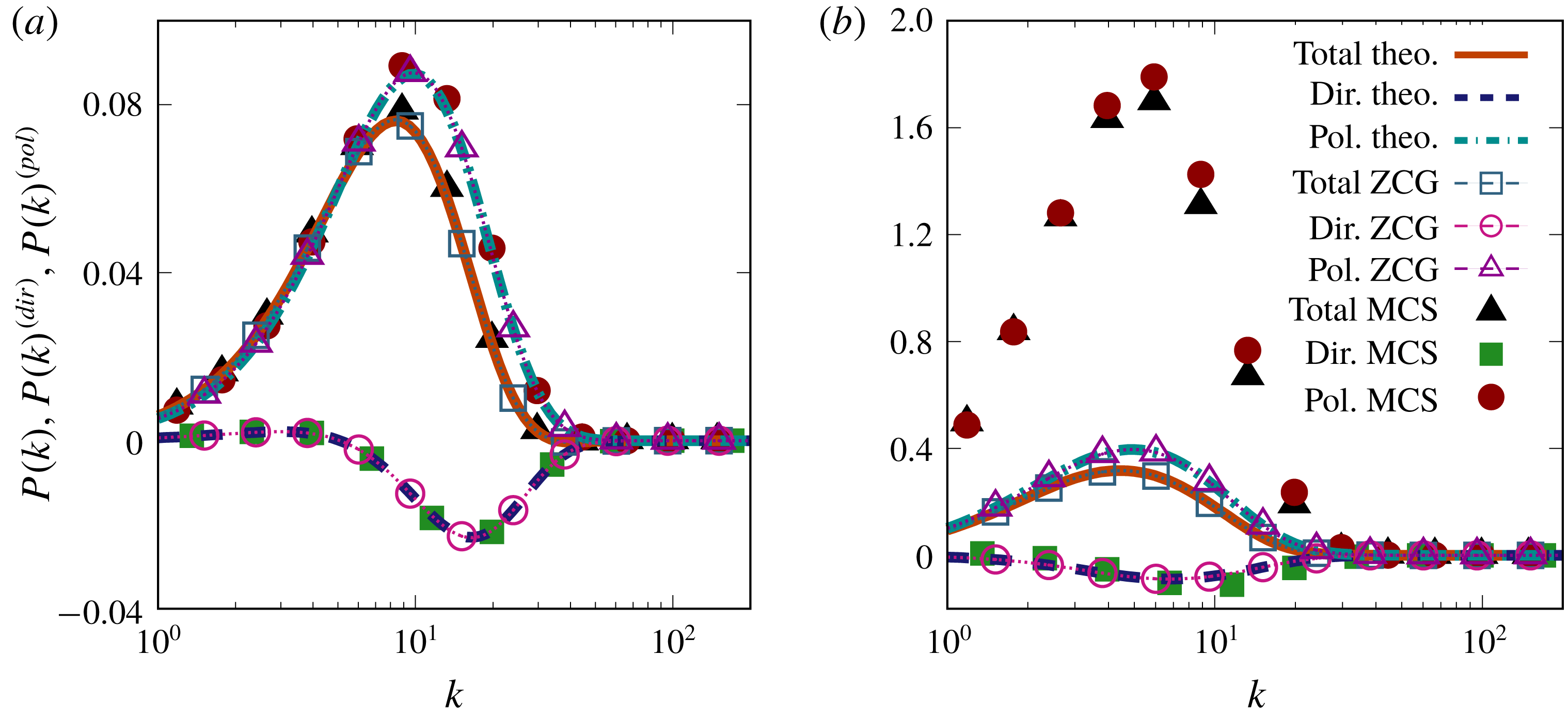
Figure 11. Spherically averaged spectra
$P(k)$
of the production term, with both directional and polarization anisotropies for non-rotating shear case
$R=0$
in viscous linear limit. MCS–ZCG–theoretical solution comparisons at (a)
$St=0.5$
and (b)
$St=5$
.
Figure 12. Spherically averaged production spectra
$P(k)$
and their directional and polarization anisotropy contents in viscous linear limit. Comparison of results at
$St=5$
from the ZCG and MCS models with: (a)
$R=0$
; (b)
$R=-0.5$
; (c)
$R=-1$
; (d)
$R=-5$
.
4.2 Nonlinear dynamics for the rotating shear cases
Figure 13. Time evolution of turbulent kinetic energy with: (a)
$R=0$
; (b)
$R=-0.5$
; (c)
$R=-1$
; and (d)
$R=-5$
. Comparisons of results from the fully nonlinear models: full ZCG, MCS, Weinstock’s model, hybrid model, DNS and viscous linear ZCG.
The addition of a Coriolis force dramatically changes the linear dynamics with respect to the pure shear case. It is expected that the most difficult term to account for in SLT equation for second-order statistics is the stropholysis factor
$-\text{i}kZ(\boldsymbol{k},t)((\boldsymbol{W}+4\unicode[STIX]{x1D734})\boldsymbol{\cdot }\unicode[STIX]{x1D736}-2\unicode[STIX]{x1D6FA}_{E})$
in (2.6b
), which reflects the direct effect of mean vorticity, shear vorticity as well as system vorticity. As already discussed by Leblanc & Cambon (Reference Leblanc and Cambon1998), both absolute mean vorticity
$\boldsymbol{W}+2\unicode[STIX]{x1D6FA}$
and tilting mean vorticity
$\boldsymbol{W}+4\unicode[STIX]{x1D6FA}$
are called into play. The result in figure 6 suggests that the simplest case without the stropholysis term explains the good behaviour of MCS. Unfortunately, the stropholysis effect includes also the
$\unicode[STIX]{x1D6FA}_{E}$
term in (2.6b
), which is non-zero in our first system of axes. To identify more clearly stropholysis and tilting mean vorticity, the mean plane shear is changed to
$A_{ij}=S\unicode[STIX]{x1D6FF}_{i1}\unicode[STIX]{x1D6FF}_{j3}$
in the following fully nonlinear cases so that
$\unicode[STIX]{x1D6FA}_{E}$
vanishes. In addition, the robustness of the present ZCG model can be tested and one can also obtain simpler analytical linear solutions with this mean-velocity configuration.
Consequently, in this new configuration, indices 2 and 3 refer to spanwise and cross-gradient directions, and the Coriolis force is along axis 2. Accordingly, the ratio
$R$
changes to
$2\unicode[STIX]{x1D6FA}/S$
. The relevant component for single-point anisotropy then becomes
$\unicode[STIX]{x1D623}_{13}$
instead of
$\unicode[STIX]{x1D623}_{12}$
and the corresponding production spectrum is
$P(k,t)=-2SE(k,t)\unicode[STIX]{x1D60F}_{13}(k,t)$
. The initial energy spectrum is the same as in the direct numerical simulations (DNS) by Salhi et al. (Reference Salhi, Jacobitz, Schneider and Cambon2014) and we use the flow parameters from the linear cases since some computational parameters of the DNS are not document in their article.
Results for the nonlinear evolution of turbulent kinetic energy are presented in figure 13, for quantitative comparisons between DNS, MCS and the ZCG model, and with ZCG in the viscous linear limit. First of all, figure 13(d) shows that all approaches agree for the
$R=-5$
case, showing that the flow regime is mostly viscous linear with very small production, also echoed by the small amplitude of the production spectrum in figure 12(d). This is not the case for other flows at
$R=0,-1/2$
and
$-1$
in which nonlinearity and anisotropy are larger. Figure 13(a–c) for these flows shows a very good agreement between DNS and ZCG, although in the pure shear case the ZCG model saturates in terms of kinetic energy with respect to DNS which suggests an exponential re-growth. The MCS model predictions are not satisfactory in the most unstable case, in spite of its good behaviour in the linear limit (figure 6
b for
$R=-1/2$
). The disappointing behaviour of the ZCG model for the case
$R=0$
without system rotation (figure 13) suggests to add a term of forced return to isotropy in the ZCG model, in line with the proposition of Weinstock (Reference Weinstock2013). This motivated the introduction of the hybrid model described in § 2.2, and figure 13 will be discussed further in § 5 along with Weinstock’s model results.
5 Discussion for pure shear cases
Figure 14. Time development of (a) the deviatoric part of the Reynolds-stress tensor component,
$\unicode[STIX]{x1D623}_{13}$
, typical of production-related term; (b) directional and (c) polarization anisotropies by the different fully nonlinear models in the non-rotating shear case
$R=0$
. Predictions by MCS–ZCG–Weinstock’s and hybrid models.
Going back to figure 13(a), the results of both Weinstock’s and the hybrid model are plotted. Weinstock’s model misses the exponential regrowth, as does our ZCG model, but a very satisfactory result is given by the hybrid model. The hybrid model remains satisfactory in all cases with system rotation, and the slight underestimation of energy from DNS can partly result from slightly dissimilar flow parameters between our simulations and DNS. The fact that the hybrid model performs better than ZCG or Weinstock’s model alone indicates that both models have complementary features that add up correctly to produce a better model compared to MCS for pure shear turbulence.
Still focusing on the case without system rotation, the deviatoric part of the Reynolds-stress tensor is plotted in figure 14. Unfortunately, this information is not available from DNS, but the hybrid model gives the clearer steady limit of
$\unicode[STIX]{x1D623}_{13}=-0.14$
that is consistent with the exponential re-growth of energy, with a value very close to the classically expected one, in the range
$[-0.16;-0.1]$
(see table p. 443 in Sagaut & Cambon Reference Sagaut and Cambon2018). This stabilization of
$\unicode[STIX]{x1D623}_{13}$
to a constant by the hybrid model explains the constant rate of exponential growth equal to
$-2\unicode[STIX]{x1D623}_{13}-\unicode[STIX]{x1D700}/(S{\mathcal{K}})$
((4.4), allowing for the change of 2 and 3 reference directions). Contribution of polarization anisotropy is dominant (figure 14
c), and overestimated only by MCS, as usual, with a negative sign opposite to the one of directional contribution. The latter is correctly reproduced by MCS as well.
Figure 15. Time development of spherically averaged energy spectra in the non-rotating shear case. Comparisons of the results among different fully nonlinear models, viscous linear and DNS: (a) DNS; (b) ZCG viscous linear; (c) MCS; and (d) hybrid model.
Figure 16. Spherically averaged spectrum
$P(k)$
of the production term with both directional and polarization anisotropies in pure shear case at
$St=5$
. Comparisons of the results among different fully nonlinear models, DNS and viscous linear ZCG: (a) DNS, (b) ZCG (viscous linear), (c) MCS and (d) hybrid model.
The spherically averaged energy spectrum
$E(k,t)$
is plotted in figure 15 at increasing times
$St=0$
, 3, 5, 8. Some differences between the results of various models with respect to the DNS ones are partly due to a forced isotropic precomputation only performed in DNS, in order to increase the Reynolds number before applying the mean shear. Accordingly, the initial spectrum (at
$St=0$
) is closer to the one before the forced isotropic precomputation than the actual one in DNS. Nevertheless, qualitative comparisons remain informative. In figure 15(c), the MCS model again is not relevant, especially at large scales up to wavenumbers of approximately 10, and at small scales where too much evolution is observed. The ZCG model in its viscous linear limit (figure 15
b) satisfactorily predicts the large scales growth, but not the decrease of the smallest scales. The latter decrease continuously instead of being saturated, as in DNS in figure 15(a). The prediction of large-scale evolution is almost unchanged with respect to the linear behaviour in the ZCG model (not shown) and in the hybrid model (figure 15
d), but the collapse of smallest scales at increasing times is very well reproduced by the hybrid model, slightly better than in the ZCG and Weinstock models. Because all models except MCS reproduce correctly the linear dynamics, dominant at large scales, it is difficult to distinguish them from this viewpoint. The scrambling of large scales in DNS, due to the poor discretization at small wavenumber, and cumulated errors of remeshing, especially at long times, does not permit a hierarchy of the models’ predictions quality in the dissipation range. One can however focus on the large-scale growth, or equivalently on the decrease of the wavenumber
$k_{p}$
at the peak of
$E(k)$
. DNS does predict the expected decrease of
$k_{p}$
in time, from
$k_{p}\simeq 16$
at
$St=0$
to
$k_{p}\simeq 4.2$
at
$St=8$
, and so do the ZCG and hybrid models (
$k_{p}\simeq 4.1$
at
$St=8$
for the latter), but the decrease by the linear ZCG model is smaller (
$k_{p}\simeq 5.3$
at
$St=8$
), and similarly for Weinstock’s model (not shown).
Finally, the production spectrum
$P(k,t)$
is plotted in figure 16 for DNS, viscous linear ZCG, MCS and hybrid models, at a significantly large non-dimensional time
$St=5$
. Again, all models behave satisfactorily at first glance, except MCS due to the polarization contribution to production (figure 16
c), which is overestimated, as in the linear limit. Close examination of directional terms still shows small differences between the models, e.g. the peak production occurs at larger scales in Weinstock’s model, and the complete ZCG model decreases both directional and polarization production slightly (not shown), but the amplitudes and shapes of production spectra are very similar to that of DNS in all models but MCS.
6 Conclusions and perspectives
Spectral modelling seems to be a powerful and promising approach to statistics of two-point second-order correlations for homogeneous anisotropic turbulence, in the presence of uniform mean gradients and body forces, using a smart combination of SLT and EDQNM closure. This allows a scale-by-scale and angle-dependent analysis of anisotropy, disentangling directional and polarization anisotropy. Given the complexity and numerical cost of models in which the full angle dependence of spectra is retained, especially for the EDQNM part, simplified models in terms of spherically averaged descriptors are favoured. This was illustrated by Cambon, Jeandel & Mathieu (Reference Cambon, Jeandel and Mathieu1981) and further developed by MCS using truncated spherical harmonics expansions. Our approach and detailed calculations in the present paper first confirm the following general tendencies:
(i) When the linear dynamics gives exponential growth, models similar to MCS (in terms of spherically averaged descriptors) work well. Generally, the nonlinear evolution results in a reduction of the exponential growth rate of energy, but without saturation. This is illustrated in figure 6, in which the maximum destabilization case (figure 6 b) merits further discussion.
(ii) On the contrary, models perform poorly when the linear dynamics yields algebraic growth, best illustrated with the plane shear flow without rotation: any model using a truncated expansion in terms of spherical harmonics wrongly gives an exponential growth. In spite of satisfactory results at short time, MC – even with further introduction of fourth-degree harmonics (Briard et al. Reference Briard, Gréa, Mons, Cambon, Gomez and Sagaut2018) – is disqualified for a quantitative comparison with DNS. A similar comment applies to the other ‘neutral case’ (figure 6 c), although to a lower extent. This is confirmed in our paper, thanks to the accurate calculation of exact SLT.
The second point (ii) suggested to focus on the pure shear case, in which the exponential re-growth is mediated by nonlinear mechanisms. We thus combined exact calculation of linear terms in the
$({\mathcal{E}},Z)$
equations, and MCS model for reconstructing the nonlinear transfer terms from EDQNM at the degree 2. But this was not sufficient and kinetic energy was found to saturate, without re-growth. This disappointing result is attributed to insufficient scale-by-scale return to isotropy. There is indeed a large consensus on the fact that RTI is essential for redistributing the kinetic energy from the streamwise component of the RST to the vertical (cross-gradient) one. The nonlinear feeding of this vertical component is the key for obtaining the re-growth, even if the ‘Rotta operator’ damps all components of RST anisotropy, including the production-related one (
$\unicode[STIX]{x1D623}_{12}$
in § 4.1,
$\unicode[STIX]{x1D623}_{13}$
in § 4.2). This suggested the recourse to Weinstock’s model, in which the spectral RTI is prescribed, and yields two new results:
(iii) Weinstock’s model alone does not work, when implemented, with a saturation of kinetic energy instead of regrowth (figure 13 a). This result is obtained by employing an accurate calculation of the linear terms.
(iv) Satisfactory results were eventually obtained by an hybrid of our first ZCG model, with a spectral RTI restricted to higher-degree harmonics. This means that the nonlinear closure needs an elaborate degree-two expansion (in MCS but absent in Weinstock’s model), but supplemented by a spectral RTI term for clipping higher-degree terms (as in Weinstock, and ignored in ZCG).
The latter result is perhaps our best achievement. It merits more specific studies for the pure shear, with parametric analysis and comparison with additional DNS simulations, extrapolated to very high Reynolds number by our hybrid model. Fortunately, our hybrid model does not require new adjustable parameters: a single isotropic eddy-damping time scale is used in MCS and in the return-to-isotropy coefficient
$\unicode[STIX]{x1D711}^{\mathit{RTI}}$
(2.13) proposed by Weinstock.
Other perspectives concern the improvement of simpler models, keeping the description in terms of angular harmonics but with ad hoc corrections, and a possible outcome for the improvement of single-point closures is expected as well. Further studies on inhomogeneous flows in physical space inspired from the current work can also be expected. For instance, the frameworks of anisotropic spectra and anisotropic structure functions may be bridged via the expansion in terms of spherical harmonics: the so-called Wiener–Kinchin expansions can be used and adapted to this context. Regarding inhomogeneous flows in geophysics, astrophysics or wall-bounded turbulence, the feedback from fluctuation to mean field is essential and ought to be restored, but the interaction between fluctuation and itself is almost ignored or roughly mimicked by effective diffusivities in such studies. Alternately, an elaborate anisotropic EDQNM model for this nonlinear interaction can be coupled with a model for feedback interaction; this is the case of unstably stratified homogeneous turbulence (Burlot et al. Reference Burlot, Gréa, Godeferd, Cambon and Griffond2015) coupled with the rapid acceleration model by Gréa (Reference Gréa2013).
The latter study in buoyancy-driven flows suggests similar fully coupled models in weakly inhomogeneous shear-driven flows.
Acknowledgement
Y.Z. is supported by the Chinese Scholarship Council (Fellowship #201506020093).
Appendix A. EDQNM background and detailed equations for MCS
The closed system of equations from MCS (Mons et al.
Reference Mons, Cambon and Sagaut2016) for
$(E,\unicode[STIX]{x1D60F}_{ij}^{(dir)},\unicode[STIX]{x1D60F}_{ij}^{(pol)})$
is:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+2\unicode[STIX]{x1D708}k^{2}\right)E(k,t)=S^{L}(k,t)+T(k,t),\\ \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+2\unicode[STIX]{x1D708}k^{2}\right)E(k,t)\unicode[STIX]{x1D60F}_{ij}^{(dir)}(k,t)=S^{L(dir)}(k,t)+\mathit{S}_{ij}^{\mathit{NL(dir)}}(k,t),\\ \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+2\unicode[STIX]{x1D708}k^{2}\right)E(k,t)\unicode[STIX]{x1D60F}_{ij}^{(pol)}(k,t)=S^{L(pol)}(k,t)+\mathit{S}_{ij}^{\mathit{NL(pol)}}(k,t),\end{array}\right\}\end{eqnarray}$$
in which linear terms in the left-hand sides of (2.6a
) and (2.6b
) give contributions
$S^{L}$
,
$S_{ij}^{L(dir)}$
and
$S_{ij}^{L(pol)}$
, whereas nonlinear contributions yield the transfer terms
$T$
,
$S_{ij}^{\mathit{NL(dir)}}$
and
$S_{ij}^{\mathit{NL(pol)}}$
. A convenient way to write the model in (2.12) is to use the spectra
$\tilde{S}_{ij}^{\mathit{NL(dir)}}=S_{ij}^{\mathit{NL(dir)}}/T$
and
$\tilde{S}_{ij}^{\mathit{NL(pol)}}=S_{ij}^{\mathit{NL(pol)}}/T$
.
The linear terms in (A 1) are:
$$\begin{eqnarray}{\mathcal{S}}^{L}(k,t)=-2S_{lm}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE\unicode[STIX]{x1D60F}_{lm}^{(dir)})-2ES_{lm}(\unicode[STIX]{x1D60F}_{lm}^{(dir)}+\unicode[STIX]{x1D60F}_{lm}^{(pol)}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{ij}^{L(dir)}(k,t) & = & \displaystyle \frac{2}{15}\mathit{S}_{ij}E-\frac{2}{7}E\left(S_{jl}\unicode[STIX]{x1D60F}_{il}^{(pol)}+S_{il}\unicode[STIX]{x1D60F}_{jl}^{(pol)}-\frac{2}{3}S_{lm}\unicode[STIX]{x1D60F}_{lm}^{(pol)}\unicode[STIX]{x1D6FF}_{ij}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2}{7}\left(S_{il}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE\unicode[STIX]{x1D60F}_{lj}^{(dir)})+S_{lj}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE\unicode[STIX]{x1D60F}_{li}^{(dir)})-\frac{2}{3}S_{lm}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE\unicode[STIX]{x1D60F}_{lm}^{(dir)})\unicode[STIX]{x1D6FF}_{ij}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{7}E\left(S_{jl}\unicode[STIX]{x1D60F}_{li}^{(dir)}+S_{il}\unicode[STIX]{x1D60F}_{lj}^{(dir)}-\frac{2}{3}S_{lm}\unicode[STIX]{x1D60F}_{lm}^{(dir)}\unicode[STIX]{x1D6FF}_{ij}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}E(\unicode[STIX]{x1D716}_{jmn}W_{m}\unicode[STIX]{x1D60F}_{ni}^{(dir)}+\unicode[STIX]{x1D716}_{imn}W_{m}\unicode[STIX]{x1D60F}_{jn}^{(dir)})-\frac{1}{15}\mathit{S}_{ij}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{ij}^{L(pol)}(k,t) & = & \displaystyle -\frac{2}{5}E\mathit{S}_{ij}-\frac{12}{7}E\left(S_{lj}\unicode[STIX]{x1D60F}_{li}^{(dir)}+S_{il}\unicode[STIX]{x1D60F}_{lj}^{(dir)}-\frac{2}{3}S_{lm}\unicode[STIX]{x1D60F}_{lm}^{(dir)}\unicode[STIX]{x1D6FF}_{ij}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2}{7}\left(S_{jl}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE\unicode[STIX]{x1D60F}_{il}^{(pol)})+S_{il}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE\unicode[STIX]{x1D60F}_{lj}^{(pol)})-\frac{2}{3}S_{ln}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}(kE\unicode[STIX]{x1D60F}_{ln}^{(pol)})\unicode[STIX]{x1D6FF}_{ij}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{7}E\left(S_{il}\unicode[STIX]{x1D60F}_{lj}^{(pol)}+S_{jl}\unicode[STIX]{x1D60F}_{li}^{(pol)}-\frac{2}{3}S_{lm}\unicode[STIX]{x1D60F}_{lm}^{(pol)}\unicode[STIX]{x1D6FF}_{ij}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{6}E(\unicode[STIX]{x1D716}_{iml}W_{m}\unicode[STIX]{x1D60F}_{lj}^{(pol)}+\unicode[STIX]{x1D716}_{jml}W_{m}\unicode[STIX]{x1D60F}_{li}^{(pol)})-\frac{4}{3}E(\unicode[STIX]{x1D716}_{iml}\unicode[STIX]{x1D6FA}_{m}\unicode[STIX]{x1D60F}_{lj}^{(pol)}+\unicode[STIX]{x1D716}_{jml}\unicode[STIX]{x1D6FA}_{m}\unicode[STIX]{x1D60F}_{il}^{(pol)}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
$E=E(k,t)$
,
$\unicode[STIX]{x1D60F}_{ij}^{(dir)}=\unicode[STIX]{x1D60F}_{ij}^{(dir)}(k,t)$
,
$\unicode[STIX]{x1D60F}_{ij}^{(pol)}=\unicode[STIX]{x1D60F}_{ij}^{(pol)}(k,t)$
. In the presence of additional system vorticity, only the contribution from polarization anisotropy is affected, with the last term in
$\unicode[STIX]{x1D734}$
added in (A 4) with respect to the equation in Mons et al. (Reference Mons, Cambon and Sagaut2016).
Nonlinear terms are
$$\begin{eqnarray}T(k,t)=\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}16\unicode[STIX]{x03C0}^{2}p^{2}k^{2}q(xy+z^{3}){\mathcal{E}}_{0}^{\prime \prime }({\mathcal{E}}_{0}^{\prime }-{\mathcal{E}}_{0})\,\text{d}p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{ij}^{\mathit{NL(dir)}}(k,t) & = & \displaystyle \int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}4\unicode[STIX]{x03C0}^{2}p^{2}k^{2}q{\mathcal{E}}_{0}^{\prime \prime }[(y^{2}-1)(xy+z^{3})({\mathcal{E}}_{0}^{\prime }-{\mathcal{E}}_{0})\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime \prime }}\nonumber\\ \displaystyle & & \displaystyle +\,z(1-z^{2})^{2}{\mathcal{E}}_{0}^{\prime }\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime }}\!]\text{d}p\,\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}8\unicode[STIX]{x03C0}^{2}p^{2}k^{2}q(xy+z^{3}){\mathcal{E}}_{0}^{\prime \prime }[(3y^{2}-1)({\mathcal{E}}_{0}^{\prime }-{\mathcal{E}}_{0})\unicode[STIX]{x1D60F}_{ij}^{(dir)^{\prime \prime }}\nonumber\\ \displaystyle & & \displaystyle +\,(3z^{2}-1){\mathcal{E}}_{0}^{\prime }\unicode[STIX]{x1D60F}_{ij}^{(dir)^{\prime }}-2{\mathcal{E}}_{0}\unicode[STIX]{x1D60F}_{ij}^{(dir)}\! ]\text{d}p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{ij}^{\mathit{NL(pol)}}(k,t) & = & \displaystyle \int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}4\unicode[STIX]{x03C0}^{2}p^{2}k^{2}q{\mathcal{E}}_{0}^{\prime \prime }[(xy+z^{3})((1+z^{2}){\mathcal{E}}_{0}^{\prime }\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime }}-4{\mathcal{E}}_{0}\unicode[STIX]{x1D60F}_{ij}^{(pol)})\nonumber\\ \displaystyle & & \displaystyle +\,z(z^{2}-1)(1+y^{2})({\mathcal{E}}_{0}^{\prime }-{\mathcal{E}}_{0})\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime \prime }}+2z(z^{2}-y^{2}){\mathcal{E}}_{0}^{\prime }\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime }}\nonumber\\ \displaystyle & & \displaystyle +\,2yx(z^{2}-1){\mathcal{E}}_{0}\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime \prime }}\!]\text{d}p\,\text{d}q\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}24\unicode[STIX]{x03C0}^{2}p^{2}k^{2}qz(z^{2}-1){\mathcal{E}}_{0}^{\prime \prime }[(y^{2}-1)({\mathcal{E}}_{0}^{\prime }-{\mathcal{E}}_{0})\unicode[STIX]{x1D60F}_{ij}^{(dir)^{\prime \prime }}\nonumber\\ \displaystyle & & \displaystyle +\,(z^{2}-1){\mathcal{E}}_{0}^{\prime }\unicode[STIX]{x1D60F}_{ij}^{(dir)^{\prime }}\!]\text{d}p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{ij}(k,t) & = & \displaystyle \int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}16\unicode[STIX]{x03C0}^{2}p^{2}k^{2}q(yz+x){\mathcal{E}}_{0}^{\prime \prime }[\!{\mathcal{E}}_{0}^{\prime }(y(z^{2}-y^{2})(6\unicode[STIX]{x1D60F}_{ij}^{(dir)^{\prime \prime }}+\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime \prime }})\nonumber\\ \displaystyle & & \displaystyle -\,(xz+y)\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime \prime }}\!)-y(z^{2}-x^{2}){\mathcal{E}}_{0}(6\unicode[STIX]{x1D60F}_{ij}^{(dir)^{\prime \prime }}+\unicode[STIX]{x1D60F}_{ij}^{(pol)^{\prime \prime }}\!)\!]\text{d}p\,\text{d}q,\end{eqnarray}$$
with
${\mathcal{E}}_{0}=E(k,t)/4\unicode[STIX]{x03C0}k^{2}$
,
${\mathcal{E}}_{0}^{\prime }=E(p,t)/4\unicode[STIX]{x03C0}p^{2}$
,
${\mathcal{E}}_{0}^{\prime \prime }=E(q,t)/4\unicode[STIX]{x03C0}q^{2}$
,
$\unicode[STIX]{x1D60F}_{ij}^{()}=\unicode[STIX]{x1D60F}_{ij}^{()}(k,t)$
,
$\unicode[STIX]{x1D60F}_{ij}^{()^{\prime }}=\unicode[STIX]{x1D60F}_{ij}^{()}(p,t)$
and
$\unicode[STIX]{x1D60F}_{ij}^{()^{\prime \prime }}=\unicode[STIX]{x1D60F}_{ij}^{()}(q,t)$
, where
$\unicode[STIX]{x1D60F}_{ij}^{()}$
may refer to either
$\unicode[STIX]{x1D60F}_{ij}^{(dir)}$
or
$\unicode[STIX]{x1D60F}_{ij}^{(pol)}$
. The integrals over
$p$
and
$q$
are performed over the domain
$\unicode[STIX]{x1D6E5}_{k}$
so that
$k$
,
$p$
and
$q$
are the lengths of the sides of the triangle formed by
$\boldsymbol{k}$
,
$\boldsymbol{p}$
and
$\boldsymbol{q}$
.
In addition, the characteristic decorrelation time is
$\unicode[STIX]{x1D703}_{kpq}=(\unicode[STIX]{x1D707}_{kpq})^{-1}$
as in the isotropic EDQNM model, with
$\unicode[STIX]{x1D707}_{kpq}=\unicode[STIX]{x1D708}(k^{2}+p^{2}+q^{2})+\unicode[STIX]{x1D702}(k,t)+\unicode[STIX]{x1D702}(p,t)+\unicode[STIX]{x1D702}(q,t)$
, and the eddy damping coefficient is
$\unicode[STIX]{x1D702}(k,t)=A(\int _{0}^{k}p^{2}E(p,t)\,\text{d}p)^{1/2}$
following Pouquet et al. (Reference Pouquet, Lesieur, André and Basdevant1975). The only parameter of the model is set to
$A=0.36$
to recover the well-admitted value of the Kolmogorov constant (André & Lesieur Reference André and Lesieur1977), and is the same in all the EDQNM models, hence is not used as a tuning parameter.
Appendix B. Elements of spectral linear theory
The equations for the fluctuating velocity in physical and spectral space are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}t}+A_{jk}x_{k}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}+A_{ij}u_{j}+\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+2\unicode[STIX]{x1D700}_{imn}\unicode[STIX]{x1D6FA}_{m}u_{n}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\hat{u} _{i}(\boldsymbol{k},t)}{\unicode[STIX]{x2202}t}-A_{ln}k_{l}\frac{\unicode[STIX]{x2202}\hat{u} _{i}(\boldsymbol{k},t)}{\unicode[STIX]{x2202}k_{n}}+M_{in}(\boldsymbol{k})\hat{u} _{n}(\boldsymbol{k},t)=0. & \displaystyle\end{eqnarray}$$
They permit the definition of characteristic lines in physical space and Fourier space:
$$\begin{eqnarray}\dot{x_{i}}=\frac{\text{d}x_{i}}{\text{d}t}=A_{ik}x_{k}\quad \text{and}\quad \dot{k_{i}}=\frac{\text{d}k_{i}}{\text{d}t}=-A_{ji}k_{j}.\end{eqnarray}$$
The characteristic lines can be expressed by the Cauchy matrix
$\unicode[STIX]{x1D60D}_{ij}(t,t_{0})$
with
$x_{i}=\unicode[STIX]{x1D60D}_{ij}(t,t_{0})X_{j}$
and
$k_{i}(t)=\unicode[STIX]{x1D60D}_{ji}^{-1}(t,t_{0})K_{j}$
, where
$X_{j}=x_{j}(t_{0})$
and
$K_{j}=k_{j}(t_{0})$
. For the spectral wavenumber evolution, one gets
$$\begin{eqnarray}\dot{k_{i}}=-A_{ji}k_{j}\quad \text{and}\quad \frac{\text{d}\hat{u} _{i}(\boldsymbol{k}(t),t)}{\text{d}t}=-M_{in}(t)\hat{u} _{n}(\boldsymbol{k}(t),t).\end{eqnarray}$$
Consequently, the linear solution for
$\hat{u} _{i}(\boldsymbol{k}(t),t)$
can be obtained as
$$\begin{eqnarray}\hat{u} _{i}(\boldsymbol{k}(t),t)=\unicode[STIX]{x1D60E}_{ij}(\boldsymbol{k},t,t_{0})\hat{u} _{j}(\boldsymbol{K},t_{0})\quad \text{with }\unicode[STIX]{x1D60E}_{ij}(\boldsymbol{k},t_{0},t_{0})=\unicode[STIX]{x1D6FF}_{ij}-\frac{K_{i}K_{j}}{K^{2}},\end{eqnarray}$$
when Green’s function
$\unicode[STIX]{x1D642}$
is solved, and the general solution for the second-order spectral tensor is therefore
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)=\unicode[STIX]{x1D60E}_{ik}(\boldsymbol{k},t,t_{0})\unicode[STIX]{x1D60E}_{jl}(\boldsymbol{k},t,t_{0})\hat{\unicode[STIX]{x1D619}}_{kl}(\boldsymbol{K},t_{0}).\end{eqnarray}$$
In this solution, viscous decay can easily be inserted as a multiplying exponential term.
For instance, for the shear case without rotation
$$\begin{eqnarray}[A_{ij}]=\left[\begin{array}{@{}ccc@{}}0 & S & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}k_{1}(t)=K_{1},\quad k_{2}(t)=K_{2}-StK_{1},\quad k_{3}(t)=K_{3},\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{d}\hat{u} _{1}(\boldsymbol{k}(t),t)}{\text{d}t}}=\left({\displaystyle \frac{2k_{1}^{2}}{k^{2}}}-1\right)S\hat{u} _{2}(\boldsymbol{k}(t),t),\\ {\displaystyle \frac{\text{d}\hat{u} _{2}(\boldsymbol{k}(t),t)}{\text{d}t}}={\displaystyle \frac{2k_{1}k_{2}}{k^{2}}}S\hat{u} _{2}(\boldsymbol{k}(t),t),\\ {\displaystyle \frac{\text{d}\hat{u} _{1}(\boldsymbol{k}(t),t)}{\text{d}t}}=-{\displaystyle \frac{2k_{1}k_{3}}{k^{2}}}S\hat{u} _{2}(\boldsymbol{k}(t),t),\end{array}\right\}\end{eqnarray}$$
and since
$\dot{k^{2}}=2k_{i}\dot{k_{i}}=-Sk_{1}k_{2}$
, one finds that
$k^{2}\hat{u} _{2}(\boldsymbol{k},t)$
is conservative, so that
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}\hat{u} _{1}(\boldsymbol{k},t)\\ \hat{u} _{2}(\boldsymbol{k},t)\\ \hat{u} _{3}(\boldsymbol{k},t)\end{array}\right)=\left[\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D60E}_{12} & 0\\ 0 & {\displaystyle \frac{K^{2}}{k^{2}}} & 0\\ 0 & \unicode[STIX]{x1D60E}_{32} & 1\end{array}\right]\left(\begin{array}{@{}c@{}}\hat{u} _{1}(\boldsymbol{K},0)\\ \hat{u} _{2}(\boldsymbol{K},0)\\ \hat{u} _{3}(\boldsymbol{K},0)\end{array}\right),\end{eqnarray}$$
where the Green’s function components are
$$\begin{eqnarray}\unicode[STIX]{x1D60E}_{12}=-S\int \left(1-2{\displaystyle \frac{K_{1}^{2}}{k^{2}}}\right){\displaystyle \frac{K^{2}}{k^{2}}}\,\text{d}t,\quad \unicode[STIX]{x1D60E}_{32}=2S{\displaystyle \frac{K_{1}K_{3}}{K^{2}}}\int {\displaystyle \frac{K^{4}}{k^{4}}}\,\text{d}t.\end{eqnarray}$$
The analytical solution comes from the integrals of
$\int \!(1/k^{2})\,\text{d}t$
and
$\int \!(1/k^{4})\,\text{d}t$
, and we finally obtain
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}\unicode[STIX]{x1D60E}_{12}\, & =\, & {\displaystyle \frac{K^{2}}{K_{1}^{2}+K_{3}^{2}}}\left(-{\displaystyle \frac{K_{3}^{2}}{K_{1}\sqrt{K_{1}^{2}+K_{3}^{2}}}}\arctan {\displaystyle \frac{K_{1}St\sqrt{K_{1}^{2}+K_{3}^{2}}}{K^{2}-K_{1}K_{2}St}}\right.\\ \, & \, & +\left.\vphantom{{\displaystyle \frac{K_{1}St\sqrt{K_{1}^{2}+K_{3}^{2}}}{K^{2}-K_{1}K_{2}St}}}{\displaystyle \frac{StK_{1}^{2}(K^{2}-2K_{1}^{2}+StK_{1}K_{2})}{K^{2}k^{2}}}\right),\\ \unicode[STIX]{x1D60E}_{32}\, & =\, & {\displaystyle \frac{K_{1}K_{3}}{K_{1}^{2}+K_{3}^{2}}}\left({\displaystyle \frac{K^{2}}{K_{1}\sqrt{K_{1}^{2}+K_{3}^{2}}}}\arctan {\displaystyle \frac{K_{1}St\sqrt{K_{1}^{2}+K_{3}^{2}}}{K^{2}-K_{1}K_{2}St}}\right.\\ \, & \, & +\left.\vphantom{{\displaystyle \frac{K_{1}St\sqrt{K_{1}^{2}+K_{3}^{2}}}{K^{2}-K_{1}K_{2}St}}}{\displaystyle \frac{St(K^{2}-2K_{1}^{2}+StK_{1}K_{2})}{k^{2}}}\right).\end{array}\right\}\end{eqnarray}$$
For the 2-D modes such that
$K_{1}=0$
, the simple solution is
$k/K=1$
,
$\unicode[STIX]{x1D60E}_{12}=-St$
and
$\unicode[STIX]{x1D60E}_{32}=0$
.
