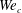1 Introduction and observations: ubiquity of non-isolated impacts
The outcome of the impact of a drop depends on its impacting energy and the surface wetting properties. Upon impact on a solid surface, a drop expands into a sheet, a corona, which can rebound, stick or splash and fragment into secondary droplets (Rioboo, Marengo & Tropea Reference Rioboo, Marengo and Tropea2002; Yarin Reference Yarin2006). Numerous studies have focused on impacts of single drops on superhydrophobic surfaces to understand when and how splash, rebound or coating occurs. This is important for spray-coating, deicing, pesticide spraying (Zable Reference Zable1977; Eggers & Villermaux Reference Eggers and Villermaux2008; Josserand & Thoroddsen Reference Josserand and Thoroddsen2016), and for environmental and health processes such as erosion (Furbish et al.
Reference Furbish, Hammer, Schmeeckle, Borosund and Mudd2007) or contaminant dissemination by secondary pathogen-bearing droplets (Bourouiba & Bush Reference Bourouiba, Bush and Fernando2013; Bourouiba, Dehandschoewercker & Bush Reference Bourouiba, Dehandschoewercker and Bush2014; Gilet & Bourouiba Reference Gilet and Bourouiba2014, Reference Gilet and Bourouiba2015; Scharfman et al.
Reference Scharfman, Techet, Bush and Bourouiba2016). However, most natural and indoor surfaces have average-wetting – neither superhydrophobic nor superhydrophilic – properties and support sessile drops. The physics of a single drop impact on most surfaces can be dramatically changed by the presence of adjacent sessile drops (Sivakumar & Tropea Reference Sivakumar and Tropea2002; Moreira, Moita & Panão Reference Moreira, Moita and Panão2010; Gilet & Bourouiba Reference Gilet and Bourouiba2014; Liang & Mudawar Reference Liang and Mudawar2016). Yet, little attention has been paid to interactions between impacting drops and sessile drops surrounding them on average-wetting surfaces (Charalampous & Hardalupas Reference Charalampous and Hardalupas2016). Instead, the focus has been on the impact of isolated drops on surfaces, predicting, for example, the maximum radius of expansion of the corona they form upon impact,
$r_{max}$
, and the number of corrugations,
$N$
, that appear on the rim surrounding such expanding corona. Here, we focus on the neglected case of drop impact on surfaces of average wetting that hold sessile drops.
1.1 Types of drop–drop impact
Two types of impact on a leaf supporting a sessile drop are illustrated experimentally in figure 1(a,b). A rain or irrigation spray drop, of radius
$r_{1}$
, can either impact a sessile drop of radius
$r_{2}$
head-on, at its centre (figure 1
a), or off-centre, leading to a crescent-moon fragmentation (figure 1
b). When off-centre, with an interdrop distance
$d$
, the impacting drop viewed from the bottom (figure 2
c) spreads into a circular corona which collides with the sessile drop (figures 1
b, 2
c). Viewed from the side, the collision results in lift of the sessile drop from the surface to form an arched sheet (figures 1
b, 2
b) expanding in the air with a profile shaped as a crescent-moon (figure 2
a), which eventually fragments into droplets. Viewed from below, quickly following the lift of the sessile drop, two filaments emerge at the edge of the foot of the crescent-moon sheet and grow (figures 1
a and 2
c). A few studies have reported the interaction of coronas (Barnes et al.
Reference Barnes, Hardalupas, Taylor and Wilkins1999) or head-on collisions of trains of drops on surfaces (Yarin & Weiss Reference Yarin and Weiss1995; Fujimoto, Ito & Takezaki Reference Fujimoto, Ito and Takezaki2002).
Figure 1. Drop–drop interactions on a leaf. (a) A drop hits a sessile drop right at its centre, forming a head-on collision. (b) A drop hits a sessile drop off-centre, leading to a crescent-moon with universal sheet lift and growth of a pair of bounding ligaments. The scale bar is 5 mm.
Figure 2. Crescent-moon formation. (a) From impacting clear drop, to lift of the blue sessile drop, to its stretching and onset of fragmentation. Both drops are made of water with density
$\unicode[STIX]{x1D70C}=1.0\times 10^{3}~\text{kg}~\text{m}^{-3}$
, viscosity
$\unicode[STIX]{x1D708}=1.0\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
and surface tension
$\unicode[STIX]{x1D70E}=72~\text{mNm}^{-1}$
. The radii are
$r_{1}=2.24$
mm and
$r_{2}=1.95$
mm for the impacting and sessile drop respectively. (b) Side view of the crescent-moon formation shown in (a), displaying the stretching of the sessile drop into an arched sheet as it lifts from the surface. (c) Bottom view of the expanding corona of the impacting drop lifting the sessile drop, at distance
$d=5.65$
mm from impact, and emergence of the pair of ligaments bounding the base of the crescent-moon sheet. Here,
$r_{max}$
is the maximum radius of the corona and
$\unicode[STIX]{x1D706}$
is the average wavelength (distance) between rim corrugations at the maximum radius. The time interval is 0.12 ms and the scale bar is 5 mm.
However, the probability of an off-centre impact such as in figure 2(a–c) is much higher than that of a head-on impact. Hence, crescent-moon fragmentation is a more frequent and efficient source of secondary droplets in spray- or rain-induced foliar disease transmission (Gilet & Bourouiba Reference Gilet and Bourouiba2015). Indeed, common leaves have average wetting – neither superhydrophobic nor superhydrophilic – and support sessile drops (Gilet & Bourouiba Reference Gilet and Bourouiba2014). The physics of the crescent-moon generalizes beyond impacts on leaves and provides an explanation of difficulties in achieving uniform coatings or suppressing undesired secondary droplet ejection from most common surfaces of average wetting (figure 2
a). Even when the impacting drop is below the splash limit, the presence of a sessile drop in the vicinity can still generate undesired ejection of secondary droplets (figure 2
a–c), thus making it important to gain an understanding of this recently discovered phenomenon. Before discussing our observations further, we start by reviewing the body of literature on isolated drop impact on surfaces, with a particular focus on the maximum corona radius
$r_{max}$
they reach, and the number of corrugations
$N$
observed on the rim of their corona.
1.2 Maximum corona radius and corrugations: prior literature results
We consider the impact of an isolated drop of radius
$r_{1}$
with normal impact Weber number
$We=\unicode[STIX]{x1D70C}u_{1}^{2}(2r_{1})/\unicode[STIX]{x1D70E}$
, where
$r_{1}$
is the radius of the impacting drop,
$u_{1}$
is the impact speed, and
$\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D70E}$
are the density, kinematic viscosity and surface tension of the drop respectively. Upon impact, the drop expands in the form of a corona which reaches a maximum radius
$r_{max}$
(figure 2
c). Two particular regimes of such corona spreading have been predominantly discussed in the literature (table 1): a viscous dominated regime and a capillary dominated regime. In the capillary dominated regime, viscous effects are neglected. In this first regime, lossless conversion of the impacting drop kinetic energy to the corona surface energy is assumed to set
$r_{max}$
, leading to
$R_{max}=r_{max}/r_{1}\sim We^{1/2}$
first derived by Madejski (Reference Madejski1976). Lastakowski et al. (Reference Lastakowski, Boyer, Biance, Pirat and Ybert2014) more recently reported
$R_{max}\sim We^{1/2}$
based on experiments on superheated surfaces which reduce viscous stresses. Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004) proposed a scaling
$R_{max}\sim We^{1/4}$
on superhydrophobic surfaces based on mass conservation and considering an average corona thickness
$h=\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}a}$
, with
$a=u_{1}^{2}/d_{1}$
the impact acceleration and
$d_{1}$
the impacting drop diameter. The
$R_{max}$
observed in their experiments was smaller than their prediction. These authors conjectured that the missing energy was converted to internal circulation in the corona. In the viscous regime, surface tension is neglected. In this second regime, Madejski (Reference Madejski1976) and Chandra & Avedisian (Reference Chandra and Avedisian1991) predicted
$R_{max}\sim Re^{1/5}$
by considering full viscous dissipation of the impacting drop kinetic energy, where
$Re=(2r_{1})u_{1}/\unicode[STIX]{x1D708}$
is the Reynolds number and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of the fluid. This scaling is also consistent with the experimental data reported by Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004).
Table 1. Summary of scaling laws proposed in prior work for the maximum spreading of isolated impacting drops on surfaces,
$R_{max}=r_{max}/r_{1}$
, where
$r_{1}$
is the impacting drop radius.
Eggers et al. (Reference Eggers, Fontelos, Josserand and Zaleski2010) attempted to combine the viscous and capillary dominated regimes and proposed a unified expression
$R_{max}=Re^{1/5}f(P)$
, with
$P=We\,Re^{-2/5}$
when energy conservation holds as in Madejski (Reference Madejski1976) or
$P=We\,Re^{-4/5}$
when impact inertia is dominant as in Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004). More recently, Laan et al. (Reference Laan, De Bruin, Bartolo, Josserand and Bonn2014) collapsed all of the experimental data available on
$R_{max}$
from both the viscous and capillary dominated regimes and also proposed a unified scaling as
$$\begin{eqnarray}R_{max}=Re^{1/5}f(P),\quad \text{with}~P=We\,Re^{-2/5},\end{eqnarray}$$
where the empirical expression of
$f(P)$
was proposed using the Padé approximant,
$$\begin{eqnarray}f_{c}(P)=\frac{P^{1/2}}{A+P^{1/2}},\end{eqnarray}$$
with fitting parameter
$A=1.24\pm 0.02$
. Lee et al. (Reference Lee, Derome, Dolatabadi and Carmeliet2016) extended the Padé approximant of Laan et al. (Reference Laan, De Bruin, Bartolo, Josserand and Bonn2014) by incorporating surface wetting via a contact angle
$\unicode[STIX]{x1D703}_{e}$
, leading to
$\tilde{R}_{max}=(R_{max}^{2}-R_{v\rightarrow 0}^{2})^{1/2}$
, where
$R_{v\rightarrow 0}$
is the drop dimensionless radius when deposited (without inertia) on the surface,
$$\begin{eqnarray}\tilde{R}_{max}=f_{c}(We)=\frac{We^{1/2}}{B+We^{1/2}},\end{eqnarray}$$
with fitting parameter
$B=7.6$
.
Scheller & Bousfield (Reference Scheller and Bousfield1995) considered drop impacts on a range of materials from glass to plastic and for the widest range of Weber number from 50 to 2500. The initial fit to their data for maximum radius led to
$$\begin{eqnarray}R_{max}=0.61(Re^{2}Oh)^{1/6}=0.61\,Re^{1/5}(We\,Re^{-2/5})^{1/6},\end{eqnarray}$$
which can also be expressed as
$R_{max}=Re^{1/5}f(P)$
in the form proposed by Eggers et al. (Reference Eggers, Fontelos, Josserand and Zaleski2010). Scheller & Bousfield (Reference Scheller and Bousfield1995) also discussed a prediction of
$R_{max}$
based on a ‘squeeze flow model’, assuming that the impacting drop squeezes in the form of a cylindrical column. This geometry, combined with conservation of mass and momentum, and considering viscous stress and surface tension as external forces, leads to
$$\begin{eqnarray}R_{max}=(Re^{2}Oh)^{0.123},\end{eqnarray}$$
which is close to the best fit of their experimental data (1.4). In summary, we can re-express (1.1), (1.3) and (1.4) as
$$\begin{eqnarray}R_{max}=\frac{We^{1/2}}{1.24+We^{2/5}Oh^{1/5}},\quad \tilde{R}_{max}=\frac{We^{2/5}Oh^{-1/5}}{7.6+We^{1/2}},\quad R_{max}=0.61\left(\frac{We}{Oh}\right)^{1/6}\end{eqnarray}$$
respectively. These expressions are summarized with additional details in table 1.
Table 2. Summary of literature scaling laws proposed to quantify the number of rim corrugations,
$N$
, surrounding the corona of a single impacting drop.
In the literature, the number of corrugations,
$N$
, at maximum corona radius
$r_{max}$
was linked to the destabilization wavelength of the rim,
$N=2\unicode[STIX]{x03C0}r_{max}/\unicode[STIX]{x1D706}$
(see figure 2
c for illustration of
$\unicode[STIX]{x1D706}$
). A summary of prior literature predictions of
$N$
is given in table 2. In particular, Marmanis & Thoroddsen (Reference Marmanis and Thoroddsen1996) first conducted an experimental study of the corrugations for drop impacts on paper and found
$N$
to scale with the ‘impact Reynolds number’
$Re_{I}=u_{1}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$
, where
$\unicode[STIX]{x1D6FF}=\sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}_{c}}$
is the boundary layer thickness based on the drop free oscillation period, essentially the capillary timescale
$\unicode[STIX]{x1D70F}_{c}=\sqrt{\unicode[STIX]{x1D70C}8r_{1}^{3}/\unicode[STIX]{x1D70E}}$
, yielding
$$\begin{eqnarray}N=B(Re_{I})^{3/4}=B(Re^{1/2}We^{1/4})^{3/4}=B\left(\frac{We}{Oh}\right)^{3/8},\end{eqnarray}$$
where the coefficient
$B$
was not explicitly given by the authors.
Bhola & Chandra (Reference Bhola and Chandra1999) estimated
$N=2\unicode[STIX]{x03C0}r_{max}/\unicode[STIX]{x1D706}$
, with
$r_{max}/r_{1}\sim Re^{1/4}$
proposed in their study, with
$\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}\sqrt{3\unicode[STIX]{x1D70E}/a\unicode[STIX]{x1D70C}}$
the wavelength characteristic of the Rayleigh–Taylor instability with a characteristic acceleration
$a=u_{1}^{2}/2r_{1}$
, leading to
$$\begin{eqnarray}N=\frac{Re^{1/4}We^{1/2}}{4\sqrt{3}}=\frac{We^{5/8}}{4\sqrt{3}\,Oh^{1/4}}.\end{eqnarray}$$
Mehdizadeh et al. (Reference Mehdizadeh, Chandra and Mostaghimi2004) conducted a theoretical study of the temporal evolution of the corrugations by considering small initial perturbations of the corona rim and using a linear Rayleigh instability analysis. They inferred a decreasing value of
$N$
with corona expansion, but did not express
$N$
at maximum corona radius explicitly.
In this study, combining experiments and theory, we show that an impacting drop that would not splash in isolation, but coat the surface, can still lead to secondary droplets in the presence of a sessile drop. Our focus is on the impact of rain or irrigation drops on intermediate-wetting surfaces supporting sessile contaminated drops with potential for secondary contaminated drop ejection. We revisit the predictions of maximum corona radius
$R_{max}$
and corrugations
$N$
for impacts on average-wetting surfaces. We identify four regimes of drop–drop interaction: head-on collision, crescent-moon fragmentation, touch-and-flop collision and no collision (§ 2). We combine experiments and theory to derive the conditions under which these regimes occur, and find that a subtle combination of geometry and momentum transfer determines a critical drop–drop impact force governing the existence and inter-regime boundaries and the physics of the crescent-moon new splash phenomenon (§ 3). We introduce a horizontal critical collision Weber number
$We_{c}$
which determines when crescent-moon fragmentation can occur. The critical collision Weber number
$We_{c}$
is defined based on the force per unit length upon collision of the corona rim on the sessile drop (§§ 3.3.1–3.3.2). Finally, we also predict key properties of the crescent-moon fragmentation: the extension of its base (§ 4) and the length of the pair of ligaments always surrounding its base (§ 5). These properties are important for study of the highly efficient fragmentation process that is the crescent-moon (§ 6).
Table 3. The experimental conditions for the water drop–drop impact experiments. Deionized water was used for both the falling drops and the sessile drops with density, kinematic viscosity and surface tension
$\unicode[STIX]{x1D70C}=1.0\times 10^{3}~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D708}=1.0\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
and
$\unicode[STIX]{x1D70E}=72~\text{mN}~\text{m}^{-1}$
respectively. The Weber number
$We=\unicode[STIX]{x1D70C}u_{1}^{2}(2r_{1})/\unicode[STIX]{x1D70E}$
, Reynolds number
$Re=(2r_{1})u_{1}/\unicode[STIX]{x1D708}$
and Ohnesorge number
$Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D70E}(2r_{1})}$
involved are also given. The averaged wetting of the surface used was similar to that of plant leaves supporting crescent-moon fragmentation (figure 1).
2 Experimental set-up and observations: regimes of drop–drop interaction
We conducted systematic collision experiments involving a water drop impacting in the vicinity of sessile drops of increasing viscosity (from water to pure glycerol), with properties summarized in tables 3 and 4. The impacts were recorded by two high-speed cameras from side and bottom views (figures 4 and 2). An impacting drop of radius
$r_{1}$
was released from a height of 0.3–2.2 m onto an impact point at distance
$d$
from the centre of a sessile drop of radius
$r_{2}$
(table 3). The sessile drop was deposited on surfaces of average wetting with static equilibrium contact angles
$45^{\circ }\leqslant \unicode[STIX]{x1D703}_{E}\leqslant 82^{\circ }$
. Upon expansion of the impacting drop, the expanding corona grows and reaches a maximum radius
$r_{max}$
(figure 2
c). For every impacting drop speed
$u_{1}$
and size
$r_{1}$
, the distance
$d$
between the impact point and the centre of the sessile drop and the size of the sessile drop
$r_{2}$
were varied. Our large set of experiments allowed us to identify four drop–drop interaction regimes: head-on collision, crescent-moon fragmentation, touch-and-flop collision and no collision (figure 3
a–h).
Figure 3. The four possible scenarios of drop–drop interaction. In each quadrant, the upper two panels are imaged from below, while the lower panels are imaged simultaneously from the side. The red impacting drop radius is
$r_{1}=2.27$
, 2.29, 2.31, 2.31 mm for (a), (c), (e), (g) respectively. The blue sessile drop radius is
$r_{2}=2.29$
, 2.24, 2.60, 2.16 mm for (a), (c), (e), (g) respectively. The drop–drop distance is
$d=2.51$
, 6.85, 11.51, 17.68 mm for (a), (c), (e), (g) respectively.
Table 4. The experimental parameters used for drop–drop collisions with sessile drops of increasing viscosity and with a solid drop-analogue. Mixture 1 is made of a 1 : 1 volume ratio of water to glycerol. Mixture 2 has a 1 : 2 volume ratio. The density, kinematic viscosity and surface tension of the falling drops are the same as those given in table 3, with corresponding
$We=1063\pm 26$
,
$Re=(1.89\pm 0.04)\times 10^{4}$
and
$Oh=(1.73\pm 0.03)\times 10^{-3}$
.
Figure 4. Schematic of the experimental set-up. The inset shows the scheme of the impact phenomenon viewed from the top. The red circle indicates the impacting drop and the blue circle the sessile drop. The radii of the impacting drop and the sessile drop are
$r_{1}$
and
$r_{2}$
respectively. The centre-to-centre offset between the sessile drop and the impact point is
$d$
;
$r_{max}$
is the maximum radius of the expanding corona.
3 Boundary between the regimes of drop–drop interaction
3.1 Head-on collision
We capture the transition between the four regimes (figure 3) with only two parameters: the impact Weber number
$We=\unicode[STIX]{x1D70C}u_{1}^{2}(2r_{1})/\unicode[STIX]{x1D70E}$
and the dimensionless drop–drop distance
$D=(d-r_{2})/r_{1}$
. If the impacting drop contacts the sessile drop prior to touch-down on the surface, then a head-on drop–drop interaction occurs (figures 1
a and 3
a,b). This regime emerges for drop–drop offsets
$d$
that are smaller than the sum of the radii of the two drops, namely for
$$\begin{eqnarray}d<r_{1}+r_{2}\quad \text{or}\quad D<1.\end{eqnarray}$$
Depending on the relative drop sizes, the impact is analogous to (i) an isolated drop impact on a surface, where the expanding corona of the impacting drop seamlessly swallows the sessile drop (
$r_{1}/r_{2}\gg 1$
), (ii) an impact on thin film (
$r_{1}/r_{2}\ll 1$
) or (iii) an asymmetric non-isolated drop impact on a solid surface (
$r_{1}/r_{2}\sim O(1)$
), as seen in figures 1(b) and 3(a,b).
Figure 5. Comparison of our measured isolated drop
$R_{max}=r_{max}/r_{1}$
as a function of impact Weber number
$We$
(black dots) with literature predictions summarized in table 1. Our data, obtained with the conditions summarized in table 5, are best captured by
$R_{max}=0.61(We/Oh)^{1/6}$
from Scheller & Bousfield (Reference Scheller and Bousfield1995). Here, the Weber number
$We=\unicode[STIX]{x1D70C}u_{1}^{2}(2r_{1})/\unicode[STIX]{x1D70E}$
and the Ohnesorge number
$Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D70E}(2r_{1})}$
.
Table 5. Experimental conditions and number of experiments in the present study used to quantify the maximum radius
$R_{max}=r_{max}/r_{1}$
(§ 3.2) and the number of ligaments
$N$
(figure 9) of the impacting drop expanding corona. Given our focus on the impact of rain and irrigation drops, the density, kinematic viscosity and surface tension of the impacting drops are those of water:
$\unicode[STIX]{x1D70C}=1.0\times 10^{3}~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D708}=1.0\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
and
$\unicode[STIX]{x1D70E}=72~\text{mN}~\text{m}^{-1}$
respectively.
3.2 No collision and maximum corona radius
If the impacting drop corona is smaller than the drop–drop distance, no collision occurs, making this an isolated drop impact. This scenario (figure 3 g,h) is captured by
$$\begin{eqnarray}d>r_{max}+r_{2}\quad \text{or}\quad D>\frac{r_{max}}{r_{1}}=R_{max},\end{eqnarray}$$
where
$R_{max}$
is the dimensionless spreading of the impacting drop. A number of prior studies have examined isolated drop impacts on solid surfaces and aimed to express
$R_{max}=r_{max}/r_{1}$
as a function of the impact Weber and Reynolds numbers,
$We=\unicode[STIX]{x1D70C}u_{1}^{2}(2r_{1})/\unicode[STIX]{x1D70E}$
and
$Re=(2r_{1})u_{1}/\unicode[STIX]{x1D708}$
respectively (table 1 and § 1.2).
Given the disparities in prior literature predictions of maximum corona radius for a range of eclectic surfaces and fluids, and our focus on impacts of water drops on surfaces of average wetting relevant for irrigation or washing of crop and fresh produce, we proceed to conduct more than a hundred isolated water drop impact experiments to determine the relevant maximum radius on our surfaces (table 5). The impacting drop viscosity
$\unicode[STIX]{x1D707}$
, surface tension
$\unicode[STIX]{x1D70E}$
and size
$r_{1}$
are such that
$Oh=(1.74\pm 0.01)\times 10^{-3}$
is fixed, while
$We$
ranges from 240 to 2020 (see table 5 for the full list of parameters).
Figure 5 shows our experimental measurements of maximum corona radius
$R_{max}$
as a function of drop impact
$We$
. When compared with the literature (table 1), our results are consistent with the scaling of Scheller & Bousfield (Reference Scheller and Bousfield1995) and Laan et al. (Reference Laan, De Bruin, Bartolo, Josserand and Bonn2014), and are best captured by
$R_{max}\sim We^{1/6}$
from Scheller & Bousfield (Reference Scheller and Bousfield1995), who conducted experiments over an analogous range of impact
$We$
and
$Re$
to our study (tables 1 and 5). From figure 5, we obtain
$$\begin{eqnarray}R_{max}=\frac{r_{max}}{r_{1}}=C_{R}\,We^{1/6},\end{eqnarray}$$
with
$C_{R}=0.61/Oh^{1/6}=1.75$
given (1.6) and
$Oh=1.75\times 10^{-3}$
, which is fixed here (table 3). The experiments presented in this section allow us to fix the expression for
$R_{max}$
as (3.3) with
$C_{R}=1.75$
for the remainder of this study.
3.3 Boundary between crescent-moon and touch-and-flop collision
Crescent-moon fragmentation and touch-and-flop collision can only exist for
$1<D<R_{max}$
. Crescent-moon fragmentation occurs if the sessile drop is lifted and transformed into an expanding arched sheet, ultimately fragmenting into secondary droplets (figures 2
a–c, 3
c,d). The onset of the touch-and-flop collision is similar to that of the crescent-moon, with an initial lift of the sessile drop; however, the sessile drop remains a coherent bulk without topological change into a thin sheet. This results in the sessile fluid being simply displaced to form another sessile drop in the vicinity of the original one (figure 3
e,f). We summarize in figure 6 our results and prediction of transition criteria between drop–drop interaction regimes in a phase diagram of
$We$
versus
$D$
.
Figure 6. Regime map of the outcome of drop–drop interaction as a function of
$D=(d-r_{2})/r_{1}$
,
$R_{max}=r_{max}/r_{1}$
and
$We=\unicode[STIX]{x1D70C}u_{1}^{2}(2r_{1})/\unicode[STIX]{x1D70E}$
. The collision threshold Weber number
$We_{c}=25$
derived in the text is used to analytically derive the boundaries between the regimes. All experimental values are found in tables 3–5. The boundaries between the regimes are elucidated and derived one by one in § 3.
Figure 7. (a) Top view of the expanding corona, the contour of which is detected using image processing, allowing us to deduce a radial expansion velocity
$u=\text{d}r/\text{d}t$
, where
$r$
is the radius of the corona. This radius was determined by measurement of the temporal evolution of the corona area
$A$
and
$r=\sqrt{A/\unicode[STIX]{x03C0}}$
. (b) The side view allows us to measure the radius of the corona at the time of collision with the sessile drop,
$r_{c}$
, and to track the evolution of the thickness of the corona edge
$h$
(c). These side and top views allow us to define a force of impact per unit arclength of corona,
$f_{c}=\unicode[STIX]{x1D70C}hu^{2}$
. (d–f) The time evolution of the dimensionless (d) corona radius
$R=r/r_{1}$
, (e) radial speed
$U=u/u_{1}$
and (f) edge thickness
$H=h/r_{1}$
for different Weber numbers. Here,
$T=t/\unicode[STIX]{x1D70F}$
is the dimensionless time, with impact time
$\unicode[STIX]{x1D70F}=r_{1}/u_{1}$
.
3.3.1 Physical picture and threshold impact force
To understand the more subtle transition between the crescent-moon and the touch-and-flop collision, we consider the following. Upon impact with a given
$We$
, the impacting drop expands into a corona. This expansion is decelerated by surface viscous stresses and surface tension. As it decelerates, the force of impact with the sessile drop along the way decreases with the distance of expansion
$r$
(figure 7
a). The impact
$We$
determines the radial speed of corona expansion
$u=\text{d}r/\text{d}t$
in addition to its maximum extension
$r_{max}$
(figure 7
b). The interplay of the corona expansion speed
$u$
and the drop–drop offset
$d$
determines the force of impact between the corona and the sessile drop. In particular, for a given impact
$We$
, the larger the interdrop distance
$d$
is, the smaller the momentum transfer from the edge of the corona to its neighbouring sessile drop upon impact is.
We can formalize this physical picture further by defining a horizontal collision Weber number
$We_{c}$
characterizing the competition between the inertia of the corona edge and the interfacial forces of the sessile drop. For a given impact
$We$
, there should exist a critical collision distance,
$r_{c}$
, such that
$r_{1}+r_{2}<d-r_{2}<r_{c}<r_{max}$
, below which
$We_{c}$
is high enough for the horizontal collision to impart high enough inertia to the sessile drop to overcome capillarity, transforming the sessile drop into an expanding sheet in the air. For an interdrop distance
$r_{c}$
such that
$r_{c}<d-r_{2}<r_{max}$
, this would not be the case and only a touch-and-flop collision could occur.
Figure 8. (a) The collision Weber number
$We_{c}$
as a function of the dimensionless corona radius
$R$
. The collision Weber number
$We_{c}$
is the ratio of the rate of change of momentum (collision force) per unit arclength
$\unicode[STIX]{x1D70C}u^{2}h$
and surface tension
$\unicode[STIX]{x1D70E}$
. (b) The critical distance above which crescent-moon fragmentation cannot occur,
$R_{c}$
, as a function of the impact
$We$
and at which
$We_{c}=25$
. Below the impacting drop
$We=417$
, crescent-moon fragmentation cannot occur regardless of the radial drop–drop interdistance.
We quantify this process with an expression for the drop–drop impact force of the corona per unit arclength,
$$\begin{eqnarray}f_{c}=\unicode[STIX]{x1D70C}hu^{2},\end{eqnarray}$$
where
$h$
and
$u$
are the thickness and velocity of the corona edge respectively (figure 7
a–c). This force allows us to derive an expression for the impact horizontal Weber number,
$$\begin{eqnarray}We_{c}=\frac{f_{c}}{\unicode[STIX]{x1D70E}}=\frac{\unicode[STIX]{x1D70C}hu^{2}}{\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
By analogy with impacts normal to a surface, we expect
$We_{c}$
of the order of 1–10 or lower not to allow for sufficient force to transform the sessile drop into a sheet, thus restricting the drop–drop impact outcome to a touch-and-flop. Similarly, we expect values of
$We_{c}$
higher than order 10 to enable crescent-moon sheet formation. We test this expectation in the next section.
3.3.2 Quantification of threshold impact force from spatiotemporal corona expansion
Combining top and side analysis of the spatiotemporal corona expansion with detailed calibration of thickness and feature extraction as illustrated in figure 7(a–c) (Wang & Bourouiba Reference Wang and Bourouiba2017), we measured the following: the time evolution of the corona area
$A$
and its radius
$r=\sqrt{A/\unicode[STIX]{x03C0}}$
, its edge radial velocity
$u=\text{d}r/\text{d}t$
and its average thickness
$h$
. The results are shown in figure 7(d–f) for a range of impact
$We$
. From these results, we can deduce the dependence of the horizontal collision Weber number
$We_{c}$
on the corona radius
$R=r/r_{1}$
, as shown in figure 8(a), and compute the threshold corona radius
$r_{c}$
above which
$We_{c}$
is too small to induce crescent-moon sheet formation (figure 8
b). We find that the corresponding threshold value for crescent-moon formation is
$We_{c}=\unicode[STIX]{x1D70C}hu^{2}/\unicode[STIX]{x1D70E}=25$
, associated with a local drop–drop threshold collision force
$f_{c}=1.2~\text{kg}~\text{s}^{-2}$
per unit arclength. It should be noted that
$We_{c}=25$
is consistent with our expectation of a threshold Weber number of the order of 1–10 by analogy with the classical splash of isolated drops upon impact normal to a solid surface (Yarin Reference Yarin2006; Josserand & Thoroddsen Reference Josserand and Thoroddsen2016). However, here, as the drop–drop collision is tangential to a solid surface, we expect more dissipation from tangential surface friction and longitudinal wave propagation in the sessile drop; hence, the critical
$We_{c}=25$
for the tangential on-surface drop–drop collision is slightly higher compared with normal single drop impacts
$We=1{-}10$
. Figure 8(a) also shows that no crescent-moon can occur if
$We$
is too small (
$We<417$
here), regardless of the drop–drop interdistance. In summary, the boundary between crescent-moon and touch-and-flop regimes is for
$$\begin{eqnarray}1<D=R_{c}=0.043(We-417)^{0.58}+1<R_{max},\end{eqnarray}$$
where
$R_{c}=r_{c}/r_{1}$
. This expression when overlaid on the
$D$
–
$We$
regime map of figure 6 is in very good agreement with the data, hence supporting the physical picture of drop–drop impact presented in this section.
4 Crescent-moon: universality of opening angle
To better understand crescent-moon fragmentation, we now turn to the factors governing its features. At impacting drop maximum corona radius
$r_{max}$
, the base of the sheet of the crescent-moon is prescribed by an opening angle
$\unicode[STIX]{x1D703}_{f}$
and is surrounded by two ligaments of length
$l_{l}$
(figure 9
a). The values of
$\unicode[STIX]{x1D703}_{f}$
and
$l_{l}$
can depend on a range of parameters
$d$
,
$r_{1},r_{2},u_{1},r_{max},f_{c}$
of this complex problem (see figures 2 and 9
a).
Figure 9. (a) Overlay of bottom views of the crescent-moon collision, where the opening angle evolves from (4.1) at initial contact between the red corona and the blue sessile drop to (4.3) at maximum corona radius (
$r_{max}$
). The scale bar is 4 mm. The corrugation angle of the corona rim is
$\unicode[STIX]{x1D703}_{c}=(\unicode[STIX]{x1D703}_{f}-\unicode[STIX]{x1D703})/2$
. (b) Comparison between the measured and predicted number of corrugations
$N$
from the literature:
$N=4.1We^{3/8}$
is the scaling from Marmanis & Thoroddsen (Reference Marmanis and Thoroddsen1996) and
$N=1.14We^{1/2}$
is from Mehdizadeh et al. (Reference Mehdizadeh, Chandra and Mostaghimi2004);
$N=3.36We^{3/8}$
is the best fit of the experimental data of the present study. The left inset shows the normalized power spectrum of rim corrugations at the maximum corona radius (right inset) as a function of wavenumber. The wavenumber with the peak of the spectrum gives the number of ligaments
$N$
.
We first elucidate the crescent-moon angle
$\unicode[STIX]{x1D703}_{f}$
via a geometrical relation between the falling drop of size
$r_{1}$
at a distance
$d$
from the sessile drop of size
$r_{2}$
. The view from below in figure 9(a) shows
$\unicode[STIX]{x1D703}$
, the angle between the two tangent lines to the sessile drop (
$r_{2}$
) originating from the centre of the impacting drop at radial distance
$d$
. Simple geometry yields
$$\begin{eqnarray}\unicode[STIX]{x1D703}=2\,\text{arcsin}\left(\frac{r_{2}}{d}\right).\end{eqnarray}$$
The inset to figure 10(a) compares the predicted opening angle
$\unicode[STIX]{x1D703}$
(4.1) and its measurement
$\unicode[STIX]{x1D703}_{f}$
as in figure 9(a). The prediction and observation differ by a systematic bias. We elucidate this bias by closer inspection of the corona of the impacting drop. Prior studies have documented the appearance of corrugations surrounding the expanding coronas of isolated impacting drops on solids, as summarized in table 2. We observe that during corona expansion, the angle
$\unicode[STIX]{x1D703}$
(4.1) defining the base of the crescent-moon sheet is stretched outward (figure 9
a). The fluid accumulated in the flaps surrounding the sessile drop settles and is entrained and absorbed into the two closest corrugations of the corona rim. This process is further discussed in § 5.
Figure 10. (a) The match between prediction (4.1)–(4.3) and measurement of crescent-moon opening angle
$\unicode[STIX]{x1D703}_{f}$
as a function of
$r_{2}/d$
. (b) Robustness of the prediction to increase of sessile drop fluid viscosity and for impact with a solid analogue sessile drop. (c) Bottom views of the crescent-moon with sessile drops of increasing viscosity (left to right) and a solid (rightmost), showing the robustness and universality of
$\unicode[STIX]{x1D703}_{f}$
and the emerging pair of ligaments. The scale bar is 4 mm.
To elucidate the systematic bias of the prediction of the opening angle in figure 10(a inset), we analyse the average angle
$\unicode[STIX]{x1D703}_{c}$
between rim corrugations at maximum corona radius
$r_{max}$
,
$\unicode[STIX]{x1D703}_{c}=2\unicode[STIX]{x03C0}/N$
, where
$N$
is the total number of rim corrugations (figure 9
b). To measure the total number of ligaments systematically, we take the Fourier transform of the rim corrugations, leading to a power spectrum as a function of the wavenumber
$n=2\unicode[STIX]{x03C0}r_{max}/\unicode[STIX]{x1D706}_{n}$
(figure 9
b inset), where
$\unicode[STIX]{x1D706}_{n}$
is the wavelength. We use the dominant mode (wavenumber corresponding to the peak of the spectrum) as the number of ligaments
$N$
. Correction of the prediction (4.1) by the obtained intercorrugation angle
$\unicode[STIX]{x1D703}_{c}=2\unicode[STIX]{x03C0}/N$
leads to figure 10(a). The opening angle predicted,
$\unicode[STIX]{x1D703}+2\unicode[STIX]{x1D703}_{c}$
, and that measured match very well.
In addition, our Fourier analysis shows that the number of rim corrugations
$N$
at maximum corona radius is well captured by
$$\begin{eqnarray}N=C_{N}\,We^{3/8},\end{eqnarray}$$
with
$C_{N}=3.36$
as seen in figure 9(b). Equation (4.2) falls between prior scalings proposed in the literature (§ 1.2 and table 2) and matches the empirical expression proposed by Marmanis & Thoroddsen (Reference Marmanis and Thoroddsen1996) particularly well. We expect
$C_{N}$
to be sensitive to surface roughness, wetting and temperature. The value of
$C_{N}=3.36$
obtained in this paper was, however, robust to the range of contact angles of average wetting of interest herein,
$45^{\circ }\leqslant \unicode[STIX]{x1D703}_{e}\leqslant 82^{\circ }$
(discussed thereafter in figure 12). The value of
$C_{N}=3.36$
is fixed for the remainder of the study.
Hence, we can predict the opening angle of the crescent-moon,
$\unicode[STIX]{x1D703}_{f}$
, completely from the geometric parameters
$d$
and
$r_{2}$
and the dynamic parameter
$We$
as
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{f}=2\,\text{arcsin}\left(\frac{r_{2}}{d}\right)+\frac{4\unicode[STIX]{x03C0}}{C_{N}We^{3/8}},\end{eqnarray}$$
with
$C_{N}=3.36$
fixed, which is robust to change of the impact Weber number, as shown in figure 10(a). To investigate further the robustness of the prediction, we conducted an extensive series of experiments where the sessile drop was changed from inviscid to viscous, to a solid drop-analogue with similar size and geometry to the sessile drop as seen from below in figure 10(c) (see table 4 for the fluids and solids used). We found that the prediction of
$\unicode[STIX]{x1D703}_{f}$
(4.3) is robust to change of sessile fluid properties and is even robust for impacts of expanding coronas on sessile solids, as shown in figure 10(b,c). This robust match confirms that crescent-moon fragmentation is governed by geometry at first order and governed by dynamics, via impacting drop corona destabilization, at second order.
5 Crescent-moon: universality of ligament length
We now turn to the length of the ligaments,
$l_{l}$
(figure 11
a). Upon impact with the sessile drop, the impacting drop corona is obstructed. Close observation reveals that the fluid in the crescent-moon sheet is from the sessile drop, while the fluid in the ligaments surrounding its base is from the impacting drop corona (figures 2
c, 3
c, 9
a and 10
c). We conducted an extensive set of experiments and predicted the length
$l_{l}$
of the two ligaments bounding the crescent-moon (figure 10
c).
Careful observation (e.g. figure 11
a inset) reveals that the fluid of the obstructed corona (pink in figure 11
a) is diverted as it flows out along the sides of the lifted sessile drop (blue in figure 11
a), where the sessile drop and the expanding drop sheet connect. The two regions, or flaps, surrounding the sessile drop (blue shadowed flaps in figure 11
a) are initially formed around the sessile drop sheet suspended in the air (e.g. figure 11
b inset). When the corona sheet reaches maximum radius
$r_{max}$
, the fluid settles down on the surface and flows radially outward in the corona sheet. On reaching and entering the rim, the fluid is reoriented to flow along the rim, reaching and feeding the closest corrugation. The two surrounding rim corrugations of thickness
$w_{c}$
indeed grow into crescent-moon ligaments of length
$l_{l}$
as a result. We report that the thickness of the two ligaments is similar to that of the rim corrugations,
$$\begin{eqnarray}w_{c}=\frac{2\unicode[STIX]{x03C0}r_{max}}{2N}=\frac{\unicode[STIX]{x03C0}r_{max}}{N},\end{eqnarray}$$
as shown in figures 9(a) and 11(b). Based on this physical picture, the resulting volume of fluid expected to be in the two flaps in the air surrounding the crescent-moon sheet should be equal to the volume of the two bounding ligaments.
Figure 11. (a) The impacting drop (dark red) of maximum corona radius
$r_{max}$
(light red) with rim corrugations of width
$w_{c}$
is shown with a sessile drop (blue) of radius
$r_{2}$
at distance
$d$
and the crescent-moon pair of cylindrical ligaments of length
$l_{l}$
and width
$w_{c}$
. The fluid in the flaps surrounding the crescent-moon sheet (blue shadow region) is originally lifted up. (b) Impact of an expanding corona on a sessile drop (upper panel) and a solid drop-analogue (lower panel). At corona radius
$r_{max}$
, the fluid in the flaps settles and feeds the pair of ligaments. The scale bar is 4 mm.
Figure 12. (a) Side view of a sessile drop on a solid surface. A circle is fitted to the drop. The contact angle is measured on both sides and averaged such that
$\unicode[STIX]{x1D703}_{e}=\arctan (r_{2}/h_{c})$
, where
$r_{2}$
is the radius of the base of the sessile drop and
$h_{c}$
is the distance between the surface plane and the centre of the circle. (b) The contour of the sessile drop in (a) detected using an image processing algorithm. (c) The agreement between our prediction of ligament length (5.8) at maximum corona radius and our experimental data.
From geometry (figure 11 a shadowed blue regions), the volume of fluid in the flaps surrounding the crescent-moon sheet is
$$\begin{eqnarray}V_{s}=A_{s}h,\end{eqnarray}$$
where
$h$
is the average thickness of the corona at maximum radius and
$A_{s}$
is the area of the flaps, which can be expressed by
$$\begin{eqnarray}A_{s}\approx (r_{max}-d)r_{max}\sin \left(\frac{\unicode[STIX]{x1D703}_{f}-\unicode[STIX]{x1D703}}{2}\right).\end{eqnarray}$$
At maximum corona radius
$r_{max}$
, the average corona thickness is
$$\begin{eqnarray}h=V/\unicode[STIX]{x03C0}r_{max}^{2}=\frac{4}{3}r_{1}^{3}/r_{max}^{2},\end{eqnarray}$$
with
$V=(4/3)\unicode[STIX]{x03C0}r_{1}^{3}$
the initial impacting drop volume.
The volume of the ligaments (figure 11 a) is
$$\begin{eqnarray}V_{f}=2A_{f}l_{l},\end{eqnarray}$$
with cross-sectional area
$A_{f}=C_{s}w_{c}^{2}$
, by assuming their shape to be semicylindrical of width
$w_{c}$
, as shown in figure 11(a). The geometrical coefficient
$C_{s}$
can be expressed as
$$\begin{eqnarray}C_{s}={\textstyle \frac{1}{4}}(\unicode[STIX]{x1D703}_{e}\csc ^{2}\unicode[STIX]{x1D703}_{e}-\cot \unicode[STIX]{x1D703}_{e}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D703}_{e}$
is the equilibrium contact angle of the fluid on the surface. We measured the contact angle using image processing on the two sides of the sessile drops as shown in figure 12(a,b). Our measurements give a mean contact angle of
$\unicode[STIX]{x1D703}_{e}=60^{\circ }$
, and thus
$C_{s}=0.2047$
, with a maximum angle of
$82^{\circ }$
and a minimum angle of
$45^{\circ }$
.
By equating the volume of the flaps
$V_{s}$
to the volume of the ligaments
$V_{l}$
, we obtain a prediction for the length of the ligaments as
$$\begin{eqnarray}\frac{l_{l}}{r_{max}}=\frac{2}{3C_{s}}\left(\frac{N}{\unicode[STIX]{x03C0}}\right)^{2}\left(\frac{r_{1}}{r_{max}}\right)^{3}\left(1-\frac{d}{r_{max}}\right)\sin \left[\frac{\unicode[STIX]{x1D703}_{f}-\unicode[STIX]{x1D703}}{2}\right].\end{eqnarray}$$
It should be recalled that we have already determined and fixed the constants associated with the dimensionless maximum corona radius
$R_{max}=r_{max}/r_{1}$
in (3.3) (figure 5) and the number of corrugations,
$N$
, of the corona at its maximum radius
$R_{max}$
in (4.2) (figure 9
b and § 4). By leveraging these prior findings, the ligament length predicted is
$$\begin{eqnarray}\frac{l_{l}}{r_{max}}=C_{L}We^{1/4}\left(1-\frac{d}{r_{max}}\right)\sin \left[\frac{\unicode[STIX]{x1D703}_{f}-\unicode[STIX]{x1D703}}{2}\right]\end{eqnarray}$$
or
$$\begin{eqnarray}\frac{l_{l}}{r_{1}}=C_{R}C_{L}We^{5/12}\left(1-\frac{d}{r_{1}C_{R}}We^{-1/6}\right)\sin \left[\underbrace{\frac{2\unicode[STIX]{x03C0}}{C_{N}}}_{{\approx}2}We^{-3/8}\right],\end{eqnarray}$$
in terms of initial impact parameters. The constants are interdependent, with
$$\begin{eqnarray}C_{L}=\frac{2}{3\unicode[STIX]{x03C0}^{2}C_{s}}\left(\frac{C_{N}^{2}}{C_{R}^{3}}\right),\end{eqnarray}$$
where all constants are fixed by our prior measurements (no free parameter) and given by (5.6), (3.3) and (4.2) with
$C_{L}=0.69$
for
$C_{s}=0.2047$
,
$C_{R}=1.75$
and
$C_{N}=3.36$
. Figure 12(c) shows the very good agreement between our prediction (5.8) and our experimental measurements. The dashed lines show the prediction of the length of ligaments corresponding to the minimum and maximum values of contact angle measured (figure 12
a,b). Our data fall within our range of prediction (5.8).
Interestingly, the size of the sessile drop,
$r_{2}$
, does not prescribe the length of the crescent-moon ligaments. Returning to the schematic in figure 11(a), one can see that, regardless of
$r_{2}$
, the flap regions of corona fluid forming the ligaments are indeed independent of
$r_{2}$
. They depend directly on the corona extension
$r_{max}$
(fixed by
$r_{1}$
and impact
$We$
), its corrugation wavelength
$\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}r_{max}/N$
and the interdrop distance
$d$
. Prediction (5.8) is robust to increase of sessile drop viscosity up to approximately 30 times that of water (figures 12
c and 10
c). The lengths of the ligaments for impacts on solid sessile objects and sessile drops of viscosity 1400 times that of water (i.e. pure glycerol) differ however. This is expected given that (5.8) is based on the key observation that the ligaments are formed of the fluid of the lifted flaps surrounding the deformed sessile drop (figure 11
a,b). The lift of the sessile drop and formation of flaps continues to be the dominant feature of the crescent-moon regime for sessile drop viscosities of up to 30 times that of water (mixtures 1 and 2 in figure 10
c and table 4), but can no longer occur for pure glycerol and rigid objects. In addition, one of the underlying assumptions of our model is that both interacting drops have comparable sizes (as found in sprays and rainfalls), and both are assumed to be of the order of or smaller than the capillary length. By construction, equation (5.9) is established for the crescent-moon
$We$
–
$D$
regime (figure 6). Finally, one last underlying assumption is that the corona corrugation wavelength is smaller than the typical sessile drop size considered:
$\unicode[STIX]{x1D706}<r_{2}$
. This last assumption is clearly always true for the water drops of interest for sprays and rainfalls motivating the present study.
6 Conclusion
Drop impacts on surfaces are ubiquitous in agriculture, coating and pathogen transport. Most extensive research on drop impacts has focused on idealized superhydrophobic or fully wetting surfaces. Despite the ubiquity of surfaces of intermediate wetting (not fully wetting or superhydrophobic) in nature, indoors and in industry, little is understood about the physics of impacts on them. Combining experiments and modelling, we show that such surfaces, which support sessile drops, lead to dramatically different regimes of coating and splash from those inferred from isolated impacts. We showed that four regimes of drop–drop interaction emerge: head-on collision, crescent-moon fragmentation, touch-and-flop collision and no collision (figures 3 and 6). These regimes include novel fragmentation phenomena only recently identified as ubiquitous in impacts on plant surfaces (Gilet & Bourouiba Reference Gilet and Bourouiba2015), such as the crescent-moon fragmentation. Herein, we have predicted the transitions between these four regimes accurately based on two dimensionless parameters: the impacting drop Weber number and the normalized interdistance between the two drops (figure 6). We have shown that a critical drop–drop impact force governs the existence and physics of the crescent-moon fragmentation and that this force is shaped by a subtle combination of geometry and momentum transfer. We introduced a horizontal critical collision Weber number
$We_{c}$
below which crescent-moon fragmentation cannot occur. The horizontal critical collision Weber number
$We_{c}$
is defined based on the force per unit length upon collision of the rim of the expanding corona onto the sessile drop. Below
$We_{c}=25$
, the momentum imparted to the sessile drop is not sufficient to transform its bulk into an expanding sheet characteristic of a crescent-moon. Using the geometric constraint of the drop–drop interaction and volume conservation, we also predicted and validated the models governing two peculiar features of crescent-moon fragmentation: the width of the base of its expanding sheet in the air and the length of the pair of ligaments surrounding its base. We showed that the predictions of these two properties are robust to a wide range of surface average wettings and sessile drop fluid viscosities. Prediction of these properties is important for the study of crescent-moon fragmentation, which is a highly efficient producer of secondary droplets.
Our findings bring a fundamental understanding to a ubiquitous, yet so far neglected, drop–drop interaction physical phenomena. Our results suggest a new paradigm: impacts on most surfaces can make a splash of a new kind – a crescent-moon – for any impact velocity when neighbouring sessile drops are present. Hence, interactions between sessile and impacting drops of comparable sizes can alter the washing and coating of surfaces significantly, while increasing spray drift or rain-induced pathogen transmission from contaminated surfaces in agriculture. Elucidation of the final stages of drop–drop impact fragmentation in this agricultural context is our current focus.
Acknowledgements
This research was partially supported by NSF CBET-1546990 and the USDA-NIFA Specialty Crop Research Initiative Grant Award No. MDW-2016-04938. Y.W. is grateful for the partial support of the MIT J. S. Hennessy ODGE Fellowship.
