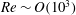1. Introduction
It has been reported that the perturbation by rising bubbles substantially modulates the hydrodynamic properties (e.g. turbulence) of the liquid phase in gas–liquid flows (Rensen, Luther & Lohse Reference Rensen, Luther and Lohse2005; Balachandar & Eaton Reference Balachandar and Eaton2010; Hosokawa & Tomiyama Reference Hosokawa and Tomiyama2013), if the ratio of bubble size to the integral length scale of the liquid phase is larger than
${\sim}0.1$
(Gore & Crowe Reference Gore and Crowe1989). Therefore, in various engineering systems (e.g. power plants, bioreactors, mineral processing, waste water treatment and air-lift systems) which involve the transport of mass, momentum and heat between two phases, the accurate evaluation of bubble motion and the subsequent gas void-fraction distribution are very important.
So far, the rise of a bubble driven by buoyancy in a still liquid has been investigated mainly for an unbounded configuration. Despite its simple appearance, interestingly the shape and trajectory of a bubble show quite complex trends depending on the relative dominance among inertia, viscosity and surface tension, and also the contamination of the bubble surface (Clift, Grace & Weber Reference Clift, Grace and Weber1978; Magnaudet & Eames Reference Magnaudet and Eames2000). In clean water, a small bubble whose diameter is less than
${\sim}1.3~\text{mm}$
tends to retain a spherical shape and to follow a simple rectilinear trajectory. As the bubble size increases, however, its shape changes to an oblate ellipsoid and it follows a plane zigzag and/or three-dimensional helical path. This so-called path instability is attributed to the asymmetry of the vortical structures in the wake (i.e. wake instability) caused by the excess vorticity accumulated on the bubble surface (Ellingsen & Risso Reference Ellingsen and Risso2001; Mougin & Magnaudet Reference Mougin and Magnaudet2002, Reference Mougin and Magnaudet2006; Yang & Prosperetti Reference Yang and Prosperetti2007; Zenit & Magnaudet Reference Zenit and Magnaudet2008; Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012).
In many practical situations, on the other hand, the rising bubbles encounter solid boundaries (e.g. vertical walls). Without concerning their hydrodynamics in detail, early works focused on the retarding of the rise velocity of the bubble due to the wall (Uno & Kinter Reference Uno and Kinter1956; Krishna et al. Reference Krishna, Urseanu, van Baten and Ellenberger1999). However, it is well known that the wall effect, combined with the wake instability, may cause a more complex path instability for the rising bubbles. For example, de Vries (Reference de Vries2001) observed that a bubble slides or bounces a few times on a wall depending on the bubble size and the initial distance between the bubble and wall.
Previous studies successfully explained the mechanism of repulsive and attractive lift (i.e. wall-normal) forces which cause different near-wall movements of a spherical bubble rising at very small Reynolds numbers of
$\mathit{O}({\leqslant}10)$
; otherwise it would rise in a straight line without the wall. When the Reynolds number (
$\mathit{Re}$
), based on the rise velocity and the equivalent bubble diameter, is small (
${\lesssim}30$
) so that the viscous effects are dominant, the rising bubble migrates away from the wall due to the repulsive lift caused by strong diffusion of the vorticity in the interaction between the wall and bubble wake (Takemura et al.
Reference Takemura, Takagi, Magnaudet and Matsumoto2002; Takemura & Magnaudet Reference Takemura and Magnaudet2003). As
$\mathit{Re}$
increases, however, the vorticity generated remains confined in a thin boundary layer on the bubble surface and instead a finite liquid velocity is induced between the bubble and the wall. The wall-normal pressure gradient due to this velocity distribution around the bubble (which is well-predicted by the potential flow theory) causes the bubble to be attracted toward the wall (Takemura & Magnaudet Reference Takemura and Magnaudet2003). When the gap between the bubble and the wall becomes much narrower because of this attraction, on the other hand, the sign of lift force is reversed due to the effect of viscosity in the thin liquid layer between the bubble and the wall (lubrication theory), and the rising bubble bounces off the wall (Takemura & Magnaudet Reference Takemura and Magnaudet2003; Sugiyama & Takemura Reference Sugiyama and Takemura2010).
For high-
$\mathit{Re}$
(and high Weber number,
$\mathit{We}$
) bubbles, the circumstances are more complex due to the shape instability (i.e. deformation) (Magnaudet & Eames Reference Magnaudet and Eames2000). Moctezuma, Lima-Ochoterena & Zenit (Reference Moctezuma, Lima-Ochoterena and Zenit2005) modelled the bouncing motion of a spherical bubble near a vertical wall in still water using the potential flow theory, representing the case of high
$\mathit{Re}$
and low
$\mathit{We}$
, and pointed out the importance of effects of viscosity in predicting the bubble’s bouncing behaviour accurately. Zaruba et al. (Reference Zaruba, Lucasa, Prasser and Höhne2007) constructed the equation of motion for a rising bubble (
$\mathit{Re}=220{-}1000$
) near a vertical wall, under an upward shear, by considering associated force components acting on the bubble. They predicted the changes in the bubble’s bouncing motion with varying liquid velocity, and hypothesized that at a low liquid velocity, the bubble obtains additional energy from the shape oscillation to compensate the damping effect during bubble–wall collisions and maintains the bouncing amplitude almost constant. Figueroa-Espinoza, Zenit & Legendre (Reference Figueroa-Espinoza, Zenit and Legendre2008) also found that at
$\mathit{Re}>100$
, the strong wall effect imposes a transition between attractive and repulsive lift forces on a rising bubble in a confined (by two closely spaced sidewalls) condition, which triggers a path instability at lower
$\mathit{Re}~({\sim}70)$
than that
$({\sim}660)$
(Duineveld Reference Duineveld1995) of a freely rising bubble in pure water.
On the other hand, the changes in the bubble–wall collision dynamics with wall boundary condition have been tested for the normal bouncing on a horizontal top-wall (Krasowska & Malysa Reference Krasowska and Malysa2007; Zawala et al. Reference Zawala, Krasowska, Dabros and Malysa2007). In these studies, the rising bubble was originally spherical and deformed only when it collided with the horizontal wall. Krasowska & Malysa (Reference Krasowska and Malysa2007) reported that air pockets trapped on a slippery wall cause the approaching bubble to attach on the wall after a smaller number of bounces than on a no-slip wall. Zawala et al. (Reference Zawala, Krasowska, Dabros and Malysa2007) estimated the transfer of kinetic energy to surface energy during those collisions. In the case of a hydrophobic surface, the energy transfer was small (i.e. large energy loss) such that the approaching bubble attaches to the wall, but the bubble stayed under the hydrophilic wall after multiple collisions where the energy transfer is larger (i.e. smaller loss of energy). For the normal bubble collision, an interesting analysis was given by Zenit & Legendre (Reference Zenit and Legendre2009) who investigated the ratio of the wall-normal velocities of the bubble after and before the impact, as an indirect measure of energy dissipation, resulting from the bubble–wall collision. They found that the process of normal collision is well characterized by the modified Stokes number (where the added-mass effect is considered as well) and the capillary number, which is different from the collision of solid particles.
Despite these previous intensive efforts, more investigations on the near-wall dynamics of a rising bubble are still necessary. First, most previous studies on the interaction between a rising bubble and a vertical wall focused on a spherical bubble (whose Reynolds and Weber numbers ranged from small to moderate), thus the reference bubble trajectory (without the wall) is considered to be straight and the shape deformation is negligible (or mild). Thus it is necessary to study the wall-induced path variation on a large deformable bubble further. In addition, a systematic investigation on the effect of initial distance between the bubble and the wall would be informative. Second, previous studies have considered walls with a conventional no-slip boundary condition, and the effects of having a different material (i.e. different boundary condition) on the movement of rising bubbles have not been studied.
Therefore, in the present study, the path of a single bubble rising near a vertical wall is experimentally investigated in a quiescent water tank. We specifically consider the rise of a large deformable bubble, i.e. the reference bubble (without the wall) already has its own path (two-dimensional zigzag path) and shape instabilities, and systematically vary the initial distance between the bubble and the wall. The considered
$\mathit{Re}$
and
$\mathit{We}$
are high enough for the bubble to become an oblate ellipsoid and deform as well. Four different types of wall are considered to change the boundary condition at the surface, such as a no-slip, porous and hydrophobic ones. The initial distance between the bubble centre and the wall is also varied for each wall. This approach will help the understanding of wall-induced path instability for a high-
$\mathit{Re}$
and high-
$\mathit{We}$
(large and deformable) bubble, and furthermore the predicting or controlling of the near-wall void fraction distribution in gas–liquid flow systems. Also, we hope that the current results can be extended to a wide range of applications such as power conversion systems, cavitating flows, waste water treatment, oil extraction, mineral processing, froth flotation, and reactors. In these systems, commonly, (i) the consequence of bubble–wall collision or the underlying dynamics is very important in assessing their performance and (ii) complex mass transfer between agents is important.
2. Experimental set-up and procedures
2.1. Single bubble rising in quiescent water
The experimental set-up is composed of a water tank, a high-speed camera (Troubleshooter, Fastec Imaging Co.) and a halogen lamp to facilitate high-speed shadowgraph imaging (figure 1
a). The water tank is an acrylic cube container (
$500\times 500\times 500~\text{mm}^{3}$
) with a stainless steel nozzle (inner diameter of 0.8 mm) located at the centre of the bottom. A bubble, generated from compressed air through the nozzle, rises due to buoyancy in quiescent water. The size of the bubble and the frequency of bubble generation are controlled by a pressure regulator and a solenoid valve. The container is fully filled up with tap water to minimize the free-surface effect on the bubble motion.
Figure 1. (a) Experimental set-up for a single bubble rising near a vertical wall in a stagnant water tank. (b) Reference zigzag motion of a freely rising bubble at
$\mathit{Re}\simeq 1100$
. (c) Modelling of a periodically bouncing bubble’s trajectory with a sinusoidal function and definitions of bubble geometry.
We fix the bubble Reynolds number as
$\mathit{Re}=Ud_{eq}{\it\nu}^{-1}\simeq 1100$
based on the equivalent diameter (
$d_{eq}$
) and the mean rise velocity (
$U=0.284~\text{m}~\text{s}^{-1}$
) of a freely rising (i.e. without the wall) bubble (
${\it\nu}$
is the kinematic viscosity of water). Corresponding Weber and Eötvös numbers are
$\mathit{We}={\it\rho}_{l}U^{2}d_{eq}{\it\sigma}^{-1}\simeq 4.4$
and
$\mathit{Eo}=g({\it\rho}_{l}-{\it\rho}_{g})d_{eq}^{2}{\it\sigma}^{-1}\simeq 2.1$
, respectively, which are higher than those considered in previous studies. Here,
${\it\rho}_{l}$
and
${\it\sigma}$
are the density and surface tension of water, respectively,
$g$
is the gravitational acceleration, and
${\it\rho}_{g}$
is the density of air. The equivalent diameter is estimated from the projected shape as
$d_{eq}=(d_{h}^{2}d_{v})^{1/3}\simeq 3.92~\text{mm}$
, where
$d_{h}$
and
$d_{v}$
are the length of horizontal (major) and vertical (minor) axes of an oblate ellipsoidal bubble, respectively (see figure 1
c). The typical wobbling shape of the bubble (see figures 1
b and 3) in the present set-up is in a good agreement with the classification of the bubble shape depending on
$\mathit{Re}$
and
$\mathit{Eo}$
, proposed by Clift et al. (Reference Clift, Grace and Weber1978). Note that the present wobbling bubble shape is approximated as an oblate ellipsoid and its geometric variables are calculated accordingly, as done by many previous studies (Zaruba et al.
Reference Zaruba, Lucasa, Prasser and Höhne2007; Zenit & Magnaudet Reference Zenit and Magnaudet2008; Cano-Lozano, Bohorquez & Martínez-Bazán Reference Cano-Lozano, Bohorquez and Martínez-Bazán2013). On the other hand, for the present
$d_{eq}$
and
$\mathit{Re}$
, it is known that a freely rising bubble follows an in-plane zigzag oscillation (Clift et al.
Reference Clift, Grace and Weber1978; Ellingsen & Risso Reference Ellingsen and Risso2001; Zenit & Magnaudet Reference Zenit and Magnaudet2008), which we also confirmed (figure 1
b).
In air–water two-phase flows where the surface tension is relatively high, surfactants (i.e. bubble surface contamination) may cause a drastic change in the hydrodynamics of the flow (Clift et al. Reference Clift, Grace and Weber1978; Cuenot, Magnaudet & Spennato Reference Cuenot, Magnaudet and Spennato1997; Magnaudet & Eames Reference Magnaudet and Eames2000; Takagi & Matsumoto Reference Takagi and Matsumoto2010). As understood by the Marangoni effect due to the localized contamination of bubble surface, the effects of surfactants on the motion of a single bubble are summarized as (i) the reduction of the rise velocity (increase of drag) and (ii) the change in the lateral migration (decrease of lift) in the presence of liquid shear (Takagi & Matsumoto Reference Takagi and Matsumoto2010). Since the surrounding water is stationary in the present set-up, the effect of surface contamination may be indirectly examined through the bubble’s rise velocity. We compared the rise velocity of the current bubble with the empirical estimation by Clift et al. (Reference Clift, Grace and Weber1978) and confirmed that the current condition is close to that of a clean bubble.
On the other hand, the time that the bubble has travelled in the liquid (Bachhuber & Sanford Reference Bachhuber and Sanford1974) and the bubble size (Duineveld Reference Duineveld1994) are also important factors to determine the effect of surface contamination. According to them, if a bubble diameter is large enough (
${\gtrsim}2.5~\text{mm}$
) and the experiment duration is not too long, the behaviour of bubbles rising in tap water can be approximated as that in pure water. Currently, we think that the bubble motion was not filmed for a long enough time for the surfactants to have a great influence. In the present study, no special care was taken to maintain the bubble surface super-clean (but the tap water was replaced for each data set); however, based on the above reasoning, we may say that the surface of the present bubble is not fully immobilized.
2.2. Characterization of different types of wall
To establish the wall effect on the dynamics of a rising bubble in detail, we consider two parameters: (i) the distance (
$s$
) between the wall and the centre of nozzle exit (i.e. the initial distance between the bubble centre and the wall) and (ii) the wall boundary condition. The normalized initial distance (
$s^{\ast }=s/r_{eq}$
, where
$r_{eq}=0.5d_{eq}$
) is varied from 0.26 to 4.08. As material for the wall, we consider an acrylic, a polyurethane sponge, polytetrafluoroethylene (PTFE) and roughened PTFE to obtain the wall boundary condition as no-slip, porous, hydrophobic and enhanced hydrophobic, respectively. The porous characteristics and its applications in flow control of a regular polyurethane sponge (foam) have been well documented previously (Saleh, Thovert & Adler Reference Saleh, Thovert and Adler1993; Manes, Poggi & Ridolfi Reference Manes, Poggi and Ridolfi2011). As a hydrophobic surface, we use a Teflon® which is a commercially available patented PTFE. It is well known that the addition of roughness enhances the hydrophobicity of the surface (Cassie & Baxter Reference Cassie and Baxter1944). The so-called Cassie–Baxter model states that, in the de-wetted (or fakir) state, the surface roughness makes the surface appear more hydrophobic (i.e. the apparent contact angle (CA) is larger than the intrinsic CA of the surface). We modified the surface of a regular Teflon plate with an abrasive paper (grit No. 80) and achieved an increase of the apparent CA of a water droplet from 95° to 120° (figure 2). Achievement of enhanced hydrophobicity by this simple manipulation of a Teflon® surface has been proposed by Nilsson, Daniello & Rothstein (Reference Nilsson, Daniello and Rothstein2010). Figure 2 shows scanning electron microscopy (SEM) images of the considered sponge and PTFE walls, and the shape of a water droplet on them to measure the static CA. For the PTFE walls, the root-mean-square size of the roughness is calculated to be
${\sim}3.7~{\rm\mu}\text{m}$
and
${\sim}42~{\rm\mu}\text{m}$
for the regular and roughened surface, respectively, based on cross-sectional SEM images.
Figure 2. SEM images (
$100\times$
) (top) and measurement of the contact angle (CA) of a water droplet (bottom) for three of the wall types considered: (a) polyurethane sponge; (b) regular PTFE; (c) roughened PTFE.
Figure 3. Variations in the trajectories (in the
$x{-}y$
plane) of a rising bubble with
$s^{\ast }$
near a vertical wall of (a) acrylic, (b) polyurethane sponge, (c) PTFE and (d) roughened PTFE. The time interval between adjacent bubbles is 10 ms (i.e. 100 f.p.s.), being reduced from the raw 500 f.p.s. videos. The insets next to the first column of (c) and (d) show a close-up view of the sliding bubble shape.
Figure 4. Variations in the trajectories (in the
$x{-}z$
plane) of a rising bubble with
$s^{\ast }$
near the acrylic wall at (a)
$90\lesssim x^{\ast }\lesssim 165$
; (b)
$10\lesssim x^{\ast }\lesssim 80$
. The time interval between adjacent bubbles is 10 ms (i.e. 100 f.p.s.), being reduced from the raw 500 f.p.s. videos. Clearly, the oscillation in the
$x{-}z$
plane is much smaller that in the
$x{-}y$
plane.
2.3. Image capture and data processing
In the present study, the shadowgraph images (induced by a halogen lamp) of a rising bubble in the
$x{-}y$
plane (figure 1) are captured by a high-speed camera (
$640~\text{pixel}\times 480~\text{pixel}$
) at 500 f.p.s. The spatial resolution of the camera is set to be about
$280~{\rm\mu}\text{m pixel}^{-1}$
so that the field of view (FoV) has a size of
$177~\text{mm}\times 133~\text{mm}$
(which is equivalent to about
$70r_{eq}$
in the vertical (
$x$
) direction), positioned at 20 mm above the nozzle exit. The location of the measurement plane was determined to be near the nozzle to exclude the possibility of having a transition from a zigzag to a helical path due to external perturbations, if any.
To analyse the shape and motion of a rising bubble qualitatively, we processed sequential shadow images of the bubble using the method introduced by Bröder & Sommerfeld (Reference Bröder and Sommerfeld2007). First, we set the optimal threshold of the grey value to distinguish the bubble from the background by which the raw images are binarized. Then we apply the Sobel filter which evaluates the grey-value gradient on each pixel to detect the edge of the bubble. Based on the detected contour of the bubble, we pick a number of points on the bubble edge with a uniform spacing. Connecting each point on the edge to a certain point inside the bubble (i.e. a guessed bubble centre), the bubble can be divided into several segments. As a result, the actual bubble centre is determined by calculating the centre of gravity on each segment. The trajectory of the bubble is tracked based on the bubble centre at each instant and the bubble shape deformation is indirectly evaluated by calculating the aspect ratio,
${\it\chi}=d_{h}/d_{v}$
(figure 1
c).
On the other hand, for the case of a periodically rebounding bubble which was observed to collide against the wall 1–4 times within the considered FoV, its trajectory is fitted with a harmonic function (figure 1
c), where
$h$
,
${\it\lambda}$
and
$r$
are the amplitude, wavelength and wall-normal shift of the periodic bouncing, respectively. The sinusoidal modelling of a periodic rebounding motion of a bubble has been also adopted by Takemura & Magnaudet (Reference Takemura and Magnaudet2003) and Figueroa-Espinoza et al. (Reference Figueroa-Espinoza, Zenit and Legendre2008).
3. Results and discussion
Shown in figure 3 are representative trajectories of a rising bubble in the
$x{-}y$
plane with increasing
$s^{\ast }$
for each considered wall type. We measured the bubble’s trajectory more than 10 times for each case and the repeatability error is within 5 % in terms of the rise velocity. To check the two-dimensionality of the bubble motion, maintaining the same conditions such as
$r_{eq}$
and
$s^{\ast }$
, the shadow images (trajectories) of a rising bubble were taken in the
$x{-}z$
plane (i.e. out-of-plane movement) for the acrylic wall (figure 4). Due to the limited accessibility of the high-speed camera, the trajectories in figure 4 were not taken at the same instants as those in figure 3. However, it is adequate to check the two- or three-dimensionality of the measured trajectories. As shown in the figure, it is clear that the bubble motion in the
$x{-}z$
plane is almost straight for the considered
$s^{\ast }$
values, even after a collision against the wall (highlighted with dashed-line boxes at
$s^{\ast }=0.26$
), and shows a slight oscillation at large
$s^{\ast }$
(figure 4
b). This is interesting because the vertical wall could encourage the instability of the bubble path to evolve into the three-dimensional one, but this did not occur. As introduced above, the path instability of a rising bubble is a direct consequence of the vortex dynamics in the bubble wake (i.e. wake instability) (Zenit & Magnaudet Reference Zenit and Magnaudet2008). Therefore, it is conceivable that the collision against the wall does not produce three-dimensional vortical structures in the bubble wake. The modification of flow structures due to the presence of the wall (known as a ground effect) has been investigated for various geometries. For the wake behind a sphere (similar to the present bubble), it has been reported that the vortical structures are stabilized (i.e. wake instability is not triggered) in the close vicinity of the wall, both at low (Lee Reference Lee2012) and high (Tsutsui Reference Tsutsui2008) Reynolds numbers. Similar stabilization of the wake structure has been reported for the flow behind a two-dimensional circular cylinder located very close to the wall (Bearman & Zdravkovich Reference Bearman and Zdravkovich1978; Huang & Sung Reference Huang and Sung2007). Thus, we may attribute the two-dimensional bubble motion even in the vicinity of the wall to the stabilizing effect of the wall, which should be confirmed through the detailed measurement of the liquid velocity field between the bubble and the wall in the future. Thus, in the present set-up, it is understood that the out-of-plane movement of the bubble is negligibly small compared to the in-plane movement, i.e. two-dimensional. By moving the camera vertically, it is also confirmed that the same behaviours of the bubbles are retained at
$90\lesssim x^{\ast }\lesssim 165$
(figure 4
a), above the original location of measurement (
$0\lesssim x^{\ast }\lesssim 70$
) (figure 4
b). Although it was not possible to observe the bubble motions in the
$x{-}z$
plane for other types of wall material due to their opacity, we think that the two-dimensionality of the bubble motion is still valid for them.
Based on the data in figure 3, it is found that the effect of different wall materials on the bubble motion is significant at
$s^{\ast }\lesssim 2.0$
and becomes less at
$s^{\ast }>2.0$
. Thus, we start by analysing the near-wall rising motions in these regimes separately.
3.1. Near-wall rising behaviour of a large deformable bubble at
$s^{\ast }\lesssim 2.0$
3.1.1. Rebounding bubbles
At
$s^{\ast }\lesssim 2.0$
, a rising bubble near the acrylic and polyurethane sponge walls shows periodic or non-periodic rebounding motions (figure 3
a,b). The periodic bouncing motions are nicely fitted with a sinusoidal function (selected examples are plotted in figure 5
a) and the variations of corresponding parameters (amplitude and wavelength) are plotted in figure 5(b,c). The cases of non-periodic bouncing were not plotted. In addition to the visual confirmation, we used the value of
$r/r_{eq}$
to determine whether the bubble actually collides with the wall or not; that is,
$r/r_{eq}<1.0$
for all the cases shown in figure 5(b,c), and the same criterion has been used by Takemura & Magnaudet (Reference Takemura and Magnaudet2003).
Figure 5. (a) Measured trace (symbols) of a bubble (selected from figure 2) and corresponding curve fit (lines): ○, ——, acrylic at
$s^{\ast }=0.26$
; ♦, – ⋅ – ⋅ –, polyurethane sponge at 0.26; ▵, - - - -, PTFE at 1.53; ▪,
$\cdots \cdots$
, roughened PTFE at 2.04. Variations of the (b) normalized amplitude (
$h^{\ast }$
) and (c) wavelength (
${\it\lambda}$
) with
$s^{\ast }$
are plotted for acrylic (○), sponge (♦), PTFE (▵) and roughened PTFE (▪) walls. In (b) and (c), dashed lines denote
$h^{\ast }$
and
${\it\lambda}$
of a freely rising bubble (i.e. without the wall) at the same
$\mathit{Re}$
and
$\mathit{We}$
. Here, superscript
$\ast$
denotes normalization by the equivalent bubble radius (
$r_{eq}$
).
For the acrylic wall (having a conventional no-slip boundary condition at the surface), the rising bubble bounces off the wall repeatedly at
$s^{\ast }\leqslant 2.04$
(figure 3
a). Among them, the example (
$s^{\ast }=0.26$
) of periodic bouncing motion (
$0.26\leqslant s^{\ast }\leqslant 1.53$
) is shown to be nicely fitted with a sinusoidal function in figure 5(a). Except in the close vicinity of the wall (i.e.
$s^{\ast }=0.26$
), the non-dimensional amplitude (
$h^{\ast }=h/r_{eq}$
) of the periodic bouncing is maintained roughly the same at
$s^{\ast }\leqslant 1.53$
(figure 5
b). On the other hand, the wavelength (
${\it\lambda}$
) tends to increase with increasing
$s^{\ast }$
(figure 5
c). It is noted that the bubble still bounces on the acrylic wall at
$s^{\ast }=2.04$
, but its trajectory oscillates non-periodically.
Figure 3(b) shows the case of arising bubble near a polyurethane sponge wall. Similar to the case of the acrylic wall, when
$s^{\ast }\leqslant 0.51$
the rising bubble bounces repeatedly off the wall with an approximately constant
$h^{\ast }$
and
${\it\lambda}$
which are smaller than those for the acrylic wall at the same
$s^{\ast }$
value (figure 5
b,c). Functionally, the effective boundary condition on a porous wall, such as the present polyurethane sponge, felt by the fluid flow over it, has been modelled as a slip velocity in a tangential direction (Beavers & Joseph Reference Beavers and Joseph1967; Hahn, Je & Choi Reference Hahn, Je and Choi2002; Gangloff, Hwang & Advani Reference Gangloff, Hwang and Advani2014), and has been also validated through a direct simulation using a continuum approach (Breugem, Boersma & Uittenbogaard Reference Breugem, Boersma and Uittenbogaard2006) and experimental measurement (Manes et al.
Reference Manes, Poggi and Ridolfi2011). On the other hand, according to Gangloff et al. (Reference Gangloff, Hwang and Advani2014), the tangential slip boundary condition is only valid when the bubble is separated sufficiently from the wall, because seepage (i.e. non-zero wall-normal velocity) into the wall may happen as the bubble approaches the wall. Since the surrounding water is static and the fluid flow over the porous wall is solely induced by the bubble motion in the present set-up, the effective boundary condition on the sponge wall is hypothesized as the combination of tangential slip (when the bubble is away from the wall) and non-zero wall-normal velocity (when the bubble is approaching the wall). Therefore, at the same
$s^{\ast }$
value, the smaller amplitude and wavelength of bouncing motion on the polyurethane sponge wall than on the acrylic wall is thought to be caused by the interaction between the non-zero water velocity (induced at the wall) and the bubble wake.
In this regime of
$s^{\ast }\;({\lesssim}2.0)$
, considering that the reference bubble trajectory is a two-dimensional zigzag, it is interesting to see that the existence of a vertical wall (with no-slip and porous boundary conditions) does not drastically change the bubble motion, such as the transition to a three-dimensional helical motion; instead, only the amplitude and wavelength of lateral oscillation are affected while elastic rebounding motion occurs. Further discussion on the effects of wall boundary conditions on the bubble motion, in terms of energy components, will be provided in § 3.5.
3.1.2. Sliding bubbles
When the wall has hydrophobicity (figure 3
c), interestingly, the rising bubble slides on the wall, at small
$s^{\ast }\;({\leqslant}0.51)$
, while being slanted slightly. Previously, de Vries (Reference de Vries2001) and Zaruba et al. (Reference Zaruba, Lucasa, Prasser and Höhne2007) observed that a spherical rising bubble (
$d_{eq}<1~\text{mm}$
), smaller than the current one, also slides on the wall after a few bounces with gradually decreasing amplitudes. They attributed the cause of a transition from bouncing to sliding to the weakened inertia compared to the surface tension (de Vries Reference de Vries2001) or the balance between the wall-normal lift and drag forces (Zaruba et al.
Reference Zaruba, Lucasa, Prasser and Höhne2007). Although the present bubble is much larger (
${\sim}3.9~\text{mm}$
) and bouncing amplitude tends to be maintained approximately constant (i.e. the inertia is not lessened significantly), we were able to make the bubble slide by changing the wall boundary condition, i.e. possibly based on a different mechanism from those previously suggested, which will be discussed below. As
$s^{\ast }$
increases, on the other hand, transitions to periodic bouncing (
$1.02\leqslant s^{\ast }\leqslant 2.04$
) and then to irregular oscillations (
$s^{\ast }\geqslant 2.55$
) appear in turn. For periodic bounces,
$h^{\ast }$
is roughly similar, but
${\it\lambda}$
increases with
$s^{\ast }$
(figure 5
b,c).
Figure 3(d) shows the case when the hydrophobicity of the wall is enhanced, i.e. the roughened PTFE wall. When
$s^{\ast }$
is small (
${\leqslant}0.51$
), the rising bubble also slides on the wall, but the bubble deforms more (see the insets in figure 3
c,d, at
$s^{\ast }=0.26$
; a larger perimeter of the bubble is in contact with the roughened PTFE). Due to the enhanced hydrophobicity, unlike the regular PTFE wall, the transition from bouncing to sliding is observed at a fixed
$s^{\ast }~(1.02\leqslant s^{\ast }\leqslant 2.04)$
. Even if the transition to sliding is not captured in the present FoV, the bouncing amplitude is gradually reduced after each collision even at larger
$s^{\ast }\;({\geqslant}2.55)$
, and the bubble will eventually slide on the wall outside of the present FoV. For the cases of periodic rebounding on the roughened PTFE wall (
$2.04\leqslant s^{\ast }\leqslant 2.55$
), on the other hand,
$h^{\ast }$
and
${\it\lambda}$
is smaller and larger, respectively, than those on the regular PTFE wall (figure 5
b,c).
As mentioned above, next we discuss the cause of bubble sliding. As the bubble approaches closer to the wall, the liquid layer between the bubble and the wall thins (figure 6). Below the critical thickness of this liquid layer, a three-phase (gas–liquid–solid) contact (TPC) is formed, the dynamics of which is an important phenomenon used in (i) adhesion, spreading of droplets and bubbles on solid substrate (Wasan & Nikolov Reference Wasan and Nikolov2003; Stancik & Fuller Reference Stancik and Fuller2004) and (ii) bubble–particle flotation separation processes (Leja Reference Leja1982; Nguyen & Schulze Reference Nguyen and Schulze2004; Malysa, Kraswska & Krzan Reference Malysa, Kraswska and Krzan2005; Krasowska & Malysa Reference Krasowska and Malysa2007). The temporal rate of change in the thickness (
$h_{l}$
) of the liquid layer between the (no-slip) soild wall and gas bubble (free surface) has been suggested by Sheludko (Reference Sheludko1967), as
$$\begin{eqnarray}\frac{\text{d}(1/h_{l}^{2})}{\text{d}t}=\frac{16}{3{\it\mu}R_{F}^{2}}{\rm\Delta}P,\end{eqnarray}$$
where
${\it\mu}$
is the viscosity of the liquid,
$R_{F}$
is the radius of the liquid film, and
${\rm\Delta}P\;(\simeq 2{\it\sigma}/r_{eq})$
is the difference between the pressures in the thin layer and in the bulk region. According to Princen (Reference Princen, Matijevic and Eirich1969),
$R_{F}^{2}\simeq (r_{eq}/{\rm\pi}{\it\sigma})F$
, where
$r_{eq}$
is the radius of the bubble,
${\it\sigma}$
is the surface tension, and
$F$
is the force causing the thinning of the liquid layer (figure 6). As mentioned above, for the formation of TPC and subsequent bubble adhesion to the wall, the intervening liquid layer between the bubble and the wall should reach a critical thickness of a rupture (Leja Reference Leja1982; Nguyen & Schulze Reference Nguyen and Schulze2004). Although it may vary depending on the conditions such as the surface roughness of the wall and liquid viscosity, the critical thickness has been reported as roughly
$\mathit{O}({\lesssim}1~{\rm\mu}\text{m})$
(Schulze, Stockelhuber & Wenger Reference Schulze, Stockelhuber and Wenger2001; Krasowska, Zawala & Malysa Reference Krasowska, Zawala and Malysa2009). Once the rupture occurs, the TPC nucleus (i.e. hole in the liquid) is formed and expands until the wetting perimeter of the bubble becomes long enough to make the bubble attach to the wall (Leja Reference Leja1982; Nguyen & Schulze Reference Nguyen and Schulze2004).
Figure 6. Conceptual schematic to describe the thinning liquid layer between the rising bubble and the wall. Here the driving force (
$F$
) mainly originates from the circulation by the vortices in the bubble wake (drawn not to scale).
As shown by many studies, on the other hand, a counter-rotating vortex pair is formed in the wake behind a laterally oscillating bubble while rising (de Vries Reference de Vries2001; Ellingsen & Risso Reference Ellingsen and Risso2001; Mougin & Magnaudet Reference Mougin and Magnaudet2002, Reference Mougin and Magnaudet2006; Magnaudet & Mougin Reference Magnaudet and Mougin2007; Yang & Prosperetti Reference Yang and Prosperetti2007; Cano-Lozano et al.
Reference Cano-Lozano, Bohorquez and Martínez-Bazán2013). Clearly, the same vortical structure would not exist under the interaction with the wall. As explained above, known as the ground effect, the rebounds and diffusion of a single vortex near the no-slip or slip surface (Barker & Crow Reference Barker and Crow1977; Peace & Riley Reference Peace and Riley1983) and the stabilization of wake vortices behind a sphere in the vicinity of the wall (Tsutsui Reference Tsutsui2008; Lee Reference Lee2012) have been well reported. However, it is reasonable to assume that the force that contributes most to induce the thinning of liquid layer is the wake-induced lift (i.e. wall-normal) force (
$F$
), which is the main cause of the oscillating (zigzagging in the present study) bubble path (Mougin & Magnaudet Reference Mougin and Magnaudet2006). Since the liquid velocity fields are not available, to calculate the wake-induced force (Mougin & Magnaudet Reference Mougin and Magnaudet2006), we roughly estimate
$F$
based on the circulation (
${\it\Gamma}\simeq 2{\rm\pi}v_{i}r_{eq}$
) in the wake, where
$v_{i}$
is the lateral component of induced liquid velocity in the wake and the equivalent bubble radius (
$r_{eq}$
) is used as a characteristic length (figure 6). Then, the wall-normal force
$F$
is estimated as an inviscid lift force (by the Kutta–Joukowski theorem),
$F\simeq {\it\rho}_{l}u{\it\Gamma}r_{eq}=2{\rm\pi}{\it\rho}_{l}ur_{eq}^{2}v_{i}$
, where
$u$
is the bubble’s rise velocity. Using these relations, (3.1) is integrated to yield
$$\begin{eqnarray}\frac{1}{h_{l}^{2}}\simeq \frac{16}{3}\frac{{\it\sigma}^{2}}{{\it\mu}{\it\rho}_{l}uv_{i}r_{eq}^{4}}t,\end{eqnarray}$$
where
$t$
is the duration of bubble–wall collision. Let us first estimate
$h_{l}$
for a bouncing bubble on the acrylic wall (
$s^{\ast }=0.26$
). From the current measurements, the contact duration (
$t$
) is about 10 ms and the bubble’s rise velocity is
$u\simeq 0.27~\text{m}~\text{s}^{-1}$
(see figure 9
a below). For a zigzagging bubble, the maximum induced liquid velocity in the wake is
$v_{i}\simeq (0.05{-}0.1)u$
(Ellingsen & Risso Reference Ellingsen and Risso2001). The wake structure would be affected by the interaction with the wall, but we think the order of magnitude estimation based on this value would be valid. As a result, the liquid layer thickness corresponding to bubble–wall collision is estimated to be
$h_{l}\simeq 15{-}20~{\rm\mu}\text{m}$
, which is one order of magnitude larger than the critical thickness for rupture. In the case of an acrylic wall, therefore, the bubble–wall collision time is too short to form a TPC, and thus the bubble just bounces off the wall, due to the high pressure in the liquid layer (lubrication theory) (Takemura & Magnaudet Reference Takemura and Magnaudet2003; Sugiyama & Takemura Reference Sugiyama and Takemura2010). Similarly, many previous studies have shown evidence that the most critical parameter in TPC formation is the bubble–wall contact duration, which should be long enough to ensure the expansion of the TPC for stable bubble attachment.
On the other hand, for the roughened PTFE wall, the increase of the bubble–wall collision time (
${\gtrsim}100~\text{ms}$
) is clearly shown (figures 3
d, 5
a) and the estimated liquid layer thickness is
$h_{l}\lesssim 3~{\rm\mu}\text{m}$
, which is of similar order to the reported critical thickness. It is well known that air pockets are trapped on the rough hydrophobic surface when immersed underwater (Rothstein Reference Rothstein2010; Park, Sun & Kim Reference Park, Sun and Kim2014, to name only a few), and this air layer would encourage the formation of a TPC through the lengthening of the contact time (Krasowska & Malysa Reference Krasowska and Malysa2007; Krasowska et al.
Reference Krasowska, Zawala and Malysa2009). Therefore, the sliding motion and deformed bubble shape indicate that the main mechanism of a large bubble sliding on a hydrophobic wall at small
$s^{\ast }$
is related to the fast formation of a TPC. Also, it is interesting to see that the submicron-sized air pockets, possibly existing on the regular (not perfectly smooth) Teflon®, are enough to promote bubble sliding (figure 3
c).
In the context of having a surface slip boundary condition, as stated above, the porous (polyurethane sponge) wall is similar to the current hydrophobic walls on which the effective slip is generated on the interface between water and trapped air pockets. Most numerical approaches have used the same slip boundary condition to model both the porous (Beavers & Joseph Reference Beavers and Joseph1967; Hahn et al. Reference Hahn, Je and Choi2002; Bruneau & Mortazavi Reference Bruneau and Mortazavi2008) and hydrophobic (Min & Kim Reference Min and Kim2004; Martell, Perot & Rothstein Reference Martell, Perot and Rothstein2009; Park, Parn & Kim Reference Park, Parn and Kim2013) walls. However, as shown in figure 3(b), the rising bubble does not slide on the sponge wall. This is because the fully immersed porous wall does not have air pockets physically. Therefore, even with the same slip boundary condition, functionally, the behaviour of a rising bubble shows a different trend.
3.2. Near-wall rising behaviour of a large deformable bubble at
$s^{\ast }>2.0$
As
$s^{\ast }$
increases further (
${>}2.0$
), the rebounding motion of a rising bubble on the acrylic wall transitions. That is, the rising bubble oscillates in the wall-normal direction non-periodically and does not touch the wall (figure 3
a). When
$s^{\ast }$
is relatively large enough, it is assumed that the hydrodynamic forces on the rising bubble, induced by the wall (e.g. wall-induced lift and drag forces) are reduced. A weaker hydrodynamic force then indicates that the bubble is more susceptible to the path and shape instabilities that already persist in the considered
$\mathit{Re}$
and
$\mathit{We}$
regime. This would cause the bubble trajectory to appear non-periodic and unpredictable, as shown. However, it is necessary to measure the liquid velocity fields in detail to assess the exact cause of these phenomena. Interestingly the bubble trajectories under the reduced wall effect are not exactly same as the reference case of a two-dimensional zigzag path (figure 1
b) nor do they evolve into the three-dimensional helical one. At
$s^{\ast }=4.08$
, slight out-of-plane motion of the bubble is observed (figure 4), but it is different from the typical three-dimensional helical path and thus the bubble trajectory can be assumed to be roughly two-dimensional.
A similar change of the bubble motion occurs for the other types of wall, as
$s^{\ast }$
increases in this regime. However, compared to other cases, the rising bubble starts to move away from the polyurethane sponge wall at the smaller
$s^{\ast }=1.53$
(figure 3
b). In addition, the gradual migration of the rising bubble (while oscillating in the wall-normal direction) away from the polyurethane sponge wall is also observed, as clearly shown at
$s^{\ast }=1.02,1.53$
and 4.08 (figure 3
b), which is not observed for the other types of wall. For the roughened PTFE wall, the successive rebounding motion with gradually decreasing bouncing amplitude persists to
$s^{\ast }=3.57$
and the irregular oscillation starts to occur at
$s^{\ast }=4.08$
.
In summary, the near-wall behaviour of a rising deformable bubble at high
$\mathit{Re}$
and
$\mathit{We}$
is described as a transition from periodic bouncing to non-periodic oscillation without colliding against the wall, and the critical
$s^{\ast }$
for transition varies depending on the wall boundary condition. The repeated bouncing of a rising bubble on the vertical wall are similar to the trajectory of two bubbles rising side by side (Duineveld Reference Duineveld, Biesheuvel and van Heijst1998; Legendre, Magnaudet & Mougin Reference Legendre, Magnaudet and Mougin2003; Sanada et al.
Reference Sanada, Sato, Shirota and Watanabe2009; Hallez & Legendre Reference Hallez and Legendre2011). As
$\mathit{Re}$
and
$\mathit{We}$
increase, two interacting rising bubbles tend to avoid coalescence and bounce off each other. It has been claimed that for a certain condition, this bubble–bubble bounce triggers the path (i.e. wake) instability of the bubbles to make them rebound repeatedly, similar to the present rebounding bubbles. However, a detailed comparison between the two phenomena is beyond the scope of the present study, but would be interesting as a future study. On the other hand, at small
$s^{\ast }$
, it is also found that hydrophobicity causes the bubble to slide on the wall before periodic bouncing appears, and the rising bubble migrates away from the wall in the case of the porous wall. As shown in figure 5,
${\it\lambda}$
of the periodic bouncing gradually increases (i.e. the bubble collision frequency decreases) with increasing
$s^{\ast }$
, but
$h^{\ast }$
shows a wide scatter depending on the wall boundary condition. Moctezuma et al. (Reference Moctezuma, Lima-Ochoterena and Zenit2005) also predicted that
${\it\lambda}$
of periodic bouncing increases with increasing
$s^{\ast }$
and explained the reason as the reduced hydrodynamic forces, like the wall-induced lift force. Compared to the reference in-plane zigzag motion of a freely rising bubble without a wall (dashed lines in figure 5
b,c), a comparable magnitude of
$h^{\ast }$
is obtained in some cases for the acrylic and PTFE walls; however, in general, we find that
$h^{\ast }$
of oscillation is reduced due to the wall. On the other hand, due to the wall,
${\it\lambda}$
of oscillation becomes smaller than that of a freely rising bubble at
$s^{\ast }\lesssim 2.0$
(when the effect of wall boundary condition is relatively strong) but becomes larger at
$s^{\ast }>2.0$
(when the rising bubble no longer touches the wall).
Figure 7. Typical motion of a bubble when it is closest to the wall during its oscillatory rise, which includes bouncing and sliding, depending on wall type, at
$s^{\ast }=$
(a) 0.26; (b) 1.02; (c) 2.04. The solid lines on the bubbles illustrate their horizontal axis (
$d_{h}$
). (d) Definition of the inclination angle (
${\it\beta}$
).
3.3. Bubble orientation
In this section, we discuss the variation of bubble’s orientation during its rise. Since the current bubble has an oblate ellipsoidal shape and deforms greatly during rising, its movement (i.e. orientation) shows a specific dependence on the wall boundary condition, especially when the bubble is closest to the wall during its oscillatory rise. Figure 7 shows close-up views of the typical motion of bouncing bubble on each type of the wall, at three different
$s^{\ast }$
values. As shown, the bubble’s orientation appears to vary as the bubble approaches towards and migrates away from the wall. There are obvious differences in the collision dynamics depending on the wall boundary condition, such as the sliding with the increased collision time for hydrophobic surfaces (see the cases of roughened PTFE in figure 7
b,c), related to the formation of a TPC as mentioned above. However, irrespective of the wall type, the rising bubble tends to align along its trajectory in the same way, i.e. its major axis (denoted as
$d_{h}$
in figure 7
d) becomes perpendicular to the direction of motion. During the collision, interestingly, it is observed that the bubble actually rolls over the wall (the advancing and receding side of the bubble is reversed after the collision), not just simply bounce off. In the reference two-dimensional zigzag path, the orientation of the bubble is not reversed during its rise (figure 1
b). As the rising bubble does not touch the wall at larger
$s^{\ast }$
, it is observed that the bubble’s orientation is not reversed (see the cases of acrylic and sponge in figure 7
b,c). Previously, Zaruba et al. (Reference Zaruba, Lucasa, Prasser and Höhne2007) showed that the orientation of a rising bubble near a vertical wall, under an upward shear, varies depending on the liquid velocity. For example, the bubble tends to stretch along the liquid flow direction (i.e. tries to maintain a fixed orientation) when the liquid velocity is high. At low liquid velocity, on the other hand, the bubble’s orientation fluctuates much during the rise, which somewhat agrees with the current findings. For the sliding bubble, on the other hand, the inclination angle
${\it\beta}$
(see figure 7
d) is about 120° on the regular PTFE wall and about 90° on the roughened PTFE wall, indicating that the adhesion of the bubble becomes stronger.
To quantify the effect of the wall on the bubble’s orientation during its rise further, we analyse the history of inclination angle (
${\it\beta}$
), defined as the angle between the horizontal axis of the oblate bubble shape and the vertical wall (figure 7
d). Figure 8 shows the variation of
${\it\beta}$
for the cases of rebounding (figure 8
a,c,e,g) and non-periodic oscillations without touching the wall (figure 8
b,d, f,h) for each wall type. For the rebounding cases (i.e. at
$s^{\ast }\lesssim 2.0$
), analysis at the same
$s^{\ast }$
is not possible since the bubble shows different behaviour such as bouncing, sliding and migrating away, depending on the wall material (see figure 3 and § 3.1). Thus, we chose to discuss the trend at the smallest
$s^{\ast }$
at which the bubble experiences a discernible bouncing for each wall type (figure 8
a,c,e,g).
Figure 8. Variation of inclination angle (
${\it\beta}$
) with bubble trajectory: (a) acrylic wall at
$s^{\ast }=0.26$
and (b) at 4.08; (c) polyurethane sponge wall at 0.26 and (d) at 4.08; (e) PTFE wall at 1.02 and (f) at 4.08; (g) roughened PTFE wall at 2.04 and (h) at 4.08. Here, ○ denotes
${\it\beta}$
and the solid line the trajectory of the bubble centre.
When the bubble bounces off the wall, in general,
${\it\beta}$
increases as the bubble approaches the wall and drops down suddenly at the instant of collision (figure 8
a,c,e,g). After the impact,
${\it\beta}$
recovers back as the bubble moves away from the wall. Depending on the wall type, on the other hand, the detailed trend in
${\it\beta}$
differs. For example,
${\it\beta}$
increases gradually after the collision for an acrylic wall (figure 8
a); however, for the polyurethane sponge wall, it is maintained approximately constant while the bubble moves away from the wall and increases sharply as the bubble is attracted toward the wall (figure 8
c). For hydrophobic surfaces,
${\it\beta}$
remains constant as the bubble moves away from and toward the wall (i.e.
${\it\beta}$
does not experience a sharp increase after the impact), respectively (figure 8
e,g), indicating that the wall effect is strong enough to balance the hydrodynamic forces acting on the bubble and keep the same orientation. This is also associated with the lengthened contact time due to the formation of a TPC during the collision. Based on the data in figure 8(a,c,e,g), the change in
${\it\beta}$
across the bubble–wall collision is calculated for each wall type as
$95^{\circ }\pm 12^{\circ }$
for the acrylic,
$70^{\circ }\pm 10^{\circ }$
for the sponge,
$125^{\circ }\pm 15^{\circ }$
for the PTFE, and
$144^{\circ }\pm 15^{\circ }$
for the roughened PTFE. This indicates that compared to the conventional no-slip surface, the bouncing bubble rotates less (i.e. smaller angular momentum is required) on the porous wall; however, it rotates more (i.e. larger angular momentum is required) on the hydrophobic surfaces. This is related to the wall effect on the energy dissipation during the bubble–wall collision, as explained in § 3.5.
When the rising bubble does not touch the wall as
$s^{\ast }$
increases, the variation of
${\it\beta}$
becomes less significant during the rise. At
$s^{\ast }=4.08$
, for example, where the bubble’s movement becomes irregular (figure 3) without colliding against the wall, the bubble still tends to be aligned along its trajectory (the horizontal axis of the bubble is perpendicular to its trajectory) (figure 8
b,d, f,h). Compared to the cases of rebounding, however, the correlation between
${\it\beta}$
and bubble trajectory is weaker and no discernible dependence on the wall material is measured, which indicates that the wall effect is reduced.
3.4. Instantaneous and mean velocities of rising bubbles
The history of instantaneous bubble velocity (decomposed into vertical (
$u$
) and wall-normal (
$v$
) components) is calculated and shown in figures 9 and 10. For all cases, it is measured that the oscillation of vertical velocity is relatively mild but the wall-normal velocity (although its absolute value is smaller than the vertical one) varies significantly according to the oscillating bubble path.
Figure 9. History of instantaneous velocity of rising bubble near the (a,c,e,g) acrylic and (b,d,f,h) polyurethane sponge walls, at
$s^{\ast }=$
(a,b) 0.26; (c,d) 1.53; (e, f) 2.55; (g,h) 4.08. Here, ○ and ● denote the vertical (
$u$
) and wall-normal (
$v$
) components of the velocity, respectively, and the solid line the corresponding trajectory of the bubble centre. In (a–c), the dashed-line boxes highlight the bubble–wall collisions.
Figure 10. History of instantaneous velocity of rising bubble near the (a,c,e,g) PTFE and (b,d,f,h) roughened PTFE walls, at
$s^{\ast }=$
(a,b) 0.26; (c,d) 1.53; (e,f) 2.55; (g,h) 4.08. Here, ○ and ● denote the vertical (
$u$
) and wall-normal (
$v$
) components of the velocity, respectively, and the solid line the corresponding trajectory of the bubble centre. In (c,d,f), the dashed-line boxes highlight the bubble–wall collisions.
For the rebounding bubbles on the acrylic (figure 9
a) and sponge (figure 9
b) walls (at
$s^{\ast }=0.26$
), the wall-normal velocity (
$v$
) is accelerated, towards the wall, as the bubble is attracted to the wall. Then
$v$
reaches its negative peak before the collision. From this moment on, during collision,
$v$
is instantly reduced and changes its sign to approach the positive (out of the wall) peak (highlighted with dashed-line boxes in figure 9
a,b). As the bubble is shifted to the maximum distance from the wall after the collision,
$v$
remains almost constant and the same process is repeated as the bubble rebounds. After each collision, no significant reductions of
$u$
or
$v$
are measured in the present configuration. Since the bubble–wall contact time on the sponge wall is slightly longer than on the acrylic wall, the rate of change in wall-normal velocity across the collision on the sponge wall is less sharp than that on the acrylic wall. Although a slight deceleration of
$u$
is captured during the bubble–wall collision, its variation is not strong compared to that of
$v$
. As
$s^{\ast }$
increases, the unsteady scattering of
$u$
becomes more pronounced (figure 9
e–h), which is consistent with the findings that the bubble trajectory is less regulated at
$s^{\ast }>2.0$
(figure 3
a,b).
On the other hand, figure 10 shows the variation of bubble velocity near the hydrophobic walls. When the bubble shows the sliding motion (at
$s^{\ast }=0.26$
), the vertical (
$u$
) and wall-normal (
$v$
) velocities remain almost constant during the rising and the wall-normal velocity is zero (figure 10
a,b). As
$s^{\ast }$
increases to 1.53, the bubble velocity on the regular PTFE wall shows the same trend (figure 10
c) as those of rebounding bubbles on the acrylic and sponge walls (note that a similar trend is shown at
$s^{\ast }=2.55$
for the roughened PTFE wall (figure 10
f)). At the same
$s^{\ast }$
, the bouncing–sliding transition on the roughened PTFE wall is also clearly captured by the bubble velocity variation; that is,
$u$
is reduced more than 50 % and
$v$
becomes zero after the transition (figure 10
d). On increasing
$s^{\ast }$
further, the bubble velocity still aligns with the irregular bubble motion but the unsteady scattering of the data is pronounced.
Next, to see the global effect of the wall on the bubble dynamics, the mean rise velocity (
$\bar{u}$
) of the bubble, normalized by that (
$U$
) of a freely rising bubble (without the wall) is plotted in figure 11. In general, the existence of the wall reduces the rise velocity of the bubble (
$\bar{u}/U<1$
) as shown by Uno & Kinter (Reference Uno and Kinter1956) and Krishna et al. (Reference Krishna, Urseanu, van Baten and Ellenberger1999). In addition, we can classify two regimes depending on the variation of rise velocity with
$s^{\ast }$
, as we did in §§ 3.1 and 3.2. Very close to the wall (
$s^{\ast }\lesssim 2.0$
) where the rising bubble bounces periodically or slides on the wall (figure 3), the rise velocity of the bubble is significantly affected by the wall boundary condition, i.e. the bouncing bubble rises faster than the sliding one. In this regime, the bubble near the sponge wall rises faster than the other cases, which is consistent with the smaller
$h$
of the bouncing on the sponge wall (figure 11), i.e.
$u\sim {\it\lambda}/h$
from the sinusoidal curve fitting of the periodic bouncing motion. By modelling the porous wall as a slip boundary condition, Gangloff et al. (Reference Gangloff, Hwang and Advani2014) also numerically showed that the rise velocity of a bubble near the wall increases due to its porosity. For a bubble rising near the PTFE wall, the rise velocity is the slowest when it slides on the wall (
$s^{\ast }\lesssim 0.5$
) but increases sharply as the transition to the periodic bouncing happens. For other (acrylic, roughened PTFE and sponge) cases, the rise velocity remains almost constant with
$s^{\ast }$
in this regime. At
$s^{\ast }>2.0$
where the bubble’s oscillating trajectory loses its periodicity without colliding with the wall, on the other hand, the effects of wall boundary condition and
$s^{\ast }$
on the rise velocity become relatively small, although the rise velocity of a bubble near the PTFE wall is slower than those of the other walls which are approximately constant with
$s^{\ast }$
. The transient (unsteady) behaviour of the bubble seems unpredictable in this regime as mentioned above, but the global features, like the mean rise velocity, are not affected much by the wall.
Figure 11. Variations of the normalized mean rise velocity (
$\bar{u}/U$
) with
$s^{\ast }$
: ○, acrylic; ♦, polyurethane sponge; ▵, PTFE; ▪, roughened PTFE walls.
3.5. Energy components associated with the rise of a bubble near a wall
As a bubble (while deforming as well in the present case) approaches a wall, the surrounding fluid is accelerated with it (the so-called added-mass effect, Batchelor Reference Batchelor1967; Clift et al.
Reference Clift, Grace and Weber1978) and thus the transport between the kinetic (
$E_{k}$
) and surface (
$E_{s}$
) energies and to dissipation (
$E_{D}$
), are closely associated with the behaviour of a rising bubble under the wall effect, especially at the instant of collision. Here, we investigate the interplay between the above-mentioned energies to understand the physics of near-wall bubble motions, observed in figure 3. First, the kinetic energy (
$E_{k}$
) is calculated as
$$\begin{eqnarray}E_{k}=\frac{{\rm\pi}}{12}({\it\rho}_{g}+c_{m}{\it\rho}_{l})d_{eq}^{3}(u^{2}+v^{2})=E_{ku}+E_{kv},\end{eqnarray}$$
where
$E_{ku}$
and
$E_{kv}$
denote the contributions of vertical (
$u$
) and wall-normal (
$v$
) velocities to
$E_{k}$
. For the added-mass coefficient (
$c_{m}$
), we use the following relation between
$c_{m}$
and
${\it\chi}$
(Milne-Thomson Reference Milne-Thomson1968):
$$\begin{eqnarray}c_{m}=\frac{{\it\alpha}}{2-{\it\alpha}},\quad {\it\alpha}=\frac{2{\it\chi}^{2}}{{\it\chi}^{2}-1}\left(1-\frac{1}{\sqrt{{\it\chi}^{2}-1}}\cos ^{-1}(1/{\it\chi})\right).\end{eqnarray}$$
Here, the aspect ratio (
${\it\chi}=d_{h}/d_{v}$
) of the bubble is defined as the ratio of the length of the horizontal (major) to vertical (minor) axes of the approximated oblate ellipsoidal shape (see figure 1
c). On the other hand, the surface energy (
$E_{s}$
) is calculated as
$E_{s}={\it\sigma}A$
, where
${\it\sigma}$
is the surface tension at the air–water interface. The surface area (
$A$
) of an oblate ellipsoid is expressed as a function of
$d_{h}$
and
${\it\chi}$
:
$$\begin{eqnarray}A=\frac{{\rm\pi}d_{h}^{2}}{2}\left(1+\frac{1-e^{2}}{e}\tanh ^{-1}e\right),\quad e^{2}=1-1/{\it\chi}^{2}.\end{eqnarray}$$
If we define
$E_{t}$
as the sum of kinetic and surface energies as
$E_{t}=E_{ku}+E_{kv}+E_{s}$
, then the energy would be balanced as
$E=E_{t}+E_{D}$
where
$E_{D}$
is the energy dissipated due to the viscosity (
$E_{v}$
) and wall effect (
$E_{w}$
), for instance. The viscous dissipation (
$E_{v}$
) is defined as
$$\begin{eqnarray}E_{v}=\int _{0}^{t}\int _{V}{\it\Phi}\,\text{d}v\,\text{d}t,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Phi} & = & \displaystyle 2{\it\mu}\left[\left(\frac{\partial u}{\partial x}\right)^{2}+\left(\frac{\partial v}{\partial y}\right)^{2}+\left(\frac{\partial w}{\partial z}\right)^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\left\{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\right)^{2}+\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)^{2}\right\}\right],\end{eqnarray}$$
where
$V$
is the control volume which includes the bubble. To fully evaluate
$E_{D}$
, therefore, the spatially and temporally resolved velocity field data inside and outside the bubble are required (Nam, Kim & Shin Reference Nam, Kim and Shin2013; Zawala & Dabros Reference Zawala and Dabros2013), which are not available in the present study. Therefore, as an alternative way, we try to roughly estimate
$E_{D}$
as the deficit of
$E_{t}$
, expressed as
$E_{D}=E_{to}-E_{t}$
where
$E_{to}$
is the value of
$E_{t}$
when the bubble is displaced furthest from the wall, as an index for dissipated energy, especially for the purpose of focusing on the loss due to the wall. Since the buoyancy identically applies to all cases, once the volume and the location of the bubble are fixed, the potential energy due to the buoyancy is not considered here.
The variations of each energy component (
$E_{ku}$
,
$E_{kv}$
,
$E_{s}$
, and
$E_{D}$
) for selected cases of a rebounding bubble (at the smallest
$s^{\ast }$
where the rebounding initiates for each wall type) are plotted in figures 12 and 13. In each figure, the corresponding bubble trajectory is also plotted (in subfigure i) and the instants of bubble–wall collision are highlighted with dashed-line boxes.
Figure 12. Variations in energy components along
$x^{\ast }$
for (a) acrylic wall at
$s^{\ast }=0.26$
and (b) polyurethane sponge wall at 0.26: (i) ●,
$E_{ku}/E_{k}$
; ○,
$E_{kv}/E_{k}$
; (ii) ●,
$E_{ku}/E_{t}$
; ○,
$E_{kv}/E_{t}$
; ▵,
$E_{s}/E_{t}$
; (iii) ●,
${\it\chi}$
; (iv) ▪,
$E_{s}$
; (v) ▫,
$E_{t}$
; (vi) ♢,
$E_{D}/E_{to}$
. In (i), the solid lines denote the corresponding bubble trajectory.
Figure 13. Variations in energy components along
$x^{\ast }$
for (a) PTFE wall at
$s^{\ast }=1.02$
and (b) roughened PTFE wall at 2.04: (i) ●,
$E_{ku}/E_{k}$
; ○,
$E_{kv}/E_{k}$
; (ii) ●,
$E_{ku}/E_{t}$
; ○,
$E_{kv}/E_{t}$
; ▵,
$E_{s}/E_{t}$
; (iii) ●,
${\it\chi}$
; (iv) ▪,
$E_{s}$
; (v) ▫,
$E_{t}$
; (vi) ♢,
$E_{D}/E_{to}$
. In (i), the solid lines denote the corresponding bubble trajectory.
3.5.1. Typical trends in the variations of energy components for bouncing bubbles
Let us first describe the typical trends of energy components for bouncing bubbles, which are found to be highly correlated with each other. Due to the deforming nature of a high-
$\mathit{Re}$
and high-
$\mathit{We}$
bubble, the aspect ratio (
${\it\chi}$
) of the present bubble fluctuates greatly during its rise (the aspect ratio of the reference bubble is measured to vary within
$2.5\pm 0.6$
) but also shows a trend specific to the bouncing motion; that is, as the bubble approaches the wall,
${\it\chi}$
decreases and then increases as the bubble moves away from the wall after the collision (subfigure iii in figures 12 and 13). As expected from (3.5), the surface energy (
$E_{s}$
) also follows this trend, especially across a bubble–wall collision, i.e. as the bubble approaches the wall,
$E_{s}$
decreases with
${\it\chi}$
(subfigure iv in figures 12 and 13). Although it is clearly observed that
$E_{s}$
has a local minimum during the collision, its fluctuating nature makes it difficult to discern any characteristic trend relevant to the bubble motion. After trying many parameters to explain the role of
$E_{s}$
in the bubble motion, we find that the ratio of
$E_{s}$
to
$E_{t}$
(where
$E_{t}$
is the sum of
$E_{s}$
and
$E_{k}$
) shows a good correlation with the bubble motion. As shown in subfigure (ii) in figures 12 and 13,
$E_{s}/E_{t}$
varies periodically according to the rebounding trajectory of the bubble, and
$E_{s}$
has a larger contribution to
$E_{t}$
than
$E_{ku}$
and
$E_{kv}$
, indicating that
$E_{s}$
is a dominant source for maintaining the present rebounding bubble motion.
Interestingly,
$E_{s}/E_{t}$
shows the opposite trend to
$E_{s}$
during the bubble–wall collisions. As the bubble moves away from the wall,
$E_{s}/E_{t}$
decreases (
$E_{s}$
increases) while
${\it\chi}$
increases, and is kept to a moderate level (
${\sim}0.5$
); however, it increases significantly as the bubble approaches the wall while
${\it\chi}$
decreases. After the collision,
$E_{s}/E_{t}$
decreases back and this oscillating behaviour is repeated along the bubble’s rise.
On the other hand,
$E_{ku}/E_{t}$
(the contribution of the vertical component of bubble kinetic energy to
$E_{t}$
) shows the opposite trend to that of
$E_{s}/E_{t}$
(subfigure ii in figures 12 and 13). That is,
$E_{ku}/E_{t}$
decreases as the bubble is attracted toward the wall and recovers after the collision, in step with
$E_{s}/E_{t}$
. This sharp decrease of rise velocity, i.e.
$E_{ku}$
, just before the bubble–wall collision has been also reported by Moctezuma et al. (Reference Moctezuma, Lima-Ochoterena and Zenit2005) and Figueroa-Espinoza et al. (Reference Figueroa-Espinoza, Zenit and Legendre2008). The wall-normal component of
$E_{k}~(E_{kv})$
contributes less to
$E_{t}$
than the others, but shows a small peak just before the collision.
When the instant of bubble–wall collision is examined closely (see the dashed-line boxes in figures 12 and 13), we can discuss the transport between energy components and the opposite trend of
$E_{s}/E_{t}$
to
$E_{s}$
. Closer to the collision, both
$E_{s}$
and
$E_{ku}$
are reduced while
$E_{kv}$
and energy dissipation (
$E_{D}$
) increase (subfigures i, ii and vi in figures 12 and 13). Then, the increase of
$E_{s}/E_{t}$
before the collision indicates that the loss of
$E_{ku}$
(to
$E_{D}$
, for example) is larger than the release of
$E_{s}$
. Although it is difficult to quantitatively characterize the transport between energy components, it is thought that some of the deficits of
$E_{s}$
and
$E_{ku}$
are converted to
$E_{kv}$
before the collision and also some are dissipated. Across the collision,
$E_{ku}/E_{t}$
and
$E_{kv}/E_{t}$
become very small and
$E_{s}$
contributes most to
$E_{t}$
, indicating that most of
$E_{k}(=E_{ku}+E_{kv})$
has dissipated. Just after the impact, most of
$E_{kv}$
and
$E_{ku}$
is recovered. As the bubble moves away from the wall after the collision, both
$E_{s}$
and
$E_{ku}$
increase while
$E_{D}$
and
$E_{kv}$
are reduced. Based on the reduction of
$E_{s}/E_{t}$
at this stage, we can say that the recovery of
$E_{ku}$
is larger than the increased
$E_{s}$
(i.e. the enlarged bubble surface area). When the bubble is shifted furthest from the wall (when
$E_{D}$
is smallest), therefore, the deformation-related force (energy) is small while the hydrodynamic forces (wake-induced forces, for example) prevail again, which eventually attracts the bubble toward the wall for rebounding motion. Therefore, it is understood that the accumulation of available (or excess) kinetic energy in the shape deformation (i.e.
$E_{s}$
) and then the transport back to
$E_{kv}$
across the collision is responsible for the rebounding motion with a large amplitude, even considering the large energy dissipation during the process (Zaruba et al.
Reference Zaruba, Lucasa, Prasser and Höhne2007).
3.5.2. Variation in energy components with wall configuration
We now look into the variation of energy components specific to each wall type. Figure 12(a) shows the result for the rebounding bubble on the acrylic wall at
$s^{\ast }=0.26$
. This case fits well the general picture explained above. That is,
$E_{k}$
is mostly dominated by the vertical component (
$E_{ku}$
) except just before the collision when
$E_{kv}$
takes up to 40 % of
$E_{k}$
(figure 12
a i), which is similar to the suggestion by Figueroa-Espinoza et al. (Reference Figueroa-Espinoza, Zenit and Legendre2008) that the bubble may experience an enhanced bouncing (i.e. larger amplitude) due to the transfer from vertical to horizontal (i.e. wall-normal) momentum, despite the obvious loss of energy during collisions. Note that in the previous section, we approximately described the transport between
$E_{ku}$
,
$E_{kv}$
,
$E_{s}$
and
$E_{D}$
. The contribution of
$E_{s}$
to
$E_{t}$
becomes almost 90 % at the instant of collision but that of
$E_{ku}$
recovers to be comparable to that of
$E_{s}$
when the bubble is at the maximum distance from the wall (figure 12
a ii). The variations of
$E_{s}/E_{k}$
and
$E_{k}/E_{t}$
are well correlated with the change in
${\it\chi}$
(in figure 12
a iii) along the bubble trajectory. As the bubble approaches the wall,
${\it\chi}$
decreases while
$E_{s}/E_{t}$
and
$E_{ku}/E_{t}$
increase and decrease, respectively. The trend is reversed after the collision.
$E_{t}$
shows a local minimum during the bubble–wall collision (figure 12
a v), while the wall effect (i.e.
$E_{D}$
) shows a sharp peak at the instant of collision (figure 12
a vi).
For a porous wall at
$s^{\ast }=0.26$
(figure 12
b), general trends of energy components are similar to those for the acrylic wall. However, the rates of change of each energy component are not significant, compared to those on the no-slip wall; the contribution of
$E_{kv}$
to
$E_{t}~(E_{kv}/E_{t})$
and the reduction of
$E_{ku}$
just before the collision become smaller than those on the acrylic wall (figure 12
b i), which indirectly indicates the existence of non-negligible wall-normal velocity (i.e. seepage effect) into the wall (Gangloff et al.
Reference Gangloff, Hwang and Advani2014). And this will result in the reduced repulsive force that makes the bouncing amplitude become smaller than others (see figure 5
a). Since the bubble’s momentum is spent less on the bouncing (and also on the bubble’s rolling movement during the collision, see figure 8), estimated
$E_{D}$
is smaller than other cases and thus the large
$E_{t}$
is achieved (figure 12
b v,vi).
Figures 13(a) and 13(b) show the rebounding and bouncing–sliding transition events on the regular and roughened PTFE walls, respectively. For both walls, the trends of each energy component with bubble trajectory are similar, but the reduction of
$E_{ku}$
is measured to be larger than on the acrylic and sponge walls. On the other hand, the role of hydrophobicity is identified more clearly for the roughened PTFE wall. For example, after the first two collisions with a broad peak in
$E_{D}$
(note that
$E_{D}$
had a relatively sharp peak for the acrylic and sponge walls), the kinetic energy (and also the bouncing amplitude) is reduced gradually and the bubble starts to slide when the available inertia (or
$E_{kv}$
) does not preclude the formation of a TPC (figure 13
b i,ii). When the bubble slides,
$E_{s}$
contributes to
$E_{t}$
more than 90 % and
$E_{D}$
remains very large. As shown in figure 3(d), the rate of shape deformation is very large (figure 13
b iii) for the roughened PTFE wall. As a result, it is understood that the hydrophobicity increases
$E_{D}$
on a bouncing bubble, compared to that of the rebounding bubble on the acrylic wall, i.e. at
$1.02\leqslant s^{\ast }\leqslant 2.04$
for regular PTFE and at
$2.04\leqslant s^{\ast }\leqslant 2.55$
for roughened PTFE (figure 14).
Figure 14. Variations of
$E_{D}/E_{to}$
with
$s^{\ast }$
for its (a) average and (b) maximum peak: ○, acrylic; ♦, polyurethane sponge, ▵, PTFE and ▪, roughened PTFE walls.
3.5.3. Wall effect on the energy dissipation
Shown in subfigure (v) in figures 12(a,b) and 13(a,b) are the variations of
$E_{t}$
along
$x^{\ast }$
. It is calculated that
$E_{t}$
is maintained approximately constant during the rise but decreases locally at the collision and thus the wall effect (
$E_{w}$
) on the energy (i.e. loss,
$E_{D}$
) shows a peak at that time (subfigure vi in figures 12
a,b and 13
a,b). There may be various sources of the energy loss during the bubble’s rise near the wall, such as a viscous dissipation (especially in a thin liquid film between the bubble and the wall), damping due to surface deformation and the diffusion of fluid energy into the secondary vortices generated by the interaction between the bubble and the wall. Contrary to the unsteady liquid droplet motion in air (Nam et al.
Reference Nam, Kim and Shin2013), the viscous dissipation due to the motion inside the air bubble is assumed to be relatively small. In the present case, on the other hand, the wall effect (
$E_{w}$
) is thought to be dominant, because
$E_{D}$
decreases remarkably with increasing
$s^{\ast }$
. Note also that a sharp change in the bubble orientation (due to the tumbling motion) accompanies the bubble–wall collision (figure 8). As shown in (3.6), detailed velocity field measurements around the bubble and the wall are required to identify the exact causes. However, the current estimation of
$E_{D}$
according to various wall configurations would also provide useful insight.
Figures 14(a) and 14(b) show the variations of normalized
$E_{D}$
with
$s^{\ast }$
, for its average and maximum peak, respectively. The maximum peak occurs during the bubble–wall collision. As shown, the maximum peak and average values of normalized
$E_{D}$
show the same trend with
$s^{\ast }$
and wall boundary condition, indicating that the trend of
$E_{D}$
explained here is not limited to local events during the collision. As
$s^{\ast }$
increases, in general,
$E_{D}$
tends to decrease, indicating the reduced wall effect on the energy dissipation. According to Figueroa-Espinoza et al. (Reference Figueroa-Espinoza, Zenit and Legendre2008), the wall-induced vorticity decreases as
$(s^{\ast })^{3}$
, which might be one of the explanations for the trend in figure 14.
As can be expected from the different bubble rises depending on the wall boundary conditions at
$s^{\ast }\lesssim 2.0$
, the estimated
$E_{D}$
also shows a discernible deviation at smaller
$s^{\ast }$
values. As shown in figure 14, for example, normalized
$E_{D}$
on the porous wall is smaller than that on the acrylic wall. Less energy loss seems to be related to the slip boundary condition at the porous wall. That is, the interaction between the bubble wake and the porous wall may produce a weaker secondary vortex than that for the no-slip wall, due to the apparent surface slip. Also, we showed that the slip condition requires less angular momentum to be used for the bubble during the collision (figure 8). Therefore, the wall-induced energy loss on the porous wall is smaller than for the other walls, and this agrees well with the fact that the bubble rises faster over the sponge wall than the other cases (figure 11).
An interesting trend of
$E_{D}$
is found on hydrophobic walls. As shown in figure 14, the energy dissipation on the hydrophobic surfaces is larger than that on the no-slip surface at
$s^{\ast }\lesssim 2.0$
for regular PTFE and at
$s^{\ast }\lesssim 2.5$
for roughened PTFE walls. In these ranges of
$s^{\ast }$
, the bubble actually touches the wall for sliding or bouncing. As explained in § 3.1.2, the three-phase-contact (TPC) formation encouraged by the air pockets trapped on the hydrophobic surface will retard the rebounding motion of the bubble, which is evidenced by the elongated bubble–wall contact time (figure 3
d) and larger change rate in the bubble orientation during collision (figure 8). Therefore, even with the same (functionally) slip boundary condition as the porous wall, the existence of air pockets on the surface induces strong energy dissipation when colliding. When the bubble does not touch the hydrophobic surface (
$s^{\ast }>2.0$
for regular PTFE and
$s^{\ast }>2.5$
for roughened PTFE walls), conversely,
$E_{D}$
becomes smaller than that on the no-slip surface (figure 14). Now the bubble does not touch the wall, and thus the direct contact with the trapped air pockets has little effect on
$E_{D}$
while the slip boundary condition is in place. With the same reason for small
$E_{D}$
on the porous wall, the hydrophobic surfaces impose smaller
$E_{D}$
on the rising bubbles than that imposed by the no-slip wall.
As
$s^{\ast }$
increases (
${\gtrsim}3.0$
), on the other hand, the difference in
$E_{D}$
with wall boundary condition is reduced, and the dominating variable affecting
$E_{D}$
seems to be
$s^{\ast }$
. In previous sections, we showed that the bubble motion and variation of mean rise velocity are also classified with a similar criterion for
$s^{\ast }$
.
3.5.4. Coefficient of restitution
In previous sections, we discussed that the interplay between the energy storage (i.e. transport between surface and kinetic energies) and the energy dissipation determines the detailed motion of a rising bubble near a wall. The same conclusion has been drawn from studies of the dynamics of normal bouncing of solid (Joseph et al.
Reference Joseph, Zenit, Hunt and Rosenwinkel2001; Gondret, Lance & Petit Reference Gondret, Lance and Petit2002) and liquid (Legendre, Daniel & Guiraud Reference Legendre, Daniel and Guiraud2005) particles on a horizontal wall. These studies adopted the coefficient of restitution (
${\it\epsilon}$
), defined as
${\it\epsilon}=|v_{departure}/v_{approach}|$
, as an indirect measure of energy dissipation resulting from a collision. Here,
$v_{departure}$
and
$v_{approach}$
denote the wall-normal velocity of the particle, after and before the collision, respectively. For example,
${\it\epsilon}$
of a solid particle scales well as
${\it\epsilon}\sim f(St)$
, where the impact Stokes number (ratio of the particle inertia to the viscous forces) is defined as
$\mathit{St}={\it\rho}_{p}d_{eq}v_{approach}/(9{\it\mu})$
based on the particle density
${\it\rho}_{p}$
(Joseph et al.
Reference Joseph, Zenit, Hunt and Rosenwinkel2001; Gondret et al.
Reference Gondret, Lance and Petit2002). As
$\mathit{St}$
increases,
${\it\epsilon}$
increases sharply. On the other hand, for the normal collision of a liquid droplet, Legendre et al. (Reference Legendre, Daniel and Guiraud2005) suggested a correlation of
${\it\epsilon}\sim f(\mathit{St}^{\ast })$
, where the modified Stokes number includes the effect of added mass such that
$\mathit{St}^{\ast }=({\it\rho}_{p}+c_{m}{\it\rho})d_{eq}v_{approach}/(9{\it\mu})$
. Here,
$c_{m}$
is the added mass coefficient (3.4). Unlike the solid particle, the normal bouncing of a liquid droplet was highly dissipative and thus the added-mass effect should be considered.
Zenit & Legendre (Reference Zenit and Legendre2009) tried to show that the above correlation also works for the normal bouncing of a gas bubble. From a wide range of experiments (
$\mathit{Re}=4{-}540;\mathit{We}=0.02{-}3.52$
), they found the relationship
$-\log \,{\it\epsilon}\sim (\mathit{Ca}/\mathit{St}^{\ast })^{1/2}$
, where
$\mathit{Ca}={\it\mu}U/{\it\sigma}$
is the capillary number.
Although the bubble considered herein collides with the vertical wall (i.e. lateral bouncing) (figure 3), it would be interesting to study the bubble–wall collision events in terms of
${\it\epsilon}$
. Figure 15 shows the variation of
${\it\epsilon}$
with modified Stokes number,
$\mathit{St}^{\ast }$
, for all rebounding (
${\it\epsilon}>0$
) and bouncing–sliding transition (
${\it\epsilon}=0$
) events measured for all types of wall. As shown, even the lateral bouncing of the large deformable bubble is well presented in terms of
$\mathit{St}^{\ast }$
; that is,
$\log {\it\epsilon}\sim \mathit{St}^{\ast }$
. Here,
$\mathit{St}^{\ast }$
is calculated for each event, based on the maximum wall-normal velocity of the bubble approaching the wall. The best fit is given by
${\it\epsilon}=\exp (5\mathit{St}^{\ast })/30$
. Compared to the acrylic wall,
${\it\epsilon}$
(and the corresponding
$\mathit{St}^{\ast }$
) on the sponge wall are larger, indicating that the dominance of inertia over the viscous effect is more pronounced (i.e. less energy loss). On the other hand,
${\it\epsilon}$
on the hydrophobic walls is smaller than on the acrylic wall and the corresponding
$\mathit{St}^{\ast }$
is small to represent the increased viscous effect (i.e. more energy loss). Clearly, this trend is closely associated with the analysis of transports between energy components in previous sections.
Figure 15. Variation of the coefficient of restitution (
${\it\epsilon}$
) with the modified impact Stokes number (
$\mathit{St}^{\ast }$
) for the rebounding and bouncing–sliding transition events: ○, acrylic; ♦, polyurethane sponge; ▵, PTFE and ▪, roughened PTFE walls.
In the present analysis, we find that the correlation between
${\it\epsilon}$
and
$\mathit{Ca}/\mathit{St}^{\ast }$
, as suggested by Zenit & Legendre (Reference Zenit and Legendre2009), is not clear as that with
$\mathit{St}^{\ast }$
. This may due to the difference between normal and lateral bouncing or the fact that the present bubble (
$d_{eq}\simeq 3.9~\text{mm}$
) is larger than the capillary length of an air–water system,
${\it\lambda}_{c}=\sqrt{{\it\sigma}/{\it\rho}g}\simeq 2.7~\text{mm}$
. In Zenit & Legendre (Reference Zenit and Legendre2009), the size of the bubble considered was smaller than or equivalent to
${\it\lambda}_{c}$
.
4. Conclusions
In the present study, the near-wall rising behaviour of a large deformable bubble has been measured and analysed while varying the initial bubble–wall distance (
$s$
) and boundary condition (no-slip, porous and hydrophobic). In the present set-up, the rising bubble already oscillates laterally (i.e. with an instability path that is a two-dimensional zigzag) even without the wall, and more complex path variations (i.e. sliding, periodic rebounding, migrating away, and non-periodic oscillation without collisions) due to the wall effect were observed. First of all, the wall effect on the bubble motion depended on the initial bubble–wall distance. That is, at
$s/r_{eq}\lesssim 2.0$
, the bubble motion changes significantly with the wall boundary condition; however, the variation is reduced when
$s/r_{eq}>2.0$
. In the regime where the wall effect is strong, especially on the hydrophobic surface, trapped air pockets encouraged the fast formation of a TPC such that a large air bubble slides on the wall, accompanied by a significant shape deformation. Investigation of the bubble inclination angle and energy components shows that the hydrophobicity enhances or reduces the wall effect (loss of inertia) depending on the distance to the wall, but the porosity (i.e. combination of tangential slip and wall-normal seepage) only reduces it. In addition, the effect of relative dominance of inertia and viscous forces on the bubble motion is examined in terms of a restitution coefficient and a good correlation with the modified Stokes number is established.
Previously, in a low-
$\mathit{Re}$
regime, the attraction and repulsion of the bubble with respect to the wall was attributed to the wall-normal pressure gradient predicted by the potential theory and viscous effects from the lubrication theory, respectively (Takemura & Magnaudet Reference Takemura and Magnaudet2003; Sugiyama & Takemura Reference Sugiyama and Takemura2010); however, the shape deformation (surface energy) contributed significantly to the oscillatory motion of the current bubble in a high-
$\mathit{Re}$
and high-
$\mathit{We}$
regime. As a result, a much larger oscillating amplitude (
$h/r_{eq}\sim 2.5{-}3$
) for the rebounding bubble was achieved than that (
${\sim}0.5$
) for a low-
$\mathit{Re}$
bubble (Takemura & Magnaudet Reference Takemura and Magnaudet2003). Also, despite the apparent loss of momentum during bubble–wall collisions, the rising bubble was able to obtain additional energy from the surface deformation and could retain an almost constant rebounding motion, within the observed field of view.
The significant changes in bubble motion identified, caused by modifying the wall configuration, may provide an idea for a way of predicting or controlling the near-wall gas void fraction distribution in gas–liquid flow systems. To deepen our understanding, a future study performing detailed velocity measurements around a rising bubble near a wall by two-phase particle image velocimetry would be worthwhile. For example, it has been previously shown that the vorticity in the two counter-rotating vortices in the bubble wake changes its sign twice during one period of the zigzagging path (Mougin & Magnaudet Reference Mougin and Magnaudet2002, Reference Mougin and Magnaudet2006). In the present study, we measured that the period (i.e. wavelength) of the lateral oscillation (i.e. periodic bouncing) increases or decreases depending on the wall interaction, indicating a substantial change in the wake structures (e.g. the ground effect). Thus it would be informative to see how the bubble wake structure is modified near the wall, depending on the wall configurations considered here. Also, it would be interesting to investigate how the existence of the wall affects the dynamics of a rising bubble in a helical (three-dimensional) motion.
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (NRF-2012M2A8A4055647, NRF-2013R1A1A1008373) via SNU-IAMD, and the Aspiring Researcher Program through Seoul National University (SNU) in 2014, Korea. The authors thank Professor H.-Y. Kim for fruitful comments on the manuscript.
