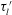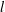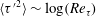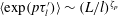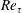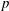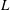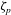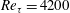1 Introduction
The phenomenological explanation of the transfer of turbulent kinetic energy from large to small scales was introduced in the classical paper by Kolmogorov (Reference Kolmogorov1941) (from now on K41) but the concept of a turbulent cascade in terms of interactions among eddies was proposed earlier by Richardson (Reference Richardson1922), and later by Obukhov (Reference Obukhov1941). Since then, many detailed investigations, mostly in isotropic turbulence (HIT), have greatly advanced our understanding of high-Reynolds-number turbulent flows (Onsager Reference Onsager1949; Batchelor Reference Batchelor1953; Heisenberg Reference Heisenberg1985; Mandelbrot Reference Mandelbrot1999; Jiménez Reference Jiménez2012), with some of them even testing the original idea of Richardson (Reference Richardson1922) in terms of eddies merging and splitting as in Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014b ).
There have been many different attempts to unravel the physical mechanism behind the cascade with varying but complementary tools. A classic physical explanation is given in terms of vortex stretching, where the strain at a given scale stretches vortices at a smaller scale. This interaction induces higher velocities by the conservation of angular momentum, resulting in a net energy transfer from large to small scales (Goto Reference Goto2012; Leung, Swaminathan & Davidson Reference Leung, Swaminathan and Davidson2012; Lozano-Durán, Holzner & Jiménez Reference Lozano-Durán, Holzner and Jiménez2016). It has also been known for some time that the cascade is not one-directional from large to small scales, but that there is a balance between direct and inverse transfers. Most of the evidence for this backscatter originates from filtering techniques in scale space (Piomelli et al. Reference Piomelli, Cabot, Moin and Lee1991; Aoyama et al. Reference Aoyama, Ishihara, Kaneda, Yokokawa and Uno2005; Cardesa et al. Reference Cardesa, Vela-Martín, Dong and Jiménez2015). Other interpretations of the cascade are rooted in statistical mechanics, as the works by Leith (Reference Leith1967) and Orszag (Reference Orszag1970), where energy transfer is modelled as an entropy-driven random process in phase space, with the energy tending to equipartition while drifting either up or down in scale.
In the present work, we focus on the multifractal formalism (Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1991; Frisch & Donnelly Reference Frisch and Donnelly1996; Mandelbrot Reference Mandelbrot1999), which has been successful in characterizing the inertial energy cascade. Within this framework, statistical properties of the flow such as the central moments of the two-point velocity increments and the coarse-grained energy dissipation have been reasonably well estimated. However, instead of energy, here we will study another often-encountered cascading process in wall-bounded turbulence, that is, the momentum. In this case, momentum is transferred from the large energy-containing eddies to smaller scales until it is drained at the wall.
The momentum cascade and the energy cascade are, in many ways, analogous. The sizes of the energy-containing motions are the only relevant length scales in the inertial range; consequently, the energy flux is nearly constant across all scales in the inertial range. The analogous range of scales in wall-bounded flows is the logarithmic range. In the log-region, eddy sizes scale with their distance from the wall and the momentum flux
![]() $-\langle u^{\prime }v^{\prime }\rangle$
is almost constant, where
$-\langle u^{\prime }v^{\prime }\rangle$
is almost constant, where
![]() $u$
,
$u$
,
![]() $v$
are the velocities in the streamwise and wall-normal directions, the superscript
$v$
are the velocities in the streamwise and wall-normal directions, the superscript
![]() $\prime$
indicates fluctuating quantities and
$\prime$
indicates fluctuating quantities and
![]() $\langle \cdot \rangle$
denotes ensemble average. Fluid motions in the inertial range are self-similar, as is also the case for structures in the log-region (see e.g. Del Álamo et al.
Reference Del Álamo, Jimenez, Zandonade and Moser2006; Lozano-Durán, Flores & Jiménez Reference Lozano-Durán, Flores and Jiménez2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013; Baars, Hutchins & Marusic Reference Baars, Hutchins and Marusic2017; Morrill-Winter, Philip & Klewicki Reference Morrill-Winter, Philip and Klewicki2017), consistent with the attached-eddy hypothesis scenario proposed by Townsend (Reference Townsend1980) and extended by Perry & Chong (Reference Perry and Chong1982) and Marusic & Perry (Reference Marusic and Perry1995). Dissipation drains energy at viscous scales
$\langle \cdot \rangle$
denotes ensemble average. Fluid motions in the inertial range are self-similar, as is also the case for structures in the log-region (see e.g. Del Álamo et al.
Reference Del Álamo, Jimenez, Zandonade and Moser2006; Lozano-Durán, Flores & Jiménez Reference Lozano-Durán, Flores and Jiménez2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013; Baars, Hutchins & Marusic Reference Baars, Hutchins and Marusic2017; Morrill-Winter, Philip & Klewicki Reference Morrill-Winter, Philip and Klewicki2017), consistent with the attached-eddy hypothesis scenario proposed by Townsend (Reference Townsend1980) and extended by Perry & Chong (Reference Perry and Chong1982) and Marusic & Perry (Reference Marusic and Perry1995). Dissipation drains energy at viscous scales
![]() $(\unicode[STIX]{x1D708}^{3}/\langle \unicode[STIX]{x1D716}\rangle )^{1/4}$
, where
$(\unicode[STIX]{x1D708}^{3}/\langle \unicode[STIX]{x1D716}\rangle )^{1/4}$
, where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
![]() $\unicode[STIX]{x1D716}$
is the energy dissipation. Momentum, on the other hand, is drained at the wall by fluid motions of viscous scales
$\unicode[STIX]{x1D716}$
is the energy dissipation. Momentum, on the other hand, is drained at the wall by fluid motions of viscous scales
![]() ${\sim}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
, where
${\sim}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
, where
![]() $u_{\unicode[STIX]{x1D70F}}$
is the friction velocity. Both dissipation and wall-stress fluctuations are known to be intermittent (see e.g. Park et al. (Reference Park, Wallace, Wu and Moin2012) and Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013) for discussion on the wall-stress fluctuations).
$u_{\unicode[STIX]{x1D70F}}$
is the friction velocity. Both dissipation and wall-stress fluctuations are known to be intermittent (see e.g. Park et al. (Reference Park, Wallace, Wu and Moin2012) and Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013) for discussion on the wall-stress fluctuations).
Despite the many common features, four decades after the work of Mandelbrot (Reference Mandelbrot1972), the multifractal formalism has not been extended to modelling of the momentum cascade in wall-bounded flows. Even the basic idea of momentum cascade has not been used as much as its energy counterpart by the wall-bounded turbulence community (see e.g. Flores & Jiménez (Reference Flores and Jiménez2010) and Jiménez (Reference Jiménez2012) for some discussion on the difference and common features between the momentum cascade and the energy cascade).
In the present work, the momentum cascade in wall-bounded flows at high Reynolds numbers is investigated using the multifractal framework. A brief introduction to the multifractality is included in § 2. In § 3, an analogy is formally made between the energy cascade and the momentum cascade. The multifractal formalism is then extended to modelling the momentum cascade. Estimates of the scalings of the low-pass filtered wall-shear stress are presented and tested in a direct numerical simulation (DNS) of channel flow at friction Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}=4200$
. Finally, a short discussion and summary are given in § 4.
$Re_{\unicode[STIX]{x1D70F}}=4200$
. Finally, a short discussion and summary are given in § 4.
2 The energy cascade and the multifractal formalism
The cascade process of Richardson (Reference Richardson1922) is sketched in figure 1. In such sketches, eddies of different sizes are often displaced for illustration purposes, as is done in figure 1(b) (see e.g. Frisch & Donnelly Reference Frisch and Donnelly1996; Pope Reference Pope2001).

Figure 1. (a) A sketch of the Richardson cascade. (b) A typical sketch of the Richardson cascade in textbooks. Eddies of different sizes are displaced. (c) A schematic of the energy cascade according to the multifractal formalism.
![]() $\unicode[STIX]{x1D716}_{nj}$
is the volume-averaged dissipation rate in eddy
$\unicode[STIX]{x1D716}_{nj}$
is the volume-averaged dissipation rate in eddy
![]() $W_{nj}$
.
$W_{nj}$
.
![]() $m_{nj}$
is a multiplicative.
$m_{nj}$
is a multiplicative.
![]() $W_{11}$
is the first of the hierarchy. Three hierarchies are sketched.
$W_{11}$
is the first of the hierarchy. Three hierarchies are sketched.
Developments after the celebrated K41 phenomenology have led to the fractal and multifractal formalism (see Frisch & Donnelly Reference Frisch and Donnelly1996) as well as Navier–Stokes-based statistical models including the direct interaction approximation and the shell model (Kraichnan Reference Kraichnan1991, Reference Kraichnan1965; Biferale Reference Biferale2003). The discussion in this section is limited to multifractal models. Figure 1(c) is a schematic of the cascade process according to the multifractal formalism. We define the volume-averaged energy transfer (including both forward cascading and backward scattering) in an eddy
![]() $W_{nj}$
as
$W_{nj}$
as
where
![]() $V_{nj}$
is the volume of eddy
$V_{nj}$
is the volume of eddy
![]() $W_{nj}$
, and the subscript
$W_{nj}$
, and the subscript
![]() $n$
and
$n$
and
![]() $j$
indicate the
$j$
indicate the
![]() $j$
th eddy at the
$j$
th eddy at the
![]() $n$
th cascade step, respectively. Without loss of generality,
$n$
th cascade step, respectively. Without loss of generality,
![]() $\unicode[STIX]{x1D6F1}_{11}=1$
. Analogously the volume-averaged dissipation rate is defined as
$\unicode[STIX]{x1D6F1}_{11}=1$
. Analogously the volume-averaged dissipation rate is defined as
For statistically stationary flows,
![]() $\langle \unicode[STIX]{x1D716}_{nj}\rangle =\langle \unicode[STIX]{x1D6F1}_{nj}\rangle$
by energy conservation. When
$\langle \unicode[STIX]{x1D716}_{nj}\rangle =\langle \unicode[STIX]{x1D6F1}_{nj}\rangle$
by energy conservation. When
![]() $W_{11}$
breaks into
$W_{11}$
breaks into
![]() $W_{21}$
,
$W_{21}$
,
![]() $W_{22}$
, the energy flux is not necessarily equally split into the daughter eddies. The volume-averaged dissipation rates in
$W_{22}$
, the energy flux is not necessarily equally split into the daughter eddies. The volume-averaged dissipation rates in
![]() $W_{21}$
and
$W_{21}$
and
![]() $W_{22}$
are therefore not
$W_{22}$
are therefore not
![]() $1$
in general. Without loss of generality, in eddy
$1$
in general. Without loss of generality, in eddy
![]() $W_{21}$
,
$W_{21}$
,
![]() $\unicode[STIX]{x1D716}_{21}=1\cdot m_{12}$
and in eddy
$\unicode[STIX]{x1D716}_{21}=1\cdot m_{12}$
and in eddy
![]() $W_{22}$
,
$W_{22}$
,
![]() $\unicode[STIX]{x1D716}_{22}=1\cdot m_{22}$
. According to figure 1(a),
$\unicode[STIX]{x1D716}_{22}=1\cdot m_{22}$
. According to figure 1(a),
![]() $\unicode[STIX]{x1D716}_{21}V_{21}+\unicode[STIX]{x1D716}_{22}V_{22}=\unicode[STIX]{x1D716}_{11}V_{11}$
. This cascade process continues, giving rise to eddy
$\unicode[STIX]{x1D716}_{21}V_{21}+\unicode[STIX]{x1D716}_{22}V_{22}=\unicode[STIX]{x1D716}_{11}V_{11}$
. This cascade process continues, giving rise to eddy
![]() $W_{3j}$
and fluid motions of lesser sizes.
$W_{3j}$
and fluid motions of lesser sizes.
After
![]() $n$
steps of this cascade process, the size of the energy-containing eddies decreases to
$n$
steps of this cascade process, the size of the energy-containing eddies decreases to
![]() $l=L/r^{n}$
, where
$l=L/r^{n}$
, where
![]() $L$
is the characteristic length of eddy
$L$
is the characteristic length of eddy
![]() $W_{11}$
and
$W_{11}$
and
![]() $r$
is a constant. Following Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1991),
$r$
is a constant. Following Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1991),
![]() $r$
is set to be 2. The volume-averaged dissipation rate in eddy
$r$
is set to be 2. The volume-averaged dissipation rate in eddy
![]() $W_{nj}$
is
$W_{nj}$
is
where
![]() $j_{1}$
,
$j_{1}$
,
![]() $j_{2},\ldots ,j_{n}$
are indices of the multiplicatives at the 1st, 2nd, and
$j_{2},\ldots ,j_{n}$
are indices of the multiplicatives at the 1st, 2nd, and
![]() $n$
th cascade step that lead to
$n$
th cascade step that lead to
![]() $W_{nj}$
. According to (2.3), the energy cascade is a multiplicative process and only interactions among neighbouring scales are accounted for. For
$W_{nj}$
. According to (2.3), the energy cascade is a multiplicative process and only interactions among neighbouring scales are accounted for. For
![]() $l=L/r^{n}$
in the inertial range, the cascade process is self-similar and
$l=L/r^{n}$
in the inertial range, the cascade process is self-similar and
![]() $m_{ij}$
’s are identically distributed multiplicatives and equal to
$m_{ij}$
’s are identically distributed multiplicatives and equal to
![]() $m$
. Then, equation (2.3) leads to the following scaling laws
$m$
. Then, equation (2.3) leads to the following scaling laws
where the eddy index
![]() $j$
is dropped,
$j$
is dropped,
![]() $\unicode[STIX]{x1D716}_{n}$
is the volume-averaged energy dissipation of a typical eddy at the
$\unicode[STIX]{x1D716}_{n}$
is the volume-averaged energy dissipation of a typical eddy at the
![]() $n$
th cascade step and
$n$
th cascade step and
![]() $p>0$
is an integer.
$p>0$
is an integer.
![]() $\unicode[STIX]{x1D701}_{p}$
is the so-called ‘anomalous exponent’. According to K41, the energy flux is equally split into the daughter eddies at every cascade step, which implies
$\unicode[STIX]{x1D701}_{p}$
is the so-called ‘anomalous exponent’. According to K41, the energy flux is equally split into the daughter eddies at every cascade step, which implies
![]() $m\equiv 1$
and
$m\equiv 1$
and
![]() $\langle \unicode[STIX]{x1D716}_{l}^{p}\rangle =\langle \unicode[STIX]{x1D716}_{1}\rangle ^{p}$
. Later, Kolmogorov (Reference Kolmogorov1962) modelled
$\langle \unicode[STIX]{x1D716}_{l}^{p}\rangle =\langle \unicode[STIX]{x1D716}_{1}\rangle ^{p}$
. Later, Kolmogorov (Reference Kolmogorov1962) modelled
![]() $\log (m)$
as a Gaussian random variable. According to this log-normal model,
$\log (m)$
as a Gaussian random variable. According to this log-normal model,
![]() $\unicode[STIX]{x1D701}_{p}=c_{1}p^{2}+c_{2}p$
, where
$\unicode[STIX]{x1D701}_{p}=c_{1}p^{2}+c_{2}p$
, where
![]() $c_{1}$
,
$c_{1}$
,
![]() $c_{2}$
are constants. The reader is directed to Frisch & Donnelly (Reference Frisch and Donnelly1996) for detailed discussions on other fractal and multifractal models including the
$c_{2}$
are constants. The reader is directed to Frisch & Donnelly (Reference Frisch and Donnelly1996) for detailed discussions on other fractal and multifractal models including the
![]() $\unicode[STIX]{x1D6FD}$
model (Frisch, Sulem & Nelkin Reference Frisch, Sulem and Nelkin1978), the
$\unicode[STIX]{x1D6FD}$
model (Frisch, Sulem & Nelkin Reference Frisch, Sulem and Nelkin1978), the
![]() $p$
-model (Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1987), etc. The brief overview here is merely a short introduction to the basic ideas behind the multifractal formalism and is not meant to be a comprehensive review of the work on the topic of energy cascade.
$p$
-model (Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1987), etc. The brief overview here is merely a short introduction to the basic ideas behind the multifractal formalism and is not meant to be a comprehensive review of the work on the topic of energy cascade.
3 The momentum cascade
Figure 2 is a schematic of the momentum cascade in high-Reynolds-number wall-bounded turbulence. The streamwise momentum is carried by the large-scale eddies in the boundary layer, then passed to small-scale and lesser-scale eddies and last drained at the wall. The momentum transfer in wall turbulence is governed by the flux term
![]() $(-\langle u(v+V_{r})\rangle +\unicode[STIX]{x1D708}\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)$
, where
$(-\langle u(v+V_{r})\rangle +\unicode[STIX]{x1D708}\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y)$
, where
![]() $V_{r}$
is the wall-normal velocity of the frame of reference. Although it is the wall-normal derivative of the flux term that enters the momentum equation, whose sign is independent of the frame of reference, the sign of the flux term itself does depend on
$V_{r}$
is the wall-normal velocity of the frame of reference. Although it is the wall-normal derivative of the flux term that enters the momentum equation, whose sign is independent of the frame of reference, the sign of the flux term itself does depend on
![]() $V_{r}$
(Jiménez Reference Jiménez2016). To avoid ambiguity, we consider the momentum cascade of the fluctuating velocities in this study, as is usually done for the energy cascade in HIT. In this case, the mean velocity does not play a role, and the direction of the momentum transfer is determined by the flux term
$V_{r}$
(Jiménez Reference Jiménez2016). To avoid ambiguity, we consider the momentum cascade of the fluctuating velocities in this study, as is usually done for the energy cascade in HIT. In this case, the mean velocity does not play a role, and the direction of the momentum transfer is determined by the flux term
![]() $\langle u^{\prime }v^{\prime }\rangle$
, which is independent of the frame of reference. In wall-bounded flows, where positive
$\langle u^{\prime }v^{\prime }\rangle$
, which is independent of the frame of reference. In wall-bounded flows, where positive
![]() $y$
is the wall-normal direction and points away from the wall,
$y$
is the wall-normal direction and points away from the wall,
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
are negatively correlated on average. This determines the momentum transfer, on average, being from the bulk region to the wall. Unless noted otherwise, wall units are used for normalization.
$v^{\prime }$
are negatively correlated on average. This determines the momentum transfer, on average, being from the bulk region to the wall. Unless noted otherwise, wall units are used for normalization.

Figure 2. A schematic of the momentum cascade from large-scale eddies to small-scale eddies in wall-bounded flows. The shear stresses on the wall bear footprints of eddies of all scales (lightly shaded grey).
The quantity of interest here is the low-pass filtered streamwise wall-stress fluctuation, which is defined as
where
![]() $\unicode[STIX]{x1D70F}$
is the wall-shear stress in the flow direction,
$\unicode[STIX]{x1D70F}$
is the wall-shear stress in the flow direction,
![]() $G_{l}$
is a filtering kernel, and the subscript
$G_{l}$
is a filtering kernel, and the subscript
![]() $l$
is the filtering length scale.
$l$
is the filtering length scale.
![]() $\unicode[STIX]{x1D70F}_{l}^{\prime }=0$
for
$\unicode[STIX]{x1D70F}_{l}^{\prime }=0$
for
![]() $l/\unicode[STIX]{x1D6FF}\rightarrow \infty$
and
$l/\unicode[STIX]{x1D6FF}\rightarrow \infty$
and
![]() $\unicode[STIX]{x1D70F}_{l}^{\prime }=\unicode[STIX]{x1D70F}^{\prime }$
for
$\unicode[STIX]{x1D70F}_{l}^{\prime }=\unicode[STIX]{x1D70F}^{\prime }$
for
![]() $l/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})\rightarrow 0$
. We model the low-pass filtered wall-stress fluctuation as an additive process (see Yang, Marusic & Meneveau Reference Yang, Marusic and Meneveau2016a
, for other flow quantities that follow additive processes)
$l/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})\rightarrow 0$
. We model the low-pass filtered wall-stress fluctuation as an additive process (see Yang, Marusic & Meneveau Reference Yang, Marusic and Meneveau2016a
, for other flow quantities that follow additive processes)
where both
![]() $\unicode[STIX]{x1D70F}_{l}^{\prime }$
and the addends
$\unicode[STIX]{x1D70F}_{l}^{\prime }$
and the addends
![]() $a_{i}$
are functions of spatial coordinates at the wall (
$a_{i}$
are functions of spatial coordinates at the wall (
![]() $x$
and
$x$
and
![]() $z$
), an addend
$z$
), an addend
![]() $a_{i}$
is an increment in
$a_{i}$
is an increment in
![]() $\unicode[STIX]{x1D70F}_{l}^{\prime }$
due to an eddy of height
$\unicode[STIX]{x1D70F}_{l}^{\prime }$
due to an eddy of height
![]() ${\sim}\unicode[STIX]{x1D6FF}/2^{i}$
.
${\sim}\unicode[STIX]{x1D6FF}/2^{i}$
.
![]() $\unicode[STIX]{x1D6FF}$
is the boundary layer height and the number of addends is
$\unicode[STIX]{x1D6FF}$
is the boundary layer height and the number of addends is
![]() $n_{l}\sim \log _{2}(\unicode[STIX]{x1D6FF}/l)$
. The spatial dependence will be dropped hereafter for brevity. Following the multifractal formalism, the addends
$n_{l}\sim \log _{2}(\unicode[STIX]{x1D6FF}/l)$
. The spatial dependence will be dropped hereafter for brevity. Following the multifractal formalism, the addends
![]() $a_{i}$
are identically and independently distributed (i.i.d.) and equal to
$a_{i}$
are identically and independently distributed (i.i.d.) and equal to
![]() $a$
. Filtering at the viscous scale
$a$
. Filtering at the viscous scale
![]() ${\sim}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
gives back the unfiltered wall-shear stress
${\sim}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
gives back the unfiltered wall-shear stress
![]() $\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{C\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}}^{\prime }$
, where
$\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{C\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}}^{\prime }$
, where
![]() $C$
is an
$C$
is an
![]() $O(1)$
constant. According to (3.2), the variance of the wall-shear stress fluctuations in boundary layer flows follows
$O(1)$
constant. According to (3.2), the variance of the wall-shear stress fluctuations in boundary layer flows follows
where
![]() $\langle a_{i}a_{j}\rangle =0$
for
$\langle a_{i}a_{j}\rangle =0$
for
![]() $i\neq j$
. It then follows that STD
$i\neq j$
. It then follows that STD
![]() $(\unicode[STIX]{x1D70F}^{\prime })\equiv \sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }\sim \sqrt{\log (Re_{\unicode[STIX]{x1D70F}})}$
. This is in contrast to the scaling suggested by Schlatter & Örlü (Reference Schlatter and Örlü2010)
$(\unicode[STIX]{x1D70F}^{\prime })\equiv \sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }\sim \sqrt{\log (Re_{\unicode[STIX]{x1D70F}})}$
. This is in contrast to the scaling suggested by Schlatter & Örlü (Reference Schlatter and Örlü2010)
and the one proposed by Alfredsson et al. (Reference Alfredsson, Johansson, Haritonidis and Eckelmann1988), STD
![]() $(\unicode[STIX]{x1D70F}^{\prime })=0.4$
. Figures 3(a,b) show respectively the standard deviation and the variance of the wall-shear stress fluctuations in boundary layer flows as functions of the friction Reynolds number. Both scalings in (3.3), (3.4) provide reasonably good fits for the data from low to moderate Reynolds numbers. Considering this, including DNS data, which are between
$(\unicode[STIX]{x1D70F}^{\prime })=0.4$
. Figures 3(a,b) show respectively the standard deviation and the variance of the wall-shear stress fluctuations in boundary layer flows as functions of the friction Reynolds number. Both scalings in (3.3), (3.4) provide reasonably good fits for the data from low to moderate Reynolds numbers. Considering this, including DNS data, which are between
![]() $Re_{\unicode[STIX]{x1D70F}}\approx 180$
(Kim, Moin & Moser Reference Kim, Moin and Moser1987) and
$Re_{\unicode[STIX]{x1D70F}}\approx 180$
(Kim, Moin & Moser Reference Kim, Moin and Moser1987) and
![]() $Re_{\unicode[STIX]{x1D70F}}\approx 5200$
(Lee & Moser Reference Lee and Moser2015) is not very useful here. Predictions according to (3.3), (3.4) are only tellingly different at high Reynolds numbers (
$Re_{\unicode[STIX]{x1D70F}}\approx 5200$
(Lee & Moser Reference Lee and Moser2015) is not very useful here. Predictions according to (3.3), (3.4) are only tellingly different at high Reynolds numbers (
![]() $Re_{\unicode[STIX]{x1D70F}}>10^{5}$
), where only one data point is available. The available data generally favour (3.3). The evidence here, however, is not conclusive, because the data from Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013) are not direct measurements but are inferred results based on a calibrated near-wall small-scale signal and a modulation model. Future confirmation/refutation of the scaling in (3.3) will need measurements of the wall-shear stresses from one same facility at friction Reynolds numbers that span at least two decades (from
$Re_{\unicode[STIX]{x1D70F}}>10^{5}$
), where only one data point is available. The available data generally favour (3.3). The evidence here, however, is not conclusive, because the data from Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013) are not direct measurements but are inferred results based on a calibrated near-wall small-scale signal and a modulation model. Future confirmation/refutation of the scaling in (3.3) will need measurements of the wall-shear stresses from one same facility at friction Reynolds numbers that span at least two decades (from
![]() $Re_{\unicode[STIX]{x1D70F}}\approx 10^{3}$
to
$Re_{\unicode[STIX]{x1D70F}}\approx 10^{3}$
to
![]() $10^{5}$
and higher), an investigation that may be done at CICLoPE (Vinuesa, Duncan & Nagib Reference Vinuesa, Duncan and Nagib2016).
$10^{5}$
and higher), an investigation that may be done at CICLoPE (Vinuesa, Duncan & Nagib Reference Vinuesa, Duncan and Nagib2016).

Figure 3. (a)
![]() $\sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }$
as a function of
$\sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }$
as a function of
![]() $Re_{\unicode[STIX]{x1D70F}}$
. The data are reported in Österlund (Reference Österlund1999) and Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013). The dotted line corresponds to
$Re_{\unicode[STIX]{x1D70F}}$
. The data are reported in Österlund (Reference Österlund1999) and Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013). The dotted line corresponds to
![]() $\sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }=0.4$
from Alfredsson et al. (Reference Alfredsson, Johansson, Haritonidis and Eckelmann1988). The dashed line corresponds to the scaling
$\sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }=0.4$
from Alfredsson et al. (Reference Alfredsson, Johansson, Haritonidis and Eckelmann1988). The dashed line corresponds to the scaling
![]() $\sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }=0.24+0.018\ln (Re_{\unicode[STIX]{x1D70F}})$
(Schlatter & Örlü Reference Schlatter and Örlü2010). The solid line is the least-square fit of the data according to (3.3) and is
$\sqrt{\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle }=0.24+0.018\ln (Re_{\unicode[STIX]{x1D70F}})$
(Schlatter & Örlü Reference Schlatter and Örlü2010). The solid line is the least-square fit of the data according to (3.3) and is
![]() $\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle =0.10+0.68\ln (Re_{\unicode[STIX]{x1D70F}})$
. (b)
$\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle =0.10+0.68\ln (Re_{\unicode[STIX]{x1D70F}})$
. (b)
![]() $\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle$
as a function of
$\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle$
as a function of
![]() $Re_{\unicode[STIX]{x1D70F}}$
. The dashed line and the solid line are straight lines in (a) and (b), respectively.
$Re_{\unicode[STIX]{x1D70F}}$
. The dashed line and the solid line are straight lines in (a) and (b), respectively.
It is worth noting that according to (3.2),
![]() $\exp (\unicode[STIX]{x1D70F}_{l}^{\prime })$
follows a multiplicative process. Therefore
$\exp (\unicode[STIX]{x1D70F}_{l}^{\prime })$
follows a multiplicative process. Therefore
![]() $\exp (\unicode[STIX]{x1D70F}_{l}^{\prime })$
is formally analogous to the energy dissipation rate in HIT. Figure 4(a) shows
$\exp (\unicode[STIX]{x1D70F}_{l}^{\prime })$
is formally analogous to the energy dissipation rate in HIT. Figure 4(a) shows
![]() $\exp (\unicode[STIX]{x1D70F}^{\prime })$
as a function of the spanwise coordinate. The signal resembles dissipation signals in HIT (see e.g. figure 1(b) in Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1991) for comparison). The data are from the DNS of Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014a
) of channel flow at
$\exp (\unicode[STIX]{x1D70F}^{\prime })$
as a function of the spanwise coordinate. The signal resembles dissipation signals in HIT (see e.g. figure 1(b) in Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1991) for comparison). The data are from the DNS of Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014a
) of channel flow at
![]() $Re_{\unicode[STIX]{x1D70F}}\approx 4200$
.
$Re_{\unicode[STIX]{x1D70F}}\approx 4200$
.

Figure 4.
![]() $\exp (\unicode[STIX]{x1D70F}^{\prime })$
as a function of the spanwise coordinate in channel flow at
$\exp (\unicode[STIX]{x1D70F}^{\prime })$
as a function of the spanwise coordinate in channel flow at
![]() $Re_{\unicode[STIX]{x1D70F}}=4200$
. The dashed line corresponds to
$Re_{\unicode[STIX]{x1D70F}}=4200$
. The dashed line corresponds to
![]() $\unicode[STIX]{x1D70F}^{\prime }=0$
.
$\unicode[STIX]{x1D70F}^{\prime }=0$
.
We have examined
![]() $\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle$
as a function of the friction Reynolds number in figure 3 and
$\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle$
as a function of the friction Reynolds number in figure 3 and
![]() $\exp (p\unicode[STIX]{x1D70F}^{\prime })$
qualitatively in figure 4. Next, we investigate the scaling behaviour of the moment generating function
$\exp (p\unicode[STIX]{x1D70F}^{\prime })$
qualitatively in figure 4. Next, we investigate the scaling behaviour of the moment generating function
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
, which is a useful statistical tool in general and central moments can be derived by
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
, which is a useful statistical tool in general and central moments can be derived by
![]() $\langle \unicode[STIX]{x1D719}^{n}\rangle =\text{d}\langle \exp (p\unicode[STIX]{x1D719})\rangle /\text{d}p|_{p=0}$
, where
$\langle \unicode[STIX]{x1D719}^{n}\rangle =\text{d}\langle \exp (p\unicode[STIX]{x1D719})\rangle /\text{d}p|_{p=0}$
, where
![]() $\unicode[STIX]{x1D719}$
is a generic random statistical quantity. To make predictions of the scaling behaviour of
$\unicode[STIX]{x1D719}$
is a generic random statistical quantity. To make predictions of the scaling behaviour of
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as a function of
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as a function of
![]() $l$
, we follow the same steps that lead to (2.4). Considering addends being i.i.d.,
$l$
, we follow the same steps that lead to (2.4). Considering addends being i.i.d.,
 $$\begin{eqnarray}\displaystyle \langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle & {\sim} & \displaystyle \langle \exp (pa_{1})\rangle \langle \exp (pa_{2})\rangle \langle \exp (pa_{3})\rangle \cdots \langle \exp (pa_{n_{l}})\rangle \nonumber\\ \displaystyle & {\sim} & \displaystyle \langle \exp (pa)\rangle ^{n_{l}}\sim (\unicode[STIX]{x1D6FF}/l)^{\log _{2}(\langle \exp (pa)\rangle )}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FF}/l)^{\unicode[STIX]{x1D701}_{p}},\quad \unicode[STIX]{x1D701}_{p}=\log _{2}(\langle \exp (pa)\rangle ).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle & {\sim} & \displaystyle \langle \exp (pa_{1})\rangle \langle \exp (pa_{2})\rangle \langle \exp (pa_{3})\rangle \cdots \langle \exp (pa_{n_{l}})\rangle \nonumber\\ \displaystyle & {\sim} & \displaystyle \langle \exp (pa)\rangle ^{n_{l}}\sim (\unicode[STIX]{x1D6FF}/l)^{\log _{2}(\langle \exp (pa)\rangle )}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FF}/l)^{\unicode[STIX]{x1D701}_{p}},\quad \unicode[STIX]{x1D701}_{p}=\log _{2}(\langle \exp (pa)\rangle ).\end{eqnarray}$$
While isotropy is expected at small scales in the bulk region (at scales
![]() $\ll y$
, see Saddoughi & Veeravalli (Reference Saddoughi and Veeravalli1994) for detailed discussion), at the wall, isotropy is not expected at any scale because of the dominating effect of shear. Because isotropy is lost, spatial filtering in wall-bounded flows is not as straightforward as it is in HIT. As the channel is populated with long-living elongated streaks that span the entire periodic domain, filtering flow quantities in the
$\ll y$
, see Saddoughi & Veeravalli (Reference Saddoughi and Veeravalli1994) for detailed discussion), at the wall, isotropy is not expected at any scale because of the dominating effect of shear. Because isotropy is lost, spatial filtering in wall-bounded flows is not as straightforward as it is in HIT. As the channel is populated with long-living elongated streaks that span the entire periodic domain, filtering flow quantities in the
![]() $x$
direction needs many independent realizations for convergence. Limited by the number of DNS samples, the streamwise wall-shear stress is low-pass filtered in the spanwise direction only. Filtering in the streamwise direction leads to less converged data and limits the analysis to small
$x$
direction needs many independent realizations for convergence. Limited by the number of DNS samples, the streamwise wall-shear stress is low-pass filtered in the spanwise direction only. Filtering in the streamwise direction leads to less converged data and limits the analysis to small
![]() $|p|$
values. However, similar observations can still be made and none of the conclusions here are affected if the wall-shear stress is filtered in the streamwise direction. Figure 5(a) shows
$|p|$
values. However, similar observations can still be made and none of the conclusions here are affected if the wall-shear stress is filtered in the streamwise direction. Figure 5(a) shows
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
for
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
for
![]() $p=-4$
,
$p=-4$
,
![]() $-3$
,
$-3$
,
![]() $1$
,
$1$
,
![]() $1.5$
as functions of the filtering length. Power-law behaviour is found in the enclosed region between
$1.5$
as functions of the filtering length. Power-law behaviour is found in the enclosed region between
![]() $l^{+}\approx 350$
and
$l^{+}\approx 350$
and
![]() $l/\unicode[STIX]{x1D6FF}=0.8$
, thus providing direct support to (3.2). The bounds of the power-law scalings in flat-plate boundary layer flows are expected to be flow-dependent but not Reynolds-number-dependent (see e.g. de Silva et al.
Reference de Silva, Marusic, Woodcock and Meneveau2015). In flows where the wall is curved, the length scale imposed by the surface curvature
$l/\unicode[STIX]{x1D6FF}=0.8$
, thus providing direct support to (3.2). The bounds of the power-law scalings in flat-plate boundary layer flows are expected to be flow-dependent but not Reynolds-number-dependent (see e.g. de Silva et al.
Reference de Silva, Marusic, Woodcock and Meneveau2015). In flows where the wall is curved, the length scale imposed by the surface curvature
![]() $l_{R}$
might limit the size of the attached eddies, thus limiting the range of the scalings to
$l_{R}$
might limit the size of the attached eddies, thus limiting the range of the scalings to
![]() ${\sim}O(l_{R})$
.
${\sim}O(l_{R})$
.

Figure 5. (a)
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as functions of the filtering length for
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as functions of the filtering length for
![]() $p=-4$
,
$p=-4$
,
![]() $-3$
,
$-3$
,
![]() $1$
,
$1$
,
![]() $1.5$
. The enclosed region corresponds to
$1.5$
. The enclosed region corresponds to
![]() $340<l_{z}^{+}$
and
$340<l_{z}^{+}$
and
![]() $l/\unicode[STIX]{x1D6FF}<0.8$
. The stress is low-pass filtered in the spanwise direction. The bold line indicates the slope of
$l/\unicode[STIX]{x1D6FF}<0.8$
. The stress is low-pass filtered in the spanwise direction. The bold line indicates the slope of
![]() $\langle \exp (-4\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
in the enclosed region and the slope is 0.14. (b)
$\langle \exp (-4\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
in the enclosed region and the slope is 0.14. (b)
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as functions of
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as functions of
![]() $\langle \exp (-4\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
for
$\langle \exp (-4\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
for
![]() $p=-4$
,
$p=-4$
,
![]() $-3$
,
$-3$
,
![]() $-2$
,
$-2$
,
![]() $-1$
. The corresponding values of the reference scaling at
$-1$
. The corresponding values of the reference scaling at
![]() $l=\unicode[STIX]{x1D6FF}$
,
$l=\unicode[STIX]{x1D6FF}$
,
![]() $0.1\unicode[STIX]{x1D6FF}$
and
$0.1\unicode[STIX]{x1D6FF}$
and
![]() $l^{+}=100$
,
$l^{+}=100$
,
![]() $10$
are indicated using thin vertical lines.
$10$
are indicated using thin vertical lines.
The power-law scalings shown in figure 5(a) are often referred to as ‘strong self-similarity’. The existence of ‘strong self-similarity’ depends on firstly the multifractal formalism, equation (3.2), and secondly the additives being i.i.d. As the addends are only i.i.d. in the log-region, ‘strong self-similarity’ can only be observed in the log-region and the corresponding range of spanwise scales, assuming that the momentum carrying eddies have an average spanwise-to-wall-normal aspect ratio 2–3 (Del Álamo et al.
Reference Del Álamo, Jimenez, Zandonade and Moser2006; Lozano-Durán et al.
Reference Lozano-Durán, Flores and Jiménez2012). Even supposing that the low-pass filtered streamwise stress fluctuation does follow an additive process across all scales, the addends of eddies in the bulk and the viscosity-affected regions are not expected to be statistically similar to those in the log-region. As a result, ‘strong self-similarity’ fails at viscosity-affected scales (
![]() $l^{+}\lesssim 300$
) and at integral scales (
$l^{+}\lesssim 300$
) and at integral scales (
![]() $l\sim O(\unicode[STIX]{x1D6FF})$
). At these scales, the multifractal formalism may be examined using the so-called extended self-similarity (ESS), which are power-law scalings of
$l\sim O(\unicode[STIX]{x1D6FF})$
). At these scales, the multifractal formalism may be examined using the so-called extended self-similarity (ESS), which are power-law scalings of
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as functions of
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
as functions of
![]() $\langle \exp (p_{o}\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
for fixed
$\langle \exp (p_{o}\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
for fixed
![]() $p_{o}$
. ESS does not depend critically on the addends being i.i.d. (see detailed discussion in Yang et al.
Reference Yang, Meneveau, Marusic and Biferale2016c
), and therefore it is often referred to as ‘weak self-similarity’. Figure 5(b) shows the ESS scalings for
$p_{o}$
. ESS does not depend critically on the addends being i.i.d. (see detailed discussion in Yang et al.
Reference Yang, Meneveau, Marusic and Biferale2016c
), and therefore it is often referred to as ‘weak self-similarity’. Figure 5(b) shows the ESS scalings for
![]() $p_{o}=-4$
. In contrast to ‘strong self-similarity’, which is only found in the log-region, ESS scalings are found across all scales from
$p_{o}=-4$
. In contrast to ‘strong self-similarity’, which is only found in the log-region, ESS scalings are found across all scales from
![]() $l^{+}=10$
to
$l^{+}=10$
to
![]() $l=\unicode[STIX]{x1D6FF}$
. This suggests that the low-pass filtered streamwise stress fluctuations may be modelled using (3.2) across all scales, although the large-scale flow motions and the viscosity affect the statistical properties of the addends in the bulk region and the near-wall region, respectively.
$l=\unicode[STIX]{x1D6FF}$
. This suggests that the low-pass filtered streamwise stress fluctuations may be modelled using (3.2) across all scales, although the large-scale flow motions and the viscosity affect the statistical properties of the addends in the bulk region and the near-wall region, respectively.
ESS provides a measure of
![]() $\unicode[STIX]{x1D701}_{p}/\unicode[STIX]{x1D701}_{p_{o}}$
. Therefore, the anomalous exponent
$\unicode[STIX]{x1D701}_{p}/\unicode[STIX]{x1D701}_{p_{o}}$
. Therefore, the anomalous exponent
![]() $\unicode[STIX]{x1D701}_{p}$
is known given a
$\unicode[STIX]{x1D701}_{p}$
is known given a
![]() $\unicode[STIX]{x1D701}_{p_{o}}$
(Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). While HIT admits an exact scaling
$\unicode[STIX]{x1D701}_{p_{o}}$
(Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). While HIT admits an exact scaling
![]() $\langle \unicode[STIX]{x1D716}_{n}\rangle \sim \langle \unicode[STIX]{x1D716}\rangle$
, the same is not true for the momentum cascade counterpart (except for the trivial case of
$\langle \unicode[STIX]{x1D716}_{n}\rangle \sim \langle \unicode[STIX]{x1D716}\rangle$
, the same is not true for the momentum cascade counterpart (except for the trivial case of
![]() $p=0$
,
$p=0$
,
![]() $\langle \exp (0\cdot \unicode[STIX]{x1D70F}_{l})\rangle =1$
). As a result, the analogous anomalous exponent defined in (3.5) needs to be measured directly by fitting the data in the enclosed region in figure 5(a). The measured exponent
$\langle \exp (0\cdot \unicode[STIX]{x1D70F}_{l})\rangle =1$
). As a result, the analogous anomalous exponent defined in (3.5) needs to be measured directly by fitting the data in the enclosed region in figure 5(a). The measured exponent
![]() $\unicode[STIX]{x1D701}_{p}$
is shown as a function of the power exponent
$\unicode[STIX]{x1D701}_{p}$
is shown as a function of the power exponent
![]() $p$
in figure 6(a), which, according to the multifractal formalism,
$p$
in figure 6(a), which, according to the multifractal formalism,
![]() $\unicode[STIX]{x1D701}_{p}=\log _{2}(\langle \exp (pa)\rangle )$
. The anomalous exponent
$\unicode[STIX]{x1D701}_{p}=\log _{2}(\langle \exp (pa)\rangle )$
. The anomalous exponent
![]() $\unicode[STIX]{x1D701}_{p}$
was defined for the MGF of the streamwise velocity fluctuation (Yang, Marusic & Meneveau Reference Yang, Marusic and Meneveau2016b
), which was subsequently found to be universal (Krug et al.
Reference Krug, Yang, de Silva, Ostilla-Monico, Verzicco, Marusic and Lohse2017). While the universality of the anomalous exponent defined here has not been tested, it is likely that
$\unicode[STIX]{x1D701}_{p}$
was defined for the MGF of the streamwise velocity fluctuation (Yang, Marusic & Meneveau Reference Yang, Marusic and Meneveau2016b
), which was subsequently found to be universal (Krug et al.
Reference Krug, Yang, de Silva, Ostilla-Monico, Verzicco, Marusic and Lohse2017). While the universality of the anomalous exponent defined here has not been tested, it is likely that
![]() $\unicode[STIX]{x1D701}_{p}$
for the wall-shear stress is also universal. It should be noted that without invoking the multifractal assumption,
$\unicode[STIX]{x1D701}_{p}$
for the wall-shear stress is also universal. It should be noted that without invoking the multifractal assumption,
![]() $a$
is a constant, and
$a$
is a constant, and
![]() $\unicode[STIX]{x1D701}_{p}$
is a linear function of
$\unicode[STIX]{x1D701}_{p}$
is a linear function of
![]() $p$
. Following Kolmogorov (Reference Kolmogorov1962), and modelling the addends
$p$
. Following Kolmogorov (Reference Kolmogorov1962), and modelling the addends
![]() $a$
as Gaussian random variables, it is straightforward to show that
$a$
as Gaussian random variables, it is straightforward to show that
![]() $\unicode[STIX]{x1D701}_{p}=C_{LN}p^{2}$
, where
$\unicode[STIX]{x1D701}_{p}=C_{LN}p^{2}$
, where
![]() $C_{LN}$
is a constant. As is seen,
$C_{LN}$
is a constant. As is seen,
![]() $C_{LN}=0.0089$
gives a fairly good fit for the measured exponents. Because rare events are not fully accounted for in a log-normal model (Landau & Lifshitz Reference Landau and Lifshitz1987), the fact that log-normal model fits the measurements well suggests that the momentum cascade is less intermittent than the energy cascade counterpart.
$C_{LN}=0.0089$
gives a fairly good fit for the measured exponents. Because rare events are not fully accounted for in a log-normal model (Landau & Lifshitz Reference Landau and Lifshitz1987), the fact that log-normal model fits the measurements well suggests that the momentum cascade is less intermittent than the energy cascade counterpart.

Figure 6. (a) Anomalous exponent as a function of the power exponent
![]() $p$
. The solid line corresponds to
$p$
. The solid line corresponds to
![]() $0.0098p^{2}$
. (b) Premultiplied p.d.f. of
$0.0098p^{2}$
. (b) Premultiplied p.d.f. of
![]() $\exp (p\unicode[STIX]{x1D70F}^{\prime })$
for
$\exp (p\unicode[STIX]{x1D70F}^{\prime })$
for
![]() $p=-4$
and
$p=-4$
and
![]() $p=1.5$
. The magnitude of the premultiplied p.d.f. is not relevant for the present work and is not shown here.
$p=1.5$
. The magnitude of the premultiplied p.d.f. is not relevant for the present work and is not shown here.
Finally, the data convergence can be examined using the premultiplied probability density function (p.d.f.). Figure 6(b) shows the premultiplied p.d.f.s of
![]() $\exp (p\unicode[STIX]{x1D70F}^{\prime })$
for
$\exp (p\unicode[STIX]{x1D70F}^{\prime })$
for
![]() $p=-4$
and
$p=-4$
and
![]() $1.5$
. Because
$1.5$
. Because
![]() $\exp (p\unicode[STIX]{x1D70F}^{\prime })$
emphasizes fluctuations that have the same sign as
$\exp (p\unicode[STIX]{x1D70F}^{\prime })$
emphasizes fluctuations that have the same sign as
![]() $p$
,
$p$
,
![]() $\langle \exp (p_{1}\unicode[STIX]{x1D70F}^{\prime })\rangle$
converges more slowly than
$\langle \exp (p_{1}\unicode[STIX]{x1D70F}^{\prime })\rangle$
converges more slowly than
![]() $\langle \exp (p_{2}\unicode[STIX]{x1D70F}^{\prime })\rangle$
for
$\langle \exp (p_{2}\unicode[STIX]{x1D70F}^{\prime })\rangle$
for
![]() $|p_{1}|>|p_{2}|$
,
$|p_{1}|>|p_{2}|$
,
![]() $p_{1}p_{2}>0$
. Also, because low-pass filtering damps fluctuations in a signal,
$p_{1}p_{2}>0$
. Also, because low-pass filtering damps fluctuations in a signal,
![]() $\langle \exp (p\unicode[STIX]{x1D70F}^{\prime })\rangle$
converges more slowly than
$\langle \exp (p\unicode[STIX]{x1D70F}^{\prime })\rangle$
converges more slowly than
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
(see O’Neil & Meneveau (Reference O’Neil and Meneveau1993), Yang et al. (Reference Yang, Marusic and Meneveau2016b
) for detailed discussion). As
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
(see O’Neil & Meneveau (Reference O’Neil and Meneveau1993), Yang et al. (Reference Yang, Marusic and Meneveau2016b
) for detailed discussion). As
![]() $\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
is the area under the its premultiplied p.d.f., figure 6(b) suggests that both
$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle$
is the area under the its premultiplied p.d.f., figure 6(b) suggests that both
![]() $\langle \exp (-4\unicode[STIX]{x1D70F}^{\prime })\rangle$
and
$\langle \exp (-4\unicode[STIX]{x1D70F}^{\prime })\rangle$
and
![]() $\langle \exp (1.5\unicode[STIX]{x1D70F}^{\prime })\rangle$
are statistically converged. Then, by the reasoning above, all the statistics shown in figure 5(a) are converged. Limited by the number of DNS samples, statistics for
$\langle \exp (1.5\unicode[STIX]{x1D70F}^{\prime })\rangle$
are statistically converged. Then, by the reasoning above, all the statistics shown in figure 5(a) are converged. Limited by the number of DNS samples, statistics for
![]() $p<-4$
and
$p<-4$
and
![]() $p>1.5$
are poorly converged and therefore are not reported here.
$p>1.5$
are poorly converged and therefore are not reported here.
4 Discussion and summary
In the present work, we have argued that the momentum cascade in wall-bounded turbulence is analogous to the energy cascade in HIT, and that it can be modelled as an additive process within the multifractal formalism. Analogous to the coarse-grained dissipation rates, the statistics associated to the exponential of the coarse-grained wall stresses follows power-law scalings. This leads to a new prediction for the variance of the wall-shear stress, that should scale as
![]() $\log (Re_{\unicode[STIX]{x1D70F}})$
, in contrast to previous works, where the prediction holds for the standard deviation instead (Schlatter & Örlü Reference Schlatter and Örlü2010). In addition, we have shown that the wall stress satisfies reasonably well the ‘strong self-similarity’ hypothesis for scales spanning along the log-layer, and that the ‘extended self-similarity’ holds at all scales.
$\log (Re_{\unicode[STIX]{x1D70F}})$
, in contrast to previous works, where the prediction holds for the standard deviation instead (Schlatter & Örlü Reference Schlatter and Örlü2010). In addition, we have shown that the wall stress satisfies reasonably well the ‘strong self-similarity’ hypothesis for scales spanning along the log-layer, and that the ‘extended self-similarity’ holds at all scales.
Despite the similarities between the energy and momentum cascades, there are many features in the former that are not present in the latter. (1) While the flow is roughly isotropic in the inertial range, the momentum cascade is hardly isotropic due to the effect of the shear. (2) The momentum cascade follows fairly well an additive process but the energy cascade is better represented by a multiplicative one. (3) Because
![]() $\unicode[STIX]{x1D70F}^{\prime }$
is not positive definite, back-scattering is allowed at dissipative scales in the momentum cascade but energy back-scattering hardly happens close to the dissipative scales. The consequence of this last point is that subgrid scale (SGS) modelling of the momentum cascade (in today’s term, LES wall modelling, see e.g. Piomelli & Balaras (Reference Piomelli and Balaras2002)) is probably more challenging than the conventional eddy-viscosity SGS modelling formulated in terms of the dissipation (Meneveau & Katz Reference Meneveau and Katz2000). (4) Velocities at the wall, because of the non-slip condition, equal the velocity of the wall, making it difficult to formulate the momentum cascade using a Lagrangian frame of reference, which has shown to be quite successful in SGS modelling (Meneveau, Lund & Cabot Reference Meneveau, Lund and Cabot1996). In this sense, the results presented here might be a useful tool for LES wall modelling of many problems, where not only the mean stress but also the fluctuations are of interest. In this context, it is worth noting that currently available LES wall models underpredict wall-shear stress fluctuations (Park & Moin Reference Park and Moin2016) and the present work can be used to augment the subgrid stresses that are not resolved by the LES grids. (5) The anomalous exponent in the momentum cascade may be modelled as a parabolic function of the power exponent
$\unicode[STIX]{x1D70F}^{\prime }$
is not positive definite, back-scattering is allowed at dissipative scales in the momentum cascade but energy back-scattering hardly happens close to the dissipative scales. The consequence of this last point is that subgrid scale (SGS) modelling of the momentum cascade (in today’s term, LES wall modelling, see e.g. Piomelli & Balaras (Reference Piomelli and Balaras2002)) is probably more challenging than the conventional eddy-viscosity SGS modelling formulated in terms of the dissipation (Meneveau & Katz Reference Meneveau and Katz2000). (4) Velocities at the wall, because of the non-slip condition, equal the velocity of the wall, making it difficult to formulate the momentum cascade using a Lagrangian frame of reference, which has shown to be quite successful in SGS modelling (Meneveau, Lund & Cabot Reference Meneveau, Lund and Cabot1996). In this sense, the results presented here might be a useful tool for LES wall modelling of many problems, where not only the mean stress but also the fluctuations are of interest. In this context, it is worth noting that currently available LES wall models underpredict wall-shear stress fluctuations (Park & Moin Reference Park and Moin2016) and the present work can be used to augment the subgrid stresses that are not resolved by the LES grids. (5) The anomalous exponent in the momentum cascade may be modelled as a parabolic function of the power exponent
![]() $p$
, whereas in the energy cascade, a super-Gaussian model has to be employed. This suggests that the momentum cascade is less dominated by extreme events and hence is not as intermittent as the energy cascade.
$p$
, whereas in the energy cascade, a super-Gaussian model has to be employed. This suggests that the momentum cascade is less dominated by extreme events and hence is not as intermittent as the energy cascade.
Finally, despite the knowledge gained on the energy cascade in the past century and the analogy made here, the interscale transfer of momentum is still a problem of its own merits and much work remains to be done to fully understand this flow phenomenon.
Acknowledgements
The work is funded by the US AFOSR, grant no. 1194592-1-TAAHO monitored by Dr I. Leyva, and NASA, grant no. NNX15AU93A. X. Yang would like to acknowledge P. Moin and P. Johnson for their generous help and fruitful discussions.