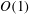1 Introduction
The hydrodynamics of swimming microorganisms near interfaces/walls is intriguing because of its applications in biological systems, so there has been an immense amount of research in this field (Lighthill Reference Lighthill1976; Brennen & Winet Reference Brennen and Winet1977; Lauga & Powers Reference Lauga and Powers2009; Li, Karimi & Ardekani Reference Li, Karimi and Ardekani2014; Lauga Reference Lauga2016). For instance, the reorientation of Escherichia coli (pusher swimmer) near a plane wall and attraction to the wall was observed and explained theoretically (Berke et al. Reference Berke, Turner, Berg and Lauga2008). Swimming of bacteria (E. coli) in circles, in a clockwise direction (when viewed from above) near a plane wall (Lauga et al. Reference Lauga, DiLuzio, Whitesides and Stone2006) and in a counter-clockwise direction near a plane air–water interface (Di Leonardo et al. Reference Di Leonardo, Dell’Arciprete, Angelani and Iebba2011) were also observed. Attraction/repulsion, reorientation and swimming in circles by microorganisms (mainly pusher swimmers) near complex interfaces (interfaces covered with surfactant) was studied using far-field hydrodynamic interactions (Lopez & Lauga Reference Lopez and Lauga2014). Motion of a two-dimensional (2-D) treadmilling swimmer near a plane wall was analysed theoretically, with the observation of nonlinear periodic swimming orbits (Crowdy & Or Reference Crowdy and Or2010; Crowdy Reference Crowdy2011). Also, Ferracci et al. (Reference Ferracci, Ueno, Numayama-Tsuruta, Imai, Yamaguchi and Ishikawa2013) observed the trapping of fresh water ciliates (Tetrahymena thermophila) near a water–air interface.
Among the few works which focused on the motion of swimmers near a deforming stress-free interface, Trouilloud et al. (Reference Trouilloud, Yu, Hosoi and Lauga2008) studied the motion of a time-reversible swimmer near such an interface. Using scaling arguments and experiments, they reported that the dimensionless time-averaged swimming velocities can be
![]() $O(1)$
(non-dimensionalized using the product of characteristic length scale and actuation frequency of the deformation of the swimmer) if
$O(1)$
(non-dimensionalized using the product of characteristic length scale and actuation frequency of the deformation of the swimmer) if
![]() $Ca>1$
, where
$Ca>1$
, where
![]() $Ca$
is the capillary number. They did not study the effect of the interface deformation on the orientational dynamics of the swimmer. Lee et al. (Reference Lee, Bush, Hosoi and Lauga2008) studied the locomotion of water snails that crawl beneath the water–air interface using lubrication theory. Later, Crowdy et al. (Reference Crowdy, Lee, Samson, Lauga and Hosoi2011) analysed the motion of swimmers which propel by performing steady surface deformations near a stress-free interface. Representing the swimmer by a 2-D stresslet and using complex variables and a conformal mapping approach, they concluded that such swimmers can swim steadily in a direction parallel to the undeformed interface. Even though their analysis is valid for arbitrary values of
$Ca$
is the capillary number. They did not study the effect of the interface deformation on the orientational dynamics of the swimmer. Lee et al. (Reference Lee, Bush, Hosoi and Lauga2008) studied the locomotion of water snails that crawl beneath the water–air interface using lubrication theory. Later, Crowdy et al. (Reference Crowdy, Lee, Samson, Lauga and Hosoi2011) analysed the motion of swimmers which propel by performing steady surface deformations near a stress-free interface. Representing the swimmer by a 2-D stresslet and using complex variables and a conformal mapping approach, they concluded that such swimmers can swim steadily in a direction parallel to the undeformed interface. Even though their analysis is valid for arbitrary values of
![]() $Ca$
and interface deformation, their approach is only correct for distances of the swimmer from the interface that are much larger in comparison to the swimmer’s size. At the other end of the spectrum, the motion of a rigid sphere near a plane interface is very well understood (Lee, Chadwick & Leal Reference Lee, Chadwick and Leal1979; Lee & Leal Reference Lee and Leal1980). These solutions were used to study the force and torque experienced by a sphere due to weak interface deformations (Berdan & Leal Reference Berdan and Leal1982), weak non-Newtonian and weak inertial effects (Becker, McKinley & Stone Reference Becker, McKinley and Stone1996). Following the similar analogy, we first derive the flow field due to the motion of spherical model microorganisms (squirmers) near a plane interface. Even though one can study the influence of all three above-mentioned effects on the dynamics of a swimmer, in this work, we focus only on the effect of weak interface deformations (valid assumption if either
$Ca$
and interface deformation, their approach is only correct for distances of the swimmer from the interface that are much larger in comparison to the swimmer’s size. At the other end of the spectrum, the motion of a rigid sphere near a plane interface is very well understood (Lee, Chadwick & Leal Reference Lee, Chadwick and Leal1979; Lee & Leal Reference Lee and Leal1980). These solutions were used to study the force and torque experienced by a sphere due to weak interface deformations (Berdan & Leal Reference Berdan and Leal1982), weak non-Newtonian and weak inertial effects (Becker, McKinley & Stone Reference Becker, McKinley and Stone1996). Following the similar analogy, we first derive the flow field due to the motion of spherical model microorganisms (squirmers) near a plane interface. Even though one can study the influence of all three above-mentioned effects on the dynamics of a swimmer, in this work, we focus only on the effect of weak interface deformations (valid assumption if either
![]() $Ca\ll 1$
or
$Ca\ll 1$
or
![]() $Ca/Bo\ll 1$
, where
$Ca/Bo\ll 1$
, where
![]() $Bo$
is the gravitational Bond number) on the dynamics of a swimmer. We note that our approach is valid for arbitrary values of the distances of the swimmer from the interface.
$Bo$
is the gravitational Bond number) on the dynamics of a swimmer. We note that our approach is valid for arbitrary values of the distances of the swimmer from the interface.
Our mathematical modelling is inspired by the work of Berdan & Leal (Reference Berdan and Leal1982) for the motion of a rigid sphere near a weakly deforming interface. Here, we analyse the motion of the swimmer near a weakly deforming interface using two approaches: (i) the bipolar coordinate approach (Lee & Leal Reference Lee and Leal1980) and (ii) the method of reflections (referred to as the Lorentz reciprocal theorem approach in the original paper) (Lee et al.
Reference Lee, Chadwick and Leal1979). Importantly, through such an analysis, one can estimate the accuracy of the method of reflections (MOR) approach in comparison to the exact solution. In particular, we identify that MOR is most accurate when the interface is stress free and forces due to a density difference dominate the interfacial tension forces. It is to be noted that the MOR used in this work is different from the method of images (MOI) commonly used in the literature to analyse the motion of swimmers near boundaries. Notably, the MOI approach has its origins in the earlier works of Blake & Chwang (Reference Blake and Chwang1974) on finding the images of a Stokeslet near a plane wall and Aderogba & Blake (Reference Aderogba and Blake1978) on finding the images of Stokeslet near a fluid–fluid interface (Aderogba & Blake Reference Aderogba and Blake1978). On the other hand, the MOR used in this work is based on the lemma proposed by Lee et al. (Reference Lee, Chadwick and Leal1979) which gives us the solution of Stokes equations near a plane fluid interface if we know the solution of Stokes equations in an unbounded fluid. As both approaches give the same solution, it does not matter which approach is used. Even though MOI/MOR is not accurate when the swimmer is very close to the interface, its simplicity and ability to predict experimental observations consistently have made it a popular technique that has been extensively used in the past. For instance, Berke et al. (Reference Berke, Turner, Berg and Lauga2008) studied the motion of a swimmer near a plane wall. Using MOI, they predicted that the swimmer reorients itself in such a way that it eventually gets attracted to the wall, in agreement with their experimental observations. Recent experiments of Takagi et al. (Reference Takagi, Palacci, Braunschweig, Shelley and Zhang2014) showed that synthetic swimmers follow complex trajectories in the field of spherical colloids. In an attempt to understand this, Spagnolie et al. (Reference Spagnolie, Moreno-Flores, Bartolo and Lauga2015) studied the motion of swimmers near spherical obstacles using MOI/MOR, thereby estimating the scaling laws for critical colloid size and basin of attraction for subcritical interactions. Mathijssen et al. (Reference Mathijssen, Doostmohammadi, Yeomans and Shendruk2016) studied the hydrodynamics of microswimmers in films using both MOI and exact solutions. There are very few works in the literature which use other methods such as an exact solution or numerical simulations to estimate the accuracy of the MOI approach. Spagnolie & Lauga (Reference Spagnolie and Lauga2012) use the method of regularized Stokeslets to analyse the motion of a swimmer near a plane wall or a stress-free interface. They concluded that the MOI is accurate for the distances of the swimmer from the undeformed interface as small as
![]() $O(1)$
, thereby proving the usefulness of MOI. In the spirit of these works, we obtain an exact solution of Stokes equations using the bipolar coordinate approach (valid for any value of
$O(1)$
, thereby proving the usefulness of MOI. In the spirit of these works, we obtain an exact solution of Stokes equations using the bipolar coordinate approach (valid for any value of
![]() $l$
, where
$l$
, where
![]() $l$
is the distance between the centre of the swimmer and the undeformed interface) so as to eventually estimate the accuracy of MOR (valid for
$l$
is the distance between the centre of the swimmer and the undeformed interface) so as to eventually estimate the accuracy of MOR (valid for
![]() $l\gg 1$
) for the motion of swimmer near a deforming interface.
$l\gg 1$
) for the motion of swimmer near a deforming interface.
Noting that our analysis is valid for a swimmer with an arbitrary time-dependent squirming gait, we hereby present the dynamics of a swimmer for two examples: (i) steady (time independent) and (ii) time-reversible squirming gaits. As the velocity of swimmer due to the interface deformation is an order of magnitude smaller than its velocity near a plane interface, we note that the dynamics of a swimmer with steady squirming gait near a weakly deforming interface is the same as that near a plane interface as long as the swimmer is far away from the interface. We thereafter analyse the motion of a swimmer with a time-reversible squirming gait. Analysing the long-time dynamics of a time-reversible swimmer, we divide its phase space (in terms of swimmers position and orientation) into regions of attraction towards and repulsion from the interface. Also, the long-time orientation of a time-reversible swimmer that is moving towards the interface depends on its initial orientation. We analyse the time-averaged dynamics of the time-reversible swimmer by either fixing its position and orientation over one time period (simple approach) (Trouilloud et al. Reference Trouilloud, Yu, Hosoi and Lauga2008; Yazdi, Ardekani & Borhan Reference Yazdi, Ardekani and Borhan2014) or by averaging the swimmer’s instantaneous velocity over one time period (exact approach). We show that the simple time-averaging approach cannot accurately estimate the long-time dynamics of the swimmer.
This paper is organized as follows. In § 2.1, we explain the governing equations and boundary conditions for the motion of a spherical swimmer near a weakly deforming interface. After describing the non-dimensionalization scheme, we explain the perturbation method providing the
![]() $O(1)$
and
$O(1)$
and
![]() $O(\unicode[STIX]{x1D716})$
equations and boundary conditions. In § 2.2, we explain the reciprocal theorem used to obtain the
$O(\unicode[STIX]{x1D716})$
equations and boundary conditions. In § 2.2, we explain the reciprocal theorem used to obtain the
![]() $O(\unicode[STIX]{x1D716})$
swimmer velocities without explicitly solving the
$O(\unicode[STIX]{x1D716})$
swimmer velocities without explicitly solving the
![]() $O(\unicode[STIX]{x1D716})$
flow fields. Finally, we describe the solution method used for solving the
$O(\unicode[STIX]{x1D716})$
flow fields. Finally, we describe the solution method used for solving the
![]() $O(1)$
flow fields using the bipolar coordinate approach in § 2.3 and method of reflections in § 2.4. In § 3.1, we analyse the interface deformation for various swimmer orientations, viscosity ratios, various values of
$O(1)$
flow fields using the bipolar coordinate approach in § 2.3 and method of reflections in § 2.4. In § 3.1, we analyse the interface deformation for various swimmer orientations, viscosity ratios, various values of
![]() $Ca$
,
$Ca$
,
![]() $Ca/Bo$
and distances of the swimmer from the interface. We thereafter study the dynamics of a swimmer with steady squirming modes in § 3.2, and with time-reversible squirming modes in § 3.3, focusing on time-averaged velocities in § 3.3.1 and instantaneous velocities in § 3.3.2. We conclude with some discussions in § 4, followed by technical derivations in the appendices A–C.
$Ca/Bo$
and distances of the swimmer from the interface. We thereafter study the dynamics of a swimmer with steady squirming modes in § 3.2, and with time-reversible squirming modes in § 3.3, focusing on time-averaged velocities in § 3.3.1 and instantaneous velocities in § 3.3.2. We conclude with some discussions in § 4, followed by technical derivations in the appendices A–C.
2 Mathematical model
2.1 Governing equations and boundary conditions
Consider the motion of a swimmer near a weakly deforming fluid–fluid interface, with the swimmer fully immersed in the lower fluid (fluid 2). The flow field in both fluids is governed by the Stokes equation and the incompressibility condition
where the superscript
![]() $k=1$
or 2 indicates fluid 1
$k=1$
or 2 indicates fluid 1
![]() $(z>0)$
or 2
$(z>0)$
or 2
![]() $(z<0)$
and
$(z<0)$
and
![]() $p^{(k)}$
,
$p^{(k)}$
,
![]() $\boldsymbol{u}^{(k)}$
and
$\boldsymbol{u}^{(k)}$
and
![]() $\unicode[STIX]{x1D707}^{(k)}$
denote the pressure, velocity and the dynamic viscosity of the kth fluid. In this work, we consider swimmers that propel themselves by means of a slip velocity
$\unicode[STIX]{x1D707}^{(k)}$
denote the pressure, velocity and the dynamic viscosity of the kth fluid. In this work, we consider swimmers that propel themselves by means of a slip velocity
![]() $\boldsymbol{u}_{s}$
on their surface. Because of this slip velocity, the swimmer moves with a translation velocity
$\boldsymbol{u}_{s}$
on their surface. Because of this slip velocity, the swimmer moves with a translation velocity
![]() $(\boldsymbol{U})$
and rotational velocity
$(\boldsymbol{U})$
and rotational velocity
![]() $(\unicode[STIX]{x1D734})$
, so the boundary condition on its surface is given by
$(\unicode[STIX]{x1D734})$
, so the boundary condition on its surface is given by
In addition, there are hydrodynamic force-free and torque-free constraints on the swimmer, given by
Here,
![]() $\boldsymbol{x}^{s}$
is a position vector from the centre of the swimmer to its surface,
$\boldsymbol{x}^{s}$
is a position vector from the centre of the swimmer to its surface,
![]() $\unicode[STIX]{x1D64F}^{(2)}$
denotes the stress tensor in fluid 2,
$\unicode[STIX]{x1D64F}^{(2)}$
denotes the stress tensor in fluid 2,
![]() $S_{p}$
denotes the surface of the swimmer,
$S_{p}$
denotes the surface of the swimmer,
![]() $\boldsymbol{n}$
is the unit normal vector to the surface of the swimmer that is pointing into the fluid and dS is an infinitesimal surface area on the surface of the swimmer. For describing the surface deformation, we use the traditional ‘squirmer’ model (Lighthill Reference Lighthill1952; Blake Reference Blake1971) which assigns a tangential velocity on the surface of the swimmer as a manifestation of the metachronal beating of cilia on its surface. A periodic stroke on the surface of a swimmer can be described using two different approaches: (i) in a reference frame fixed to the swimmer, we prescribe at each instant, a periodic surface velocity. This description is referred to as the Eulerian periodic stroke in Michelin & Lauga (Reference Michelin and Lauga2013). (ii) Otherwise, one can prescribe periodic trajectories of material surface points. This description is referred to as the Lagrangian periodic stroke in Michelin & Lauga (Reference Michelin and Lauga2013). Because of its simplicity and its widespread usage in modelling swimmers with steady surface and flow velocities (Ishikawa, Simmonds & Pedley Reference Ishikawa, Simmonds and Pedley2006; Short et al.
Reference Short, Solari, Ganguly, Powers, Kessler and Goldstein2006; Doostmohammadi, Stocker & Ardekani Reference Doostmohammadi, Stocker and Ardekani2012), we choose Eulerian periodic strokes to model a swimmer. We truncate the infinite series in the slip velocity to first two terms (Ishikawa et al.
Reference Ishikawa, Simmonds and Pedley2006; Li & Ardekani Reference Li and Ardekani2014; Matas-Navarro et al.
Reference Matas-Navarro, Golestanian, Liverpool and Fielding2014). This slip velocity is given by
$\boldsymbol{n}$
is the unit normal vector to the surface of the swimmer that is pointing into the fluid and dS is an infinitesimal surface area on the surface of the swimmer. For describing the surface deformation, we use the traditional ‘squirmer’ model (Lighthill Reference Lighthill1952; Blake Reference Blake1971) which assigns a tangential velocity on the surface of the swimmer as a manifestation of the metachronal beating of cilia on its surface. A periodic stroke on the surface of a swimmer can be described using two different approaches: (i) in a reference frame fixed to the swimmer, we prescribe at each instant, a periodic surface velocity. This description is referred to as the Eulerian periodic stroke in Michelin & Lauga (Reference Michelin and Lauga2013). (ii) Otherwise, one can prescribe periodic trajectories of material surface points. This description is referred to as the Lagrangian periodic stroke in Michelin & Lauga (Reference Michelin and Lauga2013). Because of its simplicity and its widespread usage in modelling swimmers with steady surface and flow velocities (Ishikawa, Simmonds & Pedley Reference Ishikawa, Simmonds and Pedley2006; Short et al.
Reference Short, Solari, Ganguly, Powers, Kessler and Goldstein2006; Doostmohammadi, Stocker & Ardekani Reference Doostmohammadi, Stocker and Ardekani2012), we choose Eulerian periodic strokes to model a swimmer. We truncate the infinite series in the slip velocity to first two terms (Ishikawa et al.
Reference Ishikawa, Simmonds and Pedley2006; Li & Ardekani Reference Li and Ardekani2014; Matas-Navarro et al.
Reference Matas-Navarro, Golestanian, Liverpool and Fielding2014). This slip velocity is given by
Here,
![]() $B_{n}(t)$
is the swimming gait for the
$B_{n}(t)$
is the swimming gait for the
![]() $n$
th squirming mode, while
$n$
th squirming mode, while
![]() $P_{n}^{\prime }$
denotes the derivative of the Legendre polynomial with respect to its argument,
$P_{n}^{\prime }$
denotes the derivative of the Legendre polynomial with respect to its argument,
![]() $\boldsymbol{e}$
denotes the direction of the head of the swimmer. If the squirming gait,
$\boldsymbol{e}$
denotes the direction of the head of the swimmer. If the squirming gait,
![]() $B_{n}$
, is proportional to
$B_{n}$
, is proportional to
![]() $\sin (\unicode[STIX]{x1D714}t)$
, such a swimmer cannot swim on an average according to Purcell’s scallop theorem (Purcell Reference Purcell1977). However, the nonlinearities due to the interface deformation break the scallop theorem leading to the motion of a swimmer performing time-reversible surface deformation. The slip velocity of a squirmer can be written in terms of the spherical coordinates whose origin is at the centre of the swimmer as
$\sin (\unicode[STIX]{x1D714}t)$
, such a swimmer cannot swim on an average according to Purcell’s scallop theorem (Purcell Reference Purcell1977). However, the nonlinearities due to the interface deformation break the scallop theorem leading to the motion of a swimmer performing time-reversible surface deformation. The slip velocity of a squirmer can be written in terms of the spherical coordinates whose origin is at the centre of the swimmer as
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{s} & = & \displaystyle u_{s\unicode[STIX]{x1D703}}\boldsymbol{i}_{\unicode[STIX]{x1D703}}+u_{s\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\nonumber\\ \displaystyle & = & \displaystyle \{[-\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\sin (\unicode[STIX]{x1D703}_{z})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}\nonumber\\ \displaystyle & & \displaystyle \times \,\{B_{1}(t)+B_{2}(t)[\sin (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\cos (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{s} & = & \displaystyle u_{s\unicode[STIX]{x1D703}}\boldsymbol{i}_{\unicode[STIX]{x1D703}}+u_{s\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\nonumber\\ \displaystyle & = & \displaystyle \{[-\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\sin (\unicode[STIX]{x1D703}_{z})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}\nonumber\\ \displaystyle & & \displaystyle \times \,\{B_{1}(t)+B_{2}(t)[\sin (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\cos (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\}.\end{eqnarray}$$

Figure 1. Schematic of the problem. The interface shown is weakly deforming. ‘
![]() $O$
’ is the origin of the Cartesian and cylindrical coordinate systems, both fixed at the undeformed interface.
$O$
’ is the origin of the Cartesian and cylindrical coordinate systems, both fixed at the undeformed interface.
![]() $O^{\prime }$
is the origin of the spherical coordinate system, fixed at the centre of the sphere. The swimmer is at a distance of
$O^{\prime }$
is the origin of the spherical coordinate system, fixed at the centre of the sphere. The swimmer is at a distance of
![]() $l$
from the undeformed interface.
$l$
from the undeformed interface.
Here,
![]() $\unicode[STIX]{x1D703}_{z}$
is the angle made by the head of the swimmer (
$\unicode[STIX]{x1D703}_{z}$
is the angle made by the head of the swimmer (
![]() $\boldsymbol{e}$
) with the interface-fixed
$\boldsymbol{e}$
) with the interface-fixed
![]() $z$
-axis (pointing from fluid 2 to fluid 1), while
$z$
-axis (pointing from fluid 2 to fluid 1), while
![]() $\unicode[STIX]{x1D719}_{x}$
is the angle made by the projection of
$\unicode[STIX]{x1D719}_{x}$
is the angle made by the projection of
![]() $\boldsymbol{e}$
in the
$\boldsymbol{e}$
in the
![]() $xy$
plane (equivalently
$xy$
plane (equivalently
![]() $XY$
plane) with the
$XY$
plane) with the
![]() $x$
-axis (equivalently
$x$
-axis (equivalently
![]() $X$
-axis). The origin of
$X$
-axis). The origin of
![]() $xyz$
coordinate system is at the undeformed interface, while the origin of
$xyz$
coordinate system is at the undeformed interface, while the origin of
![]() $XYZ$
coordinate system is at the centre of the swimmer. Without loss of generality, we consider
$XYZ$
coordinate system is at the centre of the swimmer. Without loss of generality, we consider
![]() $\unicode[STIX]{x1D719}_{x}=0$
. Also,
$\unicode[STIX]{x1D719}_{x}=0$
. Also,
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D719}$
are the coordinate variables in spherical coordinates fixed at the centre of the swimmer,
$\unicode[STIX]{x1D719}$
are the coordinate variables in spherical coordinates fixed at the centre of the swimmer,
![]() $\boldsymbol{i}_{\unicode[STIX]{x1D703}}$
and
$\boldsymbol{i}_{\unicode[STIX]{x1D703}}$
and
![]() $\boldsymbol{i}_{\unicode[STIX]{x1D719}}$
are the unit vectors in the polar and azimuthal directions as shown in figure 1. As the swimmer is moving in a quiescent fluid, the flow field far from the swimmer is given by
$\boldsymbol{i}_{\unicode[STIX]{x1D719}}$
are the unit vectors in the polar and azimuthal directions as shown in figure 1. As the swimmer is moving in a quiescent fluid, the flow field far from the swimmer is given by
The shape of the interface is represented by
![]() $F\equiv z-f(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t;l)=0$
, the boundary conditions at the interface are given by (Leal Reference Leal2007)
$F\equiv z-f(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t;l)=0$
, the boundary conditions at the interface are given by (Leal Reference Leal2007)
where
![]() $\unicode[STIX]{x1D70E}$
is the interfacial tension between the two fluids,
$\unicode[STIX]{x1D70E}$
is the interfacial tension between the two fluids,
![]() $g$
is the acceleration due to gravity,
$g$
is the acceleration due to gravity,
![]() $t$
is time,
$t$
is time,
![]() $\unicode[STIX]{x1D70C}^{(k)}$
denotes the density of the
$\unicode[STIX]{x1D70C}^{(k)}$
denotes the density of the
![]() $k$
th fluid,
$k$
th fluid,
![]() $\boldsymbol{n}=\unicode[STIX]{x1D735}F/|\unicode[STIX]{x1D735}F|$
denotes the unit vector normal to the interface,
$\boldsymbol{n}=\unicode[STIX]{x1D735}F/|\unicode[STIX]{x1D735}F|$
denotes the unit vector normal to the interface,
![]() $(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z)$
are the coordinate variables of the cylindrical coordinate system with the origin fixed at the undeformed interface and
$(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z)$
are the coordinate variables of the cylindrical coordinate system with the origin fixed at the undeformed interface and
![]() $l$
denotes the distance of the centre of the swimmer from the undeformed interface.
$l$
denotes the distance of the centre of the swimmer from the undeformed interface.
We hereby non-dimensionalize the governing equations and boundary conditions. For this purpose, we use
![]() $u_{ref}=b_{1}$
(assuming
$u_{ref}=b_{1}$
(assuming
![]() $B_{n}=b_{n}\unicode[STIX]{x1D6FD}_{n}(t)$
),
$B_{n}=b_{n}\unicode[STIX]{x1D6FD}_{n}(t)$
),
![]() $l_{ref}=R$
(radius of the squirmer),
$l_{ref}=R$
(radius of the squirmer),
![]() $p_{ref}^{(k)}=T_{ref}^{(k)}=\unicode[STIX]{x1D707}^{(k)}u_{ref}/R$
and
$p_{ref}^{(k)}=T_{ref}^{(k)}=\unicode[STIX]{x1D707}^{(k)}u_{ref}/R$
and
![]() $t_{ref}=R/u_{ref}$
as the characteristic scales for velocity, length, stress field and time, respectively. Additionally, any forces and torques (especially encountered in the complementary Stokes problem of the reciprocal theorem) are non-dimensionalized by
$t_{ref}=R/u_{ref}$
as the characteristic scales for velocity, length, stress field and time, respectively. Additionally, any forces and torques (especially encountered in the complementary Stokes problem of the reciprocal theorem) are non-dimensionalized by
![]() $\unicode[STIX]{x1D707}^{(2)}u_{ref}R$
and
$\unicode[STIX]{x1D707}^{(2)}u_{ref}R$
and
![]() $\unicode[STIX]{x1D707}^{(2)}u_{ref}R^{2}$
, respectively. We hereby denote the dimensionless variables by the same symbols as used for the dimensional ones. All the variables appearing hereafter are dimensionless variables. The dimensionless governing equations are given as
$\unicode[STIX]{x1D707}^{(2)}u_{ref}R^{2}$
, respectively. We hereby denote the dimensionless variables by the same symbols as used for the dimensional ones. All the variables appearing hereafter are dimensionless variables. The dimensionless governing equations are given as
The boundary conditions on the surface of the swimmer, the force-free and torque-free conditions and the slip velocity on the surface of the swimmer are given by
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{s} & = & \displaystyle u_{s\unicode[STIX]{x1D703}}\boldsymbol{i}_{\unicode[STIX]{x1D703}}+u_{s\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\nonumber\\ \displaystyle & = & \displaystyle \{[-\text{cos}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\sin (\unicode[STIX]{x1D703}_{z})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}\nonumber\\ \displaystyle & & \displaystyle \times \,\{\unicode[STIX]{x1D6FD}_{1}(t)+\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6FD}_{2}(t)[\sin (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\cos (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{s} & = & \displaystyle u_{s\unicode[STIX]{x1D703}}\boldsymbol{i}_{\unicode[STIX]{x1D703}}+u_{s\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\nonumber\\ \displaystyle & = & \displaystyle \{[-\text{cos}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\sin (\unicode[STIX]{x1D703}_{z})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}\nonumber\\ \displaystyle & & \displaystyle \times \,\{\unicode[STIX]{x1D6FD}_{1}(t)+\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6FD}_{2}(t)[\sin (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})+\cos (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703}_{z})]\},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6EC}=b_{2}/b_{1}$
. The flow field far from the swimmer is still given by
$\unicode[STIX]{x1D6EC}=b_{2}/b_{1}$
. The flow field far from the swimmer is still given by
The boundary conditions at the interface are given by (Lee et al. Reference Lee, Chadwick and Leal1979; Lee & Leal Reference Lee and Leal1980; Berdan & Leal Reference Berdan and Leal1982; Leal Reference Leal2007)
where
![]() $\unicode[STIX]{x1D6FD}=Ca^{-1}=\unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D707}^{(2)}u_{ref});\unicode[STIX]{x1D6FC}=Bo/Ca=(gR^{2}(\unicode[STIX]{x1D70C}^{(2)}-\unicode[STIX]{x1D70C}^{(1)}))/(\unicode[STIX]{x1D707}^{(2)}u_{ref});\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}^{(1)}/\unicode[STIX]{x1D707}^{(2)}$
.
$\unicode[STIX]{x1D6FD}=Ca^{-1}=\unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D707}^{(2)}u_{ref});\unicode[STIX]{x1D6FC}=Bo/Ca=(gR^{2}(\unicode[STIX]{x1D70C}^{(2)}-\unicode[STIX]{x1D70C}^{(1)}))/(\unicode[STIX]{x1D707}^{(2)}u_{ref});\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}^{(1)}/\unicode[STIX]{x1D707}^{(2)}$
.
For
![]() $\unicode[STIX]{x1D6FD}\gg 1$
or
$\unicode[STIX]{x1D6FD}\gg 1$
or
![]() $\unicode[STIX]{x1D6FC}\gg 1$
, the deformation of the interface is very small, so we define
$\unicode[STIX]{x1D6FC}\gg 1$
, the deformation of the interface is very small, so we define
![]() $\unicode[STIX]{x1D716}=1/(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})$
to consider the influence of either
$\unicode[STIX]{x1D716}=1/(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})$
to consider the influence of either
![]() $\unicode[STIX]{x1D6FC}$
or
$\unicode[STIX]{x1D6FC}$
or
![]() $\unicode[STIX]{x1D6FD}$
. For
$\unicode[STIX]{x1D6FD}$
. For
![]() $\unicode[STIX]{x1D716}\ll 1$
, we can write
$\unicode[STIX]{x1D716}\ll 1$
, we can write
![]() $f(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t;l)=\unicode[STIX]{x1D716}f_{1}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719};t,l)+\unicode[STIX]{x1D716}^{2}f_{2}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719};t,l)+\cdots \,.$
Expanding all the flow field variables and the swimmer velocities as a regular perturbation series in
$f(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t;l)=\unicode[STIX]{x1D716}f_{1}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719};t,l)+\unicode[STIX]{x1D716}^{2}f_{2}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719};t,l)+\cdots \,.$
Expanding all the flow field variables and the swimmer velocities as a regular perturbation series in
![]() $\unicode[STIX]{x1D716}$
, we get (Berdan & Leal Reference Berdan and Leal1982)
$\unicode[STIX]{x1D716}$
, we get (Berdan & Leal Reference Berdan and Leal1982)
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}^{(k)}=\boldsymbol{u}_{0}^{(k)}+\unicode[STIX]{x1D716}\boldsymbol{u}_{1}^{(k)}+\cdots \,,\\ \displaystyle p^{(k)}=p_{0}^{(k)}+\unicode[STIX]{x1D716}p_{1}^{(k)}+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D64F}^{(k)}=\unicode[STIX]{x1D64F}_{0}^{(k)}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D64F}_{1}^{(k)}+\cdots \,,\\ \displaystyle \{\boldsymbol{U},\unicode[STIX]{x1D734}\}=\{\boldsymbol{U}_{0},\unicode[STIX]{x1D734}_{0}\}+\unicode[STIX]{x1D716}\{\boldsymbol{U}_{1},\unicode[STIX]{x1D734}_{1}\}+\cdots \,.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}^{(k)}=\boldsymbol{u}_{0}^{(k)}+\unicode[STIX]{x1D716}\boldsymbol{u}_{1}^{(k)}+\cdots \,,\\ \displaystyle p^{(k)}=p_{0}^{(k)}+\unicode[STIX]{x1D716}p_{1}^{(k)}+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D64F}^{(k)}=\unicode[STIX]{x1D64F}_{0}^{(k)}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D64F}_{1}^{(k)}+\cdots \,,\\ \displaystyle \{\boldsymbol{U},\unicode[STIX]{x1D734}\}=\{\boldsymbol{U}_{0},\unicode[STIX]{x1D734}_{0}\}+\unicode[STIX]{x1D716}\{\boldsymbol{U}_{1},\unicode[STIX]{x1D734}_{1}\}+\cdots \,.\end{array}\right\}\end{eqnarray}$$
Note that the subscript denotes the order of perturbation, whereas the superscript denotes fluid 1 or 2. For small interface deformations, we write the boundary conditions at the interface, equations (2.15)–(2.17) as a series of boundary conditions applied at an undeformed interface using Taylor series expansion about
![]() $z=0$
. We then substitute the regular perturbation expansion of the flow field variables, equation (2.18) in the governing equations and the boundary conditions (applied at the undeformed interface) and we eventually collect the terms at each order of
$z=0$
. We then substitute the regular perturbation expansion of the flow field variables, equation (2.18) in the governing equations and the boundary conditions (applied at the undeformed interface) and we eventually collect the terms at each order of
![]() $\unicode[STIX]{x1D716}$
(the usual domain perturbation methodology). At
$\unicode[STIX]{x1D716}$
(the usual domain perturbation methodology). At
![]() $O(1)$
, the boundary condition at the surface of the swimmer and at the interface are given as (Berdan & Leal Reference Berdan and Leal1982)
$O(1)$
, the boundary condition at the surface of the swimmer and at the interface are given as (Berdan & Leal Reference Berdan and Leal1982)
At the undeformed interface,
where
![]() $\unicode[STIX]{x1D716}=1/(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})$
and
$\unicode[STIX]{x1D716}=1/(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})$
and
![]() $\unicode[STIX]{x1D6FB}_{2}^{2}$
is a 2-D Laplacian in cylindrical coordinates for a constant
$\unicode[STIX]{x1D6FB}_{2}^{2}$
is a 2-D Laplacian in cylindrical coordinates for a constant
![]() $z$
. The normal component of (2.22) is used for finding the leading-order interface deformation. Assuming that the slip velocity on the surface of the swimmer is
$z$
. The normal component of (2.22) is used for finding the leading-order interface deformation. Assuming that the slip velocity on the surface of the swimmer is
![]() $O(1)$
, the boundary conditions at
$O(1)$
, the boundary conditions at
![]() $O(\unicode[STIX]{x1D716})$
on the surface of the swimmer and at the interface are given as (Berdan & Leal Reference Berdan and Leal1982)
$O(\unicode[STIX]{x1D716})$
on the surface of the swimmer and at the interface are given as (Berdan & Leal Reference Berdan and Leal1982)
At the undeformed interface, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{i}_{z}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(1)}+\boldsymbol{i}_{z}\boldsymbol{\cdot }f_{1}\frac{\unicode[STIX]{x2202}\boldsymbol{u}_{0}^{(1)}}{\unicode[STIX]{x2202}z}-\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{u}_{0}^{(1)}-\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{u}_{0}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{i}_{z}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(2)}+\boldsymbol{i}_{z}\boldsymbol{\cdot }f_{1}\frac{\unicode[STIX]{x2202}\boldsymbol{u}_{0}^{(2)}}{\unicode[STIX]{x2202}z}-\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{u}_{0}^{(2)}-\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{u}_{0}^{(2)}=\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{i}_{z}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(1)}+\boldsymbol{i}_{z}\boldsymbol{\cdot }f_{1}\frac{\unicode[STIX]{x2202}\boldsymbol{u}_{0}^{(1)}}{\unicode[STIX]{x2202}z}-\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{u}_{0}^{(1)}-\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{u}_{0}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{i}_{z}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(2)}+\boldsymbol{i}_{z}\boldsymbol{\cdot }f_{1}\frac{\unicode[STIX]{x2202}\boldsymbol{u}_{0}^{(2)}}{\unicode[STIX]{x2202}z}-\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{u}_{0}^{(2)}-\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{u}_{0}^{(2)}=\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D706}\boldsymbol{i}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{1}^{(1)}-\boldsymbol{i}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{1}^{(2)}+\unicode[STIX]{x1D706}f_{1}\boldsymbol{i}_{z}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D64F}_{0}^{(1)}}{\unicode[STIX]{x2202}z}-f_{1}\boldsymbol{i}_{z}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D64F}_{0}^{(2)}}{\unicode[STIX]{x2202}z}-\unicode[STIX]{x1D706}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(1)}-\unicode[STIX]{x1D706}\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(2)}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(2)}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}\left[-f_{1}\left(\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\right)+f_{2}\boldsymbol{i}_{z}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}\left[(\unicode[STIX]{x1D6FB}_{2}^{2}f_{1})\left(\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\right)-\unicode[STIX]{x1D6FB}_{2}^{2}f_{2}\boldsymbol{i}_{z}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D706}\boldsymbol{i}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{1}^{(1)}-\boldsymbol{i}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{1}^{(2)}+\unicode[STIX]{x1D706}f_{1}\boldsymbol{i}_{z}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D64F}_{0}^{(1)}}{\unicode[STIX]{x2202}z}-f_{1}\boldsymbol{i}_{z}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D64F}_{0}^{(2)}}{\unicode[STIX]{x2202}z}-\unicode[STIX]{x1D706}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(1)}-\unicode[STIX]{x1D706}\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(2)}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}_{0}^{(2)}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}\left[-f_{1}\left(\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\right)+f_{2}\boldsymbol{i}_{z}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}\left[(\unicode[STIX]{x1D6FB}_{2}^{2}f_{1})\left(\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\boldsymbol{i}_{\unicode[STIX]{x1D70C}}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}\boldsymbol{i}_{\unicode[STIX]{x1D719}}\right)-\unicode[STIX]{x1D6FB}_{2}^{2}f_{2}\boldsymbol{i}_{z}\right].\end{eqnarray}$$
It can be seen that the
![]() $O(1)$
problem is the motion of the swimmer near a plane interface. This is a linear problem so if
$O(1)$
problem is the motion of the swimmer near a plane interface. This is a linear problem so if
![]() $\boldsymbol{u}^{s}$
is time reversible, we expect the swimmer velocities at this order
$\boldsymbol{u}^{s}$
is time reversible, we expect the swimmer velocities at this order
![]() $(\boldsymbol{U}_{0},\unicode[STIX]{x1D734}_{0})$
to also be time reversible, i.e., the time-averaged swimmer velocities to be zero. Consequently, on an average, the swimmer will not move, consistent with the predictions of the scallop theorem at
$(\boldsymbol{U}_{0},\unicode[STIX]{x1D734}_{0})$
to also be time reversible, i.e., the time-averaged swimmer velocities to be zero. Consequently, on an average, the swimmer will not move, consistent with the predictions of the scallop theorem at
![]() $O(1)$
. Besides this, we need to solve the
$O(1)$
. Besides this, we need to solve the
![]() $O(\unicode[STIX]{x1D716})$
problem to find the leading-order effect of the interface deformation on the swimmer velocities,
$O(\unicode[STIX]{x1D716})$
problem to find the leading-order effect of the interface deformation on the swimmer velocities,
![]() $(\boldsymbol{U}_{1},\unicode[STIX]{x1D734}_{1})$
. This, however, requires the solution of the
$(\boldsymbol{U}_{1},\unicode[STIX]{x1D734}_{1})$
. This, however, requires the solution of the
![]() $O(1)$
problem as the boundary conditions at
$O(1)$
problem as the boundary conditions at
![]() $O(\unicode[STIX]{x1D716})$
involve flow variables at
$O(\unicode[STIX]{x1D716})$
involve flow variables at
![]() $O(1)$
. Before explaining the solution methodology to solve the
$O(1)$
. Before explaining the solution methodology to solve the
![]() $O(1)$
problem, we first describe the reciprocal theorem used for obtaining the
$O(1)$
problem, we first describe the reciprocal theorem used for obtaining the
![]() $O(\unicode[STIX]{x1D716})$
swimmer velocities directly without solving for the
$O(\unicode[STIX]{x1D716})$
swimmer velocities directly without solving for the
![]() $O(\unicode[STIX]{x1D716})$
flow fields. This reciprocal theorem is similar to that obtained for the motion of rigid sphere near a weakly deforming interface (Berdan & Leal Reference Berdan and Leal1982).
$O(\unicode[STIX]{x1D716})$
flow fields. This reciprocal theorem is similar to that obtained for the motion of rigid sphere near a weakly deforming interface (Berdan & Leal Reference Berdan and Leal1982).
2.2 Reciprocal theorem for a swimmer near a deforming interface
We begin with the generalized reciprocal theorem between two Stokes flows
![]() $(\boldsymbol{u}^{\prime },\unicode[STIX]{x1D64F}^{\prime }),(\boldsymbol{u}^{\prime \prime },\unicode[STIX]{x1D64F}^{\prime \prime })$
in the same flow geometry given by
$(\boldsymbol{u}^{\prime },\unicode[STIX]{x1D64F}^{\prime }),(\boldsymbol{u}^{\prime \prime },\unicode[STIX]{x1D64F}^{\prime \prime })$
in the same flow geometry given by
As we would like to find the velocity of a squirmer at
![]() $O(\unicode[STIX]{x1D716})$
near a weakly deforming interface using the reciprocal theorem, we define
$O(\unicode[STIX]{x1D716})$
near a weakly deforming interface using the reciprocal theorem, we define
![]() $(\boldsymbol{u}^{\prime },\unicode[STIX]{x1D64F}^{\prime })\equiv (\boldsymbol{u}_{1}^{(k)},\unicode[STIX]{x1D64F}_{1}^{(k)})$
. We also consider the auxiliary problem (or the complementary Stokes problem) as the motion of a rigid sphere near a flat interface, we denote this problem by variables with a hat over them,
$(\boldsymbol{u}^{\prime },\unicode[STIX]{x1D64F}^{\prime })\equiv (\boldsymbol{u}_{1}^{(k)},\unicode[STIX]{x1D64F}_{1}^{(k)})$
. We also consider the auxiliary problem (or the complementary Stokes problem) as the motion of a rigid sphere near a flat interface, we denote this problem by variables with a hat over them,
![]() $(\boldsymbol{u}^{\prime \prime },\unicode[STIX]{x1D64F}^{\prime \prime })=(\hat{\boldsymbol{u}}^{(k)},\hat{\unicode[STIX]{x1D64F}}^{(k)})$
. Applying the reciprocal theorem in fluid 1, we have
$(\boldsymbol{u}^{\prime \prime },\unicode[STIX]{x1D64F}^{\prime \prime })=(\hat{\boldsymbol{u}}^{(k)},\hat{\unicode[STIX]{x1D64F}}^{(k)})$
. Applying the reciprocal theorem in fluid 1, we have
whereas the application of reciprocal theorem in fluid 2 gives
where
![]() $A_{F}$
is the area of the flat interface,
$A_{F}$
is the area of the flat interface,
![]() $A_{2}$
includes the area of the flat interface and the area of the sphere
$A_{2}$
includes the area of the flat interface and the area of the sphere
![]() $(A_{2}=A_{F}+S_{p})$
. Multiplying (2.28) with
$(A_{2}=A_{F}+S_{p})$
. Multiplying (2.28) with
![]() $\unicode[STIX]{x1D706}$
and subtracting from (2.29), we have
$\unicode[STIX]{x1D706}$
and subtracting from (2.29), we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \iint _{A_{F}}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D64F}_{1}^{(1)}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{1}+\unicode[STIX]{x1D706}\hat{\unicode[STIX]{x1D64F}}^{(1)}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(1)}+\unicode[STIX]{x1D64F}_{1}^{(2)}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{(2)}-\hat{\unicode[STIX]{x1D64F}}^{(2)}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(2)})\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle \quad =-\!\iint _{S_{p}}(\unicode[STIX]{x1D64F}_{1}^{(2)}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{(2)}-\hat{\unicode[STIX]{x1D64F}}^{(2)}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(2)})\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \iint _{A_{F}}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D64F}_{1}^{(1)}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{1}+\unicode[STIX]{x1D706}\hat{\unicode[STIX]{x1D64F}}^{(1)}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(1)}+\unicode[STIX]{x1D64F}_{1}^{(2)}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{(2)}-\hat{\unicode[STIX]{x1D64F}}^{(2)}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(2)})\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle \quad =-\!\iint _{S_{p}}(\unicode[STIX]{x1D64F}_{1}^{(2)}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{(2)}-\hat{\unicode[STIX]{x1D64F}}^{(2)}\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(2)})\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S.\end{eqnarray}$$
Using the boundary condition on the surface of the swimmer,
![]() $\boldsymbol{u}_{1}^{(2)}=\boldsymbol{U}_{1}+\unicode[STIX]{x1D734}_{1}\times \boldsymbol{x}$
, on the surface of the rigid sphere in the complementary Stokes problem,
$\boldsymbol{u}_{1}^{(2)}=\boldsymbol{U}_{1}+\unicode[STIX]{x1D734}_{1}\times \boldsymbol{x}$
, on the surface of the rigid sphere in the complementary Stokes problem,
![]() $\hat{\boldsymbol{u}}^{(2)}=\hat{\boldsymbol{U}}+\hat{\unicode[STIX]{x1D734}}\times \boldsymbol{x}$
and the boundary conditions at the interface in the complementary Stokes problem, equation (2.30) can be simplified to
$\hat{\boldsymbol{u}}^{(2)}=\hat{\boldsymbol{U}}+\hat{\unicode[STIX]{x1D734}}\times \boldsymbol{x}$
and the boundary conditions at the interface in the complementary Stokes problem, equation (2.30) can be simplified to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \iint _{A_{F}}\boldsymbol{i}_{z}\boldsymbol{\cdot }(\unicode[STIX]{x1D64F}_{1}^{(2)}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D64F}_{1}^{(1)})\boldsymbol{\cdot }\hat{\boldsymbol{u}}\,\text{d}S+\iint _{A_{F}}\boldsymbol{i}_{z}\boldsymbol{\cdot }(\unicode[STIX]{x1D706}\hat{\unicode[STIX]{x1D64F}}^{(1)}-\hat{\unicode[STIX]{x1D64F}}^{(2)})\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(1)}\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle \quad +\,\iint _{A_{F}}\boldsymbol{i}_{z}\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D64F}}^{(2)}\boldsymbol{\cdot }(\boldsymbol{u}_{1}^{(1)}-\boldsymbol{u}_{1}^{(2)})\,\text{d}S=-\hat{\boldsymbol{F}}\boldsymbol{\cdot }\boldsymbol{U}_{1}-\hat{\boldsymbol{L}}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \iint _{A_{F}}\boldsymbol{i}_{z}\boldsymbol{\cdot }(\unicode[STIX]{x1D64F}_{1}^{(2)}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D64F}_{1}^{(1)})\boldsymbol{\cdot }\hat{\boldsymbol{u}}\,\text{d}S+\iint _{A_{F}}\boldsymbol{i}_{z}\boldsymbol{\cdot }(\unicode[STIX]{x1D706}\hat{\unicode[STIX]{x1D64F}}^{(1)}-\hat{\unicode[STIX]{x1D64F}}^{(2)})\boldsymbol{\cdot }\boldsymbol{u}_{1}^{(1)}\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle \quad +\,\iint _{A_{F}}\boldsymbol{i}_{z}\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D64F}}^{(2)}\boldsymbol{\cdot }(\boldsymbol{u}_{1}^{(1)}-\boldsymbol{u}_{1}^{(2)})\,\text{d}S=-\hat{\boldsymbol{F}}\boldsymbol{\cdot }\boldsymbol{U}_{1}-\hat{\boldsymbol{L}}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{1},\end{eqnarray}$$
where
![]() $\hat{\boldsymbol{u}}=\hat{\boldsymbol{u}}^{(1)}=\hat{\boldsymbol{u}}^{(2)}$
(on the interface),
$\hat{\boldsymbol{u}}=\hat{\boldsymbol{u}}^{(1)}=\hat{\boldsymbol{u}}^{(2)}$
(on the interface),
![]() $\hat{\boldsymbol{F}},\hat{\boldsymbol{L}}$
are the force and torque acting on the rigid sphere in the complementary Stokes problem. Using the boundary conditions at the interface for
$\hat{\boldsymbol{F}},\hat{\boldsymbol{L}}$
are the force and torque acting on the rigid sphere in the complementary Stokes problem. Using the boundary conditions at the interface for
![]() $O(\unicode[STIX]{x1D716})$
problem, equations (2.24)–(2.26), along with (2.31), we see that we only need to know the solution of
$O(\unicode[STIX]{x1D716})$
problem, equations (2.24)–(2.26), along with (2.31), we see that we only need to know the solution of
![]() $O(1)$
problem and complementary Stokes flow problem to find the swimmer velocity at
$O(1)$
problem and complementary Stokes flow problem to find the swimmer velocity at
![]() $O(\unicode[STIX]{x1D716})$
.
$O(\unicode[STIX]{x1D716})$
.
Below, we outline the methodology used for solving the
![]() $O(1)$
problem corresponding to the motion of a swimmer near a plane interface which is governed by (2.10), (2.12)–(2.14), (2.19)–(2.22). We use two approaches: (i) the bipolar coordinate approach and (ii) the method of reflections. Corresponding approaches are used for solving the complementary Stokes problem of the motion of a rigid sphere near a plane interface. These complementary Stokes problems were already solved using the bipolar coordinate approach (Lee & Leal Reference Lee and Leal1980), and also using Lorentz reciprocal theorem approach (Lee et al.
Reference Lee, Chadwick and Leal1979). So, we will not repeat the solution of the complementary Stokes problem here.
$O(1)$
problem corresponding to the motion of a swimmer near a plane interface which is governed by (2.10), (2.12)–(2.14), (2.19)–(2.22). We use two approaches: (i) the bipolar coordinate approach and (ii) the method of reflections. Corresponding approaches are used for solving the complementary Stokes problem of the motion of a rigid sphere near a plane interface. These complementary Stokes problems were already solved using the bipolar coordinate approach (Lee & Leal Reference Lee and Leal1980), and also using Lorentz reciprocal theorem approach (Lee et al.
Reference Lee, Chadwick and Leal1979). So, we will not repeat the solution of the complementary Stokes problem here.
2.3 Swimmer near a plane interface: bipolar coordinate approach
Following the traditional approach (Lauga & Powers Reference Lauga and Powers2009), we divide the
![]() $O(1)$
problem into two subproblems. The first subproblem, also known as the thrust problem, consists of a swimmer fixed in space. As the swimmer is fixed in space, it will experience a hydrodynamic force and torque
$O(1)$
problem into two subproblems. The first subproblem, also known as the thrust problem, consists of a swimmer fixed in space. As the swimmer is fixed in space, it will experience a hydrodynamic force and torque
![]() $(\boldsymbol{F}_{T},\boldsymbol{L}_{T})$
. The second subproblem, also known as the drag problem, consists of the motion of a rigid sphere with unknown translational and rotational velocities of the swimmer, thereby experiencing a drag force and torque
$(\boldsymbol{F}_{T},\boldsymbol{L}_{T})$
. The second subproblem, also known as the drag problem, consists of the motion of a rigid sphere with unknown translational and rotational velocities of the swimmer, thereby experiencing a drag force and torque
![]() $(\boldsymbol{F}_{D},\boldsymbol{L}_{D})$
. As the swimmer itself is force free and torque free, we have
$(\boldsymbol{F}_{D},\boldsymbol{L}_{D})$
. As the swimmer itself is force free and torque free, we have
Knowing the force and torque experienced by the swimmer in the drag problem, the unknown swimmer's translational and rotational velocities can be found using the linear relations between forces and velocities given by
where
![]() $\unicode[STIX]{x1D646}_{T},\unicode[STIX]{x1D646}_{C},\unicode[STIX]{x1D646}_{R}$
are second-order tensors known as the resistance tensors. The appropriate form of these tensors for the motion of a rigid sphere near a plane interface are given by Lee & Leal (Reference Lee and Leal1980) using the bipolar coordinate approach. Thus, we do not repeat the derivation of these resistance tensors. We rather focus on deriving the force experienced by the swimmer in the thrust problem using the bipolar coordinate approach.
$\unicode[STIX]{x1D646}_{T},\unicode[STIX]{x1D646}_{C},\unicode[STIX]{x1D646}_{R}$
are second-order tensors known as the resistance tensors. The appropriate form of these tensors for the motion of a rigid sphere near a plane interface are given by Lee & Leal (Reference Lee and Leal1980) using the bipolar coordinate approach. Thus, we do not repeat the derivation of these resistance tensors. We rather focus on deriving the force experienced by the swimmer in the thrust problem using the bipolar coordinate approach.
For the motion of a sphere near a plane interface, we represent the velocity field in cylindrical coordinates, which in turn is expressed in terms of bispherical eigensolutions. The transformation between cylindrical and bipolar coordinates is given by (Happel & Brenner Reference Happel and Brenner1981)
where
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702},\unicode[STIX]{x1D719})$
are the bispherical coordinate variables. In these coordinates, the surface of the sphere is at
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702},\unicode[STIX]{x1D719})$
are the bispherical coordinate variables. In these coordinates, the surface of the sphere is at
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{0}=-\text{cosh}^{-1}(l)$
, the plane interface is at
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{0}=-\text{cosh}^{-1}(l)$
, the plane interface is at
![]() $\unicode[STIX]{x1D702}=0$
and
$\unicode[STIX]{x1D702}=0$
and
![]() $c=\sqrt{l^{2}-1}$
. A general solution of the Stokes equation for fluid 2 for the motion of a sphere near a plane interface is given by (even though flow field variables in
$c=\sqrt{l^{2}-1}$
. A general solution of the Stokes equation for fluid 2 for the motion of a sphere near a plane interface is given by (even though flow field variables in
![]() $O(1)$
problem are denoted by
$O(1)$
problem are denoted by
![]() $\boldsymbol{u}_{0}^{(k)}$
and
$\boldsymbol{u}_{0}^{(k)}$
and
![]() $p_{0}^{(k)}$
, in this section, for the purposes of brevity, we denote the
$p_{0}^{(k)}$
, in this section, for the purposes of brevity, we denote the
![]() $O(1)$
flow variables in fluid 2 by
$O(1)$
flow variables in fluid 2 by
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $p$
)
$p$
)
where
![]() $(u,v,w)$
are the
$(u,v,w)$
are the
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $\unicode[STIX]{x1D719}$
, and
$\unicode[STIX]{x1D719}$
, and
![]() $z$
components of the velocity field,
$z$
components of the velocity field,
![]() $\unicode[STIX]{x1D701}=\cos (\unicode[STIX]{x1D709})$
,
$\unicode[STIX]{x1D701}=\cos (\unicode[STIX]{x1D709})$
,
![]() $P_{n}^{m}$
is the associated Legendre polynomial of degree
$P_{n}^{m}$
is the associated Legendre polynomial of degree
![]() $n$
and order
$n$
and order
![]() $m$
, while
$m$
, while
![]() $\unicode[STIX]{x1D6FC}_{m}$
are the constants and
$\unicode[STIX]{x1D6FC}_{m}$
are the constants and
A similar set of equations can also be obtained for the motion of fluid above the interface, fluid 1. Satisfying the boundary conditions, continuity equation and boundedness of the flow field provides us with an infinite set of linear algebraic equations among the constants
![]() $A_{n}^{m}$
,
$A_{n}^{m}$
,
![]() $B_{n}^{m}$
,
$B_{n}^{m}$
,
![]() $C_{n}^{m}$
,
$C_{n}^{m}$
,
![]() $E_{n}^{m}$
,
$E_{n}^{m}$
,
![]() $F_{n}^{m}$
,
$F_{n}^{m}$
,
![]() $G_{n}^{m}$
and
$G_{n}^{m}$
and
![]() $H_{n}^{m}$
. As these equations were already derived by Lee & Leal (Reference Lee and Leal1980), we hereby do not repeat them. Since the order of magnitude of these constants for large values of
$H_{n}^{m}$
. As these equations were already derived by Lee & Leal (Reference Lee and Leal1980), we hereby do not repeat them. Since the order of magnitude of these constants for large values of
![]() $n$
is very small, we, therefore, truncate these infinite series to some finite number
$n$
is very small, we, therefore, truncate these infinite series to some finite number
![]() $N$
such that the error in evaluating these constants is
$N$
such that the error in evaluating these constants is
![]() $O(10^{-6})$
. As the major difference in this work is due to the boundary conditions at the surface of the swimmer, we, therefore, proceed to describe the methodology in applying the boundary conditions at the surface of the swimmer in the thrust problem, given by
$O(10^{-6})$
. As the major difference in this work is due to the boundary conditions at the surface of the swimmer, we, therefore, proceed to describe the methodology in applying the boundary conditions at the surface of the swimmer in the thrust problem, given by
The surface velocity can be written in terms of bispherical eigenfunctions as
Hence, for
![]() $m=0$
, we expand
$m=0$
, we expand
![]() $u_{s}^{0}$
and
$u_{s}^{0}$
and
![]() $v_{s}^{0}$
as
$v_{s}^{0}$
as
whereas for
![]() $m\geqslant 1$
, we have
$m\geqslant 1$
, we have
while for all
![]() $m$
, we have
$m$
, we have
The boundary condition on the surface of the swimmer determines the values of constants
![]() $X_{n}^{m}$
,
$X_{n}^{m}$
,
![]() $Y_{n}^{m}$
and
$Y_{n}^{m}$
and
![]() $Z_{n}^{m}$
, which in turn determine the constants
$Z_{n}^{m}$
, which in turn determine the constants
![]() $A_{n}^{m}$
,
$A_{n}^{m}$
,
![]() $B_{n}^{m}$
,
$B_{n}^{m}$
,
![]() $C_{n}^{m}$
,
$C_{n}^{m}$
,
![]() $E_{n}^{m}$
,
$E_{n}^{m}$
,
![]() $F_{n}^{m}$
,
$F_{n}^{m}$
,
![]() $G_{n}^{m}$
and
$G_{n}^{m}$
and
![]() $H_{n}^{m}$
. We, therefore, describe in detail the derivation of constants
$H_{n}^{m}$
. We, therefore, describe in detail the derivation of constants
![]() $X_{n}^{m}$
,
$X_{n}^{m}$
,
![]() $Y_{n}^{m}$
and
$Y_{n}^{m}$
and
![]() $Z_{n}^{m}$
for a squirming boundary condition at the surface of the sphere in appendix A.
$Z_{n}^{m}$
for a squirming boundary condition at the surface of the sphere in appendix A.
2.4 Swimmer near a plane interface: method of reflections
In this section we solve the
![]() $O(1)$
problem for the motion of the squirmer near a plane interface up to an accuracy of
$O(1)$
problem for the motion of the squirmer near a plane interface up to an accuracy of
![]() $O(1/l^{3})$
, using the Lorentz reciprocal theorem. Such a method was used by Lee et al. (Reference Lee, Chadwick and Leal1979) for solving the motion of a rigid sphere near a plane interface. The authors proposed a lemma using which one can find the solution of creeping flow equations for the motion of an arbitrarily shaped particle near a plane interface if one already knows the solution of creeping flow equations for the motion of the same particle in an unbounded medium. If
$O(1/l^{3})$
, using the Lorentz reciprocal theorem. Such a method was used by Lee et al. (Reference Lee, Chadwick and Leal1979) for solving the motion of a rigid sphere near a plane interface. The authors proposed a lemma using which one can find the solution of creeping flow equations for the motion of an arbitrarily shaped particle near a plane interface if one already knows the solution of creeping flow equations for the motion of the same particle in an unbounded medium. If
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $p$
are the solutions of creeping flow equations for the motion of a particle in an infinite fluid 2, then the solutions near a plane interface are given by
$p$
are the solutions of creeping flow equations for the motion of a particle in an infinite fluid 2, then the solutions near a plane interface are given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}^{(2)}=(\boldsymbol{u}+\boldsymbol{u}^{\ast })-\frac{\unicode[STIX]{x1D706}}{1+\unicode[STIX]{x1D706}}(\boldsymbol{u}^{\ast }-\tilde{\boldsymbol{u}}^{\ast })\\ \displaystyle p^{(2)}=(p+p^{\ast })-\frac{\unicode[STIX]{x1D706}}{1+\unicode[STIX]{x1D706}}(p^{\ast }-\tilde{p}^{\ast })\end{array}\right\}\quad \text{for }z<0.\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}^{(2)}=(\boldsymbol{u}+\boldsymbol{u}^{\ast })-\frac{\unicode[STIX]{x1D706}}{1+\unicode[STIX]{x1D706}}(\boldsymbol{u}^{\ast }-\tilde{\boldsymbol{u}}^{\ast })\\ \displaystyle p^{(2)}=(p+p^{\ast })-\frac{\unicode[STIX]{x1D706}}{1+\unicode[STIX]{x1D706}}(p^{\ast }-\tilde{p}^{\ast })\end{array}\right\}\quad \text{for }z<0.\end{eqnarray}$$
For the purposes of brevity, we again denote the flow field variables in the
![]() $O(1)$
problem of motion of a swimmer near a plane interface as
$O(1)$
problem of motion of a swimmer near a plane interface as
![]() $\boldsymbol{u}^{(k)}$
and
$\boldsymbol{u}^{(k)}$
and
![]() $p^{(k)}$
. Here
$p^{(k)}$
. Here
![]() $(\tilde{\boldsymbol{u}},\tilde{p})$
is the associated solution of
$(\tilde{\boldsymbol{u}},\tilde{p})$
is the associated solution of
![]() $(\boldsymbol{u},p)$
and is defined as (Lee et al.
Reference Lee, Chadwick and Leal1979)
$(\boldsymbol{u},p)$
and is defined as (Lee et al.
Reference Lee, Chadwick and Leal1979)
and
![]() $(\boldsymbol{u}^{\ast },p^{\ast })$
is the reflected image solution of
$(\boldsymbol{u}^{\ast },p^{\ast })$
is the reflected image solution of
![]() $(\boldsymbol{u},p)$
given by
$(\boldsymbol{u},p)$
given by
where
![]() $(\tilde{\boldsymbol{u}}^{\ast },\tilde{p}^{\ast })$
is the associated solution of
$(\tilde{\boldsymbol{u}}^{\ast },\tilde{p}^{\ast })$
is the associated solution of
![]() $(\boldsymbol{u}^{\ast },p^{\ast })$
. The operator
$(\boldsymbol{u}^{\ast },p^{\ast })$
. The operator
![]() $\boldsymbol{J}$
is defined as
$\boldsymbol{J}$
is defined as
![]() $J_{ij}\equiv \unicode[STIX]{x1D6FF}_{ij}-2\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}$
, where
$J_{ij}\equiv \unicode[STIX]{x1D6FF}_{ij}-2\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}$
, where
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta. These solutions satisfy the continuity of velocity, shear stress and zero normal velocity at the plane interface.
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta. These solutions satisfy the continuity of velocity, shear stress and zero normal velocity at the plane interface.
The creeping flow equations for the motion of the squirmer in an unbounded fluid were already solved in the literature (Blake Reference Blake1971; Ishikawa et al.
Reference Ishikawa, Simmonds and Pedley2006; Pak & Lauga Reference Pak and Lauga2014). For two squirming modes
![]() $(B_{1},B_{2})$
, this solution can be readily written in terms of point force singularities located at the centre of the squirmer as
$(B_{1},B_{2})$
, this solution can be readily written in terms of point force singularities located at the centre of the squirmer as
where
![]() $\boldsymbol{x}_{+}=(x,y,z+l)$
and
$\boldsymbol{x}_{+}=(x,y,z+l)$
and
![]() $\boldsymbol{u}_{SS},\boldsymbol{u}_{D},\boldsymbol{u}_{D4}$
are the flow fields due to stresslet, source dipole and source quadrupole, respectively. Their expressions are provided in appendix B. Here, the subscript denotes the level of approximation in the context of normal reflection calculation procedure. For instance,
$\boldsymbol{u}_{SS},\boldsymbol{u}_{D},\boldsymbol{u}_{D4}$
are the flow fields due to stresslet, source dipole and source quadrupole, respectively. Their expressions are provided in appendix B. Here, the subscript denotes the level of approximation in the context of normal reflection calculation procedure. For instance,
![]() $\boldsymbol{u}_{0}^{(k)}$
denotes the flow field in an unbounded domain,
$\boldsymbol{u}_{0}^{(k)}$
denotes the flow field in an unbounded domain,
![]() $\boldsymbol{u}_{1}^{(k)}$
denotes the (first) reflection from the interface,
$\boldsymbol{u}_{1}^{(k)}$
denotes the (first) reflection from the interface,
![]() $\boldsymbol{u}_{2}^{(k)}$
denotes the (second) reflection from the sphere. Even though these velocity fields are dimensionless, i.e.,
$\boldsymbol{u}_{2}^{(k)}$
denotes the (second) reflection from the sphere. Even though these velocity fields are dimensionless, i.e.,
![]() $B_{1}=\unicode[STIX]{x1D6FD}_{1}(t)$
and
$B_{1}=\unicode[STIX]{x1D6FD}_{1}(t)$
and
![]() $B_{2}=\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6FD}_{2}(t)$
, we write them in terms of
$B_{2}=\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6FD}_{2}(t)$
, we write them in terms of
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
to see the correspondence with the dimensional velocities. Using the lemma and the above solution, one can derive the solution of creeping flow equations for the motion of a squirmer near a plane interface. After subtracting the flow field in an unbounded fluid, equations (2.60)–(2.62) from the solution calculated using the lemma, we obtain the flow field due to the interface (denoted as
$B_{2}$
to see the correspondence with the dimensional velocities. Using the lemma and the above solution, one can derive the solution of creeping flow equations for the motion of a squirmer near a plane interface. After subtracting the flow field in an unbounded fluid, equations (2.60)–(2.62) from the solution calculated using the lemma, we obtain the flow field due to the interface (denoted as
![]() $\boldsymbol{u}_{1}^{(k)},p_{1}^{(k)}$
). Using the Faxen’s laws with the flow field due to the interface in fluid 2
$\boldsymbol{u}_{1}^{(k)},p_{1}^{(k)}$
). Using the Faxen’s laws with the flow field due to the interface in fluid 2
![]() $(\boldsymbol{u}_{1}^{(2)},p_{1}^{(2)})$
and the force-free, torque-free condition on the squirmer, we obtain the corrections to the swimmer velocity because of the presence of the interface which are given as
$(\boldsymbol{u}_{1}^{(2)},p_{1}^{(2)})$
and the force-free, torque-free condition on the squirmer, we obtain the corrections to the swimmer velocity because of the presence of the interface which are given as
 $$\begin{eqnarray}\displaystyle U_{x} & = & \displaystyle \frac{2}{3}B_{1}\sin (\unicode[STIX]{x1D703}_{z})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{8}\frac{\sin (\unicode[STIX]{x1D703}_{z})(B_{2}\cos (\unicode[STIX]{x1D703}_{z})[l^{4}\unicode[STIX]{x1D706}+(-\unicode[STIX]{x1D706}-\frac{1}{3})l^{2}+\frac{5}{9}\unicode[STIX]{x1D706}]-\frac{2}{9}B_{1}l[(\unicode[STIX]{x1D706}+\frac{1}{2})l^{2}-\unicode[STIX]{x1D706}])}{l^{6}(1+\unicode[STIX]{x1D706})},\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U_{x} & = & \displaystyle \frac{2}{3}B_{1}\sin (\unicode[STIX]{x1D703}_{z})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{8}\frac{\sin (\unicode[STIX]{x1D703}_{z})(B_{2}\cos (\unicode[STIX]{x1D703}_{z})[l^{4}\unicode[STIX]{x1D706}+(-\unicode[STIX]{x1D706}-\frac{1}{3})l^{2}+\frac{5}{9}\unicode[STIX]{x1D706}]-\frac{2}{9}B_{1}l[(\unicode[STIX]{x1D706}+\frac{1}{2})l^{2}-\unicode[STIX]{x1D706}])}{l^{6}(1+\unicode[STIX]{x1D706})},\qquad\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle U_{z} & = & \displaystyle \frac{2}{3}B_{1}\cos (\unicode[STIX]{x1D703}_{z})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{48l^{6}(1+\unicode[STIX]{x1D706})}\left(\begin{array}{@{}c@{}}(27B_{2}\cos (\unicode[STIX]{x1D703}_{z})^{2}-9B_{2})[(\unicode[STIX]{x1D706}+\frac{2}{3})l^{4}+(-\frac{4}{3}\unicode[STIX]{x1D706}-\frac{1}{3})l^{2}+\frac{5}{9}\unicode[STIX]{x1D706}]\\ -16B_{1}l\cos (\unicode[STIX]{x1D703}_{z})[(\unicode[STIX]{x1D706}+\frac{1}{4})l^{2}-\frac{1}{2}\unicode[STIX]{x1D706}]\end{array}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U_{z} & = & \displaystyle \frac{2}{3}B_{1}\cos (\unicode[STIX]{x1D703}_{z})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{48l^{6}(1+\unicode[STIX]{x1D706})}\left(\begin{array}{@{}c@{}}(27B_{2}\cos (\unicode[STIX]{x1D703}_{z})^{2}-9B_{2})[(\unicode[STIX]{x1D706}+\frac{2}{3})l^{4}+(-\frac{4}{3}\unicode[STIX]{x1D706}-\frac{1}{3})l^{2}+\frac{5}{9}\unicode[STIX]{x1D706}]\\ -16B_{1}l\cos (\unicode[STIX]{x1D703}_{z})[(\unicode[STIX]{x1D706}+\frac{1}{4})l^{2}-\frac{1}{2}\unicode[STIX]{x1D706}]\end{array}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

Figure 2. Velocities of a swimmer moving near a plane interface, (a)
![]() $U_{z}$
and (b)
$U_{z}$
and (b)
![]() $\unicode[STIX]{x1D6FA}_{y}$
for
$\unicode[STIX]{x1D6FA}_{y}$
for
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
,
$\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
,
![]() $\unicode[STIX]{x1D706}=10^{-3},1$
and 10. Lines indicate bipolar coordinate results while symbols denote the method of reflections results.
$\unicode[STIX]{x1D706}=10^{-3},1$
and 10. Lines indicate bipolar coordinate results while symbols denote the method of reflections results.
These expressions in the limit
![]() $\unicode[STIX]{x1D706}\rightarrow \infty$
or
$\unicode[STIX]{x1D706}\rightarrow \infty$
or
![]() $\unicode[STIX]{x1D706}=0$
are identical to the expressions derived by Spagnolie & Lauga (Reference Spagnolie and Lauga2012) for the motion of a swimmer (represented by force dipole, source dipole and source quadrupole) near a plane wall and plane interface, respectively. In the case of a stresslet near a plane interface, these expressions reduce to those derived by Lopez & Lauga (Reference Lopez and Lauga2014), for arbitrary values of viscosity ratios. Additionally, in figure 2, we compare these expressions of swimmer velocities with the bipolar coordinate results, for various values of viscosity ratios. The flow field due to the interface in fluid 2
$\unicode[STIX]{x1D706}=0$
are identical to the expressions derived by Spagnolie & Lauga (Reference Spagnolie and Lauga2012) for the motion of a swimmer (represented by force dipole, source dipole and source quadrupole) near a plane wall and plane interface, respectively. In the case of a stresslet near a plane interface, these expressions reduce to those derived by Lopez & Lauga (Reference Lopez and Lauga2014), for arbitrary values of viscosity ratios. Additionally, in figure 2, we compare these expressions of swimmer velocities with the bipolar coordinate results, for various values of viscosity ratios. The flow field due to the interface in fluid 2
![]() $(\boldsymbol{u}_{1}^{(2)},p_{1}^{(2)})$
, however, does not satisfy the boundary conditions on the surface of the squirmer given by
$(\boldsymbol{u}_{1}^{(2)},p_{1}^{(2)})$
, however, does not satisfy the boundary conditions on the surface of the squirmer given by
![]() $\boldsymbol{U}_{1}+\unicode[STIX]{x1D734}_{1}\times \boldsymbol{x}^{s}$
. Consequently, we need to put additional singularities at the centre of the squirmer to satisfy the boundary conditions on its surface
$\boldsymbol{U}_{1}+\unicode[STIX]{x1D734}_{1}\times \boldsymbol{x}^{s}$
. Consequently, we need to put additional singularities at the centre of the squirmer to satisfy the boundary conditions on its surface
![]() $(\boldsymbol{U}_{1}+\unicode[STIX]{x1D734}_{1}\times \boldsymbol{x}^{s}-\boldsymbol{u}_{1}^{(2)}(\boldsymbol{x}^{s}))$
. We expand this boundary condition in terms of
$(\boldsymbol{U}_{1}+\unicode[STIX]{x1D734}_{1}\times \boldsymbol{x}^{s}-\boldsymbol{u}_{1}^{(2)}(\boldsymbol{x}^{s}))$
. We expand this boundary condition in terms of
![]() $1/l$
, and we choose singularities located at the centre of the squirmer only to cancel the first term of this boundary condition expressed in terms of
$1/l$
, and we choose singularities located at the centre of the squirmer only to cancel the first term of this boundary condition expressed in terms of
![]() $1/l$
. The non-zero velocity on the surface of the squirmer expanded in terms of
$1/l$
. The non-zero velocity on the surface of the squirmer expanded in terms of
![]() $1/l$
is given as
$1/l$
is given as
 $$\begin{eqnarray}\displaystyle u_{1}^{(2)} & = & \displaystyle \frac{1}{l^{3}}\left[\frac{B_{2}(15\cos (\unicode[STIX]{x1D703}_{z})^{2}\unicode[STIX]{x1D706}+6\cos (\unicode[STIX]{x1D703}_{z})^{2}-7\unicode[STIX]{x1D706}-2)x}{32+32\unicode[STIX]{x1D706}}-\frac{9B_{2}\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})(\unicode[STIX]{x1D706}+\frac{1}{3})(z+l)}{16+16\unicode[STIX]{x1D706}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\frac{1}{l^{4}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{1}^{(2)} & = & \displaystyle \frac{1}{l^{3}}\left[\frac{B_{2}(15\cos (\unicode[STIX]{x1D703}_{z})^{2}\unicode[STIX]{x1D706}+6\cos (\unicode[STIX]{x1D703}_{z})^{2}-7\unicode[STIX]{x1D706}-2)x}{32+32\unicode[STIX]{x1D706}}-\frac{9B_{2}\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})(\unicode[STIX]{x1D706}+\frac{1}{3})(z+l)}{16+16\unicode[STIX]{x1D706}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\frac{1}{l^{4}}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle w_{1}^{(2)} & = & \displaystyle \frac{1}{l^{3}}\left[-\frac{9B_{2}\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})(\unicode[STIX]{x1D706}+\frac{1}{3})x}{16+16\unicode[STIX]{x1D706}}-\frac{B_{2}(3\cos (\unicode[STIX]{x1D703}_{z})^{2}-1)(2\unicode[STIX]{x1D706}+1)(z+l)}{8+8\unicode[STIX]{x1D706}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\frac{1}{l^{4}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w_{1}^{(2)} & = & \displaystyle \frac{1}{l^{3}}\left[-\frac{9B_{2}\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})(\unicode[STIX]{x1D706}+\frac{1}{3})x}{16+16\unicode[STIX]{x1D706}}-\frac{B_{2}(3\cos (\unicode[STIX]{x1D703}_{z})^{2}-1)(2\unicode[STIX]{x1D706}+1)(z+l)}{8+8\unicode[STIX]{x1D706}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\frac{1}{l^{4}}\right).\end{eqnarray}$$
The flow field satisfying these boundary conditions on the surface of the sphere and the Stokes flow equations can be written as a linear combination of shear flow and extensional flow past a sphere. A shear flow past a sphere can be represented by a stresslet, rotlet and a potential quadrupole located at the centre of the sphere, while an extensional flow past a sphere can be generated by a stresslet and a potential quadrupole kept at the centre of the sphere (Chwang & Wu Reference Chwang and Wu1975). Consequently, we find that this boundary condition can be satisfied by a suitable combination of stresslet and a potential quadrupole located at the centre of the squirmer, given by
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{2}^{(2)} & = & \displaystyle \frac{A}{l^{3}}\left[-\frac{5}{2}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})-\frac{1}{2}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{C}{l^{3}}\left[-\frac{5}{3}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})-\frac{1}{3}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{D}{l^{3}}\left[\frac{5}{6}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})+\frac{1}{6}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{2}^{(2)} & = & \displaystyle \frac{A}{l^{3}}\left[-\frac{5}{2}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})-\frac{1}{2}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{C}{l^{3}}\left[-\frac{5}{3}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})-\frac{1}{3}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{D}{l^{3}}\left[\frac{5}{6}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})+\frac{1}{6}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})\right],\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D71E}_{1}=\boldsymbol{i}_{x}-\boldsymbol{i}_{z};\unicode[STIX]{x1D71E}_{2}=\frac{5}{6}(\boldsymbol{i}_{x}+\boldsymbol{i}_{z})$
and
$\unicode[STIX]{x1D71E}_{1}=\boldsymbol{i}_{x}-\boldsymbol{i}_{z};\unicode[STIX]{x1D71E}_{2}=\frac{5}{6}(\boldsymbol{i}_{x}+\boldsymbol{i}_{z})$
and
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle A=\frac{B_{2}(9\cos (\unicode[STIX]{x1D703}_{z})^{2}\unicode[STIX]{x1D706}+6\cos (\unicode[STIX]{x1D703}_{z})^{2}-\unicode[STIX]{x1D706}-2)}{32(1+\unicode[STIX]{x1D706})},\\ \displaystyle C=\frac{3B_{2}\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})(3\unicode[STIX]{x1D706}+1)}{16(1+\unicode[STIX]{x1D706})},\\ \displaystyle D=-\frac{3B_{2}\unicode[STIX]{x1D706}\sin (\unicode[STIX]{x1D703}_{z})^{2}}{16(1+\unicode[STIX]{x1D706})}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle A=\frac{B_{2}(9\cos (\unicode[STIX]{x1D703}_{z})^{2}\unicode[STIX]{x1D706}+6\cos (\unicode[STIX]{x1D703}_{z})^{2}-\unicode[STIX]{x1D706}-2)}{32(1+\unicode[STIX]{x1D706})},\\ \displaystyle C=\frac{3B_{2}\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})(3\unicode[STIX]{x1D706}+1)}{16(1+\unicode[STIX]{x1D706})},\\ \displaystyle D=-\frac{3B_{2}\unicode[STIX]{x1D706}\sin (\unicode[STIX]{x1D703}_{z})^{2}}{16(1+\unicode[STIX]{x1D706})}.\end{array}\right\}\end{eqnarray}$$
In summary, the singularities required to represent the flow field due to a squirmer near a plane interface, accurate to
![]() $O(1/l^{3})$
, are given by
$O(1/l^{3})$
, are given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{stresslet}:-\frac{B_{2}}{2}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})+\frac{1}{l^{3}}\left[\begin{array}{@{}c@{}}\displaystyle -\frac{5A}{2}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})-\frac{5C}{3}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})\\ \displaystyle +\frac{5D}{6}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})\end{array}\right],\\ \displaystyle \text{source dipole}:\frac{B_{1}}{3}\boldsymbol{u}_{D}(\boldsymbol{x}_{+};\boldsymbol{e}),\\ \displaystyle \text{source quadrupole}:-\frac{B_{2}}{6}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})+\frac{1}{l^{3}}\left[\begin{array}{@{}c@{}}\displaystyle -\frac{A}{2}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})-\frac{C}{3}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})\\ \displaystyle +\frac{D}{6}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})\end{array}\right].\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{stresslet}:-\frac{B_{2}}{2}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})+\frac{1}{l^{3}}\left[\begin{array}{@{}c@{}}\displaystyle -\frac{5A}{2}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})-\frac{5C}{3}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})\\ \displaystyle +\frac{5D}{6}\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})\end{array}\right],\\ \displaystyle \text{source dipole}:\frac{B_{1}}{3}\boldsymbol{u}_{D}(\boldsymbol{x}_{+};\boldsymbol{e}),\\ \displaystyle \text{source quadrupole}:-\frac{B_{2}}{6}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})+\frac{1}{l^{3}}\left[\begin{array}{@{}c@{}}\displaystyle -\frac{A}{2}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{z},\boldsymbol{i}_{z})-\frac{C}{3}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\boldsymbol{i}_{x},\boldsymbol{i}_{z})\\ \displaystyle +\frac{D}{6}\boldsymbol{u}_{D4}(\boldsymbol{x}_{+};\unicode[STIX]{x1D71E}_{1},\unicode[STIX]{x1D71E}_{2})\end{array}\right].\end{array}\right\}\end{eqnarray}$$
For simplicity, we will derive the velocity of the squirmer near a weakly deforming interface, accurate to
![]() $O(1/l)$
. For this purpose, we will need the flow field due to the motion of a squirmer near a plane interface, accurate to
$O(1/l)$
. For this purpose, we will need the flow field due to the motion of a squirmer near a plane interface, accurate to
![]() $O(1/l)$
. From the above expressions, we can clearly see that such a flow field, accurate up to
$O(1/l)$
. From the above expressions, we can clearly see that such a flow field, accurate up to
![]() $O(1/l)$
, is given by
$O(1/l)$
, is given by
![]() $-(B_{2}/2)\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})+(B_{1}/3)\boldsymbol{u}_{D}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})$
.
$-(B_{2}/2)\boldsymbol{u}_{SS}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})+(B_{1}/3)\boldsymbol{u}_{D}(\boldsymbol{x}_{+};\boldsymbol{e},\boldsymbol{e})$
.
3 Results and discussion
We note that the solution derived is valid for the squirming modes,
![]() $B_{1}(t)$
and
$B_{1}(t)$
and
![]() $B_{2}(t)$
, that are arbitrary functions of time. In this section, we analysed two examples of these solutions: a swimmer with constant squirming modes and a squirmer with time-reversible squirming modes. The reason for analysing a time-reversible swimmer is that such a swimmer does not move (in a time-averaged sense) near plane interfaces but it can move due to the interface deformations (Scallop theorem is broken solely due to its hydrodynamic interactions with a flexible interface).
$B_{2}(t)$
, that are arbitrary functions of time. In this section, we analysed two examples of these solutions: a swimmer with constant squirming modes and a squirmer with time-reversible squirming modes. The reason for analysing a time-reversible swimmer is that such a swimmer does not move (in a time-averaged sense) near plane interfaces but it can move due to the interface deformations (Scallop theorem is broken solely due to its hydrodynamic interactions with a flexible interface).
3.1 Interface deformation
The leading-order interface shape is given by the solution of differential equation which is obtained from the
![]() $O(1)$
normal stress balance at the interface, given by
$O(1)$
normal stress balance at the interface, given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}\left(\frac{\unicode[STIX]{x2202}^{2}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{2}}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}+\frac{1}{\unicode[STIX]{x1D70C}^{2}}\frac{\unicode[STIX]{x2202}^{2}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}^{2}}\right)+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}f_{1}=(\unicode[STIX]{x1D706}T_{zz0}^{(1)}-T_{zz0}^{(2)})\nonumber\\ \displaystyle & & \displaystyle \quad =g_{0}(\unicode[STIX]{x1D70C},t)+g_{1}(\unicode[STIX]{x1D70C},t)\cos (\unicode[STIX]{x1D719})+g_{2}(\unicode[STIX]{x1D70C},t)\cos (2\unicode[STIX]{x1D719}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}\left(\frac{\unicode[STIX]{x2202}^{2}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{2}}+\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}+\frac{1}{\unicode[STIX]{x1D70C}^{2}}\frac{\unicode[STIX]{x2202}^{2}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}^{2}}\right)+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}f_{1}=(\unicode[STIX]{x1D706}T_{zz0}^{(1)}-T_{zz0}^{(2)})\nonumber\\ \displaystyle & & \displaystyle \quad =g_{0}(\unicode[STIX]{x1D70C},t)+g_{1}(\unicode[STIX]{x1D70C},t)\cos (\unicode[STIX]{x1D719})+g_{2}(\unicode[STIX]{x1D70C},t)\cos (2\unicode[STIX]{x1D719}).\end{eqnarray}$$
The expressions for
![]() $g_{0}$
,
$g_{0}$
,
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{2}$
using the method of reflections are given by
$g_{2}$
using the method of reflections are given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle g_{0}(\unicode[STIX]{x1D70C},t)=A_{1}(t)\left(\frac{2l^{3}-3l\unicode[STIX]{x1D70C}^{2}}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{7/2}}\right);\\ A_{1}(t)=-9B_{2}(t)\cos (\unicode[STIX]{x1D703}_{z})^{2}l+4B_{1}(t)\cos (\unicode[STIX]{x1D703}_{z})+3B_{2}(t)l,\\ \displaystyle g_{1}(\unicode[STIX]{x1D70C},t)=C_{1}(t)\left(\frac{-\unicode[STIX]{x1D70C}^{3}+4l^{2}\unicode[STIX]{x1D70C}}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{7/2}}\right);\quad C_{1}(t)=4\sin (\unicode[STIX]{x1D703}_{z})(-3B_{2}(t)l\cos (\unicode[STIX]{x1D703}_{z})+B_{1}(t)),\\ \displaystyle g_{2}(\unicode[STIX]{x1D70C},t)=D_{1}(t)\frac{\unicode[STIX]{x1D70C}}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{7/2}};\quad D_{1}(t)=-15B_{2}(t)l^{2}\sin (\unicode[STIX]{x1D703}_{z})^{2}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle g_{0}(\unicode[STIX]{x1D70C},t)=A_{1}(t)\left(\frac{2l^{3}-3l\unicode[STIX]{x1D70C}^{2}}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{7/2}}\right);\\ A_{1}(t)=-9B_{2}(t)\cos (\unicode[STIX]{x1D703}_{z})^{2}l+4B_{1}(t)\cos (\unicode[STIX]{x1D703}_{z})+3B_{2}(t)l,\\ \displaystyle g_{1}(\unicode[STIX]{x1D70C},t)=C_{1}(t)\left(\frac{-\unicode[STIX]{x1D70C}^{3}+4l^{2}\unicode[STIX]{x1D70C}}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{7/2}}\right);\quad C_{1}(t)=4\sin (\unicode[STIX]{x1D703}_{z})(-3B_{2}(t)l\cos (\unicode[STIX]{x1D703}_{z})+B_{1}(t)),\\ \displaystyle g_{2}(\unicode[STIX]{x1D70C},t)=D_{1}(t)\frac{\unicode[STIX]{x1D70C}}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{7/2}};\quad D_{1}(t)=-15B_{2}(t)l^{2}\sin (\unicode[STIX]{x1D703}_{z})^{2}.\end{array}\right\}\end{eqnarray}$$
The solution of equation (3.1) for any arbitrary values of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
is given by
$\unicode[STIX]{x1D6FD}$
is given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle f_{1}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t)=[h_{0}(\unicode[STIX]{x1D70C},t)+h_{1}(\unicode[STIX]{x1D70C},t)\cos (\unicode[STIX]{x1D719})+h_{2}(\unicode[STIX]{x1D70C},t)\cos (2\unicode[STIX]{x1D719})],\\ \displaystyle h_{m}(\unicode[STIX]{x1D70C},t)=\frac{\text{I}_{m}(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{ref})}{\unicode[STIX]{x1D6FD}}\int _{\unicode[STIX]{x1D70C}}^{\infty }yg_{m}(y,t)\text{K}_{m}(y/\unicode[STIX]{x1D70C}_{ref})\,\text{d}y\\ \displaystyle \hspace{55.00008pt}+\,\frac{\text{K}_{m}(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{ref})}{\unicode[STIX]{x1D6FD}}\int _{0}^{\unicode[STIX]{x1D70C}}yg_{m}(y,t)\text{I}_{m}(y/\unicode[STIX]{x1D70C}_{ref})\,\text{d}y,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle f_{1}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t)=[h_{0}(\unicode[STIX]{x1D70C},t)+h_{1}(\unicode[STIX]{x1D70C},t)\cos (\unicode[STIX]{x1D719})+h_{2}(\unicode[STIX]{x1D70C},t)\cos (2\unicode[STIX]{x1D719})],\\ \displaystyle h_{m}(\unicode[STIX]{x1D70C},t)=\frac{\text{I}_{m}(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{ref})}{\unicode[STIX]{x1D6FD}}\int _{\unicode[STIX]{x1D70C}}^{\infty }yg_{m}(y,t)\text{K}_{m}(y/\unicode[STIX]{x1D70C}_{ref})\,\text{d}y\\ \displaystyle \hspace{55.00008pt}+\,\frac{\text{K}_{m}(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{ref})}{\unicode[STIX]{x1D6FD}}\int _{0}^{\unicode[STIX]{x1D70C}}yg_{m}(y,t)\text{I}_{m}(y/\unicode[STIX]{x1D70C}_{ref})\,\text{d}y,\end{array}\right\}\end{eqnarray}$$
where,
![]() $m=0$
, 1 or 2,
$m=0$
, 1 or 2,
![]() $\unicode[STIX]{x1D70C}_{ref}=\sqrt{\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D70C}_{ref}=\sqrt{\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC}}$
,
![]() $\text{I}_{m}$
and
$\text{I}_{m}$
and
![]() $\text{K}_{m}$
are the modified Bessel functions of first and second kind of order
$\text{K}_{m}$
are the modified Bessel functions of first and second kind of order
![]() $m$
. The interface shape for the limiting values of
$m$
. The interface shape for the limiting values of
![]() $\unicode[STIX]{x1D6FC}\ll \unicode[STIX]{x1D6FD}$
is given by
$\unicode[STIX]{x1D6FC}\ll \unicode[STIX]{x1D6FD}$
is given by
 $$\begin{eqnarray}\displaystyle f_{1}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t) & = & \displaystyle \frac{1}{3}\frac{lA_{1}(t)}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{3/2}}+\left[\frac{1}{3}\frac{\unicode[STIX]{x1D70C}C_{1}(t)}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{3/2}}\right]\cos (\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle -\,\left[\frac{2}{15}\frac{((-15l^{2}-15\unicode[STIX]{x1D70C}^{2})\sqrt{l^{2}+\unicode[STIX]{x1D70C}^{2}}+l^{3}+\frac{3}{2}l\unicode[STIX]{x1D70C}^{2})D_{1}(t)}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{3/2}l\unicode[STIX]{x1D70C}^{2}}\right]\cos (2\unicode[STIX]{x1D719}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{1}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},t) & = & \displaystyle \frac{1}{3}\frac{lA_{1}(t)}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{3/2}}+\left[\frac{1}{3}\frac{\unicode[STIX]{x1D70C}C_{1}(t)}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{3/2}}\right]\cos (\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle -\,\left[\frac{2}{15}\frac{((-15l^{2}-15\unicode[STIX]{x1D70C}^{2})\sqrt{l^{2}+\unicode[STIX]{x1D70C}^{2}}+l^{3}+\frac{3}{2}l\unicode[STIX]{x1D70C}^{2})D_{1}(t)}{(l^{2}+\unicode[STIX]{x1D70C}^{2})^{3/2}l\unicode[STIX]{x1D70C}^{2}}\right]\cos (2\unicode[STIX]{x1D719}),\end{eqnarray}$$
and for
![]() $\unicode[STIX]{x1D6FC}\gg \unicode[STIX]{x1D6FD}$
is given by
$\unicode[STIX]{x1D6FC}\gg \unicode[STIX]{x1D6FD}$
is given by
For the motion of a rigid sphere normal to the undeformed interface, Aderogba & Blake (Reference Aderogba and Blake1978) remarked that if we set
![]() $\unicode[STIX]{x1D6FC}$
identically to zero in the differential equation for the interface deformation, then the interface deformation has a log singularity and it has no solution which is both finite at the origin and zero as
$\unicode[STIX]{x1D6FC}$
identically to zero in the differential equation for the interface deformation, then the interface deformation has a log singularity and it has no solution which is both finite at the origin and zero as
![]() $\unicode[STIX]{x1D70C}$
goes to infinity. Note that when
$\unicode[STIX]{x1D70C}$
goes to infinity. Note that when
![]() $\unicode[STIX]{x1D6FC}$
is identically zero, the flow field is dominated by interfacial tension. Berdan & Leal (Reference Berdan and Leal1982) suggested that the interfacial tension can only restrict the surface curvature but not the surface deformation, thereby allowing the occurrence of a log singularity as predicted by Aderogba & Blake (Reference Aderogba and Blake1978). We note that there is no such log singularity in the interface deformation when
$\unicode[STIX]{x1D6FC}$
is identically zero, the flow field is dominated by interfacial tension. Berdan & Leal (Reference Berdan and Leal1982) suggested that the interfacial tension can only restrict the surface curvature but not the surface deformation, thereby allowing the occurrence of a log singularity as predicted by Aderogba & Blake (Reference Aderogba and Blake1978). We note that there is no such log singularity in the interface deformation when
![]() $\unicode[STIX]{x1D6FC}$
is set identically to zero in (3.1), for the motion of a squirmer near a deforming interface. To generalize, one cannot find an interface deformation satisfying all the boundary conditions for a Stokeslet (far-field approximation of a rigid sphere) oriented normal to an undeformed interface. However, this is not the case for a Stokes dipole (far-field approximation of a swimmer) oriented normal to an undeformed interface. Such an ill-posed problem for rigid bodies versus a well-posed problem for swimmers can also be found for the motion of two-dimensional bodies. For instance, the translational motion of an infinitely long cylinder in an unbounded fluid is an ill-posed problem (Happel & Brenner Reference Happel and Brenner1981; Guazzelli, Morris & Pic Reference Guazzelli, Morris and Pic2011). On the contrary, the motion of a cylindrical swimmer in an unbounded fluid is a well-posed problem which can also be solved using a reciprocal theorem framework (Elfring Reference Elfring2015).
$\unicode[STIX]{x1D6FC}$
is set identically to zero in (3.1), for the motion of a squirmer near a deforming interface. To generalize, one cannot find an interface deformation satisfying all the boundary conditions for a Stokeslet (far-field approximation of a rigid sphere) oriented normal to an undeformed interface. However, this is not the case for a Stokes dipole (far-field approximation of a swimmer) oriented normal to an undeformed interface. Such an ill-posed problem for rigid bodies versus a well-posed problem for swimmers can also be found for the motion of two-dimensional bodies. For instance, the translational motion of an infinitely long cylinder in an unbounded fluid is an ill-posed problem (Happel & Brenner Reference Happel and Brenner1981; Guazzelli, Morris & Pic Reference Guazzelli, Morris and Pic2011). On the contrary, the motion of a cylindrical swimmer in an unbounded fluid is a well-posed problem which can also be solved using a reciprocal theorem framework (Elfring Reference Elfring2015).

Figure 3. Interface deformation for various orientations of swimmer at
![]() $l=2$
,
$l=2$
,
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. The orientations of the swimmer are (a)
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. The orientations of the swimmer are (a)
![]() $\unicode[STIX]{x1D703}_{z}=0$
, (b)
$\unicode[STIX]{x1D703}_{z}=0$
, (b)
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/3$
, (c)
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/3$
, (c)
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/2$
and (d)
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/2$
and (d)
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}$
. Interface shape is axisymmetric when
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}$
. Interface shape is axisymmetric when
![]() $\unicode[STIX]{x1D703}_{z}=0$
or
$\unicode[STIX]{x1D703}_{z}=0$
or
![]() $\unicode[STIX]{x03C0}$
.
$\unicode[STIX]{x03C0}$
.
In this section, we study the interface deformation for steady squirming modes. Figure 3 shows the interface deformation for the squirmer orientations of
![]() $\unicode[STIX]{x1D703}_{z}=0,\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}$
and
$\unicode[STIX]{x1D703}_{z}=0,\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}$
and
![]() $\unicode[STIX]{x03C0}/3$
. When
$\unicode[STIX]{x03C0}/3$
. When
![]() $\unicode[STIX]{x1D703}_{z}$
is 0 or
$\unicode[STIX]{x1D703}_{z}$
is 0 or
![]() $\unicode[STIX]{x03C0}$
, the problem is axisymmetric, hence it can be seen from (3.3) that
$\unicode[STIX]{x03C0}$
, the problem is axisymmetric, hence it can be seen from (3.3) that
![]() $f_{1}=h_{0}$
(as
$f_{1}=h_{0}$
(as
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{2}$
are zero, so
$g_{2}$
are zero, so
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
are zero). Hence, the interface shape is the same for these two orientations but the magnitude of the interface deformation is larger for
$h_{2}$
are zero). Hence, the interface shape is the same for these two orientations but the magnitude of the interface deformation is larger for
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}$
due to a corresponding larger magnitude of
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}$
due to a corresponding larger magnitude of
![]() $A_{1}$
when
$A_{1}$
when
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}$
(note that
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}$
(note that
![]() $h_{0}\propto g_{0}\propto A_{1}$
).
$h_{0}\propto g_{0}\propto A_{1}$
).

Figure 4. The effect of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
on the interface deformation for the motion of a squirmer near an interface. The values of parameters are taken as:
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
on the interface deformation for the motion of a squirmer near an interface. The values of parameters are taken as:
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
and
$\unicode[STIX]{x1D706}=1$
and
![]() $l=3$
. Lines denote the bipolar coordinate results while symbols denote the MOR results.
$l=3$
. Lines denote the bipolar coordinate results while symbols denote the MOR results.
We hereby study the effect of the relative importance of density difference and the interfacial tension on the interfacial deformation, i.e., the effect of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
on
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
on
![]() $f_{1}$
. For this purpose, we fix the sum
$f_{1}$
. For this purpose, we fix the sum
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
as 20 (equivalent to fixing
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
as 20 (equivalent to fixing
![]() $\unicode[STIX]{x1D716}=0.05$
) and study the interfacial deformation as
$\unicode[STIX]{x1D716}=0.05$
) and study the interfacial deformation as
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
is varied from 0.01 to
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
is varied from 0.01 to
![]() $\infty$
. We note that
$\infty$
. We note that
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
implies that the physics is determined by the interfacial tension forces while
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
implies that the physics is determined by the interfacial tension forces while
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
means that the density difference is the dominating factor. Figure 4 shows the variation of interfacial deformation with radial coordinate (in cylindrical coordinates) for
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
means that the density difference is the dominating factor. Figure 4 shows the variation of interfacial deformation with radial coordinate (in cylindrical coordinates) for
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01,0.1,1,10$
and
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01,0.1,1,10$
and
![]() $\infty$
,
$\infty$
,
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $l=3$
and
$l=3$
and
![]() $B_{2}/B_{1}=4$
. As deformation itself is two-dimensional as shown in figure 3, for simplicity, we study the behaviour of deformation as observed from the equatorial plane
$B_{2}/B_{1}=4$
. As deformation itself is two-dimensional as shown in figure 3, for simplicity, we study the behaviour of deformation as observed from the equatorial plane
![]() $(\unicode[STIX]{x1D719}=0,\unicode[STIX]{x03C0})$
. It is to be noted that the behaviour of the interface deformation with
$(\unicode[STIX]{x1D719}=0,\unicode[STIX]{x03C0})$
. It is to be noted that the behaviour of the interface deformation with
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
is qualitatively the same for all other combination of parameters not reported here. It can be seen from the figure that the maximum deformation is obtained when the forces due to the interfacial tension are dominant, i.e.,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
is qualitatively the same for all other combination of parameters not reported here. It can be seen from the figure that the maximum deformation is obtained when the forces due to the interfacial tension are dominant, i.e.,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
while the minimum deformation is obtained when the forces due to both interfacial tension and density difference are of the same order of magnitude, i.e.,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
while the minimum deformation is obtained when the forces due to both interfacial tension and density difference are of the same order of magnitude, i.e.,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=O(1)$
. This result needs to be contrasted with the interface deformation for the motion of a rigid sphere near an interface. In the latter case, the maximum deformation occurs for
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=O(1)$
. This result needs to be contrasted with the interface deformation for the motion of a rigid sphere near an interface. In the latter case, the maximum deformation occurs for
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
but the minimum deformation is obtained for
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
but the minimum deformation is obtained for
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
. Berdan & Leal (Reference Berdan and Leal1982) gave a reason for such an observation by saying that the forces due to the density difference act directly in restricting the interface deformation (thereby giving a minimum deformation when
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
. Berdan & Leal (Reference Berdan and Leal1982) gave a reason for such an observation by saying that the forces due to the density difference act directly in restricting the interface deformation (thereby giving a minimum deformation when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
) but the interfacial tension forces act to restrict the surface curvature but not the deformation (thereby giving a maximum deformation when
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
) but the interfacial tension forces act to restrict the surface curvature but not the deformation (thereby giving a maximum deformation when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
). Even though the physical nature of forces due to the interfacial tension and density difference are still the same in both problems, the minimum interface deformation occurs when
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
). Even though the physical nature of forces due to the interfacial tension and density difference are still the same in both problems, the minimum interface deformation occurs when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
for the motion of a squirmer near an interface. As shown in figure 4, the MOR results predict the interface deformation quite accurately for all values of
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
for the motion of a squirmer near an interface. As shown in figure 4, the MOR results predict the interface deformation quite accurately for all values of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
, for the given parameters of interest.
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
, for the given parameters of interest.

Figure 5. (a) The role of the distance of the squirmer from the undeformed interface on the interface deformation. The values of the parameters are taken as
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $l=2$
, 3 and 4. (b) Effect of viscosity ratio on the interface deformation. The values of most of the parameters are the same as those of panel (a) except
$l=2$
, 3 and 4. (b) Effect of viscosity ratio on the interface deformation. The values of most of the parameters are the same as those of panel (a) except
![]() $l$
is fixed at 2 and
$l$
is fixed at 2 and
![]() $\unicode[STIX]{x1D706}$
is varied from
$\unicode[STIX]{x1D706}$
is varied from
![]() $10^{-3}$
to
$10^{-3}$
to
![]() $10^{4}$
. Again the lines indicate the bipolar coordinate solutions while symbols indicate the MOR solutions.
$10^{4}$
. Again the lines indicate the bipolar coordinate solutions while symbols indicate the MOR solutions.
Now, we study the effect of distance of the centre of the squirmer from the undeformed interface on the interfacial deformation as shown in figure 5(a) for
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
![]() $\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
$\unicode[STIX]{x1D703}_{z}=\unicode[STIX]{x03C0}/6$
,
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $l=2$
, 3 and 4. As expected, the interface deformation decreases with the distance of the squirmer from the undeformed interface. It can also be seen in figure 5(a) that the error in predictions of interface deformation using MOR decreases with the distance of the squirmer from the interface. This is expected as the MOR results are accurate when the squirmer is far away from the interface. In figure 5(b), we study the effect of viscosity ratio on the interface deformation when
$l=2$
, 3 and 4. As expected, the interface deformation decreases with the distance of the squirmer from the undeformed interface. It can also be seen in figure 5(a) that the error in predictions of interface deformation using MOR decreases with the distance of the squirmer from the interface. This is expected as the MOR results are accurate when the squirmer is far away from the interface. In figure 5(b), we study the effect of viscosity ratio on the interface deformation when
![]() $\unicode[STIX]{x1D706}$
is varied from
$\unicode[STIX]{x1D706}$
is varied from
![]() $10^{-3}$
to
$10^{-3}$
to
![]() $10^{4}$
. We note that
$10^{4}$
. We note that
![]() $\unicode[STIX]{x1D706}\ll 1$
corresponds to an air–water interface, whereas
$\unicode[STIX]{x1D706}\ll 1$
corresponds to an air–water interface, whereas
![]() $\unicode[STIX]{x1D706}\gg 1$
corresponds to an oil–water interface (e.g. for a crude oil–water interface,
$\unicode[STIX]{x1D706}\gg 1$
corresponds to an oil–water interface (e.g. for a crude oil–water interface,
![]() $\unicode[STIX]{x1D706}=12$
). The interface deformation predicted using bipolar coordinates varies negligibly with the viscosity ratio. On the other hand, the MOR results predict that the interface deformation is independent of the viscosity ratio. This can also be seen from the expression for the interface deformation, equation (3.3) which does not depend on the viscosity ratio. However, the MOR results for the motion of a rigid sphere near an interface predict that the interface deformation does vary, even though slowly with the viscosity ratio. These different behaviours of interface deformation with the viscosity ratio predicted by the MOR in the two cases can be understood by looking at the singularities that occur in the
$\unicode[STIX]{x1D706}=12$
). The interface deformation predicted using bipolar coordinates varies negligibly with the viscosity ratio. On the other hand, the MOR results predict that the interface deformation is independent of the viscosity ratio. This can also be seen from the expression for the interface deformation, equation (3.3) which does not depend on the viscosity ratio. However, the MOR results for the motion of a rigid sphere near an interface predict that the interface deformation does vary, even though slowly with the viscosity ratio. These different behaviours of interface deformation with the viscosity ratio predicted by the MOR in the two cases can be understood by looking at the singularities that occur in the
![]() $O(1)$
problem. The singularities that enter into the solution due to the reflections from the surface of the squirmer (i.e. to satisfy the boundary condition in (2.66)–(2.68)) are
$O(1)$
problem. The singularities that enter into the solution due to the reflections from the surface of the squirmer (i.e. to satisfy the boundary condition in (2.66)–(2.68)) are
![]() $O(1/l^{3})$
or lower. Thus, these singularities do not enter into the
$O(1/l^{3})$
or lower. Thus, these singularities do not enter into the
![]() $O(\unicode[STIX]{x1D716})$
problem, because of which the interfacial deformation does not depend on the viscosity ratio as predicted by the MOR. Such a phenomenon does not happen for the motion of a rigid sphere near an interface.
$O(\unicode[STIX]{x1D716})$
problem, because of which the interfacial deformation does not depend on the viscosity ratio as predicted by the MOR. Such a phenomenon does not happen for the motion of a rigid sphere near an interface.
3.2 Swimming with steady squirming modes
Once the leading-order interface deformation is determined, we can derive the
![]() $O(\unicode[STIX]{x1D716})$
swimming velocities using the reciprocal theorem, equation (2.31). As the swimming dynamics (attraction/repulsion to the interface and reorientation) near an interface is governed by
$O(\unicode[STIX]{x1D716})$
swimming velocities using the reciprocal theorem, equation (2.31). As the swimming dynamics (attraction/repulsion to the interface and reorientation) near an interface is governed by
![]() $U_{z}$
and
$U_{z}$
and
![]() $\unicode[STIX]{x1D6FA}_{y}$
, we report only these two velocities. In general, the swimming velocity is of the form
$\unicode[STIX]{x1D6FA}_{y}$
, we report only these two velocities. In general, the swimming velocity is of the form
 $$\begin{eqnarray}\displaystyle \boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t) & = & \displaystyle \overbrace{\boldsymbol{M}_{1}(z,\unicode[STIX]{x1D703}_{z})B_{1}(t)+\boldsymbol{M}_{2}(z,\unicode[STIX]{x1D703}_{z})B_{2}(t)}^{\text{velocity}\;\text{of}\;\text{the}\;\text{swimmer}\;\text{near}\;\text{a}\;\text{plane}\;\text{interface}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D716}\underbrace{\left[\begin{array}{@{}c@{}}\displaystyle \boldsymbol{N}_{1}(z,\unicode[STIX]{x1D703}_{z})\frac{\text{d}B_{1}}{\text{d}t}+\boldsymbol{N}_{2}(z,\unicode[STIX]{x1D703}_{z})\frac{\text{d}B_{2}}{\text{d}t}\\ \displaystyle +\,\boldsymbol{K}_{11}(z,\unicode[STIX]{x1D703}_{z})B_{1}(t)^{2}+\boldsymbol{K}_{22}(z,\unicode[STIX]{x1D703}_{z})B_{2}(t)^{2}+\boldsymbol{K}_{12}(z,\unicode[STIX]{x1D703}_{z})B_{1}(t)B_{2}(t)\end{array}\right]\!,}_{\text{velocity}\;\text{of}\;\text{the}\;\text{swimmer}\;\text{due}\;\text{to}\;\text{interface}\;\text{deformations}}\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t) & = & \displaystyle \overbrace{\boldsymbol{M}_{1}(z,\unicode[STIX]{x1D703}_{z})B_{1}(t)+\boldsymbol{M}_{2}(z,\unicode[STIX]{x1D703}_{z})B_{2}(t)}^{\text{velocity}\;\text{of}\;\text{the}\;\text{swimmer}\;\text{near}\;\text{a}\;\text{plane}\;\text{interface}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D716}\underbrace{\left[\begin{array}{@{}c@{}}\displaystyle \boldsymbol{N}_{1}(z,\unicode[STIX]{x1D703}_{z})\frac{\text{d}B_{1}}{\text{d}t}+\boldsymbol{N}_{2}(z,\unicode[STIX]{x1D703}_{z})\frac{\text{d}B_{2}}{\text{d}t}\\ \displaystyle +\,\boldsymbol{K}_{11}(z,\unicode[STIX]{x1D703}_{z})B_{1}(t)^{2}+\boldsymbol{K}_{22}(z,\unicode[STIX]{x1D703}_{z})B_{2}(t)^{2}+\boldsymbol{K}_{12}(z,\unicode[STIX]{x1D703}_{z})B_{1}(t)B_{2}(t)\end{array}\right]\!,}_{\text{velocity}\;\text{of}\;\text{the}\;\text{swimmer}\;\text{due}\;\text{to}\;\text{interface}\;\text{deformations}}\qquad\end{eqnarray}$$
where the functions
![]() $\boldsymbol{M}_{1}$
,
$\boldsymbol{M}_{1}$
,
![]() $\boldsymbol{M}_{2}$
,
$\boldsymbol{M}_{2}$
,
![]() $\boldsymbol{N}_{1}$
,
$\boldsymbol{N}_{1}$
,
![]() $\boldsymbol{N}_{2}$
,
$\boldsymbol{N}_{2}$
,
![]() $\boldsymbol{K}_{11}$
,
$\boldsymbol{K}_{11}$
,
![]() $\boldsymbol{K}_{12}$
and
$\boldsymbol{K}_{12}$
and
![]() $\boldsymbol{K}_{22}$
are obtained either from bipolar coordinate approach or from the method of reflections. Now if
$\boldsymbol{K}_{22}$
are obtained either from bipolar coordinate approach or from the method of reflections. Now if
![]() $B_{1},B_{2}\propto j(t)$
, then the swimmer velocity is given by
$B_{1},B_{2}\propto j(t)$
, then the swimmer velocity is given by
![]() $\boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t)=\boldsymbol{M}(z,\unicode[STIX]{x1D703}_{z})j(t)+\unicode[STIX]{x1D716}[\boldsymbol{N}(z,\unicode[STIX]{x1D703}_{z})(\unicode[STIX]{x2202}j/\unicode[STIX]{x2202}t)+\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z})j^{2}]$
, where
$\boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t)=\boldsymbol{M}(z,\unicode[STIX]{x1D703}_{z})j(t)+\unicode[STIX]{x1D716}[\boldsymbol{N}(z,\unicode[STIX]{x1D703}_{z})(\unicode[STIX]{x2202}j/\unicode[STIX]{x2202}t)+\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z})j^{2}]$
, where
![]() $\boldsymbol{M}=\boldsymbol{M}_{1}+\unicode[STIX]{x1D6EC}\boldsymbol{M}_{2}$
,
$\boldsymbol{M}=\boldsymbol{M}_{1}+\unicode[STIX]{x1D6EC}\boldsymbol{M}_{2}$
,
![]() $\boldsymbol{N}=\boldsymbol{N}_{1}+\unicode[STIX]{x1D6EC}\boldsymbol{N}_{2}$
and
$\boldsymbol{N}=\boldsymbol{N}_{1}+\unicode[STIX]{x1D6EC}\boldsymbol{N}_{2}$
and
![]() $\boldsymbol{K}=\boldsymbol{K}_{11}+\unicode[STIX]{x1D6EC}\boldsymbol{K}_{12}+\unicode[STIX]{x1D6EC}^{2}\boldsymbol{K}_{22}$
. Also, if
$\boldsymbol{K}=\boldsymbol{K}_{11}+\unicode[STIX]{x1D6EC}\boldsymbol{K}_{12}+\unicode[STIX]{x1D6EC}^{2}\boldsymbol{K}_{22}$
. Also, if
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
are constants (independent of time), then the swimmer velocity is given by
$B_{2}$
are constants (independent of time), then the swimmer velocity is given by
![]() $\boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t)=\boldsymbol{M}(z,\unicode[STIX]{x1D703}_{z})+\unicode[STIX]{x1D716}\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z})$
. We note that the velocity of the swimmer located far away from a plane interface is
$\boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t)=\boldsymbol{M}(z,\unicode[STIX]{x1D703}_{z})+\unicode[STIX]{x1D716}\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z})$
. We note that the velocity of the swimmer located far away from a plane interface is
![]() $O(1)$
while the velocity due to the interface deformations is
$O(1)$
while the velocity due to the interface deformations is
![]() $O(\unicode[STIX]{x1D716})$
. Hence the dynamics of a swimmer with steady squirming gait near a weakly deforming interface is similar to that near a plane interface except if it is very close to the interface.
$O(\unicode[STIX]{x1D716})$
. Hence the dynamics of a swimmer with steady squirming gait near a weakly deforming interface is similar to that near a plane interface except if it is very close to the interface.
3.3 Swimming with time-reversible squirming modes
3.3.1 Time-averaged velocities
In this section, we study the dynamics of a swimmer with time-reversible squirming modes,
![]() $B_{1},B_{2}\propto \sin (t)$
. Here, we use
$B_{1},B_{2}\propto \sin (t)$
. Here, we use
![]() $t_{ref}=1/\unicode[STIX]{x1D714}$
, where
$t_{ref}=1/\unicode[STIX]{x1D714}$
, where
![]() $\unicode[STIX]{x1D714}$
is the frequency of surface velocity. In this case, the swimming velocity is of the form
$\unicode[STIX]{x1D714}$
is the frequency of surface velocity. In this case, the swimming velocity is of the form
![]() $\boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t)=\boldsymbol{M}(z,\unicode[STIX]{x1D703}_{z})\sin (t)+\unicode[STIX]{x1D716}[\boldsymbol{N}(z,\unicode[STIX]{x1D703}_{z})\cos (t)+\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z})\sin ^{2}(t)]$
. In line with the previous literature on the locomotion of time-reversible swimmers near a wall in viscoelastic fluids (Yazdi et al.
Reference Yazdi, Ardekani and Borhan2014) and near a deforming interface in a Newtonian fluid (Trouilloud et al.
Reference Trouilloud, Yu, Hosoi and Lauga2008), we investigate the time-averaged velocities in this section. Specifically, this time average is obtained by fixing
$\boldsymbol{U}(z,\unicode[STIX]{x1D703}_{z},t)=\boldsymbol{M}(z,\unicode[STIX]{x1D703}_{z})\sin (t)+\unicode[STIX]{x1D716}[\boldsymbol{N}(z,\unicode[STIX]{x1D703}_{z})\cos (t)+\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z})\sin ^{2}(t)]$
. In line with the previous literature on the locomotion of time-reversible swimmers near a wall in viscoelastic fluids (Yazdi et al.
Reference Yazdi, Ardekani and Borhan2014) and near a deforming interface in a Newtonian fluid (Trouilloud et al.
Reference Trouilloud, Yu, Hosoi and Lauga2008), we investigate the time-averaged velocities in this section. Specifically, this time average is obtained by fixing
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D703}_{z}$
for one time period and is given by
$\unicode[STIX]{x1D703}_{z}$
for one time period and is given by
![]() $\langle \boldsymbol{U}\rangle =(\unicode[STIX]{x1D716}\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z}))/2$
, where
$\langle \boldsymbol{U}\rangle =(\unicode[STIX]{x1D716}\boldsymbol{K}(z,\unicode[STIX]{x1D703}_{z}))/2$
, where
![]() $\langle \text{}\rangle$
denotes the time-averaged quantity. Clearly, this time-averaged velocity is valid only if
$\langle \text{}\rangle$
denotes the time-averaged quantity. Clearly, this time-averaged velocity is valid only if
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D703}_{z}$
vary slowly with time. Even though this averaging procedure is very simple, we see that it captures some of the physics. Later in this section, we report the exact time-averaged velocity by integrating the instantaneous velocity over the time period of surface deformation.
$\unicode[STIX]{x1D703}_{z}$
vary slowly with time. Even though this averaging procedure is very simple, we see that it captures some of the physics. Later in this section, we report the exact time-averaged velocity by integrating the instantaneous velocity over the time period of surface deformation.

Figure 6. Vector field of
![]() $\langle \bar{\unicode[STIX]{x1D6FA}}_{y}\rangle =\langle \unicode[STIX]{x1D6FA}_{y}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
,
$\langle \bar{\unicode[STIX]{x1D6FA}}_{y}\rangle =\langle \unicode[STIX]{x1D6FA}_{y}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
,
![]() $\langle \bar{U}_{z}\rangle =\langle U_{z}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
for
$\langle \bar{U}_{z}\rangle =\langle U_{z}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
for
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. The contour plot shows the magnitude of the vector
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. The contour plot shows the magnitude of the vector
![]() $(\langle \unicode[STIX]{x1D6FA}_{y}\rangle ,\langle U_{z}\rangle )$
, i.e.,
$(\langle \unicode[STIX]{x1D6FA}_{y}\rangle ,\langle U_{z}\rangle )$
, i.e.,
![]() $\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
obtained using (a) the bipolar coordinates and (b) MOR.
$\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
obtained using (a) the bipolar coordinates and (b) MOR.
Figure 6(a,b) shows the vector fields of time-averaged swimmer velocities for different positions and orientations of the swimmer along with the contour plot of the magnitude of the velocity,
![]() $\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
. The horizontal component of the vector denotes
$\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
. The horizontal component of the vector denotes
![]() $\langle \bar{\unicode[STIX]{x1D6FA}}_{y}\rangle =\langle \unicode[STIX]{x1D6FA}_{y}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
, whereas the vertical component denotes
$\langle \bar{\unicode[STIX]{x1D6FA}}_{y}\rangle =\langle \unicode[STIX]{x1D6FA}_{y}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
, whereas the vertical component denotes
![]() $\langle \bar{U}_{z}\rangle =\langle U_{z}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
. Figure 6(a) shows the results obtained using bipolar coordinates whereas figure 6(b) shows the results obtained using MOR. The results are reported for
$\langle \bar{U}_{z}\rangle =\langle U_{z}\rangle /\sqrt{\langle \unicode[STIX]{x1D6FA}_{y}\rangle ^{2}+\langle U_{z}\rangle ^{2}}$
. Figure 6(a) shows the results obtained using bipolar coordinates whereas figure 6(b) shows the results obtained using MOR. The results are reported for
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. It can be seen from figure 6(a) that the
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. It can be seen from figure 6(a) that the
![]() $\langle U_{z}\rangle$
velocity is always positive. This indicates that the time-averaged swimmer velocity is directed towards the interface for all orientations. This result is a generalization of that predicted by Trouilloud et al. (Reference Trouilloud, Yu, Hosoi and Lauga2008) for the time-averaged swimming velocity of parallel force dipole near a deforming interface using the scaling analysis. According to them, the time-averaged velocity of a parallel force dipole is directed towards the interface when it is oriented either parallel or perpendicular to the interface. We, however, observe that such a force dipole has a time-averaged velocity directed towards the interface irrespective of its orientation. It can also be seen that
$\langle U_{z}\rangle$
velocity is always positive. This indicates that the time-averaged swimmer velocity is directed towards the interface for all orientations. This result is a generalization of that predicted by Trouilloud et al. (Reference Trouilloud, Yu, Hosoi and Lauga2008) for the time-averaged swimming velocity of parallel force dipole near a deforming interface using the scaling analysis. According to them, the time-averaged velocity of a parallel force dipole is directed towards the interface when it is oriented either parallel or perpendicular to the interface. We, however, observe that such a force dipole has a time-averaged velocity directed towards the interface irrespective of its orientation. It can also be seen that
![]() $\langle \unicode[STIX]{x1D6FA}_{y}\rangle \ll \langle U_{z}\rangle$
. So, the orientation of the swimmer changes by a very small amount in one time period. Berdan & Leal (Reference Berdan and Leal1982) reported a similar observation for the motion of a rigid sphere near an interface. According to them, the drag force correction due to the interface deformation for either a translation of sphere parallel to the plane (undeformed) interface or rotation about an axis parallel to an undeformed interface is much smaller than the drag force correction due to the translation of sphere normal to the undeformed interface. From the contour plot, we see that the magnitude of the velocity is large when the swimmer is close to the interface. The interface deformation increases with the decrease of the distance between the swimmer and the undeformed interface leading to the increase in the magnitude of the swimmer velocity.
$\langle \unicode[STIX]{x1D6FA}_{y}\rangle \ll \langle U_{z}\rangle$
. So, the orientation of the swimmer changes by a very small amount in one time period. Berdan & Leal (Reference Berdan and Leal1982) reported a similar observation for the motion of a rigid sphere near an interface. According to them, the drag force correction due to the interface deformation for either a translation of sphere parallel to the plane (undeformed) interface or rotation about an axis parallel to an undeformed interface is much smaller than the drag force correction due to the translation of sphere normal to the undeformed interface. From the contour plot, we see that the magnitude of the velocity is large when the swimmer is close to the interface. The interface deformation increases with the decrease of the distance between the swimmer and the undeformed interface leading to the increase in the magnitude of the swimmer velocity.

Figure 7. Variation of time-averaged swimming velocities (a)
![]() $\langle U_{z}\rangle$
and (b)
$\langle U_{z}\rangle$
and (b)
![]() $\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
with the distance of the swimmer from the interface for
$\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
with the distance of the swimmer from the interface for
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, 0.1, 1 and 10,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, 0.1, 1 and 10,
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. The lines indicate bipolar coordinate results whereas the symbols indicate the MOR results. A corresponding plot of the change in the swimmer’s position and orientation in one time period is given in figure 12 of appendix C.
$\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. The lines indicate bipolar coordinate results whereas the symbols indicate the MOR results. A corresponding plot of the change in the swimmer’s position and orientation in one time period is given in figure 12 of appendix C.
Figure 7(a,b) shows the variation of time-averaged swimmer velocities with the distance of the swimmer from the undeformed interface for various values of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
ranging from 0.01 to 10 and fixing the values of other parameters at
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
ranging from 0.01 to 10 and fixing the values of other parameters at
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
and
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
and
![]() $\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. This figure also quantitatively compares the MOR and bipolar coordinate results, where lines denote bipolar coordinate results and symbols denote MOR results. The decrease of interface deformation with the distance of the squirmer from an undeformed interface causes a decrease in the magnitude of time-averaged swimming velocities as shown in figure 7(a,b). After all, a swimmer which is far away from the interface does not cause the interface to deform, thereby does not swim in a time-averaged sense. For a swimmer far away from the interface
$\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. This figure also quantitatively compares the MOR and bipolar coordinate results, where lines denote bipolar coordinate results and symbols denote MOR results. The decrease of interface deformation with the distance of the squirmer from an undeformed interface causes a decrease in the magnitude of time-averaged swimming velocities as shown in figure 7(a,b). After all, a swimmer which is far away from the interface does not cause the interface to deform, thereby does not swim in a time-averaged sense. For a swimmer far away from the interface
![]() $(l\sim 4)$
, we see that the maximum value of
$(l\sim 4)$
, we see that the maximum value of
![]() $\langle U_{z}\rangle$
occurs at a minimum value of
$\langle U_{z}\rangle$
occurs at a minimum value of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, while the minimum value of
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, while the minimum value of
![]() $\langle U_{z}\rangle$
occurs at a maximum value of
$\langle U_{z}\rangle$
occurs at a maximum value of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=10$
. This result of
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=10$
. This result of
![]() $\langle U_{z}\rangle$
is consistent with that of interface deformation which is again maximum at
$\langle U_{z}\rangle$
is consistent with that of interface deformation which is again maximum at
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
. Berdan & Leal (Reference Berdan and Leal1982) also reported similar result for the drag force correction due to the interface deformation, due to the motion of a rigid sphere near an interface. They reported that the drag force is maximum when
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
. Berdan & Leal (Reference Berdan and Leal1982) also reported similar result for the drag force correction due to the interface deformation, due to the motion of a rigid sphere near an interface. They reported that the drag force is maximum when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
, while it is minimum when
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\ll 1$
, while it is minimum when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
. When we are close to the interface
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
. When we are close to the interface
![]() $(l\sim 1.5)$
, it seems that the value of
$(l\sim 1.5)$
, it seems that the value of
![]() $\langle U_{z}\rangle$
is insensitive to the value of
$\langle U_{z}\rangle$
is insensitive to the value of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
as shown in figure 7(a). Additionally, the error in the predictions of
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
as shown in figure 7(a). Additionally, the error in the predictions of
![]() $\langle U_{z}\rangle$
velocity by MOR decreases with the distance of the squirmer from the undeformed interface. Even though MOR, in principle should be valid for the swimmer distances from the undeformed interface of the order of 10, i.e.,
$\langle U_{z}\rangle$
velocity by MOR decreases with the distance of the squirmer from the undeformed interface. Even though MOR, in principle should be valid for the swimmer distances from the undeformed interface of the order of 10, i.e.,
![]() $l=O(10)$
, we see from figure 7(a) that MOR predicts
$l=O(10)$
, we see from figure 7(a) that MOR predicts
![]() $\langle U_{z}\rangle$
velocities quite accurately even when
$\langle U_{z}\rangle$
velocities quite accurately even when
![]() $l\approx 3$
. MOR, however, fails when
$l\approx 3$
. MOR, however, fails when
![]() $l\leqslant 3$
, overpredicting
$l\leqslant 3$
, overpredicting
![]() $\langle U_{z}\rangle$
velocities by large extent (absolute error
$\langle U_{z}\rangle$
velocities by large extent (absolute error
![]() $=$
$=$
![]() $O(0.1)$
). Spagnolie & Lauga (Reference Spagnolie and Lauga2012) have also reported a similar observation. According to them, the velocity of the swimmer moving near a plane wall/stress-free surface predicted using the method of images is accurate even when
$O(0.1)$
). Spagnolie & Lauga (Reference Spagnolie and Lauga2012) have also reported a similar observation. According to them, the velocity of the swimmer moving near a plane wall/stress-free surface predicted using the method of images is accurate even when
![]() $l=O(1)$
. Even though the MOR predicts
$l=O(1)$
. Even though the MOR predicts
![]() $\langle U_{z}\rangle$
velocity quite accurately, it seems that the error in predictions of the
$\langle U_{z}\rangle$
velocity quite accurately, it seems that the error in predictions of the
![]() $\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
velocity by the MOR depends on
$\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
velocity by the MOR depends on
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
. When
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
. When
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=10$
, the MOR predictions of the
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=10$
, the MOR predictions of the
![]() $\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
velocity is quite close to that of bipolar coordinates predictions. However, when
$\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
velocity is quite close to that of bipolar coordinates predictions. However, when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, these two predictions fall far apart. In fact, when
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, these two predictions fall far apart. In fact, when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, the MOR predicts
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, the MOR predicts
![]() $\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
which is of opposite sign to that predicted by the bipolar coordinate method. In summary, we conclude that the MOR predicts the swimming velocities accurately when the forces due to density differences dominate the forces due to the interfacial tension, i.e., when
$\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
which is of opposite sign to that predicted by the bipolar coordinate method. In summary, we conclude that the MOR predicts the swimming velocities accurately when the forces due to density differences dominate the forces due to the interfacial tension, i.e., when
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
.
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
.

Figure 8. Variation of time-averaged swimming velocities (a)
![]() $\langle U_{z}\rangle$
and (b)
$\langle U_{z}\rangle$
and (b)
![]() $\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
with the distance of the swimmer from the interface for
$\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
with the distance of the swimmer from the interface for
![]() $\unicode[STIX]{x1D706}=10^{-3}$
, 1, 10 and
$\unicode[STIX]{x1D706}=10^{-3}$
, 1, 10 and
![]() $10^{4}$
,
$10^{4}$
,
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. The lines indicate bipolar coordinate results and the symbols indicate the MOR results. A corresponding plot of the change in the swimmer’s position and orientation in one time period is given in figure 13 of appendix C.
$\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. The lines indicate bipolar coordinate results and the symbols indicate the MOR results. A corresponding plot of the change in the swimmer’s position and orientation in one time period is given in figure 13 of appendix C.
Figure 8(a,b) shows the variation of time-averaged swimming velocities with the viscosity ratio of two fluids. The parameters used in this figure are the same as that of figure 7 except
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
is fixed at 1 and
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
is fixed at 1 and
![]() $\unicode[STIX]{x1D706}$
is varied in the range
$\unicode[STIX]{x1D706}$
is varied in the range
![]() $10^{-3}$
–
$10^{-3}$
–
![]() $10^{4}$
. From figure 8(a), for a swimmer far away from the interface
$10^{4}$
. From figure 8(a), for a swimmer far away from the interface
![]() $(l\sim 4)$
, the value of
$(l\sim 4)$
, the value of
![]() $\langle U_{z}\rangle$
is minimum at
$\langle U_{z}\rangle$
is minimum at
![]() $\unicode[STIX]{x1D706}=10^{-3}$
and its value is insensitive to
$\unicode[STIX]{x1D706}=10^{-3}$
and its value is insensitive to
![]() $\unicode[STIX]{x1D706}$
for
$\unicode[STIX]{x1D706}$
for
![]() $\unicode[STIX]{x1D706}$
in the range of 1–
$\unicode[STIX]{x1D706}$
in the range of 1–
![]() $10^{4}$
. This result is similar to the corrected drag ratio acting on a sphere translating normal to the interface as reported by Berdan & Leal (Reference Berdan and Leal1982). For a swimmer close to the interface
$10^{4}$
. This result is similar to the corrected drag ratio acting on a sphere translating normal to the interface as reported by Berdan & Leal (Reference Berdan and Leal1982). For a swimmer close to the interface
![]() $(l\sim 1.5)$
, the value of
$(l\sim 1.5)$
, the value of
![]() $\langle U_{z}\rangle$
does not depend on
$\langle U_{z}\rangle$
does not depend on
![]() $\unicode[STIX]{x1D706}$
for all values of
$\unicode[STIX]{x1D706}$
for all values of
![]() $\unicode[STIX]{x1D706}$
investigated. We should note that the interface deformation is also independent of viscosity ratio. For
$\unicode[STIX]{x1D706}$
investigated. We should note that the interface deformation is also independent of viscosity ratio. For
![]() $l>2$
, the magnitude of
$l>2$
, the magnitude of
![]() $\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
decreases with
$\langle \unicode[STIX]{x1D6FA}_{y}\rangle$
decreases with
![]() $\unicode[STIX]{x1D706}$
as seen in figure 8(b). The MOR results are in good agreement with bipolar coordinate results for a swimmer far away from the interface, as seen from figure 8(a,b). However, the error in the predictions of the MOR depends on the viscosity ratio,
$\unicode[STIX]{x1D706}$
as seen in figure 8(b). The MOR results are in good agreement with bipolar coordinate results for a swimmer far away from the interface, as seen from figure 8(a,b). However, the error in the predictions of the MOR depends on the viscosity ratio,
![]() $\unicode[STIX]{x1D706}$
. In particular, when
$\unicode[STIX]{x1D706}$
. In particular, when
![]() $\unicode[STIX]{x1D706}=10^{-3}$
, the error in the predictions of the MOR are so small that these results are in good agreement with the bipolar coordinate results even at
$\unicode[STIX]{x1D706}=10^{-3}$
, the error in the predictions of the MOR are so small that these results are in good agreement with the bipolar coordinate results even at
![]() $l=1.3$
, as seen in figure 8(a,b). However, the error in the predictions of the MOR is large when
$l=1.3$
, as seen in figure 8(a,b). However, the error in the predictions of the MOR is large when
![]() $\unicode[STIX]{x1D706}=10^{4}$
. Observations from figures 7 and 8 conclude that the MOR is quite accurate to study the locomotion of swimming microorganisms near a stress-free interface (as
$\unicode[STIX]{x1D706}=10^{4}$
. Observations from figures 7 and 8 conclude that the MOR is quite accurate to study the locomotion of swimming microorganisms near a stress-free interface (as
![]() $\unicode[STIX]{x1D706}\approx 0$
) such as an air–water interface when the interfacial tension between the two fluids is very small compared to the force due to the density difference (i.e.
$\unicode[STIX]{x1D706}\approx 0$
) such as an air–water interface when the interfacial tension between the two fluids is very small compared to the force due to the density difference (i.e.
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
).
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}\gg 1$
).
3.3.2 Instantaneous velocities
In the previous section, we analysed the time-averaged velocities which were obtained by fixing
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D703}_{z}$
while integrating velocities with respect to time. In this work, we have access to swimmer instantaneous velocities. As a first step to understand the instantaneous swimmer velocities, we plot in figure 9, trajectories of the swimmer when released from
$\unicode[STIX]{x1D703}_{z}$
while integrating velocities with respect to time. In this work, we have access to swimmer instantaneous velocities. As a first step to understand the instantaneous swimmer velocities, we plot in figure 9, trajectories of the swimmer when released from
![]() $z=-2.6$
for different orientations at time
$z=-2.6$
for different orientations at time
![]() $t_{in}=0$
for
$t_{in}=0$
for
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. It can be seen from the figure that for some values of
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. It can be seen from the figure that for some values of
![]() $\unicode[STIX]{x1D703}_{z}=4\unicode[STIX]{x03C0}/11,9\unicode[STIX]{x03C0}/11$
and
$\unicode[STIX]{x1D703}_{z}=4\unicode[STIX]{x03C0}/11,9\unicode[STIX]{x03C0}/11$
and
![]() $10\unicode[STIX]{x03C0}/11$
, the swimmer moves away from the interface in a time-averaged sense. Such an observation of swimmer moving away from the interface is not captured by the simplified analysis of the previous section (figure 6
a).
$10\unicode[STIX]{x03C0}/11$
, the swimmer moves away from the interface in a time-averaged sense. Such an observation of swimmer moving away from the interface is not captured by the simplified analysis of the previous section (figure 6
a).

Figure 9. Trajectories of swimmer when released from
![]() $z_{in}=-2.6$
,
$z_{in}=-2.6$
,
![]() $t_{in}=0$
for time duration
$t_{in}=0$
for time duration
![]() $\unicode[STIX]{x0394}t=200$
. The other parameters used in this figure are
$\unicode[STIX]{x0394}t=200$
. The other parameters used in this figure are
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. The markers
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
. The markers
![]() $\times$
show the initial position and orientation of the swimmer. When released at
$\times$
show the initial position and orientation of the swimmer. When released at
![]() $\unicode[STIX]{x1D703}_{in}=4\unicode[STIX]{x03C0}/11,9\unicode[STIX]{x03C0}/11$
and
$\unicode[STIX]{x1D703}_{in}=4\unicode[STIX]{x03C0}/11,9\unicode[STIX]{x03C0}/11$
and
![]() $10\unicode[STIX]{x03C0}/11$
, the swimmer moves away from the interface in a time-averaged sense.
$10\unicode[STIX]{x03C0}/11$
, the swimmer moves away from the interface in a time-averaged sense.

Figure 10. Vector fields of
![]() $(\unicode[STIX]{x0394}\bar{\unicode[STIX]{x1D703}}_{z},\unicode[STIX]{x0394}\bar{z})$
(their definitions being given in the main text) along with the contours of
$(\unicode[STIX]{x0394}\bar{\unicode[STIX]{x1D703}}_{z},\unicode[STIX]{x0394}\bar{z})$
(their definitions being given in the main text) along with the contours of
![]() $\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}}$
obtained using bipolar coordinates, for (a) puller swimmer (
$\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}}$
obtained using bipolar coordinates, for (a) puller swimmer (
![]() $B_{2}/B_{1}=4$
), (b) pusher swimmer (
$B_{2}/B_{1}=4$
), (b) pusher swimmer (
![]() $B_{2}/B_{1}=-4$
) and (c) neutral swimmer (
$B_{2}/B_{1}=-4$
) and (c) neutral swimmer (
![]() $B_{2}/B_{1}=0$
). The values of the parameters used in these plots are
$B_{2}/B_{1}=0$
). The values of the parameters used in these plots are
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $t_{in}=0$
. A corresponding plot of vector fields obtained using the MOR is provided in figure 11 of appendix C.
$t_{in}=0$
. A corresponding plot of vector fields obtained using the MOR is provided in figure 11 of appendix C.
Now, we release the swimmer at all possible positions and orientations at time
![]() $t_{in}=0$
and plot the vector fields of
$t_{in}=0$
and plot the vector fields of
![]() $(\unicode[STIX]{x0394}\bar{\unicode[STIX]{x1D703}}_{z},\unicode[STIX]{x0394}\bar{z})=(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}/\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}},\unicode[STIX]{x0394}z/\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}})$
in figure 10. Here,
$(\unicode[STIX]{x0394}\bar{\unicode[STIX]{x1D703}}_{z},\unicode[STIX]{x0394}\bar{z})=(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}/\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}},\unicode[STIX]{x0394}z/\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}})$
in figure 10. Here,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
denotes a change in the orientation of the swimmer, while
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
denotes a change in the orientation of the swimmer, while
![]() $\unicode[STIX]{x0394}z$
denotes a change in the position of the swimmer in one time period. Dimensionless time-averaged velocities are calculated as
$\unicode[STIX]{x0394}z$
denotes a change in the position of the swimmer in one time period. Dimensionless time-averaged velocities are calculated as
![]() $\langle U_{z}\rangle =\unicode[STIX]{x0394}z/(2\unicode[STIX]{x03C0}),\langle \unicode[STIX]{x1D6FA}_{y}\rangle =\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}/(2\unicode[STIX]{x03C0})$
. Unlike the time-averaged velocities reported in the previous section, which are only valid under the separation of time scales, this calculation of time-averaged velocity does not have such a limitation. The white region in these figures shows that the swimmer goes very close to the interface (
$\langle U_{z}\rangle =\unicode[STIX]{x0394}z/(2\unicode[STIX]{x03C0}),\langle \unicode[STIX]{x1D6FA}_{y}\rangle =\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}/(2\unicode[STIX]{x03C0})$
. Unlike the time-averaged velocities reported in the previous section, which are only valid under the separation of time scales, this calculation of time-averaged velocity does not have such a limitation. The white region in these figures shows that the swimmer goes very close to the interface (
![]() $z<1.1$
) during one time period when released at that position and orientation. In these cases, due to computational cost, we did not calculate
$z<1.1$
) during one time period when released at that position and orientation. In these cases, due to computational cost, we did not calculate
![]() $\unicode[STIX]{x0394}z$
,
$\unicode[STIX]{x0394}z$
,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
over one time period. These plots, in essence, show how the swimmer’s position and orientation vary over one time period when released at time
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
over one time period. These plots, in essence, show how the swimmer’s position and orientation vary over one time period when released at time
![]() $t_{in}=0$
. It can be seen from these plots that there is no stable fixed point in the phase plane.
$t_{in}=0$
. It can be seen from these plots that there is no stable fixed point in the phase plane.
We hereby investigate the long-time dynamics of a swimmer near a weakly deforming interface. From figure 10(a,b), we see that if the initial orientation and position of the swimmer fall outside the region bounded by the blue curves, it moves towards the interface, otherwise it moves away from the interface. If the distance of the centre of the swimmer from the interface after a long time is less than 1.1, we say it is moving towards the interface. On the other hand, if it is greater than 10, we say it is moving away from the interface. Furthermore, we can investigate the long-time orientation of a swimmer that is moving towards the interface. In general, we can write the long-time orientation of the swimmer
![]() $(\unicode[STIX]{x1D703}_{z}^{\infty })$
in terms of its critical orientation
$(\unicode[STIX]{x1D703}_{z}^{\infty })$
in terms of its critical orientation
![]() $(\unicode[STIX]{x1D703}_{z}^{c})$
, where
$(\unicode[STIX]{x1D703}_{z}^{c})$
, where
![]() $\unicode[STIX]{x1D703}_{z}^{c}$
is the orientation of the swimmer at which it moves towards the interface with zero angular velocity. For instance, if a puller (pusher) swimmer is initially oriented towards the interface (
$\unicode[STIX]{x1D703}_{z}^{c}$
is the orientation of the swimmer at which it moves towards the interface with zero angular velocity. For instance, if a puller (pusher) swimmer is initially oriented towards the interface (
![]() $0<\unicode[STIX]{x1D703}_{z}<\unicode[STIX]{x03C0}/2$
), its critical orientation is normal and pointing towards the interface, i.e.,
$0<\unicode[STIX]{x1D703}_{z}<\unicode[STIX]{x03C0}/2$
), its critical orientation is normal and pointing towards the interface, i.e.,
![]() $\unicode[STIX]{x1D703}_{z}^{c}=0$
(parallel to the interface, i.e.,
$\unicode[STIX]{x1D703}_{z}^{c}=0$
(parallel to the interface, i.e.,
![]() $\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}/2$
). On the other hand, if a puller (pusher) swimmer is initially oriented away from the interface (
$\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}/2$
). On the other hand, if a puller (pusher) swimmer is initially oriented away from the interface (
![]() $\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D703}_{z}<\unicode[STIX]{x03C0}$
), its critical orientation is parallel to the interface, i.e.,
$\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D703}_{z}<\unicode[STIX]{x03C0}$
), its critical orientation is parallel to the interface, i.e.,
![]() $\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}/2$
(normal but pointing away from the interface, i.e.,
$\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}/2$
(normal but pointing away from the interface, i.e.,
![]() $\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}$
). From figure 10(c), it can be seen that if the initial orientation and position of a neutral swimmer lie in the region bounded by the blue curve, it moves towards the interface with a critical orientation that is parallel to the interface, i.e.,
$\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}$
). From figure 10(c), it can be seen that if the initial orientation and position of a neutral swimmer lie in the region bounded by the blue curve, it moves towards the interface with a critical orientation that is parallel to the interface, i.e.,
![]() $\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}/2$
. Otherwise it moves away from the interface. Additionally, the width of the region where the swimmer moves away from the interface increases with the distance of the swimmer from the interface.
$\unicode[STIX]{x1D703}_{z}^{c}=\unicode[STIX]{x03C0}/2$
. Otherwise it moves away from the interface. Additionally, the width of the region where the swimmer moves away from the interface increases with the distance of the swimmer from the interface.
One can compare the long-time swimming dynamics with that of a force dipole (specifically pusher swimmer) near a plane interface. It was reported that, after long time, the force dipole aligns parallel to the interface and always moves towards the interface (Berke et al. Reference Berke, Turner, Berg and Lauga2008). However, we see that the long-time orientation of a time-reversible swimmer near a weakly deforming interface depends on the type of the swimmer and even for a given swimmer, it depends on its initial orientation.
4 Conclusions
The motion of swimming microorganisms (swimmers) near an interface can cause the interface to deform. For instance, in the presence of ultralow interfacial tension (Rosen et al.
Reference Rosen, Wang, Shen and Zhu2005)
![]() $(10^{-3}{-}10^{-2}~\text{mN}~\text{m}^{-1})$
, bacteria or protozoa of size
$(10^{-3}{-}10^{-2}~\text{mN}~\text{m}^{-1})$
, bacteria or protozoa of size
![]() $O(10{-}100)~\unicode[STIX]{x03BC}\text{m}$
(Lauga & Powers Reference Lauga and Powers2009) moving with speed
$O(10{-}100)~\unicode[STIX]{x03BC}\text{m}$
(Lauga & Powers Reference Lauga and Powers2009) moving with speed
![]() $O(10{-}1000)~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$
near a surfactant covered aqueous solution–oil interface correspond to the conditions
$O(10{-}1000)~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$
near a surfactant covered aqueous solution–oil interface correspond to the conditions
![]() $Ca\approx 10^{-3}{-}1$
and
$Ca\approx 10^{-3}{-}1$
and
![]() $Ca/Bo\approx 10^{-4}{-}10$
, hence the interface deformation can be finite (when
$Ca/Bo\approx 10^{-4}{-}10$
, hence the interface deformation can be finite (when
![]() $Ca\sim O(1)$
and
$Ca\sim O(1)$
and
![]() $Ca/Bo\sim O(1)$
). Bacteria and spermatozoa swimming in mucus with a large apparent viscosity (Clift & Hart Reference Clift and Hart1953) correspond to
$Ca/Bo\sim O(1)$
). Bacteria and spermatozoa swimming in mucus with a large apparent viscosity (Clift & Hart Reference Clift and Hart1953) correspond to
![]() $Ca$
and
$Ca$
and
![]() $Ca/Bo\sim O(1)$
, where the interface deformation can be large. To understand the motion of microorganism near a weakly deforming interface, we model the microorganism as a spherical squirmer with only two squirming modes. We thereby provide a methodology to evaluate the velocity of the swimmer near a weakly deforming interface. This consists of (i) deriving the flow field due to a swimmer near a plane interface and (ii) applying the reciprocal theorem with a suitable auxiliary problem. A similar approach can be used to study the influence of weak inertial and non-Newtonian effects on the dynamics of the swimmer near a plane interface. We apply this methodology using an exact solution of Stokes equations (bipolar coordinates approach) and using an approximate solution (the method of reflections).
$Ca/Bo\sim O(1)$
, where the interface deformation can be large. To understand the motion of microorganism near a weakly deforming interface, we model the microorganism as a spherical squirmer with only two squirming modes. We thereby provide a methodology to evaluate the velocity of the swimmer near a weakly deforming interface. This consists of (i) deriving the flow field due to a swimmer near a plane interface and (ii) applying the reciprocal theorem with a suitable auxiliary problem. A similar approach can be used to study the influence of weak inertial and non-Newtonian effects on the dynamics of the swimmer near a plane interface. We apply this methodology using an exact solution of Stokes equations (bipolar coordinates approach) and using an approximate solution (the method of reflections).
Using the instantaneous velocity of the swimmer near a weakly deforming interface, we explore two examples: steady squirmer as well as a time-reversible squirmer. We observe that the weak interface deformations do not influence the dynamics of a steady squirmer if it is far away from the interface. This is not the case for a time-reversible swimmer. For instance, the long-time dynamics of a time-reversible swimmer is such that it either moves towards or away from the interface. We thereby divide its phase space into regions of attraction (repulsion) towards (from) the interface. Also, the long-time orientation of a time-reversible swimmer that is moving towards the interface depends on its initial orientation. We further note that the MOR is accurate to capture the dynamics of a swimmer even if the distance of the centre of the swimmer from the interface is of the order of the swimmer size. It is of interest to investigate the role of higher squirming modes in a future work as they can modify the swimming dynamics close to an interface and the results may be gait specific.
Acknowledgements
We would like to thank Dr S. Kim, Dr A. Bandopadhyay, Dr U. Ghosh and Dr G. Li for useful discussions. This research was made possible by grants from the Gulf of Mexico Research Initiative and the NSF, CBET-1445955-CAREER and CBET-1604423. V.A.S. would like to thank the Perry fellowship for partial support. Data are publicly available through the Gulf of Mexico Research Initiative Information & Data Cooperative (GRIIDC) at https://data.gulfresearchinitiative.org (doi:10.7266/N73R0QZ5).
Appendix A. Squirming boundary condition in bipolar coordinates
A.1
 $B_{1}$
squirming mode
$B_{1}$
squirming mode
For
![]() $B_{1}$
squirming mode, the boundary condition at the surface of the swimmer is given by
$B_{1}$
squirming mode, the boundary condition at the surface of the swimmer is given by
We split this into two subproblems, where the boundary condition on the swimmer for each subproblem is given by
so that the flow field due to
![]() $B_{1}$
mode is given by
$B_{1}$
mode is given by
where
![]() $\{\text{}\}_{k}$
denote the variables corresponding to
$\{\text{}\}_{k}$
denote the variables corresponding to
![]() $k$
th subproblem.
$k$
th subproblem.
A.1.1 Subproblem 0
In this case, the boundary condition on the swimmer can be rewritten in terms of cylindrical coordinates as
Thus, the non-zero terms in the general solution are those only with
![]() $m=0$
and
$m=0$
and
![]() $\unicode[STIX]{x1D6FC}_{0}=0$
. Using this equation we obtain
$\unicode[STIX]{x1D6FC}_{0}=0$
. Using this equation we obtain
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{0}=-\frac{2\sqrt{2}}{3}\sinh \unicode[STIX]{x1D702}_{0}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}[(2n+1)\sinh \unicode[STIX]{x1D702}_{0}+3\cosh \unicode[STIX]{x1D702}_{0}],\\ \displaystyle Z_{n}^{0}=\frac{4\sqrt{2}}{3}\sinh \unicode[STIX]{x1D702}_{0}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}[(n^{2}+n+1)\sinh \unicode[STIX]{x1D702}_{0}+(2n+1)\cosh \unicode[STIX]{x1D702}_{0}],\\ \displaystyle Y_{n}^{0}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{0}=-\frac{2\sqrt{2}}{3}\sinh \unicode[STIX]{x1D702}_{0}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}[(2n+1)\sinh \unicode[STIX]{x1D702}_{0}+3\cosh \unicode[STIX]{x1D702}_{0}],\\ \displaystyle Z_{n}^{0}=\frac{4\sqrt{2}}{3}\sinh \unicode[STIX]{x1D702}_{0}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}[(n^{2}+n+1)\sinh \unicode[STIX]{x1D702}_{0}+(2n+1)\cosh \unicode[STIX]{x1D702}_{0}],\\ \displaystyle Y_{n}^{0}=0.\end{array}\right\}\end{eqnarray}$$
A.1.2 Subproblem 1
In this case, the boundary condition on the swimmer can be written in terms of cylindrical coordinates as
Thus, the non-zero terms in the general solution are those only with
![]() $m=1$
and
$m=1$
and
![]() $\unicode[STIX]{x1D6FC}_{1}=-\unicode[STIX]{x1D719}_{x}$
. Using this equation, we obtain
$\unicode[STIX]{x1D6FC}_{1}=-\unicode[STIX]{x1D719}_{x}$
. Using this equation, we obtain
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{1}={\textstyle \frac{4}{3}}\sqrt{2}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\sinh ^{2}(\unicode[STIX]{x1D702}_{0}),\\ \displaystyle \hspace{-240.0pt}Y_{n}^{1}=-\frac{4\sqrt{2}}{3}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{30.0pt}\times \left((n^{2}+n+1)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})+(2n+1)\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})-n^{2}-n+\frac{1}{2}\right),\\ \displaystyle Z_{n}^{1}=-{\textstyle \frac{2}{3}}(2\sinh (\unicode[STIX]{x1D702}_{0})n+\sinh (\unicode[STIX]{x1D702}_{0})+3\cosh (\unicode[STIX]{x1D702}_{0}))\sqrt{2}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\sinh (\unicode[STIX]{x1D702}_{0}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{1}={\textstyle \frac{4}{3}}\sqrt{2}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\sinh ^{2}(\unicode[STIX]{x1D702}_{0}),\\ \displaystyle \hspace{-240.0pt}Y_{n}^{1}=-\frac{4\sqrt{2}}{3}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{30.0pt}\times \left((n^{2}+n+1)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})+(2n+1)\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})-n^{2}-n+\frac{1}{2}\right),\\ \displaystyle Z_{n}^{1}=-{\textstyle \frac{2}{3}}(2\sinh (\unicode[STIX]{x1D702}_{0})n+\sinh (\unicode[STIX]{x1D702}_{0})+3\cosh (\unicode[STIX]{x1D702}_{0}))\sqrt{2}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\sinh (\unicode[STIX]{x1D702}_{0}).\end{array}\right\}\end{eqnarray}$$
The expressions for force and torque acting on the swimmer due to all the squirming modes can be readily obtained by integrating the traction vector and the first moment of the traction vector on the surface of the swimmer. As these expressions are lengthy, we do not report them here.
A.2
 $B_{2}$
squirming mode
$B_{2}$
squirming mode
For
![]() $B_{2}$
squirming mode, the boundary condition at the surface of the swimmer is given by
$B_{2}$
squirming mode, the boundary condition at the surface of the swimmer is given by
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{s} & = & \displaystyle \left(\cos ^{2}(\unicode[STIX]{x1D703}_{z})-\frac{\sin ^{2}(\unicode[STIX]{x1D703}_{z})}{2}\right)\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703})\boldsymbol{i}_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})\{[-\text{cos}^{2}(\unicode[STIX]{x1D703})+\sin ^{2}(\unicode[STIX]{x1D703})]\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\sin ^{2}(\unicode[STIX]{x1D703}_{z})}{2}\{-\text{cos}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D703})\sin (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{s} & = & \displaystyle \left(\cos ^{2}(\unicode[STIX]{x1D703}_{z})-\frac{\sin ^{2}(\unicode[STIX]{x1D703}_{z})}{2}\right)\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703})\boldsymbol{i}_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,\sin (\unicode[STIX]{x1D703}_{z})\cos (\unicode[STIX]{x1D703}_{z})\{[-\text{cos}^{2}(\unicode[STIX]{x1D703})+\sin ^{2}(\unicode[STIX]{x1D703})]\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\sin ^{2}(\unicode[STIX]{x1D703}_{z})}{2}\{-\text{cos}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D703})\sin (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}}\}.\end{eqnarray}$$
We split this problem into three subproblems, with the boundary condition on the swimmer for each subproblem given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{Subproblem 0:}\;\boldsymbol{u}_{0}^{s}=\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703})\boldsymbol{i}_{\unicode[STIX]{x1D703}},\\ \displaystyle \text{Subproblem 1:}\;\boldsymbol{u}_{1}^{s}=(-\text{cos}^{2}(\unicode[STIX]{x1D703})+\sin ^{2}(\unicode[STIX]{x1D703}))\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}},\\ \text{Subproblem 2:}\;\boldsymbol{u}_{2}^{s}=-\text{cos}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D703})\sin (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{Subproblem 0:}\;\boldsymbol{u}_{0}^{s}=\sin (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D703})\boldsymbol{i}_{\unicode[STIX]{x1D703}},\\ \displaystyle \text{Subproblem 1:}\;\boldsymbol{u}_{1}^{s}=(-\text{cos}^{2}(\unicode[STIX]{x1D703})+\sin ^{2}(\unicode[STIX]{x1D703}))\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}},\\ \text{Subproblem 2:}\;\boldsymbol{u}_{2}^{s}=-\text{cos}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D703}}+\sin (\unicode[STIX]{x1D703})\sin (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x})\boldsymbol{i}_{\unicode[STIX]{x1D719}},\end{array}\right\}\end{eqnarray}$$
so that the flow field due to
![]() $B_{2}$
mode is given by
$B_{2}$
mode is given by
where again
![]() $\{\text{}\}_{k}$
denote the variables corresponding to
$\{\text{}\}_{k}$
denote the variables corresponding to
![]() $k$
th subproblem.
$k$
th subproblem.
A.2.1 Subproblem 0
In this case, the boundary condition on the swimmer can be rewritten in terms of cylindrical coordinates as
Thus, the non-zero terms in the general solution are those only with
![]() $m=0$
and
$m=0$
and
![]() $\unicode[STIX]{x1D6FC}_{0}=0$
. Using this equation, we obtain
$\unicode[STIX]{x1D6FC}_{0}=0$
. Using this equation, we obtain
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \hspace{-180.0pt}X_{n}^{0}=-\frac{8\sqrt{2}}{15}\sinh (\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{48.0pt}\times \left((n^{2}+n+4)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})+(4n+2)\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})-\left(n+\frac{1}{2}\right)^{2}\right),\\ \displaystyle \hspace{-180.0pt}Z_{n}^{0}=\frac{8\sqrt{2}}{15}\sinh (\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{18.0pt}\times \left(\begin{array}{@{}c@{}}(n+\frac{1}{2})(n^{2}+n+6)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})\\ +\,\frac{9}{2}\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})(n^{2}+n+\frac{2}{3})-(n+\frac{1}{2})(n^{2}+n+3)\end{array}\right),\\ Y_{n}^{0}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \hspace{-180.0pt}X_{n}^{0}=-\frac{8\sqrt{2}}{15}\sinh (\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{48.0pt}\times \left((n^{2}+n+4)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})+(4n+2)\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})-\left(n+\frac{1}{2}\right)^{2}\right),\\ \displaystyle \hspace{-180.0pt}Z_{n}^{0}=\frac{8\sqrt{2}}{15}\sinh (\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{18.0pt}\times \left(\begin{array}{@{}c@{}}(n+\frac{1}{2})(n^{2}+n+6)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})\\ +\,\frac{9}{2}\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})(n^{2}+n+\frac{2}{3})-(n+\frac{1}{2})(n^{2}+n+3)\end{array}\right),\\ Y_{n}^{0}=0.\end{array}\right\}\end{eqnarray}$$
A.2.2 Subproblem 1
In this case, the boundary condition on the swimmer can be rewritten in terms of cylindrical coordinates as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{s}=[-(z+l)^{3}+\unicode[STIX]{x1D70C}^{2}(z+l)]\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x}),\\ v_{s}=(z+l)\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x}),\\ w_{s}=[(z+l)^{2}\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{3}]\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{s}=[-(z+l)^{3}+\unicode[STIX]{x1D70C}^{2}(z+l)]\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x}),\\ v_{s}=(z+l)\sin (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x}),\\ w_{s}=[(z+l)^{2}\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{3}]\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{x}).\end{array}\right\}\end{eqnarray}$$
Thus, the non-zero terms in the general solution are those only with
![]() $m=1$
and
$m=1$
and
![]() $\unicode[STIX]{x1D6FC}_{1}=-\unicode[STIX]{x1D719}_{x}$
. Using this equation, we obtain
$\unicode[STIX]{x1D6FC}_{1}=-\unicode[STIX]{x1D719}_{x}$
. Using this equation, we obtain
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{1}={\textstyle \frac{8}{15}}\text{e}^{1/2(2n+1)\unicode[STIX]{x1D702}_{0}}\sqrt{2}(2\sinh (\unicode[STIX]{x1D702}_{0})n+\sinh (\unicode[STIX]{x1D702}_{0})+5\cosh (\unicode[STIX]{x1D702}_{0}))(\sinh (\unicode[STIX]{x1D702}_{0}))^{2},\\ \displaystyle Y_{n}^{1}=-\frac{2\sqrt{2}}{15}\text{e}^{1/2\unicode[STIX]{x1D702}_{0}(2n-5)}\left(\begin{array}{@{}c@{}}\text{e}^{6\unicode[STIX]{x1D702}_{0}}n^{3}+6\text{e}^{6\unicode[STIX]{x1D702}_{0}}n^{2}+11\text{e}^{6\unicode[STIX]{x1D702}_{0}}n-3\text{e}^{4\unicode[STIX]{x1D702}_{0}}n^{3}+6\text{e}^{6\unicode[STIX]{x1D702}_{0}}-9\text{e}^{4\unicode[STIX]{x1D702}_{0}}n^{2}\\ +\,3\text{e}^{4\unicode[STIX]{x1D702}_{0}}n+3\text{e}^{2\unicode[STIX]{x1D702}_{0}}n^{3}+9\text{e}^{4\unicode[STIX]{x1D702}_{0}}-12\text{e}^{2\unicode[STIX]{x1D702}_{0}}n-n^{3}+3n^{2}-2n\end{array}\right),\\ \displaystyle Z_{n}^{1}=-\frac{\sqrt{2}\text{e}^{1/2\unicode[STIX]{x1D702}_{0}(2n-5)}}{15}\left(\begin{array}{@{}c@{}}2\text{e}^{6\unicode[STIX]{x1D702}_{0}}n^{2}+10\text{e}^{6\unicode[STIX]{x1D702}_{0}}n+12\text{e}^{6\unicode[STIX]{x1D702}_{0}}-6\text{e}^{4\unicode[STIX]{x1D702}_{0}}n^{2}-14\text{e}^{4\unicode[STIX]{x1D702}_{0}}n-13\text{e}^{4\unicode[STIX]{x1D702}_{0}}\\ +\,6\text{e}^{2\unicode[STIX]{x1D702}_{0}}n^{2}-2\text{e}^{2\unicode[STIX]{x1D702}_{0}}n+5\text{e}^{2\unicode[STIX]{x1D702}_{0}}-2n^{2}+6n-4\end{array}\right).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{1}={\textstyle \frac{8}{15}}\text{e}^{1/2(2n+1)\unicode[STIX]{x1D702}_{0}}\sqrt{2}(2\sinh (\unicode[STIX]{x1D702}_{0})n+\sinh (\unicode[STIX]{x1D702}_{0})+5\cosh (\unicode[STIX]{x1D702}_{0}))(\sinh (\unicode[STIX]{x1D702}_{0}))^{2},\\ \displaystyle Y_{n}^{1}=-\frac{2\sqrt{2}}{15}\text{e}^{1/2\unicode[STIX]{x1D702}_{0}(2n-5)}\left(\begin{array}{@{}c@{}}\text{e}^{6\unicode[STIX]{x1D702}_{0}}n^{3}+6\text{e}^{6\unicode[STIX]{x1D702}_{0}}n^{2}+11\text{e}^{6\unicode[STIX]{x1D702}_{0}}n-3\text{e}^{4\unicode[STIX]{x1D702}_{0}}n^{3}+6\text{e}^{6\unicode[STIX]{x1D702}_{0}}-9\text{e}^{4\unicode[STIX]{x1D702}_{0}}n^{2}\\ +\,3\text{e}^{4\unicode[STIX]{x1D702}_{0}}n+3\text{e}^{2\unicode[STIX]{x1D702}_{0}}n^{3}+9\text{e}^{4\unicode[STIX]{x1D702}_{0}}-12\text{e}^{2\unicode[STIX]{x1D702}_{0}}n-n^{3}+3n^{2}-2n\end{array}\right),\\ \displaystyle Z_{n}^{1}=-\frac{\sqrt{2}\text{e}^{1/2\unicode[STIX]{x1D702}_{0}(2n-5)}}{15}\left(\begin{array}{@{}c@{}}2\text{e}^{6\unicode[STIX]{x1D702}_{0}}n^{2}+10\text{e}^{6\unicode[STIX]{x1D702}_{0}}n+12\text{e}^{6\unicode[STIX]{x1D702}_{0}}-6\text{e}^{4\unicode[STIX]{x1D702}_{0}}n^{2}-14\text{e}^{4\unicode[STIX]{x1D702}_{0}}n-13\text{e}^{4\unicode[STIX]{x1D702}_{0}}\\ +\,6\text{e}^{2\unicode[STIX]{x1D702}_{0}}n^{2}-2\text{e}^{2\unicode[STIX]{x1D702}_{0}}n+5\text{e}^{2\unicode[STIX]{x1D702}_{0}}-2n^{2}+6n-4\end{array}\right).\end{array}\right\}\end{eqnarray}$$
A.2.3 Subproblem 2
In this case, the boundary condition on the swimmer can be rewritten in terms of cylindrical coordinates as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{s}=-(z+l)^{2}\unicode[STIX]{x1D70C}\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x}),\\ v_{s}=\unicode[STIX]{x1D70C}\sin (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x}),\\ w_{s}=\unicode[STIX]{x1D70C}^{2}(z+l)\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{s}=-(z+l)^{2}\unicode[STIX]{x1D70C}\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x}),\\ v_{s}=\unicode[STIX]{x1D70C}\sin (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x}),\\ w_{s}=\unicode[STIX]{x1D70C}^{2}(z+l)\cos (2\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D719}_{x}).\end{array}\right\}\end{eqnarray}$$
Thus, the non-zero terms in the general solution are those only with
![]() $m=2$
and
$m=2$
and
![]() $\unicode[STIX]{x1D6FC}_{2}=-2\unicode[STIX]{x1D719}_{x}$
. Using this equation, we obtain
$\unicode[STIX]{x1D6FC}_{2}=-2\unicode[STIX]{x1D719}_{x}$
. Using this equation, we obtain
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{2}=-\frac{8\sqrt{2}\sinh ^{3}(\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}}{15},\\ \displaystyle \hspace{-120.0pt}Y_{n}^{2}=\frac{8\sqrt{2}}{15}\sinh (\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{60.0pt}\times \left(\begin{array}{@{}c@{}}(n^{2}+n+4)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})+(4n+2)\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})\\ -\,n^{2}-n+\frac{7}{2}\end{array}\right),\\ \displaystyle Z_{n}^{2}=\frac{4\sqrt{2}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}(2\sinh (\unicode[STIX]{x1D702}_{0})n+5\cosh (\unicode[STIX]{x1D702}_{0})+\sinh (\unicode[STIX]{x1D702}_{0}))\sinh ^{2}(\unicode[STIX]{x1D702}_{0})}{15}.\end{array}\right\}\quad\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle X_{n}^{2}=-\frac{8\sqrt{2}\sinh ^{3}(\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}}{15},\\ \displaystyle \hspace{-120.0pt}Y_{n}^{2}=\frac{8\sqrt{2}}{15}\sinh (\unicode[STIX]{x1D702}_{0})\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}\\ \displaystyle \hspace{60.0pt}\times \left(\begin{array}{@{}c@{}}(n^{2}+n+4)\cosh ^{2}(\unicode[STIX]{x1D702}_{0})+(4n+2)\sinh (\unicode[STIX]{x1D702}_{0})\cosh (\unicode[STIX]{x1D702}_{0})\\ -\,n^{2}-n+\frac{7}{2}\end{array}\right),\\ \displaystyle Z_{n}^{2}=\frac{4\sqrt{2}\text{e}^{(n+(1/2))\unicode[STIX]{x1D702}_{0}}(2\sinh (\unicode[STIX]{x1D702}_{0})n+5\cosh (\unicode[STIX]{x1D702}_{0})+\sinh (\unicode[STIX]{x1D702}_{0}))\sinh ^{2}(\unicode[STIX]{x1D702}_{0})}{15}.\end{array}\right\}\quad\end{eqnarray}$$

Figure 11. Vector fields of
![]() $(\unicode[STIX]{x0394}\bar{\unicode[STIX]{x1D703}}_{z},\unicode[STIX]{x0394}\bar{z})$
(their definitions being given in the main text) along with the contours of
$(\unicode[STIX]{x0394}\bar{\unicode[STIX]{x1D703}}_{z},\unicode[STIX]{x0394}\bar{z})$
(their definitions being given in the main text) along with the contours of
![]() $\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}}$
obtained using the MOR, for (a) puller swimmer (
$\sqrt{(\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z})^{2}+(\unicode[STIX]{x0394}z)^{2}}$
obtained using the MOR, for (a) puller swimmer (
![]() $B_{2}/B_{1}=4$
), (b) pusher swimmer (
$B_{2}/B_{1}=4$
), (b) pusher swimmer (
![]() $B_{2}/B_{1}=-4$
) and (c) neutral swimmer (
$B_{2}/B_{1}=-4$
) and (c) neutral swimmer (
![]() $B_{2}/B_{1}=0$
). The values of parameters used in these plots are
$B_{2}/B_{1}=0$
). The values of parameters used in these plots are
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $t_{in}=0$
.
$t_{in}=0$
.

Figure 12. Change in (a) swimmer position
![]() $\unicode[STIX]{x0394}z$
and (b) orientation
$\unicode[STIX]{x0394}z$
and (b) orientation
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
in one time period for
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
in one time period for
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, 1 and 10,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=0.01$
, 1 and 10,
![]() $B_{2}/B_{1}=4$
,
$B_{2}/B_{1}=4$
,
![]() $\unicode[STIX]{x1D706}=1$
,
$\unicode[STIX]{x1D706}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. The lines indicate the bipolar coordinate results and the symbols indicate the MOR results.
$\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8$
. The lines indicate the bipolar coordinate results and the symbols indicate the MOR results.

Figure 13. Change in (a) swimmer position
![]() $\unicode[STIX]{x0394}z$
and (b) orientation
$\unicode[STIX]{x0394}z$
and (b) orientation
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
in one time period for
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}$
in one time period for
![]() $\unicode[STIX]{x1D706}=10^{-3}$
, 1 and 10,
$\unicode[STIX]{x1D706}=10^{-3}$
, 1 and 10,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}=1$
,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=20$
,
![]() $\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8,B_{2}/B_{1}=4$
. The lines indicate bipolar coordinate results and the symbols indicate the MOR results.
$\unicode[STIX]{x1D703}_{z}=3\unicode[STIX]{x03C0}/8,B_{2}/B_{1}=4$
. The lines indicate bipolar coordinate results and the symbols indicate the MOR results.
Appendix B. Point force singularities
B.1 Source dipole
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})=-\frac{\unicode[STIX]{x1D739}}{R^{3}}+\frac{3(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}\boldsymbol{x};\quad R=|\boldsymbol{x}|,\\ \displaystyle p_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})=-\frac{\unicode[STIX]{x1D739}}{R^{3}}+\frac{3(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}\boldsymbol{x};\quad R=|\boldsymbol{x}|,\\ \displaystyle p_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})=0.\end{array}\right\}\end{eqnarray}$$
B.2 Stresslet
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{ss}(\boldsymbol{x};\unicode[STIX]{x1D738},\unicode[STIX]{x1D739})=\left[-\frac{\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D739}}{R^{3}}+\frac{3(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}\right]\boldsymbol{x},\\ \displaystyle p_{ss}(\boldsymbol{x};\unicode[STIX]{x1D738},\unicode[STIX]{x1D739})=2\left[-\frac{\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D739}}{R^{3}}+\frac{3(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}\right].\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{ss}(\boldsymbol{x};\unicode[STIX]{x1D738},\unicode[STIX]{x1D739})=\left[-\frac{\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D739}}{R^{3}}+\frac{3(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}\right]\boldsymbol{x},\\ \displaystyle p_{ss}(\boldsymbol{x};\unicode[STIX]{x1D738},\unicode[STIX]{x1D739})=2\left[-\frac{\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D739}}{R^{3}}+\frac{3(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}\right].\end{array}\right\}\end{eqnarray}$$
B.3 Source quadrupole
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \hspace{-180.0pt}\boldsymbol{u}_{D4}(\boldsymbol{x};\unicode[STIX]{x1D739},\unicode[STIX]{x1D738})=\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D735}[\boldsymbol{u}_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})]\\ \displaystyle \hspace{42.0pt}=\frac{3\unicode[STIX]{x1D739}(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})+3(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\unicode[STIX]{x1D738})\boldsymbol{x}+3\unicode[STIX]{x1D738}(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}-\frac{15(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{x}}{R^{7}},\\ \displaystyle p_{D4}(\boldsymbol{x};\unicode[STIX]{x1D739},\unicode[STIX]{x1D738})=\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \hspace{-180.0pt}\boldsymbol{u}_{D4}(\boldsymbol{x};\unicode[STIX]{x1D739},\unicode[STIX]{x1D738})=\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D735}[\boldsymbol{u}_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})]\\ \displaystyle \hspace{42.0pt}=\frac{3\unicode[STIX]{x1D739}(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})+3(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\unicode[STIX]{x1D738})\boldsymbol{x}+3\unicode[STIX]{x1D738}(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})}{R^{5}}-\frac{15(\unicode[STIX]{x1D739}\boldsymbol{\cdot }\boldsymbol{x})(\unicode[STIX]{x1D738}\boldsymbol{\cdot }\boldsymbol{x})\boldsymbol{x}}{R^{7}},\\ \displaystyle p_{D4}(\boldsymbol{x};\unicode[STIX]{x1D739},\unicode[STIX]{x1D738})=\unicode[STIX]{x1D738}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{D}(\boldsymbol{x};\unicode[STIX]{x1D739})=0.\end{array}\right\}\end{eqnarray}$$
Appendix C. Instantaneous velocities of a time-reversible squirmer: method of reflections
We present the changes in the position and orientation of the swimmer in one time period, obtained using the method of reflections, in figures 11–13. We also compare these results with those obtained using bipolar coordinates for various values of
![]() $B_{2}/B_{1}$
,
$B_{2}/B_{1}$
,
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.