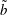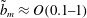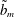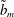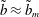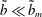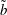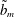1 Introduction
A classical problem of dynamic wetting is the spreading of a droplet when it is placed in contact with a smooth and chemically homogeneous substrate (Chen Reference Chen1988; Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). For complete wetting, with a vanishing equilibrium contact angle, the spreading process follows the well-known Tanner’s law (Voinov Reference Voinov1976; Tanner Reference Tanner1979) stating that the contact line radius
![]() $R$
grows in time
$R$
grows in time
![]() $t$
as a power law
$t$
as a power law
![]() $R\sim t^{1/10}$
. This asymptotically valid relation is derived with the assumption that the droplet maintains a spherical-cap-shaped profile during spreading, except in the vicinity of the moving contact line, where the interface is deformed strongly due to viscous stresses. The general assumptions of a quasistatic macroscopic interface profile and a quasisteady viscous flow in the region close to the contact line have been central guidelines in studies of dynamic wetting problems (Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009; Snoeijer & Andreotti Reference Snoeijer and Andreotti2013; Sui, Ding & Spelt Reference Sui, Ding and Spelt2014). Examples include industrial applications such as oil recovery (Sahimi Reference Sahimi1993), immersion lithography (Winkels et al.
Reference Winkels, Peters, Evangelista, Riepen, Daerr, Limat and Snoeijer2011) and coating (Weinstein & Ruschak Reference Weinstein and Ruschak2004), as well as natural phenomena (Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009) such as liquid droplets sliding on the surface of a leaf. The basis of these assumptions lies in the wide separation of length scales between the extension of the interface and a microscopic length to relax the singularity of infinite viscous dissipation (Huh & Scriven Reference Huh and Scriven1971) at the contact line. As specifically discussed here, this microscopic length scale may be the slip length, defined as the ratio between the fluid velocity parallel to the substrate and the shear rate at the boundary. In cases where a no-slip condition is assumed for the solid/liquid boundary, other microscopic length scales in specific models have been proposed as reviewed in Bonn et al. (Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009), Snoeijer & Andreotti (Reference Snoeijer and Andreotti2013) and Sui et al. (Reference Sui, Ding and Spelt2014).
$R\sim t^{1/10}$
. This asymptotically valid relation is derived with the assumption that the droplet maintains a spherical-cap-shaped profile during spreading, except in the vicinity of the moving contact line, where the interface is deformed strongly due to viscous stresses. The general assumptions of a quasistatic macroscopic interface profile and a quasisteady viscous flow in the region close to the contact line have been central guidelines in studies of dynamic wetting problems (Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009; Snoeijer & Andreotti Reference Snoeijer and Andreotti2013; Sui, Ding & Spelt Reference Sui, Ding and Spelt2014). Examples include industrial applications such as oil recovery (Sahimi Reference Sahimi1993), immersion lithography (Winkels et al.
Reference Winkels, Peters, Evangelista, Riepen, Daerr, Limat and Snoeijer2011) and coating (Weinstein & Ruschak Reference Weinstein and Ruschak2004), as well as natural phenomena (Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009) such as liquid droplets sliding on the surface of a leaf. The basis of these assumptions lies in the wide separation of length scales between the extension of the interface and a microscopic length to relax the singularity of infinite viscous dissipation (Huh & Scriven Reference Huh and Scriven1971) at the contact line. As specifically discussed here, this microscopic length scale may be the slip length, defined as the ratio between the fluid velocity parallel to the substrate and the shear rate at the boundary. In cases where a no-slip condition is assumed for the solid/liquid boundary, other microscopic length scales in specific models have been proposed as reviewed in Bonn et al. (Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009), Snoeijer & Andreotti (Reference Snoeijer and Andreotti2013) and Sui et al. (Reference Sui, Ding and Spelt2014).
In the context of hydrodynamics, slippage refers to the phenomenon that fluids may flow with non-zero velocity along a solid/liquid boundary. Although the microscopic origin of slippage depends on the material parameters of solid/liquid pair under consideration (Lauga, Brenner & Stone Reference Lauga, Brenner, Stone, Tropea, Foss and Yarin2007), there have been extensive studies on the measurement of the slip length due to the development of new experimental techniques in recent years (Neto et al. Reference Neto, Evans, Bonaccurso, Butt and Craig2005; Bocquet & Charlaix Reference Bocquet and Charlaix2009; Guo et al. Reference Guo, Gao, Xiong, Wang, Wang, Sheng and Tong2013). Interestingly, slip lengths as large as a few micrometres have been reported in some studies using polymer melts (Reiter & Sharma Reference Reiter and Sharma2001; Leger Reference Leger2003; Fetzer et al. Reference Fetzer, Jacobs, Münch, Wagner and Witelski2005, Reference Fetzer, Münch, Wagner, Rauscher and Jacobs2007; Bäumchen, Fetzer & Jacobs Reference Bäumchen, Fetzer and Jacobs2009; Haefner et al. Reference Haefner, Benzaquen, Bäumchen, Salez, Peters, McGraw, Jacobs, Raphaël and Dalnoki-Veress2015). These findings raise fundamental questions on the description of the contact line motion and the evolution of the interface profile, particularly in micrometric (Cuenca & Bodiguel Reference Cuenca and Bodiguel2013; Setu et al. Reference Setu, Dullens, Hernández-Machado, Pagonabarraga, Aarts and Ledesma-Aguilar2015) or nanometric (Falk et al. Reference Falk, Sedlmeier, Joly, Netz and Bocquet2010) systems, for which the separation of length scales may not be fulfilled.
The opposite process of spreading (wetting), called dewetting, occurs when the driving forces tend to decrease the contact area between the liquid and the solid (de Gennes, Brochart-Wyart & Quéré Reference de Gennes, Brochart-Wyart and Quéré2003). Dewetting has been commonly studied in the geometry of liquid films (Redon, Brochard-Wyart & Rondelez Reference Redon, Brochard-Wyart and Rondelez1991; Snoeijer & Eggers Reference Snoeijer and Eggers2010; Rivetti et al.
Reference Rivetti, Salez, Benzaquen, Raphaël and Bäumchen2015). In these situations, due to the accumulation of mass in the contact line region, a bump of liquid is naturally formed in a rim. In the case of no slip or weak slip, namely the slip length is orders of magnitude smaller than the height of the bump; the bump maintains a static shape with a growing size (i.e. quasistatic), and the contact line moves at a constant speed (Redon et al.
Reference Redon, Brochard-Wyart and Rondelez1991; Snoeijer & Eggers Reference Snoeijer and Eggers2010). Recently, the dewetting of flat droplets on a solid surface has been studied in detail (Edwards et al.
Reference Edwards, Ledesma-Aguilar, Newton, Brown and McHale2016). In that study, the ratio between the slip length (
![]() ${\approx}1$
nm) and the central height of the droplets is approximately
${\approx}1$
nm) and the central height of the droplets is approximately
![]() $10^{-5}$
. The dewetting process has been found to be similar to that of liquid films (Redon et al.
Reference Redon, Brochard-Wyart and Rondelez1991; Snoeijer & Eggers Reference Snoeijer and Eggers2010), except the final state is a single droplet. In this weak-slip regime, the slip length effectively acts as a cutoff length for the contact line singularity, and only has a weak effect (logarithmic dependence) on the dynamics. A recent study on dewetting polymer microdroplets (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016), however, showed that the transient droplet shape evolution, in the regime where the slip length is comparable to or larger than the typical droplet size (i.e.
$10^{-5}$
. The dewetting process has been found to be similar to that of liquid films (Redon et al.
Reference Redon, Brochard-Wyart and Rondelez1991; Snoeijer & Eggers Reference Snoeijer and Eggers2010), except the final state is a single droplet. In this weak-slip regime, the slip length effectively acts as a cutoff length for the contact line singularity, and only has a weak effect (logarithmic dependence) on the dynamics. A recent study on dewetting polymer microdroplets (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016), however, showed that the transient droplet shape evolution, in the regime where the slip length is comparable to or larger than the typical droplet size (i.e.
![]() $\tilde{b}\approx O(0.1{-}10)$
), is much richer than one expects under the assumptions of quasistatic profiles and dissipation localized near the contact line. The transient droplet profiles are indeed found to be non-spherical (i.e. non-quasistatic), and highly dependent on the precise value of the slip length. One characteristic feature of the dewetting process is the development of a transient ridge for relatively small slip lengths. The ridge was found to be more pronounced when the slip length is smaller, and avoided for larger slip lengths due to elongational flow inside the droplet. On the other hand, as discussed above, when the slip length is many orders of magnitude smaller than the droplet size, one expects to recover the typical quasistatic sequence of spherical-cap-shaped profiles.
$\tilde{b}\approx O(0.1{-}10)$
), is much richer than one expects under the assumptions of quasistatic profiles and dissipation localized near the contact line. The transient droplet profiles are indeed found to be non-spherical (i.e. non-quasistatic), and highly dependent on the precise value of the slip length. One characteristic feature of the dewetting process is the development of a transient ridge for relatively small slip lengths. The ridge was found to be more pronounced when the slip length is smaller, and avoided for larger slip lengths due to elongational flow inside the droplet. On the other hand, as discussed above, when the slip length is many orders of magnitude smaller than the droplet size, one expects to recover the typical quasistatic sequence of spherical-cap-shaped profiles.
In this article, we study the dewetting of a flat viscous droplet for a wide range of slip lengths and various equilibrium contact angles employing the boundary element method. We elucidate the transition between the quasistatic and non-quasistatic evolutions of a dewetting droplet. The non-sphericity of the droplet increases when the slip length is first decreased from the full-slip limit. Further decreasing the slip length, we observe a new feature with respect to previous works (McGraw et al. Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016): the non-sphericity reaches a maximum and then starts to decrease. This behaviour is demonstrated for different equilibrium contact angles. We give explanations for these results in terms of flow structures and the spreading of a localized ridge.
2 Formulation
As an initial condition, we consider a spherical-cap-shaped droplet sitting on a plane and smooth substrate with a contact angle
![]() $\unicode[STIX]{x1D703}_{i}$
, which is smaller than the equilibrium contact angle
$\unicode[STIX]{x1D703}_{i}$
, which is smaller than the equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}$
. In order to minimize the surface energy, the droplet starts to retract and approaches a spherical cap with the equilibrium contact angle. Because of the homogeneous and planar substrate, the shape of the droplet remains axisymmetric during its evolution. The droplet profile is described by the height,
$\unicode[STIX]{x1D703}_{e}$
. In order to minimize the surface energy, the droplet starts to retract and approaches a spherical cap with the equilibrium contact angle. Because of the homogeneous and planar substrate, the shape of the droplet remains axisymmetric during its evolution. The droplet profile is described by the height,
![]() $h(r,t)$
, of the liquid with respect to the substrate as a function of the radial distance from the central axis
$h(r,t)$
, of the liquid with respect to the substrate as a function of the radial distance from the central axis
![]() $r$
and time
$r$
and time
![]() $t$
. We further assume the liquid inside the droplet to be a highly viscous and incompressible Newtonian liquid so that the flow obeys the Stokes equation,
$t$
. We further assume the liquid inside the droplet to be a highly viscous and incompressible Newtonian liquid so that the flow obeys the Stokes equation,
and the continuity equation which reads
where
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $p$
are the velocity field and the pressure field in the liquid, respectively, and
$p$
are the velocity field and the pressure field in the liquid, respectively, and
![]() $\unicode[STIX]{x1D702}$
is the dynamic viscosity of the liquid.
$\unicode[STIX]{x1D702}$
is the dynamic viscosity of the liquid.
To solve for the flow fields and the evolution of the interface profile, one needs to specify appropriate boundary conditions. First, the stress tensor
![]() $\unicode[STIX]{x1D748}$
in Cartesian coordinates is given as
$\unicode[STIX]{x1D748}$
in Cartesian coordinates is given as
and the stress
![]() $\boldsymbol{f}$
at the boundary reads
$\boldsymbol{f}$
at the boundary reads
Here
![]() $\hat{\boldsymbol{n}}$
is the unit vector normal to the boundary of the droplet pointing into the enclosed fluid.
$\hat{\boldsymbol{n}}$
is the unit vector normal to the boundary of the droplet pointing into the enclosed fluid.
Assuming the surrounding air flow is negligible, the tangential stress vanishes at the liquid/air boundary. The normal stress
![]() $f_{n}^{free}\equiv \boldsymbol{f}^{free}\boldsymbol{\cdot }\hat{\boldsymbol{n}}$
at the free surface is balanced by the surface tension, leading to the Young–Laplace law:
$f_{n}^{free}\equiv \boldsymbol{f}^{free}\boldsymbol{\cdot }\hat{\boldsymbol{n}}$
at the free surface is balanced by the surface tension, leading to the Young–Laplace law:
where
![]() $\unicode[STIX]{x1D6FE}$
denotes the interfacial tension and
$\unicode[STIX]{x1D6FE}$
denotes the interfacial tension and
![]() $\unicode[STIX]{x1D705}$
the mean curvature of the free surface, which is defined as
$\unicode[STIX]{x1D705}$
the mean curvature of the free surface, which is defined as
 $$\begin{eqnarray}\unicode[STIX]{x1D705}=\frac{{\displaystyle \frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}r^{2}}}}{2\left(1+\left({\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}r}}\right)^{2}\right)^{3/2}}+\frac{{\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}r}}}{2r\left(1+\left({\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}r}}\right)^{2}\right)^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}=\frac{{\displaystyle \frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}r^{2}}}}{2\left(1+\left({\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}r}}\right)^{2}\right)^{3/2}}+\frac{{\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}r}}}{2r\left(1+\left({\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}r}}\right)^{2}\right)^{1/2}}.\end{eqnarray}$$
Note that disjoining pressures are not considered in this model. The evolution of the interface profile is given by the kinematic condition along the free interface, that is
At the solid/liquid boundary, the velocity normal to the wall vanishes. Regarding the velocity component parallel to the wall
![]() $u_{t}^{wall}\hat{\boldsymbol{r}}$
, we impose a Navier-slip condition which reads
$u_{t}^{wall}\hat{\boldsymbol{r}}$
, we impose a Navier-slip condition which reads
where
![]() $\hat{\boldsymbol{r}}$
is the unit vector in the radial direction,
$\hat{\boldsymbol{r}}$
is the unit vector in the radial direction,
![]() $f_{t}^{wall}\equiv \boldsymbol{f}^{wall}\boldsymbol{\cdot }\hat{\boldsymbol{r}}$
is the shear stress at the wall and the slip length,
$f_{t}^{wall}\equiv \boldsymbol{f}^{wall}\boldsymbol{\cdot }\hat{\boldsymbol{r}}$
is the shear stress at the wall and the slip length,
![]() $b$
, is assumed to be a constant. To complete the hydrodynamic problem, we impose the condition that the free surface touches the wall with a finite contact angle. This angle is assumed to be the same as the equilibrium contact angle
$b$
, is assumed to be a constant. To complete the hydrodynamic problem, we impose the condition that the free surface touches the wall with a finite contact angle. This angle is assumed to be the same as the equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}$
, independent of the contact line velocity. Moreover, since the substrate surface is smooth and chemically homogeneous,
$\unicode[STIX]{x1D703}_{e}$
, independent of the contact line velocity. Moreover, since the substrate surface is smooth and chemically homogeneous,
![]() $\unicode[STIX]{x1D703}_{e}$
is also independent of the contact line position.
$\unicode[STIX]{x1D703}_{e}$
is also independent of the contact line position.
2.1 Boundary element method (BEM)
The Stokes equation (2.1) and the continuity equation (2.2) can be formulated in the form of the boundary integral equations; a method which has been used extensively to study many interfacial flow problems (Pozrikidis Reference Pozrikidis1992). In this approach the velocity
![]() $\boldsymbol{u}(\boldsymbol{s}_{0})$
at any point
$\boldsymbol{u}(\boldsymbol{s}_{0})$
at any point
![]() $\boldsymbol{s}_{0}$
can be written in terms of integrals involving the stress
$\boldsymbol{s}_{0}$
can be written in terms of integrals involving the stress
![]() $\boldsymbol{f}$
and the velocity on the boundary. For the axisymmetric Stokes flow problem we study in this article, the boundary integral equations (Pozrikidis Reference Pozrikidis1992) read
$\boldsymbol{f}$
and the velocity on the boundary. For the axisymmetric Stokes flow problem we study in this article, the boundary integral equations (Pozrikidis Reference Pozrikidis1992) read
where the subscripts
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D701}$
represent either the radial (
$\unicode[STIX]{x1D701}$
represent either the radial (
![]() $r$
) or the vertical (
$r$
) or the vertical (
![]() $z$
) components in cylindrical coordinates, and
$z$
) components in cylindrical coordinates, and
![]() $c$
is the contour line (boundary) over which the integration takes place. The repeated Greek indices conform to the Einstein summation convention, that is they are summed over the radial and the vertical components. For the expression of the tensor components
$c$
is the contour line (boundary) over which the integration takes place. The repeated Greek indices conform to the Einstein summation convention, that is they are summed over the radial and the vertical components. For the expression of the tensor components
![]() $\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
$\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
![]() $\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
, we refer to § A.1. The value of
$\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
, we refer to § A.1. The value of
![]() $A$
depends on the position
$A$
depends on the position
![]() $\boldsymbol{s}_{0}$
:
$\boldsymbol{s}_{0}$
:
We note that
![]() $\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
$\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
![]() $\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
are singular at
$\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
are singular at
![]() $\boldsymbol{s}=\boldsymbol{s}_{0}$
; the integral over the singular point is thus computed analytically by expanding the tensor components in series about
$\boldsymbol{s}=\boldsymbol{s}_{0}$
; the integral over the singular point is thus computed analytically by expanding the tensor components in series about
![]() $\boldsymbol{s}=\boldsymbol{s}_{0}$
(Lee & Leal Reference Lee and Leal1982; van Lengerich & Steen Reference van Lengerich and Steen2012).
$\boldsymbol{s}=\boldsymbol{s}_{0}$
(Lee & Leal Reference Lee and Leal1982; van Lengerich & Steen Reference van Lengerich and Steen2012).
The main advantage of the boundary element method is that the velocity field is explicitly written in terms of the velocities and the stresses on the boundary. No discretization of elements inside the droplet is required to solve for the flow fields. As given by the boundary conditions, not all the velocities and stresses at the boundary of the liquid domain are known. For example, the velocities at the free interface are unknowns, yet the unknown quantities can be found by solving (2.9) for the case that
![]() $\boldsymbol{s}_{0}$
lies on the boundary. For a numerical treatment of the problem, the contour is discretized into small linear elements. The velocity and the stress are taken to be constant within the same element. A system of linear equations is then obtained from (2.9), and the unknown quantities can be computed. Note that the normal stress for the numerical element of the liquid/air interface containing the contact line is computed with the boundary condition of the imposed equilibrium contact angle
$\boldsymbol{s}_{0}$
lies on the boundary. For a numerical treatment of the problem, the contour is discretized into small linear elements. The velocity and the stress are taken to be constant within the same element. A system of linear equations is then obtained from (2.9), and the unknown quantities can be computed. Note that the normal stress for the numerical element of the liquid/air interface containing the contact line is computed with the boundary condition of the imposed equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}$
. Once the velocities at the free surface have been computed, one can determine the profile evolution using the kinematic condition (2.7).
$\unicode[STIX]{x1D703}_{e}$
. Once the velocities at the free surface have been computed, one can determine the profile evolution using the kinematic condition (2.7).
Initially, the droplet has a spherical-cap shape with a contact angle
![]() $\unicode[STIX]{x1D703}_{i}$
. Due to the small molecular relaxation time scale at the contact line, the contact angle quickly reaches the equilibrium contact angle
$\unicode[STIX]{x1D703}_{i}$
. Due to the small molecular relaxation time scale at the contact line, the contact angle quickly reaches the equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}$
microscopically (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016). To approximate this initial microscopic contact angle in our numerical computations, we assume that at
$\unicode[STIX]{x1D703}_{e}$
microscopically (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016). To approximate this initial microscopic contact angle in our numerical computations, we assume that at
![]() $t=0$
, there is a kink in the interface profile at the contact line position. The line connecting the first numerical marker point and the contact line makes an angle
$t=0$
, there is a kink in the interface profile at the contact line position. The line connecting the first numerical marker point and the contact line makes an angle
![]() $\unicode[STIX]{x1D703}_{e}$
with the substrate. Due to this kink, the magnitude of the approximated interfacial curvature near the contact line is larger than that on the rest of the interface, thus the Laplace pressure is unbalanced and the pressure gradient initiates a flow. Hence, the contact line starts to move towards the centre. The kink then quickly relaxes to a smooth shape due to surface tension. This type of initial profile is a natural choice as it smoothly connects the boundary condition at the contact line and the initial spherical-cap shape of the droplet. Note that our model is not able to describe the physics happening in the very vicinity of the contact line at earlier times. A different approach from hydrodynamics is required to solve that specific problem, such as molecular dynamics simulations.
$\unicode[STIX]{x1D703}_{e}$
with the substrate. Due to this kink, the magnitude of the approximated interfacial curvature near the contact line is larger than that on the rest of the interface, thus the Laplace pressure is unbalanced and the pressure gradient initiates a flow. Hence, the contact line starts to move towards the centre. The kink then quickly relaxes to a smooth shape due to surface tension. This type of initial profile is a natural choice as it smoothly connects the boundary condition at the contact line and the initial spherical-cap shape of the droplet. Note that our model is not able to describe the physics happening in the very vicinity of the contact line at earlier times. A different approach from hydrodynamics is required to solve that specific problem, such as molecular dynamics simulations.
We non-dimensionalize the problem as follows: all lengths are rescaled by the initial maximum height of the droplet
![]() $h_{0}$
and all the times by the viscous capillary time scale
$h_{0}$
and all the times by the viscous capillary time scale
![]() $h_{0}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D6FE}$
. All these dimensionless variables are denoted with a tilde. We are thus left with three independent dimensionless parameters. In the following, we consider the initial contact angle
$h_{0}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D6FE}$
. All these dimensionless variables are denoted with a tilde. We are thus left with three independent dimensionless parameters. In the following, we consider the initial contact angle
![]() $\unicode[STIX]{x1D703}_{i}$
, the equilibrium contact angle
$\unicode[STIX]{x1D703}_{i}$
, the equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}$
and the rescaled slip length
$\unicode[STIX]{x1D703}_{e}$
and the rescaled slip length
![]() $\tilde{b}\equiv b/h_{0}$
as the control parameters. For all our numerical computations, 300 marker points are used to describe the interface profile of the droplet. The vertical separation between two marker points is approximately 0.003. For smaller separations, the profile evolution becomes unstable. We then set the smallest rescaled slip length to
$\tilde{b}\equiv b/h_{0}$
as the control parameters. For all our numerical computations, 300 marker points are used to describe the interface profile of the droplet. The vertical separation between two marker points is approximately 0.003. For smaller separations, the profile evolution becomes unstable. We then set the smallest rescaled slip length to
![]() $\tilde{b}=0.023$
, which is about ten times the marker separation. Hence for all our computations, the rescaled slip length is varied in a range
$\tilde{b}=0.023$
, which is about ten times the marker separation. Hence for all our computations, the rescaled slip length is varied in a range
![]() $\tilde{b}>0.023$
. We also check the conservation of volume in our numerics. The difference between the initial and the final volumes of the droplets is less than 1 %. Further demonstrations of the numerical precision of our BEM, and a comparison to analytical results, are shown in § A.2.
$\tilde{b}>0.023$
. We also check the conservation of volume in our numerics. The difference between the initial and the final volumes of the droplets is less than 1 %. Further demonstrations of the numerical precision of our BEM, and a comparison to analytical results, are shown in § A.2.

Figure 1. Evolution of the droplet profiles. The initial shape of the droplet is a flat spherical cap with contact angle
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. The final equilibrium droplet has contact angle
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. The final equilibrium droplet has contact angle
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. One of the profiles in each figure is plotted with a dashed line to emphasize the difference between the transient shapes. (a)
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. One of the profiles in each figure is plotted with a dashed line to emphasize the difference between the transient shapes. (a)
![]() $\tilde{b}=0.46$
. The time interval
$\tilde{b}=0.46$
. The time interval
![]() $\unicode[STIX]{x1D6FF}\tilde{t}$
between two neighbouring curves is 3.48. (b)
$\unicode[STIX]{x1D6FF}\tilde{t}$
between two neighbouring curves is 3.48. (b)
![]() $\tilde{b}=23.2$
and
$\tilde{b}=23.2$
and
![]() $\unicode[STIX]{x1D6FF}\tilde{t}=1.28$
. Insets: the contact line position
$\unicode[STIX]{x1D6FF}\tilde{t}=1.28$
. Insets: the contact line position
![]() $\tilde{R}(\tilde{t})$
as a function of time
$\tilde{R}(\tilde{t})$
as a function of time
![]() $\tilde{t}$
.
$\tilde{t}$
.
3 Results and discussion
In this section, we present the results of our numerical computations. In § 3.1, we revisit the interfacial profile evolution as studied by McGraw et al. (Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016). We characterize and quantify the deviation of the transient droplet profiles from a spherical cap. Then we investigate the temporal evolution of the non-sphericity and how the non-sphericity depends on the slip length and the equilibrium contact angle. The early time dynamics of the transient ridge is studied in § 3.2. In § 3.3 we rationalize the behaviour of the non-sphericity in terms of the flow structure and the spreading of the ridge.
3.1 Interfacial profile evolution and non-sphericity of the profiles
Here we briefly consider the droplet geometries studied in McGraw et al. (Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016), namely an initial spherical cap with
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
and an equilibrium contact angle
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
and an equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. As discussed in McGraw et al. (Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016), the main feature of the profile evolution is the appearance, or absence, of a transient ridge, defined as the fluid region in between the contact line and the outermost inflection point of the droplet profile (i.e.
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. As discussed in McGraw et al. (Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016), the main feature of the profile evolution is the appearance, or absence, of a transient ridge, defined as the fluid region in between the contact line and the outermost inflection point of the droplet profile (i.e.
![]() $\unicode[STIX]{x2202}^{2}\tilde{h}/\unicode[STIX]{x2202}\tilde{r}^{2}|_{\tilde{r}=\tilde{r}_{inf}}=0$
). The ridge may develop to a global bump, characterized by a maximum in the height profile at
$\unicode[STIX]{x2202}^{2}\tilde{h}/\unicode[STIX]{x2202}\tilde{r}^{2}|_{\tilde{r}=\tilde{r}_{inf}}=0$
). The ridge may develop to a global bump, characterized by a maximum in the height profile at
![]() $\tilde{r}\neq 0$
. The properties of the global bump will be discussed in § 3.4. We first look at two different rescaled slip lengths,
$\tilde{r}\neq 0$
. The properties of the global bump will be discussed in § 3.4. We first look at two different rescaled slip lengths,
![]() $\tilde{b}=0.46$
and 23.2, which respectively demonstrate the formation or absence of a transient ridge. The evolution of the free interface profiles
$\tilde{b}=0.46$
and 23.2, which respectively demonstrate the formation or absence of a transient ridge. The evolution of the free interface profiles
![]() $\tilde{h}(\tilde{r},\tilde{t})$
is shown in figure 1(a) for
$\tilde{h}(\tilde{r},\tilde{t})$
is shown in figure 1(a) for
![]() $\tilde{b}=0.46$
and in figure 1(b) for
$\tilde{b}=0.46$
and in figure 1(b) for
![]() $\tilde{b}=23.2$
. The main difference between the two cases is that, for
$\tilde{b}=23.2$
. The main difference between the two cases is that, for
![]() $\tilde{b}=0.46$
, the profile around the centre does not change appreciably at early times. The fluid accumulates in a rim as the contact line moves towards the centre of the droplet and forms a transient ridge. In contrast, for
$\tilde{b}=0.46$
, the profile around the centre does not change appreciably at early times. The fluid accumulates in a rim as the contact line moves towards the centre of the droplet and forms a transient ridge. In contrast, for
![]() $\tilde{b}=23.2$
, the height of the interface profile at the centre of the droplet increases at early times due to elongational flow (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016). No ridge is developed in this case.
$\tilde{b}=23.2$
, the height of the interface profile at the centre of the droplet increases at early times due to elongational flow (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016). No ridge is developed in this case.

Figure 2. (a) The non-sphericity,
![]() $\unicode[STIX]{x0394}V/V$
, versus the rescaled contact line displacement
$\unicode[STIX]{x0394}V/V$
, versus the rescaled contact line displacement
![]() $(\tilde{R}(0)-\tilde{R}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
for
$(\tilde{R}(0)-\tilde{R}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
for
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
and for three different slip lengths. The maxima are indicated by solid symbols. (b) The maximum of
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
and for three different slip lengths. The maxima are indicated by solid symbols. (b) The maximum of
![]() $\unicode[STIX]{x0394}V/V$
shown in (a),
$\unicode[STIX]{x0394}V/V$
shown in (a),
![]() $\unicode[STIX]{x0394}V_{m}/V$
, as a function of slip length
$\unicode[STIX]{x0394}V_{m}/V$
, as a function of slip length
![]() $\tilde{b}$
for different equilibrium contact angles
$\tilde{b}$
for different equilibrium contact angles
![]() $\unicode[STIX]{x1D703}_{e}$
. For both (a) and (b), the initial contact angle is
$\unicode[STIX]{x1D703}_{e}$
. For both (a) and (b), the initial contact angle is
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
.
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
.
The transient profiles of the droplets in both cases shown in figure 1 deviate significantly from the shape of a spherical cap. To quantify the non-sphericity of the droplet, we introduce an observable
![]() $\unicode[STIX]{x0394}V$
in the following way. For each time
$\unicode[STIX]{x0394}V$
in the following way. For each time
![]() $\tilde{t}$
, we determine the spherical cap of profile
$\tilde{t}$
, we determine the spherical cap of profile
![]() $\tilde{z}=\tilde{S}(\tilde{r},\tilde{t};\tilde{\unicode[STIX]{x1D70C}},\tilde{S}_{0})$
that best fits the profile of the droplet;
$\tilde{z}=\tilde{S}(\tilde{r},\tilde{t};\tilde{\unicode[STIX]{x1D70C}},\tilde{S}_{0})$
that best fits the profile of the droplet;
![]() $\tilde{S}$
is given implicitly by
$\tilde{S}$
is given implicitly by
![]() $\tilde{\unicode[STIX]{x1D70C}}^{2}=\tilde{r}^{2}+(\tilde{S}-\tilde{S}_{0})^{2}$
, where
$\tilde{\unicode[STIX]{x1D70C}}^{2}=\tilde{r}^{2}+(\tilde{S}-\tilde{S}_{0})^{2}$
, where
![]() $\tilde{S}_{0}$
is the vertical shift of the sphere centre while
$\tilde{S}_{0}$
is the vertical shift of the sphere centre while
![]() $\tilde{\unicode[STIX]{x1D70C}}$
is its radius of curvature. We introduce
$\tilde{\unicode[STIX]{x1D70C}}$
is its radius of curvature. We introduce
![]() $\unicode[STIX]{x0394}V$
as the total volume of the non-overlapped region between the droplet and the corresponding spherical cap. The spherical cap is selected under the condition that the total non-overlapped volume is minimized. More precisely, we define
$\unicode[STIX]{x0394}V$
as the total volume of the non-overlapped region between the droplet and the corresponding spherical cap. The spherical cap is selected under the condition that the total non-overlapped volume is minimized. More precisely, we define
under the constraint of identical total volumes:
Note that
where
![]() $\tilde{R}(\tilde{t})$
and
$\tilde{R}(\tilde{t})$
and
![]() $\tilde{R}_{cap}(\tilde{t};\tilde{\unicode[STIX]{x1D70C}},\tilde{S}_{0})$
are the contact line radius of the droplet and the spherical cap respectively.
$\tilde{R}_{cap}(\tilde{t};\tilde{\unicode[STIX]{x1D70C}},\tilde{S}_{0})$
are the contact line radius of the droplet and the spherical cap respectively.
In figure 2(a),
![]() $\unicode[STIX]{x0394}V$
rescaled by the volume of the droplet is plotted as a function of the contact line displacement
$\unicode[STIX]{x0394}V$
rescaled by the volume of the droplet is plotted as a function of the contact line displacement
![]() $\tilde{R}(0)-\tilde{R}(\tilde{t})$
normalized by the total displacement
$\tilde{R}(0)-\tilde{R}(\tilde{t})$
normalized by the total displacement
![]() $\tilde{R}(0)-\tilde{R}(\infty )$
for
$\tilde{R}(0)-\tilde{R}(\infty )$
for
![]() $\tilde{b}=0.023$
, 0.20 and 23.2. For all three cases,
$\tilde{b}=0.023$
, 0.20 and 23.2. For all three cases,
![]() $\unicode[STIX]{x0394}V/V$
is zero at
$\unicode[STIX]{x0394}V/V$
is zero at
![]() $\tilde{t}=0$
and at equilibrium because of the spherical-cap shape of the droplets. During the evolution, the non-sphericity attains a maximum. This maximal non-sphericity,
$\tilde{t}=0$
and at equilibrium because of the spherical-cap shape of the droplets. During the evolution, the non-sphericity attains a maximum. This maximal non-sphericity,
![]() $\unicode[STIX]{x0394}V_{m}/V$
, occurs at smaller contact line displacements for smaller slip lengths.
$\unicode[STIX]{x0394}V_{m}/V$
, occurs at smaller contact line displacements for smaller slip lengths.
A full investigation of
![]() $\unicode[STIX]{x0394}V_{m}/V$
as a function of
$\unicode[STIX]{x0394}V_{m}/V$
as a function of
![]() $\tilde{b}$
is shown in figure 2(b) for various
$\tilde{b}$
is shown in figure 2(b) for various
![]() $\unicode[STIX]{x1D703}_{e}$
. We observe that this maximal non-sphericity of the droplet evolution is non-monotonic with
$\unicode[STIX]{x1D703}_{e}$
. We observe that this maximal non-sphericity of the droplet evolution is non-monotonic with
![]() $\tilde{b}$
for all
$\tilde{b}$
for all
![]() $\unicode[STIX]{x1D703}_{e}$
investigated. We note furthermore the presence of a well-defined maximum at a slip length that we denote by
$\unicode[STIX]{x1D703}_{e}$
investigated. We note furthermore the presence of a well-defined maximum at a slip length that we denote by
![]() $\tilde{b}_{m}(\unicode[STIX]{x1D703}_{e})$
. For
$\tilde{b}_{m}(\unicode[STIX]{x1D703}_{e})$
. For
![]() $\tilde{b}>\tilde{b}_{m}$
,
$\tilde{b}>\tilde{b}_{m}$
,
![]() $\unicode[STIX]{x0394}V_{m}/V$
decreases with
$\unicode[STIX]{x0394}V_{m}/V$
decreases with
![]() $\tilde{b}$
and asymptotically saturates to a finite
$\tilde{b}$
and asymptotically saturates to a finite
![]() $\unicode[STIX]{x0394}V_{m}(\infty )/V$
. For
$\unicode[STIX]{x0394}V_{m}(\infty )/V$
. For
![]() $\tilde{b}<\tilde{b}_{m}$
,
$\tilde{b}<\tilde{b}_{m}$
,
![]() $\unicode[STIX]{x0394}V_{m}/V$
decreases with decreasing
$\unicode[STIX]{x0394}V_{m}/V$
decreases with decreasing
![]() $\tilde{b}$
. As expected, the non-sphericity becomes smaller as the equilibrium contact angle
$\tilde{b}$
. As expected, the non-sphericity becomes smaller as the equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}$
approaches the initial contact angle
$\unicode[STIX]{x1D703}_{e}$
approaches the initial contact angle
![]() $\unicode[STIX]{x1D703}_{i}$
.
$\unicode[STIX]{x1D703}_{i}$
.

Figure 3. After two different rescalings, the data in figure 2(b) collapse onto a single function for two different regions, namely
![]() $\tilde{b}>\tilde{b}_{m}$
as shown in (a) and for
$\tilde{b}>\tilde{b}_{m}$
as shown in (a) and for
![]() $0.023<\tilde{b}<\tilde{b}_{m}$
as shown in (c). (a)
$0.023<\tilde{b}<\tilde{b}_{m}$
as shown in (c). (a)
![]() $V_{1}$
, defined as
$V_{1}$
, defined as
![]() $(\unicode[STIX]{x0394}V_{m}/V-\unicode[STIX]{x0394}V_{m}(\infty )/V)/V_{d}$
, versus
$(\unicode[STIX]{x0394}V_{m}/V-\unicode[STIX]{x0394}V_{m}(\infty )/V)/V_{d}$
, versus
![]() $k_{1}\tilde{b}$
. (b) The dependence of
$k_{1}\tilde{b}$
. (b) The dependence of
![]() $V_{d}$
and
$V_{d}$
and
![]() $k_{1}$
on the equilibrium contact angle
$k_{1}$
on the equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}$
. (c)
$\unicode[STIX]{x1D703}_{e}$
. (c)
![]() $V_{2}$
, defined as
$V_{2}$
, defined as
![]() $\unicode[STIX]{x0394}V_{m}/V$
rescaled by
$\unicode[STIX]{x0394}V_{m}/V$
rescaled by
![]() $\unicode[STIX]{x0394}V_{m}(\tilde{b}_{m})/V$
, versus
$\unicode[STIX]{x0394}V_{m}(\tilde{b}_{m})/V$
, versus
![]() $(\tilde{b}/\tilde{b}_{m})^{k_{2}}$
. (d)
$(\tilde{b}/\tilde{b}_{m})^{k_{2}}$
. (d)
![]() $\tilde{b}_{m}$
and
$\tilde{b}_{m}$
and
![]() $k_{2}$
as a function of
$k_{2}$
as a function of
![]() $\unicode[STIX]{x1D703}_{e}$
.
$\unicode[STIX]{x1D703}_{e}$
.
The similar features of
![]() $\unicode[STIX]{x0394}V_{m}/V$
as a function of
$\unicode[STIX]{x0394}V_{m}/V$
as a function of
![]() $\tilde{b}$
for different equilibrium contact angles
$\tilde{b}$
for different equilibrium contact angles
![]() $\unicode[STIX]{x1D703}_{e}$
suggest possible collapse of the curves after certain rescalings. First, we shift
$\unicode[STIX]{x1D703}_{e}$
suggest possible collapse of the curves after certain rescalings. First, we shift
![]() $\unicode[STIX]{x0394}V_{m}/V$
by
$\unicode[STIX]{x0394}V_{m}/V$
by
![]() $\unicode[STIX]{x0394}V_{m}(\infty )/V$
such that all the curves have the same reference level in the full-slip limit. Then we rescale the shifted
$\unicode[STIX]{x0394}V_{m}(\infty )/V$
such that all the curves have the same reference level in the full-slip limit. Then we rescale the shifted
![]() $\unicode[STIX]{x0394}V_{m}/V$
by
$\unicode[STIX]{x0394}V_{m}/V$
by
![]() $V_{d}\equiv \unicode[STIX]{x0394}V_{m}(\tilde{b}_{m})/V-\unicode[STIX]{x0394}V_{m}(\infty )/V$
. We hence introduce a rescaled quantity
$V_{d}\equiv \unicode[STIX]{x0394}V_{m}(\tilde{b}_{m})/V-\unicode[STIX]{x0394}V_{m}(\infty )/V$
. We hence introduce a rescaled quantity
![]() $V_{1}(\tilde{b})$
as the following:
$V_{1}(\tilde{b})$
as the following:
The maximum of
![]() $V_{1}$
is unity for any equilibrium contact angles. When plotting
$V_{1}$
is unity for any equilibrium contact angles. When plotting
![]() $V_{1}$
versus
$V_{1}$
versus
![]() $\tilde{b}$
multiplied by a scaling factor
$\tilde{b}$
multiplied by a scaling factor
![]() $k_{1}(\unicode[STIX]{x1D703}_{e})$
in figure 3(a), we observe that the curves for different
$k_{1}(\unicode[STIX]{x1D703}_{e})$
in figure 3(a), we observe that the curves for different
![]() $\unicode[STIX]{x1D703}_{e}$
collapse into a single function for
$\unicode[STIX]{x1D703}_{e}$
collapse into a single function for
![]() $\tilde{b}>\tilde{b}_{m}$
. The dependence of
$\tilde{b}>\tilde{b}_{m}$
. The dependence of
![]() $V_{d}$
and
$V_{d}$
and
![]() $k_{1}$
on
$k_{1}$
on
![]() $\unicode[STIX]{x1D703}_{e}$
is shown in figure 3(b). Note that
$\unicode[STIX]{x1D703}_{e}$
is shown in figure 3(b). Note that
![]() $k_{1}$
is not unique. The effect of
$k_{1}$
is not unique. The effect of
![]() $k_{1}$
is shifting the curve horizontally. Multiplying
$k_{1}$
is shifting the curve horizontally. Multiplying
![]() $k_{1}$
by an arbitrary factor will still collapse all the curves. Here we take
$k_{1}$
by an arbitrary factor will still collapse all the curves. Here we take
![]() $k_{1}=1$
for
$k_{1}=1$
for
![]() $\unicode[STIX]{x1D703}_{e}=17^{\circ }$
, which is the smallest equilibrium contact angle considered here.
$\unicode[STIX]{x1D703}_{e}=17^{\circ }$
, which is the smallest equilibrium contact angle considered here.
For
![]() $0.023<\tilde{b}<\tilde{b}_{m}$
, a different rescaling is required to reach a collapse of the curves. In figure 3(c),
$0.023<\tilde{b}<\tilde{b}_{m}$
, a different rescaling is required to reach a collapse of the curves. In figure 3(c),
![]() $V_{2}$
, defined as
$V_{2}$
, defined as
![]() $\unicode[STIX]{x0394}V_{m}/V$
rescaled by
$\unicode[STIX]{x0394}V_{m}/V$
rescaled by
![]() $\unicode[STIX]{x0394}V_{m}(\tilde{b}_{m})/V$
, is plotted as a function of
$\unicode[STIX]{x0394}V_{m}(\tilde{b}_{m})/V$
, is plotted as a function of
![]() $(\tilde{b}/\tilde{b}_{m})^{k_{2}}$
; a single curve is thus obtained for
$(\tilde{b}/\tilde{b}_{m})^{k_{2}}$
; a single curve is thus obtained for
![]() $0.023<\tilde{b}<\tilde{b}_{m}$
. This rescaling suggests a relation of the form
$0.023<\tilde{b}<\tilde{b}_{m}$
. This rescaling suggests a relation of the form
![]() $V_{2}/k_{2}\sim \log (\tilde{b}/\tilde{b}_{m})$
. Such a logarithmic relation is reminiscent of the weak-slip models for non-equilibrium droplets (de Gennes Reference de Gennes1985; Cox Reference Cox1986), in which the contact line dynamics and the interface profile also depend on the slip length logarithmically. The dependence of
$V_{2}/k_{2}\sim \log (\tilde{b}/\tilde{b}_{m})$
. Such a logarithmic relation is reminiscent of the weak-slip models for non-equilibrium droplets (de Gennes Reference de Gennes1985; Cox Reference Cox1986), in which the contact line dynamics and the interface profile also depend on the slip length logarithmically. The dependence of
![]() $\tilde{b}_{m}$
and
$\tilde{b}_{m}$
and
![]() $k_{2}$
on
$k_{2}$
on
![]() $\unicode[STIX]{x1D703}_{e}$
is shown in figure 3(d). The different rescalings for
$\unicode[STIX]{x1D703}_{e}$
is shown in figure 3(d). The different rescalings for
![]() $\tilde{b}<\tilde{b}_{m}$
and
$\tilde{b}<\tilde{b}_{m}$
and
![]() $\tilde{b}>\tilde{b}_{m}$
indicate the existence of different regimes of the droplet retraction dynamics. The details will be discussed in the following sections.
$\tilde{b}>\tilde{b}_{m}$
indicate the existence of different regimes of the droplet retraction dynamics. The details will be discussed in the following sections.
3.2 The transient ridge and early time dynamics

Figure 4. (a) Rescaled contact line displacement
![]() $(\tilde{R}_{0}-\tilde{R}(\tilde{t}))/(\tilde{R}_{0}-\tilde{R}_{\infty })$
as a function of
$(\tilde{R}_{0}-\tilde{R}(\tilde{t}))/(\tilde{R}_{0}-\tilde{R}_{\infty })$
as a function of
![]() $\tilde{t}$
in log–log scale for different
$\tilde{t}$
in log–log scale for different
![]() $\tilde{b}$
and fixed
$\tilde{b}$
and fixed
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. The early time data for intermediate slip lengths around
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. The early time data for intermediate slip lengths around
![]() $\tilde{b}_{m}$
can be described by a power law. A single power law becomes less pronounced for large and small slip lengths away from
$\tilde{b}_{m}$
can be described by a power law. A single power law becomes less pronounced for large and small slip lengths away from
![]() $\tilde{b}_{m}$
. (b–d) Rescaled profiles for
$\tilde{b}_{m}$
. (b–d) Rescaled profiles for
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
in (b),
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
in (b),
![]() $\unicode[STIX]{x1D703}_{e}=40^{\circ }$
in (c) and
$\unicode[STIX]{x1D703}_{e}=40^{\circ }$
in (c) and
![]() $\unicode[STIX]{x1D703}_{e}=23^{\circ }$
in (d);
$\unicode[STIX]{x1D703}_{e}=23^{\circ }$
in (d);
![]() $\tilde{b}=0.46$
in all cases.
$\tilde{b}=0.46$
in all cases.
As the initial driving force is at the contact line, it is important to examine the growth of the rim once the contact line has started to move. We first look at the motion of the contact line. To resolve the contact line motion for early times, we investigate the rescaled contact line displacement
![]() ${\mathcal{R}}(\tilde{t})\equiv (\tilde{R}(0)-\tilde{R}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
. For given
${\mathcal{R}}(\tilde{t})\equiv (\tilde{R}(0)-\tilde{R}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
. For given
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
and
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
and
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
,
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
,
![]() ${\mathcal{R}}(\tilde{t})$
as a function of time is plotted in figure 4(a) in log–log scale for different
${\mathcal{R}}(\tilde{t})$
as a function of time is plotted in figure 4(a) in log–log scale for different
![]() $\tilde{b}$
. For large
$\tilde{b}$
. For large
![]() $\tilde{b}$
, the slope of the curves decreases with time. A power law is observed for intermediate slip lengths in the vicinity of
$\tilde{b}$
, the slope of the curves decreases with time. A power law is observed for intermediate slip lengths in the vicinity of
![]() $\tilde{b}_{m}$
corresponding to the maximal non-sphericity,
$\tilde{b}_{m}$
corresponding to the maximal non-sphericity,
![]() $\unicode[STIX]{x0394}V_{m}$
. We recall that
$\unicode[STIX]{x0394}V_{m}$
. We recall that
![]() $\tilde{b}_{m}=0.21$
for
$\tilde{b}_{m}=0.21$
for
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. For example, for
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. For example, for
![]() $\tilde{b}=0.46$
and
$\tilde{b}=0.46$
and
![]() $0.12<\tilde{t}<30$
, the relation, i.e.
$0.12<\tilde{t}<30$
, the relation, i.e.
![]() ${\mathcal{R}}\sim \tilde{t}^{\unicode[STIX]{x1D6FD}}$
, describes the data with
${\mathcal{R}}\sim \tilde{t}^{\unicode[STIX]{x1D6FD}}$
, describes the data with
![]() $\unicode[STIX]{x1D6FD}=0.59$
. The power-law relation becomes less pronounced when decreasing
$\unicode[STIX]{x1D6FD}=0.59$
. The power-law relation becomes less pronounced when decreasing
![]() $\tilde{b}$
for
$\tilde{b}$
for
![]() $\tilde{b}<\tilde{b}_{m}$
. For
$\tilde{b}<\tilde{b}_{m}$
. For
![]() $\tilde{b}=0.023$
, the curve is seen to bend upward with time. Similar features are also observed for other equilibrium contact angles. The exponent
$\tilde{b}=0.023$
, the curve is seen to bend upward with time. Similar features are also observed for other equilibrium contact angles. The exponent
![]() $\unicode[STIX]{x1D6FD}$
is found to be 0.57 for
$\unicode[STIX]{x1D6FD}$
is found to be 0.57 for
![]() $\unicode[STIX]{x1D703}_{e}=40^{\circ }$
and 0.54 for
$\unicode[STIX]{x1D703}_{e}=40^{\circ }$
and 0.54 for
![]() $\unicode[STIX]{x1D703}_{e}=23^{\circ }$
, when
$\unicode[STIX]{x1D703}_{e}=23^{\circ }$
, when
![]() $\tilde{b}=0.46$
.
$\tilde{b}=0.46$
.
Given these power-law relations for slip lengths around
![]() $\tilde{b}_{m}$
, it is instructive to investigate whether the interface profiles near the contact line can be described by a similarity solution. Assuming a similarity solution of the form
$\tilde{b}_{m}$
, it is instructive to investigate whether the interface profiles near the contact line can be described by a similarity solution. Assuming a similarity solution of the form
![]() $\tilde{h}=\tilde{t}^{\unicode[STIX]{x1D6FC}}f((\tilde{R}(\tilde{t})-\tilde{r})/\tilde{t}^{\unicode[STIX]{x1D6FC}})$
, we found that the rescaled profiles in the rim region collapse best for values of
$\tilde{h}=\tilde{t}^{\unicode[STIX]{x1D6FC}}f((\tilde{R}(\tilde{t})-\tilde{r})/\tilde{t}^{\unicode[STIX]{x1D6FC}})$
, we found that the rescaled profiles in the rim region collapse best for values of
![]() $\unicode[STIX]{x1D6FC}=0.64$
for
$\unicode[STIX]{x1D6FC}=0.64$
for
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
, 0.59 for
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
, 0.59 for
![]() $\unicode[STIX]{x1D703}_{e}=40^{\circ }$
and 0.49 for
$\unicode[STIX]{x1D703}_{e}=40^{\circ }$
and 0.49 for
![]() $\unicode[STIX]{x1D703}_{e}=23^{\circ }$
. The corresponding rescaled profiles are shown in figure 4(b–d). Note that these exponents are slightly different from the exponent
$\unicode[STIX]{x1D703}_{e}=23^{\circ }$
. The corresponding rescaled profiles are shown in figure 4(b–d). Note that these exponents are slightly different from the exponent
![]() $\unicode[STIX]{x1D6FD}$
for the contact line. The exponent 0.49 for the case of
$\unicode[STIX]{x1D6FD}$
for the contact line. The exponent 0.49 for the case of
![]() $\unicode[STIX]{x1D703}_{e}=23^{\circ }$
, in which the interfacial slope is small, is close to the
$\unicode[STIX]{x1D703}_{e}=23^{\circ }$
, in which the interfacial slope is small, is close to the
![]() $\unicode[STIX]{x1D6FC}=1/2$
scaling predicted from the lubrication calculation for intermediate slip, namely when the dissipation is dominated by the friction at the substrate (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016).
$\unicode[STIX]{x1D6FC}=1/2$
scaling predicted from the lubrication calculation for intermediate slip, namely when the dissipation is dominated by the friction at the substrate (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016).
3.3 Physical explanation for the behaviour of the non-sphericity: flow structures and the spreading of the ridge
In this section, we rationalize the non-monotonic behaviour of the non-sphericity in terms of the flow structure and the spreading of the ridge.
We compute the velocity field inside the droplet using the boundary integral equation (2.9) with
![]() $A=1/2$
. The flow fields inside the droplet when the contact line position
$A=1/2$
. The flow fields inside the droplet when the contact line position
![]() $\tilde{R}=10.82$
are shown in figure 5 for three different rescaled slip lengths
$\tilde{R}=10.82$
are shown in figure 5 for three different rescaled slip lengths
![]() $\tilde{b}=0.023$
, 0.21 and 23.2, and with the same equilibrium contact angle
$\tilde{b}=0.023$
, 0.21 and 23.2, and with the same equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. For
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. For
![]() $\tilde{b}\gg \tilde{b}_{m}$
, low friction at the substrate promotes an elongational flow which affects the whole droplet in a very short time, see figure 5 for
$\tilde{b}\gg \tilde{b}_{m}$
, low friction at the substrate promotes an elongational flow which affects the whole droplet in a very short time, see figure 5 for
![]() $\tilde{b}=23.2$
. Therefore, the central height of the droplet increases even at early times due to the upward flow in the centre. This prevents mass accumulation at the edge of the droplet. When decreasing
$\tilde{b}=23.2$
. Therefore, the central height of the droplet increases even at early times due to the upward flow in the centre. This prevents mass accumulation at the edge of the droplet. When decreasing
![]() $\tilde{b}$
, the elongational flow becomes less dominant. The flow is concentrated in the rim, see figure 5 for
$\tilde{b}$
, the elongational flow becomes less dominant. The flow is concentrated in the rim, see figure 5 for
![]() $\tilde{b}=0.023$
and 0.21. Mass is thus accumulated in the rim while the contact line is moving towards the droplet centre. As a consequence, a pronounced transient ridge is observed and the non-sphericity,
$\tilde{b}=0.023$
and 0.21. Mass is thus accumulated in the rim while the contact line is moving towards the droplet centre. As a consequence, a pronounced transient ridge is observed and the non-sphericity,
![]() $\unicode[STIX]{x0394}V_{m}/V$
, becomes larger when decreasing
$\unicode[STIX]{x0394}V_{m}/V$
, becomes larger when decreasing
![]() $\tilde{b}$
for
$\tilde{b}$
for
![]() $\tilde{b}>\tilde{b}_{m}$
.
$\tilde{b}>\tilde{b}_{m}$
.

Figure 5. The flow fields for three different rescaled slip lengths
![]() $\tilde{b}=$
0.023, 0.21 and 23.2. The initial contact angle is
$\tilde{b}=$
0.023, 0.21 and 23.2. The initial contact angle is
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
and the equilibrium contact angle is
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
and the equilibrium contact angle is
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. The contact line position is
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. The contact line position is
![]() $\tilde{R}=10.82$
.
$\tilde{R}=10.82$
.
For
![]() $\tilde{b}$
close to
$\tilde{b}$
close to
![]() $\tilde{b}_{m}$
, the ridge profiles in the early times can be described by similarity solutions as shown in § 3.2. For small equilibrium contact angles, the similarity solutions can be obtained from the intermediate-slip lubrication model in which the dissipation by the friction at the substrate becomes dominant (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016).
$\tilde{b}_{m}$
, the ridge profiles in the early times can be described by similarity solutions as shown in § 3.2. For small equilibrium contact angles, the similarity solutions can be obtained from the intermediate-slip lubrication model in which the dissipation by the friction at the substrate becomes dominant (McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016).
When further decreasing
![]() $\tilde{b}$
from
$\tilde{b}$
from
![]() $\tilde{b}_{m}$
, the non-sphericity becomes less pronounced. For those small
$\tilde{b}_{m}$
, the non-sphericity becomes less pronounced. For those small
![]() $\tilde{b}$
cases, the flow is more confined to the contact line region and presents a vertical parabolic profile associated with strong shear dissipation, see figure 5 for
$\tilde{b}$
cases, the flow is more confined to the contact line region and presents a vertical parabolic profile associated with strong shear dissipation, see figure 5 for
![]() $\tilde{b}=0.023$
. In addition, similarity solutions cannot describe the early ridge profiles anymore. The question of how much mass is accumulated at the ridge depends on the contact line speed and how fast the mass is redistributed to the central part of the droplet by shear flow. This type of mass redistribution can be observed from the spreading of the ridge. One can imagine a situation when a contact line is pinned from a certain moment, the accumulated mass then has enough time to redistribute to the central part of the droplet and the development of a pronounced global ridge is avoided. Along this line of reasoning, we can understand the decrease of
$\tilde{b}=0.023$
. In addition, similarity solutions cannot describe the early ridge profiles anymore. The question of how much mass is accumulated at the ridge depends on the contact line speed and how fast the mass is redistributed to the central part of the droplet by shear flow. This type of mass redistribution can be observed from the spreading of the ridge. One can imagine a situation when a contact line is pinned from a certain moment, the accumulated mass then has enough time to redistribute to the central part of the droplet and the development of a pronounced global ridge is avoided. Along this line of reasoning, we can understand the decrease of
![]() $\unicode[STIX]{x0394}V_{m}/V$
with decreasing
$\unicode[STIX]{x0394}V_{m}/V$
with decreasing
![]() $\tilde{b}$
. The characteristic speed of the contact line decreases logarithmically with decreasing
$\tilde{b}$
. The characteristic speed of the contact line decreases logarithmically with decreasing
![]() $\tilde{b}$
for small
$\tilde{b}$
for small
![]() $\tilde{b}$
(McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016), which means that the disturbance at the contact line will have more time to spread for smaller
$\tilde{b}$
(McGraw et al.
Reference McGraw, Chan, Maurer, Salez, Benzaquen, Raphaël, Brinkmann and Jacobs2016), which means that the disturbance at the contact line will have more time to spread for smaller
![]() $\tilde{b}$
. This result is demonstrated in figure 6(a,b) for the case of
$\tilde{b}$
. This result is demonstrated in figure 6(a,b) for the case of
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. In figure 6(a), several interface profiles are shown at the same contact line position for
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. In figure 6(a), several interface profiles are shown at the same contact line position for
![]() $\tilde{b}=0.023$
and 0.14. For both cases, the slip lengths are smaller than
$\tilde{b}=0.023$
and 0.14. For both cases, the slip lengths are smaller than
![]() $\tilde{b}_{m}$
, so the shear dissipation dominates over the elongational one. One clearly sees that the ridge spreads wider for the smaller slip length, namely
$\tilde{b}_{m}$
, so the shear dissipation dominates over the elongational one. One clearly sees that the ridge spreads wider for the smaller slip length, namely
![]() $\tilde{b}=0.023$
.
$\tilde{b}=0.023$
.

Figure 6. (a) Droplet profiles for
![]() $\tilde{b}=0.023$
and 0.14. The profiles are compared when they have the same contact line position. (b) The rescaled displacement of the inflection point
$\tilde{b}=0.023$
and 0.14. The profiles are compared when they have the same contact line position. (b) The rescaled displacement of the inflection point
![]() $(\tilde{R}(0)-\tilde{r}_{inf}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
versus the rescaled contact line displacement
$(\tilde{R}(0)-\tilde{r}_{inf}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
versus the rescaled contact line displacement
![]() $(\tilde{R}(0)-\tilde{R}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
.
$(\tilde{R}(0)-\tilde{R}(\tilde{t}))/(\tilde{R}(0)-\tilde{R}(\infty ))$
.
From the profiles of figure 6(a), we observe an outermost inflection point where
![]() $\text{d}^{2}\tilde{h}/\text{d}\tilde{r}^{2}=0$
. The position of the inflection point
$\text{d}^{2}\tilde{h}/\text{d}\tilde{r}^{2}=0$
. The position of the inflection point
![]() $\tilde{r}_{inf}(\tilde{t})$
is used to characterize the extent of the ridge. The displacement of this inflection point
$\tilde{r}_{inf}(\tilde{t})$
is used to characterize the extent of the ridge. The displacement of this inflection point
![]() $(\tilde{R}(0)-\tilde{r}_{inf}(\tilde{t}))$
normalized by
$(\tilde{R}(0)-\tilde{r}_{inf}(\tilde{t}))$
normalized by
![]() $(\tilde{R}(0)-\tilde{R}(\infty ))$
is plotted as a function of the rescaled contact line displacement in figure 6(b). It is found that first, the inflection point moves faster than the contact line for both cases, and second, for the same contact line position, the inflection point displaces more for
$(\tilde{R}(0)-\tilde{R}(\infty ))$
is plotted as a function of the rescaled contact line displacement in figure 6(b). It is found that first, the inflection point moves faster than the contact line for both cases, and second, for the same contact line position, the inflection point displaces more for
![]() $\tilde{b}=0.023$
compared to
$\tilde{b}=0.023$
compared to
![]() $\tilde{b}=0.14$
. This result shows again that mass is redistributed over a wider extent for the smaller slip length,
$\tilde{b}=0.14$
. This result shows again that mass is redistributed over a wider extent for the smaller slip length,
![]() $\tilde{b}=0.023$
. Hence the non-sphericity decreases with decreasing
$\tilde{b}=0.023$
. Hence the non-sphericity decreases with decreasing
![]() $\tilde{b}$
. Although we are numerically limited to the smallest
$\tilde{b}$
. Although we are numerically limited to the smallest
![]() $\tilde{b}=0.023$
, from the trends shown in figure 2(b), we expect that
$\tilde{b}=0.023$
, from the trends shown in figure 2(b), we expect that
![]() $\unicode[STIX]{x0394}V_{m}/V$
diminishes in the limit of vanishing
$\unicode[STIX]{x0394}V_{m}/V$
diminishes in the limit of vanishing
![]() $\tilde{b}$
. Our study thus indicates a crossover from a non-quasistatic regime to a quasistatic regime when
$\tilde{b}$
. Our study thus indicates a crossover from a non-quasistatic regime to a quasistatic regime when
![]() $\tilde{b}$
is small.
$\tilde{b}$
is small.
3.4 Characteristic of the global bump

Figure 7. The global-bump height
![]() $h_{b}$
versus
$h_{b}$
versus
![]() $\tilde{b}$
for
$\tilde{b}$
for
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. The equilibrium contact angle is
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. The equilibrium contact angle is
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
in (a),
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
in (a),
![]() $\unicode[STIX]{x1D703}_{e}=34.5^{\circ }$
or
$\unicode[STIX]{x1D703}_{e}=34.5^{\circ }$
or
![]() $36.2^{\circ }$
in (b). (c) Phase diagram showing the with-global-bump region and the without-global-bump region. The vertical dashed line indicates the initial contact angle
$36.2^{\circ }$
in (b). (c) Phase diagram showing the with-global-bump region and the without-global-bump region. The vertical dashed line indicates the initial contact angle
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. The horizontal dashed line indicates the smallest
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. The horizontal dashed line indicates the smallest
![]() $\tilde{b}$
we have computed for, which is 0.023. Circles are
$\tilde{b}$
we have computed for, which is 0.023. Circles are
![]() $b^{\ast }$
as a function of
$b^{\ast }$
as a function of
![]() $\unicode[STIX]{x1D703}_{e}$
. Squares are
$\unicode[STIX]{x1D703}_{e}$
. Squares are
![]() $\tilde{b}_{L}^{\ast }$
as a function of
$\tilde{b}_{L}^{\ast }$
as a function of
![]() $\unicode[STIX]{x1D703}_{e}$
. (d) Zoom on the region where
$\unicode[STIX]{x1D703}_{e}$
. (d) Zoom on the region where
![]() $\tilde{b}_{L}^{\ast }$
is computed. Note that
$\tilde{b}_{L}^{\ast }$
is computed. Note that
![]() $\tilde{b}$
(
$\tilde{b}$
(
![]() $y$
-axis) is in log scale.
$y$
-axis) is in log scale.
In this section we discuss the properties of the global bump, which reflects a global feature of the droplet profile. Understanding of this feature might be useful for droplet manipulations in micro- and nanofluidics. One can characterize the size of the global bump by measuring the difference between the maximum height of the profile and the central height of the droplet, which we refer to as the global-bump height. Like the non-sphericity
![]() $\unicode[STIX]{x0394}V_{m}/V$
, the global-bump height attains a maximum value, denoted as
$\unicode[STIX]{x0394}V_{m}/V$
, the global-bump height attains a maximum value, denoted as
![]() $h_{b}$
, throughout the profile evolution. A typical behaviour of
$h_{b}$
, throughout the profile evolution. A typical behaviour of
![]() $h_{b}$
as a function of slip length
$h_{b}$
as a function of slip length
![]() $\tilde{b}$
is shown in figure 7(a) for
$\tilde{b}$
is shown in figure 7(a) for
![]() $\unicode[STIX]{x1D703}=62^{\circ }$
. The behaviours of
$\unicode[STIX]{x1D703}=62^{\circ }$
. The behaviours of
![]() $\unicode[STIX]{x0394}V_{m}/V$
and
$\unicode[STIX]{x0394}V_{m}/V$
and
![]() $h_{b}$
are similar. The maximum bump height
$h_{b}$
are similar. The maximum bump height
![]() $h_{b}$
is a non-monotonic function of the slip length and the maximum of
$h_{b}$
is a non-monotonic function of the slip length and the maximum of
![]() $h_{b}$
occurs at almost the same
$h_{b}$
occurs at almost the same
![]() $\tilde{b}$
as for
$\tilde{b}$
as for
![]() $\unicode[STIX]{x0394}V_{m}/V$
. This indicates that the behaviour of both quantities have the same physical origin, namely the change of the flow structure when varying the slip length as discussed in § 3.3. For
$\unicode[STIX]{x0394}V_{m}/V$
. This indicates that the behaviour of both quantities have the same physical origin, namely the change of the flow structure when varying the slip length as discussed in § 3.3. For
![]() $\tilde{b}$
larger than the point of the maximum, we define the slip length at which
$\tilde{b}$
larger than the point of the maximum, we define the slip length at which
![]() $h_{b}$
goes to zero as
$h_{b}$
goes to zero as
![]() $\tilde{b}\equiv \tilde{b}^{\ast }$
, which equals to 2.81 for the case of
$\tilde{b}\equiv \tilde{b}^{\ast }$
, which equals to 2.81 for the case of
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. No transient global bump is observed for
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
. No transient global bump is observed for
![]() $\tilde{b}>\tilde{b}^{\ast }$
.
$\tilde{b}>\tilde{b}^{\ast }$
.
Accessing more values of the equilibrium contact angle, we find an additional transition when
![]() $\tilde{b}$
is further decreased from
$\tilde{b}$
is further decreased from
![]() $\tilde{b}^{\ast }$
. For example, for
$\tilde{b}^{\ast }$
. For example, for
![]() $\unicode[STIX]{x1D703}_{e}=34.5^{\circ }$
,
$\unicode[STIX]{x1D703}_{e}=34.5^{\circ }$
,
![]() $\tilde{b}^{\ast }=0.79$
, we observe a transition from ‘with global bump’ to ‘without global bump’ at a certain
$\tilde{b}^{\ast }=0.79$
, we observe a transition from ‘with global bump’ to ‘without global bump’ at a certain
![]() $\tilde{b}$
, which is denoted as
$\tilde{b}$
, which is denoted as
![]() $\tilde{b}_{L}^{\ast }$
here, and equals 0.050 in this case. This result means a transient global bump exists only when
$\tilde{b}_{L}^{\ast }$
here, and equals 0.050 in this case. This result means a transient global bump exists only when
![]() $\tilde{b}_{L}^{\ast }<\tilde{b}<\tilde{b}^{\ast }$
. This interesting behaviour can be observed clearly in figure 7(b) where the bump height
$\tilde{b}_{L}^{\ast }<\tilde{b}<\tilde{b}^{\ast }$
. This interesting behaviour can be observed clearly in figure 7(b) where the bump height
![]() $h_{b}$
is plotted as a function of
$h_{b}$
is plotted as a function of
![]() $\tilde{b}$
. To summarize the results, a phase diagram is plotted in figure 7(c,d) that indicates whether a global transient bump can be observed or not, for the specific case of
$\tilde{b}$
. To summarize the results, a phase diagram is plotted in figure 7(c,d) that indicates whether a global transient bump can be observed or not, for the specific case of
![]() $\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. When
$\unicode[STIX]{x1D703}_{i}=10^{\circ }$
. When
![]() $\unicode[STIX]{x1D703}_{e}$
is close to
$\unicode[STIX]{x1D703}_{e}$
is close to
![]() $\unicode[STIX]{x1D703}_{i}$
, namely
$\unicode[STIX]{x1D703}_{i}$
, namely
![]() $\unicode[STIX]{x1D703}_{e}<32.1^{\circ }$
, no global bump appears for any value of
$\unicode[STIX]{x1D703}_{e}<32.1^{\circ }$
, no global bump appears for any value of
![]() $\tilde{b}$
. In these cases, a ridge is observed at the early stage for small slip lengths. However, a global bump (with a profile maximum not at
$\tilde{b}$
. In these cases, a ridge is observed at the early stage for small slip lengths. However, a global bump (with a profile maximum not at
![]() $\tilde{r}=0$
) does not form because the initial and the final droplet shapes are too similar. In figure 7(d), one can observe the ‘with-global-bump’ region starts from
$\tilde{r}=0$
) does not form because the initial and the final droplet shapes are too similar. In figure 7(d), one can observe the ‘with-global-bump’ region starts from
![]() $\unicode[STIX]{x1D703}_{e}=32.1^{\circ }$
. Although the second transition is not observed for
$\unicode[STIX]{x1D703}_{e}=32.1^{\circ }$
. Although the second transition is not observed for
![]() $\unicode[STIX]{x1D703}_{e}>36.2^{\circ }$
due to numerical limitations, we expect the bump to diminish in magnitude also for very small slip lengths in this case; the decrease of
$\unicode[STIX]{x1D703}_{e}>36.2^{\circ }$
due to numerical limitations, we expect the bump to diminish in magnitude also for very small slip lengths in this case; the decrease of
![]() $h_{b}$
in figure 7(a) for small
$h_{b}$
in figure 7(a) for small
![]() $\tilde{b}$
supports this argument. Nevertheless, the slip length below which the global bump disappears is expected to be extremely small if the difference between the initial contact angle and the equilibrium contact angle is large. A recent study has demonstrated that a pronounced global bump exists in the dewetting of very flat droplets (
$\tilde{b}$
supports this argument. Nevertheless, the slip length below which the global bump disappears is expected to be extremely small if the difference between the initial contact angle and the equilibrium contact angle is large. A recent study has demonstrated that a pronounced global bump exists in the dewetting of very flat droplets (
![]() $h_{0}/R(0)\approx 0.02{-}0.1$
) even though the slip length is very small (
$h_{0}/R(0)\approx 0.02{-}0.1$
) even though the slip length is very small (
![]() $\tilde{b}\approx 10^{-5}$
) (Edwards et al.
Reference Edwards, Ledesma-Aguilar, Newton, Brown and McHale2016). In such cases, the transient global bump itself can be treated as quasistatic, as is the case in dewetting rims of thin liquid films (Redon et al.
Reference Redon, Brochard-Wyart and Rondelez1991; Snoeijer & Eggers Reference Snoeijer and Eggers2010; Rivetti et al.
Reference Rivetti, Salez, Benzaquen, Raphaël and Bäumchen2015).
$\tilde{b}\approx 10^{-5}$
) (Edwards et al.
Reference Edwards, Ledesma-Aguilar, Newton, Brown and McHale2016). In such cases, the transient global bump itself can be treated as quasistatic, as is the case in dewetting rims of thin liquid films (Redon et al.
Reference Redon, Brochard-Wyart and Rondelez1991; Snoeijer & Eggers Reference Snoeijer and Eggers2010; Rivetti et al.
Reference Rivetti, Salez, Benzaquen, Raphaël and Bäumchen2015).
4 Conclusion
In this article, we study numerically the dewetting of a droplet, with an initial contact angle smaller than the equilibrium contact angle, using the boundary element method for axisymmetric Stokes flow. We impose the Navier-slip boundary condition at the solid/liquid boundary, and a time-independent equilibrium contact angle at the contact line position. The profile evolution is computed for a wide range of slip lengths (
![]() $2.3\times 10^{-2}<\tilde{b}<10^{4}$
) and various equilibrium contact angles. For all our computations, the transient droplet profiles are found to deviate significantly from a spherical cap. We find that when decreasing the slip length, the typical non-sphericity first increases, reaches a maximum at a characteristic slip length
$2.3\times 10^{-2}<\tilde{b}<10^{4}$
) and various equilibrium contact angles. For all our computations, the transient droplet profiles are found to deviate significantly from a spherical cap. We find that when decreasing the slip length, the typical non-sphericity first increases, reaches a maximum at a characteristic slip length
![]() $\tilde{b}_{m}$
, and then decreases. This non-monotonic behaviour is found for all of the equilibrium contact angles investigated in this study, from
$\tilde{b}_{m}$
, and then decreases. This non-monotonic behaviour is found for all of the equilibrium contact angles investigated in this study, from
![]() $17^{\circ }\leqslant \unicode[STIX]{x1D703}_{e}\leqslant 69^{\circ }$
.
$17^{\circ }\leqslant \unicode[STIX]{x1D703}_{e}\leqslant 69^{\circ }$
.
The dependence of the non-sphericity on the slip length for different equilibrium contact angles can be described by two universal relations, one for
![]() $\tilde{b}>\tilde{b}_{m}$
and the other one for
$\tilde{b}>\tilde{b}_{m}$
and the other one for
![]() $0.023<\tilde{b}<\tilde{b}_{m}$
. This result indicates the existence of different flow structures depending on the value of
$0.023<\tilde{b}<\tilde{b}_{m}$
. This result indicates the existence of different flow structures depending on the value of
![]() $\tilde{b}$
. For
$\tilde{b}$
. For
![]() $\tilde{b}\gg \tilde{b}_{m}$
, the flow is dominated by elongational flow. For
$\tilde{b}\gg \tilde{b}_{m}$
, the flow is dominated by elongational flow. For
![]() $\tilde{b}\lesssim \tilde{b}_{m}$
, the elongational flow becomes less important and the flow is confined in the rim at the beginning of the dewetting. Around
$\tilde{b}\lesssim \tilde{b}_{m}$
, the elongational flow becomes less important and the flow is confined in the rim at the beginning of the dewetting. Around
![]() $\tilde{b}_{m}$
, the dissipation is dominated by the friction at the substrate as shown by the similarity solutions for the rim profile evolution at early times. When
$\tilde{b}_{m}$
, the dissipation is dominated by the friction at the substrate as shown by the similarity solutions for the rim profile evolution at early times. When
![]() $\tilde{b}<\tilde{b}_{m}$
, shear flow becomes more important. We rationalize the decrease of the non-sphericity with decreasing
$\tilde{b}<\tilde{b}_{m}$
, shear flow becomes more important. We rationalize the decrease of the non-sphericity with decreasing
![]() $\tilde{b}$
in terms of the spreading of the ridge and the contact line velocity. For smaller slip lengths, the accumulated mass due the movement of the contact line is redistributed to a wider extent, thus the droplet profile is closer to a spherical cap.
$\tilde{b}$
in terms of the spreading of the ridge and the contact line velocity. For smaller slip lengths, the accumulated mass due the movement of the contact line is redistributed to a wider extent, thus the droplet profile is closer to a spherical cap.
Although our numerical computations are limited to the smallest
![]() $\tilde{b}=0.023$
we can access, the trend of the non-sphericity for
$\tilde{b}=0.023$
we can access, the trend of the non-sphericity for
![]() $\tilde{b}<\tilde{b}_{m}$
implies that the transient droplet profile will be close to a spherical-cap shape when
$\tilde{b}<\tilde{b}_{m}$
implies that the transient droplet profile will be close to a spherical-cap shape when
![]() $\tilde{b}$
is very small, consistent with the expectation from the quasistatic approach. However, for a large difference between the initial and the equilibrium contact angles, the slip length below which the global bump disappears can be extremely small. In that case, the evolution of the global bump itself can be treated as quasistatic for small slip lengths. Our study thus brings a first prediction on the connection between the quasistatic and non-quasistatic regimes of droplet dewetting.
$\tilde{b}$
is very small, consistent with the expectation from the quasistatic approach. However, for a large difference between the initial and the equilibrium contact angles, the slip length below which the global bump disappears can be extremely small. In that case, the evolution of the global bump itself can be treated as quasistatic for small slip lengths. Our study thus brings a first prediction on the connection between the quasistatic and non-quasistatic regimes of droplet dewetting.
Acknowledgements
The authors thank S. Maurer, M. Benzaquen, E. Raphaël and K. Jacobs for a previous joint study on the topic. The authors also thank the Alexander von Humboldt Foundation and NSERC of Canada for financial support. The authors also acknowledge financial support from the Global Station for Soft Matter – a project of Global Institution for Collaborative Research and Education at Hokkaido University. J.D.M. was supported by LabEX ENS-ICFP: ANR-10-LABX-0010/ANR-10-IDEX-0001-02 PSL.
Appendix A
A.1 Expressions of
 $\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
$\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
 $\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
$\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
For the axisymmetric Stokes flow problem we study in this article, the boundary integral equation is quoted in (2.9). Here, we provide the standard expressions of the tensors
![]() $\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
$\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
![]() $\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
. Note that different symbols are used for these tensors in the book of Pozrikidis (Reference Pozrikidis1992). First, we introduce a function
$\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
. Note that different symbols are used for these tensors in the book of Pozrikidis (Reference Pozrikidis1992). First, we introduce a function
![]() $I_{mn}$
, which is defined as
$I_{mn}$
, which is defined as
![]() $k$
is given as
$k$
is given as
and
![]() $z_{d}\equiv z-z_{0}$
. Here
$z_{d}\equiv z-z_{0}$
. Here
![]() $(r,z)$
and
$(r,z)$
and
![]() $(r_{0},z_{0})$
are the coordinates of
$(r_{0},z_{0})$
are the coordinates of
![]() $\boldsymbol{s}$
and
$\boldsymbol{s}$
and
![]() $\boldsymbol{s}_{0}$
respectively.
$\boldsymbol{s}_{0}$
respectively.
For
![]() $\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
,
$\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
,
For
![]() $\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
,
$\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
,
The tensors
![]() $\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
$\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
![]() $\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
have singular points at
$\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
have singular points at
![]() $\boldsymbol{s}=\boldsymbol{s}_{0}$
and
$\boldsymbol{s}=\boldsymbol{s}_{0}$
and
![]() $\boldsymbol{s}=0$
. Around these points, the boundary integral equation (2.9) is performed analytically by expanding
$\boldsymbol{s}=0$
. Around these points, the boundary integral equation (2.9) is performed analytically by expanding
![]() $\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
$\bar{\unicode[STIX]{x1D60E}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
![]() $\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
in series (van Lengerich & Steen Reference van Lengerich and Steen2012).
$\bar{\unicode[STIX]{x1D61B}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}}$
in series (van Lengerich & Steen Reference van Lengerich and Steen2012).
A.2 Validation of the numerical method
A.2.1 Number of marker points

Figure 8. The contact line position
![]() $\tilde{R}$
as a function of time
$\tilde{R}$
as a function of time
![]() $\tilde{t}$
for
$\tilde{t}$
for
![]() $\unicode[STIX]{x1D703}_{e}=62^{\circ }$
and
$\unicode[STIX]{x1D703}_{e}=62^{\circ }$
and
![]() $\tilde{b}=0.023$
.
$\tilde{b}=0.023$
.
The number of marker points
![]() $M$
for the liquid/air interface used in the computations presented in this paper is
$M$
for the liquid/air interface used in the computations presented in this paper is
![]() $M=300$
. The convergence has been checked, see figure 8. The maximum difference between the curves for
$M=300$
. The convergence has been checked, see figure 8. The maximum difference between the curves for
![]() $M=300$
and for
$M=300$
and for
![]() $M=400$
is 0.4 %, we thus conclude that
$M=400$
is 0.4 %, we thus conclude that
![]() $M=300$
is sufficient to describe accurately the droplet evolution.
$M=300$
is sufficient to describe accurately the droplet evolution.
A.2.2 Relaxation of a free droplet
To validate our BEM, we consider the relaxation of a viscous ellipsoidal droplet of viscosity
![]() $\unicode[STIX]{x1D702}$
surrounded by a inviscid fluid. The droplet is axisymmetric and the profile is described by
$\unicode[STIX]{x1D702}$
surrounded by a inviscid fluid. The droplet is axisymmetric and the profile is described by
![]() $h(r,t)$
. For small deformations, the profile maintains a shape of ellipse with the major axis denoted by
$h(r,t)$
. For small deformations, the profile maintains a shape of ellipse with the major axis denoted by
![]() $a(t)$
and the minor axis denoted by
$a(t)$
and the minor axis denoted by
![]() $b(t)$
, namely
$b(t)$
, namely
for
![]() $0\leqslant r\leqslant a(t)$
. We define
$0\leqslant r\leqslant a(t)$
. We define
![]() $D(t)\equiv (a(t)-b(t))/(a(t)+b(t))$
. Applying Stokes equations, it has been proved analytically that
$D(t)\equiv (a(t)-b(t))/(a(t)+b(t))$
. Applying Stokes equations, it has been proved analytically that
![]() $D(t)$
rescaled by the initial value
$D(t)$
rescaled by the initial value
![]() $D_{0}=D(t=0)$
follows asymptotically the relation (Taylor Reference Taylor1934; Guido & Villone Reference Guido and Villone1999)
$D_{0}=D(t=0)$
follows asymptotically the relation (Taylor Reference Taylor1934; Guido & Villone Reference Guido and Villone1999)
Here
![]() $t$
is the time rescaled by
$t$
is the time rescaled by
![]() $R_{0}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D6FE}$
, where
$R_{0}\unicode[STIX]{x1D702}/\unicode[STIX]{x1D6FE}$
, where
![]() $R_{0}$
is the radius of the droplet (of spherical shape) at
$R_{0}$
is the radius of the droplet (of spherical shape) at
![]() $t\rightarrow \infty$
.
$t\rightarrow \infty$
.

Figure 9. (a) The initial droplet profile and a profile close to a sphere at
![]() $t=4$
. (b) Time series of
$t=4$
. (b) Time series of
![]() $a(t)$
and
$a(t)$
and
![]() $b(t)$
computed by BEM. (c) The variable
$b(t)$
computed by BEM. (c) The variable
![]() $D(t)/D_{0}$
computed by BEM and (A 14).
$D(t)/D_{0}$
computed by BEM and (A 14).
To validate our BEM, we compare our computation with the above analytical formula (A 14). For our computation, we take the rescaled slip length
![]() $\tilde{b}=10\,000$
and the equilibrium contact angle
$\tilde{b}=10\,000$
and the equilibrium contact angle
![]() $\unicode[STIX]{x1D703}_{e}=90^{\circ }$
. As an initial condition, we consider
$\unicode[STIX]{x1D703}_{e}=90^{\circ }$
. As an initial condition, we consider
![]() $a(t=0)=1.1$
and
$a(t=0)=1.1$
and
![]() $b(t=0)=1$
. Figures 9(a) and 9(b) show the droplet profiles and the time series of
$b(t=0)=1$
. Figures 9(a) and 9(b) show the droplet profiles and the time series of
![]() $a(t)$
and
$a(t)$
and
![]() $b(t)$
respectively. In figure 9(c), the variable
$b(t)$
respectively. In figure 9(c), the variable
![]() $D(t)/D_{0}$
computed by BEM is shown to agree well with the analytical result of (A 14) with no free fitting parameter.
$D(t)/D_{0}$
computed by BEM is shown to agree well with the analytical result of (A 14) with no free fitting parameter.