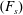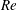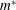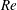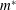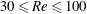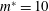1 Introduction
1.1 Vortex-induced vibration
Vortex shedding from a bluff body and vortex-induced vibration (VIV) are ubiquitous and have a broad range of applications in numerous fields such as offshore, wind and aerospace engineering. Apart from their great practical importance, these phenomena have a fundamental value in fluid mechanics due to the vast richness of their vorticity dynamics and coupled nonlinear physics. Asymmetric vortex shedding from a bluff body causes a large unsteady transverse load, which in turn may lead to structural vibrations when the structure is free to vibrate in the transverse direction (Sarpkaya Reference Sarpkaya2004; Williamson & Govardhan Reference Williamson and Govardhan2004; Bearman Reference Bearman2011). These large VIVs can lead to damage and potential risk to structures, in particular for ocean structures such as marine risers, subsea pipelines and cables. When the natural frequency of the structure is close the vortex shedding frequency, the phenomenon of VIV results in a complex evolution of the shedding frequency, which deviates from the Strouhal relation of its stationary counterpart. In this frequency lock-in regime, the vortex formation locks on to the natural frequency of the body within a range of the Strouhal frequency and there exists a strong coupling between the fluid and the structure (Sarpkaya Reference Sarpkaya2004). This frequency lock-in phenomenon leads to high-amplitude and self-sustained vibrations; thus, there is a need to understand the origin and different regimes during the lock-in process. The lock-in process is self-excited and is characterized by a matching of the frequency of periodic vortex shedding and the oscillation frequency of the body (Khalak & Williamson Reference Khalak and Williamson1999).
The flow over a single elastically mounted two-dimensional bluff body has served as a generic VIV model for both numerical and experimental investigations. In this canonical configuration, it is often convenient to consider the elastically mounted cylinder as two coupled oscillators, whereby one system is the oscillating body and the other is the wake. Numerous studies have been conducted to understand the frequency lock-in phenomenon for this simplified fluid–structure system. This VIV model problem manifests a complex dynamical behaviour, which has still been the subject of active research over the past decade (Williamson & Govardhan Reference Williamson and Govardhan2004; Bearman Reference Bearman2011). Apart from the fundamental physics of a single-cylinder VIV (Blackburn & Henderson Reference Blackburn and Henderson1999; Shiels, Leonard & Roshko Reference Shiels, Leonard and Roshko2001; Singh & Mittal Reference Singh and Mittal2005; Leontini, Thompson & Hourigan Reference Leontini, Thompson and Hourigan2006), the topics for numerical investigations range from the development of coupling procedures for the Navier–Stokes and structural equations (He, Zhou & Bao Reference He, Zhou and Bao2012; Jaiman, Sen & Gurugubelli Reference Jaiman, Sen and Gurugubelli2015; Jaiman, Guan & Miyanawala Reference Jaiman, Guan and Miyanawala2016a ; Jaiman, Pillalamarri & Guan Reference Jaiman, Pillalamarri and Guan2016b ) to the modelling of near-wall proximity effects (Tham et al. Reference Tham, Gurugubelli, Li and Jaiman2015), multiple-cylinder arrangements (Liu & Jaiman Reference Liu and Jaiman2016; Mysa, Kaboudian & Jaiman Reference Mysa, Kaboudian and Jaiman2016) and suppression devices (Yu et al. Reference Yu, Xie, Yan, Constantinides, Oakley and Karniadakis2015; Law & Jaiman Reference Law and Jaiman2017). High-fidelity computational fluid dynamics (CFD) can reveal a vast amount of physical insight in terms of the vorticity distribution, the force dynamics, the frequency characteristics and phase relations, and the shape of the VIV trajectory. Despite improved algorithms and powerful supercomputers, state-of-the-art CFD-based VIV simulation is less attractive with regard to parametric optimization and the development of control strategies. The primary motivation behind the present work is (i) to develop an efficient low-order model for the VIV lock-in of a circular-shaped bluff body and (ii) to generalize the eigenvalue analysis of the VIV lock-in mechanism for other two-dimensional bluff bodies.
1.2 The VIV mechanism and control
A simple interpretation of frequency lock-in during VIV is attributed to the classical resonance or synchronization with a well-defined frequency. The structural response amplitude should grow gradually as the natural frequency of the structure,
![]() $f_{N}$
, approaches the alternate vortex shedding frequency,
$f_{N}$
, approaches the alternate vortex shedding frequency,
![]() $f_{vs}$
, and should attain its maximum value when
$f_{vs}$
, and should attain its maximum value when
![]() $f_{N}/f_{vs}\approx 1$
. However, VIV simulations (Singh & Mittal Reference Singh and Mittal2005; Tham et al.
Reference Tham, Gurugubelli, Li and Jaiman2015) at
$f_{N}/f_{vs}\approx 1$
. However, VIV simulations (Singh & Mittal Reference Singh and Mittal2005; Tham et al.
Reference Tham, Gurugubelli, Li and Jaiman2015) at
![]() $Re=100$
reveal that the circular cylinder acquires its maximum amplitude at
$Re=100$
reveal that the circular cylinder acquires its maximum amplitude at
![]() $f_{N}/f_{vs}\approx 1.3$
, or in the vicinity of VIV lock-in onset, which is not consistent with the simple resonance interpretation. Therefore, the classical resonance is not adequate to interpret the underlying VIV lock-in mechanism and the large amplitude during the lock-in process. Through a linear global stability analysis of the flow past an elastically mounted cylinder, Cossu & Morino (Reference Cossu and Morino2000) identified two modes in the fluid–structure system, namely a nearly structural mode and the von Karman wake mode. De Langre (Reference De Langre2006) investigated the mechanism of lock-in to a coupled-mode flutter by using a simple linear wake-oscillator model for a transversely vibrating circular cylinder. The VIV analysis by De Langre (Reference De Langre2006) was performed by considering an empirical wake-oscillator model while neglecting nonlinear and viscous terms. Analogously to the plunging and pitching instability of an airfoil in the classical aeroelasticity, De Langre (Reference De Langre2006) attributed the root cause of VIV lock-in to the mode coupling between the transverse periodic motion and the continuous rotation of the separation point along the smooth contour of the circular cylinder.
$f_{N}/f_{vs}\approx 1.3$
, or in the vicinity of VIV lock-in onset, which is not consistent with the simple resonance interpretation. Therefore, the classical resonance is not adequate to interpret the underlying VIV lock-in mechanism and the large amplitude during the lock-in process. Through a linear global stability analysis of the flow past an elastically mounted cylinder, Cossu & Morino (Reference Cossu and Morino2000) identified two modes in the fluid–structure system, namely a nearly structural mode and the von Karman wake mode. De Langre (Reference De Langre2006) investigated the mechanism of lock-in to a coupled-mode flutter by using a simple linear wake-oscillator model for a transversely vibrating circular cylinder. The VIV analysis by De Langre (Reference De Langre2006) was performed by considering an empirical wake-oscillator model while neglecting nonlinear and viscous terms. Analogously to the plunging and pitching instability of an airfoil in the classical aeroelasticity, De Langre (Reference De Langre2006) attributed the root cause of VIV lock-in to the mode coupling between the transverse periodic motion and the continuous rotation of the separation point along the smooth contour of the circular cylinder.
Using a standard asymptotic analysis, Meliga & Chomaz (Reference Meliga and Chomaz2011) confirmed the existence of the two modes identified by Cossu & Morino (Reference Cossu and Morino2000) and termed them as the wake mode (WM) and the structure mode (SM). For weak fluid–structure interaction in the limit of large solid-to-fluid mass ratio, the eigenvalue of the WM was found to be similar to the leading eigenvalue computed for the flow past a fixed cylinder, whereas the eigenvalue of the SM approached the natural eigenvalue of the cylinder-only system. Inspired by the semi-analytical findings of De Langre (Reference De Langre2006), Zhang et al. (Reference Zhang, Li, Ye and Jiang2015) recently employed a linear reduced-order model (ROM)-based CFD method to provide further evidence of the frequency lock-in phenomenon of a circular cylinder at
![]() $Re=60$
, and two regimes were confirmed in the VIV response, namely resonance-induced lock-in and flutter-induced lock-in. The resonance regime is related to the vorticity dynamics of the wake flow, whereas the flutter regime may be interpreted as an inertial coupling between the structure and the global wake flow. In another recent work by Navrose & Mittal (Reference Mittal2016), the lock-in phenomenon was investigated via a linear stability and direct time integration, and two leading eigenmodes referred to as the fluid mode and the elastic mode were classified for a transversely vibrating circular cylinder. These two leading modes were found to have a strong coupling for low mass ratios, and a clear demarcation of the fluid (wake) mode or elastic (structure) mode was found to be non-trivial. As opposed to the decoupled modes (WM and SM) for high mass ratios, these modes were termed as coupled modes for low mass ratios (Navrose & Mittal Reference Mittal2016).
$Re=60$
, and two regimes were confirmed in the VIV response, namely resonance-induced lock-in and flutter-induced lock-in. The resonance regime is related to the vorticity dynamics of the wake flow, whereas the flutter regime may be interpreted as an inertial coupling between the structure and the global wake flow. In another recent work by Navrose & Mittal (Reference Mittal2016), the lock-in phenomenon was investigated via a linear stability and direct time integration, and two leading eigenmodes referred to as the fluid mode and the elastic mode were classified for a transversely vibrating circular cylinder. These two leading modes were found to have a strong coupling for low mass ratios, and a clear demarcation of the fluid (wake) mode or elastic (structure) mode was found to be non-trivial. As opposed to the decoupled modes (WM and SM) for high mass ratios, these modes were termed as coupled modes for low mass ratios (Navrose & Mittal Reference Mittal2016).
Due to the complexity of VIV with regard to fluid–structure interaction, a unified description of the frequency lock-in still remains unclear for arbitrary shaped bluff bodies and general physical conditions. It is of particular interest in this study to understand some elementary aspects of the self-sustained VIV oscillations by considering a linear aspect of the lock-in process. The linear instability plays a key role in the origin of self-sustained VIV oscillation arising from a coupled fluid–structure system. Once the fluid–structure system rises to a high-amplitude VIV response, the nonlinearity begins to dominate and the system transforms into a fully developed (self-limiting) limit-cycle state. Some key questions with regard to the generality of the VIV lock-in process have remained unexplained, such as how the geometry of the bluff body influences the frequency lock-in in VIV, why the VIV behaviour of a square cylinder is different from its circular counterpart, and whether the resonance and flutter regimes always exist or are actually influenced by the Reynolds number and the geometry of the bluff body? In this article, we attempt to answer these questions and understand more general aspects of the linear VIV mechanism via our proposed eigensystem realization algorithm (ERA)-based ROM procedure.
An understanding of the VIV mechanism can help in developing flow control techniques based on both passive and active control schemes, whereby the passive schemes require no energy input and the active schemes rely on continuous energy input. Due to the complexity of VIV, the control schemes are generally ad hoc, and a good understanding of the dynamical behaviour with respect to the flow and structure parameters is required. Although a high-fidelity CFD model is able to resolve physical features of interest, a linear model based on the model reduction provides a way to perform stability analysis for the flow past a bluff body and to design active control strategies (Marquet, Sipp & Jacquin Reference Marquet, Sipp and Jacquin2008; Mettot, Renac & Sipp Reference Mettot, Renac and Sipp2014; Thompson et al. Reference Thompson, Radi, Rao, Sheridan and Hourigan2014; Flinois & Morgans Reference Flinois and Morgans2016). Two ways exist to derive a linear model of the original nonlinear system. While the first one is to derive a linear governing equation and then discretize the system of equations, the second approach is to discretize the nonlinear model first and then to obtain the linear model from it. The latter method is widely used in the aeroelastic research community to construct the linear model by the automatic differencing method. However, both types of method are expensive and are not attractive for parametric study and the development of VIV control strategies. A low-order model based on the minimal state-space dimension has the potential to become a practical alternative to understand the VIV mechanism and to design a proper control procedure. A model-based control design can help to regulate and stabilize alternate vortex formation and the near-wake dynamics. Such a model relies on the smallest state-space dimension of realized systems that have similar input–output relations within a specified degree of precision. As shown in Ho & Kalman (Reference Ho and Kalman1966), the minimum problem represents the problem of identifying the sequence of real matrices, also known as the Markov parameters, based on the impulse response of a dynamic system.
1.3 Model order reduction
The model order reduction (MOR) technique consists of approximating the original full-order (high-dimensional) system with a low-order model, which retains the significant dynamics of the original system and provides order of magnitude efficiency improvement for the construction of the essential dynamics of the system. As discussed in Flinois & Morgans (Reference Flinois and Morgans2016), we can categorize previous studies on the linear MOR into two main approaches. The first ROM construction approach is based on Galerkin projection of the full-order system onto a small subspace spanned by mode vectors. The mode vector can be obtained by proper orthogonal decomposition (POD), balanced truncation (Moore Reference Moore1981) or dynamic mode decomposition (DMD) (Rowley et al. Reference Rowley, Mezic, Bagheri, Schlatter and Henningson2009; Schmid Reference Schmid2010). One of the drawbacks of conventional POD/Galerkin models is that while they capture the most energetic modes based on a user-defined energy norm, low-energy features may be crucial to the dynamics of the underlying problem. Compared with the POD method, which only extracts modes from snapshots of the primary system, the balance truncation method derives the modes by collecting snapshots of both the primary and the adjoint systems. This feature of the balance truncation method allows identification of the modes that are dynamically important. Based on the work of Moore (Reference Moore1981), Willcox & Peraire (Reference Willcox and Peraire2002) and Rowley (Reference Rowley2005) further extended the balance truncation concept to a large system by approximating the system observable and controllable Gramians via two sets of snapshots from a linearized forward simulation and a companion adjoint simulation. This algorithm is usually referred to as the balanced proper orthogonal decomposition (BPOD) and provides two sets of modes, namely primal and adjoint modes.
The second approach is based on the system identification method, which only requires input and output information and considers the original system as a black box via the input–output dynamical relationship. From a time-domain formulation and the realization of a state-space model, an ROM of the dynamic system can be constructed on the basis of input–output data. One widely used system identification method is the ERA introduced by Juang & Pappa (Reference Juang and Pappa1985) for the model reduction using a Hankel-matrix-based decomposition. The ERA essentially extends the well-known algorithm of Ho & Kalman (Reference Ho and Kalman1966) from control theory and creates a minimal realization that follows the evolution of the system output when it is subjected to an impulse input. In a recent theoretical study, Ma, Ahuja & Rowley (Reference Ma, Ahuja and Rowley2011) proved that the ERA constructs an ROM that is mathematically equivalent to the BPOD method. With regard to recent fluid dynamics applications, the ERA has been considered for unsteady problems by Yao & Marques (Reference Yao and Marques2015) and Flinois & Morgans (Reference Flinois and Morgans2016).
The aforementioned methods were originally developed for stable linear systems. Extensions have been made to circumvent this restriction of the model reduction for unstable systems by either partitioning the unstable and stable subspaces or inverting the large linear system (Barbagallo, Sipp & Schmid Reference Barbagallo, Sipp and Schmid2009; Ahuja & Rowley Reference Ahuja and Rowley2010; Dergham et al. Reference Dergham, Sipp, Robinet and Barbagallo2011). In a recent work by Flinois, Morgans & Schmid (Reference Flinois, Morgans and Schmid2015), a theoretical analysis was presented to show that the unmodified balance truncation (designed for stable systems) method can be applied to an unstable system. Following this analysis and the work of Ma et al. (Reference Ma, Ahuja and Rowley2011), the ERA was recently employed for active control of the unstable wake behind a bluff body (Flinois & Morgans Reference Flinois and Morgans2016). Compared with the ROM method used in Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), which lacks mathematical rigour and is highly sensitive to the training trajectory, the ERA has a theoretical foundation for unstable linear systems generated by the unsteady wake dynamics and VIVs. Therefore, following Flinois et al. (Reference Flinois, Morgans and Schmid2015) and the findings of Ma et al. (Reference Ma, Ahuja and Rowley2011), the ERA is adopted in this paper to construct the low-order fluid model.
1.4 Contributions and organization
In this work, we present physical insight and the underlying mechanism of VIV by exploiting a unified description of frequency lock-in for elastically mounted cylinders. We introduce the ERA-based ROM to capture just enough physics to extract the stability properties of the fluid–structure systems of two-dimensional bluff bodies consisting of sharp corners and smooth curves. It is of particular interest to provide a generalized description of these frequency lock-in regimes at low Reynolds numbers via a model reduction technique. Unlike the wake-oscillator model, the present technique does not rely on any empirical formulation and captures the physical effects related to the added-mass and damping forces naturally through solution of the Navier–Stokes equations. We first employ the ERA-based ROM for unstable wake flow over a stationary circular cylinder and predict the critical Reynolds number
![]() $Re_{cr}$
of vortex shedding. We then perform stability analysis of the fluid–structure system via the ERA-based ROM to analyse the effects of the Reynolds number
$Re_{cr}$
of vortex shedding. We then perform stability analysis of the fluid–structure system via the ERA-based ROM to analyse the effects of the Reynolds number
![]() $Re$
, the mass ratio
$Re$
, the mass ratio
![]() $m^{\ast }$
and the rounding of a square cylinder. To examine the accuracy and reliability of the low-order model, we assess the ROM results against full-order simulations performed by the variationally coupled Navier–Stokes and rigid-body equations.
$m^{\ast }$
and the rounding of a square cylinder. To examine the accuracy and reliability of the low-order model, we assess the ROM results against full-order simulations performed by the variationally coupled Navier–Stokes and rigid-body equations.
We will show in this paper that the two frequency lock-in regimes associated with resonance and flutter characteristics only exist when certain conditions are satisfied. These regimes have a strong dependence on the shape of the bluff body, the Reynolds number and the mass ratio. The presence of sharp corners on a square cylinder greatly alters the VIV lock-in characteristics compared with the circular counterpart with smooth curves. We report that the frequency lock-in of a square cylinder is found to be dominated by the resonance regime without any coupled-mode flutter at low Reynolds number (
![]() $Re\leqslant 80$
). This indicates that the previous theoretical findings by De Langre (Reference De Langre2006) on the root cause of frequency lock-in due to the coupled flutter do not hold for a transversely vibrating sharp-cornered square cylinder. Apart from the frequency lock-in regimes, we qualitatively visualize the spatio-temporal evolution of vortex shedding and leading eigenmodes to link the lock-in process with the intrinsic wake dynamics. To understand the influence of geometry on the frequency lock-in regimes, we present a stability phase diagram for five two-dimensional bluff bodies, namely circle, square, ellipse, forward triangle and diamond. Compared with the circular cylinder, we show that the flutter mode is more pronounced in the elliptical cylinder, while the lock-in/synchronization is galloping-dominated for the forward triangle configuration. The proposed ERA-based ROM is general and efficient for fluid–structure systems without the need for a linearized flow or an adjoint solver, which allows the method to be applicable even for physical experiments.
$Re\leqslant 80$
). This indicates that the previous theoretical findings by De Langre (Reference De Langre2006) on the root cause of frequency lock-in due to the coupled flutter do not hold for a transversely vibrating sharp-cornered square cylinder. Apart from the frequency lock-in regimes, we qualitatively visualize the spatio-temporal evolution of vortex shedding and leading eigenmodes to link the lock-in process with the intrinsic wake dynamics. To understand the influence of geometry on the frequency lock-in regimes, we present a stability phase diagram for five two-dimensional bluff bodies, namely circle, square, ellipse, forward triangle and diamond. Compared with the circular cylinder, we show that the flutter mode is more pronounced in the elliptical cylinder, while the lock-in/synchronization is galloping-dominated for the forward triangle configuration. The proposed ERA-based ROM is general and efficient for fluid–structure systems without the need for a linearized flow or an adjoint solver, which allows the method to be applicable even for physical experiments.
The paper is structured as follows. Section 2 introduces the full-order model, the state-space formulation for the model reduction and the ERA for the wake flow and VIV. Section 3 describes the VIV problem set-up and presents the convergence and the numerical verification of the ERA-based ROM model. A systematic analysis of the frequency lock-in mechanism as a function of the Reynolds number, and the effects of rounding and geometry is provided in § 4. Concluding remarks are presented in § 5.
2 Numerical methodology
For the sake of completeness, we first summarize the formulation for the high-dimensional full-order model (FOM) and describe the implementation of the numerical schemes used for the coupled variational fluid–structure solver. Later, we present the ERA for the construction of the ROM using the Navier–Stokes and rigid-body equations.
2.1 Full-order model formulation
To study the interaction of an elastically mounted cylinder with a fluid, we consider a variational fluid formulation based on the arbitrary Lagrangian–Eulerian (ALE) description and semi-discrete time stepping (Liu, Jaiman & Gurugubelli Reference Liu, Jaiman and Gurugubelli2014; Jaiman et al.
Reference Jaiman, Sen and Gurugubelli2015). We consider a fluid domain
![]() $\unicode[STIX]{x1D6FA}^{f}(t)$
with spatial and temporal coordinates denoted by
$\unicode[STIX]{x1D6FA}^{f}(t)$
with spatial and temporal coordinates denoted by
![]() $\boldsymbol{x}^{f}$
and
$\boldsymbol{x}^{f}$
and
![]() $t$
respectively. The Navier–Stokes (NS) equations governing an incompressible flow in the ALE reference frame are
$t$
respectively. The Navier–Stokes (NS) equations governing an incompressible flow in the ALE reference frame are
where
![]() $\unicode[STIX]{x1D70C}^{f}$
,
$\unicode[STIX]{x1D70C}^{f}$
,
![]() $\boldsymbol{u}^{f}$
,
$\boldsymbol{u}^{f}$
,
![]() $\boldsymbol{w}$
,
$\boldsymbol{w}$
,
![]() $\unicode[STIX]{x1D748}^{f}$
and
$\unicode[STIX]{x1D748}^{f}$
and
![]() $\boldsymbol{b}^{f}$
are the fluid density, the fluid velocity, the ALE mesh velocity, the Cauchy stress tensor and the body force per unit mass respectively. For the partial time derivative in (2.1), the ALE referential coordinate
$\boldsymbol{b}^{f}$
are the fluid density, the fluid velocity, the ALE mesh velocity, the Cauchy stress tensor and the body force per unit mass respectively. For the partial time derivative in (2.1), the ALE referential coordinate
![]() $\unicode[STIX]{x1D74C}$
is held fixed and for a Newtonian fluid
$\unicode[STIX]{x1D74C}$
is held fixed and for a Newtonian fluid
![]() $\unicode[STIX]{x1D748}^{f}$
is defined as
$\unicode[STIX]{x1D748}^{f}$
is defined as
where
![]() $p$
,
$p$
,
![]() $\unicode[STIX]{x1D707}^{f}$
and
$\unicode[STIX]{x1D707}^{f}$
and
![]() $\unicode[STIX]{x1D644}$
are the pressure, the dynamic viscosity of the fluid and an identity tensor respectively. A rigid-body structure submerged in the fluid experiences unsteady fluid forces and consequently may undergo flow-induced vibrations if the body is mounted elastically. To simulate translational motion of a two-dimensional rigid body about its centre of mass, the Lagrangian motion along the Cartesian axes is given by
$\unicode[STIX]{x1D644}$
are the pressure, the dynamic viscosity of the fluid and an identity tensor respectively. A rigid-body structure submerged in the fluid experiences unsteady fluid forces and consequently may undergo flow-induced vibrations if the body is mounted elastically. To simulate translational motion of a two-dimensional rigid body about its centre of mass, the Lagrangian motion along the Cartesian axes is given by
where
![]() $\boldsymbol{u}^{s}(t)$
represents the velocity of the immersed rigid body in the fluid domain,
$\boldsymbol{u}^{s}(t)$
represents the velocity of the immersed rigid body in the fluid domain,
![]() $\unicode[STIX]{x1D753}^{s}(t)$
denotes the position of the centre of the rigid body at time
$\unicode[STIX]{x1D753}^{s}(t)$
denotes the position of the centre of the rigid body at time
![]() $t$
, and
$t$
, and
![]() $\unicode[STIX]{x1D662},\unicode[STIX]{x1D658}$
,
$\unicode[STIX]{x1D662},\unicode[STIX]{x1D658}$
,
![]() $\unicode[STIX]{x1D660}$
are mass, damping and stiffness coefficient matrices for the translational motions. Here,
$\unicode[STIX]{x1D660}$
are mass, damping and stiffness coefficient matrices for the translational motions. Here,
![]() $\boldsymbol{F}^{s}$
is the fluid force on the rigid body.
$\boldsymbol{F}^{s}$
is the fluid force on the rigid body.
Let
![]() $\unicode[STIX]{x1D6E4}(t)$
be the fluid–structure interface at time
$\unicode[STIX]{x1D6E4}(t)$
be the fluid–structure interface at time
![]() $t$
. The coupled system needs to satisfy the continuity of velocity and the force equilibrium at the fluid–body interface
$t$
. The coupled system needs to satisfy the continuity of velocity and the force equilibrium at the fluid–body interface
![]() $\unicode[STIX]{x1D6E4}$
as follows:
$\unicode[STIX]{x1D6E4}$
as follows:
where
![]() $\boldsymbol{n}$
is the outer normal to the fluid–body interface. In (2.7), the first term represents the force exerted by the fluid and the second term is the solid load vector applied in (2.4). The ALE mesh nodes on the fluid domain
$\boldsymbol{n}$
is the outer normal to the fluid–body interface. In (2.7), the first term represents the force exerted by the fluid and the second term is the solid load vector applied in (2.4). The ALE mesh nodes on the fluid domain
![]() $\unicode[STIX]{x1D6FA}^{f}(\boldsymbol{x}^{f},t)$
can be updated by solving a linear steady pseudo-elastic material model,
$\unicode[STIX]{x1D6FA}^{f}(\boldsymbol{x}^{f},t)$
can be updated by solving a linear steady pseudo-elastic material model,
where
![]() $\unicode[STIX]{x1D748}^{m}$
is the stress experienced by the ALE mesh due to the strain induced by the rigid-body movement,
$\unicode[STIX]{x1D748}^{m}$
is the stress experienced by the ALE mesh due to the strain induced by the rigid-body movement,
![]() $\boldsymbol{\unicode[STIX]{x1D702}}^{f}$
represents the ALE mesh node displacement and
$\boldsymbol{\unicode[STIX]{x1D702}}^{f}$
represents the ALE mesh node displacement and
![]() $k_{m}$
is a mesh stiffness variable chosen as a function of the element area to limit the distortion of small elements located in the immediate vicinity of the fluid–body interface.
$k_{m}$
is a mesh stiffness variable chosen as a function of the element area to limit the distortion of small elements located in the immediate vicinity of the fluid–body interface.
The weak variational form of (2.1) is discretized in space using
![]() $\mathbb{P}_{n}/\mathbb{P}_{n-1}$
iso-parametric finite elements for the fluid velocity and pressure, where
$\mathbb{P}_{n}/\mathbb{P}_{n-1}$
iso-parametric finite elements for the fluid velocity and pressure, where
![]() $\mathbb{P}_{n}$
denotes the standard
$\mathbb{P}_{n}$
denotes the standard
![]() $n$
th order Lagrange finite element space on the discretized fluid domain. To satisfy the inf–sup condition, a
$n$
th order Lagrange finite element space on the discretized fluid domain. To satisfy the inf–sup condition, a
![]() $\mathbb{P}_{2}/\mathbb{P}_{1}$
finite element mesh is adopted and the second-order backward scheme is used for the time discretization of the NS system (Liu et al.
Reference Liu, Jaiman and Gurugubelli2014). In the present study, a partitioned staggered scheme is considered for the full-order simulations of the fluid–structure interaction (Jaiman et al.
Reference Jaiman, Geubelle, Loth and Jiao2011). The motion of the structure is driven by the traction forces exerted by the flowing fluid at the fluid–structure interface
$\mathbb{P}_{2}/\mathbb{P}_{1}$
finite element mesh is adopted and the second-order backward scheme is used for the time discretization of the NS system (Liu et al.
Reference Liu, Jaiman and Gurugubelli2014). In the present study, a partitioned staggered scheme is considered for the full-order simulations of the fluid–structure interaction (Jaiman et al.
Reference Jaiman, Geubelle, Loth and Jiao2011). The motion of the structure is driven by the traction forces exerted by the flowing fluid at the fluid–structure interface
![]() $\unicode[STIX]{x1D6E4}$
, whereby the structural motion predicts the new interface position and the geometry changes for the ALE fluid domain at each time step. The movement of the internal ALE fluid nodes is accommodated such that the mesh quality does not deteriorate as the motion of the solid structure becomes large. The above coupled variational formulation completes the presentation of the FOM for the direct numerical simulation of the fluid–structure interaction. We next present a state-space formulation of the model reduction using a system identification technique based on the input–output dynamics.
$\unicode[STIX]{x1D6E4}$
, whereby the structural motion predicts the new interface position and the geometry changes for the ALE fluid domain at each time step. The movement of the internal ALE fluid nodes is accommodated such that the mesh quality does not deteriorate as the motion of the solid structure becomes large. The above coupled variational formulation completes the presentation of the FOM for the direct numerical simulation of the fluid–structure interaction. We next present a state-space formulation of the model reduction using a system identification technique based on the input–output dynamics.
2.2 Basic state-space formulation and model reduction
The linear time-invariant (LTI) and multiple-input multiple-output (MIMO) model represented in a state-space form at discrete times
![]() $t=k\unicode[STIX]{x0394}t$
,
$t=k\unicode[STIX]{x0394}t$
,
![]() $k=0,1,2,\ldots ,$
with a constant sampling time
$k=0,1,2,\ldots ,$
with a constant sampling time
![]() $\unicode[STIX]{x0394}t$
reads as
$\unicode[STIX]{x0394}t$
reads as
where
![]() $\unicode[STIX]{x1D66D}_{r}$
is an
$\unicode[STIX]{x1D66D}_{r}$
is an
![]() $n_{r}$
-dimensional state vector,
$n_{r}$
-dimensional state vector,
![]() $\unicode[STIX]{x1D66A}$
denotes a
$\unicode[STIX]{x1D66A}$
denotes a
![]() $q$
-dimensional input vector and
$q$
-dimensional input vector and
![]() $\unicode[STIX]{x1D66E}_{r}$
is a
$\unicode[STIX]{x1D66E}_{r}$
is a
![]() $p$
-dimensional output vector. The integer
$p$
-dimensional output vector. The integer
![]() $k$
is a sample index for the time stepping. The system matrices are
$k$
is a sample index for the time stepping. The system matrices are
![]() $(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
, whereby the transition matrix
$(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
, whereby the transition matrix
![]() $\unicode[STIX]{x1D63C}_{r}$
characterizes the dynamics of the system. Here,
$\unicode[STIX]{x1D63C}_{r}$
characterizes the dynamics of the system. Here,
![]() $\unicode[STIX]{x1D63D}_{r}$
,
$\unicode[STIX]{x1D63D}_{r}$
,
![]() $\unicode[STIX]{x1D63E}_{r}$
and
$\unicode[STIX]{x1D63E}_{r}$
and
![]() $\unicode[STIX]{x1D63F}_{r}$
denote the input, output and feed-through matrices respectively. For the given output vector
$\unicode[STIX]{x1D63F}_{r}$
denote the input, output and feed-through matrices respectively. For the given output vector
![]() $\unicode[STIX]{x1D66E}_{r}$
, the statement of system realization is to construct the system matrices
$\unicode[STIX]{x1D66E}_{r}$
, the statement of system realization is to construct the system matrices
![]() $(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
such that the vector
$(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
such that the vector
![]() $\unicode[STIX]{x1D66E}_{r}$
is reproduced by the state-space model. In a discrete-time setting, the state-space realization matrices
$\unicode[STIX]{x1D66E}_{r}$
is reproduced by the state-space model. In a discrete-time setting, the state-space realization matrices
![]() $(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
of the dynamical system are constructed by the ERA, in which only the impulse response function (IRF) of the original full-order system is required for the system realization. The impulse response of the full-order linear system is first defined as
$(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
of the dynamical system are constructed by the ERA, in which only the impulse response function (IRF) of the original full-order system is required for the system realization. The impulse response of the full-order linear system is first defined as
![]() $\unicode[STIX]{x1D66E}=[\unicode[STIX]{x1D66E}_{1},\unicode[STIX]{x1D66E}_{2},\unicode[STIX]{x1D66E}_{3},\ldots ,\unicode[STIX]{x1D66E}_{n_{i}}]$
, where
$\unicode[STIX]{x1D66E}=[\unicode[STIX]{x1D66E}_{1},\unicode[STIX]{x1D66E}_{2},\unicode[STIX]{x1D66E}_{3},\ldots ,\unicode[STIX]{x1D66E}_{n_{i}}]$
, where
![]() $n_{i}$
represents the length of the impulse response and
$n_{i}$
represents the length of the impulse response and
![]() $\unicode[STIX]{x1D66E}_{i}$
denotes the IRF with the dimension
$\unicode[STIX]{x1D66E}_{i}$
denotes the IRF with the dimension
![]() $p\times q$
. Based on the impulse response, the generalized block Hankel matrices
$p\times q$
. Based on the impulse response, the generalized block Hankel matrices
![]() $r\times s$
can be constructed as
$r\times s$
can be constructed as
 $$\begin{eqnarray}\unicode[STIX]{x1D643}(k-1)=\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D66E}_{k+1} & \unicode[STIX]{x1D66E}_{k+2} & \cdots \, & \unicode[STIX]{x1D66E}_{k+s}\\ \unicode[STIX]{x1D66E}_{k+2} & \unicode[STIX]{x1D66E}_{k+3} & \cdots \, & \unicode[STIX]{x1D66E}_{k+s+1}\\ \vdots & \vdots & \ddots & \vdots \\ \unicode[STIX]{x1D66E}_{k+r} & \unicode[STIX]{x1D66E}_{k+r+1} & \cdots \, & \unicode[STIX]{x1D66E}_{k+(s+r-1)}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D643}(k-1)=\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D66E}_{k+1} & \unicode[STIX]{x1D66E}_{k+2} & \cdots \, & \unicode[STIX]{x1D66E}_{k+s}\\ \unicode[STIX]{x1D66E}_{k+2} & \unicode[STIX]{x1D66E}_{k+3} & \cdots \, & \unicode[STIX]{x1D66E}_{k+s+1}\\ \vdots & \vdots & \ddots & \vdots \\ \unicode[STIX]{x1D66E}_{k+r} & \unicode[STIX]{x1D66E}_{k+r+1} & \cdots \, & \unicode[STIX]{x1D66E}_{k+(s+r-1)}\end{array}\right].\end{eqnarray}$$
From the partitioned singular value decomposition of the Hankel matrix
![]() $\unicode[STIX]{x1D643}(0)$
, we have
$\unicode[STIX]{x1D643}(0)$
, we have
where the diagonal matrices
![]() $\unicode[STIX]{x1D72E}$
are the Hankel singular values (HSVs)
$\unicode[STIX]{x1D72E}$
are the Hankel singular values (HSVs)
![]() $\unicode[STIX]{x1D70E}_{i}$
, which represent the dynamical significance through sorting such that
$\unicode[STIX]{x1D70E}_{i}$
, which represent the dynamical significance through sorting such that
![]() $\unicode[STIX]{x1D70E}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70E}_{n}\geqslant 0$
. The block matrix
$\unicode[STIX]{x1D70E}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70E}_{n}\geqslant 0$
. The block matrix
![]() $\unicode[STIX]{x1D72E}_{2}$
contains the zeros or negligible elements. By truncating the dynamically less significant states, we estimate
$\unicode[STIX]{x1D72E}_{2}$
contains the zeros or negligible elements. By truncating the dynamically less significant states, we estimate
![]() $\unicode[STIX]{x1D643}(0)\approx \unicode[STIX]{x1D650}_{1}\unicode[STIX]{x1D72E}_{1}\unicode[STIX]{x1D651}_{1}^{\ast }$
. The reduced system matrices
$\unicode[STIX]{x1D643}(0)\approx \unicode[STIX]{x1D650}_{1}\unicode[STIX]{x1D72E}_{1}\unicode[STIX]{x1D651}_{1}^{\ast }$
. The reduced system matrices
![]() $(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
are then defined as
$(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
are then defined as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D63C}_{r}=\unicode[STIX]{x1D72E}_{1}^{-1/2}\unicode[STIX]{x1D650}_{1}^{\ast }\unicode[STIX]{x1D643}(1)\unicode[STIX]{x1D651}_{1}\unicode[STIX]{x1D72E}_{1}^{-1/2},\\ \displaystyle \unicode[STIX]{x1D63D}_{r}=\unicode[STIX]{x1D72E}_{1}^{1/2}\unicode[STIX]{x1D651}_{1}^{\ast }\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D662}},\\ \displaystyle \unicode[STIX]{x1D63E}_{r}=\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D669}}^{\ast }\unicode[STIX]{x1D650}_{1}\unicode[STIX]{x1D72E}_{1}^{1/2},\\ \displaystyle \unicode[STIX]{x1D63F}_{r}=\unicode[STIX]{x1D66E}_{1}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D63C}_{r}=\unicode[STIX]{x1D72E}_{1}^{-1/2}\unicode[STIX]{x1D650}_{1}^{\ast }\unicode[STIX]{x1D643}(1)\unicode[STIX]{x1D651}_{1}\unicode[STIX]{x1D72E}_{1}^{-1/2},\\ \displaystyle \unicode[STIX]{x1D63D}_{r}=\unicode[STIX]{x1D72E}_{1}^{1/2}\unicode[STIX]{x1D651}_{1}^{\ast }\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D662}},\\ \displaystyle \unicode[STIX]{x1D63E}_{r}=\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D669}}^{\ast }\unicode[STIX]{x1D650}_{1}\unicode[STIX]{x1D72E}_{1}^{1/2},\\ \displaystyle \unicode[STIX]{x1D63F}_{r}=\unicode[STIX]{x1D66E}_{1}.\end{array}\right\}\end{eqnarray}$$
Here,
![]() $\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D662}}^{\ast }=[\unicode[STIX]{x1D644}_{q}\;\mathbf{0}]_{q\times N}$
and
$\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D662}}^{\ast }=[\unicode[STIX]{x1D644}_{q}\;\mathbf{0}]_{q\times N}$
and
![]() $\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D669}}^{\ast }=[\unicode[STIX]{x1D644}_{p}\;\mathbf{0}]_{p\times M}$
, where
$\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D669}}^{\ast }=[\unicode[STIX]{x1D644}_{p}\;\mathbf{0}]_{p\times M}$
, where
![]() $N=s\times q$
,
$N=s\times q$
,
![]() $M=r\times p$
, and
$M=r\times p$
, and
![]() $\unicode[STIX]{x1D644}_{p}$
and
$\unicode[STIX]{x1D644}_{p}$
and
![]() $\unicode[STIX]{x1D644}_{q}$
are the identity matrices. We next present the ERA to construct the fluid ROM, which relies on the incompressible NS equations to represent the dynamics of a small-amplitude perturbation around the equilibrium base flow.
$\unicode[STIX]{x1D644}_{q}$
are the identity matrices. We next present the ERA to construct the fluid ROM, which relies on the incompressible NS equations to represent the dynamics of a small-amplitude perturbation around the equilibrium base flow.
2.3 The ERA-based model reduction for VIV
In the present work, we only consider the transverse motion of a cylinder in a flowing stream for the sake of simplicity. However, the formulation of the ERA-based ROM is general for any fluid–structure system. The cylinder is mounted on a spring system in the cross-flow direction, which allows the cylinder to vibrate through unsteady lift comprising the pressure and shear stresses of the fluid. Due to the direct solution of the NS equations, the effects of added-mass and added-damping forces are implicitly captured in the present model. To perform linear stability analysis, the fluid ROM constructed by the ERA is coupled with the linear structural model. The non-dimensional structural equation for a transversely vibrating cylinder with one degree of freedom can be written as
where
![]() $Y$
is the transverse displacement,
$Y$
is the transverse displacement,
![]() $C_{l}$
is the lift coefficient,
$C_{l}$
is the lift coefficient,
![]() $m^{\ast }$
and
$m^{\ast }$
and
![]() $\unicode[STIX]{x1D701}$
are the ratio of the mass of the vibrating structure to the mass of the displaced fluid and the damping coefficient respectively and
$\unicode[STIX]{x1D701}$
are the ratio of the mass of the vibrating structure to the mass of the displaced fluid and the damping coefficient respectively and
![]() $F_{s}$
is the reduced natural frequency of the structure, defined as
$F_{s}$
is the reduced natural frequency of the structure, defined as
![]() $F_{s}=f_{N}D/U=1/U_{r}$
, where
$F_{s}=f_{N}D/U=1/U_{r}$
, where
![]() $U_{r}$
is the reduced velocity which is an alternative parameter to describe the frequency lock-in phenomenon. The mass ratio
$U_{r}$
is the reduced velocity which is an alternative parameter to describe the frequency lock-in phenomenon. The mass ratio
![]() $m^{\ast }$
is a key parameter for VIV lock-in and it is defined as the ratio of the mass of the vibrating structure to the mass of the displaced fluid. The characteristic length scale factor
$m^{\ast }$
is a key parameter for VIV lock-in and it is defined as the ratio of the mass of the vibrating structure to the mass of the displaced fluid. The characteristic length scale factor
![]() $a_{s}$
is related to the geometry of the body. For example, the values are
$a_{s}$
is related to the geometry of the body. For example, the values are
![]() $a_{s}=2/\unicode[STIX]{x03C0}$
for a circular cylinder and
$a_{s}=2/\unicode[STIX]{x03C0}$
for a circular cylinder and
![]() $a_{s}=0.5$
for a square cylinder. There exists a complex dynamical relation between the transverse amplitude
$a_{s}=0.5$
for a square cylinder. There exists a complex dynamical relation between the transverse amplitude
![]() $Y$
and the lift force
$Y$
and the lift force
![]() $C_{l}$
. One of the main objectives of this work is to construct a state-space relationship between the transverse force and the amplitude directly from the NS equations subject to an impulse. We next proceed to the model reduction of the fluid–structure system.
$C_{l}$
. One of the main objectives of this work is to construct a state-space relationship between the transverse force and the amplitude directly from the NS equations subject to an impulse. We next proceed to the model reduction of the fluid–structure system.
The non-dimensional structural equation (2.13) can be cast into a state-space formulation as
where the state matrices and vectors are
It is straightforward to solve (2.14) using a standard time integrator (Yao & Jaiman Reference Yao and Jaiman2016). In the present work, an exact state-space discretization of (2.14) is considered as follows:
where the state matrices are
![]() $\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}\unicode[STIX]{x1D659}}=\text{e}^{\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}\unicode[STIX]{x0394}t}$
,
$\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}\unicode[STIX]{x1D659}}=\text{e}^{\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}\unicode[STIX]{x0394}t}$
,
![]() $\unicode[STIX]{x1D63D}_{\unicode[STIX]{x1D668}\unicode[STIX]{x1D659}}={\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}}^{-1}(\text{e}^{\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}\unicode[STIX]{x0394}t}-\unicode[STIX]{x1D644})\unicode[STIX]{x1D63D}_{\unicode[STIX]{x1D668}}$
at discrete times
$\unicode[STIX]{x1D63D}_{\unicode[STIX]{x1D668}\unicode[STIX]{x1D659}}={\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}}^{-1}(\text{e}^{\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}\unicode[STIX]{x0394}t}-\unicode[STIX]{x1D644})\unicode[STIX]{x1D63D}_{\unicode[STIX]{x1D668}}$
at discrete times
![]() $t=k\unicode[STIX]{x0394}t$
,
$t=k\unicode[STIX]{x0394}t$
,
![]() $k=0,1,2,\ldots ,$
with a constant sampling time
$k=0,1,2,\ldots ,$
with a constant sampling time
![]() $\unicode[STIX]{x0394}t$
,
$\unicode[STIX]{x0394}t$
,
![]() $\unicode[STIX]{x1D644}$
is an identity matrix of the same size as
$\unicode[STIX]{x1D644}$
is an identity matrix of the same size as
![]() $\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}$
, and
$\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D668}}$
, and
![]() $\unicode[STIX]{x1D63E}_{\unicode[STIX]{x1D668}\unicode[STIX]{x1D659}}=[1\;0]$
. Through the input–output dynamics, the fluid ROM is derived by the ERA method as described in (2.9). The input for the ROM is the transverse displacement
$\unicode[STIX]{x1D63E}_{\unicode[STIX]{x1D668}\unicode[STIX]{x1D659}}=[1\;0]$
. Through the input–output dynamics, the fluid ROM is derived by the ERA method as described in (2.9). The input for the ROM is the transverse displacement
![]() $Y$
, and the output is the lift coefficient
$Y$
, and the output is the lift coefficient
![]() $C_{l}$
. The ERA-based ROM with the single input and single output (SISO) can reformulated as
$C_{l}$
. The ERA-based ROM with the single input and single output (SISO) can reformulated as
By substituting (2.17) into (2.16), the resultant ROM can be expressed as
where
![]() $(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
are the ROM matrices defined by the ERA method as given in (2.9),
$(\unicode[STIX]{x1D63C}_{r},\unicode[STIX]{x1D63D}_{r},\unicode[STIX]{x1D63E}_{r},\unicode[STIX]{x1D63F}_{r})$
are the ROM matrices defined by the ERA method as given in (2.9),
![]() $\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}$
denotes the coupled fluid–structure matrix in the discrete state-space form and
$\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}$
denotes the coupled fluid–structure matrix in the discrete state-space form and
![]() $\unicode[STIX]{x1D66D}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}=[\unicode[STIX]{x1D66D}_{\unicode[STIX]{x1D668}}\;\;\unicode[STIX]{x1D66D}_{r}]^{\text{T}}$
.
$\unicode[STIX]{x1D66D}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}=[\unicode[STIX]{x1D66D}_{\unicode[STIX]{x1D668}}\;\;\unicode[STIX]{x1D66D}_{r}]^{\text{T}}$
.
The present ERA-based ROM reproduces the input–output dynamics of the full-order system. The linear stability analysis of the VIV system can be expressed as an eigenvalue problem of (2.18). The eigenvalue distribution of the coupled fluid–structure matrix
![]() $\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}$
characterizes the stability of the VIV system. Here, (
$\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}$
characterizes the stability of the VIV system. Here, (
![]() $\unicode[STIX]{x1D706},\widehat{\unicode[STIX]{x1D66D}}$
) correspond to continuous-time eigenvalue/eigenvectors of
$\unicode[STIX]{x1D706},\widehat{\unicode[STIX]{x1D66D}}$
) correspond to continuous-time eigenvalue/eigenvectors of
![]() $\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}$
, whereby the spatial structure is characterized by the complex vector field
$\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}$
, whereby the spatial structure is characterized by the complex vector field
![]() $\widehat{\unicode[STIX]{x1D66D}}$
and the temporal behaviour by the complex scalar
$\widehat{\unicode[STIX]{x1D66D}}$
and the temporal behaviour by the complex scalar
![]() $\unicode[STIX]{x1D706}$
. The stability analysis can be easily accomplished by tracing the trajectory of the complex eigenvalue
$\unicode[STIX]{x1D706}$
. The stability analysis can be easily accomplished by tracing the trajectory of the complex eigenvalue
![]() $\unicode[STIX]{x1D706}$
in the complex plane, whereby
$\unicode[STIX]{x1D706}$
in the complex plane, whereby
![]() $\widehat{\unicode[STIX]{x1D66D}}$
provides the spatial global modes of the ROM. Based on the leading global mode or least damped eigenvalue of the ERA-based ROM, we define a growth (amplification) rate
$\widehat{\unicode[STIX]{x1D66D}}$
provides the spatial global modes of the ROM. Based on the leading global mode or least damped eigenvalue of the ERA-based ROM, we define a growth (amplification) rate
![]() $\unicode[STIX]{x1D70E}=Re(\unicode[STIX]{x1D706})$
and frequency
$\unicode[STIX]{x1D70E}=Re(\unicode[STIX]{x1D706})$
and frequency
![]() $f=\text{Im}(\unicode[STIX]{x1D706}/2\unicode[STIX]{x03C0})$
. The construction of the above ERA-based ROM model is computationally efficient as it only relies on the impulse response of the FOM. While the aforementioned formulation is presented for transverse-only vibration of the structure, it is general for any coupled fluid–structure system. After reviewing the mathematical formulation and ERA-based ROM technique, we next present the numerical set-up and verification of our solver.
$f=\text{Im}(\unicode[STIX]{x1D706}/2\unicode[STIX]{x03C0})$
. The construction of the above ERA-based ROM model is computationally efficient as it only relies on the impulse response of the FOM. While the aforementioned formulation is presented for transverse-only vibration of the structure, it is general for any coupled fluid–structure system. After reviewing the mathematical formulation and ERA-based ROM technique, we next present the numerical set-up and verification of our solver.
3 Numerical set-up and verification
3.1 Problem definition
Figure 1 shows a schematic diagram of the set-up used in our simulation study for an elastically mounted bluff body with various cross-sections in a flowing stream. The coordinate origin is located at the geometric centre of the bluff body. The streamwise and transverse directions are denoted
![]() $x$
and
$x$
and
![]() $y$
respectively. A stream of incompressible fluid enters into the domain from an inlet boundary
$y$
respectively. A stream of incompressible fluid enters into the domain from an inlet boundary
![]() $\unicode[STIX]{x1D6E4}_{in}$
at a horizontal velocity
$\unicode[STIX]{x1D6E4}_{in}$
at a horizontal velocity
![]() $(u,v)=(U,0)$
, where
$(u,v)=(U,0)$
, where
![]() $u$
and
$u$
and
![]() $v$
denote the streamwise and transverse velocities respectively. The bluff body with mass
$v$
denote the streamwise and transverse velocities respectively. The bluff body with mass
![]() $m$
and characteristic diameter
$m$
and characteristic diameter
![]() $D$
is mounted on a linear spring in the transverse direction. The damping coefficient
$D$
is mounted on a linear spring in the transverse direction. The damping coefficient
![]() $\unicode[STIX]{x1D701}$
is set to zero in the present work. The computational domain and the boundary conditions are also illustrated in figure 1. A no-slip wall condition is implemented on the surfaces of the bluff body and a traction-free boundary condition is implemented along the outlet
$\unicode[STIX]{x1D701}$
is set to zero in the present work. The computational domain and the boundary conditions are also illustrated in figure 1. A no-slip wall condition is implemented on the surfaces of the bluff body and a traction-free boundary condition is implemented along the outlet
![]() $\unicode[STIX]{x1D6E4}_{out}$
, while a slip wall condition is implemented on the top
$\unicode[STIX]{x1D6E4}_{out}$
, while a slip wall condition is implemented on the top
![]() $\unicode[STIX]{x1D6E4}_{top}$
and bottom
$\unicode[STIX]{x1D6E4}_{top}$
and bottom
![]() $\unicode[STIX]{x1D6E4}_{bottom}$
boundaries. The numerical domain extends from
$\unicode[STIX]{x1D6E4}_{bottom}$
boundaries. The numerical domain extends from
![]() $-10D$
at the inlet to
$-10D$
at the inlet to
![]() $30D$
at the outlet and from
$30D$
at the outlet and from
![]() $-15D$
to
$-15D$
to
![]() $15D$
in the transverse direction. Except when stated otherwise, all positions and length scales are normalized by the characteristic dimension
$15D$
in the transverse direction. Except when stated otherwise, all positions and length scales are normalized by the characteristic dimension
![]() $D$
, velocities by the free-stream velocity
$D$
, velocities by the free-stream velocity
![]() $U$
and frequencies by
$U$
and frequencies by
![]() $U/D$
. The Reynolds number
$U/D$
. The Reynolds number
![]() $Re$
of the flow is based on the characteristic dimension
$Re$
of the flow is based on the characteristic dimension
![]() $D$
, the kinematic viscosity of the fluid and the free-stream speed
$D$
, the kinematic viscosity of the fluid and the free-stream speed
![]() $U$
.
$U$
.

Figure 1. Schematic diagram of a representative bluff body of an elastically mounted cylinder in a uniform horizontal flow. The computational domain and boundary conditions are shown.
3.2 Linear stability analysis
We verify the validity of our ERA-based ROM by investigating the stability of the laminar wake behind a two-dimensional circular cylinder. To study the mesh convergence for our simulation study, we consider three representative discretizations
![]() $M1$
,
$M1$
,
![]() $M2$
and
$M2$
and
![]() $M3$
consisting of 9517, 22 004 and 41 132
$M3$
consisting of 9517, 22 004 and 41 132
![]() $\mathbb{P}_{2}/\mathbb{P}_{1}$
iso-parametric elements. A representative M2 mesh is shown in figure 2, and the corresponding central square represents the fine mesh region around the cylinder body. The mesh in the cylinder wake is appropriately refined to resolve the alternate vortex shedding. The quality of the mesh convergence is determined by the prediction of the growth rate
$\mathbb{P}_{2}/\mathbb{P}_{1}$
iso-parametric elements. A representative M2 mesh is shown in figure 2, and the corresponding central square represents the fine mesh region around the cylinder body. The mesh in the cylinder wake is appropriately refined to resolve the alternate vortex shedding. The quality of the mesh convergence is determined by the prediction of the growth rate
![]() $\unicode[STIX]{x1D70E}$
and the frequency
$\unicode[STIX]{x1D70E}$
and the frequency
![]() $f$
of the fluid ROM for the flow past a circular cylinder at
$f$
of the fluid ROM for the flow past a circular cylinder at
![]() $Re=60$
. The non-dimensional time-step size is
$Re=60$
. The non-dimensional time-step size is
![]() $\unicode[STIX]{x0394}t=0.05$
. Based on the procedure described in the previous section, we next briefly describe the process of extracting ROMs from the incompressible NS equations.
$\unicode[STIX]{x0394}t=0.05$
. Based on the procedure described in the previous section, we next briefly describe the process of extracting ROMs from the incompressible NS equations.

Figure 2. A representative finite element mesh with
![]() $\mathbb{P}_{2}/\mathbb{P}_{1}$
discretization: (a) full domain discretization and (b) close-up view of the finite element mesh in the vicinity of the cylinder. All other meshes for different bluff-body geometries are similarly created.
$\mathbb{P}_{2}/\mathbb{P}_{1}$
discretization: (a) full domain discretization and (b) close-up view of the finite element mesh in the vicinity of the cylinder. All other meshes for different bluff-body geometries are similarly created.

Figure 3. Base flow of a stationary circular cylinder at
![]() $Re=60$
; the streamwise velocity contours are shown. The contour levels are from
$Re=60$
; the streamwise velocity contours are shown. The contour levels are from
![]() $-$
0.1 to 1.2 in increments of 0.1 and the flow is from left to right.
$-$
0.1 to 1.2 in increments of 0.1 and the flow is from left to right.
The ERA-based ROM is constructed in the neighbourhood of the base flow, which is computed via fixed-point iteration without the time-dependent term in (2.1). At
![]() $Re=60$
with the
$Re=60$
with the
![]() $M2$
mesh, figure 3 shows the streamwise velocity contours of the base flow with a symmetric recirculation bubble. The bubble length (measured from the centre of the cylinder) is
$M2$
mesh, figure 3 shows the streamwise velocity contours of the base flow with a symmetric recirculation bubble. The bubble length (measured from the centre of the cylinder) is
![]() $L_{w}=4.1$
, which agrees reasonably well with literature values (
$L_{w}=4.1$
, which agrees reasonably well with literature values (
![]() $L_{w}=4.2$
, Giannetti & Luchini (Reference Giannetti and Luchini2007);
$L_{w}=4.2$
, Giannetti & Luchini (Reference Giannetti and Luchini2007);
![]() $L_{w}=4.1$
, Mao & Blackburn (Reference Mao and Blackburn2014)). The Hankel matrix shown in (2.10) is obtained from the output lift signal (
$L_{w}=4.1$
, Mao & Blackburn (Reference Mao and Blackburn2014)). The Hankel matrix shown in (2.10) is obtained from the output lift signal (
![]() $C_{l}$
) subject to the impulse input of the transverse displacement
$C_{l}$
) subject to the impulse input of the transverse displacement
![]() $Y$
. A sufficiently small amplitude (
$Y$
. A sufficiently small amplitude (
![]() $\unicode[STIX]{x1D6FF}=10^{-4}$
) is considered such that the flow evolves linearly for a relatively large time. To ensure that the unstable modes start to dominate the essential dynamics of the input–output relationship, an adequate number of cycles is required to capture the linear dynamics of the system. However, an excessively long simulation time should be avoided before the nonlinearity appears via exponential growth of the unstable modes.
$\unicode[STIX]{x1D6FF}=10^{-4}$
) is considered such that the flow evolves linearly for a relatively large time. To ensure that the unstable modes start to dominate the essential dynamics of the input–output relationship, an adequate number of cycles is required to capture the linear dynamics of the system. However, an excessively long simulation time should be avoided before the nonlinearity appears via exponential growth of the unstable modes.
The linearity of the unstable system is confirmed by comparing the response subject to two impulse inputs with
![]() $\unicode[STIX]{x1D6FF}=10^{-4}$
and
$\unicode[STIX]{x1D6FF}=10^{-4}$
and
![]() $\unicode[STIX]{x1D6FF}=10^{-3}$
. A set of
$\unicode[STIX]{x1D6FF}=10^{-3}$
. A set of
![]() $1000$
impulse response outputs (
$1000$
impulse response outputs (
![]() $C_{l}$
) is then stacked at each time step
$C_{l}$
) is then stacked at each time step
![]() $\unicode[STIX]{x0394}t=0.05$
, resulting in the final simulation time
$\unicode[STIX]{x0394}t=0.05$
, resulting in the final simulation time
![]() $tU/D=50$
. The adequate number of simulation cycles is then determined by examining the convergence of the fluid unstable eigenvalues computed from Hankel matrices with dimensions of
$tU/D=50$
. The adequate number of simulation cycles is then determined by examining the convergence of the fluid unstable eigenvalues computed from Hankel matrices with dimensions of
![]() $500\times 20$
,
$500\times 20$
,
![]() $500\times 50$
,
$500\times 50$
,
![]() $500\times 150$
and
$500\times 150$
and
![]() $500\times 200$
. It is found that the
$500\times 200$
. It is found that the
![]() $500\times 150$
Hankel matrix is sufficient, which corresponds to 32.5 convective time units. The order of the ERA-based ROM is then determined by examining the singular values (HSVs) of the Hankel
$500\times 150$
Hankel matrix is sufficient, which corresponds to 32.5 convective time units. The order of the ERA-based ROM is then determined by examining the singular values (HSVs) of the Hankel
![]() $500\times 150$
matrix. As shown in figure 4(a), the output lift signal
$500\times 150$
matrix. As shown in figure 4(a), the output lift signal
![]() $C_{l}$
gradually diverges as a function of the convective time
$C_{l}$
gradually diverges as a function of the convective time
![]() $tU/D$
at
$tU/D$
at
![]() $Re=60$
. This asymptotic divergence behaviour indicates that the wake flow begins to lose its stability via a Hopf bifurcation, which breaks the symmetry of the flow field and gives rise to a periodic vortex street. The first
$Re=60$
. This asymptotic divergence behaviour indicates that the wake flow begins to lose its stability via a Hopf bifurcation, which breaks the symmetry of the flow field and gives rise to a periodic vortex street. The first
![]() $30$
singular values are shown in figure 4(b). The rapidly decaying singular values indicate that a low-order ROM can be constructed. To further confirm the accuracy, the ERA-based ROM with a number of modes of
$30$
singular values are shown in figure 4(b). The rapidly decaying singular values indicate that a low-order ROM can be constructed. To further confirm the accuracy, the ERA-based ROM with a number of modes of
![]() $n_{r}=25$
is compared with the FOM result in figure 4(a). A good match between the impulse responses of the ROM and FOM can be seen in the figure. It is worth noting that it is not necessary for the Hankel matrix to be a square matrix for the suitability of the ERA-based ROM (Juang & Pappa Reference Juang and Pappa1985). As pointed by Juang & Pappa (Reference Juang and Pappa1985), further consideration is required to determine the optimal
$n_{r}=25$
is compared with the FOM result in figure 4(a). A good match between the impulse responses of the ROM and FOM can be seen in the figure. It is worth noting that it is not necessary for the Hankel matrix to be a square matrix for the suitability of the ERA-based ROM (Juang & Pappa Reference Juang and Pappa1985). As pointed by Juang & Pappa (Reference Juang and Pappa1985), further consideration is required to determine the optimal
![]() $r$
and
$r$
and
![]() $s$
in (2.10). Therefore, the Hankel matrix can be tall (
$s$
in (2.10). Therefore, the Hankel matrix can be tall (
![]() $r>s$
), wide (
$r>s$
), wide (
![]() $r<s$
) or square (
$r<s$
) or square (
![]() $r=s$
). In the present study, the dimension
$r=s$
). In the present study, the dimension
![]() $r$
is fixed while
$r$
is fixed while
![]() $s$
is tuned to obtain a reasonably converged unstable eigenvalue for a good match between the impulse response of the FOM and ROM.
$s$
is tuned to obtain a reasonably converged unstable eigenvalue for a good match between the impulse response of the FOM and ROM.

Figure 4. The ERA-based ROM for the unstable wake behind a stationary circular cylinder at
![]() $Re=60$
: (a) lift history of the FOM and the ROM based on linearized dynamics subject to the impulse response and (b) HSV distribution corresponding to a
$Re=60$
: (a) lift history of the FOM and the ROM based on linearized dynamics subject to the impulse response and (b) HSV distribution corresponding to a
![]() $500\times 150$
Hankel matrix.
$500\times 150$
Hankel matrix.
Table 1 summarizes the comparison of the growth rate and frequency, which shows that the difference between
![]() $M2$
and
$M2$
and
![]() $M3$
is less than
$M3$
is less than
![]() $1\,\%$
. Therefore, the mesh
$1\,\%$
. Therefore, the mesh
![]() $M2$
is adequate for the stability analysis of VIV. This study also confirms the convergence properties of our ERA-based ROM procedure for unstable wake flow. For further verification, we next show that the ERA-based ROM is able to accurately predict the onset of the unstable wake state due to a Hopf bifurcation. The onset of the unstable wake is commonly determined by the linearized NS equations in the literature (Giannetti & Luchini Reference Giannetti and Luchini2007; Marquet et al.
Reference Marquet, Sipp and Jacquin2008; Mettot et al.
Reference Mettot, Renac and Sipp2014). The growth rate
$M2$
is adequate for the stability analysis of VIV. This study also confirms the convergence properties of our ERA-based ROM procedure for unstable wake flow. For further verification, we next show that the ERA-based ROM is able to accurately predict the onset of the unstable wake state due to a Hopf bifurcation. The onset of the unstable wake is commonly determined by the linearized NS equations in the literature (Giannetti & Luchini Reference Giannetti and Luchini2007; Marquet et al.
Reference Marquet, Sipp and Jacquin2008; Mettot et al.
Reference Mettot, Renac and Sipp2014). The growth rate
![]() $\unicode[STIX]{x1D70E}$
and the frequency
$\unicode[STIX]{x1D70E}$
and the frequency
![]() $f$
are plotted as a function of the Reynolds number in figure 5. Instability of the base flow occurs when the growth rate crosses the
$f$
are plotted as a function of the Reynolds number in figure 5. Instability of the base flow occurs when the growth rate crosses the
![]() $\unicode[STIX]{x1D70E}=0$
line at the critical Reynolds number
$\unicode[STIX]{x1D70E}=0$
line at the critical Reynolds number
![]() $Re_{cr}\approx 46.8$
, which is in good agreement with the numerical prediction of Giannetti & Luchini (Reference Giannetti and Luchini2007) and Marquet et al. (Reference Marquet, Sipp and Jacquin2008) and the experimental measurement of Williamson (Reference Williamson1996). The frequency predicted by the ERA-based ROM at this critical Reynolds number is
$Re_{cr}\approx 46.8$
, which is in good agreement with the numerical prediction of Giannetti & Luchini (Reference Giannetti and Luchini2007) and Marquet et al. (Reference Marquet, Sipp and Jacquin2008) and the experimental measurement of Williamson (Reference Williamson1996). The frequency predicted by the ERA-based ROM at this critical Reynolds number is
![]() $f=0.119$
, which matches quite well with the results of Giannetti & Luchini (Reference Giannetti and Luchini2007) and Marquet et al. (Reference Marquet, Sipp and Jacquin2008). However, it is worth noting that the frequency given by the linear model is only valid in the vicinity of the critical Reynolds number and fails to capture the frequency in the region far away from the critical point, where nonlinear effects start to dominate the wake dynamics.
$f=0.119$
, which matches quite well with the results of Giannetti & Luchini (Reference Giannetti and Luchini2007) and Marquet et al. (Reference Marquet, Sipp and Jacquin2008). However, it is worth noting that the frequency given by the linear model is only valid in the vicinity of the critical Reynolds number and fails to capture the frequency in the region far away from the critical point, where nonlinear effects start to dominate the wake dynamics.
To extract the most energetic structures via the POD method, snapshots of the flow solutions are stored during the process of the ROM construction, i.e. the flow solution is recorded at each physical time step subjected to the impulse response. For the unstable wake case at
![]() $Re_{cr}\approx 46.8$
, the first POD mode corresponding to the streamwise and cross-flow velocity is shown in figure 6. The spatial structures are antisymmetric and they travel downstream with the formation of Kelvin–Helmholtz instabilities.
$Re_{cr}\approx 46.8$
, the first POD mode corresponding to the streamwise and cross-flow velocity is shown in figure 6. The spatial structures are antisymmetric and they travel downstream with the formation of Kelvin–Helmholtz instabilities.

Figure 5. Prediction of the critical Reynolds number via the ERA-based ROM for the flow past a stationary circular cylinder: (a) growth rate
![]() $\unicode[STIX]{x1D70E}$
and (b) frequency
$\unicode[STIX]{x1D70E}$
and (b) frequency
![]() $f$
. The cylinder wake becomes unstable when the growth rate crosses the
$f$
. The cylinder wake becomes unstable when the growth rate crosses the
![]() $\unicode[STIX]{x1D70E}=0$
line at the critical
$\unicode[STIX]{x1D70E}=0$
line at the critical
![]() $Re_{cr}\approx 46.8$
and vortex shedding emanates.
$Re_{cr}\approx 46.8$
and vortex shedding emanates.

Figure 6. The first POD mode at
![]() $Re_{cr}\approx 46.8$
: (a) streamwise velocity and (b) cross-stream velocity. The flow is from left to right.
$Re_{cr}\approx 46.8$
: (a) streamwise velocity and (b) cross-stream velocity. The flow is from left to right.
Table 1. Mesh convergence study: comparison of growth rate and frequency for meshes
![]() $M1$
,
$M1$
,
![]() $M2$
and
$M2$
and
![]() $M3$
for the flow past a stationary circular cylinder at
$M3$
for the flow past a stationary circular cylinder at
![]() $Re=60$
.
$Re=60$
.

3.3 Unstable flow past a stationary cylinder
As discussed in § 3.2, the wake flow becomes unstable through a Hopf bifurcation when
![]() $Re>Re_{cr}$
and vortex shedding appears behind a stationary cylinder at the frequency
$Re>Re_{cr}$
and vortex shedding appears behind a stationary cylinder at the frequency
![]() $f_{vs}$
. The unstable flow finally reaches a fully nonlinear state with the alternate time-periodic vortex shedding. The flow field in the whole domain behaves like a global oscillator, which causes unsteady lift and drag forces on the immersed body. To further establish the validity of the numerical method and the desired accuracy for the VIV simulation, the dimensionless vortex shedding frequency
$f_{vs}$
. The unstable flow finally reaches a fully nonlinear state with the alternate time-periodic vortex shedding. The flow field in the whole domain behaves like a global oscillator, which causes unsteady lift and drag forces on the immersed body. To further establish the validity of the numerical method and the desired accuracy for the VIV simulation, the dimensionless vortex shedding frequency
![]() $St=f_{vs}D/U$
and the root mean square (r.m.s.) value of the lift coefficient
$St=f_{vs}D/U$
and the root mean square (r.m.s.) value of the lift coefficient
![]() $C_{l}$
are compared with the works of Williamson (Reference Williamson1989) and Zhang et al. (Reference Zhang, Fey, Noack, Knig and Eckelmann1995) for the Reynolds number
$C_{l}$
are compared with the works of Williamson (Reference Williamson1989) and Zhang et al. (Reference Zhang, Fey, Noack, Knig and Eckelmann1995) for the Reynolds number
![]() $Re<180$
. The results are summarized in table 2, which demonstrates good agreement with the literature. This further confirms that the numerical methodology and the mesh discretization are adequate to capture the vortex dynamics and the stability characteristics of the VIV response.
$Re<180$
. The results are summarized in table 2, which demonstrates good agreement with the literature. This further confirms that the numerical methodology and the mesh discretization are adequate to capture the vortex dynamics and the stability characteristics of the VIV response.
Table 2. Comparison of the r.m.s. value of the lift coefficient (
![]() $C_{l}$
) and the Strouhal number
$C_{l}$
) and the Strouhal number
![]() $(St)$
obtained with previous studies for a range of Reynolds numbers. A constant time-step size
$(St)$
obtained with previous studies for a range of Reynolds numbers. A constant time-step size
![]() $\unicode[STIX]{x0394}t=0.05$
is employed for the present computations.
$\unicode[STIX]{x0394}t=0.05$
is employed for the present computations.

4 Results and discussion
4.1 Assessment of the ERA-based ROM
In this section, the constructed ERA-based ROM is first applied to analyse the stability properties of a transversely vibrating circular cylinder at
![]() $(Re,m^{\ast })=(60,10)$
. Consistent with the previous literature of Meliga & Chomaz (Reference Meliga and Chomaz2011) and Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), we use the terminology of SM and WM to classify the distinct eigenvalue trajectories of the linear fluid–structure system governed by (2.18). When the eigenvalue of the fluid–structure system approaches that of the stationary cylinder, the resulting mode is defined as a WM. The fluid–structure mode is considered as an SM if the eigenvalue comes close to the natural frequency of the cylinder-alone system.
$(Re,m^{\ast })=(60,10)$
. Consistent with the previous literature of Meliga & Chomaz (Reference Meliga and Chomaz2011) and Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), we use the terminology of SM and WM to classify the distinct eigenvalue trajectories of the linear fluid–structure system governed by (2.18). When the eigenvalue of the fluid–structure system approaches that of the stationary cylinder, the resulting mode is defined as a WM. The fluid–structure mode is considered as an SM if the eigenvalue comes close to the natural frequency of the cylinder-alone system.
As discussed in Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), VIV lock-in may result either from instability of the WM alone or via simultaneous existence of unstable SM and WM. In the event of the first scenario, the lock-in occurs due to the closeness of the frequencies of the WM and SM. This type of VIV branch is termed as resonance-induced lock-in. For the second scenario, the instability to sustain the VIV lock-in occurs via combined mode instability of the SM and WM, which is referred to as flutter-induced lock-in or coupled-mode flutter (De Langre Reference De Langre2006). In the present study, the WM is also considered as the leading mode of the unstable fluid system.
We consider the continuous-time eigenvalues in the context of linear stability analysis via the ERA-based ROM. Using the fluid–structure matrix (2.18), the eigenvalue is obtained from
![]() $\unicode[STIX]{x1D706}=\text{log}(\text{eig}(\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}))/\unicode[STIX]{x0394}t$
, where
$\unicode[STIX]{x1D706}=\text{log}(\text{eig}(\unicode[STIX]{x1D63C}_{\unicode[STIX]{x1D65B}\unicode[STIX]{x1D668}}))/\unicode[STIX]{x0394}t$
, where
![]() $\unicode[STIX]{x0394}t=0.05$
is the time step. To graphically depict the dynamical behaviour, we study the eigenvalue distribution of the system in the complex plane via the root locus. The positions of the eigenvalues provide the information about the stability of the fluid–structure system. For example, the roots in the right half-plane depict the unstable modes of the system, whereas the roots on the real axis characterize the asymptotic (non-oscillatory) behaviour. Roots that are closest to the right half-plane are lightly damped oscillatory modes.
$\unicode[STIX]{x0394}t=0.05$
is the time step. To graphically depict the dynamical behaviour, we study the eigenvalue distribution of the system in the complex plane via the root locus. The positions of the eigenvalues provide the information about the stability of the fluid–structure system. For example, the roots in the right half-plane depict the unstable modes of the system, whereas the roots on the real axis characterize the asymptotic (non-oscillatory) behaviour. Roots that are closest to the right half-plane are lightly damped oscillatory modes.

Figure 7. Eigenspectrum of the ERA-based ROM for a circular cylinder at
![]() $(Re,m^{\ast })=(60,10)$
: (a) root loci as a function of the reduced natural frequency
$(Re,m^{\ast })=(60,10)$
: (a) root loci as a function of the reduced natural frequency
![]() $F_{s}$
, where the unstable right half-plane
$F_{s}$
, where the unstable right half-plane
![]() $(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
$(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
![]() $F_{s}$
; (b) real and imaginary parts of the root loci, where the lock-in region is shaded in grey colour. Two branches of lock-in, namely resonance and flutter, can be seen in (b).
$F_{s}$
; (b) real and imaginary parts of the root loci, where the lock-in region is shaded in grey colour. Two branches of lock-in, namely resonance and flutter, can be seen in (b).
Figure 7(a) shows the eigenvalue trajectory of the fluid–structure system as a function of the reduced natural frequency
![]() $F_{s}$
with
$F_{s}$
with
![]() $0.05\leqslant F_{s}\leqslant 0.25$
and the increment is
$0.05\leqslant F_{s}\leqslant 0.25$
and the increment is
![]() $\unicode[STIX]{x0394}F_{s}=0.025$
. In the figure, the WM branch originates in the vicinity of the eigenvalue of the stationary cylinder (uncoupled WM) and loops back as the reduced natural frequency
$\unicode[STIX]{x0394}F_{s}=0.025$
. In the figure, the WM branch originates in the vicinity of the eigenvalue of the stationary cylinder (uncoupled WM) and loops back as the reduced natural frequency
![]() $F_{s}$
increases. It is expected that the WM will finally recover to the eigenvalue of the stationary cylinder as
$F_{s}$
increases. It is expected that the WM will finally recover to the eigenvalue of the stationary cylinder as
![]() $F_{s}$
approaches infinity or the cylinder becomes stationary (i.e. without elastic mounting). It is also evident that the WM remains unstable (
$F_{s}$
approaches infinity or the cylinder becomes stationary (i.e. without elastic mounting). It is also evident that the WM remains unstable (
![]() $\unicode[STIX]{x1D70E}>0$
) throughout the sweeping as
$\unicode[STIX]{x1D70E}>0$
) throughout the sweeping as
![]() $Re=60>Re_{cr}$
. On the other hand, the SM branch rises from the bottom of the complex plane (low-frequency regime) to the upper complex plane (high-frequency regime). As elucidated in figure 7(b), the SM becomes unstable only when
$Re=60>Re_{cr}$
. On the other hand, the SM branch rises from the bottom of the complex plane (low-frequency regime) to the upper complex plane (high-frequency regime). As elucidated in figure 7(b), the SM becomes unstable only when
![]() $0.147<F_{s}\leqslant 0.179$
, which is determined by the real part of the eigenvalue. As mentioned earlier, the unstable SM phenomenon can be considered as coupled-mode flutter or combined mode instability. As shown in figure 7(b), the imaginary part of the eigenvalue as a function of
$0.147<F_{s}\leqslant 0.179$
, which is determined by the real part of the eigenvalue. As mentioned earlier, the unstable SM phenomenon can be considered as coupled-mode flutter or combined mode instability. As shown in figure 7(b), the imaginary part of the eigenvalue as a function of
![]() $F_{s}$
reveals that two distinct frequencies (WM and SM frequencies) co-exist in the combined mode instability. In addition, figure 7(b) also indicates that the frequencies of the WM and SM come closer when
$F_{s}$
reveals that two distinct frequencies (WM and SM frequencies) co-exist in the combined mode instability. In addition, figure 7(b) also indicates that the frequencies of the WM and SM come closer when
![]() $0.11\leqslant F_{s}\leqslant 0.147$
, which is recognized as the resonance mode. It should be noted that the lower left boundary of the resonance mode cannot be pinpointed precisely from the ROM due to the overlapping of the SM and WM trajectories. Thus, we determine the frequency at the lower left boundary from the FOM simulation, which is found to be
$0.11\leqslant F_{s}\leqslant 0.147$
, which is recognized as the resonance mode. It should be noted that the lower left boundary of the resonance mode cannot be pinpointed precisely from the ROM due to the overlapping of the SM and WM trajectories. Thus, we determine the frequency at the lower left boundary from the FOM simulation, which is found to be
![]() $F_{s}=0.11$
.
$F_{s}=0.11$
.
To further verify the stability results predicted by the ERA-based ROM, the VIV response is computed by direct numerical simulation using the FOM. As shown in figure 8(a), the vortex shedding frequency begins to synchronize with the natural frequency of the structure at
![]() $F_{s}=0.11$
and recovers to the vortex shedding frequency at
$F_{s}=0.11$
and recovers to the vortex shedding frequency at
![]() $F_{s}=0.179$
. As the nonlinearity starts to dominate the VIV response, the two distinct frequencies of the WM and SM corresponding to the flutter mode are eventually synchronized with the natural frequency of the structure
$F_{s}=0.179$
. As the nonlinearity starts to dominate the VIV response, the two distinct frequencies of the WM and SM corresponding to the flutter mode are eventually synchronized with the natural frequency of the structure
![]() $F_{s}$
. Figure 8(b) suggests that the cylinder rises to the peak VIV amplitude at
$F_{s}$
. Figure 8(b) suggests that the cylinder rises to the peak VIV amplitude at
![]() $F_{s}=0.179$
(lock-in onset
$F_{s}=0.179$
(lock-in onset
![]() $U_{r}\approx 5.59$
), which compares accurately with the upper boundary of the flutter mode predicted by the present ERA-based ROM.
$U_{r}\approx 5.59$
), which compares accurately with the upper boundary of the flutter mode predicted by the present ERA-based ROM.
It is worth mentioning that the cylinder acquires the maximum amplitude at
![]() $F_{s}=0.179$
or
$F_{s}=0.179$
or
![]() $F_{s}/St=1.31$
, which is not at
$F_{s}/St=1.31$
, which is not at
![]() $F_{s}/St\approx 1$
, as expected from the classical resonance interpretation of VIV lock-in. This phenomenon suggests that the onset of VIV lock-in results from the amplification of energy input as a consequence of an unstable SM, in which the structure is able to optimally absorb energy from the surrounding fluid system. This is analogous to the pitch and plunge flutter observed in the aeroelastic airfoil configuration. The flutter mode of VIV lock-in results from the coupling of periodic vortex shedding and the structural transverse displacement. In the flutter regime (
$F_{s}/St\approx 1$
, as expected from the classical resonance interpretation of VIV lock-in. This phenomenon suggests that the onset of VIV lock-in results from the amplification of energy input as a consequence of an unstable SM, in which the structure is able to optimally absorb energy from the surrounding fluid system. This is analogous to the pitch and plunge flutter observed in the aeroelastic airfoil configuration. The flutter mode of VIV lock-in results from the coupling of periodic vortex shedding and the structural transverse displacement. In the flutter regime (
![]() $1.07<F_{s}/St\leqslant 1.31$
), the unstable SM and WM jointly sustain VIV lock-in, whereas the WM dominates the resonance regime (
$1.07<F_{s}/St\leqslant 1.31$
), the unstable SM and WM jointly sustain VIV lock-in, whereas the WM dominates the resonance regime (
![]() $0.8\leqslant F_{s}/St\leqslant 1.07$
) until the VIV goes into the lock-out region.
$0.8\leqslant F_{s}/St\leqslant 1.07$
) until the VIV goes into the lock-out region.

Figure 8. The VIV results as a function of the reduced natural frequency
![]() $F_{s}$
using the FOM at
$F_{s}$
using the FOM at
![]() $(Re,m^{\ast })=(60,10)$
: variation of (a) the normalized vortex shedding frequency
$(Re,m^{\ast })=(60,10)$
: variation of (a) the normalized vortex shedding frequency
![]() $f$
and (b) the r.m.s. value of the lift coefficient (
$f$
and (b) the r.m.s. value of the lift coefficient (
![]() $C_{l}$
) and the normalized maximum amplitude (
$C_{l}$
) and the normalized maximum amplitude (
![]() $Y_{max}$
). The lock-in is shaded in grey colour.
$Y_{max}$
). The lock-in is shaded in grey colour.
More quantitative insight into the VIV lock-in mechanism can be obtained from figure 9(a), which shows the phase angle
![]() $\unicode[STIX]{x1D719}$
estimated by the ERA-based ROM (see appendix A). The phase angle
$\unicode[STIX]{x1D719}$
estimated by the ERA-based ROM (see appendix A). The phase angle
![]() $\unicode[STIX]{x1D719}$
of the ROM is a function of (
$\unicode[STIX]{x1D719}$
of the ROM is a function of (
![]() $F_{s},\unicode[STIX]{x1D706}$
) and its sign is determined by the real part of the eigenvalues. The instantaneous phase angle of the FOM is obtained by the Hilbert transformation of lift and displacement, as described in Tham et al. (Reference Tham, Gurugubelli, Li and Jaiman2015). In figure 9(a), we present the phase angles of the FOM and ROM as functions of
$F_{s},\unicode[STIX]{x1D706}$
) and its sign is determined by the real part of the eigenvalues. The instantaneous phase angle of the FOM is obtained by the Hilbert transformation of lift and displacement, as described in Tham et al. (Reference Tham, Gurugubelli, Li and Jaiman2015). In figure 9(a), we present the phase angles of the FOM and ROM as functions of
![]() $F_{s}$
at
$F_{s}$
at
![]() $(Re,m^{\ast })=(60,10)$
. Compared with the FOM result, the WM trajectory yields a continuous transition from
$(Re,m^{\ast })=(60,10)$
. Compared with the FOM result, the WM trajectory yields a continuous transition from
![]() $0^{\circ }$
to
$0^{\circ }$
to
![]() $180^{\circ }$
as
$180^{\circ }$
as
![]() $F_{s}$
decreases in the lock-in region. In contrast, the phase angle of the SM remains positive only within the flutter mode (
$F_{s}$
decreases in the lock-in region. In contrast, the phase angle of the SM remains positive only within the flutter mode (
![]() $0.147<F_{s}\leqslant 0.179$
).
$0.147<F_{s}\leqslant 0.179$
).

Figure 9. The VIV results as a function of the reduced natural frequency
![]() $F_{s}$
at
$F_{s}$
at
![]() $(Re,m^{\ast })=(60,10)$
: (a) comparison of phase angle difference
$(Re,m^{\ast })=(60,10)$
: (a) comparison of phase angle difference
![]() $\unicode[STIX]{x1D719}$
between the ERA-based ROM and the FOM, where the lock-in is shaded in grey colour; (b) lift
$\unicode[STIX]{x1D719}$
between the ERA-based ROM and the FOM, where the lock-in is shaded in grey colour; (b) lift
![]() $C_{l}$
history at two representative frequencies
$C_{l}$
history at two representative frequencies
![]() $F_{s}=(0.14,0.177)$
. In (a), (– - – - –) represents
$F_{s}=(0.14,0.177)$
. In (a), (– - – - –) represents
![]() $F_{s}=0.13$
.
$F_{s}=0.13$
.
It is also interesting to note from figure 8(b) that the lift coefficient is significantly amplified in the vicinity of the VIV lock-in onset reduced velocity (
![]() $U_{r}\approx 5.59$
). A gradual decrease and eventually recovery to the value of the stationary cylinder counterpart as
$U_{r}\approx 5.59$
). A gradual decrease and eventually recovery to the value of the stationary cylinder counterpart as
![]() $U_{r}$
increases (
$U_{r}$
increases (
![]() $F_{s}$
decreases) can be seen in the figure. To further assess the behaviour of the lift coefficient in the flutter and resonance regimes, the lift histories for two representative reduced frequencies
$F_{s}$
decreases) can be seen in the figure. To further assess the behaviour of the lift coefficient in the flutter and resonance regimes, the lift histories for two representative reduced frequencies
![]() $F_{s}=0.177$
and 0.140 are compared in figure 9(b). The minimum r.m.s. value of the lift coefficient
$F_{s}=0.177$
and 0.140 are compared in figure 9(b). The minimum r.m.s. value of the lift coefficient
![]() $C_{l}$
occurs at
$C_{l}$
occurs at
![]() $F_{s}\approx 0.13$
or
$F_{s}\approx 0.13$
or
![]() $F_{s}/St\approx 0.95$
, which coincides with the phase angle jump, as shown in figure 9(a). Therefore, we can infer that the reduction in the r.m.s. lift coefficient has a direct relation with the phase angle. In § 4.2, we further confirm that the lift reduction is not associated with the resonance mode.
$F_{s}/St\approx 0.95$
, which coincides with the phase angle jump, as shown in figure 9(a). Therefore, we can infer that the reduction in the r.m.s. lift coefficient has a direct relation with the phase angle. In § 4.2, we further confirm that the lift reduction is not associated with the resonance mode.
Geometric and physical parameters such as the cross-sectional shape and mass ratio play an important role with regard to the coupling strength of the fluid–structure interaction. A classification of the fluid–structure eigenmodes as WM and SM is suitable for weak fluid–structure interaction (e.g. very large mass ratio), which is elucidated in figure 7 by two distinct eigenvalue branches of the WM and SM. Owing to weaker fluid–structure coupling at large
![]() $m^{\ast }$
(i.e. in the limit of
$m^{\ast }$
(i.e. in the limit of
![]() $m^{\ast }\rightarrow \infty$
), the eigenfrequency of the WM approaches that of the stationary cylinder wake for all values of
$m^{\ast }\rightarrow \infty$
), the eigenfrequency of the WM approaches that of the stationary cylinder wake for all values of
![]() $F_{s}$
and the frequency of the SM comes close to the natural frequency of the cylinder-only system. However, the root loci of the WM and SM can coalesce and form coupled modes in certain conditions, such as in the limit of low mass ratio (Meliga & Chomaz Reference Meliga and Chomaz2011; Navrose & Mittal Reference Mittal2016) and for different geometrical shapes, as demonstrated in § 4.4. These coupled modes do not offer distinct characteristics of the WM and SM, since the two branches exchange their roles when coalescence of eigenvalue occurs. Similarly to Navrose & Mittal (Reference Mittal2016), we term these mixed or coupled modes as wake–structure mode I (WSMI) and wake–structure mode II (WSMII). For higher values of
$F_{s}$
and the frequency of the SM comes close to the natural frequency of the cylinder-only system. However, the root loci of the WM and SM can coalesce and form coupled modes in certain conditions, such as in the limit of low mass ratio (Meliga & Chomaz Reference Meliga and Chomaz2011; Navrose & Mittal Reference Mittal2016) and for different geometrical shapes, as demonstrated in § 4.4. These coupled modes do not offer distinct characteristics of the WM and SM, since the two branches exchange their roles when coalescence of eigenvalue occurs. Similarly to Navrose & Mittal (Reference Mittal2016), we term these mixed or coupled modes as wake–structure mode I (WSMI) and wake–structure mode II (WSMII). For higher values of
![]() $F_{s}$
, WSMI behaves as the WM and WSMII recovers to the SM. On the other hand, for a smaller
$F_{s}$
, WSMI behaves as the WM and WSMII recovers to the SM. On the other hand, for a smaller
![]() $F_{s}$
range, WSMI and WSMII represent the SM and WM respectively. A characteristic anticrossing with a frequency splitting can be also observed at low mass ratios, which is one of the traits of strongly coupled harmonic oscillators (Novotny Reference Novotny2010). To demonstrate the effect of the mass ratio, further details on the coupled modes WSMI and WSMII are discussed in appendix B.
$F_{s}$
range, WSMI and WSMII represent the SM and WM respectively. A characteristic anticrossing with a frequency splitting can be also observed at low mass ratios, which is one of the traits of strongly coupled harmonic oscillators (Novotny Reference Novotny2010). To demonstrate the effect of the mass ratio, further details on the coupled modes WSMI and WSMII are discussed in appendix B.

Figure 10. The effect of the Reynolds number on the eigenspectrum of the ERA-based ROM at
![]() $Re=(60,70,100)$
and
$Re=(60,70,100)$
and
![]() $m^{\ast }=10$
: (a) root loci as a function of the reduced natural frequency
$m^{\ast }=10$
: (a) root loci as a function of the reduced natural frequency
![]() $F_{s}$
, where the unstable right half-plane
$F_{s}$
, where the unstable right half-plane
![]() $(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
$(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
![]() $F_{s}$
; (b) the real and imaginary parts of the root loci. The SM data points are denoted by the filled symbols with the same shape as the WM points in (a,b). The boundary of
$F_{s}$
; (b) the real and imaginary parts of the root loci. The SM data points are denoted by the filled symbols with the same shape as the WM points in (a,b). The boundary of
![]() $\text{Re}(\unicode[STIX]{x1D706})>0$
for SM at
$\text{Re}(\unicode[STIX]{x1D706})>0$
for SM at
![]() $Re=70$
is defined at
$Re=70$
is defined at
![]() $F_{s}=0.106$
(– – –) and
$F_{s}=0.106$
(– – –) and
![]() $F_{s}=0.187$
(– - – - –) in the real parts of the root loci in (b).
$F_{s}=0.187$
(– - – - –) in the real parts of the root loci in (b).
In this section, the ERA-based ROM is successfully employed to perform linear stability analysis of the VIV of a transversely vibrating circular cylinder. Consistent with the previous study of Zhang et al. (Reference Zhang, Li, Ye and Jiang2015) on the mechanism of VIV, we clearly observe two distinct lock-in patterns of the flutter and the resonance from our eigenmode analysis. However, the regime classification of Zhang et al. (Reference Zhang, Li, Ye and Jiang2015) was only based on the VIV linear analysis at
![]() $Re=60$
. In the next section, we extend the existence and dependence of the two distinct lock-in modes to a larger parameter space of Reynolds number in the laminar flow regime.
$Re=60$
. In the next section, we extend the existence and dependence of the two distinct lock-in modes to a larger parameter space of Reynolds number in the laminar flow regime.
4.2 Effect of Reynolds number
As shown in figure 5(a), the growth rate is amplified as
![]() $Re$
increases, which indicates that the coupling between the WM and the SM tends to become stronger for higher
$Re$
increases, which indicates that the coupling between the WM and the SM tends to become stronger for higher
![]() $Re$
. To further investigate the effect of Reynolds number, the VIV ROMs for
$Re$
. To further investigate the effect of Reynolds number, the VIV ROMs for
![]() $Re=(70,100)$
and
$Re=(70,100)$
and
![]() $m^{\ast }=10$
are constructed and a stability analysis similar to that for
$m^{\ast }=10$
are constructed and a stability analysis similar to that for
![]() $Re=60$
is carried out. The root loci as a function of the natural frequency
$Re=60$
is carried out. The root loci as a function of the natural frequency
![]() $F_{s}$
are shown in figure 10(b). Compared with the root loci at
$F_{s}$
are shown in figure 10(b). Compared with the root loci at
![]() $Re=60$
, figure 10(b) shows that the range of unstable SM or flutter mode increases slightly to
$Re=60$
, figure 10(b) shows that the range of unstable SM or flutter mode increases slightly to
![]() $0.106\leqslant F_{s}\leqslant 0.187$
or
$0.106\leqslant F_{s}\leqslant 0.187$
or
![]() $0.71\leqslant F_{s}/St\leqslant 1.25$
and covers the entire lock-in region. This is also evident from the FOM results, as shown in figure 11, where the lock-in region is
$0.71\leqslant F_{s}/St\leqslant 1.25$
and covers the entire lock-in region. This is also evident from the FOM results, as shown in figure 11, where the lock-in region is
![]() $0.11\leqslant F_{s}\leqslant 0.192$
or
$0.11\leqslant F_{s}\leqslant 0.192$
or
![]() $0.73\leqslant F_{s}/St\leqslant 0.128$
. This new finding from the present work suggests that the extents of the flutter and resonance modes are highly sensitive to the Reynolds number. This can be further elucidated by looking into the stability region where the magnitude of the velocity leading eigenmode is large (Giannetti & Luchini Reference Giannetti and Luchini2007). The complex modal velocity components, the streamwise velocity
$0.73\leqslant F_{s}/St\leqslant 0.128$
. This new finding from the present work suggests that the extents of the flutter and resonance modes are highly sensitive to the Reynolds number. This can be further elucidated by looking into the stability region where the magnitude of the velocity leading eigenmode is large (Giannetti & Luchini Reference Giannetti and Luchini2007). The complex modal velocity components, the streamwise velocity
![]() $\widehat{u}$
and the transverse velocity
$\widehat{u}$
and the transverse velocity
![]() $\widehat{v}$
, are computed from the linearized NS equations around the base flow. To visualize the magnitude of the leading modal velocity, we first compute the amplitudes of the complex modal velocity components (
$\widehat{v}$
, are computed from the linearized NS equations around the base flow. To visualize the magnitude of the leading modal velocity, we first compute the amplitudes of the complex modal velocity components (
![]() $|\widehat{u}|$
and
$|\widehat{u}|$
and
![]() $|\widehat{v}|$
) and then evaluate the pointwise modal velocity magnitude as
$|\widehat{v}|$
) and then evaluate the pointwise modal velocity magnitude as
![]() $|\widehat{U}|=\sqrt{|\widehat{u}|^{2}+|\widehat{v}|^{2}}$
. As shown in figure 12, the stability region shifts gradually to the bluff body, which indicates that the coupling effect between the unstable wake and the bluff body is enhanced as
$|\widehat{U}|=\sqrt{|\widehat{u}|^{2}+|\widehat{v}|^{2}}$
. As shown in figure 12, the stability region shifts gradually to the bluff body, which indicates that the coupling effect between the unstable wake and the bluff body is enhanced as
![]() $Re$
increases.
$Re$
increases.

Figure 11. The VIV results as a function of the reduced natural frequency
![]() $F_{s}$
from the FOM at
$F_{s}$
from the FOM at
![]() $(Re,m^{\ast })=(70,10)$
: variation of (a) the normalized vortex shedding frequency
$(Re,m^{\ast })=(70,10)$
: variation of (a) the normalized vortex shedding frequency
![]() $f$
, (b) the r.m.s. value of the lift coefficient (
$f$
, (b) the r.m.s. value of the lift coefficient (
![]() $C_{l}$
) and the maximum amplitude (
$C_{l}$
) and the maximum amplitude (
![]() $Y_{max}$
), and (c) the phase angle (
$Y_{max}$
), and (c) the phase angle (
![]() $\unicode[STIX]{x1D719}$
). The lock-in is shaded in grey colour.
$\unicode[STIX]{x1D719}$
). The lock-in is shaded in grey colour.
Figure 10 shows that the unstable SM branch becomes gradually more pronounced and covers the lock-in region as the Reynolds number increases, whereas the size of the WM loop becomes smaller. The threshold Reynolds number is approximately
![]() $Re=70$
when the resonance mode ceases to exist for
$Re=70$
when the resonance mode ceases to exist for
![]() $m^{\ast }=10$
. This result suggests that the frequency lock-in VIV is pure flutter mode instability for
$m^{\ast }=10$
. This result suggests that the frequency lock-in VIV is pure flutter mode instability for
![]() $Re\geqslant 70$
, which is consistent with the theoretical analysis of De Langre (Reference De Langre2006) using the wake-oscillator model. However, due to the simplification in the wake-oscillator model and without nonlinear and dissipative terms, a general statement on VIV lock-in as a coupled flutter mode may not be valid for all flow conditions. On the other hand, the numerical study of Zhang et al. (Reference Zhang, Li, Ye and Jiang2015) is only valid for
$Re\geqslant 70$
, which is consistent with the theoretical analysis of De Langre (Reference De Langre2006) using the wake-oscillator model. However, due to the simplification in the wake-oscillator model and without nonlinear and dissipative terms, a general statement on VIV lock-in as a coupled flutter mode may not be valid for all flow conditions. On the other hand, the numerical study of Zhang et al. (Reference Zhang, Li, Ye and Jiang2015) is only valid for
![]() $Re_{cr}<Re<70$
. Table 3 summarizes the existence of flutter and resonance modes at different Reynolds numbers for a vibrating circular cylinder.
$Re_{cr}<Re<70$
. Table 3 summarizes the existence of flutter and resonance modes at different Reynolds numbers for a vibrating circular cylinder.

Figure 12. The influence of the Reynolds number on the stability regions defined by the pointwise modal velocity magnitude
![]() $|\widehat{U}|$
of the leading eigenmodes for
$|\widehat{U}|$
of the leading eigenmodes for
![]() $Re=$
(a) 60 and (b) 70. The flow is from left to right.
$Re=$
(a) 60 and (b) 70. The flow is from left to right.

Figure 13. Full-order results for a circular cylinder at
![]() $(Re,m^{\ast })=(70,10)$
. Instantaneous vorticity contours at
$(Re,m^{\ast })=(70,10)$
. Instantaneous vorticity contours at
![]() $F_{s}=$
(a) 0.13, (b) 0.15, (c) 0.17 and (d) 0.19. The contour levels are from
$F_{s}=$
(a) 0.13, (b) 0.15, (c) 0.17 and (d) 0.19. The contour levels are from
![]() $-$
0.5 to 0.5 in increments of 0.077 and the flow is from left to right.
$-$
0.5 to 0.5 in increments of 0.077 and the flow is from left to right.
Table 3. The VIV lock-in regimes of a circular cylinder for Reynolds number in the range
![]() $30\leqslant Re\leqslant 100$
and mass ratio
$30\leqslant Re\leqslant 100$
and mass ratio
![]() $m^{\ast }=10$
. For
$m^{\ast }=10$
. For
![]() $Re>Re_{cr}$
, the flutter regime comprises both unstable eigenvalues
$Re>Re_{cr}$
, the flutter regime comprises both unstable eigenvalues
![]() $(Re(\unicode[STIX]{x1D706})>0)$
of the WM and SM, whereas the resonance regime has only unstable WM.
$(Re(\unicode[STIX]{x1D706})>0)$
of the WM and SM, whereas the resonance regime has only unstable WM.

It is also interesting to note from figure 11(b) that a reduction in the r.m.s. value of the lift coefficient also appears, although the resonance regime does not exist at
![]() $Re=70$
. This observation suggests that the reduction of the r.m.s. lift force does not interlink with the flutter or resonance regime, which is different from the conclusion reached by Zhang et al. (Reference Zhang, Li, Ye and Jiang2015) that the r.m.s. lift coefficient is attenuated in the resonance regime but amplified in the flutter region. As shown in figure 11(b,c), the minimum lift coefficient appears at
$Re=70$
. This observation suggests that the reduction of the r.m.s. lift force does not interlink with the flutter or resonance regime, which is different from the conclusion reached by Zhang et al. (Reference Zhang, Li, Ye and Jiang2015) that the r.m.s. lift coefficient is attenuated in the resonance regime but amplified in the flutter region. As shown in figure 11(b,c), the minimum lift coefficient appears at
![]() $F_{s}\approx 0.135$
or
$F_{s}\approx 0.135$
or
![]() $F_{s}/St\approx 0.92$
, where the phase angle changes from
$F_{s}/St\approx 0.92$
, where the phase angle changes from
![]() $0^{\circ }$
to
$0^{\circ }$
to
![]() $180^{\circ }$
. This further confirms that the lift reduction phenomenon is explicitly linked with the phase angle.
$180^{\circ }$
. This further confirms that the lift reduction phenomenon is explicitly linked with the phase angle.
Furthermore, figure 13 shows the instantaneous patterns of vortex shedding investigated for a broad range of reduced natural frequencies. We adopt the classical terminology of Williamson & Roshko (Reference Williamson and Roshko1988) to identify the vortex shedding patterns. In the 2S mode, a single vortex is alternately shed from each side of the cylinder per shedding cycle, whereas the vortices start to coalesce in the far wake in the C(2S) mode. As reported by Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), the 2S mode is observed in the resonance regime, whereas the C(2S) mode appears in the flutter region. However, we argue that the vorticity topology changes gradually from the C(2S) to the 2S mode as
![]() $F_{s}$
decreases from 0.19 to 0.13, which indicates that the topology variation is associated with the vibration amplitude. The C(2S) mode starts to appear at VIV lock-in onset
$F_{s}$
decreases from 0.19 to 0.13, which indicates that the topology variation is associated with the vibration amplitude. The C(2S) mode starts to appear at VIV lock-in onset
![]() $U_{r}\approx 5.21$
(
$U_{r}\approx 5.21$
(
![]() $F_{s}=0.192$
) and gradually transits to the 2S mode as the amplitude decreases. To further generalize our ERA-based ROM for the VIV lock-in regime, we next investigate the influence of rounding in the VIV lock-in mechanism of a square cylinder.
$F_{s}=0.192$
) and gradually transits to the 2S mode as the amplitude decreases. To further generalize our ERA-based ROM for the VIV lock-in regime, we next investigate the influence of rounding in the VIV lock-in mechanism of a square cylinder.
4.3 Effect of rounding
In the previous section, the effects of Reynolds number and mass ratio have been considered for the transverse VIV of a circular cylinder. It is interesting to explore whether the aforementioned VIV lock-in regimes of a circular cylinder still apply to an elastically mounted square cylinder. It is known that the presence of sharp corners on a square cylinder vastly alters the flow dynamics compared with the dynamics for cylinders with circular/elliptical sections having smooth curves. Besides the angle of incidence, the sharp corners are important contributing factors in the geometry of bluff body, as they affect the flow separation points, which in turn dictate the wake dynamics. By gradual removal of the sharp corners of a square cylinder, a circular cross-section can be recovered. As reported in Jaiman et al. (Reference Jaiman, Sen and Gurugubelli2015), the VIV response of a square cylinder is dramatically different in comparison with its circular cylinder counterpart. For example, the lock-in region of a square cylinder is narrower and the amplitude is smaller for similar VIV operational parameters (
![]() $Re,m^{\ast },\unicode[STIX]{x1D701}$
), as extensively discussed in Jaiman et al. (Reference Jaiman, Guan and Miyanawala2016a
,Reference Jaiman, Pillalamarri and Guan
b
). Recently, a rounded square was also numerically studied in terms of primary and secondary instabilities (Park & Yang Reference Park and Yang2016); it was shown that sharp corners alter the flow topology significantly, subsequently changing the stability properties of the wake dynamics. It is therefore important to consider the effect of rounding the corners of a square cylinder for the VIV mechanism. The VIV stability properties of five different cross-sections including a circle and a square are explored in the context of eigenvalue distributions.
$Re,m^{\ast },\unicode[STIX]{x1D701}$
), as extensively discussed in Jaiman et al. (Reference Jaiman, Guan and Miyanawala2016a
,Reference Jaiman, Pillalamarri and Guan
b
). Recently, a rounded square was also numerically studied in terms of primary and secondary instabilities (Park & Yang Reference Park and Yang2016); it was shown that sharp corners alter the flow topology significantly, subsequently changing the stability properties of the wake dynamics. It is therefore important to consider the effect of rounding the corners of a square cylinder for the VIV mechanism. The VIV stability properties of five different cross-sections including a circle and a square are explored in the context of eigenvalue distributions.

Figure 14. Square-section bluff body with projected width
![]() $D$
and rounding radius
$D$
and rounding radius
![]() $r_{s}$
in uniform flow. Rounding is introduced by inscribing a quarter circle with
$r_{s}$
in uniform flow. Rounding is introduced by inscribing a quarter circle with
![]() $r_{s}$
at each edge of the square geometry. The square and circular cylinders correspond to rounding radii of
$r_{s}$
at each edge of the square geometry. The square and circular cylinders correspond to rounding radii of
![]() $r_{s}=0$
and
$r_{s}=0$
and
![]() $r_{s}=0.5D$
respectively.
$r_{s}=0.5D$
respectively.
Figure 14 schematically depicts a square cylinder with a rounding radius
![]() $r_{s}$
. The edge length of the square with sharp corners is denoted by
$r_{s}$
. The edge length of the square with sharp corners is denoted by
![]() $D$
. Rounding is introduced by inscribing a quarter circle with
$D$
. Rounding is introduced by inscribing a quarter circle with
![]() $r_{s}$
at each edge of the square geometry, where
$r_{s}$
at each edge of the square geometry, where
![]() $r_{s}=0.5D$
corresponds to a circular shape and
$r_{s}=0.5D$
corresponds to a circular shape and
![]() $r_{s}=0$
recovers to the basic square shape. The characteristic dimension
$r_{s}=0$
recovers to the basic square shape. The characteristic dimension
![]() $D$
of all of the cross-sections is identical, where
$D$
of all of the cross-sections is identical, where
![]() $D$
is the maximum dimension of the cylinder normal to the flow. The origin of the Cartesian coordinate system coincides with the centre of the square.
$D$
is the maximum dimension of the cylinder normal to the flow. The origin of the Cartesian coordinate system coincides with the centre of the square.

Figure 15. The effect of the rounding
![]() $r_{s}$
on the eigenspectrum of the ERA-based ROM at
$r_{s}$
on the eigenspectrum of the ERA-based ROM at
![]() $(Re,m^{\ast })=(60,10)$
: (a) root loci as a function of the reduced natural frequency
$(Re,m^{\ast })=(60,10)$
: (a) root loci as a function of the reduced natural frequency
![]() $F_{s}$
, where the unstable right half-plane
$F_{s}$
, where the unstable right half-plane
![]() $(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey and the hollow arrow indicates increasing
$(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey and the hollow arrow indicates increasing
![]() $F_{s}$
, and (b) the real and imaginary parts of the root loci. In (a), the unstable eigenvalues of the stationary square cylinder (uncoupled WM) with different rounding values are connected by a black curve with a solid arrow indicating increasing
$F_{s}$
, and (b) the real and imaginary parts of the root loci. In (a), the unstable eigenvalues of the stationary square cylinder (uncoupled WM) with different rounding values are connected by a black curve with a solid arrow indicating increasing
![]() $r_{s}$
. The SM is denoted by filled symbols with the same shape as those for the WM in (a,b).
$r_{s}$
. The SM is denoted by filled symbols with the same shape as those for the WM in (a,b).

Figure 16. The VIV results for a square cylinder with sharp corners using the FOM at
![]() $(Re,m^{\ast })=(60,10)$
: variation of (a) the normalized vortex shedding frequency
$(Re,m^{\ast })=(60,10)$
: variation of (a) the normalized vortex shedding frequency
![]() $f$
, (b) the r.m.s. value of the lift coefficient (
$f$
, (b) the r.m.s. value of the lift coefficient (
![]() $C_{l}$
) and the maximum amplitude (
$C_{l}$
) and the maximum amplitude (
![]() $Y_{max}$
), and (c) the phase angle (
$Y_{max}$
), and (c) the phase angle (
![]() $\unicode[STIX]{x1D719}$
). The lock-in is shaded in grey colour.
$\unicode[STIX]{x1D719}$
). The lock-in is shaded in grey colour.
To begin with, the VIV linear analysis is conducted for a square cylinder with sharp corners at (
![]() $Re,m^{\ast }$
) = (60, 10). It is evident from figure 15(a) that the SM is stable, which suggests that the lock-in is entirely dominated by the resonance mode. Due to the absence of lock-in via the flutter mode, the onset reduced velocity (
$Re,m^{\ast }$
) = (60, 10). It is evident from figure 15(a) that the SM is stable, which suggests that the lock-in is entirely dominated by the resonance mode. Due to the absence of lock-in via the flutter mode, the onset reduced velocity (
![]() $U_{r}$
) for a square cylinder may not be clearly recognized compared with its circular cylinder counterpart. Furthermore, the region of the WM loop for the square cylinder is smaller than its circular cylinder counterpart, implying that the coupling between the fluid and the structure is reduced due to the sharp corners. In figure 15, the root loci for the fluid–structure system of a square cylinder provide an explanation that the lock-in only consists of the resonance mode and the flutter state disappears due to the presence of sharp corners for
$U_{r}$
) for a square cylinder may not be clearly recognized compared with its circular cylinder counterpart. Furthermore, the region of the WM loop for the square cylinder is smaller than its circular cylinder counterpart, implying that the coupling between the fluid and the structure is reduced due to the sharp corners. In figure 15, the root loci for the fluid–structure system of a square cylinder provide an explanation that the lock-in only consists of the resonance mode and the flutter state disappears due to the presence of sharp corners for
![]() $(Re,m^{\ast })=(60,10)$
. As expected, the sharp corners suppress the continuous movement of separation points, whereby the smooth circular cylinder promotes the movement of separation points. Figure 16 shows the frequency, the VIV response and the lift coefficient from the FOM simulation for a vibrating square cylinder. The extent of the lock-in region can be observed as
$(Re,m^{\ast })=(60,10)$
. As expected, the sharp corners suppress the continuous movement of separation points, whereby the smooth circular cylinder promotes the movement of separation points. Figure 16 shows the frequency, the VIV response and the lift coefficient from the FOM simulation for a vibrating square cylinder. The extent of the lock-in region can be observed as
![]() $0.11\leqslant F_{s}\leqslant 0.154$
or
$0.11\leqslant F_{s}\leqslant 0.154$
or
![]() $0.87\leqslant F_{s}/St\leqslant 1.21$
. The results illustrate that the maximum amplitude is also acquired approximately at the lock-in onset (
$0.87\leqslant F_{s}/St\leqslant 1.21$
. The results illustrate that the maximum amplitude is also acquired approximately at the lock-in onset (
![]() $U_{r}\approx 6.49$
) even if no flutter regime exists. It is notable that the maximum amplitude is smaller and the lock-in region is narrower than its circular cylinder counterpart, which is observed earlier for the square cylinder (Zhao, Cheng & Zhou Reference Zhao, Cheng and Zhou2013; Jaiman et al.
Reference Jaiman, Pillalamarri and Guan2016b
).
$U_{r}\approx 6.49$
) even if no flutter regime exists. It is notable that the maximum amplitude is smaller and the lock-in region is narrower than its circular cylinder counterpart, which is observed earlier for the square cylinder (Zhao, Cheng & Zhou Reference Zhao, Cheng and Zhou2013; Jaiman et al.
Reference Jaiman, Pillalamarri and Guan2016b
).
Similarly to its circular counterpart, the lift coefficient for a square cylinder also experiences an amplification in the vicinity of lock-in onset,
![]() $U_{r}\approx 6.49$
, and gradually recovers to its stationary counterpart as
$U_{r}\approx 6.49$
, and gradually recovers to its stationary counterpart as
![]() $F_{s}$
decreases (
$F_{s}$
decreases (
![]() $U_{r}$
increases). The maximum value of the r.m.s. lift coefficient is
$U_{r}$
increases). The maximum value of the r.m.s. lift coefficient is
![]() $C_{l}=0.314$
, as shown in figure 16(b), which is approximately 3.1 times larger than the stationary square cylinder value (
$C_{l}=0.314$
, as shown in figure 16(b), which is approximately 3.1 times larger than the stationary square cylinder value (
![]() $C_{l}=0.1$
). For the VIV of the circular cylinder, on the other hand, the amplification of the r.m.s. lift coefficient is approximately
$C_{l}=0.1$
). For the VIV of the circular cylinder, on the other hand, the amplification of the r.m.s. lift coefficient is approximately
![]() $5.9$
times that of the stationary circular cylinder, as shown in figure 8
b. To understand the direction of energy transfer between the fluid and the square cylinder, the phase angle is shown in figure 16(c). Similarly to the circular cylinder, there is a sudden jump from
$5.9$
times that of the stationary circular cylinder, as shown in figure 8
b. To understand the direction of energy transfer between the fluid and the square cylinder, the phase angle is shown in figure 16(c). Similarly to the circular cylinder, there is a sudden jump from
![]() $0^{\circ }$
to
$0^{\circ }$
to
![]() $180^{\circ }$
during the lock-in region around
$180^{\circ }$
during the lock-in region around
![]() $F_{s}\approx 0.125$
or
$F_{s}\approx 0.125$
or
![]() $F_{s}/St\approx 0.98$
, where the r.m.s. lift coefficient acquires the minimum value.
$F_{s}/St\approx 0.98$
, where the r.m.s. lift coefficient acquires the minimum value.

Figure 17. Full-order results for the square cylinder at
![]() $(Re,m^{\ast })=(60,10)$
. Instantaneous vorticity contours at
$(Re,m^{\ast })=(60,10)$
. Instantaneous vorticity contours at
![]() $F_{s}=$
(a) 0.12, (b) 0.13, (c) 0.14 and (d) 0.15. The contour levels are from
$F_{s}=$
(a) 0.12, (b) 0.13, (c) 0.14 and (d) 0.15. The contour levels are from
![]() $-$
0.5 to 0.5 in increments of 0.077 and the flow is from left to right.
$-$
0.5 to 0.5 in increments of 0.077 and the flow is from left to right.
For the range of
![]() $F_{s}$
considered, two counter-rotating vortices (2S mode) are released every oscillation cycle from the rear of each cylinder, as shown in figure 17. From the vorticity fields, separations along the front corners of lateral edges for the square with sharp corners can be observed for the considered cases. While the C(2S) mode is observed in the vicinity of lock-in onset for the circular cylinder, the classic 2S mode is dominant for the square cylinder. This is consistent with our previous hypothesis that the wake pattern is closely related to the vibration amplitude. We next elucidate the influence of rounding on the distribution of the eigenspectrum and the unstable global modes.
$F_{s}$
considered, two counter-rotating vortices (2S mode) are released every oscillation cycle from the rear of each cylinder, as shown in figure 17. From the vorticity fields, separations along the front corners of lateral edges for the square with sharp corners can be observed for the considered cases. While the C(2S) mode is observed in the vicinity of lock-in onset for the circular cylinder, the classic 2S mode is dominant for the square cylinder. This is consistent with our previous hypothesis that the wake pattern is closely related to the vibration amplitude. We next elucidate the influence of rounding on the distribution of the eigenspectrum and the unstable global modes.

Figure 18. Stability regions shown by the spatial distribution of the pointwise modal velocity amplitude
![]() $|\widehat{U}|$
at
$|\widehat{U}|$
at
![]() $Re=60$
for different rounding parameters
$Re=60$
for different rounding parameters
![]() $r_{s}=$
(a) 0.0, (b)
$r_{s}=$
(a) 0.0, (b)
![]() $0.1D$
, (c)
$0.1D$
, (c)
![]() $0.2D$
and (d)
$0.2D$
and (d)
![]() $0.4D$
. The flow is from left to right.
$0.4D$
. The flow is from left to right.
As shown in figure 15(a), the SM trajectory moves gradually towards the positive real axis
![]() $(Re(\unicode[STIX]{x1D706})>0)$
as the rounding radius
$(Re(\unicode[STIX]{x1D706})>0)$
as the rounding radius
![]() $r_{s}$
increases. Meanwhile, the flutter region starts to appear and achieves its maximum extent for the rounding radius
$r_{s}$
increases. Meanwhile, the flutter region starts to appear and achieves its maximum extent for the rounding radius
![]() $r_{s}=0.5D$
. As expected, the rounding of the corners delays the onset of separation; hence, the rounding aids in reducing the bluffness of the square cylinder. It is also worth noting that the unstable SM and WM loops are both more pronounced, indicating that the coupling effect between the fluid and the structure becomes stronger. However, the growth rate of the uncoupled WM does not increase monotonically from the square (
$r_{s}=0.5D$
. As expected, the rounding of the corners delays the onset of separation; hence, the rounding aids in reducing the bluffness of the square cylinder. It is also worth noting that the unstable SM and WM loops are both more pronounced, indicating that the coupling effect between the fluid and the structure becomes stronger. However, the growth rate of the uncoupled WM does not increase monotonically from the square (
![]() $r_{s}=0$
) to the circular (
$r_{s}=0$
) to the circular (
![]() $r_{s}=0.5D$
) configuration, as shown by a black curve with a solid arrow in figure 15(a). The growth rate first decreases, then increases and eventually recovers to the growth rate of the circular cylinder.
$r_{s}=0.5D$
) configuration, as shown by a black curve with a solid arrow in figure 15(a). The growth rate first decreases, then increases and eventually recovers to the growth rate of the circular cylinder.
By examining the real parts of the root loci in figure 15(b), it can be seen that the onset of lock-in starts to move towards the low reduced velocity (high
![]() $F_{s}$
) as the rounding radius
$F_{s}$
) as the rounding radius
![]() $r_{s}$
increases. In figure 18, from the comparison of stability regions through the contours of
$r_{s}$
increases. In figure 18, from the comparison of stability regions through the contours of
![]() $|\widehat{U}|$
, we observe that the rounding has significant effects on the wake topology, subsequently altering the stability properties. The separation point can move widely as the rounding radius increases, indicating that the flutter mode is more pronounced. It is also shown that the stability region gradually moves closer to the rear of the bluff body as
$|\widehat{U}|$
, we observe that the rounding has significant effects on the wake topology, subsequently altering the stability properties. The separation point can move widely as the rounding radius increases, indicating that the flutter mode is more pronounced. It is also shown that the stability region gradually moves closer to the rear of the bluff body as
![]() $r_{s}$
increases, which is similar to the effect of
$r_{s}$
increases, which is similar to the effect of
![]() $Re$
, as discussed in § 4.2. Consequently, the level of fluid and structure interaction is enhanced. This trend is monotonic compared with the growth rate, suggesting that the flutter mode becomes gradually more pronounced. This explains why the SM trajectory moves towards the right half-plane monotonically. The WM branch, on the other hand, moves towards the imaginary axis positive or higher-frequency direction, monotonically. For similar VIV operating parameters, the circular cylinder is much easier to perturb compared with its square counterpart at the same Reynolds number.
$Re$
, as discussed in § 4.2. Consequently, the level of fluid and structure interaction is enhanced. This trend is monotonic compared with the growth rate, suggesting that the flutter mode becomes gradually more pronounced. This explains why the SM trajectory moves towards the right half-plane monotonically. The WM branch, on the other hand, moves towards the imaginary axis positive or higher-frequency direction, monotonically. For similar VIV operating parameters, the circular cylinder is much easier to perturb compared with its square counterpart at the same Reynolds number.

Figure 19. Schematics of bluff-body geometries with relevant dimensions. The representative elliptical cylinder (a) has aspect ratio
![]() $AR=0.5$
; the forward triangle (b) is equilateral with angle
$AR=0.5$
; the forward triangle (b) is equilateral with angle
![]() $60^{\circ }$
; the diamond (c) represents a square cylinder with sharp corners at
$60^{\circ }$
; the diamond (c) represents a square cylinder with sharp corners at
![]() $45^{\circ }$
flow incidence.
$45^{\circ }$
flow incidence.
While the rounding generally stabilizes the wake flow for a stationary square cylinder, it promotes the movement of separation points along the smooth rounded surface of the vibrating cylinder. Analogously to the aeroelastic flutter with plunge-torsion mode coupling for an airfoil configuration, as described by De Langre (Reference De Langre2006), the transverse periodic displacement and the movement of separation points can form a similar dynamics for a transversely vibrating circular cylinder. The square cylinder with sharp corners restricts the free motion of separation points and is relatively stable in the sense that the lock-in onset reduced velocity
![]() $U_{r}$
is greater than its circular counterpart. Moreover, compared with the circular cylinder at
$U_{r}$
is greater than its circular counterpart. Moreover, compared with the circular cylinder at
![]() $(Re,m^{\ast })=(60,10)$
, the lock-in range of the square cylinder is narrower and only a resonance regime exists. To further generalize our findings, we next examine the lock-in regimes from the eigenvalue distributions for additional bluff bodies for the smooth curve geometry of an elliptic cylinder and two sharp corner shapes of forward triangle and diamond cylinders.
$(Re,m^{\ast })=(60,10)$
, the lock-in range of the square cylinder is narrower and only a resonance regime exists. To further generalize our findings, we next examine the lock-in regimes from the eigenvalue distributions for additional bluff bodies for the smooth curve geometry of an elliptic cylinder and two sharp corner shapes of forward triangle and diamond cylinders.
4.4 Effect of geometry
In this section, a set of three representative two-dimensional geometries is assessed to elucidate the frequency lock-in regimes and to demonstrate the ability of the developed ERA-based ROM. The three additional geometries, namely an ellipse as a smooth curve and a forward triangle and a diamond with sharp corners, are shown in figure 19. The major axis with length
![]() $D$
of the elliptic cylinder is placed normal to the flow direction and the aspect ratio
$D$
of the elliptic cylinder is placed normal to the flow direction and the aspect ratio
![]() $AR=0.5$
is defined by the ratio of the minor,
$AR=0.5$
is defined by the ratio of the minor,
![]() $D/2$
, to the major axis length. The forward triangle is equilateral and has an edge with length
$D/2$
, to the major axis length. The forward triangle is equilateral and has an edge with length
![]() $D$
normal to the flow; the peak corner is on the leeward side. Similarly to Zhao et al. (Reference Zhao, Cheng and Zhou2013), the diamond geometry is considered as a square cylinder with
$D$
normal to the flow; the peak corner is on the leeward side. Similarly to Zhao et al. (Reference Zhao, Cheng and Zhou2013), the diamond geometry is considered as a square cylinder with
![]() $45^{\circ }$
flow incidence and the Reynolds number is defined by the edge length
$45^{\circ }$
flow incidence and the Reynolds number is defined by the edge length
![]() $D$
as the characteristic length scale. Similarly to the circular and square cylinders, the new geometries of the ellipse, forward triangle and diamond cylinders undergo unsteady wake transition via a Hopf bifurcation at a critical Reynolds number
$D$
as the characteristic length scale. Similarly to the circular and square cylinders, the new geometries of the ellipse, forward triangle and diamond cylinders undergo unsteady wake transition via a Hopf bifurcation at a critical Reynolds number
![]() $Re_{cr}$
, which is responsible for the onset of the time-periodic vortex shedding phenomenon. Table 4 shows the critical Reynolds numbers
$Re_{cr}$
, which is responsible for the onset of the time-periodic vortex shedding phenomenon. Table 4 shows the critical Reynolds numbers
![]() $Re_{cr}$
for the different geometries computed by our ERA-based ROM, which match reasonably well with previous studies. It is worth noting that the forward triangle has the lowest critical Reynolds number for the initial wake transition from steady to unsteady flow. The unsteady transitions of the ellipse with aspect ratio
$Re_{cr}$
for the different geometries computed by our ERA-based ROM, which match reasonably well with previous studies. It is worth noting that the forward triangle has the lowest critical Reynolds number for the initial wake transition from steady to unsteady flow. The unsteady transitions of the ellipse with aspect ratio
![]() $AR=0.5$
and the diamond with sharp corners occur lower than their circular and square counterparts. Due to unsteady lift and drag forces, the three geometries can undergo flow-induced vibration if mounted on elastic supports.
$AR=0.5$
and the diamond with sharp corners occur lower than their circular and square counterparts. Due to unsteady lift and drag forces, the three geometries can undergo flow-induced vibration if mounted on elastic supports.
Table 4. Comparison of critical Reynolds numbers
![]() $Re_{cr}$
between the available literature and the predicted values by the ERA-based ROM for different topologies of bluff bodies. The onset reduced velocity
$Re_{cr}$
between the available literature and the predicted values by the ERA-based ROM for different topologies of bluff bodies. The onset reduced velocity
![]() $U_{r}$
of VIV lock-in from the present study is also outlined in the final row.
$U_{r}$
of VIV lock-in from the present study is also outlined in the final row.

To further elucidate the lock-in mechanism, we plot the root loci and the real and imaginary parts of the eigenvalues for the additional three bluff bodies in figure 20. The figure clearly shows that the geometry of the bluff body has a significant impact on the eigenvalue trajectory. The elliptical configuration has the lowest lock-in onset
![]() $U_{r}$
followed by the diamond and forward triangle configurations, as shown in table 4. Compared with the circular cylinder at identical conditions of
$U_{r}$
followed by the diamond and forward triangle configurations, as shown in table 4. Compared with the circular cylinder at identical conditions of
![]() $(Re,m^{\ast })=(60,10)$
, the root loci of the SM and WM coalesce for the diamond, ellipse and forward triangle configurations. Similarly to the low mass ratio effect during the VIV of the circular cylinder, the two branches exchange their roles and no distinction can be made between the WM and the SM for the three geometries. Therefore, we consider the coupled modes WSMI and WSMII to classify the stability characteristics for these geometries. When the intersection of the growth rate curves corresponding to WSMI and WSMII occurs in figure 20(b) (top), the stability roles of WSMI and WSMII switch at a specific value of
$(Re,m^{\ast })=(60,10)$
, the root loci of the SM and WM coalesce for the diamond, ellipse and forward triangle configurations. Similarly to the low mass ratio effect during the VIV of the circular cylinder, the two branches exchange their roles and no distinction can be made between the WM and the SM for the three geometries. Therefore, we consider the coupled modes WSMI and WSMII to classify the stability characteristics for these geometries. When the intersection of the growth rate curves corresponding to WSMI and WSMII occurs in figure 20(b) (top), the stability roles of WSMI and WSMII switch at a specific value of
![]() $F_{s}$
for the three geometries. As shown in figure 20(b) (bottom), the two curves of
$F_{s}$
for the three geometries. As shown in figure 20(b) (bottom), the two curves of
![]() $\text{Im}(\unicode[STIX]{x1D706})$
for the three geometries no longer cross, in comparison to the circular cylinder counterpart in identical conditions. Due to stronger coupling, there is a characteristic anticrossing with a frequency splitting between WSMI and WSMII for the three geometries. In addition, the forward triangle branch departs further away from the line
$\text{Im}(\unicode[STIX]{x1D706})$
for the three geometries no longer cross, in comparison to the circular cylinder counterpart in identical conditions. Due to stronger coupling, there is a characteristic anticrossing with a frequency splitting between WSMI and WSMII for the three geometries. In addition, the forward triangle branch departs further away from the line
![]() $f=2\unicode[STIX]{x03C0}F_{s}$
compared with the diamond and elliptical cylinders.
$f=2\unicode[STIX]{x03C0}F_{s}$
compared with the diamond and elliptical cylinders.
In contrast to the square cylinder (
![]() $0^{\circ }$
degree flow incidence) at
$0^{\circ }$
degree flow incidence) at
![]() $(Re,m^{\ast })=(60,10)$
, the diamond configuration has a flutter-dominated VIV lock-in. This difference in the lock-in behaviour can be attributed to the boundary layer movement over the front edges of the diamond cylinder, whereby the square cylinder has flow separations at the upstream corners and inhibits the co-existence of flutter and resonance regimes.
$(Re,m^{\ast })=(60,10)$
, the diamond configuration has a flutter-dominated VIV lock-in. This difference in the lock-in behaviour can be attributed to the boundary layer movement over the front edges of the diamond cylinder, whereby the square cylinder has flow separations at the upstream corners and inhibits the co-existence of flutter and resonance regimes.

Figure 20. Effect of geometry on the eigenspectrum of the ERA-based ROM at
![]() $(Re,m^{\ast })=(60,10)$
: (a) root loci as a function of the reduced natural frequency
$(Re,m^{\ast })=(60,10)$
: (a) root loci as a function of the reduced natural frequency
![]() $F_{s}$
, where the unstable right half-plane
$F_{s}$
, where the unstable right half-plane
![]() $(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
$(\text{Re}(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
![]() $F_{s}$
; (b) real and imaginary parts of the root loci. The WSMI data are denoted by filled symbols with the same shapes as those for WSMII in (a,b). The onset
$F_{s}$
; (b) real and imaginary parts of the root loci. The WSMI data are denoted by filled symbols with the same shapes as those for WSMII in (a,b). The onset
![]() $U_{r}$
is computed on
$U_{r}$
is computed on
![]() $F_{s}=0.184$
(forward triangle – - – - –, blue),
$F_{s}=0.184$
(forward triangle – - – - –, blue),
![]() $F_{s}=0.216$
(diamond – - – - –, red) and
$F_{s}=0.216$
(diamond – - – - –, red) and
![]() $F_{s}=0.239$
(ellipse – - – - –, green) in the real parts of the root loci in (b).
$F_{s}=0.239$
(ellipse – - – - –, green) in the real parts of the root loci in (b).

Figure 21. The VIV results for the forward triangle configuration using the FOM at
![]() $(Re,m^{\ast })=(60,10)$
: variation of (a) the normalized vortex shedding frequency
$(Re,m^{\ast })=(60,10)$
: variation of (a) the normalized vortex shedding frequency
![]() $f$
and (b) the r.m.s. value of the lift coefficient (
$f$
and (b) the r.m.s. value of the lift coefficient (
![]() $C_{l}$
) and the maximum amplitude (
$C_{l}$
) and the maximum amplitude (
![]() $Y_{max}$
). The lock-in is shaded in grey colour.
$Y_{max}$
). The lock-in is shaded in grey colour.
For the forward triangle configuration, it is notable that WSMI and WSMII remain unstable for
![]() $F_{s}\leqslant 0.184$
or
$F_{s}\leqslant 0.184$
or
![]() $U_{r}\geqslant 5.43$
, as predicted by the ERA-based ROM, which indicates that flutter-dominated VIV persists. Therefore, the forward triangle is of particular interest for the present study. These linear stability results have been confirmed by the FOM simulations, as shown in figure 21. The amplitude grows continually for
$U_{r}\geqslant 5.43$
, as predicted by the ERA-based ROM, which indicates that flutter-dominated VIV persists. Therefore, the forward triangle is of particular interest for the present study. These linear stability results have been confirmed by the FOM simulations, as shown in figure 21. The amplitude grows continually for
![]() $F_{s}\leqslant 0.184$
or
$F_{s}\leqslant 0.184$
or
![]() $U_{r}\geqslant 5.43$
and the lift coefficient reaches its maximum value at the lock-in onset
$U_{r}\geqslant 5.43$
and the lift coefficient reaches its maximum value at the lock-in onset
![]() $U_{r}$
, which is similar to the circular and square cylinders. The vortex shedding frequency starts to synchronize with the natural frequency of the structure and there exists 1:1 frequency synchronization, whereby the body is synchronized with the vortex shedding frequency. The transverse amplitude grows continually as
$U_{r}$
, which is similar to the circular and square cylinders. The vortex shedding frequency starts to synchronize with the natural frequency of the structure and there exists 1:1 frequency synchronization, whereby the body is synchronized with the vortex shedding frequency. The transverse amplitude grows continually as
![]() $F_{s}$
decreases (
$F_{s}$
decreases (
![]() $U_{r}$
increases), which is referred to as galloping-dominated flow-induced vibration. This galloping regime is characterized by a low-frequency and high-amplitude vibration, whereas a circular cross-section is not susceptible to galloping. For
$U_{r}$
increases), which is referred to as galloping-dominated flow-induced vibration. This galloping regime is characterized by a low-frequency and high-amplitude vibration, whereas a circular cross-section is not susceptible to galloping. For
![]() $F_{s}<0.085$
(
$F_{s}<0.085$
(
![]() $U_{r}>11.76$
), the amplitude experiences a small but distinct increase in amplitude, and 1:3 synchronization gradually appears, as shown in figure 22. In this regime, there is net energy transfer from the base flow with the frequency component at three times the body oscillation frequency. During this energy transfer, the fluid force performs work on the body, which stores the energy in the form of kinetic energy as well as the potential energy in the spring. To further elucidate the high harmonic response for the forward triangle, figure 22 depicts motion and lift force traces with their corresponding spectra. In the figure, there is a clear third-harmonic frequency in the lift force where the body oscillates with a dominant frequency. Figure 23 shows the instantaneous vorticity contours at different values of the reduced natural frequency
$U_{r}>11.76$
), the amplitude experiences a small but distinct increase in amplitude, and 1:3 synchronization gradually appears, as shown in figure 22. In this regime, there is net energy transfer from the base flow with the frequency component at three times the body oscillation frequency. During this energy transfer, the fluid force performs work on the body, which stores the energy in the form of kinetic energy as well as the potential energy in the spring. To further elucidate the high harmonic response for the forward triangle, figure 22 depicts motion and lift force traces with their corresponding spectra. In the figure, there is a clear third-harmonic frequency in the lift force where the body oscillates with a dominant frequency. Figure 23 shows the instantaneous vorticity contours at different values of the reduced natural frequency
![]() $F_{s}$
. The vortex shedding mode is 2S for
$F_{s}$
. The vortex shedding mode is 2S for
![]() $F_{s}=0.17$
, and remains 2S for
$F_{s}=0.17$
, and remains 2S for
![]() $F_{s}=0.15$
with somewhat increased spacing between the vortices shed alternately from each side of the cylinder. By further decreasing
$F_{s}=0.15$
with somewhat increased spacing between the vortices shed alternately from each side of the cylinder. By further decreasing
![]() $F_{s}$
to 0.1, the strong SM and WM interactions result in a larger vibration amplitude and the flow diverges to a wide vortex street.
$F_{s}$
to 0.1, the strong SM and WM interactions result in a larger vibration amplitude and the flow diverges to a wide vortex street.

Figure 22. Full-order VIV results for a forward triangle with 1:3 synchronization: temporal variation of (a) the transverse amplitude and (c) the lift coefficient; normalized power spectrum
![]() $P$
versus
$P$
versus
![]() $f^{\ast }$
of (b) the transverse amplitude and (d) the lift coefficient at
$f^{\ast }$
of (b) the transverse amplitude and (d) the lift coefficient at
![]() $F_{s}=0.05$
, where
$F_{s}=0.05$
, where
![]() $f^{\ast }=f/F_{s}$
is the frequency of lift and transverse displacement normalized by the reduced natural frequency
$f^{\ast }=f/F_{s}$
is the frequency of lift and transverse displacement normalized by the reduced natural frequency
![]() $F_{s}$
. A third-harmonic frequency is evident in
$F_{s}$
. A third-harmonic frequency is evident in
![]() $C_{l}$
.
$C_{l}$
.

Figure 23. Full-order results for the forward triangle cylinder at
![]() $(Re,m^{\ast })=(60,10)$
. Instantaneous vorticity contours at
$(Re,m^{\ast })=(60,10)$
. Instantaneous vorticity contours at
![]() $F_{s}=$
(a) 0.05, (b) 0.1, (c) 0.15 and (d) 0.17. The contour levels are from
$F_{s}=$
(a) 0.05, (b) 0.1, (c) 0.15 and (d) 0.17. The contour levels are from
![]() $-$
0.5 to 0.5 in increments of 0.077 and the flow is from left to right.
$-$
0.5 to 0.5 in increments of 0.077 and the flow is from left to right.
The geometry of the bluff body alters the flow structures significantly in the vicinity of the base flow, resulting in different root loci and subsequently changing the stability properties. For example, as shown in figure 15, the sharp corner of the square stabilizes the flow and the resonance mode dominates the entire lock-in for
![]() $(Re,m^{\ast })=(60,10)$
. This can be further elucidated by looking into the magnitude of the leading modal velocity
$(Re,m^{\ast })=(60,10)$
. This can be further elucidated by looking into the magnitude of the leading modal velocity
![]() $|\widehat{U}|$
for the different geometrical configurations. As illustrated in figure 24, the stability regions of the ellipse, diamond and triangle geometries shift upstream in comparison with the circular geometry, indicating that the coupling effect is enhanced. The stationary configurations of the ellipse, diamond and forward triangle have quite similar stability regions. The forward triangle is easier to perturb from the flow unsteadiness, or by a Hopf bifurcation for alternate vortex shedding. However, the sharp corners generally stabilize the fluid–structure system, as the separation point is constrained and there is less freedom for the interaction of flow and structural modes. Due to this attribute in the forward triangle configuration, there is a delay in lock-in onset
$|\widehat{U}|$
for the different geometrical configurations. As illustrated in figure 24, the stability regions of the ellipse, diamond and triangle geometries shift upstream in comparison with the circular geometry, indicating that the coupling effect is enhanced. The stationary configurations of the ellipse, diamond and forward triangle have quite similar stability regions. The forward triangle is easier to perturb from the flow unsteadiness, or by a Hopf bifurcation for alternate vortex shedding. However, the sharp corners generally stabilize the fluid–structure system, as the separation point is constrained and there is less freedom for the interaction of flow and structural modes. Due to this attribute in the forward triangle configuration, there is a delay in lock-in onset
![]() $U_{r}$
with identical operating parameters
$U_{r}$
with identical operating parameters
![]() $(Re,m^{\ast })$
compared with the elliptical cylinder.
$(Re,m^{\ast })$
compared with the elliptical cylinder.

Figure 24. Stability regions shown by the spatial distribution of pointwise modal velocity amplitude
![]() $|\widehat{U}|$
at
$|\widehat{U}|$
at
![]() $Re=60$
: contours of modal velocity for the (a) circle, (b) ellipse, (c) diamond and (d) forward triangle configurations. The flow is from left to right.
$Re=60$
: contours of modal velocity for the (a) circle, (b) ellipse, (c) diamond and (d) forward triangle configurations. The flow is from left to right.

Figure 25. Stability phase diagram of VIV lock-in for transversely vibrating two-dimensional bluff bodies with smooth curves and sharp corners for
![]() $30\leqslant Re\leqslant 100$
,
$30\leqslant Re\leqslant 100$
,
![]() $m^{\ast }=10$
and
$m^{\ast }=10$
and
![]() $0.05\leqslant F_{s}\leqslant 0.25$
. Here, the solid curve (——) represents the critical Reynolds number (
$0.05\leqslant F_{s}\leqslant 0.25$
. Here, the solid curve (——) represents the critical Reynolds number (
![]() $Re_{cr}$
) of the fixed bluff body, and flutter- and resonance-induced regimes are demarcated, where ▫ represents the co-existence of flutter and resonance regimes, ○ denotes the resonance regime and ▵ represents the flutter regime. For
$Re_{cr}$
) of the fixed bluff body, and flutter- and resonance-induced regimes are demarcated, where ▫ represents the co-existence of flutter and resonance regimes, ○ denotes the resonance regime and ▵ represents the flutter regime. For
![]() $Re>Re_{cr}$
, the flutter regime comprises both unstable eigenvalues
$Re>Re_{cr}$
, the flutter regime comprises both unstable eigenvalues
![]() $(\text{Re}(\unicode[STIX]{x1D706})>0)$
of the WM and SM, whereas the resonance regime has only unstable WM.
$(\text{Re}(\unicode[STIX]{x1D706})>0)$
of the WM and SM, whereas the resonance regime has only unstable WM.
Figure 25 summarizes the stability regimes of transversely vibrating bluff bodies for the Reynolds number range
![]() $30\leqslant Re\leqslant 100$
. In this figure, the solid curve (——) depicts the trend for the critical Reynolds number. The following observations can be made from the stability phase diagram. The circle, ellipse and diamond geometries exhibit the flutter and mixed resonance–flutter modes. In contrast to its square counterpart, the diamond geometry has a movement of asymmetric boundary layers on the front lateral edges which allows the co-existence of flutter and resonance modes. For the elliptic cylinder, the mixed flutter–resonance regime occurs at a lower Reynolds number in comparison with the circular cylinder. Notably, the forward triangle configuration only shows the flutter-induced lock-in regime for this range of Reynolds number and the edges are on the leeward side with separated flow. Finally, the square-section body shows a predominant resonance regime for approximately
$30\leqslant Re\leqslant 100$
. In this figure, the solid curve (——) depicts the trend for the critical Reynolds number. The following observations can be made from the stability phase diagram. The circle, ellipse and diamond geometries exhibit the flutter and mixed resonance–flutter modes. In contrast to its square counterpart, the diamond geometry has a movement of asymmetric boundary layers on the front lateral edges which allows the co-existence of flutter and resonance modes. For the elliptic cylinder, the mixed flutter–resonance regime occurs at a lower Reynolds number in comparison with the circular cylinder. Notably, the forward triangle configuration only shows the flutter-induced lock-in regime for this range of Reynolds number and the edges are on the leeward side with separated flow. Finally, the square-section body shows a predominant resonance regime for approximately
![]() $30\leqslant Re\leqslant 80$
, which turns into the flutter state for
$30\leqslant Re\leqslant 80$
, which turns into the flutter state for
![]() $Re>80$
.
$Re>80$
.
The present ERA-based ROM study has been concerned with two-dimensional bluff-body configurations for which only two directions in space are resolved. All of the notions of the ROM, such as base flows and eigenvalue realization, can be easily extended to full three-dimensional settings. Thus, the present method does not pose any theoretical limitation except that there may be numerical ones with respect to memory requirements and CPU time to solve the generalized eigenvalue problem.
5 Concluding remarks
In this study, we presented an ERA-based model reduction for coupled fluid–structure analysis to investigate the stability characteristics of the VIVs of bluff bodies. The ERA-based ROM relies on the singular value decomposition of a Hankel matrix constructed from the impulse response of the NS equations. The present study has remarkably demonstrated the effectiveness of the ERA-based ROM for predicting the unstable wake flow behind a stationary circular cylinder. The critical Reynolds number and the flow dynamics were well predicted and excellent agreement was found with the FOM and the available literature. We next employed the ROM for a unified description of the lock-in phenomenon as a function of the Reynolds number
![]() $Re$
, the mass ratio
$Re$
, the mass ratio
![]() $m^{\ast }$
and for the investigation of the effect of rounding and various geometrical shapes. To investigate the VIV mechanism, the ERA-based ROM was extended to construct the fluid ROM and coupled with a linear structure to form a reduced fluid–structure system in the state-space format. Two distinct lock-in patterns of flutter- and resonance-induced regimes were investigated by the ERA-based ROM for a transversely vibrating circular cylinder at the baseline parameters of
$m^{\ast }$
and for the investigation of the effect of rounding and various geometrical shapes. To investigate the VIV mechanism, the ERA-based ROM was extended to construct the fluid ROM and coupled with a linear structure to form a reduced fluid–structure system in the state-space format. Two distinct lock-in patterns of flutter- and resonance-induced regimes were investigated by the ERA-based ROM for a transversely vibrating circular cylinder at the baseline parameters of
![]() $(Re,m^{\ast })=(60,10)$
. While the resonance state has the unstable WM together with the stable SM in the range
$(Re,m^{\ast })=(60,10)$
. While the resonance state has the unstable WM together with the stable SM in the range
![]() $0.11\leqslant F_{s}\leqslant 0.147$
, the flutter regime has the co-existence of the unstable SM and WM in the range
$0.11\leqslant F_{s}\leqslant 0.147$
, the flutter regime has the co-existence of the unstable SM and WM in the range
![]() $0.147<F_{s}\leqslant 0.179$
. In comparison with the linear ROM used in Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), which is sensitive to the training trajectory, the proposed ERA-based ROM is sufficiently accurate and only requires the impulse response of the unstable fluid system. To generalize the proposed ERA-based ROM for VIV linear stability analysis, the effects of the Reynolds number, the rounding of a square cylinder and the geometry have been systematically examined and compared against the full-order simulations. Based on the systematic parametric study, the following conclusions can be drawn.
$0.147<F_{s}\leqslant 0.179$
. In comparison with the linear ROM used in Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), which is sensitive to the training trajectory, the proposed ERA-based ROM is sufficiently accurate and only requires the impulse response of the unstable fluid system. To generalize the proposed ERA-based ROM for VIV linear stability analysis, the effects of the Reynolds number, the rounding of a square cylinder and the geometry have been systematically examined and compared against the full-order simulations. Based on the systematic parametric study, the following conclusions can be drawn.
-
(i) The study on the effect of the Reynolds number demonstrates that the flutter and resonance regimes do not always exist during the lock-in phenomenon. For
 $m^{\ast }=10$
, it was found that the flutter and resonance regimes co-exist for
$m^{\ast }=10$
, it was found that the flutter and resonance regimes co-exist for
 $Re_{cr}<Re<70$
. The flutter-induced regime gradually dominates the entire lock-in region when
$Re_{cr}<Re<70$
. The flutter-induced regime gradually dominates the entire lock-in region when
 $Re\geqslant 70$
. The finding is consistent with the theoretical analysis of De Langre (Reference De Langre2006) for high Reynolds numbers. The stability region provides an explanation that it shifts upstream as
$Re\geqslant 70$
. The finding is consistent with the theoretical analysis of De Langre (Reference De Langre2006) for high Reynolds numbers. The stability region provides an explanation that it shifts upstream as
 $Re$
increases, indicating that the coupling between the unstable wake and the bluff body is enhanced. Another observation is that the reduction of the r.m.s. value of lift force is not associated with either the resonance or the flutter state, but is closely related to the phase angle jump from
$Re$
increases, indicating that the coupling between the unstable wake and the bluff body is enhanced. Another observation is that the reduction of the r.m.s. value of lift force is not associated with either the resonance or the flutter state, but is closely related to the phase angle jump from
 $0^{\circ }$
to
$0^{\circ }$
to
 $180^{\circ }$
, which is also demonstrated during the lock-in of the square cylinder.
$180^{\circ }$
, which is also demonstrated during the lock-in of the square cylinder. -
(ii) The analysis on the rounding effect of the square cylinder at
 $(Re,m^{\ast })=(60,10)$
shows that the rounding has a remarkable impact on the flutter and resonance regimes. The flutter regime can be promoted by gradually removing the sharp corners. The sharp corners suppress the continuous movement of separation points, and the WM loop of the square cylinder is smaller than the circular cylinder counterpart. As the rounding radius
$(Re,m^{\ast })=(60,10)$
shows that the rounding has a remarkable impact on the flutter and resonance regimes. The flutter regime can be promoted by gradually removing the sharp corners. The sharp corners suppress the continuous movement of separation points, and the WM loop of the square cylinder is smaller than the circular cylinder counterpart. As the rounding radius
 $r_{s}$
increases, the SM trajectory moves gradually towards the positive real axis and the flutter region starts to appear. From the comparison of leading modes, it can be seen that the stability region shifts downstream as the rounding radius
$r_{s}$
increases, the SM trajectory moves gradually towards the positive real axis and the flutter region starts to appear. From the comparison of leading modes, it can be seen that the stability region shifts downstream as the rounding radius
 $r_{s}$
decreases. There is a reduction in the coupling strength between the fluid and the structure due to the presence of sharp corners, which inhibit the movement of separation points and the susceptibility to inertial coupling. In comparison with the VIV of a circular cylinder, this study also explains why the lock-in onset
$r_{s}$
decreases. There is a reduction in the coupling strength between the fluid and the structure due to the presence of sharp corners, which inhibit the movement of separation points and the susceptibility to inertial coupling. In comparison with the VIV of a circular cylinder, this study also explains why the lock-in onset
 $U_{r}$
is larger and the lock-in region is narrower for a square cylinder.
$U_{r}$
is larger and the lock-in region is narrower for a square cylinder. -
(iii) The geometry study reveals that the cross-sectional shape significantly alters the VIV and the galloping instability. The ERA-based ROM can effectively capture the stability properties and the lock-in regimes for the elliptical, forward triangle and diamond-shaped configurations. It is found that the root loci of the WM and SM coalesce and form coupled modes for these geometries. We have provided further insights into the phenomena of flow-induced vibration by the ERA-based ROM for these bluff-body geometries. The elliptical cylinder was found to have the lowest
 $U_{r}$
for the lock-in onset, followed by the diamond and forward triangle configurations. It is of particular note that, for the forward triangle VIV, the ROM predicts that the flutter-dominated VIV persists for
$U_{r}$
for the lock-in onset, followed by the diamond and forward triangle configurations. It is of particular note that, for the forward triangle VIV, the ROM predicts that the flutter-dominated VIV persists for
 $F_{s}\leqslant 0.184$
or
$F_{s}\leqslant 0.184$
or
 $U_{r}\geqslant 5.43$
. A low-frequency galloping instability and a kink in the amplitude response associated with 1:3 synchronization were observed in the forward triangle configuration. We presented a summary phase diagram to characterize the effects of geometry on the VIV stability regimes based on the eigenspectrum distribution. Such a phase diagram based on the linear dynamics of the lock-in process provides insight to help in developing a unified description of flow-induced vibration. The phase diagram shows that the resonance mode only exists for a certain range of Reynolds number. The VIV lock-in mechanism is eventually dominated by the flutter mode as the Reynolds number increases.
$U_{r}\geqslant 5.43$
. A low-frequency galloping instability and a kink in the amplitude response associated with 1:3 synchronization were observed in the forward triangle configuration. We presented a summary phase diagram to characterize the effects of geometry on the VIV stability regimes based on the eigenspectrum distribution. Such a phase diagram based on the linear dynamics of the lock-in process provides insight to help in developing a unified description of flow-induced vibration. The phase diagram shows that the resonance mode only exists for a certain range of Reynolds number. The VIV lock-in mechanism is eventually dominated by the flutter mode as the Reynolds number increases.
The proposed ERA-based ROM is demonstrated to be accurate and efficient for the VIV linear stability analysis of bluff bodies, which has relevance in the development of flow control strategies. By shifting the unstable eigenvalues of the WM and SM to the stable left half-complex-plane, suppression of vortex streets and VIV can be achieved by the model. The simplicity of the model permits investigation of a range of geometries and parameters for the VIV mechanism and paves the way to a bottom-up approach for the development of control devices. We would like to emphasize that we have considered only linear dynamical systems in this study; a possible future direction would include an extension of the system identification process to nonlinear systems. In the future, there will also be a need for further investigation at high Reynolds numbers to expand the proposed model reduction approach to a generalized lock-in description with a wider parameter space of the mass-damping parameter.
Acknowledgement
The first author would like to acknowledge Singapore Maritime Institute Grant (SMI-2014-OF-04) for the financial support.
Appendix A. Derivation of the phase angle for VIV
By considering the cylinder motion and fluid forcing as sinusoidal functions, the displacement and lift coefficient can be obtained for the VIV linear system as
where
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{r}+\text{i}\unicode[STIX]{x1D706}_{i}$
is the eigenvalue with real
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{r}+\text{i}\unicode[STIX]{x1D706}_{i}$
is the eigenvalue with real
![]() $\unicode[STIX]{x1D706}_{r}$
and imaginary
$\unicode[STIX]{x1D706}_{r}$
and imaginary
![]() $\unicode[STIX]{x1D706}_{i}$
components, and
$\unicode[STIX]{x1D706}_{i}$
components, and
![]() ${\hat{Y}}$
and
${\hat{Y}}$
and
![]() $\hat{C_{l}}$
denote the magnitudes of the eigenmodes. The phase angle
$\hat{C_{l}}$
denote the magnitudes of the eigenmodes. The phase angle
![]() $\unicode[STIX]{x1D719}$
can be derived by plugging (A 1) into the structural equation (2.13) as
$\unicode[STIX]{x1D719}$
can be derived by plugging (A 1) into the structural equation (2.13) as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left[{\hat{Y}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}(\unicode[STIX]{x1D706}_{r}^{2}-\unicode[STIX]{x1D706}_{i}^{2}+4\unicode[STIX]{x03C0}\unicode[STIX]{x1D701}F_{s}\unicode[STIX]{x1D706}_{r}+(2\unicode[STIX]{x03C0}F_{s})^{2})-\frac{a_{s}\hat{C_{l}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}\cos \unicode[STIX]{x1D719}}{m^{\ast }}\right]\cos \unicode[STIX]{x1D706}_{i}t\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[{\hat{Y}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}(-2\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D706}_{i}-4\unicode[STIX]{x03C0}\unicode[STIX]{x1D701}F_{s}\unicode[STIX]{x1D706}_{i})+\frac{a_{s}\hat{C_{l}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}\sin \unicode[STIX]{x1D719}}{m^{\ast }}\right]\sin \unicode[STIX]{x1D706}_{i}t=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[{\hat{Y}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}(\unicode[STIX]{x1D706}_{r}^{2}-\unicode[STIX]{x1D706}_{i}^{2}+4\unicode[STIX]{x03C0}\unicode[STIX]{x1D701}F_{s}\unicode[STIX]{x1D706}_{r}+(2\unicode[STIX]{x03C0}F_{s})^{2})-\frac{a_{s}\hat{C_{l}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}\cos \unicode[STIX]{x1D719}}{m^{\ast }}\right]\cos \unicode[STIX]{x1D706}_{i}t\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[{\hat{Y}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}(-2\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D706}_{i}-4\unicode[STIX]{x03C0}\unicode[STIX]{x1D701}F_{s}\unicode[STIX]{x1D706}_{i})+\frac{a_{s}\hat{C_{l}}\text{e}^{\unicode[STIX]{x1D706}_{r}t}\sin \unicode[STIX]{x1D719}}{m^{\ast }}\right]\sin \unicode[STIX]{x1D706}_{i}t=0.\end{eqnarray}$$
By equating the coefficients of
![]() $\cos (\unicode[STIX]{x1D706}_{i}t)$
and
$\cos (\unicode[STIX]{x1D706}_{i}t)$
and
![]() $\sin (\unicode[STIX]{x1D706}_{i}t)$
to zero, we obtain the following relations:
$\sin (\unicode[STIX]{x1D706}_{i}t)$
to zero, we obtain the following relations:
By solving (A 4) and setting
![]() $\unicode[STIX]{x1D701}=0$
,
$\unicode[STIX]{x1D701}=0$
,
![]() $\sin \unicode[STIX]{x1D719}$
and
$\sin \unicode[STIX]{x1D719}$
and
![]() $\cos \unicode[STIX]{x1D719}$
can be obtained as
$\cos \unicode[STIX]{x1D719}$
can be obtained as
Through the trigonometric identity
![]() $\cos ^{2}\unicode[STIX]{x1D719}+\sin ^{2}\unicode[STIX]{x1D719}=1$
, the term
$\cos ^{2}\unicode[STIX]{x1D719}+\sin ^{2}\unicode[STIX]{x1D719}=1$
, the term
![]() $\sin \unicode[STIX]{x1D719}$
can be further simplified in terms of
$\sin \unicode[STIX]{x1D719}$
can be further simplified in terms of
![]() $(\unicode[STIX]{x1D706},F_{s})$
as follows:
$(\unicode[STIX]{x1D706},F_{s})$
as follows:

Figure 26. The effect of the mass ratio on the eigenspectrum of the ERA-based ROM for a circular cylinder at
![]() $m^{\ast }=(5,7.6,20)$
and
$m^{\ast }=(5,7.6,20)$
and
![]() $Re=60$
: (a) the root loci as a function of the reduced natural frequency
$Re=60$
: (a) the root loci as a function of the reduced natural frequency
![]() $F_{s}$
, where the unstable right half-plane
$F_{s}$
, where the unstable right half-plane
![]() $(Re(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
$(Re(\unicode[STIX]{x1D706})>0)$
is shaded in grey colour and the hollow arrow indicates increasing
![]() $F_{s}$
; (b) the real and imaginary parts of the root loci. In (b), the growth rate
$F_{s}$
; (b) the real and imaginary parts of the root loci. In (b), the growth rate
![]() $\text{Re}(\unicode[STIX]{x1D706})$
curves of WSMI and WSMII intersect at
$\text{Re}(\unicode[STIX]{x1D706})$
curves of WSMI and WSMII intersect at
![]() $F_{s}=0.175$
(– – –) and the flutter regime is defined between
$F_{s}=0.175$
(– – –) and the flutter regime is defined between
![]() $F_{s}=0.197$
(– - – - –) and
$F_{s}=0.197$
(– - – - –) and
![]() $F_{s}=0.165$
(
$F_{s}=0.165$
(
![]() $\cdots \cdots$
) for
$\cdots \cdots$
) for
![]() $m^{\ast }=5$
. The frequency anticrossing is shown in the inset of the
$m^{\ast }=5$
. The frequency anticrossing is shown in the inset of the
![]() $\text{Im}(\unicode[STIX]{x1D706})$
plot. The WSMI and SM branches are denoted by filled symbols with the same shapes as the WSMII and WM symbols in (a,b).
$\text{Im}(\unicode[STIX]{x1D706})$
plot. The WSMI and SM branches are denoted by filled symbols with the same shapes as the WSMII and WM symbols in (a,b).
Appendix B. Effect of mass ratio
For illustration of the ERA-based ROM, the effect of the mass ratio is shown in figure 26 for
![]() $m^{\ast }=(5,7.6,20)$
at
$m^{\ast }=(5,7.6,20)$
at
![]() $Re=60$
. Figure 26(b) shows the real and imaginary parts of the root loci as a function of the reduced frequency
$Re=60$
. Figure 26(b) shows the real and imaginary parts of the root loci as a function of the reduced frequency
![]() $F_{s}$
. It indicates that the lock-in onset starts to move to the lower reduced velocity (
$F_{s}$
. It indicates that the lock-in onset starts to move to the lower reduced velocity (
![]() $U_{r}=1/F_{s}$
) regime as the mass ratio
$U_{r}=1/F_{s}$
) regime as the mass ratio
![]() $m^{\ast }$
decreases. As expected, due to weaker fluid–structure coupling for larger mass ratio
$m^{\ast }$
decreases. As expected, due to weaker fluid–structure coupling for larger mass ratio
![]() $m^{\ast }=20$
, the eigenfrequency of the WM recovers to the frequency of the stationary cylinder and the frequency of the SM approaches the natural frequency of the cylinder-only system as
$m^{\ast }=20$
, the eigenfrequency of the WM recovers to the frequency of the stationary cylinder and the frequency of the SM approaches the natural frequency of the cylinder-only system as
![]() $F_{s}$
increases. As the mass ratio decreases further, figure 26(a) shows that the root loci of the SM and WM gradually coalesce and form a coupled mode due to the increased strength of the fluid–structure coupling. The approximate threshold mass ratio is
$F_{s}$
increases. As the mass ratio decreases further, figure 26(a) shows that the root loci of the SM and WM gradually coalesce and form a coupled mode due to the increased strength of the fluid–structure coupling. The approximate threshold mass ratio is
![]() $m^{\ast }\approx 7.6$
for the coupled mode, which is very close to the predicted
$m^{\ast }\approx 7.6$
for the coupled mode, which is very close to the predicted
![]() $m^{\ast }=7.3$
in Zhang et al. (Reference Zhang, Li, Ye and Jiang2015). The phenomenon is termed as the mixed WM/SM (Meliga & Chomaz Reference Meliga and Chomaz2011) or the coupled fluid–elastic mode (Navrose & Mittal Reference Mittal2016). As illustrated in figure 26(b), for the mass ratio
$m^{\ast }=7.3$
in Zhang et al. (Reference Zhang, Li, Ye and Jiang2015). The phenomenon is termed as the mixed WM/SM (Meliga & Chomaz Reference Meliga and Chomaz2011) or the coupled fluid–elastic mode (Navrose & Mittal Reference Mittal2016). As illustrated in figure 26(b), for the mass ratio
![]() $m^{\ast }=5$
, the coupled wake–structure modes WSMI and WSMII resemble the SM and WM respectively for
$m^{\ast }=5$
, the coupled wake–structure modes WSMI and WSMII resemble the SM and WM respectively for
![]() $F_{s}\leqslant 0.175$
, whereas WSMI and WSMII resemble the standard WM and SM respectively for
$F_{s}\leqslant 0.175$
, whereas WSMI and WSMII resemble the standard WM and SM respectively for
![]() $F_{s}>0.175$
. This finding suggests that the stability roles of the WM and the SM switch at a specific value of
$F_{s}>0.175$
. This finding suggests that the stability roles of the WM and the SM switch at a specific value of
![]() $F_{s}$
, where the two growth rate
$F_{s}$
, where the two growth rate
![]() $Re(\unicode[STIX]{x1D706})$
curves of WSMI and WSMII intersect. The flutter regime for
$Re(\unicode[STIX]{x1D706})$
curves of WSMI and WSMII intersect. The flutter regime for
![]() $m^{\ast }=5$
is then defined by
$m^{\ast }=5$
is then defined by
![]() $0.165<F_{s}\leqslant 0.197$
(
$0.165<F_{s}\leqslant 0.197$
(
![]() $5.08\leqslant U_{r}<6.07$
), as shown in figure 26(b), which matches well with the results of Navrose & Mittal (Reference Mittal2016) (
$5.08\leqslant U_{r}<6.07$
), as shown in figure 26(b), which matches well with the results of Navrose & Mittal (Reference Mittal2016) (
![]() $5.0\leqslant U_{r}<6.0$
) in identical conditions. In figure 26(b) (bottom), the two curves of
$5.0\leqslant U_{r}<6.0$
) in identical conditions. In figure 26(b) (bottom), the two curves of
![]() $\text{Im}(\unicode[STIX]{x1D706})$
for
$\text{Im}(\unicode[STIX]{x1D706})$
for
![]() $m^{\ast }=(5,7.6)$
no longer cross and there is a characteristic anticrossing with a frequency splitting (
$m^{\ast }=(5,7.6)$
no longer cross and there is a characteristic anticrossing with a frequency splitting (
![]() $\unicode[STIX]{x0394}f$
) between WSMI and WSMII. This phenomenon of anticrossing is an intrinsic property of strong coupling at low mass ratio, as reported for generic coupled mechanical oscillators in Novotny (Reference Novotny2010).
$\unicode[STIX]{x0394}f$
) between WSMI and WSMII. This phenomenon of anticrossing is an intrinsic property of strong coupling at low mass ratio, as reported for generic coupled mechanical oscillators in Novotny (Reference Novotny2010).