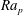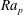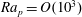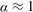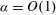1. Introduction
There are numerous heat transfer systems where the heat flow is driven by spatially distributed heating. Efficient heat removal from components installed on computer motherboards represents one typical situation. Natural convection is preferred due to its passive character but it can rarely handle the required heat load. Weather phenomena associated with non-uniform heating of the ground represent another example. This effect is related to the presence of patterns of roofs–streets–parks in an urban environment and forests–lakes–fields in a rural environment. The use of flow patterning for biological applications such as cell analysers provides an interesting application in microfluidics (Krishnan, Ugaz & Burns Reference Krishnan, Ugaz and Burns2002). Understanding of the motions of fluids over geometrically, chemically and thermally patterned surfaces is of vital interest in their design. Of particular importance is how convective motions develop and how they affect the transport of passive scalar quantities along regularly structured surfaces (Beltrame et al. Reference Beltrame, Knobloch, Hänggi and Thiele2011). It is known in geological applications that a system of fractures, leads and polynyas in sea ice leads to convection in both the ocean and the atmosphere, with small leads of the order of several metres being more efficient than larger ones of the order of several hundred metres (Marcq & Weiss Reference Marcq and Weiss2012). The insulating effect of continents on mantle convection within the Earth is another example of a spatially structured convection occurring in nature (Lenardic et al. Reference Lenardic, Moresi, Jellinek and Manga2005).
The heat transport in the case of pure natural convection is driven by the buoyancy force. Convection occurring in a stationary fluid layer subject to spatially homogeneous heating from below represents the reference case. This is the so-called Rayleigh–Bénard (RB) convection (Bénard Reference Bénard1900; Rayleigh Reference Rayleigh1916). The conductive state of equilibrium undergoes transition to convective motion if the critical conditions expressed in terms of a suitably defined Rayleigh number are met; see Bodenschatz, Pesch & Ahlers (Reference Bodenschatz, Pesch and Ahlers2000), Ahlers, Grossmann & Lohse (Reference Ahlers, Grossmann and Lohse2009), Lohse & Xia (Reference Lohse and Xia2010) and Chilla & Schumacher (Reference Chilla and Schumacher2012) for recent reviews. The RB convection can be combined with inhomogeneities in the boundary temperatures, but this concept has been used only to study the effects of small inhomogeneities (or boundary imperfections) on the symmetry breakup in the RB convection rather than to investigate convection dominated by such inhomogeneities (Hossain & Floryan Reference Hossain and Floryan2013b ). The introduction of forced motion (mixed convection) gives preference to rolls with axes parallel to the flow direction but does not affect the critical conditions (Gage & Reid Reference Gage and Reid1968); see Kelly (Reference Kelly1994) for a complete review.
Inhomogeneous heating creates horizontal temperature variations, which lead to different vertical pressure distributions at different horizontal locations, giving rise to horizontal pressure gradients. Such configurations are statically unstable, resulting in fluid movement regardless of the intensity of the heating and leading to motion frequently referred to as horizontal convection (Maxworthy Reference Maxworthy1997; Siggers, Kerswell & Balmforth Reference Siggers, Kerswell and Balmforth2004; Hughes & Griffiths Reference Hughes and Griffiths2008; Winters & Young Reference Winters and Young2009). The first study of such convection that we are aware of used asymptotic approximation in the analysis of long-wavelength heating (Kelly & Pal Reference Kelly and Pal1976a
,Reference Kelly and Pal
b
). A detailed analysis of convection resulting from application of heating with arbitrary wavelength and with arbitrary Prandtl number has been given only recently (Hossain & Floryan Reference Hossain and Floryan2013a
). It has been shown that the heat transfer strongly depends on the wavenumber; it rapidly decreases when the wavenumber is either too small or too large. The primary convection undergoes transition to secondary convection whose structure strongly depends on the heating wavenumber (Hossain & Floryan Reference Hossain and Floryan2013b
). For large wavenumbers, the primary convection creates a conduction zone above a thin boundary layer adjacent to the heated wall, resulting in the dominance of the RB mechanism. When heating wavenumbers are
![]() $O(1)$
, the spatial parametric resonance dominates, resulting in the formation of oblique rolls with the wavevector having a component orthogonal to the wavevector of the primary convection. Such oblique structures are rarely observed in pattern-forming systems, where they lead to the three-dimensionalization of the otherwise two-dimensional flow problem. It has been shown that wavenumber locking between the primary and secondary convection occurs under certain conditions. A qualitatively similar problem with spatial variability resulting from the use of mixed insulating and conducting boundary conditions has been studied by Ripesi et al. (Reference Ripesi, Biferale, Sbragaglia and Wirth2014) using numerical simulations.
$O(1)$
, the spatial parametric resonance dominates, resulting in the formation of oblique rolls with the wavevector having a component orthogonal to the wavevector of the primary convection. Such oblique structures are rarely observed in pattern-forming systems, where they lead to the three-dimensionalization of the otherwise two-dimensional flow problem. It has been shown that wavenumber locking between the primary and secondary convection occurs under certain conditions. A qualitatively similar problem with spatial variability resulting from the use of mixed insulating and conducting boundary conditions has been studied by Ripesi et al. (Reference Ripesi, Biferale, Sbragaglia and Wirth2014) using numerical simulations.
In many applications, spatially distributed heating is combined with forced motion. It has been shown recently that spatially periodic heating gives rise to the superthermohydrophobic effect (Floryan Reference Floryan2012; Hossain, Floryan & Floryan Reference Hossain, Floryan and Floryan2012), which leads to a significant drag reduction for small
![]() $\mathit{Re}$
flows and thus could lead to the design of a new class of microfluidic devices. These predictions remain valid as long as the flow does not undergo transition to secondary states. The first study of secondary states that we are aware of is due to Hasnaoui et al. (Reference Hasnaoui, Rilgen, Vasseur and Robillard1991), who used two-dimensional direct numerical simulations and observed a number of complex secondary states. Their analysis cannot capture oblique rolls as well as rolls with axes parallel to the flow direction, which play the dominant role in mixed convection with uniform heating (Gage & Reid Reference Gage and Reid1968; Kelly Reference Kelly1994). It can be concluded that the characteristics of mixed convection in a system subject to spatially periodic heating are not known. The conditions leading to transition to secondary states as well as flow patterns resulting from such transition remain to be determined.
$\mathit{Re}$
flows and thus could lead to the design of a new class of microfluidic devices. These predictions remain valid as long as the flow does not undergo transition to secondary states. The first study of secondary states that we are aware of is due to Hasnaoui et al. (Reference Hasnaoui, Rilgen, Vasseur and Robillard1991), who used two-dimensional direct numerical simulations and observed a number of complex secondary states. Their analysis cannot capture oblique rolls as well as rolls with axes parallel to the flow direction, which play the dominant role in mixed convection with uniform heating (Gage & Reid Reference Gage and Reid1968; Kelly Reference Kelly1994). It can be concluded that the characteristics of mixed convection in a system subject to spatially periodic heating are not known. The conditions leading to transition to secondary states as well as flow patterns resulting from such transition remain to be determined.
The main objective of this analysis is to determine the basic characteristics of fluid movement and the resulting heat transfer process associated with mixed convection in a simple system consisting of an infinitely long horizontal channel where the flow is driven by a pressure gradient and the channel is subject to heating that is periodic in the flow direction. We shall focus our attention on fluids with
![]() $\mathit{Pr}=0.71$
and consider a simple sinusoidal temperature variation applied at the lower wall, as this reduces the number of parameters to just three, i.e. the heating wavenumber
$\mathit{Pr}=0.71$
and consider a simple sinusoidal temperature variation applied at the lower wall, as this reduces the number of parameters to just three, i.e. the heating wavenumber
![]() ${\it\alpha}$
, the heating intensity expressed in terms of the Rayleigh number
${\it\alpha}$
, the heating intensity expressed in terms of the Rayleigh number
![]() $\mathit{Ra}_{p}$
, and the flow Reynolds number
$\mathit{Ra}_{p}$
, and the flow Reynolds number
![]() $\mathit{Re}$
. The convective motion resulting from the applied heating can be viewed as a forced response or, alternatively, it can be referred to as the primary convection. It is known that convective flows are highly unstable, and thus the analysis is extended to include determination of conditions leading to secondary convection as well as determination of the possible patterns of secondary motions. The analysis is carried out using a model problem where the heating is applied at the lower wall. Generalization of the results to the heating applied at the upper wall is discussed, as the system exhibits up–down symmetries (Howard & Krishnamurti Reference Howard and Krishnamurti1986; Hossain & Floryan Reference Hossain and Floryan2014).
$\mathit{Re}$
. The convective motion resulting from the applied heating can be viewed as a forced response or, alternatively, it can be referred to as the primary convection. It is known that convective flows are highly unstable, and thus the analysis is extended to include determination of conditions leading to secondary convection as well as determination of the possible patterns of secondary motions. The analysis is carried out using a model problem where the heating is applied at the lower wall. Generalization of the results to the heating applied at the upper wall is discussed, as the system exhibits up–down symmetries (Howard & Krishnamurti Reference Howard and Krishnamurti1986; Hossain & Floryan Reference Hossain and Floryan2014).
The rest of this paper is organized as follows. Section 2 discusses the forced response of the fluid, i.e. the primary convection. Section 3 discusses transition to secondary states as well as flow topologies associated with these states using linear stability theory as the main methodology. Section 4 provides a summary of the main conclusions.
2. Primary convection
The external heating of interest is a function of the streamwise coordinate and it results in a two-dimensional steady primary convection. The three-dimensional secondary convection is discussed in § 3.
2.1. Problem formulation with heating applied at the lower wall
Consider fluid contained in a slot between two parallel plates extending to
![]() $\pm \infty$
in the
$\pm \infty$
in the
![]() $x$
and
$x$
and
![]() $z$
directions and placed at a distance
$z$
directions and placed at a distance
![]() $2h$
apart from each other, with the gravitational acceleration
$2h$
apart from each other, with the gravitational acceleration
![]() $g$
acting in the negative
$g$
acting in the negative
![]() $y$
direction, as shown in figure 1. The fluid is driven in the positive
$y$
direction, as shown in figure 1. The fluid is driven in the positive
![]() $x$
direction by a constant pressure gradient, resulting in a two-dimensional motion. The upper plate is kept isothermal with the constant temperature
$x$
direction by a constant pressure gradient, resulting in a two-dimensional motion. The upper plate is kept isothermal with the constant temperature
![]() $T_{U}$
, while the lower plate is subject to periodic heating resulting in its temperature
$T_{U}$
, while the lower plate is subject to periodic heating resulting in its temperature
![]() $T_{L}$
of the form
$T_{L}$
of the form
where
![]() ${\it\lambda}=2{\rm\pi}/{\it\alpha}$
is the wavelength of the heating. The fluid is incompressible and Newtonian, with thermal conductivity
${\it\lambda}=2{\rm\pi}/{\it\alpha}$
is the wavelength of the heating. The fluid is incompressible and Newtonian, with thermal conductivity
![]() $k$
, specific heat
$k$
, specific heat
![]() $c$
, thermal diffusivity
$c$
, thermal diffusivity
![]() ${\it\kappa}=k/{\it\rho}c$
, kinematic viscosity
${\it\kappa}=k/{\it\rho}c$
, kinematic viscosity
![]() ${\it\nu}$
, dynamic viscosity
${\it\nu}$
, dynamic viscosity
![]() ${\it\mu}$
, thermal expansion coefficient
${\it\mu}$
, thermal expansion coefficient
![]() ${\it\Gamma}$
and variations of the density
${\it\Gamma}$
and variations of the density
![]() ${\it\rho}$
that follow the Boussinesq approximation. All material properties are taken at the reference temperature
${\it\rho}$
that follow the Boussinesq approximation. All material properties are taken at the reference temperature
![]() $T_{U}$
.
$T_{U}$
.

Figure 1. Sketch of the flow system.
The dimensionless form of the velocity and pressure fields in the absence of the heating are expressed as
where
![]() $\boldsymbol{v}_{0}$
denotes the velocity vector scaled with the maximum of the
$\boldsymbol{v}_{0}$
denotes the velocity vector scaled with the maximum of the
![]() $x$
velocity
$x$
velocity
![]() $U_{max}$
,
$U_{max}$
,
![]() $p_{0}$
stands for the pressure scaled with
$p_{0}$
stands for the pressure scaled with
![]() ${\it\rho}U_{max}^{2}$
, half of the distance between the plates
${\it\rho}U_{max}^{2}$
, half of the distance between the plates
![]() $h$
has been chosen as the length scale and the Reynolds number is defined as
$h$
has been chosen as the length scale and the Reynolds number is defined as
![]() $\mathit{Re}=U_{max}h/{\it\nu}$
.
$\mathit{Re}=U_{max}h/{\it\nu}$
.
Introduction of the heating modifies the above fields, which can be represented as a superposition of the pressure-gradient-driven and the buoyancy-driven motions. The temperature field can be represented, for convenience of interpretation, as a superposition of the conductive field
![]() ${\it\theta}_{0}$
corresponding to the external heating and modifications associated with the movement of the fluid. Here
${\it\theta}_{0}$
corresponding to the external heating and modifications associated with the movement of the fluid. Here
![]() ${\it\theta}_{0}=(T-T_{U})$
stands for the relative temperature. The complete flow quantities are identified using the subscript
${\it\theta}_{0}=(T-T_{U})$
stands for the relative temperature. The complete flow quantities are identified using the subscript
![]() $B$
and have the form
$B$
and have the form
where
![]() $(u_{1},v_{1})$
,
$(u_{1},v_{1})$
,
![]() $p_{1}$
and
$p_{1}$
and
![]() ${\it\theta}_{1}$
stand for the part of the velocity vector, the pressure and the temperature associated with the buoyancy effects. The complete velocity vector
${\it\theta}_{1}$
stand for the part of the velocity vector, the pressure and the temperature associated with the buoyancy effects. The complete velocity vector
![]() $(u_{B},v_{B})$
and the velocity modifications
$(u_{B},v_{B})$
and the velocity modifications
![]() $(u_{1},v_{1})$
have been scaled using the convective velocity scale
$(u_{1},v_{1})$
have been scaled using the convective velocity scale
![]() $U_{v}={\it\nu}/h$
, where
$U_{v}={\it\nu}/h$
, where
![]() $U_{max}/U_{v}=\mathit{Re}$
, the complete pressure field
$U_{max}/U_{v}=\mathit{Re}$
, the complete pressure field
![]() $p_{B}$
as well as the pressure modifications
$p_{B}$
as well as the pressure modifications
![]() $p_{1}$
have been scaled using
$p_{1}$
have been scaled using
![]() ${\it\rho}U_{v}^{2}$
, the complete temperature field
${\it\rho}U_{v}^{2}$
, the complete temperature field
![]() ${\it\theta}_{B}$
as well as the temperature modifications
${\it\theta}_{B}$
as well as the temperature modifications
![]() ${\it\theta}_{1}$
have been scaled with the convective temperature scale
${\it\theta}_{1}$
have been scaled with the convective temperature scale
![]() $T_{v}=T_{d}{\it\nu}/{\it\kappa}$
, while the conductive temperature field has been scaled with
$T_{v}=T_{d}{\it\nu}/{\it\kappa}$
, while the conductive temperature field has been scaled with
![]() $T_{d}$
as the relevant scale, where
$T_{d}$
as the relevant scale, where
![]() $T_{v}/T_{d}=\mathit{Pr}$
and
$T_{v}/T_{d}=\mathit{Pr}$
and
![]() $\mathit{Pr}$
stands for the Prandtl number. The reader may note that the maximum of
$\mathit{Pr}$
stands for the Prandtl number. The reader may note that the maximum of
![]() ${\it\theta}_{B}$
in this scaling is always
${\it\theta}_{B}$
in this scaling is always
![]() $(2\mathit{Pr})^{-1}$
. The conductive temperature field is described by the system
$(2\mathit{Pr})^{-1}$
. The conductive temperature field is described by the system
where
![]() ${\rm\nabla}^{2}$
denotes the Laplace operator. Its solution has the form
${\rm\nabla}^{2}$
denotes the Laplace operator. Its solution has the form
and demonstrates that conductive effects do not generate net heat flow across the channel. The dimensionless field equations for the flow and temperature modifications take the form
The relevant boundary conditions include the no-slip and the no-penetration conditions as well as the thermal boundary of the form
Solution of (2.6)–(2.8) results in the simultaneous determination of the velocity and temperature fields, followed by determination of the heat flow characteristics. The limit of
![]() $\mathit{Re}\rightarrow 0$
corresponds to a pure natural convection studied by Hossain & Floryan (Reference Hossain and Floryan2013a
,Reference Hossain and Floryan
b
). An increase of
$\mathit{Re}\rightarrow 0$
corresponds to a pure natural convection studied by Hossain & Floryan (Reference Hossain and Floryan2013a
,Reference Hossain and Floryan
b
). An increase of
![]() $\mathit{Re}$
leads to an increase in the importance of the forced flow. Elimination of the heating corresponds to the limit
$\mathit{Re}$
leads to an increase in the importance of the forced flow. Elimination of the heating corresponds to the limit
![]() $\mathit{Ra}_{p}\rightarrow 0$
, which results in
$\mathit{Ra}_{p}\rightarrow 0$
, which results in
![]() $u_{1}=v_{1}=p_{1}={\it\theta}_{1}=0$
with the flow field being described by (2.2a,b
).
$u_{1}=v_{1}=p_{1}={\it\theta}_{1}=0$
with the flow field being described by (2.2a,b
).
2.2. Numerical solution method
The numerical algorithm used in this analysis is similar to that employed by Hossain & Floryan (Reference Hossain and Floryan2013b
) and thus the following presentation is limited to a short outline. Introduction of the stream function
![]() ${\it\psi}(x,y)$
, defined in the usual manner, i.e.
${\it\psi}(x,y)$
, defined in the usual manner, i.e.
![]() $u_{1}=\partial {\it\psi}/\partial y$
,
$u_{1}=\partial {\it\psi}/\partial y$
,
![]() $v_{1}=-\partial {\it\psi}/\partial x$
, and elimination of pressure brings the governing equations to the form
$v_{1}=-\partial {\it\psi}/\partial x$
, and elimination of pressure brings the governing equations to the form
and
![]() $\langle \cdots \rangle$
denotes products. The solution is assumed to be in the form of Fourier expansions
$\langle \cdots \rangle$
denotes products. The solution is assumed to be in the form of Fourier expansions
where
![]() $u_{1}^{(n)}=\text{D}{\it\varphi}^{(n)}$
,
$u_{1}^{(n)}=\text{D}{\it\varphi}^{(n)}$
,
![]() $v_{1}^{(n)}=-\text{i}n{\it\alpha}{\it\varphi}^{(n)}$
,
$v_{1}^{(n)}=-\text{i}n{\it\alpha}{\it\varphi}^{(n)}$
,
![]() ${\it\varphi}^{(n)}={\it\varphi}^{(-n)\ast }$
,
${\it\varphi}^{(n)}={\it\varphi}^{(-n)\ast }$
,
![]() $u_{1}^{(n)}=u_{1}^{(-n)\ast }$
,
$u_{1}^{(n)}=u_{1}^{(-n)\ast }$
,
![]() $v_{1}^{(n)}=v_{1}^{(-n)\ast }$
,
$v_{1}^{(n)}=v_{1}^{(-n)\ast }$
,
![]() ${\it\phi}^{(n)}={\it\phi}^{(-n)\ast }$
,
${\it\phi}^{(n)}={\it\phi}^{(-n)\ast }$
,
![]() $p_{1}^{(n)}=p_{1}^{(-n)\ast }$
, and the asterisk denotes the complex conjugate. The products are expressed using Fourier expansions of the form
$p_{1}^{(n)}=p_{1}^{(-n)\ast }$
, and the asterisk denotes the complex conjugate. The products are expressed using Fourier expansions of the form
Substitution of (2.12) into (2.9) and separation of Fourier components results in a system of ordinary differential equations for the modal functions for
![]() $-\infty <n<\infty$
of the form
$-\infty <n<\infty$
of the form
where the conditions for
![]() ${\it\varphi}^{(0)}$
represent the stream function normalization condition and the flow-rate constraint. System (2.13) and (2.14) needs to be solved numerically.
${\it\varphi}^{(0)}$
represent the stream function normalization condition and the flow-rate constraint. System (2.13) and (2.14) needs to be solved numerically.
For the purpose of numerical solution, the expansions (2.12) have been truncated after
![]() $N_{M}$
terms. The discretization method in the
$N_{M}$
terms. The discretization method in the
![]() $y$
direction uses the Chebyshev collocation technique based on
$y$
direction uses the Chebyshev collocation technique based on
![]() $N_{T}$
collocation points. The resulting nonlinear algebraic system is solved using an iterative technique combined with under-relaxation of the form
$N_{T}$
collocation points. The resulting nonlinear algebraic system is solved using an iterative technique combined with under-relaxation of the form
![]() ${\it\Phi}_{j+1}={\it\Phi}_{j}+\text{RF}({\it\Phi}_{comp}-{\it\Phi}_{j})$
, where
${\it\Phi}_{j+1}={\it\Phi}_{j}+\text{RF}({\it\Phi}_{comp}-{\it\Phi}_{j})$
, where
![]() ${\it\Phi}=\{{\it\varphi}^{(n)},{\it\phi}^{(n)}\}$
is the vector of unknowns,
${\it\Phi}=\{{\it\varphi}^{(n)},{\it\phi}^{(n)}\}$
is the vector of unknowns,
![]() ${\it\Phi}_{comp}$
denotes the current solution,
${\it\Phi}_{comp}$
denotes the current solution,
![]() ${\it\Phi}_{j}$
denotes the previous solution,
${\it\Phi}_{j}$
denotes the previous solution,
![]() ${\it\Phi}_{j+1}$
stands for the accepted value of the next iteration and RF denotes the relaxation factor. The solution process represents the first-order fixed point method, i.e. the full iteration step involves solution of (2.13) with the nonlinear terms on the right-hand side taken from the most recent iteration (they are ignored in the first iteration), evaluation of the new approximation of the velocity and temperature fields, and evaluation of the new values of the nonlinear terms. This process is continued until a convergence criterion in the form
${\it\Phi}_{j+1}$
stands for the accepted value of the next iteration and RF denotes the relaxation factor. The solution process represents the first-order fixed point method, i.e. the full iteration step involves solution of (2.13) with the nonlinear terms on the right-hand side taken from the most recent iteration (they are ignored in the first iteration), evaluation of the new approximation of the velocity and temperature fields, and evaluation of the new values of the nonlinear terms. This process is continued until a convergence criterion in the form
![]() $\max (|{\it\Phi}_{comp}-{\it\Phi}_{j}|)<\text{TOL}$
is satisfied, where TOL denotes the specified error. The number of collocation points and the number of Fourier modes used in the solution were selected through numerical experiments so that the flow quantities of interest were determined with at least six-digit accuracy. Typically
$\max (|{\it\Phi}_{comp}-{\it\Phi}_{j}|)<\text{TOL}$
is satisfied, where TOL denotes the specified error. The number of collocation points and the number of Fourier modes used in the solution were selected through numerical experiments so that the flow quantities of interest were determined with at least six-digit accuracy. Typically
![]() $N_{T}=50$
provided sufficient accuracy. The required value of
$N_{T}=50$
provided sufficient accuracy. The required value of
![]() $N_{M}$
strongly depends on
$N_{M}$
strongly depends on
![]() ${\it\alpha}$
,
${\it\alpha}$
,
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $\mathit{Ra}$
and can be as large as
$\mathit{Ra}$
and can be as large as
![]() $N_{M}=30$
.
$N_{M}=30$
.
The evaluation of the nonlinear terms requires evaluation of products of two Fourier series. It is more efficient to evaluate these products in physical space rather than in Fourier space. The required quantities were computed in physical space on a suitable grid based on the collocation points in the
![]() $y$
direction and on a uniformly distributed set of points in the
$y$
direction and on a uniformly distributed set of points in the
![]() $x$
direction, and the relevant products were evaluated. The fast Fourier transform (FFT) algorithm was used to express these products in terms of Fourier expansions (2.12). The aliasing error was controlled using a discrete FFT transform with
$x$
direction, and the relevant products were evaluated. The fast Fourier transform (FFT) algorithm was used to express these products in terms of Fourier expansions (2.12). The aliasing error was controlled using a discrete FFT transform with
![]() $N_{p}$
rather than
$N_{p}$
rather than
![]() $N_{M}$
points, where
$N_{M}$
points, where
![]() $N_{p}\geqslant 3N_{M}/2$
.
$N_{p}\geqslant 3N_{M}/2$
.
2.3. Description of the primary convection when the lower wall is heated
Figure 2 illustrates typical flow patterns. The pattern for purely natural convection (
![]() $\mathit{Re}=0$
) consists of a pair of counter-rotating rolls with fluid rising above the hot spots (figure 2
a). The introduction of forced convection results in the formation of stream tube meandering between separation bubbles whose origin can be traced to the convection rolls, e.g. see the flow pattern in figure 2(b) for
$\mathit{Re}=0$
) consists of a pair of counter-rotating rolls with fluid rising above the hot spots (figure 2
a). The introduction of forced convection results in the formation of stream tube meandering between separation bubbles whose origin can be traced to the convection rolls, e.g. see the flow pattern in figure 2(b) for
![]() $\mathit{Re}=5$
. A further increase of
$\mathit{Re}=5$
. A further increase of
![]() $\mathit{Re}$
results in the removal of the separation bubbles (figure 2
c) and nearly complete elimination of the transverse motion.
$\mathit{Re}$
results in the removal of the separation bubbles (figure 2
c) and nearly complete elimination of the transverse motion.

Figure 2. Flow patterns for
![]() $\mathit{Ra}_{p}=1000$
,
$\mathit{Ra}_{p}=1000$
,
![]() ${\it\alpha}=1$
and
${\it\alpha}=1$
and
![]() $\mathit{Re}=0$
(a), 5 (b) and 20 (c), respectively. The complete stream function
$\mathit{Re}=0$
(a), 5 (b) and 20 (c), respectively. The complete stream function
![]() ${\it\Psi}(x,y)=\mathit{Re}(-y^{3}/3+y+2/3)+{\it\psi}(x,y)$
is normalized by its maximum,
${\it\Psi}(x,y)=\mathit{Re}(-y^{3}/3+y+2/3)+{\it\psi}(x,y)$
is normalized by its maximum,
![]() ${\it\Psi}_{max}=6.52$
(a), 8.56 (b) and 26.27 (c), respectively.
${\it\Psi}_{max}=6.52$
(a), 8.56 (b) and 26.27 (c), respectively.
The main quantities of interest are the net heat transfer between the walls and the horizontal heat transfer along the heated wall. The former is expressed in terms of the average Nusselt number
![]() $\mathit{Nu}_{av}$
based on the conductive temperature scale, i.e.
$\mathit{Nu}_{av}$
based on the conductive temperature scale, i.e.
The latter is measured by evaluating the periodic part of the heat flow coming out of the wall per half wavelength and is expressed in terms of the horizontal Nusselt number
![]() $\mathit{Nu}_{h}$
defined as
$\mathit{Nu}_{h}$
defined as
 $$\begin{eqnarray}\displaystyle \mathit{Nu}_{h} & = & \displaystyle \frac{2}{{\it\lambda}}\mathit{Pr}\int _{-{\it\lambda}/4}^{{\it\lambda}/4}(-\text{D}{\it\theta}_{B}|_{y=-1})\,\text{d}x+\mathit{Pr}\text{D}{\it\phi}^{(0)}|_{y=-1}\nonumber\\ \displaystyle & = & \displaystyle \frac{{\it\alpha}}{2{\rm\pi}}[\text{coth}({\it\alpha})+\text{tanh}({\it\alpha})]+\left[\frac{2}{{\it\lambda}}\mathit{Pr}\int _{-{\it\lambda}/4}^{{\it\lambda}/4}(-\text{D}{\it\theta}_{1}|_{y=-1})\,\text{d}x+\mathit{Pr}\text{D}{\it\phi}^{(0)}|_{y=-1}\right]\nonumber\\ \displaystyle & = & \displaystyle \mathit{Nu}_{h,cond}+\mathit{Nu}_{h,conv}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{Nu}_{h} & = & \displaystyle \frac{2}{{\it\lambda}}\mathit{Pr}\int _{-{\it\lambda}/4}^{{\it\lambda}/4}(-\text{D}{\it\theta}_{B}|_{y=-1})\,\text{d}x+\mathit{Pr}\text{D}{\it\phi}^{(0)}|_{y=-1}\nonumber\\ \displaystyle & = & \displaystyle \frac{{\it\alpha}}{2{\rm\pi}}[\text{coth}({\it\alpha})+\text{tanh}({\it\alpha})]+\left[\frac{2}{{\it\lambda}}\mathit{Pr}\int _{-{\it\lambda}/4}^{{\it\lambda}/4}(-\text{D}{\it\theta}_{1}|_{y=-1})\,\text{d}x+\mathit{Pr}\text{D}{\it\phi}^{(0)}|_{y=-1}\right]\nonumber\\ \displaystyle & = & \displaystyle \mathit{Nu}_{h,cond}+\mathit{Nu}_{h,conv}.\end{eqnarray}$$
In the above, the first term on the right-hand side accounts for the conductive heat flow, and the second accounts for the convective heat flow. The reader may note alternative methods for estimation of the horizontal heat fluxes (Maxworthy Reference Maxworthy1997; Siggers et al. Reference Siggers, Kerswell and Balmforth2004; Hughes & Griffiths Reference Hughes and Griffiths2008; Winters & Young Reference Winters and Young2009).
The qualitative analysis of
![]() $\mathit{Nu}_{av}$
can be carried out by extracting mode zero from (2.13b
), i.e.
$\mathit{Nu}_{av}$
can be carried out by extracting mode zero from (2.13b
), i.e.
Double integration and application of the boundary conditions results in
and leads to
The function
![]() $M$
can be referred to as the heat transport function and its form demonstrates explicitly the essential role played by the vertical velocity component in creating the net heat transfer. We shall now investigate how the convective motion is affected by the characteristics of the applied heating.
$M$
can be referred to as the heat transport function and its form demonstrates explicitly the essential role played by the vertical velocity component in creating the net heat transfer. We shall now investigate how the convective motion is affected by the characteristics of the applied heating.
2.3.1. Long-wavelength heating
 $({\it\alpha}\rightarrow 0)$
$({\it\alpha}\rightarrow 0)$
We begin the analysis by identifying the range of
![]() ${\it\alpha}$
that leads to the most intense heat transfer. In the case of long-wavelength heating (
${\it\alpha}$
that leads to the most intense heat transfer. In the case of long-wavelength heating (
![]() ${\it\alpha}\rightarrow 0$
), the conductive field (i.e. (2.5)) can be approximated as
${\it\alpha}\rightarrow 0$
), the conductive field (i.e. (2.5)) can be approximated as
where the definitions of
![]() ${\it\theta}_{00}$
,
${\it\theta}_{00}$
,
![]() ${\it\theta}_{02}$
and
${\it\theta}_{02}$
and
![]() ${\it\theta}_{04}$
are given in appendix A and
${\it\theta}_{04}$
are given in appendix A and
![]() $X={\it\alpha}x$
denotes the slow scale. The field equations, with
$X={\it\alpha}x$
denotes the slow scale. The field equations, with
![]() $x$
replaced by the slow scale, assume the form
$x$
replaced by the slow scale, assume the form
where
![]() $\mathit{Nu}_{L}$
is the local Nusselt number. The above expansions are substituted into (2.19), with the leading-order system being of the form
$\mathit{Nu}_{L}$
is the local Nusselt number. The above expansions are substituted into (2.19), with the leading-order system being of the form
with the proper boundary conditions and the flow-rate constraint. The solution is of the form
with definitions of
![]() $F_{U1}$
,
$F_{U1}$
,
![]() $F_{V2}$
,
$F_{V2}$
,
![]() $F_{P0}$
and
$F_{P0}$
and
![]() $F_{{\it\Theta}1}$
given in appendix A. Here
$F_{{\it\Theta}1}$
given in appendix A. Here
![]() $U_{1}$
,
$U_{1}$
,
![]() $V_{2}$
and
$V_{2}$
and
![]() $P_{0}$
describe the natural convection, which is unaffected by the forced convection at this level of approximation, and
$P_{0}$
describe the natural convection, which is unaffected by the forced convection at this level of approximation, and
![]() ${\it\Theta}_{1}$
describes modifications of the temperature field created by the forced convection. There is no net heat transfer between the walls. The next-order system has the form
${\it\Theta}_{1}$
describes modifications of the temperature field created by the forced convection. There is no net heat transfer between the walls. The next-order system has the form
A similar solution process leads to
with the definitions of
![]() $F_{U21}$
,
$F_{U21}$
,
![]() $F_{U22}$
,
$F_{U22}$
,
![]() $F_{V31}$
,
$F_{V31}$
,
![]() $F_{V32}$
,
$F_{V32}$
,
![]() $F_{P1}$
,
$F_{P1}$
,
![]() $F_{{\it\Theta}21}$
,
$F_{{\it\Theta}21}$
,
![]() $F_{{\it\Theta}22}$
and
$F_{{\it\Theta}22}$
and
![]() $F_{{\it\Theta}23}$
given in appendix A. Here
$F_{{\it\Theta}23}$
given in appendix A. Here
![]() $F_{U21}$
,
$F_{U21}$
,
![]() $F_{V31}$
and
$F_{V31}$
and
![]() $F_{P1}$
arise because of temperature changes created by the forced convection,
$F_{P1}$
arise because of temperature changes created by the forced convection,
![]() $F_{U22}$
,
$F_{U22}$
,
![]() $F_{V32}$
and
$F_{V32}$
and
![]() $F_{P1}$
arise because of the interaction of the natural and forced convective motions,
$F_{P1}$
arise because of the interaction of the natural and forced convective motions,
![]() $F_{{\it\Theta}22}$
accounts for the temperature changes created by the forced convection, and
$F_{{\it\Theta}22}$
accounts for the temperature changes created by the forced convection, and
![]() $F_{{\it\Theta}21}$
and
$F_{{\it\Theta}21}$
and
![]() $F_{{\it\Theta}23}$
account for changes in the conductive temperature field created by the natural convection. There is a net heat transfer between both walls at this level of approximation. The next-order system has the form
$F_{{\it\Theta}23}$
account for changes in the conductive temperature field created by the natural convection. There is a net heat transfer between both walls at this level of approximation. The next-order system has the form
 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\partial ^{2}{\it\Theta}_{3}}{\partial y^{2}} & = & \displaystyle \mathit{Re}\left[\mathit{Pr}\,u_{0}\frac{\partial {\it\Theta}_{2}}{\partial X}-u_{0}{\it\theta}_{02}\sin (X)\right]+\mathit{Pr}\left(U_{1}\frac{\partial {\it\Theta}_{1}}{\partial X}+V_{2}\frac{\partial {\it\Theta}_{1}}{\partial y}\right)\nonumber\\ \displaystyle \displaystyle & & \displaystyle -\,U_{2}{\it\theta}_{00}\sin (X)+\text{D}{\it\theta}_{00}V_{3}\cos (X)-\frac{\partial ^{2}{\it\Theta}_{1}}{\partial X^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\partial ^{2}{\it\Theta}_{3}}{\partial y^{2}} & = & \displaystyle \mathit{Re}\left[\mathit{Pr}\,u_{0}\frac{\partial {\it\Theta}_{2}}{\partial X}-u_{0}{\it\theta}_{02}\sin (X)\right]+\mathit{Pr}\left(U_{1}\frac{\partial {\it\Theta}_{1}}{\partial X}+V_{2}\frac{\partial {\it\Theta}_{1}}{\partial y}\right)\nonumber\\ \displaystyle \displaystyle & & \displaystyle -\,U_{2}{\it\theta}_{00}\sin (X)+\text{D}{\it\theta}_{00}V_{3}\cos (X)-\frac{\partial ^{2}{\it\Theta}_{1}}{\partial X^{2}}.\end{eqnarray}$$
Its solution can be written as
 $$\begin{eqnarray}\displaystyle \frac{\partial ^{2}{\it\Theta}_{4}}{\partial y^{2}} & = & \displaystyle \mathit{Re}\mathit{Pr}\,u_{0}\frac{\partial {\it\Theta}_{3}}{\partial X}+\mathit{Pr}\left(U_{1}\frac{\partial {\it\Theta}_{2}}{\partial X}+U_{2}\frac{\partial {\it\Theta}_{1}}{\partial X}+V_{2}\frac{\partial {\it\Theta}_{2}}{\partial y}+V_{3}\frac{\partial {\it\Theta}_{1}}{\partial y}\right)\nonumber\\ \displaystyle & & \displaystyle -\,({\it\theta}_{02}U_{1}+{\it\theta}_{00}U_{3})\sin (X)+(\text{D}{\it\theta}_{02}V_{2}+\text{D}{\it\theta}_{00}V_{4})\cos (X)-\frac{\partial ^{2}{\it\Theta}_{2}}{\partial X^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}{\it\Theta}_{4}}{\partial y^{2}} & = & \displaystyle \mathit{Re}\mathit{Pr}\,u_{0}\frac{\partial {\it\Theta}_{3}}{\partial X}+\mathit{Pr}\left(U_{1}\frac{\partial {\it\Theta}_{2}}{\partial X}+U_{2}\frac{\partial {\it\Theta}_{1}}{\partial X}+V_{2}\frac{\partial {\it\Theta}_{2}}{\partial y}+V_{3}\frac{\partial {\it\Theta}_{1}}{\partial y}\right)\nonumber\\ \displaystyle & & \displaystyle -\,({\it\theta}_{02}U_{1}+{\it\theta}_{00}U_{3})\sin (X)+(\text{D}{\it\theta}_{02}V_{2}+\text{D}{\it\theta}_{00}V_{4})\cos (X)-\frac{\partial ^{2}{\it\Theta}_{2}}{\partial X^{2}}.\end{eqnarray}$$
The aperiodic term on the right-hand side is responsible for the net heat flow and it results in
The expression for
![]() $\mathit{Nu}_{L,4}$
is not given due to its length. The results displayed in figure 3 demonstrate that (2.20) provides a good approximation for
$\mathit{Nu}_{L,4}$
is not given due to its length. The results displayed in figure 3 demonstrate that (2.20) provides a good approximation for
![]() $\mathit{Nu}_{av}$
when
$\mathit{Nu}_{av}$
when
![]() ${\it\alpha}<0.2$
.
${\it\alpha}<0.2$
.

Figure 3. Variations of the average Nusselt number
![]() $\mathit{Nu}_{av}$
as a function of
$\mathit{Nu}_{av}$
as a function of
![]() ${\it\alpha}$
for
${\it\alpha}$
for
![]() $\mathit{Ra}_{p}=200$
, 400 and 1000 with
$\mathit{Ra}_{p}=200$
, 400 and 1000 with
![]() $\mathit{Re}=1$
(a) and
$\mathit{Re}=1$
(a) and
![]() $R=10$
(b). The asymptotes for
$R=10$
(b). The asymptotes for
![]() ${\it\alpha}\rightarrow 0$
and
${\it\alpha}\rightarrow 0$
and
![]() ${\it\alpha}\rightarrow \infty$
are marked using dotted lines. The curves for
${\it\alpha}\rightarrow \infty$
are marked using dotted lines. The curves for
![]() $\mathit{Re}=0$
and
$\mathit{Re}=0$
and
![]() $\mathit{Re}=1$
overlap within the resolution of panel (a).
$\mathit{Re}=1$
overlap within the resolution of panel (a).
2.3.2. Short-wavelength heating (
 ${\it\alpha}\rightarrow \infty$
)
${\it\alpha}\rightarrow \infty$
)
In the case of the short-wavelength heating, the conductive temperature field, i.e. (2.5), can be approximated as
The
![]() $x$
variations of the buoyancy force are confined to a thin boundary layer adjacent to the lower wall, and the natural convection is confined to the same layer. All the field variables above the boundary layer can be functions of the vertical coordinate only. The solution is expressed as an expansion in terms of
$x$
variations of the buoyancy force are confined to a thin boundary layer adjacent to the lower wall, and the natural convection is confined to the same layer. All the field variables above the boundary layer can be functions of the vertical coordinate only. The solution is expressed as an expansion in terms of
![]() ${\it\alpha}^{-1}$
and using the method of matched asymptotic expansions leads to the determination of the expansion terms. It can be shown through matching with the inner solution that the outer solution can be simplified to the following form:
${\it\alpha}^{-1}$
and using the method of matched asymptotic expansions leads to the determination of the expansion terms. It can be shown through matching with the inner solution that the outer solution can be simplified to the following form:
Similarly, the Nusselt number can be represented as
Substitution of (2.29) and (2.30) into the field equations and separation of terms of equal order of magnitude leads to the following systems:
with solution of the form
where
![]() $\tilde{B}_{3}$
is to be determined from matching with the inner solution. The heat transport in the outer zone is driven by the vertical conduction with a non-zero boundary condition at the edge of the boundary layer created by the boundary layer phenomena.
$\tilde{B}_{3}$
is to be determined from matching with the inner solution. The heat transport in the outer zone is driven by the vertical conduction with a non-zero boundary condition at the edge of the boundary layer created by the boundary layer phenomena.
Analysis of the boundary layer begins with the introduction of the fast scale
![]() ${\it\xi}={\it\alpha}x$
in the horizontal direction and the stretched coordinate centred at the lower wall
${\it\xi}={\it\alpha}x$
in the horizontal direction and the stretched coordinate centred at the lower wall
![]() ${\it\eta}={\it\alpha}(1+y)$
in the vertical direction. The externally imposed temperature and velocity fields expressed in the
${\it\eta}={\it\alpha}(1+y)$
in the vertical direction. The externally imposed temperature and velocity fields expressed in the
![]() $({\it\xi},{\it\eta})$
coordinate system have the form
$({\it\xi},{\it\eta})$
coordinate system have the form
 $$\begin{eqnarray}\displaystyle \frac{\partial ^{2}u_{1}}{\partial {\it\xi}^{2}}+\frac{\partial ^{2}u_{1}}{\partial {\it\eta}^{2}}-{\it\alpha}^{-1}\frac{\partial p_{1}}{\partial {\it\xi}} & = & \displaystyle {\it\alpha}^{-1}[\mathit{Re}({\it\alpha}^{-1}2{\it\eta}-{\it\alpha}^{-2}{\it\eta}^{2})+u_{1}]\frac{\partial u_{1}}{\partial {\it\xi}}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\alpha}^{-2}\left[\mathit{Re}(2-{\it\alpha}^{-1}2{\it\eta})+{\it\alpha}\frac{\partial u_{1}}{\partial {\it\eta}}\right]v_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}u_{1}}{\partial {\it\xi}^{2}}+\frac{\partial ^{2}u_{1}}{\partial {\it\eta}^{2}}-{\it\alpha}^{-1}\frac{\partial p_{1}}{\partial {\it\xi}} & = & \displaystyle {\it\alpha}^{-1}[\mathit{Re}({\it\alpha}^{-1}2{\it\eta}-{\it\alpha}^{-2}{\it\eta}^{2})+u_{1}]\frac{\partial u_{1}}{\partial {\it\xi}}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\alpha}^{-2}\left[\mathit{Re}(2-{\it\alpha}^{-1}2{\it\eta})+{\it\alpha}\frac{\partial u_{1}}{\partial {\it\eta}}\right]v_{1},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\partial ^{2}v_{1}}{\partial {\it\xi}^{2}}+\frac{\partial ^{2}v_{1}}{\partial {\it\eta}^{2}}-{\it\alpha}^{-1}\frac{\partial p_{1}}{\partial {\it\eta}} & = & \displaystyle {\it\alpha}^{-1}[\mathit{Re}\,({\it\alpha}^{-1}2{\it\eta}-{\it\alpha}^{-2}{\it\eta}^{2})+u_{1}]\frac{\partial v_{1}}{\partial {\it\xi}}+{\it\alpha}^{-1}v_{1}\frac{\partial v_{1}}{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle -\,{\it\alpha}^{-2}\mathit{Ra}_{p}{\it\theta}_{1}+{\it\alpha}^{-2}\frac{1}{2}\mathit{Ra}_{p}\mathit{Pr}^{-1}\text{e}^{-{\it\eta}}\cos ({\it\xi}),\hspace{36.0pt}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}v_{1}}{\partial {\it\xi}^{2}}+\frac{\partial ^{2}v_{1}}{\partial {\it\eta}^{2}}-{\it\alpha}^{-1}\frac{\partial p_{1}}{\partial {\it\eta}} & = & \displaystyle {\it\alpha}^{-1}[\mathit{Re}\,({\it\alpha}^{-1}2{\it\eta}-{\it\alpha}^{-2}{\it\eta}^{2})+u_{1}]\frac{\partial v_{1}}{\partial {\it\xi}}+{\it\alpha}^{-1}v_{1}\frac{\partial v_{1}}{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle -\,{\it\alpha}^{-2}\mathit{Ra}_{p}{\it\theta}_{1}+{\it\alpha}^{-2}\frac{1}{2}\mathit{Ra}_{p}\mathit{Pr}^{-1}\text{e}^{-{\it\eta}}\cos ({\it\xi}),\hspace{36.0pt}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\partial ^{2}{\it\theta}_{1}}{\partial {\it\xi}^{2}}+\frac{\partial ^{2}{\it\theta}_{1}}{\partial {\it\eta}^{2}} & = & \displaystyle {\it\alpha}^{-1}[\mathit{Re}\,({\it\alpha}^{-1}2{\it\eta}-{\it\alpha}^{-2}{\it\eta}^{2})+u_{1}]\left[-\frac{1}{2}\text{e}^{-{\it\eta}}\sin ({\it\xi})+\mathit{Pr}\frac{\partial {\it\theta}_{1}}{\partial {\it\xi}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,{\it\alpha}^{-2}v_{1}\left[-\frac{1}{2}{\it\alpha}\text{e}^{-{\it\eta}}\cos ({\it\xi})+{\it\alpha}\,\mathit{Pr}\frac{\partial {\it\theta}_{1}}{\partial {\it\eta}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}{\it\theta}_{1}}{\partial {\it\xi}^{2}}+\frac{\partial ^{2}{\it\theta}_{1}}{\partial {\it\eta}^{2}} & = & \displaystyle {\it\alpha}^{-1}[\mathit{Re}\,({\it\alpha}^{-1}2{\it\eta}-{\it\alpha}^{-2}{\it\eta}^{2})+u_{1}]\left[-\frac{1}{2}\text{e}^{-{\it\eta}}\sin ({\it\xi})+\mathit{Pr}\frac{\partial {\it\theta}_{1}}{\partial {\it\xi}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,{\it\alpha}^{-2}v_{1}\left[-\frac{1}{2}{\it\alpha}\text{e}^{-{\it\eta}}\cos ({\it\xi})+{\it\alpha}\,\mathit{Pr}\frac{\partial {\it\theta}_{1}}{\partial {\it\eta}}\right].\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle [u_{1,inner}({\it\xi},{\it\eta}),v_{1,inner}({\it\xi},{\it\eta}),{\it\theta}_{1,inner}({\it\xi},{\it\eta})]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=2}^{3}{\it\alpha}^{-n}[U_{n}({\it\xi},{\it\eta}),V_{n}({\it\xi},{\it\eta}),{\it\Theta}_{n}({\it\xi},{\it\eta})]+O({\it\alpha}^{-4}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle [u_{1,inner}({\it\xi},{\it\eta}),v_{1,inner}({\it\xi},{\it\eta}),{\it\theta}_{1,inner}({\it\xi},{\it\eta})]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=2}^{3}{\it\alpha}^{-n}[U_{n}({\it\xi},{\it\eta}),V_{n}({\it\xi},{\it\eta}),{\it\Theta}_{n}({\it\xi},{\it\eta})]+O({\it\alpha}^{-4}),\end{eqnarray}$$
Its solution
demonstrates that the natural convection is confined to the boundary layer and thus is unable to alter the net heat transfer between the walls. The system
![]() $O({\it\alpha}^{-3})$
has the form
$O({\it\alpha}^{-3})$
has the form
and leads to the solution
 $$\begin{eqnarray}\displaystyle {\it\Theta}_{3}({\it\xi},{\it\eta}) & = & \displaystyle \left[\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}+B_{3}{\it\eta}-\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}(1+2{\it\eta}+2{\it\eta}^{2})\text{e}^{-2{\it\eta}}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\mathit{Re}}{4}\left(\frac{{\it\eta}}{2}+\frac{{\it\eta}^{2}}{2}+\frac{{\it\eta}^{3}}{3}\right)\text{e}^{-{\it\eta}}\sin ({\it\xi})+\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}\left(\frac{{\it\eta}}{2}+{\it\eta}^{2}\right)\text{e}^{-2{\it\eta}}\cos (2{\it\xi}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Theta}_{3}({\it\xi},{\it\eta}) & = & \displaystyle \left[\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}+B_{3}{\it\eta}-\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}(1+2{\it\eta}+2{\it\eta}^{2})\text{e}^{-2{\it\eta}}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\mathit{Re}}{4}\left(\frac{{\it\eta}}{2}+\frac{{\it\eta}^{2}}{2}+\frac{{\it\eta}^{3}}{3}\right)\text{e}^{-{\it\eta}}\sin ({\it\xi})+\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}\left(\frac{{\it\eta}}{2}+{\it\eta}^{2}\right)\text{e}^{-2{\it\eta}}\cos (2{\it\xi}).\end{eqnarray}$$
Constant
![]() $B_{3}$
is determined from matching with the outer solution, leading to the uniformly valid expression for the temperature, i.e.
$B_{3}$
is determined from matching with the outer solution, leading to the uniformly valid expression for the temperature, i.e.
 $$\begin{eqnarray}\displaystyle {\it\theta}_{1}(x,y) & = & \displaystyle {\it\alpha}^{-3}\left[\vphantom{\displaystyle \left[\frac{1}{2}\right]}\frac{\mathit{Ra}_{p}}{512\mathit{Pr}}(1-y)-\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}[1+2{\it\alpha}(1+y)+2{\it\alpha}^{2}(1+y)^{2}]\text{e}^{-2{\it\alpha}(1+y)}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\mathit{Re}}{4}\left[\frac{1}{2}{\it\alpha}(1+y)+\frac{1}{2}{\it\alpha}^{2}(1+y)^{2}+\frac{1}{3}{\it\alpha}^{3}(1+y)^{3}\right]\text{e}^{-{\it\alpha}(1+y)}\sin ({\it\alpha}x)\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{\mathit{Ra}_{p}}{256\,\mathit{Pr}}\left[\frac{1}{2}{\it\alpha}(1+y)+{\it\alpha}^{2}(1+y)^{2}\right]\text{e}^{-2{\it\alpha}(1+y)}\cos (2{\it\alpha}\,x)\right]+O({\it\alpha}^{-4}).\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\theta}_{1}(x,y) & = & \displaystyle {\it\alpha}^{-3}\left[\vphantom{\displaystyle \left[\frac{1}{2}\right]}\frac{\mathit{Ra}_{p}}{512\mathit{Pr}}(1-y)-\frac{\mathit{Ra}_{p}}{256\mathit{Pr}}[1+2{\it\alpha}(1+y)+2{\it\alpha}^{2}(1+y)^{2}]\text{e}^{-2{\it\alpha}(1+y)}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\mathit{Re}}{4}\left[\frac{1}{2}{\it\alpha}(1+y)+\frac{1}{2}{\it\alpha}^{2}(1+y)^{2}+\frac{1}{3}{\it\alpha}^{3}(1+y)^{3}\right]\text{e}^{-{\it\alpha}(1+y)}\sin ({\it\alpha}x)\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{\mathit{Ra}_{p}}{256\,\mathit{Pr}}\left[\frac{1}{2}{\it\alpha}(1+y)+{\it\alpha}^{2}(1+y)^{2}\right]\text{e}^{-2{\it\alpha}(1+y)}\cos (2{\it\alpha}\,x)\right]+O({\it\alpha}^{-4}).\qquad\end{eqnarray}$$
The above expression demonstrates explicitly that the outer zone sees the edge of the boundary layer as a uniformly heated wall. The net heat transfer between the two walls can now be expressed as
The above expression provides a good approximation for
![]() $\mathit{Nu}_{av}$
when
$\mathit{Nu}_{av}$
when
![]() ${\it\alpha}>7$
(see figure 3).
${\it\alpha}>7$
(see figure 3).
2.3.3. Weak heating
The above discussion demonstrates, together with the results presented in figure 3, that the net heat transfer becomes marginal if the heating wavelength is either too short or too long. We shall now consider a heating wavelength
![]() $O(1)$
. The heat transfer occurs due to the vertical fluid movement, as demonstrated in § 2.3. The forced motion increases the horizontal fluid movement, which competes with the vertical movement. A very strong horizontal motion may negate any transverse motion and thus may alter the heat transport qualitatively. It is convenient to start discussion of these processes by considering weak heating.
$O(1)$
. The heat transfer occurs due to the vertical fluid movement, as demonstrated in § 2.3. The forced motion increases the horizontal fluid movement, which competes with the vertical movement. A very strong horizontal motion may negate any transverse motion and thus may alter the heat transport qualitatively. It is convenient to start discussion of these processes by considering weak heating.
The natural convection is driven by nonlinear effects and thus its strength is not directly related to the magnitude of
![]() $\mathit{Ra}_{p}$
;
$\mathit{Ra}_{p}$
;
![]() $\mathit{Ra}_{p}$
of order
$\mathit{Ra}_{p}$
of order
![]() $O(1)$
may generate convection with negligible nonlinear interactions. In the following analysis, the strength of the natural convection is measured using
$O(1)$
may generate convection with negligible nonlinear interactions. In the following analysis, the strength of the natural convection is measured using
![]() ${\it\varepsilon}\ll 1$
. The flow quantities are represented as expansions in powers of
${\it\varepsilon}\ll 1$
. The flow quantities are represented as expansions in powers of
![]() ${\it\varepsilon}$
of the form
${\it\varepsilon}$
of the form
Substitution of (2.44) into (2.6) and retention of the terms of the two highest orders of magnitude lead to a system
![]() $O({\it\varepsilon})$
of the form
$O({\it\varepsilon})$
of the form
The solution process starts with the energy equation (2.45c
), which is decoupled from the rest of the system. Since
![]() ${\it\varepsilon}$
is undefined, this equation is rearranged into the form
${\it\varepsilon}$
is undefined, this equation is rearranged into the form
where
![]() $\tilde{{\it\Theta}}_{1}={\it\varepsilon}{\it\Theta}_{1}$
. The known forcing on the right-hand side of (2.47) leads to a solution of the form
$\tilde{{\it\Theta}}_{1}={\it\varepsilon}{\it\Theta}_{1}$
. The known forcing on the right-hand side of (2.47) leads to a solution of the form
where
![]() $\tilde{{\it\Theta}}_{1}^{(1)}$
is defined by the following problem,
$\tilde{{\it\Theta}}_{1}^{(1)}$
is defined by the following problem,
and c.c. stands for the complex conjugate. The solution has been determined using the spectral collocation method identical to that described in § 2.2. Determination of the net heat transfer requires analysis of the next-order problem, i.e. (2.46c
). The coefficients of (2.46c
) include the
![]() $U_{1}$
and
$U_{1}$
and
![]() $V_{1}$
velocity components, which need to be determined from the solution of (2.45a,b,d
). Introduction of the stream function, defined as
$V_{1}$
velocity components, which need to be determined from the solution of (2.45a,b,d
). Introduction of the stream function, defined as
![]() $u_{1}=\partial {\it\psi}/\partial y$
and
$u_{1}=\partial {\it\psi}/\partial y$
and
![]() $v_{1}=-\partial {\it\psi}/\partial x$
, and elimination of the pressure results in a single equation of the form
$v_{1}=-\partial {\it\psi}/\partial x$
, and elimination of the pressure results in a single equation of the form
The character of the forcing on the right-hand side of (2.50) suggests a solution of the form
Substitution of (2.5), (2.48) and (2.49) into (2.50) leads to the problem
where
![]() $\tilde{{\it\Theta}}_{2}={\it\varepsilon}{\it\Theta}_{2}$
and the right-hand side represents the known forcing
$\tilde{{\it\Theta}}_{2}={\it\varepsilon}{\it\Theta}_{2}$
and the right-hand side represents the known forcing
![]() $F(x,y)$
, which can be written explicitly as
$F(x,y)$
, which can be written explicitly as
where
The solution of (2.54) has the form
i.e. it consists of a non-periodic term, which determines the net heat flow, and the first superharmonic of the imposed heating. Substitution of (2.55) and (2.56) into (2.54) and mode separation leads to equations for the modal functions of the form
Before attempting solution, (2.57) is rearranged, i.e.
Since the function
![]() $M^{(0)}$
is available, integration and application of boundary conditions leads to a solution of the form
$M^{(0)}$
is available, integration and application of boundary conditions leads to a solution of the form
Explicit evaluations of (2.60) have been carried out using the fourth-order-accurate extension of the trapezoid rule. Similarly, (2.58) is arranged into the form
The average Nusselt number can be evaluated as
without the need for an explicit determination of
![]() ${\it\varepsilon}$
. The above analysis shows that
${\it\varepsilon}$
. The above analysis shows that
![]() $\mathit{Nu}_{av}$
increases proportionally to
$\mathit{Nu}_{av}$
increases proportionally to
![]() $\mathit{Ra}_{p}$
for small enough
$\mathit{Ra}_{p}$
for small enough
![]() $\mathit{Ra}_{p}$
. The approximation is sufficiently accurate for
$\mathit{Ra}_{p}$
. The approximation is sufficiently accurate for
![]() $\mathit{Ra}_{p}\approx 500$
as shown in figure 4.
$\mathit{Ra}_{p}\approx 500$
as shown in figure 4.

Figure 4. Variations of the average Nusselt number
![]() $\mathit{Nu}_{av}$
as a function of
$\mathit{Nu}_{av}$
as a function of
![]() $\mathit{Ra}_{p}$
for
$\mathit{Ra}_{p}$
for
![]() ${\it\alpha}=1$
.
${\it\alpha}=1$
.
Equation (2.62) demonstrates that the net heat flow results from the nonlinear effects associated with the buoyancy-driven motion. The heat transport function
![]() $M^{(0)}$
represents energy carried by the transverse movement of the fluid averaged over one heating wavelength in the
$M^{(0)}$
represents energy carried by the transverse movement of the fluid averaged over one heating wavelength in the
![]() $x$
direction. Integration of this function between the walls gives the net energy transfer between the walls. The magnitude of
$x$
direction. Integration of this function between the walls gives the net energy transfer between the walls. The magnitude of
![]() $M^{(0)}$
depends on the magnitudes of
$M^{(0)}$
depends on the magnitudes of
![]() ${\it\theta}_{0}^{(1)}$
,
${\it\theta}_{0}^{(1)}$
,
![]() $\tilde{{\it\Theta}}_{1}^{(1)}$
and
$\tilde{{\it\Theta}}_{1}^{(1)}$
and
![]() $\tilde{V}_{1}^{(-1)}$
as well as on the phase difference between the temperature field and the vertical velocity component. The conductive temperature
$\tilde{V}_{1}^{(-1)}$
as well as on the phase difference between the temperature field and the vertical velocity component. The conductive temperature
![]() ${\it\theta}_{0}^{(1)}$
is always real, i.e.
${\it\theta}_{0}^{(1)}$
is always real, i.e.
![]() ${\it\theta}_{0}^{(1)}={\it\theta}_{0}^{(-1)}$
, while the phase of
${\it\theta}_{0}^{(1)}={\it\theta}_{0}^{(-1)}$
, while the phase of
![]() $\tilde{{\it\Theta}}_{1}^{(1)}$
changes depending on the strength of the forced motion.
$\tilde{{\it\Theta}}_{1}^{(1)}$
changes depending on the strength of the forced motion.
2.3.4. Effects of the Reynolds number
 $\mathit{Re}$
$\mathit{Re}$
The introduction of a forced convection results in the formation of a continuous stream tube directed from left to right, which reduces the size of the rolls and separates vortex pairs into distinct objects that can be viewed as separation bubbles (see figure 2). The motion in the interior of these bubbles is driven by both the buoyancy and the shear created by the forced convection. The transverse motion, which is responsible for the vertical heat transfer, occurs in the interior of the bubbles as well as in the stream tube that meanders in the upwards and downwards directions. An increase of
![]() $\mathit{Re}$
increases the size of the stream tube and makes this stream tube more rectilinear, and, as a result, the size of the rolls significantly decreases. The overall transverse motion decreases and the heat may be carried only by conduction across the stream tube.
$\mathit{Re}$
increases the size of the stream tube and makes this stream tube more rectilinear, and, as a result, the size of the rolls significantly decreases. The overall transverse motion decreases and the heat may be carried only by conduction across the stream tube.
The mechanics of the heat transfer changes as the presence of the forced motion modifies the temperature field (i.e.
![]() $\tilde{{\it\Theta}}_{1}^{(1)}\neq 0$
in (2.49)), alters the buoyancy-driven motion and changes the phase difference between the temperature and the vertical velocity component. We shall now discuss these processes in detail for the case of weak heating.
$\tilde{{\it\Theta}}_{1}^{(1)}\neq 0$
in (2.49)), alters the buoyancy-driven motion and changes the phase difference between the temperature and the vertical velocity component. We shall now discuss these processes in detail for the case of weak heating.
Assume initially that
![]() $\mathit{Re}$
is small but finite. Separate
$\mathit{Re}$
is small but finite. Separate
![]() $\tilde{{\it\Theta}}_{1}^{(1)}$
into real and imaginary parts and represent each as an expansion in terms of powers of
$\tilde{{\it\Theta}}_{1}^{(1)}$
into real and imaginary parts and represent each as an expansion in terms of powers of
![]() $\mathit{Re}$
, i.e.
$\mathit{Re}$
, i.e.
Substitution of (2.63) into (2.49) and retention of terms proportional to the two lowest powers of
![]() $\mathit{Re}$
results in the following systems:
$\mathit{Re}$
results in the following systems:
Analysis of (2.64a
) and (2.65b
) shows that
![]() ${\it\Theta}_{r1}=0$
and
${\it\Theta}_{r1}=0$
and
![]() ${\it\Theta}_{i2}=0$
. The modification temperature
${\it\Theta}_{i2}=0$
. The modification temperature
![]() $\tilde{{\it\Theta}}_{1}^{(1)}$
assumes non-zero values for small but finite
$\tilde{{\it\Theta}}_{1}^{(1)}$
assumes non-zero values for small but finite
![]() $\mathit{Re}$
, with its imaginary part playing the dominant role. Now separate the stream function into real and imaginary parts and represent them as expansions in terms of powers of
$\mathit{Re}$
, with its imaginary part playing the dominant role. Now separate the stream function into real and imaginary parts and represent them as expansions in terms of powers of
![]() $\mathit{Re}$
, i.e.
$\mathit{Re}$
, i.e.
Substitution of (2.66) into (2.52) and retention of those terms proportional to the two lowest powers of
![]() $\mathit{Re}$
results in the following systems:
$\mathit{Re}$
results in the following systems:
The forced motion affects both the temperature and the velocity fields at
![]() $O(\mathit{Re})$
but these changes contribute only to a small phase shift and thus do not affect the heat flow. The heat flow is affected at
$O(\mathit{Re})$
but these changes contribute only to a small phase shift and thus do not affect the heat flow. The heat flow is affected at
![]() $O(\mathit{Re}^{2})$
and the change occurs due to (i) correction in the vertical velocity component that is in phase with the conductive field (the first term in the brackets in (2.70)), (ii) the part of the temperature modification that is in phase with the conductive temperature field (the second term in the brackets), and (iii) interaction between the parts of the velocity and temperature modifications that are out of phase with the conductive temperature field (the third term in the brackets). The importance of the third term is expected to rise as
$O(\mathit{Re}^{2})$
and the change occurs due to (i) correction in the vertical velocity component that is in phase with the conductive field (the first term in the brackets in (2.70)), (ii) the part of the temperature modification that is in phase with the conductive temperature field (the second term in the brackets), and (iii) interaction between the parts of the velocity and temperature modifications that are out of phase with the conductive temperature field (the third term in the brackets). The importance of the third term is expected to rise as
![]() $\mathit{Re}$
increases. The conclusion that the heat transfer approaches a constant limit corresponding to the pure natural convection when
$\mathit{Re}$
increases. The conclusion that the heat transfer approaches a constant limit corresponding to the pure natural convection when
![]() $\mathit{Re}\rightarrow 0$
is supported by the results presented in figure 5.
$\mathit{Re}\rightarrow 0$
is supported by the results presented in figure 5.

Figure 5. Variations of the average Nusselt number
![]() $\mathit{Nu}_{av}$
as a function of
$\mathit{Nu}_{av}$
as a function of
![]() $\mathit{Re}$
for
$\mathit{Re}$
for
![]() ${\it\alpha}=1$
and
${\it\alpha}=1$
and
![]() $\mathit{Ra}_{p}=200$
, 400 and 1000. The asymptotes for
$\mathit{Ra}_{p}=200$
, 400 and 1000. The asymptotes for
![]() $\mathit{Re}\rightarrow 0$
and
$\mathit{Re}\rightarrow 0$
and
![]() $\mathit{Re}\rightarrow \infty$
are marked using dotted lines.
$\mathit{Re}\rightarrow \infty$
are marked using dotted lines.
Variations of the heat transport for large
![]() $\mathit{Re}$
are more complex but can nevertheless be explained in qualitative terms. Equation (2.49) describing the temperature field has a variable coefficient containing the product
$\mathit{Re}$
are more complex but can nevertheless be explained in qualitative terms. Equation (2.49) describing the temperature field has a variable coefficient containing the product
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $u_{0}$
, and an inhomogeneous term with a similar product. When
$u_{0}$
, and an inhomogeneous term with a similar product. When
![]() $\mathit{Re}\rightarrow \infty$
, these two terms are large everywhere except close to the walls where
$\mathit{Re}\rightarrow \infty$
, these two terms are large everywhere except close to the walls where
![]() $u_{0}\approx 0$
and thus temperature boundary layers may form. It can be shown that the temperature modal function
$u_{0}\approx 0$
and thus temperature boundary layers may form. It can be shown that the temperature modal function
![]() $\tilde{{\it\Theta}}_{1}^{(1)}=({\it\Theta}_{r}+\text{i}{\it\Theta}_{i})$
is equal to the conductive temperature modal function, i.e.
$\tilde{{\it\Theta}}_{1}^{(1)}=({\it\Theta}_{r}+\text{i}{\it\Theta}_{i})$
is equal to the conductive temperature modal function, i.e.
everywhere except near the lower wall; this is due to the fact that
![]() ${\it\theta}_{0}^{(1)}\rightarrow 0.5$
but
${\it\theta}_{0}^{(1)}\rightarrow 0.5$
but
![]() ${\it\Theta}_{r}\rightarrow 0$
when
${\it\Theta}_{r}\rightarrow 0$
when
![]() $y\rightarrow -1$
. This leads to the formation of the temperature boundary layer at the lower wall. The flow becomes nearly isothermal outside the boundary layer, leading to the elimination of the buoyancy force in the bulk of the fluid. This force must overcome dissipation in the whole flow domain in order to drive natural convection. Clearly, the intensity of this convection must be decreasing rapidly as
$y\rightarrow -1$
. This leads to the formation of the temperature boundary layer at the lower wall. The flow becomes nearly isothermal outside the boundary layer, leading to the elimination of the buoyancy force in the bulk of the fluid. This force must overcome dissipation in the whole flow domain in order to drive natural convection. Clearly, the intensity of this convection must be decreasing rapidly as
![]() $\mathit{Re}$
increases. As a result, the Nusselt number must also be decreasing. This process is illustrated in figure 5, where the numerically determined decrease rate is proportional to
$\mathit{Re}$
increases. As a result, the Nusselt number must also be decreasing. This process is illustrated in figure 5, where the numerically determined decrease rate is proportional to
![]() $\mathit{Re}^{-1.71}$
for
$\mathit{Re}^{-1.71}$
for
![]() $\mathit{Re}\rightarrow \infty$
.
$\mathit{Re}\rightarrow \infty$
.
2.3.5. Mixed convection under arbitrary heating conditions
We shall now consider mixed convection for an arbitrary combination of transport parameters. The discussion presented in the previous sections demonstrate that
![]() $\mathit{Nu}_{av}$
rapidly decreases for large
$\mathit{Nu}_{av}$
rapidly decreases for large
![]() $\mathit{Re}$
and both small and large
$\mathit{Re}$
and both small and large
![]() ${\it\alpha}$
. This defines the range of parameters that are relevant for potential applications. Figure 6 illustrates variations of
${\it\alpha}$
. This defines the range of parameters that are relevant for potential applications. Figure 6 illustrates variations of
![]() $\mathit{Nu}_{av}$
as a function of
$\mathit{Nu}_{av}$
as a function of
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() ${\it\alpha}$
and clearly identifies the magnitudes of the net heat transfer driven by periodic heating. Figure 7 illustrates variations of
${\it\alpha}$
and clearly identifies the magnitudes of the net heat transfer driven by periodic heating. Figure 7 illustrates variations of
![]() $\mathit{Nu}_{av}$
as a function of
$\mathit{Nu}_{av}$
as a function of
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() $\mathit{Ra}_{p}$
for fixed
$\mathit{Ra}_{p}$
for fixed
![]() $\mathit{Re}$
and defines the conditions under which secondary motions are expected to set in. Figure 8 illustrates the magnitude of the horizontal heat flux and demonstrates that the overall heat flux is dominated by the conductive effects. The convective part of this flux (
$\mathit{Re}$
and defines the conditions under which secondary motions are expected to set in. Figure 8 illustrates the magnitude of the horizontal heat flux and demonstrates that the overall heat flux is dominated by the conductive effects. The convective part of this flux (
![]() $\mathit{Nu}_{h,conv}$
) has a similar magnitude and characteristics as
$\mathit{Nu}_{h,conv}$
) has a similar magnitude and characteristics as
![]() $\mathit{Nu}_{av}$
.
$\mathit{Nu}_{av}$
.

Figure 6. Variations of the average Nusselt number
![]() $\mathit{Nu}_{av}$
as a function of
$\mathit{Nu}_{av}$
as a function of
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() $\mathit{Re}$
for
$\mathit{Re}$
for
![]() $\mathit{Ra}_{p}=1000$
.
$\mathit{Ra}_{p}=1000$
.

Figure 7. Variations of the average Nusselt number
![]() $\mathit{Nu}_{av}$
as a function of
$\mathit{Nu}_{av}$
as a function of
![]() $\mathit{Ra}_{p}{\it\alpha}^{-3}$
and
$\mathit{Ra}_{p}{\it\alpha}^{-3}$
and
![]() ${\it\alpha}$
for
${\it\alpha}$
for
![]() $\mathit{Re}=1$
(a), 5 (b) and 10 (c). The thick solid lines identify the critical stability conditions for the transverse rolls.
$\mathit{Re}=1$
(a), 5 (b) and 10 (c). The thick solid lines identify the critical stability conditions for the transverse rolls.

Figure 8. Variations of (a) the horizontal heat flux along the heated wall expressed in terms of the horizontal Nusselt number
![]() $\mathit{Nu}_{h}$
and (b) the convective part of this heat flux expressed in terms of the horizontal convective Nusselt number
$\mathit{Nu}_{h}$
and (b) the convective part of this heat flux expressed in terms of the horizontal convective Nusselt number
![]() $\mathit{Nu}_{h,conv}$
.
$\mathit{Nu}_{h,conv}$
.
2.4. Heating applied at the upper wall
Consider the same problem as discussed above but apply the external heating at the upper wall. The conduction problem (2.4) needs to be replaced by
while the rest of the formulation remains the same. The similarity of the flow response to that found in the case of heating applied from below can be demonstrated by (i) reversing the direction of gravity, i.e.
![]() $\mathit{Ra}_{p}\rightarrow -\mathit{Ra}_{p}$
, and (ii) changing the sign of the temperature, i.e.
$\mathit{Ra}_{p}\rightarrow -\mathit{Ra}_{p}$
, and (ii) changing the sign of the temperature, i.e.
![]() ${\it\theta}\rightarrow -{\it\theta}$
. The latter condition implies a change of the sign of the temperature imposed at the lower plate and results in a shift of the temperature field by half a cycle in the
${\it\theta}\rightarrow -{\it\theta}$
. The latter condition implies a change of the sign of the temperature imposed at the lower plate and results in a shift of the temperature field by half a cycle in the
![]() $x$
direction. As a result, the global convection characteristics for the system heated from above are identical to those found in the case of the system heated from below (Hossain & Floryan Reference Hossain and Floryan2014).
$x$
direction. As a result, the global convection characteristics for the system heated from above are identical to those found in the case of the system heated from below (Hossain & Floryan Reference Hossain and Floryan2014).
3. Stability of the primary convection
The linear stability theory is used to identify the onset conditions and to predict the form of the secondary motions. We begin with convection resulting from heating applied at the lower wall.
3.1. Problem formulation
The stability analysis begins with the momentum equations written in the vorticity transport form supplemented by the energy and the continuity equations, i.e.
where
![]() $\boldsymbol{j}$
is the unit vector along the vertical direction, and
$\boldsymbol{j}$
is the unit vector along the vertical direction, and
![]() ${\bf\omega}$
and
${\bf\omega}$
and
![]() $\boldsymbol{v}$
are the vorticity and velocity vectors, respectively. Unsteady three-dimensional disturbances are superposed on the base flow in the form (Floryan Reference Floryan1997)
$\boldsymbol{v}$
are the vorticity and velocity vectors, respectively. Unsteady three-dimensional disturbances are superposed on the base flow in the form (Floryan Reference Floryan1997)
where subscripts 2 refer to the disturbance fields,
![]() $\boldsymbol{v}_{2}=(u_{2},v_{2},w_{2})$
is the disturbance velocity vector,
$\boldsymbol{v}_{2}=(u_{2},v_{2},w_{2})$
is the disturbance velocity vector,
![]() ${\bf\omega}_{2}=({\it\omega}_{x2},{\it\omega}_{y2},{\it\omega}_{z2})$
is the disturbance vorticity vector and
${\bf\omega}_{2}=({\it\omega}_{x2},{\it\omega}_{y2},{\it\omega}_{z2})$
is the disturbance vorticity vector and
![]() ${\it\theta}_{2}$
stands for the temperature disturbance. The flow quantities (3.2) are substituted into (3.1), the components containing the primary convection are subtracted, and the equations are linearized. The resulting disturbance equations have the form
${\it\theta}_{2}$
stands for the temperature disturbance. The flow quantities (3.2) are substituted into (3.1), the components containing the primary convection are subtracted, and the equations are linearized. The resulting disturbance equations have the form
and are subject to the homogeneous boundary conditions
at the walls. The disturbance equations (3.3) have coefficients that are functions of
![]() $x$
and
$x$
and
![]() $y$
, and thus the solution can be written in the form
$y$
, and thus the solution can be written in the form
The disturbance wavevector has components (
![]() ${\it\delta},{\it\beta}$
) in the (
${\it\delta},{\it\beta}$
) in the (
![]() $x,z$
) directions,
$x,z$
) directions,
![]() $\boldsymbol{V}_{2}(x,y)$
,
$\boldsymbol{V}_{2}(x,y)$
,
![]() ${\it\bf\Omega}_{2}(x,y)$
and
${\it\bf\Omega}_{2}(x,y)$
and
![]() ${\it\Theta}_{2}(x,y)$
are the
${\it\Theta}_{2}(x,y)$
are the
![]() $x$
-periodic amplitude functions modulated by the heating, the exponent
$x$
-periodic amplitude functions modulated by the heating, the exponent
![]() ${\it\sigma}$
is assumed to be complex
${\it\sigma}$
is assumed to be complex
![]() $({\it\sigma}={\it\sigma}_{r}+\text{i}{\it\sigma}_{i})$
with imaginary and real parts describing the rate of growth and the frequency of disturbances, respectively, and c.c. stands for the complex conjugate. Positive
$({\it\sigma}={\it\sigma}_{r}+\text{i}{\it\sigma}_{i})$
with imaginary and real parts describing the rate of growth and the frequency of disturbances, respectively, and c.c. stands for the complex conjugate. Positive
![]() ${\it\sigma}_{i}$
identifies instability.
${\it\sigma}_{i}$
identifies instability.
The set (
![]() ${\it\delta},{\it\beta},{\it\sigma}$
) represents the eigenvalues for the specified heating conditions (
${\it\delta},{\it\beta},{\it\sigma}$
) represents the eigenvalues for the specified heating conditions (
![]() $\mathit{Re},\mathit{Pr},\mathit{Ra}_{p},{\it\alpha}$
), creating a large parameter space; the size of this space is reduced in this analysis by setting
$\mathit{Re},\mathit{Pr},\mathit{Ra}_{p},{\it\alpha}$
), creating a large parameter space; the size of this space is reduced in this analysis by setting
![]() $\mathit{Pr}=0.71$
. The relevant eigenvalue problem for the partial differential equations (3.3) can be easily derived. Rather than solving this problem directly, we take advantage of the periodicity of the amplitude functions and represent them in terms of Fourier expansions
$\mathit{Pr}=0.71$
. The relevant eigenvalue problem for the partial differential equations (3.3) can be easily derived. Rather than solving this problem directly, we take advantage of the periodicity of the amplitude functions and represent them in terms of Fourier expansions
where
 $$\begin{eqnarray}\displaystyle I_{v}^{(m-n)} & = & \displaystyle k_{m-n}^{-2}[\text{i}n{\it\alpha}({\it\beta}^{2}-t_{m}t_{m-n})\text{D}u_{1}^{(n)}\text{D}+k_{m}^{2}({\it\beta}^{2}+t_{m-n}t_{m-2n})v_{1}^{(n)}\text{D}]\nonumber\\ \displaystyle & & \displaystyle +\,k_{m-n}^{-2}[\text{i}(-k_{m-n}^{2}t_{m}+2n{\it\alpha}{\it\beta}^{2})u_{1}^{(n)}\text{D}^{2}+(n{\it\alpha}t_{m}-k_{m}^{2})v_{1}^{(n)}\text{D}^{3}]\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}k_{m}^{2}t_{m-2n}u_{1}^{(n)}+\text{i}t_{m}\text{D}^{2}u_{1}^{(n)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{v}^{(m-n)} & = & \displaystyle k_{m-n}^{-2}[\text{i}n{\it\alpha}({\it\beta}^{2}-t_{m}t_{m-n})\text{D}u_{1}^{(n)}\text{D}+k_{m}^{2}({\it\beta}^{2}+t_{m-n}t_{m-2n})v_{1}^{(n)}\text{D}]\nonumber\\ \displaystyle & & \displaystyle +\,k_{m-n}^{-2}[\text{i}(-k_{m-n}^{2}t_{m}+2n{\it\alpha}{\it\beta}^{2})u_{1}^{(n)}\text{D}^{2}+(n{\it\alpha}t_{m}-k_{m}^{2})v_{1}^{(n)}\text{D}^{3}]\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}k_{m}^{2}t_{m-2n}u_{1}^{(n)}+\text{i}t_{m}\text{D}^{2}u_{1}^{(n)},\end{eqnarray}$$
The above formulation is analogous to the Bloch theory (Bloch Reference Bloch1928) for systems with spatially periodic coefficients. It can also be interpreted in terms of the Floquet theory (Coddington & Levinson Reference Coddington and Levinson1965).
3.2. Method of solution
Equations (3.7a–c
), together with the boundary conditions (3.8), are truncated after
![]() $N_{M}$
modes. The dispersion relation is determined numerically through solution of the relevant eigenvalue problem. For the purposes of calculations, the problem is posed as an eigenvalue problem for
$N_{M}$
modes. The dispersion relation is determined numerically through solution of the relevant eigenvalue problem. For the purposes of calculations, the problem is posed as an eigenvalue problem for
![]() ${\it\sigma}$
. Equations (3.7a–c
) are discretized with spectral accuracy using the Chebyshev collocation method with
${\it\sigma}$
. Equations (3.7a–c
) are discretized with spectral accuracy using the Chebyshev collocation method with
![]() $N_{T}$
collocation points. The discretization procedure results in a matrix eigenvalue problem
$N_{T}$
collocation points. The discretization procedure results in a matrix eigenvalue problem
![]() ${\it\bf\Xi}x=0$
, where
${\it\bf\Xi}x=0$
, where
![]() ${\it\bf\Xi}({\it\sigma})$
represents the coefficient matrix. This matrix is linear in
${\it\bf\Xi}({\it\sigma})$
represents the coefficient matrix. This matrix is linear in
![]() ${\it\sigma}$
, i.e.
${\it\sigma}$
, i.e.
![]() ${\it\bf\Xi}={\it\bf\Xi}_{0}+{\it\bf\Xi}_{1}{\it\sigma}$
, where
${\it\bf\Xi}={\it\bf\Xi}_{0}+{\it\bf\Xi}_{1}{\it\sigma}$
, where
![]() ${\it\bf\Xi}_{0}={\it\bf\Xi}(0)$
and
${\it\bf\Xi}_{0}={\it\bf\Xi}(0)$
and
![]() ${\it\bf\Xi}_{1}={\it\bf\Xi}(1)-{\it\bf\Xi}_{0}$
. The
${\it\bf\Xi}_{1}={\it\bf\Xi}(1)-{\it\bf\Xi}_{0}$
. The
![]() ${\it\sigma}$
spectrum is determined by solving a general eigenvalue problem of the form
${\it\sigma}$
spectrum is determined by solving a general eigenvalue problem of the form
![]() ${\it\bf\Xi}_{0}x={\it\sigma}{\it\bf\Xi}_{1}x$
. The individual eigenvalues are determined by finding the zeros of the determinant of
${\it\bf\Xi}_{0}x={\it\sigma}{\it\bf\Xi}_{1}x$
. The individual eigenvalues are determined by finding the zeros of the determinant of
![]() ${\it\bf\Xi}$
. The computed eigenvalues are further refined using the inverse iteration technique.
${\it\bf\Xi}$
. The computed eigenvalues are further refined using the inverse iteration technique.
Two methods of tracing the eigenvalues in the parameter space have been used (Floryan Reference Floryan2003). In both of them we start with a small change of one of the dimensionless numbers. Then, in the first method, we produce an approximation for the eigenvalue, which is improved iteratively by searching for the nearby zero of the determinant using a Newton–Raphson search procedure. A reasonable guess for the unknown eigenvalue is essential for the convergence. In the second method, the inverse iterations method, we compute an approximation for the eigenvector
![]() ${\it\bf\Lambda}_{a}$
corresponding to the unknown eigenvalue
${\it\bf\Lambda}_{a}$
corresponding to the unknown eigenvalue
![]() ${\it\sigma}_{a}$
using an iterative process in the form
${\it\sigma}_{a}$
using an iterative process in the form
![]() $({\it\bf\Xi}_{0}-{\it\sigma}_{0}{\it\bf\Xi}_{1}){\it\bf\Lambda}^{(k+1)}={\it\bf\Xi}_{1}{\it\bf\Lambda}^{(k)}$
, where
$({\it\bf\Xi}_{0}-{\it\sigma}_{0}{\it\bf\Xi}_{1}){\it\bf\Lambda}^{(k+1)}={\it\bf\Xi}_{1}{\it\bf\Lambda}^{(k)}$
, where
![]() ${\it\sigma}_{0}$
and
${\it\sigma}_{0}$
and
![]() ${\it\bf\Lambda}^{(0)}$
are the eigenvalue and the eigenvector (an eigenpair) corresponding to the unaltered flow. If
${\it\bf\Lambda}^{(0)}$
are the eigenvalue and the eigenvector (an eigenpair) corresponding to the unaltered flow. If
![]() ${\it\sigma}_{a}$
is the eigenvalue closest to
${\it\sigma}_{a}$
is the eigenvalue closest to
![]() ${\it\sigma}_{0}$
,
${\it\sigma}_{0}$
,
![]() ${\it\bf\Lambda}^{(k)}$
converges to
${\it\bf\Lambda}^{(k)}$
converges to
![]() ${\it\bf\Lambda}_{a}$
. The eigenvalue
${\it\bf\Lambda}_{a}$
. The eigenvalue
![]() ${\it\sigma}_{a}$
is evaluated using the formula
${\it\sigma}_{a}$
is evaluated using the formula
![]() ${\it\sigma}_{a}={\it\bf\Lambda}_{a}^{\ast }{\it\bf\Xi}_{0}{\it\bf\Lambda}_{a}/{\it\bf\Lambda}_{a}^{\ast }{\it\bf\Xi}_{1}{\it\bf\Lambda}_{a}$
, where the asterisk denotes the complex conjugate transpose. The inverse iterations method was found to be generally more efficient. The relevant numerical parameters (i.e.
${\it\sigma}_{a}={\it\bf\Lambda}_{a}^{\ast }{\it\bf\Xi}_{0}{\it\bf\Lambda}_{a}/{\it\bf\Lambda}_{a}^{\ast }{\it\bf\Xi}_{1}{\it\bf\Lambda}_{a}$
, where the asterisk denotes the complex conjugate transpose. The inverse iterations method was found to be generally more efficient. The relevant numerical parameters (i.e.
![]() $N_{M}$
and
$N_{M}$
and
![]() $N_{T}$
) have been selected through numerical convergence studies to guarantee at least four-digit eigenvalue accuracy.
$N_{T}$
) have been selected through numerical convergence studies to guarantee at least four-digit eigenvalue accuracy.
3.3. Description of flow stability characteristics
It is convenient to start the discussion with descriptions of two reference states, i.e. the natural convection (
![]() $\mathit{Re}=0$
) driven by periodic heating and the forced convection in a channel with a uniformly heated lower plate.
$\mathit{Re}=0$
) driven by periodic heating and the forced convection in a channel with a uniformly heated lower plate.
3.3.1. Natural convection driven by a periodic heating
 $(\mathit{Re}=0)$
$(\mathit{Re}=0)$
Two instability mechanisms are active in the case of periodic heating described by (2.1), i.e. the RB mechanism and the spatial parametric resonance mechanism (Hossain & Floryan Reference Hossain and Floryan2013b
). Three types of structures can be created at the onset, i.e. longitudinal rolls (rolls parallel to the primary rolls) driven primarily by the RB mechanism, transverse rolls (rolls orthogonal to the primary rolls) also driven primarily by the RB mechanism, and oblique rolls driven primarily by the spatial parametric resonance. Figure 9 illustrates variations of the critical Rayleigh number
![]() $\mathit{Ra}_{p,cr}$
and the critical wavenumbers
$\mathit{Ra}_{p,cr}$
and the critical wavenumbers
![]() ${\it\delta}_{cr}$
and
${\it\delta}_{cr}$
and
![]() ${\it\beta}_{cr}$
as functions of
${\it\beta}_{cr}$
as functions of
![]() ${\it\alpha}$
for these rolls. The oblique rolls play the critical role for
${\it\alpha}$
for these rolls. The oblique rolls play the critical role for
![]() ${\it\alpha}=O(1)$
, the longitudinal rolls play such a role in a small interval of
${\it\alpha}=O(1)$
, the longitudinal rolls play such a role in a small interval of
![]() ${\it\alpha}$
centred around
${\it\alpha}$
centred around
![]() ${\it\alpha}\approx 4$
and the transverse rolls become critical for larger
${\it\alpha}\approx 4$
and the transverse rolls become critical for larger
![]() ${\it\alpha}$
. In the limit of
${\it\alpha}$
. In the limit of
![]() ${\it\alpha}\rightarrow \infty$
, the primary convection is confined to a thin boundary layer adjacent to the lower wall with the conduction state emerging above this layer (see § 2.3.2) resulting in the dominance of the RB mechanism. As a result, the critical stability curves approach an asymptote for
${\it\alpha}\rightarrow \infty$
, the primary convection is confined to a thin boundary layer adjacent to the lower wall with the conduction state emerging above this layer (see § 2.3.2) resulting in the dominance of the RB mechanism. As a result, the critical stability curves approach an asymptote for
![]() ${\it\alpha}\rightarrow \infty$
, which can be predicted on the basis of the RB instability (Pellew & Southwell Reference Pellew and Southwell1940; Koschmieder Reference Koschmieder1993). Wavenumber lock-in between the primary rolls and the component of the disturbance wavevector parallel to the primary convection wavevector occurs for
${\it\alpha}\rightarrow \infty$
, which can be predicted on the basis of the RB instability (Pellew & Southwell Reference Pellew and Southwell1940; Koschmieder Reference Koschmieder1993). Wavenumber lock-in between the primary rolls and the component of the disturbance wavevector parallel to the primary convection wavevector occurs for
![]() ${\it\alpha}=O(1)$
.
${\it\alpha}=O(1)$
.

Figure 9. Variations of (a) the critical Rayleigh number
![]() $\mathit{Ra}_{p,cr}$
and (b) the critical wavenumbers
$\mathit{Ra}_{p,cr}$
and (b) the critical wavenumbers
![]() ${\it\delta}_{cr}$
and
${\it\delta}_{cr}$
and
![]() ${\it\beta}_{cr}$
as functions of
${\it\beta}_{cr}$
as functions of
![]() ${\it\alpha}$
for the periodically heated layer with
${\it\alpha}$
for the periodically heated layer with
![]() $\mathit{Re}=0$
(see § 3.3.1). Curves 1, 2 and 3 correspond to the longitudinal, transverse and oblique rolls, respectively.
$\mathit{Re}=0$
(see § 3.3.1). Curves 1, 2 and 3 correspond to the longitudinal, transverse and oblique rolls, respectively.

Figure 10. Variations of (a) the critical Rayleigh number
![]() $\mathit{Ra}_{cr}$
and (b) the critical wavenumbers
$\mathit{Ra}_{cr}$
and (b) the critical wavenumbers
![]() ${\it\delta}_{cr}$
and
${\it\delta}_{cr}$
and
![]() ${\it\beta}_{cr}$
, and the frequency
${\it\beta}_{cr}$
, and the frequency
![]() ${\it\sigma}_{r}$
as functions of the Reynolds number
${\it\sigma}_{r}$
as functions of the Reynolds number
![]() $\mathit{Re}$
for the uniformly heated fluid layer (see § 3.3.2). Curves 1, 2, 3 and 4 correspond to the parallel rolls, the 60° oblique rolls, the 30° oblique rolls, and the orthogonal rolls, respectively. In panel (b), the thick solid, dashed and dash-dotted lines identify
$\mathit{Re}$
for the uniformly heated fluid layer (see § 3.3.2). Curves 1, 2, 3 and 4 correspond to the parallel rolls, the 60° oblique rolls, the 30° oblique rolls, and the orthogonal rolls, respectively. In panel (b), the thick solid, dashed and dash-dotted lines identify
![]() ${\it\delta}_{cr}$
,
${\it\delta}_{cr}$
,
![]() ${\it\beta}_{cr}$
and
${\it\beta}_{cr}$
and
![]() ${\it\sigma}_{r}$
, respectively; the limit points A, B, C and D (marked using ●, ♢, ○, ▵) correspond to
${\it\sigma}_{r}$
, respectively; the limit points A, B, C and D (marked using ●, ♢, ○, ▵) correspond to
![]() $({\it\delta}_{cr},{\it\beta}_{cr},{\it\sigma}_{r})=(0,1.56,0)$
,
$({\it\delta}_{cr},{\it\beta}_{cr},{\it\sigma}_{r})=(0,1.56,0)$
,
![]() $(0.51,0.89,1565)$
,
$(0.51,0.89,1565)$
,
![]() $(0.89,0.51,1554)$
and
$(0.89,0.51,1554)$
and
![]() $(1.02,0,1554)$
, respectively.
$(1.02,0,1554)$
, respectively.
3.3.2. Forced convection driven by uniform heating
Conditions leading to the onset of natural convection in the case of a uniformly heated lower wall and in the absence of forced convection are expressed in terms of the Rayleigh number defined as
![]() $\mathit{Ra}=g{\it\Gamma}h^{3}{\rm\Delta}T/{\it\nu}{\it\kappa}$
, where
$\mathit{Ra}=g{\it\Gamma}h^{3}{\rm\Delta}T/{\it\nu}{\it\kappa}$
, where
![]() ${\rm\Delta}T$
stands for the temperature difference between the walls. The Rayleigh number
${\rm\Delta}T$
stands for the temperature difference between the walls. The Rayleigh number
![]() $\mathit{Ra}$
has to reach the critical value of
$\mathit{Ra}$
has to reach the critical value of
![]() $\mathit{Ra}_{cr}=213.5$
in order to initiate any movement of the fluid (Pellew & Southwell Reference Pellew and Southwell1940; Koschmieder Reference Koschmieder1993). The pattern of the resulting motion cannot be determined on the basis of linear stability theory; various symmetry-breaking mechanisms may affect this process (Freund, Pesch & Zimmermann Reference Freund, Pesch and Zimmermann2011; Weiss, Seiden & Bodenschatz Reference Weiss, Seiden and Bodenschatz2012). Introduction of forced motion provides another symmetry-breaking mechanism and gives preference to rolls with their axes parallel to the direction of the forced flow (Gage & Reid Reference Gage and Reid1968). The evolution of the critical conditions as a function of
$\mathit{Ra}_{cr}=213.5$
in order to initiate any movement of the fluid (Pellew & Southwell Reference Pellew and Southwell1940; Koschmieder Reference Koschmieder1993). The pattern of the resulting motion cannot be determined on the basis of linear stability theory; various symmetry-breaking mechanisms may affect this process (Freund, Pesch & Zimmermann Reference Freund, Pesch and Zimmermann2011; Weiss, Seiden & Bodenschatz Reference Weiss, Seiden and Bodenschatz2012). Introduction of forced motion provides another symmetry-breaking mechanism and gives preference to rolls with their axes parallel to the direction of the forced flow (Gage & Reid Reference Gage and Reid1968). The evolution of the critical conditions as a function of
![]() $\mathit{Re}$
is illustrated in figure 10. Three types of roll are shown: (i) rolls with axes parallel to the flow direction are referred to as parallel rolls (they correspond to the transverse rolls in the case of periodic heating), (ii) rolls with axes orthogonal to the flow direction are referred to as orthogonal rolls (they correspond to the longitudinal rolls in the case of periodic heating), and (iii) oblique rolls. The obliqueness angle
$\mathit{Re}$
is illustrated in figure 10. Three types of roll are shown: (i) rolls with axes parallel to the flow direction are referred to as parallel rolls (they correspond to the transverse rolls in the case of periodic heating), (ii) rolls with axes orthogonal to the flow direction are referred to as orthogonal rolls (they correspond to the longitudinal rolls in the case of periodic heating), and (iii) oblique rolls. The obliqueness angle
![]() ${\it\chi}$
is defined as
${\it\chi}$
is defined as
![]() $\tan ({\it\chi})={\it\beta}/{\it\delta}$
and thus
$\tan ({\it\chi})={\it\beta}/{\it\delta}$
and thus
![]() ${\it\chi}=0^{\circ }$
corresponds to orthogonal rolls and
${\it\chi}=0^{\circ }$
corresponds to orthogonal rolls and
![]() ${\it\chi}=90^{\circ }$
to parallel rolls. The critical conditions for all rolls approach the same limit of
${\it\chi}=90^{\circ }$
to parallel rolls. The critical conditions for all rolls approach the same limit of
![]() $\mathit{Re}_{cr}=213.5$
,
$\mathit{Re}_{cr}=213.5$
,
![]() $\sqrt{{\it\delta}_{cr}^{2}+{\it\beta}_{cr}^{2}}=1.56$
,
$\sqrt{{\it\delta}_{cr}^{2}+{\it\beta}_{cr}^{2}}=1.56$
,
![]() ${\it\sigma}_{r}=0$
when
${\it\sigma}_{r}=0$
when
![]() $\mathit{Re}\rightarrow 0$
. The critical conditions for the parallel rolls remain independent of
$\mathit{Re}\rightarrow 0$
. The critical conditions for the parallel rolls remain independent of
![]() $\mathit{Re}$
and such rolls always remain stationary. All other rolls travel in the downstream direction when
$\mathit{Re}$
and such rolls always remain stationary. All other rolls travel in the downstream direction when
![]() $\mathit{Re}>0$
with
$\mathit{Re}>0$
with
![]() ${\it\sigma}_{r}$
increasing with
${\it\sigma}_{r}$
increasing with
![]() $\mathit{Re}$
; their
$\mathit{Re}$
; their
![]() $\mathit{Ra}_{cr}$
increases with increase of
$\mathit{Ra}_{cr}$
increases with increase of
![]() $\mathit{Re}$
, reaches a maximum and then drops off rapidly, as shown in figure 10. The orthogonal rolls are of the most interest as their
$\mathit{Re}$
, reaches a maximum and then drops off rapidly, as shown in figure 10. The orthogonal rolls are of the most interest as their
![]() $\mathit{Ra}_{cr}$
drop to zero at the smallest
$\mathit{Ra}_{cr}$
drop to zero at the smallest
![]() $\mathit{Re}$
, i.e. at
$\mathit{Re}$
, i.e. at
![]() $\mathit{Re}=5772$
, and this point corresponds to the shear instability beginning to play the critical role. The results displayed in figure 10 well illustrate the morphing of the orthogonal rolls into the two-dimensional Tollmien–Schlichting (TS) waves as
$\mathit{Re}=5772$
, and this point corresponds to the shear instability beginning to play the critical role. The results displayed in figure 10 well illustrate the morphing of the orthogonal rolls into the two-dimensional Tollmien–Schlichting (TS) waves as
![]() $\mathit{Re}$
increases. In summary, the parallel rolls play the critical role when
$\mathit{Re}$
increases. In summary, the parallel rolls play the critical role when
![]() $\mathit{Re}<5772$
, and the transition to the secondary state for such conditions is driven by the RB mechanism. The two-dimensional travelling waves play the critical role for
$\mathit{Re}<5772$
, and the transition to the secondary state for such conditions is driven by the RB mechanism. The two-dimensional travelling waves play the critical role for
![]() $\mathit{Re}>5772$
, and for such conditions the transition is driven by viscous shear. One should note that flow with parallel rolls is subject to secondary instabilities (Clever & Busse Reference Clever and Busse1991).
$\mathit{Re}>5772$
, and for such conditions the transition is driven by viscous shear. One should note that flow with parallel rolls is subject to secondary instabilities (Clever & Busse Reference Clever and Busse1991).

Figure 11. The flow structures associated with (a) the primary convection and (b) the secondary convection in the form of transverse rolls at the onset in a flow with
![]() $\mathit{Re}=1$
. (a) The stream function normalized by its maximum; (b) the second invariant of the velocity gradient tensor (see (3.21)). The heating has the wavenumber
$\mathit{Re}=1$
. (a) The stream function normalized by its maximum; (b) the second invariant of the velocity gradient tensor (see (3.21)). The heating has the wavenumber
![]() ${\it\alpha}=5$
, requires the intensity corresponding to
${\it\alpha}=5$
, requires the intensity corresponding to
![]() $\mathit{Ra}_{p,cr}=3317$
and generates the secondary convection with wavenumber
$\mathit{Ra}_{p,cr}=3317$
and generates the secondary convection with wavenumber
![]() ${\it\beta}_{cr}=1.6$
.
${\it\beta}_{cr}=1.6$
.

Figure 12. The onset conditions required for the formation of the secondary convection in the form of transverse rolls in the fluid flowing through a periodically heated channel at different Reynolds numbers
![]() $\mathit{Re}$
(see § 3.3.3): variations of (a) the critical Rayleigh number
$\mathit{Re}$
(see § 3.3.3): variations of (a) the critical Rayleigh number
![]() $\mathit{Ra}_{cr}$
and (b) the critical wavenumber
$\mathit{Ra}_{cr}$
and (b) the critical wavenumber
![]() ${\it\beta}_{cr}$
as functions of the heating wavenumber
${\it\beta}_{cr}$
as functions of the heating wavenumber
![]() ${\it\alpha}$
.
${\it\alpha}$
.
3.3.3. Transverse rolls
We shall now return to the periodic heating and enquire how the introduction of forced convection affects the onset conditions when compared with natural convection, and identify the form of the unstable motion at the onset. We begin the presentation with the transverse rolls; such rolls are parallel to the direction of the forced convection and are orthogonal to the primary rolls, and thus may exhibit some of the features of the parallel rolls generated by uniform heating. The form of these rolls is illustrated in figure 11, where the second invariant of the velocity gradient tensor
![]() ${\it\vartheta}$
(Dubief & Delcayre Reference Dubief and Delcayre2000), defined as
${\it\vartheta}$
(Dubief & Delcayre Reference Dubief and Delcayre2000), defined as
where
![]() ${\it\Phi}_{ij}=(u_{i,j}-u_{j,i})/2$
,
${\it\Phi}_{ij}=(u_{i,j}-u_{j,i})/2$
,
![]() ${\it\varpi}_{ij}=(u_{i,j}+u_{j,i})/2$
, has been plotted with the disturbance velocity field normalized by the condition
${\it\varpi}_{ij}=(u_{i,j}+u_{j,i})/2$
, has been plotted with the disturbance velocity field normalized by the condition
![]() $\max (g_{2u}^{(1)})=1$
. Figure 12(a) illustrates variations of
$\max (g_{2u}^{(1)})=1$
. Figure 12(a) illustrates variations of
![]() $\mathit{Ra}_{cr}$
as a function of
$\mathit{Ra}_{cr}$
as a function of
![]() ${\it\alpha}$
; the form of the critical curves suggests the existence of two characteristic zones. In the limit of
${\it\alpha}$
; the form of the critical curves suggests the existence of two characteristic zones. In the limit of
![]() ${\it\alpha}\rightarrow \infty$
these curves reach the same asymptote for all
${\it\alpha}\rightarrow \infty$
these curves reach the same asymptote for all
![]() $\mathit{Re}$
considered and, in this sense, the properties of these rolls resemble the properties of the parallel rolls of § 3.3.2. The asymptote can be determined analytically by taking advantage of (2.43) (for details see Hossain & Floryan Reference Hossain and Floryan2013b
). This is due to the fact that in this limit the temperature field splits into a thin boundary layer adjacent to the heated wall and a conduction zone with a constant vertical temperature gradient above the boundary layer. As a result, the spatial parametric resonance is practically eliminated and the instability is driven by the RB mechanism. The results displayed in figure 12(b) demonstrate that the critical wavenumbers reach the limit
$\mathit{Re}$
considered and, in this sense, the properties of these rolls resemble the properties of the parallel rolls of § 3.3.2. The asymptote can be determined analytically by taking advantage of (2.43) (for details see Hossain & Floryan Reference Hossain and Floryan2013b
). This is due to the fact that in this limit the temperature field splits into a thin boundary layer adjacent to the heated wall and a conduction zone with a constant vertical temperature gradient above the boundary layer. As a result, the spatial parametric resonance is practically eliminated and the instability is driven by the RB mechanism. The results displayed in figure 12(b) demonstrate that the critical wavenumbers reach the limit
![]() ${\it\beta}_{cr}\rightarrow 1.56$
when
${\it\beta}_{cr}\rightarrow 1.56$
when
![]() ${\it\alpha}\rightarrow \infty$
, which is identical to that found in the case of uniform heating. The situation is more complex when
${\it\alpha}\rightarrow \infty$
, which is identical to that found in the case of uniform heating. The situation is more complex when
![]() ${\it\alpha}=O(1)$
, as the strength of the primary rolls is largest under such conditions (see § 2.3) and this strengthens the spatial parametric resonance. The critical curves displayed in figure 12(a) show large variations of form as a function of
${\it\alpha}=O(1)$
, as the strength of the primary rolls is largest under such conditions (see § 2.3) and this strengthens the spatial parametric resonance. The critical curves displayed in figure 12(a) show large variations of form as a function of
![]() $\mathit{Re}$
for
$\mathit{Re}$
for
![]() ${\it\alpha}=O(1)$
. A small increase of
${\it\alpha}=O(1)$
. A small increase of
![]() $\mathit{Re}$
may destabilize the system and expand the unstable zone to smaller
$\mathit{Re}$
may destabilize the system and expand the unstable zone to smaller
![]() ${\it\alpha}$
values, but its further increase stabilizes the system due to the washing out of the separation bubbles, as illustrated in figures 2, 5 and 6. The complexity of this process is illustrated in figure 12(b), which displays variations of
${\it\alpha}$
values, but its further increase stabilizes the system due to the washing out of the separation bubbles, as illustrated in figures 2, 5 and 6. The complexity of this process is illustrated in figure 12(b), which displays variations of
![]() ${\it\beta}_{cr}$
as a function of
${\it\beta}_{cr}$
as a function of
![]() ${\it\alpha}$
for several values of
${\it\alpha}$
for several values of
![]() $\mathit{Re}$
. The strong role of the parametric resonance is underlined by the rapid change in the character of variations of
$\mathit{Re}$
. The strong role of the parametric resonance is underlined by the rapid change in the character of variations of
![]() ${\it\beta}_{cr}$
for
${\it\beta}_{cr}$
for
![]() $\mathit{Re}=0$
at
$\mathit{Re}=0$
at
![]() ${\it\alpha}\approx 4$
. Introduction of forced convection, regardless of how small
${\it\alpha}\approx 4$
. Introduction of forced convection, regardless of how small
![]() $\mathit{Re}$
might be, leads to the qualitative change in the variations of
$\mathit{Re}$
might be, leads to the qualitative change in the variations of
![]() ${\it\beta}_{cr}$
(figure 12
b) and to an increase rather than a decrease of
${\it\beta}_{cr}$
(figure 12
b) and to an increase rather than a decrease of
![]() ${\it\beta}_{cr}$
as the magnitude of
${\it\beta}_{cr}$
as the magnitude of
![]() ${\it\alpha}$
decreases to
${\it\alpha}$
decreases to
![]() ${\it\alpha}<4$
.
${\it\alpha}<4$
.
Figure 13 illustrates effects of
![]() $\mathit{Re}$
more explicitly. When
$\mathit{Re}$
more explicitly. When
![]() $\mathit{Re}=O(1)$
and
$\mathit{Re}=O(1)$
and
![]() ${\it\alpha}=O(1)$
, the parametric resonance is active and results in the formation of a variety of critical curves as shown in figure 13(a). An increase of
${\it\alpha}=O(1)$
, the parametric resonance is active and results in the formation of a variety of critical curves as shown in figure 13(a). An increase of
![]() $\mathit{Re}$
while keeping
$\mathit{Re}$
while keeping
![]() $\mathit{Ra}_{p}$
fixed results in the washing away of the primary rolls and the formation of a boundary layer at the lower wall (§ 2.3.4). These rolls can be maintained in the whole channel if an increase of
$\mathit{Ra}_{p}$
fixed results in the washing away of the primary rolls and the formation of a boundary layer at the lower wall (§ 2.3.4). These rolls can be maintained in the whole channel if an increase of
![]() $\mathit{Re}$
is accompanied by an appropriate increase of
$\mathit{Re}$
is accompanied by an appropriate increase of
![]() $\mathit{Ra}_{p}$
. The second effect in play involves variations of
$\mathit{Ra}_{p}$
. The second effect in play involves variations of
![]() ${\it\alpha}$
; its increase results in the formation of a different boundary layer at the lower wall and a conduction zone above it. An increase of both
${\it\alpha}$
; its increase results in the formation of a different boundary layer at the lower wall and a conduction zone above it. An increase of both
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() ${\it\alpha}$
reduces the spatial flow modulations and eliminates the spatial parametric resonance. As a result, the secondary motion is driven by the RB effect and all of the critical curves approach a similar asymptote for
${\it\alpha}$
reduces the spatial flow modulations and eliminates the spatial parametric resonance. As a result, the secondary motion is driven by the RB effect and all of the critical curves approach a similar asymptote for
![]() $\mathit{Re}\rightarrow \infty$
, as illustrated in figure 13(a); the asymptote has been determined numerically. On the other hand, variations of
$\mathit{Re}\rightarrow \infty$
, as illustrated in figure 13(a); the asymptote has been determined numerically. On the other hand, variations of
![]() ${\it\beta}_{cr}$
always show a strong dependence on
${\it\beta}_{cr}$
always show a strong dependence on
![]() ${\it\alpha}$
, as illustrated in figure 13(b); this variability does not disappear even in the limit of
${\it\alpha}$
, as illustrated in figure 13(b); this variability does not disappear even in the limit of
![]() $\mathit{Re}\rightarrow \infty$
. The results displayed in figure 14 demonstrate the existence of different
$\mathit{Re}\rightarrow \infty$
. The results displayed in figure 14 demonstrate the existence of different
![]() ${\it\beta}_{cr}$
for different
${\it\beta}_{cr}$
for different
![]() ${\it\alpha}$
even when
${\it\alpha}$
even when
![]() $\mathit{Re}=10^{5}$
.
$\mathit{Re}=10^{5}$
.

Figure 13. The onset conditions required for the formation of the secondary convection in the form of transverse rolls in the fluid flowing through a channel subject to periodic heating of different wavelength (see § 3.3.3): variations of (a) the critical Rayleigh number
![]() $\mathit{Ra}_{p,cr}$
and (b) the critical wavenumber
$\mathit{Ra}_{p,cr}$
and (b) the critical wavenumber
![]() ${\it\beta}_{cr}$
as functions of the Reynolds number
${\it\beta}_{cr}$
as functions of the Reynolds number
![]() $\mathit{Re}$
. The asymptote for large
$\mathit{Re}$
. The asymptote for large
![]() $\mathit{Re}$
is marked in panel (a) using the dashed line. No asymptote has been identified in panel (b) (see figure 14 for further explanations).
$\mathit{Re}$
is marked in panel (a) using the dashed line. No asymptote has been identified in panel (b) (see figure 14 for further explanations).

Figure 14. Demonstration that an
![]() ${\it\alpha}$
-independent asymptote for
${\it\alpha}$
-independent asymptote for
![]() ${\it\beta}_{cr}$
for large
${\it\beta}_{cr}$
for large
![]() $\mathit{Re}$
does not exist. This figure displays variations of the amplification rate
$\mathit{Re}$
does not exist. This figure displays variations of the amplification rate
![]() ${\it\sigma}_{i}$
as a function of the wavenumber
${\it\sigma}_{i}$
as a function of the wavenumber
![]() ${\it\beta}$
of transverse rolls resulting from the application of heating with wavenumbers
${\it\beta}$
of transverse rolls resulting from the application of heating with wavenumbers
![]() ${\it\alpha}=1$
, 2, 5 and 10 for three values of the Reynolds number, i.e.
${\it\alpha}=1$
, 2, 5 and 10 for three values of the Reynolds number, i.e.
![]() $\mathit{Re}=10^{4}$
,
$\mathit{Re}=10^{4}$
,
![]() $5\times 10^{4}$
and
$5\times 10^{4}$
and
![]() $10^{5}$
. Heating with the Rayleigh number corresponding to the critical conditions for each combination of
$10^{5}$
. Heating with the Rayleigh number corresponding to the critical conditions for each combination of
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() $\mathit{Re}$
has been used. It can be seen that an increase of
$\mathit{Re}$
has been used. It can be seen that an increase of
![]() $\mathit{Re}$
results in
$\mathit{Re}$
results in
![]() ${\it\beta}_{cr}\rightarrow 1.74$
, 1.58, 1.51 and 1.50 for
${\it\beta}_{cr}\rightarrow 1.74$
, 1.58, 1.51 and 1.50 for
![]() ${\it\alpha}=1$
, 2, 5 and 10.
${\it\alpha}=1$
, 2, 5 and 10.

Figure 15. The flow structures associated with (a) the primary convection and (b) the secondary convection in the form of longitudinal rolls at the onset in a flow with
![]() $\mathit{Re}=1$
. (a) The stream function normalized with its maximum; (b) the second invariant of the velocity gradient tensor (see (3.21)). The heating has the wavenumber
$\mathit{Re}=1$
. (a) The stream function normalized with its maximum; (b) the second invariant of the velocity gradient tensor (see (3.21)). The heating has the wavenumber
![]() ${\it\alpha}=3.6$
, requires an intensity corresponding to
${\it\alpha}=3.6$
, requires an intensity corresponding to
![]() $\mathit{Ra}_{p,cr}=3191$
and generates the secondary convection with wavenumber
$\mathit{Ra}_{p,cr}=3191$
and generates the secondary convection with wavenumber
![]() ${\it\delta}_{cr}=1.8$
(the lock-in conditions). The rolls are pushed downstream with the phase speed corresponding to
${\it\delta}_{cr}=1.8$
(the lock-in conditions). The rolls are pushed downstream with the phase speed corresponding to
![]() ${\it\sigma}_{r}=0.0015$
. This speed increases with an increase of
${\it\sigma}_{r}=0.0015$
. This speed increases with an increase of
![]() $\mathit{Re}$
.
$\mathit{Re}$
.

Figure 16. The onset conditions required for the formation of the secondary convection in the form of longitudinal rolls in a fluid driven through a periodically heated channel at different Reynolds numbers
![]() $\mathit{Re}$
(see § 3.3.4). (a) Variations of the critical Rayleigh number
$\mathit{Re}$
(see § 3.3.4). (a) Variations of the critical Rayleigh number
![]() $\mathit{Ra}_{cr}$
as a function of the heating wavenumber
$\mathit{Ra}_{cr}$
as a function of the heating wavenumber
![]() ${\it\alpha}$
. The thick solid line identifies the reference state of
${\it\alpha}$
. The thick solid line identifies the reference state of
![]() $\mathit{Re}=0$
. (b) Variations of the critical wavenumber
$\mathit{Re}=0$
. (b) Variations of the critical wavenumber
![]() ${\it\delta}_{cr}$
(solid lines) as a function of the heating wavenumber
${\it\delta}_{cr}$
(solid lines) as a function of the heating wavenumber
![]() ${\it\alpha}$
, with the thick solid line corresponding to the reference state of
${\it\alpha}$
, with the thick solid line corresponding to the reference state of
![]() $\mathit{Re}=0$
. Also shown are variations of the critical frequency
$\mathit{Re}=0$
. Also shown are variations of the critical frequency
![]() ${\it\sigma}_{cr}$
as a function of the heating wavenumber
${\it\sigma}_{cr}$
as a function of the heating wavenumber
![]() ${\it\alpha}$
(dashed lines). The reference state of
${\it\alpha}$
(dashed lines). The reference state of
![]() $\mathit{Re}=0$
is marked using the dotted line (
$\mathit{Re}=0$
is marked using the dotted line (
![]() ${\it\sigma}_{cr}=0$
).
${\it\sigma}_{cr}=0$
).
3.3.4. Longitudinal rolls
We shall now turn our attention to the longitudinal rolls. Such rolls are parallel to the primary rolls and thus they are orthogonal to the direction of the forced flow (see figure 15). These rolls correspond to the orthogonal rolls in the case of uniform heating. Figure 16 displays variations of the critical conditions as a function of
![]() ${\it\alpha}$
. It can be seen that the rolls are stationary for
${\it\alpha}$
. It can be seen that the rolls are stationary for
![]() $\mathit{Re}=0$
but begin to be pushed downstream when forced convection is introduced (figure 16
b). The speed of the downstream movement increases with
$\mathit{Re}=0$
but begin to be pushed downstream when forced convection is introduced (figure 16
b). The speed of the downstream movement increases with
![]() $\mathit{Re}$
for the complete range of
$\mathit{Re}$
for the complete range of
![]() ${\it\alpha}$
studied. There is a finite range of
${\it\alpha}$
studied. There is a finite range of
![]() ${\it\alpha}$
bounded from below, which can lead to the formation of such rolls when
${\it\alpha}$
bounded from below, which can lead to the formation of such rolls when
![]() $\mathit{Re}=0$
(figure 16
a). An increase of
$\mathit{Re}=0$
(figure 16
a). An increase of
![]() $\mathit{Re}$
expands this range towards smaller
$\mathit{Re}$
expands this range towards smaller
![]() ${\it\alpha}$
s. The minimum of
${\it\alpha}$
s. The minimum of
![]() $\mathit{Ra}_{p,cr}$
occurs for
$\mathit{Ra}_{p,cr}$
occurs for
![]() $\mathit{Re}\approx 5$
and further increase of
$\mathit{Re}\approx 5$
and further increase of
![]() $\mathit{Re}$
stabilizes the flow, at least in the range of
$\mathit{Re}$
stabilizes the flow, at least in the range of
![]() ${\it\alpha}$
studied. There is an interesting evolution of the disturbance pattern at the onset, as illustrated in figure 16(b). In the case of natural convection (
${\it\alpha}$
studied. There is an interesting evolution of the disturbance pattern at the onset, as illustrated in figure 16(b). In the case of natural convection (
![]() $\mathit{Re}=0$
) and for
$\mathit{Re}=0$
) and for
![]() ${\it\alpha}<4.2$
, the disturbance wavenumber is locked in with the wavenumber of the primary convection according to the relation
${\it\alpha}<4.2$
, the disturbance wavenumber is locked in with the wavenumber of the primary convection according to the relation
![]() ${\it\delta}_{cr}={\it\alpha}/2$
(figure 16
b). Heating with larger
${\it\delta}_{cr}={\it\alpha}/2$
(figure 16
b). Heating with larger
![]() ${\it\alpha}$
generates rolls with
${\it\alpha}$
generates rolls with
![]() ${\it\delta}_{cr}$
exhibiting a rather complex dependence on
${\it\delta}_{cr}$
exhibiting a rather complex dependence on
![]() ${\it\alpha}$
and with the limit point of
${\it\alpha}$
and with the limit point of
![]() ${\it\delta}_{cr}\rightarrow 1.56$
for
${\it\delta}_{cr}\rightarrow 1.56$
for
![]() ${\it\alpha}\rightarrow \infty$
(Hossain & Floryan Reference Hossain and Floryan2013b
). A small increase of
${\it\alpha}\rightarrow \infty$
(Hossain & Floryan Reference Hossain and Floryan2013b
). A small increase of
![]() $\mathit{Re}$
up to
$\mathit{Re}$
up to
![]() $\mathit{Re}=5$
maintains a similar structure of variations of
$\mathit{Re}=5$
maintains a similar structure of variations of
![]() ${\it\delta}_{cr}$
but with the lock-in point moved towards smaller
${\it\delta}_{cr}$
but with the lock-in point moved towards smaller
![]() ${\it\alpha}$
and the limit point for
${\it\alpha}$
and the limit point for
![]() ${\it\alpha}\rightarrow \infty$
slightly increasing (figure 16
b). A further increase of
${\it\alpha}\rightarrow \infty$
slightly increasing (figure 16
b). A further increase of
![]() $\mathit{Re}$
completely eliminates the lock-in phenomenon and leads to an increase of
$\mathit{Re}$
completely eliminates the lock-in phenomenon and leads to an increase of
![]() ${\it\delta}_{cr}$
for
${\it\delta}_{cr}$
for
![]() ${\it\alpha}<4.2$
. This is due to the elimination of the separation bubbles and thus elimination of the spatial parametric resonance, as has already been discussed in the previous section. At the same time, the limit of
${\it\alpha}<4.2$
. This is due to the elimination of the separation bubbles and thus elimination of the spatial parametric resonance, as has already been discussed in the previous section. At the same time, the limit of
![]() ${\it\delta}_{cr}$
for
${\it\delta}_{cr}$
for
![]() ${\it\alpha}\rightarrow \infty$
increases above the reference value of 1.56 found in the case of natural convection.
${\it\alpha}\rightarrow \infty$
increases above the reference value of 1.56 found in the case of natural convection.

Figure 17. The onset conditions required for the formation of the secondary convection in the form of longitudinal rolls in a fluid driven through a channel subject to periodic heating of different wavelength (see § 3.3.4). (a) Variations of the critical Rayleigh number
![]() $\mathit{Ra}_{p,cr}$
, (b) variations of the critical wavenumber
$\mathit{Ra}_{p,cr}$
, (b) variations of the critical wavenumber
![]() ${\it\delta}_{cr}$
and (c) variations of the critical frequency
${\it\delta}_{cr}$
and (c) variations of the critical frequency
![]() ${\it\sigma}_{r}$
as functions of the Reynolds number
${\it\sigma}_{r}$
as functions of the Reynolds number
![]() $\mathit{Re}$
. Correlation
$\mathit{Re}$
. Correlation
![]() $\mathit{Ra}_{p,cr}={\it\alpha}^{0.2}(61.1\mathit{Re}^{1.386}-7.2\times 10^{-7}\mathit{Re}^{3.48})$
valid for
$\mathit{Ra}_{p,cr}={\it\alpha}^{0.2}(61.1\mathit{Re}^{1.386}-7.2\times 10^{-7}\mathit{Re}^{3.48})$
valid for
![]() $250<\mathit{Re}<5772$
is marked in panel (a) using the dotted line. The limit points A, B and C in panel (b) are located at
$250<\mathit{Re}<5772$
is marked in panel (a) using the dotted line. The limit points A, B and C in panel (b) are located at
![]() $(\mathit{Re},{\it\delta}_{cr})=(5772,1.02)$
,
$(\mathit{Re},{\it\delta}_{cr})=(5772,1.02)$
,
![]() $(0,2)$
and
$(0,2)$
and
![]() $(0,1.66)$
, respectively, and the limit point D in panel (d) is located at
$(0,1.66)$
, respectively, and the limit point D in panel (d) is located at
![]() $(\mathit{Re},{\it\sigma}_{r})=(5772,1554)$
.
$(\mathit{Re},{\it\sigma}_{r})=(5772,1554)$
.
Figure 17 illustrates more explicitly the variations of the critical conditions as a function of
![]() $\mathit{Re}$
. The results displayed in figure 17(a) demonstrate a complex dependence of
$\mathit{Re}$
. The results displayed in figure 17(a) demonstrate a complex dependence of
![]() $\mathit{Ra}_{p,cr}$
on
$\mathit{Ra}_{p,cr}$
on
![]() $\mathit{Re}$
. For small
$\mathit{Re}$
. For small
![]() $\mathit{Re}~(\mathit{Re}<5)$
,
$\mathit{Re}~(\mathit{Re}<5)$
,
![]() $\mathit{Ra}_{p,cr}$
either does not depend on
$\mathit{Ra}_{p,cr}$
either does not depend on
![]() $\mathit{Re}$
or decreases with
$\mathit{Re}$
or decreases with
![]() $\mathit{Re}$
depending on
$\mathit{Re}$
depending on
![]() ${\it\alpha}$
. Increase of
${\it\alpha}$
. Increase of
![]() $\mathit{Re}$
above
$\mathit{Re}$
above
![]() $\mathit{Re}=5$
results in an increase of
$\mathit{Re}=5$
results in an increase of
![]() $\mathit{Ra}_{p,cr}$
for all
$\mathit{Ra}_{p,cr}$
for all
![]() ${\it\alpha}$
considered. All critical curves exhibit a similar form for
${\it\alpha}$
considered. All critical curves exhibit a similar form for
![]() $\mathit{Re}>250$
, which leads to a correlation of the form
$\mathit{Re}>250$
, which leads to a correlation of the form
![]() $\mathit{Ra}_{p,cr}={\it\alpha}^{0.2}(61.1\,\mathit{Re}^{1.386}-7.2\times 10^{-7}\,\mathit{Re}^{3.48})$
. When
$\mathit{Ra}_{p,cr}={\it\alpha}^{0.2}(61.1\,\mathit{Re}^{1.386}-7.2\times 10^{-7}\,\mathit{Re}^{3.48})$
. When
![]() $\mathit{Re}$
approaches the limiting value of 5772,
$\mathit{Re}$
approaches the limiting value of 5772,
![]() $\mathit{Ra}_{p,cr}$
rapidly drops off for all
$\mathit{Ra}_{p,cr}$
rapidly drops off for all
![]() ${\it\alpha}$
as the instability becomes dominated by shear, similar to the case of uniform heating (§ 3.3.2). The variations of
${\it\alpha}$
as the instability becomes dominated by shear, similar to the case of uniform heating (§ 3.3.2). The variations of
![]() ${\it\delta}_{cr}$
displayed in figure 17(b) underline the complexity of the dependence of the critical conditions on
${\it\delta}_{cr}$
displayed in figure 17(b) underline the complexity of the dependence of the critical conditions on
![]() $\mathit{Re}$
. There is a wide range of variations of
$\mathit{Re}$
. There is a wide range of variations of
![]() ${\it\delta}_{cr}$
as a function of
${\it\delta}_{cr}$
as a function of
![]() $\mathit{Re}$
for
$\mathit{Re}$
for
![]() $\mathit{Re}<5$
, dependent on the heating wavenumber. This is followed by rapid but qualitatively similar variations of
$\mathit{Re}<5$
, dependent on the heating wavenumber. This is followed by rapid but qualitatively similar variations of
![]() ${\it\delta}_{cr}$
for all
${\it\delta}_{cr}$
for all
![]() ${\it\alpha}$
for
${\it\alpha}$
for
![]() $\mathit{Re}$
between 5 and 250, and different but also qualitatively similar variations for
$\mathit{Re}$
between 5 and 250, and different but also qualitatively similar variations for
![]() $\mathit{Re}>250$
with the critical curves approaching the same limit point
$\mathit{Re}>250$
with the critical curves approaching the same limit point
![]() $({\it\delta}_{cr},\mathit{Re})=(1.02,5772)$
for all
$({\it\delta}_{cr},\mathit{Re})=(1.02,5772)$
for all
![]() ${\it\alpha}$
. Figure 17(c) illustrates the evolution of the complex frequency from
${\it\alpha}$
. Figure 17(c) illustrates the evolution of the complex frequency from
![]() ${\it\sigma}_{r}=0$
at
${\it\sigma}_{r}=0$
at
![]() $\mathit{Re}=0$
to
$\mathit{Re}=0$
to
![]() ${\it\sigma}_{r}=1554$
at
${\it\sigma}_{r}=1554$
at
![]() $\mathit{Re}=5772$
. These changes illustrate morphing of the stationary longitudinal rolls at
$\mathit{Re}=5772$
. These changes illustrate morphing of the stationary longitudinal rolls at
![]() $\mathit{Re}=0$
into travelling waves driven by shear for
$\mathit{Re}=0$
into travelling waves driven by shear for
![]() $\mathit{Re}>5772$
.
$\mathit{Re}>5772$
.
3.3.5. Oblique rolls
The previous two sections discussed the properties of two special classes of rolls, i.e. longitudinal and transverse rolls. The instability can generate rolls with any orientation, i.e. oblique rolls (see figure 18). Figure 19 displays variations of
![]() $\mathit{Ra}_{p,cr}$
as a function of roll orientation for
$\mathit{Ra}_{p,cr}$
as a function of roll orientation for
![]() ${\it\alpha}=3.5$
for
${\it\alpha}=3.5$
for
![]() $\mathit{Re}=0$
, 1 and 10. The obliqueness angle
$\mathit{Re}=0$
, 1 and 10. The obliqueness angle
![]() ${\it\chi}$
used in this figure is defined as
${\it\chi}$
used in this figure is defined as
![]() $\tan ({\it\chi})={\it\beta}/{\it\delta}$
and thus
$\tan ({\it\chi})={\it\beta}/{\it\delta}$
and thus
![]() ${\it\chi}=0^{\circ }$
corresponds to longitudinal rolls and
${\it\chi}=0^{\circ }$
corresponds to longitudinal rolls and
![]() ${\it\chi}=90^{\circ }$
to transverse rolls. Results of this type permit identification of the roll orientation at the onset and variations of the critical roll orientation as a function of
${\it\chi}=90^{\circ }$
to transverse rolls. Results of this type permit identification of the roll orientation at the onset and variations of the critical roll orientation as a function of
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() ${\it\alpha}$
. In the case of this particular heating wavenumber, the oblique rolls play the critical role at
${\it\alpha}$
. In the case of this particular heating wavenumber, the oblique rolls play the critical role at
![]() $\mathit{Re}=0$
and
$\mathit{Re}=0$
and
![]() $\mathit{Re}=1$
, to be replaced by the transverse rolls at
$\mathit{Re}=1$
, to be replaced by the transverse rolls at
![]() $\mathit{Re}=10$
. Figure 20 displays the critical curves that identify both the critical roll orientation and the corresponding
$\mathit{Re}=10$
. Figure 20 displays the critical curves that identify both the critical roll orientation and the corresponding
![]() $\mathit{Ra}_{p,cr}$
as a function of
$\mathit{Ra}_{p,cr}$
as a function of
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() ${\it\alpha}$
. This figure is limited only to those conditions where the oblique rolls play the critical role. The limit points where either longitudinal or transverse rolls become critical are marked with a black dot.
${\it\alpha}$
. This figure is limited only to those conditions where the oblique rolls play the critical role. The limit points where either longitudinal or transverse rolls become critical are marked with a black dot.

Figure 18. The flow structures associated with (a) the primary convection and (b) the secondary convection in the form of oblique rolls at the onset in a flow with
![]() $\mathit{Re}=1$
. (a) The stream function normalized by its maximum; (b) the second invariant of the velocity gradient tensor (see (3.21)). The heating has the wavenumber
$\mathit{Re}=1$
. (a) The stream function normalized by its maximum; (b) the second invariant of the velocity gradient tensor (see (3.21)). The heating has the wavenumber
![]() ${\it\alpha}=2.5$
, requires an intensity corresponding to
${\it\alpha}=2.5$
, requires an intensity corresponding to
![]() $\mathit{Ra}_{p,cr}=2513$
and generates the secondary convection with wavenumbers
$\mathit{Ra}_{p,cr}=2513$
and generates the secondary convection with wavenumbers
![]() ${\it\delta}_{cr}=1.25$
and
${\it\delta}_{cr}=1.25$
and
![]() ${\it\beta}_{cr}=0.77$
.
${\it\beta}_{cr}=0.77$
.

Figure 19. The onset conditions required for the formation of the secondary convection in the form of oblique rolls in a fluid driven through a periodically heated channel (see § 3.3.5). (a–c) Variations of the critical Rayleigh number
![]() $\mathit{Ra}_{p,cr}$
as a function of the magnitude of the disturbance wavevector
$\mathit{Ra}_{p,cr}$
as a function of the magnitude of the disturbance wavevector
![]() $|\boldsymbol{q}|=\sqrt{{\it\delta}^{2}+{\it\beta}^{2}}$
and its orientation angle
$|\boldsymbol{q}|=\sqrt{{\it\delta}^{2}+{\it\beta}^{2}}$
and its orientation angle
![]() ${\it\chi}$
, defined as
${\it\chi}$
, defined as
![]() $\tan ({\it\chi})={\it\beta}/{\it\delta}$
, for the heating with the wavenumber
$\tan ({\it\chi})={\it\beta}/{\it\delta}$
, for the heating with the wavenumber
![]() ${\it\alpha}=3.5$
for the flow Reynolds number
${\it\alpha}=3.5$
for the flow Reynolds number
![]() $\mathit{Re}=0$
(a), 1 (b) and 10 (c), respectively.
$\mathit{Re}=0$
(a), 1 (b) and 10 (c), respectively.

Figure 20. The onset conditions required for the formation of the secondary convection in the form of oblique rolls in a fluid driven through a periodically heated channel (see § 3.3.5). Variations of (a) the critical Rayleigh number
![]() $\mathit{Ra}_{p,cr}$
and (b) the critical wavenumbers
$\mathit{Ra}_{p,cr}$
and (b) the critical wavenumbers
![]() ${\it\delta}_{cr}$
and
${\it\delta}_{cr}$
and
![]() ${\it\beta}_{cr}$
as functions of the heating wavenumber
${\it\beta}_{cr}$
as functions of the heating wavenumber
![]() ${\it\alpha}$
. The critical curves for
${\it\alpha}$
. The critical curves for
![]() $\mathit{Re}>6$
consist of two segments with the dash-dotted lines used to identify the left segment. Symbols (●) identify the limit points on the
$\mathit{Re}>6$
consist of two segments with the dash-dotted lines used to identify the left segment. Symbols (●) identify the limit points on the
![]() ${\it\alpha}$
axis where the oblique rolls cease to play the critical role.
${\it\alpha}$
axis where the oblique rolls cease to play the critical role.
In all the cases considered, the critical oblique rolls are stationary, i.e.
![]() ${\it\sigma}_{r}=0$
. The critical wavevector has
${\it\sigma}_{r}=0$
. The critical wavevector has
![]() $x$
component locked in with the wavevector of the primary instability according to the relation
$x$
component locked in with the wavevector of the primary instability according to the relation
![]() ${\it\delta}_{cr}={\it\alpha}/2$
, which is a characteristic feature of the spatial resonance (figure 20
b), while variations of the
${\it\delta}_{cr}={\it\alpha}/2$
, which is a characteristic feature of the spatial resonance (figure 20
b), while variations of the
![]() $z$
component do not follow any regular path. The appearance of the
$z$
component do not follow any regular path. The appearance of the
![]() $z$
component results in the three-dimensionalization of the disturbance velocity field, which is another characteristic feature of the spatial resonance (Manor, Hagberg & Meron Reference Manor, Hagberg and Meron2008, Reference Manor, Hagberg and Meron2009). An increase of
$z$
component results in the three-dimensionalization of the disturbance velocity field, which is another characteristic feature of the spatial resonance (Manor, Hagberg & Meron Reference Manor, Hagberg and Meron2008, Reference Manor, Hagberg and Meron2009). An increase of
![]() $\mathit{Re}$
results in the transfer of the limit points towards smaller
$\mathit{Re}$
results in the transfer of the limit points towards smaller
![]() ${\it\alpha}$
; an increase of
${\it\alpha}$
; an increase of
![]() $\mathit{Re}$
from
$\mathit{Re}$
from
![]() $\mathit{Re}=0$
to
$\mathit{Re}=0$
to
![]() $\mathit{Re}=3$
results in the reduction of
$\mathit{Re}=3$
results in the reduction of
![]() $\mathit{Ra}_{p,cr}$
, which can be achieved at any
$\mathit{Ra}_{p,cr}$
, which can be achieved at any
![]() ${\it\alpha}$
(see figure 20
a), but a further increase of
${\it\alpha}$
(see figure 20
a), but a further increase of
![]() $\mathit{Re}$
leads to an increase of
$\mathit{Re}$
leads to an increase of
![]() $\mathit{Ra}_{p,cr}$
. The flow stabilization, which is due to an increase of
$\mathit{Ra}_{p,cr}$
. The flow stabilization, which is due to an increase of
![]() $\mathit{Re}$
and, at the same time, due to the reduction of
$\mathit{Re}$
and, at the same time, due to the reduction of
![]() ${\it\alpha}$
, is consistent with the weakening of the parametric resonance mechanism. It has already been pointed out in the previous two sections that an increase of
${\it\alpha}$
, is consistent with the weakening of the parametric resonance mechanism. It has already been pointed out in the previous two sections that an increase of
![]() $\mathit{Re}$
reduces the strength of the separation bubbles, which leads to the reduction of the magnitude of the spatial flow modulation, and this results in the reduction of the strength of the spatial resonance.
$\mathit{Re}$
reduces the strength of the separation bubbles, which leads to the reduction of the magnitude of the spatial flow modulation, and this results in the reduction of the strength of the spatial resonance.
The special feature of the oblique rolls is the division of the critical curves into two segments for
![]() $\mathit{Re}>5$
. As
$\mathit{Re}>5$
. As
![]() $\mathit{Re}$
increases above
$\mathit{Re}$
increases above
![]() $\mathit{Re}=3$
, the instability expands into smaller
$\mathit{Re}=3$
, the instability expands into smaller
![]() ${\it\alpha}$
, with the critical curve acquiring two minima (see curve for
${\it\alpha}$
, with the critical curve acquiring two minima (see curve for
![]() $\mathit{Re}=4$
in figure 20
a). A further increase of
$\mathit{Re}=4$
in figure 20
a). A further increase of
![]() $\mathit{Re}$
amplifies this division (see curve for
$\mathit{Re}$
amplifies this division (see curve for
![]() $\mathit{Re}=5$
in figure 20
a) and leads to separation of the critical curves into two segments (see curves for
$\mathit{Re}=5$
in figure 20
a) and leads to separation of the critical curves into two segments (see curves for
![]() $\mathit{Re}=6{-}10$
in figure 20
a). These segments might join each other at much higher
$\mathit{Re}=6{-}10$
in figure 20
a). These segments might join each other at much higher
![]() $\mathit{Ra}_{p}$
, but this question has not been investigated. The formation of the left segment of the critical curve, which extends into
$\mathit{Ra}_{p}$
, but this question has not been investigated. The formation of the left segment of the critical curve, which extends into
![]() ${\it\alpha}$
values much smaller than those found for
${\it\alpha}$
values much smaller than those found for
![]() $\mathit{Re}=0$
, suggests that another instability mechanism may contribute to the system dynamics. In this case the primary convection has the form of very elongated rolls (Hossain & Floryan Reference Hossain and Floryan2013a
), the spatial resonance remains active (see the form of the critical wavevector in figure 20
b) and so the most likely mechanism is the reinvigorated RB mechanism. This question has not been pursued any further in this study.
$\mathit{Re}=0$
, suggests that another instability mechanism may contribute to the system dynamics. In this case the primary convection has the form of very elongated rolls (Hossain & Floryan Reference Hossain and Floryan2013a
), the spatial resonance remains active (see the form of the critical wavevector in figure 20
b) and so the most likely mechanism is the reinvigorated RB mechanism. This question has not been pursued any further in this study.
The role of
![]() $\mathit{Re}$
in the onset of oblique rolls is illustrated in figure 21. These rolls play the critical role for very small
$\mathit{Re}$
in the onset of oblique rolls is illustrated in figure 21. These rolls play the critical role for very small
![]() $\mathit{Re}$
and undergo a very rapid
$\mathit{Re}$
and undergo a very rapid
![]() ${\it\alpha}$
-dependent transformation due to small changes of
${\it\alpha}$
-dependent transformation due to small changes of
![]() $\mathit{Re}$
. Generally, they cease to play the critical role for
$\mathit{Re}$
. Generally, they cease to play the critical role for
![]() $\mathit{Re}<10$
, but these conditions vary greatly with
$\mathit{Re}<10$
, but these conditions vary greatly with
![]() ${\it\alpha}$
.
${\it\alpha}$
.

Figure 21. The onset conditions required for the formation of the secondary convection in the form of oblique rolls in a fluid driven through a periodically heated channel (see § 3.3.5). Variations of (a) the critical Rayleigh number
![]() $\mathit{Ra}_{p,cr}$
and (b) the critical wavenumber
$\mathit{Ra}_{p,cr}$
and (b) the critical wavenumber
![]() ${\it\beta}_{cr}$
as functions of the Reynolds number
${\it\beta}_{cr}$
as functions of the Reynolds number
![]() $\mathit{Re}$
. Symbols (●) identify the limit points on the
$\mathit{Re}$
. Symbols (●) identify the limit points on the
![]() $\mathit{Re}$
axis where the oblique rolls cease to play the critical role. Note that
$\mathit{Re}$
axis where the oblique rolls cease to play the critical role. Note that
![]() ${\it\delta}_{cr}={\it\alpha}/2$
for oblique rolls.
${\it\delta}_{cr}={\it\alpha}/2$
for oblique rolls.
3.3.6. The critical conditions
The final question to be discussed is the identification of the type of rolls that is generated at the onset, i.e. discussion of the competition between different rolls and the identification of patterns of motion that result from the instability. The discussion presented in the previous sections demonstrates a rapid change in the instability patterns for small
![]() $\mathit{Re}$
, with the transverse rolls eventually winning the competition. This process is illustrated in figure 22. When
$\mathit{Re}$
, with the transverse rolls eventually winning the competition. This process is illustrated in figure 22. When
![]() $\mathit{Re}=0$
, the oblique rolls dominate for
$\mathit{Re}=0$
, the oblique rolls dominate for
![]() ${\it\alpha}<4.03$
, the longitudinal rolls dominate for
${\it\alpha}<4.03$
, the longitudinal rolls dominate for
![]() $4.03<{\it\alpha}<4.46$
and the transverse rolls dominate for
$4.03<{\it\alpha}<4.46$
and the transverse rolls dominate for
![]() ${\it\alpha}>4.46$
. At
${\it\alpha}>4.46$
. At
![]() $\mathit{Re}=1$
the changeover points are at
$\mathit{Re}=1$
the changeover points are at
![]() ${\it\alpha}=3.77$
and
${\it\alpha}=3.77$
and
![]() ${\it\alpha}=4.34$
. The longitudinal rolls cease to play the critical role at
${\it\alpha}=4.34$
. The longitudinal rolls cease to play the critical role at
![]() $\mathit{Re}=2$
and the changeover between the oblique and transverse rolls occurs at
$\mathit{Re}=2$
and the changeover between the oblique and transverse rolls occurs at
![]() ${\it\alpha}=3.68$
. The changeover point moves to
${\it\alpha}=3.68$
. The changeover point moves to
![]() ${\it\alpha}=3.16$
, 2.77, 2.38, 1.72 and 1.2 for
${\it\alpha}=3.16$
, 2.77, 2.38, 1.72 and 1.2 for
![]() $\mathit{Re}=3$
, 4, 5, 6 and 8, respectively. The transverse rolls dominate at
$\mathit{Re}=3$
, 4, 5, 6 and 8, respectively. The transverse rolls dominate at
![]() $\mathit{Re}=10$
. These predictions are correct assuming that there are no additional effects that may provide a preference for certain type of rolls.
$\mathit{Re}=10$
. These predictions are correct assuming that there are no additional effects that may provide a preference for certain type of rolls.

Figure 22. The onset conditions for the secondary convection (see § 3.3.6). (a–i) Variations of the critical conditions for the transverse, longitudinal and oblique rolls as a function of the heating wavenumber
![]() ${\it\alpha}$
for the flow Reynolds number
${\it\alpha}$
for the flow Reynolds number
![]() $\mathit{Re}=0$
, 1, 2, 3, 4, 5, 6, 8 and 10, respectively. Labels 1, 2 and 3 identify the longitudinal, transverse and oblique rolls, respectively. Points A, B, C, D, E, F, G, H, I and J have coordinates
$\mathit{Re}=0$
, 1, 2, 3, 4, 5, 6, 8 and 10, respectively. Labels 1, 2 and 3 identify the longitudinal, transverse and oblique rolls, respectively. Points A, B, C, D, E, F, G, H, I and J have coordinates
![]() $({\it\alpha},\mathit{Ra}_{p,cr})=(4.46,3192)$
,
$({\it\alpha},\mathit{Ra}_{p,cr})=(4.46,3192)$
,
![]() $(4.03,3032)$
,
$(4.03,3032)$
,
![]() $(4.34,3156)$
,
$(4.34,3156)$
,
![]() $(3.77,3201)$
,
$(3.77,3201)$
,
![]() $(3.68,3178)$
,
$(3.68,3178)$
,
![]() $(3.16,3162)$
,
$(3.16,3162)$
,
![]() $(2.77,3251)$
,
$(2.77,3251)$
,
![]() $(2.38,3623)$
,
$(2.38,3623)$
,
![]() $(1.72,8234)$
and
$(1.72,8234)$
and
![]() $(1.2,8040)$
, respectively.
$(1.2,8040)$
, respectively.
3.4. Transition to secondary states with heating applied at the upper wall
It can be shown that the transformation discussed in § 2.4 applies also to the analysis of stability of the primary convection. As a result, the transition to secondary states occurs under the same conditions as in the case of heating applied at the lower wall, while the disturbance flow patterns exhibit phase differences similar to those discussed by Hossain & Floryan (Reference Hossain and Floryan2014).
4. Summary
Mixed convection in a channel exposed to heating that is periodic in the flow direction has been analysed. The heating can be applied either at the lower or at the upper wall and results in a sinusoidal wall temperature distribution characterized by the wavenumber
![]() ${\it\alpha}$
and the amplitude expressed in terms of the Rayleigh number
${\it\alpha}$
and the amplitude expressed in terms of the Rayleigh number
![]() $\mathit{Ra}_{p}$
. The primary convection represents a forced response to the applied heating and has the form of counter-rotating rolls whose pattern is dictated by the pattern of the heating. This convection occurs regardless of the magnitude of the heating. Detailed results have been presented for fluids with Prandtl number
$\mathit{Ra}_{p}$
. The primary convection represents a forced response to the applied heating and has the form of counter-rotating rolls whose pattern is dictated by the pattern of the heating. This convection occurs regardless of the magnitude of the heating. Detailed results have been presented for fluids with Prandtl number
![]() $\mathit{Pr}=0.71$
. The largest heat transfer across the channel occurs for the natural convection (
$\mathit{Pr}=0.71$
. The largest heat transfer across the channel occurs for the natural convection (
![]() $\mathit{Re}=0$
) and diminishes with an increase of the forced flow component (increase of
$\mathit{Re}=0$
) and diminishes with an increase of the forced flow component (increase of
![]() $\mathit{Re}$
). The most effective heating wavenumber is
$\mathit{Re}$
). The most effective heating wavenumber is
![]() ${\it\alpha}\approx 1$
, with the heat transfer rapidly decreasing for smaller and larger
${\it\alpha}\approx 1$
, with the heat transfer rapidly decreasing for smaller and larger
![]() ${\it\alpha}$
. The magnitude of the heat transfer is proportional to
${\it\alpha}$
. The magnitude of the heat transfer is proportional to
![]() $\mathit{Ra}_{p}$
for small enough heating intensity but its growth saturates for
$\mathit{Ra}_{p}$
for small enough heating intensity but its growth saturates for
![]() $\mathit{Ra}_{p}=O(10^{3})$
. Heating with large
$\mathit{Ra}_{p}=O(10^{3})$
. Heating with large
![]() ${\it\alpha}$
leads to the formation of a boundary layer adjacent to the heated wall and formation of a conduction zone in the remaining part of the channel where the temperature varies only in the vertical direction.
${\it\alpha}$
leads to the formation of a boundary layer adjacent to the heated wall and formation of a conduction zone in the remaining part of the channel where the temperature varies only in the vertical direction.
The primary convection with large enough
![]() $\mathit{Ra}_{p}$
undergoes transition to a secondary convection, which changes the heat transfer process in a qualitative sense. This transition is driven by a mix of the RB mechanism, which dominates for large
$\mathit{Ra}_{p}$
undergoes transition to a secondary convection, which changes the heat transfer process in a qualitative sense. This transition is driven by a mix of the RB mechanism, which dominates for large
![]() ${\it\alpha}$
, with the spatial parametric resonance, which dominates for
${\it\alpha}$
, with the spatial parametric resonance, which dominates for
![]() ${\it\alpha}=O(1)$
. The critical conditions have been determined for the range of
${\it\alpha}=O(1)$
. The critical conditions have been determined for the range of
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() $\mathit{Re}$
of practical interest. Three types of rolls can be formed at the onset, i.e. longitudinal, transverse and oblique rolls, depending on
$\mathit{Re}$
of practical interest. Three types of rolls can be formed at the onset, i.e. longitudinal, transverse and oblique rolls, depending on
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() $\mathit{Re}$
. The detailed characteristics of these rolls have been given for the range of
$\mathit{Re}$
. The detailed characteristics of these rolls have been given for the range of
![]() $\mathit{Re}$
where the heating determines the onset conditions. The longitudinal rolls are stationary at
$\mathit{Re}$
where the heating determines the onset conditions. The longitudinal rolls are stationary at
![]() $\mathit{Re}=0$
but begin to travel in the downstream direction as
$\mathit{Re}=0$
but begin to travel in the downstream direction as
![]() $\mathit{Re}$
increases. These rolls undergo morphing into TS waves as
$\mathit{Re}$
increases. These rolls undergo morphing into TS waves as
![]() $\mathit{Re}$
increases, with transition completed at
$\mathit{Re}$
increases, with transition completed at
![]() $\mathit{Re}=5772$
. Wavenumber locking between the primary and secondary convection is observed for small enough
$\mathit{Re}=5772$
. Wavenumber locking between the primary and secondary convection is observed for small enough
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() ${\it\alpha}$
; an increase of
${\it\alpha}$
; an increase of
![]() $\mathit{Re}$
above
$\mathit{Re}$
above
![]() $\mathit{Re}=5$
eliminates the lock-in phenomenon. The transverse rolls remain stationary as
$\mathit{Re}=5$
eliminates the lock-in phenomenon. The transverse rolls remain stationary as
![]() $\mathit{Re}$
increases; the corresponding critical
$\mathit{Re}$
increases; the corresponding critical
![]() $\mathit{Ra}_{p}$
approaches an asymptote for
$\mathit{Ra}_{p}$
approaches an asymptote for
![]() ${\it\alpha}\rightarrow \infty$
, which can be predicted analytically by taking advantage of knowledge about the formation of the conduction zone away from the heated wall. An increase of
${\it\alpha}\rightarrow \infty$
, which can be predicted analytically by taking advantage of knowledge about the formation of the conduction zone away from the heated wall. An increase of
![]() $\mathit{Re}$
leads to the formation of another type of boundary layer; the corresponding
$\mathit{Re}$
leads to the formation of another type of boundary layer; the corresponding
![]() $\mathit{Ra}_{p}$
approaches an asymptote as
$\mathit{Ra}_{p}$
approaches an asymptote as
![]() $\mathit{Re}\rightarrow \infty$
whose form has been determined numerically. Oblique rolls play a critical role only for small enough
$\mathit{Re}\rightarrow \infty$
whose form has been determined numerically. Oblique rolls play a critical role only for small enough
![]() $\mathit{Re}$
and small enough
$\mathit{Re}$
and small enough
![]() ${\it\alpha}$
. The character of the instability motion undergoes rapid
${\it\alpha}$
. The character of the instability motion undergoes rapid
![]() ${\it\alpha}$
-dependent changes for small
${\it\alpha}$
-dependent changes for small
![]() $\mathit{Re}$
. A sufficient increase of
$\mathit{Re}$
. A sufficient increase of
![]() $\mathit{Re}$
results in the dominance of the transverse rolls, assuming that no symmetry-breaking effects are present. The heat transfer properties of the saturation states remain to be determined.
$\mathit{Re}$
results in the dominance of the transverse rolls, assuming that no symmetry-breaking effects are present. The heat transfer properties of the saturation states remain to be determined.
The system response is the same regardless of whether the heating is applied at the lower or at the upper wall.
Acknowledgements
This work has been carried out with the financial support of the Natural Sciences and Engineering Research Council (NSERC) of Canada.
Appendix A
Definitions of functions used in § 2.3:
 $$\begin{eqnarray}\displaystyle F_{U21}(y) & = & \displaystyle -\frac{y^{8}}{26\,880}+\frac{y^{7}}{10\,080}+\frac{y^{6}}{2880}-\frac{y^{5}}{480}-\frac{7y^{4}}{1152}+\frac{5y^{3}}{288}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{107y^{2}}{100\,800}-\frac{31y}{2016}-\frac{1}{6400},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{U21}(y) & = & \displaystyle -\frac{y^{8}}{26\,880}+\frac{y^{7}}{10\,080}+\frac{y^{6}}{2880}-\frac{y^{5}}{480}-\frac{7y^{4}}{1152}+\frac{5y^{3}}{288}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{107y^{2}}{100\,800}-\frac{31y}{2016}-\frac{1}{6400},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{U22}(y) & = & \displaystyle -\frac{y^{8}}{8960}+\frac{y^{7}}{2016}+\frac{7y^{6}}{14\,400}-\frac{y^{5}}{480}-\frac{y^{4}}{1152}+\frac{y^{3}}{288}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{19y^{2}}{33\,600}-\frac{19y}{10\,080}-\frac{29}{403\,200},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{U22}(y) & = & \displaystyle -\frac{y^{8}}{8960}+\frac{y^{7}}{2016}+\frac{7y^{6}}{14\,400}-\frac{y^{5}}{480}-\frac{y^{4}}{1152}+\frac{y^{3}}{288}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{19y^{2}}{33\,600}-\frac{19y}{10\,080}-\frac{29}{403\,200},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V31}(y) & = & \displaystyle -\frac{y^{9}}{241\,920}+\frac{y^{8}}{80\,640}+\frac{y^{7}}{20\,160}-\frac{y^{6}}{2880}-\frac{7y^{5}}{28\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{5y^{4}}{1152}+\frac{107y^{3}}{302\,400}-\frac{31y^{2}}{4032}-\frac{y}{6400}+\frac{33}{8960},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V31}(y) & = & \displaystyle -\frac{y^{9}}{241\,920}+\frac{y^{8}}{80\,640}+\frac{y^{7}}{20\,160}-\frac{y^{6}}{2880}-\frac{7y^{5}}{28\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{5y^{4}}{1152}+\frac{107y^{3}}{302\,400}-\frac{31y^{2}}{4032}-\frac{y}{6400}+\frac{33}{8960},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V32}(y) & = & \displaystyle -\frac{y^{9}}{80\,640}+\frac{y^{8}}{16\,128}+\frac{y^{7}}{14\,400}-\frac{y^{6}}{2880}-\frac{y^{5}}{5760}+\frac{y^{4}}{1152}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{19y^{3}}{100\,800}-\frac{19y^{2}}{20\,160}-\frac{29y}{403\,200}+\frac{29}{80\,640},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V32}(y) & = & \displaystyle -\frac{y^{9}}{80\,640}+\frac{y^{8}}{16\,128}+\frac{y^{7}}{14\,400}-\frac{y^{6}}{2880}-\frac{y^{5}}{5760}+\frac{y^{4}}{1152}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{19y^{3}}{100\,800}-\frac{19y^{2}}{20\,160}-\frac{29y}{403\,200}+\frac{29}{80\,640},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}21} & = & \displaystyle \frac{y^{7}}{26\,880}-\frac{y^{6}}{3840}+\frac{y^{5}}{6400}+\frac{y^{4}}{1280}-\frac{y^{3}}{1280}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{y^{2}}{1280}+\frac{79y}{134\,400}+\frac{1}{3840},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}21} & = & \displaystyle \frac{y^{7}}{26\,880}-\frac{y^{6}}{3840}+\frac{y^{5}}{6400}+\frac{y^{4}}{1280}-\frac{y^{3}}{1280}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{y^{2}}{1280}+\frac{79y}{134\,400}+\frac{1}{3840},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}22} & = & \displaystyle \frac{1}{201\,600} (35y^{9}-75y^{8}-260y^{7}+980y^{6}+714y^{5}-3850y^{4}\nonumber\\ \displaystyle & & \displaystyle -\,980y^{3}+10\,500y^{2}+491y-7555),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}22} & = & \displaystyle \frac{1}{201\,600} (35y^{9}-75y^{8}-260y^{7}+980y^{6}+714y^{5}-3850y^{4}\nonumber\\ \displaystyle & & \displaystyle -\,980y^{3}+10\,500y^{2}+491y-7555),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}23} & = & \displaystyle -\frac{y^{7}}{40\,320}+\frac{y^{6}}{5760}-\frac{y^{5}}{4800}-\frac{y^{4}}{2880}+\frac{y^{3}}{1152}-\frac{y^{2}}{1920}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{y}{1575}+\frac{1}{1440},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}23} & = & \displaystyle -\frac{y^{7}}{40\,320}+\frac{y^{6}}{5760}-\frac{y^{5}}{4800}-\frac{y^{4}}{2880}+\frac{y^{3}}{1152}-\frac{y^{2}}{1920}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{y}{1575}+\frac{1}{1440},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{U32}(y) & = & \displaystyle -\frac{y^{12}}{4561\,920}+\frac{y^{11}}{1478\,400}+\frac{23y^{10}}{7257\,600}-\frac{y^{9}}{48\,384}-\frac{31y^{8}}{1612\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{31y^{7}}{120\,960}+\frac{949y^{6}}{18\,144\,000}-\frac{y^{5}}{1152}-\frac{73y^{4}}{967\,680}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{323y^{3}}{241\,920}+\frac{181\,171y^{2}}{4036\,032\,000}-\frac{1337y}{1900\,800}-\frac{398\,309}{72\,648\,576\,000},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{U32}(y) & = & \displaystyle -\frac{y^{12}}{4561\,920}+\frac{y^{11}}{1478\,400}+\frac{23y^{10}}{7257\,600}-\frac{y^{9}}{48\,384}-\frac{31y^{8}}{1612\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{31y^{7}}{120\,960}+\frac{949y^{6}}{18\,144\,000}-\frac{y^{5}}{1152}-\frac{73y^{4}}{967\,680}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{323y^{3}}{241\,920}+\frac{181\,171y^{2}}{4036\,032\,000}-\frac{1337y}{1900\,800}-\frac{398\,309}{72\,648\,576\,000},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{U33}(y) & = & \displaystyle -\frac{y^{12}}{1520\,640}+\frac{y^{11}}{295\,680}+\frac{37y^{10}}{7257\,600}-\frac{19y^{9}}{725\,760}-\frac{29y^{8}}{1612\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{11y^{7}}{120\,960}+\frac{71y^{6}}{2016\,000}-\frac{y^{5}}{5760}-\frac{199y^{4}}{4838\,400}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{47y^{3}}{241\,920}+\frac{323y^{2}}{14\,676\,480}-\frac{709y}{7983\,360}-\frac{185\,711}{72\,648\,576\,000},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{U33}(y) & = & \displaystyle -\frac{y^{12}}{1520\,640}+\frac{y^{11}}{295\,680}+\frac{37y^{10}}{7257\,600}-\frac{19y^{9}}{725\,760}-\frac{29y^{8}}{1612\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{11y^{7}}{120\,960}+\frac{71y^{6}}{2016\,000}-\frac{y^{5}}{5760}-\frac{199y^{4}}{4838\,400}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{47y^{3}}{241\,920}+\frac{323y^{2}}{14\,676\,480}-\frac{709y}{7983\,360}-\frac{185\,711}{72\,648\,576\,000},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{U34}(y) & = & \displaystyle -\frac{y^{12}}{7603\,200}+\frac{y^{11}}{2661\,120}+\frac{13y^{10}}{7257\,600}-\frac{y^{9}}{103\,680}-\frac{17y^{8}}{1612\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{11y^{7}}{120\,960}+\frac{7y^{6}}{172\,800}-\frac{y^{5}}{1152}-\frac{491y^{4}}{4838\,400}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1511y^{3}}{241\,920}+\frac{15\,661y^{2}}{192\,192\,000}-\frac{8717y}{1596\,672}-\frac{120\,749}{10\,378\,368\,000},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{U34}(y) & = & \displaystyle -\frac{y^{12}}{7603\,200}+\frac{y^{11}}{2661\,120}+\frac{13y^{10}}{7257\,600}-\frac{y^{9}}{103\,680}-\frac{17y^{8}}{1612\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{11y^{7}}{120\,960}+\frac{7y^{6}}{172\,800}-\frac{y^{5}}{1152}-\frac{491y^{4}}{4838\,400}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1511y^{3}}{241\,920}+\frac{15\,661y^{2}}{192\,192\,000}-\frac{8717y}{1596\,672}-\frac{120\,749}{10\,378\,368\,000},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{U35}(y) & = & \displaystyle \frac{y^{10}}{14\,515\,200}-\frac{y^{9}}{1451\,520}+\frac{y^{8}}{806\,400}+\frac{y^{7}}{302\,400}-\frac{y^{6}}{69\,120}+\frac{y^{5}}{57\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{4}}{18\,900}-\frac{y^{3}}{4320}-\frac{197y^{2}}{4224\,000}+\frac{307y}{1451\,520}+\frac{2749}{399\,168\,000},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{U35}(y) & = & \displaystyle \frac{y^{10}}{14\,515\,200}-\frac{y^{9}}{1451\,520}+\frac{y^{8}}{806\,400}+\frac{y^{7}}{302\,400}-\frac{y^{6}}{69\,120}+\frac{y^{5}}{57\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{4}}{18\,900}-\frac{y^{3}}{4320}-\frac{197y^{2}}{4224\,000}+\frac{307y}{1451\,520}+\frac{2749}{399\,168\,000},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{U36}(y) & = & \displaystyle \frac{y^{10}}{8294\,400}-\frac{y^{9}}{829\,440}+\frac{23y^{8}}{6451\,200}+\frac{y^{7}}{483\,840}-\frac{49y^{6}}{6912\,000}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{5}}{230\,400}-\frac{y^{4}}{55\,296}-\frac{y^{3}}{69\,120}+\frac{1021y^{2}}{39\,424\,000}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{269y}{29\,030\,400}-\frac{14\,083}{3193\,344\,000},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{U36}(y) & = & \displaystyle \frac{y^{10}}{8294\,400}-\frac{y^{9}}{829\,440}+\frac{23y^{8}}{6451\,200}+\frac{y^{7}}{483\,840}-\frac{49y^{6}}{6912\,000}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{5}}{230\,400}-\frac{y^{4}}{55\,296}-\frac{y^{3}}{69\,120}+\frac{1021y^{2}}{39\,424\,000}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{269y}{29\,030\,400}-\frac{14\,083}{3193\,344\,000},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V41}(y) & = & \displaystyle -\frac{y^{7}}{6720}+\frac{y^{6}}{960}+\frac{11y^{5}}{14\,400}-\frac{5y^{4}}{576}-\frac{109y^{3}}{100\,800}+\frac{41y^{2}}{2880}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{47y}{100\,800}-\frac{19}{2880},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V41}(y) & = & \displaystyle -\frac{y^{7}}{6720}+\frac{y^{6}}{960}+\frac{11y^{5}}{14\,400}-\frac{5y^{4}}{576}-\frac{109y^{3}}{100\,800}+\frac{41y^{2}}{2880}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{47y}{100\,800}-\frac{19}{2880},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V42}(y) & = & \displaystyle \frac{y^{13}}{59\,304\,960}-\frac{y^{12}}{17\,740\,800}-\frac{23y^{11}}{79\,833\,600}+\frac{y^{10}}{483\,840}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{31y^{9}}{14\,515\,200}-\frac{31y^{8}}{967\,680}-\frac{949y^{7}}{127\,008\,000}+\frac{y^{6}}{6912}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{73y^{5}}{4838\,400}-\frac{323y^{4}}{967\,680}-\frac{181\,171y^{3}}{12\,108\,096\,000}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1337y^{2}}{3\,801\,600}+\frac{398\,309y}{72\,648\,576\,000}-\frac{1411}{10\,644\,480},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V42}(y) & = & \displaystyle \frac{y^{13}}{59\,304\,960}-\frac{y^{12}}{17\,740\,800}-\frac{23y^{11}}{79\,833\,600}+\frac{y^{10}}{483\,840}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{31y^{9}}{14\,515\,200}-\frac{31y^{8}}{967\,680}-\frac{949y^{7}}{127\,008\,000}+\frac{y^{6}}{6912}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{73y^{5}}{4838\,400}-\frac{323y^{4}}{967\,680}-\frac{181\,171y^{3}}{12\,108\,096\,000}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1337y^{2}}{3\,801\,600}+\frac{398\,309y}{72\,648\,576\,000}-\frac{1411}{10\,644\,480},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V43}(y) & = & \displaystyle \frac{y^{13}}{19\,768\,320}-\frac{y^{12}}{3548\,160}-\frac{37y^{11}}{79\,833\,600}+\frac{19y^{10}}{7257\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{29y^{9}}{14\,515\,200}-\frac{11y^{8}}{967\,680}-\frac{71y^{7}}{14\,112\,000}+\frac{y^{6}}{34\,560}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{199y^{5}}{24\,192\,000}-\frac{47y^{4}}{967\,680}-\frac{323y^{3}}{44\,029\,440}+\frac{709y^{2}}{15\,966\,720}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{185\,711y}{72\,648\,576\,000}-\frac{359}{22\,809\,600},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V43}(y) & = & \displaystyle \frac{y^{13}}{19\,768\,320}-\frac{y^{12}}{3548\,160}-\frac{37y^{11}}{79\,833\,600}+\frac{19y^{10}}{7257\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{29y^{9}}{14\,515\,200}-\frac{11y^{8}}{967\,680}-\frac{71y^{7}}{14\,112\,000}+\frac{y^{6}}{34\,560}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{199y^{5}}{24\,192\,000}-\frac{47y^{4}}{967\,680}-\frac{323y^{3}}{44\,029\,440}+\frac{709y^{2}}{15\,966\,720}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{185\,711y}{72\,648\,576\,000}-\frac{359}{22\,809\,600},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V44}(y) & = & \displaystyle \frac{y^{13}}{98\,841\,600}-\frac{y^{12}}{31\,933\,440}-\frac{13y^{11}}{79\,833\,600}+\frac{y^{10}}{1036\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{17y^{9}}{14\,515\,200}-\frac{11y^{8}}{967\,680}-\frac{y^{7}}{172\,800}+\frac{y^{6}}{6912}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{491y^{5}}{24\,192\,000}-\frac{1511y^{4}}{967\,680}-\frac{15\,661y^{3}}{576\,576\,000}+\frac{8717y^{2}}{3193\,344}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{120\,749y}{10\,378\,368\,000}-\frac{69\,323}{53\,222\,400},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V44}(y) & = & \displaystyle \frac{y^{13}}{98\,841\,600}-\frac{y^{12}}{31\,933\,440}-\frac{13y^{11}}{79\,833\,600}+\frac{y^{10}}{1036\,800}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{17y^{9}}{14\,515\,200}-\frac{11y^{8}}{967\,680}-\frac{y^{7}}{172\,800}+\frac{y^{6}}{6912}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{491y^{5}}{24\,192\,000}-\frac{1511y^{4}}{967\,680}-\frac{15\,661y^{3}}{576\,576\,000}+\frac{8717y^{2}}{3193\,344}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{120\,749y}{10\,378\,368\,000}-\frac{69\,323}{53\,222\,400},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V45}(y) & = & \displaystyle -\frac{y^{11}}{79\,833\,600}+\frac{y^{10}}{7257\,600}-\frac{y^{9}}{3628\,800}-\frac{y^{8}}{1209\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{7}}{241\,920}-\frac{y^{6}}{172\,800}-\frac{y^{5}}{47\,250}+\frac{y^{4}}{8640}+\frac{197y^{3}}{6336\,000}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{307y^{2}}{1451\,520}-\frac{2749y}{199\,584\,000}+\frac{53}{518\,400},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V45}(y) & = & \displaystyle -\frac{y^{11}}{79\,833\,600}+\frac{y^{10}}{7257\,600}-\frac{y^{9}}{3628\,800}-\frac{y^{8}}{1209\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{7}}{241\,920}-\frac{y^{6}}{172\,800}-\frac{y^{5}}{47\,250}+\frac{y^{4}}{8640}+\frac{197y^{3}}{6336\,000}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{307y^{2}}{1451\,520}-\frac{2749y}{199\,584\,000}+\frac{53}{518\,400},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{V46}(y) & = & \displaystyle -\frac{y^{11}}{45\,619\,200}+\frac{y^{10}}{4147\,200}-\frac{23y^{9}}{29\,030\,400}-\frac{y^{8}}{1935\,360}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{7y^{7}}{3456\,000}-\frac{y^{6}}{691\,200}+\frac{y^{5}}{138\,240}+\frac{y^{4}}{138\,240}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1021y^{3}}{59\,136\,000}-\frac{269y^{2}}{29\,030\,400}+\frac{14\,083y}{1596\,672\,000}+\frac{109}{29\,030\,400},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{V46}(y) & = & \displaystyle -\frac{y^{11}}{45\,619\,200}+\frac{y^{10}}{4147\,200}-\frac{23y^{9}}{29\,030\,400}-\frac{y^{8}}{1935\,360}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{7y^{7}}{3456\,000}-\frac{y^{6}}{691\,200}+\frac{y^{5}}{138\,240}+\frac{y^{4}}{138\,240}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1021y^{3}}{59\,136\,000}-\frac{269y^{2}}{29\,030\,400}+\frac{14\,083y}{1596\,672\,000}+\frac{109}{29\,030\,400},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}32}(y) & = & \displaystyle \frac{y^{13}}{898\,560}-\frac{y^{12}}{354\,816}-\frac{59y^{11}}{4435\,200}+\frac{211y^{10}}{3628\,800}+\frac{487y^{9}}{7257\,600}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{23y^{8}}{53\,760}-\frac{121y^{7}}{604\,800}+\frac{41y^{6}}{17\,280}+\frac{1471y^{5}}{4032\,000}-\frac{3611y^{4}}{483\,840}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{491y^{3}}{1209\,600}+\frac{1511y^{2}}{80\,640}+\frac{966\,443y}{5189\,184\,000}-\frac{1059\,757}{79\,833\,600},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}32}(y) & = & \displaystyle \frac{y^{13}}{898\,560}-\frac{y^{12}}{354\,816}-\frac{59y^{11}}{4435\,200}+\frac{211y^{10}}{3628\,800}+\frac{487y^{9}}{7257\,600}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{23y^{8}}{53\,760}-\frac{121y^{7}}{604\,800}+\frac{41y^{6}}{17\,280}+\frac{1471y^{5}}{4032\,000}-\frac{3611y^{4}}{483\,840}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{491y^{3}}{1209\,600}+\frac{1511y^{2}}{80\,640}+\frac{966\,443y}{5189\,184\,000}-\frac{1059\,757}{79\,833\,600},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}33}(y) & = & \displaystyle \frac{y^{11}}{10\,6444\,800}-\frac{y^{10}}{29\,030\,400}-\frac{y^{9}}{5806\,080}+\frac{y^{8}}{645\,120}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{7}}{691\,200}-\frac{y^{6}}{27\,648}-\frac{107y^{5}}{24\,192\,000}+\frac{31y^{4}}{193\,536}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{3}}{153\,600}-\frac{33y^{2}}{71\,680}-\frac{769y}{228\,096\,000}+\frac{9721}{29\,030\,400},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}33}(y) & = & \displaystyle \frac{y^{11}}{10\,6444\,800}-\frac{y^{10}}{29\,030\,400}-\frac{y^{9}}{5806\,080}+\frac{y^{8}}{645\,120}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{7}}{691\,200}-\frac{y^{6}}{27\,648}-\frac{107y^{5}}{24\,192\,000}+\frac{31y^{4}}{193\,536}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{3}}{153\,600}-\frac{33y^{2}}{71\,680}-\frac{769y}{228\,096\,000}+\frac{9721}{29\,030\,400},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}34}(y) & = & \displaystyle \frac{y^{11}}{35\,481\,600}-\frac{y^{10}}{5806\,080}-\frac{y^{9}}{4147\,200}+\frac{y^{8}}{645\,120}+\frac{y^{7}}{967\,680}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{y^{6}}{138\,240}-\frac{19y^{5}}{8064\,000}+\frac{19y^{4}}{967\,680}+\frac{29y^{3}}{9676\,800}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{29y^{2}}{645\,120}-\frac{2333y}{1596\,672\,000}+\frac{181}{5806\,080},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}34}(y) & = & \displaystyle \frac{y^{11}}{35\,481\,600}-\frac{y^{10}}{5806\,080}-\frac{y^{9}}{4147\,200}+\frac{y^{8}}{645\,120}+\frac{y^{7}}{967\,680}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{y^{6}}{138\,240}-\frac{19y^{5}}{8064\,000}+\frac{19y^{4}}{967\,680}+\frac{29y^{3}}{9676\,800}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{29y^{2}}{645\,120}-\frac{2333y}{1596\,672\,000}+\frac{181}{5806\,080},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}35}(y) & = & \displaystyle -\frac{y^{11}}{2027\,520}+\frac{23y^{10}}{6451\,200}-\frac{3y^{9}}{716\,800}-\frac{y^{8}}{36\,864}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{47y^{7}}{645\,120}+\frac{37y^{6}}{460\,800}-\frac{259y^{5}}{768\,000}+\frac{163y^{4}}{9676\,800}+\frac{13\,033y^{3}}{19\,353\,600}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{217y^{2}}{307\,200}-\frac{430\,411y}{1064\,448\,000}+\frac{12\,247}{19\,353\,600},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}35}(y) & = & \displaystyle -\frac{y^{11}}{2027\,520}+\frac{23y^{10}}{6451\,200}-\frac{3y^{9}}{716\,800}-\frac{y^{8}}{36\,864}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{47y^{7}}{645\,120}+\frac{37y^{6}}{460\,800}-\frac{259y^{5}}{768\,000}+\frac{163y^{4}}{9676\,800}+\frac{13\,033y^{3}}{19\,353\,600}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{217y^{2}}{307\,200}-\frac{430\,411y}{1064\,448\,000}+\frac{12\,247}{19\,353\,600},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F_{{\it\Theta}36}(y) & = & \displaystyle -\frac{y^{11}}{7884\,800}+\frac{7y^{10}}{8294\,400}-\frac{y^{9}}{58\,060\,800}-\frac{37y^{8}}{6451\,200}+\frac{y^{7}}{276\,480}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{6}}{55\,296}-\frac{293y^{5}}{16\,128\,000}-\frac{247y^{4}}{9676\,800}+\frac{731y^{3}}{19\,353\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{29y^{2}}{6451\,200}-\frac{73\,691y}{3193\,344\,000}+\frac{13}{1658\,880}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\Theta}36}(y) & = & \displaystyle -\frac{y^{11}}{7884\,800}+\frac{7y^{10}}{8294\,400}-\frac{y^{9}}{58\,060\,800}-\frac{37y^{8}}{6451\,200}+\frac{y^{7}}{276\,480}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{y^{6}}{55\,296}-\frac{293y^{5}}{16\,128\,000}-\frac{247y^{4}}{9676\,800}+\frac{731y^{3}}{19\,353\,600}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{29y^{2}}{6451\,200}-\frac{73\,691y}{3193\,344\,000}+\frac{13}{1658\,880}.\end{eqnarray}$$