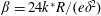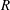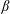1 Introduction
Many applications in chemical engineering, water filtration and biology involve the motion of solid particles suspended in a Newtonian fluid near a porous slab or membrane. For instance, in filtration technology the problem of membrane clogging appears when particles approach very close to the membrane. This leads to membrane fouling (see for instance Le-Clech, Chen & Fane (Reference Le-Clech, Chen and Fane2006) and references therein).
The filtration flow field of a viscous fluid near an isotropic porous slab is usually modelled using Navier–Stokes equations in the fluid and either Darcy (Reference Darcy1856) or Brinkman (Reference Brinkman1947) equations in the porous medium. In the Darcy equation the isotropic porous medium is characterized by its (positive) permeability, denoted here as
![]() $k^{\ast }$
. The size of pores is of order
$k^{\ast }$
. The size of pores is of order
![]() $\sqrt{k^{\ast }}$
. The more complicated case of an anisotropic porous medium is modelled with a permeability matrix; see e.g. Karmakar & Raja Sekhar (Reference Karmakar and Raja Sekhar2018).
$\sqrt{k^{\ast }}$
. The more complicated case of an anisotropic porous medium is modelled with a permeability matrix; see e.g. Karmakar & Raja Sekhar (Reference Karmakar and Raja Sekhar2018).
The Brinkman equation being mathematically more general than the Darcy equation, the matching of the fluid and porous domains is simply done by prescribing continuity of the velocity and stress across the permeable interface. On the other hand, the use of the Darcy equation requires specific boundary conditions on the interface. Thus, there is a large body of literature devoted to this topic; see e.g. Nield & Bejan (Reference Nield and Bejan2006). The conditions depend in general on the interface curvature. Henceforth, attention is restricted to a plane interface. The simplest boundary conditions are the continuity of normal velocity and pressure together with the no-slip condition for the tangential velocity. These conditions, which are physically valid at scales much larger than the size of pores, are widely employed. For instance Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), whose results will be compared to the present work, use such conditions. A more elaborate set of conditions valid at pore size was proposed by Saffman (Reference Saffman1971). This allows a slip of the tangential velocity on the fluid side of the interface. As shown by Saffman (Reference Saffman1971), this is the next approximation in an expansion for small
![]() $\sqrt{k^{\ast }}/a$
, where
$\sqrt{k^{\ast }}/a$
, where
![]() $a$
is a typical length scale in the fluid (for instance, the size of a particle embedded in the fluid). Note also that the Saffman slip condition is an extension of the Navier (Reference Navier1823) slip condition for an impermeable wall. The Navier condition involves a slip length. This model has been shown to be also relevant for rough walls (see Lecoq et al. (Reference Lecoq, Anthore, Cichocki, Szymczak and Feuillebois2004)). Even more general conditions were proposed either for the tangential velocity by Beavers & Joseph (Reference Beavers and Joseph1967) or for the shear stress by Ochoa-Tapia & Whitaker (Reference Ochoa-Tapia and Whitaker1995a
,Reference Ochoa-Tapia and Whitaker
b
) and this is an ongoing research field. These more refined model conditions will not be considered here. Theoretically, the slip length of a linear shear flow along a porous wall is obtained by dividing the (tangent) slip velocity on the wall by the local shear rate. Practically, the needed shear flow profile near the porous wall is obtained by different experimental techniques. For instance, Carotenuto & Minale (Reference Carotenuto and Minale2011) used measurement from a constant-stress rheometer to infer the velocity profile and Wu & Mirbod (Reference Wu and Mirbod2018) measured directly the velocity profile by particle image velocimetry. For anisotropic porous media the interface might also be anisotropic and another anisotropic Saffman-like slip condition would then apply, generalizing the case of an impermeable anisotropic plane slip wall (see Bazant & Vinagradova (Reference Bazant and Vinagradova2008)).
$a$
is a typical length scale in the fluid (for instance, the size of a particle embedded in the fluid). Note also that the Saffman slip condition is an extension of the Navier (Reference Navier1823) slip condition for an impermeable wall. The Navier condition involves a slip length. This model has been shown to be also relevant for rough walls (see Lecoq et al. (Reference Lecoq, Anthore, Cichocki, Szymczak and Feuillebois2004)). Even more general conditions were proposed either for the tangential velocity by Beavers & Joseph (Reference Beavers and Joseph1967) or for the shear stress by Ochoa-Tapia & Whitaker (Reference Ochoa-Tapia and Whitaker1995a
,Reference Ochoa-Tapia and Whitaker
b
) and this is an ongoing research field. These more refined model conditions will not be considered here. Theoretically, the slip length of a linear shear flow along a porous wall is obtained by dividing the (tangent) slip velocity on the wall by the local shear rate. Practically, the needed shear flow profile near the porous wall is obtained by different experimental techniques. For instance, Carotenuto & Minale (Reference Carotenuto and Minale2011) used measurement from a constant-stress rheometer to infer the velocity profile and Wu & Mirbod (Reference Wu and Mirbod2018) measured directly the velocity profile by particle image velocimetry. For anisotropic porous media the interface might also be anisotropic and another anisotropic Saffman-like slip condition would then apply, generalizing the case of an impermeable anisotropic plane slip wall (see Bazant & Vinagradova (Reference Bazant and Vinagradova2008)).
Consider now particles near a plane impermeable or permeable solid boundary. Assuming a dilute suspension of spheres, we are concerned with a single solid impermeable sphere located close to a plane surface on which one of the above boundary conditions applies.
The case of a sphere near an impermeable slip plane has been handled in several works. Starting with the axisymmetric problem of a slip sphere translating normal to an impermeable plane slip wall (using the Navier condition for both impermeable surfaces), Goren (Reference Goren1973), Hocking (Reference Hocking1973) and Vinogradova (Reference Vinogradova1995) considered the lubrication problem when the sphere is very close to the wall. Note that Goren (Reference Goren1973) and Vinogradova (Reference Vinogradova1995) allow two different slip lengths on the sphere and on the wall, as opposed to Hocking (Reference Hocking1973). Moreover, Goren (Reference Goren1973) implemented the bipolar coordinates technique to solve the problem of arbitrary sphere–wall gap for equal slip lengths. The asymmetric problem of a sphere translating and/or rotating parallel to a plane impermeable wall has been solved, using bipolar coordinates, by Davis, Kezirian & Brenner (Reference Davis, Kezirian and Brenner1994) when there is slip either on the wall or on the sphere. The asymmetric case of a slip sphere immersed in an ambient shear flow above a slip plane impermeable wall was also treated in Luo & Pozrikidis (Reference Luo and Pozrikidis2008) by resorting to a boundary element method. Finally, the asymmetric case of a no-slip sphere embedded in an ambient linear and quadratic shear flow parallel to a slip impermeable wall was solved by Loussaief, Pasol & Feuillebois (Reference Loussaief, Pasol and Feuillebois2015) and Ghalia, Feuillebois & Sellier (Reference Ghalia, Feuillebois and Sellier2016), respectively, using the bipolar coordinates technique.
The case of a no-slip impermeable sphere located near a plane permeable surface (for instance near a porous half-space or near a porous slab or membrane with finite thickness and parallel plane boundaries) has also been the subject of various articles. The axisymmetric problem of a sphere translating normal to a no-slip permeable plane has been solved, using bipolar coordinates for non-zero gap and tangent bipolar coordinates for the contact problem: for the case of a thin no-slip permeable membrane we may cite Goren (Reference Goren1979) for arbitrary sphere–plane gap and Nir (Reference Nir1981) for a sphere in contact. In a similar way, the problem of a sphere near a porous half-space was considered by Sherwood (Reference Sherwood1988) for the contact case and Michalopoulou, Burganos & Payatakes (Reference Michalopoulou, Burganos and Payatakes1992) otherwise. The axisymmetric problem of a sphere translating towards the permeable and no-slip plane upper surface of a porous slab with finite thickness is more involved, since it also requires the modelling of the fluid flow inside the slab, by using either Darcy or Brinkman equations. For a sphere close to the slab, a lubrication analysis of the flow field in the thin liquid film is possible. Such an analysis can be derived from Lin, Lu & Yang (Reference Lin, Lu and Yang2001) for a no-slip boundary condition at the motionless lower slab surface and a Brinkman model inside the slab. Another lubrication analysis was performed by Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) who deal with a Darcy model in a thin slab with the no-slip boundary condition on its upper boundary and a prescribed uniform pressure on its lower boundary. The same flow field configuration, but for the more general case of a sphere at some distance of the slab, was solved by Debbech, Elasmi & Feuillebois (Reference Debbech, Elasmi and Feuillebois2010) using the method of fundamental solution. This solution is based on the calculation of the Green tensor for the Stokes flow near a Darcy porous slab by Elasmi & Feuillebois (Reference Elasmi and Feuillebois2001). The more general case of a porous slab of arbitrary thickness with the same boundary condition (in particular no slip on the upper boundary and uniform pressure at the lower boundary) was solved later by Elasmi & Feuillebois (Reference Elasmi and Feuillebois2003) using the boundary integral method.
For a small wall–particle gap (around of
![]() $5\,\%$
of the sphere radius), the boundary integral method suffers from some lack of accuracy. This is the incentive to propose here a lubrication analysis for the axisymmetric problem of a sphere translating normal and close to a thin porous slab. The Darcy equation applies in the thin slab and the Saffman slip condition is prescribed on its upper side.
$5\,\%$
of the sphere radius), the boundary integral method suffers from some lack of accuracy. This is the incentive to propose here a lubrication analysis for the axisymmetric problem of a sphere translating normal and close to a thin porous slab. The Darcy equation applies in the thin slab and the Saffman slip condition is prescribed on its upper side.
The paper is organized as follows. The addressed filtration problem and adopted numerical method are presented in § 2. Asymptotic predictions for large and small normalized permeability and numerical results obtained for the pressure on the sphere and the resulting drag force are presented in § 3. The settling of the sphere is then examined in § 4 and finally conclusions are given in § 5.
2 Filtration problem and numerical procedure
This section presents the problem of the pressure distribution on a solid sphere translating towards a permeable slip porous slab and the solving numerical procedure.
2.1 Considered axisymmetric flow fields
Consider, as sketched in figure 1, a Newtonian fluid (liquid or gas), with uniform density
![]() $\unicode[STIX]{x1D70C}$
and viscosity
$\unicode[STIX]{x1D70C}$
and viscosity
![]() $\unicode[STIX]{x1D707}$
, embedding a porous slab domain
$\unicode[STIX]{x1D707}$
, embedding a porous slab domain
![]() ${\mathcal{S}}$
with thickness
${\mathcal{S}}$
with thickness
![]() $e>0$
in
$e>0$
in
![]() $-e<z<0$
and two open fluid domains in
$-e<z<0$
and two open fluid domains in
![]() $z<-e$
and
$z<-e$
and
![]() $z>0$
. In the absence of the sphere, the fluid velocity is uniform, i.e.
$z>0$
. In the absence of the sphere, the fluid velocity is uniform, i.e.
![]() $-V_{0}\boldsymbol{e}_{z}$
in each domain. The fluid pressure is a constant
$-V_{0}\boldsymbol{e}_{z}$
in each domain. The fluid pressure is a constant
![]() $p_{0}>0$
for
$p_{0}>0$
for
![]() $z>0$
, zero for
$z>0$
, zero for
![]() $z<-e$
and obeys the Darcy equation in the slab with uniform Darcy permeability
$z<-e$
and obeys the Darcy equation in the slab with uniform Darcy permeability
![]() $k^{\ast }>0$
. The pressure
$k^{\ast }>0$
. The pressure
![]() $Q$
in the slab therefore reads
$Q$
in the slab therefore reads
![]() $Q=\unicode[STIX]{x1D707}V_{0}(z+e)/k^{\ast }$
. Finally, the fluid pressure is continuous across the porous slab boundaries
$Q=\unicode[STIX]{x1D707}V_{0}(z+e)/k^{\ast }$
. Finally, the fluid pressure is continuous across the porous slab boundaries
![]() $z=-e$
and
$z=-e$
and
![]() $z=0$
, called here the lower and upper surfaces
$z=0$
, called here the lower and upper surfaces
![]() $\unicode[STIX]{x1D6F4}_{l}$
and
$\unicode[STIX]{x1D6F4}_{l}$
and
![]() $\unicode[STIX]{x1D6F4}_{u}$
, respectively. Thus, the so-called background permeation velocity
$\unicode[STIX]{x1D6F4}_{u}$
, respectively. Thus, the so-called background permeation velocity
![]() $V_{0}$
in the whole space, imposed by the pressure
$V_{0}$
in the whole space, imposed by the pressure
![]() $p_{0}$
, is given by
$p_{0}$
, is given by
![]() $V_{0}=p_{0}k^{\ast }/(\unicode[STIX]{x1D707}e)$
.
$V_{0}=p_{0}k^{\ast }/(\unicode[STIX]{x1D707}e)$
.

Figure 1. A solid sphere with radius
![]() $R$
settling towards a permeable porous slab
$R$
settling towards a permeable porous slab
![]() ${\mathcal{S}}$
with permeability
${\mathcal{S}}$
with permeability
![]() $k^{\ast }>0$
and thickness
$k^{\ast }>0$
and thickness
![]() $e$
.
$e$
.
A solid sphere, with centre
![]() $O^{\prime }$
and radius
$O^{\prime }$
and radius
![]() $R$
, is immersed above the slab in the ambient permeation flow
$R$
, is immersed above the slab in the ambient permeation flow
![]() $-V_{0}\boldsymbol{e}_{z}$
. It translates towards the slab at the steady velocity
$-V_{0}\boldsymbol{e}_{z}$
. It translates towards the slab at the steady velocity
![]() $-V_{p}\boldsymbol{e}_{z}$
. The resulting perturbed fluid flow has a quasi-steady velocity
$-V_{p}\boldsymbol{e}_{z}$
. The resulting perturbed fluid flow has a quasi-steady velocity
![]() $\boldsymbol{u}-V_{0}\boldsymbol{e}_{z}$
and a pressure
$\boldsymbol{u}-V_{0}\boldsymbol{e}_{z}$
and a pressure
![]() $p_{0}+p$
in the fluid domain
$p_{0}+p$
in the fluid domain
![]() ${\mathcal{D}}$
above the slab and a quasi-steady velocity
${\mathcal{D}}$
above the slab and a quasi-steady velocity
![]() $\boldsymbol{u}^{\prime }-V_{0}\boldsymbol{e}_{z}$
and a pressure
$\boldsymbol{u}^{\prime }-V_{0}\boldsymbol{e}_{z}$
and a pressure
![]() $Q+p^{\prime }$
in the slab
$Q+p^{\prime }$
in the slab
![]() ${\mathcal{S}}$
. As will be shown below, it is irrelevant to consider in the present work the velocity and pressure disturbances occurring below the slab (i.e. in the
${\mathcal{S}}$
. As will be shown below, it is irrelevant to consider in the present work the velocity and pressure disturbances occurring below the slab (i.e. in the
![]() $z<-e$
domain) and such quantities are thus henceforth discarded. The flow is governed by the quasi-steady Navier–Stokes and Darcy equations in
$z<-e$
domain) and such quantities are thus henceforth discarded. The flow is governed by the quasi-steady Navier–Stokes and Darcy equations in
![]() ${\mathcal{D}}$
and
${\mathcal{D}}$
and
![]() ${\mathcal{S}}$
, respectively. Accordingly,
${\mathcal{S}}$
, respectively. Accordingly,
The problem (2.1)–(2.2) must be supplemented with proper boundary conditions. Denoting by
![]() $S$
the sphere boundary, the following far-field condition and no-slip boundary condition on the sphere apply:
$S$
the sphere boundary, the following far-field condition and no-slip boundary condition on the sphere apply:
Additional conditions on the permeable
![]() $z=0$
upper surface
$z=0$
upper surface
![]() $\unicode[STIX]{x1D6F4}_{u}$
are also needed. The continuity of both the velocity component normal to the slab and the pressure holds there
$\unicode[STIX]{x1D6F4}_{u}$
are also needed. The continuity of both the velocity component normal to the slab and the pressure holds there
In the present work we also impose on
![]() $\unicode[STIX]{x1D6F4}_{u}$
the Saffman (Reference Saffman1971) (SA) slip boundary condition for the velocities
$\unicode[STIX]{x1D6F4}_{u}$
the Saffman (Reference Saffman1971) (SA) slip boundary condition for the velocities
![]() $\boldsymbol{u}_{t}=\boldsymbol{u}-(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{z})\boldsymbol{e}_{z}$
tangent to the slab. This condition reads
$\boldsymbol{u}_{t}=\boldsymbol{u}-(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{z})\boldsymbol{e}_{z}$
tangent to the slab. This condition reads
where the dimensionless slip parameter
![]() $\unicode[STIX]{x1D70E}$
is positive. In practice, the Darcy law is obtained when the porous slab thickness
$\unicode[STIX]{x1D70E}$
is positive. In practice, the Darcy law is obtained when the porous slab thickness
![]() $e$
is much larger than the typical length of the pores
$e$
is much larger than the typical length of the pores
![]() $r_{p}=\sqrt{k^{\ast }}$
. Accordingly, we assume that
$r_{p}=\sqrt{k^{\ast }}$
. Accordingly, we assume that
![]() $e\gg \sqrt{k^{\ast }}$
. In addition, the Saffman condition suggests introducing the so-called slab slip length
$e\gg \sqrt{k^{\ast }}$
. In addition, the Saffman condition suggests introducing the so-called slab slip length
![]() $l=\sqrt{k^{\ast }}/\unicode[STIX]{x1D70E}$
which means that
$l=\sqrt{k^{\ast }}/\unicode[STIX]{x1D70E}$
which means that
![]() $\unicode[STIX]{x1D70E}=r_{p}/l$
. The widely employed Navier (Reference Navier1823) slip condition on a solid and impermeable wall with given slip length
$\unicode[STIX]{x1D70E}=r_{p}/l$
. The widely employed Navier (Reference Navier1823) slip condition on a solid and impermeable wall with given slip length
![]() $l>0$
is retrieved by taking
$l>0$
is retrieved by taking
![]() $\unicode[STIX]{x1D70E}=\sqrt{k^{\ast }}/l$
and letting
$\unicode[STIX]{x1D70E}=\sqrt{k^{\ast }}/l$
and letting
![]() $k^{\ast }$
vanish. The case of a permeable and no-slip slab, considered in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), is retrieved from the Saffman boundary condition with
$k^{\ast }$
vanish. The case of a permeable and no-slip slab, considered in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), is retrieved from the Saffman boundary condition with
![]() $k^{\ast }>0$
and
$k^{\ast }>0$
and
![]() $\unicode[STIX]{x1D70E}\rightarrow \infty$
. In summary, the retained assumptions are
$\unicode[STIX]{x1D70E}\rightarrow \infty$
. In summary, the retained assumptions are
For symmetry reasons both flows
![]() $(\boldsymbol{u},p)$
and
$(\boldsymbol{u},p)$
and
![]() $(\boldsymbol{u}^{\prime },p^{\prime })$
are axisymmetric, with no swirl, about the
$(\boldsymbol{u}^{\prime },p^{\prime })$
are axisymmetric, with no swirl, about the
![]() $(O,\boldsymbol{e}_{z})$
axis. We use Cartesian coordinates
$(O,\boldsymbol{e}_{z})$
axis. We use Cartesian coordinates
![]() $(O,x,y,z)$
and cylindrical coordinates
$(O,x,y,z)$
and cylindrical coordinates
![]() $(r,z)$
with the unit local vector
$(r,z)$
with the unit local vector
![]() $\boldsymbol{e}_{r}$
such that
$\boldsymbol{e}_{r}$
such that
![]() $r=\{x^{2}+{y^{2}\}}^{1/2}$
and
$r=\{x^{2}+{y^{2}\}}^{1/2}$
and
![]() $\boldsymbol{x}=z\boldsymbol{e}_{z}+r\boldsymbol{e}_{r}$
. Accordingly,
$\boldsymbol{x}=z\boldsymbol{e}_{z}+r\boldsymbol{e}_{r}$
. Accordingly,
![]() $p(\boldsymbol{x})=p(r,z)$
and
$p(\boldsymbol{x})=p(r,z)$
and
![]() $\boldsymbol{u}(\boldsymbol{x})=u_{r}(r,z)\boldsymbol{e}_{r}+w(r,z)\boldsymbol{e}_{z}$
with similar properties for
$\boldsymbol{u}(\boldsymbol{x})=u_{r}(r,z)\boldsymbol{e}_{r}+w(r,z)\boldsymbol{e}_{z}$
with similar properties for
![]() $p^{\prime }$
and
$p^{\prime }$
and
![]() $\boldsymbol{u}^{\prime }$
, the cylindrical components of which are
$\boldsymbol{u}^{\prime }$
, the cylindrical components of which are
![]() $u_{r}^{\prime }$
and
$u_{r}^{\prime }$
and
![]() $w^{\prime }$
. The stress tensor of the flow field
$w^{\prime }$
. The stress tensor of the flow field
![]() $(\boldsymbol{u},p)$
is denoted as
$(\boldsymbol{u},p)$
is denoted as
![]() $\unicode[STIX]{x1D748}$
. For symmetry reasons, the force
$\unicode[STIX]{x1D748}$
. For symmetry reasons, the force
![]() $\boldsymbol{F}_{s}$
experienced by the translating sphere then reads
$\boldsymbol{F}_{s}$
experienced by the translating sphere then reads
![]() $\boldsymbol{F}_{s}=F_{s}\boldsymbol{e}_{z}$
with
$\boldsymbol{F}_{s}=F_{s}\boldsymbol{e}_{z}$
with
where
![]() $\boldsymbol{n}$
denotes the unit normal vector on
$\boldsymbol{n}$
denotes the unit normal vector on
![]() $S$
pointing into the liquid (see figure 1). The sphere centre is
$S$
pointing into the liquid (see figure 1). The sphere centre is
![]() $O^{\prime }$
and each point
$O^{\prime }$
and each point
![]() $M$
on its boundary
$M$
on its boundary
![]() $S$
is specified by an angle
$S$
is specified by an angle
![]() $\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}]$
with
$\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}]$
with
![]() $\boldsymbol{O}^{\prime }\boldsymbol{M}=R\boldsymbol{n}$
and
$\boldsymbol{O}^{\prime }\boldsymbol{M}=R\boldsymbol{n}$
and
![]() $\boldsymbol{n}=\sin \unicode[STIX]{x1D703}\boldsymbol{e}_{r}+\cos \unicode[STIX]{x1D703}\boldsymbol{e}_{z}$
. Consequently,
$\boldsymbol{n}=\sin \unicode[STIX]{x1D703}\boldsymbol{e}_{r}+\cos \unicode[STIX]{x1D703}\boldsymbol{e}_{z}$
. Consequently,
2.2 Lubrication approximation and resulting problem for the pressure
In our notation, the continuity equation in (2.1) becomes the linear relation
while the momentum equation in (2.1) is nonlinear and thus much less tractable. Now, for a near-contact sphere the well-known lubrication approximation is relevant and makes it possible to solely retain the linear part of this equation. From the assumption that the sphere–slab gap
![]() $\unicode[STIX]{x1D6FF}$
is small compared with the sphere radius
$\unicode[STIX]{x1D6FF}$
is small compared with the sphere radius
![]() $R$
, the classical (see Taylor, G. I., private communication cited in Handy & Bircumshaw Reference Handy and Bircumshaw1925) lubrication analysis consists of asymptotically expanding in terms of the small parameter
$R$
, the classical (see Taylor, G. I., private communication cited in Handy & Bircumshaw Reference Handy and Bircumshaw1925) lubrication analysis consists of asymptotically expanding in terms of the small parameter
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D6FF}/R$
the flow velocity components
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D6FF}/R$
the flow velocity components
![]() $(u_{r},w)$
and pressure
$(u_{r},w)$
and pressure
![]() $p$
in the vicinity of the origin
$p$
in the vicinity of the origin
![]() $O$
(recall figure 1), i.e. for
$O$
(recall figure 1), i.e. for
![]() $z=O(\unicode[STIX]{x1D6FF})$
and
$z=O(\unicode[STIX]{x1D6FF})$
and
![]() $r=O(R)$
. In the present paper the analysis is restricted to the first-order approximation. Let
$r=O(R)$
. In the present paper the analysis is restricted to the first-order approximation. Let
![]() $U$
and
$U$
and
![]() $W$
denote the typical magnitudes of the velocity components
$W$
denote the typical magnitudes of the velocity components
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{z}$
in the lubrication domain. The continuity equation (2.9) first gives
$u_{z}$
in the lubrication domain. The continuity equation (2.9) first gives
![]() $W=\unicode[STIX]{x1D716}U$
. In approximating the momentum equation in (2.1) with boundary condition (2.3), the following Reynolds number
$W=\unicode[STIX]{x1D716}U$
. In approximating the momentum equation in (2.1) with boundary condition (2.3), the following Reynolds number
![]() $Re_{0}$
arises:
$Re_{0}$
arises:
![]() $Re_{0}=\unicode[STIX]{x1D70C}|V_{0}-V_{p}|\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D707}$
. We assume that
$Re_{0}=\unicode[STIX]{x1D70C}|V_{0}-V_{p}|\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D707}$
. We assume that
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D6FF}/R$
is small enough so that
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D6FF}/R$
is small enough so that
![]() $Re_{0}\ll 1$
. Then, the nonlinear term on the left-hand side of the momentum equation (2.1) vanishes in the first approximation and, at the leading order in
$Re_{0}\ll 1$
. Then, the nonlinear term on the left-hand side of the momentum equation (2.1) vanishes in the first approximation and, at the leading order in
![]() $\unicode[STIX]{x1D716}$
, this equation becomes
$\unicode[STIX]{x1D716}$
, this equation becomes
In the lubrication domain the following scalings, also obtained using (2.9)–(2.10), hold:
In the lubrication approximation the leading contribution to the force
![]() $F_{s}$
given by (2.8) is due to the part of the sphere located near the slab, i.e. to points of
$F_{s}$
given by (2.8) is due to the part of the sphere located near the slab, i.e. to points of
![]() $S$
for which
$S$
for which
![]() $r=R\sin \unicode[STIX]{x1D703}$
with
$r=R\sin \unicode[STIX]{x1D703}$
with
![]() $\unicode[STIX]{x1D703}$
close to
$\unicode[STIX]{x1D703}$
close to
![]() $\unicode[STIX]{x03C0}$
. Furthermore, using (2.11) on the sphere boundary
$\unicode[STIX]{x03C0}$
. Furthermore, using (2.11) on the sphere boundary
![]() $S$
shows that it is possible to retain only the pressure term on the right-hand side of (2.8). Upon performing the change of variable
$S$
shows that it is possible to retain only the pressure term on the right-hand side of (2.8). Upon performing the change of variable
![]() $r=r(\unicode[STIX]{x1D703})$
, and recalling from (2.10) that the pressure
$r=r(\unicode[STIX]{x1D703})$
, and recalling from (2.10) that the pressure
![]() $p$
is independent of
$p$
is independent of
![]() $z$
in the lubrication domain gives
$z$
in the lubrication domain gives
In (2.12) the upper limit
![]() ${\mathcal{R}}$
is large compared with
${\mathcal{R}}$
is large compared with
![]() $\unicode[STIX]{x1D6FF}$
. It will be shown below, after (2.20), that the present (inner) expansion at scale
$\unicode[STIX]{x1D6FF}$
. It will be shown below, after (2.20), that the present (inner) expansion at scale
![]() $\unicode[STIX]{x1D6FF}$
is valid for
$\unicode[STIX]{x1D6FF}$
is valid for
![]() ${\mathcal{R}}\rightarrow \infty$
.
${\mathcal{R}}\rightarrow \infty$
.
In summary, the task in this work reduces to the determination of the approximated lubrication pressure
![]() $p$
and velocities
$p$
and velocities
![]() $(u_{r},w)$
governed by the linear equations (2.9) and (2.7) and the far-field behaviour and boundary conditions (2.3)–(2.5).
$(u_{r},w)$
governed by the linear equations (2.9) and (2.7) and the far-field behaviour and boundary conditions (2.3)–(2.5).
The conditions (2.5) may be recast into the following form:
Now, the second equation (2.10) yields
![]() $p=p(r)$
. Integrating twice the first equation (2.10) and taking into account (2.13) give the velocity profile
$p=p(r)$
. Integrating twice the first equation (2.10) and taking into account (2.13) give the velocity profile
At this stage the velocity
![]() $u_{r}(r,0)$
on the interface is still unknown. It is obtained here by enforcing the boundary condition (2.3) on the sphere surface
$u_{r}(r,0)$
on the interface is still unknown. It is obtained here by enforcing the boundary condition (2.3) on the sphere surface
![]() $S$
in the radial direction. As shown in figure 1, this surface is described near the porous slab side by the equation
$S$
in the radial direction. As shown in figure 1, this surface is described near the porous slab side by the equation
![]() $z=h(r)$
. Therefore, equation (2.3) requires that
$z=h(r)$
. Therefore, equation (2.3) requires that
![]() $u_{r}(r,h)=0$
. With this condition the result for the radial velocity profile is
$u_{r}(r,h)=0$
. With this condition the result for the radial velocity profile is
Next, integrating the continuity equation (2.9) over
![]() $z$
in
$z$
in
![]() $[0,h(r)]$
yields
$[0,h(r)]$
yields
The boundary condition (2.3), when projected on the
![]() $z$
direction, also provides
$z$
direction, also provides
![]() $w(r,h)=V_{0}-V_{p}$
while the first condition (2.4) gives
$w(r,h)=V_{0}-V_{p}$
while the first condition (2.4) gives
![]() $w(r,0)=w^{\prime }(r,0)$
. This latter quantity is given by the Darcy law (see first equation (2.2)), i.e. by
$w(r,0)=w^{\prime }(r,0)$
. This latter quantity is given by the Darcy law (see first equation (2.2)), i.e. by
![]() $w^{\prime }(r,0)=-(k^{\ast }/\unicode[STIX]{x1D707})(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}$
. As in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), we assume a linear variation of the pressure
$w^{\prime }(r,0)=-(k^{\ast }/\unicode[STIX]{x1D707})(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}$
. As in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), we assume a linear variation of the pressure
![]() $p^{\prime }$
across the slab:
$p^{\prime }$
across the slab:
![]() $(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}\sim [p^{\prime }(r,0)-p^{\prime }(r,-e)]/e$
. As shown in appendix B, this assumption actually requires that
$(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}\sim [p^{\prime }(r,0)-p^{\prime }(r,-e)]/e$
. As shown in appendix B, this assumption actually requires that
![]() $e\ll R$
; that is, the porous slab thickness is small compared with the sphere radius. We also consider that the fluid below the slab imposes the pressure on the slab lower surface
$e\ll R$
; that is, the porous slab thickness is small compared with the sphere radius. We also consider that the fluid below the slab imposes the pressure on the slab lower surface
![]() $\unicode[STIX]{x1D6F4}_{l}(z=-e)$
, i.e. that
$\unicode[STIX]{x1D6F4}_{l}(z=-e)$
, i.e. that
![]() $p^{\prime }(r,-e)=0$
. Then we obtain the additional link
$p^{\prime }(r,-e)=0$
. Then we obtain the additional link
![]() $w^{\prime }(r,0)=-k^{\ast }p^{\prime }(r,0)/(\unicode[STIX]{x1D707}e)$
. Noting that
$w^{\prime }(r,0)=-k^{\ast }p^{\prime }(r,0)/(\unicode[STIX]{x1D707}e)$
. Noting that
![]() $p^{\prime }(r,0)=p(r,0)=p(r)$
, the combination of (2.16) and (2.15) provides the governing equation for the pressure
$p^{\prime }(r,0)=p(r,0)=p(r)$
, the combination of (2.16) and (2.15) provides the governing equation for the pressure
![]() $p$
in the lubrication domain
$p$
in the lubrication domain
Equation (2.17) may be seen as an extension of the classical Reynolds equation (Reynolds Reference Reynolds1886; Nguyen Reference Nguyen2000). There is no mass injection on the
![]() $(O,\boldsymbol{e}_{z})$
axis and thus
$(O,\boldsymbol{e}_{z})$
axis and thus
![]() $u_{r}^{\prime }(r,0)=0$
at
$u_{r}^{\prime }(r,0)=0$
at
![]() $r=0$
. By symmetry,
$r=0$
. By symmetry,
![]() $(\text{d}p/\text{d}r)(r=0)$
vanishes. In addition
$(\text{d}p/\text{d}r)(r=0)$
vanishes. In addition
![]() $p$
should vanish for large
$p$
should vanish for large
![]() $r$
. From the small normalized sphere–wall gap
$r$
. From the small normalized sphere–wall gap
![]() $\unicode[STIX]{x1D6FF}/R$
assumption,
$\unicode[STIX]{x1D6FF}/R$
assumption,
![]() $h(r)\sim \unicode[STIX]{x1D6FF}+r^{2}/(2R)$
in the vicinity of the origin
$h(r)\sim \unicode[STIX]{x1D6FF}+r^{2}/(2R)$
in the vicinity of the origin
![]() $O$
, namely for
$O$
, namely for
![]() $r\leqslant O(\sqrt{\unicode[STIX]{x1D6FF}R})$
as classically found. As in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), we henceforth use the lengths
$r\leqslant O(\sqrt{\unicode[STIX]{x1D6FF}R})$
as classically found. As in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), we henceforth use the lengths
![]() $(l_{2},k)$
and the dimensionless parameter
$(l_{2},k)$
and the dimensionless parameter
![]() $\unicode[STIX]{x1D6FD}$
, length
$\unicode[STIX]{x1D6FD}$
, length
![]() $s$
and pressure
$s$
and pressure
![]() $P$
such that
$P$
such that
Henceforth, the reduced permeability
![]() $\unicode[STIX]{x1D6FD}$
is simply called the permeability while
$\unicode[STIX]{x1D6FD}$
is simply called the permeability while
![]() $k$
is the permeance. In addition, we also introduce the dimensionless sphere-to-slab gap
$k$
is the permeance. In addition, we also introduce the dimensionless sphere-to-slab gap
![]() $\tilde{\unicode[STIX]{x1D706}}$
:
$\tilde{\unicode[STIX]{x1D706}}$
:
and then obtain for
![]() $P$
the following dimensionless boundary value problem:
$P$
the following dimensionless boundary value problem:
with
![]() $H=1+s^{2}$
the normalized sphere-to-wall distance at position
$H=1+s^{2}$
the normalized sphere-to-wall distance at position
![]() $s$
. The governing problem (2.20) extends that considered in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) by applying the Saffman slip boundary condition. Not surprisingly, taking
$s$
. The governing problem (2.20) extends that considered in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) by applying the Saffman slip boundary condition. Not surprisingly, taking
![]() $\tilde{\unicode[STIX]{x1D706}}\rightarrow \infty$
in (2.20) recovers the Ramon formulation.
$\tilde{\unicode[STIX]{x1D706}}\rightarrow \infty$
in (2.20) recovers the Ramon formulation.
The problem (2.20) is well-posed for large
![]() $s$
as may be proven by considering its asymptotic expansion for
$s$
as may be proven by considering its asymptotic expansion for
![]() $s\gg 1$
. Then
$s\gg 1$
. Then
![]() $H\sim s^{2}$
and the differential equation may be recast in terms of the variable
$H\sim s^{2}$
and the differential equation may be recast in terms of the variable
![]() $H$
$H$
For
![]() $H\gg 1$
the first term takes over and the formal solution behaves like
$H\gg 1$
the first term takes over and the formal solution behaves like
![]() $P\sim H^{-2}\sim s^{-4}$
. Thus, the condition at infinity in (2.20) can indeed be applied and the lubrication problem is regular as expected. Moreover, in the integral (2.12) for the force
$P\sim H^{-2}\sim s^{-4}$
. Thus, the condition at infinity in (2.20) can indeed be applied and the lubrication problem is regular as expected. Moreover, in the integral (2.12) for the force
![]() $F_{s}$
the upper limit
$F_{s}$
the upper limit
![]() ${\mathcal{R}}$
is rejected to infinity.
${\mathcal{R}}$
is rejected to infinity.
As in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), the force
![]() $F_{s}$
is normalized by that obtained for an impermeable no-slip wall. Using our previous scalings (2.11) and (2.18) for
$F_{s}$
is normalized by that obtained for an impermeable no-slip wall. Using our previous scalings (2.11) and (2.18) for
![]() $s$
and
$s$
and
![]() $P$
, the normalized force
$P$
, the normalized force
![]() $F$
is
$F$
is
In this paper we focus on the normalized force
![]() $F$
which, by virtue of (2.19)–(2.22), depends on the sphere–slab gap
$F$
which, by virtue of (2.19)–(2.22), depends on the sphere–slab gap
![]() $\unicode[STIX]{x1D6FF}$
, the sphere radius
$\unicode[STIX]{x1D6FF}$
, the sphere radius
![]() $R$
and the porous slab properties
$R$
and the porous slab properties
![]() $(k^{\ast },e,\unicode[STIX]{x1D70E})$
through the dimensionless parameters
$(k^{\ast },e,\unicode[STIX]{x1D70E})$
through the dimensionless parameters
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\tilde{\unicode[STIX]{x1D706}}$
. The validity of the present formulation however brings some additional restrictions to the previously mentioned ones in (2.6). First, we must recall the condition, discussed after (2.16), of a sufficiently thin slab with
$\tilde{\unicode[STIX]{x1D706}}$
. The validity of the present formulation however brings some additional restrictions to the previously mentioned ones in (2.6). First, we must recall the condition, discussed after (2.16), of a sufficiently thin slab with
![]() $e\ll R$
. Second, the lubrication approximation is valid for
$e\ll R$
. Second, the lubrication approximation is valid for
![]() $r\leqslant O(l_{2})$
and the associated domain on the upper slab boundary
$r\leqslant O(l_{2})$
and the associated domain on the upper slab boundary
![]() $z=0$
must contain a large number of pores, i.e.
$z=0$
must contain a large number of pores, i.e.
![]() $r_{p}=\sqrt{k^{\ast }}\ll l_{2}$
. In summary, we require in the present paper that for a slip porous slab
$r_{p}=\sqrt{k^{\ast }}\ll l_{2}$
. In summary, we require in the present paper that for a slip porous slab
The particular value
![]() $\unicode[STIX]{x1D70E}=\infty$
is here employed with
$\unicode[STIX]{x1D70E}=\infty$
is here employed with
![]() $k^{\ast }>0$
to retrieve the no-slip permeable slab (case
$k^{\ast }>0$
to retrieve the no-slip permeable slab (case
![]() $l=0$
) handled in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013).
$l=0$
) handled in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013).
2.3 Numerical implementation and tests
For the no-slip permeable slab case (Saffman case with
![]() $\tilde{\unicode[STIX]{x1D706}}=\infty$
) the solution of (2.20) for the lubrication pressure
$\tilde{\unicode[STIX]{x1D706}}=\infty$
) the solution of (2.20) for the lubrication pressure
![]() $P$
is obtained in closed form. This solution, surprisingly not reported in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), is given in appendix A. In all other cases, equation (2.20) has to be solved numerically. This is achieved using a truncated domain
$P$
is obtained in closed form. This solution, surprisingly not reported in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), is given in appendix A. In all other cases, equation (2.20) has to be solved numerically. This is achieved using a truncated domain
![]() $0\leqslant s\leqslant L$
and a
$0\leqslant s\leqslant L$
and a
![]() $O(h^{2})$
second-order finite-difference scheme with
$O(h^{2})$
second-order finite-difference scheme with
![]() $N+1$
nodal points
$N+1$
nodal points
![]() $s_{n}=nh$
(taking
$s_{n}=nh$
(taking
![]() $n=0,1,\ldots ,N$
) and
$n=0,1,\ldots ,N$
) and
![]() $h=L/N$
. We then calculate the normalized force
$h=L/N$
. We then calculate the normalized force
![]() $F$
taking as
$F$
taking as
![]() $L$
the upper value of the domain of integration in the integral occurring on the right-hand side of (2.22). This procedure is benchmarked for
$L$
the upper value of the domain of integration in the integral occurring on the right-hand side of (2.22). This procedure is benchmarked for
![]() $\unicode[STIX]{x1D6FD}=1,100$
against the force obtained for the no-slip permeable case. That force is obtained here by integrating, using Maple computer algebra software and taking
$\unicode[STIX]{x1D6FD}=1,100$
against the force obtained for the no-slip permeable case. That force is obtained here by integrating, using Maple computer algebra software and taking
![]() $L=\infty$
, the product
$L=\infty$
, the product
![]() $P(s)s$
with
$P(s)s$
with
![]() $P$
the analytical lubrication pressure displayed in appendix A.
$P$
the analytical lubrication pressure displayed in appendix A.
As shown in table 1, the numerical results converge as
![]() $L$
increases and become very close to the analytical results. In view of these results we henceforth take
$L$
increases and become very close to the analytical results. In view of these results we henceforth take
![]() $L=80$
which is sufficient for a three-digit accuracy.
$L=80$
which is sufficient for a three-digit accuracy.
3 Results for the pressure field and drag force
The normalized force,
![]() $F$
, solely depends upon the positive dimensionless permeability
$F$
, solely depends upon the positive dimensionless permeability
![]() $\unicode[STIX]{x1D6FD}$
and slip parameter
$\unicode[STIX]{x1D6FD}$
and slip parameter
![]() $\tilde{\unicode[STIX]{x1D706}}$
given by
$\tilde{\unicode[STIX]{x1D706}}$
given by
In practice, these parameters take values in the interval
![]() $[0,\infty [$
.
$[0,\infty [$
.
3.1 Asymptotic expansion for
 $\unicode[STIX]{x1D6FD}\gg 1$
$\unicode[STIX]{x1D6FD}\gg 1$
As achieved in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) for the no-slip case, it is worth estimating for the Saffman slip case the resulting normalized lubrication pressure
![]() $P$
and force
$P$
and force
![]() $F$
for either large or small values of the permeability
$F$
for either large or small values of the permeability
![]() $\unicode[STIX]{x1D6FD}$
. In this subsection we consider the case of a sphere translating towards a near-contact permeable slab
$\unicode[STIX]{x1D6FD}$
. In this subsection we consider the case of a sphere translating towards a near-contact permeable slab
![]() $(k=k^{\ast }/e>0)$
in the limit
$(k=k^{\ast }/e>0)$
in the limit
![]() $\unicode[STIX]{x1D6FD}\gg 1$
of large permeability. In such circumstances asymptotic expansions for
$\unicode[STIX]{x1D6FD}\gg 1$
of large permeability. In such circumstances asymptotic expansions for
![]() $P$
and
$P$
and
![]() $F$
can be derived by extending the treatment proposed in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013). Curtailing the details, the pressure
$F$
can be derived by extending the treatment proposed in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013). Curtailing the details, the pressure
![]() $P$
takes, for
$P$
takes, for
![]() $\unicode[STIX]{x1D6FD}$
large, the following form:
$\unicode[STIX]{x1D6FD}$
large, the following form:
with, using Maple software, the functions
 $$\begin{eqnarray}\displaystyle P_{2}^{\ast }(\unicode[STIX]{x1D702}) & = & \displaystyle -\frac{1}{256\unicode[STIX]{x1D702}^{10}}\left[9-58\unicode[STIX]{x1D702}^{2}+4\unicode[STIX]{x1D702}^{4}+\frac{1}{\tilde{\unicode[STIX]{x1D706}}}(18-116\unicode[STIX]{x1D702}^{2}+8\unicode[STIX]{x1D702}^{4})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{1}{\tilde{\unicode[STIX]{x1D706}}^{2}}(9+122\unicode[STIX]{x1D702}^{2}+68\unicode[STIX]{x1D702}^{4})\right]\text{e}^{-1/(2\unicode[STIX]{x1D702}^{2})}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{2}^{\ast }(\unicode[STIX]{x1D702}) & = & \displaystyle -\frac{1}{256\unicode[STIX]{x1D702}^{10}}\left[9-58\unicode[STIX]{x1D702}^{2}+4\unicode[STIX]{x1D702}^{4}+\frac{1}{\tilde{\unicode[STIX]{x1D706}}}(18-116\unicode[STIX]{x1D702}^{2}+8\unicode[STIX]{x1D702}^{4})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{1}{\tilde{\unicode[STIX]{x1D706}}^{2}}(9+122\unicode[STIX]{x1D702}^{2}+68\unicode[STIX]{x1D702}^{4})\right]\text{e}^{-1/(2\unicode[STIX]{x1D702}^{2})}.\end{eqnarray}$$
Of course, letting
![]() $\tilde{\unicode[STIX]{x1D706}}$
tend to infinity in (3.2)–(3.4) retrieves the asymptotics given in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013). Observe that for (3.2) to be an asymptotic expansion,
$\tilde{\unicode[STIX]{x1D706}}$
tend to infinity in (3.2)–(3.4) retrieves the asymptotics given in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013). Observe that for (3.2) to be an asymptotic expansion,
![]() $\tilde{\unicode[STIX]{x1D706}}$
cannot vanish (inspect
$\tilde{\unicode[STIX]{x1D706}}$
cannot vanish (inspect
![]() $P_{1}^{\ast }$
in (3.3) and
$P_{1}^{\ast }$
in (3.3) and
![]() $P_{2}^{\ast }$
in (3.4)). In practice, the expansion (3.2) is valid for
$P_{2}^{\ast }$
in (3.4)). In practice, the expansion (3.2) is valid for
![]() $\sqrt{\unicode[STIX]{x1D6FD}}\gg \text{Max}(1,\tilde{\unicode[STIX]{x1D706}}^{-1})$
. On the basis of (3.2)–(3.4), an asymptotic expansion is derived for the dimensionless drag force from (2.22):
$\sqrt{\unicode[STIX]{x1D6FD}}\gg \text{Max}(1,\tilde{\unicode[STIX]{x1D706}}^{-1})$
. On the basis of (3.2)–(3.4), an asymptotic expansion is derived for the dimensionless drag force from (2.22):
Let us introduce the dimensionless permeability
![]() $\overline{k}=24k/R=24k^{\ast }/(eR)>0$
which compares the porous slab typical pore size
$\overline{k}=24k/R=24k^{\ast }/(eR)>0$
which compares the porous slab typical pore size
![]() $r_{p}=\sqrt{k^{\ast }}$
with the length
$r_{p}=\sqrt{k^{\ast }}$
with the length
![]() $\sqrt{eR}$
. From our second assumption (2.23), it turns out that
$\sqrt{eR}$
. From our second assumption (2.23), it turns out that
![]() $k^{\ast }\ll eR$
, i.e. that
$k^{\ast }\ll eR$
, i.e. that
![]() $\overline{k}\ll 24$
. The requirement
$\overline{k}\ll 24$
. The requirement
![]() $\sqrt{\unicode[STIX]{x1D6FD}}\gg \text{Max}(1,\tilde{\unicode[STIX]{x1D706}}^{-1})$
then becomes
$\sqrt{\unicode[STIX]{x1D6FD}}\gg \text{Max}(1,\tilde{\unicode[STIX]{x1D706}}^{-1})$
then becomes
![]() $\sqrt{\overline{k}}\gg \text{Max}(\unicode[STIX]{x1D6FF}/R,l/R)$
. These constraints tell us to what extent the ratio
$\sqrt{\overline{k}}\gg \text{Max}(\unicode[STIX]{x1D6FF}/R,l/R)$
. These constraints tell us to what extent the ratio
![]() $k^{\ast }/(eR)$
must be large enough for given parameters
$k^{\ast }/(eR)$
must be large enough for given parameters
![]() $(\unicode[STIX]{x1D6FF}/R,l/R)$
. Using (2.22) and (3.5) provides the following approximation of the dimensional force
$(\unicode[STIX]{x1D6FF}/R,l/R)$
. Using (2.22) and (3.5) provides the following approximation of the dimensional force
![]() $F_{s}$
experienced by a sphere translating normal and very close to a permeable (porous) slab with upper surface subject to the Saffman condition:
$F_{s}$
experienced by a sphere translating normal and very close to a permeable (porous) slab with upper surface subject to the Saffman condition:
 $$\begin{eqnarray}\displaystyle F_{s} & {\sim} & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(V_{p}-V_{0})R\left\{\frac{4}{(\overline{k})^{1/2}}-\frac{6(\tilde{\unicode[STIX]{x1D706}}+1)}{\tilde{\unicode[STIX]{x1D706}}\overline{k}}\left(\frac{\unicode[STIX]{x1D6FF}}{R}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{3}{2(\overline{k})^{3/2}}\left[\frac{17+\tilde{\unicode[STIX]{x1D706}}(2+\tilde{\unicode[STIX]{x1D706}})}{\tilde{\unicode[STIX]{x1D706}}^{2}}\right]\left(\frac{\unicode[STIX]{x1D6FF}}{R}\right)^{2}\right\}\quad \text{for }\sqrt{\overline{k}}\gg \text{Max}(\unicode[STIX]{x1D6FF}/R,l/R).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{s} & {\sim} & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(V_{p}-V_{0})R\left\{\frac{4}{(\overline{k})^{1/2}}-\frac{6(\tilde{\unicode[STIX]{x1D706}}+1)}{\tilde{\unicode[STIX]{x1D706}}\overline{k}}\left(\frac{\unicode[STIX]{x1D6FF}}{R}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{3}{2(\overline{k})^{3/2}}\left[\frac{17+\tilde{\unicode[STIX]{x1D706}}(2+\tilde{\unicode[STIX]{x1D706}})}{\tilde{\unicode[STIX]{x1D706}}^{2}}\right]\left(\frac{\unicode[STIX]{x1D6FF}}{R}\right)^{2}\right\}\quad \text{for }\sqrt{\overline{k}}\gg \text{Max}(\unicode[STIX]{x1D6FF}/R,l/R).\end{eqnarray}$$
According to (3.2)–(3.6), the first approximations of the lubrication pressure and of the resulting force exerted on a sphere close to the permeable
![]() $(k>0)$
porous slab are independent of the slip parameter
$(k>0)$
porous slab are independent of the slip parameter
![]() $\tilde{\unicode[STIX]{x1D706}}$
. For a large permeability this was not a priori expected on physical grounds. The Saffman condition is found to affect the lubrication pressure and dimensional force only at the next order.
$\tilde{\unicode[STIX]{x1D706}}$
. For a large permeability this was not a priori expected on physical grounds. The Saffman condition is found to affect the lubrication pressure and dimensional force only at the next order.
Table 1. Normalized force
![]() $F$
versus the length
$F$
versus the length
![]() $L$
for the no-slip permeable case (i.e. as in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013)) and
$L$
for the no-slip permeable case (i.e. as in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013)) and
![]() $\unicode[STIX]{x1D6FD}=1,100$
. For
$\unicode[STIX]{x1D6FD}=1,100$
. For
![]() $L<\infty$
the lubrication pressure is calculated numerically by solving (2.20) for the Saffman boundary condition
$L<\infty$
the lubrication pressure is calculated numerically by solving (2.20) for the Saffman boundary condition
![]() $(\unicode[STIX]{x1D6FF}_{BJ}=0)$
and
$(\unicode[STIX]{x1D6FF}_{BJ}=0)$
and
![]() $\tilde{\unicode[STIX]{x1D706}}\rightarrow \infty$
. The last column for
$\tilde{\unicode[STIX]{x1D706}}\rightarrow \infty$
. The last column for
![]() $L=\infty$
is the analytical lubrication pressure given in appendix A.
$L=\infty$
is the analytical lubrication pressure given in appendix A.

The range of validity of the asymptotic expansion (3.5) is evaluated by comparing in table 2 its predictions against the numerical results of three-digit accuracy . Clearly, the asymptotic expansion does not actually hold for
![]() $\tilde{\unicode[STIX]{x1D706}}=1$
when
$\tilde{\unicode[STIX]{x1D706}}=1$
when
![]() $\unicode[STIX]{x1D6FD}=10,50$
. (This is actually still the case when
$\unicode[STIX]{x1D6FD}=10,50$
. (This is actually still the case when
![]() $\tilde{\unicode[STIX]{x1D706}}=0.1$
for
$\tilde{\unicode[STIX]{x1D706}}=0.1$
for
![]() $\unicode[STIX]{x1D6FD}=1000$
with
$\unicode[STIX]{x1D6FD}=1000$
with
![]() $F=0.0930$
and
$F=0.0930$
and
![]() $F_{a}=0.1421$
and also for
$F_{a}=0.1421$
and also for
![]() $\unicode[STIX]{x1D6FD}=5000$
with
$\unicode[STIX]{x1D6FD}=5000$
with
![]() $F=0.0474$
and
$F=0.0474$
and
![]() $F_{a}=0.0507$
. In contrast, for
$F_{a}=0.0507$
. In contrast, for
![]() $\tilde{\unicode[STIX]{x1D706}}=0.1$
and
$\tilde{\unicode[STIX]{x1D706}}=0.1$
and
![]() $\unicode[STIX]{x1D6FD}=10\,000$
the closer values
$\unicode[STIX]{x1D6FD}=10\,000$
the closer values
![]() $F=0.0348$
and
$F=0.0348$
and
![]() $F_{a}=0.0360$
are obtained.) However, as seen in table 2, the asymptotic expansion provides already for
$F_{a}=0.0360$
are obtained.) However, as seen in table 2, the asymptotic expansion provides already for
![]() $\unicode[STIX]{x1D6FD}=50$
and
$\unicode[STIX]{x1D6FD}=50$
and
![]() $\tilde{\unicode[STIX]{x1D706}}\geqslant 10$
the same three-digit accuracy and may therefore be seen as a handy formula in the range
$\tilde{\unicode[STIX]{x1D706}}\geqslant 10$
the same three-digit accuracy and may therefore be seen as a handy formula in the range
![]() $\unicode[STIX]{x1D6FD}\geqslant 50$
for this domain of the slip parameter
$\unicode[STIX]{x1D6FD}\geqslant 50$
for this domain of the slip parameter
![]() $\tilde{\unicode[STIX]{x1D706}}$
. It also nicely matches the numerics for
$\tilde{\unicode[STIX]{x1D706}}$
. It also nicely matches the numerics for
![]() $\tilde{\unicode[STIX]{x1D706}}\geqslant 1$
when
$\tilde{\unicode[STIX]{x1D706}}\geqslant 1$
when
![]() $\unicode[STIX]{x1D6FD}\geqslant 100$
.
$\unicode[STIX]{x1D6FD}\geqslant 100$
.
Table 2. Computed normalized force in the Saffman case,
![]() $F$
, for a large range of values of the dimensionless permeability,
$F$
, for a large range of values of the dimensionless permeability,
![]() $\unicode[STIX]{x1D6FD}$
, and asymptotic estimate,
$\unicode[STIX]{x1D6FD}$
, and asymptotic estimate,
![]() $F_{a}$
, for either
$F_{a}$
, for either
![]() $\unicode[STIX]{x1D6FD}\gg 1$
(§ 3.1) or
$\unicode[STIX]{x1D6FD}\gg 1$
(§ 3.1) or
![]() $\unicode[STIX]{x1D6FD}\ll 1$
(§ 3.2), both for various values of the parameter
$\unicode[STIX]{x1D6FD}\ll 1$
(§ 3.2), both for various values of the parameter
![]() $\tilde{\unicode[STIX]{x1D706}}$
(see (2.19)). The asymptotic values
$\tilde{\unicode[STIX]{x1D706}}$
(see (2.19)). The asymptotic values
![]() $F_{a}$
for
$F_{a}$
for
![]() $\unicode[STIX]{x1D6FD}\leqslant 1$
have been obtained using the small
$\unicode[STIX]{x1D6FD}\leqslant 1$
have been obtained using the small
![]() $\unicode[STIX]{x1D6FD}$
approximation given in § 3.2. Each line with a
$\unicode[STIX]{x1D6FD}$
approximation given in § 3.2. Each line with a
![]() $\ast$
symbol reports the closed-form (order
$\ast$
symbol reports the closed-form (order
![]() $O(\unicode[STIX]{x1D6FD})$
) approximation in small
$O(\unicode[STIX]{x1D6FD})$
) approximation in small
![]() $\unicode[STIX]{x1D6FD}$
obtained by retaining only the first two terms in (3.10).
$\unicode[STIX]{x1D6FD}$
obtained by retaining only the first two terms in (3.10).

3.2 Asymptotic expansion for
 $\unicode[STIX]{x1D6FD}\ll 1$
$\unicode[STIX]{x1D6FD}\ll 1$
For a vanishing porous slab permeance
![]() $k=k^{\ast }/e$
, the dimensionless permeability
$k=k^{\ast }/e$
, the dimensionless permeability
![]() $\unicode[STIX]{x1D6FD}$
might be small compared with unity even for a very small normalized sphere–slab gap
$\unicode[STIX]{x1D6FD}$
might be small compared with unity even for a very small normalized sphere–slab gap
![]() $\unicode[STIX]{x1D6FF}/R$
(see (2.23)). More precisely, since
$\unicode[STIX]{x1D6FF}/R$
(see (2.23)). More precisely, since
![]() $\unicode[STIX]{x1D6FD}=\overline{k}(R/\unicode[STIX]{x1D6FF})^{2}$
the condition
$\unicode[STIX]{x1D6FD}=\overline{k}(R/\unicode[STIX]{x1D6FF})^{2}$
the condition
![]() $\unicode[STIX]{x1D6FD}\ll 1$
is ensured for
$\unicode[STIX]{x1D6FD}\ll 1$
is ensured for
![]() $\sqrt{\overline{k}}\ll \unicode[STIX]{x1D6FF}/R$
. In such circumstances a regular expansion of the problem (2.20) for small
$\sqrt{\overline{k}}\ll \unicode[STIX]{x1D6FF}/R$
. In such circumstances a regular expansion of the problem (2.20) for small
![]() $\unicode[STIX]{x1D6FD}$
is worked out, as also done in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) for the no-slip case. Omitting the details, the pressure
$\unicode[STIX]{x1D6FD}$
is worked out, as also done in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) for the no-slip case. Omitting the details, the pressure
![]() $P$
is approximated as
$P$
is approximated as
with the zeroth-order pressure
![]() $P_{0}$
and first-order pressure
$P_{0}$
and first-order pressure
![]() $P_{1}$
derived in closed form (again using the Maple software), that is
$P_{1}$
derived in closed form (again using the Maple software), that is
and a much more complicated form for
![]() $P_{1}$
given in appendix C. Finally, the second-order pressure
$P_{1}$
given in appendix C. Finally, the second-order pressure
![]() $P_{2}$
was calculated numerically using a finite-difference scheme (as in § 2.3) to solve the following problem (from the extended Reynolds equation (2.20)):
$P_{2}$
was calculated numerically using a finite-difference scheme (as in § 2.3) to solve the following problem (from the extended Reynolds equation (2.20)):
Following (3.7) and applying (2.22), the expansion for the normalized force
![]() $F$
reads
$F$
reads
Although the analytical expression for the pressure
![]() $P_{1}$
is very involved (see appendix C), it is nevertheless possible to find a simple expression for
$P_{1}$
is very involved (see appendix C), it is nevertheless possible to find a simple expression for
![]() $F_{1}(\tilde{\unicode[STIX]{x1D706}})$
. The results are
$F_{1}(\tilde{\unicode[STIX]{x1D706}})$
. The results are
By inspection of (3.11)–(3.12) and as shown in figure 2 it is observed that both coefficients
![]() $F_{0}$
and
$F_{0}$
and
![]() $F_{1}$
remain of the order of unity in the entire range
$F_{1}$
remain of the order of unity in the entire range
![]() $\tilde{\unicode[STIX]{x1D706}}\geqslant 0$
.
$\tilde{\unicode[STIX]{x1D706}}\geqslant 0$
.
It should be noted that
![]() $F_{0}(\tilde{\unicode[STIX]{x1D706}})$
is actually the normalized force experienced by a sphere located close to (i.e. in the lubrication regime
$F_{0}(\tilde{\unicode[STIX]{x1D706}})$
is actually the normalized force experienced by a sphere located close to (i.e. in the lubrication regime
![]() $\unicode[STIX]{x1D6FF}\ll R$
) an impermeable surface on which the usual Navier slip condition holds. In this case the result (3.11) is recovered from Vinogradova (Reference Vinogradova1995) lubrication analysis (see equations (3.18)–(3.19) there), by letting in her notation
$\unicode[STIX]{x1D6FF}\ll R$
) an impermeable surface on which the usual Navier slip condition holds. In this case the result (3.11) is recovered from Vinogradova (Reference Vinogradova1995) lubrication analysis (see equations (3.18)–(3.19) there), by letting in her notation
![]() $R_{2}\rightarrow \infty ,b\rightarrow 0$
and
$R_{2}\rightarrow \infty ,b\rightarrow 0$
and
![]() $k\rightarrow \infty$
with
$k\rightarrow \infty$
with
![]() $kb=l$
being the slip length. We used Maple computer algebra software to check this limit. In principle, we should also retrieve the function
$kb=l$
being the slip length. We used Maple computer algebra software to check this limit. In principle, we should also retrieve the function
![]() $F_{0}(\tilde{\unicode[STIX]{x1D706}})$
from Goren (Reference Goren1973) lubrication results (his equation (17)), converting his notation with
$F_{0}(\tilde{\unicode[STIX]{x1D706}})$
from Goren (Reference Goren1973) lubrication results (his equation (17)), converting his notation with
![]() $K\!n_{s}=l/R,h=\unicode[STIX]{x1D6FF}$
and
$K\!n_{s}=l/R,h=\unicode[STIX]{x1D6FF}$
and
![]() $K\!n_{w}\rightarrow 0$
. (We could not however succeed in retrieving his result and suspect a misprint in his equation (17) for two reasons: first, there are two analogous terms
$K\!n_{w}\rightarrow 0$
. (We could not however succeed in retrieving his result and suspect a misprint in his equation (17) for two reasons: first, there are two analogous terms
![]() $4ST$
and
$4ST$
and
![]() $2ST$
in the same parentheses and, second, his results from table 1 are not recovered from his formula (17).)
$2ST$
in the same parentheses and, second, his results from table 1 are not recovered from his formula (17).)
As
![]() $\tilde{\unicode[STIX]{x1D706}}$
becomes large the no-slip boundary condition applies and the zeroth-order pressure
$\tilde{\unicode[STIX]{x1D706}}$
becomes large the no-slip boundary condition applies and the zeroth-order pressure
![]() $P_{0}$
tends to the function obtained in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) while
$P_{0}$
tends to the function obtained in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013) while
![]() $F_{0}(\tilde{\unicode[STIX]{x1D706}})\sim 1$
and
$F_{0}(\tilde{\unicode[STIX]{x1D706}})\sim 1$
and
![]() $F_{1}(\tilde{\unicode[STIX]{x1D706}})\sim -1/24$
. We also recover the results by Goren (Reference Goren1979) for a very thin membrane.
$F_{1}(\tilde{\unicode[STIX]{x1D706}})\sim -1/24$
. We also recover the results by Goren (Reference Goren1979) for a very thin membrane.
Like
![]() $P_{0}$
and
$P_{0}$
and
![]() $P_{1}$
, the pressure
$P_{1}$
, the pressure
![]() $P_{2}$
solution of (3.9) is of order unity whatever the value of
$P_{2}$
solution of (3.9) is of order unity whatever the value of
![]() $\tilde{\unicode[STIX]{x1D706}}\geqslant 0$
. Therefore, and in contrast to the previous case of large permeability
$\tilde{\unicode[STIX]{x1D706}}\geqslant 0$
. Therefore, and in contrast to the previous case of large permeability
![]() $\unicode[STIX]{x1D6FD}$
, no restriction bearing on the slip parameter
$\unicode[STIX]{x1D6FD}$
, no restriction bearing on the slip parameter
![]() $\tilde{\unicode[STIX]{x1D706}}$
appears here for the expansions (3.7) and (3.10) to be valid. Again invoking (2.22) eventually provides the following expansion for the dimensionless force:
$\tilde{\unicode[STIX]{x1D706}}$
appears here for the expansions (3.7) and (3.10) to be valid. Again invoking (2.22) eventually provides the following expansion for the dimensionless force:
 $$\begin{eqnarray}\displaystyle F_{s} & = & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(V_{p}-V_{0})R\left\{F_{0}(\tilde{\unicode[STIX]{x1D706}})\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)+F_{1}(\tilde{\unicode[STIX]{x1D706}})\overline{k}\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)^{3}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,F_{2}(\tilde{\unicode[STIX]{x1D706}})\overline{k}^{2}\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)^{5}+O\left(\overline{k}^{3}\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)^{7}\right)\right\}\quad \text{for }\unicode[STIX]{x1D6FD}\ll 1.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{s} & = & \displaystyle 6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(V_{p}-V_{0})R\left\{F_{0}(\tilde{\unicode[STIX]{x1D706}})\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)+F_{1}(\tilde{\unicode[STIX]{x1D706}})\overline{k}\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)^{3}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,F_{2}(\tilde{\unicode[STIX]{x1D706}})\overline{k}^{2}\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)^{5}+O\left(\overline{k}^{3}\left(\frac{R}{\unicode[STIX]{x1D6FF}}\right)^{7}\right)\right\}\quad \text{for }\unicode[STIX]{x1D6FD}\ll 1.\end{eqnarray}$$
As for the case of large permeability, the asymptotic estimate (3.10) of the normalized force
![]() $F$
for
$F$
for
![]() $\unicode[STIX]{x1D6FD}\ll 1$
was tested against the numerical predictions. The results displayed in table 2 show the approximation (3.10) both at
$\unicode[STIX]{x1D6FD}\ll 1$
was tested against the numerical predictions. The results displayed in table 2 show the approximation (3.10) both at
![]() $O(\unicode[STIX]{x1D6FD}^{2})$
‘first order’ and
$O(\unicode[STIX]{x1D6FD}^{2})$
‘first order’ and
![]() $O(\unicode[STIX]{x1D6FD}^{3})$
‘second order’. From table 2 the agreement between the three-digit numerics and both (first-order and second-order) asymptotic approximations for the normalized force turns out to be amazingly good (that is, within
$O(\unicode[STIX]{x1D6FD}^{3})$
‘second order’. From table 2 the agreement between the three-digit numerics and both (first-order and second-order) asymptotic approximations for the normalized force turns out to be amazingly good (that is, within
![]() $O(10^{-4})$
accuracy) up to
$O(10^{-4})$
accuracy) up to
![]() $\unicode[STIX]{x1D6FD}=0.1$
in the entire range
$\unicode[STIX]{x1D6FD}=0.1$
in the entire range
![]() $\tilde{\unicode[STIX]{x1D706}}\geqslant 1$
. Note also that the first-order approximation, obtained by retaining the first two terms on the right-hand side of (3.10), may be considered as a handy formula for practical use.
$\tilde{\unicode[STIX]{x1D706}}\geqslant 1$
. Note also that the first-order approximation, obtained by retaining the first two terms on the right-hand side of (3.10), may be considered as a handy formula for practical use.
3.3 Numerical results
In practice the permeability parameter
![]() $\unicode[STIX]{x1D6FD}$
can take values in the entire range
$\unicode[STIX]{x1D6FD}$
can take values in the entire range
![]() $\unicode[STIX]{x1D6FD}\geqslant 0$
. For
$\unicode[STIX]{x1D6FD}\geqslant 0$
. For
![]() $\unicode[STIX]{x1D6FD}$
neither small nor large the lubrication pressure
$\unicode[STIX]{x1D6FD}$
neither small nor large the lubrication pressure
![]() $P$
and resulting normalized force
$P$
and resulting normalized force
![]() $F$
have to be calculated numerically. This is achieved in the present work, with a three-digit accuracy, using the numerical method described in § 2.3.
$F$
have to be calculated numerically. This is achieved in the present work, with a three-digit accuracy, using the numerical method described in § 2.3.
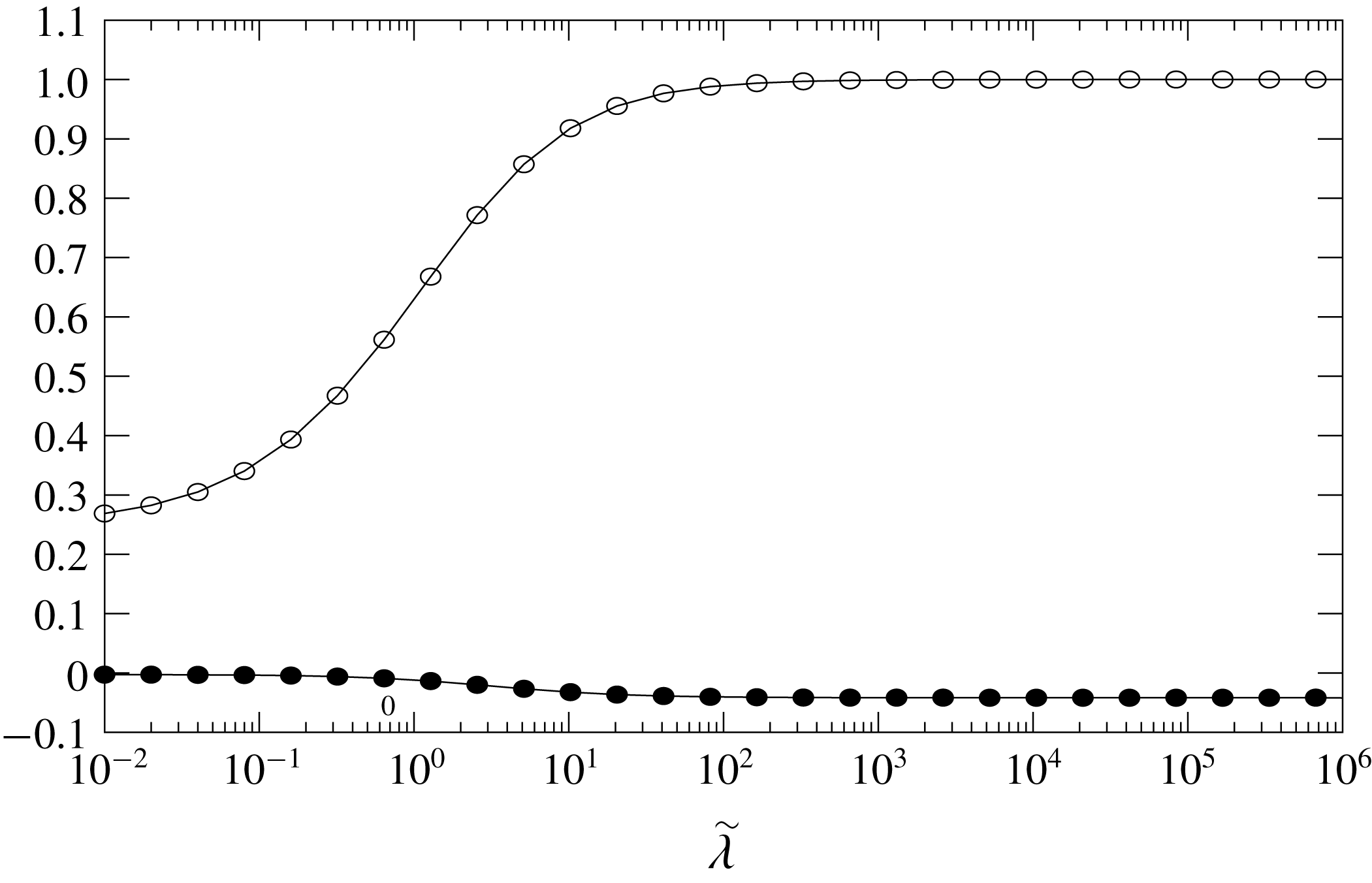
Figure 3 displays the force
![]() $F$
versus
$F$
versus
![]() $\unicode[STIX]{x1D6FD}$
in the range
$\unicode[STIX]{x1D6FD}$
in the range
![]() $[0.01,1000]$
for the Saffman slip case
$[0.01,1000]$
for the Saffman slip case
![]() $\tilde{\unicode[STIX]{x1D706}}=0.1,1,10,100$
and also for the Ramon no-slip case (associated with the value
$\tilde{\unicode[STIX]{x1D706}}=0.1,1,10,100$
and also for the Ramon no-slip case (associated with the value
![]() $\tilde{\unicode[STIX]{x1D706}}=\infty$
). The slip parameter is also written
$\tilde{\unicode[STIX]{x1D706}}=\infty$
). The slip parameter is also written
![]() $\tilde{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6FF}/l$
with
$\tilde{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6FF}/l$
with
![]() $l$
the porous slab slip length. The curves in figure 3 reveal that
$l$
the porous slab slip length. The curves in figure 3 reveal that
![]() $F$
is deeply sensitive to the ratio
$F$
is deeply sensitive to the ratio
![]() $\unicode[STIX]{x1D6FF}/l$
in a wide range (say here in the range
$\unicode[STIX]{x1D6FF}/l$
in a wide range (say here in the range
![]() $[0.01,100]$
) of the permeability
$[0.01,100]$
) of the permeability
![]() $\unicode[STIX]{x1D6FD}$
. Not surprisingly, at given values of
$\unicode[STIX]{x1D6FD}$
. Not surprisingly, at given values of
![]() $\unicode[STIX]{x1D6FD}$
and of the small sphere–slab gap
$\unicode[STIX]{x1D6FD}$
and of the small sphere–slab gap
![]() $\unicode[STIX]{x1D6FF}$
, the normalized force decreases as the slip increases (i.e. as
$\unicode[STIX]{x1D6FF}$
, the normalized force decreases as the slip increases (i.e. as
![]() $l$
increases). Moreover, at given slip parameter
$l$
increases). Moreover, at given slip parameter
![]() $\tilde{\unicode[STIX]{x1D706}}$
the force quickly reaches for
$\tilde{\unicode[STIX]{x1D706}}$
the force quickly reaches for
![]() $\unicode[STIX]{x1D6FD}\leqslant O(1)$
its limit value for the impermeable
$\unicode[STIX]{x1D6FD}\leqslant O(1)$
its limit value for the impermeable
![]() $(\unicode[STIX]{x1D6FD}=0)$
slab case. This limit value agrees with the one obtained by Vinogradova (Reference Vinogradova1995) for the impermeable slipping wall case. Of course, as shown by the leading order in expansion (3.5), all curves collapse as
$(\unicode[STIX]{x1D6FD}=0)$
slab case. This limit value agrees with the one obtained by Vinogradova (Reference Vinogradova1995) for the impermeable slipping wall case. Of course, as shown by the leading order in expansion (3.5), all curves collapse as
![]() $\unicode[STIX]{x1D6FD}$
becomes large enough. Moreover, it is observed in figure 3 that curves for
$\unicode[STIX]{x1D6FD}$
becomes large enough. Moreover, it is observed in figure 3 that curves for
![]() $\tilde{\unicode[STIX]{x1D706}}\geqslant 1$
almost coincide as soon as
$\tilde{\unicode[STIX]{x1D706}}\geqslant 1$
almost coincide as soon as
![]() $\unicode[STIX]{x1D6FD}\geqslant 1000$
.
$\unicode[STIX]{x1D6FD}\geqslant 1000$
.

Figure 3. Normalized force
![]() $F$
versus the permeability parameter
$F$
versus the permeability parameter
![]() $\unicode[STIX]{x1D6FD}$
for
$\unicode[STIX]{x1D6FD}$
for
![]() $\tilde{\unicode[STIX]{x1D706}}=0.1$
(○),
$\tilde{\unicode[STIX]{x1D706}}=0.1$
(○),
![]() $\tilde{\unicode[STIX]{x1D706}}=1$
(▫),
$\tilde{\unicode[STIX]{x1D706}}=1$
(▫),
![]() $\tilde{\unicode[STIX]{x1D706}}=10$
(▵) and
$\tilde{\unicode[STIX]{x1D706}}=10$
(▵) and
![]() $\tilde{\unicode[STIX]{x1D706}}=100$
(solid curve). For comparison purposes, a few values obtained for the no-slip Ramon case (associated with
$\tilde{\unicode[STIX]{x1D706}}=100$
(solid curve). For comparison purposes, a few values obtained for the no-slip Ramon case (associated with
![]() $\tilde{\unicode[STIX]{x1D706}}=\infty$
) are also indicated by
$\tilde{\unicode[STIX]{x1D706}}=\infty$
) are also indicated by
![]() $\ast$
symbols.
$\ast$
symbols.
The lubrication pressure
![]() $P(s)$
is also displayed in figure 4 versus the normalized radial coordinate in the gap,
$P(s)$
is also displayed in figure 4 versus the normalized radial coordinate in the gap,
![]() $s$
, for
$s$
, for
![]() $\unicode[STIX]{x1D6FD}=1,100$
and the same values of
$\unicode[STIX]{x1D6FD}=1,100$
and the same values of
![]() $\tilde{\unicode[STIX]{x1D706}}$
as in figure 3. As shown for
$\tilde{\unicode[STIX]{x1D706}}$
as in figure 3. As shown for
![]() $\unicode[STIX]{x1D6FD}=1$
in figure 4(a), the pressure is strongly sensitive to the value of
$\unicode[STIX]{x1D6FD}=1$
in figure 4(a), the pressure is strongly sensitive to the value of
![]() $\tilde{\unicode[STIX]{x1D706}}$
but is mainly exerted in the narrow domain
$\tilde{\unicode[STIX]{x1D706}}$
but is mainly exerted in the narrow domain
![]() $s\leqslant 1.5$
close to the symmetry axis. In contrast, figure 4(b) reveals that for
$s\leqslant 1.5$
close to the symmetry axis. In contrast, figure 4(b) reveals that for
![]() $\unicode[STIX]{x1D6FD}=100$
the pressure becomes less sensitive to the parameter
$\unicode[STIX]{x1D6FD}=100$
the pressure becomes less sensitive to the parameter
![]() $\tilde{\unicode[STIX]{x1D706}}$
but is mainly distributed in the extended range
$\tilde{\unicode[STIX]{x1D706}}$
but is mainly distributed in the extended range
![]() $s\leqslant 3$
.
$s\leqslant 3$
.

Figure 4. Lubrication pressure
![]() $P$
versus
$P$
versus
![]() $s$
for
$s$
for
![]() $\tilde{\unicode[STIX]{x1D706}}=0.1$
(○),
$\tilde{\unicode[STIX]{x1D706}}=0.1$
(○),
![]() $\tilde{\unicode[STIX]{x1D706}}=1$
(▫),
$\tilde{\unicode[STIX]{x1D706}}=1$
(▫),
![]() $\tilde{\unicode[STIX]{x1D706}}=10$
(▵),
$\tilde{\unicode[STIX]{x1D706}}=10$
(▵),
![]() $\tilde{\unicode[STIX]{x1D706}}=100$
(solid curve) and also for the
$\tilde{\unicode[STIX]{x1D706}}=100$
(solid curve) and also for the
![]() $\tilde{\unicode[STIX]{x1D706}}=\infty$
case (no curve but * symbols). (a) Case
$\tilde{\unicode[STIX]{x1D706}}=\infty$
case (no curve but * symbols). (a) Case
![]() $\unicode[STIX]{x1D6FD}=1$
. (b) Case
$\unicode[STIX]{x1D6FD}=1$
. (b) Case
![]() $\unicode[STIX]{x1D6FD}=100$
.
$\unicode[STIX]{x1D6FD}=100$
.
4 Settling of a solid sphere near a porous slab
This section considers the settling of a solid sphere towards a near-contact porous slab. There is no background permeation
![]() $(V_{0}=0)$
and the uniform gravity field
$(V_{0}=0)$
and the uniform gravity field
![]() $\boldsymbol{g}=-g\boldsymbol{e}_{z}$
is normal to the slab.
$\boldsymbol{g}=-g\boldsymbol{e}_{z}$
is normal to the slab.
4.1 Time-dependent problem and numerical treatment
As displayed in figure 1, the sphere centre is
![]() $O^{\prime }$
with
$O^{\prime }$
with
![]() $\boldsymbol{O}\boldsymbol{O}^{\prime }=(R+\unicode[STIX]{x1D6FF})\boldsymbol{e}_{z}$
. The sphere–slab gap
$\boldsymbol{O}\boldsymbol{O}^{\prime }=(R+\unicode[STIX]{x1D6FF})\boldsymbol{e}_{z}$
. The sphere–slab gap
![]() $\unicode[STIX]{x1D6FF}$
now depends on time
$\unicode[STIX]{x1D6FF}$
now depends on time
![]() $t$
. The sphere density
$t$
. The sphere density
![]() $\unicode[STIX]{x1D70C}_{s}$
is uniform, so that the sphere settles without rotating at the translational velocity
$\unicode[STIX]{x1D70C}_{s}$
is uniform, so that the sphere settles without rotating at the translational velocity
![]() $-V_{p}\boldsymbol{e}_{z}$
with
$-V_{p}\boldsymbol{e}_{z}$
with
![]() $V_{p}=-\text{d}\unicode[STIX]{x1D6FF}/\text{d}t$
. Since the fluid has a uniform density
$V_{p}=-\text{d}\unicode[STIX]{x1D6FF}/\text{d}t$
. Since the fluid has a uniform density
![]() $\unicode[STIX]{x1D70C}$
the sphere buoyancy-corrected mass is
$\unicode[STIX]{x1D70C}$
the sphere buoyancy-corrected mass is
![]() $m=4\unicode[STIX]{x03C0}(\unicode[STIX]{x1D70C}_{s}-\unicode[STIX]{x1D70C})R^{3}/3$
. Accounting for gravity, the flow field perturbed by the sphere is
$m=4\unicode[STIX]{x03C0}(\unicode[STIX]{x1D70C}_{s}-\unicode[STIX]{x1D70C})R^{3}/3$
. Accounting for gravity, the flow field perturbed by the sphere is
![]() $(\boldsymbol{u},p+\unicode[STIX]{x1D70C}\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{x})$
in the fluid domain
$(\boldsymbol{u},p+\unicode[STIX]{x1D70C}\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{x})$
in the fluid domain
![]() ${\mathcal{D}}$
and
${\mathcal{D}}$
and
![]() $(\boldsymbol{u}^{\prime },p^{\prime }+\unicode[STIX]{x1D70C}\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{x})$
in the slab
$(\boldsymbol{u}^{\prime },p^{\prime }+\unicode[STIX]{x1D70C}\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{x})$
in the slab
![]() ${\mathcal{S}}$
with
${\mathcal{S}}$
with
![]() $(\boldsymbol{u},p)$
and
$(\boldsymbol{u},p)$
and
![]() $(\boldsymbol{u}^{\prime },p^{\prime })$
still governed by (2.2)–(2.5) and the lubrication approximation (2.10). The total (hydrodynamic plus gravity) force exerted on the sphere with volume
$(\boldsymbol{u}^{\prime },p^{\prime })$
still governed by (2.2)–(2.5) and the lubrication approximation (2.10). The total (hydrodynamic plus gravity) force exerted on the sphere with volume
![]() ${\mathcal{V}}$
is
${\mathcal{V}}$
is
![]() $(F_{s}+\unicode[STIX]{x1D70C}{\mathcal{V}}g)\boldsymbol{e}_{z}$
where
$(F_{s}+\unicode[STIX]{x1D70C}{\mathcal{V}}g)\boldsymbol{e}_{z}$
where
![]() $F_{s}$
is related to the normalized force
$F_{s}$
is related to the normalized force
![]() $F$
by (2.22) (in which one sets
$F$
by (2.22) (in which one sets
![]() $V_{0}=0$
). Neglecting the sphere inertia, which corresponds to either a liquid or a gas at low Stokes number, the time-dependent sphere ‘location’
$V_{0}=0$
). Neglecting the sphere inertia, which corresponds to either a liquid or a gas at low Stokes number, the time-dependent sphere ‘location’
![]() $\unicode[STIX]{x1D6FF}(t)$
is the solution to the following problem:
$\unicode[STIX]{x1D6FF}(t)$
is the solution to the following problem:
with
![]() $\unicode[STIX]{x1D6FF}_{0}$
the prescribed initial sphere–slab gap.
$\unicode[STIX]{x1D6FF}_{0}$
the prescribed initial sphere–slab gap.
As outlined after (2.22), the normalized force
![]() $F$
solely depends upon
$F$
solely depends upon
![]() $\unicode[STIX]{x1D6FF}/R$
and the dimensionless parameters
$\unicode[STIX]{x1D6FF}/R$
and the dimensionless parameters
![]() $(\unicode[STIX]{x1D6FD},\tilde{\unicode[STIX]{x1D706}})$
. From the definitions (3.1), the time-dependent normalized sphere ‘location’
$(\unicode[STIX]{x1D6FD},\tilde{\unicode[STIX]{x1D706}})$
. From the definitions (3.1), the time-dependent normalized sphere ‘location’
![]() $\overline{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D6FF}/R$
is thus determined by the time scale
$\overline{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D6FF}/R$
is thus determined by the time scale
![]() $\unicode[STIX]{x1D70F}_{g}=\sqrt{24}\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}R^{2}/(mg)$
as in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), the given initial sphere location
$\unicode[STIX]{x1D70F}_{g}=\sqrt{24}\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}R^{2}/(mg)$
as in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), the given initial sphere location
![]() $\overline{\unicode[STIX]{x1D6FF}}_{0}=\unicode[STIX]{x1D6FF}_{0}/R$
and the auxiliary parameters
$\overline{\unicode[STIX]{x1D6FF}}_{0}=\unicode[STIX]{x1D6FF}_{0}/R$
and the auxiliary parameters
![]() $(k/R,l/R)$
. For convenience, the normalized time
$(k/R,l/R)$
. For convenience, the normalized time
![]() $\overline{t}=t/\unicode[STIX]{x1D70F}_{g}$
is introduced. From (4.1), we obtain the ratio
$\overline{t}=t/\unicode[STIX]{x1D70F}_{g}$
is introduced. From (4.1), we obtain the ratio
![]() $\overline{\unicode[STIX]{x1D6FF}}$
versus
$\overline{\unicode[STIX]{x1D6FF}}$
versus
![]() $\overline{t}$
, for given quantities
$\overline{t}$
, for given quantities
![]() $(\overline{\unicode[STIX]{x1D6FF}}_{0},k/R,l/R)$
, by solving the problem
$(\overline{\unicode[STIX]{x1D6FF}}_{0},k/R,l/R)$
, by solving the problem
Except for a no-slip and impermeable slab (see below), this task requires a numerical procedure. In the present work we resort to a predictor–corrector marching-in-time algorithm (except for the first two time steps for which a second-order Runge–Kutta scheme is used) to solve (4.2). This procedure is benchmarked against the analytical solution available for a no-slip and impermeable slab (i.e. for the case of a usual no-slip solid boundary wall
![]() $\unicode[STIX]{x1D6F4}_{u}$
). Indeed, in such circumstances
$\unicode[STIX]{x1D6F4}_{u}$
). Indeed, in such circumstances
![]() $k=\unicode[STIX]{x1D6FD}=0$
while
$k=\unicode[STIX]{x1D6FD}=0$
while
![]() $\tilde{\unicode[STIX]{x1D706}}\rightarrow \infty$
so that (recall (3.10) and our discussion after (3.12))
$\tilde{\unicode[STIX]{x1D706}}\rightarrow \infty$
so that (recall (3.10) and our discussion after (3.12))
![]() $F=1$
whatever
$F=1$
whatever
![]() $\overline{\unicode[STIX]{x1D6FF}}$
. Analytically solving (4.2) thus becomes possible and yields the analytical solution
$\overline{\unicode[STIX]{x1D6FF}}$
. Analytically solving (4.2) thus becomes possible and yields the analytical solution
![]() $\overline{\unicode[STIX]{x1D6FF}}_{a}=\overline{\unicode[STIX]{x1D6FF}}_{0}\text{e}^{-\sqrt{2/3}\overline{t}}$
.
$\overline{\unicode[STIX]{x1D6FF}}_{a}=\overline{\unicode[STIX]{x1D6FF}}_{0}\text{e}^{-\sqrt{2/3}\overline{t}}$
.
As shown in table 3, the analytical solution
![]() $\overline{\unicode[STIX]{x1D6FF}}_{a}$
is accurately retrieved by the numerics.
$\overline{\unicode[STIX]{x1D6FF}}_{a}$
is accurately retrieved by the numerics.
Table 3. Analytical and numerical values of normalized sphere–slab gap
![]() $\overline{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D6FF}/R$
at different dimensionless times
$\overline{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D6FF}/R$
at different dimensionless times
![]() $\bar{t}=1,2,3,5,10$
in the impermeable
$\bar{t}=1,2,3,5,10$
in the impermeable
![]() $(\unicode[STIX]{x1D6FD}=0)$
and no-slip
$(\unicode[STIX]{x1D6FD}=0)$
and no-slip
![]() $(\overline{\unicode[STIX]{x1D706}}=\infty )$
case. Here
$(\overline{\unicode[STIX]{x1D706}}=\infty )$
case. Here
![]() $\overline{\unicode[STIX]{x1D6FF}}_{0}=0.2$
and (4.2) is solved numerically by the marching-in-time algorithm taking for the dimensionless force
$\overline{\unicode[STIX]{x1D6FF}}_{0}=0.2$
and (4.2) is solved numerically by the marching-in-time algorithm taking for the dimensionless force
![]() $F$
either (i) its analytical value
$F$
either (i) its analytical value
![]() $F=1;$
or (ii) its numerical Ramon value (as in table 1); or (iii) its numerical value calculated for the Saffman condition with
$F=1;$
or (ii) its numerical Ramon value (as in table 1); or (iii) its numerical value calculated for the Saffman condition with
![]() $\tilde{\unicode[STIX]{x1D706}}=\infty$
.
$\tilde{\unicode[STIX]{x1D706}}=\infty$
.

We compute the sphere trajectory
![]() $\overline{\unicode[STIX]{x1D6FF}}(\overline{t})$
for prescribed sphere initial location
$\overline{\unicode[STIX]{x1D6FF}}(\overline{t})$
for prescribed sphere initial location
![]() $\overline{\unicode[STIX]{x1D6FF}}_{0}$
and parameters
$\overline{\unicode[STIX]{x1D6FF}}_{0}$
and parameters
![]() $(k/R,l/R)$
. Both parameters
$(k/R,l/R)$
. Both parameters
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\tilde{\unicode[STIX]{x1D706}}$
evolve on the trajectory with, as the sphere approaches the slab, an increase of
$\tilde{\unicode[STIX]{x1D706}}$
evolve on the trajectory with, as the sphere approaches the slab, an increase of
![]() $\unicode[STIX]{x1D6FD}$
and a decrease of
$\unicode[STIX]{x1D6FD}$
and a decrease of
![]() $\tilde{\unicode[STIX]{x1D706}}$
. The product
$\tilde{\unicode[STIX]{x1D706}}$
. The product
![]() $C=\unicode[STIX]{x1D6FD}\tilde{\unicode[STIX]{x1D706}}^{2}/24=(k/R)/(l/R)^{2}\geqslant 0$
is however constant on each trajectory with a value entirely prescribed by the parameters
$C=\unicode[STIX]{x1D6FD}\tilde{\unicode[STIX]{x1D706}}^{2}/24=(k/R)/(l/R)^{2}\geqslant 0$
is however constant on each trajectory with a value entirely prescribed by the parameters
![]() $(k/R,l/R)$
(i.e. indepently of the initial location
$(k/R,l/R)$
(i.e. indepently of the initial location
![]() $\overline{\unicode[STIX]{x1D6FF}}_{0}$
).
$\overline{\unicode[STIX]{x1D6FF}}_{0}$
).
For a permeable slab (that is, for a positive slab permeance ratio
![]() $k/R$
), note that
$k/R$
), note that
![]() $\unicode[STIX]{x1D6FD}\rightarrow \infty$
as the sphere approaches the slab. Moreover, for a sufficiently small sphere–slab normalized gap
$\unicode[STIX]{x1D6FD}\rightarrow \infty$
as the sphere approaches the slab. Moreover, for a sufficiently small sphere–slab normalized gap
![]() $\overline{\unicode[STIX]{x1D6FF}}$
then
$\overline{\unicode[STIX]{x1D6FF}}$
then
![]() $\sqrt{\unicode[STIX]{x1D6FD}}$
becomes large enough for (3.5) to hold with
$\sqrt{\unicode[STIX]{x1D6FD}}$
becomes large enough for (3.5) to hold with
![]() $F\sim 4\unicode[STIX]{x1D6FD}^{-1/2}=(2/3)^{1/2}(k/R)^{-1/2}\overline{\unicode[STIX]{x1D6FF}}$
and the sphere normalized velocity
$F\sim 4\unicode[STIX]{x1D6FD}^{-1/2}=(2/3)^{1/2}(k/R)^{-1/2}\overline{\unicode[STIX]{x1D6FF}}$
and the sphere normalized velocity
![]() $[\text{d}\overline{\unicode[STIX]{x1D6FF}}/\text{d}\overline{t}]\boldsymbol{e}_{z}$
therefore adopts the time-independent value
$[\text{d}\overline{\unicode[STIX]{x1D6FF}}/\text{d}\overline{t}]\boldsymbol{e}_{z}$
therefore adopts the time-independent value
![]() $-V_{pc}\boldsymbol{e}_{z}$
with
$-V_{pc}\boldsymbol{e}_{z}$
with
![]() $V_{pc}=\sqrt{k/R}$
. As found in § 3.1, the sphere velocity
$V_{pc}=\sqrt{k/R}$
. As found in § 3.1, the sphere velocity
![]() $V_{p}$
tends to
$V_{p}$
tends to
![]() $V_{pc}$
for
$V_{pc}$
for
![]() $\sqrt{\overline{k}}\gg \text{Max}(\overline{\unicode[STIX]{x1D6FF}},l/R)$
with
$\sqrt{\overline{k}}\gg \text{Max}(\overline{\unicode[STIX]{x1D6FF}},l/R)$
with
![]() $\overline{k}=24k/R$
.
$\overline{k}=24k/R$
.
4.2 Settling trajectories
The sphere trajectory sensitivity to the parameters
![]() $k/R$
and
$k/R$
and
![]() $l/R$
is illustrated in figure 5 which plots
$l/R$
is illustrated in figure 5 which plots
![]() $\overline{\unicode[STIX]{x1D6FF}}$
versus
$\overline{\unicode[STIX]{x1D6FF}}$
versus
![]() $\overline{t}$
for the initial location
$\overline{t}$
for the initial location
![]() $\overline{\unicode[STIX]{x1D6FF}}_{0}=0.2$
and various values of the permeability parameter
$\overline{\unicode[STIX]{x1D6FF}}_{0}=0.2$
and various values of the permeability parameter
![]() $k/R=0.001,0.01$
and of the slip parameter
$k/R=0.001,0.01$
and of the slip parameter
![]() $l/R=0,0.01,0.1$
.
$l/R=0,0.01,0.1$
.

Figure 5. Normalized sphere–slab gap
![]() $\overline{\unicode[STIX]{x1D6FF}}$
versus dimensionless time
$\overline{\unicode[STIX]{x1D6FF}}$
versus dimensionless time
![]() $\overline{t}$
for a no-slip and impermeable
$\overline{t}$
for a no-slip and impermeable
![]() $(k/R=0)$
slab (dashed curve) and for a permeable slab, with either
$(k/R=0)$
slab (dashed curve) and for a permeable slab, with either
![]() $k/R=0.001$
(a) or
$k/R=0.001$
(a) or
![]() $k/R=0.01$
(b). The permeable slab is either no-slip with
$k/R=0.01$
(b). The permeable slab is either no-slip with
![]() $l/R=0$
(*) or slipping with the Saffman boundary condition with normalized slip length
$l/R=0$
(*) or slipping with the Saffman boundary condition with normalized slip length
![]() $l/R=0.01$
(▫) and
$l/R=0.01$
(▫) and
![]() $l/R=0.1$
(▵). Here
$l/R=0.1$
(▵). Here
![]() $\overline{\unicode[STIX]{x1D6FF}}_{0}=0.2$
and the fictitious straight trajectory
$\overline{\unicode[STIX]{x1D6FF}}_{0}=0.2$
and the fictitious straight trajectory
![]() $\unicode[STIX]{x1D6EC}$
(see § 4.1) of a sphere settling at the constant velocity
$\unicode[STIX]{x1D6EC}$
(see § 4.1) of a sphere settling at the constant velocity
![]() $-V_{pc}\boldsymbol{e}_{z}$
is also displayed (straight dash-dotted line).
$-V_{pc}\boldsymbol{e}_{z}$
is also displayed (straight dash-dotted line).
As expected, the sphere settles faster towards a porous slab than towards a no-slip impermeable (dashed line) plane wall. In addition, for a given value of
![]() $k/R$
the sphere approaches faster the slap as the slip parameter
$k/R$
the sphere approaches faster the slap as the slip parameter
![]() $l/R$
increases. Trajectories for a slipping slab either for
$l/R$
increases. Trajectories for a slipping slab either for
![]() $l/R=0.01$
or
$l/R=0.01$
or
![]() $l/R=0.1$
differ either weakly or moderately, respectively, from the one prevailing in the no-slip case (see Ramon et al.
Reference Ramon, Huppert, Lister and Stone2013). Moreover, these differences decrease in magnitude as
$l/R=0.1$
differ either weakly or moderately, respectively, from the one prevailing in the no-slip case (see Ramon et al.
Reference Ramon, Huppert, Lister and Stone2013). Moreover, these differences decrease in magnitude as
![]() $k/R$
increases.
$k/R$
increases.
The slopes of trajectories for slip and no-slip porous slabs approach each other as
![]() $\overline{\unicode[STIX]{x1D6FF}}$
decreases. This can be observed by tracking on a trajectory for given
$\overline{\unicode[STIX]{x1D6FF}}$
decreases. This can be observed by tracking on a trajectory for given
![]() $l>0$
the slope ratio (see (4.2))
$l>0$
the slope ratio (see (4.2))
![]() $s_{r}(\overline{\unicode[STIX]{x1D6FF}})=F(\infty ,\unicode[STIX]{x1D6FD})/F(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})>1$
versus the pair
$s_{r}(\overline{\unicode[STIX]{x1D6FF}})=F(\infty ,\unicode[STIX]{x1D6FD})/F(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})>1$
versus the pair
![]() $(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})$
which evolves as
$(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})$
which evolves as
![]() $\overline{\unicode[STIX]{x1D6FF}}$
drops. This can be done using table 4 and then figure 3.
$\overline{\unicode[STIX]{x1D6FF}}$
drops. This can be done using table 4 and then figure 3.
Table 4. Values of
![]() $\overline{k}^{1/2},\unicode[STIX]{x1D6FD}$
and
$\overline{k}^{1/2},\unicode[STIX]{x1D6FD}$
and
![]() $\tilde{\unicode[STIX]{x1D706}}$
for different parameters
$\tilde{\unicode[STIX]{x1D706}}$
for different parameters
![]() $k/R,l/R$
and normalized gap
$k/R,l/R$
and normalized gap
![]() $\overline{\unicode[STIX]{x1D6FF}}$
. Here
$\overline{\unicode[STIX]{x1D6FF}}$
. Here
![]() $\unicode[STIX]{x1D6FD}_{n}$
and
$\unicode[STIX]{x1D6FD}_{n}$
and
![]() $\tilde{\unicode[STIX]{x1D706}}_{n}$
are obtained for
$\tilde{\unicode[STIX]{x1D706}}_{n}$
are obtained for
![]() $\overline{\unicode[STIX]{x1D6FF}}=10^{-n}$
with
$\overline{\unicode[STIX]{x1D6FF}}=10^{-n}$
with
![]() $n=1,2,3$
.
$n=1,2,3$
.

Hence, for the
![]() $l/R=0.1$
trajectory in figure 5(a) note that, from table 4,
$l/R=0.1$
trajectory in figure 5(a) note that, from table 4,
![]() $(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})=(\tilde{\unicode[STIX]{x1D706}}_{1},\unicode[STIX]{x1D6FD}_{1})=(1,2.4)$
for
$(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})=(\tilde{\unicode[STIX]{x1D706}}_{1},\unicode[STIX]{x1D6FD}_{1})=(1,2.4)$
for
![]() $\overline{\unicode[STIX]{x1D6FF}}=0.1$
and
$\overline{\unicode[STIX]{x1D6FF}}=0.1$
and
![]() $(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})=(\tilde{\unicode[STIX]{x1D706}}_{2},\unicode[STIX]{x1D6FD}_{2})=(0.1,240)$
for
$(\tilde{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6FD})=(\tilde{\unicode[STIX]{x1D706}}_{2},\unicode[STIX]{x1D6FD}_{2})=(0.1,240)$
for
![]() $\overline{\unicode[STIX]{x1D6FF}}=0.01$
. From inspection of figure 3, it thus follows that
$\overline{\unicode[STIX]{x1D6FF}}=0.01$
. From inspection of figure 3, it thus follows that
![]() $s_{t}(\overline{\unicode[STIX]{x1D6FF}}_{1})>s_{t}(\overline{\unicode[STIX]{x1D6FF}}_{2})$
.
$s_{t}(\overline{\unicode[STIX]{x1D6FF}}_{1})>s_{t}(\overline{\unicode[STIX]{x1D6FF}}_{2})$
.
As predicted at the end of § 4.1, each trajectory slope tends to the time-independent limit
![]() $-V_{pc}$
for
$-V_{pc}$
for
![]() $\overline{\unicode[STIX]{x1D6FF}}$
sufficiently small in the following sense:
$\overline{\unicode[STIX]{x1D6FF}}$
sufficiently small in the following sense:
![]() $\sqrt{\overline{k}}\gg \text{Max}(\overline{\unicode[STIX]{x1D6FF}},l/R)$
. This trend is checked by also plotting in figure 5(a,b) the fictitious straight trajectory
$\sqrt{\overline{k}}\gg \text{Max}(\overline{\unicode[STIX]{x1D6FF}},l/R)$
. This trend is checked by also plotting in figure 5(a,b) the fictitious straight trajectory
![]() $\unicode[STIX]{x1D6EC}$
of a sphere that would settle with the previous time-independent velocity
$\unicode[STIX]{x1D6EC}$
of a sphere that would settle with the previous time-independent velocity
![]() $V_{pc}=\sqrt{k/R}$
. For
$V_{pc}=\sqrt{k/R}$
. For
![]() $\overline{\unicode[STIX]{x1D6FF}}\sim 0.01$
the slopes of
$\overline{\unicode[STIX]{x1D6FF}}\sim 0.01$
the slopes of
![]() $\unicode[STIX]{x1D6EC}$
and the trajectories for a permeable slab become close for
$\unicode[STIX]{x1D6EC}$
and the trajectories for a permeable slab become close for
![]() $k/R=0.001$
and very close for
$k/R=0.001$
and very close for
![]() $k/R=0.01$
, respectively. This is because, as shown in table 4, the condition
$k/R=0.01$
, respectively. This is because, as shown in table 4, the condition
![]() $\sqrt{\overline{k}}\geqslant \text{Max}(0.01,l/R)$
or
$\sqrt{\overline{k}}\geqslant \text{Max}(0.01,l/R)$
or
![]() $\sqrt{\overline{k}}\gg \text{Max}(0.01,l/R)$
is met for
$\sqrt{\overline{k}}\gg \text{Max}(0.01,l/R)$
is met for
![]() $k/R=0.001$
or
$k/R=0.001$
or
![]() $k/R=0.01$
, respectively.
$k/R=0.01$
, respectively.
5 Conclusions
The governing problem for the pressure exerted on a sphere translating towards a porous slab at close range is solved within the lubrication approximation using also the assumption of a thin slab. This latter assumption makes it possible to circumvent the determination of the flows inside and below the slab. Using the Saffman slip boundary condition on the porous slab upper interface, the pressure is obtained by solving a Reynolds-like equation and the drag force is obtained therefrom. These quantities solely depend on the dimensionless permeability
![]() $\unicode[STIX]{x1D6FD}=24kR/\unicode[STIX]{x1D6FF}^{2}$
and sphere–slab gap parameter
$\unicode[STIX]{x1D6FD}=24kR/\unicode[STIX]{x1D6FF}^{2}$
and sphere–slab gap parameter
![]() $\tilde{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6FF}/l$
.
$\tilde{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6FF}/l$
.
Handy formulae are proposed for the normalized force at large and small permeability
![]() $\unicode[STIX]{x1D6FD}$
. These formulae agree well with the computed results which are valid in the entire range
$\unicode[STIX]{x1D6FD}$
. These formulae agree well with the computed results which are valid in the entire range
![]() $\unicode[STIX]{x1D6FD}>0$
.
$\unicode[STIX]{x1D6FD}>0$
.
For vanishing permeability
![]() $\unicode[STIX]{x1D6FD}$
our asymptotics retrieve the result of Vinogradova (Reference Vinogradova1995) whatever the slip length. For small permeability
$\unicode[STIX]{x1D6FD}$
our asymptotics retrieve the result of Vinogradova (Reference Vinogradova1995) whatever the slip length. For small permeability
![]() $\unicode[STIX]{x1D6FD}$
and a vanishing slip length our asymptotic results agree with those of Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013).
$\unicode[STIX]{x1D6FD}$
and a vanishing slip length our asymptotic results agree with those of Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013).
Based on the preceding results, the sphere settling trajectory is found to depend significantly upon the slip length ratio
![]() $l/R$
, especially at low permeance ratio (low
$l/R$
, especially at low permeance ratio (low
![]() $k/R$
).
$k/R$
).
This work is restricted to the analysis of a thin slab
![]() $(e/R\ll 1)$
therefore simplifying the flow field in the slab and disregarding that below the slab. It would be useful to relax this thin-slab condition. This task however requires the determination of the axisymmetric Stokes flows above and below the slab, coupled with the Darcy flow in the slab through the Saffman slip condition on both permeable interfaces. This challenging issue is therefore postponed to another work.
$(e/R\ll 1)$
therefore simplifying the flow field in the slab and disregarding that below the slab. It would be useful to relax this thin-slab condition. This task however requires the determination of the axisymmetric Stokes flows above and below the slab, coupled with the Darcy flow in the slab through the Saffman slip condition on both permeable interfaces. This challenging issue is therefore postponed to another work.
Appendix A. Closed-form lubrication pressure for the permeable no-slip thin-slab case
The case of the no-slip thin permeable slab, handled in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), is obtained using the Saffman slip condition with
![]() $\tilde{\unicode[STIX]{x1D706}}=\infty$
. Setting
$\tilde{\unicode[STIX]{x1D706}}=\infty$
. Setting
![]() $v=[\unicode[STIX]{x1D6FD}s^{2}/(1+s^{2})]^{1/2}$
and using Maple software, the lubrication pressure
$v=[\unicode[STIX]{x1D6FD}s^{2}/(1+s^{2})]^{1/2}$
and using Maple software, the lubrication pressure
![]() $P(s)$
solution to (2.20) in this case is found to be
$P(s)$
solution to (2.20) in this case is found to be
with
![]() $I_{0}$
and
$I_{0}$
and
![]() $I_{1}$
the usual modified Bessel functions (of the first kind) of zeroth and first order, respectively (see Abramowitz & Stegun (Reference Abramowitz and Stegun1965)).
$I_{1}$
the usual modified Bessel functions (of the first kind) of zeroth and first order, respectively (see Abramowitz & Stegun (Reference Abramowitz and Stegun1965)).
Appendix B. Approximation of
 $(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}$
for a thin porous slab
$(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}$
for a thin porous slab
Using a Taylor expansion of the pressure
![]() $p^{\prime }(r,z)$
in the porous slab yields the approximation
$p^{\prime }(r,z)$
in the porous slab yields the approximation
From equations (2.2), it is classical that
![]() $p^{\prime }$
is harmonic in the porous slab. With our cylindrical coordinates
$p^{\prime }$
is harmonic in the porous slab. With our cylindrical coordinates
![]() $(r,z)$
this property reads
$(r,z)$
this property reads
If
![]() $p^{\prime }$
scales like
$p^{\prime }$
scales like
![]() $P^{\prime }$
in the slab, in which
$P^{\prime }$
in the slab, in which
![]() $r$
has typical size
$r$
has typical size
![]() $R$
, the scale of the last term in (B 1) is thus
$R$
, the scale of the last term in (B 1) is thus
![]() $e^{2}P^{\prime }/R^{2}$
. Accordingly, for
$e^{2}P^{\prime }/R^{2}$
. Accordingly, for
![]() $e\ll R$
the expansion (B 1) becomes, as discussed after (2.16),
$e\ll R$
the expansion (B 1) becomes, as discussed after (2.16),
![]() $(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}\sim [p^{\prime }(r,0)-p^{\prime }(r,-e)]/e$
.
$(\unicode[STIX]{x2202}p^{\prime }/\unicode[STIX]{x2202}z)_{z=0}\sim [p^{\prime }(r,0)-p^{\prime }(r,-e)]/e$
.
Appendix C. Pressure term
 $P_{1}$
for vanishing
$P_{1}$
for vanishing
 $\unicode[STIX]{x1D6FD}$
$\unicode[STIX]{x1D6FD}$
Defining the dilogarithmic function dilog as (Abramowitz & Stegun Reference Abramowitz and Stegun1965)
and setting
![]() $u=s^{2}$
, the pressure term
$u=s^{2}$
, the pressure term
![]() $P_{1}$
is found by running Maple software to take the following form:
$P_{1}$
is found by running Maple software to take the following form:
 $$\begin{eqnarray}\displaystyle P_{1}(s) & = & \displaystyle \frac{3\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{1024}[\text{dilog}(H)-\text{dilog}(1+\tilde{\unicode[STIX]{x1D706}}H/4)]+\frac{3\tilde{\unicode[STIX]{x1D706}}(4+\tilde{\unicode[STIX]{x1D706}}^{2})}{1024(4+\tilde{\unicode[STIX]{x1D706}})}\text{dilog}\left(\frac{4+\tilde{\unicode[STIX]{x1D706}}H}{4+\tilde{\unicode[STIX]{x1D706}}}\right)\nonumber\\ \displaystyle & & \displaystyle -\left\{\frac{3\tilde{\unicode[STIX]{x1D706}}^{3}[7\tilde{\unicode[STIX]{x1D706}}+256\,Y(\tilde{\unicode[STIX]{x1D706}})]}{32768(4+\tilde{\unicode[STIX]{x1D706}})}+\frac{3\tilde{\unicode[STIX]{x1D706}}(4+\tilde{\unicode[STIX]{x1D706}}H)}{32768H^{2}}[H(7\tilde{\unicode[STIX]{x1D706}}+8)+4]\right\}\log (4+\tilde{\unicode[STIX]{x1D706}}H)\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\left[\frac{3\tilde{\unicode[STIX]{x1D706}}(\tilde{\unicode[STIX]{x1D706}}-4)-16}{128}\right]Y(\tilde{\unicode[STIX]{x1D706}})+\frac{3\tilde{\unicode[STIX]{x1D706}}[1+2(1+\tilde{\unicode[STIX]{x1D706}})H]+4H^{2}}{2048H^{2}}\right\}\log (H)\nonumber\\ \displaystyle & & \displaystyle -\,\left\{\frac{3\tilde{\unicode[STIX]{x1D706}}[16+7\tilde{\unicode[STIX]{x1D706}}(4-\tilde{\unicode[STIX]{x1D706}})]}{32768}\right\}\log (H)+\frac{1+\tilde{\unicode[STIX]{x1D706}}}{2(4+\tilde{\unicode[STIX]{x1D706}})}\left[Y(\tilde{\unicode[STIX]{x1D706}})+\frac{3\tilde{\unicode[STIX]{x1D706}}-2}{128}\right]\log (H-1)\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{2+H(4+3\tilde{\unicode[STIX]{x1D706}})}{32H^{2}}\right]Y(\tilde{\unicode[STIX]{x1D706}})-\frac{3\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{512}(\log 2)^{2}-\frac{\unicode[STIX]{x03C0}^{2}\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{2048}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{9\tilde{\unicode[STIX]{x1D706}}}{65536}\log (\tilde{\unicode[STIX]{x1D706}})\log (4+\tilde{\unicode[STIX]{x1D706}}H)+\frac{3\tilde{\unicode[STIX]{x1D706}}^{2}}{65536}[2(8+7\tilde{\unicode[STIX]{x1D706}})-3\tilde{\unicode[STIX]{x1D706}}^{2}\log (\tilde{\unicode[STIX]{x1D706}})]\log (\tilde{\unicode[STIX]{x1D706}}H)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{2048}\left[(\log (H))^{2}-4\log 2\log (\tilde{\unicode[STIX]{x1D706}}H)-\log (4+\tilde{\unicode[STIX]{x1D706}})\log \left(\frac{4+\tilde{\unicode[STIX]{x1D706}}}{(H-1)^{2}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{8192H^{3}}\left[(42\tilde{\unicode[STIX]{x1D706}}^{2}+36\tilde{\unicode[STIX]{x1D706}}-16)H^{2}+4(3\tilde{\unicode[STIX]{x1D706}}-2)H-\frac{16}{3}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{1}(s) & = & \displaystyle \frac{3\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{1024}[\text{dilog}(H)-\text{dilog}(1+\tilde{\unicode[STIX]{x1D706}}H/4)]+\frac{3\tilde{\unicode[STIX]{x1D706}}(4+\tilde{\unicode[STIX]{x1D706}}^{2})}{1024(4+\tilde{\unicode[STIX]{x1D706}})}\text{dilog}\left(\frac{4+\tilde{\unicode[STIX]{x1D706}}H}{4+\tilde{\unicode[STIX]{x1D706}}}\right)\nonumber\\ \displaystyle & & \displaystyle -\left\{\frac{3\tilde{\unicode[STIX]{x1D706}}^{3}[7\tilde{\unicode[STIX]{x1D706}}+256\,Y(\tilde{\unicode[STIX]{x1D706}})]}{32768(4+\tilde{\unicode[STIX]{x1D706}})}+\frac{3\tilde{\unicode[STIX]{x1D706}}(4+\tilde{\unicode[STIX]{x1D706}}H)}{32768H^{2}}[H(7\tilde{\unicode[STIX]{x1D706}}+8)+4]\right\}\log (4+\tilde{\unicode[STIX]{x1D706}}H)\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\left[\frac{3\tilde{\unicode[STIX]{x1D706}}(\tilde{\unicode[STIX]{x1D706}}-4)-16}{128}\right]Y(\tilde{\unicode[STIX]{x1D706}})+\frac{3\tilde{\unicode[STIX]{x1D706}}[1+2(1+\tilde{\unicode[STIX]{x1D706}})H]+4H^{2}}{2048H^{2}}\right\}\log (H)\nonumber\\ \displaystyle & & \displaystyle -\,\left\{\frac{3\tilde{\unicode[STIX]{x1D706}}[16+7\tilde{\unicode[STIX]{x1D706}}(4-\tilde{\unicode[STIX]{x1D706}})]}{32768}\right\}\log (H)+\frac{1+\tilde{\unicode[STIX]{x1D706}}}{2(4+\tilde{\unicode[STIX]{x1D706}})}\left[Y(\tilde{\unicode[STIX]{x1D706}})+\frac{3\tilde{\unicode[STIX]{x1D706}}-2}{128}\right]\log (H-1)\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{2+H(4+3\tilde{\unicode[STIX]{x1D706}})}{32H^{2}}\right]Y(\tilde{\unicode[STIX]{x1D706}})-\frac{3\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{512}(\log 2)^{2}-\frac{\unicode[STIX]{x03C0}^{2}\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{2048}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{9\tilde{\unicode[STIX]{x1D706}}}{65536}\log (\tilde{\unicode[STIX]{x1D706}})\log (4+\tilde{\unicode[STIX]{x1D706}}H)+\frac{3\tilde{\unicode[STIX]{x1D706}}^{2}}{65536}[2(8+7\tilde{\unicode[STIX]{x1D706}})-3\tilde{\unicode[STIX]{x1D706}}^{2}\log (\tilde{\unicode[STIX]{x1D706}})]\log (\tilde{\unicode[STIX]{x1D706}}H)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3\tilde{\unicode[STIX]{x1D706}}(1+\tilde{\unicode[STIX]{x1D706}})}{2048}\left[(\log (H))^{2}-4\log 2\log (\tilde{\unicode[STIX]{x1D706}}H)-\log (4+\tilde{\unicode[STIX]{x1D706}})\log \left(\frac{4+\tilde{\unicode[STIX]{x1D706}}}{(H-1)^{2}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{8192H^{3}}\left[(42\tilde{\unicode[STIX]{x1D706}}^{2}+36\tilde{\unicode[STIX]{x1D706}}-16)H^{2}+4(3\tilde{\unicode[STIX]{x1D706}}-2)H-\frac{16}{3}\right],\end{eqnarray}$$
where it is recalled that
![]() $H=1+s^{2}$
and the new quantity
$H=1+s^{2}$
and the new quantity
![]() $Y(\tilde{\unicode[STIX]{x1D706}})$
is defined as
$Y(\tilde{\unicode[STIX]{x1D706}})$
is defined as
![]() $Y(\tilde{\unicode[STIX]{x1D706}})=[2-3\tilde{\unicode[STIX]{x1D706}}++3\tilde{\unicode[STIX]{x1D706}}(4+\tilde{\unicode[STIX]{x1D706}})\log (4+\tilde{\unicode[STIX]{x1D706}})/4]/128$
.
$Y(\tilde{\unicode[STIX]{x1D706}})=[2-3\tilde{\unicode[STIX]{x1D706}}++3\tilde{\unicode[STIX]{x1D706}}(4+\tilde{\unicode[STIX]{x1D706}})\log (4+\tilde{\unicode[STIX]{x1D706}})/4]/128$
.