1. Introduction
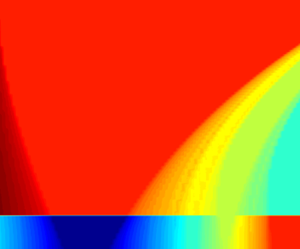
Combustion instability is a catastrophic phenomenon characterised by self-sustained, large-amplitude pressure oscillations. When pressure fluctuations in the flow field are in-phase with heat release rate fluctuations, there is a growth of the oscillation amplitude, described by the Rayleigh criterion (Rayleigh Reference Rayleigh1878). Although several active and passive control techniques (Crocco Reference Crocco1969; Candel Reference Candel1992; Schadow & Gutmark Reference Schadow and Gutmark1992; Dowling & Morgans Reference Dowling and Morgans2005) are proposed to mitigate combustion instability, understanding the mechanism of instability in a given configuration is still a difficult task. This is partly owing to a variety of mechanisms such as flame–surface fluctuations, equivalence ratio fluctuations and hydrodynamic instabilities (Candel Reference Candel2002; Lieuwen & Yang Reference Lieuwen and Yang2005) that drive combustion instability either individually or in a combined fashion. Vortex shedding is one such driving mechanism. Gas turbine combustion chambers involve carefully designed geometries that facilitate the mixing of air, fuel and hot products for efficient burning, stable anchored flame and low ![]() $\textrm {NO}_{x}$ emissions. Flame anchoring requires recirculation zones. In the afterburners of jet engines and ramjets, the flame is stabilised behind bluff bodies (Hertzberg, Shepherd & Talbot Reference Hertzberg, Shepherd and Talbot1991; Schadow & Gutmark Reference Schadow and Gutmark1992). Recirculation zones formed behind them facilitate vortex shedding (figure 1). Gas turbine main combustors have a dump plane with a swirl burner that creates vortex shedding (Huang et al. Reference Huang, Sung, Hsieh and Yang2003; Huang & Yang Reference Huang and Yang2009). In such designs, large vortex structures act as a driving element for instability.
$\textrm {NO}_{x}$ emissions. Flame anchoring requires recirculation zones. In the afterburners of jet engines and ramjets, the flame is stabilised behind bluff bodies (Hertzberg, Shepherd & Talbot Reference Hertzberg, Shepherd and Talbot1991; Schadow & Gutmark Reference Schadow and Gutmark1992). Recirculation zones formed behind them facilitate vortex shedding (figure 1). Gas turbine main combustors have a dump plane with a swirl burner that creates vortex shedding (Huang et al. Reference Huang, Sung, Hsieh and Yang2003; Huang & Yang Reference Huang and Yang2009). In such designs, large vortex structures act as a driving element for instability.

Figure 1. Schematic of the nature of vortex shedding often observed in V-gutters of turbojet afterburners and backward-facing step of swirl-stabilised combustors. The physical features described by the lower-order model (Matveev & Culick Reference Matveev and Culick2003) are illustrated in (b,d).
The earliest experiments on premixed dump combustors (flame anchored over a backward-facing step) by Zukoski (Reference Zukoski1985) indicated a general mechanism that triggers vortex-driven combustion instability. They observed that the shear layer formed at the edge of the dump plane rolls up to form a vortex structure. The fuel–air mixture is trapped in this vortex. The recirculation zone formed just downstream of the dump plane has hot products formed owing to the presence of flame. The presence of high shear in the vortex does not allow the trapped reactants and products in the recirculation zone to mix. When this convecting vortex impinges on sidewalls and obstacles, it disintegrates, leading to quick mixing between hot products and reactants. This mechanism leads to a sudden heat release rate. In turn, this unsteady heat release creates acoustic waves. The upstream propagating wave perturbs the shear layer, which in turn generates vortices. This perturbation alters the vortex shedding frequency and the phase of shedding (Anderson & Yang Reference Anderson and Yang1995; Keller Reference Keller1995). A feedback loop is formed between the vortex shedding and the acoustic waves, which overcomes damping in the system and leads to combustion instability. Poinsot et al. (Reference Poinsot, Trouve, Veynante, Candel and Esposito1987) introduced the concept of vortex-acoustic lock-in through their experiments performed in premixed dump combustors. Their results indicated that during instability, vortex shedding occurs at the frequency of the acoustic mode of the combustor. Heat release rate fluctuations also occur in synchronisation with vortex shedding, confirming that the latter drives instability. Similar investigations on lock-in were reported by Chakravarthy et al. (Reference Chakravarthy, Shreenivasan, Boehm, Dreizler and Janicka2007) for a non-premixed half-dump combustor. They observed that the dominant frequency moved from vortex shedding to acoustic mode during the onset of lock-in. Previous investigators have performed experiments, wherein the main idea was to show vortex shedding occurring at the frequency of the chamber acoustic mode. Recently, our group has performed experiments (Singh & Mariappan Reference Singh and Mariappan2021) on a premixed, axisymmetric bluff-body stabilised combustor, where the system is progressively taken from a no lock-in to a lock-in region. In this study, various identifiable intermediate regions on route to lock-in were observed. In all of the aforementioned experimental investigations, it was found that the frequency of the acoustic mode was hardly altered. Therefore, the self-excited problem of vortex-acoustic lock-in can be replaced by an equivalent externally forced problem, where the external excitation (mostly in the form of velocity fluctuations) represents the acoustic field. The excitation is mostly realised in the form of velocity fluctuations upstream of the separation edge, where the genesis of the vortex begins. The response of the shedding process is measured in terms of the vortex shedding frequency.
Two academic groups, the Georgia Institute of Technology and Cambridge University, have performed significant investigations to understand lock-in under external excitation. Emerson et al. (Reference Emerson, O'Connor, Noble and Lieuwen2012) experimentally reported that vortex shedding occurs at the forcing frequency when the latter is near the natural vortex shedding frequency. This lock-in is found to be weakened when the density ratio between the unburnt and burnt gas increases. On the other hand, Emerson, Murphy & Lieuwen (Reference Emerson, Murphy and Lieuwen2013) and Emerson & Lieuwen (Reference Emerson and Lieuwen2015) reported abatement in heat release rate oscillations during lock-in. This observation is contradictory with the conventional perception that the response of the flame is strong when excited near the natural hydrodynamic instability frequency.
The other group performed experiments, where they externally excited reacting (Li & Juniper Reference Li and Juniper2013b; Balusamy et al. Reference Balusamy, Li, Han, Juniper and Hochgreb2015) and non-reacting (Li & Juniper Reference Li and Juniper2013a,Reference Li and Juniperc) jets. The reacting case was self-excited owing to the feedback from the acoustic field. In this case, the external excitation was studied from the context of active control of the self-excited instability. In these studies, the flow field was subjected to a single-frequency (![]() $f$) sinusoidal excitation of known amplitude (
$f$) sinusoidal excitation of known amplitude (![]() $A$). Its response was reported in terms of pressure and heat release rate (in the reacting flow case) fluctuations. They observed that heat release fluctuations occurred at the forcing frequency (lock-in) when the excitation amplitude had a particular threshold value. In the
$A$). Its response was reported in terms of pressure and heat release rate (in the reacting flow case) fluctuations. They observed that heat release fluctuations occurred at the forcing frequency (lock-in) when the excitation amplitude had a particular threshold value. In the ![]() $A - f$ plane, the threshold amplitude represented a V-shape boundary stemmed at
$A - f$ plane, the threshold amplitude represented a V-shape boundary stemmed at ![]() $f=1$ (
$f=1$ (![]() $f$ being normalised by the natural hydrodynamic frequency). When the forcing parameters were within this boundary, the self-excited system responded at the forcing frequency. These experimental results were shown to compare well with lower-order mathematical models (Van der Pol and Landau–Stuart model). In addition, the route to lock-in from the perspective of the attractor in phase space was studied. Recent experimental investigations (Guan, Murugesan & Li Reference Guan, Murugesan and Li2018) show the transition from lock-in to non-chaotic and chaotic dynamics at large-amplitude excitation. Furthermore, Guan et al. (Reference Guan, He, Murugesan, Li, Liu and Li2019b) used large-amplitude forcing for a short time period to switch from a large-amplitude unstable mode to a lower-amplitude mode. In this case, the forcing locks the system to the latter lower-amplitude mode. Therefore, this short-term forcing was proposed as a control strategy.
$f$ being normalised by the natural hydrodynamic frequency). When the forcing parameters were within this boundary, the self-excited system responded at the forcing frequency. These experimental results were shown to compare well with lower-order mathematical models (Van der Pol and Landau–Stuart model). In addition, the route to lock-in from the perspective of the attractor in phase space was studied. Recent experimental investigations (Guan, Murugesan & Li Reference Guan, Murugesan and Li2018) show the transition from lock-in to non-chaotic and chaotic dynamics at large-amplitude excitation. Furthermore, Guan et al. (Reference Guan, He, Murugesan, Li, Liu and Li2019b) used large-amplitude forcing for a short time period to switch from a large-amplitude unstable mode to a lower-amplitude mode. In this case, the forcing locks the system to the latter lower-amplitude mode. Therefore, this short-term forcing was proposed as a control strategy.
Matveev & Culick (Reference Matveev and Culick2003) introduced a reduced-order mathematical model that gives the circulation strength of the vortex dependant on the unsteady flow field. For a dump combustor model, they performed a mathematical study using the reduced-order model, considering vortex shedding, acoustic field and combustion as driving mechanisms of the instability in the combustor. Using the one-dimensional wave equation, they obtained the amplitude of pressure fluctuations in the combustion chamber and compared their results with the available experimental data. The lock-in characteristics of the model compare well with the experimental results. Therefore, this commendable lower-order model is frequently used for numerical analyses of combustion instability driven by vortex shedding (Pastrone, Casalino & Carmicino Reference Pastrone, Casalino and Carmicino2014; Nair & Sujith Reference Nair and Sujith2015; Pawar et al. Reference Pawar, Seshadri, Unni and Sujith2017).
Our group used the aforementioned Matveev model to obtain analytical predictions of the onset of lock-in (Singaravelu & Mariappan Reference Singaravelu and Mariappan2016), which compared well with the experimental results of Chakravarthy et al. (Reference Chakravarthy, Shreenivasan, Boehm, Dreizler and Janicka2007). Since the analysis was linear, the extent of lock-in could not be determined. Later, nonlinear terms describing vortex shedding were included (Britto & Mariappan Reference Britto and Mariappan2019a); however, the self-excited thermoacoustic system was replaced by a forced system for analytical tractability. Lock-in characteristics such as onset and extent were determined for single-frequency (![]() $f$) velocity excitation at various amplitudes (
$f$) velocity excitation at various amplitudes (![]() $A$). Analytical expressions for
$A$). Analytical expressions for ![]() $1\,{:}\,1, 2\,{:}\,1, \ldots , p\,{:}\,1$ lock-in boundaries in the
$1\,{:}\,1, 2\,{:}\,1, \ldots , p\,{:}\,1$ lock-in boundaries in the ![]() $A - f$ plane were presented. A general p : q lock-in (in the context of single-frequency excitation) indicates that forcing and vortex shedding frequencies are in the ratio
$A - f$ plane were presented. A general p : q lock-in (in the context of single-frequency excitation) indicates that forcing and vortex shedding frequencies are in the ratio ![]() $p/q$, where
$p/q$, where ![]() $p/q$ is a rational number. In comparison to the previous models presented for lock-in (Li & Juniper Reference Li and Juniper2013a), the Matveev & Culick (Reference Matveev and Culick2003) model shows two additional features. (1) The presence of a critical excitation frequency (given as
$p/q$ is a rational number. In comparison to the previous models presented for lock-in (Li & Juniper Reference Li and Juniper2013a), the Matveev & Culick (Reference Matveev and Culick2003) model shows two additional features. (1) The presence of a critical excitation frequency (given as ![]() $f_{min}$ in § 3 of Britto & Mariappan Reference Britto and Mariappan2019a), below which lock-in did not occur for any excitation amplitude. (2) There was an upper critical amplitude, above which a transition out of lock-in occurred. This critical amplitude was found to depend on the particular p : 1 lock-in state. Experiments performed by Guan et al. (Reference Guan, Murugesan and Li2018) showed the latter feature. Apart from lock-in behaviour, Britto & Mariappan (Reference Britto and Mariappan2019b) identified that for physically relevant forcing parameters (
$f_{min}$ in § 3 of Britto & Mariappan Reference Britto and Mariappan2019a), below which lock-in did not occur for any excitation amplitude. (2) There was an upper critical amplitude, above which a transition out of lock-in occurred. This critical amplitude was found to depend on the particular p : 1 lock-in state. Experiments performed by Guan et al. (Reference Guan, Murugesan and Li2018) showed the latter feature. Apart from lock-in behaviour, Britto & Mariappan (Reference Britto and Mariappan2019b) identified that for physically relevant forcing parameters (![]() $0\leqslant A \leqslant 1$), the Matveev & Culick (Reference Matveev and Culick2003) model does not exhibit chaotic dynamics.
$0\leqslant A \leqslant 1$), the Matveev & Culick (Reference Matveev and Culick2003) model does not exhibit chaotic dynamics.
All the previously mentioned investigations focused on the study of lock-in in the presence of single-frequency excitation. However, even in a simple laminar self-excited premixed flame, multiple frequency peaks in thermoacoustic oscillations were reported (Kabiraj & Sujith Reference Kabiraj and Sujith2012; Kabiraj et al. Reference Kabiraj, Saurabh, Wahi and Sujith2012a; Kabiraj, Sujith & Wahi Reference Kabiraj, Sujith and Wahi2012b). These peaks occur owing to the presence of quasi-periodic (incommensurate dominant frequencies ![]() $f_1$ and
$f_1$ and ![]() $f_2$), higher-periodic (
$f_2$), higher-periodic (![]() $f_1,f_2=f_1/2$), superharmonic (
$f_1,f_2=f_1/2$), superharmonic (![]() $f_1, f_2=2f_1$) oscillations and their combinations. Furthermore, chaotic oscillations were reported, which also presents multiple peaks. Practical combustors do exhibit multiple peaks (Lieuwen Reference Lieuwen2003). A brief discussion on the experimental and theoretical investigations pertaining to the study of flame response to multiple-frequency excitation is made subsequently.
$f_1, f_2=2f_1$) oscillations and their combinations. Furthermore, chaotic oscillations were reported, which also presents multiple peaks. Practical combustors do exhibit multiple peaks (Lieuwen Reference Lieuwen2003). A brief discussion on the experimental and theoretical investigations pertaining to the study of flame response to multiple-frequency excitation is made subsequently.
The following experimental studies explore the effects of multiple-frequency excitation on combustion instability: Joos & Vortmeyer (Reference Joos and Vortmeyer1986), Balachandran, Dowling & Mastorakos (Reference Balachandran, Dowling and Mastorakos2008), Kim (Reference Kim2017). Balachandran et al. (Reference Balachandran, Dowling and Mastorakos2008) studied the response of a lean premixed flame to two-frequency inlet velocity perturbations. Depending on the excitation amplitude, the introduction of a second forcing component (harmonic of the first) altered vortex formation, shedding frequency and flame response. In the works of Kim (Reference Kim2017) on both premixed and partially premixed flame, nonlinear interactions between the fundamental and higher harmonics of pressure, velocity and heat release fluctuations were analysed. Kim (Reference Kim2017) observed that the interaction between the fundamental and higher harmonics of the inlet velocity fluctuation leads to a transition of heat release response from a linear to a nonlinear regime. This transition marked a significant increase in the pressure fluctuations of the combustion chamber.
On the theoretical front, Moeck & Paschereit (Reference Moeck and Paschereit2012), Orchini & Juniper (Reference Orchini and Juniper2016), Acharya, Bothien & Lieuwen (Reference Acharya, Bothien and Lieuwen2018), and Haeringer, Merk & Polifke (Reference Haeringer, Merk and Polifke2019) presented methodologies to predict limit-cycle oscillations in thermoacoustic systems, containing multiple frequencies in the velocity field. These works were dedicated to modelling a flame using a multi-input flame describing function, having multiple (velocity) excitation inputs at various frequencies. Using the aforementioned flame model, Moeck & Paschereit (Reference Moeck and Paschereit2012) and Orchini & Juniper (Reference Orchini and Juniper2016) presented a harmonic-balance approach to calculate the amplitude and frequency of limit-cycle oscillations having multiple unstable thermoacoustic modes. Their approach was shown to effectively predict the interactions between the two unstable modes observed in experiments. Recently, a multi-input model describing the function and harmonic balance framework was employed successfully to predict limit-cycle amplitudes in an annular combustor, configured to exhibit mode interactions and mode switching (Humbert et al. Reference Humbert, Gensini, Andreini, Paschereit and Orchini2021).
Limit-cycle oscillations caused by additional frequency components in the flow field are also studied using coupled oscillator models (Acharya et al. Reference Acharya, Bothien and Lieuwen2018). In this mathematical work, time-dependant Galerkin modes of acoustic pressure and velocity fluctuation are considered as two sinusoidal functions with time-varying amplitude and frequency. Two amplitude equations are obtained, through which several observations were presented in relation to the spacing effect between the frequencies. Interestingly, they identified that the first unstable mode exhibited dominance in the limit-cycle oscillations for a larger frequency spacing, although the second mode had a higher linear growth rate.
The above literature review emphasises that the presence of additional frequency components with comparable amplitudes to that of the primary component significantly affects the flame response. Therefore, we believe that they also have an important impact on vortex-acoustic lock-in. To the best of the authors’ knowledge, there have been no formal studies performed to understand lock-in caused by multiple frequency excitation. As a first step, we attempt to study it from a theoretical perspective using the Matveev & Culick (Reference Matveev and Culick2003) model. Specifically, we explore the difference in lock-in characteristics between single- and two-frequency excitations. The aforementioned reduced-order mathematical model is chosen, as it describes several experimentally reported dynamics associated with vortex-acoustic lock-in under single-frequency excitation (Britto & Mariappan Reference Britto and Mariappan2019a). External periodic velocity excitation that consists of two sinusoidal components, namely primary and secondary excitation, is introduced. Although the theoretical study made in this paper is applicable for any general two-frequency excitations, which are commensurate, the results are presented only for sub- and superharmonic secondary excitations. The effect of these components on the vortex shedding behaviour is studied in terms of cobweb diagrams.
The rest of the paper is arranged as follows. Section 2 begins with using the Matveev & Culick (Reference Matveev and Culick2003) model to derive a discrete map equation that relates the time instances of successive vortex shedding in a two-frequency excited flow. In § 3, we study phase portraits of the vortex shedding time period using numerically obtained iterations. Critical differences between single- and two-frequency excitations are highlighted. The phenomenon of lock-in is studied in the context of phase lock-in. It is identified as synchronisation of the generalised phase, obtained using the Hilbert transform. Its details are discussed in § 4. The dynamics of phase points during the excitation is studied geometrically, and an analytical condition to identify a generalised p : q lock-in in terms of these phase points is derived. In § 5, the occurrence of lock-in and subsequent bifurcations are studied using return maps and cobweb diagrams. A detailed explanation of the bifurcations that are observed during two-frequency excitation is presented in § 5.1. In § 6, we provide analytical solutions for a few geometrical characteristic features of the lock-in boundary observed during two-frequency excitation. Finally, the notable results and conclusions of this paper are summarised in § 7.
2. Governing equation for vortex shedding
A mathematical model for the vortex shedding process in inviscid flows was introduced by Matveev & Culick (Reference Matveev and Culick2003) to study combustion instability in dump combustors. The non-dimensional form of the equations governing the vortex shedding process is given as follows:
Non-dimensionalisation is performed with mean flow velocity ![]() $\bar {u}$ and steady-state vortex shedding frequency
$\bar {u}$ and steady-state vortex shedding frequency ![]() $1/\Delta t_{st}$ as reference parameters. Further details are discussed in Britto & Mariappan (Reference Britto and Mariappan2019a). The variables
$1/\Delta t_{st}$ as reference parameters. Further details are discussed in Britto & Mariappan (Reference Britto and Mariappan2019a). The variables ![]() $\varGamma _{m}$ and
$\varGamma _{m}$ and ![]() $\varGamma _{sep}$ are the non-dimensional circulation strength of the
$\varGamma _{sep}$ are the non-dimensional circulation strength of the ![]() $m$th vortex and the circulation threshold for shedding, respectively. Non-dimensional velocity fluctuations in the flow near the separation edge of the step/bluff body geometry are given by
$m$th vortex and the circulation threshold for shedding, respectively. Non-dimensional velocity fluctuations in the flow near the separation edge of the step/bluff body geometry are given by ![]() $u'(t)$.
$u'(t)$.
Figure 1(a) is a schematic of a turbojet afterburner designed with a V-gutter for flame stabilisation. Local velocity fluctuations near the separation edge of the V-gutter cause hydrodynamic fluctuations, leading to fluctuations in vortex shedding frequency. A similar physical mechanism occurs in combustors designed with a swirled flow over a backward-facing step (shown in (c)). In such configurations, the recirculation zone holds the flame owing to its low-velocity region. The velocity gradient between the recirculation zone and the flow causes hydrodynamic fluctuations, which alter the vortex shedding frequency. Idealised versions represented by Matveev & Culick (Reference Matveev and Culick2003) of the previous two configurations (a,c) are shown in (b) and (d), respectively. In the ideal case, the shed vortex is assumed to convect downstream with the base-flow velocity, with a constant circulation strength. As already mentioned, in this paper, we focus on two-frequency excitation, where the external velocity perturbation ![]() $u'(t)$ is chosen as a sum of two sinusoidal forcings of the form shown below,
$u'(t)$ is chosen as a sum of two sinusoidal forcings of the form shown below,
where ![]() $f_p$ and
$f_p$ and ![]() $f_s$ are primary and secondary excitation frequencies, respectively. Similarly,
$f_s$ are primary and secondary excitation frequencies, respectively. Similarly, ![]() $A_p$ and
$A_p$ and ![]() $A_s$ are their respective excitation amplitudes. Henceforth, the two terms in (2.3) are called primary (subscript
$A_s$ are their respective excitation amplitudes. Henceforth, the two terms in (2.3) are called primary (subscript ![]() $p$) and secondary (subscript
$p$) and secondary (subscript ![]() $s$) excitation components in this paper. It should be noted that these terminologies are chosen based on the excitation frequency rather than amplitude. We use the term ‘primary excitation’ when the excitation forcing frequency is near the natural vortex shedding frequency. For the secondary excitation, its frequency is rationally related (
$s$) excitation components in this paper. It should be noted that these terminologies are chosen based on the excitation frequency rather than amplitude. We use the term ‘primary excitation’ when the excitation forcing frequency is near the natural vortex shedding frequency. For the secondary excitation, its frequency is rationally related (![]() $f_s=p_f f_p/q_f$,
$f_s=p_f f_p/q_f$, ![]() $p_f$ and
$p_f$ and ![]() $q_f$ are integers) to the primary excitation frequency. The initial phase difference between
$q_f$ are integers) to the primary excitation frequency. The initial phase difference between ![]() $f_p$ and
$f_p$ and ![]() $f_s$ is denoted by
$f_s$ is denoted by ![]() $\gamma$. Although the initial phase does influence the results, we have chosen
$\gamma$. Although the initial phase does influence the results, we have chosen ![]() $\gamma =0$ throughout this paper. The reason for this choice is discussed in § 5.
$\gamma =0$ throughout this paper. The reason for this choice is discussed in § 5.
Equations (2.1) and (2.2) together represent an integrate and fire model. The value of ![]() $\varGamma _{m}(t)$, associated with the
$\varGamma _{m}(t)$, associated with the ![]() $m$th vortex increases nonlinearly in time, till a threshold value (
$m$th vortex increases nonlinearly in time, till a threshold value (![]() $\varGamma _{sep}(t$)) is attained (defined by (2.2)). When
$\varGamma _{sep}(t$)) is attained (defined by (2.2)). When ![]() $\varGamma _{m}(t)=\varGamma _{sep}(t)$, the
$\varGamma _{m}(t)=\varGamma _{sep}(t)$, the ![]() $m$th vortex is shed. Specifically, for
$m$th vortex is shed. Specifically, for ![]() $m=1$,
$m=1$, ![]() $\varGamma _{1}(t)$ increases from 0 (at
$\varGamma _{1}(t)$ increases from 0 (at ![]() $t=0$) until a time
$t=0$) until a time ![]() $t_1$, when
$t_1$, when ![]() $\varGamma _{1}(t_1)=\varGamma _{sep}(t_1)$. At
$\varGamma _{1}(t_1)=\varGamma _{sep}(t_1)$. At ![]() $t_1$, the first vortex is considered to be shed instantly and the circulation of the second vortex
$t_1$, the first vortex is considered to be shed instantly and the circulation of the second vortex ![]() $\varGamma _{2}$ is reset to zero. Similar to the first vortex, the increase in circulation and subsequent shedding of the second vortex is calculated. The corresponding shedding time
$\varGamma _{2}$ is reset to zero. Similar to the first vortex, the increase in circulation and subsequent shedding of the second vortex is calculated. The corresponding shedding time ![]() $t_2$ is noted. The procedure is repeated to obtain shedding instances (
$t_2$ is noted. The procedure is repeated to obtain shedding instances (![]() $t_m$) of an
$t_m$) of an ![]() $m$th vortex. The time period between successive shed vortices is called an instantaneous vortex shedding time period:
$m$th vortex. The time period between successive shed vortices is called an instantaneous vortex shedding time period: ![]() $\Delta t_m=t_m-t_{m-1}$.
$\Delta t_m=t_m-t_{m-1}$.
Figure 2(a) illustrates the evolution and reset of ![]() $\varGamma _{m}$ (black curve) over time
$\varGamma _{m}$ (black curve) over time ![]() $t$ for single-frequency excitation having the parameters
$t$ for single-frequency excitation having the parameters ![]() $f_p=0.8$,
$f_p=0.8$, ![]() $A_p=0.5$ and
$A_p=0.5$ and ![]() $A_s=0$. The evolution of threshold circulation
$A_s=0$. The evolution of threshold circulation ![]() $\varGamma _{sep}(t)$ is shown as a blue curve. Vortex shedding time instances (
$\varGamma _{sep}(t)$ is shown as a blue curve. Vortex shedding time instances (![]() $\varGamma _{m}=\varGamma _{sep}$) are illustrated with blue dots. The corresponding shedding time periods are indicated as
$\varGamma _{m}=\varGamma _{sep}$) are illustrated with blue dots. The corresponding shedding time periods are indicated as ![]() $\Delta t_1,\Delta t_2,\ldots$. The continuous nonlinear growth of
$\Delta t_1,\Delta t_2,\ldots$. The continuous nonlinear growth of ![]() $\varGamma _m(t)$ and its reset, resulting in discrete vortex shedding events can be observed in panel (a).
$\varGamma _m(t)$ and its reset, resulting in discrete vortex shedding events can be observed in panel (a).

Figure 2. Time evolution of ![]() $\varGamma _{sep}$ and
$\varGamma _{sep}$ and ![]() $\varGamma _{m}$ for
$\varGamma _{m}$ for ![]() $f_p=0.8$,
$f_p=0.8$, ![]() $A_p=0.5$, (a)
$A_p=0.5$, (a) ![]() $A_s=0$. Here,
$A_s=0$. Here, ![]() $\varGamma _{m}(t)$ and threshold circulation
$\varGamma _{m}(t)$ and threshold circulation ![]() $\varGamma _{sep}(t)$ are shown using black and blue curves, respectively. Vortex shedding time instances (
$\varGamma _{sep}(t)$ are shown using black and blue curves, respectively. Vortex shedding time instances (![]() $\varGamma _{m}=\varGamma _{sep}$) obtained from (3.1) are marked with blue dots. The vortex shedding time period is obtained from the relation
$\varGamma _{m}=\varGamma _{sep}$) obtained from (3.1) are marked with blue dots. The vortex shedding time period is obtained from the relation ![]() $\Delta t_m=t_m-t_{m-1}$ after every reset of
$\Delta t_m=t_m-t_{m-1}$ after every reset of ![]() $\varGamma _{m}$. Arrows indicate the course of
$\varGamma _{m}$. Arrows indicate the course of ![]() $\varGamma _m(t)$ over time. In (b), a comparison of
$\varGamma _m(t)$ over time. In (b), a comparison of ![]() $\varGamma _{sep}(t)$ between single- (blue curve,
$\varGamma _{sep}(t)$ between single- (blue curve, ![]() $A_s=0$) and two-frequency (red curve,
$A_s=0$) and two-frequency (red curve, ![]() $A_s=0.1,f_s=2f_p$) excitation is shown. The evolution of shedding time period
$A_s=0.1,f_s=2f_p$) excitation is shown. The evolution of shedding time period ![]() $\Delta t_m$ in comparison with single- and two-frequency excitation is shown in (c).
$\Delta t_m$ in comparison with single- and two-frequency excitation is shown in (c).
In figure 2(b), a comparison of shedding time instances between single- (a) and two-frequency (![]() $f_s=2 f_p$,
$f_s=2 f_p$, ![]() $A_s=0.1$, other parameters are the same as in (a)) excitations is illustrated. For clarity, only the
$A_s=0.1$, other parameters are the same as in (a)) excitations is illustrated. For clarity, only the ![]() $\varGamma _{sep}$ curves are shown. Here,
$\varGamma _{sep}$ curves are shown. Here, ![]() $\varGamma _{sep}$ and shedding instances for single- and two-frequency excitations are indicated as blue/red curves and blue/red dots, respectively. Note that the amplitude of the secondary excitation is
$\varGamma _{sep}$ and shedding instances for single- and two-frequency excitations are indicated as blue/red curves and blue/red dots, respectively. Note that the amplitude of the secondary excitation is ![]() $20\,\%$ of the primary excitation and
$20\,\%$ of the primary excitation and ![]() $\varGamma _{sep}(t)$ is found to change slightly in shape. This alters the shedding dynamics to a large extent. Shedding occurs at far different time instances between single (blue dots) and two-frequency (red dots) excitations (b). The impact of the secondary component on the vortex shedding time period
$\varGamma _{sep}(t)$ is found to change slightly in shape. This alters the shedding dynamics to a large extent. Shedding occurs at far different time instances between single (blue dots) and two-frequency (red dots) excitations (b). The impact of the secondary component on the vortex shedding time period ![]() $\varDelta t_m$ is illustrated in (c). The iterations (
$\varDelta t_m$ is illustrated in (c). The iterations (![]() $m$) of
$m$) of ![]() $\Delta t_m$ during single-frequency excitation appear to reach a constant value indicating that vortex shedding occurs at a constant frequency (period-1 state). Whereas, owing to the inclusion of a secondary component, the period-1 state collapses and shedding exhibits a higher-periodic behaviour. To understand the overall influence of secondary excitation, we perform a systematic study as follows.
$\Delta t_m$ during single-frequency excitation appear to reach a constant value indicating that vortex shedding occurs at a constant frequency (period-1 state). Whereas, owing to the inclusion of a secondary component, the period-1 state collapses and shedding exhibits a higher-periodic behaviour. To understand the overall influence of secondary excitation, we perform a systematic study as follows.
3. Numerical investigation of secondary excitation
In this section, we numerically study the response of vortex shedding in terms of its shedding time period ![]() $\Delta t_m$ for a range of primary excitation components (
$\Delta t_m$ for a range of primary excitation components (![]() $f_p$ and
$f_p$ and ![]() $A_p$) at given secondary excitation parameters (
$A_p$) at given secondary excitation parameters (![]() $f_s$ and
$f_s$ and ![]() $A_s$). An implicit dynamical map (similar to that discussed in Britto & Mariappan Reference Britto and Mariappan2019a) in
$A_s$). An implicit dynamical map (similar to that discussed in Britto & Mariappan Reference Britto and Mariappan2019a) in ![]() $\Delta t_m$ is obtained. We substitute (2.3) into (2.1) and (2.2), and integrate (2.1) between the events: just after the shedding of the
$\Delta t_m$ is obtained. We substitute (2.3) into (2.1) and (2.2), and integrate (2.1) between the events: just after the shedding of the ![]() $(m-1)$th vortex (limits
$(m-1)$th vortex (limits ![]() $\varGamma _m=0$ at
$\varGamma _m=0$ at ![]() $t_{m-1}$) and just before the shedding of the
$t_{m-1}$) and just before the shedding of the ![]() $m$th vortex (limits
$m$th vortex (limits ![]() $\varGamma _m=\varGamma _{sep}$ at
$\varGamma _m=\varGamma _{sep}$ at ![]() $t_{m}$), to obtain
$t_{m}$), to obtain
 \begin{align}
&\frac{\left[\sin \left( 4{\rm \pi} f_{p}t_{m-1}\right) - \sin \left(4{\rm \pi}
f_{p}t_{m} \right) -4{\rm \pi} f_p \left( t_{m-1}-t_{m} \right) \right]{A_p}^{2}}{16{\rm \pi} f_p}
\nonumber\\
&\qquad +\frac{\left[\cos \left( 2{\rm \pi} f_p{t_{m-1}} \right) -\cos \left( 2{\rm \pi} f_p{t_{m}}\right)
\right]A_p}{{2{\rm \pi} f_p}}\nonumber\\
&\qquad + \frac{\left[\sin \left( 2{\rm \pi} f_s{t_{m-1}}+\gamma \right) \cos
\left( 2{\rm \pi} f_p{t_{m-1}} \right) -\sin \left( 2{\rm \pi}
f_s{t_{m}}+\gamma \right) \cos \left( 2{\rm \pi} f_p{t_{m}}
\right) \right] f_p A_p A_s}{{2{\rm \pi} f_p}^{2}-{2{\rm \pi}
f_s}^{2}}\nonumber\\
&\qquad - \frac{ \left[\cos \left( 2{\rm \pi} f_s{t_{m-1}} +\gamma \right) \sin \left( 2{\rm \pi}
f_p{t_{m-1}} \right) -\cos \left( 2{\rm \pi}
f_s{t_{m}}+\gamma\right) \sin \left( 2{\rm \pi} f_p{t_{m}}
\right) \right] f_s A_p A_s}{{2{\rm \pi} f_p}^{2}-{2{\rm \pi}
f_s}^{2}} \nonumber\\
&\qquad+ \frac{ \left[\sin \left(
4{\rm \pi} f_s{t_{m-1}}+2\gamma \right) - \sin \left( 4{\rm \pi}
f_s{t_{m}} + 2 \gamma\right) -4{\rm \pi} f_s \left(
{t_{m-1}}-{t_{m}} \right) \right] A_s^{2}}{16{\rm \pi} f_s} \nonumber\\
&\qquad +\frac{\left[ \cos \left( 2{\rm \pi} f_s{t_{m-1}} +\gamma\right) -\cos \left( 2{\rm \pi} f_s{t_{m}}
+\gamma\right) \right] A_s}{{2{\rm \pi} f_s}}-{\frac{\left( {t_{m-1}}-{t_{m}} \right)}{2}} \nonumber\\
&\quad=\frac{1}{2}\left[1+A_p \sin\left(2{\rm \pi} f_p t_{m}\right) +A_s \sin \left(2{\rm \pi} f_s
t_m+\gamma\right)\right].
\end{align}
\begin{align}
&\frac{\left[\sin \left( 4{\rm \pi} f_{p}t_{m-1}\right) - \sin \left(4{\rm \pi}
f_{p}t_{m} \right) -4{\rm \pi} f_p \left( t_{m-1}-t_{m} \right) \right]{A_p}^{2}}{16{\rm \pi} f_p}
\nonumber\\
&\qquad +\frac{\left[\cos \left( 2{\rm \pi} f_p{t_{m-1}} \right) -\cos \left( 2{\rm \pi} f_p{t_{m}}\right)
\right]A_p}{{2{\rm \pi} f_p}}\nonumber\\
&\qquad + \frac{\left[\sin \left( 2{\rm \pi} f_s{t_{m-1}}+\gamma \right) \cos
\left( 2{\rm \pi} f_p{t_{m-1}} \right) -\sin \left( 2{\rm \pi}
f_s{t_{m}}+\gamma \right) \cos \left( 2{\rm \pi} f_p{t_{m}}
\right) \right] f_p A_p A_s}{{2{\rm \pi} f_p}^{2}-{2{\rm \pi}
f_s}^{2}}\nonumber\\
&\qquad - \frac{ \left[\cos \left( 2{\rm \pi} f_s{t_{m-1}} +\gamma \right) \sin \left( 2{\rm \pi}
f_p{t_{m-1}} \right) -\cos \left( 2{\rm \pi}
f_s{t_{m}}+\gamma\right) \sin \left( 2{\rm \pi} f_p{t_{m}}
\right) \right] f_s A_p A_s}{{2{\rm \pi} f_p}^{2}-{2{\rm \pi}
f_s}^{2}} \nonumber\\
&\qquad+ \frac{ \left[\sin \left(
4{\rm \pi} f_s{t_{m-1}}+2\gamma \right) - \sin \left( 4{\rm \pi}
f_s{t_{m}} + 2 \gamma\right) -4{\rm \pi} f_s \left(
{t_{m-1}}-{t_{m}} \right) \right] A_s^{2}}{16{\rm \pi} f_s} \nonumber\\
&\qquad +\frac{\left[ \cos \left( 2{\rm \pi} f_s{t_{m-1}} +\gamma\right) -\cos \left( 2{\rm \pi} f_s{t_{m}}
+\gamma\right) \right] A_s}{{2{\rm \pi} f_s}}-{\frac{\left( {t_{m-1}}-{t_{m}} \right)}{2}} \nonumber\\
&\quad=\frac{1}{2}\left[1+A_p \sin\left(2{\rm \pi} f_p t_{m}\right) +A_s \sin \left(2{\rm \pi} f_s
t_m+\gamma\right)\right].
\end{align} Equation (3.1) represents the implicit map connecting ![]() $t_{m-1}$ and
$t_{m-1}$ and ![]() $t_m$. For a given set of primary and secondary excitation parameters, and for initial time
$t_m$. For a given set of primary and secondary excitation parameters, and for initial time ![]() $t_1=0$, we obtain the subsequent vortex shedding time instances (
$t_1=0$, we obtain the subsequent vortex shedding time instances (![]() $t_2,t_3,\ldots$) from the solution of (3.1). For every parametric set, (3.1) is solved for 2000 iterations and the first 1000 iterations are discarded to eliminate the effect of transients. Secondary excitations are restricted to be super- and subharmonics of the primary excitations. This restriction allows us to study vortex dynamics analytically in a framework using return maps and cobweb diagrams, described in this paper. Moreover, often experiments of combustion instability report multiple frequency peaks, which are either super- or subharmonic of the primary peak.
$t_2,t_3,\ldots$) from the solution of (3.1). For every parametric set, (3.1) is solved for 2000 iterations and the first 1000 iterations are discarded to eliminate the effect of transients. Secondary excitations are restricted to be super- and subharmonics of the primary excitations. This restriction allows us to study vortex dynamics analytically in a framework using return maps and cobweb diagrams, described in this paper. Moreover, often experiments of combustion instability report multiple frequency peaks, which are either super- or subharmonic of the primary peak.
3.1. Superharmonic secondary excitation
Figure 3 shows the Feigenbaum diagrams across a range of primary excitation amplitudes ![]() $A_p=0-1$ at
$A_p=0-1$ at ![]() $f_p=0.9$. In these panels, we consider superharmonic secondary excitation with frequency
$f_p=0.9$. In these panels, we consider superharmonic secondary excitation with frequency ![]() $f_s=2f_p$ and amplitude
$f_s=2f_p$ and amplitude ![]() $A_s=0$, 0.05, 0.1 and
$A_s=0$, 0.05, 0.1 and ![]() $0.15$ (figure 3a–d). During single-frequency excitation (figure 3a), shedding occurs at the natural vortex shedding time period (period-1 state) when
$0.15$ (figure 3a–d). During single-frequency excitation (figure 3a), shedding occurs at the natural vortex shedding time period (period-1 state) when ![]() $A_p=0$. As the amplitude
$A_p=0$. As the amplitude ![]() $A_p$ is gradually increased, torus birth bifurcation occurs, and shedding endures a quasi-periodic route, which is evident from the dense points near the low
$A_p$ is gradually increased, torus birth bifurcation occurs, and shedding endures a quasi-periodic route, which is evident from the dense points near the low ![]() $A_p$ range. This quasi-periodic behaviour is found to extend to
$A_p$ range. This quasi-periodic behaviour is found to extend to ![]() $A_p=0.119$.
$A_p=0.119$.

Figure 3. Plots showing the last 1000 iterations (Feigenbaum diagrams) of ![]() $\Delta t_m$ across
$\Delta t_m$ across ![]() $A_p$ for superharmonic secondary excitation frequency
$A_p$ for superharmonic secondary excitation frequency ![]() $f_s=2f_p$. With
$f_s=2f_p$. With ![]() $f_p=0.9$, each panel indicates Feigenbaum diagrams for a fixed secondary excitation
$f_p=0.9$, each panel indicates Feigenbaum diagrams for a fixed secondary excitation ![]() $(a)$
$(a)$ ![]() $A_s=0$,
$A_s=0$, ![]() $(b)$
$(b)$ ![]() $A_s=0.05$,
$A_s=0.05$, ![]() $(c)$
$(c)$ ![]() $A_s=0.1$ and
$A_s=0.1$ and ![]() $(d)$
$(d)$ ![]() $A_s=0.15$. Panels (e–h) show the phase portraits between
$A_s=0.15$. Panels (e–h) show the phase portraits between ![]() $\Delta t_{m}$ and
$\Delta t_{m}$ and ![]() $\Delta t_{m-1}$ for amplitudes associated with (a–d), respectively, at
$\Delta t_{m-1}$ for amplitudes associated with (a–d), respectively, at ![]() $A_p=0.02$ (shown with red dashed line in (a–d)).
$A_p=0.02$ (shown with red dashed line in (a–d)).
A second bifurcation occurs (saddle-node bifurcation as reported in our previous study Britto & Mariappan Reference Britto and Mariappan2019a) when the amplitude ![]() $A_p$ is increased further. In this amplitude region, shedding exhibits a period-1 state, locked-in with the excitation frequency
$A_p$ is increased further. In this amplitude region, shedding exhibits a period-1 state, locked-in with the excitation frequency ![]() $f_p$. Finally, when
$f_p$. Finally, when ![]() $A_p$ is increased above
$A_p$ is increased above ![]() $0.75$, a transition from period-1 state to a higher-periodic orbit is observed. It is observed in various dynamical systems that are susceptible to lock-in (Gollub & Benson Reference Gollub and Benson1980; Franceschini Reference Franceschini1983; Anishchenko, Safonova & Chua Reference Anishchenko, Safonova and Chua1993; Guan et al. Reference Guan, Murugesan and Li2018).
$0.75$, a transition from period-1 state to a higher-periodic orbit is observed. It is observed in various dynamical systems that are susceptible to lock-in (Gollub & Benson Reference Gollub and Benson1980; Franceschini Reference Franceschini1983; Anishchenko, Safonova & Chua Reference Anishchenko, Safonova and Chua1993; Guan et al. Reference Guan, Murugesan and Li2018).
In figure 3(b), we have introduced non-zero secondary excitation (![]() $A_s=0.05$). Since the total excitation amplitude of
$A_s=0.05$). Since the total excitation amplitude of ![]() $u'$ starts from
$u'$ starts from ![]() $0.05$ at
$0.05$ at ![]() $A_p=0$, vortex shedding never occurs at its natural time period. Quasi-periodic behaviour is observed right from
$A_p=0$, vortex shedding never occurs at its natural time period. Quasi-periodic behaviour is observed right from ![]() $A_p=0$. Comparing figure 3(a–d), the extent of quasi-periodicity reduces with an increase in secondary excitation amplitude (
$A_p=0$. Comparing figure 3(a–d), the extent of quasi-periodicity reduces with an increase in secondary excitation amplitude (![]() $0< A_p<0.085$ for
$0< A_p<0.085$ for ![]() $A_s=0.05$ and
$A_s=0.05$ and ![]() $0< A_p<0.022$ for
$0< A_p<0.022$ for ![]() $A_s=0.1$). Finally, after a certain amplitude
$A_s=0.1$). Finally, after a certain amplitude ![]() $A_s$, quasi-periodicity ceases to exist, and shedding begins to occur at the locked-in time period
$A_s$, quasi-periodicity ceases to exist, and shedding begins to occur at the locked-in time period ![]() $1/2f_s$ (2 : 1 lock-in) as shown in figure 3(d).
$1/2f_s$ (2 : 1 lock-in) as shown in figure 3(d).
Figure 3(e–h) shows phase portraits ![]() $\Delta t_m-\Delta t_{m-1}$ at
$\Delta t_m-\Delta t_{m-1}$ at ![]() $A_p=0.02$ (indicated in red dashed line in figure 3a–d). Referring to figure 4 of Britto & Mariappan (Reference Britto and Mariappan2019a), it was reported that during single-frequency excitation, the phase portrait in the quasi-periodic region exhibits a two-dimensional torus. With the increase in amplitude
$A_p=0.02$ (indicated in red dashed line in figure 3a–d). Referring to figure 4 of Britto & Mariappan (Reference Britto and Mariappan2019a), it was reported that during single-frequency excitation, the phase portrait in the quasi-periodic region exhibits a two-dimensional torus. With the increase in amplitude ![]() $A_p$, the size of the torus increases with its shape being retained. In the current scenario, we observe that the additional secondary excitation changes the shape of the torus as it evolves to a 2-quasi-periodic curve (f). Similar shape change was reported by Gardini et al. (Reference Gardini, Lupini, Mammana and Messia1987), Van Veen (Reference Van Veen2005) and Gyllenberg, Jiang & Niu (Reference Gyllenberg, Jiang and Niu2020). In the Lotka–Voltera model, Gardini et al. (Reference Gardini, Lupini, Mammana and Messia1987) first reported that the quasi-periodic curve (two-dimensional torus in the phase portrait) undergoes a Hopf bifurcation and the curve rounds twice to exhibit a 2-quasiperiodic curve (named recently by Gyllenberg et al. Reference Gyllenberg, Jiang and Niu2020). Subsequently, when the parameters are varied, the system undergoes a cascade of Hopf bifurcations and attains chaos (similar to classical period-doubling bifurcation to chaos). In the present model, as the secondary amplitude is increased gradually, the shape of the two-dimensional torus evolves and a bifurcation occurs therein, and the curve in the phase portrait rounds twice retaining its dense points, thereby exhibiting a 2-quasi-periodic curve. Unlike Lotka–Voltera model, we do not observe quasi-period-doubling. Whereas, when the amplitude
$A_p$, the size of the torus increases with its shape being retained. In the current scenario, we observe that the additional secondary excitation changes the shape of the torus as it evolves to a 2-quasi-periodic curve (f). Similar shape change was reported by Gardini et al. (Reference Gardini, Lupini, Mammana and Messia1987), Van Veen (Reference Van Veen2005) and Gyllenberg, Jiang & Niu (Reference Gyllenberg, Jiang and Niu2020). In the Lotka–Voltera model, Gardini et al. (Reference Gardini, Lupini, Mammana and Messia1987) first reported that the quasi-periodic curve (two-dimensional torus in the phase portrait) undergoes a Hopf bifurcation and the curve rounds twice to exhibit a 2-quasiperiodic curve (named recently by Gyllenberg et al. Reference Gyllenberg, Jiang and Niu2020). Subsequently, when the parameters are varied, the system undergoes a cascade of Hopf bifurcations and attains chaos (similar to classical period-doubling bifurcation to chaos). In the present model, as the secondary amplitude is increased gradually, the shape of the two-dimensional torus evolves and a bifurcation occurs therein, and the curve in the phase portrait rounds twice retaining its dense points, thereby exhibiting a 2-quasi-periodic curve. Unlike Lotka–Voltera model, we do not observe quasi-period-doubling. Whereas, when the amplitude ![]() $A_s$ is further increased, the size of the 2-quasi-periodic curve increases gradually and it breaks into a higher-periodic orbit (seen in figure 3(g,h)) before it encounters lock-in. Similar behaviour is observed when the secondary excitation frequency is switched to a subharmonic of the primary component (
$A_s$ is further increased, the size of the 2-quasi-periodic curve increases gradually and it breaks into a higher-periodic orbit (seen in figure 3(g,h)) before it encounters lock-in. Similar behaviour is observed when the secondary excitation frequency is switched to a subharmonic of the primary component (![]() $f_s=f_p/2$), as described next.
$f_s=f_p/2$), as described next.
3.2. Subharmonic secondary excitation
Figure 4(a–d) shows the Feigenbaum diagrams of ![]() $\Delta t_m$ across
$\Delta t_m$ across ![]() $A_p=0-1$ for
$A_p=0-1$ for ![]() $A_s=0$, 0.05, 0.1 and
$A_s=0$, 0.05, 0.1 and ![]() $0.2$. When a subharmonic (
$0.2$. When a subharmonic (![]() $f_s=f_p/2$) secondary excitation is introduced, the lock-in region becomes a period-2 orbit. For comparison, primary excitation frequency
$f_s=f_p/2$) secondary excitation is introduced, the lock-in region becomes a period-2 orbit. For comparison, primary excitation frequency ![]() $f_p=0.9$ is kept the same as that of the superharmonic excitation. We observe the following similarities with the superharmonic case (§ 3.1): (1) before the onset of lock-in, a quasi-periodic behaviour is observed; (2) in the presence of (non-zero) secondary excitation (b–d), shedding does not occur at its natural frequency (even at
$f_p=0.9$ is kept the same as that of the superharmonic excitation. We observe the following similarities with the superharmonic case (§ 3.1): (1) before the onset of lock-in, a quasi-periodic behaviour is observed; (2) in the presence of (non-zero) secondary excitation (b–d), shedding does not occur at its natural frequency (even at ![]() $A_p=0$); (3) from the phase portraits (
$A_p=0$); (3) from the phase portraits (![]() $\Delta t_{m-2}-\Delta t_m$ considering period-2 orbit) in the quasi-periodic regime, shown in figure 4(e–h), the two-dimensional torus undergoes a fold and evolves into a 2-quasi-periodic curve (f) as secondary excitation is introduced; and (4) when
$\Delta t_{m-2}-\Delta t_m$ considering period-2 orbit) in the quasi-periodic regime, shown in figure 4(e–h), the two-dimensional torus undergoes a fold and evolves into a 2-quasi-periodic curve (f) as secondary excitation is introduced; and (4) when ![]() $A_s$ is increased further, the size of the 2-quasi-periodic curve increases and transitions to a higher-periodic orbit (g,h). However, unlike the superharmonic case, quasi-periodic shedding never disappears in the subharmonic secondary excitation (compare 3d and 4d).
$A_s$ is increased further, the size of the 2-quasi-periodic curve increases and transitions to a higher-periodic orbit (g,h). However, unlike the superharmonic case, quasi-periodic shedding never disappears in the subharmonic secondary excitation (compare 3d and 4d).

Figure 4. Plots showing the last 1000 iterations (Feigenbaum diagrams) of ![]() $\Delta t_m$ across
$\Delta t_m$ across ![]() $A_p$ for subharmonic secondary excitation frequency
$A_p$ for subharmonic secondary excitation frequency ![]() $f_s=f_p/2$. With
$f_s=f_p/2$. With ![]() $f_p=0.9$, each panel shows the Feigenbaum diagram for a fixed secondary excitation amplitude
$f_p=0.9$, each panel shows the Feigenbaum diagram for a fixed secondary excitation amplitude ![]() $(a)$
$(a)$ ![]() $A_s=0$,
$A_s=0$, ![]() $(b)$
$(b)$ ![]() $A_s=0.05$,
$A_s=0.05$, ![]() $(c)$
$(c)$ ![]() $A_s=0.1$ and
$A_s=0.1$ and ![]() $(d)$
$(d)$ ![]() $A_s=0.2$. Panels (e–h) show the phase portraits for amplitudes associated with (a–d), respectively at
$A_s=0.2$. Panels (e–h) show the phase portraits for amplitudes associated with (a–d), respectively at ![]() $A_p=0.1$ (red dashed line).
$A_p=0.1$ (red dashed line).
Furthermore, we observe the following differences between single- and two-frequency excitation from Feigenbaum diagrams and phase portraits: (1) the reduction in the extent and subsequent disappearance of the quasi-periodic nature followed by a lock-in observed during superharmonic excitation (figure 3, (a) and (b–d)) highlights an important quantitative difference; and (2) the absence of a natural vortex shedding frequency and the appearance of folds in the phase portraits (observed both in subharmonic and superharmonic excitation) indicates a significant qualitative difference ((a) and (b–d) of figures 3 and 4).
In addition, we observe the following difference between subharmonic and superharmonic excitation. For ![]() $f_p=0.9$, the gradual increase in
$f_p=0.9$, the gradual increase in ![]() $A_s$ decreases the critical amplitude at which the onset of lock-in occurs and it leads to early lock-in (figure 3a–d). This behaviour is absent in the subharmonic excitation case. In contrast, the quasi-periodic nature with intermediate periodic windows never disappears during subharmonic excitation, whereas, when
$A_s$ decreases the critical amplitude at which the onset of lock-in occurs and it leads to early lock-in (figure 3a–d). This behaviour is absent in the subharmonic excitation case. In contrast, the quasi-periodic nature with intermediate periodic windows never disappears during subharmonic excitation, whereas, when ![]() $A_s$ is gradually increased, the shedding occurs at a wider range of time period before the onset of lock-in (figure 4a–d).
$A_s$ is gradually increased, the shedding occurs at a wider range of time period before the onset of lock-in (figure 4a–d).
These differences motivated further analyses that are presented in the rest of this paper. Since multiple frequencies are involved in excitation, lock-in is investigated from the perspective of phase lock-in. In the next section, we introduce the phase lock-in phenomenon often observed in interacting dynamical systems. The procedure to identify it in the current model is discussed in detail.
4. Phase lock-in owing to two-frequency excitation
In our previous work (Britto & Mariappan Reference Britto and Mariappan2019a), we stated that 1:1 frequency lock-in is encountered when vortex shedding and excitation time periods (![]() $1/f_p$) are equal. However, in the current scenario, the excitation signal has two-frequency components. Therefore, we study lock-in behaviour using the concept of phase. Phase lock-in is a common phenomenon observed in dynamical systems that are susceptible to external excitation. During phase lock-in, phases of the interacting systems are in a certain relation with each other (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007). This behaviour is well understood in various physical (Strogatz et al. Reference Strogatz, Abrams, McRobie, Eckhardt and Ott2005) and biological systems (Daan, Beersma & Borbély Reference Daan, Beersma and Borbély1984; Graves et al. Reference Graves, Glass, Laporta, Meloche and Grassino1986). For hydrodynamic systems, Li & Juniper (Reference Li and Juniper2013c) and recently Mondal, Pawar & Sujith (Reference Mondal, Pawar and Sujith2019) studied phase-locking behaviour in a self-excited low-density jet and Rijke tube, respectively, under single-frequency periodic excitation. When the system (low-density jet or Rijke tube) is subjected to external excitation, Li & Juniper (Reference Li and Juniper2013c) measured the streamwise velocity fluctuation as the response of the jet and Mondal et al. (Reference Mondal, Pawar and Sujith2019) measured the acoustic pressure fluctuations inside the Rijke tube. In both the studies, the forcing frequency was kept near the system natural frequency. They summarised their observations as two categories of behaviours across the parametric plane (the
$1/f_p$) are equal. However, in the current scenario, the excitation signal has two-frequency components. Therefore, we study lock-in behaviour using the concept of phase. Phase lock-in is a common phenomenon observed in dynamical systems that are susceptible to external excitation. During phase lock-in, phases of the interacting systems are in a certain relation with each other (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007). This behaviour is well understood in various physical (Strogatz et al. Reference Strogatz, Abrams, McRobie, Eckhardt and Ott2005) and biological systems (Daan, Beersma & Borbély Reference Daan, Beersma and Borbély1984; Graves et al. Reference Graves, Glass, Laporta, Meloche and Grassino1986). For hydrodynamic systems, Li & Juniper (Reference Li and Juniper2013c) and recently Mondal, Pawar & Sujith (Reference Mondal, Pawar and Sujith2019) studied phase-locking behaviour in a self-excited low-density jet and Rijke tube, respectively, under single-frequency periodic excitation. When the system (low-density jet or Rijke tube) is subjected to external excitation, Li & Juniper (Reference Li and Juniper2013c) measured the streamwise velocity fluctuation as the response of the jet and Mondal et al. (Reference Mondal, Pawar and Sujith2019) measured the acoustic pressure fluctuations inside the Rijke tube. In both the studies, the forcing frequency was kept near the system natural frequency. They summarised their observations as two categories of behaviours across the parametric plane (the ![]() $A - f$ plane): (i) when the forcing frequency (
$A - f$ plane): (i) when the forcing frequency (![]() $f$) is close to the natural frequency (
$f$) is close to the natural frequency (![]() $f_n$) of the oscillating jet, they observe phase slipping, where the phase difference between the response and the forcing stays nearly constant with time, followed by discrete rapid jumps by
$f_n$) of the oscillating jet, they observe phase slipping, where the phase difference between the response and the forcing stays nearly constant with time, followed by discrete rapid jumps by ![]() $2{\rm \pi}$; and (ii) when
$2{\rm \pi}$; and (ii) when ![]() $f$ is far away from
$f$ is far away from ![]() $f_n$, there was no phase slipping, whereas phase trapping was observed. In this case, the phase difference oscillates periodically and remains bounded throughout in time. Both phase slipping and trapping behaviour were observed before the onset of lock-in. After (phase) lock-in, the phase difference becomes constant with time. In the following section, we examine lock-in in the present model through the previously described concept of phase, first for single-frequency excitation and later extended for two-frequency excitation.
$f_n$, there was no phase slipping, whereas phase trapping was observed. In this case, the phase difference oscillates periodically and remains bounded throughout in time. Both phase slipping and trapping behaviour were observed before the onset of lock-in. After (phase) lock-in, the phase difference becomes constant with time. In the following section, we examine lock-in in the present model through the previously described concept of phase, first for single-frequency excitation and later extended for two-frequency excitation.
4.1. Hilbert transform for single- and two-frequency excitation
As mentioned in the previous paragraph, phase lock-in is identified by the difference between the phase of the system's response and excitation. In the present case, the system's response are the shedding time instances ![]() $t_1,t_2,\ldots$. Between two successive shedding instances, say
$t_1,t_2,\ldots$. Between two successive shedding instances, say ![]() $t_{m-1}$ and
$t_{m-1}$ and ![]() $t_m$, the circulation of the
$t_m$, the circulation of the ![]() $m$th vortex begins to grow from zero and reaches
$m$th vortex begins to grow from zero and reaches ![]() $\varGamma _{sep}$, after which the vortex sheds. This forms a cycle, and the associated phase increases by
$\varGamma _{sep}$, after which the vortex sheds. This forms a cycle, and the associated phase increases by ![]() $2{\rm \pi}$. Therefore, phase (
$2{\rm \pi}$. Therefore, phase (![]() $\psi _{R,m}$) of the response is defined only at vortex shedding instances (
$\psi _{R,m}$) of the response is defined only at vortex shedding instances (![]() $t_m$s), given as
$t_m$s), given as ![]() $\psi _{R,m}=2m{\rm \pi}$ where
$\psi _{R,m}=2m{\rm \pi}$ where ![]() $m=1,2,3,~\dots$ indicates vortex shedding events. Subscripts
$m=1,2,3,~\dots$ indicates vortex shedding events. Subscripts ![]() $R$ and
$R$ and ![]() $m$ represent response and
$m$ represent response and ![]() $m$th vortex, respectively.
$m$th vortex, respectively.
On the other hand, the phase of the excitation signal ![]() $u'$ is obtained using the concept of the analytic signal (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007). An analytic signal
$u'$ is obtained using the concept of the analytic signal (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007). An analytic signal ![]() $\zeta (t)$ is constructed from a signal or time series
$\zeta (t)$ is constructed from a signal or time series ![]() $u'(t)$ as below:
$u'(t)$ as below:
where ![]() $H(u'(t))$ is the Hilbert transform of
$H(u'(t))$ is the Hilbert transform of ![]() $u'(t)$. As usual
$u'(t)$. As usual ![]() ${i}=\sqrt {-1}$. The instantaneous phase (
${i}=\sqrt {-1}$. The instantaneous phase (![]() $\psi _E(t$), subscript
$\psi _E(t$), subscript ![]() $E$ stands for excitation signal) of
$E$ stands for excitation signal) of ![]() $u'$ is given by the following:
$u'$ is given by the following:
For the functional form of ![]() $u'$ (2.3),
$u'$ (2.3), ![]() $H(u'(t))=-A_p \cos (2 {\rm \pi}f_p t)-A_s \cos (2{\rm \pi} f_s t+\gamma )$, and
$H(u'(t))=-A_p \cos (2 {\rm \pi}f_p t)-A_s \cos (2{\rm \pi} f_s t+\gamma )$, and ![]() $\psi _E(t)$ is, in general, a continuous function of time. We calculate it at discrete vortex shedding time instances
$\psi _E(t)$ is, in general, a continuous function of time. We calculate it at discrete vortex shedding time instances ![]() $t_1,t_2,\ldots$ to obtain the phase of excitation signal,
$t_1,t_2,\ldots$ to obtain the phase of excitation signal, ![]() $\psi _{E,m}=\psi _E (t_m)$.
$\psi _{E,m}=\psi _E (t_m)$.
To identify 1:1 phase lock-in, the phase difference (![]() $\Delta \psi _{m}$) between excitation signal and response at vortex shedding time instances is calculated as
$\Delta \psi _{m}$) between excitation signal and response at vortex shedding time instances is calculated as ![]() $\Delta \psi _{m}=\psi _{E,m}-\psi _{R,m}$. The dynamics of
$\Delta \psi _{m}=\psi _{E,m}-\psi _{R,m}$. The dynamics of ![]() $\Delta \psi _{m}$ with
$\Delta \psi _{m}$ with ![]() $m$ allows one to identify phase lock-in. The same idea can be extended to identify a general p : q phase lock-in, where
$m$ allows one to identify phase lock-in. The same idea can be extended to identify a general p : q phase lock-in, where ![]() $\Delta \psi _{m}=q\psi _{E,m}-p\psi _{R,m}$ is a constant value.
$\Delta \psi _{m}=q\psi _{E,m}-p\psi _{R,m}$ is a constant value.
In the subsequent sections, we first discuss the dynamics of ![]() $\Delta \psi _m$ in the vicinity of the 1:1 lock-in region in the
$\Delta \psi _m$ in the vicinity of the 1:1 lock-in region in the ![]() $A_p - f_p$ plane. In § 4.3, we explore the nature of p : q lock-in during two-frequency excitation.
$A_p - f_p$ plane. In § 4.3, we explore the nature of p : q lock-in during two-frequency excitation.
4.2. Phase lock-in during single-frequency excitation
Identification of phase lock-in through ![]() $\Delta \psi$ is first demonstrated in single-frequency excitation (
$\Delta \psi$ is first demonstrated in single-frequency excitation (![]() $A_s=0$). The lock-in region (represented by green in figure 5a) is obtained from the analytical solution discussed in our previous paper (Britto & Mariappan Reference Britto and Mariappan2019a). Phase difference
$A_s=0$). The lock-in region (represented by green in figure 5a) is obtained from the analytical solution discussed in our previous paper (Britto & Mariappan Reference Britto and Mariappan2019a). Phase difference ![]() $\Delta \psi$ is evaluated at three significant regions in
$\Delta \psi$ is evaluated at three significant regions in ![]() $A_p - f_p$ plane: (i) before the onset of lock-in; and (ii) inside the lock-in region and (iii) in the region after the transition from lock-in. In the following discussions, we highlight the behaviour of
$A_p - f_p$ plane: (i) before the onset of lock-in; and (ii) inside the lock-in region and (iii) in the region after the transition from lock-in. In the following discussions, we highlight the behaviour of ![]() $\Delta \psi$ at these locations.
$\Delta \psi$ at these locations.

Figure 5. Phase lock-in during single-frequency excitation. Lock-in boundary is shown in (a). Phase difference ![]() $\Delta \psi _m$ for various forcing amplitudes and excitation frequency (b)
$\Delta \psi _m$ for various forcing amplitudes and excitation frequency (b) ![]() $f=0.8$ and (c)
$f=0.8$ and (c) ![]() $f=1.1$ are illustrated. Excitation amplitudes chosen in (b,c) are colour coded and are shown in (a) using cross symbols with the corresponding colours. Lock-in region is obtained from the analytical expression given in Britto & Mariappan (Reference Britto and Mariappan2019a).
$f=1.1$ are illustrated. Excitation amplitudes chosen in (b,c) are colour coded and are shown in (a) using cross symbols with the corresponding colours. Lock-in region is obtained from the analytical expression given in Britto & Mariappan (Reference Britto and Mariappan2019a).
For two primary excitation frequencies on either side of ![]() $f_p=1$ (
$f_p=1$ (![]() $f_p=0.8$ and
$f_p=0.8$ and ![]() $f_p=1.1$), the evolution of
$f_p=1.1$), the evolution of ![]() $\Delta \psi _m/2{\rm \pi}$ with
$\Delta \psi _m/2{\rm \pi}$ with ![]() $m$ at the selected locations in the
$m$ at the selected locations in the ![]() $A_p - f_p$ plane is illustrated in figure 5(b,c). The colour of the curves corresponds to the cross symbols shown in the
$A_p - f_p$ plane is illustrated in figure 5(b,c). The colour of the curves corresponds to the cross symbols shown in the ![]() $A_p - f_p$ plane of (a). For
$A_p - f_p$ plane of (a). For ![]() $f_p=0.8$, we begin with a low amplitude,
$f_p=0.8$, we begin with a low amplitude, ![]() $A_p=0.1$ (illustrated with a blue marker). Clearly, there is no lock-in, and
$A_p=0.1$ (illustrated with a blue marker). Clearly, there is no lock-in, and ![]() $\Delta \psi _m$ increases unboundedly, exhibiting a large positive slope (blue curve in (b)). This phenomenon is called phase drifting (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007; Li & Juniper Reference Li and Juniper2013c). As the amplitude is increased gradually, the slope of
$\Delta \psi _m$ increases unboundedly, exhibiting a large positive slope (blue curve in (b)). This phenomenon is called phase drifting (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007; Li & Juniper Reference Li and Juniper2013c). As the amplitude is increased gradually, the slope of ![]() $\Delta \psi _m$ approaches zero. This phenomenon is called frequency pulling (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007; Li & Juniper Reference Li and Juniper2013c), where the average frequency of the shedding is pulled towards the forcing frequency. Finally, the instantaneous phase difference,
$\Delta \psi _m$ approaches zero. This phenomenon is called frequency pulling (Pikovsky & Rosenblum Reference Pikovsky and Rosenblum2007; Li & Juniper Reference Li and Juniper2013c), where the average frequency of the shedding is pulled towards the forcing frequency. Finally, the instantaneous phase difference, ![]() $\Delta \psi _{m}$, attains a constant value leading to phase lock-in (green curve). Near the lock-in boundary (in the unlocked state),
$\Delta \psi _{m}$, attains a constant value leading to phase lock-in (green curve). Near the lock-in boundary (in the unlocked state), ![]() $\Delta \psi _m$ is almost constant with phase slips occurring at discrete instances (red and yellow curves). During a phase slip,
$\Delta \psi _m$ is almost constant with phase slips occurring at discrete instances (red and yellow curves). During a phase slip, ![]() $\Delta \psi _m$ jumps by
$\Delta \psi _m$ jumps by ![]() $2{\rm \pi}$. Phase slips occur less frequently as one approaches the lock-in boundary (compare red and yellow curves). This indicates that shedding begins to exhibit intermittent, long epochs of lock-in between phase slips as
$2{\rm \pi}$. Phase slips occur less frequently as one approaches the lock-in boundary (compare red and yellow curves). This indicates that shedding begins to exhibit intermittent, long epochs of lock-in between phase slips as ![]() $A_p$ approaches the lock-in boundary. In the phase lock-in region (green shaded portion),
$A_p$ approaches the lock-in boundary. In the phase lock-in region (green shaded portion), ![]() $\Delta \psi _m$ remains constant without any phase slips. When the amplitude reaches higher values, a transition out of lock-in occurs. The black marker in panel
$\Delta \psi _m$ remains constant without any phase slips. When the amplitude reaches higher values, a transition out of lock-in occurs. The black marker in panel ![]() $a$ is outside the lock-in boundary, and the corresponding
$a$ is outside the lock-in boundary, and the corresponding ![]() $\Delta \psi _m$ shows phase slips. It must be noted that for all
$\Delta \psi _m$ shows phase slips. It must be noted that for all ![]() $A_p$ in
$A_p$ in ![]() $f_p<1$,
$f_p<1$, ![]() $\Delta \psi _m$ remains positive. Since
$\Delta \psi _m$ remains positive. Since ![]() $f_p$ is less than the natural vortex shedding frequency, the phase of the excitation signal
$f_p$ is less than the natural vortex shedding frequency, the phase of the excitation signal ![]() $\psi _E (t)$ is greater than
$\psi _E (t)$ is greater than ![]() $\psi _R (t)$. Hence the positive slope is consistent in no lock-in amplitudes. The three salient features of phase that are observed in the current model, namely phase drifting, phase slipping and frequency pulling, were reported in experiments (Li & Juniper Reference Li and Juniper2013c).
$\psi _R (t)$. Hence the positive slope is consistent in no lock-in amplitudes. The three salient features of phase that are observed in the current model, namely phase drifting, phase slipping and frequency pulling, were reported in experiments (Li & Juniper Reference Li and Juniper2013c).
In (c), the above exercise is repeated for ![]() $f_p=1.1$ (a case where
$f_p=1.1$ (a case where ![]() $f_p>1$), we see that
$f_p>1$), we see that ![]() $\Delta \psi _m$ exhibits similar characteristics as that for
$\Delta \psi _m$ exhibits similar characteristics as that for ![]() $f_p=0.8$, but with the slope of
$f_p=0.8$, but with the slope of ![]() $\Delta \psi _m$ negative before the onset of lock-in (since
$\Delta \psi _m$ negative before the onset of lock-in (since ![]() $\psi _E (t) < \psi _R (t)$). However, during the transition out of lock-in, the phase difference exhibits a positive slope similar to the
$\psi _E (t) < \psi _R (t)$). However, during the transition out of lock-in, the phase difference exhibits a positive slope similar to the ![]() $f_p<1$ case. Overall, we have shown that the identification of a lock-in region through
$f_p<1$ case. Overall, we have shown that the identification of a lock-in region through ![]() $\Delta \psi _m$ is possible for single-frequency excitation. We now proceed to extend the same idea during two-frequency excitation.
$\Delta \psi _m$ is possible for single-frequency excitation. We now proceed to extend the same idea during two-frequency excitation.
4.3. Phase lock-in during two-frequency excitation
Figure 6(a) shows the boundary of lock-in in the ![]() $A_p - f_p$ plane, during a two-frequency excitation. In this case, the excitation signal, apart from the primary frequency
$A_p - f_p$ plane, during a two-frequency excitation. In this case, the excitation signal, apart from the primary frequency ![]() $(f_p)$ contains a secondary superharmonic component with amplitude
$(f_p)$ contains a secondary superharmonic component with amplitude ![]() $A_s=0.05$ and frequency
$A_s=0.05$ and frequency ![]() $f_s=2f_p$. Similar to the previous single-frequency excitation, we consider two cases for the frequency of primary excitation:
$f_s=2f_p$. Similar to the previous single-frequency excitation, we consider two cases for the frequency of primary excitation: ![]() $f_p<1$ and
$f_p<1$ and ![]() $f_p>1$. The corresponding evolution of phase difference
$f_p>1$. The corresponding evolution of phase difference ![]() $\Delta \psi _m$ is shown in (b) and (c), respectively. Considering first the case at
$\Delta \psi _m$ is shown in (b) and (c), respectively. Considering first the case at ![]() $f_p=0.85$ in the no lock-in,
$f_p=0.85$ in the no lock-in, ![]() $\Delta \psi _{m}$ (blue curve in (b)) increases with time, and exhibits phase slipping with an intermediate
$\Delta \psi _{m}$ (blue curve in (b)) increases with time, and exhibits phase slipping with an intermediate ![]() $2{\rm \pi}$ jump. As
$2{\rm \pi}$ jump. As ![]() $A_p$ is increased, the interval between the jump increases (refer to red and yellow curves). Finally during lock-in (green curve),
$A_p$ is increased, the interval between the jump increases (refer to red and yellow curves). Finally during lock-in (green curve), ![]() $\Delta \psi _{m}$ attains a constant value. Overall, both for
$\Delta \psi _{m}$ attains a constant value. Overall, both for ![]() $f_p<1$ and
$f_p<1$ and ![]() $f_p>1$ (see (b,c)),
$f_p>1$ (see (b,c)), ![]() $\Delta \psi _{m}$ follows qualitatively similar characteristics as that of their single-frequency excitation counterpart. It is important to mention the following observation. For the case,
$\Delta \psi _{m}$ follows qualitatively similar characteristics as that of their single-frequency excitation counterpart. It is important to mention the following observation. For the case, ![]() $f_p=1.4$ which is relatively far (in comparison with the case,
$f_p=1.4$ which is relatively far (in comparison with the case, ![]() $f_p=0.85$) from the natural vortex shedding frequency,
$f_p=0.85$) from the natural vortex shedding frequency, ![]() $\Delta \psi _{m}$ becomes constant during lock-in (
$\Delta \psi _{m}$ becomes constant during lock-in (![]() $A_p=0.25$, green curve in (c)) and decreases unboundedly near the lock-in boundary (
$A_p=0.25$, green curve in (c)) and decreases unboundedly near the lock-in boundary (![]() $A_p=0.24$, pink curve in (c)). This shows that the current model does not exhibit phase trapping, a behaviour in which
$A_p=0.24$, pink curve in (c)). This shows that the current model does not exhibit phase trapping, a behaviour in which ![]() $\Delta \psi _{m}$ remains bounded but fluctuates near the lock-in boundary. The same observation is found in our previous investigation (Britto & Mariappan Reference Britto and Mariappan2019a) which involved single-frequency excitation.
$\Delta \psi _{m}$ remains bounded but fluctuates near the lock-in boundary. The same observation is found in our previous investigation (Britto & Mariappan Reference Britto and Mariappan2019a) which involved single-frequency excitation.

Figure 6. Phase lock-in during two-frequency excitation. Lock-in boundary is shown in (a). Phase difference ![]() $\Delta \psi _{m}$ obtained for various forcing amplitudes and excitation frequency
$\Delta \psi _{m}$ obtained for various forcing amplitudes and excitation frequency ![]() $f_s=2f_p$ (b)
$f_s=2f_p$ (b) ![]() $f_p=0.85$ and (c)
$f_p=0.85$ and (c) ![]() $f_p=1.4$. Lock-in region can be identified when the phase difference is constant. The chosen excitation amplitudes in (b,c) are colour-coded and are marked in (a) using cross symbols with the corresponding colours.
$f_p=1.4$. Lock-in region can be identified when the phase difference is constant. The chosen excitation amplitudes in (b,c) are colour-coded and are marked in (a) using cross symbols with the corresponding colours.
Unlike the case of single-frequency excitation, where the lock-in boundary is obtained analytically (Britto & Mariappan Reference Britto and Mariappan2019a), the boundary for the case of two (or multiple)-frequency excitation is identified by tracking the evolution of ![]() $\Delta \psi _{m}$.
$\Delta \psi _{m}$.
To find lock-in regions in multiple-frequency excitation, we use the criteria ![]() $\Delta \psi _m=C$, where
$\Delta \psi _m=C$, where ![]() $C$ is a constant. Throughout this study, we restrict ourselves to only rational relations between primary and secondary excitation frequencies,
$C$ is a constant. Throughout this study, we restrict ourselves to only rational relations between primary and secondary excitation frequencies, ![]() $f_s=p_f f_p/q_f$, where
$f_s=p_f f_p/q_f$, where ![]() $p_f$ and
$p_f$ and ![]() $q_f$ are integers. A discussion on such a choice of secondary excitation is provided in § 4.4. During phase lock-in, the iterations of
$q_f$ are integers. A discussion on such a choice of secondary excitation is provided in § 4.4. During phase lock-in, the iterations of ![]() $\Delta \psi _m$ are period-
$\Delta \psi _m$ are period-![]() $q_f$ and bounded. Therefore, a p : q lock-in region is identified using the following relations:
$q_f$ and bounded. Therefore, a p : q lock-in region is identified using the following relations:
To identify a given p : q lock-in, ![]() $\Delta \psi _m-\Delta \psi _{m-q_f}=K$ is plotted in the
$\Delta \psi _m-\Delta \psi _{m-q_f}=K$ is plotted in the ![]() $A_p - f_p$ plane. For illustration, we choose
$A_p - f_p$ plane. For illustration, we choose ![]() $f_s=2f_p$ for superharmonic and
$f_s=2f_p$ for superharmonic and ![]() $f_s=f_p/2$ for subharmonic excitations. Consequently, we expect 1:1, 2 : 1 and 1:1, 1 : 2 lock-in for super- and subharmonic excitations, respectively. Figures 7(a,b) and (d,e) show the contour plots of
$f_s=f_p/2$ for subharmonic excitations. Consequently, we expect 1:1, 2 : 1 and 1:1, 1 : 2 lock-in for super- and subharmonic excitations, respectively. Figures 7(a,b) and (d,e) show the contour plots of ![]() $K$ corresponding to superharmonic and subharmonic secondary excitation, respectively, with
$K$ corresponding to superharmonic and subharmonic secondary excitation, respectively, with ![]() $A_s=0.05$. The dark blue region (
$A_s=0.05$. The dark blue region (![]() $K=0$) in the contour represents phase lock-in regions. The corresponding boundary of lock-in is shown in figure 7(c,f). This boundary is obtained by increasing
$K=0$) in the contour represents phase lock-in regions. The corresponding boundary of lock-in is shown in figure 7(c,f). This boundary is obtained by increasing ![]() $A_p$ gradually till
$A_p$ gradually till ![]() $K=0$ is attained for the first time, at each
$K=0$ is attained for the first time, at each ![]() $f_p$, blue and red curves represent 1:1 and 2 : 1/1 : 2 lock-in, respectively, in figures 7(c) and 7(f).
$f_p$, blue and red curves represent 1:1 and 2 : 1/1 : 2 lock-in, respectively, in figures 7(c) and 7(f).

Figure 7. Illustration of boundary of lock-in obtained using the condition (4.3). Panels (a–c) and (d–f) correspond to the superharmonic and subharmonic secondary excitation, respectively, with ![]() $A_s=0.05$. In (a,d), the dark blue region (
$A_s=0.05$. In (a,d), the dark blue region (![]() $K=0$) represents 1:1 phase lock-in. Similarly, in (b,e), it represents 2 : 1 and 1 : 2 phase lock-in, respectively. The boundary of blue regions in these panels are mapped in (c,f).
$K=0$) represents 1:1 phase lock-in. Similarly, in (b,e), it represents 2 : 1 and 1 : 2 phase lock-in, respectively. The boundary of blue regions in these panels are mapped in (c,f).
The following observations are common to both variants of secondary excitations: (i) when ![]() $A_p< A_s$, the system exhibits 2 : 1 or 1 : 2 lock-in for super- and subharmonic excitation, respectively; and (ii) when
$A_p< A_s$, the system exhibits 2 : 1 or 1 : 2 lock-in for super- and subharmonic excitation, respectively; and (ii) when ![]() $A_p>A_s$, vortex shedding encounters 1:1 lock-in. For superharmonic excitation (a,b), both 1:1 and 2 : 1 lock-in regions show a plateau boundary (upper and lower plateau) at their onsets (c). On the other hand, a prominent plateau boundary is observed only at the onset of the 1:1 lock-in boundary (upper plateau) for subharmonic excitation (f). Our simulations indicate that the lower plateau is so small that it appears to be absent.
$A_p>A_s$, vortex shedding encounters 1:1 lock-in. For superharmonic excitation (a,b), both 1:1 and 2 : 1 lock-in regions show a plateau boundary (upper and lower plateau) at their onsets (c). On the other hand, a prominent plateau boundary is observed only at the onset of the 1:1 lock-in boundary (upper plateau) for subharmonic excitation (f). Our simulations indicate that the lower plateau is so small that it appears to be absent.
Furthermore, in contrast to the lock-in boundary of single-frequency excitation (figure 5a), we observe the following difference in its shape during two-frequency excitation (the differences are common in both super- and subharmonic secondary excitation). The 1:1 lock-in forms a plateau boundary at ![]() $A_p=A_s$ which is in contrast to the classical
$A_p=A_s$ which is in contrast to the classical ![]() $V$-shaped boundary at
$V$-shaped boundary at ![]() $f_p=1$ during single-frequency excitation (figure 5a). Although the contribution of secondary excitation is present throughout the
$f_p=1$ during single-frequency excitation (figure 5a). Although the contribution of secondary excitation is present throughout the ![]() $A_p - f_p$ plane, it is dominant in the region where
$A_p - f_p$ plane, it is dominant in the region where ![]() $A_p< A_s$. This dominance restricts the 1:1 lock-in region to the
$A_p< A_s$. This dominance restricts the 1:1 lock-in region to the ![]() $A_p>A_s$ region. This behaviour is observed for other superharmonic (
$A_p>A_s$ region. This behaviour is observed for other superharmonic (![]() $f_s=3f_p$) and subharmonic (
$f_s=3f_p$) and subharmonic (![]() $f_s=f_p/3$) secondary excitation (figure 8). The same figure shows that the 1:1 lock-in boundary stemmed at
$f_s=f_p/3$) secondary excitation (figure 8). The same figure shows that the 1:1 lock-in boundary stemmed at ![]() $f_p=1$ for single-frequency excitation, detaches from
$f_p=1$ for single-frequency excitation, detaches from ![]() $(A_p,f_p)=(0,1)$ and shifts to a value of
$(A_p,f_p)=(0,1)$ and shifts to a value of ![]() $A_p=A_s$, forming a plateau.
$A_p=A_s$, forming a plateau.

Figure 8. The 1:1 phase lock-in regions for (a) ![]() $f_s=2f_p$, (b)
$f_s=2f_p$, (b) ![]() $f_s=3f_p$, (c)
$f_s=3f_p$, (c) ![]() $f_s=f_p/2$ and (d)
$f_s=f_p/2$ and (d) ![]() $f_s=f_p/3$. Three different secondary excitation amplitudes are chosen to illustrate the variation of lock-in boundary.
$f_s=f_p/3$. Three different secondary excitation amplitudes are chosen to illustrate the variation of lock-in boundary.
At this point, it is worth to mention the parallels with the experimental study by Guan et al. (Reference Guan, Gupta, Wan and Li2019a). They periodically forced a ducted laminar premixed flame, exhibiting quasi-periodic unforced (natural) oscillations. The parallel is that the shape of the lock-in boundary is altered by the presence of two natural frequencies. This is similar to the present altered lock-in boundary (figure 8), where there is a change in the order of lock-in. In our investigations, two forcing frequencies are used, while in Guan et al. (Reference Guan, Gupta, Wan and Li2019a), two natural frequencies are present. In both studies, three modes are involved.
These results show the possibility of controlling and tailoring the lock-in region by introducing a secondary excitation component in the flow stream. Since some of the previous experimental results do indicate the occurrence of 1:1 lock-in during combustion instability (Poinsot et al. Reference Poinsot, Trouve, Veynante, Candel and Esposito1987; Singh & Mariappan Reference Singh and Mariappan2021), the above method can be considered as active control for its mitigation.
In order to understand the formation of a plateau in the lock-in boundary, analytical investigation through first return maps is performed in § 5. This requires a geometrical interpretation of phase difference ![]() $\Delta \psi _m$, discussed in the next section.
$\Delta \psi _m$, discussed in the next section.
4.4. Geometric interpretation of  $\Delta \psi _m$
$\Delta \psi _m$
We begin by studying the geometrical interpretation of the phase of the excitation signal ![]() $\psi _{E,m}$. As explained in § 2, vortex shedding time instances
$\psi _{E,m}$. As explained in § 2, vortex shedding time instances ![]() $(t_m)$ are identified by the condition
$(t_m)$ are identified by the condition ![]() $\varGamma _m (t_m)= \varGamma _{sep}(t_m)$,
$\varGamma _m (t_m)= \varGamma _{sep}(t_m)$, ![]() $\varGamma _{sep}(t_m)$ is linearly related to excitation
$\varGamma _{sep}(t_m)$ is linearly related to excitation ![]() $u'$. Since the excitation is sinusoidal, for a particular set of
$u'$. Since the excitation is sinusoidal, for a particular set of ![]() $A_p$,
$A_p$, ![]() $f_p$,
$f_p$, ![]() $A_s$ and
$A_s$ and ![]() $f_s$,
$f_s$, ![]() $\varGamma _{sep}(t_m)$ can be located as phase points on a geometry consisting of two circles: primary and secondary (figure 9). The primary excitation along with the steady base flow is represented by the primary circle of radius
$\varGamma _{sep}(t_m)$ can be located as phase points on a geometry consisting of two circles: primary and secondary (figure 9). The primary excitation along with the steady base flow is represented by the primary circle of radius ![]() $A_p/2$, centred (point
$A_p/2$, centred (point ![]() $O$) at 1/2 from the origin (point
$O$) at 1/2 from the origin (point ![]() $S$) in the vertical direction. The shift 1/2 is to accommodate the steady flow velocity in
$S$) in the vertical direction. The shift 1/2 is to accommodate the steady flow velocity in ![]() $\varGamma _{sep}(t_m)$. The vertical distance between points
$\varGamma _{sep}(t_m)$. The vertical distance between points ![]() $P$ and
$P$ and ![]() $S$ equals
$S$ equals ![]() $1/2+A_p\sin (2{\rm \pi} f_p)/2$, which represents the contribution of steady and primary frequency components of
$1/2+A_p\sin (2{\rm \pi} f_p)/2$, which represents the contribution of steady and primary frequency components of ![]() $u'$ excitation in
$u'$ excitation in ![]() $\varGamma _{sep}(t_m)$ (refer to (a)). Over time
$\varGamma _{sep}(t_m)$ (refer to (a)). Over time ![]() $t$, the point
$t$, the point ![]() $P$ traces over the primary circle and forms an angle
$P$ traces over the primary circle and forms an angle ![]() $2 {\rm \pi}f_p t$. Similarly, the presence of the secondary component (
$2 {\rm \pi}f_p t$. Similarly, the presence of the secondary component (![]() $A_s \sin (2{\rm \pi} f_s t$)) can be represented by another point
$A_s \sin (2{\rm \pi} f_s t$)) can be represented by another point ![]() $Q$ lying on the secondary circle having a radius
$Q$ lying on the secondary circle having a radius ![]() $A_s/2$. This circle is centred at the primary phase point
$A_s/2$. This circle is centred at the primary phase point ![]() $P$, allowing the secondary circle to move along the primary circle. Geometrically, the vertical distance between points
$P$, allowing the secondary circle to move along the primary circle. Geometrically, the vertical distance between points ![]() $Q$ and
$Q$ and ![]() $S$ equals
$S$ equals ![]() $\varGamma _{sep}(t_m)=1/2+A_p\sin {(2{\rm \pi} f_p t_m)}/2+A_s\sin {(2{\rm \pi} f_s t_m+\gamma )}/2$ (refer to (b)). Therefore, the evolution of
$\varGamma _{sep}(t_m)=1/2+A_p\sin {(2{\rm \pi} f_p t_m)}/2+A_s\sin {(2{\rm \pi} f_s t_m+\gamma )}/2$ (refer to (b)). Therefore, the evolution of ![]() $\varGamma _{sep}$ is the movement of point
$\varGamma _{sep}$ is the movement of point ![]() $Q$ with time. Crucially, the angle (
$Q$ with time. Crucially, the angle (![]() $\phi _{m}$) subtended between the line joining points
$\phi _{m}$) subtended between the line joining points ![]() $Q$ and
$Q$ and ![]() $O$ with the horizontal (
$O$ with the horizontal (![]() $OR$) equals
$OR$) equals
where ![]() $X=A_p \cos (2{\rm \pi} f_p t_m)+A_s \cos ( 2{\rm \pi} f_s t_m +\gamma )$ and
$X=A_p \cos (2{\rm \pi} f_p t_m)+A_s \cos ( 2{\rm \pi} f_s t_m +\gamma )$ and ![]() $Y=A_p \sin (2{\rm \pi} f_p t_m)+A_s \sin (2{\rm \pi} f_s t_m +\gamma )$ (b). Now,
$Y=A_p \sin (2{\rm \pi} f_p t_m)+A_s \sin (2{\rm \pi} f_s t_m +\gamma )$ (b). Now, ![]() $\phi _m$ at time instances
$\phi _m$ at time instances ![]() $t_m$, where
$t_m$, where ![]() $m=1,2,3,\ldots$ are the phase points of the vortex shedding events on the
$m=1,2,3,\ldots$ are the phase points of the vortex shedding events on the ![]() $\varGamma _{sep}(t)$. The angle
$\varGamma _{sep}(t)$. The angle ![]() $\phi _m$ can be related to the phase
$\phi _m$ can be related to the phase ![]() $\psi _{E,m}$ of the excitation signal
$\psi _{E,m}$ of the excitation signal ![]() $u'$ using (4.2):
$u'$ using (4.2):

Figure 9. Time instances of vortex shedding are illustrated as phase points on the circle. (a) The circle centred at ![]() $O$ represents the primary excitation signal with the parameters
$O$ represents the primary excitation signal with the parameters ![]() $A_p$ and
$A_p$ and ![]() $f_p$. The inclusion of a secondary component results in an additional circle of radius
$f_p$. The inclusion of a secondary component results in an additional circle of radius ![]() $A_s$ with frequency
$A_s$ with frequency ![]() $f_s$ centred at the point
$f_s$ centred at the point ![]() $P$. Over time
$P$. Over time ![]() $t$ points
$t$ points ![]() $P$ and
$P$ and ![]() $Q$ trace over the primary and secondary circle, respectively. (b) At any time instant
$Q$ trace over the primary and secondary circle, respectively. (b) At any time instant ![]() $t$, the phase point
$t$, the phase point ![]() $Q$ lies at a vertical distance
$Q$ lies at a vertical distance ![]() $\varGamma _{sep}(t)$ from
$\varGamma _{sep}(t)$ from ![]() $S$. The angle subtended by
$S$. The angle subtended by ![]() $QO$ with
$QO$ with ![]() $OR$ is
$OR$ is ![]() $\phi _m$.
$\phi _m$.
As discussed in § 4.1, a p : q lock-in is identified when ![]() $\Delta \psi _m$ is constant. For a secondary excitation given by
$\Delta \psi _m$ is constant. For a secondary excitation given by ![]() $f_s=p_f/q_f f_p$, where
$f_s=p_f/q_f f_p$, where ![]() $p_f$ and
$p_f$ and ![]() $q_f$ are integers, the constant phase criteria translates to
$q_f$ are integers, the constant phase criteria translates to ![]() $\Delta \psi _m-\Delta \psi _{m-q_f}=0$, from which we obtain the following relation between
$\Delta \psi _m-\Delta \psi _{m-q_f}=0$, from which we obtain the following relation between ![]() $\phi _m$ and
$\phi _m$ and ![]() $\phi _{m-q_f}$:
$\phi _{m-q_f}$:
 \begin{equation} \left.\begin{gathered} q \left(\psi_{E,m}-\psi_{E,m-q_f}\right)-p\left(\psi_{R,m}-\psi_{R,m-q_f}\right)=0,\\ q \left(\phi_{m}+\frac{\rm \pi}{2}-\phi_{m-q_f}-\frac{\rm \pi}{2}\right)-p\left(q_f 2{\rm \pi}\right)=0,\\ \implies \phi_m-\phi_{m-q_f}=\frac{2{\rm \pi} p q_f}{q}. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} q \left(\psi_{E,m}-\psi_{E,m-q_f}\right)-p\left(\psi_{R,m}-\psi_{R,m-q_f}\right)=0,\\ q \left(\phi_{m}+\frac{\rm \pi}{2}-\phi_{m-q_f}-\frac{\rm \pi}{2}\right)-p\left(q_f 2{\rm \pi}\right)=0,\\ \implies \phi_m-\phi_{m-q_f}=\frac{2{\rm \pi} p q_f}{q}. \end{gathered}\right\} \end{equation}Equation (4.6) is similar to that of the phase relation reported for single-frequency excitation during p : q lock-in (Britto & Mariappan Reference Britto and Mariappan2019a).
Specifically, for the superharmonic excitations considered in this paper, ![]() $q_f=1$ (refer to figure 8a,b). The phase relation becomes
$q_f=1$ (refer to figure 8a,b). The phase relation becomes ![]() $\phi _m-\phi _{m-1}={2{\rm \pi} p/q}$. Furthermore, in the present vortex shedding model, we always observed lock-in with
$\phi _m-\phi _{m-1}={2{\rm \pi} p/q}$. Furthermore, in the present vortex shedding model, we always observed lock-in with ![]() $q=1$. Therefore, in a p : 1 lock-in, the consecutive phases
$q=1$. Therefore, in a p : 1 lock-in, the consecutive phases ![]() $\phi _m$s are
$\phi _m$s are ![]() $2{\rm \pi} p$ radians apart. On the other hand, for the present subharmonic excitations,
$2{\rm \pi} p$ radians apart. On the other hand, for the present subharmonic excitations, ![]() $p_f=1$ (refer to figure 8c,d). Therefore, the condition for lock-in becomes
$p_f=1$ (refer to figure 8c,d). Therefore, the condition for lock-in becomes ![]() $\phi _m-\phi _{m-q_f}=2{\rm \pi} q_f/q$. Specifically, during 1 : 2 lock-in, owing to subharmonic (
$\phi _m-\phi _{m-q_f}=2{\rm \pi} q_f/q$. Specifically, during 1 : 2 lock-in, owing to subharmonic (![]() $f_s=f_p/2$) secondary excitation, the phase follows
$f_s=f_p/2$) secondary excitation, the phase follows ![]() $\phi _{m}-\phi _{m-2}={2{\rm \pi} }$. Therefore, phases
$\phi _{m}-\phi _{m-2}={2{\rm \pi} }$. Therefore, phases ![]() $\phi _m$s are
$\phi _m$s are ![]() $2{\rm \pi}$ radians apart for every two iterations. Depending on the lock-in order and frequency ratio, the phase relation exhibits different periodicity. Overall, the period of
$2{\rm \pi}$ radians apart for every two iterations. Depending on the lock-in order and frequency ratio, the phase relation exhibits different periodicity. Overall, the period of ![]() $\phi _m$ is equivalent to the lowest frequency among the primary and secondary excitation signals. This behaviour was recently reported by Kashinath, Li & Juniper (Reference Kashinath, Li and Juniper2018) in a model oscillator subjected to large amplitude forcing. Hence, an appropriate modulo operation (modulo
$\phi _m$ is equivalent to the lowest frequency among the primary and secondary excitation signals. This behaviour was recently reported by Kashinath, Li & Juniper (Reference Kashinath, Li and Juniper2018) in a model oscillator subjected to large amplitude forcing. Hence, an appropriate modulo operation (modulo ![]() $2{\rm \pi} , ~4{\rm \pi} ,~6{\rm \pi} ,\ldots$) on
$2{\rm \pi} , ~4{\rm \pi} ,~6{\rm \pi} ,\ldots$) on ![]() $\phi _m$ leads to a fixed point during lock-in. We utilise this fact to study bifurcations across the lock-in boundary in § 5.
$\phi _m$ leads to a fixed point during lock-in. We utilise this fact to study bifurcations across the lock-in boundary in § 5.
Since the condition of lock-in can be expressed elegantly using (4.6), we prefer to study a map relating ![]() $\phi _{m-q_f}$ and
$\phi _{m-q_f}$ and ![]() $\phi _{m}$, instead of investigating (3.1) in time
$\phi _{m}$, instead of investigating (3.1) in time ![]() $t$. Furthermore, the transformation allows us to conveniently study dynamical features of lock-in, such as bifurcations, through first return maps (discussed in § 5).
$t$. Furthermore, the transformation allows us to conveniently study dynamical features of lock-in, such as bifurcations, through first return maps (discussed in § 5).
At this point, it is necessary to highlight lock-in in the presence of quasi-periodic excitations. Quasi-periodic behaviour of oscillations were reported during combustion instability in multiple previous investigations Kabiraj & Sujith (Reference Kabiraj and Sujith2012). During lock-in, under a non-zero secondary excitation (![]() $f_s=p_f f_p/q_f$), (4.6) implies that the oscillations (
$f_s=p_f f_p/q_f$), (4.6) implies that the oscillations (![]() $\phi _m$) are
$\phi _m$) are ![]() $q_f$ periodic. As
$q_f$ periodic. As ![]() $q_f$ is infinite for the quasi-periodic excitation, it is not possible to study phase lock-in in the current framework (refer to (4.6)). In fact, only frequency lock-in is viable during the quasi-periodic excitation, which is shown in figure 10.
$q_f$ is infinite for the quasi-periodic excitation, it is not possible to study phase lock-in in the current framework (refer to (4.6)). In fact, only frequency lock-in is viable during the quasi-periodic excitation, which is shown in figure 10.

Figure 10. Response caused by quasi-periodic excitation with ![]() $f_p=0.9$,
$f_p=0.9$, ![]() $f_s=\sqrt {2} f_p$ and
$f_s=\sqrt {2} f_p$ and ![]() $A_s=0.05$. Panel (a) shows the evolution of
$A_s=0.05$. Panel (a) shows the evolution of ![]() $\Delta \psi _m$ with
$\Delta \psi _m$ with ![]() $A_p=0.08 - 0.12$. Panels (b–d) show the corresponding phase portrait between
$A_p=0.08 - 0.12$. Panels (b–d) show the corresponding phase portrait between ![]() $\Delta t_m$ and
$\Delta t_m$ and ![]() $\Delta t_{m-1}$ for amplitudes associated with (a) (curves are colour coded in (a)).
$\Delta t_{m-1}$ for amplitudes associated with (a) (curves are colour coded in (a)).
Figure 10(a) represents the evolution of the instantaneous phase difference ![]() $\Delta \psi _m$ for
$\Delta \psi _m$ for ![]() $f_p=0.9$,
$f_p=0.9$, ![]() $A_s=0.05$ and
$A_s=0.05$ and ![]() $f_s=\sqrt {2} f_p$. At the lowest amplitude
$f_s=\sqrt {2} f_p$. At the lowest amplitude ![]() $A_p=0.08$,
$A_p=0.08$, ![]() $\Delta \psi _m$ decreases unboundedly indicating phase drifting (unlocked state). When the amplitude is increased gradually, the slope of
$\Delta \psi _m$ decreases unboundedly indicating phase drifting (unlocked state). When the amplitude is increased gradually, the slope of ![]() $\Delta \psi _m$ moves towards zero. At
$\Delta \psi _m$ moves towards zero. At ![]() $A_p=0.12$,
$A_p=0.12$, ![]() $\Delta \psi _m$ becomes bounded, although fluctuating about a mean. The bounded nature indicates frequency lock-in, while the fluctuations show the absence of phase lock-in. Panels (b–d) show the corresponding phase portraits between
$\Delta \psi _m$ becomes bounded, although fluctuating about a mean. The bounded nature indicates frequency lock-in, while the fluctuations show the absence of phase lock-in. Panels (b–d) show the corresponding phase portraits between ![]() $\Delta t_m - \Delta t_{m-1}$, which reveal the occurrence of frequency lock-in. At the lowest amplitude (
$\Delta t_m - \Delta t_{m-1}$, which reveal the occurrence of frequency lock-in. At the lowest amplitude (![]() $A_p=0.08$), we observe that the iterations occupy a dense region in the phase portrait, exhibiting three frequency quasi-periodicity (3-tori shown in (b,c)). During frequency lock-in (d), the phase portrait collapses to a 2-torus quasi-periodic orbit. Since the present framework allows us to study only phase lock-in, we restrict ourselves to super- and subharmonic secondary excitations, which are rational multiples of the primary.
$A_p=0.08$), we observe that the iterations occupy a dense region in the phase portrait, exhibiting three frequency quasi-periodicity (3-tori shown in (b,c)). During frequency lock-in (d), the phase portrait collapses to a 2-torus quasi-periodic orbit. Since the present framework allows us to study only phase lock-in, we restrict ourselves to super- and subharmonic secondary excitations, which are rational multiples of the primary.
It is found that a dynamical map between ![]() $\phi _{m-q_f}$ and
$\phi _{m-q_f}$ and ![]() $\phi _m$ for the two-frequency excitation cannot be obtained explicitly. However, the map can be indirectly determined. For this purpose, we introduce
$\phi _m$ for the two-frequency excitation cannot be obtained explicitly. However, the map can be indirectly determined. For this purpose, we introduce ![]() $\alpha _m=2{\rm \pi} f_p t_m$ and
$\alpha _m=2{\rm \pi} f_p t_m$ and ![]() $\beta _m=2 {\rm \pi}f_s t_m+\gamma$ as notations for phase angles of points P and Q, respectively, in their corresponding circles (refer to figure 9). The following relation between
$\beta _m=2 {\rm \pi}f_s t_m+\gamma$ as notations for phase angles of points P and Q, respectively, in their corresponding circles (refer to figure 9). The following relation between ![]() $\alpha _m$ and
$\alpha _m$ and ![]() $\beta _m$ exists:
$\beta _m$ exists:
where ![]() $\gamma$ is the initial (
$\gamma$ is the initial (![]() $t=0$) relative phase between the primary and secondary excitation. Using the above notations in (3.1), the map equation connecting successive vortex shedding events become
$t=0$) relative phase between the primary and secondary excitation. Using the above notations in (3.1), the map equation connecting successive vortex shedding events become
The full implicit equation (4.8) is given in Appendix A. The parameters ![]() $A_p$,
$A_p$, ![]() $A_s$,
$A_s$, ![]() $f_p$ and
$f_p$ and ![]() $f_s$, along with the initial condition
$f_s$, along with the initial condition ![]() $\gamma$ govern the successive instantaneous phase
$\gamma$ govern the successive instantaneous phase ![]() $\alpha _m$ of vortex shedding. In the next section, the influence of these parameters on the dynamics of
$\alpha _m$ of vortex shedding. In the next section, the influence of these parameters on the dynamics of ![]() $\alpha _m$, and hence
$\alpha _m$, and hence ![]() $\phi _m$, is studied in detail using return maps and cobweb diagrams.
$\phi _m$, is studied in detail using return maps and cobweb diagrams.
5. Analysis of return maps
A ![]() $q_f$th return map is a mapping between
$q_f$th return map is a mapping between ![]() $\phi _{m}$ and its previous
$\phi _{m}$ and its previous ![]() $\phi _{m-q_f}$ iteration. We use the following approach to obtain it. It should be noted that (4.8) is
$\phi _{m-q_f}$ iteration. We use the following approach to obtain it. It should be noted that (4.8) is ![]() $2{\rm \pi}$ or
$2{\rm \pi}$ or ![]() $2{\rm \pi} q_f$ periodic for super- or subharmonic secondary excitation. Therefore, using (4.8), we solve for
$2{\rm \pi} q_f$ periodic for super- or subharmonic secondary excitation. Therefore, using (4.8), we solve for ![]() $\alpha _m$ in the range of
$\alpha _m$ in the range of ![]() $\alpha _{m-1}\epsilon [0,2{\rm \pi} ]$ and
$\alpha _{m-1}\epsilon [0,2{\rm \pi} ]$ and ![]() $\alpha _{m-1}\epsilon [0,2{\rm \pi} q_f]$ to study p : 1 and 1 : q lock-in, respectively. It is to be noted that
$\alpha _{m-1}\epsilon [0,2{\rm \pi} q_f]$ to study p : 1 and 1 : q lock-in, respectively. It is to be noted that ![]() $\alpha _m$ solved from (4.8) contains harmonic terms, leading to the occurrence of multiple solutions, where
$\alpha _m$ solved from (4.8) contains harmonic terms, leading to the occurrence of multiple solutions, where ![]() $\alpha _m$ closest to the previous iteration
$\alpha _m$ closest to the previous iteration ![]() $\alpha _{m-1}$ is the correct solution, while other
$\alpha _{m-1}$ is the correct solution, while other ![]() $\alpha _m$ are termed as forbidden solutions. The correct solution is extracted numerically through a careful choice of algorithm, the details of which were given in Appendix A by Britto & Mariappan (Reference Britto and Mariappan2019a).
$\alpha _m$ are termed as forbidden solutions. The correct solution is extracted numerically through a careful choice of algorithm, the details of which were given in Appendix A by Britto & Mariappan (Reference Britto and Mariappan2019a).
It is found that the relative phase ![]() $\gamma$ in (4.8) influence the shape of
$\gamma$ in (4.8) influence the shape of ![]() $\varGamma _{sep}$. Therefore, it is true that
$\varGamma _{sep}$. Therefore, it is true that ![]() $\gamma$ does affect vortex shedding behaviour and subsequent lock-in. Figure 11 illustrates the effect of
$\gamma$ does affect vortex shedding behaviour and subsequent lock-in. Figure 11 illustrates the effect of ![]() $\gamma$ on the evolution of
$\gamma$ on the evolution of ![]() $\Delta \psi _m$. The parameters
$\Delta \psi _m$. The parameters ![]() $f_s=2f_p$,
$f_s=2f_p$, ![]() $f_p=0.9$ and
$f_p=0.9$ and ![]() $A_s=0.05$ are fixed, while the primary amplitude
$A_s=0.05$ are fixed, while the primary amplitude ![]() $A_p$ is increased until lock-in is encountered; (a) corresponds to
$A_p$ is increased until lock-in is encountered; (a) corresponds to ![]() $\gamma =0$ and lock-in is attained at
$\gamma =0$ and lock-in is attained at ![]() $A_p=0.09$ (purple curve). On the other hand, when
$A_p=0.09$ (purple curve). On the other hand, when ![]() $\gamma$ is set to
$\gamma$ is set to ![]() ${\rm \pi} /2$ (b),
${\rm \pi} /2$ (b), ![]() $\Delta \psi _m$ exhibits similar qualitative behaviour with a delayed lock-in occurring at a larger amplitude
$\Delta \psi _m$ exhibits similar qualitative behaviour with a delayed lock-in occurring at a larger amplitude ![]() $A_p=0.18$. Although
$A_p=0.18$. Although ![]() $\gamma$ does influence the onset of lock-in, we choose its value to be zero in this paper. This choice provides considerable simplification and analytical tractability (see § 6). The authors believe that the influence of the initial phase on lock-in during multiple-frequency excitation can be studied as a separate work. Figure 12 shows a map between
$\gamma$ does influence the onset of lock-in, we choose its value to be zero in this paper. This choice provides considerable simplification and analytical tractability (see § 6). The authors believe that the influence of the initial phase on lock-in during multiple-frequency excitation can be studied as a separate work. Figure 12 shows a map between ![]() $\phi _{m}$ and
$\phi _{m}$ and ![]() $\phi _{m-1}$ for parameters
$\phi _{m-1}$ for parameters ![]() $f_s=2f_p$,
$f_s=2f_p$, ![]() $f_p=0.9$ and
$f_p=0.9$ and ![]() $A_s=0.15$,
$A_s=0.15$, ![]() $A_p=0.1$. The iterations of
$A_p=0.1$. The iterations of ![]() $\alpha _m$,
$\alpha _m$, ![]() $\beta _m$ and
$\beta _m$ and ![]() $\phi _m$ are evaluated from (4.8), (4.7) and (4.4), respectively. The successive iterations
$\phi _m$ are evaluated from (4.8), (4.7) and (4.4), respectively. The successive iterations ![]() $\phi _{1},\phi _{2},\ldots$ are obtained using
$\phi _{1},\phi _{2},\ldots$ are obtained using ![]() $\alpha _{0},\alpha _{1},\ldots$, respectively. The lines connecting these iterations are called cobwebs and are shown as black lines. As mentioned before, multiple solutions for a given
$\alpha _{0},\alpha _{1},\ldots$, respectively. The lines connecting these iterations are called cobwebs and are shown as black lines. As mentioned before, multiple solutions for a given ![]() $\alpha _{m-1}$ are possible. The correct solution is represented by green curves, while the other solution, termed as the forbidden solution is shown in red (a). Initially, the cobweb jumps vertically from
$\alpha _{m-1}$ are possible. The correct solution is represented by green curves, while the other solution, termed as the forbidden solution is shown in red (a). Initially, the cobweb jumps vertically from ![]() $\phi _0=0$ (for
$\phi _0=0$ (for ![]() $t_1=0$ and
$t_1=0$ and ![]() $\gamma =0$) to its correct solution
$\gamma =0$) to its correct solution ![]() $\phi _1$ that lie on the first return map (green curve). Since
$\phi _1$ that lie on the first return map (green curve). Since ![]() $\phi _1$ is the initial condition to the next iteration (
$\phi _1$ is the initial condition to the next iteration (![]() $\phi _2$), the cobweb jumps horizontally to the
$\phi _2$), the cobweb jumps horizontally to the ![]() $\phi _{m}=\phi _{m-1}$ line shown using black dashed line. The flow of the cobwebs now follow alternate vertical and horizontal jumps from the first return map to the dashed line, respectively; the arrows indicate the direction of flow.
$\phi _{m}=\phi _{m-1}$ line shown using black dashed line. The flow of the cobwebs now follow alternate vertical and horizontal jumps from the first return map to the dashed line, respectively; the arrows indicate the direction of flow.

Figure 11. The effect of initial relative phase ![]() $\gamma$ on the onset of lock-in. Phase difference
$\gamma$ on the onset of lock-in. Phase difference ![]() $\Delta \psi _{m}$ obtained for various forcing amplitude at excitation frequency
$\Delta \psi _{m}$ obtained for various forcing amplitude at excitation frequency ![]() $f_s=2f_p$ with (a)
$f_s=2f_p$ with (a) ![]() $\gamma =0$ and (b)
$\gamma =0$ and (b) ![]() $\gamma ={\rm \pi} /2$. Lock-in is identified when
$\gamma ={\rm \pi} /2$. Lock-in is identified when ![]() $\Delta \psi _m$ is constant.
$\Delta \psi _m$ is constant.

Figure 12. First return map and cobweb diagrams to illustrate the flow of ![]() $\phi _{m}$. The primary and secondary excitation components are
$\phi _{m}$. The primary and secondary excitation components are ![]() $f_p=0.9$,
$f_p=0.9$, ![]() $A_p=0.1$,
$A_p=0.1$, ![]() $f_s=2f_p$ and
$f_s=2f_p$ and ![]() $A_s=0.15$. Map between
$A_s=0.15$. Map between ![]() $\phi _{m}-\phi _{m-1}$ obtained using (4.8) and (4.4) is shown in (a). Correct and forbidden solutions are represented by green and red curves, respectively. Since the chosen parameters lie in the 2 : 1 lock-in region, a modulo
$\phi _{m}-\phi _{m-1}$ obtained using (4.8) and (4.4) is shown in (a). Correct and forbidden solutions are represented by green and red curves, respectively. Since the chosen parameters lie in the 2 : 1 lock-in region, a modulo ![]() $4{\rm \pi}$ operation is chosen in compliance with (4.6) to observe the fixed point. (b) The map
$4{\rm \pi}$ operation is chosen in compliance with (4.6) to observe the fixed point. (b) The map ![]() $\phi _{m}-\phi _{m-1}$ spans from
$\phi _{m}-\phi _{m-1}$ spans from ![]() $0 - 4{\rm \pi}$. Only the correct solution is shown. Arrows indicate the direction of cobwebs.
$0 - 4{\rm \pi}$. Only the correct solution is shown. Arrows indicate the direction of cobwebs.
The chosen parameters in figure 12 lie in the 2 : 1 lock-in region. Hence, a modulo ![]() $4{\rm \pi}$ operation is chosen in compliance with (4.6). This further helps the illustration of the lock-in process elegantly. Panel (b) represents the first return map (only the correct solution is shown in the present and subsequent figures), along with cobwebs of (a), after the modulo operation. A stable fixed point (shown as a green circle) at
$4{\rm \pi}$ operation is chosen in compliance with (4.6). This further helps the illustration of the lock-in process elegantly. Panel (b) represents the first return map (only the correct solution is shown in the present and subsequent figures), along with cobwebs of (a), after the modulo operation. A stable fixed point (shown as a green circle) at ![]() $\phi _m=\phi _{m-1}$ is observed.
$\phi _m=\phi _{m-1}$ is observed.
Using the geometry of return maps, we study the bifurcations across the lock-in boundary observed in figure 8. First, the dynamics inside the lock-in boundary below ![]() $A_p< A_s$ is studied. Subsequently, we analyse the bifurcations that occur across
$A_p< A_s$ is studied. Subsequently, we analyse the bifurcations that occur across ![]() $A_p=A_s$ and
$A_p=A_s$ and ![]() $A_p>A_s$ regions.
$A_p>A_s$ regions.
5.1. Bifurcations in the  $A_p - f_p$ plane
$A_p - f_p$ plane
In previous work (Britto & Mariappan Reference Britto and Mariappan2019a), for a single-frequency excitation case, we observed the birth of stable and unstable fixed points in the return maps at the onset of lock-in. This occurred through a saddle-node bifurcation. An analytical stability analysis was performed to confirm the same. In this study, we follow a similar procedure and analyse our return maps. Since a functional relation between ![]() $\phi _{m}$ and
$\phi _{m}$ and ![]() $\phi _{m-1}$ (or
$\phi _{m-1}$ (or ![]() $\phi _{m}$ and
$\phi _{m}$ and ![]() $\phi _{m-2}$) is not available, we rely entirely on the geometry of return maps and cobweb diagrams to study bifurcations. In the present study, we observed two orders of lock-in in three regions of the
$\phi _{m-2}$) is not available, we rely entirely on the geometry of return maps and cobweb diagrams to study bifurcations. In the present study, we observed two orders of lock-in in three regions of the ![]() $A_p - f_p$ plane (refer to figure 7). Therefore, we explore the nature of bifurcations across these regions:
$A_p - f_p$ plane (refer to figure 7). Therefore, we explore the nature of bifurcations across these regions: ![]() $A_p< A_s$,
$A_p< A_s$, ![]() $A_p=A_s$ and
$A_p=A_s$ and ![]() $A_p>A_s$. First, we study the geometry of return maps in the
$A_p>A_s$. First, we study the geometry of return maps in the ![]() $A_p< A_s$ region where the secondary excitation is dominant over the primary (discussed in figure 7). Further, the bifurcation associated when both primary and secondary excitation amplitudes are equal across
$A_p< A_s$ region where the secondary excitation is dominant over the primary (discussed in figure 7). Further, the bifurcation associated when both primary and secondary excitation amplitudes are equal across ![]() $A_p=A_s$. In the end, the bifurcation beyond the
$A_p=A_s$. In the end, the bifurcation beyond the ![]() $A_p>A_s$ region is studied.
$A_p>A_s$ region is studied.
5.1.1. Phase dynamics in the  $A_p< A_s$ region
$A_p< A_s$ region
Figure 13(a) shows the lock-in region in focus. Using criteria (4.6), we find the occurrence of 2 : 1 lock-in for ![]() $A_p< A_s$. To illustrate the occurrence of bifurcations, we choose
$A_p< A_s$. To illustrate the occurrence of bifurcations, we choose ![]() $A_p=0.01< A_s=0.05$ with
$A_p=0.01< A_s=0.05$ with ![]() $f_s=2f_p$ (superharmonic excitation). As we increase the primary excitation frequency, from
$f_s=2f_p$ (superharmonic excitation). As we increase the primary excitation frequency, from ![]() $f_p=0.935 - 1.07$ (refer to (b–h)), the first return map exhibits a series of saddle-node bifurcations (
$f_p=0.935 - 1.07$ (refer to (b–h)), the first return map exhibits a series of saddle-node bifurcations (![]() $SN_1-SN_4$) (see supplementary movie 1, available at https://doi.org/10.1017/jfm.2021.624). Using (4.6), we have set modulo
$SN_1-SN_4$) (see supplementary movie 1, available at https://doi.org/10.1017/jfm.2021.624). Using (4.6), we have set modulo ![]() $4{\rm \pi}$ on
$4{\rm \pi}$ on ![]() $\phi _m$ to observe fixed points on return maps during 2 : 1 lock-in. Initially, in (b),
$\phi _m$ to observe fixed points on return maps during 2 : 1 lock-in. Initially, in (b), ![]() $f_p=0.935$ lies outside the lock-in region and, hence, there are no fixed points in the first return map. The flow of cobwebs occupy a dense region in the map representing quasi-periodic behaviour. The parameter
$f_p=0.935$ lies outside the lock-in region and, hence, there are no fixed points in the first return map. The flow of cobwebs occupy a dense region in the map representing quasi-periodic behaviour. The parameter ![]() $f_p$ now enters the 2 : 1 phase lock-in region illustrated in (c). The return map, in turn, intersects with
$f_p$ now enters the 2 : 1 phase lock-in region illustrated in (c). The return map, in turn, intersects with ![]() $\phi _m=\phi _{m-1}$ at two locations (solid and hollow green circles), marking the formation of two new fixed points through saddle-node bifurcation (
$\phi _m=\phi _{m-1}$ at two locations (solid and hollow green circles), marking the formation of two new fixed points through saddle-node bifurcation (![]() $SN_1$). At one of the fixed points (hollow circle), the return map has a slope greater than one, identifying it as linearly unstable. Therefore, the cobwebs flow towards the stable fixed point (solid circle), where the slope is less than one (solid green circle). The dynamics governed by the geometry of the first return map alters once
$SN_1$). At one of the fixed points (hollow circle), the return map has a slope greater than one, identifying it as linearly unstable. Therefore, the cobwebs flow towards the stable fixed point (solid circle), where the slope is less than one (solid green circle). The dynamics governed by the geometry of the first return map alters once ![]() $f_p$ enters the blue shaded region shown in (a). Although
$f_p$ enters the blue shaded region shown in (a). Although ![]() $f_p$ lies inside the 2 : 1 phase lock-in region, a new pair of fixed points (solid and hollow orange circles) are formed through a second saddle-node bifurcation (
$f_p$ lies inside the 2 : 1 phase lock-in region, a new pair of fixed points (solid and hollow orange circles) are formed through a second saddle-node bifurcation (![]() $SN_2$), in addition to the existing set (d). This causes the cobweb to choose between the two stable fixed points (between solid green and orange circles). The flow of cobwebs now depends on the initial
$SN_2$), in addition to the existing set (d). This causes the cobweb to choose between the two stable fixed points (between solid green and orange circles). The flow of cobwebs now depends on the initial ![]() $\phi _0$, which defines a bistable region that exists throughout the blue shaded region shown in (a). When the cobweb switches from one fixed point to another, it changes the vortex shedding phase instances as illustrated in (i), through threshold curve
$\phi _0$, which defines a bistable region that exists throughout the blue shaded region shown in (a). When the cobweb switches from one fixed point to another, it changes the vortex shedding phase instances as illustrated in (i), through threshold curve ![]() $\varGamma _{sep} (t)$. Although
$\varGamma _{sep} (t)$. Although ![]() $\varGamma _{m}$ remains almost same, both
$\varGamma _{m}$ remains almost same, both ![]() $\phi _m$s and, hence,
$\phi _m$s and, hence, ![]() $t_m$s change with the initial condition (
$t_m$s change with the initial condition (![]() $\phi _0$). This behaviour is critical from the perspective of combustion instability. The phase of heat release in comparison to the acoustic pressure fluctuation in the combustion chamber largely alters the Rayleigh criterion (Lieuwen Reference Lieuwen2012), which governs the growth/decay of pressure oscillations. If the conditions are right, one of the fixed points can have an appropriate
$\phi _0$). This behaviour is critical from the perspective of combustion instability. The phase of heat release in comparison to the acoustic pressure fluctuation in the combustion chamber largely alters the Rayleigh criterion (Lieuwen Reference Lieuwen2012), which governs the growth/decay of pressure oscillations. If the conditions are right, one of the fixed points can have an appropriate ![]() $\phi _m$ for the occurrence of instability. So the bistable region has the potential to exhibit pulsed combustion instability (Culick, Burnley & Swenson Reference Culick, Burnley and Swenson1995).
$\phi _m$ for the occurrence of instability. So the bistable region has the potential to exhibit pulsed combustion instability (Culick, Burnley & Swenson Reference Culick, Burnley and Swenson1995).

Figure 13. Illustration of bifurcations occurring in region ![]() $A_p< A_s$. (a) The bistability region is shown using blue shade. It lies within the 2 : 1 lock-in boundary. (b–h) Return maps and cobweb diagrams for superharmonic secondary excitation
$A_p< A_s$. (a) The bistability region is shown using blue shade. It lies within the 2 : 1 lock-in boundary. (b–h) Return maps and cobweb diagrams for superharmonic secondary excitation ![]() $f_s=2f_p$. With the primary excitation amplitude set to
$f_s=2f_p$. With the primary excitation amplitude set to ![]() $A_p=0.01$,
$A_p=0.01$, ![]() $f_p$ is swept across the lock-in boundary (the chosen
$f_p$ is swept across the lock-in boundary (the chosen ![]() $f_p$s are marked using red cross symbols in (a)). Appearances of stable and unstable fixed points are marked using solid and hollow circles, respectively. Saddle-node bifurcations marked
$f_p$s are marked using red cross symbols in (a)). Appearances of stable and unstable fixed points are marked using solid and hollow circles, respectively. Saddle-node bifurcations marked ![]() $SN_1-SN_4$ are shown in (c–g). Vortex shedding time instances for two initial conditions
$SN_1-SN_4$ are shown in (c–g). Vortex shedding time instances for two initial conditions ![]() $\phi _0=0$,
$\phi _0=0$, ![]() $0.5$ corresponding to (d) are shown using green and orange circles in (i). Refer to supplementary movie 1 showing the continuous variation of the return map with
$0.5$ corresponding to (d) are shown using green and orange circles in (i). Refer to supplementary movie 1 showing the continuous variation of the return map with ![]() $f_p$, along with the occurrence of saddle-node bifurcations.
$f_p$, along with the occurrence of saddle-node bifurcations.
Now, as the primary excitation frequency crosses ![]() $f_p=1$, the shape of the first return map begins to exhibit another transformation (see (e–h)). The curve of the first return map near the first fixed point (green circle) begins to detach from the
$f_p=1$, the shape of the first return map begins to exhibit another transformation (see (e–h)). The curve of the first return map near the first fixed point (green circle) begins to detach from the ![]() $\phi _m=\phi _{m-1}$ line. This causes another saddle-node bifurcation (
$\phi _m=\phi _{m-1}$ line. This causes another saddle-node bifurcation (![]() $SN_3$), and the first fixed point disappears (g), marking the end of bistability. Hence, the cobweb flows towards the second fixed point (orange circle). Finally, when
$SN_3$), and the first fixed point disappears (g), marking the end of bistability. Hence, the cobweb flows towards the second fixed point (orange circle). Finally, when ![]() $f_p$ is increased beyond the lock-in boundary, the second fixed point disappears through the final saddle-node bifurcation (
$f_p$ is increased beyond the lock-in boundary, the second fixed point disappears through the final saddle-node bifurcation (![]() $SN_4$) and causes the cobweb to occupy a dense region in the map (h). It should be noted that bistability is only observed during superharmonic secondary excitation when
$SN_4$) and causes the cobweb to occupy a dense region in the map (h). It should be noted that bistability is only observed during superharmonic secondary excitation when ![]() $A_p< A_s$. In subharmonic secondary excitation, we observe only
$A_p< A_s$. In subharmonic secondary excitation, we observe only ![]() $SN_1$ and
$SN_1$ and ![]() $SN_4$ bifurcations.
$SN_4$ bifurcations.
The origin of the bistability region is comprehended using the return maps. In figure 14(a–d) represent return maps for super- (![]() $f_s=2f_p$) and subharmonic (
$f_s=2f_p$) and subharmonic (![]() $f_s=f_p/2$) secondary excitations, respectively. According to (4.6), modulo
$f_s=f_p/2$) secondary excitations, respectively. According to (4.6), modulo ![]() $4{\rm \pi}$ and
$4{\rm \pi}$ and ![]() $2{\rm \pi}$ operations must be performed on the corresponding return maps. However, we use modulo
$2{\rm \pi}$ operations must be performed on the corresponding return maps. However, we use modulo ![]() $2{\rm \pi}$ operation throughout (a–d) to illustrate better the origin of bistability. Consequently, the curves that span from
$2{\rm \pi}$ operation throughout (a–d) to illustrate better the origin of bistability. Consequently, the curves that span from ![]() $0 - 2{\rm \pi}$ and
$0 - 2{\rm \pi}$ and ![]() $2{\rm \pi} - 4{\rm \pi}$ are shown in blue and red colours, respectively. We begin with
$2{\rm \pi} - 4{\rm \pi}$ are shown in blue and red colours, respectively. We begin with ![]() $A_p=0$, which corresponds to the single-frequency excitation. In this scenario, we observe that the return map (a,c) that spans between
$A_p=0$, which corresponds to the single-frequency excitation. In this scenario, we observe that the return map (a,c) that spans between ![]() $\phi _m=2{\rm \pi} - 4{\rm \pi}$ (red curve) overlaps with the curve that lies within
$\phi _m=2{\rm \pi} - 4{\rm \pi}$ (red curve) overlaps with the curve that lies within ![]() $0 - 2{\rm \pi}$ (blue curve). Hence, the two sets (both stable and unstable) of fixed points formed between
$0 - 2{\rm \pi}$ (blue curve). Hence, the two sets (both stable and unstable) of fixed points formed between ![]() $\phi _m=0 - 4{\rm \pi}$ are the same (solid and hollow red circles). This observation is common for both sub- and superharmonic secondary excitations.
$\phi _m=0 - 4{\rm \pi}$ are the same (solid and hollow red circles). This observation is common for both sub- and superharmonic secondary excitations.

Figure 14. Origin of bistability owing to the inclusion of primary excitation. Panels (a–d) represent the return maps for super- and subharmonic secondary excitations, respectively. In both the cases, the primary excitation frequency is set at ![]() $f_p=1.01$ and
$f_p=1.01$ and ![]() $A_p$ is increased from
$A_p$ is increased from ![]() $0$ to
$0$ to ![]() $0.02$. Panels (e,g) and (f,h) represent the threshold circulation strength
$0.02$. Panels (e,g) and (f,h) represent the threshold circulation strength ![]() $\varGamma _{sep}$ for super- (
$\varGamma _{sep}$ for super- (![]() $f_s=2 f_p$) and subharmonic (
$f_s=2 f_p$) and subharmonic (![]() $f_s=f_p/2$) secondary excitations, respectively. Panels in the rows (e,f) and (g,h) correspond to primary excitation amplitudes
$f_s=f_p/2$) secondary excitations, respectively. Panels in the rows (e,f) and (g,h) correspond to primary excitation amplitudes ![]() $A_p=0.01$ and
$A_p=0.01$ and ![]() $0.045$, respectively. The evolution of
$0.045$, respectively. The evolution of ![]() $\varGamma _{sep}$ is shown as a blue solid curve, while black and red dashed curves correspond to the contributions from primary and secondary excitations, respectively.
$\varGamma _{sep}$ is shown as a blue solid curve, while black and red dashed curves correspond to the contributions from primary and secondary excitations, respectively.
Bistability occurs when a non-zero primary excitation is introduced into the flow field (![]() $A_p=0.02$, refer to (b,d)). In the superharmonic excitation, the
$A_p=0.02$, refer to (b,d)). In the superharmonic excitation, the ![]() $2{\rm \pi}$ periodicity is broken as the first return map begins to exhibit
$2{\rm \pi}$ periodicity is broken as the first return map begins to exhibit ![]() $4{\rm \pi}$ periodicity (blue and red curves do not overlap). This behaviour is in line with the lock-in criterion given in (4.6). In (b), it can be observed that the return map and fixed points (blue and red circles) exhibit a slight difference between them. Therefore, it creates a bistable region during superharmonic secondary excitation. The absence of this behaviour during subharmonic secondary excitation (refer to (d)) is discussed below.
$4{\rm \pi}$ periodicity (blue and red curves do not overlap). This behaviour is in line with the lock-in criterion given in (4.6). In (b), it can be observed that the return map and fixed points (blue and red circles) exhibit a slight difference between them. Therefore, it creates a bistable region during superharmonic secondary excitation. The absence of this behaviour during subharmonic secondary excitation (refer to (d)) is discussed below.
Panels (e–h) represents the time evolution of threshold circulation strength ![]() $\varGamma _{sep}$ (blue curve) for super- (e,g) and subharmonic (f,h) secondary excitations, respectively. In both cases, the primary excitation is increased from
$\varGamma _{sep}$ (blue curve) for super- (e,g) and subharmonic (f,h) secondary excitations, respectively. In both cases, the primary excitation is increased from ![]() $A_p=0.01$ to
$A_p=0.01$ to ![]() $0.045$. In the considered parametric regime (
$0.045$. In the considered parametric regime (![]() $A_p< A_s$), secondary excitation is dominant, which dictates the vortex shedding. The presence of the primary excitation modulates
$A_p< A_s$), secondary excitation is dominant, which dictates the vortex shedding. The presence of the primary excitation modulates ![]() $\varGamma _{sep}$. This can be observed by the evolution of the contributions of primary (black dashed curve) and secondary (red dashed curve) excitations to
$\varGamma _{sep}$. This can be observed by the evolution of the contributions of primary (black dashed curve) and secondary (red dashed curve) excitations to ![]() $\varGamma _{sep}$, shown in (e–h). In our current model, we observe that the period of oscillation of
$\varGamma _{sep}$, shown in (e–h). In our current model, we observe that the period of oscillation of ![]() $\phi _m$ (also in
$\phi _m$ (also in ![]() $\varGamma _{sep}$) corresponds to that of the lowest frequency of excitation (also reported in Kashinath et al. Reference Kashinath, Li and Juniper2018). In the superharmonic case (
$\varGamma _{sep}$) corresponds to that of the lowest frequency of excitation (also reported in Kashinath et al. Reference Kashinath, Li and Juniper2018). In the superharmonic case (![]() $f_s=2f_p$), the lowest frequency corresponds to the primary component
$f_s=2f_p$), the lowest frequency corresponds to the primary component ![]() $A_p$ (black dashed curve). Hence, the non-zero primary excitation creates a change in the periodicity of the return map, leading to two stable solutions (bistability). Whereas, in the subharmonic case, the lowest frequency is caused by the dominant secondary excitation (red dashed curve). Hence, the introduction of the primary (having a larger frequency) does not break the
$A_p$ (black dashed curve). Hence, the non-zero primary excitation creates a change in the periodicity of the return map, leading to two stable solutions (bistability). Whereas, in the subharmonic case, the lowest frequency is caused by the dominant secondary excitation (red dashed curve). Hence, the introduction of the primary (having a larger frequency) does not break the ![]() $2{\rm \pi}$ periodicity in the corresponding return maps (c,d). Therefore, the presence of two-frequency excitation causes bistability only in the superharmonic case.
$2{\rm \pi}$ periodicity in the corresponding return maps (c,d). Therefore, the presence of two-frequency excitation causes bistability only in the superharmonic case.
5.1.2. Phase dynamics across  $A_p=A_s$
$A_p=A_s$
In this section, we discuss the dynamics of ![]() $\phi _m$ across the
$\phi _m$ across the ![]() $A_p=A_s$ line that separates the relative dominance of the two excitation signals. As discussed in § 4.3, there are two orders of lock-in regions within the lock-in boundary in the
$A_p=A_s$ line that separates the relative dominance of the two excitation signals. As discussed in § 4.3, there are two orders of lock-in regions within the lock-in boundary in the ![]() $A_p - f_p$ plane (discussed in figure 7). This indicates a jump in the order of lock-in across
$A_p - f_p$ plane (discussed in figure 7). This indicates a jump in the order of lock-in across ![]() $A_p=A_s$. Using the analytical criterion given in (4.6), for a superharmonic (or subharmonic) excitation
$A_p=A_s$. Using the analytical criterion given in (4.6), for a superharmonic (or subharmonic) excitation ![]() $f_s=2f_p$ (
$f_s=2f_p$ (![]() $f_s=f_p/2$), the iterations of
$f_s=f_p/2$), the iterations of ![]() $\phi _m$ exhibit a phase difference of
$\phi _m$ exhibit a phase difference of ![]() $4{\rm \pi}$ (
$4{\rm \pi}$ (![]() $2{\rm \pi}$) and
$2{\rm \pi}$) and ![]() $2{\rm \pi}$ (
$2{\rm \pi}$ (![]() $4{\rm \pi}$) in 2 : 1 (1 : 2) and 1:1 (1:1) lock-in regions. Hence, we use the appropriate modulo operation on their return maps to study the behaviour of fixed points and the flow of cobwebs. In figure 15, we have set
$4{\rm \pi}$) in 2 : 1 (1 : 2) and 1:1 (1:1) lock-in regions. Hence, we use the appropriate modulo operation on their return maps to study the behaviour of fixed points and the flow of cobwebs. In figure 15, we have set ![]() $A_s=0.05$ and varied
$A_s=0.05$ and varied ![]() $A_p$ in the range 0.048–0.051. In the superharmonic excitation (a,b), the first return map spans from
$A_p$ in the range 0.048–0.051. In the superharmonic excitation (a,b), the first return map spans from ![]() $0 - 4{\rm \pi}$ and
$0 - 4{\rm \pi}$ and ![]() $0 - 2{\rm \pi}$ when
$0 - 2{\rm \pi}$ when ![]() $A_p< A_s$ and
$A_p< A_s$ and ![]() $A_p>A_s$, respectively (refer to (4.6)). First, during 2 : 1 lock-in, a stable fixed point (slope less than one) exists at
$A_p>A_s$, respectively (refer to (4.6)). First, during 2 : 1 lock-in, a stable fixed point (slope less than one) exists at ![]() $\phi _{m-1}=10.15$ (green solid circle in figure 15a). When
$\phi _{m-1}=10.15$ (green solid circle in figure 15a). When ![]() $A_p$ is increased gradually, the shape of the first return map changes slightly (not shown). As
$A_p$ is increased gradually, the shape of the first return map changes slightly (not shown). As ![]() $A_p$ crosses
$A_p$ crosses ![]() $A_s$, the geometry of the first return map changes drastically and becomes
$A_s$, the geometry of the first return map changes drastically and becomes ![]() $2{\rm \pi}$ periodic as shown in (b). A new pair of fixed points are formed at
$2{\rm \pi}$ periodic as shown in (b). A new pair of fixed points are formed at ![]() $\phi _{m-1}=1.14{\rm \pi}$ (solid green circle) and
$\phi _{m-1}=1.14{\rm \pi}$ (solid green circle) and ![]() $1.85{\rm \pi}$ (hollow green circle) (refer to figure 15b). It should be noted that previously, there was no fixed point below
$1.85{\rm \pi}$ (hollow green circle) (refer to figure 15b). It should be noted that previously, there was no fixed point below ![]() $\phi _{m-1}=2{\rm \pi}$ (illustrated using vertical dashed line in (a)). This indicates that the map undergoes a saddle-node bifurcation when
$\phi _{m-1}=2{\rm \pi}$ (illustrated using vertical dashed line in (a)). This indicates that the map undergoes a saddle-node bifurcation when ![]() $A_p$ is increased across the
$A_p$ is increased across the ![]() $A_p=A_s$ line. The aforementioned can be observed in supplementary movie 2, where the return maps between
$A_p=A_s$ line. The aforementioned can be observed in supplementary movie 2, where the return maps between ![]() $\phi _{m-1}-\phi _{m}$ (superharmonic, left panel) and
$\phi _{m-1}-\phi _{m}$ (superharmonic, left panel) and ![]() $\phi _{m-2}-\phi _{m}$ (subharmonic, right panel) are animated in blue. Note that both the axes are between
$\phi _{m-2}-\phi _{m}$ (subharmonic, right panel) are animated in blue. Note that both the axes are between ![]() $0 - 4{\rm \pi}$. To highlight the occurrence of
$0 - 4{\rm \pi}$. To highlight the occurrence of ![]() $2{\rm \pi}$ periodicity, the map between
$2{\rm \pi}$ periodicity, the map between ![]() $2{\rm \pi} - 4{\rm \pi}$ is re-plotted between
$2{\rm \pi} - 4{\rm \pi}$ is re-plotted between ![]() $0 - 2{\rm \pi}$ in red. From the movie, one can observe at
$0 - 2{\rm \pi}$ in red. From the movie, one can observe at ![]() $A_p=A_s$, the first return map (left panel) changes its periodicity from
$A_p=A_s$, the first return map (left panel) changes its periodicity from ![]() $4{\rm \pi}$ to
$4{\rm \pi}$ to ![]() $2{\rm \pi}$ (shown by the overlap between blue and red curves in
$2{\rm \pi}$ (shown by the overlap between blue and red curves in ![]() $0 - 4{\rm \pi}$). A contrasting behaviour is observed during subharmonic secondary excitation shown in figure 15(c,d). Since
$0 - 4{\rm \pi}$). A contrasting behaviour is observed during subharmonic secondary excitation shown in figure 15(c,d). Since ![]() $q_f=2$, we now study the second return map and its corresponding cobweb diagram in
$q_f=2$, we now study the second return map and its corresponding cobweb diagram in ![]() $\phi _m - \phi _{m-2}$ plane. When
$\phi _m - \phi _{m-2}$ plane. When ![]() $A_p< A_s$ (c), the return map lies within
$A_p< A_s$ (c), the return map lies within ![]() $0 - 2{\rm \pi}$ with a fold near
$0 - 2{\rm \pi}$ with a fold near ![]() $\phi _{m-2}={\rm \pi} /2 - 3{\rm \pi} /2$ (between red vertical dashed lines in (c)). There are two stable fixed points (orange and green solid circles) that lie within
$\phi _{m-2}={\rm \pi} /2 - 3{\rm \pi} /2$ (between red vertical dashed lines in (c)). There are two stable fixed points (orange and green solid circles) that lie within ![]() $0 - 2{\rm \pi}$. When
$0 - 2{\rm \pi}$. When ![]() $A_p$ is increased above
$A_p$ is increased above ![]() $0.05$, the return map unfolds and stretches between
$0.05$, the return map unfolds and stretches between ![]() $0 - 4{\rm \pi}$ (d). One of the stable fixed points (solid green circle), along with its unstable counterpart, disappears and a new pair of fixed points is formed at
$0 - 4{\rm \pi}$ (d). One of the stable fixed points (solid green circle), along with its unstable counterpart, disappears and a new pair of fixed points is formed at ![]() $\phi _{m-2}=11.14$ and
$\phi _{m-2}=11.14$ and ![]() $11.61$ (hollow and solid pink circles). Therefore, a saddle-node bifurcation is observed when the primary excitation amplitude is increased across the
$11.61$ (hollow and solid pink circles). Therefore, a saddle-node bifurcation is observed when the primary excitation amplitude is increased across the ![]() $A_p=A_s$ line (refer to the right panel of supplementary movie 2). In the next section, we study the bifurcation observed beyond
$A_p=A_s$ line (refer to the right panel of supplementary movie 2). In the next section, we study the bifurcation observed beyond ![]() $A_p=A_s$.
$A_p=A_s$.

Figure 15. Return maps and cobweb diagrams for (a,b) superharmonic ![]() $f_s=2f_p$ and (c,d) subharmonic secondary excitation. With the primary excitation frequency set to
$f_s=2f_p$ and (c,d) subharmonic secondary excitation. With the primary excitation frequency set to ![]() $f_p=1.05$,
$f_p=1.05$, ![]() $A_p$ is swept across
$A_p$ is swept across ![]() $A_s=0.05$. The transformation in the periodicity of the first return map and the flow of cobwebs are illustrated in supplementary movie 2.
$A_s=0.05$. The transformation in the periodicity of the first return map and the flow of cobwebs are illustrated in supplementary movie 2.
5.1.3. Bifurcations in the  $A_p>A_s$ region
$A_p>A_s$ region
We set the excitation amplitudes at ![]() $A_p=0.07$ and
$A_p=0.07$ and ![]() $A_s=0.05$. For the superharmonic secondary excitation, the iterations
$A_s=0.05$. For the superharmonic secondary excitation, the iterations ![]() $\phi _m$ are
$\phi _m$ are ![]() $2{\rm \pi}$ periodic (refer to (4.6)). First, we start from
$2{\rm \pi}$ periodic (refer to (4.6)). First, we start from ![]() $f_p=0.88$ and increase
$f_p=0.88$ and increase ![]() $f_p$ across the lock-in boundary. figure 16(a) shows the two frequencies considered across the 1:1 lock-in boundary (green and pink cross symbols). Initially, at
$f_p$ across the lock-in boundary. figure 16(a) shows the two frequencies considered across the 1:1 lock-in boundary (green and pink cross symbols). Initially, at ![]() $f_p=0.88$, cobwebs densely fill a region (as observed in § 5.1.1) of the return map indicating quasi-periodic nature of vortex shedding (b). Subsequently, when
$f_p=0.88$, cobwebs densely fill a region (as observed in § 5.1.1) of the return map indicating quasi-periodic nature of vortex shedding (b). Subsequently, when ![]() $f_p$ is increased to
$f_p$ is increased to ![]() $f_p=0.92$ (c), the map intersects
$f_p=0.92$ (c), the map intersects ![]() $\phi _{m-1}=\phi _{m}$ (dashed line) at two locations, indicated as solid and hollow green circles. They represent the stable and unstable fixed points of the map. The cobwebs converge to the solid green circle. In (b), there are no fixed points, while in (c) two fixed points (stable and unstable) occur. Therefore, 1:1 lock-in occurs through a saddle-node bifurcation.
$\phi _{m-1}=\phi _{m}$ (dashed line) at two locations, indicated as solid and hollow green circles. They represent the stable and unstable fixed points of the map. The cobwebs converge to the solid green circle. In (b), there are no fixed points, while in (c) two fixed points (stable and unstable) occur. Therefore, 1:1 lock-in occurs through a saddle-node bifurcation.

Figure 16. Occurrence of saddle-node bifurcation through the appearance of a stable and unstable fixed point in the ![]() $A_p>A_s$ region. Panel (a) shows the lock-in boundary for
$A_p>A_s$ region. Panel (a) shows the lock-in boundary for ![]() $f_s=2f_p$ and
$f_s=2f_p$ and ![]() $A_s=0.05$. The chosen parameters in (b,c) are represented using green and pink cross symbols. First return maps for (b)
$A_s=0.05$. The chosen parameters in (b,c) are represented using green and pink cross symbols. First return maps for (b) ![]() $f_p=0.88$ and (c)
$f_p=0.88$ and (c) ![]() $f_p=0.92$ with cobweb diagrams show the presence of saddle-node bifurcation.
$f_p=0.92$ with cobweb diagrams show the presence of saddle-node bifurcation.
A similar behaviour is observed during subharmonic secondary excitation ![]() $f_s=f_p/2$ (not shown). Since
$f_s=f_p/2$ (not shown). Since ![]() $q_f=2$, the iterations are of period-2 and second return maps in the
$q_f=2$, the iterations are of period-2 and second return maps in the ![]() $\phi _m - \phi _{m-2}$ plane are used to identify saddle-node bifurcation.
$\phi _m - \phi _{m-2}$ plane are used to identify saddle-node bifurcation.
Throughout, we have dealt with two-frequency excitation using the phase of the excitation signal. Using the geometric interpretation of phase ![]() $\phi _m$, we observed various dynamics of return map and cobweb diagrams across the phase lock-in boundary. We observed plateaus at (i)
$\phi _m$, we observed various dynamics of return map and cobweb diagrams across the phase lock-in boundary. We observed plateaus at (i) ![]() $A_p=0$ during superharmonic secondary excitation (the extent of the plateau is comparably small during subharmonic secondary excitation) and (ii)
$A_p=0$ during superharmonic secondary excitation (the extent of the plateau is comparably small during subharmonic secondary excitation) and (ii) ![]() $A_p=A_s$ during both super- and subharmonic secondary excitation (refer to figure 8). In the next section, we obtain analytical relations for lock-in boundaries.
$A_p=A_s$ during both super- and subharmonic secondary excitation (refer to figure 8). In the next section, we obtain analytical relations for lock-in boundaries.
6. Analytical relations for the boundary of lock-in
In this section, we use the discrete difference equation (4.8) and obtain analytical relations for the boundary of lock-in. Furthermore, we present analytical solutions for the frequencies associated with the ends of upper and lower plateaus observed in figures 7(c) and 8. Owing to the form of the sinusoidal terms present in (4.8), it is found that analytical relations are limited only to superharmonic secondary excitation (![]() $f_s=p_f f_p$). When a superharmonic component (
$f_s=p_f f_p$). When a superharmonic component (![]() $f_s=p_f f_p$) is included along with the primary excitation signal, we observe a period-1 response (shown in the cobweb diagrams of figures 13, 15 and 16). This implies that the phase points
$f_s=p_f f_p$) is included along with the primary excitation signal, we observe a period-1 response (shown in the cobweb diagrams of figures 13, 15 and 16). This implies that the phase points ![]() $\phi _m$ and, hence,
$\phi _m$ and, hence, ![]() $\alpha _m$ make
$\alpha _m$ make ![]() $2{\rm \pi} p$ and
$2{\rm \pi} p$ and ![]() $2{\rm \pi}$ rotations, respectively, in each iteration. Therefore, we revisit (4.8) and substitute
$2{\rm \pi}$ rotations, respectively, in each iteration. Therefore, we revisit (4.8) and substitute ![]() $\alpha _{m}=\alpha _{m-1}+2{\rm \pi}$ as the criterion for lock-in. Equation (4.8) reduces to the following form for
$\alpha _{m}=\alpha _{m-1}+2{\rm \pi}$ as the criterion for lock-in. Equation (4.8) reduces to the following form for ![]() $f_s=p_f f_p$:
$f_s=p_f f_p$:
For a given ![]() $A_p$,
$A_p$, ![]() $A_s$ and
$A_s$ and ![]() $\alpha _{m-1}$, the sinusoidal terms in (6.1) govern the positive values of
$\alpha _{m-1}$, the sinusoidal terms in (6.1) govern the positive values of ![]() $f_p$. Therefore, collecting all the harmonic terms together, we obtain the following:
$f_p$. Therefore, collecting all the harmonic terms together, we obtain the following:
Note that the right-hand side of (6.2) is a function of ![]() $\alpha _{m-1}$ and bounded between
$\alpha _{m-1}$ and bounded between ![]() $\pm M$, where
$\pm M$, where ![]() $M$ is the maximum value of
$M$ is the maximum value of ![]() $|A_p\sin (\alpha _{m-1})+A_s\sin (p_f \alpha _{m-1})|$, maximised over
$|A_p\sin (\alpha _{m-1})+A_s\sin (p_f \alpha _{m-1})|$, maximised over ![]() $\alpha _{m-1}$. From our previous investigation for single-frequency excitation (Britto & Mariappan Reference Britto and Mariappan2019a), we found that the boundary of lock-in occurs at the extreme values:
$\alpha _{m-1}$. From our previous investigation for single-frequency excitation (Britto & Mariappan Reference Britto and Mariappan2019a), we found that the boundary of lock-in occurs at the extreme values: ![]() $\pm M$. We now assume that the same is valid for the present case (two-frequency excitation). This assumption is found to be fairly accurate, as shown in figure 17. An analytical expression to determine the frequency range
$\pm M$. We now assume that the same is valid for the present case (two-frequency excitation). This assumption is found to be fairly accurate, as shown in figure 17. An analytical expression to determine the frequency range ![]() $f_{p,b}-f_{p,e}$ (refer to 6.3), inside which lock-in occurs (subscript
$f_{p,b}-f_{p,e}$ (refer to 6.3), inside which lock-in occurs (subscript ![]() $b$ and
$b$ and ![]() $e$ indicate beginning and end) is found as follows:
$e$ indicate beginning and end) is found as follows:
 \begin{equation} \left.\begin{gathered} f_{p,b}=\frac{A_p^{2}+A_s^{2}+2}{2(1+M)} {{,}} \quad f_p<1 \\ f_{p,e}=\frac{A_p^{2}+A_s^{2}+2}{2(1-M)}{{,}} \quad f_p>1 \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} f_{p,b}=\frac{A_p^{2}+A_s^{2}+2}{2(1+M)} {{,}} \quad f_p<1 \\ f_{p,e}=\frac{A_p^{2}+A_s^{2}+2}{2(1-M)}{{,}} \quad f_p>1 \end{gathered}\right\}\end{equation}
where ![]() $M$ depends on
$M$ depends on ![]() $p_f,~A_p$ and
$p_f,~A_p$ and ![]() $A_s$. Figure 17 shows comparison between analytical (red curve obtained using (6.3)) and numerical (black dashed curve, evaluated through the procedure mentioned in § 4.3) solutions of the lock-in boundary for
$A_s$. Figure 17 shows comparison between analytical (red curve obtained using (6.3)) and numerical (black dashed curve, evaluated through the procedure mentioned in § 4.3) solutions of the lock-in boundary for ![]() $f_s=2f_p, A_s=0.05$ (panel a) and
$f_s=2f_p, A_s=0.05$ (panel a) and ![]() $A_s=0.15$ (panel b). A good comparison is observed at lower amplitudes (a), while it deteriorates as we move higher, as shown in (b) (reason discussed later). Subsequently, at the upper (
$A_s=0.15$ (panel b). A good comparison is observed at lower amplitudes (a), while it deteriorates as we move higher, as shown in (b) (reason discussed later). Subsequently, at the upper (![]() $A_p=A_s$) and lower (
$A_p=A_s$) and lower (![]() $A_p=0$) plateaus in the lock-in boundary, the expression for lock-in frequency range is obtained as below:
$A_p=0$) plateaus in the lock-in boundary, the expression for lock-in frequency range is obtained as below:
 \begin{gather} \left.\begin{gathered} f_{p,U_b}= \frac{{A_p}^{2}+1}{(1+M)},\quad f_p<1\\ f_{p,U_e}= \frac{{A_p}^{2}+1}{(1-M)},\quad f_p>1 \end{gathered}\right\}\end{gather}
\begin{gather} \left.\begin{gathered} f_{p,U_b}= \frac{{A_p}^{2}+1}{(1+M)},\quad f_p<1\\ f_{p,U_e}= \frac{{A_p}^{2}+1}{(1-M)},\quad f_p>1 \end{gathered}\right\}\end{gather} \begin{gather} \left.\begin{gathered} f_{p,L_b}= \frac{{A_s}^{2}+2}{2(1+A_s)},\quad f_p<1\\ f_{p,L_e}= \frac{{A_s}^{2}+2}{2(1-A_s)},\quad f_p>1 \end{gathered}\right\}\end{gather}
\begin{gather} \left.\begin{gathered} f_{p,L_b}= \frac{{A_s}^{2}+2}{2(1+A_s)},\quad f_p<1\\ f_{p,L_e}= \frac{{A_s}^{2}+2}{2(1-A_s)},\quad f_p>1 \end{gathered}\right\}\end{gather}
where the subscripts ![]() $U$ and
$U$ and ![]() $L$ are short notations for upper and lower plateaus, respectively, and the subscripts
$L$ are short notations for upper and lower plateaus, respectively, and the subscripts ![]() $b$ and
$b$ and ![]() $e$ denote the beginning and the endpoint of the plateaus, respectively.
$e$ denote the beginning and the endpoint of the plateaus, respectively.
Figure 18 shows a comparison of the frequencies (![]() $f_{p,U_b}$,
$f_{p,U_b}$, ![]() $f_{p,U_e}$,
$f_{p,U_e}$, ![]() $f_{p,L_b}$,
$f_{p,L_b}$, ![]() $f_{p,L_e}$, represented as pink and black circles) at the ends of the plateaus obtained through (6.4)–(6.5) with the numerical lock-in boundary for secondary excitation amplitudes,
$f_{p,L_e}$, represented as pink and black circles) at the ends of the plateaus obtained through (6.4)–(6.5) with the numerical lock-in boundary for secondary excitation amplitudes, ![]() $A_s=0.05$, 0.1, 0.15 and 0.2 at
$A_s=0.05$, 0.1, 0.15 and 0.2 at ![]() $f_s=2f_p$ (a–d) and
$f_s=2f_p$ (a–d) and ![]() $f_s=3f_p$ (e–h). The solid and dashed curves represent p : 1 and 1:1 lock-in boundaries, respectively. The analytical expression for the frequency range of the upper plateau (6.4) depends on
$f_s=3f_p$ (e–h). The solid and dashed curves represent p : 1 and 1:1 lock-in boundaries, respectively. The analytical expression for the frequency range of the upper plateau (6.4) depends on ![]() $p_f$ (through
$p_f$ (through ![]() $M$), whereas for the lower plateau (6.5), it is independent of
$M$), whereas for the lower plateau (6.5), it is independent of ![]() $p_f$. This is observed through figure 18, where the range of the lower plateau is the same for
$p_f$. This is observed through figure 18, where the range of the lower plateau is the same for ![]() $p_f=2$,
$p_f=2$, ![]() $3$ at a given
$3$ at a given ![]() $A_s$. As mentioned before, the comparison between the numerical and analytical lock-in boundaries at the plateaus deteriorates for higher amplitudes. This deterioration is studied using the first return map of
$A_s$. As mentioned before, the comparison between the numerical and analytical lock-in boundaries at the plateaus deteriorates for higher amplitudes. This deterioration is studied using the first return map of ![]() $\alpha _m$ and its cobweb diagrams for the upper plateau (similar behaviour is observed in lower plateau) in figure 19.
$\alpha _m$ and its cobweb diagrams for the upper plateau (similar behaviour is observed in lower plateau) in figure 19.

Figure 18. Comparison of frequencies (![]() $f_{p,U_b}$,
$f_{p,U_b}$, ![]() $f_{p,U_e}$,
$f_{p,U_e}$, ![]() $f_{p,L_b}$,
$f_{p,L_b}$, ![]() $f_{p,L_e}$, represented as pink and black circles) at the ends of the plateaus obtained through (6.4)–(6.5) with the numerical lock-in boundary for secondary excitation amplitudes,
$f_{p,L_e}$, represented as pink and black circles) at the ends of the plateaus obtained through (6.4)–(6.5) with the numerical lock-in boundary for secondary excitation amplitudes, ![]() $A_s=0.05$, 0.1, 0.15 and 0.2 at
$A_s=0.05$, 0.1, 0.15 and 0.2 at ![]() $f_s=2f_p$ (a–d) and
$f_s=2f_p$ (a–d) and ![]() $f_s=3f_p$ (e–h). Solid and dashed curve represent p : 1 and 1:1 lock-in boundaries, respectively.
$f_s=3f_p$ (e–h). Solid and dashed curve represent p : 1 and 1:1 lock-in boundaries, respectively.

Figure 19. First return map and cobweb diagrams to illustrate the discrepancy between analytically (6.4) and numerically obtained lock-in boundaries. Panels (a–c) show the flow of cobwebs on the first return map of ![]() $\alpha _m-\alpha _{m-1}$ for
$\alpha _m-\alpha _{m-1}$ for ![]() $f_s=2f_p$ and
$f_s=2f_p$ and ![]() $A_p=A_s=0.2$. Rightward protrusion of the upper branch over the stable fixed point (orange circle) is observed in (a). Although the cobwebs approach the stable fixed point (in the forbidden region of the solution), it is thrown away from it by the protrusion. The location of the stable fixed point is highlighted using an orange vertical dashed line for reference. The protrusion keeps retracting towards the stable fixed point (a,b). In (c), the upper branch of the map falls to the left of the stable fixed point, and the cobwebs flow towards the stable fixed point. Black arrows indicate the flow of cobwebs, while pink arrows represent the movement of the protrusion.
$A_p=A_s=0.2$. Rightward protrusion of the upper branch over the stable fixed point (orange circle) is observed in (a). Although the cobwebs approach the stable fixed point (in the forbidden region of the solution), it is thrown away from it by the protrusion. The location of the stable fixed point is highlighted using an orange vertical dashed line for reference. The protrusion keeps retracting towards the stable fixed point (a,b). In (c), the upper branch of the map falls to the left of the stable fixed point, and the cobwebs flow towards the stable fixed point. Black arrows indicate the flow of cobwebs, while pink arrows represent the movement of the protrusion.
Primary and secondary excitations are fixed at ![]() $A_p=A_s=0.2$ with
$A_p=A_s=0.2$ with ![]() $f_s=2f_p$. The primary excitation frequency
$f_s=2f_p$. The primary excitation frequency ![]() $f_p$ is increased from
$f_p$ is increased from ![]() $f_{p,U_b}$ to the actual (numerical) end of the plateau (for
$f_{p,U_b}$ to the actual (numerical) end of the plateau (for ![]() $f_p<1$). The chosen parameters lie along the upper plateau in figure 18(d). As discussed in § 5,
$f_p<1$). The chosen parameters lie along the upper plateau in figure 18(d). As discussed in § 5, ![]() $\alpha _m$ solved from (4.8) contains harmonic terms, leading to multiple solutions: correct (green) and forbidden (red) solutions shown in figure 19); the
$\alpha _m$ solved from (4.8) contains harmonic terms, leading to multiple solutions: correct (green) and forbidden (red) solutions shown in figure 19); the ![]() $\alpha _m$ closest to the previous iteration
$\alpha _m$ closest to the previous iteration ![]() $\alpha _{m-1}$ is the correct solution. At
$\alpha _{m-1}$ is the correct solution. At ![]() $f_{p,U_b}$, although the first return map exhibits a stable fixed point (orange circle), the cobwebs are not attracted to it (figure 19a). This is owing to the rightward protrusion of the upper branch of the map (shown in (a)) over the fixed point (observe the orange dashed line for reference). This protrusion also forces the fixed point to lie in the forbidden solution. The protrusion persists on further increase in
$f_{p,U_b}$, although the first return map exhibits a stable fixed point (orange circle), the cobwebs are not attracted to it (figure 19a). This is owing to the rightward protrusion of the upper branch of the map (shown in (a)) over the fixed point (observe the orange dashed line for reference). This protrusion also forces the fixed point to lie in the forbidden solution. The protrusion persists on further increase in ![]() $f_p$; however, the upper branch keeps retracting (leftward) towards the fixed point (b). Finally, the cobwebs flow towards the stable fixed point as the upper branch falls behind the fixed point (c). This parameter location
$f_p$; however, the upper branch keeps retracting (leftward) towards the fixed point (b). Finally, the cobwebs flow towards the stable fixed point as the upper branch falls behind the fixed point (c). This parameter location ![]() $f_p=0.863$ corresponds to the beginning of the upper plateau obtained numerically (solid pink curve in figure 18d). The analytical expression for the frequency at the beginning of the plateau (given by
$f_p=0.863$ corresponds to the beginning of the upper plateau obtained numerically (solid pink curve in figure 18d). The analytical expression for the frequency at the beginning of the plateau (given by ![]() $f_{p,U_b}$ and
$f_{p,U_b}$ and ![]() $f_{p,L_b}$) marks only the birth of the stable fixed point (figure 19a). However, the cobwebs never reach this fixed point as they are hindered by the protrusion of the upper branch of the map over the fixed point. This causes the discrepancy in the comparison between the analytically and numerically obtained lock-in boundaries. The effect of this protrusion is more prominent at large excitation amplitudes. The same behaviour is observed for
$f_{p,L_b}$) marks only the birth of the stable fixed point (figure 19a). However, the cobwebs never reach this fixed point as they are hindered by the protrusion of the upper branch of the map over the fixed point. This causes the discrepancy in the comparison between the analytically and numerically obtained lock-in boundaries. The effect of this protrusion is more prominent at large excitation amplitudes. The same behaviour is observed for ![]() $f_s=3f_p$, although the discrepancy begins to become dominant at still higher amplitudes (compared with
$f_s=3f_p$, although the discrepancy begins to become dominant at still higher amplitudes (compared with ![]() $f_s=2f_p$). It should be noted that in single-frequency excitation, the previously discussed nature of the first return map is encountered, which causes a transition out of lock-in (refer to § 4 of Britto & Mariappan Reference Britto and Mariappan2019a) at large excitation amplitudes.
$f_s=2f_p$). It should be noted that in single-frequency excitation, the previously discussed nature of the first return map is encountered, which causes a transition out of lock-in (refer to § 4 of Britto & Mariappan Reference Britto and Mariappan2019a) at large excitation amplitudes.
7. Conclusion
In this paper, the dynamics of vortex shedding under two-frequency (primary and secondary) excitation is studied using geometrical, numerical and analytical techniques. The low-order model given by Matveev & Culick (Reference Matveev and Culick2003) is converted to a map equation that governs successive time instances of vortex shedding behind the bluff body/step. The map equation is implicit and nonlinear. It has two sets of input parameters, associated with primary and secondary excitation quantities: ![]() $A_p$,
$A_p$, ![]() $f_p$ and
$f_p$ and ![]() $A_s$,
$A_s$, ![]() $f_s$, respectively, where
$f_s$, respectively, where ![]() $A$ and
$A$ and ![]() $f$ indicate excitation amplitude and frequency, respectively, and the subscripts
$f$ indicate excitation amplitude and frequency, respectively, and the subscripts ![]() $p$ and
$p$ and ![]() $s$ represent primary and secondary excitation, respectively. We consider secondary excitations having
$s$ represent primary and secondary excitation, respectively. We consider secondary excitations having ![]() $f_s=p_ff_p/q_f$, (
$f_s=p_ff_p/q_f$, (![]() $p_f,q_f=1,2,3,\ldots$), which comprise super- and subharmonic frequencies observed during combustion instability. For a given input, the iterations of instantaneous vortex shedding time periods are monitored as the output. Lock-in is defined as phase synchronisation between these iterations and the excitation velocity. Through numerical simulations, we observed that the addition of secondary excitation leads to the occurrence of multiple orders of lock-in existing within the lock-in boundary. This is the striking difference between single- and multiple-frequency excitations.
$p_f,q_f=1,2,3,\ldots$), which comprise super- and subharmonic frequencies observed during combustion instability. For a given input, the iterations of instantaneous vortex shedding time periods are monitored as the output. Lock-in is defined as phase synchronisation between these iterations and the excitation velocity. Through numerical simulations, we observed that the addition of secondary excitation leads to the occurrence of multiple orders of lock-in existing within the lock-in boundary. This is the striking difference between single- and multiple-frequency excitations.
We begin the analytical investigation of phase synchronisation by obtaining the instantaneous phase of the input velocity excitation through the Hilbert transform (![]() $\psi _{E,m}$). At successive vortex shedding instants (output), their phase (
$\psi _{E,m}$). At successive vortex shedding instants (output), their phase (![]() $\psi _{R,m}$) is increased by
$\psi _{R,m}$) is increased by ![]() $2{\rm \pi}$. A p : qth order lock-in is identified, when the phase difference between the output and input,
$2{\rm \pi}$. A p : qth order lock-in is identified, when the phase difference between the output and input, ![]() $\Delta \psi _m=q\psi _{E,m}-p\psi _{R,m}$ is
$\Delta \psi _m=q\psi _{E,m}-p\psi _{R,m}$ is ![]() $q_f$-periodic. Contours of
$q_f$-periodic. Contours of ![]() $\Delta \psi _m-\Delta \psi _{m-q_f}$ revealed two orders of lock-in region (1:1 and p : 1 or 1 : q in this paper). This transition between the orders occurs when both the excitation amplitudes are equal, identified as an upper plateau formed at
$\Delta \psi _m-\Delta \psi _{m-q_f}$ revealed two orders of lock-in region (1:1 and p : 1 or 1 : q in this paper). This transition between the orders occurs when both the excitation amplitudes are equal, identified as an upper plateau formed at ![]() $A_p=A_s$ in the lock-in boundary. This plateau also forms the lower bound of the 1:1 lock-in region. In addition, another (lower) plateau at
$A_p=A_s$ in the lock-in boundary. This plateau also forms the lower bound of the 1:1 lock-in region. In addition, another (lower) plateau at ![]() $A_p=0$ exists during both super- and subharmonic excitations. However, its extent during subharmonic excitation is comparatively small.
$A_p=0$ exists during both super- and subharmonic excitations. However, its extent during subharmonic excitation is comparatively small.
As an analytical interpretation, we observe that the dynamics of instantaneous vortex shedding periods can be represented by the movement of phase points on a secondary circle, whose centre also moves along a primary circle. The angle ![]() $\phi _m$ subtended by the phase point with the centre of the primary circle is used to indicate the map dynamics. Return maps,
$\phi _m$ subtended by the phase point with the centre of the primary circle is used to indicate the map dynamics. Return maps, ![]() $\phi _m-\phi _{m-q_f}$ and their cobweb diagrams are used to identify bifurcations occurring across and within lock-in boundary. We identify two lock-in regions: (i)
$\phi _m-\phi _{m-q_f}$ and their cobweb diagrams are used to identify bifurcations occurring across and within lock-in boundary. We identify two lock-in regions: (i) ![]() $A_p< A_s$ and (ii)
$A_p< A_s$ and (ii) ![]() $A_p>A_s$. In the former, p : 1 or 1 : q lock-in is observed for super- and subharmonic excitations, respectively. Furthermore, in the superharmonic case, a region of bistability exists, and the two stable solutions have different vortex shedding phase instances (with respect to velocity excitation). The latter region (
$A_p>A_s$. In the former, p : 1 or 1 : q lock-in is observed for super- and subharmonic excitations, respectively. Furthermore, in the superharmonic case, a region of bistability exists, and the two stable solutions have different vortex shedding phase instances (with respect to velocity excitation). The latter region (![]() $A_p>A_s$) contains only 1:1 lock-in. The geometry of the return map shows that all the transitions: (a) from no lock-in to lock-in, (b) p : 1 or 1 : q to 1:1 lock-in and (c) bistable region inside
$A_p>A_s$) contains only 1:1 lock-in. The geometry of the return map shows that all the transitions: (a) from no lock-in to lock-in, (b) p : 1 or 1 : q to 1:1 lock-in and (c) bistable region inside ![]() $A_p< A_s$ occur through saddle-node bifurcations. In the end, we obtained analytical relations that give the shape of the lock-in boundary during superharmonic excitation. These relations exhibit a fair comparison with the actual shape of the lock-in boundary, capturing the occurrence of plateaus. Furthermore, various identified new features such as a change in the order of lock-in and the existence of a bistable region within a lock-in boundary can be explored with experiments, which might perhaps lead to new methods of instability mitigation in vortex shedding combustors.
$A_p< A_s$ occur through saddle-node bifurcations. In the end, we obtained analytical relations that give the shape of the lock-in boundary during superharmonic excitation. These relations exhibit a fair comparison with the actual shape of the lock-in boundary, capturing the occurrence of plateaus. Furthermore, various identified new features such as a change in the order of lock-in and the existence of a bistable region within a lock-in boundary can be explored with experiments, which might perhaps lead to new methods of instability mitigation in vortex shedding combustors.
Supplementary data
Supplementary movies are available at https://doi.org/10.1017/jfm.2021.624.
Declaration of interests
The authors report no conflict of interest.
Appendix A
An explicit expression for ![]() $F$, which is used in (4.8) is given as follows:
$F$, which is used in (4.8) is given as follows:
 \begin{align} F&={\frac{ \left[ \sin
\left( 2\alpha_{m-1} \right) - \sin \left( 2\alpha_m
\right) -2\left( {\alpha_{m-1}}-{\alpha_{m}} \right)
\right] {{A_p}}^{2}}{16 {{\rm \pi} f_p}}} \nonumber\\ &\quad
+{\frac{\left[\cos \left( \alpha_{m-1} \right) -\cos
\left(\alpha_{m}\right) -{\rm \pi} f_p
\sin(\alpha_{m})\right]A_p}{{2{\rm \pi} f_p}}} \nonumber\\
&\quad + \frac{ \left[ \sin \left( \gamma +p_f\alpha_{m-1}/
q_f \right) \cos \left(\alpha_{m-1} \right) -\sin \left(
\gamma +p_f\alpha_{m}/ q_f \right) \cos
\left(\alpha_{m}\right) \right]{f_p A_p
A_s}}{2{\rm \pi}\left({f_p}^{2}-{f_s}^{2}\right)}\nonumber\\
&\quad - \frac{ \left[\cos \left( \gamma +p_f \alpha_{m-1}/
q_f \right) \sin \left(\alpha_{m-1}\right) -\cos \left(
\gamma +p_f\alpha_{m}/ q_f\right) \sin \left( \alpha_{m}
\right) \right] {f_s A_p
A_s}}{2{\rm \pi}\left({f_p}^{2}-{f_s}^{2}\right)} \nonumber\\
&\quad +{\frac{ \left[\sin \left(2\gamma +2
p_f\alpha_{m-1}/ q_f\right) \,{-}\, \sin \left( 2\gamma +2
p_f\alpha_{m}/ q_f \right) \,{-}\, 2\left( {p_f\alpha_{m-1}/
q_f} \,{-}\, {p_f \alpha_{m}/ q_f} \right) \right] {{A_s}}^{2}}{16
{\rm \pi} f_s}} \nonumber\\ &\quad +{\frac{ \left[ \cos
\left(\gamma +p_f\alpha_{m-1}/ q_f \right) -\cos \left(
\gamma +p_f\alpha_{m}/ q_f \right) -{\rm \pi} f_s\sin
\left(\gamma +p_f\alpha_{m}/ q_f\right) \right]
{A_s}}{{2{\rm \pi} f_s}}}\nonumber\\ &\quad -\frac{\left(
{\alpha_{m-1}}-{\alpha_{m}}+2{\rm \pi} f_p \right) }{4 {\rm \pi}
f_p}. \end{align}
\begin{align} F&={\frac{ \left[ \sin
\left( 2\alpha_{m-1} \right) - \sin \left( 2\alpha_m
\right) -2\left( {\alpha_{m-1}}-{\alpha_{m}} \right)
\right] {{A_p}}^{2}}{16 {{\rm \pi} f_p}}} \nonumber\\ &\quad
+{\frac{\left[\cos \left( \alpha_{m-1} \right) -\cos
\left(\alpha_{m}\right) -{\rm \pi} f_p
\sin(\alpha_{m})\right]A_p}{{2{\rm \pi} f_p}}} \nonumber\\
&\quad + \frac{ \left[ \sin \left( \gamma +p_f\alpha_{m-1}/
q_f \right) \cos \left(\alpha_{m-1} \right) -\sin \left(
\gamma +p_f\alpha_{m}/ q_f \right) \cos
\left(\alpha_{m}\right) \right]{f_p A_p
A_s}}{2{\rm \pi}\left({f_p}^{2}-{f_s}^{2}\right)}\nonumber\\
&\quad - \frac{ \left[\cos \left( \gamma +p_f \alpha_{m-1}/
q_f \right) \sin \left(\alpha_{m-1}\right) -\cos \left(
\gamma +p_f\alpha_{m}/ q_f\right) \sin \left( \alpha_{m}
\right) \right] {f_s A_p
A_s}}{2{\rm \pi}\left({f_p}^{2}-{f_s}^{2}\right)} \nonumber\\
&\quad +{\frac{ \left[\sin \left(2\gamma +2
p_f\alpha_{m-1}/ q_f\right) \,{-}\, \sin \left( 2\gamma +2
p_f\alpha_{m}/ q_f \right) \,{-}\, 2\left( {p_f\alpha_{m-1}/
q_f} \,{-}\, {p_f \alpha_{m}/ q_f} \right) \right] {{A_s}}^{2}}{16
{\rm \pi} f_s}} \nonumber\\ &\quad +{\frac{ \left[ \cos
\left(\gamma +p_f\alpha_{m-1}/ q_f \right) -\cos \left(
\gamma +p_f\alpha_{m}/ q_f \right) -{\rm \pi} f_s\sin
\left(\gamma +p_f\alpha_{m}/ q_f\right) \right]
{A_s}}{{2{\rm \pi} f_s}}}\nonumber\\ &\quad -\frac{\left(
{\alpha_{m-1}}-{\alpha_{m}}+2{\rm \pi} f_p \right) }{4 {\rm \pi}
f_p}. \end{align}