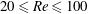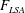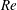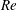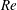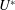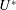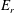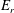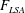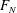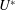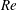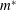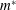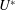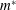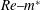1 Introduction
Lock-in/synchronization/wake-capture is an important phenomenon associated with vortex-induced vibrations (VIV) of bluff bodies. It is characterized by a high amplitude of structural vibrations. These vibrations can cause fatigue and may lead to catastrophic failure of structures. Lock-in, therefore, has been a subject of numerous computational and experimental studies in the past. For a detailed review on the various works that have been carried out related to synchronization in VIV, the interested reader is referred to articles by Bearman (Reference Bearman1984, Reference Bearman2011), Sarpkaya (Reference Sarpkaya2004), Williamson & Govardhan (Reference Williamson and Govardhan2004) and Wu, Ge & Hong (Reference Wu, Ge and Hong2012). Most of the earlier studies on VIV have focused on characterizing the lock-in regime, and its dependence on various parameters. In this paper, we explore the mechanism that leads to the phenomenon of lock-in.
First, we present a very brief review of the studies that mainly focus on characterizing
the fluid–structure system within the lock-in regime. The behaviour of the
fluid–structure system depends very significantly on the Reynolds number (
![]() $Re$
) and mass of the cylinder. As a result, depending on the parameter
range over which the various studies have been carried out, several definitions of
lock-in have been proposed/used in the literature. The pioneering work by Bishop
& Hassan (Reference Bishop and Hassan1964) and Feng (Reference Feng1968) shows that during lock-in, the frequency of
cylinder oscillation is close to the natural frequency of the oscillator. In these two
studies the fluid medium surrounding the cylinder was air. Hence, the mass ratio,
$Re$
) and mass of the cylinder. As a result, depending on the parameter
range over which the various studies have been carried out, several definitions of
lock-in have been proposed/used in the literature. The pioneering work by Bishop
& Hassan (Reference Bishop and Hassan1964) and Feng (Reference Feng1968) shows that during lock-in, the frequency of
cylinder oscillation is close to the natural frequency of the oscillator. In these two
studies the fluid medium surrounding the cylinder was air. Hence, the mass ratio,
![]() $m^{\ast }$
, defined as the ratio of the mass of the moving structure to the mass
of the displaced fluid is high (
$m^{\ast }$
, defined as the ratio of the mass of the moving structure to the mass
of the displaced fluid is high (
![]() $m^{\ast }\sim O(100)$
). Khalak & Williamson (Reference Khalak and Williamson1997, Reference Khalak and Williamson1999) carried out experiments with
relatively low mass ratios (
$m^{\ast }\sim O(100)$
). Khalak & Williamson (Reference Khalak and Williamson1997, Reference Khalak and Williamson1999) carried out experiments with
relatively low mass ratios (
![]() $m^{\ast }\sim O(10)$
) by conducting experiments in water. The range of Reynolds number for
these experiments varied between
$m^{\ast }\sim O(10)$
) by conducting experiments in water. The range of Reynolds number for
these experiments varied between
![]() $5000\leqslant Re\leqslant 16\,000$
. They observed large amplitude oscillations of the cylinder with a
frequency that is significantly higher than the natural frequency of the oscillator in
water. In such cases, they found that the pattern of vortex shedding is different from
that of the flow past a stationary cylinder and repeats after each cycle of cylinder
oscillation. Subsequently, Khalak & Williamson (Reference Khalak and Williamson1999) defined lock-in as the matching of the frequency of the
periodic wake vortex mode and the oscillation frequency of the body. This is in line
with the definition used by Sarpkaya (Reference Sarpkaya1995) where
the force frequency matches the oscillation frequency of the structure in the lock-in
regime.
$5000\leqslant Re\leqslant 16\,000$
. They observed large amplitude oscillations of the cylinder with a
frequency that is significantly higher than the natural frequency of the oscillator in
water. In such cases, they found that the pattern of vortex shedding is different from
that of the flow past a stationary cylinder and repeats after each cycle of cylinder
oscillation. Subsequently, Khalak & Williamson (Reference Khalak and Williamson1999) defined lock-in as the matching of the frequency of the
periodic wake vortex mode and the oscillation frequency of the body. This is in line
with the definition used by Sarpkaya (Reference Sarpkaya1995) where
the force frequency matches the oscillation frequency of the structure in the lock-in
regime.
As is the case at large
![]() $Re$
, computational studies in the laminar regime and
$Re$
, computational studies in the laminar regime and
![]() $m^{\ast }=10$
(Singh & Mittal Reference Singh and Mittal2005; Prasanth & Mittal Reference Prasanth and Mittal2008;
Prasanth, Premchandran & Mittal Reference Prasanth, Premchandran and Mittal2011;
Navrose et al.
Reference Yogeswaran, Sen and Mittal2014) show that the frequency of cylinder
oscillation and vortex shedding are identical in the lock-in regime. They are quite
close to the natural frequency of the oscillator in vacuum. Outside the lock-in regime,
the cylinder exhibits very low amplitude oscillations at a frequency that is nearly
equal to the vortex shedding frequency of flow past a stationary cylinder. The present
study is confined to the laminar flow regime. The lock-in regime is identified using the
metrics that have been proposed and utilized in the earlier studies: relatively high
amplitude of cylinder oscillation and, matching of the cylinder oscillation and vortex
shedding frequency. Figure 1 shows the
amplitude of vibration and frequency ratio of a cylinder exhibiting VIV for
$m^{\ast }=10$
(Singh & Mittal Reference Singh and Mittal2005; Prasanth & Mittal Reference Prasanth and Mittal2008;
Prasanth, Premchandran & Mittal Reference Prasanth, Premchandran and Mittal2011;
Navrose et al.
Reference Yogeswaran, Sen and Mittal2014) show that the frequency of cylinder
oscillation and vortex shedding are identical in the lock-in regime. They are quite
close to the natural frequency of the oscillator in vacuum. Outside the lock-in regime,
the cylinder exhibits very low amplitude oscillations at a frequency that is nearly
equal to the vortex shedding frequency of flow past a stationary cylinder. The present
study is confined to the laminar flow regime. The lock-in regime is identified using the
metrics that have been proposed and utilized in the earlier studies: relatively high
amplitude of cylinder oscillation and, matching of the cylinder oscillation and vortex
shedding frequency. Figure 1 shows the
amplitude of vibration and frequency ratio of a cylinder exhibiting VIV for
![]() $(Re,m^{\ast })=(100,10)$
. The lock-in regime is highlighted via shading.
$(Re,m^{\ast })=(100,10)$
. The lock-in regime is highlighted via shading.

Figure 1. Flow past a freely vibrating cylinder for
![]() $Re=100$
and
$Re=100$
and
![]() $m^{\ast }=10$
: variation of (a) normalized
maximum amplitude of cylinder oscillation, and
(b) frequency ratio,
$m^{\ast }=10$
: variation of (a) normalized
maximum amplitude of cylinder oscillation, and
(b) frequency ratio,
![]() $f^{\ast }$
, with reduced velocity.
$f^{\ast }$
, with reduced velocity.
![]() $f^{\ast }$
is the ratio between the cylinder vibration frequency and the
natural frequency of the oscillator in vacuum. Results are shown for the
computations when
$f^{\ast }$
is the ratio between the cylinder vibration frequency and the
natural frequency of the oscillator in vacuum. Results are shown for the
computations when
![]() $U^{\ast }$
is increased in small increments as well as when it is
decreased in small decrements. The lock-in regime obtained via the increasing
$U^{\ast }$
is increased in small increments as well as when it is
decreased in small decrements. The lock-in regime obtained via the increasing
![]() $U^{\ast }$
approach is shaded: initial branch (magenta) and lower branch
(grey). Hysteresis is shown only in (a), and not
in (b) to avoid clutter.
$U^{\ast }$
approach is shaded: initial branch (magenta) and lower branch
(grey). Hysteresis is shown only in (a), and not
in (b) to avoid clutter.
There have been relatively fewer studies that investigate the mechanism(s) underlying
the lock-in phenomenon in free vibrations, i.e. what causes lock-in in free
vibrations? Cossu & Morino (Reference Cossu and Morino2000)
carried out linear stability analysis for the flow past an elastically mounted cylinder
in the laminar flow regime. They identified two modes that may be responsible for the
onset of instability in the fluid–structure system and referred to them as
the von Kármán and nearly structural modes. It was demonstrated
that vortex shedding accompanied with a large amplitude of cylinder oscillation is
possible for subcritical
![]() $Re$
and low
$Re$
and low
![]() $m^{\ast }$
owing to the instability of the nearly structural mode. Meliga
& Chomaz (Reference Meliga and Chomaz2011), using asymptotic
analysis, corroborated the existence of the two modes reported by Cossu &
Morino (Reference Cossu and Morino2000) and renamed them the wake mode (WM)
and structure mode (SM), respectively. The identification of the modes is based on their
characteristics in the limit of very large mass ratio. For large
$m^{\ast }$
owing to the instability of the nearly structural mode. Meliga
& Chomaz (Reference Meliga and Chomaz2011), using asymptotic
analysis, corroborated the existence of the two modes reported by Cossu &
Morino (Reference Cossu and Morino2000) and renamed them the wake mode (WM)
and structure mode (SM), respectively. The identification of the modes is based on their
characteristics in the limit of very large mass ratio. For large
![]() $m^{\ast }$
, the eigenvalue of the SM tends to the natural eigenvalue of the
cylinder-only system. On the other hand, the eigenvalue of WM, in the limit of large
$m^{\ast }$
, the eigenvalue of the SM tends to the natural eigenvalue of the
cylinder-only system. On the other hand, the eigenvalue of WM, in the limit of large
![]() $m^{\ast }$
, tends to the leading eigenvalue computed for the flow past a
stationary cylinder. Therefore, to identify the two modes for a given value of
$m^{\ast }$
, tends to the leading eigenvalue computed for the flow past a
stationary cylinder. Therefore, to identify the two modes for a given value of
![]() $Re$
and reduced speed (
$Re$
and reduced speed (
![]() $U^{\ast }$
), the eigenvalue of the modes need to be followed up to large values
of
$U^{\ast }$
), the eigenvalue of the modes need to be followed up to large values
of
![]() $m^{\ast }$
. For certain combinations of
$m^{\ast }$
. For certain combinations of
![]() $Re$
and
$Re$
and
![]() $U^{\ast }$
, the eigenvalues may coalesce at a mass ratio. Naturally, in this
situation the classification of modes as wake and structure mode is not possible. Meliga
& Chomaz (Reference Meliga and Chomaz2011) also carried out an
approximate nonlinear analysis in the regime of linear instability of the
fluid–structure system and proposed a criterion based on the amplitude of
cylinder oscillation to identify the lock-in regime.
$U^{\ast }$
, the eigenvalues may coalesce at a mass ratio. Naturally, in this
situation the classification of modes as wake and structure mode is not possible. Meliga
& Chomaz (Reference Meliga and Chomaz2011) also carried out an
approximate nonlinear analysis in the regime of linear instability of the
fluid–structure system and proposed a criterion based on the amplitude of
cylinder oscillation to identify the lock-in regime.
Recently, Zhang et al. (Reference Zhang, Li, Ye and Jiang2015), carried out linear stability analysis of the fluid–structure
system utilizing a reduced-order model for the wake. They suggested that at
![]() $Re=60$
, lock-in may result either from the instability of WM only or both WM
and SM. They proposed that in the first situation, lock-in occurs because of the
vicinity of the frequency of WM to the natural frequency of the oscillator. This kind of
lock-in was referred to as resonance-induced lock-in. In the other case, instability
results from the interaction of SM and WM. This was referred to as flutter-induced
lock-in. The criterion used for the identification of lock-in by Zhang
et al. (Reference Zhang, Li, Ye and Jiang2015) is
based entirely on frequency considerations. However, it has been well established in
earlier studies (for example, Govardhan & Williamson Reference Govardhan and Williamson2000) that, the frequency of the fluid–structure system in
the lock-in regime may depend significantly on the mass ratio. In fact, at low enough
mass ratio, the cylinder can vibrate with large oscillation amplitude and frequency that
can be several times the natural frequency of the oscillator (Govardhan &
Williamson Reference Govardhan and Williamson2002). Therefore, a criteria for
lock-in that is based on frequency only may not be suitable for systems with moderate to
low value of mass ratio.
$Re=60$
, lock-in may result either from the instability of WM only or both WM
and SM. They proposed that in the first situation, lock-in occurs because of the
vicinity of the frequency of WM to the natural frequency of the oscillator. This kind of
lock-in was referred to as resonance-induced lock-in. In the other case, instability
results from the interaction of SM and WM. This was referred to as flutter-induced
lock-in. The criterion used for the identification of lock-in by Zhang
et al. (Reference Zhang, Li, Ye and Jiang2015) is
based entirely on frequency considerations. However, it has been well established in
earlier studies (for example, Govardhan & Williamson Reference Govardhan and Williamson2000) that, the frequency of the fluid–structure system in
the lock-in regime may depend significantly on the mass ratio. In fact, at low enough
mass ratio, the cylinder can vibrate with large oscillation amplitude and frequency that
can be several times the natural frequency of the oscillator (Govardhan &
Williamson Reference Govardhan and Williamson2002). Therefore, a criteria for
lock-in that is based on frequency only may not be suitable for systems with moderate to
low value of mass ratio.
In the present study we investigate the phenomenon of lock-in via linear stability
analysis (LSA) and direct time integration (DTI) of the equations that govern the flow
and response of the structure. No empirical model is used. Most of the earlier studies
that explore lock-in consider variation with reduced speed while holding mass ratio
fixed. The present analysis is carried out over a relatively wide range of
![]() $m^{\ast }$
and
$m^{\ast }$
and
![]() $Re$
, including the subcritical and supercritical regimes with respect to
onset of vortex shedding. Using these results, a classification of the modes is
presented. It is observed that, for large mass ratios, the modes corresponding to the
two leading eigenvalues are quite distinct and maintain this distinction as
$Re$
, including the subcritical and supercritical regimes with respect to
onset of vortex shedding. Using these results, a classification of the modes is
presented. It is observed that, for large mass ratios, the modes corresponding to the
two leading eigenvalues are quite distinct and maintain this distinction as
![]() $U^{\ast }$
is varied. In this sense, the two leading modes are decoupled from
each other. We refer to the two eigenmodes as the fluid mode (FM) and elastic mode (EM).
The FM resembles the mode corresponding to the leading eigenvalue of the flow past a
stationary cylinder. For low mass ratios, the two leading eigenmodes do not exhibit a
clear distinction in terms of their affiliation to being either class fluid or class
elastic. We refer to them as coupled modes.
$U^{\ast }$
is varied. In this sense, the two leading modes are decoupled from
each other. We refer to the two eigenmodes as the fluid mode (FM) and elastic mode (EM).
The FM resembles the mode corresponding to the leading eigenvalue of the flow past a
stationary cylinder. For low mass ratios, the two leading eigenmodes do not exhibit a
clear distinction in terms of their affiliation to being either class fluid or class
elastic. We refer to them as coupled modes.
The linear instability of the coupled fluid–structure system results in free
vibrations. Depending on the operational parameters (
![]() $m^{\ast }$
,
$m^{\ast }$
,
![]() $U^{\ast }$
,
$U^{\ast }$
,
![]() $Re$
) there may be several unstable modes. As the amplitude of vibration
increases, nonlinear terms become significant and the response of the system is altered
from its linear behaviour. As a consequence, the fluid–structure system
achieves a limit cycle. However, not all unstable eigenmodes lead to high amplitude
response of the cylinder. Only those unstable eigenmodes whose
$Re$
) there may be several unstable modes. As the amplitude of vibration
increases, nonlinear terms become significant and the response of the system is altered
from its linear behaviour. As a consequence, the fluid–structure system
achieves a limit cycle. However, not all unstable eigenmodes lead to high amplitude
response of the cylinder. Only those unstable eigenmodes whose
![]() $E_{r}$
a higher than a certain threshold value lead to lock-in. We also study
the phase angle between the cylinder displacement and lift force corresponding to an
eigenmode. The phase angle is found to be related to the direction of energy transfer
between the fluid and structure. DTI is initiated with the disturbance field
corresponding to the unstable eigenmodes. The phase angle undergoes a change as the
amplitude of cylinder vibration increases.
$E_{r}$
a higher than a certain threshold value lead to lock-in. We also study
the phase angle between the cylinder displacement and lift force corresponding to an
eigenmode. The phase angle is found to be related to the direction of energy transfer
between the fluid and structure. DTI is initiated with the disturbance field
corresponding to the unstable eigenmodes. The phase angle undergoes a change as the
amplitude of cylinder vibration increases.
2 The governing equations
2.1 Incompressible flow equations
To investigate the interaction between the fluid and the oscillating cylinder, linear
stability analysis of the governing equations is carried out in a moving frame
attached to the cylinder. Such an approach has been used earlier to study
vortex-induced vibration of a cylinder (Étienne & Pelletier
Reference Étienne and Pelletier2012; Lu & Papadakis Reference Lu and Papadakis2014). Let
![]() $\boldsymbol{x}$
and
$\boldsymbol{x}$
and
![]() $t$
denote the spatial and temporal coordinates respectively. The
spatial domain is represented by
$t$
denote the spatial and temporal coordinates respectively. The
spatial domain is represented by
![]() ${\it\Omega}\subset \mathbb{R}^{2}$
.
${\it\Omega}\subset \mathbb{R}^{2}$
.
![]() ${\it\Gamma}$
represents the boundary of
${\it\Gamma}$
represents the boundary of
![]() ${\it\Omega}$
. The temporal domain is represented by
${\it\Omega}$
. The temporal domain is represented by
![]() $(0,T)$
. The Navier–Stokes equations governing an incompressible
flow in the absence of body forces are
$(0,T)$
. The Navier–Stokes equations governing an incompressible
flow in the absence of body forces are
Here,
![]() ${\it\rho}$
,
${\it\rho}$
,
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() ${\bf\sigma}$
are the density, velocity and stress tensor, respectively.
${\bf\sigma}$
are the density, velocity and stress tensor, respectively.
![]() $\boldsymbol{U}_{b}$
denotes the instantaneous velocity of the cylinder. For a Newtonian
fluid the stress tensor is given as
$\boldsymbol{U}_{b}$
denotes the instantaneous velocity of the cylinder. For a Newtonian
fluid the stress tensor is given as
![]() ${\bf\sigma}=-p\boldsymbol{I}+2{\it\mu}{\bf\varepsilon}(\boldsymbol{u})$
, where,
${\bf\sigma}=-p\boldsymbol{I}+2{\it\mu}{\bf\varepsilon}(\boldsymbol{u})$
, where,
![]() ${\bf\varepsilon}$
is the strain rate given as
${\bf\varepsilon}$
is the strain rate given as
![]() ${\bf\varepsilon}(\boldsymbol{u})=((\boldsymbol{{\rm\nabla}}\boldsymbol{u})+(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}})/2$
and,
${\bf\varepsilon}(\boldsymbol{u})=((\boldsymbol{{\rm\nabla}}\boldsymbol{u})+(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}})/2$
and,
![]() $p$
and
$p$
and
![]() ${\it\mu}$
are the pressure and coefficient of dynamic viscosity,
respectively.
${\it\mu}$
are the pressure and coefficient of dynamic viscosity,
respectively.
Unlike the LSA, the DTI of the governing equations is carried out in an inertial frame of reference. Therefore, the third term in (2.1) is dropped. More details on the same can be found in our earlier work (Prasanth & Mittal Reference Prasanth and Mittal2008). The computational domain along with the boundary conditions are shown in figure 2. No-slip condition is applied on the velocity at the surface of the cylinder. The location of the cylinder and its velocity are updated at each nonlinear iteration of the solution to the flow equations.

Figure 2. Flow past a freely vibrating cylinder: (a) finite element mesh that has been employed for the computations in this work, (b) close-up view of the mesh near the surface of the cylinder. The mesh consists of 12 814 nodes and 12 540 quadrilateral elements. The location of the various boundaries and boundary conditions are also shown.
2.2 The equations of motion for the structure
The motion of the cylinder mounted on elastic supports, in the two directions along the Cartesian axes, is governed by the following system of equations:
Here,
![]() $F_{N}$
is the reduced natural frequency of the oscillator,
$F_{N}$
is the reduced natural frequency of the oscillator,
![]() ${\it\zeta}$
the structural damping ratio and
${\it\zeta}$
the structural damping ratio and
![]() $m^{\ast }$
the non-dimensional mass of the body.
$m^{\ast }$
the non-dimensional mass of the body.
![]() $\boldsymbol{C}_{\boldsymbol{F}}$
is the instantaneous coefficient of fluid force acting on the
cylinder. The fluid force is computed by integrating stress on the boundary of the
cylinder.
$\boldsymbol{C}_{\boldsymbol{F}}$
is the instantaneous coefficient of fluid force acting on the
cylinder. The fluid force is computed by integrating stress on the boundary of the
cylinder.
![]() $\boldsymbol{X}$
denotes the normalized displacement. The displacement and velocity
are normalized by the diameter of the cylinder,
$\boldsymbol{X}$
denotes the normalized displacement. The displacement and velocity
are normalized by the diameter of the cylinder,
![]() $D$
, and the free-stream speed
$D$
, and the free-stream speed
![]() $U$
, respectively.
$U$
, respectively.
![]() $F_{N}$
is related to the natural frequency of the spring mass system (
$F_{N}$
is related to the natural frequency of the spring mass system (
![]() $f_{N}$
) as
$f_{N}$
) as
![]() $F_{N}=f_{N}D/U$
. Another related parameter is the reduced velocity,
$F_{N}=f_{N}D/U$
. Another related parameter is the reduced velocity,
![]() $U^{\ast }$
. It is defined as
$U^{\ast }$
. It is defined as
![]() $U^{\ast }=U/(f_{N}D)=1/F_{N}$
. Although the formulation presented here is general, results are
presented for transverse-only oscillation of the structure.
$U^{\ast }=U/(f_{N}D)=1/F_{N}$
. Although the formulation presented here is general, results are
presented for transverse-only oscillation of the structure.
2.3 Global LSA
We carry out a global linear stability analysis of the fluid–structure
system represented by (2.1)–(2.4). A
similar approach was employed by Cossu & Morino (Reference Cossu and Morino2000). The unsteady flow variables,
![]() $(\boldsymbol{u},p)$
are decomposed as a combination of the steady and the disturbance
field:
$(\boldsymbol{u},p)$
are decomposed as a combination of the steady and the disturbance
field:
![]() $\boldsymbol{u}=\boldsymbol{U}+\boldsymbol{u}^{\prime }$
and
$\boldsymbol{u}=\boldsymbol{U}+\boldsymbol{u}^{\prime }$
and
![]() $p=P+p^{\prime }$
.
$p=P+p^{\prime }$
.
![]() $(\boldsymbol{U},P)$
, the steady flow past a stationary cylinder, is obtained by
dropping the unsteady terms in (2.1) and (2.2).
$(\boldsymbol{U},P)$
, the steady flow past a stationary cylinder, is obtained by
dropping the unsteady terms in (2.1) and (2.2).
![]() $\boldsymbol{u}^{\prime }$
and
$\boldsymbol{u}^{\prime }$
and
![]() $p^{\prime }$
are the perturbation fields of the velocity and pressure,
respectively. In the steady state the cylinder is at rest at its equilibrium
position. Therefore,
$p^{\prime }$
are the perturbation fields of the velocity and pressure,
respectively. In the steady state the cylinder is at rest at its equilibrium
position. Therefore,
![]() $\boldsymbol{U}_{b}$
is also the disturbance in the velocity of the cylinder. In the
equilibrium state, the spring is in a stretched position,
$\boldsymbol{U}_{b}$
is also the disturbance in the velocity of the cylinder. In the
equilibrium state, the spring is in a stretched position,
![]() $\boldsymbol{X}_{\boldsymbol{e}\boldsymbol{q}}$
, due to the steady force acting on the cylinder. In general, for a
circular cylinder in uniform flow, this force is along the streamwise direction. The
displacement of the cylinder, therefore, can be decomposed as
$\boldsymbol{X}_{\boldsymbol{e}\boldsymbol{q}}$
, due to the steady force acting on the cylinder. In general, for a
circular cylinder in uniform flow, this force is along the streamwise direction. The
displacement of the cylinder, therefore, can be decomposed as
![]() $\boldsymbol{X}=\boldsymbol{X}_{\boldsymbol{e}\boldsymbol{q}}+\boldsymbol{x}^{\prime }$
, where
$\boldsymbol{X}=\boldsymbol{X}_{\boldsymbol{e}\boldsymbol{q}}+\boldsymbol{x}^{\prime }$
, where
![]() $\boldsymbol{x}^{\prime }$
represents the disturbance field of the cylinder displacement.
Substituting for the decomposition of flow and the structural variables
in (2.1)–(2.4), and
subtracting from them, the equations for steady flow, the equations for the evolution
of the disturbance field can be obtained. We assume that the disturbances are small
and drop the nonlinear terms. We also assume that the system is devoid of any
structural damping. This leads to the following linearized equations of the
disturbance field:
$\boldsymbol{x}^{\prime }$
represents the disturbance field of the cylinder displacement.
Substituting for the decomposition of flow and the structural variables
in (2.1)–(2.4), and
subtracting from them, the equations for steady flow, the equations for the evolution
of the disturbance field can be obtained. We assume that the disturbances are small
and drop the nonlinear terms. We also assume that the system is devoid of any
structural damping. This leads to the following linearized equations of the
disturbance field:
 $$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{U}}_{b}+(2{\rm\pi}F_{N})^{2}\boldsymbol{x}^{\prime }=\frac{2\left(\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial \boldsymbol{U}_{\boldsymbol{b}}}\boldsymbol{\cdot }\boldsymbol{U}_{\boldsymbol{b}}+\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial p^{\prime }}p^{\prime }\right)}{{\rm\pi}m^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{U}}_{b}+(2{\rm\pi}F_{N})^{2}\boldsymbol{x}^{\prime }=\frac{2\left(\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial \boldsymbol{U}_{\boldsymbol{b}}}\boldsymbol{\cdot }\boldsymbol{U}_{\boldsymbol{b}}+\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial p^{\prime }}p^{\prime }\right)}{{\rm\pi}m^{\ast }}, & \displaystyle\end{eqnarray}$$
In the equation above,
![]() ${\bf\sigma}^{\prime }$
represents the stress tensor due to disturbance field of the flow.
The variation in non-dimensional forces because of change in the velocity of the
cylinder with respect to the equilibrium state is denoted by the matrix
${\bf\sigma}^{\prime }$
represents the stress tensor due to disturbance field of the flow.
The variation in non-dimensional forces because of change in the velocity of the
cylinder with respect to the equilibrium state is denoted by the matrix
![]() $\partial \boldsymbol{C}_{\boldsymbol{F}}/\partial \boldsymbol{U}_{\boldsymbol{b}}$
. Similarly, the variation in forces because of the change in the
pressure on the surface of the cylinder is
$\partial \boldsymbol{C}_{\boldsymbol{F}}/\partial \boldsymbol{U}_{\boldsymbol{b}}$
. Similarly, the variation in forces because of the change in the
pressure on the surface of the cylinder is
![]() $\partial \boldsymbol{C}_{\boldsymbol{F}}/\partial p^{\prime }$
. For conducting the global LSA of the combined
fluid–cylinder system, we assume the disturbance field of the following
form:
$\partial \boldsymbol{C}_{\boldsymbol{F}}/\partial p^{\prime }$
. For conducting the global LSA of the combined
fluid–cylinder system, we assume the disturbance field of the following
form:
Substituting this form of the disturbance in (2.5)–(2.8) we obtain:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}\hat{\boldsymbol{U}}_{b}+(2{\rm\pi}F_{N})^{2}\hat{\boldsymbol{x}}=\frac{2\left(\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial \hat{\boldsymbol{U}}_{b}}\boldsymbol{\cdot }\hat{\boldsymbol{U}}_{b}+\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial \hat{p}}p^{\prime }\right)}{{\rm\pi}m^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}\hat{\boldsymbol{U}}_{b}+(2{\rm\pi}F_{N})^{2}\hat{\boldsymbol{x}}=\frac{2\left(\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial \hat{\boldsymbol{U}}_{b}}\boldsymbol{\cdot }\hat{\boldsymbol{U}}_{b}+\displaystyle \frac{\partial \boldsymbol{C}_{\boldsymbol{F}}}{\partial \hat{p}}p^{\prime }\right)}{{\rm\pi}m^{\ast }}, & \displaystyle\end{eqnarray}$$
Here,
![]() ${\it\lambda}$
is the eigenvalue of the coupled fluid–structure system
and governs its stability. In general,
${\it\lambda}$
is the eigenvalue of the coupled fluid–structure system
and governs its stability. In general,
![]() ${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
, where
${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
, where
![]() ${\it\lambda}_{r}$
and
${\it\lambda}_{r}$
and
![]() ${\it\lambda}_{i}$
are the real and imaginary parts, respectively. We define the
non-dimensional frequency of the eigenmode as
${\it\lambda}_{i}$
are the real and imaginary parts, respectively. We define the
non-dimensional frequency of the eigenmode as
![]() $F_{LSA}={\it\lambda}_{i}/2{\rm\pi}$
. The corresponding reduced velocity is represented by
$F_{LSA}={\it\lambda}_{i}/2{\rm\pi}$
. The corresponding reduced velocity is represented by
![]() $U_{LSA}^{\ast }=2{\rm\pi}/{\it\lambda}_{i}=1/F_{LSA}$
. In this study, we restrict the motion of the cylinder in the
direction transverse to the free-stream flow. This is commonly referred to as
$U_{LSA}^{\ast }=2{\rm\pi}/{\it\lambda}_{i}=1/F_{LSA}$
. In this study, we restrict the motion of the cylinder in the
direction transverse to the free-stream flow. This is commonly referred to as
![]() $Y$
-only oscillations. A typical global eigenmode of the
fluid–structure system is thus represented as (
$Y$
-only oscillations. A typical global eigenmode of the
fluid–structure system is thus represented as (
![]() $\hat{\boldsymbol{u}}(\boldsymbol{x})$
,
$\hat{\boldsymbol{u}}(\boldsymbol{x})$
,
![]() $\hat{p}(\boldsymbol{x})$
,
$\hat{p}(\boldsymbol{x})$
,
![]() $\hat{{\dot{Y}}}$
,
$\hat{{\dot{Y}}}$
,
![]() ${\hat{Y}}$
).
${\hat{Y}}$
).
3 The finite element formulation
A stabilized finite element method has been utilized to carry out the time integration of the governing equations as well as their linear stability analyses. The numerical stabilizations are based on SUPG (streamline-upwind/Petrov–Galerkin) and PSPG (pressure-stabilizing/Petrov–Galerkin) techniques (Tezduyar et al. Reference Tezduyar, Mittal, Ray and Shih1992c ). All the stabilizations used in this work are residual based. Therefore, they lead to a consistent formulation in the sense that the exact solution satisfies the finite element formulation. The steady state about which stability analysis is carried out is obtained by simply dropping the unsteady term in the governing equations. For carrying out direct time integration, a space–time version of the stabilized finite element method is employed (Tezduyar et al. Reference Tezduyar, Behr, Mittal and Liou1992a ; Tezduyar, Liou & Behr Reference Tezduyar, Liou and Behr1992b ). We rewrite (2.1) and (2.2) in the stationary frame. The equations of motion for the oscillator are also cast in the space–time formulation as described in the articles by Mittal & Tezduyar (Reference Mittal and Tezduyar1992a ,Reference Mittal and Tezduyar b ) and Tezduyar et al. (Reference Tezduyar, Mittal, Ray and Shih1992c ). This method allows us to carry out computations that involve moving boundaries and interfaces. The finite element mesh that has been employed for all the computations is shown in figure 2.
The finite element formulation of the linear stability analysis of flow equations is the
extension of that presented in our earlier studies (Mittal & Kumar Reference Mittal and Kumar2007; Mittal & Verma Reference Mittal and Verma2014). The stabilization coefficients for the
formulation are based on the steady-state velocity field,
![]() $\boldsymbol{U}^{h}$
. In this work the formulation is extended to include (2.12) and (2.13) for the structure. The finite element discretization of
(2.10)–(2.13) leads to a generalized eigenvalue
problem of the form
$\boldsymbol{U}^{h}$
. In this work the formulation is extended to include (2.12) and (2.13) for the structure. The finite element discretization of
(2.10)–(2.13) leads to a generalized eigenvalue
problem of the form
![]() $\unicode[STIX]{x1D63C}X-{\it\lambda}\unicode[STIX]{x1D63D}X=0$
, where
$\unicode[STIX]{x1D63C}X-{\it\lambda}\unicode[STIX]{x1D63D}X=0$
, where
![]() $\unicode[STIX]{x1D63C}$
and
$\unicode[STIX]{x1D63C}$
and
![]() $\unicode[STIX]{x1D63D}$
are non-symmetric matrices. We use a shift-invert transformation in
conjunction with the subspace iteration method to track the fastest growing eigenmodes.
The growth rate of the eigenmodes obtained from LSA is confirmed by tracking the growth
rate of the energy of the disturbance from the DTI of the governing equations. This is
illustrated for a few cases in § 8 by initiating computations with the eigenmodes obtained from
LSA.
$\unicode[STIX]{x1D63D}$
are non-symmetric matrices. We use a shift-invert transformation in
conjunction with the subspace iteration method to track the fastest growing eigenmodes.
The growth rate of the eigenmodes obtained from LSA is confirmed by tracking the growth
rate of the energy of the disturbance from the DTI of the governing equations. This is
illustrated for a few cases in § 8 by initiating computations with the eigenmodes obtained from
LSA.
4 Eigenmodes from the linear stability analysis
4.1 Classification of modes
Compared to the fluid alone, LSA of the fluid–structure model is
associated with two additional eigenmodes. Cossu & Morino (Reference Cossu and Morino2000) and Meliga & Chomaz (Reference Meliga and Chomaz2011) presented a classification of the
eigenmodes based on their characteristics in the limit of very large
![]() $m^{\ast }$
. To identify the class to which an eigenmode belongs for a given
value of
$m^{\ast }$
. To identify the class to which an eigenmode belongs for a given
value of
![]() $Re$
and
$Re$
and
![]() $U^{\ast }$
, the eigenvalue has to be followed up to large values of
$U^{\ast }$
, the eigenvalue has to be followed up to large values of
![]() $m^{\ast }$
. Most studies on VIV that explore the characteristics of the
fluid–structure system in lock-in regime consider its variation with
reduced speed while holding the mass ratio fixed. A different perspective towards
mode classification is adopted in this work wherein
$m^{\ast }$
. Most studies on VIV that explore the characteristics of the
fluid–structure system in lock-in regime consider its variation with
reduced speed while holding the mass ratio fixed. A different perspective towards
mode classification is adopted in this work wherein
![]() $m^{\ast }$
is fixed and the eigenmodes are computed over a wide range of
$m^{\ast }$
is fixed and the eigenmodes are computed over a wide range of
![]() $U^{\ast }$
. The present classification makes it relatively easier to compare
the characteristics of fluid–structure system in the lock-in regime with
the properties of the unstable modes. It is observed that for systems with large
$U^{\ast }$
. The present classification makes it relatively easier to compare
the characteristics of fluid–structure system in the lock-in regime with
the properties of the unstable modes. It is observed that for systems with large
![]() $m^{\ast }$
, the modes corresponding to two leading eigenvalues are quite
distinct and maintain this distinction for all
$m^{\ast }$
, the modes corresponding to two leading eigenvalues are quite
distinct and maintain this distinction for all
![]() $U^{\ast }$
. That is, in terms of variation with
$U^{\ast }$
. That is, in terms of variation with
![]() $U^{\ast }$
, the two leading eigenmodes are decoupled. We refer to the two
modes as fluid mode and elastic mode. The frequency of FM remains nearly constant
with
$U^{\ast }$
, the two leading eigenmodes are decoupled. We refer to the two
modes as fluid mode and elastic mode. The frequency of FM remains nearly constant
with
![]() $U^{\ast }$
. The frequency of EM, on the other hand, varies inversely with
$U^{\ast }$
. The frequency of EM, on the other hand, varies inversely with
![]() $U^{\ast }$
. For low
$U^{\ast }$
. For low
![]() $m^{\ast }$
, the two leading eigenmodes do not exhibit a clear distinction in
terms of their affiliation to being either class elastic or class fluid. We refer to
such modes as coupled modes and denote them by fluid–elastic mode I (FEMI)
and fluid–elastic mode II (FEMII). For small
$m^{\ast }$
, the two leading eigenmodes do not exhibit a clear distinction in
terms of their affiliation to being either class elastic or class fluid. We refer to
such modes as coupled modes and denote them by fluid–elastic mode I (FEMI)
and fluid–elastic mode II (FEMII). For small
![]() $U^{\ast }$
, FEMI resembles fluid mode and FEMII is similar to elastic mode.
However, for large
$U^{\ast }$
, FEMI resembles fluid mode and FEMII is similar to elastic mode.
However, for large
![]() $U^{\ast }$
, the characteristics of FEMI and FEMII resemble EM and FM
respectively. A detailed description of decoupled and coupled modes for the
$U^{\ast }$
, the characteristics of FEMI and FEMII resemble EM and FM
respectively. A detailed description of decoupled and coupled modes for the
![]() $Re=60$
flow is presented for two values of mass ratio,
$Re=60$
flow is presented for two values of mass ratio,
![]() $m^{\ast }=20$
and
$m^{\ast }=20$
and
![]() $5$
. The modes are decoupled for
$5$
. The modes are decoupled for
![]() $m^{\ast }=20$
, while they are coupled for
$m^{\ast }=20$
, while they are coupled for
![]() $m^{\ast }=5$
. In the discussion that follows, we refer to the mode responsible
for the onset of global instability in the flow past a stationary cylinder as the
stationary wake mode.
$m^{\ast }=5$
. In the discussion that follows, we refer to the mode responsible
for the onset of global instability in the flow past a stationary cylinder as the
stationary wake mode.

Figure 3. Linear stability analysis of the steady flow past a
fluid–structure system: stability characteristics for
(a,c)
![]() $(Re,m^{\ast })=(60,20)$
, (b,d)
$(Re,m^{\ast })=(60,20)$
, (b,d)
![]() $(Re,m^{\ast })=(60,5)$
.
$(Re,m^{\ast })=(60,5)$
.
![]() ${\it\lambda}_{r}$
represents the growth rate and
${\it\lambda}_{r}$
represents the growth rate and
![]() $F_{LSA}={\it\lambda}_{i}/2{\rm\pi}$
represents the non-dimensional frequency.
$F_{LSA}={\it\lambda}_{i}/2{\rm\pi}$
represents the non-dimensional frequency.
Figure 3(a) shows
the variation of the growth rate of the fluid and the elastic mode with
![]() $U^{\ast }$
for
$U^{\ast }$
for
![]() $(Re,m^{\ast })=(60,20)$
. The fluid mode is unstable for all
$(Re,m^{\ast })=(60,20)$
. The fluid mode is unstable for all
![]() $U^{\ast }$
. It achieves maximum growth rate for
$U^{\ast }$
. It achieves maximum growth rate for
![]() $U^{\ast }=8.0$
. The growth rate of FM approaches the growth rate of the stationary
wake mode for
$U^{\ast }=8.0$
. The growth rate of FM approaches the growth rate of the stationary
wake mode for
![]() $Re=60$
for very small and very large values of
$Re=60$
for very small and very large values of
![]() $U^{\ast }$
. The elastic mode is unstable for
$U^{\ast }$
. The elastic mode is unstable for
![]() $5.8<U^{\ast }<7.3$
. This mode attains highest growth rate for
$5.8<U^{\ast }<7.3$
. This mode attains highest growth rate for
![]() $U^{\ast }=7.0$
. Figure 3(c) shows the variation of non-dimensional frequency,
$U^{\ast }=7.0$
. Figure 3(c) shows the variation of non-dimensional frequency,
![]() $F_{LSA}={\it\lambda}_{i}/2{\rm\pi}$
, with
$F_{LSA}={\it\lambda}_{i}/2{\rm\pi}$
, with
![]() $U^{\ast }$
. The frequency of the fluid mode remains close to the frequency of
the stationary wake mode for all
$U^{\ast }$
. The frequency of the fluid mode remains close to the frequency of
the stationary wake mode for all
![]() $U^{\ast }$
. It is noted that the growth rate of both modes achieve maximum
within the range of
$U^{\ast }$
. It is noted that the growth rate of both modes achieve maximum
within the range of
![]() $U^{\ast }$
where the frequencies of the two modes are close to each other.
Figure 4 shows the vorticity field
for the real and imaginary parts of the unstable eigenmode for the steady flow past a
stationary cylinder at
$U^{\ast }$
where the frequencies of the two modes are close to each other.
Figure 4 shows the vorticity field
for the real and imaginary parts of the unstable eigenmode for the steady flow past a
stationary cylinder at
![]() $Re=60$
. Figure 5 shows the
vorticity field for FM and EM for different
$Re=60$
. Figure 5 shows the
vorticity field for FM and EM for different
![]() $U^{\ast }$
at
$U^{\ast }$
at
![]() $(Re,m^{\ast })=(60,20)$
. It is observed that the shape of the eigenmode is closely related
to its frequency (
$(Re,m^{\ast })=(60,20)$
. It is observed that the shape of the eigenmode is closely related
to its frequency (
![]() $F_{LSA}$
). If the frequency associated with the eigenmode is relatively
larger, then the region of large perturbation associated with the mode is closer to
the cylinder. As the frequency of the eigenmode decreases, the large perturbation
region shifts downstream with respect to the cylinder. The frequency of FM remains
close to that of the
$F_{LSA}$
). If the frequency associated with the eigenmode is relatively
larger, then the region of large perturbation associated with the mode is closer to
the cylinder. As the frequency of the eigenmode decreases, the large perturbation
region shifts downstream with respect to the cylinder. The frequency of FM remains
close to that of the
![]() $Re=60$
stationary wake mode for all values of
$Re=60$
stationary wake mode for all values of
![]() $U^{\ast }$
. Therefore, the mode shape of FM resembles the stationary wake mode
(figure 4) for all reduced speeds.
On the other hand, the frequency of EM follows the natural frequency of the
structure-only system over a wide range of
$U^{\ast }$
. Therefore, the mode shape of FM resembles the stationary wake mode
(figure 4) for all reduced speeds.
On the other hand, the frequency of EM follows the natural frequency of the
structure-only system over a wide range of
![]() $U^{\ast }$
. As a result, with increase in
$U^{\ast }$
. As a result, with increase in
![]() $U^{\ast }$
the region of large perturbation associated with EM moves
downstream to the cylinder. For
$U^{\ast }$
the region of large perturbation associated with EM moves
downstream to the cylinder. For
![]() $U^{\ast }$
values where the frequency of FM and EM are close to each other, no
perceptible difference is observed in the structure of the two modes.
$U^{\ast }$
values where the frequency of FM and EM are close to each other, no
perceptible difference is observed in the structure of the two modes.

Figure 4. Linear stability analysis of the
![]() $Re=60$
steady flow past a circular cylinder: vorticity field for
the (a) real and
(b) imaginary parts of the eigenmode
corresponding to the stationary wake mode. The flow is from left to
right.
$Re=60$
steady flow past a circular cylinder: vorticity field for
the (a) real and
(b) imaginary parts of the eigenmode
corresponding to the stationary wake mode. The flow is from left to
right.

Figure 5. Linear stability analysis of the steady flow past a
fluid–structure system for
![]() $(Re,m^{\ast })=(60,20)$
: spanwise vorticity field of the EM
(a,c,e) and the FM
(b,d,f) for
(a,b)
$(Re,m^{\ast })=(60,20)$
: spanwise vorticity field of the EM
(a,c,e) and the FM
(b,d,f) for
(a,b)
![]() $U^{\ast }=5.5$
, (c,d)
$U^{\ast }=5.5$
, (c,d)
![]() $U^{\ast }=7.0$
and (e,f)
$U^{\ast }=7.0$
and (e,f)
![]() $U^{\ast }=8.0$
. The flow is from left to right.
$U^{\ast }=8.0$
. The flow is from left to right.
Figure 3(b,d) shows the stability characteristics
of FEMI and FEMII for
![]() $(Re,m^{\ast })=(60,5)$
. The vorticity field of the eigenmodes for different values of
$(Re,m^{\ast })=(60,5)$
. The vorticity field of the eigenmodes for different values of
![]() $U^{\ast }$
are shown in figure 6. The growth rate, frequency and mode shape of FEMI resemble the stationary
wake mode for low
$U^{\ast }$
are shown in figure 6. The growth rate, frequency and mode shape of FEMI resemble the stationary
wake mode for low
![]() $U^{\ast }$
. In the same
$U^{\ast }$
. In the same
![]() $U^{\ast }$
regime, FEMII is stable and its frequency follows the
structure-only system. Concomitantly, the region of large perturbation associated
with FEMII moves downstream to the cylinder with increase in reduced speed. The
growth rate of FEMI decreases with increase in
$U^{\ast }$
regime, FEMII is stable and its frequency follows the
structure-only system. Concomitantly, the region of large perturbation associated
with FEMII moves downstream to the cylinder with increase in reduced speed. The
growth rate of FEMI decreases with increase in
![]() $U^{\ast }$
and the mode becomes stable beyond
$U^{\ast }$
and the mode becomes stable beyond
![]() $U^{\ast }=6.0$
. FEMII is unstable for
$U^{\ast }=6.0$
. FEMII is unstable for
![]() $U^{\ast }\geqslant 5.0$
. Towards the higher-
$U^{\ast }\geqslant 5.0$
. Towards the higher-
![]() $U^{\ast }$
end, growth rate, frequency and mode shape of FEMII resemble the
stationary wake mode. For FEMI, at large values of
$U^{\ast }$
end, growth rate, frequency and mode shape of FEMII resemble the
stationary wake mode. For FEMI, at large values of
![]() $U^{\ast }$
, the large perturbation region associated with the eigenmode moves
downstream with increase in
$U^{\ast }$
, the large perturbation region associated with the eigenmode moves
downstream with increase in
![]() $U^{\ast }$
. For
$U^{\ast }$
. For
![]() $6.0\leqslant U^{\ast }\leqslant 9.0$
, the frequencies of the two modes are close to each other and their
variations with
$6.0\leqslant U^{\ast }\leqslant 9.0$
, the frequencies of the two modes are close to each other and their
variations with
![]() $U^{\ast }$
are also similar. The growth rate of the unstable FEMII achieves
maximum within this range.
$U^{\ast }$
are also similar. The growth rate of the unstable FEMII achieves
maximum within this range.

Figure 6. Linear stability analysis of the steady flow past a
fluid–structure system for
![]() $(Re,m^{\ast })=(60,5)$
: spanwise vorticity field of FEMI
(a,c,e) and FEMII
(b,d,f) for
(a,b)
$(Re,m^{\ast })=(60,5)$
: spanwise vorticity field of FEMI
(a,c,e) and FEMII
(b,d,f) for
(a,b)
![]() $U^{\ast }=4.0$
, (c,d)
$U^{\ast }=4.0$
, (c,d)
![]() $U^{\ast }=6.8$
and (e,f)
$U^{\ast }=6.8$
and (e,f)
![]() $U^{\ast }=10.0$
. The flow is from left to right.
$U^{\ast }=10.0$
. The flow is from left to right.

Figure 7. Linear stability analysis of the steady flow past a
fluid–structure system: variation of
![]() $U_{LSA}^{\ast }=2{\rm\pi}/{\it\lambda}_{i}=1/F$
with
$U_{LSA}^{\ast }=2{\rm\pi}/{\it\lambda}_{i}=1/F$
with
![]() $U^{\ast }$
for (a)
$U^{\ast }$
for (a)
![]() $(Re,m^{\ast })=(60,20)$
and (b)
$(Re,m^{\ast })=(60,20)$
and (b)
![]() $(Re,m^{\ast })=(60,5)$
. The point corresponding to stationary wake mode is shown
in bull’s eye symbol.
$(Re,m^{\ast })=(60,5)$
. The point corresponding to stationary wake mode is shown
in bull’s eye symbol.
To further bring out the distinction between the coupled and decoupled modes we
replot the results shown in figure 3
on the
![]() ${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane;
${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane;
![]() $U_{LSA}^{\ast }(=1/F_{LSA})$
is the reduced velocity based on the frequency of the eigenmode.
Figure 7 shows the variation of
the growth rate with
$U_{LSA}^{\ast }(=1/F_{LSA})$
is the reduced velocity based on the frequency of the eigenmode.
Figure 7 shows the variation of
the growth rate with
![]() $U_{LSA}^{\ast }$
for
$U_{LSA}^{\ast }$
for
![]() $(Re,m^{\ast })=(60,20)$
and
$(Re,m^{\ast })=(60,20)$
and
![]() $(60,5)$
. The end points of the curves are tagged with
$(60,5)$
. The end points of the curves are tagged with
![]() $A{-}B$
for FM,
$A{-}B$
for FM,
![]() $C{-}D$
for EM,
$C{-}D$
for EM,
![]() $P{-}Q$
for FEMI and
$P{-}Q$
for FEMI and
![]() $R{-}S$
for FEMII. The location of these points in figure 3 is also marked. In the case of decoupled modes,
the end points of the fluid mode, at the low (point
$R{-}S$
for FEMII. The location of these points in figure 3 is also marked. In the case of decoupled modes,
the end points of the fluid mode, at the low (point
![]() $A$
) and high end of
$A$
) and high end of
![]() $U^{\ast }$
(point
$U^{\ast }$
(point
![]() $B$
), approach each other with increase in the range of
$B$
), approach each other with increase in the range of
![]() $U^{\ast }$
. For the limiting case when the reduced velocity spans from zero to
infinity, FM would appear as a closed ring, separate from EM, on
$U^{\ast }$
. For the limiting case when the reduced velocity spans from zero to
infinity, FM would appear as a closed ring, separate from EM, on
![]() ${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane. The point where the end points of the ring merge,
corresponds to that for the stationary wake mode (shown as bull’s eye
symbol in figure 3). For the case of
coupled modes, with increase in the range of
${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane. The point where the end points of the ring merge,
corresponds to that for the stationary wake mode (shown as bull’s eye
symbol in figure 3). For the case of
coupled modes, with increase in the range of
![]() $U^{\ast }$
, the end point of FEMII (point
$U^{\ast }$
, the end point of FEMII (point
![]() $S$
) and the beginning of FEMI (point
$S$
) and the beginning of FEMI (point
![]() $P$
) approach the point corresponding to the stationary wake mode. In
the limiting case when the reduced velocity spans from zero to infinity, the two
modes would merge at the point corresponding to stationary wake mode on
$P$
) approach the point corresponding to the stationary wake mode. In
the limiting case when the reduced velocity spans from zero to infinity, the two
modes would merge at the point corresponding to stationary wake mode on
![]() ${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane and appear as a single curve. Figure 7 clearly brings out the distinction between the
coupled and decoupled modes and the identification of the two branches.
${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane and appear as a single curve. Figure 7 clearly brings out the distinction between the
coupled and decoupled modes and the identification of the two branches.
4.2 Regime of coupled and decoupled modes
In general, whether the modes are coupled or decoupled depends on
![]() $m^{\ast }$
and
$m^{\ast }$
and
![]() $Re$
. At a given
$Re$
. At a given
![]() $Re$
, the modes are coupled for relatively low
$Re$
, the modes are coupled for relatively low
![]() $m^{\ast }$
and get decoupled to EM and FM at larger
$m^{\ast }$
and get decoupled to EM and FM at larger
![]() $m^{\ast }$
. We define critical mass ratio,
$m^{\ast }$
. We define critical mass ratio,
![]() $m_{c}^{\ast }$
, as the largest mass ratio for which modes are coupled at a certain
$m_{c}^{\ast }$
, as the largest mass ratio for which modes are coupled at a certain
![]() $Re$
. We also define
$Re$
. We also define
![]() $Re_{o}$
as the Reynolds number beyond which the stationary wake mode
becomes unstable. The value of
$Re_{o}$
as the Reynolds number beyond which the stationary wake mode
becomes unstable. The value of
![]() $Re_{o}$
estimated with the mesh employed in the present study is
$Re_{o}$
estimated with the mesh employed in the present study is
![]() $Re_{o}=47.5$
. The value of
$Re_{o}=47.5$
. The value of
![]() $Re_{o}$
from the study reported by Kumar & Mittal (Reference Kumar and Mittal2006), independent of mesh and blockage effects,
is
$Re_{o}$
from the study reported by Kumar & Mittal (Reference Kumar and Mittal2006), independent of mesh and blockage effects,
is
![]() $Re_{o}=47$
. The two values are in very good agreement. The small difference
between the two studies is attributed to the slightly lower spatial resolution in the
present study. Compared to the flow past stationary cylinder, the coupled
fluid–structure system has additional degrees of freedom corresponding to
cylinder displacement and velocity. In addition, these degrees of freedom are
strongly coupled with the flow variables at the surface of the cylinder. Therefore,
LSA of the coupled fluid–structure problem is relatively more demanding on
computational resources as compared to the fluid-only and structure-only problems.
One of the factors in choosing the finite element mesh used in the present study is
that with the computational resources at our disposal, we should be able to carry out
LSA over a wide range of the various parameters of interest (
$Re_{o}=47$
. The two values are in very good agreement. The small difference
between the two studies is attributed to the slightly lower spatial resolution in the
present study. Compared to the flow past stationary cylinder, the coupled
fluid–structure system has additional degrees of freedom corresponding to
cylinder displacement and velocity. In addition, these degrees of freedom are
strongly coupled with the flow variables at the surface of the cylinder. Therefore,
LSA of the coupled fluid–structure problem is relatively more demanding on
computational resources as compared to the fluid-only and structure-only problems.
One of the factors in choosing the finite element mesh used in the present study is
that with the computational resources at our disposal, we should be able to carry out
LSA over a wide range of the various parameters of interest (
![]() $Re$
,
$Re$
,
![]() $U^{\ast }$
,
$U^{\ast }$
,
![]() $m^{\ast }$
). A mesh convergence study is carried out to check the adequacy of
the mesh against a mesh of finer spatial resolution. The details of the mesh
convergence study are presented in appendix A. The results from the two meshes are found to be in very good
agreement. The effect of
$m^{\ast }$
). A mesh convergence study is carried out to check the adequacy of
the mesh against a mesh of finer spatial resolution. The details of the mesh
convergence study are presented in appendix A. The results from the two meshes are found to be in very good
agreement. The effect of
![]() $m^{\ast }$
on (de-)coupling of modes is presented with
$m^{\ast }$
on (de-)coupling of modes is presented with
![]() $Re$
. To account for the offset in the value of
$Re$
. To account for the offset in the value of
![]() $Re_{o}$
compared to that reported by Kumar & Mittal (Reference Kumar and Mittal2006), we additionally present the results with
respect to
$Re_{o}$
compared to that reported by Kumar & Mittal (Reference Kumar and Mittal2006), we additionally present the results with
respect to
![]() $Re/Re_{o}$
. Marais et al. (Reference Marais, Godoy-Diana, Barkley and Wesfreid2011) used a similar approach to present their results on
stability analysis. They recorded a value of
$Re/Re_{o}$
. Marais et al. (Reference Marais, Godoy-Diana, Barkley and Wesfreid2011) used a similar approach to present their results on
stability analysis. They recorded a value of
![]() $Re_{o}=64$
in their experiments because of confinement and blockage effects.
$Re_{o}=64$
in their experiments because of confinement and blockage effects.
Figure 8(a) shows
the regions in
![]() $Re{-}m^{\ast }$
plane where the modes are coupled or decoupled. We describe the
procedure used to generate this figure. For several values of
$Re{-}m^{\ast }$
plane where the modes are coupled or decoupled. We describe the
procedure used to generate this figure. For several values of
![]() $Re$
, computations are carried out for many values of
$Re$
, computations are carried out for many values of
![]() $m^{\ast }$
that are separated by a step size of
$m^{\ast }$
that are separated by a step size of
![]() ${\rm\Delta}m^{\ast }=5.0$
. At each of these
${\rm\Delta}m^{\ast }=5.0$
. At each of these
![]() $(Re,m^{\ast })$
values, LSA is carried out over a wide range of reduced speed. The
variation of
$(Re,m^{\ast })$
values, LSA is carried out over a wide range of reduced speed. The
variation of
![]() ${\it\lambda}_{r}$
with
${\it\lambda}_{r}$
with
![]() $U_{LSA}^{\ast }$
is utilized to identify coupled/decoupled modes. In the range of
$U_{LSA}^{\ast }$
is utilized to identify coupled/decoupled modes. In the range of
![]() $m^{\ast }$
where the system transits between coupled and decoupled modes,
computations are carried out for more
$m^{\ast }$
where the system transits between coupled and decoupled modes,
computations are carried out for more
![]() $m^{\ast }$
values that are separated by a finer step size of
$m^{\ast }$
values that are separated by a finer step size of
![]() ${\rm\Delta}m^{\ast }=1.0$
. These are utilized to estimate the critical mass ratio,
${\rm\Delta}m^{\ast }=1.0$
. These are utilized to estimate the critical mass ratio,
![]() $m_{c}^{\ast }$
, beyond which the modes are decoupled for a given
$m_{c}^{\ast }$
, beyond which the modes are decoupled for a given
![]() $Re$
. These values are shown in figure 8(a) by solid circles. We note that
$Re$
. These values are shown in figure 8(a) by solid circles. We note that
![]() $m_{c}^{\ast }$
decreases as one moves away from
$m_{c}^{\ast }$
decreases as one moves away from
![]() $Re_{o}$
. Figure 8(b–d) shows the variation of
$Re_{o}$
. Figure 8(b–d) shows the variation of
![]() ${\it\lambda}_{r}$
with
${\it\lambda}_{r}$
with
![]() $U_{LSA}^{\ast }$
for
$U_{LSA}^{\ast }$
for
![]() $m^{\ast }=75$
at
$m^{\ast }=75$
at
![]() $Re=37.5$
, 47 and 56.5, respectively. For
$Re=37.5$
, 47 and 56.5, respectively. For
![]() $Re=37.5$
and 56.5 the modes are decoupled. While the fluid mode is stable
for former, it is unstable in the latter case. For
$Re=37.5$
and 56.5 the modes are decoupled. While the fluid mode is stable
for former, it is unstable in the latter case. For
![]() $Re=47.0$
(
$Re=47.0$
(
![]() $Re/Re_{o}=1.0$
), the modes are coupled. The value of
$Re/Re_{o}=1.0$
), the modes are coupled. The value of
![]() ${\it\lambda}_{r}$
at the junction, where the branches corresponding to modes FEMI and
FEMII meet, is equal to zero. The transition from the regime of coupled modes to
decoupled modes with increase in mass ratio is demonstrated in
figure 9 for
${\it\lambda}_{r}$
at the junction, where the branches corresponding to modes FEMI and
FEMII meet, is equal to zero. The transition from the regime of coupled modes to
decoupled modes with increase in mass ratio is demonstrated in
figure 9 for
![]() $Re=42$
and 52 by the evolution of the topology of the curves.
$Re=42$
and 52 by the evolution of the topology of the curves.

Figure 8. Linear stability analysis of the steady flow past a
fluid–cylinder system: (a) the
regions of mode coupling/decoupling. The variation of growth rate of modes
with
![]() $U_{LSA}^{\ast }$
for
$U_{LSA}^{\ast }$
for
![]() $m^{\ast }=75$
at (b)
$m^{\ast }=75$
at (b)
![]() $Re=37.5$
, (c)
$Re=37.5$
, (c)
![]() $Re=Re_{o}=47$
and (d)
$Re=Re_{o}=47$
and (d)
![]() $Re=56.5$
.
$Re=56.5$
.

Figure 9. Linear stability analysis of the steady flow past a
fluid–cylinder system: variation of growth rate with
![]() $U_{LSA}^{\ast }$
of modes for for (a)
$U_{LSA}^{\ast }$
of modes for for (a)
![]() $(Re,m^{\ast })=(42,10)$
, (c)
$(Re,m^{\ast })=(42,10)$
, (c)
![]() $(Re,m^{\ast })=(42,25)$
, (e)
$(Re,m^{\ast })=(42,25)$
, (e)
![]() $(Re,m^{\ast })=(42,50)$
, (b)
$(Re,m^{\ast })=(42,50)$
, (b)
![]() $(Re,m^{\ast })=(52,10)$
, (d)
$(Re,m^{\ast })=(52,10)$
, (d)
![]() $(Re,m^{\ast })=(52,25)$
, (f)
$(Re,m^{\ast })=(52,25)$
, (f)
![]() $(Re,m^{\ast })=(52,40)$
.
$(Re,m^{\ast })=(52,40)$
.
The term critical mass ratio has been used in earlier studies on free vibrations in
different contexts. For example, Govardhan & Williamson (Reference Govardhan and Williamson2000) introduced a critical mass ratio,
![]() $m_{crit}^{\ast }$
, below which synchronization is observed for values of
$m_{crit}^{\ast }$
, below which synchronization is observed for values of
![]() $U^{\ast }$
up to infinity. Prasanth et al. (Reference Prasanth, Premchandran and Mittal2011) introduced a critical mass ratio,
$U^{\ast }$
up to infinity. Prasanth et al. (Reference Prasanth, Premchandran and Mittal2011) introduced a critical mass ratio,
![]() $m_{cr}^{\ast }$
, below which hysteresis between the initial and lower branch, at
low
$m_{cr}^{\ast }$
, below which hysteresis between the initial and lower branch, at
low
![]() $Re$
and in an unbounded domain, disappears. The term critical mass
ratio, in the present work, is not related to these two phenomena. In the following
sections most of the results and figures are presented for the case of coupled modes.
The general argument can be extended to the case of coupled modes as well.
$Re$
and in an unbounded domain, disappears. The term critical mass
ratio, in the present work, is not related to these two phenomena. In the following
sections most of the results and figures are presented for the case of coupled modes.
The general argument can be extended to the case of coupled modes as well.
5 Lock-in regime
As a first step towards exploring the connection between the lock-in phenomenon and linear instability of the fluid–structure system, we identify the lock-in regime in the cylinder response obtained from the DTI of governing equations. Later in the section, we present a comparison of the lock-in regime obtained from DTI with that estimated from the results of LSA. In the linear regime the fluid and the structure system are associated with the same growth rate and frequency (2.9). A positive growth rate, via linear theory, would necessarily lead to very large oscillations of the fluid–structure system at sufficiently large times. Therefore, it is appropriate to conclude that in the linear regime, instability is synonymous with lock-in/synchronization. However, as the disturbance field becomes large the nonlinear terms in the governing equations become significant; the system can no longer be approximated by dropping the nonlinear effects. In fact, the nonlinear terms drive the system to a limit cycle with finite amplitude of oscillation and with modified frequency. This may change the lock-in range as compared to that predicted by LSA. Figures 10–12 show the lock-in regime predicted by LSA and DTI of the governing equations. The results shown for DTI are the ones when the oscillations have reached a limit cycle. The three figures are discussed in detail below.

Figure 10. Flow past a fluid–cylinder system for
![]() $(Re,m^{\ast })=(40,10)$
: variation of (a) normalized
maximum amplitude of cylinder response and
(b) frequency ratio with reduced velocity obtained
from DTI. The lock-in regime from DTI, in the presence of nonlinear effects, is
shaded in grey in (a,b). The
variation of growth rate and frequency ratio of the eigenmodes with reduced
velocity are shown in (c)
and (d), respectively. The stable and unstable
eigenmodes are denoted by hollow and solid symbols, respectively. The range of
$(Re,m^{\ast })=(40,10)$
: variation of (a) normalized
maximum amplitude of cylinder response and
(b) frequency ratio with reduced velocity obtained
from DTI. The lock-in regime from DTI, in the presence of nonlinear effects, is
shaded in grey in (a,b). The
variation of growth rate and frequency ratio of the eigenmodes with reduced
velocity are shown in (c)
and (d), respectively. The stable and unstable
eigenmodes are denoted by hollow and solid symbols, respectively. The range of
![]() $U^{\ast }$
over which the system is linearly unstable is shaded
in (c,d).
$U^{\ast }$
over which the system is linearly unstable is shaded
in (c,d).

Figure 11. Flow past a fluid–cylinder system for
![]() $(Re,m^{\ast })=(60,20)$
: variation of (a) normalized
maximum amplitude of cylinder response and
(b) frequency ratio with reduced velocity obtained
from DTI. The lock-in regime from DTI, in the presence of nonlinear effects, is
shaded in grey in (a,b). The variation of
growth rate and frequency ratio of the eigenmodes with reduced velocity are
shown in (c) and (d), respectively. The
stable and unstable eigenmodes are denoted by hollow and solid symbols,
respectively. The range of
$(Re,m^{\ast })=(60,20)$
: variation of (a) normalized
maximum amplitude of cylinder response and
(b) frequency ratio with reduced velocity obtained
from DTI. The lock-in regime from DTI, in the presence of nonlinear effects, is
shaded in grey in (a,b). The variation of
growth rate and frequency ratio of the eigenmodes with reduced velocity are
shown in (c) and (d), respectively. The
stable and unstable eigenmodes are denoted by hollow and solid symbols,
respectively. The range of
![]() $U^{\ast }$
over which the system is linearly unstable is shaded
in (c,d).
$U^{\ast }$
over which the system is linearly unstable is shaded
in (c,d).

Figure 12. Flow past a fluid–cylinder system for
![]() $(Re,m^{\ast })=(60,5)$
: variation of (a) normalized
maximum amplitude of cylinder response and
(b) frequency ratio with reduced velocity obtained
from DTI. The lock-in regime from DTI, in the presence of nonlinear effects, is
shaded in grey in (a,b). The
variation of growth rate and frequency ratio of the eigenmodes with reduced
velocity are shown in (c)
and (d), respectively. The stable and unstable
eigenmodes are denoted by hollow and solid symbols, respectively. The range of
$(Re,m^{\ast })=(60,5)$
: variation of (a) normalized
maximum amplitude of cylinder response and
(b) frequency ratio with reduced velocity obtained
from DTI. The lock-in regime from DTI, in the presence of nonlinear effects, is
shaded in grey in (a,b). The
variation of growth rate and frequency ratio of the eigenmodes with reduced
velocity are shown in (c)
and (d), respectively. The stable and unstable
eigenmodes are denoted by hollow and solid symbols, respectively. The range of
![]() $U^{\ast }$
over which the system is linearly unstable is shaded
in (c,d).
$U^{\ast }$
over which the system is linearly unstable is shaded
in (c,d).
![]() $Re\leqslant Re_{o}$
: Figure 10(a,b) shows the variation of normalized
maximum amplitude of transverse oscillation and frequency ratio with
$Re\leqslant Re_{o}$
: Figure 10(a,b) shows the variation of normalized
maximum amplitude of transverse oscillation and frequency ratio with
![]() $U^{\ast }$
for
$U^{\ast }$
for
![]() $(Re,m^{\ast })=(40,10)$
obtained from DTI. The frequency ratio,
$(Re,m^{\ast })=(40,10)$
obtained from DTI. The frequency ratio,
![]() $f_{DTI}^{\ast }$
, is defined as the ratio of the frequency of the cylinder oscillation
to the natural frequency of the oscillator in vacuum. It is observed that
lock-in/synchronization occurs for
$f_{DTI}^{\ast }$
, is defined as the ratio of the frequency of the cylinder oscillation
to the natural frequency of the oscillator in vacuum. It is observed that
lock-in/synchronization occurs for
![]() $5.9<U^{\ast }<10.1$
. Outside this range of
$5.9<U^{\ast }<10.1$
. Outside this range of
![]() $U^{\ast }$
the flow is steady and the cylinder is at rest. In the lock-in regime,
the cylinder oscillations are accompanied with vortex shedding and the frequency ratio
is close to unity. As shown in figure 10(a,c), LSA predicts instability of the
fluid–structure system in exactly the same regime of
$U^{\ast }$
the flow is steady and the cylinder is at rest. In the lock-in regime,
the cylinder oscillations are accompanied with vortex shedding and the frequency ratio
is close to unity. As shown in figure 10(a,c), LSA predicts instability of the
fluid–structure system in exactly the same regime of
![]() $U^{\ast }$
as computed from DTI. The instability sets in via the elastic mode. We
note that the fluid mode is stable for all
$U^{\ast }$
as computed from DTI. The instability sets in via the elastic mode. We
note that the fluid mode is stable for all
![]() $U^{\ast }$
for subcritical
$U^{\ast }$
for subcritical
![]() $Re$
. The frequency ratio,
$Re$
. The frequency ratio,
![]() $f_{LSA}^{\ast }={\it\lambda}_{i}/(2{\rm\pi}F_{N})$
, of EM is also close to unity as is
$f_{LSA}^{\ast }={\it\lambda}_{i}/(2{\rm\pi}F_{N})$
, of EM is also close to unity as is
![]() $f_{DTI}^{\ast }$
. However, the two values are different (figure 10
c,d). The
difference is attributed to nonlinear effects that are associated with DTI. The effect
of nonlinearities on the frequency response of the fluid–structure system has
been explored by Meliga & Chomaz (Reference Meliga and Chomaz2011) for systems with relatively large mass ratio. In the scenario of coupled
modes, lock-in occurs via FEMII while FEMI is stable for all
$f_{DTI}^{\ast }$
. However, the two values are different (figure 10
c,d). The
difference is attributed to nonlinear effects that are associated with DTI. The effect
of nonlinearities on the frequency response of the fluid–structure system has
been explored by Meliga & Chomaz (Reference Meliga and Chomaz2011) for systems with relatively large mass ratio. In the scenario of coupled
modes, lock-in occurs via FEMII while FEMI is stable for all
![]() $U^{\ast }$
.
$U^{\ast }$
.
![]() $Re>Re_{o}$
: Figure 11(a,b) shows the variation of
$Re>Re_{o}$
: Figure 11(a,b) shows the variation of
![]() $Y_{max}/D$
and
$Y_{max}/D$
and
![]() $f_{DTI}^{\ast }$
with
$f_{DTI}^{\ast }$
with
![]() $U^{\ast }$
for
$U^{\ast }$
for
![]() $(Re,m^{\ast })=(60,20)$
. The amplitude and the frequency of the cylinder response show that
lock-in occurs over
$(Re,m^{\ast })=(60,20)$
. The amplitude and the frequency of the cylinder response show that
lock-in occurs over
![]() $5.8<U^{\ast }<9.3$
. The cylinder exhibits large amplitude of vibration within the lock-in
regime. The frequency ratio in the lock-in regime is closer to unity than outside the
range of lock-in. LSA, in this case, shows that FM is unstable for all
$5.8<U^{\ast }<9.3$
. The cylinder exhibits large amplitude of vibration within the lock-in
regime. The frequency ratio in the lock-in regime is closer to unity than outside the
range of lock-in. LSA, in this case, shows that FM is unstable for all
![]() $U^{\ast }$
; suggesting lock-in forever (figure 11
c). The elastic mode is unstable over
$U^{\ast }$
; suggesting lock-in forever (figure 11
c). The elastic mode is unstable over
![]() $5.8<U^{\ast }<7.3$
. Figure 12(a,b) shows the variation of
$5.8<U^{\ast }<7.3$
. Figure 12(a,b) shows the variation of
![]() $Y_{max}/D$
and
$Y_{max}/D$
and
![]() $f_{DTI}^{\ast }$
with
$f_{DTI}^{\ast }$
with
![]() $U^{\ast }$
for
$U^{\ast }$
for
![]() $(Re,m^{\ast })=(60,5)$
. In this case also the fluid–structure system is linearly
unstable for all
$(Re,m^{\ast })=(60,5)$
. In this case also the fluid–structure system is linearly
unstable for all
![]() $U^{\ast }$
. For low values of
$U^{\ast }$
. For low values of
![]() $U^{\ast }$
, the instability occurs via FEMI while for large
$U^{\ast }$
, the instability occurs via FEMI while for large
![]() $U^{\ast }$
, FEMII is unstable. The results from DTI show that lock-in for
$U^{\ast }$
, FEMII is unstable. The results from DTI show that lock-in for
![]() $(Re,m^{\ast })=(60,5)$
occurs over
$(Re,m^{\ast })=(60,5)$
occurs over
![]() $5.0<U^{\ast }<8.8$
. Compared to free vibrations at subcritical
$5.0<U^{\ast }<8.8$
. Compared to free vibrations at subcritical
![]() $Re$
, the oscillations for
$Re$
, the oscillations for
![]() $Re>Re_{o}$
are different on two major counts.
$Re>Re_{o}$
are different on two major counts.
-
(1) The
 $U^{\ast }$
-range of lock-in from DTI and LSA are different: for
$U^{\ast }$
-range of lock-in from DTI and LSA are different: for
 $Re\leqslant Re_{o}$
, prediction of the lock-in range from LSA matches the range
observed from DTI. This is not so for
$Re\leqslant Re_{o}$
, prediction of the lock-in range from LSA matches the range
observed from DTI. This is not so for
 $Re>Re_{o}$
. The fluid–structure system is linearly unstable
for all
$Re>Re_{o}$
. The fluid–structure system is linearly unstable
for all
 $U^{\ast }$
. However, nonlinear effects lead to saturation of oscillation
amplitude of the cylinder to relatively low values outside the lock-in regime.
More specifically, the phase between the lift and displacement as well as the
frequency undergo a significant change due to the nonlinear effects leading the
system to desynchronization. Desynchronization is indicated by a strong
departure of
$U^{\ast }$
. However, nonlinear effects lead to saturation of oscillation
amplitude of the cylinder to relatively low values outside the lock-in regime.
More specifically, the phase between the lift and displacement as well as the
frequency undergo a significant change due to the nonlinear effects leading the
system to desynchronization. Desynchronization is indicated by a strong
departure of
 $f^{\ast }$
from unity (results for DTI in figure 11
b). A question that
arises from this observation is, ‘Is there any feature in the
unstable eigenmodes from LSA that might indicate whether it will eventually
lead to lock-in or no lock-in?’ We explore this in the next section
by studying the relative distribution of energy in an eigenmode between the
fluid and the structure.
$f^{\ast }$
from unity (results for DTI in figure 11
b). A question that
arises from this observation is, ‘Is there any feature in the
unstable eigenmodes from LSA that might indicate whether it will eventually
lead to lock-in or no lock-in?’ We explore this in the next section
by studying the relative distribution of energy in an eigenmode between the
fluid and the structure. -
(2) The mode that leads to synchronization: for
 $Re\leqslant Re_{o}$
, only one mode is unstable and it controls the dynamics;
instability sets in via EM for decoupled modes and FEMII for the case of
coupled modes. However, for
$Re\leqslant Re_{o}$
, only one mode is unstable and it controls the dynamics;
instability sets in via EM for decoupled modes and FEMII for the case of
coupled modes. However, for
 $Re>Re_{o}$
, multiple eigenmodes may be unstable depending on the
operational
$Re>Re_{o}$
, multiple eigenmodes may be unstable depending on the
operational
 $U^{\ast }$
. For
$U^{\ast }$
. For
 $(Re,m^{\ast })=(60,20)$
, towards the lower
$(Re,m^{\ast })=(60,20)$
, towards the lower
 $U^{\ast }$
end of lock-in, both EM and FM are unstable (
$U^{\ast }$
end of lock-in, both EM and FM are unstable (
 $5.8<U^{\ast }<7.3$
). Similarly, for
$5.8<U^{\ast }<7.3$
). Similarly, for
 $(Re,m^{\ast })=(60,5)$
, both FEMI and FEMII are unstable for
$(Re,m^{\ast })=(60,5)$
, both FEMI and FEMII are unstable for
 $5.0<U^{\ast }<6.0$
. In next section we explore the question as to
‘which of the two modes leads to lock-in?’ It is shown
that for
$5.0<U^{\ast }<6.0$
. In next section we explore the question as to
‘which of the two modes leads to lock-in?’ It is shown
that for
 $(Re,m^{\ast })=(60,20)$
, compared to FM, EM is associated with higher energy transfer
from the fluid to the cylinder. Therefore, for
$(Re,m^{\ast })=(60,20)$
, compared to FM, EM is associated with higher energy transfer
from the fluid to the cylinder. Therefore, for
 $5.9\leqslant U^{\ast }\leqslant 7.2$
, the elastic mode leads to lock-in. For
$5.9\leqslant U^{\ast }\leqslant 7.2$
, the elastic mode leads to lock-in. For
 $7.2<U^{\ast }\leqslant 9.2$
, lock-in occurs via the fluid mode as it is the only unstable
mode. In the case of coupled modes, lock-in occurs via FEMII as it is
associated with higher energy transfer than FEMI.
$7.2<U^{\ast }\leqslant 9.2$
, lock-in occurs via the fluid mode as it is the only unstable
mode. In the case of coupled modes, lock-in occurs via FEMII as it is
associated with higher energy transfer than FEMI.
6 Energy considerations related to eigenmodes
6.1 Energy ratio
We consider the disturbance field given by (2.9). In general, the eigenvalues/eigenmodes are complex. The total energy
of the fluid–oscillator system associated with the disturbance field is
the sum of the structural energy,
![]() $E_{s}$
, and the kinetic energy of the fluid,
$E_{s}$
, and the kinetic energy of the fluid,
![]() $E_{f}$
. The two components are defined as:
$E_{f}$
. The two components are defined as:
In (6.1) the first term on the right-hand side is the contribution of the kinetic energy of the cylinder while the second term arises from the potential energy of the spring. Equations (6.1) and (6.2) can be rewritten as
where
![]() $\hat{E}_{s}$
and
$\hat{E}_{s}$
and
![]() $\hat{E}_{f}$
are given as,
$\hat{E}_{f}$
are given as,
We define the energy ratio as
![]() $E_{r}=E_{s}(t)/(E_{s}(t)+E_{f}(t))$
. It denotes the fraction of the total energy of the disturbance
field contained in the structure;
$E_{r}=E_{s}(t)/(E_{s}(t)+E_{f}(t))$
. It denotes the fraction of the total energy of the disturbance
field contained in the structure;
![]() $(1-E_{r})$
is the fraction of the total energy of the disturbance due to the
motion of the fluid. We note that
$(1-E_{r})$
is the fraction of the total energy of the disturbance due to the
motion of the fluid. We note that
![]() $E_{r}$
is constant with respect to time and can also be computed via
$E_{r}$
is constant with respect to time and can also be computed via
![]() $E_{r}=\hat{E}_{s}/(\hat{E}_{s}+\hat{E}_{f})$
. The evolution of
$E_{r}=\hat{E}_{s}/(\hat{E}_{s}+\hat{E}_{f})$
. The evolution of
![]() $E_{s}(t)$
, therefore, depends on
$E_{s}(t)$
, therefore, depends on
![]() $E_{r}$
and
$E_{r}$
and
![]() ${\it\lambda}_{r}$
. If
${\it\lambda}_{r}$
. If
![]() ${\it\lambda}_{r}$
is positive,
${\it\lambda}_{r}$
is positive,
![]() $E_{s}$
, grows with time. However, the nonlinear terms become significant
when the disturbance field becomes relatively large. As a consequence, the
fluid–structure system tends towards a limit cycle. The saturated
oscillation amplitude of the spring mass oscillator significantly depends on
$E_{s}$
, grows with time. However, the nonlinear terms become significant
when the disturbance field becomes relatively large. As a consequence, the
fluid–structure system tends towards a limit cycle. The saturated
oscillation amplitude of the spring mass oscillator significantly depends on
![]() $E_{r}$
of the unstable mode. We will show later in the paper that systems
with relatively large
$E_{r}$
of the unstable mode. We will show later in the paper that systems
with relatively large
![]() $E_{r}$
, coupled with positive growth rate, attain large amplitude
oscillations resulting in synchronization. The threshold value of
$E_{r}$
, coupled with positive growth rate, attain large amplitude
oscillations resulting in synchronization. The threshold value of
![]() $E_{r}$
beyond which the unstable eigenmodes lead to lock-in state depends
on
$E_{r}$
beyond which the unstable eigenmodes lead to lock-in state depends
on
![]() $Re$
and
$Re$
and
![]() $m^{\ast }$
. For example for
$m^{\ast }$
. For example for
![]() $(Re,m^{\ast })=(60,20)$
, all unstable eigenmodes that are associated with
$(Re,m^{\ast })=(60,20)$
, all unstable eigenmodes that are associated with
![]() $E_{r}>2\times 10^{-4}$
lead to lock-in. Figure 13(a) shows the variation of
$E_{r}>2\times 10^{-4}$
lead to lock-in. Figure 13(a) shows the variation of
![]() $E_{r}$
with
$E_{r}$
with
![]() $U^{\ast }$
for the elastic and fluid mode for
$U^{\ast }$
for the elastic and fluid mode for
![]() $(Re,m^{\ast })=(60,20)$
. The same for the case of coupled modes at
$(Re,m^{\ast })=(60,20)$
. The same for the case of coupled modes at
![]() $(Re,m^{\ast })=(60,5)$
is shown in figure 13(b). To clearly bring out the features in the variation
of
$(Re,m^{\ast })=(60,5)$
is shown in figure 13(b). To clearly bring out the features in the variation
of
![]() $E_{r}$
with
$E_{r}$
with
![]() $U^{\ast }$
and the relative behaviour of the two eigenmodes, the vertical axis
is shown in log scale. Also shown in the figures, via shading, is the lock-in regime
obtained from DTI. The stable and the unstable eigenmodes are denoted by hollow and
solid symbols, respectively.
$U^{\ast }$
and the relative behaviour of the two eigenmodes, the vertical axis
is shown in log scale. Also shown in the figures, via shading, is the lock-in regime
obtained from DTI. The stable and the unstable eigenmodes are denoted by hollow and
solid symbols, respectively.
![]() $E_{r}$
of the unstable eigenmodes is relatively low outside the lock-in
regime. Within the lock-in regime, for each
$E_{r}$
of the unstable eigenmodes is relatively low outside the lock-in
regime. Within the lock-in regime, for each
![]() $U^{\ast }$
, the energy ratio of at least one unstable eigenmode has a large
value. For
$U^{\ast }$
, the energy ratio of at least one unstable eigenmode has a large
value. For
![]() $(Re,m^{\ast })=(60,20)$
, EM has high
$(Re,m^{\ast })=(60,20)$
, EM has high
![]() $E_{r}$
for
$E_{r}$
for
![]() $U^{\ast }$
up to 7.3 approximately. Beyond
$U^{\ast }$
up to 7.3 approximately. Beyond
![]() $U^{\ast }\sim 7.3$
, EM is stable and is not expected to play any role in lock-in. In
this flow regime, though,
$U^{\ast }\sim 7.3$
, EM is stable and is not expected to play any role in lock-in. In
this flow regime, though,
![]() $E_{r}$
for the fluid mode is large and is expected to drive the system
towards lock-in. For
$E_{r}$
for the fluid mode is large and is expected to drive the system
towards lock-in. For
![]() $(Re,m^{\ast })=(60,5)$
, FEMII has a significantly large values of
$(Re,m^{\ast })=(60,5)$
, FEMII has a significantly large values of
![]() $E_{r}$
over the entire lock-in regime. Lock-in in this case, therefore, is
expected via FEMII.
$E_{r}$
over the entire lock-in regime. Lock-in in this case, therefore, is
expected via FEMII.

Figure 13. Linear stability analysis of the steady flow past a
fluid–cylinder system: variation of energy ratio of the
eigenmodes with
![]() $U^{\ast }$
for (a)
$U^{\ast }$
for (a)
![]() $(Re,m^{\ast })=(60,20)$
and (b)
$(Re,m^{\ast })=(60,20)$
and (b)
![]() $(Re,m^{\ast })=(60,5)$
. The stable and the unstable eigenmodes are shown as
hollow and solid symbols, respectively. The lock-in regime from DTI, in the
presence of nonlinear effects, is shaded in the figures.
$(Re,m^{\ast })=(60,5)$
. The stable and the unstable eigenmodes are shown as
hollow and solid symbols, respectively. The lock-in regime from DTI, in the
presence of nonlinear effects, is shaded in the figures.
6.2 Energy transfer per oscillation cycle
The key to self-excited nature of free vibrations is the net energy transfer over a
cycle from the fluid to the oscillator (Williamson & Roshko Reference Williamson and Roshko1988; Morse & Williamson Reference Morse and Williamson2009). The time evolution of cylinder
displacement and lift coefficient corresponding to an eigenmode (
![]() $\hat{\boldsymbol{u}},\hat{p},\hat{{\dot{Y}}},{\hat{Y}}$
) is given as:
$\hat{\boldsymbol{u}},\hat{p},\hat{{\dot{Y}}},{\hat{Y}}$
) is given as:
Here,
![]() ${\hat{C}}_{L}$
is the lift coefficient calculated by integrating the stress
corresponding to the eigenmode at the boundary of the cylinder. In general,
${\hat{C}}_{L}$
is the lift coefficient calculated by integrating the stress
corresponding to the eigenmode at the boundary of the cylinder. In general,
![]() ${\hat{Y}}$
and
${\hat{Y}}$
and
![]() ${\hat{C}}_{L}$
are complex and c.c. represents the complex conjugate. Let
${\hat{C}}_{L}$
are complex and c.c. represents the complex conjugate. Let
![]() $|{\hat{Y}}|$
and
$|{\hat{Y}}|$
and
![]() $|{\hat{C}}_{L}|$
represent the magnitude of
$|{\hat{C}}_{L}|$
represent the magnitude of
![]() ${\hat{Y}}$
and
${\hat{Y}}$
and
![]() ${\hat{C}}_{L}$
, respectively. Further, let
${\hat{C}}_{L}$
, respectively. Further, let
![]() ${\it\theta}$
and
${\it\theta}$
and
![]() ${\it\theta}+{\it\phi}$
denote the argument of
${\it\theta}+{\it\phi}$
denote the argument of
![]() ${\hat{Y}}$
and
${\hat{Y}}$
and
![]() ${\hat{C}}_{L}$
, respectively, where
${\hat{C}}_{L}$
, respectively, where
![]() ${\it\phi}$
is the phase angle between the cylinder displacement and lift
coefficient. We recall that
${\it\phi}$
is the phase angle between the cylinder displacement and lift
coefficient. We recall that
![]() ${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
. Equations (6.7) and (6.8) can be
rearranged and written as:
${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
. Equations (6.7) and (6.8) can be
rearranged and written as:
The non-dimensional energy transfer from the fluid to the oscillator
over a time interval,
![]() $T_{1}$
–
$T_{1}$
–
![]() $T_{2}$
is defined as:
$T_{2}$
is defined as:
We now consider the non-dimensional energy transfer over a time
period of cylinder oscillation from that part of
![]() $C_{L}$
and
$C_{L}$
and
![]() $Y$
that excludes the exponential growth/decay. The time period of
cylinder oscillation is related to
$Y$
that excludes the exponential growth/decay. The time period of
cylinder oscillation is related to
![]() ${\it\lambda}_{i}$
as
${\it\lambda}_{i}$
as
![]() $T_{c}=2{\rm\pi}/{\it\lambda}_{i}$
. We define
$T_{c}=2{\rm\pi}/{\it\lambda}_{i}$
. We define
![]() $E_{c}$
, energy transfer per oscillation cycle, as:
$E_{c}$
, energy transfer per oscillation cycle, as:
![]() $E_{c}$
and
$E_{c}$
and
![]() $E_{\mathit{transfer}}$
are related as
$E_{\mathit{transfer}}$
are related as
Plugging in the expressions of
![]() $C_{L_{o}}$
and
$C_{L_{o}}$
and
![]() $Y_{o}$
from (6.9) and
(6.10) in (6.12), it can be shown that
$Y_{o}$
from (6.9) and
(6.10) in (6.12), it can be shown that
It is noted that
![]() $E_{c}$
is directly proportional to
$E_{c}$
is directly proportional to
![]() $\sin {\it\phi}$
. For
$\sin {\it\phi}$
. For
![]() $0^{\circ }<{\it\phi}<180^{\circ }$
,
$0^{\circ }<{\it\phi}<180^{\circ }$
,
![]() $E_{c}>0$
and the energy transfer per cycle of oscillation is from the flow
to the oscillator. In this case, the amplitude of cylinder oscillation grows with
time. Instead, for
$E_{c}>0$
and the energy transfer per cycle of oscillation is from the flow
to the oscillator. In this case, the amplitude of cylinder oscillation grows with
time. Instead, for
![]() $-180^{\circ }<{\it\phi}<0^{\circ }$
,
$-180^{\circ }<{\it\phi}<0^{\circ }$
,
![]() $E_{c}$
is negative and the energy is transferred to the fluid by the
oscillator. As a result the oscillation of cylinder decays with time leading to a
steady state. Figure 14(a) shows the variation of
$E_{c}$
is negative and the energy is transferred to the fluid by the
oscillator. As a result the oscillation of cylinder decays with time leading to a
steady state. Figure 14(a) shows the variation of
![]() $E_{c}$
with
$E_{c}$
with
![]() $U^{\ast }$
for
$U^{\ast }$
for
![]() $(Re,m^{\ast })=(60,20)$
. The lock-in regime based on DTI is also shaded in the figure.
$(Re,m^{\ast })=(60,20)$
. The lock-in regime based on DTI is also shaded in the figure.
![]() $E_{c}$
can be written in terms of the growth rate and frequency of the
eigenmode (details in appendix C)
as:
$E_{c}$
can be written in terms of the growth rate and frequency of the
eigenmode (details in appendix C)
as:
Equation (6.15) shows that the sign of
![]() $E_{c}$
is determined by the sign of
$E_{c}$
is determined by the sign of
![]() ${\it\lambda}_{r}$
. Therefore,
${\it\lambda}_{r}$
. Therefore,
![]() $E_{c}$
is positive for unstable eigenmode and negative for stable
eigenmodes. If an eigenmode is unstable (
$E_{c}$
is positive for unstable eigenmode and negative for stable
eigenmodes. If an eigenmode is unstable (
![]() ${\it\lambda}_{r}>0$
), a net energy transfer takes place from the base flow to the
fluid–oscillator system. A part of this energy, determined by the energy
ratio
${\it\lambda}_{r}>0$
), a net energy transfer takes place from the base flow to the
fluid–oscillator system. A part of this energy, determined by the energy
ratio
![]() $E_{r}$
, is transferred to the structure. This energy transfer is via the
work done by the fluid force in displacing the oscillator. The energy transferred to
the oscillator adds up to its kinetic energy as well as the potential energy of the
spring. We note that the variation of
$E_{r}$
, is transferred to the structure. This energy transfer is via the
work done by the fluid force in displacing the oscillator. The energy transferred to
the oscillator adds up to its kinetic energy as well as the potential energy of the
spring. We note that the variation of
![]() $E_{c}$
with
$E_{c}$
with
![]() $U^{\ast }$
can be quite different than the variation of
$U^{\ast }$
can be quite different than the variation of
![]() ${\it\lambda}_{r}$
with
${\it\lambda}_{r}$
with
![]() $U^{\ast }$
, even though they are of the same sign. Therefore, the
$U^{\ast }$
, even though they are of the same sign. Therefore, the
![]() $U^{\ast }$
for largest growth rate may not necessarily coincide with that for
maximum energy transfer. It is noted that
$U^{\ast }$
for largest growth rate may not necessarily coincide with that for
maximum energy transfer. It is noted that
![]() $E_{c}$
of the EM is generally higher than that of the fluid mode in the
regime of instability of the elastic mode (
$E_{c}$
of the EM is generally higher than that of the fluid mode in the
regime of instability of the elastic mode (
![]() $5.8<U^{\ast }<7.3$
). However, we recall here that the growth rate of FM is higher than
the elastic mode for all
$5.8<U^{\ast }<7.3$
). However, we recall here that the growth rate of FM is higher than
the elastic mode for all
![]() $U^{\ast }$
(figure 11
c). This suggests that for
$U^{\ast }$
(figure 11
c). This suggests that for
![]() $5.8<U^{\ast }<7.3$
initially FM would dominate the temporal evolution of cylinder
displacement. However, as time progresses, EM is expected to drive the structural
response towards lock-in. This is confirmed by direct time integration
in § 8.3.
The variation of
$5.8<U^{\ast }<7.3$
initially FM would dominate the temporal evolution of cylinder
displacement. However, as time progresses, EM is expected to drive the structural
response towards lock-in. This is confirmed by direct time integration
in § 8.3.
The variation of
![]() $E_{c}$
with
$E_{c}$
with
![]() $U^{\ast }$
for the case of coupled modes is shown in figure 14(b). FEMII is expected to
dominate the dynamics of the fluid–structure system in this case.
$U^{\ast }$
for the case of coupled modes is shown in figure 14(b). FEMII is expected to
dominate the dynamics of the fluid–structure system in this case.

Figure 14. Linear stability analysis of the steady flow past a
fluid–cylinder system: variation of energy transfer per cycle of
cylinder oscillation with
![]() $U^{\ast }$
for (a)
$U^{\ast }$
for (a)
![]() $(Re,m^{\ast })=(60,20)$
and (b)
$(Re,m^{\ast })=(60,20)$
and (b)
![]() $(Re,m^{\ast })=(60,5)$
. The stable and the unstable eigenmodes are shown as
hollow and solid symbols, respectively. The lock-in regime from DTI, in the
presence of nonlinear effects, is shaded in the figures.
$(Re,m^{\ast })=(60,5)$
. The stable and the unstable eigenmodes are shown as
hollow and solid symbols, respectively. The lock-in regime from DTI, in the
presence of nonlinear effects, is shaded in the figures.
7 Phase angle between cylinder displacement and lift
In free vibrations, the phase angle between the lift and cylinder displacement is
closely related to the energy transfer between the fluid and the oscillator. Morse
& Williamson (Reference Morse and Williamson2009), using the
approximation that cylinder motion and fluid forcing are sinusoidal functions, showed
that the energy transfer from the fluid to the cylinder over one cycle of cylinder
oscillation is given by,
![]() $E_{IN}={\rm\pi}AF\sin {\it\phi}$
. Here,
$E_{IN}={\rm\pi}AF\sin {\it\phi}$
. Here,
![]() $A$
and
$A$
and
![]() $F$
are the amplitude of cylinder displacement and lift force,
respectively;
$F$
are the amplitude of cylinder displacement and lift force,
respectively;
![]() ${\it\phi}$
denotes the phase difference between the two functions. In the fully
developed state, where the system oscillates with constant amplitude and frequency, the
energy input to the structural system should exactly balance the energy dissipated by
it. Since, in the present study there is no structural damping,
${\it\phi}$
denotes the phase difference between the two functions. In the fully
developed state, where the system oscillates with constant amplitude and frequency, the
energy input to the structural system should exactly balance the energy dissipated by
it. Since, in the present study there is no structural damping,
![]() $E_{IN}$
is identically zero in the fully developed state. This implies that
$E_{IN}$
is identically zero in the fully developed state. This implies that
![]() ${\it\phi}$
can admit only two solutions, 0° or 180°. In
general,
${\it\phi}$
can admit only two solutions, 0° or 180°. In
general,
![]() ${\it\phi}$
is close to zero towards the lower-
${\it\phi}$
is close to zero towards the lower-
![]() $U^{\ast }$
end of the lock-in regime. However, near the middle of lock-in regime,
$U^{\ast }$
end of the lock-in regime. However, near the middle of lock-in regime,
![]() ${\it\phi}$
suffers a jump of approximately 180°, and remain close to
180° for higher values of
${\it\phi}$
suffers a jump of approximately 180°, and remain close to
180° for higher values of
![]() $U^{\ast }$
. These observations have been reported in earlier articles by
Govardhan & Williamson (Reference Govardhan and Williamson2000) and
Prasanth & Mittal (Reference Prasanth and Mittal2008).
$U^{\ast }$
. These observations have been reported in earlier articles by
Govardhan & Williamson (Reference Govardhan and Williamson2000) and
Prasanth & Mittal (Reference Prasanth and Mittal2008).
Phase angle can be also be defined for eigenmodes obtained from LSA. By substituting (6.7) and (6.8) into the equation describing the motion of the oscillator (2.3) and (2.4), it can be shown that the phase angle related to eigenmodes is given by:
The details of the derivation are given in appendix C. We denote the phase angle estimated from DTI and
that from the eigenmodes as
![]() ${\it\phi}_{DTI}$
and
${\it\phi}_{DTI}$
and
![]() ${\it\phi}_{LSA}$
, respectively. As discussed
in § 6.2, the
eigenmodes are usually associated with non-zero energy transfer. The relationship
between
${\it\phi}_{LSA}$
, respectively. As discussed
in § 6.2, the
eigenmodes are usually associated with non-zero energy transfer. The relationship
between
![]() $E_{c}$
and the phase angle is described by (6.14). For unstable eigenmodes the phase angle lies between
$E_{c}$
and the phase angle is described by (6.14). For unstable eigenmodes the phase angle lies between
![]() $0^{\circ }<{\it\phi}_{LSA}<180^{\circ }$
. Figure 15 shows the
variation of phase angle of eigenmodes with
$0^{\circ }<{\it\phi}_{LSA}<180^{\circ }$
. Figure 15 shows the
variation of phase angle of eigenmodes with
![]() $U^{\ast }$
for
$U^{\ast }$
for
![]() $(Re,m^{\ast })=(40,10)$
and
$(Re,m^{\ast })=(40,10)$
and
![]() $(60,20)$
. For comparison
$(60,20)$
. For comparison
![]() ${\it\phi}_{DTI}$
is also plotted. Unlike in DTI, where a phase jump from 0°
to 180° occurs during lock-in,
${\it\phi}_{DTI}$
is also plotted. Unlike in DTI, where a phase jump from 0°
to 180° occurs during lock-in,
![]() ${\it\phi}_{LSA}$
varies rather smoothly with
${\it\phi}_{LSA}$
varies rather smoothly with
![]() $U^{\ast }$
. Figure 15 shows that
$U^{\ast }$
. Figure 15 shows that
![]() ${\it\phi}_{DTI}$
undergoes a jump close to that value of
${\it\phi}_{DTI}$
undergoes a jump close to that value of
![]() $U^{\ast }$
where
$U^{\ast }$
where
![]() ${\it\phi}_{LSA}$
crosses 90°. It appears that, in most cases, the nonlinear
effects drive
${\it\phi}_{LSA}$
crosses 90°. It appears that, in most cases, the nonlinear
effects drive
![]() ${\it\phi}_{DTI}$
to a near-zero value if
${\it\phi}_{DTI}$
to a near-zero value if
![]() ${\it\phi}_{LSA}<90^{\circ }$
and to 180° if
${\it\phi}_{LSA}<90^{\circ }$
and to 180° if
![]() ${\it\phi}_{LSA}>90^{\circ }$
to maintain zero energy transfer in the limit cycle.
${\it\phi}_{LSA}>90^{\circ }$
to maintain zero energy transfer in the limit cycle.

Figure 15. Flow past a freely vibrating cylinder: variation of phase angle from DTI and
phase angle of eigenmodes with
![]() $U^{\ast }$
for (a)
$U^{\ast }$
for (a)
![]() $(Re,m^{\ast })=(40,10)$
and (b)
$(Re,m^{\ast })=(40,10)$
and (b)
![]() $(Re,m^{\ast })=(60,20)$
. The stable and unstable eigenmodes are denoted by hollow and
solid symbols, respectively. The lock-in regime from DTI, in the presence of
nonlinear effects, is shaded in the figures.
$(Re,m^{\ast })=(60,20)$
. The stable and unstable eigenmodes are denoted by hollow and
solid symbols, respectively. The lock-in regime from DTI, in the presence of
nonlinear effects, is shaded in the figures.
Close to the phase jump, the frequency spectrum of the lift force in the fully developed
state shows multiple peaks. In general, the phase difference between the lift force and
cylinder displacement corresponding to each frequency component is different. The phase
angle (
![]() ${\it\phi}_{DTI}$
) shown in figure 15
corresponds to the fundamental frequency which is usually the most dominant one. It is
observed that for
${\it\phi}_{DTI}$
) shown in figure 15
corresponds to the fundamental frequency which is usually the most dominant one. It is
observed that for
![]() $U^{\ast }$
close to the phase jump,
$U^{\ast }$
close to the phase jump,
![]() ${\it\phi}_{DTI}$
exhibits offset from 0° or 180° despite
${\it\phi}_{DTI}$
exhibits offset from 0° or 180° despite
![]() $E_{IN}$
being equal to zero. We note that the condition of
$E_{IN}$
being equal to zero. We note that the condition of
![]() ${\it\phi}_{DTI}=0^{\circ }$
or 180° for free vibrations has been derived for the
situation when the time histories of cylinder displacement and lift force are associated
with only one frequency. The offset, therefore, may be attributed to the interaction of
components of energy at various frequency.
${\it\phi}_{DTI}=0^{\circ }$
or 180° for free vibrations has been derived for the
situation when the time histories of cylinder displacement and lift force are associated
with only one frequency. The offset, therefore, may be attributed to the interaction of
components of energy at various frequency.

Figure 16.
![]() $(Re,m^{\ast })=(60,20)$
flow past a freely vibrating cylinder for
(a,b)
$(Re,m^{\ast })=(60,20)$
flow past a freely vibrating cylinder for
(a,b)
![]() $U^{\ast }=5.5$
and (c,d)
$U^{\ast }=5.5$
and (c,d)
![]() $U^{\ast }=8.0$
: time evolution of
(a,c) cylinder displacement,
Strouhal number based on frequency of cylinder oscillation and
(b,d) structural energy. The
time instant beyond which the nonlinear terms become significant is marked in
broken lines. Also shown in inset
in (b,d) is the close-up view of
the evolution of structural energy in the linear regime. The line with slope
two times the growth rate of the wake mode is shown in blue colour.
$U^{\ast }=8.0$
: time evolution of
(a,c) cylinder displacement,
Strouhal number based on frequency of cylinder oscillation and
(b,d) structural energy. The
time instant beyond which the nonlinear terms become significant is marked in
broken lines. Also shown in inset
in (b,d) is the close-up view of
the evolution of structural energy in the linear regime. The line with slope
two times the growth rate of the wake mode is shown in blue colour.
8 Effect of nonlinearities and relative significance of eigenmodes
8.1 When do nonlinear terms become significant?
In the preceding sections we have shown that there are differences between LSA and
DTI with respect to the frequency, phase and the extent of lock-in regime. These
differences are attributed to the nonlinear terms in DTI of the governing equations.
We recall that the oscillator used in the present study is associated with linear
spring and damper. Therefore, the nonlinearity in the fluid–oscillator
system results entirely from the convection terms in (2.1). We assume that the nonlinear terms involving the
disturbance field become relatively significant when their magnitude exceeds
10 % of the size of the other terms, i.e.
![]() $O(|\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }|)\sim 0.1O(|\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}|)$
. Based on this assumption, the time at which the nonlinear effects
are expected to become significant is estimated to be:
$O(|\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }|)\sim 0.1O(|\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}|)$
. Based on this assumption, the time at which the nonlinear effects
are expected to become significant is estimated to be:
The details for the derivation of
![]() $T_{nl}$
are presented in appendix B. We now present an estimate of
$T_{nl}$
are presented in appendix B. We now present an estimate of
![]() $T_{nl}$
for
$T_{nl}$
for
![]() $(Re,m^{\ast })=(60,20)$
for two values of reduced velocity. Figure 16 shows the estimate of
$(Re,m^{\ast })=(60,20)$
for two values of reduced velocity. Figure 16 shows the estimate of
![]() $T_{nl}$
for
$T_{nl}$
for
![]() $U^{\ast }=5.5$
and
$U^{\ast }=5.5$
and
![]() $8.0$
. While
$8.0$
. While
![]() $U^{\ast }=5.5$
lies before the onset of synchronization, the oscillator
experiences lock-in for
$U^{\ast }=5.5$
lies before the onset of synchronization, the oscillator
experiences lock-in for
![]() $U^{\ast }=8.0$
(see figure 11
a). From figure 16 we observe that up to
$U^{\ast }=8.0$
(see figure 11
a). From figure 16 we observe that up to
![]() $t=T_{nl}$
the fluid–structure system indeed retains its linear
behaviour. This is most evident from the time variation of the structural energy,
$t=T_{nl}$
the fluid–structure system indeed retains its linear
behaviour. This is most evident from the time variation of the structural energy,
![]() $E_{s}$
. The structural energy at any instant is the sum of the kinetic
energy and potential energy of the oscillator. As seen from (6.3), the slope of
$E_{s}$
. The structural energy at any instant is the sum of the kinetic
energy and potential energy of the oscillator. As seen from (6.3), the slope of
![]() $\ln (E_{s})$
versus
$\ln (E_{s})$
versus
![]() $t$
is
$t$
is
![]() $2{\it\lambda}_{r}$
in the linear regime. The match between the two slopes, from DTI
and the estimate via LSA, is excellent. Beyond
$2{\it\lambda}_{r}$
in the linear regime. The match between the two slopes, from DTI
and the estimate via LSA, is excellent. Beyond
![]() $t=T_{nl}$
, the nonlinear terms cause saturation in the oscillation amplitude
and
$t=T_{nl}$
, the nonlinear terms cause saturation in the oscillation amplitude
and
![]() $E_{s}$
, leading to a limit cycle. The saturation in the Strouhal number
and the added mass coefficient is also observed for
$E_{s}$
, leading to a limit cycle. The saturation in the Strouhal number
and the added mass coefficient is also observed for
![]() $t>T_{nl}$
.
$t>T_{nl}$
.
We note that much of the increase in the amplitude of transverse vibration takes
place in the linear regime (
![]() $t<T_{nl}$
). For example, for
$t<T_{nl}$
). For example, for
![]() $U^{\ast }=5.5$
, the amplitude of cylinder response increases eightfold during
$U^{\ast }=5.5$
, the amplitude of cylinder response increases eightfold during
![]() $0\leqslant t\leqslant T_{nl}$
and only by a factor of 1.5 beyond
$0\leqslant t\leqslant T_{nl}$
and only by a factor of 1.5 beyond
![]() $T_{nl}$
up to the attainment of limit cycle. These numbers for
$T_{nl}$
up to the attainment of limit cycle. These numbers for
![]() $U^{\ast }=8.0$
are 17 and 3, approximately.
$U^{\ast }=8.0$
are 17 and 3, approximately.

Figure 17. Flow past a freely vibrating cylinder: distribution of energy ratio with the
growth rate of the eigenmodes for (a)
![]() $(Re,m^{\ast })=(60,20)$
, and (b)
$(Re,m^{\ast })=(60,20)$
, and (b)
![]() $(Re,m^{\ast })=(60,5)$
. All unstable eigenmodes that lead to lock-in with respect
to the fully developed state are shown in solid symbols. These eigenmodes
are characterized by energy ratio that is greater than a threshold value,
$(Re,m^{\ast })=(60,5)$
. All unstable eigenmodes that lead to lock-in with respect
to the fully developed state are shown in solid symbols. These eigenmodes
are characterized by energy ratio that is greater than a threshold value,
![]() $E_{rt}$
.
$E_{rt}$
.
8.2 What causes lock-in?
The observations from the preceding section motivate us to propose a hypothesis to as
to why lock-in occurs for a certain range of
![]() $U^{\ast }$
, and not for others. We believe that
$U^{\ast }$
, and not for others. We believe that
![]() $E_{r}$
(fraction of energy in the structural part of the eigenmode)
determines if a certain disturbance field will lead to attainment of lock-in. To
demonstrate the relevance of the energy ratio,
$E_{r}$
(fraction of energy in the structural part of the eigenmode)
determines if a certain disturbance field will lead to attainment of lock-in. To
demonstrate the relevance of the energy ratio,
![]() $E_{r}$
, we consider the case of
$E_{r}$
, we consider the case of
![]() $(Re,m^{\ast })=(60,20)$
. The two modes that, in general, govern the aeroelastic instability
of the fluid–structure system for various
$(Re,m^{\ast })=(60,20)$
. The two modes that, in general, govern the aeroelastic instability
of the fluid–structure system for various
![]() $U^{\ast }$
are EM and FM. Figure 17(a) shows the points for the two eigenmodes on the
$U^{\ast }$
are EM and FM. Figure 17(a) shows the points for the two eigenmodes on the
![]() $E_{r}{-}{\it\lambda}_{r}$
plane, for various
$E_{r}{-}{\it\lambda}_{r}$
plane, for various
![]() $U^{\ast }$
. DTI is carried out for each case. The initial condition is the
steady flow superimposed with the eigenmode:
$U^{\ast }$
. DTI is carried out for each case. The initial condition is the
steady flow superimposed with the eigenmode:
![]() $s$
is a scalar and is used to control the magnitude of the initial
disturbance. Unless stated otherwise, a value of 1.0 is assigned to
$s$
is a scalar and is used to control the magnitude of the initial
disturbance. Unless stated otherwise, a value of 1.0 is assigned to
![]() $s$
for all the cases presented in this work. In
figure 17(a) the
eigenmodes that lead to lock-in are marked in solid symbols and the ones that do not
cause lock-in are marked in hollow symbol. It is noted that all unstable eigenmodes,
irrespective of their growth rate, that have an
$s$
for all the cases presented in this work. In
figure 17(a) the
eigenmodes that lead to lock-in are marked in solid symbols and the ones that do not
cause lock-in are marked in hollow symbol. It is noted that all unstable eigenmodes,
irrespective of their growth rate, that have an
![]() $E_{r}$
beyond a threshold value of
$E_{r}$
beyond a threshold value of
![]() $2\times 10^{-4}$
lead to lock-in. Interestingly, the case that leads to maximum
oscillation amplitude is associated with smallest positive value of
$2\times 10^{-4}$
lead to lock-in. Interestingly, the case that leads to maximum
oscillation amplitude is associated with smallest positive value of
![]() ${\it\lambda}_{r}$
, but the largest value of
${\it\lambda}_{r}$
, but the largest value of
![]() $E_{r}$
. Similarly, modes that are associated with relatively large
$E_{r}$
. Similarly, modes that are associated with relatively large
![]() ${\it\lambda}_{r}$
, but with
${\it\lambda}_{r}$
, but with
![]() $E_{r}$
below the threshold value, do not lead to lock-in. The region in
the
$E_{r}$
below the threshold value, do not lead to lock-in. The region in
the
![]() $E_{r}{-}{\it\lambda}_{r}$
plane that leads to lock-in is marked in figure 17(a). Figure 17(b) shows the same for
$E_{r}{-}{\it\lambda}_{r}$
plane that leads to lock-in is marked in figure 17(a). Figure 17(b) shows the same for
![]() $(Re,m^{\ast })=(60,5)$
. Similar observations hold for this figure as well. The value of
$(Re,m^{\ast })=(60,5)$
. Similar observations hold for this figure as well. The value of
![]() $E_{rt}$
in this case is
$E_{rt}$
in this case is
![]() $1\times 10^{-3}$
. We note that the threshold value of
$1\times 10^{-3}$
. We note that the threshold value of
![]() $E_{r}$
, required for lock-in depends on
$E_{r}$
, required for lock-in depends on
![]() $m^{\ast }$
, and possibly on
$m^{\ast }$
, and possibly on
![]() $Re$
.
$Re$
.
8.3 Eigenmodes responsible for lock-in
For subcritical
![]() $Re$
(
$Re$
(
![]() $Re\leqslant Re_{o}$
), the instability of the fluid–structure system, if any,
is caused by only one unstable eigenmode. In the scenario of coupled modes, FEMII is
responsible for lock-in. For large mass ratios, where the modes are decoupled,
lock-in is attributed to the growth of EM. For supercritical
$Re\leqslant Re_{o}$
), the instability of the fluid–structure system, if any,
is caused by only one unstable eigenmode. In the scenario of coupled modes, FEMII is
responsible for lock-in. For large mass ratios, where the modes are decoupled,
lock-in is attributed to the growth of EM. For supercritical
![]() $Re$
(
$Re$
(
![]() $Re>Re_{o}$
), the situation becomes complicated as LSA predicts lock-in for all
$Re>Re_{o}$
), the situation becomes complicated as LSA predicts lock-in for all
![]() $U^{\ast }$
. Further, in certain flow regimes multiple eigenmodes are unstable.
We now study in more detail the mechanism of how an unstable eigenmode leads to
lock-in for
$U^{\ast }$
. Further, in certain flow regimes multiple eigenmodes are unstable.
We now study in more detail the mechanism of how an unstable eigenmode leads to
lock-in for
![]() $Re>Re_{o}$
. We carry out DTI for
$Re>Re_{o}$
. We carry out DTI for
![]() $(Re,m^{\ast })=(60,20)$
for various values of
$(Re,m^{\ast })=(60,20)$
for various values of
![]() $U^{\ast }$
in the lock-in regime. As shown in figure 11(c), for
$U^{\ast }$
in the lock-in regime. As shown in figure 11(c), for
![]() $(Re,m^{\ast })=(60,20)$
, LSA predicts the instability of the FM for the
fluid–structure system for all values of
$(Re,m^{\ast })=(60,20)$
, LSA predicts the instability of the FM for the
fluid–structure system for all values of
![]() $U^{\ast }$
. The EM is unstable for
$U^{\ast }$
. The EM is unstable for
![]() $5.8<U^{\ast }<7.3$
. The growth rate of FM is higher than that of EM in the entire
$5.8<U^{\ast }<7.3$
. The growth rate of FM is higher than that of EM in the entire
![]() $U^{\ast }$
regime. However, the energy ratio,
$U^{\ast }$
regime. However, the energy ratio,
![]() $E_{r}$
, that has been shown to be very relevant for determining the
amplitude of cylinder oscillation in the limit cycle, is larger for EM than for FM,
and above the threshold value for
$E_{r}$
, that has been shown to be very relevant for determining the
amplitude of cylinder oscillation in the limit cycle, is larger for EM than for FM,
and above the threshold value for
![]() $5.8<U^{\ast }<7.2$
. This is shown in figure 13(a). Figure 17(a) shows that lock-in occurs only when
$5.8<U^{\ast }<7.2$
. This is shown in figure 13(a). Figure 17(a) shows that lock-in occurs only when
![]() $E_{r}$
for the concerned mode exceeds the threshold value. The range for
lock-in for
$E_{r}$
for the concerned mode exceeds the threshold value. The range for
lock-in for
![]() $(Re,m^{\ast })=(60,20)$
is
$(Re,m^{\ast })=(60,20)$
is
![]() $5.8<U^{\ast }<9.3$
.
$5.8<U^{\ast }<9.3$
.
8.3.1 Lock-in via fluid mode
For
![]() $(Re,m^{\ast })=(60,20)$
, lock-in via the fluid mode occurs for
$(Re,m^{\ast })=(60,20)$
, lock-in via the fluid mode occurs for
![]() $7.3\leqslant U^{\ast }<9.3$
. In this regime, the energy ratio of FM is larger than the
threshold value while the elastic mode is stable. Figure 16 shows the time evolution of the cylinder
response, Strouhal number and energy of the structure for DTI initiated with the
steady flow superimposed with FM for
$7.3\leqslant U^{\ast }<9.3$
. In this regime, the energy ratio of FM is larger than the
threshold value while the elastic mode is stable. Figure 16 shows the time evolution of the cylinder
response, Strouhal number and energy of the structure for DTI initiated with the
steady flow superimposed with FM for
![]() $U^{\ast }=5.5$
and 8.0. In both cases, the time variation of
$U^{\ast }=5.5$
and 8.0. In both cases, the time variation of
![]() $E_{s}$
, in the linear regime, is consistent with the response predicted
by LSA. Lock-in is observed at
$E_{s}$
, in the linear regime, is consistent with the response predicted
by LSA. Lock-in is observed at
![]() $U^{\ast }=8.0$
and is accompanied with large amplitude vibration of the
cylinder. No lock-in is obtained for
$U^{\ast }=8.0$
and is accompanied with large amplitude vibration of the
cylinder. No lock-in is obtained for
![]() $U^{\ast }=5.5$
.
$U^{\ast }=5.5$
.
8.3.2 Lock-in via elastic mode
For
![]() $(Re,m^{\ast })=(60,20)$
, both the elastic and the fluid mode are unstable for
$(Re,m^{\ast })=(60,20)$
, both the elastic and the fluid mode are unstable for
![]() $5.8<U^{\ast }<7.3$
. In this regime
$5.8<U^{\ast }<7.3$
. In this regime
![]() $E_{r}$
of the elastic mode is above the threshold energy for lock-in
(figure 17
a).
The fluid mode, though unstable, has energy ratio lower than
$E_{r}$
of the elastic mode is above the threshold energy for lock-in
(figure 17
a).
The fluid mode, though unstable, has energy ratio lower than
![]() $E_{rt}$
. Hence, lock-in over this regime results from the instability of
EM. To elucidate this, we carry out computations for
$E_{rt}$
. Hence, lock-in over this regime results from the instability of
EM. To elucidate this, we carry out computations for
![]() $U^{\ast }=6.0$
with two initial conditions. In the first case, the simulation
is initiated with the elastic mode superimposed on the steady solution. The value
of
$U^{\ast }=6.0$
with two initial conditions. In the first case, the simulation
is initiated with the elastic mode superimposed on the steady solution. The value
of
![]() $s$
(8.2) used for
this case is 10.0. Figure 18
shows the time evolution of
$s$
(8.2) used for
this case is 10.0. Figure 18
shows the time evolution of
![]() $Y/D$
and
$Y/D$
and
![]() $E_{s}$
. It is observed that the amplitude of cylinder oscillation
increases with time up to
$E_{s}$
. It is observed that the amplitude of cylinder oscillation
increases with time up to
![]() $t=T_{nl}$
with a rate that matches the growth rate of EM. Concomitantly,
the structural energy grows with twice the growth rate of EM over this time
interval. Beyond
$t=T_{nl}$
with a rate that matches the growth rate of EM. Concomitantly,
the structural energy grows with twice the growth rate of EM over this time
interval. Beyond
![]() $t=T_{nl}$
, the response of the fluid–structure system
approaches a limit cycle where the cylinder exhibits relatively large amplitude of
oscillation with frequency that is close to the natural frequency of the
oscillator in vacuum. The fluid–structure system is in a state of
lock-in in the limit cycle. Simulations with lower value of
$t=T_{nl}$
, the response of the fluid–structure system
approaches a limit cycle where the cylinder exhibits relatively large amplitude of
oscillation with frequency that is close to the natural frequency of the
oscillator in vacuum. The fluid–structure system is in a state of
lock-in in the limit cycle. Simulations with lower value of
![]() $s$
(for example,
$s$
(for example,
![]() $s=1$
) lead to an interesting evolution. The numerical inaccuracies in
the eigenmodes act as noise and excite other modes, including FM. Since FM has a
higher growth rate than EM, for this case, the FM grows very rapidly compared to
EM. Therefore, in the linear regime for
$s=1$
) lead to an interesting evolution. The numerical inaccuracies in
the eigenmodes act as noise and excite other modes, including FM. Since FM has a
higher growth rate than EM, for this case, the FM grows very rapidly compared to
EM. Therefore, in the linear regime for
![]() $s=1.0$
, the growth of amplitude of the cylinder exhibits the growth
rate of EM at low
$s=1.0$
, the growth of amplitude of the cylinder exhibits the growth
rate of EM at low
![]() $t$
followed by a growth rate corresponding to that of FM up to the
end of the linear regime. On the other hand, with
$t$
followed by a growth rate corresponding to that of FM up to the
end of the linear regime. On the other hand, with
![]() $s=10.0$
, even though the FM grows faster than the EM, the growth is
dominated by EM owing to its significantly larger initial strength.
$s=10.0$
, even though the FM grows faster than the EM, the growth is
dominated by EM owing to its significantly larger initial strength.

Figure 18. Flow past a freely vibrating cylinder for
![]() $(Re,m^{\ast },U^{\ast })=(60,20,6.0)$
initiated with EM: time evolution of
(a) cylinder displacement, Strouhal number
based on frequency of cylinder oscillation and
(b) structural energy. The time instant
beyond which the nonlinear terms become significant is marked in
dash-dotted lines. The line with slope two times the growth rate of the
elastic mode is shown in green colour.
$(Re,m^{\ast },U^{\ast })=(60,20,6.0)$
initiated with EM: time evolution of
(a) cylinder displacement, Strouhal number
based on frequency of cylinder oscillation and
(b) structural energy. The time instant
beyond which the nonlinear terms become significant is marked in
dash-dotted lines. The line with slope two times the growth rate of the
elastic mode is shown in green colour.

Figure 19. Flow past a freely vibrating cylinder for
![]() $(Re,m^{\ast },U^{\ast })=(60,20,6.0)$
initiated with FM: time evolution of
(a) cylinder displacement, Strouhal number
based on frequency of cylinder oscillation and
(b) structural energy. The time instant
beyond which the nonlinear terms become significant is marked in
dash-dotted lines. The different flow regions are demarcated by broken
lines. The line with slope two times the growth rate of the elastic mode
is shown in green colour. Also shown in inset is the evolution of
structural energy in the linear regime. The line with slope two times the
growth rate of the fluid mode is shown in blue colour.
$(Re,m^{\ast },U^{\ast })=(60,20,6.0)$
initiated with FM: time evolution of
(a) cylinder displacement, Strouhal number
based on frequency of cylinder oscillation and
(b) structural energy. The time instant
beyond which the nonlinear terms become significant is marked in
dash-dotted lines. The different flow regions are demarcated by broken
lines. The line with slope two times the growth rate of the elastic mode
is shown in green colour. Also shown in inset is the evolution of
structural energy in the linear regime. The line with slope two times the
growth rate of the fluid mode is shown in blue colour.
In the second case, the computations are initiated with the fluid mode
superimposed on the steady solution. Figure 19 shows the time history of
![]() $Y/D$
and
$Y/D$
and
![]() $E_{s}$
for this case. It is observed that the initial growth of the
amplitude of cylinder oscillation is governed by the fluid mode. This is shown as
region I in the figure (also shown in the inset). In this region, the contribution
of nonlinear terms based on the analysis, described earlier, is negligible. In
region II, the oscillations achieve a state where the amplitude and the structural
energy are nearly constant. It is further observed that
$E_{s}$
for this case. It is observed that the initial growth of the
amplitude of cylinder oscillation is governed by the fluid mode. This is shown as
region I in the figure (also shown in the inset). In this region, the contribution
of nonlinear terms based on the analysis, described earlier, is negligible. In
region II, the oscillations achieve a state where the amplitude and the structural
energy are nearly constant. It is further observed that
![]() $Y/D$
and
$Y/D$
and
![]() $E_{s}$
in region II are comparable to that observed for
$E_{s}$
in region II are comparable to that observed for
![]() $U^{\ast }=5.5$
in the fully developed state; the latter corresponds to a
lock-in state. Beyond region II, the response of the cylinder exhibit beats. The
frequency spectrum of
$U^{\ast }=5.5$
in the fully developed state; the latter corresponds to a
lock-in state. Beyond region II, the response of the cylinder exhibit beats. The
frequency spectrum of
![]() $Y/D$
show two prominent peaks: one at 0.136 and the other at 0.157.
The former is equal to the frequency of oscillation in region II, while the latter
matches the frequency of the elastic mode for
$Y/D$
show two prominent peaks: one at 0.136 and the other at 0.157.
The former is equal to the frequency of oscillation in region II, while the latter
matches the frequency of the elastic mode for
![]() $U^{\ast }=6.0$
. It is noted that the structural energy, in region III, grows
almost linearly with twice the growth rate of the elastic mode. The linear growth
becomes more clear in region IV. Further the frequency spectrum in region IV is
dominated by the elastic mode. These observations suggest that the dynamics of the
fluid–structure system in regions III and IV is governed by the elastic
mode. The transition of the system from region II to region IV may be attributed
to transfer of the energy from FM to EM due to nonlinear effects which become
significant beyond
$U^{\ast }=6.0$
. It is noted that the structural energy, in region III, grows
almost linearly with twice the growth rate of the elastic mode. The linear growth
becomes more clear in region IV. Further the frequency spectrum in region IV is
dominated by the elastic mode. These observations suggest that the dynamics of the
fluid–structure system in regions III and IV is governed by the elastic
mode. The transition of the system from region II to region IV may be attributed
to transfer of the energy from FM to EM due to nonlinear effects which become
significant beyond
![]() $T_{nl}$
. We recall that the energy transfer per cycle of cylinder
oscillation (
$T_{nl}$
. We recall that the energy transfer per cycle of cylinder
oscillation (
![]() $E_{c}$
) for EM is quite large (figure 14). As a result, the structural energy of the system
increases significantly in region IV. At the end of region IV the oscillation
amplitude and structural energy are similar to the values observed at the end of
the linear regime for computations started with the elastic mode. Finally, in
region
$E_{c}$
) for EM is quite large (figure 14). As a result, the structural energy of the system
increases significantly in region IV. At the end of region IV the oscillation
amplitude and structural energy are similar to the values observed at the end of
the linear regime for computations started with the elastic mode. Finally, in
region
![]() $V$
, the oscillations achieve a limit cycle with amplitude
$V$
, the oscillations achieve a limit cycle with amplitude
![]() $Y/D\sim 0.5$
. In summary, the computations initiated with the FM drive the
system to an intermediate state corresponding to no lock-in. The system then
transitions to a state of lock-in via the elastic mode.
$Y/D\sim 0.5$
. In summary, the computations initiated with the FM drive the
system to an intermediate state corresponding to no lock-in. The system then
transitions to a state of lock-in via the elastic mode.
9 Conclusions
The phenomenon of synchronization/lock-in in transverse-only free vibrations of a
circular cylinder is investigated in the laminar flow regime. DTI and LSA, of the
equations governing the dynamics of the coupled aeroelastic system, is carried out.
Lock-in is identified from the results of DTI using the metrics that have been proposed
and utilized in earlier studies. It is characterized by relatively high amplitude of
cylinder response and the matching of the frequencies of the periodic wake vortex mode
and cylinder oscillation (Khalak & Williamson Reference Khalak and Williamson1999) when it has achieved a limit cycle. Figure 20 shows an example each of the lock-in regime for
the sub and supercritical
![]() $Re$
.
$Re$
.

Figure 20. Flow past a freely vibrating cylinder: different response regimes and the
eigenmodes responsible for them for (a)
![]() $(Re,m^{\ast })=(40,10)$
and (b)
$(Re,m^{\ast })=(40,10)$
and (b)
![]() $(Re,m^{\ast })=(60,20)$
. The lock-in regime from DTI, in the presence of nonlinear
effects, is shaded in the figure.
$(Re,m^{\ast })=(60,20)$
. The lock-in regime from DTI, in the presence of nonlinear
effects, is shaded in the figure.
A stabilized finite element method for carrying out LSA of an aeroelastic system has
been presented. The linear instability of the aeroelastic system implies that in the
absence of nonlinear effects, the system achieves very large amplitude oscillations. The
nonlinear terms in the equations governing the flow of fluid, become significant when
the disturbance field grows beyond a certain limit. They tend to saturate the growth of
the disturbance field and drive the system to a limit cycle. The oscillation amplitude
of the cylinder, in the limit cycle, is quite large over a certain range of
![]() $U^{\ast }$
. During synchronization, the frequency of the system evolves from
$U^{\ast }$
. During synchronization, the frequency of the system evolves from
![]() $F_{LSA}$
to close to
$F_{LSA}$
to close to
![]() $F_{N}$
. Outside the lock-in regime, however, the frequency evolves to a value
that is close to the vortex shedding frequency for the flow past a stationary cylinder.
The reason as to why this happens is not clear from this study. We speculate that this
might be an outcome of the fluid–structure system attempting to find a state
where the fluid faces least resistance from the structure and achieves this by
minimization of the added mass during the limit cycle in free vibrations.
$F_{N}$
. Outside the lock-in regime, however, the frequency evolves to a value
that is close to the vortex shedding frequency for the flow past a stationary cylinder.
The reason as to why this happens is not clear from this study. We speculate that this
might be an outcome of the fluid–structure system attempting to find a state
where the fluid faces least resistance from the structure and achieves this by
minimization of the added mass during the limit cycle in free vibrations.
A method, based on the order-of-magnitude analysis of the governing equations, to
estimate the time beyond which nonlinear terms become significant has been presented. It
is observed, via computations initiated with an unstable eigenmode, that the increase in
the amplitude of cylinder oscillation occurs mainly in the linear regime. Further, not
all unstable eigenmodes lead to lock-in in the limit cycle. We define energy ratio as
the fraction of the total energy of the eigenmode that is contained in the structure as
kinetic and potential energy. Only those unstable eigenmodes for which the energy ratio
is above a certain threshold value result in lock-in in the saturated state. This
behaviour is found to be independent of the value of the growth rate of the unstable
eigenmode. For subcritical
![]() $Re$
, the regime of
$Re$
, the regime of
![]() $U^{\ast }$
for which lock-in occurs, coincides with the region of linear
instability of the fluid–structure system. In this case, only one mode is
linearly unstable and that too for a finite range of
$U^{\ast }$
for which lock-in occurs, coincides with the region of linear
instability of the fluid–structure system. In this case, only one mode is
linearly unstable and that too for a finite range of
![]() $U^{\ast }$
. For supercritical
$U^{\ast }$
. For supercritical
![]() $Re$
, the aeroelastic system in unstable for all
$Re$
, the aeroelastic system in unstable for all
![]() $U^{\ast }$
. However, lock-in occurs over a finite range of
$U^{\ast }$
. However, lock-in occurs over a finite range of
![]() $U^{\ast }$
. Lock-in, in this case, is caused by different eigenmodes for
different regimes of
$U^{\ast }$
. Lock-in, in this case, is caused by different eigenmodes for
different regimes of
![]() $U^{\ast }$
. This is shown in figure 20. In the flow regime where multiple modes are unstable, the energy transfer
from the fluid to the structure corresponding to the eigenmode is found to have
significant effect on the time evolution of the response.
$U^{\ast }$
. This is shown in figure 20. In the flow regime where multiple modes are unstable, the energy transfer
from the fluid to the structure corresponding to the eigenmode is found to have
significant effect on the time evolution of the response.
Compared to the stationary cylinder, the transversely oscillating cylinder is associated
with two additional eigenmodes. A new approach to classification of modes is presented
wherein
![]() $Re$
and
$Re$
and
![]() $m^{\ast }$
are fixed and LSA is carried out over a wide range of
$m^{\ast }$
are fixed and LSA is carried out over a wide range of
![]() $U^{\ast }$
. The present classification makes it relatively easier to compare the
characteristics of fluid–structure system in the lock-in regime. It is
observed that for certain combinations of
$U^{\ast }$
. The present classification makes it relatively easier to compare the
characteristics of fluid–structure system in the lock-in regime. It is
observed that for certain combinations of
![]() $Re$
and
$Re$
and
![]() $m^{\ast }$
, the eigenmodes corresponding to the two leading eigenvalues are
distinct and maintain the distinction for all
$m^{\ast }$
, the eigenmodes corresponding to the two leading eigenvalues are
distinct and maintain the distinction for all
![]() $U^{\ast }$
. The two modes, in this situation, are referred to as the fluid mode,
FM and the elastic mode, EM. The frequency of the fluid mode remains close to that of
the stationary wake mode for all reduced velocities. The frequency of the elastic mode,
on the other hand, varies inversely with
$U^{\ast }$
. The two modes, in this situation, are referred to as the fluid mode,
FM and the elastic mode, EM. The frequency of the fluid mode remains close to that of
the stationary wake mode for all reduced velocities. The frequency of the elastic mode,
on the other hand, varies inversely with
![]() $U^{\ast }$
. However, for certain combinations of
$U^{\ast }$
. However, for certain combinations of
![]() $Re$
and
$Re$
and
![]() $m^{\ast }$
, it may not be possible to classify the two modes as either FM or EM.
In this situation we refer to the two modes as coupled modes. The evolution of modes is
better understood on
$m^{\ast }$
, it may not be possible to classify the two modes as either FM or EM.
In this situation we refer to the two modes as coupled modes. The evolution of modes is
better understood on
![]() ${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane. On this plane, in the case of decoupled modes, the fluid mode
appears like a ring, separate from the elastic mode. In the case of coupled modes, the
two modes appear to be parts of a single curve. In general, coupled modes are observed
for low
${\it\lambda}_{r}{-}U_{LSA}^{\ast }$
plane. On this plane, in the case of decoupled modes, the fluid mode
appears like a ring, separate from the elastic mode. In the case of coupled modes, the
two modes appear to be parts of a single curve. In general, coupled modes are observed
for low
![]() $m^{\ast }$
and decoupled modes for relatively large
$m^{\ast }$
and decoupled modes for relatively large
![]() $m^{\ast }$
. We define critical mass ratio,
$m^{\ast }$
. We define critical mass ratio,
![]() $m_{c}^{\ast }$
, as the largest mass ratio for which the modes are coupled.
$m_{c}^{\ast }$
, as the largest mass ratio for which the modes are coupled.
![]() $m_{c}^{\ast }$
is found to be very large for
$m_{c}^{\ast }$
is found to be very large for
![]() $Re_{o}$
, the critical
$Re_{o}$
, the critical
![]() $Re$
for the onset of vortex shedding past a stationary cylinder. It
decreases as
$Re$
for the onset of vortex shedding past a stationary cylinder. It
decreases as
![]() $Re$
deviates further from
$Re$
deviates further from
![]() $Re_{o}$
.
$Re_{o}$
.
The phase angle related to the eigenmodes has been defined. The phase angle of the
eigenmode is found to be related to the energy transfer per oscillation cycle of the
cylinder oscillation. Unlike in the nonlinear regime where a jump in phase with
![]() $U^{\ast }$
is observed, the
$U^{\ast }$
is observed, the
![]() ${\it\Phi}$
for the eigenmodes for LSA varies smoothly with
${\it\Phi}$
for the eigenmodes for LSA varies smoothly with
![]() $U^{\ast }$
. It is observed in most cases that in the limit cycle the nonlinear
processes drive the phase angle to near zero value if the phase angle is less than
90°, and to 180° if the phase angle is greater than
90°. The phenomenon of phase jump in the limit cycle response is observed
when the phase angle of an unstable eigenmode crosses 90°.
$U^{\ast }$
. It is observed in most cases that in the limit cycle the nonlinear
processes drive the phase angle to near zero value if the phase angle is less than
90°, and to 180° if the phase angle is greater than
90°. The phenomenon of phase jump in the limit cycle response is observed
when the phase angle of an unstable eigenmode crosses 90°.
Acknowledgements
The use of computational resources at High Performance Computing facility, Computer Center, Indian Institute of Technology Kanpur that is set up with assistance from DST, India is acknowledged. The authors are also grateful to Dr D. Philip, Department of Industrial and Management Engineering for providing access to his computational resources.
Appendix A. Convergence studies
The computations in this study have been carried out over a wide range of parameter
space (
![]() $20\leqslant Re\leqslant 100$
,
$20\leqslant Re\leqslant 100$
,
![]() $1.0\leqslant m^{\ast }\leqslant 300$
,
$1.0\leqslant m^{\ast }\leqslant 300$
,
![]() $2.0\leqslant U^{\ast }\leqslant 15.0$
). Prasanth & Mittal (Reference Prasanth and Mittal2008) carried out a detailed domain and mesh convergence study for
numerical simulations at
$2.0\leqslant U^{\ast }\leqslant 15.0$
). Prasanth & Mittal (Reference Prasanth and Mittal2008) carried out a detailed domain and mesh convergence study for
numerical simulations at
![]() $60\leqslant Re\leqslant 100$
. They reported that a computational domain with blockage less than
2 % can successfully simulate an unbounded flow. In the present study, we
have used a computational domain that has a blockage of 1 %. The spatial
resolution of the mesh used for carrying out direct time integration is higher than
the one used by Prasanth & Mittal (Reference Prasanth and Mittal2008). It consists of 12 814 nodes and 12 540 elements.
The same mesh is used for carrying out linear stability analysis. We name this mesh
M1. To establish the adequacy of mesh M1 for LSA, its performance is compared to a
mesh with higher spatial resolution. The finer mesh is denoted by M2. The number of
nodes and elements in mesh M2 are 15 004 and 14 710,
respectively. The computational domain as well as the structure of the mesh is same
in the two cases. The difference is mostly in the grid points close to the cylinder.
Table 1 shows the effect of
spatial resolution on the growth rate and frequency of the eigenmodes computed at
$60\leqslant Re\leqslant 100$
. They reported that a computational domain with blockage less than
2 % can successfully simulate an unbounded flow. In the present study, we
have used a computational domain that has a blockage of 1 %. The spatial
resolution of the mesh used for carrying out direct time integration is higher than
the one used by Prasanth & Mittal (Reference Prasanth and Mittal2008). It consists of 12 814 nodes and 12 540 elements.
The same mesh is used for carrying out linear stability analysis. We name this mesh
M1. To establish the adequacy of mesh M1 for LSA, its performance is compared to a
mesh with higher spatial resolution. The finer mesh is denoted by M2. The number of
nodes and elements in mesh M2 are 15 004 and 14 710,
respectively. The computational domain as well as the structure of the mesh is same
in the two cases. The difference is mostly in the grid points close to the cylinder.
Table 1 shows the effect of
spatial resolution on the growth rate and frequency of the eigenmodes computed at
![]() $U^{\ast }=7.0$
for
$U^{\ast }=7.0$
for
![]() $(Re,m^{\ast })=(60,20)$
. The value of
$(Re,m^{\ast })=(60,20)$
. The value of
![]() $U^{\ast }$
is close to the one for which maximum growth rate is obtained for
EM. Results from the two meshes are in very good agreement. The maximum difference of
0.5 % is noted in the growth rate of EM. In view of the difference being
small enough, mesh M1 is employed for all computations in the present work.
$U^{\ast }$
is close to the one for which maximum growth rate is obtained for
EM. Results from the two meshes are in very good agreement. The maximum difference of
0.5 % is noted in the growth rate of EM. In view of the difference being
small enough, mesh M1 is employed for all computations in the present work.
Table 1.
![]() $(Re,m^{\ast },U^{\ast })=(60,20,7.0)$
LSA of a fluid–structure system: effect of mesh
resolution on the rightmost eigenvalue of different modes. Meshes M1 and M2
consist of 12 814 and 15 004 nodes, respectively.
$(Re,m^{\ast },U^{\ast })=(60,20,7.0)$
LSA of a fluid–structure system: effect of mesh
resolution on the rightmost eigenvalue of different modes. Meshes M1 and M2
consist of 12 814 and 15 004 nodes, respectively.

Appendix B. Derivation of
 $T_{nl}$
$T_{nl}$
We present a method to obtain an a priori estimate of the time
beyond which the nonlinear terms are expected to become significant. Let
![]() $\boldsymbol{U}$
represent the base flow velocity and
$\boldsymbol{U}$
represent the base flow velocity and
![]() $L$
denote a suitable length scale. Then the convection term in the
base flow is of the order
$L$
denote a suitable length scale. Then the convection term in the
base flow is of the order
![]() $|\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}|\sim O({U_{\infty }}^{2}/L)$
; where
$|\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}|\sim O({U_{\infty }}^{2}/L)$
; where
![]() $U_{\infty }$
is the free-stream speed. For the flow regime considered in the
present work, this is also the magnitude of the largest term in the flow equations.
We assume that the nonlinear terms involving the disturbance field become relatively
significant when their magnitude exceeds 10 % size of the other terms, i.e.
$U_{\infty }$
is the free-stream speed. For the flow regime considered in the
present work, this is also the magnitude of the largest term in the flow equations.
We assume that the nonlinear terms involving the disturbance field become relatively
significant when their magnitude exceeds 10 % size of the other terms, i.e.
![]() $O(|\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }|)\sim 0.1O(|\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}|)$
. This implies that the nonlinear terms gain significance when
$O(|\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\prime }|)\sim 0.1O(|\boldsymbol{U}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}|)$
. This implies that the nonlinear terms gain significance when
![]() $O(|\boldsymbol{u}^{\prime }|)\sim 0.33U_{\infty }$
. We consider the situation when the computations are initiated with
the steady base flow superimposed with a disturbance field corresponding to the
eigenmode from LSA. Therefore, in the linear regime the disturbance evolves as
$O(|\boldsymbol{u}^{\prime }|)\sim 0.33U_{\infty }$
. We consider the situation when the computations are initiated with
the steady base flow superimposed with a disturbance field corresponding to the
eigenmode from LSA. Therefore, in the linear regime the disturbance evolves as
![]() $\boldsymbol{u}^{\prime }=\hat{\boldsymbol{u}}\text{e}^{{\it\lambda}t}$
. The estimate of the size of the disturbance at any time is given
as:
$\boldsymbol{u}^{\prime }=\hat{\boldsymbol{u}}\text{e}^{{\it\lambda}t}$
. The estimate of the size of the disturbance at any time is given
as:
![]() $O(|\boldsymbol{u}^{\prime }|)\sim O(|\hat{\boldsymbol{u}}|)\text{e}^{{\it\lambda}_{r}t}$
. The nonlinear terms are expected to become locally important as
soon as
$O(|\boldsymbol{u}^{\prime }|)\sim O(|\hat{\boldsymbol{u}}|)\text{e}^{{\it\lambda}_{r}t}$
. The nonlinear terms are expected to become locally important as
soon as
![]() $\hat{\boldsymbol{u}}$
becomes large enough at that local location. This will occur at the
spatial location where
$\hat{\boldsymbol{u}}$
becomes large enough at that local location. This will occur at the
spatial location where
![]() $|\hat{\boldsymbol{u}}|$
is the largest. We, therefore, locate the maxima of
$|\hat{\boldsymbol{u}}|$
is the largest. We, therefore, locate the maxima of
![]() $|\hat{\boldsymbol{u}}|$
, and represent it as
$|\hat{\boldsymbol{u}}|$
, and represent it as
![]() $|\hat{\boldsymbol{u}}_{max}|$
. Let
$|\hat{\boldsymbol{u}}_{max}|$
. Let
![]() $T_{nl}$
be the time at which the nonlinear terms gain significance. At that
time instant,
$T_{nl}$
be the time at which the nonlinear terms gain significance. At that
time instant,
![]() $O(|\boldsymbol{u}^{\prime }|)\sim |\hat{\boldsymbol{u}}_{max}|\text{e}^{{\it\lambda}_{r}T_{nl}}$
and the disturbance becomes large locally as
$O(|\boldsymbol{u}^{\prime }|)\sim |\hat{\boldsymbol{u}}_{max}|\text{e}^{{\it\lambda}_{r}T_{nl}}$
and the disturbance becomes large locally as
![]() ${\sim}0.33U_{\infty }$
. Therefore, the estimate of
${\sim}0.33U_{\infty }$
. Therefore, the estimate of
![]() $T_{nl}$
is
$T_{nl}$
is
Appendix C. Amplitude and frequency equations
The time evolution of cylinder displacement and lift coefficient corresponding to an
eigenmode (
![]() $\hat{\boldsymbol{u}},\hat{p},\hat{{\dot{Y}}},{\hat{Y}}$
) is given as:
$\hat{\boldsymbol{u}},\hat{p},\hat{{\dot{Y}}},{\hat{Y}}$
) is given as:
Here,
![]() ${\hat{C}}_{L}$
is the lift coefficient calculated by integrating the stress
corresponding to the eigenmode around the boundary of the cylinder. In general,
${\hat{C}}_{L}$
is the lift coefficient calculated by integrating the stress
corresponding to the eigenmode around the boundary of the cylinder. In general,
![]() ${\hat{Y}}$
and
${\hat{Y}}$
and
![]() ${\hat{C}}_{L}$
are complex and c.c. represents the complex conjugate. Let
${\hat{C}}_{L}$
are complex and c.c. represents the complex conjugate. Let
![]() $|{\hat{Y}}|$
and
$|{\hat{Y}}|$
and
![]() $|{\hat{C}}_{L}|$
represent the magnitude of
$|{\hat{C}}_{L}|$
represent the magnitude of
![]() ${\hat{Y}}$
and
${\hat{Y}}$
and
![]() ${\hat{C}}_{L}$
, respectively. Further, let
${\hat{C}}_{L}$
, respectively. Further, let
![]() ${\it\theta}$
and
${\it\theta}$
and
![]() ${\it\theta}+{\it\phi}$
denote the argument of
${\it\theta}+{\it\phi}$
denote the argument of
![]() ${\hat{Y}}$
and
${\hat{Y}}$
and
![]() ${\hat{C}}_{L}$
, respectively, where
${\hat{C}}_{L}$
, respectively, where
![]() ${\it\phi}$
is the phase angle between the cylinder displacement and lift
coefficient. We recall that
${\it\phi}$
is the phase angle between the cylinder displacement and lift
coefficient. We recall that
![]() ${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
. Equations (C 1) and (C 2) can be rewritten as
${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
. Equations (C 1) and (C 2) can be rewritten as
Substituting (C 3) and (C 4) in the equations describing the motion of the cylinder (2.3) and (2.4), and assuming the structural damping coefficient to be zero, we obtain:
 $$\begin{eqnarray}\displaystyle & & \displaystyle |{\hat{Y}}|\text{e}^{{\it\lambda}_{r}t}[({{\it\lambda}_{r}}^{2}-{{\it\lambda}_{i}}^{2})\cos ({\it\lambda}_{i}t+{\it\theta})-2{\it\lambda}_{r}{\it\lambda}_{i}\sin ({\it\lambda}_{i}t+{\it\theta})]+(2{\rm\pi}F_{N})^{2}|{\hat{Y}}|\text{e}^{{\it\lambda}_{r}t}\cos ({\it\lambda}_{i}t+{\it\theta})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{|{\hat{C}}_{L}|\text{e}^{{\it\lambda}_{r}t}}{{\rm\pi}m^{\ast }}[\cos ({\it\lambda}_{i}t+{\it\theta})\cos {\it\phi}-\sin ({\it\lambda}_{i}t+{\it\theta})\sin {\it\phi}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |{\hat{Y}}|\text{e}^{{\it\lambda}_{r}t}[({{\it\lambda}_{r}}^{2}-{{\it\lambda}_{i}}^{2})\cos ({\it\lambda}_{i}t+{\it\theta})-2{\it\lambda}_{r}{\it\lambda}_{i}\sin ({\it\lambda}_{i}t+{\it\theta})]+(2{\rm\pi}F_{N})^{2}|{\hat{Y}}|\text{e}^{{\it\lambda}_{r}t}\cos ({\it\lambda}_{i}t+{\it\theta})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{|{\hat{C}}_{L}|\text{e}^{{\it\lambda}_{r}t}}{{\rm\pi}m^{\ast }}[\cos ({\it\lambda}_{i}t+{\it\theta})\cos {\it\phi}-\sin ({\it\lambda}_{i}t+{\it\theta})\sin {\it\phi}].\end{eqnarray}$$
Since (C 5) holds for all
time, we collect the terms involving
![]() $\cos ({\it\lambda}_{i}t+{\it\theta})$
and
$\cos ({\it\lambda}_{i}t+{\it\theta})$
and
![]() $\sin ({\it\lambda}_{i}t+{\it\theta})$
and equate them to zero. This leads to
$\sin ({\it\lambda}_{i}t+{\it\theta})$
and equate them to zero. This leads to
where,
![]() ${\it\alpha}=[({{\it\lambda}_{r}}^{2}-(|{\hat{C}}_{L}|\cos {\it\phi})/(|{\hat{Y}}|{\rm\pi}m^{\ast }))/(2{\rm\pi}F_{N}^{2})]-1$
. We refer (C 6) and (C 7) as the amplitude and frequency equation following the
nomenclature proposed by Khalak & Williamson (Reference Khalak and Williamson1999). While (C 6) defines the phase between the cylinder displacement and
the lift acting on it, (C 7) relates the frequency of the response of the
fluid–structure system to its natural frequency in the vacuum.
${\it\alpha}=[({{\it\lambda}_{r}}^{2}-(|{\hat{C}}_{L}|\cos {\it\phi})/(|{\hat{Y}}|{\rm\pi}m^{\ast }))/(2{\rm\pi}F_{N}^{2})]-1$
. We refer (C 6) and (C 7) as the amplitude and frequency equation following the
nomenclature proposed by Khalak & Williamson (Reference Khalak and Williamson1999). While (C 6) defines the phase between the cylinder displacement and
the lift acting on it, (C 7) relates the frequency of the response of the
fluid–structure system to its natural frequency in the vacuum.
Using (C 6), the energy
transfer per cycle of cylinder oscillation for an eigenmode,
![]() $E_{c}$
, that is given by (6.14), can also be written as
$E_{c}$
, that is given by (6.14), can also be written as