2.1. Physical model

The physical model comes from Genin's experiment and considers a liquid metal flow along a horizontal electrically insulating pipe subject to bottom uniform heating with heat flux intensity $q$ and an external constant transverse magnetic field $\boldsymbol {B}_0$, as shown in figure 1. Mixed convection flow would be produced by a combined action of a pressure driven flow and thermal buoyancy due to huge temperature gradients with strong magnetic fields, then such a flow is usually called MHD mixed convection. The liquid metal is not a magnetizable liquid and is considered as an incompressible, electrically conducting Newtonian viscous fluid with constant kinematic viscosity $\nu$, electric conductivity $\sigma$ and thermal conductivity $\kappa$. The pipe wall is assumed to be electrically insulating, the upper half of the wall is assumed to be thermally insulating and the lower half of the wall has an imposed constant and uniform heat flux.

Figure 1. The flow configuration. The pipe is placed horizontally and heated from below with a constant heat flux $q$, and the upper half of the pipe wall is assumed to be insulated. Uniform magnetic field $\boldsymbol B$ is imposed in the transverse horizontal direction and gravity field $\boldsymbol g$ has a vertical downward direction.

The Oberbeck–Boussinesq approximation is applied for the buoyancy force and the quasi-static model is adopted for the electromagnetic interactions. Then the dimensional governing equations for the liquid metal pipe flow can be described by the Navier–Stokes system

(2.1)\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{v}} = 0, \end{gather}

(2.2)\begin{gather} \rho_0\left[\frac{\partial {\boldsymbol{v}}}{\partial t} + {\boldsymbol{v}} \boldsymbol{\cdot} \boldsymbol{\nabla} {\boldsymbol{v}}\right] ={-} \boldsymbol{\nabla} p + \rho_0\nu \nabla^2 {\boldsymbol{v}} + \boldsymbol{F}_b + \boldsymbol{F}_l, \end{gather}

(2.3)\begin{gather} \rho_0 c_p \left[\frac{\partial T}{\partial t} + {\boldsymbol{v}} \boldsymbol{\cdot} \boldsymbol{\nabla} T\right] = \boldsymbol{\nabla} \boldsymbol{\cdot} (\kappa \boldsymbol{\nabla} T) + \frac{1}{\sigma}{\boldsymbol{j}}^2 + \varPhi + Q. \end{gather}

Here, ${\boldsymbol {v}}$, $p$ and $T$ are the fields of velocity, pressure and temperature, $\rho _0$ is the reference value of the fluid mass density, $c_p$ is the specific heat capacity, $({1}/{\sigma }){\boldsymbol {j}}^2$ is the loss of magnetic energy due to Joule dissipation, $\varPhi$ is the loss of kinetic energy due to viscous dissipation and $Q$ is other sources of volumetric energy release such as nuclear radiation or chemical reactions. The buoyancy force $\boldsymbol {F}_b$ with the Oberbeck–Boussinesq approximation is assumed to vary linearly with temperature and is represented as

(2.4a,b)\begin{equation} \boldsymbol{F}_b =(\rho-\rho_0)\boldsymbol{g},\quad \rho = \rho_0\left[1-\beta(T-T_0) \right], \end{equation}

where $\beta$ is the thermal expansion coefficient and $\boldsymbol {g}$ is the gravitational acceleration in the negative vertical direction. The Lorentz force $\boldsymbol {F}_l$ with the quasi-static model is represented as

(2.5)\begin{gather} \boldsymbol{F}_l = {\boldsymbol{j}}\times \boldsymbol{B}_0, \end{gather}

(2.6)\begin{gather} {\boldsymbol{j}} = \sigma\left( -\boldsymbol{\nabla}\phi + {\boldsymbol{v}}\times \boldsymbol{B}_0 \right), \end{gather}

where ${\boldsymbol {j}}$ is the induced electric current density, $\phi$ is the electrostatic potential. It is clearly seen that, using the quasi-static model, the induced magnetic field can be neglected and the magnetic field remains undisturbed in the expressions of the Lorentz force (2.5) and Ohm's law (2.6). The quasi-static model has been proven to be sufficiently accurate when the magnetic Reynolds and Prandtl numbers are both small (Roberts Reference Roberts1967; Davidson Reference Davidson2001). In most laboratory experiments, the magnetic Reynolds number is relatively small and the induced magnetic field is much weaker than the imposed field.

The current density can be considered to be solenoidal by neglecting displacement currents and assuming the fluid to be electrically neutral, i.e.

(2.7)\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{j}}=0. \end{equation}

Then by substituting the Ohm's law into above solenoidal relation, a Poisson equation for the electrostatic potential is obtained as follows

(2.8)\begin{equation} \nabla^2 \phi = \boldsymbol{\nabla} \boldsymbol{\cdot} ( {\boldsymbol{v}}\times \boldsymbol{B}_0 ) . \end{equation}

By neglecting all energy dissipation and other energy sources except the Fourier diffusion term, the temperature equation (2.3) is reduced to

(2.9)\begin{equation} \frac{\partial T}{\partial t} + {\boldsymbol{v}} \boldsymbol{\cdot} \boldsymbol{\nabla} T = \chi \nabla^2 T . \end{equation}

Here, $\chi =\kappa /\rho _0 c_p$ is the thermal diffusivity.

The boundary conditions on the lower half of the wall include the no-slip condition for the velocity and constant heat flux for the temperature, i.e.

(2.10)\begin{equation} \kappa \frac{\partial T}{\partial n} = q, \end{equation}

and the boundary conditions on the upper half of the wall are no slip and thermally insulated, i.e.

(2.11)\begin{equation} \frac{\partial T}{\partial n} = 0. \end{equation}

2.2. Model non-dimensionalization and reduction

The dimensional governing equations can be further non-dimensionalized by using the pipe diameter $d$ as the length scale, mean streamwise velocity $U_m$ as the velocity scale, $qd/\kappa$ as the temperature scale, $B_0$ as the scale of the magnetic field strength and $dB_0U_m$ as the scale of the electric potential. Then the dimensionless governing equations can be written as

(2.12)\begin{gather} \frac{\partial {\boldsymbol{v}}}{\partial t} + {\boldsymbol{v}} \boldsymbol{\cdot} \boldsymbol{\nabla} {\boldsymbol{v}} ={-}\boldsymbol{\nabla} p + \frac{1}{Re} \nabla^2 {\boldsymbol{v}} + \boldsymbol{f}_b + \boldsymbol{f}_l, \end{gather}

(2.13)\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{v}} = 0, \end{gather}

(2.14)\begin{gather} \frac{\partial T}{\partial t} + {\boldsymbol{v}} \boldsymbol{\cdot} \boldsymbol{\nabla} T = \frac{1}{Pe} \nabla^2 T . \end{gather}

The buoyancy and Lorentz forces are dimensionalized as

(2.15a,b)\begin{equation} \boldsymbol{f}_b = \frac{Gr}{Re^2}T \boldsymbol{e}_y \quad \text{and} \quad \boldsymbol{f}_l = \frac{Ha^2}{Re} {\boldsymbol{j}}\times \boldsymbol{e}_x, \end{equation}

where the dimensionless parameters including the Reynolds number, Prandtl number, Péclet number, Grashof number and Hartmann number are defined as

(2.16a–c)\begin{gather} Re= \frac{U_m d}{\nu},\quad Pr=\frac{\nu}{\chi}, \quad Pe = \frac{U_m d}{\chi}=Re\cdot Pr, \end{gather}

(2.17a,b)\begin{gather} Gr = \frac{g\beta qd^4}{\nu^2\kappa},\quad Ha = B_0 d\left(\frac{\sigma}{\rho\nu}\right)^{1/2}. \end{gather}

In order to compare our results with those of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013), the same dimensionless parameters for the Reynolds number and Prandtl number are selected, with $Re=9046$ and $Pr=0.022$ in this work.

The boundary conditions at the pipe wall include the no-slip conditions for velocity and the condition of perfect electric insulation

(2.18)\begin{equation} {\boldsymbol{v}} = 0,\quad \frac{\partial \phi}{\partial r}=0, \quad \text{at}\ r=\sqrt{x^2+y^2}=1/2. \end{equation}

Here, $x$ and $y$ are horizontal and vertical coordinates in the cross-section, respectively. For the temperature, the condition on the lower half of the wall is

(2.19)\begin{equation} \frac{\partial T}{\partial r}=1, \quad \text{at}\ r=1/2, \end{equation}

while for the upper thermally insulating half of the wall we have

(2.20)\begin{equation} \frac{\partial T}{\partial r}=0, \quad \text{at}\ r=1/2. \end{equation}

The temperature field can be further decomposed as a sum of the mean mixed temperature and the resulting temperature deviation

(2.21)\begin{equation} T(\boldsymbol{x},t) = T_m(z) + \theta(\boldsymbol{x},t). \end{equation}

The mean mixed temperature is assumed to be a linear function of the streamwise coordinate $z$, which makes the overall energy balance between the heat transfer across the lower half of the wall with constant heat flux and the streamwise convection heat transfer. Then its streamwise gradient is given by

(2.22)\begin{equation} \frac{{\rm d}T_m}{{\rm d}z} = \frac{\texttt{P}}{A\cdot Pe}, \end{equation}

where $\texttt {P}={\rm \pi} /2$ is the perimeter of the heated portion of the wall and $A={\rm \pi} /4$ is the cross-sectional area of the pipe. Then the temperature governing equation is written as

(2.23)\begin{equation} \frac{\partial \theta}{\partial t} + {\boldsymbol{v}} \boldsymbol{\cdot} \boldsymbol{\nabla} \theta = \frac{1}{Pe} \nabla^2 \theta - w \frac{{\rm d}T_m}{{\rm d}z}. \end{equation}

The pressure can also be decomposed into three parts as follows:

(2.24)\begin{equation} p= \tilde{p}(z) + \breve{p}(y,z) + p(\boldsymbol{x},t). \end{equation}

The first part is a linear function of $z$ corresponding to a spatially uniform streamwise gradient ${\rm d}\tilde {p}/{\rm d}z$ which pushes the pipe flow. The second part is used to balance with the buoyancy force from the mean mixed temperature

(2.25)\begin{equation} \breve{p}(y,z) = \frac{Gr}{Re^2}y\, T_m + {\rm cons.} \end{equation}

Also, the forcing in the streamwise direction from the second part is deduced with

(2.26)\begin{equation} \frac{\partial\breve{p}}{\partial z} = \frac{Gr}{Re^2}\frac{{\rm d}T_m}{{\rm d}z} y. \end{equation}

We look for the 2-D steady-state solutions in which the velocity, pressure, temperature (excluding the linear part coming from the bottom heating) and electrostatic potential are independent of streamwise coordinate, as follows:

(2.27)\begin{gather} {\boldsymbol{v}}_b = {\boldsymbol{V}}(x,y) = (\boldsymbol{U}(x,y),W(x,y)), \end{gather}

(2.28a–c)\begin{gather} p=P(x,y),\quad \theta=\varTheta(x,y),\quad \phi = \varPhi(x,y). \end{gather}

Here, $\boldsymbol{U}=(U,V)$ is the cross-sectional velocity, and $W$ is the streamwise velocity. Thus the 2-D steady governing systems for the steady flow state are obtained as follows:

(2.29)\begin{gather} (\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla}_s)W={-}{\rm d}\tilde{p}/{\rm d}z - \frac{Gr}{Re^2}\frac{{\rm d}T_m}{{\rm d}z} y +\frac{1}{Re}\boldsymbol{\nabla}_s^2 W + \frac{Ha^2}{Re} F_z, \end{gather}

(2.30)\begin{gather} (\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla}_s)\boldsymbol{U}={-}\boldsymbol{\nabla}_s P +\frac{1}{Re}\boldsymbol{\nabla}_s^2 \boldsymbol{U} + \frac{Gr}{Re^2}\varTheta \boldsymbol{e}_y + \frac{Ha^2}{Re} \boldsymbol{f}, \end{gather}

(2.31)\begin{gather} (\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla}_s)\varTheta=\frac{1}{Pe}\boldsymbol{\nabla}_s^2 \varTheta -W\frac{{\rm d}T_m}{{\rm d}z}, \end{gather}

(2.32)\begin{gather} \boldsymbol{\nabla}_s \boldsymbol{\cdot} \boldsymbol{U} = 0, \end{gather}

(2.33)\begin{gather} \boldsymbol{F} = (-\boldsymbol{\nabla} \varPhi + {\boldsymbol{v}}_b \times \boldsymbol{e}_x)\times \boldsymbol{e}_x, \end{gather}

(2.34)\begin{gather} \nabla^2 \varPhi = \boldsymbol{\nabla} \boldsymbol{\cdot} ( {\boldsymbol{v}}_b \times \boldsymbol{e}_x ) . \end{gather}

Here, $\boldsymbol {\nabla }_s=(\partial _x,\partial _y)$, $\boldsymbol{F}=(\boldsymbol{f},F_z)$ and $\boldsymbol{f}=(F_x,F_y)$. The corresponding boundary conditions on the walls are the no-slip condition for the velocity

(2.35)\begin{equation} {\boldsymbol{v}}_b = 0,\quad \text{at}\ r=1/2, \end{equation}

fixed heat flux for constant-rate heating on the lower half of the wall and thermal insulation on the upper half of the wall

(2.36)\begin{gather} \frac{\partial\varTheta}{\partial r} = 1,\quad \text{at}\ r=1/2,\ y<0, \end{gather}

(2.37)\begin{gather} \frac{\partial\varTheta}{\partial r} = 0,\quad \text{at}\ r=1/2,\ y>0, \end{gather}

as well as zero current flux due to the electrically insulating walls

(2.38)\begin{equation} \frac{\partial\varPhi}{\partial r} = 0,\quad \text{at}\ r=1/2. \end{equation}

3.1. Finite-element method for linear global stability analysis

For linear global stability analysis of the MHD mixed convection in a circular pipe, the 2-D steady-state solutions of the governing equations should be computed. The Taylor–Hood finite-element method is used for spatial discretization for the steady governing equations, and the Newton method is adopted to solve the derived nonlinear system when the cross-sectional velocity is not zero. A high-level integrated software FreeFem++ (Pironneau, Hecht & Morice Reference Pironneau, Hecht and Morice2013) for the numerical solution of nonlinear multiphysics partial differential equations is adopted for the computation of the steady-state solutions. The bi-dimensional anisotropic mesh generator BAMG built into FreeFem++ is used to define the circular cross-section geometry and generate the 2-D triangular meshes. Three borders are first defined for the 2-D mesh generation, one is the outer wall boundary with $r=0.5$, the other two are internal circles with $r=0.4$ and $r=0.3$. Then, discrete mesh points are uniformly distributed on these borders with different numbers. The numbers of mesh points can be used to control the mesh resolution and further be defined as $n_r$, $0.5n_r$ and $0.3n_r$, respectively. This will produce a much larger mesh size for the border with the smaller circle radius. It is easily seen from figure 1 that the triangular mesh with $n_r=100$ has a much smaller mesh size near the pipe wall. Obviously, finer mesh resolution near the pipe wall is realized and beneficial to improve the numerical accuracy.

Because the mean streamwise velocity is adopted as the velocity scale, it should be noted that the uniform streamwise pressure gradient ${\rm d}\tilde {p}/{\rm d}z$ should be adjusted to make the average streamwise velocity to be positive one, i.e.

(3.1)\begin{equation} \frac{1}{A}\int_A W\, \mathrm{d} A = 1. \end{equation}

A simple bisection process can be used to satisfy relation (3.1). The Newton iterative method needs a good initial guess, then the steady-state solutions are computed continuously from small dimensionless parameters to large ones. In order to verify the correctness of the 2-D steady-state solutions, the same cases as Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013) for $Re=9046$, $Pr=0.022$, $Gr = 8.298\times 10^7$ with different Hartmann numbers are considered. Base flow solution of the streamwise velocity and temperature field along the cross-section for $Ha=102$ is first plotted in figure 2, which has the same spatial distribution as Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013). A detailed comparison of the profiles of the streamwise velocity $W$ of the base flow along horizontal and vertical lines drawn through the pipe axis is presented in figure 3. It is clearly seen from these figures that the steady-state solutions obtained by the finite-element method agree very well with those by direct numerical simulations of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013).

Figure 2. Base flow solution of the streamwise velocity (a) and temperature (b) field along the cross-section; $Re=9046$, $Pr=0.022$, $Gr = 8.298\times 10^7$ and $Ha=102$.

Figure 3. Profiles of the streamwise velocity $W$ of the base flow along horizontal (a) and vertical (b) lines drawn through the pipe axis; solid line is obtained by the finite element method with FreeFem++ software, while triangle symbols are from direct numerical simulations of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013); $Re=9046$, $Pr=0.022$, $Gr = 8.298\times 10^7$ and $Ha=102$.

In order to study the asymptotic behaviour in time of generic small-amplitude perturbations of $({\boldsymbol {V}}', P', \varTheta ', \varPhi ')$ imposed on the steady-state mixed convection, these perturbations can be expanded as normal modes in the streamwise direction as follows:

(3.2)\begin{equation} ({\boldsymbol{V}}', P', \varTheta', \varPhi') = (\hat{{\boldsymbol{v}}}, \hat{p}, \hat{\theta}, \hat{\phi})\exp({\rm i}kz+\gamma t), \end{equation}

where $k$ is the wavenumber in the streamwise direction, and $\gamma =\gamma _r + {\rm i}\gamma _i$ is the corresponding complex growth rate. By substituting the expressions of the disturbed flow field ${\boldsymbol {V}} + {\boldsymbol {V}}',P+P',\varTheta +\varTheta ',\varPhi +\varPhi '$ into the governing system, the full global linear stability equations are obtained as follows:

(3.3)$$\begin{gather} \gamma \hat{u} +\left( \boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla}_s + {\rm i}kW \right)\hat{u} +\left( \boldsymbol{\hat{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}_s \right) U ={-}\frac{\partial \hat{p}}{\partial x}\nonumber\\ +\frac{1}{Re}\left(\boldsymbol{\nabla}_s^2-k^2\right)\hat{u}, \end{gather}$$

(3.4)$$\begin{gather} \gamma \hat{v} +\left( \boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla}_s + {\rm i}kW \right)\hat{v} +\left( \boldsymbol{\hat{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}_s \right) V ={-}\frac{\partial \hat{p}}{\partial y}\nonumber\\ +\frac{1}{Re}\left(\boldsymbol{\nabla}_s^2-k^2\right)\hat{v} +\frac{Ha^2}{Re}\left(-{\rm i}k\hat{\phi}-\hat{v} \right), \end{gather}$$

(3.5)$$\begin{gather} \gamma \hat{w} +\left( \boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla}_s + {\rm i}kW \right)\hat{w} +\left( \boldsymbol{\hat{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}_s \right) W ={-}{\rm i}k\hat{p}\nonumber\\ +\frac{1}{Re}\left(\boldsymbol{\nabla}_s^2-k^2\right)\hat{w}+\frac{Gr}{Re^2}\hat{\theta} +\frac{Ha^2}{Re}\left(\frac{\partial\hat{\phi}}{\partial y}-\hat{w} \right), \end{gather}$$

(3.6)$$\begin{gather} \gamma \hat{\theta} +\left( \boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla}_s + {\rm i}kW \right)\hat{\theta} +\left( \boldsymbol{\hat{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}_s \right) \varTheta\nonumber\\ = \frac{1}{Pe}\left(\boldsymbol{\nabla}_s^2-k^2\right)\hat{\theta}-\hat{w}\frac{{\rm d}T_m}{{\rm d}z}, \end{gather}$$

(3.7)\begin{gather} \frac{\partial \hat{u}}{\partial x}+\frac{\partial \hat{v}}{\partial y} + {\rm i}k\hat{w} = 0, \end{gather}

(3.8)\begin{gather} \left(\boldsymbol{\nabla}_s^2-k^2\right)\hat{\phi} - \left(\frac{\partial\hat{w}}{\partial y}-{\rm i}k\hat{v} \right)=0. \end{gather}

Here, $\hat {{\boldsymbol {v}}}=(\boldsymbol{\hat {u}},\hat {w})=(\hat {u},\hat {v},\hat {w})$, and the boundary conditions are given by

(3.9)\begin{equation} \hat{{\boldsymbol{v}}}=\frac{\partial\hat{\theta}}{\partial r}=\frac{\partial\hat{\phi}}{\partial r} = 0, \quad \text{at}\ r=1/2. \end{equation}

The spatial discretization of Taylor–Hood finite elements can also be used for the global linear stability equations. After the spatial discretization of the linear stability equations, a generalized eigenvalue problem has to be solved in the matrix form as follows:

(3.10)\begin{equation} {\boldsymbol{A}}\hat{{\boldsymbol{q}}} = \gamma {\boldsymbol{B}} \hat{{\boldsymbol{q}}}, \end{equation}

where $\hat {{\boldsymbol {q}}}=(\hat {{\boldsymbol {v}}}, \hat {p}, \hat {\theta }, \hat {\phi })$ is the eigenvector collecting the velocity components, pressure, temperature and electrostatic potential of each degree of freedom of the discrete problem, ${\boldsymbol {A}}$ and ${\boldsymbol {B}}$ are large sparse complex matrices. In order to facilitate the extraction of the desired eigenvalues for unstable modes, spectral transformations should be introduced into the generalized eigenvalue problem. Theofilis (Reference Theofilis2011) has reviewed a lot of spectral transformations commonly utilized in the global instability analysis of fluid flows. Most commonly used is the shift-and-invert strategy which transforms the generalized eigenvalue problem into a standard eigenvalue problem as follows:

(3.11)\begin{equation} ({\boldsymbol{A}}-\mu{\boldsymbol{B}})^{{-}1}{\boldsymbol{B}} \hat{{\boldsymbol{q}}} = (\gamma-\mu)^{{-}1} \hat{{\boldsymbol{q}}}. \end{equation}

The shift matrix can be solved by the UMFPACK or MUMPS sparse LU solver and the standard eigenvalue problem solved with an implicitly restarted Arnoldi algorithm as provided in the ARPACK software library (Lehoucq, Sorensen & Yang Reference Lehoucq, Sorensen and Yang1998). Thus, the largest eigenvalues of the transformed matrix now correspond to those eigenvalues of the original generalized eigenvalue equation which are the closest to the shift value $\mu$.

In order to validate the computation of the eigenspectrum, the linear growth rate and phase velocity of most unstable mode as a function of wavenumber are plotted in figure 4 for $Re=9046$, $Pr=0.022$, $Gr = 8.298\times 10^7$ and $Ha=306$. Compared with the numerical simulation results of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013), it is easily found that the linear growth rates we get from FreeFem++ software are a little higher than their results, this is especially obvious near the maximum growth rate. It is noticed that Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013) used two different streamwise grid numbers, the larger one ($N=64$) is for long-wave perturbations while the smaller one ($N=32$) is for short-wave perturbations. Under these two mesh resolutions, their phase velocity results of most unstable mode are obviously different, also specifically for moderate wavenumbers ($k=5\sim 7$) where large exponential growth occurs. Interestingly, it is found that a good agreement between our eigenspectrum results and numerical simulations of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013) occurs when the exponential perturbation growth is not very strong.

Figure 4. Linear growth rate (a) and phase velocity (b) of most unstable mode as a function of wavenumber; solid line is obtained by the finite-element method with FreeFem++ software, while rectangle and triangle symbols are from direct numerical simulations of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013) with respect to the streamwise grid numbers $N=32$ and $N=64$; $Re=9046$, $Pr=0.022$, $Gr = 8.298\times 10^7$ and $Ha=306$.

3.2. Fourier-spectral finite-difference method for direct numerical simulation

For direct numerical simulations, we solve the dimensionless governing equations in cylindrical coordinates where $r,\beta$,$z$ denote the radial (i.e. wall-normal), azimuthal and axial directions, respectively. Then, the velocity field would be denoted with ${\boldsymbol {v}}=(u_r,u_\beta,u_z)$. We use a Fourier-spectral finite-difference method for discretizing the equations. Field variables, i.e. ${\boldsymbol {v}}$, $p$, $\phi$ and $\theta$, are expanded with a twofold Fourier expansion

(3.12)\begin{equation} A(r,\beta,z,t)=\sum_{k={-}K}^{K}\sum_{m={-}M}^{M}\hat A(r,t)_{k,m} \exp{\{{\rm i}k\alpha z+{\rm i}m\beta}\}, \end{equation}

in which $\hat A(r,t)_{k,m}$ is the Fourier coefficient of the $(k,m)$ Fourier mode and is a function of $r$ and $t$, $\alpha$ would determine spatial periodicity. In the radial direction, we use a 9-stencil high-order finite-difference method for the discretization. The nonlinear terms are calculated using the pseudo-spectral technique with the $3/2$-rule for dealiasing. Also, $2K$ and $2M$ give the total number of Fourier modes used in the axial and azimuthal directions, respectively. We use the finite-difference scheme, the singularity-removal technique at the pipe axis and the message passing interface (MPI) parallelization strategy of OPENPIPEFLOW (Willis Reference Willis2017). In particular, the singularity removal is achieved by avoiding a grid point at the pipe axis $r=0$ and imposing proper parity conditions on the velocity, electric potential and temperature in the neighbourhood of the pipe axis. To be clear, near the pipe axis $u_r$ and $u_\beta$ are odd for even $m$ and even for odd $m$, whereas $u_z$, $\phi$ and $\theta$ are even for even $m$ and are odd for odd $m$. Technically, the parity condition is implemented by imposing a homogeneous Dirichlet condition for odd functions and a homogeneous Neumann condition for even functions at $r=0$. The details can be found in the documentation of OPENPIPEFLOW (Willis Reference Willis2017).

For the time integration of the Navier–Stokes equations and the heat equation, a semi-implicit three-level Adams–Bashforth time-integration scheme is adopted. Linear terms are treated implicitly and the nonlinear term is treated explicitly using a backward differentiation scheme. The incompressibility condition is imposed using a projection method (Hugues & Randriamampianina Reference Hugues and Randriamampianina1998). Since only the lower half-pipe wall is heated and the upper half-pipe wall is thermally insulated, there will exist a discontinuity with respect to the heat flux ${\partial T}/{\partial r}$ at the boundary between the heated and insulated parts of the pipe wall. In order to use the Fourier-spectral method, we adopt a steep tanh function to approximate this discontinuity. Assuming the heated part is located at $\beta \in [{{\rm \pi} }/{2}, {3{\rm \pi} }/{2}]$, then the distribution of the heat flux around the whole pipe wall is given by

(3.13)\begin{equation} q=\dfrac{\partial \theta}{\partial r}(\beta)=0.5-0.5\tanh{\dfrac{|\beta-{\rm \pi}|-\dfrac{\rm \pi}{2}}{\delta}}, \end{equation}

where the parameter $\delta$ is a control parameter which determines the steepness at the approximated discontinuity boundary. As shown in figure 5, it is clearly seen that smaller parameter $\delta$ gives rise to steeper boundary for the heat flux. However, a much smaller parameter $\delta$ would need more azimuthal collocation points near the approximated discontinuity boundary and then should be properly chosen to balance the accuracy and computational cost.

Figure 5. The distribution of the heat flux around the whole pipe wall used for direct numerical simulations with the spectral finite-difference method.

As the steady base flow is streamwise invariant, we can choose to only solve the $k = 0$ modes to obtain the base flow. It is obvious that the base flow would have 2-D stability in the cross-section. As a validation, we compare our calculations using the spectral method with the results using the finite-element method in the previous subsection. The flow parameters of the test case are $Ha=204$, $Re=9046$, $Gr=8.298\times 10^7$, $Pr=0.022$. The resolution of the spectral simulation is $N=144$ and $M=96$ (i.e. 144 grid points on the radius and $2M=192$ grid points in the azimuthal direction before dealiasing). The steepness parameter $\delta =0.05$ and this azimuthal resolution give approximately six grid points within the smoothing region of the approximated discontinuity of heat flux. Figure 6(a,b) shows the visualization of the base flow in our spectral simulations for the streamwise velocity and temperature field in the cross-section. It is seen that the basic streamwise velocity becomes uniform along the magnetic field direction in the bulk of the circular pipe for large Hartmann numbers. In figure 6(c,d), the streamwise velocity and temperature distributions along the vertical and horizontal lines of the cross-section are compared between our spectral simulation and the finite-element calculation. The agreement between the two sets of results is excellent with a deviation below 0.5 %. This agreement validates our methods and particularly the smoothing of the heat flux in our spectral methods, at least for the base flow calculation.

Figure 6. The base flow calculated using the spectral method and finite-element method. Contours of temperature (a) and streamwise velocity (b) on the pipe cross-section. Data are from our spectral method simulation. (c) Comparison of temperature distribution on the vertical and horizontal lines through the pipe centre. (d) Comparison of streamwise velocity on the vertical and horizontal lines through the pipe centre. In (c,d), symbols are data from our spectral method simulation and lines are from the finite-element simulation.

After obtaining the base flow, we can perturb the base flow with small perturbations in the spectral space, i.e. small Fourier coefficient of a given mode with the wavenumber $(k\alpha, m)$ is set to give the initial condition of direct numerical simulations. Then, the linear growth rate of the unstable mode at a fixed wavenumber can be calculated from the modal kinetic energy variation between two different time instances, i.e.

(3.14)\begin{equation} \gamma=\frac{1}{2}\frac{\log{KE(t_2)}-\log{KE(t_1)}}{t_2-t_1}, \end{equation}

where $\gamma$ denotes the linear growth rate, $KE=\int _V({\boldsymbol {v}}-{\boldsymbol {v}}_b)\,{\rm d}V$ is the modal kinetic energy and $t_1$ and $t_2$ are two time instants in the exponentially growing stage. The phase speed of the leading eigenmode can be calculated as

(3.15)\begin{equation} c=\frac{\lambda}{T}, \end{equation}

with the streamwise wavelength $\lambda$ and the period of oscillation $T$ which can be measured by monitoring the velocity at a fixed point in the flow domain. For the same case with $Ha=306$, $Re=9046$, $Gr=8.298\times 10^7$ and $Pr=0.022$ as in Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013), the linear growth rates and phase speeds with respect to different wavenumbers can be computed through both the eigenvalue computation of the linear stability equations and the numerical simulations with the spectral method, as shown in figure 7. Although the two approaches are different and performed independently, it is clearly seen that a good agreement is obtained and can be used as a cross-validation of these two approaches. A further convergence test for the linear growth rate with respect to the steepness parameter $\delta$ is given in table 1, which shows $\delta =0.5$ with $M=96$ can yield good calculation accuracy. An additional validation of our spectral method against an asymptotic solution of the basic flow for the MHD pipe flow (without the heating and buoyancy) can be found in Appendix A. All these tests confirm the correctness of our basic flow calculations.

Figure 7. The linear growth rate (a) and the phase speed (b) of the leading eigenmode with respect to different wavenumbers. Here, the solid line is obtained with the eigenvalue computation of the linear stability equations while discrete circle symbols are the results by direct numerical simulations using the spectral method. The dimensionless parameters $Ha=306$, $Re=9046$, $Gr=8.298\times 10^7$ and $Pr=0.022$ are adopted, while the steepness parameter $\delta =0.05$ is used for direct numerical simulations.

Table 1. Convergence of the linear growth rate about the smoothing width $\delta$. The flow parameters are $Ha=306$, $Re=9046$, $Gr=8.298\times 10^7$ and $Pr=0.022$, and the streamwise wavelength of $\lambda =1.0$ is considered for this convergence test.

4.1. Linear stability boundary of the MHD mixed convection

Linear stability boundary of the MHD mixed convection is determined by the most unstable mode, which can be easily computed if there exists only one unstable mode for the parameters under investigation. However, if there exist more than one unstable modes and especially if they have close linear growth rates, then the linear stability boundary may become complex and is difficult to obtain. The critical curves for the linear stability of the MHD mixed convection are first plotted in the $Gr$–$Ha$ parameter space with $Re=9046$ and $Pr=0.022$ as shown figure 8. It is clearly seen that there exist three critical curves located at small and large Hartmann numbers. All the critical curves have been validated by our direct numerical simulations. The critical curve for large Hartmann number is determined by the only unstable mode denoted by mode I, which was first revealed by the numerical simulations of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013). It is easily found that the unstable mode I occurs above a threshold of the Hartmann number of approximately $Ha=136.33$. Across the threshold, the unstable region for the Grashof number becomes larger and larger with the increase of the Hartmann number. The upper boundary of the unstable region increases nearly exponentially while the lower boundary decreases very slowly. The other two critical curves are located at small Hartmann numbers and determined by different unstable modes. They intersect at $Ha=37.46$ and are denoted by mode II and mode III, respectively. The critical Grashof number on these two critical curves increases nearly exponentially with the increase of the Hartmann number, from $Gr_c\sim 1.2\times 10^6$ at $Ha=20$ to $Gr_c\sim 1.8\times 10^8$ at $Ha=80$. Within the unstable region bounded by the critical curves for the small Hartmann number, there exist many other unstable modes which are not presented here.

Figure 8. The critical curves of the most unstable modes in the $Gr$–$Ha$ parameter space with $Re=9046$ and $Pr=0.022$.

Along all the critical curves of the most unstable modes in the $Gr$–$Ha$ parameter space, the corresponding wavenumber and phase speed as a function of Hartmann number can be plotted, as shown in figure 9. It is clearly seen that both the critical wavenumber and phase velocity for small Hartmann numbers are much smaller than those for large Hartmann numbers. Then, for small Hartmann numbers, long-wave instabilities first occur at the threshold, and the critical wavenumber is found to increase with the increase of the Hartmann number. Meanwhile, the phase velocity of these long-wave instabilities even decreases with the increase of the Hartmann number for the unstable mode II. It is also seen that at $Ha=67.7$ there exists a jump of the critical wavenumber and phase velocity of mode II. It is carefully checked that this jump is not due to eigenmode transiton, but a rapid change of the critical parameters for the same unstable mode.

Figure 9. Critical wavenumber (a) and phase velocity (b) of most unstable modes along all the critical curves as a function of Hartmann number with $Re=9046$ and $Pr=0.022$.

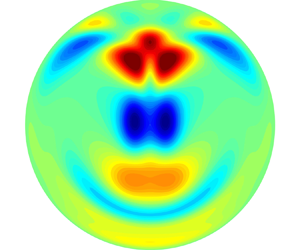
Spatial structure of the 3-D unstable mode for the perturbations of temperature and vertical velocity in the horizontal cross-section passing through the axis of the pipe is presented in figures 10 and 11 at two critical points with large and small Hartmann numbers, respectively. It is easily seen that the spatial structure for the critical case of $Ha=136.33$ is very similar to the simulation result by Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013) for $Ha = 306$ and $\lambda = 1.0$. Specifically, the simulation result for large Hartmann number has a more uniform distribution of vertical velocity along the magnetic field direction. Obviously, there exists only one unstable mode which results in such a similar spatial structure for different large Hartmann numbers. However, the spatial structure for the critical case of $Ha=50$ is very different, as shown in figure 11. It is easily seen that the temperature perturbation is distributed near the lateral walls and in the central region, while the perturbations of three velocity components concentrate in the central region. Different spatial structures of different critical eigenmodes imply different destabilization mechanisms, which are further studied in following subsection.

Figure 10. Spatial structure of the 3-D unstable mode for the perturbations of temperature (a) and vertical velocity (b) in the horizontal cross-section passing through the axis of the pipe at a critical point of $k_c=5.8$, $Ha=136.33$, $Gr=5.14\times 10^7$, $Re=9046$ and $Pr=0.022$.

Figure 11. Spatial structure of the 3-D unstable mode for the perturbations of temperature (a), vertical velocity (b) and streamwise velocity (c) in the horizontal cross-section passing through the axis of the pipe at a critical point of $k_c=1.69$, $Ha=50$, $Gr=2.898\times 10^7$, $Re=9046$ and $Pr=0.022$.

4.2. Energy budget analyses at the critical unstable thresholds

In order to obtain the physical destabilization mechanism, it is usual to perform energy budget analyses at the critical thresholds for the most unstable mode. First, the linear stability equations (3.3)–(3.5) are multiplied by the complex conjugate of the velocity perturbation $\hat {{\boldsymbol {v}}}^*$ and then integrated on the cross-section $A$. After some simplifications, an equation giving the rate of change of the fluctuating kinetic energy can be derived. At the critical threshold ($\mathrm {Re}(\lambda )=0$) for any unstable mode, kinetic energy budgets can be further obtained as

(4.1)\begin{equation} E_{su} + E_{sv} + E_{sw} + E_{b} + E_{m} + E_d = 0, \end{equation}

where $E_{su}$, $E_{sv}$ and $E_{sw}$ are the productions of fluctuating kinetic energy by shear of the basic flow, $E_{b}$ is the production of fluctuating kinetic energy by buoyancy, $E_{m}$ is the dissipation of fluctuating kinetic energy by magnetic forces and $E_d$ is the viscous dissipation of fluctuating kinetic energy. They are defined as follows:

(4.2)\begin{gather} E_{su} ={-}\mathrm{Re}\left(\int_A \left[\hat{u}\frac{\partial U}{\partial x}\hat{u}^* + \hat{v}\frac{\partial U}{\partial y}\hat{u}^*\right] \,{\rm d}x\,{\rm d}y\right), \end{gather}

(4.3)\begin{gather} E_{sv} ={-}\mathrm{Re}\left(\int_A \left[\hat{u}\frac{\partial V}{\partial x}\hat{v}^* + \hat{v}\frac{\partial V}{\partial y}\hat{v}^*\right] \,{\rm d}x\,{\rm d}y\right), \end{gather}

(4.4)\begin{gather} E_{sw} ={-}\mathrm{Re}\left(\int_A \left[\hat{u}\frac{\partial W}{\partial x}\hat{w}^* + \hat{v}\frac{\partial W}{\partial y}\hat{w}^*\right] \,{\rm d}x\,{\rm d}y\right), \end{gather}

(4.5)\begin{gather} E_{b} = \mathrm{Re}\left(\int_A \frac{Gr}{Re^2}\hat{\theta}\hat{v}^* \,{\rm d}x\,{\rm d}y\right), \end{gather}

(4.6)\begin{gather} E_{m} = \mathrm{Re}\left(\int_A \frac{Ha^2}{Re} \left[(-\boldsymbol{\nabla} \hat{\phi} + \hat{{\boldsymbol{v}}} \times \boldsymbol{e}_x)\times \boldsymbol{e}_x\right] \hat{{\boldsymbol{v}}}^* \,{\rm d}x\,{\rm d}y\right), \end{gather}

(4.7)\begin{gather} E_{d} ={-}\mathrm{Re}\left(\int_A \frac{1}{Re}\frac{\partial \hat{v}_i}{\partial x_j}\frac{\partial \hat{v}_i^*}{\partial x_j} \,{\rm d}x\,{\rm d}y\right). \end{gather}

All these terms can be further normalized by the viscous dissipation of fluctuating kinetic energy $E_d$, then a normalized kinetic energy budget equation is written as

(4.8)\begin{equation} E'_{su} + E'_{sv} + E'_{sw} + E'_{b} + E'_{m} = 1, \end{equation}

where $E'_{su}=E_{su}/|E_d|$, $E'_{sv}=E_{sv}/|E_d|$, $E'_{sw}=E_{sw}/|E_d|$, $E'_{b}=E_{b}/|E_d|$, $E'_{m}=E_{m}/|E_d|$.

The kinetic energy budgets by shear of the basic flow, buoyancy and magnetic forces at the critical points of the least stable 3-D modes are presented for different Hartmann numbers in table 2. For all cases of mode I, it is easily seen that the production of fluctuating kinetic energy by buoyancy $E'_{b}$ is the dominant destabilizing term, the production of fluctuating kinetic energy by the streamwise shear of the basic flow $E'_{sw}$ gives a significant stabilization effect and the production of fluctuating kinetic energy by the cross-sectional shear of the basic flow $E'_{su}$ and $E'_{sv}$ is very small and thus has little effect on the flow stability. According to the values of the stabilizing term $E'_{m}$, the cases on the lower boundary of mode I have a much weaker stabilization effect due to magnetic forces than those on the upper boundary of mode I. For the cases of mode II and mode III, it is found that the streamwise shear of the basic flow gives the dominant production of fluctuating kinetic energy due to positive large values of $E'_{sw}$. Then, the dominant destabilization mechanism is the streamwise shear of the basic flow instead of buoyancy with negligible terms $E'_{b}$. It is also found that, with the increase of Hartmann number along the critical curves of mode II and mode III, the values of the destabilization term $E'_{su}$ as well as stabilization terms $E'_{sv}$ and $E'_{m}$ become larger and larger.

Table 2. Kinetic energy budgets by shear of the basic flow $E'_{su}$, $E'_{sv}$, $E'_{sw}$, buoyancy $E'_{b}$ and magnetic forces $E'_{m}$ at the critical point of the most unstable 3-D mode for different Hartmann numbers with $Re=5000$ and $Pr=0.0321$.

Now the dominant destabilization mechanism is revealed to be buoyancy for mode I as well as streamwise shear of basic flow for mode II and mode III. It is necessary to plot the spatial distribution of local buoyancy and the local streamwise shear of the basic flow i.e. the integral terms in the integral formula (4.4) and (4.5), at the critical points for these modes. As shown in figure 12(a), it is clearly seen that the local buoyancy $E_b$ for the production of fluctuating kinetic energy is mainly located in the middle and lower parts of the pipe for mode I. However, the local streamwise shear of the basic flow $E_{sw}$ for mode II is situated at the upper part of the pipe, as seen in figure 12(b).

Figure 12. Spatial distribution of (a) the local buoyancy $E_b$ and (b) local streamwise shear of the basic flow $E_{sw}$ at the critical points of the 3-D unstable modes for (a) mode I with $k_c=5.8$, $Ha=136.33$, $Gr=5.14\times 10^7$ and (b) mode II with $k_c=1.69$, $Ha=50$, $Gr=2.898\times 10^7$; where $Re=9046$ and $Pr=0.022$.

5.1. Low-$Ha$ branch

Starting from a point close to the neutral stability boundary at $(Ha, Gr)=(45, 2\times 10^7)$, we explore horizontally at $(Ha, Gr)=(40, 2\times 10^7)$ and $(30, 2\times 10^7)$. For all simulations in this subsection, the pipe length is chosen to be 12.2 pipe diameters, which is three times the wavelength of the most unstable mode at $(Ha, Gr)=(45, 2\times 10^7)$.

5.1.1. The case $(Ha, Gr)=(45, 2\times 10^7)$

The streamwise velocity fields for the nonlinear flow state and the most unstable mode are both computed by direct numerical simulations and shown in figure 14. It is clearly seen that the nonlinear saturated flow exhibits a travelling wave structure that is symmetric about the vertical plane through the pipe axis. The spatial distributions of the streamwise velocity in all cross-sections are very similar with respect to both the saturated flow state and the most unstable mode. Obviously, the reason is that the nonlinear effect is very weak and the nonlinear flow state is thus dominated by the most unstable mode when the parameters are very close to the linear stability boundary.

Figure 14. The streamwise velocity on the pipe cross-sections at $(Ha, Gr)=(45, 2\times 10^7)$. The full velocity is plotted in the $r$–$\beta$ cross-section (a), vertical $r$–$z$ cross-section (i.e. the $y$–$z$ plane through the pipe axis) (b) and horizontal $r$–$z$ cross-section (i.e. the $x$–$z$ plane through the pipe axis) (c). The deviation with respect to the basic laminar flow is shown in (d–f) and the most unstable linear mode is visualized in (g–i). The location of the maximum deviation of $u_z$ from the basic laminar flow is shitted to the left end of the pipe in all the plots in the $r$–$z$ cross-sections. Panels (a,d,g) are plotted at the left end of the pipe.

5.1.2. The case $(Ha, Gr)=(40, 2\times 10^7)$

At this parameter point, we find that the saturated flow state seems to have a strong dependence on the initial condition. Direct numerical simulations for this case are performed with two different initial conditions. The temporal evolution of the flow is monitored using the kinetic energy $KE_{3D}=\int _V({\boldsymbol {v}}-<{\boldsymbol {v}}>_z)\,{\rm d}V$ associated with the streamwise dependent velocity components, see figure 15.

Figure 15. The kinetic energy of the 3-D flow components (streamwise dependent ones), $KE_{3D}$, of two simulations starting from different initial conditions at $(Ha, Gr)=(40, 2\times 10^7)$. One starts from a fully turbulent flow simulated at $Ha=30$ and the other from a slightly perturbed laminar basic flow, see the blue and red curves, respectively.

The first simulation begins with a fully turbulent state and the kinetic energy $KE_{3D}$ is plotted as the blue curve in figure 15. The flow remains turbulent for several hundred time units, and then seems to approach a periodic state with large kinetic energy oscillations. Flow fields for the streamwise velocity at four time instants (marked with four symbols in figure 15) are visualized in figure 16. The first two columns correspond to the time instants marked with red circle and green triangle, respectively. Although both of them are at the peaks of the oscillation in $KE_{3D}$, the flow field is not identical to that seen in the $r$–$\beta$ cross-section. Nevertheless, by looking at the flow fields in the vertical and horizontal $r$–$z$ cross-sections, it can be observed that the two flow fields are nearly identical up to a phase shift. Therefore, the period of the oscillation of $KE_{3D}$ is not equal to the period of the flow field. Furthermore, we compare the flow fields of the first column and the fourth column corresponding to the two time instants marked with the red circle and blue square (both are at peaks). These two flow fields seem identical up to a reflection about the vertical plane through the pipe axis. This means that the two flow fields are separated by half a period in phase. Then, it can be inferred that the period of the flow field should correspond to four periods of the oscillation in $KE_{3D}$, which is nearly 380 time units. The third column corresponding to the black diamond in figure 15 shows the flow field at the trough of the oscillation in $KE_{3D}$, where the velocity perturbations are much weaker than those at other three peak instants. It seems that the periodic state only maintains one cycle, and then the flow begins to leave the periodic orbit after $t=1400$ because the oscillation becomes irregular at later times. The temporal evolution of this nonlinear flow state indicates that there exists an unstable nonlinear periodic solution at the given flow parameters.

Figure 16. The quasi-periodic flow state at $(Ha, Gr)=(40, 2\times 10^7)$. The visualization of the streamwise velocity field at the four time instants marked by the four symbols on the blue curve in figure 15. Each column corresponds to a time instant. Panels (a–l) share the same colour scale. From (a,d,g,j) to (c, f,i,l), $r$–$\beta$ cross-section at the left end of the pipe, vertical $r$–$z$ cross-section and horizontal $r$–$z$ cross-section.

The second simulation starts from random small perturbations and is shown as the red curve in figure 15. It is clearly seen that there is no high-amplitude periodic oscillation up to 1100 time units. The flow field is visualized at $t=966$ in figure 17. Compared with the first simulation, although there are some similarities in the spatial distributions of the flow fields in the cross-sections, there does not exist any regular or periodic structure in either the signal of $KE_{3D}$ or the flow fields visualized in the pipe cross-sections. However, it should be noted that we cannot rule out the possibility that the non-periodic state would also approach some periodic orbits at some time in the future. Both nonlinear states show little similarity in flow structure with the linear eigenmode (which is similar to figure 14g–i).

Figure 17. Visualization of the flow field of the non-periodic flow state at $(Ha, Gr)=(40, 2\times 10^7)$, which was started from a small random perturbation, see the red curve in figure 15. Data are taken at $t=966$. Panels (a–c) to (j–l) show full $u_z$, full $\theta$, $u_z$ deviation and $\theta$ deviation, respectively.

5.1.3. The case $(Ha, Gr)=(30, 2\times 10^7)$

When $Ha$ is further decreased to 30, several different initial conditions are used for direct numerical simulations and the flow evolves into a fully turbulent state in all the cases. The turbulent flow field is visualized in figure 18. The first column shows an instantaneous $u_z$ field, and the second column shows the corresponding temperature $\theta$ field. One can see that, although the turbulent $u_z$ fluctuations (turbulent fluctuation refers to the deviation from the turbulent mean flow, where the turbulent mean flow refers to the flow averaged in time and streamwise direction) seem to be homogeneous in the vertical $r$–$z$ cross-section, the turbulent temperature $\theta$ fluctuations seem to be significant only close to the bottom heated wall. The third column shows the deviation of the mean flow from the basic laminar flow. It can be seen that the mean streamwise velocity is faster than the basic flow mainly close to the top wall, is slower than the basic flow in the middle and only slightly deviates from the basic flow near the bottom wall. The mean temperature is higher than the basic laminar flow mainly near the bottom wall, and only slightly deviates from the basic laminar flow in the upper part of the pipe.

Figure 18. Visualization of the fully turbulent flow field at $(Ha, Gr)=(30, 2\times 10^7)$. Panels (a–c) show the full $u_z$ in the $r$–$\beta$ cross-section (a), in the vertical $r$–$z$ cross-section (b) and the turbulent fluctuations of $u_z$ in the vertical $r$–$z$ cross-section (c). Panels (d–f) show the full $\theta$ field in the same cross-sections. Panels (g,h) shows the deviation of the turbulent mean of $u_z$ and $\theta$ with respect to their basic laminar counterparts, respectively.

5.2. High-$Ha$ branch

Within the unstable region of mode I at large $Ha$, as seen in figure 13, three Hartmann numbers $Ha=150$, $180$ and $306$ with a fixed Grashof number $Gr=8.298\times 10^7$ are considered to investigate the nonlinear flow states. Obviously, nonlinear flow states are responsible for the low-frequency high-amplitude fluctuations of temperature appearing in the experiment of Genin et al. (Reference Genin, Zhilin, Ivochkin, Razuvanov, Belyaev, Listratov and Sviridov2011). In order to explain that the high-amplitude fluctuations originally come from the global instability mode, it is necessary to compare the nonlinear flow states with the global unstable eigenmode with respect to the spatial structure of the flow field.

5.2.1. The case $(Ha,Gr)=(150, 8.298\times 10^7)$

This set of parameters is close to the linear stability boundary, and the saturated nonlinear flow state exhibits a nonlinear travelling wave, as shown in figure 19. From the second column of this figure, the amplitude of the deviation $u_z$ is relatively small and thus indicates that the nonlinear flow field is only slightly deviated from the basic laminar flow. Comparing the deviation of $u_z$ with the most unstable linear eigenmode (mode I) in all cross-sections, as shown in the second and third columns, one can see that their spatial distributions are very similar. Therefore, the saturated nonlinear flow is mainly dominated by the most unstable eigenmode and the nonlinearity is too weak to change the spatial structure significantly. This observation is similar to the case with $(Ha,Gr)=(45, 2\times 10^7)$, which is close to the linear stability boundary curves of the low-$Ha$ branch. However, noticeable differences in the flow field from the case with $(Ha,Gr)=(45, 2\times 10^7)$ can be observed. Firstly, the dominant flow structures of the large-$Ha$ case have a much larger streamwise wavenumber, i.e. smaller streamwise wavelength. Secondly, the flow structures in the $r$–$\beta$ cross-section show much simpler symmetrical structures, which are nearly aligned with the magnetic field. Thirdly, the flow structures extend along the whole horizontal pipe cross-section, rather than being localized in a narrow region around the vertical $r$–$z$ cross-section as in the case with $(Ha,Gr)=(45, 2\times 10^7)$.

Figure 19. Visualization of the streamwise velocity field at $(Ha, Gr)=(150, 8.298\times 10^7)$. Panels (a–c) to (g–i) show the full $u_z$, $u_z$ deviation and $u_z$ of the most unstable eigenmode. From (a,d,g) to (c, f,i), $r$–$\beta$, vertical $r$–$z$, and horizontal $r$–$z$ cross-sections.

5.2.2. The case $(Ha,Gr)=(180, 8.298\times 10^7)$

The case with $Ha=180$ is farther from the linear stability boundary compared with the $Ha=150$ case. The simulation is started with small random perturbations, and strong temporal oscillations in $KE_{3D}$ are observed when the flow develops into a nonlinear state, as shown in figure 20. The flow fields at three time instants between the trough and peak of an oscillation (see the symbols in figure 20) are visualized in figure 21. While the high-amplitude oscillation of $KE_{3D}$ is temporally quasi-periodic, the spatial structure of flow flied is also quasi-periodic, as shown in the second row for $u_z$ deviation. The most unstable linear eigenmode is visualized in the rightmost column for comparison. It can be seen that the spatial structure of the flow at the trough of the oscillation is similar to the linear eigenmode, whereas it deviates noticeably from the linear eigenmode at the other two time instants, especially at the peak of the oscillation. Besides, the dominant streamwise wavelength of the quasi-periodic structures seems to slightly differ from that of the most unstable eigenmode. It can be considered that the quasi-periodic spatio-temporal structure results from nonlinear modulations of the linear global eigenmode and may be described by a weak nonlinear analysis. Compared with the $Ha=150$ case, the flow structures become more uniform along the direction of the magnetic field due to the larger Hartmann number.

Figure 20. The value of $KE_{3D}$ of the case at $(Ha, Gr)=(180, 8.298\times 10^7)$. The symbols mark three time instants at which the flow is visualized in figure 21.

Figure 21. Panels (a–c), (d–f) and (g–i) show the visualization of the streamwise velocity field at the three time instants marked in figure 20. Panels ( j–l) shows the velocity field of the most unstable linear eigenmode in the pipe. From (a,d,g,j) to (c, f,i,l) are $r$–$\beta$, vertical $r$–$z$ and horizontal $r$–$z$ cross-sections. In panels (a–l), only $u_z$ deviation is plotted.

5.2.3. The case $(Ha,Gr)=(306, 8.298\times 10^7)$

Compared with the $(Ha, Gr)=(180, 8.298\times 10^7)$ case as seen in figure 21 and figure 22, the flow for this case shows a much stronger streamwise modulation such that the velocity fluctuations nearly form localized clusters interspersed with quiescent flow regions. Inside the clusters, the flow shows some similarities to the flow at the peak of the oscillation for the $(Ha, Gr)=(180, 8.298\times 10^7)$ case, as shown in the third columns of both figures. However, the flow field does not oscillate in time as in the $Ha=180$ case. Moreover, the velocity and temperature structures are nearly uniform along the magnetic field.

Figure 22. Visualization of the streamwise velocity and temperature at $(Ha, Gr)=(306, 8.298\times 10^7)$. Panels (a–c) to (j–l) show the full $u_z$, full $\theta$, $u_z$ deviation and $\theta$ deviation, respectively. From (a,d,g,j) to (c–l) are $r$–$\beta$, vertical $r$–$z$ and horizontal $r$–$z$ cross-sections.

The most unstable linear global mode for this case is plotted in figure 23 to compare with the deviations from the basic flow in the nonlinear state, as seen from the third and fourth columns of figure 22. It can be seen that the linear flow structures are also nearly uniform along the magnetic field. However, there are noticeable differences in the distributions of streamwise velocity and temperature in the vertical $r$–$z$ plane. From the fourth column in figure 22 and figure 23(e), the temperature fluctuations are mainly located close to the centreline of the vertical $r$–$z$ plane in the linear mode, whereas they are mainly located close to the top and bottom pipe walls for the nonlinear state. Besides, in the linear case, the high and low temperature regions are arranged alternately along the pipe axis, whereas for the nonlinear case, the temperature in the lower half of the pipe is always lower than that of the basic laminar flow while is always higher than the latter in the upper half of the pipe. These obvious differences of the flow field structure indicate strong nonlinear effects.

Figure 23. The most unstable mode in the pipe shown in figure 22 at $(Ha, Gr)=(306, 8.298\times 10^7)$. (a–c) The streamwise velocity in the $r$–$\beta$, vertical $r$–$z$ and horizontal $r$–$z$ cross-sections. (d–f) Temperature in the $r$–$\beta$, vertical $r$–$z$ and horizontal $r$–$z$ cross-sections.

This case has been studied by Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013) also, and the authors reported nonlinear flow structures in the form of convection roll cells. They concluded that the flow structure of the nonlinear state is very similar to that of the linear unstable mode. However, as explained above, the structure of the fully developed nonlinear state greatly deviates from that of the linear mode, although the flow still forms convection roll-cell structures. The principal reason for the difference is that the setting of their numerical simulations is different from ours. They adopted a computational domain of 50 pipe diameters with only a part (approximately 40 diameters) subject to a uniform bottom heating and transverse magnetic field, without a periodic boundary condition in the streamwise direction, in order to mimic the experiments of Genin et al. (Reference Genin, Zhilin, Ivochkin, Razuvanov, Belyaev, Listratov and Sviridov2011). Therefore, what they obtained is a nonlinear flow developing from linear instability instead of a fully developed nonlinear state. Our simulations adopt a much shorter ($4{\rm \pi}$ diameters) periodic pipe but with a longer evolution time for the flow, and the target is the fully developed nonlinear flow state, which has not been reached in the set-up of Zikanov et al. (Reference Zikanov, Listratov and Sviridov2013).