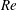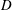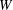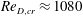1 Introduction
A rectangular finite-span open cavity has been used extensively as a simplified model to understand flow in aircraft bays. Despite the apparent simplicity of the geometry, a multitude of physical phenomena arise, involving the shear layer emanating from the upstream cavity lip and its interaction with the downstream cavity corner, the boundary layers on the cavity walls, shock waves and expansion waves potentially existing at appropriate flow regimes, and acoustic waves generated at the cavity and propagating at long distances from it. From an engineering point of view, either of these aspects in isolation or their interaction can be seen at distinct flow regimes to affect noise emission from the cavity, structural integrity of landing gears, and safe release of stores.
Extensive research efforts over more than half a century have employed experimentation, numerical simulation and linear instability analysis in order to understand and control cavity flow physics. Table 1 summarizes a representative list of studies which have, at least partially, focused on flow instability in open cavities. While most practical applications use the full (three-dimensional, rectangular, finite-span) geometry, linear instability analyses of cavity flows to date have resorted to additional assumptions which make the resulting theoretical problem tractable. Most often spanwise flow homogeneity has been assumed, or flow over a two-dimensional cavity has been considered. The present work employs for the first time the theoretical TriGlobal instability analysis framework, which is appropriate for finite-span open cavities, as will be discussed shortly.
Table 1. A representative list of works describing linear instabilities in rectangular open cavity flows, using linear and nonlinear instability analysis, simulations and experiments;
$ax$
denotes axisymmetric geometry and
$sh$
indicates three-dimensional cavity in which spanwise-homogeneous flow is assumed.
$\mathit{Re}$
is based on
$D$
.
Research into open cavity flows commenced in the 1950s (Krishnamurty Reference Krishnamurty1955; Roshko Reference Roshko1955) and has continued incessantly since. In an early significant contribution, Rossiter (Reference Rossiter1964) described a flow-acoustic resonance mechanism involving the interaction of the shear layer with the downstream cavity corner and derived a semi-empirical formula to predict the resonance frequencies, a work that has been extended by a number of authors since (e.g. Alvarez, Kerschen & Tumin Reference Alvarez, Kerschen and Tumin2004). Sarohia (Reference Sarohia1975, Reference Sarohia1977) performed experiments and inviscid local linear instability analysis of laminar flow in a shallow axisymmetric cavity geometry and found that a large lateral motion of the shear layer occurs near the downstream lip. This three-dimensional motion results in a periodic shedding of vortices at a frequency of cavity oscillation different from those predicted by the Rossiter frequencies. In their classic experiment, Gharib & Roshko (Reference Gharib and Roshko1987) also employed the axisymmetric cavity geometry and described a flow behaviour, termed wake mode, which was found to be qualitatively distinct from that described by the quasi-parallel shear layer emanating from the upstream cavity lip. Rowley et al. (Reference Rowley, Colonuis and Basu2002), in their two-dimensional direct numerical simulations (DNS), described both the shear-layer instabilities and those of the bluff-body-like wake mode, and associated the latter with absolute instability in the sense of Huerre & Monkewitz (Reference Huerre and Monkewitz1990), but did not employ the latter theory, applicable to one-dimensional base flow profiles, to describe the wake mode physics.
The linear instability analysis of Brés & Colonius (Reference Brés and Colonius2008) employed modal BiGlobal theory to reveal a centrifugal instability mechanism associated with the main recirculation eddy inside the cavity, which was responsible for the loss of stability of two-dimensional cavity flows to three-dimensional instabilities. The frequency of this centrifugal instability, the characteristics of which were documented for a wide range of subsonic Mach numbers, was found to be one order of magnitude lower than that of the shear-layer mode. The periodic spanwise structure formation predicted in the analysis was found to be in good agreement with experimental observations in the same geometry (Faure et al. Reference Faure, Adrianos, Lusseyran and Pastur2007, Reference Faure, Pastur, Lusseyran, Fraigneau and Bisch2009). Meseguer et al. (Reference Meseguer, de Vicente, Valero and Theofilis2014) and Citro et al. (Reference Citro, Brandt and Luchini2015) have focused on the incompressible regime of spanwise-homogeneous flow and presented detailed linear BiGlobal instability analyses of the centrifugal linear instability mechanism; the latter work also discussed the means for theoretically founded control of this instability mechanism. Yamouni et al. (Reference Yamouni, Sipp and Jacquin2013) revisited compressible flow over a rectangular open cavity and connected the global modes identified in their analysis with those predicted by the earlier cavity acoustics theories.
Experimentally, vortex shedding phenomena with a lateral motion downstream of the cavity were observed in a series of experiments performed in an axisymmetric cavity by Zhang & Naguib (Reference Zhang and Naguib2008) and a wall-bounded version of the same geometry by Zhang & Naguib (Reference Zhang and Naguib2011). The detected frequencies were consistent with those found by Sarohia (Reference Sarohia1977) but different from those predicted by the Rossiter theory. In this context, the numerical experiments of Yao et al. (Reference Yao, Cooper and Raghunathan2004) on unsteady incompressible three-dimensional cavity flow indicated that, at sufficiently high Reynolds number, both three-dimensional centrifugal modes and shear-layer modes may co-exist and interact. In an analogous vein, the experimental work of George et al. (Reference George, Ukeiley, Cattafesta and Taira2015) employed stereo particle image velocimetry (PIV) measurements to show that the effect of the sidewalls in the cavity flow is also relevant; their experiments revealed that the frequency of the dominant Rossiter mode varies when comparing different spanwise aspect ratio cavities, with and without lateral walls. The experiments of Ashcroft & Zhang (Reference Ashcroft and Zhang2005) employed PIV measurements to analyse turbulent flow over a large-width cavity and documented the presence of shear-layer instabilities in turbulent flow. Özsoy et al. (Reference Özsoy, Rambaud, Stitou and Riethmuller2005) also experimented with turbulent flow and described vortex motions inside the cavity. Crook, Kelso & Drobik (Reference Crook, Kelso, Drobik, Jacobs, Mclntyre and Cleary2007), Crook et al. (Reference Crook, Lau and Kelso2013) performed experiments with the full three-dimensional geometry and postulated that a single vortex located near the cavity centreline was responsible for asymmetries observed in the cavity flow. The observed asymmetry in the time-mean flow was due to the asymmetries in the instantaneous flow field, which switched between two extremes at low frequency. These authors associated this motion with centrifugal instability, but with a more three-dimensional complex pattern. De Vicente et al. (Reference De Vicente, Basley, Meseguer, Soria and Theofilis2014) further described the centrifugal instability in a combined theoretical and experimental work, while very recently Douay et al. (Reference Douay, Pastur and Lusseyran2016) have performed experimental work exclusively dedicated to the description of this mechanism. Large-scale simulations have employed DNS to fully resolve the two-dimensional (Sun et al. Reference Sun, Nair, Taira, Cattafesta, Ukeiley and Brés2014) or three-dimensional spanwise-homogeneous (Zhang et al. Reference Zhang, Sun, Arora, Cattafesta, Taira and Ukeiley2015) and finite-span cavity (Yao et al. Reference Yao, Cooper and Raghunathan2004), as well as large eddy simulation for the latter geometry (Forestier et al. Reference Forestier, Jacquin and Geffroy2003; Larchevêque et al. Reference Larchevêque, Sagaut, Lê and Comte2004, Reference Larchevêque, Sagaut and Labbé2007; Nayyar, Barakos & Badcock Reference Nayyar, Barakos and Badcock2007). Useful as they may be in the identification of physical mechanisms, large-scale simulations are hardly appropriate for parametric studies of the dependence of instability characteristics on geometric or flow parameters. A full discussion of the intense efforts to control cavity flow, also by exploiting the hitherto understood linear instability mechanisms, may be found in the excellent reviews of Cattafesta et al. (Reference Cattafesta, Song, William, Rowley and Alvi2008) and the related work on actuators of Cattafesta & Sheplak (Reference Cattafesta and Sheplak2011).
Despite this intense activity, to date the question of the origins of laminar–turbulent transition in the cavity model closest mimicking the desired application, namely a three-dimensional, rectangular, finite-span open cavity, is still open. Evidence does exist in the literature to suggest that the lateral walls have a profound influence on the flow features, and hence on their instability modes. Motivated by the fact that all linear instability work on open cavities has been performed either in a local framework, or assuming flow homogeneity along the span, the present work employs for the first time the TriGlobal modal analysis framework (Theofilis Reference Theofilis2003) appropriate for rectangular finite-span open cavities.
Section 2 defines the geometric and flow parameters considered. The cavity geometry employed by Crook et al. (Reference Crook, Lau and Kelso2013) and others in their experiments is chosen in order to facilitate comparisons, albeit qualitative on account of the lower Reynolds numbers at which instabilities have been identified; flow topology is used to relate the two sets of results. Three-dimensional DNS is performed in § 3.1 in order to obtain the base flows to be analysed, either by time-marching the full equations of motion until convergence in the subcritical regime, or by employing a selective frequency damping (SFD) technique in order to obtain steady unstable three-dimensional flows beyond the first bifurcation. Linear instability analysis results are presented in § 3.2 and their relation to those obtained by assuming spanwise-homogeneous flow is discussed in § 3.3. Topological reconstruction of the main flow features is used to provide a qualitative comparison of the present theoretical results with the available experimental results. A short discussion in § 4 closes the present contribution.
2 Problem formulation
A sketch of the rectangular finite-span open cavity flow configuration walls is shown in figure 1. The cavity geometry is characterized by a length
$L$
to depth
$D$
to width
$W$
ratios of
$L$
:
$W$
:
$D$
$=$
6 : 2 : 1. A Cartesian coordinate system with
$(x,y,z)$
the streamwise, wall-normal and spanwise direction, respectively, is considered and the origin
$(0,0,0)$
is fixed at the upstream left corner of the cavity. The velocity vector
$\boldsymbol{u}(x,y,z,t)$
comprises the corresponding Cartesian components
$(u,v,w)^{\text{T}}$
, all of which are inhomogeneous functions of the three spatial coordinates and time. The length, height and width of the computational domain are denoted by
$L_{x}$
,
$L_{y}$
and
$L_{z}$
, respectively. The domain boundaries
$\mathscr{D}_{in},\mathscr{D}_{w},\mathscr{D}_{f},\mathscr{D}_{out}$
and
$\mathscr{D}_{fs}$
denote inflow, wall, far-field, outflow and side wall boundaries, respectively. The flow is governed by three-dimensional incompressible Navier–Stokes and continuity equations, and the Reynolds number is based on the cavity depth
$\mathit{Re}=UD/{\it\nu}$
, where
$U=1$
is the streamwise velocity in the far field and
${\it\nu}$
is the kinematic viscosity. A laminar Blasius boundary layer is imposed at the inflow boundary and the flow parameters are chosen such that no boundary layer instabilities develop prior to the upstream cavity lip. The parameter ratio of cavity length to initial boundary layer momentum thickness,
$L/{\it\theta}$
, boundary layer displacement thickness
${\it\delta}^{\ast }$
and displacement thickness Reynolds number
$Re_{{\it\delta}^{\ast }}=U{\it\delta}^{\ast }/{\it\nu}$
are fixed at the values listed in table 2.
Figure 1. Configuration of the three-dimensional open cavity.
Table 2. Summary of the flow parameters considered in the analysis. Subscript 0 refers to conditions at the upstream edge of the cavity.
Direct numerical simulations are performed with the spectral element code Nek5000 (Fischer & Ronquist Reference Fischer and Ronquist1994). The boundary conditions used to obtain the solutions analysed are homogeneous Dirichlet on the wall boundary
$\mathscr{D}_{w}$
,
$(u,v,w)=(u_{B},v_{B},0)$
at the inflow boundary
$\mathscr{D}_{in}$
,
$(u,\partial v/\partial n,w)=(U,0,0)$
on the far-field boundary
$\mathscr{D}_{f}$
,
$(\partial u/\partial n,\partial v/\partial n,w)=\mathbf{0}$
on the lateral boundaries
$\mathscr{D}_{fs}$
and
$(p-(1/\mathit{Re})\boldsymbol{{\rm\nabla}}\boldsymbol{u})\boldsymbol{\cdot }\boldsymbol{n}=0$
on the outflow boundary
$\mathscr{D}_{out}$
. The subscript
$B$
denotes Blasius boundary layer profile. The computational domain above the cavity is initialized with an incompressible Blasius boundary layer profile, while the flow inside the cavity is initially taken to be at rest.
The linear instability of the flow to small-amplitude perturbations has been analysed using a modal TriGlobal approach (Theofilis Reference Theofilis2003, Reference Theofilis2011), following which flow is decomposed into a steady base flow
$\bar{\boldsymbol{u}}$
and a small amplitude time-varying three-dimensional perturbation
$\hat{\boldsymbol{u}}$
according to
$$\begin{eqnarray}\boldsymbol{u}(x,y,z,t)=\bar{\boldsymbol{u}}(x,y,z)+{\it\epsilon}\hat{\boldsymbol{u}}(x,y,z)\text{e}^{{\it\lambda}t}+\text{c.c.}\end{eqnarray}$$
Here
${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$
, where
${\it\lambda}_{r}$
denotes the temporal amplification/damping rate of the perturbations,
${\it\lambda}_{i}$
is the perturbation frequency, c.c. denotes the complex conjugate and
${\it\epsilon}\ll 1$
. Introduction of this decomposition into the equations of motion and linearization yields the linearized Navier–Stokes equations (LNSE), which can be recast as the three-dimensional eigenvalue problem
$$\begin{eqnarray}\boldsymbol{A}\hat{\boldsymbol{u}}={\it\lambda}\hat{\boldsymbol{u}},\end{eqnarray}$$
at
$O({\it\epsilon})$
, in which the operator
$\boldsymbol{A}$
is an abbreviation for the Jacobian. The boundary conditions closing (2.2) are homogeneous Dirichlet on all perturbation velocity components on
$\mathscr{D}_{in}$
and
$\mathscr{D}_{w}$
alongside
$(\hat{u} ,\partial \hat{v}/\partial n,{\hat{w}})=\mathbf{0}$
on
$\mathscr{D}_{f}$
,
$(\partial \hat{u} /\partial n,\partial \hat{v}/\partial n,{\hat{w}})=\mathbf{0}$
on
$\mathscr{D}_{fs}$
and
$(\hat{p}-(1/\mathit{Re})\boldsymbol{{\rm\nabla}}\hat{\boldsymbol{u}})\boldsymbol{\cdot }\boldsymbol{n}=0$
on
$\mathscr{D}_{out}$
. The eigenvalue problem (2.2) is solved for the recovery of
${\it\lambda}$
and
$\hat{\boldsymbol{u}}$
using the time-stepping methods provided in Nek5000 (Peplinski et al.
Reference Peplinski, Schlatter, Fischer and Henningson2014).
For comparison purposes with the more commonly employed BiGlobal linear modal analysis framework for the analysis of open cavity flow, the related Ansatz is also presented here. In the case of spanwise homogeneous base flow, linear global modal perturbations satisfy the expansion
$$\begin{eqnarray}\boldsymbol{u}(x,y,z,t)=\bar{\boldsymbol{u}}(x,y)+{\it\epsilon}\hat{\boldsymbol{u}_{\mathbf{2}\boldsymbol{d}}}(x,y)\text{e}^{\text{i}({\it\beta}z+{\it\lambda}_{i}t)}\text{e}^{{\it\lambda}_{r}t}+\text{c.c.}\end{eqnarray}$$
The eigenvalue problem resulting from substituting (2.3) into the LNSE has also been solved here and results will be discussed in the next section. In the present work the BiGlobal eigenvalue problem is also solved by a time-stepping approach, in a three-dimensional domain in which the base flow is uniform along
$z$
. Periodic boundary conditions are imposed along the spanwise spatial direction, which, for a given wavenumber of interest,
${\it\beta}$
, is taken to have a length of
$L_{z}=2{\rm\pi}/{\it\beta}$
. Consequently, modes corresponding to
${\it\beta}=0$
or multiples of the imposed
${\it\beta}$
may appear in the results.
3 Results
3.1 Base flow
At the set of flow parameters chosen our first concern has been to establish independence of the steady base flows analysed from the choice of size of computational domain and polynomial order used to resolve the base state and its gradients. As regards the extent of the domain, it was found that
$L_{x}=13$
,
$L_{y}=5$
and
$L_{z}=4$
are the lowest values in the three spatial directions which ensure that the base state obtained in the cavity is independent of the lateral, top and downstream boundary locations.
Once the minimum domain size has been established, the genbox utility of nek5000 has been used to create a mesh comprising a total of 9696 elements. This has been kept constant in the subsequent computations, while the polynomial order has been varied between
$p=5$
, 7 and 9, until convergence of the vorticity components at randomly chosen locations within the domain was obtained; details may be found in Liu (Reference Liu2016). In order to maintain the computing cost at a minimum while convergence is ensured,
$p=7$
has been selected for the computations that follow.
Preliminary work on the same geometry and flow conditions has identified the critical Reynolds number at
$\mathit{Re}\approx 1100$
(Liu, Gómez & Theofilis Reference Liu, Gómez and Theofilis2015). Below this value direct DNS have been performed until convergence to a steady state has been reached, while above this value the selective frequency damping (SFD) algorithm (Åkervik et al.
Reference Åkervik, Brandt, Henningson and Hœpffner2006), as implemented in the nek5000 code, has been used to obtain steady unstable three-dimensional flows that will subsequently be analysed. It should be noted in this context that the critical Reynolds number of an
$L$
:
$D$
$=$
6 : 1 cavity, in which spanwise-homogeneous flow is considered, is
$\mathit{Re}\approx 790$
(Sun et al.
Reference Sun, Nair, Taira, Cattafesta, Ukeiley and Brés2014), as extrapolated from the results of these authors at the limit Mach number
$M\rightarrow 0$
, a point which will be discussed further in what follows.
Figure 2(a) presents DNS results at
$\mathit{Re}=1050$
and 1100. Shown is the perturbation energy
${\rm\Delta}E_{k}=|E_{k}(t)-\bar{E}_{k}|$
, where
$E_{k}=\int _{{\it\Omega}}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}{\it\Omega}$
and
$\bar{E}_{k}$
is the solution at convergence. At
$\mathit{Re}=1050$
, a linearly decaying signal is observed, which results in a steady state being obtained at convergence. By contrast, at
$\mathit{Re}=1100$
the flow attains a saturated state in which both a low-frequency and a high-frequency oscillation are visible. Fourier transforming the signal, two frequencies may be identified,
$St={\it\lambda}_{i}D/U\approx 0.004$
and
$St\approx 0.23$
, as shown in figure 2(b). Isosurfaces
${\rm\Delta}w=\pm 0.008$
of the spanwise component of the fluctuating velocity vector are presented in figure 2(c) and will be discussed in what follows.
Figure 2. (a) Convergence history of
$\ln ({\rm\Delta}E_{k})$
against time. (b) Power spectral density of
$\ln ({\rm\Delta}E_{k})$
at
$\mathit{Re}=1100$
. (c) Spanwise fluctuation velocity component.
Table 3. The leading eigenvalues of the centrifugal steady (CS), centrifugal travelling (CT) and shear-layer travelling (ST) mode in the Reynolds number range examined.
3.2 Linear instability analysis
Results of TriGlobal linear modal instability analysis performed for the stationary base flows at
$\mathit{Re}=900$
, 950, 1000 and 1050, and the steady unstable base flow obtained with the SFD algorithm, using filter width
${\it\Delta}=2$
and force control parameter
${\it\chi}=0.8$
, at
$\mathit{Re}=1100$
are shown in table 3. At
$\mathit{Re}=900$
and 950, the leading global mode is stable and stationary, having a spatial structure reminiscent of the centrifugal instability known from analyses of the spanwise-homogeneous cavity, as has been discussed by Brés & Colonius (Reference Brés and Colonius2008) and earlier related work (e.g. Barkley, Gomez & Henderson Reference Barkley, Gomez and Henderson2002). This mode is referred to as the centrifugal stationary (CS) eigenmode. Additional modes having low frequencies and analogous spatial structure of the eigenfunctions, but being stronger damped, have also been recovered. The next of them is referred to as the centrifugal travelling (CT) mode. When the Reynolds number is increased to
$\mathit{Re}=1000$
, the leading mode is still the CS perturbation, however, besides this and the CT mode, a new global mode appears in the subset of the eigenspectrum recovered, having a relatively higher frequency than the CT mode,
$St\approx 0.23$
. Owing to the spatial structure of its amplitude function, this mode is termed the shear-layer travelling (ST) eigenmode. When the flow Reynolds number is further increased to
$\mathit{Re}=1050$
, the ST mode becomes the leading eigenvalue, its
${\it\lambda}_{r}$
exceeding the damping rates of both of the CT and CS instabilities, and finally becoming unstable, leading flow to a modally unstable state and ultimately to laminar–turbulent transition. The critical Reynolds number is obtained using linear interpolation of the damping/growth rate results of the ST mode either side of the
${\it\lambda}_{r}=0$
axis, as shown in figure 3. The zero crossing of the
${\it\lambda}_{r,ST}$
eigenvalue in this open cavity configuration is estimated to occur at
$\mathit{Re}_{cr}\approx 1080$
.
Figure 3. Dependence of
${\it\lambda}_{r}$
on
$Re$
for the cavity modes ST, CS and CT.
Figure 4. Spanwise amplitude functions of the leading cavity eigenmodes at
$\mathit{Re}=1050$
.
The spatial structure of the amplitude functions of global modes ST, CS and CT at
$\mathit{Re}=1050$
is illustrated in figure 4. Eigenfunctions are normalized with their respective
$\max |\hat{u} |$
values and isosurfaces
$\hat{u} =\pm 0.1$
,
$\hat{v},{\hat{w}}=\pm 0.05$
are shown. Visual inspection of the amplitude functions reveals that the velocity field of the ST mode corresponds to three-dimensional shedding oscillations near the downstream corner of the cavity, which exhibit typical shear-layer mode characteristics. However, the mode structure is different from an idealized spanwise-homogeneous Kelvin–Helmholtz perturbation, as it has a more complex spatial structure owing to the proximity of the lateral walls. Such behaviour can be interpreted as being qualitatively related to that found in earlier experimental work (Sarohia Reference Sarohia1977; Zhang & Naguib Reference Zhang and Naguib2008), according to which no vortex structures are to be observed in the neighbourhood of the leading edge of the cavity, while self-sustained oscillations are seen near the downstream cavity corner, caused by convective waves accompanied by a large lateral flapping motion. The present results identify the origin of the latter motion in the existence of the spanwise perturbation velocity
${\hat{w}}_{ST}$
of the ST mode.
The amplitude functions of the CS and CT modes, also shown in figure 4, are three-dimensional structures mainly confined inside the cavity, which peak in the neighbourhood of the three-dimensional base flow recirculation region of the cavity (Liu Reference Liu2016). The characteristic structure of the
${\hat{w}}$
perturbation component of both of these modes is reminiscent of the pattern found in the spanwise-homogeneous cavity (Brés & Colonius Reference Brés and Colonius2008), although in the latter case alternating maxima and minima of the spanwise perturbation velocity are repeated, in line with the imposed periodicity wavenumber. By contrast, in the present lateral-wall-bounded cavity, only one such structure, symmetric about the plane
$z=1$
, can be seen in the
${\hat{w}}$
amplitude functions of both of the CS and CT eigenmodes.
Returning to the ST mode, additional evidence regarding its potential relevance to transition in the open cavity at higher Reynolds numbers is provided by the fact that its frequency is found to remain approximately constant in the instability analysis at
$\mathit{Re}=1000$
and 1050, and is practically identical to the highest of the frequencies extracted by post-processing the DNS signal of nonlinearly saturated flow at
$\mathit{Re}=1100$
, shown in figure 2(b). In other words, the dynamics of flow at
$\mathit{Re}=1100$
appears to be dominated by the ST mode, a conjecture corroborated by the comparison of the spatial structure of the spanwise velocity component obtained in the DNS at
$\mathit{Re}=1100$
, shown in figure 2(c) with the amplitude function of the
${\hat{w}}_{ST}$
component of the perturbation velocity at
$\mathit{Re}=1050$
, shown in figure 4; the respective three-dimensional functions are practically indistinguishable.
Next, an attempt is made to relate the present finding of linear instability of the ST mode with the result of earlier experimental work of Crook et al. (Reference Crook, Kelso, Drobik, Jacobs, Mclntyre and Cleary2007) in which the exact same geometry has been utilized, albeit at an order-of-magnitude higher Reynolds number value. Topological bifurcations (Délery Reference Délery2013) exerted by the ST, CS and CT modes on the underlying steady three-dimensional base flow have been examined by Liu (Reference Liu2016), using a methodology analogous to that employed in earlier analyses of three-dimensional separated flows (Theofilis, Hein & Dallmann Reference Theofilis, Hein and Dallmann2000; Rodríguez & Theofilis Reference Rodríguez and Theofilis2011; Le Clainche et al.
Reference Le Clainche, Li, Theofilis and Soria2015). The near-wall-streamline pattern of a composite three-dimensional field is computed, in which the base state and its leading eigenmode are superposed linearly at an arbitrary but small amplitude parameter
${\it\epsilon}$
.
Figure 5. (a) Wall streamlines of the composite field constructed with the ST mode at
$\mathit{Re}=1050$
. (b) Streamlines depicted in the experiments of Crook et al. (Reference Crook, Kelso, Drobik, Jacobs, Mclntyre and Cleary2007) at
$\mathit{Re}\approx 1.66\times 10^{4}$
(reproduced with permission).
Figure 5(a) shows the wall-streamline result for the ST mode at an amplitude
${\it\epsilon}=0.1$
, while in (b) the experimental result of Crook et al. (Reference Crook, Kelso, Drobik, Jacobs, Mclntyre and Cleary2007) is presented. Compared with their counterparts constructed using the CS and CT modes (Liu Reference Liu2016), the wall-streamline pattern of the composite field corresponding to the ST mode is that which closest resembles the streamline curvature pattern seen in the experiment. The two vortices predicted experimentally to exist near the downstream corners of the cavity (cf. Crook et al.
Reference Crook, Lau and Kelso2013) can also be identified as greyscale pressure minimum contours in the theoretical results. At the higher Reynolds number of the experiment, additional eigenmodes may have become unstable and will modify the theoretical wall-streamline pattern, such that the qualitative agreement presented may still be fortuitous. Nevertheless, this result motivates renewed combined theoretical and experimental efforts at the exact same parameters, in order to further elucidate the laminar–turbulent transition scenario in this flow.
3.3 Instability in spanwise-homogeneous cavities
Instability analysis of flow over spanwise-homogeneous cavities has been performed in order to enable quantitative comparisons with the results of the lateral-wall-bounded open cavity discussed in the previous sections. Two spanwise-homogeneous configurations have been chosen, the square cavity discussed by Citro et al. (Reference Citro, Brandt and Luchini2015) at
$\mathit{Re}=4140$
,
${\it\beta}=22$
with which comparisons of the leading eigenmodes have been performed, as well as a cavity with aspect ratio
$L$
:
$D$
$=$
6 : 1 (Sun et al.
Reference Sun, Nair, Taira, Cattafesta, Ukeiley and Brés2014) in which analysis has been performed at
$\mathit{Re}=1000$
,
${\it\beta}={\rm\pi}$
. The conditions examined in both configurations correspond to linearly unstable flow; the eigenvalue spectrum is presented in the former work, while a critical Reynolds number
$502\leqslant \mathit{Re}\leqslant 634$
has been reported in the latter at Mach number
$M=0.1$
. In the present analysis, three-dimensional DNS making use of the SFD algorithm is used to obtain the basic states in both configurations.
The leading members of the eigenvalue spectrum obtained in the first configuration were found to be in good agreement with the results reproduced graphically from Citro et al. (Reference Citro, Brandt and Luchini2015) and shown alongside our results for both open cavity configurations in table 4 (Liu Reference Liu2016). Of particular interest in the present context is the second configuration, in which the spanwise periodicity length,
${\it\Lambda}=2{\rm\pi}/{\it\beta}=2$
, is identical to the width
$W=2$
of the wall-bounded cavity analysed in the earlier sections. Comparing the results of table 3 at
$\mathit{Re}=1000$
and those of table 4 for the
$L$
:
$D$
$=$
6 : 1 cavity, it is seen that the leading eigenvalues of the former cavity, pertinent to the (linearly stable) lateral-wall-bounded flow and those of the (linearly unstable) spanwise-homogeneous flow in the
$L$
:
$D$
$=$
6 : 1 cavity with periodicity length
${\it\Lambda}=2$
, bear no resemblance to each other. Besides the opposite signs of the amplification rates
${\it\lambda}_{r}$
of all three modes, none of the frequencies,
${\it\lambda}_{i}$
, in either set of results coincides with any mode pertaining to the other configuration. The stationary perturbation in the lateral-wall-bounded flow is altogether absent in the spanwise-homogeneous case. On the other hand, the fact that the frequencies of the travelling modes in the two configurations are of the same order of magnitude may be considered as being fortuitous.
Figure 6. Streamwise perturbation velocities of the leading three modes of a
$L$
:
$D$
$=$
6 : 1 spanwise-homogeneous cavity at
$\mathit{Re}=1000$
whose eigenvalues are shown in table 4.
Table 4. Leading eigenvalues in the spanwise-periodic open cavity
$L$
:
$D$
$=$
1 : 1 at
$\mathit{Re}=4140$
,
${\it\beta}=22$
and in the
$L$
:
$D$
$=$
6 : 1 cavity at
$\mathit{Re}=1000$
,
${\it\beta}={\rm\pi}$
.
The last statement is strengthened by reference to the amplitude functions obtained in BiGlobal linear modal analysis of the spanwise homogeneous open cavity flow. The streamwise perturbation velocity components of the three modes pertinent to the
$L$
:
$D$
$=$
6 : 1 cavity shown in table 4 are presented in figure 6 as isosurfaces
$\hat{u} =\pm 0.2$
, after being scaled with their respective
$\max (\hat{u} )$
values. The first two modes are seen to correspond to
${\it\beta}=0$
and be independent of the
$z$
-spatial direction, a fact that is certainly not true in any of the corresponding eigenfunctions shown in figure 4. Indeed, Modes I and II of the spanwise-homogeneous base flow are typical Rossiter modes further discussed by Liu (Reference Liu2016), while the well-defined spanwise-periodic structure of Mode III, known from earlier analyses and experiments to be related to centrifugal instability, is also different from the spatial structure of the amplitude functions of the CS or CT modes, in which the lateral-wall effect are evident.
4 Discussion and conclusions
Incompressible flow over a three-dimensional rectangular finite-span open cavity with
$L$
:
$W$
:
$D$
$=$
6 : 2 : 1 has been analysed with respect to its linear instability from subcritical to supercritical conditions. TriGlobal linear analysis has been employed for the first time to this class of flows, and the critical Reynolds number was determined to be
$\mathit{Re}_{cr}\sim 1080$
. The mode responsible for the first bifurcation from steady to unsteady flow that may lead to laminar–turbulent flow transition at higher Reynolds numbers is akin to the well-known shear-layer instability, although the lateral walls have a strong effect on the amplitude function. Direct numerical simulations at supercritical Reynolds numbers confirmed the existence and predominance of the shear-layer mode. Linear amplification of the leading shear-layer eigenmode gives rise to large lateral motions near the downstream cavity wall, while wall-streamline patterns corresponding to the linear superposition of the base flow and this mode are reminiscent of experimental results at one order of magnitude higher Reynolds number. Additional eigenmodes have been discovered, arising from centrifugal instability associated with the three-dimensional laminar separation bubble forming inside the cavity. The centrifugal instabilities are less damped than the shear-layer mode at lower Reynolds numbers, but have not become unstable in the Reynolds number range examined presently. Results of the present analysis have been compared with those pertinent to the well-understood spanwise homogeneous open cavity configuration having the same length-to-depth ratio. Strong differences were documented both in the critical Reynolds number values of the two configurations, as well as in the frequencies and spatial structure of the amplitude functions of all modes identified in the respective analyses, a result which underlines the need to employ modal TriGlobal linear stability theory in order to understand the origins of laminar–turbulent flow transition in three-dimensional open cavity geometries.
Acknowledgements
Q.L. gratefully acknowledges a research scholarship of the Chinese Scholarship Council and additional support from Nu-Modelling SL, in the framework of Grant FA9550-13-1-0059 of the Air Force Office of Scientific Research, Air Force Material Command, USAF and Subaward A12494 of Rensselaer Polytechnic Institute. The US Government is authorized to reproduce and distribute reprints for Governmental purpose not withstanding any copyright notation thereon.
