2.1.1. Unbounded models

The hydrodynamic lift force is an inertia-induced force that reduces to zero for rigid particles in Stokes flow (Bretherton Reference Bretherton1962). When inertia is present, a particle that either leads or lags the fluid flow can experience a lift force in unbounded linear shear flows (figure 1a). Accounting for this, Saffman (Reference Saffman1965) proposed an asymptotic expression for the lift force ($F_{L}$)

(2.1)\begin{align} {F_{L}^{{\ast}}} = \frac{F_{{L}} \rho}{\mu^2} ={-}\text{sgn}({\gamma^{{\ast}}})2.255\times \frac{9}{\rm \pi} { {Re_\gamma}}^{{1}/{2}}Re_{slip} + \text{sgn}({\gamma^{{\ast}}}) \frac{11}{8}Re_\gamma Re_{slip} - {\rm \pi}Re_\omega Re_{slip} \end{align}

valid for low slip, shear and rotational Reynolds numbers ($Re_{slip}, Re_\gamma , Re_\omega \ll 1$). Here,

(2.2a–c)\begin{equation} Re_{{slip}} = \frac{|u_{{slip}}|a}{\nu},\quad Re_{\gamma} = \frac{|\gamma| a^2}{\nu},\quad Re_{\omega} = \frac{\omega a^2}{\nu}, \end{equation}

and $u_{{slip}}$, $\omega$, $a$, $\mu$, $\nu$ and $\gamma$ are the particle slip velocity, particle angular rotation, particle radius, dynamic viscosity, fluid kinematic viscosity and fluid shear rate, respectively corresponding to the flow geometry of figure 1(a). Here, the particle slip velocity refers to the velocity of particle relative to the local undisturbed flow velocity ($u_{{slip}} = u_{{p}} - u_{{f}}$). The shear rate normalised by the slip velocity $\gamma ^{\ast } =\gamma a/u_{slip}$, depends on both the slip velocity and shear rate, with the direction of the lift force determined by the sign of $\gamma ^{\ast }$. Hence, in two-dimensional Cartesian flow system, Reference SaffmanSaffman's (Reference Saffman1965) first-order lift solution (first term of (2.1)) predicts a lift force in the direction of increasing fluid velocity ($+y$ direction) for a lagging particle in a positive shear ($u_{slip} < 0, \gamma > 0$) or for a leading particle in a negative shear ($u_{slip} > 0, \gamma < 0$), where $\gamma = {\textrm {d} u_{{f,x}}}/{\textrm {d}y}$, and the reader is refereed to figure 1(a) for coordinate directions. Hereafter, for convenience, any lift force acting in the positive $+y$ direction will be defined as positive. If both the slip and shear have the same sign (i.e. $\gamma ^{\ast } > 0$), the lift direction reverses and the Saffman (Reference Saffman1965) first-order lift solution predicts a negative lift force.

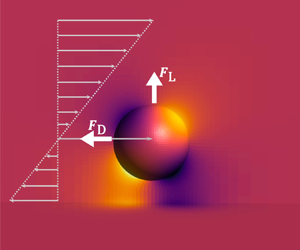
Figure 1. Schematic of a translating sphere of radius $a$ moving at velocity $u_{p}$ in (a) an unbounded linear shear flow (b) a wall-bounded quiescent flow and (c) a wall-bounded linear shear flow.

Saffman's model is an outer-region-based lift model, in which the boundary of the inner and outer region is located at $min(L_{{G}},L_{{S}})$ from the particle. Here, $L_{{S}}={\nu }/{|u_{slip}|}$ and $L_{{G}} = \sqrt {{\nu }/{|\gamma |}}$ are the Stokes and Saffman length scales, respectively. In addition to the small particle Reynolds number constraints, inertial effects due to shear must be higher than the inertial effects generated by the slip velocity ($\epsilon = \sqrt {\lvert {Re\gamma }\rvert }/Re_{slip} \gg 1$ or equivalently ${L_{G}} \ll {L_{S}}$) for the model to be valid.

The first and second terms on the right-hand side of (2.1) are both due to fluid slip-shear effects, while the third term, similar to the lift model of Reference Rubinow and KellerRubinow & Keller, is due to the particle rotation. Saffman (Reference Saffman1965) illustrated that the lift force due to rotation is less than that due to the shear by an order of magnitude, unless the rotational speed of a particle is much greater than the shear rate. Since the self-induced rotation of a freely rotating particle was shown to be small compared to the slip-shear lift for the condition $Re_\gamma \ll 1$, many studies neglect the third term when considering a freely translating and rotating particle. Additionally, the second term in (2.1) is less important than the first when $\epsilon \gg 1$ (McLaughlin Reference McLaughlin1991), and as a consequence, many outer-region studies focus solely on the first term of (2.1).

Relaxing the constrains of $\epsilon \gg 1$ in the Saffman (Reference Saffman1965) first-order solution and using the Oseen approximation, McLaughlin (Reference McLaughlin1991) and Asmolov (Reference Asmolov1990) independently proposed modified unbounded lift models in the form of,

(2.3)\begin{equation} {F_{L}^{{\ast}}} ={-}\text{sgn}({\gamma}^{{\ast}})\frac{9}{\rm \pi} Re_\gamma^{{1}/{2}}Re_{slip} J(\epsilon),\end{equation}

valid for non-rotating particles at $Re_{slip}, Re_\gamma \ll 1$. This force can be written in terms of a slip-shear lift force coefficient for unbounded flow, defined by

(2.4)\begin{equation} {C}^{ub}_{L,2} =\frac{F_{L}^{{\ast}}}{-\text{sgn}(\gamma^{{\ast}})Re_{slip}^2} = \frac{9}{\rm \pi} \epsilon J(\epsilon).\end{equation}

The function $J(\epsilon )$ needs to be evaluated analytically or numerically. Currently available expressions based on asymptotic solutions and empirical fitting functions for $J(\epsilon )$ are presented in table 1. These expressions, along with previous direct numerical simulation and experimental results, are plotted in figure 2. At the limit $\epsilon \rightarrow \infty$ (or equivalently at the limit $Re_\gamma \gg Re_{slip}$), $J(\epsilon )$ reduces to the Reference SaffmanSaffman's limit of 2.255, whereas $J(\epsilon )$ decreases to zero rapidly as $\epsilon$ decreases.

Figure 2. Comparison of $J(\epsilon )$ values from experimental and DNS data for $Re_{slip} <1$ with empirical and theoretical correlations. Asymptotic solution ($\circ$) and asymptotic limits (--------) by McLaughlin (Reference McLaughlin1991). DNS: Legendre & Magnaudet (Reference Legendre and Magnaudet1998) ($\square$, red), Cherukat, McLaughlin & Dandy (Reference Cherukat, McLaughlin and Dandy1999) ($\square$, light blue), Kurose & Komori (Reference Kurose and Komori1999) ($\square$, light green). Experiments: Cherukat, McLaughlin & Graham (Reference Cherukat, McLaughlin and Graham1994) (+, light grey), empirical fits by Mei (Reference Mei1992) (--------, blue), Shi & Rzehak (Reference Shi and Rzehak2019) (--------, Lime green) and Legendre & Magnaudet (Reference Legendre and Magnaudet1998) (--------, red).

Table 1. Correlations for $J(\epsilon )$.

In the McLaughlin (Reference McLaughlin1991) and Asmolov (Reference Asmolov1990) studies, the integral expression for $J(\epsilon )$ was evaluated numerically. In addition, McLaughlin (Reference McLaughlin1991) also provided two analytical solutions for $J(\epsilon )$ at the limits of $\epsilon \ll 1$ and $\epsilon \gg 1$ (see figure 2). The values obtained from numerical evaluations suggested a positive $J(\epsilon )$ for $\epsilon > 0.23$ and a negative $J(\epsilon )$ for $\epsilon < 0.23$. Based on Reference McLaughlinMcLaughlin's (Reference McLaughlin1991) theoretical results, specifically given for the range $0.1<\epsilon <20$, Mei (Reference Mei1992) proposed a fitting function for $J(\epsilon )$. In a similar vein, the same integral expression of $J(\epsilon )$ was re-evaluated numerically by Shi & Rzehak (Reference Shi and Rzehak2019) who proposed another fitting function to capture both negative and positive values accurately. Note, however, these asymptotic solutions derived for $Re_\gamma , Re_{slip} \ll 1$ may not be valid for larger Reynolds numbers, specifically for the ${O}(10^{-1})$ ranges relevant to this study.

Direct numerical simulation (DNS) studies, whereby the flow around an individual particle is simulated, provide better estimations of $J(\epsilon )$ for $Re_{slip}, Re_\gamma \lesssim 1$ in unbounded linear shear flows, as they do not rely on the Oseen approximation (Dandy & Dwyer Reference Dandy and Dwyer1990; Legendre & Magnaudet Reference Legendre and Magnaudet1998; Cherukat et al. Reference Cherukat, McLaughlin and Dandy1999; Kurose & Komori Reference Kurose and Komori1999). Dandy & Dwyer (Reference Dandy and Dwyer1990) performed the first DNS study of the flow around a rigid sphere in an unbounded linear shear flow. However, the values obtained for the lift at small Reynolds numbers were later shown by subsequent DNS studies to be significantly in error due to the small domain size (25 particle radii) employed (Legendre & Magnaudet Reference Legendre and Magnaudet1998; Cherukat et al. Reference Cherukat, McLaughlin and Dandy1999). Legendre & Magnaudet (Reference Legendre and Magnaudet1998) performed simulations for a clean spherical bubble using large domain sizes (100 particle radii and 200 particle radii, Shi & Rzehak Reference Shi and Rzehak2019). Note that these results for bubble simulations were used to interpret lift forces on rigid spheres by considering the $J(\epsilon )$ function which applies to both bubbles and rigid particles, as shown in Legendre & Magnaudet (Reference Legendre and Magnaudet1997). The numerical data and theoretical estimations from McLaughlin (Reference McLaughlin1991) were in good agreement for $\epsilon \geq 0.5$, however, the negative $J(\epsilon )$ values for $0<\epsilon <0.23$ predicted by the theoretical studies were not observed. Citing reasons for this discrepancy, Legendre & Magnaudet (Reference Legendre and Magnaudet1998), and later Takemura & Magnaudet (Reference Takemura and Magnaudet2009), explained that the theoretical integral expression obtained for $J(\epsilon )$ is based on the Oseen approximation, which is not sufficiently accurate to evaluate the small lift forces that exists at low shear rates. They illustrated that this approximation cannot capture the higher-order terms in the lift force expansion (i.e. second term in (2.1)) which are important when $\epsilon$ is very small ($Re_{slip} \gg \sqrt {Re_\gamma }$) (McLaughlin Reference McLaughlin1991; Legendre & Magnaudet Reference Legendre and Magnaudet1998). Comparing their numerical data with theoretical values, Legendre & Magnaudet (Reference Legendre and Magnaudet1998) suggested that the lower bound of validity in the asymptotic solution is $\epsilon \approx 0.7$. In the same study an empirical fit for $J(\epsilon )$ was suggested, based on their numerical results for $0.2 < \epsilon < 0.6$ at $Re_{slip} < 1$ and the McLaughlin (Reference McLaughlin1991) theoretical results for $\epsilon > 0.8$. The resulting correlation predicts a positive lift force for all $\epsilon$ values. Both Kurose & Komori (Reference Kurose and Komori1999) and Cherukat et al. (Reference Cherukat, McLaughlin and Dandy1999) performed DNSs specifically for a rigid sphere translating in unbounded linear shear flows. Cherukat et al. (Reference Cherukat, McLaughlin and Dandy1999) used large domains (75 and 105 particle radii) and tested for low slip and shear Reynolds number combinations ($0.01 < Re_{slip} < 1$, $0.01<Re_\gamma <0.025$). The computed $J(\epsilon )$ values were positive for all $\epsilon$ at $Re_{slip}, Re_\gamma < 1$, as illustrated in figure 2. However, the results for $\epsilon \geq 2$ deviated from other asymptotic predictions. The discrepancy has been explained as a domain truncation error (Cherukat et al. Reference Cherukat, McLaughlin and Dandy1999). Kurose & Komori (Reference Kurose and Komori1999) performed simulations for relatively large slip Reynolds numbers $0.25< Re_{slip} < 250$, using relatively small domain sizes (10, 20 particle radii), and found the computed $J(\epsilon )$ values agreed well with other numerical studies.

Experimentally, Cherukat et al. (Reference Cherukat, McLaughlin and Graham1994) investigated the variation of $J(\epsilon )$ at small $Re_\gamma$ and $Re_{slip}$ numbers in unbounded flows. The migration velocities of a small negatively buoyant particle sedimenting in a linear shear flow were measured. To allow comparison with theory, these migration velocities have been converted to $J(\epsilon )$ values using (2.3) and Stokes’ law, and the results are plotted in figure 2. As illustrated in the figure, the experimental values for $J(\epsilon )$ closely follow the asymptotic theories up to $\epsilon \sim 1$, but beyond this there is a difference between the two results. Cherukat et al. (Reference Cherukat, McLaughlin and Graham1994) explained that the inconsistencies between experimental and theoretical values in this region could be due to experimental errors in the measurements of low migration velocities at low $Re_{slip}$. Consistent with the DNS results, negative $J(\epsilon )$ values were not observed in any of these experiments, specifically for $\epsilon <0.23$. This again suggests that any analytical solution or empirical correlation based on Oseen's approximation are not accurate for low $\epsilon$.

For relatively large slip Reynolds numbers with weak shear, a significant change in the lift coefficient and the direction were observed numerically beyond a specific value of $Re_{slip}$ ($Re_{slip} >50$) (Kurose & Komori Reference Kurose and Komori1999; Bagchi & Balachandar Reference Bagchi and Balachandar2002). Accounting for these numerical results, Loth (Reference Loth2008) and recently Shi & Rzehak (Reference Shi and Rzehak2019) proposed correlations for lift force coefficient, ${C}^{ub}_{L,2}$, valid for $Re_{slip}>50$. Also, for the inviscid limit and weak shear ($Re_{slip} \rightarrow \infty$), Auton (Reference Auton1987) suggested a theoretical estimation for a rigid spherical particle's lift coefficient.

2.1.2. Wall-bounded models

In bounded flows (i.e. near a wall), particles moving at a finite slip velocity experience an additional lift force even in the absence of shear. This wall-slip lift is greatest near the wall and reduces rapidly to zero away from the wall. Note that while a particle slip velocity can be in any direction relative to a wall, in this study we only consider slip lift due to slip velocity in the direction parallel to a wall.

2.1.2.1 Outer region

The wall-slip lift for a spherical particle sedimenting in a quiescent fluid ($Re_\gamma = 0$) with a single wall located in the outer region ($l>L_{S}$) was first investigated by Vasseur & Cox (Reference Vasseur and Cox1977). Here, $l$ is the distance between the particle centre and the wall. Singular perturbation techniques were used to determine the migration velocity and the equivalent lift force was then calculated using Stokes’ law. The deduced lift force valid for $Re_{slip} \ll 1$ was given as

(2.9)\begin{equation} {F_{L}^{{\ast}}} = C_{L,3}^{wb,out}(l/L_{S})Re_{slip}^2 .\end{equation}

The integral expression for $C_{L,3}^{wb,out}$ was evaluated numerically as a function of separation distance normalised by the Stokes length $l/L_{S}$. In the same study, the asymptotic behaviour at small and large values of ${L}_{S}$ was obtained analytically considering the inner and outer boundary limits of the outer region ($l/L_{S} \ll 1$ and $l/L_{S} \gg 1$, respectively). Although a rotating sphere was originally considered, Vasseur & Cox (Reference Vasseur and Cox1977) illustrated that the calculated lift force is independent of rotation as long as the angular velocity is less than ${O}(Re_{slip})$ in the outer region. Hence, (2.9) is applicable for a non-rotating sphere as well. Several studies have developed empirical fitting correlations for $C_{L,3}^{wb,out}$ by solving the integral expression for $C_{L,3}^{wb,out}$ numerically (Takemura & Magnaudet Reference Takemura and Magnaudet2003; Takemura Reference Takemura2004; Shi & Rzehak Reference Shi and Rzehak2020). These expressions are listed in table 2, in addition to the analytical solutions obtained for the asymptotic limits, and the predictions of these correlations show that a leading or lagging particle in quiescent flows always moves away from the wall. Hence, the deduced lift coefficient $C_{L,3}^{wb,out}$ is positive irrespective of the slip velocity direction, but reduces to zero as $l/L_{S} \rightarrow \infty$. Vasseur & Cox (Reference Vasseur and Cox1977) and later Takemura (Reference Takemura2004) conducted experiments to measure the migration velocity of a rigid particle sedimenting in a quiescent flow. While the first study obtained migration velocities of a particle falling relatively far away from the wall, the latter study focused mainly on obtaining experimental results for the inner region. The experimental measurements of Vasseur & Cox (Reference Vasseur and Cox1977) obtained mainly for $l/L_{S} > 1$ agreed well with the outer-region-based $C_{L,3}^{wb,out}$ correlations. The presence of a wall also affects the slip-shear lift force acting on a particle in a linear shear flow. A non-rotating sphere in a single-wall-bounded linear shear flow with the wall lying in the outer region was first investigated by Drew (Reference Drew1988), and later by Asmolov (Reference Asmolov1989) and McLaughlin (Reference McLaughlin1993). The latter two studies used the method of matched asymptotic expansions, and considered a leading and a lagging particle in a positive shear field. These cases correspond to ${\gamma }^{\ast }>0$ and ${\gamma }^{\ast }<0$ respectively. In the outer region, the effect of rotation was shown to be less significant, and hence the developed models are applicable for both freely rotating or non-rotating particles. Drew (Reference Drew1988) considered the problem in the limit of $\epsilon \gg 1$ while McLaughlin (Reference McLaughlin1993) and Asmolov (Reference Asmolov1989) considered a range of $\epsilon$ values. Based on the Oseen approximation, an analytical solution for $l \gg L_{{G}}$ and $\epsilon \gg 1$ (but not necessarily $Re_{slip} = 0$) was also provided in the McLaughlin (Reference McLaughlin1993) study.

Table 2. Correlations for outer-region-based wall-slip lift coefficient $C_{L,3}^{wb,out}$.

For $Re_\gamma , Re_{slip} \ll 1$ and $l \gg min(L_{{G}},L_{{S}})$ (i.e. in the outer region) the wall-bounded slip lift force can be presented as,

(2.14)\begin{equation} {F_{L}^{{\ast}}} ={-} \text{sgn}({\gamma}^{{\ast}})C_{L,2}^{wb,out}Re_{slip}^2. \end{equation}

The numerical values obtained for $C_{L,2}^{wb,out}$ by solving Airy functions indicated that the unbounded slip-shear lift varies as $l/L_{G}$ changes (Asmolov Reference Asmolov1989; McLaughlin Reference McLaughlin1993). For $\epsilon \gg 1$, $C_{L,2}^{wb,out}$ monotonically reduced from the unbounded values to near zero values for small enough $l/L_{G}$, irrespective of the sign of ${\gamma }^{\ast }$. McLaughlin (Reference McLaughlin1993) showed that these near zero values are similar to the outer boundary values of the inner-region solutions of Cox & Hsu (Reference Cox and Hsu1977) when $l/L_{G} <1$ and $\epsilon > 1$. Based on the numerical data tabulated in McLaughlin (Reference McLaughlin1993), for both ${\gamma }^{\ast } > 0$ and ${\gamma }^{\ast } < 0$, and considering the asymptotic inner-region solution of Cox & Hsu (Reference Cox and Hsu1977) valid for $l < L_{G}$, both Takemura, Magnaudet & Dimitrakopoulos (Reference Takemura, Magnaudet and Dimitrakopoulos2009) and Shi & Rzehak (Reference Shi and Rzehak2020) proposed semi-empirical fits for $C_{L,2}^{wb,out}$ for $\epsilon > 1$ in the form of

(2.15)\begin{equation} C_{L,2}^{wb,out} = f(\epsilon, l/L_{G})C_{L,2}^{ub}.\end{equation}

Table 3 summarises the available theoretical and empirical correlations for $f(\epsilon , l/L_{G})$.

Table 3. Numerical correlations for $f(\epsilon , L_{G})$.

Noting that when shear is negligibly small ($\epsilon \rightarrow 0$, or $Re_\gamma \rightarrow 0$) the lift contribution should be entirely due to the disturbance produced by the wall and slip effects, several studies have attempted to combine (2.14) and (2.9) such that $\text {sgn}(\gamma ^{\ast })C_{L,2}^{wb,out}$ tends towards to $C_{L,3}^{wb,out}$ in the limit of $\epsilon \rightarrow 0$. Using (2.12) and (2.20) for $C_{L,3}^{wb,out}$ and $C_{L,2}^{wb,out}$ respectively, Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) combined these two coefficients using a fitting function ($\,f_{2}({\epsilon ,l/L_{S}})$) as

(2.16a)\begin{equation} F_{L}^{{\ast}} = \left(-\text{sgn}({\gamma}^{{\ast}})C_{L,2}^{wb,out} + f_2({\epsilon,l/L_{S}})C_{L,3}^{wb,out}\right)Re_{{slip}}^2, \end{equation}

where

(2.16b)\begin{equation} f_{2}({\epsilon,l/L_{S}}) = \exp{({-}0.22 \epsilon^{3.3} (l/L_{S})^{2.5})}, \end{equation}

(2.16a) can be expressed as a force coefficient,

(2.16c)\begin{equation} C_{L,23}^{{wb,out}} = \frac{F_{L}^{{\ast}}}{Re_{{slip}}^2} ={-}\text{sgn}({\gamma}^{{\ast}})C_{L,2}^{wb,out} + f_2({\epsilon,l/L_{S}})C_{L,3}^{wb,out}, \end{equation}

with the lift normalised by the slip Reynolds number. The outer-region-based lift model given by (2.16) performs well for small and intermediate $\epsilon \gtrsim 1$ (Takemura et al. Reference Takemura, Magnaudet and Dimitrakopoulos2009; Shi & Rzehak Reference Shi and Rzehak2020), however, it is worth noting that this model predicts a zero lift force in the absence of slip which is not the case for non-zero shear rates (Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020).

The lift force acting on a spherical particle translating with zero-slip velocity ($Re_{slip} =0$ or equivalently $\epsilon = \infty$) in the outer region of a positive shear flow has also been studied theoretically and numerically. Asymptotic studies for $Re_\gamma \ll 1$ (Asmolov Reference Asmolov1999) and DNS studies for $10^{-3}< Re_\gamma < 10^{-1}$ (Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) find a lift force that decays rapidly to zero with increasing separation distance. Based on numerical lift results, Ekanayake et al. (Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) proposed an outer-region-based lift model accounting for both shear and wall effects

(2.17a)\begin{equation} {F_{L}^{{\ast}}} = C_{L,1}^{wb,out}(l/L_{G})Re_\gamma^2, \end{equation}

where

(2.17b)\begin{equation} C_{L,1}^{wb,out} = 2.231 \exp({({-}0.1054(l/L_{G})^2-0.3859(l/L_{G}))}), \end{equation}

for non-rotating particles and

(2.17c)\begin{equation} C_{L,1}^{wb,out} = 1.982 \exp({({-}0.115(l/L_{G})^2-0.2771(l/L_{G}))}), \end{equation}

for freely rotating particles, with $C_{L,1}^{wb,out}$ approaching zero as $l/L_{G}$ increases. Similar to the slip-based lift coefficient ($C_{L,3}^{wb,out}$), the shear-based lift coefficient $C_{L,1}^{wb,out}$ remains positive for both negative and positive shear rates, favouring particle migration away from the wall.

2.1.2.2 Inner region

Inner-region-based models require a particle to be located close to the wall such that $l \ll$ $min(L_{{G}},L_{{S}})$ and $Re_{{slip}}, Re_{\gamma } \ll 1$ (Cox & Brenner Reference Cox and Brenner1968). In these models the lift force on both freely rotating and non-rotating particles is obtained by coupling the two flow disturbances that originate from particle slip and fluid shear in a nonlinear manner. These inner-region-based lift models present the lift as (Cherukat & McLaughlin Reference Cherukat and McLaughlin1994; Magnaudet, Takagi & Legendre Reference Magnaudet, Takagi and Legendre2003)

(2.22)\begin{equation} F_{L}^{{\ast}} = C_{L,1}^{wb,in}Re_{\gamma}^2+\text{sgn}(\gamma^\ast)C_{L,2}^{wb,in} Re_{\gamma}Re_{{slip}}+C_{L,3}^{wb,in}Re_{{slip}}^2, \end{equation}

where the three lift coefficients, $C_{L,1}^{wb,in},C_{L,2}^{wb,in}$ and $C_{L,3}^{wb,in}$ are functions of separation distance. The first and last terms on the right-hand side of (2.22) originate from the disturbance induced by the presence of the wall in a shear flow field and by the presence of the wall in quiescent flow, respectively. The corresponding lift coefficients $C_{L,1}^{wb,in}$ and $C_{L,3}^{wb,in}$ are therefore associated with a force in the absence of slip ($Re_{slip}=0$) and a force in the absence of shear ($Re_\gamma =0$), respectively. The second term depends on both the slip velocity and shear rate, and the corresponding coefficient $C_{L,2}^{{wb,in}}$ is associated with a force when both the slip and shear are of the same order of magnitude. The first and last terms in (2.22) produce forces directed away from the wall, promoting positive lift, whereas the lift force due to the second term depends on both slip and shear rate directions, with the direction of this force captured by the sign of $(\gamma ^*)$. The available correlations for $C_{L,2}^{wb,in}$ and $C_{L,3}^{wb,in}$ are summarised in table 4. Correlations available for $C_{L,1}^{wb,in}$ are tabulated in our previous study (Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) and hence not detailed further here.

Table 4. Slip-based lift coefficients ($C_{L,2}^{wb,in}$ and $C_{L,3}^{wb,in}$) of inner-region studies.

$^{a}$Minor corrections were provided by Lovalenti in the Appendix of Cherukat & McLaughlin (Reference Cherukat and McLaughlin1994)

In the theoretical context, Cox & Brenner (Reference Cox and Brenner1968) were the first to obtain an implicit expression for the lift forces in the inner region by using point force approximations at $l/a \gg 1$. Later, Cox & Hsu (Reference Cox and Hsu1977) simplified this and presented closure expressions for lift coefficients with the leading-order term proportional to ${l/a}$. The model is valid only when the separation distance is large compared to the sphere radius ($l/a \gg 1$). Accounting for the finite size of the particle, several other inner-region studies considered higher-order contributions to the flow disturbances, and proposed lift correlations that are valid for a particle almost in contact with the wall ($l/a \gtrsim 1$) (Leighton & Acrivos Reference Leighton and Acrivos1985; Cherukat & McLaughlin Reference Cherukat and McLaughlin1994; Krishnan & Leighton Reference Krishnan and Leighton1995; Magnaudet et al. Reference Magnaudet, Takagi and Legendre2003). Unlike for the outer-region models, rotation has a significant effect on lift coefficients within the inner region, particularly when the particle is close to the wall. Overall, as the inner-region models require a particle to be close to a wall, these models cannot be used to predict unbounded results as ${l/a}$ becomes large even at $Re_{{slip}}, Re_{\gamma } \ll 1$.

To summarise, the above analysis on existing lift force theories shows that all the presented lift models are limited to specific ranges of wall separation distance, fluid shear rate and particle slip velocity. For example, lift coefficients currently available for quiescent flows ($C_{L,3}$) are region specific (i.e. either inner region or outer region based) and do not account for any slip-based inertial corrections particular when a particle translates closer to a wall (i.e. towards and within the inner region). For linear shear flows, existing slip-shear-based lift coefficients ($C_{L,2}$) are also region specific and hence cannot capture the slip- or shear-based inertial dependence when a particle translates closer to a wall. The $C_{L,2}$ correlations that capture the inertial dependence of slip and shear are always limited to the systems where slip is stronger than shear, and thereby fail to capture the lift forces when shear is strong (i.e. freely translating neutrally buoyant particles in shear flows). Hence, a generalised lift model valid for arbitrary particle–wall separation distances is necessary to make accurate predictions of particle distributions in industrial applications where $Re_{{slip}},Re_\gamma <10^{-1}$.

2.2.1. Unbounded models

The drag force acting on a rigid sphere translating with a finite slip velocity in an unbounded quiescent flow was first examined by Stokes (Reference Stokes1851). The study only considered the inner region of the disturbed flow and assumed $Re_{slip} \ll 1$. The finite inertial effects in the outer region of the disturbed flow were later analysed by Oseen (Reference Oseen1910), who proposed a first-order slip-based inertial correction to the Stokes expression. Accounting for both inner and outer regions of the disturbed flow, a higher-order inertial correction for the drag force was suggested by Proudman & Pearson (Reference Proudman and Pearson1957), using a matched asymptotic method. The drag force predicted by Reference Proudman and PearsonProudman & Pearson's model reduces to Stokes’ expression or Oseen's drag results, depending on the magnitude of $Re_{slip}$. Of note, these theoretical models are strictly limited to $Re_{slip} \ll 1$ and their predictions rapidly deviate from the measured drag forces for $Re_{slip} > 1$. Therefore, for $Re_{slip} \gtrsim 1$, empirical inertial corrections based on experimental and numerical data are more commonly used to capture the drag force variation (Schiller Reference Schiller1933; Clift, Grace & Weber Reference Clift, Grace and Weber1978). The drag force ($F_{D}$) acting on a spherical particle with a finite slip in an unbounded flow is generally presented as

(2.30)\begin{equation} {{F}_{D}^\ast} = \frac{{F}_{D} \rho}{\mu^2} ={-} \text{sgn} (u_{slip})Re_{slip}C_{D,2}^{ub}(Re_{slip}), \end{equation}

where $C_{D,2}^{ub}$ is the unbounded drag coefficient. Various theoretical and empirical correlations for $C_{D,2}^{ub}$, particularly for $Re_{slip} \lesssim 10$, are listed in the table 5.

Table 5. Theoretical and empirical inertial corrections for $C_{D,2}^{ub}$.

In unbounded linear shear flows, the effect of shear on the drag force is extremely weak for small slip Reynolds numbers ($Re_{slip}\lesssim 1$) (Dandy & Dwyer Reference Dandy and Dwyer1990; Legendre & Magnaudet Reference Legendre and Magnaudet1998; Kurose & Komori Reference Kurose and Komori1999). However, for relatively large slip values ($Re_{slip} > 5$) and $Re_\gamma /Re_{slip} \sim {O}(1)$, a noticeable effect from shear on the drag force occurs (Kurose & Komori Reference Kurose and Komori1999). For these large slip velocities theoretical arguments predict the drag as (Legendre & Magnaudet Reference Legendre and Magnaudet1998)

(2.36)\begin{equation} {{F}_{D}^\ast} ={-}\text{sgn} (u_{slip})Re_{slip}C_{D,2}^{ub}(Re_{slip})[1+K_{0}(Re_\gamma/Re_{slip})^2]. \end{equation}

The numerical results of Kurose & Komori (Reference Kurose and Komori1999) suggested that $K_{0}$ is of the order of unity for $Re_{slip}) \sim {O}(1)$ and $K_{0} \simeq 0$ for $Re_{slip} \ll 1$.

2.2.2. Bounded models

The effect of walls on the drag force was first examined by Faxen (Reference Faxen1922) for a particle translating with a finite slip velocity parallel to a wall. The study considered a non-inertial ($Re_{slip} \ll 1$), quiescent flow ($Re_\gamma = 0$) with the walls located in the inner region of the disturbed flow of the particle. In Faxen's study, the unbounded drag model, (2.30) was modified to incorporate wall effects via (Happel & Brenner Reference Happel and Brenner1981)

(2.37)\begin{equation} {{F}_{D}^\ast} ={-}\text{sgn} (u_{slip})Re_{slip}[C_{D,2}^{ub}(Re_{slip})+C_{D,2}^{wb,in}(a/l)].\end{equation}

Thus, the net drag coefficient in a quiescent flow can be written as

(2.38)\begin{equation} C_{D,2} = \frac{{F}_{D}^\ast}{ -\text{sgn} (u_{slip})Re_{slip}} = C_{D,2}^{ub}+C_{D,2}^{wb,in}.\end{equation}

The wall-bounded drag coefficient derived by Faxen, $C_{D,2}^{wb,in}$ consists of higher-order terms of separation distance up to ${O}((a/l)^5)$ in the drag force expansion

(2.39)\begin{equation} \frac{C_{D,2}^{wb,in}}{6 {\rm \pi}} = \left[1-\frac{9}{16}\left(\frac{a}{l}\right)+ \frac{1}{8}\left(\frac{a}{l}\right)^3-\frac{45}{256}\left(\frac{a}{l}\right)^4- \frac{1}{16}\left(\frac{a}{l}\right)^5\right]^{{-}1} -1.\end{equation}

This correlation is in good agreement with experimental data up to $Re_{slip} = 0.1$ (Ambari, Gauthier & Guyon Reference Ambari, Gauthier and Guyon1984; Takemura Reference Takemura2004). Vasseur & Cox (Reference Vasseur and Cox1977) analysed the effects of walls located in the outer region of the flow on the drag force. The study considered a quiescent flow and used a method of matched asymptotic expansions together with the Oseen approximation. The integral expression obtained for the drag force by solving the outer-region velocity field was numerically evaluated and plotted as a function of $l/L_{S}$. Two analytical models valid in the limits of $l \ll L_{S}$ and $l\gg L_{S}$ were also suggested in the same study. Later, Takemura (Reference Takemura2004) suggested an empirical fit for the Vasseur & Cox (Reference Vasseur and Cox1977) outer-region-based wall-bounded drag coefficient. The model was presented as a function of $l/L_{S}$ and considered numerical values up to $l/L_{S} \ll 10$

(2.40)\begin{equation} C_{D,2}^{wb,out} = 6{\rm \pi}\left(\frac{a}{l}\right)\left[\frac{9}{16+11.13(l/L_{S})+ 0.584(l/L_{S})^2+0.371(l/L_{S})^3}\right]. \end{equation}

The net drag coefficient under Reference TakemuraTakemura's outer-region models is obtained by replacing the $C_{D,2}^{wb,in}$ by $C_{D,2}^{wb,out}$ in (2.38) (Takemura Reference Takemura2004). The theoretical predictions of $C_{D,2}^{wb,in}$ and $C_{D,2}^{wb,out}$, given via (2.39) and (2.40), reduce to zero with increasing separation distance, while the net drag coefficient, $C_{D,2}$, reduces to the unbounded drag coefficient value $C_{D,2}^{ub}$. Note, however, that, as the slip Reynolds number increases, the net drag coefficient predicted using $C_{D,2}^{wb,out}$ tends to reach the unbounded Stokes limit much faster than that predicted via the inner region $C_{D,2}^{wb,in}$.

Equations (2.39) and (2.40) are specific to the inner and outer regions, respectively, and hence cannot represent the drag across all separation distances. Based on experimental results at $Re_{slip} \sim 0.09 - 0.5$, Takemura (Reference Takemura2004) suggested a modification to $C_{D,2}^{wb}$ as follows:

(2.41)\begin{equation} \frac{C_{D,2}^{wb}}{6 {\rm \pi}} = \left[1-\left(\frac{ C_{D,2}^{wb,out}}{6 {\rm \pi}} \frac{l}{a}\right)\left(\frac{a}{l}\right)+\frac{1}{8}\left(\frac{a}{l}\right)^3- \frac{45}{256}\left(\frac{a}{l}\right)^4-\frac{1}{16}\left(\frac{a}{l}\right)^5\right]^{{-}1} -1. \end{equation}

In this modification, the $9/16$ coefficient of the inner-region model represented by (2.39) was replaced by $C_{D,2}^{wb,out}$ to capture the transition behaviour of the $C_{D,2}^{wb}$ when a particle shifts from the inner to the outer region.

For wall-bounded linear shear flows, Magnaudet et al. (Reference Magnaudet, Takagi and Legendre2003) presented an additional contribution to the drag force due to wall shear applicable to the inner region of the disturbed flow when $Re_\gamma \ll 1$. The force was given by

(2.42)\begin{equation} {{F}_{D}^\ast} ={-}\text{sgn} (\gamma)Re_\gamma{}C_{D,1}^{wb,in}(Re_\gamma,a/l)-\text{sgn} (u_{slip})Re_{slip}C_{D,2}(Re_{slip},a/l), \end{equation}

with the wall-shear-based drag coefficient, $C_{D,1}^{wb,in}$ given as a function of $(a/l)$ as,

(2.43)\begin{equation} C_{D,1}^{wb,in} = \frac{15{\rm \pi}}{8}\left(\frac{a}{l}\right)^2 \left[1+\frac{9}{16}\left(\frac{a}{l}\right)\right] .\end{equation}

This function reduces rapidly to zero moving away from the wall (Magnaudet et al. Reference Magnaudet, Takagi and Legendre2003). In our previous numerical study, Ekanayake et al. (Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) modified this coefficient by including higher-order terms of separation distance and introduced an inertial correction for shear, resulting in an expression valid for inner, outer and unbounded regions as

(2.44)\begin{align} C_{D,1} &= \frac{15{\rm \pi}}{8}\left(\frac{a}{l}\right)^2 \left[1+\frac{9}{16}\left(\frac{a}{l}\right)+0.5801\left(\frac{a}{l}\right)^2-3.34 \left(\frac{a}{l}\right)^3+4.15\left(\frac{a}{l}\right)^4\right] \nonumber\\ &\quad +(3.001Re_\gamma^2 -1.025Re_\gamma). \end{align}

Note that this shear-based wall drag creates a negative slip velocity near a wall for force-free particles. Despite the considerable past research in this area, existing drag models require further work to cover practically relevant moderate inertial ranges. For particles moving in quiescent flows, the influence of finite slip inertial effects on the $C_{D,2}$ drag coefficient requires further validation, particularly for $Re_{{slip}}<10^{-1}$. For particles moving in linear shear flows, the influence of both finite slip and shear inertial effects on the overall $C_{D}$ drag coefficient also requires further validation, again for the relevant ranges of $Re_{{slip}},Re_\gamma <10^{-1}$.

4.2.1. Lift force

In figure 3, the lift coefficients $C_{L,3}$ computed for both non-rotating and a freely rotating particles in a quiescent flow are plotted as a function of non-dimensional separation distance (${l^{\ast }}$). The numerical results are compared against the available inner-region correlations listed in table 4 that are valid for $Re_{{slip}} \ll 1$. In general, the lift coefficient values predicted via most of the analytical solutions slightly underestimate the numerically computed lift forces, particularly for $Re_{{slip}} < 10^{-2}$ near the wall. For example, the lowest slip Reynolds number ($Re_{{slip}} = 10^{-3}$) simulation conducted at the smallest distance to the wall (${l^{\ast }} = 1.2$) gives a $C_{{L,3}}$ of $1.755$ ($1.682$) for a non-rotating (freely rotating) particle, which is $\sim 1.68\,\%$ ($0.48\,\%$) higher than the asymptotic value of $1.726$ ($1.674$) predicted for a non-rotating (freely rotating) particle at ${l^{\ast }} = 1.2$ (Cherukat & McLaughlin Reference Cherukat and McLaughlin1994). The Cox & Hsu (Reference Cox and Hsu1977) first-order lift expression, which does not account for the finite particle size, produces a lift coefficient independent of ${l^{\ast }}$ for both non-rotating and a freely rotating particles. The value agrees to a certain extent with the present numerical and other theoretical predictions, but is not particularly accurate near the wall. When a particle is almost in contact with the wall ($l^{\ast } = 1$), the Krishnan & Leighton (Reference Krishnan and Leighton1995) study gives a $C_{L,3}$ of $1.755$ for a non-rotating particle, which is reasonably consistent with the present numerical results obtained at $l^{\ast } = 1.2$. For a freely rotating particle at $l^{\ast } = 1$, Krishnan & Leighton (Reference Krishnan and Leighton1995) also predict a value of $C_{L,3} = 0.236$, which is nearly an order of magnitude less than the non-rotating $C_{L,3}$ value, and is far from ours and the other inner-region model predictions in this region. Although the rotation of the sphere acts to decrease this lift for a particle near the wall, the reason for the significant deviation between these two theoretical analyses is not clear. For a freely rotating particle the Magnaudet et al. (Reference Magnaudet, Takagi and Legendre2003) lift correlation predicts a lift coefficient which is larger than the available asymptotic inner-region theories for $Re_{slip} \ll 1$ (figure 3b). A similar over-prediction is observed for $C_{L,1}$ near the wall (see Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) which may be caused by the neglect of higher-order separation distance terms (${O}(1/{l^{\ast }}) > 2$) that are significant when in the vicinity of the wall.

Figure 3. Lift coefficient ($C_{{L,3}}$) for different shear Reynolds number as a function of non-dimensional separation distance (${l^{\ast }}$) for (a) non-rotating and (b) freely rotating spheres. Simulations: $Re_{slip} = 10^{-3}$ ($\circ$, red), $10^{-2}$ ($\triangle$, red) and $10^{-1}$ ($\square$, red). Numerical predictions by Fischer & Rosenberger (Reference Fischer and Rosenberger1987) that included small inertial effects at $Re_\gamma \ll 1$ ($\ast$, black star). Analytical predictions of Cox & Hsu (Reference Cox and Hsu1977) ($\cdot \!\cdot \!\cdot \!\cdot \!\cdot \!\cdot$, (2.23), (2.24)), Cherukat & McLaughlin (Reference Cherukat and McLaughlin1994) (-$\cdot$-$\cdot$, grey, (2.25), (2.26)), Krishnan & Leighton (Reference Krishnan and Leighton1995) (--------, grey, (2.27)) and Magnaudet et al. (Reference Magnaudet, Takagi and Legendre2003) (- - -, grey, (2.29)). Present numerical fit for inner region (--------, blue, (4.3a), (4.3b)). Present numerical fit for all regions (--------, red, (4.4a), (4.4b)).

For the non-rotating case (figure 3a), the lift results are also compared with numerical predictions based on a boundary element method (BEM) which included small inertial effects ($Re_\gamma \ll 1$) (Fischer & Rosenberger Reference Fischer and Rosenberger1987). The computed lift coefficient values for the lowest slip Reynolds number ($Re_{slip} = 10^{-3}$) are consistent with the BEM results for small separation distances (figure 3a). However, a considerable difference between the present results and BEM predictions is apparent at larger separation distances (${l^{\ast }} \sim 10$). This could be possibly due to insufficient numerical accuracy of a Gauss–Legendre product formula used by Fischer & Rosenberger (Reference Fischer and Rosenberger1987), as suggested by Shi & Rzehak (Reference Shi and Rzehak2020). However, to our knowledge there are no numerical data available for a freely rotating particle at these low slip Reynolds numbers for additional verification. We also note from our domain dependence study that the errors in our numerical simulations are also highest at these large $l^{\ast }$ and small $Re_{slip}$ values.

As $Re_{{slip}}$ increases, the computed lift coefficients deviate significantly from the asymptotic inner-region correlations as inertial effects become significant, in both the non-rotating and freely rotating cases. Although most of our numerical data are well within the inner region, the computed lift force coefficient decreases with $Re_{slip}$ number in contrast to the inner-region models which predict lift coefficients that are independent of $Re_{slip}$. The discrepancy between simulation and theory arises as the force expansion used in the inner-region models does not satisfy the boundary conditions at large distances from the wall. With increasing slip velocity and separation distance, the walls move to the outer region, and the inner-region-based theoretical lift models then fail to capture the lift coefficient variation.

The numerical lift coefficient values and the outer-region asymptotic predictions valid for $Re_{slip} \ll 1$ are plotted in figure 4 as a function of $l^{\ast }/{L_{S}}^{\ast }$. Here, ${L_{S}}^{\ast } (={L_{S}}/a)$ is the normalised Stokes length by the particle radius. Although all the computed results are in inner region, the coefficients closer to the outer boundary ($l^{\ast }/{L_{S}}^{\ast } \sim 1$), particularly at $Re_{slip} = 10^{-1}$, trend towards the outer-region theoretical predictions. In this boundary limit, the difference between a non-rotating and freely rotating lift coefficient value is less significant and the lift results are consistent with outer-region theory (Vasseur & Cox Reference Vasseur and Cox1977). Since the outer-region asymptotic models are strictly valid for $l^{\ast }/{L_{S}}^{\ast } \gg 1$, variations in the lift correlation observed to occur in the inner region are thus not captured. This further highlights the need for a model capable of capturing both inner and outer-region slip lift behaviours simultaneously. Based on our lift results obtained for the lowest slip Reynolds number ($Re_{slip} = 10^{-3}$), we first propose a numerical fit for the wall-slip lift force in the inner region as a function of separation distance ($l^{\ast }$). The proposed correlations are given by

(4.3a)\begin{equation} C_{L,3}^{wb,in}=1.774 + 0.4353\left(\frac{1}{l^{{\ast}}}\right) -1.198\left(\frac{1}{l^{{\ast}}}\right)^2 + 0.7792\left(\frac{1}{l^{{\ast}}}\right)^3, \end{equation}

for a non-rotating particle and

(4.3b)\begin{equation} C_{L,3}^{wb,in}=1.764 + 0.4757\left(\frac{1}{l^{{\ast}}}\right) -1.268\left(\frac{1}{l^{{\ast}}}\right)^2 + 0.683\left(\frac{1}{l^{{\ast}}}\right)^3, \end{equation}

for a freely rotating particle. Figure 3 indicates that there is no significant variation of the numerical results for $C_{L,3}$ when the slip Reynolds number increases from $Re_{slip} = 10^{-3}$ to $10^{-2}$. This behaviour suggests that the proposed inner-region-based correlations, shown in figure 3, can be used for very small slip Reynolds numbers ($Re_{slip} \ll 1$) as the numerical lift results are almost independent of slip for $Re_{slip}<10^{-2}$.

Figure 4. Lift coefficient ($C_{{L,3}}$) for slip Reynolds number values of $Re_{slip} = 10^{-3}$ ($\circ$), $10^{-2}$ ($\triangle$) and $10^{-1}$ ($\square$) as a function of separation distance non-dimensionalised by the Stokes length scale ($l^{\ast }/{L_{{S}}}^{\ast }$). Red and blue symbols are for freely rotating and non-rotating particles, respectively. Asymptotic models for $Re_{slip} \ll 1$ by Vasseur & Cox (Reference Vasseur and Cox1977) (--------, grey, (2.10)), Takemura & Magnaudet (Reference Takemura and Magnaudet2003) (- - -, grey, (2.11)), Takemura (Reference Takemura2004) ($\cdot \!\cdot \!\cdot \!\cdot \!\cdot \!\cdot$, grey, (2.12)) and Shi & Rzehak (Reference Shi and Rzehak2020) (-$\cdot$-$\cdot$, grey, (2.13)). Present numerical fit for non-rotating particles (--------, blue, (4.4a)) and freely rotating particles (--------, red, (4.4b)).

Next, by replacing the constant in the proposed inner-region lift model (4.3) with the Takemura (Reference Takemura2004) outer-region model (2.12), the following correlation is proposed to account for the inertial dependency over all wall separation distances as:

(4.4a)\begin{equation} C_{L,3}= C_{L,3}^{wb,out} + 0.4353\left(\frac{1}{l^{{\ast}}}\right) -1.198\left(\frac{1}{l^{{\ast}}}\right)^2 + 0.7792\left(\frac{1}{l^{{\ast}}}\right)^3, \end{equation}

for a non-rotating particle and

(4.4b)\begin{equation} C_{L,3}=C_{L,3}^{wb,out} + 0.4757\left(\frac{1}{l^{{\ast}}}\right) -1.268\left(\frac{1}{l^{{\ast}}}\right)^2 + 0.683\left(\frac{1}{l^{{\ast}}}\right)^3, \end{equation}

for a freely rotating particle. Here, the Takemura (Reference Takemura2004) outer-region model (2.12) gives a definition for $C_{L,3}^{wb,out}$ as

(4.4c)\begin{equation} C_{L,3}^{wb,out} = \frac{18{\rm \pi}}{32+2\left(\dfrac{l^{{\ast}}}{L_{S}^{{\ast}}}\right)+3.8 \left(\dfrac{l^{{\ast}}}{L_{S}^{{\ast}}}\right)^2+0.049\left(\dfrac{l^\ast}{L_{S}\ast}\right)^3}. \end{equation}

These correlations are also plotted in figures 3 and 4, demonstrating that inertial effects are accurately predicted as a particle moves from the inner to the outer region, and the correct limit of $C_{L,3} \rightarrow 0$ for $l^{\ast }/L_{S}^{\ast } \rightarrow \infty$ is achieved. When a particle is very close to the wall for the smallest Reynolds number, i.e. $l^{\ast }/L_{S}^{\ast } \rightarrow 0$ and $l^\ast = 1$, (4.4a) (4.4b) calculates the lift coefficient as 1.784 (1.659) for a non-rotating (freely rotating) particle, a value that is just $2.3\,\% (0.1\,\%)$ higher (lower) than the asymptotic inner-region result of Cherukat & McLaughlin (Reference Cherukat and McLaughlin1994, Reference Cherukat and McLaughlin1995).

4.2.2. Drag force

In this section, we validate existing drag models using the numerical data obtained for quiescent flows. Under these conditions there is no shear and hence $C_{D,1}=0$. Figure 5 shows the variation in net drag coefficient, $C_{D,2}$, as a function of dimensionless separation distance ($l^{\ast }$) for both non-rotating and freely rotating particles. The inset in the figure shows the variation as a function of separation distance ($l^{\ast }/L_{S}^{\ast }$). The results are compared against the wall-bounded inner-region analytical correlation of Faxen (Happel & Brenner Reference Happel and Brenner1981) (2.39) and the outer-region empirical drag model of Takemura (Reference Takemura2004) (2.40). The predictions of the Takemura (Reference Takemura2004) inner–outer-based theoretical model given by (2.41) for low slip Reynolds numbers are also shown.

Figure 5. Drag force coefficient of a spherical particle in the absence of shear ($C_{{D,2}}$). Simulations: non-rotating ($\circ$), freely rotating (+). Analytical prediction: Faxen inner-region correlation (Happel & Brenner Reference Happel and Brenner1981) (--------, (2.39)), Takemura (Reference Takemura2004) outer-region correlation (--------, blue, (2.40)) and Takemura (Reference Takemura2004) inner–outer-region correlation (- - -, red, (2.41)). Unbounded Stokes drag ($\cdot \!\cdot \!\cdot \!\cdot \!\cdot \!\cdot$, (2.31)).

For each of the slip Reynolds numbers, the highest numerical value for $C_{D,2}$ is reported when the particle is close to the wall, and with increasing wall distance, these coefficients asymptote to the unbounded Stokes limit ($C_{D,2}=6{\rm \pi}$) for both non-rotating and freely rotating particles. The effect of rotation on the drag force is hardly discernible for all separation distances. As indicated in figure 5, no inertial dependency is observed in the computed drag coefficients for all tested $Re_{slip}$ values. The numerical drag results are in good agreement with the analytical inner-region correlation, (2.39), noting that all the numerical results are inside the region $l^{\ast }/L_{S}^{\ast } < 1$ (inset of figure 5). However, even in the outer boundary limit (when $l^{\ast }/L_{S}^{\ast } \sim 1$), the results given for $Re_{{slip}} = 10^{-1}$ do not significantly deviate from the inner-region predictions (2.39) or follow the transition behaviour predicted by Takemura (Reference Takemura2004) in (2.40). Note that (2.40) was originally validated for relatively large slip Reynolds numbers ($0.09 \leq Re_{{slip}} \leq 0.5$), compared to our simulated slip range. Hence, we conclude that the correlation given by (2.39) is valid up to $Re_{{slip}} = 10^{-1}$ for both rotating and freely rotating particles without requiring correction any further for inertial effects.

4.3.1. Lift force

Figure 6 shows the variation in dimensionless lift force ($F_{L}^{\ast }$) for a freely rotating particle as a function of $l^{\ast }$ for different combinations of slip and shear Reynolds numbers. Figure 6(a) and figure 6(b) present results for a leading ($u_{slip} > 0$) and a lagging particle ($u_{slip}<0$) respectively, in a positive shear field ($\gamma > 0$). The numerical results are compared against the available inner and outer-region lift models that are valid for $Re_\gamma , Re_{slip} \ll 1$. Here, the inner-region model of Cherukat & McLaughlin (Reference Cherukat and McLaughlin1995) given by (2.22), and the outer-region model of Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) given by (2.16) are included for comparison.

Figure 6. Non-dimensional lift force ($F_{{L}}^{\ast }$) of a freely rotating particle; $Re_\gamma$ and $Re_{slip}$ increase in the order of $10^{-3}, 10^{-2}, 10^{-1}$ from left to right and top to bottom respectively. Simulations: inner region ($\circ$, red) and outer region ($\bullet$, red) for each plot. Analytical predictions: inner-region model of Cherukat & McLaughlin (Reference Cherukat and McLaughlin1995) (- - -, grey, (2.22)), outer-region model of Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) (-$\cdot$-$\cdot$, grey, (2.16)). Present model prediction (--------, red, (4.6)). (a) Leading particle in a positive shear field (${\gamma }^{\ast } > 0$) and (b) lagging particle in a positive shear field (${\gamma }^{\ast } < 0$).

For $Re_{slip}, Re_{\gamma } < 10^{-2}$, the numerically computed lift forces in the region close to the wall (${l^{\ast }} < 5$) agree reasonably well with the asymptotic values predicted by the inner-region model (Cherukat & McLaughlin Reference Cherukat and McLaughlin1995) for both positive and negative slip velocities. As $Re_{slip}$ and $Re_{\gamma }$ increase and inertial effects become more significant, the computed lift coefficients deviate significantly from the inner-region theoretical values. With increasing slip, shear and separation distance, the walls move to the outer region ($l^{\ast }>min({L_{G}}^{\ast },{L_{S}}^{\ast })$) and unsurprisingly, the inner-region-based models fail to capture the lift coefficient variations accurately. Here, ${L_{G}}^{\ast } (={L_{G}}/a)$ is the normalised Saffman length by the particle radius. At $Re_{slip}$ and $Re_\gamma >10^{-2}$ and $l^{\ast } \gtrsim 5$, the computed results coincide reasonably well with values predicted by the Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) outer-region correlation. However, for the largest shear Reynolds numbers and smallest slip Reynolds numbers (i.e. results for $Re_\gamma > 10^{-2}, Re_{slip} < 10^{-1}$), the existing outer-region model significantly underestimates the simulated lift results.

In order to better understand the outer-region behaviour, in figure 7 we plot the computed lift force coefficients against the separation distance normalised using the Saffman length scale ($l^{\ast }/L_{{G}}^{\ast }$). The numerical results are compared against two existing outer-region-based correlations, namely $C_{L,23}^{wb,out}$ given via (2.16) and $C_{L,2}^{wb,out}$ given via (2.15). However, while $C_{L,23}^{wb,out}$ is valid for both small and large $\epsilon$ values, $C_{L,2}^{wb,out}$ is only valid when shear dominates ($\epsilon > 1$). In both cases $J(\epsilon )$ is evaluated using the Legendre & Magnaudet (Reference Legendre and Magnaudet1998) correlation (2.7) and $f(\epsilon ,l/L_{G})$ is evaluated using the Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) correlation, (2.20). Equation (2.12) is used to evaluate $C_{L,3}^{{wb,out}}$, present in the expression for $C_{L,23}^{wb,out}$. As $(l^{\ast }/L_{G}^{\ast })$ increases, the theoretical lift force results for positive and negative $\gamma ^{\ast } (=\gamma /u_{slip})$, obtained by varying only the slip direction, asymptote to the negative and positive unbounded lift forces, respectively. Although the theoretical model given by (2.16) fails to capture the numerical lift variation in the transition region ($l^{\ast }\sim L_{G}^{\ast }$) when $|\gamma ^{\ast }| \geq 10$, the same model predicts the numerical data reasonably well when $|\gamma ^{\ast }| \leq 1$. On the other hand, the predictions of (2.15) coincide with the numerical data only when $|\gamma ^{\ast }| \sim 1$ ($Re_\gamma \sim Re_{slip}$) (see figure 7a).

Figure 7. Lift force coefficient ($C_{{L}}=F_{{L}}^{\ast }/Re_{slip}^2$) of a freely rotating particle as a function of separation distance non-dimensionalised by Saffman length scale ($l^{\ast }/{L_{{G}}}^{\ast }$). Simulations: inner region ($\circ$) and outer region ($\bullet$). Analytical outer-region correlation of Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) (- - -, (2.16)) and ($\cdot \!\cdot \!\cdot \!\cdot \!\cdot \!\cdot$, (2.15)). Present model predictions (--------, (4.6)). (a) Leading particle in a positive shear field (${\gamma }^{\ast } > 0$) and (b) lagging particle in a positive shear field (${\gamma }^{\ast } < 0$).

No existing models capture the force variation in both the inner and outer regions successfully for all of the Reynolds numbers considered here. Recalling our definition for the net lift force given by (4.1), since the coefficients $C_{L,1}$ and $C_{L,3}$ capture the lift contributions due to finite shear and finite slip conditions in the limits of $\gamma ^{\ast } \rightarrow \infty$ and $\gamma ^{\ast } = 0$, respectively, the remaining coefficient $C_{L,2}$ is found by subtracting the force contributions due to $C_{L,1}$ and $C_{L,3}$, from the present numerical results (see figure 8). Here, $C_{L,1}$ and $C_{L,3}$ are evaluated using (3.3) in Ekanayake et al. (Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) and (4.4) in the present study respectively.

Figure 8. Lift force coefficient $C_{{L,2}}$ of a freely rotating particle; $Re_\gamma$ and $Re_{slip}$ increase in the order of $10^{-3}, 10^{-2}, 10^{-1}$ from left to right and top to bottom respectively. Simulations: inner region ($\circ$, red) and outer region ($\bullet$, red) for each subplot. Analytical predictions: inner-region $C_{{L,2}}$ model of Cherukat & McLaughlin (Reference Cherukat and McLaughlin1995) (- - -, grey, (2.26)), outer-region model of Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) (-$\cdot$-$\cdot$, grey, (2.15)). Present model prediction (--------, red, (4.5b)). (a) Leading particle in a positive shear field (${\gamma }^{\ast } > 0$) and (b) lagging particle in a positive shear field (${\gamma }^{\ast } < 0$).

We define a new correlation for $C_{{L,2}}$ in the following manner. To capture the variation of the remaining force contributions and the inner- and outer-region transition behaviour, the outer-region-based, wall-bounded lift coefficient $C_{L,2}^{wb,out}$ given by (2.15) is substituted into the lowest-order term of the Cherukat & McLaughlin (Reference Cherukat and McLaughlin1995) inner-region slip-shear lift $C_{L,2}^{wb,in}$ correlation given by (2.25) for a non-rotating particle and (2.26) for a freely rotating particle. Noting that $C_{L,2}^{wb,out}$ in (2.15) scales with $Re_{slip}^2$, the outer-region coefficient is divided by $|\gamma ^{\ast }|$ to match the inner-region lift correlation scaling. The resulting slip-shear-based net lift coefficient $C_{L,2}$, which is valid for all three regions (i.e. inner, outer and unbounded) is,

(4.5a)\begin{equation} C_{L,2}={-}{C_{L,2}^{wb,out}}\frac{1}{\lvert{\gamma}^{{\ast}}\rvert} -1.1450-2.0840 \left(\frac{1}{l^{{\ast}}}\right)+0.9059\left(\frac{1}{l^{{\ast}}}\right)^{2},\end{equation}

for a non-rotating particle and

(4.5b)\begin{equation} C_{L,2}={-}{C_{L,2}^{wb,out}}\frac{1}{\lvert{\gamma}^{{\ast}}\rvert} -2.6729-0.8373 \left(\frac{1}{l^{{\ast}}}\right)+0.4683\left(\frac{1}{l^{{\ast}}}\right)^{2},\end{equation}

for a freely rotating particle. The new $C_{L,2}$ correlation proposed for the freely rotating particle is plotted as a function of $l^{\ast }$ in figure 8 and as a function of the normalised Saffman length $l^{\ast }/L_{G}^{\ast }$ in figure 9. Given that the new correlation for $C_{L,2}$ (4.5) captures the variation of the remaining lift force contributions reasonably well for most of the slip and shear Reynolds numbers considered, we substitute this force model into the main net lift force correlation. The performance of the net lift correlation (4.1) is then examined for a freely rotating particle by plotting the force (${F}_{L}^{\ast }$) predictions in figure 6. The overall lift coefficient (${C}_{L}$), obtained by normalising the net lift force by the slip Reynolds number,

(4.6)\begin{equation} {C}_{L} = \frac{{F}_{L}^{{\ast}}}{Re_{{slip}}^2} = {\gamma^{{\ast}}}^2 {C}_{L,1} + \gamma^{{\ast}}{C}_{L,2} + {C}_{L,3}, \end{equation}

is shown in figure 7. Here again, the lift coefficients, $C_{L,1}$ and $C_{L,3}$ are evaluated using (4.1) from our previous study (Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) and (4.4b) from § 4.2. For reference a summary of all the lift correlations used in the net lift force calculations are provided in Appendix A.

Figure 9. Lift force coefficient $C_{{L,2}}$ of a freely rotating particle as a function of separation distance non-dimensionalised by the Saffman length scale ($l^{\ast }/{L_{{G}}}^{\ast }$). Simulations: inner region ($\circ$) and outer region ($\bullet$). Analytical outer-region correlation of Takemura et al. (Reference Takemura, Magnaudet and Dimitrakopoulos2009) (- - -, (2.15)). Present model predictions (--------, (4.5)). (a) Leading particle in a positive shear field (${\gamma }^{\ast } > 0$) and (b) lagging particle in a positive shear field (${\gamma }^{\ast } < 0$).

As shown in both figures 6 and 7, the new model captures the inner–outer transition behaviour of the computed lift results well. Referring to figure 6, for low slip and shear values ($Re_\gamma$ and $Re_{slip} \lesssim 10^{-2}$), the model performs well for both positive and negative $\gamma ^{\ast }$. For large slip values and for small shear rates (i.e. $Re_{slip} = 10^{-1}$ and $Re_\gamma = 10^{-3}$), the model slightly overestimates (underestimates) the simulated results with a maximum deviation of $4.96\,\%$ $(3.67\,\%)$ for $\gamma ^{\ast } > 0$ ($\gamma ^{\ast } < 0$) when the particle is furthest from the wall. With increasing shear rate (i.e. $Re_\gamma \sim 10^{-1}$) for the same large slip values, this deviation rapidly reduces for ${\gamma }^{\ast } > 0$, but increases to $24.03\,\%$ for ${\gamma }^{\ast } < 0$.

As well as the force magnitudes, the change of the lift force direction is more accurately predicted (i.e. ${Re_\gamma } = 10^{-1}$) using the new correlation than any other available model. Note that a positive lift ($F_{L}^{\ast }>0$) and a negative lift ($F_{L}^{\ast } <0$) represent a force directed away from and a force acting towards the wall, respectively. In figure 6(a), the lift forces computed for ${\gamma }^{\ast } > 0$ indicate a change of the lift force direction and a decrease in the force with increasing separation distance. However, for the same $Re_\gamma$ and $Re_{slip}$ values, the numerical data given in figure 6(b) for ${\gamma }^{\ast } < 0$, only indicate positive lift forces for the selected range of separation distances, and generally an increase in the lift force with increasing separation distance.

The force variations shown in figures 6 and 7 can be explained by examining the behaviour of the three theoretical lift coefficients ($C_{L,1}, C_{L,2}$ and $C_{L,3}$) separately. The coefficients $C_{L,1}$ and $C_{L,3}$, responsible for the lift due to pure shear and pure slip, respectively, always remain positive irrespective of the direction of both slip and shear. Thus, the lift forces due to these two coefficients will always act to push a particle away from the wall. However, with increasing separation distance, the values of these two lift coefficients rapidly reduce to zero (Vasseur & Cox Reference Vasseur and Cox1977; Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020). Therefore $C_{L,1}$ and $C_{L,3}$ are only important close to the wall. The remaining slip-shear lift coefficient, $C_{L,2}$, behaves differently. Unlike the other two coefficients, $C_{L,2}$ is sensitive to the direction of slip and shear (determined by sgn(${\gamma }^{\ast }$)), and also has a finite negative or positive value in the unbounded limit. Hence, at large separation distances, the net lift force mainly depends on the $C_{L,2}$ coefficient and its corresponding sign. However, near a wall, the net lift force magnitude and the direction strongly depend upon the inner-region contributions of all three coefficients.

Including all lift contributions covering the inner and outer regions means that the present lift model predicts the correct lift coefficient variation with $Re_\gamma , Re_{slip}$ and $l^{\ast }$, over the wide range of parameters considered in this study (figures 6 and 7).

4.3.2. Drag force

The drag force on a freely rotating spherical particle moving parallel to a wall in a linear shear flow is analysed in this section. Here, the drag force normalised by the slip Reynolds number

(4.7)\begin{equation} {C}_{D} = \frac{{F}_{D}^{{\ast}}}{Re_{slip}} ={-}\gamma^{{\ast}}C_{D,1}-C_{D,2} \end{equation}

is used to define the net drag coefficients. Results are presented for positive and negative slip velocities in a positive shear field, noting that results for a negative shear field are identical to the presented positive shear field results with the sign of the slip velocity swapped. Figure 10 shows the variation in the net drag coefficient $C_{D}$ for slip and shear Reynolds numbers in the range $10^{-3} - 10^{-1}$ as a function of wall separation distance normalised by Saffman's length. A positive slip in the presence of the wall produces a force on a leading particle that is in the opposite direction to the flow (figure 10a). The largest negative values for $C_{D}$ are obtained when the particle is close to the wall, reducing to the unbounded Stokes drag result with increasing wall distance. Both positive and negative values for $C_{D}$ are reported for a lagging particle close to the wall (figure 10b), with the direction of the force depending on both the $C_{D,1}$ and $C_{D,2}$ magnitudes. Although a lagging particle results in a positive slip-drag force contribution, the positive shear produces a force in the opposite direction to the flow. As a result negative net drag forces are obtained near the wall at high $\gamma ^{\ast }$.

Figure 10. Drag force coefficient ($C_{{D}}$) of a freely rotating particle as a function of separation distance non-dimensionalised by the Saffman length scale ($l^{\ast }/{L_{{G}}}^{\ast }$). Simulations: inner region ($\circ$) and outer region ($\bullet$). Inner-region analytical predictions when $C_{D,1}$ is evaluated by (2.44) (--------) and by (2.43) (- - -). For both cases $C_{D,2}$ is evaluated by (2.39). Outer-region analytical prediction when $C_{D,2}$ and $C_{D,1}$ are evaluated by (2.40) and (2.44), respectively (-$\cdot$-$\cdot$). (a) Leading particle in a positive shear field (${\gamma }^{\ast } > 0$) and (b) lagging particle in a positive shear field (${\gamma }^{\ast } < 0$).

The simulated drag coefficient results are also compared against the inner-region- and outer-region-based theoretical drag correlations at low $Re_{\gamma } \ll 1$. Two correlations, (2.44) and (2.43), for $C_{D,1}$ are first tested while using an inner-region-based Faxen drag coefficient for $C_{D,2}$ (2.39). As shown in figure 10, (2.44) for $C_{D,1}$ performs better than (2.43) when predicting the lift results for high $\gamma ^{\ast }$. However, no significant difference between these two models is observed for small $\gamma ^{\ast }$. The outer-region-based drag model of Takemura (Reference Takemura2004) (2.40) is also tested for $C_{D,2}$ in combination with (2.44) for $C_{D,1}$. Unsurprisingly, this model fails to capture the inner-region behaviour in either slip direction, particularly closer to the wall, although the model predictions agree reasonably well with other theoretical models for large $l^{\ast }/{L_{{G}}}^{\ast }$ values. In summary, for the considered range of slip and shear Reynolds numbers, the most accurate drag predictions are obtained using the Ekanayake et al. (Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020) model (2.44) for $C_{D,1}$ and the Faxen (Reference Faxen1922) model (2.39) for $C_{D,2}$, respectively.