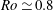1 Introduction
Baroclinic three-dimensional vortices are stable coherent structures in vertically stratified and horizontally rotating geophysical flows (e.g. Carton Reference Carton and Flór2010). Persistence of these rotating structures has motivated the mathematical development of vortex models. Two convenient properties are often required in these vortex models, namely isolation from the background flow and stability to small perturbations. Vortex isolation implies that the amount of potential vorticity anomaly (henceforth PVA) in the vortex volume must sum up to zero, so that the radial PVA density distribution must change sign at some distance from the vortex centre in axisymmetric flows. The PVA density gradient must change sign as well. However, sign changing PVA density gradients lead to flow instability, and hence the paradox, noticed by Benilov (Reference Benilov2003), arises, that geophysical vortex models, if isolated, must be unstable, a result apparently contradicting the long persistence of these vortices (e.g. Richardson, Bower & Zenk Reference Richardson, Bower and Zenk2000). The purpose of this paper is to show that some isolated baroclinic vortices can develop flow instability and yet remain coherent for long time periods even for high Rossby numbers
![]() $Ro\equiv |\unicode[STIX]{x1D701}|_{max}/f\simeq 0.8$
, where
$Ro\equiv |\unicode[STIX]{x1D701}|_{max}/f\simeq 0.8$
, where
![]() $\unicode[STIX]{x1D701}$
is the relative vertical vorticity and
$\unicode[STIX]{x1D701}$
is the relative vertical vorticity and
![]() $f$
is the planetary vorticity.
$f$
is the planetary vorticity.
First, we introduce a new family of isolated vortices (§ 2) under the requirement of zero amount of PVA on every isopycnal. Mesoscale or submesoscale vortices are never found exactly isolated in the real ocean due to the ubiquitous existence of inertia–gravity waves, baroclinic tides, background horizontally and vertically sheared currents, surface wind stress, or even the close presence of other eddies or density fronts. Frequently, however, as suggested by the long persistence of these vortices, these external processes have only a perturbative second-order effect on the vortex dynamics, which justifies the investigation on theoretical models of baroclinic continuously stratified isolated vortices that remain stable to small perturbations. Furthermore, experimental data suggest that some long-life mesoscale subsurface eddies in the ocean display an outer PVA region of sign opposite to that of the vortex core (Paillet et al. Reference Paillet, Cann, Carton, Morel and Serpette2002), which further supports the zero PVA amount vortex model.
The theoretical development and numerical algorithm used to analyse the vortex evolution and stability properties (§ 3) are based on a fully three-dimensional non-hydrostatic approach and on the explicit conservation of PVA on isopycnals. This PVA conservative method is therefore very well suited for this particular vortex application. The time evolution of a particular member of this vortex family (§ 4), with a high Rossby number
![]() $Ro\simeq 0.8$
, and therefore out of the range of application of the quasigeostrophic (QG) approximation, and initially subjected to small perturbations, displays temporary growth of flow instabilities at the critical levels and subsequent inner-core vortex axisymmetrization. For high Rossby numbers, non-QG terms substantially affect the vortex stability properties (Tsang & Dritschel Reference Tsang and Dritschel2014). The final vortex state is, however, that of marginal stability, with an elliptic-like inner-core vortex experiencing precession and nutation, and forcing a second-mode vertical velocity field. Our purpose here is only to describe a representative case of an isolated marginally stable vortex with a high Rossby number, and no attempt is made to generate a stability classification, similar to that made in Yim, Billant & Ménesguen (Reference Yim, Billant and Ménesguen2016), in the parametric space of this vortex family. Finally, concluding remarks are given in § 5.
$Ro\simeq 0.8$
, and therefore out of the range of application of the quasigeostrophic (QG) approximation, and initially subjected to small perturbations, displays temporary growth of flow instabilities at the critical levels and subsequent inner-core vortex axisymmetrization. For high Rossby numbers, non-QG terms substantially affect the vortex stability properties (Tsang & Dritschel Reference Tsang and Dritschel2014). The final vortex state is, however, that of marginal stability, with an elliptic-like inner-core vortex experiencing precession and nutation, and forcing a second-mode vertical velocity field. Our purpose here is only to describe a representative case of an isolated marginally stable vortex with a high Rossby number, and no attempt is made to generate a stability classification, similar to that made in Yim, Billant & Ménesguen (Reference Yim, Billant and Ménesguen2016), in the parametric space of this vortex family. Finally, concluding remarks are given in § 5.
2 Initial conditions: the vortex family
 $\unicode[STIX]{x1D71B}_{p,q}$
$\unicode[STIX]{x1D71B}_{p,q}$
The vortex initial conditions define the stability properties of the vortex. We introduce the isolated vortex family
![]() $\unicode[STIX]{x1D71B}_{p,q}$
as a set of initial conditions having some members leading to marginally stable vortices. To avoid an excess of notation, the parameters
$\unicode[STIX]{x1D71B}_{p,q}$
as a set of initial conditions having some members leading to marginally stable vortices. To avoid an excess of notation, the parameters
![]() $(p,q)$
, whose meaning is explained below, are omitted, with a few exceptions, in the dependent variables symbols. Since the initial base conditions are axisymmetric and the vortices are defined in the isopycnal space, we work with isopycnal coordinates
$(p,q)$
, whose meaning is explained below, are omitted, with a few exceptions, in the dependent variables symbols. Since the initial base conditions are axisymmetric and the vortices are defined in the isopycnal space, we work with isopycnal coordinates
![]() $(\mathfrak{r},\mathfrak{z})$
of radial distance
$(\mathfrak{r},\mathfrak{z})$
of radial distance
![]() $\mathfrak{r}$
and isopycnal
$\mathfrak{r}$
and isopycnal
![]() $\mathfrak{z}$
. The two-dimensional base PVA distribution
$\mathfrak{z}$
. The two-dimensional base PVA distribution
![]() $\tilde{\unicode[STIX]{x1D71B}}_{b}(\mathfrak{r},\mathfrak{z})$
satisfies the boundary conditions
$\tilde{\unicode[STIX]{x1D71B}}_{b}(\mathfrak{r},\mathfrak{z})$
satisfies the boundary conditions
where
![]() $\tilde{\unicode[STIX]{x1D71B}}_{0}(\mathfrak{z})$
in (2.1a
) defines the PVA profile along the vortex vertical axis and (2.1b
) is required for PVA continuity at the vortex outer limit
$\tilde{\unicode[STIX]{x1D71B}}_{0}(\mathfrak{z})$
in (2.1a
) defines the PVA profile along the vortex vertical axis and (2.1b
) is required for PVA continuity at the vortex outer limit
![]() $\mathfrak{r}_{0}(\mathfrak{z})$
. The radial dependence of
$\mathfrak{r}_{0}(\mathfrak{z})$
. The radial dependence of
![]() $\tilde{\unicode[STIX]{x1D71B}}_{b}$
is specified by its degree of smoothness along the radial direction at the vortex origin
$\tilde{\unicode[STIX]{x1D71B}}_{b}$
is specified by its degree of smoothness along the radial direction at the vortex origin
![]() $\mathfrak{r}=0$
(parameter
$\mathfrak{r}=0$
(parameter
![]() $p$
) and at the vortex outer limit
$p$
) and at the vortex outer limit
![]() $\mathfrak{r}_{0}(\mathfrak{z})$
(parameter
$\mathfrak{r}_{0}(\mathfrak{z})$
(parameter
![]() $q$
) on isopycnals,
$q$
) on isopycnals,
Besides the above conditions we impose zero amount of PVA on every isopycnic layer,
Thus, the isopycnal gradient of the PVA assumes both signs along the vortex radius and satisfies the Charney–Stern necessary condition for the growth of disturbances (Charney & Stern Reference Charney and Stern1962).

Figure 1. Four representative functions of (a) the base horizontal PVA
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}(p,q;\unicode[STIX]{x1D718})$
and (b) its derivative
$\tilde{\unicode[STIX]{x1D71B}}_{B}(p,q;\unicode[STIX]{x1D718})$
and (b) its derivative
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}^{\prime }(p,q;\unicode[STIX]{x1D718})$
for
$\tilde{\unicode[STIX]{x1D71B}}_{B}^{\prime }(p,q;\unicode[STIX]{x1D718})$
for
![]() $(p,q)=(2,2)$
(dashed, not labelled),
$(p,q)=(2,2)$
(dashed, not labelled),
![]() $(2,4)$
,
$(2,4)$
,
![]() $(4,2)$
and
$(4,2)$
and
![]() $(4,4)$
.
$(4,4)$
.
The PVA solution
![]() $\tilde{\unicode[STIX]{x1D71B}}_{b}(\mathfrak{r},\mathfrak{z})$
for monopolar one-core potential vorticity (PV) vortices with a single outer PV shield can be decomposed, in the isopycnal space, into horizontal and vertical components
$\tilde{\unicode[STIX]{x1D71B}}_{b}(\mathfrak{r},\mathfrak{z})$
for monopolar one-core potential vorticity (PV) vortices with a single outer PV shield can be decomposed, in the isopycnal space, into horizontal and vertical components
In this equation,
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}$
defines the horizontal spatial PVA distribution in terms of the radial distance
$\tilde{\unicode[STIX]{x1D71B}}_{B}$
defines the horizontal spatial PVA distribution in terms of the radial distance
![]() $\mathfrak{r}$
normalized by the radius vortex
$\mathfrak{r}$
normalized by the radius vortex
![]() $\mathfrak{r}_{0}(\mathfrak{z})$
on each isopycnal
$\mathfrak{r}_{0}(\mathfrak{z})$
on each isopycnal
![]() $\mathfrak{z}$
, and is given (appendix A) by
$\mathfrak{z}$
, and is given (appendix A) by
 $$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D71B}}_{B}(\unicode[STIX]{x1D718}) & \equiv & \displaystyle 1+\frac{(p+q+4)(p+1)}{2(q+1)}I(p+2,q+1;\unicode[STIX]{x1D718})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(p+q+2)(p+3)}{2(q+1)}I(p+1,q+1;\unicode[STIX]{x1D718}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D71B}}_{B}(\unicode[STIX]{x1D718}) & \equiv & \displaystyle 1+\frac{(p+q+4)(p+1)}{2(q+1)}I(p+2,q+1;\unicode[STIX]{x1D718})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(p+q+2)(p+3)}{2(q+1)}I(p+1,q+1;\unicode[STIX]{x1D718}),\end{eqnarray}$$
where
![]() $I(p,q;\unicode[STIX]{x1D718})$
is the normalized incomplete Beta function. Some examples of
$I(p,q;\unicode[STIX]{x1D718})$
is the normalized incomplete Beta function. Some examples of
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}(p,q;\unicode[STIX]{x1D718})$
and its derivative
$\tilde{\unicode[STIX]{x1D71B}}_{B}(p,q;\unicode[STIX]{x1D718})$
and its derivative
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}^{\prime }(p,q;\unicode[STIX]{x1D718})$
are shown in figure 1. It should be noted that we may generalize
$\tilde{\unicode[STIX]{x1D71B}}_{B}^{\prime }(p,q;\unicode[STIX]{x1D718})$
are shown in figure 1. It should be noted that we may generalize
![]() $p,q\in \mathbb{R}$
so that these symbols in (2.2) must be understood as their corresponding integer part. The function
$p,q\in \mathbb{R}$
so that these symbols in (2.2) must be understood as their corresponding integer part. The function
![]() $\tilde{\unicode[STIX]{x1D71B}}_{0}(\mathfrak{z})$
in (2.4) defines the PVA amplitude along the vortex vertical axis, or the vertical structure of the vortex. The simplest PVA surface geometry is spheroidal, so that both the normalized vortex horizontal radius
$\tilde{\unicode[STIX]{x1D71B}}_{0}(\mathfrak{z})$
in (2.4) defines the PVA amplitude along the vortex vertical axis, or the vertical structure of the vortex. The simplest PVA surface geometry is spheroidal, so that both the normalized vortex horizontal radius
![]() $\mathfrak{r}_{0}(\mathfrak{z})/r_{0}$
and the normalized vertical axis PVA
$\mathfrak{r}_{0}(\mathfrak{z})/r_{0}$
and the normalized vertical axis PVA
![]() $\tilde{\unicode[STIX]{x1D71B}}_{0}(\mathfrak{z})/\unicode[STIX]{x1D71B}_{0}$
are given by the same function
$\tilde{\unicode[STIX]{x1D71B}}_{0}(\mathfrak{z})/\unicode[STIX]{x1D71B}_{0}$
are given by the same function
where constant
![]() $r_{0}\equiv \mathfrak{r}_{0}(0)$
is the vortex radius at the middle isopycnal
$r_{0}\equiv \mathfrak{r}_{0}(0)$
is the vortex radius at the middle isopycnal
![]() $\mathfrak{z}=0$
,
$\mathfrak{z}=0$
,
![]() $\unicode[STIX]{x1D71B}_{0}\equiv \tilde{\unicode[STIX]{x1D71B}}_{0}(0)$
is the PVA at the vortex centre
$\unicode[STIX]{x1D71B}_{0}\equiv \tilde{\unicode[STIX]{x1D71B}}_{0}(0)$
is the PVA at the vortex centre
![]() $(\mathfrak{r},\mathfrak{z})=(0,0)$
and
$(\mathfrak{r},\mathfrak{z})=(0,0)$
and
![]() $\mathfrak{z}_{0}$
is the deepest vortex isopycnal (located at a depth
$\mathfrak{z}_{0}$
is the deepest vortex isopycnal (located at a depth
![]() $z_{0}$
in the reference configuration, as explained in the next section). The vertical to horizontal vortex aspect ratio
$z_{0}$
in the reference configuration, as explained in the next section). The vertical to horizontal vortex aspect ratio
![]() $z_{0}/r_{0}$
, the PVA at the vortex centre
$z_{0}/r_{0}$
, the PVA at the vortex centre
![]() $\unicode[STIX]{x1D71B}_{0}$
and the horizontal structure parameters
$\unicode[STIX]{x1D71B}_{0}$
and the horizontal structure parameters
![]() $(p,q)$
complete the parameter set of the vortex family
$(p,q)$
complete the parameter set of the vortex family
![]() $\unicode[STIX]{x1D71B}_{p,q}$
.
$\unicode[STIX]{x1D71B}_{p,q}$
.
3 Numerical algorithm
The three-dimensional baroclinic geophysical (rotating and stably stratified) volume-preserving non-hydrostatic vortex flow, under the Boussinesq and
![]() $f$
-plane approximations, is simulated using a triply periodic numerical model (Dritschel & Viúdez Reference Dritschel and Viúdez2003) initialized using the PV initialization approach (Viúdez & Dritschel Reference Viúdez and Dritschel2003). The PV is represented by contours lying on isopycnals. We use a
$f$
-plane approximations, is simulated using a triply periodic numerical model (Dritschel & Viúdez Reference Dritschel and Viúdez2003) initialized using the PV initialization approach (Viúdez & Dritschel Reference Viúdez and Dritschel2003). The PV is represented by contours lying on isopycnals. We use a
![]() $256^{3}$
grid, with 256 isopycnals, in a domain of vertical extent
$256^{3}$
grid, with 256 isopycnals, in a domain of vertical extent
![]() $L_{z}=2\unicode[STIX]{x03C0}$
(which defines the unit of length) and horizontal extents
$L_{z}=2\unicode[STIX]{x03C0}$
(which defines the unit of length) and horizontal extents
![]() $L_{x}=L_{y}=cL_{z}$
, where
$L_{x}=L_{y}=cL_{z}$
, where
![]() $c_{0}\equiv 10$
is the ratio of the mean Brunt–Väisälä to the constant Coriolis frequency
$c_{0}\equiv 10$
is the ratio of the mean Brunt–Väisälä to the constant Coriolis frequency
![]() $c_{0}\equiv N/f$
. We take the buoyancy period (
$c_{0}\equiv N/f$
. We take the buoyancy period (
![]() $1~\text{bp}\equiv 2\unicode[STIX]{x03C0}/N$
) as the unit of time by setting
$1~\text{bp}\equiv 2\unicode[STIX]{x03C0}/N$
) as the unit of time by setting
![]() $N\equiv 2\unicode[STIX]{x03C0}$
. One inertial period (
$N\equiv 2\unicode[STIX]{x03C0}$
. One inertial period (
![]() $1~\text{ip}\equiv 2\unicode[STIX]{x03C0}/f$
) equals 10 bp. The time step
$1~\text{ip}\equiv 2\unicode[STIX]{x03C0}/f$
) equals 10 bp. The time step
![]() $\unicode[STIX]{x1D6FF}t=0.01$
and the initialization time
$\unicode[STIX]{x1D6FF}t=0.01$
and the initialization time
![]() $t_{i}=5~\text{ip}$
. The initialization time is the minimum time required for the fluid to reach its initial prescribed PVA state with minimal generation of inertia–gravity waves.
$t_{i}=5~\text{ip}$
. The initialization time is the minimum time required for the fluid to reach its initial prescribed PVA state with minimal generation of inertia–gravity waves.
The vertical displacement
![]() ${\mathcal{D}}$
of isopycnals with respect to the reference density configuration is
${\mathcal{D}}$
of isopycnals with respect to the reference density configuration is
![]() ${\mathcal{D}}(\boldsymbol{x},t)\equiv z-d(\boldsymbol{x},t)$
, where
${\mathcal{D}}(\boldsymbol{x},t)\equiv z-d(\boldsymbol{x},t)$
, where
![]() $d(\boldsymbol{x},t)\equiv (\unicode[STIX]{x1D70C}(\boldsymbol{x},t)-\unicode[STIX]{x1D70C}_{0})/\unicode[STIX]{x1D71A}_{z}=\mathfrak{z}$
is the depth, or vertical location, that an isopycnal located at
$d(\boldsymbol{x},t)\equiv (\unicode[STIX]{x1D70C}(\boldsymbol{x},t)-\unicode[STIX]{x1D70C}_{0})/\unicode[STIX]{x1D71A}_{z}=\mathfrak{z}$
is the depth, or vertical location, that an isopycnal located at
![]() $\boldsymbol{x}$
at time
$\boldsymbol{x}$
at time
![]() $t$
has in the reference density configuration defined by
$t$
has in the reference density configuration defined by
![]() $\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D71A}_{z}z$
, where
$\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D71A}_{z}z$
, where
![]() $\unicode[STIX]{x1D70C}$
is the mass density and
$\unicode[STIX]{x1D70C}$
is the mass density and
![]() $\unicode[STIX]{x1D70C}_{0}>0$
and
$\unicode[STIX]{x1D70C}_{0}>0$
and
![]() $\unicode[STIX]{x1D71A}_{z}<0$
are background density and background density stratification constants that do not need to be specified in this approach. It should be noted that
$\unicode[STIX]{x1D71A}_{z}<0$
are background density and background density stratification constants that do not need to be specified in this approach. It should be noted that
![]() ${\mathcal{D}}$
is triply periodic but
${\mathcal{D}}$
is triply periodic but
![]() $d$
is not. Static instability occurs when
$d$
is not. Static instability occurs when
![]() ${\mathcal{D}}_{z}\equiv \unicode[STIX]{x2202}{\mathcal{D}}/\unicode[STIX]{x2202}z>1$
. The Rossby number
${\mathcal{D}}_{z}\equiv \unicode[STIX]{x2202}{\mathcal{D}}/\unicode[STIX]{x2202}z>1$
. The Rossby number
![]() ${\mathcal{R}}\equiv \unicode[STIX]{x1D701}/f$
and the Froude number
${\mathcal{R}}\equiv \unicode[STIX]{x1D701}/f$
and the Froude number
![]() ${\mathcal{F}}\equiv \unicode[STIX]{x1D714}_{h}/{\mathcal{N}}$
, where
${\mathcal{F}}\equiv \unicode[STIX]{x1D714}_{h}/{\mathcal{N}}$
, where
![]() $\unicode[STIX]{x1D714}_{h}$
and
$\unicode[STIX]{x1D714}_{h}$
and
![]() $\unicode[STIX]{x1D701}$
are the horizontal and vertical components of the relative vorticity
$\unicode[STIX]{x1D701}$
are the horizontal and vertical components of the relative vorticity
![]() $\unicode[STIX]{x1D74E}$
respectively and
$\unicode[STIX]{x1D74E}$
respectively and
![]() ${\mathcal{N}}$
is the total Brunt–Väisälä frequency. The PVA
${\mathcal{N}}$
is the total Brunt–Väisälä frequency. The PVA
![]() $\unicode[STIX]{x1D71B}\equiv \unicode[STIX]{x1D6F1}-1$
, where
$\unicode[STIX]{x1D71B}\equiv \unicode[STIX]{x1D6F1}-1$
, where
![]() $\unicode[STIX]{x1D6F1}\equiv (\unicode[STIX]{x1D74E}/f+\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}d$
is the dimensionless total potential vorticity. The PVA
$\unicode[STIX]{x1D6F1}\equiv (\unicode[STIX]{x1D74E}/f+\boldsymbol{k})\boldsymbol{\cdot }\unicode[STIX]{x1D735}d$
is the dimensionless total potential vorticity. The PVA
![]() $\unicode[STIX]{x1D71B}$
is represented by contours in every isopycnal. The state variables are the components of the vector potential
$\unicode[STIX]{x1D71B}$
is represented by contours in every isopycnal. The state variables are the components of the vector potential
![]() $\unicode[STIX]{x1D753}=(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},\unicode[STIX]{x1D719})$
that provide the velocity
$\unicode[STIX]{x1D753}=(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},\unicode[STIX]{x1D719})$
that provide the velocity
![]() $\boldsymbol{u}\propto \unicode[STIX]{x1D735}\times \unicode[STIX]{x1D753}$
and the vertical displacement of isopycnals
$\boldsymbol{u}\propto \unicode[STIX]{x1D735}\times \unicode[STIX]{x1D753}$
and the vertical displacement of isopycnals
![]() ${\mathcal{D}}\propto \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D753}$
. This approach, briefly described in appendix B and in detail in Dritschel & Viúdez (Reference Dritschel and Viúdez2003), has been applied to the study of a variety of ageostrophic flows in the atmosphere and oceans (e.g. Viúdez Reference Viúdez2007).
${\mathcal{D}}\propto \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D753}$
. This approach, briefly described in appendix B and in detail in Dritschel & Viúdez (Reference Dritschel and Viúdez2003), has been applied to the study of a variety of ageostrophic flows in the atmosphere and oceans (e.g. Viúdez Reference Viúdez2007).
4 Evolution of the isolated marginally stable vortex
In this section, we describe the time evolution of an oblate vortex
![]() $\unicode[STIX]{x1D71B}_{2,2}$
, which is a smooth vortex compared with higher-order vortices having larger PVA gradients (figure 1). The main purpose of this section is to show that an initially perturbed
$\unicode[STIX]{x1D71B}_{2,2}$
, which is a smooth vortex compared with higher-order vortices having larger PVA gradients (figure 1). The main purpose of this section is to show that an initially perturbed
![]() $\unicode[STIX]{x1D71B}_{2,2}$
vortex experiences several unsteady processes, similar to those experienced by similar vortices, but it nevertheless remains marginally stable for long time periods. The specific
$\unicode[STIX]{x1D71B}_{2,2}$
vortex experiences several unsteady processes, similar to those experienced by similar vortices, but it nevertheless remains marginally stable for long time periods. The specific
![]() $\unicode[STIX]{x1D71B}_{2,2}$
vortex chosen is a large-amplitude anticyclone with PVA amplitude
$\unicode[STIX]{x1D71B}_{2,2}$
vortex chosen is a large-amplitude anticyclone with PVA amplitude
![]() $\unicode[STIX]{x1D71B}_{0}=-0.8$
, which implies a high maximum absolute Rossby number of
$\unicode[STIX]{x1D71B}_{0}=-0.8$
, which implies a high maximum absolute Rossby number of
![]() $Ro\approx 0.8$
and oblate geometry
$Ro\approx 0.8$
and oblate geometry
![]() $(r_{0}/c_{0},z_{0})=(2,-0.9)$
in the QG space of coordinates
$(r_{0}/c_{0},z_{0})=(2,-0.9)$
in the QG space of coordinates
![]() $(r/c_{0},z)$
. It should be noticed that, although the PVA distribution in the isopycnal space is oblate (figure 2
a), the inner PVA core (
$(r/c_{0},z)$
. It should be noticed that, although the PVA distribution in the isopycnal space is oblate (figure 2
a), the inner PVA core (
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}<0$
) is approximately spherical, and indeed the azimuthal velocity distribution
$\tilde{\unicode[STIX]{x1D71B}}_{B}<0$
) is approximately spherical, and indeed the azimuthal velocity distribution
![]() $v_{B}(r,z)$
is prolate in the QG physical space (figure 2
b). We notice that this particular parameter set
$v_{B}(r,z)$
is prolate in the QG physical space (figure 2
b). We notice that this particular parameter set
![]() $\{p,q,\unicode[STIX]{x1D71B}_{0},|z_{0}c_{0}/r_{0}|\}=\{2,2,-0.8,0.9/2\}$
is an extremal case of a marginally stable vortex with a high Rossby number. Numerical experiments on vortices with larger
$\{p,q,\unicode[STIX]{x1D71B}_{0},|z_{0}c_{0}/r_{0}|\}=\{2,2,-0.8,0.9/2\}$
is an extremal case of a marginally stable vortex with a high Rossby number. Numerical experiments on vortices with larger
![]() $z_{0}$
(more prolate) or more negative
$z_{0}$
(more prolate) or more negative
![]() $\unicode[STIX]{x1D71B}_{0}$
(higher Rossby number) turned out to be unstable, while vortices with shorter
$\unicode[STIX]{x1D71B}_{0}$
(higher Rossby number) turned out to be unstable, while vortices with shorter
![]() $z_{0}$
(more oblate) or less negative
$z_{0}$
(more oblate) or less negative
![]() $\unicode[STIX]{x1D71B}_{0}$
(lower Rossby number) continued to be marginally stable. Increasing the parameters
$\unicode[STIX]{x1D71B}_{0}$
(lower Rossby number) continued to be marginally stable. Increasing the parameters
![]() $(p,q)$
with the other parameters remaining unchanged caused larger horizontal PVA gradients and resulted in unstable vortices. For example, both
$(p,q)$
with the other parameters remaining unchanged caused larger horizontal PVA gradients and resulted in unstable vortices. For example, both
![]() $\unicode[STIX]{x1D71B}_{3,3}$
and
$\unicode[STIX]{x1D71B}_{3,3}$
and
![]() $\unicode[STIX]{x1D71B}_{4,4}$
vortices were unstable and, after breaking their positive and negative PVA cores, evolved,
$\unicode[STIX]{x1D71B}_{4,4}$
vortices were unstable and, after breaking their positive and negative PVA cores, evolved,
![]() $\unicode[STIX]{x1D71B}_{4,4}$
more rapidly than
$\unicode[STIX]{x1D71B}_{4,4}$
more rapidly than
![]() $\unicode[STIX]{x1D71B}_{3,3}$
, into two departing dipoles in a way similar to the two-dimensional zero circulation Rankine vortices in Morel & Carton (Reference Morel and Carton1994).
$\unicode[STIX]{x1D71B}_{3,3}$
, into two departing dipoles in a way similar to the two-dimensional zero circulation Rankine vortices in Morel & Carton (Reference Morel and Carton1994).

Figure 2. (a) The base 2D PVA
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}(\mathfrak{r},\mathfrak{z})$
for vortex
$\tilde{\unicode[STIX]{x1D71B}}_{B}(\mathfrak{r},\mathfrak{z})$
for vortex
![]() $\unicode[STIX]{x1D71B}_{2,2}$
. Contour lines
$\unicode[STIX]{x1D71B}_{2,2}$
. Contour lines
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}<0$
(continuous),
$\tilde{\unicode[STIX]{x1D71B}}_{B}<0$
(continuous),
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}=0$
(thick) and
$\tilde{\unicode[STIX]{x1D71B}}_{B}=0$
(thick) and
![]() $\tilde{\unicode[STIX]{x1D71B}}_{B}>0$
(dashed); contour interval
$\tilde{\unicode[STIX]{x1D71B}}_{B}>0$
(dashed); contour interval
![]() $\unicode[STIX]{x1D6E5}=0.1$
. (b) The base azimuthal velocity component
$\unicode[STIX]{x1D6E5}=0.1$
. (b) The base azimuthal velocity component
![]() $v_{B}(r,z)$
. Contour lines
$v_{B}(r,z)$
. Contour lines
![]() $v_{B}<0$
(continuous) and
$v_{B}<0$
(continuous) and
![]() $v_{B}=0$
(dashed); contour interval
$v_{B}=0$
(dashed); contour interval
![]() $\unicode[STIX]{x1D6E5}=0.1$
;
$\unicode[STIX]{x1D6E5}=0.1$
;
![]() $v_{B}(r,z)\in [-0.97,0.032]$
. The thick dashed line indicates the critical level
$v_{B}(r,z)\in [-0.97,0.032]$
. The thick dashed line indicates the critical level
![]() $r_{cr}(z)$
where
$r_{cr}(z)$
where
![]() $v_{B}(r_{cr}(z),z)/r_{cr}(z)=\dot{\unicode[STIX]{x1D717}}_{0}$
. The spatial extent shown is only a part of the whole domain of the numerical simulation whose spatial intervals are
$v_{B}(r_{cr}(z),z)/r_{cr}(z)=\dot{\unicode[STIX]{x1D717}}_{0}$
. The spatial extent shown is only a part of the whole domain of the numerical simulation whose spatial intervals are
![]() $\unicode[STIX]{x0394}X/c_{0}=\unicode[STIX]{x0394}Y/c_{0}=\unicode[STIX]{x0394}Z=[-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$
.
$\unicode[STIX]{x0394}X/c_{0}=\unicode[STIX]{x0394}Y/c_{0}=\unicode[STIX]{x0394}Z=[-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$
.
A small PVA jump
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D71B}\simeq 1.24\times 10^{-2}$
is used to correctly discretize the PVA in the outer vortex. This small PVA jump implies a large number of PVA contours in every isopycnal. For example, the number of contours
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D71B}\simeq 1.24\times 10^{-2}$
is used to correctly discretize the PVA in the outer vortex. This small PVA jump implies a large number of PVA contours in every isopycnal. For example, the number of contours
![]() $n_{c}$
between PVA extrema
$n_{c}$
between PVA extrema
![]() $\unicode[STIX]{x1D71B}_{0}$
and
$\unicode[STIX]{x1D71B}_{0}$
and
![]() $\unicode[STIX]{x1D71B}_{min}$
in the middle layer
$\unicode[STIX]{x1D71B}_{min}$
in the middle layer
![]() $\mathfrak{z}=0$
(figure 3) is
$\mathfrak{z}=0$
(figure 3) is
![]() $n_{c}=80$
. The PVA minimum location (A 5) is
$n_{c}=80$
. The PVA minimum location (A 5) is
![]() $\unicode[STIX]{x1D718}_{e}=5/8=0.625$
and its value
$\unicode[STIX]{x1D718}_{e}=5/8=0.625$
and its value
![]() $\unicode[STIX]{x1D71B}_{min}=\unicode[STIX]{x1D71B}(\unicode[STIX]{x1D718}_{e},0)\simeq -0.24$
. Although numerical truncation inherent to any discrete computer algorithm causes a lack of precision and accuracy large enough to trigger the vortex unsteadiness at long times (e.g. Reinaud Reference Reinaud2017), we added a small perturbation consisting of a small horizontal displacement of the PVA contours by an amplitude
$\unicode[STIX]{x1D71B}_{min}=\unicode[STIX]{x1D71B}(\unicode[STIX]{x1D718}_{e},0)\simeq -0.24$
. Although numerical truncation inherent to any discrete computer algorithm causes a lack of precision and accuracy large enough to trigger the vortex unsteadiness at long times (e.g. Reinaud Reference Reinaud2017), we added a small perturbation consisting of a small horizontal displacement of the PVA contours by an amplitude
![]() $\unicode[STIX]{x1D6FF}r=0.1$
and vertical wavenumbers 2 and 3, in order to speed up the unsteady motion leading to the marginally stable vortex.
$\unicode[STIX]{x1D6FF}r=0.1$
and vertical wavenumbers 2 and 3, in order to speed up the unsteady motion leading to the marginally stable vortex.
The time evolution of the vortex (figure 3, supplementary movie 1 available at https://doi.org/10.1017/jfm.2017.440) shows that, as expected, instability develops at the radius of maximum PVA, the critical level (Benilov Reference Benilov2003; Nguyen et al.
Reference Nguyen, Hua, Schopp and Carton2012), and the inner core acquires a mode 2 perturbation. However, both the inner negative and outer positive PVA regions remain largely stable for long time periods. In this case, the vortex was stable through the complete simulation period of 365 ip, reaching Rossby numbers
![]() ${\mathcal{R}}\in [-0.77,0.23]$
and maximum Froude number
${\mathcal{R}}\in [-0.77,0.23]$
and maximum Froude number
![]() ${\mathcal{F}}_{max}=0.24$
.
${\mathcal{F}}_{max}=0.24$
.

Figure 3. The distribution of the PVA jumps on the middle isopycnal
![]() $\mathfrak{z}=0$
at times
$\mathfrak{z}=0$
at times
![]() $t=0$
, 60 and 140 ip for vortex
$t=0$
, 60 and 140 ip for vortex
![]() $\unicode[STIX]{x1D71B}_{2,2}$
.
$\unicode[STIX]{x1D71B}_{2,2}$
.
Prior to the PVA wave breaking at the critical level, the inner vortex experiences layering (Nguyen et al.
Reference Nguyen, Hua, Schopp and Carton2012; Hua et al.
Reference Hua, Ménesguen, Gentil, Schopp, Marsset and Aiki2013; Meunier et al.
Reference Meunier, Ménesguen, Schopp and Le Gentil2015) above and below the middle depth (figure 4). Layering, or stacking of the PVA, as recently found by Nguyen et al. (Reference Nguyen, Hua, Schopp and Carton2012), has a helical structure. Here, we observe, very clearly due to the large number of PVA contours on every isopycnal, the time evolution of the spiral stacking consisting of a spiral with growing radial wavenumber. The spiral pattern is noticed as early as
![]() $t=10~\text{ip}$
with a radial wavenumber of approximately 2, and grows approximately as
$t=10~\text{ip}$
with a radial wavenumber of approximately 2, and grows approximately as
![]() $t/(5~\text{ip})$
. It should be noted that layering occurs in most parts of the inner vortex and not only close to the critical level radius. These are probably vortex Rossby waves (Tung Reference Tung1983; Montgomery & Kallenbach Reference Montgomery and Kallenbach1997; McWilliams, Graves & Montgomery Reference McWilliams, Graves and Montgomery2003), taking place in the presence of PVA gradients and having an increasing radial wavenumber. The vortex Rossby waves develop and grow in the inner core but only break at the critical, or stagnation, radius, where the phase speed (given below) of the PVA mode 2 perturbation equals the angular velocity of the background azimuthal vortex motion. The averaged kinetic energy in the outer shell of positive PVA (
$t/(5~\text{ip})$
. It should be noted that layering occurs in most parts of the inner vortex and not only close to the critical level radius. These are probably vortex Rossby waves (Tung Reference Tung1983; Montgomery & Kallenbach Reference Montgomery and Kallenbach1997; McWilliams, Graves & Montgomery Reference McWilliams, Graves and Montgomery2003), taking place in the presence of PVA gradients and having an increasing radial wavenumber. The vortex Rossby waves develop and grow in the inner core but only break at the critical, or stagnation, radius, where the phase speed (given below) of the PVA mode 2 perturbation equals the angular velocity of the background azimuthal vortex motion. The averaged kinetic energy in the outer shell of positive PVA (
![]() $\unicode[STIX]{x1D71B}\geqslant 0.1$
) increases at the expense of the potential energy of both this outer shell and the inner negative PVA vortex core.
$\unicode[STIX]{x1D71B}\geqslant 0.1$
) increases at the expense of the potential energy of both this outer shell and the inner negative PVA vortex core.
Other vortex configurations, depending on the four parameters
![]() $\{p,q,\unicode[STIX]{x1D71B}_{0},z_{0}c_{0}/r_{0}\}$
of this vortex family, lead to vortices that become unstable and transform into a tripole, a pair of dipoles, etc., in ways similar to other vortices and dynamics described in previous studies (Carnevale & Kloosterziel Reference Carnevale and Kloosterziel1994; Morel & Carton Reference Morel and Carton1994; Reinaud Reference Reinaud2017). These instability processes will not be analysed here.
$\{p,q,\unicode[STIX]{x1D71B}_{0},z_{0}c_{0}/r_{0}\}$
of this vortex family, lead to vortices that become unstable and transform into a tripole, a pair of dipoles, etc., in ways similar to other vortices and dynamics described in previous studies (Carnevale & Kloosterziel Reference Carnevale and Kloosterziel1994; Morel & Carton Reference Morel and Carton1994; Reinaud Reference Reinaud2017). These instability processes will not be analysed here.

Figure 4. The distribution of the PVA jumps on the lower isopycnal
![]() $\mathfrak{z}\simeq -0.4$
(isopycnal numerical index
$\mathfrak{z}\simeq -0.4$
(isopycnal numerical index
![]() $i_{\mathfrak{z}}=102$
) at times
$i_{\mathfrak{z}}=102$
) at times
![]() $t=10$
, 20, 30 and 40 ip for vortex
$t=10$
, 20, 30 and 40 ip for vortex
![]() $\unicode[STIX]{x1D71B}_{2,2}$
. Vortex revolution is observed here as a slight mismatch between the vortex and domain geometrical centres.
$\unicode[STIX]{x1D71B}_{2,2}$
. Vortex revolution is observed here as a slight mismatch between the vortex and domain geometrical centres.
In order to describe the unsteady PVA disturbances, we define the PVA centre of the inner vortex, at every depth
![]() $z$
, by its normalized first moment
$z$
, by its normalized first moment
![]() $\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)$
,
$\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)$
,
 $$\begin{eqnarray}\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)\equiv \frac{\displaystyle \int _{{\mathcal{S}}_{h}(z,t)}(x\boldsymbol{i}+y\,\boldsymbol{j})\,\unicode[STIX]{x1D71B}(x,y,z,t)\,\text{d}x\,\text{d}y}{\displaystyle \int _{{\mathcal{S}}_{h}(z,t)}\unicode[STIX]{x1D71B}(x,y,z,t)\,\text{d}x\,\text{d}y},\end{eqnarray}$$
$$\begin{eqnarray}\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)\equiv \frac{\displaystyle \int _{{\mathcal{S}}_{h}(z,t)}(x\boldsymbol{i}+y\,\boldsymbol{j})\,\unicode[STIX]{x1D71B}(x,y,z,t)\,\text{d}x\,\text{d}y}{\displaystyle \int _{{\mathcal{S}}_{h}(z,t)}\unicode[STIX]{x1D71B}(x,y,z,t)\,\text{d}x\,\text{d}y},\end{eqnarray}$$
where
![]() ${\mathcal{S}}_{h}(z,t)$
is the spatial horizontal surface where
${\mathcal{S}}_{h}(z,t)$
is the spatial horizontal surface where
![]() $\unicode[STIX]{x1D71B}(x,y,z,t)<0$
and its absolute value
$\unicode[STIX]{x1D71B}(x,y,z,t)<0$
and its absolute value
![]() $|\unicode[STIX]{x1D71B}(x,y,z,t)|$
is larger than a threshold value
$|\unicode[STIX]{x1D71B}(x,y,z,t)|$
is larger than a threshold value
![]() $\unicode[STIX]{x1D71B}_{T}\equiv 0.1(|\text{max}(\unicode[STIX]{x1D71B})|+|\text{min}(\unicode[STIX]{x1D71B})|)/2$
; that is,
$\unicode[STIX]{x1D71B}_{T}\equiv 0.1(|\text{max}(\unicode[STIX]{x1D71B})|+|\text{min}(\unicode[STIX]{x1D71B})|)/2$
; that is,
![]() ${\mathcal{S}}_{h}(z,t)=\{(x,y)\mid \unicode[STIX]{x1D71B}(x,y,z,t)\leqslant -\unicode[STIX]{x1D71B}_{T}\}$
. The horizontal phase functions
${\mathcal{S}}_{h}(z,t)=\{(x,y)\mid \unicode[STIX]{x1D71B}(x,y,z,t)\leqslant -\unicode[STIX]{x1D71B}_{T}\}$
. The horizontal phase functions
![]() $\hat{\unicode[STIX]{x1D703}}(z,t)\equiv \arctan (\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)\boldsymbol{\cdot }\boldsymbol{j},\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)\boldsymbol{\cdot }\boldsymbol{i})$
are not plotted since these are visually indistinguishable from a single straight line. The phase functions are vertically averaged to provide the averaged phase
$\hat{\unicode[STIX]{x1D703}}(z,t)\equiv \arctan (\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)\boldsymbol{\cdot }\boldsymbol{j},\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)\boldsymbol{\cdot }\boldsymbol{i})$
are not plotted since these are visually indistinguishable from a single straight line. The phase functions are vertically averaged to provide the averaged phase
![]() $\langle \hat{\unicode[STIX]{x1D703}}\rangle (t)$
and hence the averaged phase speed
$\langle \hat{\unicode[STIX]{x1D703}}\rangle (t)$
and hence the averaged phase speed
![]() $\dot{\unicode[STIX]{x1D703}}(t)\equiv \text{d}\langle \hat{\unicode[STIX]{x1D703}}\rangle /\text{d}t$
, which, using a linear model fit to
$\dot{\unicode[STIX]{x1D703}}(t)\equiv \text{d}\langle \hat{\unicode[STIX]{x1D703}}\rangle /\text{d}t$
, which, using a linear model fit to
![]() $\langle \hat{\unicode[STIX]{x1D703}}\rangle (t)$
, gives an average phase speed
$\langle \hat{\unicode[STIX]{x1D703}}\rangle (t)$
, gives an average phase speed
![]() $\dot{\unicode[STIX]{x1D703}}_{0}\simeq -0.3045~\text{ip}^{-1}$
, equivalent to a period
$\dot{\unicode[STIX]{x1D703}}_{0}\simeq -0.3045~\text{ip}^{-1}$
, equivalent to a period
![]() $T_{0}\simeq 20.63~\text{ip}$
.
$T_{0}\simeq 20.63~\text{ip}$
.

Figure 5. The vertical velocity
![]() $w(x,y,z,t)$
at time
$w(x,y,z,t)$
at time
![]() $t=140~\text{ip}$
on (a) the horizontal plane
$t=140~\text{ip}$
on (a) the horizontal plane
![]() $z=0$
and (b) the vertical section
$z=0$
and (b) the vertical section
![]() $y=0$
. Here,
$y=0$
. Here,
![]() $w\in [-2.1,2.1]\times 10^{-3}$
and the contour interval
$w\in [-2.1,2.1]\times 10^{-3}$
and the contour interval
![]() $\unicode[STIX]{x1D6E5}=0.2\times 10^{-3}$
.
$\unicode[STIX]{x1D6E5}=0.2\times 10^{-3}$
.
An alternative way to measure the phase speed of the PVA disturbance is through the vertical velocity field
![]() $w(x,y,z,t)$
, which is an appropriate quantity to measure the vortex perturbation because the
$w(x,y,z,t)$
, which is an appropriate quantity to measure the vortex perturbation because the
![]() $w$
of the vortex base state is zero, and
$w$
of the vortex base state is zero, and
![]() $w$
only develops due to the vortex deviation from its base state. The vertical velocity pattern (figure 5, movie 2) is basically dipolar and rotates with the vortex phase speed. Defining the positive and negative
$w$
only develops due to the vortex deviation from its base state. The vertical velocity pattern (figure 5, movie 2) is basically dipolar and rotates with the vortex phase speed. Defining the positive and negative
![]() $w$
centres
$w$
centres
![]() $\boldsymbol{r}_{wh}^{\pm }(z,t)$
, the mean location or vortex centre
$\boldsymbol{r}_{wh}^{\pm }(z,t)$
, the mean location or vortex centre
![]() $\overline{\boldsymbol{r}}_{wh}(z,t)$
and the vector from negative to positive centres
$\overline{\boldsymbol{r}}_{wh}(z,t)$
and the vector from negative to positive centres
![]() $\hat{\boldsymbol{r}}_{wh}(z,t)$
as
$\hat{\boldsymbol{r}}_{wh}(z,t)$
as
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{r}_{wh}^{\pm }(z,t)\equiv \frac{\displaystyle \int _{{\mathcal{S}}_{h}^{\pm }(z,t)}(x\boldsymbol{i}+y\,\boldsymbol{j})w(x,y,z,t)\,\text{d}x\,\text{d}y}{\displaystyle \int _{{\mathcal{S}}_{h}^{\pm }(z,t)}w(x,y,z,t)\,\text{d}x\,\text{d}y}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{r}_{wh}^{\pm }(z,t)\equiv \frac{\displaystyle \int _{{\mathcal{S}}_{h}^{\pm }(z,t)}(x\boldsymbol{i}+y\,\boldsymbol{j})w(x,y,z,t)\,\text{d}x\,\text{d}y}{\displaystyle \int _{{\mathcal{S}}_{h}^{\pm }(z,t)}w(x,y,z,t)\,\text{d}x\,\text{d}y}, & \displaystyle\end{eqnarray}$$
it is also possible to trace the motion of the disturbance vortex. Above
![]() ${\mathcal{S}}_{h}^{\pm }(z,t)$
is the spatial horizontal surface where the vertical velocity magnitude has a minimum threshold value
${\mathcal{S}}_{h}^{\pm }(z,t)$
is the spatial horizontal surface where the vertical velocity magnitude has a minimum threshold value
![]() $w_{T}\equiv 0.1(|\text{max}(w)|+|\text{min}(w)|)/2$
; that is,
$w_{T}\equiv 0.1(|\text{max}(w)|+|\text{min}(w)|)/2$
; that is,
![]() ${\mathcal{S}}_{h}^{\pm }(z,t)=(x,y)|\pm w(x,y,z,t)\geqslant w_{T}$
. The phase velocity computed from the vertical velocity moments is very similar to
${\mathcal{S}}_{h}^{\pm }(z,t)=(x,y)|\pm w(x,y,z,t)\geqslant w_{T}$
. The phase velocity computed from the vertical velocity moments is very similar to
![]() $\dot{\unicode[STIX]{x1D703}}_{0}\simeq -0.30~\text{ip}^{-1}$
. The critical radius
$\dot{\unicode[STIX]{x1D703}}_{0}\simeq -0.30~\text{ip}^{-1}$
. The critical radius
![]() $r_{cr}$
is where the angular velocity
$r_{cr}$
is where the angular velocity
![]() $v(r_{cr},z)/r_{cr}=\dot{\unicode[STIX]{x1D703}}_{0}$
. At the plane
$v(r_{cr},z)/r_{cr}=\dot{\unicode[STIX]{x1D703}}_{0}$
. At the plane
![]() $z=0$
, this happens at
$z=0$
, this happens at
![]() $r_{cr}\simeq 1.2c_{0}$
, where
$r_{cr}\simeq 1.2c_{0}$
, where
![]() $v(r_{cr},0)\simeq -0.3$
. The critical radius
$v(r_{cr},0)\simeq -0.3$
. The critical radius
![]() $r_{cr}(z)$
decreases with depth
$r_{cr}(z)$
decreases with depth
![]() $z$
, and is included in figure 2(a).
$z$
, and is included in figure 2(a).
The marginally stable vortex state is reached after an initial adjustment period of approximately 60 ip during which the vortex experiences the process of axisymmetrization towards a vertically tilted axial precession vortex. Vortex precession is a known process in unsteady baroclinic geophysical vortices (e.g. Päschke et al.
Reference Päschke, Marschalik, Owinoh and Klein2012). The time evolution of the angle
![]() $\unicode[STIX]{x1D719}(z,t)\equiv \arctan (|\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)|/z)$
that forms the three-dimensional vortex axis vectors
$\unicode[STIX]{x1D719}(z,t)\equiv \arctan (|\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)|/z)$
that forms the three-dimensional vortex axis vectors
![]() $\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)+z\,\boldsymbol{k}$
with the vertical direction
$\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z,t)+z\,\boldsymbol{k}$
with the vertical direction
![]() $\boldsymbol{k}$
(declination or axial tilt, figure 6
a) shows the initial adjustment period, the axial precession with a mean declination
$\boldsymbol{k}$
(declination or axial tilt, figure 6
a) shows the initial adjustment period, the axial precession with a mean declination
![]() $\langle \langle \unicode[STIX]{x1D719}\rangle \rangle \simeq 0.115$
(measured in the QG stretched space) and oscillations of
$\langle \langle \unicode[STIX]{x1D719}\rangle \rangle \simeq 0.115$
(measured in the QG stretched space) and oscillations of
![]() $\langle \unicode[STIX]{x1D719}\rangle (t)$
around the mean
$\langle \unicode[STIX]{x1D719}\rangle (t)$
around the mean
![]() $\langle \langle \unicode[STIX]{x1D719}\rangle \rangle$
, which indicate nutation of the rotation axis. Visual inspection of
$\langle \langle \unicode[STIX]{x1D719}\rangle \rangle$
, which indicate nutation of the rotation axis. Visual inspection of
![]() $\langle \unicode[STIX]{x1D719}\rangle (t)$
in figure 6(a) reveals two kinds of nutations, namely a fast low-amplitude and a slow large-amplitude oscillation. The time spectrum of
$\langle \unicode[STIX]{x1D719}\rangle (t)$
in figure 6(a) reveals two kinds of nutations, namely a fast low-amplitude and a slow large-amplitude oscillation. The time spectrum of
![]() $\langle \unicode[STIX]{x1D719}\rangle (t)$
(figure 6
b) confirms the two nutation frequencies
$\langle \unicode[STIX]{x1D719}\rangle (t)$
(figure 6
b) confirms the two nutation frequencies
![]() $\unicode[STIX]{x1D717}_{n1}\simeq 0.023~\text{cyc}/\text{ip}$
(period
$\unicode[STIX]{x1D717}_{n1}\simeq 0.023~\text{cyc}/\text{ip}$
(period
![]() $T_{n1}\simeq 43.5~\text{ip}$
) and
$T_{n1}\simeq 43.5~\text{ip}$
) and
![]() $\unicode[STIX]{x1D717}_{n2}\simeq 0.013~\text{cyc}/\text{ip}$
(period
$\unicode[STIX]{x1D717}_{n2}\simeq 0.013~\text{cyc}/\text{ip}$
(period
![]() $T_{n2}\simeq 76.9~\text{ip}$
), which are presumably related to the inner negative PVA vortex and outer positive PVA vortex respectively. It should be noted that both nutation periods
$T_{n2}\simeq 76.9~\text{ip}$
), which are presumably related to the inner negative PVA vortex and outer positive PVA vortex respectively. It should be noted that both nutation periods
![]() $T_{ni}$
are larger than the precession period
$T_{ni}$
are larger than the precession period
![]() $T_{p}\simeq 20.6~\text{ip}$
.
$T_{p}\simeq 20.6~\text{ip}$
.
The inner vortex also experiences revolution, which may be noticed in figure 4 as a slight departure of the centre of the most interior vortex contour lines from the geometrical centre of the domain. Vortex revolution may be measured from the vertical average
![]() $\langle \hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}\rangle (t)$
. The rotary spectra of
$\langle \hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}\rangle (t)$
. The rotary spectra of
![]() $\langle \hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}\rangle (t)$
show that the revolution is anticyclonic with an amplitude of approximately 0.1 and period
$\langle \hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}\rangle (t)$
show that the revolution is anticyclonic with an amplitude of approximately 0.1 and period
![]() $T_{R}\simeq 20.9~\text{ip}$
, which, considering sampling errors (three-dimensional numerical fields are saved every inertial period), is indiscernible from the PVA vortex period
$T_{R}\simeq 20.9~\text{ip}$
, which, considering sampling errors (three-dimensional numerical fields are saved every inertial period), is indiscernible from the PVA vortex period
![]() $T_{0}\simeq 20.6~\text{ip}$
computed earlier, so that the vortex revolution and precession axis are in phase.
$T_{0}\simeq 20.6~\text{ip}$
computed earlier, so that the vortex revolution and precession axis are in phase.

Figure 6. (a) The angle
![]() $\unicode[STIX]{x1D719}(z,t)$
computed from vectors in the lower (
$\unicode[STIX]{x1D719}(z,t)$
computed from vectors in the lower (
![]() $z<0$
, blue points) and upper (
$z<0$
, blue points) and upper (
![]() $z>0$
, red points) part of the vortex. The black curve is the mean
$z>0$
, red points) part of the vortex. The black curve is the mean
![]() $\langle \unicode[STIX]{x1D719}\rangle (t)$
, having a time-mean
$\langle \unicode[STIX]{x1D719}\rangle (t)$
, having a time-mean
![]() $\langle \langle \unicode[STIX]{x1D719}\rangle \rangle \simeq 0.115$
. The grey dashed curve
$\langle \langle \unicode[STIX]{x1D719}\rangle \rangle \simeq 0.115$
. The grey dashed curve
![]() $\overline{\unicode[STIX]{x1D719}}(t)\simeq \langle \unicode[STIX]{x1D719}\rangle (t)$
is the angle of the straight line resulting from the least-squares fit to the locations
$\overline{\unicode[STIX]{x1D719}}(t)\simeq \langle \unicode[STIX]{x1D719}\rangle (t)$
is the angle of the straight line resulting from the least-squares fit to the locations
![]() $\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z_{i},t)+z_{i}\,\boldsymbol{k}$
for
$\hat{\boldsymbol{r}}_{\unicode[STIX]{x1D71B}}(z_{i},t)+z_{i}\,\boldsymbol{k}$
for
![]() $z_{i}$
in the inner vortex. (b) The time spectrum of
$z_{i}$
in the inner vortex. (b) The time spectrum of
![]() $\langle \unicode[STIX]{x1D719}\rangle (t)$
, showing the two peaks at both nutation frequencies.
$\langle \unicode[STIX]{x1D719}\rangle (t)$
, showing the two peaks at both nutation frequencies.
5 Concluding remarks
Long-term stability of isolated oceanic vortices has been a topic of fruitful research in fluid dynamics and physical oceanography in recent decades. Here, we have seen that, in some vortex configurations, sign reversal in the radial gradient of the PVA, as implied by the isolation requirement, leads to vortex unsteadiness but does not break the vortex coherence, and the vortex remains marginally stable even for high Rossby numbers. The marginally stable vortices are some elements of the new isolated vortex family
![]() $\unicode[STIX]{x1D71B}_{p,q}$
characterized by a zero amount of PVA on every isopycnal. Confidence in the numerical stability results is sustained by the reproduction of phenomena occurring in the vortex evolution towards the marginally stable final state. Spiral waves (apparently vortex Rossby waves) and axial symmetrization play an essential part in this evolution. The marginally stable final state is characterized by an unsteady vortex whose inner one-signed PV part experiences revolution, rotation, precession and nutation. Curiously, in this sense, the inner vortex experiences the same four motions as the solid Earth. Moreover, we do not discard flow instabilities that may break the vortex at very long times, say at
$\unicode[STIX]{x1D71B}_{p,q}$
characterized by a zero amount of PVA on every isopycnal. Confidence in the numerical stability results is sustained by the reproduction of phenomena occurring in the vortex evolution towards the marginally stable final state. Spiral waves (apparently vortex Rossby waves) and axial symmetrization play an essential part in this evolution. The marginally stable final state is characterized by an unsteady vortex whose inner one-signed PV part experiences revolution, rotation, precession and nutation. Curiously, in this sense, the inner vortex experiences the same four motions as the solid Earth. Moreover, we do not discard flow instabilities that may break the vortex at very long times, say at
![]() $O(t)=10^{3}~\text{ip}$
, since we have not investigated this aspect with very long numerical integrations. However, at these very long time scales, the amplitude of ocean vortices decays due to turbulent viscosity or temperature and salinity diffusion, which are not considered in our PV conserving approach which is strictly valid for inviscid adiabatic flows.
$O(t)=10^{3}~\text{ip}$
, since we have not investigated this aspect with very long numerical integrations. However, at these very long time scales, the amplitude of ocean vortices decays due to turbulent viscosity or temperature and salinity diffusion, which are not considered in our PV conserving approach which is strictly valid for inviscid adiabatic flows.
In this marginally stable state, the vertical velocity has a dipolar pattern with maxima at
![]() $z=0$
. This dipolar pattern is related to the upward and downward motion of almost plane isopycnals caused by the axial precession of a spheroidal vortex. This dipolar pattern contrasts with the octopolar pattern of vertical velocity characteristic of ellipsoidal PVA, not precessing, vortices, which is due to the motion of fluid particles on ellipsoidal isopycnals at a speed faster than the vortex phase speed, and is therefore zero at
$z=0$
. This dipolar pattern is related to the upward and downward motion of almost plane isopycnals caused by the axial precession of a spheroidal vortex. This dipolar pattern contrasts with the octopolar pattern of vertical velocity characteristic of ellipsoidal PVA, not precessing, vortices, which is due to the motion of fluid particles on ellipsoidal isopycnals at a speed faster than the vortex phase speed, and is therefore zero at
![]() $z=0$
where isopycnals are horizontal.
$z=0$
where isopycnals are horizontal.
The question of how well this mathematical vortex model fits oceanic vortices must be evaluated only after experimental acquisition and careful analysis of high-resolution density and velocity data, allowing detailed computation of the PVA along vortex vertical radial sections. We note that, although the vortex unsteadiness may look drastic in the PVA contours, the unsteady velocity perturbations are only of second order relative to the vortex flow. In the particular case analysed here, the maximum flow speed is of order
![]() $|\boldsymbol{u}|\approx 1$
, while the corresponding speed perturbations are only
$|\boldsymbol{u}|\approx 1$
, while the corresponding speed perturbations are only
![]() $|\unicode[STIX]{x0394}\boldsymbol{u}|\approx 0.1$
. Thus, experimental data analysis should be able to discriminate this intrinsic vortex velocity perturbation from external perturbations due to inertia–gravity waves, tides or wind stress induced currents.
$|\unicode[STIX]{x0394}\boldsymbol{u}|\approx 0.1$
. Thus, experimental data analysis should be able to discriminate this intrinsic vortex velocity perturbation from external perturbations due to inertia–gravity waves, tides or wind stress induced currents.
Acknowledgements
I thank four anonymous referees for their very helpful comments. Partial support for this study was obtained through project CTM2014-56987-P (Spanish Ministry of Science and Innovation).
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2017.440.
Appendix A. Base PVA distribution
The base PVA
![]() $\tilde{\unicode[STIX]{x1D71B}}_{b}(\mathfrak{r},\mathfrak{z})$
is constructed from the one-dimensional function
$\tilde{\unicode[STIX]{x1D71B}}_{b}(\mathfrak{r},\mathfrak{z})$
is constructed from the one-dimensional function
![]() $\unicode[STIX]{x1D71B}_{B}(\unicode[STIX]{x1D718})$
, where the variable
$\unicode[STIX]{x1D71B}_{B}(\unicode[STIX]{x1D718})$
, where the variable
![]() $\unicode[STIX]{x1D718}=\tilde{\unicode[STIX]{x1D718}}(\mathfrak{r},\mathfrak{z})\equiv \mathfrak{r}/\mathfrak{r}_{0}(\mathfrak{z})$
is the radial distance scaled by the vortex radius
$\unicode[STIX]{x1D718}=\tilde{\unicode[STIX]{x1D718}}(\mathfrak{r},\mathfrak{z})\equiv \mathfrak{r}/\mathfrak{r}_{0}(\mathfrak{z})$
is the radial distance scaled by the vortex radius
![]() $\mathfrak{r}_{0}(\mathfrak{z})$
on isopycnal
$\mathfrak{r}_{0}(\mathfrak{z})$
on isopycnal
![]() $\mathfrak{z}$
. The function
$\mathfrak{z}$
. The function
![]() $\unicode[STIX]{x1D71B}_{B}$
must satisfy boundary conditions
$\unicode[STIX]{x1D71B}_{B}$
must satisfy boundary conditions
and
and the integral condition
For monopolar vortices with a single PVA core and one PVA annulus of opposite PVA sign, the PVA
![]() $\unicode[STIX]{x1D71B}_{B}$
on every isopycnal must have one zero and, subjected to the above conditions, only one interior extremum. Thus,
$\unicode[STIX]{x1D71B}_{B}$
on every isopycnal must have one zero and, subjected to the above conditions, only one interior extremum. Thus,
![]() $\unicode[STIX]{x1D71B}_{B}(\unicode[STIX]{x1D718})$
has only one interior extremum, say at
$\unicode[STIX]{x1D71B}_{B}(\unicode[STIX]{x1D718})$
has only one interior extremum, say at
![]() $\unicode[STIX]{x1D718}=\unicode[STIX]{x1D718}_{e}$
, and
$\unicode[STIX]{x1D718}=\unicode[STIX]{x1D718}_{e}$
, and
![]() $\unicode[STIX]{x1D71B}_{B}^{\prime }(\unicode[STIX]{x1D718})$
must be of the form
$\unicode[STIX]{x1D71B}_{B}^{\prime }(\unicode[STIX]{x1D718})$
must be of the form
The extremum
![]() $\unicode[STIX]{x1D718}_{e}$
is found from the integral condition (A 3b
), resulting in
$\unicode[STIX]{x1D718}_{e}$
is found from the integral condition (A 3b
), resulting in
where
![]() $B(p,q)$
is the Beta function. Integration of (A 4), with boundary conditions (A 1a,b
), leads to (2.5).
$B(p,q)$
is the Beta function. Integration of (A 4), with boundary conditions (A 1a,b
), leads to (2.5).
Appendix B. Theoretical basis of the numerical algorithm
By combining the non-hydrostatic balance of linear momentum in a rotating frame under the
![]() $f$
-plane and Boussinesq approximations, the mass conservation equation and the isochoric condition we obtain the rate of change of
$f$
-plane and Boussinesq approximations, the mass conservation equation and the isochoric condition we obtain the rate of change of
![]() $\boldsymbol{{\mathcal{A}}}={\mathcal{A}}\boldsymbol{i}+{\mathcal{B}}\,\boldsymbol{j}+{\mathcal{C}}\,\boldsymbol{k}\equiv \unicode[STIX]{x1D74E}/f-c_{0}^{2}\unicode[STIX]{x1D735}{\mathcal{D}}$
,
$\boldsymbol{{\mathcal{A}}}={\mathcal{A}}\boldsymbol{i}+{\mathcal{B}}\,\boldsymbol{j}+{\mathcal{C}}\,\boldsymbol{k}\equiv \unicode[STIX]{x1D74E}/f-c_{0}^{2}\unicode[STIX]{x1D735}{\mathcal{D}}$
,
The horizontal component of (B 1), namely the rate of change of
![]() $\boldsymbol{{\mathcal{A}}}_{h}=({\mathcal{A}},{\mathcal{B}})$
, is numerically integrated using an explicit leapfrog scheme, together with a weak Robert–Asselin time filter to avoid decoupling between even and odd time levels. Spatial derivatives are carried out in the spectral space. A biharmonic hyperdiffusion term, providing a small damping rate (
$\boldsymbol{{\mathcal{A}}}_{h}=({\mathcal{A}},{\mathcal{B}})$
, is numerically integrated using an explicit leapfrog scheme, together with a weak Robert–Asselin time filter to avoid decoupling between even and odd time levels. Spatial derivatives are carried out in the spectral space. A biharmonic hyperdiffusion term, providing a small damping rate (
![]() $e$
folding) per ip at the highest wavenumber equal to
$e$
folding) per ip at the highest wavenumber equal to
![]() $e_{f}=50$
, is added to the horizontal component of (B 1). The third prognostic equation is the explicit material conservation of PVA by contour advection on isopycnals (
$e_{f}=50$
, is added to the horizontal component of (B 1). The third prognostic equation is the explicit material conservation of PVA by contour advection on isopycnals (
![]() $\text{d}\unicode[STIX]{x1D71B}/\text{d}t=0$
), so that large PV gradients are not severely smoothed by diffusion. The locations of the PV contours are numerically integrated in time using a standard third-order three-time-level Adams–Bashforth scheme. The horizontal potentials
$\text{d}\unicode[STIX]{x1D71B}/\text{d}t=0$
), so that large PV gradients are not severely smoothed by diffusion. The locations of the PV contours are numerically integrated in time using a standard third-order three-time-level Adams–Bashforth scheme. The horizontal potentials
![]() $\unicode[STIX]{x1D753}_{h}=(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
are recovered from the inversion, in the spectral space, of
$\unicode[STIX]{x1D753}_{h}=(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
are recovered from the inversion, in the spectral space, of
![]() $\boldsymbol{{\mathcal{A}}}_{h}=\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D753}_{h}$
, while the vertical potential
$\boldsymbol{{\mathcal{A}}}_{h}=\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D753}_{h}$
, while the vertical potential
![]() $\unicode[STIX]{x1D719}$
is obtained from the inversion of the PVA definition
$\unicode[STIX]{x1D719}$
is obtained from the inversion of the PVA definition
![]() $\unicode[STIX]{x1D71B}\equiv \unicode[STIX]{x1D6F1}-1=(\unicode[STIX]{x1D74E}/f+\boldsymbol{k})\boldsymbol{\cdot }(\boldsymbol{k}-\unicode[STIX]{x1D735}{\mathcal{D}})-1$
in terms of the potentials,
$\unicode[STIX]{x1D71B}\equiv \unicode[STIX]{x1D6F1}-1=(\unicode[STIX]{x1D74E}/f+\boldsymbol{k})\boldsymbol{\cdot }(\boldsymbol{k}-\unicode[STIX]{x1D735}{\mathcal{D}})-1$
in terms of the potentials,
![]() $\unicode[STIX]{x1D71B}=\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D753}}\{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},\unicode[STIX]{x1D719}\}$
. The main advantage of these prognostic equations is that they allow us to use the potential vector
$\unicode[STIX]{x1D71B}=\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D753}}\{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},\unicode[STIX]{x1D719}\}$
. The main advantage of these prognostic equations is that they allow us to use the potential vector
![]() $\unicode[STIX]{x1D753}$
, so that volume conservation is implicit, both three-dimensional velocity and vertical displacement are obtained directly from
$\unicode[STIX]{x1D753}$
, so that volume conservation is implicit, both three-dimensional velocity and vertical displacement are obtained directly from
![]() $\unicode[STIX]{x1D753}$
, and the inversion of the horizontal potentials is easy (symbolically,
$\unicode[STIX]{x1D753}$
, and the inversion of the horizontal potentials is easy (symbolically,
![]() $\unicode[STIX]{x1D753}_{h}=\unicode[STIX]{x1D6FB}^{-2}\boldsymbol{{\mathcal{A}}}_{h}$
). The disadvantage of this formulation is that the computation of the (horizontal component) right-hand side of (B 1) and the inversion of the PVA (symbolically
$\unicode[STIX]{x1D753}_{h}=\unicode[STIX]{x1D6FB}^{-2}\boldsymbol{{\mathcal{A}}}_{h}$
). The disadvantage of this formulation is that the computation of the (horizontal component) right-hand side of (B 1) and the inversion of the PVA (symbolically
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D753}}^{-1}\{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},\unicode[STIX]{x1D71B}\}$
) are numerically costly.
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D753}}^{-1}\{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},\unicode[STIX]{x1D71B}\}$
) are numerically costly.