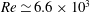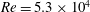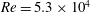1 Introduction
Stability and sensitivity analysis can be rigorously applied to a baseflow which is at incipient instability. As the baseflow departs from that condition the predictions provided by stability analysis become progressively less accurate. This is shown for instance in Sipp & Lebedev (Reference Sipp and Lebedev2007) for the flow past a circular cylinder. However, there are classes of oscillators characterised by the peculiarity that, if the stability analysis is applied to the mean flow field, even if the contribution of the Reynolds stresses is neglected in the stability equations, the analysis predicts a nearly marginally stable mode with a frequency which is similar to that of the nonlinearly saturated instability.
Conditions for this behaviour to hold are investigated by Sipp & Lebedev (Reference Sipp and Lebedev2007) and, more recently, by Turton, Tuckerman & Barkley (Reference Turton, Tuckerman and Barkley2015). In this last work it is shown that when a flow is characterised by energetically dominant quasi-monochromatic oscillations, thus leading to peaked temporal power spectra, the characteristics of the global mode leading to the oscillations can be predicted by the stability analysis of the mean flow. For instance, this behaviour is typical for a bluff-body wake. This was first noticed for wake flows in Hammond & Redekopp (Reference Hammond and Redekopp1997), Pier (Reference Pier2002), where the local linear criterion for weakly non-parallel flows (Monkewitz, Huerre & Chomaz Reference Monkewitz, Huerre and Chomaz1993), applied to the mean flow field, is shown to yield the correct prediction of the saturated wake instability. The same behaviour was observed, by global stability analysis, for the flow past a circular cylinder up to
$Re=180$
by Barkley (Reference Barkley2006), Sipp & Lebedev (Reference Sipp and Lebedev2007), Mittal (Reference Mittal2008), and it was confirmed up to
$Re=600$
in Leontini, Thompson & Hourigan (Reference Leontini, Thompson and Hourigan2010). In the referenced papers the mean flow field was computed by direct numerical simulation (DNS) and stability analysis was carried out on the mean (i.e. time-averaged) flow field. In Khor et al. (Reference Khor, Sheridan, Thompson and Hourigan2008) local spatio-temporal analysis is applied to mean wake profiles fitting experimental measurements in the wake past a circular cylinder in the range
$600\leqslant Re\leqslant 4600$
, showing good agreement between the predicted and the measured vortex shedding frequency. In Emerson, Lieuwen & Juniper (Reference Emerson, Lieuwen and Juniper2016) stability and sensitivity analysis is applied to the experimental mean velocity and density fields in reacting bluff-body wakes, showing good agreement in the prediction of the vortex shedding frequency and of the associated flow fluctuations. In Camarri, Fallenius & Fransson (Reference Camarri, Fallenius and Fransson2013) global stability analysis is performed on experimental particle image velocimetry (PIV) mean flow fields past a porous circular cylinder at
$Re=3.5\times 10^{3}$
for different transpiration velocities through the cylinder surface, showing discrepancies between predicted and measured vortex shedding frequencies which are less than
$15\,\%$
. In Camarri et al. (Reference Camarri, Fallenius and Fransson2013) it is also shown that the inclusion of a very crude eddy-viscosity model in the stability analysis of the mean flow leads to an improved prediction of the vortex shedding frequency. The same conclusion concerning the use of an eddy-viscosity model in the global stability analysis has been recently confirmed for instance in Tammisola & Juniper (Reference Tammisola and Juniper2016) for a swirling injector and in Rukes, Paschereit & Oberleithner (Reference Rukes, Paschereit and Oberleithner2016) for strongly swirling flows.
To the authors knowledge, the first work conjecturing the property of marginal stability of a mean flow field is documented in Malkus (Reference Malkus1956). In the specific context of bluff-body wakes, an interpretation of the above behaviour was reported in Noack et al. (Reference Noack, Afanasiev, Morzynski, Tadmor and Thiele2003), suggesting that the amplitude of the oscillating wake saturates precisely when the mean flow becomes nearly marginally stable. The same conjecture has been recently used in Mantič-Lugo, Arratia & Gallaire (Reference Mantič-Lugo, Arratia and Gallaire2014) in order to formulate a self-consistent model for the vortex shedding in the laminar flow past a circular cylinder.
When the considered wakes are turbulent, a formally consistent approach to justify the stability analysis of mean flow fields was originally proposed in Reynolds & Hussain (Reference Reynolds and Hussain1972) (see also Reau & Tumin Reference Reau and Tumin2002), where a triple decomposition is used for the flow variables, separating the following contributions: (i) the time-averaged flow field, (ii) the large-scale coherent part and (iii) the fluctuating part. This decomposition is well suited for wakes, as they show self-sustained oscillations which are strongly periodic and related to large-scale flow structures. The occurrence of this kind of instability can be detected in the framework of the triple decomposition by applying stability analysis to the linearised equations for the coherent velocity fluctuations evolving on the mean flow field.
Provided that the stability analysis of mean flow fields in a bluff-body wake leads to a realistic prediction of the vortex shedding frequency, techniques based on sensitivity analysis (see e.g. the review in Camarri Reference Camarri2015) can be applied for its control. Conversely, no information is directly provided on the action of the control on the saturated amplitude of the periodic motion. As shown in Marquet, Sipp & Jacquin (Reference Marquet, Sipp and Jacquin2008), in order to estimate the effect on vortex shedding of a passive control that might be obtained by introducing a small control cylinder in the wake, it is necessary to have a model for the simulation of the mean flow. This is done for instance in Meliga, Pujals & Serre (Reference Meliga, Pujals and Serre2012) for reproducing the experimental results documented in Parezanović & Cadot (Reference Parezanović and Cadot2012, Reference Parezanović and Cadot2009). In the experiments the sensitivity of the global characteristics of the turbulent wake past a plane D-shaped cylinder at
$Re=13\,000$
was investigated by placing a small control cylinder in generic positions of the wake. In Meliga et al. (Reference Meliga, Pujals and Serre2012) the sensitivity map of the vortex shedding to a generic placement of the control cylinder is estimated on the basis of a sensitivity analysis of the Reynolds averaged Navier–Stokes (RANS) equations governing the problem. The RANS equations are closed using the Spalart–Allmaras (SA) one equation closure (see Spalart & Allmaras Reference Spalart and Allmaras1994) and they are used in order to compute an approximation of the same mean flow field of the experiments in Parezanović & Cadot (Reference Parezanović and Cadot2009, Reference Parezanović and Cadot2012). The linearisation of the RANS equations (including the additional equation for the SA model) around the mean flow field is used to carry out a global stability and sensitivity analysis. The control cylinder is modelled as a pure drag force estimated on the basis of a constant drag coefficient, of the size of the cylinder and of the local velocity. The resulting sensitivity map shows a good agreement with the experiments, thus demonstrating the potential of the described strategy to predict control of large-scale instability in the turbulent wake past a bluff body.
The main objective of the present work is to derive and validate experimentally the sensitivity map of the vortex shedding frequency in a bluff-body wake similarly to what is done in Meliga et al. (Reference Meliga, Pujals and Serre2012), but basing the analysis solely on available PIV flow fields of the uncontrolled flow. Thus, we renounce using the mean flow field obtained numerically by a set of a priori closed RANS equations, and instead derive a numerical model of the mean flow which incorporates the PIV measurements available from the experiments, and in particular the mean flow field itself and the phase-averaged Reynolds stresses. The objective of the proposed model is to provide the (linearised) variation of the mean flow as a small control cylinder. This is done for a generic position of the cylinder using the same adjoint methods as described in Meliga et al. (Reference Meliga, Pujals and Serre2012). The mean flow model is built starting from the triple decomposition of the flow and closing the equations for the mean flow field by an eddy-viscosity closure. The eddy viscosity is successively found by an optimisation algorithm, thus minimising the discrepancies between the mean flow field given by the model and the reference mean flow field available from the experiments.
Following the modelling documented in Viola et al. (Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014), the same eddy viscosity, tuned so as to build the mean flow model, is included in a physically consistent way in the stability analysis of the mean flow field. As a second objective of this paper we show that the inclusion of this turbulence model in the stability equations, derived by the calibration of the mean flow model, leads to a significant improvement in the accuracy of the predicted vortex shedding frequency and of the associated eigenmode. As a final output, this paper also confirms that, when turbulence is not included in the analysis, the predictions of the vortex shedding frequency based on the PIV mean flow fields is acceptable for Reynolds numbers up to
$5.3\times 10^{4}$
. Lastly, the mean flow model and the stability analysis are used here to derive a control map for the vortex shedding frequency in the considered wake flow, and results are compared to the corresponding map derived experimentally similarly to what has been done in Meliga et al. (Reference Meliga, Pujals and Serre2012) and in Parezanović & Cadot (Reference Parezanović and Cadot2012, Reference Parezanović and Cadot2009).
As a prototype flow for the analysis described above we have considered the flow past a rectangular forebody with a smooth leading edge and a blunt trailing edge, which offers the possibility to modify the boundary layer on the upper and lower sides of the body through wall suction from the perforated surfaces. A modification of the boundary layers prior to separation results in an altered near-wake topology and, consequently, a change of the vortex shedding frequency (Fallenius, Trip & Fransson Reference Fallenius, Trip and Fransson2014; Trip & Fransson Reference Trip and Fransson2014; Trip & Fransson Reference Trip and Fransson2016). The range of considered Reynolds numbers,
$Re\simeq 6.6\times 10^{3}{-}5.3\times 10^{4}$
, is chosen so as to include both laminar and turbulent boundary layers detaching from the body and impinging onto the wake. For each considered value of the flow Reynolds number, the flow at issue is investigated for different levels of suction from the body surface, which implies different values of the vortex shedding frequencies and different mean flow fields. The available experimental database permits one to test the robustness of the proposed method and its performance for a wide range of wakes.
The experimental set-up employed to obtain mean and phase-averaged velocity fields will be introduced first, followed by a detailed description of the theoretical tools, i.e. the ad hoc tuned model for the mean flow and the sensitivity analysis for predicting the effect of a small control rod on the vortex shedding frequency. The results obtained by the application of these tools are successively presented in § 5.
2 Experimental set-up
The experiments were carried out in the Boundary Layer (BL) wind tunnel at the Odqvist Laboratory, located at the Royal Institute of Technology (KTH). The BL tunnel has a background turbulence intensity of 0.04 % and 0.06 % in the streamwise and cross-flow directions, respectively, at a free-stream velocity of
$25~\text{m}~\text{s}^{-1}$
.
The perforated, thick, plate is best described as a
$2.3~\text{m}$
long rectangular forebody with a smooth leading edge and a blunt trailing edge. The plate is mounted horizontally in the
$4\;\text{m}$
long test section, with a cross-sectional area of
$0.5\;\text{m}$
in width and
$0.75\;\text{m}$
in height, see figure 1. The body is
$h\,=\;4\,\text{cm}$
thick and spans the entire width of the test section. Boundary layer modification by means of wall suction and/or blowing is possible through perforations in the top and bottom titanium surfaces with a porosity of
$0.5\,\%$
. The perforations constitute of laser-drilled discrete holes of
$60~\unicode[STIX]{x03BC}\text{m}$
in diameter. A detailed description of the test section and of the rectangular forebody is given by Fallenius et al. (Reference Fallenius, Trip and Fransson2014).
In the present study, we limit ourselves to cases of wall suction, and a pressure drop over the surface of at most 500 Pa. A measure of the wall-normal velocity
$V_{0}$
, which was found to be in the range
$-3.3\;\text{cm}~\text{s}^{-1}{-}0\;\text{cm}~\text{s}^{-1}$
, was obtained. Different experimental cases are referred to ‘UXDpY’, where X and Y correspond to the free-stream velocity
$(\text{m}~\text{s}^{-1})$
and the pressure difference (Pa) over the perforated surface.
2.1 Vortex shedding frequency
To obtain the frequency of vortex shedding, a hot-wire probe was mounted
$6h$
downstream of the body,
$3h$
above the wake centreline. The hot-wire probe, with a wire that is
$0.5~\text{mm}$
long and
$2.5~\unicode[STIX]{x03BC}\text{m}$
in diameter, is built in-house. It was operated in combination with a Dantec Dynamics StreamLine 90N10 system, equipped with a Constant Temperature Anemometer (CTA) module. A total of 91 250 samples were recorded at a sampling frequency of
$1\;\times \;10^{4}\;\text{Hz}$
. The time signal was converted to the frequency spectrum employing a Welch algorithm. A bin size of
$2^{15}$
was used, which corresponds to a frequency resolution of
$0.3~\text{Hz}$
.
Figure 1. A schematic drawing of the experimental set-up, with: (1) the perforated surface of the rectangular forebody, (2) the hot-wire probe, and (3) and (4) the cameras and laser of the PIV system, respectively, aligned as to capture the field of view delineated with dash-dotted lines.
Figure 2. Frequency-premultiplied power spectral energy estimated via the Welch method for two hot-wire signals measured at (a)
$2.5~\text{m}~\text{s}^{-1}$
(case U2.5Dp0) and (b)
$20.0~\text{m}~\text{s}^{-1}$
(case U20Dp0) without suction from the body wall.
Two examples of frequency-premultiplied power energy spectra obtained from hot-wire signals at the lowest (2.5
$\text{m}~\text{s}^{-1}$
, case U2.5Dp0) and highest (20.0
$\text{m}~\text{s}^{-1}$
, case U20Dp0) speed, without suction from the wall, are shown in figure 2. As can be seen from the spectra in figure 2, vortex shedding is strongly periodic, the power spectra are narrow-banded around the vortex shedding frequency, and the related energy peak in the spectra are by far dominant over all other frequency components. Note that in figure 2(b) there are other peaks distributed at
$150~\text{Hz}$
,
$250~\text{Hz}$
,
$350~\text{Hz}$
and so on. These peaks are due to the PIV system which was activated at a frequency of
$150~\text{Hz}$
while the hot-wire signal was measuring, and the higher frequencies are caused by the interaction between the PIV frequency at
$150~\text{Hz}$
and the vortex shedding frequency, which is close to
$100~\text{Hz}$
, and thus they are not related to flow structures. More details on the spectral characteristics of hot-wire signals for this flow case, even when suction is applied from the wall, can be found in Trip & Fransson (Reference Trip and Fransson2014).
2.2 Phase-averaged flow
The time-resolved hot-wire signal was recorded simultaneously to the PIV experiment, and can therefore be conveniently used as a phase indicator to sort the PIV images. The PIV snapshots of a complete ensemble are subdivided into 16 discrete phase bins, based on their phase angle in the shedding cycle. The mean of the snapshots in each bin is approximately equal to the phase average of the velocity field. The independence of the phase average from the number of phase bins was checked by increasing the number of phase bins up to 128. An example of the phase-averaged flow field, at a generic phase, obtained for the flow case U2.5Dp0 is given in figure 3, where the velocity vectors and the vorticity fields are reported, together with the identification of the wake vortices through the
$\unicode[STIX]{x1D706}_{2}$
criterion (see Jeong & Hussain Reference Jeong and Hussain1995) plotted with a black line on the figures. As highlighted by figure 3, the phase-averaged flow field is smooth enough for the application of differential operators (i.e. so as to derive the vorticity field) and the vortices which dominates the wake dynamics are clearly visible.
Figure 3. Flow case U2.5Dp0: phase-averaged velocity (a) and vorticity (b) fields at a generic phase angle; black line indicates the wake vortices identified by the
$\unicode[STIX]{x1D706}_{2}$
criterion (see Jeong & Hussain Reference Jeong and Hussain1995).
As additional information on the unsteadiness of the flow field, the components of the Reynolds stresses resolved by PIV for case U2.5Dp0 have been reported in figure 4(a), together with the contribution given solely by the phase-averaged velocity field (b) and that given by the residual velocity fluctuations (c), in the spirit of the triple decomposition of the flow variables (see the following for more details).
Figure 4. Flow case U2.5Dp0: experimentally resolved Reynolds stresses in column (a), contribution given by the phase-averaged velocity field in column (b) and by the residual velocity fluctuations in column (c).
2.3 Maps for passive control
To study the effect of a small body on the vortex shedding frequency, a control cylinder is introduced into the wake of the body. The control cylinder, with a diameter equal to
$d^{\ast }=3$
mm, is rigid such that it can be clamped between the wind tunnel walls. The minimum diameter of the cylinder, which is the one adopted here, is dictated by technological realisability of the experiment. However, from an aerodynamic viewpoint this cylinder is rather intrusive. Indeed, the maximum Reynolds number, based on its diameter, ranges between
$5\times 10^{2}$
and
$4\times 10^{3}$
depending on the flow case. An experimental sensitivity map for the considered passive control is obtained by recording the vortex shedding frequency with the control cylinder placed on a
$15\times 11$
rectangular grid extending
$1h$
from the wake centreline in the wall-normal direction and
$2h$
downstream of the trailing edge of the plate in the streamwise direction. The resulting map is reported later in figure 10(b) for case U2.5Dp0 and commented in § 5.4.
3 Theoretical tools
In this section we describe the theoretical tools proposed in order to predict the control map providing the variation of the vortex shedding frequency consequent to the local introduction of a small control rod. The proposed tools are based on the triple decomposition of the flow variables. In particular, given the velocity flow field
$\boldsymbol{U}(\boldsymbol{x},t)$
, we decompose it into a mean part
$\overline{\boldsymbol{U}}(\boldsymbol{x})$
, a time-periodic part
$\tilde{\boldsymbol{u}}(\boldsymbol{x},t)=\tilde{\boldsymbol{u}}(\boldsymbol{x},t+T)$
(
$T$
being the period), and a residual part,
$\boldsymbol{u}^{\prime }(\boldsymbol{x},t)$
:
$$\begin{eqnarray}\boldsymbol{U}=\overline{\boldsymbol{U}}(\boldsymbol{x})+\tilde{\boldsymbol{u}}(\boldsymbol{x},t)+\boldsymbol{u}^{\prime }(\boldsymbol{x},t),\end{eqnarray}$$
where
$\overline{\cdot }$
and
$\tilde{\cdot }$
indicate the operators of time and phase averages, respectively. The same decomposition applies for all the other flow variables. The basic assumption for using the triple decomposition consists in assuming that the considered flow has a nearly periodic energetically dominant component, so that we can isolate that component through a phase average. For the flow at issue this characteristic is demonstrated by the energy spectra reported in figure 2. Moreover, for the objectives of the present work, the requirements on the flow for using the triple decomposition are even milder. Indeed, here we use the equations governing the linearised dynamics of a time-periodic flow component only to inspect the stability properties of the mean flow field and to check the possible existence of a periodic-in-time flow component on top of the mean flow field.
Following the derivation in Viola et al. (Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014), manipulating the Navier–Stokes equations for incompressible Newtonian flows and using the triple decomposition, it is possible to derive the equations for both the mean velocity field and the time-periodic velocity. In particular, the mean flow field is governed by the following set of equations in normalised form:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\boldsymbol{U}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\underbrace{\overline{\tilde{\boldsymbol{u}}~\tilde{\boldsymbol{u}}}}_{(a)}+\underbrace{\overline{\boldsymbol{u}^{\prime }~\boldsymbol{u}^{\prime }}}_{(b)}\right)+\unicode[STIX]{x1D735}\overline{p}-\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\overline{\boldsymbol{U}}=0. & \displaystyle\end{eqnarray}$$
The terms (a) and (b) in (3.3) need to be measured or modelled in order to close the set of equations, as discussed below. All quantities are scaled using the plate thickness
$h$
and the velocity
$U_{\infty }$
on which the flow Reynolds number is based (
$Re=U_{\infty }\,h\,/\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
being the kinematic viscosity of the fluid).
The equations governing the dynamics of the time-periodic component of the flow in non-dimensional form are given by:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\tilde{\boldsymbol{u}}}{\unicode[STIX]{x2202}t}+\overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}+\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}=-\unicode[STIX]{x1D735}\tilde{p}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\tilde{\boldsymbol{u}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\tilde{\boldsymbol{u}}\,\tilde{\boldsymbol{u}}-\overline{\tilde{\boldsymbol{u}}\,\tilde{\boldsymbol{u}}}\right)-\underbrace{\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\widetilde{\boldsymbol{u}^{\prime }\,\boldsymbol{u}^{\prime }}-\overline{\boldsymbol{u}^{\prime }\,\boldsymbol{u}^{\prime }}\right)}_{(c)}. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
As for the mean flow, terms (c) in (3.5) need to be modelled so as to close the set of equations.
In the present work we have chosen to close the above equations following the Boussinesq approximation via an eddy-viscosity model. Following the derivation detailed in Viola et al. (Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014), which is based on the properties of the time-average and phase-average operators, it is possible to model term (b) in (3.3) as follows:
$$\begin{eqnarray}-\overline{\boldsymbol{u}^{\prime }\boldsymbol{u}^{\prime }}+{\textstyle \frac{2}{3}}\overline{q_{t}}\unicode[STIX]{x1D644}\simeq \unicode[STIX]{x1D708}_{\boldsymbol{t}}(\boldsymbol{x})\left(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}^{\text{T}}\hspace{0.7pt}\overline{\boldsymbol{U}}\right),\end{eqnarray}$$
where
$\overline{q_{t}}$
is the turbulent kinetic energy,
$\unicode[STIX]{x1D644}$
is the
$3\times 3$
identity matrix and
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
is the non-dimensional distribution of turbulent eddy viscosity, which is a scalar field that needs to be assigned for the closure of the equations. If the term
$(2/3)\overline{q_{t}}\unicode[STIX]{x1D644}$
is included in the mean pressure
$\overline{p}$
, as is standard in this type of turbulence closure, we arrive at the following set of equations for the mean flow:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\boldsymbol{U}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}\overline{p}-\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\overline{\boldsymbol{U}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})\left(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}^{\text{T}}\hspace{0.7pt}\overline{\boldsymbol{U}}\right)\right]+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\overline{\tilde{\boldsymbol{u}}~\tilde{\boldsymbol{u}}})=0. & \displaystyle\end{eqnarray}$$
Following the derivation in Viola et al. (Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014) it is possible to show that the linearised dynamics of the time-periodic flow field can be closed with the same distribution of eddy viscosity used for the mean flow field,
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
, and the resulting equations can be written as follows (see also Rukes et al.
Reference Rukes, Paschereit and Oberleithner2016):
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\tilde{\boldsymbol{u}}}{\unicode[STIX]{x2202}t}+\overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}+\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}=-\unicode[STIX]{x1D735}\tilde{p}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\underbrace{\left(\frac{1}{Re}+\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})\right)}_{\frac{1}{Re_{eq}}}\left(\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}+\unicode[STIX]{x1D735}^{\text{T}}\tilde{\boldsymbol{u}}\right)\right]. & \displaystyle\end{eqnarray}$$
In deriving equations (3.9) and (3.10) it is assumed that the eddy viscosity is independent of the mean flow field.
In Viola et al. (Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014) an eddy-viscosity model and a mixing length model, both assumed to vary only in the streamwise direction, are used to close the equations, leading in this last case to a set of equations slightly different from (3.9) and (3.10). In the present work the more general case of an eddy viscosity which varies generically in space is considered. This closure, which is more general than the one proposed in Viola et al. (Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014), also leads to a more complex optimisation problem when tuning the eddy viscosity, as shown in the following. Lastly, the presence of the field
$\unicode[STIX]{x1D708}_{t}$
permits one to define a variable local Reynolds number,
$Re_{eq}(\boldsymbol{x})=Re/(1+Re\,\unicode[STIX]{x1D708}_{t}(\boldsymbol{x}))$
which takes into account both the molecular (
$Re$
) and the turbulent (
$\unicode[STIX]{x1D708}_{t}$
) contributions in (3.10).
3.1 A model for the mean flow field
In the present work the mean flow field and its phase average (with respect to vortex shedding) is always available from the experiments through dedicated PIV measurements. Relying on the available experimental information we want to derive a mathematical model for the mean flow field. The model proposed here is based on the governing equations (3.7)–(3.8) and makes use of all the information available from experiments.
In particular the only unknown term in (3.7)–(3.8) is the eddy-viscosity field
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
, which cannot be obtained experimentally since the time resolution of the PIV measurements inevitably acts as a filter on the flow variables which prevents obtaining fully resolved Reynolds stresses. For this reason
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
is a free field on which it is possible to act so as to change the output of (3.7)–(3.8). Consequently,
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
is estimated so as to minimise the differences between the target mean flow field coming from the experiments,
$\overline{\boldsymbol{U}}^{(\text{T})}$
, and the simulated flow field,
$\overline{\boldsymbol{U}}$
. The target flow
$\overline{\boldsymbol{U}}^{(\text{T})}$
can be the raw experimental mean field,
$\overline{\boldsymbol{U}}^{(E)}$
, or a regularised field,
$\overline{\boldsymbol{U}}^{(R)}$
, as explained later. The considered objective function to be minimised in the resulting optimisation problem is the following one:
$$\begin{eqnarray}I=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}\left(\overline{\boldsymbol{U}}^{(\text{T})}-\overline{\boldsymbol{U}}\right)^{2}\text{d}\unicode[STIX]{x1D6FA}.\end{eqnarray}$$
The cost function
$I$
must be minimised considering that
$\overline{\boldsymbol{U}}$
is the solution of (3.7)–(3.8), and this constraint is taken into account by a classical Lagrangian approach, i.e. defining an augmented functional as follows:
$$\begin{eqnarray}\displaystyle & & \displaystyle J=I-\int _{\unicode[STIX]{x1D6FA}}\left(q\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\boldsymbol{U}}\right)\text{d}\unicode[STIX]{x1D6FA}\nonumber\\ \displaystyle & & \displaystyle \quad -\int _{\unicode[STIX]{x1D6FA}}\vec{V}\boldsymbol{\cdot }\left[\overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}\overline{p}-\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\overline{\boldsymbol{U}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})\left(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}^{\text{T}}\hspace{0.7pt}\overline{\boldsymbol{U}}\right)\right]+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\overline{\tilde{\boldsymbol{u}}~\tilde{\boldsymbol{u}}})\right]\text{d}\unicode[STIX]{x1D6FA},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$\vec{V}$
and
$q$
are Lagrangian multipliers.
By applying standard variational methods to (3.12) it is possible to derive the adjoint equations for the Lagrange multipliers
$(\vec{V},q)$
and the associated boundary conditions. In particular, the equations for
$(\vec{V},q)$
are written as follows:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\vec{V}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D735}\overline{\boldsymbol{U}}\boldsymbol{\cdot }\vec{V}-\overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\vec{V}-\unicode[STIX]{x1D735}q\nonumber\\ \displaystyle & & \displaystyle \quad \quad -\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[2\left(\frac{1}{Re}+\unicode[STIX]{x1D708}_{t}\right)\left(\frac{\unicode[STIX]{x1D735}\vec{V}+\unicode[STIX]{x1D735}^{\text{T}}\vec{V}}{2}\right)\right]-\left(\overline{\boldsymbol{U}}^{(\text{T})}-\overline{\boldsymbol{U}}\right)=0.\end{eqnarray}$$
As we will see in the following sections, two types of boundary conditions are used for the mean flow equations. One type is a Dirichlet type (boundary
$\unicode[STIX]{x1D6E4}_{D}$
), such that the mean velocity
$\overline{\boldsymbol{U}}$
is forced to assume a prescribed value. The other type, on
$\unicode[STIX]{x1D6E4}_{o}$
, is a stress-free condition, and it can be written as follows:
$\overline{p}\boldsymbol{n}-\left((1/Re)+\unicode[STIX]{x1D708}_{t}\right)[\boldsymbol{n}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}^{\text{T}}\overline{\boldsymbol{U}})]=\mathbf{0}$
. On the boundary
$\unicode[STIX]{x1D6E4}_{D}$
it can be shown that the natural boundary conditions for
$\vec{V}$
are homogeneous Dirichlet conditions, i.e.
$\vec{V}=\mathbf{0}$
. On
$\unicode[STIX]{x1D6E4}_{o}$
we have the following conditions:
$q\boldsymbol{n}-\left((1/Re)+\unicode[STIX]{x1D708}_{t}\right)[\boldsymbol{n}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\vec{V}+\unicode[STIX]{x1D735}^{\text{T}}\vec{V})]=-\!\left(\overline{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n}\right)\vec{V}$
.
Once the Lagrangian multipliers
$(\vec{V},q)$
are found, the variation
$\unicode[STIX]{x1D6FF}I$
of the cost function
$I$
in (3.11) with respect to a generic variation in the spatial distribution of
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
, is given as follows:
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D6FF}I=-\int _{\unicode[STIX]{x1D6FA}}\left[2\left(\frac{\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}^{\text{T}}\overline{\boldsymbol{U}}}{2}\right)\left(\frac{\unicode[STIX]{x1D735}\vec{V}+\unicode[STIX]{x1D735}^{\text{T}}\vec{V}}{2}\right)\right]\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{t}\text{d}\unicode[STIX]{x1D6FA}\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{\unicode[STIX]{x1D6E4}_{o}}\left[2\vec{V}\boldsymbol{\cdot }\left(\left(\frac{\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}+\unicode[STIX]{x1D735}^{\text{T}}\overline{\boldsymbol{U}}}{2}\right)\boldsymbol{\cdot }\boldsymbol{n}\right)\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{t}\right]\text{d}\unicode[STIX]{x1D6E4}.\end{eqnarray}$$
The optimal distribution of
$\unicode[STIX]{x1D708}_{t}$
can thus be obtained using a gradient-based method based on (3.15). At each step of the gradient method,
$\unicode[STIX]{x1D708}_{t}$
is varied moving towards the steepest descent for
$I$
and the length of the step in the direction of the gradient is found by searching numerically for the optimality condition in the direction specified by the gradient, which is computed by (3.15).
It is important to underline that the distribution of
$\unicode[STIX]{x1D708}_{t}$
obtained by the procedure described above is aimed at modelling the unresolved small-scales Reynolds stresses, which is the most important contribution needed in (3.8) so as to reproduce accurately the reference mean flow. However, since the field
$\unicode[STIX]{x1D708}_{t}$
is the result of an optimisation process, it also compensates for all the elements, which prevents equations (3.7)–(3.8) from reproducing exactly the experimental mean flow even if the exact unresolved stresses were introduced directly in the equations. These elements can be, for instance, the experimental uncertainty or the errors due to the numerical discretisation of the equations, including domain truncation.
Since the mean experimental flow fields are affected by noise, which may amplify as they are differentiated in space, they have been usually regularised before being employed as target flows in the calibration of the mean flow model. The regularisation applied here is a variational form of the Tikhonov regularisation smoothing first-order spatial derivatives, as proposed for instance in Wang (Reference Wang, Kirby and Johnson2011) for inverse electrocardiographic applications. If not explicitly stated, regularised fields are always used here instead of raw experimental data. Moreover, again if not explicitly commented, we have also imposed that the regularised mean velocity fields are divergence-free. In principle, since we are measuring the flow in the symmetry plane and, moreover, the considered flow should approximate a nominally plane wake, it is expected that the experimental mean flow will be two-dimensional and, thus, divergence-free in the measurement plane. This may not be the case due to measurement and differentiation errors. For this reason, even if tests reported later prove that this is not an important aspect, we decided to add the divergence-free constraint to the regularised fields. Lastly, even if the target flow was not divergence-free, the tuned model flow is so by definition (see equation (3.7)) and, thus, the projection of the reference flow on a divergence-free subspace has no significant influence on the resulting tuned flow model. This aspect is also investigated later. Indicating with
$\overline{\boldsymbol{U}}^{(E)}$
the PIV measurements and with
$\overline{\boldsymbol{U}}^{(R)}$
the regularised field, the regularisation problem consists in searching for
$\overline{\boldsymbol{U}}^{(R)}$
which minimises
$I_{G}$
given as follows:
$$\begin{eqnarray}\displaystyle I_{G} & = & \displaystyle \frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}\left(\overline{\boldsymbol{U}}^{(R)}-\overline{\boldsymbol{U}}^{(E)}\right)^{2}\text{d}\unicode[STIX]{x1D6FA}+\frac{\unicode[STIX]{x1D706}_{r}^{2}}{2}\int _{\unicode[STIX]{x1D6FA}}\left(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}^{(R)}\boldsymbol{ : }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}^{(R)}\right)\text{d}\unicode[STIX]{x1D6FA}\nonumber\\ \displaystyle & & \displaystyle -\,\int _{\unicode[STIX]{x1D6FA}}q\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\boldsymbol{U}}^{(R)}\right)\text{d}\unicode[STIX]{x1D6FA},\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}_{r}$
is an arbitrary penalisation constant which regulates the amount of regularisation of the procedure and
$q$
is a Lagrangian multiplier. Here the value of
$\unicode[STIX]{x1D706}_{r}$
has been selected heuristically.
3.2 Stability analysis of the mean flow field
The stability problem, which is related to the existence of a periodic flow component, is governed by the linearised equations (3.9) and (3.10).
The associated boundary conditions are of the same type as those imposed on the base flow equations, but they are homogeneous. Considering the boundary conditions used in the present work, which are either boundaries where the velocity field is specified,
$\unicode[STIX]{x1D6E4}_{D}$
(i.e. inflow boundaries or solid walls) or stress-free boundaries,
$\unicode[STIX]{x1D6E4}_{O}$
(i.e. outflow boundaries), we have the following conditions:
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\boldsymbol{u}}=\mathbf{0},\quad \text{on}~\unicode[STIX]{x1D71E}_{\boldsymbol{D}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{p}\boldsymbol{n}-Re_{eq}^{-1}[\boldsymbol{n}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}+\unicode[STIX]{x1D735}^{\text{T}}\tilde{\boldsymbol{u}})]=0,\quad \text{on}~\unicode[STIX]{x1D6E4}_{O}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\boldsymbol{u}}\left(\boldsymbol{x},t\right)=\hat{\boldsymbol{u}}(\boldsymbol{x})\exp \left(\unicode[STIX]{x1D70E}t\right)\!, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{p}\left(\boldsymbol{x},t\right)=\hat{p}(\boldsymbol{x})\exp \left(\unicode[STIX]{x1D70E}t\right)\!. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}\hat{\boldsymbol{u}}+\overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}+\hat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{1}{Re_{eq}(\boldsymbol{x})}\left(\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}+\unicode[STIX]{x1D735}^{\text{T}}\hat{\boldsymbol{u}}\right)\right]=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{u}}=0, & \displaystyle\end{eqnarray}$$
$\tilde{\boldsymbol{u}}$
,
$\tilde{p}$
) in (3.17). Equations (3.19), together with the boundary conditions, form an eigenvalue problem. Any solution
$(\hat{\boldsymbol{u}},\hat{p})$
, associated to the eigenvalue
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D706}+\text{i}\unicode[STIX]{x1D714}$
, is a global mode with time growth rate equal to
$\unicode[STIX]{x1D706}$
(
$\unicode[STIX]{x1D706}>0$
indicates an unstable mode) and angular frequency
$\unicode[STIX]{x1D714}$
. Note that the associated frequency is given by
$f=\unicode[STIX]{x1D714}/(2\unicode[STIX]{x03C0})$
, and is given directly in non-dimensional form as a Strouhal number based on the same velocity and length reference quantities used to normalise the Navier–Stokes (NS) equations.
3.3 Passive control of vortex shedding instability
The objective of this section is to estimate the effect of placing a small control rod in the flow on the eigenvalue identified by the stability analysis of the mean flow that is related to the vortex shedding instability. This is carried out using an adjoint-based sensitivity analysis analogous to that proposed in Marquet et al. (Reference Marquet, Sipp and Jacquin2008).
As a device for passive control we consider a cylinder of diameter
$d^{\ast }$
positioned on a generic point
$(x_{0},y_{0})$
. The cylinder diameter is assumed to be small enough so that its action on the flow can be described by a linearised approach. Moreover, it is not directly simulated, but its effect is modelled by introducing the force that it exerts on the flow explicitly in the NS equations. This force is assumed to be a pure drag force, which depends on the local flow conditions. Consequently the control cylinder, when invested by a flow velocity
$\boldsymbol{U}$
, is assumed to exert a localised drag force of the following form:
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\boldsymbol{F}(\boldsymbol{x}_{0})=-\!\left[{\textstyle \frac{1}{2}}C_{D}d^{\ast }\Vert \boldsymbol{U}\Vert \,\boldsymbol{U}\,\right]\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}_{0}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}_{0})$
is the Dirac function centred on the position of the control cylinder,
$\boldsymbol{x}_{0}$
. The notation
$\unicode[STIX]{x1D6FF}\boldsymbol{F}$
is used in (3.20) so as to emphasise that this force is a small perturbation of the uncontrolled configuration. As concerns the drag coefficient, this can be generally assumed to be a function of the flow Reynolds number, i.e.
$C_{D}(Re_{d\ast })$
. In this paper we have assumed a constant value equal to
$C_{D}\simeq 1.2$
, which is representative of the drag of the control cylinder in the considered flow, as will be illustrated in the following. For quantitative indications on the drag coefficient of circular cylinders, we refer to the ESDU database (ESDU 1986). Note that (3.20) is a quasi-static model, in the sense that the unsteady load
$\unicode[STIX]{x1D6FF}\boldsymbol{F}$
is proportional to the local time-varying velocity field
$\boldsymbol{U}$
through a constant drag coefficient
$C_{D}$
, which in this case is an averaged drag coefficient. The use of a quasi-static model for similar cases is common in the literature (see e.g. the review in Camarri Reference Camarri2015, and its bibliography) and is loosely justified by the scale separation existing between the flow to be controlled and the control cylinder.
In the framework of the triple decomposition of the flow variables, assuming further that turbulent fluctuations can be neglected in the estimation of the force experienced by the control cylinder, we consider the drag force given by (3.20) linearised with respect to
$\tilde{\boldsymbol{u}}$
(see the decomposition in (3.1)), which is consistent with the assumptions made for the stability equations (3.19):
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\boldsymbol{F}\approx \underbrace{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FC}\left(\Vert \overline{\boldsymbol{U}}\Vert \overline{\boldsymbol{U}}\right)\,\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}_{0})}_{\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{M}}}\underbrace{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FC}\left[\Vert \overline{\boldsymbol{U}}\Vert \tilde{\boldsymbol{u}}+\left(\frac{\overline{\boldsymbol{U}}}{\Vert \overline{\boldsymbol{U}}\Vert }\boldsymbol{\cdot }\tilde{\boldsymbol{u}}\right)\overline{\boldsymbol{U}}\right]\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}_{0})}_{\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{F}}},\end{eqnarray}$$
in which
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FC}=(1/2)d^{\ast }C_{D}(Re_{d^{\ast }})$
.
By inspecting equation (3.21) it is possible to notice that the force
$\unicode[STIX]{x1D6FF}\boldsymbol{F}$
is composed of two contributions:
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{M}}$
, which depends on
$\overline{\boldsymbol{U}}$
and is independent of
$\tilde{\boldsymbol{u}}$
, and
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{F}}$
, which depends linearly on
$\tilde{\boldsymbol{u}}$
. Consequently, the term
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{M}}$
acts as a forcing on the mean flow equations (3.7)–(3.8) and the term
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{F}}$
acts directly as a structural perturbation of the stability equations (3.19). Thus, the control cylinder affects the stability characteristics of the mean flow in two ways: via a modification of the mean flow itself caused by the term
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{M}}$
and via a modification of the stability equations caused by the term
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{F}}$
. The resulting global effect on a particular eigenvalue
$\unicode[STIX]{x1D70E}$
can be estimated in a linear framework by an adjoint-based sensitivity analysis.
Let us focus on a particular global mode
$\unicode[STIX]{x1D70E},(\hat{\boldsymbol{u}},\hat{p})$
of the uncontrolled mean flow field (
$\overline{\boldsymbol{U}}$
,
$\overline{p}$
). As the control is applied, both the mode and the mean flow field are perturbed, resulting in
$\unicode[STIX]{x1D70E}^{\prime \prime },(\hat{\boldsymbol{u}}^{\prime \prime },\hat{p}^{\prime \prime })$
and (
$\overline{\boldsymbol{U}}^{\prime \prime }$
,
$\overline{p}^{\prime \prime }$
), respectively. The coupled governing equations for the perturbed mean flow and stability problem can be written as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }(\overline{\boldsymbol{U}}^{\prime \prime }\overline{\boldsymbol{U}}^{\prime \prime })+\unicode[STIX]{x1D735}\overline{p}^{\prime \prime }-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{1}{Re_{eq}}\left(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}^{\prime \prime }+\unicode[STIX]{x1D735}^{\text{T}}\overline{\boldsymbol{U}}^{\prime \prime }\right)\right]+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\overline{\tilde{\boldsymbol{u}}~\tilde{\boldsymbol{u}}}\right)=\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{M}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\boldsymbol{U}}^{\prime \prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}^{\prime \prime }\hat{\boldsymbol{u}}^{\prime \prime }+\overline{\boldsymbol{U}}^{\prime \prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{\prime \prime }+\hat{\boldsymbol{u}}^{\prime \prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}^{\prime \prime }-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{1}{Re_{eq}(\boldsymbol{x})}\left(\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{\prime \prime }+\unicode[STIX]{x1D735}^{\text{T}}\hat{\boldsymbol{u}}^{\prime \prime }\right)\right]+\unicode[STIX]{x1D735}\hat{p}^{\prime \prime }=\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{ F}}, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{\prime \prime }=0. & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70E}$
of the eigenvalue
$\unicode[STIX]{x1D70E}$
induced by control, i.e.
$\unicode[STIX]{x1D70E}^{\prime \prime }=\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70E}$
. Using an adjoint-based sensitivity analysis it is possible to show that (see Marquet et al.
Reference Marquet, Sipp and Jacquin2008, for details): 
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70E}=S(\boldsymbol{x}_{0})=\int _{\unicode[STIX]{x1D6FA}}\left[(\overline{\boldsymbol{U}}^{+})^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{ M}}\right]\,\text{d}\unicode[STIX]{x1D6FA}+\int _{\unicode[STIX]{x1D6FA}}\left[(\hat{\boldsymbol{u}}^{+})^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{ F}}\right]\text{d}\unicode[STIX]{x1D6FA},\end{eqnarray}$$
where
$\overline{\boldsymbol{U}}^{+}$
and
$\hat{\boldsymbol{u}}^{+}$
are the adjoint mean flow and eigenmode, respectively,
$\unicode[STIX]{x1D6FA}$
is the flow domain and
$(~)^{\ast }$
stands for complex-conjugate quantities. Equation (3.23) is very convenient from a computational viewpoint because it is linear with respect to the parameter
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FC}$
and provides an answer for a generic position of the control cylinder (
$\boldsymbol{x}_{0}$
) without the need to perform integration, since both
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{M}}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{H}_{\boldsymbol{F}}$
, defined in (3.21), are proportional to
$\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}_{0})$
. Thus, once the diameter of the control cylinder is fixed, equation (3.23) provides directly a control map
$S(\boldsymbol{x})$
which gives the shift
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70E}$
of the identified eigenvalue versus a generic placement of the control cylinder in the flow domain. The use of equation (3.23) requires the estimation of the vector fields
$\overline{\boldsymbol{U}}^{+}$
and
$\hat{\boldsymbol{u}}^{+}$
. The field
$\overline{\boldsymbol{U}}^{+}$
is solution of the following system of equations:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\overline{\boldsymbol{U}}\boldsymbol{\cdot }\overline{\boldsymbol{U}}^{+}-\overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}^{+}+\unicode[STIX]{x1D735}\overline{p}^{+}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{1}{Re_{eq}}\left(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}^{+}+\unicode[STIX]{x1D735}^{\text{T}}\hspace{0.7pt}\overline{\boldsymbol{U}}^{+}\right)\right]=\unicode[STIX]{x1D735}_{\overline{\boldsymbol{U}}}\unicode[STIX]{x1D70E}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\boldsymbol{U}}^{+}=0, & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D735}_{\overline{\boldsymbol{U}}}\unicode[STIX]{x1D70E}$
is given by: 
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{\overline{\boldsymbol{U}}}\unicode[STIX]{x1D70E}=-\hat{\boldsymbol{u}}^{+}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\hat{\boldsymbol{u}})^{H}+\hat{\boldsymbol{u}}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{+},\end{eqnarray}$$
equations (3.24) are supplemented with homogeneous boundary conditions at the inlet and on the solid wall and the following condition on the outflow boundary:
$$\begin{eqnarray}\displaystyle \overline{p}^{+}\boldsymbol{n}-Re_{eq}^{-1}\left[\boldsymbol{n}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}^{+}+\unicode[STIX]{x1D735}^{\text{T}}\hspace{0.7pt}\overline{\boldsymbol{U}}^{+}\right)\right]=-(\overline{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n})\overline{\boldsymbol{U}}^{+}+(\hat{\boldsymbol{u}}^{\ast }\boldsymbol{\cdot }\boldsymbol{n})\hat{\boldsymbol{u}}^{+}. & & \displaystyle\end{eqnarray}$$
The adjoint eigenmode
$\{\unicode[STIX]{x1D70E}^{\ast },(\hat{\boldsymbol{u}}^{+},\hat{p}^{+})\}$
is the solution of the following eigenvalue problem:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}^{\ast }\hat{\boldsymbol{u}}^{+}-\overline{\boldsymbol{U}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{+}+\unicode[STIX]{x1D735}\overline{\boldsymbol{U}}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{+}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{1}{Re_{eq}(\boldsymbol{x})}\left(\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{+}+\unicode[STIX]{x1D735}^{\text{T}}\hat{\boldsymbol{u}}^{+}\right)\right]+\unicode[STIX]{x1D735}\hat{p}^{+}=0, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{+}=0. & \displaystyle\end{eqnarray}$$
As concerns the boundary conditions,
$\hat{\boldsymbol{u}}^{+}=\mathbf{0}$
on the same boundaries on which
$\hat{\boldsymbol{u}}=\mathbf{0}$
. At the outflow we have:
$\hat{p}^{+}\boldsymbol{n}-Re_{eq}^{-1}[\boldsymbol{n}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{+}+\unicode[STIX]{x1D735}^{\text{T}}\hat{\boldsymbol{u}}^{+})]=(\overline{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n})\hat{\boldsymbol{u}}^{+}$
. Moreover, the velocity field
$\hat{\boldsymbol{u}}^{+}$
is normalised such that:
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}}\left[(\hat{\boldsymbol{u}}^{+})^{\ast }\boldsymbol{\cdot }\hat{\boldsymbol{u}}\right]\text{d}\unicode[STIX]{x1D6FA}=1.\end{eqnarray}$$
4 Numerical tools
All the systems of PDEs proposed in this work and solved numerically, i.e. the mean flow model in (3.7)–(3.8), equations (3.13)–(3.14) for the Lagrangian multiplier
$\vec{V}$
, the Tikhonov regularisation, the direct and adjoint stability problems in equations (3.19) and (3.27), and the adjoint mean flow problem in (3.24), are discretised in space by a second-order finite-element formulation employing Taylor–Hood triangular Lagrangian elements, in which velocity and pressure are represented with P2 and P1 elements, respectively. The finite-element formulation have been developed using FreeFem++ software (see www.freefem.org), which employs triangular grids and permits mesh adaptivity. Mesh adaptivity is particularly useful here because it permits a proper discretisation of high-gradient regions of the mean flow field and of the resulting stability modes at reasonable computational costs.
The computational domain used, which is common for all PDEs, coincides with the PIV window used in the experiments. Considering the frame of reference in figure 1, for the case with free-stream velocity equal to
$2.5~\text{m}~\text{s}^{-1}$
the PIV window extends in the range
$0.03h\leqslant x\leqslant 3.4h$
and
$-1.3h\leqslant y\leqslant 1.3h$
, while for
$20~\text{m}~\text{s}^{-1}$
it extends in the range
$0.03h\leqslant x\leqslant 3.4h$
and
$-1.9h\leqslant y\leqslant 1.9h$
. Note that the window comprises only the rear face of the body, and its size is sufficient to include the mean recirculation region of the wake. Although its size is small if compared to the wake characteristic evolution length, it can be shown following Camarri et al. (Reference Camarri, Fallenius and Fransson2013) that it includes the instability core which is confined in the recirculation region, and this grants the possibility to apply stability analysis to the resulting mean flow field.
The nonlinear problem for the mean flow, equations (3.7)–(3.8), is solved numerically by a standard Newton method. All the remaining linear PDEs are solved by a direct sparse LU factorisation method. The eigenvalue problems in (3.19) and (3.27) are solved using the Implicitly Restarted Arnoldi Method implemented in the Arpack library, and a shift-invert strategy in the complex plane is used to accelerate convergence to the desired eigenvalue.
The calibration of the mean flow model implies the identification of the eddy-viscosity field
$\unicode[STIX]{x1D708}_{t}$
which is optimal in the sense that it minimises the difference in the norm between the predicted and the experimental mean velocity fields. This optimum problem is solved numerically using a gradient method, where the gradient of the cost function
$I$
in (3.11) with respect to a generic variation
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
is estimated by (3.15). The initial guess for
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
is computed by minimising, in a least square sense, the residuals of the model RANS eqs. (3.7)–(3.8) when they are applied to the experimental mean flow field. The problem of finding
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
is ill-posed and is regularised by applying, at each descent step of the gradient method, a Tikhonov regularisation to the field
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
of the same type as the one applied to the mean velocity field. That kind of regularisation acts as a smoothing of the spatial fluctuations of
$\unicode[STIX]{x1D708}_{t}$
. Lastly, the optimal
$\unicode[STIX]{x1D708}_{t}$
is obtained by forcing the simulated mean flow field to be equal to the experimental one on all boundaries except at the outflow, where null-stress conditions are applied.
5 Results
5.1 Tuning of the mean flow model
The mean flow model has been tuned here for two cases without suction from the wall: a case with laminar boundary layers at the separation point from the body, U2.5Dp0 (
$U_{\infty }=2.5\,\text{m}~\text{s}^{-1}$
), and a case with turbulent boundary layers, U20Dp0 (
$U_{\infty }=20\,\text{m}~\text{s}^{-1}$
).
In both cases, the reference experimental mean flow fields have been regularised by Tikhonov regularisation and by forcing the divergence-free constraint as detailed in (§ 3.1). The constant
$\unicode[STIX]{x1D706}_{r}$
in (3.16) has been heuristically fixed to
$\unicode[STIX]{x1D706}_{r}^{2}=10^{-3}$
. A sensitivity analysis by varying this parameter has been carried out showing that results in terms of distribution of the resulting
$\unicode[STIX]{x1D708}_{t}$
and of the minimum value of the functional
$I$
(see equation (3.11)) are in very good approximation independent of the choice of
$\unicode[STIX]{x1D706}_{r}$
around the value fixed heuristically. This result is not detailed here for the sake of brevity.
An example of the effects of the regularisation of the mean flow field for the case U20Dp0 is shown in figure 5. In particular, figure 5(a,b) shows the velocity components of the mean flow field derived by the PIV measurements directly. Figure 5(c,d) shows the equivalent fields when the flow field is regularised using
$\unicode[STIX]{x1D706}_{r}^{2}=10^{-3}$
and without imposing the constraint that the resulting regularised flow field is divergence-free at discrete level. Finally, figure 5(e,f) shows the result when it is also forced that the resulting regularised flow field is divergence-free. In this last case, as evident from the comparison with figure 5(a,b), the regularisation has a stronger effect on the resulting velocity fields. Nevertheless, differences with respect to the original velocity field are of limited amount and, in any case, their effects on the results of the stability analysis have been investigated in the following.
Figure 5. Mean velocity field for the case U20Dp0 (
$U_{\infty }=20\,\text{m}~\text{s}^{-1}$
, no suction from the body): mean horizontal and vertical velocity of the original PIV measurements (a,b), of the regularised field (
$\unicode[STIX]{x1D706}_{r}^{2}=10^{-3}$
) without imposing the constraint of being divergence-free at discrete level (c,d) and also imposing the divergence-free constraint (e,f).
Figure 6. Mean velocity field for the case U20Dp0 (
$U_{\infty }=20\,\text{m}~\text{s}^{-1}$
, no suction from the body): regularised PIV
$\bar{U}$
and
$\bar{V}$
fields (a,b) and equivalent fields simulated by the calibrated mean flow model (c,d).
As an example of the calibration of the mean flow model, for case U20Dp0 we show in figure 6 both the target flow field (a,b) and the simulated flow field (c,d) through the mean flow model. As can be deduced by their comparison, the mean flow model leads to flow fields which are difficult to distinguish from the original ones. The main differences can be evidenced near the outflow boundary of the computational domain. Such differences, which do not affect stability results since they are far from the core of the instability (see e.g. Camarri et al.
Reference Camarri, Fallenius and Fransson2013), are related to the use of stress-free boundary conditions on
$\unicode[STIX]{x1D6E4}_{O}$
. This aspect can be further improved by including the reference data in the applied boundary conditions for that boundary, but this option has not been tested here. From a quantitative viewpoint, the difference in norm between the experimental and the simulated mean velocity fields for this case is equal to
$I\simeq 2.8\times 10^{-4}$
, which can be considered a very small value.
Figure 7. Mean velocity field for the case U2.5Dp0 (
$U_{\infty }=2.5\,\text{m}~\text{s}^{-1}$
, no suction from the body): regularised PIV
$\bar{U}$
and
$\bar{V}$
fields (a,b) and equivalent fields simulated by the calibrated mean flow model (c,d).
Similar considerations can be done for the case U2.5Dp0, whose results are reported in figure 7. In this case the final value of the functional
$I$
is
$I\simeq 3.1\times 10^{-4}$
, which is of the same order of magnitude as the previous case.
As concerns the distribution of
$\unicode[STIX]{x1D708}_{t}$
obtained by the calibration of the mean flow model, we have reported in figure 8 the field of the equivalent Reynolds number
$Re_{eq}(\boldsymbol{x})$
obtained for the two cases mentioned above. It can be noticed that the level of turbulent eddy viscosity obtained for the case U2.5Dp0, in which laminar boundary layers detach from the body, is correctly lower than that of U20Dp0, in which the boundary layers detaching from the body are already turbulent. In both cases the turbulent eddy viscosity increases in the streamwise direction, and consequently the value of
$Re_{eq}$
decreases, reaching the minimum values on the outflow boundary. We think that in that region the obtained value of
$\unicode[STIX]{x1D708}_{t}$
can be affected by domain truncation.
Figure 8. Fields of
$Re_{eq}(\boldsymbol{x})$
obtained by tuning the mean flow model for the case U2.5Dp0 (a) and U20Dp0 (b).
5.2 Estimation of the vortex shedding frequency from the mean flow field
As a first step we have applied stability analysis to the mean flow fields obtained by PIV considering only the molecular viscosity in the stability analysis, i.e. neglecting turbulence effects (
$Re_{eq}=Re$
). Concerning grid convergence of the results, all the reported cases are fully converged and for each one it has been verified that by doubling the number of degrees of freedom (dofs) the predicted Strouhal number of the vortex shedding instability changes only at the fourth decimal digit. Concerning the boundary conditions, in all cases homogeneous Dirichlet boundary conditions are imposed for the stability modes at the inflow of the domain, and stress-free conditions are applied at the outlet boundary.
Results of the stability analyses described above are reported in table 1 for the flow configurations with free-stream velocity equal to
$2.5~\text{m}~\text{s}^{-1}$
. All the identified modes are nearly unstable and in all cases only one couple of complex-conjugate unstable modes has been identified, thus there was no ambiguity in identifying the stability mode associated with vortex shedding. In case 2 homogeneous Dirichlet boundary conditions are applied to the stability eigenmodes on the lateral boundaries (i.e. in the
$y$
direction), as suggested in Camarri et al. (Reference Camarri, Fallenius and Fransson2013), and raw PIV flow fields are used. Comparison with the experiments shows that, except for a peak of approximately
$12\,\%$
at
$\unicode[STIX]{x1D6E4}=0.0$
, the error in the prediction of the Strouhal number of vortex shedding is less than
$2.5\,\%$
. The accuracy in the prediction of
$St$
of approximately
$15\,\%$
is in line with what is known in the literature about this kind of problems, as widely discussed in the review by Camarri (Reference Camarri2015) and in the related references (see also Emerson et al.
Reference Emerson, Lieuwen and Juniper2016).
Sensitivity of the results to the boundary conditions applied on the lateral boundaries can be appreciated by comparing case 2 with case 1, which was obtained by applying stress-free conditions on the lateral boundaries. Differences in the predictions between case 1 and case 2 are very limited, and they decrease as suction is applied from the body, which reduces the size of the recirculation bubble and, thus, the size of the core of the instability; this, in turn, makes the computational domain progressively more appropriate, decreasing the sensitivity of the results to domain truncation in the lateral direction. In all cases it was checked that the computational domain contains appropriately the instability core as it is defined as in Giannetti & Luchini (Reference Giannetti and Luchini2007).
Concerning the regularisation of the reference PIV flow fields, this is applied only in case 3, while in cases 1 and 2 raw PIV fields are used. Thus, the effect of regularisation on the results of the stability analysis can be appreciated by comparing cases 2 and 3, the maximum relative variation in terms of predicted Strouhal number being of approximately
$4.4\,\%$
for the case with the highest suction. Thus, the effect of regularisation can be considered acceptably small. Moreover, this result indicates that the regularisation is not required for the stability analysis alone, as already observed in Camarri et al. (Reference Camarri, Fallenius and Fransson2013).
Table 1. Result obtained from the linear stability analysis of the mean flow field of the wake, compared with experimental values, for cases in which the boundary layers detaching from the body are laminar. In case 1 stress-free boundary conditions are applied on the lateral boundaries, while homogeneous Dirichlet conditions are applied on the same boundary in case 2 and 3. Case 3 differs from case 2 because stability analysis is carried out on regularised PIV mean flow field. Case 4 is similar to case 3, but the tuned eddy viscosity
$\unicode[STIX]{x1D708}_{t}$
is included in the stability analysis.
The same tests documented in table 1 have been repeated for all the flow configurations that have been considered in the experiments. As an other example, we report here in table 2 the case with the highest free-stream velocity,
$20\,\text{m}~\text{s}^{-1}$
. As can be deduced from the table, for this case the errors with respect to the experiments are significantly higher if compared to the case in table 1. In particular they range between
$9\,\%$
and
$16\,\%$
, and this is expected to be an effect of turbulence which is completely neglected in the analysis. In the case reported in table 2 the PIV window is larger than that for the case reported in table 1, and the core of the instability is located at a larger distance from the lateral boundaries of the PIV window. This explains why the results are more insensitive to the boundary conditions applied on the lateral boundaries, as can be deduced by comparing cases 1 and 2 in table 2. Concerning the effects of the regularisation of the baseflow, variations of the predicted Strouhal numbers between cases 2 and 3 are within
$1.5\,\%$
for
$\unicode[STIX]{x1D6E4}\leqslant 5.7$
, and they increase to approximately
$10\,\%$
for
$\unicode[STIX]{x1D6E4}\geqslant 9.4$
. However, the same comments made on this point for the results in table 1 hold for this case as well.
Finally, the performance and characteristics of the stability results for all other free-stream velocities considered in the experiments, and not reported here for the sake of brevity, are intermediate between the two cases discussed here and quantified in table 1 and table 2.
Table 2. Result obtained from the linear stability analysis of the mean flow field of the wake, compared with experimental values, for cases in which the boundary layers detaching from the body are turbulent. In case 1 stress-free boundary conditions are applied on the lateral boundaries, while homogeneous Dirichlet conditions are applied on the same boundary in case 2 and 3. Case 3 differs from case 2 because stability analysis is carried out on regularised PIV mean flow field. Case 4 is similar to case 3, but the tuned eddy viscosity
$\unicode[STIX]{x1D708}_{t}$
is included in the stability analysis.
Results obtained including the eddy-viscosity field derived by the mean flow model in the stability analysis are reported with the label ‘Case 4’ in table 1 and table 2, and they are obtained imposing homogeneous Dirichlet boundary conditions to the eigenmodes on the lateral boundaries. As shown by a direct comparison with the experiments, the inclusion of field
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
leads to an impressive improvement in the prediction of the vortex shedding frequency, both in the cases with laminar and turbulent boundary layers detaching from the body. In the second configuration the improvement in the predicted value is particularly significant, leading to an error lower than
$1\,\%$
, as shown in table 2. As concerns the growth factors, when
$\unicode[STIX]{x1D708}_{t}$
is included in the stability analysis the modes associated with vortex shedding are again unambiguously identified and are slightly stable, conversely to the case without eddy viscosity in which the modes are slightly unstable. In order to provide a rough indication of the values of growth factors, despite the fact that these values are sensitive to the different numerical parameters and are not interesting for the analysis carried out here, we have
$\unicode[STIX]{x1D706}\simeq 0.1$
without eddy viscosity and
$\unicode[STIX]{x1D706}\simeq -0.1$
when eddy viscosity is included in the analysis.
In order to highlight the sensitivity of the stability results to the different parameters involved in the tuning of the mean flow model, and thus in the derivation of the field
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
, we refer to table 3, which is related to the flow configuration U20Dp0. In particular, case 4a differs from case 4 for the number of degrees of freedom involved in both the mean flow tuning and in the stability analysis, which passes from approximately
$26\,000$
for each velocity component in case 4 to
$60\,000$
in case 4a, thus increasing by a factor
$2.3$
. Comparing the results it is possible to note that the variation in the predicted value of the Strouhal number is negligible, thus indicating that the calculation can be considered at grid convergence. In case 4b the parameter
$\unicode[STIX]{x1D706}_{r}^{2}$
of the regularisation is decreased by a factor
$10$
, i.e.
$\unicode[STIX]{x1D706}_{r}^{2}=10^{-4}$
. Also in this case the variation in terms of
$St$
is negligible, indicating an independence of the results with respect to this parameter. In case 4c the constraint that the regularised flow field is divergence-free is eliminated. As a result, the global effect on the predicted value of
$St$
is still very small, of the order of
$1.7\,\%$
. Finally, case 4d differs from case 4 in the sense that the stability analysis is carried out on the original PIV flow field without any regularisation, while regularisation is applied only to tune the mean flow model and, thus, to derive
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
. The resulting effect on
$St$
is approximately equal to
$1.2\,\%$
, and thus negligible.
Table 3. Predictions of the vortex shedding frequency for case U20Dp0: different cases, from 4 to 4d, are discussed in details in the text. Reference case, case 4, is also reported in table 2.
5.3 Analysis of the stability eigenmodes
Section 5.2 shows that the stability analysis applied to the experimental mean flow field leads to reasonable predictions of the vortex shedding frequency and, when the eddy viscosity is included in the analysis, the predictions are systematically improved. In this section we further validate the results of the stability analysis and the beneficial effects of introducing an eddy viscosity by inspecting the resulting eigenmodes, which are related to the vortex shedding process. In order to have reference flow fields for comparing the stability eigenmodes, in each case proper orthogonal decomposition (POD) has been applied to the instantaneous snapshots of the database. Since the flow is strongly dominated by vortex shedding, as also discussed in § 2, in all cases POD leads to the identification of a couple of energetically dominant modes which represent two flow snapshots of the mean vortex shedding process which are shifted in phase by an angle equal to
$\unicode[STIX]{x03C0}/2$
(once the mean flow has been subtracted). These two POD modes play the same role as the real and imaginary parts of one of the two complex-conjugate eigenmodes identified by the stability analysis. Their linear combination, weighted by the cosine and sine of a generic phase angle, results in an instantaneous flow field of the phase-averaged vortex shedding process.
As a representative example, we have considered here the flow case U2.5Dp0. As expected, two strongly dominant eigenmodes are unambiguously identified in the POD energy spectrum and a combination of the two for a generic phase angle of the vortex shedding is obtained and plotted in figure 9(a) (
$x$
-component of velocity) and figure 9(d) (
$y$
-component). This field will be a reference so as to evaluate how well the stability eigenmodes represent the features of the mean vortex shedding process.
For comparison with the stability analysis, we have considered cases 2 and 4 of table 1. In both cases, the two complex-conjugate eigenmodes associated to vortex shedding have been normalised so that the maximum velocity norm is equal to that of the POD reference field. Moreover, the phase angles of the stability modes have been tuned to be equal to that of the POD field. The flow field so obtained is reported in figure 9(b,e) for case 2. As can be seen by comparison with the POD field, the
$y$
positions of the flow structures in the
$x$
-component of the velocity, i.e. figure 9(b), which are related to the position of the centres of the vortices shed by the body, are markedly closer to the centreline
$y=0$
if compared to the POD field (figure 9
a). Their spacing in the streamwise direction is slightly shifted, as can be noticed also from figure 9(e) for the
$y$
-component of the velocity in comparison with figure 9(b). The fact that the shed vortices in the eigenmode are shifted with respect to the centreline is in agreement with the error in the predicted vortex shedding frequency for case 2 reported in table 1. Finally, the eigenmode for case 2, especially figure 9(b), shows regions with very large gradients associated with some minor irregularities in the isocontours which are due to the fact that the stability analysis is carried out using the laminar flow Reynolds number, which is quite high and equal to
$6.7\times 10^{3}$
, and they result from a lack of dissipation in the equations since turbulence is completely neglected. When the field
$\unicode[STIX]{x1D708}_{t}(\boldsymbol{x})$
is introduced in the analysis, the resulting flow field associated to the stability eigenmodes is reported in figure 9(c,f). As can be seen, in this case the eigenmode matches reasonably well with the POD reference field, and the
$x$
and
$y$
spacing of the wake vortical structures are now in agreement with the experiments. As a consequence, the vortex shedding frequency is also well predicted, as shown in table 1. Finally, isocontours are regular and smooth since now the equivalent flow Reynolds number
$Re_{eq}$
is markedly lower than
$6.7\times 10^{3}$
, as also shown in figure 8(a), and the dissipation due to small-scale turbulence is taken into account via the eddy-viscosity model.
As a conclusion, the analysis documented in this section demonstrates that the stability analysis of the mean flow field is able to predict not only the vortex shedding frequency but also the spatial structure of the phase-averaged flow fields, and the prediction is markedly improved as the eddy viscosity deriving from the mean flow model is included in the stability analysis.
Figure 9. Flow configuration U2.5Dp0; velocity components
$x$
(a–c) and
$y$
(d–f) at a generic vortex shedding phase angle of: the POD mode (a,d) and, with reference to table 1, case 2 (b,e) and case 4 (c,f).
5.4 Estimation of the maps for passive control
In this section the mean flow model is used, together with the results of the stability analysis, in order to derive theoretically the sensitivity of the vortex shedding frequency to the introduction of a small control cylinder in a generic position of the flow. The prediction is done following the theoretical method illustrated in § 3.3. In particular, the imaginary part of
$S(\boldsymbol{x})$
defined in (3.23) indicates the variation in the vortex shedding frequency with respect to the local introduction of a small control body in the flow. The map
$\text{Im}\left[S(\boldsymbol{x})\right]$
is plotted for the flow configuration U2.5Dp0 in figure 10(a). In this derivation we have assumed a constant drag coefficient for the control body equal to
$C_{D}=1.2$
and we have assumed that its diameter is equal to
$d^{\ast }/h=7.5\times 10^{-2}$
, in agreement with the reference experiment. As shown in figure 10(a), sensitivity is concentrated in the shear layers bounding the mean wake. The values in the legend indicate the direct variation in terms of Strouhal number.
Figure 10. Control maps indicating the sensitivity of the vortex shedding frequency to the introduction of a small control cylinder of diameter equal to
$3~\text{mm}$
in the flow field of configuration U2.5Dp0: (a) theoretical prediction, (b) experimental map with the same colourmap as in (a).
As described in § 2.3, a similar map has been obtained experimentally by using a control cylinder of the same size as chosen for the numerical estimation, i.e.
$d^{\ast }/h=7.5\times 10^{-2}$
. Actually, due to technical constraints in the experiments, the size of this control cylinder is large for an accurate description of its effects by using the map in figure 10(a). Indeed, the local Reynolds number is estimated to be large enough to have vortex shedding also from the control cylinder, at least in some of the positions that have been tested experimentally, leading to an additional high-frequency load component that is not taken into account in the theoretical analysis. Nevertheless, despite the many possible sources of error, the experimental map, which is reported in figure 10(b), compares reasonably well with the map estimated theoretically, which is obtained by taking into account only the quasi-steady drag of the control cylinder. Actually the two maps are fairly similar in shape and they agree in identifying the region of maximum sensitivity, which leads to a decrease in the vortex shedding frequency in the controlled case, as indicated by the blue region extending in the range
$0.6\leqslant y/h\leqslant 0.8$
and
$0\leqslant x/h\leqslant 1$
. In the remaining spatial regions the experiments predict a slight decrease in the vortex shedding frequency, by an amount of approximately
$-0.02$
, while the theoretical map predicts an increase of approximately
$0.015$
. From the comparison between figure 10(a) and figure 10(b) the experimental and the theoretical maps seem to differ mainly by a constant and low shift value. This aspect could be related to a slight difference in the prediction of the absolute value of the vortex shedding frequency in the uncontrolled case, which is subtracted from the value measured in the controlled case in order to derive the sensitivity map. The important conclusion that we can draw by the previous analysis is that the high-sensitivity region is well identified and quantified by the proposed method, and the results shown here indicate that the method proposed has a good potential in estimating the effect of passive control on the basis of a database measured for the uncontrolled configuration.
For completeness, we also report in figure 11 the theoretical control map for the flow configuration U20Dp0. In this specific case there are no experimental results for validation, thus the only possible analysis is in comparison with case U2.5Dp0. This comparison shows that the sensitivity of case U20Dp0 has a similar distribution, i.e. localised on the boundaries of the recirculation bubble of the mean flow, and also compares quite well from a quantitative viewpoint.
Figure 11. Control map indicating the sensitivity of the vortex shedding frequency to the introduction of a small control cylinder of diameter equal to
$3~\text{mm}$
in the flow field of case U20Dp0.
6 Conclusions
In this paper we propose a strategy to estimate the effect of a passive control on the vortex shedding frequency in turbulent bluff-body wakes. Differently to previous works in the literature, the methodology proposed here relies entirely on the knowledge of the mean and phase-averaged flow fields measured in the uncontrolled case. The method is based on well-known tools, and its originality consists in the formulation of an ad hoc model for the mean flow which is tuned on the basis of the experimental results. The method also suggests a consistent way to introduce the effects of turbulence in the stability analysis of the mean flow field, even if this aspect is already known in the literature, and it has been previously applied for convectively unstable flows (see for instance Viola et al.
Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014). The proposed strategy is applied to the flow past a thick and perforated flat plate. The possibility to apply suction from the plate surface permits one to have a set of different wakes for each considered value of the flow Reynolds number. Experiments are available for laminar as well as turbulent separating boundary layers, thus for a wide range of flow complexity. It is also shown that the global stability of the mean flow fields, which are measured in a PIV window which fully includes the wake, predicts a nearly marginal unstable mode with a frequency that is close to that of vortex shedding from the body even neglecting the turbulence effects. This result extends the work in Camarri et al. (Reference Camarri, Fallenius and Fransson2013) up to flow Reynolds numbers equal to
$5.3\times 10^{4}$
. When laminar boundary layers detach from the body the errors in terms of predicted Strouhal number are generally less than
$3\,\%$
, while the errors grow with the flow complexity up to approximately
$15\,\%$
for cases at
$Re=5.3\times 10^{4}$
. When turbulence is included in the analysis, the ad hoc turbulence closure being a side result obtained by the tuning of the corresponding mean flow model, the errors in the predicted value of
$St$
are drastically and systematically reduced, especially for the turbulent case, where they become less than
$3\,\%$
. Finally, the combination of the mean flow model and of the stability analysis leads to the prediction of the effects on the vortex shedding frequency that could be obtained by introducing a small control cylinder in the wake. The theoretical sensitivity map, which is predicted using the measurements available for the uncontrolled case, is compared with the equivalent one derived experimentally. Although the control cylinder used in the experiments is rather intrusive, the comparison shows that the region of maximum sensitivity is well predicted, and compares reasonably well also from a quantitative viewpoint. In the areas of low sensitivity the maps show some discrepancies, but globally the two maps, i.e. the experimental and the theoretical one, seem to differ mainly by a constant and low shift value. This aspect could be related to a slight difference in the prediction of the absolute value of the vortex shedding frequency in the uncontrolled case, which is subtracted from the value measured in the controlled case so as to derive the sensitivity map. Nevertheless, results obtained are in our opinion more than satisfactory, considering that this analysis entirely relies on experimental PIV flow fields taken in the uncontrolled case at high values of the flow Reynolds number, and considering the size of the control cylinder used in the experiments.
We remark that the same control map estimated in the present paper might be obtained by tuning a time-periodic eddy viscosity so as to fit the experimental phase-averaged flow field and by linearising the resulting RANS equations around the limit cycle representing the saturated vortex shedding process, following the work in Luchini, Giannetti & Pralits (Reference Luchini, Giannetti, Pralits, Braza and Hourigan2009). This second approach, however, is definitely more complex than the one proposed here, and leads to cumbersome optimisation problems, as time is also involved.
Finally, even if not considered in this work, the proposed mean flow model provides an estimation of the pressure field in the PIV window and on the body surface. This final output of the model could be used to estimate the pressure on the body when suction is applied and near the separation points, i.e. where it is very challenging to measure pressure experimentally. The validation of this additional output of the model will be the subject of future investigations.
