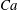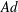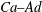1 Introduction
Margination, defined as the migration of a particle in blood flow towards the periphery of the blood vessel, allows the particle to come close to the endothelium, and then adhere to the vessel wall (Du Trochet Reference Du Trochet, marquis1824; Koumoutsakos, Pivkin & Milde Reference Koumoutsakos, Pivkin and Milde2013). It is of significant importance to understand such physiological processes for curing relevant diseases. For example, in the inflammation process, margination of leukocytes towards the vessel wall is the precondition for an organism to perform defence functions, such as adhering to vascular endothelium and transmigrating into the tissues (Ley & Tedder Reference Ley and Tedder1995; Fedosov, Fornleitner & Gompper Reference Fedosov, Fornleitner and Gompper2012). In atherosclerosis, the thrombosis, formed by the clot, is caused by the margination and accumulation of numerous platelets responding quickly to events on the vessel wall, e.g. injury (Wootton & Ku Reference Wootton and Ku1999; Fogelson & Neeves Reference Fogelson and Neeves2015). Additionally, margination has extensive applications in microfluidic devices for the removal of pathogens and the separation of cells (Bhagat et al. Reference Bhagat, Bow, Hou, Tan, Han and Lim2010; Gossett et al. Reference Gossett, Weaver, Mach, Hur, Tse, Lee, Amini and Di Carlo2010; Hou et al. Reference Hou, Bhagat, Chong, Mao, Tan, Han and Lim2010).
The root cause of margination has not been completely revealed so far. In blood flow, every component of blood such as plasma and red blood cells (RBCs) may contribute to margination (Farutin & Misbah Reference Farutin and Misbah2013). Generally speaking, three major factors, i.e. hydrodynamic forces, wall effects and adhesive interactions between ligands and receptors, are considered to be responsible for the margination of micro-particles (MPs). Here, another most important effect, Brownian interaction in nanoparticles, can be ignored due to the large size of MPs (Ramakrishnan et al. Reference Ramakrishnan, Wang, Eckmann, Ayyaswamy and Radhakrishnan2017). Hence, when placing the MP in the blood flow through injection or other administration, the dynamics of MPs is governed by the complex interplay among these three factors. The performance of the MP will be affected by its physiological properties, such as size, shape, stiffness and surface functionality – also known as the ‘4S’ parameters (Li et al. Reference Li, Lian, Zhang, Aldousari, Hedia, Asiri and Liu2016; Ye et al. Reference Ye, Shen, Yu, Wei and Li2018c ). These properties play different roles, depending on the specific physiological conditions. For example, Decuzzi et al. (Reference Decuzzi, Godin, Tanaka, Lee, Chiappini, Liu and Ferrari2010) found that, in an in vivo experiment, discoidal particles demonstrated the strongest accumulation in most organs, such as spleen and kidney; whereas in the liver, cylindrical particles outperformed the other kinds of particles. Therefore, investigations of the ‘4S’ parameters become crucial in the optimal design of MPs acting as drug carriers in biomedical application.
Among the ‘4S’ parameters, stiffness attracts relatively less attention compared to the other parameters. It should play an important role in the margination process of MPs. Owing to deformability, the symmetry of the Stokes flow is broken. According to the mirror symmetry time reversal theorem proposed by Bretherton (Reference Bretherton1962), the elastic MP will experience a lateral force in the near-wall region. For example, usually the leukocyte is assumed to marginate towards the vessel wall in blood flow (Freund Reference Freund2007; Fedosov et al. Reference Fedosov, Fornleitner and Gompper2012; Marth, Aland & Voigt Reference Marth, Aland and Voigt2016). Recently it has been discovered that the reversal of margination (migration from the near-wall region to the centre of a vessel) happens when the stiffness is reduced by reorganization of cellular cortical actins (Fay et al. Reference Fay, Myers, Kumar, Turbyfield, Byler, Crawford, Mannino, Laohapant, Tyburski and Sakurai2016).
The dynamics of an elastic particle is more complex than that of a rigid one. The shape of an elastic MP is not given a priori and continuously deforms in flow. The evolution of shape is determined by the dynamic balance between the interfacial force and fluid stress, depending on the local flow environment. Additionally, a large number of RBCs occupy the blood flow. Thus, the deformation and motion of RBCs influence the flow field around MPs. Hydrodynamic interaction can also happen between RBCs and elastic MPs. Poiseuille (Reference Poiseuille1836) recognized that blood corpuscles in the capillaries tended to migrate away from the wall due to deformation-induced migration stemming from viscous effects. Nevertheless, this stiffness-dependent migration of particles has attracted extensive attention very recently. Owing to the similar behaviour of RBCs under flow, a series of elastic particles, such as capsules and vesicles, have been investigated in regard to their migration motion by experimental (Abkarian, Lartigue & Viallat Reference Abkarian, Lartigue and Viallat2002; Callens et al.
Reference Callens, Minetti, Coupier, Mader, Dubois, Misbah and Podgorski2008; Coupier et al.
Reference Coupier, Kaoui, Podgorski and Misbah2008; Kantsler, Segre & Steinberg Reference Kantsler, Segre and Steinberg2008), analytical (Olla Reference Olla1997a
,Reference Olla
b
; Seifert Reference Seifert1999; Vlahovska & Gracia Reference Vlahovska and Gracia2007; Danker, Vlahovska & Misbah Reference Danker, Vlahovska and Misbah2009; Farutin & Misbah Reference Farutin and Misbah2011, Reference Farutin and Misbah2013; Qi & Shaqfeh Reference Qi and Shaqfeh2017) and numerical studies (Cantat & Misbah Reference Cantat and Misbah1999; Sukumaran & Seifert Reference Sukumaran and Seifert2001; Secomb, Styp-Rekowska & Pries Reference Secomb, Styp-Rekowska and Pries2007; Doddi & Bagchi Reference Doddi and Bagchi2008; Kaoui et al.
Reference Kaoui, Ristow, Cantat, Misbah and Zimmermann2008; Zhao, Spann & Shaqfeh Reference Zhao, Spann and Shaqfeh2011; Nix et al.
Reference Nix, Imai, Matsunaga, Yamaguchi and Ishikawa2014; Singh, Li & Sarkar Reference Singh, Li and Sarkar2014). Quantitative determination of the deformation-induced migration is instrumental in revealing the underlying mechanism of the migration behaviours of erythrocytes and leukocytes in blood flow. Abkarian et al. (Reference Abkarian, Lartigue and Viallat2002) used light microscopy to study the tank-treading motion and deformation of vesicles in linear shear flow. Upon increasing the shear rate of flow, the vesicle tilted with respect to the substrate, and further incrementation of shear rate
![]() $\dot{\unicode[STIX]{x1D6FE}}$
made vesicle migrate away from the substrate. These observations revealed the existence of deformation-induced migration. They found that the magnitude of the deformation-induced migration depended on the viscosity
$\dot{\unicode[STIX]{x1D6FE}}$
made vesicle migrate away from the substrate. These observations revealed the existence of deformation-induced migration. They found that the magnitude of the deformation-induced migration depended on the viscosity
![]() $\unicode[STIX]{x1D702}$
of the fluid, the radius
$\unicode[STIX]{x1D702}$
of the fluid, the radius
![]() $R$
of the vesicle, the distance
$R$
of the vesicle, the distance
![]() $h$
from the substrate and a monotonically decreasing function
$h$
from the substrate and a monotonically decreasing function
![]() $f(1-v)$
of the reduced volume
$f(1-v)$
of the reduced volume
![]() $v$
. On the basis of these direct observations, Farutin & Misbah (Reference Farutin and Misbah2013) derived the migration velocity of a vesicle near the wall. From the method using the stresslet of a droplet in a Couette device (Smart & Leighton Jr Reference Smart and Leighton1991), they employed an asymptotic method to derive the expression for the migration velocity by determining the stresslet in a power series of the shape parameter
$v$
. On the basis of these direct observations, Farutin & Misbah (Reference Farutin and Misbah2013) derived the migration velocity of a vesicle near the wall. From the method using the stresslet of a droplet in a Couette device (Smart & Leighton Jr Reference Smart and Leighton1991), they employed an asymptotic method to derive the expression for the migration velocity by determining the stresslet in a power series of the shape parameter
![]() $\unicode[STIX]{x1D6E4}$
of the vesicles. This parameter
$\unicode[STIX]{x1D6E4}$
of the vesicles. This parameter
![]() $\unicode[STIX]{x1D6E4}$
quantifies the deflation of a vesicle from a sphere with the same volume. In the leading order of
$\unicode[STIX]{x1D6E4}$
quantifies the deflation of a vesicle from a sphere with the same volume. In the leading order of
![]() $\unicode[STIX]{x1D6E4}$
, the migration velocity
$\unicode[STIX]{x1D6E4}$
, the migration velocity
![]() ${\sim}\dot{\unicode[STIX]{x1D6FE}}R^{3}/h^{2}$
. The theoretical analysis was implemented on the basis of the assumption that the deflation
${\sim}\dot{\unicode[STIX]{x1D6FE}}R^{3}/h^{2}$
. The theoretical analysis was implemented on the basis of the assumption that the deflation
![]() $\unicode[STIX]{x1D6E4}$
is small. This means that if the shear modulus of the particles, such as that of the capsule, is not high, the expression should not be valid. More recently, Singh et al. (Reference Singh, Li and Sarkar2014) corrected the analytical migration velocity by fitting the results obtained from a series of numerical simulations for capsules with different elastic capillary numbers
$\unicode[STIX]{x1D6E4}$
is small. This means that if the shear modulus of the particles, such as that of the capsule, is not high, the expression should not be valid. More recently, Singh et al. (Reference Singh, Li and Sarkar2014) corrected the analytical migration velocity by fitting the results obtained from a series of numerical simulations for capsules with different elastic capillary numbers
![]() $Ca$
. They found that there existed a critical
$Ca$
. They found that there existed a critical
![]() $Ca_{cr}$
splitting the migration velocity into two distinct regimes. When
$Ca_{cr}$
splitting the migration velocity into two distinct regimes. When
![]() $Ca<Ca_{cr}$
, migration velocity
$Ca<Ca_{cr}$
, migration velocity
![]() ${\sim}Ca$
and
${\sim}Ca$
and
![]() ${\sim}\dot{\unicode[STIX]{x1D6FE}}R^{3}/h^{2}$
, which is similar to the analytical relation for vesicles. However, when
${\sim}\dot{\unicode[STIX]{x1D6FE}}R^{3}/h^{2}$
, which is similar to the analytical relation for vesicles. However, when
![]() $Ca>Ca_{cr}$
, migration velocity
$Ca>Ca_{cr}$
, migration velocity
![]() ${\sim}Ca^{0.6}$
and
${\sim}Ca^{0.6}$
and
![]() ${\sim}\dot{\unicode[STIX]{x1D6FE}}R^{2.35}/h^{1.35}$
. Hence, if the capsule is soft (large
${\sim}\dot{\unicode[STIX]{x1D6FE}}R^{2.35}/h^{1.35}$
. Hence, if the capsule is soft (large
![]() $Ca$
), the analytic relation is not valid for the capsule any more. Also, a detailed study for lift velocity of RBCs through simulations has been proposed by Qi & Shaqfeh (Reference Qi and Shaqfeh2017). Here, the elastic MPs pertain to capsules, and will be discussed in detail later.
$Ca$
), the analytic relation is not valid for the capsule any more. Also, a detailed study for lift velocity of RBCs through simulations has been proposed by Qi & Shaqfeh (Reference Qi and Shaqfeh2017). Here, the elastic MPs pertain to capsules, and will be discussed in detail later.
According to Farutin & Misbah (Reference Farutin and Misbah2013), in addition to deformation-induced migration, hydrodynamic interaction is an additional governing mechanism of particle migration in simple shear flow. Hydrodynamic interaction results in hydrodynamic diffusion, which is induced by collisions between particles. Collisions between two identical particles, namely homogeneous collisions, such as between capsules (Singh & Sarkar Reference Singh and Sarkar2015) and between vesicles (Farutin & Misbah Reference Farutin and Misbah2013), have been investigated numerically and theoretically, respectively. These homogeneous collisions are not essential in particle migration and segregation, because the migrations of the two collision partners are the same. Kumar & Graham (Reference Kumar and Graham2011, Reference Kumar and Graham2012b ) and Sinha & Graham (Reference Sinha and Graham2016) extended this to heterogeneous collisions between capsules with the same volume but different membrane rigidities and shapes, respectively. In a binary suspension of soft and stiff capsules, the stiff particles were observed to accumulate in the near-wall region in a suspension of primarily soft particles, whereas soft particles were found to concentrate on the centreline in a suspension of primarily stiff particles. This segregation behaviour was attributed to larger cross-stream displacement in heterogeneous collisions of stiff particles than that of soft particles. Furthermore, Vahidkhah & Bagchi (Reference Vahidkhah and Bagchi2015) proposed that a binary collision between an RBC and a rigid MP should be one of the reasons for the shape-dependent margination behaviour of MPs. The result presented that spherical and oblate MPs marginated more than prolate MPs after several collisions. In terms of the elastic MPs, the collisions between MPs and RBCs will be more complex, and should play an important role in the margination behaviour of elastic MPs. However, it remains largely unexplored so far.
After the particle marginates, it has a chance to interact with the vessel wall and adhere to it, depending on the ligand–receptor binding properties. Adhesion behaviour has been studied extensively using the Bell model (Bell Reference Bell1978), developed by adhesive dynamics which was first employed to understand the dynamics of leukocyte adhesion under flow (Hammer & Lauffenburger Reference Hammer and Lauffenburger1987; King & Hammer Reference King and Hammer2001; Hammer Reference Hammer2014). A number of studies in drug delivery systems focus on the adhesion process (Decuzzi & Ferrari Reference Decuzzi and Ferrari2006; Charoenphol, Huang & Eniola-Adefeso Reference Charoenphol, Huang and Eniola-Adefeso2010; Fedosov Reference Fedosov2010; Charoenphol et al.
Reference Charoenphol, Onyskiw, Carrasco-Teja and Eniola-Adefeso2012; Luo & Bai Reference Luo and Bai2016; Coclite et al.
Reference Coclite, Mollica, Ranaldo, Pascazio, de Tullio and Decuzzi2017). In human blood, MPs with diameters of
![]() $3~\unicode[STIX]{x03BC}\text{m}$
were found to be the ideal choice for spherical, rigid particles to adhere to vessel walls rather than nanoparticles (Charoenphol et al.
Reference Charoenphol, Huang and Eniola-Adefeso2010, Reference Charoenphol, Onyskiw, Carrasco-Teja and Eniola-Adefeso2012). In addition to spherical particles, Decuzzi & Ferrari (Reference Decuzzi and Ferrari2006) investigated the effects of particle size and shape on the adhesion behaviour from the viewpoint of specific adhesive interaction strength. They predicted that, for a fixed shape (e.g. spherical or ellipsoidal), there existed an optimal volume (size) making the adhesive strength reach a maximum. Additionally, they found that non-spherical particles can carry a larger amount of drugs than spherical particles with the same adhesive strength. More recently, Coclite et al. (Reference Coclite, Mollica, Ranaldo, Pascazio, de Tullio and Decuzzi2017) constructed a two-dimensional lattice Boltzmann–immersed boundary model to systematically predict the near-wall dynamics of circulating particles with different shapes and adhesive strengths. As for the adhesion behaviour of deformable particles, a variety of dynamic phenomena, including detachment, rolling, firm adhesion and stop-and-go motion (Fedosov Reference Fedosov2010; Luo & Bai Reference Luo and Bai2016), were found. Luo & Bai (Reference Luo and Bai2016) combined the front-tracking finite element method and adhesion kinetics model to investigate capsule dynamics in flow and adhesive dynamics, respectively. It was found that, for a particle with low
$3~\unicode[STIX]{x03BC}\text{m}$
were found to be the ideal choice for spherical, rigid particles to adhere to vessel walls rather than nanoparticles (Charoenphol et al.
Reference Charoenphol, Huang and Eniola-Adefeso2010, Reference Charoenphol, Onyskiw, Carrasco-Teja and Eniola-Adefeso2012). In addition to spherical particles, Decuzzi & Ferrari (Reference Decuzzi and Ferrari2006) investigated the effects of particle size and shape on the adhesion behaviour from the viewpoint of specific adhesive interaction strength. They predicted that, for a fixed shape (e.g. spherical or ellipsoidal), there existed an optimal volume (size) making the adhesive strength reach a maximum. Additionally, they found that non-spherical particles can carry a larger amount of drugs than spherical particles with the same adhesive strength. More recently, Coclite et al. (Reference Coclite, Mollica, Ranaldo, Pascazio, de Tullio and Decuzzi2017) constructed a two-dimensional lattice Boltzmann–immersed boundary model to systematically predict the near-wall dynamics of circulating particles with different shapes and adhesive strengths. As for the adhesion behaviour of deformable particles, a variety of dynamic phenomena, including detachment, rolling, firm adhesion and stop-and-go motion (Fedosov Reference Fedosov2010; Luo & Bai Reference Luo and Bai2016), were found. Luo & Bai (Reference Luo and Bai2016) combined the front-tracking finite element method and adhesion kinetics model to investigate capsule dynamics in flow and adhesive dynamics, respectively. It was found that, for a particle with low
![]() $Ca$
, deformation promoted the transition from rolling to firm adhesion; while deformation would inhibit both the rolling to firm adhesion and the detachment to rolling transitions when the
$Ca$
, deformation promoted the transition from rolling to firm adhesion; while deformation would inhibit both the rolling to firm adhesion and the detachment to rolling transitions when the
![]() $Ca$
of the particle was relatively high. Because the particle with high
$Ca$
of the particle was relatively high. Because the particle with high
![]() $Ca$
would collapse on the substrate, and in the middle of the particle, a ligand–receptor free region formed. Further increment of
$Ca$
would collapse on the substrate, and in the middle of the particle, a ligand–receptor free region formed. Further increment of
![]() $Ca$
made the rolling motion vanish and the particle shape largely deviate from spherical.
$Ca$
made the rolling motion vanish and the particle shape largely deviate from spherical.
In general, margination is thought to be the necessary precondition for adhesion (Müller, Fedosov & Gompper Reference Müller, Fedosov and Gompper2016). Before a particle can interact with a vessel wall, it should marginate into the near-wall region, e.g. the cell-free layer (CFL) in the blood flow. The CFL is a thin layer near the vessel wall with no RBCs inside, which forms due to the deformability of RBCs. However, adhesion can also, in turn, affect the margination process. In engineering applications, micrometre-sized particles are often used as drug carriers due to their better performance over nanometre-sized particles in the margination process (Tasciotti et al.
Reference Tasciotti, Liu, Bhavane, Plant, Leonard, Price, Cheng, Decuzzi, Tour and Robertson2008). The thickness of the CFL is also measured in micrometres (approximately
![]() $1.5{-}5.0~\unicode[STIX]{x03BC}\text{m}$
) in the human vasculature (Fedosov et al.
Reference Fedosov, Caswell, Popel and Karniadakis2010b
). Hence, when a particle moves close to or enters the CFL, the particle can interact with the vessel wall through ligand–receptor binding. Additionally, in terms of deformation of the particle, the elastic MP may move away from the wall to the centre of blood flow due to deformation-induced migration. But adhesion may play a role in preventing it escaping from the CFL. Thus, adhesion will affect the choice of elastic MP located near the CFL: entering or departing from the CFL? Such a phenomenon was also reported in previous work (Müller et al.
Reference Müller, Fedosov and Gompper2016), but without discussion. Researchers pay more attention to the effects of particle ‘4S’ properties on either margination or adhesion (Decuzzi & Ferrari Reference Decuzzi and Ferrari2006; Müller, Fedosov & Gompper Reference Müller, Fedosov and Gompper2014; Vahidkhah & Bagchi Reference Vahidkhah and Bagchi2015).
$1.5{-}5.0~\unicode[STIX]{x03BC}\text{m}$
) in the human vasculature (Fedosov et al.
Reference Fedosov, Caswell, Popel and Karniadakis2010b
). Hence, when a particle moves close to or enters the CFL, the particle can interact with the vessel wall through ligand–receptor binding. Additionally, in terms of deformation of the particle, the elastic MP may move away from the wall to the centre of blood flow due to deformation-induced migration. But adhesion may play a role in preventing it escaping from the CFL. Thus, adhesion will affect the choice of elastic MP located near the CFL: entering or departing from the CFL? Such a phenomenon was also reported in previous work (Müller et al.
Reference Müller, Fedosov and Gompper2016), but without discussion. Researchers pay more attention to the effects of particle ‘4S’ properties on either margination or adhesion (Decuzzi & Ferrari Reference Decuzzi and Ferrari2006; Müller, Fedosov & Gompper Reference Müller, Fedosov and Gompper2014; Vahidkhah & Bagchi Reference Vahidkhah and Bagchi2015).
Considering the above aspects, we focus on the performance of elastic MPs in the whole process from margination to adhesion. We combine the lattice Boltzmann method (LBM) and molecular dynamics to solve the fluid dynamics and particle dynamics (RBCs and elastic MPs), respectively. These two parts are coupled by the immersed boundary method (IBM). In our simulation, the most expensive part is solving the fluid dynamics. The LBM is adopted due to its high natural parallelism. In the past two decades, it has been confirmed as an efficient and accurate numerical solver to handle fluid dynamics problems (Higuera, Succi & Benzi Reference Higuera, Succi and Benzi1989; Benzi, Succi & Vergassola Reference Benzi, Succi and Vergassola1992; Chen & Doolen Reference Chen and Doolen1998). Its application in simulating blood flow has achieved significant progress (Zhang, Johnson & Popel Reference Zhang, Johnson and Popel2007, Reference Zhang, Johnson and Popel2008; Lorenz, Hoekstra & Caiazzo Reference Lorenz, Hoekstra and Caiazzo2009; MacMeccan et al.
Reference MacMeccan, Clausen, Neitzel and Aidun2009; Aidun & Clausen Reference Aidun and Clausen2010; Clausen, Reasor & Aidun Reference Clausen, Reasor and Aidun2010; Melchionna et al.
Reference Melchionna, Bernaschi, Succi, Kaxiras, Rybicki, Mitsouras, Coskun and Feldman2010; Czaja et al.
Reference Czaja, Závodszky, Tarksalooyeh and Hoekstra2018; de Haan et al.
Reference de Haan, Zavodszky, Azizi and Hoekstra2018). In the absence of large numbers of RBCs, Melchionna et al. (Reference Melchionna, Bernaschi, Succi, Kaxiras, Rybicki, Mitsouras, Coskun and Feldman2010) took a hydrokinetic approach (Bernaschi et al.
Reference Bernaschi, Melchionna, Succi, Fyta, Kaxiras and Sircar2009) to model large-scale cardiovascular blood flow to recognize the key relevance to the localization and progression of major cardiovascular diseases, such as atherosclerosis. Borgdorff et al. (Reference Borgdorff, Mamonski, Bosak, Kurowski, Belgacem, Chopard, Groen, Coveney and Hoekstra2014) provided a multiscale coupling library and environment to make possible the simulation of an extra-large-scale vasculature network. Furthermore, considering the existence of RBCs, Zhang et al. (Reference Zhang, Johnson and Popel2007, Reference Zhang, Johnson and Popel2008) conducted simulations from the aggregation of multiple RBCs to the rheology of an RBC suspension in two-dimensional blood flow. MacMeccan et al. (Reference MacMeccan, Clausen, Neitzel and Aidun2009) and Clausen et al. (Reference Clausen, Reasor and Aidun2010) extended it to three-dimensional blood flow by coupling the LBM with the finite element method. Additionally, the adhesive dynamics of elastic MPs to a vessel wall is governed by the probabilistic model proposed by Hammer & Lauffenburger (Reference Hammer and Lauffenburger1987). The diameter of MPs is set as
![]() $2~\unicode[STIX]{x03BC}\text{m}$
, and the haematocrit of blood flow is 30 %, in which the thickness of the CFL is comparable to the particle size. To clarify the influence of near-wall adhesion on the localization of MPs, the particle size and blood flow conditions are fixed. The
$2~\unicode[STIX]{x03BC}\text{m}$
, and the haematocrit of blood flow is 30 %, in which the thickness of the CFL is comparable to the particle size. To clarify the influence of near-wall adhesion on the localization of MPs, the particle size and blood flow conditions are fixed. The
![]() $Ca$
is tuned by changing the shear modulus of elastic MPs, and we vary the adhesion strength to adjust
$Ca$
is tuned by changing the shear modulus of elastic MPs, and we vary the adhesion strength to adjust
![]() $Ad$
. The interplay of adhesion strength and particle deformability leads to two optimal margination regimes. One is with moderate
$Ad$
. The interplay of adhesion strength and particle deformability leads to two optimal margination regimes. One is with moderate
![]() $Ca$
and high
$Ca$
and high
![]() $Ad$
, and the other is with small
$Ad$
, and the other is with small
![]() $Ca$
and moderate
$Ca$
and moderate
![]() $Ad$
. This may shed light on the optimal design of MPs favouring high localization at the wall in blood flow.
$Ad$
. This may shed light on the optimal design of MPs favouring high localization at the wall in blood flow.
The paper is organized as follows. In § 2 we describe the physical problem involving the transport of elastic MPs in blood flow and the numerical methods that we employ to solve the fluid flow, particle dynamics and adhesive dynamics. We validate our computational method in § 3. Furthermore, § 4 presents the margination and adhesion results. A detailed discussion of the underlying physical mechanisms is also provided. In § 5, conclusions are given.
2 Physical problem and computational method
2.1 Physical problem

Figure 1. Transport of elastic MPs in blood flow. (a) Computational model of margination and adhesion of elastic MPs in blood flow. The zoomed panels give the detailed adhesion behaviour of an elastic MP under a stochastic ligand–receptor binding effect. (b) Schematic of transport process of an elastic MP from the centre of the bloodstream (denoted (C)) to the cell-free layer (F), and then reaching the adhesion layer.
In blood flow, most parts of the vessel are occupied by a large number of RBCs. In a normal human blood vessel, the volume fraction of RBCs (haematocrit
![]() $Ht$
) is approximately 20 %–45 %. Under the interplay effect of the flow and the vessel wall, RBCs move from the near-wall region to the centre of the vessel due to deformation-induced migration. This results in the formation of a cell-free layer (CFL). The CFL plays the role of a lubricant layer and reduces the blood flow resistance, which is also called the Fåhraeus–Lindqvist effect (Fåhraeus & Lindqvist Reference Fåhraeus and Lindqvist1931). When elastic MPs, acting as drug carriers, are injected into a vein, they move with the bulk flow as shown in figure 1(a). The elastic MPs deform under the shear stress and collide with RBCs. The deformation depends on the local flow environment. Additionally, the MPs may move in the cross-stream direction, migrating either towards the wall or to the centre of the channel. Once MPs migrate to the near-wall region, i.e. CFL, the ligands decorated on their surfaces have the chance to interact with the receptors on endothelial cells distributed on the vessel wall (figure 1
a). This ligand–receptor binding is required for the further release of drug molecules into tumour sites through a vascular targeting strategy (Schnitzer Reference Schnitzer1998; Neri & Bicknell Reference Neri and Bicknell2005). However, reaching the CFL cannot guarantee that such interactions will occur. Only when an MP reaches a closer distance to the vessel wall, in which ligands can interact with receptors, does the interaction occur. This distance is determined by the reaction distance between ligands and receptors. We name the layer within this distance as the adhesion layer (
$Ht$
) is approximately 20 %–45 %. Under the interplay effect of the flow and the vessel wall, RBCs move from the near-wall region to the centre of the vessel due to deformation-induced migration. This results in the formation of a cell-free layer (CFL). The CFL plays the role of a lubricant layer and reduces the blood flow resistance, which is also called the Fåhraeus–Lindqvist effect (Fåhraeus & Lindqvist Reference Fåhraeus and Lindqvist1931). When elastic MPs, acting as drug carriers, are injected into a vein, they move with the bulk flow as shown in figure 1(a). The elastic MPs deform under the shear stress and collide with RBCs. The deformation depends on the local flow environment. Additionally, the MPs may move in the cross-stream direction, migrating either towards the wall or to the centre of the channel. Once MPs migrate to the near-wall region, i.e. CFL, the ligands decorated on their surfaces have the chance to interact with the receptors on endothelial cells distributed on the vessel wall (figure 1
a). This ligand–receptor binding is required for the further release of drug molecules into tumour sites through a vascular targeting strategy (Schnitzer Reference Schnitzer1998; Neri & Bicknell Reference Neri and Bicknell2005). However, reaching the CFL cannot guarantee that such interactions will occur. Only when an MP reaches a closer distance to the vessel wall, in which ligands can interact with receptors, does the interaction occur. This distance is determined by the reaction distance between ligands and receptors. We name the layer within this distance as the adhesion layer (
![]() $\unicode[STIX]{x1D712}$
). Usually the thickness of the adhesion layer is in the range of tens to hundreds of nanometres (Decuzzi & Ferrari Reference Decuzzi and Ferrari2006; Müller et al.
Reference Müller, Fedosov and Gompper2014, Reference Müller, Fedosov and Gompper2016). Here, it is set as
$\unicode[STIX]{x1D712}$
). Usually the thickness of the adhesion layer is in the range of tens to hundreds of nanometres (Decuzzi & Ferrari Reference Decuzzi and Ferrari2006; Müller et al.
Reference Müller, Fedosov and Gompper2014, Reference Müller, Fedosov and Gompper2016). Here, it is set as
![]() $1.0~\unicode[STIX]{x03BC}\text{m}$
according to the reaction distance that we used in the computational model. This is reasonable compared to that used in the previous work of Müller et al. (Reference Müller, Fedosov and Gompper2014).
$1.0~\unicode[STIX]{x03BC}\text{m}$
according to the reaction distance that we used in the computational model. This is reasonable compared to that used in the previous work of Müller et al. (Reference Müller, Fedosov and Gompper2014).
The numerical study is employed to study the transport of elastic MPs due to its flexibility in tuning the properties of MPs and adhesive interactions. Blood flow is considered as a suspension of RBCs. Owing to limited computational resources, a small part of the vessel is taken into account and modelled as a rectangular channel. The size of the channel is of height
![]() $36~\unicode[STIX]{x03BC}\text{m}$
, width
$36~\unicode[STIX]{x03BC}\text{m}$
, width
![]() $27~\unicode[STIX]{x03BC}\text{m}$
and length
$27~\unicode[STIX]{x03BC}\text{m}$
and length
![]() $54~\unicode[STIX]{x03BC}\text{m}$
. Periodic boundary conditions are applied in the width (
$54~\unicode[STIX]{x03BC}\text{m}$
. Periodic boundary conditions are applied in the width (
![]() $x$
) and length (
$x$
) and length (
![]() $y$
) directions. The height (
$y$
) directions. The height (
![]() $z$
) direction is bounded by two flat plates. The bottom plate (vessel wall, also named substrate) is fixed and the flow is driven by the moving of the upper one with a constant velocity
$z$
) direction is bounded by two flat plates. The bottom plate (vessel wall, also named substrate) is fixed and the flow is driven by the moving of the upper one with a constant velocity
![]() $U$
. In all of the simulations, shear rates stay at
$U$
. In all of the simulations, shear rates stay at
![]() $200~\text{s}^{-1}$
. A total of 162 RBCs and 80 identical elastic MPs are placed inside the channel. The haematocrit is approximately 30 %. MPs are initially set to a spherical shape with radius
$200~\text{s}^{-1}$
. A total of 162 RBCs and 80 identical elastic MPs are placed inside the channel. The haematocrit is approximately 30 %. MPs are initially set to a spherical shape with radius
![]() $1~\unicode[STIX]{x03BC}\text{m}$
, and their total volume fraction is approximately 0.64 % in the channel. Additionally, the ligands and receptors are uniformly distributed on the surfaces of MPs and substrate, respectively. The densities of ligands and receptors are listed in table 1.
$1~\unicode[STIX]{x03BC}\text{m}$
, and their total volume fraction is approximately 0.64 % in the channel. Additionally, the ligands and receptors are uniformly distributed on the surfaces of MPs and substrate, respectively. The densities of ligands and receptors are listed in table 1.
Table 1. Parameters used in adhesive model for ligand–receptor binding.

2.2 Computational method
2.2.1 Lattice Boltzmann method for fluid flow
The RBCs are immersed within blood plasma in the blood flow. The other components, such as the white blood cells and platelets, are negligible due to their low volume fractions compared to that of RBCs. The plasma is usually considered as a Newtonian fluid. Its dynamics is described by the continuity equation and incompressible Navier–Stokes (NS) equation:
where
![]() $\unicode[STIX]{x1D70C}$
is the plasma density, and
$\unicode[STIX]{x1D70C}$
is the plasma density, and
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $p$
represent the velocity and pressure of the flow, respectively. The term
$p$
represent the velocity and pressure of the flow, respectively. The term
![]() $F$
on the right-hand side of (2.2) is the external force;
$F$
on the right-hand side of (2.2) is the external force;
![]() $\unicode[STIX]{x1D707}$
is the dynamic viscosity of the plasma and is set as 1.2 cP. The LBM is employed to solve the NS equation due to its high efficiency and accuracy in handling incompressible Newtonian flow (Higuera et al.
Reference Higuera, Succi and Benzi1989; Benzi et al.
Reference Benzi, Succi and Vergassola1992; Chen & Doolen Reference Chen and Doolen1998). By discretizing the velocity of the linearized Boltzmann equation, a finite difference scheme is obtained:
$\unicode[STIX]{x1D707}$
is the dynamic viscosity of the plasma and is set as 1.2 cP. The LBM is employed to solve the NS equation due to its high efficiency and accuracy in handling incompressible Newtonian flow (Higuera et al.
Reference Higuera, Succi and Benzi1989; Benzi et al.
Reference Benzi, Succi and Vergassola1992; Chen & Doolen Reference Chen and Doolen1998). By discretizing the velocity of the linearized Boltzmann equation, a finite difference scheme is obtained:
where
![]() $f_{i}(\boldsymbol{x},t)$
is the distribution function and
$f_{i}(\boldsymbol{x},t)$
is the distribution function and
![]() $\boldsymbol{e}_{i}$
is the discretized velocity. In the current simulation, the D3Q19 velocity model is used (Mackay, Ollila & Denniston Reference Mackay, Ollila and Denniston2013), and the fluid particles have the possible discrete velocities stated in Mackay et al. (Reference Mackay, Ollila and Denniston2013). In (2.3)
$\boldsymbol{e}_{i}$
is the discretized velocity. In the current simulation, the D3Q19 velocity model is used (Mackay, Ollila & Denniston Reference Mackay, Ollila and Denniston2013), and the fluid particles have the possible discrete velocities stated in Mackay et al. (Reference Mackay, Ollila and Denniston2013). In (2.3)
![]() $\unicode[STIX]{x1D70F}$
denotes the non-dimensional relaxation time, which is related to the dynamic viscosity in the NS equation as follows:
$\unicode[STIX]{x1D70F}$
denotes the non-dimensional relaxation time, which is related to the dynamic viscosity in the NS equation as follows:
Also in (2.3)
![]() $f_{i}^{eq}(\boldsymbol{x},t)$
is the equilibrium distribution function and
$f_{i}^{eq}(\boldsymbol{x},t)$
is the equilibrium distribution function and
![]() $F_{i}$
is the discretized scheme of the external force. In the current simulation, the equilibrium distribution function adopts the form
$F_{i}$
is the discretized scheme of the external force. In the current simulation, the equilibrium distribution function adopts the form
where the weighting coefficients are
![]() $\unicode[STIX]{x1D714}_{0}=1/3$
,
$\unicode[STIX]{x1D714}_{0}=1/3$
,
![]() $\unicode[STIX]{x1D714}_{i}=1/18~(i=1{-}6)$
and
$\unicode[STIX]{x1D714}_{i}=1/18~(i=1{-}6)$
and
![]() $\unicode[STIX]{x1D714}_{i}=1/36~(i=7{-}18)$
. The term
$\unicode[STIX]{x1D714}_{i}=1/36~(i=7{-}18)$
. The term
![]() $c_{s}$
represents the sound speed, which equals
$c_{s}$
represents the sound speed, which equals
![]() $\unicode[STIX]{x0394}x/(\sqrt{3}\unicode[STIX]{x0394}t)$
. The external forcing term can be discretized by the form (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002):
$\unicode[STIX]{x0394}x/(\sqrt{3}\unicode[STIX]{x0394}t)$
. The external forcing term can be discretized by the form (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002):
Equation (2.3) is advanced through the algorithm proposed by Ollila et al. (Reference Ollila, Denniston, Karttunen and Ala-Nissila2011). Here, the solver of the LBM is embedded in a large-scale atomic/molecular massively parallel simulator (LAMMPS) (Plimpton Reference Plimpton1995), which is implemented by Mackay et al. (Reference Mackay, Ollila and Denniston2013). After the particle density distributions are known in the whole fluid domain, the properties of the fluid, such as fluid density and velocity, can be calculated as
2.2.2 Coarse-grained models for RBC and MP
To capture the dynamics and deformation of RBCs and elastic MPs, we develop a coarse-grained model and implement it into LAMMPS (Ye, Shen & Li Reference Ye, Shen and Li2018b
). The RBC is modelled as a liquid-filled coarse-grained membrane, and its equilibrium shape is biconcave. The diameter of an RBC is
![]() $7.8~\unicode[STIX]{x03BC}\text{m}$
, and the thickness is approximately
$7.8~\unicode[STIX]{x03BC}\text{m}$
, and the thickness is approximately
![]() $2.1~\unicode[STIX]{x03BC}\text{m}$
. The surface area and volume of an RBC are
$2.1~\unicode[STIX]{x03BC}\text{m}$
. The surface area and volume of an RBC are
![]() $134.1~\unicode[STIX]{x03BC}\text{m}^{2}$
and
$134.1~\unicode[STIX]{x03BC}\text{m}^{2}$
and
![]() $94.1~\unicode[STIX]{x03BC}\text{m}^{3}$
, respectively (Evans & Skalak Reference Evans and Skalak1980). In the simulation, the membrane is discretized into 3286 vertices and 6568 triangular elements.
$94.1~\unicode[STIX]{x03BC}\text{m}^{3}$
, respectively (Evans & Skalak Reference Evans and Skalak1980). In the simulation, the membrane is discretized into 3286 vertices and 6568 triangular elements.
To capture the in-plane shear property of an RBC, a stretching potential
![]() $U_{stretching}$
is used. It includes two parts, namely an attractive nonlinear spring potential (wormlike chain model, WLC) and a repulsive power potential (power function, POW) (Fedosov, Caswell & Karniadakis Reference Fedosov, Caswell and Karniadakis2010a
; Fedosov et al.
Reference Fedosov, Pan, Caswell, Gompper and Karniadakis2011b
). They can be expressed as
$U_{stretching}$
is used. It includes two parts, namely an attractive nonlinear spring potential (wormlike chain model, WLC) and a repulsive power potential (power function, POW) (Fedosov, Caswell & Karniadakis Reference Fedosov, Caswell and Karniadakis2010a
; Fedosov et al.
Reference Fedosov, Pan, Caswell, Gompper and Karniadakis2011b
). They can be expressed as
where
![]() $k_{B}T$
is the basic energy unit,
$k_{B}T$
is the basic energy unit,
![]() $x=l/l_{m}\in (0,1)$
,
$x=l/l_{m}\in (0,1)$
,
![]() $l$
is the length of the spring,
$l$
is the length of the spring,
![]() $l_{m}$
is the maximum spring extension,
$l_{m}$
is the maximum spring extension,
![]() $p$
is the persistence length, and
$p$
is the persistence length, and
![]() $k_{p}$
is the POW force coefficient. Applying the bending potential
$k_{p}$
is the POW force coefficient. Applying the bending potential
the out-of-plane bending property of an RBC is reflected. Here
![]() $k_{b}$
is the bending stiffness,
$k_{b}$
is the bending stiffness,
![]() $\unicode[STIX]{x1D703}_{k}$
is the dihedral angle between two adjacent triangular elements, and
$\unicode[STIX]{x1D703}_{k}$
is the dihedral angle between two adjacent triangular elements, and
![]() $\unicode[STIX]{x1D703}_{0}$
is the initial value of the dihedral angle. In the following, subscript
$\unicode[STIX]{x1D703}_{0}$
is the initial value of the dihedral angle. In the following, subscript
![]() $0$
represents the corresponding initial value; and
$0$
represents the corresponding initial value; and
![]() $N_{s}$
denotes the total number of dihedral angles.
$N_{s}$
denotes the total number of dihedral angles.
Besides the above, the bulk properties, such as surface area and volume conservation, are ensured by introducing the penalty forms:
and
where the first term in (2.10) represents the local area constraint,
![]() $A_{k}$
and
$A_{k}$
and
![]() $A_{k0}$
denote the area of the
$A_{k0}$
denote the area of the
![]() $k$
th element and its initial area, respectively, and
$k$
th element and its initial area, respectively, and
![]() $k_{d}$
is the corresponding spring constant. The second term in (2.10) is the global area constraint,
$k_{d}$
is the corresponding spring constant. The second term in (2.10) is the global area constraint,
![]() $A_{t}$
is the total area, and
$A_{t}$
is the total area, and
![]() $k_{a}$
is the spring constant. In (2.11),
$k_{a}$
is the spring constant. In (2.11),
![]() $k_{v}$
is the spring constant and
$k_{v}$
is the spring constant and
![]() $V$
is the total volume.
$V$
is the total volume.
Then the total energy
![]() $U$
is
$U$
is
The nodal forces exerted on each vertex of the RBC membrane are derived from
where
![]() $X_{i}$
denotes the vertex of the RBC membrane. Thus, if we know the positions of the membrane vertices, we can calculate the nodal force according to (2.13). The detailed derivation of the force formulae, such as two-point stretching force and three-point bending force, are presented in Ye et al. (Reference Ye, Shen and Li2018b
).
$X_{i}$
denotes the vertex of the RBC membrane. Thus, if we know the positions of the membrane vertices, we can calculate the nodal force according to (2.13). The detailed derivation of the force formulae, such as two-point stretching force and three-point bending force, are presented in Ye et al. (Reference Ye, Shen and Li2018b
).
The elastic MPs adopt the same model as RBCs, but with 828 vertices and changeable in-plane shear strength. Before we choose the parameters for the coarse-grained model of RBCs and elastic MPs, we should know the corresponding macroscopic properties through experiments a priori. According to the relationships between coarse-grained model parameters and macroscopic properties (Allen & Tildesley Reference Allen and Tildesley1989; Dao, Li & Suresh Reference Dao, Li and Suresh2006; Fedosov et al. Reference Fedosov, Caswell and Karniadakis2010a ) we have
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D707}_{0}={\displaystyle \frac{\sqrt{3}k_{B}T}{4pl_{m}x_{0}}}\left({\displaystyle \frac{x_{0}}{2(1-x_{0})^{3}}}-{\displaystyle \frac{1}{4(1-x_{0})^{2}}}+{\displaystyle \frac{1}{4}}\right)+{\displaystyle \frac{3\sqrt{3}k_{p}}{4l_{0}^{3}}},\\ K=2\unicode[STIX]{x1D707}_{0}+k_{a}+k_{d},\\ Y={\displaystyle \frac{4K\unicode[STIX]{x1D707}_{0}}{K+\unicode[STIX]{x1D707}_{0}}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D707}_{0}={\displaystyle \frac{\sqrt{3}k_{B}T}{4pl_{m}x_{0}}}\left({\displaystyle \frac{x_{0}}{2(1-x_{0})^{3}}}-{\displaystyle \frac{1}{4(1-x_{0})^{2}}}+{\displaystyle \frac{1}{4}}\right)+{\displaystyle \frac{3\sqrt{3}k_{p}}{4l_{0}^{3}}},\\ K=2\unicode[STIX]{x1D707}_{0}+k_{a}+k_{d},\\ Y={\displaystyle \frac{4K\unicode[STIX]{x1D707}_{0}}{K+\unicode[STIX]{x1D707}_{0}}},\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{0}$
is the shear modulus,
$\unicode[STIX]{x1D707}_{0}$
is the shear modulus,
![]() $K$
represents the area compression modulus and
$K$
represents the area compression modulus and
![]() $Y$
denotes the Young’s modulus. Therefore, the potential parameters can be chosen on the basis of the physical quantities. The parameters used in the simulation are listed in table 2.
$Y$
denotes the Young’s modulus. Therefore, the potential parameters can be chosen on the basis of the physical quantities. The parameters used in the simulation are listed in table 2.
The accuracy of this model for RBCs and elastic MPs has been validated in our previous works (Ye et al. Reference Ye, Shen, Yu, Wei and Li2017a ; Ye, Shen & Li Reference Ye, Shen and Li2018a ; Ye et al. Reference Ye, Shen and Li2018b ). In § 3, we will show two more validations to confirm the convergence of both the fluid and membrane meshes and modelling of the rheology of blood flow. Details about the computational efficiency and cost are discussed in § 5 and Ye et al. (Reference Ye, Shen and Li2018b ). In addition to the above potentials, it is necessary to employ intermolecular interactions between RBCs to characterize their interactions. Here we use the Morse potential as intermolecular interaction (Liu & Liu Reference Liu and Liu2006; Fedosov et al. Reference Fedosov, Pan, Caswell, Gompper and Karniadakis2011b ; Tan, Thomas & Liu Reference Tan, Thomas and Liu2012), in the form
where
![]() $D_{0}$
represents the depth of the potential energy well and
$D_{0}$
represents the depth of the potential energy well and
![]() $\unicode[STIX]{x1D6FD}$
controls its width,
$\unicode[STIX]{x1D6FD}$
controls its width,
![]() $r$
is the distance between the two particles,
$r$
is the distance between the two particles,
![]() $r_{0}$
is the equilibrium distance, and
$r_{0}$
is the equilibrium distance, and
![]() $r_{c}$
is the cutoff distance. Additionally, a short-range and purely repulsive Lennard-Jones potential is applied to prevent overlap between RBCs and MPs (Ye et al.
Reference Ye, Shen and Li2018b
).
$r_{c}$
is the cutoff distance. Additionally, a short-range and purely repulsive Lennard-Jones potential is applied to prevent overlap between RBCs and MPs (Ye et al.
Reference Ye, Shen and Li2018b
).
Table 2. Coarse-grained potential parameters for RBCs and elastic MPs, and their corresponding physical values.

2.2.3 Immersed boundary method for fluid–structure interaction
The IBM is used to couple the LBM with LAMMPS to account for fluid–structure interaction (Peskin Reference Peskin2002; Krüger, Varnik & Raabe Reference Krüger, Varnik and Raabe2011; Krüger, Kaoui & Harting Reference Krüger, Kaoui and Harting2014; Ye et al.
Reference Ye, Wei, Huang and Lu2017b
). We use the Lagrangian (
![]() $X$
) and Eulerian (
$X$
) and Eulerian (
![]() $x$
) mesh points in the computational domain to represent RBCs (or MPs) and fluid particles, respectively. The Eulerian fluid mesh is uniform and the resolution is
$x$
) mesh points in the computational domain to represent RBCs (or MPs) and fluid particles, respectively. The Eulerian fluid mesh is uniform and the resolution is
![]() $\unicode[STIX]{x0394}x=250~\text{nm}$
in all directions. The Lagrangian mesh for RBCs or MPs is generated by MATLAB code (Persson & Strang Reference Persson and Strang2004; Persson Reference Persson2005). The mesh is approximately uniform and the mesh size is set at approximately
$\unicode[STIX]{x0394}x=250~\text{nm}$
in all directions. The Lagrangian mesh for RBCs or MPs is generated by MATLAB code (Persson & Strang Reference Persson and Strang2004; Persson Reference Persson2005). The mesh is approximately uniform and the mesh size is set at approximately
![]() $\unicode[STIX]{x0394}X=(0.6{-}0.8)\unicode[STIX]{x0394}x$
. Then there are approximately 32 Eulerian points across one RBC in diametral direction. That is sufficient to resolve the deformation and motion of an RBC (MacMeccan et al.
Reference MacMeccan, Clausen, Neitzel and Aidun2009; Vahidkhah & Bagchi Reference Vahidkhah and Bagchi2015). The coupling is fulfilled by the interpolation of velocity and force distributions between Lagrangian and Eulerian mesh points (Mittal & Iaccarino Reference Mittal and Iaccarino2005).
$\unicode[STIX]{x0394}X=(0.6{-}0.8)\unicode[STIX]{x0394}x$
. Then there are approximately 32 Eulerian points across one RBC in diametral direction. That is sufficient to resolve the deformation and motion of an RBC (MacMeccan et al.
Reference MacMeccan, Clausen, Neitzel and Aidun2009; Vahidkhah & Bagchi Reference Vahidkhah and Bagchi2015). The coupling is fulfilled by the interpolation of velocity and force distributions between Lagrangian and Eulerian mesh points (Mittal & Iaccarino Reference Mittal and Iaccarino2005).
To ensure a no-slip boundary condition, the membrane vertex
![]() $X$
with Lagrangian coordinate
$X$
with Lagrangian coordinate
![]() $s$
should move at the same velocity as the fluid around it, that is
$s$
should move at the same velocity as the fluid around it, that is
The velocity can be interpolated by the fluid velocity through a smoothed Dirac delta function
![]() $\unicode[STIX]{x1D6FF}$
:
$\unicode[STIX]{x1D6FF}$
:
This condition will cause the membrane to move and deform. The membrane force density
![]() $F(s,t)$
is obtained by derivation of potential functions such as (2.13), and is distributed to the surrounding fluid mesh points by
$F(s,t)$
is obtained by derivation of potential functions such as (2.13), and is distributed to the surrounding fluid mesh points by
2.2.4 Adhesive model for ligand–receptor binding
The ligand–receptor binding is described by the association and dissociation of biological bonds, and it is governed by the probabilistic adhesion model (Hammer & Lauffenburger Reference Hammer and Lauffenburger1987). Figure 1(a) gives a schematic of the adhesive model. When the ligands on the MP approach the receptors on the vessel wall, they have the chance to bind together, which is determined by the probability
![]() $P_{on}$
. In the reverse situation, the existing bond has a probability
$P_{on}$
. In the reverse situation, the existing bond has a probability
![]() $P_{off}$
to break. They can be expressed as
$P_{off}$
to break. They can be expressed as
Here
![]() $\unicode[STIX]{x0394}t$
is the time step in the simulation,
$\unicode[STIX]{x0394}t$
is the time step in the simulation,
![]() $d_{on}$
and
$d_{on}$
and
![]() $d_{off}$
are the cutoffs for bond creation and breakup, respectively, and
$d_{off}$
are the cutoffs for bond creation and breakup, respectively, and
![]() $k_{on}$
and
$k_{on}$
and
![]() $k_{off}$
are the association and dissociation rates with the forms
$k_{off}$
are the association and dissociation rates with the forms
where
![]() $\unicode[STIX]{x1D70E}_{on}$
and
$\unicode[STIX]{x1D70E}_{on}$
and
![]() $\unicode[STIX]{x1D70E}_{off}$
are the effective on and off strengths, representing a decrease and increase of the corresponding rates within
$\unicode[STIX]{x1D70E}_{off}$
are the effective on and off strengths, representing a decrease and increase of the corresponding rates within
![]() $d_{on}$
and
$d_{on}$
and
![]() $d_{off}$
, respectively, and
$d_{off}$
, respectively, and
![]() $k_{on}^{0}$
and
$k_{on}^{0}$
and
![]() $k_{off}^{0}$
are the reaction rates at the equilibrium length
$k_{off}^{0}$
are the reaction rates at the equilibrium length
![]() $l=l_{0}$
between ligand and receptor. The mechanical properties of the biological bond are described by a harmonic spring. The equilibrium length is
$l=l_{0}$
between ligand and receptor. The mechanical properties of the biological bond are described by a harmonic spring. The equilibrium length is
![]() $l_{0}$
, and the force exerted on the receptor and ligand is
$l_{0}$
, and the force exerted on the receptor and ligand is
![]() $F_{b}=k_{s}(l-l_{0})$
. Here,
$F_{b}=k_{s}(l-l_{0})$
. Here,
![]() $k_{s}$
represents the adhesive strength. This model and the relevant parameters (cf. table 1) are chosen according to the previous works of Fedosov (Reference Fedosov2010) and Fedosov, Caswell & Karniadakis (Reference Fedosov, Caswell and Karniadakis2011a
).
$k_{s}$
represents the adhesive strength. This model and the relevant parameters (cf. table 1) are chosen according to the previous works of Fedosov (Reference Fedosov2010) and Fedosov, Caswell & Karniadakis (Reference Fedosov, Caswell and Karniadakis2011a
).
There are three dimensionless parameters:
Considering the physiological environment surrounding the cell, the fluid flow is considered as a Stokes flow. Thus,
![]() $Re$
is very small, and we fix its value as
$Re$
is very small, and we fix its value as
![]() $Re=0.0134$
to approximately represent the Stokes regime. The capillary number represents the ratio of the shear stress exerted on the surface of an elastic MP to the elastic force induced by the deformation of the elastic MP; and
$Re=0.0134$
to approximately represent the Stokes regime. The capillary number represents the ratio of the shear stress exerted on the surface of an elastic MP to the elastic force induced by the deformation of the elastic MP; and
![]() $\unicode[STIX]{x1D707}_{0}$
is the shear modulus of the MP. The higher the
$\unicode[STIX]{x1D707}_{0}$
is the shear modulus of the MP. The higher the
![]() $Ca$
, the softer the particle. The adhesion number denotes the ratio of adhesive strength to shear stress of the flow. Thus, the higher the
$Ca$
, the softer the particle. The adhesion number denotes the ratio of adhesive strength to shear stress of the flow. Thus, the higher the
![]() $Ad$
, the stronger the adhesion strength. In our simulations,
$Ad$
, the stronger the adhesion strength. In our simulations,
![]() $Ca$
is tuned by varying the shear modulus
$Ca$
is tuned by varying the shear modulus
![]() $\unicode[STIX]{x1D707}_{0}$
, and
$\unicode[STIX]{x1D707}_{0}$
, and
![]() $Ad$
is varied by changing the adhesive strength
$Ad$
is varied by changing the adhesive strength
![]() $k_{s}$
.
$k_{s}$
.
3 Validation of numerical method
Grid independence studies of the fluid and RBC membrane are conducted. We perform a case study in which a single RBC with diameter
![]() $D_{r}$
moves in simple shear flow
$D_{r}$
moves in simple shear flow
![]() $v(z)=\dot{\unicode[STIX]{x1D6FE}}z$
, as shown in figure 2(a). Here the RBC is discretized with different numbers of vertices as presented in figure 2(b). To exclude the size effect of the channel, we adopt the same channel and same shear rate as the margination studies of MPs. First, we vary the mesh size
$v(z)=\dot{\unicode[STIX]{x1D6FE}}z$
, as shown in figure 2(a). Here the RBC is discretized with different numbers of vertices as presented in figure 2(b). To exclude the size effect of the channel, we adopt the same channel and same shear rate as the margination studies of MPs. First, we vary the mesh size
![]() $\unicode[STIX]{x0394}x$
of the fluid, and track the trajectories of the centre of the RBC in the height direction (
$\unicode[STIX]{x0394}x$
of the fluid, and track the trajectories of the centre of the RBC in the height direction (
![]() $z$
direction). Figure 2(c) shows that, when the mesh is coarse (
$z$
direction). Figure 2(c) shows that, when the mesh is coarse (
![]() $\unicode[STIX]{x0394}x=1/8D_{r}$
), the trajectory is obviously different from those with fine meshes, and it is not smooth compared to those with fine meshes. Further increase of mesh resolution (
$\unicode[STIX]{x0394}x=1/8D_{r}$
), the trajectory is obviously different from those with fine meshes, and it is not smooth compared to those with fine meshes. Further increase of mesh resolution (
![]() $\unicode[STIX]{x0394}x=1/16D_{r}$
) leads to a more consistent trajectory, and only a small difference of trajectory exists between it and with the finer mesh. When the mesh resolution increases to
$\unicode[STIX]{x0394}x=1/16D_{r}$
) leads to a more consistent trajectory, and only a small difference of trajectory exists between it and with the finer mesh. When the mesh resolution increases to
![]() $\unicode[STIX]{x0394}x=1/32D_{r}$
, the difference between it and with the finer mesh can be negligible. Thus, the current study adopts the mesh size
$\unicode[STIX]{x0394}x=1/32D_{r}$
, the difference between it and with the finer mesh can be negligible. Thus, the current study adopts the mesh size
![]() $\unicode[STIX]{x0394}x=1/32D_{r}$
. Furthermore, we change the number of discretized vertices of the RBC membrane. Four cases
$\unicode[STIX]{x0394}x=1/32D_{r}$
. Furthermore, we change the number of discretized vertices of the RBC membrane. Four cases
![]() $V=766$
, 1418, 3286 and 9864 are investigated here;
$V=766$
, 1418, 3286 and 9864 are investigated here;
![]() $V$
and
$V$
and
![]() $T$
represent the numbers of vertices and triangular elements of the RBC membrane, respectively. Again, we track the trajectories of the centre of the RBC in the height direction. We find that the discretization of the membrane has a weak influence on the motion of an RBC under the current scheme (
$T$
represent the numbers of vertices and triangular elements of the RBC membrane, respectively. Again, we track the trajectories of the centre of the RBC in the height direction. We find that the discretization of the membrane has a weak influence on the motion of an RBC under the current scheme (
![]() $766<V<9864$
). There is only a small difference for the case of
$766<V<9864$
). There is only a small difference for the case of
![]() $V=766$
, compared to other cases. To ensure enough convergence of the membrane mesh, we adopt a relatively fine mesh
$V=766$
, compared to other cases. To ensure enough convergence of the membrane mesh, we adopt a relatively fine mesh
![]() $V=3286$
. In the following simulations, the fluid mesh size is
$V=3286$
. In the following simulations, the fluid mesh size is
![]() $\unicode[STIX]{x0394}x=1/32D_{r}$
and the discretization of the RBC membrane is
$\unicode[STIX]{x0394}x=1/32D_{r}$
and the discretization of the RBC membrane is
![]() $V=3286$
.
$V=3286$
.

Figure 2. Grid independence studies. (a) Model of motion of a single RBC in simple shear flow. (b) Discretization of an RBC membrane with different numbers of vertices. (c) Grid independence of fluid mesh. (d) Grid independence of RBC discretization.

Figure 3. Fåhraeus and Fåhraeus–Lindqvist effects. (a) Snapshots to show the tube flow with different diameters under haematocrit 15 %. (b) Fåhraeus effect: discharge haematocrit comparison. (c) Fåhraeus–Lindqvist effect: relative viscosity validation.
Here, we study the Fåhraeus effect and the Fåhraeus–Lindqvist effect of blood flow with different haematocrits (15 % and 30 %) in a tube with different diameters (
![]() $10$
,
$10$
,
![]() $20$
and
$20$
and
![]() $40~\unicode[STIX]{x03BC}\text{m}$
) to validate our numerical method in terms of rheology of blood flow. The length of the tube is fixed as three times the diameter.
$40~\unicode[STIX]{x03BC}\text{m}$
) to validate our numerical method in terms of rheology of blood flow. The length of the tube is fixed as three times the diameter.
The Fåhraeus effect presented an increased value of discharge haematocrit (
![]() $H_{d}$
) measured at the tube exit in comparison with that before the tube entrance. It was first discovered in in vitro experiments of blood flow in a tube (Fåhraeus Reference Fåhraeus1929). In our simulation, we take the same definition as that in Fedosov et al. (Reference Fedosov, Caswell, Popel and Karniadakis2010b
) to calculate the discharge haematocrit:
$H_{d}$
) measured at the tube exit in comparison with that before the tube entrance. It was first discovered in in vitro experiments of blood flow in a tube (Fåhraeus Reference Fåhraeus1929). In our simulation, we take the same definition as that in Fedosov et al. (Reference Fedosov, Caswell, Popel and Karniadakis2010b
) to calculate the discharge haematocrit:
where
![]() $\bar{v}=Q/A$
is the mean velocity of the blood flow, and
$\bar{v}=Q/A$
is the mean velocity of the blood flow, and
![]() $\bar{v}_{c}$
is the average cell velocity averaged in time in the steady-state regime.
$\bar{v}_{c}$
is the average cell velocity averaged in time in the steady-state regime.
The Fåhraeus–Lindqvist effect stated that apparent blood viscosity decreased with decrease of tube diameter found in experiments (Fåhraeus & Lindqvist Reference Fåhraeus and Lindqvist1931; Pries, Neuhaus & Gaehtgens Reference Pries, Neuhaus and Gaehtgens1992; Pries et al. Reference Pries, Secomb, Gessner, Sperandio, Gross and Gaehtgens1994). It is usually convenient to calculate the relative apparent viscosity to investigate this effect, which is defined as
where the apparent viscosity
![]() $\unicode[STIX]{x1D702}_{apparent}=\unicode[STIX]{x0394}PD_{tube}^{2}/32\bar{v}L$
, with
$\unicode[STIX]{x1D702}_{apparent}=\unicode[STIX]{x0394}PD_{tube}^{2}/32\bar{v}L$
, with
![]() $\unicode[STIX]{x0394}P$
and
$\unicode[STIX]{x0394}P$
and
![]() $L$
the pressure difference between inlet and outlet of the tube and the length of the tube, respectively.
$L$
the pressure difference between inlet and outlet of the tube and the length of the tube, respectively.
In figure 3(a), we show snapshots of blood flow in a tube with different diameters under haematocrit 15 %. We calculate the discharge haematocrit and relative viscosity of the blood flow, and compare our results with those in experiment (Pries et al. Reference Pries, Neuhaus and Gaehtgens1992) and numerical (Fedosov et al. Reference Fedosov, Caswell, Popel and Karniadakis2010b ; Czaja et al. Reference Czaja, Závodszky, Tarksalooyeh and Hoekstra2018) studies in figure 3(b,c). As for the relative viscosity of the blood flow, we also provide the empirical viscosity from experiment (Pries et al. Reference Pries, Secomb, Gessner, Sperandio, Gross and Gaehtgens1994). We find that our results are more consistent with an empirical value under low haematocrit 15 % compared with that under haematocrit 30 %. What is more, the results are more consistent with the numerical results than with the empirical results. The discrepancies between numerical simulations and experiments may be induced by the interaction between an RBC and the tube wall, and the estimation method in experiments (Fedosov et al. Reference Fedosov, Caswell, Popel and Karniadakis2010b ). However, the current study has adequate accuracy to model the blood flow from the above comparison.
4 Results and discussion
We study the margination behaviours of elastic MPs (i) without (
![]() $Ad=0$
) and (ii) with (
$Ad=0$
) and (ii) with (
![]() $Ad=0.07{-}32.8$
) adhesion. The stiffness of the elastic MPs is varied by changing the shear modulus
$Ad=0.07{-}32.8$
) adhesion. The stiffness of the elastic MPs is varied by changing the shear modulus
![]() $\unicode[STIX]{x1D707}_{0}$
, which makes
$\unicode[STIX]{x1D707}_{0}$
, which makes
![]() $Ca$
range from 0.00037 to 3.7. This corresponds to the shear modulus of an MP from
$Ca$
range from 0.00037 to 3.7. This corresponds to the shear modulus of an MP from
![]() $6.3\times 10^{-4}$
to
$6.3\times 10^{-4}$
to
![]() $6.3\times 10^{-8}~\text{N}~\text{m}^{-1}$
(note that the shear modulus of an RBC is
$6.3\times 10^{-8}~\text{N}~\text{m}^{-1}$
(note that the shear modulus of an RBC is
![]() $6.3\times 10^{-6}~\text{N}~\text{m}^{-1}$
). The elastic MPs are randomly placed among RBCs in the whole channel at the beginning of all simulations. For MPs with different shear moduli, they have the same initial configurations. This eliminates the influence of the initial condition on the margination results.
$6.3\times 10^{-6}~\text{N}~\text{m}^{-1}$
). The elastic MPs are randomly placed among RBCs in the whole channel at the beginning of all simulations. For MPs with different shear moduli, they have the same initial configurations. This eliminates the influence of the initial condition on the margination results.

Figure 4. Snapshots to show the margination behaviour of an elastic MP (
![]() $Ca=0.0037$
) without effect of adhesion.
$Ca=0.0037$
) without effect of adhesion.
4.1 Margination of elastic MPs without adhesion
The margination of MPs without adhesion is first investigated. The margination process of a typical case of MPs with
![]() $Ca=0.0037$
is shown in figure 4. In these snapshots, at
$Ca=0.0037$
is shown in figure 4. In these snapshots, at
![]() $t=0~\text{s}$
, we can see that MPs are randomly distributed as well as RBCs. The RBCs and MPs are considered at their equilibrium states. The shapes of RBCs and MPs are biconcave and spherical, respectively. At time
$t=0~\text{s}$
, we can see that MPs are randomly distributed as well as RBCs. The RBCs and MPs are considered at their equilibrium states. The shapes of RBCs and MPs are biconcave and spherical, respectively. At time
![]() $t=1.0~\text{s}$
, the fluid flow is developed. A large deformation has been observed for RBCs. Under the shear flow, we find that RBCs align their major axes along the flow direction. Though the deformation of MPs is small due to their high stiffness (small
$t=1.0~\text{s}$
, the fluid flow is developed. A large deformation has been observed for RBCs. Under the shear flow, we find that RBCs align their major axes along the flow direction. Though the deformation of MPs is small due to their high stiffness (small
![]() $Ca=0.0037$
), they should deform under the shear stress; and the deformation will be significant for the case with high
$Ca=0.0037$
), they should deform under the shear stress; and the deformation will be significant for the case with high
![]() $Ca$
. In addition to the deformation, RBCs and MPs both demonstrate cross-stream migration, but towards the opposite directions. RBCs migrate from the near-wall region to the centre of the channel, while MPs move towards the wall. We also find that the CFL becomes clear and that some MPs reach the CFL quickly. As simulation time further advances, at
$Ca$
. In addition to the deformation, RBCs and MPs both demonstrate cross-stream migration, but towards the opposite directions. RBCs migrate from the near-wall region to the centre of the channel, while MPs move towards the wall. We also find that the CFL becomes clear and that some MPs reach the CFL quickly. As simulation time further advances, at
![]() $t=2.0~\text{s}$
, the CFL is fully developed and MPs start to accumulate at the CFL.
$t=2.0~\text{s}$
, the CFL is fully developed and MPs start to accumulate at the CFL.
Localization of MPs at the wall is characterized by margination probability
![]() $\unicode[STIX]{x1D6F7}(t)$
, which is defined as
$\unicode[STIX]{x1D6F7}(t)$
, which is defined as
where
![]() $n_{f}(t)$
represents the number of MPs with centres locating in the CFL at time
$n_{f}(t)$
represents the number of MPs with centres locating in the CFL at time
![]() $t$
, and
$t$
, and
![]() $N$
denotes the total number of MPs in the channel. Before quantifying the margination probability, the thickness of the CFL is estimated in the absence of MPs. We use the same method as proposed by Fedosov et al. (Reference Fedosov, Caswell, Popel and Karniadakis2010b
); the thickness of the CFL is approximately
$N$
denotes the total number of MPs in the channel. Before quantifying the margination probability, the thickness of the CFL is estimated in the absence of MPs. We use the same method as proposed by Fedosov et al. (Reference Fedosov, Caswell, Popel and Karniadakis2010b
); the thickness of the CFL is approximately
![]() $2.8~\unicode[STIX]{x03BC}\text{m}$
for current blood flow with
$2.8~\unicode[STIX]{x03BC}\text{m}$
for current blood flow with
![]() $Ht=30\,\%$
. This is consistent with previous numerical studies (Lee et al.
Reference Lee, Choi, Kopacz, Yun, Liu and Decuzzi2013; Müller et al.
Reference Müller, Fedosov and Gompper2014). Figure 5(a) gives the evolution of margination probabilities
$Ht=30\,\%$
. This is consistent with previous numerical studies (Lee et al.
Reference Lee, Choi, Kopacz, Yun, Liu and Decuzzi2013; Müller et al.
Reference Müller, Fedosov and Gompper2014). Figure 5(a) gives the evolution of margination probabilities
![]() $\unicode[STIX]{x1D6F7}$
for three different stiffnesses (
$\unicode[STIX]{x1D6F7}$
for three different stiffnesses (
![]() $Ca=0.00037$
, 0.037 and 3.7). We find that the margination process can be split into two stages. In the first stage, the margination probability increases very fast, which signifies that there are more and more particles moving from the centre to the CFL. We note that, in this stage, the margination probabilities of softer particles increase faster (
$Ca=0.00037$
, 0.037 and 3.7). We find that the margination process can be split into two stages. In the first stage, the margination probability increases very fast, which signifies that there are more and more particles moving from the centre to the CFL. We note that, in this stage, the margination probabilities of softer particles increase faster (
![]() $Ca=0.037$
and 3.7) than that of stiff particles (
$Ca=0.037$
and 3.7) than that of stiff particles (
![]() $Ca=0.00037$
). However, the duration of this stage for stiff particles is longer than those of soft particles. Therefore, when the first stage ends, the margination probability of stiff particles is higher than those of soft ones. In the second stage, the margination probabilities of both stiff and soft particles increase slower than those in the first stage. Also, the growth rates for these particles are almost the same.
$Ca=0.00037$
). However, the duration of this stage for stiff particles is longer than those of soft particles. Therefore, when the first stage ends, the margination probability of stiff particles is higher than those of soft ones. In the second stage, the margination probabilities of both stiff and soft particles increase slower than those in the first stage. Also, the growth rates for these particles are almost the same.

Figure 5. Margination behaviour of elastic MPs with different stiffnesses. (a) Evolution of margination probabilities for elastic MPs. (b) Mean-square displacement of elastic MPs during margination. (c) Probabilities of two types of motion: centre to cell-free layer (C–F) and cell-free layer to centre (F–C). (d) Time-averaged margination probability in the steady-state regime.
To investigate this stiffness dependence of margination behaviour, the mean-square displacements (MSDs) for MPs with different stiffnesses are calculated. The deformation of RBCs in the blood flow induces the fluctuation of flow around them. This is considered as the root cause of migration of rigid particles such as platelets in blood flow (Zhao, Shaqfeh & Narsimhan Reference Zhao, Shaqfeh and Narsimhan2012). From figure 5(b), we find that there are no obvious differences among MSDs for all of the MPs. At the initial stage (
![]() $t<1.0~\text{s}$
), the MSDs are almost the same. After that, the MSDs for MPs become different, but with only small variations. We calculated the diffusivities, defined as
$t<1.0~\text{s}$
), the MSDs are almost the same. After that, the MSDs for MPs become different, but with only small variations. We calculated the diffusivities, defined as
![]() $D=\langle \unicode[STIX]{x0394}z^{2}\rangle /2t$
, and they range from approximately 0.9 to
$D=\langle \unicode[STIX]{x0394}z^{2}\rangle /2t$
, and they range from approximately 0.9 to
![]() $1.2\times 10^{-7}~\text{cm}^{-2}~\text{s}^{-1}$
for these MPs. This is in good agreement with previous studies (Zhao & Shaqfeh Reference Zhao and Shaqfeh2011; Vahidkhah & Bagchi Reference Vahidkhah and Bagchi2015). The diffusivity is approximately two orders of magnitude higher than the Brownian diffusivity, which means that the existence of RBCs augments the diffusion of MPs. However, from these results, RBC augmentation of diffusion is stiffness-independent. Thus, diffusion alone cannot explain the observed stiffness dependence of margination behaviour.
$1.2\times 10^{-7}~\text{cm}^{-2}~\text{s}^{-1}$
for these MPs. This is in good agreement with previous studies (Zhao & Shaqfeh Reference Zhao and Shaqfeh2011; Vahidkhah & Bagchi Reference Vahidkhah and Bagchi2015). The diffusivity is approximately two orders of magnitude higher than the Brownian diffusivity, which means that the existence of RBCs augments the diffusion of MPs. However, from these results, RBC augmentation of diffusion is stiffness-independent. Thus, diffusion alone cannot explain the observed stiffness dependence of margination behaviour.
To gain a better insight into the margination behaviour, the types of motion of MPs in blood flow are studied. Compared to rigid particles in blood flow, elastic MPs may experience deformation-induced migration, which can drive them to move away from the vessel wall (Coupier et al.
Reference Coupier, Kaoui, Podgorski and Misbah2008; Kumar & Graham Reference Kumar and Graham2012b
). This is the essential mechanism for CFL formation in a blood vessel. Here the motion of elastic MPs can be classified into four types: (i) staying in the centre; (ii) staying in the CFL; (iii) moving from the centre to the CFL (C–F); and (iv) moving from the CFL to the centre (F–C). Obviously, the first two types cannot contribute to the localization of MPs at the wall. The margination probability is attributed to the difference between the last two types as shown in figure 5(c). We find that the probabilities of F–C motion for all of the elastic MPs are the same and the values are almost 0. This indicates that there are only a few particles migrating from the CFL to the centre region. We also observe that the C–F motion has the same tendency as the margination probability
![]() $\unicode[STIX]{x1D6F7}$
. All these results lead to the conclusion that localization of MPs at the wall in the current study is determined by the C–F motion. This is different from our previous study in Ye et al. (Reference Ye, Shen, Yu, Wei and Li2017a
), in which F–C motion at some time can dominate the margination behaviour of particles. The reason for this difference mainly lies in the size of the particle and the haematocrit of blood flow. If the size of the particle is large (
$\unicode[STIX]{x1D6F7}$
. All these results lead to the conclusion that localization of MPs at the wall in the current study is determined by the C–F motion. This is different from our previous study in Ye et al. (Reference Ye, Shen, Yu, Wei and Li2017a
), in which F–C motion at some time can dominate the margination behaviour of particles. The reason for this difference mainly lies in the size of the particle and the haematocrit of blood flow. If the size of the particle is large (
![]() $2~\unicode[STIX]{x03BC}\text{m}$
in diameter), and the haematocrit is high (30 %), there is no available space for the particle to stay in the centre of the channel, because, under shear flow, most parts of the centre region are occupied by RBCs. Hence, F–C motion is not significant in the present study.
$2~\unicode[STIX]{x03BC}\text{m}$
in diameter), and the haematocrit is high (30 %), there is no available space for the particle to stay in the centre of the channel, because, under shear flow, most parts of the centre region are occupied by RBCs. Hence, F–C motion is not significant in the present study.
To quantify the stiffness effect on margination probability, the mean margination probabilities
![]() $\langle \unicode[STIX]{x1D6F7}\rangle$
are calculated and are given in figure 5(d). The mean value takes the time-averaged value of margination probability, which is estimated in a time interval within the steady-state regime. We can see that the margination process of MPs reaches a steady state after approximately
$\langle \unicode[STIX]{x1D6F7}\rangle$
are calculated and are given in figure 5(d). The mean value takes the time-averaged value of margination probability, which is estimated in a time interval within the steady-state regime. We can see that the margination process of MPs reaches a steady state after approximately
![]() $t=2.5~\text{s}$
. The localization of MPs at the wall decreases dramatically when the particles are very stiff (small
$t=2.5~\text{s}$
. The localization of MPs at the wall decreases dramatically when the particles are very stiff (small
![]() $Ca$
). With further decrease of stiffness (increase of
$Ca$
). With further decrease of stiffness (increase of
![]() $Ca$
), there is no obvious change of the margination probability.
$Ca$
), there is no obvious change of the margination probability.
The underlying mechanism of this stiffness dependence of margination behaviour relies on the interplay of collision with RBCs and deformation-induced lateral migration of elastic MPs (Qi & Shaqfeh Reference Qi and Shaqfeh2017). At the beginning of the simulation, the RBCs near the wall of the channel sense the shear flow, and then deform under the shear stress. The existence of the wall makes RBCs move away from the wall, and then the CFL forms. According to the previous study (Katanov, Gompper & Fedosov Reference Katanov, Gompper and Fedosov2015), the time needed to fully form the CFL is approximately
![]() $0.8~\text{s}$
under the conditions (channel size and haematocrit) in the current study (Ye et al.
Reference Ye, Shen, Yu, Wei and Li2017a
). This signals that the first stage of margination probability corresponds to the development of the CFL (cf. figure 5
a). In this stage, a large number of RBCs move from the near-wall region to the centre of the channel. The migration of RBCs should induce a reverse flow moving from the centre to the CFL in the regions around RBCs, due to the mass conservation of the fluid. Hence, if the MPs are located in these reverse flow regions, they will move along with the flow from the centre to the CFL. This phenomenon looks like the exclusion effect that particles are excluded by RBCs from the near-wall region to the centre of the channel (Crowl & Fogelson Reference Crowl and Fogelson2011). Specifically, the exclusion effect appears more significant for soft particles than for stiff particles. Here soft MPs have stronger alignment with the flow due to deformation. This is the reason why, in the first stage, the soft MPs marginate faster than stiff ones. In the second stage, the CFL is fully formed and the flow is fully developed. The soft MPs in the near-wall region may experience deformation-induced migration due to the existence of the wall. This results in low accumulation of soft MPs in the CFL. However, when the stiffness of the MPs decreases to a critical value (approximately
$0.8~\text{s}$
under the conditions (channel size and haematocrit) in the current study (Ye et al.
Reference Ye, Shen, Yu, Wei and Li2017a
). This signals that the first stage of margination probability corresponds to the development of the CFL (cf. figure 5
a). In this stage, a large number of RBCs move from the near-wall region to the centre of the channel. The migration of RBCs should induce a reverse flow moving from the centre to the CFL in the regions around RBCs, due to the mass conservation of the fluid. Hence, if the MPs are located in these reverse flow regions, they will move along with the flow from the centre to the CFL. This phenomenon looks like the exclusion effect that particles are excluded by RBCs from the near-wall region to the centre of the channel (Crowl & Fogelson Reference Crowl and Fogelson2011). Specifically, the exclusion effect appears more significant for soft particles than for stiff particles. Here soft MPs have stronger alignment with the flow due to deformation. This is the reason why, in the first stage, the soft MPs marginate faster than stiff ones. In the second stage, the CFL is fully formed and the flow is fully developed. The soft MPs in the near-wall region may experience deformation-induced migration due to the existence of the wall. This results in low accumulation of soft MPs in the CFL. However, when the stiffness of the MPs decreases to a critical value (approximately
![]() $Ca=0.037$
), the deformation-induced migration dominates the motion of MPs. Therefore, under this circumstance, changing stiffness of MPs will not result in an obvious difference of the margination probability.
$Ca=0.037$
), the deformation-induced migration dominates the motion of MPs. Therefore, under this circumstance, changing stiffness of MPs will not result in an obvious difference of the margination probability.
4.2 Adhesion effect on localization of elastic MPs at wall

Figure 6. Snapshots for the margination behaviour of elastic MPs (
![]() $Ca=0.37$
) under the influence of adhesion: (a)
$Ca=0.37$
) under the influence of adhesion: (a)
![]() $Ad=0.07$
and (b)
$Ad=0.07$
and (b)
![]() $Ad=32.8$
.
$Ad=32.8$
.
In figure 5(a), it is obvious that the evolution of margination probability oscillates. In some time intervals, the oscillation amplitude can reach approximately 20 % of the margination probability. This indicates that many MPs are travelling between the centre of the channel and the CFL. Under this circumstance, MPs near the CFL have a chance to interact with the vessel wall through ligand–receptor binding. Since the diameter of an MP is
![]() $2.0~\unicode[STIX]{x03BC}\text{m}$
, when it moves near the CFL, part of its surface will be located inside the adhesion layer according to the thicknesses of the CFL (
$2.0~\unicode[STIX]{x03BC}\text{m}$
, when it moves near the CFL, part of its surface will be located inside the adhesion layer according to the thicknesses of the CFL (
![]() $2.8~\unicode[STIX]{x03BC}\text{m}$
) and adhesion layer (
$2.8~\unicode[STIX]{x03BC}\text{m}$
) and adhesion layer (
![]() $1.0~\unicode[STIX]{x03BC}\text{m}$
).
$1.0~\unicode[STIX]{x03BC}\text{m}$
).
To have a direct comparison, figure 6 presents the adhesion effect on the localization of elastic MPs. In figure 6(a,b), the stiffnesses of MPs are the same
![]() $Ca=0.37$
, while the adhesion strengths are different: (a)
$Ca=0.37$
, while the adhesion strengths are different: (a)
![]() $Ad=0.07$
and (b)
$Ad=0.07$
and (b)
![]() $Ad=32.8$
. We find that there are more MPs entering and staying inside the CFL when increasing the adhesion strength
$Ad=32.8$
. We find that there are more MPs entering and staying inside the CFL when increasing the adhesion strength
![]() $Ad$
. With small
$Ad$
. With small
![]() $Ad=0.07$
, when MPs move into the CFL, only a small contact area forms between the MP and the substrate. The ligand–receptor binding is not strong, and these MPs move freely near the substrate. However, with strong adhesion
$Ad=0.07$
, when MPs move into the CFL, only a small contact area forms between the MP and the substrate. The ligand–receptor binding is not strong, and these MPs move freely near the substrate. However, with strong adhesion
![]() $Ad=32.8$
, the MPs collapse on the substrate like a droplet on the ground. It should be emphasized that this collapse phenomenon only happens for soft MPs. If the MP is stiff or rigid, it cannot deform any more. They can only roll on the substrate (King & Hammer Reference King and Hammer2001; Decuzzi & Ferrari Reference Decuzzi and Ferrari2006; Coclite et al.
Reference Coclite, Mollica, Ranaldo, Pascazio, de Tullio and Decuzzi2017). However, elastic MPs can either roll or firmly adhere on the substrate, depending on the adhesion strength
$Ad=32.8$
, the MPs collapse on the substrate like a droplet on the ground. It should be emphasized that this collapse phenomenon only happens for soft MPs. If the MP is stiff or rigid, it cannot deform any more. They can only roll on the substrate (King & Hammer Reference King and Hammer2001; Decuzzi & Ferrari Reference Decuzzi and Ferrari2006; Coclite et al.
Reference Coclite, Mollica, Ranaldo, Pascazio, de Tullio and Decuzzi2017). However, elastic MPs can either roll or firmly adhere on the substrate, depending on the adhesion strength
![]() $Ad$
.
$Ad$
.

Figure 7. Margination probabilities of elastic MPs with adhesion effect. (a) Margination probability against adhesion strength with different MP stiffnesses. (b) Margination probability against MP stiffness with different adhesion strengths.
To differentiate the margination probability of MPs with and without adhesion, we use
![]() $\unicode[STIX]{x1D6F1}$
rather than
$\unicode[STIX]{x1D6F1}$
rather than
![]() $\unicode[STIX]{x1D6F7}$
to represent the margination probability with the adhesion effect. The interplay of stiffness and adhesion strength effects is isolated in figure 7. Figure 7(a) gives the relationship between the margination probability and the adhesion strength for MPs with different stiffnesses. We use
$\unicode[STIX]{x1D6F7}$
to represent the margination probability with the adhesion effect. The interplay of stiffness and adhesion strength effects is isolated in figure 7. Figure 7(a) gives the relationship between the margination probability and the adhesion strength for MPs with different stiffnesses. We use
![]() $\langle \,\cdot \,\rangle$
to denote the mean value over a time interval, and subscript
$\langle \,\cdot \,\rangle$
to denote the mean value over a time interval, and subscript
![]() $m$
represents margination. We find that the margination probabilities have the same tendencies with increment of adhesion strength for MPs with different stiffness. Under relatively low adhesion strength (
$m$
represents margination. We find that the margination probabilities have the same tendencies with increment of adhesion strength for MPs with different stiffness. Under relatively low adhesion strength (
![]() $Ad<5$
), the margination probability dramatically increases with increasing adhesion strength; while further increment of adhesion strength makes the margination probability slowly decrease (
$Ad<5$
), the margination probability dramatically increases with increasing adhesion strength; while further increment of adhesion strength makes the margination probability slowly decrease (
![]() $5<Ad<23$
). But when the adhesion strength exceeds a critical value, the margination probability will increase with the increment of adhesion strength again. The critical value differs among MPs with different stiffnesses. The margination probability against stiffness is given in figure 7(b) for MPs with different adhesion strengths. The margination probability result of MPs without adhesion (
$5<Ad<23$
). But when the adhesion strength exceeds a critical value, the margination probability will increase with the increment of adhesion strength again. The critical value differs among MPs with different stiffnesses. The margination probability against stiffness is given in figure 7(b) for MPs with different adhesion strengths. The margination probability result of MPs without adhesion (
![]() $Ad=0$
) is also presented to allow a comparison. We find that, with the same adhesion strength, the margination probabilities increase with the increment of
$Ad=0$
) is also presented to allow a comparison. We find that, with the same adhesion strength, the margination probabilities increase with the increment of
![]() $Ca$
when MPs are stiff (relatively small
$Ca$
when MPs are stiff (relatively small
![]() $Ca$
); while a further increase of
$Ca$
); while a further increase of
![]() $Ca$
results in the decrease of margination probability. Though the margination probability has a decrement when the MP is soft (high
$Ca$
results in the decrease of margination probability. Though the margination probability has a decrement when the MP is soft (high
![]() $Ca$
), it is still higher than that of an MP without adhesion. The difference of margination probability between the cases with and without adhesion is determined by the adhesion strength. These relationships remain to be discussed in detail later.
$Ca$
), it is still higher than that of an MP without adhesion. The difference of margination probability between the cases with and without adhesion is determined by the adhesion strength. These relationships remain to be discussed in detail later.

Figure 8. Contours of margination probability on the
![]() $Ca{-}Ad$
plane.
$Ca{-}Ad$
plane.
Furthermore, we summarize the results of margination probabilities in the contours on the
![]() $Ca{-}Ad$
plane as shown in figure 8. We find that two peaks exist in the contours for the margination probability. One is in the region with high adhesion strength
$Ca{-}Ad$
plane as shown in figure 8. We find that two peaks exist in the contours for the margination probability. One is in the region with high adhesion strength
![]() $Ad$
and moderate stiffness (moderate
$Ad$
and moderate stiffness (moderate
![]() $Ca$
), namely I; the other one is located in the region with moderate adhesion strength
$Ca$
), namely I; the other one is located in the region with moderate adhesion strength
![]() $Ad$
and large stiffness (small
$Ad$
and large stiffness (small
![]() $Ca$
), denoted as II. These two regions, which favour margination behaviour, are determined by the interplay of the adhesion effect and deformability. To investigate the underlying mechanisms, the adhesion behaviour of elastic MPs is first examined.
$Ca$
), denoted as II. These two regions, which favour margination behaviour, are determined by the interplay of the adhesion effect and deformability. To investigate the underlying mechanisms, the adhesion behaviour of elastic MPs is first examined.
4.3 Adhesion behaviour of elastic MPs

Figure 9. Identification of motion types of elastic MPs. (a) Snapshots for firm adhesion (FA), stop-and-go motion (SG), stable rolling (SR) and free motion (FM). (b) Corresponding trajectories of the four different types of motion for elastic MPs along the flow direction.
The adhesion behaviour should be influenced by the deformability according to previous studies (Ndri, Shyy & Tran-Son-Tay Reference Ndri, Shyy and Tran-Son-Tay2003; Khismatullin & Truskey Reference Khismatullin and Truskey2005; Balsara, Banton & Eggleton Reference Balsara, Banton and Eggleton2016; Luo & Bai Reference Luo and Bai2016; Ye et al.
Reference Ye, Shen and Li2018a
). The deformability of MPs can affect the hydrodynamics, which balances the spring force exerted by the biological bonds. It is revealed that deformation of an MP can promote the adhesion of the MP to the substrate. Previous studies (Ndri et al.
Reference Ndri, Shyy and Tran-Son-Tay2003; Khismatullin & Truskey Reference Khismatullin and Truskey2005) demonstrated that when an elastic MP moved near the substrate, the bottom of the MP was flattened. This resulted in a large contact area between the MP and the substrate. Then the adhesion became strong. Before we present the adhesion behaviour of elastic MPs in blood flow, the classification of the types of motion of elastic MPs is shown first. On the basis of our adhesive model, the probabilistic model (Hammer & Lauffenburger Reference Hammer and Lauffenburger1987), there are a total of four motion types of elastic MPs, which are presented in figure 9(a). They are characterized by the snapshots at
![]() $t=0.01$
, 0.02, 0.03 and 0.04 s along the flow (
$t=0.01$
, 0.02, 0.03 and 0.04 s along the flow (
![]() $y$
) direction. In the case of firm adhesion (FA), the MP collapses on the substrate like a droplet and cannot move any more. The MP can slowly move at some time intervals despite collapsing on to the substrate in stop-and-go motion (SG). However, in stable rolling (SR), the MP moves on the substrate. Additionally, the MP deforms like an ellipsoid under shear stress with a flattened contact area between MP and substrate. In the free motion (FM), the MP totally becomes an ellipsoid, and it moves freely near the substrate. Under FM, there is no obvious contact between the MP and the substrate. These motions are distinguished by calculating the velocity of the MP’s centre (cf. figure 9
b) along the flow direction (
$y$
) direction. In the case of firm adhesion (FA), the MP collapses on the substrate like a droplet and cannot move any more. The MP can slowly move at some time intervals despite collapsing on to the substrate in stop-and-go motion (SG). However, in stable rolling (SR), the MP moves on the substrate. Additionally, the MP deforms like an ellipsoid under shear stress with a flattened contact area between MP and substrate. In the free motion (FM), the MP totally becomes an ellipsoid, and it moves freely near the substrate. Under FM, there is no obvious contact between the MP and the substrate. These motions are distinguished by calculating the velocity of the MP’s centre (cf. figure 9
b) along the flow direction (
![]() $y$
direction). In FA, the velocity is nearly zero through the simulation time. When the velocity is non-zero at some time intervals and zero at other time intervals, it is referred to as SG. As for the SR and FM, there is no difference in terms of trajectories of the MP’s centre, while their velocities are not identical. If the velocity of the MP’s centre is the same as the fluid velocity at the same location, it is defined as FM. Otherwise, it is SR motion. The detailed classification of these adhesion types is discussed in the supporting information (supplementary material is available at https://doi.org/10.1017/jfm.2018.890).
$y$
direction). In FA, the velocity is nearly zero through the simulation time. When the velocity is non-zero at some time intervals and zero at other time intervals, it is referred to as SG. As for the SR and FM, there is no difference in terms of trajectories of the MP’s centre, while their velocities are not identical. If the velocity of the MP’s centre is the same as the fluid velocity at the same location, it is defined as FM. Otherwise, it is SR motion. The detailed classification of these adhesion types is discussed in the supporting information (supplementary material is available at https://doi.org/10.1017/jfm.2018.890).
The adhesion probability is used to quantify the behaviours of MPs near the substrate; it is defined as
where
![]() $n_{a}(t)$
represents the number of elastic MPs that have interactions with the substrate at time
$n_{a}(t)$
represents the number of elastic MPs that have interactions with the substrate at time
![]() $t$
,
$t$
,
![]() $N$
is the total number of elastic MPs, and subscript
$N$
is the total number of elastic MPs, and subscript
![]() $a$
is adopted to distinguish it from margination probability. The formation of a biological bond between the ligand and the receptor is an indication of interaction between the MP and the substrate. Additionally, the adhesion probability of the four motion types of MPs on the substrate is defined as the number fraction of MPs with definite motion types. In the following, for simplicity, the type names of the MPs represent the corresponding adhesion probability. Figure 10 presents the adhesion probabilities for elastic MPs and the motion types. In figure 10(a), the adhesion strength is weak (
$a$
is adopted to distinguish it from margination probability. The formation of a biological bond between the ligand and the receptor is an indication of interaction between the MP and the substrate. Additionally, the adhesion probability of the four motion types of MPs on the substrate is defined as the number fraction of MPs with definite motion types. In the following, for simplicity, the type names of the MPs represent the corresponding adhesion probability. Figure 10 presents the adhesion probabilities for elastic MPs and the motion types. In figure 10(a), the adhesion strength is weak (
![]() $Ad=0.7$
). We find that when the MPs are stiff (low
$Ad=0.7$
). We find that when the MPs are stiff (low
![]() $Ca$
), FM and SR dominate the motion of MPs compared to SG and FA; almost no MP has FA. But when the MPs become soft (increasing
$Ca$
), FM and SR dominate the motion of MPs compared to SG and FA; almost no MP has FA. But when the MPs become soft (increasing
![]() $Ca$
), FM and SR decrease; and the FM can even vanish when
$Ca$
), FM and SR decrease; and the FM can even vanish when
![]() $Ca$
is large enough. When MPs are very soft (high
$Ca$
is large enough. When MPs are very soft (high
![]() $Ca$
), SG and FA start to increase, and SG can exceed SR and FM. One thing that should be noted is that the sum of the adhesion probabilities of all four motion types should be equal to the total adhesion probability. The tendency is consistent with previous studies that deformability can promote the firm adhesion of particles on the substrate (Ndri et al.
Reference Ndri, Shyy and Tran-Son-Tay2003; Khismatullin & Truskey Reference Khismatullin and Truskey2005; Shen et al.
Reference Shen, Ye, Kröger and Li2018). However, when the adhesion strength increases (cf. figure 10
b), the adhesion probabilities have the opposite trend compared to that under weak adhesion. FA and SG dominate the motion of MPs when MPs are stiff. When MPs become soft (increasing
$Ca$
), SG and FA start to increase, and SG can exceed SR and FM. One thing that should be noted is that the sum of the adhesion probabilities of all four motion types should be equal to the total adhesion probability. The tendency is consistent with previous studies that deformability can promote the firm adhesion of particles on the substrate (Ndri et al.
Reference Ndri, Shyy and Tran-Son-Tay2003; Khismatullin & Truskey Reference Khismatullin and Truskey2005; Shen et al.
Reference Shen, Ye, Kröger and Li2018). However, when the adhesion strength increases (cf. figure 10
b), the adhesion probabilities have the opposite trend compared to that under weak adhesion. FA and SG dominate the motion of MPs when MPs are stiff. When MPs become soft (increasing
![]() $Ca$
), SG and FA start to decrease, but SR and FM increase. When MPs are soft enough (high
$Ca$
), SG and FA start to decrease, but SR and FM increase. When MPs are soft enough (high
![]() $Ca$
), SR can outperform FA and SG. This results in the opposite conclusion that a stiff MP demonstrates superior adhesion compared to soft particles when adhesion strength is strong.
$Ca$
), SR can outperform FA and SG. This results in the opposite conclusion that a stiff MP demonstrates superior adhesion compared to soft particles when adhesion strength is strong.

Figure 10. Adhesion probabilities for elastic MPs and corresponding adhesion probabilities of different motion types: (a)
![]() $Ad=0.7$
and (b)
$Ad=0.7$
and (b)
![]() $Ad=32.8$
.
$Ad=32.8$
.

Figure 11. (a) Phase diagram for motion type of elastic MPs on
![]() $Ca{-}Ad$
plane. (b) Adhesion probability contours of elastic MPs on
$Ca{-}Ad$
plane. (b) Adhesion probability contours of elastic MPs on
![]() $Ca{-}Ad$
plane.
$Ca{-}Ad$
plane.
To have detailed motion type distributions with different adhesion strengths and stiffnesses, we give the phase diagram of motion types on the
![]() $Ca{-}Ad$
plane in figure 11(a). The type is chosen as follows: for example, when
$Ca{-}Ad$
plane in figure 11(a). The type is chosen as follows: for example, when
![]() $Ca=0.037$
and
$Ca=0.037$
and
![]() $Ad=32.8$
, the adhesion probability of FA dominates compared to the other three motion types, and then we use FA to represent the motion type of MPs under the specific adhesion strength and stiffness. Comparing figure 11(a) with the margination probability contour under the adhesion effect (cf. figure 8), we find that the two regions favouring margination are just the FA and SG regions corresponding to the motion type phase diagram. This means that the adhesion-favouring region is also the margination-favouring region. Additionally, the adhesion probability contour is provided in figure 11(b). We find that in the regions where the margination probabilities are high, the adhesion probabilities are also high. Thus high margination should be a prerequisite for high adhesion, but the intrinsic relationship between margination and adhesion is not clear. We will discuss it in detail below.
$Ad=32.8$
, the adhesion probability of FA dominates compared to the other three motion types, and then we use FA to represent the motion type of MPs under the specific adhesion strength and stiffness. Comparing figure 11(a) with the margination probability contour under the adhesion effect (cf. figure 8), we find that the two regions favouring margination are just the FA and SG regions corresponding to the motion type phase diagram. This means that the adhesion-favouring region is also the margination-favouring region. Additionally, the adhesion probability contour is provided in figure 11(b). We find that in the regions where the margination probabilities are high, the adhesion probabilities are also high. Thus high margination should be a prerequisite for high adhesion, but the intrinsic relationship between margination and adhesion is not clear. We will discuss it in detail below.

Figure 12. (a) Interaction modes of elastic MPs in blood flow. (b) Three mechanisms dominating the motion of elastic MPs near the wall of a channel.
4.4 Mechanism of localization of elastic MPs under adhesion
When the elastic MP is located in the blood flow, it can interact with other objects, such as RBCs, the wall of the channel and other MPs. Particularly, considering the adhesion effect, the elastic MPs can also interact with the wall through ligand–receptor binding. We give a simple schematic to show the interaction modes of an elastic MP with other objects in figure 12(a). Here, the interaction mode between MP and MP is negligible due to the low volume fraction (less than 1 %). When the MP is located in the centre region of the channel, it can only interact with RBCs through hydrodynamic collision, which is denoted as interaction mode
![]() $A$
in figure 12(a). We define a near-wall region
$A$
in figure 12(a). We define a near-wall region
![]() $\unicode[STIX]{x1D6E5}$
, in which the existence of the wall will influence the motion of objects within it. The thickness of
$\unicode[STIX]{x1D6E5}$
, in which the existence of the wall will influence the motion of objects within it. The thickness of
![]() $\unicode[STIX]{x1D6E5}$
is approximately three times the radius of the object (Singh et al.
Reference Singh, Li and Sarkar2014). If an MP enters the region
$\unicode[STIX]{x1D6E5}$
is approximately three times the radius of the object (Singh et al.
Reference Singh, Li and Sarkar2014). If an MP enters the region
![]() $\unicode[STIX]{x1D6E5}$
, it can experience deformation-induced migration besides a hydrodynamic collision with an RBC. We name this mode as
$\unicode[STIX]{x1D6E5}$
, it can experience deformation-induced migration besides a hydrodynamic collision with an RBC. We name this mode as
![]() $B$
. Further moving towards the wall makes an elastic MP locate around the interface of the CFL (
$B$
. Further moving towards the wall makes an elastic MP locate around the interface of the CFL (
![]() $\unicode[STIX]{x1D6FF}$
). An MP in this region has complicated interactions with its surroundings. It not only collides with an RBC and experiences deformation-induced migration, but also starts to interact with the wall through ligand–receptor binding. The interaction mode in this region is symbolized as
$\unicode[STIX]{x1D6FF}$
). An MP in this region has complicated interactions with its surroundings. It not only collides with an RBC and experiences deformation-induced migration, but also starts to interact with the wall through ligand–receptor binding. The interaction mode in this region is symbolized as
![]() $C$
. After the MP moves into the CFL and adheres on the substrate, it experiences both adhesive interaction and deformation-induced migration. We call this interaction mode
$C$
. After the MP moves into the CFL and adheres on the substrate, it experiences both adhesive interaction and deformation-induced migration. We call this interaction mode
![]() $D$
. We focus on mode
$D$
. We focus on mode
![]() $C$
and isolate it in figure 12(b). Here we believe that the motion of an elastic MP with mode
$C$
and isolate it in figure 12(b). Here we believe that the motion of an elastic MP with mode
![]() $C$
is complex but crucial to the margination and adhesion process. The region where this mode happens is located around the interface of the CFL and adhesion layer. If the MP moves away from the wall, it will not be counted as an MP having localization. While, when it moves towards the wall, it will be regarded as an MP owing to margination and adhesion. The moving direction is attributed to the competition among three mechanisms: (i) deformation-induced migration; (ii) adhesion effect; and (iii) near-wall hydrodynamic collision with an RBC. The deformation-induced migration makes an MP move away from the wall, and thus hampers localization. The adhesion effect plays a role through biological bond, and it facilitates localization. As for the near-wall hydrodynamic collision with an RBC, because there is no RBC within the CFL, then the collision should be a one-sided collision. The RBCs are always located on one side of the MP. Furthermore, it is confirmed that three-body and higher-order collision schemes can be negligible under the current circumstances (
$C$
is complex but crucial to the margination and adhesion process. The region where this mode happens is located around the interface of the CFL and adhesion layer. If the MP moves away from the wall, it will not be counted as an MP having localization. While, when it moves towards the wall, it will be regarded as an MP owing to margination and adhesion. The moving direction is attributed to the competition among three mechanisms: (i) deformation-induced migration; (ii) adhesion effect; and (iii) near-wall hydrodynamic collision with an RBC. The deformation-induced migration makes an MP move away from the wall, and thus hampers localization. The adhesion effect plays a role through biological bond, and it facilitates localization. As for the near-wall hydrodynamic collision with an RBC, because there is no RBC within the CFL, then the collision should be a one-sided collision. The RBCs are always located on one side of the MP. Furthermore, it is confirmed that three-body and higher-order collision schemes can be negligible under the current circumstances (
![]() $Ht=30\,\%$
) (Kumar & Graham Reference Kumar and Graham2012a
; Rivera, Zhang & Graham Reference Rivera, Zhang and Graham2016; Qi & Shaqfeh Reference Qi and Shaqfeh2017). Therefore, only a side pair collision is considered here. According to the locations of the RBC and MP, the pair collision hinders the penetration of the MP into the centre of the channel, and thus promotes localization.
$Ht=30\,\%$
) (Kumar & Graham Reference Kumar and Graham2012a
; Rivera, Zhang & Graham Reference Rivera, Zhang and Graham2016; Qi & Shaqfeh Reference Qi and Shaqfeh2017). Therefore, only a side pair collision is considered here. According to the locations of the RBC and MP, the pair collision hinders the penetration of the MP into the centre of the channel, and thus promotes localization.

Figure 13. (a) Numerical experiment for pair collision between an RBC and an elastic MP. (b) Collision displacement of an RBC and an elastic MP with different stiffnesses. (c) Comparison of collision displacement and deformation-induced migration displacement of elastic MPs. (d) Number of biological bonds established when elastic MPs adhere on a substrate with different adhesion strengths against stiffness of elastic MP.
The side pair collision is first examined systematically for elastic MPs with different stiffnesses. Figure 13(a) gives the side pair collision illustration. In this numerical experiment, the channel and the flow condition are the same as in the above simulations for margination of elastic MPs. A single RBC and an elastic MP are placed in the centre of the channel to eliminate the wall effect. The centre distance between their initial positions in the height direction (
![]() $z$
direction) is
$z$
direction) is
![]() $\unicode[STIX]{x1D70E}=2~\unicode[STIX]{x03BC}\text{m}$
. During the simulation, the trajectories of the centres of the RBC and the MP are tracked. The displacement of the centres of the RBC and the MP in the z direction refers to the collision displacement. The evolution of collision displacements for the RBC (
$\unicode[STIX]{x1D70E}=2~\unicode[STIX]{x03BC}\text{m}$
. During the simulation, the trajectories of the centres of the RBC and the MP are tracked. The displacement of the centres of the RBC and the MP in the z direction refers to the collision displacement. The evolution of collision displacements for the RBC (
![]() $\unicode[STIX]{x1D6E5}_{R}$
) and the elastic MP (
$\unicode[STIX]{x1D6E5}_{R}$
) and the elastic MP (
![]() $\unicode[STIX]{x1D6E5}_{S}$
) are presented in figure 13(b). As for the RBC, we find that the collision displacements are almost the same; and they are much smaller compared to all of the elastic MPs. They have no dependence on the stiffness of MPs. This is attributed to the small size of an MP compared to the RBC. The trajectories of MPs with different stiffnesses have the same trend. The first approach between the RBC and the MP makes the MP abruptly migrate towards the wall. After collision ends, it can partially restore towards its initial position. It is located in a specific equilibrium position between the initial and maximum migration positions. We denote the distance between this equilibrium position and the initial position as the collision displacement, which is based on the definition in Loewenberg & Hinch (Reference Loewenberg and Hinch1997), Kumar & Graham (Reference Kumar and Graham2011, Reference Kumar and Graham2012a
,Reference Kumar and Graham
b
) and Zhao & Shaqfeh (Reference Zhao and Shaqfeh2013). From the zoom in figure 13(b), we can see that the difference of collision displacements among MPs with different stiffnesses is small. But this is an individual collision between an RBC and an MP. Repeated collisions between RBCs and MPs will distinguish the collision displacement with a large value for MPs with different stiffnesses. The result is shown in figure 13(c),
$\unicode[STIX]{x1D6E5}_{S}$
) are presented in figure 13(b). As for the RBC, we find that the collision displacements are almost the same; and they are much smaller compared to all of the elastic MPs. They have no dependence on the stiffness of MPs. This is attributed to the small size of an MP compared to the RBC. The trajectories of MPs with different stiffnesses have the same trend. The first approach between the RBC and the MP makes the MP abruptly migrate towards the wall. After collision ends, it can partially restore towards its initial position. It is located in a specific equilibrium position between the initial and maximum migration positions. We denote the distance between this equilibrium position and the initial position as the collision displacement, which is based on the definition in Loewenberg & Hinch (Reference Loewenberg and Hinch1997), Kumar & Graham (Reference Kumar and Graham2011, Reference Kumar and Graham2012a
,Reference Kumar and Graham
b
) and Zhao & Shaqfeh (Reference Zhao and Shaqfeh2013). From the zoom in figure 13(b), we can see that the difference of collision displacements among MPs with different stiffnesses is small. But this is an individual collision between an RBC and an MP. Repeated collisions between RBCs and MPs will distinguish the collision displacement with a large value for MPs with different stiffnesses. The result is shown in figure 13(c),
![]() $L_{p}$
represents the collision displacement. We find that when
$L_{p}$
represents the collision displacement. We find that when
![]() $Ca<0.037$
, the collision displacement increases with the increment of
$Ca<0.037$
, the collision displacement increases with the increment of
![]() $Ca$
, while when
$Ca$
, while when
![]() $Ca>0.037$
, it decreases slightly with the increment of
$Ca>0.037$
, it decreases slightly with the increment of
![]() $Ca$
. Hence, there is an optimal stiffness for the pair collision of an elastic MP and an RBC (results in the supporting information point out that this optimal
$Ca$
. Hence, there is an optimal stiffness for the pair collision of an elastic MP and an RBC (results in the supporting information point out that this optimal
![]() $Ca$
is a bit larger than 0.037).
$Ca$
is a bit larger than 0.037).
As far as we know, this is the first time that a hydrodynamic collision between an RBC and an elastic MP has been presented. There are also a number of previous studies showing the pair collision between particles with either the same volume or the same shape (Kumar & Graham Reference Kumar and Graham2011, Reference Kumar and Graham2012b
; Sinha & Graham Reference Sinha and Graham2016). The collision result can be explained as follows. Owing to the size difference between an RBC (diameter
![]() $8~\unicode[STIX]{x03BC}\text{m}$
) and an elastic MP (diameter
$8~\unicode[STIX]{x03BC}\text{m}$
) and an elastic MP (diameter
![]() $2~\unicode[STIX]{x03BC}\text{m}$
), the motion of the elastic MP is probably governed by the fluctuation of the flow field near the RBC induced by its deformation. The RBC should perform a tank-treading motion under shear flow, and the flow field around it is presented in figure 13(a). When
$2~\unicode[STIX]{x03BC}\text{m}$
), the motion of the elastic MP is probably governed by the fluctuation of the flow field near the RBC induced by its deformation. The RBC should perform a tank-treading motion under shear flow, and the flow field around it is presented in figure 13(a). When
![]() $Ca<0.037$
, with the increment of
$Ca<0.037$
, with the increment of
![]() $Ca$
, it is easier for a soft MP to align itself with the flow field, thus the collision displacement increases. However, further increase of
$Ca$
, it is easier for a soft MP to align itself with the flow field, thus the collision displacement increases. However, further increase of
![]() $Ca$
makes the tank-treading motion of a soft MP become significant (Fedosov et al.
Reference Fedosov, Caswell and Karniadakis2010a
). The tank-treading motion of a soft MP can also induce the fluctuation of flow around it, but with the opposite direction to the flow field induced by RBC motion. It acts as resistance to the alignment of the MP with the flow field. Therefore, further increase of
$Ca$
makes the tank-treading motion of a soft MP become significant (Fedosov et al.
Reference Fedosov, Caswell and Karniadakis2010a
). The tank-treading motion of a soft MP can also induce the fluctuation of flow around it, but with the opposite direction to the flow field induced by RBC motion. It acts as resistance to the alignment of the MP with the flow field. Therefore, further increase of
![]() $Ca$
will lead to the decrease of the collision displacement of an MP.
$Ca$
will lead to the decrease of the collision displacement of an MP.
When an elastic MP is placed in the flow, the shape cannot be analytically captured, especially for an MP with large deformation. Therefore, the deformation-induced migration, which is highly dependent on the shape of the MP, can hardly be determined. In the literature, numerical simulations are employed to study the deformation-induced migration of an elastic MP in a flow (Doddi & Bagchi Reference Doddi and Bagchi2008; Kaoui et al.
Reference Kaoui, Ristow, Cantat, Misbah and Zimmermann2008; Nix et al.
Reference Nix, Imai, Matsunaga, Yamaguchi and Ishikawa2014; Singh et al.
Reference Singh, Li and Sarkar2014; Qi & Shaqfeh Reference Qi and Shaqfeh2017). Here, an empirical relationship in Singh et al. (Reference Singh, Li and Sarkar2014) is adopted, due to its systematics. In their study, the lateral migration velocity of the deformable capsule is a function of its stiffness (
![]() $Ca$
) and distance away from the wall (
$Ca$
) and distance away from the wall (
![]() $h$
). A phenomenological formula for migration velocity is given as
$h$
). A phenomenological formula for migration velocity is given as
 $$\begin{eqnarray}\frac{V_{d}}{\dot{\unicode[STIX]{x1D6FE}}a}=\left\{\begin{array}{@{}ll@{}}(0.65Ca+0.021)\left({\displaystyle \frac{a}{h}}\right)^{2},\quad & Ca\leqslant Ca_{cr},\\ V_{cr}^{\ast }+0.02(Ca-Ca_{cr})^{0.6}\left({\displaystyle \frac{a}{h}}\right)^{1.35},\quad & Ca>Ca_{cr},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\frac{V_{d}}{\dot{\unicode[STIX]{x1D6FE}}a}=\left\{\begin{array}{@{}ll@{}}(0.65Ca+0.021)\left({\displaystyle \frac{a}{h}}\right)^{2},\quad & Ca\leqslant Ca_{cr},\\ V_{cr}^{\ast }+0.02(Ca-Ca_{cr})^{0.6}\left({\displaystyle \frac{a}{h}}\right)^{1.35},\quad & Ca>Ca_{cr},\end{array}\right.\end{eqnarray}$$
where
![]() $V_{cr}^{\ast }=(V_{d}/\dot{\unicode[STIX]{x1D6FE}}a)|_{Ca=Ca_{cr}}$
. Their simulation results pointed out a power-law relation for the capsule velocity. There exists a critical stiffness,
$V_{cr}^{\ast }=(V_{d}/\dot{\unicode[STIX]{x1D6FE}}a)|_{Ca=Ca_{cr}}$
. Their simulation results pointed out a power-law relation for the capsule velocity. There exists a critical stiffness,
![]() $Ca_{cr}$
, of the capsule; here we choose it as
$Ca_{cr}$
, of the capsule; here we choose it as
![]() $Ca_{cr}=0.15$
according to the proposed regime in Singh et al. (Reference Singh, Li and Sarkar2014). When
$Ca_{cr}=0.15$
according to the proposed regime in Singh et al. (Reference Singh, Li and Sarkar2014). When
![]() $Ca\leqslant Ca_{cr}$
, the migration velocity is linearly proportional to
$Ca\leqslant Ca_{cr}$
, the migration velocity is linearly proportional to
![]() $Ca$
and related to
$Ca$
and related to
![]() $h^{-2}$
, while when
$h^{-2}$
, while when
![]() $Ca>Ca_{cr}$
, the velocity has 0.6 and
$Ca>Ca_{cr}$
, the velocity has 0.6 and
![]() $-1.35$
power scalings with
$-1.35$
power scalings with
![]() $Ca$
and
$Ca$
and
![]() $h$
, respectively. On the basis of this relation, we set
$h$
, respectively. On the basis of this relation, we set
![]() $h=2~\unicode[STIX]{x03BC}\text{m}$
, which corresponds to a position between the adhesion layer and the CFL, and then integrate (4.3) from
$h=2~\unicode[STIX]{x03BC}\text{m}$
, which corresponds to a position between the adhesion layer and the CFL, and then integrate (4.3) from
![]() $t=0$
to
$t=0$
to
![]() $t=0.1$
. The deformation-induced migration displacement
$t=0.1$
. The deformation-induced migration displacement
![]() $L_{d}$
against stiffness of the elastic MP is obtained and is shown in figure 13(c), denoted as a blue line.
$L_{d}$
against stiffness of the elastic MP is obtained and is shown in figure 13(c), denoted as a blue line.
To study the adhesion effect, we also conduct simulation experiments to investigate the adhesion behaviour of a single elastic MP on a substrate under shear flow. The flow and the channel size are the same as in the above margination study. The interaction between an elastic MP and the substrate is established by the biological bonds formed in the adhesion process, and the bond is modelled as a linear spring. The number of bonds can be used to quantify the adhesion effect. Figure 13(d) shows the relationship between the number of bonds and the stiffness of the elastic MP under different adhesion strengths. We find that the number of bonds increases with the increment of
![]() $Ca$
when
$Ca$
when
![]() $Ca$
is not large (
$Ca$
is not large (
![]() $Ca<0.037$
). However, further increase of
$Ca<0.037$
). However, further increase of
![]() $Ca$
does not significantly affect the number of bonds. When the adhesion strength is very strong (
$Ca$
does not significantly affect the number of bonds. When the adhesion strength is very strong (
![]() $Ad=32.8$
), the number of bonds may slightly decrease with increment of
$Ad=32.8$
), the number of bonds may slightly decrease with increment of
![]() $Ca$
.
$Ca$
.
The results given above demonstrate the strength of three mechanisms against the stiffness of MPs. They are combined to explain the margination results in figure 7(b). When the MP is relatively stiff (low
![]() $Ca<0.037$
), with the increment of
$Ca<0.037$
), with the increment of
![]() $Ca$
, the collision displacement increases, the adhesion effect increases, and the deformation-induced migration displacement remains almost unchanged. Two promoting factors of localization increase and one impeding factor remains unchanged. Thus, the margination probability increases with the increment of
$Ca$
, the collision displacement increases, the adhesion effect increases, and the deformation-induced migration displacement remains almost unchanged. Two promoting factors of localization increase and one impeding factor remains unchanged. Thus, the margination probability increases with the increment of
![]() $Ca$
. However, when
$Ca$
. However, when
![]() $Ca$
exceeds the critical value
$Ca$
exceeds the critical value
![]() $Ca=0.037$
, the MP becomes relatively soft. With the increment of
$Ca=0.037$
, the MP becomes relatively soft. With the increment of
![]() $Ca$
, the collision displacement decreases, the adhesion effect stays almost unchanged, and the deformation-induced migration drastically increases. The impeding factor of localization dominates compared to the other two promoting factors. Hence, in this circumstance, the localization of the MP decreases with the increment of
$Ca$
, the collision displacement decreases, the adhesion effect stays almost unchanged, and the deformation-induced migration drastically increases. The impeding factor of localization dominates compared to the other two promoting factors. Hence, in this circumstance, the localization of the MP decreases with the increment of
![]() $Ca$
.
$Ca$
.

Figure 14. (a) Deformation of particles with
![]() $Ca=0.037$
under different adhesion strengths. Dashed lines are used as a guide to show the deformation of particles. (b) Number of biological bonds established when elastic MPs adhere on a substrate against adhesion strengths for particles with different stiffnesses.
$Ca=0.037$
under different adhesion strengths. Dashed lines are used as a guide to show the deformation of particles. (b) Number of biological bonds established when elastic MPs adhere on a substrate against adhesion strengths for particles with different stiffnesses.
Furthermore, the relationship between margination behaviour and adhesion strength is isolated for investigation. With the same
![]() $Ca$
, the side pair collision displacements for MPs under different adhesion strengths should be the same, because the collision displacement is independent of the adhesion, while the deformation-induced migration displacement should be influenced by the adhesion strength. From (4.3), it seems that the deformation-induced migration velocity is only relevant to
$Ca$
, the side pair collision displacements for MPs under different adhesion strengths should be the same, because the collision displacement is independent of the adhesion, while the deformation-induced migration displacement should be influenced by the adhesion strength. From (4.3), it seems that the deformation-induced migration velocity is only relevant to
![]() $Ca$
. But this is not true. The root cause of deformation-induced migration is the deformation of the MP under shear flow. Here, considering the adhesion effect, the deformation of the MP is affected not only by
$Ca$
. But this is not true. The root cause of deformation-induced migration is the deformation of the MP under shear flow. Here, considering the adhesion effect, the deformation of the MP is affected not only by
![]() $Ca$
, but also by the adhesion strength
$Ca$
, but also by the adhesion strength
![]() $Ad$
. Figure 14(a) presents the configurations of the MP with the same
$Ad$
. Figure 14(a) presents the configurations of the MP with the same
![]() $Ca=0.037$
, but under different adhesion strengths. We find that, when the adhesion strength is weak (
$Ca=0.037$
, but under different adhesion strengths. We find that, when the adhesion strength is weak (
![]() $Ad=0.07$
), the deformation of the MP is small. With the increment of adhesion strength (
$Ad=0.07$
), the deformation of the MP is small. With the increment of adhesion strength (
![]() $Ad=0.7{-}13.2$
), the deformation becomes significant and increases, while further increase of
$Ad=0.7{-}13.2$
), the deformation becomes significant and increases, while further increase of
![]() $Ad$
will not cause any further increment of MP deformation. This result reveals that the adhesion effect plays a role in the localization of MPs through influencing the deformation of the MP. Additionally, the relationship between the number of bonds and the adhesion strength for MPs with different stiffnesses is displayed in figure 14(b). We find that, when the adhesion strength is small (
$Ad$
will not cause any further increment of MP deformation. This result reveals that the adhesion effect plays a role in the localization of MPs through influencing the deformation of the MP. Additionally, the relationship between the number of bonds and the adhesion strength for MPs with different stiffnesses is displayed in figure 14(b). We find that, when the adhesion strength is small (
![]() $Ad<3.3$
), the number of bonds dramatically increases with the increment of
$Ad<3.3$
), the number of bonds dramatically increases with the increment of
![]() $Ad$
; while further increment of
$Ad$
; while further increment of
![]() $Ad$
also results in the increase of number of bonds, but with a slow growth rate.
$Ad$
also results in the increase of number of bonds, but with a slow growth rate.
Apart from the collision effect, the adhesion effect and deformation-induced migration are combined to reveal the underlying mechanism of margination probability against adhesion strength for MPs with different stiffnesses in figure 7(a). When
![]() $Ad$
is small (
$Ad$
is small (
![]() $Ad\sim 0.7$
), the deformation-induced migration displacements are almost the same, but the adhesion effect dramatically increases, and thus the margination probability grows rapidly with the increment of adhesion strength. When
$Ad\sim 0.7$
), the deformation-induced migration displacements are almost the same, but the adhesion effect dramatically increases, and thus the margination probability grows rapidly with the increment of adhesion strength. When
![]() $Ad$
becomes relatively large (
$Ad$
becomes relatively large (
![]() $Ad\sim 0.7{-}13.2$
), the adhesion effect slowly increases, while the deformation of particles is significant, leading to large deformation-induced migration displacement. Therefore, in this regime, the margination probability decreases with the increment of adhesion strength. With the further increase of
$Ad\sim 0.7{-}13.2$
), the adhesion effect slowly increases, while the deformation of particles is significant, leading to large deformation-induced migration displacement. Therefore, in this regime, the margination probability decreases with the increment of adhesion strength. With the further increase of
![]() $Ad$
, the deformation-induced migration displacements are almost constant, but adhesion effects still slowly increase. Hence, the margination probability should increase with the increment of adhesion strength in this regime.
$Ad$
, the deformation-induced migration displacements are almost constant, but adhesion effects still slowly increase. Hence, the margination probability should increase with the increment of adhesion strength in this regime.
5 Conclusion
We present numerical results on the localization of elastic MPs without and with effect of adhesion. Margination probability is adopted to quantify the localization of elastic MPs. Without adhesion effects, the margination probabilities of MPs decrease with the increment of
![]() $Ca$
. This stiffness dependence of margination behaviour is found to rely on the interplay of collisions with RBCs and deformation-induced lateral migration of elastic MPs. We find that the evolution of margination can be split into two stages. The first stage corresponds to the development of the CFL. And in this stage, a soft MP marginates more readily than a stiff one. This is attributed to the exclusion of RBCs moving from the CFL to the centre of the channel. The volume exclusion effect is more significant for soft MPs than for stiff MPs, because the deformation of soft MPs demonstrates stronger alignment with the flow direction. However, in the second stage, the CFL is fully formed and the flow is fully developed. The soft MPs in the near-wall region will experience deformation-induced migration due to the existence of the wall. This results in the low accumulation of soft MPs in the CFL. Thus, the margination probability decreases with the increment of
$Ca$
. This stiffness dependence of margination behaviour is found to rely on the interplay of collisions with RBCs and deformation-induced lateral migration of elastic MPs. We find that the evolution of margination can be split into two stages. The first stage corresponds to the development of the CFL. And in this stage, a soft MP marginates more readily than a stiff one. This is attributed to the exclusion of RBCs moving from the CFL to the centre of the channel. The volume exclusion effect is more significant for soft MPs than for stiff MPs, because the deformation of soft MPs demonstrates stronger alignment with the flow direction. However, in the second stage, the CFL is fully formed and the flow is fully developed. The soft MPs in the near-wall region will experience deformation-induced migration due to the existence of the wall. This results in the low accumulation of soft MPs in the CFL. Thus, the margination probability decreases with the increment of
![]() $Ca$
. After the MP becomes softer (high
$Ca$
. After the MP becomes softer (high
![]() $Ca$
), the deformation-induced lateral migration dominates the motion of MPs; therefore, the margination probabilities almost remain the same with the change of
$Ca$
), the deformation-induced lateral migration dominates the motion of MPs; therefore, the margination probabilities almost remain the same with the change of
![]() $Ca$
.
$Ca$
.
Furthermore, localization of elastic MPs under the adhesion effect is studied. We obtain the margination probability contours by systematically varying the capillary number
![]() $Ca$
and the adhesion number
$Ca$
and the adhesion number
![]() $Ad$
. We find that there are two optimal regimes favouring high margination probability on the
$Ad$
. We find that there are two optimal regimes favouring high margination probability on the
![]() $Ca{-}Ad$
plane. It is concluded that the existence of optimal regimes is induced by the interplay of MP deformability and adhesion. The underlying mechanism is explained as competition among three factors: (i) near-wall hydrodynamic collisions between RBCs and MPs; (ii) deformation-induced migration due to the existence of the wall; (iii) adhesive interaction between MPs and the substrate. For MPs with the same adhesion strengths
$Ca{-}Ad$
plane. It is concluded that the existence of optimal regimes is induced by the interplay of MP deformability and adhesion. The underlying mechanism is explained as competition among three factors: (i) near-wall hydrodynamic collisions between RBCs and MPs; (ii) deformation-induced migration due to the existence of the wall; (iii) adhesive interaction between MPs and the substrate. For MPs with the same adhesion strengths
![]() $Ad$
, when they are relatively stiff (low
$Ad$
, when they are relatively stiff (low
![]() $Ca=0.00037{-}0.037$
), the collision displacements increase with the increment of
$Ca=0.00037{-}0.037$
), the collision displacements increase with the increment of
![]() $Ca$
. At the same time, the adhesion effects increase. The deformation-induced migration displacements almost remain the same. Thus, the margination probability will increase with the increment of
$Ca$
. At the same time, the adhesion effects increase. The deformation-induced migration displacements almost remain the same. Thus, the margination probability will increase with the increment of
![]() $Ca$
. However, after
$Ca$
. However, after
![]() $Ca$
of MPs exceeds the critical value
$Ca$
of MPs exceeds the critical value
![]() $Ca=0.037$
, the MPs become softer. With the increment of
$Ca=0.037$
, the MPs become softer. With the increment of
![]() $Ca$
, the collision displacements decrease and the adhesion effects have no obvious difference, while deformation-induced migration displacements dramatically increase. Hence, the margination probability decreases with the increment of
$Ca$
, the collision displacements decrease and the adhesion effects have no obvious difference, while deformation-induced migration displacements dramatically increase. Hence, the margination probability decreases with the increment of
![]() $Ca$
. Additionally, the dependence of the adhesion effect is investigated by fixing the stiffness of the MP. As the collision displacement only depends on the stiffness of the MP, we ignore its influence here. When
$Ca$
. Additionally, the dependence of the adhesion effect is investigated by fixing the stiffness of the MP. As the collision displacement only depends on the stiffness of the MP, we ignore its influence here. When
![]() $Ad$
is small, the deformation-induced migration displacements are almost the same, while the adhesion effects increase quickly; then the margination probabilities dramatically increase with the increment of
$Ad$
is small, the deformation-induced migration displacements are almost the same, while the adhesion effects increase quickly; then the margination probabilities dramatically increase with the increment of
![]() $Ad$
. Furthermore, when
$Ad$
. Furthermore, when
![]() $Ad$
becomes relatively large, the adhesion effects slowly increase, while the deformation of the MPs is significant. Therefore, in this regime, the margination probabilities decrease with the increase of
$Ad$
becomes relatively large, the adhesion effects slowly increase, while the deformation of the MPs is significant. Therefore, in this regime, the margination probabilities decrease with the increase of
![]() $Ad$
. With the further increase of
$Ad$
. With the further increase of
![]() $Ad$
, the deformation-induced migration displacements are almost the same. Although the growth rates are small, the adhesion effects continuously increase. Thus, the margination probabilities can slowly increase with the increment of
$Ad$
, the deformation-induced migration displacements are almost the same. Although the growth rates are small, the adhesion effects continuously increase. Thus, the margination probabilities can slowly increase with the increment of
![]() $Ad$
.
$Ad$
.
For computational studies of blood flow, there are still some limitations in the current numerical model. In normal human vasculature, the viscosity inside the RBC is 4–6 times larger than in the plasma outside the RBC. This viscosity contrast can affect the rheology of the RBC suspension. This is one of the reasons why our simulation results are not exactly the same as experimental results in the validation part. Besides, the blood vessel is usually tubular. Thus, the results obtained from the rectangular channel in our model may have some discrepancies with those in a tube. Tube flow deserves to be investigated in the future.
The findings in this work, especially the optimal regimes favouring localization, suggest that a softer MP or stronger adhesion is not always the best choice for the localization of MPs. This could offer further guidance to design efficient drug carriers in biomedical application, in which high localization is needed.
Acknowledgements
This work was supported by the National Science Foundation (OAC-1755779). The authors thank A. Fisher for proofreading the manuscript. Z.S., H.Y. and Y.L. are all grateful for the support from the Department of Mechanical Engineering at the University of Connecticut. Z.S. and H.Y. acknowledge partial financial support from the GE Fellowship for Innovation. This research benefited in part from the computational resources and staff contributions provided by the Booth Engineering Center for Advanced Technology (BECAT) at the University of Connecticut. Part of this work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation grant no. ACI-1053575.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2018.890.