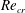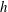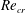1. Introduction
The close relation between vortex breakdown (VB) and hydrodynamic stability was recognized from early VB studies. The visualization of the flow above a delta wing by Lambourne & Brayer (Reference Lambourne and Brayer1961) demonstrated two VB patterns: helical and bubble-like. The transformation of an axisymmetric vortex core into a helix or multi-helix structure can occur only due to the three-dimensional (3D) instability. The nature of bubble-like VB was not so obvious and different conjectures were proposed to explain it: (a) inertial wave roll-up (Benjamin Reference Benjamin1962), (b) collapse of the near-axis boundary layer (Hall Reference Hall1972), (c) flow separation (Leibovich Reference Leibovich1984), (d) fold catastrophe (Trigub Reference Trigub1985), and (e) transition from convective to absolute instability (Olendraru et al. Reference Olendraru, Sellier, Rossi and Huerre1996). More detailed discussions of VB interpretations can be found in Escudier’s (Reference Escudier1988) review and in Shtern (Reference Shtern2012).
A breakthrough in the understanding of the nature of VB was achieved due to the fundamental studies of swirling flows in a sealed cylindrical container. The advantages of exploring VB in a confined flow are that (i) the role of control parameters can be easily recognized in the absence of ambient disturbances and (ii) the flow geometry and the boundary conditions are simple and well defined, allowing meaningful comparisons of experimental and numerical results.
The VB flow driven by one rotating end disk was first experimentally studied by Vogel (Reference Vogel1968). The comprehensive experiments by Escudier (Reference Escudier1984) discovered a variety of VB patterns depending on the aspect ratio,
![]() $h=H/R$
, and the Reynolds number,
$h=H/R$
, and the Reynolds number,
![]() $\mathit{Re}={\it\Omega}R^{2}/{\it\nu}$
, where
$\mathit{Re}={\it\Omega}R^{2}/{\it\nu}$
, where
![]() $H$
and
$H$
and
![]() $R$
are the cylinder length and radius,
$R$
are the cylinder length and radius,
![]() ${\it\Omega}$
is the angular velocity of the rotating disk, and
${\it\Omega}$
is the angular velocity of the rotating disk, and
![]() ${\it\nu}$
is the kinematic viscosity of the fluid. Numerical simulations, starting from the pioneering paper of Lopez (Reference Lopez1990), agreed with the experimental results and helped to better understand the VB nature.
${\it\nu}$
is the kinematic viscosity of the fluid. Numerical simulations, starting from the pioneering paper of Lopez (Reference Lopez1990), agreed with the experimental results and helped to better understand the VB nature.
The stability investigations by Gelfgat, Bar-Yoseph & Solan (Reference Gelfgat, Bar-Yoseph and Solan1996, Reference Gelfgat, Bar-Yoseph and Solan2001) clearly demonstrated that the appearance of a VB bubble is a manifestation of local flow reversal, which can occur in steady axisymmetric flow with no instability, while the instability does not necessarily result in the appearance of a VB bubble.
It was recently argued that the swirl-decay mechanism (SDM) causes counterflows in swirling motions and, in particular, the emergence of VB bubbles. In a few words, the SDM is the following. In a rapidly rotating flow, the centrifugal force induces a radial gradient of pressure
![]() $p$
, according to the cyclostrophic balance,
$p$
, according to the cyclostrophic balance,
![]() $\partial p/\partial r={\it\rho}v^{2}/r$
, where
$\partial p/\partial r={\it\rho}v^{2}/r$
, where
![]() ${\it\rho}$
is the fluid density,
${\it\rho}$
is the fluid density,
![]() $v$
is the swirl velocity, and
$v$
is the swirl velocity, and
![]() $r$
is the distance from the rotation axis. The reduction of pressure near the axis, compared with its peripheral value, is larger (smaller) in the vicinity (downstream) of a swirl source because the swirl decays, e.g. due to friction at the sidewall. Therefore, the near-axis pressure is smaller (larger) in the vicinity of (away from) the swirl source. This pressure difference drives the backflow near the axis. If a swirling flow converges to the axis, the near-axis pressure reduces, decelerating and reversing the downstream flow, i.e. a VB bubble develops.
$r$
is the distance from the rotation axis. The reduction of pressure near the axis, compared with its peripheral value, is larger (smaller) in the vicinity (downstream) of a swirl source because the swirl decays, e.g. due to friction at the sidewall. Therefore, the near-axis pressure is smaller (larger) in the vicinity of (away from) the swirl source. This pressure difference drives the backflow near the axis. If a swirling flow converges to the axis, the near-axis pressure reduces, decelerating and reversing the downstream flow, i.e. a VB bubble develops.
The SDM theory initially aimed to explain the elongated counterflows occurring in hydrocyclones and vortex tubes (Shtern & Borissov Reference Shtern and Borissov2010a ,Reference Shtern and Borissov b ). Then SMD helped explain the development of double counterflows in a vortex combustor and in a vortex trap (Shtern, Torregrosa & Herrada Reference Shtern, Torregrosa and Herrada2011a ,Reference Shtern, Torregrosa and Herrada b ). Next, it was found that SMD helps to understand the chain-like process of the emergence of VB bubbles in the Vogel–Escudier flow (Shtern, Torregrosa & Herrada Reference Shtern, Torregrosa and Herrada2012). The analysis of experimental results by Mununga et al. (Reference Mununga, Lo Jacono, Sørensen, Leweke, Thompson and Hourigan2014) revealed that SMD helps explain the opposite VB-control effects caused by (a) a small disk, embedded in the still endwall, whose co-rotation enhances VB, and (b) a central rod, whose co-rotation suppresses VB (Husain, Shtern & Hussain Reference Husain, Shtern and Hussain2003). Thus, SDM has been shown to be relevant for understanding VB physics and different control strategies.
The experimental and numerical studies by Escudier (Reference Escudier1984), Sorensen, Naumov & Mikkelsen (Reference Sorensen, Naumov and Mikkelsen2006), Sorensen et al. (Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009), and Sorensen, Naumov & Okulov (Reference Sorensen, Naumov and Okulov2011) documented that, as
![]() $\mathit{Re}$
increases, the steady axisymmetric VB bubble first develops for
$\mathit{Re}$
increases, the steady axisymmetric VB bubble first develops for
![]() $h<3.2$
. For larger
$h<3.2$
. For larger
![]() $h$
, the flow first becomes unstable with respect to 3D time-oscillatory disturbances with
$h$
, the flow first becomes unstable with respect to 3D time-oscillatory disturbances with
![]() $m=3$
for
$m=3$
for
![]() $3.2<h<4.3$
,
$3.2<h<4.3$
,
![]() $m=2$
for
$m=2$
for
![]() $4.3<h<5.2$
, and
$4.3<h<5.2$
, and
![]() $m=4$
for
$m=4$
for
![]() $5.2<h<5.5$
, with
$5.2<h<5.5$
, with
![]() $m$
being the azimuthal wavenumber. The fact that the flow becomes 3D and time-dependent for
$m$
being the azimuthal wavenumber. The fact that the flow becomes 3D and time-dependent for
![]() $\mathit{Re}$
exceeding its critical value
$\mathit{Re}$
exceeding its critical value
![]() $Re_{cr}$
, does not prevent the emergence of a VB bubble (which is 3D and time-dependent here) as
$Re_{cr}$
, does not prevent the emergence of a VB bubble (which is 3D and time-dependent here) as
![]() $\mathit{Re}$
further increases (Kulikov et al.
Reference Kulikov, Mikkelsen, Naumov and Okulov2014).
$\mathit{Re}$
further increases (Kulikov et al.
Reference Kulikov, Mikkelsen, Naumov and Okulov2014).
Thus, the prior studies revealed a number of interesting and important stability features. However, the shear-layer character of the Vogel–Escudier-flow instability has not been described. The goal of this paper is to explore and highlight the nature of this instability. To this end, we consider elongated cylindrical containers (
![]() $h\gg 1$
) where three flow regions can be clearly distinguished at
$h\gg 1$
) where three flow regions can be clearly distinguished at
![]() $\mathit{Re}=\mathit{Re}_{cr}$
: the Kármán boundary layer near the rotating disk, the creeping motion near the stationary disk, and the circulation region (CR) in between. It is found that the instability emerges in the CR central part and the critical characteristics, namely
$\mathit{Re}=\mathit{Re}_{cr}$
: the Kármán boundary layer near the rotating disk, the creeping motion near the stationary disk, and the circulation region (CR) in between. It is found that the instability emerges in the CR central part and the critical characteristics, namely
![]() $\mathit{Re}_{cr}\approx 3100$
,
$\mathit{Re}_{cr}\approx 3100$
,
![]() $m=4$
and
$m=4$
and
![]() ${\it\omega}=0.4$
, are nearly
${\it\omega}=0.4$
, are nearly
![]() $h$
-invariant for
$h$
-invariant for
![]() $h>5$
, where
$h>5$
, where
![]() ${\it\omega}$
is the disturbance frequency.
${\it\omega}$
is the disturbance frequency.
In the CR, (a) the flow dependence on the axial coordinate
![]() $z$
is weak compared with that near the end disks and (b) the radial velocity is significantly smaller than the axial and swirl velocities. Features (a) and (b) allow an analysis of the circulatory flow stability in the framework of known instability mechanisms working in parallel flows. In particular, we also consider the stability of a
$z$
is weak compared with that near the end disks and (b) the radial velocity is significantly smaller than the axial and swirl velocities. Features (a) and (b) allow an analysis of the circulatory flow stability in the framework of known instability mechanisms working in parallel flows. In particular, we also consider the stability of a
![]() $z$
-independent swirling counterflow and compare the results with those for the Vogel–Escudier flow. Based on this analysis, we argue that the Vogel–Escudier-flow instability is of the shear-layer type.
$z$
-independent swirling counterflow and compare the results with those for the Vogel–Escudier flow. Based on this analysis, we argue that the Vogel–Escudier-flow instability is of the shear-layer type.
Finally, we explore effects of additional co-rotation of the sidewall on the base-flow pattern and stability. It is known that the co-rotation suppresses VBs (Shtern et al.
Reference Shtern, Torregrosa and Herrada2012). Here we show that the co-rotation suppresses instability as well. As the co-rotation intensifies, the centrifugal instability first develops as
![]() $\mathit{Re}$
increases.
$\mathit{Re}$
increases.
In this paper, we formulate the problem (§ 2), describe the numerical technique (§ 3), explore the base-flow features (§ 4) and its stability (§ 5), and the stability of a related one-dimensional flow (§ 6), describe the effects of additional rotation of the sidewall (§ 7), and summarize the results (§ 8).
2. Problem formulation
2.1. Flow geometry
Figure 1 is a schematic drawing of the problem geometry. We consider the flow of a viscous incompressible fluid in a cylindrical container of length
![]() $H$
and radius
$H$
and radius
![]() $R$
driven by the end disk at
$R$
driven by the end disk at
![]() $z=0$
, which rotates with angular velocity
$z=0$
, which rotates with angular velocity
![]() ${\it\Omega}$
. The two main control parameters are the aspect ratio
${\it\Omega}$
. The two main control parameters are the aspect ratio
![]() $h=H/R$
and the Reynolds number,
$h=H/R$
and the Reynolds number,
![]() $\mathit{Re}={\it\Omega}R^{2}/{\it\nu}$
, characterizing the swirl strength, where
$\mathit{Re}={\it\Omega}R^{2}/{\it\nu}$
, characterizing the swirl strength, where
![]() ${\it\nu}$
is the fluid kinematic viscosity. We also consider the flow with additional co-rotation of the sidewall (§ 7). The co-rotation parameter,
${\it\nu}$
is the fluid kinematic viscosity. We also consider the flow with additional co-rotation of the sidewall (§ 7). The co-rotation parameter,
![]() ${\it\Omega}_{s}$
, is the sidewall-to-disk angular velocity ratio.
${\it\Omega}_{s}$
, is the sidewall-to-disk angular velocity ratio.

Figure 1. Schematic of the problem.
2.2. Governing equations
Using
![]() $R,1/{\it\Omega},{\it\Omega}R$
, and
$R,1/{\it\Omega},{\it\Omega}R$
, and
![]() ${\it\rho}{\it\Omega}^{2}R^{2}$
as scales for length, time, velocity, and pressure, respectively, renders all variables dimensionless. The flow is governed by the Navier–Stokes equations for a viscous incompressible fluid, whose dimensionless form is:
${\it\rho}{\it\Omega}^{2}R^{2}$
as scales for length, time, velocity, and pressure, respectively, renders all variables dimensionless. The flow is governed by the Navier–Stokes equations for a viscous incompressible fluid, whose dimensionless form is:
where subscripts ‘
![]() $b$
’ and ‘
$b$
’ and ‘
![]() $d$
’ denote the base flow and a disturbance, respectively;
$d$
’ denote the base flow and a disturbance, respectively;
![]() $\text{c.c.}$
denotes the complex conjugate of the preceding term;
$\text{c.c.}$
denotes the complex conjugate of the preceding term;
![]() ${\it\varepsilon}\ll 1$
is an amplitude; integer
${\it\varepsilon}\ll 1$
is an amplitude; integer
![]() $m$
is an azimuthal wavenumber; and
$m$
is an azimuthal wavenumber; and
![]() ${\it\omega}={\it\omega}_{r}+\text{i}{\it\omega}_{i}$
is a complex number to be found, with frequency
${\it\omega}={\it\omega}_{r}+\text{i}{\it\omega}_{i}$
is a complex number to be found, with frequency
![]() ${\it\omega}_{r}$
and growth rate of disturbance
${\it\omega}_{r}$
and growth rate of disturbance
![]() ${\it\omega}_{i}$
. For a decaying (growing) disturbance,
${\it\omega}_{i}$
. For a decaying (growing) disturbance,
![]() ${\it\omega}_{i}$
is negative (positive). The equations governing the base flow result from substituting (2.5) in system (2.1)–(2.4) and setting
${\it\omega}_{i}$
is negative (positive). The equations governing the base flow result from substituting (2.5) in system (2.1)–(2.4) and setting
![]() ${\it\varepsilon}=0$
. The terms of order
${\it\varepsilon}=0$
. The terms of order
![]() $O({\it\varepsilon})$
constitute equations governing infinitesimal disturbances.
$O({\it\varepsilon})$
constitute equations governing infinitesimal disturbances.
2.3. Boundary conditions
The conditions for the base flow are the following.
-
(i) No-slip at the walls:
 $u_{b}=v_{b}=w_{b}=0$
at
$u_{b}=v_{b}=w_{b}=0$
at
 $z=h$
and
$z=h$
and
 $0<r<1$
(still disk),
$0<r<1$
(still disk), $u_{b}=v_{b}=w_{b}=0$
at
$u_{b}=v_{b}=w_{b}=0$
at
 $r=1$
and
$r=1$
and
 $0<z<h$
(sidewall),
$0<z<h$
(sidewall), $u_{b}=w_{b}=0$
,
$u_{b}=w_{b}=0$
,
 $v_{b}=r$
at
$v_{b}=r$
at
 $z=0$
and
$z=0$
and
 $0<r<1$
(rotating disk).
$0<r<1$
(rotating disk). -
(ii) Regularity at the axis:
 $u_{b}=v_{b}=0$
,
$u_{b}=v_{b}=0$
,
 $\partial w_{b}/\partial r=0$
at
$\partial w_{b}/\partial r=0$
at
 $r=0$
and
$r=0$
and
 $0<z<h$
.
$0<z<h$
.
For the problem where the sidewall also rotates, the conditions at the sidewall are modified to
![]() $u_{b}=w_{b}=0$
and
$u_{b}=w_{b}=0$
and
![]() $v_{b}={\it\Omega}_{s}$
at
$v_{b}={\it\Omega}_{s}$
at
![]() $r=1$
and
$r=1$
and
![]() $0<z<h$
.
$0<z<h$
.
The conditions for disturbances are the following.
-
(i) No-slip at all walls:
 $u_{d}=v_{d}=w_{d}=0$
.
$u_{d}=v_{d}=w_{d}=0$
. -
(ii) Regularity at the axis:
 $u_{d}=v_{d}=\partial w_{d}/\partial r=0$
at
$u_{d}=v_{d}=\partial w_{d}/\partial r=0$
at
 $m=0$
;
$m=0$
; $w_{d}=0$
,
$w_{d}=0$
,
 $\partial u_{d}/\partial r=0$
, and
$\partial u_{d}/\partial r=0$
, and
 $u_{d}+mv_{d}=0$
at
$u_{d}+mv_{d}=0$
at
 $|m|=1$
;
$|m|=1$
; $u_{d}=v_{d}=w_{d}=0$
for
$u_{d}=v_{d}=w_{d}=0$
for
 $|m|>1$
.
$|m|>1$
.
Since the equations and boundary conditions are uniform for disturbances, there is a trivial (zero) solution. Non-zero solutions exist at eigenvalues of
![]() ${\it\omega}$
. A disturbance with
${\it\omega}$
. A disturbance with
![]() ${\it\omega}_{i}=0$
is neutral. Neutral disturbances corresponding to the minimal Re at prescribed
${\it\omega}_{i}=0$
is neutral. Neutral disturbances corresponding to the minimal Re at prescribed
![]() $m$
are marginal. The marginal disturbance corresponding to the minimal Re among all
$m$
are marginal. The marginal disturbance corresponding to the minimal Re among all
![]() $m$
values is critical. Corresponding parameters
$m$
values is critical. Corresponding parameters
![]() ${\it\omega}_{r}$
and
${\it\omega}_{r}$
and
![]() $m$
are also named as marginal and critical (Sorensen et al.
Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009).
$m$
are also named as marginal and critical (Sorensen et al.
Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009).
3. Numeric technique
Equations for both the basic flow and disturbances are discretized using the same spatial mesh with
![]() $nr$
and
$nr$
and
![]() $nz$
Chebyshev collocation points along the
$nz$
Chebyshev collocation points along the
![]() $r$
and
$r$
and
![]() $z$
axes, respectively. We mostly use
$z$
axes, respectively. We mostly use
![]() $nr=41$
and
$nr=41$
and
![]() $nz=66$
. For prescribed Re,
$nz=66$
. For prescribed Re,
![]() $h$
, and
$h$
, and
![]() ${\it\Omega}_{s}$
, the resulting set of
${\it\Omega}_{s}$
, the resulting set of
![]() $4(nr\times nz)$
discrete nonlinear equations for the basic flow are solved iteratively using a Newton–Raphson procedure. Once the base flow is computed, and given an azimuthal wavenumber
$4(nr\times nz)$
discrete nonlinear equations for the basic flow are solved iteratively using a Newton–Raphson procedure. Once the base flow is computed, and given an azimuthal wavenumber
![]() $m$
, we use MATLAB subroutine EIGS to calculate the eigenvalues of the system of
$m$
, we use MATLAB subroutine EIGS to calculate the eigenvalues of the system of
![]() $4(nr\times nz)$
discrete linear equations.
$4(nr\times nz)$
discrete linear equations.
At a prescribed
![]() $m$
, fixing
$m$
, fixing
![]() $h$
(or
$h$
(or
![]() ${\it\Omega}_{s}$
) and changing
${\it\Omega}_{s}$
) and changing
![]() ${\it\Omega}_{s}$
(or
${\it\Omega}_{s}$
(or
![]() $h$
) to compute the marginal
$h$
) to compute the marginal
![]() $\mathit{Re}_{cr}$
, the function
$\mathit{Re}_{cr}$
, the function
![]() $f(\mathit{Re})={\it\omega}_{i}^{\ast }$
, where
$f(\mathit{Re})={\it\omega}_{i}^{\ast }$
, where
![]() ${\it\omega}_{i}^{\ast }$
is the largest imaginary part of eigenvalues for a given
${\it\omega}_{i}^{\ast }$
is the largest imaginary part of eigenvalues for a given
![]() $m$
, is driven to zero,
$m$
, is driven to zero,
![]() $f(\mathit{Re})=0$
, by using a Newton–Raphson method. This method fails when the marginal curve has folding points. In the folding case, a different approach is used. Both the basic and the perturbation problems are solved in the (
$f(\mathit{Re})=0$
, by using a Newton–Raphson method. This method fails when the marginal curve has folding points. In the folding case, a different approach is used. Both the basic and the perturbation problems are solved in the (
![]() $h,\mathit{Re}$
) or (
$h,\mathit{Re}$
) or (
![]() ${\it\Omega}_{s},\mathit{Re}$
) plane in the region of interest to compute the surface
${\it\Omega}_{s},\mathit{Re}$
) plane in the region of interest to compute the surface
![]() ${\it\omega}_{i}^{\ast }(h,\mathit{Re})$
(or
${\it\omega}_{i}^{\ast }(h,\mathit{Re})$
(or
![]() ${\it\omega}_{i}^{\ast }({\it\Omega}_{s},\mathit{Re})$
). Cubic interpolation is then used to draw the contour
${\it\omega}_{i}^{\ast }({\it\Omega}_{s},\mathit{Re})$
). Cubic interpolation is then used to draw the contour
![]() ${\it\omega}_{i}^{\ast }(h,\mathit{Re})$
which provide the marginal curve.
${\it\omega}_{i}^{\ast }(h,\mathit{Re})$
which provide the marginal curve.
The numerical technique was verified by using independent codes and by comparing our results with the numerical and experimental results obtained by Sorensen et al. (Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009), presented in figure 12, and PIV measurements by Kulikov et al. (Reference Kulikov, Mikkelsen, Naumov and Okulov2014) related to
![]() $\mathit{Re}_{cr}$
and
$\mathit{Re}_{cr}$
and
![]() ${\it\omega}_{r}$
. To draw streamlines of base flow, we use the Stokes stream function,
${\it\omega}_{r}$
. To draw streamlines of base flow, we use the Stokes stream function,
![]() ${\it\Psi}$
,
${\it\Psi}$
,
![]() $u_{b}=-r^{-1}\partial {\it\Psi}/\partial z$
,
$u_{b}=-r^{-1}\partial {\it\Psi}/\partial z$
,
![]() $w_{b}=r^{-1}\partial {\it\Psi}/\partial r$
.
$w_{b}=r^{-1}\partial {\it\Psi}/\partial r$
.
4. Features of the Vogel–Escudier flow in elongated cylinders
To understand the instability nature of the Vogel–Escudier flow, it is helpful to consider an elongated container. In this section, we discuss some important features of the base flow in cylinders with
![]() $h\gg 1$
.
$h\gg 1$
.
4.1. Formation of global counterflow
It is known that a swirling flow in a long cylindrical container with one rotating end disk is multicellular for
![]() $\mathit{Re}\ll 1$
(Hills Reference Hills2001). We show here how this multicellular flow transforms into a global counterflow as Re increases. Figure 2 represents streamlines, i.e. contours of
$\mathit{Re}\ll 1$
(Hills Reference Hills2001). We show here how this multicellular flow transforms into a global counterflow as Re increases. Figure 2 represents streamlines, i.e. contours of
![]() ${\it\Psi}=\text{const.}$
, of the meridional motion driven by the rotating disk located at
${\it\Psi}=\text{const.}$
, of the meridional motion driven by the rotating disk located at
![]() $z=0$
in a cylinder with
$z=0$
in a cylinder with
![]() $h=10$
.
$h=10$
.

Figure 2. Development of global counterflow as Re increases at
![]() $h=10$
;
$h=10$
;
![]() $\mathit{Re}=1$
(a), 2000 (b), 4000 (c), and 5000 (d).
$\mathit{Re}=1$
(a), 2000 (b), 4000 (c), and 5000 (d).
Figure 2(a) depicts the six flow cells existing at
![]() $\mathit{Re}=1$
. Our simulations show that the magnitude of
$\mathit{Re}=1$
. Our simulations show that the magnitude of
![]() ${\it\Psi}$
rapidly decays as
${\it\Psi}$
rapidly decays as
![]() $z$
increases. This agrees with the known feature that
$z$
increases. This agrees with the known feature that
![]() ${\it\Psi}$
decays at least as
${\it\Psi}$
decays at least as
![]() $\exp (-{\it\lambda}_{r}z)$
and oscillates as
$\exp (-{\it\lambda}_{r}z)$
and oscillates as
![]() $\sin ({\it\lambda}_{i}z)$
for small
$\sin ({\it\lambda}_{i}z)$
for small
![]() $\mathit{Re}$
;
$\mathit{Re}$
;
![]() ${\it\lambda}_{r}=4.466$
and
${\it\lambda}_{r}=4.466$
and
![]() ${\it\lambda}_{i}=1.468$
(Shankar Reference Shankar1998). In order to better observe the slow motion near the stationary disk, located at
${\it\lambda}_{i}=1.468$
(Shankar Reference Shankar1998). In order to better observe the slow motion near the stationary disk, located at
![]() $z=10$
,
$z=10$
,
![]() ${\it\Psi}$
is multiplied by
${\it\Psi}$
is multiplied by
![]() $\exp ({\it\lambda}_{r}z)$
in figure 2(a).
$\exp ({\it\lambda}_{r}z)$
in figure 2(a).
As Re increases, the cell adjacent to the rotating disk (left-hand cell in figure 2
a–d) extends while the other cells move toward the stationary disk, shrink, and disappear. There are three cells at
![]() $\mathit{Re}=2000$
(figure 2
b), one large and two small cells for
$\mathit{Re}=2000$
(figure 2
b), one large and two small cells for
![]() $\mathit{Re}=4000$
(figure 2
c). The second cell shown in figure 2(b) separates from the axis and shrinks near the sidewall as Re further increases, as figure 2(c) illustrates for
$\mathit{Re}=4000$
(figure 2
c). The second cell shown in figure 2(b) separates from the axis and shrinks near the sidewall as Re further increases, as figure 2(c) illustrates for
![]() $\mathit{Re}=4000$
. The near-sidewall cell disappears, the large and small cells merge, and the flow becomes one-cellular at
$\mathit{Re}=4000$
. The near-sidewall cell disappears, the large and small cells merge, and the flow becomes one-cellular at
![]() $\mathit{Re}=5000$
(figure 2
d).
$\mathit{Re}=5000$
(figure 2
d).
The solid curve in figure 3 depicts the dependence on Re of maximal axial extent
![]() $L$
of the cell adjacent to the rotating disk. Here,
$L$
of the cell adjacent to the rotating disk. Here,
![]() $L$
is the distance from the rotating disk to the point where the velocity at the axis changes its sign the first time (see figure 2
a). The dependence
$L$
is the distance from the rotating disk to the point where the velocity at the axis changes its sign the first time (see figure 2
a). The dependence
![]() $L(\mathit{Re})$
can be approximated by the linear relation,
$L(\mathit{Re})$
can be approximated by the linear relation,
![]() $L=4+0.00134\,\mathit{Re}$
, depicted by the dots in figure 3. In the range
$L=4+0.00134\,\mathit{Re}$
, depicted by the dots in figure 3. In the range
![]() $2000<\mathit{Re}<4480$
, the curve and dots merge within the accuracy displayed in figure 3.
$2000<\mathit{Re}<4480$
, the curve and dots merge within the accuracy displayed in figure 3.

Figure 3. Dependence of
![]() $L$
(see figure 2
a) on the Reynolds number. The dotted discrete points represent the linear approximation of the numerical data (solid curve).
$L$
(see figure 2
a) on the Reynolds number. The dotted discrete points represent the linear approximation of the numerical data (solid curve).
Below we discuss an important feature for the instability development: the appearance of a local maximum of the swirl vorticity as Re increases.
4.2. Formation of a local maximum of swirl vorticity
At the axis, the swirl vorticity is
![]() ${\it\omega}_{z}=2{\it\Omega}_{a}$
, where
${\it\omega}_{z}=2{\it\Omega}_{a}$
, where
![]() ${\it\Omega}_{a}$
is the angular velocity at
${\it\Omega}_{a}$
is the angular velocity at
![]() $r=0$
, which is prescribed at the rotating disk (
$r=0$
, which is prescribed at the rotating disk (
![]() $z=0$
) as
$z=0$
) as
![]() ${\it\Omega}_{a}=1$
. Figure 4 presents the distribution of
${\it\Omega}_{a}=1$
. Figure 4 presents the distribution of
![]() ${\it\Omega}_{a}$
along the axis in the vicinity of
${\it\Omega}_{a}$
along the axis in the vicinity of
![]() $z=0$
for the Re values shown near the curves. Curve
$z=0$
for the Re values shown near the curves. Curve
![]() $\mathit{Re}=1$
in figure 4 depicts the distribution mostly governed by viscous diffusion of
$\mathit{Re}=1$
in figure 4 depicts the distribution mostly governed by viscous diffusion of
![]() ${\it\omega}_{z}$
from the rotating disk; the role of meridional circulation (figure 2) is negligible for
${\it\omega}_{z}$
from the rotating disk; the role of meridional circulation (figure 2) is negligible for
![]() $\mathit{Re}\leqslant 1$
. As Re increases, the circulation contribution becomes remarkable. The backflow near the axis transports
$\mathit{Re}\leqslant 1$
. As Re increases, the circulation contribution becomes remarkable. The backflow near the axis transports
![]() ${\it\omega}_{z}$
toward the disk thus diminishing the diffusion of
${\it\omega}_{z}$
toward the disk thus diminishing the diffusion of
![]() ${\it\omega}_{z}$
away from the disk. Comparison of curves
${\it\omega}_{z}$
away from the disk. Comparison of curves
![]() $\mathit{Re}=1$
and
$\mathit{Re}=1$
and
![]() $\mathit{Re}=100$
in figure 4 illustrates this effect:
$\mathit{Re}=100$
in figure 4 illustrates this effect:
![]() ${\it\Omega}_{a}$
is significantly reduced near the disk at
${\it\Omega}_{a}$
is significantly reduced near the disk at
![]() $\mathit{Re}=100$
compared with that at
$\mathit{Re}=100$
compared with that at
![]() $\mathit{Re}=1$
.
$\mathit{Re}=1$
.

Figure 4. Development of a local maximum of angular velocity
![]() ${\it\Omega}_{a}$
on the axis as Re (shown near the curves) increases; the dashed curve corresponds to the Kármán boundary layer.
${\it\Omega}_{a}$
on the axis as Re (shown near the curves) increases; the dashed curve corresponds to the Kármán boundary layer.
For larger Re, the boundary layer develops near the rotating disk (von Kármán Reference von Kármán1921). The dashed curve in figure 4 depicts the distribution of
![]() ${\it\Omega}_{a}$
, corresponding to Kármán’s solution at
${\it\Omega}_{a}$
, corresponding to Kármán’s solution at
![]() $\mathit{Re}=500$
. This curve and those for
$\mathit{Re}=500$
. This curve and those for
![]() $\mathit{Re}=1$
and 100 illustrate the formation of the boundary layer as Re increases.
$\mathit{Re}=1$
and 100 illustrate the formation of the boundary layer as Re increases.
The distribution of
![]() ${\it\Omega}_{a}$
, depicted by solid curve
${\it\Omega}_{a}$
, depicted by solid curve
![]() $\mathit{Re}=500$
in figure 4, qualitatively differs from those shown by the other curves: there is a local maximum of
$\mathit{Re}=500$
in figure 4, qualitatively differs from those shown by the other curves: there is a local maximum of
![]() ${\it\Omega}_{a}$
near
${\it\Omega}_{a}$
near
![]() $z=0.8$
. The maximum appears due to the intensified meridional circulation, as discussed below.
$z=0.8$
. The maximum appears due to the intensified meridional circulation, as discussed below.
The circulatory flow (left-hand cell in figure 2
a–d) transports the angular momentum,
![]() $rv$
, from the disk periphery along the sidewall and then toward the axis, thus increasing the swirl vorticity there. As figure 5 illustrates, the backflow velocity magnitude,
$rv$
, from the disk periphery along the sidewall and then toward the axis, thus increasing the swirl vorticity there. As figure 5 illustrates, the backflow velocity magnitude,
![]() $-w_{a}$
, at the axis,
$-w_{a}$
, at the axis,
![]() $r=0$
, is maximal in the vicinity of the local maximum of
$r=0$
, is maximal in the vicinity of the local maximum of
![]() ${\it\Omega}_{a}$
(figure 4). The dashed curve in figure 5 depicts Kármán’s solution for
${\it\Omega}_{a}$
(figure 4). The dashed curve in figure 5 depicts Kármán’s solution for
![]() $-w_{a}$
, which saturates to
$-w_{a}$
, which saturates to
![]() $0.885/\mathit{Re}^{1/2}$
outside the boundary layer as
$0.885/\mathit{Re}^{1/2}$
outside the boundary layer as
![]() $z$
increases.
$z$
increases.

Figure 5. Velocity on the axis near the rotating disk at
![]() $\mathit{Re}=500$
; the dashed curve corresponds to the Kármán boundary layer.
$\mathit{Re}=500$
; the dashed curve corresponds to the Kármán boundary layer.
The difference between the solid and dashed curves in figures 4 and 5 is provided by the meridional circulation which develops due to the presence of the sidewall. This flow transformation causes an important change in the pressure pattern discussed next.
4.3. Alteration of local minimum of pressure
The local maximum of swirl vorticity results in a local minimum of pressure. The cyclostrophic balance,
![]() $\partial p/\partial r=v^{2}/r$
, and the solid-body swirl distribution,
$\partial p/\partial r=v^{2}/r$
, and the solid-body swirl distribution,
![]() $v={\it\Omega}_{a}r$
, occurring near the axis, yield that
$v={\it\Omega}_{a}r$
, occurring near the axis, yield that
![]() $\partial p/\partial r={\it\Omega}_{a}^{2}r$
, i.e. the pressure is minimal on the axis at the
$\partial p/\partial r={\it\Omega}_{a}^{2}r$
, i.e. the pressure is minimal on the axis at the
![]() $z$
value where
$z$
value where
![]() ${\it\Omega}_{a}$
is maximal. Figure 6 illustrates that the location of the pressure minimum at the axis,
${\it\Omega}_{a}$
is maximal. Figure 6 illustrates that the location of the pressure minimum at the axis,
![]() $r=0$
, shifts away from the rotating disk,
$r=0$
, shifts away from the rotating disk,
![]() $z=0$
, as Re increases. This shift occurs because the pressure drop across the Kármán boundary layer,
$z=0$
, as Re increases. This shift occurs because the pressure drop across the Kármán boundary layer,
![]() ${\rm\Delta}p_{K}=0.3825/\mathit{Re}$
, decreases while the pressure drop due to the meridional circulation,
${\rm\Delta}p_{K}=0.3825/\mathit{Re}$
, decreases while the pressure drop due to the meridional circulation,
![]() ${\rm\Delta}p_{c}$
, increases, as Re grows. For example,
${\rm\Delta}p_{c}$
, increases, as Re grows. For example,
![]() ${\rm\Delta}p_{K}=0.000765$
and
${\rm\Delta}p_{K}=0.000765$
and
![]() ${\rm\Delta}p_{c}=0.005$
at
${\rm\Delta}p_{c}=0.005$
at
![]() $\mathit{Re}=500$
. The
$\mathit{Re}=500$
. The
![]() $p_{min}$
location at
$p_{min}$
location at
![]() $\mathit{Re}=500$
(figure 6
b) is close to the
$\mathit{Re}=500$
(figure 6
b) is close to the
![]() ${\it\Omega}_{amax}$
location (figure 4). As Re further increases, the pressure minimum location moves away from the rotating disk.
${\it\Omega}_{amax}$
location (figure 4). As Re further increases, the pressure minimum location moves away from the rotating disk.

Figure 6. Pressure contours near the rotating disk for
![]() $\mathit{Re}=1$
(a) and 500 (b). The pressure minimum location on the axis,
$\mathit{Re}=1$
(a) and 500 (b). The pressure minimum location on the axis,
![]() $r=0$
, shifts for larger
$r=0$
, shifts for larger
![]() $z$
as Re increases.
$z$
as Re increases.
4.4. Base-flow features at
 $\mathit{Re}=3100$
and
$\mathit{Re}=3100$
and
 $h=8$
$h=8$
Figure 7(a) depicts contours of azimuthal vorticity
![]() ${\it\omega}_{{\it\phi}}=\partial u/\partial z-\partial w/\partial r$
, which is positive (dark contours) near the rotating disk and the sidewall, and negative (light contours) near the axis. It is important to remark for the following stability study that the negative vorticity has a local minimum at
${\it\omega}_{{\it\phi}}=\partial u/\partial z-\partial w/\partial r$
, which is positive (dark contours) near the rotating disk and the sidewall, and negative (light contours) near the axis. It is important to remark for the following stability study that the negative vorticity has a local minimum at
![]() $r=0.46$
and
$r=0.46$
and
![]() $z=2.95$
(bold black point in figure 7
a).
$z=2.95$
(bold black point in figure 7
a).

Figure 7. Azimuthal vorticity (a) and stream function (b) contours at
![]() $\mathit{Re}=3100$
and
$\mathit{Re}=3100$
and
![]() $h=8$
. The dark contours are positive and the light contours negative.
$h=8$
. The dark contours are positive and the light contours negative.
Figure 7(b) depicts streamlines,
![]() ${\it\Psi}=\text{const.}$
, at these Re and
${\it\Psi}=\text{const.}$
, at these Re and
![]() $h$
. The rotating disk (
$h$
. The rotating disk (
![]() $z=0$
) pushes the fluid to the periphery near the disk and develops the clockwise circulation. The streamlines are packed in the Kármán boundary layer near the rotating disk, form the annular jet near the sidewall (
$z=0$
) pushes the fluid to the periphery near the disk and develops the clockwise circulation. The streamlines are packed in the Kármán boundary layer near the rotating disk, form the annular jet near the sidewall (
![]() $r=1$
), turn around, and constitute the backflow near the axis (
$r=1$
), turn around, and constitute the backflow near the axis (
![]() $r=0$
). Here,
$r=0$
). Here,
![]() ${\it\Psi}$
reaches its maximal magnitude at
${\it\Psi}$
reaches its maximal magnitude at
![]() $r=0.68$
and
$r=0.68$
and
![]() $z=1.58$
(bold black point in figure 7
b).
$z=1.58$
(bold black point in figure 7
b).
Figure 8 depicts the
![]() $z$
-dependence at the axis,
$z$
-dependence at the axis,
![]() $r=0$
, of
$r=0$
, of
![]() $w_{a}$
,
$w_{a}$
,
![]() ${\it\Omega}_{a}$
, and
${\it\Omega}_{a}$
, and
![]() $p$
. Pressure
$p$
. Pressure
![]() $p$
is multiplied by 15 for convenient observation. Functions
$p$
is multiplied by 15 for convenient observation. Functions
![]() ${\it\Omega}_{a}(z)$
and
${\it\Omega}_{a}(z)$
and
![]() $w_{a}(z)$
have large-magnitude derivatives near
$w_{a}(z)$
have large-magnitude derivatives near
![]() $z=0$
, related to the Kármán boundary layer (see the dashed curves in figures 4 and 5). In this layer,
$z=0$
, related to the Kármán boundary layer (see the dashed curves in figures 4 and 5). In this layer,
![]() ${\it\Omega}_{a}$
drops from 1 at
${\it\Omega}_{a}$
drops from 1 at
![]() $z=0$
down to its local minimum 0.033 at
$z=0$
down to its local minimum 0.033 at
![]() $z=z_{K}=0.17=9.2/\mathit{Re}^{1/2}$
.
$z=z_{K}=0.17=9.2/\mathit{Re}^{1/2}$
.

Figure 8. Distribution of velocity
![]() $w_{a}$
, angular velocity
$w_{a}$
, angular velocity
![]() ${\it\Omega}_{a}$
, and pressure
${\it\Omega}_{a}$
, and pressure
![]() $p$
, as labelled, at the axis for
$p$
, as labelled, at the axis for
![]() $\mathit{Re}=3100$
.
$\mathit{Re}=3100$
.
Pressure
![]() $p$
and axial velocity
$p$
and axial velocity
![]() $w_{a}$
reach their minimal values at
$w_{a}$
reach their minimal values at
![]() $z=2.5$
and 2.7 respectively, while
$z=2.5$
and 2.7 respectively, while
![]() ${\it\Omega}_{a}$
reaches its local maximum at
${\it\Omega}_{a}$
reaches its local maximum at
![]() $z=2.7$
. Therefore, near these
$z=2.7$
. Therefore, near these
![]() $z$
values, the circulation flow is strong. All quantities presented in figure 8 are negligibly small for
$z$
values, the circulation flow is strong. All quantities presented in figure 8 are negligibly small for
![]() $z>z_{c}\approx 7$
where
$z>z_{c}\approx 7$
where
![]() ${\it\Omega}_{a}<1/\mathit{Re}$
, i.e. the flow is creeping in the region,
${\it\Omega}_{a}<1/\mathit{Re}$
, i.e. the flow is creeping in the region,
![]() $z_{c}<z<h$
.
$z_{c}<z<h$
.
4.5. Three sub-regions of base flow
Summarizing the above results, we can distinguish the following flow regions for
![]() $h\gg 1$
:
$h\gg 1$
:
-
(i) a Kármán boundary layer in the range
 $0<z<z_{K}=9.2/\mathit{Re}^{1/2}$
;
$0<z<z_{K}=9.2/\mathit{Re}^{1/2}$
; -
(ii) circulation flow in the range
 $z_{K}<z<z_{c}$
;
$z_{K}<z<z_{c}$
; -
(iii) creeping flow in the range
 $z_{c}<z<h$
.
$z_{c}<z<h$
.
The strength of the circulation flow (ii) can be characterized by the maximal magnitude of velocity at the axis,
![]() $|w_{a}|_{max}$
, or by
$|w_{a}|_{max}$
, or by
![]() $\mathit{Re}_{a}=|w_{a}|_{max}\mathit{Re}$
. For example, we have
$\mathit{Re}_{a}=|w_{a}|_{max}\mathit{Re}$
. For example, we have
![]() $|w_{a}|_{max}=0.0734$
and
$|w_{a}|_{max}=0.0734$
and
![]() $\mathit{Re}_{a}=227$
at
$\mathit{Re}_{a}=227$
at
![]() $\mathit{Re}=3100$
. As shown below, the instability emerges in the middle of the circulation region (ii).
$\mathit{Re}=3100$
. As shown below, the instability emerges in the middle of the circulation region (ii).
5. Instability nature
5.1. Critical parameters for
 $h>3$
$h>3$
Figure 9 depicts numerical data for the dependence of (a) critical Reynolds number,
![]() $\mathit{Re}_{cr}$
, and (b) critical disturbance frequency,
$\mathit{Re}_{cr}$
, and (b) critical disturbance frequency,
![]() ${\it\omega}$
, on cylinder aspect ratio
${\it\omega}$
, on cylinder aspect ratio
![]() $h$
. The filled square symbols represent our results, which are also denoted by letter ‘M’. The other symbols, denoted by letter ‘S’, correspond to the results of Sorensen et al. (Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009). Numbers next to ‘M’ and ‘S’ in figure 9 indicate the values of
$h$
. The filled square symbols represent our results, which are also denoted by letter ‘M’. The other symbols, denoted by letter ‘S’, correspond to the results of Sorensen et al. (Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009). Numbers next to ‘M’ and ‘S’ in figure 9 indicate the values of
![]() $m$
for the critical disturbances. Our results agree with results of Sorensen et al. (Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009) for
$m$
for the critical disturbances. Our results agree with results of Sorensen et al. (Reference Sorensen, Gelfgat, Naumov and Mikkelsen2009) for
![]() $h\leqslant 5.5$
and reveal that
$h\leqslant 5.5$
and reveal that
![]() $\mathit{Re}_{cr}$
,
$\mathit{Re}_{cr}$
,
![]() ${\it\omega}_{cr}$
, and
${\it\omega}_{cr}$
, and
![]() $m_{cr}$
are nearlly
$m_{cr}$
are nearlly
![]() $h$
-independent for
$h$
-independent for
![]() $h>5.5$
, as can be checked with the numerical values shown in table 1.
$h>5.5$
, as can be checked with the numerical values shown in table 1.

Figure 9. Critical values of (a) Reynolds number (
![]() $\mathit{Re}_{cr}$
) and (b) disturbance frequency (
$\mathit{Re}_{cr}$
) and (b) disturbance frequency (
![]() ${\it\omega}$
) for cylinder aspect ratio
${\it\omega}$
) for cylinder aspect ratio
![]() $3.2<h<8$
. Letters mark our (M) and Sorensen et al.’s (S) results, respectively. Numbers next to ‘M’ and ‘S’ indicate helix value
$3.2<h<8$
. Letters mark our (M) and Sorensen et al.’s (S) results, respectively. Numbers next to ‘M’ and ‘S’ indicate helix value
![]() $m$
.
$m$
.
Table 1. Dependence of critical stability characteristics on aspect ratio
![]() $h$
.
$h$
.

5.2. Spatial distribution of disturbance energy
To help understand why the critical parameters, presented in figure 9 and table 1, are nearly
![]() $h$
-independent, figure 10 depicts contours
$h$
-independent, figure 10 depicts contours
![]() $E_{d}=\text{const.}$
on the
$E_{d}=\text{const.}$
on the
![]() $r{-}z$
plane for
$r{-}z$
plane for
![]() $h$
varying from 5.5 to 8 at
$h$
varying from 5.5 to 8 at
![]() $\mathit{Re}=3100$
;
$\mathit{Re}=3100$
;
![]() $E_{d}$
is the time-averaged kinetic energy of critical disturbance normalized by its maximal value,
$E_{d}$
is the time-averaged kinetic energy of critical disturbance normalized by its maximal value,
![]() $E_{dm}$
. The outermost contours in figure 10 correspond to
$E_{dm}$
. The outermost contours in figure 10 correspond to
![]() $E_{d}=0.1E_{dm}$
and show that
$E_{d}=0.1E_{dm}$
and show that
![]() $E_{d}$
is localized in the middle of circulation flow region (ii). The maximum
$E_{d}$
is localized in the middle of circulation flow region (ii). The maximum
![]() $E_{d}$
is located at
$E_{d}$
is located at
![]() $r=r_{E}=0.52$
and
$r=r_{E}=0.52$
and
![]() $z=z_{E}=2.3$
. These values and the
$z=z_{E}=2.3$
. These values and the
![]() $E_{d}$
contours are nearly the same for all
$E_{d}$
contours are nearly the same for all
![]() $h$
in figure 10.
$h$
in figure 10.

Figure 10. Contours of constant kinetic energy
![]() $E_{d}$
of critical disturbance for
$E_{d}$
of critical disturbance for
![]() $h=5.5$
(a), 6 (b), 6.5 (c), 7 (d), 7.5 (e), and 8 (f) at
$h=5.5$
(a), 6 (b), 6.5 (c), 7 (d), 7.5 (e), and 8 (f) at
![]() $\mathit{Re}=3100$
.
$\mathit{Re}=3100$
.
Figure 11 depicts the
![]() $z$
-dependence of
$z$
-dependence of
![]() $E_{d}$
and the base-flow velocity at the axis,
$E_{d}$
and the base-flow velocity at the axis,
![]() $-w_{a}$
. Both
$-w_{a}$
. Both
![]() $E_{d}$
and
$E_{d}$
and
![]() $-w_{a}$
are normalized by their maximal values. Here,
$-w_{a}$
are normalized by their maximal values. Here,
![]() $E_{d}$
is shown at the radial coordinate of the
$E_{d}$
is shown at the radial coordinate of the
![]() $E_{d}$
peak, i.e.
$E_{d}$
peak, i.e.
![]() $r=0.52$
(figure 10). Figure 11 confirms that the disturbance energy is localized in the middle of circulatory flow region (ii) and shows that
$r=0.52$
(figure 10). Figure 11 confirms that the disturbance energy is localized in the middle of circulatory flow region (ii) and shows that
![]() $E_{d}$
vanishes both in the Kármán boundary layer region (i) and in the region (iii) near
$E_{d}$
vanishes both in the Kármán boundary layer region (i) and in the region (iii) near
![]() $z=h$
where the flow is creeping. This feature helps understand why the critical parameters are invariant for
$z=h$
where the flow is creeping. This feature helps understand why the critical parameters are invariant for
![]() $5.5<h<8$
(figure 9), and indicates that the invariance can be expected for larger
$5.5<h<8$
(figure 9), and indicates that the invariance can be expected for larger
![]() $h$
as well.
$h$
as well.

Figure 11.
![]() $z$
-dependence of base flow velocity,
$z$
-dependence of base flow velocity,
![]() $w_{a}$
, at axis
$w_{a}$
, at axis
![]() $r=0$
, and kinetic energy of critical disturbance,
$r=0$
, and kinetic energy of critical disturbance,
![]() $E_{d}$
, at
$E_{d}$
, at
![]() $r=0.52$
; for
$r=0.52$
; for
![]() $h=8$
and
$h=8$
and
![]() $\mathit{Re}=\mathit{Re}_{cr}$
.
$\mathit{Re}=\mathit{Re}_{cr}$
.
Figure 12 depicts the
![]() $r$
-dependence of base-flow velocities
$r$
-dependence of base-flow velocities
![]() $u,v,w$
, and disturbance energy
$u,v,w$
, and disturbance energy
![]() $E_{d}$
at
$E_{d}$
at
![]() $z=2.3$
, which is the axial coordinate of the
$z=2.3$
, which is the axial coordinate of the
![]() $E_{d}$
peak, for
$E_{d}$
peak, for
![]() $h=8$
and
$h=8$
and
![]() $\mathit{Re}=\mathit{Re}_{cr}$
(table 1). The velocities are normalized by
$\mathit{Re}=\mathit{Re}_{cr}$
(table 1). The velocities are normalized by
![]() $|w(0)|$
and
$|w(0)|$
and
![]() $E_{d}$
is normalized by its maximal value. Figure 12 reveals that the radial velocity
$E_{d}$
is normalized by its maximal value. Figure 12 reveals that the radial velocity
![]() $u$
of the base flow is very small compared to the axial
$u$
of the base flow is very small compared to the axial
![]() $w$
and swirl
$w$
and swirl
![]() $v$
velocities, while maximal magnitudes of
$v$
velocities, while maximal magnitudes of
![]() $w$
and
$w$
and
![]() $v$
are comparable. Figure 12 also shows that
$v$
are comparable. Figure 12 also shows that
![]() $E_{d}$
is localized in the radial direction as well.
$E_{d}$
is localized in the radial direction as well.

Figure 12.
![]() $r$
-dependence of base-flow velocities
$r$
-dependence of base-flow velocities
![]() $u,v,w$
, and kinetic energy of critical disturbance
$u,v,w$
, and kinetic energy of critical disturbance
![]() $E_{d}$
at
$E_{d}$
at
![]() $z=2.3$
, for
$z=2.3$
, for
![]() $h=8$
and
$h=8$
and
![]() $\mathit{Re}=\mathit{Re}_{cr}$
.
$\mathit{Re}=\mathit{Re}_{cr}$
.
The peak location of
![]() $E_{d}$
(figure 10) is close to the location of minimum base-flow azimuthal vorticity (see the bold black point in figure 7
a). This feature implies that the instability could be of the shear-layer type, caused by the presence of an inflection point in the radial profile of axial velocity (see curve for
$E_{d}$
(figure 10) is close to the location of minimum base-flow azimuthal vorticity (see the bold black point in figure 7
a). This feature implies that the instability could be of the shear-layer type, caused by the presence of an inflection point in the radial profile of axial velocity (see curve for
![]() $w$
in figure 12).
$w$
in figure 12).
Since
![]() $E_{d}$
is localized in
$E_{d}$
is localized in
![]() $1<z<4$
(figure 11), we guess that the instability is a result of the strong counterflow developing in the central part of circulatory region (ii). The central part of the flow also remains nearly invariant as
$1<z<4$
(figure 11), we guess that the instability is a result of the strong counterflow developing in the central part of circulatory region (ii). The central part of the flow also remains nearly invariant as
![]() $h$
increases from 5.5 to 8. A suitable characteristic of the strong counterflow is
$h$
increases from 5.5 to 8. A suitable characteristic of the strong counterflow is
![]() $\mathit{Re}_{a}=|w_{a}|_{max}\,\mathit{Re}$
, whose critical value is 239 at
$\mathit{Re}_{a}=|w_{a}|_{max}\,\mathit{Re}$
, whose critical value is 239 at
![]() $h=8$
.
$h=8$
.
6. Instability of a
 $z$
-independent flow model
$z$
-independent flow model
To test the above conjecture, we consider the
![]() $z$
-independent flow,
$z$
-independent flow,
![]() $u=0$
,
$u=0$
,
![]() $v=V(r)$
,
$v=V(r)$
,
![]() $w=W(r)$
, in an unbounded pipe, where
$w=W(r)$
, in an unbounded pipe, where
![]() $V(r)$
and
$V(r)$
and
![]() $W(r)$
are the swirl and axial velocities depicted by curves
$W(r)$
are the swirl and axial velocities depicted by curves
![]() $v$
and
$v$
and
![]() $w$
in figure 12. To study the instability of this flow, we use the representation
$w$
in figure 12. To study the instability of this flow, we use the representation
which is similar to (2.5), but modified for the
![]() $z$
-independent base flow. Substituting (6.1) in system (2.1)–(2.4) yields (to
$z$
-independent base flow. Substituting (6.1) in system (2.1)–(2.4) yields (to
![]() $O({\it\varepsilon})$
) ordinary differential equations describing the stability of the
$O({\it\varepsilon})$
) ordinary differential equations describing the stability of the
![]() $z$
-independent flow to infinitesimal disturbances. The uniform boundary conditions for the disturbances are no-slip at the pipe wall,
$z$
-independent flow to infinitesimal disturbances. The uniform boundary conditions for the disturbances are no-slip at the pipe wall,
![]() $r=1$
, and regularity at the axis,
$r=1$
, and regularity at the axis,
![]() $r=0$
.
$r=0$
.
To numerically solve this stability problem, we use a technique similar to that described by Herrada, Pérez-Saborid & Barrero (Reference Herrada, Pérez-Saborid and Barrero2004). The equations and boundary conditions are discretized by expanding the fields in terms of a truncated Chebyshev series in the
![]() $r$
direction. The resulting problem is solved using MATLAB subroutine EIGS, which provides the entire spectrum of both eigenvalues and eigenfunctions. Spurious eigenvalues are ruled out by comparing the results for different numbers,
$r$
direction. The resulting problem is solved using MATLAB subroutine EIGS, which provides the entire spectrum of both eigenvalues and eigenfunctions. Spurious eigenvalues are ruled out by comparing the results for different numbers,
![]() $nr$
, of collocation points in the
$nr$
, of collocation points in the
![]() $r$
direction. After some calibration,
$r$
direction. After some calibration,
![]() $nr=40$
is used.
$nr=40$
is used.
The minimal (critical) marginal
![]() $\mathit{Re}_{a}$
, corresponding to
$\mathit{Re}_{a}$
, corresponding to
![]() $m=1$
, is rather small. This feature is typical of the shear-layer instability. At
$m=1$
, is rather small. This feature is typical of the shear-layer instability. At
![]() $m=0$
, the marginal
$m=0$
, the marginal
![]() $\mathit{Re}_{a}$
is large compared with those for
$\mathit{Re}_{a}$
is large compared with those for
![]() $m\neq 0$
, i.e. three-dimensional disturbances are more dangerous than the axisymmetric disturbances as table 2 illustrates.
$m\neq 0$
, i.e. three-dimensional disturbances are more dangerous than the axisymmetric disturbances as table 2 illustrates.
Figure 13 depicts the neutral curves for
![]() $m=1$
, 2, 3 and 4 (shown near the curves). Since in the 2D problem, the strong counterflow and the disturbance energy have limited axial extent, for a reasonable comparison we focus on neutral disturbances of small wavelength, i.e. large
$m=1$
, 2, 3 and 4 (shown near the curves). Since in the 2D problem, the strong counterflow and the disturbance energy have limited axial extent, for a reasonable comparison we focus on neutral disturbances of small wavelength, i.e. large
![]() $k$
, in the one-dimensional problem. To this end, we compare the upper branches of the neutral curves for different
$k$
, in the one-dimensional problem. To this end, we compare the upper branches of the neutral curves for different
![]() $m$
presented in figure 13. The larger the
$m$
presented in figure 13. The larger the
![]() $m$
, the larger the range of
$m$
, the larger the range of
![]() $k$
for growing disturbances will be. For example, at
$k$
for growing disturbances will be. For example, at
![]() $m=4$
, the
$m=4$
, the
![]() $k$
-range of growing disturbances saturates to
$k$
-range of growing disturbances saturates to
![]() $0<k<5$
as
$0<k<5$
as
![]() $\mathit{Re}_{a}\rightarrow \infty$
. This wide range, indicating the instability inviscid character, is also typical for the shear-layer instability.
$\mathit{Re}_{a}\rightarrow \infty$
. This wide range, indicating the instability inviscid character, is also typical for the shear-layer instability.

Figure 13. Neutral curves of
![]() $z$
-independent base flow for the
$z$
-independent base flow for the
![]() $m$
values shown near the curves.
$m$
values shown near the curves.
It is reasonable that the critical
![]() $\mathit{Re}_{a}$
for the
$\mathit{Re}_{a}$
for the
![]() $z$
-independent flow is smaller than that for the Vogel–Escudier flow (see
$z$
-independent flow is smaller than that for the Vogel–Escudier flow (see
![]() $\mathit{Re}_{a}$
in the
$\mathit{Re}_{a}$
in the
![]() ${\it\Omega}_{s}=0$
row in table 3) because the latter flow weakens for
${\it\Omega}_{s}=0$
row in table 3) because the latter flow weakens for
![]() $z<z_{w}$
and
$z<z_{w}$
and
![]() $z>z_{w}$
(see
$z>z_{w}$
(see
![]() $z_{w}$
value in table 3, discussed in the next section). Based on the above results, we conclude that the shear-layer nature of instability is common for the Vogel–Escudier and
$z_{w}$
value in table 3, discussed in the next section). Based on the above results, we conclude that the shear-layer nature of instability is common for the Vogel–Escudier and
![]() $z$
-independent flows.
$z$
-independent flows.
7. Stabilizing effect of additional co-rotation of sidewall
It is known that an additional co-rotation of the sidewall is an efficient means to suppress VBs in the Vogel–Escudier flow (Shtern et al. Reference Shtern, Torregrosa and Herrada2012). Here we explore whether the sidewall co-rotation can suppress the flow instability.
7.1. Shear-layer instability
Table 3 shows how the critical parameters depend on sidewall-to-disk angular velocity ratio
![]() ${\it\Omega}_{s}$
at
${\it\Omega}_{s}$
at
![]() $h=8$
. There
$h=8$
. There
![]() $z_{w}~(z_{E})$
is the axial coordinate where the magnitude of base-flow axial velocity
$z_{w}~(z_{E})$
is the axial coordinate where the magnitude of base-flow axial velocity
![]() $w$
(disturbance energy
$w$
(disturbance energy
![]() $E_{d}$
) reaches its maximal value. Table 3 reveals that even a weak co-rotation causes a significant increase in
$E_{d}$
) reaches its maximal value. Table 3 reveals that even a weak co-rotation causes a significant increase in
![]() $\mathit{Re}_{cr}$
. In contrast to
$\mathit{Re}_{cr}$
. In contrast to
![]() $\mathit{Re}_{cr}$
, the critical
$\mathit{Re}_{cr}$
, the critical
![]() $\mathit{Re}_{a}$
is nearly invariant and even slightly decreases as
$\mathit{Re}_{a}$
is nearly invariant and even slightly decreases as
![]() ${\it\Omega}_{s}$
grows.
${\it\Omega}_{s}$
grows.
Table 2. Marginal and critical (bold) stability parameters for
![]() $z$
-independent flow.
$z$
-independent flow.

Table 3. Dependence of marginal and critical (bold) parameters on sidewall co-rotation
![]() ${\it\Omega}_{s}$
for shear-layer instability at
${\it\Omega}_{s}$
for shear-layer instability at
![]() $h=8$
.
$h=8$
.

Note that the
![]() $z$
-location of the
$z$
-location of the
![]() $E_{d}$
peak (
$E_{d}$
peak (
![]() $z_{E}$
) is smaller than that for the maximum of
$z_{E}$
) is smaller than that for the maximum of
![]() $-w_{a}$
(
$-w_{a}$
(
![]() $z_{w}$
) for all
$z_{w}$
) for all
![]() ${\it\Omega}_{s}$
values in table 3. Therefore, the instability develops where the base flow decelerates near the axis. This feature agrees with the destabilizing effect of base-flow deceleration typical of swirling and swirl-free jets (Shtern Reference Shtern2012).
${\it\Omega}_{s}$
values in table 3. Therefore, the instability develops where the base flow decelerates near the axis. This feature agrees with the destabilizing effect of base-flow deceleration typical of swirling and swirl-free jets (Shtern Reference Shtern2012).
Figure 14 depicts the
![]() $z$
-dependence of (a) velocity
$z$
-dependence of (a) velocity
![]() $w_{a}$
, (b) angular velocity
$w_{a}$
, (b) angular velocity
![]() ${\it\Omega}_{a}$
, and (c) pressure
${\it\Omega}_{a}$
, and (c) pressure
![]() $p$
along the axis,
$p$
along the axis,
![]() $r=0$
, of the base flow for the parameter values listed in table 3. Figure 14 reveals the following effects of the sidewall co-rotation.
$r=0$
, of the base flow for the parameter values listed in table 3. Figure 14 reveals the following effects of the sidewall co-rotation.
-
(a) The co-rotation kills creeping flow in the region (iii) and induces a tornado-like motion near the stationary disk. The swirling flow converges to the axis near the disk and forms a strong near-axis jet directed away from the disk. The motion mechanism is similar to that driving the Bödewadt flow. According to the Bödewadt (Reference Bödewadt1940) solution, the flow characteristics are ‘wavy’ at the axis. The dotted lines in figure 14(b,c) are also ‘wavy’, having local minima and maxima, near the stationary disk located at
 $z=h=8$
.
$z=h=8$
. -
(b) The
 $w$
maximal magnitude decreases as the co-rotation increases. This feature follows from the swirl decay mechanism, SDM, which drives the meridional circulation (§ 1). The co-rotation increases angular velocity
$w$
maximal magnitude decreases as the co-rotation increases. This feature follows from the swirl decay mechanism, SDM, which drives the meridional circulation (§ 1). The co-rotation increases angular velocity
 ${\it\Omega}_{a}$
near the stationary disk (figure 14
b) and thus reduces the swirl decay and the magnitude of pressure variations in the
${\it\Omega}_{a}$
near the stationary disk (figure 14
b) and thus reduces the swirl decay and the magnitude of pressure variations in the
 $z$
direction (figure 14
c). This weakens circulation flow in the region (ii).
$z$
direction (figure 14
c). This weakens circulation flow in the region (ii). -
(c) The location of the
 $w$
maximal magnitude shifts toward the stationary disk as
$w$
maximal magnitude shifts toward the stationary disk as
 ${\it\Omega}_{s}$
increases. A local maximum of
${\it\Omega}_{s}$
increases. A local maximum of
 $w_{a}$
emerges near the rotating disk (dotted and dashed curves in figure 14
a). This is a precursor of a VB developing as
$w_{a}$
emerges near the rotating disk (dotted and dashed curves in figure 14
a). This is a precursor of a VB developing as
 ${\it\Omega}_{s}$
further increases (dash-dotted curve in figure 14
a).
${\it\Omega}_{s}$
further increases (dash-dotted curve in figure 14
a).

Figure 14. Effect of sidewall co-rotation on
![]() $z$
-dependence of (a) base-flow velocity
$z$
-dependence of (a) base-flow velocity
![]() $w_{a}$
, (b) angular velocity
$w_{a}$
, (b) angular velocity
![]() ${\it\Omega}_{a}$
, and (c) pressure
${\it\Omega}_{a}$
, and (c) pressure
![]() $p$
on axis
$p$
on axis
![]() $r=0$
; for
$r=0$
; for
![]() ${\it\Omega}_{s}=0$
, 0.01, 0.02 and 0.025 at critical parameters listed in table 3.
${\it\Omega}_{s}=0$
, 0.01, 0.02 and 0.025 at critical parameters listed in table 3.
It is known that as Re increases in elongated (
![]() $h>2.7$
) cylinders with one rotating disk and the other walls being stationary, a VB first develop near the rotating disk (Iwatsu Reference Iwatsu2005). Even for the unsteady 3D flow in the
$h>2.7$
) cylinders with one rotating disk and the other walls being stationary, a VB first develop near the rotating disk (Iwatsu Reference Iwatsu2005). Even for the unsteady 3D flow in the
![]() $h=4.5$
cylinder, a VB first develops near the rotating disk at
$h=4.5$
cylinder, a VB first develops near the rotating disk at
![]() $\mathit{Re}_{VB1}=3200$
and then near the stationary disk at
$\mathit{Re}_{VB1}=3200$
and then near the stationary disk at
![]() $\mathit{Re}_{VB2}=3800$
(Kulikov et al.
Reference Kulikov, Mikkelsen, Naumov and Okulov2014). It is interesting that these numbers are only slightly smaller than those for the steady axisymmetric flow.
$\mathit{Re}_{VB2}=3800$
(Kulikov et al.
Reference Kulikov, Mikkelsen, Naumov and Okulov2014). It is interesting that these numbers are only slightly smaller than those for the steady axisymmetric flow.
The physical reason for VB development as
![]() ${\it\Omega}_{s}$
increases is also the SDM. The solid curve in figure 14(b) shows that
${\it\Omega}_{s}$
increases is also the SDM. The solid curve in figure 14(b) shows that
![]() ${\it\Omega}_{a}$
sharply drops from its maximal value
${\it\Omega}_{a}$
sharply drops from its maximal value
![]() ${\it\Omega}_{a}=1$
at
${\it\Omega}_{a}=1$
at
![]() $z=0$
, as
$z=0$
, as
![]() $z$
increases within the Kármán boundary layer. Figure 14(b) also shows that
$z$
increases within the Kármán boundary layer. Figure 14(b) also shows that
![]() ${\it\Omega}_{a}$
drops from its local maximum at the centre of the circulation flow region (ii) (at
${\it\Omega}_{a}$
drops from its local maximum at the centre of the circulation flow region (ii) (at
![]() $z=2.7$
in figure 14
b) as
$z=2.7$
in figure 14
b) as
![]() $z$
decreases. For larger Re, these
$z$
decreases. For larger Re, these
![]() ${\it\Omega}_{a}$
maxima become more separated and the in-between minimal
${\it\Omega}_{a}$
maxima become more separated and the in-between minimal
![]() ${\it\Omega}_{a}$
decreases. Accordingly, pressure has two local minima separated by the local maximum. The fluid moves against the increasing pressure as
${\it\Omega}_{a}$
decreases. Accordingly, pressure has two local minima separated by the local maximum. The fluid moves against the increasing pressure as
![]() $z$
decreases from 3.52 down to 0.4 (see dotted line in figure 14
c) which decelerates the backflow (weakened by effect b) and causes its reversal as Re further increases.
$z$
decreases from 3.52 down to 0.4 (see dotted line in figure 14
c) which decelerates the backflow (weakened by effect b) and causes its reversal as Re further increases.
This emergence of a VB does not contradict the result of Shtern et al. (Reference Shtern, Torregrosa and Herrada2012) that the sidewall co-rotation suppresses VBs, because as
![]() ${\it\Omega}_{s}$
increases in that work Re is fixed, while here Re significantly grows. This growth occurs because increasing
${\it\Omega}_{s}$
increases in that work Re is fixed, while here Re significantly grows. This growth occurs because increasing
![]() ${\it\Omega}_{s}$
weakens circulation flow (ii) and thus suppresses the shear-layer instability. For this instability,
${\it\Omega}_{s}$
weakens circulation flow (ii) and thus suppresses the shear-layer instability. For this instability,
![]() $\mathit{Re }=7361$
is marginal at
$\mathit{Re }=7361$
is marginal at
![]() ${\it\Omega}_{s}=0.025$
(table 3), but the flow is centrifugally unstable at these Re and
${\it\Omega}_{s}=0.025$
(table 3), but the flow is centrifugally unstable at these Re and
![]() ${\it\Omega}_{s}$
as discussed below.
${\it\Omega}_{s}$
as discussed below.
7.2. Centrifugal instability
The square symbols and curve K4 in figure 15 represent the marginal and critical Reynolds numbers of the shear-layer instability listed in table 3. The other symbols and curves in figure 15 represent the marginal and critical Reynolds numbers related to a different kind of instability. They are marked by letter ‘T’ followed by the corresponding value of
![]() $m$
. The letters denote the Kelvin (K) and Taylor (T) instabilities. The critical and marginal Re values, related to the new (T) instability, are smaller than those related to the shear-layer (K) instability for
$m$
. The letters denote the Kelvin (K) and Taylor (T) instabilities. The critical and marginal Re values, related to the new (T) instability, are smaller than those related to the shear-layer (K) instability for
![]() ${\it\Omega}_{s}>0.0212$
.
${\it\Omega}_{s}>0.0212$
.

Figure 15. Dependence on sidewall angular velocity
![]() ${\it\Omega}_{s}$
of marginal and critical Reynolds numbers for the shear-layer (K) and centrifugal (T) instabilities at
${\it\Omega}_{s}$
of marginal and critical Reynolds numbers for the shear-layer (K) and centrifugal (T) instabilities at
![]() $h=8$
. Azimuthal wavenumbers
$h=8$
. Azimuthal wavenumbers
![]() $m$
of marginal disturbances are shown next to T and K.
$m$
of marginal disturbances are shown next to T and K.
To clarify the nature of T-instability, it is helpful to explore the spatial distribution of time-averaged kinetic energy
![]() $E_{d}$
for marginal disturbances. As an example, figure 16 depicts the
$E_{d}$
for marginal disturbances. As an example, figure 16 depicts the
![]() $E_{d}$
contours of the disturbance at
$E_{d}$
contours of the disturbance at
![]() ${\it\Omega}_{s}=0.03$
,
${\it\Omega}_{s}=0.03$
,
![]() $m=4$
and
$m=4$
and
![]() $\mathit{Re}=4633$
. This Re is the smallest among those corresponding to the diamond symbols in figure 15.
$\mathit{Re}=4633$
. This Re is the smallest among those corresponding to the diamond symbols in figure 15.

Figure 16. Energy contours for marginal disturbance at
![]() ${\it\Omega}_{s}=0.03$
,
${\it\Omega}_{s}=0.03$
,
![]() $\mathit{Re}=4633$
, and
$\mathit{Re}=4633$
, and
![]() $m=4$
.
$m=4$
.
The energy distribution, depicted in figure 16, indicates that this disturbance is localized near the sidewall. The maximum of disturbance energy
![]() $E_{d}$
is located at
$E_{d}$
is located at
![]() $r=r_{E}=0.91$
and
$r=r_{E}=0.91$
and
![]() $z=z_{E}=1.85$
(compare with
$z=z_{E}=1.85$
(compare with
![]() $r_{E}=0.52$
and
$r_{E}=0.52$
and
![]() $z_{E}=2.3$
for the shear-layer instability in figure 10). Therefore, it is instructive to analyse
$z_{E}=2.3$
for the shear-layer instability in figure 10). Therefore, it is instructive to analyse
![]() $r$
-profiles of base-flow velocity components at
$r$
-profiles of base-flow velocity components at
![]() $z=z_{E}=1.85$
, depicted in figure 17.
$z=z_{E}=1.85$
, depicted in figure 17.

Figure 17.
![]() $r$
-dependence of base-flow velocities
$r$
-dependence of base-flow velocities
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
at
$w$
at
![]() $z=1.85$
for
$z=1.85$
for
![]() $h=8$
,
$h=8$
,
![]() ${\it\Omega}_{s}=0.03$
, and
${\it\Omega}_{s}=0.03$
, and
![]() $\mathit{Re}=4633$
.
$\mathit{Re}=4633$
.
It is clear from figure 17 that the instability is not due to radial velocity
![]() $u$
, since
$u$
, since
![]() $u$
is negligibly small compared with
$u$
is negligibly small compared with
![]() $v$
and
$v$
and
![]() $w$
. The maximal swirl velocity,
$w$
. The maximal swirl velocity,
![]() $v_{m}=0.109$
, is about three times the maximal axial velocity,
$v_{m}=0.109$
, is about three times the maximal axial velocity,
![]() $w_{m}=0.0367$
. The fact that
$w_{m}=0.0367$
. The fact that
![]() $v_{m}$
is significantly larger than swirl velocity
$v_{m}$
is significantly larger than swirl velocity
![]() $v=0.03$
of the sidewall,
$v=0.03$
of the sidewall,
![]() $r=1$
, indicates that the angular momentum at
$r=1$
, indicates that the angular momentum at
![]() $z=1.85$
is mostly provided by the flow transport from the rotating disk.
$z=1.85$
is mostly provided by the flow transport from the rotating disk.
The dominance of
![]() $v$
over
$v$
over
![]() $u$
and
$u$
and
![]() $w$
points out that the swirl velocity distribution might be responsible for the instability. The instability can be centrifugal, similar to that occurring in the Taylor–Couette flow (Chandrasekhar Reference Chandrasekhar1961). To check this guess, figure 18 depicts the
$w$
points out that the swirl velocity distribution might be responsible for the instability. The instability can be centrifugal, similar to that occurring in the Taylor–Couette flow (Chandrasekhar Reference Chandrasekhar1961). To check this guess, figure 18 depicts the
![]() $r$
-profiles of the base-flow squared angular momentum
$r$
-profiles of the base-flow squared angular momentum
![]() $(rv)^{2}$
and marginal-disturbance energy
$(rv)^{2}$
and marginal-disturbance energy
![]() $E_{d}$
at
$E_{d}$
at
![]() $z=z_{E}=1.85$
. Both
$z=z_{E}=1.85$
. Both
![]() $(rv)^{2}$
and
$(rv)^{2}$
and
![]() $E_{d}$
are normalized by their maximal values in figure 18.
$E_{d}$
are normalized by their maximal values in figure 18.

Figure 18.
![]() $r$
-dependence of base-flow squared angular momentum
$r$
-dependence of base-flow squared angular momentum
![]() $(rv)^{2}$
and energy
$(rv)^{2}$
and energy
![]() $E_{d}$
of marginal disturbance at
$E_{d}$
of marginal disturbance at
![]() $z=1.85$
for
$z=1.85$
for
![]() ${\it\Omega}_{s}=0.03$
,
${\it\Omega}_{s}=0.03$
,
![]() $\mathit{Re}=4633$
,
$\mathit{Re}=4633$
,
![]() $m=4$
, and
$m=4$
, and
![]() $h=8$
.
$h=8$
.
According to the Rayleigh criterion, no centrifugal instability can develop if
![]() $(rv)^{2}$
grows with
$(rv)^{2}$
grows with
![]() $r$
(Chandrasekhar Reference Chandrasekhar1961). The necessary condition for the centrifugal instability is the decaying of
$r$
(Chandrasekhar Reference Chandrasekhar1961). The necessary condition for the centrifugal instability is the decaying of
![]() $(rv)^{2}$
as
$(rv)^{2}$
as
![]() $r$
increases (as occurs in the Taylor–Couette flow where the inner (outer) cylinder is rotating (stationary)). The pattern in figure 18 exactly matches the Rayleigh criterion:
$r$
increases (as occurs in the Taylor–Couette flow where the inner (outer) cylinder is rotating (stationary)). The pattern in figure 18 exactly matches the Rayleigh criterion:
![]() $E_{d}$
peaks in the middle of the region where
$E_{d}$
peaks in the middle of the region where
![]() $(rv)^{2}$
reduces as
$(rv)^{2}$
reduces as
![]() $r$
increases; and
$r$
increases; and
![]() $E_{d}$
becomes negligibly small in the region where
$E_{d}$
becomes negligibly small in the region where
![]() $(rv)^{2}$
grows with
$(rv)^{2}$
grows with
![]() $r$
.
$r$
.
In addition, the centrifugal instability induces Taylor cells in the circular Couette flow (Chandrasekhar Reference Chandrasekhar1961). Similarly, figure 16 shows two peaks of
![]() $E_{d}$
, indicative of two cells of disturbance motion. The Taylor cells are steady, but become unsteady if the base flow includes an axial stream. The frequency of time oscillations increases with the base-flow axial velocity. This feature agrees with that found here: the above discussed marginal disturbance has low frequency,
$E_{d}$
, indicative of two cells of disturbance motion. The Taylor cells are steady, but become unsteady if the base flow includes an axial stream. The frequency of time oscillations increases with the base-flow axial velocity. This feature agrees with that found here: the above discussed marginal disturbance has low frequency,
![]() ${\it\omega}_{i}=-0.096$
, compared to
${\it\omega}_{i}=-0.096$
, compared to
![]() ${\it\omega}_{i}=0.405$
for the shear-layer mode. It is reasonable that the frequency is low because the axial flow is weak in relation to the swirl (compare figures 12 and 17).
${\it\omega}_{i}=0.405$
for the shear-layer mode. It is reasonable that the frequency is low because the axial flow is weak in relation to the swirl (compare figures 12 and 17).
Based on the above analysis, we conclude that the low-frequency instability is centrifugal. The centrifugal instability also develops in the Vogel–Escudier flow, i.e. at
![]() ${\it\Omega}_{s}=0$
(see curves T3 and T4 in figure 15 and data in table 4 at
${\it\Omega}_{s}=0$
(see curves T3 and T4 in figure 15 and data in table 4 at
![]() ${\it\Omega}_{s}=0$
), but for larger Re than
${\it\Omega}_{s}=0$
), but for larger Re than
![]() $\mathit{Re}_{cr}=3100$
at which the shear-layer instability emerges. As
$\mathit{Re}_{cr}=3100$
at which the shear-layer instability emerges. As
![]() ${\it\Omega}_{s}$
increases, the azimuthal wavenumber
${\it\Omega}_{s}$
increases, the azimuthal wavenumber
![]() $m$
of critical disturbances also increases, as figure 15 and table 4 show.
$m$
of critical disturbances also increases, as figure 15 and table 4 show.
Table 4. Dependence of marginal and critical (bold) parameters on sidewall co-rotation
![]() ${\it\Omega}_{s}$
for centrifugal instability at
${\it\Omega}_{s}$
for centrifugal instability at
![]() $h=8$
.
$h=8$
.

The critical Re values correspond to the shear-layer disturbance modes with
![]() $m=4$
for
$m=4$
for
![]() $0<{\it\Omega}_{s}<0.0212$
, and to the centrifugal disturbance modes with
$0<{\it\Omega}_{s}<0.0212$
, and to the centrifugal disturbance modes with
![]() $m=3$
for
$m=3$
for
![]() $0.0212<{\it\Omega}_{s}<0.0505$
,
$0.0212<{\it\Omega}_{s}<0.0505$
,
![]() $m=4$
for
$m=4$
for
![]() $0.0505<{\it\Omega}_{s}<0.085$
,
$0.0505<{\it\Omega}_{s}<0.085$
,
![]() $m=5$
for
$m=5$
for
![]() $0.085<{\it\Omega}_{s}<0.1$
(and so on).
$0.085<{\it\Omega}_{s}<0.1$
(and so on).
Figure 19 depicts the energy distribution of critical disturbance at
![]() $\mathit{Re}=5192$
,
$\mathit{Re}=5192$
,
![]() ${\it\Omega}_{s}=0.1$
, and
${\it\Omega}_{s}=0.1$
, and
![]() $m=5$
. The pattern of
$m=5$
. The pattern of
![]() $E_{d}$
contours in figure 19, being similar to that in figure 16, indicates that the instability remains centrifugal as
$E_{d}$
contours in figure 19, being similar to that in figure 16, indicates that the instability remains centrifugal as
![]() ${\it\Omega}_{s}$
and
${\it\Omega}_{s}$
and
![]() $m$
increase (figure 15). There are three
$m$
increase (figure 15). There are three
![]() $E_{d}$
peaks in figure 19, while figure 16 depicts only two
$E_{d}$
peaks in figure 19, while figure 16 depicts only two
![]() $E_{d}$
peaks, i.e. the number of critical-disturbance cells grows as
$E_{d}$
peaks, i.e. the number of critical-disturbance cells grows as
![]() ${\it\Omega}_{s}$
and
${\it\Omega}_{s}$
and
![]() $m$
increase.
$m$
increase.

Figure 19. Energy contours for critical disturbance at
![]() $\mathit{Re}=5192$
,
$\mathit{Re}=5192$
,
![]() ${\it\Omega}_{s}=0.1$
, and
${\it\Omega}_{s}=0.1$
, and
![]() $m=5$
.
$m=5$
.
The sidewall co-rotation suppresses the centrifugal instability as well: critical Re grows with
![]() ${\it\Omega}_{s}$
(as figure 15 and table 4 show). The stabilizing effect is stronger (weaker) for the shear-layer (centrifugal) instability. The difference is due to the sidewall co-rotation more strongly (weakly) suppressing the meridional motion near the axis (wall) as
${\it\Omega}_{s}$
(as figure 15 and table 4 show). The stabilizing effect is stronger (weaker) for the shear-layer (centrifugal) instability. The difference is due to the sidewall co-rotation more strongly (weakly) suppressing the meridional motion near the axis (wall) as
![]() ${\it\Omega}_{s}$
increases.
${\it\Omega}_{s}$
increases.
Comparison of
![]() $w$
profiles in figures 12 and 17, shows that the velocity at the axis,
$w$
profiles in figures 12 and 17, shows that the velocity at the axis,
![]() $r=0$
, is drastically reduced at
$r=0$
, is drastically reduced at
![]() ${\it\Omega}_{s}=0.03$
compared to that at
${\it\Omega}_{s}=0.03$
compared to that at
![]() ${\it\Omega}_{s}=0$
. The significant shear-layer characteristic,
${\it\Omega}_{s}=0$
. The significant shear-layer characteristic,
![]() $w_{max}-w_{min}$
, is also reduced, being 0.067 (0.11) at
$w_{max}-w_{min}$
, is also reduced, being 0.067 (0.11) at
![]() ${\it\Omega}_{s}=0.03$
(0). These reductions, occurring despite
${\it\Omega}_{s}=0.03$
(0). These reductions, occurring despite
![]() $\mathit{Re}=4633$
(3100) being larger (smaller) at
$\mathit{Re}=4633$
(3100) being larger (smaller) at
![]() ${\it\Omega}_{s}=0.03$
(0), explain the strong suppression of the shear-layer instability by the sidewall co-rotation.
${\it\Omega}_{s}=0.03$
(0), explain the strong suppression of the shear-layer instability by the sidewall co-rotation.
In contrast,
![]() $w_{max}=0.0329$
(0.0367) at
$w_{max}=0.0329$
(0.0367) at
![]() ${\it\Omega}_{s}=0$
(0.03) increases, i.e. the near-wall flow, transporting the angular momentum from the rotation disk along the sidewall, remains rather strong as
${\it\Omega}_{s}=0$
(0.03) increases, i.e. the near-wall flow, transporting the angular momentum from the rotation disk along the sidewall, remains rather strong as
![]() ${\it\Omega}_{s}$
grows. This explains the relatively weak suppression of the centrifugal instability by the sidewall co-rotation.
${\it\Omega}_{s}$
grows. This explains the relatively weak suppression of the centrifugal instability by the sidewall co-rotation.
8. Conclusions
This paper explores the instability nature of the Vogel–Escudier flow. To this end, elongated cylinders are considered. Our numerical simulations first describe (in §§ 4.1–4.3) the development of the global circulation, where the instability occurs (§ 5), as the Reynolds number Re increases. In §§ 4.4 and 4.5, we show that at the critical
![]() $\mathit{Re}=\mathit{Re}_{cr}=3100$
, the flow consists of three parts: (i) the Kármán boundary layer near the rotating disk, (ii) the bulk circulation, and (iii) the creeping motion near the stationary disk. We focus on flow features in region (ii) where the instability is localized (§ 5).
$\mathit{Re}=\mathit{Re}_{cr}=3100$
, the flow consists of three parts: (i) the Kármán boundary layer near the rotating disk, (ii) the bulk circulation, and (iii) the creeping motion near the stationary disk. We focus on flow features in region (ii) where the instability is localized (§ 5).
The instability does not depend on the creeping flow pattern (iii) near the still disk resulting in
![]() $\mathit{Re}_{cr}$
being
$\mathit{Re}_{cr}$
being
![]() $h$
-independent and close to 3100 for
$h$
-independent and close to 3100 for
![]() $h>5.5$
(table 1 and figure 9). As figures 10 and 11 show, the instability occurs near the centre of the circulatory flow region (ii). Based on the stability analysis of the Vogel–Escudier flow (§ 5) and of the related
$h>5.5$
(table 1 and figure 9). As figures 10 and 11 show, the instability occurs near the centre of the circulatory flow region (ii). Based on the stability analysis of the Vogel–Escudier flow (§ 5) and of the related
![]() $z$
-independent flow (§ 6), we argue that the instability is of the shear-layer type, being caused by the presence of an inflection point in the radial distribution of axial velocity of the base counterflow.
$z$
-independent flow (§ 6), we argue that the instability is of the shear-layer type, being caused by the presence of an inflection point in the radial distribution of axial velocity of the base counterflow.
It is found in § 7 that there are indeed two competing types of instabilities: shear-layer (K) and centrifugal (T), which both exist (and the K-instability dominates) in the Vogel–Escudier flow. The results of § 7 provide two important additions to those in § 5: (a) they show the range of the K-instability (figure 15) and (b) they indicate the efficient control means – the sidewall co-rotation – to suppress both K- and T-instabilities.
![]() $\mathit{Re}_{cr}$
significantly increases with sidewall-to-disk angular velocity ratio
$\mathit{Re}_{cr}$
significantly increases with sidewall-to-disk angular velocity ratio
![]() ${\it\Omega}_{s}$
(tables 3 and 4). For
${\it\Omega}_{s}$
(tables 3 and 4). For
![]() ${\it\Omega}_{s}>0.0212$
, the centrifugal instability first develops as Re increases, and the azimuthal wavenumber,
${\it\Omega}_{s}>0.0212$
, the centrifugal instability first develops as Re increases, and the azimuthal wavenumber,
![]() $m$
, of critical disturbances grows with
$m$
, of critical disturbances grows with
![]() ${\it\Omega}_{s}$
(figure 15). The physical reason is provided for why the stabilizing effect of the co-rotation is stronger (weaker) for the shear-layer (centrifugal) instability (§ 7.2).
${\it\Omega}_{s}$
(figure 15). The physical reason is provided for why the stabilizing effect of the co-rotation is stronger (weaker) for the shear-layer (centrifugal) instability (§ 7.2).
Thus the obtained results explain the instability nature of the Vogel–Escudier flow and indicate efficient means to suppress this instability.
Acknowledgements
Partial support from the Ministry of Science and Education and Junta de Andalucía (Spain) through grants nos. DPI2010-21103 and P08-TEP-04128, respectively, is gratefully acknowledged.