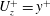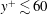1 Introduction
Many fluids do not display constant viscosity and are known as non-Newtonian fluids. They are important in many practical applications. Generalised Newtonian (GN) fluids are a class of non-Newtonian fluids in which the fluid stress is proportional to the local instantaneous strain rate via a non-uniform viscosity,
Here,
![]() $\unicode[STIX]{x1D749}$
is the stress tensor,
$\unicode[STIX]{x1D749}$
is the stress tensor,
![]() $\unicode[STIX]{x1D70C}$
is density,
$\unicode[STIX]{x1D70C}$
is density,
![]() $\unicode[STIX]{x1D708}$
is fluid kinematic viscosity and
$\unicode[STIX]{x1D708}$
is fluid kinematic viscosity and
![]() $\unicode[STIX]{x1D668}$
is the strain rate
$\unicode[STIX]{x1D668}$
is the strain rate
![]() $\unicode[STIX]{x1D668}=[\unicode[STIX]{x1D735}\boldsymbol{v}+(\unicode[STIX]{x1D735}\boldsymbol{v})^{\text{T}}]/2$
where
$\unicode[STIX]{x1D668}=[\unicode[STIX]{x1D735}\boldsymbol{v}+(\unicode[STIX]{x1D735}\boldsymbol{v})^{\text{T}}]/2$
where
![]() $\text{T}$
represents the matrix transpose. In (1.1)
$\text{T}$
represents the matrix transpose. In (1.1)
![]() $\boldsymbol{r}$
is the position vector and
$\boldsymbol{r}$
is the position vector and
![]() $t$
is time. For GN fluids, the fluid viscosity is typically defined as being a function of the strain rate,
$t$
is time. For GN fluids, the fluid viscosity is typically defined as being a function of the strain rate,
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}(\dot{\unicode[STIX]{x1D6FE}})$
where
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}(\dot{\unicode[STIX]{x1D6FE}})$
where
![]() $\dot{\unicode[STIX]{x1D6FE}}=(2\unicode[STIX]{x1D668}\boldsymbol{ : }\unicode[STIX]{x1D668})^{1/2}$
, the second invariant of the strain-rate tensor. The GN assumption implies that flows are free from elastic effects and that the response of the fluid to an applied shear stress is instantaneous. Fine particle suspensions, paints and food products such as molten chocolate, mayonnaise and tomato ketchup, are examples of GN fluids. GN fluids can be broadly categorised based on whether or not they show a yield stress i.e. the minimum shear stress required before the fluid starts to shear. In this study, we only consider fluids which do not show a yield stress.
$\dot{\unicode[STIX]{x1D6FE}}=(2\unicode[STIX]{x1D668}\boldsymbol{ : }\unicode[STIX]{x1D668})^{1/2}$
, the second invariant of the strain-rate tensor. The GN assumption implies that flows are free from elastic effects and that the response of the fluid to an applied shear stress is instantaneous. Fine particle suspensions, paints and food products such as molten chocolate, mayonnaise and tomato ketchup, are examples of GN fluids. GN fluids can be broadly categorised based on whether or not they show a yield stress i.e. the minimum shear stress required before the fluid starts to shear. In this study, we only consider fluids which do not show a yield stress.
The rheology of a GN fluid is determined experimentally using a rheogram (i.e. shear stress versus shear-rate data). Typically, a particular rheological model is fitted to the rheogram via regression. Model parameters determined via such regressions have no intrinsic physical meaning, but nevertheless are very useful in predicting flow behaviour and are extensively used. There are many rheology models available for GN fluids (see e.g. Chhabra & Richardson Reference Chhabra and Richardson2008) but for GN fluids which do not show a yield stress, in particular for shear-thinning fluids, a power-law (PL) rheology model is commonly used, despite having an infinite zero-shear viscosity that is not observed in practice. Such fluids are the focus of the present work. The PL rheology model defines the fluid viscosity as:
where the consistency
![]() $K$
and flow index
$K$
and flow index
![]() $n$
are model parameters. The PL rheology model describes shear-thinning behaviour when
$n$
are model parameters. The PL rheology model describes shear-thinning behaviour when
![]() $0<n<1$
, i.e. the viscosity of the fluid decreases with increase in shear rate, and for
$0<n<1$
, i.e. the viscosity of the fluid decreases with increase in shear rate, and for
![]() $n>1$
shear-thickening behaviour.
$n>1$
shear-thickening behaviour.
The non-uniform viscosity of PL fluids makes the choice of an appropriate viscosity scale (and hence Reynolds number) unclear. Instead of defining a viscosity scale, Metzner & Reed (Reference Metzner and Reed1955) proposed the following definition of Reynolds number (now known as the Metzner–Reed Reynolds number) for PL fluids by collapsing laminar flow friction factor data on to the Newtonian curve:
where
![]() $D$
is pipe diameter and
$D$
is pipe diameter and
![]() $U_{b}$
is the bulk velocity (flow rate per unit area). This definition is widely used, although it may be argued that it is not appropriate for turbulent flows because it is derived from a laminar flow analysis (Guzel, Frigaard & Martinez Reference Guzel, Frigaard and Martinez2009). Additionally, turbulent flow of PL fluids with different
$U_{b}$
is the bulk velocity (flow rate per unit area). This definition is widely used, although it may be argued that it is not appropriate for turbulent flows because it is derived from a laminar flow analysis (Guzel, Frigaard & Martinez Reference Guzel, Frigaard and Martinez2009). Additionally, turbulent flow of PL fluids with different
![]() $n$
but the same
$n$
but the same
![]() $Re_{MR}$
can show significantly different turbulent flow behaviour (Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004).
$Re_{MR}$
can show significantly different turbulent flow behaviour (Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004).
Another Reynolds number commonly used for GN fluids is based on the nominal wall viscosity
![]() $\unicode[STIX]{x1D708}_{w}$
(Pinho & Whitelaw Reference Pinho and Whitelaw1990; Ptasinski et al.
Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001; Pinho Reference Pinho2003; Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004). For a PL fluid it is easily shown using the mean wall shear stress
$\unicode[STIX]{x1D708}_{w}$
(Pinho & Whitelaw Reference Pinho and Whitelaw1990; Ptasinski et al.
Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001; Pinho Reference Pinho2003; Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004). For a PL fluid it is easily shown using the mean wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
and (1.2) that
$\unicode[STIX]{x1D70F}_{w}$
and (1.2) that
where
![]() $\unicode[STIX]{x1D70F}_{w}$
is determined from the mean pressure gradient in the axial (
$\unicode[STIX]{x1D70F}_{w}$
is determined from the mean pressure gradient in the axial (
![]() $z$
) direction
$z$
) direction
![]() $\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}z$
as
$\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}z$
as
![]() $\unicode[STIX]{x1D70F}_{w}=(D/4)\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}z$
. Using this viscosity scale, a generalised bulk Reynolds number
$\unicode[STIX]{x1D70F}_{w}=(D/4)\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}z$
. Using this viscosity scale, a generalised bulk Reynolds number
![]() $Re_{G}$
and a friction Reynolds number
$Re_{G}$
and a friction Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}$
are defined as
$Re_{\unicode[STIX]{x1D70F}}$
are defined as
where
![]() $R=D/2$
is pipe radius and
$R=D/2$
is pipe radius and
![]() $u^{\ast }=(\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C})^{1/2}$
is the friction velocity. Other definitions of Reynolds number have been proposed (Tomita Reference Tomita1959; Clapp Reference Clapp1961; Slatter & Lazarus Reference Slatter and Lazarus1993; Chilton & Stainsby Reference Chilton and Stainsby1998; Madlener, Frey & Ciezki Reference Madlener, Frey and Ciezki2009; Guzel et al.
Reference Guzel, Frigaard and Martinez2009), however there is no clear evidence to suggest that one definition is more useful than others in describing and collapsing data from turbulent flows of GN fluids. We adopt (1.4) and (1.5) in the present work.
$u^{\ast }=(\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C})^{1/2}$
is the friction velocity. Other definitions of Reynolds number have been proposed (Tomita Reference Tomita1959; Clapp Reference Clapp1961; Slatter & Lazarus Reference Slatter and Lazarus1993; Chilton & Stainsby Reference Chilton and Stainsby1998; Madlener, Frey & Ciezki Reference Madlener, Frey and Ciezki2009; Guzel et al.
Reference Guzel, Frigaard and Martinez2009), however there is no clear evidence to suggest that one definition is more useful than others in describing and collapsing data from turbulent flows of GN fluids. We adopt (1.4) and (1.5) in the present work.
Computational modelling of GN fluids, especially using direct numerical simulation (DNS), shows promise in helping to understand transition and turbulence in these fluids. The main benefit of using DNS is that once validated, it can be reliably used to model flow behaviour and provide a detailed picture of turbulence structure that is almost impossible to obtain in real GN fluids, which are usually opaque. DNS has the added benefit that rheological effects such as viscoelasticity (often unintentionally present, although small, in physical experiments using model GN fluids) can be excluded and the effect of modifying individual rheological parameters can be readily isolated. Additionally, the technique allows the validity of rheological models to be assessed in different flow scenarios.
DNS of GN fluids was first presented by Rudman et al. (Reference Rudman, Blackburn, Graham and Pullum2004) and Rudman & Blackburn (Reference Rudman and Blackburn2006), results of which showed that in a turbulent pipe flow, shear thinning reduced the friction factor (technically equivalent to drag reduction) at a given
![]() $Re_{G}$
. Transition to turbulence, quantified by transition
$Re_{G}$
. Transition to turbulence, quantified by transition
![]() $Re_{G}$
, was also delayed by shear thinning, which was also in agreement with experimental results of Pinho & Whitelaw (Reference Pinho and Whitelaw1990) and Rudman et al. (Reference Rudman, Graham, Blackburn and Pullum2002). The maximum Reynolds number in those studies was
$Re_{G}$
, was also delayed by shear thinning, which was also in agreement with experimental results of Pinho & Whitelaw (Reference Pinho and Whitelaw1990) and Rudman et al. (Reference Rudman, Graham, Blackburn and Pullum2002). The maximum Reynolds number in those studies was
![]() $Re_{G}\approx 8000$
, however, the flow was weakly turbulent for the moderately shear-thinning fluid (
$Re_{G}\approx 8000$
, however, the flow was weakly turbulent for the moderately shear-thinning fluid (
![]() $n=0.69$
) considered there. Additionally there were significant discrepancies between the results from DNS and experiments as discussed in Rudman & Blackburn (Reference Rudman and Blackburn2006). These discrepancies have recently been shown to be caused by a lack of high shear-rate data used in rheology characterisation (Singh et al.
Reference Singh, Rudman, Blackburn, Chryss, Pullum and Grahah2016). Local, instantaneous shear rates in turbulent pipe flow, especially near the wall, can be much higher (by an order of magnitude) than the maximum shear rate commonly used in rheology characterisation. Use of low-shear rheology in DNS implicitly involves extrapolating the rheology far outside the shear-rate range over which it is measured, leading to erroneous results. Hence, reliable high-shear rheology data are essential in matching DNS and experimental studies of turbulent flows of GN fluids. The other DNS study of PL fluids is by Gavrilov & Rudyak (Reference Gavrilov and Rudyak2016) at relatively higher
$n=0.69$
) considered there. Additionally there were significant discrepancies between the results from DNS and experiments as discussed in Rudman & Blackburn (Reference Rudman and Blackburn2006). These discrepancies have recently been shown to be caused by a lack of high shear-rate data used in rheology characterisation (Singh et al.
Reference Singh, Rudman, Blackburn, Chryss, Pullum and Grahah2016). Local, instantaneous shear rates in turbulent pipe flow, especially near the wall, can be much higher (by an order of magnitude) than the maximum shear rate commonly used in rheology characterisation. Use of low-shear rheology in DNS implicitly involves extrapolating the rheology far outside the shear-rate range over which it is measured, leading to erroneous results. Hence, reliable high-shear rheology data are essential in matching DNS and experimental studies of turbulent flows of GN fluids. The other DNS study of PL fluids is by Gavrilov & Rudyak (Reference Gavrilov and Rudyak2016) at relatively higher
![]() $Re_{G}$
(10 000 and 20 000) which observed similar results as reported by Rudman et al. (Reference Rudman, Blackburn, Graham and Pullum2004) and Rudman & Blackburn (Reference Rudman and Blackburn2006). Gavrilov & Rudyak (Reference Gavrilov and Rudyak2016) proposed that shear thinning decreases the turbulent energy transfer from the axial component to others which leads to an increased anisotropy compared to a Newtonian fluid.
$Re_{G}$
(10 000 and 20 000) which observed similar results as reported by Rudman et al. (Reference Rudman, Blackburn, Graham and Pullum2004) and Rudman & Blackburn (Reference Rudman and Blackburn2006). Gavrilov & Rudyak (Reference Gavrilov and Rudyak2016) proposed that shear thinning decreases the turbulent energy transfer from the axial component to others which leads to an increased anisotropy compared to a Newtonian fluid.
Other computational (though not DNS) studies of the turbulent flow of GN fluids are represented by Malin (Reference Malin1997), Cruz & Pinho (Reference Cruz and Pinho2003), Ohta & Miyashita (Reference Ohta and Miyashita2014) and Gnambode et al. (Reference Gnambode, Orlandi, Ould-Rouiss and Nicolas2015). Gnambode et al. (Reference Gnambode, Orlandi, Ould-Rouiss and Nicolas2015) used large eddy simulation (LES) to examine the effect of GN rheology on the turbulence flow whereas the others developed Reynolds-averaged Navier–Stokes (RANS) or LES models for GN fluids.
There is a paucity of DNS results for even first-order flow statistics, which is a gap that needs to be filled in order to understand and correctly model turbulent transport of momentum in these fluids. To overcome the limited
![]() $Re_{G}$
in Rudman et al. (Reference Rudman, Blackburn, Graham and Pullum2004) and Rudman & Blackburn (Reference Rudman and Blackburn2006), the current study considers flow at a higher Reynolds number (
$Re_{G}$
in Rudman et al. (Reference Rudman, Blackburn, Graham and Pullum2004) and Rudman & Blackburn (Reference Rudman and Blackburn2006), the current study considers flow at a higher Reynolds number (
![]() $Re_{G}\approx 12\,000$
,
$Re_{G}\approx 12\,000$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=323$
). The effects of shear thinning and shear thickening on turbulent pipe flow are considered and profiles of mean flow, turbulence intensities and budgets of mean shear stress and mean and turbulent kinetic energies are investigated.
$Re_{\unicode[STIX]{x1D70F}}=323$
). The effects of shear thinning and shear thickening on turbulent pipe flow are considered and profiles of mean flow, turbulence intensities and budgets of mean shear stress and mean and turbulent kinetic energies are investigated.
To our knowledge the present work is the first study of these budgets in turbulent pipe flow of a GN fluid. The key finding is that the effect of PL rheology on turbulent pipe flow is mainly significant in the inner, near-wall layers.
2 Mathematical formulation
2.1 Governing equations
Here, we briefly review the simulation methodology, and refer the reader to Blackburn & Sherwin (Reference Blackburn and Sherwin2004) and Rudman & Blackburn (Reference Rudman and Blackburn2006) for more detailed descriptions. Since the instantaneous viscosity is spatially varying, the incompressible Navier–Stokes equations must be written in stress-divergence form:
where
![]() $\boldsymbol{v}$
is the velocity vector,
$\boldsymbol{v}$
is the velocity vector,
![]() $p$
is the static pressure,
$p$
is the static pressure,
![]() $\unicode[STIX]{x1D749}$
is the stress tensor and
$\unicode[STIX]{x1D749}$
is the stress tensor and
![]() $\unicode[STIX]{x1D70C}\boldsymbol{g}$
is the body force. For ease of notation, we will divide
$\unicode[STIX]{x1D70C}\boldsymbol{g}$
is the body force. For ease of notation, we will divide
![]() $p$
,
$p$
,
![]() $\unicode[STIX]{x1D749}$
and
$\unicode[STIX]{x1D749}$
and
![]() $\unicode[STIX]{x1D70C}\boldsymbol{g}$
in (2.1) by the constant fluid density
$\unicode[STIX]{x1D70C}\boldsymbol{g}$
in (2.1) by the constant fluid density
![]() $\unicode[STIX]{x1D70C}$
, but refer to them as pressure, stress and body force respectively. The stress tensor
$\unicode[STIX]{x1D70C}$
, but refer to them as pressure, stress and body force respectively. The stress tensor
![]() $\unicode[STIX]{x1D749}$
is modelled with the GN assumption as:
$\unicode[STIX]{x1D749}$
is modelled with the GN assumption as:
where
![]() $\unicode[STIX]{x1D668}$
is the instantaneous strain-rate tensor and the kinematic viscosity
$\unicode[STIX]{x1D668}$
is the instantaneous strain-rate tensor and the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
is calculated using the PL model (see (1.2)). The numerically singular viscosity of PL rheology model at zero shear rate is avoided by using a ‘cutoff’ value below which the shear rate is assumed constant for calculating the viscosity. A very low value for the shear-rate cutoff (
$\unicode[STIX]{x1D708}$
is calculated using the PL model (see (1.2)). The numerically singular viscosity of PL rheology model at zero shear rate is avoided by using a ‘cutoff’ value below which the shear rate is assumed constant for calculating the viscosity. A very low value for the shear-rate cutoff (
![]() $1\times 10^{-6}$
) is used to ensure that it does not affect the flow predictions: no shear rate in the present work reaches such a low value.
$1\times 10^{-6}$
) is used to ensure that it does not affect the flow predictions: no shear rate in the present work reaches such a low value.
For numerical robustness, the convective term in (2.1) is implemented in skew-symmetric form, i.e.
![]() $(\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}\boldsymbol{v})/2$
. The axial pressure gradient is applied as a body force term via
$(\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}\boldsymbol{v})/2$
. The axial pressure gradient is applied as a body force term via
![]() $\boldsymbol{g}$
in (2.1). The form of the Navier–Stokes equations implemented in the code is written as:
$\boldsymbol{g}$
in (2.1). The form of the Navier–Stokes equations implemented in the code is written as:
The spatial discretisation uses two-dimensional spectral elements to cover the pipe cross-section as shown in figure 1 and Fourier expansion in the axial (
![]() $z$
) direction. The spectral element representation uses standard tensor-product nodal basis with Gauss–Lobatto–Legendre collocation points. The body force acts only in the axial direction giving
$z$
) direction. The spectral element representation uses standard tensor-product nodal basis with Gauss–Lobatto–Legendre collocation points. The body force acts only in the axial direction giving
![]() $g=g_{z}$
which is set to achieve a desired flow rate,
$g=g_{z}$
which is set to achieve a desired flow rate,
![]() $g$
takes the place of an axial pressure gradient and thus the pressure in (2.3) can be periodic as required by the Fourier expansion used in this direction. Execution is parallel over planar Fourier modes; product terms are computed pseudo-spectrally and not de-aliased. Time integration is second order and uses backwards differencing for approximating temporal derivatives in the velocity correction scheme (Karniadakis, Israeli & Orszag Reference Karniadakis, Israeli and Orszag1991; Guermond, Minev & Shen Reference Guermond, Minev and Shen2006). The time integration method as originally proposed by Karniadakis et al. (Reference Karniadakis, Israeli and Orszag1991) requires a spatially constant viscosity which is accommodated here by adopting a technique introduced by Leslie & Gao (Reference Leslie and Gao1988) in the context of LES. The viscosity
$g$
takes the place of an axial pressure gradient and thus the pressure in (2.3) can be periodic as required by the Fourier expansion used in this direction. Execution is parallel over planar Fourier modes; product terms are computed pseudo-spectrally and not de-aliased. Time integration is second order and uses backwards differencing for approximating temporal derivatives in the velocity correction scheme (Karniadakis, Israeli & Orszag Reference Karniadakis, Israeli and Orszag1991; Guermond, Minev & Shen Reference Guermond, Minev and Shen2006). The time integration method as originally proposed by Karniadakis et al. (Reference Karniadakis, Israeli and Orszag1991) requires a spatially constant viscosity which is accommodated here by adopting a technique introduced by Leslie & Gao (Reference Leslie and Gao1988) in the context of LES. The viscosity
![]() $\unicode[STIX]{x1D708}$
is split into a spatially constant component,
$\unicode[STIX]{x1D708}$
is split into a spatially constant component,
![]() $\unicode[STIX]{x1D708}_{ref}$
, with variable remainder
$\unicode[STIX]{x1D708}_{ref}$
, with variable remainder
![]() $\unicode[STIX]{x1D708}-\unicode[STIX]{x1D708}_{ref}$
to give the momentum equation
$\unicode[STIX]{x1D708}-\unicode[STIX]{x1D708}_{ref}$
to give the momentum equation
Following this decomposition, the term
![]() $\unicode[STIX]{x1D708}_{ref}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}$
is handled implicitly in time, while the remaining viscous term is dealt with explicitly and grouped with the nonlinear terms. One advantage of this method is that by appropriate choice of
$\unicode[STIX]{x1D708}_{ref}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}$
is handled implicitly in time, while the remaining viscous term is dealt with explicitly and grouped with the nonlinear terms. One advantage of this method is that by appropriate choice of
![]() $\unicode[STIX]{x1D708}_{ref}$
, it is possible to integrate stably with time steps close to the Courant–Friedrichs–Lewy limit, rather than at smaller values which would be determined by a fully explicit treatment of viscous diffusion.
$\unicode[STIX]{x1D708}_{ref}$
, it is possible to integrate stably with time steps close to the Courant–Friedrichs–Lewy limit, rather than at smaller values which would be determined by a fully explicit treatment of viscous diffusion.

Figure 1. Detail of a spectral element mesh used to discretise the pipe cross-section for
![]() $n=0.4{-}1.2$
, illustrating the elements (left) and grid nodes for twelfth-order element interpolation functions,
$n=0.4{-}1.2$
, illustrating the elements (left) and grid nodes for twelfth-order element interpolation functions,
![]() $N_{p}=12$
(right). The mesh used for
$N_{p}=12$
(right). The mesh used for
![]() $n=1.2$
was slightly finer and had more elements near the pipe centre.
$n=1.2$
was slightly finer and had more elements near the pipe centre.
2.2 Reynolds-averaged Navier–Stokes equation for an incompressible GN fluid
Reynolds decomposition is used to separate variables into their ensemble mean and the fluctuating components. Here, the velocity is decomposed as
![]() $\boldsymbol{v}=\boldsymbol{V}+\boldsymbol{v}^{\prime }$
; viscosity
$\boldsymbol{v}=\boldsymbol{V}+\boldsymbol{v}^{\prime }$
; viscosity
![]() $\unicode[STIX]{x1D708}=\bar{\unicode[STIX]{x1D708}}+\unicode[STIX]{x1D708}^{\prime }$
and the rate of strain tensor as
$\unicode[STIX]{x1D708}=\bar{\unicode[STIX]{x1D708}}+\unicode[STIX]{x1D708}^{\prime }$
and the rate of strain tensor as
![]() $\unicode[STIX]{x1D668}=\unicode[STIX]{x1D64E}+\unicode[STIX]{x1D668}^{\prime }$
, where
$\unicode[STIX]{x1D668}=\unicode[STIX]{x1D64E}+\unicode[STIX]{x1D668}^{\prime }$
, where
![]() $\boldsymbol{V}$
,
$\boldsymbol{V}$
,
![]() $\bar{\unicode[STIX]{x1D708}}$
and
$\bar{\unicode[STIX]{x1D708}}$
and
![]() $\unicode[STIX]{x1D64E}$
are the time-averaged quantities. Important to note for subsequent discussion is that
$\unicode[STIX]{x1D64E}$
are the time-averaged quantities. Important to note for subsequent discussion is that
![]() $\bar{\unicode[STIX]{x1D708}}_{w}\neq \unicode[STIX]{x1D708}_{w}$
, as shown later in § 4.1. Thus the Reynolds-averaged mean momentum equation for an incompressible non-Newtonian fluid is written as:
$\bar{\unicode[STIX]{x1D708}}_{w}\neq \unicode[STIX]{x1D708}_{w}$
, as shown later in § 4.1. Thus the Reynolds-averaged mean momentum equation for an incompressible non-Newtonian fluid is written as:
In (2.5), the mean stress tensor is the sum of three stress components.
As in the mean momentum equation for a Newtonian fluid, there is a mean viscous stress (
![]() $\unicode[STIX]{x1D749}^{v}$
) and a Reynolds stress (
$\unicode[STIX]{x1D749}^{v}$
) and a Reynolds stress (
![]() $\unicode[STIX]{x1D749}^{R}$
). For GN fluids a new stress term arises (
$\unicode[STIX]{x1D749}^{R}$
). For GN fluids a new stress term arises (
![]() $\unicode[STIX]{x1D749}^{fv}$
) which we call the turbulent viscous stress (
$\unicode[STIX]{x1D749}^{fv}$
) which we call the turbulent viscous stress (
![]() $\unicode[STIX]{x1D749}^{fv}$
). In the literature for viscoelastic fluids, an equivalent term is referred to as the ‘polymer stress’ (Ptasinski et al.
Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001). The terminology is not appropriate here as its contribution to the mean stress is not related to polymer addition to a carrier fluid and will be shown to have a different character to the same term in viscoelastic fluids. Unlike other stress terms,
$\unicode[STIX]{x1D749}^{fv}$
). In the literature for viscoelastic fluids, an equivalent term is referred to as the ‘polymer stress’ (Ptasinski et al.
Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001). The terminology is not appropriate here as its contribution to the mean stress is not related to polymer addition to a carrier fluid and will be shown to have a different character to the same term in viscoelastic fluids. Unlike other stress terms,
![]() $\unicode[STIX]{x1D749}^{fv}$
can be positive or negative depending on the rheology of the fluid and unlike
$\unicode[STIX]{x1D749}^{fv}$
can be positive or negative depending on the rheology of the fluid and unlike
![]() $\unicode[STIX]{x1D749}^{R}$
, it does not vanish at the wall. This is because it is a correlation between the fluctuations in viscosity
$\unicode[STIX]{x1D749}^{R}$
, it does not vanish at the wall. This is because it is a correlation between the fluctuations in viscosity
![]() $\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}-\bar{\unicode[STIX]{x1D708}}$
and shear rate
$\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}-\bar{\unicode[STIX]{x1D708}}$
and shear rate
![]() $\unicode[STIX]{x1D668}^{\prime }=\unicode[STIX]{x1D668}-\unicode[STIX]{x1D64E}$
. Both mean and fluctuating shear rates are non-zero at the wall because they are related to velocity gradients that do not vanish there. Similarly, viscosity and its fluctuations are non-zero at the wall as they depend on shear rate there. Therefore, we do not expect the correlation
$\unicode[STIX]{x1D668}^{\prime }=\unicode[STIX]{x1D668}-\unicode[STIX]{x1D64E}$
. Both mean and fluctuating shear rates are non-zero at the wall because they are related to velocity gradients that do not vanish there. Similarly, viscosity and its fluctuations are non-zero at the wall as they depend on shear rate there. Therefore, we do not expect the correlation
![]() $\unicode[STIX]{x1D70F}^{fv}$
to vanish at the wall. Using an order of magnitude analysis, Pinho (Reference Pinho2003) showed that
$\unicode[STIX]{x1D70F}^{fv}$
to vanish at the wall. Using an order of magnitude analysis, Pinho (Reference Pinho2003) showed that
![]() $\unicode[STIX]{x1D749}^{fv}$
could only be neglected in the mean flow of a non- or weakly shear-thinning fluid and for strongly shear-thinning fluids, especially in the vicinity of the wall, this term can be large. The other difference in (2.5) compared to its Newtonian version is that the mean viscous stress is formed from a spatially varying viscosity,
$\unicode[STIX]{x1D749}^{fv}$
could only be neglected in the mean flow of a non- or weakly shear-thinning fluid and for strongly shear-thinning fluids, especially in the vicinity of the wall, this term can be large. The other difference in (2.5) compared to its Newtonian version is that the mean viscous stress is formed from a spatially varying viscosity,
![]() $\bar{\unicode[STIX]{x1D708}}(r)$
.
$\bar{\unicode[STIX]{x1D708}}(r)$
.
2.3 Non-dimensional variables
For most of the analysis below, wall units are defined in a similar manner to the Newtonian analysis using the nominal wall viscosity
![]() $\unicode[STIX]{x1D708}_{w}$
(1.4) as the viscosity scale. The friction velocity
$\unicode[STIX]{x1D708}_{w}$
(1.4) as the viscosity scale. The friction velocity
![]() $u^{\ast }=(\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C})^{1/2}$
is used for the velocity scale and
$u^{\ast }=(\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C})^{1/2}$
is used for the velocity scale and
![]() $\unicode[STIX]{x1D708}_{w}/u^{\ast }$
for the length scale. Hence, the distance from the wall is expressed as
$\unicode[STIX]{x1D708}_{w}/u^{\ast }$
for the length scale. Hence, the distance from the wall is expressed as
![]() $y^{+}=(R-r)/(\unicode[STIX]{x1D708}_{w}/u^{\ast })$
, where
$y^{+}=(R-r)/(\unicode[STIX]{x1D708}_{w}/u^{\ast })$
, where
![]() $r$
is the radial distance from the centre of the pipe. The non-dimensional mean axial velocity and mean viscosity are expressed as
$r$
is the radial distance from the centre of the pipe. The non-dimensional mean axial velocity and mean viscosity are expressed as
![]() $U_{z}^{+}=U_{z}/u^{\ast }$
and
$U_{z}^{+}=U_{z}/u^{\ast }$
and
![]() $\unicode[STIX]{x1D708}^{+}=\bar{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D708}_{w}$
. Turbulence intensities are expressed in wall units as
$\unicode[STIX]{x1D708}^{+}=\bar{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D708}_{w}$
. Turbulence intensities are expressed in wall units as
![]() $u_{i}^{\prime +}=(\overline{u_{i}^{\prime ^{2}}})^{1/2}/u^{\ast }$
. Shear rate is normalised by
$u_{i}^{\prime +}=(\overline{u_{i}^{\prime ^{2}}})^{1/2}/u^{\ast }$
. Shear rate is normalised by
![]() ${u^{\ast }}^{2}/\unicode[STIX]{x1D708}_{w}$
, stress terms by
${u^{\ast }}^{2}/\unicode[STIX]{x1D708}_{w}$
, stress terms by
![]() $\unicode[STIX]{x1D70C}{u^{\ast }}^{2}$
and the energy budget terms by
$\unicode[STIX]{x1D70C}{u^{\ast }}^{2}$
and the energy budget terms by
![]() $(u^{\ast })^{4}/\unicode[STIX]{x1D708}_{w}$
. The Fanning friction factor,
$(u^{\ast })^{4}/\unicode[STIX]{x1D708}_{w}$
. The Fanning friction factor,
![]() $f$
, which is the non-dimensional wall shear stress, is defined as
$f$
, which is the non-dimensional wall shear stress, is defined as
![]() $f=2\unicode[STIX]{x1D70F}_{w}/(\unicode[STIX]{x1D70C}U_{b}^{2})$
.
$f=2\unicode[STIX]{x1D70F}_{w}/(\unicode[STIX]{x1D70C}U_{b}^{2})$
.
Although the mean wall shear stress,
![]() $\unicode[STIX]{x1D70F}_{w}$
, and the nominal wall viscosity,
$\unicode[STIX]{x1D70F}_{w}$
, and the nominal wall viscosity,
![]() $\unicode[STIX]{x1D708}_{w}$
, are chosen here for scaling, it is shown later in § 4.3 that these scalings do not maintain the fundamental
$\unicode[STIX]{x1D708}_{w}$
, are chosen here for scaling, it is shown later in § 4.3 that these scalings do not maintain the fundamental
![]() $U_{z}^{+}=y^{+}$
relation near the wall. Later we will develop a scaling that gives
$U_{z}^{+}=y^{+}$
relation near the wall. Later we will develop a scaling that gives
![]() $U_{z}^{+}=y^{+}$
, however, we choose to use
$U_{z}^{+}=y^{+}$
, however, we choose to use
![]() $\unicode[STIX]{x1D708}_{w}$
and
$\unicode[STIX]{x1D708}_{w}$
and
![]() $u^{\ast }$
in the majority of the analysis below because these can be determined a priori from the mean pressure gradient which is easily measured in experiments. This allows a direct comparison to DNS results.
$u^{\ast }$
in the majority of the analysis below because these can be determined a priori from the mean pressure gradient which is easily measured in experiments. This allows a direct comparison to DNS results.
2.4 Simulation parameters
In the present study, DNS are run for flow indices in the range
![]() $n=0.4{-}1.2$
. The governing equation (2.4) is non-dimensionalised by the friction velocity and the pipe radius
$n=0.4{-}1.2$
. The governing equation (2.4) is non-dimensionalised by the friction velocity and the pipe radius
![]() $R=0.5$
. This non-dimensionalisation gives
$R=0.5$
. This non-dimensionalisation gives
![]() $\unicode[STIX]{x1D708}_{w}=1/Re_{\unicode[STIX]{x1D70F}}$
and the non-dimensional body force
$\unicode[STIX]{x1D708}_{w}=1/Re_{\unicode[STIX]{x1D70F}}$
and the non-dimensional body force
![]() $gR/{u^{\ast }}^{2}=2$
. We chose a friction Reynolds number
$gR/{u^{\ast }}^{2}=2$
. We chose a friction Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}=323$
in the current simulations to attain a wider range of length scales in the flow than those previously reported in Rudman et al. (Reference Rudman, Blackburn, Graham and Pullum2004). The consistency
$Re_{\unicode[STIX]{x1D70F}}=323$
in the current simulations to attain a wider range of length scales in the flow than those previously reported in Rudman et al. (Reference Rudman, Blackburn, Graham and Pullum2004). The consistency
![]() $K$
for a given
$K$
for a given
![]() $n$
is calculated using the expression of the nominal wall viscosity
$n$
is calculated using the expression of the nominal wall viscosity
![]() $\unicode[STIX]{x1D708}_{w}$
(1.4). A summary of simulation conditions is given in table 1 and the fluid viscosity normalised by
$\unicode[STIX]{x1D708}_{w}$
(1.4). A summary of simulation conditions is given in table 1 and the fluid viscosity normalised by
![]() $\unicode[STIX]{x1D708}_{w}$
is plotted against shear rate (viscosity rheogram) in figure 2 for different
$\unicode[STIX]{x1D708}_{w}$
is plotted against shear rate (viscosity rheogram) in figure 2 for different
![]() $n$
. It can be seen that shear thinning affects the viscosity estimates significantly at all shear rates except for
$n$
. It can be seen that shear thinning affects the viscosity estimates significantly at all shear rates except for
![]() $\dot{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D708}_{w}$
(
$\dot{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D708}_{w}$
(
![]() $\dot{\unicode[STIX]{x1D6FE}}^{+}=1$
) for which the nominal wall viscosity is forced to be the same for all
$\dot{\unicode[STIX]{x1D6FE}}^{+}=1$
) for which the nominal wall viscosity is forced to be the same for all
![]() $n$
. The predicted bulk velocity and therefore, generalised Reynolds number
$n$
. The predicted bulk velocity and therefore, generalised Reynolds number
![]() $Re_{G}$
slightly decrease with increasing
$Re_{G}$
slightly decrease with increasing
![]() $n$
.
$n$
.
Table 1. Summary of simulation conditions for different flow indices
![]() $n$
(
$n$
(
![]() $n=1$
represents the Newtonian case).
$n=1$
represents the Newtonian case).
![]() $DR$
(drag reduction) is defined as
$DR$
(drag reduction) is defined as
![]() $(f-f_{Newt})/f_{Newt}$
where
$(f-f_{Newt})/f_{Newt}$
where
![]() $f$
is a Fanning friction factor. Friction Reynolds number
$f$
is a Fanning friction factor. Friction Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}$
, non-dimensional body force
$Re_{\unicode[STIX]{x1D70F}}$
, non-dimensional body force
![]() $gR/{u^{\ast }}^{2}$
and therefore the nominal wall viscosity
$gR/{u^{\ast }}^{2}$
and therefore the nominal wall viscosity
![]() $\unicode[STIX]{x1D708}_{w}$
are fixed at
$\unicode[STIX]{x1D708}_{w}$
are fixed at
![]() $323$
,
$323$
,
![]() $2$
and
$2$
and
![]() $1/323$
respectively.
$1/323$
respectively.


Figure 2. Non-dimensionalised viscosity plotted as a function of non-dimensional shear rate for different
![]() $n$
(see table 1) on a log–log scale. In this and subsequent figures, arrows labelled
$n$
(see table 1) on a log–log scale. In this and subsequent figures, arrows labelled
![]() $n$
indicate sense of increasing flow index.
$n$
indicate sense of increasing flow index.
2.5 Mesh design
Mesh design for these flows has been an iterative process, influenced by rules of thumb for the resolution and domain size established in Newtonian DNS (Piomelli Reference Piomelli, Liu and Liu1997); by our previous experience (Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004; Rudman & Blackburn Reference Rudman and Blackburn2006); and results from preliminary investigations over the range of flow indices investigated. Turbulence structures become finer with decreasing shear thinning (i.e. increasing
![]() $n$
). Therefore, DNS requires a higher mesh resolution as
$n$
). Therefore, DNS requires a higher mesh resolution as
![]() $n$
is increased. In case of a shear-thickening fluid, due to the lower viscosity in the core region (and hence turbulent eddies with smaller length scales) a higher mesh resolution is required in the core region compared to a Newtonian simulation at the same
$n$
is increased. In case of a shear-thickening fluid, due to the lower viscosity in the core region (and hence turbulent eddies with smaller length scales) a higher mesh resolution is required in the core region compared to a Newtonian simulation at the same
![]() $Re_{\unicode[STIX]{x1D70F}}$
. In order to ensure mesh convergence for all cases, a grid resolution study was performed for
$Re_{\unicode[STIX]{x1D70F}}$
. In order to ensure mesh convergence for all cases, a grid resolution study was performed for
![]() $n=1.0$
and the same mesh was used for
$n=1.0$
and the same mesh was used for
![]() $n=0.4{-}1.0$
which implies a more finely resolved mesh for these cases. A separate grid resolution study was conducted for
$n=0.4{-}1.0$
which implies a more finely resolved mesh for these cases. A separate grid resolution study was conducted for
![]() $n=1.2$
. The final meshes used in simulations had 300 spectral elements for
$n=1.2$
. The final meshes used in simulations had 300 spectral elements for
![]() $n=0.4-1.0$
and 384 spectral elements for
$n=0.4-1.0$
and 384 spectral elements for
![]() $n=1.2$
. All meshes used twelfth-order tensor-product shape functions and 384 axial data planes giving the near-wall mesh spacing of
$n=1.2$
. All meshes used twelfth-order tensor-product shape functions and 384 axial data planes giving the near-wall mesh spacing of
![]() $y_{w}^{+}=0.8$
in the wall-normal direction,
$y_{w}^{+}=0.8$
in the wall-normal direction,
![]() $(r\unicode[STIX]{x0394}\unicode[STIX]{x1D703})_{w}^{+}=4.5$
in the azimuthal direction and
$(r\unicode[STIX]{x0394}\unicode[STIX]{x1D703})_{w}^{+}=4.5$
in the azimuthal direction and
![]() $\unicode[STIX]{x0394}z^{+}=21$
in the axial direction for
$\unicode[STIX]{x0394}z^{+}=21$
in the axial direction for
![]() $n=0.4{-}1.0$
. The mesh resolution was slightly finer for
$n=0.4{-}1.0$
. The mesh resolution was slightly finer for
![]() $n=1.2$
in the azimuthal direction,
$n=1.2$
in the azimuthal direction,
![]() $(r\unicode[STIX]{x0394}\unicode[STIX]{x1D703})_{w}^{+}=3.5$
, and near the pipe centre. These near-wall mesh spacings in the wall normal and the azimuthal direction agree with typical values used for wall resolving DNS of Newtonian fluids (Piomelli Reference Piomelli, Liu and Liu1997; Moser, Kim & Mansour Reference Moser, Kim and Mansour1999; Chin, Monty & Ooi Reference Chin, Monty and Ooi2014). Although, the mesh in the axial direction is coarser than that used in Newtonian studies (Moser et al.
Reference Moser, Kim and Mansour1999; Chin et al.
Reference Chin, Monty and Ooi2014), our mesh resolution study showed that further mesh refinement did not change the results noticeably.
$(r\unicode[STIX]{x0394}\unicode[STIX]{x1D703})_{w}^{+}=3.5$
, and near the pipe centre. These near-wall mesh spacings in the wall normal and the azimuthal direction agree with typical values used for wall resolving DNS of Newtonian fluids (Piomelli Reference Piomelli, Liu and Liu1997; Moser, Kim & Mansour Reference Moser, Kim and Mansour1999; Chin, Monty & Ooi Reference Chin, Monty and Ooi2014). Although, the mesh in the axial direction is coarser than that used in Newtonian studies (Moser et al.
Reference Moser, Kim and Mansour1999; Chin et al.
Reference Chin, Monty and Ooi2014), our mesh resolution study showed that further mesh refinement did not change the results noticeably.
2.6 Domain length independence study
To ensure that the axial domain periodicity did not unduly influence results, a domain length independence study was carried out. Since the range of length scales in the flow decreases with decreasing
![]() $n$
,
$n$
,
![]() $n=0.6$
was chosen for this study. Results showed that a minimum domain length of
$n=0.6$
was chosen for this study. Results showed that a minimum domain length of
![]() $11D$
is required in order that streamwise correlations are sufficiently small and the turbulence statistics converge. In the final simulations, a domain length of
$11D$
is required in order that streamwise correlations are sufficiently small and the turbulence statistics converge. In the final simulations, a domain length of
![]() $L_{z}=4\unicode[STIX]{x03C0}D$
is used for
$L_{z}=4\unicode[STIX]{x03C0}D$
is used for
![]() $n=0.6{-}1.2$
which is twice that used by Eggels et al. (Reference Eggels, Unger, Wiess, Westerweel, Adrian, Friedrich and Nieuwstadt1994) in their DNS of a Newtonian fluid at
$n=0.6{-}1.2$
which is twice that used by Eggels et al. (Reference Eggels, Unger, Wiess, Westerweel, Adrian, Friedrich and Nieuwstadt1994) in their DNS of a Newtonian fluid at
![]() $Re_{\unicode[STIX]{x1D70F}}=180$
and comparable to that suggested by Chin et al. (Reference Chin, Ooi, Marusic and Blackburn2010) for DNS of a Newtonian fluid at
$Re_{\unicode[STIX]{x1D70F}}=180$
and comparable to that suggested by Chin et al. (Reference Chin, Ooi, Marusic and Blackburn2010) for DNS of a Newtonian fluid at
![]() $Re_{\unicode[STIX]{x1D70F}}=170{-}500$
. A slightly longer domain (
$Re_{\unicode[STIX]{x1D70F}}=170{-}500$
. A slightly longer domain (
![]() $L_{z}\approx 16D$
) is used for
$L_{z}\approx 16D$
) is used for
![]() $n=0.4$
due to its transitional nature (discussed later). These domain lengths are further checked for their adequacy via two point axial correlations of axial velocity fluctuations
$n=0.4$
due to its transitional nature (discussed later). These domain lengths are further checked for their adequacy via two point axial correlations of axial velocity fluctuations
![]() $\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
defined as:
$\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
defined as:
Here,
![]() $u_{z}^{\prime }$
represents the axial velocity fluctuations at time
$u_{z}^{\prime }$
represents the axial velocity fluctuations at time
![]() $t$
and
$t$
and
![]() $\langle \,\rangle$
denotes averaging. As seen in figure 3
$\langle \,\rangle$
denotes averaging. As seen in figure 3
![]() $\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
decays to zero for all
$\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
decays to zero for all
![]() $n$
. Close to the centre of the pipe (not shown)
$n$
. Close to the centre of the pipe (not shown)
![]() $\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
remains positive for much of the domain, although less than 0.1. Overall, these results indicate adequate domain length. Negative values of
$\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
remains positive for much of the domain, although less than 0.1. Overall, these results indicate adequate domain length. Negative values of
![]() $\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
in the profiles of
$\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
in the profiles of
![]() $n=0.4$
and
$n=0.4$
and
![]() $n=0.6$
indicate intermittent turbulent regions which are also seen in near-wall streaks shown later (in figure 6). The larger negative values of
$n=0.6$
indicate intermittent turbulent regions which are also seen in near-wall streaks shown later (in figure 6). The larger negative values of
![]() $\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
for
$\unicode[STIX]{x1D70C}_{u_{z}^{\prime }u_{z}^{\prime }}$
for
![]() $n=0.4$
indicate the transitional nature of this flow. Therefore we exclude the results of
$n=0.4$
indicate the transitional nature of this flow. Therefore we exclude the results of
![]() $n=0.4$
and present those only for
$n=0.4$
and present those only for
![]() $n=0.6{-}1.2$
.
$n=0.6{-}1.2$
.

Figure 3. Two point correlation coefficient of axial velocity fluctuations as a function of streamwise separation
![]() $\unicode[STIX]{x0394}z/D$
plotted for different
$\unicode[STIX]{x0394}z/D$
plotted for different
![]() $n$
(see table 1) at two different
$n$
(see table 1) at two different
![]() $y^{+}$
locations.
$y^{+}$
locations.
2.7 Temporal averaging
Initial conditions were taken from earlier simulations on different meshes or from simulations with different
![]() $n$
. Simulations were run until the calculated instantaneous total wall shear stress and the bulk velocity had reached a statistically steady value. In most cases the wall shear stress and the bulk velocity fluctuated by approximately 2 % about the mean value. The time interval required to reach this state typically corresponded to around ten to twenty domain wash-through times. Once this state had been reached, time-averaged statistics were accumulated over another fifteen to twenty transit times.
$n$
. Simulations were run until the calculated instantaneous total wall shear stress and the bulk velocity had reached a statistically steady value. In most cases the wall shear stress and the bulk velocity fluctuated by approximately 2 % about the mean value. The time interval required to reach this state typically corresponded to around ten to twenty domain wash-through times. Once this state had been reached, time-averaged statistics were accumulated over another fifteen to twenty transit times.

Figure 4. Wall scaled statistical profiles from DNS of Newtonian fluid at
![]() $Re_{\unicode[STIX]{x1D70F}}=323$
(solid line), compared to experimental results of den Toonder & Nieuwstadt (Reference den Toonder and Nieuwstadt1997, circles:
$Re_{\unicode[STIX]{x1D70F}}=323$
(solid line), compared to experimental results of den Toonder & Nieuwstadt (Reference den Toonder and Nieuwstadt1997, circles:
![]() $Re_{\unicode[STIX]{x1D70F}}=314$
). (a) Mean axial velocity; (b) axial and radial turbulence intensities; (c) Reynolds shear stress; (d) turbulent kinetic energy production.
$Re_{\unicode[STIX]{x1D70F}}=314$
). (a) Mean axial velocity; (b) axial and radial turbulence intensities; (c) Reynolds shear stress; (d) turbulent kinetic energy production.
2.8 Validation of numerical method
To provide a baseline comparison of the numerical method, statistical data for turbulent pipe flow of a Newtonian fluid at
![]() $Re_{\unicode[STIX]{x1D70F}}=323$
are compared in figure 4 to the experimental results of den Toonder & Nieuwstadt (Reference den Toonder and Nieuwstadt1997) obtained by Laser doppler anemometry (LDV) measurement at a similar
$Re_{\unicode[STIX]{x1D70F}}=323$
are compared in figure 4 to the experimental results of den Toonder & Nieuwstadt (Reference den Toonder and Nieuwstadt1997) obtained by Laser doppler anemometry (LDV) measurement at a similar
![]() $Re_{\unicode[STIX]{x1D70F}}$
of 314. As seen in the figure, profiles of mean axial velocity, turbulence intensities, Reynolds shear stress and turbulent kinetic energy production obtained from DNS agree well with the experimental results except very close to the wall, where some of the experimental results are acknowledged to be unreliable.
$Re_{\unicode[STIX]{x1D70F}}$
of 314. As seen in the figure, profiles of mean axial velocity, turbulence intensities, Reynolds shear stress and turbulent kinetic energy production obtained from DNS agree well with the experimental results except very close to the wall, where some of the experimental results are acknowledged to be unreliable.
The DNS friction factor predictions for different flow indices are compared with the Dodge and Metzner correlation (Dodge & Metzner Reference Dodge and Metzner1959) which gives the best agreement with experiments compared to others (Hartnett & Kostic Reference Hartnett and Kostic1990). As seen in table 1, DNS predictions of the friction factor for different flow indices agree well (within 5 %) with the Dodge and Metzner correlation suggesting the accuracy of the current results. Note that the errors in predicting
![]() $f$
compared to Dodge and Metzner’s correlation is lower in the current study compared to our earlier studies (Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004; Rudman & Blackburn Reference Rudman and Blackburn2006) where the flow was weakly turbulent. Since the Dodge and Metzner correlation is a semi-empirical correlation with the parameters determined using turbulent flow experiments, it is prone to give erroneous prediction in weakly turbulent flows. Results presented in Singh et al. (Reference Singh, Rudman, Blackburn, Chryss, Pullum and Grahah2016) also support the validity of the present simulation methodology for GN fluids.
$f$
compared to Dodge and Metzner’s correlation is lower in the current study compared to our earlier studies (Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004; Rudman & Blackburn Reference Rudman and Blackburn2006) where the flow was weakly turbulent. Since the Dodge and Metzner correlation is a semi-empirical correlation with the parameters determined using turbulent flow experiments, it is prone to give erroneous prediction in weakly turbulent flows. Results presented in Singh et al. (Reference Singh, Rudman, Blackburn, Chryss, Pullum and Grahah2016) also support the validity of the present simulation methodology for GN fluids.
3 Observations of instantaneous flow
The effect of flow index
![]() $n$
on instantaneous flow structures is shown in figures 5 and 6. Finer-scale structure is observed with increasing
$n$
on instantaneous flow structures is shown in figures 5 and 6. Finer-scale structure is observed with increasing
![]() $n$
, which is seen clearly in the contours of axial velocity and viscosity plotted on a pipe cross-section in figure 5 and in the near-wall streaks shown in figure 6. The finer scales also correspond to higher frequency motions, although later it will be seen they are also associated with lower turbulent kinetic energy. The longer, wider low-speed streaks seen in figure 6 for lower
$n$
, which is seen clearly in the contours of axial velocity and viscosity plotted on a pipe cross-section in figure 5 and in the near-wall streaks shown in figure 6. The finer scales also correspond to higher frequency motions, although later it will be seen they are also associated with lower turbulent kinetic energy. The longer, wider low-speed streaks seen in figure 6 for lower
![]() $n$
are associated with reduced wall-normal turbulence intensities by shear thinning which will be discussed in § 4.4. There are qualitative correlations evident between the surface contours on adjacent surfaces indicating the radial extent of these structures, which indicate the imprint of the outer flow on near-wall fluctuations (Hutchins & Marusic Reference Hutchins and Marusic2007).
$n$
are associated with reduced wall-normal turbulence intensities by shear thinning which will be discussed in § 4.4. There are qualitative correlations evident between the surface contours on adjacent surfaces indicating the radial extent of these structures, which indicate the imprint of the outer flow on near-wall fluctuations (Hutchins & Marusic Reference Hutchins and Marusic2007).

Figure 5. (a–d) Contours of instantaneous axial velocity normalised by the bulk velocity
![]() $U_{b}$
(0 is black, 1.4 is white). (e–h) Contours of instantaneous viscosity normalised by the maximum viscosity (0.1 is black, 1.0 is light grey). From left to right, flow indices are (a,e)
$U_{b}$
(0 is black, 1.4 is white). (e–h) Contours of instantaneous viscosity normalised by the maximum viscosity (0.1 is black, 1.0 is light grey). From left to right, flow indices are (a,e)
![]() $n=0.6$
, (b,f)
$n=0.6$
, (b,f)
![]() $n=0.8$
, (c,g)
$n=0.8$
, (c,g)
![]() $n=1.0$
and (d,h)
$n=1.0$
and (d,h)
![]() $n=1.2$
. The velocity and viscosity contours for a given fluid are plotted for the same time instant.
$n=1.2$
. The velocity and viscosity contours for a given fluid are plotted for the same time instant.

Figure 6. Contours of instantaneous axial velocity fluctuations normalised by the local mean axial velocity at
![]() $y^{+}=10,30,45,70,100$
(from top to bottom) for (a–e) Newtonian and (f–j)
$y^{+}=10,30,45,70,100$
(from top to bottom) for (a–e) Newtonian and (f–j)
![]() $n=0.6$
plotted on surfaces of constant
$n=0.6$
plotted on surfaces of constant
![]() $y^{+}$
. White represents positive fluctuation and black negative. Contours have been stretched azimuthally to maintain the same vertical extent.
$y^{+}$
. White represents positive fluctuation and black negative. Contours have been stretched azimuthally to maintain the same vertical extent.
The information presented in figure 6 can be quantified using the velocity integral length scale which is a measure of the characteristic correlation distance between the velocity fluctuations at two points in the flow field. Here, the streamwise velocity integral length scale,
![]() $l_{z}$
, is calculated by integrating the two point autocorrelation function (2.7) to the point where it first crosses zero. As expected from the qualitative information in figure 6,
$l_{z}$
, is calculated by integrating the two point autocorrelation function (2.7) to the point where it first crosses zero. As expected from the qualitative information in figure 6,
![]() $l_{z}$
increases with decreasing
$l_{z}$
increases with decreasing
![]() $n$
(figure 7
a,b) from approximately 60 for
$n$
(figure 7
a,b) from approximately 60 for
![]() $n=1$
to around 100 for
$n=1$
to around 100 for
![]() $n=0.6$
. This suggests that axial velocity fluctuations are correlated for a longer distance for lower
$n=0.6$
. This suggests that axial velocity fluctuations are correlated for a longer distance for lower
![]() $n$
. For all flow indices, the maximum
$n$
. For all flow indices, the maximum
![]() $l_{z}$
occurs at
$l_{z}$
occurs at
![]() $y^{+}\approx 10$
with the exact location slightly shifting away from the wall with decreasing
$y^{+}\approx 10$
with the exact location slightly shifting away from the wall with decreasing
![]() $n$
(figure 7
b). Azimuthal length scales near the pipe wall follow a similar trend with
$n$
(figure 7
b). Azimuthal length scales near the pipe wall follow a similar trend with
![]() $n$
(figure 7
c).
$n$
(figure 7
c).

Figure 7. (a,b) Streamwise integral length scales and (c) azimuthal integral length scale plotted as functions of
![]() $y^{+}$
.
$y^{+}$
.
4 Mean flow and turbulence statistics
4.1 Mean axial velocity and viscosity
The effect of
![]() $n$
is seen when the mean axial velocity,
$n$
is seen when the mean axial velocity,
![]() $U_{z}^{+}$
, is plotted in wall coordinates (figure 8
a), however,
$U_{z}^{+}$
, is plotted in wall coordinates (figure 8
a), however,
![]() $U_{z}^{+}$
profiles show little variation when plotted in outer variables (not shown). For ease of discussion, the flow domain is nominally divided into four regions – the viscous sublayer (
$U_{z}^{+}$
profiles show little variation when plotted in outer variables (not shown). For ease of discussion, the flow domain is nominally divided into four regions – the viscous sublayer (
![]() $y^{+}<5$
), buffer layer (
$y^{+}<5$
), buffer layer (
![]() $5<y^{+}<30$
), log layer (
$5<y^{+}<30$
), log layer (
![]() $30<y^{+}<200$
) and core region (
$30<y^{+}<200$
) and core region (
![]() $y^{+}>200$
). Although this flow domain subdivision is common for Newtonian fluids (Pope Reference Pope2000), it will be seen that the delineation is not as obvious for GN fluids. In all subsequent discussion, when a trend is described as occurring with shear thinning (
$y^{+}>200$
). Although this flow domain subdivision is common for Newtonian fluids (Pope Reference Pope2000), it will be seen that the delineation is not as obvious for GN fluids. In all subsequent discussion, when a trend is described as occurring with shear thinning (
![]() $n<1$
), it should be taken as read that the opposite trend occurs with shear thickening (
$n<1$
), it should be taken as read that the opposite trend occurs with shear thickening (
![]() $n>1$
).
$n>1$
).
In Newtonian fluids it is well known that the mean axial velocity profile in the viscous sublayer follows
![]() $U_{z}^{+}=y^{+}$
which is the near-wall form of the law of the wall (Pope Reference Pope2000). For PL fluids a similar viscous sublayer was anticipated in the analyses of Dodge & Metzner (Reference Dodge and Metzner1959) and Clapp (Reference Clapp1961). For
$U_{z}^{+}=y^{+}$
which is the near-wall form of the law of the wall (Pope Reference Pope2000). For PL fluids a similar viscous sublayer was anticipated in the analyses of Dodge & Metzner (Reference Dodge and Metzner1959) and Clapp (Reference Clapp1961). For
![]() $n\neq 1$
, a viscous sublayer appears in the mean axial velocity profiles (figure 8
a), however, a close examination shows that the profiles for different
$n\neq 1$
, a viscous sublayer appears in the mean axial velocity profiles (figure 8
a), however, a close examination shows that the profiles for different
![]() $n$
deviate slightly from the Newtonian case. This is more clearly seen in figure 8(b) where the difference (
$n$
deviate slightly from the Newtonian case. This is more clearly seen in figure 8(b) where the difference (
![]() $\unicode[STIX]{x0394}U_{z}^{+}$
) between
$\unicode[STIX]{x0394}U_{z}^{+}$
) between
![]() $U_{z}^{+}$
of the PL and Newtonian fluids is plotted against
$U_{z}^{+}$
of the PL and Newtonian fluids is plotted against
![]() $y^{+}$
. For all
$y^{+}$
. For all
![]() $y^{+}$
, the
$y^{+}$
, the
![]() $U_{z}^{+}$
profiles for shear-thinning GN fluids lie above the Newtonian profile (and vice versa for shear thickening).
$U_{z}^{+}$
profiles for shear-thinning GN fluids lie above the Newtonian profile (and vice versa for shear thickening).
Although the effect of flow index is seen at all
![]() $y^{+}$
,
$y^{+}$
,
![]() $\unicode[STIX]{x0394}U_{z}^{+}$
profiles deviate significantly from each other only beyond
$\unicode[STIX]{x0394}U_{z}^{+}$
profiles deviate significantly from each other only beyond
![]() $y^{+}\approx 10$
. The maximum
$y^{+}\approx 10$
. The maximum
![]() $\unicode[STIX]{x0394}U_{z}^{+}$
occurs somewhere in the log layer with the exact location depending on the value of
$\unicode[STIX]{x0394}U_{z}^{+}$
occurs somewhere in the log layer with the exact location depending on the value of
![]() $n$
. Note that the area integral of
$n$
. Note that the area integral of
![]() $\unicode[STIX]{x0394}U_{z}^{+}$
at a cross-section represents the excess bulk flow rate and therefore, higher values of
$\unicode[STIX]{x0394}U_{z}^{+}$
at a cross-section represents the excess bulk flow rate and therefore, higher values of
![]() $\unicode[STIX]{x0394}U_{z}^{+}$
indicate higher bulk flow (hence higher
$\unicode[STIX]{x0394}U_{z}^{+}$
indicate higher bulk flow (hence higher
![]() $U_{b}$
) for lower
$U_{b}$
) for lower
![]() $n$
which was seen in table 1. Since
$n$
which was seen in table 1. Since
![]() $\unicode[STIX]{x1D70F}_{w}$
is fixed in simulations, higher bulk velocity gives lower friction factor
$\unicode[STIX]{x1D70F}_{w}$
is fixed in simulations, higher bulk velocity gives lower friction factor
![]() $f$
for a more shear-thinning fluid. These results are consistent with those reported in previous studies (Dodge & Metzner Reference Dodge and Metzner1959; Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004; Rudman & Blackburn Reference Rudman and Blackburn2006). It is noted that the relative decrease in
$f$
for a more shear-thinning fluid. These results are consistent with those reported in previous studies (Dodge & Metzner Reference Dodge and Metzner1959; Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004; Rudman & Blackburn Reference Rudman and Blackburn2006). It is noted that the relative decrease in
![]() $f$
compared to the Newtonian fluid (referred to as drag reduction,
$f$
compared to the Newtonian fluid (referred to as drag reduction,
![]() $DR$
, in table 1) is approximately 14 % for
$DR$
, in table 1) is approximately 14 % for
![]() $n=0.6$
(see table 1), which is much less than that seen for viscoelastic fluids for which a drag reduction up to 70 % was observed in Ptasinski et al. (Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001) at a comparable Reynolds number (
$n=0.6$
(see table 1), which is much less than that seen for viscoelastic fluids for which a drag reduction up to 70 % was observed in Ptasinski et al. (Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001) at a comparable Reynolds number (
![]() $Re_{G}=10\,000$
).
$Re_{G}=10\,000$
).

Figure 8. Profiles of (a) mean axial velocity
![]() $U_{z}^{+}$
and (b) difference between
$U_{z}^{+}$
and (b) difference between
![]() $U_{z}^{+}$
for a PL and Newtonian fluid plotted against
$U_{z}^{+}$
for a PL and Newtonian fluid plotted against
![]() $y^{+}$
.
$y^{+}$
.
Profiles of the normalised mean viscosity,
![]() $\unicode[STIX]{x1D708}^{+}=\bar{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D708}_{w}$
(
$\unicode[STIX]{x1D708}^{+}=\bar{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D708}_{w}$
(
![]() $\bar{\unicode[STIX]{x1D708}}$
is the time-averaged viscosity), show only minor dependence on
$\bar{\unicode[STIX]{x1D708}}$
is the time-averaged viscosity), show only minor dependence on
![]() $n$
for
$n$
for
![]() $y^{+}<10$
with slightly higher values for lower
$y^{+}<10$
with slightly higher values for lower
![]() $n$
(figure 9). At
$n$
(figure 9). At
![]() $y^{+}=10$
,
$y^{+}=10$
,
![]() $\unicode[STIX]{x1D708}^{+}$
is
$\unicode[STIX]{x1D708}^{+}$
is
![]() $1.25$
(25 % higher than the nominal wall viscosity) for
$1.25$
(25 % higher than the nominal wall viscosity) for
![]() $n=0.6$
and
$n=0.6$
and
![]() $1.10$
for
$1.10$
for
![]() $n=1.2$
. Because viscosity of a shear-thinning fluid increases with decreasing shear rate, we expect the mean viscosity,
$n=1.2$
. Because viscosity of a shear-thinning fluid increases with decreasing shear rate, we expect the mean viscosity,
![]() $\unicode[STIX]{x1D708}^{+}$
, to increase monotonically towards the centre of the pipe for a shear-thinning fluid. For
$\unicode[STIX]{x1D708}^{+}$
, to increase monotonically towards the centre of the pipe for a shear-thinning fluid. For
![]() $n\neq 1$
, mean viscosity profiles deviate rapidly from the wall value beyond
$n\neq 1$
, mean viscosity profiles deviate rapidly from the wall value beyond
![]() $y^{+}=10$
. The profiles of
$y^{+}=10$
. The profiles of
![]() $\unicode[STIX]{x1D708}^{+}$
appear to display a log-like region over the range
$\unicode[STIX]{x1D708}^{+}$
appear to display a log-like region over the range
![]() $20\lesssim y^{+}\lesssim 200$
, although the reasons for this are not yet understood.
$20\lesssim y^{+}\lesssim 200$
, although the reasons for this are not yet understood.

Figure 9. Profiles of the normalised mean viscosity
![]() $\unicode[STIX]{x1D708}^{+}=\bar{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D708}_{w}$
plotted as a function of
$\unicode[STIX]{x1D708}^{+}=\bar{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D708}_{w}$
plotted as a function of
![]() $y^{+}$
. Detail in the viscous sublayer is shown in the inset figure.
$y^{+}$
. Detail in the viscous sublayer is shown in the inset figure.
4.2 Mean shear stress budget
Noting that the mean shear stress is zero at the pipe centre and
![]() $\unicode[STIX]{x1D70F}_{w}$
at the wall, integration of (2.5) leads to the following expression for the
$\unicode[STIX]{x1D70F}_{w}$
at the wall, integration of (2.5) leads to the following expression for the
![]() $(r,z)$
component of the mean non-dimensional shear stress:
$(r,z)$
component of the mean non-dimensional shear stress:
In a pipe flow, only the (
![]() $r,z$
) component of the mean shear stress component remains, therefore subscript
$r,z$
) component of the mean shear stress component remains, therefore subscript
![]() $rz$
is dropped in the following discussion for clarity.
$rz$
is dropped in the following discussion for clarity.
The effect of flow index
![]() $n$
on the mean shear stress budget is shown in figure 10 where similar profiles of
$n$
on the mean shear stress budget is shown in figure 10 where similar profiles of
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
and
$\unicode[STIX]{x1D70F}^{v^{+}}$
and
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
are seen for all
$\unicode[STIX]{x1D70F}^{R^{+}}$
are seen for all
![]() $n$
. As expected, the profile of the total mean shear stress is same for all
$n$
. As expected, the profile of the total mean shear stress is same for all
![]() $n$
and is a straight line in linear coordinates with the maximum at the wall and zero at the pipe centre.
$n$
and is a straight line in linear coordinates with the maximum at the wall and zero at the pipe centre.

Figure 10. Profiles of the
![]() $(r,z)$
component of the mean viscous stress,
$(r,z)$
component of the mean viscous stress,
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
, Reynolds shear stress,
$\unicode[STIX]{x1D70F}^{v^{+}}$
, Reynolds shear stress,
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
, and the turbulent viscous stress,
$\unicode[STIX]{x1D70F}^{R^{+}}$
, and the turbulent viscous stress,
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
, plotted for different
$\unicode[STIX]{x1D70F}^{fv^{+}}$
, plotted for different
![]() $n$
. The profile of the total mean stress
$n$
. The profile of the total mean stress
![]() $\unicode[STIX]{x1D70F}^{+}$
is linear and the same for all
$\unicode[STIX]{x1D70F}^{+}$
is linear and the same for all
![]() $n$
and is given by (4.1).
$n$
and is given by (4.1).
The mean viscous stress,
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
, is maximum at the wall and remains nearly constant until
$\unicode[STIX]{x1D70F}^{v^{+}}$
, is maximum at the wall and remains nearly constant until
![]() $y^{+}\approx 3$
and then decreases towards the centre of the pipe. For shear-thinning fluids,
$y^{+}\approx 3$
and then decreases towards the centre of the pipe. For shear-thinning fluids,
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
is higher than the Newtonian fluid across the entire radius. For the Newtonian fluid
$\unicode[STIX]{x1D70F}^{v^{+}}$
is higher than the Newtonian fluid across the entire radius. For the Newtonian fluid
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
drops to 5 % by
$\unicode[STIX]{x1D70F}^{v^{+}}$
drops to 5 % by
![]() $y^{+}=50$
, however, for
$y^{+}=50$
, however, for
![]() $n=0.6$
it is still
$n=0.6$
it is still
![]() ${\approx}15\,\%$
at
${\approx}15\,\%$
at
![]() $y^{+}=50$
. It does not drop to 5 % until
$y^{+}=50$
. It does not drop to 5 % until
![]() $y^{+}\approx 200$
, which indicates a significant thickening of the region over which the viscous stress plays a role as first suggested by Wilson & Thomas (Reference Wilson and Thomas1985). Note that
$y^{+}\approx 200$
, which indicates a significant thickening of the region over which the viscous stress plays a role as first suggested by Wilson & Thomas (Reference Wilson and Thomas1985). Note that
![]() $\unicode[STIX]{x1D70F}^{v^{+}}=2\unicode[STIX]{x1D708}^{+}S_{rz}^{+}$
, thus the increase in
$\unicode[STIX]{x1D70F}^{v^{+}}=2\unicode[STIX]{x1D708}^{+}S_{rz}^{+}$
, thus the increase in
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
with shear thinning could be a result of either increased
$\unicode[STIX]{x1D70F}^{v^{+}}$
with shear thinning could be a result of either increased
![]() $\unicode[STIX]{x1D708}^{+}$
(see figure 9) or increased
$\unicode[STIX]{x1D708}^{+}$
(see figure 9) or increased
![]() $S_{rz}^{+}=(\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+})/2$
(see figure 11). From these figures, the increase in
$S_{rz}^{+}=(\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+})/2$
(see figure 11). From these figures, the increase in
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
in the viscous sublayer is seen to be due to small increases in both
$\unicode[STIX]{x1D70F}^{v^{+}}$
in the viscous sublayer is seen to be due to small increases in both
![]() $\unicode[STIX]{x1D708}^{+}$
and
$\unicode[STIX]{x1D708}^{+}$
and
![]() $S_{rz}^{+}$
. Beyond
$S_{rz}^{+}$
. Beyond
![]() $y^{+}>10$
, the increase in
$y^{+}>10$
, the increase in
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
with shear thinning is primarily due to an increase in
$\unicode[STIX]{x1D70F}^{v^{+}}$
with shear thinning is primarily due to an increase in
![]() $\unicode[STIX]{x1D708}^{+}$
.
$\unicode[STIX]{x1D708}^{+}$
.

Figure 11. Profiles of the mean velocity gradient plotted as a function of
![]() $y^{+}$
for different
$y^{+}$
for different
![]() $n$
.
$n$
.
Outside the viscous sublayer, the increase in
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
with shear thinning is compensated for primarily by a decrease in the Reynolds shear stress,
$\unicode[STIX]{x1D70F}^{v^{+}}$
with shear thinning is compensated for primarily by a decrease in the Reynolds shear stress,
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
. The maximum value of
$\unicode[STIX]{x1D70F}^{R^{+}}$
. The maximum value of
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
for the Newtonian fluid is approximately
$\unicode[STIX]{x1D70F}^{R^{+}}$
for the Newtonian fluid is approximately
![]() $80\,\%$
which occurs at
$80\,\%$
which occurs at
![]() $y^{+}\approx 40$
. In contrast, for
$y^{+}\approx 40$
. In contrast, for
![]() $n=0.6$
, the maximum
$n=0.6$
, the maximum
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
is approximately
$\unicode[STIX]{x1D70F}^{R^{+}}$
is approximately
![]() $70\,\%$
with the location of maximum
$70\,\%$
with the location of maximum
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
moving away from the wall,
$\unicode[STIX]{x1D70F}^{R^{+}}$
moving away from the wall,
![]() $y^{+}\approx 50$
. These results are discussed further in § 4.5.
$y^{+}\approx 50$
. These results are discussed further in § 4.5.
Since the Reynolds shear stress,
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
, vanishes in the viscous sublayer, the increase here in mean viscous stress,
$\unicode[STIX]{x1D70F}^{R^{+}}$
, vanishes in the viscous sublayer, the increase here in mean viscous stress,
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
, with shear thinning is compensated by a decrease in the turbulent viscous stress,
$\unicode[STIX]{x1D70F}^{v^{+}}$
, with shear thinning is compensated by a decrease in the turbulent viscous stress,
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
. Since
$\unicode[STIX]{x1D70F}^{fv^{+}}$
. Since
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}=0$
for a Newtonian fluid, this results in increasingly negative values of
$\unicode[STIX]{x1D70F}^{fv^{+}}=0$
for a Newtonian fluid, this results in increasingly negative values of
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
for
$\unicode[STIX]{x1D70F}^{fv^{+}}$
for
![]() $n<1$
as seen in figure 10. However, the contribution of
$n<1$
as seen in figure 10. However, the contribution of
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
to the mean shear stress budget is small (approximately
$\unicode[STIX]{x1D70F}^{fv^{+}}$
to the mean shear stress budget is small (approximately
![]() $5\,\%$
at the wall for
$5\,\%$
at the wall for
![]() $n=0.6$
). Note that we expect negative values of
$n=0.6$
). Note that we expect negative values of
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}=2\overline{\unicode[STIX]{x1D708}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}$
for a shear-thinning fluid because viscosity decreases with increase in shear rate.
$\unicode[STIX]{x1D70F}^{fv^{+}}=2\overline{\unicode[STIX]{x1D708}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}$
for a shear-thinning fluid because viscosity decreases with increase in shear rate.
Overall, the effect of increased shear thinning (decreasing
![]() $n$
) on the mean shear stress budget is to increase the mean viscous stress and decrease the Reynolds shear stress. The turbulent viscous stress which is zero for a Newtonian fluid, becomes more negative with shear thinning, but is small compared to other components. It is noted that the turbulent viscous stress is determined here using the predicted viscosity and shear-rate fluctuations. It can also be determined as a deficit in the time-averaged shear stress as
$n$
) on the mean shear stress budget is to increase the mean viscous stress and decrease the Reynolds shear stress. The turbulent viscous stress which is zero for a Newtonian fluid, becomes more negative with shear thinning, but is small compared to other components. It is noted that the turbulent viscous stress is determined here using the predicted viscosity and shear-rate fluctuations. It can also be determined as a deficit in the time-averaged shear stress as
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}=r/R-\unicode[STIX]{x1D70F}^{v^{+}}-\unicode[STIX]{x1D70F}^{R^{+}}$
(see (4.1)). This can be done from experimental measurements of the mean viscous stress and the Reynolds shear stress as done by Ptasinski et al. (Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001, Reference Ptasinski, Boersma, Nieuwstadt, Hulsen, Van den Brule and Hunt2003) for viscoelastic fluids. Thus, a comparison of
$\unicode[STIX]{x1D70F}^{fv^{+}}=r/R-\unicode[STIX]{x1D70F}^{v^{+}}-\unicode[STIX]{x1D70F}^{R^{+}}$
(see (4.1)). This can be done from experimental measurements of the mean viscous stress and the Reynolds shear stress as done by Ptasinski et al. (Reference Ptasinski, Nieuwstadt, Van den Brule and Hulsen2001, Reference Ptasinski, Boersma, Nieuwstadt, Hulsen, Van den Brule and Hunt2003) for viscoelastic fluids. Thus, a comparison of
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
between DNS and experiments is possible.
$\unicode[STIX]{x1D70F}^{fv^{+}}$
between DNS and experiments is possible.
4.3 Mean velocity gradient and wall units
In the viscous sublayer, we observed a higher mean axial velocity at all
![]() $y^{+}$
for more shear-thinning fluids (see figure 8). This can be explained by considering (4.1) at the wall. Noting that
$y^{+}$
for more shear-thinning fluids (see figure 8). This can be explained by considering (4.1) at the wall. Noting that
![]() $\unicode[STIX]{x1D70F}^{v^{+}}=\unicode[STIX]{x1D708}^{+}(\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+})$
and
$\unicode[STIX]{x1D70F}^{v^{+}}=\unicode[STIX]{x1D708}^{+}(\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+})$
and
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
and
$\unicode[STIX]{x1D70F}^{R^{+}}$
and
![]() $y^{+}/R^{+}$
are zero at the wall, equation (4.1) can be used to write the mean axial velocity gradient at the wall as:
$y^{+}/R^{+}$
are zero at the wall, equation (4.1) can be used to write the mean axial velocity gradient at the wall as:
For a Newtonian fluid
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}=0$
, and hence (4.2) gives
$\unicode[STIX]{x1D70F}^{fv^{+}}=0$
, and hence (4.2) gives
![]() $\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+}=1$
which is the classical linear wall profile
$\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+}=1$
which is the classical linear wall profile
![]() $U_{z}^{+}=y^{+}$
. However,
$U_{z}^{+}=y^{+}$
. However,
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
is negative for a shear-thinning fluid and its magnitude increases with shear thinning (figure 10). Although the mean viscosity at the wall,
$\unicode[STIX]{x1D70F}^{fv^{+}}$
is negative for a shear-thinning fluid and its magnitude increases with shear thinning (figure 10). Although the mean viscosity at the wall,
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
, increases slightly with shear thinning (figure 9), it does not compensate for the increase in
$\bar{\unicode[STIX]{x1D708}}_{w}$
, increases slightly with shear thinning (figure 9), it does not compensate for the increase in
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
in (4.2). Thus higher
$\unicode[STIX]{x1D70F}^{fv^{+}}$
in (4.2). Thus higher
![]() $\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+}$
with decreasing
$\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+}$
with decreasing
![]() $n$
results in a non-unitary slope of the mean axial velocity at the wall.
$n$
results in a non-unitary slope of the mean axial velocity at the wall.
We fare no better if we replace the nominal wall viscosity,
![]() $\unicode[STIX]{x1D708}_{w}$
, used in the non-dimensionalisation by the mean wall viscosity
$\unicode[STIX]{x1D708}_{w}$
, used in the non-dimensionalisation by the mean wall viscosity
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
(
$\bar{\unicode[STIX]{x1D708}}_{w}$
(
![]() $\bar{\unicode[STIX]{x1D708}}_{w}\neq \unicode[STIX]{x1D708}_{w}$
). Doing this gives the distance from the wall in wall coordinates as
$\bar{\unicode[STIX]{x1D708}}_{w}\neq \unicode[STIX]{x1D708}_{w}$
). Doing this gives the distance from the wall in wall coordinates as
![]() $y^{\ominus }=yu^{\ast }/\bar{\unicode[STIX]{x1D708}}_{w}$
and allows (4.2) to be written as:
$y^{\ominus }=yu^{\ast }/\bar{\unicode[STIX]{x1D708}}_{w}$
and allows (4.2) to be written as:
Profiles of the mean axial velocity gradient for different
![]() $n$
are shown in figure 12(a) using the above non-dimensionalisation. Because
$n$
are shown in figure 12(a) using the above non-dimensionalisation. Because
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
is non-zero at the wall for shear-thinning fluids, it is clear from (4.3) that
$\unicode[STIX]{x1D70F}^{fv^{+}}$
is non-zero at the wall for shear-thinning fluids, it is clear from (4.3) that
![]() $\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{\ominus }\neq 1$
, thus using
$\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{\ominus }\neq 1$
, thus using
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
as the viscosity scale also does not provide the classical scaling. However, (4.3) suggests an alternative velocity scaling. Instead of using
$\bar{\unicode[STIX]{x1D708}}_{w}$
as the viscosity scale also does not provide the classical scaling. However, (4.3) suggests an alternative velocity scaling. Instead of using
![]() $\unicode[STIX]{x1D70C}u^{\ast 2}=\unicode[STIX]{x1D70F}_{w}$
, define a velocity scale via
$\unicode[STIX]{x1D70C}u^{\ast 2}=\unicode[STIX]{x1D70F}_{w}$
, define a velocity scale via
![]() $\unicode[STIX]{x1D70C}u^{\#2}=(\unicode[STIX]{x1D70F}_{w}-\unicode[STIX]{x1D70F}^{fv})$
and use
$\unicode[STIX]{x1D70C}u^{\#2}=(\unicode[STIX]{x1D70F}_{w}-\unicode[STIX]{x1D70F}^{fv})$
and use
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
as the viscosity scale. This gives a non-dimensional distance from the wall
$\bar{\unicode[STIX]{x1D708}}_{w}$
as the viscosity scale. This gives a non-dimensional distance from the wall
![]() $y^{\oplus }=yu^{\#}/\bar{\unicode[STIX]{x1D708}}_{w}$
and a non-dimensional velocity of
$y^{\oplus }=yu^{\#}/\bar{\unicode[STIX]{x1D708}}_{w}$
and a non-dimensional velocity of
![]() $U_{z}^{\oplus }=U_{z}/u^{\#}$
. Finally, it is straightforward to show that
$U_{z}^{\oplus }=U_{z}/u^{\#}$
. Finally, it is straightforward to show that
![]() $\unicode[STIX]{x2202}U_{z}^{\oplus }/\unicode[STIX]{x2202}y^{\oplus }=1$
and thus profiles of the mean axial velocity and its gradient collapse for different
$\unicode[STIX]{x2202}U_{z}^{\oplus }/\unicode[STIX]{x2202}y^{\oplus }=1$
and thus profiles of the mean axial velocity and its gradient collapse for different
![]() $n$
in the viscous sublayer (figures 12
b and 13).
$n$
in the viscous sublayer (figures 12
b and 13).

Figure 12. Profiles of the mean axial velocity gradient for different
![]() $n$
where the non-dimensionalistion used (a)
$n$
where the non-dimensionalistion used (a)
![]() $u^{\ast }$
for the velocity scale and the mean wall viscosity
$u^{\ast }$
for the velocity scale and the mean wall viscosity
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
for the viscosity scale, (b)
$\bar{\unicode[STIX]{x1D708}}_{w}$
for the viscosity scale, (b)
![]() $u^{\#}$
for the velocity scale and
$u^{\#}$
for the velocity scale and
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
for the viscosity scale.
$\bar{\unicode[STIX]{x1D708}}_{w}$
for the viscosity scale.

Figure 13. Mean axial velocity profiles plotted for different
![]() $n$
using
$n$
using
![]() $u^{\#}$
for the velocity scale and
$u^{\#}$
for the velocity scale and
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
for the viscosity scale in non-dimensionalisation.
$\bar{\unicode[STIX]{x1D708}}_{w}$
for the viscosity scale in non-dimensionalisation.
A mitigating factor against using these new scales is that they are less practical. Neither
![]() $u^{\#}$
or
$u^{\#}$
or
![]() $\bar{\unicode[STIX]{x1D708}}_{w}$
can be determined a priori in experiment or simulation. The mean shear rate and axial velocity gradient required at the wall are difficult to measure accurately in experiment. Although the new scaling collapses near wall profiles of the mean axial velocity, its gradient and the mean viscous stress, profiles of other mean flow variables and correlations do not collapse for different
$\bar{\unicode[STIX]{x1D708}}_{w}$
can be determined a priori in experiment or simulation. The mean shear rate and axial velocity gradient required at the wall are difficult to measure accurately in experiment. Although the new scaling collapses near wall profiles of the mean axial velocity, its gradient and the mean viscous stress, profiles of other mean flow variables and correlations do not collapse for different
![]() $n$
in the viscous sublayer (not shown). Finally, profiles of the total mean shear stress for different
$n$
in the viscous sublayer (not shown). Finally, profiles of the total mean shear stress for different
![]() $n$
no longer lie on top of each other because the shear stress scale
$n$
no longer lie on top of each other because the shear stress scale
![]() $\unicode[STIX]{x1D70C}{u^{\#}}^{2}$
varies with
$\unicode[STIX]{x1D70C}{u^{\#}}^{2}$
varies with
![]() $n$
. Thus in the process of recovering one fundamental Newtonian relation, another fundamental relation is lost. As a consequence of these facts
$n$
. Thus in the process of recovering one fundamental Newtonian relation, another fundamental relation is lost. As a consequence of these facts
![]() $u^{\ast }$
and
$u^{\ast }$
and
![]() $\unicode[STIX]{x1D708}_{w}$
as mentioned in § 2.3 are used in the non-dimensionalisation.
$\unicode[STIX]{x1D708}_{w}$
as mentioned in § 2.3 are used in the non-dimensionalisation.

Figure 14. Profiles of the viscous stresses,
![]() $\unicode[STIX]{x1D70F}^{v}$
and
$\unicode[STIX]{x1D70F}^{v}$
and
![]() $\unicode[STIX]{x1D70F}^{fv}$
, plotted for different
$\unicode[STIX]{x1D70F}^{fv}$
, plotted for different
![]() $n$
using
$n$
using
![]() $u^{\#}$
for the velocity scale and
$u^{\#}$
for the velocity scale and
![]() $(\bar{\unicode[STIX]{x1D708}})_{w}$
for the viscosity scale in non-dimensionalisation.
$(\bar{\unicode[STIX]{x1D708}})_{w}$
for the viscosity scale in non-dimensionalisation.
4.4 Turbulence intensities
The results presented in § 4.1 show that the mean axial velocity,
![]() $U_{z}^{+}$
, and the mean viscosity,
$U_{z}^{+}$
, and the mean viscosity,
![]() $\unicode[STIX]{x1D708}^{+}$
, are only weakly dependent on
$\unicode[STIX]{x1D708}^{+}$
, are only weakly dependent on
![]() $n$
in the viscous sublayer. However, this is not the case for the axial turbulence intensity
$n$
in the viscous sublayer. However, this is not the case for the axial turbulence intensity
![]() $u_{z}^{\prime +}$
as shown in figure 15(a). Here
$u_{z}^{\prime +}$
as shown in figure 15(a). Here
![]() $u_{z}^{\prime +}$
increases with decreasing
$u_{z}^{\prime +}$
increases with decreasing
![]() $n$
at all
$n$
at all
![]() $y^{+}$
and its peak moves further from the wall. For
$y^{+}$
and its peak moves further from the wall. For
![]() $n=0.6$
the increase in the viscous sublayer is of order 25 %.
$n=0.6$
the increase in the viscous sublayer is of order 25 %.
Unlike
![]() $u_{z}^{\prime +}$
which increased with shear thinning at all
$u_{z}^{\prime +}$
which increased with shear thinning at all
![]() $y^{+}$
, the radial and the azimuthal turbulence intensities (
$y^{+}$
, the radial and the azimuthal turbulence intensities (
![]() $u_{r}^{\prime +}$
,
$u_{r}^{\prime +}$
,
![]() $u_{\unicode[STIX]{x1D703}}^{\prime +}$
) show dependence on
$u_{\unicode[STIX]{x1D703}}^{\prime +}$
) show dependence on
![]() $n$
mainly outside the viscous sublayer, where they decrease with decreasing
$n$
mainly outside the viscous sublayer, where they decrease with decreasing
![]() $n$
(figure 15
b,c). The location where profiles of
$n$
(figure 15
b,c). The location where profiles of
![]() $u_{r}^{\prime +}$
,
$u_{r}^{\prime +}$
,
![]() $u_{\unicode[STIX]{x1D703}}^{\prime +}$
for different
$u_{\unicode[STIX]{x1D703}}^{\prime +}$
for different
![]() $n$
deviate significantly from each other coincides with the location where the mean viscosity
$n$
deviate significantly from each other coincides with the location where the mean viscosity
![]() $\unicode[STIX]{x1D708}^{+}$
also deviates. This suggests that
$\unicode[STIX]{x1D708}^{+}$
also deviates. This suggests that
![]() $u_{r}^{\prime +}$
,
$u_{r}^{\prime +}$
,
![]() $u_{\unicode[STIX]{x1D703}}^{\prime +}$
strongly depend on the mean fluid viscosity and that increased viscosity with decreasing
$u_{\unicode[STIX]{x1D703}}^{\prime +}$
strongly depend on the mean fluid viscosity and that increased viscosity with decreasing
![]() $n$
damps the velocity fluctuations normal to the mean flow direction. Note that the turbulence intensity profiles plotted in outer units (normalised by the bulk velocity
$n$
damps the velocity fluctuations normal to the mean flow direction. Note that the turbulence intensity profiles plotted in outer units (normalised by the bulk velocity
![]() $U_{b}$
) also show similar trends (figure 15
d–f). Both of these trends have been noted previously (Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004; Rudman & Blackburn Reference Rudman and Blackburn2006; Gavrilov & Rudyak Reference Gavrilov and Rudyak2016) and have been suggested as being due to decreased energy transfer from axial velocity fluctuations to transverse velocity fluctuations via pressure fluctuations (Gavrilov & Rudyak Reference Gavrilov and Rudyak2016).
$U_{b}$
) also show similar trends (figure 15
d–f). Both of these trends have been noted previously (Rudman et al.
Reference Rudman, Blackburn, Graham and Pullum2004; Rudman & Blackburn Reference Rudman and Blackburn2006; Gavrilov & Rudyak Reference Gavrilov and Rudyak2016) and have been suggested as being due to decreased energy transfer from axial velocity fluctuations to transverse velocity fluctuations via pressure fluctuations (Gavrilov & Rudyak Reference Gavrilov and Rudyak2016).

Figure 15. Profiles of turbulence intensities plotted in wall units (a–c) and in outer units (d–f) for different flow indices
![]() $n$
.
$n$
.

Figure 16. Profiles of root mean square viscosity fluctuations normalised by (a) the nominal wall viscosity
![]() $\unicode[STIX]{x1D708}_{w}$
and (b) mean viscosity,
$\unicode[STIX]{x1D708}_{w}$
and (b) mean viscosity,
![]() $\bar{\unicode[STIX]{x1D708}}(y^{+})$
plotted for different
$\bar{\unicode[STIX]{x1D708}}(y^{+})$
plotted for different
![]() $n$
.
$n$
.
For a power-law fluid, root mean square (r.m.s.) viscosity fluctuations
![]() $\unicode[STIX]{x1D708}^{\prime +}=\unicode[STIX]{x1D708}_{rms}^{\prime }/\unicode[STIX]{x1D708}_{w}$
are non-zero at all
$\unicode[STIX]{x1D708}^{\prime +}=\unicode[STIX]{x1D708}_{rms}^{\prime }/\unicode[STIX]{x1D708}_{w}$
are non-zero at all
![]() $y^{+}$
and increase with shear thinning (figure 16
a). Similar to the mean viscosity,
$y^{+}$
and increase with shear thinning (figure 16
a). Similar to the mean viscosity,
![]() $\unicode[STIX]{x1D708}^{\prime +}$
remains uniform in the viscous sublayer and increases with
$\unicode[STIX]{x1D708}^{\prime +}$
remains uniform in the viscous sublayer and increases with
![]() $y^{+}$
outside the viscous sublayer, however, except for
$y^{+}$
outside the viscous sublayer, however, except for
![]() $n=0.6$
, the rate of increase in
$n=0.6$
, the rate of increase in
![]() $\unicode[STIX]{x1D708}^{\prime +}$
with
$\unicode[STIX]{x1D708}^{\prime +}$
with
![]() $y^{+}$
is small. Profiles of
$y^{+}$
is small. Profiles of
![]() $\unicode[STIX]{x1D708}^{\prime +}$
normalised by the local mean viscosity show that
$\unicode[STIX]{x1D708}^{\prime +}$
normalised by the local mean viscosity show that
![]() $\unicode[STIX]{x1D708}^{\prime +}/\unicode[STIX]{x1D708}^{+}$
increases only up to a certain
$\unicode[STIX]{x1D708}^{\prime +}/\unicode[STIX]{x1D708}^{+}$
increases only up to a certain
![]() $y^{+}$
, which increases with decreasing
$y^{+}$
, which increases with decreasing
![]() $n$
, and then starts decreasing (figure 16
b). Higher
$n$
, and then starts decreasing (figure 16
b). Higher
![]() $\unicode[STIX]{x1D708}^{\prime +}$
suggests higher instantaneous viscosities for a more shear-thinning fluid, which is also seen in figure 5.
$\unicode[STIX]{x1D708}^{\prime +}$
suggests higher instantaneous viscosities for a more shear-thinning fluid, which is also seen in figure 5.
4.5 Quadrant analysis of Reynolds stresses
We consider the quadrant analysis of Reynolds shear stress proposed by Wallace, Eckelmann & Brodkey (Reference Wallace, Eckelmann and Brodkey1972) and define
![]() $\tilde{v_{r}}^{\prime }=-v_{r}^{\prime }$
as the instantaneous wall-normal velocity fluctuations (
$\tilde{v_{r}}^{\prime }=-v_{r}^{\prime }$
as the instantaneous wall-normal velocity fluctuations (
![]() $v_{r}^{\prime }$
has a different sign here because of the coordinate system employed). The analysis classifies the
$v_{r}^{\prime }$
has a different sign here because of the coordinate system employed). The analysis classifies the
![]() $v_{z}^{\prime }\tilde{v_{r}}^{\prime }$
signal into four different categories: Q1(
$v_{z}^{\prime }\tilde{v_{r}}^{\prime }$
signal into four different categories: Q1(
![]() $+v_{z}^{\prime }$
,
$+v_{z}^{\prime }$
,
![]() $+\tilde{v}_{r}^{\prime }$
), Q2(
$+\tilde{v}_{r}^{\prime }$
), Q2(
![]() $-v_{z}^{\prime }$
,
$-v_{z}^{\prime }$
,
![]() $+\tilde{v}_{r}^{\prime }$
), Q3(
$+\tilde{v}_{r}^{\prime }$
), Q3(
![]() $-v_{z}^{\prime }$
,
$-v_{z}^{\prime }$
,
![]() $-\tilde{v}_{r}^{\prime }$
) and Q4(
$-\tilde{v}_{r}^{\prime }$
) and Q4(
![]() $+v_{z}^{\prime }$
,
$+v_{z}^{\prime }$
,
![]() $-\tilde{v}_{r}^{\prime }$
). These quadrants are associated with different physical events. For channel flows of Newtonian fluids, it has been found that most of the Reynolds shear stress production is associated with the ejection (Q2) and sweep (Q4) of low-speed fluid near the wall. Consequently they are also termed the ejection and sweep quadrants (see Wallace Reference Wallace2016).
$-\tilde{v}_{r}^{\prime }$
). These quadrants are associated with different physical events. For channel flows of Newtonian fluids, it has been found that most of the Reynolds shear stress production is associated with the ejection (Q2) and sweep (Q4) of low-speed fluid near the wall. Consequently they are also termed the ejection and sweep quadrants (see Wallace Reference Wallace2016).
Figure 17 compares the joint probability distribution
![]() $P(-v_{r}^{\prime }/u^{\ast },v_{z}^{\prime }/u^{\ast })$
of
$P(-v_{r}^{\prime }/u^{\ast },v_{z}^{\prime }/u^{\ast })$
of
![]() $n=1.0$
and
$n=1.0$
and
![]() $n=0.6$
for values of
$n=0.6$
for values of
![]() $y^{+}=10$
, 30, 70 and 100. In the near-wall region, the major axis of
$y^{+}=10$
, 30, 70 and 100. In the near-wall region, the major axis of
![]() $P(-v_{r}^{\prime },v_{z}^{\prime })$
is less inclined in the direction of Q2–Q4 for
$P(-v_{r}^{\prime },v_{z}^{\prime })$
is less inclined in the direction of Q2–Q4 for
![]() $n=0.6$
(figure 17
e–h) compared to the Newtonian fluid (figure 17
a–d), which suggests that the shear-thinning rheology suppresses the contribution of ejection and sweep to Reynolds shear stress generation. Compared to the Newtonian fluid, a narrower spread of the marginal probability distribution
$n=0.6$
(figure 17
e–h) compared to the Newtonian fluid (figure 17
a–d), which suggests that the shear-thinning rheology suppresses the contribution of ejection and sweep to Reynolds shear stress generation. Compared to the Newtonian fluid, a narrower spread of the marginal probability distribution
![]() $P(-v_{r}^{\prime })$
for
$P(-v_{r}^{\prime })$
for
![]() $n=0.6$
in the near-wall region (seen clearly for
$n=0.6$
in the near-wall region (seen clearly for
![]() $y^{+}=10$
and
$y^{+}=10$
and
![]() $30$
) suggests that with shear thinning, axial velocity fluctuations become larger than wall-normal fluctuations (as known from figure 15). Therefore, there is a less momentum exchange via the Reynolds shear stress in the wall-normal direction.
$30$
) suggests that with shear thinning, axial velocity fluctuations become larger than wall-normal fluctuations (as known from figure 15). Therefore, there is a less momentum exchange via the Reynolds shear stress in the wall-normal direction.

Figure 17. Joint and marginal probability distributions of the axial and wall-normal velocity fluctuations (
![]() $v_{z}^{\prime }$
and
$v_{z}^{\prime }$
and
![]() $-v_{r}^{\prime }$
) plotted at
$-v_{r}^{\prime }$
) plotted at
![]() $y^{+}=10,30,70,100$
(top to bottom) for (a–d) Newtonian and (e–h)
$y^{+}=10,30,70,100$
(top to bottom) for (a–d) Newtonian and (e–h)
![]() $n=0.6$
.
$n=0.6$
.
4.6 Summary
The key results in this section are that the effect of shear thinning is to increase the mean axial velocity, mean viscosity and axial turbulence intensity but, to decrease the radial and azimuthal turbulence intensities. The mean viscous stress increases slightly in the very-near-wall region and quite significantly in the buffer layer, and the distance from the wall where it drops to of order 5 % of the total stress is significantly increased. With shear thinning, the Reynolds shear stress decreases across the pipe and the new term in the mean shear stress balance, the turbulent viscous stress, is always negative, offsetting the increased mean viscous stress very near the wall. This results in an increase in the mean axial velocity gradient and the bulk velocity (hence, the flow rate) with shear thinning.
5 Energy budgets
The total kinetic energy per unit mass is defined as
![]() $q=u_{i}u_{i}/2$
and using the Reynolds decomposition, the mean kinetic energy is written as
$q=u_{i}u_{i}/2$
and using the Reynolds decomposition, the mean kinetic energy is written as
![]() $\bar{q}=K+k$
where
$\bar{q}=K+k$
where
![]() $K=U_{i}U_{i}/2$
is the mean flow kinetic energy (MFKE) and
$K=U_{i}U_{i}/2$
is the mean flow kinetic energy (MFKE) and
![]() $k=\overline{u_{i}^{\prime }u_{i}^{\prime }}/2$
is the turbulent kinetic energy (TKE). Non-uniform viscosity and viscosity fluctuations modify the MFKE and TKE budget equations for a non-Newtonian fluid. Since MFKE and TKE are scalar quantities, the choice of the coordinate system does not influence their budget equations and a Cartesian system is chosen here for clarity.
$k=\overline{u_{i}^{\prime }u_{i}^{\prime }}/2$
is the turbulent kinetic energy (TKE). Non-uniform viscosity and viscosity fluctuations modify the MFKE and TKE budget equations for a non-Newtonian fluid. Since MFKE and TKE are scalar quantities, the choice of the coordinate system does not influence their budget equations and a Cartesian system is chosen here for clarity.
5.1 Mean flow kinetic energy budget
An equation for the MFKE can be obtained by taking the divergence of (2.5). In Cartesian coordinates this produces
 $$\begin{eqnarray}\displaystyle \overbrace{\frac{\unicode[STIX]{x2202}K}{\unicode[STIX]{x2202}t}}^{K_{t}}+\overbrace{U_{j}\frac{\unicode[STIX]{x2202}K}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{A}}_{m}} & = & \displaystyle \overbrace{-U_{j}\frac{\unicode[STIX]{x2202}P}{\unicode[STIX]{x2202}x_{j}}}^{W_{dp/dz}}+\overbrace{\left(-\frac{\unicode[STIX]{x2202}U_{i}\overline{u_{i}^{\prime }u_{j}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}\right)}^{{\mathcal{T}}^{m}}+\overbrace{2\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D708}}S_{ij}U_{i}}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{D}}^{m}}+\overbrace{(-2\bar{\unicode[STIX]{x1D708}}S_{ij}S_{ij})}^{\unicode[STIX]{x1D716}^{m}}+\overbrace{\overline{u_{i}^{\prime }u_{j}^{\prime }}S_{ij}}^{-{\mathcal{P}}}\nonumber\\ \displaystyle & & \displaystyle +\,\overbrace{2\frac{\unicode[STIX]{x2202}U_{i}\overline{\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}}^{\unicode[STIX]{x1D6F6}_{nn}^{m}}+\overbrace{(-2\overline{\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }}S_{ij})}^{\unicode[STIX]{x1D712}_{nn}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overbrace{\frac{\unicode[STIX]{x2202}K}{\unicode[STIX]{x2202}t}}^{K_{t}}+\overbrace{U_{j}\frac{\unicode[STIX]{x2202}K}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{A}}_{m}} & = & \displaystyle \overbrace{-U_{j}\frac{\unicode[STIX]{x2202}P}{\unicode[STIX]{x2202}x_{j}}}^{W_{dp/dz}}+\overbrace{\left(-\frac{\unicode[STIX]{x2202}U_{i}\overline{u_{i}^{\prime }u_{j}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}\right)}^{{\mathcal{T}}^{m}}+\overbrace{2\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D708}}S_{ij}U_{i}}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{D}}^{m}}+\overbrace{(-2\bar{\unicode[STIX]{x1D708}}S_{ij}S_{ij})}^{\unicode[STIX]{x1D716}^{m}}+\overbrace{\overline{u_{i}^{\prime }u_{j}^{\prime }}S_{ij}}^{-{\mathcal{P}}}\nonumber\\ \displaystyle & & \displaystyle +\,\overbrace{2\frac{\unicode[STIX]{x2202}U_{i}\overline{\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}}^{\unicode[STIX]{x1D6F6}_{nn}^{m}}+\overbrace{(-2\overline{\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }}S_{ij})}^{\unicode[STIX]{x1D712}_{nn}}.\end{eqnarray}$$
We use following terminology for different terms in (5.1):
-
 $K_{t}$
:
$K_{t}$
: -
local rate of change of
 $K$
;
$K$
; -
 ${\mathcal{A}}^{m}$
:
${\mathcal{A}}^{m}$
: -
mean flow advection;
-
 $W_{dp/dz}^{+}$
:
$W_{dp/dz}^{+}$
: -
the mean flow energy production;
-
 ${\mathcal{T}}^{m}$
:
${\mathcal{T}}^{m}$
: -
turbulent transport;
-
 ${\mathcal{D}}^{m}$
:
${\mathcal{D}}^{m}$
: -
the mean viscous transport;
-
 $\unicode[STIX]{x1D716}^{m}$
:
$\unicode[STIX]{x1D716}^{m}$
: -
the mean viscous dissipation;
-
 $-{\mathcal{P}}$
:
$-{\mathcal{P}}$
: -
turbulent energy transfer or negative of turbulent kinetic energy production;
-
 $\unicode[STIX]{x1D6F6}_{nn}^{m}$
:
$\unicode[STIX]{x1D6F6}_{nn}^{m}$
: -
the turbulent viscous stress transport;
-
 $\unicode[STIX]{x1D712}_{nn}$
:
$\unicode[STIX]{x1D712}_{nn}$
: -
the mean shear turbulent viscous dissipation.
A subscript
![]() $nn$
is used for terms which are non-zero only for a non-Newtonian fluid. The first two terms in (5.1) i.e.
$nn$
is used for terms which are non-zero only for a non-Newtonian fluid. The first two terms in (5.1) i.e.
![]() $K_{t}$
and
$K_{t}$
and
![]() ${\mathcal{A}}^{m}$
, are the rate of change and the mean advection of
${\mathcal{A}}^{m}$
, are the rate of change and the mean advection of
![]() $K$
both of which vanish for a pipe flow as the mean flow is temporally stationary, one component and uniform in the axial direction. The mean flow energy production,
$K$
both of which vanish for a pipe flow as the mean flow is temporally stationary, one component and uniform in the axial direction. The mean flow energy production,
![]() $W_{dp/dz}$
, is the only source of energy in (5.1). The mean flow stresses common for both Newtonian and a non-Newtonian fluid (
$W_{dp/dz}$
, is the only source of energy in (5.1). The mean flow stresses common for both Newtonian and a non-Newtonian fluid (
![]() $\unicode[STIX]{x1D70F}^{v}=2\bar{\unicode[STIX]{x1D708}}S_{ij}$
and
$\unicode[STIX]{x1D70F}^{v}=2\bar{\unicode[STIX]{x1D708}}S_{ij}$
and
![]() $\unicode[STIX]{x1D70F}^{R}=-\overline{u_{i}^{\prime }u_{j}^{\prime }}$
) appear at four places in (5.1) and play two roles; first, they redistribute the energy within the domain via the transport terms
$\unicode[STIX]{x1D70F}^{R}=-\overline{u_{i}^{\prime }u_{j}^{\prime }}$
) appear at four places in (5.1) and play two roles; first, they redistribute the energy within the domain via the transport terms
![]() ${\mathcal{D}}^{m}$
and
${\mathcal{D}}^{m}$
and
![]() ${\mathcal{T}}^{m}$
. Second, they act as a sink (
${\mathcal{T}}^{m}$
. Second, they act as a sink (
![]() $\unicode[STIX]{x1D716}^{m}$
and
$\unicode[STIX]{x1D716}^{m}$
and
![]() $-{\mathcal{P}}$
). The transport terms cannot affect the global MFKE budget because the volume integral of each transport term is zero (Pope Reference Pope2000). As we will see later,
$-{\mathcal{P}}$
). The transport terms cannot affect the global MFKE budget because the volume integral of each transport term is zero (Pope Reference Pope2000). As we will see later,
![]() $-{\mathcal{P}}$
is the negative of the only source term in the TKE budget (see (5.2)) and therefore represents the energy transfer from the mean flow to the turbulence.
$-{\mathcal{P}}$
is the negative of the only source term in the TKE budget (see (5.2)) and therefore represents the energy transfer from the mean flow to the turbulence.
The last two terms in (5.1),
![]() $\unicode[STIX]{x1D6F6}_{nn}^{m}$
and
$\unicode[STIX]{x1D6F6}_{nn}^{m}$
and
![]() $\unicode[STIX]{x1D712}_{nn}$
, appear only for a non-Newtonian fluid. They arise from the interaction between the turbulent viscous stress,
$\unicode[STIX]{x1D712}_{nn}$
, appear only for a non-Newtonian fluid. They arise from the interaction between the turbulent viscous stress,
![]() $\unicode[STIX]{x1D70F}^{fv}=2\overline{\unicode[STIX]{x1D708}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}$
, and the mean flow. The turbulent viscous transport,
$\unicode[STIX]{x1D70F}^{fv}=2\overline{\unicode[STIX]{x1D708}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}$
, and the mean flow. The turbulent viscous transport,
![]() $\unicode[STIX]{x1D6F6}_{nn}^{m}$
, is a transport term whereas the mean shear turbulent viscous dissipation,
$\unicode[STIX]{x1D6F6}_{nn}^{m}$
, is a transport term whereas the mean shear turbulent viscous dissipation,
![]() $\unicode[STIX]{x1D712}_{nn}$
, modifies the mean flow energy dissipation
$\unicode[STIX]{x1D712}_{nn}$
, modifies the mean flow energy dissipation
![]() $\unicode[STIX]{x1D716}^{m}$
. This non-Newtonian dissipation term,
$\unicode[STIX]{x1D716}^{m}$
. This non-Newtonian dissipation term,
![]() $\unicode[STIX]{x1D712}_{nn}$
, also appears in the TKE budget (see (5.2)). Note that
$\unicode[STIX]{x1D712}_{nn}$
, also appears in the TKE budget (see (5.2)). Note that
![]() $\unicode[STIX]{x1D712}_{nn}$
can be positive or negative depending on the rheology of the fluid. However, positive values of
$\unicode[STIX]{x1D712}_{nn}$
can be positive or negative depending on the rheology of the fluid. However, positive values of
![]() $\unicode[STIX]{x1D712}_{nn}$
do not imply MFKE production. The mean flow can receive energy only through the action of pressure gradient against the mean flow and positive values of
$\unicode[STIX]{x1D712}_{nn}$
do not imply MFKE production. The mean flow can receive energy only through the action of pressure gradient against the mean flow and positive values of
![]() $\unicode[STIX]{x1D712}_{nn}$
instead correspond to a reduced mean flow kinetic energy dissipation.
$\unicode[STIX]{x1D712}_{nn}$
instead correspond to a reduced mean flow kinetic energy dissipation.

Figure 18. Profiles of the mean flow kinetic energy terms from (5.1) plotted in wall units for a Newtonian fluid (top) and
![]() $n=0.6$
(bottom). Vertical lines show the location where
$n=0.6$
(bottom). Vertical lines show the location where
![]() ${\mathcal{D}}^{m^{+}}$
,
${\mathcal{D}}^{m^{+}}$
,
![]() $-{\mathcal{P}}^{+}$
and
$-{\mathcal{P}}^{+}$
and
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
intersect.
$\unicode[STIX]{x1D716}^{m^{+}}$
intersect.
To set the scene for subsequent discussion, we briefly describe the MFKE budget for a Newtonian fluid and plot the profiles of each term in figure 18. As the mean axial pressure gradient,
![]() $\text{d}P/\text{d}z$
, is independent of
$\text{d}P/\text{d}z$
, is independent of
![]() $r$
, profiles of the mean flow energy production,
$r$
, profiles of the mean flow energy production,
![]() $W_{\text{d}p/\text{d}z}^{+}$
, follow a similar trend as seen for
$W_{\text{d}p/\text{d}z}^{+}$
, follow a similar trend as seen for
![]() $U_{z}^{+}$
in figure 8(a) and
$U_{z}^{+}$
in figure 8(a) and
![]() $W_{\text{d}p/\text{d}z}^{+}$
increases with the distance from the wall. Very near the wall (
$W_{\text{d}p/\text{d}z}^{+}$
increases with the distance from the wall. Very near the wall (
![]() $y^{+}<3$
), the MFKE budget is purely a balance between the two viscous terms,
$y^{+}<3$
), the MFKE budget is purely a balance between the two viscous terms,
![]() ${\mathcal{D}}^{m^{+}}$
and
${\mathcal{D}}^{m^{+}}$
and
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
, because the Reynolds shear stress,
$\unicode[STIX]{x1D716}^{m^{+}}$
, because the Reynolds shear stress,
![]() $\unicode[STIX]{x1D70F}^{R^{+}}$
vanishes here, as do the two terms that contain it (i.e. the Reynolds stress transport,
$\unicode[STIX]{x1D70F}^{R^{+}}$
vanishes here, as do the two terms that contain it (i.e. the Reynolds stress transport,
![]() ${\mathcal{T}}^{m^{+}}$
, and the turbulent energy transfer,
${\mathcal{T}}^{m^{+}}$
, and the turbulent energy transfer,
![]() $-{\mathcal{P}}^{+}$
).
$-{\mathcal{P}}^{+}$
).
Over the range
![]() $3<y^{+}<60$
, there is a more complex balance between the Newtonian transport and dissipation terms,
$3<y^{+}<60$
, there is a more complex balance between the Newtonian transport and dissipation terms,
![]() ${\mathcal{T}}^{m^{+}}$
,
${\mathcal{T}}^{m^{+}}$
,
![]() ${\mathcal{D}}^{m^{+}}$
,
${\mathcal{D}}^{m^{+}}$
,
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
and
$\unicode[STIX]{x1D716}^{m^{+}}$
and
![]() $-{\mathcal{P}}^{+}$
. For
$-{\mathcal{P}}^{+}$
. For
![]() $y^{+}>3$
, both
$y^{+}>3$
, both
![]() ${\mathcal{T}}^{m^{+}}$
and
${\mathcal{T}}^{m^{+}}$
and
![]() $-{\mathcal{P}}^{+}$
grow in magnitude with
$-{\mathcal{P}}^{+}$
grow in magnitude with
![]() ${\mathcal{T}}^{m^{+}}$
adding energy in this region and
${\mathcal{T}}^{m^{+}}$
adding energy in this region and
![]() $-{\mathcal{P}}^{+}$
dissipating it , with both terms reaching their maximum effect at
$-{\mathcal{P}}^{+}$
dissipating it , with both terms reaching their maximum effect at
![]() $y^{+}\approx 10$
. The mean viscous transport,
$y^{+}\approx 10$
. The mean viscous transport,
![]() ${\mathcal{D}}^{m^{+}}$
, is a sink for
${\mathcal{D}}^{m^{+}}$
, is a sink for
![]() $y^{+}>8$
and source for
$y^{+}>8$
and source for
![]() $y^{+}<8$
, which means that it transports energy to the viscous sublayer because its volume integral is zero. The turbulent kinetic energy production,
$y^{+}<8$
, which means that it transports energy to the viscous sublayer because its volume integral is zero. The turbulent kinetic energy production,
![]() $-{\mathcal{P}}^{+}$
, is significant only for
$-{\mathcal{P}}^{+}$
, is significant only for
![]() $3\lesssim y^{+}\lesssim 40$
and it reaches a maximum approximately at the same location where
$3\lesssim y^{+}\lesssim 40$
and it reaches a maximum approximately at the same location where
![]() ${\mathcal{D}}^{m^{+}}$
and
${\mathcal{D}}^{m^{+}}$
and
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
cross each other as also noted in Thais, Gatski & Mompean (Reference Thais, Gatski and Mompean2013) for viscoelastic fluids.
$\unicode[STIX]{x1D716}^{m^{+}}$
cross each other as also noted in Thais, Gatski & Mompean (Reference Thais, Gatski and Mompean2013) for viscoelastic fluids.
The Reynolds shear stress transport,
![]() ${\mathcal{T}}^{m^{+}}$
, continues acting as a source up to
${\mathcal{T}}^{m^{+}}$
, continues acting as a source up to
![]() $y^{+}\approx 40$
where it changes sign due to the change in the slope of the Reynolds shear stress (see figure 10). It then acts as a sink and therefore, transports energy from
$y^{+}\approx 40$
where it changes sign due to the change in the slope of the Reynolds shear stress (see figure 10). It then acts as a sink and therefore, transports energy from
![]() $y^{+}>40$
towards the wall. For
$y^{+}>40$
towards the wall. For
![]() $y^{+}>60$
, the MFKE budget is mainly a balance between
$y^{+}>60$
, the MFKE budget is mainly a balance between
![]() ${\mathcal{T}}^{m^{+}}$
and
${\mathcal{T}}^{m^{+}}$
and
![]() $W_{\text{d}P/\text{d}z}^{+}$
because the turbulent kinetic energy production,
$W_{\text{d}P/\text{d}z}^{+}$
because the turbulent kinetic energy production,
![]() $-{\mathcal{P}}^{+}$
, is very small and approaches zero at the pipe centre.
$-{\mathcal{P}}^{+}$
, is very small and approaches zero at the pipe centre.

Figure 19. Profiles of the mean flow kinetic energy budget terms from (5.1) plotted for different flow indices
![]() $n$
in wall variables. Note that the vertical scale changes in each plot.
$n$
in wall variables. Note that the vertical scale changes in each plot.
The effect of changes in flow index on individual mean flow energy budget terms is shown in figures 18 and 19. We first discuss the effect of shear thinning on those terms that also appear for a Newtonian fluid before examining the modifications resulting to the non-Newtonian terms. As mentioned earlier also, when a trend is described as occurring with shear thinning, it should be taken as read that the opposite trend occurs with shear thickening.
As already noted in § 4.1, the mean axial velocity profile for a shear-thinning fluid lies above the Newtonian profile and consequently the mean flow energy production,
![]() $W_{\text{d}P/\text{d}z}^{+}$
, must increase with shear thinning as seen in figure 19(a). However, with the exception of
$W_{\text{d}P/\text{d}z}^{+}$
, must increase with shear thinning as seen in figure 19(a). However, with the exception of
![]() $W_{\text{d}P/\text{d}z}^{+}$
, most terms show little variation with
$W_{\text{d}P/\text{d}z}^{+}$
, most terms show little variation with
![]() $n$
beyond
$n$
beyond
![]() $y^{+}\approx 60$
although there are sufficient differences to balance the increased production, these are not obvious given the required figures axis scaling. The radial location where the two viscous terms,
$y^{+}\approx 60$
although there are sufficient differences to balance the increased production, these are not obvious given the required figures axis scaling. The radial location where the two viscous terms,
![]() ${\mathcal{D}}^{m^{+}}$
and
${\mathcal{D}}^{m^{+}}$
and
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
, intersect each other is also shifted by shear thinning as seen in figure 18.
$\unicode[STIX]{x1D716}^{m^{+}}$
, intersect each other is also shifted by shear thinning as seen in figure 18.
The mean axial velocity gradient,
![]() $\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+}$
, and hence the mean viscous stress,
$\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+}$
, and hence the mean viscous stress,
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
, increases with decreasing
$\unicode[STIX]{x1D70F}^{v^{+}}$
, increases with decreasing
![]() $n$
(figure 10), therefore, more negative
$n$
(figure 10), therefore, more negative
![]() $\unicode[STIX]{x1D716}_{m}^{v^{+}}$
is observed with decreasing
$\unicode[STIX]{x1D716}_{m}^{v^{+}}$
is observed with decreasing
![]() $n$
in figure 19(d). Since the gradient of
$n$
in figure 19(d). Since the gradient of
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
is also less negative for a more shear-thinning fluid further from the wall, higher values of
$\unicode[STIX]{x1D70F}^{v^{+}}$
is also less negative for a more shear-thinning fluid further from the wall, higher values of
![]() ${\mathcal{D}}^{m^{+}}$
result until
${\mathcal{D}}^{m^{+}}$
result until
![]() $y^{+}\approx 15{-}20$
where this term becomes slightly less negative for a more shear-thinning fluid (figure 19
c). Similarly, lower Reynolds stress with decreasing
$y^{+}\approx 15{-}20$
where this term becomes slightly less negative for a more shear-thinning fluid (figure 19
c). Similarly, lower Reynolds stress with decreasing
![]() $n$
(figure 10) results in less negative turbulent energy transfer,
$n$
(figure 10) results in less negative turbulent energy transfer,
![]() $-{\mathcal{P}}^{+}$
, (figure 19
e) and lower values of the Reynolds stress transport,
$-{\mathcal{P}}^{+}$
, (figure 19
e) and lower values of the Reynolds stress transport,
![]() ${\mathcal{T}}^{m^{+}}$
, up to approx
${\mathcal{T}}^{m^{+}}$
, up to approx
![]() $y^{+}\approx 20$
at which point the latter term becomes a little higher with shear thinning (figure 19
b). As discussed later in § 5.2,
$y^{+}\approx 20$
at which point the latter term becomes a little higher with shear thinning (figure 19
b). As discussed later in § 5.2,
![]() $-{\mathcal{P}}^{+}$
appears with opposite sign in the turbulent kinetic energy budget as a production term. Thus the decrease in magnitude of
$-{\mathcal{P}}^{+}$
appears with opposite sign in the turbulent kinetic energy budget as a production term. Thus the decrease in magnitude of
![]() $-{\mathcal{P}}^{+}$
observed here with shear thinning means there is a less energy transferred via this mechanism into turbulence. The combination of higher MFKE production,
$-{\mathcal{P}}^{+}$
observed here with shear thinning means there is a less energy transferred via this mechanism into turbulence. The combination of higher MFKE production,
![]() $W_{dP/dz}^{+}$
, and less energy transfer to turbulence via
$W_{dP/dz}^{+}$
, and less energy transfer to turbulence via
![]() $-{\mathcal{P}}^{+}$
suggests that there will be higher dissipation by the mean viscous stress (
$-{\mathcal{P}}^{+}$
suggests that there will be higher dissipation by the mean viscous stress (
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
) in case of lower
$\unicode[STIX]{x1D716}^{m^{+}}$
) in case of lower
![]() $n$
– this may be observed in figure 19(d).
$n$
– this may be observed in figure 19(d).
The two non-Newtonian terms,
![]() $\unicode[STIX]{x1D6F6}_{nn}^{m^{+}}$
and
$\unicode[STIX]{x1D6F6}_{nn}^{m^{+}}$
and
![]() $\unicode[STIX]{x1D712}_{nn}^{+}$
, vary most significantly for
$\unicode[STIX]{x1D712}_{nn}^{+}$
, vary most significantly for
![]() $y^{+}<60$
, similarly to the Newtonian transport and dissipation terms. However, their magnitude is approximately one order less than the
$y^{+}<60$
, similarly to the Newtonian transport and dissipation terms. However, their magnitude is approximately one order less than the
![]() ${\mathcal{D}}^{m^{+}}$
and
${\mathcal{D}}^{m^{+}}$
and
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
and they play a smaller role in the MFKE balance. The non-Newtonian dissipation,
$\unicode[STIX]{x1D716}^{m^{+}}$
and they play a smaller role in the MFKE balance. The non-Newtonian dissipation,
![]() $\unicode[STIX]{x1D712}_{nn}^{+}$
, is negatively related to
$\unicode[STIX]{x1D712}_{nn}^{+}$
, is negatively related to
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
which was seen to be negative for a shear-thinning fluid (figure 10). Thus we expect
$\unicode[STIX]{x1D70F}^{fv^{+}}$
which was seen to be negative for a shear-thinning fluid (figure 10). Thus we expect
![]() $\unicode[STIX]{x1D712}_{nn}^{+}$
to be positive for shear-thinning fluids (as seen in figure 19
f) and this reduces dissipation. However, the sum of
$\unicode[STIX]{x1D712}_{nn}^{+}$
to be positive for shear-thinning fluids (as seen in figure 19
f) and this reduces dissipation. However, the sum of
![]() $\unicode[STIX]{x1D716}^{m^{+}}$
and
$\unicode[STIX]{x1D716}^{m^{+}}$
and
![]() $\unicode[STIX]{x1D712}_{nn}^{+}$
(figure 20
a) shows that the net effect of these two viscous dissipation terms only slightly increases the magnitude of dissipation in the very near wall and buffer layer. The non-Newtonian transport term,
$\unicode[STIX]{x1D712}_{nn}^{+}$
(figure 20
a) shows that the net effect of these two viscous dissipation terms only slightly increases the magnitude of dissipation in the very near wall and buffer layer. The non-Newtonian transport term,
![]() $\unicode[STIX]{x1D6F6}_{nn}^{m^{+}}$
, changes sign in
$\unicode[STIX]{x1D6F6}_{nn}^{m^{+}}$
, changes sign in
![]() $y^{+}\approx 15{-}20$
(depending on
$y^{+}\approx 15{-}20$
(depending on
![]() $n$
) and for shear thinning acts as a sink of the mean flow energy for
$n$
) and for shear thinning acts as a sink of the mean flow energy for
![]() $y^{+}\lesssim 15$
and a source further away from the wall. Overall, except in a narrow region near
$y^{+}\lesssim 15$
and a source further away from the wall. Overall, except in a narrow region near
![]() $y^{+}\approx 10$
, the non-Newtonian terms act as a source for shear-thinning fluids and as a sink for the shear-thickening fluid (
$y^{+}\approx 10$
, the non-Newtonian terms act as a source for shear-thinning fluids and as a sink for the shear-thickening fluid (
![]() $n=1.2$
) in the MFKE budget at all
$n=1.2$
) in the MFKE budget at all
![]() $y^{+}$
(figure 19
h).
$y^{+}$
(figure 19
h).

Figure 20. Profiles of the sum of Newtonian and non-Newtonian (a) viscous transport and dissipation terms (b) total transport and dissipation in (5.1) plotted for different flow indices
![]() $n$
.
$n$
.
In summary, the mean flow energy production increases with shear thinning outside the buffer layer. For all other terms, the overall effect of decreasing flow index is to modify the MFKE budget terms most significantly in the near-wall region
![]() $y^{+}\lesssim 60$
. The total viscous dissipation increases with shear thinning but the turbulent energy transfer (which peaks at
$y^{+}\lesssim 60$
. The total viscous dissipation increases with shear thinning but the turbulent energy transfer (which peaks at
![]() $y^{+}\approx 10$
) becomes less negative. The magnitude of the total viscous transport is also increased with shear thinning. The turbulent transport which is the mean flow energy transfer via the Reynolds shear stress which peaks at
$y^{+}\approx 10$
) becomes less negative. The magnitude of the total viscous transport is also increased with shear thinning. The turbulent transport which is the mean flow energy transfer via the Reynolds shear stress which peaks at
![]() $y^{+}\approx 10$
and decreases with shear thinning. The non-Newtonian terms largely act as a source in the MFKE budget for shear-thinning fluids. In the total transport and dissipation profiles the shear-thinning effect almost disappears in
$y^{+}\approx 10$
and decreases with shear thinning. The non-Newtonian terms largely act as a source in the MFKE budget for shear-thinning fluids. In the total transport and dissipation profiles the shear-thinning effect almost disappears in
![]() $4\lesssim y^{+}\lesssim 10$
(figure 20
b).
$4\lesssim y^{+}\lesssim 10$
(figure 20
b).
5.2 Turbulent kinetic energy budget
The equation for the ensemble-average turbulent kinetic energy (
![]() $k=\overline{u_{i}^{\prime }u_{i}^{\prime }}/2$
) is
$k=\overline{u_{i}^{\prime }u_{i}^{\prime }}/2$
) is
 $$\begin{eqnarray}\displaystyle \overbrace{\frac{\unicode[STIX]{x2202}k}{\unicode[STIX]{x2202}t}}^{k_{t}}+\overbrace{U_{j}\frac{\unicode[STIX]{x2202}k}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{A}}} & = & \displaystyle \overbrace{-\overline{u_{i}^{\prime }u_{j}^{\prime }}S_{ij}}^{{\mathcal{P}}}+\left\{\overbrace{-\frac{1}{2}\frac{\unicode[STIX]{x2202}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{j}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{T}}}\overbrace{-\frac{\unicode[STIX]{x2202}\overline{p^{\prime }u_{j}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}}^{\unicode[STIX]{x1D6F1}}\overbrace{+\frac{\unicode[STIX]{x2202}(2\bar{\unicode[STIX]{x1D708}}\overline{s_{ij}^{\prime }u_{i}^{\prime }})}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{D}}}\right\}\overbrace{-2\bar{\unicode[STIX]{x1D708}}\overline{s_{ij}^{\prime }s_{ij}^{\prime }}}^{\unicode[STIX]{x1D716}}\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\overbrace{\frac{\unicode[STIX]{x2202}(\overline{2\unicode[STIX]{x1D708}^{\prime }u_{i}^{\prime }}S_{ij})}{\unicode[STIX]{x2202}x_{j}}}^{\unicode[STIX]{x1D709}_{nn}}+\overbrace{\frac{\unicode[STIX]{x2202}(\overline{2\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }u_{i}^{\prime }})}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{D}}_{nn}}\right\}\overbrace{-\overline{2\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }}S_{ij}}^{\unicode[STIX]{x1D712}_{nn}}\overbrace{-2\overline{\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }s_{ij}^{\prime }}}^{\unicode[STIX]{x1D716}_{nn}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overbrace{\frac{\unicode[STIX]{x2202}k}{\unicode[STIX]{x2202}t}}^{k_{t}}+\overbrace{U_{j}\frac{\unicode[STIX]{x2202}k}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{A}}} & = & \displaystyle \overbrace{-\overline{u_{i}^{\prime }u_{j}^{\prime }}S_{ij}}^{{\mathcal{P}}}+\left\{\overbrace{-\frac{1}{2}\frac{\unicode[STIX]{x2202}\overline{u_{i}^{\prime }u_{i}^{\prime }u_{j}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{T}}}\overbrace{-\frac{\unicode[STIX]{x2202}\overline{p^{\prime }u_{j}^{\prime }}}{\unicode[STIX]{x2202}x_{j}}}^{\unicode[STIX]{x1D6F1}}\overbrace{+\frac{\unicode[STIX]{x2202}(2\bar{\unicode[STIX]{x1D708}}\overline{s_{ij}^{\prime }u_{i}^{\prime }})}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{D}}}\right\}\overbrace{-2\bar{\unicode[STIX]{x1D708}}\overline{s_{ij}^{\prime }s_{ij}^{\prime }}}^{\unicode[STIX]{x1D716}}\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\overbrace{\frac{\unicode[STIX]{x2202}(\overline{2\unicode[STIX]{x1D708}^{\prime }u_{i}^{\prime }}S_{ij})}{\unicode[STIX]{x2202}x_{j}}}^{\unicode[STIX]{x1D709}_{nn}}+\overbrace{\frac{\unicode[STIX]{x2202}(\overline{2\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }u_{i}^{\prime }})}{\unicode[STIX]{x2202}x_{j}}}^{{\mathcal{D}}_{nn}}\right\}\overbrace{-\overline{2\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }}S_{ij}}^{\unicode[STIX]{x1D712}_{nn}}\overbrace{-2\overline{\unicode[STIX]{x1D708}^{\prime }s_{ij}^{\prime }s_{ij}^{\prime }}}^{\unicode[STIX]{x1D716}_{nn}}.\end{eqnarray}$$
Here, the terms in the first row appear for both Newtonian and non-Newtonian fluids and the following is the standard terminology:
-
 $k_{t}$
:
$k_{t}$
: -
rate of change of turbulence kinetic energy;
-
 ${\mathcal{A}}$
:
${\mathcal{A}}$
: -
mean flow advection;
-
 ${\mathcal{P}}$
:
${\mathcal{P}}$
: -
turbulent kinetic energy production;
-
 ${\mathcal{T}}$
:
${\mathcal{T}}$
: -
turbulent velocity transport;
-
 $\unicode[STIX]{x1D6F1}$
:
$\unicode[STIX]{x1D6F1}$
: -
pressure related transport;
-
 ${\mathcal{D}}$
:
${\mathcal{D}}$
: -
mean viscous transport;
-
 $\unicode[STIX]{x1D716}$
:
$\unicode[STIX]{x1D716}$
: -
mean viscous dissipation.
The remaining terms i.e. the terms in the second row in (5.2) are zero for a Newtonian fluid and appear only for a fluid with non-uniform viscosity. We adopt the following terminology for these terms:
-
 $\unicode[STIX]{x1D709}_{nn}$
:
$\unicode[STIX]{x1D709}_{nn}$
: -
mean shear turbulent viscous transport;
-
 ${\mathcal{D}}_{nn}$
:
${\mathcal{D}}_{nn}$
: -
turbulent viscous transport;
-
 $\unicode[STIX]{x1D712}_{nn}$
:
$\unicode[STIX]{x1D712}_{nn}$
: -
mean shear turbulent viscous dissipation;
-
 $\unicode[STIX]{x1D716}_{nn}$
:
$\unicode[STIX]{x1D716}_{nn}$
: -
turbulent viscous dissipation.
When the terms of similar nature are summed together TKE budget equation can be written as:
Here,
![]() $T^{k}={\mathcal{T}}+\unicode[STIX]{x1D6F1}+{\mathcal{D}}+{\mathcal{D}}_{nn}+\unicode[STIX]{x1D709}_{nn}$
is the total transport and
$T^{k}={\mathcal{T}}+\unicode[STIX]{x1D6F1}+{\mathcal{D}}+{\mathcal{D}}_{nn}+\unicode[STIX]{x1D709}_{nn}$
is the total transport and
![]() $\unicode[STIX]{x1D716}^{k}=\unicode[STIX]{x1D716}+\unicode[STIX]{x1D712}_{nn}+\unicode[STIX]{x1D716}_{nn}$
is the total dissipation. As with the MFKE budget (5.1), the first two terms in (5.2),
$\unicode[STIX]{x1D716}^{k}=\unicode[STIX]{x1D716}+\unicode[STIX]{x1D712}_{nn}+\unicode[STIX]{x1D716}_{nn}$
is the total dissipation. As with the MFKE budget (5.1), the first two terms in (5.2),
![]() $k_{t}$
and
$k_{t}$
and
![]() ${\mathcal{A}}$
vanish for a pipe flow and the local TKE budget is maintained by a balance between the remaining terms. As already mentioned in § 5.1, the turbulent kinetic energy production
${\mathcal{A}}$
vanish for a pipe flow and the local TKE budget is maintained by a balance between the remaining terms. As already mentioned in § 5.1, the turbulent kinetic energy production
![]() ${\mathcal{P}}$
, is the only source term in (5.2) and it couples the MFKE and the TKE budget equations. The mean viscous dissipation,
${\mathcal{P}}$
, is the only source term in (5.2) and it couples the MFKE and the TKE budget equations. The mean viscous dissipation,
![]() $\unicode[STIX]{x1D716}$
, is negative definite and as the name says, is the dissipation of TKE due to the mean viscosity. The gradient terms,
$\unicode[STIX]{x1D716}$
, is negative definite and as the name says, is the dissipation of TKE due to the mean viscosity. The gradient terms,
![]() ${\mathcal{T}}$
,
${\mathcal{T}}$
,
![]() $\unicode[STIX]{x1D6F1}$
,
$\unicode[STIX]{x1D6F1}$
,
![]() ${\mathcal{D}}$
, only redistribute TKE,
${\mathcal{D}}$
, only redistribute TKE,
![]() $k$
, within the domain. Although they cannot produce or dissipate TKE, they can be local sources or sinks in (5.2).
$k$
, within the domain. Although they cannot produce or dissipate TKE, they can be local sources or sinks in (5.2).
Remaining terms,
![]() $\unicode[STIX]{x1D709}_{nn}$
,
$\unicode[STIX]{x1D709}_{nn}$
,
![]() ${\mathcal{D}}_{nn}$
,
${\mathcal{D}}_{nn}$
,
![]() $\unicode[STIX]{x1D712}_{nn}$
and
$\unicode[STIX]{x1D712}_{nn}$
and
![]() $\unicode[STIX]{x1D716}_{nn}$
are zero for a Newtonian fluid as they depend on viscosity fluctuations. We refer these as non-Newtonian TKE budget terms. The gradient terms, the mean shear turbulent viscous transport,
$\unicode[STIX]{x1D716}_{nn}$
are zero for a Newtonian fluid as they depend on viscosity fluctuations. We refer these as non-Newtonian TKE budget terms. The gradient terms, the mean shear turbulent viscous transport,
![]() $\unicode[STIX]{x1D709}_{nn}$
, and the turbulent viscous transport,
$\unicode[STIX]{x1D709}_{nn}$
, and the turbulent viscous transport,
![]() ${\mathcal{D}}_{nn}$
either enhance or diminish the transport by the Newtonian transport terms. The mean shear turbulent viscous dissipation,
${\mathcal{D}}_{nn}$
either enhance or diminish the transport by the Newtonian transport terms. The mean shear turbulent viscous dissipation,
![]() $\unicode[STIX]{x1D712}_{nn}$
appears in both the MFKE and the TKE budgets with the same sign, meaning that it affects both energy budgets in a similar manner. Both
$\unicode[STIX]{x1D712}_{nn}$
appears in both the MFKE and the TKE budgets with the same sign, meaning that it affects both energy budgets in a similar manner. Both
![]() $\unicode[STIX]{x1D712}_{nn}$
and
$\unicode[STIX]{x1D712}_{nn}$
and
![]() $\unicode[STIX]{x1D716}_{nn}$
appear as source/sink terms in TKE budget, although neither is obviously positive (or negative) definite for shear-thinning fluids. As mentioned in § 5.1 for
$\unicode[STIX]{x1D716}_{nn}$
appear as source/sink terms in TKE budget, although neither is obviously positive (or negative) definite for shear-thinning fluids. As mentioned in § 5.1 for
![]() $\unicode[STIX]{x1D712}_{nn}$
, positive values of either of these terms does not mean that they are true sources of turbulent energy. Turbulence can only source energy from the mean flow and although
$\unicode[STIX]{x1D712}_{nn}$
, positive values of either of these terms does not mean that they are true sources of turbulent energy. Turbulence can only source energy from the mean flow and although
![]() $\unicode[STIX]{x1D712}_{nn}$
involves the mean flow via
$\unicode[STIX]{x1D712}_{nn}$
involves the mean flow via
![]() $S_{ij}$
, its genesis is in the total viscous dissipation and as such it is clearly part of the total turbulent dissipation. The turbulent viscous dissipation,
$S_{ij}$
, its genesis is in the total viscous dissipation and as such it is clearly part of the total turbulent dissipation. The turbulent viscous dissipation,
![]() $\unicode[STIX]{x1D716}_{nn}$
, has a similar genesis and is more clearly associated with dissipation.
$\unicode[STIX]{x1D716}_{nn}$
, has a similar genesis and is more clearly associated with dissipation.
The effect of flow index
![]() $n$
on the individual terms in (5.2) is shown in figure 21. Turbulence kinetic energy production,
$n$
on the individual terms in (5.2) is shown in figure 21. Turbulence kinetic energy production,
![]() ${\mathcal{P}}^{+}$
, decreases with shear thinning over
${\mathcal{P}}^{+}$
, decreases with shear thinning over
![]() $3<y^{+}<20$
with the peak shifting slightly away from the wall (figure 21
a). Production is the product
$3<y^{+}<20$
with the peak shifting slightly away from the wall (figure 21
a). Production is the product
![]() $-\overline{u_{i}^{\prime }u_{j}^{\prime }}S_{ij}$
and for a pipe flow, only the
$-\overline{u_{i}^{\prime }u_{j}^{\prime }}S_{ij}$
and for a pipe flow, only the
![]() $S_{rz}$
component survives, which gives
$S_{rz}$
component survives, which gives
![]() ${\mathcal{P}}^{+}=\unicode[STIX]{x1D70F}^{R^{+}}(\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+})/2$
. Since
${\mathcal{P}}^{+}=\unicode[STIX]{x1D70F}^{R^{+}}(\unicode[STIX]{x2202}U_{z}^{+}/\unicode[STIX]{x2202}y^{+})/2$
. Since
![]() $S_{rz}^{+}$
is little affected by shear thinning for
$S_{rz}^{+}$
is little affected by shear thinning for
![]() $3<y^{+}<20$
(figure 11), the observed decrease in
$3<y^{+}<20$
(figure 11), the observed decrease in
![]() ${\mathcal{P}}^{+}$
with shear thinning is primarily due to the decrease in Reynolds shear stress (figure 10).
${\mathcal{P}}^{+}$
with shear thinning is primarily due to the decrease in Reynolds shear stress (figure 10).

Figure 21. Profiles of the turbulent kinetic energy budget terms (see (5.2)) plotted for different flow indices
![]() $n$
in wall variables. Note that the vertical scale changes in each plot.
$n$
in wall variables. Note that the vertical scale changes in each plot.
As
![]() $n$
decreases, turbulent kinetic energy dissipation,
$n$
decreases, turbulent kinetic energy dissipation,
![]() $\unicode[STIX]{x1D716}^{+}=2\unicode[STIX]{x1D708}^{+}\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}^{+}$
, increases in magnitude for all
$\unicode[STIX]{x1D716}^{+}=2\unicode[STIX]{x1D708}^{+}\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}^{+}$
, increases in magnitude for all
![]() $y^{+}$
, although most noticeably for
$y^{+}$
, although most noticeably for
![]() $y^{+}<5$
and then less so over
$y^{+}<5$
and then less so over
![]() $20<y^{+}<100$
(figure 21
a). The increased dissipation over
$20<y^{+}<100$
(figure 21
a). The increased dissipation over
![]() $20<y^{+}<100$
is due to the increase in mean viscosity with shear thinning (figure 9) since
$20<y^{+}<100$
is due to the increase in mean viscosity with shear thinning (figure 9) since
![]() $\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}^{+}$
decreases here for all
$\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}^{+}$
decreases here for all
![]() $n$
(figure 22
a). However, the increase in
$n$
(figure 22
a). However, the increase in
![]() $\unicode[STIX]{x1D716}^{+}$
with decreasing
$\unicode[STIX]{x1D716}^{+}$
with decreasing
![]() $n$
close to the wall is due to increased strain-rate fluctuations
$n$
close to the wall is due to increased strain-rate fluctuations
![]() $\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}$
with decreasing
$\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}$
with decreasing
![]() $n$
as the mean viscosity is only weakly dependant on
$n$
as the mean viscosity is only weakly dependant on
![]() $n$
(figure 9).
$n$
(figure 9).
Profiles of the three Newtonian transport terms,
![]() ${\mathcal{D}}^{+}$
,
${\mathcal{D}}^{+}$
,
![]() ${\mathcal{T}}^{+}$
and
${\mathcal{T}}^{+}$
and
![]() $\unicode[STIX]{x1D6F1}^{+}$
, are shown in figure 21(a–c). The mean viscous transport,
$\unicode[STIX]{x1D6F1}^{+}$
, are shown in figure 21(a–c). The mean viscous transport,
![]() ${\mathcal{D}}^{+}$
, is the largest in magnitude and shows flow index dependence mostly in the viscous sublayer where it increases with shear thinning (figure 21
a), partly countering the more negative dissipation for lower
${\mathcal{D}}^{+}$
, is the largest in magnitude and shows flow index dependence mostly in the viscous sublayer where it increases with shear thinning (figure 21
a), partly countering the more negative dissipation for lower
![]() $n$
. Recalling that (i)
$n$
. Recalling that (i)
![]() ${\mathcal{D}}^{+}$
is the gradient of
${\mathcal{D}}^{+}$
is the gradient of
![]() $2\unicode[STIX]{x1D708}^{+}\overline{\unicode[STIX]{x1D634}_{ij}^{\prime +}u_{i}^{\prime +}}$
(see (5.2)), (ii) that only the radial derivative survives and (iii) that the mean viscosity,
$2\unicode[STIX]{x1D708}^{+}\overline{\unicode[STIX]{x1D634}_{ij}^{\prime +}u_{i}^{\prime +}}$
(see (5.2)), (ii) that only the radial derivative survives and (iii) that the mean viscosity,
![]() $\unicode[STIX]{x1D708}^{+}$
, is almost constant in the viscous sublayer (figure 9), we draw the conclusion that larger
$\unicode[STIX]{x1D708}^{+}$
, is almost constant in the viscous sublayer (figure 9), we draw the conclusion that larger
![]() ${\mathcal{D}}^{+}$
for lower
${\mathcal{D}}^{+}$
for lower
![]() $n$
is due to more rapid increase in
$n$
is due to more rapid increase in
![]() $\overline{s_{ri}^{\prime }u_{i}^{\prime }}^{+}$
in the viscous sublayer with shear thinning.
$\overline{s_{ri}^{\prime }u_{i}^{\prime }}^{+}$
in the viscous sublayer with shear thinning.
The main effect of decreasing
![]() $n$
on the turbulent velocity transport,
$n$
on the turbulent velocity transport,
![]() ${\mathcal{T}}^{+}$
, is flattening and broadening of the profile in
${\mathcal{T}}^{+}$
, is flattening and broadening of the profile in
![]() $8<y^{+}<50$
(figure 21
b). The contribution of the pressure related transport,
$8<y^{+}<50$
(figure 21
b). The contribution of the pressure related transport,
![]() $\unicode[STIX]{x1D6F1}^{+}$
, is small compared to the other transport terms (figure 21
c) and although its magnitude is reduced in the viscous sublayer and buffer layer with shear thinning, this has a little effect on the total turbulent energy transport.
$\unicode[STIX]{x1D6F1}^{+}$
, is small compared to the other transport terms (figure 21
c) and although its magnitude is reduced in the viscous sublayer and buffer layer with shear thinning, this has a little effect on the total turbulent energy transport.
Overall, the effect of reducing flow index on the Newtonian terms in TKE budget is to elevate the mean viscous transport,
![]() ${\mathcal{D}}^{+}$
and turbulent dissipation,
${\mathcal{D}}^{+}$
and turbulent dissipation,
![]() $\unicode[STIX]{x1D716}^{+}$
, close to the wall (
$\unicode[STIX]{x1D716}^{+}$
, close to the wall (
![]() $y^{+}<3$
), and to decrease turbulent kinetic energy production,
$y^{+}<3$
), and to decrease turbulent kinetic energy production,
![]() ${\mathcal{P}}^{+}$
, near
${\mathcal{P}}^{+}$
, near
![]() $y^{+}=10$
.
$y^{+}=10$
.
The non-Newtonian transport terms, the mean shear turbulent viscous transport,
![]() $\unicode[STIX]{x1D709}_{nn}^{+}$
, and the turbulent viscous transport,
$\unicode[STIX]{x1D709}_{nn}^{+}$
, and the turbulent viscous transport,
![]() ${\mathcal{D}}_{nn}^{+}$
, are significant only for
${\mathcal{D}}_{nn}^{+}$
, are significant only for
![]() $y^{+}\lesssim 40$
and the magnitude of both increases with shear thinning (figure 21
d,e). The contribution of
$y^{+}\lesssim 40$
and the magnitude of both increases with shear thinning (figure 21
d,e). The contribution of
![]() $\unicode[STIX]{x1D709}_{nn}^{+}$
to the turbulent kinetic energy budget at the wall is significant. It is approximately
$\unicode[STIX]{x1D709}_{nn}^{+}$
to the turbulent kinetic energy budget at the wall is significant. It is approximately
![]() $25\,\%$
of the total Newtonian transport (
$25\,\%$
of the total Newtonian transport (
![]() ${\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}$
) for
${\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}$
) for
![]() $n=0.6$
and approximately
$n=0.6$
and approximately
![]() $13\,\%$
for
$13\,\%$
for
![]() $n=0.8$
there. For
$n=0.8$
there. For
![]() $y^{+}<5$
,
$y^{+}<5$
,
![]() $\unicode[STIX]{x1D709}_{nn}^{+}$
acts opposite to the Newtonian viscous transport,
$\unicode[STIX]{x1D709}_{nn}^{+}$
acts opposite to the Newtonian viscous transport,
![]() ${\mathcal{D}}^{+}$
. At
${\mathcal{D}}^{+}$
. At
![]() $y^{+}\approx 5$
,
$y^{+}\approx 5$
,
![]() $\unicode[STIX]{x1D709}_{nn}^{+}$
changes sign (as does
$\unicode[STIX]{x1D709}_{nn}^{+}$
changes sign (as does
![]() ${\mathcal{D}}^{+}$
) and continues to act in an opposite sense to
${\mathcal{D}}^{+}$
) and continues to act in an opposite sense to
![]() ${\mathcal{D}}^{+}$
for
${\mathcal{D}}^{+}$
for
![]() $5\lesssim y^{+}\lesssim 30$
. This opposition is expected from the opposite signs of the mean viscous stress,
$5\lesssim y^{+}\lesssim 30$
. This opposition is expected from the opposite signs of the mean viscous stress,
![]() $\unicode[STIX]{x1D70F}^{v^{+}}$
, and the turbulent viscous stress,
$\unicode[STIX]{x1D70F}^{v^{+}}$
, and the turbulent viscous stress,
![]() $\unicode[STIX]{x1D70F}^{fv^{+}}$
(see figure 10). The contribution of
$\unicode[STIX]{x1D70F}^{fv^{+}}$
(see figure 10). The contribution of
![]() ${\mathcal{D}}_{nn}^{+}$
to the turbulent kinetic energy budget is small (
${\mathcal{D}}_{nn}^{+}$
to the turbulent kinetic energy budget is small (
![]() ${<}10\,\%$
of the Newtonian transport for
${<}10\,\%$
of the Newtonian transport for
![]() $n=0.8$
). It changes sign several times and acts both against and with
$n=0.8$
). It changes sign several times and acts both against and with
![]() ${\mathcal{D}}^{+}$
over different regions of
${\mathcal{D}}^{+}$
over different regions of
![]() $y^{+}$
. The sum of all transport terms (
$y^{+}$
. The sum of all transport terms (
![]() ${\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}+{\mathcal{D}}_{nn}^{+}+\unicode[STIX]{x1D709}_{nn}^{+}$
) is shown in figure 22
b where it is seen that the effect of shear thinning is to reduce the transport by the Newtonian terms for
${\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}+{\mathcal{D}}_{nn}^{+}+\unicode[STIX]{x1D709}_{nn}^{+}$
) is shown in figure 22
b where it is seen that the effect of shear thinning is to reduce the transport by the Newtonian terms for
![]() $y^{+}\lesssim 20$
and to increase it marginally over
$y^{+}\lesssim 20$
and to increase it marginally over
![]() $20\lesssim y^{+}\lesssim 70$
.
$20\lesssim y^{+}\lesssim 70$
.
The other two non-Newtonian terms, the mean shear turbulent viscous dissipation,
![]() $\unicode[STIX]{x1D712}_{nn}^{+}$
, and the turbulent viscous dissipation,
$\unicode[STIX]{x1D712}_{nn}^{+}$
, and the turbulent viscous dissipation,
![]() $\unicode[STIX]{x1D716}_{nn}^{+}$
, are positive for shear-thinning fluids and negative for shear thickening (figure 21
f,g). As previously mentioned, they are identified as dissipation terms that act to reduce the mean flow dissipation
$\unicode[STIX]{x1D716}_{nn}^{+}$
, are positive for shear-thinning fluids and negative for shear thickening (figure 21
f,g). As previously mentioned, they are identified as dissipation terms that act to reduce the mean flow dissipation
![]() $\unicode[STIX]{x1D716}^{+}$
over the entire pipe radius, but particularly for
$\unicode[STIX]{x1D716}^{+}$
over the entire pipe radius, but particularly for
![]() $y^{+}<40$
. For
$y^{+}<40$
. For
![]() $n=0.6$
they reduce the dissipation in the viscous sublayer close to the wall by approximately 40 %. Their net effect is most clearly seen in figure 22(a) where the total dissipation is seen to reduce with shear thinning for
$n=0.6$
they reduce the dissipation in the viscous sublayer close to the wall by approximately 40 %. Their net effect is most clearly seen in figure 22(a) where the total dissipation is seen to reduce with shear thinning for
![]() $y^{+}\lesssim 30$
with the reduction balancing the reduction in net transport for
$y^{+}\lesssim 30$
with the reduction balancing the reduction in net transport for
![]() $y^{+}<5$
and partially balancing the reduction in production observed around
$y^{+}<5$
and partially balancing the reduction in production observed around
![]() $y^{+}\approx 10$
.
$y^{+}\approx 10$
.
In the very near-wall region,
![]() $\unicode[STIX]{x1D709}_{nn}^{+}$
and
$\unicode[STIX]{x1D709}_{nn}^{+}$
and
![]() $\unicode[STIX]{x1D712}_{nn}^{+}$
almost cancel each other, as do
$\unicode[STIX]{x1D712}_{nn}^{+}$
almost cancel each other, as do
![]() ${\mathcal{D}}_{nn}^{+}$
and
${\mathcal{D}}_{nn}^{+}$
and
![]() $\unicode[STIX]{x1D716}_{nn}^{+}$
, resulting in no net effect of the non-Newtonian TKE budget terms at the wall. The net effect of these terms increases through the viscous sublayer reaching a maximum near
$\unicode[STIX]{x1D716}_{nn}^{+}$
, resulting in no net effect of the non-Newtonian TKE budget terms at the wall. The net effect of these terms increases through the viscous sublayer reaching a maximum near
![]() $y^{+}\approx 7$
before slowly decreasing again out to
$y^{+}\approx 7$
before slowly decreasing again out to
![]() $y^{+}\gtrsim 100$
(figure 21
h). They thus provide an additional source of energy in the TKE budget for shear-thinning fluids.
$y^{+}\gtrsim 100$
(figure 21
h). They thus provide an additional source of energy in the TKE budget for shear-thinning fluids.
A summary of the effects of flow index modification is shown in figure 22(b) where the turbulent kinetic energy production, total transport and dissipation are compared for different
![]() $n$
. They show flow index dependence only for
$n$
. They show flow index dependence only for
![]() $y^{+}\lesssim 70$
and shear thinning is seen to reduce the magnitude of each, albeit over different ranges of
$y^{+}\lesssim 70$
and shear thinning is seen to reduce the magnitude of each, albeit over different ranges of
![]() $y^{+}$
.
$y^{+}$
.

Figure 22. Profiles of (a)
![]() $\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}^{+}$
(b) turbulent kinetic energy production (
$\overline{\unicode[STIX]{x1D634}_{ij}^{\prime }\unicode[STIX]{x1D634}_{ij}^{\prime }}^{+}$
(b) turbulent kinetic energy production (
![]() ${\mathcal{P}}^{+}$
), total dissipation (
${\mathcal{P}}^{+}$
), total dissipation (
![]() $\unicode[STIX]{x1D716}^{k^{+}}=\unicode[STIX]{x1D716}^{+}+\unicode[STIX]{x1D712}_{nn}^{+}+\unicode[STIX]{x1D716}_{nn}^{+}$
) and transport (
$\unicode[STIX]{x1D716}^{k^{+}}=\unicode[STIX]{x1D716}^{+}+\unicode[STIX]{x1D712}_{nn}^{+}+\unicode[STIX]{x1D716}_{nn}^{+}$
) and transport (
![]() $T^{k^{+}}={\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}+{\mathcal{D}}_{nn}^{+}+\unicode[STIX]{x1D709}_{nn}^{+}$
) plotted in wall units.
$T^{k^{+}}={\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}+{\mathcal{D}}_{nn}^{+}+\unicode[STIX]{x1D709}_{nn}^{+}$
) plotted in wall units.

Figure 23. Profiles of the ratio of turbulent kinetic energy production to total dissipation (
![]() ${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
), total transport (
${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
), total transport (
![]() $T^{k^{+}}$
) and the turbulent kinetic energy
$T^{k^{+}}$
) and the turbulent kinetic energy
![]() $k^{+}$
plotted in wall units.
$k^{+}$
plotted in wall units.

Figure 24. Integrated budget of turbulent kinetic energy production (
![]() ${\mathcal{P}}^{+}$
), transport (
${\mathcal{P}}^{+}$
), transport (
![]() ${\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}+{\mathcal{D}}_{nn}^{+}+\unicode[STIX]{x1D709}_{nn}^{+}$
) and dissipation (
${\mathcal{T}}^{+}+\unicode[STIX]{x1D6F1}^{+}+{\mathcal{D}}^{+}+{\mathcal{D}}_{nn}^{+}+\unicode[STIX]{x1D709}_{nn}^{+}$
) and dissipation (
![]() $\unicode[STIX]{x1D716}^{+}+\unicode[STIX]{x1D712}_{nn}^{+}+\unicode[STIX]{x1D716}_{nn}^{+}$
), normalised by the total Newtonian turbulent kinetic energy production (volume integral of
$\unicode[STIX]{x1D716}^{+}+\unicode[STIX]{x1D712}_{nn}^{+}+\unicode[STIX]{x1D716}_{nn}^{+}$
), normalised by the total Newtonian turbulent kinetic energy production (volume integral of
![]() ${\mathcal{P}}^{+}$
for
${\mathcal{P}}^{+}$
for
![]() $n=1$
) plotted for different
$n=1$
) plotted for different
![]() $n$
. The primary axis on the left is for the turbulent transport budget and the secondary axis on the right is for the turbulent kinetic energy production and dissipation.
$n$
. The primary axis on the left is for the turbulent transport budget and the secondary axis on the right is for the turbulent kinetic energy production and dissipation.
Shear thinning widens the production region (where production exceeds the total dissipation) by increasing its upper bound (figure 23) whereas the lower bound remains fixed at
![]() $y^{+}\approx 6$
. In this region, the total transport becomes negative and thus carries the excess energy (
$y^{+}\approx 6$
. In this region, the total transport becomes negative and thus carries the excess energy (
![]() ${\mathcal{P}}^{+}-\unicode[STIX]{x1D716}^{k^{+}}$
) away from the production region. The ratio of production to total dissipation (
${\mathcal{P}}^{+}-\unicode[STIX]{x1D716}^{k^{+}}$
) away from the production region. The ratio of production to total dissipation (
![]() ${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
) is increased for
${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
) is increased for
![]() $15\lesssim y^{+}\lesssim 60$
but decreased for
$15\lesssim y^{+}\lesssim 60$
but decreased for
![]() $6\lesssim y^{+}\lesssim 15$
and beyond
$6\lesssim y^{+}\lesssim 15$
and beyond
![]() $y^{+}\approx 60$
with shear thinning.
$y^{+}\approx 60$
with shear thinning.
Profiles of the turbulent production, total dissipation and transport when integrated over the pipe cross-section show that shear thinning globally decreases the overall turbulent kinetic energy production and hence the total dissipation (figure 24). Beyond
![]() $y^{+}=150$
, profiles of the integrated production and total dissipation for all
$y^{+}=150$
, profiles of the integrated production and total dissipation for all
![]() $n$
are almost flat showing that most of the turbulent production and dissipation occurs for
$n$
are almost flat showing that most of the turbulent production and dissipation occurs for
![]() $y^{+}\gtrsim 150$
. Profiles of the integrated total turbulent transport (which also represents negative of the extra energy available for turbulence i.e.
$y^{+}\gtrsim 150$
. Profiles of the integrated total turbulent transport (which also represents negative of the extra energy available for turbulence i.e.
![]() $-({\mathcal{P}}^{+}-\unicode[STIX]{x1D716}^{k^{+}})$
) show that there is more energy available (
$-({\mathcal{P}}^{+}-\unicode[STIX]{x1D716}^{k^{+}})$
) show that there is more energy available (
![]() $T^{k^{+}}$
is more negative for
$T^{k^{+}}$
is more negative for
![]() $y^{+}\gtrsim 25$
) for turbulence for a more shear-thinning fluid. This suggests that shear thinning decreases dissipation more than it decreases the production.
$y^{+}\gtrsim 25$
) for turbulence for a more shear-thinning fluid. This suggests that shear thinning decreases dissipation more than it decreases the production.
Using the results of
![]() ${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
shown in figure 23, the turbulent kinetic energy profiles for different
${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
shown in figure 23, the turbulent kinetic energy profiles for different
![]() $n$
can be explained. The turbulent kinetic energy
$n$
can be explained. The turbulent kinetic energy
![]() $k^{+}$
peaks at
$k^{+}$
peaks at
![]() $y^{+}\approx 15$
which is slightly higher than the location where
$y^{+}\approx 15$
which is slightly higher than the location where
![]() ${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
attains a maximum and approximately the same location where
${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
attains a maximum and approximately the same location where
![]() ${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
profiles for different
${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
profiles for different
![]() $n$
cross each other. Over the region
$n$
cross each other. Over the region
![]() $15\lesssim y^{+}\lesssim 60$
, higher production than dissipation results in higher
$15\lesssim y^{+}\lesssim 60$
, higher production than dissipation results in higher
![]() $k^{+}$
for more shear-thinning fluids. A part of this higher
$k^{+}$
for more shear-thinning fluids. A part of this higher
![]() $k^{+}$
is transported away from the wall and part towards the wall. For
$k^{+}$
is transported away from the wall and part towards the wall. For
![]() $y^{+}>60$
, there is more dissipation for a lower
$y^{+}>60$
, there is more dissipation for a lower
![]() $n$
which dissipates the extra energy available for a more shear-thinning fluid and the
$n$
which dissipates the extra energy available for a more shear-thinning fluid and the
![]() $k^{+}$
profiles of different
$k^{+}$
profiles of different
![]() $n$
collapse on top of each other for
$n$
collapse on top of each other for
![]() $y^{+}\gtrsim 90$
. For
$y^{+}\gtrsim 90$
. For
![]() $y^{+}<15$
, there is a narrow region (
$y^{+}<15$
, there is a narrow region (
![]() $y^{+}=6-15$
) where
$y^{+}=6-15$
) where
![]() ${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
is clearly lower for a more shear-thinning fluid and therefore, the turbulent kinetic energy profiles slowly converge to a single curve towards the wall.
${\mathcal{P}}^{+}/\unicode[STIX]{x1D716}^{k^{+}}$
is clearly lower for a more shear-thinning fluid and therefore, the turbulent kinetic energy profiles slowly converge to a single curve towards the wall.
5.3 Summary of results of energy budgets
Results of the MFKE budget show that except the MFKE production, all other terms show flow index dependence only near the wall for
![]() $y^{+}\lesssim 60$
. Shear thinning increases the MFKE production and hence dissipation. The non-Newtonian terms are a source in the MFKE budget for a shear-thinning fluid and sink for the shear thickening. Similar to the MFKE budget terms, TKE budget terms are also dependent on
$y^{+}\lesssim 60$
. Shear thinning increases the MFKE production and hence dissipation. The non-Newtonian terms are a source in the MFKE budget for a shear-thinning fluid and sink for the shear thickening. Similar to the MFKE budget terms, TKE budget terms are also dependent on
![]() $n$
only near the wall. Shear thinning decreases the turbulent kinetic energy production in the buffer layer whereas it increases the turbulent transport and the mean viscous dissipation primarily in the viscous sublayer. The non-Newtonian terms act as a source in the TKE budget. The non-Newtonian dissipation terms in both MFKE and TKE are positive for a shear-thinning fluid and therefore decrease the total viscous dissipation.
$n$
only near the wall. Shear thinning decreases the turbulent kinetic energy production in the buffer layer whereas it increases the turbulent transport and the mean viscous dissipation primarily in the viscous sublayer. The non-Newtonian terms act as a source in the TKE budget. The non-Newtonian dissipation terms in both MFKE and TKE are positive for a shear-thinning fluid and therefore decrease the total viscous dissipation.
6 Conclusions
The present study investigates the effect of the flow index parameter
![]() $n$
on the turbulent pipe flow at a friction Reynolds number of
$n$
on the turbulent pipe flow at a friction Reynolds number of
![]() $323$
. DNS results of the mean flow and turbulent kinetic energy budgets are presented for turbulent pipe flow of a GN fluid for the first time. Qualitative features of the flow for different
$323$
. DNS results of the mean flow and turbulent kinetic energy budgets are presented for turbulent pipe flow of a GN fluid for the first time. Qualitative features of the flow for different
![]() $n$
exhibits quite different flow structures and the range of flow length scales increases with increasing
$n$
exhibits quite different flow structures and the range of flow length scales increases with increasing
![]() $n$
. When the results are scaled with the nominal wall viscosity
$n$
. When the results are scaled with the nominal wall viscosity
![]() $\unicode[STIX]{x1D708}_{w}$
and the traditional friction velocity
$\unicode[STIX]{x1D708}_{w}$
and the traditional friction velocity
![]() $u^{\ast }$
, the mean axial velocity profiles of a power-law fluid do not strictly follow
$u^{\ast }$
, the mean axial velocity profiles of a power-law fluid do not strictly follow
![]() $U_{z}^{+}=y^{+}$
in the viscous sublayer and the mean axial velocity gradient increases as
$U_{z}^{+}=y^{+}$
in the viscous sublayer and the mean axial velocity gradient increases as
![]() $n$
is decreased. New velocity and viscosity scales are derived, which collapse the mean axial velocity profiles in the viscous sublayer for different
$n$
is decreased. New velocity and viscosity scales are derived, which collapse the mean axial velocity profiles in the viscous sublayer for different
![]() $n$
. However, these new scales are difficult to determine in experiments and result in the total non-dimensional stress profiles no longer lying on top of each other for different
$n$
. However, these new scales are difficult to determine in experiments and result in the total non-dimensional stress profiles no longer lying on top of each other for different
![]() $n$
. Mean axial velocity profiles for different
$n$
. Mean axial velocity profiles for different
![]() $n$
show large deviation in the log layer and lie above the Newtonian profile for shear-thinning fluids. The mean viscosity increases with decreasing
$n$
show large deviation in the log layer and lie above the Newtonian profile for shear-thinning fluids. The mean viscosity increases with decreasing
![]() $n$
however, the effect is seen clearly only outside the viscous sublayer. The cause of a log-like region seen in the mean viscosity profiles remains unknown. Turbulence intensities when expressed in wall units are found to increase in the axial direction but decrease in the radial and the azimuthal direction with decreasing
$n$
however, the effect is seen clearly only outside the viscous sublayer. The cause of a log-like region seen in the mean viscosity profiles remains unknown. Turbulence intensities when expressed in wall units are found to increase in the axial direction but decrease in the radial and the azimuthal direction with decreasing
![]() $n$
. This is likely due to the decrease in the turbulent energy transfer from the axial component to others as suggested by Gavrilov & Rudyak (Reference Gavrilov and Rudyak2016).
$n$
. This is likely due to the decrease in the turbulent energy transfer from the axial component to others as suggested by Gavrilov & Rudyak (Reference Gavrilov and Rudyak2016).
The Reynolds shear stress is also found to decrease with decreasing
![]() $n$
. Due to viscosity fluctuations a new term is introduced in the mean momentum balance: the turbulent viscous stress which is negative for a shear-thinning fluid and positive for the shear-thickening fluid. The magnitude of the turbulent viscous stress is maximum at the wall, however, there is no obvious reason why this should be the case. For unreported results of other rheologies, we observed it to be maximum away from the wall. Due to increased viscosity and mean shear rate, the mean viscous stress increase with decreasing
$n$
. Due to viscosity fluctuations a new term is introduced in the mean momentum balance: the turbulent viscous stress which is negative for a shear-thinning fluid and positive for the shear-thickening fluid. The magnitude of the turbulent viscous stress is maximum at the wall, however, there is no obvious reason why this should be the case. For unreported results of other rheologies, we observed it to be maximum away from the wall. Due to increased viscosity and mean shear rate, the mean viscous stress increase with decreasing
![]() $n$
and the range of
$n$
and the range of
![]() $y^{+}$
where its effect can be ignored increases with decreasing
$y^{+}$
where its effect can be ignored increases with decreasing
![]() $n$
, which suggests the thickening of the viscous sublayer by shear thinning.
$n$
, which suggests the thickening of the viscous sublayer by shear thinning.
Except for the mean flow energy production, the effect of
![]() $n$
is seen on the mean flow energy budgets mostly for
$n$
is seen on the mean flow energy budgets mostly for
![]() $y^{+}<60$
. The mean flow energy production and dissipation increase with decreasing
$y^{+}<60$
. The mean flow energy production and dissipation increase with decreasing
![]() $n$
and the non-Newtonian terms act as a source in the mean flow kinetic energy budget for shear-thinning fluids. Similar to the mean flow kinetic energy, the turbulent kinetic energy budget terms also show flow index dependence largely for
$n$
and the non-Newtonian terms act as a source in the mean flow kinetic energy budget for shear-thinning fluids. Similar to the mean flow kinetic energy, the turbulent kinetic energy budget terms also show flow index dependence largely for
![]() $y^{+}<60$
. The flow index
$y^{+}<60$
. The flow index
![]() $n$
has a notable effect on turbulent kinetic energy production in the buffer layer, whereas it affects the mean viscous dissipation and turbulent transport largely in the viscous sublayer. The new terms introduced in the turbulent kinetic energy budget from the non-Newtonian rheology are found to add a source for a shear-thinning fluid and sink for a shear-thickening fluid. The current results for shear-thinning fluids are qualitatively similar to those for viscoelastic fluids, however, further investigation is required for the quantitative comparison between these two types of fluids.
$n$
has a notable effect on turbulent kinetic energy production in the buffer layer, whereas it affects the mean viscous dissipation and turbulent transport largely in the viscous sublayer. The new terms introduced in the turbulent kinetic energy budget from the non-Newtonian rheology are found to add a source for a shear-thinning fluid and sink for a shear-thickening fluid. The current results for shear-thinning fluids are qualitatively similar to those for viscoelastic fluids, however, further investigation is required for the quantitative comparison between these two types of fluids.
In the current simulations, the mean axial velocity profiles shift away from the Newtonian profile with shear thinning. This kind of shift has been observed even for Newtonian fluids at lower Reynolds number. Contours of the instantaneous axial velocity showed less developed turbulence in the flow for lower
![]() $n$
. Therefore, the question remains whether the observed shifting of the mean axial velocity profiles in current simulations is a Reynolds number effect or a rheology effect. Simulations at higher Reynolds numbers will answer this question. High Reynolds number simulations are also needed to show if log layer in the mean viscosity profiles is real or not. The current simulations have shown that the turbulent kinetic energy budget is affected by shear thinning only in the near-wall region (
$n$
. Therefore, the question remains whether the observed shifting of the mean axial velocity profiles in current simulations is a Reynolds number effect or a rheology effect. Simulations at higher Reynolds numbers will answer this question. High Reynolds number simulations are also needed to show if log layer in the mean viscosity profiles is real or not. The current simulations have shown that the turbulent kinetic energy budget is affected by shear thinning only in the near-wall region (
![]() $y^{+}<60$
). A question arises as to whether generalised Newtonian rheology is important only in
$y^{+}<60$
). A question arises as to whether generalised Newtonian rheology is important only in
![]() $y^{+}<60$
and the deviation in the mean axial velocity and turbulence intensity profiles with shear thinning in the log layer is due to only to what happens close to the wall. This is the focus of ongoing research.
$y^{+}<60$
and the deviation in the mean axial velocity and turbulence intensity profiles with shear thinning in the log layer is due to only to what happens close to the wall. This is the focus of ongoing research.
Acknowledgements
The first author was supported by an industry project AMIRA-P1087 funded through AMIRA International. We would like to thank J. M. J. den Toonder for supplying the experimental data used in compiling figure 4, and also J. G. M. Eggels for copies of his PhD thesis. Computations were performed at the Australian National Computational Infrastructure National Facility and the Pawsey Supercomputing Centre using resources allocated via the NCI Merit Allocation Scheme to grant d77.