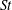1 Introduction
Inertial particles moving in a turbulent flow do not simply trace the paths of fluid elements since particle inertia allows the particles to detach from the local fluid. This causes small-scale spatial clustering even in incompressible turbulence (Maxey Reference Maxey1987; Duncan et al. Reference Duncan, Mehlig, Östlund and Wilkinson2005; Bec et al. Reference Bec, Biferale, Cencini, Lanotte, Musacchio and Toschi2007; Goto & Vassilicos Reference Goto and Vassilicos2008; Bragg & Collins Reference Bragg and Collins2014). Moreover, preferential sampling of regions with high vorticity/strain is observed for particles that are lighter/heavier than the fluid. As a result, the statistical properties of inertial heavy or light particles (for example water droplets in turbulent clouds (Shaw Reference Shaw2003) or air bubbles in water (Mazzitelli, Lohse & Toschi Reference Mazzitelli, Lohse and Toschi2003; Rensen, Luther & Lohse Reference Rensen, Luther and Lohse2005)) in turbulence are highly non-trivial both at sub-viscous and larger scales. An important example is the case of inertial-particle accelerations (Bec et al. Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a ; Qureshi et al. Reference Qureshi, Arrieta, Baudet, Cartellier, Gagne and Bourgoin2008; Gibert, Xu & Bodenschatz Reference Gibert, Xu and Bodenschatz2010, Reference Gibert, Xu and Bodenschatz2012; Volk et al. Reference Volk, Calzavarini, Leveque and Pinton2011; Prakash et al. Reference Prakash, Tagawa, Calzavarini, Mercado, Toschi, Lohse and Sun2012), see also the review by Toschi & Bodenschatz (Reference Toschi and Bodenschatz2009). At large inertia, singularities (caustics) occur in the dynamics of heavy particles (Falkovich, Fouxon & Stepanov Reference Falkovich, Fouxon and Stepanov2002; Wilkinson & Mehlig Reference Wilkinson and Mehlig2005), giving rise to large relative velocities between close particles (Sundaram & Collins Reference Sundaram and Collins1997; Falkovich & Pumir Reference Falkovich and Pumir2007; Bec et al. Reference Bec, Biferale, Cencini, Lanotte and Toschi2010a ; Gustavsson & Mehlig Reference Gustavsson and Mehlig2011, Reference Gustavsson and Mehlig2014), and leading eventually to an enhancement of collision rates (Wilkinson, Mehlig & Bezuglyy Reference Wilkinson, Mehlig and Bezuglyy2006; Bec, Homann & Ray Reference Bec, Homann and Ray2014).
The dynamics of light particles is important because of its relevance to fundamental and applied questions. Light particles can be used as small probes that preferentially track high vorticity structures, highlighting statistical and topological properties of the underlying fluid, conditioned on those structures. In the limit of high volume fractions they might also have a complex feedback on the flow, including the case of reducing the turbulent drag (van den Berg et al. Reference van den Berg, Luther, Lathrop and Lohse2005, Reference van den Berg, van Gils, Lathrop and Lohse2007; Jacob et al. Reference Jacob, Olivieri, Miozzi, Campana and Piva2010). Compared to heavy particles the dynamics of light particles is more difficult to analyse because pressure-gradient forces (Tchen Reference Tchen1947) and added-mass effects must be taken into account. Apart from the fact that light particles tend to be drawn into vortices there is little theoretical analysis of their dynamics in turbulent flows.
This motivated us to formulate a closure scheme that allows us to compute inertial accelerations of both heavy and light particles in turbulence. We describe the scheme and we test it by comparing its predictions to results of direct numerical simulations (DNS). We consider a simple model for the particle dynamics, taking into account added-mass and pressure-gradient forces, but neglecting the effect of buoyancy on the acceleration as well as the Basset–Boussinesq history force, as in many previous DNS studies (Babiano et al. Reference Babiano, Cartwright, Piro and Provenzale2000; Bec et al. Reference Bec, Celani, Cencini and Musacchio2005; Calzavarini et al. Reference Calzavarini, Cencini, Lohse and Toschi2008a , Reference Calzavarini, Volk, Bourgoin, Leveque, Pinton and Toschi2009; Volk et al. Reference Volk, Calzavarini, Verhille, Lohse, Mordant, Pinton and Toschi2008). We comment on these questions in the conclusions.
Our scheme for the inertial-particle accelerations approximates the particle paths by the Lagrangian fluid-element paths. It is a closure for the particle equation of motion that neglects inertial preferential sampling such as heavy inertial particles being centrifuged out of long-lived vortical regions of the flow (Maxey Reference Maxey1987), so that they preferentially sample straining regions, or light particles which by contrast are drawn into vortices (Calzavarini et al.
Reference Calzavarini, Cencini, Lohse and Toschi2008a
,Reference Calzavarini, Kerscher, Lohse and Toschi
b
). The latter is simply a consequence of the fact that light particles are influenced by pressure gradients in the undisturbed flow. Our approximation cannot be quantitatively correct when inertial preferential sampling is significant, but overall it yields a good qualitative description of how particle accelerations depend on the particle density relative to that of the fluid, and upon the Stokes number, a dimensionless measure of particle inertia. Moreover, and more interestingly, the closure also predicts highly non-trivial properties of the intermittent, non-Gaussian acceleration fluctuations, as the magnitude of inertial effects and the Reynolds number of the turbulence change. For example, the closure scheme predicts that the flatness of the acceleration develops a maximum or a minimum as a function of
![]() $St$
for light or heavy particles. This is in good qualitative agreement with the measurements on the DNS data. For heavy particles the closure fails when inertial preferential sampling affects inertial particle accelerations, i.e. for Stokes numbers of order unity, see figure 1(b) in Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
). In fact, for heavy particles our closure is equivalent to the ‘filtering’ mechanism discussed by Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
). For light particles, by contrast, comparisons to DNS results show that inertial preferential sampling effects are strong only at very large Stokes numbers,
$St$
for light or heavy particles. This is in good qualitative agreement with the measurements on the DNS data. For heavy particles the closure fails when inertial preferential sampling affects inertial particle accelerations, i.e. for Stokes numbers of order unity, see figure 1(b) in Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
). In fact, for heavy particles our closure is equivalent to the ‘filtering’ mechanism discussed by Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
). For light particles, by contrast, comparisons to DNS results show that inertial preferential sampling effects are strong only at very large Stokes numbers,
![]() $St\sim 10$
, leading to an enlarged range of small and intermediate values of
$St\sim 10$
, leading to an enlarged range of small and intermediate values of
![]() $St$
where the closure works qualitatively well.
$St$
where the closure works qualitatively well.
The remainder of this article is organized as follows. In the next section we formulate the problem, introduce the equations of motion and qualitatively discuss inertial preferential sampling. In § 3 we describe our Lagrangian closure scheme for inertial particle accelerations. Data from DNS of turbulent flows are analysed in § 4 together with a detailed comparison to the predictions from the closure scheme. In § 5, we assess the potentialities of the closure on a data set obtained using a stochastic surrogate for the fluid velocity field. § 6 contains the conclusions.
2 Formulation of the problem
Many studies have considered the dynamics of heavy inertial particles, much denser than the carrying fluid. When the particles are very heavy and at the same time very small (point particles) the motion is simply determined by Stokes’ drag. The dynamics of light particles by contrast is also affected by pressure gradients of the unperturbed fluid, and added-mass effects. Neglecting the effect of gravitational settling (and thus buoyancy) the equation of motion reads:
where
![]() $\boldsymbol{r}_{t}$
is the particle position at time
$\boldsymbol{r}_{t}$
is the particle position at time
![]() $t$
,
$t$
,
![]() $\boldsymbol{v}_{t}$
, is the particle velocity,
$\boldsymbol{v}_{t}$
, is the particle velocity,
![]() $\boldsymbol{u}(\boldsymbol{r}_{t},t)$
is the velocity field of the undisturbed fluid and
$\boldsymbol{u}(\boldsymbol{r}_{t},t)$
is the velocity field of the undisturbed fluid and
![]() $\text{D}_{t}\boldsymbol{u}=\partial _{t}\boldsymbol{u}+(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u}$
is the Lagrangian derivative. The dimensionless constant
$\text{D}_{t}\boldsymbol{u}=\partial _{t}\boldsymbol{u}+(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u}$
is the Lagrangian derivative. The dimensionless constant
![]() ${\it\beta}=3{\it\rho}_{f}/({\it\rho}_{f}+2{\it\rho}_{p})$
accounts for the contrast between particle density
${\it\beta}=3{\it\rho}_{f}/({\it\rho}_{f}+2{\it\rho}_{p})$
accounts for the contrast between particle density
![]() ${\it\rho}_{p}$
and fluid density
${\it\rho}_{p}$
and fluid density
![]() ${\it\rho}_{f}$
, while the Stokes number is defined as
${\it\rho}_{f}$
, while the Stokes number is defined as
![]() $St={\it\tau}_{s}/{\it\tau}_{K}$
where the particle response time is
$St={\it\tau}_{s}/{\it\tau}_{K}$
where the particle response time is
![]() ${\it\tau}_{s}=R^{2}/(3{\it\nu}{\it\beta})$
,
${\it\tau}_{s}=R^{2}/(3{\it\nu}{\it\beta})$
,
![]() $R$
is the particle radius,
$R$
is the particle radius,
![]() ${\it\nu}$
the kinematic viscosity of the flow and
${\it\nu}$
the kinematic viscosity of the flow and
![]() ${\it\tau}_{K}=\sqrt{{\it\nu}/{\it\epsilon}}$
the Kolmogorov time defined in terms of the fluid energy dissipation,
${\it\tau}_{K}=\sqrt{{\it\nu}/{\it\epsilon}}$
the Kolmogorov time defined in terms of the fluid energy dissipation,
![]() ${\it\epsilon}$
. Many studies have employed this model (Babiano et al.
Reference Babiano, Cartwright, Piro and Provenzale2000; Bec et al.
Reference Bec, Celani, Cencini and Musacchio2005; Calzavarini et al.
Reference Calzavarini, Cencini, Lohse and Toschi2008a
, Reference Calzavarini, Volk, Bourgoin, Leveque, Pinton and Toschi2009; Volk et al.
Reference Volk, Calzavarini, Verhille, Lohse, Mordant, Pinton and Toschi2008). The model takes into account added-mass effects but neglects buoyancy forces. It is an open question under which circumstances this is a quantitative model for the acceleration of small particles in turbulence.
${\it\epsilon}$
. Many studies have employed this model (Babiano et al.
Reference Babiano, Cartwright, Piro and Provenzale2000; Bec et al.
Reference Bec, Celani, Cencini and Musacchio2005; Calzavarini et al.
Reference Calzavarini, Cencini, Lohse and Toschi2008a
, Reference Calzavarini, Volk, Bourgoin, Leveque, Pinton and Toschi2009; Volk et al.
Reference Volk, Calzavarini, Verhille, Lohse, Mordant, Pinton and Toschi2008). The model takes into account added-mass effects but neglects buoyancy forces. It is an open question under which circumstances this is a quantitative model for the acceleration of small particles in turbulence.
The following analysis is based on (2.1). It is important to first understand this case before addressing more realistic situations (inclusion of buoyancy, finite particle size, collisions and feedback on the flow). The sources of the difficulties are twofold. First, even in the much simpler case of a non-turbulent Eulerian velocity field
![]() $\boldsymbol{u}(\boldsymbol{r},t)$
the particle dynamics is still complicated and often chaotic, simply because equation (2.1) are nonlinear. Second, turbulence makes the problem even harder due to the existence of substantial spatial and temporal fluctuations. This results in chaotic Lagrangian dynamics of fluid elements. Note that even though Lagrangian fluid elements sample space uniformly, their instantaneous motion is in general correlated with structures in the underlying flow. This implies that multi-time Lagrangian flow correlation functions evaluated along tracer trajectories do not coincide with the underlying Eulerian correlation functions which are evaluated at fixed positions in space. Particles that are heavier or lighter than the fluid may detach from the flow if they have inertia. This leads to the inertial preferential sampling mentioned in the introduction. As a result, the flow statistics experienced by an inertial particle differs from that of a Lagrangian fluid element.
$\boldsymbol{u}(\boldsymbol{r},t)$
the particle dynamics is still complicated and often chaotic, simply because equation (2.1) are nonlinear. Second, turbulence makes the problem even harder due to the existence of substantial spatial and temporal fluctuations. This results in chaotic Lagrangian dynamics of fluid elements. Note that even though Lagrangian fluid elements sample space uniformly, their instantaneous motion is in general correlated with structures in the underlying flow. This implies that multi-time Lagrangian flow correlation functions evaluated along tracer trajectories do not coincide with the underlying Eulerian correlation functions which are evaluated at fixed positions in space. Particles that are heavier or lighter than the fluid may detach from the flow if they have inertia. This leads to the inertial preferential sampling mentioned in the introduction. As a result, the flow statistics experienced by an inertial particle differs from that of a Lagrangian fluid element.

Figure 1. Parameter space showing available DNS data sets with
![]() $Re_{{\it\lambda}}=185$
and
$Re_{{\it\lambda}}=185$
and
![]() $Re_{{\it\lambda}}=400$
. For values of
$Re_{{\it\lambda}}=400$
. For values of
![]() $St$
smaller than
$St$
smaller than
![]() $0.05$
the
$0.05$
the
![]() $x$
axis is linear, while it is logarithmic for values of
$x$
axis is linear, while it is logarithmic for values of
![]() $St$
larger than
$St$
larger than
![]() $0.05$
. For each data set with
$0.05$
. For each data set with
![]() $Re_{{\it\lambda}}=185$
we have analysed a total of 130 000 trajectories of duration
$Re_{{\it\lambda}}=185$
we have analysed a total of 130 000 trajectories of duration
![]() $6T_{L}$
and for each data set with
$6T_{L}$
and for each data set with
![]() $Re_{{\it\lambda}}=400$
we have analysed a total of 200 000 trajectories of duration
$Re_{{\it\lambda}}=400$
we have analysed a total of 200 000 trajectories of duration
![]() $2.5T_{L}$
. Level curves
$2.5T_{L}$
. Level curves
![]() $St(1-{\it\beta})={\it\epsilon}$
for constants
$St(1-{\it\beta})={\it\epsilon}$
for constants
![]() ${\it\epsilon}=\{-1,-0.1,-0.01,0,0.01,0.1,1\}$
are plotted as black lines. Parameter families: with
${\it\epsilon}=\{-1,-0.1,-0.01,0,0.01,0.1,1\}$
are plotted as black lines. Parameter families: with
![]() $Re_{{\it\lambda}}=185$
:
$Re_{{\it\lambda}}=185$
:
![]() ${\it\beta}=0$
(red, ○),
${\it\beta}=0$
(red, ○),
![]() ${\it\beta}=0.25$
(magenta, ▵),
${\it\beta}=0.25$
(magenta, ▵),
![]() ${\it\beta}=0.5$
(cyan, ▿),
${\it\beta}=0.5$
(cyan, ▿),
![]() ${\it\beta}=0.75$
(green, ▹),
${\it\beta}=0.75$
(green, ▹),
![]() ${\it\beta}=1$
(black, ▫),
${\it\beta}=1$
(black, ▫),
![]() ${\it\beta}=1.25$
(brown, ♢),
${\it\beta}=1.25$
(brown, ♢),
![]() ${\it\beta}=1.5$
(purple, ▿),
${\it\beta}=1.5$
(purple, ▿),
![]() ${\it\beta}=2$
(orange, ▹),
${\it\beta}=2$
(orange, ▹),
![]() ${\it\beta}=2.5$
(dark green, ◃),
${\it\beta}=2.5$
(dark green, ◃),
![]() ${\it\beta}=3$
(blue, ▵). With
${\it\beta}=3$
(blue, ▵). With
![]() $Re_{{\it\lambda}}=400$
:
$Re_{{\it\lambda}}=400$
:
![]() ${\it\beta}=0$
(red,
${\it\beta}=0$
(red,
3 Lagrangian closure
Let us notice that the dynamics determined by equation (2.1) tends to the evolution of a tracer in both limits
![]() $St\rightarrow 0$
and
$St\rightarrow 0$
and
![]() ${\it\beta}\rightarrow 1$
. Indeed, in the limit
${\it\beta}\rightarrow 1$
. Indeed, in the limit
![]() ${\it\tau}_{s}\rightarrow 0$
, imposing a finite Stokes drag leads to
${\it\tau}_{s}\rightarrow 0$
, imposing a finite Stokes drag leads to
![]() $\boldsymbol{v}_{t}=\boldsymbol{u}+O({\it\tau}_{s})$
. For
$\boldsymbol{v}_{t}=\boldsymbol{u}+O({\it\tau}_{s})$
. For
![]() ${\it\beta}=1$
, by contrast we may approximate the material derivative along fluid-trace trajectories with the derivative along the trajectory of a particle,
${\it\beta}=1$
, by contrast we may approximate the material derivative along fluid-trace trajectories with the derivative along the trajectory of a particle,
![]() $\text{D}_{t}\boldsymbol{u}\sim \dot{\boldsymbol{u}}$
, and consistently check that the evolution of (2.1) leads to an exponential relaxation of the evolution of the particle to the trajectory of the tracer. Hence, the idea is to approximate the effects of inertial forces on the particle trajectory starting from the evolution of tracers. This approach cannot be exact. It is for example known that vortices are preferentially sampled by inertial particles. Nevertheless, it is important to understand and quantify how big the difference is as a function of the distance in the parameter phase space,
$\text{D}_{t}\boldsymbol{u}\sim \dot{\boldsymbol{u}}$
, and consistently check that the evolution of (2.1) leads to an exponential relaxation of the evolution of the particle to the trajectory of the tracer. Hence, the idea is to approximate the effects of inertial forces on the particle trajectory starting from the evolution of tracers. This approach cannot be exact. It is for example known that vortices are preferentially sampled by inertial particles. Nevertheless, it is important to understand and quantify how big the difference is as a function of the distance in the parameter phase space,
![]() $(St,{\it\beta})$
, from the two lines
$(St,{\it\beta})$
, from the two lines
![]() $St=0$
or
$St=0$
or
![]() ${\it\beta}=1$
where the closure must be exact (see figure 1). The starting point is to evaluate (2.1) along tracer trajectories:
${\it\beta}=1$
where the closure must be exact (see figure 1). The starting point is to evaluate (2.1) along tracer trajectories:
where
![]() $\boldsymbol{r}_{t}^{(L)}$
denotes the Lagrangian trajectory of a tracer particle. This approximation is a closure in the sense that the first equation in (3.1) is independent of the second one, and the second equation can be solved in terms of the Lagrangian velocity statistics
$\boldsymbol{r}_{t}^{(L)}$
denotes the Lagrangian trajectory of a tracer particle. This approximation is a closure in the sense that the first equation in (3.1) is independent of the second one, and the second equation can be solved in terms of the Lagrangian velocity statistics
![]() $\boldsymbol{u}(\boldsymbol{r}_{t}^{(L)},t)$
of the underlying flow. We solve (3.1) for
$\boldsymbol{u}(\boldsymbol{r}_{t}^{(L)},t)$
of the underlying flow. We solve (3.1) for
![]() $\boldsymbol{v}_{t}$
(disregarding initial conditions here and below because these do not matter for the steady-state statistics) to obtain
$\boldsymbol{v}_{t}$
(disregarding initial conditions here and below because these do not matter for the steady-state statistics) to obtain
Using this expression, the particle acceleration follows from the second of equation (3.1)
Using equation (3.3) we express two-time acceleration statistics in terms of the two-point Lagrangian acceleration correlation function
In the steady-state limit we find
 $$\begin{eqnarray}\displaystyle \langle \boldsymbol{a}_{t}\boldsymbol{\cdot }\boldsymbol{a}_{0}\rangle & = & \displaystyle {\it\beta}^{2}C_{L}(t)+\frac{1-{\it\beta}^{2}}{{\it\tau}_{s}}\left[\cosh \left[\frac{t}{{\it\tau}_{s}}\right]\int _{t}^{\infty }\text{d}t_{1}\,\text{e}^{-t_{1}/{\it\tau}_{s}}C_{L}(t_{1})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\text{e}^{-t/{\it\tau}_{s}}\int _{0}^{t}\text{d}t_{1}\,\cosh \left[\frac{t_{1}}{{\it\tau}_{s}}\right]C_{L}(t_{1})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \boldsymbol{a}_{t}\boldsymbol{\cdot }\boldsymbol{a}_{0}\rangle & = & \displaystyle {\it\beta}^{2}C_{L}(t)+\frac{1-{\it\beta}^{2}}{{\it\tau}_{s}}\left[\cosh \left[\frac{t}{{\it\tau}_{s}}\right]\int _{t}^{\infty }\text{d}t_{1}\,\text{e}^{-t_{1}/{\it\tau}_{s}}C_{L}(t_{1})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\text{e}^{-t/{\it\tau}_{s}}\int _{0}^{t}\text{d}t_{1}\,\cosh \left[\frac{t_{1}}{{\it\tau}_{s}}\right]C_{L}(t_{1})\right].\end{eqnarray}$$
The acceleration variance is obtained by letting
![]() $t\rightarrow 0$
in (3.5)
$t\rightarrow 0$
in (3.5)
Similarly, the fourth moment of the particle acceleration is obtained as:
 $$\begin{eqnarray}\displaystyle \langle |\boldsymbol{a}|^{4}\rangle & = & \displaystyle {\it\beta}^{4}C_{L}(0,0,0)-4\frac{({\it\beta}-1){\it\beta}^{3}}{{\it\tau}_{s}}\int _{0}^{\infty }\text{d}t_{1}\,\text{e}^{-t_{1}/{\it\tau}_{s}}C_{L}(-t_{1},0,0)\nonumber\\ \displaystyle & & \displaystyle +\,6\frac{({\it\beta}-1)^{2}{\it\beta}^{2}}{{\it\tau}_{s}^{2}}\int _{0}^{\infty }\text{d}t_{1}\,\int _{0}^{\infty }\text{d}t_{2}\,\text{e}^{-(t_{1}+t_{2})/{\it\tau}_{s}}C_{L}(-t_{1},-t_{2},0)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{({\it\beta}-1)^{3}(3{\it\beta}+1)}{{\it\tau}_{s}^{3}}\int _{0}^{\infty }\text{d}t_{1}\,\int _{0}^{\infty }\text{d}t_{2}\,\int _{0}^{\infty }\text{d}t_{3}\,\text{e}^{-(t_{1}+t_{2}+t_{3})/{\it\tau}_{s}}C_{L}(-t_{1},-t_{2},-t_{3}).\quad \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle |\boldsymbol{a}|^{4}\rangle & = & \displaystyle {\it\beta}^{4}C_{L}(0,0,0)-4\frac{({\it\beta}-1){\it\beta}^{3}}{{\it\tau}_{s}}\int _{0}^{\infty }\text{d}t_{1}\,\text{e}^{-t_{1}/{\it\tau}_{s}}C_{L}(-t_{1},0,0)\nonumber\\ \displaystyle & & \displaystyle +\,6\frac{({\it\beta}-1)^{2}{\it\beta}^{2}}{{\it\tau}_{s}^{2}}\int _{0}^{\infty }\text{d}t_{1}\,\int _{0}^{\infty }\text{d}t_{2}\,\text{e}^{-(t_{1}+t_{2})/{\it\tau}_{s}}C_{L}(-t_{1},-t_{2},0)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{({\it\beta}-1)^{3}(3{\it\beta}+1)}{{\it\tau}_{s}^{3}}\int _{0}^{\infty }\text{d}t_{1}\,\int _{0}^{\infty }\text{d}t_{2}\,\int _{0}^{\infty }\text{d}t_{3}\,\text{e}^{-(t_{1}+t_{2}+t_{3})/{\it\tau}_{s}}C_{L}(-t_{1},-t_{2},-t_{3}).\quad \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Here isotropy of the acceleration components
![]() $\langle a_{i}a_{j}a_{k}a_{l}\rangle =[{\it\delta}_{ij}{\it\delta}_{kl}+{\it\delta}_{ik}{\it\delta}_{jl}+{\it\delta}_{il}{\it\delta}_{jk}]\langle a_{1}^{4}\rangle /3$
was used to express
$\langle a_{i}a_{j}a_{k}a_{l}\rangle =[{\it\delta}_{ij}{\it\delta}_{kl}+{\it\delta}_{ik}{\it\delta}_{jl}+{\it\delta}_{il}{\it\delta}_{jk}]\langle a_{1}^{4}\rangle /3$
was used to express
![]() $\langle |\boldsymbol{a}|^{4}\rangle$
in terms of the four-point Lagrangian correlation function
$\langle |\boldsymbol{a}|^{4}\rangle$
in terms of the four-point Lagrangian correlation function
where
![]() $\text{D}_{t}u_{1}$
is a component of the fluid acceleration and
$\text{D}_{t}u_{1}$
is a component of the fluid acceleration and
![]() $d$
is the spatial dimension. Equations (3.5)–(3.7) express the fluctuations of inertial-particle accelerations in terms of Lagrangian correlation functions of the underlying flow, and predict how the inertial-particle accelerations depend on
$d$
is the spatial dimension. Equations (3.5)–(3.7) express the fluctuations of inertial-particle accelerations in terms of Lagrangian correlation functions of the underlying flow, and predict how the inertial-particle accelerations depend on
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $St$
. The integrals in (3.6) and (3.7) are hard to evaluate numerically for very small and for very large values of
$St$
. The integrals in (3.6) and (3.7) are hard to evaluate numerically for very small and for very large values of
![]() $St$
. When
$St$
. When
![]() $St$
is small, the exponential factors in the right-hand side of (3.6) and (3.7) become singular and one needs a very high sampling frequency of the fluid acceleration along the particle trajectory to evaluate the integrals reliably. When
$St$
is small, the exponential factors in the right-hand side of (3.6) and (3.7) become singular and one needs a very high sampling frequency of the fluid acceleration along the particle trajectory to evaluate the integrals reliably. When
![]() $St$
is large, on the other hand, the integrals sum up large-time contributions with large fluctuations due to the finite length of experimental and numerical trajectories.
$St$
is large, on the other hand, the integrals sum up large-time contributions with large fluctuations due to the finite length of experimental and numerical trajectories.
Before we proceed to a quantitative assessment of the model let us make a few general remarks about the range of applicability and accuracy of the approximation made. First, in (3.6) and (3.7) we need to evaluate the acceleration correlation function of the tracers for general values of
![]() $t$
. This might be seen as a problem because the trajectories of tracers and of inertial particles must depart on a time scale of the order of the Lyapunov time. On the other hand, the acceleration correlation function of the tracer is known to decay on a time of the order of the Kolmogorov time,
$t$
. This might be seen as a problem because the trajectories of tracers and of inertial particles must depart on a time scale of the order of the Lyapunov time. On the other hand, the acceleration correlation function of the tracer is known to decay on a time of the order of the Kolmogorov time,
![]() ${\it\tau}_{K}$
, which is ten times smaller than the typical Lyapunov time of heavy particles (Bec et al.
Reference Bec, Biferale, Boffetta, Cencini, Musacchio and Toschi2006b
) and stays close to zero in the inertial range of scales (Falkovich et al.
Reference Falkovich, Xu, Pumir, Bodenschatz, Biferale, Boffetta, Lanotte and Toschi2012). Therefore we do not see any problem in the evaluation of the integrals in the above equations. Second, we are only interested in stationary properties of the inertial particle statistics and we always assume that the initial conditions for all particles are chosen from their stationary distribution functions. As a result no influence of the initial condition should appear in the closure. The Lagrangian closure adopted here can also be applied to correlation functions of other observables of the particle, or of the flow, provided that the underlying Lagrangian correlation functions decay quickly enough. Here, we focus on the acceleration statistics because of their highly non-Gaussian properties and high sensitivity to the parameters
${\it\tau}_{K}$
, which is ten times smaller than the typical Lyapunov time of heavy particles (Bec et al.
Reference Bec, Biferale, Boffetta, Cencini, Musacchio and Toschi2006b
) and stays close to zero in the inertial range of scales (Falkovich et al.
Reference Falkovich, Xu, Pumir, Bodenschatz, Biferale, Boffetta, Lanotte and Toschi2012). Therefore we do not see any problem in the evaluation of the integrals in the above equations. Second, we are only interested in stationary properties of the inertial particle statistics and we always assume that the initial conditions for all particles are chosen from their stationary distribution functions. As a result no influence of the initial condition should appear in the closure. The Lagrangian closure adopted here can also be applied to correlation functions of other observables of the particle, or of the flow, provided that the underlying Lagrangian correlation functions decay quickly enough. Here, we focus on the acceleration statistics because of their highly non-Gaussian properties and high sensitivity to the parameters
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $St$
. Finally, let us stress that our closure is fully based on Lagrangian properties and does require the use of any Eulerian correlation function, as opposed to closures based on the fast Eulerian approach by Ferry & Balachandar (Reference Ferry and Balachandar2001) or the Lagrangian–Eulerian closure to predict two-particle distributions (Derevich Reference Derevich2000; Zaichik & Alipchenkov Reference Zaichik and Alipchenkov2003; Alipchenkov & Zaichik Reference Alipchenkov and Zaichik2007; Pan & Padoan Reference Pan and Padoan2010). To make further progress we need to determine the Lagrangian correlation functions. In § 4 we present the most important new results, we determine the Lagrangian correlation functions by DNS of inertial particle dynamics in turbulence, substitute into (3.5)–(3.7) and assess the accuracy of these equations in predicting particle acceleration fluctuations and correlations.
$St$
. Finally, let us stress that our closure is fully based on Lagrangian properties and does require the use of any Eulerian correlation function, as opposed to closures based on the fast Eulerian approach by Ferry & Balachandar (Reference Ferry and Balachandar2001) or the Lagrangian–Eulerian closure to predict two-particle distributions (Derevich Reference Derevich2000; Zaichik & Alipchenkov Reference Zaichik and Alipchenkov2003; Alipchenkov & Zaichik Reference Alipchenkov and Zaichik2007; Pan & Padoan Reference Pan and Padoan2010). To make further progress we need to determine the Lagrangian correlation functions. In § 4 we present the most important new results, we determine the Lagrangian correlation functions by DNS of inertial particle dynamics in turbulence, substitute into (3.5)–(3.7) and assess the accuracy of these equations in predicting particle acceleration fluctuations and correlations.
4 Direct numerical simulations
4.1 Simulation method
We present here the analysis of data obtained from DNS of a homogeneous and isotropic turbulent flow seeded with point-like particles with different inertia and particle–fluid density ratios (see figure 1 for a summary of the
![]() $(St,{\it\beta})$
values available). The data set was previously obtained by Bec et al. (Reference Bec, Biferale, Lanotte, Scagliarini and Toschi2010b
). The flow obeys the Navier–Stokes equations for an incompressible velocity field
$(St,{\it\beta})$
values available). The data set was previously obtained by Bec et al. (Reference Bec, Biferale, Lanotte, Scagliarini and Toschi2010b
). The flow obeys the Navier–Stokes equations for an incompressible velocity field
![]() $\boldsymbol{u}(\boldsymbol{x},t)$
:
$\boldsymbol{u}(\boldsymbol{x},t)$
:
The external forcing
![]() $\boldsymbol{f}$
is statistically homogeneous, stationary and isotropic, injecting energy in the first low wavenumber shells by keeping their spectral content constant (Chen et al.
Reference Chen, Doolen, Kraichnan and She1993). The viscosity
$\boldsymbol{f}$
is statistically homogeneous, stationary and isotropic, injecting energy in the first low wavenumber shells by keeping their spectral content constant (Chen et al.
Reference Chen, Doolen, Kraichnan and She1993). The viscosity
![]() ${\it\nu}$
is set such that the Kolmogorov length scale
${\it\nu}$
is set such that the Kolmogorov length scale
![]() ${\it\eta}\approx {\it\delta}x$
, where
${\it\eta}\approx {\it\delta}x$
, where
![]() ${\it\delta}x$
is the grid spacing. The numerical domain is
${\it\delta}x$
is the grid spacing. The numerical domain is
![]() $2{\rm\pi}$
-periodic in the three directions. We use a fully dealiased pseudospectral algorithm with second-order Adams–Bashforth time stepping. For details see Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
), Cencini et al. (Reference Cencini, Bec, Biferale, Boffetta, Celani, Lanotte, Musacchio and Toschi2006). Two series of DNS are analysed: Run I, with a numerical resolution of
$2{\rm\pi}$
-periodic in the three directions. We use a fully dealiased pseudospectral algorithm with second-order Adams–Bashforth time stepping. For details see Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
), Cencini et al. (Reference Cencini, Bec, Biferale, Boffetta, Celani, Lanotte, Musacchio and Toschi2006). Two series of DNS are analysed: Run I, with a numerical resolution of
![]() $512^{3}$
grid points and the Reynolds number at the Taylor scale
$512^{3}$
grid points and the Reynolds number at the Taylor scale
![]() $Re_{{\it\lambda}}\approx 200$
; Run II, with
$Re_{{\it\lambda}}\approx 200$
; Run II, with
![]() $2048^{3}$
resolution and
$2048^{3}$
resolution and
![]() $Re_{{\it\lambda}}\approx 400$
. Details can be found in table 1.
$Re_{{\it\lambda}}\approx 400$
. Details can be found in table 1.

Figure 2. Acceleration variance (a) and flatness (b) for DNS data at changing
![]() ${\it\beta}$
,
${\it\beta}$
,
![]() $St$
and
$St$
and
![]() $Re$
. (a) Points correspond to the DNS data (same symbols of figure 1). Solid lines (labelled with their corresponding value of
$Re$
. (a) Points correspond to the DNS data (same symbols of figure 1). Solid lines (labelled with their corresponding value of
![]() ${\it\beta}$
) show the closure scheme prediction for the acceleration variance of light and heavy particles, (3.6), normalized with the fluid variance, for all data from Run I; dashed line corresponds to the closure for Run II. (b) The flatness measured on the DNS data and the one predicted by the closure scheme, (3.7), for heavy and light particles. Thin dashed black line shows the limit of normal distributed acceleration components. Additional data for
${\it\beta}$
) show the closure scheme prediction for the acceleration variance of light and heavy particles, (3.6), normalized with the fluid variance, for all data from Run I; dashed line corresponds to the closure for Run II. (b) The flatness measured on the DNS data and the one predicted by the closure scheme, (3.7), for heavy and light particles. Thin dashed black line shows the limit of normal distributed acceleration components. Additional data for
![]() ${\it\beta}=3$
(blue,
${\it\beta}=3$
(blue,
Table 1. Eulerian parameters for the two runs analysed in this article: Run I and Run II in the text.
![]() $N$
is the number of grid points in each spatial direction;
$N$
is the number of grid points in each spatial direction;
![]() $Re_{{\it\lambda}}$
is the Taylor-scale Reynolds number;
$Re_{{\it\lambda}}$
is the Taylor-scale Reynolds number;
![]() ${\it\eta}$
is the Kolmogorov dissipative scale;
${\it\eta}$
is the Kolmogorov dissipative scale;
![]() ${\it\delta}x=\mathscr{L}/N$
is the grid spacing, with
${\it\delta}x=\mathscr{L}/N$
is the grid spacing, with
![]() $\mathscr{L}=2{\rm\pi}$
denoting the physical size of the numerical domain;
$\mathscr{L}=2{\rm\pi}$
denoting the physical size of the numerical domain;
![]() ${\it\tau}_{K}=\left({\it\nu}/{\it\varepsilon}\right)^{1/2}$
is the Kolmogorov dissipative time scale;
${\it\tau}_{K}=\left({\it\nu}/{\it\varepsilon}\right)^{1/2}$
is the Kolmogorov dissipative time scale;
![]() ${\it\varepsilon}$
is the average rate of energy injection;
${\it\varepsilon}$
is the average rate of energy injection;
![]() ${\it\nu}$
is the kinematic viscosity;
${\it\nu}$
is the kinematic viscosity;
![]() $t_{\mathit{dump}}$
is the time interval between two successive dumps along particle trajectories;
$t_{\mathit{dump}}$
is the time interval between two successive dumps along particle trajectories;
![]() ${\it\delta}t$
is the time step;
${\it\delta}t$
is the time step;
![]() $T_{L}=L/U_{0}$
is the eddy turnover time at the integral scale
$T_{L}=L/U_{0}$
is the eddy turnover time at the integral scale
![]() $L={\rm\pi}$
and
$L={\rm\pi}$
and
![]() $U_{0}$
is the typical large-scale velocity.
$U_{0}$
is the typical large-scale velocity.
4.2 Comparison for acceleration variance and flatness against DNS
In figure 2(a) we show the comparison of the acceleration variance,
![]() $\langle a^{2}\rangle$
, to DNS data as a function of
$\langle a^{2}\rangle$
, to DNS data as a function of
![]() $St$
for different values of
$St$
for different values of
![]() ${\it\beta}$
. Consider first heavy particles (
${\it\beta}$
. Consider first heavy particles (
![]() ${\it\beta}<1$
). It is clear that the closure (3.1) captures the general trend and it becomes better and better for larger Stokes numbers. Similarly, this approximation must become exact as
${\it\beta}<1$
). It is clear that the closure (3.1) captures the general trend and it becomes better and better for larger Stokes numbers. Similarly, this approximation must become exact as
![]() $St\rightarrow 0$
, but the DNS data set does not contain values of
$St\rightarrow 0$
, but the DNS data set does not contain values of
![]() $St$
small enough to reach this limit. At intermediate Stokes numbers the Lagrangian closure described in § 3 does not match the DNS results. This mismatch for Stokes numbers between
$St$
small enough to reach this limit. At intermediate Stokes numbers the Lagrangian closure described in § 3 does not match the DNS results. This mismatch for Stokes numbers between
![]() $0.1$
and
$0.1$
and
![]() $1$
is certainly due to preferential sampling, as already remarked by Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
). Yet, the closure predicts a small Reynolds-number dependency (compare solid and dashed red lines for
$1$
is certainly due to preferential sampling, as already remarked by Bec et al. (Reference Bec, Biferale, Boffetta, Celani, Cencini, Lanotte, Musacchio and Toschi2006a
). Yet, the closure predicts a small Reynolds-number dependency (compare solid and dashed red lines for
![]() ${\it\beta}=0$
) inherited by the dependency of the fluid tracers. Such a small variation is not detectable within the accuracy of our numerical data. Now consider light particles (
${\it\beta}=0$
) inherited by the dependency of the fluid tracers. Such a small variation is not detectable within the accuracy of our numerical data. Now consider light particles (
![]() ${\it\beta}>1$
). Figure 2(a) shows that also in this case the agreement between the DNS data and the closure scheme is good, except around
${\it\beta}>1$
). Figure 2(a) shows that also in this case the agreement between the DNS data and the closure scheme is good, except around
![]() $St\sim 10$
where the closure underestimates the DNS data. In this case inertial preferential sampling must be important. The reason is that light particles are drawn into vortex filaments where they experience high accelerations. Nevertheless, inertial preferential sampling must become irrelevant in the limit
$St\sim 10$
where the closure underestimates the DNS data. In this case inertial preferential sampling must be important. The reason is that light particles are drawn into vortex filaments where they experience high accelerations. Nevertheless, inertial preferential sampling must become irrelevant in the limit
![]() $St\rightarrow \infty$
as shown by the trend for very large
$St\rightarrow \infty$
as shown by the trend for very large
![]() $St$
in the same figure. It is interesting to remark that the closure scheme (solid line) becomes better and better the closer
$St$
in the same figure. It is interesting to remark that the closure scheme (solid line) becomes better and better the closer
![]() ${\it\beta}$
is to unity, and/or the smaller the Stokes number is, suggesting the possibility to develop a systematic perturbative expansion in the small parameter
${\it\beta}$
is to unity, and/or the smaller the Stokes number is, suggesting the possibility to develop a systematic perturbative expansion in the small parameter
![]() ${\it\epsilon}=St(1-{\it\beta})$
. Furthermore it is important to note that while the acceleration variance increases monotonically as both
${\it\epsilon}=St(1-{\it\beta})$
. Furthermore it is important to note that while the acceleration variance increases monotonically as both
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $St$
increase, the flatness of the acceleration, defined as
$St$
increase, the flatness of the acceleration, defined as
has a non-monotonic dependency on
![]() $St$
. In figure 2(b) we show that light particles have a maximum in their flatness at
$St$
. In figure 2(b) we show that light particles have a maximum in their flatness at
![]() $St\sim 0.5$
and heavy particles have minimum flatness for
$St\sim 0.5$
and heavy particles have minimum flatness for
![]() $St>1$
(except for the case of very heavy particles with
$St>1$
(except for the case of very heavy particles with
![]() ${\it\beta}=0$
). Importantly, our closure approximation predicts these extrema qualitatively, indicating that the non-Gaussian tails observed numerically and experimentally (Volk et al.
Reference Volk, Calzavarini, Verhille, Lohse, Mordant, Pinton and Toschi2008) in the acceleration probability distribution function of bubbles are not only due to inertial preferential sampling, which is neglected by the closure. Let us also note that the non-monotonicity shown by the model for
${\it\beta}=0$
). Importantly, our closure approximation predicts these extrema qualitatively, indicating that the non-Gaussian tails observed numerically and experimentally (Volk et al.
Reference Volk, Calzavarini, Verhille, Lohse, Mordant, Pinton and Toschi2008) in the acceleration probability distribution function of bubbles are not only due to inertial preferential sampling, which is neglected by the closure. Let us also note that the non-monotonicity shown by the model for
![]() $St\sim 0.1$
and
$St\sim 0.1$
and
![]() ${\it\beta}=0$
,
${\it\beta}=0$
,
![]() $0.25$
and
$0.25$
and
![]() $3$
are artefacts due to insufficient accuracy in the numerical evaluation of the integral in (3.7). In conclusion, remarkably, the closure approximation is in reasonable agreement with the DNS data, with the exception of those values of Stokes number where preferential sampling is important. This is an important result, supporting the idea that many key properties, including deviations from Gaussian statistics, of the acceleration statistics of inertial particles are due to the kinematic structure of the equation of motion together with the non-trivial Lagrangian properties of the fluid tracers evolution, and not only due to inertial preferential sampling.
$3$
are artefacts due to insufficient accuracy in the numerical evaluation of the integral in (3.7). In conclusion, remarkably, the closure approximation is in reasonable agreement with the DNS data, with the exception of those values of Stokes number where preferential sampling is important. This is an important result, supporting the idea that many key properties, including deviations from Gaussian statistics, of the acceleration statistics of inertial particles are due to the kinematic structure of the equation of motion together with the non-trivial Lagrangian properties of the fluid tracers evolution, and not only due to inertial preferential sampling.
In order to quantify the accuracy of the closure described in § 3 we plot in figure 3 the relative error in the prediction of the acceleration variance for both light and heavy particles:
where with
![]() $\langle \boldsymbol{a}^{2}\rangle$
we refer to the expression (3.6) and with
$\langle \boldsymbol{a}^{2}\rangle$
we refer to the expression (3.6) and with
![]() $\langle \boldsymbol{a}^{2}\rangle _{DNS}$
to the numerical value obtained from the DNS results. As one can see the approximation is never very bad, with a maximum discrepancy of the order of 30–40 % at those values where inertial preferential sampling is important, i.e. for
$\langle \boldsymbol{a}^{2}\rangle _{DNS}$
to the numerical value obtained from the DNS results. As one can see the approximation is never very bad, with a maximum discrepancy of the order of 30–40 % at those values where inertial preferential sampling is important, i.e. for
![]() $St\sim O(1)$
for heavy particles and for
$St\sim O(1)$
for heavy particles and for
![]() $St\sim O(10)$
for light particles.
$St\sim O(10)$
for light particles.
5 Statistical Eulerian velocity model
Mathematical analysis and numerical studies of the particle dynamics become easier when the turbulent fluctuations of
![]() $\boldsymbol{u}(\boldsymbol{r},t)$
are approximated by a stochastic process. Following Gustavsson & Mehlig (Reference Gustavsson and Mehlig2016) we use a smooth, homogeneous and isotropic Gaussian random velocity field with root-mean-squared speed
$\boldsymbol{u}(\boldsymbol{r},t)$
are approximated by a stochastic process. Following Gustavsson & Mehlig (Reference Gustavsson and Mehlig2016) we use a smooth, homogeneous and isotropic Gaussian random velocity field with root-mean-squared speed
![]() $u_{0}$
and typical length and time scales
$u_{0}$
and typical length and time scales
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() ${\it\tau}$
. The model is characterized by a dimensionless number, the Kubo number,
${\it\tau}$
. The model is characterized by a dimensionless number, the Kubo number,
![]() $Ku={\it\tau}/({\it\eta}/u_{0})$
, that measures the degree of persistence of flow structures in time. Very small Kubo numbers correspond to a rapidly fluctuating fluid velocity field. In this limit, the closure approximation described in § 3 is exact, inertial preferential sampling is negligible and the Lagrangian correlation functions of tracer particles are well approximated by the Eulerian correlation functions. In this limit it is also possible to perform a systematic perturbative expansion (Gustavsson & Mehlig Reference Gustavsson and Mehlig2016). In this paper we are interested in comparing the validity of the Lagrangian closure for the statistical model at
$Ku={\it\tau}/({\it\eta}/u_{0})$
, that measures the degree of persistence of flow structures in time. Very small Kubo numbers correspond to a rapidly fluctuating fluid velocity field. In this limit, the closure approximation described in § 3 is exact, inertial preferential sampling is negligible and the Lagrangian correlation functions of tracer particles are well approximated by the Eulerian correlation functions. In this limit it is also possible to perform a systematic perturbative expansion (Gustavsson & Mehlig Reference Gustavsson and Mehlig2016). In this paper we are interested in comparing the validity of the Lagrangian closure for the statistical model at
![]() $Ku\sim O(1)$
, where no analytical results can be obtained, and to further compare them with the DNS results shown in § 4. The motivation is the following. The statistical model has no ‘internal intermittency’, i.e. there is no Reynolds-number dependency on the acceleration statistics (there is not even the meaning of a Reynolds number). Nevertheless, once the Gaussian Eulerian velocity field is prescribed, we can calculate the acceleration probability density function of the fluid tracers. It turns out that this is not Gaussian and that it depends on the Kubo number, due to the effect of the quadratic advection term,
$Ku\sim O(1)$
, where no analytical results can be obtained, and to further compare them with the DNS results shown in § 4. The motivation is the following. The statistical model has no ‘internal intermittency’, i.e. there is no Reynolds-number dependency on the acceleration statistics (there is not even the meaning of a Reynolds number). Nevertheless, once the Gaussian Eulerian velocity field is prescribed, we can calculate the acceleration probability density function of the fluid tracers. It turns out that this is not Gaussian and that it depends on the Kubo number, due to the effect of the quadratic advection term,
![]() $\boldsymbol{a}_{f}=\partial _{t}\boldsymbol{u}+Ku[\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\text{T}}]\boldsymbol{u}$
. As a result, we expect that many of the properties shown by the acceleration distribution of inertial particles evolved in real turbulent flows are shared by particles evolved in a Gaussian random flow. Finally, a comparison between DNS data and the statistical model will allow us to assess further the importance of internal intermittency.
$\boldsymbol{a}_{f}=\partial _{t}\boldsymbol{u}+Ku[\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\text{T}}]\boldsymbol{u}$
. As a result, we expect that many of the properties shown by the acceleration distribution of inertial particles evolved in real turbulent flows are shared by particles evolved in a Gaussian random flow. Finally, a comparison between DNS data and the statistical model will allow us to assess further the importance of internal intermittency.
5.1 Construction of the random-velocity field
For simplicity we discuss only the two-dimensional case. Generalization to three dimensions is straightforward. The velocity field is given in terms of the streamfunction:
![]() $\boldsymbol{u}(\boldsymbol{r},t)=\boldsymbol{{\rm\nabla}}{\it\psi}(\boldsymbol{r},t)\wedge \hat{\boldsymbol{e}}_{3}\,$
, which is defined as a superposition of Fourier modes with a Gaussian cutoff,
$\boldsymbol{u}(\boldsymbol{r},t)=\boldsymbol{{\rm\nabla}}{\it\psi}(\boldsymbol{r},t)\wedge \hat{\boldsymbol{e}}_{3}\,$
, which is defined as a superposition of Fourier modes with a Gaussian cutoff,
Here the system size
![]() $L$
is
$L$
is
![]() $10{\it\eta}$
,
$10{\it\eta}$
,
![]() $k_{i}=2{\rm\pi}n_{i}/L$
and
$k_{i}=2{\rm\pi}n_{i}/L$
and
![]() $n_{i}$
are integers with an upper cutoff
$n_{i}$
are integers with an upper cutoff
![]() $|n_{i}|\leqslant 2L/{\it\eta}$
because higher-order Fourier modes are negligible. The resulting spatial correlation function of
$|n_{i}|\leqslant 2L/{\it\eta}$
because higher-order Fourier modes are negligible. The resulting spatial correlation function of
![]() ${\it\psi}$
is Gaussian, if
${\it\psi}$
is Gaussian, if
![]() $L\gg {\it\eta}$
we have:
$L\gg {\it\eta}$
we have:
![]() $\langle {\it\psi}(\boldsymbol{x},0){\it\psi}(\mathbf{0},0)\rangle =(u_{0}^{2}{\it\eta}^{2}/2)\,\text{e}^{-x^{2}/(2{\it\eta}^{2})}$
. The random coefficients
$\langle {\it\psi}(\boldsymbol{x},0){\it\psi}(\mathbf{0},0)\rangle =(u_{0}^{2}{\it\eta}^{2}/2)\,\text{e}^{-x^{2}/(2{\it\eta}^{2})}$
. The random coefficients
![]() $a_{\boldsymbol{k}}(t)$
in
$a_{\boldsymbol{k}}(t)$
in
![]() ${\it\psi}$
are drawn from random Gaussian distributions with zero means, smoothly correlated in time. To do that we used an Ornstein–Uhlenbeck process convolved with a Gaussian kernel of the form
${\it\psi}$
are drawn from random Gaussian distributions with zero means, smoothly correlated in time. To do that we used an Ornstein–Uhlenbeck process convolved with a Gaussian kernel of the form
![]() $w(t)\equiv \exp [-t^{2}/(2t_{0}^{2})]/(t_{0}\sqrt{2{\rm\pi}})\,$
to have a smooth correlation function also for the acceleration. The parameter
$w(t)\equiv \exp [-t^{2}/(2t_{0}^{2})]/(t_{0}\sqrt{2{\rm\pi}})\,$
to have a smooth correlation function also for the acceleration. The parameter
![]() $t_{0}$
must be small,
$t_{0}$
must be small,
![]() $t_{0}\ll {\it\tau}$
, in order for the flow field to decorrelate at long times in a similar fashion as in fully developed turbulence. The Eulerian autocorrelation function of
$t_{0}\ll {\it\tau}$
, in order for the flow field to decorrelate at long times in a similar fashion as in fully developed turbulence. The Eulerian autocorrelation function of
![]() $\boldsymbol{u}$
is:
$\boldsymbol{u}$
is:
where
![]() $\mathscr{F}(x)=\sqrt{{\rm\pi}}\exp (x^{2})\text{erfc}(x)$
. Note that the flow field is homogeneous in space and also in time and
$\mathscr{F}(x)=\sqrt{{\rm\pi}}\exp (x^{2})\text{erfc}(x)$
. Note that the flow field is homogeneous in space and also in time and
![]() $\langle \boldsymbol{u}(\boldsymbol{x}_{0},t)\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{x}_{0},0)\rangle$
is a function of
$\langle \boldsymbol{u}(\boldsymbol{x}_{0},t)\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{x}_{0},0)\rangle$
is a function of
![]() $|t|$
only. For
$|t|$
only. For
![]() $|t|\ll t_{0}$
this correlation function is Gaussian and for
$|t|\ll t_{0}$
this correlation function is Gaussian and for
![]() $|t|\gg t_{0}$
the correlation function is exponential:
$|t|\gg t_{0}$
the correlation function is exponential:
![]() $\langle \boldsymbol{u}(\boldsymbol{x}_{0},t)\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{x}_{0},0)\rangle \sim \text{e}^{-|t|/{\it\tau}}$
.
$\langle \boldsymbol{u}(\boldsymbol{x}_{0},t)\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{x}_{0},0)\rangle \sim \text{e}^{-|t|/{\it\tau}}$
.
5.2 Results for the random-velocity model
We consider first the acceleration variance. Simulation results for the statistical model are compared with the Lagrangian closure (3.6)–(3.7) in figure 4 by changing both
![]() $St,{\it\beta}$
for
$St,{\it\beta}$
for
![]() $Ku=5$
(panel a). We observe a good agreement between the Lagrangian closure and the numerical simulations, comparable to what was observed for the DNS data. In figure 4(b) we show the results for the flatness. It is important to stress two facts. Also here, both heavy and light particles depart from the corresponding fluid value with a qualitative trend similar to that observed for the DNS case in the previous section. Also, for the random velocity field, the Lagrangian closure works qualitatively well. The departure from the numerical data is a signature of the corresponding importance of preferential sampling at those Stokes numbers. Let us notice nevertheless an important difference with respect to the DNS data. Here the absolute values of the flatness are much smaller, due to the absence of internal intermittency. In the stochastic signal the acceleration of the fluid is non-Gaussian only because of kinematic effects. In real flows, the acceleration is more intense and more fluctuating because of the vortex stretching mechanism and of the turbulent energy cascade.
$Ku=5$
(panel a). We observe a good agreement between the Lagrangian closure and the numerical simulations, comparable to what was observed for the DNS data. In figure 4(b) we show the results for the flatness. It is important to stress two facts. Also here, both heavy and light particles depart from the corresponding fluid value with a qualitative trend similar to that observed for the DNS case in the previous section. Also, for the random velocity field, the Lagrangian closure works qualitatively well. The departure from the numerical data is a signature of the corresponding importance of preferential sampling at those Stokes numbers. Let us notice nevertheless an important difference with respect to the DNS data. Here the absolute values of the flatness are much smaller, due to the absence of internal intermittency. In the stochastic signal the acceleration of the fluid is non-Gaussian only because of kinematic effects. In real flows, the acceleration is more intense and more fluctuating because of the vortex stretching mechanism and of the turbulent energy cascade.
6 Conclusions
In this paper we have analysed a Lagrangian closure describing fluctuations and correlations of inertial-particle accelerations in turbulent flows in the diluted regime (one-way coupling), i.e. neglecting particle–particle collisions and feedback on the flow. In this way, we have a model that is able to predict some properties of the acceleration statistics of inertial particles for a large range of values of
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $St$
out of one single measurement based on fluid tracers only. We have compared the predictions of the closure to DNS of heavy and light inertial particles in turbulence. To summarize our results, the closure predictions are in overall good qualitative agreement with the results of DNS of particles. The closure neglects inertial preferential sampling, i.e. the tendency of light/heavy particles to be centrifuged in or out of vortex structures. Hence, the good agreement with the DNS data indicates that inertial preferential sampling has in general only a partial effect on inertial-particle accelerations. The main trends are essentially kinematic, a consequence of the form of the equation of motion, as also shown by the results obtained using a stochastic surrogate for the flow velocity. A closer inspection shows that there are important differences between the Lagrangian closure scheme and the DNS, revealing where inertial preferential sampling is important. The effect is larger for light particles at large Stokes numbers (
$St$
out of one single measurement based on fluid tracers only. We have compared the predictions of the closure to DNS of heavy and light inertial particles in turbulence. To summarize our results, the closure predictions are in overall good qualitative agreement with the results of DNS of particles. The closure neglects inertial preferential sampling, i.e. the tendency of light/heavy particles to be centrifuged in or out of vortex structures. Hence, the good agreement with the DNS data indicates that inertial preferential sampling has in general only a partial effect on inertial-particle accelerations. The main trends are essentially kinematic, a consequence of the form of the equation of motion, as also shown by the results obtained using a stochastic surrogate for the flow velocity. A closer inspection shows that there are important differences between the Lagrangian closure scheme and the DNS, revealing where inertial preferential sampling is important. The effect is larger for light particles at large Stokes numbers (
![]() $St\sim 10$
in our DNS) and is a consequence of the fact that light bubbles are drawn into intense vortex tubes. We mention that there is no small-scale fractal clustering for these values of
$St\sim 10$
in our DNS) and is a consequence of the fact that light bubbles are drawn into intense vortex tubes. We mention that there is no small-scale fractal clustering for these values of
![]() $St$
, i.e. particles are distributed on a three-dimensional set at scales much smaller than the Kolmogorov length. Finally, non-trivial non-monotonic behaviours of the flatness for both light and heavy particles as a function of
$St$
, i.e. particles are distributed on a three-dimensional set at scales much smaller than the Kolmogorov length. Finally, non-trivial non-monotonic behaviours of the flatness for both light and heavy particles as a function of
![]() $St$
are predicted by the closure scheme and confirmed by the DNS results, including the fact that light particles are always more intermittent than the fluid tracers and the opposite holds for heavy particles, as shown by the fact that the flatness for the former is always larger than the one of fluid tracers and vice versa for the latter. The Lagrangian closure scheme must become exact when
$St$
are predicted by the closure scheme and confirmed by the DNS results, including the fact that light particles are always more intermittent than the fluid tracers and the opposite holds for heavy particles, as shown by the fact that the flatness for the former is always larger than the one of fluid tracers and vice versa for the latter. The Lagrangian closure scheme must become exact when
![]() $St\rightarrow 0$
or
$St\rightarrow 0$
or
![]() ${\it\beta}\rightarrow 1$
, it should therefore be possible to see it as a perturbative expansion around Lagrangian tracers and proportional to a small parameter
${\it\beta}\rightarrow 1$
, it should therefore be possible to see it as a perturbative expansion around Lagrangian tracers and proportional to a small parameter
![]() ${\it\epsilon}=St(1-{\it\beta})$
, at least for quantities that depend on Lagrangian correlation functions decaying on a time scale of the order of the Kolmogorov time. In this case, one could try to develop an intermediate asymptotic where for small enough time, the difference between the two trajectories remains small and then improve the zeroth-order approximation here presented by considering also corrections induced by the velocity gradients around the Lagrangian tracers:
${\it\epsilon}=St(1-{\it\beta})$
, at least for quantities that depend on Lagrangian correlation functions decaying on a time scale of the order of the Kolmogorov time. In this case, one could try to develop an intermediate asymptotic where for small enough time, the difference between the two trajectories remains small and then improve the zeroth-order approximation here presented by considering also corrections induced by the velocity gradients around the Lagrangian tracers:
where
![]() ${\it\delta}\boldsymbol{r}=\boldsymbol{r}_{t}-\boldsymbol{r}_{t}^{(L)}$
. Work in this direction is in progress. Finally, we have also investigated the validity of the Lagrangian closure using a stochastic Gaussian surrogate for the advecting fluid velocity field. In such a case, the
${\it\delta}\boldsymbol{r}=\boldsymbol{r}_{t}-\boldsymbol{r}_{t}^{(L)}$
. Work in this direction is in progress. Finally, we have also investigated the validity of the Lagrangian closure using a stochastic Gaussian surrogate for the advecting fluid velocity field. In such a case, the
![]() $Ku$
number is another free parameter that can be tuned to increase/decrease the effects of inertial preferential sampling (effects vanish as
$Ku$
number is another free parameter that can be tuned to increase/decrease the effects of inertial preferential sampling (effects vanish as
![]() $Ku$
approaches zero). We have shown that for large Kubo numbers, corresponding to the long-lived structures in turbulent flows, the closure theory works as well as for the DNS data, even though the data for the statistical model have a much smaller flatness.
$Ku$
approaches zero). We have shown that for large Kubo numbers, corresponding to the long-lived structures in turbulent flows, the closure theory works as well as for the DNS data, even though the data for the statistical model have a much smaller flatness.
Let us add some remarks about the generality and the limitations of the approach proposed. First, there are no theoretical difficulties in incorporating buoyancy, Faxén corrections and other forces in the closure scheme as long as the dynamics can be described by a point-particle approach. We refrained from presenting here the results because of lack of DNS data to compare with. On the other hand, it is known that the equations (2.1) are not valid for all values in the (
![]() ${\it\beta},St$
) parameter space. Indeed, the two requirements that the Reynolds number based on the particle slip velocity is small:
${\it\beta},St$
) parameter space. Indeed, the two requirements that the Reynolds number based on the particle slip velocity is small:
![]() $Re_{p}=|u-v|R/{\it\nu}<O(1)$
and that the particle size is smaller than the Kolmogorov scale
$Re_{p}=|u-v|R/{\it\nu}<O(1)$
and that the particle size is smaller than the Kolmogorov scale
![]() $R/{\it\eta}<O(1)$
lead to the condition that
$R/{\it\eta}<O(1)$
lead to the condition that
![]() $St<O(1)$
if
$St<O(1)$
if
![]() ${\it\beta}>1$
. So the prediction of the model in the limit of large Stokes numbers for light particles cannot be taken on a quantitative basis. We stress nevertheless that the most interesting property highlighted by our approach, i.e. the existence of a non-monotonic behaviour for the flatness of the acceleration of light and heavy particles, develops at values of
${\it\beta}>1$
. So the prediction of the model in the limit of large Stokes numbers for light particles cannot be taken on a quantitative basis. We stress nevertheless that the most interesting property highlighted by our approach, i.e. the existence of a non-monotonic behaviour for the flatness of the acceleration of light and heavy particles, develops at values of
![]() $St$
where the model equations are still valid. It is difficult to precisely assess the value of Stokes where the approximation breaks down. For instance, recently it was found (Mathai et al.
Reference Mathai, Prakash, Brons, Sun and Lohse2015) that the acceleration variance of light particles with a size up to
$St$
where the model equations are still valid. It is difficult to precisely assess the value of Stokes where the approximation breaks down. For instance, recently it was found (Mathai et al.
Reference Mathai, Prakash, Brons, Sun and Lohse2015) that the acceleration variance of light particles with a size up to
![]() $R\sim 10{\it\eta}$
follow quite closely the point-like approximation (2.1). For even larger particle sizes a wake-driven dynamics becomes dominant. For such a range of particle parameters no theoretical models for the equations of motion are known.
$R\sim 10{\it\eta}$
follow quite closely the point-like approximation (2.1). For even larger particle sizes a wake-driven dynamics becomes dominant. For such a range of particle parameters no theoretical models for the equations of motion are known.
For instance, recently it was found (Mathai et al.
Reference Mathai, Prakash, Brons, Sun and Lohse2015) that the acceleration variance of light particles with a size up to
![]() $R\sim 10{\it\eta}$
follow quite closely the approximate dynamics (2.1).
$R\sim 10{\it\eta}$
follow quite closely the approximate dynamics (2.1).
Acknowledgements
This work was supported Vetenskapsrådet and by the grant Bottlenecks for particle growth in turbulent aerosols from the Knut and Alice Wallenberg Foundation, Dnr. KAW 2014.0048. The research leading to these results has received funding from the European Union’s Seventh Framework Programme (FP7/2007-2013) under grant agreement no 339032.