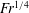1 Introduction
We examine the two-dimensional thin-film flow formed when a free laminar jet (sheet) of a Newtonian fluid impinges vertically onto, and spreads over, a horizontal hydrophobic or slippery plate. Recent studies have focused on quantifying the magnitude of the slip length and its dependence on parameters such as the wettability and surface roughness (Rothstein Reference Rothstein2010). Flowing liquid films of thickness of the order of microns or smaller can be strongly influenced by the substrate microstructure and the hydrodynamic characteristics at the solid–liquid interface (Dressaire et al. Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010). Our objective is to examine this influence on the spread of the impinging thin film and the ensuing hydraulic jump.
The liquid spreads in a thin layer until the depth increases, suddenly forming a hydraulic jump (see figure 1). The problem thus consists of examining the influence of slip on the shape of the free surface, the flow field within the film and the jump region. As the boundary layer develops from the stagnation region, it gradually absorbs the whole of the flow until the viscous forces reach the free surface and the spreading jet is in the fully viscous boundary-layer region in the form of a thin film. The flow of thin Newtonian and non-Newtonian films, in turn, has been extensively investigated in the literature (see, for instance, Khayat & Kim Reference Khayat and Kim2006 and the references therein).
An impinging jet on a hydrophilic surface has been extensively investigated in the literature. The impingement of an adhering jet was considered earlier by Watson (Reference Watson1964), who examined both the radial and the planar jet spread for steady laminar and turbulent flows. Neglecting the surface-tension effect and using a thin-film or boundary-layer approach, Watson found that for a two-dimensional jet at impinging velocity
![]() $V_{\text{0}}$
, the steady jet surface height (in units of the half jet width a) grows at a rate equal to
$V_{\text{0}}$
, the steady jet surface height (in units of the half jet width a) grows at a rate equal to
![]() $1.81/Re$
, where
$1.81/Re$
, where
![]() $Re=aV_{0}/\unicode[STIX]{x1D708}$
is the Reynolds number, with
$Re=aV_{0}/\unicode[STIX]{x1D708}$
is the Reynolds number, with
![]() $\unicode[STIX]{x1D708}$
being the kinematic viscosity. A relation between the jump location and the height was also obtained for both laminar and turbulent flows. Watson’s theory was tested in a number of experimental investigations, including those of Watson himself, Craik et al. (Reference Craik, Latham, Fawkes and Gibbon1981), Stevens & Webb (Reference Stevens and Webb1992), Bush & Aristoff (Reference Bush and Aristoff2003) and Baonga, Louahlia-Gualous & Imbert (Reference Baonga, Louahlia-Gualous and Imbert2006). In particular, Watson’s theoretical predictions for the free-surface velocity and film thickness were experimentally verified by Stevens & Webb (Reference Stevens and Webb1992) and Baonga et al. (Reference Baonga, Louahlia-Gualous and Imbert2006). Liu & Lienhard (Reference Liu and Lienhard1993) observed that Watson’s predictions are least satisfactory in the limit of relatively weak jump, specifically when the ratio of the layer depths after and before the jump is small. In an effort to improve Watson’s theory, Bush & Aristoff (Reference Bush and Aristoff2003) included the influence of surface tension for small-radius circular jumps, leading to better agreement with experiment. It is, however, generally agreed that Watson’s theory is adequate for circular jumps with large radius and height. Since only planar flow is examined in the current work, the surface-tension effect will be neglected. Other extensions have also been considered, such as the flow of an impinging jet on an inclined plane (Benilov Reference Benilov2015). For an impinging non-Newtonian jet, far fewer studies are available. The reader is referred to the work of Zhao & Khayat (Reference Zhao and Khayat2008) and the references therein.
$\unicode[STIX]{x1D708}$
being the kinematic viscosity. A relation between the jump location and the height was also obtained for both laminar and turbulent flows. Watson’s theory was tested in a number of experimental investigations, including those of Watson himself, Craik et al. (Reference Craik, Latham, Fawkes and Gibbon1981), Stevens & Webb (Reference Stevens and Webb1992), Bush & Aristoff (Reference Bush and Aristoff2003) and Baonga, Louahlia-Gualous & Imbert (Reference Baonga, Louahlia-Gualous and Imbert2006). In particular, Watson’s theoretical predictions for the free-surface velocity and film thickness were experimentally verified by Stevens & Webb (Reference Stevens and Webb1992) and Baonga et al. (Reference Baonga, Louahlia-Gualous and Imbert2006). Liu & Lienhard (Reference Liu and Lienhard1993) observed that Watson’s predictions are least satisfactory in the limit of relatively weak jump, specifically when the ratio of the layer depths after and before the jump is small. In an effort to improve Watson’s theory, Bush & Aristoff (Reference Bush and Aristoff2003) included the influence of surface tension for small-radius circular jumps, leading to better agreement with experiment. It is, however, generally agreed that Watson’s theory is adequate for circular jumps with large radius and height. Since only planar flow is examined in the current work, the surface-tension effect will be neglected. Other extensions have also been considered, such as the flow of an impinging jet on an inclined plane (Benilov Reference Benilov2015). For an impinging non-Newtonian jet, far fewer studies are available. The reader is referred to the work of Zhao & Khayat (Reference Zhao and Khayat2008) and the references therein.
To the best of our knowledge, there is no adequate study that addresses the influence of slip for a jet impinging on a hydrophobic surface. In contrast to the impinging jet of an adhering fluid, the slip condition on a hydrophobic surface prohibits a similarity solution, making the problem challenging. A closely related problem is that of the boundary-layer flow over a semi-infinite flat plate with slip, which, despite early attempts using asymptotic analysis and more recent numerical studies, remains essentially unsolved. Laurmann (Reference Laurmann1961) used a linearized approach, and solved the resulting Oseen equation using Fourier transform. However, inversion was impossible to obtain. Using a Wiener–Hopf technique, an asymptotic solution was also obtained, and was later improved by Murray (Reference Murray1965) by adding more terms. More recently, the problem was treated by incorrectly assuming local similarity while solving the Blasius equation (Martin & Boyd Reference Martin, Boyd, Bartel and Gallis2001; Ajadi, Adegoke & Aziz Reference Ajadi, Adegoke and Aziz2009).
The challenges due to the non-similar character of the boundary-layer flow are even more formidable for the impinging jet problem. Here too, various levels of approximation and assumptions have been adopted. Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010) examined the problem of a circular jet impinging on a microdecorated surface. Their measurements focused mainly on the location and size of the hydraulic jump, assessing the influence of surface roughness that consisted of regular arrays of micron-size posts. In order to accommodate a similarity solution in their theoretical model, they chose the (variable) slip length to be proportional to the film surface (see the discussion in § 3 below). Moreover, the flow field near impact was approximately imposed since only the boundary-layer height is needed. In contrast, and as we shall see, for a general slipping jet, the entire flow field must be matched at the transition point. Later, Prince, Maynes & Crockett (Reference Prince, Maynes and Crockett2012) examined the influence of constant slip length on a circular impinging jet by adopting an integral approach and assuming a cubic behaviour for the velocity profile in both the developing and viscous boundary-layer regions. While this approach is convenient, it lacks the accuracy typically resulting from the use of the Karman–Pohlhausen (K–P) approximation. Prince et al. (Reference Prince, Maynes and Crockett2012) assessed the accuracy of their approach by comparing their results with ones based on Watson’s similarity solution (1964) for an adhering jet. The K–P approach may be suitable for the estimation of the boundary-layer height; the very definition of height in this case is arbitrary despite the common acceptance that it corresponds to the location where the flow velocity reaches 99 % of the free-stream level. We shall conduct a comparison between the K–P solution and more rigorous local solutions for a planar slipping jet.
The height and position of the hydraulic jump cannot be uniquely determined in general. However, the recent measurements of Duchesne, Lebon & Limat (Reference Duchesne, Lebon and Limat2014) show that, for an adhering circular jet, the Froude number based on the jump height and velocity remains constant when the flow rate, viscosity and surface tension are varied. This remarkable result, along with their thin-film analysis, leads to the explicit dependence of the jump location and height on the flow rate and viscosity, simultaneously confirming and improving the earlier scaling of Bohr, Dimon & Putzkaradze (Reference Bohr, Dimon and Putzkaradze1993) and Rojas, Argentina & Tirapegui (Reference Rojas, Argentina and Tirapegui2013). We will take guidance from Duchesne et al. (Reference Duchesne, Lebon and Limat2014), and adopt their observations for the planar jet, which would allow the unique determination of the jump height and position.
The focus of the current study is on the interplay between inertia and slip effects for thin-film flow. Watson’s (Reference Watson1964) assumptions remain valid, particularly those of moderately large inertia effect and a jump occurring far from impingement. Consequently, the surface-tension effect will be neglected. The gravitational pressure gradient is similarly neglected except in the hydraulic-jump region. In § 2, the large-Reynolds-number limit of the conservation equations is established as well as the boundary conditions in both the streamwise and transverse directions. In § 3, asymptotic series solutions are sought in the developing boundary-layer region. The implementation of a finite-difference scheme is also discussed. The boundary-layer height and transition location are determined using a K–P approach. In § 4, we consider the fully developed viscous boundary-layer region where the flow field and film thickness are determined. In § 5, the principle of momentum conservation is applied at the hydraulic jump, and a relation is derived between the position and height of the jump. Both inviscid and viscous films are considered downstream of the jump. Finally, some concluding remarks are given in § 6.

Figure 1. Schematic illustration of the plane jet (sheet) flow impinging on a flat solid plate. The stagnation region (i), developing boundary-layer region (ii), fully viscous boundary-layer region (iii) and hydraulic-jump region (iv) are illustrated. All notations are dimensionless.
2 Problem statement and physical domain
Consider the steady laminar incompressible flow of a planar jet (sheet) of a Newtonian fluid of width
![]() $a$
, impinging at a (uniform) velocity
$a$
, impinging at a (uniform) velocity
![]() $V_{\text{0}}$
on a fixed flat plate lying normal to the jet direction. The flow configuration is depicted schematically in figure 1. The length and velocity scales are taken to be respectively a and
$V_{\text{0}}$
on a fixed flat plate lying normal to the jet direction. The flow configuration is depicted schematically in figure 1. The length and velocity scales are taken to be respectively a and
![]() $V_{\text{0}}$
in both the streamwise and transverse directions. It should be noted that dimensionless variables are used in figure 1. The
$V_{\text{0}}$
in both the streamwise and transverse directions. It should be noted that dimensionless variables are used in figure 1. The
![]() $x$
-axis is taken along the flat plate and the
$x$
-axis is taken along the flat plate and the
![]() $y$
-axis is parallel to the jet. In this case,
$y$
-axis is parallel to the jet. In this case,
![]() $u(x,y)$
and
$u(x,y)$
and
![]() $v(x,y)$
are the corresponding dimensionless velocity components. Three dimensionless groups emerge in this case, namely the Reynolds number
$v(x,y)$
are the corresponding dimensionless velocity components. Three dimensionless groups emerge in this case, namely the Reynolds number
![]() $Re=aV_{0}/\unicode[STIX]{x1D708}$
, where
$Re=aV_{0}/\unicode[STIX]{x1D708}$
, where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity, the slip parameter
$\unicode[STIX]{x1D708}$
is the kinematic viscosity, the slip parameter
![]() $S=s/a$
, where
$S=s/a$
, where
![]() $s$
is the slip length, and the Froude number
$s$
is the slip length, and the Froude number
![]() $Fr=V_{0}/\sqrt{ag}$
,
$Fr=V_{0}/\sqrt{ag}$
,
![]() $g$
being the acceleration due to gravity. The velocity at the wall is assumed to experience a first-order (Navier) slip. Hence,
$g$
being the acceleration due to gravity. The velocity at the wall is assumed to experience a first-order (Navier) slip. Hence,
![]() $u(x,y=0)=S\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y(x,y=0)$
, with
$u(x,y=0)=S\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y(x,y=0)$
, with
![]() $S$
defined such that a linear extrapolation of the velocity based on the gradient at the wall vanishes at y
$S$
defined such that a linear extrapolation of the velocity based on the gradient at the wall vanishes at y
![]() $=-S$
. There is no restriction on the order of magnitude of
$=-S$
. There is no restriction on the order of magnitude of
![]() $S$
. Thus, a relatively large slip length, which is not uncommon for superhydrophobic surfaces (Rothstein Reference Rothstein2010), can be accommodated in the present formulation. A large slip length is detected in the presence of an air–water interface in microridges. Ou & Rothstein (Reference Ou and Rothstein2005) used micro-particle image velocimetry (
$S$
. Thus, a relatively large slip length, which is not uncommon for superhydrophobic surfaces (Rothstein Reference Rothstein2010), can be accommodated in the present formulation. A large slip length is detected in the presence of an air–water interface in microridges. Ou & Rothstein (Reference Ou and Rothstein2005) used micro-particle image velocimetry (
![]() $\unicode[STIX]{x1D707}$
-PIV) measurements to examine the flow kinematics in a microchannel at length scales well below that of the microridges on the superhydrophobic surface. The flow was observed to come to rest along the microridges, but slip velocities greater than 60 % of the average velocity were detected along the air–water interface.
$\unicode[STIX]{x1D707}$
-PIV) measurements to examine the flow kinematics in a microchannel at length scales well below that of the microridges on the superhydrophobic surface. The flow was observed to come to rest along the microridges, but slip velocities greater than 60 % of the average velocity were detected along the air–water interface.
2.1 Physical domain
Following Watson (Reference Watson1964), four distinct regions of flow are identified for a slipping fluid, with smooth passage from one region to the next: a stagnation flow region (i), a developing boundary-layer region (ii) and a fully viscous thin-film region (iii). Under some flow conditions, a hydraulic jump may form in region (iv). In the vicinity of the stagnation point, in region (i),
![]() $x=O(1)$
. The speed outside the boundary layer rises rapidly from 0 at the stagnation point to the impingement velocity in the inviscid far region. For an adhering as well as a slipping jet, the impinging inviscid flow is not affected by slip, and the boundary-layer thickness remains negligibly small. Obviously, this would be the case for a jet at relatively large Reynolds number, especially for a slipping fluid. Ideally, the flow at the boundary-layer edge should correspond to the inviscid flow near the stagnating jet, with the boundary-layer leading edge coinciding with the stagnation point (Liu, Gabour & Lienhard Reference Liu, Gabour and Lienhard1993). However, the assumption of uniform horizontal flow near the wall and outside the boundary layer (as illustrated in figure 1) is not unreasonable. For an adhering jet, the flow acquires a similar character; the position or effect of the leading edge is irrelevant. This is not the case for a slipping jet, where, as we shall see, a non-similarity solution is sought subject to initial conditions at the leading edge. However, as argued above, the dominance of inertia and slip should make the assumption of uniform flow and a delayed leading edge plausible.
$x=O(1)$
. The speed outside the boundary layer rises rapidly from 0 at the stagnation point to the impingement velocity in the inviscid far region. For an adhering as well as a slipping jet, the impinging inviscid flow is not affected by slip, and the boundary-layer thickness remains negligibly small. Obviously, this would be the case for a jet at relatively large Reynolds number, especially for a slipping fluid. Ideally, the flow at the boundary-layer edge should correspond to the inviscid flow near the stagnating jet, with the boundary-layer leading edge coinciding with the stagnation point (Liu, Gabour & Lienhard Reference Liu, Gabour and Lienhard1993). However, the assumption of uniform horizontal flow near the wall and outside the boundary layer (as illustrated in figure 1) is not unreasonable. For an adhering jet, the flow acquires a similar character; the position or effect of the leading edge is irrelevant. This is not the case for a slipping jet, where, as we shall see, a non-similarity solution is sought subject to initial conditions at the leading edge. However, as argued above, the dominance of inertia and slip should make the assumption of uniform flow and a delayed leading edge plausible.
In region (ii), the boundary layer is expected to grow like
![]() $\sqrt{x/Re}$
, at a rate that diminishes with
$\sqrt{x/Re}$
, at a rate that diminishes with
![]() $S$
(see Khayat Reference Khayat2016). The elongation rate or normal stress weakens with distance, but the flow remains two-dimensional as a result of non-negligible surface curvature. The speed outside the boundary layer remains almost constant, equal to 1 (in units of
$S$
(see Khayat Reference Khayat2016). The elongation rate or normal stress weakens with distance, but the flow remains two-dimensional as a result of non-negligible surface curvature. The speed outside the boundary layer remains almost constant, equal to 1 (in units of
![]() $V_{\text{0}}$
), as the fluid here is unaffected by the viscous stresses. For
$V_{\text{0}}$
), as the fluid here is unaffected by the viscous stresses. For
![]() $x\gg 1$
, the flow field in region (ii) is not affected by the stagnation flow of region (i). The region
$x\gg 1$
, the flow field in region (ii) is not affected by the stagnation flow of region (i). The region
![]() $1\ll x<x_{\text{0}}$
will be referred to as the developing boundary-layer region, with boundary-layer thickness
$1\ll x<x_{\text{0}}$
will be referred to as the developing boundary-layer region, with boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}(x)$
, outside which the flow is inviscid and constant. Here,
$\unicode[STIX]{x1D6FF}(x)$
, outside which the flow is inviscid and constant. Here,
![]() $x_{\text{0}}$
is the location of the transition point at which viscous stresses become appreciable right up to the free surface, where the whole flow is of the boundary-layer type. At this point, for an adhering jet, the velocity profile changes from the Blasius type to the similarity profile. In contrast, a similarity profile does not exist for a slipping jet. The flow in region (iii),
$x_{\text{0}}$
is the location of the transition point at which viscous stresses become appreciable right up to the free surface, where the whole flow is of the boundary-layer type. At this point, for an adhering jet, the velocity profile changes from the Blasius type to the similarity profile. In contrast, a similarity profile does not exist for a slipping jet. The flow in region (iii),
![]() $x>x_{\text{0}}$
, which will be referred to as the fully developed boundary-layer region, is bounded by the flat plate and the free surface
$x>x_{\text{0}}$
, which will be referred to as the fully developed boundary-layer region, is bounded by the flat plate and the free surface
![]() $y=h(x)$
.
$y=h(x)$
.
Finally, the hydraulic jump in region (iv) occurs at a location
![]() $x=x_{J}$
, which can be larger or smaller than
$x=x_{J}$
, which can be larger or smaller than
![]() $x_{\text{0}}$
since the jump may occur at any point in the flow. The jump height
$x_{\text{0}}$
since the jump may occur at any point in the flow. The jump height
![]() $H(x)$
is generally not constant but different from the height immediately downstream of the jump,
$H(x)$
is generally not constant but different from the height immediately downstream of the jump,
![]() $H_{J}=H(x=x_{J})$
. In practice, the fluid is drained at the end
$H_{J}=H(x=x_{J})$
. In practice, the fluid is drained at the end
![]() $x=x_{\infty }$
(trailing edge) of the plate to maintain steady flow, with the film thickness denoted by
$x=x_{\infty }$
(trailing edge) of the plate to maintain steady flow, with the film thickness denoted by
![]() $H_{\infty }$
. Although it is common practice to assume the jump height to remain equal to
$H_{\infty }$
. Although it is common practice to assume the jump height to remain equal to
![]() $H_{J}$
, this assumption is only valid for fluids of low viscosity. In this study, we consider both an inviscid layer and a viscous layer downstream of the jump.
$H_{J}$
, this assumption is only valid for fluids of low viscosity. In this study, we consider both an inviscid layer and a viscous layer downstream of the jump.
2.2 Governing equations and boundary conditions
Unless otherwise specified,
![]() $Re$
will be assumed to be moderately large. Thus, for a thin jet, the conservation equations reduce to
$Re$
will be assumed to be moderately large. Thus, for a thin jet, the conservation equations reduce to
The gravitational effect will only be considered downstream of the jump. Here, a prime denotes total differentiation (with respect to
![]() $x$
in this case) and a subscript with respect to
$x$
in this case) and a subscript with respect to
![]() $x$
or
$x$
or
![]() $y$
denotes partial differentiation. At the plate, the (partial) slip and no-penetration conditions are assumed to hold, so that
$y$
denotes partial differentiation. At the plate, the (partial) slip and no-penetration conditions are assumed to hold, so that
The flow field is sought separately in the developing boundary-layer region
![]() $(x<x_{0})$
, fully developed viscous boundary-layer region
$(x<x_{0})$
, fully developed viscous boundary-layer region
![]() $(x>x_{0})$
and hydraulic-jump region. Consequently, the additional boundary conditions are as follows. In region (ii), or the developing boundary-layer region (
$(x>x_{0})$
and hydraulic-jump region. Consequently, the additional boundary conditions are as follows. In region (ii), or the developing boundary-layer region (
![]() $1\ll x<x_{\text{0}}$
), the flow is assumed to be sufficiently inertial for inviscid flow to prevail between the boundary-layer limit and the free surface (see figure 1). In this case, the following condition at the outer edge of the boundary layer must hold:
$1\ll x<x_{\text{0}}$
), the flow is assumed to be sufficiently inertial for inviscid flow to prevail between the boundary-layer limit and the free surface (see figure 1). In this case, the following condition at the outer edge of the boundary layer must hold:
Additionally, a boundary condition is needed at the origin (
![]() $x=0$
), namely
$x=0$
), namely
which reflects the uniformity of the flow at the leading edge of the boundary layer and will be referred to as the initial condition. For region (iii), we let
![]() $U(x)\equiv u(x>x_{0},y=h)$
and
$U(x)\equiv u(x>x_{0},y=h)$
and
![]() $V(x)\equiv v(x>x_{0},y=h)$
denote the velocity components at the free surface. In the absence of surface tension, the kinematic and dynamic conditions can be written respectively as
$V(x)\equiv v(x>x_{0},y=h)$
denote the velocity components at the free surface. In the absence of surface tension, the kinematic and dynamic conditions can be written respectively as
Here again, given the non-similar character of the flow, an initial condition is needed for the solution in region (iii), which is provided by matching the flow at the transition point:
Although the Reynolds number and slip parameter appear explicitly in problem (2.1)–(2.7), it is possible to deduce universal behaviour for the flow with respect to these two dimensionless groups. It is not difficult to show that, upon substituting
![]() $x$
by
$x$
by
![]() $x/Re$
and
$x/Re$
and
![]() $v$
by
$v$
by
![]() $Rev$
, the entire problem can be treated independently of the Reynolds number. Less obvious is the universality with respect to
$Rev$
, the entire problem can be treated independently of the Reynolds number. Less obvious is the universality with respect to
![]() $S$
, which will be discussed in the next sections.
$S$
, which will be discussed in the next sections.
2.3 Overall solution strategy
We use different solution strategies in each flow region. We propose two approaches in region (ii) to examine the boundary-layer flow, namely a rigorous series or asymptotic approach for large and small slip lengths, and a K–P approximation, the latter being most convenient to estimate the boundary-layer height and validate the series solution. A numerical approach is also implemented and discussed. However, as expected, the numerical solution performs poorly near the leading edge due to the flow singularity. The flow in the entire boundary-layer domain is obtained upon matching the flows between the developing and fully viscous boundary-layer regions. A series solution is also used in region (iii), this time taking advantage of the small film thickness. In region (iv) downstream of the hydraulic jump, inertia will be neglected, allowing an analytical solution in the presence of gravity.
3 Influence of slip on the flow in the developing boundary-layer region (
 $\boldsymbol{x}\boldsymbol{{<}}\boldsymbol{x}_{\mathbf{0}}$
)
$\boldsymbol{x}\boldsymbol{{<}}\boldsymbol{x}_{\mathbf{0}}$
)
As for an adhering jet, it is convenient to recast the problem for a slipping jet in terms of the streamfunction, and introduce the following change of coordinates:
We express
![]() $u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
and
$u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
and
![]() $v(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
in terms of the function
$v(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
in terms of the function
![]() $f(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, such that
$f(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, such that
Equation (3.2b ) is obtained upon integrating the continuity equation (2.1a ) and taking the plate as the base streamline. In this case, equation (2.1b ) as well as conditions (2.2) and (2.3) become (neglecting the gravitational effect)
Additionally, the initial condition (2.4) of uniform flow leads to
Interestingly, this initial condition satisfies both equation (3.3) and conditions (3.4), which is not the case for an adhering fluid; in the limit
![]() $S=0$
, a uniform flow is not accommodated by the no-slip condition. This is an important departure for a slipping flow from an adhering flow, reflecting the difference in the singular character at the leading edge (see below). The universality with respect to
$S=0$
, a uniform flow is not accommodated by the no-slip condition. This is an important departure for a slipping flow from an adhering flow, reflecting the difference in the singular character at the leading edge (see below). The universality with respect to
![]() $S$
mentioned earlier is now more apparent from problem (3.3)–(3.5a,b
). Indeed, it is not difficult to show that, for non-vanishing slip length (
$S$
mentioned earlier is now more apparent from problem (3.3)–(3.5a,b
). Indeed, it is not difficult to show that, for non-vanishing slip length (
![]() $S>0$
), substituting
$S>0$
), substituting
![]() $\unicode[STIX]{x1D709}$
by
$\unicode[STIX]{x1D709}$
by
![]() $\unicode[STIX]{x1D709}/S^{2}$
leads to a problem independent of
$\unicode[STIX]{x1D709}/S^{2}$
leads to a problem independent of
![]() $S$
. Both a numerical and an asymptotic approach are suggested.
$S$
. Both a numerical and an asymptotic approach are suggested.
Although (3.3) and the latter two conditions in (3.4) clearly accommodate a similarity solution, of the form
![]() $f(\unicode[STIX]{x1D702})$
, the slip condition prohibits such a solution. Surprisingly, several studies actually do carry out the solution by invoking the so-called local similarity, whereby
$f(\unicode[STIX]{x1D702})$
, the slip condition prohibits such a solution. Surprisingly, several studies actually do carry out the solution by invoking the so-called local similarity, whereby
![]() $f$
is taken to depend only on
$f$
is taken to depend only on
![]() $\unicode[STIX]{x1D702}$
, simplifying (3.3) to the Blasius equation,
$\unicode[STIX]{x1D702}$
, simplifying (3.3) to the Blasius equation,
![]() $f_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}=-f/2f_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}$
, and solving it subject to (3.4) while fixing
$f_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}=-f/2f_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}$
, and solving it subject to (3.4) while fixing
![]() $\unicode[STIX]{x1D709}$
as a parameter (see, for instance, Martin & Boyd (Reference Martin, Boyd, Bartel and Gallis2001); Ajadi et al. (Reference Ajadi, Adegoke and Aziz2009)). The slip condition in (3.4) indicates that such a similarity solution is possible only in the limit of vanishing slip length (
$\unicode[STIX]{x1D709}$
as a parameter (see, for instance, Martin & Boyd (Reference Martin, Boyd, Bartel and Gallis2001); Ajadi et al. (Reference Ajadi, Adegoke and Aziz2009)). The slip condition in (3.4) indicates that such a similarity solution is possible only in the limit of vanishing slip length (
![]() $S=0$
) or at large distance from the leading edge
$S=0$
) or at large distance from the leading edge
![]() $(\unicode[STIX]{x1D709}\rightarrow \infty )$
. In both limits, adherence is recovered. Another possibility that would allow the implementation of a similarity technique consists of taking
$(\unicode[STIX]{x1D709}\rightarrow \infty )$
. In both limits, adherence is recovered. Another possibility that would allow the implementation of a similarity technique consists of taking
![]() $S$
to vary like
$S$
to vary like
![]() $\sqrt{\unicode[STIX]{x1D709}}$
. However, this model is restrictive as it corresponds to a particular surface structure. A similar approach was proposed by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010). They assumed the slip length to be proportional to the film thickness above the posts, with the proportionality constant determined empirically as a function of the roughness porosity and aspect ratio of the posts.
$\sqrt{\unicode[STIX]{x1D709}}$
. However, this model is restrictive as it corresponds to a particular surface structure. A similar approach was proposed by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010). They assumed the slip length to be proportional to the film thickness above the posts, with the proportionality constant determined empirically as a function of the roughness porosity and aspect ratio of the posts.
3.1 Flow behaviour for large slip length
A series solution is sought by expanding the streamfunction and velocity in suitable powers of
![]() $\unicode[STIX]{x1D709}$
. For the slip velocity
$\unicode[STIX]{x1D709}$
. For the slip velocity
![]() $u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)$
to remain finite and non-zero, the slip condition in (3.4) suggests that we must have
$u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)$
to remain finite and non-zero, the slip condition in (3.4) suggests that we must have
![]() $f_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)\sim \sqrt{\unicode[STIX]{x1D709}}$
to leading order. Similarly, for
$f_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)\sim \sqrt{\unicode[STIX]{x1D709}}$
to leading order. Similarly, for
![]() $v(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
to remain finite near the origin, equation (3.2) suggests that
$v(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
to remain finite near the origin, equation (3.2) suggests that
![]() $f(\unicode[STIX]{x1D709}\rightarrow 0,\unicode[STIX]{x1D702})\sim \sqrt{\unicode[STIX]{x1D709}}$
. Thus, we set
$f(\unicode[STIX]{x1D709}\rightarrow 0,\unicode[STIX]{x1D702})\sim \sqrt{\unicode[STIX]{x1D709}}$
. Thus, we set
In this case, it is not difficult to show that the recurrence relation takes the form
The corresponding boundary conditions read
We list the first two modes for reference, namely

Figure 2. Streamfunction profiles at different positions from the leading edge of the boundary layer.
The non-similar character of the flow is perhaps best illustrated by examining the behaviour of
![]() $f(x,\unicode[STIX]{x1D702})$
. Figure 2 shows the variation of
$f(x,\unicode[STIX]{x1D702})$
. Figure 2 shows the variation of
![]() $f$
with
$f$
with
![]() $\unicode[STIX]{x1D702}$
at various
$\unicode[STIX]{x1D702}$
at various
![]() $x$
positions, with an increment of
$x$
positions, with an increment of
![]() $\unicode[STIX]{x1D6E5}=0.01/ReS^{2}$
over the range
$\unicode[STIX]{x1D6E5}=0.01/ReS^{2}$
over the range
![]() $0\leqslant x/ReS^{2}\leqslant 0.1$
. The figure illustrates clearly the dependence of
$0\leqslant x/ReS^{2}\leqslant 0.1$
. The figure illustrates clearly the dependence of
![]() $f$
on
$f$
on
![]() $x$
, and suggests that saturation occurs as the distance grows from the leading edge of the boundary layer. The saturation is a reflection of the growing viscous effect as the fluid advances, slowing the flow. More importantly, the slowing rate can be determined accurately as function of
$x$
, and suggests that saturation occurs as the distance grows from the leading edge of the boundary layer. The saturation is a reflection of the growing viscous effect as the fluid advances, slowing the flow. More importantly, the slowing rate can be determined accurately as function of
![]() $Re$
and
$Re$
and
![]() $S$
. The overall behaviour appears to be close to linear, with a slope diminishing with distance, confirming the weakening of the flow across the boundary layer, and not just at the plate.
$S$
. The overall behaviour appears to be close to linear, with a slope diminishing with distance, confirming the weakening of the flow across the boundary layer, and not just at the plate.

Figure 3. Streamwise (a) and transverse (b) velocity profiles at different distances from the leading edge in the developing boundary-layer region (ii), based on series solution. The inset in (a) shows the slip velocity against the distance along the plate.
The flow in the boundary layer is illustrated in figure 3, which displays the profiles of the streamwise (figure 3
a) and transverse (figure 3
b) velocity components over the range
![]() $0.01<x/S^{2}Re<0.1$
. As for an adhering jet,
$0.01<x/S^{2}Re<0.1$
. As for an adhering jet,
![]() $u$
and
$u$
and
![]() $v$
increase monotonically with height. While these observations essentially hold for both adhering and slipping jets, there is a dramatic departure in behaviour for a slipping jet.
$v$
increase monotonically with height. While these observations essentially hold for both adhering and slipping jets, there is a dramatic departure in behaviour for a slipping jet.
The contrast to an adhering jet becomes particularly evident when examining the flow at the plate. For this, we have included the slip velocity dependence on distance, reported in the inset of figure 3(a). The velocity is readily available from (3.6) as
![]() $u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)=1+\sum _{n=1}F_{n}^{\prime }(\unicode[STIX]{x1D702}=0)(\sqrt{\unicode[STIX]{x1D709}}/S)^{n}$
. It should be recalled that, for an adhering jet, there is a sudden drop in velocity from 1 to 0 at the leading edge of the boundary layer, accompanied by a sudden jump in the shear stress, causing in fact the emergence of the boundary layer at the leading edge. For a slipping jet, the transition is continuous for both the velocity and the shear stress, with the latter behaving like
$u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)=1+\sum _{n=1}F_{n}^{\prime }(\unicode[STIX]{x1D702}=0)(\sqrt{\unicode[STIX]{x1D709}}/S)^{n}$
. It should be recalled that, for an adhering jet, there is a sudden drop in velocity from 1 to 0 at the leading edge of the boundary layer, accompanied by a sudden jump in the shear stress, causing in fact the emergence of the boundary layer at the leading edge. For a slipping jet, the transition is continuous for both the velocity and the shear stress, with the latter behaving like
![]() $\sqrt{\unicode[STIX]{x1D709}}$
and the former remaining close to 1 near the leading edge (see the inset in figure 3
a). Consequently, it is the discontinuity in the normal stress
$\sqrt{\unicode[STIX]{x1D709}}$
and the former remaining close to 1 near the leading edge (see the inset in figure 3
a). Consequently, it is the discontinuity in the normal stress
![]() $u_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)$
, which behaves like
$u_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)$
, which behaves like
![]() $-1/\sqrt{\unicode[STIX]{x1D709}}$
near the origin, that causes the formation of the boundary layer. It should be recalled that the normal stress remains continuously zero for an adhering jet. Moreover, unlike an adhering jet, the
$-1/\sqrt{\unicode[STIX]{x1D709}}$
near the origin, that causes the formation of the boundary layer. It should be recalled that the normal stress remains continuously zero for an adhering jet. Moreover, unlike an adhering jet, the
![]() $v$
profiles in figure 3(b) display a non-zero slope at the plate. For
$v$
profiles in figure 3(b) display a non-zero slope at the plate. For
![]() $S=0$
, equation (3.2) shows that the transverse velocity component reduces to
$S=0$
, equation (3.2) shows that the transverse velocity component reduces to
![]() $2\sqrt{Re\unicode[STIX]{x1D709}}v(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=\unicode[STIX]{x1D702}f_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D702})-f(\unicode[STIX]{x1D702})$
, leading to
$2\sqrt{Re\unicode[STIX]{x1D709}}v(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=\unicode[STIX]{x1D702}f_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D702})-f(\unicode[STIX]{x1D702})$
, leading to
![]() $v_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)=0$
. More generally, for
$v_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)=0$
. More generally, for
![]() $S\geqslant 0$
, equation (3.2) leads to
$S\geqslant 0$
, equation (3.2) leads to
which confirms the singular character of an adhering fluid.

Figure 4. Dependence of the slip velocity on the position in the developing boundary-layer region (ii). The profiles based on the series solution with 1, 2 and 3 modes, the Karman–Pohlhausen approximation and the numerical solution are shown.
Figure 4 shows a comparison between the numerical and series solutions for the evolution of the slip velocity with distance. We also show the influence of the number of modes on the series solution, which reflects rapid convergence when only three modes are included. As expected, the need for higher-order modes increases as the discrepancy grows with distance. However, as we shall see below, the transition to fully developed flow occurs at a relatively short distance from the leading edge (origin), and three modes turn out to be amply sufficient for our purposes. Comparison with the numerical solution indicates an overall agreement of 2–4 %. However, there is a significant qualitative disagreement near the origin; the stress singularity at the origin is not captured by the numerical solution. Ideally, some local (asymptotic) treatment is required that would provide a suitable initial condition for the numerical integration to start at some point downstream of the origin (see Khayat Reference Khayat2016). There are additional challenges facing the implementation of a numerical approach for the present problem, particularly when matching the flow at the transition location. Further details and discussion are given in appendix A. We shall not pursue the numerical approach beyond this point.
Figure 4 also shows the slip velocity based on the K–P parabolic approximation, which will be discussed below and given in (3.22). There is good agreement with the series solution near the origin, reflecting the capability of the K–P solution to capture the singular character at the leading edge. However, it tends to underestimate the level of slip velocity overall by a few per cent. A velocity profile different from the parabolic profile (3.22) may yield closer agreement. However, in addition to the expected cumbersome manipulation of a more complicated profile, there is no physical justification or systematic approach for the generation of such a profile (Prince et al. Reference Prince, Maynes and Crockett2012).
Finally, it should be noted that the series solution (3.6) is valid for finite
![]() $S$
only; in fact, the solution is singular for
$S$
only; in fact, the solution is singular for
![]() $S=0$
. Thus, for the solution to apply close to the leading edge,
$S=0$
. Thus, for the solution to apply close to the leading edge,
![]() $S$
must be relatively large. We propose next a series solution that is valid for small
$S$
must be relatively large. We propose next a series solution that is valid for small
![]() $S$
, including the
$S$
, including the
![]() $S=0$
limit.
$S=0$
limit.
3.2 Flow behaviour for small slip length
If
![]() $S$
is small, it can be adopted as the small parameter for the problem, and we can seek a perturbation expansion of the streamfunction in powers of
$S$
is small, it can be adopted as the small parameter for the problem, and we can seek a perturbation expansion of the streamfunction in powers of
![]() $S$
. In this case, the similarity solution
$S$
. In this case, the similarity solution
![]() $f_{0}(\unicode[STIX]{x1D702})$
, corresponding to an adhering jet, is taken as the leading-order term. Clearly, this term should not be confused with the one in (A 3a,b
). Thus, the solution of (3.3) can be written as
$f_{0}(\unicode[STIX]{x1D702})$
, corresponding to an adhering jet, is taken as the leading-order term. Clearly, this term should not be confused with the one in (A 3a,b
). Thus, the solution of (3.3) can be written as
It should be recalled that the leading-order function satisfies the following similarity problem (Schlichting Reference Schlichting2000):
Upon substituting (3.12) into (3.3), and using (3.13), we obtain the following recurrence equations for the perturbation coefficients, namely, for
![]() $n\geqslant 1$
:
$n\geqslant 1$
:
 $$\begin{eqnarray}\displaystyle f_{n\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}} & = & \displaystyle \displaystyle \unicode[STIX]{x1D709}(f_{0}^{\prime }\,\,f_{n\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}}-f_{0}^{\prime \prime }f_{n\unicode[STIX]{x1D709}})-\frac{1}{2}(f_{0}f_{n\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}+f_{0}^{\prime \prime }f_{n})\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\mathop{\sum }_{m=1}^{n-1}\left[\unicode[STIX]{x1D709}(f_{m\unicode[STIX]{x1D702}}\,f_{n-m\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}}-f_{m\unicode[STIX]{x1D709}}f_{n-m\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}})-\frac{1}{2}f_{m}f_{n-m\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{n\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}} & = & \displaystyle \displaystyle \unicode[STIX]{x1D709}(f_{0}^{\prime }\,\,f_{n\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}}-f_{0}^{\prime \prime }f_{n\unicode[STIX]{x1D709}})-\frac{1}{2}(f_{0}f_{n\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}+f_{0}^{\prime \prime }f_{n})\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\mathop{\sum }_{m=1}^{n-1}\left[\unicode[STIX]{x1D709}(f_{m\unicode[STIX]{x1D702}}\,f_{n-m\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}}-f_{m\unicode[STIX]{x1D709}}f_{n-m\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}})-\frac{1}{2}f_{m}f_{n-m\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}\right].\end{eqnarray}$$
By inspecting (3.14) and corresponding boundary conditions, it is not difficult to see that the solution is of the form
![]() $f_{n}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=H_{n}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D709}^{-n/2}$
, where the coefficients
$f_{n}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=H_{n}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D709}^{-n/2}$
, where the coefficients
![]() $H_{n}$
are governed by
$H_{n}$
are governed by
We observe that for small
![]() $S$
,
$S$
,
![]() $S/\sqrt{\unicode[STIX]{x1D709}}$
must remain small for expansion (3.12) to be valid, whereas for finite
$S/\sqrt{\unicode[STIX]{x1D709}}$
must remain small for expansion (3.12) to be valid, whereas for finite
![]() $S$
, it is
$S$
, it is
![]() $\sqrt{\unicode[STIX]{x1D709}}/S$
that must be small for expansion (3.6) to hold. In other words, expansion (3.12) is valid far from the leading edge, whereas (3.6) is applicable for small distance.
$\sqrt{\unicode[STIX]{x1D709}}/S$
that must be small for expansion (3.6) to hold. In other words, expansion (3.12) is valid far from the leading edge, whereas (3.6) is applicable for small distance.
The flow is then given by

Figure 5. Influence of the slip length on the velocity profile for small
![]() $S$
, plotted at various positions along the plate in the developing boundary-layer region.
$S$
, plotted at various positions along the plate in the developing boundary-layer region.
The slip velocity is given by
![]() $u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)=0.332S/\sqrt{\unicode[STIX]{x1D709}}-0.0805S^{2}/\unicode[STIX]{x1D709}+O(S^{3}/\unicode[STIX]{x1D709}^{3/2})$
, where we recall that
$u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)=0.332S/\sqrt{\unicode[STIX]{x1D709}}-0.0805S^{2}/\unicode[STIX]{x1D709}+O(S^{3}/\unicode[STIX]{x1D709}^{3/2})$
, where we recall that
![]() $f_{0}^{\prime \prime }(\unicode[STIX]{x1D702}=0)\approx 0.332$
(Schlichting Reference Schlichting2000). As an illustration, figure 5 depicts the influence of slip length on the velocity profile for small
$f_{0}^{\prime \prime }(\unicode[STIX]{x1D702}=0)\approx 0.332$
(Schlichting Reference Schlichting2000). As an illustration, figure 5 depicts the influence of slip length on the velocity profile for small
![]() $S$
, to
$S$
, to
![]() $O(S^{3}/\unicode[STIX]{x1D709}^{3/2})$
. In particular, one should note the gradual departure from the similarity profile
$O(S^{3}/\unicode[STIX]{x1D709}^{3/2})$
. In particular, one should note the gradual departure from the similarity profile
![]() $(S^{2}Re/x=0)$
, and the contrast to figure 3(a).
$(S^{2}Re/x=0)$
, and the contrast to figure 3(a).
3.3 Boundary-layer height
A more physically insightful and reasonably accurate approach is to determine the boundary-layer height
![]() $\unicode[STIX]{x1D6FF}(x)$
using the K–P integral method. Considering the mass and force balance over the boundary-layer region, the integral form of (2.1) leads to
$\unicode[STIX]{x1D6FF}(x)$
using the K–P integral method. Considering the mass and force balance over the boundary-layer region, the integral form of (2.1) leads to
As in the case of an adhering jet, the balance of terms in (2.1b
) suggests that
![]() $\unicode[STIX]{x1D6FF}\simeq \sqrt{x/Re}$
for a slipping jet as well. In this case, letting
$\unicode[STIX]{x1D6FF}\simeq \sqrt{x/Re}$
for a slipping jet as well. In this case, letting
and recalling the slip condition in (2.2), equation (3.18) reduces to
We adopt a parabolic profile for the velocity, subject to the following conditions:
In this case,
This profile yields an error of a few per cent for
![]() $S=0$
, relative to the estimate of the boundary-layer thickness based on the similarity solution White (Reference White2015). As reported in figure 4, the same level of accuracy holds for a slipping jet as well. The slip velocity becomes
$S=0$
, relative to the estimate of the boundary-layer thickness based on the similarity solution White (Reference White2015). As reported in figure 4, the same level of accuracy holds for a slipping jet as well. The slip velocity becomes
which reflects similar qualitative flow features, distinct to a slipping jet, to the series solution (3.6). In particular, the continuity of the flow velocity and discontinuity of normal stress are ensured for a slipping jet. Thus, for
![]() $S>0$
, near the origin,
$S>0$
, near the origin,
![]() $u\sim 1$
and
$u\sim 1$
and
![]() $u_{\unicode[STIX]{x1D709}}\sim -1/\sqrt{\unicode[STIX]{x1D709}}$
. This explains the agreement between the K–P and series solutions depicted in figure 4 for small distance, and establishes the range of validity of the K–P approach. Despite its limitation, the profile (3.22) has the significant advantage of being uniformly valid for any
$u_{\unicode[STIX]{x1D709}}\sim -1/\sqrt{\unicode[STIX]{x1D709}}$
. This explains the agreement between the K–P and series solutions depicted in figure 4 for small distance, and establishes the range of validity of the K–P approach. Despite its limitation, the profile (3.22) has the significant advantage of being uniformly valid for any
![]() $S$
value. In contrast, the asymptotic solutions in §§ 3.1 and 3.2 are limited to the large and small
$S$
value. In contrast, the asymptotic solutions in §§ 3.1 and 3.2 are limited to the large and small
![]() $S$
values respectively.
$S$
values respectively.
Inserting (3.22) into (3.20), we obtain the following equation:
Assuming that
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}=0)=0$
, we finally obtain a transcendental relation for the boundary-layer height, namely
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}=0)=0$
, we finally obtain a transcendental relation for the boundary-layer height, namely
Equation (3.24) is the counterpart of equation (11) of Prince et al. (Reference Prince, Maynes and Crockett2012) for a circular jet.

Figure 6. Influence of slip on the boundary-layer thickness (a) and slip velocity (b). All curves collapse onto the
![]() $S=1$
curve when
$S=1$
curve when
![]() $\unicode[STIX]{x1D6FF}/S$
is plotted against
$\unicode[STIX]{x1D6FF}/S$
is plotted against
![]() $x/ReS^{2}$
. The large-
$x/ReS^{2}$
. The large-
![]() $S$
limit is also added as a solid (lowest) curve.
$S$
limit is also added as a solid (lowest) curve.
Figure 6 depicts the influence of slip on the profiles of the boundary layer (figure 6
a) and slip velocity (figure 6
b), including the limit of an adhering film
![]() $(S=0)$
. While the boundary-layer thickness grows indefinitely with distance, the slip velocity eventually vanishes regardless of the slip length, as also suggested by (3.23). As expected, the more slipping jet tends to exhibit a thinner boundary layer, moving faster at the plate. The drop in
$(S=0)$
. While the boundary-layer thickness grows indefinitely with distance, the slip velocity eventually vanishes regardless of the slip length, as also suggested by (3.23). As expected, the more slipping jet tends to exhibit a thinner boundary layer, moving faster at the plate. The drop in
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})$
and the jump in
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})$
and the jump in
![]() $u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)$
, relative to an adhering jet, are significant for a weakly slipping jet. For small
$u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)$
, relative to an adhering jet, are significant for a weakly slipping jet. For small
![]() $S$
and a position not too close to the leading edge
$S$
and a position not too close to the leading edge
![]() $(S\prec \sqrt{\unicode[STIX]{x1D709}})$
, equation (3.25) suggests that
$(S\prec \sqrt{\unicode[STIX]{x1D709}})$
, equation (3.25) suggests that
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{30\unicode[STIX]{x1D709}}-2S$
. In the limit
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{30\unicode[STIX]{x1D709}}-2S$
. In the limit
![]() $S=0$
, one recovers the boundary-layer height for an adhering jet, namely
$S=0$
, one recovers the boundary-layer height for an adhering jet, namely
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})=\sqrt{30\unicode[STIX]{x1D709}}$
(White Reference White2015). For small slip, (3.23) suggests that the slip velocity behaves like
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})=\sqrt{30\unicode[STIX]{x1D709}}$
(White Reference White2015). For small slip, (3.23) suggests that the slip velocity behaves like
![]() $u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)\sim S/\sqrt{30\unicode[STIX]{x1D709}}$
. In other words, both the drop in the boundary-layer height and the jump in the slip velocity are linear with respect to the slip length for weakly slipping flow. For larger slip length,
$u(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}=0)\sim S/\sqrt{30\unicode[STIX]{x1D709}}$
. In other words, both the drop in the boundary-layer height and the jump in the slip velocity are linear with respect to the slip length for weakly slipping flow. For larger slip length,
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})$
displays saturation and a non-zero limit, whereas the slip velocity reaches the free-stream value. This saturation suggests insensitivity of the flow to the effect of slip length for strongly slipping liquids, and is also evident from figure 3 of Prince et al. (Reference Prince, Maynes and Crockett2012) for a circular jet. Equations (3.23) and (3.25) indicate that the curves in figure 6 are collapsible onto one curve when
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})$
displays saturation and a non-zero limit, whereas the slip velocity reaches the free-stream value. This saturation suggests insensitivity of the flow to the effect of slip length for strongly slipping liquids, and is also evident from figure 3 of Prince et al. (Reference Prince, Maynes and Crockett2012) for a circular jet. Equations (3.23) and (3.25) indicate that the curves in figure 6 are collapsible onto one curve when
![]() $\unicode[STIX]{x1D6FF}/S$
and the slip velocity are plotted against
$\unicode[STIX]{x1D6FF}/S$
and the slip velocity are plotted against
![]() $x/ReS^{2}$
. In fact, these curves correspond to
$x/ReS^{2}$
. In fact, these curves correspond to
![]() $S=1$
in figures 6(a) and 6(b) respectively. This same universality was also exhibited by the series solution in figures 3 and 4.
$S=1$
in figures 6(a) and 6(b) respectively. This same universality was also exhibited by the series solution in figures 3 and 4.
These predictions corroborate closely the observations and measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010), who examined the flow of a circular jet impinging on smooth and microdecorated substrate surfaces, the latter consisting of a regular array of micron-size posts. They rationalized their observations by considering a leakage flow (through the posts) coupled to an effective slip length. Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) observed that the thickness of the boundary layer decreases as the slip coefficient and the leakage flow in the porous layer increase. In their experiment, the
![]() $y=0$
plane corresponds to the top of the posts. Thus, as the slip length corresponds to the distance below the actual surface at which the velocity is equal to zero, they interpreted the reduced thickness as the development of the boundary layer from a plane below the
$y=0$
plane corresponds to the top of the posts. Thus, as the slip length corresponds to the distance below the actual surface at which the velocity is equal to zero, they interpreted the reduced thickness as the development of the boundary layer from a plane below the
![]() $y=0$
plane; see below.
$y=0$
plane; see below.

Figure 7. Dependence of the boundary-layer thickness (a) and slip velocity (b) on the slip parameter at different positions
![]() $(0.1\leqslant x/Re\leqslant 1)$
. It should be noted that
$(0.1\leqslant x/Re\leqslant 1)$
. It should be noted that
![]() $\unicode[STIX]{x1D6FF}(S;x=0)=0$
and
$\unicode[STIX]{x1D6FF}(S;x=0)=0$
and
![]() $u(y=0,S;x=0)=1$
.
$u(y=0,S;x=0)=1$
.
The asymptotic behaviour depicted in figure 6 for large
![]() $S$
becomes more apparent from figure 7, where the boundary-layer height and slip velocity are plotted against
$S$
becomes more apparent from figure 7, where the boundary-layer height and slip velocity are plotted against
![]() $S$
at different streamwise distances in figures 7(a) and 7(b) respectively. This behaviour was also reported by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) for any leakage flow rate, as shown in their figure 7(b). Interestingly, the large-
$S$
at different streamwise distances in figures 7(a) and 7(b) respectively. This behaviour was also reported by Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) for any leakage flow rate, as shown in their figure 7(b). Interestingly, the large-
![]() $S$
behaviour appears to be insensitive to the leakage flow rate, as the curves converge together for large slip length. For a planar jet with large slip length, (3.27) suggests an asymptotic height
$S$
behaviour appears to be insensitive to the leakage flow rate, as the curves converge together for large slip length. For a planar jet with large slip length, (3.27) suggests an asymptotic height
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{6\unicode[STIX]{x1D709}}$
, signalling a 55 % drop from the
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{6\unicode[STIX]{x1D709}}$
, signalling a 55 % drop from the
![]() $\sqrt{30\unicode[STIX]{x1D709}}$
level for an adhering jet. Comparatively, for a circular jet, figure 7(b) of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) indicates a 77 % drop, suggesting that drag is easier to reduce for a circular jet than a liquid sheet. The linear behaviour against
$\sqrt{30\unicode[STIX]{x1D709}}$
level for an adhering jet. Comparatively, for a circular jet, figure 7(b) of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) indicates a 77 % drop, suggesting that drag is easier to reduce for a circular jet than a liquid sheet. The linear behaviour against
![]() $S$
for small slip length, discussed earlier, is evident from the current figures 7(a) and 7(b).
$S$
for small slip length, discussed earlier, is evident from the current figures 7(a) and 7(b).
3.4 Transition location
As the boundary layer grows with distance, it eventually invades the entire jet width, merging with the jet free surface at
![]() $x=x_{0}$
. For
$x=x_{0}$
. For
![]() $x<x_{0}$
and above the boundary-layer outer edge, at some
$x<x_{0}$
and above the boundary-layer outer edge, at some
![]() $y=h(x)>\unicode[STIX]{x1D6FF}(x)$
, lies the free surface. The height of the free surface is determined from volume conservation inside and outside the boundary layer, namely
$y=h(x)>\unicode[STIX]{x1D6FF}(x)$
, lies the free surface. The height of the free surface is determined from volume conservation inside and outside the boundary layer, namely
Upon using (3.22), we deduce that
For an adhering jet,
![]() $h(\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{0})=1+1/3\sqrt{30\unicode[STIX]{x1D709}}$
. More generally, for small
$h(\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{0})=1+1/3\sqrt{30\unicode[STIX]{x1D709}}$
. More generally, for small
![]() $S$
, we recall that
$S$
, we recall that
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{30\unicode[STIX]{x1D709}}-2S$
, so that
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{30\unicode[STIX]{x1D709}}-2S$
, so that
![]() $h(\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{0})\sim 1+1/3(\sqrt{30\unicode[STIX]{x1D709}}-2S)^{2}/\sqrt{30\unicode[STIX]{x1D709}}\simeq 1+1/3\sqrt{30\unicode[STIX]{x1D709}}(1-4S/\sqrt{30\unicode[STIX]{x1D709}})$
. Hence, both the boundary-layer and the film thickness in region (ii) tend to decrease linearly with the slip length. On the other hand, for large
$h(\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{0})\sim 1+1/3(\sqrt{30\unicode[STIX]{x1D709}}-2S)^{2}/\sqrt{30\unicode[STIX]{x1D709}}\simeq 1+1/3\sqrt{30\unicode[STIX]{x1D709}}(1-4S/\sqrt{30\unicode[STIX]{x1D709}})$
. Hence, both the boundary-layer and the film thickness in region (ii) tend to decrease linearly with the slip length. On the other hand, for large
![]() $S$
,
$S$
,
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{6\unicode[STIX]{x1D709}}$
, so that
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709})\sim \sqrt{6\unicode[STIX]{x1D709}}$
, so that
![]() $h(\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{0})\sim 1+2(\unicode[STIX]{x1D709}/\sqrt{6\unicode[STIX]{x1D709}}+2S)$
.
$h(\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{0})\sim 1+2(\unicode[STIX]{x1D709}/\sqrt{6\unicode[STIX]{x1D709}}+2S)$
.
The transverse velocity component at the outer edge of the boundary layer is obtained upon using (2.5) and (3.27), namely
This expression illustrates clearly the character of the flow at the leading edge of the boundary layer. For an adhering jet,
![]() $V$
is infinite at
$V$
is infinite at
![]() $x=0$
as it behaves like
$x=0$
as it behaves like
![]() $1/\sqrt{x}$
. For a slipping jet, the jump is finite with
$1/\sqrt{x}$
. For a slipping jet, the jump is finite with
![]() $V(\unicode[STIX]{x1D709}=0)=1/2S$
. The flow structure is further discussed once the solution in the fully viscous layer is determined in the next section.
$V(\unicode[STIX]{x1D709}=0)=1/2S$
. The flow structure is further discussed once the solution in the fully viscous layer is determined in the next section.

Figure 8. Influence of slip on the transition location and free-surface height,
![]() $h(x_{0})=\unicode[STIX]{x1D6FF}(x_{0})$
, at the transition point. The large-
$h(x_{0})=\unicode[STIX]{x1D6FF}(x_{0})$
, at the transition point. The large-
![]() $S$
asymptote is also shown for
$S$
asymptote is also shown for
![]() $\unicode[STIX]{x1D6FF}$
.
$\unicode[STIX]{x1D6FF}$
.
The transition point is reached when the boundary layer absorbs all of the flow. Consequently,
![]() $\unicode[STIX]{x1D709}_{0}$
and the corresponding jet thickness are determined upon setting
$\unicode[STIX]{x1D709}_{0}$
and the corresponding jet thickness are determined upon setting
![]() $h(\unicode[STIX]{x1D709}_{0})=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{0})$
in (3.27) and using (3.25), yielding
$h(\unicode[STIX]{x1D709}_{0})=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{0})$
in (3.27) and using (3.25), yielding
Figure 8 displays the influence of slip on the transition location and corresponding jet thickness. Overall, the transition location increases with slip length, and the jet becomes thinner. In the limit of an adhering jet, one recovers
![]() $h(\unicode[STIX]{x1D709}_{0})\sim 3/2$
and
$h(\unicode[STIX]{x1D709}_{0})\sim 3/2$
and
![]() $\unicode[STIX]{x1D709}_{0}\sim 3/40$
. For an infinitely slipping jet, (3.29) and (3.30) suggest that
$\unicode[STIX]{x1D709}_{0}\sim 3/40$
. For an infinitely slipping jet, (3.29) and (3.30) suggest that
![]() $h(\unicode[STIX]{x1D709}_{0})\sim 1+3/16S$
and
$h(\unicode[STIX]{x1D709}_{0})\sim 1+3/16S$
and
![]() $\unicode[STIX]{x1D709}_{0}\sim 1/6(1+3/8S)$
. The asymptote for the height is also shown in the figure.
$\unicode[STIX]{x1D709}_{0}\sim 1/6(1+3/8S)$
. The asymptote for the height is also shown in the figure.
4 Flow in the fully viscous layer region
The flow in region (iii), for
![]() $x>x_{0}$
, is determined by seeking a solution of equations (2.1) subject to boundary conditions (2.5) and (2.6), and matching the flow at the transition location. In this case, let
$x>x_{0}$
, is determined by seeking a solution of equations (2.1) subject to boundary conditions (2.5) and (2.6), and matching the flow at the transition location. In this case, let
and set
where
![]() $U(\unicode[STIX]{x1D709})$
is the streamwise velocity component at the surface and
$U(\unicode[STIX]{x1D709})$
is the streamwise velocity component at the surface and
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})$
is to be determined. Upon substituting (4.2) into the continuity equation (2.1a
) and integrating, we have
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})$
is to be determined. Upon substituting (4.2) into the continuity equation (2.1a
) and integrating, we have
In this case, (2.1b
) reduces to the desired equation for
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})$
, namely
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})$
, namely
where
![]() $G(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\equiv \int _{0}^{\unicode[STIX]{x1D701}}g(\unicode[STIX]{x1D709},z)\,\text{d}z$
. The boundary conditions become
$G(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\equiv \int _{0}^{\unicode[STIX]{x1D701}}g(\unicode[STIX]{x1D709},z)\,\text{d}z$
. The boundary conditions become
Additionally, the flow must match at the transition point according to (2.7). Thus, by equating (4.2) to (3.22) at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{0}$
, and noting that
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{0}$
, and noting that
![]() $U(\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{0})=1$
, we have
$U(\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{0})=1$
, we have
where
![]() $h(\unicode[STIX]{x1D709}_{0})$
and
$h(\unicode[STIX]{x1D709}_{0})$
and
![]() $\unicode[STIX]{x1D709}_{0}$
are given by (3.29) and (3.30) respectively. Conservation of mass dictates that
$\unicode[STIX]{x1D709}_{0}$
are given by (3.29) and (3.30) respectively. Conservation of mass dictates that
The problem (4.4)–(4.7) consists of determining
![]() $h(\unicode[STIX]{x1D709}),\,U(\unicode[STIX]{x1D709})$
and
$h(\unicode[STIX]{x1D709}),\,U(\unicode[STIX]{x1D709})$
and
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})$
for
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})$
for
![]() $\unicode[STIX]{x1D709}\geqslant \unicode[STIX]{x1D709}_{0}$
,
$\unicode[STIX]{x1D709}\geqslant \unicode[STIX]{x1D709}_{0}$
,
![]() $0\leqslant \unicode[STIX]{x1D701}\leqslant 1$
. It is of the integrodifferential type and, unlike the case of an adhering jet (Watson Reference Watson1964), does not admit a similarity solution. A numerical approach would be dauntingly challenging. Fortunately, an accurate series solution is possible as we can take advantage of the small range
$0\leqslant \unicode[STIX]{x1D701}\leqslant 1$
. It is of the integrodifferential type and, unlike the case of an adhering jet (Watson Reference Watson1964), does not admit a similarity solution. A numerical approach would be dauntingly challenging. Fortunately, an accurate series solution is possible as we can take advantage of the small range
![]() $0\leqslant \unicode[STIX]{x1D701}\leqslant 1$
.
$0\leqslant \unicode[STIX]{x1D701}\leqslant 1$
.
4.1 Series expansion in powers of
 $\unicode[STIX]{x1D701}$
$\unicode[STIX]{x1D701}$
Before seeking a series solution, it is helpful to eliminate the integral from equation (4.4) by differentiating equation (4.4) with respect to
![]() $\unicode[STIX]{x1D701}$
and reusing (4.4) to obtain
$\unicode[STIX]{x1D701}$
and reusing (4.4) to obtain
It is also convenient to make the transformation
![]() $\unicode[STIX]{x1D701}\rightarrow 1-\unicode[STIX]{x1D701}$
. In this case, equation (4.8) remains of the same form, subject to the following conditions, recast from (4.5)–(4.7) as
$\unicode[STIX]{x1D701}\rightarrow 1-\unicode[STIX]{x1D701}$
. In this case, equation (4.8) remains of the same form, subject to the following conditions, recast from (4.5)–(4.7) as
The solution of (4.8) is symmetric with respect to
![]() $\unicode[STIX]{x1D701}=0$
; that is,
$\unicode[STIX]{x1D701}=0$
; that is,
![]() $g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})=g(\unicode[STIX]{x1D709},-\unicode[STIX]{x1D701})$
. Therefore, we let
$g(\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})=g(\unicode[STIX]{x1D709},-\unicode[STIX]{x1D701})$
. Therefore, we let
which satisfy the latter two conditions in (4.9). Upon substituting (4.11) into (4.8), one arrives at the following relations for the first two coefficients:
and the recurrence relation for the remaining
![]() $G_{m\geqslant 3}$
coefficients:
$G_{m\geqslant 3}$
coefficients:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle 2(m+1)(2m+1)G_{m+1}=h^{2}UG_{m}^{\prime }+2h[(m+1)hU^{\prime }+mUh^{\prime }]G_{m}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,h\mathop{\sum }_{n=1}^{m-1}\left[\frac{2m-2n+3}{2m-2n+1}hUG_{m-n}^{\prime }+\frac{(2m+1)hU^{\prime }+2nh^{\prime }U}{2m-2n+1}G_{m-n}\right]G_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle 2(m+1)(2m+1)G_{m+1}=h^{2}UG_{m}^{\prime }+2h[(m+1)hU^{\prime }+mUh^{\prime }]G_{m}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,h\mathop{\sum }_{n=1}^{m-1}\left[\frac{2m-2n+3}{2m-2n+1}hUG_{m-n}^{\prime }+\frac{(2m+1)hU^{\prime }+2nh^{\prime }U}{2m-2n+1}G_{m-n}\right]G_{n}.\end{eqnarray}$$
Additionally, the slip condition in (4.9) and the conservation of mass relation in (4.10) lead respectively to
Finally, the following initial conditions ensue from the matching of the flow at the transition point:
This completes the set of equations needed to determine the unknown variables
![]() $U(\unicode[STIX]{x1D709})$
,
$U(\unicode[STIX]{x1D709})$
,
![]() $h(\unicode[STIX]{x1D709})$
and
$h(\unicode[STIX]{x1D709})$
and
![]() $G_{m\geqslant 1}(\unicode[STIX]{x1D709})$
. It should be noted that, despite the apparent decoupling process, the problem (4.12)–(4.16) remains highly nonlinear and constitutes a coupled algebraic–differential system. The results discussed next are obtained with an error of the order of
$G_{m\geqslant 1}(\unicode[STIX]{x1D709})$
. It should be noted that, despite the apparent decoupling process, the problem (4.12)–(4.16) remains highly nonlinear and constitutes a coupled algebraic–differential system. The results discussed next are obtained with an error of the order of
![]() $10^{-5}$
.
$10^{-5}$
.
4.2 Slip and transition flow
The influence of slip on the flow through the transition region is discussed now that the solutions have been established in the developing and fully viscous boundary layers. Figure 9 illustrates the influence of slip on the film free-surface height (figure 9
a), streamwise velocity component at the free surface (figure 9
b) and slip velocity at the plate (figure 9
c). Both regions (ii) and (iii) are covered for coherence and completeness. Figure 9(a) depicts a relatively sharp increase in jet thickness above the boundary layer near the leading edge
![]() $(x<x_{0})$
in region (ii) and a milder essentially linear growth beyond the transition point
$(x<x_{0})$
in region (ii) and a milder essentially linear growth beyond the transition point
![]() $(x>x_{0})$
in region (iii). The linear growth was also predicted by Watson (Reference Watson1964) for an adhering jet. For a more slipping jet, the film is thinner and the growth remains practically linear throughout. The velocity at the surface in figure 9(b) exhibits essentially a linear decrease with distance, at a rate diminishing with slip.
$(x>x_{0})$
in region (iii). The linear growth was also predicted by Watson (Reference Watson1964) for an adhering jet. For a more slipping jet, the film is thinner and the growth remains practically linear throughout. The velocity at the surface in figure 9(b) exhibits essentially a linear decrease with distance, at a rate diminishing with slip.

Figure 9. Influence of slip on the jet free-surface height (a), surface velocity (b) and slip velocity (c) across the developing and transition regions (ii) and (iii). The locus of transition points is also shown in (a) and (c). The limit of an adhering jet is shown in bold solid lines in all three panels.
Figure 9(c) should be contrasted to figure 6(b) where the slip velocity was only shown over the developing boundary-layer region (ii). The rather sharp drop in region (ii), as a result of the sharp increase in boundary-layer height (see figures 6 a and 9(a)), is tempered significantly in the viscous boundary-layer region (iii) as a result of the slower growth of film thickness (figure 9 a) compared with the boundary-layer height (figure 6 a).

Figure 10. Influence of slip on the jet and boundary-layer thicknesses.
This difference in growth rate between the boundary-layer height and the film thickness is evident from figure 10, where the boundary-layer profiles are shown near the leading edge. The locus of the transition points is also shown in figures 9(a) and 9(c), which indicates that the transition becomes relatively insensitive to slip for large
![]() $S$
. This saturation is also reflected in the profiles of figure 9(b) and 10, and, to a lesser extent, in the slip velocity profiles of figure 9(c). Finally, despite the difference in solution methodologies and levels of accuracy in the fully developed and viscous boundary-layer regions, the free-surface slope in figure 9(a) as well as the slopes of the slip velocity in figure 9(c) remain reasonably smooth at the transition point,
$S$
. This saturation is also reflected in the profiles of figure 9(b) and 10, and, to a lesser extent, in the slip velocity profiles of figure 9(c). Finally, despite the difference in solution methodologies and levels of accuracy in the fully developed and viscous boundary-layer regions, the free-surface slope in figure 9(a) as well as the slopes of the slip velocity in figure 9(c) remain reasonably smooth at the transition point,
![]() $x=x_{\text{0}}$
.
$x=x_{\text{0}}$
.
5 Influence of slip on hydraulic jump
In this section, we consider the planar flow in region (iv), the hydraulic-jump region. The cases of inviscid and viscous fluids will be discussed separately. In general, we denote the position of the hydraulic jump by
![]() $x=x_{J}$
. We also let
$x=x_{J}$
. We also let
![]() $h_{J}=h(x=x_{J})$
be the depth just upstream of the jump (see figure 1). Downstream of the jump, the height is generally denoted by
$h_{J}=h(x=x_{J})$
be the depth just upstream of the jump (see figure 1). Downstream of the jump, the height is generally denoted by
![]() $H(x)$
, and, at the jump, we let
$H(x)$
, and, at the jump, we let
![]() $H_{J}=H(x=x_{J})$
. The surface-tension effect is neglected, and the flow beyond the jump is assumed to be predominantly unidirectional as the film remains thin. Consequently, flow separation and the associated recirculation eddy are not considered. The present planar formulation and results can be regarded as an adequate representation for large-radius circular jumps, even with the surface-tension effect neglected.
$H_{J}=H(x=x_{J})$
. The surface-tension effect is neglected, and the flow beyond the jump is assumed to be predominantly unidirectional as the film remains thin. Consequently, flow separation and the associated recirculation eddy are not considered. The present planar formulation and results can be regarded as an adequate representation for large-radius circular jumps, even with the surface-tension effect neglected.
5.1 The case of an inviscid fluid
This case mimics the flow of a film of low viscosity, draining at a relatively high rate. Hence, the influence of slip originates from the upstream side of the jump. Following Watson (Reference Watson1964), the position of the hydraulic jump,
![]() $x=x_{J}$
, is determined by equating the rate of change of momentum to the force associated with the difference in pressure that arises from the elevation change. This assumption is legitimate provided that the width (measured in the streamwise direction) of the jump is small so that skin friction can be ignored. In this case, the height remains constant, with
$x=x_{J}$
, is determined by equating the rate of change of momentum to the force associated with the difference in pressure that arises from the elevation change. This assumption is legitimate provided that the width (measured in the streamwise direction) of the jump is small so that skin friction can be ignored. In this case, the height remains constant, with
![]() $H(x\geqslant x_{J})=H_{J}$
and
$H(x\geqslant x_{J})=H_{J}$
and
![]() $u(x>x_{J},y)=1/H$
. In this case, the integral form for the condition of momentum (2.1) is expressed as
$u(x>x_{J},y)=1/H$
. In this case, the integral form for the condition of momentum (2.1) is expressed as
The momentum outside the wave, which is
![]() $O(h/H)$
compared with that inside, will be included only approximately since it is assumed that the speed of flow immediately outside the jump is uniform. In this case, (5.1) becomes
$O(h/H)$
compared with that inside, will be included only approximately since it is assumed that the speed of flow immediately outside the jump is uniform. In this case, (5.1) becomes
The integral on the right-hand side of (5.2) must be evaluated separately for
![]() $x_{J}>x_{0}$
and
$x_{J}>x_{0}$
and
![]() $x_{J}<x_{0}$
, since the jump may occur at any point in the development of the boundary layer.
$x_{J}<x_{0}$
, since the jump may occur at any point in the development of the boundary layer.
When
![]() $x_{J}\leqslant x_{0}$
, the flow upstream of the jump consists of the developing boundary layer and external inviscid flow. In this case,
$x_{J}\leqslant x_{0}$
, the flow upstream of the jump consists of the developing boundary layer and external inviscid flow. In this case,
where
![]() $\unicode[STIX]{x1D6FF}_{J}=\unicode[STIX]{x1D6FF}(x=x_{J})$
and
$\unicode[STIX]{x1D6FF}_{J}=\unicode[STIX]{x1D6FF}(x=x_{J})$
and
![]() $\unicode[STIX]{x1D709}_{J}=x_{J}/Re$
. Although an accurate expression such as (3.9) can be used to evaluate the integral in (5.3), the approximate profile (3.22) is perhaps more physically revealing, and certainly much more convenient to use. In this case,
$\unicode[STIX]{x1D709}_{J}=x_{J}/Re$
. Although an accurate expression such as (3.9) can be used to evaluate the integral in (5.3), the approximate profile (3.22) is perhaps more physically revealing, and certainly much more convenient to use. In this case,
It should be noted that the upstream film height is determined from (3.27).
When
![]() $x_{J}\geqslant x_{o}$
, the substitution of the velocity profile from (4.11) leads to
$x_{J}\geqslant x_{o}$
, the substitution of the velocity profile from (4.11) leads to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{0}^{h_{J}}u^{2}(x_{J}>x_{0},y)\,\text{d}y=U_{J}^{2}h_{J}\int _{0}^{1}g^{2}(\unicode[STIX]{x1D709}_{J},\unicode[STIX]{x1D701})\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle \quad =U_{J}^{2}h_{J}\left[1+2\mathop{\sum }_{m=1}\frac{G_{m}(\unicode[STIX]{x1D709}_{J})}{2m+1}+\mathop{\sum }_{m=1}\mathop{\sum }_{n=1}\frac{G_{m}(\unicode[STIX]{x1D709}_{J})G_{n}(\unicode[STIX]{x1D709}_{J})}{2m+2n+1}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{0}^{h_{J}}u^{2}(x_{J}>x_{0},y)\,\text{d}y=U_{J}^{2}h_{J}\int _{0}^{1}g^{2}(\unicode[STIX]{x1D709}_{J},\unicode[STIX]{x1D701})\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle \quad =U_{J}^{2}h_{J}\left[1+2\mathop{\sum }_{m=1}\frac{G_{m}(\unicode[STIX]{x1D709}_{J})}{2m+1}+\mathop{\sum }_{m=1}\mathop{\sum }_{n=1}\frac{G_{m}(\unicode[STIX]{x1D709}_{J})G_{n}(\unicode[STIX]{x1D709}_{J})}{2m+2n+1}\right],\end{eqnarray}$$
where
![]() $U_{J}=U(x=x_{J})$
is the velocity at the surface just upstream of the jump. Since, from (4.15a,b
),
$U_{J}=U(x=x_{J})$
is the velocity at the surface just upstream of the jump. Since, from (4.15a,b
),
![]() $\sum _{m=1}G_{m}/2m+1=1/hU-1$
, (5.2) becomes, for
$\sum _{m=1}G_{m}/2m+1=1/hU-1$
, (5.2) becomes, for
![]() $\unicode[STIX]{x1D709}_{J}\geqslant \unicode[STIX]{x1D709}_{o}$
,
$\unicode[STIX]{x1D709}_{J}\geqslant \unicode[STIX]{x1D709}_{o}$
,
In this case,
![]() $h_{J}$
and
$h_{J}$
and
![]() $U_{J}$
are obtained from (4.15a,b
).
$U_{J}$
are obtained from (4.15a,b
).

Figure 11. Influence of slip on the dependence of the hydraulic-jump height on the jump position for an inviscid film. The locus of transition locations is also shown.
Figure 11 shows the influence of slip on the variation of the hydraulic-jump height with the position of the jump, incorporating the influence of the Froude number. The term
![]() $h_{J}^{2}/2Fr^{2}$
, which is the pressure thrust on the inward side of the wave jump, is only
$h_{J}^{2}/2Fr^{2}$
, which is the pressure thrust on the inward side of the wave jump, is only
![]() $O(h^{2}/H^{2})$
compared with the thrust on the outward side, and is assumed to be negligible. The locus of the transition locations is also included. It is shown that, as for an adhering jet, the hydraulic jump occurs earlier when the film depth downstream of the jump is larger. The figure illustrates that greater slip leads to farther location of the jump, as a result of reduced friction at the plate. In this case, the jet spreads more easily. These observations are in agreement with those of Prince et al. (Reference Prince, Maynes and Crockett2012) for a circular jet (see their figure 10). The influence of slip is very much like the effect of shear thinning (see figure 19(a) of Zhao & Khayat (Reference Zhao and Khayat2008)), where the level of viscosity, and not necessarily the degree of shear thinning, dictates the position of the hydraulic jump.
$O(h^{2}/H^{2})$
compared with the thrust on the outward side, and is assumed to be negligible. The locus of the transition locations is also included. It is shown that, as for an adhering jet, the hydraulic jump occurs earlier when the film depth downstream of the jump is larger. The figure illustrates that greater slip leads to farther location of the jump, as a result of reduced friction at the plate. In this case, the jet spreads more easily. These observations are in agreement with those of Prince et al. (Reference Prince, Maynes and Crockett2012) for a circular jet (see their figure 10). The influence of slip is very much like the effect of shear thinning (see figure 19(a) of Zhao & Khayat (Reference Zhao and Khayat2008)), where the level of viscosity, and not necessarily the degree of shear thinning, dictates the position of the hydraulic jump.

Figure 12. Influence of slip on the jump position for
![]() $Fr=2.75$
. The jump height is kept the same at
$Fr=2.75$
. The jump height is kept the same at
![]() $H=2.7$
for all slip lengths. The locus of transition locations is also shown.
$H=2.7$
for all slip lengths. The locus of transition locations is also shown.
Finally, figure 12 displays the influence of slip on the location of the hydraulic jump while the jump height is kept the same (
![]() $H=2.7$
) for any slip length. This corresponds to a value of
$H=2.7$
) for any slip length. This corresponds to a value of
![]() $(H^{3}+2Fr^{2})/2Fr^{2}H=0.85$
in figure 11, with
$(H^{3}+2Fr^{2})/2Fr^{2}H=0.85$
in figure 11, with
![]() $Fr=2.75$
. The locus of the transition locations is also shown, which indicates that the jump occurs in the fully developed boundary layer for
$Fr=2.75$
. The locus of the transition locations is also shown, which indicates that the jump occurs in the fully developed boundary layer for
![]() $S<0.5$
and in the fully viscous layer for the more slipping fluid.
$S<0.5$
and in the fully viscous layer for the more slipping fluid.
5.2 The case of a viscous fluid
Following Duchesne et al. (Reference Duchesne, Lebon and Limat2014), we determine the thickness distribution by adopting a thin-film approach downstream of the jump. The formulation is valid at large distance
![]() $x$
compared with the jump height. As for the ideal case, the jump height and position cannot be determined uniquely. However, the measurements of Duchesne et al. for a circular jet provide an additional relation for the unique determination of
$x$
compared with the jump height. As for the ideal case, the jump height and position cannot be determined uniquely. However, the measurements of Duchesne et al. for a circular jet provide an additional relation for the unique determination of
![]() $H_{J}$
and
$H_{J}$
and
![]() $x_{J}$
. The local Reynolds number and the local slope are both assumed to be small; they are of the order of
$x_{J}$
. The local Reynolds number and the local slope are both assumed to be small; they are of the order of
![]() $10^{\text{-2}}$
in the experiment of Duchesne et al. (Reference Duchesne, Lebon and Limat2014).
$10^{\text{-2}}$
in the experiment of Duchesne et al. (Reference Duchesne, Lebon and Limat2014).
Since experimental data are typically reported in terms of the flow rate
![]() $Q$
(Dressaire et al.
Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010; Duchesne et al.
Reference Duchesne, Lebon and Limat2014), we shall discuss our results in terms of
$Q$
(Dressaire et al.
Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010; Duchesne et al.
Reference Duchesne, Lebon and Limat2014), we shall discuss our results in terms of
![]() $Fr$
and
$Fr$
and
![]() $G\equiv Re/Fr$
(rather than
$G\equiv Re/Fr$
(rather than
![]() $Fr$
and
$Fr$
and
![]() $Re$
) given that
$Re$
) given that
![]() $G$
is independent of the flow rate. Neglecting inertia, the balance between hydrostatic pressure and viscous friction in (2.1), and the conditions of slip at the substrate (2.2) and free slip at the free surface (2.5) yield the following expressions for the velocity components and the pressure:
$G$
is independent of the flow rate. Neglecting inertia, the balance between hydrostatic pressure and viscous friction in (2.1), and the conditions of slip at the substrate (2.2) and free slip at the free surface (2.5) yield the following expressions for the velocity components and the pressure:
In addition, conservation of mass leads to
Integration between the positions of the jump
![]() $x_{J}$
and the trailing edge of the plate
$x_{J}$
and the trailing edge of the plate
![]() $x_{\infty }$
gives
$x_{\infty }$
gives
The measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for an adhering circular jet indicate that their experimental Froude number,
![]() $Fr_{J}=Q/2\unicode[STIX]{x03C0}\bar{R}_{J}\sqrt{g}\bar{H}_{J}^{3/2}$
, defined in terms of the (dimensional) jump height
$Fr_{J}=Q/2\unicode[STIX]{x03C0}\bar{R}_{J}\sqrt{g}\bar{H}_{J}^{3/2}$
, defined in terms of the (dimensional) jump height
![]() $\bar{H}_{J}$
and radius
$\bar{H}_{J}$
and radius
![]() $\bar{R}_{J}$
, remains constant when the flow rate
$\bar{R}_{J}$
, remains constant when the flow rate
![]() $Q$
is varied. Equivalently, for the current planar jet, and in terms of our (dimensionless) notations, we may then assume that
$Q$
is varied. Equivalently, for the current planar jet, and in terms of our (dimensionless) notations, we may then assume that
![]() $Fr_{J}=Fr/x_{J}H_{J}^{3/2}$
remains constant (independent of the Froude number,
$Fr_{J}=Fr/x_{J}H_{J}^{3/2}$
remains constant (independent of the Froude number,
![]() $Fr$
). This assumption is not unreasonable since planar flow is the limit of circular flow with infinite radius of curvature, and also since there does not seem to be any restriction on the jump radius in the experiment. Moreover, the insensitivity of the experimental Froude number,
$Fr$
). This assumption is not unreasonable since planar flow is the limit of circular flow with infinite radius of curvature, and also since there does not seem to be any restriction on the jump radius in the experiment. Moreover, the insensitivity of the experimental Froude number,
![]() $Fr_{J}$
, to variation of the flow rate was verified for both low- and high-viscosity liquids. It should be noted that
$Fr_{J}$
, to variation of the flow rate was verified for both low- and high-viscosity liquids. It should be noted that
![]() $Fr_{J}$
is independent of the viscosity. In this case, it is plausible to assume that the constancy of
$Fr_{J}$
is independent of the viscosity. In this case, it is plausible to assume that the constancy of
![]() $Fr_{J}$
would also hold for a slipping jet. Consequently, we assume that the value of
$Fr_{J}$
would also hold for a slipping jet. Consequently, we assume that the value of
![]() $Fr_{J}$
is the same for any
$Fr_{J}$
is the same for any
![]() $S$
. This yields the following additional relations:
$S$
. This yields the following additional relations:
which, together with (5.9), determine the jump height and position uniquely.
Admittedly, the assumptions we make here are speculative, awaiting experimental verification for an impinging liquid sheet. However, they seem to yield a realistic physical picture of the flow in the jump region. For instance, the first relation in (5.11), suggesting a decrease in the jump position with the jump height for a fixed Froude number, agrees well with the measurements and scaling arguments of Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) for the jump radius versus height at a fixed flow rate, as reported in their figure 5. Finally, the flow structure is expected to change as the jump location decreases with increasing depth (Bush & Aristoff Reference Bush and Aristoff2003). Such a change, however, cannot be captured by the current thin-film formulation.

Figure 13. Jump height (a) and position (b) behaviour with the Froude number (flow rate) for various slip lengths. Here,
![]() $G=0.2$
,
$G=0.2$
,
![]() $Fr_{J}=1$
and
$Fr_{J}=1$
and
![]() $x_{\infty }=2$
.
$x_{\infty }=2$
.
Figure 13 illustrates the dependence of the jump height and the position on
![]() $Fr$
(flow rate) for various
$Fr$
(flow rate) for various
![]() $S$
values. Here,
$S$
values. Here,
![]() $G=0.2$
,
$G=0.2$
,
![]() $Fr_{J}=1$
and
$Fr_{J}=1$
and
![]() $x_{\infty }=2$
. Both the jump height (figure 13
a) and the position (figure 13
b) increase with the Froude number, reflecting the tendency of the film to accumulate further downstream at higher flow rate. While the jump height decreases with slip, its position increases. This behaviour is typical of jets with lower viscosity, where, as in the case of slipping jets, the reduced friction enables the liquid to flow farther with diminished accumulation. The jump height becomes increasingly less sensitive to the variation of
$x_{\infty }=2$
. Both the jump height (figure 13
a) and the position (figure 13
b) increase with the Froude number, reflecting the tendency of the film to accumulate further downstream at higher flow rate. While the jump height decreases with slip, its position increases. This behaviour is typical of jets with lower viscosity, where, as in the case of slipping jets, the reduced friction enables the liquid to flow farther with diminished accumulation. The jump height becomes increasingly less sensitive to the variation of
![]() $Fr$
with slip (figure 13
a); the film behaves increasingly like an inviscid fluid, adopting a thickness closer to the film at the trailing edge. This insensitivity is contrasted by the sharper growth of the jump location with
$Fr$
with slip (figure 13
a); the film behaves increasingly like an inviscid fluid, adopting a thickness closer to the film at the trailing edge. This insensitivity is contrasted by the sharper growth of the jump location with
![]() $Fr$
. In fact, in the limit of infinite slip, (5.9) and (5.11) indicate that
$Fr$
. In fact, in the limit of infinite slip, (5.9) and (5.11) indicate that
suggesting a linear growth of jump position with flow rate, and no change in height.
The trend in figure 13(b) against
![]() $Fr$
agrees with the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) which indicate that the (average) jump radius for a circular jet also increases with the (total) flow rate. See the data reported in their figure 16(a). This observation holds for both smooth and rough substrates. The influence of slip reported in figure 13(b) is also in qualitative agreement with existing predictions, such as the K–P approach of Prince et al. (Reference Prince, Maynes and Crockett2012) and the similarity approach of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010). The latter assumed a slip length inversely proportional to the film thickness to secure a similarity solution. However, in contrast to the trend in figure 13(b), the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010), when conducted to examine the influence of topographical parameters of textured substrates on the jump radius and its dependence on flow rate, indicate that the jump radius actually decreases when roughness is added, regardless of the microtexture examined. Four square lattices were considered, with fixed post radius and different lattice spacings and post heights. In particular, they found that the jump radius decreases with increasing post height. Since the slip length is directly related to the post height, the experimental findings contradict existing theoretical predictions, including the behaviour reported in our figure 13(b) above. Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010) attributed the systematic reduction in jump radius to a reduced flow rate. They regarded the (total) flow rate as divided into a leakage flow rate through the microtexture and the flow rate of a film above the posts.
$Fr$
agrees with the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) which indicate that the (average) jump radius for a circular jet also increases with the (total) flow rate. See the data reported in their figure 16(a). This observation holds for both smooth and rough substrates. The influence of slip reported in figure 13(b) is also in qualitative agreement with existing predictions, such as the K–P approach of Prince et al. (Reference Prince, Maynes and Crockett2012) and the similarity approach of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010). The latter assumed a slip length inversely proportional to the film thickness to secure a similarity solution. However, in contrast to the trend in figure 13(b), the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010), when conducted to examine the influence of topographical parameters of textured substrates on the jump radius and its dependence on flow rate, indicate that the jump radius actually decreases when roughness is added, regardless of the microtexture examined. Four square lattices were considered, with fixed post radius and different lattice spacings and post heights. In particular, they found that the jump radius decreases with increasing post height. Since the slip length is directly related to the post height, the experimental findings contradict existing theoretical predictions, including the behaviour reported in our figure 13(b) above. Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010) attributed the systematic reduction in jump radius to a reduced flow rate. They regarded the (total) flow rate as divided into a leakage flow rate through the microtexture and the flow rate of a film above the posts.
The predictions in figure 13 corroborate well observations and findings of existing studies for an adhering jet. Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) and Rojas et al. (Reference Rojas, Argentina and Tirapegui2013) found the (dimensional) jump radius to scale roughly as
![]() $\bar{R}_{J}\sim Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
for a circular jet. More recently, Duchesne et al. (Reference Duchesne, Lebon and Limat2014) derived a more accurate estimate involving a logarithmic correction based on the thin-film approach. In the current problem, the same scaling holds for an adhering planar jet. When cast in dimensionless form, we find that the jump location behaves like
$\bar{R}_{J}\sim Q^{5/8}\unicode[STIX]{x1D708}^{-3/8}g^{-1/8}$
for a circular jet. More recently, Duchesne et al. (Reference Duchesne, Lebon and Limat2014) derived a more accurate estimate involving a logarithmic correction based on the thin-film approach. In the current problem, the same scaling holds for an adhering planar jet. When cast in dimensionless form, we find that the jump location behaves like
![]() $x_{J}\sim Fr_{J}^{-1}Fr^{5/8}G^{-3/8}$
. This behaviour corresponds to the
$x_{J}\sim Fr_{J}^{-1}Fr^{5/8}G^{-3/8}$
. This behaviour corresponds to the
![]() $S=0$
curve in figure 13(b).
$S=0$
curve in figure 13(b).
The film shape and flow downstream of the jump are now examined by first integrating (5.8) to yield the following equation for
![]() $H(x)$
:
$H(x)$
:
The velocity at the surface is determined from (5.7). In particular,
For an adhering jet, one has
which is equivalent to equation (3) of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for a circular jump.

Figure 14. Film thickness (a) and surface velocity (b) evolution with position downstream of the jump for the range
![]() $x_{J}\leqslant x\leqslant x_{\infty }$
, for different slip parameters. Here,
$x_{J}\leqslant x\leqslant x_{\infty }$
, for different slip parameters. Here,
![]() $x_{\infty }=2$
and
$x_{\infty }=2$
and
![]() $G=0.2$
. The jump position for each
$G=0.2$
. The jump position for each
![]() $S$
value is also indicated by a vertical line.
$S$
value is also indicated by a vertical line.
Figure 14 depicts the evolution of the film height (figure 14
a) and the surface velocity (figure 14
b) with position downstream of the jump. Vertical lines indicate the jump position for each slip level. The decrease in jump height with position is obviously accompanied by an increase in surface velocity that is particularly steep near the plate trailing edge. The height profile is similar to the one measured by Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for axisymmetric flow (see their figure 2a). While the jump height decreases gradually with slip, the velocity remains relatively insensitive to the variation of
![]() $S$
, except near the trailing edge of the plate. This may be surprising at first, but upon closer examination of figure 14, we observe the relatively large values of the jump height, which make the effect of slip relatively uninfluential at the surface, except near the edge where the film thickness narrows considerably. Finally, figure 14 shows the tendency of the film to become increasingly uniform with slip. In the limit of infinite slip, (5.7) and (5.8) yield
$S$
, except near the trailing edge of the plate. This may be surprising at first, but upon closer examination of figure 14, we observe the relatively large values of the jump height, which make the effect of slip relatively uninfluential at the surface, except near the edge where the film thickness narrows considerably. Finally, figure 14 shows the tendency of the film to become increasingly uniform with slip. In the limit of infinite slip, (5.7) and (5.8) yield
![]() $H(x)\sim H_{\infty }$
and
$H(x)\sim H_{\infty }$
and
![]() $u(x>x_{J},y)\sim 1/H_{\infty }$
, in correlation with (5.11a,b
).
$u(x>x_{J},y)\sim 1/H_{\infty }$
, in correlation with (5.11a,b
).
6 Concluding remarks
In this study, the flow of a planar jet impinging onto a solid flat plate with slip is examined theoretically. Navier’s slip condition is used, which mimics the flow slippage on hydrophobic surfaces. The jet is assumed to spread out in a thin layer bounded by a hydraulic jump, draining at the edge of the plate to maintain steady conditions (see figure 1). In addition to the stagnation flow region (i), the flow domain is divided into three main regions: a developing boundary-layer region (ii), a fully viscous boundary-layer region (iii) and a hydraulic-jump region (iv). In contrast to an adhering jet, a slipping jet is inherently non-similar in character. Some emphasis is placed on the flow structure in region (ii), given its fundamental relevance to boundary layers on hydrophobic surfaces in general. We show how the different scaling in each region can be used to develop separate asymptotic series expansions to obtain the flow in regions (ii) and (iii). The flow must satisfy the initial uniform flow at the leading edge of the boundary layer, and match at the transition point.
The ratio of slip length to jet width,
![]() $S$
, can be large or small. In the developing boundary-layer region (ii), we show that
$S$
, can be large or small. In the developing boundary-layer region (ii), we show that
![]() $ReS^{2}$
is the only similarity group needed in the problem. For the flow in this region, for relatively large
$ReS^{2}$
is the only similarity group needed in the problem. For the flow in this region, for relatively large
![]() $S$
or small distance
$S$
or small distance
![]() $x$
, the solution expansion is sought in fractional powers of
$x$
, the solution expansion is sought in fractional powers of
![]() $x/ReS^{2}$
. On the other hand, for small
$x/ReS^{2}$
. On the other hand, for small
![]() $S$
or large
$S$
or large
![]() $x$
, the expansion is sought in fractional powers of
$x$
, the expansion is sought in fractional powers of
![]() $ReS^{2}/x$
. The solution shows good agreement against the K–P approach (figure 4). We find that a slipping film exhibits a singularity in normal stress at the leading edge of the boundary layer, as opposed to the singularity in velocity and shear stress for an adhering film. The nature of the singularity is confirmed when using a K–P approach. We also implement a numerical finite-difference scheme along
$ReS^{2}/x$
. The solution shows good agreement against the K–P approach (figure 4). We find that a slipping film exhibits a singularity in normal stress at the leading edge of the boundary layer, as opposed to the singularity in velocity and shear stress for an adhering film. The nature of the singularity is confirmed when using a K–P approach. We also implement a numerical finite-difference scheme along
![]() $x$
, which, as expected, does not capture the singularity at the origin, but gives reasonable results further from the leading edge (see figure 4 again).
$x$
, which, as expected, does not capture the singularity at the origin, but gives reasonable results further from the leading edge (see figure 4 again).
At the leading edge, there is full slip in velocity, which decreases with downstream distance. At large distance, viscous drag causes the (slip) velocity to vanish; at that point, the Blasius similarity profile is recovered. The boundary-layer and film heights are both found to decrease with slip relative to a smooth substrate (figure 6), roughly like
![]() $\sqrt{30x/Re}-2S$
, whereas the slip velocity intensifies like
$\sqrt{30x/Re}-2S$
, whereas the slip velocity intensifies like
![]() $S\sqrt{Re/30x}$
with slip. The large-
$S\sqrt{Re/30x}$
with slip. The large-
![]() $S$
limit indicates that the boundary layer of a planar jet experiences a 55 % drop from the
$S$
limit indicates that the boundary layer of a planar jet experiences a 55 % drop from the
![]() $\sqrt{30x/Re}$
level for an adhering jet (figure 7
a). Comparatively, for a circular jet, figure 7(b) of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) indicates a 77 % drop, suggesting that drag is easier to reduce for a circular jet than a liquid sheet.
$\sqrt{30x/Re}$
level for an adhering jet (figure 7
a). Comparatively, for a circular jet, figure 7(b) of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2010) indicates a 77 % drop, suggesting that drag is easier to reduce for a circular jet than a liquid sheet.
The transition is delayed by slip, and the jet becomes thinner. In the limit of an adhering jet, one recovers
![]() $h(\unicode[STIX]{x1D709}_{0})\sim 3/2$
and
$h(\unicode[STIX]{x1D709}_{0})\sim 3/2$
and
![]() $\unicode[STIX]{x1D709}_{0}\sim 3/40$
for the film height and transition location. For an infinitely slipping jet,
$\unicode[STIX]{x1D709}_{0}\sim 3/40$
for the film height and transition location. For an infinitely slipping jet,
![]() $h(\unicode[STIX]{x1D709}_{0})\sim 1+3/16S$
and
$h(\unicode[STIX]{x1D709}_{0})\sim 1+3/16S$
and
![]() $\unicode[STIX]{x1D709}_{0}\sim 1/6(1+3/8S)$
. Beyond the transition, the flow problem in the fully viscous region (iii) is of the integro-differential type in the
$\unicode[STIX]{x1D709}_{0}\sim 1/6(1+3/8S)$
. Beyond the transition, the flow problem in the fully viscous region (iii) is of the integro-differential type in the
![]() $(\unicode[STIX]{x1D709}=x/Re,\unicode[STIX]{x1D701}=y/h(x))$
plane. A series solution is sought here in powers of
$(\unicode[STIX]{x1D709}=x/Re,\unicode[STIX]{x1D701}=y/h(x))$
plane. A series solution is sought here in powers of
![]() $\unicode[STIX]{x1D701}$
. The film height is found to decrease with slip, whereas the free-surface velocity intensifies. The slip velocity decreases at a slower rate than it would for pure boundary-layer flow (compare figures 6
b and 9
c).
$\unicode[STIX]{x1D701}$
. The film height is found to decrease with slip, whereas the free-surface velocity intensifies. The slip velocity decreases at a slower rate than it would for pure boundary-layer flow (compare figures 6
b and 9
c).
Finally, ideal and viscous liquids were examined for the flow downstream of the jump, taking into account the drainage at the trailing edge of the plate. Guided by the measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), and the scaling arguments of Bohr et al. (Reference Bohr, Dimon and Putzkaradze1993) and Rojas et al. (Reference Rojas, Argentina and Tirapegui2013), for a circular adhering jet, the hydraulic jump height and location are determined for a planar jet, and are found to increase with the Froude number (flow rate) like
![]() $Fr^{1/4}$
(figure 13
a) and
$Fr^{1/4}$
(figure 13
a) and
![]() $Fr^{5/8}$
(figure 13
b) respectively. This behaviour appears to hold independently of the slip length. While the jump height decreases with slip, its location increases (figure 13). This response is in agreement with existing predictions. However, the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010) show that the jump radius actually decreases with slip. Dressaire et al. attributed this anomalous trend to a ‘leakage’ flow through the microposts of their textured (rough) substrate.
$Fr^{5/8}$
(figure 13
b) respectively. This behaviour appears to hold independently of the slip length. While the jump height decreases with slip, its location increases (figure 13). This response is in agreement with existing predictions. However, the measurements of Dressaire et al. (Reference Dressaire, Courbin, Crest and Stone2009, Reference Dressaire, Courbin, Crest and Stone2010) show that the jump radius actually decreases with slip. Dressaire et al. attributed this anomalous trend to a ‘leakage’ flow through the microposts of their textured (rough) substrate.
Acknowledgements
The financial support of the Natural Sciences and Engineering Council of Canada is gratefully acknowledged. I am grateful to Mr Z. Zhang for carrying out the numerical solution.
Appendix A. Numerical solution
The numerical approach consists of an implicit finite-difference scheme in
![]() $\unicode[STIX]{x1D709}$
, coupled with integration of the resulting discretized equations in
$\unicode[STIX]{x1D709}$
, coupled with integration of the resulting discretized equations in
![]() $\unicode[STIX]{x1D702}$
. Equation (3.3) is discretized in the streamwise direction by using a fixed mesh interval,
$\unicode[STIX]{x1D702}$
. Equation (3.3) is discretized in the streamwise direction by using a fixed mesh interval,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D709}$
, and letting
$\unicode[STIX]{x0394}\unicode[STIX]{x1D709}$
, and letting
![]() $f_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i},\unicode[STIX]{x1D702})=f_{i+1}(\unicode[STIX]{x1D702})-f_{i}(\unicode[STIX]{x1D702})/\unicode[STIX]{x0394}\unicode[STIX]{x1D709}$
, where
$f_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{i},\unicode[STIX]{x1D702})=f_{i+1}(\unicode[STIX]{x1D702})-f_{i}(\unicode[STIX]{x1D702})/\unicode[STIX]{x0394}\unicode[STIX]{x1D709}$
, where
![]() $i$
runs over the number of nodes. The resulting problem for
$i$
runs over the number of nodes. The resulting problem for
![]() $f_{i}(\unicode[STIX]{x1D702})$
at
$f_{i}(\unicode[STIX]{x1D702})$
at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{i}$
for
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{i}$
for
![]() $i>0$
reads
$i>0$
reads
Additionally, the initial conditions (3.5a,b ) lead to
The problem (3.6)–(3.7) is of the two-point boundary-value type, and is solved using a variable-order variable-step-size finite-difference method with deferred corrections (IMSL-DBVPFD routine). Although, in principle, this method is robust and relatively easy to implement, it can be tedious and impractical. The two-point boundary-value problem must be solved at a high number of
![]() $\unicode[STIX]{x1D709}$
positions. The problem is nonlinear, therefore requiring an accurate initial guess for the solution to converge at successive
$\unicode[STIX]{x1D709}$
positions. The problem is nonlinear, therefore requiring an accurate initial guess for the solution to converge at successive
![]() $\unicode[STIX]{x1D709}_{i}$
positions. It should be noted that, although available at discrete
$\unicode[STIX]{x1D709}_{i}$
positions. It should be noted that, although available at discrete
![]() $\unicode[STIX]{x1D702}$
points, the solution
$\unicode[STIX]{x1D702}$
points, the solution
![]() $f_{i-1}(\unicode[STIX]{x1D702})$
at the previous position
$f_{i-1}(\unicode[STIX]{x1D702})$
at the previous position
![]() $\unicode[STIX]{x1D709}_{i-1}$
cannot be readily used to solve (3.6). A smooth profile must be generated out of the discrete data, which introduces errors that become significant, especially when estimating the derivative. The method becomes particularly inconvenient when calculating the boundary-layer thickness and matching the flow at
$\unicode[STIX]{x1D709}_{i-1}$
cannot be readily used to solve (3.6). A smooth profile must be generated out of the discrete data, which introduces errors that become significant, especially when estimating the derivative. The method becomes particularly inconvenient when calculating the boundary-layer thickness and matching the flow at
![]() $x=x_{\text{0}}$
, at the interface between the developing and viscous fully developed boundary layer regions (ii) and (iii), and at the hydraulic jump. Admittedly, these numerical issues may conceivably be overcome or controlled. However, there remains one serious issue that plagues the numerical approach, namely the presence of the normal stress singularity at the leading edge of the boundary layer (see § 3.1). Nevertheless, we use the method as reference despite its limited range of validity compared with the alternative semi-analytical asymptotic techniques proposed in § 3.
$x=x_{\text{0}}$
, at the interface between the developing and viscous fully developed boundary layer regions (ii) and (iii), and at the hydraulic jump. Admittedly, these numerical issues may conceivably be overcome or controlled. However, there remains one serious issue that plagues the numerical approach, namely the presence of the normal stress singularity at the leading edge of the boundary layer (see § 3.1). Nevertheless, we use the method as reference despite its limited range of validity compared with the alternative semi-analytical asymptotic techniques proposed in § 3.