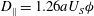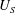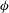1. Introduction
Hydrodynamic diffusion is a topic of ongoing interest in the study of multiphase flows, and in flowing suspensions enables the bulk migration or mixing of particles, even in the absence of Brownian motion. One well-known manifestation of lateral migration of neutrally buoyant rigid particles under flow is the Segré–Silberberg effect, where particles in Poiseuille tube flow accumulate in a thin annular region, avoiding both the wall and the centre region of the channel (Segré & Silberberg Reference Segré and Silberberg1961). While this phenomenon results from a competition between inertial lift forces and viscous drag (Ho & Leal Reference Ho and Leal1974), flow-induced migration and non-Brownian diffusion can (and do) persist even at zero Reynolds number. In Stokes flow, non-colloidal particles can migrate laterally relative to the bulk flow, first noted in shear flows by Eckstein, Bailey & Shapiro (Reference Eckstein, Bailey and Shapiro1977), who computed lateral shear-induced diffusion by monitoring a marked tracer particle in a Couette viscometer in the velocity-gradient direction. Leighton & Acrivos (Reference Leighton and Acrivos1987a
) refined the measurement of lateral shear-induced diffusion, inferring the diffusivity from the time elapsed for a marked particle to complete a circuit of the Couette device. The elapsed time can be obtained with higher precision than the velocity-gradient position coordinate, allowing Leighton and Acrivos to show that, in the dilute limit, the lateral shear-induced self-diffusion in a suspension of neutrally buoyant non-colloidal particles is proportional to
$\dot{{\it\gamma}}a^{2}{\it\phi}^{2}$
, where
$\dot{{\it\gamma}}$
is the shear rate,
${\it\phi}$
is the volume fraction of particles and
$a$
is the particle radius. Notably, the coefficient
${\it\phi}^{2}$
indicates that three-body or higher interactions are essential to shear-induced migration, a manifestation of the fore–aft symmetry of two-sphere trajectories in Stokes flow.
The requirement of at least three-body interactions for lateral shear migration applies specifically to the ‘pure-hydrodynamic’ limit; namely, where particles in suspension move and flow in the absence of Brownian motion or direct particle interactions. Lateral migration can arise from pairwise interactions in shear flow only when non-hydrodynamic forces drive particles off their Stokes-flow trajectories and in turn destroy reversibility. Such irreversibility in non-Brownian suspensions can arise from particle eccentricity (Beimfohr, Looby & Leighton Reference Beimfohr, Looby, Leighton, Plasynski, Peters and Roco1993) or roughness (Davis Reference Davis1992; da Cunha & Hinch Reference da Cunha and Hinch1996), where surface asperities that correspond to repulsive forces as short-ranged as one ten-thousandth of a particle size result in irreversible collisions. As a result, particles move past one another on trajectories that are farther in the velocity-gradient and vorticity directions than those describing the approach. No matter what the source of irreversible pairwise interactions, the appropriate scaling for lateral hydrodynamic diffusion becomes linear in the volume fraction of particles, i.e. proportional to
$\dot{{\it\gamma}}a^{2}{\it\phi}$
, with some functional dependence on the range of interparticle interactions.
Broken flow symmetry leads to anisotropic flow-induced diffusion and shear-induced migration in non-colloidal suspensions (Eckstein et al.
Reference Eckstein, Bailey and Shapiro1977; Gadala-Maria & Acrivos Reference Gadala-Maria and Acrivos1980; Leighton & Acrivos Reference Leighton and Acrivos1987a
,Reference Leighton and Acrivos
b
), but Stokes-flow symmetries may also be broken by multibody interactions. Acrivos et al. (Reference Acrivos, Batchelor, Hinch, Koch and Mauri1992) quantified part of this anisotropy: for a given pair of nearly touching spheres in simple shear flow, a second pair of particles colliding nearby disrupts the velocity-gradient coordinates of the nearly touching pair, demonstrating that hydrodynamic interactions generate longitudinal shear-induced diffusion proportional to
$\dot{{\it\gamma}}a^{2}{\it\phi}\ln ({\it\phi}^{-1})$
, much stronger than the
$O({\it\phi}^{2})$
transverse diffusion. Anisotropic diffusion has thus played an important role in understanding departures from reversibility and can be a harbinger of non-Newtonian rheology: non-zero normal stress differences and particle pressure emerge from the same sources of anisotropic diffusion in strongly sheared flows (Brady & Morris Reference Brady and Morris1997), with corresponding results obtained in microrheological flows (Zia & Brady Reference Zia and Brady2010, Reference Zia and Brady2012).
Anisotropic hydrodynamic diffusion is also observed in sedimenting suspensions with diffusion greater along the direction of body forces than transverse to it. In the direction of gravity, such diffusion has been shown to initially increase with concentration in dilute sedimenting suspensions (Ham & Homsy Reference Ham and Homsy1988), but the trend reverses and self-diffusion decreases for higher concentrations (Nicolai et al. Reference Nicolai, Herzhaft, Hinch, Oger and Guazzelli1995). When the sedimenting suspension is dense, a particle can become confined in a cage of particles as it sediments, and mechanisms for diffusion shift from single-particle fluctuations to relatively weaker collective fluctuations. Hydrodynamic diffusion in sedimenting suspensions is independent of the container size (Nicolai & Guazzelli Reference Nicolai and Guazzelli1995), as predicted by Koch & Shaqfeh (Reference Koch and Shaqfeh1991) via a ‘screening’ mechanism, where the presence of a nearby third particle destabilizes and consequently reduces the likelihood of trajectories of nearly touching particles falling in tandem. Common to these studies is the uniformity of particles in size, shape and density.
When the tracer-particle density differs from that of the background spheres, a particle pair sediments relative to one another. In the special case where the background spheres are neutrally buoyant, polydisperse sedimentation simplifies to the experimental technique of falling-ball rheometry. Resultant pairwise interactions reduce the mean fall speed (Batchelor Reference Batchelor1982; Batchelor & Wen Reference Batchelor and Wen1982; Milliken et al. Reference Milliken, Mondy, Gottlieb, Graham and Powell1989; Almog & Brenner Reference Almog and Brenner1997) and induce velocity fluctuations (Nicolai, Peysson & Guazzelli Reference Nicolai, Peysson and Guazzelli1996) and hydrodynamic diffusion (Davis Reference Davis1992; Davis & Hill Reference Davis and Hill1992; Abbott et al. Reference Abbott, Graham, Mondy and Brenner1998) in non-colloids. As is the case for suspensions of hard spheres in pure straining flow (Batchelor & Green Reference Batchelor and Green1972), the microstructure in falling-ball rheometry about a test sphere is fore–aft symmetric in the pure-hydrodynamic limit and is, in fact, spherically symmetric (Batchelor Reference Batchelor1982). This microstructural symmetry in dilute suspensions exerts a powerful influence on the macroscopic response: the material behaves as a Newtonian fluid, in contrast to the well-known non-Newtonian rheology of colloidal dispersions such as shear thinning, shear thickening and non-zero normal stress differences which persist even when Brownian motion is very weak compared with the imposed flow, owing to a highly asymmetric microstructure confined to a thin diffusive boundary layer at particle contact. Almog & Brenner (Reference Almog and Brenner1997) studied the non-colloidal (pure-hydrodynamic) limit of falling-ball rheometry: Batchelor’s spherically symmetric microstructure, which neglects a diffusive boundary layer at contact, fully determines the mean fall speed of a falling ball. From this steady fall speed, they determined the (Newtonian) intrinsic viscosity of the suspension, demonstrating the highly singular limit of infinitesimally weak Brownian motion in colloidal suspensions.
In addition to mean sedimenting motion, it has been shown that fluctuations in non-colloidal tracer velocity exist, and lead to diffusion. Encounters between the falling ball and the background particles produce velocity fluctuations, as the tracer samples a range of suspension densities, from particle-free solvent pockets to long-duration close encounters with other particles. Davis & Hill (Reference Davis and Hill1992) predicted such fluctuations in non-colloids, finding that they lead to anisotropic flow-induced diffusion, along and transverse to the force of gravity. The latter was found to be zero, consistent with the reversibility of Stokes flow. Davis (Reference Davis1992) showed that a non-zero lateral diffusion can be obtained in such systems only by breaking the fore–aft symmetry of pairwise particle trajectories. Davis & Hill (Reference Davis and Hill1992) did find tracer tracer diffusion along the direction of gravity, which scaled as
$D_{\Vert }\sim aU_{S}{\it\phi}$
, where
$U_{S}$
is the Stokes velocity of a particle of size
$a$
alone in solvent, and
${\it\phi}$
is the volume fraction of bath particles. This result is somewhat surprising given the spherical symmetry of the suspension microstructure, but the authors noted that background particles that approach the probe nearly coincident with the line of forcing contribute most strongly to the velocity variance of the probe. These particles, described as having a small ‘impact parameter,’ are able to approach most closely to the probe, and hence most significantly alter the speed of the falling ball. Purely hydrodynamic diffusion is consequently thought to arise primarily due to close encounters between particle pairs, although the trajectory analysis of Davis & Hill (Reference Davis and Hill1992) neglected thermal and entropic forces critical in nearly touching configurations, suggesting that the limit of infinitely weak Brownian motion is highly singular with respect to fluctuations as well.
A connection between the non-colloidal limit and flow-induced diffusion in colloidal suspensions can be found in recent studies of probe fluctuations in microrheology. Zia & Brady (Reference Zia and Brady2010) showed that force-induced diffusion in the limits of weak Brownian motion and no hydrodynamic interactions is anisotropic, with strong diffusion both along and transverse to the line of forcing. Both components scale as
$a_{th}U_{S}{\it\phi}$
, based on the thermodynamic size
$a_{th}$
of the probe, which is large compared with the hydrodynamic (no-slip) radius. Neglecting hydrodynamic interactions evidently gives rise to a much weaker degree of longitudinal versus transverse anisotropy, which is to be expected since even weak Brownian motion or interparticle forces easily destroy fore–aft symmetry.
In the present study, we consider force-induced diffusion in microrheology in the limit of pure hydrodynamics, where Brownian motion plays no role. To do so requires description of the mean and fluctuating suspension microstructure. Advection drives more pronounced microstructural distortion when hydrodynamic interactions are considered, with greater accumulation of pair density about the probe and stronger fluctuations. We find, however, that fluctuations driven by advection cannot induce hydrodynamic diffusion without non-hydrodynamic forces near contact. We utilize the excluded-annulus model to determine the character and value of such interparticle forces in the pure-hydrodynamic limit. We show that, while they cannot generate translational motion, interparticle forces must be present even in the pure-hydrodynamic limit: the probe particle occupies a finite region of the suspension, from which bath particles are entropically excluded. The interparticle force reconciles the non-colloidal limit of active microrheology with prior studies of falling-ball rheometry by inducing diffusion along the line of probe forcing.
The remainder of this paper is organized as follows. The theoretical framework is presented in § 2, including a review of two-sphere hydrodynamics in § 2.1. Next, statistical mechanics is utilized to study probe flux, and leads to expressions for the hydrodynamic flow-induced diffusion,
$\unicode[STIX]{x1D63F}^{\,flow}$
, in § 2.2. The Smoluchowski equation yields governing equations for both the mean and the fluctuating microstructure about the probe in § 2.3. A first look at the fluctuation field and hydrodynamic diffusion is presented in § 3.2, where all components of the force-induced diffusivity are identically zero. Because this result conflicts with experimental measurements and theoretical predictions for falling-ball rheometry, a closer look is taken in § 3.3 at the simplifying assumptions made in our model. Motivated by the findings of Davis & Hill (Reference Davis and Hill1992) that small-impact-parameter encounters most strongly contribute to diffusion, the excluded-annulus model is utilized to study relative trajectories and the balance of forces at contact. The interparticle force is shown to play a surprising role in the pure-hydrodynamic limit, where the longitudinal force-induced diffusivity is obtained from the interparticle flux. Our results are in excellent agreement with corresponding measurements for falling-ball rheometry. A comparison between the new theory and falling-ball rheometry is presented in § 4, and the study is concluded with a summary discussion in § 5.
2. Theoretical framework
We consider a suspension of volume
$V$
comprising
$N_{b}$
rigid non-colloidal spheres of radius
$a$
dispersed homogeneously in a Newtonian fluid of density
${\it\rho}$
and dynamic viscosity
${\it\eta}$
. The bath particles are external force- and torque-free. A ‘probe’ particle, also of radius
$a$
, is dragged by a constant external force
$\boldsymbol{F}^{ext}$
through the suspension, setting the fluid and particles into motion. The Reynolds number
$Re\equiv {\it\rho}Ua/{\it\eta}\ll 1$
, so the fluid mechanics are governed by the Stokes equations. Here,
$U$
is the characteristic fluid velocity set by probe motion. In the dilute limit, the volume fraction of bath particles
${\it\phi}\equiv (4{\rm\pi}a^{3}/3)N_{b}/V\ll 1$
, and only pair interactions matter. A relative coordinate system is adopted, with the probe centred at a position
$\boldsymbol{z}$
and a bath particle centred at
$\boldsymbol{r}$
relative to the probe (figure 1). Interactions with bath particles hinder mean probe motion and give rise to fluctuations in the probe trajectory. In the so-called ‘pure-hydrodynamic’ limit, encounters between probe and bath particles are strictly non-colloidal. To begin the analysis, we briefly review two-body hydrodynamic interactions.
Figure 1. Model system.
2.1. Two-body hydrodynamics
In Stokes flow, the velocity of a particle
${\it\alpha}\in \{1,2\}$
entrained by the motion of a particle
${\it\beta}\in \{1,2\}$
is linear in the forces on particle
${\it\beta}$
. Here,
$1$
and
$2$
represent the probe and bath particle respectively. The strength of entrainment is given by the hydrodynamic mobility tensor
$\unicode[STIX]{x1D648}_{{\it\alpha}{\it\beta}}^{UF}$
, which has the tensorial form
$$\begin{eqnarray}\unicode[STIX]{x1D648}_{{\it\alpha}{\it\beta}}^{UF}={\displaystyle \frac{1}{6{\rm\pi}{\it\eta}a}}[x_{{\it\alpha}{\it\beta}}^{a}(r/a)\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+y_{{\it\alpha}{\it\beta}}^{a}(r/a)(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})],\end{eqnarray}$$
where
$r=|\boldsymbol{r}|$
is the centre-to-centre separation,
$\hat{\boldsymbol{r}}=\boldsymbol{r}/r$
is the unit vector parallel to the line of centres and
$\unicode[STIX]{x1D644}$
is the second-rank identity tensor. The functions
$x_{{\it\alpha}{\it\beta}}^{a}$
and
$y_{{\it\alpha}{\it\beta}}^{a}$
are the well-known scalar mobility functions (Jeffrey & Onishi Reference Jeffrey and Onishi1984; Kim & Karrila Reference Kim and Karrila2005) describing the hydrodynamic coupling between particle motion and probe forcing parallel and transverse to the line of centres respectively. These functions depend only on geometry, and are fully characterized, for identically sized particles, by the dimensionless centre-to-centre separation
$r/a$
. If the probe and bath particles are identically sized spheres,
$\unicode[STIX]{x1D648}_{11}^{UF}=\unicode[STIX]{x1D648}_{22}^{UF}$
and
$\unicode[STIX]{x1D648}_{12}^{UF}=\unicode[STIX]{x1D648}_{21}^{UF}$
. The configuration-dependent velocity of particle
${\it\alpha}$
arising from the applied external force is given by
$\boldsymbol{U}_{{\it\alpha}}=\unicode[STIX]{x1D648}_{{\it\alpha}1}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}$
, and is independent of the absolute position
$\boldsymbol{z}$
of the probe.
The motion of a bath particle relative to the probe,
$\boldsymbol{U}_{rel}\equiv \boldsymbol{U}_{2}\,-\,\boldsymbol{U}_{1}$
, can be formed from a linear combination of the functions
$x_{{\it\alpha}{\it\beta}}^{a}$
and
$y_{{\it\alpha}{\it\beta}}^{a}$
. Following the notation of Batchelor (Reference Batchelor1982), relative motion is expressed compactly by the scalar functions
$L(r/a)$
and
$M(r/a)$
, the couplings along and transverse to the line of centres respectively,
$$\begin{eqnarray}\displaystyle L(r/a) & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \displaystyle x_{11}^{a}(r/a)-x_{21}^{a}(r/a),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M(r/a) & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \displaystyle y_{11}^{a}(r/a)-y_{21}^{a}(r/a),\end{eqnarray}$$
$\boldsymbol{F}^{ext}$
in the presence of a bath particle, 
$$\begin{eqnarray}\boldsymbol{U}_{rel}=-[L(r/a)\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+M(r/a)(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})]\boldsymbol{\cdot }\boldsymbol{U}_{S}.\end{eqnarray}$$
Here,
$\boldsymbol{U}_{S}=\boldsymbol{F}^{ext}/(6{\rm\pi}{\it\eta}a)$
is the Stokes velocity. Particle motion
$\boldsymbol{U}_{{\it\alpha}}$
induces flux
$\boldsymbol{j}_{{\it\alpha}}$
through the suspension, from which the flow-induced diffusion can be inferred.
2.2. Flux and flow-induced diffusivity
Probe motion through the bath distorts the microstructural configuration, leading to many possible distorted arrangements. The likelihood of any one arrangement
$\{\boldsymbol{z},\boldsymbol{r}\}$
of probe and bath particle at time
$t$
is given by the pair probability density
$P_{2}(\boldsymbol{z},\boldsymbol{r};t)$
. In the non-colloidal limit, advective and interparticle forces drive particle flux, but thermal fluctuations play no role in particle configuration. Translational motion of particle
${\it\alpha}$
advects pair density as defined by the flux
$\boldsymbol{j}_{{\it\alpha}}$
:
$$\begin{eqnarray}\boldsymbol{j}_{{\it\alpha}}=\boldsymbol{U}_{{\it\alpha}}P_{2}(\boldsymbol{z},\boldsymbol{r};t)=[\unicode[STIX]{x1D648}_{{\it\alpha}1}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}-(\unicode[STIX]{x1D648}_{{\it\alpha}1}^{UF}-\unicode[STIX]{x1D648}_{{\it\alpha}2}^{UF})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\boldsymbol{ r}}V(\boldsymbol{r})]P_{2}(\boldsymbol{z},\boldsymbol{r};t),\end{eqnarray}$$
where the interparticle potential,
$V(\boldsymbol{r})$
, is a function only of the position
$\boldsymbol{r}$
of a bath particle relative to the probe. In the present study, we consider hard particles that cannot overlap:
$$\begin{eqnarray}V(\boldsymbol{r})=\left\{\begin{array}{@{}ll@{}}\infty ,\quad & r\leqslant r_{min},\\ 0,\quad & r>r_{min},\end{array}\right.\end{eqnarray}$$
where the minimum-approach distance
$r_{min}$
defines the no-overlap surface. The excluded-annulus model (Russel Reference Russel1984) allows particles to interact hydrodynamically at their no-slip surfaces,
$a$
, yet also allows non-hydrodynamic forces to play a role in particle motion. Surface asperities, electrostatic layers and adsorbed polymers, for example, can prevent overlap at a surface
$r_{min}>2a$
that extends beyond the hydrodynamic radius. In the present study, the hydrodynamic (no-slip) radius coincides exactly with the no-overlap surface,
$r_{min}=2a$
, a condition that defines the model of the pure-hydrodynamic limit.
We restrict our attention to accessible configurations for which particles do not overlap. Additionally, the vanishing relative radial mobility at contact prohibits bath particles from making contact with the probe. With no interparticle forces acting beyond
$r=2a$
, the flux is purely advective:
$$\begin{eqnarray}\boldsymbol{j}_{{\it\alpha}}=\boldsymbol{U}_{{\it\alpha}}P_{2}(\boldsymbol{z},\boldsymbol{r};t)=\unicode[STIX]{x1D648}_{{\it\alpha}1}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}P_{2}(\boldsymbol{z},\boldsymbol{r};t).\end{eqnarray}$$
Transformation to Fourier space facilitates identification of the mean and fluctuating probe motion (Zia & Brady Reference Zia and Brady2010):
$$\begin{eqnarray}\tilde{\boldsymbol{j}}_{1}=\unicode[STIX]{x1D648}_{11}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}\tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t),\end{eqnarray}$$
where
$\tilde{\boldsymbol{j}}_{1}$
and
$\tilde{P_{2}}$
are the Fourier transforms of the probe flux and pair probability respectively, and
$\boldsymbol{k}$
is the wavevector.
We are interested in the flux of the probe after many encounters with bath particles; to this end, the flux
$\tilde{\boldsymbol{j}}_{1}$
is averaged over all pair configurations:
$$\begin{eqnarray}\langle \,\tilde{\boldsymbol{j}}_{1}\rangle =\boldsymbol{U}_{S}\tilde{P}_{1}(\boldsymbol{k};t)+\displaystyle \int _{\!r\geqslant 2a}[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\boldsymbol{U}_{S}\tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t)\,\text{d}\boldsymbol{r},\end{eqnarray}$$
where
$\tilde{P}_{1}(\boldsymbol{k};t)$
is the Fourier transform of the probe probability density
$P_{1}(\boldsymbol{z};t)\equiv \int P_{2}(\boldsymbol{z},\boldsymbol{r};t)\,\text{d}\boldsymbol{r}$
. The first term in (2.8) is the probe flux through pure solvent, while the integral term describes how hydrodynamic interactions with bath particles modify the average probe flux. To evaluate this integral, the detailed distribution of bath particles about the probe is required, motivating the definition of the structure function
$g_{\boldsymbol{k}}(\boldsymbol{k},\boldsymbol{r};t)$
:
$$\begin{eqnarray}\tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t)\equiv n_{b}g_{\boldsymbol{k}}(\boldsymbol{k},\boldsymbol{r};t)\tilde{P}_{1}(\boldsymbol{k};t),\end{eqnarray}$$
where
$n_{b}=3{\it\phi}/(4{\rm\pi}a^{3})$
is the number density of bath particles. Distinction between the structure function
$g_{\boldsymbol{k}}(\boldsymbol{k},\boldsymbol{r};t)$
and related quantities such as the real-space pair distribution function
$g_{\boldsymbol{z}}(\boldsymbol{z},\boldsymbol{r};t)$
and the structure factor
$S(\boldsymbol{z},\boldsymbol{q};t)$
is given by Zia & Brady (Reference Zia and Brady2010).
We are interested in the mean and fluctuating motion of the probe after many encounters with bath particles, which occur over large distances and long times, corresponding to small wavevectors
$\boldsymbol{k}$
. Expanding the structure function
$g_{\boldsymbol{k}}$
for small
$\boldsymbol{k}$
gives
$$\begin{eqnarray}g_{\boldsymbol{k}}(\boldsymbol{r},\boldsymbol{k};t)=g(\boldsymbol{r};t)+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{d}(\boldsymbol{r};t)+O(|\boldsymbol{k}|^{2}),\end{eqnarray}$$
where
$\text{i}$
is the imaginary unit. The first term on the right-hand side of (2.10) gives the mean particle configuration,
$g(\boldsymbol{r};t)$
, and describes the likelihood of finding a bath particle at
$\boldsymbol{r}$
with which to interact. The second term corresponds to fluctuations in the particle configuration – a probability-weighted displacement, or fluctuation field,
$\boldsymbol{d}(\boldsymbol{r};t)$
, giving the strength and direction of a ‘kick’ from probe–microstructure interactions.
The small-
$\boldsymbol{k}$
expansion (2.10) of the structure function is substituted into the probe flux (2.8) to give
$$\begin{eqnarray}\displaystyle \langle \,\tilde{\boldsymbol{j}}_{1}\rangle & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \left\{\left[\boldsymbol{U}_{S}+U_{S}n_{b}\displaystyle \int _{\!r\geqslant 2a}g(\boldsymbol{r};t)[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\hat{\boldsymbol{F}}\,\text{d}\boldsymbol{r}\right]\right.\nonumber\\ \displaystyle \hspace{-2.0pt} & \hspace{-2.0pt} & \displaystyle -\,\left.\text{i}\boldsymbol{k}\boldsymbol{\cdot }\left[-U_{S}n_{b}\displaystyle \int _{\!r\geqslant 2a}\boldsymbol{d}(\boldsymbol{r};t)[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\hat{\boldsymbol{F}}\,\text{d}\boldsymbol{r}\right]\right\}\tilde{P}_{1}(\boldsymbol{k};t),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$U_{S}=|\boldsymbol{U}_{S}|$
is the magnitude of the Stokes velocity and
$\hat{\boldsymbol{F}}=\boldsymbol{F}^{ext}/|\boldsymbol{F}^{ext}|$
is the unit vector parallel to the applied external force. Following Zia & Brady (Reference Zia and Brady2010), the terms in (2.11) are bracketed into two groups: the first is independent of wavevector
$\boldsymbol{k}$
and the second is
$O(\boldsymbol{k})$
. The
$O(1)$
terms describe the mean probe response to the applied external force: the Stokes velocity, plus the reduction in the probe speed due to hydrodynamic interactions with bath particles, averaged over all configurations. This term corresponds to advective flux, and is consistent with the coefficient for the mean disturbance velocity
$k_{m}$
defined by Davis & Hill (Reference Davis and Hill1992), the constant-force apparent viscosity coefficient
$k_{m}^{F}$
of Almog & Brenner (Reference Almog and Brenner1997) and the intrinsic hydrodynamic microviscosity
${\it\eta}_{i}^{H}$
of Khair & Brady (Reference Khair and Brady2006).
The
$O(\boldsymbol{k})$
integral describes fluctuations in probe motion arising from hydrodynamic flow-induced deflections of the probe. This term corresponds to diffusive flux:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\,flow}=-U_{S}n_{b}\displaystyle \int _{\!r\geqslant 2a}\boldsymbol{d}(\boldsymbol{r};t)[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\hat{\boldsymbol{F}}\,\text{d}\boldsymbol{r}.\end{eqnarray}$$
Because Brownian diffusion is absent, we identify equation (2.12) as the (strictly) hydrodynamic flow-induced diffusivity,
$\unicode[STIX]{x1D63F}^{\,flow}$
. Here, encounters between probe and bath particles cause the probe velocity to fluctuate and, in turn, drive a diffusive spread of its trajectory. These fluctuations arise due to natural variation in such encounters that depend on the so-called impact parameter (Davis & Hill Reference Davis and Hill1992): the offset between the bath-particle trajectory and the line of external forcing (figure 1). Unlike shear flow, relative trajectories in microrheology are open, indicating that the probe and bath particle always pass one another. However, the time required to approach, pass and move past a particle depends on the details of the approach and, in turn, on the longitudinal and transverse hydrodynamic couplings (2.2a
) and (2.2b
). That is, a bath particle approaching nearly along the
$z$
axis (
${\it\theta}\approxeq 0$
in figure 1) spends a longer time interacting with the probe along a pair trajectory than a bath particle offset farther in
$x$
and
$y$
(larger values of
${\it\theta}$
).
Equation (2.12) indicates that, despite the entirely deterministic motion of non-Brownian particles, the probe undergoes a random walk. The origin of randomness for this walk is the homogeneity of the suspension far from the probe: a bath-particle trajectory is equally likely to begin anywhere relative to the
$z$
axis of the probe (the line of forcing), and its trajectory is entirely determined by its initial (random) position far away. These random offsets lead to random fluctuations in probe motion. However, fore–aft symmetry of two-sphere relative trajectories prevents net migration of the probe transverse to the applied external force; that is, no lateral diffusive migration is permitted owing to the reversibility of Stokes flow. As a result, it is expected that
$\unicode[STIX]{x1D63F}^{\,flow}$
has only one non-zero component along the line of external force. The determination of the fluctuation field
$\boldsymbol{d}(\boldsymbol{r};t)$
is the next step in obtaining force-induced diffusion.
2.3. The fluctuation field
The two-particle Smoluchowski equation governs the spatiotemporal evolution of the pair probability density:
$$\begin{eqnarray}{\displaystyle \frac{\partial P_{2}(\boldsymbol{z},\boldsymbol{r};t)}{\partial t}}+\boldsymbol{{\rm\nabla}}_{\boldsymbol{z}}\boldsymbol{\cdot }\boldsymbol{j}_{1}+\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }(\boldsymbol{j}_{2}-\boldsymbol{j}_{1})=0,\end{eqnarray}$$
where the flux
$\boldsymbol{j}_{{\it\alpha}}=\unicode[STIX]{x1D648}_{{\it\alpha}1}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}P_{2}$
of particle
${\it\alpha}$
is purely advective in the pure-hydrodynamic non-colloidal regime: microstructural evolution is driven solely by the fixed external force
$\boldsymbol{F}^{ext}$
. Transforming (2.13) on the probe position
$\boldsymbol{z}$
to Fourier space gives
$$\begin{eqnarray}{\displaystyle \frac{\partial \tilde{P}_{2}(\boldsymbol{k},\boldsymbol{r};t)}{\partial t}}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\tilde{\boldsymbol{j}}_{1}+\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }(\tilde{\boldsymbol{j}}_{2}-\tilde{\boldsymbol{j}}_{1})=0.\end{eqnarray}$$
The Smoluchowski equation (2.14) is ensemble-averaged over all bath-particle configurations to yield a single-particle Smoluchowski equation for the probe:
$$\begin{eqnarray}{\displaystyle \frac{\partial \tilde{P}_{1}}{\partial t}}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{U}_{S}\tilde{P}_{1}=-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\langle (\unicode[STIX]{x1D648}_{11}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}-\boldsymbol{U}_{S})\tilde{P}_{2}\rangle -\langle \boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }(\tilde{\boldsymbol{j}}_{2}-\tilde{\boldsymbol{j}}_{1})\rangle .\end{eqnarray}$$
Scaling (2.15) on the advective time scale, substituting the definition of the structure function (2.9) and dividing all terms by
$\tilde{P}_{1}U_{S}/a$
gives
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{1}{\tilde{P}_{1}}}{\displaystyle \frac{\partial \tilde{P}_{1}}{\partial t}}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\hat{\boldsymbol{F}} & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle -{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\left(\text{i}\boldsymbol{k}\boldsymbol{\cdot }\displaystyle \int _{\!r\geqslant 2} (\hspace{1.0pt}(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(y_{11}^{a}-1)\unicode[STIX]{x1D644})\!g_{\boldsymbol{k}}\,\text{d}\boldsymbol{r}+\displaystyle \oint _{r=2}Lg_{\boldsymbol{k}}\hat{\boldsymbol{r}}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\,\text{d}S\right).\end{eqnarray}$$
Here, length and time have been made dimensionless on the particle radius
$a$
and the advective time scale
$a/U_{S}$
respectively. Length and time variables are henceforth dimensionless by these scales unless otherwise noted. Noting that the right-hand side of (2.16) is
$O({\it\phi})$
, which is small, gives
$$\begin{eqnarray}{\displaystyle \frac{1}{\tilde{P}_{1}}}{\displaystyle \frac{\partial \tilde{P}_{1}}{\partial t}}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\hat{\boldsymbol{F}}=O({\it\phi})\ll 1.\end{eqnarray}$$
Equations (2.14) and (2.17) are combined, and terms to leading order in
${\it\phi}$
are kept to obtain the dimensionless governing equation for the structure function
$g_{\boldsymbol{k}}$
:
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{\partial g_{\boldsymbol{k}}(\boldsymbol{r},\boldsymbol{k};t)}{\partial t}}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\hat{\boldsymbol{F}}g_{\boldsymbol{ k}}(\boldsymbol{r},\boldsymbol{k};t)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }([L\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+M(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})]\boldsymbol{\cdot }\hat{\boldsymbol{F}}g_{\boldsymbol{k}}(\boldsymbol{r},\boldsymbol{k};t))=0.\end{eqnarray}$$
The small-
$\boldsymbol{k}$
expansion (2.10) is substituted into (2.18); the advective terms (those independent of
$\boldsymbol{k}$
) govern the steady non-equilibrium microstructure
$g(\boldsymbol{r})$
, which at steady state reads
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }([L\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+M(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})]\boldsymbol{\cdot }\hat{\boldsymbol{F}}g(\boldsymbol{r}))=0.\end{eqnarray}$$
Terms of
$O(\boldsymbol{k})$
govern the fluctuation field
$\boldsymbol{d}(\boldsymbol{r})$
:
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }([L\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+M(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})]\boldsymbol{\cdot }\hat{\boldsymbol{F}}\boldsymbol{d}(\boldsymbol{r}))=[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\hat{\boldsymbol{F}}g(\boldsymbol{r}).\end{eqnarray}$$
Equations (2.19) and (2.20) govern the evolution of the mean microstructure and its fluctuations respectively. Each is a first-order differential equation, so at most one boundary condition may be enforced. The deformation of the suspension microstructure due to the translating probe decays over large separations
$r$
, i.e. the conditional probability density
$\tilde{P}_{1|1}(\boldsymbol{r}|\boldsymbol{k})$
approaches the unconditional probability density
$P_{1}(\boldsymbol{r})=n_{b}$
. The corresponding dimensionless boundary conditions for the steady microstructure
$g(\boldsymbol{r})$
and the fluctuation field
$\boldsymbol{d}(\boldsymbol{r})$
are
$$\begin{eqnarray}g(\boldsymbol{r})\rightarrow 1\quad \text{as }r\rightarrow \infty\end{eqnarray}$$
and
$$\begin{eqnarray}\boldsymbol{d}(\boldsymbol{r})\rightarrow \mathbf{0}\quad \text{as }r\rightarrow \infty .\end{eqnarray}$$
Having established the governing equations and boundary conditions for the mean microstructure
$g(\boldsymbol{r})$
and its fluctuations
$\boldsymbol{d}(\boldsymbol{r})$
, we may return to the hydrodynamic force-induced diffusion (2.12), which, in terms of dimensionless variables, reads
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\,flow}=-aU_{S}{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\displaystyle \int _{\!r\geqslant 2}\boldsymbol{d}(\boldsymbol{r})[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\hat{\boldsymbol{F}}\,\text{d}\boldsymbol{r}.\end{eqnarray}$$
As discussed above, the probe undergoes a random walk arising from many encounters with background bath particles. The flow-induced diffusion given by (2.23) is thus strictly hydrodynamic in origin; no Brownian motion is required, giving the advective scaling
$\unicode[STIX]{x1D63F}^{\,flow}\sim aU_{S}{\it\phi}$
in (2.23) expected for self-diffusion in non-colloids. The linear scaling in the volume fraction
${\it\phi}$
of bath particles is also expected, since only one bath particle must be present for the probe velocity to deviate from
$\boldsymbol{U}_{S}$
.
In the next section, we present the solutions of the governing equations (2.19) and (2.20) for the mean microstructure
$g(\boldsymbol{r})$
and its fluctuations
$\boldsymbol{d}(\boldsymbol{r})$
and, from them, compute the hydrodynamic flow-induced diffusivity,
$\unicode[STIX]{x1D63F}^{\,flow}$
.
3. Results
Microstructural fluctuations
$\boldsymbol{d}(\boldsymbol{r})$
produce a diffusive spread of the probe trajectory, leading to hydrodynamic force-induced diffusion
$\unicode[STIX]{x1D63F}^{\,flow}$
, and are forced by hydrodynamic interactions of the probe with the mean microstructure
$g(\boldsymbol{r})$
. Computation of
$\unicode[STIX]{x1D63F}^{\,flow}$
thus requires solution of the Smoluchowski equations for both the mean (2.19) and the fluctuating (2.20) microstructure. In the pure-hydrodynamic limit, the solution for
$g(\boldsymbol{r})$
is well known, but a brief review is presented in § 3.1 for heuristic value. This review is followed by the solution for the fluctuation field,
$\boldsymbol{d}$
, and finally the flow-induced diffusivity,
$\unicode[STIX]{x1D63F}^{\,flow}$
.
3.1. The mean microstructure
The mean microstructure about an externally forced non-Brownian probe has been studied in the analogous frameworks of sedimentation in polydisperse suspensions (Batchelor Reference Batchelor1982; Batchelor & Wen Reference Batchelor and Wen1982) and falling-ball rheometry (Davis & Hill Reference Davis and Hill1992; Almog & Brenner Reference Almog and Brenner1997). In the pure-hydrodynamic limit, the pair structure is spherically symmetric about the probe (Batchelor Reference Batchelor1982) and is given by
$$\begin{eqnarray}g(r)={\displaystyle \frac{1}{L(r)}}\exp \left[\displaystyle \int _{\!r}^{\infty }~{\displaystyle \frac{2}{z}}\left(1-{\displaystyle \frac{M(z)}{L(z)}}\right)\,\text{d}z\right].\end{eqnarray}$$
The microstructural distortion,
$g(r)-1$
, is plotted in figure 2 as a function of the surface-to-surface separation
${\it\xi}\equiv r-2$
(solid black curve). The asymptotic form for widely separated particles shows that disturbances to the microstructure decay as
$1/r^{4}$
(Batchelor Reference Batchelor1982; Almog & Brenner Reference Almog and Brenner1997):
$$\begin{eqnarray}g(r\gg 2)=1+{\textstyle \frac{15}{8}}r^{-4}+O(r^{-5}).\end{eqnarray}$$
Despite the long-range nature of hydrodynamic interactions, which entrain particles with a strength that decays slowly as
$1/r$
, accumulation of pair density about the probe decays more rapidly, as it must – the pair density depends on the divergence of the relative mobility, which describes how particles accumulate along a pair trajectory (and hence spend more time) as they come closer together. Physically, the relative velocity between the probe and bath particles decreases as the pair approaches, resulting in an accumulation of particles.
Figure 2. Strength of distortions to and fluctuations in the mean microstructure, as a function of particle separation. Solid black curve: non-equilibrium distortions
$g(r)-1$
of the mean microstructure grow weaker with increasing particle separation. When a probe and a bath particle approach one another closely,
${\it\xi}\rightarrow 0$
, the structural distortion (particle accumulation) diverges as
${\it\xi}^{-{\it\delta}}f(\log {\it\xi}^{-1})$
, where
${\it\xi}=r-2$
is the fluid gap between particle surfaces and
${\it\delta}=0.799$
for identically sized probe and bath particles. At large separations, the probe-induced structural deformation decays rapidly, as
$r^{-4}$
. Probe fluctuations also grow infinitely large near particle contact, where fluctuations along (red dashed line) and transverse to (blue dotted line) the external force scale as
${\it\xi}^{-1}$
and
${\it\xi}^{-{\it\delta}}f(\log {\it\xi}^{-1})$
respectively. At large separations, the fluctuations decay rapidly, showing that diffusion induced by hydrodynamic interactions with the mean and fluctuating microstructure is most strongly driven by near-contact encounters.
In the opposite limit of nearly touching spheres,
${\it\xi}\ll 1$
, the asymptotic form of
$g(r)$
from (3.1) is set by the lubrication expressions for the relative mobility functions
$L(r)$
and
$M(r)$
defined in (2.2a
) and (2.2b
), expressed here as functions of
${\it\xi}$
:
$$\begin{eqnarray}\displaystyle L({\it\xi}\ll 1) & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \displaystyle l_{1}{\it\xi}+O({\it\xi}^{2}\ln {\it\xi}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M({\it\xi}\ll 1) & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \displaystyle m_{0}+O((\ln {\it\xi}^{-1}-C)^{-1}),\end{eqnarray}$$
$l_{1}$
,
$m_{0}$
and
$C$
are constants that depend only on the relative size of the probe and bath particles. For same-sized particles, the constants
$l_{1}$
and
$m_{0}$
are
$2.000$
and
$0.401$
respectively. The leading-order microstructure
$g(r)$
in the lubrication limit was first reported by Batchelor (Reference Batchelor1982): 
$$\begin{eqnarray}g({\it\xi}\ll 1)\sim {\it\xi}^{-{\it\delta}}~f(\ln {\it\xi}^{-1}),\end{eqnarray}$$
where
${\it\delta}\equiv 1-m_{0}/l_{1}$
is equal to
$0.799$
for same-sized probe and bath particles. This scaling is shown by the solid black curve in figure 2 for small values of
${\it\xi}$
. The weak logarithmic correction
$f(\ln {\it\xi}^{-1})$
arises from the
$O((\ln {\it\xi}^{-1}-C)^{-1})$
terms in (3.3b
). The exact logarithmic correction was later determined by Almog & Brenner (Reference Almog and Brenner1997).
Accumulation of bath-particle density near contact as described by (3.4) may be viewed through the lens of relative trajectories: relative bath-particle motion slows during approach, speeding up again upon passing the probe. As a consequence, more time is elapsed resolving interactions in nearly touching configurations, promoting particle accumulation, while the probe and bath particles spend less time in comparatively more mobile arrangements.
Beyond the asymptotic forms for the suspension microstructure
$g(r)$
at large and small separations given by (3.2) and (3.4) respectively, Batchelor & Wen (Reference Batchelor and Wen1982) obtained a numerical solution to good approximation. Improving upon this solution, Almog & Brenner (Reference Almog and Brenner1997) developed a method utilizing recurrence relations and the twin-multipole expansion coefficients of Jeffrey & Onishi (Reference Jeffrey and Onishi1984). We leverage their approach to evaluate the fluctuation field in § 3.2.
Before continuing to fluctuations in the microstructure, it is worthwhile to comment on connections between material viscosity, microstructure and probe motion in sedimentation (Batchelor Reference Batchelor1982; Batchelor & Wen Reference Batchelor and Wen1982), falling-ball rheometry (Davis & Hill Reference Davis and Hill1992; Almog & Brenner Reference Almog and Brenner1997) and microviscosity (Squires & Brady Reference Squires and Brady2005; Khair & Brady Reference Khair and Brady2006; Swan & Zia Reference Swan and Zia2013; Zia & Brady Reference Zia and Brady2013). Analogous connections are seen here in the suspension-averaged probe flux, where we recall that the first bracketed term on the right-hand side of (2.11) relates probe velocity to structure:
$$\begin{eqnarray}\langle \boldsymbol{U}\rangle =\boldsymbol{U}_{S}\left(1+{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\displaystyle \int _{\!r\geqslant 2}g(\boldsymbol{r})[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{ : }\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\,\text{d}\boldsymbol{r}\right).\end{eqnarray}$$
Owing to a spherically symmetric structure, the rheology is Newtonian in the sense that particle pressure and normal stress differences vanish (Brady & Morris Reference Brady and Morris1997). The mean motion can thus be simplified:
$$\begin{eqnarray}\langle \boldsymbol{U}\rangle =\boldsymbol{U}_{S}\left(1+{\it\phi}\displaystyle \int _{\!2}^{\infty }g(r)[x_{11}^{a}+2y_{11}^{a}-3]r^{2}\,\text{d}r\right)=\boldsymbol{U}_{S}(1-{\it\eta}_{i}^{H}{\it\phi}),\end{eqnarray}$$
where
${\it\eta}_{i}^{H}$
can be viewed as an intrinsic hydrodynamic suspension viscosity. Prior studies examining the mean motion of a falling particle (Batchelor & Wen Reference Batchelor and Wen1982; Davis & Hill Reference Davis and Hill1992; Almog & Brenner Reference Almog and Brenner1997; Khair & Brady Reference Khair and Brady2006; Swan & Zia Reference Swan and Zia2013) all find a similar
$O({\it\phi})$
reduction of mean motion compared with the Stokes velocity. For same-sized probe and bath particles, (3.6) simplifies to
$\boldsymbol{U}_{S}(1-2.52{\it\phi})$
, where entrainment of bath particles diminishes the Stokes velocity
$\boldsymbol{U}_{S}$
as
$2.52{\it\phi}$
(Batchelor & Wen Reference Batchelor and Wen1982; Davis & Hill Reference Davis and Hill1992). That is, the apparent (micro)viscosity is independent of the forcing strength, and is thus Newtonian.
However, when the pure-hydrodynamic limit is approached in a colloidal suspension, non-Newtonian rheology persists even when Brownian motion is very weak. Khair & Brady (Reference Khair and Brady2006) and Swan & Zia (Reference Swan and Zia2013) found that the presence of a diffusive boundary layer near contact serves as a source of apparent force thickening as the pure-hydrodynamic limit is approached by increasing the strength of advection relative to diffusion, as defined by the Péclet number,
$Pe$
. The Newtonian rheology for the pure-hydrodynamic limit has been reconciled with non-Newtonian force thickening in colloidal suspensions as
$Pe\rightarrow \infty$
by recognizing that the bath-particle density inside a thin diffusive boundary layer drives force thickening. Bath particles are driven towards contact by the relative advective flux
$\hat{\boldsymbol{r}}\boldsymbol{\cdot }(\tilde{\boldsymbol{j}}_{2}-\tilde{\boldsymbol{j}}_{1})$
into the boundary layer. This relative advective flux of pair density transitions smoothly to zero at pair contact, as shown by the solid black curve in figure 3. The rheology must become Newtonian in the limit
$Pe^{-1}\equiv 0$
, as the bath-particle density advected into the diffusive boundary layer vanishes, due to a faster decay of relative velocity compared with the rate of bath-particle accumulation. Even though the no-flux boundary condition cannot be formally enforced, the fact that
$g(r)$
satisfies no flux (and thus mass conservation) is both satisfying and central to Newtonian behaviour in the pure-hydrodynamic limit. This perspective will play an important role in the analysis of structural fluctuations, taken up next.
Figure 3. Contributions to the radial relative advective flux
$\hat{\boldsymbol{r}}\boldsymbol{\cdot }(\,\tilde{\boldsymbol{j}}_{2}-\tilde{\boldsymbol{j}}_{1})\sim L(r)g_{\boldsymbol{k}}(\boldsymbol{r})$
in the pure-hydrodynamic limit from the mean
$g(r)$
, longitudinal fluctuating
$d^{\Vert }(\boldsymbol{r})$
and transverse fluctuating
$d^{\bot }(\boldsymbol{r})$
microstructure, as a function of the surface separation distance
${\it\xi}\equiv r-2$
. The longitudinal and transverse fluctuations in the relative radial fluxes are from the spherical harmonics
$d_{1}^{\Vert }(r)P_{1}(\cos {\it\theta})$
and
$d_{1}^{\bot }(r)P_{1}^{1}(\cos {\it\theta})\text{e}^{\text{i}{\it\varphi}}$
respectively. The contributions from the mean and the transverse fluctuating microstructure both decay to zero as
${\it\xi}\rightarrow 0$
, scaling as
${\it\xi}^{1-{\it\delta}}f(\ln {\it\xi}^{-1})$
. In contrast, the radial relative flux from longitudinal fluctuations approaches a constant as
${\it\xi}\rightarrow 0$
. A no-overlap condition for the longitudinal fluctuation field is not automatically satisfied by the solution of the pure-hydrodynamic Smoluchowski equation, suggesting that additional fluxes at contact driven by non-hydrodynamic forces, e.g. thermal, interparticle, etc., arise to oppose the advective flux and act to ensure probability conservation.
3.2. The fluctuation field – a first look
The Smoluchowski equations (2.19) and (2.20) govern the advective distortion of the mean microstructure and its fluctuations. Batchelor’s solution (3.1), discussed in § 3.1, describes spherically symmetric particle accumulation about the probe that reduces the mean probe motion. In this section, we examine the validity of this approach for solving (2.20) for the microstructural fluctuations
$\boldsymbol{d}(\boldsymbol{r})$
.
The fluctuation field can be expressed in terms of scalar components along and transverse to the applied external force:
$$\begin{eqnarray}\boldsymbol{d}(\boldsymbol{r})=d^{\Vert }(r,{\it\theta},{\it\varphi})\hat{\boldsymbol{F}}+\text{Re}[d^{\bot }(r,{\it\theta},{\it\varphi})]\boldsymbol{e}_{x}+\text{Im}[d^{\bot }(r,{\it\theta},{\it\varphi})]\boldsymbol{e}_{y},\end{eqnarray}$$
where
$d^{\Vert }$
and
$d^{\bot }$
are the longitudinal and transverse fluctuation fields respectively. The orthonormal basis of unit vectors
$\{\boldsymbol{e}_{x},\boldsymbol{e}_{y},\hat{\boldsymbol{F}}\}$
describes a coordinate system centred about the probe, oriented relative to the line of the external force, and
${\it\varphi}$
is the azimuthal angle about the line of external forcing as measured from the
$+x$
axis towards the
$+y$
axis. Prior studies have utilized series expansions in Legendre polynomials to numerically evaluate the mean microstructure (Khair & Brady Reference Khair and Brady2006). For the fluctuation field, the spherical harmonics
$P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}$
are a convenient set of orthogonal basis functions to describe the angular dependence of the fluctuation field, where
$P_{l}^{m}(\cos {\it\theta})$
is the associated Legendre polynomial of order
$m$
and degree
$l$
. The solution for
$d^{\Vert }(\boldsymbol{r})$
comprises an infinitude of spherical harmonics of order zero and of odd degree:
$$\begin{eqnarray}d^{\Vert }(\boldsymbol{r})=\mathop{\sum }_{n\,odd}d_{n}^{\Vert }(r)P_{n}(\cos {\it\theta}),\end{eqnarray}$$
where
$P_{n}(\cos {\it\theta})$
is the Legendre polynomial of degree
$n$
, equivalent to the associated Legendre polynomial
$P_{n}^{0}(\cos {\it\theta})$
. All other spherical harmonics are identically zero for
$d^{\Vert }(\boldsymbol{r})$
. The integral solution for the radial dependence of the
$n=1$
harmonic is
$$\begin{eqnarray}d_{1}^{\Vert }(r)=-{\displaystyle \frac{1}{r^{2}L(r)}}\int _{r}^{\infty }g(z)[x_{11}^{a}(z)+2y_{11}^{a}(z)-3]z^{2}\,\text{d}z.\end{eqnarray}$$
The solution for
$d^{\bot }(\boldsymbol{r})$
is a single spherical harmonic of degree one and order one:
$$\begin{eqnarray}d^{\bot }(\boldsymbol{r})=d_{1}^{\bot }(r)P_{1}^{1}(\cos {\it\theta})\text{e}^{\text{i}{\it\varphi}}.\end{eqnarray}$$
The integral solution for the radial dependence of
$d_{1}^{\bot }(r)$
is
$$\begin{eqnarray}d_{1}^{\bot }(r)=rg(r)(L(r)g(r))^{1/2}\displaystyle \int _{\!r}^{\infty }{\displaystyle \frac{x_{11}^{a}(z)-y_{11}^{a}(z)}{zL(z)}}(L(z)g(z))^{-1/2}\,\text{d}z.\end{eqnarray}$$
The details and methods of solution for
$d^{\Vert }(\boldsymbol{r})$
and
$d^{\bot }(\boldsymbol{r})$
are given in appendix A.
The solutions for
$d_{1}^{\Vert }(r)$
and
$d_{1}^{\bot }(r)$
from (3.9) and (3.11) are plotted alongside the mean microstructural deformation in figure 2. At large separations
$r$
, fluctuations decay as
$r^{-3}$
, indicating that widely separated particles do not influence probe fluctuations as strongly as bath particles near the probe surface. Near contact, longitudinal fluctuations (dashed red curve) are inversely proportional to the surface separation distance
${\it\xi}=r-2$
, while transverse fluctuations (dotted blue curve) scale as
${\it\xi}^{-{\it\delta}}f(\ln {\it\xi}^{-1})$
. The disparity in longitudinal and transverse fluctuations near the probe is critical in setting the degree of anisotropy in the diffusion tensor.
The fluctuation field has distinct components longitudinal and transverse to the applied external force
$\boldsymbol{F}^{ext}$
, suggesting that
$\unicode[STIX]{x1D63F}^{\,flow}$
will also be anisotropic. We begin with the transverse flow-induced diffusion
$D_{\bot }^{\,flow}$
. Since the geometry is axisymmetric, both the
$\boldsymbol{e}_{x}\boldsymbol{e}_{x}$
and the
$\boldsymbol{e}_{y}\boldsymbol{e}_{y}$
components of
$\unicode[STIX]{x1D63F}^{\,flow}$
(2.23) are equal to
$D_{\bot }^{\,flow}$
. The
$\boldsymbol{e}_{x}\boldsymbol{e}_{x}$
projection of
$\unicode[STIX]{x1D63F}^{\,flow}$
is
$$\begin{eqnarray}D_{\bot }^{\,flow}=aU_{S}{\it\phi}_{b}{\displaystyle \frac{3}{4{\rm\pi}}}\displaystyle \int _{\!r\geqslant 2}\text{Re}[d^{\bot }(\boldsymbol{r})](x_{11}^{a}(r)-y_{11}^{a}(r))\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\boldsymbol{ : }\hat{\boldsymbol{F}}\boldsymbol{e}_{x}\,\text{d}\boldsymbol{r}.\end{eqnarray}$$
The terms
$d^{\bot }(\boldsymbol{r})$
and
$\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\boldsymbol{ : }\hat{\boldsymbol{F}}\boldsymbol{e}_{x}$
appearing in (3.12) have
${\it\theta}$
dependences of
$P_{1}^{1}(\cos {\it\theta})$
and
$P_{2}^{1}(\cos {\it\theta})$
respectively. The associated Legendre polynomials are mutually orthogonal over the interval
$0\leqslant {\it\theta}\leqslant {\rm\pi}$
; thus, the transverse component of the force-induced diffusivity
$D_{\bot }^{\,flow}$
is identically zero, consistent with the findings of Davis & Hill (Reference Davis and Hill1992).
The longitudinal flow-induced diffusivity
$D_{\Vert }^{\,flow}$
is the
$\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}$
component of
$\unicode[STIX]{x1D63F}^{\,flow}$
:
$$\begin{eqnarray}D_{\Vert }^{\,flow}=aU_{S}{\it\phi}_{b}{\displaystyle \frac{3}{4{\rm\pi}}}\displaystyle \int _{\!r\geqslant 2}d^{\Vert }(\boldsymbol{r})[(x_{11}^{a}(r)-y_{11}^{a}(r))\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}(r)-1)\unicode[STIX]{x1D644}]\boldsymbol{ : }\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}\,\text{d}\boldsymbol{r}.\end{eqnarray}$$
The
${\it\theta}$
dependence of the longitudinal fluctuation field
$d^{\Vert }(\boldsymbol{r})$
is given by the odd Legendre polynomials
$P_{n}(\cos {\it\theta})$
, while the
${\it\theta}$
dependences of the products
$\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}\boldsymbol{ : }\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}$
and
$\unicode[STIX]{x1D644}\boldsymbol{ : }\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}$
appearing in (3.13) are given by
$P_{2}(\cos {\it\theta})$
and
$P_{0}(\cos {\it\theta})$
. The Legendre polynomials are mutually orthogonal over the interval
$0\leqslant {\it\theta}\leqslant {\rm\pi}$
; thus, the longitudinal force-induced diffusion
$D_{\Vert }^{\,flow}$
is also identically zero, in conflict with previous experiments in falling-ball rheometry by Abbott et al. (Reference Abbott, Graham, Mondy and Brenner1998). In addition, previous falling-ball rheometry theory put forth by Davis & Hill (Reference Davis and Hill1992) found that
$D_{\Vert }^{\,flow}=1.33aU_{S}{\it\phi}$
in the pure-hydrodynamic limit. In their trajectory analysis, Davis and Hill determined that incoming bath particles with small impact parameter give the dominant contribution to hydrodynamic diffusion. Particles that approach the probe nearly along the line of forcing are also those that move closest to contact with the probe. This suggests that our first look may have neglected forces influencing pair trajectories near contact.
The advective flux of fluctuations to the probe surface is another indicator that non-hydrodynamic forces near pair contact might matter. The relative radial advective flux
$\hat{\boldsymbol{r}}\,\boldsymbol{\cdot }\,(\tilde{\boldsymbol{j}}_{2}-\tilde{\boldsymbol{j}}_{1})$
is proportional to the product of the relative radial mobility
$L(r)$
and the structure function
$g_{\boldsymbol{k}}(\boldsymbol{r})$
. The product
$Lg_{\boldsymbol{k}}$
is plotted in figure 3. Contributions from the mean (solid black line) and the transverse (dotted blue line) fluctuating microstructure both decay to zero as
${\it\xi}\rightarrow 0$
, scaling as
${\it\xi}^{1-{\it\delta}}f(\ln {\it\xi}^{-1})$
. In contrast, the radial relative flux from longitudinal fluctuations (dashed red line) approaches a non-zero constant as
${\it\xi}\rightarrow 0$
. That is, the no-overlap (no-flux) condition is not automatically satisfied for longitudinal fluctuations by the solution of the pure-hydrodynamic Smoluchowski equation. While a no-flux condition cannot be formally enforced due to the order of the differential equation, the net probability flux into volume occupied by the probe is unsatisfying: the Smoluchowski equation is by definition a conservation statement. Other sources of particle flux at contact, driven by non-hydrodynamic forces (e.g. thermal, interparticle, etc.), oppose the advective flux and, in so doing, drive longitudinal force-induced diffusion.
3.3. The fluctuation field – a closer look
Experimental studies (Abbott et al. Reference Abbott, Graham, Mondy and Brenner1998) and theoretical models (Davis Reference Davis1992; Davis & Hill Reference Davis and Hill1992) for falling-ball rheometry report longitudinal hydrodynamic diffusion in the absence of Brownian motion. In contrast, our ‘first-approach’ microrheology theory found zero flow-induced diffusion in the corresponding pure-hydrodynamic limit. We revisit assumptions made in the formulation of the governing equations to understand this contradictory result. The importance of particle encounters via small-impact-parameter trajectories identified in falling-ball studies (Davis & Hill Reference Davis and Hill1992) provides a clue, and suggests that particle flux near contact requires a closer look.
In § 2.2, kinematic expressions for probe flux were developed. In general, external forces, hydrodynamic interactions, thermal forces and interparticle forces may all play a role in particle motion. The thermal energy
$kT$
plays no role in the non-colloidal limit, so thermal forces were neglected; hydrodynamic interactions were incorporated at the pair level via the hydrodynamic mobility; finally, interparticle forces were included, giving (2.4) for the flux of any particle in the suspension in response to external forcing and interparticle interactions.
Next, a functional form for the interparticle forces was introduced. The conservative interparticle force, derivable from a potential
$V(\boldsymbol{r})$
, gives infinitely large resistance to surface overlap at
$r=2a$
. Further, the properties of Stokes flow dictate that, in the pure-hydrodynamic limit, the relative radial mobility of two particles vanishes at contact. Thus, interparticle forces that act radially outward at particle contact can produce no relative motion. That is,
$\hat{\boldsymbol{r}}\boldsymbol{\cdot }(\unicode[STIX]{x1D648}_{2{\it\beta}}^{UF}-\unicode[STIX]{x1D648}_{1{\it\beta}}^{UF})=\mathbf{0}$
at
$r=2a$
and ensures that
$r\geqslant 2a$
. Physically, interparticle forces act at contact or not at all; when particles do make contact, the interparticle force produces no motion because the relative hydrodynamic mobility is zero there. In consequence, the interparticle force plays no role in the particle velocity in this perspective, and was thus dropped from the particle flux (2.6).
While it is true that the relative radial mobility must be zero at the surface of contact, this led us to conclude that the relative radial flux is also zero; but this somehow does not give the full picture. To take a closer look at the interparticle flux, we consider a force balance at contact comprising interparticle, external and hydrodynamic contributions. An infinitude of forms for the interparticle force satisfy the momentum balance in the pure-hydrodynamic limit, which is not surprising: the constraint of zero hydrodynamic relative mobility at contact makes it so. However, even a very weak departure (a small-but-finite relative mobility at contact) breaks this indeterminacy and thus may provide insight into what was missed. One way to model such a condition is via the so-called excluded-annulus (or excluded-shell) model (Russel Reference Russel1984), shown in figure 4, where particles interact hydrodynamically at a no-slip surface,
$2a$
, and sterically at a surface that extends beyond the hydrodynamic radius,
$r_{min}>2a$
, thus allowing non-zero hydrodynamic mobility at ‘contact’ of the surfaces of the excluded volumes. The strength of the interparticle force acting at a given value of
$r_{min}$
is then unique, and approaches a well-defined value for the pure-hydrodynamic limit as
$r_{min}\rightarrow 2a$
. The physics underlying this behaviour depends on the balance of microscopic forces at the relevant contact surfaces, and this is where we focus our closer look.
Figure 4. Model system showing excluded annuli. The excluded annulus prevents particle overlap for separations
$r<r_{min}$
. The upstream region is described by the polar angles
$0\leqslant {\it\theta}<{\rm\pi}/2$
, while the downstream region is described by the polar angles
${\rm\pi}/2<{\it\theta}\leqslant {\rm\pi}$
.
In non-colloidal suspensions where particles interact via the excluded annulus at
$r=r_{min}>2a$
, the surface that prevents overlap is different from the no-slip surface, and thus there is an annular shell around any particle through which fluid may pass but particles may not, as illustrated by the trajectories in figure 5. Bath particles that would otherwise follow the fluid and pass through the region occupied by the annulus must instead move around it. In the figure, the upstream trajectories of such particles are shaded in grey; as they move around the probe, they trace the surface of the excluded annulus, and move downstream along the innermost trajectory shown. Once a particle comes into contact with the annular surface, it maintains this contact until it reaches the downstream surface at
${\it\theta}={\rm\pi}/2$
. Here, all bath-particle trajectories in contact with the excluded-annulus surface now separate from contact on a single trajectory, and continue downstream. Four panels are shown in figure 5, beginning with a large excluded annulus corresponding to the limit of weak hydrodynamics in (a). As hydrodynamic interactions grow stronger, moving from (a) to (d), bath particles come close enough to the probe to experience hydrodynamic interactions; some bath particles are deflected without contacting the excluded annulus. When hydrodynamic interactions are strong, as shown in (d), many trajectories are deflected.
Figure 5. Bath-particle trajectories relative to the probe. The probe (grey shaded circle) is forced from left to right. Two dotted-line circles are shown: the smaller corresponds to the excluded-volume size of the probe and the larger defines the minimum-approach distance
$r_{min}$
((a)
$r_{min}=22a$
, (b)
$r_{min}=4a$
, (c)
$r_{min}=2.2a$
, (d)
$r_{min}=2.0002a$
). The solid grey circle represents the hydrodynamic radius. The solid lines in each panel represent bath-particle trajectories, and the dashed lines represent the envelope bounding the zone of filtered trajectories upstream of the probe, shaded in grey. In (a), the excluded annulus is so large that trajectories are not deflected by hydrodynamic interactions. The zone of filtered trajectories is approximately a cylinder of radius
$r_{min}$
extending upstream of the probe. As
$r_{min}$
decreases in (b–d), the zone of filtered trajectories becomes slender about the axis of forcing. Bath-particle trajectories outside the filtering envelope are deflected around the probe by hydrodynamic interactions, and do not make contact at the excluded annulus.
Figure 6. (a) The envelope of filtered trajectories about the probe for a range of
$r_{min}$
. The trajectories are plotted such that
$r_{min}$
is the same length for each envelope. The probe is forced from left to right. For large excluded annuli (blue outermost trajectories), the envelope describes a cylinder of radius
$r_{min}$
that extends indefinitely about the axis of forcing. As
$r_{min}\rightarrow 2a$
(red innermost trajectories), more bath-particle trajectories are deflected around the probe due to hydrodynamic interactions. The probe collides with fewer bath particles and the filtering envelope becomes slender. (b) The envelope of filtered trajectories collapses onto the axis of the external force only for
$r_{min}\equiv 2a$
, the pure-hydrodynamic limit. In this limit, the collapsed filtering envelope describes a single trajectory with two stagnation points directly in front of and behind the probe.
The ‘filtering envelope’ in figure 5 (dashed trajectories) separates the zone of filtered bath-particle trajectories, shaded in grey, from those that do not make contact with the excluded annulus. This envelope is defined for a given
$r_{min}$
by all trajectories that make contact with the excluded annulus only at
${\it\theta}={\rm\pi}/2$
. The envelope of filtered trajectories is plotted for a range of
$r_{min}>2a$
in figure 6(a). For
$r_{min}\rightarrow \infty$
, the filtering envelope describes a cylindrical region of radius
$r_{min}$
extending indefinitely upstream of the probe. As
$r_{min}\rightarrow 2a$
, more bath-particle trajectories are deflected around the probe due to hydrodynamic interactions. The probe collides with fewer bath particles and the filtering envelope shrinks. Eventually, in the pure-hydrodynamic limit
$r_{min}\equiv 2a$
, the filtering envelope collapses onto a single trajectory, as shown in figure 6(b). Here, the filtering envelope is coincident with the line of forcing both upstream and downstream of the probe, and traces the contact surface of the probe. This single trajectory has two stagnation points, directly in front of and behind the probe. Only in the pure-hydrodynamic limit do bath particles in contact on the upstream face remain in contact with the probe on the downstream face. This is qualitatively different from excluded annuli
$r_{min}>2a$
, where the interparticle forces are felt only on the upstream face. Because the filtering envelope is coincident with
$r=2a$
over the entire contact surface, one expects interparticle forces to act uniformly and radially outward over the entire contact surface only in the pure-hydrodynamic limit, consistent with a force derivable from an interaction potential
$V(r)$
.
To quantify the strength of interparticle forces, we consider an excluded annulus
$r_{min}>2a$
. With an excluded annulus, the strength of interparticle forces is determined uniquely from a force balance on each particle, and has a well-defined limit when approaching the pure-hydrodynamic limit as
$r_{min}\rightarrow 2a$
. We begin with a force balance on each particle,
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{F}^{ext}+\boldsymbol{F}_{1}^{P}+\boldsymbol{F}_{1}^{H}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{F}_{2}^{P}+\boldsymbol{F}_{2}^{H}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
$\boldsymbol{F}_{{\it\alpha}}^{P}$
and hydrodynamic drag
$\boldsymbol{F}_{{\it\alpha}}^{H}$
act on each particle. The hydrodynamic drag force is linear in the particle velocity
$\boldsymbol{U}_{{\it\alpha}}$
. The forces
$\boldsymbol{F}_{1}^{P}$
and
$\boldsymbol{F}_{2}^{P}$
are equal and opposite, and thus the particle velocities are obtained directly from (3.14a
) and (3.14b
): 
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{U}_{1}=\unicode[STIX]{x1D648}_{11}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}+[\unicode[STIX]{x1D648}_{11}^{UF}-\unicode[STIX]{x1D648}_{12}^{UF}]\boldsymbol{\cdot }\boldsymbol{F}_{1}^{P}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{U}_{2}=\unicode[STIX]{x1D648}_{21}^{UF}\boldsymbol{\cdot }\boldsymbol{F}^{ext}+[\unicode[STIX]{x1D648}_{21}^{UF}-\unicode[STIX]{x1D648}_{22}^{UF}]\boldsymbol{\cdot }\boldsymbol{F}_{1}^{P}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{U}_{2}-\boldsymbol{U}_{1}=-{\displaystyle \frac{1}{6{\rm\pi}{\it\eta}a}}[L(r/a)\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+M(r/a)(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})]\boldsymbol{\cdot }(\boldsymbol{F}^{ext}+2\boldsymbol{F}_{1}^{P}),\end{eqnarray}$$
shown here for same-sized probe and bath particles. Restricting our attention to configurations in which particles do not overlap, the excluded-annulus potential prevents the bath particle from moving any closer to the probe than the minimum allowable separation
$r_{min}$
. Thus, the radial component of the relative velocity at the excluded annulus
$r=r_{min}$
must be greater than or equal to zero:
$$\begin{eqnarray}\hat{\boldsymbol{r}}\boldsymbol{\cdot }(\boldsymbol{U}_{2}-\boldsymbol{U}_{1})=-{\displaystyle \frac{1}{6{\rm\pi}{\it\eta}a}}L(r_{min}/a)(\hat{\boldsymbol{r}}\boldsymbol{\cdot }\boldsymbol{F}^{ext}+2\hat{\boldsymbol{r}}\boldsymbol{\cdot }\boldsymbol{F}_{1}^{P})\geqslant 0.\end{eqnarray}$$
From (3.3a
), we may evaluate the relative radial mobility function
$L(r_{min}/a)$
at contact for small excluded annuli:
$$\begin{eqnarray}L\left({\displaystyle \frac{r_{min}}{a}}\right)=l_{1}\left({\displaystyle \frac{r_{min}}{a}}-2\right)+O\left(\left({\displaystyle \frac{r_{min}}{a}}-2\right)^{2}\right).\end{eqnarray}$$
The contact value of
$L$
is zero only when the excluded annulus is coincident with the hydrodynamic radii, i.e. when
$r_{min}=2a$
. Thus, to satisfy (3.17), for any excluded annulus
$r_{min}>2a$
, the following inequality must hold:
$$\begin{eqnarray}\hat{\boldsymbol{r}}\boldsymbol{\cdot }\boldsymbol{F}^{ext}+2\hat{\boldsymbol{r}}\boldsymbol{\cdot }\boldsymbol{F}_{1}^{P}\leqslant 0.\end{eqnarray}$$
The minimum interparticle force that meets this criterion results in the expected filtered trajectories of figure 5, and is given by
$$\begin{eqnarray}\boldsymbol{F}_{1}^{P}(r_{min}>2a)=\left\{\begin{array}{@{}ll@{}}-{\displaystyle \frac{F^{ext}}{2}}\hat{\boldsymbol{r}}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\hat{\boldsymbol{r}}{\it\delta}\left({\displaystyle \frac{r}{r_{min}}}-1\right),\quad & \hat{\boldsymbol{r}}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\geqslant 0,\\ \mathbf{0},\quad & \hat{\boldsymbol{r}}\boldsymbol{\cdot }\hat{\boldsymbol{F}}<0.\end{array}\right.\end{eqnarray}$$
The interparticle force required to maintain filtered trajectories in the non-colloidal limit has a maximum at the upstream stagnation point of
$F^{ext}/2$
, independent of the range
$r_{min}$
of excluded-volume interactions. It is this magnitude that defines the strength of the interparticle force in the pure-hydrodynamic limit, which must be uniform over the contact surface as discussed above:
$$\begin{eqnarray}\boldsymbol{F}_{1}^{P}(r_{min}=2a)=-{\displaystyle \frac{F^{ext}}{2}}\hat{\boldsymbol{r}}{\it\delta}\left({\displaystyle \frac{r}{r_{min}}}-1\right),\end{eqnarray}$$
and produces probe flux
$$\begin{eqnarray}\boldsymbol{j}_{1}^{P}\equiv (\unicode[STIX]{x1D648}_{11}^{UF}\boldsymbol{\cdot }\boldsymbol{F}_{1}^{P}+\unicode[STIX]{x1D648}_{12}^{UF}\boldsymbol{\cdot }\boldsymbol{F}_{2}^{P})P_{2}(\boldsymbol{z},\boldsymbol{r};t).\end{eqnarray}$$
Following the procedure of § 2.2, (3.22) yields a bath-averaged flux with
$O(1)$
and
$O(\boldsymbol{k})$
terms describing mean and fluctuating motion respectively:
$$\begin{eqnarray}\langle \tilde{\boldsymbol{j}}_{1}^{P}\rangle =\left(-2U_{S}{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\oint _{r=2}L(r)\hat{\boldsymbol{r}}[g(r)+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{d}(\boldsymbol{r})]\,\text{d}{\it\Omega}\right)\tilde{P}_{1}(\boldsymbol{k};t).\end{eqnarray}$$
The reduction in the mean probe motion from interparticle forces
$\langle U_{1}^{P}\rangle$
follows from the interparticle flux independent of the wavevector
$\boldsymbol{k}$
:
$$\begin{eqnarray}\langle U_{1}^{P}\rangle =-2U_{S}{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\oint _{r=2}L(r)g(r)\hat{\boldsymbol{r}}\boldsymbol{\cdot }\hat{\boldsymbol{F}}\,\text{d}{\it\Omega}.\end{eqnarray}$$
From orthogonality properties and the spherical symmetry of the microstructure in the pure-hydrodynamic limit,
$U_{1}^{P}=0$
. Additionally, the relative radial probability flux
$L(r)g(r)$
at small separations decays as
${\it\xi}^{1-{\it\delta}}$
as shown in figure 3, ensuring that, as expected, interparticle forces produce no reduction in probe motion.
The flow-induced diffusivity
$\unicode[STIX]{x1D63F}^{\,flow}$
is again defined from the
$O(\boldsymbol{k})$
terms of the interparticle flux:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\,flow}=2aU_{S}{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\oint _{r=2}L(r)\boldsymbol{d}(\boldsymbol{r})\hat{\boldsymbol{r}}\,\text{d}{\it\Omega},\end{eqnarray}$$
with the transverse component
$$\begin{eqnarray}D_{\bot }^{\,flow}=2aU_{S}{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\oint _{r=2}L(r)d_{1}^{\bot }(r)P_{1}^{1}({\it\mu})P_{1}^{1}({\it\mu})\cos ^{2}{\it\phi}\,\text{d}{\it\Omega}.\end{eqnarray}$$
The
$O(\boldsymbol{k})$
relative radial probability flux
$L(r)d_{1}^{\bot }(r)$
at small separations decays as
${\it\xi}^{1-{\it\delta}}$
as shown in figure 3, ensuring no transverse diffusion from interparticle forces at
$O({\it\phi})$
, also as expected, due to the reversibility of Stokes flow; that is,
$D_{\bot }^{\,flow}=0$
.
The longitudinal flow-induced diffusivity is the
$\hat{\boldsymbol{F}}\hat{\boldsymbol{F}}$
component of equation (3.25):
$$\begin{eqnarray}D_{\Vert }^{\,flow}=2aU_{S}{\displaystyle \frac{3{\it\phi}}{4{\rm\pi}}}\oint _{r=2}L(r)d_{1}^{\Vert }(r)P_{1}({\it\mu})P_{1}({\it\mu})\,\text{d}{\it\Omega}.\end{eqnarray}$$
Only the component
$d_{1}^{\Vert }(r)$
of the series expansion of longitudinal fluctuations is required to evaluate the flow-induced diffusivity; all other moments can be omitted from (3.27) by orthogonality of the Legendre polynomials. We can determine the contact value of
$L(r)d_{1}^{\Vert }(r)$
from (3.9):
$$\begin{eqnarray}\displaystyle \displaystyle \lim _{r\rightarrow 2}L(r)d_{1}^{\Vert }(r) & = & \displaystyle \displaystyle -{\displaystyle \frac{1}{4}}\int _{2}^{\infty }g(z)[x_{11}^{a}(z)+2y_{11}^{a}(z)-3]z^{2}\,\text{d}z\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \displaystyle {\displaystyle \frac{1}{4}}{\it\eta}_{i}^{H},\end{eqnarray}$$
${\it\eta}_{i}^{H}=2.52$
. Batchelor & Wen (Reference Batchelor and Wen1982) referred to
$-{\it\eta}_{i}^{H}$
as the sedimentation coefficient
$S_{ij}$
, while Davis & Hill (Reference Davis and Hill1992) referred to
${\it\eta}_{i}^{H}$
as the mean velocity coefficient
$k_{m}$
. Both of these studies agree with
${\it\eta}_{i}^{H}=2.52$
. Further, the limit in (3.28b
) approaching a constant is consistent with the limiting value of the relative radial flux shown in figure 3. Insertion of (3.28b
) into (3.27) gives the longitudinal force-induced diffusivity 
$$\begin{eqnarray}D_{\Vert }^{\,flow}=1.26aU_{S}{\it\phi},\end{eqnarray}$$
in excellent agreement with falling-ball measurements by Abbott et al. (Reference Abbott, Graham, Mondy and Brenner1998) and trajectory-analysis theory by Davis & Hill (Reference Davis and Hill1992), which give
$D_{\Vert }^{\,flow}=1.20aU_{S}{\it\phi}^{1.08}$
and
$D_{\Vert }^{\,flow}=1.33aU_{S}{\it\phi}$
respectively.
4. Comparison with falling-ball rheometry
The longitudinal flow-induced diffusivity
$D_{\Vert }^{\,flow}=1.26aU_{S}{\it\phi}$
as calculated from the interparticle probe flux is in excellent agreement with the experimental findings of Abbott et al. (Reference Abbott, Graham, Mondy and Brenner1998), who measured a vertical dispersivity in falling-ball experiments of
$D_{\Vert }^{\,flow}=1.20aU_{S}{\it\phi}^{1.08}$
, as well as the theoretical results of Davis & Hill (Reference Davis and Hill1992), who found
$D_{\Vert }^{\,flow}=1.33aU_{S}{\it\phi}$
via trajectory analysis for macroscopic falling-ball rheometry. In § 3.2, a key distinction between our approach and that of Davis and Hill was made clear: the non-vanishing relative radial flux at pair contact is shown only via the Smoluchowski equation. Trajectory analysis exploits the entirely deterministic relative motion between a falling ball and a bath particle; as such, Davis and Hill determined the hydrodynamic diffusion simply by multiplying the average mean-square displacement per pair encounter by the rate of encounters, the latter of which is set by the homogeneity of the dispersion far from the falling ball. No relative trajectories may pass through the falling ball due to the singularity of the contact lubrication force, thus hydrodynamic forces are sufficient to determine hydrodynamic diffusion in the trajectory analysis. In doing so, trajectory analysis misses key entropic effects revealed by fluctuations. The probe excludes bath particles from a suspension volume about its surface. This entropically excluded volume is clearly evident with a large excluded annulus, as many bath-particle trajectories collide with the excluded shell. However, the non-vanishing relative radial flux is evidence that the probe excludes a region of space from the bath particles even in the pure-hydrodynamic limit. The flux into the excluded volume can be interpreted as the probe acting as a ‘sink’ of longitudinal fluctuations. These longitudinal fluctuations cannot disappear: they manifest themselves as longitudinal force-induced diffusion via the interparticle force.
The trajectory analysis of Davis and Hill requires completely deterministic forces: even a small amount of thermal energy disrupts the relative trajectories. Computing diffusion from mean and fluctuating microstructure permits consideration of the contributions from stochastic forces, i.e. Brownian motion. The pure-hydrodynamic limit in this study defines the infinite-
$Pe$
asymptotic behaviour for studies varying the relative strengths of external and thermal forces. In addition, our approach opens the possibility of considering surface roughness and additional non-hydrodynamic forces via a finite excluded annulus.
A prior theoretical investigation by Davis (Reference Davis1992) introduced finite surface roughness into an analysis of falling-ball rheometry. In his work, two possible mechanisms of contact forces were set forth. The first, the ‘stick/rotate’ model, stipulates that a pair that come into contact adhere to one another and move in rigid-body translation and rotation. Like our analysis of finite excluded annuli, he recognized that background particles separate at
${\it\theta}={\rm\pi}/2$
because contact forces are assumed to be purely repulsive. The second, the ‘roll/slip’ model, introduces a tangential component into the contact force which, depending on the magnitude of the friction coefficient, causes the probe to roll or slip around the bath particle at contact.
Our approach is similar to the stick/rotate model of Davis (Reference Davis1992) in that we assume that there is no tangential component associated with interparticle forces. However, we do not impose the additional constraint that particles in contact undergo rigid-body rotation. Indeed, when the hydrodynamic radii of the two spheres are separated by any finite distance, they need not rotate as a pair. Additionally, their constraint of rigid-body rotation introduces contact torques, which in turn induce additional fluxes that may contribute to the flow-induced diffusivity.
In our approach, we found the flow-induced diffusivity to be linear in the
$O({\it\phi})$
reduction in the mean motion, that is
$D_{\Vert }^{\,flow}=({\it\eta}_{i}^{H}/2)aU_{S}{\it\phi}$
, where all particles are identical. Falling-ball rheometry in a dilute suspension of non-colloidal particles has been studied as a function of the relative size of the falling ball and bath particles (Batchelor & Wen Reference Batchelor and Wen1982; Davis & Hill Reference Davis and Hill1992; Almog & Brenner Reference Almog and Brenner1997). These studies showed that a falling ball that is large relative to the bath particles resembles a boundary of a sheared suspension, and the reduction in mean motion approaches Einstein’s viscosity correction of
$2.5{\it\phi}$
. When the relative size of the falling ball to the bath particles is
$O(1)$
or smaller, non-continuum effects cause the falling ball to spend progressively more time in the vicinity of a neutrally buoyant bath particle, and the increased probability of a nearby large bath particle hinders the falling ball; the effective viscosity thence diverges with the bath-to-ball size ratio (Almog & Brenner Reference Almog and Brenner1997). Notably, this flow-induced diffusivity can be computed strictly from the suspension microstructure, as the spherically symmetric microstructure
$g(r)$
found by Batchelor (Reference Batchelor1982) is sufficient for determining
${\it\eta}_{i}^{H}$
for any size ratio. These studies of the impact of particle size ratio on mean motion in falling-ball rheometry can be included in our model, although additional consideration of size dependence, for example in the interparticle forces, is needed to generalize the expression for
$D_{\Vert }^{\,flow}$
as a function of
${\it\eta}_{i}^{H}$
.
5. Conclusions
The goal of this study was to characterize force-induced diffusion in the so-called ‘pure-hydrodynamic’ limit, i.e. in the absence of thermal and interparticle forces, but as the infinite-
$Pe$
limit of active microrheology. To this end, we studied the suspension microstructure about a strongly forced microrheological probe through a dilute dispersion of identical rigid spherical non-colloidal particles. The mean-speed reduction and flow-induced diffusion were inferred from kinematic expressions for the probe flux given by integral expressions weighting the probe motion by the mean
$g$
and fluctuating
$\boldsymbol{d}$
microstructure respectively, where expressions governing both
$g(\boldsymbol{r})$
and
$\boldsymbol{d}(\boldsymbol{r})$
were derived from the Smoluchowski equation. The mean suspension microstructure, governed solely by advection from the external force, adopts a spherically symmetric steady state
$g(r)$
that leads to the well-known intrinsic hydrodynamic microviscosity, or the
$O({\it\phi})$
reduction in mean probe motion of
${\it\eta}_{i}^{H}=2.52$
.
As a first look, a similar procedure was followed to obtain the fluctuation field
$\boldsymbol{d}(\boldsymbol{r})$
. The spherically symmetric microstructure drives fluctuations transverse to and along the line of the external force:
$d^{\bot }(\boldsymbol{r})=d_{1}^{\bot }(r)P_{1}^{1}(\cos {\it\theta})\text{e}^{\text{i}{\it\phi}}$
and
$d^{\Vert }(\boldsymbol{r})=\sum _{n\,odd}d_{n}^{\Vert }(r)P_{n}(\cos {\it\theta})$
. However, upon insertion of the fluctuation field into the integral expressions of the hydrodynamic diffusivity, a puzzling result was obtained: zero hydrodynamic flow-induced diffusion. This contradicted prior experimental studies of falling-ball rheometry (Davis & Hill Reference Davis and Hill1992; Abbott et al.
Reference Abbott, Graham, Mondy and Brenner1998), which found the longitudinal hydrodynamic diffusivity to scale as
$aU_{S}{\it\phi}$
in the dilute limit, suggesting that something was missed in the first-look approach. Recalling that the theoretical study of Davis & Hill (Reference Davis and Hill1992) found that bath particles coming closest to contact dominate the contribution to the hydrodynamic diffusivity, a closer look was taken at the mean and fluctuating microstructure and relative fluxes near contact in our model. When the surface separation
${\it\xi}\equiv r-2\ll 1$
, the microstructure and the transverse fluctuation field were found to scale as
${\it\xi}^{-0.799}f(\log {\it\xi}^{-1})$
, while the longitudinal fluctuation field scales as
${\it\xi}^{-1}$
. This leads to relative radial fluxes
$Lg$
and
$Ld^{\bot }$
that vanish as
${\it\xi}^{0.201}f(\log {\it\xi}^{-1})$
when
${\it\xi}\rightarrow 0$
, and an
$O(1)$
flux of longitudinal fluctuations at contact,
$Ld^{\Vert }\sim O(1)$
, suggesting that non-hydrodynamic forces at contact must also play a role and can generate non-zero surface flux.
A close examination of force at contact reveals that interparticle forces are still present in the pure-hydrodynamic limit, because the probe and bath particles cannot occupy the same space. The corresponding interparticle potential
$V(r)$
must thence be infinite for separations
$r<2a$
and zero otherwise. In this limit, lubrication interactions alone are sufficient to prevent particle overlap as contact forces produce no relative motion. Nonetheless, the inability of interparticle forces to cause particle translation is not a sufficient criterion to neglect interparticle forces in the kinematic expressions for the probe flux. The interparticle force was determined utilizing a force balance at an excluded annulus:
$\boldsymbol{F}_{1}^{P}=-F^{ext}/2\cos {\it\theta}\hat{\boldsymbol{r}}{\it\delta}(r/r_{min}-1)$
upstream of the probe and zero downstream.
Bath-particle trajectories that contact the excluded annulus are enclosed within a ‘filtering envelope’ about the line of forcing. This filtering envelope becomes slender with a shrinking excluded annulus, eventually collapsing onto a single trajectory in the pure-hydrodynamic limit when
$r_{min}\equiv 2a$
. This collapse suggested two qualitative changes in the interparticle force in the pure-hydrodynamic limit. First, bath particles at the contact surface no longer separate at
${\it\theta}={\rm\pi}/2$
but rather remain in contact all the way around the probe. Thus, interparticle forces in the pure-hydrodynamic limit act uniformly over the entire contact surface. Second, the filtering envelope collapses onto a single trajectory along the line of forcing, so only the bath-particle trajectory approaching along
${\it\theta}=0$
terminates at the contact surface, showing that the interparticle force must be evaluated along the stagnation trajectory. In the pure-hydrodynamic limit,
$\boldsymbol{F}_{1}^{P}=-F^{ext}/2\hat{\boldsymbol{r}}{\it\delta}(r/2a-1)$
. This interparticle force induces probe flux at the contact surface, resulting in longitudinal flow-induced diffusivity.
We find that, owing to the reversibility of Stokes flow, the transverse flow-induced diffusivity vanishes in the dilute limit. In contrast, the longitudinal hydrodynamic diffusivity of a probe forced through a dilute suspension of identically sized bath particles is
$D_{\Vert }^{\,flow}=1.26aU_{S}{\it\phi}$
. Our results are in excellent agreement, both qualitatively and quantitatively, with experimental measurements (Milliken et al.
Reference Milliken, Mondy, Gottlieb, Graham and Powell1989; Abbott et al.
Reference Abbott, Graham, Mondy and Brenner1998) and theoretical studies (Davis Reference Davis1992; Davis & Hill Reference Davis and Hill1992) of falling-ball rheometry.
Interestingly, the longitudinal flow-induced diffusivity is proportional to the apparent hydrodynamic microviscosity
${\it\eta}_{i}^{H}$
, the
$O({\it\phi})$
reduction in the probe speed due to hydrodynamic interactions with the bath particles,
$D^{flow}=({\it\eta}_{i}^{H}/2)aU_{S}{\it\phi}$
, revealing that diffusion and drag arise from a common microstructural origin: bath-particle entrainment impedes the mean motion and induces fluctuations in the instantaneous speed. Indeed, this behaviour is a far from equilibrium counterpart to the same connection between fluctuation and dissipation in the Stokes–Einstein relation for a particle diffusing in a pure solvent.
The dependence of
$\unicode[STIX]{x1D63F}^{\,flow}$
on
${\it\eta}_{i}^{H}$
is puzzling, however: the interparticle force at contact produces longitudinal flow-induced diffusivity. That is, the interparticle flux leads to a purely hydrodynamic response. However, this must be so: the non-hydrodynamic force at contact must balance the non-zero relative radial flux of longitudinal fluctuations to the probe surface. No matter which non-hydrodynamic forces are evaluated near contact (thermal, interparticle, etc.), the advective flux towards the contact surface does not change. That is, the rate at which longitudinal fluctuations are brought to the surface is strictly governed by the strength of hydrodynamic interactions. Non-hydrodynamic (thermal, interparticle, etc.) forces act to balance this advective flux and consequently reveal the longitudinal flow-induced diffusivity.
Many interesting questions remain. For example, thermal fluctuations were neglected here in order to focus on the non-colloidal limit. This restriction is easily relaxed. Even weak Brownian motion is a source of microstructural asymmetry that leads to anisotropic rheology including flow-induced diffusion. Brownian motion can be modelled as an equivalent ‘thermodynamic’ force
$\boldsymbol{F}_{{\it\alpha}}^{B}=-kT\boldsymbol{{\rm\nabla}}_{{\it\alpha}}\ln P_{2}$
acting on particle
${\it\alpha}$
, generating a probability flux that counters advective flux from an interparticle potential
$V$
, thus recovering the equilibrium suspension microstructure (Batchelor Reference Batchelor1976).
The relative magnitudes of external and thermodynamic forces define a Péclet number
$Pe\equiv F^{ext}a/2kT$
that is large in the limit of weak Brownian forces. Physically, weak Brownian motion dissipates only the sharpest microstructural gradients near contact. Thus, advective and thermodynamic forces balance in a narrow
$O(aPe^{-1})$
boundary layer near the surface of the probe. The diffusive boundary layer is the origin of non-Newtonian force thickening in the limit of strong forcing (Khair & Brady Reference Khair and Brady2006); analogously, the diffusive boundary layer breaks symmetry in strongly sheared suspensions, leading to non-zero normal stress differences and particle pressure (Brady & Morris Reference Brady and Morris1997). The non-Newtonian rheology vanishes in the pure-hydrodynamic limit as
$Pe^{-0.201}$
, a consequence of the
$O(a^{3}Pe^{-1})$
volume of the boundary layer vanishing more rapidly than the bath-particle density
$O(Pe^{0.799})$
accumulates in this region. Alternatively, one may view the vanishing relative radial advective flux that acts to push bath particles into the diffusive boundary layer as defining the transition to Newtonian rheology: with no bath-particle density in the diffusive boundary layer, the apparent force thickening in microrheology must transition to a Newtonian plateau when
$Pe\rightarrow \infty$
. The transition to Newtonian rheology as viewed through a vanishing relative flux towards contact highlights the role played by entropic forces in non-Newtonian rheology, and could also provide insight and new interpretations for transient force thickening as microstructures develop, as has been done for active microrheology in non-hydrodynamically interacting suspensions (Zia & Brady Reference Zia and Brady2013).
Similarly, the
$O(\boldsymbol{k})$
flux describes how fluctuations are advected into the boundary layer. The relative radial advective flux of transverse fluctuations
$Ld^{\bot }\sim {\it\xi}^{0.201}$
also approaches zero in the pure-hydrodynamic limit: with a vanishing quantity of fluctuations advected into the boundary layer, the transverse flow-induced diffusivity must be identically zero in the limit
$Pe\rightarrow \infty$
. The relative radial flux of longitudinal fluctuations
$Ld_{1}^{\Vert }\sim {\it\xi}^{0}$
is
$O(1)$
near contact, suggesting that advection always drives an
$O(1)$
quantity of longitudinal fluctuations into the vanishingly thin diffusive boundary layer, even as
$Pe\rightarrow \infty$
. This persistence of longitudinal fluctuation density inside the diffusive boundary layer when
$Pe^{-1}\equiv 0$
emphasizes how critical the microstructural contact surface is to shaping the longitudinal flow-induced diffusivity. Indeed, Zia & Brady (Reference Zia and Brady2010) found that the fluctuation field about a strongly forced probe is identically zero everywhere outside the
$O(aPe^{-1})$
diffusive boundary layer in the absence of hydrodynamic interactions. Further studies of flow-induced diffusivity that include explicit thermodynamic forces and Brownian motion via
$Pe$
should recover our findings in the limit
$Pe\rightarrow \infty$
.
Generalization of these results to finite concentrations requires consideration of three-body and higher interactions. The presence of a third particle breaks the fore–aft symmetry of bath-particle trajectories, which leads to non-zero transverse dispersivity, even in the pure-hydrodynamic limit. Additionally, the bath-particle trajectory along the line of forcing that would have led to the stagnation point is deflected around the probe in the presence of a third particle. Bath particles that once may have spent an infinite amount of time being entrained along the stagnation streamline thus are pushed out of the way. This effect is similar to the ‘screening’ in sedimenting suspensions described by Koch & Shaqfeh (Reference Koch and Shaqfeh1991), and the mechanism can be generalized to active microrheology: a second bath particle in the vicinity of a pair comprising the probe and bath particles acts to destabilize the pair and induce a net deficit of pair density about the probe. Thus, we expect a decrease in the longitudinal flow-induced diffusivity, and non-zero transverse diffusion with increasing
${\it\phi}$
.
Prior studies of falling-ball rheometry have also investigated the effects of the relative size of probe and bath particles. Almog & Brenner (Reference Almog and Brenner1997) found that the dimensionless reduction in probe speed (the intrinsic hydrodynamic microviscosity) approaches
$5/2{\it\phi}$
for vanishingly small bath particles, recovering Einstein’s viscosity correction for a dilute dispersion of spheres. However, the reduction in probe speed diverges for vanishingly small probes. If the longitudinal flow-induced diffusivity were truly linear in the intrinsic hydrodynamic microviscosity alone, with no other size considerations, the longitudinal flow-induced diffusivity should approach a constant for small bath particles, while it should diverge for vanishingly small probes. The latter was predicted by the theory of Davis & Hill (Reference Davis and Hill1992); however, they also predicted that longitudinal dispersion vanishes for large probes. Additional size effects, including vanishingly small probe displacements from interparticle forces between large probes and small bath particles, could complete the picture of longitudinal diffusion from a fluctuation field approach. The flow-induced diffusion will be more sensitive to polydispersity than the reduction in mean motion. Davis & Hill (Reference Davis and Hill1992) found that, for small falling balls, the reduction in the mean motion diverges as
${\it\lambda}\equiv b/a$
, while the vertical diffusion diverges as
${\it\lambda}^{3}$
. Alternatively, for large falling balls, they predicted that the dominant contributions to vertical diffusion emerge from a ‘middle region’ (between the inner region where
${\it\xi}\ll {\it\lambda}$
and the outer region where
${\it\xi}\gg 1$
), which scales as
${\it\lambda}^{3}\log {\it\lambda}^{-1}$
. Our approach may treat both of these limits, when interpreting the interparticle force via the excluded-annulus model. The interparticle force must still be equal and opposite when the probe and bath particles are in contact at the excluded annulus, and the requirement for freely draining trajectories still holds, but the resulting interparticle displacements will differ for probe and bath particles. The ratio of the hydrodynamic functions
$L$
and
$G$
will emerge from our analysis when polydispersity plays a role, where
$L$
describes relative motion from a force on a single particle (i.e. displacements from the external force) and
$G$
describes relative motion from equal and opposite forces (i.e. interparticle displacements). The ratio
$L/G$
has a well-defined limit as
$r_{min}\rightarrow 2a$
which is size-ratio-dependent, so with some modification the same approach as shown in this work can be utilized. The Smoluchowski approach may lead to more accurate asymptotic expressions for the longitudinal diffusion as a function of the size ratio than that found by Davis & Hill (Reference Davis and Hill1992) (cf. figure 2 in that work).
Finally, this study found that the probe fluctuations
$\unicode[STIX]{x1D63F}^{\,flow}$
and energy dissipation
${\it\eta}_{i}^{H}$
are intimately tied in the pure-hydrodynamic limit of active microrheology. Prior work (Zia & Brady Reference Zia and Brady2012) suggests that the relation found here between
$\unicode[STIX]{x1D63F}^{\,flow}$
and
${\it\eta}_{i}^{H}$
fits in with broader connections between stress gradients, energy dissipation and particle motion. These connections should persist regardless of the strengths of the external forcing, thermal motion and interparticle interactions. Making these connections would require a thorough investigation of
$\unicode[STIX]{x1D63F}^{\,flow}$
over all strengths of forcing relative to thermal energy
$(Pe)$
and over a range of interparticle interaction distances
$(r_{min})$
. Once established, non-equilibrium connections between fluctuation and dissipation harness the full capability of active microrheology as a means for interrogating complex fluids.
Appendix A. Integral solutions for the fluctuation field
We recall that the Smoluchowski equation governs the spatiotemporal evolution of the mean
$g(\boldsymbol{r})$
and fluctuating
$\boldsymbol{d}(\boldsymbol{r})$
suspension microstructure. The governing equation for the fluctuation field
$\boldsymbol{d}(\boldsymbol{r})$
, given in (2.20), is repeated below for convenience:
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}_{\boldsymbol{r}}\boldsymbol{\cdot }([L\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+M(\unicode[STIX]{x1D644}-\hat{\boldsymbol{r}}\hat{\boldsymbol{r}})]\boldsymbol{\cdot }\hat{\boldsymbol{F}}\boldsymbol{d}(\boldsymbol{r}))=[(x_{11}^{a}-y_{11}^{a})\hat{\boldsymbol{r}}\hat{\boldsymbol{r}}+(y_{11}^{a}-1)\unicode[STIX]{x1D644}]\boldsymbol{\cdot }\hat{\boldsymbol{F}}g(\boldsymbol{r}).\end{eqnarray}$$
Equation (3.7) decomposes the vector fluctuation field
$\boldsymbol{d}(\boldsymbol{r})$
into scalar components along
$(d^{\Vert })$
and transverse to
$(d^{\bot })$
the line of external forcing. We begin with longitudinal fluctuations. The spherical harmonics
$P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}$
are a convenient orthogonal basis to describe the microstructure about the probe, where
$P_{l}^{m}(\cos {\it\theta})$
is the associated Legendre polynomial of degree
$l$
and order
$m$
. Expressing
$d^{\Vert }(r,{\it\theta},{\it\varphi})$
as a sum of spherical harmonics gives
$$\begin{eqnarray}d^{\Vert }(r,{\it\theta},{\it\varphi})=\mathop{\sum }_{l=0}^{\infty }\mathop{\sum }_{m=-l}^{+l}d_{l,m}^{\Vert }(r)P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}},\end{eqnarray}$$
where the function
$d_{l,m}^{\Vert }(r)$
describes the radial dependence of
$d^{\Vert }$
associated with the spherical harmonic
$P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}$
.
The Smoluchowski equation (A 1) is projected onto
$\hat{\boldsymbol{F}}$
to obtain a governing equation for longitudinal fluctuations, into which the series expansion for
$d^{\Vert }(\boldsymbol{r})$
, (A 2), is substituted:
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{l=0}^{\infty }\mathop{\sum }_{m=-l}^{+l}\left[W(r){\it\alpha}_{l,m}^{\Vert }(r)+L(r){\it\beta}_{l,m}^{\Vert }(r)+{\displaystyle \frac{M(r)}{r}}{\it\gamma}_{l,m}^{\Vert }(r)\right]P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{2}{3}}[x_{11}^{a}(r)-y_{11}^{a}(r)]g(r)P_{2}^{0}(\cos {\it\theta})+{\displaystyle \frac{1}{3}}[x_{11}^{a}(r)+2y_{11}^{a}(r)-3]g(r)P_{0}^{0}(\cos {\it\theta}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$W(r)=(2/r)(L(r)-M(r))+\text{d}L/\text{d}r$
is the divergence of the relative mobility, and the longitudinal advective coupling terms
${\it\alpha}_{l,m}^{\Vert }(r)$
,
${\it\beta}_{l,m}^{\Vert }(r)$
and
${\it\gamma}_{l,m}^{\Vert }(r)$
are
$$\begin{eqnarray}\displaystyle {\it\alpha}_{l,m}^{\Vert }(r) & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \displaystyle {\displaystyle \frac{l-m}{2l-1}}d_{l-1,m}^{\Vert }(r)+{\displaystyle \frac{l+m+1}{2l+3}}d_{l+1,m}^{\Vert }(r),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\beta}_{l,m}^{\Vert }(r) & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \displaystyle {\displaystyle \frac{l-m}{2l-1}}d_{l-1,m}^{\Vert \prime }(r)+{\displaystyle \frac{l+m+1}{2l+3}}d_{l+1,m}^{\Vert \prime }(r),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\gamma}_{l,m}^{\Vert }(r) & \hspace{-2.0pt}=\hspace{-2.0pt} & \displaystyle \displaystyle {\displaystyle \frac{(l-m)(1-l)}{2l-1}}d_{l-1}^{m}(r)+{\displaystyle \frac{(l+2)(l+m+1)}{2l+3}}d_{l+1,m}^{\Vert }(r).\end{eqnarray}$$
$P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}$
drives microstructural response in
$d_{l+1,m}^{\Vert }(r)$
and
$d_{l-1,m}^{\Vert }(r)$
as described by the advective coupling terms. It should be noted that the advection operator preserves the order
$m$
of the spherical harmonics; forcing with azimuthal dependence
$\text{e}^{\text{i}m{\it\phi}}$
drives microstructural harmonics of the same order. The forcing terms on the right-hand side of (A 3) comprise only the spherical harmonics,
$P_{0}^{0}(\cos {\it\theta})$
and
$P_{2}^{0}(\cos {\it\theta})$
. No forcing is present to drive any spherical harmonics of order
$m\neq 0$
in
$d^{\Vert }(\boldsymbol{r})$
from equilibrium, so we may simplify equation (A 2) recognizing that only the
$m=0$
spherical harmonics are driven from equilibrium: 
$$\begin{eqnarray}d^{\Vert }(r,{\it\theta})=\mathop{\sum }_{l=0}^{\infty }d_{l}^{\Vert }(r)P_{l}(\cos {\it\theta}).\end{eqnarray}$$
In (A 5),
$P_{l}(\cos {\it\theta})$
is the Legendre polynomial of degree
$l$
and is equivalent to
$P_{l}^{0}(\cos {\it\theta})$
. Via orthogonality, the spherical harmonic terms of degree
$l=0$
and order
$m=0$
in (A 3) define a first-order ordinary differential equation for
$d_{1}^{\Vert }(r)$
:
$$\begin{eqnarray}{\displaystyle \frac{\text{d}}{\text{d}r}}[r^{2}L(r)d_{1}^{\Vert }(r)]=r^{2}[x_{11}^{a}(r)+2y_{11}^{a}(r)-3]g(r).\end{eqnarray}$$
The solution for
$d_{1}^{\Vert }(r)$
is found by integrating equation (A 6):
$$\begin{eqnarray}d_{1}^{\Vert }(r)=-{\displaystyle \frac{1}{r^{2}L(r)}}\displaystyle \int _{\!r}^{\infty }z^{2}[x_{11}^{a}(z)+2y_{11}^{a}(z)-3]g(z)\,\text{d}z.\end{eqnarray}$$
Similarly, via orthogonality, the spherical harmonic terms of degree
$l=2$
and order
$m=0$
in (A 3) define a first-order ordinary differential equation for
$d_{3}^{\Vert }(r)$
, which is coupled to the solution for
$d_{1}^{\Vert }(r)$
. With some rearrangement, the following governing equation for
$d_{3}^{\Vert }(r)$
is obtained:
$$\begin{eqnarray}{\displaystyle \frac{1}{r^{2}}}{\displaystyle \frac{\text{d}}{\text{d}r}}[r^{2}L(r)d_{3}^{\Vert }(r)]+2{\displaystyle \frac{M(r)}{r}}d_{3}^{\Vert }(r)={\displaystyle \frac{14}{3}}\left[{\displaystyle \frac{M(r)}{r}}d_{1}^{\Vert }(r)+(1-y_{11}^{a}(r))g(r)\right].\end{eqnarray}$$
An integral solution of
$d_{3}^{\Vert }(r)$
may be found from (A 8), but is not necessary for our investigation:
$d_{3}^{\Vert }(r)$
and all higher degrees of spherical harmonics do not contribute to
$D_{\Vert }^{\,flow}$
. No other spherical harmonics are present in the forcing function on the right-hand side of (A 3). However, the advective coupling terms, (A 4a
–
c
), show that the spherical harmonic fluctuations
$d_{l-1}^{m}(r)P_{l-1}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}$
drive a higher harmonic
$d_{l+1}^{m}(r)P_{l+1}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}$
from equilibrium. Thus, an infinitude of odd Legendre polynomial modes are driven from equilibrium in the longitudinal fluctuation field, allowing for further simplification of (A 5):
$$\begin{eqnarray}d^{\Vert }(r,{\it\theta})=\mathop{\sum }_{l\,odd}^{\infty }d_{l}^{\Vert }(r)P_{l}(\cos {\it\theta}).\end{eqnarray}$$
We next consider transverse fluctuations. Expressing
$d^{\bot }(r,{\it\theta},{\it\varphi})$
as a sum of spherical harmonics gives
$$\begin{eqnarray}d^{\bot }(r,{\it\theta},{\it\varphi})=\mathop{\sum }_{l=0}^{\infty }\mathop{\sum }_{m=-l}^{+l}d_{l,m}^{\bot }(r)P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}},\end{eqnarray}$$
where the function
$d_{l,m}^{\bot }(r)$
describes the radial dependence of
$d^{\bot }$
associated with the spherical harmonic
$P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}$
.
The Smoluchowski equation (A 1) is projected onto
$\boldsymbol{e}_{x}$
or
$\boldsymbol{e}_{y}$
to obtain a governing equation for transverse fluctuations, into which the series expansion for
$d^{\bot }(\boldsymbol{r})$
, (A 10), is substituted:
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{l=0}^{\infty }\mathop{\sum }_{m=-l}^{+l}\left[W(r){\it\alpha}_{l,m}^{\bot }(r)+L(r){\it\beta}_{l,m}^{\bot }(r)+{\displaystyle \frac{M(r)}{r}}{\it\gamma}_{l,m}^{\bot }(r)\right]P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\varphi}}\nonumber\\ \displaystyle & & \displaystyle \quad =-{\displaystyle \frac{1}{3}}[x_{11}^{a}(r)-y_{11}^{a}(r)]g(r)P_{2}^{1}(\cos {\it\theta})\text{e}^{\text{i}{\it\varphi}},\end{eqnarray}$$
where the transverse advective coupling terms
${\it\alpha}_{l,m}^{\bot }(r)$
,
${\it\beta}_{l,m}^{\bot }(r)$
and
${\it\gamma}_{l,m}^{\bot }(r)$
are identical to those for longitudinal fluctuations given in (A 4a
), (A 4b
) and (A 4c
).
The forcing term on the right-hand side of (A 11) comprises a single spherical harmonic,
$P_{2}^{1}(\cos {\it\theta})\text{e}^{\text{i}{\it\varphi}}$
. No forcing is present to drive any spherical harmonics of order
$m\neq 1$
in
$d^{\bot }(\boldsymbol{r})$
from equilibrium, so we may simplify (A 10) recognizing that only the
$m=1$
spherical harmonics are driven from equilibrium:
$$\begin{eqnarray}d^{\bot }(r,{\it\theta},{\it\varphi})=\mathop{\sum }_{l=0}^{\infty }d_{l}^{\bot }(r)P_{l}^{1}(\cos {\it\theta})\text{e}^{\text{i}{\it\varphi}}.\end{eqnarray}$$
Via orthogonality, the spherical harmonic terms of degree
$l=2$
and order
$m=1$
in (A 11) define a first-order ordinary differential equation for
$d_{1}^{\bot }(r)$
and
$d_{3}^{\bot }(r)$
:
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{1}{3}}\left[W(r)d_{1}^{\bot }(r)+L(r){d_{1}^{\bot }}^{\prime }(r)-{\displaystyle \frac{M(r)}{r}}d_{1}^{\bot }(r)\right]\qquad \quad \nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{4}{7}}\left[W(r)d_{3}^{\bot }(r)+L(r){d_{3}^{\bot }}^{\prime }(r)+{\displaystyle \frac{4M(r)}{r}}d_{3}^{\bot }(r)\right]=-{\displaystyle \frac{1}{3}}(x_{11}^{a}(r)-y_{11}^{a}(r))g(r).\qquad \quad\end{eqnarray}$$
The solutions for
$d_{1}^{\bot }(r)$
and
$d_{3}^{\bot }(r)$
are
$$\begin{eqnarray}d_{1}^{\bot }(r)=rg(r)(L(r)g(r))^{1/2}\int _{r}^{\infty }{\displaystyle \frac{x_{11}^{a}(z)-y_{11}^{a}(z)}{zL(z)}}\left({\displaystyle \frac{1}{L(z)g(z)}}\right)^{1/2}\,\text{d}z\end{eqnarray}$$
and
$$\begin{eqnarray}d_{3}^{\bot }(r)=0.\end{eqnarray}$$
No other spherical harmonics are present in the forcing function on the right-hand side of (A 11). Because
$d_{3}^{\bot }(r)$
is identically zero, the advective coupling terms and absence of any other forcing terms require that all higher odd-degree spherical harmonics are identically zero. Similarly, the absence of any forcing terms to drive the even spherical harmonics in
$d^{\bot }(\boldsymbol{r})$
from equilibrium requires that all even-degree spherical harmonics are zero as well. The entire transverse fluctuation field is thus described by a single spherical harmonic:
$$\begin{eqnarray}d^{\bot }(r,{\it\theta},{\it\varphi})=d_{1}^{\bot }(r)P_{1}^{1}(\cos {\it\theta})\text{e}^{\text{i}{\it\varphi}}.\end{eqnarray}$$
Equations (A 9) and (A 16) show that advection drives an infinitude of odd spherical harmonics in the longitudinal fluctuation field and a single spherical harmonic in the transverse fluctuation field from equilibrium. In § 3.2, these solutions for
$d^{\Vert }$
and
$d^{\bot }$
are substituted into the expression for the hydrodynamic flow-induced diffusion
$\unicode[STIX]{x1D63F}^{\,flow}$
(2.23), yielding the puzzling result of zero force-induced diffusion. In order to reconcile this finding with falling-ball rheometry experiments (Abbott et al.
Reference Abbott, Graham, Mondy and Brenner1998), additional non-hydrodynamic forces need consideration to fully quantify force-induced diffusion in the pure-hydrodynamic limit.
