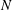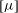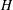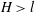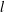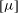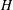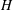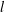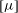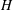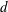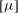1. Introduction
The effective viscosity of a suspension is usually calculated in the framework of low-Reynolds-number hydrodynamics neglecting fluid inertia, that is using the Stokes equations for fluid flows. Apart from classical results for unbounded suspensions of spheres (starting from the pioneering work of Einstein Reference Einstein1906, Reference Einstein1911), it has been found that the effective viscosity is significantly influenced by the presence of walls. There have been extensive studies of suspensions of non-Brownian spherical particles freely moving in a linear shear flow between two parallel solid walls. The effective viscosity in such a system was determined experimentally by Peyla & Verdier (Reference Peyla and Verdier2011) and numerically by Brunn (Reference Brunn1981), Tozeren & Skalak (Reference Tozeren and Skalak1983), Pasol (Reference Pasol2003), Feuillebois, Lecoq & Pasol (Reference Feuillebois, Lecoq, Pasol and Todorov2007), Zurita-Gotor, Bławzdziewicz & Wajnryb (Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2007), Davit & Peyla (Reference Davit and Peyla2008), Swan & Brady (Reference Swan and Brady2010), Sangani, Acrivos & Peyla (Reference Sangani, Acrivos and Peyla2011).
In contrast, not much work has been done to determine the wall influence on the rheology of suspensions made of non-spherical particles, even though various results exist for unbounded suspensions in geometries where confinement can be neglected. It is known that the effective viscosity of unbounded suspensions is very sensitive to the particle shape. The intrinsic viscosity of suspensions of elongated spheroidal particles in unbounded fluid was studied for instance by Sheraga (Reference Sheraga1955) and Brenner (Reference Brenner1974).
A dilute suspension of straight rods in a linear shear flow between two parallel solid walls was studied by Zurita-Gotor et al. (Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2007), using the bead model and the Cartesian-representation method developed by Bhattacharya, Bławzdziewicz & Wajnryb (Reference Bhattacharya, Bławzdziewicz and Wajnryb2005a ,Reference Bhattacharya, Bławzdziewicz and Wajnryb b ). Their study focused on systems of rods that are shorter than the distance between the walls. In particular, they have shown that the presence of walls causes a relatively small correction to the dependence of the intrinsic viscosity on the particle aspect ratio, compared to that observed for unbounded systems.
For elongated particles, it can be expected that the effective viscosity is modified whenever the particle length is larger than the distance between parallel walls, thereby limiting possible particle orientations. The goal of this theoretical paper is to determine the importance of this effect for two families of particle shapes: straight rods modelled as chains of beads, and prolate spheroids.
We consider here a quasi-steady periodic shear flow between two parallel plane walls separated by the distance
$H$
. The flow is quasi-steady in the sense that the period
$T$
is large compared with the typical time
$H^{2}/{\it\nu}$
for diffusion of vorticity, where
${\it\nu}$
denotes the fluid kinematic viscosity. The shear rate
$\dot{{\it\gamma}}>0$
is assumed to be such that the Reynolds number
$Re=\dot{{\it\gamma}}H^{2}/{\it\nu}$
is low compared with unity. In this framework we therefore neglect fluid inertia. Furthermore, we assume that the frequency
$1/T$
is high enough so that
$T\ll 1/\dot{{\it\gamma}}$
. In summary, we consider the range
$H^{2}/{\it\nu}\ll T\ll 1/\dot{{\it\gamma}},$
consistent with
$Re\ll 1$
. Recall that elongated particles immersed in an unbounded shear flow rotate with a period of order of
$1/\dot{{\it\gamma}}$
(the so-called Jeffery’s orbit; see Jeffery Reference Jeffery1922). Our high-frequency assumption implies that the particle oscillations are nearly frozen: the particles perform only small oscillations about their average orientations, so the orientation variation during an oscillation period can be neglected (see also Van der Werff et al.
Reference Van der Werff, De Kruif, Blom and Mellema1989; Shikata & Pearson Reference Shikata and Pearson1994). Consequently, any particle lateral migration due to possible changes in orientation like in Park & Butler (Reference Park and Butler2009) is also ignored. Particles are assumed to be non-Brownian. In this case there is no particle migration close to a wall from symmetry arguments (Bretherton Reference Bretherton1962). In the opposite case, there would be a lateral migration across the gap between the walls and the particle centre-of-mass distribution would be modified accordingly (Park & Butler Reference Park and Butler2009). In practice, we consider a given initial particle distribution in space and orientation. From the above assumptions this distribution will not evolve in the weakly oscillating shear flow. In this sense the ergodic assumption can be applied. Finally, the suspension is assumed to be dilute, so that hydrodynamic interactions between particles are negligible.
The outline of the paper is as follows. In § 2, a general expression for the effective viscosity of a dilute suspension bounded between parallel walls is derived in terms of the averaged stresslet on an individual particle. Methods for calculating the stresslet on a particle between walls are presented in § 3, namely the method of multipoles for interacting spheres (spheres are later assembled to form rods) and the boundary integral method for more general particle shapes (prolate spheroids are considered in the following sections). Then § 4 is concerned with the calculation and results of the effective viscosity of a bounded dilute suspension of orthotropic bodies of revolution. Based on the result of § 2, the average over positions and orientations of elongated particles is first made explicit in § 4.1. Then results for the effective viscosity are presented in § 4.2 for chains of beads and prolate spheroids. Finally, conclusions are drawn in § 5.
2. Effective viscosity of a bounded dilute suspension
In this section, we present a general expression for the effective viscosity of a bounded dilute suspension of freely moving particles embedded in the linear shear flow of a viscous fluid. The suspension is bounded by parallel walls and is homogeneous in the directions parallel to the walls.
2.1. Problem and notation
The geometry is presented in figure 1. We use a Cartesian coordinates system
$(O,x,y,z)$
with normal unit vectors
$(\boldsymbol{e}_{x},\boldsymbol{e}_{y},\boldsymbol{e}_{z})$
. The suspension is bounded by two parallel plane walls
$W_{0},W_{1}$
represented by
$z=0,H$
, respectively. It is subjected to a linear shear flow
$\boldsymbol{u}_{\infty }=\dot{{\it\gamma}}z\boldsymbol{e}_{x}$
with rate of shear
$\dot{{\it\gamma}}$
. Let
$\boldsymbol{U}_{\!\infty }=U_{\!\infty }\boldsymbol{e}_{x}=\dot{{\it\gamma}}H\boldsymbol{e}_{x}$
.
Figure 1. Sketch of a dilute suspension of particles in a linear shear flow bounded by two parallel walls. The angles
${\it\theta}$
and
${\it\varphi}$
are introduced in § 4.1. Note that
$z_{i}$
denotes the distance of the particle centre of volume
$O_{i}^{\prime }$
to the lower wall
$W_{0}$
.
Consider
$N$
particles with surfaces
$\mathscr{S}_{j}$
and centres of volume at positions
$(x_{j},y_{j},z_{j})$
,
$j=1,\dots ,N$
. The boundary conditions for the velocity of the flow field perturbed by the presence of particles are:
$$\begin{eqnarray}\text{on }W_{0}:\quad \boldsymbol{u}=\mathbf{0},\quad \text{on }W_{1}:\quad \boldsymbol{u}=\boldsymbol{U}_{\!\infty },\end{eqnarray}$$
$$\begin{eqnarray}\text{on }\mathscr{S}_{j}:\quad \boldsymbol{u}=\boldsymbol{U}_{j}+{\it\bf\Omega}_{j}\times \boldsymbol{r}_{j}\quad (\,j=1,\dots ,N),\end{eqnarray}$$
where
$\boldsymbol{r}_{j}$
is a position vector originating from the centre of volume of particle
$j$
and
$\boldsymbol{U}_{j},{\it\bf\Omega}_{j}$
are respectively the translation and rotation velocity of particle
$j$
. These velocities will be determined so that each particle
$j$
is freely moving in the flow field.
Without particles, a tangential force
${\it\mu}_{0}\dot{{\it\gamma}}\,\boldsymbol{e}_{x}$
has to be applied per unit surface of
$W_{1}$
(and an opposite force on
$W_{0}$
) to shear the fluid. The goal is to find the supplementary forces which have to be exerted on the plates in order to apply to the suspension a shear flow with the same shear rate
$\dot{{\it\gamma}}$
. In the adopted framework of the low-Reynolds-number assumption fluid inertia is neglected. Considering moreover that particle inertia is negligible and that particles are force-free and torque-free, it is equivalent to calculate either the force applied on
$W_{0}$
or that on
$W_{1}$
, since these forces are equal and opposite.
The volume fraction of the suspension is low, and we consider first-order effects. The approach to calculate the stress on either wall is an extension of that for an unbounded suspension (see Happel & Brenner Reference Happel and Brenner1973, § 9.1). The result is presented in the following sections.
2.2. Effective viscosity in terms of the averaged stresslet
Let the fluid viscosity be
${\it\mu}_{0}$
and the suspension effective viscosity be
$\langle {\it\mu}\rangle$
. For a polydisperse suspension of particles with volumes
$v_{k}~(k=1,\dots ,M)$
and volume fractions
${\it\phi}_{k}\;(k=1,\dots ,M)$
, with
${\it\phi}=\sum _{k=1}^{M}{\it\phi}_{k}$
and
${\it\phi}\ll 1$
(dilute suspension), the result for the intrinsic viscosity
$$\begin{eqnarray}[{\it\mu}]=\frac{\langle {\it\mu}\rangle -{\it\mu}_{0}}{{\it\mu}_{0}{\it\phi}}\end{eqnarray}$$
is
$$\begin{eqnarray}[{\it\mu}]=\mathop{\sum }_{k=1}^{M}\frac{{\it\phi}_{k}}{{\it\phi}}\frac{\langle \unicode[STIX]{x1D61A}_{kxz}\rangle }{{\it\mu}_{0}v_{k}\dot{{\it\gamma}}}\end{eqnarray}$$
where
$\langle \unicode[STIX]{x1D61A}_{kxz}\rangle$
is the average
$xz$
component of the stresslet tensor on a freely moving particle of type
$k$
. More precisely, the notation
$\langle \cdot \rangle$
indicates the equilibrium ensemble average over all positions and orientations of particle
$k$
. For any particle
$j=1,\dots ,N$
with surface
$\mathscr{S}_{j}$
, the stresslet tensor is defined as
$$\begin{eqnarray}\unicode[STIX]{x1D64E}_{j}=\int _{\mathscr{S}_{j}}\left[{\textstyle \frac{1}{2}}(\boldsymbol{r}_{j}\,\boldsymbol{f}+\boldsymbol{f}\,\boldsymbol{r}_{j})-{\textstyle \frac{1}{3}}\unicode[STIX]{x1D644}(\boldsymbol{r}_{j}\boldsymbol{\cdot }\boldsymbol{f})\right]\!\text{d}\mathscr{S},\end{eqnarray}$$
where
$\boldsymbol{f}={\bf\sigma}\boldsymbol{\cdot }\boldsymbol{n}$
denotes the stress applied by the fluid on
$\mathscr{S}_{j}$
. Here,
${\bf\sigma}$
is the stress tensor and
$\boldsymbol{n}$
denotes a unit normal vector on
$\mathscr{S}_{j}$
, pointing into the fluid. One should note that
$\unicode[STIX]{x1D64E}_{j}$
does not depend on the origin for
$\boldsymbol{r}_{j}$
since the particle is force-free. Let
$\unicode[STIX]{x1D61A}_{jxz}$
denote the
$xz$
component of
$\unicode[STIX]{x1D64E}_{j}$
. For a monodisperse suspension of particles of volume
$v$
, the result (2.3) then is simply
$$\begin{eqnarray}[{\it\mu}]=\frac{\langle \unicode[STIX]{x1D61A}_{xz}\rangle }{{\it\mu}_{0}v\dot{{\it\gamma}}}.\end{eqnarray}$$
This quantity will later be compared with that for an unbounded suspension,
$[{\it\mu}_{\infty }]$
.
2.3. Demonstration
A brief demonstration of (2.3) will be presented here. The perturbed Stokes flow field is sought as the sum of the unperturbed flow (with subscript
$\infty$
) and a perturbation (denoted here with a prime). The perturbed flow velocity and stress tensor are then written as
$\boldsymbol{u}=\boldsymbol{u}_{\infty }+\boldsymbol{u}^{\prime },{\bf\sigma}={\bf\sigma}_{\infty }+{\bf\sigma}^{\prime }$
.
The suspension is dilute, so that particles produce independent perturbations on the ambient flow. We therefore start by considering a single particle (in a second stage, we will sum up the analogous contributions of all particles). The boundary conditions (2.1) are supplemented by the condition that the perturbation flow vanishes at an infinite distance from the particle.
For the purpose of calculating the forces on the walls, it is expedient to apply the Lorentz reciprocal theorem (see Happel & Brenner Reference Happel and Brenner1973). The formula is written in terms of the unperturbed flow field and of the unknown perturbation flow with velocity
$\boldsymbol{u}^{\prime }$
and stress tensor
${\bf\sigma}^{\prime }$
. The fluid volume on which the theorem is applied has an embedded particle
$j$
(any of the particles
$1,\dots ,N$
) and is limited by some surface
$\mathscr{S}$
at a large distance
$r\gg H$
from the particle and by the parts of the walls
$W_{0}$
and
$W_{1}$
that are encompassed by
$\mathscr{S}\!$
, say
$\mathscr{W}_{0}$
and
$\mathscr{W}_{1}$
. Let us define
$\boldsymbol{f}_{\infty }={\bf\sigma}_{\infty }\boldsymbol{\cdot }\boldsymbol{n}$
and
$\boldsymbol{f}^{\prime }=\boldsymbol{f}-\boldsymbol{f}_{\infty }={\bf\sigma}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}$
. The theorem can then be written
$$\begin{eqnarray}\int _{(\mathscr{W}_{0}+\mathscr{W}_{1}+\mathscr{S}_{j}+\mathscr{S})}\boldsymbol{u}_{\infty }\boldsymbol{\cdot }\boldsymbol{f}^{\prime }\text{d}\mathscr{S}=\int _{(\mathscr{W}_{0}+\mathscr{W}_{1}+\mathscr{S}_{j}+\mathscr{S})}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{f}_{\infty }\text{d}\mathscr{S}.\end{eqnarray}$$
The surface area of
$\mathscr{S}$
is of order
$Hr$
. For
$r\rightarrow \infty$
, the integrals on
$\mathscr{S}$
vanish as expected because the perturbation velocity due to a freely moving particle in wall-bounded flow decays faster than that in unbounded fluid, that decays like
$1/r^{2}$
. And the perturbation stress tensor decays even faster. On the particle surface
$\mathscr{S}_{j}$
, the integral on the left-hand side of (2.6) minus that on the right-hand side gives
$$\begin{eqnarray}\int _{\mathscr{S}_{j}}(\boldsymbol{u}_{\infty }\boldsymbol{\cdot }\boldsymbol{f}^{\prime }-\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{f}_{\infty })\text{d}\mathscr{S}=\dot{{\it\gamma}}\,\unicode[STIX]{x1D61A}_{jxz},\end{eqnarray}$$
for a force-free and torque-free particle, as detailed in appendix A. From the boundary conditions on the walls, the integral on
$\mathscr{W}_{0}$
in the left-hand side of (2.6) vanishes and that on
$\mathscr{W}_{1}$
has the value
$U_{\!\infty }F_{jx}^{\prime }$
, where
$F_{jx}^{\prime }$
is the
$x$
component of the unknown tangential force exerted by the perturbation flow due to the particle
$j$
onto
$\mathscr{W}_{1}$
. The integrals on
$\mathscr{W}_{0}$
and
$\mathscr{W}_{1}$
in the right-hand side of (2.6) vanish, from the boundary conditions for
$\boldsymbol{u}^{\prime }$
. To summarize, (2.6) gives, with
$U_{\!\infty }=\dot{{\it\gamma}}H$
,
$$\begin{eqnarray}F_{jx}^{\prime }=-\frac{\unicode[STIX]{x1D61A}_{jxz}}{H}.\end{eqnarray}$$
Taking the limit
$r\rightarrow \infty$
, this result shows that the tangential force along
$x$
exerted by the perturbation flow due to particle
$j$
onto the wall
$W_{1}$
is simply related to the stresslet on particle
$j$
. It should be emphasized that this result is valid for any particle shape and position.
We turn now to the expression for the effective viscosity. Let us define a cylindrical domain
$\mathscr{D}$
bounded by
$W_{0}$
and
$W_{1}$
and containing all
$N$
particles and all particle perturbations. That is, in the fluid outside
$\mathscr{D}$
the flow field is approximately the unperturbed one. Let
$W_{0\mathscr{D}}$
and
$W_{1\mathscr{D}}$
be the part of
$W_{0}$
and
$W_{1}$
in
$\mathscr{D}$
and let
$A$
be the surface area of
$W_{0\mathscr{D}}$
and
$W_{1\mathscr{D}}$
. The
$x$
component of the total stress exerted by the perturbed flow on
$W_{1\mathscr{D}}$
is
$\mathit{f}_{x}=\mathit{f}_{\infty x}+\sum _{j=1}^{N}F_{jx}^{\prime }/A$
, where
$\mathit{f}_{\infty x}=\boldsymbol{f}_{\infty }\boldsymbol{\cdot }\boldsymbol{e}_{x}=-{\it\mu}_{0}\dot{{\it\gamma}}$
. The stress
$f_{x}$
exerted by
$W_{1\mathscr{D}}$
onto the suspension in
$\mathscr{D}$
is equal and opposite to
$\mathit{f}_{x}$
:
$$\begin{eqnarray}f_{x}=-\mathit{f}_{x}\simeq {\it\mu}_{0}\dot{{\it\gamma}}+\frac{1}{AH}\mathop{\sum }_{j=1}^{N}\unicode[STIX]{x1D61A}_{jxz}.\end{eqnarray}$$
We now extend the domain
$\mathscr{D}$
in order to encompass the infinite walls and use the assumption that the suspension is statistically homogeneous in the directions along the walls. Then the limit of (2.9) for
$\{A\rightarrow \infty ,N\rightarrow \infty \}$
and bounded
$\bar{n}=N/(AH)$
exists. Note that the neglected terms in (2.9) vanish in the limit. In this limit, the effective viscosity of the suspension is defined from the applied stress and shear rate by averaging over all possible positions and orientations of the particles:
$$\begin{eqnarray}\langle {\it\mu}\rangle =\left\langle \lim \frac{f_{x}}{\dot{{\it\gamma}}}\right\rangle .\end{eqnarray}$$
From (2.9)
$$\begin{eqnarray}\langle {\it\mu}\rangle ={\it\mu}_{0}+\left\langle \lim \frac{1}{AH\dot{{\it\gamma}}}\mathop{\sum }_{j=1}^{N}\unicode[STIX]{x1D61A}_{jxz}\right\rangle \!.\end{eqnarray}$$
Since the stresslet is proportional to the shear rate, this formula is of course independent of
$\dot{{\it\gamma}}$
. It is moreover independent of the shapes and sizes of particles. Normalizing the stresslet, the results for the intrinsic viscosity (2.2) follow in the forms (2.3) and (2.5).
3. The stresslet on a freely suspended particle
The stresslet on a freely suspended particle is calculated by solving the Stokes equations for fluid flows between two parallel solid walls using the boundary integral equation for the unknown stress
$\boldsymbol{f}$
on the particle surface. Since in this section we consider one of the particles, we omit for simplification the subscript
$j$
. The boundary integral equation (see e.g. Pozrikidis Reference Pozrikidis1992) relates
$\boldsymbol{f}$
to the particle translation and rotation velocity and the unperturbed fluid velocity at some point
$\boldsymbol{r}$
on the particle surface:
$$\begin{eqnarray}-8{\rm\pi}{\it\mu}_{0}[-\boldsymbol{u}_{\infty }+\boldsymbol{U}+{\it\bf\Omega}\times \boldsymbol{r}]=\int _{\mathscr{S}}\unicode[STIX]{x1D642}(\boldsymbol{r},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{y})\text{d}\mathscr{S}\quad \text{for }\boldsymbol{r}\text{ on }\mathscr{S}.\end{eqnarray}$$
Here,
$\boldsymbol{y}$
is a running point on
$\mathscr{S}$
and
$\unicode[STIX]{x1D642}$
is the Green tensor (with pole
$\boldsymbol{r}$
and observation point
$\boldsymbol{y})$
that vanishes at both walls (i.e.
$\unicode[STIX]{x1D642}(\boldsymbol{r},\boldsymbol{y})=0$
for
$\boldsymbol{r}$
on
$W_{0}$
and
$W_{1}$
). This Green tensor was determined by Liron & Mochon (Reference Liron and Mochon1976) and an alternative more tractable formulation was later derived by Jones (Reference Jones2004).
Solving (3.1) for
$\boldsymbol{U}={\it\bf\Omega}=\mathbf{0}$
first gives the force
$\boldsymbol{F}_{a}$
and torque
${\it\bf\Gamma}_{a}$
exerted when the particle is held fixed. By linearity, in the absence of ambient flow
$(\boldsymbol{u}_{\infty }=\mathbf{0})$
the force
$\boldsymbol{F}$
and torque
${\it\bf\Gamma}$
applied on the migrating particle are
$\boldsymbol{F}={\bf\zeta}^{tt}\boldsymbol{\cdot }\boldsymbol{U}+{\bf\zeta}^{tr}\boldsymbol{\cdot }{\it\bf\Omega}$
and
${\it\bf\Gamma}={\bf\zeta}^{rt}\boldsymbol{\cdot }\boldsymbol{U}+{\bf\zeta}^{rr}\boldsymbol{\cdot }{\it\bf\Omega}$
with second-rank tensors calculated by solving (3.1) for each of the six degrees of freedom of the particle rigid-body motion. Finally, the unknown freely suspended particle migration
$(\boldsymbol{U},{\it\bf\Omega})$
is determined by requiring the particle to be torque-free and force-free, i.e. by solving the coupled linear equations
${\bf\zeta}^{tt}\boldsymbol{\cdot }\boldsymbol{U}+{\bf\zeta}^{tr}\boldsymbol{\cdot }{\it\bf\Omega}=-\boldsymbol{F}_{a}$
and
${\bf\zeta}^{rt}\boldsymbol{\cdot }\boldsymbol{U}+{\bf\zeta}^{rr}\boldsymbol{\cdot }{\it\bf\Omega}=-{\it\bf\Gamma}_{a}$
. Once this is done,
$\boldsymbol{f}=\boldsymbol{f}_{\infty }+\boldsymbol{f}^{\prime }$
is found from (3.1) and used to compute the stresslet component
$\unicode[STIX]{x1D61A}_{xz}$
.
The boundary integral equation (3.1) is solved here using two alternative methods: the method of multipoles for chains of spheres and the boundary element technique for spheroids.
The first approach is based on the multipole expansion, corrected for lubrication to obtain a fast convergence rate (Ekiel-Jeżewska & Wajnryb Reference Ekiel-Jeżewska, Wajnryb, Feuillebois and Sellier2009). We apply the accurate method developed by Bhattacharya et al. (Reference Bhattacharya, Bławzdziewicz and Wajnryb2005a
,Reference Bhattacharya, Bławzdziewicz and Wajnryb
b
) for a system of particles between two parallel walls. It involves expanding the fluid velocity field into spherical and Cartesian fundamental sets of Stokes flows. The spherical set is used to describe the interaction of the fluid with the particles and the Cartesian set to describe the interaction with the walls. At the core of the method are transformation relationships between the spherical and Cartesian fundamental sets. The transformation formulae are used to derive a system of linear equations for the force multipoles induced on the particle surfaces. The coefficients in these equations are given in terms of lateral Fourier integrals corresponding to the directions parallel to the walls. These equations are truncated at a multipole of order
$L$
(see Ekiel-Jeżewska & Wajnryb Reference Ekiel-Jeżewska, Wajnryb, Feuillebois and Sellier2009) and solved numerically. In this work, we use
$L=4$
. The corresponding accuracy of the results for
$H/d\geqslant 2$
is better than 1 %, and for channels as narrow as
$H/d\approx 2.1$
, it is not worse than 6 %. To achieve a higher accuracy, a two-wall lubrication procedure would be needed (see Ekiel-Jeżewska et al.
Reference Ekiel-Jeżewska, Wajnryb, Bławzdziewicz and Feuillebois2008).
The second approach uses the boundary element method. For a given left-hand side, (3.1) is numerically inverted as explained in Pasol & Sellier (Reference Pasol and Sellier2006) using on
$\mathscr{S}$
an
$N$
-node mesh made of triangular and curved 6-node boundary elements.
A comparison of results of the multipole and boundary element methods is illustrated in table 1. It is observed that values of the normalized stresslet component
$\unicode[STIX]{x1D61A}_{xz}/[8{\rm\pi}{\it\mu}_{0}\dot{{\it\gamma}}a^{3}]$
for a sphere with radius
$a$
are in agreement to nearly four decimal places.
Table 1. Computed values of the normalized stress component
$\unicode[STIX]{x1D61A}_{xz}/[8{\rm\pi}{\it\mu}_{0}\dot{{\it\gamma}}a^{3}]$
for a sphere with radius
$a$
and centre distance to wall
$W_{0}$
equal to
$h=1.1a,1.3a$
. The gap between walls is
$H=3a$
and different
$N$
-node meshes on the sphere surface are used for the boundary element approach. The multipole truncation number is
$L=30$
(see Ekiel-Jeżewska & Wajnryb Reference Ekiel-Jeżewska, Wajnryb, Feuillebois and Sellier2009).
4. Viscosity of a dilute suspension of orthotropic bodies of revolution
4.1. Expression for the effective viscosity
We confine our attention to an orthotropic axisymmetric particle. Let
$\boldsymbol{e}$
be a unit vector along the particle axis of revolution. As in figure 1 for the example cases of a rod of beads and of a prolate spheroid, the particle location and orientation are described by the distance
$z$
of its centre of volume
$O^{\prime }$
to the lower wall
$W_{0}$
and the angles
$({\it\theta},{\it\varphi})$
such that
$\cos {\it\theta}=\boldsymbol{e}\boldsymbol{\cdot }\boldsymbol{e}_{z}$
and
$\sin {\it\theta}\cos {\it\varphi}=\boldsymbol{e}\boldsymbol{\cdot }\boldsymbol{e}_{x}$
with
${\it\theta}\in [0,{\rm\pi}]$
and
${\it\varphi}\in [0,2{\rm\pi}]$
.
In calculating the intrinsic viscosity
$[{\it\mu}]$
from (2.5) the average of the stresslet component
$\unicode[STIX]{x1D61A}_{xz}(z,{\it\theta},{\it\varphi})$
for the particle allowed positions
$z$
and angles
$({\it\theta},{\it\varphi})$
is obtained by assuming equally probable distributions of position and orientation.
Since the particle is orthotropic it is sufficient to take
$z_{min}\leqslant z\leqslant H/2$
where
$z_{min}>0$
denotes the lowest possible value of
$z$
over
$({\it\theta},{\it\varphi})$
when the particle touches the lower wall. Note that for each possible value of
$z$
one has
${\it\phi}\in [0,2{\rm\pi}]$
whereas
${\it\theta}\in [{\it\theta}_{1}(z),{\it\theta}_{2}(z)]$
, with angles
${\it\theta}_{1}(z)$
and
${\it\theta}_{2}(z)$
depending upon both
$z$
and the particle shape, such that
$0\leqslant {\it\theta}_{1}(z)\leqslant {\it\theta}_{2}(z)\leqslant {\rm\pi}$
. Under the previous properties and notation, the result is
$$\begin{eqnarray}[{\it\mu}]=\frac{1}{{\it\mu}_{0}v\dot{{\it\gamma}}}\left\{\displaystyle \frac{\displaystyle \int _{z_{min}}^{H/2}\left[\displaystyle \int _{{\it\theta}_{1}(z)}^{{\it\theta}_{2}(z)}\left(\displaystyle \int _{0}^{2{\rm\pi}}\unicode[STIX]{x1D61A}_{xz}(z,{\it\theta},{\it\varphi})\text{d}{\it\varphi}\right)\sin {\it\theta}\text{d}{\it\theta}\right]\!\text{d}z}{2{\rm\pi}\displaystyle \int _{z_{min}}^{H/2}\left[\displaystyle \int _{{\it\theta}_{1}(z)}^{{\it\theta}_{2}(z)}\sin {\it\theta}\text{d}{\it\theta}\right]\!\text{d}z}\right\}\!.\end{eqnarray}$$
As the reader may easily check, symmetries furthermore show that for an orthotropic axisymmetric particle the following relationship holds:
$$\begin{eqnarray}\unicode[STIX]{x1D61A}_{xz}(z,{\it\theta},{\it\varphi})=\unicode[STIX]{x1D61A}_{xz}(z,{\it\theta},0)\cos ^{2}{\it\varphi}+\unicode[STIX]{x1D61A}_{xz}(z,{\it\theta},{\rm\pi}/2)\sin ^{2}{\it\varphi}.\end{eqnarray}$$
Exploiting (4.2) then gives
$$\begin{eqnarray}\displaystyle [{\it\mu}]=\frac{B}{{\it\mu}_{0}v\dot{{\it\gamma}}A},\quad A=\int _{z_{min}}^{H/2}\!\left[\int _{{\it\theta}_{1}(z)}^{{\it\theta}_{2}(z)}\sin {\it\theta}\text{d}{\it\theta}\right]\!\text{d}z,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle B=\int _{z_{min}}^{H/2}\left[\int _{{\it\theta}_{1}(z)}^{{\it\theta}_{2}(z)}\unicode[STIX]{x1D61A}_{xz}(z,{\it\theta},{\rm\pi}/4)\sin {\it\theta}\text{d}{\it\theta}\right]\!\text{d}z. & & \displaystyle\end{eqnarray}$$
4.2. Results for chains of beads and for prolate spheroids
In this section, we analyse how two parallel solid walls influence the value of the intrinsic viscosity for a suspension of axisymmetric orthotropic particles. As illustrated in figure 1, the following two families of shapes with length
$l$
and width
$a$
are considered.
-
(i)
$N$
-bead(s) rods made of
$N\geqslant 1$
(equal touching) sphere(s) with diameter
$d=2a\leqslant H$
for which (4.5a−d )
$$\begin{eqnarray}\displaystyle v_{b}=N\left(\frac{4{\rm\pi}a^{3}}{3}\right)\!,\quad l=Nd,\quad z_{min}=a,\quad {\it\theta}_{2}(z)=\frac{{\rm\pi}}{2},\end{eqnarray}$$
(4.6)
$$\begin{eqnarray}\displaystyle & {\it\theta}_{1}(z)=\left\{\begin{array}{@{}ll@{}}0\quad & \text{for }N=1,\\ 0\quad & \text{for }Nd/2\leqslant z\leqslant H/2\text{and }N\geqslant 2,\end{array}\right. & \displaystyle\end{eqnarray}$$
(4.7)
$$\begin{eqnarray}\displaystyle & \displaystyle \cos {\it\theta}_{1}(z)=\frac{z/d-1/2}{N/2-1/2}\quad \text{for }d\leqslant 2z\leqslant H\leqslant Nd. & \displaystyle\end{eqnarray}$$
-
(ii) Prolate spheroids with semi-axis
$a\leqslant H/2$
and
$c>a$
for which (4.8a−d )
$$\begin{eqnarray}\displaystyle \displaystyle v_{s}=c\left(\frac{4{\rm\pi}a^{2}}{3}\right)\!,\quad l=2c,\quad z_{min}=a,\quad {\it\theta}_{2}(z)=\frac{{\rm\pi}}{2}, & & \displaystyle\end{eqnarray}$$
(4.9a,b )
$$\begin{eqnarray}\displaystyle \displaystyle {\it\theta}_{1}(z)=0\quad \text{ for }c\leqslant z\leqslant H/2\quad \text{and}\quad \cos {\it\theta}_{1}(z)=\sqrt{\frac{z^{2}-a^{2}}{c^{2}-a^{2}}}\quad \text{for }a\leqslant z\leqslant c. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Accordingly, a prolate spheroid with length
$l=2c$
and width
$2a$
and an
$N$
-sphere rod with the same length
$l=Nd$
and width
$2a$
have the same slenderness ratio
$l/(2a)=c/a=N$
. It is remarkable that both particles also have the same volume.
Then the integral
$A$
in (4.3) is calculated analytically for any distance
$H\geqslant 2a$
between the walls with the following results.
(i) For the
$N$
-bead rod
$$\begin{eqnarray}\displaystyle & \displaystyle A=[2H-(N+1)d]/4\quad \text{if }H\geqslant Nd, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A=\frac{(H-d)^{2}}{4d(N-1)}\quad \text{ if }d\leqslant H\leqslant Nd\quad \text{for }N\geqslant 2. & \displaystyle\end{eqnarray}$$
(ii) For the prolate spheroid with aspect ratio
${\it\beta}=c/a>1$
$$\begin{eqnarray}\displaystyle & \displaystyle A=\frac{H}{2}-c+\frac{a}{2\sqrt{{\it\beta}^{2}-1}}g({\it\beta})\quad \text{if }H\geqslant 2c, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A=\frac{a}{2\sqrt{{\it\beta}^{2}-1}}g\!\left(\frac{H}{2a}\right)\quad \text{if }H\leqslant 2c & \displaystyle\end{eqnarray}$$
$g(x)=x\sqrt{x^{2}-1}-\log [x+\sqrt{x^{2}-1}]$
for
$x\geqslant 1$
.
Finally, for both types of particles, the integral
$B$
in (4.4) is numerically evaluated using Gauss quadratures for the variables
$z$
and
$u=\cos {\it\theta}$
. In practice, for a given Gauss point
$z_{G}^{\,j}$
the selected order of quadrature in integrating over
$u=\cos {\it\theta}$
is such that the lower wall–particle gap is larger than a prescribed small and positive value for each angle
${\it\theta}_{G}^{k}$
associated with the resulting Gauss points
$u_{G}^{k}$
.
4.2.1. Results for beads
The results for beads are shown in figure 2. The variation of
$[{\it\mu}]$
exhibits a rich behaviour.
-
(a) For
$H/d\geqslant N$
it is not surprising that
$[{\it\mu}]$
increases for decreasing gap
$H/d-1$
. -
(b) For
$H/d<N$
and
$N=1,2$
the viscosity
$[{\it\mu}]$
still increases as
$H/d-1$
decreases. -
(c) For
$H/d<N$
and
$N\geqslant 3$
the intrinsic viscosity
$[{\it\mu}]$
is surprisingly found to first decrease for moderate gaps
$(2\leqslant H/d\leqslant N),$
go to a minimum and then increase for narrow gaps
$(1\leqslant H/d\leqslant 2)$
.
For narrow gaps the strong hydrodynamic coupling with the walls leads to increasing dissipation. In figure 2, the logarithmic scale is used to display the singular lubrication effect for very narrow gaps.
Figure 2. Intrinsic viscosity
$[{\it\mu}]$
of
$N$
-bead chains
$(N\leqslant 10)$
versus
$H/d-1$
with
$H$
the distance between walls and
$d$
the diameter of a bead. The logarithmic scale is used to show the lubrication behaviour for narrow gaps. The symbols for
$N=4$
in the inset refer to figure 3, that is to the values
$H/d-1=0.1$
, 1.2, 3, 3.4. The minimum is at
$H/d-1\sim 1.15$
with value
$[{\it\mu}]\sim 4.24$
.
For rods of length
$Nd$
the value of the intrinsic viscosity for unbounded liquid
$[{\it\mu}_{\infty }]$
is already reached within 2.5 % for
$H/d=20$
. Moreover, the asymptotic expression for the intrinsic viscosity at a large separation between the walls is
$$\begin{eqnarray}\displaystyle \frac{[{\it\mu}]}{[{\it\mu}_{\infty }]}\sim 1+\frac{C_{N}}{\displaystyle \frac{H}{d}-\frac{N+1}{2}}\quad \text{ for }\frac{H}{d}-\frac{N+1}{2}\gg 1, & & \displaystyle\end{eqnarray}$$
where the denominator
$H/d-(N+1)/2=2A/d$
(see (4.10)) comes from the normalization factor
$A$
given by (4.10) and the coefficients
$C_{N}$
are fitted to the numerical results. Values of
$[{\it\mu}_{\infty }]$
and
$C_{N}$
are given with a three-digit accuracy in table 2.
Table 2. Computed values of the intrinsic viscosity
$[{\it\mu}_{\infty }]$
for the
$N$
-bead rods in unbounded fluid and of the coefficients
$C_{N}$
appearing in the asymptotic formula (4.14). By comparison,
$[{\it\mu}_{\infty }]=2.58,2.79$
for prolate spheroids with aspect ratio
$c/a=2,3$
respectively from Sheraga (Reference Sheraga1955).
From figure 2, when
$N\geqslant 3$
we can define three different regimes for the intrinsic viscosity:
-
(i) a first ‘weakly confined’ regime when the chain length is smaller than the wall separation,
$Nd\leqslant H$
; -
(ii) a second ‘semi-confined’ regime where the range of possible orientations is limited, for
$H_{\mathit{min}}<H<Nd$
, with
$H_{\mathit{min}}$
the value of
$H$
at which
$[{\it\mu}]$
is minimum; -
(iii) a third ‘strongly confined’ regime for
$d\leqslant H\leqslant H_{\mathit{min}}$
.
The minimum value of
$[{\it\mu}]$
appears at the transition between the ‘semi-confined’ and ‘strongly confined’ regimes (this minimum does not appear for
$N=1,2$
).
In order to qualitatively interpret these regimes we consider now the variation of the stresslet for a four-bead
$(N=4)$
rod located at mid-channel at different orientations
${\it\theta}$
. Note that we are only considering the contribution to the intrinsic viscosity from the single position
$z=H/2$
. For this location, the angle
${\it\theta}$
assumes values
${\it\theta}_{1}\leqslant {\it\theta}\leqslant {\rm\pi}/2$
, where
$\cos {\it\theta}_{1}=\text{min}[H/d-1/N-1,1]$
. The average over the azimuthal angle
${\it\varphi}$
of the
$xz$
stresslet component,
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D61A}}_{xz}=\frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\unicode[STIX]{x1D61A}_{xz}(H/2,{\it\theta},{\it\varphi})\text{d}{\it\varphi}=\unicode[STIX]{x1D61A}_{xz}(H/2,{\it\theta},{\rm\pi}/4),\end{eqnarray}$$
normalized by
$8{\rm\pi}{\it\mu}_{0}a^{3}\dot{{\it\gamma}}$
is plotted in figure 3 versus
$\cos {\it\theta}$
for
$H/d=\infty ,4.4,4,2.2,1.1$
.
In (4.4), the integral over
${\it\theta}$
for calculating
$[{\it\mu}]$
indeed involves
$d(\cos {\it\theta})$
, and the normalization contains
$\cos {\it\theta}_{1}$
. In terms of the stretched variable
$\cos {\it\theta}/\!\cos {\it\theta}_{1}$
the contribution to the intrinsic viscosity for a selected ratio
$H/d$
is given by the area under the relevant curve in the inset of figure 3. We now examine how plots in figure 3 provide information for each regime.
-
(i) ‘Weakly confined regime’ (curves
$H/d=\infty ,4.4,4$
). For unbounded flow (
$H/d=\infty$
) the curve exhibits a maximum which comes from the average value over
${\it\varphi}$
in which the preferred value at
${\it\varphi}=0$
is
${\it\theta}={\rm\pi}/4$
(which is the direction of the pure straining motion associated with a shear flow). As
$H$
decreases the ends of the particle start to interact with the walls so that the stresslet increases near
$\cos {\it\theta}=1$
. As a consequence, the area under the curve also increases and so does
$[{\it\mu}]$
. -
(ii) ‘Semi-confined’ regime (curve
$H/d=2.2$
). When
$H$
is in the interval
$H_{\mathit{min}}<H<Nd$
contact becomes geometrically possible, but a singular behaviour of the stresslet appears at
${\it\theta}={\it\theta}_{1}$
due to lubrication. As
$H$
drops, the range of values of
${\it\theta}$
shrinks, therefore reducing the fraction of configurations with large stresslet. As a result, the area under the curve now decreases and so does
$[{\it\mu}]$
. Note (see figure 2) that the value of
$[{\it\mu}]$
for
$H/d=2.2$
is very close to the minimum. -
(iii) ‘Strongly confined’ regime (curve
$H/d=1.1$
). Finally, as
$H$
decreases below
$H_{\mathit{min}}$
, the sides of the rod (i.e. all intermediate beads) start interacting with the walls while the number of orientations weakly changes, the particle becoming nearly parallel to the walls. For very narrow rod–wall gaps the lubrication effects dramatically increase the stresslet
$\overline{\unicode[STIX]{x1D61A}}_{xz}$
and the suspension intrinsic viscosity.
Figure 3. Value of
$\overline{\unicode[STIX]{x1D61A}}_{xz}$
defined in (4.15), normalized by
$8{\rm\pi}{\it\mu}_{0}a^{3}\dot{{\it\gamma}}$
, for a four-bead rod located at the mid-channel versus
$\cos {\it\theta}$
(or
$\cos {\it\theta}/\!\cos {\it\theta}_{1}$
for the inset) for
$H/d=\infty ,4.4,4.0,2.2,1.1$
. Integration of these curves results in the contribution to the intrinsic viscosity values indicated by symbols in the inset of figure 2.
4.2.2. Results for prolate spheroids
Numerical calculations were performed for prolate spheroids with aspect ratio
$c/a=2,3,4,5,6$
. Larger aspect ratios were not considered because of the large CPU time demanded.
The ratio
$[{\it\mu}]/[{\it\mu}_{\infty }]$
of the intrinsic viscosity to that for an unbounded suspension is plotted versus the normalized gap between walls
$H/(2a)$
in figure 4. Results for chains of beads
$N=2,3,4,5,6$
are also shown for comparison. The remark that for
$c/a=N$
the prolate spheroid and the
$N$
-sphere bead have the same volume may be interesting for applications.
Similar trends are observed in figure 4 for both types of elongated particles, and the regimes (i)–(iii) for the beads also clearly appear for the prolate spheroids. Yet, for
$N\geqslant 3$
the minimum
$[{\it\mu}]/[{\it\mu}_{\infty }]$
for beads is more deep than that for the prolate spheroid with the same aspect ratio
$(c/a=N)$
. Considering integer values of
$c/a,$
for sufficiently slender particles (
$N\geqslant 5$
for beads and
$c/a\geqslant 6$
for prolate spheroids) there is a domain for narrow gaps for which the intrinsic viscosity
$[{\it\mu}]$
is even smaller than that in unbounded fluid
$[{\it\mu}_{\infty }]$
. This result might open the way to applications involving suspensions.
Figure 4. Ratio
$[{\it\mu}]/[{\it\mu}_{\infty }]$
versus
$H/(2a)$
for
$N$
-sphere beads and prolate spheroids with the same aspect ratio
$c/a=N=1,2,3,4,5,6$
. Curves (coloured online) follow this ordering from top to bottom at
$H/(2a)\rightarrow 1$
. The horizontal dashed line is the asymptote for an unbounded suspension.
5. Conclusions
Novel results are obtained for the short-time intrinsic viscosity
$[{\it\mu}]$
of a dilute suspension of non-spherical solid particles in pure linear shear flow between two parallel walls. Rods made of
$N\geqslant 1$
touching spherical bead(s) and prolate spheroids are considered. For rods with
$N\geqslant 3$
and for prolate spheroids with
$c/a\geqslant 4$
three regimes are found, depending upon the distance between the walls
$H$
:
-
(i) a ‘weakly confined’ regime for particle length
$l\leqslant H$
, where
$[{\it\mu}]$
is slightly larger for smaller
$H$
; -
(ii) a ‘semi-confined’ regime, when
$H$
becomes smaller than
$l$
, where
$[{\it\mu}]$
rapidly decreases since the limited particle orientations eliminate configurations corresponding to large stresses at the particle tips, and thus to the largest stresslets; -
(iii) a ‘strongly confined’ regime when
$H$
becomes smaller than 2–3 particle widths, where
$[{\it\mu}]$
rapidly increases because of the strong hydrodynamic interactions between the whole elongated particle and the walls.
The transition between the ‘weakly confined’ and ‘semi-confined’ regimes is a local maximum of intrinsic viscosity while the transition between the ‘semi-confined’ and ‘strongly confined’ regimes is a local minimum. This minimum may for some range of parameters be smaller than the value of the intrinsic viscosity in unbounded fluid. In this special case, the viscous dissipation for suspensions flowing in micro-channels is reduced.
Acknowledgements
J.B. would like to acknowledge financial support from National Science Foundation (NSF) Grant No. CBET 1059745. M.L.E.-J. and E.W. were supported in part by the Polish NCN Grant No. 2012/05/B/ST8/03010. M.L.E.-J. benefited from the scientific activities of the COST Action MP1106.
Appendix A. The integral providing the stresslet contribution
The goal of this appendix is to prove (2.7). The left-hand side of (2.7) can also be written as
$$\begin{eqnarray}\int _{\mathscr{S}_{j}}\left(\boldsymbol{u}_{\infty }\boldsymbol{\cdot }\boldsymbol{f}^{\prime }-\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{f}_{\infty }\right)\!\text{d}\mathscr{S}=\int _{\mathscr{S}_{j}}\boldsymbol{u}_{\infty }\boldsymbol{\cdot }\boldsymbol{f}\text{d}\mathscr{S}-\int _{\mathscr{S}_{j}}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{f}_{\infty }\text{d}\mathscr{S}.\end{eqnarray}$$
The second integral in the right-hand side of (A 1) vanishes from the boundary condition (2.1c
) for
$\boldsymbol{u}$
on
$\mathscr{S}_{j}$
and from the conditions of zero force and torque applied by the ambient flow on particle
$\mathscr{S}_{j}$
. The first integral in the right-hand side of (A 1) may be decomposed as
$$\begin{eqnarray}\displaystyle \int _{\mathscr{S}_{j}}\boldsymbol{u}_{\infty }\boldsymbol{\cdot }\boldsymbol{f}\text{d}\mathscr{S} & = & \displaystyle \int _{\mathscr{S}_{j}}\dot{{\it\gamma}}z_{j}\boldsymbol{e}_{x}\boldsymbol{\cdot }\boldsymbol{f}\text{d}\mathscr{S}+\int _{\mathscr{S}_{j}}\dot{{\it\gamma}}(z-z_{j})\boldsymbol{e}_{x}\boldsymbol{\cdot }\boldsymbol{f}\text{d}\mathscr{S}\nonumber\\ \displaystyle & = & \displaystyle \dot{{\it\gamma}}z_{j}\boldsymbol{e}_{x}\boldsymbol{\cdot }\int _{\mathscr{S}_{j}}\boldsymbol{f}\text{d}\mathscr{S}+\dot{{\it\gamma}}\boldsymbol{e}_{x}\boldsymbol{\cdot }\left[\boldsymbol{e}_{z}\boldsymbol{\cdot }\int _{\mathscr{S}_{j}}\boldsymbol{r}_{j}\,\boldsymbol{f}\text{d}\mathscr{S}\right]\!.\end{eqnarray}$$
The first integral in the right-hand side of (A 2) vanishes since the particle is force-free. The doublet
$\boldsymbol{D}_{j}=\int _{\mathscr{S}_{j}}\boldsymbol{r}_{j}\,\boldsymbol{f}\text{d}\mathscr{S}$
may be decomposed into its trace, symmetric and antisymmetric parts:
$$\begin{eqnarray}\boldsymbol{D}_{j}=\int _{\mathscr{S}_{j}}\frac{1}{3}\unicode[STIX]{x1D644}(\boldsymbol{r}_{j}\boldsymbol{\cdot }\boldsymbol{f})\text{d}\mathscr{S}+\int _{\mathscr{S}_{j}}\left[\frac{1}{2}(\boldsymbol{r}_{j}\,\boldsymbol{f}+\boldsymbol{f}\boldsymbol{r}_{j})-\frac{1}{3}\unicode[STIX]{x1D644}(\boldsymbol{r}_{j}\boldsymbol{\cdot }\boldsymbol{f})\right]\!\text{d}\mathscr{S}+\int _{\mathscr{S}_{j}}\frac{1}{2}(\boldsymbol{r}_{j}\,\boldsymbol{f}-\boldsymbol{f}\boldsymbol{r}_{j})\text{d}\mathscr{S}.\end{eqnarray}$$
The trace is ignored since its projection vanishes:
$\boldsymbol{e}_{x}\boldsymbol{\cdot }[\boldsymbol{e}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D644}(\boldsymbol{r}_{j}\boldsymbol{\cdot }\boldsymbol{f})]$
$=(\boldsymbol{e}_{x}\boldsymbol{\cdot }\boldsymbol{e}_{z})(\boldsymbol{r}_{j}\boldsymbol{\cdot }\boldsymbol{f})=0$
. The second integral in (A 3) is the stresslet
$\unicode[STIX]{x1D64E}_{j}$
and the third integral is the rotlet
$\boldsymbol{R}_{j}$
. The rotlet vanishes here since each particle
$j$
is torque-free. Thus, we are left with the
$\unicode[STIX]{x1D61A}_{ixz}=\boldsymbol{e}_{x}\boldsymbol{\cdot }[\boldsymbol{e}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}_{j}]$
component of the stresslet of the perturbation flow:
$$\begin{eqnarray}\int _{\mathscr{S}_{j}}\boldsymbol{u}_{\infty }\boldsymbol{\cdot }\boldsymbol{f}\text{d}\mathscr{S}=\dot{{\it\gamma}}\unicode[STIX]{x1D61A}_{ixz}.\end{eqnarray}$$
Finally, (2.7) is proven.
