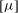1 Introduction
The way to determine the effective viscosity of a dilute suspension from the effective stress tensor was first found by Einstein (Reference Einstein1906) for spherical particles in unbounded fluid, based on the quasi-steady Stokes equations. The derived expressions are valid for any flow field. The intrinsic viscosity of ellipsoids was studied by Sheraga (Reference Sheraga1955) and Brenner (Reference Brenner1970). In this case, there appears the problem of dependence of the orientation probability distribution on the ambient flow field, and rotatory Brownian motion needs to be considered.
In a number of articles, the shear flow problem was considered in a confined geometry, i.e. between two parallel solid flat walls, see references in Feuillebois et al. (Reference Feuillebois, Ekiel-Jeżewska, Wajnryb, Sellier and Bławzdziewicz2015) (hereafter denoted as (I)). In particular, Zurita-Gotor, Bławzdziewicz & Wajnryb (Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2007) studied a dilute suspension of rods shorter than the distance between the walls, and Sangani, Acrivos & Peyla (Reference Sangani, Acrivos and Peyla2011) investigated the role of hydrodynamic particle–particle and particle–wall interactions in suspensions of spherical particles in very narrow channels. Park, Bricker & Butler (Reference Park, Bricker and Butler2007) considered polymers modelled as rigid slender bodies embedded in a shear flow near a single wall. They took into account the migration of the centre of mass of the rotating fibre because of its interaction with the wall. Park & Butler (Reference Park and Butler2009) extended their approach to fibres in either shear or Poiseuille flow between two parallel walls. However, they only used the one-wall Green tensor for determining the migration of the particle centre of mass. Pressure-driven flow of a suspension of spherical particles was considered by Bławzdziewicz & Wajnryb (Reference Bławzdziewicz and Wajnryb2008).
The important problem is to evaluate the effective viscosity of a dilute suspension, by averaging over a channel so as to obtain a quantity accessible to experiment. This approach was considered for particles in a tube by Brenner (Reference Brenner1970) and Cox & Mason (Reference Cox and Mason1971) and more recently by Navardi & Bhattacharya (Reference Navardi and Bhattacharya2010). In general, it is important to determine how large the influence of the confined geometry on the intrinsic viscosity is, and whether its value is sensitive to the method of the measurement, for example how much it differs when either in shear or in Poiseuille flow.
The goal of this article is first to derive a general formula for the effective viscosity of a dilute suspension of freely transported particles in a Poiseuille flow between parallel walls separated by a distance
$H$
.
A high-frequency flow field is considered here in the same sense as in (I). That is, the Poiseuille flow is periodic with a period
$T$
that is assumed to be small compared with
$H/u_{m}$
, where
$u_{m}$
is the maximum fluid velocity in the gap. Then, the fluid performs small oscillations. Considering elongated particles of length
$\ell \lesssim O(H)$
, their positions and orientations are practically frozen. In particular, they do not have time during a period to rotate along a Jeffery orbit (see Jeffery Reference Jeffery1922). A second assumption is that the period
$T$
is large compared with the typical time
$H^{2}/{\it\nu}$
for diffusion of vorticity across the gap, where
${\it\nu}$
is the fluid kinematic viscosity. The two preceding assumptions imply that the Reynolds number based on
$H$
and
$u_{m}$
is low compared with unity, that is
$Re=u_{m}H/{\it\nu}\ll 1$
. From these conditions, the quasi-steady Stokes equations apply. Consider, for example, a channel with gap
$H=1~\text{mm}$
containing an oil of kinematic viscosity
${\it\nu}=10^{-3}~\text{m}^{2}~\text{s}^{-1}$
, undergoing oscillatory flow with the period
$T=0.1~\text{s}$
and maximum velocity
$u_{m}=0.1~\text{mm}~\text{s}^{-1}$
. We find that
$T=(1/100)H/u_{m}$
,
$T=100\,H^{2}/{\it\nu}$
and
$Re=10^{-4}$
.
A more complicated situation, left for future studies, is when the positions and orientations of particles evolve when entrained by the flow field. This type of structure was studied by Zurita-Gotor et al. (Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2007) for non-Brownian particles in confined shear flow and by Ezhilan & Saintillan (Reference Ezhilan and Saintillan2015) for active elongated particles in Poiseuille flow. Analogous results would then have to be introduced into the calculation of the effective viscosity.
We start by considering particles of any shape between parallel walls and take into account both wall effects, which are of primary importance for confined suspensions. The general formula derived below for the effective viscosity of the dilute suspension will allow for the possibility to calculate these wall effects explicitly, using e.g. the method of multipoles for spheres or clusters of spheres and the boundary integral method for non-spherical particles.
The outline is as follows. The definition of the effective viscosity in Poiseuille flow is presented in § 2. The suspension is assumed to be dilute, that is the volume fraction is small compared with unity. In the first approximation, the contributions of particles to the stress tensor of the suspension may then be superposed. The contribution of one particle is derived in § 3. Like in Brenner (Reference Brenner1970), we use the reciprocity theorem. By superposition, the effective viscosity of the suspension is then obtained in § 4. The case of a suspension of spherical particles is described in § 5. Then, results for a suspension of axisymmetric orthotropic particles are presented in § 6. Finally, the discussion and conclusion are in § 7.
2 Definition of the effective viscosity and case of a dilute suspension
2.1 Notation for the Poiseuille flow
We consider a dilute system of rigid particles suspended in a viscous fluid bounded by two infinite parallel plane walls separated by a distance
$H$
(see figure 1). The position vector is denoted by
$\boldsymbol{x}$
, and we use a Cartesian coordinates system
$(x,y,z)$
with normal unit vectors
$(\boldsymbol{e}_{x},\boldsymbol{e}_{y},\boldsymbol{e}_{z})$
, such that the walls
$(W_{1},W_{2})$
are in the planes
$z=0$
and
$z=H$
, respectively.
Figure 1. Sketch of a dilute suspension of particles in a Poiseuille flow bounded by two parallel walls,
$\boldsymbol{u}_{0}=u_{0}(z)\boldsymbol{e}_{x}$
with (2.2).
In the absence of the particles, the parabolic fluid flow is driven by an imposed constant pressure gradient
${\rm\Delta}p_{0}/\mathscr{L}$
along the
$x$
direction, where
$\mathscr{L}$
is a length that is large compared with
$H$
. The corresponding two-dimensional Poiseuille flow velocity field is
$$\begin{eqnarray}\boldsymbol{u}_{0}=u_{0}\boldsymbol{e}_{x},\end{eqnarray}$$
where
$$\begin{eqnarray}u_{0}(z)=k_{1}z+k_{2}z^{2}\end{eqnarray}$$
is parabolic, with the coefficients
$k_{1}$
and
$k_{2}$
given by
$$\begin{eqnarray}k_{1}=-\frac{H}{2{\it\mu}_{0}}\frac{{\rm\Delta}p_{0}}{\mathscr{L}},\quad k_{2}=-\frac{k_{1}}{H}.\end{eqnarray}$$
Both these coefficients are proportional to the pressure drop per unit channel length
${\rm\Delta}p_{0}/\mathscr{L}$
and inversely proportional to the fluid viscosity
${\it\mu}_{0}$
. The local shear rate at a position
$z$
between the planes is
$$\begin{eqnarray}\dot{{\it\gamma}}(z)=k_{1}+2k_{2}z.\end{eqnarray}$$
The associated stress tensor is
$$\begin{eqnarray}{\bf\sigma}_{0}=-p_{0}(x)\unicode[STIX]{x1D644}+{\it\mu}_{0}\dot{{\it\gamma}}(z)(\boldsymbol{e}_{x}\boldsymbol{e}_{z}+\boldsymbol{e}_{z}\boldsymbol{e}_{x}),\end{eqnarray}$$
with the dynamic pressure
$$\begin{eqnarray}p_{0}(x)=2{\it\mu}_{0}k_{2}x,\end{eqnarray}$$
and the identity tensor
$\unicode[STIX]{x1D644}$
. Note that the coefficient
$k_{2}$
is negative, so that the pressure drop
${\rm\Delta}p_{0}=p_{0}(\mathscr{L}/2)-p_{0}(-\mathscr{L}/2)$
is also negative.
The volume flow rate
$\bar{u}_{0}H$
(per unit channel length in the transverse direction
$y$
) is expressed in terms of the fluid velocity averaged across the channel width,
$$\begin{eqnarray}\bar{u}_{0}=\frac{1}{H}\int _{z=0}^{H}u_{0}(z)\,\text{d}z.\end{eqnarray}$$
By inserting (2.2) and (2.3) into (2.7) we obtain the expression
$$\begin{eqnarray}\frac{{\rm\Delta}p_{0}}{\mathscr{L}}=-\frac{12}{H^{2}}{\it\mu}_{0}\bar{u}_{0}\end{eqnarray}$$
for the pressure drop per unit length of the channel. Equation (2.8) can also be considered as providing the viscosity, once the fluid volume flow rate
$\bar{u}_{0}H$
per unit length in the transverse direction and the pressure gradient in the flow direction
${\rm\Delta}p_{0}/\mathscr{L}$
are known.
2.2 Definition of the effective viscosity
In a similar way, the effective viscosity of a suspension is defined from the linear relationship between the volume flow rate
$\bar{u}_{0}H$
and the average pressure gradient on a distance
$\mathscr{L}$
such that
$\mathscr{L}/H\rightarrow \infty$
with
$H/a$
fixed, where
$a$
represents a typical particle size.
That is, for an imposed fluid volume flow rate with average velocity
$\bar{u}_{0}$
, the average of the pressure gradient
${\rm\Delta}P/\mathscr{L}$
in the suspension is expressed as
$$\begin{eqnarray}\left\langle \lim _{\mathscr{L}\rightarrow \infty }\frac{{\rm\Delta}P}{\mathscr{L}}\right\rangle =-\frac{12}{H^{2}}{\it\mu}_{eff}\bar{u}_{0},\end{eqnarray}$$
where
${\it\mu}_{eff}$
denotes the effective viscosity. In (2.9),
$\langle \cdot \rangle$
denotes an average over all possible positions and orientations of the particles.
The above global definition of the effective viscosity naturally arises when measuring the viscosity of a suspension by the classical pipe flow viscometer technique. The theoretical analysis of this quantity is the main focus of this article.
2.3 Dilute suspension and the one particle problem
Since the suspension is dilute, each particle contributes independently to the effective stress tensor of the suspension and thus to the pressure gradient.
Consider therefore only one particle labelled
$i$
with surface
$S_{i}$
and centre of mass at position
$\boldsymbol{x}_{i}=(x_{i},y_{i},z_{i})$
, as represented schematically in figure 1. Our analysis involves a finite control domain of length
$L$
in the flow direction
$x$
, width
$w$
in the transverse direction
$y$
(parallel to the walls and normal to the flow) and thickness
$H$
in the direction
$z$
. It is assumed that
$H\ll L\ll w$
. The geometry of the control domain and the corresponding notation are illustrated in figure 2. The relationship between the scale
$L$
for a single particle and the scale
$\mathscr{L}$
for the suspension will be made clear below in § 3.2.
Figure 2. Three-dimensional sketch of the control domain around a particle (centred on the line
$x=y=0$
) in a Poiseuille flow bounded by two parallel walls (the sketch is not to scale here, since
$H\ll L\ll w$
).
The flow field perturbed by the presence of particle
$i$
is sought as the sum of the unperturbed flow (indicated by the subscript
$0$
) and a perturbation (indicated by the prime). Accordingly, the perturbed flow velocity, stress tensor and pressure are written as
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}=\boldsymbol{u}_{0}+\boldsymbol{u}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\bf\sigma}={\bf\sigma}_{0}+{\bf\sigma}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p=p_{0}+p^{\prime }. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{on }W_{1}\text{ and }W_{2}:\boldsymbol{u}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{on }S_{i}:\boldsymbol{u}=\boldsymbol{U}_{i}+{\it\bf\Omega}_{i}\times (\boldsymbol{x}-\boldsymbol{x}_{i}), & \displaystyle\end{eqnarray}$$
$\boldsymbol{U}_{i}$
is the translation velocity of the centre of mass of particle
$i$
and
${\it\bf\Omega}_{i}$
is its rotation velocity. The values of these velocities will be chosen so that the particle is freely moving in the flow field.
The remaining control surfaces (see figure 2),
$$\begin{eqnarray}\displaystyle S_{L}=\{s_{x}^{-L/2}\cup s_{x}^{L/2}\}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{w}=\{s_{y}^{-w/2}\cup s_{y}^{w/2}\}, & & \displaystyle\end{eqnarray}$$
$S_{w}$
recede to infinity before the upstream and downstream control surfaces
$S_{L}$
also go to infinity. In dimensionless variables we thus have 
$$\begin{eqnarray}w/L\rightarrow \infty \quad \text{and}\quad L/H\rightarrow \infty ,\end{eqnarray}$$
with
$H/a$
fixed.
In this limit, the perturbation flow and stress fields tend to zero. Due to the slow decay of these fields at infinity (as discussed in appendix A), the boundary conditions on
$S_{L}$
and
$S_{w}$
need to be carefully specified so as to obtain in the limit a well-defined relationship between the suspension flux and average pressure drop in a multiparticle system.
We assume that the fluid volume flow rate per unit length in direction
$y$
in the suspension is the same as in the pure fluid,
${\it\Phi}=\bar{u}_{0}H$
, and search for the pressure drop
${\rm\Delta}P$
that is necessary to maintain this condition. The possibility to apply this flow rate condition in the limit of large distances is made clear below in § 3.1.2.
After taking the ensemble average in a dilute multiparticle system, this problem yields the effective suspension viscosity using (2.9).
3 Supplementary pressure gradient produced by independent rigid particles in a parallel-wall channel
In this section we first use the Lorentz reciprocity theorem to evaluate the perturbation flux and excess pressure force difference produced by a particle in terms of force multipoles induced on this particle, § 3.1. We then derive a corresponding expression for the average supplementary pressure gradient in a dilute particle system, § 3.2.
3.1 Lorentz reciprocity theorem for a single confined particle
To determine the perturbation flux and excess pressure force difference produced by a particle, we use the Lorentz reciprocity theorem for the product of the unperturbed flow
$\boldsymbol{u}_{0}$
and the perturbation flow
$\boldsymbol{u}^{\prime }$
due to the particle,
$$\begin{eqnarray}\int _{(S_{i}\cup S_{L}\cup S_{w}\cup W)}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=\int _{(S_{i}\cup S_{L}\cup S_{w}\cup W)}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }{\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S.\end{eqnarray}$$
This relationship is applied in the fluid region contained in the control domain defined above in § 2.3. The control domain contains a single suspended particle
$i$
at a position
$\boldsymbol{x}_{i}$
, and the infinite-system-size limit (2.13) is then taken. It is assumed that the unit normal vector
$\boldsymbol{n}$
is pointing into the fluid.
As shown in § B.1, the integrals over the wall surface
$W$
and the side control surfaces
$S_{w}$
vanish. Below we derive the non-zero contributions of the integrals over the particle surface
$S_{i}$
and the upstream and downstream control surfaces
$S_{L}$
.
3.1.1 The integrals over the particle surface
$S_{i}$
Using the decompositions (2.10a
) and (2.10b
) for the perturbation velocity and stress fields, the difference between the integrals over the particle surface
$S_{i}$
in the left-hand side and right-hand side of (3.1) can be expressed as
$$\begin{eqnarray}\int _{S_{i}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S-\int _{S_{i}}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }{\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=\int _{S_{i}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S-\int _{S_{i}}\boldsymbol{u}\boldsymbol{\cdot }{\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S,\end{eqnarray}$$
since the terms that involve the product of the unperturbed fields cancel out exactly. The second term on the right-hand side of the above equation vanishes,
$$\begin{eqnarray}\int _{S_{i}}\boldsymbol{u}\boldsymbol{\cdot }{\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=0,\end{eqnarray}$$
as demonstrated in § B.2. The first term can be evaluated in terms of the first three moments of the surface density of the hydrodynamic friction force
$\boldsymbol{f}={\bf\sigma}\boldsymbol{\cdot }\boldsymbol{n}$
. By expressing the unperturbed flow (2.2) as a superposition of a constant flow, shear flow and quadratic flow at the position of the particle centre,
$$\begin{eqnarray}u_{0}(z)=u_{0}(z_{i})+\dot{{\it\gamma}}(z_{i})(z-z_{i})+k_{2}(z-z_{i})^{2},\end{eqnarray}$$
we obtain
$$\begin{eqnarray}\displaystyle \int _{S_{i}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S & = & \displaystyle u_{0}(z_{i})\int _{S_{i}}\boldsymbol{e}_{x}\boldsymbol{\cdot }\boldsymbol{f}\,\text{d}S+\dot{{\it\gamma}}(z_{i})\int _{S_{i}}(z-z_{i})\boldsymbol{e}_{x}\boldsymbol{\cdot }\boldsymbol{f}\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle +\,k_{2}\int _{S_{i}}(z-z_{i})^{2}\boldsymbol{e}_{x}\boldsymbol{\cdot }\boldsymbol{f}\,\text{d}S,\end{eqnarray}$$
where
$u_{0}(z_{i})$
and
$\dot{{\it\gamma}}(z_{i})$
are the velocity (2.2) and shear rate (2.4) evaluated at the position of the particle centre
$z=z_{i}$
. Using the isotropic, symmetric and deviatoric components of the Stokes doublet to represent the second term on the right-hand side of (3.5) yields
$$\begin{eqnarray}\int _{S_{i}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=u_{0}(z_{i})F_{i,x}+\dot{{\it\gamma}}(z_{i})C_{i,y}+\dot{{\it\gamma}}(z_{i})\unicode[STIX]{x1D61A}_{i,xz}+k_{2}\unicode[STIX]{x1D618}_{i,xzz},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{F}_{i}=\int _{S_{i}}\boldsymbol{f}\,\text{d}S, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{C}_{i}=\int _{S_{i}}\boldsymbol{r}_{i}\times \boldsymbol{f}\,\text{d}S & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D61A}_{i}=\int _{S_{i}}\left[\frac{1}{2}(\boldsymbol{r}_{i}\,\boldsymbol{f}+\boldsymbol{f}\boldsymbol{r}_{i})-\frac{1}{3}(\boldsymbol{r}_{i}\boldsymbol{\cdot }\boldsymbol{f})\unicode[STIX]{x1D644}\right]\,\text{d}S\end{eqnarray}$$
is the stresslet and
$$\begin{eqnarray}\unicode[STIX]{x1D618}_{i}=\int _{S_{i}}\boldsymbol{f}\boldsymbol{r}_{i}\boldsymbol{r}_{i}\,\text{d}S\end{eqnarray}$$
is the second moment of the force distribution. In the above equations,
$\boldsymbol{r}_{i}=\boldsymbol{x}-\boldsymbol{x}_{i}$
, and the indices
$x,y,z$
denote Cartesian components of vectors and tensors. The isotropic part of the Stokes doublet does not contribute to the result (3.6), because (3.5) involves only off-diagonal terms.
Following Chwang & Wu (Reference Chwang and Wu1975), the second moment (3.9) will be called a quadrupole of stresses on particle
$S_{i}$
. Since in (3.6) the moment
$\unicode[STIX]{x1D618}_{i,xzz}$
is multiplied by the magnitude
$k_{2}$
of the parabolic flow component, the quadrupolar stresslet term is not present in linear flows.
For a freely suspended particle, the hydrodynamic force and torque (3.7) are zero, and therefore the first two terms on the right-hand side of (3.6) vanish. However, these terms yield a finite contribution for immobile particles (e.g. particles adsorbed at the channel walls).
3.1.2 The integrals over the far upstream
$s_{x}^{-L/2}$
and far downstream
$s_{x}^{L/2}$
surfaces
The integrals over the control surfaces
$S_{L}$
in (3.1) allow us to link the hydrodynamic force moments (3.7)–(3.9) with the associated correction to the pressure drop across the channel.
The integral of the product of the unperturbed velocity field
$\boldsymbol{u}_{0}$
and the perturbation stress
${\bf\sigma}^{\prime }$
is evaluated by decomposing
${\bf\sigma}^{\prime }$
as its pressure and deviatoric-stress contributions,
$$\begin{eqnarray}{\bf\sigma}^{\prime }=-p^{\prime }\unicode[STIX]{x1D644}+{\bf\sigma}_{d}^{\prime }.\end{eqnarray}$$
The integral of the deviatoric part vanishes in the infinite system limit (2.13),
$$\begin{eqnarray}\lim _{L\rightarrow \infty }\int _{S_{L}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}_{d}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=0,\end{eqnarray}$$
(where
$\boldsymbol{n}=\pm \boldsymbol{e}_{x}$
and
$\boldsymbol{u}_{0}\sim \boldsymbol{e}_{x}$
), because the perturbation flow far from the particle tends to a dipolar Hele-Shaw flow (A 3), which yields a small,
$O(L^{-3})$
projection on the
$x$
direction. It follows that
$$\begin{eqnarray}\int _{S_{L}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=-\int _{s_{x}^{-L/2}}u_{0}p^{\prime }\,\text{d}S+\int _{s_{x}^{L/2}}u_{0}p^{\prime }\,\text{d}S.\end{eqnarray}$$
The pressure
$p^{\prime }$
at large distance
$L\gg H$
from the particle is practically independent of
$z$
according to (A 3), and the external flow
$u_{0}$
depends only on
$z$
. Therefore,
$$\begin{eqnarray}\int _{s_{x}^{\pm L/2}}u_{0}(z)p^{\prime }(\pm L/2,y)\,\text{d}S=\bar{u}_{0}\,f_{\pm }^{\prime },\end{eqnarray}$$
where
$\bar{u}_{0}$
is the average unperturbed flow velocity (2.7) and
$f_{\pm }^{\prime }$
is the excess force
$$\begin{eqnarray}f_{\pm }^{\prime }=H\int _{s_{x}^{\pm L/2}}p^{\prime }(\pm L/2,y)\,\text{d}y\end{eqnarray}$$
exerted on the plane
$s^{\pm L/2}$
due to the presence of the particle. Accordingly, equation (3.12) yields
$$\begin{eqnarray}\int _{S_{L}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=\bar{u}_{0}{\rm\Delta}f^{\prime },\end{eqnarray}$$
where
$$\begin{eqnarray}{\rm\Delta}f^{\prime }=f_{+}^{\prime }-f_{-}^{\prime }\end{eqnarray}$$
is the difference in excess forces on the downstream and upstream control surfaces.
The integral of the product of the perturbation velocity field and the unperturbed stress over the surface
$S_{L}$
in (3.1) can be expressed as
$$\begin{eqnarray}\int _{S_{L}}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }{\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S={\it\Phi}^{\prime }{\rm\Delta}p_{0},\end{eqnarray}$$
where the excess fluid flux
${\it\Phi}^{\prime }$
is defined by equation
$$\begin{eqnarray}{\it\Phi}^{\prime }={\it\Phi}_{\pm }^{\prime }=\int _{s_{x}^{\pm L/2}}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{e}_{x}\,\text{d}S.\end{eqnarray}$$
The result (3.17) follows from the fact that far from the particle, the perturbation flow
$\boldsymbol{u}^{\prime }$
exponentially tends to Hele-Shaw flow (A 1) (which has only horizontal components), and from the expression (2.5), with (2.6) of the unperturbed stress tensor.
The flux
${\it\Phi}^{\prime }$
can then be set to zero
$$\begin{eqnarray}{\it\Phi}^{\prime }=0,\end{eqnarray}$$
by applying appropriate boundary conditions on the upstream and downstream surfaces
$S_{L}$
. That is, the flow rate condition for
${\it\Phi}$
may be applied in the limit of large distances.
3.2 Result for the supplementary pressure gradient
Combining (3.6), (3.15), and (3.19), the Lorentz reciprocity theorem (3.1) eventually yields
$$\begin{eqnarray}u_{0}(z_{i})F_{i,x}+\dot{{\it\gamma}}(z_{i})C_{i,y}+\dot{{\it\gamma}}(z_{i})\unicode[STIX]{x1D61A}_{i,xz}+k_{2}\unicode[STIX]{x1D618}_{i,xzz}+{\rm\Delta}f^{\prime }\bar{u}_{0}=0.\end{eqnarray}$$
Consider now
$N\gg 1$
independent particles with surfaces
$S_{i}$
and centres of mass at positions
$\boldsymbol{x}_{i}=(x_{i},y_{i},z_{i})$
,
$i=1,\ldots ,N$
. The centres are located in a portion of length
$\mathscr{L}$
of the channel, such that
$\mathscr{L}\gg L$
. (Note that for some particles near the edges of this portion of channel, the attached control domain of length
$L$
may not be included in it, which would invalidate the demonstration leading to (3.20). However, since
$\mathscr{L}\gg L$
, the number of such particles is small as compared with
$N$
.)
By linearity of Stokes equations, the relationship (3.20) can be generalised to this collection of
$N$
particles. The total force difference due to the
$N$
particles is
$$\begin{eqnarray}{\rm\Delta}F^{\prime }=-\frac{1}{\bar{u}_{0}}\mathop{\sum }_{i=1}^{N}[u_{0}(z_{i})F_{i,x}+\dot{{\it\gamma}}(z_{i})C_{i,y}+\dot{{\it\gamma}}(z_{i})\unicode[STIX]{x1D61A}_{i,xz}+k_{2}\unicode[STIX]{x1D618}_{i,xzz}].\end{eqnarray}$$
We assume that the suspension is statistically homogeneous in the
$x$
and
$y$
directions along the walls. Dividing (3.21) by the volume
$V$
containing the
$N$
particles and taking the thermodynamic limit for
$\mathscr{L}\rightarrow \infty$
(with
$N\rightarrow \infty$
and
$n=N/V$
kept constant) yields the result
$$\begin{eqnarray}\lim _{\mathscr{L}\rightarrow \infty }\frac{{\rm\Delta}P^{\prime }}{\mathscr{L}}=-\frac{1}{\bar{u}_{0}}\lim _{\mathscr{L}\rightarrow \infty }\frac{1}{V}\mathop{\sum }_{i=1}^{N}[u_{0}(z_{i})F_{i,x}+\dot{{\it\gamma}}(z_{i})C_{i,y}+\dot{{\it\gamma}}(z_{i})\unicode[STIX]{x1D61A}_{i,xz}+k_{2}\unicode[STIX]{x1D618}_{i,xzz}],\end{eqnarray}$$
in which
${\rm\Delta}P^{\prime }$
is the difference in supplementary macroscopic pressures between the downstream and upstream cross-sections. We note that individual terms on the right-hand side of (3.22) depend on the reference point representing the particle position (here chosen to be the centre of mass). However the combination of all the terms is independent of this choice, resulting in a well-defined expression for the pressure drop produced by the particles.
Results equivalent to (3.22) were derived by Bławzdziewicz & Wajnryb (Reference Bławzdziewicz and Wajnryb2008) for a confined suspension with periodic boundary conditions, using an entirely different method. Their approach combined ensemble averaging techniques with an analysis of the far-field Hele-Shaw dipolar flow produced by the particles. Moreover, the mobility formulation was used, where the particles contributed to the average flow rather than the pressure drop. Comparing the current results with the far-field analyses by Bhattacharya, Bławzdziewicz & Wajnryb (Reference Bhattacharya, Bławzdziewicz and Wajnryb2006), Bławzdziewicz & Wajnryb (Reference Bławzdziewicz and Wajnryb2008), we conclude that all hydrodynamic force multipoles on the right-hand side of (3.22) (and only those) produce the dominant far-field Hele-Shaw dipoles, which contribute to the average flow and/or average pressure drop in a confined suspension flow.
4 Intrinsic viscosity of a dilute suspension
In this section, the results of § 3 are used to determine the intrinsic viscosity of a confined suspension undergoing pressure-driven flow. We show that in a parabolic flow, in addition to the standard stresslet term, there also is a quadrupolar contribution. In this way we generalize the stresslet formula for the intrinsic viscosity of an unbounded (Batchelor Reference Batchelor1970) or bounded (Feuillebois et al. Reference Feuillebois, Ekiel-Jeżewska, Wajnryb, Sellier and Bławzdziewicz2015) suspension in linear shear flow.
4.1 General expression for the intrinsic viscosity
In what follows we consider a suspension of freely suspended particles, i.e. we assume that the particles are force and torque free,
$$\begin{eqnarray}\boldsymbol{F}_{i}=0,\quad \boldsymbol{C}_{i}=0.\end{eqnarray}$$
Thus, the first two terms under the summation sign in (3.22) vanish. Using
$P=p_{0}+P^{\prime }$
and the definition (2.9) of the intrinsic viscosity yields
$$\begin{eqnarray}\left\langle \lim _{\mathscr{L}\rightarrow \infty }\frac{{\rm\Delta}P}{\mathscr{L}}\right\rangle =\lim _{\mathscr{L}\rightarrow \infty }\frac{{\rm\Delta}p_{0}}{\mathscr{L}}+\left\langle \lim _{\mathscr{L}\rightarrow \infty }\frac{{\rm\Delta}P^{\prime }}{\mathscr{L}}\right\rangle =-\frac{12}{H^{2}}{\it\mu}_{eff}\bar{u}_{0}.\end{eqnarray}$$
Inserting (3.22) for the supplementary pressure gradient into (4.2) and applying assumption (4.1) we obtain the following key result
$$\begin{eqnarray}{\it\mu}_{eff}={\it\mu}_{0}+\frac{H^{2}}{12\bar{u}_{0}^{2}}\left\langle \lim _{\mathscr{L}\rightarrow \infty }\frac{1}{V}\mathop{\sum }_{i=1}^{N}[\dot{{\it\gamma}}(z_{i})\unicode[STIX]{x1D61A}_{i,xz}+k_{2}\unicode[STIX]{x1D618}_{i,xzz}]\right\rangle .\end{eqnarray}$$
The quadrupole singularity
$\unicode[STIX]{x1D64C}_{i}$
appears to be new in this context of the effective viscosity.
4.2 Expression for a monodisperse suspension
Consider identical particles with volume
$v$
. The volume fraction of particles is
${\it\phi}=nv$
and the suspension is dilute,
${\it\phi}\ll 1$
. The intrinsic viscosity is defined as
$$\begin{eqnarray}[{\it\mu}]=\frac{{\it\mu}_{eff}-{\it\mu}_{0}}{{\it\mu}_{0}{\it\phi}}.\end{eqnarray}$$
In a monodisperse suspension, all particle contributions are statistically equivalent, so that the expression (4.3) of the effective viscosity becomes
$$\begin{eqnarray}[{\it\mu}]=\frac{H^{2}}{12\bar{u}_{0}^{2}v{\it\mu}_{0}}\langle \dot{{\it\gamma}}(z)\unicode[STIX]{x1D61A}_{xz}+k_{2}\unicode[STIX]{x1D618}_{xzz}\rangle ,\end{eqnarray}$$
where
$z$
,
$\unicode[STIX]{x1D61A}_{xz}$
and
$\unicode[STIX]{x1D618}_{xzz}$
stand respectively for the centre position, the stresslet and the quadrupole of a test particle in an unbounded canal. Alternatively, writing all constants in terms of
$k_{1}$
, the simplified final result is
$$\begin{eqnarray}[{\it\mu}]=\frac{3}{{\it\mu}_{0}vk_{1}}\left\langle \left(1-2\frac{z}{H}\right)\unicode[STIX]{x1D61A}_{xz}-\frac{\unicode[STIX]{x1D618}_{xzz}}{H}\right\rangle .\end{eqnarray}$$
This result may be compared with that for the effective viscosity in a pure (linear) shear flow between parallel walls with a constant rate of shear
$\dot{{\it\gamma}}$
(see (I), equation (2.5)):
$$\begin{eqnarray}[{\it\mu}]_{pure\,shear}=\frac{1}{{\it\mu}_{0}v\dot{{\it\gamma}}}\langle \unicode[STIX]{x1D61A}_{xz}\rangle .\end{eqnarray}$$
In that case of a linear shear flow, the only contribution to the effective viscosity comes from stresslets. Now here, quadrupoles also appear in (4.6) because of the quadratic shear flow created by the pressure gradient. The relative importance of the quadrupole term in (4.6) compared with the stresslet term is
$({\it\mu}_{0}k_{2}/H)/({\it\mu}_{0}k_{1})\sim 1/H^{2}$
. It thus becomes important for a confined geometry, which is the focus of this article.
4.3 High-frequency flow field
Similarly to the case of a bounded shear flow in (I), we consider here a high-frequency oscillating Poiseuille flow. That is, the oscillating frequency is high enough for the distributions of particle centre-of-mass position
$z$
and orientation angles to be practically frozen, yet small enough for the flow to be quasi-steady.
Note that for a steady flow field, these distributions would evolve with the hydrodynamics. Their calculation would require supplementary efforts (see Zurita-Gotor et al. (Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2007) and Ezhilan & Saintillan (Reference Ezhilan and Saintillan2015) for examples of such calculations).
With uniform distributions, in (4.6)
$\unicode[STIX]{x1D61A}_{xz}$
is proportional to
${\it\mu}_{0}k_{1}$
and
$\unicode[STIX]{x1D618}_{xzz}/H$
is proportional to
$-{\it\mu}_{0}k_{1}/H^{2}$
, so that by (2.3) and (2.4), the result for
$[{\it\mu}]$
only depends on
$H$
and on the particle properties. The result that
$[{\it\mu}]$
is independent of the flow field tells us that the suspension has a Newtonian behaviour at first order in volume fraction
${\it\phi}$
when in a high-frequency oscillating Poiseuille flow.
4.4 Numerical methods for calculating the stresslet and quadrupole
The stresslet
$\unicode[STIX]{x1D61A}_{i,xz}$
and quadrupole
$\unicode[STIX]{x1D618}_{i,xzz}$
are calculated numerically with methods that are relevant for Stokes flow. An integral equation with the appropriate Green tensor taking into account both walls is solved by two different methods, namely the boundary element method (BEM) and the multipole method. Details about these techniques are given in (I). The calculation of the stresslet is the same here as in that preceding article. As for the additional quadrupole
$\unicode[STIX]{x1D618}_{i,xzz}$
, it is obtained by integrating on the particle the local stress which is directly provided with the BEM approach. In contrast, the multipole method requires some supplementary effort. The truncation order used for this purpose (see Ekiel-Jeżewska & Wajnryb Reference Ekiel-Jeżewska, Wajnryb, Feuillebois and Sellier2009) is
$L=6$
for all computations.
Results for normalised stresslet and quadrupole from both methods are presented in table 1 for the case of one sphere with radius
$a$
at different locations in a narrow canal with gap dimension
$H=3a$
. Results are in perfect agreement (the difference is of order
$10^{-4}$
when using
$N=1058$
meshes for the BEM and a truncation number
$L=9$
for the multipole method).
Table 1. Computed values of the normalised stresslet component
$\overline{\unicode[STIX]{x1D61A}}_{i,xz}=3\unicode[STIX]{x1D61A}_{i,xz}/[10{\rm\pi}{\it\mu}_{0}ka^{3}]$
and quadrupole component
$\overline{\unicode[STIX]{x1D618}}_{i,xzz}=-3H\unicode[STIX]{x1D618}_{i,xzz}/[8{\rm\pi}{\it\mu}_{0}ka^{5}]$
for a sphere with radius
$a$
and centre distance to wall
$W_{1}$
equal to
$z=1.1a,1.3a.$
The gap between walls is
$H=3a$
and different
$N$
-node meshes on the sphere surface are employed for the BEM while the multipole method is run with different truncation numbers
$L$
.
5 Monodisperse dilute suspension of spherical particles
As an example, consider in this section the case of a homogeneous dilute monodisperse suspension of spherical particles of radius
$a$
in Poiseuille flow. For this case, the averaging in (4.6) is only performed on the position of the sphere centre (viz. not on the particle orientation), that is by symmetry relative to the centre of the gap:
$$\begin{eqnarray}\langle f\rangle =\frac{2}{H-2a}\int _{a}^{H/2}f(z)\,\text{d}z.\end{eqnarray}$$
5.1 Neglecting interactions with walls
As a consistency check, consider in this subsection the case when hydrodynamic interactions between the particles and walls are neglected.
5.1.1 The stresslet part
The result for the
$xz$
component of the stresslet on a spherical particle in a pure straining motion with shear rate tensor
$\unicode[STIX]{x1D640}$
is (see e.g. Batchelor Reference Batchelor1970)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61A}_{xz}=5v{\it\mu}_{0}\unicode[STIX]{x1D60C}_{xz}. & & \displaystyle\end{eqnarray}$$
Now, in a linear shear flow with local shear rate
$\dot{{\it\gamma}}(z)$
, the relevant shear rate component is
$\unicode[STIX]{x1D60C}_{xz}(z)=\dot{{\it\gamma}}(z)/2$
. As for the average in the expression (4.6) of the effective viscosity, we use here the same definition (5.1) as for the full problem involving hydrodynamic interactions with walls, in order to allow below for comparisons of average quantities. Calculating the average of
$\dot{{\it\gamma}}(z)\unicode[STIX]{x1D61A}_{xz}(z)$
in (4.6), we eventually obtain the stresslet contribution to the effective viscosity:
$$\begin{eqnarray}[{\it\mu}]_{S}=\frac{5}{2}-10\left(\frac{a}{H}\right)+10\left(\frac{a}{H}\right)^{2}.\end{eqnarray}$$
In the limit
$a/H\rightarrow 0$
, we recover the Einstein result for the shear flow in an unbounded fluid:
$$\begin{eqnarray}\displaystyle [{\it\mu}]_{\infty }={\textstyle \frac{5}{2}}. & & \displaystyle\end{eqnarray}$$
The other terms in (5.3) come from the variation of the shear rate in the gap. At first order in
$a/H$
, the effective viscosity of the dilute suspension in Poiseuille flow is lower than that in unbounded fluid (the Einstein result). This may come as a surprise because the Einstein viscosity is known to be independent of the flow field. However, it should be emphasized that: (i) Einstein’s viscosity is a local one; (ii) our definition of the effective viscosity involves an average over the gap over which the shear stress varies; (iii) the variation of the shear stress decays from some value at
$z=a,H-a$
(that is close to that at infinity for large
$H/a$
) down to zero in the centre of the gap.
Recall that our definition of the effective viscosity is appropriate for experiments with the pipe flow viscometer involving measurements of the pressure drop and flow rate. Thus, even without hydrodynamic interactions with walls, corrections to Einstein’s results are to be expected in the measured results for the effective viscosity.
5.1.2 The quadrupole part
The result for the
$xzz$
component of the quadrupole on a freely moving spherical particle in a quadratic shear flow with coefficient
$k_{2}$
is derived in appendix C. From (C 6),
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D618}_{xzz}=2a^{2}v{\it\mu}_{0}k_{2}. & & \displaystyle\end{eqnarray}$$
Since it does not depend on
$z$
, then
$\langle \unicode[STIX]{x1D618}_{xzz}\rangle =\unicode[STIX]{x1D618}_{xzz}$
. The contribution of
$\unicode[STIX]{x1D618}_{xzz}$
to the intrinsic viscosity in (4.6) is
$$\begin{eqnarray}[{\it\mu}]_{Q}=-\frac{3}{{\it\mu}_{0}vk_{1}}\frac{\unicode[STIX]{x1D618}_{xzz}}{H}=6\left(\frac{ak_{2}}{k_{1}}\right)^{2}=6\left(\frac{a}{H}\right)^{2},\end{eqnarray}$$
that is of second order for small
$a/H$
. Recall that this contribution arises in Poiseuille flow because of the present definition of the effective viscosity which involves an average over the gap.
5.1.3 Result for the intrinsic viscosity
Using the preceding results (5.3) and (5.6), the intrinsic viscosity for a suspension of spherical particles in Poiseuille flow, when ignoring the interactions with walls, is
$$\begin{eqnarray}[{\it\mu}]=\frac{5}{2}-10\left(\frac{a}{H}\right)+16\left(\frac{a}{H}\right)^{2}.\end{eqnarray}$$
5.2 First-order interactions with nearest wall
An improvement over the results of § 5.1 can be obtained by considering the hydrodynamic interactions of freely moving spheres with the nearest wall. Indeed, it was shown in Pasol et al. (Reference Pasol, Martin, Ekiel-Jeżewska, Wajnryb, Bławzdziewicz and Feuillebois2011) that this approximation provides a good accuracy for the sphere translation velocity between two parallel walls in Poiseuille flow in a large range of parameters. It is then expected that this approximation also provides a good estimate of the stresslet and quadrupole on a freely moving sphere between parallel walls.
Consider then a freely moving sphere in a parabolic shear flow
$u_{0}(z)=k_{1}z+k_{2}z^{2}$
, which is the sum of a linear and parabolic shear flow. Results for the stresslets on a sphere that is freely moving in these two flow fields, say
$\unicode[STIX]{x1D61A}_{xz}^{1}$
and
$\unicode[STIX]{x1D61A}_{xz}^{2}$
, were calculated in bispherical coordinates by Pasol (Reference Pasol2003). The formal expressions in bispherical coordinates may then be expanded as series in
$a/z$
(where
$z$
represents the position of the sphere centre), using the technique shown in Feuillebois et al. (Reference Feuillebois, Ghalya, Sellier and Elasmi2012). The results are, in dimensionless form
$$\begin{eqnarray}\displaystyle & \displaystyle s_{xz}^{1}=\frac{\unicode[STIX]{x1D61A}_{xz}^{1}}{\frac{5}{2}{\it\mu}_{0}vk_{1}}=1+\frac{15}{16}\left(\frac{a}{z}\right)^{3}-\left(\frac{a}{z}\right)^{5}+\frac{225}{256}\left(\frac{a}{z}\right)^{6}\cdots & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle s_{xz}^{2}=\frac{\unicode[STIX]{x1D61A}_{xz}^{2}}{5{\it\mu}_{0}vk_{2}z}=1+\frac{15}{16}\left(\frac{a}{z}\right)^{3}-\frac{79}{64}\left(\frac{a}{z}\right)^{5}+\frac{225}{256}\left(\frac{a}{z}\right)^{6}\cdots & \displaystyle\end{eqnarray}$$
$a/z\rightarrow 0$
. It is remarkable that the two expansions (5.8a
) and (5.8b
) are identical up to order
$(a/z)^{4}$
. The stresslet on a sphere in a parabolic flow near a wall is, by linearity 
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61A}_{xz}=\unicode[STIX]{x1D61A}_{xz}^{1}+\unicode[STIX]{x1D61A}_{xz}^{2} & & \displaystyle\end{eqnarray}$$
in which we use (2.3).
This result is now introduced into the expression (4.6) for the intrinsic viscosity. Keeping only terms up to
$(a/z)^{4}$
in (5.8) and performing the average using (5.1) (this half-gap definition being well suited to this nearest wall problem), the result for the stresslet contribution is
$$\begin{eqnarray}[{\it\mu}]_{S}=\frac{5}{2}-\frac{95}{32}\left(\frac{a}{H}\right)-\frac{515}{16}\left(\frac{a}{H}\right)^{2}.\end{eqnarray}$$
Like for the result (5.3) without a wall interaction, the intrinsic viscosity decays at first order in
$a/H$
. Now, the coefficients are affected by hydrodynamic interactions: we have in (5.10)
$-95/32\simeq -2.97$
and
$-515/16\simeq -32.19$
instead of
$-10$
and
$10$
for the result (5.3) which ignores interactions with walls. At this point, we omit the contribution of the quadrupole which is not calculated in bispherical coordinates (and would require some substantial effort). It is expected that this contribution would be of order
$(a/H)^{2}$
. Considering only the
$-6.48(a/H)$
term in (5.10), as compared with the
$-10(a/H)$
in (5.3) it is found that the effective viscosity is increased. This is expected because of the increased dissipation due to the hydrodynamic interactions with the walls. Yet, the general tendency that the effective viscosity is smaller than that in unbounded fluid still holds.
5.3 Results from method of multipoles
The method of multipoles is well suited to spheres and is chosen here for its accuracy and calculation speed. It also allows to study small gaps between the particle to wall down to contact. Results from the method of multipoles for the intrinsic viscosity of suspensions of spheres are shown in figure 3 (see also figure 5 for
$N=1$
). The full result from the method of multipoles taking into account both stresslet and quadrupole is shown in figure 3 as a solid line and the partial result taking only into account the stresslet is shown as a dashed line.
Figure 3. Intrinsic viscosity
$[{\it\mu}]$
of a dilute suspension of spheres versus
$H/d$
, with
$H$
the distance between walls and
$d$
the diameter of a sphere. Solid line: from method of multipoles, taking both stresslet and quadrupole into account. At contact,
$H/d=1$
, there is a finite value (not shown) of
$[{\it\mu}]=7.09$
. Dashed line: from method of multipoles, taking only the stresslet into account. Solid line with circles: using the stresslet and quadrupole in unbounded space (viz., no wall effect), equation (5.7). Dashed line with circles: using only the stresslet in unbounded space (viz., no wall effect), equation (5.3). Dash-dotted line: first-order interactions with nearest wall, equation (5.10) up to
$a/H$
, shown here only for
$H/d>3$
.
Consider first this last quantity, say
$[{\it\mu}]_{S}$
. From (4.6) in which we put
$\unicode[STIX]{x1D618}_{xzz}=0$
, the quantity to average varies like the square of the shear rate
$\dot{{\it\gamma}}(z)^{2}=k_{1}^{2}(1-2z/H)^{2}$
. In the limit of
$H/d\rightarrow 1$
, the particle centre is in the middle of the channel where the shear rate vanishes. This is why
$[{\it\mu}]_{S}$
vanishes for
$H/d\rightarrow 1$
.
Consider now the full result for
$[{\it\mu}]$
. Then the contribution of the quadrupole becomes important for small gaps since it is related to the curvature
$k_{2}=-k_{1}/H$
of the velocity profile. In the limit
$H/d\rightarrow 1$
, the particle centre is in the middle of the channel where the curvature
$k_{2}$
is at a maximum. In this limit,
$[{\it\mu}]$
has a finite limit shown in table 3 (
$N=1$
). The solid line in figure 3, by comparison with the dashed line, clearly shows the contribution of the quadrupole.
As for large gaps, fitting the results by a polynomial in
$a/H$
, we obtain the approximation
$$\begin{eqnarray}[{\it\mu}]=\frac{5}{2}-A_{1}\left(\frac{a}{H}\right)-A_{2}\left(\frac{a}{H}\right)^{2},\end{eqnarray}$$
with
$A_{1}=3.436$
and
$A_{2}=17.72$
, valid for
$H/d>10$
. Note that the coefficient of
$(a/H)^{2}$
is negative, unlike in (5.7).
The formula (5.7) using the stresslet and quadrupole in unbounded space, which is ignoring any wall effect, is represented for comparison in figure 3 as a solid line with circles. It has the same shape as the precise result which takes hydrodynamic interactions into account. Yet, there is a displacement towards the lower viscosity, showing that hydrodynamic interactions with walls increase the viscous dissipation and thus the effective viscosity, an expected feature.
The formula (5.3) using only the stresslet in unbounded space, i.e. also ignoring any wall effect, is represented in figure 3 as a dashed line with circles. For the same reason as
$[{\it\mu}]_{S}$
, this quantity vanishes for
$H/d\rightarrow 1$
. As expected, it matches the curve for the stresslet and quadrupole for large
$H/d$
.
The formula (5.10) taking into account the first-order hydrodynamic interaction with the nearest wall, i.e.
$[{\it\mu}]=5/2-95/32(a/H)$
, is shown in figure 3 as a dash-dotted line in the range
$H/d>3$
. It has a similar shape as the other curves. It is above the no-wall approximation as expected since it models some viscous dissipation. It is different from the curve from multipoles for the ‘stresslet only’ (dashed curve) since it takes into account only a part of the dissipation due to the stresslet.
6 Suspension of axisymmetric orthotropic particles
6.1 Formulation
The general case of an arbitrarily shaped particle would be quite demanding numerically since defining its position as a solid body would require using its centre position along
$z$
plus the three Euler angles. We thus restrict our attention to the particular case of axisymmetric orthotropic particles.
The position of such a particle in the channel is defined by its centre location at
$z$
and its orientation angles
${\it\theta}$
of its symmetry axis relative to the normal to walls and
${\it\varphi}$
around the normal to walls, as depicted in figure 1. Depending upon the particle shape and its orientation, its centre position
$z$
has a minimum
$z_{min}$
when the particle touches the wall. The angle
${\it\theta}$
at
$z$
varies between bounds
${\it\theta}_{1}(z)$
and
${\it\theta}_{2}(z)$
such that
$0\leqslant {\it\theta}_{1}(z)\leqslant {\it\theta}_{2}(z)\leqslant {\rm\pi}/2$
and
${\it\varphi}$
varies in
$[0,2{\rm\pi}]$
.
The quantity to average in (4.6) depends on these quantities. Let:
$$\begin{eqnarray}\mathscr{R}(z,{\it\theta},{\it\varphi})=\left(1-2\frac{z}{H}\right)\unicode[STIX]{x1D61A}_{xz}-\frac{\unicode[STIX]{x1D618}_{xzz}}{H}.\end{eqnarray}$$
By symmetry, it is sufficient to consider
$z<H/2$
in the averaging. Like for the stresslet (see (I), equation (4.2)), it may be shown by linearity of Stokes equations and symmetries that
$$\begin{eqnarray}\mathscr{R}(z,{\it\theta},{\it\varphi})=\mathscr{R}(z,{\it\theta},0)\cos ^{2}{\it\varphi}+\mathscr{R}(z,{\it\theta},{\rm\pi}/2)\sin ^{2}{\it\varphi}.\end{eqnarray}$$
Expressing the average in (4.6) then yields an expression analogous to (4.3), (4.4) in (I):
$$\begin{eqnarray}[{\it\mu}]=\frac{3B}{{\it\mu}_{0}vk_{1}A},\quad A=\int _{z_{min}}^{H/2}\left[\int _{{\it\theta}_{1}(z)}^{{\it\theta}_{2}(z)}\sin {\it\theta}\,\text{d}{\it\theta}\right]\,\text{d}z,\end{eqnarray}$$
$$\begin{eqnarray}B=\int _{z_{min}}^{H/2}\left[\int _{{\it\theta}_{1}(z)}^{{\it\theta}_{2}(z)}\mathscr{R}(z,{\it\theta},{\rm\pi}/4)\sin {\it\theta}\,\text{d}{\it\theta}\right]\,\text{d}z.\end{eqnarray}$$
Consider in particular chains of beads and prolate spheroids. Chains of beads are constructed with
$N$
aligned touching equal spheres with radius
$a$
. The spheres are rigidly connected, that is they are not free to rotate relative to one another. Prolate spheroids have a width
$d=2a$
and a slenderness ratio
$s$
. If
$s$
is an integer
$N$
, the spheroid with the same length
$Nd$
as the chain of
$N$
beads also has the same aspect ratio and the same volume, as already noted in (I). For these particles, the geometrical formulae for
$z_{min}$
,
${\it\theta}_{1}(z)$
,
${\it\theta}_{2}(z)$
and
$A$
displayed in (4.5)–(4.9) in (I) still hold. Only
$B$
has to be calculated here.
6.2 Doublets of equal touching spheres and equivalent prolate spheroids
The results for a suspension of doublets of touching spheres of diameter
$d$
and spheroids of the same length
$2d$
and same width
$d$
are displayed in figure 4. Results for the doublets are from the method of multipoles and those for the spheroids are from the BEM. The solid curves show the full results using both the stresslet and quadrupole and the dashed curves the results using only the stresslet. For the (solid and dashed) lines with circles (for doublets) and squares (for spheroids), wall effects are ignored.
Figure 4. Intrinsic viscosity
$[{\it\mu}]$
versus
$H/d$
for suspensions of doublets of touching spheres of diameter
$d$
and suspensions of spheroids of width
$d$
and length
$2d$
. See the legend for details (Red online corresponds to doublets of spheres). For doublets at contact with walls,
$H/d=1$
, there is a finite value (not shown) of
$[{\it\mu}]=6.71$
.
The full value of
$[{\it\mu}]$
for doublets when taking both the stresslet and quadrupole into account is larger than that for spheroids. This is related to the shape difference.
The solid curve for the full value of
$[{\it\mu}]$
in figure 4 exhibits a local maximum at
$H/d\sim 2$
. This is due to the new quadrupole term since, in contrast, the dashed curve for ‘stresslet only’ has no local maximum. Note that in the case of a linear shear flow in paper (I), there is a significant local maximum due to the stresslet. Thus, the stresslet contribution to the local maximum depends on the flow field.
The bump at
$H/d\simeq 2$
on the solid lines occurs at the boundary of restricted geometrical configurations when the particle axis is normal to the walls. This bump is a local maximum for the doublets. A weaker bump also exists for spheroids at
$H/d\simeq 2$
, but it does not correspond to a maximum. For both types of particles, the bump is due to the quadrupole since it does not appear on the ‘stresslet only’ curves (the dashed curves).
Considering the curves for stresslet only (the dashed curves), that for spheroids is above that for doublets when
$H/d>3$
and below for
$H/d<3$
. For large
$H/d$
, this is related to the increased dissipation due to the configuration of doublets, as explained above for the solid curves. Now for low
$H/d$
, the influence of the quadrupole appears to be larger for spheroids.
Curves for which interactions with walls are omitted, i.e. the solid lines with circles for doublets and with triangles for spheroids, are very similar to the ones taking wall interactions into account. They are lower since the viscous dissipation from interactions with walls is omitted. The bump at
$H/d\simeq 2$
is also observed on the solid lines with circles and triangles. In this case also, it is due to the quadrupole since it does not appear on the ‘stresslet only’ curves (the dashed curves with circles and triangles).
Results from the multipoles are obtained for gaps down to contact, whereas the BEM is limited to gaps
$H/d\geqslant 1.4$
here. For
$H/d<2$
, the intrinsic viscosity first decays, then goes to a minimum (table 2 for
$N=2$
) and then increases for narrow gaps. This minimum is related to the decaying influence of the stresslet together with the growing influence of the quadrupole for decaying
$H/d$
. In the limit of contact with both walls
$H/d\rightarrow 1$
where all particles are at rest,
$[{\it\mu}]$
has a finite limit shown in table 3 (for
$N=2$
). This is in contrast to the shear flow case in (I) for which the limit
$H/d\rightarrow 1$
corresponds to moving particles with singularities at contact points leading to infinite viscosity.
Table 2. Values of
$H/d$
at the minimum of
$[{\it\mu}]$
for chains of
$N$
beads and values of this minimum when taking into account both the stresslet
$\unicode[STIX]{x1D61A}_{xz}$
and quadrupole
$\unicode[STIX]{x1D618}_{xzz}$
(third line). Values of
$[{\it\mu}]$
at these values of
$H/d$
when considering only the stresslet
$\unicode[STIX]{x1D61A}_{xz}$
(fourth line).
Table 3. Computed intrinsic viscosity
$[{\it\mu}]$
for the
$N$
-bead rods in the limit of contact
$H/d\rightarrow 1$
.
Figure 5. Intrinsic viscosity
$[{\it\mu}]$
of
$N$
-bead chains
$(N\leqslant 6)$
versus
$H/d-1$
, with
$H$
the distance between walls and
$d$
the diameter of a bead. Solid lines: taking both stresslet and quadrupole into account. Dashed lines: taking only the stresslet into account. The logarithmic scale is used to show the lubrication behaviour for narrow gaps.
6.3 Results for chains of beads
Results for the effective viscosity of chains of beads made of
$N=1,\ldots ,6$
equal touching spheres are displayed in figure 5. For
$N>2$
like for the cases
$N=1,2$
, the intrinsic viscosity taking only into account the stresslet (represented by the dashed lines) vanishes for
$H/d-1\rightarrow 0$
. This is again because the particle is then limited to the centre of the gap where the shear rate vanishes. The full results taking both stresslet and quadrupole into account show a rich behaviour:
-
(i) There is a regular variation for
$H/d\geqslant N$
, which we call the ‘weakly confined regime’. In this regime, unlike for the case of a shear flow in (I), the intrinsic viscosity
$[{\it\mu}]$
decreases for decreasing gap
$H/d-1$
. This is because the particle, being limited to the middle of the channel, is subject to a decaying shear rate; this is the influence of the varying stresslet, as explained above. -
(ii) At
$H/d\simeq N$
, there is a sudden change in slope on the solid curves. For any
$N$
, like for the case
$N=2$
considered above, this happens at the boundary of restricted geometrical configurations. This is due to the quadrupole since it does not appear on the ‘stresslet only’ curves (dashed curves). The quadrupole is effective when the particle is limited to the central region in which the curvature of the velocity profile is larger. For
$H/d>N$
, the particle position escapes this limitation and there are fewer possibilities for the quadrupole to take over and provide dissipation. Thus,
$[{\it\mu}]$
increases slower for
$H/d>N$
. -
(iii) For all values of
$N$
like in the case
$N=2$
, when
$H/d$
decays below
$N$
the intrinsic viscosity first decays, then goes to a minimum at
$H/d=H_{min}/d\simeq 1.6-1.7$
and then increases for narrow gaps. The values of the minimum are shown in table 2. Like for a shear flow in (I), the part for
$H>H_{min}$
, where the range of possible orientations is limited, may be called the ‘semi-confined’ regime and the part for
$H<H_{min}$
the ‘strongly confined’ regime. In the present case, unlike in (I), all curves have a minimum. This is related to the decaying influence of the stresslet together with the growing influence of the quadrupole for decaying
$H/d$
. Like for
$N=2$
, in the limit of contact
$H/d\rightarrow 1$
all curves have a limit (see table 3) whereas for the shear flow case in (I) the limit
$H/d\rightarrow 1$
corresponds to an infinite viscosity.
6.4 Results for prolate spheroids
Results for the intrinsic viscosity of a suspension of prolate spheroids of slenderness ratio
$s=1,1.5,2,2.5,3,4,5,6$
are plotted versus
$H/d$
in figure 6. The cases
$s=1,1.5,2,2.5$
and
$s=3,4,5,6$
are displayed separately for clarity. It is remarked that the value of
$[{\it\mu}]$
at
$H/d=10$
decays when
$s$
increases from
$1$
to
$2.5$
and increases when
$s$
increases from
$3$
to
$6$
. Values of
$[{\it\mu}]$
for the
$s=2.5$
and
$s=3$
spheroids are close for
$H/d>5$
.
Figure 6. Intrinsic viscosity
$[{\it\mu}]$
of spheroids of slenderness ratio
$s=1,1.5,2,2.5,3,4,5,6$
versus
$H/d$
, with
$H$
the distance between walls and
$d$
the width of the spheroid.
The shapes of curves are analogous to those found for chains of beads:
-
(i) For
$H/d\geqslant s$
there is a regular variation in the ‘weakly confined regime’. -
(ii) At
$H/d\simeq s$
, there is a sudden change in slope due to restricted geometrical configurations, except for the sphere (
$s=1$
). Note that the change of slope already occurs for the
$s=1.5$
spheroid, as expected. For
$s=2.5$
, there is even a minimum at
$H/d=2$
and the maximum curvature found at
$H/d=s$
for other curves is here moreover a local maximum. -
(iii) For all values of
$s$
, when
$H/d$
decays below
$s$
(for cases
$s>1$
) the intrinsic viscosity first decays, then goes to a minimum and then increases. Even though the limitation in possibilities of the BEM does not allow to study narrow gaps, it is expected that this increase would be similar to the one for chains of beads, since it is due to lubrication around the particle waist. Like for chains of beads, the part for
$H>H_{min}$
where the range of possible orientations is limited is the ‘semi-confined’ regime and the part for
$H<H_{min}$
the ‘strongly confined’ regime.
6.5 Comparison of results for chains of beads and spheroids
Comprehensive results for chains of
$N$
spheres with
$N=1,\ldots ,6$
and spheroids of the same length
$Nd$
and width
$d$
are displayed in figures 7 and 8. In figure 7, values of the intrinsic viscosity are normalized by their relevant bulk values (viz. in unbounded fluid), which are displayed in table 4.
Table 4. Values of the bulk intrinsic viscosity for chains of beads and spheroids of slenderness ratio
$1,\ldots ,6$
.
For each value of
$N$
, the curves for the chains of beads and the spheroids in figure 7 have a similar shape, with a change of slope at the same value of
$H/d=N$
and a minimum value of
$[{\it\mu}]/[{\it\mu}]_{\infty }$
(the calculation for spheroids by BEM is not numerically possible for small gaps below this minimum).
Figure 8 shows that, like for
$N=2$
(see figure 4), the value of
$[{\it\mu}]$
is for other values of
$N>2$
(and for
$H/d$
large enough) larger for chains of spheres than for spheroids. However, this effect appears to be screened by walls since figure 7 shows that the intrinsic viscosity normalised by the bulk one
$[{\it\mu}]_{\infty }$
is larger for spheroids than for chains of beads. Figure 8 also shows that there is a range of small
$H/d$
(smaller than around 3) for which the intrinsic viscosity of spheroids with
$N>2$
is larger than that of chains of beads. This difference increases with
$N$
. This may be due to the increased dissipation in the gap between the large radius of the elongated spheroid and the wall when in the lubrication regime.
Figure 7. Intrinsic viscosity
$[{\it\mu}]$
, normalised by the bulk intrinsic viscosity (in unbounded fluid)
$[{\it\mu}]_{\infty }$
, for chains of
$N$
spheres of radius
$a$
(solid lines) and suspensions of spheroids of the same length
$Nd$
and width
$d$
(solid lines with crosses), for
$N=1,\ldots ,6$
.
Figure 8. Intrinsic viscosity
$[{\it\mu}]$
for chains of
$N$
spheres of radius
$a$
(solid lines) and suspensions of spheroids of the same length
$Nd$
and width
$d$
(solid lines with crosses), for
$N=1,\ldots ,6$
.
6.6 Comparison with earlier results for pure shear flow
The comparison between results for the intrinsic viscosity of chains of beads in a pure shear flow from (I) and the present results in Poiseuille flow is displayed in figure 9. Figure 9(a), the intrinsic viscosity is normalized by its value in unbounded fluid,
$[{\it\mu}]_{\infty }$
. It is observed that the viscosity in bounded pure shear flow is generally larger than the corresponding value in unbounded flow, whereas it is the contrary for the viscosity in Poiseuille flow.
Figure 9. Intrinsic viscosity when in a shear flow (solid curves) and in Poiseuille flow (dashed curves), for chains of
$N$
spheres (
$N=1,2,6$
). (a)
$[{\it\mu}]$
, normalized by the intrinsic viscosity in unbounded fluid
$[{\it\mu}]_{\infty }$
, versus
$H/d$
. (b)
$[{\it\mu}]$
versus
$H/d-1$
.
Figure 10. Comparison of the intrinsic viscosity when in a shear flow (solid curves) and in Poiseuille flow (dashed curves), for chains of beads (lines without symbol) and spheroids (lines with crosses) of the same length
$Nd$
and width
$d$
. (a,b)
$N=2$
. (c,d)
$N=6$
. (a,c)
$[{\it\mu}]$
, normalized by the intrinsic viscosity in unbounded fluid
$[{\it\mu}]_{\infty }$
, versus
$H/d$
. (b,d)
$[{\it\mu}]$
versus
$H/d$
.
This is mainly due to two effects:
-
(i) Shear stresses between particles and walls are large in pure shear flow for small gaps because the particles are subject to a shear rate and the resulting dissipation leads to an increase in viscosity. No such shear stress is imposed on a particle in a narrow channel close to both walls in Poiseuille flow.
-
(ii) The effective viscosity in Poiseuille flow being defined in terms of an average across the gap in which the shear stress decays to zero in the centre, its value is generally smaller than the one in unbounded fluid. Only for extremely small gaps of the order of
$(H/d)-1=10^{-1}$
for
$N=1$
and
$(H/d)-1=10^{-4}$
for
$N=6$
, the lubrication stresses increase the dissipation so as to give an effective viscosity larger than the value in unbounded fluid.
The comparison for the intrinsic viscosity of chains of beads and spheroids in a pure shear flow from (I) and in Poiseuille flow is displayed in figure 10. Particles have the same length
$Nd$
and width
$d$
. Chosen values are
$N=2$
and
$N=6$
. Because of the used BEM, displayed results for spheroids are limited to the region
$1.4\leqslant H/d\leqslant 7$
. Results for chains of beads can be viewed as a zoom of those of figure 9. Like for chains of beads, the intrinsic viscosity for spheroids is generally larger for pure shear flow than for Poiseuille flow; this is also explained by the effects (i) and (ii) above. As remarked already in figures 7 and 8 for Poiseuille flow, the intrinsic viscosity for spheroids is generally smaller than that for chains of beads. Behaviours for Poiseuille flow and pure shear flow are analogous in this respect. For
$N=6$
, when in pure shear flow there is a minimum of
$[{\it\mu}]$
which is well marked for chains of beads and not so marked for spheroids. In Poiseuille flow, the minimum still exists but is much smaller.
7 Discussion and conclusion
Results show that the intrinsic viscosity
$[{\it\mu}]$
in bounded Poiseuille flow is smaller than its value
$[{\it\mu}]_{\infty }$
in unbounded flow, except for extremely narrow gaps of the order of
$(H/d)-1=10^{-1}$
for
$N=1$
and
$(H/d)-1=10^{-4}$
for
$N=6$
, when it becomes larger. In addition, the intrinsic viscosity
$[{\it\mu}]$
has a minimum for a gap
$H$
between walls of the order of 1.5–2 particle width
$d$
.
As it was observed by Feuillebois et al. (Reference Feuillebois, Ekiel-Jeżewska, Wajnryb, Sellier and Bławzdziewicz2015) for a dilute suspension in shear flow, the minimum and the shape of the curve for the intrinsic viscosity in Poiseuille flow correspond to three characteristic regimes (see figures 5 and 6). In a ‘weakly confined’ regime, with
$H$
larger than the particle length, the intrinsic viscosity slowly increases with
$H$
towards the bulk value. In a ‘semi-confined’ regime, which corresponds to smaller channel widths, a minimum of
$[{\it\mu}]$
occurs around
$H/d=1-3$
(similarly as in case of the shear flow). This is due to limited orientations of a particle when its length becomes larger than the gap. In a ‘strongly confined’ regime, for the ratio of the channel width to the particle width smaller than around 1.2, we observe a rapid (but limited) increase of
$[{\it\mu}]$
.
The lubrication regime for small gaps is well visible in figure 9(b) for chains of beads. For
$H/d\rightarrow 1$
, the viscosity increases to infinity in pure shear flow whereas it reaches a finite value in Poiseuille flow. This is due to lubrication effects (explained in item (i) in § 6.6), which are enhanced for small gaps in shear flow when both close walls moving with respect to each other not only prevent the particle from rotating, but also create a significant relative local velocity of the particle surface with respect to the wall close by. In Poiseuille flow inside a narrow channel the particle stays close to the central plane where the local shear vanishes, and therefore there is no lubrication divergence. Even though the lubrication regime cannot be calculated for spheroids by the BEM, the tendency for small gaps from figure 10 is the same and we may anticipate similar results.
The difference between the intrinsic viscosities in Poiseuille and shear flows is significant even for relatively wide channels, e.g. three times wider than the particle length as seen in figure 10. As seen in figure 9(b) for chains of beads, this difference can be neglected only if the walls are so far away from each other, that the intrinsic viscosity is practically equal to its value in the bulk fluid, which is typically for
$H/d>100$
. For thinner channels, hydrodynamic interactions with the walls have to be taken into account in the calculation of
$[{\it\mu}]$
.
The comparison of the results for spheroids and rods made of beads leads to the conclusion that for spheroids, the intrinsic viscosity is slightly smaller than for chains of beads with the same aspect ratio, with slightly less deep minima for spheroids in the weakly confined regime. However, the overall behaviour is qualitatively the same for both shapes. Therefore, in order to save significantly the computational time, a rigid chain of beads can serve as a simple model of an orthotropic particle with a more complicated shape, keeping the same volume and slenderness ratio.
Finally, we remind that the quadrupole term has to be taken into account while evaluating the intrinsic viscosity in Poiseuille flow. The results based on the stresslet term only would lead to underestimated values of
$[{\it\mu}]$
, with a large discrepancy for thin channels. The approximation based on the stresslet only is justified only in the case of very wide channels, at least one order of magnitude larger than the particle length.
The present results may be applied to some practical situations in which a small amplitude oscillatory flow is imposed to a bounded suspension. Our work moreover provides a theoretical basis for further calculations in which the particle distribution and orientation are affected by the flow field. There is no fundamental difficulty to treat that problem, on the basis of the present formulae for the averaging together with a Fokker–Planck equation for the particle position and orientation probability. The extensive numerical calculations which would have to be performed for all configurations would deserve a separate project.
Acknowledgements
E.W. and M.L.E.-J. were supported in part by the Polish NCN grant no. 2012/05/B/ST8/03010. M.L.E.-J. benefited from the scientific activities of the COST Action MP1305. J.B. would also like to acknowledge the hospitality and financial support from IPPT PAN during his summer visit.
This article is dedicated to our colleague and friend Eligiusz Wajnryb who passed away on Saturday 28th May, 2016, a few days after the paper was accepted.
Appendix A. Far-field flow produced by a particle in a parallel-wall channel
As discussed by Bhattacharya et al. (Reference Bhattacharya, Bławzdziewicz and Wajnryb2006) and by Bhattacharya & Bławzdziewicz (Reference Bhattacharya and Bławzdziewicz2008), the flow
$\boldsymbol{u}_{f}$
produced by an arbitrary bounded force distribution in a fluid confined between two parallel walls tends at large distances either to zero or to the asymptotic Hele-Shaw form,
$$\begin{eqnarray}\boldsymbol{u}^{HS}(\boldsymbol{x})=-{\textstyle \frac{1}{2}}{\it\mu}^{-1}z(H-z)\boldsymbol{{\rm\nabla}}p^{HS}(x,y),\end{eqnarray}$$
where the pressure
$p^{HS}$
is independent of
$z$
and satisfies the Laplace equation
$$\begin{eqnarray}{\rm\nabla}^{2}p^{HS}(x,y)=0.\end{eqnarray}$$
The approach of
$\boldsymbol{u}_{f}$
to the asymptotic Hele-Shaw form (A 1) is exponential on the length scale
$H$
. For a typical force distribution, the leading-order asymptotic behaviour is the Hele-Shaw flow driven by the pressure dipole,
$$\begin{eqnarray}p^{HS}(x,y)=\frac{1}{2{\rm\pi}}\boldsymbol{D}\boldsymbol{\cdot }\frac{{\bf\rho}}{{\it\rho}^{2}},\end{eqnarray}$$
where
${\bf\rho}=x\boldsymbol{e}_{x}+y\boldsymbol{e}_{y}$
,
${\it\rho}=|{\bf\rho}|$
, and
$\boldsymbol{D}$
is the dipole moment associated with the distribution of the forces applied to the fluid.
Since a solid particle in external flow can be represented in terms of induced forces distributed on the particle surface, equations (A 1)–(A 3) are valid for the scattered flow and stress fields produced by the particles in our effective viscosity problem. In particular these equations yield the following relations for the far-field behaviour of the perturbation pressure, velocity and deviatoric-stress fields,
$$\begin{eqnarray}\displaystyle p^{\prime }\sim {\it\rho}^{-1}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }\sim {\it\rho}^{-2}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}{\it\sigma}_{d,{\it\alpha}{\it\beta}}^{\prime }\sim {\it\rho}^{-3},\quad {\it\alpha},{\it\beta}=x,y,\end{eqnarray}$$
where
${\it\sigma}_{d,{\it\alpha}{\it\beta}}^{\prime }$
are the
${\it\alpha}{\it\beta}$
components of the deviatoric part of the far-field stress tensor (3.10) (evaluated in the asymptotic far-field flow regime).
The slow decay of the perturbation pressure and flow fields
$p^{\prime }$
and
$\boldsymbol{u}^{\prime }$
results in a non-trivial dependence of the average flow and pressure drop on the control domain shape and the boundary conditions in a many particle system. This non-trivial non-local dependence stems from the presence of conditionally convergent integrals and sums of
$O({\it\rho}^{-1})$
and
$O({\it\rho}^{-2})$
contributions when the infinite-system-size limit is performed (see Bhattacharya Reference Bhattacharya2008; Bławzdziewicz & Wajnryb Reference Bławzdziewicz and Wajnryb2008, for more details). In our analysis (see §§2–4) a well-defined result, equivalent to a unique local relationship between local volume flux and statistically averaged pressure gradient, is obtained by considering a cuboidal control domain in the limit (2.13).
Appendix B. Evaluation of surface integrals in Lorentz reciprocity relationship (3.1)
B.1 Integrals over the channel walls
$W$
and side control surfaces
$S_{w}$
The integrals over the wall surfaces
$W_{1}$
and
$W_{2}$
in (3.1) vanish because of the no-slip boundary conditions for the unperturbed flow
$\boldsymbol{u}_{0}$
and the perturbation flow
$\boldsymbol{u}^{\prime }$
.
To evaluate the integral over the side control surfaces
$S_{w}$
in the left-hand side of (3.1), we note that the external flow (2.1) has only the
$x$
component and that
$\boldsymbol{n}=\pm \boldsymbol{e}_{y}$
on
$S_{w}$
. Thus, by employing the decomposition (3.10) of the stress tensor as its isotropic and deviatoric components and using (A 4a,c,d
) we obtain the asymptotic behaviour of the integrand
$$\begin{eqnarray}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\sim {\it\rho}^{-1},\end{eqnarray}$$
which yields
$$\begin{eqnarray}\int _{S_{w}}\boldsymbol{u}_{0}\boldsymbol{\cdot }{\bf\sigma}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S\sim L/w.\end{eqnarray}$$
The integral (B 2) vanishes in the limit (2.13) because
$L/w\rightarrow 0$
.
A similar argument applies to the integral over the surface
$S_{w}$
in the right-hand side of (3.1). In this case, using (2.5) and the fact that in the asymptotic Hele-Shaw regime (A 1) the perturbation flow
$u^{\prime }$
has only lateral components, we find
$$\begin{eqnarray}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }{\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}\cong -p_{0}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{n}\sim {\it\rho}^{-2},\end{eqnarray}$$
according to (A 4b ). The asymptotic behaviour of the corresponding integral is
$$\begin{eqnarray}\int _{S_{w}}\boldsymbol{u}^{\prime }\boldsymbol{\cdot }{\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S\sim L^{2}/w^{2},\end{eqnarray}$$
where an additional factor
$L$
stems from the position dependence of the pressure field
$p_{0}$
. Similar to (B 2), integral (B 4) also vanishes in the limit (2.13).
B.2 Derivation of (3.3)
Using the notation
$\boldsymbol{f}_{0}={\bf\sigma}_{0}\boldsymbol{\cdot }\boldsymbol{n}$
for surface density of the hydrodynamic force and the no-slip boundary condition (2.11b
) on the particle surface, the integral on the left-hand side of (3.3) can be expressed as
$$\begin{eqnarray}\displaystyle \int _{S_{i}}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{f}_{0}\,\text{d}S & = & \displaystyle \int _{S_{i}}(\boldsymbol{U}_{i}+{\it\bf\Omega}_{i}\times \boldsymbol{r}_{i})\boldsymbol{\cdot }\boldsymbol{f}_{0}\,\text{d}S\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{U}_{i}\boldsymbol{\cdot }\int _{S_{i}}\boldsymbol{f}_{0}\,\text{d}S+{\it\bf\Omega}_{i}\boldsymbol{\cdot }\int _{S_{i}}(\boldsymbol{r}_{i}\times \boldsymbol{f}_{0})\,\text{d}S,\end{eqnarray}$$
where
$\boldsymbol{r}_{i}=\boldsymbol{x}-\boldsymbol{x}_{i}$
, and the identity
$$\begin{eqnarray}\displaystyle \int _{S_{i}}({\it\bf\Omega}_{i}\times \boldsymbol{r}_{i})\boldsymbol{\cdot }\boldsymbol{f}_{0}\,\text{d}S={\it\bf\Omega}_{i}\boldsymbol{\cdot }\int _{S_{i}}(\boldsymbol{r}_{i}\times \boldsymbol{f}_{0})\,\text{d}S & & \displaystyle\end{eqnarray}$$
has been applied. The integrals on the right-hand side of (B 5) vanish, because in the unperturbed flow the fluid enclosed by the surface in
$S_{i}$
is force and torque free.
Appendix C. Quadrupole of stresses on a sphere surface in an unbounded quadratic flow
Consider a fixed sphere in an unbounded quadratic flow with velocity
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{0}=k_{2}Z^{2}\boldsymbol{e}_{x}, & & \displaystyle\end{eqnarray}$$
where
$Z=0$
is at the sphere centre. The
$x$
component of the stress
$\boldsymbol{f}$
on the sphere is
$$\begin{eqnarray}\displaystyle & \displaystyle f_{x}^{q}=-{\textstyle \frac{1}{4}}k_{2}{\it\mu}_{0}a[2(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{x})^{2}-17(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{z})^{2}+3] & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\,2k_{2}{\it\mu}_{0}a[(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{x})^{2}-(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{z})^{2}], & \displaystyle\end{eqnarray}$$
$(r,{\it\theta},{\it\phi})$
, we have 
$$\begin{eqnarray}\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{x}=\sin {\it\theta}\cos {\it\phi},\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{y}=\sin {\it\theta}\sin {\it\phi},\quad \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{z}=\cos {\it\theta}.\end{eqnarray}$$
Since the solid spherical particle is freely moving in the quadratic flow, its velocity is from Faxen’s formula:
$(a^{2}/3)k_{2}\boldsymbol{e}_{x}$
. The stress on the sphere is uniform for the translation problem and its value (which is along
$x$
) is here
$$\begin{eqnarray}\displaystyle f_{x}^{t}=-{\textstyle \frac{1}{2}}k_{2}{\it\mu}_{0}a. & & \displaystyle\end{eqnarray}$$
The total stress on the translating sphere surface is
$$\begin{eqnarray}\displaystyle f_{x}=f_{x}^{q}+f_{x}^{t}=-{\textstyle \frac{5}{4}}k_{2}{\it\mu}_{0}a[2(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{x})^{2}-5(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{e}_{z})^{2}+1] & & \displaystyle\end{eqnarray}$$
and the required component of the quadrupole is
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D618}_{xzz} & = & \displaystyle \int _{S}ZZf_{x}\,\,\text{d}S\nonumber\\ \displaystyle & = & \displaystyle -\frac{5}{4}k_{2}{\it\mu}_{0}a^{5}\int _{{\it\theta}=0}^{{\rm\pi}}\int _{{\it\phi}=0}^{2{\rm\pi}}\cos ^{2}{\it\theta}[2(\sin {\it\theta}\cos {\it\phi})^{2}-5\,\cos ^{2}{\it\theta}+1]\sin {\it\theta}\,\text{d}{\it\theta}\,\text{d}{\it\phi}\nonumber\\ \displaystyle & = & \displaystyle \frac{8{\rm\pi}}{3}k_{2}{\it\mu}_{0}a^{5}.\end{eqnarray}$$
