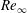1 Introduction
Low-density compressible flow conditions experienced by objects entering the atmosphere at high speed are challenging to model. The relevant non-dimensional scaling parameter is the Knudsen number (
$Kn\equiv {\it\lambda}/L$
), defined as the ratio between the mean free path of gas molecules (
${\it\lambda}$
) and a characteristic length scale of interest (
$L$
). The mean free path
${\it\lambda}$
varies by orders of magnitude between low earth orbit and sea level. Furthermore,
$L$
can be large for objects such as meteors and blunt spacecraft or can be small for space debris and sharp leading edges on flight vehicles where high heat flux becomes a design constraint.
For
$Kn>10$
the flow around the object of interest can be considered to be free-molecular, where analytical solutions exist for heat flux and shear stress (or piecewise analytic for complex geometries). For
$Kn<0.01$
the compressible Navier–Stokes equations with Newtonian and Fourier models for shear stress and heat flux are accurate and can be solved by methods from computational fluid dynamics (CFD). In the transition regime,
$0.01<Kn<10$
, the Newtonian and Fourier models become inaccurate and one must revert to the Boltzmann equation to accurately model the gas flow. Free-molecular solutions can be obtained very quickly on modern computers, whereas CFD simulations require substantially more time. Solutions to the Boltzmann equation for high-speed flows are most accurately and efficiently obtained using the direct simulation Monte Carlo (DSMC) method (Bird Reference Bird1994). Direct simulation Monte Carlo calculations are equally (and often more) expensive compared with CFD.
Although these solution methods are highly accurate, there is a need for simple correlations for heat flux and drag for the purpose of rapid engineering analysis. Such correlations are useful in early stages of design, for in-flight analysis required during space missions, satellite orbit monitoring and energy management when atmospheric conditions are highly variable, and on-board vehicle control architectures that require aerodynamic response models. The focus of this article is to develop a physics-based correlation for heat flux that can be applied across the entire
$Kn$
range for objects that can be approximated by a sphere, for example leading edges with a specific nose radius, blunt re-entry capsules, and large or small meteors and space debris.
Various correlations for predicting aero-heating have been proposed in the literature, such as those by Fay & Riddell (Reference Fay and Riddell1958) and Sutton & Graves (Reference Sutton and Graves1971), and a recent correlation developed by Brandis & Johnston (Reference Brandis and Johnston2014). Each of these correlations is based on the continuum Navier–Stokes equations. The former two correlations result from simplifying assumptions involving shock-wave and boundary-layer theory, while the recent correlation of Brandis & Johnston (Reference Brandis and Johnston2014) results from curve-fitting a large number of CFD solutions for stagnation-point heat flux. The CFD simulations included a much more precise treatment of dissociation chemistry, vibrational non-equilibrium, viscosity and thermal conductivity compared with the assumptions used in the former two correlations, and the resulting correlation was shown to be more accurate (Brandis & Johnston Reference Brandis and Johnston2014). However, the most rarefied condition contained in the CFD solution dataset that was used to fit the correlation corresponded to
$Kn=0.035$
. Therefore, the abovementioned correlations are likely to be inaccurate for higher
$Kn$
conditions as it is well established that the Navier–Stokes equations do not provide accurate solutions in the transition regime.
For flow conditions in the transition regime, analysis can be performed using equations from hydrodynamics beyond Navier–Stokes, for example through applying higher-order corrections to the Chapman–Enskog series solution (Chapman & Cowling Reference Chapman and Cowling1970) of the Boltzmann equation. The Chapman–Enskog series is an asymptotic solution of the linearized Boltzmann equation in terms of
$Kn$
. Maintaining the zeroth-, first-, second- and third-order accurate
$Kn$
terms yield the Euler, Navier–Stokes, Burnett and super-Burnett equations respectively (Chapman & Cowling Reference Chapman and Cowling1970). It is important to note that many of these hydrodynamics model equations have unresolved issues, as reported in the literature (Kogan Reference Kogan1969; Bobylev Reference Bobylev1982; Woods Reference Woods1983; Agarwal, Yun & Balakrishnan Reference Agarwal, Yun and Balakrishnan2001; Struchtrup & Torrilhon Reference Struchtrup and Torrilhon2003; Struchtrup Reference Struchtrup2005; Gu & Emerson Reference Gu and Emerson2009), for example with regards to series convergence, unknown coefficient values, etc. An article by García-Colín, Velasco & Uribe (Reference García-Colín, Velasco and Uribe2008) clearly outlines many of the strengths and limitations of these equations. In addition, these equations involve second-order (Burnett type) and third-order (super-Burnett type) derivatives of flow quantities such as density, temperature and velocity. This poses challenges for numerical solution techniques, and analytical solutions are generally not possible with few exceptions (Singh & Agrawal Reference Singh and Agrawal2014; Singh, Gavasane & Agrawal Reference Singh, Gavasane and Agrawal2014). Despite these challenges, these hydrodynamics models have been successfully applied to low-speed rarefied problems, for which a number of important rarefied phenomena have been captured (Zohar et al.
Reference Zohar, Lee, Lee, Jiang and Tong2002; He, Tang & Pu Reference He, Tang and Pu2008; Gu, Emerson & Tang Reference Gu, Emerson and Tang2009; Agrawal & Dongari Reference Agrawal and Dongari2011; Rana, Torrilhon & Struchtrup Reference Rana, Torrilhon and Struchtrup2013; Singh, Dongari & Agrawal Reference Singh, Dongari and Agrawal2013; Akintunde & Petculescu Reference Akintunde and Petculescu2014; Khalil, Garzó & Santos Reference Khalil, Garzó and Santos2014; Rahimi & Struchtrup Reference Rahimi and Struchtrup2014; Singh & Agrawal Reference Singh and Agrawal2014; Singh et al.
Reference Singh, Gavasane and Agrawal2014), and have also been applied to hypersonic flows (Agarwal et al.
Reference Agarwal, Yun and Balakrishnan2001), for which a simplified set of conventional Burnett equations was recently proposed specifically for rarefied hypersonic flows (Zhao, Chen & Agarwal Reference Zhao, Chen and Agarwal2014).
In this article we employ the Bhatnagar–Gross–Krook (BGK)–Burnett equations (Agarwal et al.
Reference Agarwal, Yun and Balakrishnan2001). We choose these equations as they have been used extensively by previous researchers, they do not suffer numerical instabilities and they include two-dimensional super-Burnett terms. We do not seek analytical or numerical solutions to the equations. Rather, we make appropriate simplifications for stagnation-point heat flux resulting from hypersonic flow over a sphere (§ 2) and quantitatively analyse the contribution from higher-order heat flux terms relative to the heat flux terms in the Navier–Stokes equations (§ 3). In this manner, the proposed correlation can be applied in combination with an existing continuum correlation of choice (for example the correlation of Brandis & Johnston Reference Brandis and Johnston2014). Burnett, super-Burnett and higher-order terms are considered, resulting in an exhaustive analysis of terms contributing to heat flux in the transitional regime. We bridge the resulting correlation to the analytical free-molecular solution in the limit of large
$Kn$
(§ 3). The new correlation is completed by fitting free parameters to existing DSMC solution data from the literature (§ 4).
2 Analysis of higher-order heat flux contributions
2.1 Relevant scaling parameters
A schematic of the flow field generated by a sphere moving at hypersonic velocity is shown in figure 1. In addition to using the sphere radius as the length scale required to define
$Kn$
and Reynolds number (
$Re$
), additional gradient length scales must be defined for the analysis of higher-order derivative terms. Length scales used in the analysis of this section, shown in figure 1, include the shock layer thickness (
$d_{s}$
), the shock-wave standoff distance (
${\it\Delta}$
), the nose radius (
$R_{N}$
) and the boundary-layer thickness (
${\it\delta}$
). Free-stream flow conditions are parametrized in terms of the Mach number (
$M_{\infty }$
), Knudsen number (
$Kn_{\infty }$
) and Reynolds number (
$Re_{\infty }$
).
It should be noted that although figure 1 shows a clear demarcation of the various layers, these layers will merge as the flow becomes more rarefied. As such rarefied effects progress, Navier–Stokes predictions for stagnation-point heat flux will become inaccurate. However, it is important to stress that simplifying assumptions should remain consistent in the limit of continuum flow. Indeed, many of the approximations made in this section are based on continuum flow theory, and it is the inclusion of higher-order terms that provides a physics-based deviation from continuum results. As the flow becomes highly rarefied, such approximations and the resulting correlations become inaccurate, and it is in this regime where we bridge to the analytical free-molecular solution (presented in § 3).
Figure 1. Schematic diagram of hypersonic flow depicting various length scales.
2.2 Analysis of the super-Burnett heat flux contribution
In this section, we carry out an order-of-magnitude analysis of the full nonlinear BGK–Burnett equation (Agarwal et al.
Reference Agarwal, Yun and Balakrishnan2001) and investigate the relative contribution of higher-order terms to the stagnation-point heat flux on a sphere moving at hypersonic speed. The
$y$
component of the super-Burnett-order heat flux vector in the BGK–Burnett equation has following form:
$$\begin{eqnarray}\displaystyle q_{sB} & = & \displaystyle \frac{{\it\mu}^{3}}{p{\it\rho}}R\left({\it\theta}_{18}T_{yyy}+{\it\theta}_{18}T_{xxy}-{\it\theta}_{18}\frac{{\it\rho}_{y}}{{\it\rho}}T_{yy}-{\it\theta}_{18}\frac{{\it\rho}_{y}}{{\it\rho}}T_{xx}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\mu}^{3}}{p{\it\rho}} ({\it\theta}_{19}v_{y}v_{yy}+{\it\theta}_{20}v_{y}u_{xy}+{\it\theta}_{6}v_{y}v_{xx}+{\it\theta}_{21}u_{x}v_{yy}+{\it\theta}_{22}u_{x}u_{xy}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\theta}_{7}u_{x}v_{xx}+{\it\theta}_{23}v_{x}u_{yy}+{\it\theta}_{24}v_{x}v_{xy}+{\it\theta}_{6}v_{x}u_{xx}+{\it\theta}_{23}u_{y}u_{yy}+{\it\theta}_{24}u_{y}v_{xy}+{\it\theta}_{6}u_{y}u_{xx} )\nonumber\\ \displaystyle & & \displaystyle -\,\frac{{\it\mu}^{3}}{p{\it\rho}}\left(\frac{{\it\rho}_{y}}{{\it\rho}}+\frac{T_{y}}{T}\right)({\it\theta}_{13}u_{x}^{2}+2{\it\theta}_{14}u_{x}v_{y}+2{\it\theta}_{17}u_{y}v_{x}+{\it\theta}_{17}u_{y}^{2}+{\it\theta}_{17}v_{x}^{2}+{\it\theta}_{13}v_{y}^{2})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\mu}^{3}}{p{\it\rho}}\frac{R}{T}({\it\theta}_{18}T_{y}T_{xx}+{\it\theta}_{18}T_{y}T_{yy}).\end{eqnarray}$$
Here,
${\it\rho}$
,
$T$
,
$p$
and
${\it\mu}$
are the gas density, temperature, pressure and viscosity, and
$R$
is the specific gas constant. The terms
$u$
and
$v$
represent the bulk gas velocity in the
$x$
-direction (normal to the stagnation line) and
$y$
-direction (parallel to the stagnation line) respectively, as depicted in figure 1. The subscripts
$x$
and
$y$
denote partial derivatives with respect to the independent variables (coordinate directions)
$x$
and
$y$
. The values of
${\it\theta}$
are constant coefficients which result from the evaluation of collision integrals in the Chapman–Enskog analysis, and in this case would be specific to the use of the BGK collision operator within the Boltzmann equation. It is important to note that the form of (2.1) is general to various forms of the BGK collision operator. Only the coefficients,
${\it\theta}$
, will have different values depending on the collision operator assumed, the collision cross-section model assumed or the interatomic potential assumed. As a result, there is uncertainty in the values of the coefficients, an important point that will be discussed in more detail later in this section.
Along the stagnation line, the flow properties
${\it\rho}$
,
$T$
,
$p$
and
$v$
are symmetric about the
$y$
-axis, while
$u$
is anti-symmetric. Symmetry dictates that
${\it\rho}_{x}$
,
$T_{x}$
,
$p_{x}$
,
$v_{x}$
and
$u_{y}$
vanish. The resulting simplified expression is
$$\begin{eqnarray}\displaystyle q_{sB} & = & \displaystyle \frac{{\it\mu}^{3}}{p{\it\rho}}R\left({\it\theta}_{18}T_{yyy}+{\it\theta}_{18}T_{xxy}-{\it\theta}_{18}\frac{{\it\rho}_{y}}{{\it\rho}}T_{yy}-{\it\theta}_{18}\frac{{\it\rho}_{y}}{{\it\rho}}~T_{xx}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\mu}^{3}}{p{\it\rho}}({\it\theta}_{19}v_{y}v_{yy}+{\it\theta}_{20}v_{y}u_{xy}+{\it\theta}_{6}v_{y}v_{xx}+{\it\theta}_{21}u_{x}v_{yy}+{\it\theta}_{22}u_{x}u_{xy}+{\it\theta}_{7}u_{x}v_{xx})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{{\it\mu}^{3}}{p{\it\rho}}\left(\frac{{\it\rho}_{y}}{{\it\rho}}+\frac{T_{y}}{T}\right)({\it\theta}_{13}u_{x}^{2}+2{\it\theta}_{14}u_{x}v_{y}+{\it\theta}_{13}v_{y}^{2})+\frac{{\it\mu}^{3}}{p{\it\rho}}\frac{R}{T}\left({\it\theta}_{18}T_{y}T_{xx}+{\it\theta}_{18}T_{y}T_{yy}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
To further simplify the heat flux expression, certain approximations can be made based on the hypersonic laminar boundary-layer solution (Matting Reference Matting1964) in the vicinity of a stagnation point. Specifically, the pressure does not vary strongly in the streamwise direction inside the boundary layer, hence
${\it\rho}_{y}/{\it\rho}=-T_{y}/T$
can be utilized for further simplification, resulting in the following form:
$$\begin{eqnarray}\displaystyle q_{sB} & = & \displaystyle \frac{{\it\mu}^{3}}{p{\it\rho}}R\left({\it\theta}_{18}T_{yyy}+{\it\theta}_{18}T_{xxy}+2{\it\theta}_{18}\frac{T_{y}}{T}~T_{yy}+2{\it\theta}_{18}\frac{T_{y}}{T}~T_{xx}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\mu}^{3}}{p{\it\rho}}({\it\theta}_{19}v_{y}v_{yy}+{\it\theta}_{20}v_{y}u_{xy}+{\it\theta}_{6}v_{y}v_{xx}+{\it\theta}_{21}u_{x}v_{yy}+{\it\theta}_{22}u_{x}u_{xy}+{\it\theta}_{7}u_{x}v_{xx}).\end{eqnarray}$$
Moreover, the hypersonic laminar boundary-layer solution (Matting Reference Matting1964) shows that
$\partial v/\partial y=-2^{J}{\it\beta}$
and
$\partial u/\partial x=-1/(2^{J}{\it\rho})\partial ({\it\rho}u)/\partial y={\it\rho}_{s}{\it\beta}/{\it\rho}$
, where
${\it\beta}$
is the tangential velocity gradient at the edge of the stagnation-point boundary layer, the subscript
$s$
denotes postshock conditions and
$J=0$
for 2D (cylinder) and
$J=1$
for 3D (sphere). For hypersonic flow,
${\it\beta}$
can be approximated in terms of the speed of sound (
$a_{s}=\sqrt{{\it\gamma}RT}$
, where
${\it\gamma}$
is the ratio of the specific heats of the gases) as
${\it\beta}=\text{d}u/\text{d}x\approx \sqrt{2/{\it\gamma}}a_{s}/R_{N}$
(Anderson Reference Anderson1989). Furthermore, the pressure being approximately constant along the stagnation streamline in the boundary layer results in approximating the velocity gradients in terms of the temperature as
$\partial u/\partial x=T{\it\beta}/T_{s}$
and
$\partial ^{2}u/\partial xy={\it\beta}/T_{s}\partial T/\partial y$
. Finally, the second-order gradients of the velocities can be now simplified as
$\partial ^{2}v/\partial y^{2}\approx 0$
and
$\partial ^{2}v/\partial x^{2}\approx 0$
, simplifying
$q_{sB}$
to the following:
$$\begin{eqnarray}q_{sB}=\frac{{\it\mu}^{3}}{p{\it\rho}}R{\it\theta}_{18}\left(T_{yyy}+T_{xxy}+2\frac{T_{y}}{T}T_{yy}+2\frac{T_{y}}{T}T_{xx}\right)+\frac{{\it\mu}^{3}}{p{\it\rho}}({\it\theta}_{20}v_{y}u_{xy}+{\it\theta}_{22}u_{x}u_{xy}).\end{eqnarray}$$
An additional assumption is made for simplification of the second- and third-order derivatives of the temperature field:
$$\begin{eqnarray}\frac{{\rm\nabla}^{2}T}{T}\approx -\frac{1}{{\it\Delta}^{2}},\end{eqnarray}$$
where
${\it\Delta}$
is a length scale which is chosen as the shock-wave standoff distance. In the transition regime, the shock thickens and merges with the boundary layer, leaving the shock-wave standoff distance as the only relevant characteristic length scale for evaluating gradients. Physically, this is the distance over which the temperature gradient between postshock conditions and the wall temperature is established. This additional assumption (2.5) reduces the super-Burnett heat flux term to the following form:
$$\begin{eqnarray}q_{sB}=\frac{{\it\mu}^{3}}{p{\it\rho}}R{\it\theta}_{18}\left(\frac{3}{{\it\Delta}^{2}}T_{y}\right)+\frac{{\it\mu}^{3}}{p{\it\rho}}\left[{\it\theta}_{20}(-2)^{J}\left(\frac{{\it\beta}_{s}^{2}}{T_{s}}\right)T_{y}+{\it\theta}_{22}T\left(\frac{{\it\beta}_{s}}{T_{s}}\right)^{2}T_{y}\right].\end{eqnarray}$$
Defining the ratio of super-Burnett (
$q_{sB}$
) and Fourier heat fluxes (
$q_{NS}$
) as a new parameter
$h_{r^{2}}$
gives
$$\begin{eqnarray}h_{r^{2}}\equiv \frac{q_{sB}}{q_{NS}}.\end{eqnarray}$$
Next, various flow properties can be related to reference values and free-stream values in the following manner. A reference temperature (
$T_{r}$
) is set as the average of the stagnation temperature (
$T_{s}$
) and the wall temperature (
$T_{w}$
). The viscosity is accurately modelled as a power-law function of temperature and is evaluated at the reference temperature,
${\it\mu}\propto T_{r}^{{\it\omega}}$
, where
${\it\omega}$
is a constant that may depend on the gas composition (
${\it\omega}$
is close to 0.75 for air). The thermal conductivity (
$k$
) for a diatomic gas can be related to its viscosity as
$k=(9{\it\gamma}-5){\it\mu}R/[4({\it\gamma}-1)]$
(Chapman & Cowling Reference Chapman and Cowling1970). Substitution leads to
$$\begin{eqnarray}\displaystyle h_{r^{2}} & = & \displaystyle -\!\left(1+\frac{T_{w}}{T_{s}}\right)^{2{\it\omega}+1}\frac{1}{2^{2{\it\omega}+1}}\left[\frac{4({\it\gamma}-1)}{9{\it\gamma}-5}\right]\left[-3{\it\theta}_{18}\left(\frac{R_{N}}{{\it\Delta}}\right)^{2}+{\it\theta}_{20}(-2)^{J}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.{\it\theta}_{22}(2)^{J}\left(1+\frac{T_{w}}{T_{s}}\right)\vphantom{\left(\frac{R_{N}}{{\it\Delta}}\right)^{2}}\right]\frac{1}{RT_{s}}\left(\frac{{\it\mu}_{s}}{{\it\rho}_{s}}\right)^{2}.\end{eqnarray}$$
Finally, dependence on the free-stream Mach number and Reynolds number (
$Re_{\infty }={\it\rho}_{\infty }V_{\infty }R_{N}/{\it\mu}_{\infty }$
) is introduced by using the normal shock-wave jump conditions for density (
${\it\rho}_{s}/{\it\rho}_{\infty }\approx ({\it\gamma}+1)/({\it\gamma}-1)$
) and temperature (
$T_{s}/T_{\infty }\approx ({\it\gamma}-1)M_{\infty }^{2}/2$
). With these approximations,
$h_{r^{2}}$
takes its final form:
$$\begin{eqnarray}h_{r^{2}}={\it\zeta}_{r^{2}}({\it\gamma},{\it\omega})C({\it\theta})\left(1+\frac{T_{w}}{T_{s}}\right)^{2{\it\omega}+1}W_{r}^{2},\end{eqnarray}$$
where we define a ‘rarefaction parameter’,
$W_{r}$
, as
$$\begin{eqnarray}W_{r}\equiv \frac{M_{\infty }^{2{\it\omega}}}{Re_{\infty }},\end{eqnarray}$$
and the two coefficient terms are given by
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\zeta}_{r^{2}}({\it\gamma},{\it\omega})=-\frac{({\it\gamma}-1)^{2{\it\omega}+3}}{2^{4{\it\omega}}}\frac{4{\it\gamma}}{9{\it\gamma}-5}\frac{1}{({\it\gamma}+1)^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C({\it\theta})=\left[-3{\it\theta}_{18}\left(\frac{{\it\Delta}}{R_{N}}\right)^{-2}+{\it\theta}_{20}(-2)^{J}+{\it\theta}_{22}\left(1+\frac{T_{w}}{T_{s}}\right)\right]. & \displaystyle\end{eqnarray}$$
Therefore, compared with the Fourier heat flux term appearing in the Navier–Stokes equations, the relative contribution from the super-Burnett heat flux term has a main dependence on
$W_{r}$
, a weak dependence on the ratio of wall to stagnation temperature, a weak dependence on gas properties through
${\it\zeta}_{r^{2}}({\it\gamma},{\it\omega})$
and, as discussed next, a weak dependence on the unknown coefficients (
${\it\theta}$
) through the expression
$C({\it\theta})$
.
In the
$C({\it\theta})$
expression, since typically in a hypersonic flow
$0.1<T_{w}/T_{s}<0.5$
, the third term will have a weak dependence on the ratio
$T_{w}/T_{s}$
and will be determined mainly by the value of
${\it\theta}_{22}$
. Likewise, the second term will be determined mainly by the value of
${\it\theta}_{20}$
. The first term includes the ratio of shock standoff distance to sphere radius. For continuum conditions this ratio ranges from 0.1 to 0.15, for example refer to the experimental data reported in Nonaka et al. (Reference Nonaka, Mizuno, Takayama and Park2000). For rarefied flow, the shock layer becomes more diffuse and the standoff distance increases with rarefaction; however, typically
${\it\Delta}/R_{N}<1$
in the transition regime. The shock standoff distance can be approximated using the inviscid model of Wen & Hornung (Reference Wen and Hornung1995), who suggest
${\it\Delta}_{inv.}=2^{(1-J)}{\it\rho}_{\infty }a_{s}/{\it\rho}_{s}{\it\beta}$
. The displacement thickness of the boundary layer,
$\hat{{\it\delta}}\approx 0.285{\it\delta}$
, can then be added to this inviscid expression to provide the following approximation for
${\it\Delta}$
:
$$\begin{eqnarray}\frac{{\it\Delta}}{R_{N}}\approx 2^{1-J}\left(\frac{{\it\gamma}}{2}\right)^{2}\frac{{\it\gamma}-1}{{\it\gamma}+1}+0.285\frac{{\it\delta}}{R_{N}}.\end{eqnarray}$$
Here,
${\it\delta}$
can be approximated as
${\it\delta}=2^{(3-J)/2}\sqrt{{\it\mu}/{\it\rho}{\it\beta}}$
and when evaluated at the reference temperature gives
$$\begin{eqnarray}\frac{{\it\delta}}{R_{N}}\approx 2^{1-J/2-{\it\omega}}\frac{{\it\gamma}^{1/4}({\it\gamma}-1)^{{\it\omega}/2+1/4}}{({\it\gamma}+1)^{1/2}}\left(1+\frac{T_{w}}{T_{s}}\right)^{{\it\omega}/2}W_{r}.\end{eqnarray}$$
In the above expressions for
${\it\Delta}/R_{N}$
(2.13) and (2.14), the dependence on
$T_{w}/T_{s}$
is very weak due to the exponent
${\it\omega}/2$
, and there is a dependence on the rarefaction parameter
$W_{r}$
, as expected. If one evaluates the above expressions for
${\it\Delta}/R_{N}$
over a range of Knudsen numbers (
$0.01<Kn<5$
), one finds
$0.1<{\it\Delta}/R_{N}<1$
, in agreement with experiment (Nonaka et al.
Reference Nonaka, Mizuno, Takayama and Park2000).
Therefore, the first term in
$C({\it\theta})$
may be the most dominant, and its value will be determined by both
${\it\Delta}/R_{N}$
and
${\it\theta}_{18}$
. The value of each
${\it\theta}$
coefficient, however, is uncertain. For the BGK–Burnett equations, the values are
${\it\theta}_{18}=4.9$
,
${\it\theta}_{20}=-0.16$
and
${\it\theta}_{22}=4.24$
. However, the BGK approximation to the collision integral in the Boltzmann equation is known to be inaccurate for realistic gases, and therefore, if the full collision integral were analysed (with accurate cross-section or interatomic potential models), the
${\it\theta}$
coefficients would certainly change. In fact, the set of coefficients for the BGK–Burnett equations is non-unique and has been proposed to ensure numerical stability and entropy consistency (Agarwal et al.
Reference Agarwal, Yun and Balakrishnan2001). Furthermore, the two sets of stable and entropy-consistent BGK–Burnett equations proposed in Balakrishnan (Reference Balakrishnan1999) have different signs for some of the coefficients. Since each term in
$C({\it\theta})$
is likely to be close to unity, and is dependent on coefficients with uncertainty in magnitude and sign, our approach in later sections will be to replace
$C({\it\theta})$
with a single fitting parameter in the correlation expression.
2.3 Analysis of the Burnett heat flux contribution
A similar analysis can be carried out for the Burnett-order heat flux term in the BGK–Burnett equations, which has the following form:
$$\begin{eqnarray}\displaystyle q_{B} & = & \displaystyle \frac{{\it\mu}^{2}}{{\it\rho}}\left({\it\Gamma}_{1}\frac{1}{T}T_{y}u_{y}+{\it\Gamma}_{2}\frac{1}{T}T_{y}v_{x}+{\it\Gamma}_{3}v_{yy}+{\it\Gamma}_{4}v_{xx}+{\it\Gamma}_{5}u_{xy}+{\it\Gamma}_{6}\frac{1}{T}T_{x}u_{y}+{\it\Gamma}_{7}\frac{1}{T}T_{x}v_{x}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.{\it\Gamma}_{8}\frac{1}{{\it\rho}}{\it\rho}_{y}v_{y}+{\it\Gamma}_{9}\frac{1}{{\it\rho}}{\it\rho}_{y}u_{x}+{\it\Gamma}_{10}\frac{1}{{\it\rho}}{\it\rho}_{x}v_{x}+{\it\Gamma}_{11}\frac{1}{{\it\rho}}{\it\rho}_{x}u_{y}\right).\end{eqnarray}$$
Here, the
${\it\Gamma}$
coefficients are determined by collision integrals in the Chapman–Enskog analysis, analogous to the
${\it\theta}$
coefficients in (2.1). Using the very same assumptions as in the previous section, the parameter (
$h_{r^{1}}$
), obtained by normalizing the Burnett-order heat flux with the Fourier heat flux, has the following form:
$$\begin{eqnarray}h_{r^{1}}\equiv \frac{q_{B}}{q_{NS}}={\it\zeta}_{r^{1}}({\it\gamma},{\it\omega})C({\it\Gamma})\left(1+\frac{T_{w}}{T_{s}}\right)^{{\it\omega}+1}W_{r},\end{eqnarray}$$
and the two coefficient terms are given by
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\zeta}_{r^{1}}({\it\gamma},{\it\omega})=\frac{({\it\gamma}-1)^{{\it\omega}+3/2}}{2^{2{\it\omega}}}\frac{4\sqrt{{\it\gamma}}}{9{\it\gamma}-5}\frac{1}{({\it\gamma}+1)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C({\it\Gamma})=\left[\frac{{\it\Gamma}_{9}}{2}\left(1+\frac{T_{w}}{T_{s}}\right)-\left({\it\Gamma}_{5}+\frac{2{\it\Gamma}_{8}}{1+T_{w}/T_{s}}\right)\right], & \displaystyle\end{eqnarray}$$
where
${\it\Gamma}_{5}=-2.8$
,
${\it\Gamma}_{8}=-1.271$
and
${\it\Gamma}_{9}=1.0$
for the BGK–Burnett equations. Following similar arguments as for
$C({\it\theta})$
, the value of
$C({\it\Gamma})$
is mainly determined by the
${\it\Gamma}$
coefficients, which are associated with a fair amount of uncertainty. It is noted that Wang, Bao & Tong (Reference Wang, Bao and Tong2010) carried out a similar analysis for the Burnett-order terms. By performing the analysis for both Burnett-order and super-Burnett-order terms (§§ 2.2 and 2.3), and noting the similarity between (2.9) and (2.16), the form of higher-order contributions can be inferred and utilized in the correlation developed in the next section.
3 A new correlation for heat flux
3.1 Higher-order contributions compared with Navier–Stokes heat flux
So far, the analysis has been presented in terms of heat flux contributions normalized with the Navier–Stokes heat flux (2.9) and (2.16). In order to evaluate the actual heat transfer coefficient, we use the recent correlation from Brandis & Johnston (Reference Brandis and Johnston2014) for the Navier–Stokes heat flux:
$$\begin{eqnarray}\displaystyle & \hat{q}=7.455\times 10^{-9}{\it\rho}_{\infty }^{0.4705}V_{\infty }^{3.089}R^{-0.52},\quad 3~\text{km}~\text{s}^{-1}\leqslant V_{\infty }<9.5~\text{km}~\text{s}^{-1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \hat{q}=1.270\times 10^{-6}{\it\rho}_{\infty }^{0.4678}V_{\infty }^{2.524}R^{-0.52},\quad 9.5~\text{km}~\text{s}^{-1}\leqslant V_{\infty }<17~\text{km}~\text{s}^{-1}, & \displaystyle\end{eqnarray}$$
where
$\hat{q}$
has units of
$\text{W}~\text{cm}^{-2}$
,
$V_{\infty }$
has units of
$\text{m}~\text{s}^{-1}$
and
$R$
has units of m. It is important to note that alternate correlations based on continuum theory, for example those by Fay & Riddell (Reference Fay and Riddell1958) and Sutton & Graves (Reference Sutton and Graves1971), could be used for
$\hat{q}$
instead.
The total heat flux including the contributions from the Burnett and super-Burnett terms is then
$$\begin{eqnarray}q=\hat{q}(1+h_{r^{1}}+h_{r^{2}}),\end{eqnarray}$$
and based on free-stream parameters we define the heat transfer coefficient
$h_{c}$
as
$$\begin{eqnarray}h_{c}=\frac{q}{\frac{1}{2}{\it\rho}_{\infty }v_{\infty }^{3}}.\end{eqnarray}$$
In figure 2 the relative significance of super-Burnett and Burnett heat flux terms compared with Navier–Stokes terms is shown along with the dependence on the ratio
$T_{w}/T_{s}$
. As is evident from figure 2(a), super-Burnett heat flux terms ((2.9) with listed
${\it\theta}$
values) are negligible for
$Kn\leqslant 1.0$
, but become significant for
$Kn\geqslant 1.0$
. These terms contribute negatively to the heat flux, which is expected since the Navier–Stokes solutions tend to overpredict the heat flux in the rarefied regime. The ratio of wall to stagnation temperature is also seen to have a noticeable effect, especially for
$Kn\geqslant 4$
. In figure 2(b), Burnett heat flux terms ((2.16) with listed
${\it\Gamma}$
values) become significant at the start of the transition regime (
$Kn\geqslant 0.1$
). The ratio of wall to stagnation temperature has a noticeable effect, although the effect is quite weak. Interestingly, the Burnett terms add to the heat transfer prediction of Navier–Stokes (i.e.
$h_{r^{1}}>0$
). This was also found by Wang et al. (Reference Wang, Bao and Tong2010) using a similar analysis. However, this is inconsistent with a number of studies showing that the heat flux in the transition regime should be lower than that predicted by the Navier–Stokes equations. Such studies include flow over a flat plate (Chen, Wang & Yu Reference Chen, Wang and Yu2014), stagnation-point heat flux for hypersonic flow over blunt bodies (Schwartzentruber, Scalabrin & Boyd Reference Schwartzentruber, Scalabrin and Boyd2008b
,Reference Schwartzentruber, Scalabrin and Boyd
c
) and hypersonic flow over a sphere (Lofthouse, Boyd & Wright Reference Lofthouse, Boyd and Wright2007; Holman & Boyd Reference Holman and Boyd2009, Reference Holman and Boyd2011). As discussed earlier, the
${\it\theta}$
and
${\it\Gamma}$
coefficients are uncertain, as are the signs of the
$C({\it\theta})$
and
$C({\it\Gamma})$
terms. This inconsistency will be remedied in the next subsection.
Figure 2. The contributions of the higher-order heat flux terms as functions of
$Kn$
. The conditions correspond to
$M_{\infty }=10.0$
,
$j=0$
and
${\it\gamma}=1.4$
. (a) Contribution from super-Burnett terms; (b) contribution from Burnett terms.
The significance of higher-order heat flux terms is presented in terms of leading-edge radius in figure 3. Here, a reduction in radius is equivalent to an increase in
$Kn$
(also plotted on the top axis in figure 3). For approximate conditions at 80 km altitude and orbital velocity, it is evident that higher-order terms begin to contribute significantly for radii less than 1 cm, with very large effects for radii of 1 mm. As noted above, the Burnett and super-Burnett terms are seen to have opposite signs. This could be due to uncertainty in the
$C({\it\theta})$
and
$C({\it\Gamma})$
coefficients and/or the need to include a more complete set of higher-order terms in the series approximation.
Figure 3. The coefficients of heat flux including higher-order terms as functions of the leading-edge radius and
$Kn$
. The conditions correspond to
$V=14\,000~\text{m}~\text{s}^{-1}$
,
${\it\rho}=10^{-5}~\text{kg}~\text{m}^{-3}$
,
$j=0$
,
${\it\gamma}=1.4$
and
$T_{w}/T_{s}=0.01$
. (a) Super-Burnett and Navier–Stokes terms; (b) Burnett and Navier–Stokes terms.
3.2 Extension to the full series of higher-order terms
The continuum equations beyond super-Burnett order are not available in the literature. Therefore it is interesting to look at the next few terms that we can obtain from the functional forms of
$h_{r^{1}}$
and
$h_{r^{2}}$
derived above. The full heat flux expression, incorporating all higher-order heat flux terms, can be expressed as
$$\begin{eqnarray}q=q_{NS}+q_{B}+q_{sB}+\cdots \,.\end{eqnarray}$$
When normalized by the Navier–Stokes heat flux (
$\bar{q}$
), this can be expressed in terms of
$h_{r^{1}}$
and
$h_{r^{2}}$
in the following manner:
$$\begin{eqnarray}\bar{q}=1+h_{r^{1}}+h_{r^{2}}+\cdots \,.\end{eqnarray}$$
From (2.9) and (2.16), it is clear that as rarefaction increases, the additional terms grow as
$W_{r}^{n}\equiv (M_{\infty }^{2{\it\omega}}/Re_{\infty })^{n}$
, where
$n=1,2,3,\,\ldots \,$
, and, furthermore, the
$n$
th term in the series can be written as
$$\begin{eqnarray}h_{r^{n}}=\left[\frac{4}{9{\it\gamma}-5}\left(1+\frac{T_{w}}{T_{s}}\right)C({\it\theta},{\it\Gamma},\ldots \,)\right]\left[\frac{\sqrt{{\it\gamma}}({\it\gamma}-1)^{{\it\omega}+3/2}}{2^{2{\it\omega}}\left({\it\gamma}+1\right)}\left(1+\frac{T_{w}}{T_{s}}\right)^{{\it\omega}}W_{r}\right]^{n}.\end{eqnarray}$$
Based on prior discussion, each term in the first square bracket is of order unity, with uncertainty in evaluating
$C({\it\theta},{\it\Gamma},\ldots )$
. It is also important to note that terms involving
${\it\gamma}$
,
${\it\omega}$
and
$T_{w}/T_{s}$
within both square brackets are not exact, rather they are the result of shock-wave and boundary-layer approximations made in the preceding analysis. In seeking an accurate yet simple correlation, it is reasonable to replace these terms by a fitting constant and maintain only the dominant terms in the functional form:
$$\begin{eqnarray}h_{r^{n}}\approx \left[{\it\beta}_{n}\frac{\sqrt{{\it\gamma}}({\it\gamma}-1)^{{\it\omega}+3/2}}{2^{2{\it\omega}}\left({\it\gamma}+1\right)}\left(1+\frac{T_{w}}{T_{s}}\right)^{{\it\omega}}W_{r}\right]^{n}.\end{eqnarray}$$
Here, the dominant terms involving gas properties (
${\it\gamma},{\it\omega}$
), wall temperature (
$T_{w}/T_{s}$
) and rarefaction parameter (
$W_{r}$
) are maintained, and the uncertain (order-unity) terms are lumped together in a fitting coefficient (
${\it\beta}_{n}$
). Since the wall temperature was shown to have minor effect (figure 2) and we are presently interested in air (
${\it\gamma}=1.4$
and
${\it\omega}\approx 0.75$
), we further combine these terms as
$$\begin{eqnarray}h_{r^{n}}\approx [{\it\alpha}_{n}W_{r}]^{n},\end{eqnarray}$$
where the
${\it\alpha}_{n}$
are a set of fitting coefficients to be determined next. Evaluating the heat flux using
$N$
higher-order terms, we have
$$\begin{eqnarray}q=q_{NS}\left[1+\mathop{\sum }_{n=1}^{n=N}h_{r^{n}}\right]=q_{NS}\left[1+\mathop{\sum }_{n=1}^{n=N}({\it\alpha}_{n}W_{r})^{n}\right]\!.\end{eqnarray}$$
One could use either (3.8) or (3.9) and determine the fitting coefficients (
${\it\beta}_{n}$
or
${\it\alpha}_{n}$
) up to a desired number of terms (
$n=1,2,\ldots ,N$
) by comparison with accurate heat flux predictions from DSMC, for example.
Finally, it is interesting that in the limit of an infinite series, if one assumes that the
${\it\alpha}_{n}$
coefficients are approximately equal, the resulting expression is simply
$$\begin{eqnarray}q=\frac{q_{NS}}{1-{\it\alpha}W_{r}}\quad \text{for }-\!1<{\it\alpha}<+1,\end{eqnarray}$$
and the coefficient of heat flux can be written as
$$\begin{eqnarray}h_{ct}=\frac{q_{NS}}{\frac{1}{2}{\it\rho}_{\infty }v_{\infty }^{3}(1-{\it\alpha}W_{r})}.\end{eqnarray}$$
In this case, only one free parameter (
${\it\alpha}$
) needs to be fitted, and, as shown later in § 4, this simple expression is able to capture the heat flux in the transition regime predicted by DSMC simulations. It is worthwhile to note that the value of
$J$
is embedded within the fitting parameter
${\it\alpha}$
. Therefore, if simulations of flow over a cylinder are used for fitting, the value of
${\it\alpha}$
may be slightly different from that when using simulations of flow over a sphere. Moreover, the choice of continuum correlation should also be consistent; for example, the correlation of Brandis & Johnston (Reference Brandis and Johnston2014) is for flow over a sphere.
3.3 Bridging function in the limit of free-molecular flow
As is evident from the expression for
$q$
in (3.11), as
$W_{r}\rightarrow 0$
,
$q$
approaches
$q_{NS}$
as desired. However, as
$W_{r}\rightarrow \infty$
,
$q$
clearly does not approach the correct free-molecular value since the correlation was derived as a deviation from the Fourier heat flux. Therefore, we force the expression for
$q$
to approach the free-molecular limit using a bridging function. The analytical expression for the heat flux in the free-molecular regime is well documented in standard textbooks (Bird Reference Bird1994) and is reproduced here for completeness:
$$\begin{eqnarray}\displaystyle q_{fm}\hspace{-2.5pt} & = & \displaystyle \hspace{-2.5pt}{\it\rho}_{\infty }\left(\sqrt{\frac{2K_{B}T}{m}}\right)^{3}\frac{1}{4\sqrt{{\rm\pi}}}\left\{\left[\frac{{\it\gamma}}{2}M_{\infty }^{2}+\frac{{\it\gamma}}{{\it\gamma}-1}-\frac{{\it\gamma}+1}{2({\it\gamma}-1)}\frac{T_{w}}{T_{\infty }}\right]\left[\vphantom{\left(\sqrt{\frac{{\rm\pi}{\it\gamma}}{2}}Ma\right)}\exp \left(-\frac{{\it\gamma}}{2}M_{\infty }^{2}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,\sqrt{\frac{{\rm\pi}{\it\gamma}}{2}}M_{\infty }\left[1+\text{erf}\left(\sqrt{\frac{{\rm\pi}{\it\gamma}}{2}}M_{\infty }\right)\right]\right]-\frac{1}{2}\exp \left(-\frac{{\it\gamma}}{2}M_{\infty }^{2}\right)\right\},\end{eqnarray}$$
where
$K_{B}$
is the Boltzmann constant and
$m$
is the molecular mass of the gas. The heat transfer coefficient based on free-stream conditions is
$$\begin{eqnarray}h_{fm}=\frac{q_{fm}}{\frac{1}{2}{\it\rho}_{\infty }v_{\infty }^{3}}.\end{eqnarray}$$
The full correlation for the stagnation-point heat transfer coefficient (
$h_{0}$
), valid for conditions ranging from continuum to free-molecular, is
$$\begin{eqnarray}h_{0}=h_{ct}+(h_{fm}-h_{ct})\max \left[\frac{W_{r}-C_{2}}{W_{r}+C_{3}},0\right].\end{eqnarray}$$
Here,
$h_{ct}$
and
$h_{fm}$
are given by (3.12) and (3.14), with
$q_{NS}$
taken from a continuum correlation such as (3.1) and (3.2),
$C_{2}$
is a constant that controls the value of
$W_{r}$
above which the bridging function becomes active and
$C_{3}$
is a constant that controls how quickly the function reaches the free-molecular limit.
4 Comparison with DSMC calculations
In this section, we compare our correlation for stagnation-point heat transfer with DSMC calculations by Glass & Moss (Reference Glass and Moss2001) and Holman & Boyd (Reference Holman and Boyd2009) for nitrogen gas. In figure 4, we plot the stagnation heat transfer coefficient against
$W_{r}\equiv M_{\infty }^{2{\it\omega}}/Re_{\infty }$
. Macrossan (Reference Macrossan2007) pointed out that the Knudsen number does not involve flow parameters and hence represents a state parameter, whereas the rarefaction parameter
$W_{r}$
involves flow parameters as well as a length scale and is therefore a better correlation parameter. In fact, this parameter is proportional to one proposed by Cheng (Reference Cheng1961) which has been used to correlate heat transfer data (Nomura Reference Nomura1983). In figure 4, it is evident that the DSMC results of Glass & Moss (Reference Glass and Moss2001) and Holman & Boyd (Reference Holman and Boyd2009) are in good agreement with the continuum correlation of Brandis & Johnston (Reference Brandis and Johnston2014) for
$W_{r}\leqslant 0.1$
. As the rarefaction parameter increases, the heat flux predicted by DSMC is lower than the continuum correlation (which is based on CFD calculations). It is noted that Wang et al. (Reference Wang, Bao and Tong2010) recently proposed the opposite trend, using similar Burnett-order analysis to that presented in § 2.3 above, where such a comparison predicted a higher heat flux compared with continuum analysis. However, the trend of lower heat flux in the transition regime, compared with continuum predictions, has been verified in a number of articles (for example Lofthouse et al.
Reference Lofthouse, Boyd and Wright2007; Schwartzentruber, Scalabrin & Boyd Reference Schwartzentruber, Scalabrin and Boyd2008a
; Schwartzentruber et al.
Reference Schwartzentruber, Scalabrin and Boyd2008b
,Reference Schwartzentruber, Scalabrin and Boyd
c
; Holman & Boyd Reference Holman and Boyd2009, Reference Holman and Boyd2011) in which DSMC calculations have been compared with matching CFD calculations where both codes used highly consistent physical models.
Figure 4. Comparison of DSMC data with Navier–Stokes (
$h_{NS}$
; no slip) based correlation and the proposed correlation (nitrogen gas;
$T_{w}=500~\text{K}$
,
$T_{\infty }=200~\text{K}$
,
$R_{N}=0.1524~\text{m}$
,
$M_{\infty }=10$
,
$V_{\infty }=2883.5~\text{m}~\text{s}^{-1}$
).
Figure 4 shows that the correlation proposed by Brandis & Johnston (Reference Brandis and Johnston2014) matches well with the DSMC results of Glass & Moss (Reference Glass and Moss2001) and Holman & Boyd (Reference Holman and Boyd2009) for
$W_{r}\leqslant 0.1$
. However, it overpredicts the heat transfer for
$W_{r}>0.1$
and quickly predicts unphysical values. By fitting our new correlation to the DSMC results of Holman & Boyd (Reference Holman and Boyd2009) together with free-molecular results, we determine the constants in our expression as
${\it\alpha}=-0.476$
,
$C_{2}=1.10$
,
$C_{3}=1.8$
. In figure 4, we see that the proposed expression for
$h_{ct}$
matches the DSMC results well in the continuum and transition regimes. However, as
$W_{r}$
becomes greater than 2.1, we observe that
$h_{ct}$
fails to capture heat flux values even qualitatively. This is no surprise since the Chapman–Enskog series solution (Chapman & Cowling Reference Chapman and Cowling1970) is based on asymptotic analysis which assumes
$Kn$
to be small in its derivation. Instead, in this range, the bridging function forces
$h_{ct}$
to smoothly asymptote to free-molecular values. As shown in figure 4, the proposed expression for the heat transfer coefficient (
$h_{0}$
) correctly captures its dependence on
$W_{r}$
in the continuum and transition regimes and dependence only on
$M_{\infty }$
in the free-molecular regime. This is evident from the close match of the correlation with the DSMC data of Glass & Moss (Reference Glass and Moss2001), which correspond to
$13\leqslant M_{\infty }\leqslant 21$
and
$0.001\leqslant Kn\leqslant 100.0$
. In the future, more DSMC simulation data could be produced in the transition regime to further validate the new heat flux correlation, improve its fitting parameters and determine its overall accuracy.
5 Conclusions
We propose an analytical correlation for stagnation-point heat flux on spherical objects travelling at high velocity which can be used for conditions ranging from continuum to free-molecular. Theoretical analysis of the Burnett and super-Burnett equations is performed using simplifications from shock-wave and boundary-layer theory to determine the relative contribution of higher-order heat flux terms compared with the Fourier heat flux (assumed in the Navier–Stokes equations). Order-of-magnitude analysis of these terms relative to the Navier–Stokes equations shows that the Burnett and super-Burnett terms become important for
$Kn\geqslant 0.1$
and
$Kn\geqslant 1.0$
respectively.
A rarefaction parameter (
$W_{r}\equiv M_{\infty }^{2{\it\omega}}/Re_{\infty }$
), based on the free-stream Mach number (
$M_{\infty }$
), Reynolds number (
$Re_{\infty }$
) and viscosity–temperature index (
${\it\omega}$
), is identified as a better correlating parameter than the Knudsen number (
$Kn$
) in the transition regime. Unlike
$Kn$
, this parameter captures the flow parameters in addition to the state parameters and the length scale. Importantly, by studying both the Burnett and super-Burnett equations, a general form for the entire series of higher-order heat flux contributions is obtained. This analysis exhausts the study of Chapman–Enskog series solutions for heat flux at the macroscopic level. The resulting heat flux expression includes terms with dependence on gas properties, the stagnation to wall-temperature ratio and a main dependence on powers of the rarefaction parameter
$W_{r}$
.
Uncertainty due to collision integral quantities and other simplifying assumptions is discussed in detail, including the fact that even the signs of the contributions from higher-order terms are uncertain. While previous analysis using only Burnett-order terms (Wang et al. Reference Wang, Bao and Tong2010) proposed that the heat flux in the transition regime was larger than that predicted by continuum (Fourier) analysis, there is ample evidence in the literature that suggests the opposite, that is, the heat flux in the transition regime should be lower than the Fourier value. Our analysis resolves this issue by acknowledging the uncertainty in various order-unity terms, replacing with appropriate coefficients to be fitted with high-quality simulation data and including all higher-order terms in a limiting expression. In the limit of this full series analysis, a simple approximate expression for the stagnation-point heat flux is determined.
The expression is applied as a correction to the Fourier heat flux and, therefore, can be combined with any continuum-based correlation of choice. In this article we use the recent CFD-based correlation from Brandis & Johnston (Reference Brandis and Johnston2014). In the free-molecular limit, a bridging function is used to ensure consistency with well-established free-molecular flow theory. A general correlation is presented which maintains dominant terms due to gas properties, the stagnation to wall-temperature ratio, powers of
$W_{r}$
and remaining (order-unity) fitting parameters that could be determined by comparison with DSMC solutions. A more simplified expression is presented, which replaces the gas properties and wall-temperature dependence by incorporating these terms into a fitting coefficient. The simplified correlation is then fitted to DSMC solutions for the stagnation-point heat flux in high-speed nitrogen flows. The correlation is shown to accurately capture the variation in heat flux predicted by DSMC in the transition regime, while limiting to both continuum and free-molecular values.
Future effort could be devoted to obtaining more DSMC results or experimental data for the heat flux in the transitional regime in order to further validate the correlation, improve the fitting accuracy, generalize to different gas mixtures and different stagnation to wall-temperature ratios, and investigate any effects due to dissociation.
