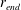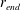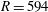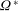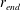1. Introduction
One of the few relatively simple exact similarity solutions of the nonlinear Navier–Stokes equations can be formulated for the flow developing on a rotating infinite disk; due to the disk’s rotation, the flow experiences an outward radial force which accelerates the flow outwards and in turn draws in fluid towards the surface. The corresponding laminar velocity profiles arising over such a rotating disk are shown in figure 1 and constitute the solution of the cylindrical Navier–Stokes equations first formulated by von Kármán (Reference von Kármán1921). This three-dimensional boundary layer, also referred to as the von Kármán flow, serves as a model for other three-dimensional boundary layers due to its simplicity, as shown, for example, by Gregory, Stuart & Walker (Reference Gregory, Stuart and Walker1955). This rotating-disk boundary layer belongs to a family of rotating flows called, here and elsewhere, the BEK boundary layers, where BEK stands for Bödewadt, Ekman and von Kármán. Bödewadt (Reference Bödewadt1940) studied the flow over an infinite stationary plane, where fluid rotated with a uniform angular velocity to an infinite distance above the plane; Ekman (Reference Ekman1905) studied the influence of the Earth’s rotation on ocean currents, which can be reformulated into a study of the flow over a rotating disk when the fluid at infinity rotates with almost the same rotation rate as the disk itself, and, as already mentioned, von Kármán (Reference von Kármán1921) studied the flow over a rotating disk when the fluid at infinity approaches a non-rotating condition. These BEK boundary layers for infinite-radius disks all have an exact solution of the Navier–Stokes equations for the mean flow.
Figure 1. The laminar velocity profiles of the similarity solution for the flow over a rotating disk. Here,
$U$
is the radial velocity component,
$V$
is the azimuthal velocity component and the vertical greyscale lines indicate the amplitude of the wall-normal velocity component
$W$
(white denotes zero velocity). The cylindrical coordinates are given by
$r$
,
${\it\theta}$
and
$z$
, and the rotation rate is defined by
${\rm\Omega}$
. A part of the spectral-element mesh used is also illustrated, for which more details are given later.
For the rotating-disk (von Kármán) flow extensive theoretical investigations, e.g. Malik (Reference Malik1986), Lingwood (Reference Lingwood1995a ), Pier (Reference Pier2003), and experimental studies, e.g. Wilkinson & Malik (Reference Wilkinson and Malik1985), Lingwood (Reference Lingwood1996), Othman & Corke (Reference Othman and Corke2006), Siddiqui et al. (Reference Siddiqui, Mukund, Scott and Pier2013), Imayama, Alfredsson & Lingwood (Reference Imayama, Alfredsson and Lingwood2014a ), have focused on various aspects of the instability characteristics and laminar–turbulent transition. There have also been several investigations of the turbulent rotating-disk flow, e.g. Littell & Eaton (Reference Littell and Eaton1994), Imayama, Lingwood & Alfredsson (Reference Imayama, Lingwood and Alfredsson2014b ). In the present work, however, we will restrict investigations to the purely linear regime in order to focus on the global-stability characteristics of a rotating disk in a domain that is not infinite, in the present case delimited by a front mimicking the appearance of turbulence further downstream.
Lingwood (Reference Lingwood1995a
) performed a linear stability analysis of the laminar locally homogeneous base flow and found in her spatio-temporal analysis that there is a linear absolute instability with a critical Reynolds number (
$R_{c}$
) of 507 (first given as 510 and then corrected in Lingwood (Reference Lingwood1997)). The Reynolds number for the rotating-disk flow is here defined as
$$\begin{eqnarray}R=r^{\ast }\sqrt{\frac{{\rm\Omega}^{\ast }}{{\it\nu}}}=r,\end{eqnarray}$$
where
$^{\ast }$
refers to a dimensional quantity,
$r^{\ast }$
is the radial position on the disk and
$\sqrt{{\it\nu}/{\rm\Omega}^{\ast }}$
is the length scale used, where
${\it\nu}$
is the (dimensional) kinematic viscosity of the fluid and
${\rm\Omega}^{\ast }$
is the angular velocity of the disk. The theoretical
$R_{c}$
found by Lingwood (Reference Lingwood1995a
) for the onset of the absolute instability agrees well with the experimentally observed location for the onset of nonlinearity,
$R=502{-}514$
(Lingwood Reference Lingwood1996) and
$R=510{-}520$
(Imayama, Alfredsson & Lingwood Reference Imayama, Alfredsson and Lingwood2013), which indicates that the absolute instability is indeed relevant to the transition process. This is particularly interesting since the rotating-disk flow was the first boundary layer found that exhibited absolutely unstable behaviour, as opposed to, say, flat-plate boundary layers, which are convectively unstable. In 2003, a direct numerical simulation (DNS) of the linearized Navier–Stokes equations was reported (Davies & Carpenter Reference Davies and Carpenter2003), computing both the local and global flow behaviour. The local behaviour exactly corresponded to that of Lingwood (Reference Lingwood1995a
), showing an absolute instability above a critical Reynolds number of
$R_{c}=507$
. However, the global behaviour was found to give no evidence of the local absolute instability giving rise to an unstable global oscillator. It was thus suggested that the rotating-disk boundary layer did not produce a linear amplified global mode in the same manner as described by Huerre & Monkewitz (Reference Huerre and Monkewitz1990). The results of Davies & Carpenter (Reference Davies and Carpenter2003) led to further work to determine whether their finding of global stability was a consequence of the linear approximation, and also to determine whether a disk’s finite radius plays a significant role, e.g. Pier (Reference Pier2003), Othman & Corke (Reference Othman and Corke2006), Davies, Thomas & Carpenter (Reference Davies, Thomas and Carpenter2007), Healey (Reference Healey2010), Imayama et al. (Reference Imayama, Alfredsson and Lingwood2013), Pier (Reference Pier2013). Moreover, Thomas & Davies (Reference Thomas and Davies2010, Reference Thomas and Davies2013) continued to investigate the rotating-disk boundary layer via DNS by looking at the effects of either suction and injection or, in the latter case, an axial magnetic field.
For fixed rotation rate, the linear radial variation in Reynolds number leads to spatial inhomogeneity, which (by analogy with, say, the Blasius boundary layer) is often called the non-parallel effect despite the similarity solution for the rotating-disk flow being physically parallel. Considering the previously described linear global stability, Davies et al. (Reference Davies, Thomas and Carpenter2007) showed that this stability might occur due to ‘detuning’ arising from the radial variation of the temporal absolute frequency. Thus, Davies et al. (Reference Davies, Thomas and Carpenter2007) argued that the non-parallel effects might stabilize the flow, allowing it to remain globally stable (within a linear framework). However, in effectively creating an infinite-radius domain, Davies & Carpenter (Reference Davies and Carpenter2003) neglected inward-travelling disturbances from the outer radial boundary (see their page 299), disturbances that are fundamental to the absolute instability mechanism (Lingwood Reference Lingwood1995a ). Healey (Reference Healey2010) used the linearized Ginzburg–Landau model to reproduce the convective behaviour, i.e. linear global stability, in an infinite domain similar to Davies & Carpenter’s (Reference Davies and Carpenter2003) findings. Then, he also modelled the behaviour in a finite domain, in which the disturbances propagate first through the absolutely unstable region as in the unbounded case but, on reaching the downstream boundary, an unstable global mode is excited (shown in his figure 2c). From his findings, Healey (Reference Healey2010) argued that linear global instability can be created by local absolute instability at the edge of the disk provided the absolutely unstable region is sufficiently large prior to the edge.
Healey (Reference Healey2010) also investigated the effect of nonlinearity using a simple model and found a (supercritical) nonlinear front appearing at the onset of absolute instability when the disk edge was far from the front itself. He also found that when the disk edge approaches
$R_{c}$
the onset of absolute instability moves radially outwards, i.e. the proximity of the edge stabilizes the flow. Experiments by Imayama et al. (Reference Imayama, Alfredsson and Lingwood2013), however, showed no obvious variation in the transition Reynolds number due to the proximity of the edge of the disk, although Pier (Reference Pier2013) found in his experiments that the edge of the disk acted as a strong source of fluctuations and suggested that the nonlinear results of Healey (Reference Healey2010) and Imayama et al. (Reference Imayama, Alfredsson and Lingwood2013) could align if a downstream boundary condition could be modelled such that it acted as a source of random noise.
Earlier work by Pier (Pier & Huerre Reference Pier and Huerre2001; Pier Reference Pier2003, Reference Pier2007) has extensively discussed the nonlinear-stability behaviour of the flow over a rotating disk and routes to turbulence. These latter studies (the latest undertaken within a context where the rotating-disk flow was thought to be linearly globally stable) predict a (sub-critical) nonlinear so-called ‘elephant’ global mode characterized by a stationary front located at
$R_{c}$
, which saturates and is itself absolutely unstable to secondary instabilities, as has more recently been found in the DNS by Viaud, Serre & Chomaz (Reference Viaud, Serre and Chomaz2011) in an open rotating cavity.
In the current study, the linear DNS results presented by Davies & Carpenter (Reference Davies and Carpenter2003) are reproduced using a different numerical method and extended to longer integration times. Of particular interest is the behaviour of the flow in a non-infinite domain, e.g. in the case when downstream turbulence needs to be considered. In contrast to Davies & Carpenter (Reference Davies and Carpenter2003), we do not neglect inward-travelling disturbances from the outer boundary, or in our case from the downstream turbulence, which allows us to study the upstream effect of the outer nonlinear region of the flow on the linear global-instability properties of the rotating-disk system; our work can therefore be compared with the work presented by Healey (Reference Healey2010).
This paper is organized as follows. In § 2 the set-up of the simulations used within this study is described in terms of the mesh, boundary conditions and initial disturbance. Results are presented in § 3 from various simulations, and a discussion of these results is also included. To close, § 4 provides a summary and conclusions.
2. Method
Our simulations are performed with the massively parallel code Nek5000 (Fischer, Lottes & Kerkemeier Reference Fischer, Lottes and Kerkemeier2012). The code Nek5000 solves the incompressible Navier–Stokes equations via a Legendre polynomial-based spectral-element method (SEM). The SEM was introduced by Patera (Reference Patera1984) and combines the geometrical flexibility of finite-element methods with the accuracy of spectral methods. The orthogonal basis of Legendre polynomials up to degree
$N$
is used within each element, where
$N=7$
in our study to optimize both resolution and computation time. The solution to the Navier–Stokes equations is then approximated as an expansion of Lagrange interpolants. The pressure is expanded in polynomials of order
$N$
, as in the standard
$P_{N}$
–
$P_{N}$
method (Maday & Patera Reference Maday, Patera, Noor and Oden1989). Between the various elements,
$C_{0}$
continuity is maintained, meaning that the values correspond at the element borders whereas the derivatives may be discontinuous. However, the difference in the derivatives decreases spectrally fast. The temporal discretization scheme BDF/EXT of second order is used (Ho Reference Ho1989), based on operator splitting, where the nonlinear convective terms are treated explicitly via a projection scheme, and the viscous and divergence operators are treated implicitly (Deville, Fischer & Mund Reference Deville, Fischer and Mund2002).
The code Nek5000 is optimized for MPI-based (message passing interface) usage on supercomputers (Tufo & Fischer Reference Tufo and Fischer2001), and all linear simulations in the present work were performed on 528 cores; the nonlinear simulation was performed on 2112 cores.
2.1. Governing equations
One nonlinear simulation was run to verify the behaviour of our radial outer boundary condition for the linear simulations, a so-called ‘sponge region’. The full Navier–Stokes equations were then solved within the Nek5000 code,
$$\begin{eqnarray}\frac{\partial \boldsymbol{U}_{\boldsymbol{x}}}{\partial t}+\boldsymbol{U}_{\boldsymbol{x}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}_{\boldsymbol{x}}=-\boldsymbol{{\rm\nabla}}p+\frac{1}{R}{\rm\nabla}^{2}\boldsymbol{U}_{\boldsymbol{x}}+\boldsymbol{f}_{\boldsymbol{x}}.\end{eqnarray}$$
The nonlinear terms can be turned off so that the code is run in only a linear fashion. This is the approach taken for our linear simulations presented here. The flow then consists of a base flow and a perturbation on top of this flow. The von Kármán similarity solutions were used as base-flow components (
$\boldsymbol{U}=(U,V,W)$
). The Navier–Stokes perturbation equations, which Nek5000 was used to solve, are
$$\begin{eqnarray}\frac{\partial \boldsymbol{u}_{\boldsymbol{x}}}{\partial t}+\boldsymbol{U}_{\boldsymbol{x}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}_{\boldsymbol{x}}+\boldsymbol{u}_{\boldsymbol{x}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{U}_{\boldsymbol{x}}=-\boldsymbol{{\rm\nabla}}p+\frac{1}{R}{\rm\nabla}^{2}\boldsymbol{u}_{\boldsymbol{x}}+\boldsymbol{f}_{\boldsymbol{x}}\end{eqnarray}$$
together with the continuity equation
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}_{\boldsymbol{x}}=0,\end{eqnarray}$$
where
$\boldsymbol{u}_{\boldsymbol{x}}=(u_{x},u_{y},w)$
are the perturbation velocities in Cartesian coordinates,
$p$
is the pressure and
$\boldsymbol{f}_{\boldsymbol{x}}$
is a forcing term used in connection with the initial disturbance and sponge regions used together with the radial boundary conditions. The von Kármán base flow is translated to Cartesian coordinates (
$\boldsymbol{U}\rightarrow \boldsymbol{U}_{\boldsymbol{x}}$
) before entering Nek5000, and when the simulations are finished, the perturbation velocities are translated to cylindrical coordinates for further analysis (
$\boldsymbol{u}_{\boldsymbol{x}}\rightarrow \boldsymbol{u}$
).
For the case of the rotating-disk flow, the non-dimensionalizing perturbation velocity, pressure and time scales are
$r^{\ast }{\rm\Omega}^{\ast }$
,
${\it\rho}r^{\ast 2}{\rm\Omega}^{\ast 2}$
and
$L^{\ast }/({\rm\Omega}^{\ast }r^{\ast })$
respectively. Here,
${\it\rho}$
is the dimensional density. The time scale within Nek5000 is then such that
$t$
corresponds to the number of radians through which the disk has rotated. Here,
$T=t/(2{\rm\pi})$
is also used as the number of full rotations of the disk.
2.2. Mesh
The spectral-element mesh used for the current simulations is schematically illustrated in figure 1. Even though the simulations are defined on a segment of an annulus, the solver itself is based on Cartesian coordinates. The angle of the domain is
$2{\rm\pi}/68$
, where 68 is chosen as this is the azimuthal wavenumber at the onset of local absolute instability. More details on the spectral mesh can be found in tables 1 and 2 for the linear and nonlinear simulations respectively. In particular, in the radial direction the physical domain extends from a position
$r_{s}=400$
to
$r_{d}$
, which is the outer radial boundary of the domain and depends on the simulation. The ratio
$r{\rm\Delta}{\it\theta}/{\rm\Delta}r$
of an element is
$0.85$
for the spectral mesh of the linear simulations at the inner part and increases outwards with the maximum ratio for a simulation presented in this paper of 1.77 (
$r_{d}=830$
). In the wall-normal, or
$z$
, direction the elements are stretched according to
$$\begin{eqnarray}z_{n}=\mathop{\sum }_{i=1}^{n}{\rm\Delta}zs^{i-1},\end{eqnarray}$$
where
$s$
is the stretching factor,
$z_{n}$
is the coordinate at position
$n$
above the wall and
$z_{1}={\rm\Delta}z$
is the height of the spectral element closest to the wall. For our linear simulations
${\rm\Delta}z=0.2$
with 20 elements taken to a height of
$z=20.5$
with
$s=1.15$
. Table 3 gives further details for the various linear simulations made, including the number of elements used in the radial direction
$(N_{r})$
together with the total number of spectral elements for each simulation. The mesh structure and resolution were chosen based on additional simulations assessing the adequacy of the resolution; for instance, the stretching of the spectral elements was tested by comparing with simulations based on constant aspect ratio elements. A higher number of elements was also used and the results turned out to be unaffected. In the above described mesh, a high-order polynomial mapping from square elements to curved ones was employed to match the geometry.
Table 1. Summary of the spectral-element mesh for the linear simulations in terms of size of the domain [min max], number of spectral elements (
$N_{r}$
,
$N_{{\it\theta}}$
and
$N_{z}$
in the
$r$
,
${\it\theta}$
and
$z$
directions respectively) and resolution of the spectral elements in the radial, azimuthal and wall-normal directions.
Table 2. Summary of the spectral-element mesh for the nonlinear simulation, again in terms of size of the domain [min max], number of spectral elements (
$N_{r}$
,
$N_{{\it\theta}}$
and
$N_{z}$
in the
$r$
,
${\it\theta}$
and
$z$
directions respectively) and resolution of the spectral elements in the radial, azimuthal and wall-normal directions.
Table 3. Summary of the parameters for the linear simulations. The radial outer boundary of the domain is indicated by
$r_{d}$
, inward of this there is a sponge stretching for
${\rm\Delta}r=100$
for all cases. From figure 5(b), the value of
$r_{end}$
was estimated as the outer radial position inward of which the impact of the annular-sponge boundary condition could be neglected, i.e. approximately
${\rm\Delta}r=125$
less than
$r_{d}$
. The location of the initial impulsive disturbance is
$r_{ex}$
, and
$N_{r}$
is the number of elements in the
$r$
direction.
The Legendre polynomials are calculated within each spectral element on Gauss–Lobatto–Legendre (GLL) quadrature points to obtain spectral accuracy. The solution is a sum of these polynomials, and using spectral interpolation this solution can be obtained everywhere in space. There is an advantage in interpolating to an equidistant mesh for post-processing. This approach was taken for the simulations presented in this paper. The simulation fields were saved 320 times per rotation of the disk.
2.3. Boundary conditions
One of the major difficulties when simulating an open flow is to find boundary conditions that preserve the physical flow characteristics within the domain of interest. The approach taken here is to have a sponge region just ahead of the outer radial boundary that forces the flow back to the von Kármán similarity solutions and, therefore, damps out all the flow perturbations. The use of a sponge in this way can prevent reflections of downstream disturbances from the outflow boundary (Kloker & Konzelmann Reference Kloker and Konzelmann1993) and reduces the instantaneous influence the pressure can have in an incompressible flow. In our simulations, the sponge function was adapted from Chevalier et al. (Reference Chevalier, Schlatter, Lundbladh and Henningson2007) and was used as
$$\begin{eqnarray}\boldsymbol{f}=-{\it\lambda}(r)\boldsymbol{u},\end{eqnarray}$$
designed to damp the perturbations to zero. The sponge function
${\it\lambda}$
is described by
$$\begin{eqnarray}{\it\lambda}(r)={\it\lambda}_{max}\left[S\left(\frac{r-r_{start}}{{\rm\Delta}_{rise}}\right)\right],\end{eqnarray}$$
where the maximum strength of the damping is
${\it\lambda}_{max}$
, the radial position where the sponge region starts is
$r_{start}$
and
${\rm\Delta}_{rise}$
corresponds to the rise distance of the damping function. This boundary condition has also been used for simulations of convective stationary instabilities in the rotating-disk boundary layer. There, the adequacy of the boundary condition was tested on a domain up to
$r=500$
where the physics was verified by both experiments and theory; see Appelquist (Reference Appelquist2014). In figure 2,
${\it\lambda}(r)$
is shown and
${\it\lambda}_{max}$
is the maximum value of this curve. Moreover, the location of
$r_{start}$
,
$r_{d}$
and the span of
${\rm\Delta}_{rise}$
are included in this figure, where all values are taken from the linear run r02 included in table 3. The value of
$r_{end}$
will be defined later. The smooth step function
$S$
, using
$x$
as the argument, is
$$\begin{eqnarray}S(x)=\left\{\begin{array}{@{}ll@{}}0,\quad & x\leqslant 0,\\ 1/(1+\text{e}^{1/(x-1)+1/x}),\quad & 0<x<1,\\ 1,\quad & x\geqslant 1.\end{array}\right.\end{eqnarray}$$
For the linear simulations, the outflow sponge region starts at a distance
${\rm\Delta}r=100$
ahead of the end of the radial domain, giving
$r_{start}=r_{d}-100$
for all simulations. Also,
${\rm\Delta}_{rise}=40$
and
${\it\lambda}_{max}=28$
. For the nonlinear simulation, the outflow sponge region starts
${\rm\Delta}r=80$
ahead of the end of the radial domain giving
$r_{start}=700$
for this simulation. Moreover,
${\rm\Delta}_{rise}=40$
and
${\it\lambda}_{max}=10$
. A sponge was also used for the inflow region where the function (2.6) was turned to damp in the opposite direction. Then,
$r_{start}=420$
,
${\rm\Delta}_{rise}=10$
was used in the negative
$r$
direction, and
${\it\lambda}_{max}=0.8$
for all simulations. The reason for this inflow sponge is to damp low-amplitude upstream propagating waves, which can possibly be reflected at the inner radial boundary.
Figure 2. The sponge forcing function
${\it\lambda}(r)$
as given by (2.6). The sponge parameters
$r_{start}$
and
${\rm\Delta}_{rise}$
are also included, along with
$r_{d}$
, denoting the end of the domain, and
$r_{end}$
, denoting the position where the global mode crosses the local absolute unstable location; see figure 5(b).
For the outer radial boundary, two more boundary conditions were tested, both with different effects on the flow field, and both were rejected in favour of the sponge regions described above. In the first case, the base flow was kept as the von Kármán similarity solution and a homogeneous outflow Neumann boundary condition was included for the perturbations in the flow field. This had an unstable impact on the flow field, giving the same qualitative results (without any advantages) as with our chosen boundary condition. In the second case, an outer finite edge of the disk was modelled, where the Dirichlet boundary condition imposed for the rotation of the disk at
$z=0$
was for
$r>630$
changed to a symmetric boundary condition:
$\partial u_{x}/\partial z=0$
,
$\partial u_{y}/\partial z=0$
and
$w=0$
. This boundary condition was included for both the base flow and the perturbations, modelling an infinitely thin disk. Nonlinear simulations converged to a steady state since the base flow beyond the edge (
$r>630$
) turned out to be stable for this set-up. Intuitively, global stabilization might have been expected in these circumstances, but later results show that any such intuitive views should not be relied upon, in particular in the case of unavoidable modifications of the upstream boundary condition and base flow.
There are two more boundaries to consider for the rotating-disk flow. For the top boundary condition a combination of Dirichlet and stress-free conditions was used. In the wall-parallel directions the von Kármán solution was used, whereas in the linear case the perturbation velocities were set to zero (
$u_{x}=0$
and
$u_{y}=0$
); the wall-normal velocity was set to follow the stress-free Neumann boundary condition d
$w/$
d
$z=p$
(linear) or d
$W/$
d
$z=p$
(nonlinear). A segmentation of the domain from the full rotating disk to only
$2{\rm\pi}/68$
radians, to decrease the overall size of the computations, was made possible through cyclic boundary conditions in the azimuthal direction, which are essentially periodic boundary conditions but involve an appropriate rotation of the velocities across the boundary.
2.4. Initial conditions
The stability of the rotating-disk flow was studied in the current work by means of an impulse response, i.e. by observing the evolution of the flow disturbances due to an initial condition. This initial condition was applied, for numerical simplicity, as a volume force active only during a very short initial time. The force was located at a relatively small radial position close to the disk surface, and was fixed in the rotating frame of the disk. In both the
$r$
and
$z$
directions the spatial shape was a Gaussian function, and in the azimuthal direction a sinusoidal wavefunction was introduced. In this way, the volume force resembles the action of an impulsive annular ‘roughness’ rotating with the disk (but only for a short period of time). Formally, the strength of the forcing was defined as
$$\begin{eqnarray}{\it\eta}=\text{Re}[a(r)\cdot b(z)\cdot c(t)\cdot d({\it\theta},t)],\end{eqnarray}$$
where
$a$
,
$b$
and
$c$
are functions of either space (
$r$
,
$z$
) or time (
$t$
), and
$d$
is a function of both
${\it\theta}$
and
$t$
(due to the simulations being conducted in the laboratory frame). The separate terms are defined as
$$\begin{eqnarray}\displaystyle & a(r)=\text{e}^{-{\it\lambda}(r-r_{ex})^{2}}\text{e}^{\text{i}{\it\alpha}(r-r_{ex})}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & b(z)=\text{e}^{-{\it\mu}(z-z_{ex})^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & c(t)=(1-\text{e}^{-{\it\sigma}t^{2}})\text{e}^{-{\it\sigma}t^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & d({\it\theta},t)=\text{e}^{\text{i}[{\it\beta}({\it\theta}-{\rm\Omega}t)]}. & \displaystyle\end{eqnarray}$$
$r_{ex}$
and
$z_{ex}=0$
set the excitation location of the disturbance in the radial and wall-normal directions respectively, whereas
${\it\lambda}=0.5$
,
${\it\mu}=25$
and
${\it\sigma}=50$
give the extent of the forcing in space (
$r$
and
$z$
directions) and time. The value of
$r_{ex}$
is given in table 3. The wavenumbers in the radial and azimuthal directions are
${\it\alpha}=0.213$
and
${\it\beta}=68$
respectively. The non-dimensional rotation rate of the disk is
${\rm\Omega}=1$
. Here,
${\rm\Omega}t$
is the azimuthal movement of the forcing disturbance, which is needed since the simulations are made in the laboratory frame while the forcing disturbance is stationary with respect to the disk, which is described by (2.12). The radial growth rate (
${\it\alpha}_{i}$
) of the forcing was here taken to be zero.
The shape of the disturbance in time at a fixed position on the disk, i.e. in the rotating reference frame, is seen in figure 3(a), where the peak is shown to be at
$t=0.12$
. The forcing is set to zero for
$t>0.4$
and
${\it\eta}<10^{-6}$
. Figure 3(b) shows the resulting forcing function
$\boldsymbol{f}$
at this peak acting according to
$$\begin{eqnarray}\boldsymbol{f}={\it\eta}(\boldsymbol{U}_{\boldsymbol{d}}-\boldsymbol{U}_{\boldsymbol{s}}),\end{eqnarray}$$
where
$\boldsymbol{U}_{\boldsymbol{d}}=(0,1,0)$
is the velocity of the disk and
$\boldsymbol{U}_{\boldsymbol{s}}$
is the current simulation velocity. In figure 3,
$\boldsymbol{U}_{\boldsymbol{s}}$
is assumed to be the laminar profiles
$\boldsymbol{U}_{\boldsymbol{s}}=(U,V,W)$
.
Figure 3. (a) The time dependence of the forcing
${\it\eta}$
, see (2.8), (2.11). (b) The forcing-function amplitude for the peak of
${\it\eta}$
acting on the laminar similarity profiles
$\boldsymbol{U}_{\boldsymbol{s}}=(U,V,W)$
according to (2.13). Key:
$f_{r}$
$--$
;
$f_{{\it\theta}}$
—;
$f_{z}$
$-\cdot -$
.
2.5. Simulations
One nonlinear simulation was conducted with
$r_{ex}=490$
to allow comparison in particular with the linear run r02. The various linear runs are described in table 3. The two main variables that vary between runs are the outflow position,
$r_{d}$
, and the location of the initial impulsive disturbance of the flow,
$r_{ex}$
, although more simulations were conducted to check the mesh structure, mesh resolution and boundary conditions, and one simulation in the rotating reference frame (rather than the laboratory frame) was run for verification. Data are only shown up to the point where the sponge region starts,
$r_{d}-100$
in the linear simulations and
$r=700$
in the nonlinear simulation.
3. Results and discussion
The root mean square (r.m.s.) of the total azimuthal velocity at a specific radial position is here defined as
$$\begin{eqnarray}\mathscr{V}_{\mathit{rms}}(r;z)=\frac{1}{r}\left[\frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}(V(r;z)-\overline{V}(r;z))^{2}\text{d}{\it\theta}\right]^{1/2},\end{eqnarray}$$
where
$V$
now denotes the total azimuthal velocity rather than the laminar velocity and the bar denotes the mean value. The kinetic energy of the fluctuations at a specific radial position is here defined as
$$\begin{eqnarray}E(r)=\int _{0}^{2{\rm\pi}}\int _{0}^{Z}\frac{1}{2}\left[\left(\frac{u}{r}\right)^{2}+\left(\frac{v}{r}\right)^{2}+\left(\frac{w}{r}\right)^{2}\right]\!\text{d}z\text{d}{\it\theta},\end{eqnarray}$$
where
$u$
,
$v$
and
$w$
represent the velocity perturbations obtained from the DNS and
$Z$
is the total height of the domain. The velocities are thus normalized by the local radius before further calculation. The reason for this normalization is to calculate a measure that is comparable with local theory where there is no underlying linear radial increase as for the global case. Figure 4(a) shows
$\log \mathscr{V}_{\mathit{rms}}(r;z=1.3)$
for all radial positions as a function of time for the nonlinear simulation. In this space–time diagram, it is possible to see the introduction of the disturbance at
$r_{ex}=490$
. The time is indicated as the number of complete disk rotations, where data up to
$T=2.5$
are included. Initially, the disturbance amplitude is growing in time as it is convected away from the excitation source. The flow becomes turbulent at large
$r$
before
$T=1$
. At this time, the behaviour in the simulation starts to change, and at approximately
$T=1.5$
is is clear that contours that were previously indicating convectively unstable behaviour, i.e. leaning to the right, have turned through the vertical to lean slightly to the left, showing growth in time at fixed position similar to a locally absolutely unstable behaviour. Figure 4(b) shows
$\log E(r)/2$
for all radial positions as a function of time for the linear simulation r02 (see table 3). It is again possible to see the introduction of the disturbance at
$r_{ex}=490$
. The figure can be compared with the global linear simulations presented by Davies & Carpenter (Reference Davies and Carpenter2003), which show only data up to
$T=1.6$
(e.g. see their figure 17). Interestingly, around
$T=1.6$
in figure 4, it is possible to see the same change in the disturbance behaviour as in the nonlinear simulation, that is a change from a convectively to a locally absolutely unstable behaviour. Davies & Carpenter (Reference Davies and Carpenter2003) also mentioned such temporal growth but connected it to ‘unwanted feedback’ from the outer radial edge of their computational domain. In their local (parallel) simulations, the absolute instability was shown immediately after the impulse response with both its upstream and downstream modes. Here, in our global simulations, the linear globally unstable behaviour seems to require a triggering of the upstream mode from a more unstable downstream region before the global mode grows, possibly due to a frequency selection mechanism. As shown in figure 4, the quantitatively similar behaviour of the nonlinear and linear simulations indicates that the sponge region models the influence of upstream turbulence on the flow field effectively. This can be understood by comparing the mechanisms of the turbulent region with the sponge region; a turbulent region, viewed from the perspective of a linear disturbance, has a damping effect (as, for example, used in an eddy-viscosity approach) on larger scales. In the linear framework, this corresponds to an extraction of energy, which is precisely the effect of the sponge region, albeit achieved by a volume force. Having shown the correspondence in behaviour between an outer region of turbulence and a sponge, the focus will now turn to the linear simulations in order to compare various simulations and investigate the linear regime further.
Figure 4. (a) Space–time diagram of
$\log \mathscr{V}_{\mathit{rms}}(r;z=1.3)$
from the nonlinear simulation. (b) Space–time diagram of
$\log E(r)/2$
from simulation r02. (c) Time derivative of
$\ln E(r)/2$
;
$(\text{d}[\ln E(r)]/\text{d}t)/2$
, from the same simulation, where the black line shows the zero contour. The dashed black line indicates
$r_{end}=605$
.
Figure 4(c) shows the growth rate in time of disturbances in (b),
$(\text{d}[\ln E(r)]/\text{d}t)/2$
, with the black line showing the zero contour growth rate. At small times, it is possible to see the short-time response of the simulation to the initial impulse. At approximately
$T=1.6$
the zero contour line clearly changes direction from going in the positive
$r$
direction with time to the negative
$r$
direction, indicating a change from convectively to absolutely unstable behaviour. Eventually, as the absolute instability contaminates the whole domain, there is a positive temporal growth rate throughout. Figure 4(c) thus shows the development in time of an unstable linear global mode with a single complex global frequency
${\it\omega}$
, which can be compared with Healey’s (Reference Healey2010) figure 2(c) and which would be expected eventually to be limited by nonlinearity, if nonlinearity were included in the simulation.
For a closer look, and to compare the various linear runs in table 3, growth-rate data in time and space at specific
$r$
and
$T$
are presented in figure 5(a,b). Figure 5(a) shows the growth rate in time of the various runs at
$r=530$
. All simulations ran until
$T=2.5$
except for r04 and r05, which needed longer to reach an approximately constant final value. The impulsive forcing for r03 is at
$r=530$
, while for the other cases it is at
$r=490$
, leading to the different characteristics for r03 at small times in figure 5(a). Between approximately
$T=0.8$
and 1.2 in figure 5(a), all cases are shown to become convectively unstable rather than absolutely unstable (i.e. negative temporal growth rate at fixed
$r$
). Each case has a growth-rate minimum in time at different positions, and the final temporal growth rates increase with
$r_{d}$
. Case r01 has a final negative temporal growth rate and therefore exhibits global stability at large times; all other cases have positive final temporal growth rate and therefore exhibit global instability at large time. The value of
$r_{d}$
where the final temporal growth rate in time is zero, i.e. neutral, is estimated to be between r01 and r02/r03 at 719 for our boundary conditions, which corresponds to an end of the linear domain,
$r_{end}$
, of approximately 594.
Figure 5. Growth rate in time (a),
$(\text{d}[\ln E(r)]/\text{d}t)/2$
, and in space (b),
$(\text{d}[\ln E(r)]/\text{d}r)/2$
, for all runs given in table 3. The data for (a) are taken at
$r=530$
and are shown together with an arrow indicating the anticipated behaviour for
$r_{end}=\infty$
. The data for (b) for cases r01–r05 are taken at the final time of each simulation, and local theory data (
$-{\it\alpha}_{i}$
) for the absolute instability pinch points for
${\it\beta}=68$
are also included (black line,
$++$
) together with data from the spatial modes contributing to the pinch points at
$r_{end}$
for each simulation (grey lines,
$--$
). (c) The time to the turn-around (
$T_{t}$
) at
$r_{end}$
as a function of the distance to
$r_{end}$
from
$r_{ex}$
, with a linear fit to the points (black line,
$--$
).
Figure 5(b) shows
$(\text{d}[\ln E(r)]/\text{d}r)/2$
at the final time of each simulation. The simulations r01–r03 show radial lines with growth rates that decrease with
$r$
through most of the domain (the lines for r02 and r03 lie on top of each other). For r04 and r05, the radial growth-rate lines in figure 5(b) are slightly wavy, which we associate with amplified numerical errors in these two simulations since the spatial growth inside the domain reaches higher than the dynamic range of double-precision numbers, i.e.
$10^{16}$
. Only the data from the maximum 16 orders are shown. This puts a limit on the maximum Reynolds number that can be simulated in such a linear set-up. Of course, in the presence of nonlinearity one expects saturation of the amplitude. Figure 5(b) also contains data from a local theoretical stability analysis similar to Lingwood (Reference Lingwood1997), showing values of
$-{\it\alpha}_{i}$
for local absolute instability for given
$r$
and
${\it\beta}=68$
as in the present set-up, and also spatial modes contributing to the absolute instability at the end of the linear domain for each case. The modes with the highest spatial growth rates at low radial positions have similar values to the simulation data for each run. These modes have a negative group velocity and are the upstream modes (inward-travelling) in contrast to the lower growth-rate modes with a positive group velocity (i.e. the downstream or outward-travelling modes). In each case (r01–r05) the downturn in radial growth rate at high
$r$
in figure 5(b) corresponds to the damping effect of the annular-sponge region.
The minima in the temporal growth rates at
$r=530$
(figure 5
a) occur later in time when the distance between
$r_{ex}$
and
$r_{d}$
increases. However, we have an annular-sponge region inbound of the domain boundary
$r_{d}$
, and are interested in finding relationships within the numerical domain not containing a sponge or its upstream damping effect. The estimated end of our ‘undisturbed’ numerical domain,
$r_{end}$
, is thus taken in each case as the position where the local theoretical absolute growth rate in
$r$
meets the simulation data, i.e. intersections of the simulation curves with the local theory line (black,
$++$
) in figure 5(b), hypothesizing that any perturbation of the flow caused by the end of the numerical domain would obtain its properties from this location. The spatial growth rates of the upstream (inward-travelling) modes contributing to the absolute instabilities at these positions (grey,
$--$
) are shown to match the simulations well. The values of
$r_{end}$
from the intersections are given in table 3, and the estimated value for
$r_{end}$
to be neutrally growing in time, i.e.
${\it\omega}_{i}=0$
, is 594.
Relating the time at the turn-around at
$r_{end}$
(
$T_{t}$
) in each case, e.g. approximately 1.6 for r02 in figure 4(c), to the distance between
$r_{end}$
and
$r_{ex}$
in each case gives a linear relation, as depicted in figure 5(c). For r03, the disturbance is placed closer to
$r_{end}$
than for r02 (although
$r_{d}$
is the same for the two cases), and the turn-around appears at earlier
$T_{t}$
, as expected. The slope of this line gives the velocity at which the convective disturbances propagate outwards, inducing an absolutely unstable mode at the end.
On extrapolating the results of figure 5(c) to an infinite domain, i.e.
$r_{end}-r_{ex}\rightarrow \infty$
, the turn-around would not occur (in finite time) and purely convective behaviour would be seen, as indicated by the arrow in figure 5(a). This infinite-domain solution is effectively the result obtained by Davies & Carpenter (Reference Davies and Carpenter2003) as they finished their simulations before the absolutely unstable mode at the end could propagate inwards.
Figure 6(a) visualizes the last instantaneous field of the azimuthal perturbation velocity (log
$|v|$
) from r02 at a height of
$z=1.3$
(at this height the largest perturbation velocities are found, see the eigenfunctions in figure 8), and shows the different orders of magnitude of the velocity within the domain of interest (
$r=420{-}630$
, not including the sponges), ranging from
$|v|=10^{-12}$
to
$10^{4}$
(two orders larger than figure 4(b) since here the perturbation velocity is not divided by
$r$
), which includes the whole range of double-precision values possible. Figure 6(a) shows three full wavelengths in the azimuthal direction, i.e.
$3\cdot 2{\rm\pi}/68$
. Moreover, figure 6(b) shows for each simulation case the angle
${\it\varepsilon}$
at which the disturbances propagate, and (c) shows the values of
${\it\alpha}_{r}$
derived from these wave angles since
$$\begin{eqnarray}{\it\varepsilon}=\text{tan}^{-1}\left(\frac{{\it\beta}}{r}\frac{1}{{\it\alpha}_{r}}\right)=\frac{{\rm\Delta}r}{r{\rm\Delta}{\it\theta}}.\end{eqnarray}$$
The latter definition of
${\it\varepsilon}$
was used to calculate the angle from the simulations, using a smoothing running mean taken over
${\rm\Delta}r=21$
, thus showing data only up to
$r_{d}-110$
for each simulation. Moreover, data 16 orders smaller than the values at
$r_{d}-100$
were removed from runs r04 and r05 when calculating the angle due to the double-precision limit. The dashed lines in both figure 6(b) and (c) correspond to the spatial modes from local theory closest to the simulation data in figure 5(b), which were determined by the pinching absolute instabilities at
$r_{end}$
. There is a slight discrepancy between the simulation data and the theoretical mode; however, this was expected since the simulation and end-determined-theory curves in figure 5(b) do not agree perfectly. For simulation r05, the low-
$r$
data deviate more significantly from the theoretical results. This is again associated with the double-precision limitations on the simulations.
Figure 6. (a) Contours of log
$|v|$
at
$z=1.3$
from run r02. The domain shown (without the sponge regions) is from
$r=420$
to
$630$
, and is repeated three times in the azimuthal direction. (b) The wave angle
${\it\varepsilon}$
for each simulation at which the disturbances seen in (a) propagate. (c) The value of
${\it\alpha}_{r}$
derived from
${\it\varepsilon}$
. In both (b) and (c) solid lines correspond to DNS data and the dashed lines indicate the theoretical end modes given in figure 5(b) closest to the simulation data.
Figure 7 gives theoretical local absolute instability results as a function of
$R$
(or
$r$
). In (a) the neutral curve for the onset of local absolute instability is shown for various
${\it\beta}$
and in (b)
${\it\omega}$
corresponding to
${\it\beta}=68$
is shown as solid lines. For
${\it\beta}=68$
, a pocket region with a positive growth rate, i.e. a pocket of local absolute instability, is depicted in the range
$507<R<1580$
. The frequency (
${\it\omega}_{r}$
) of the wave shown in figure 6 was determined by adding numerical probes at radial positions
$r=465,490,508,515,540,550$
and
$575$
at a height of
$z=1.3$
. Figure 7(b) shows these data for all runs. These frequencies were calculated over
$t=2{\rm\pi}$
(i.e.
$T=1$
). However, to compare the global results with the local absolute instability theoretical work first conducted by Lingwood (Reference Lingwood1995a
), which was in the rotating frame, the azimuthal wavenumber (
${\it\beta}=68$
) must be subtracted from our calculated frequencies to shift from the stationary to the rotating frame. The resulting values of
${\it\omega}_{r}$
(in the rotating-disk frame) were approximately constant in
$r$
for each simulation, as expected for a global mode, and were then summarized as an average value, in figure 7(b). Moreover, the associated global temporal growth rates (
${\it\omega}_{i}$
), evaluated at the same radial positions, are also shown in figure 7(b) as an average value for each case. For both cases, the error bar was within the marker size and is therefore not shown. In figure 7(b), the values of
${\it\omega}_{r}$
and
${\it\omega}_{i}$
from each simulation are plotted against the relevant value of
$r_{end}$
, showing the correspondence with the theoretical absolute instability values there. Healey’s (Reference Healey2010) linear finite-radius disk model (complex Ginzburg–Landau equation) showed that if the edge position considered is sufficiently greater than
$R_{c}=507$
there will be linear global instability. Furthermore, the linear global instability has a global frequency and growth rate determined at leading order by the local absolute instability at the edge of the disk. While the details of the outer radial boundary conditions differ between our study (a sponge for the outer
${\rm\Delta}r=100$
modelling turbulence) and Healey’s (Reference Healey2010) point-like boundary condition, with vanishing fluctuations at the outer radius modelling a disk edge, our results confirm that the presence of a limited linear region can lead to linear global instability, with the global frequency and growth rate determined approximately by the local absolute instability at
$r_{end}$
. Healey (Reference Healey2010) noted that the choice of outer boundary conditions only affects a correction term in his model, so we should not expect this difference to affect the fundamental result.
Figure 7. (a) Neutral curve for the absolutely unstable region, where
${\it\beta}=68$
is indicated by a dashed line. (b) Variation of the local absolute frequency with radius for
${\it\beta}=68$
together with simulation data. The real temporal frequency
${\it\omega}_{r}$
was found by using numerical probes at various radial positions around the final time of the simulations. The final growth rates of the global modes,
${\it\omega}_{i}$
, were extracted at the same radial positions as the asymptotic state shown in, e.g., figure 5(a). The two smaller panels are magnifications of the relevant regions in (b).
Figure 8. Eigenfunctions as a function of wall-normal position evaluated from the r.m.s. values in each direction,
$r$
,
${\it\theta}$
and
$z$
(a–c). In each figure, there are data from three positions,
$r=555$
, 580 and 605, shown from left to right. The simulation data are taken from r02 and the theoretical data correspond to
${\it\omega}=-15.0+\text{i}0.708$
,
${\it\alpha}=0.135-\text{i}0.159$
,
${\it\alpha}=0.154-\text{i}0.150$
,
${\it\alpha}=0.190-\text{i}0.133$
and
${\it\beta}=68$
, from left to right. The profiles are normalized by the maximum value of the azimuthal profile (
$v$
) for theory and simulations separately.
Ideally, we would have more points on the curves in figure 7(b) to allow greater comparison. However, increase of
$r_{d}$
with our (linear) set-up has two limitations: (i) the double-precision limit and (ii) wavenumbers that are multiples of
${\it\beta}=68$
are unstable at high
$R$
(Lingwood Reference Lingwood1995b
) and would enter the flow field and grow. For our larger numerical domains, r04 and r05, disturbances with
${\it\beta}=136$
become absolutely unstable (from local theory) at the outermost part of the domain; however, this wavelength was not found in the simulations. This second point reminds us that for a full disk, all integer azimuthal wavenumbers are possible and there will therefore always be absolutely unstable modes at
$r_{end}$
(provided
$r_{end}$
${>}R_{c}$
), which could result in linear global instability if the flow is sufficiently absolutely unstable at
$r_{end}$
. Without a limited linear region, however, i.e. with
$r_{end}$
at infinity, the mechanism for generating inward-travelling modes to interact with the outward-propagating modes is removed and linear global stability results as for Davies & Carpenter (Reference Davies and Carpenter2003).
Looking at the vertical structure of the flow at the positions
$r=555,580\text{ and }605$
for r02, the eigenfunctions are extracted from the r.m.s. of each perturbation velocity component,
$$\begin{eqnarray}\displaystyle \hspace{-18.0pt}\left.\begin{array}{@{}c@{}}\displaystyle u_{\mathit{rms}}(r;z)=\frac{1}{r}\left[\frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\!\!u(r;z)^{2}\text{d}{\it\theta}\right]^{1/2}\!\!,\quad v_{\mathit{rms}}(r;z)=\frac{1}{r}\left[\frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\!\!v(r;z)^{2}\text{d}{\it\theta}\right]^{1/2}\\ \displaystyle \text{and}\quad w_{\mathit{rms}}(r;z)=\frac{1}{r}\left[\frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}w(r;z)^{2}\text{d}{\it\theta}\right]^{1/2}\end{array}\right\}. & & \displaystyle\end{eqnarray}$$
These quantities are shown in figure 8 together with local theory data. The shapes of the eigenfunctions from the simulations and local theory correspond well, e.g. the heights of the maximum values for the three functions show good agreement. However, both the
$u_{\mathit{rms}}$
and
$w_{\mathit{rms}}$
profiles have slightly higher amplitude from the simulations than from local theory, with the agreement being best at low
$r$
. It is possible that this is an effect of the sponge, or a local versus global effect, i.e. the solutions from the DNS (global) must be continuous in
$r$
while local theory results are discrete solutions in
$r$
, which may allow larger changes between radial positions (e.g. see figure 8
a).
The entirely linear framework here is somewhat artificial, but a possible contribution from the linear behaviour to the (nonlinear) laminar–turbulent transition of the flow was discussed in Lingwood (Reference Lingwood1996), believing that small disturbances entering the boundary layer will (above
$R_{c}$
) be absolutely amplified. Since all real-world cases of the rotating-disk flow where turbulence transition occurs have an end of the linear region, such behaviour corresponds to the results seen in our simulations, provided there is a large enough absolute instability region prior to the end, i.e. small disturbances being linearly globally unstable due to the upstream effect of the nonlinear regime. There are two experiments known to the authors that look at an impulse response in the rotating-disk boundary layer: Lingwood (Reference Lingwood1996) and Othman & Corke (Reference Othman and Corke2006). The behaviour observed by Lingwood (Reference Lingwood1996) corresponded to absolutely unstable behaviour, whereas the behaviour observed by Othman & Corke (Reference Othman and Corke2006) corresponded to convectively unstable behaviour. One of the main differences between the two experiments is the edge position. Lingwood (Reference Lingwood1996) had an edge Reynolds number greater than 752 and Othman & Corke (Reference Othman and Corke2006) had their edge at
$R=587$
. The results presented here could therefore explain the discrepancy between the two experiments, suggesting that the edge Reynolds number in the experiments by Othman & Corke (Reference Othman and Corke2006) was not sufficiently larger than
$R_{c}$
for the linear global instability to dominate; we show here that there is a need for a nonlinear turbulent region above approximately 594 for linear global instability. In the case of Lingwood (Reference Lingwood1996), with the larger edge Reynolds number, the presence of linear global instability could then have allowed (via a supercritical mechanism) a direct route to a nonlinear global mode irrespective of the background noise level. In the case of Othman & Corke (Reference Othman and Corke2006), the route to nonlinearity would have required sufficient levels of disturbance to create (via a sub-critical mechanism) a nonlinear global instability at
$R_{c}$
, as described by Pier (Reference Pier2003); however, this could not be fully verified by Othman & Corke’s (Reference Othman and Corke2006) results for large-amplitude impulse disturbance. These interpretations, however, need to be viewed with caution as real disk flows always excite stationary vortices triggered by roughness elements, which complicate the situation.
4. Summary and conclusions
In this paper, the linear-stability properties of the laminar flow over a rotating disk (von Kármán flow) are studied numerically. Starting with the results by Lingwood (Reference Lingwood1995a
), who found a local absolute instability above a critical Reynolds number
$R_{c}=507$
, it has been conjectured to what extent non-local effects, and in particular also the size of the disk, might influence the results. Using linear direct numerical simulations, Davies & Carpenter (Reference Davies and Carpenter2003) have already studied this particular flow. However, here this previous work has been extended to longer integration times with the specific aim of studying the long-time evolution and to examine the upstream effects of a non-infinite disk using the modelled influence of a downstream turbulent region. Our results correspond well with Healey’s (Reference Healey2010) results using the linearized Ginzburg–Landau equation. However, there is a difference in the sense that his model links the edge of the disk to the generation of the inward-travelling modes and a linear global instability, while we show inward-travelling modes generated by a modelled turbulence outer ring, creating a linear global instability. Without the presence of the damping region in our simulations, these inward-travelling modes would not be excited. Moreover, it is shown that the global-mode frequencies and temporal growth rates appear to be linked to the local absolute instability frequencies and temporal growth rates at the end of the linear domain
$r_{end}$
. When the end is close to
$R_{c}=507$
, e.g. our run r01, the flow is shown to be globally stable, remaining convective in behaviour. When the end is positioned farther out, e.g. our runs r02–r05, the flow is shown to become (linearly) globally unstable. Neutral temporal growth would correspond to
$r_{end}=594$
. Extrapolation to the case of an infinite linear domain leads to linear global stability, despite the presence of local absolute instability, because of the lack of perturbation of the flow in the outer region, which is consistent with Davies & Carpenter (Reference Davies and Carpenter2003), where an infinite domain is inadvertently created by stopping the simulations early to prevent unwanted inward propagation of disturbances.
Our results thus show that there needs to be a large enough pocket region of absolute instability prior to
$r_{end}$
for the global flow to be linearly unstable in agreement with Healey (Reference Healey2010). Interestingly, the results presented here and the results presented by Healey (Reference Healey2010) seem to be largely independent of the details of the outer boundary conditions as long as this boundary is sufficiently far from
$R_{c}$
. Similar feedback from an outer radial edge in a numerical domain has been found for swirling jets (Healey Reference Healey2008). From our work the effect of a physically finite radial edge is, however, still unclear, at least in the case that there is no extended turbulent region upstream of the disk edge. The flow beyond the edge can be either stable or unstable, inducing different effects on the upstream flow. When it comes to the current simulations, there are, however, limitations to our linearized simulation set-up applied to this flow configuration associated with the high spatial growth rates, which prohibit longer simulations and those with larger
$r_{d}$
. Nevertheless, our simulations now confirm that the rotating-disk boundary layer can produce a linear amplified global mode. It would be interesting to investigate whether the rotating cavity simulated by Viaud, Serre & Chomaz (Reference Viaud, Serre and Chomaz2008), for example, can be shown to become globally linearly unstable by moving the edge radially outwards, allowing the disturbances to grow, saturate and produce turbulence prior to the end of their domain.
We also used a linear-stability code to find the theoretical modes corresponding to the local absolute instability at the end of the linear domain. Comparison of the results from simulations with this theoretical mode shows good agreement, with some differences that might be products of the global versus local approaches. It should be noted that the simulated modes are entirely chosen by the flow.
Since the work of Davies & Carpenter (Reference Davies and Carpenter2003), the rotating-disk boundary layer has been considered to be linearly globally stable, which is true for an infinite disk but, as indicated by Healey (Reference Healey2010) and shown herein, not for a disk of limited linear extent, e.g. where there is downstream turbulence (and the disk is sufficiently large), and therefore not necessarily for experiments where turbulence is always present for large disks. Since the theoretical research by Mack (Reference Mack1985) there should be no surprise in finding an upstream mode in the rotating-disk boundary layer. The recognition that linear global instability can exist for the rotating-disk flow means that now, alongside the (sub-critical) nonlinear global instability for sufficiently large background disturbances (see, e.g., Pier Reference Pier2003), there is a mechanism leading directly to (supercritical) nonlinear global instability regardless of the background disturbance levels. The full implications of our linear results for the nonlinear regime and finally for experiments are, however, still unclear.
It is important to recognize that with the exception of validating our outer radial boundary condition, the current study is deliberately restricted to linear simulations to address open questions about the linear global stability, or otherwise, of the rotating-disk flow, and further nonlinear DNS investigations are left for future publication. These will allow comparison with physical experiments, addressing nonlinear effects as well as the transition to turbulence.
Acknowledgements
This work is supported by the Swedish Research Council through the ASTRID project and the Linné FLOW Centre. Computer time was provided by the Swedish National Infrastructure for Computing (SNIC). Discussions with C. Davies and S. Imayama are also gratefully acknowledged.
